PCC173 - Otimização em Redes
|
|
|
- Micaela Gusmão Gabeira
- 9 Há anos
- Visualizações:
Transcrição
1 PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 27 de abril de 2016 Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
2 Avisos Site da disciplina: Moodle: Lista de s: Para solicitar acesso: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
3 Conteúdo 1 Subgrafos 2 Conectividade e Caminhos 3 Alcançabilidade 4 Conexidade ou Conectividade Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
4 Avisos Semana que vem não haverá aula: Segunda: atividades de quinta; Quarta: workshop da computação. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
5 Subgrafo Definição Um grafo G s = (V s, A s ) é dito ser um subgrafo de um grafo G = (V, A) se todos os vértices e todas as arestas de G s estão em G, ou seja, se V s V e A s A Observações: Todo grafo é subgrafo de si próprio; O subgrafo G s2 de um subgrafo G s de G também é subgrafo de G; Um vértice simples de G é um subgrafo de G; Uma aresta simples de G (juntamente com suas extremidades) é um subgrafo de G. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
6 Subgrafo Encontre todos os subgrafos. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
7 Subgrafos Subgrafos Disjuntos de Arestas Dois (ou mais) subgrafos g 1 e g 2 de um grafo G são disjuntos de arestas se g 1 e g 2 não tiverem nenhuma aresta em comum. g 1 e g 2 podem ter vértices em comum? Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
8 Subgrafos Subgrafos Disjuntos de Vértices Dois (ou mais) subgrafos g 1 e g 2 de um grafo G são disjuntos de vértices se g 1 e g 2 não tiverem nenhum vértice em comum. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
9 Subgrafos Subgrafo Induzido por Vértices Contém um subconjunto dos vértices do grafo original e todas as ligações entre eles que figurarem no mesmo grafo. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
10 Subgrafos Subgrafo Induzido por Arestas Contém um subconjunto das arestas do grafo original e todos os vértices adjacentes a elas no mesmo grafo. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
11 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
12 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
13 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
14 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
15 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
16 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
17 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
18 Definições a b c e 3 d 4 Passeio (aka percurso ou walk) Um passeio é uma sequência finita de vértices e arestas. Cada vértice da sequência é incidente a aresta que o precede e a aresta seguinte. Essa sequência deve acabar e iniciar em um vértice (não necessariamente os mesmos). Ex.: 1 - a c d d e - 5 ou: O Passeio pode ser: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
19 Definições a 1 2 b 3 c d 4 Cadeia (chain) Um passeio que não repete arestas. e Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
20 Definições a 1 2 b 3 c d 4 Cadeia (chain) Um passeio que não repete arestas. e Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
21 Definições a 1 2 b 3 c d 4 Cadeia (chain) Um passeio que não repete arestas. e Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
22 Definições a 1 2 b 3 c d 4 Cadeia (chain) Um passeio que não repete arestas. e Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
23 Definições a 1 2 b 3 c d 4 Cadeia (chain) Um passeio que não repete arestas. e Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
24 Definições a 1 2 b 3 c d 4 Cadeia (chain) Um passeio que não repete arestas. e Ex.: Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
25 Definições a b c e 3 d 4 Caminho (path) Uma cadeia sem repetição de vértices. Ex.: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: comprimento : o comprimento de um caminho é o número de arestas que o mesmo inclui. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
26 Definições a b c e 3 d 4 Caminho (path) Uma cadeia sem repetição de vértices. Ex.: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: comprimento : o comprimento de um caminho é o número de arestas que o mesmo inclui. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
27 Definições a b c e 3 d 4 Caminho (path) Uma cadeia sem repetição de vértices. Ex.: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: comprimento : o comprimento de um caminho é o número de arestas que o mesmo inclui. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
28 Definições a b c e 3 d 4 Caminho (path) Uma cadeia sem repetição de vértices. Ex.: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: comprimento : o comprimento de um caminho é o número de arestas que o mesmo inclui. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
29 Definições a b c e 3 d 4 Caminho (path) Uma cadeia sem repetição de vértices. Ex.: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: comprimento : o comprimento de um caminho é o número de arestas que o mesmo inclui. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
30 Definições a b c e 3 d 4 Caminho (path) Uma cadeia sem repetição de vértices. Ex.: aberto : quando inicia e acaba em vértices diferentes (o caso acima) fechado : quando inicia e acaba no mesmo vértice. Ex.: comprimento : o comprimento de um caminho é o número de arestas que o mesmo inclui. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
31 Relembrando... Passeio Sequência finita de vértices e arestas. Cadeia Um passeio que não repete arestas. Caminho Uma cadeia sem repetição de vértices. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
32 Caminhos e Circuitos Teorema 1 Se um grafo possui exatamente 2 vértices de grau ímpar, existe um caminho entre esses dois vértices. Teorema 2 O número mínimo de arestas de um grafo simples com n vértices e k componentes é n k. Teorema 3 Um grafo simples com n vértices e k componentes possui no máximo (n k)(n k + 1)/2 arestas (caso trivial); Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
33 Caminhos e Circuitos Teorema 1 Se um grafo possui exatamente 2 vértices de grau ímpar, existe um caminho entre esses dois vértices. Teorema 2 O número mínimo de arestas de um grafo simples com n vértices e k componentes é n k. Teorema 3 Um grafo simples com n vértices e k componentes possui no máximo (n k)(n k + 1)/2 arestas (caso trivial); Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
34 Caminhos e Circuitos Teorema 1 Se um grafo possui exatamente 2 vértices de grau ímpar, existe um caminho entre esses dois vértices. Teorema 2 O número mínimo de arestas de um grafo simples com n vértices e k componentes é n k. Teorema 3 Um grafo simples com n vértices e k componentes possui no máximo (n k)(n k + 1)/2 arestas (caso trivial); Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
35 Ciclos Definição Um ciclo é um caminho fechado. Alguns autores, utilizam o termo circuito para o caso de grafos orientados. Grafo Ciclo: Um grafo ciclo C n é um grafo com n vértices formado por apenas um ciclo passando por todos os vértices. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
36 Ciclos Definições A cintura de um grafo é o comprimento do menor ciclo existente no mesmo. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
37 Ciclos Definições A circunferência de um grafo é o comprimento do maior ciclo existente no mesmo. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
38 Alcançabilidade Definição Um vértice w é alcançável a partir do vértice v se houver um caminho entre w e v. Definição O conjunto de vértices alcançáveis a partir de v é, portanto, formado pelos sucessores de v, os sucessores dos sucessores e assim por diante. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
39 Alcançabilidade Definição Um vértice w é alcançável a partir do vértice v se houver um caminho entre w e v. Definição O conjunto de vértices alcançáveis a partir de v é, portanto, formado pelos sucessores de v, os sucessores dos sucessores e assim por diante. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
40 Alcançabilidade Transitividade Se w é alcançável a partir de v; e se x é alcançável de w; então x é alcançável a partir de v. Transitividade Relação de Alcançabilidade é transitiva. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
41 Alcançabilidade Transitividade Se w é alcançável a partir de v; e se x é alcançável de w; então x é alcançável a partir de v. Transitividade Relação de Alcançabilidade é transitiva. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
42 Fecho Transitivo de um Vértice - Grafo Não Direcionado Definição O Fecho Transitivo de um vértice v (denotado por ˆΓ(v)) é o conjunto dos vértices de um grafo alcançáveis a partir de v. ˆΓ(1) = {2, 3, 4} ˆΓ(5) = {} Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
43 Fecho Transitivo de um Vértice - Grafo Direcionado Fecho Transitivo Direto O Fecho Transitivo Direto de um vértice v (denotado por ˆΓ + (v)) é o conjunto dos vértices de um grafo alcançáveis a partir de v. Os vértices em ˆΓ + (v) são chamados de descendentes de v. Fecho Transitivo Indireto O Fecho Transitivo Indireto de um vértice v (denotado por ˆΓ (v)) é o conjunto dos vértices de um grafo a partir dos quais v é alcançável. Os vértices em ˆΓ (v) são chamados de ascendentes de v. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
44 Fecho Transitivo Direto e Indireto ˆΓ + (1) = {2, 3, 4, 5, 7, 9, 10, 13} ˆΓ (10) = {1, 4} Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
45 Conexidade em Grafos Não Direcionados Definição Em um GND conexo, todos os vértices são alcançáveis a partir de qualquer outro. Em um GND conexo, sempre é possível fazer um passeio fechado que inclua todos os vértices. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
46 Conexidade Ponte Uma ponte de um grafo G é uma aresta cuja remoção resulta no aumento do número de componentes de G. A aresta u 1 é uma ponte. As arestas u 3 e u 4 não são. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
47 Conexidade em Grafos Direcionados Grafo Simplesmente Conexo: s-conexo O grafo subjacente não-direcionado obtido através da substituição de todas as arestas de G por arestas não direcionadas é um grafo conexo. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
48 Conexidade em Grafos Direcionados Grafo Semi-Fortemente Conexo: sf-conexo Para cada par de vértices (v 1, v 2 ), existe um caminho de v 1 para v 2 ou de v 2 para v 1. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
49 Conexidade em Grafos Direcionados Grafo Fortemente Conexo: f-conexo Para cada par de vértices (v 1, v 2 ), existe um caminho direcionado de v 1 para v 2 e de v 2 para v 1. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
50 Conexidade ou Conectividade Exemplo Conceito aplicado a Grafos Não Direcionados; Indica o quanto um grafo é conexo. Definição A conexidade ou conectividade κ(g) de um grafo G = (V, E) é o menor número de vértices cuja remoção desconecta G ou o reduz a um único vértice. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
51 Conexidade ou Conectividade Exemplo Conceito aplicado a Grafos Não Direcionados; Indica o quanto um grafo é conexo. Definição A conexidade ou conectividade κ(g) de um grafo G = (V, E) é o menor número de vértices cuja remoção desconecta G ou o reduz a um único vértice. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
52 Conexidade ou Conectividade Exemplos de remoções de conjuntos de vértices que desconectam o grafo. Neste caso, κ(g) = 1 (figura 2). Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
53 Conexidade ou Conectividade Grafos Completos Para grafos completos com n vértices, κ(k n ) = n 1. Grafos Não Completos Para grafos não completos haverá um par (v 1, v 2 ) de vértices não adjacentes, então temos que: κ(g) n 2 G K n Limite superior para κ(g) em qualquer grafo: a δ(g) : menor grau em um GND. κ(g) δ(g) a Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
54 Conexidade ou Conectividade Grafos Completos Para grafos completos com n vértices, κ(k n ) = n 1. Grafos Não Completos Para grafos não completos haverá um par (v 1, v 2 ) de vértices não adjacentes, então temos que: κ(g) n 2 G K n Limite superior para κ(g) em qualquer grafo: a δ(g) : menor grau em um GND. κ(g) δ(g) a Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
55 Conexidade ou Conectividade Grafos Completos Para grafos completos com n vértices, κ(k n ) = n 1. Grafos Não Completos Para grafos não completos haverá um par (v 1, v 2 ) de vértices não adjacentes, então temos que: κ(g) n 2 G K n Limite superior para κ(g) em qualquer grafo: a δ(g) : menor grau em um GND. κ(g) δ(g) a Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
56 Conexidade ou Conectividade Caminhos Disjuntos Dois percursos entre os vértices v e w de um grafo são disjuntos se não houver interseção de arestas. Teorema Um grafo G = (V, E) é k-conexo se e somente se para todo para v, w V, v w existirem ao menos k percursos disjuntos. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
57 Conexidade ou Conectividade 1-Conexo 2-Conexo 3-Conexo Grafo k-conexo Para todo grafo k-conexo: κ(g) δ(g) κ(g) k Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
58 Conexidade ou Conectividade Grafo k-conexo Grafo borboleta: 2-conexo K 7 : 6-conexo, mas também é 1-conexo, 2-conexo, 3-conexo, 4-conexo, 5-conexo... k κ(g) δ(g) Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
59 Exercícios 1 Quantos caminhos existem entre os vértices b e f? b e f a c d g 2 Dê um exemplo de um grafo conexo G cuja remoção de qualquer aresta torna G desconexo. Quantas arestas possui um grafo com estas características? Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
60 Exercícios 1 Com relação ao grafo abaixo, responda: v4 v1 v3 v2 v5 v6 v7 a) O grafo é simples? b) Completo? c) Regular? d) Conexo? e) Encontre 2 caminhos entre v3 e v6. f) Encontre 1 ciclo. g) Indique 1 aresta cuja remoção tornará o grafo desconexo. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
61 Exercício Quantos grafos ciclos (não isomorfos) são subgrafos do grafo abaixo? Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
62 Exercícios 1 Qual a cintura e a circunferência do grafo abaixo? c 2 Mostre que não é possível ter um grupo de 7 pessoas no qual cada um conhece exatamente outras 3 pessoas. 3 Prove que quaisquer dois grafos conexos com n vértices, todos de grau 2, são isomorfos. Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
63 Exercícios Qual a conectividade do grafo abaixo? Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
64 Dúvidas? Marco Antonio M. Carvalho (UFOP) PCC de abril de / 40
Percursos em um grafo
Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Percursos em um grafo
Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Grafos Orientados (digrafos)
Grafos Orientados (digrafos) Grafo Orientado ou digrafo Consiste em um grafo G = (V,A) onde V = {v 1,, v n } é um conjunto de vértices e A = {a 1,, a k } é um conjunto de arcos tais que a k, k=1,,m é representado
Parte B Teoria dos Grafos
45 Parte B Teoria dos Grafos B. Grafos e Subgrafos Um grafo G é uma tripla ordenada (V(G), E(G), ), constituindo de um conjunto não vazio V(G) de vértices, um conjunto disjunto E(G) das arestas e uma função
GRAFOS Aula 04 Caminhos, Conexidade e Distância Max Pereira
Ciência da Computação GRAFOS Aula 04 Caminhos, Conexidade e Distância Max Pereira Um grafo é dito conexo se for possível visitar qualquer vértice, partindo de um outro qualquer, passando pelas suas arestas.
Instituto de Computação - Universidade Federal Fluminense Teoria dos Grafos - Lista de exercícios
Instituto de Computação - Universidade Federal Fluminense Teoria dos Grafos - Lista de exercícios 1 Conceitos 1. Prove o Teorema da Amizade: em qualquer festa com pelo menos seis pessoas, ou três se conhecem
Instituto de Computação - Universidade Federal Fluminense Teoria dos Grafos - Lista de exercícios
Instituto de Computação - Universidade Federal Fluminense Teoria dos Grafos - Lista de exercícios 1 Conceitos 1. Prove o Teorema da Amizade: em qualquer festa com pelo menos seis pessoas, ou três se conhecem
GRAFOS ORIENTADOS. PSfrag replacements. Figura 1: Exemplo de um grafo orientado.
Introdução à Teoria dos Grafos Bacharelado em Ciência da Computação UFMS, 2005 GRAFOS ORIENTAOS Resumo Existem ocasiões onde grafos não são apropriados para descrever certas situações. Por exemplo, um
Teoria dos Grafos AULA 3
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada [email protected], [email protected] AULA 3 Trajetos, Caminhos, Circuitos, Grafos Conexos Preparado
CONCEITOS BÁSICOS EM GRAFOS
Um grafo (simples) G é formado por um conjunto de vértices, denotado por V(G), e um conjunto de arestas, denotado por E(G). Cada aresta é um par (não ordenado) de vértices distintos. Se xy é uma aresta,
Comunicação e redes. Aula 2: Teoria dos Grafos Conceitos básicos. Professor: Guilherme Oliveira Mota.
Comunicação e redes Aula 2: Teoria dos Grafos Conceitos básicos Professor: Guilherme Oliveira Mota [email protected] Aula passada Redes complexas Grafo G: Conjunto de pontos e linhas ligando esses pontos
MATEMÁTICA DISCRETA. Patrícia Ribeiro 2018/2019. Departamento de Matemática, ESTSetúbal 1 / 47
1 / 47 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 47 1 Combinatória 2 Aritmética Racional 3 3 / 47 Capítulo 3 4 / 47 não orientados Um grafo não orientado
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada [email protected], [email protected] Grafos Eulerianos Preparado a partir do texto: Rangel, Socorro.
Introdução a Grafos Letícia Rodrigues Bueno
Introdução a Grafos Letícia Rodrigues Bueno UFABC Teoria dos Grafos - Motivação Objetivo: aprender a resolver problemas; Como: usando grafos para modelar os problemas; Grafos: ferramenta fundamental de
CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo:
![CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo:](/thumbs/54/34072329.jpg "CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo:")
Matemática Discreta ESTiG\IPB Cap4. Elementos da Teoria de Grafos pg 1 CAP4. ELEMENTOS DA TEORIA DE GRAFOS Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E), sendo: Exemplos
GRAFOS: UMA INTRODUÇÃO
GRAFOS: UMA INTRODUÇÃO Vilmar Trevisan -Instituto de Matemática - UFRGS Junho de 2006 Grafos: uma introdução Informalmente, um grafo é um conjunto de pontos no plano ligados entre por flechas ou por segmentos
TEORIA DOS GRAFOS TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS MATEMÁTICA DISCRETA II PROFº MARCOS NASCIMENTO
TEORIA DOS GRAFOS TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS MATEMÁTICA DISCRETA II PROFº MARCOS NASCIMENTO Por que estudar grafos? Importante ferramenta matemática com aplicação em diversas áreas
BCC204 - Teoria dos Grafos
BCC204 - Teoria dos Grafos Marco Antonio M. Carvalho (baseado nas notas de aula do prof. Haroldo Gambini Santos) Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal
Instituto de Computação Universidade Federal Fluminense. Notas de Aula de Teoria dos Grafos. Prof. Fábio Protti Niterói, agosto de 2015.
Instituto de Computação Universidade Federal Fluminense Notas de Aula de Teoria dos Grafos Niterói, agosto de 2015. Conteúdo 1 Conceitos Básicos 5 1.1 Grafos, vértices, arestas..................... 5 1.2
Teoria dos Grafos. Edson Prestes
Edson Prestes Introdução Um passeio entre os nós i e j é uma seqüência alternada de nós e arestas que começa no nó i e termina no nó j. G 1 G 2 Um exemplo de passeio entre os nós 1 e 4 do grafo G 1 é (1,(1,3),3,(2,3),2,(1,2),1,(1,4),4).
Teoria dos Grafos. Aulas 3 e 4. Profa. Alessandra Martins Coelho
Teoria dos Grafos Aulas 3 e 4 Profa. Alessandra Martins Coelho fev/2014 Passeio ou percurso Um passeio ou percurso é uma sequência finita de vértices e arestas Exemplo Em (1) o passeio inicia pelo vértice
Combinando relações. Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações
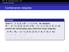1 / 11 Combinando relações Combinando relações Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações R 1 = {(1, 1), (2, 2), (3, 3)} e R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} podem ser combinadas para
Cap. 2 Conceitos Básicos em Teoria dos Grafos
Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
CI065 CI755 Algoritmos e Teoria dos Grafos
CI065 CI755 Algoritmos e Teoria dos Grafos Exercícios 11 de outubro de 2017 1 Fundamentos 1. Seja S = {S 1,..., S n } uma família de conjuntos. O grafo intercessão de S é o grafo G S cujo conjunto de vértices
Definição e Conceitos Básicos
Definição e Conceitos Básicos Grafos e Algoritmos Computacionais Prof. Flávio Humberto Cabral Nunes [email protected] 1 Conceitos Básicos Em grafos ocorrem dois tipos de elementos: Vértices ou nós;
BCC204 - Teoria dos Grafos
BCC204 - Teoria dos Grafos Marco Antonio M. Carvalho (baseado nas notas de aula do prof. Haroldo Gambini Santos) Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal
Conceito Básicos da Teoria de Grafos
1 Conceito Básicos da Teoria de Grafos GRAFO Um grafo G(V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w),
Definições Básicas para Grafos
Definições Básicas para rafos RAFO Um grafo (V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w), v e w V:
Árvores: Conceitos Básicos e Árvore Geradora
Árvores: Conceitos Básicos e Árvore Geradora Grafos e Algoritmos Computacionais Prof. Flávio Humberto Cabral Nunes [email protected] 1 Introdução No dia a dia aparecem muitos problemas envolvendo árvores:
Conteúdo. Histórico. Notas. Teoria dos Grafos BCC204. Notas. Notas. 1736: Euler e as Pontes de Königsberg
Teoria dos Grafos BCC204 Haroldo Gambini Santos Universidade Federal de Ouro Preto - UFOP 15 de março de 2011 1 / 31 Conteúdo 1 Introdução 2 Exemplos 3 4 Representação 2 / 31 Histórico 1736: Euler e as
Estrutura de Dados e Algoritmos e Programação e Computadores II. Aula 10: Introdução aos Grafos
Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 10: Introdução aos Grafos História O assunto que se constitui no marco inicial da teoria de grafos é na realidade um problema algorítmico.
x y Grafo Euleriano Figura 1
Grafo Euleriano Um caminho simples ou um circuito simples é dito euleriano se ele contém todas as arestas de um grafo. Um grafo que contém um circuito euleriano é um grafo euleriano. Um grafo que não contém
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO. 5 a Lista de Exercícios
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO MATEMÁTICA COMBINATÓRIA 5 a Lista de Exercícios 1. O grafo de intersecção de uma coleção de conjuntos A 1,..., A n é o grafo
Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 45
Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 45 Introdução a Grafos Muitos problemas de otimização podem ser analisados utilizando-se uma estrutura denominada grafo ou rede. Problemas
Doutorado em Ciência da Computação. Algoritmos e Grafos. Raimundo Macêdo LaSiD/DCC/UFBA
Doutorado em Ciência da Computação Algoritmos e Grafos Raimundo Macêdo LaSiD/DCC/UFBA Grafo Completo Grafo simples cujos vértices são dois a dois adjacentes. Usa-se a notação K n para um grafo completo
BCC204 - Teoria dos Grafos
BCC204 - Teoria dos Grafos Marco Antonio M. Carvalho (baseado nas notas de aula do prof. Haroldo Gambini Santos) Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal
Teoria dos Grafos Aula 5
Teoria dos Grafos Aula Aula passada Explorando grafos Mecanismos genéricos Ideias sobre BFS, DFS Aula de hoje Busca em grafos Busca em largura (BFS Breadth First Search) Propriedades Busca em Grafos Problema
Pesquisa Operacional II. Professor João Soares de Mello
Pesquisa Operacional II Professor João Soares de Mello http://www.uff.br/decisao/notas.htm Ementa Teoria dos grafos (pré-requisitos: PO I, Álgebra Linear) Programação não linear (pré-requisitos: PO I,
GRAFOS. Prof. André Backes. Como representar um conjunto de objetos e as suas relações?
8/0/06 GRAFOS Prof. André Backes Definição Como representar um conjunto de objetos e as suas relações? Diversos tipos de aplicações necessitam disso Um grafo é um modelo matemático que representa as relações
Teoria dos Grafos Conceitos Básicos
Teoria dos Grafos Conceitos Básicos Profª. Alessandra Martins Coelho fev/2014 Grafos com apelidos diamante Grafos com apelidos Grafos com apelidos diamante casinha Grafos com apelidos diamante casinha
Teoria dos Grafos Caminhos. Profª. Alessandra Martins Coelho
Teoria dos Grafos Caminhos Profª. Alessandra Martins Coelho junho/2014 Conexidade Em grande parte de aplicações do modelo em grafos, as relações que envolvem os vértices formam uma estrutura contínua;
IFRN. Conexidade e Distância. Prof. Edmilson Campos
IFRN Conexidade e Distância Prof. Edmilson Campos Conteúdo Grafo Conexo Componente Conexa e Algoritmos Grafo F-Conexo Componente F-Conexa Antecessor, Sucessor, Fecho Transitivo Algoritmo Grafo Reduzido
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Capítulo 5: Grafos Conexos. Departamento de Matemática Aplicada
Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 5: Grafos Conexos Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Circuitos Eulerianos Ciclos Hamiltonianos O Problema do Caixeiro Viajante CAMINHAMENTOS BASEADO EM TOWNSEND (1987), CAP. 7.
Matemática Discreta Capítulo 7 SUMÁRIO CAMINHAMENTOS BASEADO EM TOWNSEND (1987), CAP. 7 Circuitos Eulerianos Ciclos Hamiltonianos O Problema do Caixeiro Viajante Newton José Vieira 30 de julho de 2007
Grafos Eulerianos e o Problema do Carteiro Chinês
Prof. Ademir A. Constantino DIN - UEM 1 Grafos Eulerianos e o Problema do Carteiro Chinês Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Prof. Ademir A. Constantino
Conceitos Básicos da Teoria de Grafos
Conceitos Básicos da Teoria de Grafos Universidade Federal do Pampa - UNIPAMPA Engenharia da Computação Estrutura de Dados Profª Sandra Piovesan Grafos Uma noção simples, abstrata e intuitiva. Representa
Teorema 1 - Todo corte de arestas de um grafo conexo G contém pelo menos uma aresta em comum com qualquer árvore geradora de G. Exemplo 2 - Seja T:
12 - Conjuntos de Corte o estudarmos árvores geradoras, nós estávamos interessados em um tipo especial de subgrafo de um grafo conexo: um subgrafo que mantivesse todos os vértices do grafo interligados.
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
Teoria dos Grafos Valeriano A de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilceunespbr, socorro@ibilceunespbr Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro
Teoria dos Grafos Aula 2
Teoria dos Grafos Aula 2 Aula passada Logística, regras Objetivos Grafos, o que são? Formando pares Encontrando caminhos Aula de hoje Outro problema real Definições importantes Algumas propriedades Grafo
Matemática Discreta. Aula 06: Teoria dos Grafos. Tópico 01: Grafos e suas Representações. Observação
Aula 06: Teoria dos Grafos Tópico 01: Grafos e suas Representações Nesta aula nós passamos a estudar um outro assunto, mas que também tem muita aplicação na vida prática, a Teoria dos Grafos. Para esta
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Departamento de Matemática Aplicada
Teoria dos Grafos Valeriano A de Oliveira, Socorro Rangel, Silvio A de Araujo Departamento de Matemática Aplicada Capítulo 12: Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro Teoria do
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Capítulo 11: Grafos Eulerianos. Departamento de Matemática Aplicada
Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 11: Grafos Eulerianos Preparado a partir do texto: Rangel, Socorro. Teoria do
Teoria dos Grafos Introdu c ao
Teoria dos Grafos Introdução Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications,
As Pontes de Königsberg
As Pontes de Königsberg Anderson Freitas Ferreira e Lívia Minami Borges 13 de junho de 2015 Resumo A teoria de grafos teve seu início em 1736, quando Euler utilizou uma estrutura para resolver o Problema
GRAFOS. Introdução Conceitos Fundamentais
GRAFOS Introdução Conceitos Fundamentais Uma aplicação do produto de matrizes Agora é a sua vez... Considere o diagrama seguinte Determine, o número de formas diferentes de ir de a 1 até e 2 e de a 2
GRAFOS Aula 08 Árvore Geradora Mínima: Algoritmos de Kruskal e Prim-Jarnik Max Pereira
Ciência da Computação GRAFOS Aula 08 Árvore Geradora Mínima: Algoritmos de Kruskal e Prim-Jarnik Max Pereira Árvore Geradora (spanning tree) É um subconjunto de um grafo G que possui todos os vértices
Matemática Discreta. Aula nº 22 Francisco Restivo
Matemática Discreta Aula nº 22 Francisco Restivo 2006-05-26 Definição: Um grafo cujos vértices são pontos no plano e cujos lados são linhas no plano que só se encontram nos vértices do grafo são grafos
Teoria dos Grafos. Edson Prestes
Edson Prestes Introdução Um passeio entre os nós i e j é uma seqüência alternada de nós e arestas que começa no nó i e termina no nó j. G 1 G 2 Um exemplo de passeio entre os nós 1 e 4 do grafo G 1 é (1,(1,3),3,(2,3),2,(1,2),1,(1,4),4).
BCC204 - Teoria dos Grafos
BCC204 - Teoria dos Grafos Marco Antonio M. Carvalho (baseado nas notas de aula do prof. Haroldo Gambini Santos) Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal
Teoria dos Grafos. Conjuntos de Corte e Conectividade
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada [email protected], [email protected], [email protected] Conjuntos de
Lista de Exercícios 9 (Extra): Soluções Grafos
UFMG/ICEx/DCC DCC111 Matemática Discreta Lista de Exercícios 9 (Extra): Soluções Grafos Ciências Exatas & Engenharias 1 o Semestre de 018 Para cada uma das seguintes armações, diga se é verdadeira ou falsa
Noções da Teoria dos Grafos. André Arbex Hallack
Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 1.1 Introdução histórica..................................... 1 1.2 Passeios
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada [email protected], [email protected] Grafos direcionados (Digrafos) Preparado a partir do texto:
CI065 CI755 Algoritmos e Teoria dos Grafos
CI065 CI755 Algoritmos e Teoria dos Grafos Exercícios 10 de junho de 2018 1 Fundamentos 1. Seja S = {S 1,..., S n } uma família de conjuntos. O grafo intercessão de S é o grafo G S cujo conjunto de vértices
BCC204 - Teoria dos Grafos
BCC204 - Teoria dos Grafos Marco Antonio M. Carvalho (baseado nas notas de aula do prof. Haroldo Gambini Santos) Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal
Noções da Teoria dos Grafos
Noções da Teoria dos Grafos André Arbex Hallack Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 7 3 Árvores 11 4 Emparelhamento em grafos 15 5 Grafos planares: Colorindo
GRAFOS E ALGORITMOS TEORIA DE GRAFOS
GRAFOS E ALGORITMOS TEORIA DE GRAFOS 1a. PARTE Prof. Ronaldo R. Goldschmidt [email protected] [email protected] ROTEIRO 1. INTRODUÇÃO E MOTIVAÇÃO 2. FUNDAMENTOS 3. CONECTIVIDADE 4.
2 Relação entre soma dos graus e número de arestas
Rio de Janeiro, 24 de Outubro de 2011. LISTA DE ESTRUTURAS DISCRETAS PROFESSOR: EDUARDO LABER OBSERVAÇÕES: Exercícios marcados com são mais complicados. 1 Isomorfismo 1. Seja G =(V,E) um grafo simples.