C 3 C 3. De acordo com o teorema de Euler, um grafo não orientado admite um ciclo de Euler se e só for conexo e não tiver vértices de grau ímpar.
|
|
|
- Theodoro Caiado de Sá
- 6 Há anos
- Visualizações:
Transcrição
1 rafos ircuito e iclo de uler X. ircuito e iclo de uler Um grafo orientado diz-se euleriano se há um circuito que contenha todos os seus arcos uma e só uma vez (circuito euleriano ).O grafo da figura é euleriano porque admite o circuito,,,. 1 2 e acordo com o teorema de uler, um grafo orientado admite um circuito de uler se e só se for fortemente conexo e pseudo simétrico 1 (diz-se que o grafo é euleriano ). Um grafo não orientado diz-se euleriano se há um ciclo que contenha todas as suas arestas uma e só uma vez (ciclo euleriano ).O grafo da figura é euleriano porque admite, por exemplo, o ciclo,,,. 1 2 e acordo com o teorema de uler, um grafo não orientado admite um ciclo de uler se e só for conexo e não tiver vértices de grau ímpar. 1. ircuito de uler onsidere-se que a figura seguinte representa uma zona da cidade onde uma equipa terá que fazer recolha de lixo em todos os arruamentos existentes (observando o sentido indicado para o trânsito). m cada um dos arruamentos está indicada a distância (centenas de metros) entre os vértices extremos. dmitindo que se pretende que o percurso de limpeza comece e termine em qual é o circuito óptimo? O circuito óptimo será um circuito de uler (em que se percorrerão todos os arruamentos uma única vez). Se existir, a distância total óptima será de 2 centenas de metros (somatório de todas as distâncias associadas a cada um dos arcos do grafo). ste grafo será euleriano?. 1 Um grafo orientado em que qualquer dos vértices tem semigrau interior e exterior iguais, diz-se grafo pseudo simétrico. NVSTÇÃO OPRONL (MS) X-1
2 rafos ircuito e iclo de uler Na matriz do grafo, verifica-se se o grafo é conexo e, em caso afirmativo, determinam-se os semigraus de cada um dos vértices : + v Γ^ i ^ 1 Γ v i Porque o grafo é conexo e todos os vértices têm semigraus iguais, de acordo com o teorema de uler o grafo é euleriano. Para estabelecer um circuito de uler, que sabemos existir, actue-se do seguinte modo: 1. Registar em coluna, para cada vértice, os seus sucessores (1º quadro) 2. Organizar um 2º quadro para registar, sucessivamente, os arcos do circuito (início em por exemplo) Ordem 1º 2º º º º º º º echo Vértice. scolher sucessivamente sucessores do último vértice atingido, impedindo circuitos parasitas Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice X-2 NVSTÇÃO OPRONL (MS)
3 rafos ircuito e iclo de uler Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice O vértice não tem sucessores; estabeleceu-se prematuramente o circuito parasita,,,.. O vértice é deslocado para a última casa livre do 2º quadro. O último vértice do circuito é agora Ordem 1º 2º º º º º º º echo Vértice Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice NVSTÇÃO OPRONL (MS) X-
4 rafos ircuito e iclo de uler O vértice não tem sucessores; estabeleceu-se o circuito parasita,,,. O vértice é deslocado para a última casa livre do 2º quadro. O último vértice do circuito é agora Ordem 1º 2º º º º º º º echo Vértice Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice Seleccionar o arco ; eliminar no 1º quadro e registar no 2º quadro; último vértice é Ordem 1º 2º º º º º º º echo Vértice Todos os arcos foram seleccionados. Neste último quadro tem-se o circuito de uler com início e fim no vértice. Veja-se agora a situação anterior mas noutra zona da cidade: ste grafo será euleriano? X- NVSTÇÃO OPRONL (MS)
5 rafos ircuito e iclo de uler omecemos por organizar a matriz booleana do grafo da zona de limpeza, verificar se o grafo é fortemente conexo e registar o semigrau interior e exterior de cada vértice: Γ^ + v i ^ 1 Γ v i intersecção dos fechos transitivos directo e inverso do vértice é o conjunto {,,,,,,,, }) pelo que o grafo é fortemente conexo. Nos vértices,,,, e os semigraus exterior e interior são diferentes pelo que não há circuito de uler ou seja para fazer o circuito,., será necessário repetir a passagem em um ou mais dos arruamentos (arcos). O problema é então saber quais os arruamentos a repetir de forma a que o aumento na distância total seja o menor possível. O cálculo da solução óptima deste problema implica a eulerização do grafo que consiste em calcular quais os arcos a repetir entre vértices da rede (repetição de arruamentos) por forma a que, em todos eles, haja igualdade de semigraus (grafo euleriano ). Recorrendo à teoria de fluxos em rede, os vértices com semigraus diferentes serão Origem ou estino de fluxo consoante o semigrau exterior é, respectivamente, menor ou maior do que o semigrau interior. ssim, por exemplo, o vértice necessita ser considerado como Origem de luxo com oferta de uma unidade de fluxo. e facto, porque é origem de 2 arcos e fim de arcos, é necessário repetir a passagem num dos arcos de que é origem para ficar equilibrado o número de saídas de com o número de entradas em. No quadro seguinte, sistematiza-se esta pesquisa prévia: + v i v i onsiderar Oferta / Procura = < Origem 2 = < 2 Origem 1 2 = = > 2 estino 2 = > 1 estino 2 1 = = > 2 estino 2 = < 2 Origem 1 2 = 1 NVSTÇÃO OPRONL (MS) X-
6 rafos ircuito e iclo de uler Nota: Veja-se que a disponibilidade de fluxo dos vértices classificados como origem de fluxo tal como a necessidade de fluxo dos vértices classificados como destino de fluxo é igual ao valor absoluto da diferença entre os semigraus do vértice. Para calcular o fluxo máximo com menor distância total, define-se a entrada fictícia na rede, X, que é ligada com arcos às origens de fluxo (,, ) e a saída fictícia da rede, Y, que é ligada aos destinos de fluxo (,, ). capacidades destes arcos de ligação é igual à oferta/procura do vértice a que estão associados. Os restantes arcos da rede têm capacidade ilimitada. Y ap = 1 ap = 1 ap = 1 ap = 1 ap = 1 X ap = 1 O fluxo máximo com menor encargo (distância neste caso) pode obter-se recorrendo a um modelo de programação inteira (PLP) em que as variáveis de decisão, não negativas, indicam o fluxo que percorre cada arco da rede. tendendo a que, obrigatoriamente, as variáveis X, X, X, Y, Y e Y terão valor de 1 unidade (tanto quanto é o valor absoluto da diferença entre os semigraus), o modelo a utilizar é o seguinte: Min Obs = 1 Origem = 1 Origem = 1 Origem = = = = 1 estino = 1 estino = 1 estino solução óptima 1 =2, ===1 indica para cada um destes arruamentos o número de vezes que devem ser repetidos para obter o circuito desejado com a distância total óptima de 10 centenas de metros ( dos arruamentos e 1 das repetições de arruamentos). Para calcular o circuito é necessário aumentar o grafo com 2 1 Obtida pelo método out of kilter. Pode utilizar-se o modelo de Transhipment. X- NVSTÇÃO OPRONL (MS)
7 rafos ircuito e iclo de uler arcos ligando a, 1 arco ligando a, 1 arco ligando a e 1 arco ligando a pois deste modo todos os vértices ficam com semigraus iguais (grafo euleriano ): ste grafo aumentado admite o circuito de uler:,,,,,,,,,,,,,,,,,,,,,,, que se representa na figura seguinte (nos arcos está registada a ordem porque são percorridos): 1º 21º 12º 1º º º º º 1º 22º 20º 1º 11º 1º º º 1º 19º 2º 10º 1º 2º 9º Nota: veja-se que, nos vértices,,,, e são iguais os semigraus interior e exterior (pseudo simetria) Se se optasse pelo modelo de Transhipment para calcular os arruamentos a repetir, usava-se a matriz inicial: Oferta Observações distância associada às ligações inexistentes 0 é considerada infinita 0 (ig M ) Procura Nota: uffer= ; Origens e Transhipment:,, ; estinos e Transhipment:,, obtendo-se a solução óptima seguinte (veja-se =2, ===1; Min f(x)=1 ): NVSTÇÃO OPRONL (MS) X-
8 rafos ircuito e iclo de uler 2. iclo de uler onsidere-se agora a mesma zona da cidade mas em que os arruamentos permitem transitar nos dois sentidos (arestas). dmitindo desejar que o percurso de limpeza de todos os arruamentos comece e termine em qual é o ciclo óptimo? O ciclo óptimo será um ciclo de uler (em que se percorrerão todos os arruamentos uma única vez). Se existir, a distância total óptima será de centenas de metros (somatório de todas as distâncias associadas a cada um dos arcos do grafo). ste grafo admite ciclo de uler? O grau de cada um dos vértices (número de arestas de que o vértice é extremo) é o seguinte: rau Obs Ímpar Ímpar Ímpar Ímpar Ímpar Ímpar Nota: atente-se que em qualquer grafo não orientado, é sempre par o número de vértices de grau ímpar, caso existam (teorema de uler) Porque há pelo menos um vértice de grau ímpar não há ciclo de uler para a limpeza ou seja para fazer o ciclo,., será necessário repetir a passagem em um ou mais dos arruamentos. O problema é então saber quais os arruamentos a repetir de forma a que o aumento na distância total seja o menor possível. O cálculo da solução óptima deste problema implica a eulerização do grafo que consiste em calcular quais as arestas a repetir entre vértices da rede (repetição de arruamentos) por forma a que, todos eles, tenham grau par (admitindo então um ciclo de uler). X- NVSTÇÃO OPRONL (MS)
9 rafos ircuito e iclo de uler técnica a usar, que difere da utilizada para grafos orientados, é a seguinte: 1. calcular a distância mínima entre cada par de vértices da rede 2. organizar pares de vértices, de grau ímpar, de forma a que : cada um dos vértices não pertença a mais do que um par seja mínima a soma das distâncias mínimas associadas a cada um dos pares Utilizando um algoritmo de encaminhamento (loyd por exemplo) obtêm-se as seguintes matrizes de distâncias mínimas e de precedências: (Matriz inicial) (Matriz de distâncias mínimas) (Matriz de precedências) Para organizar os pares de vértices de grau ímpar recorre-se a algoritmia adequada (minimum weighted perfect matching) ou a um modelo de PL (programação linear inteira binária). Neste último, consideram-se os pares possíveis (i,j) como sendo as variáveis de decisão (binárias: com valor 1 organiza-se o par (i,j) ; com valor 0 não se organiza o par (i,j) ). O modelo de PL a utilizar é o seguinte: NVSTÇÃO OPRONL (MS) X-9
10 rafos ircuito e iclo de uler f= Vértice = = = = = = 1 Nota: Para cada vértice de grau ímpar é estabelecida uma restrição com todas as variáveis em que este vértice é o 1º ou o 2º vértice do par. este modo só uma dessas variáveis poderá ter valor 1 impedindo que o vértice pertença a mais do que um par. Os coeficientes da função objectivo, a minimizar, são as distâncias mínimas entre cada um dos pares de vértices em estudo (ver matriz de distâncias mínimas). Se, no óptimo, o par (i,j) tiver o valor 1 é necessário recorrer à matriz de precedências para saber o encaminhamento associado à distância mínima (que é coeficiente do par na função objectivo). s arestas deste encaminhamento serão duplicadas alcançando-se a desejada paridade dos vértices para se calcular o ciclo óptimo como se de um ciclo de uler se tratasse. solução óptima do modelo de PL é =1, =1; =1 com valor mínimo da função igual a 11 centenas de metros. Recorrendo à matriz de precedências, o encaminhamento óptimo entre estes pares de vértices é: : ligação directa com distância óptima de centenas de metros : ligação directa com distância óptima de centenas de metros : ligação directa com distância óptima de centenas de metros figura seguinte mostra o grafo aumentado com a indicação da ordem porque cada arruamento deve ser percorrido pelo pessoal da limpeza (ciclo de uler). distância total a percorrer será de 99 centenas de metros (+11). X-10 NVSTÇÃO OPRONL (MS)
11 rafos ircuito e iclo de uler. uto Teste a. Qual é o grau do vértice? b. O grafo seguinte admite um ciclo de uler? m caso negativo, quantas arestas são necessárias para eulerizálo? c. Qual é o mínimo de repetições de arestas necessárias para eulerizar o grafo seguinte? d. omente a afirmação seguinte: No grafo não orientado com 10 vértices de grau ímpar é necessário repetir arestas para eulerizar o mesmo. e. omente a afirmação seguinte: No grafo não orientado com 10 vértices de grau ímpar é necessário, no mínimo, repetir arestas para eulerizar o mesmo. f. ulerize o grafo seguinte: J K L NVSTÇÃO OPRONL (MS) X-11
12 rafos ircuito e iclo de uler g. alcule um ciclo óptimo de limpeza na região urbana que o grafo seguinte representa (arestas com distâncias em centenas de metros): J h. Numa fábrica as ligações exteriores existentes são as indicadas na matriz seguinte (arestas com distâncias em metros) s instalações da segurança nocturna estão localizadas em. alcule o encaminhamento óptimo para a segurança sair e regressar às instalações percorrendo todos os arruamentos exteriores. i. alcule o circuito óptimo no grafo com a seguinte matriz de custos (u.m.): X-12 NVSTÇÃO OPRONL (MS)
13 rafos ircuito e iclo de uler j. alcule o circuito postal óptimo no grafo com a seguinte matriz de tempos (u.t.): J K L J 0 10 K 0 L 20 NVSTÇÃO OPRONL (MS) X-1
14 rafos ircuito e iclo de uler. Solução do uto Teste a. O grau do vértice é o número de arcos/arestas de que o vértice é extremo. O vértice tem grau. b. Os vértices e têm grau ímpar, pelo que não há ciclo de uler. Porque e são adjacentes euleriza-se o grafo repetindo a aresta : c. Os vértices com grau ímpar são e. cadeia de menor comprimento tem duas arestas ( e ) pelo que é necessário repetir estas duas arestas: d. rrado (ver a questão anterior). e. orrecto (ver a questão anterior). f. Reutilizar as arestas,,, L, LK ou,,, K, são soluções óptimas. J K L J K L X-1 NVSTÇÃO OPRONL (MS)
15 rafos ircuito e iclo de uler g. Não há ciclo de uler (,, e têm grau ímpar). Para eulerizar o grafo é necessário calcular a matriz de encaminhamentos de distância mínima entre cada par de vértices e, de seguida, organizar os vértices de grau ímpar em dois pares complementares. Para tal, a ligação - deve desdobrar-se ficando do seguinte modo: matriz inicial de distâncias para cálculo do grau de cada vértice e encaminhamento de distância mínima entre cada par de vértices é a seguinte: J rau 2 Ímpar 10 Ímpar 10 Par 2 Par 10 Ímpar Par 2 0 Par 1 0 Par 2 0 Par Par 10 9 Ímpar J Par Os pares óptimos (,) e (,) são os arruamentos a repetir. distância total óptima é de 12 centenas de metros (11 dos arruamentos; 10 das repetições). NVSTÇÃO OPRONL (MS) X-1
16 rafos ircuito e iclo de uler O grafo aumentado a seguir apresentado (conexo e com todos os vértices de grau par) admite o ciclo de uler,definido a partir de : J 21º 22º º º 1º 1º 1º 20º º 9º 1º 2º 1º 1º 19º º º º 10º 11º 12º 1º J h. Não há ciclo de uler pois há vértices de grau ímpar ( e ). O grafo e matriz inicial são os seguintes: Para eulerizar o grafo é necessário calcular a distância mínima entre os dois únicos vértices de grau ímpar (é de 00 metros por,,, ). O grafo é aumentado com as arestas, e que representam os arruamentos a repetir durante a ronda. O ciclo óptimo (ciclo de uler) é de 900 metros (100+00):,,,,,,,,,,,, X-1 NVSTÇÃO OPRONL (MS)
17 rafos ircuito e iclo de uler i. á circuito de uler com valor de 9 u.m. (grafo conexo; todos os vértices com grau par): j. Não há circuito de uler pois há vértices com semigraus interior e exterior diferentes (só, e têm semigraus iguais). O grafo aumentado é o seguinte: J K L Nº de arcos a repetir para ; para ; 20 1 para ; para ; 0 20 para ; 1 para ; para ; J para ; K 0 2 para J; L 20 1 para K; Neste grafo, aumentado, o circuito postal óptimo tem 0 unidades de tempo das quais 20 são devidas à repetição de arcos: J L K J K J L K J NVSTÇÃO OPRONL (MS) X-1
Investigação Operacional
 nvestigação Operacional Optimização em Redes e rafos Licenciatura em ngenharia ivil Licenciatura em ngenharia do Território Licenciatura em ngenharia e rquitectura Naval / ntrodução à Teoria dos rafos
nvestigação Operacional Optimização em Redes e rafos Licenciatura em ngenharia ivil Licenciatura em ngenharia do Território Licenciatura em ngenharia e rquitectura Naval / ntrodução à Teoria dos rafos
Selecciona-se dos vértices ainda não seleccionados o vértice v k que está à menor distância de v i,
 V. Problema do caixeiro-viajante Grafos - Problema do caixeiro-viajante onsidere-se um grafo em que os vértices representam cidades e as arestas (ou arcos) representam as estradas de uma dada região (a
V. Problema do caixeiro-viajante Grafos - Problema do caixeiro-viajante onsidere-se um grafo em que os vértices representam cidades e as arestas (ou arcos) representam as estradas de uma dada região (a
Grafos Orientados (digrafos)
 Grafos Orientados (digrafos) Grafo Orientado ou digrafo Consiste em um grafo G = (V,A) onde V = {v 1,, v n } é um conjunto de vértices e A = {a 1,, a k } é um conjunto de arcos tais que a k, k=1,,m é representado
Grafos Orientados (digrafos) Grafo Orientado ou digrafo Consiste em um grafo G = (V,A) onde V = {v 1,, v n } é um conjunto de vértices e A = {a 1,, a k } é um conjunto de arcos tais que a k, k=1,,m é representado
Problemas de Fluxo em Redes
 CAPÍTULO 7 1. Conceitos fundamentais de grafos Em muitos problemas que nos surgem, a forma mais simples de o descrever, é representá-lo em forma de grafo, uma vez que um grafo oferece uma representação
CAPÍTULO 7 1. Conceitos fundamentais de grafos Em muitos problemas que nos surgem, a forma mais simples de o descrever, é representá-lo em forma de grafo, uma vez que um grafo oferece uma representação
Considere-se a relação dos exames requeridos, na mesma época, pelos alunos de uma escola: Número do Cadeiras requeridas
 X. olorir os Vértices de um Grafo a. Número cromático do grafo onsidere-se que um aluno necessita frequentar as cadeiras, e. Quantos momentos diferentes necessitam ser reservados no horário para que o
X. olorir os Vértices de um Grafo a. Número cromático do grafo onsidere-se que um aluno necessita frequentar as cadeiras, e. Quantos momentos diferentes necessitam ser reservados no horário para que o
W 8. Nas colunas "k =1 a n" executar: Nas linhas "i =1 a m" executar: Em cada linha "i" de "j=1 a n" executar: z = c ik + c kj
 VI. Encaminhamentos de encargo total mínimo Considere-se um grafo (orientado ou não) em que se associa a cada um dos seus arcos (arestas) um dado encargo real (distância, custo, tempo, etc.); admita-se
VI. Encaminhamentos de encargo total mínimo Considere-se um grafo (orientado ou não) em que se associa a cada um dos seus arcos (arestas) um dado encargo real (distância, custo, tempo, etc.); admita-se
Cap. 2 Conceitos Básicos em Teoria dos Grafos
 Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
Redes. ADSA António Câmara
 Redes ADSA António Câmara Redes Método do caminho mais curto Localização de equipamentos Minimum spanning tree Carteiro chinês Caixeiro viajante Links Redes Redes são sistemas de linhas (arcos) ligando
Redes ADSA António Câmara Redes Método do caminho mais curto Localização de equipamentos Minimum spanning tree Carteiro chinês Caixeiro viajante Links Redes Redes são sistemas de linhas (arcos) ligando
Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree
 Investigação Operacional Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree Slide Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Árvore
Investigação Operacional Árvore de Suporte de Comprimento Mínimo Minimal Spanning Tree Slide Transparências de apoio à leccionação de aulas teóricas Maria Antónia Carravilla José Fernando Oliveira Árvore
Capítulo 2- Modelos de grafos.
 Capítulo 2- Modelos de grafos. 2.1- Introdução (pág. 8) [Vídeo 24] Grafo- é um esquema constituído por pontos (ou vértices) e por segmentos (ou arestas). (8) Exemplo 1(pág.8) Um grafo diz-se conexo se
Capítulo 2- Modelos de grafos. 2.1- Introdução (pág. 8) [Vídeo 24] Grafo- é um esquema constituído por pontos (ou vértices) e por segmentos (ou arestas). (8) Exemplo 1(pág.8) Um grafo diz-se conexo se
76) 1.1 Sim 1.2 Não 1.3 Não
 6) 1.1 Sim 1.2 Não 1. Não 2.1 2.2 2.. Os grafos dos exercícios 2.1 e 2.2 são conexos, pois existe sempre uma sequência de arestas a unir quaisquer dois vértices. 4.1 Grafo I vértices: ; arestas: 2 Grafo
6) 1.1 Sim 1.2 Não 1. Não 2.1 2.2 2.. Os grafos dos exercícios 2.1 e 2.2 são conexos, pois existe sempre uma sequência de arestas a unir quaisquer dois vértices. 4.1 Grafo I vértices: ; arestas: 2 Grafo
2. Desenhe o grafo orientado G = (X, Γ) para: 3. Em cada alínea dois grafos são iguais. Identifique-os. (a) (b) (c)
 1. Desenhe o grafo não orientado G = (X, Γ) para: (a) X = {a, b, c, d} e Γ = {{a, b}, {b, c}, {c, d}}. (b) X = {a, b, c, d} e Γ = φ. (c) X = {1, 2, 3, 4, 5, 6, 7, 8} e Γ = {{1, 2}, {2, 2}, {2, 3}, {3,
1. Desenhe o grafo não orientado G = (X, Γ) para: (a) X = {a, b, c, d} e Γ = {{a, b}, {b, c}, {c, d}}. (b) X = {a, b, c, d} e Γ = φ. (c) X = {1, 2, 3, 4, 5, 6, 7, 8} e Γ = {{1, 2}, {2, 2}, {2, 3}, {3,
Matemática Aplicada às Ciências Sociais- 11º ano (Versão: para o manual a partir de 2016/17)
 Matemática Aplicada às Ciências Sociais- 11º ano (Versão: para o manual a partir de 2016/17) Professor: Pedro Nóia Livro adotado: Matemática Aplicada às Ciências Sociais- 11º ano Elisabete Longo e Isabel
Matemática Aplicada às Ciências Sociais- 11º ano (Versão: para o manual a partir de 2016/17) Professor: Pedro Nóia Livro adotado: Matemática Aplicada às Ciências Sociais- 11º ano Elisabete Longo e Isabel
2º Trabalho Prático - Algoritmos em grafos
 Page of LEIC - AEDII - 00/003 - º Semestre º Trabalho Prático - Algoritmos em grafos Introdução Conteúdo do trabalho O segundo trabalho consiste no desenvolvimento de um programa em Java de aplicação de
Page of LEIC - AEDII - 00/003 - º Semestre º Trabalho Prático - Algoritmos em grafos Introdução Conteúdo do trabalho O segundo trabalho consiste no desenvolvimento de um programa em Java de aplicação de
x y Grafo Euleriano Figura 1
 Grafo Euleriano Um caminho simples ou um circuito simples é dito euleriano se ele contém todas as arestas de um grafo. Um grafo que contém um circuito euleriano é um grafo euleriano. Um grafo que não contém
Grafo Euleriano Um caminho simples ou um circuito simples é dito euleriano se ele contém todas as arestas de um grafo. Um grafo que contém um circuito euleriano é um grafo euleriano. Um grafo que não contém
PERCURSOS. André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré
 PERCURSOS André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré Serra 2011 Índice 1...O que é caminho e circuito 1.1...Caminho 1.2...Circuito 1.3...Classificação 2...Caminhos Eulerianos 2.1...Definição
PERCURSOS André Falcão, Carlos Augusto, Rafael Broédel e Lucas Dipré Serra 2011 Índice 1...O que é caminho e circuito 1.1...Caminho 1.2...Circuito 1.3...Classificação 2...Caminhos Eulerianos 2.1...Definição
ESTRUTURAS DISCRETAS (INF 1631) GRAFOS. 1. O que é um grafo? Defina um grafo orientado. Defina um grafo não-orientado.
 PUC-Rio Departamento de Informática Profs. Marcus Vinicius S. Poggi de Aragão Período: 0. Horário: as-feiras e as-feiras de - horas de maio de 0 ESTRUTURAS DISCRETAS (INF 6) a Lista de Exercícios Procure
PUC-Rio Departamento de Informática Profs. Marcus Vinicius S. Poggi de Aragão Período: 0. Horário: as-feiras e as-feiras de - horas de maio de 0 ESTRUTURAS DISCRETAS (INF 6) a Lista de Exercícios Procure
Teoria dos Grafos. Aula 5 - Estruturas de Dados para Grafos. Profª. Alessandra Martins Coelho. março/2013
 Teoria dos Grafos Aula 5 - Estruturas de Dados para Grafos Profª. Alessandra Martins Coelho março/2013 Estrutura é o que caracteriza o próprio grafo e independe da forma como ele é representado. A representação
Teoria dos Grafos Aula 5 - Estruturas de Dados para Grafos Profª. Alessandra Martins Coelho março/2013 Estrutura é o que caracteriza o próprio grafo e independe da forma como ele é representado. A representação
PROPOSTA DE RESOLUÇÃO DA PROVA DO ENSINO SECUNDÁRIO DE MATEMÁTICA APLICADA Às CIÊNCIAS SOCIAIS (CÓDIGO DA PROVA 835) 1ª FASE 23 DE JUNHO 2016
 PROPOSTA DE RESOLUÇÃO DA PROVA DO ENSINO SECUNDÁRIO DE MATEMÁTICA APLICADA Às CIÊNCIAS SOCIAIS (CÓDIGO DA PROVA 835) 1ª FASE 23 DE JUNHO 2016 1. Considerando as preferências dos 900 internautas considerados
PROPOSTA DE RESOLUÇÃO DA PROVA DO ENSINO SECUNDÁRIO DE MATEMÁTICA APLICADA Às CIÊNCIAS SOCIAIS (CÓDIGO DA PROVA 835) 1ª FASE 23 DE JUNHO 2016 1. Considerando as preferências dos 900 internautas considerados
64.2. Designando a sequência por (Pn) podemos escrever: , 1, 2, 4, 7, 13, Designando a sequência por (Tn) podemos escrever:
 11 Pág 70 Dia Tempo de treino (em minutos) 1 30 2 40 3 50 4 60 5 70 6 80 7 90 12 Dia 8: 100 min dia 9: 110 min dia 10: 120 min (2 horas) Ao fim de 10 dias 13 20 + 10n 14 n = 14, logo 20 + 10 14 = 20 +
11 Pág 70 Dia Tempo de treino (em minutos) 1 30 2 40 3 50 4 60 5 70 6 80 7 90 12 Dia 8: 100 min dia 9: 110 min dia 10: 120 min (2 horas) Ao fim de 10 dias 13 20 + 10n 14 n = 14, logo 20 + 10 14 = 20 +
Matemática Discreta - Exercícios de Grafos
 UALG - 0/0 1. Seja G o grafo cuja matriz de adjacência é: 1 8 9 1 8 9 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
UALG - 0/0 1. Seja G o grafo cuja matriz de adjacência é: 1 8 9 1 8 9 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 0 1 0 1 1 0 1 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
Programa. 1 Parte 1 - Conjuntos e Aplicações. 1 Conjuntos. 4 Indução Matemática e Divisibilidade. 5 Congruências Lineares
 Programa Matemática Discreta 2008/09 Jorge Manuel L. André FCT/UNL 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução Matemática e Divisibilidade 5 Congruências Lineares
Programa Matemática Discreta 2008/09 Jorge Manuel L. André FCT/UNL 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução Matemática e Divisibilidade 5 Congruências Lineares
PROPOSTA DE RESOLUÇÃO DA PROVA DO ENSINO SECUNDÁRIO DE MATEMÁTICA APLICADA Às CIÊNCIAS SOCIAIS (CÓDIGO DA PROVA 835) 1ª FASE 23 DE JUNHO 2016
 Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 27-A 1500-236 Lisboa Tel.: +351 21 716 36 90 / 21 711 03 77 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO DA PROVA
Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 27-A 1500-236 Lisboa Tel.: +351 21 716 36 90 / 21 711 03 77 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO DA PROVA
Percursos em um grafo
 Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Oalgoritmo de Dijkstra
 Dijkstra Oalgoritmo de Dijkstra O algoritmo de Dijkstra, concebido pelo cientista da computação holandês Edsger Dijkstra em 1956 e publicado em 1959, soluciona o problema do caminho mais curto num grafo
Dijkstra Oalgoritmo de Dijkstra O algoritmo de Dijkstra, concebido pelo cientista da computação holandês Edsger Dijkstra em 1956 e publicado em 1959, soluciona o problema do caminho mais curto num grafo
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010
 DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
Resoluções Atividades do Manual
 Resoluções Atividades do Manual Tema 3 Atividade 1 10) Sugerimos que esta atividade seja desenvolvida em grupo, podendo cada um apresentar mais do que uma solução. Algumas das soluções possíveis são: 1.1
Resoluções Atividades do Manual Tema 3 Atividade 1 10) Sugerimos que esta atividade seja desenvolvida em grupo, podendo cada um apresentar mais do que uma solução. Algumas das soluções possíveis são: 1.1
MATEMÁTICA DISCRETA. Patrícia Ribeiro 2018/2019. Departamento de Matemática, ESTSetúbal 1 / 47
 1 / 47 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 47 1 Combinatória 2 Aritmética Racional 3 3 / 47 Capítulo 3 4 / 47 não orientados Um grafo não orientado
1 / 47 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 47 1 Combinatória 2 Aritmética Racional 3 3 / 47 Capítulo 3 4 / 47 não orientados Um grafo não orientado
Pesquisa Operacional II. Professor João Soares de Mello
 Pesquisa Operacional II Professor João Soares de Mello http://www.uff.br/decisao/notas.htm Ementa Teoria dos grafos (pré-requisitos: PO I, Álgebra Linear) Programação não linear (pré-requisitos: PO I,
Pesquisa Operacional II Professor João Soares de Mello http://www.uff.br/decisao/notas.htm Ementa Teoria dos grafos (pré-requisitos: PO I, Álgebra Linear) Programação não linear (pré-requisitos: PO I,
Percursos em um grafo
 Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
ESTRUTURAS DE DADOS. prof. Alexandre César Muniz de Oliveira. 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8.
 ESTRUTURAS DE DADOS prof. Alexandre César Muniz de Oliveira 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8. Grafos Sugestão bibliográfica: ESTRUTURAS DE DADOS USANDO C Aaron
ESTRUTURAS DE DADOS prof. Alexandre César Muniz de Oliveira 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8. Grafos Sugestão bibliográfica: ESTRUTURAS DE DADOS USANDO C Aaron
MÓDULO 3 - PROBLEMAS DE TRANSPORTE
 UNESA Sistemas de Transportes Currículo 08 / 009- MÓDULO 3 - PROBLEMAS DE TRANSPORTE. PROBLEMA CLÁSSICO DE TRANSPORTE O Problema de Transporte constitui uma das principais aplicações da PL para auxiliar
UNESA Sistemas de Transportes Currículo 08 / 009- MÓDULO 3 - PROBLEMAS DE TRANSPORTE. PROBLEMA CLÁSSICO DE TRANSPORTE O Problema de Transporte constitui uma das principais aplicações da PL para auxiliar
Estrutura de Dados e Algoritmos e Programação e Computadores II. Aula 10: Introdução aos Grafos
 Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 10: Introdução aos Grafos História O assunto que se constitui no marco inicial da teoria de grafos é na realidade um problema algorítmico.
Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 10: Introdução aos Grafos História O assunto que se constitui no marco inicial da teoria de grafos é na realidade um problema algorítmico.
Problemas de Optimização em redes
 Problemas de ptimização em Redes V., V.Lobo, N / ISGI, 8 Problemas de ptimização em redes Problemas de optimização em redes onceito de grafo Muitos problemas Muitas aplicações aminho mais curto Qual o
Problemas de ptimização em Redes V., V.Lobo, N / ISGI, 8 Problemas de ptimização em redes Problemas de optimização em redes onceito de grafo Muitos problemas Muitas aplicações aminho mais curto Qual o
Número de mandatos: Coligação C+E Número de votos da eventual coligação: =
 Proposta de Resolução do Exame de Matemática Aplicada às Ciências Sociais Cód. 835-1ª Fase 2011 1.1 Para a análise da situação descrita fez-se a distribuição dos mandatos com as hipóteses de coligação
Proposta de Resolução do Exame de Matemática Aplicada às Ciências Sociais Cód. 835-1ª Fase 2011 1.1 Para a análise da situação descrita fez-se a distribuição dos mandatos com as hipóteses de coligação
A resposta para este problema envolve a partição do conjunto de arestas de tal forma que arestas adjacentes não pertençam a um mesmo conjunto.
 6 - oloração de restas e Emparelhamentos onsidere o seguinte problema: Problema - o final do ano acadêmico, cada estudante deve fazer um exame oral com seus professores. Suponha que existam 4 estudantes
6 - oloração de restas e Emparelhamentos onsidere o seguinte problema: Problema - o final do ano acadêmico, cada estudante deve fazer um exame oral com seus professores. Suponha que existam 4 estudantes
Resolução do Exame de Matemática Aplicada às Ciências Sociais 10 ọ /11 ọ Ano 2012 (2 ạ Fase)
 Resolução do Exame de Matemática Aplicada às Ciências Sociais 10 ọ /11 ọ Ano 01 ( ạ Fase) 1. 1.1. No método de Hondt divide-se o número de votos de cada lista por 1,,, 4, 5, 6, 7, 8, 9, etc: Divisores
Resolução do Exame de Matemática Aplicada às Ciências Sociais 10 ọ /11 ọ Ano 01 ( ạ Fase) 1. 1.1. No método de Hondt divide-se o número de votos de cada lista por 1,,, 4, 5, 6, 7, 8, 9, etc: Divisores
Problemas de Transportes e de Afectação
 CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
Grafos Direcionados. > Grafos Direcionados Representações Computacionais 1/36
 Grafos Direcionados > Grafos Direcionados Representações Computacionais 1/36 Grafos Direcionados Em muitas aplicações, é importante ter direção nas arestas: Ruas de mão única Grafos modelando páginas da
Grafos Direcionados > Grafos Direcionados Representações Computacionais 1/36 Grafos Direcionados Em muitas aplicações, é importante ter direção nas arestas: Ruas de mão única Grafos modelando páginas da
Combinando relações. Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações
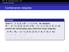 1 / 11 Combinando relações Combinando relações Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações R 1 = {(1, 1), (2, 2), (3, 3)} e R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} podem ser combinadas para
1 / 11 Combinando relações Combinando relações Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações R 1 = {(1, 1), (2, 2), (3, 3)} e R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} podem ser combinadas para
Grafos Hamiltonianos e o Problema do Caixeiro Viajante. Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá
 Grafos Hamiltonianos e o Problema do Caixeiro Viajante Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Grafo Hamiltoniano Definição: Um circuito hamiltoniano em um
Grafos Hamiltonianos e o Problema do Caixeiro Viajante Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Grafo Hamiltoniano Definição: Um circuito hamiltoniano em um
Pesquisa em profundidade. 1 - Grafos não dirigidos
 Pesquisa em profundidade void dfs( Vertex v ) //epth-first search v.visited = true; for each w adjacent to v if(! w.visited ) dfs( w ); generalização da travessia em pré-ordem squema básico da pesquisa
Pesquisa em profundidade void dfs( Vertex v ) //epth-first search v.visited = true; for each w adjacent to v if(! w.visited ) dfs( w ); generalização da travessia em pré-ordem squema básico da pesquisa
Algoritmos em Grafos COM11087-Tópicos Especiais em Programação I
 Algoritmos em Grafos COM11087-Tópicos Especiais em Programação I edmar.kampke@ufes.br Introdução Teoria dos Grafos é o estudo das propriedades e estruturas dos grafos. O objetivo é, após modelar um problema
Algoritmos em Grafos COM11087-Tópicos Especiais em Programação I edmar.kampke@ufes.br Introdução Teoria dos Grafos é o estudo das propriedades e estruturas dos grafos. O objetivo é, após modelar um problema
Tópicos de Matemática Finita 1 a Chamada 30 de Junho de 2001
 Código do Exame: 02 Tópicos de Matemática Finita a Chamada 30 de Junho de 200 Nome: Número: Curso: O exame que vai realizar tem a duração de 3 horas. consiste em: 2 questões de ecolha múltipla, valendo
Código do Exame: 02 Tópicos de Matemática Finita a Chamada 30 de Junho de 200 Nome: Número: Curso: O exame que vai realizar tem a duração de 3 horas. consiste em: 2 questões de ecolha múltipla, valendo
Teoria dos Grafos. Edson Prestes
 Edson Prestes As arestas possuem a função de indicar o relacionamento(espacial, comportamental, temporal) entre os elementos de um grafo. Em diversas situações esta relação não é simétrica, ou seja, par
Edson Prestes As arestas possuem a função de indicar o relacionamento(espacial, comportamental, temporal) entre os elementos de um grafo. Em diversas situações esta relação não é simétrica, ou seja, par
Tópicos de Matemática Finita 1 a Chamada 30 de Junho de 2001
 Código do Exame: 0 Tópicos de Matemática Finita a Chamada 30 de Junho de 200 Nome: Número: Curso: O exame que vai realizar tem a duração de 3 horas. consiste em: 2 questões de ecolha múltipla, valendo
Código do Exame: 0 Tópicos de Matemática Finita a Chamada 30 de Junho de 200 Nome: Número: Curso: O exame que vai realizar tem a duração de 3 horas. consiste em: 2 questões de ecolha múltipla, valendo
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL
 INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL Teste A CURSOS: EMP e EEM 00/00 Data: 1 de Novembro de 00 Duração: 19:0 às 1:0 Instruções:
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL Teste A CURSOS: EMP e EEM 00/00 Data: 1 de Novembro de 00 Duração: 19:0 às 1:0 Instruções:
Problemas de Fluxos em Redes
 Investigação Operacional Problemas de Fluxos em Redes Slide Transparências de apoio à leccionação de aulas teóricas Problemas de fluxos em redes Rede: Conjunto de pontos (vértices) ligados por linhas ou
Investigação Operacional Problemas de Fluxos em Redes Slide Transparências de apoio à leccionação de aulas teóricas Problemas de fluxos em redes Rede: Conjunto de pontos (vértices) ligados por linhas ou
ALGORITMO DE DIJKSTRA
 LGORITMO IJKSTR por runo Miguel Pacheco Saraiva de arvalho epartamento de ngenharia Informática Universidade de oimbra oimbra, Portugal brunomig@student.dei.uc.pt Resumo escreve-se o funcionamento do algoritmo
LGORITMO IJKSTR por runo Miguel Pacheco Saraiva de arvalho epartamento de ngenharia Informática Universidade de oimbra oimbra, Portugal brunomig@student.dei.uc.pt Resumo escreve-se o funcionamento do algoritmo
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Representação de Relações Definição: Uma relação binária de um conjunto A num conjunto
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Representação de Relações Definição: Uma relação binária de um conjunto A num conjunto
X - D U A L I D A D E
 X - D U A L I D A D E 1 - Introdução. Regras de transformação "Primal - Dual" Consideremos os dois problemas P1 e P2 de Programação Linear seguintes: P1 : n Maximizar F = Σ ck. Xk k = 1 n Σ aik. Xk bi
X - D U A L I D A D E 1 - Introdução. Regras de transformação "Primal - Dual" Consideremos os dois problemas P1 e P2 de Programação Linear seguintes: P1 : n Maximizar F = Σ ck. Xk k = 1 n Σ aik. Xk bi
Análise e Síntese de Algoritmos
 Análise e Síntese de Algoritmos Problemas NP-Completos CLRS, Cap. 34 Contexto Algoritmos em Grafos Estruturas de Dados para Conjuntos Disjuntos Programação Linear Programação Dinâmica Algoritmos Greedy
Análise e Síntese de Algoritmos Problemas NP-Completos CLRS, Cap. 34 Contexto Algoritmos em Grafos Estruturas de Dados para Conjuntos Disjuntos Programação Linear Programação Dinâmica Algoritmos Greedy
PCC173 - Otimização em Redes
 PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 31 de maio de 2017 Marco Antonio M. Carvalho
PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 31 de maio de 2017 Marco Antonio M. Carvalho
Programação Linear M É T O D O S : E S T A T Í S T I C A E M A T E M Á T I C A A P L I C A D A S D e 1 1 d e m a r ç o a 2 9 d e a b r i l d e
 Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
Escola Básica e Secundária Mouzinho da Silveira. MACS 11.º Ano Problema do Caixeiro Viajante
 Escola Básica e Secundária Mouzinho da Silveira MACS 11.º Ano Problema do Caixeiro Viajante Problema do Caixeiro Viajante Trata-se de um problema matemático que consiste, sendo dado um conjunto de cidades
Escola Básica e Secundária Mouzinho da Silveira MACS 11.º Ano Problema do Caixeiro Viajante Problema do Caixeiro Viajante Trata-se de um problema matemático que consiste, sendo dado um conjunto de cidades
Análise e Síntese de Algoritmos. Problemas NP-Completos CLRS, Cap. 34
 Análise e Síntese de Algoritmos Problemas NP-Completos CLRS, Cap. 34 Contexto Revisões [CLRS, Cap. 1-10] Algoritmos em Grafos [CLRS, Cap. 22-26] Algoritmos elementares Árvores abrangentes Caminhos mais
Análise e Síntese de Algoritmos Problemas NP-Completos CLRS, Cap. 34 Contexto Revisões [CLRS, Cap. 1-10] Algoritmos em Grafos [CLRS, Cap. 22-26] Algoritmos elementares Árvores abrangentes Caminhos mais
1 Trajeto Euleriano. > Trajeto Euleriano 0/20
 Conteúdo 1 Trajeto Euleriano > Trajeto Euleriano 0/20 Um trajeto Euleriano em um grafo G é um trajeto que utiliza todas as arestas do grafo. Definição Um grafo G é Euleriano se e somente se possui um trajeto
Conteúdo 1 Trajeto Euleriano > Trajeto Euleriano 0/20 Um trajeto Euleriano em um grafo G é um trajeto que utiliza todas as arestas do grafo. Definição Um grafo G é Euleriano se e somente se possui um trajeto
Matemática Discreta. Aula nº 22 Francisco Restivo
 Matemática Discreta Aula nº 22 Francisco Restivo 2006-05-26 Definição: Um grafo cujos vértices são pontos no plano e cujos lados são linhas no plano que só se encontram nos vértices do grafo são grafos
Matemática Discreta Aula nº 22 Francisco Restivo 2006-05-26 Definição: Um grafo cujos vértices são pontos no plano e cujos lados são linhas no plano que só se encontram nos vértices do grafo são grafos
Teoria e Algoritmos em Grafos
 Teoria e Algoritmos em Grafos 2018.2 Conjunto Independente Conjuntos Independentes são subconjuntos de vértices de um grafo no qual nenhum vértice é adjacente entre si. Conjunto Independente Conjuntos
Teoria e Algoritmos em Grafos 2018.2 Conjunto Independente Conjuntos Independentes são subconjuntos de vértices de um grafo no qual nenhum vértice é adjacente entre si. Conjunto Independente Conjuntos
Teoria dos Grafos. Árvores
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br, saraujo@ibilce.unesp.br Preparado a partir
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br, saraujo@ibilce.unesp.br Preparado a partir
1. Dos grafos seguintes, qual representa também o problema de Königsberg?
 Matemática plicada às iências Sociais 1. os grafos seguintes, qual representa também o problema de Königsberg?. Vão realizar-se, na escola, reuniões de onselho de turma. Na tabela que se segue, o símbolo
Matemática plicada às iências Sociais 1. os grafos seguintes, qual representa também o problema de Königsberg?. Vão realizar-se, na escola, reuniões de onselho de turma. Na tabela que se segue, o símbolo
O grau de saída d + (v) de um vértice v é o número de arcos que tem
 Grafos Direcionados Definição (Grau de Entrada) O grau de entrada d (v) de um vértice v é o número de arcos que tem v como cabeça. Definição (Grau de Saída) O grau de saída d + (v) de um vértice v é o
Grafos Direcionados Definição (Grau de Entrada) O grau de entrada d (v) de um vértice v é o número de arcos que tem v como cabeça. Definição (Grau de Saída) O grau de saída d + (v) de um vértice v é o
Teoria dos Grafos. Profa. Alessandra Martins Coelho
 Teoria dos Grafos Profa. Alessandra Martins Coelho fev/2014 Avaliação 2 Provas 30 pontos cada; 3 Implementações 10 pontos cada; 1 Seminário 10 pontos; Listas de exercícios Listas não valem nota, entretanto...
Teoria dos Grafos Profa. Alessandra Martins Coelho fev/2014 Avaliação 2 Provas 30 pontos cada; 3 Implementações 10 pontos cada; 1 Seminário 10 pontos; Listas de exercícios Listas não valem nota, entretanto...
GRAFOS Aula 04 Caminhos, Conexidade e Distância Max Pereira
 Ciência da Computação GRAFOS Aula 04 Caminhos, Conexidade e Distância Max Pereira Um grafo é dito conexo se for possível visitar qualquer vértice, partindo de um outro qualquer, passando pelas suas arestas.
Ciência da Computação GRAFOS Aula 04 Caminhos, Conexidade e Distância Max Pereira Um grafo é dito conexo se for possível visitar qualquer vértice, partindo de um outro qualquer, passando pelas suas arestas.
2º Semestre 2002/2003 Problemas Resolvidos
 RESOLUÇÂO DO PROBLEMA Nº 19 Determinado problema de Programação Linear depois de formulado permitiu obter as seguintes expressões: Max L = 4x 1-2x 2 + 2x 3 -x 4 s.a. R 1: x 1 - x 2 + 2x 3 +x 4 10 R 2:
RESOLUÇÂO DO PROBLEMA Nº 19 Determinado problema de Programação Linear depois de formulado permitiu obter as seguintes expressões: Max L = 4x 1-2x 2 + 2x 3 -x 4 s.a. R 1: x 1 - x 2 + 2x 3 +x 4 10 R 2:
Problema do Caminho Mínimo
 Departamento de Engenharia de Produção UFPR 63 Problema do Caminho Mínimo O problema do caminho mínimo ou caminho mais curto, shortest path problem, consiste em encontrar o melhor caminho entre dois nós.
Departamento de Engenharia de Produção UFPR 63 Problema do Caminho Mínimo O problema do caminho mínimo ou caminho mais curto, shortest path problem, consiste em encontrar o melhor caminho entre dois nós.
Tabela 3 Tabela 4. Evolução do depósito do senhor Manuel (instituição A)
 3. O senhor Jerónimo e o senhor Manuel depositaram, cada um, a quantia de 25000,00 em contas em duas instituições financeiras diferentes, A e B, respectivamente. Os depósitos evoluíram como se apresenta
3. O senhor Jerónimo e o senhor Manuel depositaram, cada um, a quantia de 25000,00 em contas em duas instituições financeiras diferentes, A e B, respectivamente. Os depósitos evoluíram como se apresenta
CAPÍTULO 3. Método Simplex
 CAPÍTULO 3 1. Soluções Básicas Admissíveis Considere um problema de PL representado nas suas formas padrão e matricial. Uma base é um conjunto de m variáveis, tais que a matriz dos coeficientes do sistema
CAPÍTULO 3 1. Soluções Básicas Admissíveis Considere um problema de PL representado nas suas formas padrão e matricial. Uma base é um conjunto de m variáveis, tais que a matriz dos coeficientes do sistema
1. Realizou-se uma Assembleia-geral de uma associação cultural, com o objectivo de
 1. Realizou-se uma Assembleia-geral de uma associação cultural, com o objectivo de eleger uma pessoa para representar a associação em sessões oficiais. Apresentaram-se três candidatos, o Rui, o Luís e
1. Realizou-se uma Assembleia-geral de uma associação cultural, com o objectivo de eleger uma pessoa para representar a associação em sessões oficiais. Apresentaram-se três candidatos, o Rui, o Luís e
Lista de Exercícios Programação Inteira. x 2 0 e inteiros.
 Lista de Exercícios Programação Inteira ) Resolva os problemas a seguir usando o método B&B a) Max z = 5 x + 2 y s.a x + y 2 x + y 5 x, y 0, x e y inteiros b) Max z = 2 x + y s.a x + 2y 0 x + y 25 x, y
Lista de Exercícios Programação Inteira ) Resolva os problemas a seguir usando o método B&B a) Max z = 5 x + 2 y s.a x + y 2 x + y 5 x, y 0, x e y inteiros b) Max z = 2 x + y s.a x + 2y 0 x + y 25 x, y
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO. 5 a Lista de Exercícios
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO MATEMÁTICA COMBINATÓRIA 5 a Lista de Exercícios 1. O grafo de intersecção de uma coleção de conjuntos A 1,..., A n é o grafo
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO DEPARTAMENTO DE CIÊNCIAS DA COMPUTAÇÃO MATEMÁTICA COMBINATÓRIA 5 a Lista de Exercícios 1. O grafo de intersecção de uma coleção de conjuntos A 1,..., A n é o grafo
INSTITUTO SUPERIOR TÉCNICO
 INSTITUTO SUPERIOR TÉCNICO DEPARTAMENTO DE ENGENHARIA CIVIL INVESTIGAÇÃO OPERACIONAL I OPTIMIZAÇÃO EM REDES E GRAFOS Algoritmos para os problemas de - Fluxo máximo - Caminho mais curto - Árvore de ligações
INSTITUTO SUPERIOR TÉCNICO DEPARTAMENTO DE ENGENHARIA CIVIL INVESTIGAÇÃO OPERACIONAL I OPTIMIZAÇÃO EM REDES E GRAFOS Algoritmos para os problemas de - Fluxo máximo - Caminho mais curto - Árvore de ligações
Tópicos de Matemática Finita Data: I II-1 II-2 II-3 II-4 III-1 III-2 III-3 III-4 IV-1 IV-2 IV-3 IV-4 Nota Final
 Tópicos de Matemática Finita Data: 5-07-2003 2 a Época Correcção Código: 2D Nome: Número: Curso: O exame que vai realizar tem a duração de três horas. As respostas às perguntas do grupo I não necessitam
Tópicos de Matemática Finita Data: 5-07-2003 2 a Época Correcção Código: 2D Nome: Número: Curso: O exame que vai realizar tem a duração de três horas. As respostas às perguntas do grupo I não necessitam
Universidade dos Açores Departamento de Matemática
 Universidade dos Açores Departamento de Matemática Grafos, Problemas de Optimização Combinatória e Algoritmos Elaboração: Abel Carneiro Orientação: Armando Mendes Ponta Delgada Junho de 001 When I was
Universidade dos Açores Departamento de Matemática Grafos, Problemas de Optimização Combinatória e Algoritmos Elaboração: Abel Carneiro Orientação: Armando Mendes Ponta Delgada Junho de 001 When I was
Alguns probleminhas...
 Introdução Vários problemas da computação, com aplicações em diversos problemas importantes, nasceram de jogos ou brincadeiras. Hoje veremos uma pequana amostra deste fato. Alguns probleminhas... Problema
Introdução Vários problemas da computação, com aplicações em diversos problemas importantes, nasceram de jogos ou brincadeiras. Hoje veremos uma pequana amostra deste fato. Alguns probleminhas... Problema
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Professora: Susana Costa
 Escola Secundária/3 Rainha Santa Isabel Planificação a Médio Prazo 201/2017 Matemática Aplicada às Ciências Sociais BLOCO II (11º ano) Turmas - 11º C e 11º D Professora: Susana Costa Planificação a Médio
Escola Secundária/3 Rainha Santa Isabel Planificação a Médio Prazo 201/2017 Matemática Aplicada às Ciências Sociais BLOCO II (11º ano) Turmas - 11º C e 11º D Professora: Susana Costa Planificação a Médio
Investigação Operacional
 Métodos de Programação Linear: Big M, Fases, S Dual (Licenciatura) Tecnologias e Sistemas de Informação http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Simplex
Métodos de Programação Linear: Big M, Fases, S Dual (Licenciatura) Tecnologias e Sistemas de Informação http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Simplex
Departamento de Engenharia de Produção UFPR 22
 Departamento de Engenharia de Produção UFPR 22 Geralmente, temos três objetivos i. Redução de custos (custos variáveis) Redução de capital (investimento, custos fixos) i Melhoria do serviço (pode conflitar
Departamento de Engenharia de Produção UFPR 22 Geralmente, temos três objetivos i. Redução de custos (custos variáveis) Redução de capital (investimento, custos fixos) i Melhoria do serviço (pode conflitar
Ficha de Exercícios nº 1
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Alguns passos da prova do Teorema de Runge
 Alguns passos da prova do Teorema de Runge Roberto Imbuzeiro Oliveira 15 de Junho de 2011 1 Os principais passos da prova Teorema 1 Sejam U C aberto, K U compacto e f : U C holomorfa Seja A C \U tal que
Alguns passos da prova do Teorema de Runge Roberto Imbuzeiro Oliveira 15 de Junho de 2011 1 Os principais passos da prova Teorema 1 Sejam U C aberto, K U compacto e f : U C holomorfa Seja A C \U tal que
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL
 INSTITUTO POLITÉCNICO DE SETÚBL ESCOL SUPERIOR DE TECNOLOGI DEPRTMENTO DE MTEMÁTIC INVESTIGÇÃO OPERCIONL TESTE CURSOS: EMP, EEM e EME 2005/2006 Data: 4 de Novembro de 2005 Duração: 19:0 às 21:0 Instruções:
INSTITUTO POLITÉCNICO DE SETÚBL ESCOL SUPERIOR DE TECNOLOGI DEPRTMENTO DE MTEMÁTIC INVESTIGÇÃO OPERCIONL TESTE CURSOS: EMP, EEM e EME 2005/2006 Data: 4 de Novembro de 2005 Duração: 19:0 às 21:0 Instruções:
Problema de Optimização. Metodologias de Apoio à Decisão 1. Slide 1
 Metodologias de Apoio à Decisão Optimização Combinatória Slide Transparências de apoio à leccionação de aulas teóricas José Fernando Oliveira Maria Antónia Carravilla Problemas de Optimização Instância
Metodologias de Apoio à Decisão Optimização Combinatória Slide Transparências de apoio à leccionação de aulas teóricas José Fernando Oliveira Maria Antónia Carravilla Problemas de Optimização Instância
PROPOSTA DE RESOLUÇÃO DO EXAME DE MATEMÁTICA APLICADA ÀS CIÊNCIAS SOCIAIS (PROVA 835) ªFASE. Grupo I
 PROPOSTA DE RESOLUÇÃO DO EXAME DE MATEMÁTICA APLICADA ÀS CIÊNCIAS SOCIAIS (PROA 835) 2013 1ªFASE Grupo I 1. 1.1. De acordo com o método apresentado, a contagem de pontos de cada tema, incluindo o tema
PROPOSTA DE RESOLUÇÃO DO EXAME DE MATEMÁTICA APLICADA ÀS CIÊNCIAS SOCIAIS (PROA 835) 2013 1ªFASE Grupo I 1. 1.1. De acordo com o método apresentado, a contagem de pontos de cada tema, incluindo o tema
Grafos Eulerianos e o Problema do Carteiro Chinês
 Prof. Ademir A. Constantino DIN - UEM 1 Grafos Eulerianos e o Problema do Carteiro Chinês Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Prof. Ademir A. Constantino
Prof. Ademir A. Constantino DIN - UEM 1 Grafos Eulerianos e o Problema do Carteiro Chinês Prof. Ademir Constantino Departamento de Informática Universidade Estadual de Maringá Prof. Ademir A. Constantino
Pesquisa Operacional
 Faculdade de Engenharia - Campus de Guaratinguetá Pesquisa Operacional Livro: Introdução à Pesquisa Operacional Capítulo 3 - Teoria dos Grafos Fernando Marins fmarins@feg.unesp.br Departamento de Produção
Faculdade de Engenharia - Campus de Guaratinguetá Pesquisa Operacional Livro: Introdução à Pesquisa Operacional Capítulo 3 - Teoria dos Grafos Fernando Marins fmarins@feg.unesp.br Departamento de Produção
Estrutura de Dados e Algoritmos e Programação e Computadores II. Aula 11: Introdução aos Grafos
 Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 11: Introdução aos Grafos Indução Finita Indução Finita é uma técnica para provar teoremas também usada no projecto de algoritmos. Suponha
Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 11: Introdução aos Grafos Indução Finita Indução Finita é uma técnica para provar teoremas também usada no projecto de algoritmos. Suponha
Problema do Caminho Mais Curto. Problema do Caminho Mais Curto
 Problema do Caminho Mais Curto " Podemos afectar pesos" aos arcos de um grafo, por exemplo, para representar uma distância entre cidades numa rede ferroviária: ria: Chicago 650 600 700 Toronto 200 New
Problema do Caminho Mais Curto " Podemos afectar pesos" aos arcos de um grafo, por exemplo, para representar uma distância entre cidades numa rede ferroviária: ria: Chicago 650 600 700 Toronto 200 New
Problemas de Decisão em Redes 18
 Problemas de Decisão em Redes 8 Problemas de Fluxo Máximo Slide Problemas de Fluxo Máximo Definição: Dada uma rede, com um nó de entrada e um nó de saída, com capacidades associadas a cada ramo, pretende-se
Problemas de Decisão em Redes 8 Problemas de Fluxo Máximo Slide Problemas de Fluxo Máximo Definição: Dada uma rede, com um nó de entrada e um nó de saída, com capacidades associadas a cada ramo, pretende-se
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios. Cap. IV Modelo Dual
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
Prova Escrita de Matemática Aplicada às Ciências Sociais
 EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 74/004, de 6 de março Prova Escrita de Matemática Aplicada às Ciências Sociais 10.º e 11.º Anos de Escolaridade Prova 835/.ª Fase Critérios de Classificação
EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 74/004, de 6 de março Prova Escrita de Matemática Aplicada às Ciências Sociais 10.º e 11.º Anos de Escolaridade Prova 835/.ª Fase Critérios de Classificação
Comunicação e redes. Aula 2: Teoria dos Grafos Conceitos básicos. Professor: Guilherme Oliveira Mota.
 Comunicação e redes Aula 2: Teoria dos Grafos Conceitos básicos Professor: Guilherme Oliveira Mota g.mota@ufabc.edu.br Aula passada Redes complexas Grafo G: Conjunto de pontos e linhas ligando esses pontos
Comunicação e redes Aula 2: Teoria dos Grafos Conceitos básicos Professor: Guilherme Oliveira Mota g.mota@ufabc.edu.br Aula passada Redes complexas Grafo G: Conjunto de pontos e linhas ligando esses pontos
Simplex. Investigação Operacional José António Oliveira Simplex
 18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
Estruturas de Dados Grafos
 Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
SUMÁRIO. Fundamentos Árvores Binárias Árvores Binárias de Busca
 ÁRVORES SUMÁRIO Fundamentos Árvores Binárias Árvores Binárias de Busca 2 ÁRVORES Utilizadas em muitas aplicações Modelam uma hierarquia entre elementos árvore genealógica Diagrama hierárquico de uma organização
ÁRVORES SUMÁRIO Fundamentos Árvores Binárias Árvores Binárias de Busca 2 ÁRVORES Utilizadas em muitas aplicações Modelam uma hierarquia entre elementos árvore genealógica Diagrama hierárquico de uma organização
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilce.unesp.br, socorro@ibilce.unesp.br Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Optimização em Redes e Não Linear
 Departamento de Matemática da Universidade de Aveiro Optimização em Redes e Não Linear Ano Lectivo 005/006, o semestre Folha - Optimização em Redes - Árvores de Suporte. Suponha que uma dada companhia
Departamento de Matemática da Universidade de Aveiro Optimização em Redes e Não Linear Ano Lectivo 005/006, o semestre Folha - Optimização em Redes - Árvores de Suporte. Suponha que uma dada companhia
Tópicos de Matemática Finita 2 a Época 20 de Julho de 2001
 Código do Exame: 301 Tópicos de Matemática Finita 2 a Época 20 de Julho de 2001 Nome: Número: Curso: O exame que vai realizar tem a duração de 3 horas. consiste em: 12 questões de ecolha múltipla, valendo
Código do Exame: 301 Tópicos de Matemática Finita 2 a Época 20 de Julho de 2001 Nome: Número: Curso: O exame que vai realizar tem a duração de 3 horas. consiste em: 12 questões de ecolha múltipla, valendo
x 1 + b a 2 a 2 : declive da recta ;
 - O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
- O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
