Lógica Matemática e Álgebra de Boole: uma Breve Introdução
|
|
|
- Maria dos Santos de Abreu do Amaral
- 6 Há anos
- Visualizações:
Transcrição
1 Lógica Matemática e Álgebra de Boole: uma Breve Introdução Rodrigo Costa Ferreira Resumo O presente texto realizará um estudo introdutório da lógica matemática booleana com fulcro nos trabalhos de Boole (2008), Rasiowa (1963: 220) e Jónsson e Tarski (1951: , 1952: ). Após motivações históricas e filosóficas, definiremos formalmente a álgebra de Boole conforme Oliveira (2004) e Burris (1981: ), bem como apresentaremos alguns teoremas fundamentais dessa álgebra. Na sequência, discutiremos como é possível por intermédio da álgebra de Boole construir uma semântica algébrica apropriada à lógica proposicional clássica. Ao final, provaremos os teoremas da correção e da completude a partir da álgebra de Lindenbaum, uma espécie de álgebra de Boole. Palavras-chave: Lógica Proposicional Clássica; Lógica Matemática; Álgebra de Boole. 1 Introdução Se é verdade que os raciocínios e argumentos matemáticos utilizam alguma lógica ou regras lógicas de inferência, não é esse o aspecto mais desenvolvido daquilo que modernamente se entende por lógica matemática. De certo, esta lógica progressivamente vem assumindo também um caráter de disciplina matemática à qual não são estranhas, portanto, as técnicas abstratas da matemática, de forma que alguns afirmam, com certo excesso, que a lógica matemática é mais uma matemática lógica do que lógica matemática. Contudo, é melhor que se entenda que esses dois aspectos completam-se e enriquecem-se a todo instante, uma vez que a matemática corrente tem evoluído de modo a se tornar cada vez mais abstrata e rigorosa, aproximando-se, por si mesma, da lógica 1. A lógica acha-se intimamente correlacionada com a matemática. Assim, quando buscamos aproximar a lógica e a matemática, pretendemos, tão-somente Mestre em Lógica Matemática pela UFPB, Doutorando em Lógica Deôntica pela UFPB- UFRN-UFPE, Professor Assistente na Universidade Federal do Semi-árido (UFERSA). rocosfer@yahoo.com.br 1 Oliveira (2004: 203). 1
2 2 sublinhar que elas se acham correlacionadas entre si de maneira profunda, tanto pelos objetos como pelos seus métodos. No fundo, uma das causas da aproximação que se verificou, a contar do século XVII e seguintes, entre a lógica e a matemática, radica no uso básico que ambas fazem do método axiomático e da formalização 2. De acordo com a tradição, a lógica matemática tem início nos trabalhos do filósofo e matemático alemão Gottfried Wilhelm Leibniz ( ). Tendo compreendido que a lógica, com os seus termos, proposições e silogismos, guarda uma certa semelhança com a álgebra, a partir da sua De Arte Combinatoria, escrita em 1666, Leibniz procura aplicar à lógica o modelo de cálculo algébrico de sua época. Nessa obra introdutória, o filósofo tenta implantar a ambiciosa construção de uma lingua philosophica com characteristica universalis, uma espécie de sistema exato e universal de notação concebido para expressar de forma clara o pensamento humano. Em paralelo, propõe o desenvolvimento de um calculus ratiocinator (cálculo da razão), uma espécie de cálculo que permitiria inferir, quase que mecanicamente, das premissas (combinações simbólicas convenientes) representadas na lingua philosophica, por conclusão, todas as coisas pensadas. Apesar do programa lógico-matemático de Leibniz, na forma como foi introduzido no século XVII, não ser teoricamente exequível, o calculus ratiocinator constituiu um importante precursor na metodologia da lógica matemática contemporânea 3. Passados dois séculos da proposta de Leibniz, a lógica matemática tem uma formulação formal mais precisa no ano de 1847 com a publicação do livro The Mathematical Analysis of Logic de George Boole ( ). Neste trabalho inovador, Boole estabelece a lógica matemática como uma espécie de cálculo lógico de classes. No mesmo ano, Augustus De Morgan ( ) publica o tratado Formal Logic no qual desenvolve importantes estudos sobre a lógica das relações. No ano de 1854, George Boole publica o artigo An Investigation into the Laws of thought on which are Founded the Mathematical Theories of Logic and Probability complementando as teorias do seu livro de Anos depois, com Ernst Schröder ( ), no volumoso tratado Vorlesungen über die Algebra der Logic publicado no período entre 1890 e 1895, as noções lógicas booleanas recebem um refinamento notável 4. Uma abordagem simbólica moderna à lógica matemática é encontrada nos trabalhos do alemão Gottlob Frege ( ), em particular no Begriffsschrift de 1879 e no Grundgesetze der Arithmetik publicado no período entre 1879 e 1903, e nas pesquisas de Giuseppe Peano ( ) com o extenso Formulaire de Mathématiques publicado a partir de Em suma, o trabalho de Peano almeja expressar toda a matemática em termos de um cálculo lógico, ao passo que o trabalho de Frege deriva da necessidade de uma fundamentação mais sólida à matemática. Os trabalhos iniciados por Frege e Peano impulsionam a construção da monumental obra Principia Mathematica publicada entre os anos de 1910 e 1913 por Alfred North Whitehead ( ) e Bertrand Russell ( ). A identificação de grande parte da matemática com a lógica é a idéia básica dessa obra. Nessa abordagem, os conceitos e teoremas matemáticos são desenvolvidos a partir de idéias lógicas, começando com o cálculo das proposições, passando pela teoria das classes e teoria das relações. No período entre 1934 e 1939 aparece o abrangente 2 Para mais detalhes: Newton C. A. da Costa (1994: 19-21). 3 Eves (2004: 669).; Mortari (2001: 33).; e D Ottaviano (2008). 4 Para mais detalhes: Kneale (1980: ).
3 3 Grundlagen der Mathematik de David Hilbert ( ) e Paul Bernays ( ). O ambicioso programa formalista de Hilbert e Bernays tinha como objetivo fundamentar toda a matemática mediante a aplicação de sistemas formais fundamentados no método axiomático. Os anos que se sucederam às pesquisas de Bernays e Hilbert são seguidos por inúmeros outros importantes trabalhos em lógica matemática, entre os quais, para citar alguns, o artigo Über Formal Unentscheidbare Sätze der Principia Mathematica und Verwandter Systeme I (1931) do matemático Kurt Gödel ( ) 5 e os trabalhos On Some Fundamental Concepts of Metamathematics (1930), The Concept of Truth in Formalized Languages (1935), Boolean Algebras with Operators (1952), entre outros, do lógico polonês Alfred Tarski ( ) 6. Assim, em particular, de modo introdutório o presente artigo pretende esboçar alguns aspectos formais da lógica matemática de Boole. Num primeiro momento (seção 2), apresentaremos algumas fundamentações filosóficas à construção da álgebra de Boole. Em seguida, em termos formais (seção 3), definiremos a estrutura da álgebra de Boole e exporemos alguns dos seus teoremas. Num segundo momento (subseção 4.1), enunciaremos uma linguagem proposicional L, sendo-lhe fixada os símbolos primitivos, as regras de formação, esquemas de axiomas, a regra de inferência modus ponens e a consequência sintática: definição de teorema, conceito de demonstração, teorema da dedução. Define-se, na seqüência, a semântica proposicional clássica. Ao final, por intermédio da álgebra de Lindenbaum o cálculo proposicional apresentado será algebrizado, bem como provaremos o teorema da correção e o teorema da completude. 2 Motivações Filosóficas à Lógica de Boole A lógica algébrica de Boole tem como fundamento a concepção intuitiva de classes de objetos. Por exemplo, nesta lógica um dado produto xy denota uma classe de objetos que pertencem a classe x e a classe y, por outras palavras, se x, por ora, representa a classe dos objetos brancos e y a classe dos ursos, então xy representa a classe dos ursos brancos. Percebe-se, claramente, e de modo interessante, que a lei comutativa xy = yx permanece válida mesmo quando aplicada a classes de objetos. Mas será que deste pequeno fato podemos afirmar existir uma íntima relação entre as leis da lógica e da álgebra? Vejamos. Na lógica algébrica booleana, nascida da analogia das leis da álgebra com as leis relativas às classes de objetos, a lei xx = x é verdadeira para quaisquer valores de x, uma vez que a classe formada com objetos que pertencem a classe x é a própria classe x. Todavia, na álgebra essa lei não é totalmente válida. A equação x 2 = x tem apenas duas soluções, a saber, x = 0 ou x = 1. Tomando esse fato em conta, Boole concluiu que na lógica algébrica são válidas as leis da álgebra matemática quando os valores se limitam a 0 e 1. A lógica booleana interpretou os símbolos 1 e 0 como classes especiais, de modo que 1 representa a classe de todos os objetos (o universo) e 0 representa a classe a que nenhum objeto pertença (a classe vazia). Assim, considerando x y uma classe formada com dois objetos da classe x, 5 Para mais detalhes sobre o metateorema da completude semântica de Gödel e algumas de suas conseqüências: Kneale (1980: ). 6 Para mais detalhes: Tarski (1956); e Jónsson e Tarski (1951: , 1952: ).
4 4 retirado os objetos da classe y, então, pela notação, 1 x seria a classe construída por todos objetos (do universo) que não fazem parte da classe x. Se de xx = x, por exemplo, subtraírmos de cada membro desta equação x, teríamos x xx = xx x, ou seja, x(1 x) = 0 uma legítima inferência; pois se, por exemplo, x é a classe dos homens, então 1 x é a classe dos objetos que não são homens. Certamente, esse produto deve ser a classe vazia, posto que não se pode, ao menos na lógica clássica, exisitr um objeto que seja simultaneamente homem e não-homem (princípio da não contradição) 7. 3 Álgebra de Boole Nesta seção, definiremos formalmente a álgebra de Boole e apresentaremos alguns dos seus teoremas. DEFINIÇÃO 1 Uma Álgebra de Boole B é uma sêxtupla ordenada B = B,,,, 0, 1 que compreende 8 : (1) um conjunto não-vazio: B; (2) duas operações binárias sobre B:, ; (3) um operador unário sobre B: ; (4) dois elementos distintos de B: 0 e 1; Ademais, para quaisquer {x, y, z} B, vale o seguinte: (Ax B 1) Comutatividade. Para todo {x, y} B, temos x y = y x; (Ax B 2) Comutatividade. Para todo {x, y} B, temos x y = y x; (Ax B 3) Distributividade. Para todo {x, y, z} B, temos x (y z) = (x y) (x z); (Ax B 4) Distributividade. Para todo {x, y, z} B, temos x (y z) = (x y) (x z); (Ax B 5) Identidade. Para todo {x, 0} B, temos x 0 = 0 x = x; (Ax B 6) Identidade. Para todo {x, 1} B, temos 7 Para mais detalhes: Boole (2008); Anderson (1962: ); e Burris (1981: ). 8 Para mais detalhes: Boole (2008). Textos consultados: Anderson (1962: ); e Burris (1981: ).
5 5 x 1 = 1 x = x; (Ax B 7) Complementariedade. Para todo x B, temos x x = 1; (Ax B 8) Complementariedade. Para todo x B, temos x x = 0. Uma álgebra de Boole é dita degenerada quando os elemento neutros para as operações e são iguais, isto é, 0 = 1. Consideremos, aqui, apenas álgebras não degeneradas (0 1). São teoremas da Álgebra de Boole: (T1) Princípio da Dualidade. Todo resultado dedutível dos axiomas da álgebra de Boole permanece válido se nele trocamos por e 0 por 1, e vice-versa. (T2) Indempotência. Para todo x em B, x x = x e x x = x; (T3) Identidade. Para todo x em B, x 0 = 0 e x 1 = 1; (T4) Absorção. Para todo x, y e z em B, (x y) x = x e (x y) x = x; (T5) Associatividade. Para todo x, y e z em B, x (y z) = (x y) z x (y z) = (x y) z; e (T6) Maximum. Para todo x em B, x 1; (T7) Minimum. Para todo x em B, x 0; (T8) Duplo Complemento. Para todo x em B, ( x) = x; (T9) Leis de De Morgan. Para todo x e y em B, (x y) = x y e (x y) = x y. 4 Cálculo Proposicional Clássico e a Álgebra de Boole 4.1 Sintaxe da Lógica Proposicional Linguagem e Axiomática DEFINIÇÃO 2 Linguagem do cálculo proposicional clássico. A linguagem proposicional do Cálculo Proposicional Clássico (CPC) será denotada por L. Os símbolos primitivo de L são os seguintes: (1) Variáveis proposicionais: A, B, C,...; (2) Conectivos lógicos:, ; (3) Símbolos de pontuação: (, ).
6 6 DEFINIÇÃO 3 Regras de formação. Dada uma linguagem proposicional L, dizemos que CPC: (1) uma variável proposicional é uma fórmula bem formada (fbf); (2) se A é uma fbf, então A também o é; (3) se A e B são fórmulas bem formadas (fbfs), então (A B) é uma fbf; (4) somente as fórmulas construídas segundo os itens acima são fbfs. Podemos acrescentar outros conectivos lógicos mediante definição; assim ( ) A B = def (A B); ( ) A B = def ( A B). Nós usaremos a convenção padrão de escrever as fórmulas sem os parênteses mais exteriores e onde não houver ambiguidade, como se encontra em qualquer livro texto de lógica. O conjunto de todas as fórmulas proposicionais no FOR; subconjuntos de fórmulas serão denotados por Γ e. DEFINIÇÃO 4 Axiomas. Dentre as fbfs, são esquemas de axiomas do CPC: (Ax 1) A (B A); (Ax 2) (A (B C)) ((A B) (A C)); (Ax 3) ( B A) (( B A) B). DEFINIÇÃO 5 Regra de inferência: para o CPC a regra: A, A B / B. Modus Ponens (MP). Admite-se Consequência Sintática DEFINIÇÃO 6 Demonstração. Uma demonstração de A no CPD é uma sequência finita de fbfs na linguagem L, do tipo A 1,..., A i,..., A n para todo i tal que 1 i n: (1) A i é axioma, ou; (2) A i é uma consequência imediata de fbfs precedentes, pela regra de inferência MP; (3) A n = A. DEFINIÇÃO 7 Teorema. A é um teorema no CPC se, e somente se, existir uma demonstração de A no CPC; escreve-se A. Se A não é um teorema no CPD, escreve-se A. DEFINIÇÃO 8 Dedução a partir de Γ. Uma dedução de A a partir de Γ é uma seqüência finita de fórmulas bem formadas na linguagem L, do tipo A 1,..., A i,..., A n, para todo i tal que 1 i n, em que cada A i satisfaz uma das seguintes condições:
7 7 (1) A i é um axioma, ou; (2) A i pertence a Γ, ou; (3) A i é obtida de fbfs anteriores na seqüência, pela regra de inferência MP; (4) A n = A. DEFINIÇÃO 9 Dedução a partir de Γ. Uma dedução de A a partir de Γ é uma sequência finita de fbfs na linguagem L, do tipo A 1,..., A i,..., A n, para todo i tal que 1 i n, em que cada A i satisfaz uma das seguintes condições: (1) A i é um axioma, ou; (2) A i pertence a Γ, ou; (3) A i é obtida de fbfs anteriores na sequência, pela regra de inferência MP; (4) A n = A. DEFINIÇÃO 10 Consequência sintática. A é uma consequência sintática de Γ se, e somente se, A é uma fbf numa dedução a partir de Γ. Escreve-se Γ A. Sendo Γ vazio, em lugar da notação Ø A, escreve-se A. TEOREMA 1 Teorema da dedução. Se Γ, A B, então Γ A B. Prova. Mendelson (1997: 37-40) Semântica Proposicional Clássica DEFINIÇÃO 11 Dada uma linguagem proposicional L para o CPC, a valoração v é uma aplicação do conjunto de todas as fórmulas proposicionais FOR no conjunto dos valores lógicos,, isto é, v é uma função do tipo v : FOR 2, conhecida como função-verdade, que atribui a cada fórmula proposicional um valor de verdade (falso) ou (verdadeiro), calculado em decorrência da matriz lógica de cada conectivo. Nestes termos, v satisfaz as seguintes condições: ( ) v ( A) = se, e somente se, v (A) = ; ( ) v (A B) = se, e somente se, v (A) = ou v (B) = ; ( ) v (A B) = se, e somente se, v (A) = v (B) = ; ( ) v (A B) = se, e somente se, v (A) = ou v (B) = ; Nós dizemos que uma fórmula A é válida, ou tautologia, se, e somente se, para toda valoração v, v(a) =. Mediante tabelas de verdade, pode-se verificar se uma determinada fórmula do CPC é válida ou não. Um modo muito interessante de prover outra semântica para o CPC é mediante o uso de ferramentas algébricas. Isso é feito na próxima subseção.
8 8 4.2 Semântica Algébrica Booleana Um modo muito interessante de prover uma semântica para o Cálculo Proposicional Clássico (CPC) é mediante o uso de ferramentas algébricas. É possível, sob dadas circunstâncias (RASIOWA, 1963: 220), determinar um homomorfismo entre a álgebra das fórmulas proposicionais do CPC ( FOR,,,,, ) e a álgebra de Lindenbaum ( FOR /,,,, 0, 1, com um conjunto quociente de todas as fbfs proposicionais munido de duas operações binárias ( e ) associativas e comutativas, um operador unário ( ), dois elementos distinguidos (0 e 1) e determinadas condições axiomáticas), isto é, verifica-se a correspondência entre as leis da lógica proposicional clássica e as leis da álgebra de Boole. Vejamos. Para FOR define-se a seguinte relação de equivalência : A B se, e somente se, A B e B A. Dada relação de equivalência definida acima, podemos agora realizar a partição de FOR, de modo a construir um conjunto quociente deste. O conjunto quociente de FOR é dado como FOR / = {[A] A FOR}, no qual a classe de equivalência de A é [A], isto é, [A] = {B FOR A B}. Forma-se, assim, uma partição disjunta de FOR em classes de equivalências. Em FOR / é possível definir a seguinte relação: [A] [B] se, e somente se, A B, em FOR. Como definida, é uma ordem parcial em FOR / : (1) é reflexiva: [A] [A]; isto é, A A; (2) é simétrica: se [A] [B] e [B] [A], então, por definição, A B e B A; segue-se que A B e, assim, [A] = [B]; (3) é transitiva: se [A] [B] e [B] [C], então, por definição, A B e B C, segue-se que A C; logo, [A] [C]. PROPOSIÇÃO 1 Álgebra de Lindenbaum. A partir da algebrização do CPC é possível definir a estrutura B = FOR,,,,,, A(B) = FOR /,,,, 0, 1, chamada de álgebra de Lindenbaum para a lógica proposicional clássica. A(B) é uma álgebra de Boole que admite as seguintes operações de classes: (1) Complemento de classes. [A] = [ A];
9 9 (2) Reunião de classes. [A] [B] = [A B]; (3) Interseção de classes. [A] [B] = [A B]; (4) Classes das contradições. 0 = [A A]; (5) Classes das tautologias. 1 = [A A]; Prova. As proposições (1) (6) são justificadas como segue-se: (1) : [A] [B] se, e somente se, [A] [B] = [B] (I). Por outro lado, A B se, e somente se, A B B (II). A equação (II) pode ser redefinida em FOR / como [A B] = [B] (III). Logo, aplicando (III) em (I), temos [A] [B] = [A B]; (2) : Dual a (1); (3) : [A] [A] se, e somente se, [A] [A] = [A] em FOR /. Se [A] = [ A], então de [A] [ A] = [A] temos [A A] = [A] pela proposição (1). Como em FOR ocorre A A se, e somente se, A A A, logo [A] = [ A]; (4) : 1. A A A A em FOR 2. [A A] = [A A] em FOR / 3. [A A] = [A] [ A] pela proposição (2) 4. [A A] = [A] [A] pela proposição (3) 5. [A A] = 0 pelo Ax B 8 (5) : Dual a (4). TEOREMA 2 [A] = 1 se, e somente se, A. Prova 9. Se [A] é a classe de uma fórmula numa álgebra A(B), uma álgebra de Boole, que é equivalente à classe da unidade 1 de A(B), então A é um teorema do cálculo proposicional. Assim, [A] = 1 se, e somente se, A. Ou seja, temos A, desde que A(B) tenha identificado o elemento 1, isto é, [A] = 1. Como 1. A Hipótese 2. A (B A) Ax 1 3. A ((A A) A) substituição em 2 4. (A A) A MP em 1 e 3, então (A A) A e [A A] [A]. Em lógica clássica temos a seguinte equivalência A A A A. Logo, a expressão [A A] [A] pode ser redefinida como [A A] [A], ou seja, pela Proposição 83 (5), temos [A] 1. Dado também que 1. A (B A) Ax 1 2. A (A A) substituição em 1 então A (A A) e [A] [A A]. Como em lógica clássica temos a seguinte equivalência A A A A, podemos representar a expressão [A] [A A] como [A] [A A], ou seja, pela Proposição 1 (5), temos 1 [A]. 9 O presente resultado está relacionado diretamente com a semântica de valorações, tomando-se = 1 e = 0. Este teorema diz que uma fórmula é demonstrável se sua classe de equivalência for idêntica à classe 1 numa álgebra de Boole. Como veremos adiante, o resultado geral é que uma fórmula é demonstrável se, e somente se, for tautologia (ou válida).
10 10 Temos, ao final, dado o exposto, [A] = 1. Como vimos, com a álgebra de Lindenbaum podemos estabelecer uma relação entre a álgebra de Boole (B) e a lógica proposicional clássica. Para tanto, associamos, por exemplo, a cada fórmula bem formada atômica A do cálculo proposicional clássico uma classe de equivalência [A] que, por sua vez, corresponde a um membro da álgebra booleana A(B). Operações numa álgebra booleana podem ser usadas para generalizar a semântica da lógica proposicional clássica de forma que [A] = v (A), isto é, escrito de outra forma, x = [A] = v (A), na qual x é um membro de uma álgebra de Boole. DEFINIÇÃO 12 Uma fbf A do cálculo proposicional clássico é válida numa álgebra de Boole se, e somente se, para toda valoração v, temos v ([A]) = 1, noutras palavras, se, e somente se, para toda v (A) =. Portanto, à luz do exposto, é possível construir uma semântica algébrica para a lógica proposicional clássica por intermédio da álgebra de Boole, desde que para uma dada linguagem proposicional do CPC à valoração v de fórmulas proposicionais bem formadas, compostas por A e B, por exemplo, seja associada elementos do tipo [A] e [B] de B da álgebra B, de forma que v satisfaça as seguintes condições: ( ) v ( A) = [A]; ( ) v (A B) = [A] [B]; ( ) v (A B) = [A] [B]; ( ) v (A B) = [A] [B]. A seguir, mostraremos que o cálculo proposicional é correto, ou seja, que todos os seus teoremas são válidos na semântica algébrica sugerida. TEOREMA 3 Teorema da correção. Se A, então B = A. Prova. Para demonstrarmos o teorema da correção, é necessário mostrarmos que todos os esquemas de axiomas da lógica proposicional (i) (iii) são válidos, e que a regra modus ponens (iv) preserva a validade na semântica proposta. Neste sentido, teremos: (i) (Ax 1) A (B A) Prova (i). 1. x ( y x) por Def. 2. x (x y) Ax B 2 3. ( x x) y Ax B y Ax B T2 (ii) (Ax 2) (A (B C)) ((A B) (A C)); Prova (ii). 1. [ x ( x z)] [ ( x y) ( x z)] por Def. 2. [ x ( x z)] [(x y) ( x z)] T 5 e T 4
11 11 3. [ x ( x z)] [(x ( x z)) ( y ( x z))] Ax B 4 4. [ x ( x z)] [((x x) z) (( y x) z))] T 3 5. [ x ( x z)] [(1 z) (( y x) z))] Ax B 9 e Ax B 2 6. [ x ( x z)] [1 (( x ( y z))] T 2 e T 3 7. [ x ( x z)] [ x ( y z)] Ax B Ax B 9 (iii) (Ax 3) ( B A) (( B A) B). Prova (iii). 1. ( y x) ( y x) y por Def. 2. (y x) (y x) y T 4 3. (y x) ( y x) y T 5 4. (y x) ( y y) (y x) Ax B 2 e Ax B 4 5. (y x) 1 (y x) Ax B 9 6. (y x) (y x) Ax B Ax B 9 (iv) Regra de inferência modus ponens. A, A B B. Prova (iv). Seja v uma valoração tal que v (A) = x = 1 e v (A B) = 1, devemos provar que v (B) = x y = 1 por Def y = 1 subs. x por y = 1 T 6 4. y = 1 Ax B 5 Provada a correção do cálculo proposicional, passaremos à completude deste, provando que toda fórmula válida, segundo a semântica algébrica proposta, é um teorema do cálculo proposicional clássico. TEOREMA 4 Teorema da completude. Se B = A, então A. Prova. Pelo Teorema 2, provamos que [A] = 1 se, e somente se, A. A expressão [A] = 1 pode ser redefinida como [A] = [A A], pela Proposição 1 (5). A expressão anterior pode ser escrita, ainda, como [A] = [A] [A], segundo a Proposição 1 (1)-(3). Valorando ambos os membros, temos v ([A]) = v ([A] [A]), isto é, v (A) =. Por conseguinte, v (A) = se, e somente se A, ou seja, de modo particular, se B = A, então A. Referências 1. Anderson, John M.; Johnstone, Henry W. Natural deduction: the logic basis of Axiom Systems. Clifornia: Wadsworth, 1962.
12 12 2. BOOLE, George. The mathematical Analysis of logic: being an essay toward a calculus of deductive reasoning. Disponível em: < archive.org/details/mathematicalanal00booluoft.> Acesso em: 10 de março de BURRIS, S; SANKPPANAVAR, H. P. A course in universal algebra. New York: Springer-Verlag, DA COSTA, N. C. A. Ensaios sobre os fundamentos da lógica. São Paulo: Hucitec, DAGHLIAN, Jacob. Lógica e álgebra de Boole. São Paulo: Atlas, D OTTAVIANO, L. M. Ítala e FEITOSA, A. Hércules. Sobre a história da lógica, a lógica clássica e o surgimento das lógicas não-clássicas. Disponível em: < ftp://ftp.cle.unicamp.br/pub/arquivos/educacional/artgt. pdf >. Acesso em: 30 de junho de EVES, Howard. Introdução à história da matemática. Trad. Higyno H. Domingues. São Paulo: Editora da UNICAMP, KNEALE, W. e KNEALE, M. O Desenvolvimento da Lógica. Trad. M. S. Lourenço. Lisboa: Fundação Calouste Gulbenkian, MENDELSON, E. Introduction to Mathematical Logic. New Jersey: Van Nostrand Company, JÓNSSON, B. e TARSKI, A. Boolean algebras with operators in American Journal of Mathematics, I - II, 73, 74, 1951: , 1952: MORTARI, Cezar A. Introdução à lógica. São Paulo: Unesp, OLIVEIRA, A.J.F. Lógica e aritmética. Brasília: Unb, RASIOWA, H.; SIKORSKI, R. The mathematics of metamathematics. Warszawa: Państwowe Wydawnictwo Naukowe - Polish Scientific, TARSKI, A. Logic, semantics, metamathematics. Trad. J. H. Woodger. Oxford: Clarendon Press,
(A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x
 Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Dedução Natural e Sistema Axiomático Pa(Capítulo 6)
 Dedução Natural e Sistema Axiomático Pa(Capítulo 6) LÓGICA APLICADA A COMPUTAÇÃO Professor: Rosalvo Ferreira de Oliveira Neto Estrutura 1. Definições 2. Dedução Natural 3. Sistemas axiomático Pa 4. Lista
Dedução Natural e Sistema Axiomático Pa(Capítulo 6) LÓGICA APLICADA A COMPUTAÇÃO Professor: Rosalvo Ferreira de Oliveira Neto Estrutura 1. Definições 2. Dedução Natural 3. Sistemas axiomático Pa 4. Lista
Lógica e Raciocínio. Introdução. Universidade da Madeira.
 Lógica e Raciocínio Universidade da Madeira http://dme.uma.pt/edu/ler/ Introdução 1 Lógica... é a ciência que estuda os princípios e aproximações para estabelecer a validez da inferência e demonstração:
Lógica e Raciocínio Universidade da Madeira http://dme.uma.pt/edu/ler/ Introdução 1 Lógica... é a ciência que estuda os princípios e aproximações para estabelecer a validez da inferência e demonstração:
Prof.Letícia Garcia Polac. 6 de abril de 2017
 Fundamentos de Lógica e Conjuntos Prof.Letícia Garcia Polac Universidade Federal de Uberlândia UFU-MG 6 de abril de 2017 Sumário 1 EMENTA 2 BIBLIOGRAFIA 3 AVALIAÇÕES 4 INTRODUÇÃO EMENTA Ementa 1. Lógica
Fundamentos de Lógica e Conjuntos Prof.Letícia Garcia Polac Universidade Federal de Uberlândia UFU-MG 6 de abril de 2017 Sumário 1 EMENTA 2 BIBLIOGRAFIA 3 AVALIAÇÕES 4 INTRODUÇÃO EMENTA Ementa 1. Lógica
4 AULA. Regras de Inferência e Regras de Equivalência LIVRO. META: Introduzir algumas regras de inferência e algumas regras de equivalência.
 1 LIVRO Regras de Inferência e Regras de Equivalência 4 AULA META: Introduzir algumas regras de inferência e algumas regras de equivalência. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de:
1 LIVRO Regras de Inferência e Regras de Equivalência 4 AULA META: Introduzir algumas regras de inferência e algumas regras de equivalência. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de:
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções
 Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) joao.carvalho@inesc.pt Álgebra de Boole Binária A Álgebra de Boole binária
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) joao.carvalho@inesc.pt Álgebra de Boole Binária A Álgebra de Boole binária
A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS.
 A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS. SANDRO MARCOS GUZZO RESUMO. A construção dos conjuntos numéricos é um assunto clássico na matemática, bem como o estudo das propriedades das operações
A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS. SANDRO MARCOS GUZZO RESUMO. A construção dos conjuntos numéricos é um assunto clássico na matemática, bem como o estudo das propriedades das operações
Lógica Computacional
 Aula Teórica 4: Semântica da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática,
Aula Teórica 4: Semântica da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática,
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES
 MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Teoria de Conjuntos Um conjunto é uma colecção de objectos/elementos/membros. (Cantor
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Teoria de Conjuntos Um conjunto é uma colecção de objectos/elementos/membros. (Cantor
Lógica Proposicional
 Lógica Proposicional Lógica Computacional Carlos Bacelar Almeida Departmento de Informática Universidade do Minho 2007/2008 Carlos Bacelar Almeida, DIUM LÓGICA PROPOSICIONAL- LÓGICA COMPUTACIONAL 1/28
Lógica Proposicional Lógica Computacional Carlos Bacelar Almeida Departmento de Informática Universidade do Minho 2007/2008 Carlos Bacelar Almeida, DIUM LÓGICA PROPOSICIONAL- LÓGICA COMPUTACIONAL 1/28
Lógica para Computação
 Lógica para Computação Prof. Celso Antônio Alves Kaestner, Dr. Eng. celsokaestner (at) utfpr (dot) edu (dot) br Sistemas Dedutivos Um Sistema Dedutivo (SD) tem por objetivo obter, a partir de um conjunto
Lógica para Computação Prof. Celso Antônio Alves Kaestner, Dr. Eng. celsokaestner (at) utfpr (dot) edu (dot) br Sistemas Dedutivos Um Sistema Dedutivo (SD) tem por objetivo obter, a partir de um conjunto
Lógica Proposicional
 Slides da disciplina Lógica para Computação, ministrada pelo Prof. Celso Antônio Alves Kaestner, Dr. Eng. (kaestner@dainf.ct.utfpr.edu.br) entre 2007 e 2008. Alterações feitas em 2009 pelo Prof. Adolfo
Slides da disciplina Lógica para Computação, ministrada pelo Prof. Celso Antônio Alves Kaestner, Dr. Eng. (kaestner@dainf.ct.utfpr.edu.br) entre 2007 e 2008. Alterações feitas em 2009 pelo Prof. Adolfo
LÓGICA I. André Pontes
 LÓGICA I André Pontes 1. Conceitos fundamentais O que é a Lógica? A LÓGICA ENQUANTO DISCIPLINA Estudo das leis de preservação da verdade. [Frege; O Pensamento] Estudo das formas válidas de argumentos.
LÓGICA I André Pontes 1. Conceitos fundamentais O que é a Lógica? A LÓGICA ENQUANTO DISCIPLINA Estudo das leis de preservação da verdade. [Frege; O Pensamento] Estudo das formas válidas de argumentos.
Matemática Discreta - 07
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 07 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Tópicos de Matemática. Teoria elementar de conjuntos
 Tópicos de Matemática Lic. em Ciências da Computação Teoria elementar de conjuntos Carla Mendes Dep. Matemática e Aplicações Universidade do Minho 2010/2011 Tóp. de Matemática - LCC - 2010/2011 Dep. Matemática
Tópicos de Matemática Lic. em Ciências da Computação Teoria elementar de conjuntos Carla Mendes Dep. Matemática e Aplicações Universidade do Minho 2010/2011 Tóp. de Matemática - LCC - 2010/2011 Dep. Matemática
Introdução à Computação: Álgebra Booleana
 Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza (bfmartins@inf.ufes.br) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza (bfmartins@inf.ufes.br) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
Fundamentos de Lógica Matemática
 Webconferência 3-01/03/2012 Inferência Lógica Prof. L. M. Levada http://www.dc.ufscar.br/ alexandre Departamento de Computação (DC) Universidade Federal de São Carlos (UFSCar) 2012/1 Objetivos Análise
Webconferência 3-01/03/2012 Inferência Lógica Prof. L. M. Levada http://www.dc.ufscar.br/ alexandre Departamento de Computação (DC) Universidade Federal de São Carlos (UFSCar) 2012/1 Objetivos Análise
Lógica. Cálculo Proposicional. Introdução
 Lógica Cálculo Proposicional Introdução Lógica - Definição Formalização de alguma linguagem Sintaxe Especificação precisa das expressões legais Semântica Significado das expressões Dedução Provê regras
Lógica Cálculo Proposicional Introdução Lógica - Definição Formalização de alguma linguagem Sintaxe Especificação precisa das expressões legais Semântica Significado das expressões Dedução Provê regras
Notas de aula de MAC0329 Álgebra Booleana e Aplicações
 Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
Fundamentos de Álgebra Moderna Profª Ana Paula CONJUNTOS
 Fundamentos de Álgebra Moderna Profª Ana Paula CONJUNTOS O conjunto é um conceito fundamental em todos os ramos da matemática. Intuitivamente, um conjunto é uma lista, coleção ou classe de objetods bem
Fundamentos de Álgebra Moderna Profª Ana Paula CONJUNTOS O conjunto é um conceito fundamental em todos os ramos da matemática. Intuitivamente, um conjunto é uma lista, coleção ou classe de objetods bem
A LINGUAGEM DO DISCURSO MATEMÁTICO E SUA LÓGICA
 MAT1513 - Laboratório de Matemática - Diurno Professor David Pires Dias - 2017 Texto sobre Lógica (de autoria da Professora Iole de Freitas Druck) A LINGUAGEM DO DISCURSO MATEMÁTICO E SUA LÓGICA Iniciemos
MAT1513 - Laboratório de Matemática - Diurno Professor David Pires Dias - 2017 Texto sobre Lógica (de autoria da Professora Iole de Freitas Druck) A LINGUAGEM DO DISCURSO MATEMÁTICO E SUA LÓGICA Iniciemos
Conjunto Quociente e Classe de Equivalência (Alguns Exemplos e Definições)
 Exemplos Definições Conjunto Quociente e Classe de Equivalência (Alguns Exemplos e Definições) Matemática Elementar - EAD Departamento de Matemática Universidade Federal da Paraíba 4 de setembro de 2014
Exemplos Definições Conjunto Quociente e Classe de Equivalência (Alguns Exemplos e Definições) Matemática Elementar - EAD Departamento de Matemática Universidade Federal da Paraíba 4 de setembro de 2014
Teoria Elementar dos Conjuntos
 Teoria Elementar dos Conjuntos Este capítulo visa oferecer uma breve revisão sobre teoria elementar dos conjuntos. Além de conceitos básicos importantes em matemática, a sua imprtância reside no fato da
Teoria Elementar dos Conjuntos Este capítulo visa oferecer uma breve revisão sobre teoria elementar dos conjuntos. Além de conceitos básicos importantes em matemática, a sua imprtância reside no fato da
Lógica e Metodologia Jurídica
 Lógica e Metodologia Jurídica Argumentos e Lógica Proposicional Prof. Juliano Souza de Albuquerque Maranhão julianomaranhao@gmail.com Quais sentenças abaixo são argumentos? 1. Bruxas são feitas de madeira.
Lógica e Metodologia Jurídica Argumentos e Lógica Proposicional Prof. Juliano Souza de Albuquerque Maranhão julianomaranhao@gmail.com Quais sentenças abaixo são argumentos? 1. Bruxas são feitas de madeira.
Prof. Leonardo Augusto Casillo
 UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 6 Álgebra de Boole Prof. Leonardo Augusto Casillo Álgebra de Boole (ou Boleana) Desenvolvida pelo matemático britânico George
UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 6 Álgebra de Boole Prof. Leonardo Augusto Casillo Álgebra de Boole (ou Boleana) Desenvolvida pelo matemático britânico George
Lógicas Construtivas: Intuicionismo, uma
 Lógicas Construtivas: Intuicionismo, uma Introdução Ricardo Bianconi 1 Introdução Vamos tratar agora de Lógicas Construtivas, ou seja, aquelas em que se admitem apenas argumentos construtivos. O que seriam
Lógicas Construtivas: Intuicionismo, uma Introdução Ricardo Bianconi 1 Introdução Vamos tratar agora de Lógicas Construtivas, ou seja, aquelas em que se admitem apenas argumentos construtivos. O que seriam
n. 25 DIAGRAMAS DE VENN
 n. 25 DIAGRAMAS DE VENN Foi o matemático inglês John Venn (1834-1923) que criou os diagramas, com o intuito de facilitar a compreensão na relação de união e intersecção entre conjuntos. John Venn desenvolveu
n. 25 DIAGRAMAS DE VENN Foi o matemático inglês John Venn (1834-1923) que criou os diagramas, com o intuito de facilitar a compreensão na relação de união e intersecção entre conjuntos. John Venn desenvolveu
Vimos que a todo o argumento corresponde uma estrutura. Por exemplo ao argumento. Se a Lua é cúbica, então os humanos voam.
 Matemática Discreta ESTiG\IPB 2012/13 Cap1 Lógica pg 10 Lógica formal (continuação) Vamos a partir de agora falar de lógica formal, em particular da Lógica Proposicional e da Lógica de Predicados. Todos
Matemática Discreta ESTiG\IPB 2012/13 Cap1 Lógica pg 10 Lógica formal (continuação) Vamos a partir de agora falar de lógica formal, em particular da Lógica Proposicional e da Lógica de Predicados. Todos
Fórmulas da lógica proposicional
 Fórmulas da lógica proposicional As variáveis proposicionais p, q, são fórmulas (V P rop ) é fórmula (falso) α e β são fórmulas, então são fórmulas (α β), (α β), (α β) e ( α) DCC-FCUP -TAI -Sistemas Dedutivos
Fórmulas da lógica proposicional As variáveis proposicionais p, q, são fórmulas (V P rop ) é fórmula (falso) α e β são fórmulas, então são fórmulas (α β), (α β), (α β) e ( α) DCC-FCUP -TAI -Sistemas Dedutivos
1 Conjuntos, Números e Demonstrações
 1 Conjuntos, Números e Demonstrações Definição 1. Um conjunto é qualquer coleção bem especificada de elementos. Para qualquer conjunto A, escrevemos a A para indicar que a é um elemento de A e a / A para
1 Conjuntos, Números e Demonstrações Definição 1. Um conjunto é qualquer coleção bem especificada de elementos. Para qualquer conjunto A, escrevemos a A para indicar que a é um elemento de A e a / A para
Lógica Matemática UNIDADE II. Professora: M. Sc. Juciara do Nascimento César
 Lógica Matemática UNIDADE II Professora: M. Sc. Juciara do Nascimento César 1 1 - Álgebra das Proposições 1.1 Propriedade da Conjunção Sejam p, q e r proposições simples quaisquer e sejam t e c proposições
Lógica Matemática UNIDADE II Professora: M. Sc. Juciara do Nascimento César 1 1 - Álgebra das Proposições 1.1 Propriedade da Conjunção Sejam p, q e r proposições simples quaisquer e sejam t e c proposições
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO Álgebra de Boole Disciplina: Lógica Professora Dr.ª: Donizete
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO Álgebra de Boole Disciplina: Lógica Professora Dr.ª: Donizete
Introdução aos Métodos de Prova
 Introdução aos Métodos de Prova Renata de Freitas e Petrucio Viana IME-UFF, Niterói/RJ II Colóquio de Matemática da Região Sul UEL, Londrina/PR 24 a 28 de abril 2012 Sumário Provas servem, principalmente,
Introdução aos Métodos de Prova Renata de Freitas e Petrucio Viana IME-UFF, Niterói/RJ II Colóquio de Matemática da Região Sul UEL, Londrina/PR 24 a 28 de abril 2012 Sumário Provas servem, principalmente,
LÓGICA I ANDRÉ PONTES
 LÓGICA I ANDRÉ PONTES 3. Introdução à Teoria dos Conjuntos Um conjunto é uma coleção ou um agregado de objetos. Introduzindo Conjuntos Ex.: O conjunto das vogais; O conjuntos de pessoas na sala; O conjunto
LÓGICA I ANDRÉ PONTES 3. Introdução à Teoria dos Conjuntos Um conjunto é uma coleção ou um agregado de objetos. Introduzindo Conjuntos Ex.: O conjunto das vogais; O conjuntos de pessoas na sala; O conjunto
Afirmações Matemáticas
 Afirmações Matemáticas Na aula passada, vimos que o objetivo desta disciplina é estudar estruturas matemáticas, afirmações sobre elas e como provar essas afirmações. Já falamos das estruturas principais,
Afirmações Matemáticas Na aula passada, vimos que o objetivo desta disciplina é estudar estruturas matemáticas, afirmações sobre elas e como provar essas afirmações. Já falamos das estruturas principais,
Lógica para computação
 Lógica para computação PROPRIEDADES SEMÂNTICAS DA LÓGICA PROPOSICIONAL Professor Marlon Marcon Introdução Esta seção considera a análise de algumas propriedades semânticas da LP que relacionam os resultados
Lógica para computação PROPRIEDADES SEMÂNTICAS DA LÓGICA PROPOSICIONAL Professor Marlon Marcon Introdução Esta seção considera a análise de algumas propriedades semânticas da LP que relacionam os resultados
Abaixo descreveremos 6 portas lógicas: AND, OR, NOT, NAND, NOR e XOR.
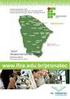 9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
INF 1771 Inteligência Artificial
 Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 06 Lógica Proposicional Lógica Proposicional Lógica simples. A sentenças são formadas por conectivos como: e, ou, então.
Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 06 Lógica Proposicional Lógica Proposicional Lógica simples. A sentenças são formadas por conectivos como: e, ou, então.
Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos. Teoria dos Conjuntos
 Pode-se dizer que a é em grande parte trabalho de um único matemático: Georg Cantor (1845-1918). noção de conjunto não é suscetível de definição precisa a partir d noções mais simples, ou seja, é uma noção
Pode-se dizer que a é em grande parte trabalho de um único matemático: Georg Cantor (1845-1918). noção de conjunto não é suscetível de definição precisa a partir d noções mais simples, ou seja, é uma noção
LÓGICA PROPOSICIONAL
 LÓGICA PROPOSICIONAL Prof. Cesar Tacla/UTFPR/Curitiba Slides baseados no capítulo 1 de DA SILVA, F. S. C.; FINGER M. e de MELO A. C. V.. Lógica para Computação. Thomson Pioneira Editora, 2006. Conceitos
LÓGICA PROPOSICIONAL Prof. Cesar Tacla/UTFPR/Curitiba Slides baseados no capítulo 1 de DA SILVA, F. S. C.; FINGER M. e de MELO A. C. V.. Lógica para Computação. Thomson Pioneira Editora, 2006. Conceitos
Números Inteiros Axiomas e Resultados Simples
 Números Inteiros Axiomas e Resultados Simples Apresentamos aqui diversas propriedades gerais dos números inteiros que não precisarão ser provadas quando você, aluno, for demonstrar teoremas nesta disciplina.
Números Inteiros Axiomas e Resultados Simples Apresentamos aqui diversas propriedades gerais dos números inteiros que não precisarão ser provadas quando você, aluno, for demonstrar teoremas nesta disciplina.
Números Reais. Gláucio Terra. Departamento de Matemática IME - USP. Números Reais p. 1/2
 Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
Capítulo 1. Os Números. 1.1 Notação. 1.2 Números naturais não nulos (inteiros positivos) Última atualização em setembro de 2017 por Sadao Massago
 Capítulo 1 Os Números Última atualização em setembro de 2017 por Sadao Massago 1.1 Notação Números naturais: Neste texto, N = {0, 1, 2, 3,...} e N + = {1, 2, 3, }. Mas existem vários autores considerando
Capítulo 1 Os Números Última atualização em setembro de 2017 por Sadao Massago 1.1 Notação Números naturais: Neste texto, N = {0, 1, 2, 3,...} e N + = {1, 2, 3, }. Mas existem vários autores considerando
Unidade: Proposições Logicamente Equivalentes. Unidade I:
 Unidade: Proposições Logicamente Equivalentes Unidade I: 0 Unidade: Proposições Logicamente Equivalentes Nesta unidade, veremos a partir de nossos estudos em tabelas-verdade as proposições logicamente
Unidade: Proposições Logicamente Equivalentes Unidade I: 0 Unidade: Proposições Logicamente Equivalentes Nesta unidade, veremos a partir de nossos estudos em tabelas-verdade as proposições logicamente
Inteligência Artificial IA II. LÓGICA DE PREDICADOS PARA REPRESENTAÇÃO DO CONHECIMENTO
 Inteligência Artificial IA Prof. João Luís Garcia Rosa II. LÓGICA DE PREDICADOS PARA REPRESENTAÇÃO DO CONHECIMENTO 2004 Representação do conhecimento Para representar o conhecimento do mundo que um sistema
Inteligência Artificial IA Prof. João Luís Garcia Rosa II. LÓGICA DE PREDICADOS PARA REPRESENTAÇÃO DO CONHECIMENTO 2004 Representação do conhecimento Para representar o conhecimento do mundo que um sistema
Álgebra de Boole. João Paulo Cerquinho Cajueiro 19 de agosto de 2009
 Álgebra de Boole João Paulo Cerquinho Cajueiro 19 de agosto de 2009 A álgebra de Boole foi desenvolvida por George Boole(1815 1864) em seu livro An Investigation of the Laws of Thought on Which are Founded
Álgebra de Boole João Paulo Cerquinho Cajueiro 19 de agosto de 2009 A álgebra de Boole foi desenvolvida por George Boole(1815 1864) em seu livro An Investigation of the Laws of Thought on Which are Founded
sumário 1 introdução e conceitos básicos 1 2 noções de lógica e técnicas de demonstração introdução à matemática discreta...
 sumário 1 introdução e conceitos básicos 1 1.1 introdução à matemática discreta... 2 1.2 conceitos básicos de teoria dos conjuntos... 3 1.2.1 conjuntos...3 1.2.2 pertinência...5 1.2.3 alguns conjuntos
sumário 1 introdução e conceitos básicos 1 1.1 introdução à matemática discreta... 2 1.2 conceitos básicos de teoria dos conjuntos... 3 1.2.1 conjuntos...3 1.2.2 pertinência...5 1.2.3 alguns conjuntos
Lógica Matemática. Conceitos Gerais. Prof. Guilherme Tomaschewski Netto
 Lógica Matemática Conceitos Gerais Prof. Guilherme Tomaschewski Netto guilherme.netto@gmail.com Roteiro! Apresentação dos Objetivos! Definições! Aspectos Históricos! Principais tendências Legendas! Nesta
Lógica Matemática Conceitos Gerais Prof. Guilherme Tomaschewski Netto guilherme.netto@gmail.com Roteiro! Apresentação dos Objetivos! Definições! Aspectos Históricos! Principais tendências Legendas! Nesta
Pontifícia Universidade Católica do Rio Grande do Sul
 Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Matemática - Departamento de Matemática Estruturas Algébricas Prof. M.Sc. Guilherme Luís Roëhe Vaccaro e-mail: vaccaro@mat.pucrs.br Prof.
Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Matemática - Departamento de Matemática Estruturas Algébricas Prof. M.Sc. Guilherme Luís Roëhe Vaccaro e-mail: vaccaro@mat.pucrs.br Prof.
Ordem dos Inteiros AULA. 4.1 Introdução. 4.2 Ordem Ordem dos Inteiros
 META: Apresentar ordem nos números inteiros e os Princípio de indução e do Menor elemento. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Usar o processo de indução finita dos Inteiros. Justificar
META: Apresentar ordem nos números inteiros e os Princípio de indução e do Menor elemento. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Usar o processo de indução finita dos Inteiros. Justificar
1 Lógica de primeira ordem
 1 Lógica de primeira ordem 1.1 Sintaxe Para definir uma linguagem de primeira ordem é necessário dispor de um alfabeto. Este alfabeto introduz os símbolos à custa dos quais são construídos os termos e
1 Lógica de primeira ordem 1.1 Sintaxe Para definir uma linguagem de primeira ordem é necessário dispor de um alfabeto. Este alfabeto introduz os símbolos à custa dos quais são construídos os termos e
Matemática Discreta. Lógica Proposicional. Profa. Sheila Morais de Almeida. agosto DAINF-UTFPR-PG
 Matemática Discreta Lógica Proposicional Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2016 Tautologias Tautologia é uma fórmula proposicional que é verdadeira para todos os possíveis valores-verdade
Matemática Discreta Lógica Proposicional Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2016 Tautologias Tautologia é uma fórmula proposicional que é verdadeira para todos os possíveis valores-verdade
Lógica Formal. Matemática Discreta. Prof. Vilson Heck Junior
 Lógica Formal Matemática Discreta Prof. Vilson Heck Junior vilson.junior@ifsc.edu.br Objetivos Utilizar símbolos da lógica proposicional; Encontrar o valor lógico de uma expressão em lógica proposicional;
Lógica Formal Matemática Discreta Prof. Vilson Heck Junior vilson.junior@ifsc.edu.br Objetivos Utilizar símbolos da lógica proposicional; Encontrar o valor lógico de uma expressão em lógica proposicional;
Lógica para Computação
 Lógica para Computação Prof. Celso Antônio Alves Kaestner, Dr. Eng. celsokaestner (at) utfpr (dot) edu (dot) br Linguagem informal x linguagem formal; Linguagem proposicional: envolve proposições e conectivos,
Lógica para Computação Prof. Celso Antônio Alves Kaestner, Dr. Eng. celsokaestner (at) utfpr (dot) edu (dot) br Linguagem informal x linguagem formal; Linguagem proposicional: envolve proposições e conectivos,
5 AULA. Teorias Axiomáticas LIVRO. META: Apresentar teorias axiomáticas.
 1 LIVRO Teorias Axiomáticas 5 AULA META: Apresentar teorias axiomáticas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Criar teorias axiomáticas; Provar a independência dos axiomas de uma
1 LIVRO Teorias Axiomáticas 5 AULA META: Apresentar teorias axiomáticas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Criar teorias axiomáticas; Provar a independência dos axiomas de uma
Notas de Aula Álgebra Linear. Elton José Figueiredo de Carvalho Escola de Ciências e Tecnologia Universidade Federal do Rio Grande do Norte
 Notas de Aula Álgebra Linear Elton José Figueiredo de Carvalho Escola de Ciências e Tecnologia Universidade Federal do Rio Grande do Norte Versão 201608221232c de 22 de agosto de 2016 Parte I Espaços vetoriais
Notas de Aula Álgebra Linear Elton José Figueiredo de Carvalho Escola de Ciências e Tecnologia Universidade Federal do Rio Grande do Norte Versão 201608221232c de 22 de agosto de 2016 Parte I Espaços vetoriais
INF 1771 Inteligência Artificial
 INF 1771 Inteligência Artificial Aula 06 Lógica Proposicional Edirlei Soares de Lima Lógica Proposicional Lógica muito simplificada. A sentenças são formadas por conectivos como:
INF 1771 Inteligência Artificial Aula 06 Lógica Proposicional Edirlei Soares de Lima Lógica Proposicional Lógica muito simplificada. A sentenças são formadas por conectivos como:
Lógica Computacional
 Aula Teórica 9: Forma Normal Conjuntiva Departamento de Informática 21 de Março de 2011 O problema Como determinar eficazmente a validade de uma fórmula? Objectivo Determinar a validade de raciocínios
Aula Teórica 9: Forma Normal Conjuntiva Departamento de Informática 21 de Março de 2011 O problema Como determinar eficazmente a validade de uma fórmula? Objectivo Determinar a validade de raciocínios
Lógica Computacional
 Aula Teórica 13: Dedução Natural em Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de
Aula Teórica 13: Dedução Natural em Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de
Cálculo Diferencial e Integral Química Notas de Aula
 Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
SMA Elementos de Matemática Notas de Aulas. Ires Dias - Sandra Maria Semensato de Godoy
 SMA - 341 - Elementos de Matemática Notas de Aulas Ires Dias - Sandra Maria Semensato de Godoy 2006 Capítulo 1 Noções de Lógica Lógica é a higiene usada pelos matemáticos para conservar suas idéias saudáveis
SMA - 341 - Elementos de Matemática Notas de Aulas Ires Dias - Sandra Maria Semensato de Godoy 2006 Capítulo 1 Noções de Lógica Lógica é a higiene usada pelos matemáticos para conservar suas idéias saudáveis
Proposições e Conectivos
 Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Proposições e Conectivos Lógica Computacional 1 Site: http://jeiks.net E-mail: jacsonrcsilva@gmail.com
Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Proposições e Conectivos Lógica Computacional 1 Site: http://jeiks.net E-mail: jacsonrcsilva@gmail.com
AS ÁLGEBRAS DOS OPERADORES DE CONSEQÜÊNCIA
 AS ÁLGEBRAS DOS OPERADORES DE CONSEQÜÊNCIA Mauri Cunha do NASCIMENTO 1 Hércules de Araújo FEITOSA 1 RESUMO: Neste trabalho, introduzimos as TK-álgebras associadas com os operadores de conseqüência de Tarski,
AS ÁLGEBRAS DOS OPERADORES DE CONSEQÜÊNCIA Mauri Cunha do NASCIMENTO 1 Hércules de Araújo FEITOSA 1 RESUMO: Neste trabalho, introduzimos as TK-álgebras associadas com os operadores de conseqüência de Tarski,
Lógica Computacional
 Lógica Computacional Aula Teórica 6: Semântica da Lógica Proposicional António Ravara Simão Melo de Sousa Marco Giunti Departamento de Informática, Faculdade de Ciências e Tecnologia, NOVA LINCS, Universidade
Lógica Computacional Aula Teórica 6: Semântica da Lógica Proposicional António Ravara Simão Melo de Sousa Marco Giunti Departamento de Informática, Faculdade de Ciências e Tecnologia, NOVA LINCS, Universidade
INTRODUÇÃO À TEORIA DOS CONJUNTOS
 1 INTRODUÇÃO À TEORIA DOS CONJUNTOS Gil da Costa Marques 1.1 Introdução 1.2 Conceitos básicos 1.3 Subconjuntos e intervalos 1.4 O conjunto dos números reais 1.4.1 A relação de ordem em 1.5 Intervalos 1.5.1
1 INTRODUÇÃO À TEORIA DOS CONJUNTOS Gil da Costa Marques 1.1 Introdução 1.2 Conceitos básicos 1.3 Subconjuntos e intervalos 1.4 O conjunto dos números reais 1.4.1 A relação de ordem em 1.5 Intervalos 1.5.1
Material Teórico - Módulo: Vetores em R 2 e R 3. Operações Envolvendo Vetores. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Operações Envolvendo Vetores Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Adição de vetores Na aula anterior
Material Teórico - Módulo: Vetores em R 2 e R 3 Operações Envolvendo Vetores Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Adição de vetores Na aula anterior
Lógica Computacional
 Aula Teórica 2: Sintaxe da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática,
Aula Teórica 2: Sintaxe da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática,
Lógica Matemática. Definição. Origem. Introdução
 Lógica Matemática Introdução 1 Definição A Lógica tem, por objeto de estudo, as leis gerais do pensamento, e as formas de aplicar essas leis corretamente na investigação da verdade. 2 Origem Aristóteles
Lógica Matemática Introdução 1 Definição A Lógica tem, por objeto de estudo, as leis gerais do pensamento, e as formas de aplicar essas leis corretamente na investigação da verdade. 2 Origem Aristóteles
Lógica Computacional
 Aula Teórica 8: Forma Normal Conjuntiva António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática, Faculdade
Aula Teórica 8: Forma Normal Conjuntiva António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática, Faculdade
Produtos de potências racionais. números primos.
 MATEMÁTICA UNIVERSITÁRIA n o 4 Dezembro/2006 pp. 23 3 Produtos de potências racionais de números primos Mário B. Matos e Mário C. Matos INTRODUÇÃO Um dos conceitos mais simples é o de número natural e
MATEMÁTICA UNIVERSITÁRIA n o 4 Dezembro/2006 pp. 23 3 Produtos de potências racionais de números primos Mário B. Matos e Mário C. Matos INTRODUÇÃO Um dos conceitos mais simples é o de número natural e
A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há
 1 Produto Cartesiano Par Ordenado A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há casos entretanto em que a ordem é importante. Daí a necessidade de se introduzir
1 Produto Cartesiano Par Ordenado A ordem em que os elementos se apresentam em um conjunto não é levada em consideração. Há casos entretanto em que a ordem é importante. Daí a necessidade de se introduzir
Matemática Computacional. Introdução
 Matemática Computacional Introdução 1 Definição A Lógica tem, por objeto de estudo, as leis gerais do pensamento, e as formas de aplicar essas leis corretamente na investigação da verdade. 2 Origem Aristóteles
Matemática Computacional Introdução 1 Definição A Lógica tem, por objeto de estudo, as leis gerais do pensamento, e as formas de aplicar essas leis corretamente na investigação da verdade. 2 Origem Aristóteles
Prof. Jorge Cavalcanti
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 01 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 01 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Sumário. 1 CAPÍTULO 1 Revisão de álgebra
 Sumário 1 CAPÍTULO 1 Revisão de álgebra 2 Conjuntos numéricos 2 Conjuntos 3 Igualdade de conjuntos 4 Subconjunto de um conjunto 4 Complemento de um conjunto 4 Conjunto vazio 4 Conjunto universo 5 Interseção
Sumário 1 CAPÍTULO 1 Revisão de álgebra 2 Conjuntos numéricos 2 Conjuntos 3 Igualdade de conjuntos 4 Subconjunto de um conjunto 4 Complemento de um conjunto 4 Conjunto vazio 4 Conjunto universo 5 Interseção
RACIOCÍNIO LÓGICO. Curso Superior de Tecnologia. Aula 02 TEORIA DOS CONJUNTOS
 Aula 02 TEORIA DOS CONJUNTOS 1. Definição de Conjuntos 2. Como se representa um Conjunto 3. Subconjunto, Pertinência e Continência 4. Conjunto das Partes 5. Operação com Conjuntos 1. União ou Reunião (Conjunção)
Aula 02 TEORIA DOS CONJUNTOS 1. Definição de Conjuntos 2. Como se representa um Conjunto 3. Subconjunto, Pertinência e Continência 4. Conjunto das Partes 5. Operação com Conjuntos 1. União ou Reunião (Conjunção)
SMA Elementos de Matemática Notas de Aulas
 Universidade de São Paulo Instituto de Ciências Matemáticas e de Computação SMA 341 - Elementos de Matemática Notas de Aulas Ires Dias Sandra Maria Semensato de Godoy São Carlos 2009 Sumário 1 Noções
Universidade de São Paulo Instituto de Ciências Matemáticas e de Computação SMA 341 - Elementos de Matemática Notas de Aulas Ires Dias Sandra Maria Semensato de Godoy São Carlos 2009 Sumário 1 Noções
1 TEORIA DOS CONJUNTOS
 1 TEORIA DOS CONJUNTOS Definição de Conjunto: um conjunto é uma coleção de zero ou mais objetos distintos, chamados elementos do conjunto, os quais não possuem qualquer ordem associada. Em outras palavras,
1 TEORIA DOS CONJUNTOS Definição de Conjunto: um conjunto é uma coleção de zero ou mais objetos distintos, chamados elementos do conjunto, os quais não possuem qualquer ordem associada. Em outras palavras,
Curso de Matemática Aplicada.
 Aula 1 p.1/25 Curso de Matemática Aplicada. Margarete Oliveira Domingues PGMET/INPE Sistema de números reais e complexos Aula 1 p.2/25 Aula 1 p.3/25 Conjuntos Conjunto, classe e coleção de objetos possuindo
Aula 1 p.1/25 Curso de Matemática Aplicada. Margarete Oliveira Domingues PGMET/INPE Sistema de números reais e complexos Aula 1 p.2/25 Aula 1 p.3/25 Conjuntos Conjunto, classe e coleção de objetos possuindo
Álgebra Linear e Geometria Analítica
 Álgebra Linear e Geometria Analítica Engenharia Electrotécnica Escola Superior de Tecnologia de Viseu www.estv.ipv.pt/paginaspessoais/lucas lucas@mat.estv.ipv.pt 2007/2008 Álgebra Linear e Geometria Analítica
Álgebra Linear e Geometria Analítica Engenharia Electrotécnica Escola Superior de Tecnologia de Viseu www.estv.ipv.pt/paginaspessoais/lucas lucas@mat.estv.ipv.pt 2007/2008 Álgebra Linear e Geometria Analítica
Lógica Proposicional. Prof. Dr. Silvio do Lago Pereira. Departamento de Tecnologia da Informação Faculdade de Tecnologia de São Paulo
 Lógica Proposicional Prof. Dr. Silvio do Lago Pereira Departamento de Tecnologia da Informação aculdade de Tecnologia de São Paulo Motivação IA IA estuda estuda como como simular simular comportamento
Lógica Proposicional Prof. Dr. Silvio do Lago Pereira Departamento de Tecnologia da Informação aculdade de Tecnologia de São Paulo Motivação IA IA estuda estuda como como simular simular comportamento
Os números inteiros. Capítulo 2
 6 Capítulo 2 Os números inteiros Intuitivamente, o conjunto Z dos números inteiros é composto pelos números naturais e pelos "negativos". Como justificamos de uma forma simples qual a origem dos números
6 Capítulo 2 Os números inteiros Intuitivamente, o conjunto Z dos números inteiros é composto pelos números naturais e pelos "negativos". Como justificamos de uma forma simples qual a origem dos números
Aula 1 Conjuntos. Meta. Introduzir as noções básicas de conjunto e produto cartesiano de. conjuntos. Objetivos
 Conjuntos AULA 1 Aula 1 Conjuntos Meta conjuntos. Introduzir as noções básicas de conjunto e produto cartesiano de Objetivos Ao final desta aula, você deve ser capaz de: Definir as noções básicas de conjunto
Conjuntos AULA 1 Aula 1 Conjuntos Meta conjuntos. Introduzir as noções básicas de conjunto e produto cartesiano de Objetivos Ao final desta aula, você deve ser capaz de: Definir as noções básicas de conjunto
Lógica Fuzzy. Conectivos e Inferência. Professor: Mário Benevides. Monitores: Bianca Munaro Diogo Borges Jonas Arêas Renan Iglesias Vanius Farias
 Lógica Fuzzy Conectivos e Inferência Professor: Mário Benevides Monitores: Bianca Munaro Diogo Borges Jonas Arêas Renan Iglesias Vanius Farias Conectivos O que são conectivos? São operadores que conectam
Lógica Fuzzy Conectivos e Inferência Professor: Mário Benevides Monitores: Bianca Munaro Diogo Borges Jonas Arêas Renan Iglesias Vanius Farias Conectivos O que são conectivos? São operadores que conectam
Números - Aula 03. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Números - Aula 03 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 28 de Fevereiro de 2014 Primeiro Semestre de 2014 Turma 2013106 - Engenharia Mecânica Corpos Vimos que o
Números - Aula 03 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 28 de Fevereiro de 2014 Primeiro Semestre de 2014 Turma 2013106 - Engenharia Mecânica Corpos Vimos que o
ENFOQUE USANDO CORTES DE DEDEKIND
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação eletrônica do KIT http://www.dma.uem.br/kit CONSTRUÇÃO DOS REAIS: UM ENFOQUE
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação eletrônica do KIT http://www.dma.uem.br/kit CONSTRUÇÃO DOS REAIS: UM ENFOQUE
Complementos sobre Números Complexos
 Complementos sobre Números Complexos Ementa 1 Introdução Estrutura Algébrica e Completude 1 O Corpo dos números complexos Notações 3 Interpretação Geométrica e Completude de C 4 Forma Polar de um Número
Complementos sobre Números Complexos Ementa 1 Introdução Estrutura Algébrica e Completude 1 O Corpo dos números complexos Notações 3 Interpretação Geométrica e Completude de C 4 Forma Polar de um Número
O TRATAMENTO MATERIAL DA LPC Valorações como interpretações para a linguagem.
 COMPLEMENTO DO ARQUIVO ANTERIOR Texto Outras noções sintáticas que desempenharão um papel importante no futuro são as de esquema de fórmulas e de instância de um esquema. Um esquema de fórmula é uma expressão
COMPLEMENTO DO ARQUIVO ANTERIOR Texto Outras noções sintáticas que desempenharão um papel importante no futuro são as de esquema de fórmulas e de instância de um esquema. Um esquema de fórmula é uma expressão
XII Semana de Matemática II Semana de Estatística. Minicurso
 XII Semana de Matemática II Semana de Estatística Minicurso Uma pequena introdução à Lógica Moderna: Lógica Clássica, Lógica Trivalente e Lógica Fuzzy Prof. Angelo de Oliveira Universidade Federal de Rondônia
XII Semana de Matemática II Semana de Estatística Minicurso Uma pequena introdução à Lógica Moderna: Lógica Clássica, Lógica Trivalente e Lógica Fuzzy Prof. Angelo de Oliveira Universidade Federal de Rondônia
Resumo. Parte 2 Introdução à Teoria da Probabilidade. Ramiro Brito Willmersdorf Introdução.
 Parte 2 Introdução à Teoria da Probabilidade Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2011.2 Resumo 1 Introdução 2 Espaço
Parte 2 Introdução à Teoria da Probabilidade Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2011.2 Resumo 1 Introdução 2 Espaço
10 AULA. Operações com Conjuntos: Produto Cartesiano LIVRO. META: Introduzir propriedades para o produto cartesiano de conjuntos.
 1 LIVRO Operações com Conjuntos: Produto Cartesiano META: Introduzir propriedades para o produto cartesiano de conjuntos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Demonstrar propriedades
1 LIVRO Operações com Conjuntos: Produto Cartesiano META: Introduzir propriedades para o produto cartesiano de conjuntos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Demonstrar propriedades
Lógica. Fernando Fontes. Universidade do Minho. Fernando Fontes (Universidade do Minho) Lógica 1 / 65
 Lógica Fernando Fontes Universidade do Minho Fernando Fontes (Universidade do Minho) Lógica 1 / 65 Outline 1 Introdução 2 Implicações e Equivalências Lógicas 3 Mapas de Karnaugh 4 Lógica de Predicados
Lógica Fernando Fontes Universidade do Minho Fernando Fontes (Universidade do Minho) Lógica 1 / 65 Outline 1 Introdução 2 Implicações e Equivalências Lógicas 3 Mapas de Karnaugh 4 Lógica de Predicados
Lógica Proposicional. LEIC - Tagus Park 2 o Semestre, Ano Lectivo 2007/08. c Inês Lynce c Luísa Coheur
 Capítulo 2 Lógica Proposicional Lógica para Programação LEIC - Tagus Park 2 o Semestre, Ano Lectivo 2007/08 c Inês Lynce c Luísa Coheur Programa Apresentação Conceitos Básicos Lógica Proposicional ou Cálculo
Capítulo 2 Lógica Proposicional Lógica para Programação LEIC - Tagus Park 2 o Semestre, Ano Lectivo 2007/08 c Inês Lynce c Luísa Coheur Programa Apresentação Conceitos Básicos Lógica Proposicional ou Cálculo
TEMA 2 PROPRIEDADES DE ORDEM NO CONJUNTO DOS NÚMEROS REAIS
 TEMA 2 PROPRIEDADES DE ORDEM NO CONJUNTO DOS NÚMEROS REAIS O conjunto dos números reais,, que possui as seguintes propriedades:, possui uma relação menor ou igual, denotada por O1: Propriedade Reflexiva:
TEMA 2 PROPRIEDADES DE ORDEM NO CONJUNTO DOS NÚMEROS REAIS O conjunto dos números reais,, que possui as seguintes propriedades:, possui uma relação menor ou igual, denotada por O1: Propriedade Reflexiva:
Apresentar o conceito de anel, suas primeiras definições, diversos exemplos e resultados. Aplicar as propriedades dos anéis na relação de problemas.
 Aula 10 O CONCEITO DE ANEL META Apresentar o conceito de anel, suas primeiras definições, diversos exemplos e resultados. OBJETIVOS Definir, exemplificar e classificar anéis. Aplicar as propriedades dos
Aula 10 O CONCEITO DE ANEL META Apresentar o conceito de anel, suas primeiras definições, diversos exemplos e resultados. OBJETIVOS Definir, exemplificar e classificar anéis. Aplicar as propriedades dos
Cálculo proposicional
 O estudo da lógica é a análise de métodos de raciocínio. No estudo desses métodos, a lógica esta interessada principalmente na forma e não no conteúdo dos argumentos. Lógica: conhecimento das formas gerais
O estudo da lógica é a análise de métodos de raciocínio. No estudo desses métodos, a lógica esta interessada principalmente na forma e não no conteúdo dos argumentos. Lógica: conhecimento das formas gerais
Lógica Matemática e Elementos de Lógica Digital
 Lógica Matemática e Elementos de Lógica Digital Curso: Ciência da Computação Lívia Lopes Azevedo livia@ufmt.br Apresentação Plano de ensino Curso Conceitos básicos de lógica lógica proposicional Comportamento
Lógica Matemática e Elementos de Lógica Digital Curso: Ciência da Computação Lívia Lopes Azevedo livia@ufmt.br Apresentação Plano de ensino Curso Conceitos básicos de lógica lógica proposicional Comportamento
ÁLGEBRA DE BOOLE POSTULADOS, TEOREMAS E PROPRIEDADES
 ÁLGEBRA DE BOOLE POSTULADOS, TEOREMAS E PROPRIEDADES A aplicação principal da álgebra de Boole é o estudo e a simplificação algébrica de circuitos lógicos. As variáveis booleanas podem assumir apenas dois
ÁLGEBRA DE BOOLE POSTULADOS, TEOREMAS E PROPRIEDADES A aplicação principal da álgebra de Boole é o estudo e a simplificação algébrica de circuitos lógicos. As variáveis booleanas podem assumir apenas dois
