AULA 01 Introdução & Modelo de regressão simples
|
|
|
- Ronaldo Canto Bacelar
- 9 Há anos
- Visualizações:
Transcrição
1 1 AULA 01 Introdução & Modelo de regressão simples Ernesto F. L. Amaral 15 de julho de 2013 Análise de Regressão Linear (MQ 2013) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem moderna. São Paulo: Cengage Learning, Capítulo 1 (1-17) e Capítulo 2 (pp.19-63).
2 ESTRUTURA DO LIVRO 2 Introdução: principais conceitos em econometria (capítulo 1). Parte 1: trata de análise de regressão com dados de corte transversal (capítulos 2 ao 9). Parte 2: análise de regressão com dados de séries temporais (capítulos 10 ao 12). Parte 3: tópicos avançados (capítulos 13 ao 19).
3 DOCUMENTAÇÃO DO LIVRO 3 UCLA Academic Technology Services: Introductory Econometrics: A Modern Approach by Jeffrey M. Wooldridge:
4 DOCUMENTAÇÃO PARA EXERCÍCIO Vamos utilizar a Pesquisa Nacional por Amostra de Domicílios (PNAD) de 2007 de Minas Gerais para as demonstrações em sala de aula e a PNAD de 2011 do Brasil para o exercício final do curso. 4 Os bancos de dados, questionário, livro de códigos e demais arquivos estão disponíveis no site do Instituto Brasileiro de Geografia e Estatística (IBGE):
5 CAPÍTULO 1 - WOOLDRIDGE INTRODUÇÃO: PRINCIPAIS CONCEITOS EM ECONOMETRIA 5
6 ECONOMETRIA 6 A econometria evoluiu como uma disciplina separada da estatística matemática, porque enfoca problemas inerentes à coleta e à análise de dados econômicos não-experimentais. Dados não-experimentais não são acumulados por meio de experimentos controlados de indivíduos, firmas ou segmentos da economia. Dados não-experimentais são também chamados de dados observacionais para enfatizar o fato de que o pesquisador é um coletor passivo de dados. Dados experimentais são frequentemente coletados em ambientes de laboratório nas ciências naturais, mas são muito mais difíceis de serem obtidos nas ciências sociais. O método de análise da regressão múltipla é utilizado por econometristas e estatísticos matemáticos, mas o foco e interpretação pode diferir significantemente.
7 ANÁLISE ECONÔMICA EMPÍRICA 7 Os métodos econométricos são usados para testar uma teoria econômica ou para analisar relações que apresentam importância para análises de políticas públicas. Uma análise empírica usa dados para testar uma teoria ou estimar uma relação. O primeiro passo em qualquer análise empírica é a formulação cuidadosa da questão de interesse, a qual pode ser a de testar efeitos de uma política governamental ou, até mesmo, de testar hipóteses e teorias. O modelo econômico formal consiste em equações matemáticas que descrevem relações para testar teorias.
8 MICROECONOMIA 8 Os indivíduos fazem escolhas para maximizar seu bemestar (maximização da utilidade), sujeitas às restrições de recursos. Isso oferece um arcabouço para criar modelos econômicos para fazer previsões entre variáveis. A maximização da utilidade leva a um conjunto de equações de demanda, no contexto das decisões de consumo. Em uma equação de demanda, a quantidade demandada de cada produto depende do seu próprio preço, do preço dos bens substitutos e complementares, da renda do consumidor e das características individuais que influem no gosto.
9 MODELO ECONÔMICO O modelo econômico é a formulação teórica de uma relação entre variáveis econômicas. A quantidade de tempo gasto na atividade criminosa é uma função de vários fatores (Gary Becker 1968): y=f(x 1, x 2, x 3, x 4, x 5, x 6, x 7 ), 9 y = horas gastas em atividades criminosas. x 1 = salário por hora ocupada em atividade criminosa. x 2 = salário-hora em emprego legal. x 3 = renda de outras atividades que não o crime ou um emprego legal. x 4 = probabilidade de ser capturado. x 5 = probabilidade de ser condenado se capturado. x 6 = sentença esperada se condenado. x 7 = idade.
10 MODELO ECONOMÉTRICO Após elaborar o modelo econômico, é especificado um modelo econométrico, que será aplicado a dados existentes. A forma da função f(.) deveria ser especificada antes de realizar uma análise econométrica. Se uma variável não pode ser obtida, é possível utilizar uma variável que se aproxima desta que se quer medir (proxy). Outros fatores são considerados no termo de erro u (ou termo de disturbância): Erro amostral é a diferença entre o resultado amostral e o verdadeiro resultado da população (devidos ao acaso). Erro não-amostral ocorre quando os dados amostrais são coletados, registrados ou analisados incorretamente. Modelo econométrico de Becker (1968): crime = β 0 + β 1 salário + β 2 outrenda + β 3 freqpris + β 4 freqcond + β 5 sentmed + β 6 idade + u 10
11 MODELO ECONOMÉTRICO NA PRÁTICA 11 Na maioria dos casos, a análise econométrica começa pela especificação de um modelo econométrico, sem consideração de detalhes da criação do modelo econômico. É comum começar com um modelo econométrico e usar o raciocínio econômico e conhecimentos científicos como guias para escolher as variáveis. Após a especificação do modelo econométrico, várias hipóteses podem ser formuladas em termos das direções e influências dos parâmetros desconhecidos (independentes) sobre a variável de interesse (dependente). Após os dados terem sido coletados, os métodos econométricos são usados para estimar os parâmetros do modelo econométrico e para testar as hipóteses de interesse.
12 DESENHOS BÁSICOS DE SURVEY: BANCOS DE DADOS 12 Após especificar os objetivos e unidades de análise da pesquisa, é preciso escolher entre diversos desenhos diferentes: Surveys interseccionais (cross-sectional). Surveys longitudinais (tendências, coortes ou painel). Surveys interseccionais servindo como longitudinais. Wooldridge (2008) classifica os dados econômicos em: Dados de corte transversal = surveys interseccionais. Cortes transversais agrupados = estudos de tendências. Dados de séries de tempo = estudos de coortes. Dados de painel ou longitudinais = estudos de painel.
13 DADOS DE CORTE TRANSVERSAL (Wooldridge) SURVEYS INTERSECCIONAIS (Babbie) Um conjunto de dados de corte transversal consiste em uma amostra de uma unidade de análise, tomada em um determinado ponto no tempo. Esses dados são muito utilizados em economia e em outras ciências sociais. Dados em um determinado ponto do tempo são importantes para testar hipóteses e avaliar políticas. Dados podem ter problemas de seleção amostral, no caso de determinados indivíduos não revelarem informações acuradas. Amostragem deve ser realizada de forma acurada para evitar que coleta se concentre em unidades com características semelhantes. 13
14 EXEMPLO DE DADOS DE CORTE TRANSVERSAL 14 Conjunto de dados de corte transversal para o ano de 1976 de 526 trabalhadores (Wooldridge 2008): Anos de Número da observação Salário por hora Anos de escolaridade experiência no mercado Feminino Estado civil (casado) de trabalho 1 3, , , , , , ,
15 CORTES TRANSVERSAIS AGRUPADOS (Wooldridge) ESTUDOS DE TENDÊNCIAS (Babbie) Uma população pode ser amostrada e estudada em ocasiões diferentes. Um mesmo conjunto de variáveis é coletado em diferentes períodos do tempo, em distintas amostras aleatórias de uma mesma população (Censo Demográfico, Pesquisa Nacional por Amostra de Domicílios PNAD). Agrupar cortes transversais de diferentes anos é eficaz para analisar os efeitos de uma política pública. O ideal é coletar dados de anos anteriores e posteriores a uma importante mudança de política governamental. Além de aumentar o tamanho da amostra, a análise de corte transversal agrupada é importante para estimar como uma relação fundamental mudou ao longo do tempo. Geralmente são utilizados dados secundários, coletados por outros pesquisadores ou instituições. 15
16 EXEMPLO DE CORTES TRANSVERSAIS AGRUPADOS 16 Conjunto de dados sobre os preços da moradia em 1993 e 1995 nos Estados Unidos (Wooldridge 2008): Número da observação Ano Preço comercializado Imppro Arquad Quantidade de dormitórios Quantidade de banheiros , , , , , , , ,5
17 DADOS DE SÉRIES DE TEMPO (Wooldridge) ESTUDOS DE COORTES (Babbie) Um conjunto de dados de séries de tempo consiste em observações sobre variáveis ao longo do tempo. Como eventos passados podem influenciar eventos futuros, o tempo é uma dimensão importante em um conjunto de dados de séries de tempo. A análise desses dados pode ser dificultada, porque observações econômicas não são independentes ao longo do tempo (variáveis possuem padrões sazonais). Há uma série de frequências possíveis: diárias, semanais, mensais, trimestrais, anuais, decenais... Estes dados são também chamados de estudos de coorte, em que mesma população é analisada, mas amostras estudadas podem ser diferentes: Pessoas com 10 anos em 2000, 20 anos em 2010, 30 anos em 2020, 40 anos em
18 EXEMPLO DE DADOS DE SÉRIES DE TEMPO 18 Conjunto de dados de séries de tempo sobre efeitos do salário mínimo em Porto Rico (apud Wooldridge 2008): Número da observação Ano Salário mínimo médio no ano Taxa de trabalhadores cobertos pela lei de salário mínimo Taxa de desemprego Produto Nacional Bruto (PNB) ,20 20,1 15,4 878, ,21 20,7 16,0 925, ,23 22,6 14, , ,35 58,1 18, , ,35 58,2 16, ,7
19 DADOS DE PAINEL OU LONGITUDINAIS (Wooldridge) ESTUDOS DE PAINEL (Babbie) Um conjunto de dados de painel consiste em uma série de tempo para cada membro do corte transversal. Os dados de painel são distintos dos dados de corte transversal agrupados (tendências) e de séries de tempo (coortes), porque as mesmas unidades são acompanhadas ao longo de um determinado período. Dados de painel podem ser coletados para indivíduos, domicílios, instituições ou unidades geográficas. Esses dados são os mais sofisticados para fins explicativos, mas são mais difíceis e caros de se obter. Pode haver problema de grande número de não respostas nas últimas ondas de entrevistas. A análise dos dados pode se tornar complicada quando se tentar avaliar as mudanças dos indivíduos no tempo. 19
20 EXEMPLO DE DADOS DE PAINEL OU LONGITUDINAIS 20 Conjunto de dados de painel sobre crime e estatísticas relacionadas em 1986 e 1990 em 150 cidades nos Estados Unidos (Wooldridge 2008): Número da observação Cidade Ano Homicídios População Desemprego Polícia , , , , , , , ,2 493
21 CORTE TRANSVERSAL USADO COMO LONGITUDINAL 21 Alguns mecanismos podem ser utilizados num survey interseccional (corte transversal) para aproximar o estudo de processo ou mudança (longitudinal). Podem ser realizadas perguntas referentes ao passado (renda no ano anterior, local de residência anterior): Há problemas de erro de memória. Os dados devem ser interpretados como amostra da população atual, e não de população passada. Por exemplo, é possível utilizar um único banco de dados de corte transversal para comparar pessoas de diferentes idades (jovens e idosos) e coortes (calouros e veteranos).
22 VARIAÇÕES DOS DESENHOS BÁSICOS 22 Os desenhos básicos de pesquisa apresentados anteriormente podem ser modificados para se enquadrarem aos objetivos de um estudo: Amostras paralelas: amostras separadas de populações diferentes, utilizando mesmo questionário (exemplo é a pesquisa sobre preconceito na UFMG). Estudos contextuais: uso de dados sobre o ambiente ou meio da pessoa para descrever o contexto do indivíduo. Estudos sociométricos: intenção é de observar as interrelações entre membros da população estudada (redes de amizades, por exemplo).
23 ESCOLHENDO O DESENHO APROPRIADO 23 Dados de corte transversal são mais apropriados se objetivo é descrição de tempo único. Mudanças ao longo do tempo são mais difíceis de realizar, porque dados de painel exigem tempo e recursos: É possível utilizar dados de corte transversal e comparar pessoas que passaram por uma experiência no passado, com aqueles que não passaram. Estudos de painel são mais viáveis economicamente quando o fenômeno estudado tem duração curta (por exemplo, opinião de voto durante uma campanha eleitoral). Estudos de tendências podem ser realizados quando dados antigos são complementados com dados coletados pelo pesquisador.
24 CAUSALIDADE 24 Na avaliação de políticas públicas, o objetivo do pesquisador é inferir que uma variável tem um efeito causal sobre outra variável. Encontrar uma associação entre duas ou mais variáveis pode ser sugestivo (correlação), mas somente será convincente se for possível estabelecer uma causalidade. A noção de ceteris paribus é importante, já que significa outros fatores (relevantes) permanecendo iguais. Se outros fatores não forem mantidos fixos, não poderemos conhecer o efeito causal de uma variável sobre outra. Como a maioria dos dados coletados nas ciências sociais são não-experimentais (não são experimentos controlados como nas ciências naturais), descobrir relações causais é uma tarefa complexa.
25 CAPÍTULO 2 - WOOLDRIDGE MODELO DE REGRESSÃO SIMPLES 25
26 MODELO DE REGRESSÃO SIMPLES O modelo de regressão linear simples explica uma variável (y) com base em modificações em outra variável (x). 26 Ou seja, é usado para avaliar a relação entre duas variáveis. Esse tipo de regressão não é muito utilizada em ciências sociais aplicadas, devido à sua simplicidade. No entanto, serve como ponto de partida, já que sua álgebra e interpretações são fáceis de entender. O entendimento do modelo de regressão simples é importante para estudar a regressão múltipla.
27 PREMISSA E EXEMPLOS 27 Premissa da análise econométrica: y e x são duas variáveis que representam uma população. Estamos interessados em explicar y em termos de x. Ou seja, queremos estudar como y varia com variações em x. Exemplos: y é o rendimento do trabalhador, e x são os anos de escolaridade. y é a escala ideológica esquerda/direita, e x é o partido político do deputado. y é o índice de tradicionalismo/secularismo, e x é o nível de escolaridade.
28 PERGUNTAS IMPORTANTES Como nunca há uma relação exata entre duas variáveis, como consideramos outros fatores que afetam y? 28 Qual é a relação funcional entre y e x? Como podemos estar certos de que estamos capturando uma relação ceteris paribus (outros fatores constantes) entre y e x?
29 MODELO DE REGRESSÃO LINEAR SIMPLES Também chamado de modelo de regressão linear de duas variáveis ou modelo de regressão linear bivariada. 29 Terminologia: y x Uso Variável Dependente Variável Independente Econometria Variável Explicada Variável Explicativa Variável de Resposta Variável de Controle Ciências Experimentais Variável Prevista Variável Previsora Regressando Regressor Covariável
30 VOLTANDO ÀS PERGUNTAS IMPORTANTES Como nunca há uma relação exata entre duas variáveis, como consideramos outros fatores que afetam y? 30 Variável u é o termo erro ou perturbação da relação. Na análise de regressão simples, todos fatores (além de x) que afetam y são tratados como não-observados.
31 OUTRA PERGUNTA Qual é a relação funcional entre y e x? 31 Se os outros fatores em u são mantidos fixos, de modo que a variação em u é zero ( u=0), então x tem um efeito linear sobre y, tal como: y=β 1 x; se u=0. A linearidade do modelo de regressão linear simples implica que uma variação de uma unidade em x tem o mesmo efeito sobre y, independentemente do valor inicial de x. Isso não é realista. Por exemplo, o próximo ano de escolaridade teria um efeito maior sobre os salários, em relação ao anterior. Esse problema será tratado adiante.
32 E O PROBLEMA DO CETERIS PARIBUS? Estamos capturando uma relação ceteris paribus (outros fatores constantes) entre y e x? 32 A variação em y é β 1 multiplicado pela variação em x. β 1 : parâmetro de inclinação da relação entre y e x, mantendo fixos os outros fatores em u. β 0 : parâmetro de intercepto é raramente analisado. β 1 mede o efeito de x sobre y, mantendo todos os outros fatores (em u) fixos. No entanto, estamos ignorando todos os outros fatores. Os estimadores de β 0 e β 1 serão confiáveis em uma amostra aleatória, se o termo não-observável (u) estiver relacionado à variável explicativa (x) de modo que o valor médio de u na população seja zero: E(u)=0.
33 HIPÓTESE SOBRE A RELAÇÃO ENTRE x E u Se u e x não estão correlacionados, então (como variáveis aleatórias) não são linearmente relacionados. No entanto, a correlação mede somente a dependência linear entre u e x. Na correlação, é possível que u seja não-correlacionado com x e seja correlacionado com funções de x, tal como x 2. Melhor seria pensar na distribuição condicional de u, dado qualquer valor de x. Para um valor de x, podemos obter o valor esperado (ou médio) de u para um grupo da população. A hipótese é que o valor médio de u não depende de x: E(u x) = E(u) = 0 Ou seja, para qualquer valor de x, a média dos fatores nãoobserváveis é a mesma e, portanto, é igual ao valor médio de u na população (hipótese de média condicional zero). 33
34 FUNÇÃO DE REGRESSÃO POPULACIONAL Quando E(u x)=e(u)=0 é verdadeiro, é útil dividir y em: Parte sistemática (parte de y explicada por x): β 0 + β 1 x Parte não-sistemática (parte de y não explicada por x): u 34 Considerando o valor esperado de y=β 0 +β 1 x+u condicionado a x, e usando E(u x)=0, temos a função de regressão populacional (FRP), que é uma função linear de x: E(y x) = β 0 + β 1 x Linearidade: o aumento de uma unidade em x faz com que o valor esperado de y varie segundo a magnitude de β 1. Para qualquer valor de x, a distribuição de y está centrada ao redor de E(y x).
35 35
36 ESTIMATIVA DE MÍNIMOS QUADRADOS ORDINÁRIOS Para a estimação dos parâmetros β 0 e β 1, é preciso considerar uma amostra da população: 36 {(x i, y i ): i=1,..., n} A equação do modelo de regressão simples é escrito como: u i é o termo erro para a observação i, já que contém todos os fatores, além de x i, que afetam y i. Um exemplo é a poupança anual para a família i (y i ), dependendo da renda anual desta família (x i ), em um determinado ano.
37 37
38 ESTIMATIVA DE MÍNIMOS QUADRADOS ORDINÁRIOS Como obter estimativas do intercepto (β 0 ) e da inclinação (β 1 ) na regressão populacional da poupança sobre a renda? 38 Na população, u tem média zero. O valor esperado de u é zero: E(u)=0 Além disso, u é não-correlacionado com x. A covariância entre x e u é zero: Cov(x,u)=E(xu)=0 E(u)=0 pode ser escrita como: E(y-β 0 -β 1 x)=0 Cov(x,u)=E(xu)=0 pode ser escrita como: E[x(y-β 0 -β 1 x)]=0 Como há dois parâmetros desconhecidos para estimar (β 0 e β 1 ), é possível utilizar uma amostra de dados para calcular as estimativas: e
39 EQUAÇÕES DA POPULAÇÃO E AMOSTRA Média de u na população: 39 Média de u na amostra: Covariância entre x e u na população: Covariância entre x e u na amostra:
40 ESTIMATIVAS DE E 40
41 ESTIMATIVAS DE MQO DE E 41 Covariância amostral entre x e y Variância amostral de x Se x e y são positivamente correlacionados na amostra, é positivo e vice-versa.
42 VARIÂNCIA DE x DEVE SER MAIOR QUE ZERO 42 A hipótese necessária para calcular estimativas de mínimos quadrados ordinários (MQO) é que a variância amostral de x seja maior que zero. Ou seja, os valores de x i na amostra não devem ser todos iguais a um mesmo valor.
43 43
44 VALORES ESTIMADOS E RESÍDUOS Encontrados o intercepto e a inclinação, teremos um valor estimado para y para cada observação (x) na amostra: 44 O resíduo é a diferença entre o valor verdadeiro de y i e seu valor estimado:
45 45
46 MINIMIZANDO A SOMA DOS RESÍDUOS QUADRADOS Suponha que escolhemos o intercepto e a inclinação estimados com o propósito de tornar a soma dos resíduos quadrados: 46 O nome mínimos quadrados ordinários é utilizado porque as estimativas do intercepto e da inclinação minimizam a soma dos resíduos quadrados. Não é utilizada a minimização dos valores absolutos dos resíduos, porque a teoria estatística para isto seria muito complicada.
47 MINIMIZANDO A SOMA DOS RESÍDUOS QUADRADOS Reta de regressão de MQO ou função de regressão amostral (FRA) é a versão estimada da função de regressão populacional (FRP): 47 O coeficiente de inclinação indica o quanto o valor estimado (previsto) de y varia quando x aumenta em uma unidade: Da mesma forma, dada qualquer variação em x, podemos calcular a variação prevista em y:
48 48
49 49 Fonte: Hamilton, 1992: 52.
50 50 Fonte: Hamilton, 1992: 53.
51 PROPRIEDADES ALGÉBRICAS DAS ESTATÍSTICAS A soma dos resíduos de MQO é zero, já que as estimativas de MQO de e são escolhidas para fazer com que a soma dos resíduos seja zero: 51 A covariância amostral entre os regressores e os resíduos de MQO é zero: Se inserirmos a média de x no lugar de x i, o valor estimado é a média de y (este ponto está sempre sobre a reta):
52 SOMAS DOS QUADRADOS Soma dos quadrados total (SQT) é uma medida da variação amostral total em y i (mede a dispersão dos y i na amostra): 52 Soma dos quadrados explicada (SQE) mede a variação amostral em: Soma dos quadrados dos resíduos (SQR) mede a variação amostral em: Variação total em y é a soma da variação explicada e da variação não-explicada: SQT = SQE + SQR
53 GRAU DE AJUSTE Visa mensurar o quanto a variável independente (x) explica a variável dependente (y). 53 É um número que resume o quão bem a reta de regressão de MQO se ajusta aos dados. R 2 : razão entre a variação explicada (SQE) e a variação total (SQT). R 2 : fração da variação amostral em y que é explicada por x. SQT = SQE + SQR SQT /SQT = (SQE + SQR)/SQT 1 = SQE/SQT + SQR/SQT SQE/SQT = 1 - SQR/SQT Usar o R 2 como principal padrão de medida de sucesso de uma análise econométrica pode levar a confusões.
54 MUDANÇAS DAS UNIDADES DE MEDIDA Ao mudar unidades de medida das variáveis dependente e/ou independente, estimativas de MQO são afetadas. 54 Se a variável dependente é multiplicada pela constante c (cada valor na amostra é multiplicado por c), então as estimativas de MQO de intercepto e de inclinação também são multiplicadas por c. Se a variável independente é dividida (ou multiplicada) por alguma constante diferente de zero (c) então o coeficiente de inclinação de MQO é multiplicado (ou dividido) por c, respectivamente. Mudar as unidades de medida da variável independente não afeta o intercepto. O grau de ajuste do modelo (R 2 ) não depende das unidades de medida das variáveis.
55 NÃO-LINEARIDADE NA REGRESSÃO SIMPLES Formas funcionais populares usadas em economia e outras ciências sociais aplicadas podem ser incorporadas à análise de regressão. 55 Até agora foram analisadas relações lineares entre as variáveis dependente e independente. No entanto, relações lineares não são suficientes para todas as aplicações econômicas e sociais. É fácil incorporar não-linearidade na análise de regressão simples.
56 EXEMPLO DE NÃO-LINEARIDADE Para cada ano adicional de educação, há um aumento fixo no salário. Esse é o aumento tanto para o primeiro ano de educação quanto para anos mais avançados: 56 Suponha que o aumento percentual no salário é o mesmo, dado um ano a mais de educação formal. Um modelo que gera um efeito percentual constante é dado por: Se, então: Para cada ano adicional de educação, há um aumento de?% sobre o salário.
57 Como a variação percentual no salário é a mesma para cada ano adicional de educação, a variação no salário aumenta quando a educação formal aumenta. 57
58 INTERPRETAÇÃO DOS COEFICIENTES Aumento de uma unidade em x aumenta y em β 1 unidades: 58 Aumento de 1% em x aumenta y em (β 1 /100) unidades: Aumento de uma unidade em x aumenta y em (100*β 1 )%. O cálculo da semi-elasticidade {[exp(β 1 ) 1]*100} indica a diferença percentual exata: Aumento de 1% em x aumenta y em β 1 % (modelo de elasticidade constante): Elasticidade é a razão entre o percentual de mudança em uma variável e o percentual de mudança em outra variável.
59 59 FORMAS FUNCIONAIS ENVOLVENDO LOGARITMOS Modelo Variável Dependente Variável Independente Interpretação de β 1 nível-nível y x y=β 1 x nível-log y log(x) y=(β 1 /100)% x log-nível log(y) x % y=(100β 1 ) x log-log log(y) log(x) % y=β 1 % x
60 SIGNIFICADO DE REGRESSÃO LINEAR O modelo de regressão linear permite relações não-lineares. 60 Esse modelo é linear nos parâmetros: β 0 e β 1. Não há restrições de como y e x se relacionam com as variáveis dependente e independente originais, já que podemos utilizar: logaritmo natural, quadrado, raiz quadrada... A interpretação dos coeficientes depende das definições de como x e y são construídos. É muito mais importante tornar-se proficiente em interpretar coeficientes do que eficiente no cálculo de fórmulas. (Wooldridge, 2008: 45)
61 UTILIZAÇÃO DE PESOS 61
62 DIFERENTES PESOS 62 Indivíduo Número de observações coletadas na amostra Peso para expandir para o tamanho da população (N) Peso para manter o tamanho da amostra (n) João 1 4 0,8 Maria 1 6 1,2 Total EXEMPLO: Peso amostral do João = Peso de frequência do João * (Peso amostral total / Peso de frequência total)
63 FWEIGHT: PESO DE FREQUÊNCIA NO STATA Expande os resultados da amostra para o tamanho populacional. Utilizado em tabelas para gerar frequências. O uso desse peso é importante na amostra do Censo Demográfico e na Pesquisa Nacional por Amostra de Domicílios (PNAD) do Instituto Brasileiro de Geografia e Estatística (IBGE) para expandir a amostra para o tamanho da população do país, por exemplo. Somente pode ser usado em tabelas de frequência quando o peso é uma variável discreta (não decimal). 63 tab x [fweight = peso]
64 PESO AMOSTRAL PARA PROGRAMADORES NO STATA IWEIGHT: Não tem uma explicação estatística formal. Esse peso é utilizado por programadores que precisam implementar técnicas analíticas próprias. Pode ser utilizado em tabelas de frequência, mesmo que o peso seja decimal. 64 tab x [iweight = peso]
65 AWEIGHT: PESO AMOSTRAL ANALÍTICO NO STATA Inversamente proporcional à variância da observação. Número de observações na regressão é escalonado para permanecer o mesmo que o número no banco. Utilizado para estimar uma regressão linear quando os dados são médias observadas, tais como: Ao invés de: group x y n group x y
66 UM POUCO MAIS SOBRE O AWEIGHT De uma forma geral, não é correto utilizar o AWEIGHT como um peso amostral, porque as fórmulas utilizadas por esse comando assumem que pesos maiores se referem a observações medidas de forma mais acurada. Uma observação em uma amostra não é medida de forma mais cuidadosa que nenhuma outra observação, já que todas fazem parte do mesmo plano amostral. Usar o AWEIGHT para especificar pesos amostrais fará com que o Stata estime valores incorretos de variância e de erros padrões para os coeficientes, assim como valores incorretos de "p" para os testes de hipótese. regress y x1 x2 [aweight = peso] 66
67 PESO AMOSTRAL NAS REGRESSÕES DO STATA PWEIGHT: Ideal para ser usado nas regressões do Stata. Usa o peso amostral como o número de observações na população que cada observação representa. São estimadas proporções, médias e parâmetros da regressão corretamente. Há o uso de uma técnica de estimação robusta da variância que automaticamente ajusta para as características do plano amostral, de tal forma que variâncias, erros padrões e intervalos de confiança são calculados de forma mais precisa. É o inverso da probabilidade da observação ser incluída no banco, devido ao desenho amostral. regress y x1 x2 [pweight = peso] 67
68 OUTRAS OBSERVAÇÕES SOBRE PESOS NO STATA 68 PESOS EM TABELAS DE FREQUÊNCIA Tipo do peso Discreto Decimal Expandir para o tamanho da população (N) fweight iweight Manter o tamanho da amostra (n) aweight PESOS EM MODELOS DE REGRESSÃO devem manter o tamanho da amostra (n) Erro padrão robusto pweight reg y x, robust R 2 ajustado, SQT, SQE, SQR aweight outreg2
69 PLANO AMOSTRAL COMPLEXO Estatísticas descritivas e modelos de regressão devem levar em consideração a estrutura de planos amostrais complexos. PNAD tem amostra complexa (Silva, Pessoa, Lila, 2002): Considerar variáveis de estrato de município autorrepresentativo e não autorrepresentativo (v4617) e de unidade primária de amostragem (v4618), do banco de domicílios. Agregar variáveis acima ao banco de pessoas, o qual possui peso da pessoa (v4729). Lidar com problema de alguns estratos terem somente uma unidade primária de amostragem. Pode-se especificar média deste estrato como sendo a média geral, ao invés da média do próprio estrato. svyset [pweight=v4729], strata(v4617) psu(v4618) singleunit(centered) Tabelas e regressões devem ser precedidas de svy:. 69
70 EXEMPLOS COM PNAD DE MINAS GERAIS DE 2007 O banco de dados de pessoas possui informação de anos de escolaridade (anest), rendimento no trabalho principal (renpri), logaritmo do rendimento no trabalho principal (lnrenpri) e peso da pessoa (v4729): 70...
71 EXEMPLO 1: PNAD DE MINAS GERAIS DE 2007 Escolaridade explicando rendimento: 71. reg renpri anest [aweight=v4729] (sum of wgt is e+06) Source SS df MS Number of obs = F( 1, 16230) = Model e e+09 Prob > F = Residual e R-squared = Adj R-squared = Total e Root MSE = renpri Coef. Std. Err. t P> t [95% Conf. Interval] anest _cons
72 EXEMPLO 1: PNAD DE MINAS GERAIS DE 2007 Renda predita por anos de escolaridade: 72 renpre anest anest renpri renpre
73 EXEMPLO 1: PNAD DE MINAS GERAIS DE 2007 Resíduos por renda predita: 73 Residuals renpre
74 EXEMPLO 2: PNAD DE MINAS GERAIS DE 2007 Escolaridade explicando logaritmo do rendimento: 74. reg lnrenpri anest [aweight=v4729] (sum of wgt is e+06) Source SS df MS Number of obs = F( 1, 16230) = Model Prob > F = Residual R-squared = Adj R-squared = Total Root MSE = lnrenpri Coef. Std. Err. t P> t [95% Conf. Interval] anest _cons
75 EXEMPLO 2: PNAD DE MINAS GERAIS DE 2007 Renda predita por anos de escolaridade: lnrenpre anest anest lnrenpri lnrenpre explnrenpre anest anest renpri explnrenpre
76 Residuals 2 4 EXEMPLO 2: PNAD DE MINAS GERAIS DE 2007 Resíduos por renda predita: -4 Residuals lnrenpre explnrenpre
77 ... GRÁFICOS FORAM GERADOS COM ESTAS VARIÁVEIS Cálculo do valor predito: y-predito = β 0 + β 1 x Cálculo do resíduo: u = y-observado y-predito Na 2ª regressão, calculamos ainda o exponencial do predito. 77
AULAS 14 E 15 Modelo de regressão simples
 1 AULAS 14 E 15 Modelo de regressão simples Ernesto F. L. Amaral 30 de abril e 02 de maio de 2013 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem
1 AULAS 14 E 15 Modelo de regressão simples Ernesto F. L. Amaral 30 de abril e 02 de maio de 2013 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem
AULAS 20 E 21 Modelo de regressão simples
 1 AULAS 20 E 21 Modelo de regressão simples Ernesto F. L. Amaral 22 e 24 de outubro de 2013 Metodologia de Pesquisa (DCP 854B) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem moderna.
1 AULAS 20 E 21 Modelo de regressão simples Ernesto F. L. Amaral 22 e 24 de outubro de 2013 Metodologia de Pesquisa (DCP 854B) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem moderna.
AULAS 14 E 15 Modelo de regressão simples
 1 AULAS 14 E 15 Modelo de regressão simples Ernesto F. L. Amaral 18 e 23 de outubro de 2012 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem
1 AULAS 14 E 15 Modelo de regressão simples Ernesto F. L. Amaral 18 e 23 de outubro de 2012 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem
AULA 01 Principais Conceitos em Econometria
 1 AULA 01 Principais Conceitos em Econometria Ernesto F. L. Amaral 02 de março de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
1 AULA 01 Principais Conceitos em Econometria Ernesto F. L. Amaral 02 de março de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
AULA 06 Modelos para a avaliação de impactos
 1 AULA 06 Modelos para a avaliação de impactos Ernesto F. L. Amaral 12 de setembro de 2013 Avaliação de Políticas Públicas (DCP 046) Fonte: Babbie, Earl. Métodos de Pesquisas de Survey. 1999. Belo Horizonte:
1 AULA 06 Modelos para a avaliação de impactos Ernesto F. L. Amaral 12 de setembro de 2013 Avaliação de Políticas Públicas (DCP 046) Fonte: Babbie, Earl. Métodos de Pesquisas de Survey. 1999. Belo Horizonte:
AULAS 17 E 18 Análise de regressão múltipla: estimação
 1 AULAS 17 E 18 Análise de regressão múltipla: estimação Ernesto F. L. Amaral 22 e 24 de outubro de 2013 Avaliação de Políticas Públicas (DCP 046) Fonte: Cohen, Ernesto, e Rolando Franco. 2000. Avaliação
1 AULAS 17 E 18 Análise de regressão múltipla: estimação Ernesto F. L. Amaral 22 e 24 de outubro de 2013 Avaliação de Políticas Públicas (DCP 046) Fonte: Cohen, Ernesto, e Rolando Franco. 2000. Avaliação
AULA 03 Análise de regressão múltipla: estimação
 1 AULA 03 Análise de regressão múltipla: estimação Ernesto F. L. Amaral 17 de julho de 2013 Análise de Regressão Linear (MQ 2013) www.ernestoamaral.com/mq13reg.html Fonte: Cohen, Ernesto, e Rolando Franco.
1 AULA 03 Análise de regressão múltipla: estimação Ernesto F. L. Amaral 17 de julho de 2013 Análise de Regressão Linear (MQ 2013) www.ernestoamaral.com/mq13reg.html Fonte: Cohen, Ernesto, e Rolando Franco.
Correlação e Regressão linear simples
 Metodologia de Diagnóstico e Elaboração de Relatório FASHT Correlação e Regressão linear simples Prof. Cesaltina Pires [email protected] Plano da Apresentação Correlação linear Diagrama de dispersão Covariância
Metodologia de Diagnóstico e Elaboração de Relatório FASHT Correlação e Regressão linear simples Prof. Cesaltina Pires [email protected] Plano da Apresentação Correlação linear Diagrama de dispersão Covariância
Plano da Apresentação. Correlação e Regressão linear simples. Correlação linear. Associação entre hábitos leitura e escolaridade.
 Metodologia de Diagnóstico e Elaboração de Relatório FASHT Correlação e Plano da Apresentação Correlação linear Diagrama de dispersão Covariância Coeficiente de correlação de Pearson Teste de correlação
Metodologia de Diagnóstico e Elaboração de Relatório FASHT Correlação e Plano da Apresentação Correlação linear Diagrama de dispersão Covariância Coeficiente de correlação de Pearson Teste de correlação
Análise de Regressão. Notas de Aula
 Análise de Regressão Notas de Aula 2 Modelos de Regressão Modelos de regressão são modelos matemáticos que relacionam o comportamento de uma variável Y com outra X. Quando a função f que relaciona duas
Análise de Regressão Notas de Aula 2 Modelos de Regressão Modelos de regressão são modelos matemáticos que relacionam o comportamento de uma variável Y com outra X. Quando a função f que relaciona duas
Análise de Regressão Linear Simples III
 Análise de Regressão Linear Simples III Aula 03 Gujarati e Porter Capítulos 4 e 5 Wooldridge Seção.5 Suposições, Propriedades e Teste t Suposições e Propriedades RLS.1 O modelo de regressão é linear nos
Análise de Regressão Linear Simples III Aula 03 Gujarati e Porter Capítulos 4 e 5 Wooldridge Seção.5 Suposições, Propriedades e Teste t Suposições e Propriedades RLS.1 O modelo de regressão é linear nos
AULAS 06, 07, 08 E 09 Análise de Regressão Múltipla: Estimação e Inferência
 1 AULAS 06, 07, 08 E 09 Análise de Regressão Múltipla: Estimação e Inferência Ernesto F. L. Amaral 18, 23, 25 e 30 de março de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte:
1 AULAS 06, 07, 08 E 09 Análise de Regressão Múltipla: Estimação e Inferência Ernesto F. L. Amaral 18, 23, 25 e 30 de março de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte:
AULAS 19, 20, 21 E 22 Análise de Regressão Múltipla com Informações Qualitativas
 1 AULAS 19, 20, 21 E 22 Análise de Regressão Múltipla com Informações Qualitativas Ernesto F. L. Amaral 13, 18, 20 e 25 de maio de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D)
1 AULAS 19, 20, 21 E 22 Análise de Regressão Múltipla com Informações Qualitativas Ernesto F. L. Amaral 13, 18, 20 e 25 de maio de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D)
AULAS 02 E 03 Modelo de Regressão Simples
 1 AULAS 02 E 03 Modelo de Regressão Simples Ernesto F. L. Amaral 04 e 09 de março de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução à
1 AULAS 02 E 03 Modelo de Regressão Simples Ernesto F. L. Amaral 04 e 09 de março de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução à
PARTE 1 ANÁLISE DE REGRESSÃO COM DADOS DE CORTE TRANSVERSAL CAPÍTULO 2 O MODELO DE REGRESSÃO SIMPLES
 PARTE 1 ANÁLISE DE REGRESSÃO COM DADOS DE CORTE TRANSVERSAL CAPÍTULO 2 O MODELO DE REGRESSÃO SIMPLES 2.1 DEFINIÇÃO DO MODELO DE REGRESSÃO SIMPLES Duas variáveis: y e x Análise explicar y em termos de x
PARTE 1 ANÁLISE DE REGRESSÃO COM DADOS DE CORTE TRANSVERSAL CAPÍTULO 2 O MODELO DE REGRESSÃO SIMPLES 2.1 DEFINIÇÃO DO MODELO DE REGRESSÃO SIMPLES Duas variáveis: y e x Análise explicar y em termos de x
AULAS 20 E 21 Análise de regressão múltipla: problemas adicionais
 1 AULAS 20 E 21 Análise de regressão múltipla: problemas adicionais Ernesto F. L. Amaral 08 e 13 de novembro de 2012 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à
1 AULAS 20 E 21 Análise de regressão múltipla: problemas adicionais Ernesto F. L. Amaral 08 e 13 de novembro de 2012 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à
Regressão linear múltipla. Prof. Tatiele Lacerda
 Regressão linear múltipla Prof Tatiele Lacerda Yi = B + Bx + B3X3 + u Plano de resposta E(Y i ) = 0,00 Y i i 0 (,33;,67) Y i 0 X i Xi X p i, p i 3 Modelo de regressão linear múltipla em termos matriciais,
Regressão linear múltipla Prof Tatiele Lacerda Yi = B + Bx + B3X3 + u Plano de resposta E(Y i ) = 0,00 Y i i 0 (,33;,67) Y i 0 X i Xi X p i, p i 3 Modelo de regressão linear múltipla em termos matriciais,
Como rodar a regressão no gretl. Usando o Console para calcular elasticidade. Elasticidade. Usando o Console para calcular predição
 Como rodar a regressão no gretl Alguns tópicos do gretl Usando o console: Comando: ols y const 3 Estima uma função linear usando o método de Mínimos Quadrados Ordinários. Elasticidade Intuição: resposta
Como rodar a regressão no gretl Alguns tópicos do gretl Usando o console: Comando: ols y const 3 Estima uma função linear usando o método de Mínimos Quadrados Ordinários. Elasticidade Intuição: resposta
Análise de Regressão Múltipla com informação qualitativa: variáveis binárias (dummy)
 Análise de Regressão Múltipla com informação qualitativa: variáveis binárias (dummy) 1 Como descrever informações qualitativas? Fatores qualitativos podem ser incorporados a modelos de regressão. Neste
Análise de Regressão Múltipla com informação qualitativa: variáveis binárias (dummy) 1 Como descrever informações qualitativas? Fatores qualitativos podem ser incorporados a modelos de regressão. Neste
Plano de Ensino PROBABILIDADE E ESTATÍSTICA APLICADA À ENGENHARIA - CCE0292
 Plano de Ensino PROBABILIDADE E ESTATÍSTICA APLICADA À ENGENHARIA - CCE0292 Título PROBABILIDADE E ESTATÍSTICA APLICADA À ENGENHARIA Código da disciplina SIA CCE0292 16 Número de semanas de aula 4 Número
Plano de Ensino PROBABILIDADE E ESTATÍSTICA APLICADA À ENGENHARIA - CCE0292 Título PROBABILIDADE E ESTATÍSTICA APLICADA À ENGENHARIA Código da disciplina SIA CCE0292 16 Número de semanas de aula 4 Número
AULA 17 Tipos de desenhos de pesquisas
 1 AULA 17 Tipos de desenhos de pesquisas Ernesto F. L. Amaral 13 de maio de 2010 Metodologia (DCP 033) Fonte: Babbie, Earl. Métodos de Pesquisas de Survey. 1999. Belo Horizonte: Editora UFMG. pp.93-111.
1 AULA 17 Tipos de desenhos de pesquisas Ernesto F. L. Amaral 13 de maio de 2010 Metodologia (DCP 033) Fonte: Babbie, Earl. Métodos de Pesquisas de Survey. 1999. Belo Horizonte: Editora UFMG. pp.93-111.
AULA 11 Experimentos Multinomiais e Tabelas de Contingência
 1 AULA 11 Experimentos Multinomiais e Tabelas de Contingência Ernesto F. L. Amaral 24 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG)
1 AULA 11 Experimentos Multinomiais e Tabelas de Contingência Ernesto F. L. Amaral 24 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG)
AULA 12 Inferência a Partir de Duas Amostras
 1 AULA 12 Inferência a Partir de Duas Amostras Ernesto F. L. Amaral 15 de setembro de 2011 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
1 AULA 12 Inferência a Partir de Duas Amostras Ernesto F. L. Amaral 15 de setembro de 2011 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
Curso de Análise Estatística Comparação entre variáveis contínuas: correlação e regressão Linear
 NÚCLEO DE ESTATÍSTICA E METODOLOGIA APLICADAS Desenvolvendo conhecimento para a excelência dos cuidados em saúde mental UNIVERSIDADE FEDERAL DE SÃO PAULO Curso de Análise Estatística Comparação entre variáveis
NÚCLEO DE ESTATÍSTICA E METODOLOGIA APLICADAS Desenvolvendo conhecimento para a excelência dos cuidados em saúde mental UNIVERSIDADE FEDERAL DE SÃO PAULO Curso de Análise Estatística Comparação entre variáveis
AMOSTRAGEM: DIMENSIONAMENTO DE AMOSTRAS. SELEÇÃO DOS ELEMENTOS DE UMA AMOSTRA. ESTIMATIVA DA CARACTERÍSTICA TOTAL DA POPULAÇÃO INVESTIGADA
 AMOSTRAGEM: DIMENSIONAMENTO DE AMOSTRAS. SELEÇÃO DOS ELEMENTOS DE UMA AMOSTRA. ESTIMATIVA DA CARACTERÍSTICA TOTAL DA POPULAÇÃO INVESTIGADA META Dimensionar o tamanho ideal de amostra para cada população.
AMOSTRAGEM: DIMENSIONAMENTO DE AMOSTRAS. SELEÇÃO DOS ELEMENTOS DE UMA AMOSTRA. ESTIMATIVA DA CARACTERÍSTICA TOTAL DA POPULAÇÃO INVESTIGADA META Dimensionar o tamanho ideal de amostra para cada população.
1 Introdução. 1.1 Importância da Utilização da Amostragem
 1 Introdução Um dos principais objetivos da maioria dos estudos, análises ou pesquisas estatísticas é fazer generalizações seguras com base em amostras, sobre as populações das quais as amostras foram
1 Introdução Um dos principais objetivos da maioria dos estudos, análises ou pesquisas estatísticas é fazer generalizações seguras com base em amostras, sobre as populações das quais as amostras foram
Capítulo 4 Inferência Estatística
 Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a variância de
Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a variância de
Medidas de Tendência Central. Introdução Média Aritmética Moda Mediana
 Medidas de Tendência Central Introdução Média Aritmética Moda Mediana Introdução A maioria dos dados apresenta uma tendência de se concentrar em torno de um ponto central Portanto, é possível selecionar
Medidas de Tendência Central Introdução Média Aritmética Moda Mediana Introdução A maioria dos dados apresenta uma tendência de se concentrar em torno de um ponto central Portanto, é possível selecionar
BIOESTATÍSTICA. Parte 1 - Estatística descritiva e análise exploratória dos dados
 BIOESTATÍSTICA Parte 1 - Estatística descritiva e análise exploratória dos dados Aulas Teóricas de 17/02/2011 a 03/03/2011 1.1. População, amostra e dados estatísticos. Dados qualitativos e quantitativos
BIOESTATÍSTICA Parte 1 - Estatística descritiva e análise exploratória dos dados Aulas Teóricas de 17/02/2011 a 03/03/2011 1.1. População, amostra e dados estatísticos. Dados qualitativos e quantitativos
Medidas de Localização
 MATEMÁTICA APLICADA ÀS CIÊNCIAS SOCIAIS RESUMO Estatística 2 Medidas de Localização e Dispersão 10º ano Cláudia Henriques Medidas de Localização Estatísticas Medidas que se calculam a partir dos dados
MATEMÁTICA APLICADA ÀS CIÊNCIAS SOCIAIS RESUMO Estatística 2 Medidas de Localização e Dispersão 10º ano Cláudia Henriques Medidas de Localização Estatísticas Medidas que se calculam a partir dos dados
AULAS 21 E 22 Análise de Regressão Múltipla: Estimação
 1 AULAS 21 E 22 Análise de Regressão Múltipla: Estimação Ernesto F. L. Amaral 28 de outubro e 04 de novembro de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Cohen, Ernesto, e Rolando Franco. 2000. Avaliação
1 AULAS 21 E 22 Análise de Regressão Múltipla: Estimação Ernesto F. L. Amaral 28 de outubro e 04 de novembro de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Cohen, Ernesto, e Rolando Franco. 2000. Avaliação
Para mais de duas variáveis independentes, em função de uma variável dependente.
 MÉTODOS QUANTlTATlVOS APLlCADOS À CONTABlLlDADE Prof. Héber Lavor Moreira Plano de Aula TEMA: REGRESSÃO MÚLTlPLA - Caso Multiplan S/A lntrodução Em muitos casos uma variável pode estar relacionada com
MÉTODOS QUANTlTATlVOS APLlCADOS À CONTABlLlDADE Prof. Héber Lavor Moreira Plano de Aula TEMA: REGRESSÃO MÚLTlPLA - Caso Multiplan S/A lntrodução Em muitos casos uma variável pode estar relacionada com
Análise de Regressão Múltipla: Mínimos Quadrados Ordinários
 1 Análise de Regressão Múltipla: Mínimos Quadrados Ordinários Ernesto F. L. Amaral Magna M. Inácio 26 de agosto de 2010 Tópicos Especiais em Teoria e Análise Política: Problema de Desenho e Análise Empírica
1 Análise de Regressão Múltipla: Mínimos Quadrados Ordinários Ernesto F. L. Amaral Magna M. Inácio 26 de agosto de 2010 Tópicos Especiais em Teoria e Análise Política: Problema de Desenho e Análise Empírica
IV Regressão e correlação IV.4. (cont.) Significância Estatística e Regressão Múltipla
 IV Regressão e correlação IV.4. (cont.) Significância Estatística e Regressão Múltipla Significância Estatística Existe uma estatítica, o t-estatístico,associado a cada estimativa O t-estatístico mede
IV Regressão e correlação IV.4. (cont.) Significância Estatística e Regressão Múltipla Significância Estatística Existe uma estatítica, o t-estatístico,associado a cada estimativa O t-estatístico mede
Métodos Quantitativos Aplicados a Custos Análise Estatística como um auxiliar valioso nas decisões
 Métodos Quantitativos Aplicados a Custos Análise Estatística como um auxiliar valioso nas decisões Que métodos estatísticos podem auxiliar as análises de custos? Qual a relação entre regressão e correlação?
Métodos Quantitativos Aplicados a Custos Análise Estatística como um auxiliar valioso nas decisões Que métodos estatísticos podem auxiliar as análises de custos? Qual a relação entre regressão e correlação?
AULA 32 Problemas Adicionais de Especificação e de Dados
 1 AULA 32 Problemas Adicionais de Especificação e de Dados Ernesto F. L. Amaral Metodologia de Pesquisa (DCP 854B) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem moderna. São Paulo:
1 AULA 32 Problemas Adicionais de Especificação e de Dados Ernesto F. L. Amaral Metodologia de Pesquisa (DCP 854B) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem moderna. São Paulo:
ROTEIRO PARA ELABORAÇÃO DO PROJETO DE PESQUISA
 ROTEIRO PARA ELABORAÇÃO DO PROJETO DE PESQUISA O objetivo desse roteiro é orientar os estudantes de Estatística para a realização do trabalho proposto conforme previsto no plano de ensino da disciplina.
ROTEIRO PARA ELABORAÇÃO DO PROJETO DE PESQUISA O objetivo desse roteiro é orientar os estudantes de Estatística para a realização do trabalho proposto conforme previsto no plano de ensino da disciplina.
Análise estatística. Aula de Bioestatística. 17/9/2008 (2.ª Parte) Paulo Nogueira
 Análise estatística Aula de Bioestatística 17/9/2008 (2.ª Parte) Paulo Nogueira Testes de Hipóteses Hipótese Estatística de teste Distribuição da estatística de teste Decisão H 0 : Não existe efeito vs.
Análise estatística Aula de Bioestatística 17/9/2008 (2.ª Parte) Paulo Nogueira Testes de Hipóteses Hipótese Estatística de teste Distribuição da estatística de teste Decisão H 0 : Não existe efeito vs.
Regressão, Interpolação e Extrapolação Numéricas
 , e Extrapolação Numéricas Departamento de Física Universidade Federal da Paraíba 29 de Maio de 2009, e Extrapolação Numéricas O problema Introdução Quem é quem Um problema muito comum na física é o de
, e Extrapolação Numéricas Departamento de Física Universidade Federal da Paraíba 29 de Maio de 2009, e Extrapolação Numéricas O problema Introdução Quem é quem Um problema muito comum na física é o de
Quanto aos objetivos TIPO DE PESQUISA
 TIPO DE PESQUISA Quanto aos objetivos Segundo Gil (2002), uma pesquisa, tendo em vista seus objetivos, pode ser classificada da seguinte forma: a) Pesquisa exploratória: Esta pesquisa tem como objetivo
TIPO DE PESQUISA Quanto aos objetivos Segundo Gil (2002), uma pesquisa, tendo em vista seus objetivos, pode ser classificada da seguinte forma: a) Pesquisa exploratória: Esta pesquisa tem como objetivo
AULA 04 Estimativas e Tamanhos Amostrais
 1 AULA 04 Estimativas e Tamanhos Amostrais Ernesto F. L. Amaral 27 de agosto de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario
1 AULA 04 Estimativas e Tamanhos Amostrais Ernesto F. L. Amaral 27 de agosto de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario
AULA 07 Procedimentos de Pesquisa em Ciências Sociais
 1 AULA 07 Procedimentos de Pesquisa em Ciências Sociais Ernesto F. L. Amaral 25 de março de 2010 Metodologia (DCP 033) Fonte: Banco Mundial. Monitorização e Avaliação: algumas ferramentas, métodos e abordagens.
1 AULA 07 Procedimentos de Pesquisa em Ciências Sociais Ernesto F. L. Amaral 25 de março de 2010 Metodologia (DCP 033) Fonte: Banco Mundial. Monitorização e Avaliação: algumas ferramentas, métodos e abordagens.
Matemática Aplicada às Ciências Sociais
 ESCOLA SECUNDÁRIA DE AMORA PLANIFICAÇÃO ANUAL Matemática Aplicada às Ciências Sociais Ensino Regular Curso Geral de Ciências Sociais e Humanas 11º ANO Ano Letivo 2014 / 2015 PLANIFICAÇÃO A LONGO PRAZO
ESCOLA SECUNDÁRIA DE AMORA PLANIFICAÇÃO ANUAL Matemática Aplicada às Ciências Sociais Ensino Regular Curso Geral de Ciências Sociais e Humanas 11º ANO Ano Letivo 2014 / 2015 PLANIFICAÇÃO A LONGO PRAZO
Estimação. Como definir um estimador. Como obter estimativas pontuais. Como construir intervalos de confiança
 Estimação Como definir um estimador. Como obter estimativas pontuais. Como construir intervalos de confiança Motivação A partir da média de uma a amostra em uma colheita recente, o conselho de qualidade
Estimação Como definir um estimador. Como obter estimativas pontuais. Como construir intervalos de confiança Motivação A partir da média de uma a amostra em uma colheita recente, o conselho de qualidade
AULA 05 Análise de regressão múltipla: inferência
 1 AULA 05 Análise de regressão múltipla: inferência Ernesto F. L. Amaral 19 de julho de 2013 Análise de Regressão Linear (MQ 2013) www.ernestoamaral.com/mq13reg.html Fonte: Wooldridge, Jeffrey M. Introdução
1 AULA 05 Análise de regressão múltipla: inferência Ernesto F. L. Amaral 19 de julho de 2013 Análise de Regressão Linear (MQ 2013) www.ernestoamaral.com/mq13reg.html Fonte: Wooldridge, Jeffrey M. Introdução
Capítulo 1. Uma Introdução à Econometria
 Capítulo 1 Uma Introdução à Econometria Livro Texto:Econometria Hill, Grifith e Judge Editora Saraiva 1a. Edição 1999. Software: GRETL 1.1 Por que se estuda Econometria? Econometria é um conjunto de ferramentas
Capítulo 1 Uma Introdução à Econometria Livro Texto:Econometria Hill, Grifith e Judge Editora Saraiva 1a. Edição 1999. Software: GRETL 1.1 Por que se estuda Econometria? Econometria é um conjunto de ferramentas
Aula Prática: Regressão Linear Simples
 Universidade Federal do Rio de Janeiro Faculdade de Medicina Departamento de Medicina Preventiva Núcleo de Estudos de Saúde Coletiva Disciplina: Modelos de Regressão em saúde Aula Prática: Regressão Linear
Universidade Federal do Rio de Janeiro Faculdade de Medicina Departamento de Medicina Preventiva Núcleo de Estudos de Saúde Coletiva Disciplina: Modelos de Regressão em saúde Aula Prática: Regressão Linear
Modelos de Probabilidade e Inferência Estatística
 Modelos de Probabilidade e Inferência Estatística Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Distribuições Qui-quadrado, t-student e F de Snedecor 04/14
Modelos de Probabilidade e Inferência Estatística Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Distribuições Qui-quadrado, t-student e F de Snedecor 04/14
Consumo. Revisão e Modelo Ciclo de Vida. Wilson Correa. April 26, 2016
 Consumo Revisão e Modelo Ciclo de Vida Wilson Correa April 26, 2016 Revisão Propensão a consumir é a relação funcional entre o determinado nível de renda e o gasto para consumo. Montante gasto em consumo
Consumo Revisão e Modelo Ciclo de Vida Wilson Correa April 26, 2016 Revisão Propensão a consumir é a relação funcional entre o determinado nível de renda e o gasto para consumo. Montante gasto em consumo
Medidas de dispersão e assimetria
 Metodologia de Diagnóstico e Elaboração de Relatório FASHT Medidas de dispersão e assimetria Profª Cesaltina Pires [email protected] Plano da Apresentação Medidas de dispersão Variância Desvio padrão Erro
Metodologia de Diagnóstico e Elaboração de Relatório FASHT Medidas de dispersão e assimetria Profª Cesaltina Pires [email protected] Plano da Apresentação Medidas de dispersão Variância Desvio padrão Erro
SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO DE CIÊNCIAS BIOLÓGICAS DECB
 Governo do Estado do Rio Grande do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNVERSDADE DO ESTADO DO RO GRANDE DO NORTE UERN FACULDADE DE CÊNCAS EXATAS E NATURAS FANAT DEPARTAMENTO DE
Governo do Estado do Rio Grande do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNVERSDADE DO ESTADO DO RO GRANDE DO NORTE UERN FACULDADE DE CÊNCAS EXATAS E NATURAS FANAT DEPARTAMENTO DE
Avaliação e Desempenho Aula 1 - Simulação
 Avaliação e Desempenho Aula 1 - Simulação Introdução à simulação Geração de números aleatórios Lei dos grandes números Geração de variáveis aleatórias O Ciclo de Modelagem Sistema real Criação do Modelo
Avaliação e Desempenho Aula 1 - Simulação Introdução à simulação Geração de números aleatórios Lei dos grandes números Geração de variáveis aleatórias O Ciclo de Modelagem Sistema real Criação do Modelo
O QUE É AMOSTRAGEM? PARTE I
 O QUE É AMOSTRAGEM? PARTE I! Teoria da amostragem! População x Amostra! O problema do censo! Amostragem probabilística e não probabilística Francisco Cavalcante([email protected]) Administrador de Empresas
O QUE É AMOSTRAGEM? PARTE I! Teoria da amostragem! População x Amostra! O problema do censo! Amostragem probabilística e não probabilística Francisco Cavalcante([email protected]) Administrador de Empresas
PERSISTÊNCIA DO PODER POLÍTICO E DESENVOLVIMENTO ECONÔMICO: O CASO DA TRANSIÇÃO DE REGIME NO BRASIL
 PERSISTÊNCIA DO PODER POLÍTICO E DESENVOLVIMENTO ECONÔMICO: O CASO DA TRANSIÇÃO DE REGIME NO BRASIL Aluno: Rafael Campos de Mattos Orientador: Claudio Ferraz Introdução Nas últimas décadas, observou-se
PERSISTÊNCIA DO PODER POLÍTICO E DESENVOLVIMENTO ECONÔMICO: O CASO DA TRANSIÇÃO DE REGIME NO BRASIL Aluno: Rafael Campos de Mattos Orientador: Claudio Ferraz Introdução Nas últimas décadas, observou-se
3 Modelos de Simulação
 43 3 Modelos de Simulação 3.1 Simulação de Monte Carlo O método de Monte Carlo foi concebido com este nome nos anos 40 por John Von Neumann, Stanislaw Ulam e Nicholas Metropolis durante o projeto de pesquisa
43 3 Modelos de Simulação 3.1 Simulação de Monte Carlo O método de Monte Carlo foi concebido com este nome nos anos 40 por John Von Neumann, Stanislaw Ulam e Nicholas Metropolis durante o projeto de pesquisa
IND 1115 Inferência Estatística Aula 8
 Conteúdo IND 5 Inferência Estatística Aula 8 Setembro 4 Mônica Barros O - aproximação da Binomial pela Este teorema é apenas um caso particular do teorema central do limite, pois uma variável aleatória
Conteúdo IND 5 Inferência Estatística Aula 8 Setembro 4 Mônica Barros O - aproximação da Binomial pela Este teorema é apenas um caso particular do teorema central do limite, pois uma variável aleatória
Aula 12: Correlação e Regressão
 Aula 12: Correlação e Regressão Sumário Aula 12: Correlação e Regressão... 1 12.l Correlação... 2 12.2 Diagrama de dispersão... 2 12.3 Correlação linear... 3 12.3.1 Coeficiente de correlação linear...
Aula 12: Correlação e Regressão Sumário Aula 12: Correlação e Regressão... 1 12.l Correlação... 2 12.2 Diagrama de dispersão... 2 12.3 Correlação linear... 3 12.3.1 Coeficiente de correlação linear...
Testes de variância e Análise de Variância (ANOVA)
 Testes de variância e Análise de Variância (ANOVA) Introdução à Inferência Estatística Introdução à Inferência Estatística TESTE DE VARIÂNCIAS E DISTRIBUIÇÃO F Testes sobre variâncias Problema: queremos
Testes de variância e Análise de Variância (ANOVA) Introdução à Inferência Estatística Introdução à Inferência Estatística TESTE DE VARIÂNCIAS E DISTRIBUIÇÃO F Testes sobre variâncias Problema: queremos
Experimento. Guia do professor. Quantos peixes há no lago? Secretaria de Educação a Distância. Ministério da Ciência e Tecnologia
 Análise de dados e probabilidade Guia do professor Experimento Quantos peixes há no lago? Objetivos da unidade Introduzir um método que permite estimar o tamanho de uma deter minada população. licença
Análise de dados e probabilidade Guia do professor Experimento Quantos peixes há no lago? Objetivos da unidade Introduzir um método que permite estimar o tamanho de uma deter minada população. licença
DISTRIBUIÇÃO DE FREQUÊNCIA DE VARIÁVEIS QUALITATIVAS E QUANTITATIVAS DISCRETAS (TABELAS E GRÁFICOS)
 DISTRIBUIÇÃO DE FREQUÊNCIA DE VARIÁVEIS QUALITATIVAS E QUANTITATIVAS DISCRETAS (TABELAS E GRÁFICOS) O QUE É ESTATÍSTICA Estatística é a ciência de obter conclusões a partir de dados. Envolve métodos para
DISTRIBUIÇÃO DE FREQUÊNCIA DE VARIÁVEIS QUALITATIVAS E QUANTITATIVAS DISCRETAS (TABELAS E GRÁFICOS) O QUE É ESTATÍSTICA Estatística é a ciência de obter conclusões a partir de dados. Envolve métodos para
Estatística. Conjunto de métodos e processos quantitativos que serve para estudar e medir os fenômenos coletivos ou de massa.
 Faculdade de Tecnologia Senac Pelotas Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas Matemática Aplicada Prof. Edécio Fernando Iepsen Estatística Variáveis Qualitativas, Quantitativas
Faculdade de Tecnologia Senac Pelotas Curso Superior de Tecnologia em Análise e Desenvolvimento de Sistemas Matemática Aplicada Prof. Edécio Fernando Iepsen Estatística Variáveis Qualitativas, Quantitativas
MOQ 13 PROBABILIDADE E ESTATÍSTICA. Professor: Rodrigo A. Scarpel
 MOQ 13 PROBABILIDADE E ESTATÍSTICA Professor: Rodrigo A. Scarpel [email protected] www.mec.ita.br/~rodrigo Probabilidade e Estatística The Science of collecting and analyzing data for the purpose of drawing
MOQ 13 PROBABILIDADE E ESTATÍSTICA Professor: Rodrigo A. Scarpel [email protected] www.mec.ita.br/~rodrigo Probabilidade e Estatística The Science of collecting and analyzing data for the purpose of drawing
Estatística AMOSTRAGEM
 Estatística AMOSTRAGEM Estatística: É a ciência que se preocupa com a coleta, a organização, descrição (apresentação), análise e interpretação de dados experimentais e tem como objetivo fundamental o estudo
Estatística AMOSTRAGEM Estatística: É a ciência que se preocupa com a coleta, a organização, descrição (apresentação), análise e interpretação de dados experimentais e tem como objetivo fundamental o estudo
AULA 06 A Ciência e as Ciências Sociais
 1 AULA 06 A Ciência e as Ciências Sociais Ernesto F. L. Amaral 20 de agosto de 2010 Metodologia (DCP 033) Fonte: Babbie, Earl. Métodos de Pesquisas de Survey. 2001. Belo Horizonte: Editora UFMG. pp.57-76.
1 AULA 06 A Ciência e as Ciências Sociais Ernesto F. L. Amaral 20 de agosto de 2010 Metodologia (DCP 033) Fonte: Babbie, Earl. Métodos de Pesquisas de Survey. 2001. Belo Horizonte: Editora UFMG. pp.57-76.
PARTICIPAÇÃO FEMININA NO MERCADO DE TRABALHO BRASILEIRO 1
 PARTICIPAÇÃO FEMININA NO MERCADO DE TRABALHO BRASILEIRO 1 Ana Luiza Neves de Holanda Barbosa 2 1 INTRODUÇÃO Nas últimas décadas o papel da mulher na economia e na sociedade como um todo tem passado por
PARTICIPAÇÃO FEMININA NO MERCADO DE TRABALHO BRASILEIRO 1 Ana Luiza Neves de Holanda Barbosa 2 1 INTRODUÇÃO Nas últimas décadas o papel da mulher na economia e na sociedade como um todo tem passado por
REGRESSÃO. Análise de Correlação
 REGRESSÃO Linear, Não linear, simples e múltipla Análise de Correlação 2 Correlação Indica a força e a direção do relacionamento linear entre dois atributos Trata-se de uma medida da relação entre dois
REGRESSÃO Linear, Não linear, simples e múltipla Análise de Correlação 2 Correlação Indica a força e a direção do relacionamento linear entre dois atributos Trata-se de uma medida da relação entre dois
Métodos Quantitativos Aplicados
 Métodos Quantitativos Aplicados Aula 2 http://www.iseg.ulisboa.pt/~vescaria/mqa/ Tópicos da apresentação Fontes de informação típicas para análise Fontes de informação típicas para análise Informação secundária
Métodos Quantitativos Aplicados Aula 2 http://www.iseg.ulisboa.pt/~vescaria/mqa/ Tópicos da apresentação Fontes de informação típicas para análise Fontes de informação típicas para análise Informação secundária
Erros e Incertezas. Rafael Alves Batista Instituto de Física Gleb Wataghin Universidade Estadual de Campinas (Dated: 10 de Julho de 2011.
 Rafael Alves Batista Instituto de Física Gleb Wataghin Universidade Estadual de Campinas (Dated: 10 de Julho de 2011.) I. INTRODUÇÃO Quando se faz um experimento, deseja-se comparar o resultado obtido
Rafael Alves Batista Instituto de Física Gleb Wataghin Universidade Estadual de Campinas (Dated: 10 de Julho de 2011.) I. INTRODUÇÃO Quando se faz um experimento, deseja-se comparar o resultado obtido
Universidade Federal do Amazonas Instituto de Ciências Exatas Departamento de Estatística
 PLANO DE ENSINO 1. IDENTIFICAÇÃO Disciplina: PROBABILIDADE E ESTATÍSTICA Código: IEE001 Pré-Requisito: IEM011 - CÁLCULO I N O de Créditos: 4 Número de Aulas Teóricas: 60 Práticas: 0 Semestre: 1 O Ano:
PLANO DE ENSINO 1. IDENTIFICAÇÃO Disciplina: PROBABILIDADE E ESTATÍSTICA Código: IEE001 Pré-Requisito: IEM011 - CÁLCULO I N O de Créditos: 4 Número de Aulas Teóricas: 60 Práticas: 0 Semestre: 1 O Ano:
Método dos mínimos quadrados Wikipédia, a enciclopédia livre
 1 de 5 25/12/2012 20:27 Método dos mínimos quadrados Origem: Wikipédia, a enciclopédia livre. O Método dos Mínimos Quadrados, ou Mínimos Quadrados Ordinários (MQO) ou OLS (do inglês Ordinary Least Squares)
1 de 5 25/12/2012 20:27 Método dos mínimos quadrados Origem: Wikipédia, a enciclopédia livre. O Método dos Mínimos Quadrados, ou Mínimos Quadrados Ordinários (MQO) ou OLS (do inglês Ordinary Least Squares)
INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA. Prof. Anderson Rodrigo da Silva [email protected]
 INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA Prof. Anderson Rodrigo da Silva [email protected] Tipos de Pesquisa Censo: é o levantamento de toda população. Aqui não se faz inferência e sim uma descrição
INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA Prof. Anderson Rodrigo da Silva [email protected] Tipos de Pesquisa Censo: é o levantamento de toda população. Aqui não se faz inferência e sim uma descrição
Estatística. Aula 1 -Fundamentos e conceitos básicos (Notas de aula) Prof. Idemauro Antonio Rodrigues de Lara
 Estatística Aula 1 -Fundamentos e conceitos básicos (Notas de aula) Prof. Idemauro Antonio Rodrigues de Lara Objetivo da disciplina Adquirir conhecimento dos fundamentos da Estatística, em seus campos
Estatística Aula 1 -Fundamentos e conceitos básicos (Notas de aula) Prof. Idemauro Antonio Rodrigues de Lara Objetivo da disciplina Adquirir conhecimento dos fundamentos da Estatística, em seus campos
AGRUPAMENTO DE ESCOLAS DA SÉ GUARDA. MATEMÁTICA B Curso de Artes Visuais
 Direção-Geral dos Estabelecimentos Escolares Direção de Serviços da Região Centro AGRUPAMENTO DE ESCOLAS DA SÉ GUARDA MATEMÁTICA B Curso de Artes Visuais ANO LECTIVO: 2015/2016 11º ANO 1º PERÍODO PLANIFICAÇÃO
Direção-Geral dos Estabelecimentos Escolares Direção de Serviços da Região Centro AGRUPAMENTO DE ESCOLAS DA SÉ GUARDA MATEMÁTICA B Curso de Artes Visuais ANO LECTIVO: 2015/2016 11º ANO 1º PERÍODO PLANIFICAÇÃO
MAE116 - Noções de Estatística
 MAE116 - Noções de Estatística Grupo A - 1 semestre de 2015 Gabarito da Lista de exercícios 10 - Introdução à Estatística Descritiva - CASA Exercício 1. (2 pontos) Sabe-se que, historicamente, 18% dos
MAE116 - Noções de Estatística Grupo A - 1 semestre de 2015 Gabarito da Lista de exercícios 10 - Introdução à Estatística Descritiva - CASA Exercício 1. (2 pontos) Sabe-se que, historicamente, 18% dos
AULA 26 Análise de Regressão Múltipla: Problemas Adicionais
 1 AULA 26 Análise de Regressão Múltipla: Problemas Adicionais Ernesto F. L. Amaral 13 de novembro de 2012 Metodologia de Pesquisa (DCP 854B) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma
1 AULA 26 Análise de Regressão Múltipla: Problemas Adicionais Ernesto F. L. Amaral 13 de novembro de 2012 Metodologia de Pesquisa (DCP 854B) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma
SOCIOLOGIA A SOCIOLOGIA EM AÇÃO
 SOCIOLOGIA A SOCIOLOGIA EM AÇÃO A SOCIOLOGIA É estudo científico dos fatos sociais e, portanto, da própria sociedade. Exerce influência: na ação de governos, na educação, na vida política, na religião,
SOCIOLOGIA A SOCIOLOGIA EM AÇÃO A SOCIOLOGIA É estudo científico dos fatos sociais e, portanto, da própria sociedade. Exerce influência: na ação de governos, na educação, na vida política, na religião,
Relatório das Provas da 2ª. Fase - Vestibular 2016
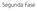 Relatório das Provas da 2ª. Fase - Vestibular 2016 Resumo Executivo O presente relatório apresenta os resultados da segunda fase do Vestibular UNICAMP 2016 constituída por três provas. Esta etapa do vestibular
Relatório das Provas da 2ª. Fase - Vestibular 2016 Resumo Executivo O presente relatório apresenta os resultados da segunda fase do Vestibular UNICAMP 2016 constituída por três provas. Esta etapa do vestibular
Stela Adami Vayego DEST/UFPR
 Resumo 5 - Análise Bivariada (Bidimensional) 5.1. Introdução O principal objetivo das análises nessa situação é explorar relações (similaridades) entre duas variáveis. A distribuição conjunta das freqüências
Resumo 5 - Análise Bivariada (Bidimensional) 5.1. Introdução O principal objetivo das análises nessa situação é explorar relações (similaridades) entre duas variáveis. A distribuição conjunta das freqüências
ESTATÍSTICA PARTE 1 OBJETIVO DA DISCIPLINA
 ESTATÍSTICA PARTE 1 OBJETIVO DA DISCIPLINA Apresentar a Estatística no contexto do dia-a-dia e fazendo uso da planilha Excel. Espera-se que o estudante ao término do curso esteja apto a usar a planilha
ESTATÍSTICA PARTE 1 OBJETIVO DA DISCIPLINA Apresentar a Estatística no contexto do dia-a-dia e fazendo uso da planilha Excel. Espera-se que o estudante ao término do curso esteja apto a usar a planilha
AULA 19 E 20 Análise de Regressão Múltipla: Problemas Adicionais
 1 AULA 19 E 20 Análise de Regressão Múltipla: Problemas Adicionais Ernesto F. L. Amaral 19 e 24 de maio de 2011 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
1 AULA 19 E 20 Análise de Regressão Múltipla: Problemas Adicionais Ernesto F. L. Amaral 19 e 24 de maio de 2011 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
PLANO DE ENSINO CONTEÚDO PROGRAMÁTICO. Unidade 1: MEDIDAS E GRANDEZAS. 1.1.- Introdução. 1.2.- Padrões usados para avaliar grandezas físicas
 PLANO DE ENSINO FACULDADE: CIÊNCIAS DA SAÚDE DE JUIZ DE FORA CURSO: FARMÁCIA Período: 2º DISCIPLINA: MATEMÁTICA E BIOESTATÍSTICA Ano: 2015 CARGA HORÁRIA: 40 H PRÉ-REQUISITO: - SEMANAL: 02 T TOTAL: 02 AULAS
PLANO DE ENSINO FACULDADE: CIÊNCIAS DA SAÚDE DE JUIZ DE FORA CURSO: FARMÁCIA Período: 2º DISCIPLINA: MATEMÁTICA E BIOESTATÍSTICA Ano: 2015 CARGA HORÁRIA: 40 H PRÉ-REQUISITO: - SEMANAL: 02 T TOTAL: 02 AULAS
Teste de Hipótese e Intervalo de Confiança. Parte 2
 Teste de Hipótese e Intervalo de Confiança Parte 2 Questões para discutirmos em sala: O que é uma hipótese estatística? O que é um teste de hipótese? Quem são as hipóteses nula e alternativa? Quando devemos
Teste de Hipótese e Intervalo de Confiança Parte 2 Questões para discutirmos em sala: O que é uma hipótese estatística? O que é um teste de hipótese? Quem são as hipóteses nula e alternativa? Quando devemos
Desvio Padrão ou Erro Padrão
 NOTAS METODOLÓGICAS ISSN 0871-3413 ArquiMed, 2006 Desvio Padrão ou Erro Padrão Nuno Lunet, Milton Severo, Henrique Barros Serviço de Higiene e Epidemiologia da Faculdade de Medicina da Universidade do
NOTAS METODOLÓGICAS ISSN 0871-3413 ArquiMed, 2006 Desvio Padrão ou Erro Padrão Nuno Lunet, Milton Severo, Henrique Barros Serviço de Higiene e Epidemiologia da Faculdade de Medicina da Universidade do
Faculdade de Odontologia Mestrado em Odontologia - Ortodontia. Projeto de Pesquisa. Titulo. Pesquisador:
 Faculdade de Odontologia Mestrado em Odontologia - Ortodontia Projeto de Pesquisa Titulo Pesquisador: Niterói 2014 1 PROJETO DE PESQUISA 1-Titulo: 2- Resumo Objetivos: Aquilo que se quer descobrir com
Faculdade de Odontologia Mestrado em Odontologia - Ortodontia Projeto de Pesquisa Titulo Pesquisador: Niterói 2014 1 PROJETO DE PESQUISA 1-Titulo: 2- Resumo Objetivos: Aquilo que se quer descobrir com
é 4. Portanto, o desvio padrão é 2. Neste caso 100% dos valores da população estão a um desvio padrão da média.
 Desvio Padrão From Wikipedia, the free encyclopedia probabilidade e estatística, o desvio padrão de uma distribuição de probabilidade, de uma variável aleatória, ou população é uma medida do espalhamento
Desvio Padrão From Wikipedia, the free encyclopedia probabilidade e estatística, o desvio padrão de uma distribuição de probabilidade, de uma variável aleatória, ou população é uma medida do espalhamento
Contabilometria. Análise Discriminante
 Contabilometria Análise Discriminante Fonte: Corrar, L. J.; Theóphilo, C. R. Pesquisa Operacional para Decisão em Contabilidade e Administração, Editora Atlas, São Paulo, 010 Cap. 3 Análise Discriminante
Contabilometria Análise Discriminante Fonte: Corrar, L. J.; Theóphilo, C. R. Pesquisa Operacional para Decisão em Contabilidade e Administração, Editora Atlas, São Paulo, 010 Cap. 3 Análise Discriminante
Objetivo. tica 3º ano EM. Oficina de Matemática
 Oficina de Matemática tica 3º ano EM Objetivo Análise, interpretação e utilização dos resultados do SAEPE para promoção da equidade e melhoria da qualidade da educação dos estudantes pernambucanos. Prof
Oficina de Matemática tica 3º ano EM Objetivo Análise, interpretação e utilização dos resultados do SAEPE para promoção da equidade e melhoria da qualidade da educação dos estudantes pernambucanos. Prof
PARTE I - EVOLUÇÃO DO PENSAMENTO. Curso Análise de Dados e Políticas Públicas. Ementa. Metodologia. Plano de Aula
 Curso Análise de Dados e Políticas Públicas Professor: Pablo Cerdeira Ementa O que Matemática tem a ver com Direito? Muita coisa. Neste curso de Análise de Dados e Políticas Públicas abordaremos três importantes
Curso Análise de Dados e Políticas Públicas Professor: Pablo Cerdeira Ementa O que Matemática tem a ver com Direito? Muita coisa. Neste curso de Análise de Dados e Políticas Públicas abordaremos três importantes
validade, acuracidade, ou exatidao viés ou vicio (Bolfarine e Bussab, 2005) 1.1 Palavras-chave
 (Bolfarine e Bussab, 2005) 1.1 Palavras-chave 1 amostra 2 amostragem por quotas 3 amostra probabilística 4 amostra representativa 5 amostragem 6 7 amostragem probabilistica característica de interesse
(Bolfarine e Bussab, 2005) 1.1 Palavras-chave 1 amostra 2 amostragem por quotas 3 amostra probabilística 4 amostra representativa 5 amostragem 6 7 amostragem probabilistica característica de interesse
A Significância Estatística do Proger na Redução da Taxa de Desemprego por Haroldo Feitosa Tajra
 A Significância Estatística do Proger na Redução da Taxa de Desemprego por Haroldo Feitosa Tajra 1. INTRODUÇÃO O objetivo desta análise é verificar a significância estatística das aplicações do Programa
A Significância Estatística do Proger na Redução da Taxa de Desemprego por Haroldo Feitosa Tajra 1. INTRODUÇÃO O objetivo desta análise é verificar a significância estatística das aplicações do Programa
Coeficiente de Assimetria e Curtose. Rinaldo Artes. Padronização., tem as seguintes propriedades: Momentos
 Coeficiente de Assimetria e Curtose Rinaldo Artes 2014 Padronização Seja X uma variável aleatória com E(X)=µ e Var(X)=σ 2. Então a variável aleatória Z, definida como =, tem as seguintes propriedades:
Coeficiente de Assimetria e Curtose Rinaldo Artes 2014 Padronização Seja X uma variável aleatória com E(X)=µ e Var(X)=σ 2. Então a variável aleatória Z, definida como =, tem as seguintes propriedades:
MEDIDAS DE DISPERSÃO. o grau de variabilidade, ou dispersão, dos valores em torno da média.
 UNIVERSIDADE FEDERAL DA PARAÍBA MEDIDAS DESCRITIVAS Departamento de Estatística Tarciana Liberal As medidas de posição apresentadas fornecem a informação dos dados apenas a nível pontual, sem ilustrar
UNIVERSIDADE FEDERAL DA PARAÍBA MEDIDAS DESCRITIVAS Departamento de Estatística Tarciana Liberal As medidas de posição apresentadas fornecem a informação dos dados apenas a nível pontual, sem ilustrar
Capítulo 5. Inferência no Modelo de Regressão Simples: Estimação de Intervalos, Teste de Hipóteses e Previsão
 Capítulo 5 Inferência no Modelo de Regressão Simples: Estimação de Intervalos, Teste de Hipóteses e Previsão Hipóteses do Modelo de Regressão Linear Simples RS1. y x e t 1 t t RS. RS3. RS4. RS5. RS6. Ee
Capítulo 5 Inferência no Modelo de Regressão Simples: Estimação de Intervalos, Teste de Hipóteses e Previsão Hipóteses do Modelo de Regressão Linear Simples RS1. y x e t 1 t t RS. RS3. RS4. RS5. RS6. Ee
Maio 2004. São Paulo. Instituto Brasileiro de Geografia e Estatística - IBGE
 Pesquisa Mensal de Emprego Maio 2004 Região Metropolitana de São Paulo Instituto Brasileiro de Geografia e Estatística - IBGE 1 I) INTRODUÇÃO PESQUISA MENSAL DE EMPREGO ESTIMATIVAS PARA O MÊS DE MAIO DE
Pesquisa Mensal de Emprego Maio 2004 Região Metropolitana de São Paulo Instituto Brasileiro de Geografia e Estatística - IBGE 1 I) INTRODUÇÃO PESQUISA MENSAL DE EMPREGO ESTIMATIVAS PARA O MÊS DE MAIO DE
Variáveis Frequências Gráficos Medidas de Posição Medidas de Dispersão Medidas Complementares Inferência
 Tipos de Variáveis Problema Motivador: Um pesquisador está interessado em fazer um levantamento sobre aspectos sócio-econômicos dos empregados da seção de orçamentos de uma companhia (vide tabela). Algumas
Tipos de Variáveis Problema Motivador: Um pesquisador está interessado em fazer um levantamento sobre aspectos sócio-econômicos dos empregados da seção de orçamentos de uma companhia (vide tabela). Algumas
Experimento. Guia do professor. Séries temporais. Governo Federal. Ministério da Educação. Secretaria de Educação a Distância
 Análise de dados e probabilidade Guia do professor Experimento Séries temporais Objetivos da unidade 1. Discutir e propagar, através de uma atividade, alguns conceitos de estatística; 2. Desenvolver a
Análise de dados e probabilidade Guia do professor Experimento Séries temporais Objetivos da unidade 1. Discutir e propagar, através de uma atividade, alguns conceitos de estatística; 2. Desenvolver a
