MAT Álgebra I para Licenciatura 2 a Lista de exercícios
|
|
|
- Roberto Tuschinski
- 5 Há anos
- Visualizações:
Transcrição
1 MAT Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3. Para todo n Z, calcular: (a) mmc (n, n + 1); (b) mmc (2n 1, 2n + 1); (c) mmc (nc, (n + 1)c). 4. Decidir se as afirmações abaixo são verdadeiras ou falsas dando a demonstração ou um contraexemplo. Sejam a, b, d Z: (a) Se existem r, s Z tais que d = ar + bs, então d = mdc (a, b); (b) Se existem r, s Z tais que 1 = ar + bs, então 1 = mdc (a, b); 5. Sejam a, b Z tais que mdc (a, b) = 1. Prove que: (a) mdc (a ± b, ab) = 1; (b) mdc (a + b, a b) = 1 ou 2; (c) mdc (a + b, a 2 + ab + b 2 ) = 1; (d) mdc (2a + b, a + 2b) = 1 ou Sejam a, b, c Z tais que a e b são relativamente primos entre si. Prove que: (a) Se 87a bc, então a c; (b) Se c a + b, então mdc (a, c) = mdc (b, c) = 1; (c) mdc (ac, b) = mdc (c, b); (d) mdc (a, b) = mdc (a, a ± b). 7. Sejam a, b, n Z tais que a e b são relativamente primos entre si. Calcule: (a) mdc (a + nb, a + (n + 1)b); 1
2 (b) mdc (a + nb, a + (n + 2)b). 8. Determinar: (a) a, b Z tais que ab = 9900 e mmc (a, b) = 330; (b) a, b Z tais que a + b = 581 e mmc (a, b) mdc (a, b) = Determinar todos os inteiros positivos a e b tais que mmc (a, b) = 72 e mdc (a, b) = Dados a, b Z não nulos, prove que:: (a) mdc (a, b) = mmc (a, b) se e somente se a = b ; (b) Para todo k Z, k 0, então mmc (ka, kb) = k mmc (a, b); ( a (c) Se k a e k b, então mmc k, b ) mmc (a, b) =. k k 11. A teoria dos números é um dos ramos mais antigos da matemática, muitos dos seus problemas nasceram mais ligados a questões místicas do que a considerações de caráter científico. Quando se perguntou a Pitágoras o que é um amigo, ele respondeu - áquele que é como o outro eu, como acontece com 220 e Pitágora quis dizer o seguinte: a soma dos divisores 1 < a < 284 de 284 é 220 e a soma dos divisores 1 < b < 220 de 220 é 284. Dois números nestas condições são chamados de amigos. Um conceito semelhante é o número perfeito. Um número dizse perfeito se ele é amigo de si mesmo. Os prímeros números perfeitos são 6 e 28 e alguns estudiosos da Bíbllia atribuem a esta propriedade o papel destes números na descrição da criação do Universo. (a) Seja a = p n 1 1 p n 2 2 p nt t da Aritmética. Mostre que: a decomposição de a > 1 nas condições do Teorema Fundamental N(a) = (n 1 + 1)(n 2 + 1) (n t + 1), é o número dos divisores positivos de a; S(a) = pn p 1 1 p n p 2 1 pnt t 1, é a soma de todos os divisores positivos de a. p t 1 (b) Prove que se 2 n 1 é primo, então 2 n 1 (2 n 1) é perfeito. (c) Determinar os inteiros a e b tais que a tem 21 divisores, b tem 10 divisores e mdc (a, b) = Sejam a e b inteiros tais que mdc (a, b) = p, onde p é primo. Calcular mdc (a 2, b) e mdc (a 2, b 2 ). 2
3 13. Prove que 4k + 3 e 5k + 4 são primos entre si para todo k. 14. Mostre que três inteiros positivos ímpares consecutidos não podem ser todos primos, com exceção de 3, 5 e Sejam p e q primos tais que p q 5. Prove que 24 (p 2 q 2 ). 16. Seja n um inteiro positivo. Prove que: (a) Se n > 4 e não é primo, então n (n 1)!; (b) Nenhum inteiro da forma 8 n + 1 é primo; (c) Se o ineiro 2 n 1 é primo, então n é primo; (d) Todo inteiro da forma n 4 + 4, com n > 1 é composto; (e) Todo inteiro n > 11 pode ser escrito como soma de dois números compostos positivos; (f) Todo primo da forma 3n + 1 é também da forma 6m + 1, para algum m Z; (g) Todo inteiro da forma 3n + 2 tem um fator primo desta forma; (h) O único primo da forma n 3 1 é 7; (i) O único primo n tal que 3n + 1 é um quadrado perfeito é Prove que: (a) Se p > 3 é um primo, então p é composto; (b) Se p 5 é um primo ímpar, então 10 (p 2 1) ou 10 (p 2 + 1). 18. Determinar a maior potência de 14 que divide 100!. 19. Determinar todos os primos que dividem 50!. 20. Sejam a e b primos entre si e m > 0. Prove que na progressão b, a + b, 2a + b,..., ka + b,... existem infinitos termos relativamente primos com m. 21. Prove que se a b, existem infinitos inteiros positivos n tais que a + n e b + n são primos entre si. 22. Se mdc (m, n) = 1 e mn é quadrado perfeito, então m e n são quadrados perfeitos. 3
4 23. Um inteiro diz-se livre de quadrados se não é divisível pelo quadrado de nenhum inteiro maior do que 1. Prove que: (a) Um inteiro é livre de quadrados se e somente se pode ser fatorado em um produto de primos distintos; (b) Todo inteiro é produto de um inteiro livre de quadrados por um quadrado perfeito. 24. Mostre que dado um inteiro n e um primo p, n pode ser escrito na forma n = p k m, onde k 0 e p m. 25. Decidir se 1009 é um número primo ou não. 26. Seja n > 0 tal que nenhum primo p 3 n divide n. Prove que n é um primo ou um produto de dois primos. 27. Demonstrar que existem infinitos primos da forma 4n Demonstrar que existem infinitos primos da forma 3n Prove que se 2 m + 1 é primo para algum m > 0, então m é uma potência de Seja p 1 = 2, p 2 = 3, p 3 = 5, p 4, p 5,... a seqüência dos números primos positivos em sua ordem natural. Mostre que: (a) p n+1 p 1 p 1 p n + 1; (b) p n 2 2n 1 para todo n 1; (c) Existem pelo menos n + 1 primos menores que 2 2n. 31. Consideremos a seqüência de inteiros positivos: n 1 = 2, n 2 = n 1 + 1, n 3 = n 1 n 2 + 1,..., n k = n 1 n 2 n k 1 + 1,... (a) Prove que, se i < k, então mdc (n i, n k ) = 1; (b) Concluir que o conjunto dos números primos é infinito. 32. Seja {p 1,..., p n } um conjunto de primos positivos. Sejam A o produto de r quaisquer destes primos e B = p 1 p n A. (a) Prove que p k divide A ou B, mas não ambos; 4
5 (b) Prove que A + B tem um divisor primo p {p 1,..., p n } ; (c) Concluir que o conjunto dos primos é infinito. 33. Sejam a e b inteiros positivos relativamente primos (primos entre si). Prove que S(ab) = S(a)S(b), onde S(a) é a soma dos divisores positivos de A; 34. Seja n > 0 par e perfeito. Mostre que: (a) n = 2 k 1 m, onde k 2, mdc (2, m) = 1 e 2 k 1 m. (b) S(m) = m + m, onde m = (c) Concluir que m é primo. m 2 k Resolver as seguintes equações diofantinas: (a) 2X + 3Y = 9; (b) 8X 7Y = 3; (c) 47X + 29Y = Seja k > 0 primo. Prove que a equação X 4 + 4Y 4 = k tem solução inteira se e somente se k = 5. Neste caso, determine o conjunto solução. 37. Determinar todos os múltiplos positivos de 11 e de 49 cuja soma seja Determinar todos os naturais menores que 1000 que têm restos: 9 na divisão por 37 e 15 na divisão por Escrever o número 100 como soma de dois inteiros positivos de modo que o primeiro seja divisível por 7 e o segundo por Certo senhor, ao descontar um cheque em seu banco, recebeu, sem notar, o número de reais trocados pelo número de centavos e vice-versa. Em seguida, gastou R$1,50 e observou, surpreso, que tinha o dobro da quantia original do cheque. Determinar o menor valor possível com o qual o cheque foi preenchido. 41. Sejam a, b > 0 primos entre si. Provar que a equação diofantina ax by = c tem infinitas soluções nos inteiros positivos. 5
6 42. (a) Provar que a equação diofantina ax + by + cz = d tem solução não vazia se e somente se mdc(a, b, c) d; (b) Determinar todas as soluções inteiras de 15X + 12Y + 30Z = Um pescador tenta pescar um cardume de peixes jogando diversas redes na água. Se cair exatamente um peixe em cada rede, salvam-se ainda n peixes. Se cairem n peixes em cada rede, sobram n redes vazias. Quantas são as redes? Quantos são os peixes? 44. (a) A que número entre 0 e 6 é congruente módulo 7 o produto ? (b) A que número entre 0 e 3 é congruente módulo 4 a soma ? 45. Sejam a, b, r inteiros e s um inteiro não nulo. Prove que a b (mod r) se e somente se as bs (mod rs). 46. Seja a Z. Prove que: (a) a 2 é congruente a 0, 1 ou 4 módulo 8; (b) Se a é simultaneamente um quadrado e um cubo, então a 2 é congruente a 0, 1, 9 ou 28 módulo 36.; (c) Se 2 a e 3 a, então a 2 1 (mod 24). 47. Determinar todos os inteiros positivos m tais que toda solução da congruência X 2 0 (mod m) também é solução da congruência X 0 (mod m). 48. Sejam m 1, m 2 primos entre si e seja a Z. Prove que a 0 (mod m 1 m 2 ) se e somente se a 0 (mod m 1 ) e a 0 (mod m 2 ). Mostrar por meio de um exemplo que a hipótese mdc (m 1, m 2 ) = 1 é essencial. 49. Prove que n 7 n (mod 42), par todo inteiro n. 50. Determinar os restos das divisões: (a) de 2 50 por 7; (b) de por 7; (c) de por 4. 6
7 51. Usar congruências para verificar que: (a) 84 (2 44 1); (b) 97 (2 48 1); (c) 23 (2 11 1). 52. Se a é ímpar, prove que a 2n 1 (mod 2 n+2 ), para todo n Resolva as seguintes congruências lineares: (a) 25X 15 (mod 29); (b) 5X 2 (mod 26); (c) 140X 133 (mod 301). 54. Resolva a congruência linear 17X 3 (mod ). 55. Resolva os seguintes sistemas de congruências lineares: (a) X 1 (mod 3), X 2 (mod 5), X 3 (mod 7); (b) X 5 (mod 6), X 4 (mod 11), X 3 (mod 17). 56. (a) Determinar três inteiros consecutivos tais que um deles seja divisível por um quadrado perfeito; (b) Determinar três inteiros consecutivos tais que o primeiro seja divisível por um cubo e o terceiro por uma quarta potência; (c) Provar que as congruências X a (mod m) e X b (mod n) têm solução comum se e somente se mdc (m, n) (a b). Provar também que a solução é única módulo mmc (m, n). 57. Se de uma cesta com ovos retiram-se duas unidades por vez, sobra um ovo. O mesmo acontece se os ovos são retirados 3 a 3, 4 a 4, 5 a 5 ou 6 a 6, mas não resta nenhum ovo quando se retiram 7 por vez. Encontrar o menor número possível de ovos que tem na cesta. 58. Seja a Z. Prove que: (a) a 21 a (mod 15), a 7 a (mod 42); (b) Se mdc (a, 35) = 1, então a 12 1 (mod 35), (c) Se mdc (a, 42) = 1, então (a 6 1). 7
8 59. (a) Sejam a, b Z e p um primo, tais que mdc (a, p) = 1. Verificar que uma solução da congruência ax b (mod p) é dada por X a p 2 b (mod p); (b) Resolver as congruências: 2X 1 (mod 31), 6X 5 (mod 11) e 3X 17 (mod 29). 60. Sejam p um primo e a, b Z. Prove que, se a p b p (mod p), então a b (mod p). 61. Seja p um primo. Prove que 1 p + 2 p + + (p 1) p 0 (mod p). 62. (a) Mostrar que (mod 17), (mod 17) Consequentemente, dados um inteiro a e um primo p que não divide a, p 1 não é, em geral, o menor inteiro positivo tal que a p 1 1 (mod p). Compare com o Teorema de Fermat. (b) Sejam p um primo e a Z tal que p a. Prove que: i. Se p > 2, a p (mod p) ou a p (mod p); ii. O menor inteiro positivo k tal que a k 1 (mod p) é divisor de p 1; iii. Se k é o menor inteiro positivo como acima, então todo inteiro m tal que a m 1 (mod p) é múltiplo de k. 63. Sejam p, q primos distintos e ímpares tais que p 1 q 1. Se mdc (a, pq) = 1, prove que a q 1 1 (mod pq). 64. Seja a Z. Prove que: (a) a 37 a (mod 1729); (b) a 13 a (mod 2730); (c) Se a é ímpar, a 33 a (mod 4080); 65. Sejam a, n Z tais que mdc (a, n) = mdc (a 1, n) = 1. Prove que 1 + a + + a φ(n) 1 0 (mod n). 66. Sejam a, n Z primos entre si. Prove que m φ(n) + n φ(m) 1 (mod mn). 67. Seja p primo tal que p 2 e p 5. Mostre que p divide infinitos inteiros da seqüência 1, 11, 111, 1111, Determinar r Z tal que a = bq + r, com 0 r < b quando: 8
9 (a) a = 15! e b = 17, (b) a = 2.26! e b = Mostrar que 18! 1 (mod 437). 70. Seja p um primo. Prove que: (a) (p 1)! p 1 (mod (p 1)); (b) Para todo a Z, p (a p + (p 1)! a) e p (a p (p 1)! + a); (c) Se p 2, então (p 2) 2 ( 1) p+1 2 (mod p). 9
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
MA14 - Aritmética Lista 1. Unidades 1 e 2
 MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 42
 1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
Matemática Discreta. Introdução à Teoria de Números - Exercícios 1 o ano /2011
 Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática
 UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática Segunda Lista de Exercícios de ITN: Números Inteiros Prof. Marnei Luis Mandler Segundo
UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática Segunda Lista de Exercícios de ITN: Números Inteiros Prof. Marnei Luis Mandler Segundo
MATEMÁTICA 1 MÓDULO 2. Divisibilidade. Professor Matheus Secco
 MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
Se mdc(a,m) = 1, como a é invertível módulo m, a equação. ax b (mod m)
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
ALGORITMO DE EUCLIDES
 Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
é uma proposição verdadeira. tal que: 2 n N k, Φ(n) = Φ(n + 1) é uma proposição verdadeira. com n N k, tal que:
 Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
, com k 1, p 1, p 2,..., p k números primos e α i, β i 0 inteiros, as factorizações de dois números inteiros a, b maiores do que 1.
 Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
NÚMEROS INTEIROS. Álgebra Abstrata - Verão 2012
 NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
Roteiro da segunda aula presencial - ME
 PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz. EST Setúbal / IPS Maio 2012
 MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz EST Setúbal / IPS 21 27 Maio 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) 21 27 Maio 2012 1 / 15 Congruências Lineares De nição
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz EST Setúbal / IPS 21 27 Maio 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) 21 27 Maio 2012 1 / 15 Congruências Lineares De nição
MATEMÁTICA MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA. Professor Matheus Secco
 MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
Aritmética dos Restos. Problemas com Congruências. Tópicos Adicionais
 Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
XIX Semana Olímpica de Matemática. Nível 3. Polinômios Ciclotômicos e Congruência Módulo p. Samuel Feitosa
 XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
Programa Combinatória Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 52
 1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
1. O que podemos dizer sobre a imagem da função. f : Z Z, f(x) = x 2 + x + 1?
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
CENTRO EDUCACIONAL GIRASSOL TD de Matemática Prof.: Tiago Rodrigues
 CENTRO EUCACIONAL GIRASSOL T de Matemática Prof.: Tiago Rodrigues proftiagorodrigues@gmail.com IVISIBILIAE E RESTO. Introdução O assunto divisibilidade no Conjunto dos Inteiros ( ) é extremamente importante
CENTRO EUCACIONAL GIRASSOL T de Matemática Prof.: Tiago Rodrigues proftiagorodrigues@gmail.com IVISIBILIAE E RESTO. Introdução O assunto divisibilidade no Conjunto dos Inteiros ( ) é extremamente importante
a) Falsa. Por exemplo, para n = 2, temos 3n = 3 2 = 6, ou seja, um número par.
 Matemática Unidade I Álgebra Série - Teoria dos números 01 a) Falsa. Por exemplo, para n =, temos 3n = 3 = 6, ou seja, um número par. b) Verdadeira. Por exemplo, para n = 1, temos n = 1 =, ou seja, um
Matemática Unidade I Álgebra Série - Teoria dos números 01 a) Falsa. Por exemplo, para n =, temos 3n = 3 = 6, ou seja, um número par. b) Verdadeira. Por exemplo, para n = 1, temos n = 1 =, ou seja, um
Teorema Chinês dos Restos. Tópicos Adicionais
 Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
MA14 - Aritmética Unidade 15 - Parte 1 Resumo. Congruências
 MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
matematicaconcursos.blogspot.com
 Professor: Rômulo Garcia Email: machadogarcia@gmail.com Conteúdo Programático: Teoria dos Números Exercícios e alguns conceitos imortantes Números Perfeitos Um inteiro ositivo n diz-se erfeito se e somente
Professor: Rômulo Garcia Email: machadogarcia@gmail.com Conteúdo Programático: Teoria dos Números Exercícios e alguns conceitos imortantes Números Perfeitos Um inteiro ositivo n diz-se erfeito se e somente
1 Congruência. 2. m mmc(n, m) m a b. De 1) e 2) segue que: a b mod n e a b mod m.
 1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
Aritmética dos Restos. Pequeno Teorema de Fermat. Tópicos Adicionais
 Aritmética dos Restos Pequeno Teorema de Fermat Tópicos Adicionais Aritmética dos Restos Pequeno Teorema de Fermat 1 Exercícios Introdutórios Exercício 1. Encontre os restos da divisão de 2 24 por a) 5
Aritmética dos Restos Pequeno Teorema de Fermat Tópicos Adicionais Aritmética dos Restos Pequeno Teorema de Fermat 1 Exercícios Introdutórios Exercício 1. Encontre os restos da divisão de 2 24 por a) 5
Aritmética. Somas de Quadrados
 Aritmética Somas de Quadrados Carlos Humberto Soares Júnior PROFMAT - SBM Objetivo Determinar quais números naturais são soma de dois quadrados. PROFMAT - SBM Aritmética, Somas de Quadrados slide 2/14
Aritmética Somas de Quadrados Carlos Humberto Soares Júnior PROFMAT - SBM Objetivo Determinar quais números naturais são soma de dois quadrados. PROFMAT - SBM Aritmética, Somas de Quadrados slide 2/14
Polos Olímpicos de Treinamento. Aula 6. Curso de Teoria dos Números - Nível 2. Congruências II. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências II Na aula de hoje, aprenderemos um dos teoremas mais importantes do curso: o pequeno teorema
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências II Na aula de hoje, aprenderemos um dos teoremas mais importantes do curso: o pequeno teorema
MATEMÁTICA MÓDULO 1 TEORIA DOS NÚMEROS 1. DIVISIBILIDADE 1.1. DEFINIÇÃO 1.2. CRITÉRIOS DE DIVISIBILIDADE
 TEORIA DOS NÚMEROS 1. DIVISIBILIDADE Neste momento inicial, nosso interesse será em determinar quando a divisão entre dois números inteiros é exata, ou seja, quando o resto da divisão é 0. Antes de mais
TEORIA DOS NÚMEROS 1. DIVISIBILIDADE Neste momento inicial, nosso interesse será em determinar quando a divisão entre dois números inteiros é exata, ou seja, quando o resto da divisão é 0. Antes de mais
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
CIC 111 Análise e Projeto de Algoritmos II
 CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 21 Number theory Primes and factors Modular arithmetic Solving equations Other results
CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 21 Number theory Primes and factors Modular arithmetic Solving equations Other results
Propostas de resolução. Capítulo 1 Números racionais Avalia o que sabes
 Capítulo Números racionais 0 + 0 Avalia o que sabes Pág. 8. Analisemos cada uma das seguintes opções: Opção A: Se a é múltiplo de b, então existe um número natural n tal que a n b. Logo, a b. Exclui-se
Capítulo Números racionais 0 + 0 Avalia o que sabes Pág. 8. Analisemos cada uma das seguintes opções: Opção A: Se a é múltiplo de b, então existe um número natural n tal que a n b. Logo, a b. Exclui-se
Equações Diofantinas. Patrícia Cristina Souza dos Santos. Fabíola Ribeiro. Orientador: Igor Lima. Matemática-UFG-CAC. Introdução
 Equações Diofantinas Patrícia Cristina Souza dos Santos Fabíola Ribeiro Orientador: Igor Lima Matemática-UFG-CAC Introdução Será falado sobre a principal aplicação do Máximo divisor comum que é a resolução
Equações Diofantinas Patrícia Cristina Souza dos Santos Fabíola Ribeiro Orientador: Igor Lima Matemática-UFG-CAC Introdução Será falado sobre a principal aplicação do Máximo divisor comum que é a resolução
MATEMÁTICA. Aula 4. Professor : Dêner Rocha. Monster Concursos 1
 MATEMÁTICA Aula 4 Professor : Dêner Rocha Monster Concursos 1 Divisibilidade Critérios de divisibilidade São critérios que nos permite verificar se um precisarmos efetuar grandes divisões. número é divisível
MATEMÁTICA Aula 4 Professor : Dêner Rocha Monster Concursos 1 Divisibilidade Critérios de divisibilidade São critérios que nos permite verificar se um precisarmos efetuar grandes divisões. número é divisível
Elementos de Matemática Finita ( ) Exercícios resolvidos
 Elementos de Matemática Finita (2016-2017) Exercícios resolvidos Ficha 3-2. Em que classes de congruência mod 8 estão os quadrados perfeitos? 4926834923 poderá ser a soma de dois quadrados perfeitos? Resolução:
Elementos de Matemática Finita (2016-2017) Exercícios resolvidos Ficha 3-2. Em que classes de congruência mod 8 estão os quadrados perfeitos? 4926834923 poderá ser a soma de dois quadrados perfeitos? Resolução:
Notas sobre teoria dos números (2)
 1 / 29 Notas sobre teoria dos números (2) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 29 Maior divisor
1 / 29 Notas sobre teoria dos números (2) Fonte: livros do L. Lóvasz e Kenneth Rosen (ref. completa na página) Centro de Informática Universidade Federal de Pernambuco 2007.1 / CIn-UFPE 2 / 29 Maior divisor
Polos Olímpicos de Treinamento. Aula 7. Curso de Teoria dos Números - Nível 2. Aula de Revisão e Aprofundamento. Prof.
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 7 Aula de Revisão e Aprofundamento Observação 1. É recomendável que o professor instigue seus alunos a pensarem
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 7 Aula de Revisão e Aprofundamento Observação 1. É recomendável que o professor instigue seus alunos a pensarem
(Ciência de Computadores) 2005/ Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação
 Álgebra (Ciência de Computadores) 2005/2006 Números inteiros 1. Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação (a) {inteiros positivos impares}; (b) {inteiros negativos pares};
Álgebra (Ciência de Computadores) 2005/2006 Números inteiros 1. Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação (a) {inteiros positivos impares}; (b) {inteiros negativos pares};
Colégio Naval 2008/2009 (PROVA VERDE)
 Colégio Naval 008/009 (PROVA VERDE) 01) Um triângulo retângulo, de lados expressos por números inteiros consecutivos, está inscrito em um triângulo eqüilátero T de lado x. Se o maior cateto é paralelo
Colégio Naval 008/009 (PROVA VERDE) 01) Um triângulo retângulo, de lados expressos por números inteiros consecutivos, está inscrito em um triângulo eqüilátero T de lado x. Se o maior cateto é paralelo
Notas de Aulas. Prof a Maria Julieta Ventura Carvalho de Araujo. Prof. Frederico Sercio Feitosa (colaborador)
 Notas de Aulas Introdução à Álgebra Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) 2009 ii i Introdução à Álgebra (MAT128) Introdução à Teoria dos Números
Notas de Aulas Introdução à Álgebra Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) 2009 ii i Introdução à Álgebra (MAT128) Introdução à Teoria dos Números
XXIX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 2 (7ª. e 8ª. séries) GABARITO
 XXIX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (ª e ª séries) GABARITO GABARITO NÍVEL ) E ) E ) B ) D ) E ) E ) C ) D ) B ) D ) E ) C ) C ) A ) B ) D ) A ) C ) B ) Anulada ) B 0) E ) A 0)
XXIX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (ª e ª séries) GABARITO GABARITO NÍVEL ) E ) E ) B ) D ) E ) E ) C ) D ) B ) D ) E ) C ) C ) A ) B ) D ) A ) C ) B ) Anulada ) B 0) E ) A 0)
Notas de Aulas. Prof a Maria Julieta Ventura Carvalho de Araujo. Prof. Frederico Sercio Feitosa (colaborador)
 Notas de Aulas Introdução à Teoria dos Números Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) Prof a Beatriz Casulari da Motta Ribeiro (colaboradora) 2016
Notas de Aulas Introdução à Teoria dos Números Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) Prof a Beatriz Casulari da Motta Ribeiro (colaboradora) 2016
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito. a(x x 0) = b(y 0 y).
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016.1 Gabarito Questão 01 [ 1,00 ::: (a)=0,50; (b)=0,50 ] (a) Seja x 0, y 0 uma solução da equação diofantina ax + by = c, onde a, b são inteiros
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016.1 Gabarito Questão 01 [ 1,00 ::: (a)=0,50; (b)=0,50 ] (a) Seja x 0, y 0 uma solução da equação diofantina ax + by = c, onde a, b são inteiros
Congruências I. Por exemplo, 7 2 (mod 5), 9 3 (mod 6), 37 7 (mod 10) mas 5 3 (mod 4). Veja que a b (mod m) se, e somente se, m a b.
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências I Definição 1. Dizemos que os inteiros a e b são congrentes módulo m se eles deixam o mesmo
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências I Definição 1. Dizemos que os inteiros a e b são congrentes módulo m se eles deixam o mesmo
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
Denominamos equação polinomial ou equação algébrica de grau n a toda equação da forma:
 EQUAÇÕES POLINOMIAIS. EQUAÇÃO POLINOMIAL OU ALGÉBRICA Denominamos equação polinomial ou equação algébrica de grau n a toda equação da forma: p(x) = a n x n + a n x n +a n x n +... + a x + a 0 = 0 onde
EQUAÇÕES POLINOMIAIS. EQUAÇÃO POLINOMIAL OU ALGÉBRICA Denominamos equação polinomial ou equação algébrica de grau n a toda equação da forma: p(x) = a n x n + a n x n +a n x n +... + a x + a 0 = 0 onde
11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA
 Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO GLOBAL Múltiplos e divisores. Critérios de divisibilidade. - Escrever múltiplos
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO GLOBAL Múltiplos e divisores. Critérios de divisibilidade. - Escrever múltiplos
Soma de Quadrados. Faculdade de Matemática, UFU, MG
 Soma de Quadrados Stela Zumerle Soares 1 Antônio Carlos Nogueira (stelazs@gmailcom (anogueira@ufubr Faculdade de Matemática, UFU, MG 1 Resultados Preliminares Historicamente, um problema que tem recebido
Soma de Quadrados Stela Zumerle Soares 1 Antônio Carlos Nogueira (stelazs@gmailcom (anogueira@ufubr Faculdade de Matemática, UFU, MG 1 Resultados Preliminares Historicamente, um problema que tem recebido
Colégio Naval 2003 (prova verde)
 Colégio Naval 00 (prova verde) 01) Analise as seguintes afirmativas sobre um sistema S se duas equações do primeiro grau com duas incógnitas X e Y. I - S sempre terá ao menos uma solução, se os seus termos
Colégio Naval 00 (prova verde) 01) Analise as seguintes afirmativas sobre um sistema S se duas equações do primeiro grau com duas incógnitas X e Y. I - S sempre terá ao menos uma solução, se os seus termos
Equações Diofantinas II
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 1 Equações Diofantinas II Continuaremos nosso estudo das equações diofantinas abordando agora algumas equações
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 1 Equações Diofantinas II Continuaremos nosso estudo das equações diofantinas abordando agora algumas equações
Números Inteiros Algoritmo da Divisão e suas Aplicações
 Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016. Gabarito Questão 01 [ 1,00 ] A secretaria de educação de um município recebeu uma certa quantidade de livros para distribuir entre as escolas
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016. Gabarito Questão 01 [ 1,00 ] A secretaria de educação de um município recebeu uma certa quantidade de livros para distribuir entre as escolas
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO ANUAL Planificação 7º ano 2010/2011 Página 1 DOMÍNIO TEMÁTICO: NÚMEROS
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA 7.º ANO PLANIFICAÇÃO ANUAL Planificação 7º ano 2010/2011 Página 1 DOMÍNIO TEMÁTICO: NÚMEROS
MA14 - Aritmética Unidade 20 Resumo. Teoremas de Euler e de Wilson
 MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Matemática Discreta. Fundamentos e Conceitos da Teoria dos Números. Universidade do Estado de Mato Grosso. 4 de setembro de 2017
 Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
MA14 - Unidade 2 Divisão Euclidiana Semana de 08/08 a 14/08
 MA14 - Unidade 2 Divisão Euclidiana Semana de 08/08 a 14/08 Divisão Euclidiana Mesmo quando um número natural a não divide o número natural b, Euclides 1, nos seus Elementos, utiliza, sem enunciá-lo explicitamente,
MA14 - Unidade 2 Divisão Euclidiana Semana de 08/08 a 14/08 Divisão Euclidiana Mesmo quando um número natural a não divide o número natural b, Euclides 1, nos seus Elementos, utiliza, sem enunciá-lo explicitamente,
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ
 NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ GABARITO LISTA 6: ALGORITMO CHINÊS DO RESTO 1. Ver gabarito das questões do livro. 2. Aplique o Algoritmo de Fermat para encontrar 999367 = 911 1097. Como 911 e 1097
NÚMEROS INTEIROS E CRIPTOGRAFIA UFRJ GABARITO LISTA 6: ALGORITMO CHINÊS DO RESTO 1. Ver gabarito das questões do livro. 2. Aplique o Algoritmo de Fermat para encontrar 999367 = 911 1097. Como 911 e 1097
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2017.1 Gabarito Questão 01 [ 1,25 ] Determine as equações das duas retas tangentes à parábola de equação y = x 2 2x + 4 que passam pelo ponto (2,
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2017.1 Gabarito Questão 01 [ 1,25 ] Determine as equações das duas retas tangentes à parábola de equação y = x 2 2x + 4 que passam pelo ponto (2,
NÚMEROS DE FERMAT. (Pedro H. O. Pantoja, Universidade de Lisboa, Portugal)
 NÚMEROS DE FERMAT (Pedro H. O. Pantoja, Universidade de Lisboa, Portugal) Intrudução: O matemático francês Pierre de fermat (1601-1665) é famoso pelo seu extensivo trabalho em teoria dos números. Suas
NÚMEROS DE FERMAT (Pedro H. O. Pantoja, Universidade de Lisboa, Portugal) Intrudução: O matemático francês Pierre de fermat (1601-1665) é famoso pelo seu extensivo trabalho em teoria dos números. Suas
Números Primos, Fatores Primos, MDC e MMC
 Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo. 1) 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo. 2) 17 tem apenas os divisores 1 e 17,
Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo. 1) 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo. 2) 17 tem apenas os divisores 1 e 17,
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b Z denotamos por a b : a divide b ou
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b Z denotamos por a b : a divide b ou
ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ]
![ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ] ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ]](/thumbs/67/56480825.jpg) MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 017 Gabarito Questão 01 [ 1,5 ] Encontre as medidas dos lados e ângulos de dois triângulos ABC diferentes tais que AC = 1, BC = e A BC = 0 Considere
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 017 Gabarito Questão 01 [ 1,5 ] Encontre as medidas dos lados e ângulos de dois triângulos ABC diferentes tais que AC = 1, BC = e A BC = 0 Considere
XIX Semana Olímpica de Matemática. Nível 2. Equações Diofantinas Lineares e o Teorema Chinês dos Restos. Samuel Feitosa
 XIX Semana Olímpica de Matemática Nível Equações Diofantinas Lineares e o Teorema Chinês dos Restos Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 016
XIX Semana Olímpica de Matemática Nível Equações Diofantinas Lineares e o Teorema Chinês dos Restos Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 016
ax + by 347 = 0 k = text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: DOCENTES: Gilda Ferreira e Ana Nunes
 text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: 21082 DOCENTES: Gilda Ferreira e Ana Nunes Resolução e Critérios de Correção 1. Sejam a, b Z tais que mdc(a, b) = 12. Relativamente à equação ax + by
text UNIDADE CURRICULAR: Matemática Finita CÓDIGO: 21082 DOCENTES: Gilda Ferreira e Ana Nunes Resolução e Critérios de Correção 1. Sejam a, b Z tais que mdc(a, b) = 12. Relativamente à equação ax + by
Álgebra A - Aula 12 Sistemas de congruências
 Álgebra A - Aula 12 Sistemas de congruências Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Equações lineares ax b (mod n) Se a possui um inverso α em Z n, então: α(ax) αb
Álgebra A - Aula 12 Sistemas de congruências Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Equações lineares ax b (mod n) Se a possui um inverso α em Z n, então: α(ax) αb
PLANO DE ENSINO E APRENDIZAGEM
 SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO DE E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR DA DISCIPLINA:
SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO DE E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR DA DISCIPLINA:
1. Métodos de prova: Construção; Contradição.
 Universidade Estadual de Santa Cruz Departamento de Ciências Exatas e Tecnológicas Bacharelado em Ciência da Computação Fundamentos Matemáticos para Computação 1. Métodos de prova: Construção; Contradição.
Universidade Estadual de Santa Cruz Departamento de Ciências Exatas e Tecnológicas Bacharelado em Ciência da Computação Fundamentos Matemáticos para Computação 1. Métodos de prova: Construção; Contradição.
Portal da OBMEP. Material Teórico - Módulo de Divisibilidade. MDC e MMC - Parte 1. Sexto Ano
 Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Máximo divisor comum Nesta aula, estudaremos métodos para
Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Máximo divisor comum Nesta aula, estudaremos métodos para
obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero.
 Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
Números Primos, MDC e MMC. O próximo teorema nos diz que os primos são as peças fundamentais dos números inteiros:
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 4 Números Primos, MDC e MMC. Definição 1. Um inteiro p > 1 é chamado número primo se não possui um divisor d
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 4 Números Primos, MDC e MMC. Definição 1. Um inteiro p > 1 é chamado número primo se não possui um divisor d
Note-se que pelo Teorema de Euler. a φ(n) 1 (mod n) logo existe k nas condições da definição acima e. Raízes Primitivas. Ordem de um elemento
 Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Primeiro Desao Mestre Kame
 Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
Introdução à Teoria dos Números - Notas 4 Máximo Divisor Comum e Algoritmo de Euclides
 Introdução à Teoria dos Números - Notas 4 Máximo Divisor Comum e Algoritmo de Euclides 1 Máximo Divisor Comum Definição 1.1 Sendo a um número inteiro, D a indicará o conjunto de seus divisores positivos,
Introdução à Teoria dos Números - Notas 4 Máximo Divisor Comum e Algoritmo de Euclides 1 Máximo Divisor Comum Definição 1.1 Sendo a um número inteiro, D a indicará o conjunto de seus divisores positivos,
Ciclo 3 Encontro 1 NÚMEROS PRIMOS, FATORAÇÃO ÚNICA EM PRIMOS, MDC E MMC VIA FATORAÇÃO EM PRIMOS
 1 Ciclo 3 Encontro 1 NÚMEROS PRIMOS, FATORAÇÃO ÚNICA EM PRIMOS, MDC E MMC VIA FATORAÇÃO EM PRIMOS Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Números primos, fatoração única em primos,
1 Ciclo 3 Encontro 1 NÚMEROS PRIMOS, FATORAÇÃO ÚNICA EM PRIMOS, MDC E MMC VIA FATORAÇÃO EM PRIMOS Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Números primos, fatoração única em primos,
Este material é apenas um resumo de parte do conteúdo da disciplina.
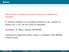 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
Aula 4 - Números Primos, MDC e MMC
 Polos Olímpicos de Treinamento Intensivo (POTI) Curso de Teoria dos Números - Nível Aula 4 - Números Primos, MDC e MMC Prof. Samuel Feitosa Arquivo Original 1 1 Documento:...gaia/educacional/matematica/teoria
Polos Olímpicos de Treinamento Intensivo (POTI) Curso de Teoria dos Números - Nível Aula 4 - Números Primos, MDC e MMC Prof. Samuel Feitosa Arquivo Original 1 1 Documento:...gaia/educacional/matematica/teoria
Álgebra A - Aula 02 Teorema da fatoração única, Propriedade fundamental dos primos, números primos
 Álgebra A - Aula 02 Teorema da fatoração única, Propriedade fundamental dos primos, números primos Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Teorema da fatoração única
Álgebra A - Aula 02 Teorema da fatoração única, Propriedade fundamental dos primos, números primos Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Teorema da fatoração única
TEOREMA FUNDAMENTAL DA ARITMÉTICA: APLICAÇÕES
 4. TEOREMA FUNDAMENTAL DA ARITMÉTICA: APLICAÇÕES 1). Achando os divisores de um número natural 2). Quantidade de divisores de um número natural 3). Decidindo se um número natural divide outro 4). Extrema
4. TEOREMA FUNDAMENTAL DA ARITMÉTICA: APLICAÇÕES 1). Achando os divisores de um número natural 2). Quantidade de divisores de um número natural 3). Decidindo se um número natural divide outro 4). Extrema
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
GABARITO E PAUTA DE CORREÇÃO DO ENQ Questão 2 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo.
![GABARITO E PAUTA DE CORREÇÃO DO ENQ Questão 2 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo. GABARITO E PAUTA DE CORREÇÃO DO ENQ Questão 2 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo.](/thumbs/70/62605338.jpg) GABARITO E PAUTA DE CORREÇÃO DO ENQ-014. Questão 1 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo. Demonstre que: (a) se p não divide a, então (p, a) = 1. (b) se p ab, então p a ou
GABARITO E PAUTA DE CORREÇÃO DO ENQ-014. Questão 1 [ 1,0 pt ::: (a)=0,5; (b)=0,5 ] Sejam a, b, p inteiros, com p primo. Demonstre que: (a) se p não divide a, então (p, a) = 1. (b) se p ab, então p a ou
Proposição 0 (Divisão Euclidiana): Dados a b, b b * existem q, r b unicamente determinados tais que 0 r < b e a = bq + r
 "!$#%& '!)( * +-,/.10 2/3"456387,:9;2 .1?/@.1, ACB DFEHG IJDLK8MHNLK8OHP Q RTSVUVWYXVZ\[^]_W Este artigo se roõe a ser uma referência sobre os temas citados no título, que aarecem naturalmente em diversos
"!$#%& '!)( * +-,/.10 2/3"456387,:9;2 .1?/@.1, ACB DFEHG IJDLK8MHNLK8OHP Q RTSVUVWYXVZ\[^]_W Este artigo se roõe a ser uma referência sobre os temas citados no título, que aarecem naturalmente em diversos
Conjuntos e Aritmética (resolução)
 Revisão 01 Conjuntos e Aritmética (resolução) 01. O conjunto A tem os seguintes elementos Assim sendo, temos 1, 2, 3, {1, 2}, {3, 4} a) {3} A verdadeira, pois 3 A b) {1, 2, 3} A verdadeira, pois 1, 2,
Revisão 01 Conjuntos e Aritmética (resolução) 01. O conjunto A tem os seguintes elementos Assim sendo, temos 1, 2, 3, {1, 2}, {3, 4} a) {3} A verdadeira, pois 3 A b) {1, 2, 3} A verdadeira, pois 1, 2,
VICE-REITORIA DE ENSINO DE GRADUAÇÃO E CORPO DISCENTE COORDENAÇÃO DE EDUCAÇÃO A DISTÂNCIA. teoria dos números. Conteudista Isidorio Rodrigues Queiros
 VICE-REITORIA DE ENSINO DE GRADUAÇÃO E CORPO DISCENTE COORDENAÇÃO DE EDUCAÇÃO A DISTÂNCIA teoria dos números Conteudista Isidorio Rodrigues Queiros Rio de Janeiro / 2008 Todos os direitos reservados à
VICE-REITORIA DE ENSINO DE GRADUAÇÃO E CORPO DISCENTE COORDENAÇÃO DE EDUCAÇÃO A DISTÂNCIA teoria dos números Conteudista Isidorio Rodrigues Queiros Rio de Janeiro / 2008 Todos os direitos reservados à
8 8 (mod 17) e 3 34 = (3 17 ) 2 9 (mod 17). Daí que 2 67 + 3 34 8 + 9 0 (mod 17), o que significa que 2 67 + 3 34 é múltiplo de 17.
 Prova Teoria de Números 23/04/203 Nome: RA: Escolha 5 questões.. Mostre que 2 67 + 3 34 é múltiplo de 7. Solução: Pelo teorema de Fermat 2 6 (mod 7 e 3 7 3 (mod 7. Portanto, 2 67 = 2 64+3 = ( 2 6 4 8 8
Prova Teoria de Números 23/04/203 Nome: RA: Escolha 5 questões.. Mostre que 2 67 + 3 34 é múltiplo de 7. Solução: Pelo teorema de Fermat 2 6 (mod 7 e 3 7 3 (mod 7. Portanto, 2 67 = 2 64+3 = ( 2 6 4 8 8
Lista 2 - Bases Matemáticas
 Lista 2 - Bases Matemáticas (Última versão: 14/6/2017-21:00) Elementos de Lógica e Linguagem Matemática Parte I 1 Atribua valores verdades as seguintes proposições: a) 5 é primo e 4 é ímpar. b) 5 é primo
Lista 2 - Bases Matemáticas (Última versão: 14/6/2017-21:00) Elementos de Lógica e Linguagem Matemática Parte I 1 Atribua valores verdades as seguintes proposições: a) 5 é primo e 4 é ímpar. b) 5 é primo
Inteiros. Inteiros. Congruência. Discrete Mathematics with Graph Theory Edgar Goodaire e Michael Parmenter, 3rd ed 2006.
 Inteiros Inteiros. Congruência. Referência: Capítulo: 4 Discrete Mathematics with Graph Theory Edgar Goodaire e Michael Parmenter, 3rd ed 2006 1 Números reais A relação binária em R é uma ordem parcial
Inteiros Inteiros. Congruência. Referência: Capítulo: 4 Discrete Mathematics with Graph Theory Edgar Goodaire e Michael Parmenter, 3rd ed 2006 1 Números reais A relação binária em R é uma ordem parcial
5 Congruências lineares. Programa. 1 Parte 1 - Conjuntos e Aplicações. 1 Conjuntos. 4 Indução matemática e divisibilidade
 Matemática Discreta 2008/09 Jorge André & Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Programa 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução matemática
Matemática Discreta 2008/09 Jorge André & Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Programa 1 Parte 1 - Conjuntos e Aplicações 1 Conjuntos 2 Relações Binárias 3 Aplicações 4 Indução matemática
Lista 2 - Álgebra I para Computação - IME -USP -2011
 Lista 2 - Álgebra I para Computação - IME -USP -2011 (A) Relações de Equivalência e Quocientes 1. Seja N = {0, 1, 2,...} o conjunto dos números naturais e considere em X = N N a seguinte relação: (a, b)
Lista 2 - Álgebra I para Computação - IME -USP -2011 (A) Relações de Equivalência e Quocientes 1. Seja N = {0, 1, 2,...} o conjunto dos números naturais e considere em X = N N a seguinte relação: (a, b)
Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c.
 Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Polos Olímpicos de Treinamento. Aula 9. Curso de Teoria dos Números - Nível 2. O Teorema de Euler. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
Equação algébrica Equação polinomial ou algébrica é toda equação na forma anxn + an 1 xn 1 + an 2 xn a 2 x 2 + a 1 x + a 0, sendo x
 EQUAÇÃO POLINOMIAL Equação algébrica Equação polinomial ou algébrica é toda equação na forma a n x n + a n 1 x n 1 + a n 2 x n 2 +... + a 2 x 2 + a 1 x + a 0, sendo x C a incógnita e a n, a n 1,..., a
EQUAÇÃO POLINOMIAL Equação algébrica Equação polinomial ou algébrica é toda equação na forma a n x n + a n 1 x n 1 + a n 2 x n 2 +... + a 2 x 2 + a 1 x + a 0, sendo x C a incógnita e a n, a n 1,..., a
QUESTÃO 16 (SARESP-SP adaptado) Uma população de bactérias cresce com o decorrer do tempo, de acordo com a função:
 Nome: N.º: endereço: data: Telefone: E-mail: Colégio PARA QUEM CURSARÁ A ạ SÉRIE DO ENSINO MÉDIO EM 0 Disciplina: MaTeMÁTiCa Prova: desafio nota: QUESTÃO 6 (SARESP-SP adaptado) Uma população de bactérias
Nome: N.º: endereço: data: Telefone: E-mail: Colégio PARA QUEM CURSARÁ A ạ SÉRIE DO ENSINO MÉDIO EM 0 Disciplina: MaTeMÁTiCa Prova: desafio nota: QUESTÃO 6 (SARESP-SP adaptado) Uma população de bactérias
Lista 1 - Bases Matemáticas
 Lista 1 - Bases Matemáticas Elementos de Lógica e Linguagem Matemática Parte I 1 Atribua valores verdades as seguintes proposições: a) 5 é primo e 4 é ímpar. b) 5 é primo ou 4 é ímpar. c) (Não é verdade
Lista 1 - Bases Matemáticas Elementos de Lógica e Linguagem Matemática Parte I 1 Atribua valores verdades as seguintes proposições: a) 5 é primo e 4 é ímpar. b) 5 é primo ou 4 é ímpar. c) (Não é verdade
Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira
 Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira 1 Introdução à Aritmética modular Definição 1 Sejam a e b inteiros positivos. Nós denotamos a mod m como o resto quando
Notas sobre teoria dos números - Aritmática Modular (2) Anjolina Grisi de Oliveira 1 Introdução à Aritmética modular Definição 1 Sejam a e b inteiros positivos. Nós denotamos a mod m como o resto quando
Recorrências - Parte I
 Polos Olímpicos de Treinamento Curso de Álgebra - Nível Prof. Marcelo Mendes Aula 4 Recorrências - Parte I Na aula anterior, vimos alguns exemplos de sequências. Em alguns deles, os termos são dados em
Polos Olímpicos de Treinamento Curso de Álgebra - Nível Prof. Marcelo Mendes Aula 4 Recorrências - Parte I Na aula anterior, vimos alguns exemplos de sequências. Em alguns deles, os termos são dados em
