Proposição 0 (Divisão Euclidiana): Dados a b, b b * existem q, r b unicamente determinados tais que 0 r < b e a = bq + r
|
|
|
- Maria da Assunção de Oliveira Cordeiro
- 6 Há anos
- Visualizações:
Transcrição
1 "!$#%& '!)( * +-,/.10 2/3"456387,:9;2 <=2>.1?/@.1, ACB DFEHG IJDLK8MHNLK8OHP Q RTSVUVWYXVZ\[^]_W Este artigo se roõe a ser uma referência sobre os temas citados no título, que aarecem naturalmente em diversos roblemas de Matemática elementar, alguns dos quais serão exlicitamente tratados aqui. O estilo é mais conciso do que a maioria dos outros artigos desta revista, o que ode tornar a leitura mais difícil, mas não desanime! Procure entender os enunciados das roosições e os roblemas resolvidos e buscar sua roria solução ara eles, além de ensar nos roblemas roostos e enviar-nos suas soluções. Em caso de qualquer dúvida não deixe de escrever-nos. Seção 1: Divisão euclidiana e o teorema fundamental da aritmética Os resultados que seguem têm como base o seguinte fato sobre os inteiros: Dados a `, b a * existem q, r b com 0 r < b e a = bq + r. Tais q e r estão unicamente determinados. De fato, q = [a/b] e r = a bq (aqui [x] denota o único inteiro k tal que k x < k + 1). Como conseqüência temos a Proosição 0 (Divisão Euclidiana): Dados a b, b b * existem q, r b unicamente determinados tais que 0 r < b e a = bq + r Definição: Dados dois inteiros a e b, com a 0 dizemos que a divide b (denotamos a b) se existe c inteiro tal que b = ac. Proosição 1: Dados a, b b não ambos nulos existe d a * tal que d a, d b e, ara todo c a *, c a, c b c d. Além disso existem x, y b com d = ax + by. (Esse d é chamado o máximo divisor comum entre a e b : d = mdc (a, b). )
2 Demonstração: Seja A = {k > 0 x, y c tais que k = ax + by} e seja d = ax 0 + by 0 o menor elemento de A. Mostraremos que d a. Como d d *, existem q, r e com a = dq + r e 0 r < d. Queremos mostrar que r = 0. De fato, se r > 0, r = a dq = a (1 qx 0 ) + b( qy 0 ) A, contradizendo o fato de d ser o menor elemento de A. Portanto, r = 0 e a = dq d a. Do mesmo modo rova-se que d b. Suonha agora que c a e c b. Então c ax 0 + by 0 = d, como queríamos rovar Lema: Se mdc (q, n) = 1 e n qk então n k. Prova do Lema: Como mdc(q, n) = 1, existem x, y e com qx + ny = 1, logo qkx + nky = k, ortanto n k (ois qkx e n nky) Corolário: Sejam um número rimo e a, b e. Se ab então a ou b Teorema fundamental da aritmética: Todo número natural n 2 ossui uma única fatoração (a menos da ordem dos fatores), como roduto de rimos. Demonstração: n = 2 é rimo. Vamos mostrar a existencia da fatoração or rimos or indução: Se n é rimo não há o que rovar. Se n é comosto, n = ab, a, b f, a < n, b < n e, or hiótese de indução, a e b se decomõem como roduto de rimos, ortanto n se decomõe como roduto de rimos. Vamos agora mostrar a unicidade, também or indução: Suonha que n admita duas fatorações n = 1 2 r e n = q 1 q 2 q s como roduto de rimos. O Corolário acima mostra que, como 1 q 1 q 2 q r, 1 deve dividir algum q i e ortanto 1 = q i (ois são ambos números rimos) e, como n/ 1 = n/q i < n admite uma única fatoração rima, or hiótese de indução, concluímos que a fatoração de n é única Proosição 2: O conjunto dos números rimos é infinito.
3 Demonstração: Suonha que o conjunto dos números rimos seja finito, digamos { 1, 2,, n }. Nesse caso, o número N = 1 2 n +1 seria maior que todos os rimos, mas não divisível or nenhum deles, ois i ( 1 2 n + 1) i 1, absurdo. Teríamos então um natural N > 2 que não seria múltilo de nenhum rimo, contradizendo o teorema fundamental da aritmética Obs.: As idéias desta seção odem ser utilizadas em situações mais gerais, como no estudo de olinômios (or exemlo com coeficientes racionais), onde existe um algoritmo de divisão, a artir do qual ode-se rovar de modo análogo resultados corresondentes aos aqui aresentados sobre máximo divisor comum, existência e unicidade de fatoração. Seção 2: Congruências Definição: Sejam a, b, n g, n > 0. Dizemos que a é congruente a b (módulo n) (denota-se a b (módulo n)) se n (b a) Obs: a a (módulo n), a b (módulo n) b a (módulo n), a b (módulo n), b c (módulo n) a c (módulo n), ou seja, congruência (módulo n) é uma relação de equivalência. Proosição: Se a b (módulo n) e c d (módulo n) então a + c b + d (módulo n) e ac bd (módulo n). Demonstração: n (b a), n (d c) n (b + d) (a + c) (a + c) (b + d) (módulo n), e bd ac = b(d c) + ((b a) n (bd ac) bd ac (módulo n) Definição: Dados n, a g n > 0, definimos a = a (módulo n) = = {k g k a (módulo n)}. Dados a, b g definimos a + b = a + b e a b = ab ( estas oerações de soma e roduto estão bem definidas ela roosição anterior). Definimos ainda h /nh = { a (módulo n), a h }={ 0, 1, 2, n 1}. Cada a é chamada uma classe de congruência módulo n.
4 Definição: Sejam n, a i, n > 0. Dizemos que a é invertível módulo n se existe b i com ab 1(módulo n) (ou seja, tal que a b = 1). Dizemos que b é o inverso de a em i /ni. Definição: (i /ni )* ={ a a i e a é invertível (módulo n)}. Obs. a é invertível (módulo n) mdc (a, n) =1. De fato, mdc (a, n) = 1 x, y i tais que ax + ny = 1 a x = 1 (módulo n). Notação: Dado um conjunto finito X, escrevemos # X ara significar o número de elementos de X. Definição: A função ϕ de Euler, ϕ: j j é definida or ϕ(n) = # (i /ni )* = # {k i 0 k < n e mdc (k, n) = 1}. Notemos que se é um número rimo e k j então ϕ( k ) = k k 1 = k (1 1/). De fato, mdc (r, k ) = 1 se e só se não divide r. Logo ϕ( k ) = #{r i 0 r < k e mdc (r, k ) =1} = # {r i 0 r < k } # {r i 0 r < k e r} = k k 1. Definição: n números inteiros a 1, a 2, a n formam um sistema comleto de resíduos (s.c.r.) módulo n se { a 1, a 2,, a n }= i /ni isto é, se os a reresentam todas as classes de congruência módulo n ( or exemlo, 0,1,2, n 1 formam um s.c.r. (módulo n)). ϕ(n) números inteiros b 1, b 2, b ϕ(n) formam um sistema comleto de invertíveis (s.c.i.) módulo n se { b 1, b 2, b ϕ(n) } = (i /ni )*, isto é, se os b i reresentam todas as classes de congruências invertíveis módulo n. Proosição: Sejam q, r, n i, n > 0, q invertível módulo n, a 1, a 2,,a n um s.c.r. (módulo n) e b 1, b 2,,b ϕ(n) um s.c.i. (módulo n). Então qa 1 + r, qa 2 + r,, qa n + r formam um s.c.r. (módulo n) e qb 1, qb 2, qb ϕ(n) formam um s.c.i. (módulo n).
5 Demonstração: Vamos rovar que se a 1, a n formam um s.c.r. (módulo n) então qa 1 + r, qa n + r formam um s.c.r. (módulo n). Basta rovar que qa i + r qa j + r (módulo n) i = j, ois nesse caso teremos n classes de congruências distintas módulo n, que devem ser todas as classes de k /nk. Seja y k tal que qy 1 (módulo n). Temos qa i = qa i + r r qa j + r r = qa j (módulo n) qya i qya j (módulo n) a i a j (módulo n) i = j. Seja agora b 1, b 2, b ϕ(n) um s.c.r. (módulo n). Temos que qb i é invertível módulo n. ara todo i,1 i ϕ(n), ois se x i é tal que b i x i 1 (módulo n). então (qb i ) (x i y) = (qy) (b i x i ) 1 (módulo n). Por outro lado, se qb i qb j (módulo n) então b i yqb i yqb j b j (módulo n) i = j, e ortanto qb 1, qb 2, qb ϕ(n) é um s.c.i. (módulo n) Teorema (Euler): Sejam a, n k, n > 0, tais que mdc (a, n) = 1. Então a ϕ(n) 1 (módulo n). Demonstração: Seja b 1, b 2, b ϕ(n) um s.c.i. (módulo n) Pela roosição anterior, (ab 1 ), (ab 2 ),,(ab ϕ(n) ) formam um s.c.i. (módulo n), e temos { b 1, b 2,, b ϕ(n) } = { ab 1, ab 2, ab ϕ(n) } = (k /nk )* b 1 b 2. b ϕ(n) = ab1 ab 2. ab ϕ(n) = a ϕ(n) b 1 b 2 b ϕ(n) b 1 b 2 b ϕ(n) ( a ϕ(n) 1) = 0 a ϕ(n) = 1 ois b 1, b 2, b ϕ(n) são invertíveis (módulo n) a ϕ(n) 1 (módulo n) Corolário: (Pequeno Teorema de Fermat): Se a k e é rimo então a a (módulo ). Prova : Se a, então a a 0 (módulo ). Se não divide a, então mdc (a, ) =1 a 1 1 (módulo ) a a (módulo ) Exercício resolvido: Exiba n l tal que 2 n tenha mais de duas mil casas decimais e tenha entre suas 2000 últimas casas decimais 1000 zeros consecutivos. 5 ) Solução: 2 1 ϕ ( 2000 (módulo ), elo teorema de Euler. Portanto,
6 5 ) existe b m com 2 ϕ = b + 1, e teremos 2 ( últimos dígitos de 2 no máximo 667 dígitos, ois ϕ (5 ) ϕ (5 ) = b , e ortanto os coincidem com a reresentação decimal de , que tem 2 3 < < < ϕ (5 ). Desta forma, 2 tem elo menos = 1333 zeros consecutivos dentre as 2000 últimas casas decimais, de modo que n = satisfaz as condições do enunciado (ois ϕ( ) = ) Teorema Chinês dos restos: Se mdc (m, n) = 1 então f: n /mnn n /mn n /nn, f ( a (módulo n)) = ( a (módulo m), a (módulo n)) é uma bijeção. Demonstração: f está bem definida, ois se a = b (módulo mn) então a b (módulo m) e a b (módulo n). Como n /mnn e n /mn n /nn têm mn elementos cada, é suficiente verificar que f é injetiva. E, de fato, se a b (módulo m) e a b (módulo n) então m (b a) e n (b a) b a = = mk, n mk n k, ois mdc (m, n) = 1 mn (b a) a b (módulo mn) 2000 Corolário: Se m 1, m 2,, m r 1 são inteiros, e mdc (m i, m j ) = 1 ara i j então f: n /m 1 m 2, m r n n /m 1 n n /m 2 n n /m r n, f ( a (módulo m 1 m 2.. m r )) = ( a (módulo m 1 ),, a (módulo m r )) é uma bijeção Notemos que este Corolário mostra que, dados inteiros a 1, a 2, a r, existe um inteiro n com n = a 1 (módulo m 1 ), n a 2 (módulo m 2 ),, n a r (módulo m r ). Proosição: Temos f ((n /mnn )*) = (n /mn )* (n /nn )* ara a função f definida acima. Demonstração: Isto segue do fato de que a é rimo com mn se e só se a é rimo com m e a é rimo com n Corolário: mdc (m, n) = 1 ϕ (mn) = ϕ (m) ϕ (n) α1 α2 αk Como conseqüência, se n = 1, 2... k onde 1, 2, k são rimos distintos, α 1, α 2, α k o * então ϕ(n) = n (1 1/ 1 ) (1 1/ 2 ) (1 1/ k ). Em articular, se n 3 então ϕ(n) é ar Vamos mostrar um roblema cuja solução usa de modo não trivial o teorema chinês dos restos: Problema: Prove que dado n existe um conjunto de n elementos A q tal que ara todo B A, B, x é uma otência não trivial (isto é, um número da forma m k, onde m, k x B são inteiros maiores ou iguais a 2), ou seja, A = {x 1, x 2, x n } tal que x 1, x 2, x n, x 1 + x 2, x 1 +x 3,, x n 1 + xn,,x 1 + x 2 + x n são todos otências não triviais. Solução: A = {4} é solução ara n = 1, A = {9,16} é solução ara n = 2. Vamos rovar a existencia de um tal conjunto or indução em n. Suonha que A={x 1,, x n } é um conjunto
7 t t com n elementos e ara todo B A, B, x = m x B kb B Vamos mostrar que existe c r tal que o conjunto à ={cx 1, cx 2,, cx n, c} satisfaz o enunciado. Seja s = mmc {k B, B A, B } o mínimo múltilo comum de todos os exonentes k B. Para cada B A, B associamos um número rimo B > s, de forma que B 1 B 2, e associamos um natural r com r B 0 (módulo x ), X B, s r B (módulo B1 B 2 B ) (tal r B existe elo teorema chinês dos restos), e tomamos c = (1 + B A B kb r m B B ) Como c é uma otência u -ésima, c é uma otência k B -ésima ara todo B A, B, ortanto, ara B {cx 1, cx 2,,cx n }, B, teremos B = {cx x B} ara algum B A, B. Logo x será uma otência k B -ésima. x B' Além disso, K B 1 (1 ) K X rx + (1 ) KB rb x = c + mb = + (1 + ) mx t mb, X B' U{ c} X X A, B que é uma otência B -ésima, ois r X é múltilo de B ara X B e u r B + 1 é múltilo de B Seção 3: Ordens e raízes rimitivas. Dados n v * e a w com mcd (a, n) = 1, definimos a ordem de a módulo n, ord n a: = min {t v * a t 1(módulo n)}. Dado a (w /nw )* definidos ord a = ord n a. Proosição: {t v * a t 1(módulo n)}={k.ord n a, k v *}. ord Demonstração: Como n a a 1 (módulo n), ara todo k v tem-se k. ordna ordna k k a = ( a ) 1 = 1 (módulo n). Por outro lado, se t n, a t 1 (módulo n), existe k v com t k. ordna r r t = k ord na + r,0 r < ord na a = a a 1. a (módulo n), ortanto r = 0 ( ois 0 < r < k. ord n a Corolário: ord n a ϕ(n) a r (módulo n) a r 1 ord n a contradiria a minimalidade de ord n a ), e t = Definição: Se ord n a = ϕ(n), dizemos que a é raiz rimitiva módulo n. Exemlos: 2 é raiz rimitiva módulo 5, ois 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16, que é a rimeira otência de 2 congruente a 1 módulo 5 e 4 = ϕ(5). 1 é raiz rimitiva módulo 2, ois ord 2 1 =1 = ϕ(2). 3 é raiz rimitiva módulo 4, ois ord 4 3 = 2 = ϕ(4).
8 Proosição 3.1: a é raiz rimitiva módulo n { a t, t x } = (y /ny )*. Demonstração: Para todo a y com mdc (a, n) = 1 temos { a t, t x } (y /ny )*. Se a é raiz rimitiva módulo n então os números 1, a, a 2, a ϕ(n) 1 são distintos (módulo n) ois a i = a j (módulo n), com 0 i < j < ϕ(n) a j i 1 (módulo n) com 0 < j i < ϕ(n), absurdo {a t, t x } = (y /ny )*. Por outro lado, #{ a t, t x } ord n a (o argumento acima mostra que de fato vale a igualdade), e ortanto { a t, t x } = (y /ny )* ord n a = ϕ(n) Corolário 1: Se m divide n e a é a raiz rimitiva módulo n então a é raiz rimitiva módulo m Corolário 2: Se k 3, então não existe nenhuma raiz rimitiva módulo 2 k. Prova: Pelo corolário anterior, basta rovar que não existe raiz rimitiva módulo 8, e isso segue do fato que se a é ímar, a = 2r + 1, r y a 2 = 4r ( r + 1) (módulo 8) Proosição 3.2: Sejam um número rimo, e a y raiz rimitiva módulo. Então a ou a + é raiz rimitiva módulo 2. Demonstração: Por hiótese, ord a = ord (a+ ) = ϕ() = 1. Portanto 1 ord 2 a (ois a t 1 (módulo 2 ) a t 1(módulo )), e, como ord 2 a ϕ( 2 ) = ( 1), devemos ter ord 2 a = 1 ou ord 2 a = ( 1) = ϕ( 2 ). Do mesmo modo, ord 2 (a + ) = 1 ou ord 2 (a + ) = ( 1) = ϕ( 2 ). Basta rovar, ortanto, que Suonha que ord 2 a (a + ) 1 = a 1 + ( 1) a 2 + C ord 2 a 1 ou ord 2 ( a + ) 1. = 1. Portanto, a 1 1 (módulo 2 ), e então 2 1 a ( 1) a 2 (módulo 2 ), ortanto (a + ) 1 não é congruente a 1(módulo 2 ), ois 2 não divide ( 1) a 2, donde ord 2 (a + ) 1 Proosição 3.3: Se é um número rimo ímar e a é raiz rimitiva módulo 2 então a é raiz rimitiva módulo k ara todo k x. Demonstração: temos a 1 1 (módulo ), mas a 1 não é congruente a 1 (módulo 2 ), ortanto a 1 = 1 + b 1, onde não divide b 1. Vamos mostrar or indução que a k 1 ( 1) = 1+ bk k, onde não divide b k, ara todo k 1 k k k k + 1 b k + C bk bk (módulo k + 2 ). Logo ( 1) k 1: Temos a k = ( a k ( 1) 1 ) = (1 + b ) = = 1+ ( 1) k + 1 a k = 1+ bk, com b k +1 b k (módulo ). Segue-se que não divide b k +1. Vamos agora mostrar or indução que a é raiz rimitiva módulo k ara todo k 2. Suonha que a seja raiz rimitiva módulo k. Então temos
9 k 1 ( 1) = ϕ( k ) = ord k a ord k a ϕ( k +1 ) = k ( 1). Portanto, + 1 ord k a = k 1 ( 1) ou ord a + k = k ( 1) = ϕ( k+1 ), mas o rimeiro caso é imossível, + ois 1 a k 1 ( 1) = 1+ bk k 1,que não é congruente a 1 módulo k+1, ois não divide b k. Portanto ord k a = ϕ( k+1 ) e a é raiz rimitiva módulo k Exemlo: 2 é raiz rimitiva módulo 5 k, k z. De fato, 2 é raiz rimitiva módulo 5, e, como 2 4 = 16 1 (módulo 25), 2 é raiz rimitiva módulo 25 = 5 2 (como na roosição 3.2). Portanto, ela roosição 3.3, 2 é raiz rimitiva módulo 5 k, k z. Exercício resolvido: Mostre que existe n natural tal que os mil últimos dígitos de 2 n ertencem a {1, 2}. Solução: Observamos inicialmente que ara todo k z existe um número m k de k algarismos, todos 1 ou 2, divisível or 2 k. De fato, m 1 = 2 e m 2 = 12 satisfazem o enunciado. Seja m k = 2 k r k, r k z. Se r k é ar, tome m k+1 = 2 10 k + m k = 2 k+1 (5 k + r k /2), e se r k é ímar, tome m k+1 = 10 k + m k =2 k+1 (5 k + r k )/2. Como m (módulo 10), 5 não divide r 1000 = m 1000 / Como 2 é raiz rimitiva módulo , existe k z com 2 k r 1000 (módulo ). Logo 2 k = b r 1000, ara algum b z. Portanto, 2 k+1000 = b r 1000 = b m 1000, e as 1000 últimas casas de 2 k+1000 são as 1000 casas de m 1000, que ertencem todas a {1, 2} Observação: Se é rimo ímar, k z e a é um inteiro ímar tal que a é raiz rimitiva módulo k então a é raiz rimitiva módulo 2 k, ois ϕ( k )= ord k a ord a k ϕ(2 k ) = ϕ ( k ) ord k a = ϕ(2 k ). Isso imlica que se a é raiz rimitiva módulo k então a ou a + k é 2 raiz rimitiva módulo 2 k ( ois a e a + k são raízes rimitivas módulo k e um deles é ímar.) Proosição 3.4: Se n = ab, com a 3 e b 3 inteiros tais que mdc(a, b) = 1, então não existe raiz rimitiva módulo n. Demonstração: Temos ϕ(n) = ϕ(a) ϕ(b) e, como a 3 e b 3, ϕ(a) e ϕ(b) são ares. Se mdc (k, n) = 1 então temos k ϕ(n)/2 = (k ϕ(b)/2 ) ϕ(a) 1 (módulo a), e k ϕ(n)/2 = (k ϕ(a)/2 ) ϕ(b) 1 (módulo b). Assim, k ϕ(n)/2 = 1(módulo n), e ortanto ord n k ϕ(n)/2 < ϕ(n) Teorema: Existe alguma raiz rimitiva módulo n se, e só se, n = 2, n = 4, n = k ou n = 2 k onde é rimo ímar. Prova: Pelos resultados anteriores, basta rovar que se é rimo ímar então existe raiz rimitiva módulo, ou seja, existe a ({ /{ )* com ord a = 1. Para cada a ({ /{ )*, tem-se ord a ( 1). Seja d um divisor de 1. Definimos N(d) = # { a ({ /{ )* ord a = d}. 2
10 Temos ortanto 1 = d 1 N(d). O resultado seguirá dos dois lemas seguintes: Lema 1: N(d) ϕ(d) ara todo d divisor de 1. Prova: Se N(d) > 0 então existe a ( / )* com ord a. Se ord a = d, então a d = 1 e, ara 0 k < d, as classes de a k são todas distintas módulo, e ( a k ) d = 1. Como a equação x d 1 = 0 tem no máximo d raízes distintas em / (ois / é um coro), suas raízes são exatamente a k, 0 k < d. Por outro lado, ord a k = d mcd(k, d) = 1, ois se r > 1 é tal que r k e r d então (a k ) d/r = (a d ) k/r 1(módulo ), logo ord (a k ) d/r < d. Desta forma, { b ( / )* ord b = d} { a k, 0 k < d e mcd (k,d) = 1}, ortanto N(d) ϕ(d) Lema 2: ϕ(d) = n, ara todo n }. d n Prova do Lema 2: Considere os n números racionais 1/n, 2/n,,n/n. Ao simlificá-los, aarecem exatamente ϕ(d) deles com denominador d, ara cada divisor d de n. Portanto, d n ϕ(d) = n Fim da rova do teorema: Do Lema 2 segue que d 1 ϕ(d) = 1 e, como 1= d 1 N(d) e N(d) ϕ(d) ara todo d, devemos ter N(d) = ϕ(d) ara todo d. Em articular, N( 1) = ϕ( 1) > 0 existem raízes rimitivas módulo ~8 ƒ \ 8 % ˆ 1) Prove que existem infinitos números rimos congruentes a 3 Š> módulo 4. Œ> Determine todos os n naturais tais que (2 n 1)/n é inteiro. > Determine todos os n naturais tais que (2 n + 1)/n 2 é inteiro. Prove que se a e b são naturais e (a 2 + b 2 ) / (ab + 1) é inteiro então (a 2 + b 2 ) / (ab + 1) é quadrado erfeito. Ž xk Sejam a, n } *. Considere a sequência (x n ) definida or x 1 = a, x k+1 = a, k }. Mostre que existe N } tal que x k+1 x k (módulo n), ara todo k N. Obs.: Os roblemas 3 e 4 foram roostos na 31 a. e na 29 a. Olimíada Internacional de Matemática (1990 e 1988) resectivamente.
matematicaconcursos.blogspot.com
 Professor: Rômulo Garcia Email: machadogarcia@gmail.com Conteúdo Programático: Teoria dos Números Exercícios e alguns conceitos imortantes Números Perfeitos Um inteiro ositivo n diz-se erfeito se e somente
Professor: Rômulo Garcia Email: machadogarcia@gmail.com Conteúdo Programático: Teoria dos Números Exercícios e alguns conceitos imortantes Números Perfeitos Um inteiro ositivo n diz-se erfeito se e somente
Devemosconsiderardoiscasos: 7 k ou7 k+1. Alémdisso, lembremo-nosdoseguintefato:
 Polos Olímicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 18 Resíduos Quadráticos Definição 1. Para todos a tais que mdc(a,m) = 1, a é chamado resíduo quadrático módulo
Polos Olímicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 18 Resíduos Quadráticos Definição 1. Para todos a tais que mdc(a,m) = 1, a é chamado resíduo quadrático módulo
Ordens e raízes primitivas
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 7 Ordens e raízes primitivas 1 Polinômios Dado um anel comutativo K, definimos o anel comutativo K[x] como
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 7 Ordens e raízes primitivas 1 Polinômios Dado um anel comutativo K, definimos o anel comutativo K[x] como
XIX Semana Olímpica de Matemática. Nível 3. Polinômios Ciclotômicos e Congruência Módulo p. Samuel Feitosa
 XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
Se mdc(a,m) = 1, como a é invertível módulo m, a equação. ax b (mod m)
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
Por que você deveria ter resolvido oproblema2daobm2007
 Por que você deveria ter resolvido oroblemadaobm007 Vamos fazer um tratado geral sobre raízes rimitivas e resíduos quadráticos em geral e deois resolveremos o roblema acima. Aroveitamos ara tratar de outros
Por que você deveria ter resolvido oroblemadaobm007 Vamos fazer um tratado geral sobre raízes rimitivas e resíduos quadráticos em geral e deois resolveremos o roblema acima. Aroveitamos ara tratar de outros
Valores e vectores próprios
 Valores e Vectores Prórios - Matemática II- /5 Valores e vectores rórios De nem-se valores e vectores rórios aenas ara matrizes quadradas, elo que, ao longo deste caítulo e quando mais nada seja eseci
Valores e Vectores Prórios - Matemática II- /5 Valores e vectores rórios De nem-se valores e vectores rórios aenas ara matrizes quadradas, elo que, ao longo deste caítulo e quando mais nada seja eseci
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
, com k 1, p 1, p 2,..., p k números primos e α i, β i 0 inteiros, as factorizações de dois números inteiros a, b maiores do que 1.
 Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Roteiro da segunda aula presencial - ME
 PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
NÚMEROS INTEIROS. Álgebra Abstrata - Verão 2012
 NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
Aritmética. Lei da Reciprocidade Quadrática
 Aritmética Lei da Recirocidade Quadrática Carlos Humberto Soares Júnior PROFMAT - SBM Objetivo Determinar uma ( ) fórmula ara calcular o símbolo de Legendre a, em que é um rimo ímar. PROFMAT - SBM Aritmética,
Aritmética Lei da Recirocidade Quadrática Carlos Humberto Soares Júnior PROFMAT - SBM Objetivo Determinar uma ( ) fórmula ara calcular o símbolo de Legendre a, em que é um rimo ímar. PROFMAT - SBM Aritmética,
M odulo de Potencia c ao e D ızimas Peri odicas Nota c ao Cient ıfica e D ızimas Oitavo Ano
 Módulo de Potenciação e Dízimas Periódicas Notação Científica e Dízimas Oitavo Ano Exercícios Introdutórios Exercício. Escreva os seguintes números na notação científica: a) 4673. b) 0, 0034. c). d) 0,
Módulo de Potenciação e Dízimas Periódicas Notação Científica e Dízimas Oitavo Ano Exercícios Introdutórios Exercício. Escreva os seguintes números na notação científica: a) 4673. b) 0, 0034. c). d) 0,
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
MATEMÁTICA 1 MÓDULO 2. Divisibilidade. Professor Matheus Secco
 MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
MA14 - Aritmética Lista 1. Unidades 1 e 2
 MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n + 3.4 n+2 + 5 2.
é uma proposição verdadeira. tal que: 2 n N k, Φ(n) = Φ(n + 1) é uma proposição verdadeira. com n N k, tal que:
 Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Corpos estendidos no espaço em grupos respostas dos exercícios
 Corpos estendidos no espaço em grupos respostas dos exercícios Carlos Shine Não se assuste com o tamanho das soluções a seguir. Eu tentei colocar o máximo de informação relacionada possível nas soluções
Corpos estendidos no espaço em grupos respostas dos exercícios Carlos Shine Não se assuste com o tamanho das soluções a seguir. Eu tentei colocar o máximo de informação relacionada possível nas soluções
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b, c Z denotamos por a b : a divide b
Algoritmos. OBMEP Teoria dos números - Parte I. Algoritmo da divisão:
 OBMEP Teoria dos números - Parte I Elaine Pimentel 1 o Semestre - 2006 Algoritmos Algoritmo = processo de cálculo baseado em regras formais Especificação de um algoritmo: entrada + instruções + saída Perguntas:
OBMEP Teoria dos números - Parte I Elaine Pimentel 1 o Semestre - 2006 Algoritmos Algoritmo = processo de cálculo baseado em regras formais Especificação de um algoritmo: entrada + instruções + saída Perguntas:
11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA
 Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Somas de números naturais consecutivos
 Julho 006 - nº 5 Somas de números naturais consecutivos António Pereira Rosa Escola Secundária Maria Amália Vaz de Carvalho, Lisboa. Introdução O objectivo deste trabalho é abordar o roblema da reresentação
Julho 006 - nº 5 Somas de números naturais consecutivos António Pereira Rosa Escola Secundária Maria Amália Vaz de Carvalho, Lisboa. Introdução O objectivo deste trabalho é abordar o roblema da reresentação
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz. EST Setúbal / IPS Maio 2012
 MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz EST Setúbal / IPS 21 27 Maio 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) 21 27 Maio 2012 1 / 15 Congruências Lineares De nição
MATEMÁTICA DISCRETA ARITMÉTICA RACIONAL (6/6) Carlos Luz EST Setúbal / IPS 21 27 Maio 2012 Carlos Luz (EST Setúbal / IPS) Aritmética Racional (6/6) 21 27 Maio 2012 1 / 15 Congruências Lineares De nição
MATEMÁTICA 3 MÓDULO 1. Lógica. Professor Renato Madeira
 MATEMÁTICA 3 Professor Renato Madeira MÓDULO 1 Lógica SUMÁRIO 1. Proosição. Negação 3. Conectivos 4. Condicionais 4.1. Relação de imlicação 4.. Relação de equivalência 5. Álgebra das roosições 6. Quantificadores
MATEMÁTICA 3 Professor Renato Madeira MÓDULO 1 Lógica SUMÁRIO 1. Proosição. Negação 3. Conectivos 4. Condicionais 4.1. Relação de imlicação 4.. Relação de equivalência 5. Álgebra das roosições 6. Quantificadores
LIMITAÇÃO DE QUALQUER FATOR PRIMO DE UM NÚMERO PERFEITO ÍMPAR
 2013: Trabalho de Conclusão de Curso do Mestrado Profissional em Matemática - PROFMAT Universidade Federal de São João del-rei - UFSJ Sociedade Brasileira de Matemática - SBM LIMITAÇÃO DE QUALQUER FATOR
2013: Trabalho de Conclusão de Curso do Mestrado Profissional em Matemática - PROFMAT Universidade Federal de São João del-rei - UFSJ Sociedade Brasileira de Matemática - SBM LIMITAÇÃO DE QUALQUER FATOR
Primos, LTE e Outras Histórias
 Primos, LTE e Outras Histórias Semana Olímpica 09 Rafael Filipe - rafaelfilipedoss@gmailcom O objetivo desse material é apresentar algumas ideias recentes que tem aparecido nos problemas de Teoria dos
Primos, LTE e Outras Histórias Semana Olímpica 09 Rafael Filipe - rafaelfilipedoss@gmailcom O objetivo desse material é apresentar algumas ideias recentes que tem aparecido nos problemas de Teoria dos
MDC, MMC, Algoritmo de Euclides e o Teorema de Bachet-Bézout
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 3 MDC, MMC, Algoritmo de Euclides e o Teorema de Bachet-Bézout 1 mdc, mmc e Algoritmo de Euclides Dados
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 3 MDC, MMC, Algoritmo de Euclides e o Teorema de Bachet-Bézout 1 mdc, mmc e Algoritmo de Euclides Dados
Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 42
 1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
Por outras palavras, iremos desenvolver a operação inversa da derivação conhecida por primitivação.
 RIMITIVS Definições No caítulo anterior, centramos a nossa atenção no seguinte roblema: dada uma função, determinar a sua função derivada Neste caítulo, vamos considerar o roblema inverso, ou seja, determinar
RIMITIVS Definições No caítulo anterior, centramos a nossa atenção no seguinte roblema: dada uma função, determinar a sua função derivada Neste caítulo, vamos considerar o roblema inverso, ou seja, determinar
1 Congruência. 2. m mmc(n, m) m a b. De 1) e 2) segue que: a b mod n e a b mod m.
 1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
1 Congruência Exercício 1.1. Proposição 23. (7) a b mod n e a b mod m a b mod mmc(n, m) De fato, ( ) Se a b mod n n a b, se a b mod n m a b. nm a b, como mmc(n, m) nm então mmc(n, m) a b a b mod mmc(n,
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero.
 Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
Neste pequeno artigo resolveremos o problema 2 da USAMO (USA Mathematical Olympiad) 2005: (x 3 + 1)(x 3 + y) = 147 157 (x 3 + y)(1 + y) = 157 147 z 9
 Ésófatorar... Serámesmo? Neste equeno artigo resolveremos o roblema 2 da USAMO (USA Mathematical Olymiad) 2005: Problema. Prove que o sistema x 6 + x + x y + y = 147 157 x + x y + y 2 + y + z 9 = 157 147
Ésófatorar... Serámesmo? Neste equeno artigo resolveremos o roblema 2 da USAMO (USA Mathematical Olymiad) 2005: Problema. Prove que o sistema x 6 + x + x y + y = 147 157 x + x y + y 2 + y + z 9 = 157 147
MAT Álgebra I para Licenciatura 2 a Lista de exercícios
 MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
1. O que podemos dizer sobre a imagem da função. f : Z Z, f(x) = x 2 + x + 1?
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Elementos de Matemática Finita Exercícios Resolvidos 1 - Algoritmo de Euclides; Indução Matemática; Teorema Fundamental da Aritmética 1. Considere os inteiros a 406 e b 654. (a) Encontre d mdc(a,b), o
Polos Olímpicos de Treinamento. Aula 6. Curso de Teoria dos Números - Nível 2. Congruências II. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências II Na aula de hoje, aprenderemos um dos teoremas mais importantes do curso: o pequeno teorema
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências II Na aula de hoje, aprenderemos um dos teoremas mais importantes do curso: o pequeno teorema
Semana Olímpica 2019
 Semana Olímpica 2019 Prof a Ana Paula Chaves apchaves.math@gmail.com Nível 1 Congruência 1. Divisibilidade e Aritmética Modular Um dos tópicos mais fundamentais da teoria dos números é, sem dúvidas, a
Semana Olímpica 2019 Prof a Ana Paula Chaves apchaves.math@gmail.com Nível 1 Congruência 1. Divisibilidade e Aritmética Modular Um dos tópicos mais fundamentais da teoria dos números é, sem dúvidas, a
Sequências recorrentes e testes de primalidade
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 18 Sequências recorrentes e testes de primalidade 1 A Sequência de Fibonacci A sequência de Fibonacci é
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 18 Sequências recorrentes e testes de primalidade 1 A Sequência de Fibonacci A sequência de Fibonacci é
Matemática Discreta. Introdução à Teoria de Números - Exercícios 1 o ano /2011
 Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
1 Lógica e teoria dos conjuntos
 Lógica e teoria dos conjuntos.. Introdução à lógica bivalente Pág. 0 Atividade de diagnóstico.. N..,5 Z.. 5.. Q.5. π R π.6. Q + +.7. Z.8. 0 Z 0.......... x = 5 x+ = 5 x = 5 x = S = { } x + = 0 ( x ) 9
Lógica e teoria dos conjuntos.. Introdução à lógica bivalente Pág. 0 Atividade de diagnóstico.. N..,5 Z.. 5.. Q.5. π R π.6. Q + +.7. Z.8. 0 Z 0.......... x = 5 x+ = 5 x = 5 x = S = { } x + = 0 ( x ) 9
Aula 10. variáveis; a resultante fatoração única em Z[x]
![Aula 10. variáveis; a resultante fatoração única em Z[x] Aula 10. variáveis; a resultante fatoração única em Z[x]](/thumbs/80/81530074.jpg) Aula 10 fatoração única em várias variáveis; a resultante (Anterior: Gauss. ) 10.1 fatoração única em Z[x] 1. Prop. Seja f Z[x], deg f > 0. Então existem m Z e polinômios irredutíveis p 1,..., p t Z[x]
Aula 10 fatoração única em várias variáveis; a resultante (Anterior: Gauss. ) 10.1 fatoração única em Z[x] 1. Prop. Seja f Z[x], deg f > 0. Então existem m Z e polinômios irredutíveis p 1,..., p t Z[x]
a = bq + r e 0 r < b.
 1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b Z denotamos por a b : a divide b ou
1 Aritmética dos Inteiros 1.1 Lema da Divisão e o Algoritmo de Euclides Recorde-se que a, o módulo ou valor absoluto de a, designa a se a N a = a se a / N Dados a, b Z denotamos por a b : a divide b ou
Números inteiros. Sandro Marcos Guzzo
 Números inteiros Sandro Marcos Guzzo Cascavel - Pr Agosto de 2013 1 Construção do conjunto dos números inteiros O conjunto dos números inteiros, designado por Z será aqui construído a partir do conjunto
Números inteiros Sandro Marcos Guzzo Cascavel - Pr Agosto de 2013 1 Construção do conjunto dos números inteiros O conjunto dos números inteiros, designado por Z será aqui construído a partir do conjunto
Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c.
 Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Álgebra A - Aula 02 Teorema da fatoração única, Propriedade fundamental dos primos, números primos
 Álgebra A - Aula 02 Teorema da fatoração única, Propriedade fundamental dos primos, números primos Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Teorema da fatoração única
Álgebra A - Aula 02 Teorema da fatoração única, Propriedade fundamental dos primos, números primos Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Teorema da fatoração única
MATEMÁTICA MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA. Professor Matheus Secco
 MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
Matemática Discreta. Fundamentos e Conceitos da Teoria dos Números. Universidade do Estado de Mato Grosso. 4 de setembro de 2017
 Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Primeiro Desao Mestre Kame
 Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
Note-se que pelo Teorema de Euler. a φ(n) 1 (mod n) logo existe k nas condições da definição acima e. Raízes Primitivas. Ordem de um elemento
 Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Polinômios Ciclotômicos e o Teorema dos Primos de Dirichlet
 Polinômios Ciclotômicos e o Teorema dos Primos de Dirichlet Antonio Caminha 15 de fevereiro de 2003 Resumo Neste artigo definimos e provamos as principais propriedades dos polinômios ciclotômicos, objetivando
Polinômios Ciclotômicos e o Teorema dos Primos de Dirichlet Antonio Caminha 15 de fevereiro de 2003 Resumo Neste artigo definimos e provamos as principais propriedades dos polinômios ciclotômicos, objetivando
Apostila TEORIA DOS NÚMEROS
 1 Apostila TEORIA DOS NÚMEROS Notas de Aula 1ª Parte Prof. Caetano Rodrigues MORAÚJO - CE Sumário ITEM ASSUNTO PAG 1 PRINCIPIO DA BOA ORDENANÇA 3 DIVISIBILIDADE 4 3 ALGORITIMO DA DIVISÃO 4 4 MÁXIMO DIVISOR
1 Apostila TEORIA DOS NÚMEROS Notas de Aula 1ª Parte Prof. Caetano Rodrigues MORAÚJO - CE Sumário ITEM ASSUNTO PAG 1 PRINCIPIO DA BOA ORDENANÇA 3 DIVISIBILIDADE 4 3 ALGORITIMO DA DIVISÃO 4 4 MÁXIMO DIVISOR
II Colóquio de Matemática do Centro Oeste 07-11/11/2011. Introdução à Teoria dos Números e Criptografia
 II Colóquio de Matemática do Centro Oeste 07-11/11/2011 Introdução à Teoria dos Números e Criptografia José Gilvan de Oliveira, Elisabete Sousa Freitas Sumário 1 Introdução 1 2 Números Inteiros 2 1 Propriedades.........................................
II Colóquio de Matemática do Centro Oeste 07-11/11/2011 Introdução à Teoria dos Números e Criptografia José Gilvan de Oliveira, Elisabete Sousa Freitas Sumário 1 Introdução 1 2 Números Inteiros 2 1 Propriedades.........................................
MATEMÁTICA COMENTÁRIO DA PROVA
 COMENTÁRIO DA PROVA Os objetivos desta rova discursiva foram lenamente alcançados. Os conteúdos rinciais foram contemlados, inclusive comlementando os tóicos abordados na ª. fase, mostrando uma conveniente
COMENTÁRIO DA PROVA Os objetivos desta rova discursiva foram lenamente alcançados. Os conteúdos rinciais foram contemlados, inclusive comlementando os tóicos abordados na ª. fase, mostrando uma conveniente
ALGORITMO DE EUCLIDES
 Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n).
![1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n). 1 Congruências de Grau Superior. Dado um polinômio f(x) Z[x] e um número natural n, vamos estudar condições para que a congruência. f(x) 0 (mod n).](/thumbs/98/136620653.jpg) Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 10 Congruências de Grau Superior 1 Congruências de Grau Superior Dado um polinômio f(x Z[x] e um número
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 10 Congruências de Grau Superior 1 Congruências de Grau Superior Dado um polinômio f(x Z[x] e um número
Congruências de grau 2 e reciprocidade quadrática. Seja p > 2 um número primo e a,b,c Z com a não divisívelpor p. Resolver
 Polos Olímicos de Treinmento Curso de Teori dos Números - Nível 3 Crlos Gustvo Moreir Aul 9 Congruêncis de gru e recirocidde qudrátic 1 Congruêncis de Gru Sej > um número rimo e,b,c Z com não divisívelor.
Polos Olímicos de Treinmento Curso de Teori dos Números - Nível 3 Crlos Gustvo Moreir Aul 9 Congruêncis de gru e recirocidde qudrátic 1 Congruêncis de Gru Sej > um número rimo e,b,c Z com não divisívelor.
AV1 - MA 14-2011. (1,0) (a) Determine o maior número natural que divide todos os produtos de três números naturais consecutivos.
 Questão 1 (1,0) (a) Determine o maior número natural que divide todos os rodutos de três números naturais consecutivos (1,0) (b) Resonda à mesma questão no caso do roduto de quatro números naturais consecutivos
Questão 1 (1,0) (a) Determine o maior número natural que divide todos os rodutos de três números naturais consecutivos (1,0) (b) Resonda à mesma questão no caso do roduto de quatro números naturais consecutivos
Teorema Chinês dos Restos. Tópicos Adicionais
 Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Números Inteiros Algoritmo da Divisão e suas Aplicações
 Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
Números Inteiros Algoritmo da Divisão e suas Aplicações Diferentemente dos números reais (R), o conjunto dos inteiros (Z) não é fechado para a divisão. Esse não-fechamento faz com que a divisão entre inteiros
Programa Combinatória Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 52
 1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
Análise I Solução da 1ª Lista de Exercícios
 FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Matemática Análise I 0- Solução da ª Lista de Eercícios. ATENÇÃO: O enunciado
FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Matemática Análise I 0- Solução da ª Lista de Eercícios. ATENÇÃO: O enunciado
Teorema 1.1 (Teorema de divisão de Euclides). Dados n Z e d N, existe uma única dupla q Z, r. n = qd + r
 Matemática Discreta September 18, 2018 1 1 Divisão de inteiros Teorema 1.1 (Teorema de divisão de Euclides). Dados n Z e d N, existe uma única dupla q Z, r {0,..., d 1} tal que n = qd + r Dizemos que a
Matemática Discreta September 18, 2018 1 1 Divisão de inteiros Teorema 1.1 (Teorema de divisão de Euclides). Dados n Z e d N, existe uma única dupla q Z, r {0,..., d 1} tal que n = qd + r Dizemos que a
02 Um paralelogramo está inscrito em uma circunferência e um de seus ângulos internos mede em graus 7 x 20º. O valor de x é : "1 "1 7 (C)
 01 Um quadrilátero é circunscritível a um círculo e tem os lados roorcionais aos números 6, 18, e 6 e a soma das medidas de dois lados oostos dá 1. Podemos dizer que o roduto dos dois lados maiores dá
01 Um quadrilátero é circunscritível a um círculo e tem os lados roorcionais aos números 6, 18, e 6 e a soma das medidas de dois lados oostos dá 1. Podemos dizer que o roduto dos dois lados maiores dá
II Bienal da Sociedade Brasileira de Matemática. Frações Contínuas: algumas propriedades e aplicações
 II Bienal da Sociedade Brasileira de Matemática Universidade Federal da Bahia, Salvador - BA 25 a 29 de outubro de 2004 Frações Contínuas: algumas propriedades e aplicações Eliana Xavier Linhares de Andrade
II Bienal da Sociedade Brasileira de Matemática Universidade Federal da Bahia, Salvador - BA 25 a 29 de outubro de 2004 Frações Contínuas: algumas propriedades e aplicações Eliana Xavier Linhares de Andrade
Corpos estendidos no espaço em grupos
 Corpos estendidos no espaço em grupos Carlos Shine Vamos ver como conceitos de teoria dos números (especialmente números mod p) podem ser generalizados com conceitos de Álgebra. 1 Corpos Em termos simples,
Corpos estendidos no espaço em grupos Carlos Shine Vamos ver como conceitos de teoria dos números (especialmente números mod p) podem ser generalizados com conceitos de Álgebra. 1 Corpos Em termos simples,
12 E 13 DE DEZEMBRO DE 2015
 PROBLEMAS DO 1 o TORNEIO CARIOCA DE MATEMÁTICA 12 E 13 DE DEZEMBRO DE 2015 Conteúdo Notações 1 1 O suer-mdc 1 2 Os Reis do etróleo 2 3 Quadraturas de Triângulos 3 4 Um roblema bimodular 4 5 Sistemas de
PROBLEMAS DO 1 o TORNEIO CARIOCA DE MATEMÁTICA 12 E 13 DE DEZEMBRO DE 2015 Conteúdo Notações 1 1 O suer-mdc 1 2 Os Reis do etróleo 2 3 Quadraturas de Triângulos 3 4 Um roblema bimodular 4 5 Sistemas de
Aritmética dos Restos. Problemas com Congruências. Tópicos Adicionais
 Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
Apontamentos de Álgebra Linear
 Aontamentos de Álgebra Linear (inclui as alicações não avaliadas) Nuno Martins Deartamento de Matemática Instituto Suerior Técnico Dezembro de 08 Índice Matrizes: oerações e suas roriedades Resolução de
Aontamentos de Álgebra Linear (inclui as alicações não avaliadas) Nuno Martins Deartamento de Matemática Instituto Suerior Técnico Dezembro de 08 Índice Matrizes: oerações e suas roriedades Resolução de
Notas de Aulas. Prof a Maria Julieta Ventura Carvalho de Araujo. Prof. Frederico Sercio Feitosa (colaborador)
 Notas de Aulas Introdução à Teoria dos Números Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) Prof a Beatriz Casulari da Motta Ribeiro (colaboradora) 2016
Notas de Aulas Introdução à Teoria dos Números Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) Prof a Beatriz Casulari da Motta Ribeiro (colaboradora) 2016
Teoria Combinatória dos Números
 Teoria Combinatória dos Números Samuel Feitosa, Yuri Lima, Davi Nogueira 27 de fevereiro de 2004 O objetivo deste artigo é mostrar algumas propriedades dos números inteiros, que combinadas podem originar
Teoria Combinatória dos Números Samuel Feitosa, Yuri Lima, Davi Nogueira 27 de fevereiro de 2004 O objetivo deste artigo é mostrar algumas propriedades dos números inteiros, que combinadas podem originar
IST-2010/11-1 o Semestre-MArq Matemática I 1 o TESTE (VERSÃO A) 6 de Novembro de 2010
 IST-00/- o Semestre-MArq Matemática I o TESTE (VERSÃO A) 6 de Novembro de 00 Nome: Número: Sala: O teste que vai realizar tem a duração de hora e 0 minutos e consiste de 5 roblemas. Os roblemas,, e 4 deverão
IST-00/- o Semestre-MArq Matemática I o TESTE (VERSÃO A) 6 de Novembro de 00 Nome: Número: Sala: O teste que vai realizar tem a duração de hora e 0 minutos e consiste de 5 roblemas. Os roblemas,, e 4 deverão
Soluções dos Exercícios do Capítulo 2
 A MATEMÁTICA DO ENSINO MÉDIO Volume 1 Soluções dos Exercícios do Capítulo 2 2.1. Seja X = {n N; a + n Y }. Como a Y, segue-se que a + 1 Y, portanto 1 X. Além disso n X a + n Y (a + n) + 1 Y n + 1 X. Logo
A MATEMÁTICA DO ENSINO MÉDIO Volume 1 Soluções dos Exercícios do Capítulo 2 2.1. Seja X = {n N; a + n Y }. Como a Y, segue-se que a + 1 Y, portanto 1 X. Além disso n X a + n Y (a + n) + 1 Y n + 1 X. Logo
Notas de Aulas. Prof a Maria Julieta Ventura Carvalho de Araujo. Prof. Frederico Sercio Feitosa (colaborador)
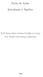 Notas de Aulas Introdução à Álgebra Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) 2009 ii i Introdução à Álgebra (MAT128) Introdução à Teoria dos Números
Notas de Aulas Introdução à Álgebra Prof a Maria Julieta Ventura Carvalho de Araujo Prof. Frederico Sercio Feitosa (colaborador) 2009 ii i Introdução à Álgebra (MAT128) Introdução à Teoria dos Números
Tópicos de Matemática Elementar
 Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Soma de Quadrados. Faculdade de Matemática, UFU, MG
 Soma de Quadrados Stela Zumerle Soares 1 Antônio Carlos Nogueira (stelazs@gmailcom (anogueira@ufubr Faculdade de Matemática, UFU, MG 1 Resultados Preliminares Historicamente, um problema que tem recebido
Soma de Quadrados Stela Zumerle Soares 1 Antônio Carlos Nogueira (stelazs@gmailcom (anogueira@ufubr Faculdade de Matemática, UFU, MG 1 Resultados Preliminares Historicamente, um problema que tem recebido
Polos Olímpicos de Treinamento. Aula 9. Curso de Teoria dos Números - Nível 2. O Teorema de Euler. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
PUC-Rio Desafio em Matemática 1 de outubro de 2017
 PUC-Rio Desafio em Matemática 1 de outubro de 017 Nome: GABARITO Assinatura: Inscrição: Identidade: Questão Valor Nota Revisão 1 1,5 1,5 3 1,5 4 1,5 5,0 6,0 Nota final 10,0 Instruções Mantenha seu celular
PUC-Rio Desafio em Matemática 1 de outubro de 017 Nome: GABARITO Assinatura: Inscrição: Identidade: Questão Valor Nota Revisão 1 1,5 1,5 3 1,5 4 1,5 5,0 6,0 Nota final 10,0 Instruções Mantenha seu celular
Divisibilidade e Números primos. George Darmiton da Cunha Cavalcanti CIn - UFPE
 Divisibilidade e Números primos George Darmiton da Cunha Cavalcanti CIn - UFPE Divisibilidade de inteiros Sejam a e b dois inteiros. Dizemos que a divide b, a é um divisor de b ou b é um múltiplo de a
Divisibilidade e Números primos George Darmiton da Cunha Cavalcanti CIn - UFPE Divisibilidade de inteiros Sejam a e b dois inteiros. Dizemos que a divide b, a é um divisor de b ou b é um múltiplo de a
Luís Diogo, Carlos Florentino e Diogo Veloso. 8 de Novembro de 2006
 E S A C N O G L A A I D L Formas Quadráticas e Fracções Contínuas Luís Diogo, Carlos Florentino e Diogo Veloso 8 de Novembro de 2006 Resumo Este artigo é baseado no curso Quadratic Forms and Continued
E S A C N O G L A A I D L Formas Quadráticas e Fracções Contínuas Luís Diogo, Carlos Florentino e Diogo Veloso 8 de Novembro de 2006 Resumo Este artigo é baseado no curso Quadratic Forms and Continued
1 Grupos (23/04) Sim(R 2 ) T T
 1 Grupos (23/04) Definição 1.1. Um grupo é um conjunto G não-vazio com uma operação binária : G G G que satisfaz as seguintes condições: 1. (associatividade) g (h k) = (g h) k para todos g, h, k G; 2.
1 Grupos (23/04) Definição 1.1. Um grupo é um conjunto G não-vazio com uma operação binária : G G G que satisfaz as seguintes condições: 1. (associatividade) g (h k) = (g h) k para todos g, h, k G; 2.
Elementos de Matemática Finita
 Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Elementos de Matemática Finita Exercícios Resolvidos - Princípio de Indução; Algoritmo de Euclides 1. Seja ( n) k n! k!(n k)! o coeficiente binomial, para n k 0. Por convenção, assumimos que, para outros
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
MA14 - Aritmética Unidade 2 Resumo. Divisão Euclidiana
 MA14 - Aritmética Unidade 2 Resumo Divisão Euclidiana Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte da disciplina e o seu estudo não garante o domínio do assunto. O material
MA14 - Aritmética Unidade 2 Resumo Divisão Euclidiana Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte da disciplina e o seu estudo não garante o domínio do assunto. O material
Polos Olímpicos de Treinamento. Aula 1. Curso de Teoria dos Números - Nível 2. Divisibilidade I. Samuel Barbosa Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Samuel Barbosa Feitosa Aula 1 Divisibilidade I Teorema 1. (Algoritmo da Divisão) Para quaisquer inteiros positivos a e b, existe um
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Samuel Barbosa Feitosa Aula 1 Divisibilidade I Teorema 1. (Algoritmo da Divisão) Para quaisquer inteiros positivos a e b, existe um
Notas sobre os anéis Z m
 Capítulo 1 Notas sobre os anéis Z m Estas notas complementam o texto principal, no que diz respeito ao estudo que aí se faz dos grupos e anéis Z m. Referem algumas propriedades mais específicas dos subanéis
Capítulo 1 Notas sobre os anéis Z m Estas notas complementam o texto principal, no que diz respeito ao estudo que aí se faz dos grupos e anéis Z m. Referem algumas propriedades mais específicas dos subanéis
m 1 Grupo A é 3, então ( P + Q R) Como o maior expoente da variável x do polinômio P + Q R Analogamente ao item a, (PQ) = 3.
 Grupo A. Seja x o grau do divisor, então p x + q x p q. Sendo r o grau do resto, então r
Grupo A. Seja x o grau do divisor, então p x + q x p q. Sendo r o grau do resto, então r
...Lista 7... Elaborado por Tiago Miranda. 1 Geometria
 .................................Lista 7................................. Elaborado or Tiago Miranda Geometria Problema G.9 Um quadrilátero tem seus vértices nos quatro lados de um quadrado de lado medindo.
.................................Lista 7................................. Elaborado or Tiago Miranda Geometria Problema G.9 Um quadrilátero tem seus vértices nos quatro lados de um quadrado de lado medindo.
Teorema. Existe alguma raiz primitiva módulo n se, e só se, n = 2, n = 4, n = p k ou n = 2p k onde p é primo ímpar.
 raízes primitivas Uma raiz primitiva módulo n é um inteiro b tal que {1, b, b 2,... ( mod n)} = U(n). Teorema. Existe alguma raiz primitiva módulo n se, e só se, n = 2, n = 4, n = p k ou n = 2p k onde
raízes primitivas Uma raiz primitiva módulo n é um inteiro b tal que {1, b, b 2,... ( mod n)} = U(n). Teorema. Existe alguma raiz primitiva módulo n se, e só se, n = 2, n = 4, n = p k ou n = 2p k onde
UNIVERSIDADE ESTADUAL VALE DO ACARAÚ. 1 a Lista de Exercícios - Comentada - Estruturas Algébricas II Professor Márcio Nascimento
 UNIVERSIDADE ESTADUAL VALE DO ACARAÚ Coordenação de Matemática 1 a Lista de Exercícios - Comentada - Estruturas Algébricas II - 214.1 Professor Márcio Nascimento 1. Sejam a G com o(a) = n 1 e m Z. Se a
UNIVERSIDADE ESTADUAL VALE DO ACARAÚ Coordenação de Matemática 1 a Lista de Exercícios - Comentada - Estruturas Algébricas II - 214.1 Professor Márcio Nascimento 1. Sejam a G com o(a) = n 1 e m Z. Se a
Resolução dos Exercícios 31/05-09/06.
 Resolução dos Exercícios 31/05-09/06. 1. Seja A um domínio de integridade. Mostre que todo subgrupo finito de U(A) é cíclico. Seja K o corpo de frações de A. Então A é um subanel de K (identificado com
Resolução dos Exercícios 31/05-09/06. 1. Seja A um domínio de integridade. Mostre que todo subgrupo finito de U(A) é cíclico. Seja K o corpo de frações de A. Então A é um subanel de K (identificado com
Introdução à Teoria de Grupos Grupos cíclicos Grupos de permutações Isomorfismos
 Observação Como para k > 1 se tem (a 1, a 2,..., a k ) = (a 1, a k )(a 1, a k 1 ) (a 1, a 2 ), um ciclo de comprimento par é uma permutação ímpar e um ciclo de comprimento ímpar é uma permutação par. Proposição
Observação Como para k > 1 se tem (a 1, a 2,..., a k ) = (a 1, a k )(a 1, a k 1 ) (a 1, a 2 ), um ciclo de comprimento par é uma permutação ímpar e um ciclo de comprimento ímpar é uma permutação par. Proposição
CIC 111 Análise e Projeto de Algoritmos II
 CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 21 Number theory Primes and factors Modular arithmetic Solving equations Other results
CIC 111 Análise e Projeto de Algoritmos II Prof. Roberto Affonso da Costa Junior Universidade Federal de Itajubá AULA 21 Number theory Primes and factors Modular arithmetic Solving equations Other results
Álgebra A - Aula 01 Algoritmo da divisão de Euclides e Algoritmo Euclideano estendido
 Álgebra A - Aula 01 Algoritmo da divisão de Euclides e Algoritmo Euclideano estendido Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Introdução Objetivo: estudar o método
Álgebra A - Aula 01 Algoritmo da divisão de Euclides e Algoritmo Euclideano estendido Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Introdução Objetivo: estudar o método
Teoria de Anéis Notas de Aula Departamento de Matemática Universidade Federal do Paraná
 Teoria de Anéis 2013 - Notas de Aula Departamento de Matemática Universidade Federal do Paraná Prof. Marcelo Muniz Silva Alves digitação: Marcelo Muniz Silva Alves Francieli Triches Milayne Guimarães 1.
Teoria de Anéis 2013 - Notas de Aula Departamento de Matemática Universidade Federal do Paraná Prof. Marcelo Muniz Silva Alves digitação: Marcelo Muniz Silva Alves Francieli Triches Milayne Guimarães 1.
Polinômios irredutíveis
 Polinômios irredutíveis Sérgio Tadao Martins 23 de janeiro de 2009 1 Introdução: polinômios em uma variável Um polinômio de grau n em uma variável x é uma expressão da forma p(x) = a 0 + a 1 x + a 2 x
Polinômios irredutíveis Sérgio Tadao Martins 23 de janeiro de 2009 1 Introdução: polinômios em uma variável Um polinômio de grau n em uma variável x é uma expressão da forma p(x) = a 0 + a 1 x + a 2 x
MA14 - Unidade 1 Divisibilidade Semana de 08/08 a 14/08
 MA14 - Unidade 1 Divisibilidade Semana de 08/08 a 14/08 Neste curso, consideraremos o conjunto dos números naturais como sendo o conjunto N = {0, 1, 2, 3,... }, denotando por N o conjunto N \ {0}. Como
MA14 - Unidade 1 Divisibilidade Semana de 08/08 a 14/08 Neste curso, consideraremos o conjunto dos números naturais como sendo o conjunto N = {0, 1, 2, 3,... }, denotando por N o conjunto N \ {0}. Como
