Segunda Lista de Exercícios de Física Matemática I Soluções (Séries de Fourier) IFUSP - 28 Março { 1 se 0 x < h f(x) = 0 se h x < 2π, Sf(x) =
|
|
|
- Judite Castelo
- 5 Há anos
- Visualizações:
Transcrição
1 Segunda Lista de Exercícios de Física Matemática I Soluções (Séries de Fourier) IFUSP - 28 Março 29 Exercício Seja f : R R uma função periódica tal que { se x < h f(x) = se h x <, onde h (, ) é uma constante. (i) A série de Fourier de f na forma complexa Sf(x) = n= tem seus coeficientes calculados no intervalo [, ]: c n = = = c n e inx () f(x)e inx dx e inx dx e inh, in para n e c = f(x)dx. (ii) Podemos então escrever a série de Fourier () de f como Sf(x) = c + ( cn e inx + c n e inx) ( e inh e inx ) e inh e inx 2in 2in e inx e inx + einh e inx e inh e inx n 2i 2i (sin nx + sin n(h x)), (2) n devido à lei do produto de exponenciais: e z e w = e z+w e às fórmulas de Euler: e ±iα = cos α ± i sin α. (iii) A série de Fourier de f em senos e cossenos no intervalo [, ) é dada por Sf(x) = a 2 + (a n cos nx + b n sin nx) (3)
2 onde para n, a = f(x) dx = dx ; a n = = f(x) cos nx dx cos nx dx e = sin nh n b n = = Substituindo os coeficientes na série (3), resulta Sf(x) + f(x) sin nx dx sin nx dx = ( cos nh). n ( n sin nx + ) (sin nh cos nx cos nh sin nx n a mesma expressão (2), devido a relação trigonométrica: sin(a b) = sin a cos b cos a sin b. Sabemos que, se g(x) denota a função periódica tal que g() = e g(x) = ( x/) /2 em (, ), então a série de Fourier de g(x) é Sg(x) = sin nx. Por conta disso, a série de n Fourier (2) de f(x) pode ser escrita como Sf(x) + Sg(x) Sg(h x). Sabemos que, pelo teste de Dirichlet juntamente com a unicidade dos coeficientes de Fourier, Sg(x) converge uniformemente para g(x) em todo intervalo [a, b] onde g(x) é contínua. Logo Sf(x) converge uniformemente para f(x) /() + g(x) g(h x) em todo intervalo [a, b] onde f(x) é contínua. Observe que, nos pontos de continuidade de f, a derivada de ambos os lados desta igualdade se anula e os limites quando x tende à e h pela direita são f(+) h + g(+) g(h ) = h = f(h + ) h + g(h + ) g( ) = + 2 h 2 =, confirmando que ambas funções coincidem em (, h) e (h, ). 2
3 Exercício 2 Seja f : R R uma função periódica tal que no intervalo simétrico x. f(x) = cos αx, α R (4) (i) Calculemos a série de Fourier (3) de f(x) em senos e cossenos. O n ésimo coeficiente desta série (par e ímpar) a n = b n = f(x) cos nx dx, (5) f(x) sin nx dx (6) está definido pois, qualquer que seja α, cos αx é integrável e absolutamente integrável em [, ]. Substituindo (4) nas integrais (5) e (6), temos para n a n = = = = cos αx cos nx dx cos αx cos nx dx (cos(α + n)x + cos(α n)x) dx (α + n) sin(α + n) + sin(α n) (α n) (α n) + sin α cos n (α + n) α sin α cos n α 2 n2 = 2( )n α sin α, (7) α 2 n2 onde usamos a paridade do integrando e as relações trigonométricas cos αx cos nx = (cos(α + n)x + cos(α n)x) /2 sin(α ± n) = sin α cos n ± cos α sin n = sin α cos n ; Devido a paridade do integrando, os coeficientes ímpares se anulam: b n = cos αx sin nx dx =. (8) 3
4 Para n =, a = cos αx dx cos αx dx = 2 sin α. (9) α Substituindo os a n s e b n s em (3), a série de Fourier de f(x) pode ser escrita como Sf(x) = α sin α + 2α sin α ( ) n cos nx. () α 2 n2 Note que, devido a f(x) ser par, os coeficientes c n da série de Fourier () de f complexa tem a mesma paridade: c n = c n (veja Proposição. do texto Complementos em marchett/fismat, Notas de Aula). Por conta disso, podemos concluir da periodicidade e paridade de f(x) que a série de Fourier Sf(x) de f(x) é uma função periódica e par e a mesma expressão () seria obtida caso empregassemos esta forma. (ii) Com base neste fato, evidente pela expansão (), vamos mostrar (por contradição) que Sf(x) é contínua nos pontos extremos ± do intervalo [, ]. Suponhamos que Sf(x) seja descontinua em x =, isto é, Sf( + ) Sf( ). Então, pela periodicidade de Sf(x), Sf( +) = Sf( +) e, pela hipótese de descontinuidade, Sf( +) Sf( ), em contradição com sua paridade: Sf( x) = Sf(x) em x =. (iii) Suponhamos que Sf(x) convirja para f(x) (veja ítem (v)), isto é, que a sequência de séries parciais (S N f(x)) N converge para f(x) qualquer que seja x R. Tomando x = na igualdade f(x) = Sf(x), temos cos α = α sin α + 2α sin α α 2 n 2 onde usamos cos 2 n = ( ) 2n =. Para α / Z, sin α e podemos dividir a igualdade por esta quantidade concluindo cot α = α 2α n 2 α 2 (iv) Fazendo α = /2 na última igualdade, temos cot /2 = cos /2 sin /2 = e n 2 (/2) 2 4 4n 2 de onde se conclui 4n 2 = 2. 4
5 (v) Pelo teste M de Weierstrass Sf(x) é uniformemente convergente em [, ] se a série majorante de () M n = α + 2 α n 2 α 2 n= cujos coeficientes satisfazem < 2 c n = a n M n, devido a sin α, for convergente. A série n2 α 2, por sua vez, é majorada da seguinte forma. Seja n α o inteiro n mais próximo de α e defina C = (α/nα ) 2. Note que < C <. Temos n= M n = α + 2 α que é finita pelo teste da convergência integral n 2 (α/n) 2 α + 2 α C n + 2 x dx = 2. 2 Por outro lado, a série de Fourier Sf(x) converge uniformemente para f(x) pela unicidade das funções f s, periódicas e contínuas, que possuem coeficientes de Fourier dados por (9), (7) e (8). n 2 5
CAPÍTULO 9. Exercícios se. 01 e. Seja f( x) Temos. 1 n n n n n n. n n. A série de Fourier da função dada é: cos. nx 4
 CAPÍTULO 9 Exercícios 9.. Ï0, x e. Seja f( x) Ìx, se x0 Ó, se 0x Temos È 0 f x dx x dx dx ( ) Í ( ) Î 0 È 0 ù an f x dx x dx dx ( ) cos Í Î ( ) cos cos ú 0 û n n n an È cos sen ù Ê cos ˆ ÎÍ n ûú Ë È 0
CAPÍTULO 9 Exercícios 9.. Ï0, x e. Seja f( x) Ìx, se x0 Ó, se 0x Temos È 0 f x dx x dx dx ( ) Í ( ) Î 0 È 0 ù an f x dx x dx dx ( ) cos Í Î ( ) cos cos ú 0 û n n n an È cos sen ù Ê cos ˆ ÎÍ n ûú Ë È 0
Departamento de Matemática da Universidade de Aveiro
 Departamento de Matemática da Universidade de Aveiro ANÁLISE MATEMÁTICA II 7/8 Folha 4 - soluções: Séries de Fourier; notação complexa. Vamos mostrar que se f e g são funções periódicas de período T, fg
Departamento de Matemática da Universidade de Aveiro ANÁLISE MATEMÁTICA II 7/8 Folha 4 - soluções: Séries de Fourier; notação complexa. Vamos mostrar que se f e g são funções periódicas de período T, fg
Suponhamos que f é uma função que pode ser representada por uma série trigonométrica da forma. ) + B nsen( 2nπx )]. (2)
![Suponhamos que f é uma função que pode ser representada por uma série trigonométrica da forma. ) + B nsen( 2nπx )]. (2) Suponhamos que f é uma função que pode ser representada por uma série trigonométrica da forma. ) + B nsen( 2nπx )]. (2)](/thumbs/67/57907746.jpg) Séries de Fourier Os fenómenos periódicos aparecem nas mais variadas situações: ondas de som, movimento da erra, batimento cardíaco,... Frequentemente uma função periódica pode ser representada por meio
Séries de Fourier Os fenómenos periódicos aparecem nas mais variadas situações: ondas de som, movimento da erra, batimento cardíaco,... Frequentemente uma função periódica pode ser representada por meio
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Séries de Fourier. Universidade Tecnológica Federal do Paraná Câmpus Francisco Beltrão. Cálculo Diferencial e Integral 4A
 Séries de Fourier Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke As séries de Fourier são a ferramente básica para se representar as funções periódicas, as quais desempenham um importante
Séries de Fourier Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke As séries de Fourier são a ferramente básica para se representar as funções periódicas, as quais desempenham um importante
35 a Aula AMIV LEAN, LEC Apontamentos
 35 a Aula 4.1.1 AMIV LEAN, LEC Apontamentos (icardo.coutinho@math.ist.utl.pt) 35.1 Série de Fourier na forma de exponenciais complexas Seja f definida em [, ], parasimplificar notação, integrável neste
35 a Aula 4.1.1 AMIV LEAN, LEC Apontamentos (icardo.coutinho@math.ist.utl.pt) 35.1 Série de Fourier na forma de exponenciais complexas Seja f definida em [, ], parasimplificar notação, integrável neste
Séries de Fourier. Matemática Aplicada. Artur M. C. Brito da Cruz. Escola Superior de Tecnologia Instituto Politécnico de Setúbal 2014/2015 1
 Séries de Fourier Matemática Aplicada Artur M. C. Brito da Cruz Escola Superior de Tecnologia Instituto Politécnico de Setúbal 14/15 1 1 versão 16 de Dezembro de 17 Conteúdo 1 Séries de Fourier...............................
Séries de Fourier Matemática Aplicada Artur M. C. Brito da Cruz Escola Superior de Tecnologia Instituto Politécnico de Setúbal 14/15 1 1 versão 16 de Dezembro de 17 Conteúdo 1 Séries de Fourier...............................
Séries de Fourier. Victor Rios Silva
 Séries de Fourier Victor Rios Silva victorrios@live.com Universidade Federal Fluminense (UFF) Instituto de Matemática (IM) Departamento de Matemática Aplicada (GMA) Rua Mário Santos Braga, S/N Valonguinho
Séries de Fourier Victor Rios Silva victorrios@live.com Universidade Federal Fluminense (UFF) Instituto de Matemática (IM) Departamento de Matemática Aplicada (GMA) Rua Mário Santos Braga, S/N Valonguinho
COMPLEMENTOS DE MATEMÁTICA MÓDULO 1. Equações Diferenciais com Derivadas Parciais
 Complementos de Matemática 1 COMPLEMENTOS DE MATEMÁTICA MÓDULO 1 Séries de Fourier Equações Diferenciais com Derivadas Parciais Complementos de Matemática 2 Jean Baptiste Joseph Fourier (1768-1830) viveu
Complementos de Matemática 1 COMPLEMENTOS DE MATEMÁTICA MÓDULO 1 Séries de Fourier Equações Diferenciais com Derivadas Parciais Complementos de Matemática 2 Jean Baptiste Joseph Fourier (1768-1830) viveu
Convergência de séries de Fourier
 Recorde-se que: Convergência de séries de Fourier Sendo f uma função definida num intervalo a,b, excepto, eventualmente, num número finito de pontos, diz-se que f é seccionalmente contínua em a, b se:
Recorde-se que: Convergência de séries de Fourier Sendo f uma função definida num intervalo a,b, excepto, eventualmente, num número finito de pontos, diz-se que f é seccionalmente contínua em a, b se:
Séries Potências II. por Abílio Lemos. Universidade Federal de Viçosa. Departamento de Matemática UFV. Aulas de MAT
 Séries Potências II por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2018 26 e 28 de setembro de 2018 Se a série de potências c n (x a) n tiver um raio de convergência
Séries Potências II por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2018 26 e 28 de setembro de 2018 Se a série de potências c n (x a) n tiver um raio de convergência
SÉRIES DE FOURIER. Fabio Cardoso D Araujo Martins, Fernando Sergio Cardoso Cunha, Paula Rodrigues. Ferreira Alves, Rafael Caveari Gomes
 SÉRIES DE FOURIER Fabio Cardoso D Araujo Martins, Fernando Sergio Cardoso Cunha, Paula Rodrigues Ferreira Alves, Rafael Caveari Gomes UFF - Universidade Federal Fluminense Neste artigo mostramos com diversos
SÉRIES DE FOURIER Fabio Cardoso D Araujo Martins, Fernando Sergio Cardoso Cunha, Paula Rodrigues Ferreira Alves, Rafael Caveari Gomes UFF - Universidade Federal Fluminense Neste artigo mostramos com diversos
Polinómio e série de Taylor
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA II - o Semestre 05/06 Exercícios Suplementares (Eng a Física Tecnológica, Matemática Aplicada e Computação
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA II - o Semestre 05/06 Exercícios Suplementares (Eng a Física Tecnológica, Matemática Aplicada e Computação
5.3 Séries (trigonométricas) de Fourier
 Derivando termo a termo, obtemos (cosx) = ( 1) n x n 1 (n 1)! = ( 1) n+1 x n+1 (n+1)! n=0 = senx, x R. Analogamente também se obteria (senx) = n=0 ( 1) n xn (n)! = cosx, x R. Recorrendo às séries confirmamos
Derivando termo a termo, obtemos (cosx) = ( 1) n x n 1 (n 1)! = ( 1) n+1 x n+1 (n+1)! n=0 = senx, x R. Analogamente também se obteria (senx) = n=0 ( 1) n xn (n)! = cosx, x R. Recorrendo às séries confirmamos
Vamos revisar alguns fatos básicos a respeito de séries de potências
 Seção 4 Revisão sobre séries de potências Vamos revisar alguns fatos básicos a respeito de séries de potências a n (x x ) n, que serão úteis no estudo de suas aplicações à resolução de equações diferenciais
Seção 4 Revisão sobre séries de potências Vamos revisar alguns fatos básicos a respeito de séries de potências a n (x x ) n, que serão úteis no estudo de suas aplicações à resolução de equações diferenciais
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I LMAC/MEBIOM/MEFT o Teste (VA) - 8 de Janeiro de 8-8: às : Apresente todos os cálculos que efectuar. Não é necessário simplificar os resultados. As cotações indicadas somam
Cálculo Diferencial e Integral I LMAC/MEBIOM/MEFT o Teste (VA) - 8 de Janeiro de 8-8: às : Apresente todos os cálculos que efectuar. Não é necessário simplificar os resultados. As cotações indicadas somam
Substituição trigonométrica hiperbólica. Esta é a última aula do segundo módulo da disciplina Cálculo II. Isso
 MÓDULO - AULA 30 Aula 30 Técnicas de integração Miscelânea Esta é a última aula do segundo módulo da disciplina Cálculo II. Isso significa que você está completando boa parte desta jornada. Você já enfrentou
MÓDULO - AULA 30 Aula 30 Técnicas de integração Miscelânea Esta é a última aula do segundo módulo da disciplina Cálculo II. Isso significa que você está completando boa parte desta jornada. Você já enfrentou
Nome: Erick Bordallo Tavares. Turma: 14:00 às 16:00hs. Professor: Altair
 Nome: Erick Bordallo Tavares Turma: 14:00 às 16:00hs Professor: Altair 1. SÉRIES DE FOURIER 1.1. FUNÇÕES PERIÓDICAS Exemplo: Uma função f(x) é dita periódica com um período T se f(x+t) = f(x) para qualquer
Nome: Erick Bordallo Tavares Turma: 14:00 às 16:00hs Professor: Altair 1. SÉRIES DE FOURIER 1.1. FUNÇÕES PERIÓDICAS Exemplo: Uma função f(x) é dita periódica com um período T se f(x+t) = f(x) para qualquer
Material Básico: Calculo A, Diva Fleming
 1 Limites Material Básico: Calculo A, Diva Fleming O conceito de Limite é importante na construção de muitos outros conceitos no cálculo diferencial e integral, por exemplo, as noções de derivada e de
1 Limites Material Básico: Calculo A, Diva Fleming O conceito de Limite é importante na construção de muitos outros conceitos no cálculo diferencial e integral, por exemplo, as noções de derivada e de
SÉRIE DE FOURIER. Universidade Federal Fluminense Rua Passo da Pátria, 156 São Domingos Niterói RJ, CEP
 SÉRIE DE FOURIER LUCAS NOBREGA CANELAS COSTA GUIMARÃES NATÃ DOS SANTOS LOPES GOMES RICARDO DE ALMEIDA CARVALHO WERTES MOTTA OLIVEIRA Universidade Federal Fluminense Rua Passo da Pátria, 156 São Domingos
SÉRIE DE FOURIER LUCAS NOBREGA CANELAS COSTA GUIMARÃES NATÃ DOS SANTOS LOPES GOMES RICARDO DE ALMEIDA CARVALHO WERTES MOTTA OLIVEIRA Universidade Federal Fluminense Rua Passo da Pátria, 156 São Domingos
SÉRIES DE FOURIER. 1. Uma série trigonométrica e sua sequência das somas parciais (S N ) N são dadas por
 SÉRIES DE FOURIER 1. Um série trigonométric e su sequênci ds soms prciis (S N ) N são dds por (1) c n e inx, n Z, c n C, x R ; S N = n= c n e inx. Tl série converge em x R se (S N (x)) N converge e, o
SÉRIES DE FOURIER 1. Um série trigonométric e su sequênci ds soms prciis (S N ) N são dds por (1) c n e inx, n Z, c n C, x R ; S N = n= c n e inx. Tl série converge em x R se (S N (x)) N converge e, o
AULA DE APOIO - 1 FÍSICA MATEMÁTICA I. A transformada de Fourier
 AULA DE APOIO - 1 FÍSICA MATEMÁTICA I A transformada de Fourier Assuntos da aula 1 Visão geral Motivações Linearidade e limitação uniforme 2 3 Translações, modulações, continuidade e etc. Física-Matemática.
AULA DE APOIO - 1 FÍSICA MATEMÁTICA I A transformada de Fourier Assuntos da aula 1 Visão geral Motivações Linearidade e limitação uniforme 2 3 Translações, modulações, continuidade e etc. Física-Matemática.
Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas. Paridade das Funções Seno e Cosseno. Primeiro Ano do Ensino Médio
 Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas Paridade das Funções Seno e Cosseno Primeiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio
Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas Paridade das Funções Seno e Cosseno Primeiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio
Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
2 ā Prova de MAT0220 Cálculo IV - IFUSP 2 ō semestre de /11/09 Prof. Oswaldo Rio Branco de Oliveira
 Nome : N ō USP : ā Prova de MAT00 Cálculo IV - IFUSP ō semestre de 009-3//09 Prof. Oswaldo Rio Branco de Oliveira GABARIT O Q 3 4 5 6 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Determine os valores
Nome : N ō USP : ā Prova de MAT00 Cálculo IV - IFUSP ō semestre de 009-3//09 Prof. Oswaldo Rio Branco de Oliveira GABARIT O Q 3 4 5 6 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Determine os valores
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
SÉRIES DE FOURIER. Felipe do Carmo Amorim. Fernando Soares Alves. Marcelo da Rocha Lopes. Engenharia Mecânica RESUMO
 SÉRIES DE FOURIER Felipe do Carmo Amorim Fernando Soares Alves Marcelo da Rocha Lopes Engenharia Mecânica RESUMO Apresentam-se no artigo que segue os conceitos sobre função periódica, séries trigonométricas,
SÉRIES DE FOURIER Felipe do Carmo Amorim Fernando Soares Alves Marcelo da Rocha Lopes Engenharia Mecânica RESUMO Apresentam-se no artigo que segue os conceitos sobre função periódica, séries trigonométricas,
Capítulo 4 Séries de Fourier
 Capítulo 4 Séries de Fourier Dizemos que representamos uma função real ela se expressa na série em série de Fourier quando os coeficientes são chamados de coeficientes de Fourier. Claro, a série de Fourier
Capítulo 4 Séries de Fourier Dizemos que representamos uma função real ela se expressa na série em série de Fourier quando os coeficientes são chamados de coeficientes de Fourier. Claro, a série de Fourier
Convergência das Séries de Fourier
 Convergência das Séries de Fourier Elton Gastardelli Kleis 6 de outubro de 010 1 1 Palavras-Chave Séries de Fourier, convergência de séries e convergência Resumo O objetivo do presente artigo é estudar
Convergência das Séries de Fourier Elton Gastardelli Kleis 6 de outubro de 010 1 1 Palavras-Chave Séries de Fourier, convergência de séries e convergência Resumo O objetivo do presente artigo é estudar
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
DISTRIBUIÇÃO DOS DOMÍNIOS POR PERÍODO
 DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS Planificação Anual da Disciplina de Matemática 11.º ano Ano Letivo de 2016/2017 Manual adotado: Máximo 11 Matemática A 11.º ano Maria Augusta Ferreira
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS Planificação Anual da Disciplina de Matemática 11.º ano Ano Letivo de 2016/2017 Manual adotado: Máximo 11 Matemática A 11.º ano Maria Augusta Ferreira
Notas de Análise Real. Jonas Renan Moreira Gomes
 Notas de Análise Real Jonas Renan Moreira Gomes 6 de novembro de 2008 ii Sumário 1 Séries de Fourier 1 1.1 Produto Hermitiano......................... 1 1.1.1 Definições........................... 1 1.1.2
Notas de Análise Real Jonas Renan Moreira Gomes 6 de novembro de 2008 ii Sumário 1 Séries de Fourier 1 1.1 Produto Hermitiano......................... 1 1.1.1 Definições........................... 1 1.1.2
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
{ 1 se x é racional, 0 se x é irracional. cos(k!πx) = cos(mπ) = ±1. { 1 se x Ak
 Solução dos Exercícios Capítulo 0 Exercício 0.: Seja f k : [0, ] R a função definida por Mostre que f k (x) = lim j (cos k!πx)2j. { f k (x) = se x {/k!, 2/k!,..., }, 0 senão e que f k converge pontualmente
Solução dos Exercícios Capítulo 0 Exercício 0.: Seja f k : [0, ] R a função definida por Mostre que f k (x) = lim j (cos k!πx)2j. { f k (x) = se x {/k!, 2/k!,..., }, 0 senão e que f k converge pontualmente
INTEGRAIS IMPRÓPRIAS
 Teoria INTEGRAIS IMPRÓPRIAS Intervalos Infinitos: Seja f integrável em [a, t], para todo t > a. Definimos + a f(x)dx = lim t + t a f(x)dx. Tal limite denomina-se integral imprópria de f estendida ao intervalo
Teoria INTEGRAIS IMPRÓPRIAS Intervalos Infinitos: Seja f integrável em [a, t], para todo t > a. Definimos + a f(x)dx = lim t + t a f(x)dx. Tal limite denomina-se integral imprópria de f estendida ao intervalo
Sobre Desenvolvimentos em Séries de Potências, Séries de Taylor e Fórmula de Taylor
 Sobre Desenvolvimentos em Séries de Potências, Séries de Taylor e Fórmula de Taylor Pedro Lopes Departamento de Matemática Instituto Superior Técnico o. Semestre 004/005 Estas notas constituem um material
Sobre Desenvolvimentos em Séries de Potências, Séries de Taylor e Fórmula de Taylor Pedro Lopes Departamento de Matemática Instituto Superior Técnico o. Semestre 004/005 Estas notas constituem um material
) a sucessão definida por y n
 aula 05 Sucessões 5.1 Sucessões Uma sucessão de números reais é simplesmente uma função x N R. É conveniente visualizar uma sucessão como uma sequência infinita: (x(), x(), x(), ). Neste contexto é usual
aula 05 Sucessões 5.1 Sucessões Uma sucessão de números reais é simplesmente uma função x N R. É conveniente visualizar uma sucessão como uma sequência infinita: (x(), x(), x(), ). Neste contexto é usual
Integrais. ( e 12/ )
 Integrais (21-04-2009 e 12/19-05-2009) Já estudámos a determinação da derivada de uma função. Revertamos agora o processo de derivação, isto é, suponhamos que nos é dada uma função F e que pretendemos
Integrais (21-04-2009 e 12/19-05-2009) Já estudámos a determinação da derivada de uma função. Revertamos agora o processo de derivação, isto é, suponhamos que nos é dada uma função F e que pretendemos
t 2 se t 0 Determine a expansão em série de potências para a função F (x) = ( 1) n y2n (2n)!, ( 1) n t4n (2n)! (2n)! ( 1) n t4n 2 dt = ( 1) n t 4n 2 )
 MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
A derivada da função inversa
 A derivada da função inversa Sumário. Derivada da função inversa............... Funções trigonométricas inversas........... 0.3 Exercícios........................ 7.4 Textos Complementares................
A derivada da função inversa Sumário. Derivada da função inversa............... Funções trigonométricas inversas........... 0.3 Exercícios........................ 7.4 Textos Complementares................
GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))
![GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1)) GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))](/thumbs/97/131760884.jpg) GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4 O problema de Sturm-Liouville A separação de variáveis da equação de Helmholtz,
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4 O problema de Sturm-Liouville A separação de variáveis da equação de Helmholtz,
Análise de Sinais no Tempo Contínuo: A Série de Fourier
 Análise de Sinais no Tempo Contínuo: A Série de Fourier Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Análise de Sinais no Tempo Contínuo: A Série de Fourier Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Análise Complexa e Equações Diferenciais
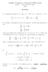 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Provas de Análise Real - Noturno - 3MAT003
 Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Convergência em espaços normados
 Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Comprimento de Arco, o Número π e as Funções Trigonométricas
 Comprimento de Arco, o Número π e as Funções Trigonométricas J. A. Verderesi Apresentaremos a seguir a medida de um ângulo como limite de poligonais inscritas e circunscritas à circunfêrencia unitária,
Comprimento de Arco, o Número π e as Funções Trigonométricas J. A. Verderesi Apresentaremos a seguir a medida de um ângulo como limite de poligonais inscritas e circunscritas à circunfêrencia unitária,
de Potências e Produtos de Funções Trigonométricas
 MÓDULO - AULA 1 Aula 1 Técnicas de Integração Integração de Potências e Produtos de Funções Trigonométricas Objetivo Aprender a integrar potências e produtos de funções trigonométricas. Na aula anterior,
MÓDULO - AULA 1 Aula 1 Técnicas de Integração Integração de Potências e Produtos de Funções Trigonométricas Objetivo Aprender a integrar potências e produtos de funções trigonométricas. Na aula anterior,
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
Cálculo Diferencial e Integral I Mestrado Integrado em Engenharia Electrotécnica e de Computadores 2 o Teste (V1) - 15 de Janeiro de h00m
 Cálculo Diferencial e Integral I Mestrado Integrado em Engenharia Electrotécnica e de Computadores 2 o Teste (V) - 5 de Janeiro de 2 - hm Resolução Problema (2,5 val.) Determine uma primitiva de cada uma
Cálculo Diferencial e Integral I Mestrado Integrado em Engenharia Electrotécnica e de Computadores 2 o Teste (V) - 5 de Janeiro de 2 - hm Resolução Problema (2,5 val.) Determine uma primitiva de cada uma
Sucessões. , ou, apenas, u n. ,u n n. Casos Particulares: 1. Progressão aritmética de razão r e primeiro termo a: o seu termo geral é u n a n1r.
 Sucessões Definição: Uma sucessão de números reais é uma aplicação u do conjunto dos números inteiros positivos,, no conjunto dos números reais,. A expressão u n que associa a cada n a sua imagem designa-se
Sucessões Definição: Uma sucessão de números reais é uma aplicação u do conjunto dos números inteiros positivos,, no conjunto dos números reais,. A expressão u n que associa a cada n a sua imagem designa-se
exercícios de análise numérica II
 exercícios de análise numérica II lic. matemática aplicada e computação (4/5) aulas práticas - capítulo Exercício. Mostre que a soma dos polinómios base de Lagrange é a função constante. Exercício. Usando
exercícios de análise numérica II lic. matemática aplicada e computação (4/5) aulas práticas - capítulo Exercício. Mostre que a soma dos polinómios base de Lagrange é a função constante. Exercício. Usando
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Notas Sobre Sequências e Séries Alexandre Fernandes
 Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
ANÁLISE MATEMÁTICA II 2007/2008. Cursos de EACI e EB
 ANÁLISE MATEMÁTICA II 2007/2008 (com Laboratórios) Cursos de EACI e EB Acetatos de Ana Matos 1ª Parte Sucessões Séries Numéricas Fórmula de Taylor Séries de Potências Série de Taylor DMAT Ana Matos - AMII0807
ANÁLISE MATEMÁTICA II 2007/2008 (com Laboratórios) Cursos de EACI e EB Acetatos de Ana Matos 1ª Parte Sucessões Séries Numéricas Fórmula de Taylor Séries de Potências Série de Taylor DMAT Ana Matos - AMII0807
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Extensão da tangente, secante, cotangente e cossecante, à reta.
 UFF/GMA Notas de aula de MB-I Maria Lúcia/Marlene 05- Trigonometria - Parte - Tan-Cot_Sec-Csc PARTE II TANGENTE COTANGENTE SECANTE COSSECANTE Agora estudaremos as funções tangente, cotangente, secante
UFF/GMA Notas de aula de MB-I Maria Lúcia/Marlene 05- Trigonometria - Parte - Tan-Cot_Sec-Csc PARTE II TANGENTE COTANGENTE SECANTE COSSECANTE Agora estudaremos as funções tangente, cotangente, secante
Números Complexos. Professores Jorge Aragona e Oswaldo R. B. de Oliveira
 úmeros Complexos Professores Jorge Aragona e Oswaldo R. B. de Oliveira Capítulo ÚMEROS COMPLEXOS 2 Capítulo 2 POLIÔMIOS 3 Capítulo 3 SEQUÊCIAS E TOPOLOGIA 4 Capítulo 4 O TEOREMA FUDAMETAL DA ÁLGEBRA E
úmeros Complexos Professores Jorge Aragona e Oswaldo R. B. de Oliveira Capítulo ÚMEROS COMPLEXOS 2 Capítulo 2 POLIÔMIOS 3 Capítulo 3 SEQUÊCIAS E TOPOLOGIA 4 Capítulo 4 O TEOREMA FUDAMETAL DA ÁLGEBRA E
PROVA EXTRAMUROS-MESTRADO (i) O tempo destinado a esta prova é de 5 horas.
 PROVA EXTRAMUROS-MESTRADO - 2016 NOME: IDENTIDADE (OU PASSAPORTE): ASSINATURA: Instruções (i) O tempo destinado a esta prova é de 5 horas. (ii) A parte I (duas questões dissertativas) corresponde a 25%
PROVA EXTRAMUROS-MESTRADO - 2016 NOME: IDENTIDADE (OU PASSAPORTE): ASSINATURA: Instruções (i) O tempo destinado a esta prova é de 5 horas. (ii) A parte I (duas questões dissertativas) corresponde a 25%
SMA333 8a. Lista - séries de Taylor 07/06/2013
 SMA333 8a Lista - séries de Taylor 7/6/213 Definição Para qualquer n = 1, 2, 3,, se uma função f tiver todas as derivadas até ordem n em algum intervalo contendo a como ponto interior, então o polinômio
SMA333 8a Lista - séries de Taylor 7/6/213 Definição Para qualquer n = 1, 2, 3,, se uma função f tiver todas as derivadas até ordem n em algum intervalo contendo a como ponto interior, então o polinômio
Séries de Termos Não-Negativos
 Séries de Termos Não-Negativos Em geral não é possível calcular explicitamente a soma duma série. O que podemos fazer é perceber se ela converge ou diverge e neste último caso, calcular aproximadamente
Séries de Termos Não-Negativos Em geral não é possível calcular explicitamente a soma duma série. O que podemos fazer é perceber se ela converge ou diverge e neste último caso, calcular aproximadamente
A integral definida Problema:
 A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Trigonometria e funções trigonométricas. Funções trigonométricas O essencial
 Trigonometria e funções trigonométricas Funções trigonométricas O essencial Funções seno e cosseno Designa-se por função seno (respetivamente, função cosseno) e representa-se por sin ou sen (respetivamente,
Trigonometria e funções trigonométricas Funções trigonométricas O essencial Funções seno e cosseno Designa-se por função seno (respetivamente, função cosseno) e representa-se por sin ou sen (respetivamente,
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Sistemas Lineares. Aula 9 Transformada de Fourier
 Sistemas Lineares Aula 9 Transformada de Fourier Séries de Fourier A Série de Fourier representa um sinal periódico como uma combinação linear de exponenciais complexas harmonicamente relacionadas. Como
Sistemas Lineares Aula 9 Transformada de Fourier Séries de Fourier A Série de Fourier representa um sinal periódico como uma combinação linear de exponenciais complexas harmonicamente relacionadas. Como
5 AULA. em Séries de Potências LIVRO. META Apresentar os principais métodos de representação de funções em séries de potências.
 LIVRO Métodos de Representação de Funções em Séries de AULA META Apresentar os principais métodos de representação de funções em séries de potências. OBJETIVOS Representar funções em séries de potências.
LIVRO Métodos de Representação de Funções em Séries de AULA META Apresentar os principais métodos de representação de funções em séries de potências. OBJETIVOS Representar funções em séries de potências.
LIMITES E CONTINIDADE
 MATEMÁTICA I LIMITES E CONTINIDADE Prof. Dr. Nelson J. Peruzzi Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Parte 2 Limites Infinitos Definição de vizinhança e ite Limites laterais Limite de função
MATEMÁTICA I LIMITES E CONTINIDADE Prof. Dr. Nelson J. Peruzzi Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Parte 2 Limites Infinitos Definição de vizinhança e ite Limites laterais Limite de função
Análise Matemática I 1 o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI)
 Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS
 Escolas João de Araújo Correia ORGANIZAÇÃO DO ANO LETIVO 16 17 GESTÃO CURRICULAR DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA A 11º ANO 1º PERÍODO ---------------------------------------------------------------------------------------------------------------------
Escolas João de Araújo Correia ORGANIZAÇÃO DO ANO LETIVO 16 17 GESTÃO CURRICULAR DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA A 11º ANO 1º PERÍODO ---------------------------------------------------------------------------------------------------------------------
Portanto, = 4 1= 2. LETRA D
 TRIGONOMETRIA PARTE QUESTÃO 0 Maior valor (cos (0,0t) -) 585 r(t) 900 + 0,5.( ) Menor valor (cos(0,0t) ) 585 r(t) 500 + 0,5.() Somando, temos: 900 + 500 000 QUESTÃO 0 P QUESTÃO 0 Queremos calcular f()
TRIGONOMETRIA PARTE QUESTÃO 0 Maior valor (cos (0,0t) -) 585 r(t) 900 + 0,5.( ) Menor valor (cos(0,0t) ) 585 r(t) 500 + 0,5.() Somando, temos: 900 + 500 000 QUESTÃO 0 P QUESTÃO 0 Queremos calcular f()
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges Depto. de Eng. Elétrica Universidade Federal de Minas Gerais Séries de Fourier Série de Fourier Qualquer função periódica f(t) pode ser representada por uma
Circuitos Elétricos III Prof. Danilo Melges Depto. de Eng. Elétrica Universidade Federal de Minas Gerais Séries de Fourier Série de Fourier Qualquer função periódica f(t) pode ser representada por uma
= 2 sen(x) (cos(x) (b) (7 pontos) Pelo item anterior, temos as k desigualdades. sen 2 (2x) sen(4x) ( 3/2) 3
 Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de 2010
 Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
Técnicas de. Integração
 Técnicas de Capítulo 7 Integração TÉCNICAS DE INTEGRAÇÃO f ( xdx ) a Na definição de integral definida, trabalhamos com uma função f definida em um intervalo limitado [a, b] e supomos que f não tem uma
Técnicas de Capítulo 7 Integração TÉCNICAS DE INTEGRAÇÃO f ( xdx ) a Na definição de integral definida, trabalhamos com uma função f definida em um intervalo limitado [a, b] e supomos que f não tem uma
Resumo das aulas dos dias 4 e 11 de abril e exercícios sugeridos
 MAT 1351 Cálculo para funções uma variável real I Curso noturno de Licenciatura em Matemática 1 semestre de 2016 Docente: Prof. Dr. Pierluigi Benevieri Resumo das aulas dos dias 4 e 11 de abril e exercícios
MAT 1351 Cálculo para funções uma variável real I Curso noturno de Licenciatura em Matemática 1 semestre de 2016 Docente: Prof. Dr. Pierluigi Benevieri Resumo das aulas dos dias 4 e 11 de abril e exercícios
1 Séries de números reais
 Universidade do Estado do Rio de Janeiro - PROFMAT MA 22 - Fundamentos de Cálculo - Professora: Mariana Villapouca Resumo Aula 0 - Profmat - MA22 (07/06/9) Séries de números reais Seja (a n ) n uma sequência
Universidade do Estado do Rio de Janeiro - PROFMAT MA 22 - Fundamentos de Cálculo - Professora: Mariana Villapouca Resumo Aula 0 - Profmat - MA22 (07/06/9) Séries de números reais Seja (a n ) n uma sequência
Diferenciais em Série de Potências
 Existência de Soluções de Equações Diferenciais em Série de Potências Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/ regi 0 de julho de
Existência de Soluções de Equações Diferenciais em Série de Potências Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/ regi 0 de julho de
Sílvia Mara da Costa Campos Victer Concurso: Matemática da Computação UERJ - Friburgo
 Convolução, Série de Fourier e Transformada de Fourier contínuas Sílvia Mara da Costa Campos Victer Concurso: Matemática da Computação UERJ - Friburgo Tópicos Sinais contínuos no tempo Função impulso Sistema
Convolução, Série de Fourier e Transformada de Fourier contínuas Sílvia Mara da Costa Campos Victer Concurso: Matemática da Computação UERJ - Friburgo Tópicos Sinais contínuos no tempo Função impulso Sistema
Teoria da Medida e Integração (MAT505)
 Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Expansão de funções em série de Taylor
 Epansão de funções em série de Talor Hudson Pimenta Silveira I. INTRODUÇÃO Neste teto, introduzirei um recurso frequentemente usado em problemas de Física: a epansão de funções em série de Talor. Muito
Epansão de funções em série de Talor Hudson Pimenta Silveira I. INTRODUÇÃO Neste teto, introduzirei um recurso frequentemente usado em problemas de Física: a epansão de funções em série de Talor. Muito
LIMITES E CONTINUIDADE
 LIMITES E CONTINUIDADE Marina Vargas R. P. Gonçalves a a Departamento de Matemática, Universidade Federal do Paraná, marina.vargas@gmail.com, http:// www.estruturas.ufpr.br PRIMEIRO LIMITE FUNDAMENTAL
LIMITES E CONTINUIDADE Marina Vargas R. P. Gonçalves a a Departamento de Matemática, Universidade Federal do Paraná, marina.vargas@gmail.com, http:// www.estruturas.ufpr.br PRIMEIRO LIMITE FUNDAMENTAL
Questão (a) 4.(b) 5.(a) 5.(b) 6.(a) 6.(b) 6.(c) 7 Cotação
 Faculdade de Ciências Exatas e da Engenharia PROVA DE AVALIAÇÃO DE CONHECIMENTOS E COMPETÊNCIAS PARA ADMISSÃO AO ENSINO SUPERIOR PARA MAIORES DE ANOS - 018 Matemática - 1/0/018 Atenção: Justifique os raciocínios
Faculdade de Ciências Exatas e da Engenharia PROVA DE AVALIAÇÃO DE CONHECIMENTOS E COMPETÊNCIAS PARA ADMISSÃO AO ENSINO SUPERIOR PARA MAIORES DE ANOS - 018 Matemática - 1/0/018 Atenção: Justifique os raciocínios
30 a OLIMPÍADA DE MATEMÁTICA DO RIO GRANDE DO NORTE PRIMEIRA FASE. NÍVEL UNIVERSITÁRIO. 35! =
 0 a OLIMPÍADA DE MATEMÁTICA DO RIO GRANDE DO NORTE 09- PRIMEIRA FASE. NÍVEL UNIVERSITÁRIO. Para cada questão, assinale uma alternativa como a resposta correta. NOME DO(A) ESTUDANTE: UNIVERSIDADE:. O fatorial
0 a OLIMPÍADA DE MATEMÁTICA DO RIO GRANDE DO NORTE 09- PRIMEIRA FASE. NÍVEL UNIVERSITÁRIO. Para cada questão, assinale uma alternativa como a resposta correta. NOME DO(A) ESTUDANTE: UNIVERSIDADE:. O fatorial
Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].
![Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3]. Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].](/thumbs/100/144026914.jpg) Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
P L A N I F I C A Ç Ã 0 E n s i n o S e c u n d á r i o
 P L A N I F I C A Ç Ã 0 E n s i n o S e c u n d á r i o 206-207 DISCIPLINA / ANO: Matemática A - ºano MANUAL ADOTADO: NOVO ESPAÇO - Matemática A º ano GESTÃO DO TEMPO Nº de Nº de Nº de tempos tempos tempos
P L A N I F I C A Ç Ã 0 E n s i n o S e c u n d á r i o 206-207 DISCIPLINA / ANO: Matemática A - ºano MANUAL ADOTADO: NOVO ESPAÇO - Matemática A º ano GESTÃO DO TEMPO Nº de Nº de Nº de tempos tempos tempos
ESCOLA SECUNDÁRIA DA AMADORA. Conteúdos programáticos/unidades
 ESCOLA SECUNDÁRIA DA AMADORA Curso Científico-Humanístico de Ciências e Tecnologias e de Ciências Socioeconómicas 018/019 Disciplina de Matemática A - 11ºAno Planificação Anual e Critérios de Avaliação
ESCOLA SECUNDÁRIA DA AMADORA Curso Científico-Humanístico de Ciências e Tecnologias e de Ciências Socioeconómicas 018/019 Disciplina de Matemática A - 11ºAno Planificação Anual e Critérios de Avaliação
ANÁLISE MATEMÁTICA IV
 ANÁLISE MATEMÁTICA IV (2 ō semestre 2006/07) LEC e LEGM Professor Responsvel: Maria João Borges http://www.math.ist.utl.pt/ mborges/amiv Sumários das Aulas Teóricas Aula 37: (05/06) Aula 36: (04/06) Continuação
ANÁLISE MATEMÁTICA IV (2 ō semestre 2006/07) LEC e LEGM Professor Responsvel: Maria João Borges http://www.math.ist.utl.pt/ mborges/amiv Sumários das Aulas Teóricas Aula 37: (05/06) Aula 36: (04/06) Continuação
Aulas n o 22: A Função Logaritmo Natural
 CÁLCULO I Aulas n o 22: A Função Logaritmo Natural Prof. Edilson Neri Júnior Prof. André Almeida 1 A Função Logaritmo Natural 2 Derivadas e Integral Propriedades dos Logaritmos 3 Gráfico Seja x > 0. Definimos
CÁLCULO I Aulas n o 22: A Função Logaritmo Natural Prof. Edilson Neri Júnior Prof. André Almeida 1 A Função Logaritmo Natural 2 Derivadas e Integral Propriedades dos Logaritmos 3 Gráfico Seja x > 0. Definimos
PLANIFICAÇÃO A MÉDIO/LONGO PRAZO
 018/019 DISCIPLINA: Matemática A ANO: 11º CURSO GERAL DE CIÊNCIAS E TECNOLOGIAS Total de aulas previstas: 15 Mês Unidades Temáticas Conteúdos Conteúdos programáticos Descritores N.º Aulas Avaliação Primeiro
018/019 DISCIPLINA: Matemática A ANO: 11º CURSO GERAL DE CIÊNCIAS E TECNOLOGIAS Total de aulas previstas: 15 Mês Unidades Temáticas Conteúdos Conteúdos programáticos Descritores N.º Aulas Avaliação Primeiro
TEMA TÓPICOS OBJETIVOS ESPECÍFICOS AVALIAÇÃO* Lei dos senos e lei dos cossenos. Extensão da definição das razões trigonométricas aos
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO Escola Básica e Secundária Dr. Vieira de Carvalho Departamento de Matemática e Ciências Experimentais Planificação Anual de Matemática A 11º ano Ano Letivo
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO Escola Básica e Secundária Dr. Vieira de Carvalho Departamento de Matemática e Ciências Experimentais Planificação Anual de Matemática A 11º ano Ano Letivo
Teoria da Medida e Integração (MAT505)
 Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
Derivadas. Derivadas. ( e )
 Derivadas (24-03-2009 e 31-03-2009) Recta Tangente Seja C uma curva de equação y = f(x). Para determinar a recta tangente a C no ponto P de coordenadas (a,f(a)), i.e, P(a, f(a)), começamos por considerar
Derivadas (24-03-2009 e 31-03-2009) Recta Tangente Seja C uma curva de equação y = f(x). Para determinar a recta tangente a C no ponto P de coordenadas (a,f(a)), i.e, P(a, f(a)), começamos por considerar
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Sequências e Séries Infinitas. Copyright Cengage Learning. Todos os direitos reservados.
 11 Sequências e Séries Infinitas Copyright Cengage Learning. Todos os direitos reservados. 11.10 Séries de Taylor e Maclaurin Copyright Cengage Learning. Todos os direitos reservados. Começaremos supondo
11 Sequências e Séries Infinitas Copyright Cengage Learning. Todos os direitos reservados. 11.10 Séries de Taylor e Maclaurin Copyright Cengage Learning. Todos os direitos reservados. Começaremos supondo
2 ō Semestre 2015/2016
 Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
