ANÁLISE MATEMÁTICA IV
|
|
|
- Ana Vitória Felícia Alcaide Palma
- 7 Há anos
- Visualizações:
Transcrição
1 ANÁLISE MATEMÁTICA IV (2 ō semestre 2006/07) LEC e LEGM Professor Responsvel: Maria João Borges mborges/amiv Sumários das Aulas Teóricas Aula 37: (05/06) Aula 36: (04/06) Continuação da aula anterior. Aplicações à equação do calor com condições de Dirichlet e de Neumann. Condições de fronteira não homogéneas. Aplicação à equação das ondas unidimensional. Equações diferenciais parciais. Resolução da equação do calor unidimensional com condições de fronteira de Dirichlet homogéneas.. Método de separação de variáveis. Aula 35: (01/06) Séries de Fourier: definição e convergência pontual. cosenos. Séries de Fourier de senos e de Aula 34: (29/05) Aula 33: (28/05) Aula 32: (25/05) Continuação da aula anterior. Equações diferenciais ordinárias lineares escalares de ordem n, com coeficientes constantes: cálculo de uma solução particular da equação não-homogénea. Fórmula da variação das constantes. Método dos coeficientes indeterminados. Equações diferenciais ordinárias lineares escalares de ordem n, com coeficientes constantes: reolução da equação homogénea. 1
2 Aula 31: (22/05) Aula 30: (21/05) Aula 29: (18/05) Aula 28: (15/05) Aula 27: (14/05) Aula 26: (11/05) Aula 25: (08/05) Equação vectorial não homogénea: fórmula de variação das constantes. Exemplo. Fórmula da variação das constantes para a equação vectorial linear de ordem 1. Equações diferenciais ordinárias lineares escalares de ordem n, com coeficientes constantes. Equivalência da equação a um sistema de ordem 1: matriz companheira, Continuação da aula anterior. Cálculo da exponencial de uma matriz. Caso não diagonalizável. Formas canónicas de Jordan. Método da variação das constantes. Método dos coeficientes indeterminados. Cálculo da exponencial de uma matriz. Caso diagonal e caso diagonalizável. Exemplo de uma matriz com valores prprios complexos. Equações vectoriais ordinárias lineares de ordem 1. Matriz solução fundamental. Equações vectoriais de coeficientes constantes. Exponencial de uma matriz (definição e rpopriedades). Solução do problema de valor inicial homogéneo para a equação de coeficientes constantes. Teorema de extensão de soluções. Comparação de soluções. Teorema de Picard-Lindelof. Existncia de solução de um problema de valor inicial de primeira ordem: Teorema de Peano. Unicidade de solução: Exemplo de um problema onde existe uma infinidade de soluções. Condição de Lipshitz. Aula 24: (07/05) Resolução de equações exactas. Equações redutíveis a exactas. Aula 23: (04/05) Aula 22: (30/04) Resolução de equações separáveis. Intervalo máximo de existência de solução. Exemplo de uma solução que explode (em tempo finito). Equações diferenciais. Notação e definições: Classificação das equações diferenciais. Solução de uma equação diferencial. Equa cões ordinárias de ordem 1. Resolução de equações lineares homogéneas e não homogéneas.. 2
3 Aula 21: (20/04) Aula 20: (17/04) Aula 19: (16/04) Aula 18: (13/04) Aula 17: (03/04) Aula 16: (02/04) Aula 15: (30/03) Aula 14: (27/03) Aula 13: (26/03) Aula 12: (23/03) Aula 11: (20/03) Revisões para o teste. Continuação da aula anterior. Integrais impróprios envolvendo funções seno e coseno. Lema de Jordan. Aplicações do teorema dos resíduos ao cálculo de integrais trigonométricos. Aplicações do teorema dos resíduos ao cálculo de integrais impróprios de funções racionais. Exemplos de aplicação do Teorema dos Resíduos. Singularidades essenciais. Exemplos. Teorema dos resíduos. Polos de ordem k.cálculo do resíduo de um polo de ordem k. Regra de Cauchy. Singularidades. Singularidades isoladas. Definição de resíduo de uma singularidade isolada. Singularidades removíveis. Demonstração do Teorema de Taylor. Séries de Laurent. Teorema de Laurent. Exemplos de séries de Laurent. Séries de potências. Teorema de Taylor e exemplos de séries de Taylor. Funções complexas definidas por séries. Convergência módulo, critério da razão e critério da raíz. Convergência uniforme. Critério de Weierstrass. Série geométrica. Aplicações da fórmula integral de Cauchy: Teorema de Morera. Teorema de Liouville. Teorema Fundamental da Álgebra. Funções harmónicas. Relação entre funções analíticas e funções harmónicas: funções harmónicas conjugadas. 3
4 Aula 10: (19/03) Aula 9: (16/03) Aula 8: (13/03) Aula 7: (12/03) Aula 6: (09/03) Aula 5: (06/03) Aula 4: (05/03) Aula 3: (02/03) Continuação da aula anterior: Teorema de Cauchy generalizado (para funções analíticas em regiões multiplamente conexas)..fórmula integral de Cauchy. Derivadas de ordem superior: fórmula integral de Cauchy generalizada. Teorema de Cauchy. Consequências do Teorema de Cauchy: independência do caminho de integração. Noção de primitiva. Teorema Fundamental do Cálculo. Curvas em C: curvas regulares, simples, curvas de Jordan. Teorema da curva de Jordan. Integração de funções complexas de variável complexa: definição do integral de uma função complexa de variável complexa, ao longo de uma curva seccionalmente regular. Propriedades elementares do integral (linearidade, aditividade, simetria). Majoração de integrais. Integrais de funções analíticas ao longo de curvas fechadas. Exemplos importantes de funções analíticas: funções polinomiais, exponencial, trigonométricas e hiperbólicas. Analiticidade das funções logaritmo. Curvas no plano complexo. Condição suficiente para a existência de derivada de uma função complexa de variável complexa. Definição de função analítica (ou holomorfa). Propriedades elementares das funes analíticas; regras de derivação. Continuidade; propriedades elementares das funções contínuas. Definição de derivada de uma função complexa de variável complexa. Condição necessária para a existência de derivada de uma função complexa de variável complexa: equações de Cauchy-Riemann. Funções trigonométricas e Funções hiperbólicas: definição e propriedades. Logaritmo complexo. Ramos da função logaritmo e valor principal. Ramos da função potência e valor principal. Funções complexas de variável complexa. Definição de limite e propriedades algébricas de limites. Raízes de um número complexo. complexo. Representação geométrica das raízes de um número Fórmula de Euler. Exponencial Complexa; definição e propriedades. 4
5 Aula 2: (27/02) Aula 1: (26/02) Conclusão da aula anterior. Representação geométrica dos números complexos. Números complexos na forma polar. Produto e quociente de números complexos na forma polar. Fórmula de Moivre. Apresentação. Estrutura algébrica do corpo dos números complexos. 5
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ
 Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
SUMÁRIO CAPÍTULO 1 CAPÍTULO 2
 SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
SUMÁRIO CAPÍTULO 1 NÚMEROS COMPLEXOS 1 Somas e produtos 1 Propriedades algébricas básicas 3 Mais propriedades algébricas 5 Vetores e módulo 8 Desigualdade triangular 11 Complexos conjugados 14 Forma exponencial
FÍSICA-MATEMÁTICA RUDI GAELZER (INSTITUTO DE FÍSICA - UFRGS)
 FÍSICA-MATEMÁTICA RUDI GAELZER (INSTITUTO DE FÍSICA - UFRGS) Apostila preparada para as disciplinas de Física- Matemática ministradas para os Cursos de Bacharelado em Física do Instituto de Física da Universidade
FÍSICA-MATEMÁTICA RUDI GAELZER (INSTITUTO DE FÍSICA - UFRGS) Apostila preparada para as disciplinas de Física- Matemática ministradas para os Cursos de Bacharelado em Física do Instituto de Física da Universidade
LOM3253 Física Matemática 2017 S2
 LOM3253 Física Matemática 2017 S2 Parte 2. Funções de variável complexa Prof. Dr. Viktor Pastoukhov EEL-USP Subconjuntos no plano complexo Geometria Analítica no plano complexo Geometria Analítica no plano
LOM3253 Física Matemática 2017 S2 Parte 2. Funções de variável complexa Prof. Dr. Viktor Pastoukhov EEL-USP Subconjuntos no plano complexo Geometria Analítica no plano complexo Geometria Analítica no plano
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas. Cálculo Combinatório: Introdução ao cálculo combinatório
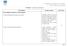 DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (12º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (13 de setembro a 15 de dezembro) Cálculo Combinatório: Introdução ao cálculo combinatório
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (12º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (13 de setembro a 15 de dezembro) Cálculo Combinatório: Introdução ao cálculo combinatório
Fichas de Análise Matemática III
 Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/15 Cursos: LEGM, MEC. Michael Paluch
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/15 Cursos: LEGM, MEC Michael Paluch Avaliação 1. Avaliação Contínua a) 1 Teste dia 11 de abril de 2015 duração 90 minutes (40% de nota final)
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/15 Cursos: LEGM, MEC Michael Paluch Avaliação 1. Avaliação Contínua a) 1 Teste dia 11 de abril de 2015 duração 90 minutes (40% de nota final)
Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA
 Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA Número da Aula Data da Aula Matéria Dada Exercícios Recomendados Obs 1 06/08 Sequências, definição, exemplos, convergência e divergência, propriedades,
Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA Número da Aula Data da Aula Matéria Dada Exercícios Recomendados Obs 1 06/08 Sequências, definição, exemplos, convergência e divergência, propriedades,
Í ndice. Capítulo 1: Os Números Reais. Generalidades. Supremo e ínfimo de um conjunto. Exercícios. Sugestões e soluções. Desigualdade do triângulo
 Í ndice Capítulo 1: Os Números Reais Generalidades Supremo e ínfimo de um conjunto e soluções Desigualdade do triângulo O princípio de indução e a desigualdade de Bernoulli. e soluções. Q é um conjunto
Í ndice Capítulo 1: Os Números Reais Generalidades Supremo e ínfimo de um conjunto e soluções Desigualdade do triângulo O princípio de indução e a desigualdade de Bernoulli. e soluções. Q é um conjunto
Provável ordem de Assuntos das Aulas e Exercícios Recomendados Cálculo II- MAC 123
 Provável ordem de Assuntos das Aulas e Exercícios Recomendados Cálculo II- MAC 123 Número da Data da Matéria Dada Exercícios Recomendados Obs Aula Aula 1 11/03 Sequências Numéricas, definição, exemplos,
Provável ordem de Assuntos das Aulas e Exercícios Recomendados Cálculo II- MAC 123 Número da Data da Matéria Dada Exercícios Recomendados Obs Aula Aula 1 11/03 Sequências Numéricas, definição, exemplos,
SUMÁRIO VOLUME II 8 MODELAGEM MATEMÁTICA COM EQUAÇÕES DIFERENCIAIS SÉRIES INFINITAS CURVAS PARAMÉTRICAS E POLARES; SEÇÕES CÔNICAS 692
 SUMÁRIO VOLUME II 8 MODELAGEM MATEMÁTICA COM EQUAÇÕES DIFERENCIAIS 561 8.1 Modelagem com equações diferenciais 561 8.2 Separação de variáveis 568 8.3 Campos de direções; método de Euler 579 8.4 Equações
SUMÁRIO VOLUME II 8 MODELAGEM MATEMÁTICA COM EQUAÇÕES DIFERENCIAIS 561 8.1 Modelagem com equações diferenciais 561 8.2 Separação de variáveis 568 8.3 Campos de direções; método de Euler 579 8.4 Equações
DISTRIBUIÇÃO DOS DOMÍNIOS POR PERÍODO
 DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS Planificação Anual da Disciplina de Matemática 11.º ano Ano Letivo de 2016/2017 Manual adotado: Máximo 11 Matemática A 11.º ano Maria Augusta Ferreira
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS Planificação Anual da Disciplina de Matemática 11.º ano Ano Letivo de 2016/2017 Manual adotado: Máximo 11 Matemática A 11.º ano Maria Augusta Ferreira
ANÁLISE MATEMÁTICA IV 1 o Teste (LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ) Justifique cuidadosamente todas as respostas.
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA IV o Teste LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ Justifique cuidadosamente todas as respostas.
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA IV o Teste LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ Justifique cuidadosamente todas as respostas.
CURRÍCULO DO CURSO. Mínimo: 7 semestres. Prof. Nereu Estanislau Burin
 Documentação: Objetivo: Titulação: Diplomado em: Curso reconhecido pelo Decreto Federal 75590 de 10/04/1975, publicado no Diário Oficial da União de 11/04/1975 Portaria Criação= 216-23/10/73-GABINETE DO
Documentação: Objetivo: Titulação: Diplomado em: Curso reconhecido pelo Decreto Federal 75590 de 10/04/1975, publicado no Diário Oficial da União de 11/04/1975 Portaria Criação= 216-23/10/73-GABINETE DO
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
12 Qua 16 mar Coordenadas retangulares, representação Funções vetoriais paramétrica
 Aula Data Aula Detalhes 1 Qua 3 fev Introdução Apresentação e avisos 2 Sex 5 fev Revisão Resumo dos pré-requisitos Qua 10 fev Feriado Carnaval 3 Sex 12 fev Soma de Riemann Área, soma superior e inferior
Aula Data Aula Detalhes 1 Qua 3 fev Introdução Apresentação e avisos 2 Sex 5 fev Revisão Resumo dos pré-requisitos Qua 10 fev Feriado Carnaval 3 Sex 12 fev Soma de Riemann Área, soma superior e inferior
INSTITUTO PUPILOS DO EXÉRCITO. Apoio ao Exame de Matemática A - Programa
 INSTITUTO PUPILOS DO EXÉRCITO Apoio ao Exame de Matemática A - Programa 10.º ANO Lógica e Teoria de Conjuntos Duração: 20 horas Proposições Valor lógico de uma proposição; Princípio de não contradição;
INSTITUTO PUPILOS DO EXÉRCITO Apoio ao Exame de Matemática A - Programa 10.º ANO Lógica e Teoria de Conjuntos Duração: 20 horas Proposições Valor lógico de uma proposição; Princípio de não contradição;
Adérito Araújo. Gonçalo Pena. Adérito Araújo. Adérito Araújo. Gonçalo Pena. Método da Bissecção. Resolução dos exercícios 2.14, 2.15, 2.16 e 2.17.
 1 2011-02-08 13:00 2h Capítulo 1 Aritmética computacional 1.1 Erros absolutos e relativos 1.2 O polinómio de Taylor Resolução do exercício 1.3 2 2011-02-08 15:00 1h30m As aulas laboratoriais só começam
1 2011-02-08 13:00 2h Capítulo 1 Aritmética computacional 1.1 Erros absolutos e relativos 1.2 O polinómio de Taylor Resolução do exercício 1.3 2 2011-02-08 15:00 1h30m As aulas laboratoriais só começam
CAPÍTULO 1 Sistemas de Coordenadas Lineares. Valor Absoluto. Desigualdades 1. CAPÍTULO 2 Sistemas de Coordenadas Retangulares 9. CAPÍTULO 3 Retas 18
 Sumário CAPÍTULO 1 Sistemas de Coordenadas Lineares. Valor Absoluto. Desigualdades 1 Sistema de Coordenadas Lineares 1 Intervalos Finitos 3 Intervalos Infinitos 3 Desigualdades 3 CAPÍTULO 2 Sistemas de
Sumário CAPÍTULO 1 Sistemas de Coordenadas Lineares. Valor Absoluto. Desigualdades 1 Sistema de Coordenadas Lineares 1 Intervalos Finitos 3 Intervalos Infinitos 3 Desigualdades 3 CAPÍTULO 2 Sistemas de
Análise Complexa e Equações Diferenciais 1 o Semestre de 2011/ o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2011, 10h,
 Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Universidade Federal do Paraná - UFPR Centro Politécnico. Departamento de Matemática Plano de curso
 Universidade Federal do Paraná - UFPR Centro Politécnico Departamento de Matemática Plano de curso Disciplina: Cálculo I Código: CM041 Turma: Honours Semestre letivo: 2017/1 Professor: Roberto Ribeiro
Universidade Federal do Paraná - UFPR Centro Politécnico Departamento de Matemática Plano de curso Disciplina: Cálculo I Código: CM041 Turma: Honours Semestre letivo: 2017/1 Professor: Roberto Ribeiro
Planificação Anual Matemática 11º Ano
 ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2018 / 2019 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 72 2º 72 3º 36 Total: 180 1º Período Total
ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2018 / 2019 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 72 2º 72 3º 36 Total: 180 1º Período Total
ANÁLISE MATEMÁTICA I
 DEMec / DEIG DEPARTAMENTO DE ENGENHARIA MECÂNICA DEPARTAMENTO DE ENGENHARIA INDUSTRIAL E GESTÃO ANÁLISE MATEMÁTICA I CONTEÚDO TEÓRICO E APLICAÇÕES Prof. Carlos A. Conceição António Setembro 2013 ii PREFÁCIO
DEMec / DEIG DEPARTAMENTO DE ENGENHARIA MECÂNICA DEPARTAMENTO DE ENGENHARIA INDUSTRIAL E GESTÃO ANÁLISE MATEMÁTICA I CONTEÚDO TEÓRICO E APLICAÇÕES Prof. Carlos A. Conceição António Setembro 2013 ii PREFÁCIO
Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA
 Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA Número da Aula Data da Aula 1 02/09 Sequências Numéricas, definição, exemplos, representação geométrica, convergência e divergência, propriedades,
Matéria das Aulas e Exercícios Recomendados Cálculo II- MAA Número da Aula Data da Aula 1 02/09 Sequências Numéricas, definição, exemplos, representação geométrica, convergência e divergência, propriedades,
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Elementos de Matemática Avançada
 Elementos de Matemática Avançada Prof. Dr. Arturo R. Samana Semestre: 2012.2 Conteúdo - Objetivos da Disciplina - Ementa curricular - Critérios de avaliação - Conteúdo programático - Programação Objetivos
Elementos de Matemática Avançada Prof. Dr. Arturo R. Samana Semestre: 2012.2 Conteúdo - Objetivos da Disciplina - Ementa curricular - Critérios de avaliação - Conteúdo programático - Programação Objetivos
Planificação Anual Matemática A 11º Ano
 ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática A 11º Ano Ano letivo 2017 / 2018 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 60 3º 48 Total: 186 1º Período Total
ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática A 11º Ano Ano letivo 2017 / 2018 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 60 3º 48 Total: 186 1º Período Total
PLANIFICAÇÃO A MÉDIO/LONGO PRAZO
 018/019 DISCIPLINA: Matemática A ANO: 11º CURSO GERAL DE CIÊNCIAS E TECNOLOGIAS Total de aulas previstas: 15 Mês Unidades Temáticas Conteúdos Conteúdos programáticos Descritores N.º Aulas Avaliação Primeiro
018/019 DISCIPLINA: Matemática A ANO: 11º CURSO GERAL DE CIÊNCIAS E TECNOLOGIAS Total de aulas previstas: 15 Mês Unidades Temáticas Conteúdos Conteúdos programáticos Descritores N.º Aulas Avaliação Primeiro
Planificação Anual Matemática 11º Ano
 ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2016/2017 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 72 3º 36 Total: 186 1º Período Total de
ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2016/2017 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 72 3º 36 Total: 186 1º Período Total de
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO
 167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
P L A N I F I C A Ç Ã 0 E n s i n o S e c u n d á r i o
 P L A N I F I C A Ç Ã 0 E n s i n o S e c u n d á r i o 206-207 DISCIPLINA / ANO: Matemática A - ºano MANUAL ADOTADO: NOVO ESPAÇO - Matemática A º ano GESTÃO DO TEMPO Nº de Nº de Nº de tempos tempos tempos
P L A N I F I C A Ç Ã 0 E n s i n o S e c u n d á r i o 206-207 DISCIPLINA / ANO: Matemática A - ºano MANUAL ADOTADO: NOVO ESPAÇO - Matemática A º ano GESTÃO DO TEMPO Nº de Nº de Nº de tempos tempos tempos
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO
 167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
TEMA TÓPICOS OBJETIVOS ESPECÍFICOS AVALIAÇÃO* Lei dos senos e lei dos cossenos. Extensão da definição das razões trigonométricas aos
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO Escola Básica e Secundária Dr. Vieira de Carvalho Departamento de Matemática e Ciências Experimentais Planificação Anual de Matemática A 11º ano Ano Letivo
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO Escola Básica e Secundária Dr. Vieira de Carvalho Departamento de Matemática e Ciências Experimentais Planificação Anual de Matemática A 11º ano Ano Letivo
2MAT017 ELEMENTOS DE MATEMÁTICA
 1ª Série 2MAT015 CÁLCULO I Os números reais e as suas propriedades. Planos coordenados e gráficos. Funções reais: limites e continuidade. Diferenciação de funções reais e aplicações. Regra de L'Hôpital.
1ª Série 2MAT015 CÁLCULO I Os números reais e as suas propriedades. Planos coordenados e gráficos. Funções reais: limites e continuidade. Diferenciação de funções reais e aplicações. Regra de L'Hôpital.
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500. Planificação Anual /Critérios de avaliação
 AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500 Planificação Anual /Critérios de avaliação Disciplina: Matemática A _ 11º ano _ CCH 2016/2017 Início
AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500 Planificação Anual /Critérios de avaliação Disciplina: Matemática A _ 11º ano _ CCH 2016/2017 Início
Unidade Curricular: Análise Matemática I
 DEPARTAMENTO DE MÉTODOS QUANTITATIVOS Unidade Curricular: Análise Matemática I DOCUMENTO DE APRESENTAÇÃO - PROGRAMA Curso de 1º Ciclo: ENGENHARIA de TELECOMUNICAÇÕES e INFORMÁTICA (ETI) e ENGENHARIA INFORMÁTICA
DEPARTAMENTO DE MÉTODOS QUANTITATIVOS Unidade Curricular: Análise Matemática I DOCUMENTO DE APRESENTAÇÃO - PROGRAMA Curso de 1º Ciclo: ENGENHARIA de TELECOMUNICAÇÕES e INFORMÁTICA (ETI) e ENGENHARIA INFORMÁTICA
PLANIFICAÇÃO A MÉDIO/LONGO PRAZO
 07/08 PLANIFICAÇÃO A MÉDIO/LONGO PRAZO DISCIPLINA: Matemática A ANO: º CURSO GERAL DE CIÊNCIAS E TECNOLOGIAS Total de aulas previstas: 53 Mês Unidades Temáticas Conteúdos Conteúdos programáticos Descritores
07/08 PLANIFICAÇÃO A MÉDIO/LONGO PRAZO DISCIPLINA: Matemática A ANO: º CURSO GERAL DE CIÊNCIAS E TECNOLOGIAS Total de aulas previstas: 53 Mês Unidades Temáticas Conteúdos Conteúdos programáticos Descritores
Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
 DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (11º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (13 de setembro a 15 de dezembro) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (11º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (13 de setembro a 15 de dezembro) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
Capítulo 2 Funções de uma variável complexa. A origem dos números complexos repousa na solução de equações algébricas
 Capítulo 2 Funções de uma variável complexa A origem dos números complexos repousa na solução de equações algébricas para. A solução da equação de 1º. grau:, remonta ao Egito antigo. Note que com os coeficientes
Capítulo 2 Funções de uma variável complexa A origem dos números complexos repousa na solução de equações algébricas para. A solução da equação de 1º. grau:, remonta ao Egito antigo. Note que com os coeficientes
Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
 DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (11º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (15 de setembro a 16 de dezembro) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (11º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (15 de setembro a 16 de dezembro) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO
 167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO.
 167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
167 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA PURA E APLICADA PLANO DE ENSINO Código MAT Nome 01167 Equações Diferenciais II Créditos/horas-aula Súmula
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
PLANO CURRICULAR DA DISCIPLINA DE MATEMÁTICA/ 5º ANO. Ano Letivo
 DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS PLANO CURRICULAR DA DISCIPLINA DE MATEMÁTICA/ 5º ANO Ano Letivo 207-208 TEMAS/ CONTEÚDOS Aulas Previstas (* ) º PERÍODO APRESENTAÇÃO/TESTE DIAGNÓSTICO/REVISÕES
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS PLANO CURRICULAR DA DISCIPLINA DE MATEMÁTICA/ 5º ANO Ano Letivo 207-208 TEMAS/ CONTEÚDOS Aulas Previstas (* ) º PERÍODO APRESENTAÇÃO/TESTE DIAGNÓSTICO/REVISÕES
Sumário. 1 CAPÍTULO 1 Revisão de álgebra
 Sumário 1 CAPÍTULO 1 Revisão de álgebra 2 Conjuntos numéricos 2 Conjuntos 3 Igualdade de conjuntos 4 Subconjunto de um conjunto 4 Complemento de um conjunto 4 Conjunto vazio 4 Conjunto universo 5 Interseção
Sumário 1 CAPÍTULO 1 Revisão de álgebra 2 Conjuntos numéricos 2 Conjuntos 3 Igualdade de conjuntos 4 Subconjunto de um conjunto 4 Complemento de um conjunto 4 Conjunto vazio 4 Conjunto universo 5 Interseção
Planificação Anual 12º Ano Área disciplinar de Matemática
 Ano letivo 2018-19 Planificação Anual 12º Ano Área disciplinar de Matemática 1.º Nº de aulas Domínios Conteúdos Atividades/Estratégias 1 Apresentação 18 CC12 16 PRB12 Cálculo Combinatório Propriedades
Ano letivo 2018-19 Planificação Anual 12º Ano Área disciplinar de Matemática 1.º Nº de aulas Domínios Conteúdos Atividades/Estratégias 1 Apresentação 18 CC12 16 PRB12 Cálculo Combinatório Propriedades
Índice. Introdução Unidade 1 Probabilidades e Cálculo Combinatório
 Índice Introdução... 9 Unidade 1 Probabilidades e Cálculo Combinatório Probabilidades Introdução ao cálculo das probabilidades...12 Experiência...13 Classificação para os acontecimentos. Espaço de acontecimentos...14
Índice Introdução... 9 Unidade 1 Probabilidades e Cálculo Combinatório Probabilidades Introdução ao cálculo das probabilidades...12 Experiência...13 Classificação para os acontecimentos. Espaço de acontecimentos...14
Metas/Objetivos/Domínios Conteúdos/Conceitos Número de Aulas
 DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: MATEMÁTICA A ANO:11.º Planificação (Conteúdos)... Período Letivo: 1.º Metas/Objetivos/Domínios Conteúdos/Conceitos Número de Aulas Trigonometria e Funções
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: MATEMÁTICA A ANO:11.º Planificação (Conteúdos)... Período Letivo: 1.º Metas/Objetivos/Domínios Conteúdos/Conceitos Número de Aulas Trigonometria e Funções
3.1 Introdução... 69
 Sumário Prefácio Agradecimentos xi xvii 1 EDOs de primeira ordem 1 1.1 Introdução.............................. 1 1.2 Existência e unicidade de soluções................. 6 1.3 A equação linear..........................
Sumário Prefácio Agradecimentos xi xvii 1 EDOs de primeira ordem 1 1.1 Introdução.............................. 1 1.2 Existência e unicidade de soluções................. 6 1.3 A equação linear..........................
ANÁLISE MATEMÁTICA IV LEEC SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS EDO S. disponível em
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
TEMA TÓPICOS OBJETIVOS ESPECÍFICOS AVALIAÇÃO* Lei dos senos e lei dos cossenos. casos de ângulos retos e obtusos. Resolução de triângulos
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO Escola Básica e Secundária Dr. Vieira de Carvalho Departamento de Matemática e Ciências Experimentais Planificação Anual de Matemática A 11º ano Ano Letivo
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO Escola Básica e Secundária Dr. Vieira de Carvalho Departamento de Matemática e Ciências Experimentais Planificação Anual de Matemática A 11º ano Ano Letivo
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS
 Escolas João de Araújo Correia ORGANIZAÇÃO DO ANO LETIVO 16 17 GESTÃO CURRICULAR DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA A 11º ANO 1º PERÍODO ---------------------------------------------------------------------------------------------------------------------
Escolas João de Araújo Correia ORGANIZAÇÃO DO ANO LETIVO 16 17 GESTÃO CURRICULAR DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA A 11º ANO 1º PERÍODO ---------------------------------------------------------------------------------------------------------------------
DEMEGI DEPARTAMENTO DE ENGENHARIA MECÂNICA E GESTÃO INDUSTRIAL ANÁLISE MATEMÁTICA I
 DEMEGI DEPARTAMENTO DE ENGENHARIA MECÂNICA E GESTÃO INDUSTRIAL ANÁLISE MATEMÁTICA I 1º Ano Licenciaturas: Engenharia Mecânica Gestão e Engenharia Industrial Ano lectivo: 2004/2005, 3ª Edição. Regente da
DEMEGI DEPARTAMENTO DE ENGENHARIA MECÂNICA E GESTÃO INDUSTRIAL ANÁLISE MATEMÁTICA I 1º Ano Licenciaturas: Engenharia Mecânica Gestão e Engenharia Industrial Ano lectivo: 2004/2005, 3ª Edição. Regente da
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Universidade de Évora Departamento de Matemática
 Universidade de Évora Departamento de Matemática Matemática I cursos bolonha: Bioquímica, Biotecnologia cursos regime antigo sem bolonha:bbg,bbi,cae,eag,eal,ebi,ezo,ebg Programa da disciplina 2009/2010
Universidade de Évora Departamento de Matemática Matemática I cursos bolonha: Bioquímica, Biotecnologia cursos regime antigo sem bolonha:bbg,bbi,cae,eag,eal,ebi,ezo,ebg Programa da disciplina 2009/2010
ESCOLA SECUNDÁRIA FERREIRA DIAS, AGUALVA SINTRA ENSINO RECORRENTE DE NÍVEL SECUNDÁRIO POR MÓDULOS CAPITALIZÁVEIS CURSO DE CIÊNCIAS E TECNOLOGIAS
 ESCOLA SECUNDÁRIA FERREIRA DIAS, AGUALVA SINTRA ENSINO RECORRENTE DE NÍVEL SECUNDÁRIO POR MÓDULOS CAPITALIZÁVEIS CURSO DE CIÊNCIAS E TECNOLOGIAS DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS DISCIPLINA
ESCOLA SECUNDÁRIA FERREIRA DIAS, AGUALVA SINTRA ENSINO RECORRENTE DE NÍVEL SECUNDÁRIO POR MÓDULOS CAPITALIZÁVEIS CURSO DE CIÊNCIAS E TECNOLOGIAS DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS DISCIPLINA
UNIVERSIDADE FEDERAL DE PERNAMBUCO. Relatório Perfil Curricular
 PERÍODO: 1º IF663- COMPUTACAO L OBRIG 0 60 60 2.0 SF451- FUNDAMENTOS DA EDUCAÇÃO OBRIG 60 0 60 4.0 INTRODUÇÃO À ANÁLISE E DISCUSSÃO DO FENÔMENO EDUCATUVO, CONSIDERANDO AS RELAÇÕES ENTRE EDUCAÇÃO E SOCIEDADE
PERÍODO: 1º IF663- COMPUTACAO L OBRIG 0 60 60 2.0 SF451- FUNDAMENTOS DA EDUCAÇÃO OBRIG 60 0 60 4.0 INTRODUÇÃO À ANÁLISE E DISCUSSÃO DO FENÔMENO EDUCATUVO, CONSIDERANDO AS RELAÇÕES ENTRE EDUCAÇÃO E SOCIEDADE
Planificação anual de Matemática A 12º ano do ensino secundário Escola Básica e Secundária de Barroselas
 Planificação anual de Matemática A 12º ano do ensino secundário Escola Básica e Secundária de Barroselas Calendário Escolar 2017-2018 1.º Período Início 13 de setembro de 2017 Termo 15 de dezembro de 2017
Planificação anual de Matemática A 12º ano do ensino secundário Escola Básica e Secundária de Barroselas Calendário Escolar 2017-2018 1.º Período Início 13 de setembro de 2017 Termo 15 de dezembro de 2017
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS DA NATUREZA CRITÉRIOS ESPECÍFICOS DE AVALIAÇÃO
 DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS DA NATUREZA CRITÉRIOS ESPECÍFICOS DE AVALIAÇÃO ( Aprovados em Conselho Pedagógico de 25 de outubro de 2016 ) AGRUPAMENTO DE CLARA DE RESENDE CÓD. 152 870 No caso específico
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS DA NATUREZA CRITÉRIOS ESPECÍFICOS DE AVALIAÇÃO ( Aprovados em Conselho Pedagógico de 25 de outubro de 2016 ) AGRUPAMENTO DE CLARA DE RESENDE CÓD. 152 870 No caso específico
Sumário VII. Introdução à Computação Álgebrica com Maple - Lenimar Andrade
 Sumário Prefácio XIII 1 Introdução ao Maple 1 1.1 Introdução.............................. 1 1.2 O menu principal.......................... 4 1.3 A barra de ferramentas....................... 5 1.4 Usando
Sumário Prefácio XIII 1 Introdução ao Maple 1 1.1 Introdução.............................. 1 1.2 O menu principal.......................... 4 1.3 A barra de ferramentas....................... 5 1.4 Usando
Universidade Estadual do Paraná Credenciada pelo Decreto Estadual nº 9538, de 05/12/2013. Campus de União da Vitória
 EDITAL Nº 01/2016 COLEGIADO DE MATEMÁTICA O Colegiado de Matemática informa, por meio deste edital, as datas, salas, horários e conteúdos dos Exames Finais. Segunda 29/02 Prof. Gabriele Terça 01/03 Prof.
EDITAL Nº 01/2016 COLEGIADO DE MATEMÁTICA O Colegiado de Matemática informa, por meio deste edital, as datas, salas, horários e conteúdos dos Exames Finais. Segunda 29/02 Prof. Gabriele Terça 01/03 Prof.
Funções Reais I. Espaços Vetoriais
 ESTRUTURA CURRICULAR Ênfase em Matemática Aplicada Funções Reais I Análise e aprofundamento dos tópicos necessários para desenvolver um estudo completo sobre funções de uma variável real, preparando os
ESTRUTURA CURRICULAR Ênfase em Matemática Aplicada Funções Reais I Análise e aprofundamento dos tópicos necessários para desenvolver um estudo completo sobre funções de uma variável real, preparando os
Capítulo 2 Funções de uma variável complexa. A origem dos números complexos repousa na solução de equações algébricas
 Capítulo 2 Funções de uma variável complexa A origem dos números complexos repousa na solução de equações algébricas para. A solução da equação de 1º. grau:, remonta ao Egito antigo. Note que com os coeficientes
Capítulo 2 Funções de uma variável complexa A origem dos números complexos repousa na solução de equações algébricas para. A solução da equação de 1º. grau:, remonta ao Egito antigo. Note que com os coeficientes
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500 Planificação Anual /Critérios de avaliação. Disciplina: Matemática A 12º ano 2016/2017
 AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500 Planificação Anual /Critérios de avaliação Disciplina: Matemática A 12º ano 2016/2017 Início Fim
AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500 Planificação Anual /Critérios de avaliação Disciplina: Matemática A 12º ano 2016/2017 Início Fim
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500. Planificação Anual /Critérios de avaliação
 AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500 Planificação Anual /Critérios de avaliação Disciplina: Matemática A 12º ano 2015/2016 Início Fim
AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS - Grupo 500 Planificação Anual /Critérios de avaliação Disciplina: Matemática A 12º ano 2015/2016 Início Fim
Resumo Elementos de Análise Infinitésimal I
 Apêndice B Os números naturais Resumo Elementos de Análise Infinitésimal I Axiomática de Peano Axioma 1 : 1 N. Axioma 2 : Se N, então + 1 N. Axioma 3 : 1 não é sucessor de nenhum N. Axioma 4 : Se + 1 =
Apêndice B Os números naturais Resumo Elementos de Análise Infinitésimal I Axiomática de Peano Axioma 1 : 1 N. Axioma 2 : Se N, então + 1 N. Axioma 3 : 1 não é sucessor de nenhum N. Axioma 4 : Se + 1 =
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
ESCOLA SECUNDÁRIA DE CALDAS DAS TAIPAS
 ESCOLA SECUNDÁRIA DE CALDAS DAS TAIPAS Ano letivo 2015/2016 PLANIFICAÇÃO ANUAL MATEMÁTICA A 12.º ANO CURSO C. H. DE CIÊNCIAS E TECNOLOGIAS CURSO C. H. DE CIÊNCIAS SOCIOECONÓMICAS António Filipe Silva Idalina
ESCOLA SECUNDÁRIA DE CALDAS DAS TAIPAS Ano letivo 2015/2016 PLANIFICAÇÃO ANUAL MATEMÁTICA A 12.º ANO CURSO C. H. DE CIÊNCIAS E TECNOLOGIAS CURSO C. H. DE CIÊNCIAS SOCIOECONÓMICAS António Filipe Silva Idalina
Equações Diferenciais com Aplicações. Discente: André Felipe Araújo Ramalho Orientadora: Profª. Jacqueline Félix de Brito.
 Universidade Federal de Campina Grande - UFCG Centro de Ciências e Tecnologia CCT Unidade Acadêmica de Matemática e Estatística UAME Programa de Educação Tutorial PET MATEMÁTICA Equações Diferenciais com
Universidade Federal de Campina Grande - UFCG Centro de Ciências e Tecnologia CCT Unidade Acadêmica de Matemática e Estatística UAME Programa de Educação Tutorial PET MATEMÁTICA Equações Diferenciais com
Universidade de Évora Departamento de Matemática
 Universidade de Évora Departamento de Matemática Matemática I Cursos: Química (cód. 166); Bioquímica (cód. 144) Biotecnologia (cód. 145); Ciências Biofísicas (cód. 178) 1. Noções topológicas em R 1.1 Vizinhança
Universidade de Évora Departamento de Matemática Matemática I Cursos: Química (cód. 166); Bioquímica (cód. 144) Biotecnologia (cód. 145); Ciências Biofísicas (cód. 178) 1. Noções topológicas em R 1.1 Vizinhança
ESCOLA SECUNDÁRIA DE CALDAS DAS TAIPAS
 ESCOLA SECUNDÁRIA DE CALDAS DAS TAIPAS Ano letivo 2016/2017 PLANIFICAÇÃO ANUAL MATEMÁTICA A 12.º ANO CURSO C. H. DE CIÊNCIAS E TECNOLOGIAS CURSO C. H. DE CIÊNCIAS SOCIOECONÓMICAS Arminda Machado José Temporão
ESCOLA SECUNDÁRIA DE CALDAS DAS TAIPAS Ano letivo 2016/2017 PLANIFICAÇÃO ANUAL MATEMÁTICA A 12.º ANO CURSO C. H. DE CIÊNCIAS E TECNOLOGIAS CURSO C. H. DE CIÊNCIAS SOCIOECONÓMICAS Arminda Machado José Temporão
UNIVERSIDADE FEDERAL DE ALFENAS PROGRAMA DE ENSINO DE DISCIPLINA
 Curso: Biotecnologia (13) Ano: 2014 Semestre: 1 Período: 1 Disciplina / Unid. Curricular / Módulo: Cálculo Diferencial e Integral I Código: DCE32 (Differential and Integral Calculus I) Carga Horária Total:
Curso: Biotecnologia (13) Ano: 2014 Semestre: 1 Período: 1 Disciplina / Unid. Curricular / Módulo: Cálculo Diferencial e Integral I Código: DCE32 (Differential and Integral Calculus I) Carga Horária Total:
GUIA DE FUNCIONAMENTO DA UNIDADE CURRICULAR
 GUIA DE FUNCIONAMENTO DA UNIDADE CURRICULAR Matemática Todos os cursos Ano lectivo: 2011/2012 Docentes Responsável Júri Vogal Vogal Responsável pela pauta Docentes que leccionam a UC Ana Maria Lebre Ana
GUIA DE FUNCIONAMENTO DA UNIDADE CURRICULAR Matemática Todos os cursos Ano lectivo: 2011/2012 Docentes Responsável Júri Vogal Vogal Responsável pela pauta Docentes que leccionam a UC Ana Maria Lebre Ana
Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 2 ō Semestre 2009/2010
 Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
