REVISÃO DE MATEMÁTICA BÁSICA
|
|
|
- João Victor Palha
- 6 Há anos
- Visualizações:
Transcrição
1 REVISÃO DE MATEMÁTICA BÁSICA Prof. Jesué Graciliano da Silva 1 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
2 2 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
3 Em uma equação tem-se uma letra que representa a variável (valor desconhecido) e um sinal de igualdade. O lado esquerdo da equação chama-se primeiro membro e o direito segundo membro. REVISÃO DE MATEMÁTICA BÁSICA Nesse anexo vamos mostrar um resumo de alguns conceitos de matemática básica como regra de três, cálculo de áreas, equações simples, volumes e uso de triângulos. 1- NOÇÕES DE ÁLGEBRA Pense no seguinte problema: Se a idade do meu pai somada com a minha é de 100 anos e a diferença entre nossas idades é de 40 anos, qual é a minha idade? Antes de responder a esta pergunta, vamos observar uma balança em equilíbrio onde temos 2 bolas de alumínio de mesma massa e um peso de 8kg no prato da esquerda e dois pesos no prato da direita, o primeiro com 8kg e o segundo com 3kg. Qual será a massa de cada bola de alumínio? A álgebra é muito útil para resolver situações deste tipo. A solução para este problema pode ser bastante facilitada através do uso de um número desconhecido representado por uma letra. A letra x é bastante utilizada como variável desconhecida. Uma análise do problema acima sugere que há equilíbrio entre os dois lados da balança, ou seja, a massa de um lado é igual à massa do outro. Se escrevermos a massa desconhecida como sendo x temos a seguinte relação: 3 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
4 2. x +8=8+3+x 2. x x= x=3 Ou seja, a partir de uma equação algébrica ficou fácil obter o valor da massa da esfera de alumínio como sendo 3kg. Outro exemplo pode ser observado a seguir: Imagine que a soma de dois números consecutivos seja 13. Quais são esses números? Observe que podemos calcular mentalmente estes dois números como sendo 6 e 7, mas isto só é possível porque os números são pequenos e inteiros. Mas quando o problema envolver outros números é comum o uso de equações algébricas como forma de facilitar os cálculos. Veja a solução. Considere que o primeiro número seja x. O segundo, sendo consecutivo só pode ser x+1. Observe ainda que foi dito no enunciado que a soma destes números é igual a 13. Logo temos: x ( x 1) x x x 12 x 6 O primeiro número é 6 e o segundo é 7 conforme já havíamos calculado mentalmente. O que acabamos de fazer chama-se equacionamento. Por definição sabemos que uma EQUAÇÃO é uma igualdade entre duas expressões matemáticas que só é satisfeita por alguns valores. No exemplo anterior, o número 6 era quem satisfazia o problema proposto. Veja por exemplo a equação: 4 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
5 2. x 2. x 2. x x 4 forma: Graficamente podemos representar o problema da seguinte Observe que podíamos trocar o peso de 10 por um de oito e outro de 2kg. Como temos dois quilogramas de cada lado, podemos tirar estes dois pesos sem mudar o equilíbrio. A massa de oito do lado direito poderia ser substituída por outras duas massas de 4kg cada. Como temos agora duas esferas de mesma massa fica claro que a massa da esfera é de 4kg. Para finalizar a equação é preciso verificar se a resposta satisfaz: Para tanto, coloque o valor 4 na posição de x da equação. Observe que o resultado fica 10 = x+ 2 = 10 5 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
6 Agora que você já aprendeu tudo isso, pense na pergunta inicial. Lembre-se que eu disse que a idade de meu pai somada com a minha dá 100 anos. A diferença entre nossas idades é de 40 anos. Para resolver o problema, basta considerar que x é a idade do filho e y é a idade do pai, logo: x y 100 y x 40 Podemos isolar o valor de y na segunda equação e substituir na primeira como segue: x 40 y 40 x x (40 x x x 60 x x) x 30 2 Logo a idade de meu filho é de 30 anos. 2- REGRAS DE OPERAÇÕES Agora que você está craque em equações é bom relembrar algumas regras de operações com números e expressões numéricas. Nesta aula vamos falar um pouco sobre propriedades das operações como comutativa, distributiva e associativa. Elas são muito importantes para uma correta análise das equações aprendidas na aula anterior. 6 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
7 Supondo que um pai vá fazer uma compra de material escolar, cujos cadernos custam R$ 18,00, os livros R$40,00 e as canetas R$32,00. Como ele deve somar todos estes valores mentalmente e de forma rápida? Isso pode ser feito sem problemas usando algumas regras matemáticas. Veja de que forma! (18 32) Observe que usamos a propriedade comutativa (trocando o 40 e o 18 de posição) e a propriedade associativa (juntando o 18 e o 32). O importante aqui é lembrar sempre que numa adição a ordem dos fatores não altera o resultado. Podemos comutar e associar termos sem problema, o que facilita a realização dos cálculos. Na multiplicação estas regras também são válidas. Por exemplo, considere um terreno de 20 metros de comprimento e 15 metros de largura em que precisamos fazer o muro em todo seu contorno. Quantos metros quadrados de alvenaria são necessários se a altura do muro fosse de 1,5m? 7 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
8 A soma das medidas laterais do terreno em metros (PERÍMETRO) é de 20m+15m+20m+15m, ou seja, 70m. A área lateral do muro será 70m de comprimento vezes 1,5m de altura, ou também 1,5m vezes 70m, o que resulta em 105m 2 de alvenaria. Observe que a ordem dos fatores também não afeta o resultado na multiplicação. Se para cada metro quadrado de construção do muro são necessários 25 tijolos, então precisamos comprar 2625 tijolos. Observe ainda que a ordem de realização das operações. Primeiro devem ser realizadas as multiplicações e as divisões para somente depois realizarmos as adições e subtrações. A seguir ilustramos uma aplicação do que acabamos de dizer: = = = 74 Para cálculos mais difíceis é importante conhecer regras na aplicação das propriedades. Para tanto utilizamos representações como ( ), [ ] e { } que são os parênteses, colchetes e chaves. Esses sinais indicam a preferência da realização dos cálculos. Observe o exemplo: Primeiramente realizamos as operações que estão entre parênteses, depois entre chaves para finalmente realizar aquelas que estão entre colchetes. 8 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
9 4. 4 )+( 36 3) = = = 15+ 8= ( + 8= 3- REGRA DE TRÊS Você já ouviu falar de regra de três? Talvez não, mas tenho certeza que você utiliza este conceito no dia a dia. Por exemplo, quando o jornalista fala na televisão que um dólar está valendo R$ 3,00. Quanto você teria em reais se tivesse guardado U$20,00? É simples, se um dólar vale 3 reais, então 20 dólares valem 60 reais. Outro exemplo é o caso de um carro que percorre uma rodovia a 80km/h. Em doze horas, quantos quilômetros ele percorrerá? Você pode resolver o problema através de um raciocínio mental ou através de uma tabela de proporcionalidade como segue: Tempo (horas) Espaço (km) x O tempo e o espaço são proporcionais, ou seja, à medida que o tempo passa o espaço percorrido também aumenta. Assim sendo temos uma relação de proporcionalidade direta e podemos montar uma proporção conforme a tabela acima. 9 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
10 x x 960 km x Observe que o nome regra de três vem dessa tabela. Ou seja, conhecemos 3 elementos e desejamos encontrar o quarto. Esse tipo de regra é muito importante nas conversões de unidades. Outro exemplo: Para aquecer 2 litros de água em 50 o C é preciso 100 kcal (k é igual a 1000). Logo, para aquecer 6 litros de água serão necessárias 300 kcal. Isto é feito diretamente porque as grandezas são proporcionais. Agora que aprendemos um pouco mais sobre regra de três fica claro o que fazer quando um catálogo diz que a capacidade do aparelho é de Btu/h e desejamos saber quanto esse valor vale em Watts, que é a unidade do Sistema Internacional. Das tabelas de conversões sabemos que Btu/h é igual a 3.517W, isto quer dizer que Btu/h vale x, ou seja, x é igual a 7014 W. Observe o quadro: Potência (Btu/h) Potência (W) x Mas nem toda regra de três é tão direta assim. Existem aquelas em que a relação de proporção é inversa. Veja o interessante caso. Um exemplo: Se 2 pintores gastam 18h para pintar uma casa. Quanto tempo levarão 4 pintores para realizar o mesmo serviço? 10 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
11 Número de pintores Tempo (h) x Observe agora que se o número de pintores aumenta é claro que o tempo do serviço cairá. Logo a relação de proporção é inversa. Se número de pintores dobra o tempo cai pela metade. 2 x x x 9h 4 18 Como estamos trabalhando com grandezas inversamente proporcionais temos que inverter a posição do x. Além da regra de três simples existe a regra de três composta, mas não entraremos em detalhes sobre o seu uso aqui. Outra aplicação importante da regra de três é no cálculo de porcentagem. Por exemplo, suponha que você aplique R$600,00 na poupança e ao final do mês a correção foi de R$21,00. Pergunto-lhe qual foi a taxa de rendimento? Observe que R$ 600,00 é o valor principal (capital) e R$21,00 é o rendimento. A taxa de rendimento (i) é dada da seguinte forma: Capital (R$) Rendimento (%) 600, ,00 X x 21,00.100% 600,00 3,5% 3, ,35 11 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
12 Observe que escrevemos 3,5% na forma fracionária (3,5/100) que é o mesmo que dizer 0,35. Cuidado com isso porque em algumas situações o valor deve ser introduzido na equação a ser trabalhada de maneira decimal. 4- CÁLCULO DE ÁREAS Para se escolher o melhor aparelho de ar condicionado para um dado ambiente o técnico necessita calcular uma série de áreas como das janelas, paredes e coberturas. Outro exemplo onde este cálculo é fundamental é na confecção dos dutos. Dessa forma é possível especificar a quantidade de chapas de aço são necessárias para a execução da obra. Não existe um equipamento para medir área, como o termômetro que serve para medir temperatura ou como a trena que serve para medir o comprimento. O que se faz é comparar a nossa superfície de interesse, uma janela, por exemplo, com um quadrado de 1 metro de lado. Olhe este exemplo: Quantos vidros de 1m por 1m cabem em uma área de janela de 3 metros de largura por 1 metro de altura? A área da janela pode ser calculada multiplicando o seu comprimento vezes sua largura. Já a área do quadrado obtida 12 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
13 através da multiplicação de seus lados. Cada quadrado tem 1 m 2, logo na janela temos 3 pedaços de 1 m 2 de vidro. 1m 1m 2 1m Observe ainda que assim como 1 metro quadrado refere-se a um quadrado de 1metro de lado, 1 km quadrado corresponde a uma superfície de um quadrado de 1 quilômetro de lado. Da mesma forma, 1cm 2 é correspondente a uma superfície de um quadrado de 1 cm de lado. Agora pense bem: Quantos cm 2 cabem em um quadrado de 1 m de lado? Lembre-se que em 1 metro cabem 10 cm. Por isso, cabem quadradinhos de 1 cm 2 no quadrado de 1metro por 1 metro de lado. Existem algumas figuras que são bastante utilizadas na prática profissional. Por isso é importante que você saiba calcular as áreas de quadrados, retângulos, triângulos, círculos, losangos e de trapézios. QUADRADO: Conforme já vimos, a área do quadrado é seu lado multiplicado por ele mesmo. Podemos utilizar letras para representar os lados destas figuras, no caso do quadrado chamamos de a o lado. Logo a área é dada por a vezes a que é igual a a Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
14 RETÂNGULO: Neste caso um lado é maior que o outro. Sendo a e b medidas destes lados podemos escrever que a área é a vezes b. b a A= b.a PARALELOGRAMO: esta figura tem como característica o fato de seus lados serem paralelos. Dessa forma o quadrado e o retângulo não deixam de ser paralelogramos com 4 ângulos retos cada (90 graus entre um lado e outro). Observe que h é a distância entre uma base até a outra na perpendicular!! Analisando a figura obtida após modificar a 14 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
15 posição do triângulo da esquerda para o lado direito temos que a área é dada por base b vezes altura h, isto é: A= b.h LOSANGO: é uma figura geométrica de lados iguais e diagonais perpendiculares. Um losango muito famoso é o da bandeira do Brasil em amarelo. Considerando que AB é a diagonal maior D e CD é a diagonal menor d podemos escrever a área do losango como: CÍRCULO: Considerando que R represente o raio do círculo, sua área pode ser calculada como sendo: Vale lembrar ainda que em relação ao círculo, uma relação importante é o perímetro da sua circunferência que é dada por: Perímetro 2.. R. D 15 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
16 TRIÂNGULO: Os triângulos são figuras geométricas muito importantes e o segredo de sua construção já era conhecido pelos antigos egípcios há 4000 anos. O seu uso é generalizado na construção do ângulo de 90 graus entre duas paredes, o mesmo princípio utilizado para construir as bases das perfeitas pirâmides regulares dos antigos faraós. Sua área é calculada por: No caso de um triângulo retângulo, quando duas dimensões do triângulo são conhecidas e uma delas não, usamos o Teorema de Pitágoras que diz que: a soma do quadrado dos catetos é igual ao quadrado da hipotenusa. 16 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
17 Observe que os arquitetos egípcios já conheciam esta relação entre os lados de um triângulo retângulo há muito tempo. a 2 b Ou seja, se conhecemos que a hipotenusa de um triângulo retângulo mede 5m e que um lado vale 3m e que o triângulo é retângulo então através do Teorema de Pitágoras temos o outro lado do: 2 c 2 Observe na figura a seguir que os egípcios utilizavam cordas com nós para fazer o esquadro das bases das pirâmides. TRAPÉZIO: um trapézio é um quadrilátero com 2 lados paralelos (base). Para o cálculo de sua área podemos usar uma equação pronta ou dividir a figura em paralelogramos e triângulos, calculando assim a área de cada figura em separado e depois somando tudo. Veja o exemplo: Nesse caso a área da figura poderia ser escrita como: 17 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
18 5- CÁLCULO DE VOLUMES Finalmente vamos comentar um pouco sobre volumes de alguns elementos geométricos bastante utilizados na vida profissional de um técnico, tais como cubos, paralelepípedos, cilindros, esferas e pirâmides. Volume de um PARALELEPÍPEDO: considere um aparelho de ar condicionado de janela. Podemos com uma trena saber que seus lados têm medidas definidas por a, b e c. O seu volume nesse caso é calculado pela multiplicação direta destes três lados, ou seja: Volume de um CILINDRO: o cilindro tem seu volume definido pela área da base multiplicada pela altura. Lembre-se que o diâmetro da base é sempre duas vezes o raio. 2 V = Ab. H = π. R. H Volume de uma ESFERA. Uma esfera é uma forma geométrica apreciada por todos. Seu volume é escrito como: V = 4. π. R 3 Volume de um CONE e de uma PIRÂMIDE. Um cone ou uma pirâmide têm seus volumes calculados através da equação: 3 18 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
19 onde H é a altura do cone ou da pirâmide. 19 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
20 EXERCÍCIOS: 1- Um duto de climatização tem 20m de comprimento e diâmetro de 80cm. Calcule qual é a área de chapas necessária para sua construção. 2- Um auditório tem 20m de comprimento por 12m de largura por 5m de altura. Se é preciso renovar o ar a uma taxa de 6 volumes de ar por hora, qual é a taxa de ar de renovação por hora? 3- Um duto de climatização tem formato oval e 12m de comprimento. Qual é a área de chapas necessária para sua construção? 4- Uma caixa d água de um tanque de termoacumulação tem 12m de altura e 2m de diâmetro. Quantos litros de água cabem nesse reservatório? 5- Uma tubulação de cobre com diâmetro interno de 3/8 e 20m de comprimento tem um volume aproximado de quantos metros cúbicos? A espessura do tubo é de 3mm (1 = 1 polegada = 25,4mm). 20 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
21 Saiba mais sobre Matemática Básica: 21 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
22 DICAS DE ESTUDO Há pessoas que aprendem melhor ouvindo do que escrevendo. Nesse caso, gravar o áudio de uma videoaula em mp3 ou gravar no celular o resumo da matéria para escutar durante o tempo livro pode contribuir para uma melhor fixação dos conteúdos. Há pessoas que aprendem fazendo resumos, outras precisam associar os conteúdos com questões concretas do dia a dia. Há estudos que afirmam que lembramos apenas uma pequena parte do que somente ouvimos e lemos. Lembramos 70% do que discutimos com outros e, aproximadamente, 90% do que nós, pessoalmente, experimentamos e ensinamos para os outros. Então, a dica é colocar em prática todo conteúdo ensinado pelos professores e estabelecer conexões concretas com o dia-a-dia. Por isso é tão importante aproveitar bem as aulas de laboratório para entender na prática os fenômenos físicos explicados em aula. No ensino tradicional, ASSISTIR AULAS muitas vezes é uma atividade passiva e coletiva. Os alunos podem estar pensando em qualquer coisa durante as aulas. O processo de ESTUDAR é uma atividade ativa e solitária. Temos que refletir sobre o assunto, fazer relações, analisar as aplicações na nossa vida. Mas isso não significa que não possamos aprender em grupo. O ideal é mesclar o estudo individual com o estudo em grupo, o que permite uma 22 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
23 rica troca de conhecimentos. Explicar o que entendemos sobre um assunto para o colega faz com que a retenção do conteúdo seja aumentada. Dizem que quem ensina o que sabe aprende duas vezes. Por muito tempo era necessário que o aluno e o professor estivessem no mesmo espaço para que o processo de ensino-aprendizagem acontecesse. Na atualidade, com a internet o estudante pode aprender também por iniciativa própria, avaliando catálogos de equipamentos, assistindo a videoaula e lendo livros e apostilas disponíveis na rede. Há excelente material no Portal do Professor (MEC), na Khan Academy e no YOUTUBE. Os estudantes podem obter grande quantidade de informações de forma rápida. Mas é preciso saber filtrar as informações úteis do lixo eletrônico disponível. Há muitas aulas disponíveis na internet para que o aluno aprenda no seu próprio ritmo ao longo de toda a vida. Há muitos blogs, grupos de Whattapps e fóruns de profissionais que estão estudando o mesmo conteúdo e isso permite o compartilhamento de experiências. Há muitos especialistas que afirmam que ALUNO (origem da palavra: a = sem, luno = luz) é um ser passivo no processo de ensinoaprendizagem. Um aluno pode estar presente, mas não estar concentrado nos assuntos tratados na aula. Já um ESTUDANTE é um ser ativo que assume a responsabilidade pelo seu aprendizado. Um ESTUDANTE pode estudar em casa e ainda ter uma postura proativa em sala de aula, acompanhando o que está sendo explicado e participando das discussões. Aproveite para tirar as dúvidas nos horários de atendimento paralelo de seus professores. Anote os horários para procurá-los sempre que for necessário. Estamos torcendo pelo seu sucesso. Uma grande caminhada começa com pequenos passos! Bom estudo! 23 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São José - IFSC
Disciplina: Matemática DIAGNÓSTICO PROF. REGENTE DOMÍNIOS / CONTEÚDOS DESCRIÇÃO DO CONTEÚDO ACOMPANHAMENTO DO PROFESSOR DA SAA. Não At.
 Escola: Nome do Aluno: Professor Regente: Tempo de Permanência no Programa: Disciplina: Matemática Turma: Data Nasc.: / / Professor da Sala de Apoio: Entrada / / Saída / / DOMÍNIOS / CONTEÚDOS DESCRIÇÃO
Escola: Nome do Aluno: Professor Regente: Tempo de Permanência no Programa: Disciplina: Matemática Turma: Data Nasc.: / / Professor da Sala de Apoio: Entrada / / Saída / / DOMÍNIOS / CONTEÚDOS DESCRIÇÃO
DEPARTAMENTO DE MATEMÁTICA INFORMÁTICA DISCIPLINA: Matemática (7º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período
 ANO LETIVO 2015/2016 DEPARTAMENTO DE MATEMÁTICA INFORMÁTICA DISCIPLINA: Matemática (7º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período Metas / Objetivos Conceitos / Conteúdos Aulas Previstas Números e
ANO LETIVO 2015/2016 DEPARTAMENTO DE MATEMÁTICA INFORMÁTICA DISCIPLINA: Matemática (7º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período Metas / Objetivos Conceitos / Conteúdos Aulas Previstas Números e
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro?
 Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
MATEMÁTICA PLANEJAMENTO 4º BIMESTRE º B - 11 Anos
 PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 4º
PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 4º
1.0. Conceitos Utilizar os critérios de divisibilidade por 2, 3, 5 e Utilizar o algoritmo da divisão de Euclides.
 Conteúdo Básico Comum (CBC) Matemática - do Ensino Fundamental do 6º ao 9º ano Os tópicos obrigatórios são numerados em algarismos arábicos Os tópicos complementares são numerados em algarismos romanos
Conteúdo Básico Comum (CBC) Matemática - do Ensino Fundamental do 6º ao 9º ano Os tópicos obrigatórios são numerados em algarismos arábicos Os tópicos complementares são numerados em algarismos romanos
TEOREMA DE PITÁGORAS AULA ESCRITA
 TEOREMA DE PITÁGORAS AULA ESCRITA 1. Introdução O Teorema de Pitágoras é uma ferramenta importante na matemática. Ele permite calcular a medida de alguma coisa que não conseguimos com o uso de trenas ou
TEOREMA DE PITÁGORAS AULA ESCRITA 1. Introdução O Teorema de Pitágoras é uma ferramenta importante na matemática. Ele permite calcular a medida de alguma coisa que não conseguimos com o uso de trenas ou
PLANO DE ESTUDOS DE MATEMÁTICA - 7.º ANO
 DE MATEMÁTICA - 7.º ANO Ano Letivo 2014 2015 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de multiplicar e dividir números racionais relativos. No domínio da Geometria e Medida,
DE MATEMÁTICA - 7.º ANO Ano Letivo 2014 2015 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de multiplicar e dividir números racionais relativos. No domínio da Geometria e Medida,
ADA 1º BIMESTRE CICLO I MATEMÁTICA 9º ANO DO ENSINO FUNDAMENTAL 2018
 ADA 1º BIMESTRE CICLO I MATEMÁTICA 9º ANO DO ENSINO FUNDAMENTAL 018 ITEM 1 DA ADA Observe potência a seguir: ( ) O resultado dessa potenciação é igual a (A) 8 1. (B) 1 8. (C) 1 81 81 (D) 1 Dada uma potência
ADA 1º BIMESTRE CICLO I MATEMÁTICA 9º ANO DO ENSINO FUNDAMENTAL 018 ITEM 1 DA ADA Observe potência a seguir: ( ) O resultado dessa potenciação é igual a (A) 8 1. (B) 1 8. (C) 1 81 81 (D) 1 Dada uma potência
Teorema de Pitágoras
 Teorema de Pitágoras Luan Arjuna 1 Introdução Uma das maiores preocupações dos matemáticos da antiguidade era a determinação de comprimentos: desde a altura de um edifício até a distância entre duas cidades,
Teorema de Pitágoras Luan Arjuna 1 Introdução Uma das maiores preocupações dos matemáticos da antiguidade era a determinação de comprimentos: desde a altura de um edifício até a distância entre duas cidades,
DEPARTAMENTO DE MATEMÁTICA INFORMÁTICA DISCIPLINA:
 ANO LETIVO 2015/2016 DEPARTAMENTO DE MATEMÁTICA INFORMÁTICA DISCIPLINA: Matemática (7º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período Metas / Objetivos Conceitos / Conteúdos Aulas Previstas Números e
ANO LETIVO 2015/2016 DEPARTAMENTO DE MATEMÁTICA INFORMÁTICA DISCIPLINA: Matemática (7º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período Metas / Objetivos Conceitos / Conteúdos Aulas Previstas Números e
PLANO DE ESTUDOS DE MATEMÁTICA 7.º ANO
 DE MATEMÁTICA 7.º ANO Ano Letivo 2015 2016 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de multiplicar e dividir números racionais relativos. No domínio da Geometria e Medida,
DE MATEMÁTICA 7.º ANO Ano Letivo 2015 2016 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de multiplicar e dividir números racionais relativos. No domínio da Geometria e Medida,
7º Ano. Planificação Matemática 2014/2015. Escola Básica Integrada de Fragoso 7º Ano
 7º Ano Planificação Matemática 2014/2015 Escola Básica Integrada de Fragoso 7º Ano Domínio Subdomínio Conteúdos Objetivos gerais / Metas Números e Operações Números racionais - Simétrico da soma e da diferença
7º Ano Planificação Matemática 2014/2015 Escola Básica Integrada de Fragoso 7º Ano Domínio Subdomínio Conteúdos Objetivos gerais / Metas Números e Operações Números racionais - Simétrico da soma e da diferença
7.º Ano. Planificação Matemática 2016/2017. Escola Básica Integrada de Fragoso 7.º Ano
 7.º Ano Planificação Matemática 201/2017 Escola Básica Integrada de Fragoso 7.º Ano Geometria e medida Números e Operações Domínio Subdomínio Conteúdos Objetivos gerais / Metas Números racionais - Simétrico
7.º Ano Planificação Matemática 201/2017 Escola Básica Integrada de Fragoso 7.º Ano Geometria e medida Números e Operações Domínio Subdomínio Conteúdos Objetivos gerais / Metas Números racionais - Simétrico
Roteiro de trabalho para o 5o ano
 Roteiro de trabalho para o 5o ano No volume do 5º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
Roteiro de trabalho para o 5o ano No volume do 5º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
Para se adicionar (ou subtrair) frações com o mesmo denominador devemos somar (ou subtrair) os numeradores e conservar o denominador comum. = - %/!
 Pontifícia Universidade Católica de Goiás Professor: Ms. Edson Vaz de Andrade Fundamentos de Matemática No estudo de Física frequentemente nos deparamos com a necessidade de realizar cálculos matemáticos
Pontifícia Universidade Católica de Goiás Professor: Ms. Edson Vaz de Andrade Fundamentos de Matemática No estudo de Física frequentemente nos deparamos com a necessidade de realizar cálculos matemáticos
Quadro de conteúdos MATEMÁTICA
 Quadro de conteúdos MATEMÁTICA 1 Apresentamos a seguir um resumo dos conteúdos trabalhados ao longo dos quatro volumes do Ensino Fundamental II, ou seja, um panorama dos temas abordados na disciplina de
Quadro de conteúdos MATEMÁTICA 1 Apresentamos a seguir um resumo dos conteúdos trabalhados ao longo dos quatro volumes do Ensino Fundamental II, ou seja, um panorama dos temas abordados na disciplina de
NOÇÕES DE GEOMETRIA PLANA
 NOÇÕES DE GEOMETRIA PLANA Polígonos são figuras planas fechadas com lados retos. Todo polígono possui os seguintes elementos: ângulos, vértices, diagonais e lados. De acordo com o número de lados o polígono
NOÇÕES DE GEOMETRIA PLANA Polígonos são figuras planas fechadas com lados retos. Todo polígono possui os seguintes elementos: ângulos, vértices, diagonais e lados. De acordo com o número de lados o polígono
Agora vamos rever alguns conceitos básicos. da Geometria, estudados ao longo do Telecurso Observe a figura abaixo e resolva a seguinte questão:
 A UA UL LA Revisão II Geometria Introdução Agora vamos rever alguns conceitos básicos da Geometria, estudados ao longo do Telecurso 2000. Observe a figura abaixo e resolva a seguinte questão: Uma formiga
A UA UL LA Revisão II Geometria Introdução Agora vamos rever alguns conceitos básicos da Geometria, estudados ao longo do Telecurso 2000. Observe a figura abaixo e resolva a seguinte questão: Uma formiga
CADERNO DE EXERCÍCIOS DE MECÂNICA DOS FLUIDOS
 CADERNO DE EXERCÍCIOS DE MECÂNICA DOS FLUIDOS Prof. Jesué Graciliano da Silva https://jesuegraciliano.wordpress.com/aulas/mecanica-dos-fluidos/ 1 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São
CADERNO DE EXERCÍCIOS DE MECÂNICA DOS FLUIDOS Prof. Jesué Graciliano da Silva https://jesuegraciliano.wordpress.com/aulas/mecanica-dos-fluidos/ 1 Prof. Jesué Graciliano da Silva Refrigeração - Câmpus São
G A B A R I T O G A B A R I T O
 Prova Anglo P-2 G A B A R I T O Tipo D-9-05/2011 01. C 07. A 13. D 19. C 02. C 08. B 14. B 20. B 03. D 09. C 15. D 21. D 04. A 10. A 16. D 22. A 05. B 11. B 17. C 00 06. D 12. C 18. A 00 841201911 PROVA
Prova Anglo P-2 G A B A R I T O Tipo D-9-05/2011 01. C 07. A 13. D 19. C 02. C 08. B 14. B 20. B 03. D 09. C 15. D 21. D 04. A 10. A 16. D 22. A 05. B 11. B 17. C 00 06. D 12. C 18. A 00 841201911 PROVA
Cubo Um paralelepípedo retângulo com todas as arestas congruentes ( a= b = c) recebe o nome de cubo. Dessa forma, as seis faces são quadrados.
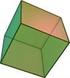 ALUNO(A) AULA 002 MATEMÁTICA DATA 18 / 10 /2013 PROFESSOR: Paulo Roberto Weissheimer AULA 002 - DE MATEMÁTICA Geometria Espacial Relação de Euler Em todo poliedro convexo é válida a relação seguinte: V
ALUNO(A) AULA 002 MATEMÁTICA DATA 18 / 10 /2013 PROFESSOR: Paulo Roberto Weissheimer AULA 002 - DE MATEMÁTICA Geometria Espacial Relação de Euler Em todo poliedro convexo é válida a relação seguinte: V
Agrupamento de Escolas de Águeda Escola Básica Fernando Caldeira
 Agrupamento de Escolas de Águeda Escola Básica Fernando Caldeira Currículo da disciplina de Matemática - 7ºano Unidade 1 Números inteiros Propriedades da adição de números racionais Multiplicação de números
Agrupamento de Escolas de Águeda Escola Básica Fernando Caldeira Currículo da disciplina de Matemática - 7ºano Unidade 1 Números inteiros Propriedades da adição de números racionais Multiplicação de números
SISTEMA ANGLO DE ENSINO G A B A R I T O
 SISTEMA ANGLO DE ENSINO Prova Anglo P-02 Tipo D9-08/2010 G A B A R I T O 01. B 07. B 13. C 19. D 02. C 08. D 14. B 20. B 03. A 09. C 15. B 21. C 04. D 10. C 16. C 22. D 05. D 11. C 17. D 00 06. B 12. A
SISTEMA ANGLO DE ENSINO Prova Anglo P-02 Tipo D9-08/2010 G A B A R I T O 01. B 07. B 13. C 19. D 02. C 08. D 14. B 20. B 03. A 09. C 15. B 21. C 04. D 10. C 16. C 22. D 05. D 11. C 17. D 00 06. B 12. A
Área: conceito e áreas do quadrado e do retângulo
 Área: conceito e áreas do quadrado e do retângulo Dada uma figura no plano, vamos definir a área desta figuracomo o resultado da comparação da figura dada como uma certa unidade de medida. No caso do conceito
Área: conceito e áreas do quadrado e do retângulo Dada uma figura no plano, vamos definir a área desta figuracomo o resultado da comparação da figura dada como uma certa unidade de medida. No caso do conceito
APOSTILA DE MATEMÁTICA PM/PA 2016
 APOSTILA DE MATEMÁTICA PM/PA 2016 Olá, tudo bem? Sou o Prof. Arthur Lima, e resumi nas próximas páginas os pontos do edital de MATEMÁTICA da POLÍCIA MILITAR DO PARÁ, cujas provas serão aplicadas pela banca
APOSTILA DE MATEMÁTICA PM/PA 2016 Olá, tudo bem? Sou o Prof. Arthur Lima, e resumi nas próximas páginas os pontos do edital de MATEMÁTICA da POLÍCIA MILITAR DO PARÁ, cujas provas serão aplicadas pela banca
Prova final de MATEMÁTICA - 3o ciclo a Fase
 Prova final de MATEMÁTICA - 3o ciclo 2016-2 a Fase Proposta de resolução Caderno 1 1. Calculando a diferença entre 3 1 e cada uma das opções apresentadas, arredondada às centésimas, temos que: 3 1 2,2
Prova final de MATEMÁTICA - 3o ciclo 2016-2 a Fase Proposta de resolução Caderno 1 1. Calculando a diferença entre 3 1 e cada uma das opções apresentadas, arredondada às centésimas, temos que: 3 1 2,2
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO
 ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO ANO 2015 PROFESSOR (a) DISCIPLINA Bruno Rezende Pereira Matemática ALUNO (a) SÉRIE 3º Ano do Ensino Médio
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO ANO 2015 PROFESSOR (a) DISCIPLINA Bruno Rezende Pereira Matemática ALUNO (a) SÉRIE 3º Ano do Ensino Médio
PLANIFICAÇÃO ANUAL DE MATEMÁTICA
 1.º Período Agrupamento de Escolas António Correia de Oliveira PLANIFICAÇÃO ANUAL DE MATEMÁTICA 7.º ANO ANO LETIVO 2016/17 Números Racionais Números e operações NO7 Números racionais - Simétrico da soma
1.º Período Agrupamento de Escolas António Correia de Oliveira PLANIFICAÇÃO ANUAL DE MATEMÁTICA 7.º ANO ANO LETIVO 2016/17 Números Racionais Números e operações NO7 Números racionais - Simétrico da soma
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MATEMÁTICA - 3o ciclo 007 - a Chamada Proposta de resolução. Como a planta está desenhada à escala de :0 e o Miguel está sentado a 3 m do televisor, ou seja 300 cm, então a distância, em
Prova final de MATEMÁTICA - 3o ciclo 007 - a Chamada Proposta de resolução. Como a planta está desenhada à escala de :0 e o Miguel está sentado a 3 m do televisor, ou seja 300 cm, então a distância, em
Geometria Euclidiana Plana
 CURSO INTRODUTÓRIO DE MTEMÁTIC PR ENGENHRI 016. Geometria Euclidiana Plana Parte II Danielly Guabiraba Dantas - Engenharia Civil Rafael lves da Silva - Engenharia Civil Introdução Desde os egípcios, que
CURSO INTRODUTÓRIO DE MTEMÁTIC PR ENGENHRI 016. Geometria Euclidiana Plana Parte II Danielly Guabiraba Dantas - Engenharia Civil Rafael lves da Silva - Engenharia Civil Introdução Desde os egípcios, que
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MATEMÁTICA - o ciclo 006-1 a Chamada Proposta de resolução 1. 1.1. Como a Marta pesa 45 kg, e para evitar lesões na coluna vertebral, o peso de uma mochila e o do material que se transporta
Prova final de MATEMÁTICA - o ciclo 006-1 a Chamada Proposta de resolução 1. 1.1. Como a Marta pesa 45 kg, e para evitar lesões na coluna vertebral, o peso de uma mochila e o do material que se transporta
Áreas parte 1. Rodrigo Lucio Silva Isabelle Araújo
 Áreas parte 1 Rodrigo Lucio Silva Isabelle Araújo Introdução Desde os egípcios, que procuravam medir e demarcar suas terras, até hoje, quando topógrafos, engenheiros e arquitetos fazem seus mapeamentos
Áreas parte 1 Rodrigo Lucio Silva Isabelle Araújo Introdução Desde os egípcios, que procuravam medir e demarcar suas terras, até hoje, quando topógrafos, engenheiros e arquitetos fazem seus mapeamentos
APOSTILA DE APOIO PEDAGÓGICO 9º ANO
 GOVERNO MUNICIPAL DE CAUCAIA SECRETARIA MUNICIPAL DE EDUCAÇÃO - SME COORDENADORIA DE DESENVOLVIMENTO PEDAGÓGICO ANOS FINAIS APOSTILA DE APOIO PEDAGÓGICO 9º ANO 2º ENCONTRO DE MATEMÁTICA PROFESSORES FORMADORES:
GOVERNO MUNICIPAL DE CAUCAIA SECRETARIA MUNICIPAL DE EDUCAÇÃO - SME COORDENADORIA DE DESENVOLVIMENTO PEDAGÓGICO ANOS FINAIS APOSTILA DE APOIO PEDAGÓGICO 9º ANO 2º ENCONTRO DE MATEMÁTICA PROFESSORES FORMADORES:
Caro(a) aluno(a), Coordenadoria de Estudos e Normas Pedagógicas CENP Secretaria da Educação do Estado de São Paulo Equipe Técnica de Matemática
 Caro(a) aluno(a), Você saberia representar a soma dos n primeiros números naturais a partir do 1? Neste Caderno você terá a oportunidade de conhecer esse e outros casos que envolvem sequências e resolvê-los
Caro(a) aluno(a), Você saberia representar a soma dos n primeiros números naturais a partir do 1? Neste Caderno você terá a oportunidade de conhecer esse e outros casos que envolvem sequências e resolvê-los
Soluções Comentadas Matemática Curso Mentor Aprendizes-Marinheiros. Barbosa, L.S.
 Soluções Comentadas Matemática Curso Mentor Aprendizes-Marinheiros Barbosa, L.S. [email protected] 6 de dezembro de 2014 2 Sumário I Provas 5 1 Matemática 2013/2014 7 2 Matemática 2014/2015
Soluções Comentadas Matemática Curso Mentor Aprendizes-Marinheiros Barbosa, L.S. [email protected] 6 de dezembro de 2014 2 Sumário I Provas 5 1 Matemática 2013/2014 7 2 Matemática 2014/2015
Grupo 1 - PIC OBMEP 2011 Módulo 2 - Geometria. Resumo do Encontro 6, 22 de setembro de Questões de geometria das provas da OBMEP
 Grupo 1 - PIC OBMEP 2011 Módulo 2 - Geometria Resumo do Encontro 6, 22 de setembro de 2012 Questões de geometria das provas da OBMEP http://www.obmep.org.br/provas.htm 1. Área: conceito e áreas do quadrado
Grupo 1 - PIC OBMEP 2011 Módulo 2 - Geometria Resumo do Encontro 6, 22 de setembro de 2012 Questões de geometria das provas da OBMEP http://www.obmep.org.br/provas.htm 1. Área: conceito e áreas do quadrado
Matéria: Matemática Concurso: Auditor Tributário ISS São José dos Campos 2018 Professor: Alex Lira
 Concurso: Professor: Alex Lira Prova comentada: Auditor Tributário ISS SÃO JOSÉ DOS CAMPOS 2018 Matemática SUMÁRIO CONTEÚDO PROGRAMÁTICO PREVISTO NO EDITAL... 3 QUESTÕES COMENTADAS... 3 LISTA DE QUESTÕES...
Concurso: Professor: Alex Lira Prova comentada: Auditor Tributário ISS SÃO JOSÉ DOS CAMPOS 2018 Matemática SUMÁRIO CONTEÚDO PROGRAMÁTICO PREVISTO NO EDITAL... 3 QUESTÕES COMENTADAS... 3 LISTA DE QUESTÕES...
Programação anual. 6 º.a n o. Sistemas de numeração Sequência dos números naturais Ideias associadas às operações fundamentais Expressões numéricas
 Programação anual 6 º.a n o 1. Números naturais 2. Do espaço para o plano Sistemas de numeração Sequência dos números naturais Ideias associadas às operações fundamentais Expressões numéricas Formas geométricas
Programação anual 6 º.a n o 1. Números naturais 2. Do espaço para o plano Sistemas de numeração Sequência dos números naturais Ideias associadas às operações fundamentais Expressões numéricas Formas geométricas
ÁREA. Unidades de medida de área. Prof. Patricia Caldana
 ÁREA Prof. Patricia Caldana Área ou superfície de uma figura plana tem a ver com o conceito (primitivo) de sua extensão (bidimensional). Usamos a área do quadrado de lado unitário como referência de unidade
ÁREA Prof. Patricia Caldana Área ou superfície de uma figura plana tem a ver com o conceito (primitivo) de sua extensão (bidimensional). Usamos a área do quadrado de lado unitário como referência de unidade
ATIVIDADES ESTRATÉGIAS
 ENSINO BÁSICO Agrupamento de Escolas Nº 1 de Abrantes ESCOLA BÁSICA DOS 2.º E 3.º CICLOS D. MIGUEL DE ALMEIDA DISCIPLINA: MATEMÁTICA ANO: 7º ANO LETIVO 2013/2014 METAS DE APRENDIZAGEM: Multiplicar e dividir
ENSINO BÁSICO Agrupamento de Escolas Nº 1 de Abrantes ESCOLA BÁSICA DOS 2.º E 3.º CICLOS D. MIGUEL DE ALMEIDA DISCIPLINA: MATEMÁTICA ANO: 7º ANO LETIVO 2013/2014 METAS DE APRENDIZAGEM: Multiplicar e dividir
EXERCICIOS - ÁREAS E ÂNGULOS:
 EXERCICIOS - ÁREAS E ÂNGULOS: 32 - Sabendo-se que um ângulo externo de um triângulo retângulo mede 287, quais os valores dos ângulos internos deste? 37 - Assinale qual dos polígonos abaixo possui todos
EXERCICIOS - ÁREAS E ÂNGULOS: 32 - Sabendo-se que um ângulo externo de um triângulo retângulo mede 287, quais os valores dos ângulos internos deste? 37 - Assinale qual dos polígonos abaixo possui todos
Exemplo Aplicando a proporcionalidade existente no Teorema de Tales, determine o valor dos segmentos AB e BC na ilustração a seguir:
 GEOMETRIA PLANA TEOREMA DE TALES O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: Se duas retas transversais são cortadas por um feixe de retas paralelas, então a razão entre
GEOMETRIA PLANA TEOREMA DE TALES O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: Se duas retas transversais são cortadas por um feixe de retas paralelas, então a razão entre
Geometria Euclidiana Plana
 CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 014. Geometria Euclidiana Plana Parte II Joyce Danielle de Araújo - Engenharia de Produção Vitor Bruno - Engenharia Civil Introdução Desde os egípcios,
CURSO INTRODUTÓRIO DE MATEMÁTICA PARA ENGENHARIA 014. Geometria Euclidiana Plana Parte II Joyce Danielle de Araújo - Engenharia de Produção Vitor Bruno - Engenharia Civil Introdução Desde os egípcios,
SOMENTE COM CANETA AZUL
 Nome completo: Turma: Unidade: SIMULADO 8 ANO - ENSINO FUNDAMENTAL Matemática Dia: 8/0 - sexta-feira º A DI 07 ORIENTAÇÕES PARA APLICAÇÃO DO SIMULADO - º TRI. A prova terá duração de horas e 0 minutos..
Nome completo: Turma: Unidade: SIMULADO 8 ANO - ENSINO FUNDAMENTAL Matemática Dia: 8/0 - sexta-feira º A DI 07 ORIENTAÇÕES PARA APLICAÇÃO DO SIMULADO - º TRI. A prova terá duração de horas e 0 minutos..
ESCOLA BÁSICA DE MAFRA 2016/2017 MATEMÁTICA (2º ciclo)
 (2º ciclo) 5º ano Operações e Medida Tratamento de Dados Efetuar com números racionais não negativos. Resolver problemas de vários passos envolvendo com números racionais representados por frações, dízimas,
(2º ciclo) 5º ano Operações e Medida Tratamento de Dados Efetuar com números racionais não negativos. Resolver problemas de vários passos envolvendo com números racionais representados por frações, dízimas,
Formação continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º ano 2º Bimestre de 2014 Plano de Trabalho
 Formação continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º ano 2º Bimestre de 2014 Plano de Trabalho Geometria Espacial Prismas e Cilindros Tarefa 2 Cursista: Maria Candida Pereira
Formação continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º ano 2º Bimestre de 2014 Plano de Trabalho Geometria Espacial Prismas e Cilindros Tarefa 2 Cursista: Maria Candida Pereira
Planejamento Anual OBJETIVO GERAL
 Planejamento Anual Componente Curricular: Matemática Ano: 6º ano Ano Letivo: 2017 Professor(a): Eni OBJETIVO GERAL Desenvolver e aprimorar estruturas cognitivas de interpretação, análise, síntese, relação
Planejamento Anual Componente Curricular: Matemática Ano: 6º ano Ano Letivo: 2017 Professor(a): Eni OBJETIVO GERAL Desenvolver e aprimorar estruturas cognitivas de interpretação, análise, síntese, relação
MATEMÁTICA PLANEJAMENTO 3º BIMESTRE º B - 11 Anos
 PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 3º
PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 3º
Agrupamento de Escolas Cego do Maio Póvoa de Varzim (Cód ) INFORMAÇÃO PROVA - PROVA EQUIVALÊNCIA À FREQUÊNCIA (PEF)
 INFORMAÇÃO PROVA - PROVA EQUIVALÊNCIA À FREQUÊNCIA (PEF) Matemática (62) MAIO DE 2019 Prova de 2019 2.º Ciclo do Ensino Básico O presente documento visa divulgar informações da prova de equivalência à
INFORMAÇÃO PROVA - PROVA EQUIVALÊNCIA À FREQUÊNCIA (PEF) Matemática (62) MAIO DE 2019 Prova de 2019 2.º Ciclo do Ensino Básico O presente documento visa divulgar informações da prova de equivalência à
PROGRAMAÇÃO CURRICULAR DE MATEMÁTICA. UNIDADE 1 Conteúdos
 PROGRAMAÇÃO CURRICULAR DE MATEMÁTICA 1. ano - 1. volume 1. ano - 2. volume UNIDADE 1 Localização espacial, utilizando o próprio corpo como referencial. Localização espacial, utilizando referenciais externos
PROGRAMAÇÃO CURRICULAR DE MATEMÁTICA 1. ano - 1. volume 1. ano - 2. volume UNIDADE 1 Localização espacial, utilizando o próprio corpo como referencial. Localização espacial, utilizando referenciais externos
Matemática GEOMETRIA PLANA. Professor Dudan
 Matemática GEOMETRIA PLANA Professor Dudan Ângulos Geometria Plana Ângulo é a região de um plano concebida pelo encontro de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo. A
Matemática GEOMETRIA PLANA Professor Dudan Ângulos Geometria Plana Ângulo é a região de um plano concebida pelo encontro de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo. A
MATEMÁTICA OFICINA ALEXSANDRO KESLLER PAZ NA ESCOLA ÁLGEBRA
 ALEXSANDRO KESLLER MATEMÁTICA OFICINA ÁLGEBRA PAZ NA ESCOLA 14.03.2019 MATEMÁTICA BÁSICA Conhecimentos Álgebricos Medidas de comprimento Transformações de unidades de medidas de comprimento Conhecimentos
ALEXSANDRO KESLLER MATEMÁTICA OFICINA ÁLGEBRA PAZ NA ESCOLA 14.03.2019 MATEMÁTICA BÁSICA Conhecimentos Álgebricos Medidas de comprimento Transformações de unidades de medidas de comprimento Conhecimentos
à situação. à situação.
 Unidade 1 Números naturais 1. Números naturais 2. Sistemas de numeração 3. Tabela simples Reconhecer os números naturais. Identificar o antecessor e o sucessor numa sequência de números naturais. Identificar
Unidade 1 Números naturais 1. Números naturais 2. Sistemas de numeração 3. Tabela simples Reconhecer os números naturais. Identificar o antecessor e o sucessor numa sequência de números naturais. Identificar
Agrupamento de Escolas da Benedita. CONTEÚDOS ANUAIS 2º Ciclo - 5º Ano ANO LETIVO 2017/2018 AULAS PREVISTAS
 CONTEÚDOS ANUAIS 2º Ciclo - 5º Ano ANO LETIVO 2017/2018 Disciplina:Matemática AULAS CONTEÚDOS PREVISTAS 5ºA 5ºB 5ºC 5ºD 5ºE 5ºF 5ºG 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP
CONTEÚDOS ANUAIS 2º Ciclo - 5º Ano ANO LETIVO 2017/2018 Disciplina:Matemática AULAS CONTEÚDOS PREVISTAS 5ºA 5ºB 5ºC 5ºD 5ºE 5ºF 5ºG 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP 1ºP 2ºP 3ºP
ESCALA DE PROFICIÊNCIA DE MATEMÁTICA 5º ANO DO ENSINO FUNDAMENTAL
 ESCALA DE PROFICIÊNCIA DE MATEMÁTICA 5º ANO DO ENSINO FUNDAMENTAL Nível* Nível 1: 125-150 Nível 2: 150-175 Nível 3: 175-200 Nível 4: 200-225 Descrição do Nível - O estudante provavelmente é capaz de: Determinar
ESCALA DE PROFICIÊNCIA DE MATEMÁTICA 5º ANO DO ENSINO FUNDAMENTAL Nível* Nível 1: 125-150 Nível 2: 150-175 Nível 3: 175-200 Nível 4: 200-225 Descrição do Nível - O estudante provavelmente é capaz de: Determinar
PADRÕES DE DESEMPENHO ESTUDANTIL. O que são Padrões de Desempenho? ABAIXO DO BÁSICO Até 150 pontos. BÁSICO De 150 até 200 pontos
 PADRÕES DE DESEMPENHO ESTUDANTIL O que são Padrões de Desempenho? Os Padrões de Desempenho constituem uma caracterização das competências e habilidades desenvolvidas pelos alunos de determinada etapa de
PADRÕES DE DESEMPENHO ESTUDANTIL O que são Padrões de Desempenho? Os Padrões de Desempenho constituem uma caracterização das competências e habilidades desenvolvidas pelos alunos de determinada etapa de
Conteúdos Ideias-Chave Objectivos específicos. múltiplo de outro número, este é divisor do primeiro.
 Capítulo 1 Números Naturais Múltiplos e Divisores Se um número natural é múltiplo de outro número, este é divisor do primeiro. Números primos e números compostos Decomposição de um número em factores primos
Capítulo 1 Números Naturais Múltiplos e Divisores Se um número natural é múltiplo de outro número, este é divisor do primeiro. Números primos e números compostos Decomposição de um número em factores primos
A adição de números naturais é associativa, ou seja, resultado da soma de três números naturais independe da ordem da soma dos números.
 . Números Naturais Para qualquer cidadão, contar faz parte da rotina da vida. Por exemplo: contamos dinheiro, contamos pessoas, contamos os itens para saber o que precisamos comprar, contamos objetos em
. Números Naturais Para qualquer cidadão, contar faz parte da rotina da vida. Por exemplo: contamos dinheiro, contamos pessoas, contamos os itens para saber o que precisamos comprar, contamos objetos em
araribá matemática Quadro de conteúdos e objetivos Quadro de conteúdos e objetivos Unidade 1 Números inteiros adição e subtração
 Unidade 1 Números inteiros adição e subtração 1. Números positivos e números negativos Reconhecer o uso de números negativos e positivos no dia a dia. 2. Conjunto dos números inteiros 3. Módulo ou valor
Unidade 1 Números inteiros adição e subtração 1. Números positivos e números negativos Reconhecer o uso de números negativos e positivos no dia a dia. 2. Conjunto dos números inteiros 3. Módulo ou valor
Revendo as operações
 A UA UL LA 61 Revendo as operações Introdução Nossa aula Assim como já vimos em muitas de nossas aulas, a Matemática é uma ciência que está sempre presente em nosso dia-adia. Na aula de hoje, recordaremos
A UA UL LA 61 Revendo as operações Introdução Nossa aula Assim como já vimos em muitas de nossas aulas, a Matemática é uma ciência que está sempre presente em nosso dia-adia. Na aula de hoje, recordaremos
Aula 30 Área de superfícies: parte I
 Aula 30 Área de superfícies: parte I Objetivos Determinar áreas de algumas superfícies curvas. Introdução Supona que um pintor utilize x litros de tinta para pintar uma parede quadrada de 1 m de lado e
Aula 30 Área de superfícies: parte I Objetivos Determinar áreas de algumas superfícies curvas. Introdução Supona que um pintor utilize x litros de tinta para pintar uma parede quadrada de 1 m de lado e
Prova final de MATEMÁTICA - 3o ciclo a Fase
 Prova final de MATEMÁTICA - 3o ciclo 017-1 a Fase Proposta de resolução Caderno 1 1. Como 9 =,5 e 5,, temos que 5 < 9 indicados na definição do conjunto, vem que: e assim, representando na reta real os
Prova final de MATEMÁTICA - 3o ciclo 017-1 a Fase Proposta de resolução Caderno 1 1. Como 9 =,5 e 5,, temos que 5 < 9 indicados na definição do conjunto, vem que: e assim, representando na reta real os
PLANIFICAÇÃO ANUAL: ANO LETIVO 2013/2014 DISCIPLINA DE MATEMÁTICA 7 º ANO
 DEPARTAMENTO DE MATEMÁTICA E TECNOLOGIAS ÁREA DISCIPLINAR DE MATEMÁTICA PLANIFICAÇÃO ANUAL: ANO LETIVO 2013/2014 DISCIPLINA DE MATEMÁTICA 7 º ANO CALENDARIZAÇÃO DO ANO LETIVO Período Início Fim Nº Semanas
DEPARTAMENTO DE MATEMÁTICA E TECNOLOGIAS ÁREA DISCIPLINAR DE MATEMÁTICA PLANIFICAÇÃO ANUAL: ANO LETIVO 2013/2014 DISCIPLINA DE MATEMÁTICA 7 º ANO CALENDARIZAÇÃO DO ANO LETIVO Período Início Fim Nº Semanas
Aula 1: Revisando o Conjunto dos Números Reais
 Aula 1: Revisando o Conjunto dos Números Reais Caro aluno, nesta aula iremos retomar um importante assunto, já estudado em anos anteriores: o conjunto dos números reais. Frequentemente, encontramo-nos
Aula 1: Revisando o Conjunto dos Números Reais Caro aluno, nesta aula iremos retomar um importante assunto, já estudado em anos anteriores: o conjunto dos números reais. Frequentemente, encontramo-nos
CADERNO DE EXERCÍCIOS 1B
 CADERNO DE EXERCÍCIOS B Ensino Médio Matemática Questão Conteúdo Habilidade da Matriz da EJA/FB Equação do º grau H7 H8 2 Teorema de Pitágoras H3 3 Área de figuras planas H3 Proporcionalidade H3 Caderno
CADERNO DE EXERCÍCIOS B Ensino Médio Matemática Questão Conteúdo Habilidade da Matriz da EJA/FB Equação do º grau H7 H8 2 Teorema de Pitágoras H3 3 Área de figuras planas H3 Proporcionalidade H3 Caderno
GABARITO DO CADERNO DE QUESTÕES
 OLÍMPIADAS DE MATEMÁTICA DO OESTE CATARINENSE GABARITO DO CADERNO DE QUESTÕES NÍVEL 3 Ensino Médio Universidade Federal da Fronteira Sul Campus Chapecó 017 OLIMPÍADA REGIONAL DE MATEMÁTICA GABARITO: 1.
OLÍMPIADAS DE MATEMÁTICA DO OESTE CATARINENSE GABARITO DO CADERNO DE QUESTÕES NÍVEL 3 Ensino Médio Universidade Federal da Fronteira Sul Campus Chapecó 017 OLIMPÍADA REGIONAL DE MATEMÁTICA GABARITO: 1.
3º TRI - MATEMATICA - LISTA MARAVILHA 20/10/16 Ensino Fundamental 9º ano A-B-C-D Profº Marcelo
 3º TRI - MATEMATICA - LISTA MARAVILHA 20/10/16 Ensino Fundamental 9º ano A-B-C-D Profº Marcelo LISTA DE ESTUDO.. Áreas 1. Calcule a área da região mais escura. 2. Um quadrado tem área de 25 cm 2. O que
3º TRI - MATEMATICA - LISTA MARAVILHA 20/10/16 Ensino Fundamental 9º ano A-B-C-D Profº Marcelo LISTA DE ESTUDO.. Áreas 1. Calcule a área da região mais escura. 2. Um quadrado tem área de 25 cm 2. O que
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO
 ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO ANO 2017 PROFESSOR (a) DISCIPLINA Bruno Rezende Pereira Matemática ALUNO (a) SÉRIE 3º Ano do Ensino Médio
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO ANO 2017 PROFESSOR (a) DISCIPLINA Bruno Rezende Pereira Matemática ALUNO (a) SÉRIE 3º Ano do Ensino Médio
32 Matemática. Programação anual de conteúdos
 Programação anual de conteúdos 2 ọ ano 1 ọ volume 1. A localização espacial e os números Construção do significado dos números e identificação da sua utilização no contexto diário Representação das quantidades
Programação anual de conteúdos 2 ọ ano 1 ọ volume 1. A localização espacial e os números Construção do significado dos números e identificação da sua utilização no contexto diário Representação das quantidades
Disciplina: Matemática. Período: I. Professor (a): Maria Aparecida Holanda Veloso e Liliane Cristina de Oliveira Vieira
 COLÉGIO LA SALLE BRASILIA Associação Brasileira de Educadores Lassalistas ABEL SGAS Q. 906 Conj. E C.P. 320 Fone: (061) 3443-7878 CEP: 70390-060 - BRASÍLIA - DISTRITO FEDERAL Disciplina: Matemática Período:
COLÉGIO LA SALLE BRASILIA Associação Brasileira de Educadores Lassalistas ABEL SGAS Q. 906 Conj. E C.P. 320 Fone: (061) 3443-7878 CEP: 70390-060 - BRASÍLIA - DISTRITO FEDERAL Disciplina: Matemática Período:
a) R$ 8,20 b) R$ 8,40 c) R$ 8,60 d) R$ 8,80 e) R$ 9,00
 Aula n ọ 03 01. Um engenheiro, precisando calcular a área de um terreno com forma quadrangular (conforme a figura abaixo), utilizou como referencial as duas ruas, A e B, que se cruzavam perpendicularmente.
Aula n ọ 03 01. Um engenheiro, precisando calcular a área de um terreno com forma quadrangular (conforme a figura abaixo), utilizou como referencial as duas ruas, A e B, que se cruzavam perpendicularmente.
PLANIFICAÇÃO ANUAL MATEMÁTICA 7.ºANO
 Escola Básica do 2.º e 3.º Ciclos Infante D. Pedro 1.º Período Apresentação. Avaliação Diagnóstica Atividades de recuperação e avaliação 54 aulas 40 aulas 9 aulas 2.º Período 4s 3s 8 aulas 3.º Período
Escola Básica do 2.º e 3.º Ciclos Infante D. Pedro 1.º Período Apresentação. Avaliação Diagnóstica Atividades de recuperação e avaliação 54 aulas 40 aulas 9 aulas 2.º Período 4s 3s 8 aulas 3.º Período
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO
 ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO ANO 2016 PROFESSOR (a) DISCIPLINA Bruno Rezende Pereira Matemática ALUNO (a) SÉRIE 3º Ano do Ensino Médio
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO 3º ANO ANO 2016 PROFESSOR (a) DISCIPLINA Bruno Rezende Pereira Matemática ALUNO (a) SÉRIE 3º Ano do Ensino Médio
ENSINO BÁSICO. ESCOLA: Secundária Dr. Solano de Abreu DISCIPLINA: Matemática ANO: 7º ANO LETIVO 2013/2014 CONTEÚDOS PROGRAMÁTICOS AULAS PREVISTAS
 ENSINO BÁSICO Agrupamento de Escolas Nº 1 de Abrantes ESCOLA: Secundária Dr. Solano de Abreu DISCIPLINA: Matemática ANO: 7º ANO LETIVO 2013/2014 CONTEÚDOS PROGRAMÁTICOS METAS DE APRENDIZAGEM ATIVIDADES
ENSINO BÁSICO Agrupamento de Escolas Nº 1 de Abrantes ESCOLA: Secundária Dr. Solano de Abreu DISCIPLINA: Matemática ANO: 7º ANO LETIVO 2013/2014 CONTEÚDOS PROGRAMÁTICOS METAS DE APRENDIZAGEM ATIVIDADES
Conteúdo: PERÍMETRO E ÁREA DE FIGURAS PLANAS
 Nome: nº Data: / / Professor: Lucas Factor Curso/Série 8º Ano Ensino Fundamental II Conteúdo: PERÍMETRO E ÁREA DE FIGURAS PLANAS Os cálculos de perímetro e área são necessários, seja para a compra de um
Nome: nº Data: / / Professor: Lucas Factor Curso/Série 8º Ano Ensino Fundamental II Conteúdo: PERÍMETRO E ÁREA DE FIGURAS PLANAS Os cálculos de perímetro e área são necessários, seja para a compra de um
1-) Uma lata metálica tem a forma de um cilindro, como mostra a figura abaixo. A opção que melhor representa a planificação do cilindro é:
 DISCIPLINA: MATEMÁTICA PROFESSORA: GIOVANA 7os. ANOS (171 e 172) ORIENTAÇÃO DE ESTUDO RECUPERAÇÃO FINAL CORPOS REDONDOS: São sólidos geométricos cujas superfícies têm ao menos uma parte arredondada (não
DISCIPLINA: MATEMÁTICA PROFESSORA: GIOVANA 7os. ANOS (171 e 172) ORIENTAÇÃO DE ESTUDO RECUPERAÇÃO FINAL CORPOS REDONDOS: São sólidos geométricos cujas superfícies têm ao menos uma parte arredondada (não
MATEMÁTICA APLICADA À AGRIMENSURA PROF. JORGE WILSON
 MATEMÁTICA APLICADA À AGRIMENSURA PROF. JORGE WILSON [email protected] DEFINIÇÕES GEOMETRIA PLANA Ponto: Um elemento do espaço que define uma posição. Reta: Conjunto infinito de pontos. Dois pontos são
MATEMÁTICA APLICADA À AGRIMENSURA PROF. JORGE WILSON [email protected] DEFINIÇÕES GEOMETRIA PLANA Ponto: Um elemento do espaço que define uma posição. Reta: Conjunto infinito de pontos. Dois pontos são
2º ANO Reconhecer e utilizar características do sistema de numeração decimal, tais como agrupamentos e trocas na base 10 e princípio do valor posicion
 PREFEITURA DA CIDADE DO RIO DE JANEIRO SECRETARIA MUNICIPAL DE EDUCAÇÃO SUBSECRETARIA DE ENSINO COORDENADORIA DE EDUCAÇÃO DESCRITORES DE MATEMÁTICA PROVA - 3º BIMESTRE 2011 2º ANO Reconhecer e utilizar
PREFEITURA DA CIDADE DO RIO DE JANEIRO SECRETARIA MUNICIPAL DE EDUCAÇÃO SUBSECRETARIA DE ENSINO COORDENADORIA DE EDUCAÇÃO DESCRITORES DE MATEMÁTICA PROVA - 3º BIMESTRE 2011 2º ANO Reconhecer e utilizar
Material de aula. Régua Compasso Par de esquadros (30 e 45 ) Borracha Lápis ou lapiseira Papel sulfite ou caderno de desenho
 Desenho Técnico Material de aula Régua Compasso Par de esquadros (30 e 45 ) Borracha Lápis ou lapiseira Papel sulfite ou caderno de desenho Geometria Conversão de unidades Polígonos e sólidos Escala Desenho
Desenho Técnico Material de aula Régua Compasso Par de esquadros (30 e 45 ) Borracha Lápis ou lapiseira Papel sulfite ou caderno de desenho Geometria Conversão de unidades Polígonos e sólidos Escala Desenho
UNICAMP Você na elite das universidades! MATEMÁTICA ELITE SEGUNDA FASE
 www.elitecampinas.com.br Fone: (19) -71 O ELITE RESOLVE IME 004 PORTUGUÊS/INGLÊS Você na elite das universidades! UNICAMP 004 SEGUNDA FASE MATEMÁTICA www.elitecampinas.com.br Fone: (19) 51-101 O ELITE
www.elitecampinas.com.br Fone: (19) -71 O ELITE RESOLVE IME 004 PORTUGUÊS/INGLÊS Você na elite das universidades! UNICAMP 004 SEGUNDA FASE MATEMÁTICA www.elitecampinas.com.br Fone: (19) 51-101 O ELITE
CADERNO DE EXERCÍCIOS DE MECÂNICA DOS FLUIDOS
 CADERNO DE EXERCÍCIOS DE MECÂNICA DOS FLUIDOS Prof. Jesué Graciliano da Silva São José, Agosto de 2018 https://jesuegraciliano.wordpress.com/aulas/mecanica-dos-fluidos/ 1 Prof. Jesué Graciliano da Silva
CADERNO DE EXERCÍCIOS DE MECÂNICA DOS FLUIDOS Prof. Jesué Graciliano da Silva São José, Agosto de 2018 https://jesuegraciliano.wordpress.com/aulas/mecanica-dos-fluidos/ 1 Prof. Jesué Graciliano da Silva
E.E.M.FRANCISCO HOLANDA MONTENEGRO PLANO DE CURSO ENSINO MÉDIO
 E.E.M.FRANCISCO HOLANDA MONTENEGRO PLANO DE CURSO ENSINO MÉDIO DISCIPLINA: GEOMETRIA SÉRIE: 1º ANO (B, C e D) 2015 PROFESSORES: Crislany Bezerra Moreira Dias BIM. 1º COMPETÊNCIAS/ HABILIDADES D48 - Identificar
E.E.M.FRANCISCO HOLANDA MONTENEGRO PLANO DE CURSO ENSINO MÉDIO DISCIPLINA: GEOMETRIA SÉRIE: 1º ANO (B, C e D) 2015 PROFESSORES: Crislany Bezerra Moreira Dias BIM. 1º COMPETÊNCIAS/ HABILIDADES D48 - Identificar
A equação da circunferência
 A UA UL LA A equação da circunferência Introdução Nas duas últimas aulas você estudou a equação da reta. Nesta aula, veremos que uma circunferência desenhada no plano cartesiano também pode ser representada
A UA UL LA A equação da circunferência Introdução Nas duas últimas aulas você estudou a equação da reta. Nesta aula, veremos que uma circunferência desenhada no plano cartesiano também pode ser representada
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
(Matemática e Ciências Naturais) Grupo 230) Ano Letivo 2017 /2018
 1 - PLANIFICAÇÃO ANUAL DE MATEMÁTICA 1.1-5º ANO Números Naturais CONTEÚDOS PERÍODO As operações: Adição, subtração, e multiplicação e divisão Expressões numéricas números pelo respetivo máximo divisor
1 - PLANIFICAÇÃO ANUAL DE MATEMÁTICA 1.1-5º ANO Números Naturais CONTEÚDOS PERÍODO As operações: Adição, subtração, e multiplicação e divisão Expressões numéricas números pelo respetivo máximo divisor
Roteiro de Recuperação do 3º Bimestre - Matemática
 Roteiro de Recuperação do 3º Bimestre - Matemática Nome: Nº 6º Ano Data: / /2015 Professores Leandro e Renan Nota: (valor 1,0) 1. Apresentação: Prezado aluno, A estrutura da recuperação bimestral paralela
Roteiro de Recuperação do 3º Bimestre - Matemática Nome: Nº 6º Ano Data: / /2015 Professores Leandro e Renan Nota: (valor 1,0) 1. Apresentação: Prezado aluno, A estrutura da recuperação bimestral paralela
ESCOLA BÁSICA INTEGRADA DE ANGRA DO HEROÍSMO Plano da Unidade
 Unidade de Ensino: OPERAÇÕES COM NÚMEROS RACIONAIS ABSOLUTOS (adição e subtracção). Tempo Previsto: 3 semanas O reconhecimento do conjunto dos racionais positivos, das diferentes formas de representação
Unidade de Ensino: OPERAÇÕES COM NÚMEROS RACIONAIS ABSOLUTOS (adição e subtracção). Tempo Previsto: 3 semanas O reconhecimento do conjunto dos racionais positivos, das diferentes formas de representação
4º. ano 1º. VOLUME. Projeto Pedagógico de Matemática 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE. Números e operações.
 4º. ano 1º. VOLUME 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE Realização de compreendendo seus significados: adição e subtração (com e sem reagrupamento) Multiplicação (como adição de parcelas
4º. ano 1º. VOLUME 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE Realização de compreendendo seus significados: adição e subtração (com e sem reagrupamento) Multiplicação (como adição de parcelas
PLANIFICAÇÃO A MÉDIO/LONGO PRAZO
 017/018 PLANIFICAÇÃO A MÉDIO/LONGO PRAZO DISCIPLINA: Matemática ANO: 7º Total de aulas previstas: 1 Unidades Temáticas Conteúdos Descritores N.º Aulas Avaliação Primeiro período 7 aulas Todos os instrumentos
017/018 PLANIFICAÇÃO A MÉDIO/LONGO PRAZO DISCIPLINA: Matemática ANO: 7º Total de aulas previstas: 1 Unidades Temáticas Conteúdos Descritores N.º Aulas Avaliação Primeiro período 7 aulas Todos os instrumentos
Soluções das Questões de Matemática do Processo Seletivo de Admissão à Escola de Aprendizes- Marinheiros PSAEAM
 Soluções das Questões de Matemática do Processo Seletivo de Admissão à Escola de Aprendizes- Marinheiros PSAEAM Questão 1 Concurso 010 Sabendo que 1 grosa é equivalente a 1 dúzias, é correto afirmar que
Soluções das Questões de Matemática do Processo Seletivo de Admissão à Escola de Aprendizes- Marinheiros PSAEAM Questão 1 Concurso 010 Sabendo que 1 grosa é equivalente a 1 dúzias, é correto afirmar que
Gabaritos das aulas 1 a 20
 Gabaritos das aulas 1 a 20 Aula 1 - Recordando operações Introdução a) adição (180 + 162) b) subtração (0-37) c) multiplicação (16 ) d) divisão (24 : 3) Eercícios a) 80 b) 37 c) - 37 d) e) 19 f) - 1 g)
Gabaritos das aulas 1 a 20 Aula 1 - Recordando operações Introdução a) adição (180 + 162) b) subtração (0-37) c) multiplicação (16 ) d) divisão (24 : 3) Eercícios a) 80 b) 37 c) - 37 d) e) 19 f) - 1 g)
CENTRO EDUCACIONAL CHARLES DARWIN ENSINO FUNDAMENTAL. DIRETRIZES CURRICULARES 1º ao 5º ANO MATEMÁTICA
 CENTRO EDUCACIONAL CHARLES DARWIN ENSINO FUNDAMENTAL 2014 DIRETRIZES CURRICULARES 1º ao 5º ANO MATEMÁTICA OBJETIVOS GERAIS Reconhecer a Matemática como instrumento de compreensão e de transformação do
CENTRO EDUCACIONAL CHARLES DARWIN ENSINO FUNDAMENTAL 2014 DIRETRIZES CURRICULARES 1º ao 5º ANO MATEMÁTICA OBJETIVOS GERAIS Reconhecer a Matemática como instrumento de compreensão e de transformação do
(Fonte: Jornal do Brasil - 02/07/95)
 AUUL AL A As médias Na aula 29, você estudou um pouco de Estatística e aprendeu que esse ramo da Matemática trabalha com dados comparativos, pesquisas de opinião, pesquisas de mercado e projeções futuras.
AUUL AL A As médias Na aula 29, você estudou um pouco de Estatística e aprendeu que esse ramo da Matemática trabalha com dados comparativos, pesquisas de opinião, pesquisas de mercado e projeções futuras.
NOÇÕES DE GEOMETRIA PLANA
 NOÇÕES DE GEOMETRIA PLANA Polígonos são figuras planas fechadas com lados retos. Todo polígono possui os seguintes elementos: ângulos, vértices, diagonais e lados. Altura de um triângulo é o segmento de
NOÇÕES DE GEOMETRIA PLANA Polígonos são figuras planas fechadas com lados retos. Todo polígono possui os seguintes elementos: ângulos, vértices, diagonais e lados. Altura de um triângulo é o segmento de
