Registro CMI Aulas 4 e 5
|
|
|
- Octavio Santarém
- 7 Há anos
- Visualizações:
Transcrição
1 Registro CMI 4317 Aulas 4 e 5 QUESTÃO 01 Seja a n uma sequência de números reais cujo termo geral é verdadeira? a) a n é uma progressão aritmética de razão 1. b) a n é uma progressão geométrica de razão 1. 4 c) a n é uma progressão geométrica de razão 4. d) a n não é uma progressão (nem geométrica, nem aritmética). e) a n é simultaneamente uma progressão aritmética e geométrica. a n 1 4 * n, n N. Qual das afirmações seguintes é QUESTÃO 0 Considere esses quatro valores x, y, 3x, y em PA crescente. Se a soma dos extremos é 0, então o terceiro termo é a) 9 b) 1 c) 15 d) 18 QUESTÃO 03 A progressão aritmética, cuja fórmula do termo geral é dada por an 5n 18, tem razão igual a 5. QUESTÃO 04 Na fabricação de mesas de reunião, uma fábrica trabalha com vários modelos e tamanhos. As mesas redondas são todas acompanhadas com uma certa quantidade de poltronas a depender do tamanho da mesa, conforme a figura abaixo: O primeiro modelo acompanha 3 poltronas, o segundo modelo acompanha 6 poltronas, o terceiro, 9 poltronas e assim sucessivamente, isto é, sempre um modelo de mesa acompanha 3 poltronas a mais em relação ao modelo anterior. Um cliente adquiriu uma unidade de cada um dos 10 primeiros modelos de mesa circular. Pág 1
2 Como todo patrimônio da sua empresa é identificado a partir de uma etiqueta adesiva, o número de adesivos que devem ser confeccionados para que cada uma das mesas e poltronas adquiridas seja devidamente etiquetadas é menor que 177. QUESTÃO 05 A sequência ( 30, 7, 4, 1, ) mantém esse padrão de comportamento para um determinado número de termos n. A soma destes n termos vale zero. Qual é esse número de termos? a) 19 b) 0 c) 1 d) QUESTÃO 06 Considere a sequência de números binários 101, , , A soma de todos os algarismos dos 0 primeiros termos dessa sequência é um múltiplo de 17. QUESTÃO Na progressão geométrica,,... existem exatos 3 termos com exatos 3 algarismos QUESTÃO 08 Considere o padrão de construção representado pelos triângulos equiláteros abaixo. O perímetro do triângulo da etapa 1 é 3 e sua altura é h; a altura do triângulo da etapa é metade da altura do triângulo da etapa 1; a altura do triângulo da etapa 3 é metade da altura do triângulo da etapa e, assim, sucessivamente. Assim, a soma dos perímetros da sequência infinita de triângulos é a). b) 3. c) 4. d) 5. e) 6. QUESTÃO 09 O valor do número x dado por x 3 é a) b) 3. 3 Pág
3 c) d) e) QUESTÃO 10 Conta uma antiga história que dois amigos caminhavam por uma rua do interior, lá pelas dez e tanto da noite, e separaram-se diante da casa de um deles. Combinavam encontrar-se na manhã do dia seguinte, bem cedo como convém àqueles que trabalham no campo, quando um deles sugeriu o seguinte: Vamos nos encontrar, no ponto do ônibus, no exato instante em que 4/11 do que restar do dia for igual ao tempo decorrido do mesmo dia. Julgue o item a seguir. Se ambos acordaram com a proposta, deveriam encontrar-se no ponto do ônibus às 6 h 14 min. QUESTÃO 11 José, Carlos e Paulo devem transportar em suas bicicletas uma certa quantidade de laranjas. Decidiram dividir o trajeto a ser percorrido em duas partes, sendo que ao final da primeira parte eles redistribuiriam a quantidade de laranjas que cada um carregava dependendo do cansaço de cada um. Na primeira parte do trajeto José, Carlos e Paulo dividiram as laranjas na proporção 6 : 5 : 4, respectivamente. Na segunda parte do trajeto José, Carlos e Paulo dividiram as laranjas na proporção 4 : 4 :, respectivamente. Julgue o item a seguir. Sabendo-se que um deles levou 50 laranjas a mais no segundo trajeto, a quantidade de laranjas que José, Carlos e Paulo, nessa ordem, transportaram na segunda parte do trajeto foi igual a 300, 300 e 150 laranjas. QUESTÃO 1 Uma mercadoria cujo preço de tabela é R$ 8.000,00 é vendida, à vista, com um desconto de x% ou em duas parcelas iguais de R$ 4.000,00, sendo a primeira no ato da compra e a segunda um mês após a compra. Suponha que o comprador dispõe do dinheiro necessário para pagar à vista e que ele sabe que a diferença entre o preço à vista e a primeira parcela pode ser aplicada no mercado financeiro a uma taxa de 5% ao mês. Nessas condições, qual o valor de x que torna indiferente comprar à vista ou a prazo? a) 5% b) 10% c) 15% d) 1,5% e) 17,5% QUESTÃO 13 ponto de partida:? (dividir por 8) (somar 1 ) 5 (multiplicar por 0,4) (subtrair 0,8) (dividir por 5) 10,4: resultado final O esquema acima mostra, passo a passo, a seqüência de operações a serem efetuadas a partir de um certo número, a fim de obter o resultado final 10,4. O número que deve ser considerado como ponto de partida está compreendido entre Pág 3
4 (A) e (B) e (C) e (D) e 1 00 (E) 1 50 e QUESTÃO 14 Uma pequena empresa fabrica camisas de um único modelo e as vende por R$ 80,00 a unidade. Devido ao aluguel e a outras despesas fixas que não dependem da quantidade produzida, a empresa tem um custo fixo anual de R$ 9.600,00. Além do custo fixo, a empresa tem de arcar com custos que dependem da quantidade produzida, chamados custos variáveis, tais como matéria-prima, por exemplo; o custo variável por camisa é R$ 40,00. O gráfico que melhor representa a função do lucro anual L em função do número n de camisas vendidas é: Pág 4
5 QUESTÃO 15 Do centro de uma cidade até o aeroporto são 40km por uma grande avenida. Os táxis que saem do aeroporto cobram R$3,60 pela bandeirada e R$0,80 por quilômetro rodado. Os que saem do centro cobram R$,00 pela bandeirada e R$0,60 por quilômetro rodado. Dois amigos se encontraram num restaurante que fica nessa avenida, sendo que um tomou o táxi que sai do aeroporto e o outro tomou o que parte do centro e, para surpresa dos dois, os seus gastos foram exatamente iguais. A distância do restaurante ao aeroporto é de a) 10 km b) 1 km c) 14 km d) 16 km e) 18 km Pág 5
6 QUESTÃO 16 QUESTÃO 17 A tabela a seguir mostra a temperatura das águas do Oceano Atlântico (ao nível do Equador) em função da profundidade: (Profundidade) - (Temperatura) Superfície 7 C 100m 1 C 500m 7 C 1000m 4 C 3000m,8 C Admitindo que a variação da temperatura seja aproximadamente linear entre cada duas das medições feitas para a profundidade, a temperatura prevista para a profundidade de 400 m é de: a)16 C b)14 C c)1,5 C d)10,5 C e) 8 C QUESTÃO 18 O gráfico abaixo representa a evolução populacional de Porto Alegre entre os anos de 199 e 010. Pág 6
7 Considerando as seguintes retas: r, determinada pelos pontos A e B; s, pelos pontos B e C; t, pelos pontos C e D; e u, pelos pontos D e E, cujos coeficientes angulares são, respectivamente, a r, a s, a t e a u, é correto afirmar que a) ar au at as b) ar au as at c) au ar at as d) au ar as at QUESTÃO 19 No plano cartesiano a seguir, estão representados o gráfico da função definida por quadrados adjacentes ABCD e DMNP. f(x) x, com x, e os vértices dos Observe que B e P são pontos do gráfico da função f e que A, B, D e M são pontos dos eixos coordenados. Desse modo, a área do polígono ABCPNM, formado pela união dos dois quadrados, é: a) 0 Pág 7
8 b) 8 c) 36 d) 40 QUESTÃO 0 O morro onde estão situadas as emissoras de TV em Porto Alegre pode ser representado graficamente, com algum prejuízo, em um sistema cartesiano, através de uma função polinomial de grau da forma y ax bx c, com a base da montanha no eixo das abscissas. Para que fique mais adequada essa representação, devemos ter a) a 0 e b) a 0 e c) a 0 e b 4ac 0 b 4ac 0 b 4ac 0 d) a 0 e b 4ac 0 QUESTÃO 1 Um restaurante francês oferece um prato sofisticado ao preço de p reais por unidade. A quantidade mensal x de pratos que é vendida relaciona-se com o preço cobrado através da função p 0,4x 00. Sejam k 1 e k os números de pratos vendidos mensalmente, para os quais a receita é igual a R$1.000,00. O valor de k1 k é: a) 450 b) 500 c) 550 d) 600 e) 650 QUESTÃO A empresa SKY transporta 400 passageiros por mês da cidade de Acrolândia a Bienvenuto. A passagem custa 0 reais, e a empresa deseja aumentar o seu preço. No entanto, o departamento de pesquisa estima que, a cada 1 real de aumento no preço da passagem, 0 passageiros deixarão de viajar pela empresa. Nesse caso, qual é o preço da passagem, em reais, que vai maximizar o faturamento da SKY? a) 75 b) 70 c) 60 d) 55 e) 50 QUESTÃO 3 A empresa SKY transporta 400 passageiros por mês da cidade de Acrolândia a Bienvenuto. A passagem custa 0 reais, e a empresa deseja aumentar o seu preço. No entanto, o departamento de pesquisa estima que, a cada 1 real de aumento no preço da passagem, 0 passageiros deixarão de viajar pela empresa. Nesse caso, qual é o preço da passagem, em reais, que vai maximizar o faturamento da SKY? a) 75 Pág 8
9 b) 70 c) 60 d) 55 e) 50 QUESTÃO 4 Um modelo matemático simplificado para o formato de um vaso sanguíneo é o de um tubo cilíndrico circular reto. Nesse modelo, devido ao atrito com as paredes do vaso, a velocidade V do sangue em um ponto P no tubo depende da distância r do ponto P ao eixo do tubo. O médico francês Jean-Louis-Marie Poiseuille ( ) propôs a seguinte lei que descreve a velocidade V em função de r: v v(r) k(r r ), Onde Ré o raio do tubo cilíndrico e ké um parâmetro que depende da diferença de pressão nos extremos do tubo, do comprimento do tubo e da viscosidade do sangue. Considerando que k é constante e positivo, assinale a alternativa que contém uma representação possível para o gráfico da função v = v(r). a) b) c) d) e) QUESTÃO 5 Um posto de combustível vende litros de álcool por dia a R$ 1,50 cada litro. Seu proprietário percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 100 litros a mais por dia. Por exemplo, no dia em que o preço do álcool foi R$ 1,48, foram vendidos litros. Considerando x o valor, em centavos, do desconto dado no preço de cada litro, e V o valor, em R$, arrecadado por dia com a venda do álcool, então a expressão que relaciona V e x é: a) V = x x. b) V = x + x. c) V = x x. d) V = x x. Pág 9
10 e) V = x + x. Pág 10
FUNÇÃO DO 2 GRAU TERÇA FEIRA
 FUNÇÃO DO GRAU TERÇA FEIRA 1. (G1 - cftmg 016) Dadas as funções reais f e g, definidas por correto afirmar que 1 a) f(x) g 0, 4 para todo x. b) f(x) 0, para todo x. f(x) 3x e g(x) 4x 1, é c) f(x) g(x),
FUNÇÃO DO GRAU TERÇA FEIRA 1. (G1 - cftmg 016) Dadas as funções reais f e g, definidas por correto afirmar que 1 a) f(x) g 0, 4 para todo x. b) f(x) 0, para todo x. f(x) 3x e g(x) 4x 1, é c) f(x) g(x),
Lista de Função Quadrática e Módulo (Prof. Pinda)
 Lista de Função Quadrática e Módulo (Prof. Pinda) 1. (Pucrj 015) Sejam as funções f(x) x 6x e g(x) x 1. O produto dos valores inteiros de x que satisfazem a desigualdade f(x) g(x) é: a) 8 b) 1 c) 60 d)
Lista de Função Quadrática e Módulo (Prof. Pinda) 1. (Pucrj 015) Sejam as funções f(x) x 6x e g(x) x 1. O produto dos valores inteiros de x que satisfazem a desigualdade f(x) g(x) é: a) 8 b) 1 c) 60 d)
Whats: (84) FUNÇÕES (GRÁFICOS)
 1.Uma empresa analisou mensalmente as vendas de um de seus produtos ao longo de 1 meses após seu lançamento. Concluiu que, a partir do lançamento, a venda mensal do produto teve um crescimento linear até
1.Uma empresa analisou mensalmente as vendas de um de seus produtos ao longo de 1 meses após seu lançamento. Concluiu que, a partir do lançamento, a venda mensal do produto teve um crescimento linear até
Aulas particulares. Conteúdo
 Conteúdo Capítulo 3...2 Funções...2 Função de 1º grau...2 Exercícios...6 Gabarito... 13 Função quadrática ou função do 2º grau... 15 Exercícios... 22 Gabarito... 29 Capítulo 3 Funções Função de 1º grau
Conteúdo Capítulo 3...2 Funções...2 Função de 1º grau...2 Exercícios...6 Gabarito... 13 Função quadrática ou função do 2º grau... 15 Exercícios... 22 Gabarito... 29 Capítulo 3 Funções Função de 1º grau
Relação de Conjuntos. Produto cartesiano A = 1,2 e o conjunto B = 2,3,4 queremos o produto cartesiano A x B
 Relação de Conjuntos Produto cartesiano A = 1,2 e o conjunto B = 2,3,4 queremos o produto cartesiano A x B A x B = { 1,2, 1,3, 1,4, 2,2, 2,3, 2,4 } A B 1 2 2 3 4 Funções Uma Relação será função se: 1.
Relação de Conjuntos Produto cartesiano A = 1,2 e o conjunto B = 2,3,4 queremos o produto cartesiano A x B A x B = { 1,2, 1,3, 1,4, 2,2, 2,3, 2,4 } A B 1 2 2 3 4 Funções Uma Relação será função se: 1.
BANCO DE QUESTÕES - ÁLGEBRA - 9º ANO - ENSINO FUNDAMENTAL
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - ÁLGEBRA - 9º ANO - ENSINO FUNDAMENTAL ============================================================================ 01- Sabe-se que o custo C para produzir
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES - ÁLGEBRA - 9º ANO - ENSINO FUNDAMENTAL ============================================================================ 01- Sabe-se que o custo C para produzir
2. Escreva em cada caso o intervalo real representado nas retas:
 ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 018 4º BIMESTRE TRABALHO DE RECUPERAÇÃO Nome: Nº Turma Data Nota Disciplina: Matemática Prof. Tallyne Siqueira Valor 1. Represente na reta real os intervalos:
ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 018 4º BIMESTRE TRABALHO DE RECUPERAÇÃO Nome: Nº Turma Data Nota Disciplina: Matemática Prof. Tallyne Siqueira Valor 1. Represente na reta real os intervalos:
TECNÓLOGO EM CONSTRUÇÃO CIVIL. Aula 5 _ Função Polinomial do 1º Grau Professor Luciano Nóbrega
 1 TECNÓLOGO EM CONSTRUÇÃO CIVIL Aula 5 _ Função Polinomial do 1º Grau Professor Luciano Nóbrega 2 FUNÇÃO POLINOMIAL DO 1º GRAU Uma função polinomial do 1º grau (ou simplesmente, função do 1º grau) é uma
1 TECNÓLOGO EM CONSTRUÇÃO CIVIL Aula 5 _ Função Polinomial do 1º Grau Professor Luciano Nóbrega 2 FUNÇÃO POLINOMIAL DO 1º GRAU Uma função polinomial do 1º grau (ou simplesmente, função do 1º grau) é uma
LISTA DE REVISÃO PROVA TRIMESTRAL DE ÁLGEBRA AULAS 30 a 38 FUNÇÕES DE 1ºGRAU
 LISTA DE REVISÃO PROVA TRIMESTRAL DE ÁLGEBRA AULAS 30 a 38 FUNÇÕES DE 1ºGRAU 1. (G1-014) O gráfico representa a função real definida por f(x) = a x + b. O valor de a + b é igual a A) 0,5. B) 1,0. C) 1,5.
LISTA DE REVISÃO PROVA TRIMESTRAL DE ÁLGEBRA AULAS 30 a 38 FUNÇÕES DE 1ºGRAU 1. (G1-014) O gráfico representa a função real definida por f(x) = a x + b. O valor de a + b é igual a A) 0,5. B) 1,0. C) 1,5.
Resposta: f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo 5, 5 5, 5 3, 3. f(g(x) = x 5.
 1. (Espcex (Aman) 016) Considere as funções reais f e g, tais que f(x) = x + 4 e f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis
1. (Espcex (Aman) 016) Considere as funções reais f e g, tais que f(x) = x + 4 e f(g(x)) = x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis
CPV O cursinho que mais aprova na GV
 O cursinho que mais aprova na GV FGV ADM Objetiva Turma A 24/outubro/2010 matemática 01. O gráfico de uma função polinomial do primeiro grau passa pelos pontos de coordenadas (x; y) dados abaixo. Podemos
O cursinho que mais aprova na GV FGV ADM Objetiva Turma A 24/outubro/2010 matemática 01. O gráfico de uma função polinomial do primeiro grau passa pelos pontos de coordenadas (x; y) dados abaixo. Podemos
LISTA DE RECUPERAÇÃO ÁLGEBRA 1º ANO 2º TRIMESTRE
 FUNÇÕES CONCEITOS INICIAIS LISTA DE RECUPERAÇÃO ÁLGEBRA 1º ANO º TRIMESTRE 1) (Espm) Numa população de 5000 alevinos de tambacu, estima-se que o número de elementos com comprimento maior ou igual a x cm
FUNÇÕES CONCEITOS INICIAIS LISTA DE RECUPERAÇÃO ÁLGEBRA 1º ANO º TRIMESTRE 1) (Espm) Numa população de 5000 alevinos de tambacu, estima-se que o número de elementos com comprimento maior ou igual a x cm
PLANTÕES DE JULHO MATEMÁTICA
 Página 1 Matemática 1 Funções do 1º e 2º grau PLANTÕES DE JULHO MATEMÁTICA Nome: Nº: Série: 1º ANO Turma: Profª CAROL MARTINS Data: JULHO 2016 1) (UFPE) No gráfico a seguir, temos o nível da água armazenada
Página 1 Matemática 1 Funções do 1º e 2º grau PLANTÕES DE JULHO MATEMÁTICA Nome: Nº: Série: 1º ANO Turma: Profª CAROL MARTINS Data: JULHO 2016 1) (UFPE) No gráfico a seguir, temos o nível da água armazenada
FUNÇÕES PROF HEY As funções nada mais são que um tipo particular de relação que possuem uma propriedade específica.
 FUNÇÕES PROF HEY As funções nada mais são que um tipo particular de relação que possuem uma propriedade específica. Uma função definida por f: R R chama-se afim quando existem constantes a, b que pertencem
FUNÇÕES PROF HEY As funções nada mais são que um tipo particular de relação que possuem uma propriedade específica. Uma função definida por f: R R chama-se afim quando existem constantes a, b que pertencem
Professor: Danilo Menezes de Oliveira Machado
 Professor: Danilo Menezes de Oliveira Machado O QUE PRECISA SER LEMBRADO Progressão aritmética: a n = a 1 + (n 1)r Parte fixa: a 1 Parte variável: (n 1)r Variável: n Tipo de variável: Discreta (IN) Juros
Professor: Danilo Menezes de Oliveira Machado O QUE PRECISA SER LEMBRADO Progressão aritmética: a n = a 1 + (n 1)r Parte fixa: a 1 Parte variável: (n 1)r Variável: n Tipo de variável: Discreta (IN) Juros
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática MAT 101 - Fundamentos de Matemática I 2012/I 2 a Lista - Funções (Parte I) 1. Dados os conjuntos M = {1, 3, 5} e N
1 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática MAT 101 - Fundamentos de Matemática I 2012/I 2 a Lista - Funções (Parte I) 1. Dados os conjuntos M = {1, 3, 5} e N
a < 0 / > 0 a < 0 / = 0 a < 0 / < 0
 FUNÇÃO DO 2 GRAU (QUADRÁTICA) a < 0 / > 0 a) Definição Denomina-se função do 2 grau toda função f : IR IR definida por f(x) = ax 2 + bx + c, com a, b, c IR e a O. b) Raízes ou zeros As raízes da função
FUNÇÃO DO 2 GRAU (QUADRÁTICA) a < 0 / > 0 a) Definição Denomina-se função do 2 grau toda função f : IR IR definida por f(x) = ax 2 + bx + c, com a, b, c IR e a O. b) Raízes ou zeros As raízes da função
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO
 ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO (NO PERÍODO DE FÉRIAS ESCOLARES) ANO 20 PROFESSOR (a) DISCIPLINA BRUNO REZENDE PEREIRA MATEMÁTICA ALUNO (a) SÉRIE
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO (NO PERÍODO DE FÉRIAS ESCOLARES) ANO 20 PROFESSOR (a) DISCIPLINA BRUNO REZENDE PEREIRA MATEMÁTICA ALUNO (a) SÉRIE
b) Determinar as raízes de f(x) = g(x) quando m = 1/2. c) Determinar, em função de m, o número de raízes da equação f(x) = g(x).
 1. (Fuvest 2000) a) Esboce, para x real, o gráfico da função f(x) = x - 2 + 2x + 1 - x - 6. O símbolo a indica o valor absoluto de um número real a e é definido por a = a, se a µ 0 e a = - a, se a < 0.
1. (Fuvest 2000) a) Esboce, para x real, o gráfico da função f(x) = x - 2 + 2x + 1 - x - 6. O símbolo a indica o valor absoluto de um número real a e é definido por a = a, se a µ 0 e a = - a, se a < 0.
b Considerando os valores log 2 = 0,30 e log 3 = 0,48, o valor de x que satisfaz a equação 36 x = 24, é: 49
 MATEMÁTICA 1 e O Sr. Paiva é proprietário de duas papelarias, A e B. Em 2002 o faturamento da unidade A foi 50% superior ao da unidade B. Em 2003, o faturamento de A aumentou 20% em relação ao seu faturamento
MATEMÁTICA 1 e O Sr. Paiva é proprietário de duas papelarias, A e B. Em 2002 o faturamento da unidade A foi 50% superior ao da unidade B. Em 2003, o faturamento de A aumentou 20% em relação ao seu faturamento
EXERCÍCIOS FUNÇÃO AFIM
 Primeiramente Bom dia! EXERCÍCIOS FUNÇÃO AFIM Questão 0 - (UNIRIO RJ/00) Um automóvel bicombustível (álcool/gasolin traz as seguintes informações sobre consumo (em quilômetros por litro) em seu manual:
Primeiramente Bom dia! EXERCÍCIOS FUNÇÃO AFIM Questão 0 - (UNIRIO RJ/00) Um automóvel bicombustível (álcool/gasolin traz as seguintes informações sobre consumo (em quilômetros por litro) em seu manual:
Quanto ela receberá de salário se ela vender um total de R$ ,00?
 Uma vendedora recebe um salário mínimo R$ 788,00 mais comissão de 5% sobre o total de suas vendas durante o mês. Se X é o quanto ela vendeu no mês, qual a lei de formação que Melhor caracteriza a lei de
Uma vendedora recebe um salário mínimo R$ 788,00 mais comissão de 5% sobre o total de suas vendas durante o mês. Se X é o quanto ela vendeu no mês, qual a lei de formação que Melhor caracteriza a lei de
9 ano E.F. Professores Cleber Assis e Tiago Miranda
 Módulo Função Quadrática Noções Básicas 9 ano E.F. Professores Cleber Assis e Tiago Miranda Função Quadrática Noções Básicas 1 Exercícios Introdutórios Exercício 1. Os coeficientes de x (a), de x (b) e
Módulo Função Quadrática Noções Básicas 9 ano E.F. Professores Cleber Assis e Tiago Miranda Função Quadrática Noções Básicas 1 Exercícios Introdutórios Exercício 1. Os coeficientes de x (a), de x (b) e
BANCO DE QUESTÕES TURMA PM-PE FUNÇÕES
 01. (ESPCEX-AMAN/016) Considere as funções reais f e g, tais que f(x) x 4 e f(g(x)) x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis valores
01. (ESPCEX-AMAN/016) Considere as funções reais f e g, tais que f(x) x 4 e f(g(x)) x 5, onde g(x) é não negativa para todo x real. Assinale a alternativa cujo conjunto contém todos os possíveis valores
Ciências da Natureza e Matemática
 Ciências da Natureza e 1 CEDAE Acompanhamento Escolar Ciências da Natureza e 2 CEDAE Acompanhamento Escolar Ciências da Natureza e 1) Numa certa cidade existem duas empresas de TV por assinatura prestando
Ciências da Natureza e 1 CEDAE Acompanhamento Escolar Ciências da Natureza e 2 CEDAE Acompanhamento Escolar Ciências da Natureza e 1) Numa certa cidade existem duas empresas de TV por assinatura prestando
MATEMÁTICA. Questão 41. O gráfico abaixo representa a evolução populacional de Porto Alegre entre os anos de 1992 e 2010.
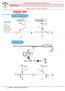
 MATEMÁTICA Questão 41 O gráfico abaixo representa a evolução populacional de Porto Alegre entre os anos de 199 e 010. Porto Alegre 1.600.000 A B C D E 1.00.000 00.000 400.000 0 199 1996 000 004 00 x Fonte:
MATEMÁTICA Questão 41 O gráfico abaixo representa a evolução populacional de Porto Alegre entre os anos de 199 e 010. Porto Alegre 1.600.000 A B C D E 1.00.000 00.000 400.000 0 199 1996 000 004 00 x Fonte:
INSTITUTO GEREMÁRIO DANTAS COMPONENTE CURRICULAR: MATEMÁTICA I EXERCÍCIOS DE RECUPERAÇÃO FINAL 2016
 INSTITUTO GEREMÁRIO DANTAS Educação Infantil, Ensino Fundamental e Médio Fone: (21) 21087900 Rio de Janeiro RJ www.igd.com.br Aluno(a): 9º Ano: Nº Professora: Maria das Graças COMPONENTE CURRICULAR: MATEMÁTICA
INSTITUTO GEREMÁRIO DANTAS Educação Infantil, Ensino Fundamental e Médio Fone: (21) 21087900 Rio de Janeiro RJ www.igd.com.br Aluno(a): 9º Ano: Nº Professora: Maria das Graças COMPONENTE CURRICULAR: MATEMÁTICA
ADA 1º BIMESTRE CICLO I MATEMÁTICA 1ª SÉRIE DO ENSINO MÉDIO 2018
 ADA 1º BIMESTRE CICLO I MATEMÁTICA 1ª SÉRIE DO ENSINO MÉDIO 2018 ITEM 1 DA ADA No desenho, a seguir, estão representados os pontos M e N que correspondem à localização de dois animais. Atividades relacionadas
ADA 1º BIMESTRE CICLO I MATEMÁTICA 1ª SÉRIE DO ENSINO MÉDIO 2018 ITEM 1 DA ADA No desenho, a seguir, estão representados os pontos M e N que correspondem à localização de dois animais. Atividades relacionadas
Exercícios de matemática - 2º ano - Ensino Médio - 4º bimestre
 Exercícios de matemática - º ano - Ensino Médio - º bimestre Pergunta de 0 - Assunto: Álgebra [0 - FUVEST-USP] Considere a matriz a a + A = [ a a + ] em que aa é um número real. Sabendo que AA admite inversa
Exercícios de matemática - º ano - Ensino Médio - º bimestre Pergunta de 0 - Assunto: Álgebra [0 - FUVEST-USP] Considere a matriz a a + A = [ a a + ] em que aa é um número real. Sabendo que AA admite inversa
( ) = 0. ( ) = 30t 3t 2 é
 QUESTÃO 01 t = 0 t +10t =1600 t 10t+1600 = 0 $ ou & t = 40 Portanto o primeiro momento em que o número de infectados é 1.600 é o 0 dia. QUESTÃO 0 9 Como D( x) = x + 18x+ 30, o valor de x que maximiza essa
QUESTÃO 01 t = 0 t +10t =1600 t 10t+1600 = 0 $ ou & t = 40 Portanto o primeiro momento em que o número de infectados é 1.600 é o 0 dia. QUESTÃO 0 9 Como D( x) = x + 18x+ 30, o valor de x que maximiza essa
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - 24 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº 12 EXERCÍCIOS 1) Um táxi começa uma corrida com o taxímetro marcando R$ 4,00. Cada quilômetro rodado custa
BANCO DE EXERCÍCIOS - 24 HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº 12 EXERCÍCIOS 1) Um táxi começa uma corrida com o taxímetro marcando R$ 4,00. Cada quilômetro rodado custa
- MATEMÁTICA - PUC-MG
 Vestibulando Web Page 1. Uma empresa deve instalar telefones de emergência a cada 42 quilômetros, ao longo da rodovia de 2.184 km, que liga Maceió ao Rio de Janeiro. Considere que o primeiro desses telefones
Vestibulando Web Page 1. Uma empresa deve instalar telefones de emergência a cada 42 quilômetros, ao longo da rodovia de 2.184 km, que liga Maceió ao Rio de Janeiro. Considere que o primeiro desses telefones
b) Determinar as raízes de f(x) = g(x) quando m = 1/2. c) Determinar, em função de m, o número de raízes da equação f(x) = g(x).
 1. (Fuvest 2004) Seja m µ 0 um número real e sejam f e g funções reais definidas por f(x) = x - 2 x + 1 e g(x) = mx + 2m. a) Esboçar, no plano cartesiano representado a seguir, os gráficos de f e de g
1. (Fuvest 2004) Seja m µ 0 um número real e sejam f e g funções reais definidas por f(x) = x - 2 x + 1 e g(x) = mx + 2m. a) Esboçar, no plano cartesiano representado a seguir, os gráficos de f e de g
MATEMÁTICA. log 2 x : logaritmo de base 2 de x. 28. Sendo a, b e c números reais, considere as seguintes afirmações.
 MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x log x : logaritmo de base de x 6 Considere que o corpo de uma determinada pessoa
MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x log x : logaritmo de base de x 6 Considere que o corpo de uma determinada pessoa
Lista de Recomendação - Verificação Suplementar Prof. Marcos Matemática
 Nome: Lista de Recomendação - Verificação Suplementar Prof. Marcos Matemática 1. O valor de x, de modo que os números 3x 1, x + 3 e x + 9 estejam, nessa ordem, em PA é: 2. O centésimo número natural par
Nome: Lista de Recomendação - Verificação Suplementar Prof. Marcos Matemática 1. O valor de x, de modo que os números 3x 1, x + 3 e x + 9 estejam, nessa ordem, em PA é: 2. O centésimo número natural par
MATEMÁTICA E RACIOCÍNIO LÓGICO
 FUNÇÕES VALOR NUMÉRICO 1 01) Dada a função f(x) 1 x, o valor f(1,5) é x + 1 igual a a) 1,7 b) 1,8 c) 1,9 d),0 e),1 0) Na função f:r R, com f(x) x² 3x + 1, o 1 valor de f a) b) 11/4 c) 3/3 d) 15/4 FUNÇÕES
FUNÇÕES VALOR NUMÉRICO 1 01) Dada a função f(x) 1 x, o valor f(1,5) é x + 1 igual a a) 1,7 b) 1,8 c) 1,9 d),0 e),1 0) Na função f:r R, com f(x) x² 3x + 1, o 1 valor de f a) b) 11/4 c) 3/3 d) 15/4 FUNÇÕES
Prova de UFRGS
 Prova de UFRGS - 212 1 Considere que o corpo de uma determinada pessoa contém 5,5 litros de sangue e 5 milhões de glóbulos vermelhos por milímetro cúbico de sangue Com base nesses dados, é correto afirmar
Prova de UFRGS - 212 1 Considere que o corpo de uma determinada pessoa contém 5,5 litros de sangue e 5 milhões de glóbulos vermelhos por milímetro cúbico de sangue Com base nesses dados, é correto afirmar
EXERCÍCIOS DE ESTRUTURA SEQUENCIAL
 EXERCÍCIOS DE ESTRUTURA SEQUENCIAL 1 - O coração humano bate em média uma vez por segundo. Desenvolva um algoritmo para calcular e escrever quantas vezes o coração de uma pessoa baterá se viver X anos.
EXERCÍCIOS DE ESTRUTURA SEQUENCIAL 1 - O coração humano bate em média uma vez por segundo. Desenvolva um algoritmo para calcular e escrever quantas vezes o coração de uma pessoa baterá se viver X anos.
Prof. Dr. Aldo Vieira
 1. Em uma determinada região do planeta, a temperatura média anual subiu de 13,35 ºC em 1995 para 13,8 ºC em 2010. Seguindo a tendência de aumento linear observada entre 1995 e 2010, a temperatura média
1. Em uma determinada região do planeta, a temperatura média anual subiu de 13,35 ºC em 1995 para 13,8 ºC em 2010. Seguindo a tendência de aumento linear observada entre 1995 e 2010, a temperatura média
INSTITUTO FEDERAL DO ESPÍRITO SANTO CAMPUS SERRA CURSO TÉCNICO EM INFORMÁTICA LISTA DE EXERCÍCIOS FUNÇÃO AFIM E FUNÇÃO QUADRÁTICA ALUNO(A):
 INSTITUTO FEDERAL DO ESPÍRITO SANTO CAMPUS SERRA CURSO TÉCNICO EM INFORMÁTICA LISTA DE EXERCÍCIOS FUNÇÃO AFIM E FUNÇÃO QUADRÁTICA ALUNO(A): 1. (Unisinos-RS) Suponha que o número de carteiros necessários
INSTITUTO FEDERAL DO ESPÍRITO SANTO CAMPUS SERRA CURSO TÉCNICO EM INFORMÁTICA LISTA DE EXERCÍCIOS FUNÇÃO AFIM E FUNÇÃO QUADRÁTICA ALUNO(A): 1. (Unisinos-RS) Suponha que o número de carteiros necessários
AULA 5 Função Afim. Se a > 0 (ou seja, se o valor de a for um número positivo), a função y = ax + b é crescente. Ex1:
 AULA 5 Função Afim Sejam a e b números reais e a 0. Dizemos que uma função f : R R é função do 1º grau ou função afim quando está definida pela lei (ou seja, quando tiver esse formato): em que : y f (
AULA 5 Função Afim Sejam a e b números reais e a 0. Dizemos que uma função f : R R é função do 1º grau ou função afim quando está definida pela lei (ou seja, quando tiver esse formato): em que : y f (
Colégio Notre Dame de Campinas Congregação de Santa Cruz PLANTÕES DE JULHO MATEMÁTICA AULA 1
 PLANTÕES DE JULHO MATEMÁTICA AULA 1 Nome: Nº: Série: 9º ANO Turma: Prof: Luis Felipe Bortoletto Data: JULHO 2018 Lista 1 1) Na figura abaixo, temos um quadrado AEDF e AC=4 e AB=6. Qual é o valor do lado
PLANTÕES DE JULHO MATEMÁTICA AULA 1 Nome: Nº: Série: 9º ANO Turma: Prof: Luis Felipe Bortoletto Data: JULHO 2018 Lista 1 1) Na figura abaixo, temos um quadrado AEDF e AC=4 e AB=6. Qual é o valor do lado
Matemática I Lista de exercícios 02
 Matemática I 2011.1 Lista de exercícios 02 1. O conjunto {( 1,2), (2,3), (3,4), (4,5), (5,6)} é um subconjunto do conjunto: (A) {( x, y) R R x = y} (B) {( x, y) R R x > y} (C) {( x, y) R R x y} (D) {(
Matemática I 2011.1 Lista de exercícios 02 1. O conjunto {( 1,2), (2,3), (3,4), (4,5), (5,6)} é um subconjunto do conjunto: (A) {( x, y) R R x = y} (B) {( x, y) R R x > y} (C) {( x, y) R R x y} (D) {(
IFRN - INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN PROFESSOR: MARCELO SILVA MATEMÁTICA LISTA FUNÇÃO
 IFRN - INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN PROFESSOR: MARCELO SILVA MATEMÁTICA LISTA FUNÇÃO 1. Dados os conjuntos G 0,1,3, 4 e 1,3 elemento de G ao seu dobro mais um em H, é dada
IFRN - INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN PROFESSOR: MARCELO SILVA MATEMÁTICA LISTA FUNÇÃO 1. Dados os conjuntos G 0,1,3, 4 e 1,3 elemento de G ao seu dobro mais um em H, é dada
REVISÃO UNIOESTE 2016 MATEMÁTICA GUSTAVO
 REVISÃO UNIOESTE 01 MATEMÁTICA GUSTAVO 1 Considere a figura: Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas quadradas de metros de lado, conforme a figura
REVISÃO UNIOESTE 01 MATEMÁTICA GUSTAVO 1 Considere a figura: Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas quadradas de metros de lado, conforme a figura
COLÉGIO ARQUIDIOCESANO S. CORAÇÃO DE JESUS
 QUESTÃO 01 Um triângulo ABC está inscrito numa semicircunferência de centro O. Como mostra o desenho abaixo. Sabe-se que a medida do segmento AB é de 12 cm. QUESTÃO 04 Numa cidade a conta de telefone é
QUESTÃO 01 Um triângulo ABC está inscrito numa semicircunferência de centro O. Como mostra o desenho abaixo. Sabe-se que a medida do segmento AB é de 12 cm. QUESTÃO 04 Numa cidade a conta de telefone é
PROCESSO SELETIVO/ O DIA GABARITO 1 1 MATEMÁTICA QUESTÕES DE 01 A 15
 PROCESSO SELETIVO/005 1 O DIA GABARITO 1 1 MATEMÁTICA QUESTÕES DE 01 A 15 01. As prefeituras das cidades A, B e C construíram uma ponte sobre o rio próximo a estas cidades. A ponte dista 10 km de A, 1
PROCESSO SELETIVO/005 1 O DIA GABARITO 1 1 MATEMÁTICA QUESTÕES DE 01 A 15 01. As prefeituras das cidades A, B e C construíram uma ponte sobre o rio próximo a estas cidades. A ponte dista 10 km de A, 1
MATEMÁTICA - 1 o ANO MÓDULO 17 FUNÇÃO DO 2 O GRAU - DEFINIÇÃO
 MATEMÁTICA - 1 o ANO MÓDULO 17 FUNÇÃO DO 2 O GRAU - DEFINIÇÃO y c x y y x x x x x x y y x =x x x =x x y y x x eixo de simetria eixo de simetria y x x v x f(x) x y v y v y v v x x v x x Como pode cair
MATEMÁTICA - 1 o ANO MÓDULO 17 FUNÇÃO DO 2 O GRAU - DEFINIÇÃO y c x y y x x x x x x y y x =x x x =x x y y x x eixo de simetria eixo de simetria y x x v x f(x) x y v y v y v v x x v x x Como pode cair
ANPAD CURSO. b) quatro desses funcionários podem ter 20 anos, quatro podem ter 35, dez podem ter 30 anos, e os demais podem ter 40 anos
 01. A média de idade de 20 funcionários de uma empresa é 30 anos. Sabendo-se que, nessa empresa, não há funcionários com menos de 18 anos de idade nem com mais de 75, pode-se afirmar que: a) necessariamente,
01. A média de idade de 20 funcionários de uma empresa é 30 anos. Sabendo-se que, nessa empresa, não há funcionários com menos de 18 anos de idade nem com mais de 75, pode-se afirmar que: a) necessariamente,
Maratona GoiásVest. Aula 03 - M A T E M Á T I C A. Questão 04 (UFF ª Fase): Questão 01 (enem-2011):
 matematica_goiasvest_ - agosto0 - Aula 0_Layout /0/0 : Page Aula 0 Questão 0 (enem-0): O medidor de energia elétrica de uma residência, conhecido por relógio de luz, é constituído de quatro pequenos relógios,
matematica_goiasvest_ - agosto0 - Aula 0_Layout /0/0 : Page Aula 0 Questão 0 (enem-0): O medidor de energia elétrica de uma residência, conhecido por relógio de luz, é constituído de quatro pequenos relógios,
MATEMÁTICA. Use este espaço para rascunho.
 MATEMÁTICA Use este espaço para rascunho 01 Cubos brancos de 1cm de aresta foram dispostos formando o paralelepípedo representado abaixo Em seguida, a superfície total desse paralelepípedo foi pintada
MATEMÁTICA Use este espaço para rascunho 01 Cubos brancos de 1cm de aresta foram dispostos formando o paralelepípedo representado abaixo Em seguida, a superfície total desse paralelepípedo foi pintada
PROCESSO DE INGRESSO NA UPE
 PROCESSO DE INGRESSO NA UPE MATEMÁTICA 2º dia 1 MATEMÁTICA 1. A figura a seguir mostra uma das peças do jogo Pentaminós. Cada peça é formada por cinco quadradinhos, e o lado de cada quadradinho mede 5cm.
PROCESSO DE INGRESSO NA UPE MATEMÁTICA 2º dia 1 MATEMÁTICA 1. A figura a seguir mostra uma das peças do jogo Pentaminós. Cada peça é formada por cinco quadradinhos, e o lado de cada quadradinho mede 5cm.
Matemática. Questão 1. 3 a série do Ensino Médio Turma. 1 o Bimestre de 2016 Data / / Escola. Aluno RESOLUÇÃO: AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO
 EM AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 3 a série do Ensino Médio Turma GOVERNO DO ESTADO DE SÃO PAULO SECRETARIA DA EDUCAÇÃO 1 o Bimestre de 2016 Data / / Escola Aluno Questão 1 Sabemos que
EM AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 3 a série do Ensino Médio Turma GOVERNO DO ESTADO DE SÃO PAULO SECRETARIA DA EDUCAÇÃO 1 o Bimestre de 2016 Data / / Escola Aluno Questão 1 Sabemos que
MATEMÁTICA. Professor Diego Viug
 MATEMÁTICA Professor Diego Viug FUNÇÃO AFIM E FUNÇÃO QUADRÁTICA FUNÇÃO AFIM Taxa de variação constante. Proporcionalidade. (usaremos semelhança) y = ax + b a coeficiente angular. b coeficiente linear.
MATEMÁTICA Professor Diego Viug FUNÇÃO AFIM E FUNÇÃO QUADRÁTICA FUNÇÃO AFIM Taxa de variação constante. Proporcionalidade. (usaremos semelhança) y = ax + b a coeficiente angular. b coeficiente linear.
x 1. Em cada uma das figuras, eles são apenas os primeiros elementos dos
 0) Nas figuras a seguir, a curva é o gráfico da função x retângulos hachurados para infinitos que possuem as mesmas características. f x. Observe atentamente o que ocorre com os x. Em cada uma das figuras,
0) Nas figuras a seguir, a curva é o gráfico da função x retângulos hachurados para infinitos que possuem as mesmas características. f x. Observe atentamente o que ocorre com os x. Em cada uma das figuras,
Colégio Notre Dame de Campinas Congregação de Santa Cruz PLANTÕES DE JULHO MATEMÁTICA AULA 1
 PLANTÕES DE JULHO MATEMÁTICA AULA 1 Nome: Nº: Série: 3º ANO Turma: Prof: Luis Felipe Bortoletto Data: JULHO 2018 Lista 1 1) Após acionar um flash de uma câmera, a bateria imediatamente começa a recarregar
PLANTÕES DE JULHO MATEMÁTICA AULA 1 Nome: Nº: Série: 3º ANO Turma: Prof: Luis Felipe Bortoletto Data: JULHO 2018 Lista 1 1) Após acionar um flash de uma câmera, a bateria imediatamente começa a recarregar
Assine e coloque seu número de inscrição no quadro abaixo. Preencha, com traços firmes, o espaço reservado a cada opção na folha de resposta.
 1 Prezado(a) candidato(a): Assine e coloque seu número de inscrição no quadro abaio. Preencha, com traços firmes, o espaço reservado a cada opção na folha de resposta. Nº de Inscrição Nome PROVA DE MATEMÁTICA
1 Prezado(a) candidato(a): Assine e coloque seu número de inscrição no quadro abaio. Preencha, com traços firmes, o espaço reservado a cada opção na folha de resposta. Nº de Inscrição Nome PROVA DE MATEMÁTICA
Matemática I Lista de exercícios 03
 Matemática I 2014.1 Lista de exercícios 03 1. O conjunto {(1,2), (2,3), (3,4), (4,5), (5,6)} é um subconjunto do conjunto: (A) {(x, y)î R R x = y} (B) {(x, y)î R R x > y} (C) {(x, y)î R R x ³ y} (D) {(x,
Matemática I 2014.1 Lista de exercícios 03 1. O conjunto {(1,2), (2,3), (3,4), (4,5), (5,6)} é um subconjunto do conjunto: (A) {(x, y)î R R x = y} (B) {(x, y)î R R x > y} (C) {(x, y)î R R x ³ y} (D) {(x,
a) b) c) d) a) 18 h. b) 19 h. c) 20 h. d) 21 h. e) 22 h. Gab: B
 01 - (UFPR/017) O gráfico ao lado representa o consumo de bateria de um celular entre as 10 h e as 16 h de um determinado dia. Supondo que o consumo manteve o mesmo padrão até a bateria se esgotar, a que
01 - (UFPR/017) O gráfico ao lado representa o consumo de bateria de um celular entre as 10 h e as 16 h de um determinado dia. Supondo que o consumo manteve o mesmo padrão até a bateria se esgotar, a que
Colégio Militar de Porto Alegre 2/11
 DE ENSINO BÁSICO, TÉCNICO E TECNOLÓGICO 013 Escolha a única resposta certa, assinalando-a com um X nos parênteses à esquerda QUESTÃO 1 O valor de 74 + 43 + 31+ 1+ 13 + 7 + 3 + 1 é igual a (A) 13 (B) 13
DE ENSINO BÁSICO, TÉCNICO E TECNOLÓGICO 013 Escolha a única resposta certa, assinalando-a com um X nos parênteses à esquerda QUESTÃO 1 O valor de 74 + 43 + 31+ 1+ 13 + 7 + 3 + 1 é igual a (A) 13 (B) 13
Exercícios de Aprofundamento Matemática Funções Quadráticas
 1. (Espcex (Aman) 015) Um fabricante de poltronas pode produzir cada peça ao custo de R$ 00,00. Se cada uma for vendida por x reais, este fabricante venderá por mês (600 x) unidades, em que 0 x 600. Assinale
1. (Espcex (Aman) 015) Um fabricante de poltronas pode produzir cada peça ao custo de R$ 00,00. Se cada uma for vendida por x reais, este fabricante venderá por mês (600 x) unidades, em que 0 x 600. Assinale
3º EM. Prof. Fabio Henrique LISTA 06. Fabio Henrique
 3º EM LISTA 06 Fabio Henrique 1. A temperatura, 2 em graus Celsius, de um objeto armazenado em um determinado local é modelada pela função x f(x) 2x 10, 12 com x dado em horas. A temperatura máxima, em
3º EM LISTA 06 Fabio Henrique 1. A temperatura, 2 em graus Celsius, de um objeto armazenado em um determinado local é modelada pela função x f(x) 2x 10, 12 com x dado em horas. A temperatura máxima, em
MATEMÁTICA I Prof. Emerson Dutra 2 semestre de 2017 EDIF01A. Lista 3 - Função Afim - 25/08/2017
 MATEMÁTICA I Prof. Emerson Dutra 2 semestre de 2017 EDIF01A Nome: RA: Lista 3 - Função Afim - 25/08/2017 Obs.: É importante fazer todos os exercícios e discutir as dúvidas existentes. 1. Dados os gráficos
MATEMÁTICA I Prof. Emerson Dutra 2 semestre de 2017 EDIF01A Nome: RA: Lista 3 - Função Afim - 25/08/2017 Obs.: É importante fazer todos os exercícios e discutir as dúvidas existentes. 1. Dados os gráficos
FUNÇÃO DO 1º GRAU INTRODUÇÃO 6,50 + 2,60 = R$ 9,10. 0, ,60 = 13,65
 FUNÇÃO DO 1º GRAU INTRODUÇÃO Larissa toma um táxi comum que cobra R$ 2,60 pela bandeirada e R$ 0,65 por quilômetro rodado. Ela quer ir à casa do namorado que fica a 10 km de onde ela está. Quanto Larissa
FUNÇÃO DO 1º GRAU INTRODUÇÃO Larissa toma um táxi comum que cobra R$ 2,60 pela bandeirada e R$ 0,65 por quilômetro rodado. Ela quer ir à casa do namorado que fica a 10 km de onde ela está. Quanto Larissa
Função do 2º grau Questões Extras
 Função do º grau Questões Extras 1. (Uemg 016) O lucro de uma empresa é dado pela expressão matemática L R C, onde L é o lucro, C o custo da produção e R a receita do produto. Uma fábrica de tratores produziu
Função do º grau Questões Extras 1. (Uemg 016) O lucro de uma empresa é dado pela expressão matemática L R C, onde L é o lucro, C o custo da produção e R a receita do produto. Uma fábrica de tratores produziu
FUNÇÕES(1) FUNÇÃO POLINOMIAL DO 2º GRAU
 FUNÇÕES(1) FUNÇÃO POLINOMIAL DO º GRAU 1. (Uece 015) Se a função real de variável real, definida por f(1) =, f() = 5 e f(3) =, então o valor de f() é a). b) 1. c) 1. d). f(x) = ax + bx + c, é tal que.
FUNÇÕES(1) FUNÇÃO POLINOMIAL DO º GRAU 1. (Uece 015) Se a função real de variável real, definida por f(1) =, f() = 5 e f(3) =, então o valor de f() é a). b) 1. c) 1. d). f(x) = ax + bx + c, é tal que.
Observação: Todos os cálculos e desenvolvimentos deverão acompanhar a Lista.
 Módulo 05. Exercícios Lista de exercícios do Módulo 05 Observação: Todos os cálculos e desenvolvimentos deverão acompanhar a Lista. 1. Se A = { todos os números reais satisfazendo x 2 8 x+12=0 }, então:
Módulo 05. Exercícios Lista de exercícios do Módulo 05 Observação: Todos os cálculos e desenvolvimentos deverão acompanhar a Lista. 1. Se A = { todos os números reais satisfazendo x 2 8 x+12=0 }, então:
1 2 Queremos calcular o valor de t para o qual se tem T = -18 C. (Q Q 0. ) = m (R R 0 (35 30) (R 2000) ( ) 200 Q 6000 = R 2000 (Q 30) =
 Resposta da questão : [A] f(x) = ax + b f(0) = 50 b = 50 55 50 5 a = = = 0 0 0 x f(x) = + 50 f() = + 50 = 5,5 9 f(9) = + 50 = 54,5 ( 5,5 + 54,5) ( 9 ) S = S = 8 Resposta da questão : [B] As taxas de desvalorização
Resposta da questão : [A] f(x) = ax + b f(0) = 50 b = 50 55 50 5 a = = = 0 0 0 x f(x) = + 50 f() = + 50 = 5,5 9 f(9) = + 50 = 54,5 ( 5,5 + 54,5) ( 9 ) S = S = 8 Resposta da questão : [B] As taxas de desvalorização
Lista de problemas sobre funções (em geral) e função afim
 COLÉGIO PEDRO II CAMPUS REALENGO II LISTA DE APROFUNDAMENTO - ENEM MATEMÁTICA PROFESSOR: ANTÔNIO ANDRADE Lista de problemas sobre funções (em geral) e função afim QUESTÃO 01 Seu José sai de casa normalmente
COLÉGIO PEDRO II CAMPUS REALENGO II LISTA DE APROFUNDAMENTO - ENEM MATEMÁTICA PROFESSOR: ANTÔNIO ANDRADE Lista de problemas sobre funções (em geral) e função afim QUESTÃO 01 Seu José sai de casa normalmente
CPV O Cursinho que Mais Aprova na GV
 CPV O Cursinho que Mais Aprova na GV FGV ADM Objetiva Prova A 11/dezembro/011 matemática 01. Os gráficos abaixo representam as funções receita mensal R(x) e custo mensal C(x) de um produto fabricado por
CPV O Cursinho que Mais Aprova na GV FGV ADM Objetiva Prova A 11/dezembro/011 matemática 01. Os gráficos abaixo representam as funções receita mensal R(x) e custo mensal C(x) de um produto fabricado por
AULA 04 FUNÇÃO DO 1º GRAU 1. Dada a função afim f(x) = - 2x + 3, determine: a) f 1 b) f(0)
 1. Dada a função afim f(x) = - 2x + 3, determine: a) f 1 b) f(0) 1 c) f 3 1 d) f - 2 2. Dada a função afim f(x) = 2x + 3, determine os valores de x para que: a) f(x) = 1 b) f(x) = 0 c) f(x) = 3 1 3. Dada
1. Dada a função afim f(x) = - 2x + 3, determine: a) f 1 b) f(0) 1 c) f 3 1 d) f - 2 2. Dada a função afim f(x) = 2x + 3, determine os valores de x para que: a) f(x) = 1 b) f(x) = 0 c) f(x) = 3 1 3. Dada
Observe na imagem a seguir, a trajetória realizada por uma bola no momento em que um jogador a chutou em direção ao gol.
 FUNÇÃO QUADRÁTICA CONTEÚDOS Função quadrática Raízes da função quadrática Gráfico de função Ponto de máximo e de mínimo de uma função AMPLIANDO SEUS CONHECIMENTOS Observe na imagem a seguir, a trajetória
FUNÇÃO QUADRÁTICA CONTEÚDOS Função quadrática Raízes da função quadrática Gráfico de função Ponto de máximo e de mínimo de uma função AMPLIANDO SEUS CONHECIMENTOS Observe na imagem a seguir, a trajetória
PROVA DE MATEMÁTICA QUESTÃO 31 QUESTÃO 32
 PROVA DE MATEMÁTICA QUESTÃO 31 Dona Margarida comprou terra adubada para sua nova jardineira, que tem a forma de um paralelepípedo retângulo, cujas dimensões internas são: 1 m de comprimento, 25 cm de
PROVA DE MATEMÁTICA QUESTÃO 31 Dona Margarida comprou terra adubada para sua nova jardineira, que tem a forma de um paralelepípedo retângulo, cujas dimensões internas são: 1 m de comprimento, 25 cm de
1. Seja f uma função afim definida por f(x) = 4x 5. Determine os valores do domínio dessa função que produzem imagem no intervalo [ 3, 3].
![1. Seja f uma função afim definida por f(x) = 4x 5. Determine os valores do domínio dessa função que produzem imagem no intervalo [ 3, 3]. 1. Seja f uma função afim definida por f(x) = 4x 5. Determine os valores do domínio dessa função que produzem imagem no intervalo [ 3, 3].](/thumbs/80/82316260.jpg) Lista de Exercícios - Função Afim 1. Seja f uma função afim definida por f(x) = 4x 5. Determine os valores do domínio dessa função que produzem imagem no intervalo [ 3, 3]. 2. As frutas que antes se compravam
Lista de Exercícios - Função Afim 1. Seja f uma função afim definida por f(x) = 4x 5. Determine os valores do domínio dessa função que produzem imagem no intervalo [ 3, 3]. 2. As frutas que antes se compravam
CPV conquista 140 vagas no insper
 CPV conquista 140 vagas no insper Prova REsolvida Insper 01/Novembro/009 Análise quantitativa 7. O gráfico abaixo representa as notas de um grupo de alunos em uma prova de matemática. A altura de cada
CPV conquista 140 vagas no insper Prova REsolvida Insper 01/Novembro/009 Análise quantitativa 7. O gráfico abaixo representa as notas de um grupo de alunos em uma prova de matemática. A altura de cada
CENTRO UNIVERSITÁRIO DE VOLTA REDONDA CENTRO INTEGRADO DE TECNOLOGIA PROGRAMA DE APOIO À APRENDIZAGEM PARA OS CURSOS DE ENGENHARIA
 LISTA DE EXERCÍCIOS Nº 06 Disciplina: MATEMÁTICA Data: 27/10/2012. 1ª Questão: Dada a função f(x)= 1-5x,calcule: a)f(0)= b)f(-1)= 2ªQuestão: O custo de um produto de uma indústria é dado por C(x)=250 +
LISTA DE EXERCÍCIOS Nº 06 Disciplina: MATEMÁTICA Data: 27/10/2012. 1ª Questão: Dada a função f(x)= 1-5x,calcule: a)f(0)= b)f(-1)= 2ªQuestão: O custo de um produto de uma indústria é dado por C(x)=250 +
COLÉGIO XIX DE MARÇO Educação do jeito que deve ser 1ª PROVA PARCIAL DE MATEMÁTICA
 COLÉGIO XIX DE MARÇO Educação do jeito que deve ser 2016 1ª PROVA PARCIAL DE MATEMÁTICA Aluno(a): Nº Ano: 9º ano Turma: Data: 09/04/16 Nota: Professor(a): LUIZ GUSTAVO Valor da Prova: 40 Pontos Orientações
COLÉGIO XIX DE MARÇO Educação do jeito que deve ser 2016 1ª PROVA PARCIAL DE MATEMÁTICA Aluno(a): Nº Ano: 9º ano Turma: Data: 09/04/16 Nota: Professor(a): LUIZ GUSTAVO Valor da Prova: 40 Pontos Orientações
Plano de Recuperação 1º Semestre EF2-2011
 Professor: Marcelo, Cebola e Natália Ano: 9º Objetivos: Proporcionar ao aluno a oportunidade de resgatar os conteúdos trabalhados em Matemática nos quais apresentou defasagens e os quais lhe servirão como
Professor: Marcelo, Cebola e Natália Ano: 9º Objetivos: Proporcionar ao aluno a oportunidade de resgatar os conteúdos trabalhados em Matemática nos quais apresentou defasagens e os quais lhe servirão como
CONCURSO VESTIBULAR UNIFICADO 2008
 QUESTÃO: 12 12. Um ônibus de 40 lugares foi fretado para uma excursão. A empresa exigiu de cada passageiro R$ 20,00 mais R$ 2,00 por lugar vago. Sobre esse contexto, analise as afirmações a se seguir:
QUESTÃO: 12 12. Um ônibus de 40 lugares foi fretado para uma excursão. A empresa exigiu de cada passageiro R$ 20,00 mais R$ 2,00 por lugar vago. Sobre esse contexto, analise as afirmações a se seguir:
Centro de Estudos Gilberto Gualberto Ancorando a sua aprendizagem LISTA FUNÇÕES
 Questão 01 - A quantidade mensalmente vendida x, em toneladas, de certo produto, relaciona-se com seu preço por tonelada p, em reais, através da equação p = 2 000 0,5x. O custo de produção mensal em reais
Questão 01 - A quantidade mensalmente vendida x, em toneladas, de certo produto, relaciona-se com seu preço por tonelada p, em reais, através da equação p = 2 000 0,5x. O custo de produção mensal em reais
2 Uma caixa d'água cúbica, de volume máximo, deve ser colocada entre o telhado e a laje de uma casa, conforme mostra a figura ao lado.
 MATEMÁTICA Uma pessoa possui a quantia de R$7.560,00 para comprar um terreno, cujo preço é de R$5,00 por metro quadrado. Considerando que os custos para obter a documentação do imóvel oneram o comprador
MATEMÁTICA Uma pessoa possui a quantia de R$7.560,00 para comprar um terreno, cujo preço é de R$5,00 por metro quadrado. Considerando que os custos para obter a documentação do imóvel oneram o comprador
Questão 2: Classifique como conjunto vazio ou conjunto unitário considerando o universo dos números naturais: a) b) c) d) e) f) g) }
 TRABALHO º ANO REGULAR - MATEMATICA Conjuntos: Questão : Escreva o conjunto expresso pela propriedade: x é um número natural par; x é um número natural múltiplo de 5 e menor do que ; x é um quadrilátero
TRABALHO º ANO REGULAR - MATEMATICA Conjuntos: Questão : Escreva o conjunto expresso pela propriedade: x é um número natural par; x é um número natural múltiplo de 5 e menor do que ; x é um quadrilátero
CPV especializado na ESPM ESPM Resolvida Prova E 16/novembro/2014
 CPV especializado na ESPM ESPM Resolvida Prova E 6/novembro/04 MATEMÁTICA. O valor da epressão + + para = 400 é igual a: 3. Se = 4, y = 3 e y = z, o valor de z é igual a: a) 0,05 b) 0,50 c) 0,0 d) 0,0
CPV especializado na ESPM ESPM Resolvida Prova E 6/novembro/04 MATEMÁTICA. O valor da epressão + + para = 400 é igual a: 3. Se = 4, y = 3 e y = z, o valor de z é igual a: a) 0,05 b) 0,50 c) 0,0 d) 0,0
EXERCÍCIOS REVISIONAIS SOBRE FUNÇÕES - 2ª PARTE
 EXERCÍCIOS REVISIONAIS SOBRE FUNÇÕES - ª PARTE. (Enem (Libras) 07) A única fonte de renda de um cabeleireiro é proveniente de seu salão. Ele cobra R$ 0,00 por cada serviço realizado e atende 00 clientes
EXERCÍCIOS REVISIONAIS SOBRE FUNÇÕES - ª PARTE. (Enem (Libras) 07) A única fonte de renda de um cabeleireiro é proveniente de seu salão. Ele cobra R$ 0,00 por cada serviço realizado e atende 00 clientes
O valor da expressão y = para x = 1,3 é: a) 2 b) 2 c) 2,6 d) 1,3 e) 1,3 Resolução. y = = = 0,7 x. Para x = 1,3 resulta y = 0,7 ( 1,3) = 0,7 + 1,3 = 2
 MATEMÁTICA a 0,9 x O valor da expressão y = para x =, é: 0,7 + x a) b) c),6 d), e), 0,9 x (0,7 + x)(0,7 x) y = = = 0,7 x. 0,7 + x (0,7 + x) Para x =, resulta y = 0,7 (,) = 0,7 +, = e A soma dos valores
MATEMÁTICA a 0,9 x O valor da expressão y = para x =, é: 0,7 + x a) b) c),6 d), e), 0,9 x (0,7 + x)(0,7 x) y = = = 0,7 x. 0,7 + x (0,7 + x) Para x =, resulta y = 0,7 (,) = 0,7 +, = e A soma dos valores
Primeiro Ano do Ensino Médio. Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto. Portal OBMEP
 Material Teórico - Módulo Função Quadrática Função Quadrática: Definições, Máximos e Mínimos Primeiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto
Material Teórico - Módulo Função Quadrática Função Quadrática: Definições, Máximos e Mínimos Primeiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto
8º Ano Ficha de Trabalho 16. fevereiro de ) Na frutaria Pomar Verde, cada quilograma de cerejas do Fundão custa 2,5.
 8º Ano Ficha de Trabalho 16 fevereiro de 2012 1) Na frutaria Pomar Verde, cada quilograma de cerejas do Fundão custa 2,5. a) No enunciado são referidas duas variáveis, a quantidade (em kg) e o preço a
8º Ano Ficha de Trabalho 16 fevereiro de 2012 1) Na frutaria Pomar Verde, cada quilograma de cerejas do Fundão custa 2,5. a) No enunciado são referidas duas variáveis, a quantidade (em kg) e o preço a
Lista de exercícios do teorema de Tales &
 Valor 2,0 Componente Curricular: Professor(a): Turno: Data: Matemática Matutino / /2013 luno(a): Nº do luno: Série: Turma: 8ª (81)(82)(83) Sucesso! Lista de Exercícios Lista de exercícios do teorema de
Valor 2,0 Componente Curricular: Professor(a): Turno: Data: Matemática Matutino / /2013 luno(a): Nº do luno: Série: Turma: 8ª (81)(82)(83) Sucesso! Lista de Exercícios Lista de exercícios do teorema de
LISTA 2 DE EXERCÍCIOS SOBRE FUNÇÕES DO 1º GRAU - PROBLEMATIZAÇÃO
 LISTA 2 DE EXERCÍCIOS SOBRE FUNÇÕES DO 1º GRAU - PROBLEMATIZAÇÃO 1. (Ucs 2014) O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor total em reais, das vendas que ele efetuar durante
LISTA 2 DE EXERCÍCIOS SOBRE FUNÇÕES DO 1º GRAU - PROBLEMATIZAÇÃO 1. (Ucs 2014) O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor total em reais, das vendas que ele efetuar durante
LISTA DE RECUPERAÇÃO ÁLGEBRA 1 ANO 3º TRIMESTRE
 LISTA DE RECUPERAÇÃO ÁLGEBRA ANO 3º TRIMESTRE ) O valor de é: A) 3 B) 3 C) 3 D) E) ) A soma das raízes reais distintas da equação x é igual a A) 0 B) C) 4 D) 6 E) 8 3) O produto das raízes da equação abaixo
LISTA DE RECUPERAÇÃO ÁLGEBRA ANO 3º TRIMESTRE ) O valor de é: A) 3 B) 3 C) 3 D) E) ) A soma das raízes reais distintas da equação x é igual a A) 0 B) C) 4 D) 6 E) 8 3) O produto das raízes da equação abaixo
Disciplina: FÍSICA Série: 2º ANO ATIVIDADES DE REVISÃO PARA A BIMESTRAL III ENSINO MÉDIO
 Professor (a): Estefânio Franco Maciel Aluno (a): Disciplina: FÍSICA Série: º ANO ATIVIDADES DE REVISÃO PARA A BIMESTRAL III ENSINO MÉDIO Data: /09/017. Questão 01) A área do polígono HGFE determinado
Professor (a): Estefânio Franco Maciel Aluno (a): Disciplina: FÍSICA Série: º ANO ATIVIDADES DE REVISÃO PARA A BIMESTRAL III ENSINO MÉDIO Data: /09/017. Questão 01) A área do polígono HGFE determinado
MATEMÁTICA. Conjunto dos números inteiros. Conjugado do número complexo z. Matriz transposta da matriz A. Matriz inversa da matriz A
 MATEMÁTICA SÍMBOLO SIGNIFICAÇÃO Z Conjunto dos números inteiros z Conjugado do número complexo z A t Matriz transposta da matriz A A 1 Matriz inversa da matriz A u.c. unidade de comprimento u.a. unidade
MATEMÁTICA SÍMBOLO SIGNIFICAÇÃO Z Conjunto dos números inteiros z Conjugado do número complexo z A t Matriz transposta da matriz A A 1 Matriz inversa da matriz A u.c. unidade de comprimento u.a. unidade
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 98/99 1ª P A R T E - MATEMÁTICA
 21 1ª P A R T E - MATEMÁTICA ITEM 01. O produto do MMC entre 30, 60 e 192 pelo MDC entre 144, 180 e 640 pode ser expresso por 2 a x 3 x 5. O valor do expoente a é a.( ) 1 b.( ) 2 c.( ) 4 d.( ) 6 e.( )
21 1ª P A R T E - MATEMÁTICA ITEM 01. O produto do MMC entre 30, 60 e 192 pelo MDC entre 144, 180 e 640 pode ser expresso por 2 a x 3 x 5. O valor do expoente a é a.( ) 1 b.( ) 2 c.( ) 4 d.( ) 6 e.( )
matemática geometria analítica pontos, baricentro do triângulo, coeficiente angular e equações da reta Exercícios de distância entre dois pontos
 Exercícios de distância entre dois pontos 1. (FUVEST 1ª fase) Sejam A = (1, ) e B = (3, ) dois pontos do plano cartesiano. Nesse plano, o segmento AC é obtido do segmento AB por uma rotação de 60º, no
Exercícios de distância entre dois pontos 1. (FUVEST 1ª fase) Sejam A = (1, ) e B = (3, ) dois pontos do plano cartesiano. Nesse plano, o segmento AC é obtido do segmento AB por uma rotação de 60º, no
H1 - Expressar a proporcionalidade direta ou inversa, como função. Q1 - A tabela a seguir informa a vazão de uma torneira aberta em relação ao tempo:
 H1 - Expressar a proporcionalidade direta ou inversa, como função Q1 - A tabela a seguir informa a vazão de uma torneira aberta em relação ao tempo: A expressão que representa a vazão em função do tempo
H1 - Expressar a proporcionalidade direta ou inversa, como função Q1 - A tabela a seguir informa a vazão de uma torneira aberta em relação ao tempo: A expressão que representa a vazão em função do tempo
Professor Diego. 01. (ENEM/2013) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do
 Professor Diego 01. (ENEM/013) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do t instante de seu desligamento (t = 0) e varia de acordo com a expressão Tt () 00,
Professor Diego 01. (ENEM/013) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do t instante de seu desligamento (t = 0) e varia de acordo com a expressão Tt () 00,
Professor (a) : César Lopes de Assis. Lista de exercícios - Geometria Analítica Ponto e Reta.
 Disciplina: Matemática/Geometria Turma: 3º Aluno: Escola SESI - Jundiaí Professor (a) : César Lopes de Assis Lista de exercícios - Geometria Analítica Ponto e Reta. 1. (Pucrj 2018) Considere os pontos
Disciplina: Matemática/Geometria Turma: 3º Aluno: Escola SESI - Jundiaí Professor (a) : César Lopes de Assis Lista de exercícios - Geometria Analítica Ponto e Reta. 1. (Pucrj 2018) Considere os pontos
C(h) = 3h + 84h 132 O maior número de clientes presentes no supermercado será dado pela ordenada máxima da função:
 Resposta da questão : [D] Reescrevendo a lei de f sob a forma canônica, vem f(x) = (x x) + 0 = (x ) +. Portanto, segue que a temperatura máxima é atingida após horas, correspondendo a C. Resposta da questão
Resposta da questão : [D] Reescrevendo a lei de f sob a forma canônica, vem f(x) = (x x) + 0 = (x ) +. Portanto, segue que a temperatura máxima é atingida após horas, correspondendo a C. Resposta da questão
