Prof. Dr. Aldo Vieira

Transcrição

1 1. Em uma determinada região do planeta, a temperatura média anual subiu de 13,35 ºC em 1995 para 13,8 ºC em Seguindo a tendência de aumento linear observada entre 1995 e 2010, a temperatura média em 2012 deverá ser de a) 13,83 ºC. b) 13,86 ºC. c) 13,92 ºC. d) 13,89 ºC. TEXTO PARA A PRÓXIMA QUESTÃO: 2. A dendrocronologia é a técnica que possibilita estimar a idade das árvores através da contagem dos anéis de crescimento. Cada anel do tronco corresponde a um ano de vida de uma árvore. Na primavera de 2011, uma árvore que foi plantada na primavera de 1991 apresenta 16 centímetros de raio na base do seu tronco. Considerando uma taxa de crescimento linear, o raio da base desse tronco, na primavera de 2026, será de: a) 22 cm b) 25 cm c) 28 cm d) 32 cm e) 44 cm 3. As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção. Considere que, independente da época ou variação de preço, certa fruta custa R$ 1,75 o quilograma. Dos gráficos a seguir, o que representa o preço m pago em reais pela compra de n quilogramas desse produto é a) Página 1 de 8

2 b) c) d) e) 4. Uma pequena empresa fabrica camisas de um único modelo e as vende por R$ 80,00 a unidade. Devido ao aluguel e a outras despesas fixas que não dependem da quantidade produzida, a empresa tem um custo fixo anual de R$ ,00. Além do custo fixo, a empresa tem que arcar com custos que dependem da quantidade produzida, chamados custos variáveis, tais como matéria-prima, por exemplo; o custo variável por camisa é R$ 40,00. Em 2009, a empresa lucrou R$ ,00. Para dobrar o lucro em 2010, em relação ao lucro de 2009, a quantidade vendida em 2010 terá de ser x% maior que a de O valor mais próximo de x é: a) 120 b) 100 c) 80 d) 60 e) O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de vagas no setor, totalizando trabalhadores com carteira assinada. Disponível em: Acesso em: 26 abr (adaptado). Suponha que o incremento de trabalhadores no setor varejista seja sempre o mesmo nos seis primeiros meses do ano. Considerando-se que y e x representam, respectivamente, as Página 2 de 8

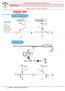
3 quantidades de trabalhadores no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante, a expressão algébrica que relaciona essas quantidades nesses meses é a) y = 4300x b) y = x c) y = x d) y = x e) y = x 6. O prefeito de uma cidade deseja construir uma rodovia para dar acesso a outro município. Para isso, foi aberta uma licitação na qual concorreram duas empresas. A primeira cobrou R$ ,00 por km construído (n), acrescidos de um valor fixo de R$ ,00, enquanto a segunda cobrou R$ ,00 por km construído (n), acrescidos de um valor fixo de R$ ,00. As duas empresas apresentam o mesmo padrão de qualidade dos serviços prestados, mas apenas uma delas poderá ser contratada. Do ponto de vista econômico, qual equação possibilitaria encontrar a extensão da rodovia que tornaria indiferente para a prefeitura escolher qualquer uma das propostas apresentadas? a) 100n = 120n b) 100n = 120n c) 100(n + 350) = 120(n + 150) d) 100(n ) = 120(n ) e) 350(n ) = 150(n ) 7. Luiza possui uma pequena confecção artesanal de bolsas. No gráfico abaixo, a reta c representa o custo total mensal com a confecção de x bolsas e a reta f representa o faturamento mensal de Luiza com a confecção de x bolsas. Com base nos dados acima, é correto afirmar que Luiza obtém lucro se, e somente se, vender a) no mínimo 2 bolsas. b) pelo menos 1 bolsa. c) exatamente 3 bolsas. d) no mínimo 4 bolsas. 8. O gráfico de uma função polinomial do primeiro grau passa pelos pontos de coordenadas (x, y) dados abaixo. X y 0 5 M k Podemos concluir que o valor de k + m é: a) 15,5 b) 16,5 Página 3 de 8

4 c) 17,5 d) 18,5 e) 19,5 TEXTO PARA AS PRÓXIMAS 2 QUESTÕES: 9. O gráfico acima mostra a evolução das notas em Matemática de dois grupos de estudantes, denominados grupo I e grupo II. Analisando o gráfico e considerando o período de 2007 a 2010, é possível afirmar: a) Os dois grupos melhoraram as notas. b) A nota do grupo I, em 2008, foi 80. c) A nota do grupo I aumentou de 2008 a 2009 e diminuiu de 2009 a d) A nota do grupo II não sofreu alteração. e) A nota do grupo I aumentou, enquanto a nota do grupo II diminuiu. 10. Em relação ao gráfico, considerando 2007 como x = 1, 2008 como x = 2 e assim, sucessivamente, a função afim y = ax + b que melhor expressa a evolução das notas em Matemática do grupo II é a) y = x b) y = x c) y = x d) y = x e) y = - 5x Acompanhando o crescimento do filho, um casal constatou que, de 0 a 10 anos, a variação da sua altura se dava de forma mais rápida do que dos 10 aos 17 anos e, a partir de 17 anos, essa variação passava a ser cada vez menor, até se tornar imperceptível. Para ilustrar essa situação, esse casal fez um gráfico relacionando as alturas do filho nas idades consideradas. Que gráfico melhor representa a altura do filho desse casal em função da idade? a) Página 4 de 8

5 b) c) d) Página 5 de 8

6 Gabarito: Resposta da questão 1: [B] Ano: Temperatura( o C): 13,35 13,80 x Temperatura anual média = 13,8 13,35 = 0,45 = 0, Em 2012, a temperatura será x = 13, ,03 = 13,86 o C. Resposta da questão 2: [C] Seja a função r(t) = at, em que r(t) é o raio do tronco, em cm, após t anos e a é a taxa de crescimento. Supondo que em 1991 (t = 0) o raio da base do tronco media 0cm, e sabendo que em (t = 20) o raio tinha 16cm, temos que a = = Portanto, na primavera de 2026 (t = 35), o raio da base desse tronco, será de 4 r(35) = 35 = 28 cm. 5 Resposta da questão 3: [E] O gráfico deverá representar a função m = f(n) = 1,75 n, onde n é o número de quilogramas comprados. O gráfico correto é: Resposta da questão 4: [E] O custo para produzir n camisas é dado por: C(n) = 40n Se o preço de venda unitário é R$ 80,00, então a receita obtida com a venda de n camisas é: R(n) = 80n. Para um lucro de R$ ,00, temos: Página 6 de 8

7 L(n) = R(n) C(n) = 80n (40n ) 40n = n = 39000, ou seja, deverão ser vendidas camisas para que a empresa lucre R$ ,00. Agora devemos calcular quantas camisas a empresa deverá vender para lucrar R$ ,00. L(n') = n' = n' = Desse modo, para dobrar o lucro a empresa deverá vender em % 38,46% a mais do que vendeu em 2009 e, portanto, o valor mais próximo de x é 40. Resposta da questão 5: [C] Admitido um crescimento constante, temos uma função de primeiro grau dada por: y = ax + b, onde a = 4300 (taxa constante) e b = = Logo, y = 4300x Resposta da questão 6: [A] Empresa A: P A = x Empresa B: P B = x Igualando os preços P A = P B, temos : x = x Resposta da questão 7: [B] c(x) = x e f(x) = 20x. Fazendo f(x) > c(x), temos: 20x > x 12x > 10 x > 10/12 Logo, deverá ser vendida pelo menos uma bolsa. Resposta da questão 8: [C] Seja f a função afim definida por f(x) = ax + b, cujo gráfico passa pelos pontos indicados na tabela. A taxa de variação da função f é dada por: k 5 a = = = m 7 0 Desse modo, Página 7 de 8

8 6 3 = 6 m 2 m = 2 k + m = 17,5. k 5 3 k = 15,5 = 7 2 Resposta da questão 9: [E] A nota do grupo I aumentou, pois a reta apresenta coeficiente angular positivo, enquanto a nota do grupo II diminuiu, pois a reta apresenta coeficiente angular negativo. Resposta da questão 10: [B] Temos então os pontos (1, 70) e (3, 65) pertencentes ao gráfico II Calculando o coeficiente angular, temos: m = = Logo a função será y = x + b. 2 Determinando agora o valor de b, temos: 70 = b b = Logo, y = x Resposta da questão 11: [A] O gráfico A é o mais adequado, pois a inclinação de 10 a 17 é maior que a inclinação para valores maiores que 17. Página 8 de 8