Tarcísio da Silva Santos ANÁLISE COMPARATIVA NO DIMENSIONAMENTO DE LAJES MACIÇAS CONVENCIONAIS E LAJES NERVURADAS APOIADAS SOBRE VIGAS
|
|
|
- Benedito das Neves Gesser
- 8 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE ESTADUAL DE FEIRA DE SANTANA DEPARTAMENTO DE TECNOLOGIA Tarcísio da Silva Santos ANÁLISE COMPARATIVA NO DIMENSIONAMENTO DE LAJES MACIÇAS CONVENCIONAIS E LAJES NERVURADAS APOIADAS SOBRE VIGAS Orientador: Prof. Clodoaldo Pereira Freitas Feira de Santana 2009
2 Tarcísio da Silva Santos ANÁLISE COMPARATIVA NO DIMENSIONAMENTO DE LAJES MACIÇAS CONVENCIONAIS E LAJES NERVURADAS APOIADAS SOBRE VIGAS Monografia solicitada para a formação no curso de graduação em Engenharia Civil da Universidade Estadual de Feira de Santana BA. Feira de Santana
3 Tarcísio da Silva Santos ANÁLISE COMPARATIVA NO DIMENSIONAMENTO DE LAJES MACIÇAS CONVENCIONAIS E LAJES NERVURADAS APOIADAS SOBRE VIGAS Trabalho Final de Curso para obtenção do Título de Bacharel em Engenharia Civil. Feira de Santana, 23 de março de 2009 Banca Examinadora: Clodoaldo Pereira Freitas Orientador Universidade Estadual de Feira de Santana Hélio Guimarães Aragão Universidade Estadual de Feira de Santana Geraldo Barros Rios Universidade Estadual de Feira de Santana 3
4 Este trabalho é dedicado àqueles que sempre estiveram ao meu lado, me apoiando e incentivando, minha família. 4
5 RESUMO Neste trabalho faz-se uma comparação entre dois sistemas estruturais empregados na atualidade, as lajes maciças convencionais e as lajes nervuradas. Para isto esboça-se sobre os conhecimentos técnicos necessários a esta análise, noções de ações e segurança em estruturas, método de grelha equivalente, particularidades e dimensionamento destes tipos de lajes e noções de orçamento de lajes. São modelados pavimentos de dois projetos distintos, utilizando em cada pavimento uma das soluções em estudo, com o objetivo de encontrar parâmetros que possibilitem a comparação: aspectos estruturais e aspectos econômicos. Por fim faz-se uma consideração, apontando sobre as vantagens e desvantagens do uso de cada solução. 5
6 ABSTRACT In this paper is presented a comparison between two structural systems currently employed, solid slabs and ribbed slabs. For both, the description of technical knowledge necessary for the analysis is made. Conceptions about active loads and structural security, method of equivalent grid, features and dimensioning of ribbed slabs and the conception about estimate cost of both models of slabs. Floors of two distinct projects were modeled having one of each solution studied with the aim to find parameters to allow the comparison: structural and economic aspects. At ending a consideration is made pointing out the advantages and disadvantages of using each model. 6
7 SUMÁRIO RESUMO... 5 ABSTRACT... 6 LISTA DE FIGURAS... 8 LISTA DE TABELAS INTRODUÇÃO JUSTIFICATIVA OBJETIVOS Objetivo Geral Objetivos Específicos METODOLOGIA NOÇÕES DE AÇÕES E SEGURANÇA EM ESTRUTURAS DE CONCRETO Estados Limites Estados Limites Últimos (ELU) Estados Limites de Serviço (ELS) Ações Valores das Ações ANALOGIA DE GRELHA GENERALIDADES E DIMENSIONAMENTO DAS LAJES LAJES MACIÇAS CONVENCIONAIS LAJES NERVURADAS ORÇAMENTO DE OBRAS MODELAGEM DAS OBRAS EM ESTUDO MODELAGEM DO PRIMEIRO PROJETO MODELAGEM DO SEGUNDO PROJETO ANÁLISE DOS RESULTADOS OBTIDOS CONCLUSÃO SUGESTÕES PARA TRABALHOS FUTUROS REFERÊNCIAS BIBLIOGRÁFICAS ANEXOS
8 LISTA DE FIGURAS Figura 1 - Pilares com capitel e painel de transição ( drop panel ) Figura 2 - Laje nervurada Figura 3 - (a) Laje Maciça; (b) Grelha Equivalente Figura 4 - Carregamento uniformemente distribuído nas barras (carga p) e carregamento concentrado nos nós (carga P1) e nas barras (carga P2) Figura 5 - Laje corredor Figura 6 - Equilíbrio da Seção Transversal Figura 7 - Dimensões Mínimas de Lajes Nervuradas Figura 8 - Planta de fôrmas de lajes maciças do primeiro pavimento Figura 9 - Deslocamentos em três dimensões nas lajes maciças Figura 10 - Armaduras positivas das lajes maciças Figura 11 - Armaduras negativas das lajes maciças Figura 12 - Seção transversal da laje nervurada Figura 13 - Planta de fôrmas de lajes nervuradas do segundo pavimento Figura 14 - Deslocamentos em três dimensões nas lajes nervuradas Figura 15 - Armaduras positivas das lajes nervuradas Figura 16 - Armaduras negativas das lajes nervuradas Figura 17 - Planta de fôrmas de lajes maciças do primeiro pavimento Figura 18 - Deslocamentos em três dimensões nas lajes maciças Figura 19 - Armaduras positivas das lajes maciças Figura 20 - Armaduras negativas das lajes maciças Figura 21 - Planta de fôrmas de lajes nervuradas do segundo pavimento Figura 22 - Deslocamentos em três dimensões nas lajes nervuradas Figura 23 - Armaduras positivas das lajes nervuradas Figura 24 - Armaduras negativas das lajes nervuradas
9 LISTA DE TABELAS Tabela 1 - Coeficientes γ f1 x γ f3 para ponderação de ações Tabela 2 - Coeficientes γ f2 para ponderação de ações Tabela 3 - Combinações últimas Tabela 4 - Combinações de serviço Tabela 5 - Taxas mínimas de armaduras Tabela 6 - Valores mínimos para armaduras de lajes Tabela 7 - Coeficientes ξ em função do tempo Tabela 8 - Valores dos deslocamentos nas lajes maciças Tabela 9 - Quantitativos das lajes maciças Tabela 10 - Índices e custos de serviços para orçamento Tabela 11 - Custos dos serviços e total geral do pavimento de lajes maciças Tabela 12 - Valores dos deslocamentos nas lajes nervuradas Tabela 13 - Quantitativos das lajes nervuradas Tabela 14 - Índices e custos de serviços para orçamento Tabela 15 - Custos dos serviços e total geral do pavimento de lajes nervuradas Tabela 16 - Valores dos deslocamentos nas lajes maciças Tabela 17 - Quantitativos das lajes maciças Tabela 18 - Custos dos serviços e total geral do pavimento de lajes maciças Tabela 19 - Valores dos deslocamentos nas lajes nervuradas Tabela 20 - Quantitativos das lajes nervuradas Tabela 21 - Custos dos serviços e total geral do pavimento de lajes maciças
10 1. INTRODUÇÃO Durante muito tempo os homens empenharam-se em diversas construções. A princípio, o homem fazia uso dos materiais que estivessem à disposição, sobretudo, madeira e pedra. No decorrer dos anos as construções começaram a ficar robustas e, com a evolução do conhecimento, novos materiais foram surgindo. O cimento, por exemplo, foi descoberto em meados do século 19. Pouco tempo depois, surgiu a idéia de associar o cimento com o aço, aparecendo assim o concreto armado. (STRAMANDINOLI, 2003) De posse deste novo material, houve um impulso no desenvolvimento das edificações. Sendo o concreto armado mais resistente aos esforços de tração, foi possível conceber novas e maiores estruturas. Com isto os edifícios de pisos múltiplos começaram a ser construídos. Com o aprimoramento e evolução das técnicas construtivas, maiores e mais desafiadoras tornaram-se as edificações, obrigando os engenheiros a empenharem-se na busca de soluções estruturais para os diversos problemas encontrados. Foi com o surgimento de tais edifícios de múltiplos pavimentos que apareceram as lajes em concreto armado. As lajes são elementos estruturais planos classificados como placas e formados por concreto armado que, segundo RÜSCH (1981), recebem solicitações perpendiculares a seu plano médio. A principal característica que a identifica como placa, são as suas dimensões. Elas possuem uma das dimensões consideravelmente menor que as outras duas. Tais elementos têm como finalidade servir como pisos em edificações, ou mesmo como cobertura de tais construções. Para atender as exigências impostas pela prática construtiva e por clientes, as lajes possuem uma espessura limitada, o que impõe uma limitação em seus vãos. Com o desenvolvimento e o avanço das necessidades humanas, foram criados vários tipos de lajes para atender às diversas solicitações impostas. Por exemplo, houve a necessidade de grandes vãos, sem a presença de pilares, por uma questão de área útil. Outra necessidade é de tetos completamente lisos, ou seja, sem a presença de vigas. Para cada uma das necessidades que foram aparecendo, surgiram soluções para satisfazê-las. 10
11 Hoje se pode destacar a existência de alguns tipos básicos de lajes. Existem as lajes planas, que são lajes maciças sem a presença de vigas. Devido à ausência de vigas, ocorrem neste tipo de laje altas tensões de cisalhamento devido à punção. Como solução, criou-se os capitéis e os painéis de transição (ou drop panel ), que consistem num alargamento da seção transversal do pilar na região do encontro deste com a laje, ou, no segundo caso, um aumento da espessura da laje na mesma região, como pode ser visto na figura 1. Outra solução empregada é o uso de vigas chatas que ficam embutidas nas lajes, servindo de apoio para estas e redistribuindo os esforços para os pilares. (HENNRICHS, 2003) Figura 1 - Pilares com capitel e painel de transição ( drop panel ) Fonte: HENNRICHS, 2003 O modelo mais empregado de laje é o sistema convencional, com lajes apoiadas sobre vigas em uma (como no caso de marquises) ou mais bordas. Quando é preciso aumentar os vãos destas lajes também ocorre um aumento da espessura, para que esta seja capaz de resistir às solicitações em questão. Tal aumento de espessura acarreta num mau aproveitamento do concreto, já que a região comprimida é pequena e ocorre um aumento do peso próprio da estrutura, segundo MOURA (1986). Assim foi criada uma alternativa construtiva para as lajes: eliminar o concreto da região onde ele não é solicitado, deixando apenas nervuras que participam da biela de compressão, equilibrando a seção transversal e preenchendo o espaço deixado com material inerte. A figura 2 mostra uma laje nervurada preenchida com material inerte. Quando este método surgiu, houve grande resistência por parte dos construtores, devido ao grande consumo de fôrmas para a concretagem das lajes. Hoje, porém, com as inovações tecnológicas a este respeito, tal custo foi reduzido devido ao desenvolvimento de diversas formas que baratearam o processo de execução, tornando esta uma solução bem empregada em edifícios de múltiplos pavimentos. 11
12 Material inerte bw lo Figura 2 - Laje nervurada Apesar de ser uma solução bem empregada, é preciso estabelecer limites para utilização destas. O modelo convencional, como visto anteriormente, apresenta limitações de dimensão de vãos, o que pode ser estendido a lajes nervuradas. Este trabalho estabelecerá uma comparação entre os dois modelos, discutindo os aspectos relativos ao comportamento estrutural (resistência, deformação e vibração) e de aspectos construtivos (custos de materiais e mão-de-obra, prazos, etc.) de forma a indicar diretrizes para escolha do modelo de laje a ser adotado em obras correntes. No capítulo Introdução é apresentado o tema da monografia, mostrando as soluções desenvolvidas para as lajes, além de apresentar a justificativa para este trabalho, bem como os objetivos e a metodologia empregada nele. O capítulo 2, Noções de Ações e Seguranças em Estruturas de Concreto apresenta a norma NBR Ações e Seguranças nas Estruturas, comentando sobre os estados limites últimos e de serviço, bem como sobre a consideração dos carregamentos utilizados nos cálculos. O terceiro capítulo, Analogia de grelha apresenta este método de análise estrutural, mostrando o princípio de cálculo deste e os fundamentos teóricos em que se baseia. O quarto capítulo, Generalidades e Dimensionamento das Lajes discorre sobre as particularidades das lajes maciças convencionais e das lajes nervuradas, destacando as considerações feitas na NBR 6118 (2003), mostrando como é feito os cálculos de armadura e as análises delas. O capítulo 5, Orçamento de Obras destaca aspectos gerais sobre orçamento. No entanto, volta sua atenção para o orçamento de lajes, que é o objeto de estudo deste trabalho, sendo indispensável para se atingir o objetivo principal. 12
13 No sexto capítulo, Modelagem das Obras em Estudo, são modelados, processados, analisados e detalhados os pavimentos de lajes maciças e nervuradas, dos projetos em estudo, dando atenção especial para os deslocamentos existentes e ao consumo de materiais. Também é feito neste capítulo o orçamento de cada pavimento, obtendo-se os quantitativos, de materiais e serviços, e os custos totais para a execução das lajes do pavimento. No capítulo seguinte, o sétimo, Análise dos Dados Obtidos, são feitas as análises dos resultados, estabelecendo a comparação entre os dois modelos empregados, além de feitas algumas considerações sobre os dois sistemas estudados. No capítulo 8, Conclusão, são feitas as considerações finais sobre o trabalho, ressaltando a importância deste e as lições tiradas da realização dele. Neste capítulo encontram-se algumas sugestões para trabalhos futuros. No último capítulo, o nono, são listadas as referências utilizadas para a confecção deste trabalho. 13
14 1.1 JUSTIFICATIVA Existem diversos tipos de lajes que são utilizados para atender as várias solicitações existentes. Dentre estes, as lajes maciças convencionais apoiadas sobre vigas nas bordas estão entre as soluções mais empregadas. No entanto existem limites a utilização destes sistemas. Quando as solicitações sobre um pavimento de edificação tornam-se muito altas ou as necessidades impõem que existam grandes vãos nas estruturas, as lajes convencionais tornam-se muito espessas para que possa atender a esta demanda. Este aumento de espessura tem algumas conseqüências. O carregamento permanente atuando sobre a estrutura torna-se maior, o que provoca a necessidade de melhorar a resistência de vigas, pilares e, conseqüentemente, da fundação. Além disso, este incremento de carga também tem efeito sobre a própria laje em questão. Visto que ocorre um aumento do carregamento suportado por ela, há um considerável acréscimo de armadura, o que vem a encarecer tal estrutura. No que dizem respeito as lajes nervuradas, estas foram desenvolvidas para vencer grandes vãos, no qual se mostram bem eficazes. No entanto é preciso analisar onde é o ponto ideal para o emprego de tal solução estrutural, pois se assim não for, o construtor estará empregando uma solução que virá a encarecer seu empreendimento. Este trabalho comparará o emprego destes tipos de lajes em projetos distintos, analisando os resultados encontrados, tanto do ponto de vista econômico como estrutural, avaliando a melhor indicação para a utilização destes sistemas. 14
15 1.2 OBJETIVOS Objetivo Geral Comparar a utilização de dois sistemas estruturais, as lajes maciças convencionais e as lajes nervuradas, do ponto de vista econômico e estrutural Objetivos Específicos Modelar e dimensionar pavimentos de projetos distintos utilizando lajes maciças convencionais. Modelar e dimensionar pavimentos dos mesmos projetos utilizando lajes nervuradas. Analisar os resultados obtidos nos dois momentos acima descritos, atentando para a economia e o modelo estrutural empregado. 15
16 1.3 METODOLOGIA Revisão bibliográfica em livros, revistas, artigos científicos, monografias, dissertações de mestrado e teses de doutorado a respeito do dimensionamento de lajes maciças convencionais e de lajes nervuradas. Modelagem e dimensionamento de lajes maciças convencionais, de projetos pré-estabelecidos, utilizando um software disponível no mercado. Modelagem e dimensionamento de lajes nervuradas nos mesmos projetos, utilizando o mesmo software. Estudo comparativo dos resultados obtidos, analisando do ponto de vista técnico, qual dimensionamento oferece maior economia e segurança. Redação da monografia. 16
17 2. NOÇÕES DE AÇÕES E SEGURANÇA EM ESTRUTURAS DE CONCRETO 2.1 Estados Limites Segundo SÜSSEKIND (1989), As obras, no seu conjunto ou em parte, devem poder resistir, com uma conveniente margem de segurança, a todas as solicitações oriundas de carregamentos aplicados ou deformações impostas durante o período de construção e futuro uso, além de não deverem apresentar deformações excessivas que possam comprometer o conforto de sua utilização, ou indesejável grau de fissuração que, por facilitar a corrosão, venha a diminuir sua durabilidade. De acordo com a NBR 8681 (2003) Ações e Segurança nas Estruturas, os estados limites de uma estrutura são aqueles a partir dos quais a estrutura apresenta desempenho inadequado às finalidades da construção. Estes estados limites podem ser estados limites últimos ou estados limites de serviço Estados Limites Últimos (ELU) Estados Limites Últimos são estados que correspondem ao esgotamento da capacidade portante da estrutura, que determine a paralisação, no todo ou em parte, do uso da estrutura. (SUSSEKIND, 1989) De acordo com a NBR 6118 (2003) Projeto de Estruturas de Concreto e a NBR 8681 (2003), este estado deve ser verificado para as seguintes situações: de perda do equilíbrio da estrutura, admitida como corpo rígido; de esgotamento da capacidade resistente da estrutura, no seu todo ou em parte, devido às solicitações normais e tangenciais; de esgotamento da capacidade resistente da estrutura, no seu todo ou em parte, considerando os efeitos de segunda ordem; provocado por solicitações dinâmicas; de colapso progressivo; 17
18 outros estados limites últimos que eventualmente possam ocorrer em casos especiais Estados Limites de Serviço (ELS) Estados Limites de Serviço são aqueles caracterizados pela impossibilidade do uso da estrutura mesmo não se tendo esgotado a capacidade resistente dela ocasionado por esta não mais oferecer as condições necessárias de conforto e/ou durabilidade especificadas para uso normal em projeto. (SUSSEKIND, 1989) De acordo com a NBR 6118 (2003) e a NBR 8681 (2003) a segurança das estruturas de concreto exige a verificação dos seguintes estados limites de serviço: Estado limite de abertura das fissuras, onde as fissuras se apresentam com aberturas iguais ou menores aos máximos especificados pela normalização, para não comprometer a durabilidade ou o aspecto estético da estrutura; Estado limite de deformações excessivas, onde as deformações respeitam os limites estabelecidos conforme normalização para a utilização normal da construção, não afetando o aspecto estético dela; Estado limite de vibrações excessivas, onde as vibrações não ultrapassem os limites estabelecidos para a utilização normal da construção gerando desconforto. 2.2 Ações Ações são influências capazes de produzirem estados de tensão e deformação em uma estrutura. De acordo com a NBR 6118 (2003): Na análise estrutural deve ser considerada a influência de todas as ações que possam produzir efeitos significativos para a segurança da estrutura em exame, levando-se em conta os possíveis estados limites últimos e os de serviço. De acordo com a NBR 8681 (2003), as ações podem ser classificadas segundo sua variabilidade no tempo, sendo permanentes, variáveis ou excepcionais. As ações permanentes são aquelas que atuam com valores praticamente constantes durante a vida útil da construção ou que crescem com o passar do tempo, 18
19 tendendo a um valor limite. Elas são compostas pelo peso próprio da estrutura e dos elementos construtivos fixados, bem como das instalações permanentes e de deformações ocorridas por retrações, fluência, deslocamentos dos apoios, imperfeições geométricas e protensão. As ações variáveis são aquelas que atuam com valores que apresentam variações significativas, durante o período de vida da construção. Estas podem ser diretas ou indiretas. As cargas acidentais de uso e de construção das estruturas, a ação do vento e das águas da chuva são chamadas de ações variáveis diretas; enquanto que as variações térmicas e ações dinâmicas são chamadas de ações variáveis indiretas. Ações excepcionais são aquelas decorrentes de explosões, choques de veículos, incêndios, enchentes e abalos sísmicos. (SILVA, 2002) Valores das Ações As ações podem ser expressas por valores representativos, podendo ser valores característicos, valores reduzidos e valores de cálculo. (NBR 8681, 2003) Os valores característicos das ações são estabelecidos em função da variabilidade de suas intensidades. Estes valores encontram-se estabelecidos em normas específicas, como na NBR 6120 (1980) Cargas para o Cálculo de Estruturas de Edificações. Os valores característicos das cargas variáveis são definidos por um estudo probabilístico. Os valores reduzidos são dados na combinação de ações para a verificação dos estados limites último e de serviço. Para a combinação de ações a NBR 8681 (2003) estabelece um coeficiente de segurança, γ f, que, por sua vez, é subdividido em três coeficientes parciais de ponderação γ f1, γ f2 e γ f3. O coeficiente γ f1 leva em conta a variabilidade das ações. O coeficiente γ f2 considera a simultaneidade das ações. O coeficiente γ f3 considera os possíveis erros de avaliação dos efeitos das ações, seja por problemas construtivos, seja por deficiência do método de cálculo empregado. A subdivisão do coeficiente de segurança γ f em coeficientes parciais de ponderação permite que os valores gerais especificados para ele possam ser discriminados, em função de peculiaridades dos diferentes tipos de estruturas e de materiais de construção considerados. Na NBR 6118 (2003) encontram-se duas tabelas de coeficientes de ponderação de ações, que considera muito baixa a probabilidade de ocorrerem simultaneamente 19
20 duas ou mais ações variáveis de natureza diferente. A tabela 1 apresenta os coeficientes γ f1 x γ f3. A tabela 2 apresenta os coeficientes de ponderação γ f2. Ações Combinações de ações Permanentes (g) Variáveis (q) Protensão D 1) F G T D F D (p) Recalques de apoio e retração F Normais 1,4 1,0 1,4 1,2 1,2 0,9 1,2 0 Especiais ou de construção 1,3 1,0 1,2 1,0 1,2 0,9 1,2 0 Excepcionais 1,2 1,0 1,0 0 1,2 0,9 0 0 Onde: D é desfavorável, F é favorável, G é geral e T é temporária. 1) Para as cargas permanentes de pequena variabilidade, como o peso próprio das estruturas, especialmente as pré-moldadas, esse coeficiente pode ser reduzido para 1,3. Tabela 1 - Coeficientes γ f1 x γ f3 para ponderação de ações Fonte: NBR 6118 (2003) Ações ψ 0 ψ 1 1) ψ 2 γ Cargas acidentais de edifícios Locais em que não há predominância de pesos de equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas 2) Locais em que há predominância de pesos de equipamentos que permanecem fixos por longos períodos de tempo, ou de elevada concentração de pessoas 3) 0,5 0,4 0,3 0,7 0,6 0,4 Biblioteca, arquivos, oficinas e garagens 0,8 0,7 0,6 Vento Pressão dinâmica do vento nas estruturas em geral 0,6 0,3 0 Temperatura Variações uniformes de temperatura em relação à média anual local 0,6 0,5 0,3 1) Para os valores de ψ relativos às pontes e principalmente aos problemas de fadiga, ver seção 23. 2) Edifícios residenciais. 3) Edifícios comerciais, de escritórios, estações e edifícios públicos. Tabela 2 - Coeficientes γ f2 para ponderação de ações Fonte: NBR 6118 (2003) As combinações são feitas de modo que as ações permanentes sejam tomadas em sua inteireza, enquanto que das ações variáveis são tomadas apenas as parcelas que surtam efeitos desfavoráveis para a segurança. (CARVALHO e FIGUEIREDO FILHO, 2004) As ações variáveis são separadas por naturezas, conforme a NBR 6118 (2003), e 20
21 em cada combinação é definido uma delas como sendo a principal, sendo as demais secundárias e, portanto, minoradas segundo os coeficientes de ponderação γ f2. De acordo com a NBR 6118 (2003): Um carregamento é definido pela combinação das ações que têm probabilidades não desprezíveis de atuarem simultaneamente sobre a estrutura, durante um período preestabelecido. A combinação das ações deve ser feita de forma que possam ser determinados os efeitos mais desfavoráveis para a estrutura; a verificação da segurança em relação aos estados limites últimos e aos estados limites de serviço deve ser realizada em função de combinações últimas e combinações de serviço, respectivamente. NBR 6118 (2003) Para as combinações últimas, a NBR 6118 (2003) preparou uma tabela, que fornece diretrizes para tal feito. Ela pode ser visualizada na tabela 3. Combinações últimas (ELU) Normais Especiais ou de construção 2) Excepcionais 2) Descrição Esgotamento da capacidade resistente para elementos estruturais de concreto armado 1) Esgotamento da capacidade resistente para elementos estruturais de concreto protendido Perda do equilíbrio como corpo rígido F d = γ g F gk + γεg Fεgk + γ q (F q1k + Σ ψ oj F qjk ) + γεq ψ o ε F εqk F d = γ g F gk + γεg Fεgk + F q1exc + γ q Σ ψ oj F qjk + γεq ψ o ε Fεqk Cálculo das solicitações F d = γ g F gk + γε g Fε gk + γ q (F q1k + Σ ψ oj F qjk ) + γεq ψ o ε F qk Deve ser considerada, quando necessário, a força de protensão como carregamento externo com os valores P kmáx e P kmin para a força desfavorável e favorável, respectivamente, conforme definido na seção 9 S (F sd ) S (F nd ) F sd = γ gs G sk + R d F nd = γ gn G nk + γ q Q nk - γ qs Q s,min, onde: Q nk = Q 1k + Σ ψ oj Q jk Onde: F d é o valor de cálculo das ações para combinação última; F gk representa as ações permanentes diretas; F εk representa as ações indiretas permanentes como a retração F εgk e variáveis como a temperatura F εqk ; F qk representa as ações variáveis diretas das quais F q1k é escolhida principal; γ g, γ εg, γ q, γ εq ver tabela 11.1; ψ oj, ψ oε - ver tabela 11.2; F sd representa as ações estabilizantes; F nd representa as ações não estabilizantes; G sk é o valor característico da ação permanente estabilizante; R d é o esforço resistente considerado como estabilizante, quando houver; G nk é o valor característico da ação permanente instabilizante; m Q nk = Q 1k + ψ oj Q jk ; j= 2 Q nk é o valor característico das ações variáveis instabilizantes; Q 1k é o valor característico da ação variável instabilizante considerada como principal; ψ oj e Q jq são as demais ações variáveis instabilizantes, consideradas com seu valor reduzido; Q s,min é o valor característico mínimo da ação variável estabilizante que acompanha obrigatoriamente uma ação variável instabilizante. 1) No caso geral, devem ser consideradas inclusive combinações onde o efeito favorável das cargas permanentes seja reduzido pela consideração de γ g = 1,0. No caso de estruturas usuais de edifícios essas combinações que consideram γ g reduzido (1,0) não precisam ser consideradas. 2) Quando F g1k ou F g1exc atuarem em tempo muito pequeno ou tiverem probabilidade de ocorrência muito baixa ψ 0j, pode ser substituído por ψ 2j. Tabela 3 - Combinações últimas Fonte: NBR 6118 (2003) 21
22 Existem três tipos de combinações últimas: normais, especiais ou de construção e excepcionais. Para cada uma delas existe uma metodologia empregada na combinação. Entretanto, pode-se notar que existem alguns pontos comuns a todas elas. Por exemplo, em todas as combinações, as cargas permanentes são consideradas majoradas pelos coeficientes encontrados na tabela 1. Outro ponto é que sempre há uma carga variável considerada em sua inteireza, ou seja, sem a minoração obtida pela multiplicação pelos coeficientes encontrados na tabela 2, sejam elas normais, especiais ou excepcionais. As demais cargas variáveis, se houver, serão consideradas minoradas pelos coeficientes ψ 0, encontrados nessa tabela. A exceção a isto é quando existem cargas permanentes ou variáveis favoráveis a segurança. Para as combinações de serviço, a NBR 6118 (2003) também fixou alguns parâmetros. Estes estão indicados na tabela 4. Combinações de serviço (ELS) Descrição Cálculo das solicitações Combinações quase permanentes de serviço (CQP) Combinações freqüentes de serviço (CF) Combinações raras de serviço (CR) Nas combinações quase permanentes de serviço, todas as ações variáveis são consideradas com seus valores quase permanentes ψ 2 F qk Nas combinações freqüentes de serviço, a ação variável principal F q1 é tomada com seu valor freqüente ψ 1 F q1k e todas as demais ações variáveis são tomadas com seus valores quase permanentes ψ 2 F qk Nas combinações raras de serviço, a ação variável principal F q1 é tomada com seu valor característico F q1k e todas as demais ações são tomadas com seus valores freqüentes Ψ 1 F qk F d, ser = Σ F gi,k + Σ ψ 2j F qj,k F d,ser = Σ F gik + ψ 1 F q1k + Σ ψ 2j F qjk F d,ser = Σ F gik + F q1k + Σ ψ 1j F qjk Onde: F d,ser é o valor de cálculo das ações para combinações de serviço; F q1k é o valor característico das ações variáveis principais diretas; ψ 1 é o fator de redução de combinação freqüente para ELS; ψ 2 é o fator de redução de combinação quase permanente para ELS. Tabela 4 - Combinações de serviço Fonte: NBR 6118 (2003) Assim como nas combinações últimas, nas de serviço também existem três combinações: as quase permanentes, as freqüentes e as raras. Nota-se que em nenhuma destas combinações são utilizados os coeficientes de majoração γ f1 e γ f3, encontrados na tabela 1. São utilizados, para as cargas variáveis, os coeficientes da tabela 2. A combinação alterna entre a utilização dos coeficientes ψ 1 e ψ 2, conforme se observa na tabela 4. Os valores de cálculo são obtidos através da multiplicação dos valores característicos pelos coeficientes de ponderação e fatores de combinação, acima citados. 22
23 3. ANALOGIA DE GRELHA Um dos métodos utilizados para o cálculo das lajes é o método de ruptura que consiste em identificar de que forma a laje chega ao colapso e calcular os esforços utilizando a teoria das charneiras plásticas. Outro método utilizado é o método elástico, que se baseia nas equações de equilíbrio de um elemento infinitesimal de placa e nas relações de compatibilidade das deformações do mesmo, segundo CARVALHO e FIGUEIREDO FILHO (2004). Neste trabalho será empregado o método elástico no cálculo dos esforços das lajes. Para a determinação dos esforços e dos deslocamentos de placas serão consideradas cargas em serviço, e será utilizado o processo de grelha equivalente (ou analogia de grelha). Este consiste em substituir o pavimento em estudo por uma malha equivalente de vigas, levando em consideração a rigidez de cada elemento do pavimento (vigas, lajes, vazios, etc.), e aplicando as cargas por influência de área em cada barra de grelha, de modo a obter o mesmo estado de deformação e os mesmos esforços nas duas estruturas. Segundo CARVALHO e FIGUEIREDO FILHO (2004): Este processo permite reproduzir o comportamento estrutural de pavimentos com praticamente qualquer geometria, seja ele composto de lajes de concreto armado maciças, com ou sem viga, ou de lajes nervuradas. Para que isto seja possível, divide-se o pavimento em questão em faixas com larguras tais que possam representar do melhor modo possível o pavimento. O número de faixas será determinado pelas dimensões e pela geometria das lajes. Daí, estas faixas são substituídas por elementos de barras, e, dessa forma, obtêm-se uma grelha equivalente ao pavimento. Na figura 3 pode-se observar um exemplo da discretização de uma laje por analogia de grelha. 23
24 Figura 3 - (a) Laje Maciça; (b) Grelha Equivalente Fonte: STRAMANDINOLI, 2003 Definida a malha da grelha equivalente, aplicam-se as rigidezes à torção e à flexão referente a cada área da laje. Deve-se levar em conta que as barras são de dois tipos: as de elemento de placa (no caso das lajes) e as de elemento viga-placa (na ligação da viga com a laje). De acordo com STRAMANDINOLI (2003), tais rigidezes são tomadas como concentradas nas barras de grelha mais próxima. As rigidezes longitudinais são aplicadas nas barras longitudinais, assim como as transversais são concentradas nas barras transversais. O processo de analogia de grelha apresenta alguns inconvenientes, pela natureza diferente das duas estruturas envolvidas. Por exemplo, o momento em uma barra depende apenas de sua curvatura, enquanto que numa laje, o momento em qualquer direção depende da curvatura naquela direção e na direção ortogonal. Outro inconveniente é que no cálculo da rigidez de elementos de placa, leva-se em consideração o coeficiente de Poisson ν, de modo que a rigidez de uma direção exerce influência sobre a direção ortogonal a esta. Isto não ocorre com elementos de barra, o que faz com que a rigidez de elementos de barra seja menor que a de uma placa. (STRAMANDINOLI, 2003) Analisando-se os resultados obtidos por pesquisadores em relação à analogia de grelha encontraram-se resultados satisfatórios desse processo, quando comparado com os resultados obtidos em análises utilizando a teoria da elasticidade. As ações atuantes nas lajes provenientes de peso-próprio, paredes, revestimento, dentre outras, podem ser aplicadas nas barras de grelha como concentradas (nos nós ou nas barras) ou distribuídas ao longo das barras. Em todo caso é preciso uma análise da 24
25 área de influência, tanto do nó como das barras, para uma correta distribuição das cargas, conforme a figura 4. Figura 4 - Carregamento uniformemente distribuído nas barras (carga p) e carregamento concentrado nos nós (carga P1) e nas barras (carga P2) Fonte: HENNRICHS,
26 4. GENERALIDADES E DIMENSIONAMENTO DAS LAJES As lajes maciças e as lajes nervuradas bidirecionais apresentam como características o fato de distribuir suas reações em todas as vigas do contorno. Isto faz com que as vigas do pavimento sejam melhor aproveitadas. Outro fator a destacar é que nestas lajes, por serem moldadas in loco, é possível executar a instalação de tubulações elétricas e hidráulicas antes da concretagem, facilitando a execução. Para o dimensionamento de lajes maciças convencionais e de lajes nervuradas é preciso estabelecer algumas hipóteses de cálculo. Embora o concreto armado seja constituído de dois materiais, o concreto e o aço, para fins de simplificação de cálculo, este pode ser considerado homogêneo. Outra hipótese é que este é um material elástico, ou seja, quando solicitado, ele sofrerá deformações, no entanto, cessada a solicitação, voltará a sua forma inicial. O concreto armado também será considerado como material isótropo, que possui as mesmas propriedades em qualquer uma das direções estudadas. (CARVALHO e FIGUEIREDO FILHO, 2004). 4.1 LAJES MACIÇAS CONVENCIONAIS Geralmente a espessura das lajes maciças convencionais varia entre L/40 e L/60 do menor vão, respeitando os limites mínimos estabelecidos na NBR 6118 (2003). Este pré-dimensionamento depende das dimensões do pavimento, sobretudo na outra direção, e dos carregamentos sobre a laje. Neste intervalo, a espessura da laje é considerada adequada para efeito de cálculo. Para a determinação dos apoios das lajes, leva-se em consideração o comprimento dos vãos. Quando a relação entre o maior e o menor vão é inferior ou igual a dois, considera-se esta laje como apoiada em duas direções. Com isto as armaduras que resistirão aos esforços de flexão serão dispostas nas duas direções. Quando a relação é superior a dois, considera-se esta laje como apoiada e armada em uma única direção. No que diz respeito ao exposto acima, o processo de analogia de grelha às vezes traz resultados inesperados. Isto ocorre pelo fato de este ser um processo que se baseia em deformações, e depender das rigidezes dos elementos envolvidos. Em regiões de lajes próximas a vigas e pilares, os resultados das análises encontrados são diferentes 26
27 dos encontrados regularmente, por causa da rigidez mais alta deste elementos, quando comparados às lajes. Como exemplo, toma-se uma situação de uma laje corredor, que seria armada em uma única direção, perpendicular ao maior vão. Se existir um pilar, que apóie uma das vigas deste maior vão, posicionado nas bordas desta laje, ao longo do maior vão, ele influenciará os momentos fletores existentes na direção deste vão, fazendo com que seja necessário armar nesta direção, não mais com armadura de distribuição, mas com armaduras destinadas a resistir aos esforços encontrados. Esta situação pode ser visualizada na figura 5. VP15 P5 3,00 7,00 VP16 VP32 P8 VP33 Figura 5 - Laje corredor O cálculo de lajes de um pavimento constituído de várias vigas, classicamente, é feito admitindo cada uma trabalhando isoladamente. Porém, de posse de processos computacionais, como neste caso o processo de analogia de grelha, é possível analisar um pavimento de uma edificação como um todo. De posse dos resultados do processamento (momentos fletores, esforços cortantes e deformações), inicia-se o cálculo das armaduras para resistir aos esforços encontrados. No que diz respeito às deformações, faz-se uma comparação dos resultados obtidos com os valores máximos prescritos em normas técnicas, para ver se estas se enquadram no estado limite de serviço. O cálculo da armadura longitudinal das lajes, nas duas direções, se faz como no caso de vigas, utilizando a teoria da flexão. Deve-se atentar que, no caso de lajes, a largura tomada para o cálculo é uma faixa unitária (geralmente um metro), devendo-se 27
28 detalhar a armadura para cada unidade de faixa padrão. No processo de grelha equivalente, a largura da faixa dos esforços dependerá da discretização da malha da grelha. Para se obter os esforços por metro, que é o usual, basta dividir os esforços encontrados pela largura da malha discretizada. A dedução da formulação utilizada para o cálculo das armaduras pode ser encontrada em SUSSEKIND (1979) e em CARVALHO e FIGUEIREDO FILHO (2004). A área de aço As necessária para uma laje de altura (espessura) h, considerando uma largura de um metro, submetida a um momento de cálculo M d é: Onde: z é o comprimento do braço de alavanca da seção transversal da laje; f γd é a tensão de escoamento de cálculo do aço utilizado. Observa-se na figura 6 uma representação da seção transversal da laje e do diagrama de tensão desta, onde nota-se a representação do braço de alavanca z, da altura da linha neutra x, das deformações do aço e do concreto ε s e ε c, respectivamente, do momento de cálculo M d aplicado, além de outros dados da seção. Com o cálculo da armadura em mãos, pode-se verificar a posição da linha neutra para ver se esta se harmoniza com os parâmetros estabelecidos na NBR 6118 (2003). var x ec Dd d h z Md Zd d' es Figura 6 - Equilíbrio da Seção Transversal Fonte: SUSSEKIND, 1989 No que diz respeito ao cálculo e detalhamento das armaduras, deve-se atentar para os limites impostos pela NBR 6118 (2003) para as armaduras mínimas. A armadura mínima para lajes se baseia nos critérios das armaduras mínimas para vigas, com algumas considerações a mais. A norma fixa um critério para o cálculo da 28
29 armadura mínima para vigas: o momento mínimo de cálculo aplicado. O objetivo desta armadura mínima é melhorar o desempenho da laje à flexão e à punção, além de controlar a fissuração, segundo a NBR 6118 (2003). O momento mínimo de cálculo aplicado é dado pela equação: onde: W o é o módulo de resistência da seção transversal bruta de concreto, relativo à fibra mais tracionada; f ctk,sup é a resistência característica superior do concreto à tração, conforme NBR 6118 (2003). Utilizando o momento mínimo de cálculo aplicado, a NBR 6118 (2003) desenvolveu uma tabela contendo uma taxa mínima de armadura. Atendendo-se a estas taxas, considera-se atendido o critério de momento mínimo. Os valores das taxas de armadura podem ser encontrados na tabela 5. Forma da seção ω mín fck Valores de ρ min 1) (A s,min /A c ) % Retangular 0,035 0,150 0,150 0,173 0,201 0,230 0,259 0,288 T (mesa comprimida) T (mesa tracionada) 0,024 0,150 0,150 0,150 0,150 0,158 0,177 0,197 0,031 0,150 0,150 0,153 0,178 0, ,255 Circular 0,070 0,230 0,288 0,345 0,403 0,460 0,518 0,575 1) Os valores de ρ min estabelecidos nesta tabela pressupõem o uso de aço CA-50, γ c = 1,4 e γ s = 1,15. Caso esses fatores sejam diferentes, ρ min deve ser recalculado com base no valor de ω mín dado. NOTA - Nas seções tipo T, a área da seção a ser considerada deve ser caracterizada pela alma acrescida da mesa colaborante. Tabela 5 - Taxas mínimas de armaduras Fonte: NBR 6118 (2003) Apesar do exposto sobre as armaduras mínimas, a NBR 6118 (2003) permite que, em alguns casos, seja utilizada uma quantidade menor de armadura. Isto ocorre em elementos estruturais superdimensionados. Para isto, deve ser feito um levantamento rigoroso dos carregamentos envolvidos, além de todas as combinações requeridas. Para o cálculo de armaduras, utiliza-se um valor de momento fletor igual ao dobro do 29
30 momento de cálculo aplicado, tendo-se cuidado com o diâmetro e o espaçamento delas por causa da fissuração. No caso de lajes, a norma estabelece uma tabela que oferece parâmetros para escolha das armaduras. Além dos critérios para armadura de distribuição, que são três: 20% da armadura principal, 0,9 cm²/m ou 0,5*ρ min, o que for maior dentre estes, as armaduras positivas sofrem uma redução, para 67% da taxa de armadura mínima, caso a laje seja armada em duas direções. Estas considerações podem ser encontradas na tabela 6. Armadura Elementos estruturais sem armaduras ativas Elementos estruturais com armadura ativa aderente Elementos estruturais com armadura ativa não aderente Armaduras negativas ρ s ρ min ρ s ρ min ρ p 0,67ρ min ρ s ρ min - 0,5ρ p 0,67ρ min (ver item ) Armaduras positivas de lajes armadas nas duas direções Armadura positiva (principal) de lajes armadas em uma direção Armadura positiva (secundária) de lajes armadas em uma direção ρ s 0,67ρ min ρ s 0,67ρ min ρ p 0,5ρ min ρ s ρ min - 0,5ρ p 0,5 ρ min ρ s ρ min ρ s ρ min ρ p 0,5ρ min ρ s ρ min - 0,5ρ p 0,5ρ min A s /s 20 % da armadura principal As/s 0,9 cm²/m - ρ s 0,5 ρ min Onde: ρ s = A s /b w h e ρ p = A p /b w h. NOTA - Os valores de ρ min constam na tabela Tabela 6 - Valores mínimos para armaduras de lajes Fonte: NBR 6118 (2003) Um ponto importante a destacar no dimensionamento de lajes é o cálculo dos deslocamentos, que será o critério utilizado para o refino da estrutura e um dos utilizados para a comparação entre os dois modelos de lajes. Segundo a NBR 6118 (2003) a verificação dos estados limites de serviço deve ser feita utilizando modelos que levem em consideração a rigidez efetiva da seção de concreto armado. Isto significa que devem ser levadas em consideração a presença da armadura, a existência de fissuras no concreto e as deformações diferidas ao longo do tempo. Deve-se ter em mente que a quantidade de variáveis para o cálculo de deformações é grande. Por isso, não se pode esperar exatidão dos resultados obtidos pelos processos analíticos. As deformações podem ser imediatas ou diferidas. A deformação imediata é a que acontece no momento de aplicação do carregamento, sendo que a diferida ocorre ao 30
31 longo do tempo de atuação deste carregamento, provocado pelos efeitos de fluência e retração do concreto. Segundo CARVALHO e FIGUEIREDO FILHO (2004) a fluência é o fenômeno em que surgem deformações em um elemento solicitado por uma tensão constante, enquanto que a retração é a variação volumétrica existente em peças de concreto devido, principalmente, à saída de água existente em seu interior. Para o cálculo da deformação imediata, a NBR 6118 (2003) indica uma equação, adaptada da equação de Branson, que leva em consideração que numa peça de concreto armado submetida à flexão, existem trechos no estádio I e trechos no estádio II. Isto é importante por que no estádio I, o concreto não se encontra fissurado, de modo que toda a seção colabora na resistência aos esforços de tração existentes, enquanto que, no estádio II, o concreto fissura, não mais colaborando com a resistência à tração. Deste modo, para o cálculo dos deslocamentos no estádio II, esta seção de concreto é desprezada, sendo necessário um cálculo de inércia equivalente, que leva em consideração o concreto da zona comprimida e o aço da zona tracionada. A equação encontrada na NBR calcula esta rigidez equivalente, para que possa ser possível encontrar o deslocamento do elemento estrutural em questão. Esta equação é dada a seguir: onde: I c é o momento de inércia da seção bruta de concreto; I II é o momento de inércia da seção fissura de concreto no estádio II; M a é o momento fletor na seção crítica do vão considerado, momento máximo no vão para elementos biapoiados ou contínuos e momento no apoio para balanços; M r é o momento de fissuração do elemento estrutural; E cs é o módulo de elasticidade secante do concreto. O momento de fissuração M r é dado por: onde: α = 1,2 para seções T ou duplo T; 31
32 α = 1,2 para seções retangulares; onde: α é o fator que correlaciona aproximadamente a resistência à tração na flexão com a resistência à tração direta; y t é a distância do centro de gravidade da seção à fibra mais tracionada; I c é o momento de inércia da seção bruta de concreto; f ct é a resistência à tração direta do concreto. De posse desta rigidez equivalente para o concreto fissurado no estádio II, podese fazer o cálculo da deformação imediata dos elementos estruturais. Vale salientar que os carregamentos utilizados para este cálculo de deslocamentos devem ser combinados segundo os critérios citados no capítulo 2, retirados da NBR 6118 (2003), sobre o estado limite de serviço. Existem muitos processos para o cálculo da flecha diferida. A NBR 6118 (2003) utiliza um método em que tal deformação é calculada pela multiplicação da flecha imediata, calculada anteriormente, por um fator α f, obtido pela equação: em que: (o valor de ρ será ponderado no vão de maneira análoga ao cálculo da inércia equivalente); A s é a área de armadura de compressão no trecho considerado; ξ é um coeficiente em função do tempo, que pode ser obtido diretamente da tabela 7, retirada na NBR 6118 (2003), ou então calculada pelas equações abaixo: sendo ; Tempo (t) meses Coeficiente ξ(t) 0 0, ,54 0,68 0,84 0,95 1,04 1,12 1,36 1,64 1,89 2 Tabela 7 - Coeficientes ξ em função do tempo Fonte: NBR 6118 (2003) 32
33 t é o tempo, em meses, quando se deseja o valor da flecha diferida; t 0 é a idade, em meses, relativa à data de aplicação da carga de longa duração. No caso de parcelas de carga de longa duração serem aplicadas em idade diferente, pode-se tomar, para t 0, o valor ponderado a seguir: onde: P i representa as parcelas de carga; t 0i é a idade em que se aplicou cada parcela P i. O valor final da flecha será determinado pela multiplicação da flecha imediata por (1 + α f ). Pode-se notar que a flecha diferida pode chegar ao dobro da flecha imediata, sendo, portanto, indispensável sua verificação. O programa utilizado para cálculo de esforços e deslocamento, neste trabalho, faz uso da formulação acima definida. Este trabalha com o método de grelha equivalente, conforme exposto no capítulo 3, discretizando o pavimento de lajes em barras de grelha. O cálculo de deslocamento se dá da seguinte forma: primeiro é aplicado 10% do carregamento da estrutura, ponderado segundo as combinações de serviço. Daí calcula-se as rigidezes de cada barra de grelha, calculando-se, após isso, os esforços e os deslocamentos. Depois, aplica-se mais 10% de carga sobre a estrutura deformada e fissurada, segundo os resultados da análise anterior. Prossegue com esta operação, aplicando-se as cargas de 10 em 10% e calculando-se as novas rigidezes, os novos deslocamentos e os novos esforços para cada incremento de carga, obtendo-se, no fim, o deslocamento final e os esforços finais, para cada elemento de grelha, sendo possível analisar como se comporta o pavimento inteiro de lajes. 4.2 LAJES NERVURADAS No concreto armado, o concreto é responsável pela absorção dos esforços de compressão na flexão, enquanto que cabe ao aço resistir aos esforços de tração. Embora o concreto resista a esforços de tração, no dimensionamento de estruturas essa 33
34 resistência é desprezada, pelo fato de esta ser pequena, se comparada à resistência do aço. Por conta disso, em estruturas de concreto submetidas à flexão, em que atuam momentos positivos, o concreto existente na região abaixo da linha neutra não tem como função resistir aos esforços de tração. Isto permitiu reduzir o concreto existente nesta região, reduzindo também o peso próprio da estrutura. Esta solução é empregada nas lajes nervuradas, que são lajes compostas por nervuras contendo, ou não, material inerte entre elas, com uma capa de concreto, denominada mesa, de espessura relativamente fina por cima. Existem muitos fabricantes que desenvolveram fôrmas para a execução deste tipo de laje, facilitando o emprego desta solução estrutural para grandes vãos, já que a retirada do concreto dispensável na flexão permitiu aumentar a espessura das lajes sem aumentar proporcionalmente o peso próprio da estrutura. Para o cálculo de lajes nervuradas, a NBR 6118 (2003) prescreve alguns critérios a serem utilizados. Estes critérios dizem respeito a dimensões mínimas empregadas nessas lajes, que ditarão a forma de calculá-las na flexão e no cisalhamento. Não tendo tubulações horizontais embutidas, a mesa pode ter espessura mínima de 1/15 da distância entre as nervuras ou de 3 cm, sendo que se houverem tubulações, a dimensão mínima passa a ser 4 cm. A espessura mínima das nervuras é de 5 cm, sendo que se houver armadura de compressão, a espessura mínima deve ser de 8 cm. Para a verificação de cisalhamento, a NBR 6118 (2003) permite que sejam utilizados os critérios de laje, desde que o espaçamento entre os eixos das nervuras seja inferior a 65 cm. Neste caso a verificação de flexão na mesa pode ser dispensada. Caso o espaçamento entre as nervuras esteja entre 65 cm e 110 cm a norma exige que seja feita a verificação da mesa à flexão, no entanto, se o espaçamento for menor que 90 cm e a largura média da nervura for superior a 12 cm, ainda permite-se a verificação das nervuras ao cisalhamento segundo os critérios de lajes; caso contrário, a verificação delas ao cisalhamento deve ser feita como vigas. Se o espaçamento entre eixos das nervuras for superior a 110 cm, a mesa deve ser dimensionada como laje maciça apoiada na grelha de vigas, respeitando-se os devidos limites de espessura desse tipo de laje. A figura 7 apresenta alguns dos critérios estabelecidos pela NBR 6118 (2003) para a mesa e as nervuras das lajes. 34
A SEGURANÇA NAS ESTRUTURAS
 A SEGURANÇA NAS ESTRUTURAS CONCEITO DE SEGURANÇA Quando uma estrutura pode ser considerada segura? SEGURANÇA: Resistência Estabilidade Durabilidade ENVOLVE DOIS CONCEITOS: Conceito Qualitativo: (Método
A SEGURANÇA NAS ESTRUTURAS CONCEITO DE SEGURANÇA Quando uma estrutura pode ser considerada segura? SEGURANÇA: Resistência Estabilidade Durabilidade ENVOLVE DOIS CONCEITOS: Conceito Qualitativo: (Método
Efeito do comportamento reológico do concreto
 Efeito do comportamento reológico do concreto FLECHAS E ELEENTOS DE CONCRETO ARADO 1 - INTRODUÇÃO Todo o cálculo das deformações de barras, devidas à fleão, tem por base a clássica equação diferencial
Efeito do comportamento reológico do concreto FLECHAS E ELEENTOS DE CONCRETO ARADO 1 - INTRODUÇÃO Todo o cálculo das deformações de barras, devidas à fleão, tem por base a clássica equação diferencial
1.1 Conceitos fundamentais... 19 1.2 Vantagens e desvantagens do concreto armado... 21. 1.6.1 Concreto fresco...30
 Sumário Prefácio à quarta edição... 13 Prefácio à segunda edição... 15 Prefácio à primeira edição... 17 Capítulo 1 Introdução ao estudo das estruturas de concreto armado... 19 1.1 Conceitos fundamentais...
Sumário Prefácio à quarta edição... 13 Prefácio à segunda edição... 15 Prefácio à primeira edição... 17 Capítulo 1 Introdução ao estudo das estruturas de concreto armado... 19 1.1 Conceitos fundamentais...
Módulo 2 Ações e Segurança e. Comportamento Básico dos Materiais. Métodos de Verificação da Segurança. Método dos Estados Limites
 NBR 68 e Comportamento Básico dos ateriais P R O O Ç Ã O Conteúdo Comportamento Básico dos ateriais étodos de Verificação da Segurança étodo dos Estados Limites Ações Coeficientes de Ponderação das Ações
NBR 68 e Comportamento Básico dos ateriais P R O O Ç Ã O Conteúdo Comportamento Básico dos ateriais étodos de Verificação da Segurança étodo dos Estados Limites Ações Coeficientes de Ponderação das Ações
CURSO TÉCNICO DE EDIFICAÇÕES. Disciplina: Projeto de Estruturas. Aula 7
 AULA 7 CURSO TÉCNICO DE EDIFICAÇÕES Disciplina: Projeto de Estruturas CLASSIFICAÇÃO DAS ARMADURAS 1 CLASSIFICAÇÃO DAS ARMADURAS ALOJAMENTO DAS ARMADURAS Armadura longitudinal (normal/flexão/torção) Armadura
AULA 7 CURSO TÉCNICO DE EDIFICAÇÕES Disciplina: Projeto de Estruturas CLASSIFICAÇÃO DAS ARMADURAS 1 CLASSIFICAÇÃO DAS ARMADURAS ALOJAMENTO DAS ARMADURAS Armadura longitudinal (normal/flexão/torção) Armadura
Estruturas de Concreto Armado. Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com
 Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados.
 LAJES DE CONCRETO ARMADO 1. Unidirecionais As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados. 1.1 Lajes em balanço Lajes em balanço são unidirecionais
LAJES DE CONCRETO ARMADO 1. Unidirecionais As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados. 1.1 Lajes em balanço Lajes em balanço são unidirecionais
e-mail: ederaldoazevedo@yahoo.com.br
 Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny
 Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
Facear Concreto Estrutural I
 1. ASSUNTOS DA AULA Durabilidade das estruturas, estádios e domínios. 2. CONCEITOS As estruturas de concreto devem ser projetadas e construídas de modo que, quando utilizadas conforme as condições ambientais
1. ASSUNTOS DA AULA Durabilidade das estruturas, estádios e domínios. 2. CONCEITOS As estruturas de concreto devem ser projetadas e construídas de modo que, quando utilizadas conforme as condições ambientais
ÍNDICE DO LIVRO CÁLCULO E DESENHO DE CONCRETO ARMADO autoria de Roberto Magnani SUMÁRIO LAJES
 ÍNDICE DO LIVRO CÁLCULO E DESENHO DE CONCRETO ARMADO autoria de Roberto Magnani SUMÁRIO LAJES 2. VINCULAÇÕES DAS LAJES 3. CARREGAMENTOS DAS LAJES 3.1- Classificação das lajes retangulares 3.2- Cargas acidentais
ÍNDICE DO LIVRO CÁLCULO E DESENHO DE CONCRETO ARMADO autoria de Roberto Magnani SUMÁRIO LAJES 2. VINCULAÇÕES DAS LAJES 3. CARREGAMENTOS DAS LAJES 3.1- Classificação das lajes retangulares 3.2- Cargas acidentais
UNIDADE 2 DIMENSIONAMENTO DE ESTRUTURAS DE CONCRETO ARMADO
 Universidade Federal de Pelotas Centro de Engenharias Curso de Engenharia Civil e Engenahria Agrícola UNIDADE 2 DIMENSIONAMENTO DE ESTRUTURAS DE CONCRETO ARMADO (AULA 2 AÇÕES E SOLICITAÇÕES) Prof. Estela
Universidade Federal de Pelotas Centro de Engenharias Curso de Engenharia Civil e Engenahria Agrícola UNIDADE 2 DIMENSIONAMENTO DE ESTRUTURAS DE CONCRETO ARMADO (AULA 2 AÇÕES E SOLICITAÇÕES) Prof. Estela
A concepção estrutural deve levar em conta a finalidade da edificação e atender, tanto quanto possível, às condições impostas pela arquitetura.
 ESTRUTURAS DE CONCRETO CAPÍTULO 4 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 2 de abril, 2003. CONCEPÇÃO ESTRUTURAL A concepção estrutural, ou simplesmente estruturação, também chamada
ESTRUTURAS DE CONCRETO CAPÍTULO 4 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 2 de abril, 2003. CONCEPÇÃO ESTRUTURAL A concepção estrutural, ou simplesmente estruturação, também chamada
SUPERESTRUTURA estrutura superestrutura infra-estrutura lajes
 SUPRSTRUTUR s estruturas dos edifícios, sejam eles de um ou vários pavimentos, são constituídas por diversos elementos cuja finalidade é suportar e distribuir as cargas, permanentes e acidentais, atuantes
SUPRSTRUTUR s estruturas dos edifícios, sejam eles de um ou vários pavimentos, são constituídas por diversos elementos cuja finalidade é suportar e distribuir as cargas, permanentes e acidentais, atuantes
O conhecimento das dimensões permite determinar os vãos equivalentes e as rigidezes, necessários no cálculo das ligações entre os elementos.
 PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
EXERCÍCIOS DE ESTRUTURAS DE MADEIRA
 UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA CIVIL,ARQUITETURA E URBANISMO Departamento de Estruturas EXERCÍCIOS DE ESTRUTURAS DE MADEIRA RAFAEL SIGRIST PONTES MARTINS,BRUNO FAZENDEIRO DONADON
UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA CIVIL,ARQUITETURA E URBANISMO Departamento de Estruturas EXERCÍCIOS DE ESTRUTURAS DE MADEIRA RAFAEL SIGRIST PONTES MARTINS,BRUNO FAZENDEIRO DONADON
2 Materiais e Métodos
 1 ANÁLISE DO COMPORTAMENTO DE VIGAS REFORÇADAS POR ACRÉSCIMO DE CONCRETO À FACE COMPRIMIDA EM FUNÇÃO DA TAXA DE ARMADURA LONGITUDINAL TRACIONADA PRÉ-EXISTENTE Elias Rodrigues LIAH; Andréa Prado Abreu REIS
1 ANÁLISE DO COMPORTAMENTO DE VIGAS REFORÇADAS POR ACRÉSCIMO DE CONCRETO À FACE COMPRIMIDA EM FUNÇÃO DA TAXA DE ARMADURA LONGITUDINAL TRACIONADA PRÉ-EXISTENTE Elias Rodrigues LIAH; Andréa Prado Abreu REIS
2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 2012 Duração prevista: até 4 horas.
 2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 212 Duração prevista: até 4 horas. Esta prova tem oito (8) questões e três (3) laudas. Consulta permitida somente ao formulário básico.
2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 212 Duração prevista: até 4 horas. Esta prova tem oito (8) questões e três (3) laudas. Consulta permitida somente ao formulário básico.
Lajes de Edifícios de Concreto Armado
 Lajes de Edifícios de Concreto Armado 1 - Introdução As lajes são elementos planos horizontais que suportam as cargas verticais atuantes no pavimento. Elas podem ser maciças, nervuradas, mistas ou pré-moldadas.
Lajes de Edifícios de Concreto Armado 1 - Introdução As lajes são elementos planos horizontais que suportam as cargas verticais atuantes no pavimento. Elas podem ser maciças, nervuradas, mistas ou pré-moldadas.
PRÉ-DIMENSIONAMENTO DA ESTRUTURA
 ECC 1008 ESTRUTURAS DE CONCRETO PRÉ-DIMENSIONAMENTO DA ESTRUTURA (Aulas 9-12) Prof. Gerson Moacyr Sisniegas Alva Algumas perguntas para reflexão... É possível obter esforços (dimensionamento) sem conhecer
ECC 1008 ESTRUTURAS DE CONCRETO PRÉ-DIMENSIONAMENTO DA ESTRUTURA (Aulas 9-12) Prof. Gerson Moacyr Sisniegas Alva Algumas perguntas para reflexão... É possível obter esforços (dimensionamento) sem conhecer
2.1. Considerações Gerais de Lajes Empregadas em Estruturas de Aço
 23 2. Sistemas de Lajes 2.1. Considerações Gerais de Lajes Empregadas em Estruturas de Aço Neste capítulo são apresentados os tipos mais comuns de sistemas de lajes utilizadas na construção civil. 2.1.1.
23 2. Sistemas de Lajes 2.1. Considerações Gerais de Lajes Empregadas em Estruturas de Aço Neste capítulo são apresentados os tipos mais comuns de sistemas de lajes utilizadas na construção civil. 2.1.1.
Módulo 6 Pilares: Estados Limites Últimos Detalhamento Exemplo. Imperfeições Geométricas Globais. Imperfeições Geométricas Locais
 NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
Resumidamente, vamos apresentar o que cada item influenciou no cálculo do PumaWin.
 Software PumaWin principais alterações O Software PumaWin está na versão 8.2, as principais mudanças que ocorreram ao longo do tempo estão relacionadas a inclusão de novos recursos ou ferramentas, correção
Software PumaWin principais alterações O Software PumaWin está na versão 8.2, as principais mudanças que ocorreram ao longo do tempo estão relacionadas a inclusão de novos recursos ou ferramentas, correção
ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE
 ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE FUNDAÇÕES Todo projeto de fundações
ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE FUNDAÇÕES Todo projeto de fundações
2 Sistema de Lajes com Forma de Aço Incorporado
 2 Sistema de Lajes com Forma de Aço Incorporado 2.1. Generalidades As vantagens de utilização de sistemas construtivos em aço são associadas à: redução do tempo de construção, racionalização no uso de
2 Sistema de Lajes com Forma de Aço Incorporado 2.1. Generalidades As vantagens de utilização de sistemas construtivos em aço são associadas à: redução do tempo de construção, racionalização no uso de
CISALHAMENTO EM VIGAS CAPÍTULO 13 CISALHAMENTO EM VIGAS
 CISALHAMENTO EM VIGAS CAPÍTULO 13 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 25 ago 2010 CISALHAMENTO EM VIGAS Nas vigas, em geral, as solicitações predominantes são o momento fletor e
CISALHAMENTO EM VIGAS CAPÍTULO 13 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 25 ago 2010 CISALHAMENTO EM VIGAS Nas vigas, em geral, as solicitações predominantes são o momento fletor e
Características do Sistema
 Características do Sistema O emprego de lajes nervuradas nas estruturas de concreto armado ganhou grande impulso nos últimos anos graças às modernas técnicas construtivas e ao desenvolvimento dos programas
Características do Sistema O emprego de lajes nervuradas nas estruturas de concreto armado ganhou grande impulso nos últimos anos graças às modernas técnicas construtivas e ao desenvolvimento dos programas
A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO
 A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO Marcos Alberto Ferreira da Silva (1) ; Jasson Rodrigues de Figueiredo Filho () ; Roberto Chust Carvalho ()
A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO Marcos Alberto Ferreira da Silva (1) ; Jasson Rodrigues de Figueiredo Filho () ; Roberto Chust Carvalho ()
Teoria das Estruturas
 Teoria das Estruturas Aula 02 Morfologia das Estruturas Professor Eng. Felix Silva Barreto ago-15 Q que vamos discutir hoje: Morfologia das estruturas Fatores Morfogênicos Funcionais Fatores Morfogênicos
Teoria das Estruturas Aula 02 Morfologia das Estruturas Professor Eng. Felix Silva Barreto ago-15 Q que vamos discutir hoje: Morfologia das estruturas Fatores Morfogênicos Funcionais Fatores Morfogênicos
Profª. Angela A. de Souza DESENHO DE ESTRUTURAS
 DESENHO DE ESTRUTURAS INTRODUÇÃO A estrutura de concreto armado é resultado da combinação entre o concreto e o aço. Porém, para a sua execução, não é suficiente apenas a presença desses dois materiais;
DESENHO DE ESTRUTURAS INTRODUÇÃO A estrutura de concreto armado é resultado da combinação entre o concreto e o aço. Porém, para a sua execução, não é suficiente apenas a presença desses dois materiais;
ESTRUTURAS MISTAS: AÇO - CONCRETO
 ESTRUTURAS MISTAS: AÇO - CONCRETO INTRODUÇÃO As estruturas mistas podem ser constituídas, de um modo geral, de concreto-madeira, concretoaço ou aço-madeira. Um sistema de ligação entre os dois materiais
ESTRUTURAS MISTAS: AÇO - CONCRETO INTRODUÇÃO As estruturas mistas podem ser constituídas, de um modo geral, de concreto-madeira, concretoaço ou aço-madeira. Um sistema de ligação entre os dois materiais
P U C R S PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL FACULDADE DE ENGENHARIA CURSO DE ENGENHARIA CIVIL CONCRETO ARMADO II FLEXÃO SIMPLES
 P U C R S PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL FACULDADE DE ENGENHARIA CURSO DE ENGENHARIA CIVIL CONCRETO ARMADO II FLEXÃO SIMPLES (OUTRA APRESENTAÇÃO) Prof. Almir Schäffer PORTO ALEGRE
P U C R S PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL FACULDADE DE ENGENHARIA CURSO DE ENGENHARIA CIVIL CONCRETO ARMADO II FLEXÃO SIMPLES (OUTRA APRESENTAÇÃO) Prof. Almir Schäffer PORTO ALEGRE
CÁLCULO DE LAJES - RESTRIÇÕES ÀS FLECHAS DAS LAJES
 CÁLCULO DE LAJES - RESTRIÇÕES ÀS FLECHAS DAS LAJES No item 4.2.3. 1.C da NB-1 alerta-se que nas lajes (e vigas) deve-se limitar as flechas das estruturas. No caso das lajes maciças, (nosso caso), será
CÁLCULO DE LAJES - RESTRIÇÕES ÀS FLECHAS DAS LAJES No item 4.2.3. 1.C da NB-1 alerta-se que nas lajes (e vigas) deve-se limitar as flechas das estruturas. No caso das lajes maciças, (nosso caso), será
MINISTERIO PÚBLICO DO TRABALHO PROCURADORIA REGIONAL DO TRABALHO 23ª REGIÃO RUA E S/N, CENTRO POLÍTICO ADMINISTRATIVO, CUIABÁ - MT
 MINISTERIO PÚBLICO DO TRABALHO PROCURADORIA REGIONAL DO TRABALHO 23ª REGIÃO RUA E S/N, CENTRO POLÍTICO ADMINISTRATIVO, CUIABÁ - MT MEMÓRIA DE CÁLCULO ESTRUTURA DE CONCRETO SUMÁRIO 1. INTRODUÇÃO 1.1. Hipóteses
MINISTERIO PÚBLICO DO TRABALHO PROCURADORIA REGIONAL DO TRABALHO 23ª REGIÃO RUA E S/N, CENTRO POLÍTICO ADMINISTRATIVO, CUIABÁ - MT MEMÓRIA DE CÁLCULO ESTRUTURA DE CONCRETO SUMÁRIO 1. INTRODUÇÃO 1.1. Hipóteses
Figura 17.1 Laje nervurada bidirecional (FRANCA & FUSCO, 1997)
 ESTRUTURAS DE CONCRETO CAPÍTULO 17 Libânio M. Pinheiro, Julio A. Razente 01 dez 2003 LAJES NERVURADAS 1. INTRODUÇÃO Uma laje nervurada é constituída por um conjunto de vigas que se cruzam, solidarizadas
ESTRUTURAS DE CONCRETO CAPÍTULO 17 Libânio M. Pinheiro, Julio A. Razente 01 dez 2003 LAJES NERVURADAS 1. INTRODUÇÃO Uma laje nervurada é constituída por um conjunto de vigas que se cruzam, solidarizadas
UNIVERSIDADE DE MARÍLIA
 UNIVERSIDADE DE MARÍLIA Faculdade de Engenharia, Arquitetura e Tecnologia SISTEMAS ESTRUTURAIS (NOTAS DE AULA) Professor Dr. Lívio Túlio Baraldi MARILIA, 2007 1. DEFINIÇÕES FUNDAMENTAIS Força: alguma causa
UNIVERSIDADE DE MARÍLIA Faculdade de Engenharia, Arquitetura e Tecnologia SISTEMAS ESTRUTURAIS (NOTAS DE AULA) Professor Dr. Lívio Túlio Baraldi MARILIA, 2007 1. DEFINIÇÕES FUNDAMENTAIS Força: alguma causa
MANUAL DE COLOCAÇÃO. Laje Treliça. Resumo Esse material tem como objetivo auxiliar no dimensionamento, montagem e concretagem da laje.
 MANUAL DE COLOCAÇÃO Laje Treliça Resumo Esse material tem como objetivo auxiliar no dimensionamento, montagem e concretagem da laje. Henrique. [Endereço de email] 1 VANTAGENS LAJE TRELIÇA É capaz de vencer
MANUAL DE COLOCAÇÃO Laje Treliça Resumo Esse material tem como objetivo auxiliar no dimensionamento, montagem e concretagem da laje. Henrique. [Endereço de email] 1 VANTAGENS LAJE TRELIÇA É capaz de vencer
ATUALIZAÇÃO EM SISTEMAS ESTRUTURAIS
 AULA 04 ATUALIZAÇÃO EM SISTEMAS ESTRUTURAIS Prof. Felipe Brasil Viegas Prof. Eduardo Giugliani http://www.feng.pucrs.br/professores/giugliani/?subdiretorio=giugliani 0 AULA 04 INSTABILIDADE GERAL DE EDIFÍCIOS
AULA 04 ATUALIZAÇÃO EM SISTEMAS ESTRUTURAIS Prof. Felipe Brasil Viegas Prof. Eduardo Giugliani http://www.feng.pucrs.br/professores/giugliani/?subdiretorio=giugliani 0 AULA 04 INSTABILIDADE GERAL DE EDIFÍCIOS
DESCRITIVO TÉCNICO - EST 1
 DESCRITIVO TÉCNICO - EST 1 1 DESCRITIVO TÉCNICO 1.1 CONSIDERAÇÕES INICIAIS Todos os cálculos e detalhamentos estão de acordo com o prescrito nas normas NBR 6118:2014 Projeto de Estruturas de Concreto -
DESCRITIVO TÉCNICO - EST 1 1 DESCRITIVO TÉCNICO 1.1 CONSIDERAÇÕES INICIAIS Todos os cálculos e detalhamentos estão de acordo com o prescrito nas normas NBR 6118:2014 Projeto de Estruturas de Concreto -
BASES PARA CÁLCULO CAPÍTULO 6 BASES PARA CÁLCULO 6.1 ESTADOS LIMITES
 BASES PARA CÁLCULO CAPÍTULO 6 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 6 maio 2003 BASES PARA CÁLCULO 6.1 ESTADOS LIMITES As estruturas de concreto armado devem ser projetadas de modo
BASES PARA CÁLCULO CAPÍTULO 6 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 6 maio 2003 BASES PARA CÁLCULO 6.1 ESTADOS LIMITES As estruturas de concreto armado devem ser projetadas de modo
Tensão para a qual ocorre a deformação de 0,2%
 O QUE É DIMENSIONAR UMA ESTRUTURA DE CONCRETO ARMADO? Dimensionar uma estrutura de concreto armado é determinar a seção de concreto (formas) e de aço (armadura) tal que: a estrutura não entre em colapso
O QUE É DIMENSIONAR UMA ESTRUTURA DE CONCRETO ARMADO? Dimensionar uma estrutura de concreto armado é determinar a seção de concreto (formas) e de aço (armadura) tal que: a estrutura não entre em colapso
3.6.1. Carga concentrada indireta (Apoio indireto de viga secundária)
 cisalhamento - ELU 22 3.6. rmadura de suspensão para cargas indiretas 3.6.1. Carga concentrada indireta (poio indireto de viga secundária) ( b w2 x h 2 ) V 1 ( b w1 x h 1 ) V d1 - viga com apoio ndireto
cisalhamento - ELU 22 3.6. rmadura de suspensão para cargas indiretas 3.6.1. Carga concentrada indireta (poio indireto de viga secundária) ( b w2 x h 2 ) V 1 ( b w1 x h 1 ) V d1 - viga com apoio ndireto
ANÁLISE ESTRUTURAL DE RIPAS PARA ENGRADAMENTO METÁLICO DE COBERTURAS
 ANÁLISE ESTRUTURAL DE RIPAS PARA ENGRADAMENTO METÁLICO DE COBERTURAS Leandro de Faria Contadini 1, Renato Bertolino Junior 2 1 Eng. Civil, UNESP-Campus de Ilha Solteira 2 Prof. Titular, Depto de Engenharia
ANÁLISE ESTRUTURAL DE RIPAS PARA ENGRADAMENTO METÁLICO DE COBERTURAS Leandro de Faria Contadini 1, Renato Bertolino Junior 2 1 Eng. Civil, UNESP-Campus de Ilha Solteira 2 Prof. Titular, Depto de Engenharia
Notas de aulas - Concreto Armado. Lançamento da Estrutura. Icléa Reys de Ortiz
 Notas de aulas - Concreto Armado 2 a Parte Lançamento da Estrutura Icléa Reys de Ortiz 1 1. Lançamento da Estrutura Antigamente costumava-se lançar vigas sob todas as paredes e assim as lajes ficavam menores
Notas de aulas - Concreto Armado 2 a Parte Lançamento da Estrutura Icléa Reys de Ortiz 1 1. Lançamento da Estrutura Antigamente costumava-se lançar vigas sob todas as paredes e assim as lajes ficavam menores
Recomendações para a Elaboração do Projeto Estrutural
 Universidade Estadual de Maringá - Centro de Tecnologia Departamento de Engenharia Civil Disciplina: Estruturas em Concreto I Professor: Rafael Alves de Souza Recomendações para a Elaboração do Projeto
Universidade Estadual de Maringá - Centro de Tecnologia Departamento de Engenharia Civil Disciplina: Estruturas em Concreto I Professor: Rafael Alves de Souza Recomendações para a Elaboração do Projeto
CUSTO COMPARADO DE ELEMENTOS PRÉ-FABRICADOS DE CONCRETO: PRÉ-LAJE PROTENDIDA X LAJE ALVEOLAR PROTENDIDA.
 CUSTO COMPARADO DE ELEMENTOS PRÉ-FABRICADOS DE CONCRETO: PRÉ-LAJE PROTENDIDA X LAJE ALVEOLAR PROTENDIDA. Adriano Mariot da Silva (1), Mônica Elizabeth Daré (2) UNESC Universidade do Extremo Sul Catarinense
CUSTO COMPARADO DE ELEMENTOS PRÉ-FABRICADOS DE CONCRETO: PRÉ-LAJE PROTENDIDA X LAJE ALVEOLAR PROTENDIDA. Adriano Mariot da Silva (1), Mônica Elizabeth Daré (2) UNESC Universidade do Extremo Sul Catarinense
Projeto estrutural de edifícios de alvenaria: decisões, desafios e impactos da nova norma de projeto
 Projeto estrutural de edifícios de alvenaria: decisões, desafios e impactos da nova norma de projeto Prof. Associado Márcio Roberto Silva Corrêa Escola de Engenharia de São Carlos Universidade de São Paulo
Projeto estrutural de edifícios de alvenaria: decisões, desafios e impactos da nova norma de projeto Prof. Associado Márcio Roberto Silva Corrêa Escola de Engenharia de São Carlos Universidade de São Paulo
ESTADOS LIMITES DE SERVIÇO SEGUNDO A NBR 6118
 Universidade Federal de Santa Maria Departamento de Estruturas e Construção Civil ESTADOS LIMITES DE SERVIÇO SEGUNDO A NBR 6118 Eng. Gerson Moacyr Sisniegas Alva MOTIVAÇÃO INICIAL Alunos de graduação Engenharia
Universidade Federal de Santa Maria Departamento de Estruturas e Construção Civil ESTADOS LIMITES DE SERVIÇO SEGUNDO A NBR 6118 Eng. Gerson Moacyr Sisniegas Alva MOTIVAÇÃO INICIAL Alunos de graduação Engenharia
Caso (2) X 2 isolado no SP
 Luiz Fernando artha étodo das Forças 6 5.5. Exemplos de solução pelo étodo das Forças Exemplo Determine pelo étodo das Forças o diagrama de momentos fletores do quadro hiperestático ao lado. Somente considere
Luiz Fernando artha étodo das Forças 6 5.5. Exemplos de solução pelo étodo das Forças Exemplo Determine pelo étodo das Forças o diagrama de momentos fletores do quadro hiperestático ao lado. Somente considere
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DOS VALES DO JEQUITINHONA E MUCURI DIAMANTINA MG ESTUDO DIRIGIDO
 MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DOS VALES DO JEQUITINHONA E MUCURI DIAMANTINA MG ESTUDO DIRIGIDO Disciplina: Construções Rurais 2011/1 Código: AGR006/AGR007 Curso (s): Agronomia e Zootecnia
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DOS VALES DO JEQUITINHONA E MUCURI DIAMANTINA MG ESTUDO DIRIGIDO Disciplina: Construções Rurais 2011/1 Código: AGR006/AGR007 Curso (s): Agronomia e Zootecnia
detalhamento da armadura longitudinal da viga
 conteúdo 36 detalhamento da armadura longitudinal da viga 36.1 Decalagem do diagrama de momentos fletores (NBR6118/2003 Item 17.4.2.2) Quando a armadura longitudinal de tração for determinada através do
conteúdo 36 detalhamento da armadura longitudinal da viga 36.1 Decalagem do diagrama de momentos fletores (NBR6118/2003 Item 17.4.2.2) Quando a armadura longitudinal de tração for determinada através do
Artigo submetido ao Curso de Engenharia Civil da UNESC - como requisito parcial para obtenção do Título de Engenheiro Civil
 ANÁLISE DO DIMENSIONAMENTO DE PILARES DE CONCRETO ARMADO PELO MÉTODO DO PILAR PADRÃO COM RIGIDEZ κ APROXIMADA E PELO MÉTODO DO PILAR PADRÃO COM CURVATURA APROXIMADA PARA EFEITOS DE 2º ORDEM Augusto Figueredo
ANÁLISE DO DIMENSIONAMENTO DE PILARES DE CONCRETO ARMADO PELO MÉTODO DO PILAR PADRÃO COM RIGIDEZ κ APROXIMADA E PELO MÉTODO DO PILAR PADRÃO COM CURVATURA APROXIMADA PARA EFEITOS DE 2º ORDEM Augusto Figueredo
O concreto armado tem inúmeras aplicações: estruturas, pavimentos, paredes, fundações, barragens, reservatórios.
 AS ESTRUTURAS DE CONCRETO ARMADO. Concreto armado - é um material da construção civil que se tornou um dos mais importantes elementos da arquitetura do século XX. É usado nas estruturas dos edifícios.
AS ESTRUTURAS DE CONCRETO ARMADO. Concreto armado - é um material da construção civil que se tornou um dos mais importantes elementos da arquitetura do século XX. É usado nas estruturas dos edifícios.
Quais são os critérios adotados pelo programa para o cálculo dos blocos de fundação?
 Assunto Quais são os critérios adotados pelo programa para o cálculo dos blocos de fundação? Artigo Segundo a NBR 6118, em seu item 22.5.1, blocos de fundação são elementos de volume através dos quais
Assunto Quais são os critérios adotados pelo programa para o cálculo dos blocos de fundação? Artigo Segundo a NBR 6118, em seu item 22.5.1, blocos de fundação são elementos de volume através dos quais
Sistemas mistos aço-concreto viabilizando estruturas para Andares Múltiplos
 viabilizando estruturas para Andares Múltiplos Vantagens Com relação às estruturas de concreto : -possibilidade de dispensa de fôrmas e escoramentos -redução do peso próprio e do volume da estrutura -aumento
viabilizando estruturas para Andares Múltiplos Vantagens Com relação às estruturas de concreto : -possibilidade de dispensa de fôrmas e escoramentos -redução do peso próprio e do volume da estrutura -aumento
DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T
 DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T Hevânio D. de Almeida a b, Rafael A. Guillou a,, Cleilson F. Bernardino
DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T Hevânio D. de Almeida a b, Rafael A. Guillou a,, Cleilson F. Bernardino
OTIMIZAÇÃO DE VIGAS CONSIDERANDO ESTADOS LIMITES ÚLTIMOS, DE UTILIZAÇÃO E DISPOSIÇÕES CONSTRUTIVAS
 OTIMIZAÇÃO DE VIGAS CONSIDERANDO ESTADOS LIMITES ÚLTIMOS, DE UTILIZAÇÃO E DISPOSIÇÕES CONSTRUTIVAS Eng. Civil Leonardo Roncetti da Silva, TECHCON Engenharia e Consultoria Ltda. Resumo Estuda-se a otimização
OTIMIZAÇÃO DE VIGAS CONSIDERANDO ESTADOS LIMITES ÚLTIMOS, DE UTILIZAÇÃO E DISPOSIÇÕES CONSTRUTIVAS Eng. Civil Leonardo Roncetti da Silva, TECHCON Engenharia e Consultoria Ltda. Resumo Estuda-se a otimização
Este curso consiste de uma introdução ao cálculo estrutural das vigas de concreto armado, ilustrada através do estudo de vigas retas de edifícios.
 Introdução 1 1. Introdução O objetivo do cálculo de uma estrutura de concreto armado é o de se garantir: uma segurança adequada contra a ruptura decorrente das solicitações; deformações decorrentes das
Introdução 1 1. Introdução O objetivo do cálculo de uma estrutura de concreto armado é o de se garantir: uma segurança adequada contra a ruptura decorrente das solicitações; deformações decorrentes das
UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil. Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV
 UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV NOTAS DE AULA MARQUISES Prof. Dr. PAULO SÉRGIO DOS SANTOS
UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV NOTAS DE AULA MARQUISES Prof. Dr. PAULO SÉRGIO DOS SANTOS
Study of structural behavior of a low height precast concrete building, considering the continuity of beam-column connections
 Study of structural behavior of a low height precast concrete building, considering the continuity of beam-column connections Universidade Federal de Viçosa - Av. P.H. Rolfs s/n - Viçosa MG - 36.570-000
Study of structural behavior of a low height precast concrete building, considering the continuity of beam-column connections Universidade Federal de Viçosa - Av. P.H. Rolfs s/n - Viçosa MG - 36.570-000
PUNÇÃO EM LAJES DE CONCRETO ARMADO
 PUNÇÃO EM LAJES DE CONCRETO ARMADO Prof. Eduardo Giugliani Colaboração Engº Fabrício Zuchetti ESTRUTURAS DE CONCRETO ARMADO III FENG / PUCRS V.02 Panorama da Fissuração. Perspectiva e Corte 1 De acordo
PUNÇÃO EM LAJES DE CONCRETO ARMADO Prof. Eduardo Giugliani Colaboração Engº Fabrício Zuchetti ESTRUTURAS DE CONCRETO ARMADO III FENG / PUCRS V.02 Panorama da Fissuração. Perspectiva e Corte 1 De acordo
TECNICAS CONSTRUTIVAS I
 Curso Superior de Tecnologia em Construção de Edifícios TECNICAS CONSTRUTIVAS I Prof. Leandro Candido de Lemos Pinheiro leandro.pinheiro@riogrande.ifrs.edu.br FUNDAÇÕES Fundações em superfície: Rasa, Direta
Curso Superior de Tecnologia em Construção de Edifícios TECNICAS CONSTRUTIVAS I Prof. Leandro Candido de Lemos Pinheiro leandro.pinheiro@riogrande.ifrs.edu.br FUNDAÇÕES Fundações em superfície: Rasa, Direta
Análise numérica de fundações diretas de aerogeradores Carlos A. Menegazzo Araujo, Dr. 1, André Puel, Msc 2, Anderson Candemil 3
 Análise numérica de fundações diretas de aerogeradores Carlos A. Menegazzo Araujo, Dr. 1, André Puel, Msc 2, Anderson Candemil 3 1 MENEGAZZO Projeto e Consultoria Ltda / carlos.menegazzo@gmail.com 2 IFSC
Análise numérica de fundações diretas de aerogeradores Carlos A. Menegazzo Araujo, Dr. 1, André Puel, Msc 2, Anderson Candemil 3 1 MENEGAZZO Projeto e Consultoria Ltda / carlos.menegazzo@gmail.com 2 IFSC
- Generalidades sobre laje Treliça
 - Generalidades sobre laje Treliça São lajes em que a viga pré-fabricada é constituída de armadura em forma de treliça, e após concretada, promove uma perfeita solidarização, tendo ainda a possibilidade
- Generalidades sobre laje Treliça São lajes em que a viga pré-fabricada é constituída de armadura em forma de treliça, e após concretada, promove uma perfeita solidarização, tendo ainda a possibilidade
PADRONIZAÇÃO DE PAINÉIS EM LIGHT STEEL FRAME
 PADRONIZAÇÃO DE PAINÉIS EM LIGHT STEEL FRAME ANITA OLIVEIRA LACERDA - anitalic@terra.com.br PEDRO AUGUSTO CESAR DE OLIVEIRA SÁ - pedrosa@npd.ufes.br 1. INTRODUÇÃO O Light Steel Frame (LSF) é um sistema
PADRONIZAÇÃO DE PAINÉIS EM LIGHT STEEL FRAME ANITA OLIVEIRA LACERDA - anitalic@terra.com.br PEDRO AUGUSTO CESAR DE OLIVEIRA SÁ - pedrosa@npd.ufes.br 1. INTRODUÇÃO O Light Steel Frame (LSF) é um sistema
CAPÍTULO III SISTEMAS ESTRUTURAIS CONSTRUÇÕES EM ALVENARIA
 1 CAPÍTULO III SISTEMAS ESTRUTURAIS CONSTRUÇÕES EM ALVENARIA I. SISTEMAS ESTRUTURAIS Podemos citar diferentes sistemas estruturais a serem adotados durante a concepção do projeto de uma edificação. A escolha
1 CAPÍTULO III SISTEMAS ESTRUTURAIS CONSTRUÇÕES EM ALVENARIA I. SISTEMAS ESTRUTURAIS Podemos citar diferentes sistemas estruturais a serem adotados durante a concepção do projeto de uma edificação. A escolha
6 Vigas: Solicitações de Flexão
 6 Vigas: Solicitações de Fleão Introdução Dando seqüência ao cálculo de elementos estruturais de concreto armado, partiremos agora para o cálculo e dimensionamento das vigas à fleão. Ações As ações geram
6 Vigas: Solicitações de Fleão Introdução Dando seqüência ao cálculo de elementos estruturais de concreto armado, partiremos agora para o cálculo e dimensionamento das vigas à fleão. Ações As ações geram
Módulo 5 Lajes: Estados Limites Últimos Estados Limites de Serviço Detalhamento Exemplo. Dimensionamento de Lajes à Punção
 NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo ELU e ELS Força Cortante em Dimensionamento de à Punção - Detalhamento - - Conclusões Estado Limite Último
NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo ELU e ELS Força Cortante em Dimensionamento de à Punção - Detalhamento - - Conclusões Estado Limite Último
Professora: Engª Civil Silvia Romfim
 Professora: Engª Civil Silvia Romfim PARTES CONSTITUINTES DE UMA COBERTURA Pode-se dizer que a cobertura é subdividida em cinco principais partes: 1. Pelo telhado, composto por vários tipos de telhas;
Professora: Engª Civil Silvia Romfim PARTES CONSTITUINTES DE UMA COBERTURA Pode-se dizer que a cobertura é subdividida em cinco principais partes: 1. Pelo telhado, composto por vários tipos de telhas;
Lajes. Marcio Varela Construção I
 Lajes Marcio Varela Construção I Lajes Aumentam o valor econômico do empreendimento; Aumentam a segurança; a; Aumentam o conforto; Tipos: Maciças; as; Pré-moldadas Protendida Nervurada, etc Lajes Maciça
Lajes Marcio Varela Construção I Lajes Aumentam o valor econômico do empreendimento; Aumentam a segurança; a; Aumentam o conforto; Tipos: Maciças; as; Pré-moldadas Protendida Nervurada, etc Lajes Maciça
PRÉ-MOLD RM PRÉ-MOLD RM PRÉ-MOLD RM PRÉ-MOLD RM
 Com mais de 20 anos de experiência na fabricação de pré-moldados em concreto, a PRÉ-MOLD RM oferece uma completa linha de produtos para a dinamização de sua obra. Laje Treliçada Bidirecional; Laje Treliçada
Com mais de 20 anos de experiência na fabricação de pré-moldados em concreto, a PRÉ-MOLD RM oferece uma completa linha de produtos para a dinamização de sua obra. Laje Treliçada Bidirecional; Laje Treliçada
O AÇO ESTRUTURAL (uma parte do material desta página foi extraída do site www.gerdau.com.br) Aços CA-50 e CA-25
 O AÇO ESTRUTURAL (uma parte do material desta página foi extraída do site www.gerdau.com.br) Os aços são classificados conforme sua resistência, definida pela sua composição e processo de fabricação. Assim,
O AÇO ESTRUTURAL (uma parte do material desta página foi extraída do site www.gerdau.com.br) Os aços são classificados conforme sua resistência, definida pela sua composição e processo de fabricação. Assim,
Vigas Altas em Alvenaria Estrutural
 Vigas Altas em Alvenaria Estrutural Fernando Fonseca, Ph.D., S.E. Brigham Young University - Utah - USA (essa é uma pegadinha) 5 Qual é o problema se a viga é alta? Distribuição das deformações na secção
Vigas Altas em Alvenaria Estrutural Fernando Fonseca, Ph.D., S.E. Brigham Young University - Utah - USA (essa é uma pegadinha) 5 Qual é o problema se a viga é alta? Distribuição das deformações na secção
PROVA DE ENGENHARIA CIVIL. Para uma viga bi-apoiada, com carga concentrada, se desprezarmos o efeito do peso próprio, é CORRETO afirmar:
 18 PROVA DE ENGENHARIA CIVIL QUESTÃO 41 Para uma viga bi-apoiada, com carga concentrada, se desprezarmos o efeito do peso próprio, é CORRETO afirmar: a) o diagrama do esforço cortante (DEC) é composto
18 PROVA DE ENGENHARIA CIVIL QUESTÃO 41 Para uma viga bi-apoiada, com carga concentrada, se desprezarmos o efeito do peso próprio, é CORRETO afirmar: a) o diagrama do esforço cortante (DEC) é composto
GALPÃO. Figura 87 instabilidade lateral
 9 CONTRAVENTAMENTO DE ESTRUTURAS DE MADEIIRA 9..1 Generalliidades 11 As estruturas reticuladas são normalmente constituídas por elementos planos. Quando são estruturas espaciais (não planas), tendem a
9 CONTRAVENTAMENTO DE ESTRUTURAS DE MADEIIRA 9..1 Generalliidades 11 As estruturas reticuladas são normalmente constituídas por elementos planos. Quando são estruturas espaciais (não planas), tendem a
Espaçador treliçado ABTC para apoio de ferragem negativa. Espaçador DL para tela soldada. Barras de transferência
 Espaçador treliçado ABTC para apoio de ferragem negativa O espaçador treliçado ABTC da FAMETH é utilizado em lajes, substituindo o ultrapassado caranguejo. É indicado para apoiar e manter o correto posicionamento
Espaçador treliçado ABTC para apoio de ferragem negativa O espaçador treliçado ABTC da FAMETH é utilizado em lajes, substituindo o ultrapassado caranguejo. É indicado para apoiar e manter o correto posicionamento
ALVENARIA ESTRUTURAL: DISCIPLINA: MATERIAIS DE CONSTRUÇÃO II PROF.: JAQUELINE PÉRTILE
 ALVENARIA ESTRUTURAL: BLOCOS DE CONCRETO DISCIPLINA: MATERIAIS DE CONSTRUÇÃO II PROF.: JAQUELINE PÉRTILE O uso de alvenaria como sistema estrutural já vem sendo usado a centenas de anos, desde as grandes
ALVENARIA ESTRUTURAL: BLOCOS DE CONCRETO DISCIPLINA: MATERIAIS DE CONSTRUÇÃO II PROF.: JAQUELINE PÉRTILE O uso de alvenaria como sistema estrutural já vem sendo usado a centenas de anos, desde as grandes
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA POLITÉCNICA Curso de Engenharia Civil Departamento de Mecânica Aplicada e Estruturas
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA POLITÉCNICA Curso de Engenharia Civil Departamento de Mecânica Aplicada e Estruturas PROJETO DE ESTRUTURAS COM GRANDES VARANDAS EDUARDO VIEIRA DA COSTA Projeto
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA POLITÉCNICA Curso de Engenharia Civil Departamento de Mecânica Aplicada e Estruturas PROJETO DE ESTRUTURAS COM GRANDES VARANDAS EDUARDO VIEIRA DA COSTA Projeto
TC 071 PONTES E ESTRUTURAS ESPECIAIS II Período: 2º semestre Professor: Jorge Luiz Ceccon Carga horária da disciplina = 120 h - 4 h por semana
 UNIVERSIDADE FEDERAL DO PARANÁ DEPARTAMENTO DE CONSTRUÇÃO CIVIL TC 071 PONTES E ESTRUTURAS ESPECIAIS II Ano: 2010 Período: 2º semestre Professor: Jorge Luiz Ceccon Carga horária da disciplina = 120 h -
UNIVERSIDADE FEDERAL DO PARANÁ DEPARTAMENTO DE CONSTRUÇÃO CIVIL TC 071 PONTES E ESTRUTURAS ESPECIAIS II Ano: 2010 Período: 2º semestre Professor: Jorge Luiz Ceccon Carga horária da disciplina = 120 h -
3.1.1.1.2 PESO DOS ELEMENTOS CONSTRUTIVOS FIXOS E DAS INSTALAÇÕES PERMANENTES
 3 AÇÕES, SOLICITAÇÕES E RESISTÊNCIAS 3.1 TIPOS DE AÇÕES Na análise estrutural deve ser considerada a influência de todas as ações que possam produzir efeitos significativos para a segurança da estrutura
3 AÇÕES, SOLICITAÇÕES E RESISTÊNCIAS 3.1 TIPOS DE AÇÕES Na análise estrutural deve ser considerada a influência de todas as ações que possam produzir efeitos significativos para a segurança da estrutura
LAJES MACIÇAS DE CONCRETO ARMADO
 CAPÍTULOS 1 A 4 Volume LAJES MACIÇAS DE CONCRETO ARMADO 1 1- Tipos usuais de lajes dos edifícios Laje h Laje maciça apoiada em vigas Vigas h Lajes nervuradas nervuras aparentes material inerte Laje Laje
CAPÍTULOS 1 A 4 Volume LAJES MACIÇAS DE CONCRETO ARMADO 1 1- Tipos usuais de lajes dos edifícios Laje h Laje maciça apoiada em vigas Vigas h Lajes nervuradas nervuras aparentes material inerte Laje Laje
ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE
 ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL CONCEITO Estacas são importantes e comuns elementos
ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL CONCEITO Estacas são importantes e comuns elementos
- Pisos e revestimentos Industriais (pinturas especiais, autonivelantes, uretânicas, vernizes...);
 A TECNIKA iniciou suas atividades em meados de 2003, impulsionada pela demanda do mercado, sempre preocupada em buscar e oferecer soluções técnicas inovadoras, tendo como focos principais as áreas de impermeabilização
A TECNIKA iniciou suas atividades em meados de 2003, impulsionada pela demanda do mercado, sempre preocupada em buscar e oferecer soluções técnicas inovadoras, tendo como focos principais as áreas de impermeabilização
DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES
 DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES EXEMPLO DE APLICAÇÃO Carlos Moutinho FEUP, Maio de 2002 1. Dados Gerais - Laje destinada a zona comercial (Q = 4 kn/m 2 ) - Peso de revestimentos e paredes
DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES EXEMPLO DE APLICAÇÃO Carlos Moutinho FEUP, Maio de 2002 1. Dados Gerais - Laje destinada a zona comercial (Q = 4 kn/m 2 ) - Peso de revestimentos e paredes
e-mail: ederaldoazevedo@yahoo.com.br
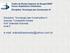 Assunto: Fundações Diretas Prof. Ederaldo Azevedo Aula 5 e-mail: ederaldoazevedo@yahoo.com.br Introdução: Todo peso de uma obra é transferido para o terreno em que a mesma é apoiada. Os esforços produzidos
Assunto: Fundações Diretas Prof. Ederaldo Azevedo Aula 5 e-mail: ederaldoazevedo@yahoo.com.br Introdução: Todo peso de uma obra é transferido para o terreno em que a mesma é apoiada. Os esforços produzidos
CÁLCULO DE VIGAS. - alvenaria de tijolos cerâmicos furados: γ a = 13 kn/m 3 ; - alvenaria de tijolos cerâmicos maciços: γ a = 18 kn/m 3.
 CAPÍTULO 5 Volume 2 CÁLCULO DE VIGAS 1 1- Cargas nas vigas dos edifícios peso próprio : p p = 25A c, kn/m ( c A = área da seção transversal da viga em m 2 ) Exemplo: Seção retangular: 20x40cm: pp = 25x0,20x0,40
CAPÍTULO 5 Volume 2 CÁLCULO DE VIGAS 1 1- Cargas nas vigas dos edifícios peso próprio : p p = 25A c, kn/m ( c A = área da seção transversal da viga em m 2 ) Exemplo: Seção retangular: 20x40cm: pp = 25x0,20x0,40
AULA A TIPOS DE LAJES
 AULA A TIPOS DE LAJES INTRODUÇÃO Lajes são partes elementares dos sistemas estruturais dos edifícios de concreto armado. As lajes são componentes planos, de comportamento bidimensional, utilizados para
AULA A TIPOS DE LAJES INTRODUÇÃO Lajes são partes elementares dos sistemas estruturais dos edifícios de concreto armado. As lajes são componentes planos, de comportamento bidimensional, utilizados para
Aços Longos. Soluções Lajes
 Aços Longos Soluções Lajes Soluções Lajes Dentre os desafios da engenharia civil, o sistema construtivo de lajes deve atender à eficiência estrutural, visando a soluções seguras, economicamente viáveis
Aços Longos Soluções Lajes Soluções Lajes Dentre os desafios da engenharia civil, o sistema construtivo de lajes deve atender à eficiência estrutural, visando a soluções seguras, economicamente viáveis
Aula 3: Forjamento e Estampagem Conceitos de Forjamento Conceitos de Estampagem
 Aula 3: Forjamento e Estampagem Conceitos de Forjamento Conceitos de Estampagem Este processo é empregado para produzir peças de diferentes tamanhos e formas, constituído de materiais variados (ferrosos
Aula 3: Forjamento e Estampagem Conceitos de Forjamento Conceitos de Estampagem Este processo é empregado para produzir peças de diferentes tamanhos e formas, constituído de materiais variados (ferrosos
Escola de Engenharia de São Carlos - Universidade de São Paulo Departamento de Engenharia de Estruturas. Alvenaria Estrutural.
 Alvenaria Estrutural Introdução CONCEITO ESTRUTURAL BÁSICO Tensões de compressão Alternativas para execução de vãos Peças em madeira ou pedra Arcos Arco simples Arco contraventado ASPECTOS HISTÓRICOS Sistema
Alvenaria Estrutural Introdução CONCEITO ESTRUTURAL BÁSICO Tensões de compressão Alternativas para execução de vãos Peças em madeira ou pedra Arcos Arco simples Arco contraventado ASPECTOS HISTÓRICOS Sistema
ESCADAS USUAIS DOS EDIFÍCIOS
 Volume 4 Capítulo 3 ESCDS USUIS DOS EDIFÍCIOS 1 3.1- INTRODUÇÃO patamar lance a b c d e Formas usuais das escadas dos edifícios armada transversalmente armada longitudinalmente armada em cruz V3 V4 Classificação
Volume 4 Capítulo 3 ESCDS USUIS DOS EDIFÍCIOS 1 3.1- INTRODUÇÃO patamar lance a b c d e Formas usuais das escadas dos edifícios armada transversalmente armada longitudinalmente armada em cruz V3 V4 Classificação
Practical formulas for calculation of deflections of reinforced concrete beams
 Teoria e Prática na Engenharia Civil, n.18, p.6-70 Novembro, 011 Fórmulas práticas para cálculo de flechas de vigas de concreto armado Practical formulas for calculation of deflections of reinforced concrete
Teoria e Prática na Engenharia Civil, n.18, p.6-70 Novembro, 011 Fórmulas práticas para cálculo de flechas de vigas de concreto armado Practical formulas for calculation of deflections of reinforced concrete
Artigo submetido ao Curso de Engenharia Civil da UNESC - Como requisito parcial para obtenção do Título de Engenheiro Civil
 Como requisito parcial para obtenção do Título de Engenheiro Civil AVALIAÇÃO DO COMPORTAMENTO DE UMA ESTRUTURA DE CONCRETO ARMADO ANALISANDO A RIGIDEZ DO ENGASTAMENTO ENTRE VIGAS E PILARES E UTILIZANDO
Como requisito parcial para obtenção do Título de Engenheiro Civil AVALIAÇÃO DO COMPORTAMENTO DE UMA ESTRUTURA DE CONCRETO ARMADO ANALISANDO A RIGIDEZ DO ENGASTAMENTO ENTRE VIGAS E PILARES E UTILIZANDO
Técnicas da Construção Civil. Aula 02
 Técnicas da Construção Civil Aula 02 Necessidades do cliente e tipos de Estruturas Taciana Nunes Arquiteta e Urbanista Necessidades do Cliente Função ou tipo de edificação? Como e quanto o cliente quer
Técnicas da Construção Civil Aula 02 Necessidades do cliente e tipos de Estruturas Taciana Nunes Arquiteta e Urbanista Necessidades do Cliente Função ou tipo de edificação? Como e quanto o cliente quer
Telas Soldadas Nervuradas
 Telas Soldadas Nervuradas Telas Soldadas Nervuradas Belgo Qualidade As Telas Soldadas de Aço Nervurado são armaduras pré-fabricadas constituídas por fios de aço Belgo 60 Nervurado, longitudinais e transversais,
Telas Soldadas Nervuradas Telas Soldadas Nervuradas Belgo Qualidade As Telas Soldadas de Aço Nervurado são armaduras pré-fabricadas constituídas por fios de aço Belgo 60 Nervurado, longitudinais e transversais,
Recomendações para Elaboração de Projetos Estruturais de Edifícios de Concreto
 Recomendações para Elaboração de Projetos Estruturais de Edifícios de Concreto INTRODUÇÃO O presente trabalho tem como objetivo fornecer aos projetistas e contratantes, recomendações básicas e orientações
Recomendações para Elaboração de Projetos Estruturais de Edifícios de Concreto INTRODUÇÃO O presente trabalho tem como objetivo fornecer aos projetistas e contratantes, recomendações básicas e orientações
Influência do tipo de laje nos custos de um edifício em aço
 ArtigoTécnico Ygor Dias da Costa Lima 1 Alex Sander Clemente de Souza 2 Silvana De Nardin 2 1 Mestre em Construção Civil pela Pós-Graduação em Construção Civil PPGCiv/UFSCar 2 Prof. Dr. Pós-Graduação em
ArtigoTécnico Ygor Dias da Costa Lima 1 Alex Sander Clemente de Souza 2 Silvana De Nardin 2 1 Mestre em Construção Civil pela Pós-Graduação em Construção Civil PPGCiv/UFSCar 2 Prof. Dr. Pós-Graduação em
2.1 O Comportamento Estrutural
 2 Vigas As vigas consistem basicamente de barras, contínuas ou não, com eixo reto ou curvo, equiibradas por um sistema de apoios, de modo a garantir que essas barras sejam, no mínimo, isostáticas. Estão
2 Vigas As vigas consistem basicamente de barras, contínuas ou não, com eixo reto ou curvo, equiibradas por um sistema de apoios, de modo a garantir que essas barras sejam, no mínimo, isostáticas. Estão
FACULDADE SUDOESTE PAULISTA Instituição Chaddad de Ensino FUNDAÇÃO RADIER
 FACULDADE SUDOESTE PAULISTA Instituição Chaddad de Ensino FUNDAÇÃO RADIER Trabalho realizado pelos alunos Alex Fabiano Ângelo, Antonangele Raimundo, Bárbara Rozzeto, Daurício Oliveira, Eduardo Brisola,
FACULDADE SUDOESTE PAULISTA Instituição Chaddad de Ensino FUNDAÇÃO RADIER Trabalho realizado pelos alunos Alex Fabiano Ângelo, Antonangele Raimundo, Bárbara Rozzeto, Daurício Oliveira, Eduardo Brisola,
NBR 7480/1996. Barras e fios de aço destinados a armaduras para concreto armado
 NBR 7480/1996 Barras e fios de aço destinados a armaduras para concreto armado OBJETIVO Fixar as condições exigíveis na encomenda, fabricação e fornecimento de barras e fios de aço destinados a armaduras
NBR 7480/1996 Barras e fios de aço destinados a armaduras para concreto armado OBJETIVO Fixar as condições exigíveis na encomenda, fabricação e fornecimento de barras e fios de aço destinados a armaduras
