APÊNDICES ATIVIDADES OBJETOS DE APRENDIZAGEM
|
|
|
- Bruno Madureira Almada
- 8 Há anos
- Visualizações:
Transcrição
1 APÊNDICES ATIVIDADES OBJETOS DE APRENDIZAGEM
2 APÊNDICE A - Análise dos softwares GeoGebra e Winplot I Objetivo: Identificar o software que será utilizado para desenvolver as atividades. II Metodologia: Iniciaremos a atividade instalando dois softwares educativos, Geogebra e Winplot, de domínio público, nos computadores. Após instalação dos softwares o aluno deverá verificar os diversos comandos de cada software, utilizá-los, e finalmente fazer a opção daquele que melhor se adaptou. III Atividade: um) Você encontrou dificuldade para instalar os programas GeoGebra e Winplot no computador? 2) Se sua resposta foi positiva, faça suas observações sobre o problema encontrado. 3) Ao verificar os programas qual deles você encontrou maior facilidade para manipular os comandos? (Justifique sua resposta)
3 APÊNDICE B Estudo da Elipse no GeoGebra I. Objetivos: Construir uma Elipse utilizando os comandos do programa GeoGebra Identificar o centro da Elipse, seus eixos e suas propriedades. Escrever os procedimentos utilizados para cada item da atividade, visando à elaboração de um objeto de aprendizagem. II. Metodologia: A atividade deve ser executada em dupla. Os alunos devem verificar na tela inicial do software os comandos necessários para a execução de cada item da atividade. Nesta atividade, os alunos devem descobrir as opções de comandos e executá-los. As dúvidas devem ser discutidas em cada dupla sem intervenção do professor pesquisador. Cada dupla deve registrar os procedimentos utilizados em cada item da atividade. Ao final, os grupos apresentarão a conclusão sobre a cônica verificada. III Atividade 1) Identifique pontos nos quatro quadrantes do plano cartesiano 1 o quadrante: 2 o quadrante: 3 o quadrante: 4 o quadrante:
4 Escreva o procedimento utilizado para identificar os pontos 2) Marque os pontos (-3, 4) e (2, 4), construa um segmento com estas extremidades, verifique sua medida e escreva o resultado encontrado. Escreva o procedimento utilizado para construir o segmento e encontrar a sua medida. 3) Construa uma Elipse utilizando os pontos (-3,4) e (1, 4), chamados focos da Elipse. Escreva o procedimento utilizado para construir a Elipse 4) Identifique o centro da Elipse 5) Construa uma reta com os dois focos da Elipse Escreva o procedimento utilizado para construir a reta 6) Encontre os pontos de interseção da reta com a Elipse
5 Escreva o procedimento utilizado para encontrar os pontos de interseção 7) Encontre a distância entre os dois pontos de interseção eixo maior da Elipse. 8) Trace a reta mediatriz do segmento cujas extremidades são os focos da Elipse Escreva o procedimento utilizado para encontrar a reta mediatriz 9) Encontre os pontos de interseção da reta mediatriz com a Elipse 10) Determine a distância entre os dois pontos encontrados eixo menor da Elipse. 11) Calcule a soma das distâncias de um ponto qualquer da Elipse aos dois focos e compare o resultado com a medida do eixo maior. Escreva as conclusões do resultado encontrado
6 APÊNDICE C - Reconhecimento de uma Elipse e estudo de suas simetrias e excentricidade I Objetivos: Reconhecer uma elipse utilizando os comandos do programa GeoGebra. Verificar as simetrias existentes. Identificar os eixos: maior e menor da Elipse. Analisar a excentricidade da Elipse. Escrever os procedimentos utilizados para cada item da atividade, visando à construção de um objeto de aprendizagem. Construir um Objeto de Aprendizagem que permita ao conjunto ampliado de alunos chegarem ao conceito de uma Elipse II Metodologia: Cada dupla deve transferir para o GeoGebra o arquivo da figura ou foto escolhida a fim de verificar se o formato da curva existente nele é uma Elipse. Utilizando o software GeoGebra os alunos devem analisar se figuras/fotos trazidas por eles tem o formato de uma elipse. Assim como na primeira atividade, os alunos devem escrever os procedimentos utilizados para a verificação da cônica. O tempo destinado à realização da atividade é de uma hora. III 1) Identifique na barra de ferramentas do GeoGebra incluir imagem e inclua a imagem que você pesquisou. Escreva o procedimento utilizado para incluir a imagem.
7 2) Como você verifica se a curva apresentada na figura é ou não uma Elipse? 3) A partir da sua resposta do item 2, construa sob a figura uma Elipse. Escreva o procedimento utilizado para construir a Elipse. 4) Faça movimentos com a Elipse utilizando recurso disponível na barra de ferramentas do GeoGebra. Escreva o procedimento utilizado para movimentar a Elipse Utilizando os focos, faça o movimento da Elipse e escreva sua conclusão.
8 5) Procure mover a Elipse com objetivo de sobrepô-la na figura inserida. Qual a sua conclusão sobre a curva existente na fotografia? 6) Construa o eixo maior e menor da Elipse. 7) Identifique as simetrias existentes na Elipse. 8) Na Elipse, construa um segmento cujos extremos são: um dos focos e uma das extremidades do eixo menor. 9) Identifique o ângulo agudo formado pelo segmento construído e pelo eixo maior. Escreva o procedimento utilizado para construir o ângulo. 10) Aumente e diminua o ângulo e descreva o que acontece com a Elipse.
9 11) No triângulo retângulo formado pelo semieixo menor (b), pelo segmento que determina a metade da distância focal (c) e pelo segmento que une um dos focos da Elipse e uma extremidade do eixo menor (a), o que acontece com a razão c/a, chamada excentricidade da Elipse, quando aumentamos e diminuímos o ângulo construído. 12) Qual a conclusão encontrada sobre a excentricidade de uma Elipse?
10 APÊNDICE D - Objeto de Aprendizagem: Reconhecimento de uma Elipse I Objetivos: Construir uma Elipse utilizando os comandos do software GeoGebra. Identificar o centro da Elipse, seus eixos e sua excentricidade. Identificar em uma figura/foto uma curva com o formato de Elipse. II Metodologia: A atividade deve ser executada em grupos de três alunos e cada aluno monitor deve acompanhar dois grupos. As dúvidas devem ser sanadas pelos alunos monitores sob o acompanhamento do professor pesquisador. Os alunos monitores devem orientar os grupos sobre utilização do arquivo com a figura/foto para análise da curva com formato de Elipse existente nele. Ao final da atividade, o professor pesquisador e os alunos monitores farão uma avaliação do Objeto de Aprendizagem executado. III Atividade: 1) Acesse o programa GeoGebra. 2) Na parte superior do vídeo clique em Exibir ; em seguida, no item Malha e no item Janela de Álgebra. 3) Marque um ponto em cada quadrante do plano cartesiano. 1 o quadrante:... 2 o quadrante:... 3 o quadrante:... 4 o quadrante:... 4) Na parte superior, clique em Arquivo e, em seguida, no item Novo. 5) Na parte superior, clique no 2 o quadro (novo ponto) e marque os pontos (-4, 2) e (4, 2). 6) Utilizando o quadro seguinte, construa um segmento unindo os dois pontos.
11 7) No oitavo quadro, identifique o comprimento do segmento traçado. Resultado:... 8) Verifique no sétimo quadro a opção Elipse e construa uma Elipse, utilizando os pontos (-4, 2) e (4, 2) como seus focos e um terceiro ponto não pertencente à reta que contém os focos. Terceiro ponto:... 9) Verifique no terceiro quadro a opção Reta Determinada por dois Pontos e construa uma reta passando pelos da Elipse. 10) Verifique no segundo quadro Interseção de dois objetos e determine a interseção entre a Elipse e a reta construída. Pontos de interseção: ) Encontre a distância entre os dois pontos de interseção, que é identificada como eixo maior da Elipse. Eixo maior:... 12) Utilizando o quarto quadro, construa uma mediatriz do eixo maior da Elipse. 13) Encontre a interseção do eixo maior com a mediatriz, que é o centro da Elipse. Centro de Elipse:... 14) Determine a interseção da mediatriz com a Elipse. Pontos de Interseção: ) Determine a distância entre os dois pontos encontrados, que é identificada como eixo menor da Elipse. Eixo menor:... 16) Identifique um ponto qualquer na Elipse e calcule as distâncias desse ponto aos focos, some o resultado e compare com a medida do eixo maior. 17) Repita esse procedimento com outro ponto qualquer, pertencente à Elipse. 18) Escreva suas conclusões sobre o resultado encontrado. 19) A partir do que foi estudado com o auxílio do GeoGebra, como você identifica uma Elipse? 20) Utilizando o arquivo com a foto, que foi disponibilizada para você, verifique se a curva existente nela tem um formato de Elipse. Caso tenha, identifique o eixo maior, eixo menor, centro e a distância entre os focos. Eixo maior:... Eixo menor:... Centro:...
12 APÊNDICE E - Objeto de Aprendizagem Estudo da Elipse I Objetivos: Construir uma Elipse utilizando outros comandos do software GeoGebra. Identificar em uma figura/foto o formato de uma Elipse. Identificar propriedades da Elipse. II Metodologia: O Objeto de aprendizagem foi desenvolvido para ser feito em grupos de três alunos. Será utilizada alternativa de comandos para a execução dos itens propostos no Objeto. Os alunos já tiveram acesso ao software na atividade quatro, com orientação dos alunos monitores; portanto, o trabalho será desenvolvido pelos grupos, onde o aluno monitor será mais um integrante desse grupo. III Atividade: 1) Acesse o programa GeoGebra. 2) Na parte inferior da tela Entrada escreva o ponto A= (-3, 4) e tecle enter. Repita o processo com os pontos B= (2,4) e C= (3,4). 3) Localize no lado direito da parte inferior da tela a palavra Comando, clique em Elipse. Na linha de Entrada, em que aparece Elipse, escreva dentro dos colchetes as letras A,B,C. Tecle enter 4) Construa o eixo menor da Elipse. 5) Utilizando a linha de comando determine os pontos de interseção da Elipse com o eixo menor. D=(...,...) e E=(...,...) 6) Construa o eixo maior da Elipse 7) Encontre o ponto G centro da Elipse 8) Determine o ângulo EGB Medida do ângulo EGB:...
13 9) Determine a excentricidade da Elipse 10) O que se pode concluir sobre a excentricidade de uma Elipse? 11) Identifique as simetrias existentes na Elipse: Simétrico em relação à reta x=... Simétrico em relação à reta y =... 12) Utilizando o arquivo com a foto, verifique se a curva existente nela tem o formato de uma Elipse. Caso tenha especifique: Eixo maior:... Eixo menor:... Focos:... Excentricidade:...
14 APÊNDICE F - Objeto de Aprendizagem Estudo da Hipérbole I Objetivos: Construir uma Hipérbole. Identificar seus eixos, focos, sua excentricidade e suas assíntotas. Identificar em uma figura/foto o formato de uma Hipérbole. Identificar na figura/foto propriedades da Hipérbole. II Metodologia: O Objeto de aprendizagem foi desenvolvido para ser feito em grupos de três alunos. Nos itens, o aluno poderá optar por utilizar o comando do GeoGebra que achar conveniente, desde que o leve à construção da Hipérbole e ao reconhecimento da curva no arquivo contendo a figura/foto. III Atividade: 1) Acesse o programa GeoGebra 2) Escolha três pontos. A= (...,...) B= (...,...) C= (...,...) 3) Construa a Hipérbole, conhecendo os pontos A, B e C. Verifique em Comando o item foco e Identifique os focos da Hipérbole ) Calcule a diferença das distâncias do ponto pertencente à Hipérbole aos seus focos.... 5) Verifique a interseção da reta que passa pelos focos com a Hipérbole. D=(...,...) E= (...,...)
15 6) Determine o comprimento do segmento que une os dois pontos de interseção, chamado eixo real da Hipérbole.... 7) Compare o resultado encontrado com a diferença das distâncias do ponto pertencente à Hipérbole aos seus focos. 8) Repita o item 3 com outro ponto da Hipérbole. 9) Tire suas conclusões e escreva como você identifica uma Hipérbole. 10) Construa a mediatriz do eixo real 11) Determine o ponto de interseção F da mediatriz com o segmento DE, centro da Hipérbole. 12) Construa uma circunferência com centro em F e raio FB 13) Construa, utilizando Comando, na parte inferior da tela, as Assíntotas da Hipérbole. 14) Encontre a interseção das Assintótas com a circunferência. (...,...) (...,...) (...,...) (...,...) 15) Construa o retângulo cujas extremidades são os pontos de interseção das assíntotas com a circunferência. 16) A interseção dos lados do retângulo, paralelos ao eixo real, com a mediatriz forma um segmento que é chamado eixo imaginário da Hipérbole. 17) Determine o comprimento desse eixo imaginário ) Calcule a razão entre a metade da distância entre os focos e a metade do eixo real. O resultado encontrado é o valor da excentricidade da Hipérbole. Excentricidade =... 19) Identifique a relação existente entre a excentricidade, a assíntota e o eixo real da Hipérbole?
16 20) O que se pode concluir sobre a excentricidade de uma Hipérbole? 21) Utilizando o comando Mover no primeiro quadro na parte superior da tela, clique em ponto da Hipérbole, faça movimentos com ele e tire suas conclusões sobre a excentricidade da Hipérbole. 22) Utilizando o arquivo com a foto, verifique se a curva existente nela tem o formato de uma Hipérbole. Justifique sua resposta:
17 I Objetivos: APÊNDICE G - Objeto de Aprendizagem Estudo da Parábola Construir uma parábola utilizando os comandos do software GeoGebra. Identificar seu eixo, foco e reta diretriz. Verificar sua excentricidade. Identificar em uma figura/foto o formato de uma parábola. Identificar propriedades da parábola. II Metodologia: O Objeto de aprendizagem foi desenvolvido para ser feito em grupos de três alunos. A atividade prevista em cada item do objeto poderá ser feita utilizando os comandos que o grupo achar conveniente. III Atividade: 1) Construa uma reta que passa por A=(-2,0) e O=(0,0). 2) Construa uma perpendicular AO, no ponto A=(-2,0). 3) Marque o ponto B=(2,0). 4) Verifique em Comando o item parábola e construa uma parábola, com foco no ponto B e a reta perpendicular ao eixo x, AO, como reta diretriz. 5) Marque um ponto na parábola e verifique a distância desse ponto à reta diretriz e a distância dele ao foco. 6) Repita o processo com mais pontos. 7) Qual foi a conclusão a que você chegou sobre o conceito de uma parábola?
18 8) Determine a razão entre a distância do ponto pertencente à parábola até a reta e a distância desse ponto ao foco.... (Excentricidade da Parábola) 9) Existe alguma simetria na parábola construída?... Em relação a quem? ) Utilizando o arquivo com a foto, verifique se a curva existente nela tem o formato de uma parábola. Justifique sua resposta:
CENTRO UNIVERSITÁRIO DA SERRA DOS ÓRGÃOS. Curso de Matemática
 Introdução ao GeoGebra software livre 0 CENTRO UNIVERSITÁRIO DA SERRA DOS ÓRGÃOS Curso de Matemática Primeiros Passos Com o Software Livre GeoGebra Março de 2010 Prof. Ilydio Pereira de Sá Introdução ao
Introdução ao GeoGebra software livre 0 CENTRO UNIVERSITÁRIO DA SERRA DOS ÓRGÃOS Curso de Matemática Primeiros Passos Com o Software Livre GeoGebra Março de 2010 Prof. Ilydio Pereira de Sá Introdução ao
UNIVERSIDADE ESTADUAL DE SANTA CRUZ - UESC DEPARTAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET GEOMETRIA ANALÍTICA ASSUNTO: CÔNICAS
 UNIVERSIDADE ESTADUAL DE SANTA CRUZ - UESC DEPARTAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET GEOMETRIA ANALÍTICA ASSUNTO: CÔNICAS. Usando a definição de parábola determinar, em cada um dos itens a
UNIVERSIDADE ESTADUAL DE SANTA CRUZ - UESC DEPARTAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET GEOMETRIA ANALÍTICA ASSUNTO: CÔNICAS. Usando a definição de parábola determinar, em cada um dos itens a
Software Régua e Compasso
 1 COORDENAÇÃO DE PESQUISA E PÓS-GRADUAÇÃO CPPG TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO- APRENDIZAGEM DE MATEMÁTICA 1ª Parte - Consulta Rápida Software Régua e Compasso A primeira
1 COORDENAÇÃO DE PESQUISA E PÓS-GRADUAÇÃO CPPG TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO- APRENDIZAGEM DE MATEMÁTICA 1ª Parte - Consulta Rápida Software Régua e Compasso A primeira
Universidade Estadual do Sudoeste da Bahia - UESB
 Universidade Estadual do Sudoeste da Bahia - UESB I Semana de Educação Matemática: Discutindo o trabalho docente aliado às novas tendências educacionais 25 a 29 de maio de 2009 Minicurso: GEOGEBRA UM FORTE
Universidade Estadual do Sudoeste da Bahia - UESB I Semana de Educação Matemática: Discutindo o trabalho docente aliado às novas tendências educacionais 25 a 29 de maio de 2009 Minicurso: GEOGEBRA UM FORTE
PROJETO SALA DE AULA
 PROJETO SALA DE AULA 1. Identificação: Título: APRENDENDO FUNÇÕES BRINCANDO Série: 1º série do Ensino Fundamental Softwares Necessários: Cabri-Géomètre, Jogos de Funções e Graphmatica Tempo previsto: Seis
PROJETO SALA DE AULA 1. Identificação: Título: APRENDENDO FUNÇÕES BRINCANDO Série: 1º série do Ensino Fundamental Softwares Necessários: Cabri-Géomètre, Jogos de Funções e Graphmatica Tempo previsto: Seis
ELIPSES INSCRITAS NUM TRIÂNGULO
 ELIPSES INSCRITAS NUM TRIÂNGULO SERGIO ALVES IME-USP Freqüentemente apresentada como um exemplo notável de sistema dedutivo, a Geometria tem, em geral, seus aspectos indutivos relegados a um segundo plano.
ELIPSES INSCRITAS NUM TRIÂNGULO SERGIO ALVES IME-USP Freqüentemente apresentada como um exemplo notável de sistema dedutivo, a Geometria tem, em geral, seus aspectos indutivos relegados a um segundo plano.
5 LG 1 - CIRCUNFERÊNCIA
 40 5 LG 1 - CIRCUNFERÊNCIA Propriedade: O lugar geométrico dos pontos do plano situados a uma distância constante r de um ponto fixo O é a circunferência de centro O e raio r. Notação: Circunf(O,r). Sempre
40 5 LG 1 - CIRCUNFERÊNCIA Propriedade: O lugar geométrico dos pontos do plano situados a uma distância constante r de um ponto fixo O é a circunferência de centro O e raio r. Notação: Circunf(O,r). Sempre
As cônicas. c, a 2 elipse é uma curva do plano em que qualquer um de seus pontos, por exemplo,, satisfaz a relação:
 As cônicas As cônicas podem ser definidas a partir de certas relações que caracterizam seus pontos. A partir delas podemos obter suas equações analíticas e, a partir delas, suas propriedades.. A elipse
As cônicas As cônicas podem ser definidas a partir de certas relações que caracterizam seus pontos. A partir delas podemos obter suas equações analíticas e, a partir delas, suas propriedades.. A elipse
Resumo. Maria Bernadete Barison apresenta aulas práticas sobre RETAS em Desenho Geométrico. Geométrica vol.1 n.1d. 2006 RETAS CAD
 1 1. INTRODUÇÃO. RETAS CAD Iniciaremos o estudo das retas construindo no CAD alguns exercícios já construídos na aula teórica utilizando a régua e o compasso. Entretanto, o nosso compasso aqui será o comando
1 1. INTRODUÇÃO. RETAS CAD Iniciaremos o estudo das retas construindo no CAD alguns exercícios já construídos na aula teórica utilizando a régua e o compasso. Entretanto, o nosso compasso aqui será o comando
As assíntotas são retas que passam no centro da hipérbole e tem coeficiente angular m = b / a e m = b / a, logo temos:
 Exercício 01. Dada à hipérbole de equação 5x 2 4y 2 20x 8y 4 = 0 determine os focos e as equações das assintotas. Escrevendo a hipérbole da maneira convencional teríamos 5[x 2 4x + 4 4] 4[y 2 + 2y + 1]
Exercício 01. Dada à hipérbole de equação 5x 2 4y 2 20x 8y 4 = 0 determine os focos e as equações das assintotas. Escrevendo a hipérbole da maneira convencional teríamos 5[x 2 4x + 4 4] 4[y 2 + 2y + 1]
Applets no Geogebra. Acesse os endereços dados a seguir e conheça exemplos de Applets. http://206.110.20.132/~dhabecker/geogebrahtml/index.
 Applets no Geogebra Sonia Regina Soares Ferreira UFBA Applet é um software aplicativo que é executado no contexto de outro programa. Os applets geralmente tem algum tipo de interface de usuário, ou fazem
Applets no Geogebra Sonia Regina Soares Ferreira UFBA Applet é um software aplicativo que é executado no contexto de outro programa. Os applets geralmente tem algum tipo de interface de usuário, ou fazem
Medida da velocidade de embarcações com o Google Earth
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Física Programa de Pós-Graduação em Ensino de Física Mestrado Profissional em Ensino de Física Medida da velocidade de embarcações com o Google Earth
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Física Programa de Pós-Graduação em Ensino de Física Mestrado Profissional em Ensino de Física Medida da velocidade de embarcações com o Google Earth
PASSO A PASSO MOVIE MAKER
 PASSO A PASSO MOVIE MAKER Nesta etapa, você deverá apresentar o programa e ajudá-los a montarem o filme. Veja como é fácil. Siga as instruções do passo-a-passo: DICA O que é o Movie Maker? Com o Microsoft
PASSO A PASSO MOVIE MAKER Nesta etapa, você deverá apresentar o programa e ajudá-los a montarem o filme. Veja como é fácil. Siga as instruções do passo-a-passo: DICA O que é o Movie Maker? Com o Microsoft
GAAL - 2013/1 - Simulado - 1 Vetores e Produto Escalar
 GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
5o Encontro da RPM 3 a 4 de junho de 2011 Salvador - BA Minicurso. Computador na sala de aula: atividades com Geometria Dinâmica
 1 5o Encontro da RPM 3 a 4 de junho de 2011 Salvador - BA Minicurso Computador na sala de aula: atividades com Geometria Dinâmica Cristina Cerri IME USP Cada vez mais estamos incorporando o computador
1 5o Encontro da RPM 3 a 4 de junho de 2011 Salvador - BA Minicurso Computador na sala de aula: atividades com Geometria Dinâmica Cristina Cerri IME USP Cada vez mais estamos incorporando o computador
1. Desativar o Firewall do computador. Clique em Iniciar Clique em Painel de Controle, como mostra a figura a seguir.
 1. Desativar o Firewall do computador Clique em Iniciar Clique em Painel de Controle, como mostra a figura a seguir. Clique em Sistema e Segurança. Clique em Firewall do Windows. Clique em Ativar ou Desativar
1. Desativar o Firewall do computador Clique em Iniciar Clique em Painel de Controle, como mostra a figura a seguir. Clique em Sistema e Segurança. Clique em Firewall do Windows. Clique em Ativar ou Desativar
RELATÓRIO. Geogebra- Uma visita aos programas de Matemática dos 2º e 3º ciclos. Formanda: Célia Rute Silva C. Sousa Formador: Luís Roçadas
 RELATÓRIO Geogebra- Uma visita aos programas de Matemática dos 2º e 3º ciclos Formanda: Célia Rute Silva C. Sousa Formador: Luís Roçadas Índice Enquadramento da actividade ------------------------------------3
RELATÓRIO Geogebra- Uma visita aos programas de Matemática dos 2º e 3º ciclos Formanda: Célia Rute Silva C. Sousa Formador: Luís Roçadas Índice Enquadramento da actividade ------------------------------------3
GUSTAVO HENRIQUE NOGUEIRA REZENDE PAIVA. Manual de atividades no Geogebra para a Educação Básica.
 GUSTAVO HENRIQUE NOGUEIRA REZENDE PAIVA Manual de atividades no Geogebra para a Educação Básica. Taguatinga, DF 2012 Novas tecnologias estão chegando às salas de aula e levando a muitas mudanças na relação
GUSTAVO HENRIQUE NOGUEIRA REZENDE PAIVA Manual de atividades no Geogebra para a Educação Básica. Taguatinga, DF 2012 Novas tecnologias estão chegando às salas de aula e levando a muitas mudanças na relação
Associação Educacional Dom Bosco Curso de Engenharia 1º ano
 Formatação condicional utilizando o valor da célula O que é? Algumas vezes é preciso destacar os valores, ou seja, como colocar em vermelho ou entre parênteses, os negativos, e de outra cor os positivos,
Formatação condicional utilizando o valor da célula O que é? Algumas vezes é preciso destacar os valores, ou seja, como colocar em vermelho ou entre parênteses, os negativos, e de outra cor os positivos,
Introdução ao GeoGebra
 Universidade Federal de Alfenas UNIFAL-MG Introdução ao GeoGebra Prof. Dr. José Carlos de Souza Junior AGOSTO 2010 Sumário 1 Primeiros Passos com o GeoGebra 4 1.1 Conhecendo o Programa............................
Universidade Federal de Alfenas UNIFAL-MG Introdução ao GeoGebra Prof. Dr. José Carlos de Souza Junior AGOSTO 2010 Sumário 1 Primeiros Passos com o GeoGebra 4 1.1 Conhecendo o Programa............................
O SOFTWARE EUCLIDEAN REALITY AUXILIANDO NA CONSTRUÇÃO DO TEOREMA DE PITÁGORAS
 O SOFTWARE EUCLIDEAN REALITY AUXILIANDO NA CONSTRUÇÃO DO TEOREMA DE PITÁGORAS Vânia de Moura Barbosa Secretaria de Educação do Estado de Pernambuco vanibosa@terra.com.br Introdução Um dos primeiros questionamentos
O SOFTWARE EUCLIDEAN REALITY AUXILIANDO NA CONSTRUÇÃO DO TEOREMA DE PITÁGORAS Vânia de Moura Barbosa Secretaria de Educação do Estado de Pernambuco vanibosa@terra.com.br Introdução Um dos primeiros questionamentos
Proposta para Abordagem da Trigonometria da Primeira Volta Utilizando o Software Sintesoft Trigonometria 2.0
 Programa de Pós-Graduação em Ensino de Ciências Exatas, Curso de Licenciatura em Ciências Exatas, com habilitação integrada em Física, Química e Matemática Atividades desenvolvidas na pesquisa Inserção
Programa de Pós-Graduação em Ensino de Ciências Exatas, Curso de Licenciatura em Ciências Exatas, com habilitação integrada em Física, Química e Matemática Atividades desenvolvidas na pesquisa Inserção
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO PUC/SP
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO PUC/SP Péricles Bedretchuk Araújo Situações de aprendizagem: a circunferência, a mediatriz e uma abordagem com o Geogebra Dissertação apresentada à Banca Examinadora
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO PUC/SP Péricles Bedretchuk Araújo Situações de aprendizagem: a circunferência, a mediatriz e uma abordagem com o Geogebra Dissertação apresentada à Banca Examinadora
Manual Sistema MLBC. Manual do Sistema do Módulo Administrativo
 Manual Sistema MLBC Manual do Sistema do Módulo Administrativo Este documento tem por objetivo descrever as principais funcionalidades do sistema administrador desenvolvido pela MLBC Comunicação Digital.
Manual Sistema MLBC Manual do Sistema do Módulo Administrativo Este documento tem por objetivo descrever as principais funcionalidades do sistema administrador desenvolvido pela MLBC Comunicação Digital.
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior
 Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 05 - Desvendando o GeoGebra PARTE 04 - COMO APAGAR OBJETOS. Ao iniciar o GeoGebra,
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 05 - Desvendando o GeoGebra PARTE 04 - COMO APAGAR OBJETOS. Ao iniciar o GeoGebra,
Barra de ferramentas padrão. Barra de formatação. Barra de desenho Painel de Tarefas
 Microsoft Power Point 2003 No Microsoft PowerPoint 2003, você cria sua apresentação usando apenas um arquivo, ele contém tudo o que você precisa uma estrutura para sua apresentação, os slides, o material
Microsoft Power Point 2003 No Microsoft PowerPoint 2003, você cria sua apresentação usando apenas um arquivo, ele contém tudo o que você precisa uma estrutura para sua apresentação, os slides, o material
Instalação - SGFLeite 1
 Instalação SGFLeite Sistema Gerenciador de Fazenda de Leite Instalação - SGFLeite 1 Resumo dos Passos para instalação do Sistema Este documento tem como objetivo auxiliar o usuário na instalação do Sistema
Instalação SGFLeite Sistema Gerenciador de Fazenda de Leite Instalação - SGFLeite 1 Resumo dos Passos para instalação do Sistema Este documento tem como objetivo auxiliar o usuário na instalação do Sistema
Aula 03 PowerPoint 2007
 Aula 03 PowerPoint 2007 Professor: Bruno Gomes Disciplina: Informática Básica Curso: Gestão de Turismo Sumário da aula: 1. Abrindo o PowerPoint; 2. Conhecendo a Tela do PowerPoint; 3. Criando uma Nova
Aula 03 PowerPoint 2007 Professor: Bruno Gomes Disciplina: Informática Básica Curso: Gestão de Turismo Sumário da aula: 1. Abrindo o PowerPoint; 2. Conhecendo a Tela do PowerPoint; 3. Criando uma Nova
Tutorial Gerar arquivo PDF. Gerando um documento pdf com várias imagens 1- Inserir imagem no Word
 Tutorial Gerar arquivo PDF. Com o objetivo de simplificar e diminuir o tamanho de arquivos anexos nos projetos, elaboramos um pequeno tutorial mostrando como gerar um único arquivo no formato pdf contendo
Tutorial Gerar arquivo PDF. Com o objetivo de simplificar e diminuir o tamanho de arquivos anexos nos projetos, elaboramos um pequeno tutorial mostrando como gerar um único arquivo no formato pdf contendo
Procedimento de Atualização - ONECLICK
 Procedimento de Atualização - ONECLICK Para começarmos a atualizar o equipamento, precisamos primeiramente realizar o download do programa necessário em sua sala de downloads. Para isso, realize o procedimento
Procedimento de Atualização - ONECLICK Para começarmos a atualizar o equipamento, precisamos primeiramente realizar o download do programa necessário em sua sala de downloads. Para isso, realize o procedimento
MANUAL DE INSTALAÇÃO DO ODONTO TECHNOLOGY
 MANUAL DE INSTALAÇÃO DO ODONTO TECHNOLOGY 1 Índice I - Prefácio...3 II - Instalação do tipo servidor...4 III Obter o nome do computador servidor...17 IV Instalação do tipo cliente...19 V Como inserir a
MANUAL DE INSTALAÇÃO DO ODONTO TECHNOLOGY 1 Índice I - Prefácio...3 II - Instalação do tipo servidor...4 III Obter o nome do computador servidor...17 IV Instalação do tipo cliente...19 V Como inserir a
MOSAICOS. RECURSO DIDÁTICO Software Geogebra (http://www.geogebra.org/cms/) 1ª TAREFA: Construção de um quadrado.
 MOSAICOS Este experimento prático visa auxiliar ao estudante desenvolver a noção de espaço, localização espacial e direção. Trabalha com as noções de translação por um vetor. O que auxilia o aluno a se
MOSAICOS Este experimento prático visa auxiliar ao estudante desenvolver a noção de espaço, localização espacial e direção. Trabalha com as noções de translação por um vetor. O que auxilia o aluno a se
Soluções com softwares geométricos de problemas apresentados por Gabriel Lamé no início do século 19
 Soluções com softwares geométricos de problemas apresentados por Gabriel Lamé no início do século 19 Eduardo Sebastiani Ferreira- esebastiani@uol.com.br Maria Zoraide M C Soares- mzsoares@uol.com.br Miriam
Soluções com softwares geométricos de problemas apresentados por Gabriel Lamé no início do século 19 Eduardo Sebastiani Ferreira- esebastiani@uol.com.br Maria Zoraide M C Soares- mzsoares@uol.com.br Miriam
Apresentando o Sistema GeoOffice GPS Profissional
 Apresentando o Sistema GeoOffice GPS Profissional O Sistema GeoOfficeGPS é uma ferramenta de automação desenvolvida pela Solution Softwares LTDA-ME para auxiliar no armazenamento e manipulação de dados
Apresentando o Sistema GeoOffice GPS Profissional O Sistema GeoOfficeGPS é uma ferramenta de automação desenvolvida pela Solution Softwares LTDA-ME para auxiliar no armazenamento e manipulação de dados
Construções Elementares com Régua e Compasso
 TERCEIRLISTDEEXERCÍCIOS Fundamentos da Matemática II MTEMÁTIC DCET UESC Humberto José ortolossi Construções Elementares com Régua e Compasso (Entregar todos os exercícios até o dia 20/04/2004) 1 Construindo
TERCEIRLISTDEEXERCÍCIOS Fundamentos da Matemática II MTEMÁTIC DCET UESC Humberto José ortolossi Construções Elementares com Régua e Compasso (Entregar todos os exercícios até o dia 20/04/2004) 1 Construindo
Você sabia que o computador pode ser uma rica ferramenta no. processo de inclusão escolar e social de crianças com necessidades
 Você sabia que o computador pode ser uma rica ferramenta no processo de inclusão escolar e social de crianças com necessidades educacionais especiais? Juliana Moraes Almeida Silva Em várias situações do
Você sabia que o computador pode ser uma rica ferramenta no processo de inclusão escolar e social de crianças com necessidades educacionais especiais? Juliana Moraes Almeida Silva Em várias situações do
UTILIZAÇÃO DE TECNOLOGIAS PARA O ENSINO DE MATEMÁTICA
 ISSN 2177-9139 UTILIZAÇÃO DE TECNOLOGIAS PARA O ENSINO DE MATEMÁTICA Natanna Silva Dutra natannabg@hotmail.com Fundação Universidade Federal do Pampa, Campus Bagé, 96413-170 Bagé, RS, Brasil Nathália Cabral
ISSN 2177-9139 UTILIZAÇÃO DE TECNOLOGIAS PARA O ENSINO DE MATEMÁTICA Natanna Silva Dutra natannabg@hotmail.com Fundação Universidade Federal do Pampa, Campus Bagé, 96413-170 Bagé, RS, Brasil Nathália Cabral
MATERIAL DIDÁTICO DE TRÂNSITO Aulas em Slide
 MANUAL MATERIAL DIDÁTICO DE TRÂNSITO Aulas em Slide 1 Sumário 1. Licença de Uso... 3 2. Pré-Requisitos... 3 3. Abrir o Material (Com Microsoft Office PowerPoint 2010)... 3 4. Instalação Power Point Viewer...
MANUAL MATERIAL DIDÁTICO DE TRÂNSITO Aulas em Slide 1 Sumário 1. Licença de Uso... 3 2. Pré-Requisitos... 3 3. Abrir o Material (Com Microsoft Office PowerPoint 2010)... 3 4. Instalação Power Point Viewer...
Como Gerar documento em PDF com várias Imagens
 Como Gerar documento em PDF com várias Imagens Para Gerar documento em PDF com várias Imagens, temos que seguir dois passos: 1. Inserir Imagens no Word 2. Gerar PDF a partir de documento do Word 1- Inserir
Como Gerar documento em PDF com várias Imagens Para Gerar documento em PDF com várias Imagens, temos que seguir dois passos: 1. Inserir Imagens no Word 2. Gerar PDF a partir de documento do Word 1- Inserir
O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem.
 TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
TUTORIAL TRACKER PIBID Walfredo v1-2.docx
 TUTORIAL TRACKER O Tracker é um software gratuito que nos auxilia a analisar conceitos da Física através do vídeo. Esse programa confecciona rapidamente gráficos a partir de dados obtidos nos vídeos e
TUTORIAL TRACKER O Tracker é um software gratuito que nos auxilia a analisar conceitos da Física através do vídeo. Esse programa confecciona rapidamente gráficos a partir de dados obtidos nos vídeos e
TUTORIAL. Dúvidas? Entre em contato com edunp@unp.br
 TUTORIAL MENU (clique sobre uma das opções) 1. CADASTRO DE LEITORES/AUTORES/AVALIADORES 2. SUBMISSÃO DE TEXTO 3. REENVIO DE TEXTO NA AVALIAÇÃO 4. REENVIO DE TEXTO NA EDIÇÃO Dúvidas? Entre em contato com
TUTORIAL MENU (clique sobre uma das opções) 1. CADASTRO DE LEITORES/AUTORES/AVALIADORES 2. SUBMISSÃO DE TEXTO 3. REENVIO DE TEXTO NA AVALIAÇÃO 4. REENVIO DE TEXTO NA EDIÇÃO Dúvidas? Entre em contato com
UNIVERSIDADE SEVERINO SOMBRA PROGRAMA DE PÓS-GRADUAÇÃO STRICTO SENSU MESTRADO PROFISSIONAL EM EDUCAÇÃO MATEMÁTICA
 UNIVERSIDADE SEVERINO SOMBRA PROGRAMA DE PÓS-GRADUAÇÃO STRICTO SENSU MESTRADO PROFISSIONAL EM EDUCAÇÃO MATEMÁTICA UNIDADE DE ENSINO POTENCIALMENTE SIGNIFICATIVA PARA SUBSIDIAR O ESTUDO DE GEOMETRIA ANALÍTICA
UNIVERSIDADE SEVERINO SOMBRA PROGRAMA DE PÓS-GRADUAÇÃO STRICTO SENSU MESTRADO PROFISSIONAL EM EDUCAÇÃO MATEMÁTICA UNIDADE DE ENSINO POTENCIALMENTE SIGNIFICATIVA PARA SUBSIDIAR O ESTUDO DE GEOMETRIA ANALÍTICA
Guia para Escolha de Fotos no PSG Request
 Gui apar aescol hadefot os com opsg Request Manualdousuár i ofi nal DLL System Guia para Escolha de Fotos no PSG Request Como escolher as fotos do CD ou DVD que você recebeu de seu Fotógrafo Suporte Técnico
Gui apar aescol hadefot os com opsg Request Manualdousuár i ofi nal DLL System Guia para Escolha de Fotos no PSG Request Como escolher as fotos do CD ou DVD que você recebeu de seu Fotógrafo Suporte Técnico
Lista de exercícios de recuperação. 3º E.M. - Matemática
 Lista de exercícios de recuperação 3º E.M. - Matemática 1) As equações das retas r e s da figura são, respectivamente, a) r: -x + y - 5 = 0 e s: x + y - 5 = 0. b) r: -5x + y - 5 = 0 e s: 5x + y - 5 = 0.
Lista de exercícios de recuperação 3º E.M. - Matemática 1) As equações das retas r e s da figura são, respectivamente, a) r: -x + y - 5 = 0 e s: x + y - 5 = 0. b) r: -5x + y - 5 = 0 e s: 5x + y - 5 = 0.
Como instalar uma impressora?
 Como instalar uma impressora? Antes de utilizar uma impressora para imprimir seus documentos, arquivos, fotos, etc. é necessário instalá-la e configurá-la no computador. Na instalação o computador se prepara
Como instalar uma impressora? Antes de utilizar uma impressora para imprimir seus documentos, arquivos, fotos, etc. é necessário instalá-la e configurá-la no computador. Na instalação o computador se prepara
Tutorial - Vetorizando uma fotografia
 Tutorial - Vetorizando uma fotografia Thiago Santos 02-2013 Vetorizando uma fotografia Meu nome é Thiago Santos e vou mostrar a vocês como vetorizar uma fotografia. O processo não é muito complicado, mas
Tutorial - Vetorizando uma fotografia Thiago Santos 02-2013 Vetorizando uma fotografia Meu nome é Thiago Santos e vou mostrar a vocês como vetorizar uma fotografia. O processo não é muito complicado, mas
Polycom RealPresence Content Sharing Suite Guia rápido do usuário
 Polycom RealPresence Content Sharing Suite Guia rápido do usuário Versão 1.2 3725-69877-001 Rev.A Novembro de 2013 Neste guia, você aprenderá a compartilhar e visualizar conteúdos durante uma conferência
Polycom RealPresence Content Sharing Suite Guia rápido do usuário Versão 1.2 3725-69877-001 Rev.A Novembro de 2013 Neste guia, você aprenderá a compartilhar e visualizar conteúdos durante uma conferência
CURSO DE INFORMÁTICA BÁSICA AULA 2 O AMBIENTE WINDOWS
 CURSO DE INFORMÁTICA BÁSICA AULA 2 O AMBIENTE WINDOWS Relembrando... Gabinete Ligando o computador São três passos básicos O ambiente Windows O Windows é um tipo de software chamado sistema operacional
CURSO DE INFORMÁTICA BÁSICA AULA 2 O AMBIENTE WINDOWS Relembrando... Gabinete Ligando o computador São três passos básicos O ambiente Windows O Windows é um tipo de software chamado sistema operacional
Objetivos. Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas e
 MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
Tutorial de desenvolvimento: Mario
 Tutorial de desenvolvimento: Mario Universidade Federal do Rio Grande do Sul Departamento de Design e Expressão Gráfica Cursos de Design Design Visual Computação Gráfica I Docente: Sérgio Leandro dos Santos
Tutorial de desenvolvimento: Mario Universidade Federal do Rio Grande do Sul Departamento de Design e Expressão Gráfica Cursos de Design Design Visual Computação Gráfica I Docente: Sérgio Leandro dos Santos
Excel Planilhas Eletrônicas
 Excel Planilhas Eletrônicas Capitulo 1 O Excel é um programa de cálculos muito utilizado em empresas para controle administrativo, será utilizado também por pessoas que gostam de organizar suas contas
Excel Planilhas Eletrônicas Capitulo 1 O Excel é um programa de cálculos muito utilizado em empresas para controle administrativo, será utilizado também por pessoas que gostam de organizar suas contas
Fluxo de trabalho do Capture Pro Software: Indexação de OCR e separação de documentos de código de correção
 Este procedimento corresponde ao fluxo de trabalho de Indexação de OCR com separação de código de correção no programa de treinamento do Capture Pro Software. As etapas do procedimento encontram-se na
Este procedimento corresponde ao fluxo de trabalho de Indexação de OCR com separação de código de correção no programa de treinamento do Capture Pro Software. As etapas do procedimento encontram-se na
Utilizando a ferramenta de criação de aulas
 http://portaldoprofessor.mec.gov.br/ 04 Roteiro Utilizando a ferramenta de criação de aulas Ministério da Educação Utilizando a ferramenta de criação de aulas Para criar uma sugestão de aula é necessário
http://portaldoprofessor.mec.gov.br/ 04 Roteiro Utilizando a ferramenta de criação de aulas Ministério da Educação Utilizando a ferramenta de criação de aulas Para criar uma sugestão de aula é necessário
Bem-vindo ao CorelDRAW, um programa abrangente de desenho e design gráfico baseado em vetor para o profissional gráfico.
 Criar um logotipo Bem-vindo ao CorelDRAW, um programa abrangente de desenho e design gráfico baseado em vetor para o profissional gráfico. Neste tutorial, você criará um logotipo para uma cafeteria imaginária.
Criar um logotipo Bem-vindo ao CorelDRAW, um programa abrangente de desenho e design gráfico baseado em vetor para o profissional gráfico. Neste tutorial, você criará um logotipo para uma cafeteria imaginária.
Eberhardt Comércio e Assist. Técnica. Ltda.
 Rua das Cerejeiras, 80 Ressacada CEP 88307-330 Itajaí SC Fone/Fax: (47) 3349 6850 Email: vendas@ecr-sc.com.br Guia de emissão de relatórios para envio ao DNPM ou arquivo e uso do software do sistema de
Rua das Cerejeiras, 80 Ressacada CEP 88307-330 Itajaí SC Fone/Fax: (47) 3349 6850 Email: vendas@ecr-sc.com.br Guia de emissão de relatórios para envio ao DNPM ou arquivo e uso do software do sistema de
Informática no Ensino da Matemática
 Informática no Ensino da Matemática Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ Lista de Exercícios 2 ATIVIDADE 1 Para poupar esforço de digitação, você pode usar o tradicional sistema
Informática no Ensino da Matemática Humberto José Bortolossi http://www.professores.uff.br/hjbortol/ Lista de Exercícios 2 ATIVIDADE 1 Para poupar esforço de digitação, você pode usar o tradicional sistema
Oficina Ensinando Geometria com Auxílio do Software GEOGEBRA. Professor Responsável: Ivan José Coser Tutora: Rafaela Seabra Cardoso Leal
 Universidade Tecnológica Federal do Paraná Câmpus Apucarana Projeto Novos Talentos Edital CAPES 55/12 Oficina Ensinando Geometria com Auxílio do Software GEOGEBRA Professor Responsável: Ivan José Coser
Universidade Tecnológica Federal do Paraná Câmpus Apucarana Projeto Novos Talentos Edital CAPES 55/12 Oficina Ensinando Geometria com Auxílio do Software GEOGEBRA Professor Responsável: Ivan José Coser
Tutorial de ilustração animada
 Tutorial ilustração animada Esse tutorial tem a finalida mostrar alguns recursos básicos e itens técnicos para os que estão tendo contato pela primeira vez com essa ferramenta. Uma vez se familiarizando,
Tutorial ilustração animada Esse tutorial tem a finalida mostrar alguns recursos básicos e itens técnicos para os que estão tendo contato pela primeira vez com essa ferramenta. Uma vez se familiarizando,
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA 5 0 Encontro da RPM TRANSFORMAÇÕES NO PLANO Jorge Costa do Nascimento Introdução Na produção desse texto utilizamos como fonte de pesquisa material
Matemática. Subtraindo a primeira equação da terceira obtemos x = 1. Substituindo x = 1 na primeira e na segunda equação obtém-se o sistema
 Matemática 01. A ilustração a seguir é de um cubo com aresta medindo 6 cm. A, B, C e D são os vértices indicados do cubo, E é o centro da face contendo C e D, e F é o pé da perpendicular a BD traçada a
Matemática 01. A ilustração a seguir é de um cubo com aresta medindo 6 cm. A, B, C e D são os vértices indicados do cubo, E é o centro da face contendo C e D, e F é o pé da perpendicular a BD traçada a
ATENÇÃO: * Arquivos com tamanho superior a 500 KB NÃO SERÃO ACEITOS * SOMENTE serão aceitos documentos do formato: PDF
 TUTORIAL DE DIGITALIZAÇÃO DIRIGIDO AO USO DO PROCESSO ELETRÔNICO Adaptado do tutorial elaborado pelo colega MAICON FALCÃO, operador de computador da subseção judiciária de Rio Grande. Introdução Este tutorial
TUTORIAL DE DIGITALIZAÇÃO DIRIGIDO AO USO DO PROCESSO ELETRÔNICO Adaptado do tutorial elaborado pelo colega MAICON FALCÃO, operador de computador da subseção judiciária de Rio Grande. Introdução Este tutorial
MICROSOFT OFFICE EXCEL 2007
 LEIAME Nenhuma informação da APOSTILA - MICROSOFT OFFICE EXCEL 2007 poderá ser copiada, movida ou modificada sem autorização prévia e escrita do autor. MICROSOFT OFFICE EXCEL 2007 Efetue cálculos, analise
LEIAME Nenhuma informação da APOSTILA - MICROSOFT OFFICE EXCEL 2007 poderá ser copiada, movida ou modificada sem autorização prévia e escrita do autor. MICROSOFT OFFICE EXCEL 2007 Efetue cálculos, analise
Apostila para uso do Power Point
 Apostila para uso do Power Point Introdução O Power Point, é um aplicativo da MicroSoft desenvolvido para a elaboração de apresentações. Possui recursos de hipertexto e multimídia como som, imagem, animação,
Apostila para uso do Power Point Introdução O Power Point, é um aplicativo da MicroSoft desenvolvido para a elaboração de apresentações. Possui recursos de hipertexto e multimídia como som, imagem, animação,
- Computador Servidor: É o computador que armazenará o banco de dados do programa. Não necessariamente precisa rodar o Hábil Enterprise.
 Hábil Enterprise Copyright 2009 2010 Koinonia Software Ltda. Fone: 0**46 3225-6234 Suporte: http://www.habilenterprise.com.br/suporte As orientações abaixo devem ser utilizadas para fazer a instalação
Hábil Enterprise Copyright 2009 2010 Koinonia Software Ltda. Fone: 0**46 3225-6234 Suporte: http://www.habilenterprise.com.br/suporte As orientações abaixo devem ser utilizadas para fazer a instalação
Poder Judiciário Tribunal Regional Federal da Terceira Região
 Poder Judiciário Tribunal Regional Federal da Terceira Região DIMI - Divisão de Microinformática e Redes Índice: O que é a Internet? 3 O que são Intranets? 3 Sobre o Nestcape Navigator 3 Para iniciar o
Poder Judiciário Tribunal Regional Federal da Terceira Região DIMI - Divisão de Microinformática e Redes Índice: O que é a Internet? 3 O que são Intranets? 3 Sobre o Nestcape Navigator 3 Para iniciar o
MANUAL DE UTILIZAÇÃO DO ESPAÇO VIRTUAL DE APRENDIZAGEM EVA
 MANUAL DE UTILIZAÇÃO DO ESPAÇO VIRTUAL DE APRENDIZAGEM EVA Sejam bem-vindos ao Núcleo de Educação a Distância da FFCL! Esse Manual tem por objetivo auxilia-los na forma de utilização do AVA. COMO FAÇO
MANUAL DE UTILIZAÇÃO DO ESPAÇO VIRTUAL DE APRENDIZAGEM EVA Sejam bem-vindos ao Núcleo de Educação a Distância da FFCL! Esse Manual tem por objetivo auxilia-los na forma de utilização do AVA. COMO FAÇO
Sistema de Recursos Humanos
 Sistema de Recursos Humanos Projeto 1 O objetivo desse sistema é gerenciar a admissão e a demissão de funcionários. Esse funcionário pode ou não ter dependentes. Esse funcionário está alocado em um departamento
Sistema de Recursos Humanos Projeto 1 O objetivo desse sistema é gerenciar a admissão e a demissão de funcionários. Esse funcionário pode ou não ter dependentes. Esse funcionário está alocado em um departamento
Construções Fundamentais. r P r
 1 Construções Fundamentais 1. De um ponto traçar a reta paralela à reta dada. + r 2. De um ponto traçar a perpendicular à reta r, sabendo que o ponto é exterior a essa reta; e de um ponto P traçar a perpendicular
1 Construções Fundamentais 1. De um ponto traçar a reta paralela à reta dada. + r 2. De um ponto traçar a perpendicular à reta r, sabendo que o ponto é exterior a essa reta; e de um ponto P traçar a perpendicular
COLÉGIO ESTADUAL PAULO LEMINSKI APOSTILA SOBRE O BROFFICE IMPRESS
 COLÉGIO ESTADUAL PAULO LEMINSKI APOSTILA SOBRE O BROFFICE IMPRESS CURITIBA 2014 2 Conteúdo Definição:... 2 Detalhando a tela:... 4 BARRA DE FERRAMENTAS DESENHO... 4 PREENCHIMENTOS... 5 RÉGUAS E GUIAS...
COLÉGIO ESTADUAL PAULO LEMINSKI APOSTILA SOBRE O BROFFICE IMPRESS CURITIBA 2014 2 Conteúdo Definição:... 2 Detalhando a tela:... 4 BARRA DE FERRAMENTAS DESENHO... 4 PREENCHIMENTOS... 5 RÉGUAS E GUIAS...
1- Tela inicial do AUTOCAD 2013
 1- Tela inicial do AUTOCAD 2013 2- Clique em NOVO 3- Para mudar a cor do fundo digite OP (de options): Se quiser veja o vídeo ilustrativo desse procedimento: http://www.youtube.com/watch?v=g7kig_yhpx4
1- Tela inicial do AUTOCAD 2013 2- Clique em NOVO 3- Para mudar a cor do fundo digite OP (de options): Se quiser veja o vídeo ilustrativo desse procedimento: http://www.youtube.com/watch?v=g7kig_yhpx4
Aula 18 Elipse. Objetivos
 MÓDULO 1 - AULA 18 Aula 18 Elipse Objetivos Descrever a elipse como um lugar geométrico. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio entre os focos e eixo
MÓDULO 1 - AULA 18 Aula 18 Elipse Objetivos Descrever a elipse como um lugar geométrico. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio entre os focos e eixo
Iniciação à Informática
 Meu computador e Windows Explorer Justificativa Toda informação ou dado trabalhado no computador, quando armazenado em uma unidade de disco, transforma-se em um arquivo. Saber manipular os arquivos através
Meu computador e Windows Explorer Justificativa Toda informação ou dado trabalhado no computador, quando armazenado em uma unidade de disco, transforma-se em um arquivo. Saber manipular os arquivos através
SISTEMA DE ABERTURA DE CHAMADOS TÉCNICOS DE INFORMÁTICA GLPI ( GESTÃO LIVRE DE PARQUE DE INFORMÁTICA ) Manual do Usuário
 SISTEMA DE ABERTURA DE CHAMADOS TÉCNICOS DE INFORMÁTICA GLPI ( GESTÃO LIVRE DE PARQUE DE INFORMÁTICA ) Manual do Usuário Setor de Tecnologia da Informação 2012 AUTORES Aurélio Ricardo Batú Maicá Laura
SISTEMA DE ABERTURA DE CHAMADOS TÉCNICOS DE INFORMÁTICA GLPI ( GESTÃO LIVRE DE PARQUE DE INFORMÁTICA ) Manual do Usuário Setor de Tecnologia da Informação 2012 AUTORES Aurélio Ricardo Batú Maicá Laura
APOSTILA DE EXCEL 2007
 APOSTILA DE EXCEL 2007 1. Introdução Quando você cria uma planilha nova, a tela do computador é dividida em linhas e colunas, formando uma grade. A interseção de uma linha e de uma coluna é chamada de
APOSTILA DE EXCEL 2007 1. Introdução Quando você cria uma planilha nova, a tela do computador é dividida em linhas e colunas, formando uma grade. A interseção de uma linha e de uma coluna é chamada de
Apostila de PowerPoint 2013
 Iniciando o Power Point 2013...01 Nova apresentação baseada no modelo...01 Escolhendo o esquema de cores do fundo do slide manualmente...02 Modificando o layout do slide... 03 Inserindo textos no slide...
Iniciando o Power Point 2013...01 Nova apresentação baseada no modelo...01 Escolhendo o esquema de cores do fundo do slide manualmente...02 Modificando o layout do slide... 03 Inserindo textos no slide...
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior
 Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 02 ATIVIDADE 01 Para poupar esforço de digitação, você pode usar o tradicional
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 02 ATIVIDADE 01 Para poupar esforço de digitação, você pode usar o tradicional
Para iniciar um Inventário, clique no botão Inserir ( primeiramente os campos solicitados na aba Identificação.
 Incluir um Inventário Para iniciar um Inventário, clique no botão Inserir ( primeiramente os campos solicitados na aba Identificação. ) e preencha Clique na aba Itens e depois no botão Carregar Produtos
Incluir um Inventário Para iniciar um Inventário, clique no botão Inserir ( primeiramente os campos solicitados na aba Identificação. ) e preencha Clique na aba Itens e depois no botão Carregar Produtos
Identificando o Buddy VS/XP Lite e Premium
 Identificando o Buddy VS/XP Lite e Premium Figura 1 - Buddy Lite VS/XP Figura 2 - Buddy Premium VS/XP O buddy Lite VS/XP é um adaptador de PS/2 para USB, para ligação do teclado e mouse da estação extra.
Identificando o Buddy VS/XP Lite e Premium Figura 1 - Buddy Lite VS/XP Figura 2 - Buddy Premium VS/XP O buddy Lite VS/XP é um adaptador de PS/2 para USB, para ligação do teclado e mouse da estação extra.
FUNDAÇÃO LUSÍADA Centro Universitário Lusíada
 O Sistema de Gerenciamento de Professores, permitirá que o docente faça o registro da nota de prova do estudante via internet. O procedimento é simples e rápido. Elaboramos esse passo a passo, o qual poderá
O Sistema de Gerenciamento de Professores, permitirá que o docente faça o registro da nota de prova do estudante via internet. O procedimento é simples e rápido. Elaboramos esse passo a passo, o qual poderá
Perspectiva isométrica de modelos com elementos diversos
 Perspectiva isométrica de modelos com elementos diversos Introdução Algumas peças apresentam partes arredondadas, elementos arredondados ou furos, como mostram os exemplos abaixo: parte arredondada furo
Perspectiva isométrica de modelos com elementos diversos Introdução Algumas peças apresentam partes arredondadas, elementos arredondados ou furos, como mostram os exemplos abaixo: parte arredondada furo
DESENHO TÉCNICO AutoCAD
 DESENHO TÉCNICO AutoCAD AULA 1 - INTRODUÇÃO Este capítulo tem como objetivo principal familiarizar o usuário com a interface do Auto-CAD, isto é, a forma como o usuário se comunica com o software e vice
DESENHO TÉCNICO AutoCAD AULA 1 - INTRODUÇÃO Este capítulo tem como objetivo principal familiarizar o usuário com a interface do Auto-CAD, isto é, a forma como o usuário se comunica com o software e vice
Lição 1 - Criação de campos calculados em consultas
 1 de 5 21-08-2011 22:15 Lição 1 - Criação de campos calculados em consultas Adição de Colunas com Valores Calculados: Vamos, inicialmente, relembrar, rapidamente alguns conceitos básicos sobre Consultas
1 de 5 21-08-2011 22:15 Lição 1 - Criação de campos calculados em consultas Adição de Colunas com Valores Calculados: Vamos, inicialmente, relembrar, rapidamente alguns conceitos básicos sobre Consultas
Manual Tabulæ Colaborativo
 Manual Tabulæ Colaborativo Estabelecendo Sessões Colaborativas em Rede Thiago Maciel de Oliveira Ulisses Dias Versão 1.0 Página 2 Manual do Tabulæ Colaborativo Sumário Uma visão geral... 5 Capítulo 1 Instalando
Manual Tabulæ Colaborativo Estabelecendo Sessões Colaborativas em Rede Thiago Maciel de Oliveira Ulisses Dias Versão 1.0 Página 2 Manual do Tabulæ Colaborativo Sumário Uma visão geral... 5 Capítulo 1 Instalando
Controle de Rifas CEOD-RN. Instalação e Manual de Uso
 Controle de Rifas CEOD-RN Instalação e Manual de Uso Primeiros Passos Extraia o arquivo RifaDeMolayMobile.apk do arquivo baixado. Conecte seu celular na porta USB. Envie o arquivo RifaDeMolayMobile.apk
Controle de Rifas CEOD-RN Instalação e Manual de Uso Primeiros Passos Extraia o arquivo RifaDeMolayMobile.apk do arquivo baixado. Conecte seu celular na porta USB. Envie o arquivo RifaDeMolayMobile.apk
Passo 3: Posicionando a Câmera na Prova Didática Teórica ou na Prova de Defesa da Produção Intelectual
 Este manual descreve um procedimento para o registro de Concursos Públicos por meio de áudio e vídeo utilizando-se recursos tecnológicos básicos i. A gravação segue o disposto na Resolução 020/09 da UFSM
Este manual descreve um procedimento para o registro de Concursos Públicos por meio de áudio e vídeo utilizando-se recursos tecnológicos básicos i. A gravação segue o disposto na Resolução 020/09 da UFSM
BREVE TUTORIAL DO PAINT PARTE I Prof. Reginaldo Brito - Informática
 BREVE TUTORIAL DO PAINT PARTE I Prof. Reginaldo Brito - Informática O Paint é o programa de edição de imagens padrão do Windows, ao instalar o sistema o Paint é instalado automaticamente. Provavelmente,
BREVE TUTORIAL DO PAINT PARTE I Prof. Reginaldo Brito - Informática O Paint é o programa de edição de imagens padrão do Windows, ao instalar o sistema o Paint é instalado automaticamente. Provavelmente,
Criar fotos em 3D no Creator
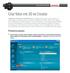 Criar fotos em 3D no Creator O aplicativo Criar fotos em 3D da Roxio torna simples produzir fotos em 3D a partir de várias origens, incluindo arquivos 3D MPO de Fujifilm FinePix REAL 3D W1, fotos digitais
Criar fotos em 3D no Creator O aplicativo Criar fotos em 3D da Roxio torna simples produzir fotos em 3D a partir de várias origens, incluindo arquivos 3D MPO de Fujifilm FinePix REAL 3D W1, fotos digitais
PÓS-GRADUAÇÃO EM MATEMÁTICA COMPUTACIONAL INFORMÁTICA INSTRUMENTAL Aula 05: Editores de Imagem Paint / GIMP
 PÓS-GRADUAÇÃO EM MATEMÁTICA COMPUTACIONAL INFORMÁTICA INSTRUMENTAL Aula 05: Editores de Imagem Paint / GIMP Desenho e Edição de Imagem Paint O Paint é um software utilizado para a criação de desenhos simples
PÓS-GRADUAÇÃO EM MATEMÁTICA COMPUTACIONAL INFORMÁTICA INSTRUMENTAL Aula 05: Editores de Imagem Paint / GIMP Desenho e Edição de Imagem Paint O Paint é um software utilizado para a criação de desenhos simples
Manual para participantes. Sala virtual multiplataforma
 Sala virtual multiplataforma Informações importantes Antes do evento: Recomendamos que entre na sala virtual que temos aberta ao público, na página principal de nosso site, evitando qualquer tipo de transtorno
Sala virtual multiplataforma Informações importantes Antes do evento: Recomendamos que entre na sala virtual que temos aberta ao público, na página principal de nosso site, evitando qualquer tipo de transtorno
Ambiente Virtual de Aprendizagem (AVA) Guia de Estudos Metodologias Jovem de Futuro
 Guia de Estudos Metodologias Jovem de Futuro Precisamos reinventar a forma de ensinar e aprender, presencial e virtualmente, diante de tantas mudanças na sociedade e no mundo do trabalho. Os modelos tradicionais
Guia de Estudos Metodologias Jovem de Futuro Precisamos reinventar a forma de ensinar e aprender, presencial e virtualmente, diante de tantas mudanças na sociedade e no mundo do trabalho. Os modelos tradicionais
Tutorial. Windows Live Mail
 Tutorial Windows Live Mail Instalação, Configuração e Utilização Windows Live Mail O Windows Live Mail permite que você envie e receba mensagens de várias contas de e-mail em um mesmo local, servindo também
Tutorial Windows Live Mail Instalação, Configuração e Utilização Windows Live Mail O Windows Live Mail permite que você envie e receba mensagens de várias contas de e-mail em um mesmo local, servindo também
Banco de Dados Microsoft Access: Criar tabelas
 Banco de Dados Microsoft Access: Criar s Vitor Valerio de Souza Campos Objetivos do curso 1. Criar uma no modo de exibição Folha de Dados. 2. Definir tipos de dados para os campos na. 3. Criar uma no modo
Banco de Dados Microsoft Access: Criar s Vitor Valerio de Souza Campos Objetivos do curso 1. Criar uma no modo de exibição Folha de Dados. 2. Definir tipos de dados para os campos na. 3. Criar uma no modo
MANUAL DE UTILIZAÇÃO DO AMBIENTE VIRTUAL DE APRENDIZAGEM AVA
 MANUAL DE UTILIZAÇÃO DO AMBIENTE VIRTUAL DE APRENDIZAGEM AVA Sejam bem-vindos ao Núcleo de Educação a Distância da FFCL! Esse Manual tem por objetivo auxilia-los na forma de utilização do AVA. COMO FAÇO
MANUAL DE UTILIZAÇÃO DO AMBIENTE VIRTUAL DE APRENDIZAGEM AVA Sejam bem-vindos ao Núcleo de Educação a Distância da FFCL! Esse Manual tem por objetivo auxilia-los na forma de utilização do AVA. COMO FAÇO
Manual de uso PSIM Client 2010
 MANUAL DE USO PSIM MESSENGER VERSÃO 2010 ÍNDICE Manual de uso PSIM Client 2010 INSTALAÇÃO...2 INSTALAÇÃO LOCAL...2 CONFIGURAÇÃO DE USUÁRIO NO PSIM CLIENT 2010...12 QUANDO O FUNCIONÁRIO JÁ ESTÁ CADASTRADO
MANUAL DE USO PSIM MESSENGER VERSÃO 2010 ÍNDICE Manual de uso PSIM Client 2010 INSTALAÇÃO...2 INSTALAÇÃO LOCAL...2 CONFIGURAÇÃO DE USUÁRIO NO PSIM CLIENT 2010...12 QUANDO O FUNCIONÁRIO JÁ ESTÁ CADASTRADO
SUMÁRIO TUTORIAL DO HQ. 2 DICAS PEDAGÓGICAS:. 2 DOWNLOAD DA INSTALAÇÃO. 2 PASSO 1 FORMULÁRIO PARA DOWNLOAD. 2 PASSO 2 ESCOLHENDO A VERSÃO.
 SUMÁRIO TUTORIAL DO HQ... 2 DICAS PEDAGÓGICAS:... 2 DOWNLOAD DA INSTALAÇÃO... 2 PASSO 1 FORMULÁRIO PARA DOWNLOAD... 2 PASSO 2 ESCOLHENDO A VERSÃO... 3 PASSO 3 INSTRUÇÕES DE INSTALAÇÃO... 4 CRIANDO NOVAS
SUMÁRIO TUTORIAL DO HQ... 2 DICAS PEDAGÓGICAS:... 2 DOWNLOAD DA INSTALAÇÃO... 2 PASSO 1 FORMULÁRIO PARA DOWNLOAD... 2 PASSO 2 ESCOLHENDO A VERSÃO... 3 PASSO 3 INSTRUÇÕES DE INSTALAÇÃO... 4 CRIANDO NOVAS
MATEMÁTICA TIPO C. 01. A função tem como domínio e contradomínio o conjunto dos números reais e é definida por ( ). Analise a
 1 MATEMÁTICA TIPO C 01. A função tem como domínio e contradomínio o conjunto dos números reais e é definida por ( ). Analise a veracidade das afirmações seguintes sobre, cujo gráfico está esboçado a seguir.
1 MATEMÁTICA TIPO C 01. A função tem como domínio e contradomínio o conjunto dos números reais e é definida por ( ). Analise a veracidade das afirmações seguintes sobre, cujo gráfico está esboçado a seguir.
Atividade 7. Figura 1 (1) Figura 2 (2)
 Atividade 7 1) PROBLEMATIZAÇÃO: No dia-a-dia não é difícil nos depararmos com situações em que há o emprego de superfícies curvas refletindo luz. Dentre elas, podem ser citados os espelhos esféricos e
Atividade 7 1) PROBLEMATIZAÇÃO: No dia-a-dia não é difícil nos depararmos com situações em que há o emprego de superfícies curvas refletindo luz. Dentre elas, podem ser citados os espelhos esféricos e
GUIA RÁPIDO DE UTILIZAÇÃO DO PORTAL DO AFRAFEP SAÚDE
 GUIA RÁPIDO DE UTILIZAÇÃO DO PORTAL DO AFRAFEP SAÚDE INTRODUÇÃO O portal do Afrafep Saúde é um sistema WEB integrado ao sistema HEALTH*Tools. O site consiste em uma área onde os Usuários e a Rede Credenciada,
GUIA RÁPIDO DE UTILIZAÇÃO DO PORTAL DO AFRAFEP SAÚDE INTRODUÇÃO O portal do Afrafep Saúde é um sistema WEB integrado ao sistema HEALTH*Tools. O site consiste em uma área onde os Usuários e a Rede Credenciada,
