FERNANDO GALLEGO DIAS MODELAGEM E SIMULAÇÃO DA DISTRIBUIÇÃO DA TEMPERATURA DO CORAÇÃO EM CIRURGIAS CARDÍACAS EM FUNÇÃO DO FLUXO CORONARIANO
|
|
|
- Lucas Vasques Canedo
- 8 Há anos
- Visualizações:
Transcrição
1 FERNANDO GALLEGO DIAS MODELAGEM E SIMULAÇÃO DA DISTRIBUIÇÃO DA TEMPERATURA DO CORAÇÃO EM CIRURGIAS CARDÍACAS EM FUNÇÃO DO FLUXO CORONARIANO Dissertação apresentada ao Programa de Pós- Graduação em Engenharia da Universidade Federal do Paraná, PIPE, omo requisito parial à obtenção do título de Mestre em Engenharia Térmia Orientador: Prof. José Viriato Coelho Vargas, Ph.D. Co-orientador: Prof. Juan Carlos Ordonez, Ph.D. CURITIBA 2007
2 TERMO DE APROVAÇÃO FERNANDO GALLEGO DIAS MODELAGEM E SIMULAÇÃO DA DISTRIBUIÇÃO DA TEMPERATURA DO CORAÇÃO EM CIRURGIAS CARDÍACAS EM FUNÇÃO DO FLUXO CORONARIANO ii
3 DEDICATÓRIA Dedio a presente dissertação à minha esposa e a toda minha família que sempre me apoiaram om sua inabalável ompreensão em todos os estágios do trabalho desenvolvido. iii
4 AGRADECIMENTOS Após trabalhar por vários anos diretamente na manutenção, instalação e exeução de projetos de sistemas de transmissão de dados, ontrole digital, teleomuniações, auxílios à navegação e equipamentos meteorológios, onsidero a experiênia adquirida om o urso de mestrado nova e extraordinária para a minha qualifiação profissional permitindo ampliar os meus onheimentos, omo também exeutar trabalhos de alta qualidade ténia aeitos em publiações internaionais de notório reonheimento no meio ientífio. Agradeço a todos que direta ou indiretamente, ontribuíram para a realização deste trabalho. Agradeço ao professor orientador José Viriato C. Vargas, produtivo pesquisador da área de Energia e Ciênias Térmias da UFPR, que teve ontribuição signifiativa sobre o desenvolvimento deste trabalho, através do aompanhamento e revisão do mesmo. Agradeço ao professor o-orientador Juan Carlos Ordonez do Departamento de Engenharia Meânia da Florida State University, que esteve sempre disponível, para sanar dúvidas e abrilhantar este trabalho. Agradeço ao Dr. Maros Brioshi pelas enriqueedoras observações e sugestões apresentadas para o presente trabalho. Agradeço ao Conselho Naional de Desenvolvimento Científio e Tenológio - CNPq que durante dois anos patroinou e permitiu a realização deste mestrado. iv
5 ÍNDICE LISTA DE TABELAS... LISTA DE ILUSTRAÇÕES... LISTA DE GRÁFICOS... LISTA DE ABREVIATURAS E SÍMBOLOS... RESUMO ABSTRACT... viii ix xii xiii xvi xvii CAPÍTULO I 1 INTRODUÇÃO CONSIDERAÇÕES INICIAIS OBJETIVOS ORGANIZAÇÃO DA DISSERTAÇÃO... 3 CAPÍTULO I I 2 REVISÃO BIBLIOGRÁFICA... 4 CAPÍTULO III 3 INTRODUÇÃO SOBRE A ANATOMIA E FISIOLOGIA CARDÍACA LOCALIZAÇÃO DO CORAÇÃO O SISTEMA CIRCULATÓRIO AS ARTÉRIAS CORONÁRIAS ANATOMIA TOPOGRÁFICA CARDÍACA Superfíie externa Interior do oração OS LADOS DIREITO E ESQUERDO DO CORAÇÃO O lado direito do oração v
6 3.5.2 O lado esquerdo do oração As válvulas de passagem CAPÍTULO IV 4 MODELO MATEMÁTICO ANÁLISE VIA ELEMENTOS FINITOS Teoria Método Numério Resultados e Disussão Conlusões ANÁLISE VIA ELEMENTOS DE VOLUME Equações governantes Elementos Fae lateral Fae de topo/fundo Cálulo do alor por evaporação da água Integração Numéria CAPÍTULO V 5 VALIDAÇÃO EXPERIMENTAL E RESULTADOS EXPERIMENTOS CIRÚRGICOS RESULTADOS DA SIMULAÇÃO DO MODELO COMPARAÇÃO NUMÉRICO-EXPERIMENTAL Comparação numério-experimental para fluxo sanguíneo normal na oronária esquerda Comparação numério-experimental para fluxo sanguíneo obstruído na oronária esquerda Avaliação do modelo vi
7 CAPÍTULO VI 6 DISCUSSÃO CAPÍTULO VII 7 CONCLUSÕES E SUGESTÕES REFERÊNCIAS BIBLIOGRÁFICAS APÊNDICES APÊNDICE 1 LISTAGEM DO ARQUIVO SYS.F (SISTEMA DE EQUAÇÕES) BIOGRAFIA vii
8 LISTA DE TABELAS TABELA 1 - DIMENSÕES DOS INCREMENTOS TABELA 2 - DISTRIBUIÇÃO DE TEMPERATURA COMPARATIVA PARA FLUXO NORMAL TABELA 3 - DISTRIBUIÇÃO DE TEMPERATURA COMPARATIVA PARA FLUXO OBSTRUÍDO viii
9 LISTA DE ILUSTRAÇÕES FIGURA 1 - LOCALIZAÇÃO DO CORAÇÃO NO MEDIASTINO... 8 FIGURA 2 - FACES ANTERIOR E INFERIOR CARDÍACAS... 9 FIGURA 3 - SISTEMAS CIRCULATÓRIOS SISTEMICO E PULMONAR FIGURA 4 - ARTÉRIAS CORONÁRIAS PRINCIPAIS FIGURA 5 - SUPERFÍCIE EXTERNA ANTERIOR CARDÍACA FIGURA 6 - SUPERFÍCIE INTERNA CORONAL CARDÍACA FIGURA 7 - FLUXO DE SANGUE NAS CÂMARAS CARDÍACAS FIGURA 8 - CORTE AXIAL DO CORAÇÃO A SER MODELADO E SUA POSIÇÃO REAL FIGURA 9 - DOMÍNIO COMPUTACIONAL REAL RETIRADO DO COMPUTADOR FIGURA 10 - VARIAÇÃO DA VISCOSIDADE DO SANGUE EM FUNÇÃO DA RAZÃO DE DEFORMAÇÃO POR CISALHAMENTO FIGURA 11 - DISTRIBUIÇÃO TÉRMICA CARDÍACA PARA CONDIÇÕES NORMAIS DA SALA DE OPERAÇÃO FIGURA 12 - VETORES INTERNOS DE FLUXO SANGUÍNEO FIGURA 13 - ELEMENTO DE VOLUME TÍPICO COM INTERAÇÕES DE TRANSFERÊNCIA DE CALOR FIGURA 14 - CÂMARA INFRAVERMELHA UTILIZADA NO EXPERIMENTO FIGURA 15 - POSICIONAMENTO DA CÂMARA INFRAVERMELHA FIGURA 16 - COMPARATIVO ENTRE IMAGEM REAL (A) E INFRAVERMELHA (B) DE UMA PONTE DE SAFENA MAGNA ix
10 FIGURA 17 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, TEMPO INICIAL (t=0 SEGUNDOS) FIGURA 18 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, APÓS 0,5 SEGUNDOS FIGURA 19 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, APÓS 1 SEGUNDO FIGURA 20 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, APÓS 2 SEGUNDOS FIGURA 21 - MODELO TRIDIMENSIONAL UTILIZADO FIGURA 22 - DESENHO (VISTAS REBATIDAS) DA MALHA DA CAIXA TORÁCICA SIMULADA FIGURA 23 - TABELA DE CORES PARA O GRADIENTE DE TEMPERATURAS EM KELVIN FIGURA 24 - RESULTADO OBTIDO NOS PLANOS x=3, x=8 E x= FIGURA 25 - RESULTADO OBTIDO NOS PLANOS y=3, y=6 E y= FIGURA 26 - RESULTADO OBTIDO NOS PLANOS z=5, z=9 E z= FIGURA 27 - RESULTADO DA UMIDADE NO PLANO XZ, PARA y=0,150 m FIGURA 28 - RESULTADO DA UMIDADE NO PLANO YZ, PARA x=0,182 m FIGURA 29 - RESULTADO DA UMIDADE NO PLANO XY, PARA Z=0,200 m FIGURA 30 - RESULTADO DA TEMPERATURA NO PLANO YZ, PARA x=0,166 m x
11 FIGURA 31 - RESULTADO DA TEMPERATURA NO PLANO XY, PARA z=0,240 m FIGURA 32 - RESULTADO 2D DA TEMPERATURA NO PLANO YZ, PARA x=0,166 m FIGURA 33 - RESULTADO 2D DA TEMPERATURA NO PLANO XY, PARA z=0,240 m FIGURA 34 - ISOMÉTRICAS DE TEMPERATURAS IGUAIS A 307 K FIGURA 35 - ISOMÉTRICAS DE TEMPERATURAS IGUAIS A 308 K FIGURA 36 - ISOMÉTRICAS DE TEMPERATURAS IGUAIS A 310 K xi
12 LISTA DE GRÁFICOS GRÁFICO 1 - CORRELAÇÃO ENTRE O FLUXO DA CORONÁRIA DESCENTENTE ANTERIOR ESQUERDA (LAD) E A TEMPERATURA PERICÁRDICA ANTERIOR ESQUERDA GRÁFICO 2 - COMPARAÇÃO ENTRE AS TEMPERATURAS ADIMENSIONAIS MEDIDAS E SIMULADAS PARA FLUXO CORONARIANO NORMAL GRÁFICO 3 - COMPARAÇÃO ENTRE AS TEMPERATURAS ADIMENSIONAIS MEDIDAS E SIMULADAS PARA FLUXO CORONARIANO OBSTRUÍDO xii
13 LISTA DE ABREVIATURAS E SÍMBOLOS A = área da superfíie do elemento de volume, m 2 = alor espeífio, J/kg.K e = espessura de parede, m g = aeleração da gravidade, m/s 2 h = oefiiente de transferênia de alor, W/m 2.K H = altura do elemento, m k = ondutividade térmia, W/m.K k ar = ondutividade térmia do ar, W/m.K l = lateral de elemento de volume, m m& = vazão em massa, kg/s N = número total de elementos de volume p v = pressão parial de vapor, N/m 2 p vs = pressão de saturação da água, N/m 2 P T = limite de preisão de temperatura, K q = fluxo de alor, W/m 2 Q & = taxa de transferênia de alor, W Ra = número de Rayleigh t = tempo, s T filme = T fluido = temperatura de filme, (T fluido + T sólido ) / 2, K temperatura de fluido, K U = oefiiente global de transferênia de alor, W/m 2.K U T = inerteza da medida de temperatura, K V = volume, m 3 x,y,z = oordenadas artesianas, m = valor absoluto α T = difusividade térmia, m 2 /s xiii
14 β = oefiiente de expansão volumétria térmia, K -1 = erro relativo de refinamento de malha δ = espaçamento de parede, m ν = visosidade inemátia, m 2 /s ρ = massa espeífia, kg/m 3 ρ ar = massa espeífia do ar, kg/m 3 φ = umidade relativa Subsritos a = número do elemento de volume adjaente av = média b = parede de baixo = número do elemento de volume sólido ond = ondução onv = onveção e = leste g = solo gen = geração em um elemento de volume i = número do elemento de volume j = parede externa l = fae do elemento de volume m = direção n = norte p = parede p,ar = ar à pressão onstante r = número do experimento s = sul t = topo xiv
15 v = substânia em volume onstante w = oeste x = direção x y = direção y z = direção z 0 = ondição iniial = ondição do ambiente externo Glossário AO = artéria aorta AP = artéria pulmonar APM = músulos papilares anteriores LAD = ramo desendente anterior da artéria oronária esquerda LV = ventríulo esquerdo OM = ramos ventriulares diagonais esquerdos PDA = ramo desendente posterior da artéria oronária direita PPM = músulos papilares posteriores RV = ventríulo direito SP = artérias septais perfurantes TCA = termo oronário angiografia VD = ventríulo direito VE = ventríulo esquerdo VHD = bano de dados humano visível xv
16 RESUMO Esta dissertação desenvolve uma análise teória e experimental, modelagem matemátia, simulação e avaliação do oração durante uma irurgia ardíaa, através de oletas de dados de temperatura no momento da irurgia e da apliação de uma ténia alternativa de simulação, denominada de modelo de elementos de volume. A ténia se baseia na ombinação de prinípios de termodinâmia lássia e de transferênia de alor, om a utilização de orrelações analítias teórias e empírias disponíveis na literatura. Utilizando omo dados de entrada fluxos oronarianos onheidos, o trabalho aplia o modelo de elementos de volume para simular a resposta térmia do oração durante a irurgia, om o tórax aberto e onsequentemente, om a metade superior do órgão ardíao, outros órgãos e teidos internos do paiente expostos ao ambiente externo, onsiderando possível irulação de ar sobre o orpo em regime de onveção natural. Um proedimento de validação experimental dos resultados numérios obtidos foi onduzido por omparação direta om medições de temperatura da superfíie dos teidos via imagens de âmara de infravermelho, em dois asos de obstruções ardiovasulares distintas. Os resultados numérios apresentam muito boa onordânia qualitativa e quantitativa om as medições experimentais dos dois asos onsiderados. Espera-se, portanto, que o ódigo omputaional desenvolvido, omo base de um próximo trabalho, venha a se transformar em um apliativo para utilização durante irurgias ardíaas para avaliar a reperfusão do órgão. Para tanto, será resolvido o problema inverso da estimativa dos fluxos oronarianos resultantes, alulados a partir das temperaturas superfiiais medidas por imagem infravermelha. xvi
17 ABSTRACT This dissertation develops a theoretial and experimental analysis, the mathematial modeling, simulation and evaluation of the heart, during a ardia surgery, through temperature data olletion in real surgery time and the appliation of an alternative simulation tehnique, namely, the volume element model. The tehnique is based on the ombination of lassial thermodynamis and heat transfer priniples, with the utilization of theoretial and empirial analytial orrelations available in the literature. Using known oronary flows as input data, the work applies the volume element model to simulate the heart thermal response during open hest surgery, and, onsequently, with the ardia organ upper half, other organs and internal tissues exposed to the external ambient, onsidering possible air irulation over the body under the natural onvetion regime. An experimental validation proedure of the obtained numerial results was onduted by diret omparison with the surfae temperature measurements of the tissues via infrared amera images, in two distint ases of ardiovasular obstrutions. The numerial results showed very good qualitative and quantitative agreement with the two experimental measurements onsidered. Therefore, it is expeted that the developed omputational ode, as the basis of a follow up work, will beome a software to be utilized during ardia surgeries to evaluate the organ reperfusion. For that, the inverse problem of the resulting oronary flows estimation will be solved, alulated from the measured surfae temperatures via infrared imaging. xvii
18 1 CAPÍTULO I 1 INTRODUÇÃO 1.1 CONSIDERAÇÕES INICIAIS O Brasil está entre os países om maior produção de irurgias ardíaas no mundo. De aordo om dados do DATASUS ( no ano de 2001 era de proedimentos foram realizados. Destes, a maioria (aproximadamente ) foram operações de revasularização do mioárdio. A omprovação trans-operatória da perfusão efetiva do mioárdio através dos enxertos realizados durante a irurgia de revasularização é um desafio ainda não resolvido. Métodos de aferição de fluxo através dos enxertos já foram exaustivamente testados sem suesso. Além da impreisão ténia, são na maioria de alto usto, prinipalmente para um país de paros reursos eonômios na área de saúde omo o Brasil. Teniamente, ao realizar a avaliação trans-operatória da perfusão mioárdia através do enxerto, o irurgião se depara om a dúvida se o fluxo através do enxerto pode não signifiar efetividade de perfusão do músulo ardíao. Desde a antiguidade, o ser humano ria e desenvolve métodos matemátios para desrever e quantifiar os fenômenos que observa na natureza bem omo para projetar e melhorar máquinas e equipamentos para os mais diversos fins. Pode-se dizer que o método dos elementos finitos, utilizado para a solução em domínio disreto de equações difereniais de vários tipos, que surgiu na déada de 60 do séulo XX, revoluionou a simulação matemátia de fenômenos físios, nas diversas áreas da iênia. Este método e, posteriormente, o método dos volumes finitos, baseado no método dos resíduos ponderados, ampliaram, qualitativa e quantitativamente, as simulações numérias que eram realizadas om o método de diferenças finitas e outros.
19 Com o aumento da omplexidade dos problemas, preisa-se de omputadores de alta veloidade de álulo, arquiteturas de hardware e geradores de malha mais sofistiados para a simulação de fenômenos espeífios, utilizando métodos numérios de domínio disretizado, que representa a dependênia espaial das variáveis do problema. Ao mesmo tempo, tem-se hoje a neessidade de simulação e otimização de sistemas omplexos, om vários omponentes interagindo entre si, uja simulação numéria através da disretização do seu inteiro domínio requer tempos omputaionais elevados, para a análise de apenas um onjunto de parâmetros de projeto e de operação. Desta maneira, fia pratiamente inviabilizado o estudo de otimização de parâmetros do sistema, que requer a análise de muitas possíveis onfigurações. O quadro aima desrito motiva a busa pelo desenvolvimento de ferramentas matemátias e omputaionais para o aprimoramento ientífio e tenológio de equipamentos e proessos. O objetivo primordial é a ombinação de preisão de simulação numéria satisfatória, baixo tempo omputaional e maior failidade de interfae do usuário om o ódigo. Dentro desse ontexto, este trabalho apresenta o desenvolvimento e análise de metodologias para avaliação da distribuição de temperatura e umidade do oração em uma irurgia ardíaa om tórax aberto, as quais subdividem o domínio a ser analisado em élulas de volume e estabelee uma únia equação diferenial para ada élula, apliando os prinípios de onservação de massa e de energia. As interações energétias entre élulas são estabeleidas através de orrelações empírias de transferênia de alor por evaporação, onveção natural, onveção forçada e ondução. O onjunto de equações difereniais ordinárias transientes obtidas em ada apliação espeífia é integrado simultaneamente. Para isso utiliza-se o método de passo adaptativo de Runge-Kutta de quarta - quinta ordem (KINCAID e CHENEY,1991), utilizando-se ondições iniiais pré-estabeleidas para as variáveis de integração. Para que uma metologia de simulação omputaional de um sistema físio seja onfiável, é neessário que a preisão dos resultados numérios seja verifiada. Para tanto, as apliações do modelo de elementos de volume são validadas por omparações diretas om temperaturas medidas por imagens 2
20 infravermelha em irurgias ardíaas om toraotomia via esternotomia, em dois asos de obstruções ardiovasulares distintas OBJETIVOS Em deorrênia das onsiderações iniiais apresentadas, esta dissertação tem por objetivo: a) avaliar a possibilidade de utilização do método de elementos finitos para simular a resposta térmia do oração a partir de fluxo oronariano onheido, em regime permanente; b) desenvolver um modelo matemátio para o oração e vizinhanças, om base no modelo de elementos de volume (VARGAS et al., 2001), para prever a resposta térmia em regime transiente do oração a partir de fluxos oronarianos onheidos; e ) validar experimentalmente o modelo matemátio desenvolvido. 1.3 ORGANIZAÇÃO DA DISSERTAÇÃO A dissertação está organizada a partir das motivações desritas neste primeiro apítulo. Iniialmente, o apítulo 2 onduz uma revisão bibliográfia pertinente aos assuntos a serem tratados nos apítulos subseqüentes. O apítulo 3 introduz uma breve apresentação sobre a anatomia e meânia de funionamento do oração. O apítulo 4 trata da apresentação e desenvolvimento dos modelos de elementos finitos e elementos de volume. A seguir, o apítulo 5 disorre sobre a validação experimental em irurgias ardíaas reais e seus resultados. O apítulo 6 disute os resultados enontrados e previstos pelo modelo, bem omo disorre sobre assuntos polêmios relaionados à obtenção de fluxos oronarianos via modelo omputaional. Finalmente, o apítulo 7 apresenta as onlusões da dissertação e as sugestões para trabalhos futuros.
21 4 CAPÍTULO II 2 REVISÃO BIBLIOGRÁFICA Através da análise da literatura relaionada om a avaliação da distribuição térmia ardíaa, onstata-se a existênia de inúmeros estudos visando desenvolver métodos de orrelação entre os fluxos oronarianos e a boa qualidade das orreções irúrgias durante o proesso operatório. Dada a importânia do assunto, ainda hoje, ontinua despertando o interesse dos pesquisadores e tremendo esforço tem sido feito no estudo das ténias de métodos que orrelaionem quantitativamente, om preisão, os efeitos de distribuição da temperatura observada na superfíie ardíaa om as diversas variáveis que denotem a qualidade da irulação sanguínea do órgão. A seguir apresenta-se um resumo bibliográfio de alguns destes estudos que ontribuíram para o desenvolvimento deste trabalho. Com a finalidade de avaliar a qualidade do enxerto (substituição de partes obstruídas das artérias oronárias om outras artérias, tais omo a artéria safena magna ou a artéria mamária), SENYK et al., em 1971, observaram a diminuição da temperatura da superfíie mioárdia após a ligadura da artéria desendente anterior e da artéria irunflexa em ães (ambas ramos da artéria oronária esquerda). Estes autores também observaram uma reação hiperêmia, ou seja, um aumento da temperatura do órgão, após a reperfusão (restabeleimento da irrigação sanguínea). ROBICSEK et al., em 1978, desobriram que a radiação infravermelha emitida pelo oração era diretamente proporional à sua temperatura, que por sua vez era diretamente proporional ao fluxo oronariano. TZIVONI et al, em 1982, ompararam alterações eletroardiográfias aos termogramas, obtidos durante olusões pariais ou totais da artéria desendente anterior, em ães. Com este estudo, observou-se que uma redução em 25% do fluxo oronariano não afeta a temperatura epiárdia (temperatura da superfíie ardíaa) nem o eletroardiograma. Entretanto, reduções de % diminuíram a
22 temperatura de superfíie e renderam alterações signifiativas no eletroardiograma. Análises quantitativas do fluxo sanguíneo passando através do mioárdio através de mapas de temperatura da superfíie epiárdia foram iniialmente estudadas por PAPP et al., em Seus resultados preliminares indiaram que a temperatura do epiárdio apresenta boa orrelação om as mudanças de fluxo oronariano. Logo após, onforme ADACHI et al., em 1987, é possível se avaliar as variações quantitativas do fluxo sanguíneo do mioárdio via alterações térmias da superfíie mioárdia, registradas através de imagens infravermelhas em tempo real, sendo que o ramo mais suseptível para tal análise é o desendente anterior da oronária esquerda. Tal análise foi omprovadamente melhor em períodos de isquemia (falta de irrigação sanguínea) seguidos de reperfusão, tal omo oorre no transorrer de uma irurgia ardíaa. Após extensa análise experimental, MOHR et al., em 1989, omprovaram o método de termo-oronário-angiografia omo um bom método a avaliação da qualidade de uma irurgia de enxerto durante o proedimento irúrgio. GORDON et al., em 1998, propuseram o primeiro modelo quantitativo que tentava orrelaionar, no transorrer de uma irurgia ardíaa om resfriamento ardíao, o fluxo oronariano da artéria desendente anterior esquerda (LAD) om a temperatura média epiárdia oletada a partir de uma âmara infravermelha. Tal modelo propunha uma orrelação exponenial entre o fluxo na LAD e a temperatura epiárdia durante a reperfusão sanguínea, e, apesar de apresentar-se omo uma boa tentativa iniial de orrelação entre as variáveis, se mostrou bastante limitado a uma pequena janela de variação, por não levar em onsideração outros parâmetros dinâmios do entro irúrgio e do paiente, tais omo a temperatura do paiente, temperatura e umidade do entro irúrgio, atividade metabólia do paiente, entre outros. TROBEC et al., em 1999, onstruíram, utilizando-se da Base de Dados Visível Humana (VHD), o primeiro modelo tridimensional ardíao ompleto, o qual, devido à sua grande preisão anatômia, seria referênia para a grande maioria dos modelos tridimensionais gráfios e matemátios a serem avaliados em futuros estudos. Tal modelo foi onstruído om base em suessivos ortes tomográfios de 5
23 grande preisão de orações normais e suas estruturas adjaentes. Conforme BRIOSCHI et al, em 2000, e BRIOSCHI e CIMBALISTA, em 2002, o elevado fluxo sangüíneo e onsiderável atividade metabólia fazem do mioárdio um exelente órgão para exame por imagem infravermelha. O termo utilizado para a avaliação da temperatura da superfíie ardíaa é termo-oronarioangiografia (TCA). Esta é uma ferramenta muito útil na monitoração qualitativa da perfusão oronária através das diferenças de emissão de alor pelo epiárdio. Elevada emissão de alor india um aumento do fluxo sangüíneo, enquanto que emissão diminuída india hipoperfusão, assim marando a termografia infravermelha omo um poderoso marador para avaliação qualitativa da perfusão ardíaa e fluxo oronariano. SUMA et al., em 2000, mostraram a grande apaidade da imagem térmia de superfíie ardíaa omo balizador para o irurgião ardíao na abordagem de irurgias de revasularização, enfatizando assim a importânia do onheimento de tal distribuição para a avaliação da qualidade de uma irurgia de implantação de enxertos. Tal afirmação foi omprovada experimentalmente por SIEBERT et al., em NAKAGAWA et al., em 2003, avaliaram qualitativamente e omprovaram a grande possibilidade de análise quantitativa do fluxo sanguíneo na artéria arótida interna via temperatura superfiial avaliada por âmaras infravermelhas om omprimento de onda detetáveis na faixa do infravermelho médio e distante. VARGAS et al., em 2001, introduziram o método de elementos de volume para avaliar a distribuição interna de temperatura e umidade em um gabinete ontendo equipamentos eletrônios. Tal método se mostrou muito promissor, e, om equaionamento simples e efiaz, onseguiu bons resultados na simulação dos proessos de troas térmias internas a tais gabinetes, om tempo omputaional reduzido. WAN, em 2002, propôs um modelo matemátio unidimensional via método de elementos finitos para a avaliação do fluxo ardiovasular. Apesar de o modelo estar limitado à irulação sanguínea somente em artérias de grande alibre, o mesmo se mostrou muito útil para prever algumas doenças ardiovasulares em função do fluxo sanguíneo difereniado nas artérias em estudo. Utilizando-se do método de elementos finitos, TRUNK et al, em 2003, 6
24 apresentaram o primeiro modelo ompleto tridimensional para avaliação das mudanças da temperatura ardíaa em função dos fluxos oronarianos e das ondições do entro irúrgio. Tal modelo, apesar de apresentar malha bastante detalhada, despendia de um grande tempo omputaional e apresentava análise de resultados restrita somente ao momento de resfriamento do órgão ardíao através de solução ardioplégia (solução fria utilizada para se interromper os movimentos ardíaos no momento da irurgia ardíaa) ou através de resfriamento tópio direto do órgão, não podendo ser utilizado em situações de fluxos e ondições onstantes do órgão ardíao. Seguindo a mesma linha de raioínio para avaliação quantitativa da perfusão do mioárdio a partir do mapeamento da temperatura epiárdia, STERK e TROBEE, 2005, desenvolveram uma simulação om alto grau de detalhamento, porém ainda demandando um alto tempo omputaional, bem omo uma interligação de alta omplexidade via proessamento paralelo. Reentemente, utilizando novamente o modelo de elementos de volume, VARGAS e BEJAN (2004) e VARGAS et. al. (2004) apresentaram e desenvolveram a simulação e otimização de estruturas internas de élulas de ombustível, mostrando que tal método é bastante onfiável para situações omplexas de transferênia de alor, bem omo apresenta uma redução signifiativa no tempo omputaional. Assim, om base na revisão bibliográfia apresentada, o objetivo prinipal desta dissertação é o de desenvolver um modelo matemátio tridimensional ardíao, om base na Base de Dados Humana Visível (TROBEC et al., 1999), om boa preisão e reduzido tempo de simulação para a aixa toráia aberta, para ser usado omo uma ferramenta de simulação e predição térmia quantitativa em tempo real, e de omplexidade omputaional reduzida. De aordo om a revisão bibliográfia realizada, não há estudos que realizem o que essa dissertação se propõe a atingir. 7
25 8 CAPÍTULO III 3 INTRODUÇÃO SOBRE ANATOMIA E FISIOLOGIA CARDÍACA 3.1 LOCALIZAÇÃO DO CORAÇÃO O oração loaliza-se na avidade toráia, no mediastino, onforme pode ser observado na Figura 1. Tal figura, bem omo todas as figuras dessa revisão ardíaa do apítulo 3 podem ser enontrados no seguinte endereço de internet: Dois terços do volume ardíao estão situados à esquerda da linha sagital mediana. Esta posição, hamada de levoárdia, é a mais freqüente. Variações na posição do oração em relação ao tórax podem oorrer. A posição mesoárdia, oorre quando a maior parte do seu volume está situada na porção mediana do tórax. A posição dextroárdia oorre quando grande parte de sua massa loaliza-se no hemitórax direito. FIGURA 1 - LOCALIZAÇÃO DO CORAÇÃO NO MEDIASTINO
26 A forma do oração é aproximadamente ônia, om a base voltada para trás e para a direita, e o ápie para a frente e para a esquerda. Há três faes no oração: a anterior ou esternoostal, onforme observada na Figura 2, sobre a qual os pulmões direito e esquerdo se sobrepõem, deixando exposta apenas uma pequena porção; a fae inferior, também observada na Figura 2, que repousa sobre o diafragma, reebendo também o nome de fae diafragmátia; e a fae lateral esquerda, formada prinipalmente pelo ventríulo esquerdo, que produz a impressão ardíaa na fae medial do pulmão esquerdo. Estas faes são delimitadas pelas margens ardíaas. A direita é bem definida, sendo hamada de aguda, enquanto que a esquerda ou obtusa é pouo definida. Anteriormente, além dos pulmões, o oração relaiona-se também om o esterno, ostelas e músulos interostais; posteriormente om a aorta desendente, esôfago e veia ázigos; e lateralmente om os pulmões, hilos pulmonares, nervos frênios e vagos. 9 FIGURA 2 - FACES ANTERIOR E INFERIOR CARDÍACAS
27 O SISTEMA CIRCULATÓRIO Todas as élulas de nosso orpo neessitam de oxigênio para viver. O papel do oração é enviar sangue rio em oxigênio a todas as élulas que ompõe o nosso organismo. As artérias são as vias por onde o sangue oxigenado é enviado. A aorta é a maior de todas as artérias, e se origina no ventríulo esquerdo. As artérias se dividem em ramos ada vez menores, até os apilares sistêmios, que são vasos extremamente finos através dos quais o oxigênio sai para os teidos. Após a retirada do oxigênio e o reebimento do gás arbônio que se enontrava nos teidos, os apilares levam o sangue até as veias. As veias transportam sangue om baixa quantidade de oxigênio e alto teor de gás arbônio, desde os teidos de volta ao oração e daí aos pulmões, hegando aos apilares pulmonares, onde o sangue volta a reeber oxigênio e a ter o gás arbônio removido, sendo o proesso reiniiado. O sangue flui ontinuamente pelo sistema irulatório, e o oração é a "bomba" que torna isso possível. Na Figura 3 podemos observar o mapa de irulação orpórea simplifiado, om o oração no entro de tal trama apilar. FIGURA 3 - SISTEMAS CIRCULATÓRIOS SISTÊMICO E PULMONAR
28 AS ARTÉRIAS CORONÁRIAS O oração, omo qualquer outro músulo do orpo, neessita de reeber oxigênio para que funione adequadamente. A musulatura do oração é nutrida através de um sistema de artérias, as artérias oronárias, que se originam da aorta. As duas artérias oronárias mais importantes são a oronária direita e a oronária esquerda - esta última se divide (mais freqüentemente) em artéria oronária desendente anterior e artéria irunflexa, onforme podemos observar na Figura 4. FIGURA 4 - ARTÉRIAS CORONÁRIAS PRINCIPAIS 3.4 ANATOMIA TOPOGRÁFICA CARDÍACA Superfíie externa Conforme pode ser observado na Figura 5, o oração é formado superfiialmente por: Veia Cava Superior (1), Veia Cava Inferior (2), Átrio Direito
29 (3), Ventríulo Direito (4), Ventríulo Esquerdo (5), Artéria Pulmonar (6), Aorta (7), Artéria Coronária Direita (8), Artéria Coronária Desendente Anterior (9), Átrio esquerdo (10) e Veias Pulmonares (11). 12 FIGURA 5 - SUPERFÍCIE EXTERNA ANTERIOR CARDÍACA Interior do Coração Conforme pode ser observado no orte oronal da Figura 6, o oração é formado internamente por Átrio Direito (1), Valva Triúspide (2), via de entrada do Ventríulo Direito (3), via do saída do Ventríulo Direito (4), Valva Pulmonar (5), Artéria Pulmonar (6), Átrio Esquerdo (7), Septo Interventriular (8), Ventríulo esquerdo (9), Valva Mitral (10) e Aorta (11).
30 13 FIGURA 6 - SUPERFÍCIE INTERNA CORONAL CARDÍACA 3.5 OS LADOS DIREITO E ESQUERDO DO CORAÇÃO O lado direito do oração O lado direito do oração reebe sangue das veias que trazem o sangue de todo o orpo. Este "sangue usado " é pobre em oxigênio e rio em gás arbônio - é hamado de sangue venoso. Como pode ser observado na Figura 7 o átrio direito (AD) é a primeira âmara ardíaa que reebe o sangue, onde a âmara se enhe a medida que seus músulos se relaxam para enher om sangue venoso que retornou de todo o orpo. Em seguida o sangue entra em uma segunda âmara musular hamada de ventríulo direito (VD), o qual é uma das duas prinipais bombas do oração, sendo que sua função é levar o sangue aos pulmões, através da artéria pulmonar (AP). Logo após, os pulmões oxigenam o sangue, restaurando a sua taxa de oxigênio, e o gás arbônio, anteriormente dissolvido em forma de biarbonato, é expirado.
31 14 FIGURA 7 - FLUXO DO SANGUE NAS CÂMARAS CARDÍACAS O lado esquerdo do oração O lado esquerdo reebe o sangue depois que ele volta dos pulmões, já oxigenado. O sangue rio em oxigênio hega ao oração por veias que vêm dos pulmões (hamadas de veias pulmonares) no átrio esquerdo, a primeira âmara do lado esquerdo. Do átrio esquerdo, o sangue segue para o ventríulo esquerdo (VE), uma âmara musular poderosa que bombeia o sangue oxigenado para todo o orpo através da artéria aorta (AO). O ventríulo esquerdo é a mais forte das âmaras do oração. Seus músulos espessos neessitam exeutar ontrações poderosas o sufiiente para bombear o sangue para todas as partes do orpo. Esta ontração forte gera a pressão sanguínea sistólia (o primeiro valor - e o mais alto - na medida da pressão arterial sanguínea). A pressão medida mais baixa, ou pressão sanguínea diastólia é enontrada quando o ventríulo esquerdo relaxa para se enher novamente om sangue. O sangue deixa o oração passando pela aorta asendente. A aorta é a prinipal artéria que alimenta de sangue o orpo inteiro.
32 As válvulas de passagem As válvulas são retalhos (flaps) musulares que se abrem e feham. Este movimento de abrir e fehar faz om que o sangue direionado de maneira orreta. O oração tem 4 válvulas: A válvula triúspide regula o fluxo do sangue entre o átrio direito e o ventríulo direito. A válvula pulmonar se abre para permitir ao sangue fluir do ventríulo direito aos pulmões. A válvula mitral regula o fluxo do sangue entre o átrio esquerdo e o ventríulo esquerdo. A válvula aórtia permite ao sangue fluir do ventríulo esquerdo à aorta.
33 16 CAPÍTULO IV 4 MODELO MATEMÁTICO 4.1 ANÁLISE VIA ELEMENTOS FINITOS Teoria A figura 8 mostra, usando radiografia marada radioativa, um orte bidimensional do oração, onde à sua direita é mostrada a linha amarela onde o orte é loalizado no oração real. RV representa o ventríulo direito, LV representa o ventríulo esquerdo, LAD representa a artéria desendente anterior esquerda, ppm e apm os músulos papilares posteriores e anteriores, respetivamente, PDA a artéria oronária desendente posterior direita, Sp as artérias perfurantes septais e OM a artéria marginal obtusa esquerda. FIGURA 8 - CORTE AXIAL DO CORAÇÃO A SER MODELADO E SUA POSIÇÃO REAL (fonte:
34 Como o modelo é onstruído utilizando um orte bidimensional do oração apresentado, é ruial para a modelagem e simulação preisas, que o orte seja representativo de todo o oração tridimensional. Portanto, em todo orte da mesma linha axial, devem haver as mesmas estruturas representadas, resultando derivadas de veloidades e temperaturas entre os ortes adjaentes nulas. A Figura 9 mostra o domínio omputaional utilizado para simular o orte da Figura 8. Como o objetivo prinipal é modelar a irurgia de peito aberto, o oração está supostamente imerso até sua metade inferior no domínio do mediastino, representado pela região (A). A região (B) representa a área do oração que está exposta ao ambiente externo do entro irúrgio. A região (C) representa o sangue em duas situações: (i) esoando do ramo da artéria oronária desendente anterior esquerda para o músulo ardíao, desemboando enfim em veias tributárias do seio oronário e (ii) no interior dos dois ventríulos. A região (D) representa o próprio músulo do oração, o mioárdio, e a região (E) representa o sangue que possui um fluxo onheido na artéria oronária desendente anterior esquerda. Este duto onetando o ramo desendente anterior esquerdo à veia tributária do seio oronário orresponde à rede de apilares do plano de orte analisado, então, em planos adjaentes, são enontradas estruturas simulares. Assim, onforme observado anteriormente, as derivadas das veloidades e temperaturas de um orte para outro são admitidas omo aproximadamente nulas, o que permite a modelagem bidimensional do problema tridimensional em pauta somente pela análise de um orte, uma vez que a mesma imagem se repete aproximadamente em todos os ortes adjaentes. O ramo LAD representa a porção do ramo desendente anterior da artéria oronária esquerda, que emite seus ramos perfurantes na porção ântero-superior do músulo ardíao, assim irrigando tal porção. Logo após, tal sangue é imediatamente oletado pelas veias tributárias do seio oronário, assim formando um duto sanguíneo no interior da porção anterior do músulo ardíao, o qual é responsável por grande parte do forneimento de alor e nutrientes para tal região. 17
35 18 FIGURA 9 - DOMÍNIO COMPUTACIONAL REAL RETIRADO DO COMPUTADOR Neste estudo, o sangue é onsiderado um fluído newtoniano. Talvez as primeiras tentativas em se estudar as propriedades de vazão do sangue foram feitas por Young e Poiseuille no séulo 17, e até a presente data a simulação real do fluxo sanguíneo em ambientes orpóreos e línios ontinua um problema de omplexidade onsiderável. Em 1963, FOX e SAIBEL, avaliaram a vazão sanguínea em ambientes orpóreos reais, onde foi plenamente estabeleido que o sangue é um fluido não newtoniano. Na Figura 10 podemos observar a variação da visosidade do sangue em função da razão de isalhamento, v1 / x 2, apliada na direção radial da artéria. Assim, onforme omparação de vários modelos de vazão sanguínea não newtonianos e modelo newtoniano feitos por JOHNSTON et al. em 2004, onlui-se que, onforme a Figura 10, para artérias de grandes e médios alibres, om geometrias simples e altas tensões deformantes de isalhamento, omo
36 é o aso das artérias oronárias ardíaas, a aproximação sanguínea via modelo newtoniano pode ser feita sem grandes perdas. É importante salientar que, onforme referênia itada anteriormente, para simulações futuras de avaliação da miro irulação mioárdia, o modelo não newtoniano da lei de potênia generalizada deverá ser onsiderado, em função das pequenas tensões de isalhamento de tal miro irulação mioárdia. 19 FIGURA 10 VARIAÇÃO DA VISCOSIDADE DO SANGUE EM FUNÇÃO DA RAZÃO DE DEFORMAÇÃO POR CISALHAMENTO (fonte: As equações governantes são as equações de massa, momento e energia que estão simplifiadas de aordo om as hipóteses de esoamento laminar inompressível bidimensional em regime permanente, dissipação visosa desprezível, propriedades onstantes no fluído e a aproximação de Boussinesq:
37 20 0, y v x u = + (1) onde u é a veloidade do fluxo na direção x, m/s; v é a veloidade do fluxo na diretação y, m/s., y u x u ν x p ρ 1 y u v x u u = + (2) onde ρ é a densidade do fluido, kg/m 3 ; p é a pressão no elemento, N/m 2 ; ν a visosidade inemátia do sangue, m 2 /s. gβt, y v x v ν y p ρ 1 y v v x v u = + (3) onde g é a aeleração da gravidade exerida na direção y, ou de empuxo, do modelo, m/s 2 ; T a temperatura do elemento, K; β o oefiiente de expansão térmia, K -1., y T x T α y T v x T u = + (4) onde α é a difusividade térmia, m 2 /s. Como próximo passo, as equações governantes são adimensionalizadas, onde as variáveis adimensionais são definidas omo:
38 (x, y) p ( X,Y) =, P =, (5) 2 L ρu 21 (U, V) 3 L 1/ 2 T T gβ(tw T )L ν = (u, v) Ra, θ =, Ra =, Pr =, (6) α T T αν α w onde (x,y) são as oordenadas artesianas, m; p a pressão, N/m 2 ; ρ a densidade do fluido, Kg/m 3 ; g a aeleração da gravidade, m/s 2 ; T a temperatura do oração, K; T a temperatura da sala de operação, K; T w a temperatura do sangue ventriular, K; β o oefiiente de exapansão térmia, K -1 ; L o omprimento do orte ardíao, m; ν a visosidade inemátia do sangue, m 2 /s and α é a difusividade térmia, m 2 /s; p é o alor espeífio, J/kg.K; µ é a visosidade absoluta, Pa.s; k é a onditividade térmia, W/m.K. A partir das Eqs. (1)-(4) obtém-se as seguintes equações adimensionais: U V + X Y = 0, (7) 1/ Ra Pr U U P U U U + V = + +, 2 2 X Y X X Y (8) Ra 1/ V V P V V 1/ U V + + Ra 2 θ, 2 2 Pr + = + X Y Y X Y (9) Ra 1/ 2 2 θ θ θ U + V = 2 X Y X 2 θ + 2 Y (10) Para ompletar a formulação do problema, são espeifiadas ondições de ontorno para o domínio omputaional do modelo da Figura 9. Note que para a
39 Região (E) é onsiderada a veloidade de 8,8 m/s, ou seja, a veloidade normal média do sangue, onforme literatura média, do ramo desendente anterior esquerdo da artéria oronária esquerda (AOKI et al., 2003): Iniialmente, foi analisada a distribuição térmia para ondições habituais de operação do entro irúrgio, isto é, temperatura da sala de operação de 25 C ( θ = 0), temperatura interna periárdia de 35,5 C ( θ = 0, ) e temperatura sanguínea de 37 C ( θ = 1). A veloidade no ramo desendente anterior da oronária esquerda foi adotada de aordo om o valor médio sugerido no parágrafo anterior, ou seja, 8,8 m/s. Assim obtém-se U 3 = 8,67.10 e V 3 = 5.10 para a entrada da região om onteúdo sanguíneo (à exeção dos ventríulos). Assim as ondições de ontorno são estabeleidas da seguinte forma: Região (A): U = 0, V = 0, θ = 0, 875 (11) Região (B): U = 0, V = 0, θ = 0 (12) Região (C): θ = 1, 0 (13) Região (D): U = 0, V = 0 (14) Região (E): U 3 3 = 8,67.10 V 5.10, = θ = 1, 0 (15) Verifia-se que as Eqs. (7)-(10) são válidas tanto para a região de fluido omo de sólido. A ondição de onservação de energia na interfae sólido-fluido é naturalmente respeitada pela equação de onservação de energia e onsiderando as diferentes propriedades do sólido e do fluido no domínio omputaional. Além disso, na região de sólido, são atribuídas veloidades nulas, onforme a Eq. (14), i.e., região (D), alulando-se apenas as temperaturas. Nas regiões de fluido,
40 portanto, as equações permitem o álulo das veloidades e das temperaturas. A ténia aqui apresentada é uma forma alternativa de tratar a interação sólido-fluido em um sistema omposto de duas fases. Espeifiada a geometria do domínio omputaional definido pelo orte da Figura 9, a resolução das Eqs (5)-(15) determina as veloidades, pressões e ampos de temperatura resultantes no domínio Método Numério A solução numéria das Eqs (5)-(15) foi obtida utilizando-se do método de elementos finitos. O primeiro passo para a implementação numéria foi a eliminação da variável pressão das Eqs. (8) e (9), através do uso do método de penalidade (HUGHES et al., 1979). É importante notar que o ampo de pressões pode ser obtido por pós proessamento, substituindo-se os valores de veloidades obtidos, e assim alulando-se a pressão. O método de penalidades, onforme desrito por REDDY E GARTLING, 2004, aproxima a Eq. (7) onforme se segue: U V + X Y = P, γ (16) onde γ é o fator de penalidade, o qual neessita ser grande o sufiiente para satisfazer aproximadamente a onservação de massa. A implementação do método de elementos finitos para a solução das Eqs (5)-(15) se iniia om a obtenção de uma forma variaional (fraa) do problema. A seguir, a forma fraa é disretizada por um método apropriado. Devido às araterístias do esoamento interno na região (C) da Figura 9, que oneta o ramo LAD à tributária do seio oronário, fisiamente, é sensato onsiderar que a solução em um ponto espeífio do modelo depende preferenialmente do que oorre à
41 frente do esoamento, onsiderando a direção do esoamento forçado. Como se sabe, o método de Galerkin, o qual é análogo ao esquema de diferenças entradas no método de diferenes finitas, não aptura este aspeto físio nas equações disretizadas. Assim, o método de disretização utilizado neste trabalho será o método upwind proposto por HUGHES (1978), onde é possível adequar a forma disreta do problema às araterístias físias do esoamento. Depois de desenvolver a forma disreta do problema, as equações algébrias resultantes são arranjadas em forma matriial para o problema bidimensional em regime permanente, omo se segue: 24 ~ ~ B C(U ~ 1 0 T ) 0 T ~ 0 C(U ~ ) U ~U 1 0 B ~ 2K11 + K 22 K 21 Kˆ K K 2K U ~U Kˆ Kˆ Kˆ ~ F, U ~U 1 1 = F 2 2 (17) D ~ (U ~ )T ~ + L ~ T ~ = G, (18) onde B 1 e B 2 são os termos de empuxo; C(U ~ ) é a matriz de apaidade que ontém os termos advetivos das equações de momento, os quais dependem de maneira não linear da solução U ~ (vetor bipartiionado: U ~ 1- direção X e U ~ 2 - direção Y, ada um om número de omponentes igual ao número de variáveis da malha); Kˆ 11,Kˆ 12, Kˆ 21 e Kˆ 22 são as matrizes om os termos de penalidades da variável pressão nas equações de momento da Eq. (4.16), que são omputados om integração reduzida (um ponto em ada direção om funções lineares) para evitar o travamento da resolução; D ~ (U ~ ) é a matriz de apaidade que ontém os termos advetivos da equação de energia; L ~ é a matriz difusiva om oefiientes onstantes (ondutividade térmia onstante), que ontém os termos difusivos da equação de energia; F 1 e F 2 são os vetores força das equações de momento que ontém as forças de ampo e as ondições de
42 ontorno para veloidade, e G ontém os termos fonte da equação de energia e as ondições de ontorno de temperatura. Por brevidade, os detalhes matemátios das omponentes das matrizes aima desritas não serão apresentados. Porém, o leitor pode se dirigir ao trabalho de REDDY E GARTLING (2004), o qual ontém toda base do presente estudo. A seguir, uma subrotina em Fortran foi esrita para implementação das equações de Navier-Stokes e energia em duas dimensões om um elemento bilinear isoparamétrio de quatro nós, o qual foi agregado ao ódigo aberto hamado finite element analysis program, FEAP, originalmente esrito por ZIENKIEWICZ E TAYLOR (1989) Resultados e Disussão Para este estudo, a malha do modelo foi dividida em três materiais distintos, ada um om as seguintes propriedades retiradas da literatura omo valores médios e de maior inidênia na população (HOLMES, 2000): Material 1 Mioárdio: ρ =1125 kg/m 3, p =3475 J/kg.K e k=0,493 W/m.K Material 2 Periárdio: ρ =900 kg/m 3, p =2650 J/kg.K e k=0,201 W/m.K Material 3 Sangue irulante: ρ =1060 kg/m 3, p =3889 J/kg.K, k=0,505 W/m.K, µ = Pa.s, β = /K e g=9,87 m/s 2 Iniialmente, foi analisada a distribuição térmia para ondições habituais de operação do entro irúrgio, isto é, temperatura da sala de operação de 25 C
43 ( θ = 0 ), temperatura interna periárdia de 35,5 C ( θ = 0, 875) e temperatura sanguínea de 37 C ( θ = 1). O fluxo no ramo desendente anterior da oronária 26 esquerda foi adotado omo U 3 = 8,67.10 e V 3 = A Figura 11 mostra os resultados obtidos da distribuição de temperatura normalizada no orte ardíao analisado. Observa-se também a malha onvergida de 2189 elementos utilizada nas simulações. Para tanto, foi alulado erro relativo da norma da solução de veloidades e temperaturas entre uma malha menos refinada e outra mais refinada. Quando o erro perentual enontrado foi menor do que 1%, adotou-se a malha menos refinada, i.e., uma malha não uniforme om 2189 elementos. FIGURA 11 - DISTRIBUIÇÃO TÉRMICA CARDÍACA PARA CONDIÇÕES NORMAIS DA SALA DE OPERAÇÃO A Figura 12 mostra os vetores obtidos que representam os fluxos internos sanguíneos no duto apilar ligando a fonte de sangue arterial om o sistema de drenagem venosa, bem omo o sangue interno aos ventríulos. Note que o entro do
44 vórtie do fluxo sanguíneo de ada ventríulo é loalizado próximo à região do gradiente de temperatura mais intenso, isto é, a área de transição entre o oração imerso no domínio periárdio e o oração exposto ao ambiente. Na verdade, esse fluxo intenso próximo às regiões de maior gradiente é expliado pelos termos de empuxo g βt na equação de momento, Eq. (3), que direiona a distribuição das derivadas da veloidade de aordo om o gradiente de temperatura. 27 FIGURA 12 - VETORES INTERNOS DE FLUXO SANGUÍNEO Como próximo passo, foi analisada a orrelação do fluxo no ramo desendente anterior da oronária esquerda (LAD) om a distribuição de temperatura no teido periárdio envolvendo a artéria em questão. O Gráfio 1 mostra a orrelação entre o fluxo sanguíneo na LAD e a temperatura periárdia anterior esquerda. O loal avaliado está imediatamente superior ao ramo LAD e inferior à porção do oração em ontato direto om o ambiente, ponto esse ideal e failmente aessível para a avaliação de temperatura em uma irurgia ardíaa. O
45 Gráfio 1 foi obtido simulando-se suessivas variações na veloidade de entrada da LAD, e assim oletando-se as temperaturas resultantes em um ponto espeífio na superfíie do periárdio. Nota-se que a tendênia obtida é orreta, em uma análise qualitativa, pois onforme a veloidade de entrada do ramo LAD aumenta o valor da temperatura do periárdio no ponto de análise também aumenta. Porém, avaliandose quantitativamente, nota-se que, onforme a veloidade varia entre 0 e 1, a temperatura varia entre 0,21 e 0,23, o que não é bom, pois se espera que exista uma variação maior na temperatura onforme se aumenta o valor da veloidade sanguínea no ramo LAD. 28 GRÁFICO 1 - CORRELAÇÃO ENTRE O FLUXO DA CORONÁRIA DESCENTENTE ANTERIOR ESQUERDA (LAD) E A TEMPERATURA PERICÁRDICA ANTERIOR ESQUERDA Conlusões O método de elementos finitos bidimensional mostrou que é apaz de
46 prover a avaliação da distribuição de temperatura ardíaa om irurgia em peito aberto, externando em regime pós-análise um modelo preiso e de fáil visualização para ondições habituais da sala irúrgia. Porém, pode ser observado pelo Gráfio 1 que o método de elementos finitos não mostrou grande preisão em orrelaionar a veloidade no ramo desendente anterior da artéria oronária esquerda om as reais distribuições resultantes após redução de veloidades, apresentando assim inapaidade para avaliação de situações de músulo mal perfundido (por exemplo um infarto do mioárdio) ou de obstruções em artérias (por exemplo ateroslerose, ou seja, fluxo sanguíneo nas oronárias limitados por uma plaa de gordura), pois, esperava-se que o sistema apresentasse grande variação na temperatura da superfíie do oração ao se variar grandemente o fluxo oronariano no ramo LAD, o que não oorreu na simulação. Notou-se também que o tempo omputaional para a avaliação do método de elementos finitos, aproximadamente 5 minutos, foi muito grande. Assim, se apliado a uma ondição real tridimensional, seria inompatível om o objetivo de se avaliar distribuições de temperatura em tempo real a partir de informações de fluxos sanguíneos. As hipóteses adotadas para a simulação bidimensional são muito fortes, portanto, os resultados não são representativos das ondições reais esperadas no oração. Em vista do exposto, partiu-se para a avaliação de distribuição térmia tridimensional do modelo ardíao via uma ténia alternativa elementos de volume (VARGAS et. al., 2001). Espera-se om isso desenvolver-se uma metodologia sufiientemente preisa e de baixo tempo omputaional, para análise em tempo real irúrgio das ondições de perfusão e temperatura resultantes no oração ANÁLISE VIA ELEMENTOS DE VOLUME O problema onsiste no álulo da distribuição da temperatura dentro da aixa toráia e ar irundante, bem omo da umidade relativa do ar. O domínio de soluções envolve uma porção onsiderável de ar irundante, uma porção do orpo e o oração, metade exposto, e metade imerso no mediastino. As distribuições são
47 determinadas por ondições ambientes externas e pela distribuição geométria dos elementos internos. O modelo físio simplifiado ombina oneitos teórios da termodinâmia lássia om oneitos teórios e orrelações empírias da meânia dos fluidos e da transferênia de alor e massa, as quais são válidas para regimes de esoamento turbulento e laminar, resultando em um onjunto de equações difereniais ordinárias. O modelo é então disretizado om um esquema simples de volume finitos om élulas entradas, em uma abordagem prátia busando maiores veloidades de omputação. Um esquema de volumes finitos tri-dimensional om élulas entradas foi usado para disretizar o domínio e numeriamente resolver o problema (FLETCHER, 1991). A inovação no presente modelo está na dimensão dos volumes de ontrole que não preisam ser extremamente reduzidos, isto é, difereniais, para obtenção de resultados sufiientemente preisos, omo é usualmente requerido por outros métodos numérios, prinipalmente na presença de grande diversidade de materiais sólidos e ar interagindo no domínio da solução. A ténia onsiste em dividir a aixa toráia em volumes de ontrole que somente ontenham ar, músulo ou sangue. A vantagem é que, om um número de elementos relativamente pequeno, a onvergênia é obtida om tempo omputaional reduzido. A ombinação do modelo físio simplifiado proposto om o esquema adotado de volumes finitos para a disretização numéria é hamada de modelo de elementos de volume (MEV). As equações governantes deorrentes dos prinípios de onservação da massa e da energia são apliadas a ada elemento de volume. O modelo leva em onta a geração de alor interna no elemento e proessos de transferênia de alor e massa através das seis faes do elemento, por ondução e onveção Equações governantes A Figura 13 mostra uma élula típia (ou elemento de volume) que pode onter tanto ar ou material sólido (músulo, sangue nos átrios, sangue nos
48 ventríulos, artérias, et.), mas nuna uma ombinação dos dois, no presente modelo. Cada elemento interage om outros elementos adjaentes, de aordo om a equação da energia (primeira lei da termodinâmia) apliada à élula, omo se segue: 31 dt i dt 1 = [Q & e + Q& w + Q& t + Q& b + Q& n + Q& s + Q& gen Q& vap ] i (ρv) +, 1 i N (19) i onde T i é a temperatura no entro de ada elemento de volume, K; ρ é a massa espeífia do material dentro do elemento de volume (ar, sólido ou sangue), kg/m 3 ;V é o volume da élula, m 3 ; pode ser o alor espeífio do sólido ou o alor espeífio a volume onstante do ar ou sangue ( v ), J/kg.K; & e,q& w,q& t,q& b,q& n,q& s, Q& gen e vap Q Q & são, respetivamente as taxas de transferênia de alor através das paredes leste, oeste, do topo, do fundo, norte, sul, por geração dentro do elemento e por evaporação da água para os elementos na amada de fronteira entre o músulo e o ar ambiente da sala irúrgia, em função do músulo ardíao sempre apresentar uma fina amada líquida sobre o mesmo, W. Considera-se o músulo omo sendo uma estrutura om miroirulação e geração metabólia própria. Portanto omo um sólido não inerte, tendo assim sua geração metabólia de alor interna, Q & gen. A temperatura interna do músulo é ontrolada indiretamente pelo hipotálamo, no enéfalo, através da liberação do hormônio TRH, e pela glândula hipófise, através da liberação do hormônio TSH, e finalmente pelo ontrole direto da glândula tireóide, através da liberação dos hormônios T 3 e T 4, em função da temperatura do elemento. Para o presente trabalho é onsiderada uma geração de alor onstante de 1,861 W/kg desde que a temperatura do músulo esteja inferior à ambiente. Tal valor é onsiderado pela literatura atual omo sendo a geração de alor média musular (GRAY, 1980).
49 FIGURA 13 - ELEMENTO DE VOLUME TÍPICO COM INTERAÇÕES DE TRANSFERÊNCIA DE CALOR 32 Q & t Q & s Q & e Q & w Q & n z y Q & b x A Equação (19) estabelee um problema de valor iniial a ser resolvido, determinando o ampo de temperaturas dentro da aixa toráia em qualquer instante do tempo, partindo de ondições iniiais onheidas T i0 (1 i N). Na seqüênia, a umidade relativa em ada elemento de ar (ampo de umidades relativas) resulta do ampo de temperaturas. Considera-se a aixa toráia e ar irundante omo um sistema fehado, e assume-se um ampo de umidades relativas iniial onheido, ϕ i0. Primeiro, a pressão de vapor iniial é alulada omo segue: p 0 v,i = φi0.p vs (Ti ), (20)
50 onde p v,i é a pressão parial de vapor da élula, ϕ i0 é a umidade relativa iniial da élula e p vs (T i0 ) é a pressão de saturação da água na temperatura T i0. Assume-se que a umidade absoluta em ada elemento de volume permanee onstante durante toda simulação. Então, a umidade relativa em ada elemento que ontém ar é alulada por: 33 p v,i φi =, (21) p (T ) vs i onde ϕ i é a umidade relativa da élula e p vs (T i ) é a pressão de saturação da água na temperatura T i. Quando o elemento de volume ontém músulo, ϕ i = 0, e quando ontém somente sangue, ϕ i = Elementos Correlações empírias (BEJAN, 1993 ; BEJAN 1995a) são utilizadas para alular as taxas de transferênia de alor através das faes de ada volume elementar. Todas alternativas possíveis foram onsideradas, i.e., três tipos de interação de energia podem oorrer: (i) fluido-músulo, (ii) fluido-fluido, ou (iii) músulo-músulo. Cada elemento de volume de número i (1 i N) possui quatro faes laterais, que foram denominadas leste, oeste, norte e sul, mais as faes topo e fundo. A análise é dividida, portanto, em faes laterais, de topo e de fundo Fae lateral O elemento pode ter ar, sangue ou músulo dentro, mas para o aso de iteração ar/ar ou músulo/músulo, somente ondução de alor oorre entre elementos adjaentes, i.e., nenhum movimento relativo entre amadas de ar laterais
51 é onsiderado. A outra possibilidade é uma interação fluido/músulo entre os dois elementos (exemplo: ar/musulo ou sangue/músulo), então a transferênia de alor através da fae do elemento é definida por onveção. Para um ontato ar/ar, o fluxo de alor é dado por: 34 Q & = U A (T T ), (22) l,i l,i l,i i a onde o índie a é o número do elemento adjaente, U l, i é o oefiiente global de transferênia de alor, W/(m 2.K); Q & l, i é o fluxo de alor entre os elementos adjaentes, W; A l, i é a área de ontato entre os elementos adjaentes, m 2 ; T i é a temperatura do elemento a ser avaliado, K; adjaente, K. T a é a temperatura do elemento U l,i k ar =, (23) (l + l ) / 2 m,i m,a onde l m,i e l m,a podem ser tanto o omprimento ou a largura da élula, de aordo om o índie m (x ou y), se a fae da élula de número i ou a é leste/oeste ou norte/sul, respetivamente. Para um ontato sólido/sólido, o fluxo de alor é também obtido a partir da Eq. (22), onde desta vez: U l,i 1 = (24) lm,i / 2 lm,a / 2 + k k i a
52 Quando o ontato é do tipo ar/sólido ou sangue/sólido, três possibilidades devem ser onsideradas, i.e., onveção natural om e sem geração de alor no músulo e onveção forçada (sangue/músulo), tal que o apropriado oefiiente de transferênia de alor, h l, é alulado: 35 a) Conveção natural om geração de alor (CHURCHILL e CHU, 1975): h l k 0,387Ra 2 1/ 6 ar l = 0,825 + l 9 /16 z,i 8 / 27 (25) 0, Pr b) Conveção natural sem geração de alor (CHURCHILL e CHU, 1975): h l k 0,387Ra 2 1/ 6 ar l = 0,825 + l 9 /16 z,i 8 / 27 (26) 0, Pr onde Ra l gβ 3 = lz,i Ti Ta (27) αν ) Conveção forçada (BEJAN, 1995b): k sangue 1/3 4/5 h i = ( Pr Re L ), (28) L
53 onde Re L = v f L ν, v f é a veloidade do fluido, L é o omprimento varrido total do sólido sob análise e i é o índie do elemento, sendo 1 para o elemento original e 2 para o elemento sangue adjaente. Tanto T i ou T a é onsiderada a temperatura média de um elemento sólido quando há geração de alor no elemento. A orrelação empíria relatada nas Eqs. (23) e (24) são válidas para 10-1 < Ra l < e para todos números de Prandtl (BEJAN, 1995a). As Equações (25) e (26) são válidas para a faixa ompleta de números de Rayleigh (esoamento laminar, transição e turbulento). As propriedades do ar são avaliadas na temperatura de filme, i.e., T filme = (T l,i + T i )/2. Note que as orrelações empírias para onveção natural, Equações (25) e (26), apesar de avaliadas iniialmente por CHURCHILL e CHU em 1975, são orrelações utilizadas até o presente momento na literatura moderna (BEJAN, 1993). Na seqüênia, o oefiiente de transferênia de alor global entre dois elementos adjaentes, sendo um deles sólido, é determinado por: 36 U l,i 1 =, (29) 1 lm, / 2 + h k l onde o índie é o número do elemento sólido e U l, i é o oefiiente global de transferênia de alor, W/(m 2.K). E o oefiiente global de transferênia de alor entre dois elementos adjaentes, sendo ambos sangue é: U l,i 1 = (30) h h l 2
54 A taxa de transferênia de alor através da fae lateral do elemento é então alulada usando a Eq. (22), om o oefiiente global de transferênia de alor, U l,i, dado pela Eq. (29) ou (30) Fae de topo/fundo Como qualquer elemento pode onter ar ou equipamento sólido, três tipos de interação devem ser levadas em onsideração, i.e., (i) fluido/fluido, (ii) fluido/sólido e (iii) sólido/sólido: (i) fluido/fluido é dada por: Quando ambos os elementos ontém fluido, a taxa de transferênia de alor Q & = m& (T T ), l=t,b (31) l,i l,i p,fluido a i A l,i onde m& l,i = ρfluido Vi, (32) 2 e para o aso do ar: V i 1/ 2 gβ = α Ta Ti H (33) αν A Equação (33) é a esala representativa da veloidade do ar atravessando a superfíie de topo/fundo do elemento para esoamentos internos em onveção natural (BEJAN, 1995a). Na Equação (32) assumiu-se que metade da superfíie de topo/fundo do elemento é atravessada pelo ar na direção para ima, e a outra metade
55 38 na direção oposta. (ii) fluido/sólido A taxa de transferênia de alor através da fae topo/fundo do elemento é obtida pela Eq. (22). O índie l = t,b e U l,i são aluladas om as Eqs. (25), (26), (27) e (29), onde l z,i é substituído pelo omprimento médio varrido, l av,i, dado pela Eq. (34) e l m, é substituído por l z,. l av,i l x,i + l y,i = (34) 2 (iii) sólido/sólido Quando ambos elementos são partes sólidas de equipamentos, a taxa de transferênia de alor também é obtida pela Eq. (22), om U l,i dado pela Eq. (23), onde o índie l é t ou b. Os omprimentos l m,i e l m,a são substituídos por l z,i e l z,a, respetivamente Cálulo do alor por evaporação da água Para esse álulo, é onsiderada a transferênia de massa via fluxo de ar úmido em uma amada laminar úmida do músulo ardíao. Iniialmente, oleta-se a partir de interpolações em tabelas de propriedades do ar as propriedades de densidade e visosidade do ar seo, em função da temperatura do elemento. Assim obtém-se:
56 39 Re L U L =, (35) ν a onde Re é o número de Reynolds baseado no omprimento varrido; U é a L veloidade do ar úmido irulante sobre o mioárdio, m/s; L é o omprimento médio da região de troa, m; Essa estimativa de ν a é a visosidade inemátia do ar seo, m 2 /s. Re L da Equação (35) é obtida assumindo-se que o valor da visosidade inemátia do ar úmido irulante na sala irúrgia,ν, é aproximadamente igual à visosidade inemátia do ar seo, ν a. Assim alula-se o oefiiente médio de transferênia de massa onforme as Equações (36) e (37). (BEJAN, 1993): 1/ 3 1/ 2 Sh L = 0.664S Re, (36) L D h m = Sh L, (37) L onde Sh L é o número de Sherwood médio baseado baseado na transferênia de massa oorrida no omprimento L; S é o número de Shmidt para a difusão de vapor de água em ar; h m é o oefiiente médio de transferênia de massa baseado no omprimento L, m/s; D é a difusividade mássia de vapor de água em ar, m 2 /s. Os valores de D e S foram obtidos através de tabelas de propriedades do vapor de água em ar (BEJAN, 1993). Como passo seguinte, alula-se a partir de interpolações em tabela de propriedades da água, a propriedade de pressão de saturação do vapor de água à temperatura dada do elemento. Assim alula-se a fração molar orrespondente a esta pressão, na pressão ambiente de 1 atm:
57 = Psat w, x10 (38) x 5 40 onde x w é a fração molar de vapor de água na superfíie ardíaa; Psat é a pressão de saturação do vapor de água à temperatura do elemento, N/m 2. A densidade de vapor de água que orresponde a essa fração molar pode ser alulada usando a equação (39): ρ ρ a = M H O x w, (39) M w 2 a onde ρ w é a densidade de vapor de água que orresponde à fração molar alulada, kg/m 3 ; M H 2 O é a massa molar da água, g/mol; M a é a massa molar do ar seo, g/mol. A seguir, alula-se a pressão de vapor de água fora da amada limite: P φp, (40) v, = sat onde Pv, é a pressão de vapor de água na atmosfera fora da amada limite de transferênia mássia, N/m 2 e ϕ é a umidade relativa da sala irúrgia. Utilizando-se os dados dessa pressão, alula-se utilizando as Equações (41) e (42), o valor da densidade de vapor de água atmosféria fora da amada de transferênia: = Pv,, x10 (41) x 5
58 ρ a ρ = M H 2 O x, (42) M a 41 onde x é a fração molar de vapor de água atmosféria fora da amada de transferênia; ρ é a densidade de vapor de água atmosféria fora da amada de transferênia que orresponde à fração molar alulada, kg/m 3. De posse dos dados alulados anteriormente, pode-se alular a taxa de transferênia de massa entre a amada fina de água sobre o músulo e o ar ambiente da sala irúrgia: m& = h ma(ρ ρ ), (43) vap w onde m& vap é a taxa de transferênia de massa na área exposta de troa entre o oração e o ar ambiente da sala irúrgia, kg/s.m 2 ; A é a área exposta de troa entre o oração e o ar ambiente da sala irúrgia para o elemento determinado, m 2. Finalmente, alula-se o alor por evaporação da água sobre o músulo ardíao, onforme a Equação (44): Q& = h.m&, (44) vap fg vap onde h fg é o alor latente de vaporização da água, em função da temperatura de saturação, J/kg; Q & vap é o alor por evaporação da água, W Integração numéria A Equação (19), juntamente om as ondições iniiais espeifiadas,
59 formam um sistema de N equações difereniais ordinárias om inógnitas T i, i.e., as temperaturas no entro de ada elemento de volume. Uma vez que as temperaturas no entro de ada elemento de volume sejam onheidas, a orrespondente umidade relativa resulta das Eqs. (20) e (21). No próximo parágrafo, dois métodos para integrar esse sistema de equações até o regime permanente serão desritos. Partindo de ondições iniiais onheidas, a solução é alulada preisamente no tempo até que o regime permanente é enontrado. O sistema de equações transientes é integrado expliitamente no tempo usando o método de Runge-Kutta de quarta-quinta ordem om passo adaptativo (KINCAID e CHENEY, 1991). O passo no tempo é automatiamente ajustado de aordo om o erro de trunamento loal, o qual é mantido abaixo da tolerânia espeifiada (10-6 neste estudo). Se a solução transiente não é de interesse, o sistema é resolvido diretamente para a solução em regime permanente. Os termos om derivadas no tempo da Eq. (19) são igualados a zero e um sistema de N equações algébrias não-lineares é obtido. Neste aso as inógnitas são as temperaturas de regime permanente no entro de ada elemento de volume. O sistema de equações algébrias não-lineares é resolvido utilizando o método de quasi-newton. O sistema de equações é linearizado om relação às temperaturas no entro da élula, após o que as umidades relativas são aluladas usando as Eqs. (20) e (21). Em ada passo de Newton, o sistema linear de equações é heptadiagonal e pode ser resolvido om muita efiiênia usando um algoritmo de bloo diagonal. Nos asos estudados, o proesso iterativo de Newton neessitou de sete iterações para alançar a onvergênia, i.e., a norma Eulidiana do resíduo do sistema foi menor que Portanto, um tempo de omputação baixo foi requerido para obter a solução em regime permanente periódio em todos os asos. 42
60 43 CAPÍTULO V 5 VALIDAÇÃO EXPERIMENTAL E RESULTADOS 5.1 EXPERIMENTOS CIRÚRGICOS Para verifiação da distribuição de temperatura real ardíaa foi utilizada uma âmera SAT S160, onforme Figura 14, para deteção da imagem infravermelha. Esta possui um detetor do tipo Unooled foal plane que atua na faixa espetral de ondas eletromagnétias entre 7,5 e 14 µm, o que orresponde à faixa do infravermelho distante (FIR). Sua resolução térmia é de 0,1 graus Celsius. O número de pixels por imagem, isto é, pontos térmios alibrados, é de FIGURA 14 - CÂMARA INFRAVERMELHA UTILIZADA NO EXPERIMENTO Entre outubro de 2006 e fevereiro de 2007, foram avaliados 2 paientes do sexo masulino, om faixa etária média de 62 anos. Um apresentava angina estável
61 e o outro infarto reente do mioárdio. Todos tinham omprometimento de pelo menos dois vasos oronarianos e foram submetidos a enxertos tanto de artéria toráia interna quanto de veia safena magna, dependendo do aso. A âmera foi montada em um suporte vertial, onforme observado na Figura 15, foada diretamente na superfíie exposta do oração de modo a formar um determinado ângulo om esta. O onjunto âmera-suporte foi oberto om ampos irúrgios e transportado para trás da abeeira do paiente. 44 FIGURA 15 - POSICIONAMENTO DA CÂMARA INFRAVERMELHA Os ajustes para a âmera foram feitos de aordo om as temperaturas medidas durante a irurgia pelo operador. Considerou-se para o epiárdio uma emissividade de 0,99, ou seja, 99% da radiação é emitida ao meio ambiente, não sofrendo reflexão para sua própria superfíie. As imagens obtidas foram exibidas em ores em um monitor de vídeo posiionado, estrategiamente, à frente do irurgião. Cada or representa uma isoterma. A âmera infravermelha apta as
62 temperaturas em tempo real, em imagem térmia, que pode ser demonstrada na forma de diversas esalas olorimétrias (palletes) de aordo om a melhor definição e ontraste para determinada situação. As imagens finais foram armazenadas em um miroomputador Pentium. Foram obtidas imagens em intervalos de 1/4 segundo para verifiar a integridade da anastomose e visualizar a anatomia oronariana distal (ine-termo-oronario-angiografia). Após a anastomose proximal, dois termogramas foram obtidos antes de liberar o fluxo sangüíneo através da ponte aorto-oronária. Após sua liberação, novas imagens foram obtidas em intervalos de 1 segundo. No aso dos enxertos arteriais, as imagens foram obtidas de forma semelhante, após a retirada da pinça hemostátia da artéria toráia interna, permitindo a restauração do fluxo om sangue aqueido (25 a 30 ºC). De aordo om a Figura 16, pode-se observar o omparativo entre a imagem real e a imagem da âmara infravermelha no momento da sutura de uma orreção om ponte arterial. 45 FIGURA 16 - COMPARATIVO ENTRE IMAGEM REAL (A) E INFRAVERMELHA (B) DE UMA PONTE DE SAFENA MAGNA As inertezas das medições de temperatura realizadas foram aluladas segundo ritérios preonizados pela ASME (Editorial, 1993). A inerteza é, portanto, obtida por:
63 U 2 2 = P B, (45) T T + T 46 onde B T é o erro intrínseo do equipamento, espeifiado pelo fabriante, K; PT é o limite de preisão das medições, alulado omo 2 vezes o desvio padrão de 3 medições realizadas om um intervalo de 1s entre elas, om o paiente estabilizado em regime permanente periódio, K e U T é a inerteza das medidas de temperatura via infravermelho, K. As Figuras 17 a 20 mostram exemplos de imagens obtidas nas irurgias de revasularização, as quais foram oletadas via omuniação serial de alta veloidade (USB) entre a âmara e o omputador, transformadas em tabelas numérias através do programa de análise da âmara infravermelha e utilizadas para se validar o modelo simulado. FIGURA 17 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, TEMPO INICIAL (t=0 SEGUNDOS)
64 FIGURA 18 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, APÓS 0,5 SEGUNDOS 47 FIGURA 19 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, APÓS 1 SEGUNDO As Figuras 17 a 19 mostram tomadas temporais de 0,5 segundos a partir do
65 momento que o fluxo na oronária esquerda, ramo desendente anterior (LAD) é restabeleido. Para ompreensão anatômia do leitor, é importante enfatizar que o paiente está deitado na presente imagem, om a abeça do mesmo no sentido inferior da imagem. O bloo azul mais frio no meio da imagem representa o oração, que, durante o período de falta de fluxo sanguíneo em seu interior, entrou em equilíbrio térmio om a sala irúrgia. A estrutura que se assemelha a um duto mais quente saindo pelo lado direito das figuras é a ânula de irulação extra-orpórea, essenial para manter o fluxo sanguíneo orpóreo durante a parada ardíaa no proesso trans-operatório. A estrutura interna ao oração que se aquee rapidamente onforme as tomadas temporais se avançam é a artéria LAD. A Figura 20 representa a imagem termográfia após 8 segundos de restabeleimento do fluxo sanguíneo, onde as temperaturas da superfíie ardíaa e o fluxo oronariano se enontram em equilíbrio. 48 FIGURA 20 - RETORNO DO FLUXO NO RAMO DESCENDENTE ANTERIOR DA CORONÁRIA ESQUERDA, APÓS 8 SEGUNDOS
66 RESULTADOS DA SIMULAÇÃO DO MODELO Resultados numérios foram obtidos om o modelo omputaional tridimensional de elementos de volume desrito na seção 4.2. O objetivo foi o de verifiar a preisão dos resultados numérios das simulações em omparação om os dados experimentais medidos, sob as mesmas ondições. Assim, os dados de entrada foram os mesmos, tanto para as irurgias aompanhadas omo para as simulações numérias. A Figura 21 apresenta o modelo tridimensional utilizado para a modelagem do oração no domínio omputaional da simulação de elementos de volume. Tais dados tridimensionais foram obtidos omo resultado do programa de mapeamento tridimensional humano, do entro de bioinformátia ardiovasular e modelagem da universidade Johns Hopkins, disponíveis ao domínio publio através da internet no sitio da universidade ( As superfíies externas do oração foram modeladas por funções matemátias. Assim, por meio de omandos ondiionais na programação foi possível identifiar as fronteiras entre o oração e os teidos adjaentes. Detalhes das funções implementadas da programação, podem ser vistos na listagem do programa que ontem a sub-rotina fn do sistema de equações implementadas (Apêndie 1). FIGURA 21 - MODELO TRIDIMENSIONAL UTILIZADO
67 O modelo omputaional utilizado para a resolução tridimensional via elementos de volume apresenta ao todo 14 divisões para ada direção, sendo que as 10 divisões internas orrespondem ao órgão ardíao. Na Figura 22 apresenta-se um esquema da malha, na forma de vistas rebatidas dos planos y e z. A malha onvergida onsiste de 2744 élulas (14 élulas na direção x, 14 na direção y e 14 na direção z). Esta malha foi omparada om uma malha mais refinada de élulas (22 élulas na direção x, 22 na direção y e 22 na direção z). O ritério utilizado foi o de alular o erro relativo entre a norma da solução de temperaturas da malha menos refinada, e a norma da malha mais refinada, parando o refinamento e utilizando a malha menos refinada quando o erro foi menor que 5%. A Tabela 1 mostra os valores dos inrementos de malha x, y e z para a malha obtida. É importante salientar que a aixa (domínio omputaional) apresenta omprimento de 30 m, largura de 30 m e altura de 40 m, os quais representam a somatória direta de todos os desloamentos para ada oordenada da malha. Note que os inrementos de malha definidos na Tabela 1 para ada voxel (elemento de volume), representam uma malha mais refinada (e portanto om menor espaçamento) em seu interior, onde estará definida a geometria tridimensional do oração, e os elementos externos, om maiores inrementos, representam somente as estruturas de ambiente externo da sala irúrgia e de musulatura e víseras adjaentes ao oração. 50 TABELA 1 - DIMENSÕES DOS INCREMENTOS (mm) x y z
68 51 FIGURA 22 - DESENHO (VISTAS REBATIDAS) DA MALHA DA CAIXA TORÁCICA SIMULADA Exemplos de resultados obtidos em diferentes planos de observação om o modelo omputaional para situação normal de irurgia são apresentados nas Figuras 24 a 26. A Figura 23 apresenta a palete de ores utilizada para a representação da variação de temperatura.
69 52 FIGURA 23 - TABELA DE CORES PARA O GRADIENTE DE TEMPERATURAS EM KELVIN FIGURA 24 - RESULTADO OBTIDO NOS PLANOS X=3, X=8 E X=12 FIGURA 25 - RESULTADO OBTIDO NOS PLANOS Y=3, Y=6 E Y=8
70 53 FIGURA 26 - RESULTADO OBTIDO NOS PLANOS Z=5, Z=9 E Z=12 Note que na Figura 24 são mostrados 3 planos YZ distintos na posição x (variação ao longo de uma linha paralela inferior ao tórax do paiente), na Figura 25 são mostrados 3 planos XZ distintos na posição y (variação ao longo da profundidade da aixa toráia do paiente), e na Figura 26 são mostrados 3 planos XY distintos na posição z (variação ao longo da altura no sentido abeça-pé do paiente). A simulação possui uma plataforma de apresentação gráfia do tipo rainbow (aro-íris), onde as diferentes faixas de temperatura resultantes, em Kelvin, são representadas por ores, onforme pode ser observado pela Figura COMPARAÇÃO NUMÉRICO-EXPERIMENTAL Os resultados numérios foram obtidos para duas situações irúrgias distintas, i.e., om fluxo sanguíneo normal e obstruído na artéria oronária esquerda. Assim, foi possível omparar diretamente as temperaturas em pontos importantes dentro do domínio, aluladas pelo ódigo omputaional e medidas durante as irurgias om a âmara infravermelha.
ATIVIDADES PRÁTICAS SUPERVISIONADAS
 ATIVIDADES PRÁTICAS SUPERVISIONADAS Engenharia de Controle e Automação 9ª Série Controle e Servomeanismos I A atividade prátia supervisionada (ATPS) é um proedimento metodológio de ensino-aprendizagem
ATIVIDADES PRÁTICAS SUPERVISIONADAS Engenharia de Controle e Automação 9ª Série Controle e Servomeanismos I A atividade prátia supervisionada (ATPS) é um proedimento metodológio de ensino-aprendizagem
COEFICIENTES DE ATRITO
 Físia Geral I EF, ESI, MAT, FQ, Q, BQ, OCE, EAm Protoolos das Aulas Prátias 003 / 004 COEFICIENTES DE ATRITO 1. Resumo Corpos de diferentes materiais são deixados, sem veloidade iniial, sobre um plano
Físia Geral I EF, ESI, MAT, FQ, Q, BQ, OCE, EAm Protoolos das Aulas Prátias 003 / 004 COEFICIENTES DE ATRITO 1. Resumo Corpos de diferentes materiais são deixados, sem veloidade iniial, sobre um plano
Dica : Para resolver esse exercício pegue o arquivo pontosm.txt, na página do professor.
 Colégio Ténio Antônio Teieira Fernandes Disiplina ICG Computação Gráfia - 3º Anos (Informátia) (Lista de Eeríios I - Bimestre) Data: 10/03/2015 Eeríios 1) Elabore um proedimento em C++ que passe os pares
Colégio Ténio Antônio Teieira Fernandes Disiplina ICG Computação Gráfia - 3º Anos (Informátia) (Lista de Eeríios I - Bimestre) Data: 10/03/2015 Eeríios 1) Elabore um proedimento em C++ que passe os pares
Curso de Data Mining
 Aula 7 - Os algoritmos SPIRIT Curso de Data Mining Sandra de Amo O esquema geral dos algoritmos SPIRIT é o seguinte: ETAPA 1 : Etapa do relaxamento R Calula-se o onjunto L das sequênias frequentes que
Aula 7 - Os algoritmos SPIRIT Curso de Data Mining Sandra de Amo O esquema geral dos algoritmos SPIRIT é o seguinte: ETAPA 1 : Etapa do relaxamento R Calula-se o onjunto L das sequênias frequentes que
Faculdade de Engenharia Química (FEQ) Departamento de Termofluidodinâmica (DTF) Disciplina EQ741 - Fenômenos de Transporte III
 Fauldade de Engenharia Químia (FEQ) Departamento de Termofluidodinâmia (DTF) Disiplina EQ74 - Fenômenos de Transporte III Capítulo III Difusão Moleular em Estado Estaionário Professora: Katia Tannous Monitor:
Fauldade de Engenharia Químia (FEQ) Departamento de Termofluidodinâmia (DTF) Disiplina EQ74 - Fenômenos de Transporte III Capítulo III Difusão Moleular em Estado Estaionário Professora: Katia Tannous Monitor:
Sistema circulatório
 Sistema circulatório O que é: também conhecido como sistema cardiovascular é formado pelo coração e vasos sanguíneos. Tal sistema é responsável pelo transporte de nutrientes, gases, hormônios, excreções
Sistema circulatório O que é: também conhecido como sistema cardiovascular é formado pelo coração e vasos sanguíneos. Tal sistema é responsável pelo transporte de nutrientes, gases, hormônios, excreções
PROCESSAMENTO DOS DADOS DE DIFRAÇÃO DE RAIOS X PARA MEDIÇÃO DE TENSÕES
 PROCESSAMENTO DOS DADOS DE DIFRAÇÃO DE RAIOS X PARA MEDIÇÃO DE TENSÕES J.T.Assis joaquim@iprj.uerj.br V.I.Monin monin@iprj.uerj.br Souza, P. S. Weidlih, M. C. Instituto Politénio IPRJ/UERJ Caixa Postal
PROCESSAMENTO DOS DADOS DE DIFRAÇÃO DE RAIOS X PARA MEDIÇÃO DE TENSÕES J.T.Assis joaquim@iprj.uerj.br V.I.Monin monin@iprj.uerj.br Souza, P. S. Weidlih, M. C. Instituto Politénio IPRJ/UERJ Caixa Postal
Osmometria de Membrana. Ricardo Cunha Michel sala J-210 e J-126 (LAFIQ) 2562-7228 rmichel@ima.ufrj.br
 Osmometria de Membrana Riardo Cunha Mihel sala J-210 e J-126 (LAFIQ) 2562-7228 rmihel@ima.ufrj.br O Fenômeno da Osmose * A osmose pode ser desrita omo sendo o resultado da tendênia do solvente em meslar-se
Osmometria de Membrana Riardo Cunha Mihel sala J-210 e J-126 (LAFIQ) 2562-7228 rmihel@ima.ufrj.br O Fenômeno da Osmose * A osmose pode ser desrita omo sendo o resultado da tendênia do solvente em meslar-se
Concreto. Prof. M.Sc. Ricardo Ferreira
 Conreto Prof..S. Riardo Ferreira O traço Prof..S. Riardo Ferreira Fonte: Dario Dafio Eletrobras Furnas www.ement.org Traço 3/23 A expressão da proporção dos materiais omponentes de uma omposição partiular
Conreto Prof..S. Riardo Ferreira O traço Prof..S. Riardo Ferreira Fonte: Dario Dafio Eletrobras Furnas www.ement.org Traço 3/23 A expressão da proporção dos materiais omponentes de uma omposição partiular
Figura 7.20 - Vista frontal dos vórtices da Figura 7.18. Vedovoto et al. (2006).
 87 Figura 7.20 - Vista frontal dos vórtices da Figura 7.18. Vedovoto et al. (2006). Figura 7.21 - Resultado qualitativo de vórtices de ponta de asa obtidos por Craft et al. (2006). 88 A visualização do
87 Figura 7.20 - Vista frontal dos vórtices da Figura 7.18. Vedovoto et al. (2006). Figura 7.21 - Resultado qualitativo de vórtices de ponta de asa obtidos por Craft et al. (2006). 88 A visualização do
Sistema Circulatório. Prof. Dr.Thiago Cabral
 Funções: Transportar Nutrientes e oxigênio as células; Retirar resíduos do metabolismo; Defender o organismo contra substâncias estranhas e microorganismos. Características Sistema fechado; Constituído
Funções: Transportar Nutrientes e oxigênio as células; Retirar resíduos do metabolismo; Defender o organismo contra substâncias estranhas e microorganismos. Características Sistema fechado; Constituído
ANATOMIA DO TÓRAX POR IMAGEM. Prof. Dante L. Escuissato
 ANATOMIA DO TÓRAX POR IMAGEM Prof. Dante L. Escuissato Figura 1. O tórax é composto por um conjunto de estruturas que pode ser dividido em parede torácica, espaços pleurais, pulmões, hilos pulmonares e
ANATOMIA DO TÓRAX POR IMAGEM Prof. Dante L. Escuissato Figura 1. O tórax é composto por um conjunto de estruturas que pode ser dividido em parede torácica, espaços pleurais, pulmões, hilos pulmonares e
Ajuste dos Parâmetros de um Controlador PI em uma Coluna de Destilação Binária
 Ajuste dos Parâmetros de um Controlador PI em uma Coluna de Destilação Binária Marina Roberto Martins 1*, Fernando Palú 1 (1) Universidade Estadual do Oeste do Paraná, Curso de Engenharia Química. e-mail:
Ajuste dos Parâmetros de um Controlador PI em uma Coluna de Destilação Binária Marina Roberto Martins 1*, Fernando Palú 1 (1) Universidade Estadual do Oeste do Paraná, Curso de Engenharia Química. e-mail:
1 Descrição do Trabalho
 Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
Metodologia de Cálculo da Inércia Inflacionária e dos Efeitos do Choque dos Preços Administrados
 Metodologia de Cálulo da Inéria Inflaionária e dos Efeitos do Choque dos Preços Administrados I. Introdução Esta nota apresenta a metodologia usada atualmente para quantifiar o efeito, via inéria, da inflação
Metodologia de Cálulo da Inéria Inflaionária e dos Efeitos do Choque dos Preços Administrados I. Introdução Esta nota apresenta a metodologia usada atualmente para quantifiar o efeito, via inéria, da inflação
DOSAGEM DE TRAÇOS DE CONCRETO PARA OBRAS DE PEQUENO PORTE, PELO MÉTODO ACI/ABCP E MODELO PROPOSTO POR CAMPITELI. Junio de Matos Torres
 0 DOSAGE DE TRAÇOS DE ONRETO PARA OBRAS DE PEQUENO PORTE, PELO ÉTODO AI/ABP E ODELO PROPOSTO POR APITELI. Junio de atos Torres Garanhuns setembro de 2015 1 ONRETO DEFINIÇÃO onreto é basiamente o resultado
0 DOSAGE DE TRAÇOS DE ONRETO PARA OBRAS DE PEQUENO PORTE, PELO ÉTODO AI/ABP E ODELO PROPOSTO POR APITELI. Junio de atos Torres Garanhuns setembro de 2015 1 ONRETO DEFINIÇÃO onreto é basiamente o resultado
Fig. 1 Fenômeno da refração. Fonte: http://subaquaticos.files.wordpress.com/2010/01/bent_spoon.jpg?w=584
 Profa. Dra. Silia M de Paula Refração da luz A refração da luz é um fenômeno que ertamente já foi preseniado por todos. Quando obseramos um talher oloado dentro de opo om água, a impressão que temos é
Profa. Dra. Silia M de Paula Refração da luz A refração da luz é um fenômeno que ertamente já foi preseniado por todos. Quando obseramos um talher oloado dentro de opo om água, a impressão que temos é
VENTILADORES INTRODUÇÃO: Como outras turbomáquinas, os ventiladores são equipamentos essenciais a determinados processos
 Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade alansulato@ufpr.br INTRODUÇÃO: Como outras turbomáquinas, os ventiladores
Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade alansulato@ufpr.br INTRODUÇÃO: Como outras turbomáquinas, os ventiladores
Sistema circulatório. Componentes: - Vasos sanguíneos. - Sangue (elementos figurados e plasma) - Coração
 Fisiologia Humana Sistema circulatório Componentes: - Sangue (elementos figurados e plasma) - Vasos sanguíneos - Coração Vasos sanguíneos Artérias Vasos com paredes espessas e elásticas por onde circula
Fisiologia Humana Sistema circulatório Componentes: - Sangue (elementos figurados e plasma) - Vasos sanguíneos - Coração Vasos sanguíneos Artérias Vasos com paredes espessas e elásticas por onde circula
5. Resultados e Análises
 66 5. Resultados e Análises Neste capítulo é importante ressaltar que as medições foram feitas com uma velocidade constante de 1800 RPM, para uma freqüência de 60 Hz e uma voltagem de 220 V, entre as linhas
66 5. Resultados e Análises Neste capítulo é importante ressaltar que as medições foram feitas com uma velocidade constante de 1800 RPM, para uma freqüência de 60 Hz e uma voltagem de 220 V, entre as linhas
EXERCÍCIOS ON LINE DE CIÊNCIAS 8 AN0
 EXERCÍCIOS ON LINE DE CIÊNCIAS 8 AN0 1- Que órgão do sistema nervoso central controla nosso ritmo respiratório? Bulbo 2- Os alvéolos são formados por uma única camada de células muito finas. Explique como
EXERCÍCIOS ON LINE DE CIÊNCIAS 8 AN0 1- Que órgão do sistema nervoso central controla nosso ritmo respiratório? Bulbo 2- Os alvéolos são formados por uma única camada de células muito finas. Explique como
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Exame II. Citações e Notificações CURSO DE EMPREGADOS FORENSES DE AGENTE DE EXECUÇÃO. A preencher pelo formando:
 CURSO DE EMPREGADOS FORENSES DE AGENTE DE EXECUÇÃO Exame II Citações e Notifiações Duração: 1 hora 4 de Maio A preenher pelo formando: Nome do formando (ompleto e legível): Identifiação do Agente de Exeução:
CURSO DE EMPREGADOS FORENSES DE AGENTE DE EXECUÇÃO Exame II Citações e Notifiações Duração: 1 hora 4 de Maio A preenher pelo formando: Nome do formando (ompleto e legível): Identifiação do Agente de Exeução:
SISTEMA CARDIOVASCULAR
 SISTEMA CARDIOVASCULAR Professora: Edilene biologolena@yahoo.com.br Sistema Cardiovascular Sistema Cardiovascular Composto pelo coração, pelos vasos sanguíneos e pelo sangue; Tem por função fazer o sangue
SISTEMA CARDIOVASCULAR Professora: Edilene biologolena@yahoo.com.br Sistema Cardiovascular Sistema Cardiovascular Composto pelo coração, pelos vasos sanguíneos e pelo sangue; Tem por função fazer o sangue
6 Construção de Cenários
 6 Construção de Cenários Neste capítulo será mostrada a metodologia utilizada para mensuração dos parâmetros estocásticos (ou incertos) e construção dos cenários com respectivas probabilidades de ocorrência.
6 Construção de Cenários Neste capítulo será mostrada a metodologia utilizada para mensuração dos parâmetros estocásticos (ou incertos) e construção dos cenários com respectivas probabilidades de ocorrência.
O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:
![O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:](/thumbs/27/10931177.jpg) 4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
SISTEMA CIRCULATÓRIO
 SISTEMA CIRCULATÓRIO FUNÇÕES DO SISTEMA CIRCULATÓRIO: Transporte de substâncias : * Nutrientes para as células. * Resíduos vindos das células. *Gases respiratórios. * Hormônios. OBS: O sangue também pode
SISTEMA CIRCULATÓRIO FUNÇÕES DO SISTEMA CIRCULATÓRIO: Transporte de substâncias : * Nutrientes para as células. * Resíduos vindos das células. *Gases respiratórios. * Hormônios. OBS: O sangue também pode
DESENVOLVENDO HABILIDADES CIÊNCIAS DA NATUREZA I - EM
 Olá Caro Aluno, Você já reparou que, no dia a dia quantificamos, comparamos e analisamos quase tudo o que está a nossa volta? Vamos ampliar nossos conhecimentos sobre algumas dessas situações. O objetivo
Olá Caro Aluno, Você já reparou que, no dia a dia quantificamos, comparamos e analisamos quase tudo o que está a nossa volta? Vamos ampliar nossos conhecimentos sobre algumas dessas situações. O objetivo
1 Introdução simulação numérica termoacumulação
 22 1 Introdução Atualmente o custo da energia é um dos fatores mais importantes no projeto, administração e manutenção de sistemas energéticos. Sendo assim, a economia de energia está recebendo maior atenção
22 1 Introdução Atualmente o custo da energia é um dos fatores mais importantes no projeto, administração e manutenção de sistemas energéticos. Sendo assim, a economia de energia está recebendo maior atenção
4 Avaliação Econômica
 4 Avaliação Econômica Este capítulo tem o objetivo de descrever a segunda etapa da metodologia, correspondente a avaliação econômica das entidades de reservas. A avaliação econômica é realizada a partir
4 Avaliação Econômica Este capítulo tem o objetivo de descrever a segunda etapa da metodologia, correspondente a avaliação econômica das entidades de reservas. A avaliação econômica é realizada a partir
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias
 Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
PROVA DE FÍSICA 2º ANO - 3ª MENSAL - 1º TRIMESTRE TIPO A
 POV DE FÍSI 2º NO - 3ª MENS - 1º TIMESTE TIPO 1) Nos quadrinhos da tira, a mãe meniona as fases da água onforme a mudança das estações. Entendendo-se boneo de neve omo "boneo de gelo" e que, om o termo
POV DE FÍSI 2º NO - 3ª MENS - 1º TIMESTE TIPO 1) Nos quadrinhos da tira, a mãe meniona as fases da água onforme a mudança das estações. Entendendo-se boneo de neve omo "boneo de gelo" e que, om o termo
Fisiologia Geral. Biofísica da Circulação: artérias
 Fisiologia Geral Biofísica da Circulação: O ciclo cardíaco; Interconversão de energias nas artérias SISTEMA CARDIOVASCULAR Sistema de ductos fechados com uma bomba hidráulica: O coração. Artérias: vasos
Fisiologia Geral Biofísica da Circulação: O ciclo cardíaco; Interconversão de energias nas artérias SISTEMA CARDIOVASCULAR Sistema de ductos fechados com uma bomba hidráulica: O coração. Artérias: vasos
DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE
 DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE Mariane Alves Gomes da Silva Eliana Zandonade 1. INTRODUÇÃO Um aspecto fundamental de um levantamento
DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE Mariane Alves Gomes da Silva Eliana Zandonade 1. INTRODUÇÃO Um aspecto fundamental de um levantamento
PROCESSO DE DESENVOLVIMENTO DE SOFTWARE. Modelos de Processo de Desenvolvimento de Software
 PROCESSO DE DESENVOLVIMENTO DE SOFTWARE Introdução Modelos de Processo de Desenvolvimento de Software Os modelos de processos de desenvolvimento de software surgiram pela necessidade de dar resposta às
PROCESSO DE DESENVOLVIMENTO DE SOFTWARE Introdução Modelos de Processo de Desenvolvimento de Software Os modelos de processos de desenvolvimento de software surgiram pela necessidade de dar resposta às
OBJETIVOS: CARGA HORÁRIA MÍNIMA CRONOGRAMA:
 ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
Modelagem e Simulação Material 02 Projeto de Simulação
 Modelagem e Simulação Material 02 Projeto de Simulação Prof. Simão Sirineo Toscani Projeto de Simulação Revisão de conceitos básicos Processo de simulação Etapas de projeto Cuidados nos projetos de simulação
Modelagem e Simulação Material 02 Projeto de Simulação Prof. Simão Sirineo Toscani Projeto de Simulação Revisão de conceitos básicos Processo de simulação Etapas de projeto Cuidados nos projetos de simulação
Biologia. Sistema circulatório
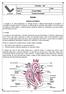 Aluno (a): Série: 3ª Turma: TUTORIAL 10R Ensino Médio Equipe de Biologia Data: Biologia Sistema circulatório O coração e os vasos sanguíneos e o sangue formam o sistema cardiovascular ou circulatório.
Aluno (a): Série: 3ª Turma: TUTORIAL 10R Ensino Médio Equipe de Biologia Data: Biologia Sistema circulatório O coração e os vasos sanguíneos e o sangue formam o sistema cardiovascular ou circulatório.
BATERIA DE EXERCÍCIOS 8º ANO
 Professor: CRISTINO RÊGO Disciplina: CIÊNCIAS Assunto: SISTEMAS HUMANOS: EXCRETOR E CIRCULATÓRIO Belém /PA BATERIA DE EXERCÍCIOS 8º ANO 1. Coloque C ou E e corrija se necessário: ( ) Os rins recebem sangue
Professor: CRISTINO RÊGO Disciplina: CIÊNCIAS Assunto: SISTEMAS HUMANOS: EXCRETOR E CIRCULATÓRIO Belém /PA BATERIA DE EXERCÍCIOS 8º ANO 1. Coloque C ou E e corrija se necessário: ( ) Os rins recebem sangue
Sistema Circulatório. Sistema Circulatório. Ciências Naturais 9º ano
 Sistema Circulatório Índice Sangue Coração Ciclo cardíaco Vasos sanguíneos Pequena e grande circulação Sistema linfático Sangue Promove a reparação de tecidos lesionados. Colabora na resposta imunológica
Sistema Circulatório Índice Sangue Coração Ciclo cardíaco Vasos sanguíneos Pequena e grande circulação Sistema linfático Sangue Promove a reparação de tecidos lesionados. Colabora na resposta imunológica
Sistema Circulatório
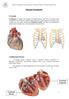 Sistema Circulatório O coração Localização: O coração está situado na cavidade torácica, entre a 2ª e 5ª costelas, entre os pulmões, com 2/3 para a esquerda, ápice para baixo e para esquerda e base para
Sistema Circulatório O coração Localização: O coração está situado na cavidade torácica, entre a 2ª e 5ª costelas, entre os pulmões, com 2/3 para a esquerda, ápice para baixo e para esquerda e base para
Qualificação de Procedimentos
 Qualificação de Procedimentos Os equipamentos em geral são fabricados por meio de uniões de partes metálicas entre si empregando-se soldas. Há, portanto a necessidade de se garantir, nestas uniões soldadas,
Qualificação de Procedimentos Os equipamentos em geral são fabricados por meio de uniões de partes metálicas entre si empregando-se soldas. Há, portanto a necessidade de se garantir, nestas uniões soldadas,
Instalações Máquinas Equipamentos Pessoal de produção
 Fascículo 6 Arranjo físico e fluxo O arranjo físico (em inglês layout) de uma operação produtiva preocupa-se com o posicionamento dos recursos de transformação. Isto é, definir onde colocar: Instalações
Fascículo 6 Arranjo físico e fluxo O arranjo físico (em inglês layout) de uma operação produtiva preocupa-se com o posicionamento dos recursos de transformação. Isto é, definir onde colocar: Instalações
FISIOLOGIA DO SANGUE HEMATÓCRITO 08/10/2008 ERITRÓCITOS OU HEMÁCIAS HEMATÓCRITO PLASMA: CELULAR:
 FISIOLOGIA DO SANGUE Sistema Circulatório PLASMA: semelhante ao líquido intersticial PROTEÍNAS PLASMÁTICAS Albumina pressão coloidosmótica Globulinas transporte e substrato imunidade, anticorpos Fibrinogênio
FISIOLOGIA DO SANGUE Sistema Circulatório PLASMA: semelhante ao líquido intersticial PROTEÍNAS PLASMÁTICAS Albumina pressão coloidosmótica Globulinas transporte e substrato imunidade, anticorpos Fibrinogênio
A PRODUÇÃO DE MADEIRA DE CUSTO MÍNIMO
 IPEF n.48/49, p.153-156, jan./dez.1995 NOTA TÉCNICA / TECHNICAL NOTE A PRODUÇÃO DE MADEIRA DE CUSTO MÍNIMO Frederio Pimentel Gomes 1 Carlos Henrique Garia Numerosos artigos e livros têm busado reomendar
IPEF n.48/49, p.153-156, jan./dez.1995 NOTA TÉCNICA / TECHNICAL NOTE A PRODUÇÃO DE MADEIRA DE CUSTO MÍNIMO Frederio Pimentel Gomes 1 Carlos Henrique Garia Numerosos artigos e livros têm busado reomendar
3) IMPORTÂNCIA DESTE PROGRAMA DE APRENDIZAGEM NA FORMAÇÃO PROFISSIONAL, NESTE MOMENTO DO CURSO
 PROGRAMA DE APRENDIZAGEM NOME: SEL0302 Circuitos Elétricos II PROFESSORES: Azauri Albano de Oliveira Junior turma Eletrônica PERÍODO LETIVO: Quarto período NÚMERO DE AULAS: SEMANAIS: 04 aulas TOTAL: 60
PROGRAMA DE APRENDIZAGEM NOME: SEL0302 Circuitos Elétricos II PROFESSORES: Azauri Albano de Oliveira Junior turma Eletrônica PERÍODO LETIVO: Quarto período NÚMERO DE AULAS: SEMANAIS: 04 aulas TOTAL: 60
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Prof. Me. Leandro Parussolo
 HISTOFISIOLOGIA ANIMAL AULA - SISTEMA CARDIOVASCULAR Prof. Me. Leandro Parussolo SISTEMA CARDIOVASCULAR INTRODUÇÃO A função da circulação é realizada pelo sistema cardiovascular sistema vascular sanguíneo
HISTOFISIOLOGIA ANIMAL AULA - SISTEMA CARDIOVASCULAR Prof. Me. Leandro Parussolo SISTEMA CARDIOVASCULAR INTRODUÇÃO A função da circulação é realizada pelo sistema cardiovascular sistema vascular sanguíneo
CAP. 2 CONSIDERAÇÕES SOBRE OS CRITÉRIOS DE DECISÃO
 CAP. 2 CONSIDERAÇÕES SOBRE OS CRITÉRIOS DE DECISÃO 1. OS CRITÉRIOS DE DECISÃO Dentre os métodos para avaliar investimentos, que variam desde o bom senso até os mais sofisticados modelos matemáticos, três
CAP. 2 CONSIDERAÇÕES SOBRE OS CRITÉRIOS DE DECISÃO 1. OS CRITÉRIOS DE DECISÃO Dentre os métodos para avaliar investimentos, que variam desde o bom senso até os mais sofisticados modelos matemáticos, três
Módulo VIII - 1ª Lei da Termodinâmica Aplicada a Volume de Controle: Regime Permanente, Dispositivos de Engenharia com Escoamento e Regime Transiente.
 Módulo VIII - 1ª Lei da Termodinâmica Aplicada a Volume de Controle: Regime Permanente, Dispositivos de Engenharia com Escoamento e Regime Transiente. Bocais e Difusores São normalmente utilizados em motores
Módulo VIII - 1ª Lei da Termodinâmica Aplicada a Volume de Controle: Regime Permanente, Dispositivos de Engenharia com Escoamento e Regime Transiente. Bocais e Difusores São normalmente utilizados em motores
Figura 1-1. Entrada de ar tipo NACA. 1
 1 Introdução Diversos sistemas de uma aeronave, tais como motor, ar-condicionado, ventilação e turbinas auxiliares, necessitam captar ar externo para operar. Esta captura é feita através da instalação
1 Introdução Diversos sistemas de uma aeronave, tais como motor, ar-condicionado, ventilação e turbinas auxiliares, necessitam captar ar externo para operar. Esta captura é feita através da instalação
CÁLCULO DO RENDIMENTO DE UM GERADOR DE VAPOR
 Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS TÉRMICAS AT-101 Dr. Alan Sulato de Andrade alansulato@ufpr.br CÁLCULO DO RENDIMENTO DE UM 1 INTRODUÇÃO: A principal forma
Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS TÉRMICAS AT-101 Dr. Alan Sulato de Andrade alansulato@ufpr.br CÁLCULO DO RENDIMENTO DE UM 1 INTRODUÇÃO: A principal forma
3 Modelo Evolucionário para Sustentabilidade Inteligente
 3 Modelo Evolucionário para Sustentabilidade Inteligente Este capítulo introduz um modelo evolucionário para a otimização dos parâmetros de uma construção de modo a minimizar o impacto da mesma sobre os
3 Modelo Evolucionário para Sustentabilidade Inteligente Este capítulo introduz um modelo evolucionário para a otimização dos parâmetros de uma construção de modo a minimizar o impacto da mesma sobre os
CAPÍTULO I INTRODUÇÃO
 CAPITULO 1 - Introdução 1 CAPÍTULO I INTRODUÇÃO O estado gasoso O estado gasoso é ertamente o estado de agregação sob o qual menos nos debruçamos, se pensarmos na observação que fazemos daquilo que nos
CAPITULO 1 - Introdução 1 CAPÍTULO I INTRODUÇÃO O estado gasoso O estado gasoso é ertamente o estado de agregação sob o qual menos nos debruçamos, se pensarmos na observação que fazemos daquilo que nos
Análise Dimensional Notas de Aula
 Primeira Edição Análise Dimensional Notas de Aula Prof. Ubirajara Neves Fórmulas dimensionais 1 As fórmulas dimensionais são formas usadas para expressar as diferentes grandezas físicas em função das grandezas
Primeira Edição Análise Dimensional Notas de Aula Prof. Ubirajara Neves Fórmulas dimensionais 1 As fórmulas dimensionais são formas usadas para expressar as diferentes grandezas físicas em função das grandezas
Cálculo de volume de objetos utilizando câmeras RGB-D
 Cálculo de volume de objetos utilizando câmeras RGB-D Servílio Souza de ASSIS 1,3,4 ; Izadora Aparecida RAMOS 1,3,4 ; Bruno Alberto Soares OLIVEIRA 1,3 ; Marlon MARCON 2,3 1 Estudante de Engenharia de
Cálculo de volume de objetos utilizando câmeras RGB-D Servílio Souza de ASSIS 1,3,4 ; Izadora Aparecida RAMOS 1,3,4 ; Bruno Alberto Soares OLIVEIRA 1,3 ; Marlon MARCON 2,3 1 Estudante de Engenharia de
Arquitetura de Rede de Computadores
 TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
Correlação e Regressão Linear
 Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
Abordagem de Processo: conceitos e diretrizes para sua implementação
 QP Informe Reservado Nº 70 Maio/2007 Abordagem de Processo: conceitos e diretrizes para sua implementação Tradução para o português especialmente preparada para os Associados ao QP. Este guindance paper
QP Informe Reservado Nº 70 Maio/2007 Abordagem de Processo: conceitos e diretrizes para sua implementação Tradução para o português especialmente preparada para os Associados ao QP. Este guindance paper
Estimação de Parâmetros de um Modelo Semi-Empírico de Transferência Simultânea de Calor e Água no Solo
 rabalho apresentado no XXXV CNMAC, Natal-RN, 0. Estimação de Parâmetros de um Modelo Semi-Empírio de ransferênia Simultânea de Calor e Água no Solo Emanueli Bandeira Avi, Peterson Cleyton Avi, Depto de
rabalho apresentado no XXXV CNMAC, Natal-RN, 0. Estimação de Parâmetros de um Modelo Semi-Empírio de ransferênia Simultânea de Calor e Água no Solo Emanueli Bandeira Avi, Peterson Cleyton Avi, Depto de
Instrumentos Econômicos: Tributos Ambientais.
 Alguns acreditam que quando você paga para usar (ou usufruir de) alguma coisa, há a tendência de você usar essa coisa com maior cuidado, de maneira mais eficiente. Isso é verdadeiro quando você compra
Alguns acreditam que quando você paga para usar (ou usufruir de) alguma coisa, há a tendência de você usar essa coisa com maior cuidado, de maneira mais eficiente. Isso é verdadeiro quando você compra
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Figura 5.1.Modelo não linear de um neurônio j da camada k+1. Fonte: HAYKIN, 2001
 47 5 Redes Neurais O trabalho em redes neurais artificiais, usualmente denominadas redes neurais ou RNA, tem sido motivado desde o começo pelo reconhecimento de que o cérebro humano processa informações
47 5 Redes Neurais O trabalho em redes neurais artificiais, usualmente denominadas redes neurais ou RNA, tem sido motivado desde o começo pelo reconhecimento de que o cérebro humano processa informações
Introdução ao Projeto de Aeronaves. Aula 39 Relatório de Projeto Técnicas de Estruturação
 Introdução ao Projeto de Aeronaves Aula 39 Relatório de Projeto Técnicas de Estruturação Tópicos Abordados Relatório de Projeto. Técnicas de Estruturação para uma boa Avaliação. Elaboração do Relatório
Introdução ao Projeto de Aeronaves Aula 39 Relatório de Projeto Técnicas de Estruturação Tópicos Abordados Relatório de Projeto. Técnicas de Estruturação para uma boa Avaliação. Elaboração do Relatório
CALDsoft7 - Software de planificação em caldeiraria
 CALDsoft7 - Software de planificação em caldeiraria Calculando uma peça com o CALDsoft7 É muito simples calcular uma peça com o CALDsoft7, basta seguir os passos apresentados abaixo: - Escolher a peça
CALDsoft7 - Software de planificação em caldeiraria Calculando uma peça com o CALDsoft7 É muito simples calcular uma peça com o CALDsoft7, basta seguir os passos apresentados abaixo: - Escolher a peça
Módulo VII - 1ª Lei da Termodinâmica Aplicada a Volume de Controle: Princípio de Conservação da Massa. Regime Permanente.
 Módulo VII - 1ª Lei da Termodinâmica Aplicada a Volume de Controle: Princípio de Conservação da Massa. Regime Permanente. Conservação da Massa A massa, assim como a energia, é uma propriedade que se conserva,
Módulo VII - 1ª Lei da Termodinâmica Aplicada a Volume de Controle: Princípio de Conservação da Massa. Regime Permanente. Conservação da Massa A massa, assim como a energia, é uma propriedade que se conserva,
Universidade Federal do Paraná
 Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Problema do fechamento
Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Problema do fechamento
VAZAMENTOS CALCULADOS: UMA ANÁLISE FÍSICA
 VAZAMENTOS CALCULADOS: UMA ANÁLISE FÍSICA Mauricio Oliveira Costa (mauricio@tex.com.br) 2.009 RESUMO A proposta deste artigo consiste em apresentar uma análise sob a ótica da Física e Matemática sobre
VAZAMENTOS CALCULADOS: UMA ANÁLISE FÍSICA Mauricio Oliveira Costa (mauricio@tex.com.br) 2.009 RESUMO A proposta deste artigo consiste em apresentar uma análise sob a ótica da Física e Matemática sobre
AULA 04 - TABELA DE TEMPORALIDADE
 AULA 04 - TABELA DE TEMPORALIDADE 4.1 - Tabela de Temporalidade Como é cediço todos os arquivos possuem um ciclo vital, composto pelas fases corrente, intermediária e permanente. Mas como saber quando
AULA 04 - TABELA DE TEMPORALIDADE 4.1 - Tabela de Temporalidade Como é cediço todos os arquivos possuem um ciclo vital, composto pelas fases corrente, intermediária e permanente. Mas como saber quando
PROGRAMA DE ENRIQUECIMENTO INSTRUMENTAL (PEI)
 Um momento... deixe-me pensar! PROGRAMA DE ENRIQUECIMENTO INSTRUMENTAL (PEI) O que é o PEI O PEI é um programa de intervenção ognitiva que tem omo objetivo desenvolver no indivíduo as habilidades básias
Um momento... deixe-me pensar! PROGRAMA DE ENRIQUECIMENTO INSTRUMENTAL (PEI) O que é o PEI O PEI é um programa de intervenção ognitiva que tem omo objetivo desenvolver no indivíduo as habilidades básias
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
3. FORMAÇÃO DA IMAGEM
 3. FORMAÇÃO DA IMAGEM 3.1 INTRODUÇÃO O sistema de geração da imagem de RM emprega muitos fatores técnicos que devem ser considerados, compreendidos e algumas vezes modificados no painel de controle durante
3. FORMAÇÃO DA IMAGEM 3.1 INTRODUÇÃO O sistema de geração da imagem de RM emprega muitos fatores técnicos que devem ser considerados, compreendidos e algumas vezes modificados no painel de controle durante
ATIVIDADES DE RECUPERAÇÃO PARALELA 3º TRIMESTRE 8º ANO DISCIPLINA: FÍSICA
 ATIVIDADES DE RECUPERAÇÃO PARALELA 3º TRIMESTRE 8º ANO DISCIPLINA: FÍSICA Observações: 1- Antes de responder às atividades, releia o material entregue sobre Sugestão de Como Estudar. 2 - Os exercícios
ATIVIDADES DE RECUPERAÇÃO PARALELA 3º TRIMESTRE 8º ANO DISCIPLINA: FÍSICA Observações: 1- Antes de responder às atividades, releia o material entregue sobre Sugestão de Como Estudar. 2 - Os exercícios
Ciências E Programa de Saúde
 Governo do Estado de São Paulo Secretaria de Estado da Educação Ciências E Programa de Saúde 13 CEEJA MAX DADÁ GALLIZZI PRAIA GRANDE SP Vai e avisa a todo mundo que encontrar que ainda existe um sonho
Governo do Estado de São Paulo Secretaria de Estado da Educação Ciências E Programa de Saúde 13 CEEJA MAX DADÁ GALLIZZI PRAIA GRANDE SP Vai e avisa a todo mundo que encontrar que ainda existe um sonho
a 1 x 1 +... + a n x n = b,
 Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
FACULDADE DE ENGENHARIA DE COMPUTAÇÃO. PROJETO FINAL I e II PLANO DE TRABALHO <NOME DO TRABALHO> <Nome do Aluno> <Nome do Orientador>
 FACULDADE DE ENGENHARIA DE COMPUTAÇÃO PROJETO FINAL I e II PLANO DE TRABALHO O Trabalho de Conclusão de Curso (TCC) a ser desenvolvido
FACULDADE DE ENGENHARIA DE COMPUTAÇÃO PROJETO FINAL I e II PLANO DE TRABALHO O Trabalho de Conclusão de Curso (TCC) a ser desenvolvido
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA ENG03108 MEDIÇÕES TÉRMICAS
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA ENG03108 MEDIÇÕES TÉRMICAS ANÁLISE DA EFICIÊNCIA TÉRMICA DE ISOLAMENTOS EM AQUECIMENTO E RESFRIAMENTO
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA MECÂNICA ENG03108 MEDIÇÕES TÉRMICAS ANÁLISE DA EFICIÊNCIA TÉRMICA DE ISOLAMENTOS EM AQUECIMENTO E RESFRIAMENTO
Prof. Eduardo Loureiro, DSc.
 Prof. Eduardo Loureiro, DSc. Transmissão de Calor é a disciplina que estuda a transferência de energia entre dois corpos materiais que ocorre devido a uma diferença de temperatura. Quanta energia é transferida
Prof. Eduardo Loureiro, DSc. Transmissão de Calor é a disciplina que estuda a transferência de energia entre dois corpos materiais que ocorre devido a uma diferença de temperatura. Quanta energia é transferida
Veja abaixo um exemplo de um endereço IP de 32 bits: 10000011 01101011 00010000 11001000
 4 Camada de Rede: O papel da camada de rede é transportar pacotes de um hospedeiro remetente a um hospedeiro destinatário. Para fazê-lo, duas importantes funções da camada de rede podem ser identificadas:
4 Camada de Rede: O papel da camada de rede é transportar pacotes de um hospedeiro remetente a um hospedeiro destinatário. Para fazê-lo, duas importantes funções da camada de rede podem ser identificadas:
Introdução. Renata Loretti Ribeiro - Enfermeira
 Introdução A função do sistema respiratório é facilitar ao organismo uma troca de gases com o ar atmosférico, assegurando permanente concentração de oxigênio no sangue, necessária para as reações metabólicas,
Introdução A função do sistema respiratório é facilitar ao organismo uma troca de gases com o ar atmosférico, assegurando permanente concentração de oxigênio no sangue, necessária para as reações metabólicas,
5 Equacionando os problemas
 A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
TRANSMISSOR ECF. Sistema de transmissão de arquivos Nota Fiscal Paulista. Manual de Utilização
 TRANSMISSOR ECF Sistema de transmissão de arquivos Nota Fiscal Paulista Manual de Utilização 1. Histórico de alterações Data Versão Alteração 04/12/2012 1 Criação do documento 28/02/2013 2 Revisão 2. Proposta
TRANSMISSOR ECF Sistema de transmissão de arquivos Nota Fiscal Paulista Manual de Utilização 1. Histórico de alterações Data Versão Alteração 04/12/2012 1 Criação do documento 28/02/2013 2 Revisão 2. Proposta
- CAPÍTULO 3 - O SISTEMA CARDIOVASCULAR. 3) ANATOMIA DO CORAÇÃO HUMANO - O coração é um órgão oco localizado no meio do peito, na cavidade torácica;
 - CAPÍTULO 3 - O SISTEMA CARDIOVASCULAR 1) FUNÇÕES DO SISTEMA CARDIOVASCULAR - Propulsão do sangue por todo o organismo; - Transporte de substâncias como o oxigênio (O 2 ), dióxido de carbono ou gás carbônico
- CAPÍTULO 3 - O SISTEMA CARDIOVASCULAR 1) FUNÇÕES DO SISTEMA CARDIOVASCULAR - Propulsão do sangue por todo o organismo; - Transporte de substâncias como o oxigênio (O 2 ), dióxido de carbono ou gás carbônico
Relatório técnico do projeto CFD-14/UFPR: testes de paralelização do código Mach2D
 Simulação numérica de escoamento reativo, transferência de calor e termoelasticidade em motor-foguete - parte 2 Projeto CFD-14/AEB-3 apoiado financeiramente pela Agência Espacial Brasileira (AEB) Anuncio
Simulação numérica de escoamento reativo, transferência de calor e termoelasticidade em motor-foguete - parte 2 Projeto CFD-14/AEB-3 apoiado financeiramente pela Agência Espacial Brasileira (AEB) Anuncio
Escola Secundária com 3º Ciclo de Madeira Torres. Ficha de Avaliação Diagnóstica de Física e Química A 2013/2014 Aluno: nº Data: Professor
 Esola Seundária om 3º Cilo de Madeira Torres. Fiha de Avaliação Diagnóstia de Físia e Químia A 203/204 Aluno: nº Data: Professor Grupo I. A figura mostra um esquema do iruito de Indianápolis, onde se realizam
Esola Seundária om 3º Cilo de Madeira Torres. Fiha de Avaliação Diagnóstia de Físia e Químia A 203/204 Aluno: nº Data: Professor Grupo I. A figura mostra um esquema do iruito de Indianápolis, onde se realizam
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 3
 Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
PERGUNTAS FREQUENTES (FAQS) Como posso entrar com dados geométricos da edificação?
 PERGUNTAS FREQUENTES (FAQS) Data de Revisão: 8/3/2013 Como posso entrar com dados geométricos da edificação? O Domus possui atualmente duas interfaces gráficas para entrada de dados geométricos. A segunda
PERGUNTAS FREQUENTES (FAQS) Data de Revisão: 8/3/2013 Como posso entrar com dados geométricos da edificação? O Domus possui atualmente duas interfaces gráficas para entrada de dados geométricos. A segunda
CÁLCULO DO VOLUME DE UM SÓLIDO DE REVOLUÇÃO: UMA ATIVIDADE USANDO OS SOFTWARES GRAPH E WINPLOT
 ISSN 2177-9139 CÁLCULO DO VOLUME DE UM SÓLIDO DE REVOLUÇÃO: UMA ATIVIDADE USANDO OS SOFTWARES GRAPH E WINPLOT Adriana Rosélia Kraisig maryshelei@yahoo.com.br Universidade Regional do Noroeste do Estado
ISSN 2177-9139 CÁLCULO DO VOLUME DE UM SÓLIDO DE REVOLUÇÃO: UMA ATIVIDADE USANDO OS SOFTWARES GRAPH E WINPLOT Adriana Rosélia Kraisig maryshelei@yahoo.com.br Universidade Regional do Noroeste do Estado
3 Conceitos Fundamentais
 3 Coneitos Fundamentais Neste aítulo são aresentados oneitos fundamentais ara o entendimento e estudo do omressor axial, assim omo sua modelagem termodinâmia 3 Máquinas de Fluxo As máquinas de fluxo odem
3 Coneitos Fundamentais Neste aítulo são aresentados oneitos fundamentais ara o entendimento e estudo do omressor axial, assim omo sua modelagem termodinâmia 3 Máquinas de Fluxo As máquinas de fluxo odem
Pesquisa com Professores de Escolas e com Alunos da Graduação em Matemática
 Pesquisa com Professores de Escolas e com Alunos da Graduação em Matemática Rene Baltazar Introdução Serão abordados, neste trabalho, significados e características de Professor Pesquisador e as conseqüências,
Pesquisa com Professores de Escolas e com Alunos da Graduação em Matemática Rene Baltazar Introdução Serão abordados, neste trabalho, significados e características de Professor Pesquisador e as conseqüências,
Segundo Pré-teste. Data de realização. 18 de Novembro de 2007. Local.
 Segundo Pré-teste Data de realização. 18 de Novembro de 2007. Local. Duas salas de aula da Pós-graduação do Departamento de Arquitetura e Urbanismo da EESC/USP. Duração: 4 horas. Dos objetivos. Envolveu
Segundo Pré-teste Data de realização. 18 de Novembro de 2007. Local. Duas salas de aula da Pós-graduação do Departamento de Arquitetura e Urbanismo da EESC/USP. Duração: 4 horas. Dos objetivos. Envolveu
7.Conclusão e Trabalhos Futuros
 7.Conclusão e Trabalhos Futuros 158 7.Conclusão e Trabalhos Futuros 7.1 Conclusões Finais Neste trabalho, foram apresentados novos métodos para aceleração, otimização e gerenciamento do processo de renderização
7.Conclusão e Trabalhos Futuros 158 7.Conclusão e Trabalhos Futuros 7.1 Conclusões Finais Neste trabalho, foram apresentados novos métodos para aceleração, otimização e gerenciamento do processo de renderização
Global T126 e GFS), executando para ambos os horários (00Z e 12Z), utilizando
 51 Figura 13 - Solicitação e resposta do http. 3.2 Método Para criação da nova metodologia de avaliação, foi utilizado trabalhos escritos por RENARD e CLARKE (1965) que dizem que é possível posicionar
51 Figura 13 - Solicitação e resposta do http. 3.2 Método Para criação da nova metodologia de avaliação, foi utilizado trabalhos escritos por RENARD e CLARKE (1965) que dizem que é possível posicionar
Nosso objetivo será mostrar como obter informações qualitativas sobre a refração da luz em um sistema óptico cilíndrico.
 Introdução Nosso objetivo será mostrar como obter informações qualitativas sobre a refração da luz em um sistema óptico cilíndrico. A confecção do experimento permitirá também a observação da dispersão
Introdução Nosso objetivo será mostrar como obter informações qualitativas sobre a refração da luz em um sistema óptico cilíndrico. A confecção do experimento permitirá também a observação da dispersão
Universidade Federal do Acre Curso de Medicina Veterinária
 Universidade Federal do Acre Curso de Medicina Veterinária Sistema Circulatório I Coração e Circulação Prof. Adj. Dr. Yuri Karaccas de Carvalho Anatomia Descritiva Animal I Objetivos da Aula Definição
Universidade Federal do Acre Curso de Medicina Veterinária Sistema Circulatório I Coração e Circulação Prof. Adj. Dr. Yuri Karaccas de Carvalho Anatomia Descritiva Animal I Objetivos da Aula Definição
14 ASPECTOS BÁSICOS PARA SELEÇÃO E ESPECIFICAÇÃO DE EQUIPAMENTOS DE PROCESSO
 14 ASPECTOS BÁSICOS PARA SELEÇÃO E ESPECIFICAÇÃO DE EQUIPAMENTOS DE PROCESSO Há certos parâmetros que são desejados em todos os tipos de equipamentos de processo, como: FUNCIONALIDADE EFICÁCIA CONFIABILIDADE
14 ASPECTOS BÁSICOS PARA SELEÇÃO E ESPECIFICAÇÃO DE EQUIPAMENTOS DE PROCESSO Há certos parâmetros que são desejados em todos os tipos de equipamentos de processo, como: FUNCIONALIDADE EFICÁCIA CONFIABILIDADE
Princípio da formação de imagem e sua aplicação na cardiologia intervencionista. Patrícia Lopes Barbosa patricialb7@gmail.com
 Princípio da formação de imagem e sua aplicação na cardiologia intervencionista Patrícia Lopes Barbosa patricialb7@gmail.com Produção dos raios X Na Cardiologia Intervencionista não existem fontes naturais
Princípio da formação de imagem e sua aplicação na cardiologia intervencionista Patrícia Lopes Barbosa patricialb7@gmail.com Produção dos raios X Na Cardiologia Intervencionista não existem fontes naturais
Convenção-Quadro das Nações Unidas sobre Mudança do Clima (CQNUMC)
 TIPO III - OUTRAS ATIVIDADES DE PROJETO Os participantes do projeto devem levar em conta a orientação geral relativa às metodologias, as informações sobre adicionalidade, as abreviaturas e a orientação
TIPO III - OUTRAS ATIVIDADES DE PROJETO Os participantes do projeto devem levar em conta a orientação geral relativa às metodologias, as informações sobre adicionalidade, as abreviaturas e a orientação
Bacharelado em Engenharia Civil
 Bacharelado em Engenharia Civil Disciplina: Fenômenos de Transporte Prof a.: Drd. Mariana de F. G. Diniz EMENTA Conceitos e definições. Análise dimensional. Fluídos estáticos. Descrição de um fluído em
Bacharelado em Engenharia Civil Disciplina: Fenômenos de Transporte Prof a.: Drd. Mariana de F. G. Diniz EMENTA Conceitos e definições. Análise dimensional. Fluídos estáticos. Descrição de um fluído em
