Curso de Data Mining

Transcrição

1 Aula 7 - Os algoritmos SPIRIT Curso de Data Mining Sandra de Amo O esquema geral dos algoritmos SPIRIT é o seguinte: ETAPA 1 : Etapa do relaxamento R Calula-se o onjunto L das sequênias frequentes que satisfazem um relaxamento R da expressão regular R original forneida pelo usuário (vamos denotar A R o autômato orrespondente a R). R pode ser : (1) o relaxamento total (algoritmo SPIRIT(N)), () o relaxamento orrespondente às sequênias legais om respeito a algum estado do autômato A R (algoritmo SPIRIT(L)), (3) o relaxamento orrespondente às sequênias válidas om respeito a algum estado do autômato A R (algoritmo SPIRIT(V)), () nenhum relaxamento, isto é, R = R (algoritmo SPIRIT(R)). ETAPA : Etapa da Restrição R Elimina-se de L as sequênias que não satisfazem R, obtendo-se assim o onjunto L das sequênias frequentes e que satisfazem R. Isto se faz através de um proedimento que dado um autômato e um string, verifia se o string é ou não aeito pelo autômato. Repare que o algoritmo SPIRIT(N) orresponde a apliar o algoritmo GSP sem nenhuma restrição na fase de geração (ETAPA 1). A ETAPA orresponden a uma etapa de pósproessamento, onde são eliminadas as sequênias que não interessam. Num outro extremo está o algoritmo SPIRIT(R), onde a ETAPA não realiza nada, pois a ETAPA 1 já fornee o onjunto L das sequênias frequentes e que satisfazem R. Resultados Experimentais Estes algoritmos foram testados em dados reais onstituídos de logs de páginas web aessadas por usuários de um Departamento de Ciênia da Computação (DCC) durante uma semana. A expressão regular R orresponde a todas as sequênias de URL s que se iniiam pelo endereço home do DCC e terminam no endereço do urso de Mestrado do DCC. O objetivo é minerar todos os aminhos mais frequentes perorridos por usuários que aessam a página do DCC e que hegam á página do urso de Mestrado. O nível mínimo de suporte foi de 0,3 % e o bano de dados de sequênias ontinha 1868 sequênias. Os resultados são ilustrados no quadro abaixo : Algo Tempo de Exe (seg.) Total de Candidatos Iterações SPIRIT (N) 156, SPIRIT (L) 3, SPIRIT (V) SPIRIT (R) 17, A partir deste quadro podemos onluir que : 1

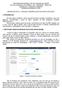
2 os algoritmos que inorporam a restrição R ou um relaxamento dela na ETAPA 1 são muito mais efiientes que o algoritmo SPIRIT(N) onde nada é feito na ETAPA 1 em termos de restringir o espaço de busa na fase de geração dos andidatos. Repare a quantidade enorme de andidatos gerados em SPIRIT(N) om relação aos outros 3 algoritmos. o algoritmo SPIRIT(V) é o mais efiiente dentre os quatro, embora seu desempenho não seja tão superior ao algoritmo SPIRIT(R), onde todo o proesso de restrição é realizado já na ETAPA 1. 1 Detalhes de Implementação de SPIRIT Maiores detalhes sobre esta seção podem ser enontrados em [?]. Já que o algoritmo SPIRIT(V) é o mais efiiente dentre os quatro da família SPIRIT, vamos detalhar as fases de geração e poda de ada iteração da ETAPA 1, somente para este algoritmo. Detalhes dos outros algoritmos podem ser enontrados no artigo : Garofalakis, Rastogi, Shim : SPIRIT: Sequential Pattern Mining with Regular Expression Constraints. Proeedings of the 5th VLDB Conferene, Edinburgh, Sotland, Fase de Geração Na iteração k, dispomos do onjunto L k 1 das sequênias frequentes de tamanho k 1 e que são válidas om respeito a algum estado do autômato A R. Sejam {q 0, q 1,..., q n } o onjunto dos estados do autômato A R. Então : L k 1 = L k 1(q 0 )... L k 1(q n ) onde L k 1 (q) denota o onjunto das sequênias frequentes de tamanho k 1 e que são válidas om respeito ao estado q do autômato A R. Para que uma sequênia < s 1, s,..., s k > de tamanho k seja válida om respeito a algum estado q 1 do autômato A R é preiso que : 1. o sufixo < s,..., s k > de tamanho k 1 seja válida om respeito a algum estado q do autômato A R e. exista uma transição no autômato indo de q 1 para q, om label s 1. Além disto, se queremos que < s 1, s,..., s k > tenha hane de ser frequente é preiso ao menos que o sufixo < s 1, s,..., s k > seja frequente. Logo, a partir desta ondição e da ondição (1) aima, é preiso exigir que este sufixo esteja em L k 1.

3 q1 s1 q s q3 s3... qk sk qf estado final o sufixo de tamanho k-1 deve estar em L k-1 Logo, o proedimento para alular os pré-andidatos C k de tamanho k a partir de L k 1 é o seguinte : Para ada estado q do autômato, identifique em L k 1 qual é o onjunto L k 1 (q). Para ada transição q a q e para ada sequênia < b 1,..., b k 1 > de L k 1 (q ) onstrua a sequênia < a, b 1,..., b k 1 >. O onjunto de todas as sequênias assim obtidas é L k (q). O onjunto L k é a união de todos os L k (q), para ada estado q do autômato. É laro que todos os pré-andidatos são válidos om respeito a algum estado do autômato A R e são potenialmente frequentes. Veja que só estamos exigindo que um pré-andidato tenha seu sufixo de tamanho k 1 frequente. É exigir muito pouo. Logo, é de se esperar que muitas sequênias não tenham hane nenhuma de serem frequentes e que serão podadas na fase de podagem. Exemplo 1.1 Considere o seguinte autômato A R : b a q1 q0 q3 a d q e Suponhamos que L = L (q 0 ) L (q 1 ) L (q ) e L (q 0 ) = {< a, >, < a, e >}, L (q 1 ) = {< b, >}, L (q ) = {< d, >, < d, e >}. 1. Consideremos q 0. Temos duas transições partindo de q 0. (a) q a 0 q 1 : neste aso onsideramos a 3-sequênia < a, b, >, já que L (q 1 ) = {< b, >}. 3

4 (b) q a 0 q : neste aso onsideramos as 3-sequênias < a, d, >, < a, d, e >, já que L (q ) = {< d, >, < d, e >}.. Consideremos q 1. Temos duas transições partindo de q 1 : b (a) q 1 q 1 : neste aso onsideramos a 3-sequênia < b, b, >, já que L (q 1 ) = {< b, >}. (b) q 1 q 3 : neste aso não onsideramos nenhuma 3-sequênia já que L (q 3 ) =. 3. Consideremos q. Temos três transições partindo de q : (a) q d q : neste aso onsideramos as 3-sequênias < d, d, >, < d, d, e >, já que L (q ) = {< d, >, < d, e >}. (b) q () q e q 3 : neste aso não onsideramos nenhuma 3-sequênia já que L (q 3 ) =. q 3 : neste aso não onsideramos nenhuma 3-sequênia já que L (q 3 ) =. Logo, o onjunto dos pré-andidatos é dado por C 3 = {< a, b, >, < a, d, >, < a, d, e >, < b, b, >, < d, d, >, < d, d, e >}. 1. Fase de Poda Vamos podar de C k as sequênias que possuem uma subsequênia om tamanho inferior a k e que não estejam em L = união dos L i para i = 1,..., k 1. Repare que, omo a ondição de satisfazer a restrição não é antimonotônia, não podemos simplesmente podar aquelas que não estão no último L k 1 (Veja problema 5 da segunda lista de exeríios). Primeiramente, portanto, para ada k-sequênia pré-andidata s preisamos alular todas as subsequênias de tamanho maximal que são válidas om respeito a algum estado do autômato A R (isto é, nenhuma subsequênia de s ontendo estritamente uma destas subsequênias será válida om relação a algum estado do autômato A R - estas são as maiores possíveis ). Depois, verifiamos se uma destas subsequênias não está em L (=união dos L i para i = 1,..., k 1), então s deverá ser podada. Por que isto? : suponha que s é uma subsequênia de s de tamanho maximal que seja válida om respeito a algum estado do autômato (todas as de tamanho superior não o são). Suponha também que s não esteja em L. É possível que s seja frequente? Ora, se s não está em L então não estará em nenhum dos L i (para i = 1,..., k 1). Se tamanho de s = N (N < k) então obviamente s não estará em L N e portanto não será frequente. Portanto, s não po derá ser frequente, já que ontém uma subsequênia s que não é frequente. Exemplo 1. Consideremos uma pequena variante do autômato que vimos na aula anterior :

5 1 a b 3 d Repare que agora o estado também é final (logo, os estados finais são : e d) Suponhamos que L = {< 1, >, <, >, <, 3 >, < 1,, >, <, 3, >}. O onjunto dos pré-andidatos C 3 é dado por : C 3 = {< 1, 1,, >, < 1,, 3, >} A sequênia < 1, 1,, > não é podada pois a únia subsequênia maximal de tamanho inferior a que é válida é {1,,} que está em L 3. Por outro lado, a sequênia < 1,, 3, > será podada pois as subsequênias maximais de tamanho inferior a que são válidas são {< 1,, 3 >, <, 3, >, < 1, >}. Uma delas, a sequênia < 1,, 3 > não está em L. Logo, < 1,, 3, > deve ser podada. Como exeríio onstate que se onsiderarmos o autômato do exemplo 1.1, nenhuma sequênia será podada de C 3 (alulado neste exemplo). Em [?] é desenvolvido um algoritmo FINDMAXSEQ (um tanto omplexo) para enontrar todas as subsequênias de uma sequênia válida s dada, que são válidas om relação a um estado do autômato A R, tenham tamanho inferior ao de s e que sejam maximais. 1.3 Condição de Parada Quando L k = o algoritmo SPIRIT(V) pára. Veja que para isso é neessário que para ada estado q do autômato, o onjunto das k-sequênias frequentes e válidas om relação a este estado q seja vazio. Por exemplo, o fato de que L (q 0 ) seja vazio não implia neessariamente que L (q 0 ) seja vazio. Basta onsiderar o autômato : onde q 0 é estado iniial e q f é estado final. q a b 0 q 1 q q 3 d q f Compare esta ondição de parada om a ondição de parada do algoritmo SPIRIT(L) (Exerçíio 10, Lista de exeríios ). A fase de geração do algoritmo SPIRIT(L) : a fase de geração para o algoritmo SPIRIT(L) é muito pareida om a do algoritmo SPIRIT(V). A idéia é ilustrada na figura abaixo : 5

6 o prefixo de tamanho k-1 deve estar em L k-1 q1 s1 q s q3 s3... qk sk qk+1 o sufixo de tamanho k-1 deve estar em L k-1 Na iteração k, dispomos do onjunto L k 1 das sequênias frequentes de tamanho k 1 e que são legais om respeito a algum estado do autômato A R. Sejam {q 0, q 1,..., q n } o onjunto dos estados do autômato A R. Então : L k 1 = L k 1(q 0 )... L k 1(q n ) Para que uma sequênia < s 1, s,..., s k > de tamanho k seja frequente e legal om respeito a algum estado q 1 do autômato A R é preiso que : 1. o sufixo < s,..., s k > de tamanho k 1 seja legal em relação a q e frequente,. o prefixo < s 1,..., s k 1 > de tamanho k 1 seja legal em relação a q 1 e frequente, 3. exista uma transição no autômato indo de q 1 para q, om label s 1. Logo, a partir das ondições (1) e () aima, é preiso exigir que o prefixo e o sufixo estejam em L k 1. Portanto, para gerar os pré-andidatos em SPIRIT(L) : Para ada estado q do autômato, identifique em L k 1 qual é o onjunto L k 1 (q). Para ada par de estados q e q : Junte sequênias de L k 1 (q) om sequênias de L k 1 (q ) se (a) retirando o primeiro elemento de uma delas e o último elemento da outra, obtemos a mesma sequênia e (b) se existe uma transição q s 1 q, onde s 1 é o primeiro elemento da primeira sequênia. O onjunto L k é a união de todos as junções de L k (q) om L k (q ), onde q e q são estados do autômato. Vamos agora ver num exemplo, onde os quatro algoritmos são exeutados sobre o mesmo input. Exemplo 1.3 Considere o bano de dados D : 6

7 Considere o autômato da aula passada: Dataset D < 1,, 3, > < 1, 1,, > <,, 3, > <, 3,, 3 > < 1, 1,, 3 > 1 a b 3 d Suponhamos também que o nível mínimo de suporte é α = 0, (0%, logo para ser frequente é preiso ser suportado por ao menos sequênias de D). Na primeira iteração, todos os algoritmos são exeutados da mesma maneira. L 1 = sequênias unitárias onstituídas dos itens frequentes = < 1 >, < >, < 3 >, < >. Na segunda iteração : o proesso é idêntio nos quatro algoritmos : ombina-se todos os elementos de L 1 obtendo-se todas as -sequênias possíveis. Depois, elimina-se aquelas que não satisfazem a ondição R. O onjunto resultante é L. A partir da tereira iteração, ada algoritmo tem sua forma própria de atuar : SPIRIT(N) : L C 3 Contador L 3 C Contador < 1, 1 > < 1, 1, 1 > 0 < 1, 1, > < 1, 1,, > 1 < 1, > < 1, 1, > < 1,, > < 1, 1,, 3 > 1 < 1, 3 > < 1, 1, 3 > 1 < 1,, 3 > <, > < 1,, > <, 3, > <, 3 > < 1,, 3 > <,, 3 > <, > <,, > 0 < 3, > <,, 3 > 0 <, 3 > <,, > 0 <, 3, > 0 <,, 3 > 0 SPIRIT(L) : 7

8 Est. L Est. C 3 Cont. Est. L 3 Est. C Cont. a < 1, 1 > a < 1, 1, 1 > 0 a < 1, 1, > a < 1, 1,, > 1 a < 1, > a < 1, 1, > a < 1,, > a < 1, 1,, 3 > 1 a <, > a < 1,, > a < 1,, 3 > a <, 3 > a < 1,, 3 > a <, 3, > b < 3, > a <, 3, > a SPIRIT(V) : Est. L Est. C 3 Cont. Est. L 3 Est. C Cont. a <, > a < 1,, > a < 1,, > a < 1, 1,, > 1 b < 3, > a <, 3, > a <, 3, > a < 1,, 3, > 0 SPIRIT(R) : L C 3 Contador L 3 C Contador <, > < 1,, > < 1,, > < 1, 1,, > 1 <, 3, > <, 3, > < 1, 1, 3, > 0 Referenes [1] Garofalakis, M.N., Rastogi, R., Shim, K. : Mining Sequential Patterns with Regular Expression Constraints. IEEE Transations on Knowledge and Data Engineering, Vol. 1, No. 3, May/June 00, pp