A Teoria Antropológica do Didático: uma Releitura Sobre a Teoria
|
|
|
- Maria do Mar Guterres Barata
- 6 Há anos
- Visualizações:
Transcrição
1 REVISTA DO PROGRAMA DE PÓS-GRADUAÇÃO EM EDUCAÇÃO MATEMÁTICA DA UNIVERSIDADE FEDERAL DE MATO GROSSO DO SUL (UFMS) Volume 8, Número Temático 2015 ISSN A Teoria Antropológica do Didático: uma Releitura Sobre a Teoria The Anthropological Theory of Didactic: a Re-reading About the Theory Marcelo Câmara dos Santos 1 Marcus Bessa de Menezes 2 Resumo Esse texto tem como objetivo apresentar os elementos da Teoria Antropológica do Didático (TAD), proposta por Yves Chevallard e que vem sendo desenvolvida por diversos pesquisadores em diferentes países. Trata-se de uma teoria desenvolvida no quadro da Didática da Matemática francesa e que permite, particularmente, analisar situações de ensino e aprendizagem da matemática escolar. A TAD foi elaborada pela necessidade de ampliação da Teoria da Transposição Didática, desenvolvida pelo mesmo autor nos anos 80, na França, e se baseia na noção de relação ao saber. Nesse texto apresentamos os elementos principais da teoria, incluindo a noção de praxeologia, buscando incluir exemplos do cotidiano da sala de aula de matemática. Palavras-chave: Teoria Antropológica do Didático. Transposição Didática. Análise Praxeológica. Abstract This text aims to present the elements of the Anthropological Theory of Didactic (TAD), proposed by Yves Chevallard and which has been developed by several researchers in different countries. It is a theory developed in the framework of the french s Didactics of Mathematics, and that allows, in particular, analyse situations of teaching and learning school mathematics. The TAD was drafted by the need of expansion of the Didactic Transposition Theory, developed by the same author in the years 80, in France, and is based on the notion of relation to know. In this text we present the main elements of the theory, including the notion of praxeology, seeking to include examples of everyday math classroom. Keywords: Anthropological Theory of Didactic. Didactic Transposition. Praxiological Analysis. 1 Doutor em Ciências da Educação pela Université Paris-X/UPX. Universidade Federal de Pernambuco/UFPE, Recife, PE, Brasil. marcelocamaraufpe@yahoo.com.br. 2 Doutor em Educação pela Universidade Federal de Pernambuco/UFPE. Universidade Federal de Campina Grande/UFCG, Campina Grande, PB, Brasil. marcusbessa@gmail.com. inma.sites.ufms.br/ppgedumat/ seer.ufms.br/index.php/pedmat
2 649 Introdução Pensando nas questões do cotidiano da prática do professor, em nosso artigo caminharemos pela Teoria Antropológica do Didático (TAD). Uma teoria apresentada por Yves Chevallard (1998), que se propõe a analisar um dos problemas do professor que é preparar seu curso de aulas e depois colocá-lo em prática, ou seja, como organizar um objeto de estudo (matemático) e fazê-lo funcionar em sala de aula? Segundo Chevallard, a sua teorização proposta na TAD deve [...] ser encarada como um desenvolvimento e uma articulação das noções cuja elaboração visa permitir pensar de maneira unificada um grande número de fenômenos didáticos, que surgem no final de múltiplas análises. (1998, p. 92). Ou seja, de acordo com o pesquisador, podemos perceber elementos da gestão do tempo, do contrato didático, da transposição didática, enfim, de diversos fenômenos didáticos que se mostram em sala de aula, a partir do olhar da TAD. Assim, podemos ver a TAD funcionando como uma forma de explicar a transposição didática (TD) no ecossistema 3 da sala de aula, ou melhor dizendo, um prolongamento da teoria da transposição didática, no momento em que amplia esses ecossistemas para relações, entre objetos de ensino, que irão além da sala de aula. Segundo o autor, Na prática, as primeiras análises propostas em la transposition didactique 4 limitavam-se a distinguir objetos «matemáticos», «paramatemáticas» e «protomatemáticos». O alargamento do quadro, levado a cabo por necessidades de análise, conduziu-me a propor uma teorização em que qualquer «objeto» pudesse aparecer: a função logarítmica é, evidentemente, um objeto («matemático»), mas existe igualmente o objeto «escola», o objeto «professor», o objeto «aprender», o objeto «saber», o objeto «dor de dente», o objeto «fazer xixi», etc. (CHEVALLARD, 1998, p.92) O autor afirma que para começar sua teorização são necessários três conceitos primitivos: os objetos O, as pessoas X e as instituições I ; e que outros virão a ser acrescentados subsequentemente. O objeto O toma uma posição privilegiada em relação aos outros temas, em virtude de ser o material de base da construção teórica. Segundo o autor, tudo é objeto, 3 Entendemos ecossistema como sendo o local onde se desenvolve um determinado sistema que possui uma ecologia própria, no caso em estudo, o sistema didático. 4 Ver Chevallard 1991.
3 650 e ele faz uma analogia com o universo matemático contemporâneo, fundado na teoria dos conjuntos, em que tudo é um conjunto. Assim também é na sua teoria, todas as coisas serão objetos ; as pessoas X e as instituições I também são objetos, assim como as outras entidades que serão introduzidas. O objeto irá existir no momento em que for reconhecido como existente por uma pessoa X ou instituição I. Com isso, aparecerão a relação pessoal de X com O, que será denotada por R(X, O), e a relação institucional de I com O, R(I, O). Ou seja, o objeto irá existir caso seja reconhecido por, pelo menos, uma pessoa X ou instituição I. Do ponto de vista da «semântica» da teoria, qualquer coisa pode ser um objeto. Um objeto existe a partir do momento em que uma pessoa X ou uma instituição I o reconhece como existente (para ela). Mais precisamente, podemos dizer que o objeto O existe para X (respectivamente, para I) se existir um objeto, que denotarei por R (X, O) (resp. R 1(O)), a que chamarei de relação pessoal de X com O (resp. relação institucional de I com O) 5. (CHEVALLARD, 1998, p 93) Assim sendo, um objeto O que identificamos como cadeira só existe porque a população (pessoa) e a sociedade (instituição) a reconhecem como tal e, assim, satisfaz a sua condição de existência. Apesar de a afirmação anterior parecer óbvia, devemos perceber que alguns objetos não existem (ou ainda não existem) para algumas instituições. Por exemplo, o Tardígrafo, animal microscópico que vive em finas películas de água, é objeto de estudo para os biólogos, mas não é conhecido pela maioria de nós. Fazendo um paralelo com a sala de aula, existem objetos de saber que ainda não são conhecidos pelos alunos (pessoa). No entanto, eles já são conhecidos pelo professor (instituição), e será a partir das relações que serão geradas em sala de aula (sujeito-objeto, sujeito-instituição, instituição-objeto) que se dará a aprendizagem. Chegamos a um ponto em que necessitamos evidenciar o que são as instituições. Segundo Chevallard (1998), uma instituição pode ser quase o que quer que seja. Devido à natureza da palavra, poderíamos dar uma conotação própria a esse personagem, ou seja, associação ou organização de caráter social, educativo, religioso, de ensino, etc. (KURY, 2002). Porém, não devemos nos surpreender ao vermos, em certos momentos, objetos tomarem o status de instituição. Uma escola é certamente uma instituição, que possui outras instituições a ela agregada, como uma sala de aula, por exemplo. 5 Grifos do autor.
4 651 O conceito de instituição pode ser explicitado como sendo um dispositivo social, total ou parcial, que impõe aos seus sujeitos formas de fazer e de pensar que são próprias a cada tipo ou forma de instituição. Para avançarmos ainda mais sobre o conceito de instituição I, devemos percebê-la não como uma estrutura homogênea, mas, sim, heterogênea, em que existem várias relações de pessoas X com objetos O que pertencem a I. Mas de que forma se relacionam os objetos O e a instituição I? (...) A cada instituição I está associado um conjunto de objetos 01, chamado conjunto dos objetos institucionais (para I), que é o conjunto dos objetos O que I conhece, ou seja, para os quais existe uma relação institucional R1(O). Um objeto O é institucional para I ou, dito de outro modo, existe para I, quando I define uma relação (institucional) com O. 6 (CHEVALLARD, 1999, p 225) O objeto O se relaciona com a instituição I por meio de suas características próprias; por exemplo, a noção de porcentagem para uma instituição financeira (um banco) pode representar taxas e lucros, enquanto para a engenharia civil pode representar proporcionalidade entre partes de uma mistura (um traço de concreto). Assim sendo, o objeto O pode estabelecer diferentes formas de relações de acordo com a instituição R1(O), R2(O), R3(O), etc. Da mesma forma, seu desenvolvimento dentro destas instituições pode vir a ser modificado com o passar do tempo, ou seja, evoluir, envelhecer ou até mesmo desaparecer. Em contrapartida, é necessário introduzir um novo termo primitivo, no qual o leitor de La transposition didactique reconhecerá uma extensão da noção de tempo didático. Para qualquer instituição I, existe aquilo a que chamarei um tempo institucional t 1 7. O conjunto O1 depende de t = t 1, e a notação O1(t) seria por isso mais exata. Com efeito, o conjunto O1(t) registra algumas das alterações que afetam I: a cada «instante» t, surgem novos objetos institucionais, enquanto outros desaparecem (para passarem a ser institucionalmente visíveis, por exemplo, apenas a partir de n. O mesmo acontece com as relações institucionais, R 1(O,t). De uma maneira geral, todas as noções relativas a I dependem de t 1. 8 (CHEVALLARD, 1999, p 225) Essas relações são permeadas por outro fenômeno didático que surge nas relações dos sujeitos X com os objetos O da instituição I, fenômeno este que se estabelece devido às expectativas que existem dentro das relações, o contrato didático. 6 Grifos do autor. 7 Podemos definir o tempo Institucional t 1 como sendo o tempo noosférico de cada instituição I, ou seja, cada Instituição I teria seu ritmo de funcionamento. 8 Grifos do autor.
5 652 Mais adiante discutiremos sobre a conformidade da relação entre a pessoa X e o objeto O (R(X, O)) sob o constrangimento da relação institucional R1(O) gerando R1(X, O), observando e analisando quais as possíveis interferências na relação R(X, O). Podem agora ser definidas duas noções essenciais (que não são termos primitivos). Elas derivam, naturalmente, das noções correspondentes de contrato didático e de meio, respectivamente introduzidas por Guy Brousseau na teoria das situações didáticas. Designa-se por C 1(t) e chama-se contrato institucional relativo a I no tempo t o conjunto dos pares (O, R 1(O,t)), em que O é um elemento de O 1(t). 9 (CHEVALLARD, 1999, p 226) Para definir o conceito de pessoa, iniciaremos diferenciando alguns de seus estágios, o indivíduo, o sujeito e a pessoa. Podemos dizer que o estágio mais primitivo seria o de Indivíduo, visto que não se sujeita nem muda com as relações cotidianas com objetos e instituições. Chevallard afirma que: Bem entendido, no curso do tempo, o sistema das relações pessoais de X evolui; objetos que não existem para ele passam a existir; outros deixam de existir; para outros enfim a relação pessoal de X muda. Nesta evolução, o invariante é o indivíduo; o que muda é a pessoa (CHEVALLARD, 1999, 226). O indivíduo se torna um sujeito quando se relaciona com uma Instituição I qualquer ou, melhor dizendo, quando se sujeita a uma Instituição I, sob suas demandas, hábitos, formas; enfim, se sujeitando a essa relação. É por meio das várias relações que o indivíduo tem com instituições diferentes que se constitui a pessoa; ou seja, o conjunto de sujeitos do indivíduo é que forma a pessoa X, que irá mudando conforme estabelece suas relações com diferentes instituições, com o passar do tempo. Uma pessoa X está sujeita a uma série de instituições. Introduzo aqui o axioma segundo o qual uma pessoa não é, na realidade, mais do que a emergência de um complexo de sujeições institucionais. Aquilo que se chama de «liberdade» da pessoa surge então com o efeito obtido em consequência de uma ou de várias sujeições institucionais contra outras. 10 (CHEVALLARD, 1999, p. 227) Uma pessoa X entra para uma instituição I, na qual existe um objeto O que é chamado de objeto institucional. Assim X, ao entrar em I, começa a viver uma relação com O sob a influência de uma relação institucional, ou seja, a relação R(X, O) irá se 9 Grifos do autor. 10 Grifos do autor.
6 653 alterar ou se construir mediante a relação R(I, O), e, de forma mais ampliada, sob a limitação do contrato institucional C. É preciso deixar claro que O poderia existir, ou não, para X antes de sua entrada em I (que analogamente podemos sugerir como conjunto vazio, sem existência). Porém, independente desse fato, a relação R(X, O) irá alterar-se. Daí então Chevallard dirá que há aprendizagem de X em relação a O. Em outras palavras, havendo alteração em R(X, O) então haverá aprendizagem da pessoa X sobre o objeto O. De forma análoga, caso R(X, O) não se altere, podemos afirmar que a pessoa nada aprendeu. Devemos observar que não há nada de didático até agora, pois a instituição I não se manifestou com intencionalidade de fazer com que R(X, O) se altere ou modifique. Para que a instituição I manifeste uma intencionalidade de fazer uma modificação ou uma alteração na relação R(X, O), é necessário que se introduza uma nova noção primitiva, a de sujeito adequado. Com isso, uma pessoa X se tornará um sujeito adequado da instituição I, relativamente ao objeto O, quando as relações R(X, O) e R(I, O) estão em conformidade. Podemos dizer que, nesse caso, o sujeito está de acordo com as expectativas desejadas pela Instituição, ele está conforme deseja a Instituição. Caso isso não esteja ocorrendo, é considerado que o sujeito está inadequado em relação ao contrato institucional C. Para melhor ilustrar as relações descritas anteriormente, pensemos um uma situação em que um jovem ao completar 18 anos alista-se nas forças armadas. Ao iniciar suas atividades, agora como militar, deverá se adequar às regras do quartel (instituição), manter o cabelo cortado, uniforme limpo, cumprir horários, enfim, as diversas obrigações que são inerentes à instituição quartel. Com isso, caso cumpra essas regras, ele se torna um sujeito daquela instituição. Também existem alguns objetos que são próprios da instituição quartel, entre eles o armamento. Apesar de poder conhecer (ou não) o armamento, o jovem passa a ter instrução de como manuseá-lo e quando utilizá-lo, de acordo com as normas previstas pelo quartel. Caso consiga exercer sua função corretamente, podemos dizer que houve uma mudança na relação que o jovem (sujeito) tinha com o armamento (objeto), assim sendo, houve aprendizagem, segundo Chevallard. Nesse exemplo, percebemos também a influência da instituição (quartel) quanto às expectativas de ser um militar, ou seja, o quartel avalia se o comportamento do jovem está adequado às suas perspectivas.
7 654 Entra então em cena a avaliação institucional. Segundo Chevallard (1999), essa avaliação é um dos mecanismos segundo os quais I é levada a pronunciar, por meio de alguns dos seus agentes, um veredicto de conformidade (ou de não conformidade) R(X, O) com R(I, O). Assim sendo, podemos pensar que a instituição sala de aula, que chamaremos a partir desse momento de I1, tem seus sujeitos X1 (os alunos), seus objetos O1 (saberes em jogo) e seus agentes que irão regular a conformidade, ou a não conformidade, com a instituição I1, de acordo com a intencionalidade estabelecida. Esses agentes são os professores, o contrato didático e o contrato institucional estabelecidos, as avaliações, entre outros, que aparecerão de acordo com o momento necessário. A avaliação, como um dos elementos controladores da conformidade, ou não conformidade, na Instituição I1, pode, nesse sentido, vir (ao contrário do que se espera) a podar todo esse interesse pelo objeto O1, fazendo com que o sujeito X1 se preocupe somente com a conformidade, ou seja, quais são os conjuntos de ações que ele deve realizar para ter a adequação esperada pela instituição. Não podemos esquecer que essa avaliação é estabelecida por meio de um contrato pedagógico e um contrato didático definidos que, de certa forma, mostra sua importância dentro de I1. Assim sendo, isso poderá comprometer a formação dos conceitos desse objeto O1 em jogo no cenário didático. Essas alterações nas relações entre o sujeito X1 e o objeto O1 vão muito além da questão epistemológica do objeto O1 (saber) ou de uma questão metodológica. Elas partem, também, de uma intencionalidade vinculada ao contrato que é estabelecido. Isso não significa que deixamos de fora esses outros fatores. Porém, é extremamente necessário, quando olharmos para o saber aprendido pelo aluno, considerarmos a relação entre os contratos (pedagógico e didático) estabelecidos; eles podem ter um peso maior nas escolhas realizadas pelos sujeitos X1 (alunos). Podemos evidenciar esse fato nas próprias escolhas que são efetuadas pelos alunos. Por exemplo, um vestibulando de medicina tem uma intencionalidade com a Matemática muito menor do que com as chamadas disciplinas das áreas afins, em virtude do peso que será dado àquelas disciplinas dentro da instituição em que ele irá exercer sua função (hospital). Depois de formado, já médico, esse saber matemático não será de muita valia no seu dia a dia; porém, os conteúdos das áreas afins serão de suma importância para seu desenvolvimento profissional. Daí vem essa intencionalidade com o saber em
8 655 jogo em um cenário didático qualquer ou, por melhor dizer, em qualquer instituição. Nesse momento estamos tratando de dois ecossistemas diferentes: a instituição escola e a instituição trabalho. Outro fator que interfere nas escolhas dos alunos é a própria maturidade deles. Quando estão no início de sua escolarização, os interesses se voltam para o sucesso na instituição escola, mesmo sem que haja uma verdadeira aquisição de conhecimento. De fato, basta ser um bom seguidor das regras estabelecidas pelo professor que se resolvem todos os problemas dentro da instituição I1. Nessa fase, o sujeito X1 não percebe, de forma clara, as necessidades futuras da aquisição desses conhecimentos que lhe são apresentados e, com isso, se permite burlar contratos e tentar enganar a instituição I1, utilizando mecanismos que indiquem falsas aquisições de saberes. Segundo Chevallard (1992), essa situação ocorre porque julgamos de forma errada os sujeitos. A este respeito, as instituições são sempre «vigarizadas» (trapaceadas) pelos seus sujeitos. Quando esperam encontrar sujeitos puros, que julgam ser inteiramente moldados por elas, deparam-se com pessoas, que lhes aparecem sempre, de uma forma ou de outra, como sujeitos desadequados. (CHEVALLARD, 1992, p. 227) Algumas relações entre sujeitos, objetos e instituição são permeadas por intencionalidades diversas, tanto por parte dos sujeitos como por parte das instituições perante os objetos em jogo nessa relação. Na sala de aula, podemos identificar vários fenômenos didáticos (contrato didático, transposição didática, gestão do tempo) que ocorrem devido a essas intencionalidades, mediante as relações entre alunos e professores diante do saber a ser ensinado. Após descrevermos como se estabelecem as relações entre objeto, pessoa e instituição, iremos apresentar a noção de praxeologia, identificando elementos que indicam como o professor dá conta de preparar suas aulas e coloca-las em prática no cenário didático. A Organização Praxeológica ou Praxeologia Podemos entender uma organização praxeológica, ou praxeologia, como a realização de certo tipo de tarefas (T) por meio de um modo de fazer, que Chevallard (1999) chama de técnica (t). Essa associação tarefa-técnica (T-t) irá definir um saberfazer próprio para esse tipo de tarefa. Porém, ela (T-t) não se mantém em estado isolado,
9 656 ou seja, não se sustentará por si só. A dupla T-t necessita de um amparo tecnológicoteórico (ou saber), que é formado por uma tecnologia (θ), que irá dar uma racionalidade e uma sustentação inteligível à técnica (t) aplicada, e uma teoria (Θ) que irá justificar e esclarecer a tecnologia (θ). Assim sendo, a organização praxeológica ou praxeologia (que a partir desse momento iremos tratar somente como praxeologia) será composta por quatro elementos, a saber: tipo de tarefa (T), técnica (t), tecnologia (θ) e teoria (Θ), articulados a partir de um bloco prático-técnico (gerando o saber-fazer) e um bloco tecnológico-teórico (amparado no saber). Segundo o autor, (...) a ecologia das tarefas e técnicas são as condições e necessidades que permitem a produção e utilização destas nas instituições e a gente supõe que, para poder existir em uma instituição, uma técnica deve ser compreensível, legível e justificada (...) essa necessidade ecológica implica na existência de um discurso descritivo e justificado das tarefas e técnicas que a gente chama de tecnologia da técnica. O postulado anunciado implica também que toda tecnologia tem necessidade de uma justificativa que a gente chama teoria da técnica e que constitui o fundamento último. (BOSCH; CHEVALLARD, 1999, p ) Podemos dizer que ao redor de um tipo de tarefa (T), se encontra, a princípio, um trio formado de, ao menos, uma técnica (t), uma tecnologia (θ) e uma teoria (Θ), formando uma praxeologia completa [T, t, θ, Θ]. Uma tal praxeologia, quando é formada ao redor de uma única tarefa é denominada pontual. Raramente encontramos praxeologias pontuais. Geralmente, em uma instituição I qualquer, uma teoria (Θ) dá conta de várias tecnologias (θj), e cada uma delas irá justificar e fazer inteligíveis várias técnicas (tij), que corresponderão a outras tantas tarefas (Tij). Assim, as praxeologias pontuais se unem, formando praxeologias locais [Ti, ti, θ, Θ], que, diferentemente das pontuais, estarão centradas em torno de uma determinada tecnologia (θ), justificada por uma mesma teoria (Θ). Em consequência, quando estivermos centrados em uma determinada teoria (Θ), teremos uma praxeologia regional [Tij, tij, θj, Θ] que mais adiante será denominada organização global [Tijk, tijk, θjk, Θk], em virtude de um complexo praxeológico obtido, em uma instituição I dada, pela agregação de diversas teorias (Θ). Para tentar exemplificar esses tipos de praxeologias, partiremos da pontual. Para isso, teremos como tarefa a resolução de uma equação de primeiro grau. Encontre o valor de x, na equação abaixo, utilizando a transposição de termos:
10 x=103 Para realizar a tarefa acima, de acordo com o enunciado, deverá ser utilizada a técnica da transposição de termos, que terá como tecnologia ou elemento tecnológico a propriedade das operações inversas em R (conjunto dos números reais). Assim, podemos perceber que nesse tipo de tarefa haverá somente uma única técnica, o que caracteriza uma praxeologia pontual. Quanto à praxeologia do tipo local, teremos como tarefa a resolução de equações do segundo grau, e três subtipos de tarefas: Resolva as equações do segundo grau abaixo: a) x²-3x=0 b) x²-4=0 c) x²+4x+4=0 Podemos perceber que para resolver a tarefa proposta, podemos utilizar diversas técnicas, tais como a fatoração das expressões, colocando em evidencia o fator comum; completar quadrados; Bháskara, entre outras. Todas essas técnicas girariam em torno de uma tecnologia ou de elementos tecnológicos que podem ser representados pelas propriedades das operações inversas em R (conjunto dos números reais). Nesse caso, teríamos a Álgebra como a teoria que justificaria esses elementos tecnológicos. Agora vamos focar na praxeologia do tipo regional. Devemos lembrar que esse tipo tem foco na teoria e, em nosso caso, a Álgebra. Buscamos uma tarefa em que a resolução de uma equação do segundo grau não seja o objetivo, porém seu conhecimento é necessário para que se alcance a solução. Assim teremos como tarefa calcular o custo de um frete: Para fazer um passeio turístico, um grupo de pessoas fretou um ônibus por R$ 1200,00. Com a adesão de mais cinco pessoas, cada um dos que já havia pago, teve restituição de R$ 20,00. Qual foi o custo do frete por pessoa? Ao buscarmos a solução da tarefa, percebemos que deveremos lançar mão de elementos tecnológicos que deram suporte à equação de segundo grau, tendo em vista que durante a resolução iremos obter a seguinte equação x²+5x-300=0. Contudo, isso não será suficiente para realizar a tarefa. Para isso, deverão ser utilizados alguns
11 658 conhecimentos do campo da matemática financeira, tais como custo, valor total, valor restituído, valor pago. Com isso, surgem outras técnicas e outros elementos tecnológicos que justificam os conhecimentos financeiros utilizados. Assim sendo, podemos identificar na resolução dessa tarefa uma praxeologia regional, que foca em uma teoria (Álgebra) e não em uma única tecnologia. Passaremos agora a praxeologia global, ou seja, que deverá ter mais uma teoria envolvida. Para tanto, teremos como tarefa calcular as dimensões de um retângulo: Quais são as dimensões de um retângulo cujo perímetro e área medem, respectivamente, 50cm e 150cm? Novamente, ao buscarmos a solução da tarefa percebemos que iremos obter uma equação de segundo grau x²-25x+150=0. Contudo, para podermos chegar a essa equação, devemos ter lançado mão de alguns conceitos da geometria, como área e perímetro. Com isso, podemos notar que é necessário mais de uma teoria para a solução, no caso, a Álgebra e a Geometria. Tal fato, irá caracterizar essa praxeologia como global. Quando colocamos em movimento as praxeologias, ou seja, passamos de uma praxeologia pontual para uma praxeologia local, colocamos em primeiro plano a tecnologia (θ), da mesma forma que no passo a seguir, passar da praxeologia local para praxeologia regional, demanda colocar em evidência a teoria (Θ). Assim sendo, nos dois casos damos uma visibilidade maior ao bloco do saber [θ, Θ], em detrimento do bloco do saber-fazer [T, t]. Componentes da praxeologia Para Chevallard (1998), a noção de tarefa, ou de tipos de tarefas, se encontra na raiz da noção de praxeologia. Podemos entender como tipo de tarefa (T), de acordo com a TAD, todo e qualquer objeto que não encontramos sua existência diretamente na natureza, ou seja, será necessário realizar procedimentos próprios, em nosso caso matemáticos, para encontrá-lo. Quando um subtipo de tarefa ( ) é parte de um tipo de tarefa T, escreveremos que є T. Segundo o autor, podemos ainda diferenciar o gênero de tarefa do tipo de tarefa ou tarefa propriamente dita. O gênero de tarefa seria caracterizado por um verbo como,
12 659 por exemplo, montar, levar, calcular, etc., sendo expresso de forma mais ampla e conteúdo não definido. Já o tipo de tarefa, ou tarefa, tem seu conteúdo estritamente especificado. Por exemplo, podemos ter como um tipo de tarefa resolver uma equação de primeiro grau, encontrar a altura de um triângulo isósceles, dentre outros. Como dito anteriormente, para se realizar uma tarefa (T), ou tipo de tarefa, os alunos devem realizar um procedimento. Assim, percebemos que essa realização tem em sua gênese uma particularidade dinâmica, o que nos leva à noção de técnica (t). Dada uma tarefa (T) qualquer, uma praxeologia relativa a T necessitará (a princípio) de um modo, ou de uma maneira, de se realizar essa tarefa. A tal maneira de se fazer T foi dado o nome de técnica (t), do grego tekhnê, saber-fazer. Segundo Chevallard (1998), uma técnica (t) pode não ser suficiente para dar conta de todos os subtipos ( ) de uma tarefa T (sendo є T). Assim, na praxeologia, poderemos ter técnicas superiores a outras. A questão da superioridade está na quantidade de subtipos ( ) de tarefas de T que uma técnica consegue realizar em relação a outra, ou seja, as técnicas superiores realizam uma quantidade maior de subtipos ( ) de tarefa de T. Para exemplificarmos a superioridade de técnicas apresentada anteriormente, tomemos o seguinte tipo de tarefa: determinar as raízes de uma equação de segundo grau. Para realizarmos esse tipo de tarefa podemos utilizar a técnica do produto nulo, da fatoração 11, da tentativa, de completar quadrados; no entanto, a escolha da técnica dependerá da forma como se apresenta a equação (incompleta, completa, com raízes inteiras). Porém, existe uma técnica que resolveria qualquer equação do segundo grau, a chamada fórmula de Bhaskara. Nesse sentido, a fórmula de Bhaskara seria superior às demais, pois realiza uma quantidade maior de subtipos de tarefas que as outras. Ainda falando sobre técnica, Chevallard afirma que: (...) uma técnica t não é necessariamente de natureza algorítmica ou quase algorítmica: isso acontece em alguns raros casos (1998, p 93). Porém, existirá quase sempre uma tendência de algoritmizar as técnicas (t) para a realização das tarefas (T). Chevallard (1998) observa ainda que um determinado tipo de técnica (t) não é universal para todas as instituições I. Em certos casos, algumas instituições não estão em 11 Nesse momento, não estamos tratando do conceito fatoração, e sim da regra da soma e produto das raízes, que comumente é chamada de fatoração.
13 660 conformidade com determinados tipos de técnicas e, assim sendo, não reconhecerão e contestarão a validade desta técnica (t). Tal exclusão é correlativa, em autores de I, de uma ilusão de naturalizar as técnicas institucionais em I fazer assim, é natural... -, em contraste com o conjunto de possíveis técnicas alternativas, que os sujeitos de I ignoram, ou, se são confrontados, lhes olharão como artificiais, e (portanto) contestáveis, inaceitáveis, etc. (CHEVALLARD, 1998, p 93) Para poder dar um suporte racional e justificar a técnica (t) aplicada para a realização de uma tarefa (T) é necessário a introdução da noção de tecnologia (θ), que é definida por Chevallard (1998) como sendo: (...) um discurso racional (logos) sobre a técnica a tekhnê t, discurso tendo por objetivo primeiro de justificar racionalmente a técnica t, e nos assegurar que ela permite o bom cumprimento das tarefas do tipo T, isto quer dizer realizar o que é pretendido. (CHEVALLARD, 1998, p 93) Sobre tecnologia (θ), Chevallard afirma que em dada instituição I uma técnica (t) para a realização de um tipo de tarefa (T) vem, frequentemente, acompanhada de vestígios ou embriões de tecnologia (θ) e, em diversos casos, na técnica (t), certos elementos tecnológicos vêm incorporados. O autor avança ainda ao afirmar que quando em uma instituição I existe, em princípio, somente uma técnica (t) que é reverenciada, reconhecida e empregada, essa técnica adquire um papel de autotecnológica, ou seja, não irá necessitar de justificativas, pois essa é a melhor maneira de se fazer nesta instituição I. (...) em uma instituição I, qualquer que seja o tipo de tarefa T, a técnica t relativa a T é sempre acompanhada de ao menos um embrião ou, mais frequentemente, de um vestígio de tecnologia θ. Em numerosos casos, certos elementos tecnológicos estão integrados na técnica. Além disso, o fato de existir em I, em princípio, somente uma técnica canônica, reconhecida e empregada, confere a esta técnica uma virtude autotecnológica : fazer assim não necessita de justificação, porque esta é a melhor maneira de fazer (em I) (CHEVALLARD, 1998, p 93, 94) Para assegurarmos o funcionamento regular de uma tecnologia (θ) em uma instituição I, necessitamos de uma nova noção que explique e justifique esta tecnologia (θ). Isso nos leva à noção de Teoria (Θ), que é a especulação abstrata da tecnologia; no plano teórico encontram-se as definições, os teoremas, as noções mais abrangentes que servem para explicar, justificar e produzir novas tecnologias. Segundo Chevallard (1998), poderíamos chegar a uma regressão absurda, na qual sempre teríamos que justificar uma coisa atrás da outra, ou seja, a técnica justificada por uma tecnologia, que é justificada por uma teoria, que seria justificada por outra teoria,
14 661 por outra e outra... Porém, o autor afirma que (...) a descrição em três níveis (técnica/tecnologia/teoria), em geral, é o suficiente para dar conta da atividade a analisar (CHEVALLARD, 1998, p 94). Análise da prática docente: um olhar pela praxeologia Para analisarmos a prática docente devemos considerar as seguintes questões: Como realizar a tarefa do tipo T? Ou, ainda, Como realizar melhor esta tarefa? Essas questões invocam uma produção de técnicas e, portanto, de praxeologias. Sendo os tipos de tarefa T, anteriormente citados, objetos matemáticos O para serem tratados em uma instituição I (uma sala de aula qualquer), podemos considerar essa análise em duas classes distintas: a) observando o primeiro questionamento com um viés pela realidade matemática, teremos uma praxeologia matemática ou organização matemática, que denominaremos como OM; b) ao observarmos o segundo questionamento, teremos um olhar sobre a didática, ou seja, de que forma encaminharemos a realidade matemática estabelecida na OM. Assim, essa realidade se denominará uma praxeologia didática ou uma organização didática OD. Praxeologia matemática ou organização matemática (OM) Chamaremos de praxeologia matemática ou organização matemática, toda realidade matemática que está envolvida na resolução de um tipo de tarefa T. Para isso, serão exigidas técnicas t, amparadas por um conjunto teórico-tecnológico [θ; Θ]. A organização matemática tem sua origem nas análises efetuadas pelos professores 12, dos documentos oficiais existentes (tais como programas e manuais escolares, além do livro didático), dos quais saem os saberes matemáticos escolhidos a serem ensinados. A partir daí o professor começa a determinar quais os tipos de tarefa que serão os condutores no processo de aquisição desses saberes escolhidos, trazendo com eles os demais componentes praxeológicos (técnica, tecnologia e teoria). Podemos exemplificar 12 Lembramos que, nesse momento em particular, estamos fazendo um olhar pela prática docente.
15 662 como um tipo de tarefa a seguinte questão: Como encontrar as raízes de uma equação de 2º grau?. Outras questões também permeiam essa atividade praxeológica: Há representatividade e clareza nos tipos de tarefas? As necessidades matemáticas propostas nos conteúdos curriculares são atendidas por esses tipos de tarefas? As técnicas propostas para a resolução dos tipos de tarefas foram efetivamente elaboradas? São suficientes para os tipos de tarefas propostos? Poderão sofrer evoluções? As tecnologias disponíveis dão conta das técnicas empregadas? As justificativas têm um distanciamento grande ou estão próximas das formas canônicas matemáticas? Esclarecem as técnicas utilizadas? Os elementos teóricos são explicitados? Justificam a tecnologia empregada? Para melhor elucidar, apresentaremos o quadro a seguir com a análise da OM de um subtipo de tarefa (T1), em que temos uma equação incompleta do segundo grau. Nele, poderemos identificar as técnicas e os elementos tecnológicos que estão presentes para a resolução da tarefa. OM1 (ax² + c = 0) TAREFA T Resolver uma equação do 2 grau Subtipo de Tarefa (T1) ax² + c = 0 RESOLUÇÃO DO TÉCNICAS PROFESSOR ax² c 0 TTC - Transpor termos, ax² c x² c a x c a invertendo as operações. SUBTÉCNICAS 13 DRE - desenvolver ou reduzir expressões. ELEMENTOS TECNOLÓGICOS POI - Propriedades das operações inversas em R (conjunto dos números reais) ou leis da transposição de termos. PR - Propriedade da Radiciação. Quadro 1 Organização Matemática de T 1 Outro ponto da prática docente será de como conduzir essa praxeologia matemática, agora estabelecida, para a sala de aula. Isto é, como transpor da realidade 13 As subtécnicas seriam técnicas que adquirem um status de auxiliar ou secundária na resolução de um tipo de tarefa que tenha uma técnica com status de principal ou primária. (BESSA DE MENEZES, 2010)
16 663 matemática para a realidade didática. Segundo Chevallard (1999), a construção da praxeologia se inicia em uma falta de técnica para a resolução de um determinado tipo de tarefa. Assim sendo, podemos pensar no exemplo dado anteriormente: Como encontrar as raízes de uma equação de 2º grau?, e fazer agora a seguinte questão: Como ensinar a encontrar as raízes de uma equação de 2º grau? Dar resposta a essa nova questão nos leva a elaborar um novo tipo de praxeologia, a praxeologia didática. Praxeologia didática ou organização didática (OD) A organização (ou praxeologia) didática surge na intenção de pôr em prática, ou de conduzir, uma organização matemática qualquer. Será ela, a OD, que irá dar conta da (re)construção ou transposição de uma determinada OM. Assim como toda praxeologia, a OD é composta de tipos de tarefas que serão resolvidas por técnicas, as quais serão explicadas pelas tecnologias e justificadas por teorias. Por organização didática podemos entender, a priori, o conjunto dos tipos de tarefas, de técnicas, de tecnologias, etc., mobilizadas para o estudo concreto em uma instituição concreta. O enfoque clássico em didática da matemática tem ignorado em geral os aspectos mais genéricos de uma organização de estudo de um tipo dado de sistemas didáticos. (CHEVALLARD, 1999, p 238) Ao pensarmos em uma OD, podemos nos perguntar: Quais são os principais tipos de tarefas que podem ocorrer? Segundo Chevallard (1999) não podemos esperar que a (re)construção, no curso de um processo de estudo, de uma OM dada se organize por ela mesma de uma maneira única. Porém, para o autor, qualquer que seja o caminho de estudo, certos tipos de situações estarão necessariamente presentes, mesmo de maneira muito variável, tanto quantitativamente como qualitativamente. Chevallard (1999) chama essas situações de momentos de estudo ou momentos didáticos, pois podemos dizer que seja qual for o caminho seguido, se chega forçosamente a um momento em que tal ou qual gesto de estudo deverá ser cumprido. A noção de momento não remete mais que em aparência à estrutura temporal do processo de estudo. Um momento, no sentido dado a palavra aqui, é em primeiro lugar uma dimensão em um espaço multidimensional (...) uma sã gestão do estudo exige que cada um dos momentos didáticos se realize no bom momento, ou mais exatamente, nos bons momentos. 14 (CHEVALLARD, 1999, p 242) 14 Grifo do autor.
17 664 O primeiro momento de estudo será aquele em que teremos o primeiro encontro com a organização matemática (OM) que está sendo posta em jogo no cenário didático. Esse primeiro encontro (ou reencontro) pode ocorrer de diversas maneiras, porém, uma dessas maneiras será a partir de pelo menos um tipo de tarefa T, que constitui a OM proposta. Esse momento com o tipo tarefa T pode ocorrer várias vezes, em virtude do entorno matemático e didático estabelecido. Segundo Chevallard (1998), se pode voltar a descobrir um tipo de tarefa como se volta a descobrir uma pessoa que se acreditava conhecer. Quais são as formas possíveis de primeiro encontro? Segundo o autor, quando a OM está expressamente organizada aparecem duas grandes formas, cujas múltiplas combinações em suas variantes desenvolvidas (ou degradadas) esgotariam o espaço de formas possíveis. Seriam elas um encontro cultural-mimético e outro por meio de situações fundamentais. O encontro cultural-mimético se dá de forma mais ou menos explícita da OM em jogo, quando em um submomento cultural o estudante tem somente relações fictícias com o objeto, que não é mais do que uma representação, seguido de um submomento mimético em que o estudante manipula efetivamente os objetos da OM. Na versão mais exigente, o encontro cultural-mimético conduz em princípio a buscar e explicitar sob o modo discursivo as razões de ser dos objetos assim encontrados, quer dizer, os motivos pelos quais este objeto tem sido construído ou aqueles pelos quais, ao menos, persiste na cultura. (CHEVALLARD, 1999, p 242) De forma contrária, o encontro a partir de situações fundamentais (que podem ser chamadas de umbilicais) afasta toda a referência de uma realidade preexistente. Assim os objetos da OM são apresentados aos olhos do aluno que, como ator principal (único ou em equipe), se permite encontrar respostas a uma série de questões determinadas. Essa forma de encontro conduz a propor uma definição do objeto da OM encontrado, que não se reduz a uma simples cópia das definições depositadas na cultura, mas, sim, é apresentado por meio de uma realidade conveniente. O segundo momento é o da exploração dos tipos de tarefas e da elaboração de técnicas relativas a esse tipo de tarefas. Segundo Chevallard, estudar problemas é um meio que permite criar e usar uma técnica relativa a problemas do mesmo tipo, ou seja, a elaboração das técnicas é um meio para resolver de maneira quase rotineira esses
18 665 problemas. Ainda segundo o pesquisador, mais do que a resolução de problemas isolados, a elaboração de técnicas é o coração da atividade matemática. O terceiro momento de estudo é o da constituição do entorno tecnológico-teórico relativo à técnica e ao tipo de tarefa proposto pela OM. Esse momento não está isolado dos outros dois anteriores, visto que ao elegermos uma determinada técnica, ela estará diretamente ligada ao bloco tecnológico-teórico, para que possa ser explicada e justificada. Para alguns professores, de acordo com suas concepções, esse momento pode se tornar a primeira etapa de estudo de uma determinada OM. O quarto momento é o momento de trabalho da técnica. Nele se deve por em prática essa técnica visando vivenciá-la e aprimorá-la, quando possível, tornando-a mais eficaz e confiável, para um tipo particular ou um corpo de tarefas adequadas tanto qualitativamente como quantitativamente. O quinto momento é o da institucionalização, ou seja, oficializar os elementos da OM em jogo no cenário didático. Esse momento de estudo tem como finalidade principal indicar com exatidão a OM elaborada. Segundo Chevallard, O momento da institucionalização é, de início, aquele que, na construção bruta que pouco a pouco, emergido do estudo, vão separar, por um movimento que compromete o porvir, o matematicamente necessário, que será conservado, e o matematicamente contingente, que logo será esquecido. (CHEVALLARD, 1999, p 244) O sexto momento é o da avaliação, que está diretamente articulado com o momento da institucionalização, pois tem o objetivo de avaliar o que de fato foi aprendido com a OM em jogo, o que tal pessoa, ou grupo de pessoas, domina(m) sobre as técnicas, tecnologias e teorias apresentadas para a realização de tipos de tarefas, propostas pela OM. Segundo Chevallard, [...] este momento de reflexibilidade, onde qualquer que seja o critério e o juiz se examina o que vale o que se já aprendeu, este momento de reflexão que, apesar das recordações de infância, não é em absoluto invenção da Escola, participa de fato da respiração mesma de toda atividade humana. (CHEVALLARD, 1999, p 245) Segundo o autor, esses momentos de estudo têm dois grandes empregos para o professor. O primeiro seria de uma cartilha ou check-list para a análise dos processos didáticos empregados no desenvolvimento da OM. O outro seria na identificação clara de problemas na realização dos diferentes momentos de estudo, que responderiam algumas perguntas, tais como: Como realizar concretamente o primeiro encontro com tal OM?
19 666 Com quais tipos de tarefa? Como conduzir o estudo exploratório de um tipo de tarefa? Como levar a cabo a institucionalização? Como realizar o momento de avaliação? Objetos ostensivos e não ostensivos A teoria antropológica do didático (TAD) não tem a pretensão de ser a única que assume que a atividade matemática é realizada recorrendo a uma diversidade de registros (o escrito, o gráfico, o verbal, o gestual, o material). Tampouco em relação às dificuldades entre a articulação dos diferentes tipos de registro do funcionamento da atividade matemática. A TAD propõe um modelo epistemológico que estabelece uma distinção dentro dos elementos que compõem uma organização (ou praxeologia) matemática, os tipos de tarefas, as técnicas, as tecnologias e as teorias. Esses elementos são feitos de objetos ostensivos e não-ostensivos. Trata-se como objetos ostensivos aqueles objetos que se percebem, se vêem, se tocam, se ouvem, etc. Ou seja, são objetos materiais ou dotados de certa materialidade, como as escrituras, os grafismos, os sons, os gestos, etc. Para generalizarmos em uma expressão, chamaremos de objetos que podem ser manipulados, apesar de serem sons, gestos, discursos, etc. Os objetos não-ostensivos são aqueles que existem institucionalmente, desde que lhes sejam atribuídos uma determinada existência. Porém, esses objetos não podem ser percebidos nem se mostram por si mesmos. São as ideias, os conceitos, as crenças, etc. Por meio da manipulação de certos objetos ostensivos podemos invocar ou evocar estes objetos não-ostensivos. Assim, podemos perceber uma co-existência permanente dos objetos ostensivos e não-ostensivos que, apesar de paradoxal, é estabelecida dentro do que Bosch e Chevallard (1999) chamam de a dialética do ostensivo e do não-ostensivo. (...) os objetos não-ostensivos emergem da manipulação de objetos ostensivos. Porém, ao mesmo tempo, tal manipulação está sempre guiada ou controlada por objetos não-ostensivos. O conceito de número inteiro ou o de função linear não existe sem toda a atividade manipulativa de ostensivos (...). Reciprocamente, toda manipulação de ostensivos vem controlada pela ativação ou evocação de objetos não-ostensivos cujas características podem ver-se modificadas ao longo da atividade. (BOSCH e CHEVALLARD, 1999, p 82)
20 667 Podemos ser levados a produzir uma conceituação simples de que os objetos ostensivos estão no nível do saber-fazer, com seus tipos de tarefas e suas técnicas próprias, deixando para os objetos não-ostensivos (conceitos, noções, ideias, etc.), a atividade de justificar e explicar, ou seja, o saber. Com isso estaríamos distribuindo os objetos ostensivos e não-ostensivos para os dois grupos que, de acordo com a TAD, formam a praxeologia, a parte prático-técnica (gerando o saber-fazer) e a parte tecnológica-teórica (amparada no saber). Ao contrário disso, os objetos ostensivos e não-ostensivos afetam todos os elementos que compõem as organizações matemáticas (OM). Bosch e Chevallard (1999) afirmam que É evidente, por exemplo, que a eleição de uma simbolização e de uma terminologia adequadas são também elementos muito importantes para a constituição e qualidade de uma tecnologia ou teoria. E, de igual modo, a realização efetiva de uma técnica pode variar enormemente, em termos de sua eficácia e robustez, segundo se ativa um objeto não-ostensivo ou outro. (BOSCH e CHEVALLARD, 1999, p 83) A TAD responde, por meio da dialética do ostensivo e do não-ostensivo, à pergunta sobre a origem dos conceitos matemáticos (não-ostensivos) e sua relação com os objetos que as representam (ostensivos). Sobre o assunto, Bosch e Chevallard (1999) avançam que (...) os conceitos surgem da manipulação de ostensivos dentro de determinadas organizações matemáticas (é dizer, como respostas a certas tarefas problemáticas e um em torno tecnológico-teórico dado) e esta mesma prática que, ao institucionalizar ou oficializar-se, estabelece vínculos entre ostensivos e não-ostensivos que permitiram aos primeiros remeter ou representar aos segundos em futuras possíveis atividades. (BOSCH e CHEVALLARD, 1999, p 82) Ao falarmos da coexistência dos ostensivos e dos não-ostensivos em todos os níveis da OM, deixamos claro que não há, em nenhum caso, uma primazia dos nãoostensivos sobre os ostensivos, pois, segundo Bosch e Chevallard (1999), não existe manipulação ostensiva (uma escrita ou um discurso) que seja a consequência direta de uma suposta possessão ou aquisição de um não-ostensivo (uma noção ou um conceito). Nem o contrário irá existir, ou seja, uma manipulação ostensiva regulada que possa prescindir de não-ostensivos. No entanto, a hipótese de coexistência entre ostensivos e não-ostensivos está vinculada à sua existência em uma instituição dada, em um momento histórico dado. Ou
21 668 seja, não há nenhuma razão que determine que o escrito f(x) seja associado ao conceito de função, porém, em uma instituição dada que considere a existência dos ostensivos e não-ostensivos correspondentes, podemos dizer que o ostensivo escrito f(x) e o ostensivo oral efe de xis formam parte da OM que se vinculam institucionalmente ao nãoostensivo função, isto é, ao não-ostensivo que invoca o ostensivo oral função. Uma pequena síntese A produção e comunicação dos saberes de referência são necessidades sociais. Esses saberes comunicados, inicialmente no mundo acadêmico e científico, trazem consigo uma necessidade de um novo tratamento, no sentido de que sua roupagem mais acadêmica seja retirada e que ele possa, após essa primeira adequação ou transformação, ser comunicado e, se possível, utilizado socialmente num período breve. Mas não é só na comunicação da comunidade científica que o saber se modifica, em sala de aula o professor também realiza algumas transformações (BESSA DE MENEZES, 2004). O saber efetivamente ensinado em sala de aula resulta das modificações feitas durante a aplicação do que estava previsto no plano de aula (um saber preparado pelo professor 15 ) para o que efetivamente ocorre na sala de aula, ou seja, a realização, ou não, das expectativas. Esse saber será impregnado, principalmente, pela relação existente entre o professor e o saber a ser ensinado, a qual irá orientar as mudanças que ocorrerão no processo de produção desse saber. Nesse momento, temos o professor como ator principal nesse processo. A característica principal do programa epistemológico consiste em considerar que o objeto primário de investigação da didática é a atividade matemática tal como se realiza em distintas instituições da sociedade. Quando se diz que a didática da matemática estuda as condições de difusão e transmissão do conhecimento matemático (Brousseau, 1994), não se considera o conhecimento do ponto de vista psicológico, como processo mental de indivíduos isolados. O conhecimento é o produto ou a cristalização de um determinado fazer humano e que está sempre caracterizado pelas atividades que surgem e pelas que permite realizar. (BOSCH, 1999, p 12). A práxis do professor está envolvida pelas transformações de saberes em sala de aula, saberes que necessitam ser adaptados, entre outros motivos, ao nível cognitivo de 15 Ver Ravel (2003)
O SABER ESCOLAR NA PERSPECTIVA DA TEORIA ANTROPOLÓGICA DO DIDÁTICO
 O SABER ESCOLAR NA PERSPECTIVA DA TEORIA ANTROPOLÓGICA DO DIDÁTICO Marcus Bessa de Menezes Marcelo Câmara dos Santos Programa de Pós-graduação em Educação/UFPE marcusbessa@gmail.com; marcelocamaraufpe@yahoo.com.br
O SABER ESCOLAR NA PERSPECTIVA DA TEORIA ANTROPOLÓGICA DO DIDÁTICO Marcus Bessa de Menezes Marcelo Câmara dos Santos Programa de Pós-graduação em Educação/UFPE marcusbessa@gmail.com; marcelocamaraufpe@yahoo.com.br
RELAÇÕES PESSOAIS DE ESTUDANTES DE SÃO PAULO DOS ENSINOS FUNDAMENTAL, MÉDIO E SUPERIOR SOBRE AS REPRESENTAÇÕES DOS NÚMEROS RACIONAIS
 SECCIÓN 1 ANÁLISIS DEL DISCURSO MATEMÁTICO ESCOLAR RELAÇÕES PESSOAIS DE ESTUDANTES DE SÃO PAULO DOS ENSINOS FUNDAMENTAL, MÉDIO E SUPERIOR SOBRE AS REPRESENTAÇÕES DOS NÚMEROS RACIONAIS José Valério Gomes
SECCIÓN 1 ANÁLISIS DEL DISCURSO MATEMÁTICO ESCOLAR RELAÇÕES PESSOAIS DE ESTUDANTES DE SÃO PAULO DOS ENSINOS FUNDAMENTAL, MÉDIO E SUPERIOR SOBRE AS REPRESENTAÇÕES DOS NÚMEROS RACIONAIS José Valério Gomes
ALGUMAS CONSIDERAÇÕES SOBRE A PROPOSTA DE ENSINO DA TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
 23 a 26 de Maio 10 e 11 de Agosto de 2017 https://sesemat.wordpress.com/ ALGUMAS CONSIDERAÇÕES SOBRE A PROPOSTA DE ENSINO DA TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Luana Vieira Ramalho Universidade do Estado
23 a 26 de Maio 10 e 11 de Agosto de 2017 https://sesemat.wordpress.com/ ALGUMAS CONSIDERAÇÕES SOBRE A PROPOSTA DE ENSINO DA TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Luana Vieira Ramalho Universidade do Estado
Diferentes praxeologias no ensino das equações de segundo grau
 Marcus Bessa de Menezes Universidade Federal de Campina Grande, Campus Sumé-PB Brasil marcusbessa@gmail.com Resumo Este trabalho se propôs a refletir sobre as semelhanças e diferenças nas práticas de professores
Marcus Bessa de Menezes Universidade Federal de Campina Grande, Campus Sumé-PB Brasil marcusbessa@gmail.com Resumo Este trabalho se propôs a refletir sobre as semelhanças e diferenças nas práticas de professores
A OPERAÇÃO POTENCIAÇÃO: UMA ANÁLISE DA ABORDAGEM EM LIVROS DIDÁTICOS DO ENSINO FUNDAMENTAL
 A OPERAÇÃO POTENCIAÇÃO: UMA ANÁLISE DA ABORDAGEM EM LIVROS DIDÁTICOS DO ENSINO FUNDAMENTAL Ana Maria Paias Pontifícia Universidade Católica de São Paulo anamariapaias@yahoo.com.br Resumo: Consideramos
A OPERAÇÃO POTENCIAÇÃO: UMA ANÁLISE DA ABORDAGEM EM LIVROS DIDÁTICOS DO ENSINO FUNDAMENTAL Ana Maria Paias Pontifícia Universidade Católica de São Paulo anamariapaias@yahoo.com.br Resumo: Consideramos
RELAÇÕES METODOLÓGICAS NA TRANSIÇÃO 5º E 6º ANO DO ENSINO FUNDAMENTAL BRASILEIRO PARA O CASO DAS FIGURAS PLANAS E FIGURAS ESPACIAIS
 SECCIÓN 1 ANÁLISIS DEL DISCURSO MATEMÁTICO ESCOLAR RELAÇÕES METODOLÓGICAS NA TRANSIÇÃO 5º E 6º ANO DO ENSINO FUNDAMENTAL BRASILEIRO PARA O CASO DAS FIGURAS PLANAS E FIGURAS ESPACIAIS Sirlene Neves de Andrade,
SECCIÓN 1 ANÁLISIS DEL DISCURSO MATEMÁTICO ESCOLAR RELAÇÕES METODOLÓGICAS NA TRANSIÇÃO 5º E 6º ANO DO ENSINO FUNDAMENTAL BRASILEIRO PARA O CASO DAS FIGURAS PLANAS E FIGURAS ESPACIAIS Sirlene Neves de Andrade,
Considerações finais
 Considerações finais Ao encerrar este estudo, acreditamos ter respondido as questões de pesquisas apresentadas, além de ter contribuído para o planejamento de ações formativas para professores em exercício.
Considerações finais Ao encerrar este estudo, acreditamos ter respondido as questões de pesquisas apresentadas, além de ter contribuído para o planejamento de ações formativas para professores em exercício.
Oficina 2B Percurso de Estudo e Pesquisa e a Formação de Professores
 Oficina 2B Percurso de Estudo e Pesquisa e a Formação de Professores Catarina Oliveira Lucas Grupo de pesquisa http://www.atd-tad.org/ Portugal, catarinalucas.mail@gmail.com Palestra com conexão: Palestra
Oficina 2B Percurso de Estudo e Pesquisa e a Formação de Professores Catarina Oliveira Lucas Grupo de pesquisa http://www.atd-tad.org/ Portugal, catarinalucas.mail@gmail.com Palestra com conexão: Palestra
Um Estudo das Organizações Didática e Matemática de Professores em Início de Docência durante as Aulas de Função. Introdução
 Um Estudo das Organizações Didática e Matemática de Professores em Início de Docência durante as Aulas de Função Introdução Adriana Barbosa de Oliveira Marilena Bittar O final de um curso de licenciatura
Um Estudo das Organizações Didática e Matemática de Professores em Início de Docência durante as Aulas de Função Introdução Adriana Barbosa de Oliveira Marilena Bittar O final de um curso de licenciatura
ÂNGULOS NOTÁVEIS NOS LIVROS DIDÁTICOS: UMA ANÁLISE PRAXEOLÓGICA.
 ÂNGULOS NOTÁVEIS NOS LIVROS DIDÁTICOS: UMA ANÁLISE PRAXEOLÓGICA. Jessie Heveny Saraiva Lima (1); Jesirreila Melo Souza do Nascimento (2); Acylena Coelho Costa (3). Universidade do Estado do Pará, Jessieheveny7@gmail.com
ÂNGULOS NOTÁVEIS NOS LIVROS DIDÁTICOS: UMA ANÁLISE PRAXEOLÓGICA. Jessie Heveny Saraiva Lima (1); Jesirreila Melo Souza do Nascimento (2); Acylena Coelho Costa (3). Universidade do Estado do Pará, Jessieheveny7@gmail.com
A ÁLGEBRA DO PROFESSOR E DO ALUNO: UM OLHAR SOB A ÓTICA DA TEORIA ANTROPOLÓGICA DO DIDÁTICO
 A ÁLGEBRA DO PROFESSOR E DO ALUNO: UM OLHAR SOB A ÓTICA DA TEORIA ANTROPOLÓGICA DO DIDÁTICO Marcus Bessa de Menezes, UFCG-CDSA, marcusbessa@ufcg.edu.br RESUMO Nesse trabalho apresentamos resultados de
A ÁLGEBRA DO PROFESSOR E DO ALUNO: UM OLHAR SOB A ÓTICA DA TEORIA ANTROPOLÓGICA DO DIDÁTICO Marcus Bessa de Menezes, UFCG-CDSA, marcusbessa@ufcg.edu.br RESUMO Nesse trabalho apresentamos resultados de
ENTREVISTA PROF. DR ELIO CARLOS RICARDO 1
 ENTREVISTA PROF. DR ELIO CARLOS RICARDO 1 Livre-docente de Ensino de Ciências e Matemática, Faculdade de Educação da USP. Entrevista concedida à TV SENAI/SC por ocasião de Formação continuada, no âmbito
ENTREVISTA PROF. DR ELIO CARLOS RICARDO 1 Livre-docente de Ensino de Ciências e Matemática, Faculdade de Educação da USP. Entrevista concedida à TV SENAI/SC por ocasião de Formação continuada, no âmbito
PANORAMA DE UM ESTUDO SOBRE A FATORAÇÃO
 23 a 26 de Maio 10 e 11 de Agosto de 2017 https://sesemat.wordpress.com/ PANORAMA DE UM ESTUDO SOBRE A FATORAÇÃO Miriam do rocio Guadagnini Universidade Anhanguera de São Paulo miriamguadagnini@hotmail.com
23 a 26 de Maio 10 e 11 de Agosto de 2017 https://sesemat.wordpress.com/ PANORAMA DE UM ESTUDO SOBRE A FATORAÇÃO Miriam do rocio Guadagnini Universidade Anhanguera de São Paulo miriamguadagnini@hotmail.com
O PAPEL E A IMPORTÂNCIA DO LIVRO DIDÁTICO NO PROCESSO DE ENSINO APRENDIZAGEM
 O PAPEL E A IMPORTÂNCIA DO LIVRO DIDÁTICO NO PROCESSO Introdução DE ENSINO APRENDIZAGEM Jefferson Dagmar Pessoa Brandão UEPB jeffdagmar@oi.com.br Parece ser consenso da importância do livro didático no
O PAPEL E A IMPORTÂNCIA DO LIVRO DIDÁTICO NO PROCESSO Introdução DE ENSINO APRENDIZAGEM Jefferson Dagmar Pessoa Brandão UEPB jeffdagmar@oi.com.br Parece ser consenso da importância do livro didático no
PLANO DE TRABALHO SOBRE EQUAÇÃO DO 2º GRAU
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ Colégio ESTADUAL ANÍBAL BENÉVOLO Professora: ANA CLÁUDIA DOS SANTOS MONÇÃO Matrículas: 0937644-3 Série: 9º ANO ENSINO FUNDAMENTAL
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ Colégio ESTADUAL ANÍBAL BENÉVOLO Professora: ANA CLÁUDIA DOS SANTOS MONÇÃO Matrículas: 0937644-3 Série: 9º ANO ENSINO FUNDAMENTAL
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE CIÊNCIA E TECNOLOGIA UNIDADE ACADÊMICA DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE EDUCAÇÃO TUTORIAL
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE CIÊNCIA E TECNOLOGIA UNIDADE ACADÊMICA DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE EDUCAÇÃO TUTORIAL TUTOR: PROF.DR. DANIEL CORDEIRO DE MORAIS FILHO ANÁLISE
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE CIÊNCIA E TECNOLOGIA UNIDADE ACADÊMICA DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE EDUCAÇÃO TUTORIAL TUTOR: PROF.DR. DANIEL CORDEIRO DE MORAIS FILHO ANÁLISE
REFLEXÕES SOBRE A PRÁTICA DOCENTE NO ENSINO FUNDAMENTAL II E MÉDIO EM ITAPETINGA-BA: FORMAÇÃO INICIAL EM FÍSICA
 REFLEXÕES SOBRE A PRÁTICA DOCENTE NO ENSINO FUNDAMENTAL II E MÉDIO EM ITAPETINGA-BA: FORMAÇÃO INICIAL EM FÍSICA Monyke Hellen dos Santos Fonsêca 1 Dulcinéia da Silva Adorni 2 INTRODUÇÃO O avanço na qualidade
REFLEXÕES SOBRE A PRÁTICA DOCENTE NO ENSINO FUNDAMENTAL II E MÉDIO EM ITAPETINGA-BA: FORMAÇÃO INICIAL EM FÍSICA Monyke Hellen dos Santos Fonsêca 1 Dulcinéia da Silva Adorni 2 INTRODUÇÃO O avanço na qualidade
AS ORGANIZAÇÕES MATEMÁTICAS PONTUAIS PARA O ENSINO DAS EQUAÇÕES DO SEGUNDO GRAU
 AS ORGANIZAÇÕES MATEMÁTICAS PONTUAIS PARA O ENSINO DAS EQUAÇÕES DO SEGUNDO GRAU Fernando Emílio Leite Almeida 1 Instituto Federal de Educação, Ciência e Tecnologia de Pernambuco, Brasil fernandoemilioleite@yahoo.com.br
AS ORGANIZAÇÕES MATEMÁTICAS PONTUAIS PARA O ENSINO DAS EQUAÇÕES DO SEGUNDO GRAU Fernando Emílio Leite Almeida 1 Instituto Federal de Educação, Ciência e Tecnologia de Pernambuco, Brasil fernandoemilioleite@yahoo.com.br
Palavras-chave: Didática da Matemática. Teoria Antropológica do Didático. Formação Inicial de professores.
 AS TEORIAS DA DIDÁTICA DA MATEMÁTICA COMO LOCUS DE REFLEXÃO E A TEORIA ANTROPOLÓGICA DO DIDÁTICO COMO PRÁXIS NA LICENCIATURA EM MATEMÁTICA GT1 Currículo e formação de professores Gladiston dos Anjos Almeida
AS TEORIAS DA DIDÁTICA DA MATEMÁTICA COMO LOCUS DE REFLEXÃO E A TEORIA ANTROPOLÓGICA DO DIDÁTICO COMO PRÁXIS NA LICENCIATURA EM MATEMÁTICA GT1 Currículo e formação de professores Gladiston dos Anjos Almeida
OS CONHECIMENTOS SUPOSTOS DISPONÍVEIS NA TRANSIÇÃO ENTRE O ENSINO MÉDIO E SUPERIOR: A NOÇÃO DE SISTEMAS DE EQUAÇÕES LINEARES
 Capítulo 1. Análisis del discurso matemático escolar OS CONHECIMENTOS SUPOSTOS DISPONÍVEIS NA TRANSIÇÃO ENTRE O ENSINO MÉDIO E SUPERIOR: A NOÇÃO DE SISTEMAS DE EQUAÇÕES LINEARES Sérgio Destácio Faro, Marlene
Capítulo 1. Análisis del discurso matemático escolar OS CONHECIMENTOS SUPOSTOS DISPONÍVEIS NA TRANSIÇÃO ENTRE O ENSINO MÉDIO E SUPERIOR: A NOÇÃO DE SISTEMAS DE EQUAÇÕES LINEARES Sérgio Destácio Faro, Marlene
Lógica Proposicional Parte 3
 Lógica Proposicional Parte 3 Nesta aula, vamos mostrar como usar os conhecimentos sobre regras de inferência para descobrir (ou inferir) novas proposições a partir de proposições dadas. Ilustraremos esse
Lógica Proposicional Parte 3 Nesta aula, vamos mostrar como usar os conhecimentos sobre regras de inferência para descobrir (ou inferir) novas proposições a partir de proposições dadas. Ilustraremos esse
VII CONGRESSO INTERNACIONAL DE ENSINO DA MATEMÁTICA
 VII CONGRESSO INTERNACIONAL DE ENSINO DA MATEMÁTICA ULBRA Canoas Rio Grande do Sul Brasil. 04, 05, 06 e 07 de outubro de 2017 Comunicação Científica ENSINO DE PROBABILIDADE: ANÁLISE PRAXEOLÓGICA DE UM
VII CONGRESSO INTERNACIONAL DE ENSINO DA MATEMÁTICA ULBRA Canoas Rio Grande do Sul Brasil. 04, 05, 06 e 07 de outubro de 2017 Comunicação Científica ENSINO DE PROBABILIDADE: ANÁLISE PRAXEOLÓGICA DE UM
OS JOGOS DE QUADROS PARA O ENSINO MÉDIO SITUAÇÕES DE APRENDIZAGEM NA CONSTRUÇÃO DE GRÁFICOS
 OS JOGOS DE QUADROS PARA O ENSINO MÉDIO SITUAÇÕES DE APRENDIZAGEM NA CONSTRUÇÃO DE GRÁFICOS Lúcia Helena Nobre Barros Universidade Bandeirantes - UNIBAN Rede pública de ensino do Estado de São Paulo, E.
OS JOGOS DE QUADROS PARA O ENSINO MÉDIO SITUAÇÕES DE APRENDIZAGEM NA CONSTRUÇÃO DE GRÁFICOS Lúcia Helena Nobre Barros Universidade Bandeirantes - UNIBAN Rede pública de ensino do Estado de São Paulo, E.
PROPOSTAS PARA AVALIAÇÃO DE APRENDIZAGEM ELABORAÇÃO DE PROVAS
 PROPOSTAS PARA AVALIAÇÃO DE APRENDIZAGEM ELABORAÇÃO DE PROVAS Para iniciar a conversa... Os objetivos determinam os tipos de atividades avaliativas. As atividades avaliativas são os veículos usados pelo
PROPOSTAS PARA AVALIAÇÃO DE APRENDIZAGEM ELABORAÇÃO DE PROVAS Para iniciar a conversa... Os objetivos determinam os tipos de atividades avaliativas. As atividades avaliativas são os veículos usados pelo
FORMAÇÃO CONTINUADA Nova Eja
 FORMAÇÃO CONTINUADA Nova Eja FUNDAÇÃO CECIERJ 1º ano /2014 Plano de Ação 2 - Unidades 3 e 4 Cursista Isa Márcia Louro Delbons Grupo - C Regional - Norte Fluminense- I Tutor Robson de Oliveira Bastos A
FORMAÇÃO CONTINUADA Nova Eja FUNDAÇÃO CECIERJ 1º ano /2014 Plano de Ação 2 - Unidades 3 e 4 Cursista Isa Márcia Louro Delbons Grupo - C Regional - Norte Fluminense- I Tutor Robson de Oliveira Bastos A
Laboratório de ensino de matemática e materiais didáticos manipuláveis. Fernanda Trevisol Ramoni Silvano
 Laboratório de ensino de matemática e materiais didáticos manipuláveis Fernanda Trevisol Ramoni Silvano INTRODUÇÃO Muitos foram os educadores que nos últimos séculos, ressaltaram a importância do apoio
Laboratório de ensino de matemática e materiais didáticos manipuláveis Fernanda Trevisol Ramoni Silvano INTRODUÇÃO Muitos foram os educadores que nos últimos séculos, ressaltaram a importância do apoio
Cálculo do Valor Acrescentado No Programa Aves Mª Conceição Silva Portela e Sandra Guerreiro
 Cálculo do Valor Acrescentado No Programa Aves Mª Conceição Silva Portela e Sandra Guerreiro 1. Valor Acrescentado Calcular o valor acrescentado de uma escola significa tentar perceber que valor a escola
Cálculo do Valor Acrescentado No Programa Aves Mª Conceição Silva Portela e Sandra Guerreiro 1. Valor Acrescentado Calcular o valor acrescentado de uma escola significa tentar perceber que valor a escola
OPEMAT. Olimpíada Pernambucana de Matemática
 OPEMAT Olimpíada Pernambucana de Matemática - 206 Nível. O ano de 206 está acabando, vamos ver se você conhece bem esse número. Para isso, julgue os itens a seguir: (V) (F) A maior potência de 2 que divide
OPEMAT Olimpíada Pernambucana de Matemática - 206 Nível. O ano de 206 está acabando, vamos ver se você conhece bem esse número. Para isso, julgue os itens a seguir: (V) (F) A maior potência de 2 que divide
ORGANIZAÇÃO PRAXEOLÓGICA SOBRE ÁREA DE FIGURAS PLANAS: UMA BREVE ABORDAGEM DO LIVRO DIDÁTICO
 ORGANIZAÇÃO PRAXEOLÓGICA SOBRE ÁREA DE FIGURAS PLANAS: UMA BREVE ABORDAGEM DO LIVRO DIDÁTICO Maria Joseane Santos Teixeira Universidade Federal de Pernambuco joseane68@hotmail.com Amanda Barbosa da Silva
ORGANIZAÇÃO PRAXEOLÓGICA SOBRE ÁREA DE FIGURAS PLANAS: UMA BREVE ABORDAGEM DO LIVRO DIDÁTICO Maria Joseane Santos Teixeira Universidade Federal de Pernambuco joseane68@hotmail.com Amanda Barbosa da Silva
Matemática I Tecnólogo em Construção de Edifícios e Tecnólogo em Refrigeração e Climatização
 35 Funções A função é um modo especial de relacionar grandezas. Por eemplo, como escrevemos o deslocamento de um móvel em movimento retilíneo variado dependendo do tempo? E se o móvel está em movimento
35 Funções A função é um modo especial de relacionar grandezas. Por eemplo, como escrevemos o deslocamento de um móvel em movimento retilíneo variado dependendo do tempo? E se o móvel está em movimento
Aspectos Didáticos do Ensino da Resolução de Problemas Usando Proporção em Livros Didáticos Atuais
 1 Aspectos Didáticos do Ensino da Resolução de Problemas Usando Proporção em Livros Didáticos Atuais Maysa Ferreira da Silva Luiz Carlos Pais 1) Considerações Iniciais Este artigo relata uma pesquisa em
1 Aspectos Didáticos do Ensino da Resolução de Problemas Usando Proporção em Livros Didáticos Atuais Maysa Ferreira da Silva Luiz Carlos Pais 1) Considerações Iniciais Este artigo relata uma pesquisa em
AS MARCAS DAS RELAÇÕES INSTITUCIONAIS SOBRE AS RELAÇÕES PESSOAIS DOS ESTUDANTES SOBRE NÚMEROS RACIONAIS NA REPRESENTAÇÃO DECIMAL.
 AS MARCAS DAS RELAÇÕES INSTITUCIONAIS SOBRE AS RELAÇÕES PESSOAIS DOS ESTUDANTES SOBRE NÚMEROS RACIONAIS NA REPRESENTAÇÃO DECIMAL. Cícera Maria dos Santos Xavier, José Valério Gomes da Silva, Rosivaldo
AS MARCAS DAS RELAÇÕES INSTITUCIONAIS SOBRE AS RELAÇÕES PESSOAIS DOS ESTUDANTES SOBRE NÚMEROS RACIONAIS NA REPRESENTAÇÃO DECIMAL. Cícera Maria dos Santos Xavier, José Valério Gomes da Silva, Rosivaldo
JUVENTUDE E ESCOLA (RELAÇÃO JUVENTUDE E ESCOLA)
 JUVENTUDE E ESCOLA (RELAÇÃO JUVENTUDE E ESCOLA) A expressão relação juventude e escola refere-se aos múltiplos aspectos envolvidos na interação entre os jovens alunos e a instituição escolar, quase sempre
JUVENTUDE E ESCOLA (RELAÇÃO JUVENTUDE E ESCOLA) A expressão relação juventude e escola refere-se aos múltiplos aspectos envolvidos na interação entre os jovens alunos e a instituição escolar, quase sempre
UMA SEQUÊNCIA DIDÁTICA PARA O ESTUDO DE RELAÇÕES EM SALA DE AULA ATRAVÉS DO EXCEL
 UMA SEQUÊNCIA DIDÁTICA PARA O ESTUDO DE RELAÇÕES EM SALA DE AULA ATRAVÉS DO EXCEL Camila Macedo Lima Nagamine Universidade Estadual de Santa Cruz cmlnagamine@uesc.br Luzia Muniz Freitas Universidade Estadual
UMA SEQUÊNCIA DIDÁTICA PARA O ESTUDO DE RELAÇÕES EM SALA DE AULA ATRAVÉS DO EXCEL Camila Macedo Lima Nagamine Universidade Estadual de Santa Cruz cmlnagamine@uesc.br Luzia Muniz Freitas Universidade Estadual
UMA ANÁLISE DA INTRODUÇÃO DE EQUAÇÕES DO PRIMEIRO GRAU COM UMA INCÓGNITA EM UM LIVRO DIDÁTICO DE MATEMÁTICA
 27 UMA ANÁLISE DA INTRODUÇÃO DE EQUAÇÕES DO PRIMEIRO GRAU COM UMA INCÓGNITA EM UM LIVRO DIDÁTICO DE MATEMÁTICA Anderson Soares Muniz - UFMS Luiz Carlos Pais - UFMS RESUMO: Este artigo procura descrever
27 UMA ANÁLISE DA INTRODUÇÃO DE EQUAÇÕES DO PRIMEIRO GRAU COM UMA INCÓGNITA EM UM LIVRO DIDÁTICO DE MATEMÁTICA Anderson Soares Muniz - UFMS Luiz Carlos Pais - UFMS RESUMO: Este artigo procura descrever
ENSINANDO FUNÇÃO EXPONENCIAL E O CONCEITO DE LIMITES DE FUNÇÕES PARA O ENSINO MÉDIO UTILIZANDO ATIVIDADES INVESTIGATIVAS
 ENSINANDO FUNÇÃO EXPONENCIAL E O CONCEITO DE LIMITES DE FUNÇÕES PARA O ENSINO MÉDIO UTILIZANDO ATIVIDADES INVESTIGATIVAS Márcio Pereira Amaral¹; Orientador: Lourenço Gonçalves Junior² Instituto Federal
ENSINANDO FUNÇÃO EXPONENCIAL E O CONCEITO DE LIMITES DE FUNÇÕES PARA O ENSINO MÉDIO UTILIZANDO ATIVIDADES INVESTIGATIVAS Márcio Pereira Amaral¹; Orientador: Lourenço Gonçalves Junior² Instituto Federal
ESTRUTURA 2. ESTRUTURA DA BNCC
 2. ESTRUTURA DA BNCC Em conformidade com os fundamentos pedagógicos apresentados na Introdução deste documento, a BNCC está estruturada de modo a explicitar as competências que os alunos devem desenvolver
2. ESTRUTURA DA BNCC Em conformidade com os fundamentos pedagógicos apresentados na Introdução deste documento, a BNCC está estruturada de modo a explicitar as competências que os alunos devem desenvolver
PLANO DE TRABALHO I GOVERNO DO ESTADO DO RIO DE JANEIRO SECRECTARIA ESTADUAL DE EDUCAÇÃO METROPOLITANA I
 PLANO DE TRABALHO I GOVERNO DO ESTADO DO RIO DE JANEIRO SECRECTARIA ESTADUAL DE EDUCAÇÃO METROPOLITANA I PROJETO SEEDUC FORMAÇÃO CONTINUADA DE PROFESSORES COLÉGIO ESTADUAL MARECHAL JUAREZ TÁVORA GRUPO
PLANO DE TRABALHO I GOVERNO DO ESTADO DO RIO DE JANEIRO SECRECTARIA ESTADUAL DE EDUCAÇÃO METROPOLITANA I PROJETO SEEDUC FORMAÇÃO CONTINUADA DE PROFESSORES COLÉGIO ESTADUAL MARECHAL JUAREZ TÁVORA GRUPO
Contrato didático e (in)disciplina. Professora: Dra. Eduarda Maria Schneider
 Contrato didático e (in)disciplina Professora: Dra. Eduarda Maria Schneider Objetivos Trabalhar o Contrato Didático como um conceito da didática e importante teoria na compreensão das diversas situações
Contrato didático e (in)disciplina Professora: Dra. Eduarda Maria Schneider Objetivos Trabalhar o Contrato Didático como um conceito da didática e importante teoria na compreensão das diversas situações
Lógica Proposicional
 Lógica Proposicional Lógica Computacional Carlos Bacelar Almeida Departmento de Informática Universidade do Minho 2007/2008 Carlos Bacelar Almeida, DIUM LÓGICA PROPOSICIONAL- LÓGICA COMPUTACIONAL 1/28
Lógica Proposicional Lógica Computacional Carlos Bacelar Almeida Departmento de Informática Universidade do Minho 2007/2008 Carlos Bacelar Almeida, DIUM LÓGICA PROPOSICIONAL- LÓGICA COMPUTACIONAL 1/28
Explorando a ideia de função
 Instituto Municipal de Ensino Superior de Catanduva SP Curso de Licenciatura em Matemática 3º ano Prática de Ensino da Matemática III Prof. M.Sc. Fabricio Eduardo Ferreira fabricio@fafica.br Explorando
Instituto Municipal de Ensino Superior de Catanduva SP Curso de Licenciatura em Matemática 3º ano Prática de Ensino da Matemática III Prof. M.Sc. Fabricio Eduardo Ferreira fabricio@fafica.br Explorando
OS CONTEXTOS EM QUE A FUNÇÃO QUADRÁTICA SE APRESENTA NAS ABORDAGENS DE LIVROS DIDÁTICOS DO ENSINO MÉDIO: UMA AMOSTRA DA ANÁLISE PRAXEOLÓGICA.
 Sociedade Brasileira de na Contemporaneidade: desafios e possibilidades São Paulo SP, 13 a 16 de julho de 016 OS CONTEXTOS EM QUE A FUNÇÃO QUADRÁTICA SE APRESENTA NAS ABORDAGENS DE LIVROS DIDÁTICOS DO
Sociedade Brasileira de na Contemporaneidade: desafios e possibilidades São Paulo SP, 13 a 16 de julho de 016 OS CONTEXTOS EM QUE A FUNÇÃO QUADRÁTICA SE APRESENTA NAS ABORDAGENS DE LIVROS DIDÁTICOS DO
Funções. Conceitos Básicos. Unidade C. Matemática I IFRS CAMPUS RIO GRANDE - FURG
 34 Unidade C Funções Conceitos Básicos Matemática I IFRS CAMPUS RIO GRANDE - FURG 35 Funções A função é um modo especial de relacionar grandezas. Por eemplo, como escrevemos o deslocamento de um móvel
34 Unidade C Funções Conceitos Básicos Matemática I IFRS CAMPUS RIO GRANDE - FURG 35 Funções A função é um modo especial de relacionar grandezas. Por eemplo, como escrevemos o deslocamento de um móvel
OS HEMISFÉRIOS CEREBRAIS
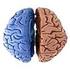 OS HEMISFÉRIOS CEREBRAIS UMA COMPARAÇÃO DAS CARACTERÍSTICAS DE CADA HEMISFÉRIO esquerdo Verbal: usa palavras para nomear, descrever e definir; Analítico: decifra as coisas de maneira sequencial e por partes;
OS HEMISFÉRIOS CEREBRAIS UMA COMPARAÇÃO DAS CARACTERÍSTICAS DE CADA HEMISFÉRIO esquerdo Verbal: usa palavras para nomear, descrever e definir; Analítico: decifra as coisas de maneira sequencial e por partes;
AGRUPAMENTO DE ESCOLAS PROF. PAULA NOGUEIRA - OLHÃO DEPARTAMENTO DE MATEMÁTICA DOS 2º E 3º CICLOS CRITÉRIOS DE AVALIAÇÃO DE MATEMÁTICA
 AGRUPAMENTO DE ESCOLAS PROF. PAULA NOGUEIRA - OLHÃO DEPARTAMENTO DE MATEMÁTICA DOS 2º E 3º CICLOS CRITÉRIOS DE AVALIAÇÃO DE MATEMÁTICA Sem prejuízo do legalmente estabelecido e sujeito aos critérios aprovados
AGRUPAMENTO DE ESCOLAS PROF. PAULA NOGUEIRA - OLHÃO DEPARTAMENTO DE MATEMÁTICA DOS 2º E 3º CICLOS CRITÉRIOS DE AVALIAÇÃO DE MATEMÁTICA Sem prejuízo do legalmente estabelecido e sujeito aos critérios aprovados
Neste artigo, a título de sugestão de abordagem do tema, apresentamos exemplos de explicitação e utilização de algumas dessas regras.
 Somo Gilda de La Roque Palis e Iaci Malta PUC - RJ Em sua autobiografia, Carl Gustav Jung 1, um dos grandes pensadores da Psicanálise, lembrando de seus tempos de colégio, diz:... o que mais me irritava
Somo Gilda de La Roque Palis e Iaci Malta PUC - RJ Em sua autobiografia, Carl Gustav Jung 1, um dos grandes pensadores da Psicanálise, lembrando de seus tempos de colégio, diz:... o que mais me irritava
Indisciplina na Escola: Desafio para a Escola e para a Família
 Indisciplina na Escola: Desafio para a Escola e para a Família Francisco Canindé de Assunção Faculdade do Norte do Paraná FACNORTE / SAPIENS canindeassuncao@gmail.com Resumo: Atualmente é comum, nas discussões
Indisciplina na Escola: Desafio para a Escola e para a Família Francisco Canindé de Assunção Faculdade do Norte do Paraná FACNORTE / SAPIENS canindeassuncao@gmail.com Resumo: Atualmente é comum, nas discussões
A RESOLUÇÃO DE PROBLEMAS E O ENSINO DA FÍSICAF
 Os processos cognitivos relacionados com o conceito geral de resolução de problemas tradicionalmente constituíam uma reserva praticamente exclusiva dos tratados de psicologia Passaram a ter um interesse
Os processos cognitivos relacionados com o conceito geral de resolução de problemas tradicionalmente constituíam uma reserva praticamente exclusiva dos tratados de psicologia Passaram a ter um interesse
CONSEQUÊNCIAS DO ESTUDO DAS EQUAÇÕES DE 2º GRAU
 CONSEQUÊNCIAS DO ESTUDO DAS EQUAÇÕES DE 2º GRAU INTRODUÇÃO No texto anterior abordamos o tema Equação de 2º grau. Lá ela foi definida, resolvida, e teve demonstradas suas propriedades. A partir de agora,
CONSEQUÊNCIAS DO ESTUDO DAS EQUAÇÕES DE 2º GRAU INTRODUÇÃO No texto anterior abordamos o tema Equação de 2º grau. Lá ela foi definida, resolvida, e teve demonstradas suas propriedades. A partir de agora,
CONEXÕES ENTRE A MATEMÁTICA DA EDUCAÇÃO BÁSICA E A MATEMÁTICA SUPERIOR: UMA REFLEXÃO A LUZ DA TEÓRIA ANTROPOLÓGICA DO DIDÁTICO.
 CONEXÕES ENTRE A MATEMÁTICA DA EDUCAÇÃO BÁSICA E A MATEMÁTICA SUPERIOR: UMA REFLEXÃO A LUZ DA TEÓRIA ANTROPOLÓGICA DO DIDÁTICO. Maria Edilane Amaral Ferreira; José Luiz Cavalcante; Rochelande Felipe Rodrigues;
CONEXÕES ENTRE A MATEMÁTICA DA EDUCAÇÃO BÁSICA E A MATEMÁTICA SUPERIOR: UMA REFLEXÃO A LUZ DA TEÓRIA ANTROPOLÓGICA DO DIDÁTICO. Maria Edilane Amaral Ferreira; José Luiz Cavalcante; Rochelande Felipe Rodrigues;
AGRUPAMENTO DE ESCOLAS GONÇALO SAMPAIO ESCOLA E.B. 2, 3 PROFESSOR GONÇALO SAMPAIO
 AGRUPAMENTO DE ESCOLAS GONÇALO SAMPAIO ESCOLA E.B. 2, 3 PROFESSOR GONÇALO SAMPAIO DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA 7º ANO PLANIFICAÇÃO ANUAL 2016/2017 PLANIFICAÇÃO ANUAL DISCIPLINA: Matemática ANO
AGRUPAMENTO DE ESCOLAS GONÇALO SAMPAIO ESCOLA E.B. 2, 3 PROFESSOR GONÇALO SAMPAIO DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA 7º ANO PLANIFICAÇÃO ANUAL 2016/2017 PLANIFICAÇÃO ANUAL DISCIPLINA: Matemática ANO
ORGANIZAÇÃO E TRATAMENTO DE DADOS
 ORGANIZAÇÃO E TRATAMENTO DE DADOS Principles and Standards for School Mathematics (2000) Este documento reforça a ênfase dada no anterior documento, da importância e da adequabilidade, às crianças mais
ORGANIZAÇÃO E TRATAMENTO DE DADOS Principles and Standards for School Mathematics (2000) Este documento reforça a ênfase dada no anterior documento, da importância e da adequabilidade, às crianças mais
O JOGO COMO RECURSO METODOLÓGICO PARA O ENSINO DA MATEMÁTICA NOS ANOS INICIAIS
 O JOGO COMO RECURSO METODOLÓGICO PARA O ENSINO DA MATEMÁTICA NOS ANOS INICIAIS Lidia Ribeiro da Silva Universidade Federal de Campina Grande, lidiaribeiroufcg@gmail.com Luana Maria Ferreira Duarte Universidade
O JOGO COMO RECURSO METODOLÓGICO PARA O ENSINO DA MATEMÁTICA NOS ANOS INICIAIS Lidia Ribeiro da Silva Universidade Federal de Campina Grande, lidiaribeiroufcg@gmail.com Luana Maria Ferreira Duarte Universidade
Caro(a) aluno(a), Coordenadoria de Estudos e Normas Pedagógicas CENP Secretaria da Educação do Estado de São Paulo Equipe Técnica de Matemática
 Caro(a) aluno(a), Você saberia representar a soma dos n primeiros números naturais a partir do 1? Neste Caderno você terá a oportunidade de conhecer esse e outros casos que envolvem sequências e resolvê-los
Caro(a) aluno(a), Você saberia representar a soma dos n primeiros números naturais a partir do 1? Neste Caderno você terá a oportunidade de conhecer esse e outros casos que envolvem sequências e resolvê-los
EAD DETERMINANTES CONCEITO:
 1 EAD DETERMINANTES CONCEITO: Dada uma Matriz Quadrada de ordem n, dizemos que Determinante de ordem n é um número associado a essa Matriz conforme determinadas leis. Representamos o Determinante de uma
1 EAD DETERMINANTES CONCEITO: Dada uma Matriz Quadrada de ordem n, dizemos que Determinante de ordem n é um número associado a essa Matriz conforme determinadas leis. Representamos o Determinante de uma
local, estreitamente associado ao saber em jogo e aos diferentes problemas em cuja resolução intervém.
 1 ESTUDO DE MOMENTOS DIDÁTICOS DE PROFESSORES DURANTE A ELABORAÇÃO DE UMA ORGANIZAÇÃO DIDÁTICA SOBRE NÚMEROS FRACIONÁRIOS SILVA, Maria José Ferreira da PUC-SP zezé@pucsp.br GT: Educação Matemática / n.19
1 ESTUDO DE MOMENTOS DIDÁTICOS DE PROFESSORES DURANTE A ELABORAÇÃO DE UMA ORGANIZAÇÃO DIDÁTICA SOBRE NÚMEROS FRACIONÁRIOS SILVA, Maria José Ferreira da PUC-SP zezé@pucsp.br GT: Educação Matemática / n.19
Concurso Público Osasco PEB I SLIDES Prof. Amarildo Vieira
 Concurso Público Osasco PEB I - 2017 SLIDES Prof. Amarildo Vieira PEDAGOGO UNIb ESPECIALIZAÇÃO EM DIDÁTICA DO ENSINO SUPERIOR PUC/SP BACHARELANDO EM DIREITO Uninove DIRETOR DE ESCOLA PMSP/SP PROFESSOR
Concurso Público Osasco PEB I - 2017 SLIDES Prof. Amarildo Vieira PEDAGOGO UNIb ESPECIALIZAÇÃO EM DIDÁTICA DO ENSINO SUPERIOR PUC/SP BACHARELANDO EM DIREITO Uninove DIRETOR DE ESCOLA PMSP/SP PROFESSOR
Conceitos Básicos INTRODUÇÃO 1 VETORES 1.1 REPRESENTAÇÃO DOS VETORES
 Conceitos Básicos INTRODUÇÃO Esse material foi criado por um motivo: o curso de álgebra linear II da UFRJ parte do princípio que o aluno de Engenharia da UFRJ que faz a disciplina já conhece alguns conceitos
Conceitos Básicos INTRODUÇÃO Esse material foi criado por um motivo: o curso de álgebra linear II da UFRJ parte do princípio que o aluno de Engenharia da UFRJ que faz a disciplina já conhece alguns conceitos
Biofísica II Turma de Biologia FFCLRP USP Prof. Antônio Roque Biologia de Populações 1 Modelo malthusiano O Modelo Malthusiano
 O Modelo Malthusiano Para começar nosso estudo de modelos matemáticos para populações, vamos estudar o modelo mais simples para mudanças no tamanho de uma população, que chamaremos de modelo malthusiano.
O Modelo Malthusiano Para começar nosso estudo de modelos matemáticos para populações, vamos estudar o modelo mais simples para mudanças no tamanho de uma população, que chamaremos de modelo malthusiano.
ARTICULAÇÃO ENTRE REPRESENTAÇÕES ALGÉBRICAS E GRÁFICAS DE UMA FUNÇÃO: CONSTRUINDO CONJECTURAS POR MEIO DO GEOGEBRA
 ARTICULAÇÃO ENTRE REPRESENTAÇÕES ALGÉBRICAS E GRÁFICAS DE UMA FUNÇÃO: CONSTRUINDO CONJECTURAS POR MEIO DO GEOGEBRA Fernanda Elisbão Silva de Souza Programa de Pós-Graduação em Educação Matemática UFMS
ARTICULAÇÃO ENTRE REPRESENTAÇÕES ALGÉBRICAS E GRÁFICAS DE UMA FUNÇÃO: CONSTRUINDO CONJECTURAS POR MEIO DO GEOGEBRA Fernanda Elisbão Silva de Souza Programa de Pós-Graduação em Educação Matemática UFMS
AS CONCEPÇÕES DOS ALUNOS COMO FACTOR CONDICIONANTE DA APRENDIZAGEM EM FÍSICA
 É útil diferenciar duas formas distintas do conhecimento prévio de um aluno: 1º) os conceitos que o aluno assimila naturalmente, através da sua interacção com o meio conceitos espontâneos 2º) os conceitos
É útil diferenciar duas formas distintas do conhecimento prévio de um aluno: 1º) os conceitos que o aluno assimila naturalmente, através da sua interacção com o meio conceitos espontâneos 2º) os conceitos
DO SABER SÁBIO AO SABER ENSINADO : QUE ESTRATÉGIAS PODEM SER ADOTADAS PARA QUE AS PESQUISAS POSSAM CONTRIBUIR PARA A PRÁTICA DO PROFESSOR?
 DO SABER SÁBIO AO SABER ENSINADO : QUE ESTRATÉGIAS PODEM SER ADOTADAS PARA QUE AS PESQUISAS POSSAM CONTRIBUIR PARA A PRÁTICA DO PROFESSOR? Celina A. A. P. Abar abarcaap@pucsp.br Pontifícia Universidade
DO SABER SÁBIO AO SABER ENSINADO : QUE ESTRATÉGIAS PODEM SER ADOTADAS PARA QUE AS PESQUISAS POSSAM CONTRIBUIR PARA A PRÁTICA DO PROFESSOR? Celina A. A. P. Abar abarcaap@pucsp.br Pontifícia Universidade
ROTEIRO DE RECUPERAÇÃO DE MATEMÁTICA (1º SEMESTRE) 9º ANO. Introdução Potenciação. Radiciação
 ROTEIRO DE RECUPERAÇÃO DE MATEMÁTICA (1º SEMESTRE) 9º ANO Nome: Nº - Série/Ano Data: / / 2017. Professor(a): Cauê / Yuri / Marcello / Diego / Rafael Os conteúdos essenciais do semestre. ÁLGEBRA: Capítulo
ROTEIRO DE RECUPERAÇÃO DE MATEMÁTICA (1º SEMESTRE) 9º ANO Nome: Nº - Série/Ano Data: / / 2017. Professor(a): Cauê / Yuri / Marcello / Diego / Rafael Os conteúdos essenciais do semestre. ÁLGEBRA: Capítulo
Uma equação nada racional!
 Reforço escolar M ate mática Uma equação nada racional! Dinâmica 5 9º Ano 1º Bimestre Professor DISCIPLINA SÉRIE CAMPO CONCEITO Matemática Ensino Fundamental 9ª Numérico Aritmético Radicais. DINÂMICA Equações
Reforço escolar M ate mática Uma equação nada racional! Dinâmica 5 9º Ano 1º Bimestre Professor DISCIPLINA SÉRIE CAMPO CONCEITO Matemática Ensino Fundamental 9ª Numérico Aritmético Radicais. DINÂMICA Equações
Introdução. Figura 1 representação geométrica de fracionários.
 Introdução Nosso interesse por números fracionários vem desde 1989, quando em pesquisa sobre o assunto, com alunos do Ensino Fundamental, percebemos suas dificuldades para se relacionar com esses números.
Introdução Nosso interesse por números fracionários vem desde 1989, quando em pesquisa sobre o assunto, com alunos do Ensino Fundamental, percebemos suas dificuldades para se relacionar com esses números.
UMA REFLEXÃO SOBRE A ATIVIDADE DE SITUAÇÕES PROBLEMA EM SISTEMA DE EQUAÇÕES LINEARES NA ESCOLA ESTADUAL MARIA DAS DORES BRASIL
 UMA REFLEXÃO SOBRE A ATIVIDADE DE SITUAÇÕES PROBLEMA EM SISTEMA DE EQUAÇÕES LINEARES NA ESCOLA ESTADUAL MARIA DAS DORES BRASIL LEITE* 1, Jardel Sousa; MENDOZA 2, Héctor José García RESUMO 1 jardelsousa562@gmail.com
UMA REFLEXÃO SOBRE A ATIVIDADE DE SITUAÇÕES PROBLEMA EM SISTEMA DE EQUAÇÕES LINEARES NA ESCOLA ESTADUAL MARIA DAS DORES BRASIL LEITE* 1, Jardel Sousa; MENDOZA 2, Héctor José García RESUMO 1 jardelsousa562@gmail.com
NOTAS DE AULA CONSTRUÇÃO DO MARCO TEÓRICO CONCEITUAL 1
 NOTAS DE AULA CONSTRUÇÃO DO MARCO TEÓRICO CONCEITUAL 1 Profa. Gláucia Russo Um projeto de pesquisa pode se organizar de diversas formas, naquela que estamos trabalhando aqui, a problematização estaria
NOTAS DE AULA CONSTRUÇÃO DO MARCO TEÓRICO CONCEITUAL 1 Profa. Gláucia Russo Um projeto de pesquisa pode se organizar de diversas formas, naquela que estamos trabalhando aqui, a problematização estaria
Planificação Anual de Matemática 7º Ano
 Temas transversais: Planificação Anual de Matemática 7º Ano Resolução de Problemas Resolver problemas usando números racionais, utilizando equações e funções em contextos matemáticos e não matemáticos,
Temas transversais: Planificação Anual de Matemática 7º Ano Resolução de Problemas Resolver problemas usando números racionais, utilizando equações e funções em contextos matemáticos e não matemáticos,
Equacionando problemas - II
 A UA UL LA Equacionando problemas - II Introdução Nossa aula Nas duas últimas aulas, resolvemos diversas equações do º grau pelo processo de completar o quadrado perfeito ou pela utilização da fórmula
A UA UL LA Equacionando problemas - II Introdução Nossa aula Nas duas últimas aulas, resolvemos diversas equações do º grau pelo processo de completar o quadrado perfeito ou pela utilização da fórmula
Miguel Dias. Como elaborar um projeto de pesquisa para TCC.
 Como elaborar um projeto de pesquisa para TCC. migdias@gmail.com www.migdias.weebly.com www.facebook.com/migueldias.pt Miguel Dias Bolsista PNPD/CAPES Universidade do Estado do Rio Grande do Norte O que
Como elaborar um projeto de pesquisa para TCC. migdias@gmail.com www.migdias.weebly.com www.facebook.com/migueldias.pt Miguel Dias Bolsista PNPD/CAPES Universidade do Estado do Rio Grande do Norte O que
CURRÍCULO DAS ÁREAS DISCIPLINARES / CRITÉRIOS DE AVALIAÇÃO
 Domínios e subdomínios Metas/Objetivos Objetivos gerais 3º Ciclo Matemática - 8º Ano Conteúdos Programáticos Critérios de Avaliação Instrumentos de Avaliação NÚMEROS E OPERAÇÕES: -Dízimas finitas, infinitas
Domínios e subdomínios Metas/Objetivos Objetivos gerais 3º Ciclo Matemática - 8º Ano Conteúdos Programáticos Critérios de Avaliação Instrumentos de Avaliação NÚMEROS E OPERAÇÕES: -Dízimas finitas, infinitas
CONSIDERAÇÕES TEÓRICAS ACERCA DE TEORIAS DAS CIÊNCIAS DA EDUCAÇÃO 1 THEORETICAL CONSIDERATIONS ABOUT THEORIES OF EDUCATION SCIENCES
 CONSIDERAÇÕES TEÓRICAS ACERCA DE TEORIAS DAS CIÊNCIAS DA EDUCAÇÃO 1 THEORETICAL CONSIDERATIONS ABOUT THEORIES OF EDUCATION SCIENCES Tailon Thiele 2, Eliane Miotto Kamphorst 3 1 Projeto de pesquisa realizado
CONSIDERAÇÕES TEÓRICAS ACERCA DE TEORIAS DAS CIÊNCIAS DA EDUCAÇÃO 1 THEORETICAL CONSIDERATIONS ABOUT THEORIES OF EDUCATION SCIENCES Tailon Thiele 2, Eliane Miotto Kamphorst 3 1 Projeto de pesquisa realizado
FIGURAS PLANAS E ESPACIAIS
 CURSO DE FORMAÇÃO CONTINUADA EM MATEMÁTICA PARA PROFESSORES DA EDUCAÇÃO BÁSICA (4º E 5º ANOS) PROFESSORA ANDRESSA CESANA CEUNES/UFES/DMA FIGURAS PLANAS E ESPACIAIS AGOSTO DE 2015 A PEDAGOGIA DO TEXTO é
CURSO DE FORMAÇÃO CONTINUADA EM MATEMÁTICA PARA PROFESSORES DA EDUCAÇÃO BÁSICA (4º E 5º ANOS) PROFESSORA ANDRESSA CESANA CEUNES/UFES/DMA FIGURAS PLANAS E ESPACIAIS AGOSTO DE 2015 A PEDAGOGIA DO TEXTO é
A ORGANIZAÇÃO DIDÁTICA DA INTRODUÇÃO DA ÁLGEBRA EM UM MANUAL DO 7º ANO DO ENSINO FUNDAMENTAL
 A ORGANIZAÇÃO DIDÁTICA DA INTRODUÇÃO DA ÁLGEBRA EM UM MANUAL DO 7º ANO DO ENSINO FUNDAMENTAL Rosane Corsini Silva Nogueira Marilena Bittar Universidade Federal de Mato Grosso do Sul RESUMO: Nesse artigo
A ORGANIZAÇÃO DIDÁTICA DA INTRODUÇÃO DA ÁLGEBRA EM UM MANUAL DO 7º ANO DO ENSINO FUNDAMENTAL Rosane Corsini Silva Nogueira Marilena Bittar Universidade Federal de Mato Grosso do Sul RESUMO: Nesse artigo
Aprendizagem significativa e aquisição da escrita
 Aprendizagem significativa e aquisição da escrita Júlio Furtado www.juliofurtado.com.br 1 O homem é a única criatura que precisa ser educada (...) Por ser dotado de instinto, um animal, ao nascer, já é
Aprendizagem significativa e aquisição da escrita Júlio Furtado www.juliofurtado.com.br 1 O homem é a única criatura que precisa ser educada (...) Por ser dotado de instinto, um animal, ao nascer, já é
Números Inteiros Axiomas e Resultados Simples
 Números Inteiros Axiomas e Resultados Simples Apresentamos aqui diversas propriedades gerais dos números inteiros que não precisarão ser provadas quando você, aluno, for demonstrar teoremas nesta disciplina.
Números Inteiros Axiomas e Resultados Simples Apresentamos aqui diversas propriedades gerais dos números inteiros que não precisarão ser provadas quando você, aluno, for demonstrar teoremas nesta disciplina.
CURRÍCULO DAS ÁREAS DISCIPLINARES / CRITÉRIOS DE AVALIAÇÃO
 Domínios e subdomínios Metas/Objetivos Objetivos gerais 3º Ciclo Matemática 7º Ano Conteúdos Programáticos Critérios de Avaliação Instrumentos de Avaliação Números e Operações: Números racionais Álgebra:
Domínios e subdomínios Metas/Objetivos Objetivos gerais 3º Ciclo Matemática 7º Ano Conteúdos Programáticos Critérios de Avaliação Instrumentos de Avaliação Números e Operações: Números racionais Álgebra:
Fundação CECIERJ/Consórcio CEDERJ
 Fundação CECIERJ/Consórcio CEDERJ Formação Continuada em Matemática Tarefa 1: Plano de Trabalho Matemática 1 Ano - 3 Bimestre/2014 Função Polinomial do 2 Grau Cursista: Soraya de Oliveira Coelho Tutor:
Fundação CECIERJ/Consórcio CEDERJ Formação Continuada em Matemática Tarefa 1: Plano de Trabalho Matemática 1 Ano - 3 Bimestre/2014 Função Polinomial do 2 Grau Cursista: Soraya de Oliveira Coelho Tutor:
Agrupamento de Escolas António Correia de Oliveira PLANIFICAÇÃO ANUAL DE MATEMÁTICA 7.º ANO ANO LETIVO 2018/19
 Agrupamento de Escolas António Correia de Oliveira PLANIFICAÇÃO ANUAL DE MATEMÁTICA 7.º ANO ANO LETIVO 2018/19 1.º PERÍODO Tema/Subtema Objetivos Essenciais de Aprendizegem Aulas previstas (45 min) Aprendizagens
Agrupamento de Escolas António Correia de Oliveira PLANIFICAÇÃO ANUAL DE MATEMÁTICA 7.º ANO ANO LETIVO 2018/19 1.º PERÍODO Tema/Subtema Objetivos Essenciais de Aprendizegem Aulas previstas (45 min) Aprendizagens
FUNDAÇÃO CECIERJ / CONSÓRCIO CEDERJ
 FORMAÇÃO CONTINUADA FUNDAÇÃO CECIERJ / CONSÓRCIO CEDERJ Matemática 9º ano 2ºBimestre / 2013 Plano de Trabalho 1 Cursista Isa Louro Delbons Grupo - 01 Tutor Emílio Rubem Batista Junior 1 Figura 1 - www.brasilescola.com
FORMAÇÃO CONTINUADA FUNDAÇÃO CECIERJ / CONSÓRCIO CEDERJ Matemática 9º ano 2ºBimestre / 2013 Plano de Trabalho 1 Cursista Isa Louro Delbons Grupo - 01 Tutor Emílio Rubem Batista Junior 1 Figura 1 - www.brasilescola.com
PERSPECTIVAS PARA O PLANEJAMENTO DE ESCRITA Autor1: Jeyza Andrade de Medeiros. Modalidade: COMUNICAÇÃO CIENTÍFICA
 PERSPECTIVAS PARA O PLANEJAMENTO DE ESCRITA Autor1: Jeyza Andrade de Medeiros Modalidade: COMUNICAÇÃO CIENTÍFICA RESUMO Neste trabalho, temos por tema o estudo do planejamento de escrita e estabelecemos
PERSPECTIVAS PARA O PLANEJAMENTO DE ESCRITA Autor1: Jeyza Andrade de Medeiros Modalidade: COMUNICAÇÃO CIENTÍFICA RESUMO Neste trabalho, temos por tema o estudo do planejamento de escrita e estabelecemos
Palavras- chaves: Geometria das abelhas, Formato hexagonal dos favos de mel, Ensinoaprendizagem.
 EXPLORANDO O FORMATO HEXAGONAL DOS FAVOS DE MEL DAS ABELHAS NA SALA DE AULA DE MATEMÁTICA Rômulo Alexandre SILVA romulo_celia@hotmail.com Cinthia Sany França XAVIER cinthiasany@gmail.com Ayze Jammylle
EXPLORANDO O FORMATO HEXAGONAL DOS FAVOS DE MEL DAS ABELHAS NA SALA DE AULA DE MATEMÁTICA Rômulo Alexandre SILVA romulo_celia@hotmail.com Cinthia Sany França XAVIER cinthiasany@gmail.com Ayze Jammylle
Resenhado por Katiele Naiara Hirsch Universidade de Santa Cruz do Sul
 SOUSA, Lucilene Bender de; GABRIEL, Rosângela. Aprendendo palavras através da leitura. Santa Cruz do Sul: EDUNISC, 2011. Resenhado por Katiele Naiara Hirsch Universidade de Santa Cruz do Sul Em Aprendendo
SOUSA, Lucilene Bender de; GABRIEL, Rosângela. Aprendendo palavras através da leitura. Santa Cruz do Sul: EDUNISC, 2011. Resenhado por Katiele Naiara Hirsch Universidade de Santa Cruz do Sul Em Aprendendo
Didática e docência: formação e trabalho de professores da educação básica
 Didática e docência: formação e trabalho de professores da educação básica Prof. Dr. José Carlos Libâneo I Simpósio sobre Ensino de Didática LEPED - Laboratório de Estudos e Pesquisas em Didática e Formação
Didática e docência: formação e trabalho de professores da educação básica Prof. Dr. José Carlos Libâneo I Simpósio sobre Ensino de Didática LEPED - Laboratório de Estudos e Pesquisas em Didática e Formação
PALAVRAS-CHAVE: Portal do Professor, Relação professor-aluno, Aula de
 RESUMO A relação professor-aluno nas aulas de Biologia Elisandra Carneiro de Freitas 1 Marilda Shuvartz 2 O presente trabalho traz resultados da investigação da dissertação de mestrado desenvolvida no
RESUMO A relação professor-aluno nas aulas de Biologia Elisandra Carneiro de Freitas 1 Marilda Shuvartz 2 O presente trabalho traz resultados da investigação da dissertação de mestrado desenvolvida no
MATEMÁTICA - 8.º Ano. Ana Soares ) Catarina Coimbra
 Salesianos de Mogofores - 2016/2017 MATEMÁTICA - 8.º Ano Ana Soares (ana.soares@mogofores.salesianos.pt ) Catarina Coimbra (catarina.coimbra@mogofores.salesianos.pt ) Rota de aprendizage m por Projetos
Salesianos de Mogofores - 2016/2017 MATEMÁTICA - 8.º Ano Ana Soares (ana.soares@mogofores.salesianos.pt ) Catarina Coimbra (catarina.coimbra@mogofores.salesianos.pt ) Rota de aprendizage m por Projetos
1). Tipos de equações. 3). Etapas na resolução algébrica de equações numéricas. 4). Os dois grandes cuidados na resolução de equações
 1). Tipos de equações LIÇÃO 7 Introdução à resolução das equações numéricas Na Matemática, nas Ciências e em olimpíadas, encontramos equações onde a incógnita pode ser número, função, matriz ou outros
1). Tipos de equações LIÇÃO 7 Introdução à resolução das equações numéricas Na Matemática, nas Ciências e em olimpíadas, encontramos equações onde a incógnita pode ser número, função, matriz ou outros
MAT ÀS DÚVIDAS: ARTICULANDO TEORIA DO CONHECIMENTO E PRÁTICA NA ESCOLA ESTADUAL MARIA CONSTANÇA BARROS MACHADO. Cleverson Borges da Silva - UFMS
 MAT ÀS DÚVIDAS: ARTICULANDO TEORIA DO CONHECIMENTO E PRÁTICA NA ESCOLA ESTADUAL MARIA CONSTANÇA BARROS MACHADO Cleverson Borges da Silva - UFMS cleverborges12@hotmail.com Emily Monge Silva emilymonge88@hotmail.com
MAT ÀS DÚVIDAS: ARTICULANDO TEORIA DO CONHECIMENTO E PRÁTICA NA ESCOLA ESTADUAL MARIA CONSTANÇA BARROS MACHADO Cleverson Borges da Silva - UFMS cleverborges12@hotmail.com Emily Monge Silva emilymonge88@hotmail.com
Diferenciar Funções lineares e não lineares. Diferenciar Funções crescentes e decrescentes. Determinar o Ponto de máximo e o Ponto de mínimo.
 MATEMÁTICA PARA NEGÓCIOS - GST1075 Semana Aula: 1 Revisão de Funções e Gráficos Tema Funções e Gráficos Palavras-chave Funções; Gráficos Objetivos Ao final desta aula, o aluno deverá ser capaz de: Diferenciar
MATEMÁTICA PARA NEGÓCIOS - GST1075 Semana Aula: 1 Revisão de Funções e Gráficos Tema Funções e Gráficos Palavras-chave Funções; Gráficos Objetivos Ao final desta aula, o aluno deverá ser capaz de: Diferenciar
PLANO DE TRABALHO SOBRE MATRIZES
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ Colégio: C.E.CONDE PEREIRA CARNEIRO Professor: RAFAEL FERREIRA DA COSTA LEITE Matrículas: 09718115 Série: 2º ANO ENSINO MÉDIO
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ Colégio: C.E.CONDE PEREIRA CARNEIRO Professor: RAFAEL FERREIRA DA COSTA LEITE Matrículas: 09718115 Série: 2º ANO ENSINO MÉDIO
Aula 02 CONCEITO DE RAÇA, ETNICIDADE E SAÚDE. 1. Definição de raça
 Aula 02 CONCEITO DE RAÇA, ETNICIDADE E SAÚDE Nas últimas décadas, diversos estudos tem mostrado diferenças raciais marcantes na morbimortalidade, no comportamento ante a doença e saúde, no acesso e uso
Aula 02 CONCEITO DE RAÇA, ETNICIDADE E SAÚDE Nas últimas décadas, diversos estudos tem mostrado diferenças raciais marcantes na morbimortalidade, no comportamento ante a doença e saúde, no acesso e uso
Material Teórico - Módulo Equações do Segundo Grau. Equações de Segundo Grau: outros resultados importantes. Nono Ano do Ensino Funcamental
 Material Teórico - Módulo Equações do Segundo Grau Equações de Segundo Grau: outros resultados importantes Nono Ano do Ensino Funcamental Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio
Material Teórico - Módulo Equações do Segundo Grau Equações de Segundo Grau: outros resultados importantes Nono Ano do Ensino Funcamental Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio
Planificação anual 2018/19
 Planificação anual Propõe-se a seguinte distribuição dos conteúdos pelos diferentes períodos: 1. Período 2. Período 3. Período Números racionais Expressões algébricas. Potenciação. Raízes quadradas e cúbicas
Planificação anual Propõe-se a seguinte distribuição dos conteúdos pelos diferentes períodos: 1. Período 2. Período 3. Período Números racionais Expressões algébricas. Potenciação. Raízes quadradas e cúbicas
OFICINA DE GEOMETRIA E MEDIDAS. Zaqueu Vieira Oliveira
 OFICINA DE GEOMETRIA E MEDIDAS Zaqueu Vieira Oliveira A TEORIA DOS VAN HEALE O CONTEXTO Teoria desenvolvida por Dina van Hiele-Geldof e Pierre M. van Hiele Pierre: aprendizagem da geometria e o fenômeno
OFICINA DE GEOMETRIA E MEDIDAS Zaqueu Vieira Oliveira A TEORIA DOS VAN HEALE O CONTEXTO Teoria desenvolvida por Dina van Hiele-Geldof e Pierre M. van Hiele Pierre: aprendizagem da geometria e o fenômeno
REFLEXÕES INICIAIS SOBRE LETRAMENTO
 REFLEXÕES INICIAIS SOBRE LETRAMENTO Jéssica Caroline Soares Coelho 1 Elson M. da Silva 2 1 Graduanda em Pedagogia pela UEG- Campus Anápolis de CSEH 2 Doutor em Educação e docente da UEG Introdução O objetivo
REFLEXÕES INICIAIS SOBRE LETRAMENTO Jéssica Caroline Soares Coelho 1 Elson M. da Silva 2 1 Graduanda em Pedagogia pela UEG- Campus Anápolis de CSEH 2 Doutor em Educação e docente da UEG Introdução O objetivo
Álgebra Linear II Apostila 2
 Álgebra Linear II Apostila 2 1 SISTEMAS LINEARES Um sistema linear é um conjunto de equações de primeiro grau, que se escrevem em função de certas variáveis. A resolução do sistema visa encontrar justamente
Álgebra Linear II Apostila 2 1 SISTEMAS LINEARES Um sistema linear é um conjunto de equações de primeiro grau, que se escrevem em função de certas variáveis. A resolução do sistema visa encontrar justamente
Primeiramente, é preciso que você estabeleça suas metas. Para isso, vamos pensar em algumas perguntas básicas.
 Sempre é hora de afinar sua maneira de estudar e sua percepção de si mesmo. Acompanhe o material criado pela orientadora profissional e psicóloga Daniela Fuschini Favaro e que é aplicado há mais de uma
Sempre é hora de afinar sua maneira de estudar e sua percepção de si mesmo. Acompanhe o material criado pela orientadora profissional e psicóloga Daniela Fuschini Favaro e que é aplicado há mais de uma
Arquitetura de Sistemas Operativos
 Arquitetura de Sistemas Operativos Sistemas Operativos 2011/2012 1 Requisitos de uma Secção Crítica Requisitos de uma Secção Crítica Antes de analisarmos as várias soluções para assegurar que um bloco
Arquitetura de Sistemas Operativos Sistemas Operativos 2011/2012 1 Requisitos de uma Secção Crítica Requisitos de uma Secção Crítica Antes de analisarmos as várias soluções para assegurar que um bloco
ÁREA EM LIVROS DIDÁTICOS BRASILEIROS DO 6º ANO: UMA ANÁLISE DE PRAXEOLOGIAS MATEMÁTICAS.
 ÁREA EM LIVROS DIDÁTICOS BRASILEIROS DO 6º ANO: UMA ANÁLISE DE PRAXEOLOGIAS MATEMÁTICAS. José Valério Gomes da Silva. valerio.gomes@yahoo.com.br UFPE Universidade Federal de Pernambuco Brasil Tema: I.
ÁREA EM LIVROS DIDÁTICOS BRASILEIROS DO 6º ANO: UMA ANÁLISE DE PRAXEOLOGIAS MATEMÁTICAS. José Valério Gomes da Silva. valerio.gomes@yahoo.com.br UFPE Universidade Federal de Pernambuco Brasil Tema: I.
OBJETIVOS DE ENSINO- APRENDIZAGEM DE CIÊNCIAS E BIOLOGIA. Docente: Dra. Eduarda Maria Schneider
 OBJETIVOS DE ENSINO- APRENDIZAGEM DE CIÊNCIAS E BIOLOGIA Docente: Dra. Eduarda Maria Schneider E-mail: emschneider@utfpr.edu.br O que são objetivos de ensino/aprendizagem? O que espero que meu aluno aprenda?
OBJETIVOS DE ENSINO- APRENDIZAGEM DE CIÊNCIAS E BIOLOGIA Docente: Dra. Eduarda Maria Schneider E-mail: emschneider@utfpr.edu.br O que são objetivos de ensino/aprendizagem? O que espero que meu aluno aprenda?
