1 Emparelhamentos em Grafos
|
|
|
- Sebastião Gama Moreira
- 6 Há anos
- Visualizações:
Transcrição
1 1 Emparelhamentos em Grafos Definição 1.1 Um emparelhamento num grafo G é um conjunto de arestas não adjacentes entre si, isto é, incidentes em pares de vértices disjuntos dois a dois. i) Um vértice incidente numa aresta do emparelhamento diz-se coberto pelo emparelhamento. ii) Um emparelhamento M é perfeito se cobre todos os vértices de G. iii) M é maximal se não existe um emparelhamento M que contenha propriamente M, e é máximo se não existe um emparelhamento com maior número de arestas. O problema de determinar um emparelhamento máximo de um grafo pode ser resolvido pelo estudo de caminhos de um tipo especial: dado um emparelhamento qualquer M (não vazio!), um caminho M-alternado é um caminho em G em que, para quaisquer duas arestas consecutivas, uma pertence a M e a outra não; se o primeiro e o último vértice de um caminho M-alternado não são cobertos por M, dizemos que é um caminho M-aumentável. Teorema 1.2 (Berge): Um emparelhamento M de um grafo G é máximo se e só se não existe em G um caminho M-aumentável. Demonstração 1.3 : Se existe um caminho M-aumentável, podemos criar um emparelhamento maior eliminando as arestas de M que pertencem ao caminho e incluindo as que não pertencem. Para provar a recíproca, suponhamos que M não é máximo e que existe portanto um outro emparelhamento M com mais arestas que M. Considere-se o grafo H que se obtém de G eliminando as arestas que pertencem a ambos os emparelhamentos e as que não pertencem a nenhum deles (ou seja, conservam-se apenas as arestas da diferença simétrica M M ); cada vértice 1
2 v de H tem grau 0, 1 ou 2 porque v pode ser incidente no máximo a uma aresta de M e uma de M ; as componentes conexas de H só podem então ser ou vértices isolados, ou ciclos de ordem par com arestas alternadamente de M e de M, ou caminhos não fechados também com arestas alternadamente de M e de M ; como M > M, o grafo H tem mais arestas de M que de M e portanto pelo menos uma das componentes de H é um caminho que começa e termina com arestas de M (que não pertencem a M); esse caminho é um caminho M-aumentável no grafo G. O conceito de caminho M-alternado aumentável está na base de um algoritmo de busca de um emparelhamento máximo num grafo. Numa descrição informal, o algoritmo tem como dados de entrada um grafo G, um emparelhamento inicial M em G (que pode ser simplesmente o emparelhamento vazio) e um vértice x não coberto por M e produz, através de uma busca em largura, uma árvore M-alternada com raiz em x. Se houver um vértice v adjacente a x não coberto por M, poderíamos substituir M por M xv (onde xv designa a aresta unindo esses dois vértices); se todos os vértices adjacentes a x já estão cobertos por M, o algoritmo cria os primeiros ramos da árvore, ligando x a todos os vértices adjacentes e cada um destes ao seu par no emparelhamento M; em seguida, o algoritmo toma sucessivamente como vértice activo cada um destes últimos vértices; se em algum passo, se encontra um vértice adjacente não coberto por M, temos um caminho M-alternado, com início em x, e podemos substituir M por um emparelhamento maior como descrito na demonstração do teorema de Berge; caso contrário, o algoritmo aumenta a árvore, ligando o vértice activo a cada um dos vértices adjacentes (ainda não pertencentes àrvore) e estes aos seus pares em M, e assim por diante. Este procedimento tem como resultado ou um novo emparelhamento maior que o inicial ou uma árvore M alternada maximal, ou seja, que não pode ser aumentada. Nesse caso, infelizmente, não se pode garantir que não existam caminhos M-alternados aumentáveis. Mas uma análise mais atenta (que se deixa como desafio) permite mostrar o seguinte: chamemos vértices vermel- 2
3 hos aos vértices da árvore criada pelo algoritmo que estão (na árvore) a uma distância par de x (incluindo o próprio x, claro). Então, se nenhum par de vértices vermelhos for adjacente em G, não existe um caminho M-alternado aumentável que contenha vértices já incluídos na árvore. Evidentemente, neste caso podemos simplesmente eliminar de G os vértices da árvore e começar de novo. Mais geralmente, as mesmas ideias permitem implementar um algoritmo que produz, em tempo polinomial, um emparelhamento máximo do grafo. Definição 1.4 Designa-se por α (G) o número máximo de arestas de um emparelhamento. Recorde-se por outro lado que β(g) é o número mínimo de vértices numa cobertura (uma cobertura é um conjunto de vértices tal que qualquer aresta do grafo incide em algum dos vértices desse conjunto). Se M for um emparelhamento, qualquer cobertura tem que conter pelo menos um dos extremos de cada aresta do emparelhamento; como isto é verdade para qualquer emparelhamento e qualquer cobertura, temos α (G) β(g). Uma outra estimativa mais interessante segue do seguinte raciocínio: suponhamos que temos em G um emparelhamento qualquer M e seja S um conjunto de vértices. O subgrafo induzido G[V \ S] pode ter várias componentes conexas; se uma dessas componentes tiver um número ímpar de vértices, pelo menos um deles não pode estar emparelhado dentro da componente, logo só poderá estar emparelhado com algum dos vértices de S; e, evidentemente, cada um destes só pode estar emparelhado com um vértice. Designando por o(g[v \ S]) o número de componentes conexas com um número ímpar de vértices daquele subgrafo, concluímos que o número de vértices não coberto por M é maior ou igual a o(g[v \ S]) S. 3
4 Como isto é verdade para qualquer emparelhamento e qualquer subconjunto S de vértices, obtém-se assim um majorante para α (G). É de facto possível demonstrar a seguinte Proposição 1.5 Fórmula de Tutte-Berge: Se G é um grafo com vértices V, α (G) = 1 min{ V (o(g[v \ S] S ) : S V } Emparelhamentos em grafos bipartidos Designamos por G[X, Y ] um grafo bipartido com partição V = X Y do conjunto dos vértices. Recordamos a seguinte caracterização de grafos bipartidos: Proposição 1.6 Um grafo é bipartido se e só se não tem ciclos de comprimento ímpar. Os problemas relacionados com emparelhamentos em grafos bipartidos têm interesse especial e também resultados específicos que convém mencionar. Dado um conjunto de vértices S, designa-se por N(S) o conjunto de todos os vértices adjacentes a algum vértice de S. Evidentemente, para que um emparelhamento em G[X, Y ] cubra todos os vértices de X, é necessário que para qualquer S X, se tenha N(S) S ; o teorema seguinte diz-nos que essa condição é também suficiente: Teorema 1.7 (Hall): G[X, Y ] tem um emparelhamento que cobre todos os vértices de X se e só se para todo o S X se tem N(S) S. 4
5 Demonstração 1.8 : Como já vimos, a condição é obviamente necessária: dado S X os vértices de S estão emparelhados com o mesmo número de vértices de Y e portanto N(S) S. Para vermos que a condição é também suficiente, suponhamos que temos um emparelhamento máximo M que não cobre todos os vértices de X e seja x um desses vértices não cobertos. Como supômos que M é máximo podemos assumir que todos os vértices adjacentes a x estão emparelhados. Seja Z o conjunto dos vértices que podem ser alcançados por um caminho M-alternado com início em x; um caminho desse tipo parte de x por uma aresta de A \ M para um vértice y Y, passa por uma aresta de M para um vértice de X, regressa a Y por uma aresta de A \ M e assim por diante. A hipótese de M ser máximo implica que x é o único vértice de Z não coberto pelo emparelhamento: se v Z X, v está coberto por M pela própria definição de caminho M-alternado; e se u Z Y não estivesse emparelhado, o caminho de x até u seria M-aumentável, contrariando a hipótese de M ser máximo. Designando S = Z X e R = Z Y concluímos que os vértices de S \ x estão emparelhados com os de R e que de facto N(S) = R; mas então N(S) = S 1 e portanto a condição não se verifica. Corolário 1.9 : Um grafo bipartido G[X, Y ] tem um emparelhamento perfeito se e só se X = Y e N(S) S, para todo o S X. Tem-se também o seguinte corolário cuja demonstração se deixa como exercício: Corolário 1.10 : Se G[X, Y ] é um grafo bipartido regular (ou seja todos os vértices têm o mesmo grau k > 0), então G[X, Y ] tem um emparelhamento perfeito. Tal como acontece com o teorema de Berge, a demonstração do Teorema de Hall pode ser posta em termos algorítmicos: dada uma ordem inicial 5
6 dos vértices de X, emparelhamos os elementos x 1, x 2, até chegarmos à situação em que um x k só tem vértices adjacentes já emparelhados; para descrever mais facilmente o algoritmo, vamos designar os vértices adjacentes de um determinado vértice como os seus vizinhos, o emparelhamento feito até aqui como M e quando um vértice está já emparelhado com outro dizemos que este é o seu par. Construímos (usando um dos algoritmos de busca em grafos) uma árvore com raiz x k do seguinte modo: ligamos a raiz a todos os seus vizinhos (que, recorde-se, já estão emparelhados), ligamos cada um destes ao seu par, ligamos cada um destes a todos os seus outros vizinhos (se existirem), e assim por diante. A condição do teorema garante que mais tarde ou mais cedo tem que haver de facto um elemento de X nesta árvore que tem um vizinho, chamemos-lhe v, ainda não emparelhado: caso contrário, cada ramo da árvore assim construída terminaria com um vértice de X que não teria mais vizinhos além do seu par e de outros vértices emparelhados com vértices de X já incluídos na árvore, o que é impossível, uma vez que nesse caso a árvore conteria, digamos, m vértices de X e apenas m 1 vértices de Y. Assim que encontramos esse v temos na árvore um caminho M-alternado que começa em x k e termina em v e podemos usá-lo para aumentar o emparelhamento. Mencionamos a seguir uma das interpretações do teorema de Hall com importância em combinatória. Definição 1.11 Dada uma família S 1, S 2,, S m de conjuntos, um sistema de representantes distintos é um conjunto x 1, x 2,, x m tal que x i S i i x i x j i j Podemos associar a uma família desse tipo um grafo bipartido G[X, Y ] em que X = {1, 2,, m}, Y = S i, e i X e u Y são adjacentes se u S i. O Teorema de Hall implica então o seguinte Teorema 1.12 : Uma família de conjuntos S 1, S 2,, S m tem um sistema de representantes distintos se e só se para qualquer subconjunto I {1, 2,, m} 6
7 se verifica a condição i I S i I O Teorema de Hall é equivalente ao seguinte resultado, de que se apresenta uma demonstração independente: Teorema 1.13 (König-Egérvary) Num grafo bipartido G[X, Y ], o número máximo de arestas num emparelhamento é igual ao número mínimo de vértices numa cobertura. Demonstração 1.14 : Em primeiro lugar, notamos que, para qualquer emparelhamento M e qualquer cobertura U num grafo G (não necessariamente bipartido), se tem M U ; de facto, cada aresta de M incide em (pelo menos) um vértice de U e arestas a e b de M não podem incidir num mesmo vértice; logo, temos uma aplicação injectiva de M em U. Para provar o Teorema basta portanto, dado um emparelhamento M máximo de G[X, Y ], encontrar uma cobertura U com M vértices. Seja então M um emparelhamento máximo em G[X, Y ] e W X o conjunto de vértices de X em que não incide uma aresta de M. Notamos que M = X W. Sejam S X e R Y os conjuntos de vértices de cada lado alcançáveis por um caminho M-alternado com início em W. Temos, por definição de caminho M-alternado, que W S; além disso, se y R, então existe uma aresta de M incidente em y: caso contrário, o caminho M alternado com início num vértice w W e fim em y seria M-aumentável, contrariando o Teorema de Berge. Podemos então considerar a aplicação h : R S \ W que a cada y R 7
8 faz corresponder o único vértice x tal que a aresta xy pertence a M, e verificamos que esta aplicação é uma bijecção: se x S \ W, a última aresta em qualquer caminho M alternado com início em W e fim em x é a aresta de M incidente em x e portanto x é a imagem por h do vértice no outro extremo dessa aresta. Concluímos que R = S W. Definimos então U = (X \S) R e verificamos que se trata de uma cobertura: designamos cada aresta por xy em que x e y são os vértices em que a aresta incide, respectivamente do lado X e do lado Y ; se x X \ S, é claro que a aresta xy está coberta por U; se x S, então x é o vértice final de um caminho M-alternado com início em W ; caso xy M, a última aresta desse caminho foi precisamente xy, logo y R; se xy / M, o caminho M-alternado que termina em x pode ser prolongado através de xy até y e portanto, mais uma vez, y R e, em qualquer dos dois casos, xy está coberta por U. Mas U = X \ S + R = X S + R = X W = M usando as igualdades deduzidas nos parágrafos anteriores. Nota 1.15 O teorema de König-Egérvary pertence a um tipo de resultados habitualmente designados por min-max que estabelecem relações de igualdade entre o máximo de uma certa grandeza e o mínimo de outra. Citamos como exemplo uma das versões do Teorema de Menger: dado um grafo G e x, y V (G), dois caminhos entre x e y dizem-se disjuntos se não têm outros vértices em comum; um conjunto de vértices S V (G) \ {x, y} separa x e y se estes dois vértices ficam em componentes conexas diferentes do grafo G \ S (que se obtém de G eliminando os vértices de S e as arestas neles incidentes). Teorema 1.16 (Menger) Dado um grafo G e x, y V (G), o número máximo de caminhos disjuntos entre x e y é igual ao número mínimo de vértices de um conjunto que separe x e y. 8
9 1.2 Emparelhamentos com prioridades ou o problema dos casamentos Vimos já que se um grafo bipartido G[X, Y ] satisfaz a condição do Teorema de Hall para X, existe um emparelhamento que cobre todos os elementos de X. No entanto, em muitas situações de aplicação deste resultado, o problema é mais complexo. Considere-se, por exemplo, a situação em que n pessoas se candidatam a m vagas; se todos os candidatos concorrem a todas as vagas, a condição para que todos fiquem colocados é simplesmente X Y. Mas é possível que cada pessoa ordene as vagas numa lista de acordo com as suas preferências; do mesmo modo, podemos supôr que as empresas ou instituições com vagas a preencher ordenam os candidatos de acordo com as suas próprias preferências. O problema de saber como preencher as vagas de modo a satisfazer o melhor possível os desejos dos candidatos, ou os das empresas, ou ambos, ficou conhecido, por razões óbvias, como o problema dos casamentos. Nessa interpretação, bastante fantasista, cada um de um conjunto X de rapazes e cada uma de um conjunto Y de raparigas (todos heterosexuais e monogâmicos!) ordena os elementos do sexo oposto por ordem de preferência e mantém essa ordem ao longo do tempo; supôe-se igualmente que todos preferem estar emparelhados do que sózinhos. Representamos os vértices masculinos por letras maiúsculas e os vértices femininos por letras minúsculas, sem qualquer intensão discriminatória. Convém, aliás, sublinhar que toda esta interpretação tem carácter meramente recreativo, não envolvendo, obviamente, qualquer juízo de valor sobre os padrões culturais nela incluídos; o autor destas linhas não assume evidentemente qualquer responsabilidade pela estabilidade e felicidade dos casamentos organizados de acordo com os resultados que se seguem... Limitamo-nos, para maior simplicidade, ao caso em que X = Y e em que todos os rapazes ordenam todas as raparigas e vice-versa. O nosso objectivo é estabelecer um emparelhamento estável: diremos que um emparelhamento (ou casamento) é estável se não contém pares Ab e Ba em que A e a se pre- 9
10 firam aos seus pares respectivos. Os matemáticos e economistas americanos Gale e Shapley apresentaram em 1962 a solução deste problema, mostrando que existe um algoritmo que tem como resultado um casamento estável. A aplicação do algoritmo na nossa interpretação reproduz as regras sociais de norma na sociedade vitoriana: cada rapaz propõe casamento à rapariga da sua preferência que não o rejeitou até aí, e cada rapariga aceita a proposta do seu pretendente favorito. Em termos mais formais, podemos representar o algoritmo como uma sucessão de passos em que nos passos ímpares os rapazes fazem as suas propostas e nos passos pares as raparigas fazem a sua escolha. Eis um exemplo muito simples: nos quadros seguintes apresentam-se as listas de preferências, seguindo-se depois a descrição da aplicação do algoritmo. Representamos uma proposta como A? a e o resultado de uma aceitação como A - a. Nas linhas pares incluímos sempre os casais formados em passos anteriores e que se mantêm, para facilitar a visualização. A - a b c d e a - C E B D A B - c a e b d b - B E D A C C - a d c b e c - D A E B C D - a b c e d d - D E A B C E - c a b d e e - E A D B C 1. A? a, B? c, C? a, D? a, E? c 2. C - a, E - c 3. A? b, B? a, D? b 4. C - a, D - b, E - c 5. A? c, B? e 10
11 6. A - c, B - e, C - a, D - b c troca E por A; 7. E? a 8. A - c, B - e, C - a, D - b a rejeita a proposta, logo nada se altera; 9. E? b 10. A - c, B - e, C - a, E - b b troca D por E; 11. D? c 12. B - e, C - a, D - c, E - b c troca A por D; 13. A? d 14. A - d, B - e, C - a, D - c, E - b todos estão emparelhados; 15. celebram-se os cinco casamentos! Alguns factos são de verificação imediata: No caso de n rapazes e m raparigas, o algoritmo termina no máximo em 2nm passos, e se n m termina com a criação de n pares; depois de comprometido, cada rapaz só muda para pior (do seu ponto de vista!) e, se n > m, só não termina emparelhado se for rejeitado por todas as raparigas; depois de se comprometer, uma rapariga nunca fica sem par e só muda para melhor (mais uma vez, de acordo com o seu ponto de vista...); Teorema 1.17 : O algoritmo de Gale-Shapley produz um emparelhamento estável. Demonstração 1.18 : Com as observações anteriores, resta provar que o emparelhamento é estável. Suponhamos que X e y não terminam emparelhados; isso só acontece se X nunca chegou a propor-se a y ou se y rejeitou X; 11
12 no primeiro caso, X está emparelhado com alguém que prefere a y, enquanto que no segundo caso é y que está emparelhada com alguém acima de X na sua lista. Num caso ou noutro a condição de estabilidade do emparelhamento está satisfeita. A observação seguinte permite-nos comparar o resultado desta aplicação do algoritmo com outros possíveis emparelhamentos estáveis (com as mesmas listas de preferências, bem entendido). Lema 1.19 : Se, na aplicação do algoritmo, y rejeitou X, então X e y não ficam emparelhados em qualquer emparelhamento estável. Demonstração 1.20 : usamos indução nos passos do algoritmo: suponhamos que estamos no primeiro passo do algoritmo em que algum y rejeitou algum X, existindo um emparelhamento estável M em que X e y estão emparelhados. Isso acontece se ou y está emparelhado com T, acima de X na sua lista; ou y estava emparelhada com X e rejeita-o por receber uma proposta de um T acima de X na sua lista. Em qualquer caso, existe um T acima de X na lista de preferências de y; mas no suposto emparelhamento M, temos o par X - y e portanto T estará emparelhado com alguma z, que tem que estar acima de y na lista de preferências de T, caso contrário M não é estável. Voltando à aplicação do algoritmo, se T não está emparelhado com z, é porque foi rejeitado por z num passo anterior, contradizendo a nossa hipótese de que y rejeita X era a primeira ocorrência desse tipo. Este resultado, juntamente com as observações anteriores, leva-nos a concluir que nenhum outro emparelhamento estável pode melhorar a situação de 12
13 qualquer dos proponentes X, ou seja, o resultado do algoritmo é o melhor emparelhamento estável para os proponentes. Por outro lado, se o algoritmo produz o par X - y também não pode existir um emparelhamento estável em que y está emparelhada com um S abaixo de X na sua lista de preferências, pois nesse emparelhamento X teria que estar emparelhado com uma z acima de y na sua lista, caso contrário o emparelhamento não seria estável. Ora isso contradiz a conclusão anterior. Portanto o resultado do algoritmo é o pior possível para as raparigas (os aceitantes de propostas), no sentido em que noutro emparelhamento estável qualquer nenhuma poderia piorar de situação. 13
O Cálculo λ sem Tipos
 Capítulo 2 O Cálculo λ sem Tipos 21 Síntaxe e Redução Por volta de 1930 o cálculo lambda sem tipos foi introduzido como uma fundação para a lógica e a matemática Embora este objectivo não tenha sido cumprido
Capítulo 2 O Cálculo λ sem Tipos 21 Síntaxe e Redução Por volta de 1930 o cálculo lambda sem tipos foi introduzido como uma fundação para a lógica e a matemática Embora este objectivo não tenha sido cumprido
Recorrendo à nossa imaginação podemos tentar escrever números racionais de modo semelhante: 1 2 = 1 + 3 + 32 +
 1 Introdução Comecemos esta discussão fixando um número primo p. Dado um número natural m podemos escrevê-lo, de forma única, na base p. Por exemplo, se m = 15 e p = 3 temos m = 0 + 2 3 + 3 2. Podemos
1 Introdução Comecemos esta discussão fixando um número primo p. Dado um número natural m podemos escrevê-lo, de forma única, na base p. Por exemplo, se m = 15 e p = 3 temos m = 0 + 2 3 + 3 2. Podemos
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS
 Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS Dois ou mais eventos são mutuamente exclusivos, ou disjuntos, se os mesmos não podem ocorrer simultaneamente. Isto é, a ocorrência de um
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS Dois ou mais eventos são mutuamente exclusivos, ou disjuntos, se os mesmos não podem ocorrer simultaneamente. Isto é, a ocorrência de um
Módulo de Equações do Segundo Grau. Equações do Segundo Grau: Resultados Básicos. Nono Ano
 Módulo de Equações do Segundo Grau Equações do Segundo Grau: Resultados Básicos. Nono Ano Equações do o grau: Resultados Básicos. 1 Exercícios Introdutórios Exercício 1. A equação ax + bx + c = 0, com
Módulo de Equações do Segundo Grau Equações do Segundo Grau: Resultados Básicos. Nono Ano Equações do o grau: Resultados Básicos. 1 Exercícios Introdutórios Exercício 1. A equação ax + bx + c = 0, com
Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios
 Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios O Método Intuitivo de elaboração de circuitos: As técnicas de elaboração de circuitos eletropneumáticos fazem parte
Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios O Método Intuitivo de elaboração de circuitos: As técnicas de elaboração de circuitos eletropneumáticos fazem parte
QUESTÕES PARA A 3ª SÉRIE ENSINO MÉDIO MATEMÁTICA 2º BIMESTE SUGESTÕES DE RESOLUÇÕES
 QUESTÕES PARA A 3ª SÉRIE ENSINO MÉDIO MATEMÁTICA 2º BIMESTE QUESTÃO 01 SUGESTÕES DE RESOLUÇÕES Descritor 11 Resolver problema envolvendo o cálculo de perímetro de figuras planas. Os itens referentes a
QUESTÕES PARA A 3ª SÉRIE ENSINO MÉDIO MATEMÁTICA 2º BIMESTE QUESTÃO 01 SUGESTÕES DE RESOLUÇÕES Descritor 11 Resolver problema envolvendo o cálculo de perímetro de figuras planas. Os itens referentes a
I. Conjunto Elemento Pertinência
 TEORI DOS CONJUNTOS I. Conjunto Elemento Pertinência Conjunto, elemento e pertinência são três noções aceitas sem definição, ou seja, são noções primitivas. idéia de conjunto é praticamente a mesma que
TEORI DOS CONJUNTOS I. Conjunto Elemento Pertinência Conjunto, elemento e pertinência são três noções aceitas sem definição, ou seja, são noções primitivas. idéia de conjunto é praticamente a mesma que
EGEA ESAPL - IPVC. Resolução de Problemas de Programação Linear, com recurso ao Excel
 EGEA ESAPL - IPVC Resolução de Problemas de Programação Linear, com recurso ao Excel Os Suplementos do Excel Em primeiro lugar deverá certificar-se que tem o Excel preparado para resolver problemas de
EGEA ESAPL - IPVC Resolução de Problemas de Programação Linear, com recurso ao Excel Os Suplementos do Excel Em primeiro lugar deverá certificar-se que tem o Excel preparado para resolver problemas de
Técnicas de Contagem I II III IV V VI
 Técnicas de Contagem Exemplo Para a Copa do Mundo 24 países são divididos em seis grupos, com 4 países cada um. Supondo que a escolha do grupo de cada país é feita ao acaso, calcular a probabilidade de
Técnicas de Contagem Exemplo Para a Copa do Mundo 24 países são divididos em seis grupos, com 4 países cada um. Supondo que a escolha do grupo de cada país é feita ao acaso, calcular a probabilidade de
PRINCÍPIOS DA MULTIPLICAÇÃO, DA ADIÇÃO E DA INCLUSÃO-
 Matemática Discreta 2009.10 Exercícios CAP2 pg 1 PRINCÍPIOS DA MULTIPLICAÇÃO, DA ADIÇÃO E DA INCLUSÃO- EXCLUSÃO 1. Quantas sequências com 5 letras podem ser escritas usando as letras A,B,C? 2. Quantos
Matemática Discreta 2009.10 Exercícios CAP2 pg 1 PRINCÍPIOS DA MULTIPLICAÇÃO, DA ADIÇÃO E DA INCLUSÃO- EXCLUSÃO 1. Quantas sequências com 5 letras podem ser escritas usando as letras A,B,C? 2. Quantos
Se inicialmente, o tanque estava com 100 litros, pode-se afirmar que ao final do dia o mesmo conterá.
 ANÁLISE GRÁFICA QUANDO y. CORRESPONDE A ÁREA DA FIGURA Resposta: Sempre quando o eio y corresponde a uma taa de variação, então a área compreendida entre a curva e o eio do será o produto y. Isto é y =
ANÁLISE GRÁFICA QUANDO y. CORRESPONDE A ÁREA DA FIGURA Resposta: Sempre quando o eio y corresponde a uma taa de variação, então a área compreendida entre a curva e o eio do será o produto y. Isto é y =
Ficha Prática 5: Cap 3.Princípios Elementares de Contagem
 Matemática Discreta - 2010/11 Cursos: Engenharia Informática, Informática de Gestão DEPARTAMENTO de MATEMÁTICA ESCOLA SUPERIOR de TECNOLOGIA e de GESTÃO - INSTITUTO POLITÉCNICO de BRAGANÇA Ficha Prática
Matemática Discreta - 2010/11 Cursos: Engenharia Informática, Informática de Gestão DEPARTAMENTO de MATEMÁTICA ESCOLA SUPERIOR de TECNOLOGIA e de GESTÃO - INSTITUTO POLITÉCNICO de BRAGANÇA Ficha Prática
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR. Prof. Angelo Augusto Frozza, M.Sc.
 PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 2 do livro de Taha (2008): Introdução O modelo de PL de duas variáveis Propriedades
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 2 do livro de Taha (2008): Introdução O modelo de PL de duas variáveis Propriedades
Subconjuntos Especiais
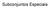 Subconjuntos Especiais Cobertura de vértices ^ C uma cobertura de vértices de um grafo é um conjunto de vértices tal que cada aresta do grafo é incidente a, pelo menos, um vértice do conjunto. É um conjunto
Subconjuntos Especiais Cobertura de vértices ^ C uma cobertura de vértices de um grafo é um conjunto de vértices tal que cada aresta do grafo é incidente a, pelo menos, um vértice do conjunto. É um conjunto
TESTES SOCIOMÉTRICOS
 TESTES SOCIOMÉTRICOS Docente: Mestre Mª João Marques da Silva Picão Oliveira TESTES SOCIOMÉTRICOS * O Teste Sociométrico ajuda-nos a avaliar o grau de integração duma criança/jovem no grupo; a descobrir
TESTES SOCIOMÉTRICOS Docente: Mestre Mª João Marques da Silva Picão Oliveira TESTES SOCIOMÉTRICOS * O Teste Sociométrico ajuda-nos a avaliar o grau de integração duma criança/jovem no grupo; a descobrir
4.4 Limite e continuidade
 4.4 Limite e continuidade Noções Topológicas em R : Dados dois pontos quaisquer (x 1, y 1 ) e (x, y ) de R indicaremos a distância entre eles por då(x 1, y 1 ), (x, y )è=(x 1 x ) + (y 1 y ). Definição
4.4 Limite e continuidade Noções Topológicas em R : Dados dois pontos quaisquer (x 1, y 1 ) e (x, y ) de R indicaremos a distância entre eles por då(x 1, y 1 ), (x, y )è=(x 1 x ) + (y 1 y ). Definição
1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431,
 1. Escreva os elementos de S 4 nas duas notações. Observe que S 4 = 4! = 24. Os elementos de S 4 tem a forma 1 a, 2 b, 3 c, 4 d onde a sequência abcd é uma das seguintes: 1234, 1243, 1324, 1342, 1423,
1. Escreva os elementos de S 4 nas duas notações. Observe que S 4 = 4! = 24. Os elementos de S 4 tem a forma 1 a, 2 b, 3 c, 4 d onde a sequência abcd é uma das seguintes: 1234, 1243, 1324, 1342, 1423,
Aula 5. Uma partícula evolui na reta. A trajetória é uma função que dá a sua posição em função do tempo:
 Aula 5 5. Funções O conceito de função será o principal assunto tratado neste curso. Neste capítulo daremos algumas definições elementares, e consideraremos algumas das funções mais usadas na prática,
Aula 5 5. Funções O conceito de função será o principal assunto tratado neste curso. Neste capítulo daremos algumas definições elementares, e consideraremos algumas das funções mais usadas na prática,
Universidade Federal de Goiás Campus Catalão Departamento de Matemática
 Universidade Federal de Goiás Campus Catalão Departamento de Matemática Disciplina: Álgebra Linear Professor: André Luiz Galdino Aluno(a): 4 a Lista de Exercícios 1. Podemos entender transformações lineares
Universidade Federal de Goiás Campus Catalão Departamento de Matemática Disciplina: Álgebra Linear Professor: André Luiz Galdino Aluno(a): 4 a Lista de Exercícios 1. Podemos entender transformações lineares
Função. Adição e subtração de arcos Duplicação de arcos
 Função Trigonométrica II Adição e subtração de arcos Duplicação de arcos Resumo das Principais Relações I sen cos II tg sen cos III cotg tg IV sec cos V csc sen VI sec tg VII csc cotg cos sen Arcos e subtração
Função Trigonométrica II Adição e subtração de arcos Duplicação de arcos Resumo das Principais Relações I sen cos II tg sen cos III cotg tg IV sec cos V csc sen VI sec tg VII csc cotg cos sen Arcos e subtração
Universidade Estadual de Campinas Departamento de Matemática. Teorema de Jacobson. Adriana Wagner(RA: 144768) Gustavo Terra Bastos(RA: 143800)
 Universidade Estadual de Campinas Departamento de Matemática Teorema de Jacobson Adriana Wagner(RA: 144768) Gustavo Terra Bastos(RA: 143800) Campinas - SP 2013 1 Resumo Nesta monografia apresentamos a
Universidade Estadual de Campinas Departamento de Matemática Teorema de Jacobson Adriana Wagner(RA: 144768) Gustavo Terra Bastos(RA: 143800) Campinas - SP 2013 1 Resumo Nesta monografia apresentamos a
2 Segmentação de imagens e Componentes conexas
 Universidade Tecnológica Federal do Paraná (UTFPR) Departamento Acadêmico de Informática (DAINF) Algoritmos II Professor: Alex Kutzke (alexk@dainf.ct.utfpr.edu.br) Especificação do Primeiro Trabalho Prático
Universidade Tecnológica Federal do Paraná (UTFPR) Departamento Acadêmico de Informática (DAINF) Algoritmos II Professor: Alex Kutzke (alexk@dainf.ct.utfpr.edu.br) Especificação do Primeiro Trabalho Prático
Entropia, Entropia Relativa
 Entropia, Entropia Relativa e Informação Mútua Miguel Barão (mjsb@di.uevora.pt) Departamento de Informática Universidade de Évora 13 de Março de 2003 1 Introdução Suponhamos que uma fonte gera símbolos
Entropia, Entropia Relativa e Informação Mútua Miguel Barão (mjsb@di.uevora.pt) Departamento de Informática Universidade de Évora 13 de Março de 2003 1 Introdução Suponhamos que uma fonte gera símbolos
Jorge Figueiredo, DSC/UFCG. Análise e Técnicas de Algoritmos 2005.1. Jorge Figueiredo, DSC/UFCG. Análise e Técnicas de Algoritmos 2005.
 Agenda Análise e Técnicas de Algoritmos Jorge Figueiredo Conceitos básicos Classes de de Complexidade P NP Redução Problemas NPC NP-Completude Introdução Existem alguns problemas computacionais que são
Agenda Análise e Técnicas de Algoritmos Jorge Figueiredo Conceitos básicos Classes de de Complexidade P NP Redução Problemas NPC NP-Completude Introdução Existem alguns problemas computacionais que são
Probabilidade. Evento (E) é o acontecimento que deve ser analisado.
 Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
3º Ano do Ensino Médio. Aula nº06
 Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº06 Assunto: Noções de Estatística 1. Conceitos básicos Definição: A estatística é a ciência que recolhe, organiza, classifica, apresenta
Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº06 Assunto: Noções de Estatística 1. Conceitos básicos Definição: A estatística é a ciência que recolhe, organiza, classifica, apresenta
Seu pé direito nas melhores Faculdades
 10 Insper 01/11/009 Seu pé direito nas melhores Faculdades análise quantitativa 40. No campeonato brasileiro de futebol, cada equipe realiza 38 jogos, recebendo, em cada partida, 3 pontos em caso de vitória,
10 Insper 01/11/009 Seu pé direito nas melhores Faculdades análise quantitativa 40. No campeonato brasileiro de futebol, cada equipe realiza 38 jogos, recebendo, em cada partida, 3 pontos em caso de vitória,
Avaliação de Empresas Profa. Patricia Maria Bortolon
 Avaliação de Empresas RISCO E RETORNO Aula 2 Retorno Total É a variação total da riqueza proporcionada por um ativo ao seu detentor. Fonte: Notas de Aula do Prof. Claudio Cunha Retorno Total Exemplo 1
Avaliação de Empresas RISCO E RETORNO Aula 2 Retorno Total É a variação total da riqueza proporcionada por um ativo ao seu detentor. Fonte: Notas de Aula do Prof. Claudio Cunha Retorno Total Exemplo 1
ActivALEA. ative e atualize a sua literacia
 ActivALEA ative e atualize a sua literacia N.º 26 A FREQUÊNCIIA RELATIIVA PARA ESTIIMAR A PROBABIILIIDADE Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL
ActivALEA ative e atualize a sua literacia N.º 26 A FREQUÊNCIIA RELATIIVA PARA ESTIIMAR A PROBABIILIIDADE Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL
Aula de Exercícios - Teorema de Bayes
 Aula de Exercícios - Teorema de Bayes Organização: Rafael Tovar Digitação: Guilherme Ludwig Primeiro Exemplo - Estagiários Três pessoas serão selecionadas aleatóriamente de um grupo de dez estagiários
Aula de Exercícios - Teorema de Bayes Organização: Rafael Tovar Digitação: Guilherme Ludwig Primeiro Exemplo - Estagiários Três pessoas serão selecionadas aleatóriamente de um grupo de dez estagiários
LOGO DO WEBSITE DA FUTURA APP
 LOGO DO WEBSITE DA FUTURA APP LexiZi é uma aplicação mobile e web que é simultaneamente uma ferramenta e um serviço. a) Ferramenta É uma ferramenta porque permite a criação de Notas em cada um dos artigos
LOGO DO WEBSITE DA FUTURA APP LexiZi é uma aplicação mobile e web que é simultaneamente uma ferramenta e um serviço. a) Ferramenta É uma ferramenta porque permite a criação de Notas em cada um dos artigos
Módulo de Princípios Básicos de Contagem. Segundo ano
 Módulo de Princípios Básicos de Contagem Combinação Segundo ano Combinação 1 Exercícios Introdutórios Exercício 1. Numa sala há 6 pessoas e cada uma cumprimenta todas as outras pessoas com um único aperto
Módulo de Princípios Básicos de Contagem Combinação Segundo ano Combinação 1 Exercícios Introdutórios Exercício 1. Numa sala há 6 pessoas e cada uma cumprimenta todas as outras pessoas com um único aperto
Árvores. ! utilizada em muitas aplicações. ! modela uma hierarquia entre elementos. ! O conceito de árvores está diretamente ligado à recursão
 Árvores 1 Árvores! utilizada em muitas aplicações! modela uma hierarquia entre elementos! árvore genealógica! diagrama hierárquico de uma organização! modelagem de algoritmos! O conceito de árvores está
Árvores 1 Árvores! utilizada em muitas aplicações! modela uma hierarquia entre elementos! árvore genealógica! diagrama hierárquico de uma organização! modelagem de algoritmos! O conceito de árvores está
XXXII Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 XXXII Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível Segunda Fase Parte A PARTE A Na parte A serão atribuídos 4 pontos para cada resposta correta e a pontuação máxima para essa
XXXII Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível Segunda Fase Parte A PARTE A Na parte A serão atribuídos 4 pontos para cada resposta correta e a pontuação máxima para essa
M =C J, fórmula do montante
 1 Ciências Contábeis 8ª. Fase Profa. Dra. Cristiane Fernandes Matemática Financeira 1º Sem/2009 Unidade I Fundamentos A Matemática Financeira visa estudar o valor do dinheiro no tempo, nas aplicações e
1 Ciências Contábeis 8ª. Fase Profa. Dra. Cristiane Fernandes Matemática Financeira 1º Sem/2009 Unidade I Fundamentos A Matemática Financeira visa estudar o valor do dinheiro no tempo, nas aplicações e
EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros exercícios)
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros eercícios) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Eercícios
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros eercícios) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Eercícios
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Produtos Notáveis; Equações; Inequações; Função; Função Afim; Paridade;
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Produtos Notáveis; Equações; Inequações; Função; Função Afim; Paridade;
Prof. Daniela Barreiro Claro
 O volume de dados está crescendo sem parar Gigabytes, Petabytes, etc. Dificuldade na descoberta do conhecimento Dados disponíveis x Análise dos Dados Dados disponíveis Analisar e compreender os dados 2
O volume de dados está crescendo sem parar Gigabytes, Petabytes, etc. Dificuldade na descoberta do conhecimento Dados disponíveis x Análise dos Dados Dados disponíveis Analisar e compreender os dados 2
Aplicações Diferentes Para Números Complexos
 Material by: Caio Guimarães (Equipe Rumoaoita.com) Aplicações Diferentes Para Números Complexos Capítulo II Aplicação 2: Complexos na Geometria Na rápida revisão do capítulo I desse artigo mencionamos
Material by: Caio Guimarães (Equipe Rumoaoita.com) Aplicações Diferentes Para Números Complexos Capítulo II Aplicação 2: Complexos na Geometria Na rápida revisão do capítulo I desse artigo mencionamos
Criar e formatar relatórios
 Treinamento Criar e formatar relatórios EXERCÍCIO 1: CRIAR UM RELATÓRIO COM A FERRAMENTA RELATÓRIO Ao ser executada, a ferramenta Relatório usa automaticamente todos os campos da fonte de dados. Além disso,
Treinamento Criar e formatar relatórios EXERCÍCIO 1: CRIAR UM RELATÓRIO COM A FERRAMENTA RELATÓRIO Ao ser executada, a ferramenta Relatório usa automaticamente todos os campos da fonte de dados. Além disso,
Métodos Formais. Agenda. Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções. Relações e Funções
 Métodos Formais Relações e Funções por Mauro Silva Agenda Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções MF - Relações e Funções 2 1 Relações Binárias Definição
Métodos Formais Relações e Funções por Mauro Silva Agenda Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções MF - Relações e Funções 2 1 Relações Binárias Definição
Testes de Hipóteses Estatísticas
 Capítulo 5 Slide 1 Testes de Hipóteses Estatísticas Resenha Hipótese nula e hipótese alternativa Erros de 1ª e 2ª espécie; potência do teste Teste a uma proporção; testes ao valor médio de uma v.a.: σ
Capítulo 5 Slide 1 Testes de Hipóteses Estatísticas Resenha Hipótese nula e hipótese alternativa Erros de 1ª e 2ª espécie; potência do teste Teste a uma proporção; testes ao valor médio de uma v.a.: σ
Resoluções A. Combinatória 1 3 os anos Blaidi/Walter Ago/09. Nome: Nº: Turma:
 Matemática Resoluções A. Combinatória 3 os anos Blaidi/Walter Ago/09 Nome: Nº: Turma: Prezadísssimos alunos e alunas, Neste bimestre, aprenderemos a resolver questões de análise combinatória com o auílio
Matemática Resoluções A. Combinatória 3 os anos Blaidi/Walter Ago/09 Nome: Nº: Turma: Prezadísssimos alunos e alunas, Neste bimestre, aprenderemos a resolver questões de análise combinatória com o auílio
Optimização e Algoritmos (2004/2005)
 Optimização e Algoritmos (2004/2005) Instituto Superior Técnico Engenharia Electrotécnica e de Computadores Série de Problemas 3 Regras de Armijo e Wolfe, Introdução às funções convexas Problema 1.[Regras
Optimização e Algoritmos (2004/2005) Instituto Superior Técnico Engenharia Electrotécnica e de Computadores Série de Problemas 3 Regras de Armijo e Wolfe, Introdução às funções convexas Problema 1.[Regras
TEORIA 5: EQUAÇÕES E SISTEMAS DO 1º GRAU MATEMÁTICA BÁSICA
 TEORIA 5: EQUAÇÕES E SISTEMAS DO 1º GRAU MATEMÁTICA BÁSICA Nome: Turma: Data / / Prof: Walnice Brandão Machado Equações de primeiro grau Introdução Equação é toda sentença matemática aberta que exprime
TEORIA 5: EQUAÇÕES E SISTEMAS DO 1º GRAU MATEMÁTICA BÁSICA Nome: Turma: Data / / Prof: Walnice Brandão Machado Equações de primeiro grau Introdução Equação é toda sentença matemática aberta que exprime
Gestão Documental. Gestão Documental
 Alcides Marques, 2007 Actualizado por Ricardo Matos em Junho de 2009 Neste capítulo pretende-se analisar a temática da, começando por apresentar um breve resumo dos conceitos subjacentes e apresentando
Alcides Marques, 2007 Actualizado por Ricardo Matos em Junho de 2009 Neste capítulo pretende-se analisar a temática da, começando por apresentar um breve resumo dos conceitos subjacentes e apresentando
Figura 4.1: Diagrama de representação de uma função de 2 variáveis
 1 4.1 Funções de 2 Variáveis Em Cálculo I trabalhamos com funções de uma variável y = f(x). Agora trabalharemos com funções de várias variáveis. Estas funções aparecem naturalmente na natureza, na economia
1 4.1 Funções de 2 Variáveis Em Cálculo I trabalhamos com funções de uma variável y = f(x). Agora trabalharemos com funções de várias variáveis. Estas funções aparecem naturalmente na natureza, na economia
Método de ordenação - objetivos:
 Método de ordenação - objetivos: Corresponde ao processo de rearranjar um conjunto de objetos em uma ordem ascendente ou descendente. Facilitar a recuperação posterior de itens do conjunto ordenado. São
Método de ordenação - objetivos: Corresponde ao processo de rearranjar um conjunto de objetos em uma ordem ascendente ou descendente. Facilitar a recuperação posterior de itens do conjunto ordenado. São
Ondas EM no Espaço Livre (Vácuo)
 Secretaria de Educação Profissional e Tecnológica Instituto Federal de Santa Catarina Campus São José Área de Telecomunicações ELM20704 Eletromagnetismo Professor: Bruno Fontana da Silva 2014-1 Ondas EM
Secretaria de Educação Profissional e Tecnológica Instituto Federal de Santa Catarina Campus São José Área de Telecomunicações ELM20704 Eletromagnetismo Professor: Bruno Fontana da Silva 2014-1 Ondas EM
LOGOTIPO OU LOGOMARCA?
 E-book para Empreendedores LOGOTIPO OU LOGOMARCA? Dicas para criar um( a ) logo de sucesso www.logovia.com.br A equipe do Logovia deseja que a leitura deste e-book seja agravável e que expanda seu entendimento
E-book para Empreendedores LOGOTIPO OU LOGOMARCA? Dicas para criar um( a ) logo de sucesso www.logovia.com.br A equipe do Logovia deseja que a leitura deste e-book seja agravável e que expanda seu entendimento
FACULDADE DE CIÊNCIAS E TECNOLOGIA. Redes de Telecomunicações (2006/2007)
 FACULDADE DE CIÊNCIAS E TECNOLOGIA Redes de Telecomunicações (2006/2007) Engª de Sistemas e Informática Trabalho nº4 (1ª aula) Título: Modelação de tráfego utilizando o modelo de Poisson Fundamentos teóricos
FACULDADE DE CIÊNCIAS E TECNOLOGIA Redes de Telecomunicações (2006/2007) Engª de Sistemas e Informática Trabalho nº4 (1ª aula) Título: Modelação de tráfego utilizando o modelo de Poisson Fundamentos teóricos
[RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013
![[RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013 [RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013](/thumbs/39/19161564.jpg) Economia I; 01/013 (º semestre) Prova da Época Recurso 3 de Julho de 013 [RESOLUÇÃO] Distribuição das respostas correctas às perguntas da Parte A (6 valores) nas suas três variantes: ER A B C P1 P P3 P4
Economia I; 01/013 (º semestre) Prova da Época Recurso 3 de Julho de 013 [RESOLUÇÃO] Distribuição das respostas correctas às perguntas da Parte A (6 valores) nas suas três variantes: ER A B C P1 P P3 P4
12 26, 62, 34, 43 21 37, 73 30 56, 65
 1 Questão 1 Solução a) Primeiro multiplicamos os algarismos de 79, obtendo 7 9 = 63, e depois somamos os algarismos desse produto, obtendo 6 + 3 = 9. Logo o transformado de é 79 é 9. b) A brincadeira de
1 Questão 1 Solução a) Primeiro multiplicamos os algarismos de 79, obtendo 7 9 = 63, e depois somamos os algarismos desse produto, obtendo 6 + 3 = 9. Logo o transformado de é 79 é 9. b) A brincadeira de
Os eixo x e y dividem a circunferência em quatro partes congruentes chamadas quadrantes, numeradas de 1 a 4 conforme figura abaixo:
 Circunferência Trigonométrica É uma circunferência de raio unitário orientada de tal forma que o sentido positivo é o sentido anti-horário. Associamos a circunferência (ou ciclo) trigonométrico um sistema
Circunferência Trigonométrica É uma circunferência de raio unitário orientada de tal forma que o sentido positivo é o sentido anti-horário. Associamos a circunferência (ou ciclo) trigonométrico um sistema
Lista de Exercícios 5: Soluções Teoria dos Conjuntos
 UFMG/ICEx/DCC DCC Matemática Discreta Lista de Exercícios 5: Soluções Teoria dos Conjuntos Ciências Exatas & Engenharias 2 o Semestre de 206. Escreva uma negação para a seguinte afirmação: conjuntos A,
UFMG/ICEx/DCC DCC Matemática Discreta Lista de Exercícios 5: Soluções Teoria dos Conjuntos Ciências Exatas & Engenharias 2 o Semestre de 206. Escreva uma negação para a seguinte afirmação: conjuntos A,
Projecto Delfos: Escola de Matemática Para Jovens 1 TEORIA DOS NÚMEROS
 Projecto Delfos: Escola de Matemática Para Jovens 1 A Teoria dos Números tem como objecto de estudo o conjunto Z dos números inteiros (a letra Z vem da palavra alemã Zahl que significa número). 1. DIVISIBILIDADE
Projecto Delfos: Escola de Matemática Para Jovens 1 A Teoria dos Números tem como objecto de estudo o conjunto Z dos números inteiros (a letra Z vem da palavra alemã Zahl que significa número). 1. DIVISIBILIDADE
Notas de aula de Lógica para Ciência da Computação. Aula 11, 2012/2
 Notas de aula de Lógica para Ciência da Computação Aula 11, 2012/2 Renata de Freitas e Petrucio Viana Departamento de Análise, IME UFF 21 de fevereiro de 2013 Sumário 1 Ineficiência das tabelas de verdade
Notas de aula de Lógica para Ciência da Computação Aula 11, 2012/2 Renata de Freitas e Petrucio Viana Departamento de Análise, IME UFF 21 de fevereiro de 2013 Sumário 1 Ineficiência das tabelas de verdade
Engenharia de Software II
 Engenharia de Software II Aula 26 http://www.ic.uff.br/~bianca/engsoft2/ Aula 26-21/07/2006 1 Ementa Processos de desenvolvimento de software Estratégias e técnicas de teste de software Métricas para software
Engenharia de Software II Aula 26 http://www.ic.uff.br/~bianca/engsoft2/ Aula 26-21/07/2006 1 Ementa Processos de desenvolvimento de software Estratégias e técnicas de teste de software Métricas para software
Manual de Utilização. Ao acessar o endereço www.fob.net.br chegaremos a seguinte página de entrada: Tela de Abertura do Sistema
 Abaixo explicamos a utilização do sistema e qualquer dúvida ou sugestões relacionadas a operação do mesmo nos colocamos a disposição a qualquer horário através do email: informatica@fob.org.br, MSN: informatica@fob.org.br
Abaixo explicamos a utilização do sistema e qualquer dúvida ou sugestões relacionadas a operação do mesmo nos colocamos a disposição a qualquer horário através do email: informatica@fob.org.br, MSN: informatica@fob.org.br
PUC-Rio Desafio em Matemática 23 de outubro de 2010
 PUC-Rio Desafio em Matemática 3 de outubro de 010 Nome: GABARITO Assinatura: Inscrição: Identidade: Questão Valor Nota Revisão 1 1,0 1,0 3 1,0 4 1,5 5 1,5 6,0 7,0 Nota final 10,0 Instruções Mantenha seu
PUC-Rio Desafio em Matemática 3 de outubro de 010 Nome: GABARITO Assinatura: Inscrição: Identidade: Questão Valor Nota Revisão 1 1,0 1,0 3 1,0 4 1,5 5 1,5 6,0 7,0 Nota final 10,0 Instruções Mantenha seu
Modelo Entidade Relacionamento (MER) Professor : Esp. Hiarly Alves
 Tópicos Apresentação Entidade, Atributo e Relacionamento Cardinalidade Representação simbólica Generalizações / Especializações Agregações Apresentação O Modelo Entidade-Relacionamento tem o objetivo de
Tópicos Apresentação Entidade, Atributo e Relacionamento Cardinalidade Representação simbólica Generalizações / Especializações Agregações Apresentação O Modelo Entidade-Relacionamento tem o objetivo de
SLOTS NA PORTELA Rui Rodrigues Site www.maquinistas.org Email rrodrigues.5@netcabo.pt Público
 SLOTS NA PORTELA Rui Rodrigues Site: www.maquinistas.org Email rrodrigues.5@netcabo.pt Público: 9 de Julho de 2007 SLOTS NA PORTELA Tem surgido na imprensa um argumento relativo à recusa de 'slots' na
SLOTS NA PORTELA Rui Rodrigues Site: www.maquinistas.org Email rrodrigues.5@netcabo.pt Público: 9 de Julho de 2007 SLOTS NA PORTELA Tem surgido na imprensa um argumento relativo à recusa de 'slots' na
AULA 07 Distribuições Discretas de Probabilidade
 1 AULA 07 Distribuições Discretas de Probabilidade Ernesto F. L. Amaral 31 de agosto de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
1 AULA 07 Distribuições Discretas de Probabilidade Ernesto F. L. Amaral 31 de agosto de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
Matemática Discreta - 08
 Universidade Federal do Vale do São Francisco urso de Engenharia da omputação Matemática Discreta - 08 Prof. Jorge avalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco urso de Engenharia da omputação Matemática Discreta - 08 Prof. Jorge avalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Corrente elétrica, potência, resistores e leis de Ohm
 Corrente elétrica, potência, resistores e leis de Ohm Corrente elétrica Num condutor metálico em equilíbrio eletrostático, o movimento dos elétrons livres é desordenado. Em destaque, a representação de
Corrente elétrica, potência, resistores e leis de Ohm Corrente elétrica Num condutor metálico em equilíbrio eletrostático, o movimento dos elétrons livres é desordenado. Em destaque, a representação de
SISTEMAS DE EQUAÇÕES DO 1º GRAU
 SISTEMAS DE EQUAÇÕES DO 1º GRAU I INTRODUÇÃO: Os sistemas de equação são ferramentas muito comuns na resolução de problemas em várias áreas ( matemática, química, física, engenharia,...) e aparecem sempre
SISTEMAS DE EQUAÇÕES DO 1º GRAU I INTRODUÇÃO: Os sistemas de equação são ferramentas muito comuns na resolução de problemas em várias áreas ( matemática, química, física, engenharia,...) e aparecem sempre
1 - POLÍGONOS REGULARES E CIRCUNFERÊNCIAS
 Matemática 2 Pedro Paulo GEOMETRIA PLANA X 1 - POLÍGONOS REGULARES E CIRCUNFERÊNCIAS 1.2 Triângulo equilátero circunscrito A seguir, nós vamos analisar a relação entre alguns polígonos regulares e as circunferências.
Matemática 2 Pedro Paulo GEOMETRIA PLANA X 1 - POLÍGONOS REGULARES E CIRCUNFERÊNCIAS 1.2 Triângulo equilátero circunscrito A seguir, nós vamos analisar a relação entre alguns polígonos regulares e as circunferências.
Prof. José Maurício S. Pinheiro - UGB - 2009
 Auditoria e Análise de Segurança da Informação Forense Computacional Prof. José Maurício S. Pinheiro - UGB - 2009 Forense Computacional 2 Forense Computacional A forense computacional pode ser definida
Auditoria e Análise de Segurança da Informação Forense Computacional Prof. José Maurício S. Pinheiro - UGB - 2009 Forense Computacional 2 Forense Computacional A forense computacional pode ser definida
IFRN. Conexidade e Distância. Prof. Edmilson Campos
 IFRN Conexidade e Distância Prof. Edmilson Campos Conteúdo Grafo Conexo Componente Conexa e Algoritmos Grafo F-Conexo Componente F-Conexa Antecessor, Sucessor, Fecho Transitivo Algoritmo Grafo Reduzido
IFRN Conexidade e Distância Prof. Edmilson Campos Conteúdo Grafo Conexo Componente Conexa e Algoritmos Grafo F-Conexo Componente F-Conexa Antecessor, Sucessor, Fecho Transitivo Algoritmo Grafo Reduzido
SUPERVISÃO Supervisão Comportamental
 ANEXO À INSTRUÇÃO N.º 12/2013 - (BO N.º 6, 17.06.2013) Temas SUPERVISÃO Supervisão Comportamental ANEXO II FICHA DE INFORMAÇÃO NORMALIZADA EM MATÉRIA DE CRÉDITO AOS CONSUMIDORES, EM CASO DE CONTRATAÇÃO
ANEXO À INSTRUÇÃO N.º 12/2013 - (BO N.º 6, 17.06.2013) Temas SUPERVISÃO Supervisão Comportamental ANEXO II FICHA DE INFORMAÇÃO NORMALIZADA EM MATÉRIA DE CRÉDITO AOS CONSUMIDORES, EM CASO DE CONTRATAÇÃO
Da linha poligonal ao polígono
 Polígonos Da linha poligonal ao polígono Uma linha poligonal é formada por segmentos de reta consecutivos, não alinhados. Polígono é uma superfície plana limitada por uma linha poligonal fechada. Dos exemplos
Polígonos Da linha poligonal ao polígono Uma linha poligonal é formada por segmentos de reta consecutivos, não alinhados. Polígono é uma superfície plana limitada por uma linha poligonal fechada. Dos exemplos
7as JORNADAS DE CLIMATIZAÇÃO Lisboa, 8 de Novembro de 2007
 7as JORNADAS DE CLIMATIZAÇÃO Lisboa, 8 de Novembro de 2007 1 Se se fecham cozinhas e restaurantes por falta de limpeza, como nos podemos permitir essa falta de limpeza no ar que respiramos todos os dias
7as JORNADAS DE CLIMATIZAÇÃO Lisboa, 8 de Novembro de 2007 1 Se se fecham cozinhas e restaurantes por falta de limpeza, como nos podemos permitir essa falta de limpeza no ar que respiramos todos os dias
aplicação arquivo Condições Gerais de Utilização
 aplicação arquivo Condições Gerais de Utilização Manual das condições gerais que regulam a utilização dos serviços disponibilizados pela aplicação Arquivo, plataforma de gestão de informação, do Municipio
aplicação arquivo Condições Gerais de Utilização Manual das condições gerais que regulam a utilização dos serviços disponibilizados pela aplicação Arquivo, plataforma de gestão de informação, do Municipio
INICIADOS - 2ª Sessão ClubeMath 7-11-2009
 INICIADOS - 2ª Sessão ClubeMath 7-11-2009 Adivinhar o dia de aniversário de outra pessoa e o mês Temos uns cartões mágicos, que vão permitir adivinhar o dia de aniversário de qualquer pessoa e outros que
INICIADOS - 2ª Sessão ClubeMath 7-11-2009 Adivinhar o dia de aniversário de outra pessoa e o mês Temos uns cartões mágicos, que vão permitir adivinhar o dia de aniversário de qualquer pessoa e outros que
Questão 1. Questão 3. Questão 2. Resposta. Resposta. Resposta. a) calcule a área do triângulo OAB. b) determine OC e CD.
 Questão Se Amélia der R$,00 a Lúcia, então ambas ficarão com a mesma quantia. Se Maria der um terço do que tem a Lúcia, então esta ficará com R$ 6,00 a mais do que Amélia. Se Amélia perder a metade do
Questão Se Amélia der R$,00 a Lúcia, então ambas ficarão com a mesma quantia. Se Maria der um terço do que tem a Lúcia, então esta ficará com R$ 6,00 a mais do que Amélia. Se Amélia perder a metade do
Probabilidade e Estatística
 Probabilidade e Estatística TESTES DE HIPÓTESES (ou Testes de Significância) Estimação e Teste de Hipóteses Estimação e teste de hipóteses (ou significância) são os aspectos principais da Inferência Estatística
Probabilidade e Estatística TESTES DE HIPÓTESES (ou Testes de Significância) Estimação e Teste de Hipóteses Estimação e teste de hipóteses (ou significância) são os aspectos principais da Inferência Estatística
10. CPU (Central Processor Unit)... 10 2 10.1 Conjunto das instruções... 10 2 10.2 Estrutura interna... 10 4 10.3 Formato das instruções...
 10. CPU (Central Processor Unit)... 10 2 10.1 Conjunto das instruções... 10 2 10.2 Estrutura interna... 10 4 10.3 Formato das instruções... 10 4 10. CPU (CENTRAL PROCESSOR UNIT) Como vimos no capítulo
10. CPU (Central Processor Unit)... 10 2 10.1 Conjunto das instruções... 10 2 10.2 Estrutura interna... 10 4 10.3 Formato das instruções... 10 4 10. CPU (CENTRAL PROCESSOR UNIT) Como vimos no capítulo
Aula 6 Propagação de erros
 Aula 6 Propagação de erros Conteúdo da aula: Como estimar incertezas de uma medida indireta Como realizar propagação de erros? Exemplo: medimos A e B e suas incertezas. Com calcular a incerteza de C, se
Aula 6 Propagação de erros Conteúdo da aula: Como estimar incertezas de uma medida indireta Como realizar propagação de erros? Exemplo: medimos A e B e suas incertezas. Com calcular a incerteza de C, se
 Manual de uso Serasa Judicial Março/2014 Controle de revisão Data da Revisão Versão Documento Versão Manager DF-e Executor Assunto Revisado 08/10/2013 1.0 Rodrigo Vieira Ambar/Gigiane Martins Criação 18/03/2104
Manual de uso Serasa Judicial Março/2014 Controle de revisão Data da Revisão Versão Documento Versão Manager DF-e Executor Assunto Revisado 08/10/2013 1.0 Rodrigo Vieira Ambar/Gigiane Martins Criação 18/03/2104
MÓDULO 2 Topologias de Redes
 MÓDULO 2 Topologias de Redes As redes de computadores de modo geral estão presentes em nosso dia adia, estamos tão acostumados a utilizá las que não nos damos conta da sofisticação e complexidade da estrutura,
MÓDULO 2 Topologias de Redes As redes de computadores de modo geral estão presentes em nosso dia adia, estamos tão acostumados a utilizá las que não nos damos conta da sofisticação e complexidade da estrutura,
Software PHC com MapPoint 2007
 Software PHC com MapPoint 2007 Descritivo completo A integração entre o Software PHC e o Microsoft MapPoint permite a análise de informação geográfica (mapas, rotas e análise de dispersão), baseada em
Software PHC com MapPoint 2007 Descritivo completo A integração entre o Software PHC e o Microsoft MapPoint permite a análise de informação geográfica (mapas, rotas e análise de dispersão), baseada em
Unidade 3 Função Afim
 Unidade 3 Função Afim Definição Gráfico da Função Afim Tipos Especiais de Função Afim Valor e zero da Função Afim Gráfico definidos por uma ou mais sentenças Definição C ( x) = 10. x + Custo fixo 200 Custo
Unidade 3 Função Afim Definição Gráfico da Função Afim Tipos Especiais de Função Afim Valor e zero da Função Afim Gráfico definidos por uma ou mais sentenças Definição C ( x) = 10. x + Custo fixo 200 Custo
Método Simplex das Duas Fases
 Notas de aula da disciplina Pesquisa Operacional 1. 2003/1 c DECOM/ICEB/UFOP. Método Simplex das Duas Fases 1 Descrição do método Suponhamos inicialmente que tenham sido efetuadas transformações no PPL,
Notas de aula da disciplina Pesquisa Operacional 1. 2003/1 c DECOM/ICEB/UFOP. Método Simplex das Duas Fases 1 Descrição do método Suponhamos inicialmente que tenham sido efetuadas transformações no PPL,
Sistemática dos seres vivos
 Sistemática dos seres vivos O mundo vivo é constituído por uma enorme variedade de organismos. Para estudar e compreender tamanha variedade, idd foi necessário agrupar os organismos de acordo com as suas
Sistemática dos seres vivos O mundo vivo é constituído por uma enorme variedade de organismos. Para estudar e compreender tamanha variedade, idd foi necessário agrupar os organismos de acordo com as suas
Matemática Básica Intervalos
 Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Raciocínio Lógico Professor: Custódio Nascimento
 Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Professor: Custódio Nascimento 1- Análise da prova Análise e Resolução da prova de Agente / PF Neste artigo, farei a análise das questões
Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Professor: Custódio Nascimento 1- Análise da prova Análise e Resolução da prova de Agente / PF Neste artigo, farei a análise das questões
Exercício. Exercício
 Exercício Exercício Aula Prática Utilizar o banco de dados ACCESS para passar o MER dos cenários apresentados anteriormente para tabelas. 1 Exercício oções básicas: ACCESS 2003 2 1 Exercício ISERIDO UMA
Exercício Exercício Aula Prática Utilizar o banco de dados ACCESS para passar o MER dos cenários apresentados anteriormente para tabelas. 1 Exercício oções básicas: ACCESS 2003 2 1 Exercício ISERIDO UMA
Modelos de Regressão Linear Simples - Erro Puro e Falta de Ajuste
 Modelos de Regressão Linear Simples - Erro Puro e Falta de Ajuste Erica Castilho Rodrigues 2 de Setembro de 2014 Erro Puro 3 Existem dois motivos pelos quais os pontos observados podem não cair na reta
Modelos de Regressão Linear Simples - Erro Puro e Falta de Ajuste Erica Castilho Rodrigues 2 de Setembro de 2014 Erro Puro 3 Existem dois motivos pelos quais os pontos observados podem não cair na reta
Modelo Relacional Normalização Diagramas E-R e Tabelas Originadas
 Informática II Modelo Relacional Normalização Diagramas E-R e Tabelas Originadas (TÓPICOS ABORDADOS NAS AULAS DE INFORMÁTICA II) Por: Artur Sousa / Jorge Loureiro Conceitos de entidade e atributo Tipos
Informática II Modelo Relacional Normalização Diagramas E-R e Tabelas Originadas (TÓPICOS ABORDADOS NAS AULAS DE INFORMÁTICA II) Por: Artur Sousa / Jorge Loureiro Conceitos de entidade e atributo Tipos
OPERAÇÕES COM FRAÇÕES
 OPERAÇÕES COM FRAÇÕES Adição A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Se inicialmente todas as frações já possuírem um denominador comum, basta que
OPERAÇÕES COM FRAÇÕES Adição A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Se inicialmente todas as frações já possuírem um denominador comum, basta que
NavegadorContábil. Sim. Não. Sim. Não. Número 13-20 de agosto de 2010. Contabilização de operações de duplicata descontada e vendor
 NavegadorContábil Número 13-20 de agosto de 2010 Contabilização de operações de duplicata descontada e vendor Introdução Muitas empresas no Brasil, na administração de seu capital de giro, fazem uso de
NavegadorContábil Número 13-20 de agosto de 2010 Contabilização de operações de duplicata descontada e vendor Introdução Muitas empresas no Brasil, na administração de seu capital de giro, fazem uso de
Capítulo I Disposições Gerais
 Regulamento Municipal do Banco Local de Voluntariado de Marco de Canaveses Preâmbulo A Lei n.º 71/98, de 3 de Novembro, estabelece as bases do enquadramento jurídico do voluntariado, visando promover e
Regulamento Municipal do Banco Local de Voluntariado de Marco de Canaveses Preâmbulo A Lei n.º 71/98, de 3 de Novembro, estabelece as bases do enquadramento jurídico do voluntariado, visando promover e
Resolução da Lista de Exercício 6
 Teoria da Organização e Contratos - TOC / MFEE Professor: Jefferson Bertolai Fundação Getulio Vargas / EPGE Monitor: William Michon Jr 10 de novembro de 01 Exercícios referentes à aula 7 e 8. Resolução
Teoria da Organização e Contratos - TOC / MFEE Professor: Jefferson Bertolai Fundação Getulio Vargas / EPGE Monitor: William Michon Jr 10 de novembro de 01 Exercícios referentes à aula 7 e 8. Resolução
Inversão de Matrizes
 Inversão de Matrizes Prof. Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2014.2 13 de
Inversão de Matrizes Prof. Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2014.2 13 de
Fundamentos de Teste de Software
 Núcleo de Excelência em Testes de Sistemas Fundamentos de Teste de Software Módulo 1- Visão Geral de Testes de Software Aula 2 Estrutura para o Teste de Software SUMÁRIO 1. Introdução... 3 2. Vertentes
Núcleo de Excelência em Testes de Sistemas Fundamentos de Teste de Software Módulo 1- Visão Geral de Testes de Software Aula 2 Estrutura para o Teste de Software SUMÁRIO 1. Introdução... 3 2. Vertentes
AV1 - MA 14-2011. (1,0) (a) Determine o maior número natural que divide todos os produtos de três números naturais consecutivos.
 Questão 1 (1,0) (a) Determine o maior número natural que divide todos os rodutos de três números naturais consecutivos (1,0) (b) Resonda à mesma questão no caso do roduto de quatro números naturais consecutivos
Questão 1 (1,0) (a) Determine o maior número natural que divide todos os rodutos de três números naturais consecutivos (1,0) (b) Resonda à mesma questão no caso do roduto de quatro números naturais consecutivos
Matrizes. matriz de 2 linhas e 2 colunas. matriz de 3 linhas e 3 colunas. matriz de 3 linhas e 1 coluna. matriz de 1 linha e 4 colunas.
 Definição Uma matriz do tipo m n (lê-se m por n), com m e n, sendo m e n números inteiros, é uma tabela formada por m n elementos dispostos em m linhas e n colunas. Estes elementos podem estar entre parênteses
Definição Uma matriz do tipo m n (lê-se m por n), com m e n, sendo m e n números inteiros, é uma tabela formada por m n elementos dispostos em m linhas e n colunas. Estes elementos podem estar entre parênteses
Prática. Exercícios didáticos ( I)
 1 Prática Exercício para início de conversa Localize na reta numérica abaixo os pontos P correspondentes aos segmentos de reta OP cujas medidas são os números reais representados por: Exercícios didáticos
1 Prática Exercício para início de conversa Localize na reta numérica abaixo os pontos P correspondentes aos segmentos de reta OP cujas medidas são os números reais representados por: Exercícios didáticos
RESUMO ABSTRACT. Vamos supor que uma caixa-preta, representada por uma relação de entrada e saída. f :!! 7!
 REALIZAÇÃO CANÔNICA DA SEQÜÊNCIA DE FIBONACCI Paulo Franca Bandel (IC) 1 & Marcos Antonio Botelho Labmat Laboratório de Matemática Experimental Departamento de Matemática Instituto Tecnológico de Aeronáutica
REALIZAÇÃO CANÔNICA DA SEQÜÊNCIA DE FIBONACCI Paulo Franca Bandel (IC) 1 & Marcos Antonio Botelho Labmat Laboratório de Matemática Experimental Departamento de Matemática Instituto Tecnológico de Aeronáutica
Condução. t x. Grupo de Ensino de Física da Universidade Federal de Santa Maria
 Condução A transferência de energia de um ponto a outro, por efeito de uma diferença de temperatura, pode se dar por condução, convecção e radiação. Condução é o processo de transferência de energia através
Condução A transferência de energia de um ponto a outro, por efeito de uma diferença de temperatura, pode se dar por condução, convecção e radiação. Condução é o processo de transferência de energia através
