Métodos Experimentais para Vibrações Mecânicas
|
|
|
- Giovanni Lancastre Álvares
- 8 Há anos
- Visualizações:
Transcrição
1 Métodos Experimentais Métodos Experimentais para Vibrações Mecânicas Prof. Aline Souza de Paula Universidade de Brasília Faculdade de Tecnologia Departamento de Engenharia Mecânica
2 Introdução A maioria das atividades humanas envolve alguma forma de vibração. Ouvimos porque o tímpano vibra; Vemos porque ondas luminosas se propagam; A respiração está associada à vibração dos pulmões; Os batimentos cardíacos são movimentos vibratórios; A fala se fundamenta na vibração das cordas vocais; As movimentos humanos envolvem oscilações de braços e pernas.
3 Introdução Em muitos outros campos da atividade humana, fenômenos apresentam variáveis cujo comportamento é oscilatório: Economia Medicina Engenharia No campo tecnológico, as aplicações de vibrações na engenharia são de grande importância: Projetos de máquinas Estruturas Motores Turbinas Sistemas de controle
4 Consequência das Vibrações A presença de vibrações frequentemente conduz a efeitos indesejáveis: Falhas mecânicas ou estruturais; Manutenção freqüente e dispendiosa de máquinas; Danos e desconforto para o homem.
5 Vibrações Modelagem Elementos concentrados de um oscilador: Inércia massa Rigidez mola Dissipação de energia amortecimento
6 SISTEMAS FÍSICOS REPRESENTADOS POR OSCILADORES
7 Fluido u Cilindro u u Fluido Corpo submerso em fluido Fluido em tudo em U
8 Sistemas Pendulares θ L m
9 Viga em balanço EI m L
10 Máquinas rotativas
11 Automóvel
12 Oscilador 1GL ζ=0 ζ=0.5
13 Consequência das Vibrações Ressonância
14 Ressonância Corpo Humano
15 Casos Escada Rio Design Barra da Tijuca / RJ
16 Casos Ponte Rio-Niterói
17 Análise Modal Teoria clássica de vibraçoes resposta dinâmica do sistema. Análise modal relacionada com as propriedades intrinsicas do sistema: Freqüências naturais Formas modais Parâmetros do sistema: Massa; Rigidez; Amortecimento.
18 Análise Modal Métodos da análise modal se caracterizam pelo cálculo direto dos parâmetros modais. Registros da excitação e resposta análise no domínio do tempo ou da frequência; Forma mais utilizada mais eficiente de investigar a análise modal: Função de Resposta em Frequência FRF.
19 Análise Modal 1 G.L. Equação de movimento: m &&+ x cx& + kx = F Para um forçamento F t = it, x t = Xe, com isso: F e 0 it tem-se uma solução do tipo it it = Xe x& t = i Xe & x x t t = Xe it Logo: it X + icx + kx e 0 m = F e it FRF: α X 1 = = F k m 0 + ic
20 Uma Função de Resposta em Freqüência FRF é uma relação causa/efeito que descreve o comportamento do sistema com uma entrada e uma saída. Receptância FRF: c i m k F X α + = = 0 1 Análise Modal 1 G.L. Mobilidade FRF: Inertância FRF: c i m k i F X Y + = = 0 & c i m k F X A + = = 0 && α A Y = =
21 Relações/definições importantes. Rigidez dinâmica: Impedância mecânica: c i m k X F α + = = 0 1 c i m k F + = = 0 1 Análise Modal 1 G.L. Impedância mecânica: Massa aparente: i c i m k Y X F + = = 0 1 & = = c i m k A X F &&
22 Análise Modal 1 G.L. Rigidez dinâmica: 1 α = k m + ic
23 Análise Modal 1 G.L. Receptância FRF: α α << 0 1 k α 1 1 = k m + ic α << >> 0 >> 0 m α 0 0log k db 0log m - 40logdB
24 Determinação do Amortecimento Fator de qualidade ou Largura de Banda: Pontos de meia potência: Gmax G 1 = G = = 1 ξ 1 = 1 1, ± ξ Equação Movimento: m &&+ x cx& + kx = F Largura de Banda: δ = ξ 1= Equação Movimento Adimensionalizada: && x + ξ x& + x = 0 0 F m
25 Determinação do Amortecimento Decremento Logaritmico Resposta Livre Decremento logaritmico: γ = 1 ln j u 1 u j +1 Coeficiente de Amortecimento viscoso: ξ = γ 4π + γ
26 Determinação do Amortecimento Decremento Linear Resposta Livre Coeficiente de Atrito Seco: µ = k u1 u k u1 u = 4mg 4N
27 Sistemas Discretos Base Modal Equações de movimento na ausência de amortecimento: [ M ]{&& x t} + [ K]{ x t} = { f t}
28 Sistemas Discretos Base Modal Equação de Movimento: [ M ]{&& x t} + [ K]{ x t} = { f t} Para um forçamento i tipo { x t} = { X } e t { f t} = { F} e, com isso: it tem-se uma solução do { x } i t i t = { X } e { x & } = i { X } e { & x } = { X } e Com isso, reescreve-se as equações de movimento: Receptância FRF: [[ K ] [ M ]]{ X} = { F} i t [ α ] = [[ K] [ M ]] 1 { X} = [ α ]{ F}
29 Resposta na coordenada i devido a uma força aplicada na coordenada j. = ] [ α α α α α α α α α α n n L L L L L L L Sistemas Discretos Base Modal i=j: ponto FRF i diferente de j: Transferência em FRF 1 1 α α α nn n n L } ]{ [ } { F X α =
30 Sistemas Discretos Base Modal Realizando a tranformação de coordenadas: { x t} = [ φ] q t onde [φ] [ M ]{&& x t} + [ K]{ x t} = { f t} é a matriz modal, obtém-se: Pré-multiplicando por [ M ][ φ ]{ q& } + [ K][ φ]{ q} = { f } [φ] T T T [ φ ] [ M ][ φ]{ q&& } + [ φ] [ K][ φ]{ q} = [ φ] { f } T = r T como [ φ ] [ M ][ φ] = [ I] e [ φ] T [ K][ φ] [ ], obtém-se que: { q&& } + r [ ]{ q} = [ φ] T { f } Problema escrito no sistema de coordenadas modais ou principais.
31 Realiza-se as mesmas transformações utilizadas para escrever o problema no sistema coordenadas modais: ] [ ]] [ ] [[ ] [ ] ][ [ ] [ 1 φ φ φ α φ = M K T T ] [ ] ][ [ ] [ = φ α φ r T T r ] ][ ][ [ ] [ φ φ α = Sistemas Discretos Base Modal Ou ainda: r ] ][ ][ [ ] [ φ φ α = = ] [ φ φ φ φ φ φ α n kn jn k j k j ij M L
32 Sistemas Discretos Base Modal Rigidez dinâmica Sistema Discreto:
33 Sistemas Discretos Base Modal Receptância FRF Sistema Discreto:
34 FRF Experimental Shaker: Acelerômetro:
35 FRF Experimental Martelo: Acelerômetro: Transdutor de força:
36 FFT Experimental Viga escala logarítmica: Máquina Rotativa escala linear:
37 Sensores Medição de Posição: Potenciômetros Encoders Sensores ópticos: sem contato. Medição de deformação: Strain gages. Medição de Velocidade: Tacômetros. Medição de Aceleração: Acelerômetro. Medição de torque e força: Células de carga.
38 Potenciômetro Converte o deslocamento linear ou angular em variação de resistência.
39 Encoder O encoder é um transdutor que converte um movimento angular ou linear em uma série de pulsos digitais elétricos. Tipos de Encoder: Absoluto Incremental
40 Encoder Incremental
41 Encoder Ligação esquemática dos sensores ao PC
42 Sensores Ópticos Medição de posição sem contato.
43 Strain Gages Os extensômetros elétricos strain gages constituem a forma mais usual de se medir deformação. Seu princípio de funcionamento baseia-se no fato de que os materiais exibem uma mudança em sua resistência elétrica quando submetidos a uma deformação mecânica. O condicionamento do sinal é feito através do uso da Ponte de Wheatstone:
44 Acelerômetro Princípio de Funcionamento Variável adotada: z t = x t y t Equação de movimento: m & z t + cz& t + k z t = my & t Movimento da base: y t = Y0 sin t && y t = Y0 sin t Equação de Movimento: m&& z t + cz& t + k z t = m Y0 sin t
45 Acelerômetro Equação de movimento: m&& z t + cz& t + k z t = m Y0 sin t Resposta do sistema: z t = Y 0 cos φ G i t n ou ainda: onde: z t = Z0 cos t φ Z0 = G i Y 0 n
46 Acelerômetro G i 1 Para, tem-se que: Z Y 0 0 n
47 Acelerômetro Piezoelétrico
48 Acelerômetros - Especificação Frequência máxima < frequência ressonância
49 Controle de Vibrações Isoladores O isolamento de vibrações envolve a inserção de um membro resiliente ou isolador entre a massa vibratória ou equipamento e a fonte da vibração de forma que a redução na resposta dinâmica do sistema é atingida sob condições específicas de excitação de vibrações.
50 Controle de Vibrações Absorvedores dinâmicos
51 Absorvedor Dinâmico de Vibrações Stockbridge: Absorvedor de vibrações para linhas de transmissão
52 Absorvedor Dinâmico de Vibrações Absorvedor de Vibrações Pendular Taipei 101, Taipei, Taiwan
53 Métodos Experimentais Métodos Experimentais para Vibrações Mecânicas Prof. Aline Souza de Paula Universidade de Brasília Faculdade de Tecnologia Departamento de Engenharia Mecânica
Que são sensores? São dispositivos que são sensíveis à um fenômeno físico (luz, temperatura, impedância elétrica etc.) e transmitem um sinal para um
 Que são sensores? São dispositivos que são sensíveis à um fenômeno físico (luz, temperatura, impedância elétrica etc.) e transmitem um sinal para um dispositivo de medição ou controle. 1 Cite 08 tipos
Que são sensores? São dispositivos que são sensíveis à um fenômeno físico (luz, temperatura, impedância elétrica etc.) e transmitem um sinal para um dispositivo de medição ou controle. 1 Cite 08 tipos
Transdutores de Deslocamento
 Transdutores de Deslocamento Potenciômetros são formados por um material condutor resistivo depositado em superfície isolante, com contatos fixos nas duas extremidades e um contato móvel (cursor) que se
Transdutores de Deslocamento Potenciômetros são formados por um material condutor resistivo depositado em superfície isolante, com contatos fixos nas duas extremidades e um contato móvel (cursor) que se
Formulário de Mecânica e Ondas MeMEC e LEAN Mário J. Pinheiro Para consulta no Teste e Exame
 1 Formulário de Mecânica e Ondas MeMEC e LEAN Mário J. Pinheiro Para consulta no Teste e Exame Constantes Físicas Fundamentais: Velocidade da luz, c.9979458 10 8 m.s 1 Constante da aceleração da gravidade,
1 Formulário de Mecânica e Ondas MeMEC e LEAN Mário J. Pinheiro Para consulta no Teste e Exame Constantes Físicas Fundamentais: Velocidade da luz, c.9979458 10 8 m.s 1 Constante da aceleração da gravidade,
Sensores de Aceleração
 Sensores de Aceleração Sensores de aceleração (acelerômetros e giroscópios) são componentes do tipo inercial que fornecem um sinal elétrico proporcional à aceleração do sistema. São transdutores que convertem
Sensores de Aceleração Sensores de aceleração (acelerômetros e giroscópios) são componentes do tipo inercial que fornecem um sinal elétrico proporcional à aceleração do sistema. São transdutores que convertem
SENSORES. Acelerômetro. Sensore de temperatura. Sensore de luminosidade. Chave de fim de curso. Interruptor de lâminas. Sensor potenciômetro
 SENSORES São dispositivos que são sensíveis à um fenômeno físico (luz, temperatura, impedância elétrica etc.) e que transmitem um sinal para um dispositivo de medição ou controle. 1 SENSORES Acelerômetro
SENSORES São dispositivos que são sensíveis à um fenômeno físico (luz, temperatura, impedância elétrica etc.) e que transmitem um sinal para um dispositivo de medição ou controle. 1 SENSORES Acelerômetro
Mecânismos A06. Prof. Nilton Ferruzzi. Prof. Nilton Ferruzzi 1
 Mecânismos A06 Prof. Nilton Ferruzzi Prof. Nilton Ferruzzi 1 Definição de Vibração Mecânica: É qualquer movimento que se repete, regular ou irregularmente, depois de um intervalo de tempo. O movimento
Mecânismos A06 Prof. Nilton Ferruzzi Prof. Nilton Ferruzzi 1 Definição de Vibração Mecânica: É qualquer movimento que se repete, regular ou irregularmente, depois de um intervalo de tempo. O movimento
AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E
 AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E SUPERCRÍTICO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 20 de março de 2013 Roteiro 1 Amortecidas forçadas Roteiro Amortecidas forçadas 1 Amortecidas
AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E SUPERCRÍTICO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 20 de março de 2013 Roteiro 1 Amortecidas forçadas Roteiro Amortecidas forçadas 1 Amortecidas
SENSORES. Acelerômetro. Sensor de temperatura. Sensor de luminosidade. Interruptor de lâminas. Sensor potenciômetro. Encoder incremental
 SENSORES São dispositivos que são sensíveis à um fenômeno físico (luz, temperatura, impedância elétrica etc.) e que transmitem um sinal para um dispositivo de medição ou controle informando a variação
SENSORES São dispositivos que são sensíveis à um fenômeno físico (luz, temperatura, impedância elétrica etc.) e que transmitem um sinal para um dispositivo de medição ou controle informando a variação
LISTA DE EXERCÍCIOS 2
 LISTA DE EXERCÍCIOS 2 Esta lista trata de vários conceitos associados ao movimento harmônico forçado e/ou amortecido. Tais conceitos são abordados no capítulo 4 do livro-texto (seções 4.1 a 4.5): Moysés
LISTA DE EXERCÍCIOS 2 Esta lista trata de vários conceitos associados ao movimento harmônico forçado e/ou amortecido. Tais conceitos são abordados no capítulo 4 do livro-texto (seções 4.1 a 4.5): Moysés
Aspectos de transdutores para medição de vibração. Prof. Paulo J. Paupitz Gonçalves
 Aspectos de transdutores para medição de vibração Prof. Paulo J. Paupitz Gonçalves Medidas de Vibração/Ruído transdutor Condicionador de Sinais Analisador Aspectos do Projeto de um Transdutor Características
Aspectos de transdutores para medição de vibração Prof. Paulo J. Paupitz Gonçalves Medidas de Vibração/Ruído transdutor Condicionador de Sinais Analisador Aspectos do Projeto de um Transdutor Características
As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um
 As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um alto-falante, ou de um instrumento de percussão. Um terremoto
As Oscilações estão presentes no nosso dia a dia como o vento que balança uma linha de transmissão elétrica, as vibrações da membrana de um alto-falante, ou de um instrumento de percussão. Um terremoto
FEP Física para Engenharia II
 FEP96 - Física para Engenharia II Prova P - Gabarito. Uma plataforma de massa m está presa a duas molas iguais de constante elástica k. A plataforma pode oscilar sobre uma superfície horizontal sem atrito.
FEP96 - Física para Engenharia II Prova P - Gabarito. Uma plataforma de massa m está presa a duas molas iguais de constante elástica k. A plataforma pode oscilar sobre uma superfície horizontal sem atrito.
2 Amortecimento Amortecimento viscoso ou proporcional Sistemas de um grau de liberdade
 2 Amortecimento Todo mecanismo de dissipação de energia introduz amortecimento na vibração de uma estrutura. Como mencionado anteriormente, em função do mecanismo relevante na dissipação de energia existem
2 Amortecimento Todo mecanismo de dissipação de energia introduz amortecimento na vibração de uma estrutura. Como mencionado anteriormente, em função do mecanismo relevante na dissipação de energia existem
CONTEÚDOS PROGRAMADOS (Acústica Ambiental - EEK603) TOTAL 45
 (Acústica Ambiental - EEK603) TOTAL 4 (Acústica Básica - EEK4) - introdução O fenômeno acústico: propagação. Nível de pressão sonora. As hipóteses acústicas. - Equacionamento Balanços de massa e quantidade
(Acústica Ambiental - EEK603) TOTAL 4 (Acústica Básica - EEK4) - introdução O fenômeno acústico: propagação. Nível de pressão sonora. As hipóteses acústicas. - Equacionamento Balanços de massa e quantidade
Transdutores de Deslocamento
 Transdutores de Deslocamento Potenciômetros são formados por um material condutor resistivo depositado em superfície isolante, com contatos fixos nas duas extremidades e um contato móvel (cursor) que se
Transdutores de Deslocamento Potenciômetros são formados por um material condutor resistivo depositado em superfície isolante, com contatos fixos nas duas extremidades e um contato móvel (cursor) que se
π rad / s. NEWLAND (1989) LISTA DE FIGURAS
 LISTA DE FIGURAS Figura 2.1 Aplicação da análise experimental de estruturas, ALMEIDA (1996) Figura 2.2 Ações determinísticas, BACHMANN; AMMANN (1987) Figura 2.3 Sistema dinâmico com um grau de liberdade,
LISTA DE FIGURAS Figura 2.1 Aplicação da análise experimental de estruturas, ALMEIDA (1996) Figura 2.2 Ações determinísticas, BACHMANN; AMMANN (1987) Figura 2.3 Sistema dinâmico com um grau de liberdade,
AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E
 AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E SUPERCRÍTICO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 26 de março de 2018 Roteiro 1 Modelo geral Amortecimento supercrítico Amortecimento subcrítico
AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E SUPERCRÍTICO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 26 de março de 2018 Roteiro 1 Modelo geral Amortecimento supercrítico Amortecimento subcrítico
Prof. Dr. Ronaldo Rodrigues Pelá. 3 de abril de 2013
 OSCILAÇÕES FORÇADAS Mecânica II (FIS-6) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 3 de abril de 013 Roteiro 1 Forçadas Roteiro 1 Resultado M: 66 DP: 0 Conceito N L 3 MB 4 B 7 R 3 I 1 D 5 Roteiro Forçadas
OSCILAÇÕES FORÇADAS Mecânica II (FIS-6) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 3 de abril de 013 Roteiro 1 Forçadas Roteiro 1 Resultado M: 66 DP: 0 Conceito N L 3 MB 4 B 7 R 3 I 1 D 5 Roteiro Forçadas
Vibrações e Dinâmica das Máquinas Aula Fundamentos de vibrações. Professor: Gustavo Silva
 Vibrações e Dinâmica das Máquinas Aula Fundamentos de vibrações Professor: Gustavo Silva 1 1.Movimentos Movimento oscilatório é qualquer movimento onde o sistema observado move-se em torno de uma certa
Vibrações e Dinâmica das Máquinas Aula Fundamentos de vibrações Professor: Gustavo Silva 1 1.Movimentos Movimento oscilatório é qualquer movimento onde o sistema observado move-se em torno de uma certa
Física para Engenharia II
 Física para Engenharia II 430196 (FEP196) Turma 01111 Sala C-13 3as 15h00 / 5as 9h0. Prof. Antonio Domingues dos Santos Depto. Física Materiais e Mecânica IF USP Ed. Mário Schemberg, sala 05 [email protected]
Física para Engenharia II 430196 (FEP196) Turma 01111 Sala C-13 3as 15h00 / 5as 9h0. Prof. Antonio Domingues dos Santos Depto. Física Materiais e Mecânica IF USP Ed. Mário Schemberg, sala 05 [email protected]
Programa Analítico de Disciplina MEC460 Vibrações Mecânicas
 Programa Analítico de Disciplina Departamento de Engenharia de Produção e Mecânica - Centro de Ciências Exatas e Tecnológicas Número de créditos: 5 Teóricas Práticas Total Duração em semanas: 15 Carga
Programa Analítico de Disciplina Departamento de Engenharia de Produção e Mecânica - Centro de Ciências Exatas e Tecnológicas Número de créditos: 5 Teóricas Práticas Total Duração em semanas: 15 Carga
Vibrações e Dinâmica das Máquinas Aula Vibração excitada harmonicamente- 1GL. Professor: Gustavo Silva
 Vibrações e Dinâmica das Máquinas Aula Vibração excitada harmonicamente- 1GL Professor: Gustavo Silva 1 1. Introdução Nesta aula estudaremos sistemas amortecidos e não amortecidos sendo excitados harmonicamente.
Vibrações e Dinâmica das Máquinas Aula Vibração excitada harmonicamente- 1GL Professor: Gustavo Silva 1 1. Introdução Nesta aula estudaremos sistemas amortecidos e não amortecidos sendo excitados harmonicamente.
FEP Física para Engenharia II
 FEP2196 - Física para Engenharia II Prova P1-25/10/2007 - Gabarito 1. Um corpo de massa 50 g está preso a uma mola de constante k = 20 N/m e oscila, inicialmente, livremente. Esse oscilador é posteriormente
FEP2196 - Física para Engenharia II Prova P1-25/10/2007 - Gabarito 1. Um corpo de massa 50 g está preso a uma mola de constante k = 20 N/m e oscila, inicialmente, livremente. Esse oscilador é posteriormente
1. Movimento Harmônico Simples
 Física Oscilações 1. Movimento Harmônico Simples Vamos analisar inicialmente a situação em que há um corpo de massa m, preso a uma mola de constante elástica K que realiza oscilações em torno de seu ponto
Física Oscilações 1. Movimento Harmônico Simples Vamos analisar inicialmente a situação em que há um corpo de massa m, preso a uma mola de constante elástica K que realiza oscilações em torno de seu ponto
NBR 7497 Vibrações mecânicas e choques
 AGO 198 NBR 7497 Vibrações mecânicas e choques ABNT-Associação Brasileira de Normas Técnicas Sede: Rio de Janeiro Av. Treze de Maio, 13-8º andar CEP 0003-900 - Caixa Postal 1680 Rio de Janeiro - RJ Tel.:
AGO 198 NBR 7497 Vibrações mecânicas e choques ABNT-Associação Brasileira de Normas Técnicas Sede: Rio de Janeiro Av. Treze de Maio, 13-8º andar CEP 0003-900 - Caixa Postal 1680 Rio de Janeiro - RJ Tel.:
TÍTULO: ANÁLISE MODAL EXPERIMENTAL CATEGORIA: CONCLUÍDO ÁREA: ENGENHARIAS E ARQUITETURA SUBÁREA: ENGENHARIAS
 TÍTULO: ANÁLISE MODAL EXPERIMENTAL CATEGORIA: CONCLUÍDO ÁREA: ENGENHARIAS E ARQUITETURA SUBÁREA: ENGENHARIAS INSTITUIÇÃO: FACULDADE ANHANGUERA DE TAUBATÉ AUTOR(ES): MARIA LAURA DA SILVA FRANÇA ORIENTADOR(ES):
TÍTULO: ANÁLISE MODAL EXPERIMENTAL CATEGORIA: CONCLUÍDO ÁREA: ENGENHARIAS E ARQUITETURA SUBÁREA: ENGENHARIAS INSTITUIÇÃO: FACULDADE ANHANGUERA DE TAUBATÉ AUTOR(ES): MARIA LAURA DA SILVA FRANÇA ORIENTADOR(ES):
U15040 Pêndulo de torção segundo Prof. Pohl
 3B SCIENTIFIC PHYSICS U15040 Pêndulo de torção segundo Prof. Pohl Instruções para o uso 1/03 ALF 9 8 7 6 5 4 bl bm bn bo bp 3 1 1 Motor do excitador Botão rotativo para o ajuste fino da tensão do excitador
3B SCIENTIFIC PHYSICS U15040 Pêndulo de torção segundo Prof. Pohl Instruções para o uso 1/03 ALF 9 8 7 6 5 4 bl bm bn bo bp 3 1 1 Motor do excitador Botão rotativo para o ajuste fino da tensão do excitador
Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula
 Aula 3 010 Movimento Harmônico Simples: Exemplos O protótipo físico do movimento harmônico simples (MHS) visto nas aulas passadas um corpo de massa m preso a uma mola executando vibrações de pequenas amplitudes
Aula 3 010 Movimento Harmônico Simples: Exemplos O protótipo físico do movimento harmônico simples (MHS) visto nas aulas passadas um corpo de massa m preso a uma mola executando vibrações de pequenas amplitudes
2 Vibrações em estacas 2.1. Frequência natural de vibração e ressonância
 2 Vibrações em estacas 2.1. Frequência natural de vibração e ressonância Todo sistema físico capaz de vibrar possui uma ou mais frequências naturais de vibração, isto é, que são características do sistema
2 Vibrações em estacas 2.1. Frequência natural de vibração e ressonância Todo sistema físico capaz de vibrar possui uma ou mais frequências naturais de vibração, isto é, que são características do sistema
Modelagem Matemática de Sistemas Mecânicos Rotacionais pela Mecânica Newtoniana
 Modelagem Matemática de Sistemas Mecânicos ranslacionais pela Mecânica ewtoniana 6 Modelagem Matemática de Sistemas Mecânicos Rotacionais pela Mecânica ewtoniana IRODUÇÃO esta apostila aprenderemos como
Modelagem Matemática de Sistemas Mecânicos ranslacionais pela Mecânica ewtoniana 6 Modelagem Matemática de Sistemas Mecânicos Rotacionais pela Mecânica ewtoniana IRODUÇÃO esta apostila aprenderemos como
WORKSHOP DA COORD. DE CÂMARAS ESPECIALIZADAS DE ENGENHARIA INDUSTRIAL - CCEEI
 CONSELHO FEDERAL DE ENGENHARIA E AGRONOMIA CONFEA WORKSHOP DA COORD. DE CÂMARAS ESPECIALIZADAS DE ENGENHARIA INDUSTRIAL - CCEEI Formação de Engenheiros para o Desenvolvimento Científico e Tecnológico de
CONSELHO FEDERAL DE ENGENHARIA E AGRONOMIA CONFEA WORKSHOP DA COORD. DE CÂMARAS ESPECIALIZADAS DE ENGENHARIA INDUSTRIAL - CCEEI Formação de Engenheiros para o Desenvolvimento Científico e Tecnológico de
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto.
 Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrer turbulência
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrer turbulência
Medição de Deformação e Força I.B De Paula
 INTRODUÇÃO O projeto de componentes sujeitos a carga para máquinas e estruturas requer informações sobre as distribuições de forças e deformações a que esses componentes estão submetidos. A mecânica dos
INTRODUÇÃO O projeto de componentes sujeitos a carga para máquinas e estruturas requer informações sobre as distribuições de forças e deformações a que esses componentes estão submetidos. A mecânica dos
INSTRUMENTAÇÃO E CONTROLE INDUSTRIAL I. Prof. Pierre Vilar Dantas Turma: 0063-A Horário: 6N ENCONTRO DE 23/03/2018
 INSTRUMENTAÇÃO E CONTROLE INDUSTRIAL I Prof. Pierre Vilar Dantas Turma: 0063-A Horário: 6N ENCONTRO DE 23/03/2018 Sensores Referências bibliográficas BRUSAMARELLO, Valner Joao; BALBINOT, Alexandre. Instrumentação
INSTRUMENTAÇÃO E CONTROLE INDUSTRIAL I Prof. Pierre Vilar Dantas Turma: 0063-A Horário: 6N ENCONTRO DE 23/03/2018 Sensores Referências bibliográficas BRUSAMARELLO, Valner Joao; BALBINOT, Alexandre. Instrumentação
SUMÁRIO APRESENTAÇÃO PREFÁCIO... 15
 SUMÁRIO APRESENTAÇÃO... 13 PREFÁCIO... 15 1 INTRODUÇÃO E DEFINIÇÕES GERAIS... 19 1.1 Aplicações da Simulação Dinâmica... 20 1.2 Tipos de Modelos para Sistemas Dinâmicos... 21 1.3 Modelos Matemáticos...
SUMÁRIO APRESENTAÇÃO... 13 PREFÁCIO... 15 1 INTRODUÇÃO E DEFINIÇÕES GERAIS... 19 1.1 Aplicações da Simulação Dinâmica... 20 1.2 Tipos de Modelos para Sistemas Dinâmicos... 21 1.3 Modelos Matemáticos...
ANÁLISE DE TENSÕES E DEFORMAÇÕES EXTENSOMETRIA ELÉTRICA-STRAIN GAGES. Extensometria é a técnica de medição de deformações na superfície dos corpos.
 ANÁLISE DE TENSÕES E DEFORMAÇÕES EXTENSOMETRIA ELÉTRICA-STRAIN GAGES Extensometria é a técnica de medição de deformações na superfície dos corpos. Fonte amplificadora SILVIO TADO ZANETIC 1 EXTENSOMETRIA-VIA
ANÁLISE DE TENSÕES E DEFORMAÇÕES EXTENSOMETRIA ELÉTRICA-STRAIN GAGES Extensometria é a técnica de medição de deformações na superfície dos corpos. Fonte amplificadora SILVIO TADO ZANETIC 1 EXTENSOMETRIA-VIA
Física para Engenharia II - Prova P a (cm/s 2 ) -10
 4320196 Física para Engenharia II - Prova P1-2012 Observações: Preencha todas as folhas com o seu nome, número USP, número da turma e nome do professor. A prova tem duração de 2 horas. Não somos responsáveis
4320196 Física para Engenharia II - Prova P1-2012 Observações: Preencha todas as folhas com o seu nome, número USP, número da turma e nome do professor. A prova tem duração de 2 horas. Não somos responsáveis
Medição de Força e Torque. Capítulo V
 Medição de Força e Torque Capítulo V 1 Métodos Básicos de Medição de Força Contrabalanceando a força gravitacional sobre massas padrões diretamente ou através de sistemas com alavancas. Medindo-se a aceleração
Medição de Força e Torque Capítulo V 1 Métodos Básicos de Medição de Força Contrabalanceando a força gravitacional sobre massas padrões diretamente ou através de sistemas com alavancas. Medindo-se a aceleração
= + Microsensores Piezoresistivos. Material Piezoresistivo. Estrutura Flexível Acoplada. Sensor Piezoresistivo. Acoplada.
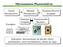 Microsensores Piezoresistivos Sensor Piezoresistivo Material Piezoresistivo + Estrutura Flexível Acoplada Exemplos: Estrutura Acoplada Transformador Mecânico Sensor de Pressão de Membrana Aplicações: microssensores
Microsensores Piezoresistivos Sensor Piezoresistivo Material Piezoresistivo + Estrutura Flexível Acoplada Exemplos: Estrutura Acoplada Transformador Mecânico Sensor de Pressão de Membrana Aplicações: microssensores
DINÂMICA DE ESTRUTURAS (SISTEMAS DE 1 GDL + MÉTODO DE RAYLEIGH)
 DEPARTAMENTO DE ENGENHARIA CIVIL TEORIA DE ESTRUTURAS II 009/010 8º Semestre DINÂMICA DE ESTRUTURAS (SISTEMAS DE 1 GDL + MÉTODO DE RAYLEIGH) Problema 1 Uma mesa pesada é suportada por quatro pernas de
DEPARTAMENTO DE ENGENHARIA CIVIL TEORIA DE ESTRUTURAS II 009/010 8º Semestre DINÂMICA DE ESTRUTURAS (SISTEMAS DE 1 GDL + MÉTODO DE RAYLEIGH) Problema 1 Uma mesa pesada é suportada por quatro pernas de
Ressonador de Helmholtz.
 Ressonador de Helmholtz. Modelo mecânico do ressonador de Helmholtz O ressonador é composto por um volume V, esférico no caso mostrado na figura, e um gargalo de seção reta S e comprimento l. A primeira
Ressonador de Helmholtz. Modelo mecânico do ressonador de Helmholtz O ressonador é composto por um volume V, esférico no caso mostrado na figura, e um gargalo de seção reta S e comprimento l. A primeira
1 ESCOLA POLITÉCNICA DA USP Sensores Eduardo L. L. Cabral ESCOLA POLITÉCNICA DA USP
 [email protected] 1 PMR2560 Robótica Sensores Eduardo L. L. Cabral [email protected] [email protected] 2 Objetivos Sensores utilizados nos robôs industriais. Sensores internos; Sensores externos. Sensores de
[email protected] 1 PMR2560 Robótica Sensores Eduardo L. L. Cabral [email protected] [email protected] 2 Objetivos Sensores utilizados nos robôs industriais. Sensores internos; Sensores externos. Sensores de
FÍSICA MÓDULO 17 OSCILAÇÕES E ONDAS. Professor Sérgio Gouveia
 FÍSICA Professor Sérgio Gouveia MÓDULO 17 OSCILAÇÕES E ONDAS MOVIMENTO HARMÔNICO SIMPLES (MHS) 1. MHS DEFINIÇÃO É o movimento oscilatório e retilíneo, tal que a aceleração é proporcional e de sentido contrário
FÍSICA Professor Sérgio Gouveia MÓDULO 17 OSCILAÇÕES E ONDAS MOVIMENTO HARMÔNICO SIMPLES (MHS) 1. MHS DEFINIÇÃO É o movimento oscilatório e retilíneo, tal que a aceleração é proporcional e de sentido contrário
Sensores Indutivos, Capacitivos e Piezoelétricos. Acelerômetros.
 Sensores Indutivos, Capacitivos e Piezoelétricos. Acelerômetros. Outubro de 21 1 Sensores Indutivos 2 Sensores Capacitivos 3 Sensores Piezoelétricos 4 Acelerômetros Sensores Indutivos I Princípio Físico
Sensores Indutivos, Capacitivos e Piezoelétricos. Acelerômetros. Outubro de 21 1 Sensores Indutivos 2 Sensores Capacitivos 3 Sensores Piezoelétricos 4 Acelerômetros Sensores Indutivos I Princípio Físico
Prof. Dr. Mário Luiz Tronco
 Sensores em Robótica Prof. Dr. Mário Luiz Tronco Mário Prof. Mário Luiz Tronco Luiz Tronco ROBÓTICA Duas Grandes Áreas do Conhecimento: Engenharias Computação Elétrica Mecânica Mecatrônica Mário Luiz Tronco
Sensores em Robótica Prof. Dr. Mário Luiz Tronco Mário Prof. Mário Luiz Tronco Luiz Tronco ROBÓTICA Duas Grandes Áreas do Conhecimento: Engenharias Computação Elétrica Mecânica Mecatrônica Mário Luiz Tronco
Aplicações: Desbalanceamento Rotativo Excitação da Base Isolamento de Vibrações
 1 17 Aplicações: Desbalanceamento Rotativo Excitação da Base Isolamento de Vibrações 1 INTRODUÇÃO A vibração pode ser um fenômeno desejável ou indesejável. Em certos situações, como no caso de britadoras,
1 17 Aplicações: Desbalanceamento Rotativo Excitação da Base Isolamento de Vibrações 1 INTRODUÇÃO A vibração pode ser um fenômeno desejável ou indesejável. Em certos situações, como no caso de britadoras,
Problemas sobre osciladores simples
 Universidade de Coimbra mecânica Clássica II 2009.2010 Problemas sobre osciladores simples 1. Um objecto com 1 kg de massa está suspenso por uma mola e é posto a oscilar. Quando a aceleração do objecto
Universidade de Coimbra mecânica Clássica II 2009.2010 Problemas sobre osciladores simples 1. Um objecto com 1 kg de massa está suspenso por uma mola e é posto a oscilar. Quando a aceleração do objecto
O reômetro capilar Análise Problemas e limitações Correções Outras informações. Reometria Capilar. Grupo de Reologia - GReo
 Reometria Capilar Grupo de Reologia - GReo Departamento de Engenharia Mecânica Pontifícia Universidade Católica - RJ 28 de julho de 2015 Sumário O reômetro capilar descrição exemplo de reômetro comerical
Reometria Capilar Grupo de Reologia - GReo Departamento de Engenharia Mecânica Pontifícia Universidade Católica - RJ 28 de julho de 2015 Sumário O reômetro capilar descrição exemplo de reômetro comerical
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto.
 Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrerem turbulência
Uma oscilação é um movimento repetitivo realizado por um corpo em torno de determinado ponto. Exemplos: pêndulos, ponte ao ser submetida à passagem de um veículo, asas de um avião ao sofrerem turbulência
 γ φ φ φ χ Φ φ φ ρ Q λ ω φ φ φ φ φ φ φ φ φ φ φ φ ( ) χ χ & + = & [ ]{&& } + ([ ] + [ ]){ & } + [ ]{ } = { } [ ] [ ] [ ] {&& } [ ] { } { } {& } γ ψ γ φ γ = ψ + φ = = ψ φ = + + = + + φ = φ
γ φ φ φ χ Φ φ φ ρ Q λ ω φ φ φ φ φ φ φ φ φ φ φ φ ( ) χ χ & + = & [ ]{&& } + ([ ] + [ ]){ & } + [ ]{ } = { } [ ] [ ] [ ] {&& } [ ] { } { } {& } γ ψ γ φ γ = ψ + φ = = ψ φ = + + = + + φ = φ
Física I 2010/2011. Aula 10. Movimento Oscilatório II
 Física I 2010/2011 Aula 10 Movimento Oscilatório II Sumário Capítulo 15: Oscilações 15-3 A Energia no Movimento Harmónico Simples 15-4 Um Oscilador Harmónico Simples Angular 15-5 O Pêndulo simples 15-7
Física I 2010/2011 Aula 10 Movimento Oscilatório II Sumário Capítulo 15: Oscilações 15-3 A Energia no Movimento Harmónico Simples 15-4 Um Oscilador Harmónico Simples Angular 15-5 O Pêndulo simples 15-7
Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia
 Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia Oscilações Movimento Oscilatório Cinemática do Movimento Harmônico Simples (MHS) MHS e Movimento
Universidade Federal de São Paulo Instituto de Ciência e Tecnologia Bacharelado em Ciência e Tecnologia Oscilações Movimento Oscilatório Cinemática do Movimento Harmônico Simples (MHS) MHS e Movimento
Oscilações, Coerência e Ressonância
 , Coerência e Ressonância 1. Por que alguns sistemas físicos oscilam e outros não?. O que caracteriza um sistema oscilatório? 3. Como se mede o período de um pêndulo? parâmetros internos Oscilaç A determinação
, Coerência e Ressonância 1. Por que alguns sistemas físicos oscilam e outros não?. O que caracteriza um sistema oscilatório? 3. Como se mede o período de um pêndulo? parâmetros internos Oscilaç A determinação
Vibrações Aula 01 Conceitos básicos de vibração
 Vibrações Conceitos básicos de vibração Prof. Dr. Thiago Andrade de Toledo https://sites.google.com/site/profthiagotoledo/home [email protected] Vibração A vibração é um movimento oscilatório
Vibrações Conceitos básicos de vibração Prof. Dr. Thiago Andrade de Toledo https://sites.google.com/site/profthiagotoledo/home [email protected] Vibração A vibração é um movimento oscilatório
Aula do cap. 16 MHS e Oscilações
 Aula do cap. 16 MHS e Oscilações Movimento harmônico simples (MHS). Equações do MHS soluções, x(t), v(t) e a(t). Relações entre MHS e movimento circular uniforme. Considerações de energia mecânica no movimento
Aula do cap. 16 MHS e Oscilações Movimento harmônico simples (MHS). Equações do MHS soluções, x(t), v(t) e a(t). Relações entre MHS e movimento circular uniforme. Considerações de energia mecânica no movimento
Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 10
 597 Física II Ondas, Fluidos e Termodinâmica USP Prof. ntônio Roque ula Oscilações acopladas e modos normais Os sistemas naturais não são isolados, mas interagem entre si. Em particular, se dois ou mais
597 Física II Ondas, Fluidos e Termodinâmica USP Prof. ntônio Roque ula Oscilações acopladas e modos normais Os sistemas naturais não são isolados, mas interagem entre si. Em particular, se dois ou mais
Sistemas de Controle (CON) Modelagem de Sistemas de Rotação e Eletromecânicos
 Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Modelagem de Sistemas de Rotação e Eletromecânicos
Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Modelagem de Sistemas de Rotação e Eletromecânicos
CONCEITOS DE VIBRAÇÃO
 CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
Questão 1. Gabarito. Considere P a potência ativa da carga e Q a potência reativa.
 Questão 1 Uma indústria tem uma carga de 1000 kva com fator de potência indutivo de 95% alimentada em 13800 V de acordo com medições efetuadas. A maneira mais fácil de representar a carga da indústria
Questão 1 Uma indústria tem uma carga de 1000 kva com fator de potência indutivo de 95% alimentada em 13800 V de acordo com medições efetuadas. A maneira mais fácil de representar a carga da indústria
Modelos Matematicos de Sistemas
 Modelos Matematicos de Sistemas Introdução; Equações Diferenciais de Sistemas Físicos; Aproximações Lineares de Sistemas Físicos; Transformada de Laplace; Função de Transferência de Sistemas Lineares;
Modelos Matematicos de Sistemas Introdução; Equações Diferenciais de Sistemas Físicos; Aproximações Lineares de Sistemas Físicos; Transformada de Laplace; Função de Transferência de Sistemas Lineares;
VIBRAÇÃO EXCITADA HARMONICAMENTE
 VIBRAÇÃO EXCITADA HARMONICAMENTE Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 6 de abril de 2018 Roteiro 1 2 Ventilador Motor Roteiro 1 2 Introdução x M F (t) Mẍ + cẋ + kx = F (t) Trata-se
VIBRAÇÃO EXCITADA HARMONICAMENTE Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 6 de abril de 2018 Roteiro 1 2 Ventilador Motor Roteiro 1 2 Introdução x M F (t) Mẍ + cẋ + kx = F (t) Trata-se
Capítulo 8 Elementos sensores
 (parte I) Instrumentação eletrônica para sistemas de medição Capítulo 8 Prof. Lélio R. Soares Júnior ENE FT UnB Introdução É o primeiro elemento do sistema de medição Está em contato e absorve energia
(parte I) Instrumentação eletrônica para sistemas de medição Capítulo 8 Prof. Lélio R. Soares Júnior ENE FT UnB Introdução É o primeiro elemento do sistema de medição Está em contato e absorve energia
Aluno Data Curso / Turma Professor
 Apostila Modelagem e Simulação de Sistemas Dinâmicos Aluno Data Curso / Turma Professor 24/10/09 Engenharia Industrial Mecânica / 2006-1 MODELAGEM MATEMÁTICA DE SISTEMAS DINÂMICOS Everton Farina, Eng.º
Apostila Modelagem e Simulação de Sistemas Dinâmicos Aluno Data Curso / Turma Professor 24/10/09 Engenharia Industrial Mecânica / 2006-1 MODELAGEM MATEMÁTICA DE SISTEMAS DINÂMICOS Everton Farina, Eng.º
Pêndulo de Pohl. Observe que as forças podem ser decompostas em componentes radiais e tangenciais, respectivamente:
 Pêndulo de Pohl Ana Caroline Manso de Carvalho - 15/0116683 e João Augusto Sobral da Silva - 15/0131895 IF-UnB/ Laboratório de Oscilações, Ondas e Fluidos - Grupo:G1 (Data: 22 de Março) Objetivos: Estudo
Pêndulo de Pohl Ana Caroline Manso de Carvalho - 15/0116683 e João Augusto Sobral da Silva - 15/0131895 IF-UnB/ Laboratório de Oscilações, Ondas e Fluidos - Grupo:G1 (Data: 22 de Março) Objetivos: Estudo
MOVIMENTO OSCILATÓRIO
 MOVIMENTO OSCILATÓRIO 1.0 Noções da Teoria da Elasticidade A tensão é o quociente da força sobre a área aplicada (N/m²): As tensões normais são tensões cuja força é perpendicular à área. São as tensões
MOVIMENTO OSCILATÓRIO 1.0 Noções da Teoria da Elasticidade A tensão é o quociente da força sobre a área aplicada (N/m²): As tensões normais são tensões cuja força é perpendicular à área. São as tensões
Prof. Dr. Ronaldo Rodrigues Pelá. 12 de março de 2013
 GIROSCÓPIO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 12 de março de 2013 Roteiro 1 2 Roteiro 1 2 Dinâmica F (ext) = M a CM τ (ext) = d L dt L = M r CM v CM + L CM τ (ext) CM = d L
GIROSCÓPIO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 12 de março de 2013 Roteiro 1 2 Roteiro 1 2 Dinâmica F (ext) = M a CM τ (ext) = d L dt L = M r CM v CM + L CM τ (ext) CM = d L
IMPORTANTE PARA O EXAME DE ANALISTA I - * IMPORTANTES PARA OS EXAMES DE ANALISTAS I E II IMPORTANTE PARA O EXAME DE ANALISTA II - #
 FUNDAÇÃO DE PESQUISA E ASSESSORAMENTO À INDÚSTRIA E INSTITUTO DE VIBRAÇÃO MTA. ORIENTAÇÃO PARA ESTUDAR PARA O EXAME DE QUALIFICAÇÃO EM ANÁLISE DE VIBRAÇÕES. ESPECIALISTAS NÍVEIS I E II IMPORTANTE PARA
FUNDAÇÃO DE PESQUISA E ASSESSORAMENTO À INDÚSTRIA E INSTITUTO DE VIBRAÇÃO MTA. ORIENTAÇÃO PARA ESTUDAR PARA O EXAME DE QUALIFICAÇÃO EM ANÁLISE DE VIBRAÇÕES. ESPECIALISTAS NÍVEIS I E II IMPORTANTE PARA
Introdução. Perturbação no primeiro dominó. Perturbação se propaga de um ponto a outro.
 Capitulo 16 Ondas I Introdução Perturbação no primeiro dominó. Perturbação se propaga de um ponto a outro. Ondas ondas é qualquer sinal (perturbação) que se transmite de um ponto a outro de um meio com
Capitulo 16 Ondas I Introdução Perturbação no primeiro dominó. Perturbação se propaga de um ponto a outro. Ondas ondas é qualquer sinal (perturbação) que se transmite de um ponto a outro de um meio com
6 Análise Dinâmica. 6.1 Modelagem computacional
 6 Análise Dinâmica O presente capítulo apresenta um estudo do comportamento dinâmico da coluna de aço estaiada, abrangendo análises modais para determinação da freqüência natural, com e sem protensão [32]
6 Análise Dinâmica O presente capítulo apresenta um estudo do comportamento dinâmico da coluna de aço estaiada, abrangendo análises modais para determinação da freqüência natural, com e sem protensão [32]
Física Geral e Experimental III
 Física Geral e Experimental III Oscilações Nosso mundo está repleto de oscilações, nas quais os objetos se movem repetidamente de um lado para outro. Eis alguns exemplos: - quando um taco rebate uma bola
Física Geral e Experimental III Oscilações Nosso mundo está repleto de oscilações, nas quais os objetos se movem repetidamente de um lado para outro. Eis alguns exemplos: - quando um taco rebate uma bola
Oscilações e ondas. FCM 0410 Física para Engenharia Ambiental. Universidade de São Paulo Instituto de Física de São Carlos - IFSC
 Universidade de São Paulo Instituto de Física de São Carlos - IFSC FCM 0410 Física para Engenharia Ambiental Oscilações e ondas Prof. Dr. José Pedro Donoso Agradescimentos O docente da disciplina, Jose
Universidade de São Paulo Instituto de Física de São Carlos - IFSC FCM 0410 Física para Engenharia Ambiental Oscilações e ondas Prof. Dr. José Pedro Donoso Agradescimentos O docente da disciplina, Jose
Departamento de Engenharia Mecatrônica da Escola Politécnica da USP PMR 2470 Prof. Larissa Driemeier, Marcilio Alves, Rafael T.
 Departamento de Engenharia Mecatrônica da Escola Politécnica da USP PMR 2470 Prof Larissa Driemeier, Marcilio Alves, Rafael T Moura LISTA DE EXERCÍCIOS Sistema de primeira ordem 1 Um termômetro de mercúrio
Departamento de Engenharia Mecatrônica da Escola Politécnica da USP PMR 2470 Prof Larissa Driemeier, Marcilio Alves, Rafael T Moura LISTA DE EXERCÍCIOS Sistema de primeira ordem 1 Um termômetro de mercúrio
Universidade de São Paulo. Instituto de Física. FEP112 - FÍSICA II para o Instituto Oceanográfico 1º Semestre de 2009
 Universidade de São Paulo Instituto de Física FEP11 - FÍSICA II para o Instituto Oceanográfico 1º Semestre de 9 Primeira Lista de Exercícios Oscilações 1) Duas molas idênticas, cada uma de constante, estão
Universidade de São Paulo Instituto de Física FEP11 - FÍSICA II para o Instituto Oceanográfico 1º Semestre de 9 Primeira Lista de Exercícios Oscilações 1) Duas molas idênticas, cada uma de constante, estão
Aula 6- Metod. tradicional de verificação da segurança de estruturas de suporte rígidas. Dimensionamento sísmico.
 Aula 6- Metod. tradicional de verificação da segurança de estruturas de suporte rígidas. Dimensionamento sísmico. Paulo Coelho - FCTUC Mestrado em Engª. Civil - Construções Civis ESTG/IPLeiria Actividade
Aula 6- Metod. tradicional de verificação da segurança de estruturas de suporte rígidas. Dimensionamento sísmico. Paulo Coelho - FCTUC Mestrado em Engª. Civil - Construções Civis ESTG/IPLeiria Actividade
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 016 Respostas esperadas Parte 1 Estas são sugestões de possíveis respostas Outras possibilidades também podem ser consideradas
INSTITUTO SUPERIOR TÉCNICO DEPARTAMENTO DE ENGENHARIA MECÂNICA. Vibrações e Ruído GUIA DE ENSAIOS EXPERIMENTAIS. Prof. Nuno Maia Prof.
 INSTITUTO SUPERIOR TÉCNICO DEPARTAMENTO DE ENGENHARIA MECÂNICA Vibrações e Ruído GUIA DE ENSAIOS EXPERIMENTAIS Prof. Nuno Maia Prof. Relógio Ribeiro IST, 2006-2007 ÍNDICE Trabalho Experimental 1 - VIBRAÇÕES
INSTITUTO SUPERIOR TÉCNICO DEPARTAMENTO DE ENGENHARIA MECÂNICA Vibrações e Ruído GUIA DE ENSAIOS EXPERIMENTAIS Prof. Nuno Maia Prof. Relógio Ribeiro IST, 2006-2007 ÍNDICE Trabalho Experimental 1 - VIBRAÇÕES
Mecânica e Ondas. Ondas estacionárias em cordas vibrantes
 Mecânica e Ondas Ondas estacionárias em cordas vibrantes Objectivo Estudo das ondas estacionárias em cordas vibrantes. Estudo da variação da frequência de ressonância da onda com a tensão e o comprimento
Mecânica e Ondas Ondas estacionárias em cordas vibrantes Objectivo Estudo das ondas estacionárias em cordas vibrantes. Estudo da variação da frequência de ressonância da onda com a tensão e o comprimento
Nota de Aula: Equações Diferenciais Ordinárias de 2 Ordem. ( Aplicações )
 Nota de Aula: Equações Diferenciais Ordinárias de Ordem ( Aplicações ) Vamos nos ater a duas aplicações de grande interesse na engenharia: Sistema massa-mola-amortecedor ( Oscilador Mecânico ) O Sistema
Nota de Aula: Equações Diferenciais Ordinárias de Ordem ( Aplicações ) Vamos nos ater a duas aplicações de grande interesse na engenharia: Sistema massa-mola-amortecedor ( Oscilador Mecânico ) O Sistema
MODELAGEM E DINÂMICA DE UM DISPOSITIVO MICRO-ELETROMECÂNICO (MEMS). MODELING AND DYNAMICS OF MICRO-ELECTROMECHANICAL DEVICE (MEMS).
 MODELAGEM E DINÂMICA DE UM DISPOSITIVO MICRO-ELETROMECÂNICO (MEMS). MODELING AND DYNAMICS OF MICRO-ELECTROMECHANICAL DEVICE (MEMS). Douglas Roca Santo 1, José Manoel Balthazar 2, Bento Rodrigues de Pontes
MODELAGEM E DINÂMICA DE UM DISPOSITIVO MICRO-ELETROMECÂNICO (MEMS). MODELING AND DYNAMICS OF MICRO-ELECTROMECHANICAL DEVICE (MEMS). Douglas Roca Santo 1, José Manoel Balthazar 2, Bento Rodrigues de Pontes
TRANSDUTORES PARA MEDIDA DE DESLOCAMENTOS LINEARES. Notas de aula
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO LEM / PEF TRANSDUTORES PARA MEDIDA DE DESLOCAMENTOS LINEARES Notas de aula Dr. Pedro Afonso de Oliveira Almeida Professor Doutor PEF-EP/USP Notas de aula
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO LEM / PEF TRANSDUTORES PARA MEDIDA DE DESLOCAMENTOS LINEARES Notas de aula Dr. Pedro Afonso de Oliveira Almeida Professor Doutor PEF-EP/USP Notas de aula
MEDIÇÃO DE DEFORMAÇÃO UTILIZANDO-SE EXTENSÔMETROS ELÉTRICOS SOLDADOS ATÉ A TEMPERATURA DE 422ºC
 MEDIÇÃO DE DEFORMAÇÃO UTILIZANDO-SE EXTENSÔMETROS ELÉTRICOS SOLDADOS ATÉ A TEMPERATURA DE 422ºC Paulo de Tarso Vida Gomes Osmar Ribeiro Lourenço Tanius Rodrigues Mansur Comissão Nacional de Energia Nuclear
MEDIÇÃO DE DEFORMAÇÃO UTILIZANDO-SE EXTENSÔMETROS ELÉTRICOS SOLDADOS ATÉ A TEMPERATURA DE 422ºC Paulo de Tarso Vida Gomes Osmar Ribeiro Lourenço Tanius Rodrigues Mansur Comissão Nacional de Energia Nuclear
D. V. Magalhães. Eng. Mecânica EESC - USP
 1. Pressão 2. Fluxo 3. Extensômetros(strain gauges) 2. Acelerômetros Piezoresistivos 3. Acelerômetros de Capacitância Variável 4. Acelerômetros Piezoelétricos Pressão Pressão Pressão Fluxo Taxa de fluxo
1. Pressão 2. Fluxo 3. Extensômetros(strain gauges) 2. Acelerômetros Piezoresistivos 3. Acelerômetros de Capacitância Variável 4. Acelerômetros Piezoelétricos Pressão Pressão Pressão Fluxo Taxa de fluxo
Exp 5 - Pêndulo de torção
 Exp 5 - Pêndulo de torção 1. Objetivos Estudo de um movimento oscilatório de torção, harmônico, sem amortecimento e também com amortecimento subcrítico, de tal forma que sejam observadas oscilações com
Exp 5 - Pêndulo de torção 1. Objetivos Estudo de um movimento oscilatório de torção, harmônico, sem amortecimento e também com amortecimento subcrítico, de tal forma que sejam observadas oscilações com
Física II (Química) FFCLRP USP Prof. Antônio Roque Aula 9
 591036 Física II (Química) FFCLRP USP Prof. Antônio Roque Aula 9 A Equação de Onda em Uma Dimensão Ondas transversais em uma corda esticada Já vimos no estudo sobre oscilações que os físicos gostam de
591036 Física II (Química) FFCLRP USP Prof. Antônio Roque Aula 9 A Equação de Onda em Uma Dimensão Ondas transversais em uma corda esticada Já vimos no estudo sobre oscilações que os físicos gostam de
