INSTRUÇÕES AOS CANDIDATOS
|
|
|
- Jónatas Candal Valverde
- 9 Há anos
- Visualizações:
Transcrição
1 MINITÉRIO D DEFE EXÉRITO RILEIRO DEP - DEP (asa de Thomaz oelho / 1889) ONURO DE DMIÃO O 1 o NO DO ENINO MÉDIO 007/008 0 DE OUTURO DE 007 PROVO DIRETOR DE ENINO OMIÃO DE ORGNIZÇÃO PREIDENTE MEMRO MEMRO INTRUÇÕE O NDIDTO 01. Duração da prova: 0 (duas) horas. 0. O candidato tem 10 (dez) minutos iniciais para tirar dúvidas, somente quanto à impressão. 0. Esta prova é constituída de 01 (um) aderno de Questões e 01 (um) artão de Respostas. 04. No artão de Respostas, ONFIR seu nome, número de inscrição e o ano (série); em seguida, assine-o. 05. Esta prova contém 0 (vinte) itens, distribuídos em 8 (Oito) folhas, incluindo a capa. 06. Marque cada resposta com atenção. Para o correto preenchimento do artão de Respostas, observe o exemplo abaixo. 00. Qual o nome da capital do rasil? () Porto legre omo você sabe, a opção correta é D. Marca-se a resposta da seguinte maneira: () Fortaleza () uiabá 00 D E (D) rasília (E) Manaus 07. s marcações deverão ser feitas, obrigatoriamente, com caneta esferográfica azul ou preta. 08. Não serão consideradas marcações rasuradas. Faça-as como no modelo acima, preenchendo todo o interior do círculo-opção sem ultrapassar os seus limites. 09. O candidato só poderá deixar o local de prova após o decurso de 80 (oitenta) minutos, o que será avisado pelo Fiscal. 10. pós o aviso acima e o término do preenchimento do artão de Respostas, retire-se da sala, entregando o artão de Respostas ao Fiscal. 11. O candidato poderá levar o aderno de Questões. 1. guarde a ordem para iniciar a prova. oa prova!
2 1 o NO (antiga 1 a série) ) O número de divisores positivos de 5 80 que, por sua vez, são divisíveis por 1 é: ) 4 ) 6 ) 48 D) 54 E) 7 ) Do quadrado de cada número natural maior do que subtraímos o sucessor desse número. Desse modo, formamos a seqüência 5, 11, 19,.... O primeiro elemento dessa seqüência que não é um número primo é o: ) Quarto ) exto ) étimo D) Nono E) Décimo ) Dada a função f(x) = ax + bx + c, com a < 0 e c > 0, podemos concluir que o gráfico desta função: ) Não intercepta o eixo dos x ) É tangente ao eixo dos x ) É secante ao eixo dos x e o intercepta em dois pontos, ambos de abscissa negativa D) É secante ao eixo dos x e o intercepta em dois pontos, ambos de abscissa positiva E) É secante ao eixo dos x e o intercepta em dois pontos, um de abscissa positiva e o outro, negativa 4) Na expansão decimal de 9 5 o 007º algarismo depois da vírgula é: ) 0 ) 1 ) D) 5 E) 8
3 1 o NO (antiga 1 a série) ) O conjunto de todos os valores de m para os quais a função f(x) = definida e é não-negativa para todo x real é: 1 ), 1 ), + ) 0, 1 D), 1 E), x x + (m + 1)x + (m + (m + 1)x + (m + ) + 4) está 6) e, ao multiplicarmos o número inteiro e positivo n por outro número inteiro e positivo de algarismos, invertermos a ordem dos algarismos deste segundo número, o resultado fica aumentado de 61. soma dos algarismos que constituem o número n será: ) 10 ) 11 ) 1 D) 1 E) ) e n + = 5, então n ) n + vale: 6 n ) 5 5 ) 18 D) 7 E) 15
4 1 o NO (antiga 1 a série) ) Na fatoração do trinômio a 5 5a + 4a aparecem os seguintes fatores: ) a + e a ) a + e a ) a + 4 e a 1 D) a + 1 e a E) a + e a 1 9) O maior inteiro que não excede a n 10n + 9, para n = , é igual a: ) ) ) D) E) ) endo = o valor de 007 ( + ) é: ) 0 ) 1 ) D) E) 4 x x y + xy = 70 11) O valor da razão na solução do sistema, considerando x < y, é: y (x + y).(x + y ) = 0 ) 0,0 ) 0,5 ) 0,0 D) 0,5 E) 0,40 4
5 1 o NO (antiga 1 a série) ) forma simplificada da expressão ) ) ) D) E) a + b ab c d c + d a b ab a b a + b d + c dc c( a a c ( b c + b d) + a d + b ) + ( abc + abd) + d( a + b ) é: 1) Dado o gráfico da função do º grau abaixo e sabendo que a área do trapézio O é 51 m, então a abscissa do vértice pertence ao intervalo: ) ] 9,5 ; 11,5 [ ) ] 11,5 ; 1,5 [ ) ] 1,5 ; 15,5 [ D) ] 15,5 ; 17,5 [ E) ] 17,5 ; 19,5 [ y 4 6 O 8 x 5
6 1 o NO (antiga 1 a série) ) abendo-se que o polígono DEF é um hexágono regular com lado medindo 8 cm, determine, em cm, a área do triângulo GH. ) 64 ) ) F H D) 1 E D G E) 8 15) Determine a área do triângulo hachurado em função da área do triângulo, sabendo que os pontos assinalados em cada lado dividem esse lado em partes iguais. ) ) 5 7 ) D) E) 15 6
7 1 o NO (antiga 1 a série) ) Em um semicírculo de centro e raio R, inscreve-se um triângulo eqüilátero, como mostra a figura. eja D o ponto onde a bissetriz do ângulo comprimento da corda D é: ˆ intercepta a semicircunferência. O ) R ) R ) R 1 D D) R 1 E) R ) Na figura abaixo, o quadrado D possui área. e F = e E =, a área hachurada mede: E F ) ) ) D) E) G D 7
8 1 o NO (antiga 1 a série) ) e o perímetro de um triângulo inscrito num círculo medir 18k cm e a soma dos senos de seus ângulos internos for igual a k, então, a área do círculo, em cm, é: ) 144 π ) 100 π ) 98 π D) 81 π E) 7 π 19) Na figura abaixo, é um diâmetro do círculo, t é tangente à circunferência em, D = 5 cm e D = 9 cm. onsiderando π =,14; Â = 40º e sen 40º = 0, 6 a medida da área hachurada é uma dízima periódica de período: D ) 4 ) 5 ) 6 D) 7 E) 8 O t 0) medida, em cm, do lado de um pentágono regular cujas diagonais medem ( + 5 ) cm é: ) 6 ) 7 ) 8 D) 9 E) 10 8
INSTRUÇÕES AOS CANDIDATOS
 MINITÉRIO DA DEFEA EXÉRCITO BRAILEIRO DEP - DEPA (Casa de Thomaz Coelho / 1889) CONCURO DE ADMIÃO AO 1 o ANO DO ENINO MÉDIO 008/009 18 DE OUTUBRO DE 008 APROVO DIRETOR DE ENINO COMIÃO DE ORGANIZAÇÃO PREIDENTE
MINITÉRIO DA DEFEA EXÉRCITO BRAILEIRO DEP - DEPA (Casa de Thomaz Coelho / 1889) CONCURO DE ADMIÃO AO 1 o ANO DO ENINO MÉDIO 008/009 18 DE OUTUBRO DE 008 APROVO DIRETOR DE ENINO COMIÃO DE ORGANIZAÇÃO PREIDENTE
00. Qual o nome do vaso sangüíneo que sai do ventrículo direito do coração humano?
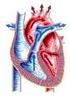 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/889) CONCURSO DE ADMISSÃO À ª SÉRIE DO ENSINO MÉDIO 006/007 DE OUTUBRO DE 006 INSTRUÇÕES AOS CANDIDATOS 0. Duração da prova: 0
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/889) CONCURSO DE ADMISSÃO À ª SÉRIE DO ENSINO MÉDIO 006/007 DE OUTUBRO DE 006 INSTRUÇÕES AOS CANDIDATOS 0. Duração da prova: 0
INSTRUÇÕES AOS CANDIDATOS
 1º ANO 009 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP DEPA (Casa de Thomaz Coelho / 1889) CONCURSO DE ADMISSÃO AO 1º ANO DO ENSINO MÉDIO 009/010 18 de outubro de 009 APROVO DIRETOR DE ENSINO COMISSÃO
1º ANO 009 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP DEPA (Casa de Thomaz Coelho / 1889) CONCURSO DE ADMISSÃO AO 1º ANO DO ENSINO MÉDIO 009/010 18 de outubro de 009 APROVO DIRETOR DE ENSINO COMISSÃO
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO D E C E x - D E P A COLÉGIO MILITAR DE MANAUS. Manaus-AM, 17 de outubro de 2010
 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO D E C E x - D E P A COLÉGIO MILITAR DE MANAUS Manaus-AM, 17 de outubro de 010 CONCURSO DE ADMISSÃO 010/011 MATEMÁTICA PREENCHIDO PELO CANDIDATO Nº de inscrição
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO D E C E x - D E P A COLÉGIO MILITAR DE MANAUS Manaus-AM, 17 de outubro de 010 CONCURSO DE ADMISSÃO 010/011 MATEMÁTICA PREENCHIDO PELO CANDIDATO Nº de inscrição
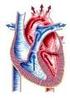
00. Qual o nome do vaso sangüíneo que sai do ventrículo direito do coração humano? (A) Veia pulmonar direita
 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/1889) CONCURSO DE ADMISSÃO À 1ª SÉRIE DO ENSINO MÉDIO 004005 DE OUTUBRO DE 004 INSTRUÇÕES AOS CANDIDATOS 01. Duração da prova:
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/1889) CONCURSO DE ADMISSÃO À 1ª SÉRIE DO ENSINO MÉDIO 004005 DE OUTUBRO DE 004 INSTRUÇÕES AOS CANDIDATOS 01. Duração da prova:
GEOMETRIA PLANA. 1) (UFRGS) Na figura abaixo, o vértice A do retângulo OABC está a 6 cm do vértice C. O raio do círculo mede
 GEOMETRI PLN 1) (UFRGS) Na figura abaixo, o vértice do retângulo O está a 6 cm do vértice. O raio do círculo mede O (a) 5 cm (b) 6 cm (c) 8 cm (d) 9 cm (e) 10 cm ) (UFRGS) Na figura abaixo, é o centro
GEOMETRI PLN 1) (UFRGS) Na figura abaixo, o vértice do retângulo O está a 6 cm do vértice. O raio do círculo mede O (a) 5 cm (b) 6 cm (c) 8 cm (d) 9 cm (e) 10 cm ) (UFRGS) Na figura abaixo, é o centro
CONCURSO DE ADMISSÃO 2003 / 2004 PROVA DE MATEMÁTICA 1ª SÉRIE DO ENSINO MÉDIO IDENTIFICAÇÃO NÚMERO DE INSCRIÇÃO: NOME COMPLETO :
 COLÉGIO MILITAR DE ELO HORIZONTE ELO HORIZONTE MG DE OUTURO DE 00 DURAÇÃO: 0 MINUTOS CONCURSO DE ADMISSÃO 00 / 00 PROVA DE MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO IDENTIFICAÇÃO NÚMERO DE INSCRIÇÃO: NOME COMPLETO
COLÉGIO MILITAR DE ELO HORIZONTE ELO HORIZONTE MG DE OUTURO DE 00 DURAÇÃO: 0 MINUTOS CONCURSO DE ADMISSÃO 00 / 00 PROVA DE MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO IDENTIFICAÇÃO NÚMERO DE INSCRIÇÃO: NOME COMPLETO
Circunferência. MA092 Geometria plana e analítica. Interior e exterior. Circunferência e círculo. Francisco A. M. Gomes
 Circunferência MA092 Geometria plana e analítica Francisco A. M. Gomes UNICAMP - IMECC Setembro de 2016 A circunferência é o conjunto dos pontos de um plano que estão a uma mesma distância (denominada
Circunferência MA092 Geometria plana e analítica Francisco A. M. Gomes UNICAMP - IMECC Setembro de 2016 A circunferência é o conjunto dos pontos de um plano que estão a uma mesma distância (denominada
INSTRUÇÕES PARA REALIZAÇÃO DA PROVA
 PROVA MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DECEx - DEPA (Casa de Thomaz Coelho/1889) CONCURSO DE ADMISSÃO AO 1º ANO DO ENSINO MÉDIO 2012/2013 11 DE NOVEMBRO DE 2012 INSTRUÇÕES PARA REALIZAÇÃO DA PROVA
PROVA MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DECEx - DEPA (Casa de Thomaz Coelho/1889) CONCURSO DE ADMISSÃO AO 1º ANO DO ENSINO MÉDIO 2012/2013 11 DE NOVEMBRO DE 2012 INSTRUÇÕES PARA REALIZAÇÃO DA PROVA
a) 64. b) 32. c) 16. d) 8. e) 4.
 GEOMETRIA PLANA 1 1) (UFRGS) Observe com atenção o retângulo ABCD, na figura abaixo. Considerando as relações existentes entre as sua dimensões e a diagonal, a área desse retângulo será igual a ) (UFRGS)
GEOMETRIA PLANA 1 1) (UFRGS) Observe com atenção o retângulo ABCD, na figura abaixo. Considerando as relações existentes entre as sua dimensões e a diagonal, a área desse retângulo será igual a ) (UFRGS)
00. Qual o nome do vaso sangüíneo que sai do ventrículo direito do coração humano? (A) Veia pulmonar direita
 MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/1889) CONCURSO DE ADMISSÃO À 1ª SÉRIE DO ENSINO MÉDIO 005/006 DE OUTUBRO DE 005 INSTRUÇÕES AOS CANDIDATOS 01. Duração da prova:
MINISTÉRIO DA DEFESA EXÉRCITO BRASILEIRO DEP - DEPA (Casa de Thomaz Coelho/1889) CONCURSO DE ADMISSÃO À 1ª SÉRIE DO ENSINO MÉDIO 005/006 DE OUTUBRO DE 005 INSTRUÇÕES AOS CANDIDATOS 01. Duração da prova:
CONCURSO PÚBLICO DE PROVAS E TÍTULOS EDITAL ESPECÍFICO 92/ CAMPUS FORMIGA PROVA OBJETIVA - PROFESSOR EBTT ÁREA DE MATEMÁTICA EDUCAÇÃO MATEMÁTICA
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE MINAS GERAIS CAMPUS FORMIGA Rua São Luiz Gonzaga, s/n Bairro São Luiz Formiga
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE MINAS GERAIS CAMPUS FORMIGA Rua São Luiz Gonzaga, s/n Bairro São Luiz Formiga
( Marque com um X, a única alternativa certa )
 (PROVA DE MATEMÁTICA DO CONCURSO DE ADMISSÃO À 1ª SÉRIE CMB ANO 004/0) MÚLTIPLA-ESCOLHA ( Marque com um X, a única alternativa certa ) QUESTÃO 01. Na figura abaixo, o círculo tem centro O, OT = 6 unidades
(PROVA DE MATEMÁTICA DO CONCURSO DE ADMISSÃO À 1ª SÉRIE CMB ANO 004/0) MÚLTIPLA-ESCOLHA ( Marque com um X, a única alternativa certa ) QUESTÃO 01. Na figura abaixo, o círculo tem centro O, OT = 6 unidades
GGM Geometria Básica - UFF Lista 4 Profa. Lhaylla Crissaff. 1. Encontre a área de um losango qualquer em função de suas diagonais. = k 2.
 1. Encontre a área de um losango qualquer em função de suas diagonais. 2. Se dois triângulos ABC e DEF são semelhantes com razão de semelhança k, mostre que A ABC A DEF = k 2. 3. Na figura 1, ABCD e EF
1. Encontre a área de um losango qualquer em função de suas diagonais. 2. Se dois triângulos ABC e DEF são semelhantes com razão de semelhança k, mostre que A ABC A DEF = k 2. 3. Na figura 1, ABCD e EF
Exercícios Propostos. Exercício 1: Cinco retas distintas em um plano cortam-se em n pontos. Determine o maior valor que n pode assumir.
 Exercícios Propostos Exercício 1: Cinco retas distintas em um plano cortam-se em n pontos. Determine o maior valor que n pode assumir. Exercício 2: As bissetrizes de dois ângulos adjacentes AÔB e BÔC são,
Exercícios Propostos Exercício 1: Cinco retas distintas em um plano cortam-se em n pontos. Determine o maior valor que n pode assumir. Exercício 2: As bissetrizes de dois ângulos adjacentes AÔB e BÔC são,
COLÉGIO SHALOM Ensino Fundamental 8 Ano Prof.º: Wesley Disciplina Geometria Aluno (a):. No.
 COLÉGIO SHALOM Ensino Fundamental 8 Ano Prof.º: Wesley Disciplina Geometria Aluno (a):. No. Trabalho de Recuperação Data: / 12/2016 Valor: Orientações: -Responder manuscrito; -Cópias de colegas, entrega
COLÉGIO SHALOM Ensino Fundamental 8 Ano Prof.º: Wesley Disciplina Geometria Aluno (a):. No. Trabalho de Recuperação Data: / 12/2016 Valor: Orientações: -Responder manuscrito; -Cópias de colegas, entrega
Exercícios Obrigatórios
 Exercícios Obrigatórios 1) (UFRGS) Na figura 1, BC é paralelo a DE e, na figura 2, GH é paralelo a IJ. x E y J a C H a (a) ab e a/b (b) ab e b/a (c) a/b e ab (d) b/a e ab (e) a/b e 1/b Então x e y valem,
Exercícios Obrigatórios 1) (UFRGS) Na figura 1, BC é paralelo a DE e, na figura 2, GH é paralelo a IJ. x E y J a C H a (a) ab e a/b (b) ab e b/a (c) a/b e ab (d) b/a e ab (e) a/b e 1/b Então x e y valem,
02 Do ponto P exterior a uma circunferência tiramos uma secante que corta a
 01 Em um triângulo AB AC 5 cm e BC cm. Tomando-se sobre AB e AC os pontos D e E, respectivamente, de maneira que DE seja paralela a BC e que o quadrilátero BCED seja circunscritível a um círculo, a distância
01 Em um triângulo AB AC 5 cm e BC cm. Tomando-se sobre AB e AC os pontos D e E, respectivamente, de maneira que DE seja paralela a BC e que o quadrilátero BCED seja circunscritível a um círculo, a distância
Polígonos PROFESSOR RANILDO LOPES 11.1
 Polígonos PROFESSOR RANILDO LOPES 11.1 Polígonos Polígono é uma figura geométrica plana e fechada formada apenas por segmentos de reta que não se cruzam no mesmo plano. Exemplos 11.1 Elementos de um polígono
Polígonos PROFESSOR RANILDO LOPES 11.1 Polígonos Polígono é uma figura geométrica plana e fechada formada apenas por segmentos de reta que não se cruzam no mesmo plano. Exemplos 11.1 Elementos de um polígono
Caderno 1: (É permitido o uso de calculadora.) Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado.
 Proposta de Resolução [dezembro - 017] Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul
Proposta de Resolução [dezembro - 017] Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul
INSTRUÇÕES. Esta prova é individual e sem consulta à qualquer material.
 OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
p q ~p ~q p q p ~ q p q ~ p q ~ p ~q F F V V F V V V F
 PROVA DE MATEMÁTICA ª ÉRIE E.M. _COLÉGIO ANCHIETA BA Elaboração: PROF. OCTAMAR MARQQUE. Resolução e comentários: PROFA. MARIA ANTÔNIA CONCEIÇÃO GOUVEIA. 01. upondo a, b, c, d R, qual das proposições a
PROVA DE MATEMÁTICA ª ÉRIE E.M. _COLÉGIO ANCHIETA BA Elaboração: PROF. OCTAMAR MARQQUE. Resolução e comentários: PROFA. MARIA ANTÔNIA CONCEIÇÃO GOUVEIA. 01. upondo a, b, c, d R, qual das proposições a
Professor Alexandre Assis. Lista de exercícios de Geometria
 1. A figura representa três círculos idênticos no interior do triângulo retângulo isósceles ABC. 3. Observando a figura a seguir, determine (em cm): a) o valor de x. b) a medida do segmento AN, sabendo
1. A figura representa três círculos idênticos no interior do triângulo retângulo isósceles ABC. 3. Observando a figura a seguir, determine (em cm): a) o valor de x. b) a medida do segmento AN, sabendo
CIRCUNFERÊNCIA E CÍRCULO
 IRUNFRÊNI ÍRUL 01 ( FUVST) medida do ângulo ˆ inscrito na circunferência de centro é, em graus, ) 100 ) 110 ) 10 ) 15 35º 0 0 ( U ) bserve a figura. la mostra dois círculos de mesmo raio com centros em
IRUNFRÊNI ÍRUL 01 ( FUVST) medida do ângulo ˆ inscrito na circunferência de centro é, em graus, ) 100 ) 110 ) 10 ) 15 35º 0 0 ( U ) bserve a figura. la mostra dois círculos de mesmo raio com centros em
PROFESSOR FLABER 2ª SÉRIE Circunferência
 PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
PROFESSOR FLABER ª SÉRIE Circunferência 01. (Fuvest SP) A reta s passa pelo ponto (0,3) e é perpendicular à reta AB onde A=(0,0) e B é o centro da circunferência x + y - x - 4y = 0. Então a equação de
13. (Uerj) Em cada ponto (x, y) do plano cartesiano, o valor de T é definido pela seguinte equação:
 1. (Ufc) Considere o triângulo cujos vértices são os pontos A(2,0); B(0,4) e C(2Ë5, 4+Ë5). Determine o valor numérico da altura relativa ao lado AB, deste triângulo. 2. (Unesp) A reta r é perpendicular
1. (Ufc) Considere o triângulo cujos vértices são os pontos A(2,0); B(0,4) e C(2Ë5, 4+Ë5). Determine o valor numérico da altura relativa ao lado AB, deste triângulo. 2. (Unesp) A reta r é perpendicular
ASSUNTO: ÂNGULOS e TRIÂNGULOS. 2) A soma de dois ângulos é 140º e um deles vale 1/3 do suplemento do outro. Determine esses ângulos.
 ASSUNTO: ÂNGULOS e TRIÂNGULOS 1) Determine: a) O complemento de 47º Resp: 43º b) O suplemento de 12º Resp: 168º c) O replemento de 3º Resp: 357º 2) A soma de dois ângulos é 140º e um deles vale 1/3 do
ASSUNTO: ÂNGULOS e TRIÂNGULOS 1) Determine: a) O complemento de 47º Resp: 43º b) O suplemento de 12º Resp: 168º c) O replemento de 3º Resp: 357º 2) A soma de dois ângulos é 140º e um deles vale 1/3 do
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
02 O resto da divisão por 11 do resultado da expressão
 0 Num colégio verificou-se que 0não alunos têm pai e mãe professores. Qual o número de alunos do colégio, sabendo-se que 55 alunos possuem pelo menos um dos pais professor e que não eistem alunos irmão?
0 Num colégio verificou-se que 0não alunos têm pai e mãe professores. Qual o número de alunos do colégio, sabendo-se que 55 alunos possuem pelo menos um dos pais professor e que não eistem alunos irmão?
PREPARATÓRIO PROFMAT/ AULA 8 Geometria
 PREPARATÓRIO PROFMAT/ AULA 8 Geometria QUESTÕES DISCURSIVAS Questão 1. (PROFMAT-2012) As figuras a seguir mostram duas circunferências distintas, com centros C 1 e C 2 que se intersectam nos pontos A e
PREPARATÓRIO PROFMAT/ AULA 8 Geometria QUESTÕES DISCURSIVAS Questão 1. (PROFMAT-2012) As figuras a seguir mostram duas circunferências distintas, com centros C 1 e C 2 que se intersectam nos pontos A e
UNIVERSIDADE FEDERAL FLUMINENSE
 UNIVERSIDADE FEDERAL FLUMINENSE REINGRESSO E MUDANÇA DE CURSO 016 MATEMÁTICA CADERNO DE QUESTÕES INSTRUÇÕES AO CANDIDATO Você deverá ter recebido o Caderno com a Proposta de Redação, a Folha de Redação,
UNIVERSIDADE FEDERAL FLUMINENSE REINGRESSO E MUDANÇA DE CURSO 016 MATEMÁTICA CADERNO DE QUESTÕES INSTRUÇÕES AO CANDIDATO Você deverá ter recebido o Caderno com a Proposta de Redação, a Folha de Redação,
NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.
![NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo. NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.](/thumbs/74/70891793.jpg) R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 99 / 00 PROVA DE CIÊNCIAS EXATAS DA. 1 a é equivalente a a
 13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
rapazes presentes. Achar a porcentagem das moças que estudam nessa Universidade, em relação ao efetivo da Universidade.
 01 Marcar a frase certa: (A) Todo número terminado em 0 é divisível por e por 5. (B) Todo número cuja soma de seus algarismos é 4 ou múltiplo de 4, é divisível por 4 (C) O produto de dois números é igual
01 Marcar a frase certa: (A) Todo número terminado em 0 é divisível por e por 5. (B) Todo número cuja soma de seus algarismos é 4 ou múltiplo de 4, é divisível por 4 (C) O produto de dois números é igual
Grupo de exercícios I.2 - Geometria plana- Professor Xanchão
 Grupo de exercícios I - Geometria plana- Professor Xanchão 1 (G1 - utfpr 013) Um triângulo isósceles tem dois lados congruentes (de medidas iguais) e o outro lado é chamado de base Se em um triângulo isósceles
Grupo de exercícios I - Geometria plana- Professor Xanchão 1 (G1 - utfpr 013) Um triângulo isósceles tem dois lados congruentes (de medidas iguais) e o outro lado é chamado de base Se em um triângulo isósceles
LISTA DE EXERCÍCIOS DE REVISÃO DE MATEMÁTICA 2º ANO PROF.: ARI
 01.: (FATEC) Um terreno retangular tem 170 m de perímetro. e a razão entre as medidas dos lados é 0,7, então a área desse terreno, em metros quadrados, é igual a: a) 7000 b) 5670 c) 4480 d) 1750 e) 1120
01.: (FATEC) Um terreno retangular tem 170 m de perímetro. e a razão entre as medidas dos lados é 0,7, então a área desse terreno, em metros quadrados, é igual a: a) 7000 b) 5670 c) 4480 d) 1750 e) 1120
CRONOGRAMA DE RECUPERAÇÃO ATIVIDADE DE RECUPERAÇÃO
 CRONOGRAMA DE RECUPERAÇÃO SÉRIE: 1ª série do EM DISCIPLINA: MATEMÁTICA 2 Cadernos Assuntos 3 e 4 Áreas e perímetros de figuras planas Lei dos senos e cossenos Trigonometria no triângulo retângulo Teorema
CRONOGRAMA DE RECUPERAÇÃO SÉRIE: 1ª série do EM DISCIPLINA: MATEMÁTICA 2 Cadernos Assuntos 3 e 4 Áreas e perímetros de figuras planas Lei dos senos e cossenos Trigonometria no triângulo retângulo Teorema
Projeto Jovem Nota 10 Áreas de Figuras Planas Lista 6 Professor Marco Costa
 1 Projeto Jovem Nota 10 1. (Fgv 97) No plano cartesiano, os vértices de um triângulo são A (5,2), B (1,3) e C (8,-4). a) Obtenha a medida da altura do triângulo, que passa por A. b) Calcule a área do triângulo
1 Projeto Jovem Nota 10 1. (Fgv 97) No plano cartesiano, os vértices de um triângulo são A (5,2), B (1,3) e C (8,-4). a) Obtenha a medida da altura do triângulo, que passa por A. b) Calcule a área do triângulo
Colégio Santa Dorotéia
 olégio Santa Dorotéia Área de Matemática Disciplina: Matemática no: 9º Ensino Fundamental Professores: Elias e Elvira Matemática tividades para Estudos utônomos Data: / 1 / 01 ORIENTÇÕES PR REUPERÇÃO FINL
olégio Santa Dorotéia Área de Matemática Disciplina: Matemática no: 9º Ensino Fundamental Professores: Elias e Elvira Matemática tividades para Estudos utônomos Data: / 1 / 01 ORIENTÇÕES PR REUPERÇÃO FINL
Matemática FUVEST. Matemática 001/001 FUVEST 2008 FUVEST 2008 Q.01. Leia atentamente as instruções abaixo Q.02
 / FUVEST 8 ª Fase Matemática (//8) Matemática LOTE SEQ. BOX / Matemática FUVEST FUNDAÇÃO UNIVERSITÁRIA PARA O VESTIBULAR Leia atentamente as instruções abaixo. Aguarde a autorização do fiscal para abrir
/ FUVEST 8 ª Fase Matemática (//8) Matemática LOTE SEQ. BOX / Matemática FUVEST FUNDAÇÃO UNIVERSITÁRIA PARA O VESTIBULAR Leia atentamente as instruções abaixo. Aguarde a autorização do fiscal para abrir
MATEMÁTICA II LISTA DE GEOMETRIA PLANA - III
 MATEMÁTICA II LISTA DE GEOMETRIA PLANA - III 0 Dois círculos de centros A e B são tangentes exteriormente e tangenciam interiormente um círculo de centro C. Se AB = cm, AC = 7 cm e BC = 3 cm, então o raio
MATEMÁTICA II LISTA DE GEOMETRIA PLANA - III 0 Dois círculos de centros A e B são tangentes exteriormente e tangenciam interiormente um círculo de centro C. Se AB = cm, AC = 7 cm e BC = 3 cm, então o raio
(PROVA DE MATEMÁTICA DO CONCURSO DE ADMISSÃO AO 1º ANO CMB 2010 / 11) MÚLTIPLA-ESCOLHA. (Marque com um X a única alternativa certa)
 (PROVA DE MATEMÁTICA DO CONCURSO DE ADMISSÃO AO 1º ANO CMB 010 / 11) MÚLTIPLA-ESCOLHA (Marque com um X a única alternativa certa) QUESTÃO 01. Uma empresa oferece serviços de acesso a internet cobrando
(PROVA DE MATEMÁTICA DO CONCURSO DE ADMISSÃO AO 1º ANO CMB 010 / 11) MÚLTIPLA-ESCOLHA (Marque com um X a única alternativa certa) QUESTÃO 01. Uma empresa oferece serviços de acesso a internet cobrando
Treino Matemático. 1. Em qual das figuras podes observar um polígono inscrito numa circunferência? (A) (B) (C) (D)
 Treino Matemático ssunto: ircunferência e círculo. 6º ano Ficha de trabalho 1. Em qual das figuras podes observar um polígono inscrito numa circunferência? () () () (). Na figura sabe-se a reta é tangente
Treino Matemático ssunto: ircunferência e círculo. 6º ano Ficha de trabalho 1. Em qual das figuras podes observar um polígono inscrito numa circunferência? () () () (). Na figura sabe-se a reta é tangente
Lista 3. Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 2.5, pág. 81 em diante.
 MA13 Exercícios das Unidades 4 e 5 2014 Lista 3 Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 2.5, pág. 81 em diante. 1) Seja ABCD um quadrilátero qualquer. Prove que os pontos médios
MA13 Exercícios das Unidades 4 e 5 2014 Lista 3 Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 2.5, pág. 81 em diante. 1) Seja ABCD um quadrilátero qualquer. Prove que os pontos médios
Projeto Jovem Nota 10 Áreas de Figuras Planas Lista 2 Professor Marco Costa
 1 Projeto Jovem Nota 10 1. (Unifesp 2004) As figuras A e B representam dois retângulos de perímetros iguais a 100 cm, porém de áreas diferentes, iguais a 400 cm e 600 cm, respectivamente. A figura C exibe
1 Projeto Jovem Nota 10 1. (Unifesp 2004) As figuras A e B representam dois retângulos de perímetros iguais a 100 cm, porém de áreas diferentes, iguais a 400 cm e 600 cm, respectivamente. A figura C exibe
2º trimestre Lista de exercícios Ensino Médio 2º ano classe: Prof. Maurício Nome: nº
 º trimestre Lista de exercícios Ensino Médio º ano classe: Prof. Maurício Nome: nº --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
º trimestre Lista de exercícios Ensino Médio º ano classe: Prof. Maurício Nome: nº --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
INSTRUÇÕES CANDIDATO, LEIA COM ATENÇÃO!
 MINISTÉRIO DA DEFESA Manaus, AM, 11 de novembro de 01 EXÉRCITO BRASILEIRO CONCURSO DE ADMISSÃO 01/013 D E C Ex D E P A COLÉGIO MILITAR DE MANAUS MATEMÁTICA 1º Ano Ensino Médio INSTRUÇÕES CANDIDATO, LEIA
MINISTÉRIO DA DEFESA Manaus, AM, 11 de novembro de 01 EXÉRCITO BRASILEIRO CONCURSO DE ADMISSÃO 01/013 D E C Ex D E P A COLÉGIO MILITAR DE MANAUS MATEMÁTICA 1º Ano Ensino Médio INSTRUÇÕES CANDIDATO, LEIA
30's Volume 9 Matemática
 30's Volume 9 Matemática www.cursomentor.com 20 de janeiro de 201 Q1. Uma pessoa adulta possui aproximadamente litros de sangue. Em uma pessoa saudável, 1 mm 3 de sangue possui, aproximadamente: milhões
30's Volume 9 Matemática www.cursomentor.com 20 de janeiro de 201 Q1. Uma pessoa adulta possui aproximadamente litros de sangue. Em uma pessoa saudável, 1 mm 3 de sangue possui, aproximadamente: milhões
TPC PÁSCOA. A função g é de proporcionalidade inversa e o ponto Os segmentos de reta OD e AB e EF. são paralelos;
 EXTERNATO JOÃO ALBERTO FARIA ARRUDA DOS VINHOS TPC PÁSCOA Ano letivo 014 / 15 1. No referencial da figura está representado um quadrilátero e um triângulo retângulo em F. A figura não está desenhada à
EXTERNATO JOÃO ALBERTO FARIA ARRUDA DOS VINHOS TPC PÁSCOA Ano letivo 014 / 15 1. No referencial da figura está representado um quadrilátero e um triângulo retângulo em F. A figura não está desenhada à
Lista de Exercícios 1 - Caio Milani e Gabriel Mendes (1º Ano)
 Lista de Exercícios 1 - Caio Milani e Gabriel Mendes (1º Ano) Polígonos 1. Calcule o número de diagonais de um icoságono (20 lados). 2. Determine o polígono cujo número de diagonais é o triplo do número
Lista de Exercícios 1 - Caio Milani e Gabriel Mendes (1º Ano) Polígonos 1. Calcule o número de diagonais de um icoságono (20 lados). 2. Determine o polígono cujo número de diagonais é o triplo do número
MATEMÁTICA - 3o ciclo Circunferência - ângulos e arcos (9 o ano)
 MTMÁTI - 3o ciclo ircunferência - ângulos e arcos (9 o ano) xercícios de provas nacionais e testes intermédios 1. Na figura ao lado, estão representados a circunferência de centro no ponto e diâmetro []
MTMÁTI - 3o ciclo ircunferência - ângulos e arcos (9 o ano) xercícios de provas nacionais e testes intermédios 1. Na figura ao lado, estão representados a circunferência de centro no ponto e diâmetro []
Datas de Avaliações 2016
 ROTEIRO DE ESTUDOS MATEMÁTICA (6ºB, 7ºA, 8ºA e 9ºA) SÉRIE 6º ANO B Conteúdo - Sucessor e Antecessor; - Representação de Conjuntos e as relações entre eles: pertinência e inclusão ( ). - Estudo da Geometria:
ROTEIRO DE ESTUDOS MATEMÁTICA (6ºB, 7ºA, 8ºA e 9ºA) SÉRIE 6º ANO B Conteúdo - Sucessor e Antecessor; - Representação de Conjuntos e as relações entre eles: pertinência e inclusão ( ). - Estudo da Geometria:
REVISÃO UNIOESTE 2016 MATEMÁTICA GUSTAVO
 REVISÃO UNIOESTE 01 MATEMÁTICA GUSTAVO 1 Considere a figura: Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas quadradas de metros de lado, conforme a figura
REVISÃO UNIOESTE 01 MATEMÁTICA GUSTAVO 1 Considere a figura: Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas quadradas de metros de lado, conforme a figura
POLÍGONOS REGULARES. Segmento: ENSINO MÉDIO. Tipo de Atividade: LISTA DE EXERCÍCIOS. 06/2017 Turma: 2 A
 Segmento: ENSINO MÉDIO Disciplina: GEOMETRIA Tipo de Atividade: LISTA DE EXERCÍCIOS Prof. Marcelo 06/017 Turma: A POLÍGONOS REGULARES 1) Considere um quadrado com 3 cm de lado, inscrito em um círculo.
Segmento: ENSINO MÉDIO Disciplina: GEOMETRIA Tipo de Atividade: LISTA DE EXERCÍCIOS Prof. Marcelo 06/017 Turma: A POLÍGONOS REGULARES 1) Considere um quadrado com 3 cm de lado, inscrito em um círculo.
Plano de Recuperação Final EF2
 Professores: Tammy, Sandra, Rafael, Bill, M Laendle, Pupo, Figo Ano: 9 ano Objetivo: Proporcionar ao aluno a oportunidade de resgatar os conteúdos trabalhados durante o ano nos quais apresentou defasagens
Professores: Tammy, Sandra, Rafael, Bill, M Laendle, Pupo, Figo Ano: 9 ano Objetivo: Proporcionar ao aluno a oportunidade de resgatar os conteúdos trabalhados durante o ano nos quais apresentou defasagens
Assinale as proposições verdadeiras some os resultados e marque na Folha de Respostas.
 PROVA DE MATEMÁTICA a AVALIAÇÃO UNIDADE 8 a SÉRIE E M _ COLÉGIO ANCHIETA-A ELAORAÇÃO DA PROVA: PROF OCTAMAR MARQUES PROFA MARIA ANTÔNIA CONCEIÇÃO GOUVEIA QUESTÕES DE A 8 Assinale as proposições verdadeiras
PROVA DE MATEMÁTICA a AVALIAÇÃO UNIDADE 8 a SÉRIE E M _ COLÉGIO ANCHIETA-A ELAORAÇÃO DA PROVA: PROF OCTAMAR MARQUES PROFA MARIA ANTÔNIA CONCEIÇÃO GOUVEIA QUESTÕES DE A 8 Assinale as proposições verdadeiras
04) 4 05) 2. ˆ B determinam o arco, portanto são congruentes, 200π 04)
 RESOLUÇÃO DA PROVA FINAL DE MATEMÁTICA - ANO 007 a SÉRIE DO E.M. _ COLÉGIO ANCHIETA BA ELABORAÇÃO: PROF. OCTAMAR MARQUES. PROFA. MARIA ANTÔNIA GOUVEIA. QUESTÃO 0) Na figura, o raio do círculo é igual a
RESOLUÇÃO DA PROVA FINAL DE MATEMÁTICA - ANO 007 a SÉRIE DO E.M. _ COLÉGIO ANCHIETA BA ELABORAÇÃO: PROF. OCTAMAR MARQUES. PROFA. MARIA ANTÔNIA GOUVEIA. QUESTÃO 0) Na figura, o raio do círculo é igual a
30's Volume 15 Matemática
 30's Volume 1 Matemática www.cursomentor.com 9 de junho de 014 Q1. Considere os segmentos AB = x, BC =, CD = x + 1 e DE = x 18 e que AB = CD. Encontre x. BC DE Q. Em um triângulo ABC, AM é bissetriz interna
30's Volume 1 Matemática www.cursomentor.com 9 de junho de 014 Q1. Considere os segmentos AB = x, BC =, CD = x + 1 e DE = x 18 e que AB = CD. Encontre x. BC DE Q. Em um triângulo ABC, AM é bissetriz interna
 Geometria Plana 1 (UEM-2013) Em um dia, em uma determinada região plana, o Sol nasce às 7 horas e se põe às 19 horas. Um observador, nessa região, deseja comparar a altura de determinados objetos com o
Geometria Plana 1 (UEM-2013) Em um dia, em uma determinada região plana, o Sol nasce às 7 horas e se põe às 19 horas. Um observador, nessa região, deseja comparar a altura de determinados objetos com o
UPE/VESTIBULAR/2002 MATEMÁTICA
 UPE/VESTIBULAR/00 MATEMÁTICA 01 Os amigos Neto, Maria Eduarda, Daniela e Marcela receberam um prêmio de R$ 1000,00, que deve ser dividido, entre eles, em partes inversamente proporcionais às respectivas
UPE/VESTIBULAR/00 MATEMÁTICA 01 Os amigos Neto, Maria Eduarda, Daniela e Marcela receberam um prêmio de R$ 1000,00, que deve ser dividido, entre eles, em partes inversamente proporcionais às respectivas
QUESTÕES OBJETIVAS. 1. Encontre uma fração equivalente a 9/5 cuja soma dos termos é igual a 196:
 QUESTÕES OBJETIVAS 1. Encontre uma fração equivalente a 9/5 cuja soma dos termos é igual a 196: (A) 96/100 (B) 106/90 (C) 116/80 (D) 16/70 (E) 136/60. Um grupo de 6 pessoas é formado por André, Bento,
QUESTÕES OBJETIVAS 1. Encontre uma fração equivalente a 9/5 cuja soma dos termos é igual a 196: (A) 96/100 (B) 106/90 (C) 116/80 (D) 16/70 (E) 136/60. Um grupo de 6 pessoas é formado por André, Bento,
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 97 / a QUESTÃO MÚLTIPLA ESCOLHA
 11 1 a QUESTÃO MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES ABAIXO. 0 Item 01. O valor de 45 é a. ( ) 1 b. ( 1 ) c. ( ) 5 d. ( 1 ) 5 e. ( ) Item 0. Num Colégio, existem
11 1 a QUESTÃO MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES ABAIXO. 0 Item 01. O valor de 45 é a. ( ) 1 b. ( 1 ) c. ( ) 5 d. ( 1 ) 5 e. ( ) Item 0. Num Colégio, existem
As cotações dos itens de cada caderno encontram-se no final do respetivo caderno.
 Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno 2). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno 2). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Entrelinha 1,5. Utiliza apenas caneta ou esferográfica de tinta indelével, azul ou preta.
 Teste Intermédio de Matemática Entrelinha 1,5 Teste Intermédio Matemática Entrelinha 1,5 (Versão única igual à Versão 1) Duração do Teste: 90 minutos 10.05.2012 9.º Ano de Escolaridade Decreto-Lei n.º
Teste Intermédio de Matemática Entrelinha 1,5 Teste Intermédio Matemática Entrelinha 1,5 (Versão única igual à Versão 1) Duração do Teste: 90 minutos 10.05.2012 9.º Ano de Escolaridade Decreto-Lei n.º
Geometria Analítica - AFA
 Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
Versão 2. Utiliza apenas caneta ou esferográfica de tinta indelével, azul ou preta.
 Teste Intermédio de Matemática Versão Teste Intermédio Matemática Versão Duração do Teste: 90 minutos 10.05.01 9.º Ano de Escolaridade Decreto-Lei n.º 6/001, de 18 de janeiro Identifica claramente, na
Teste Intermédio de Matemática Versão Teste Intermédio Matemática Versão Duração do Teste: 90 minutos 10.05.01 9.º Ano de Escolaridade Decreto-Lei n.º 6/001, de 18 de janeiro Identifica claramente, na
Grupo de exercícios I - Geometria plana- Professor Xanchão
 Grupo de exercícios I - Geometria plana- 1. (G1 - ifce 01) Na figura abaixo, R, S e T são pontos sobre a circunferência de centro O. Se x é o número real, tal que a = 5x e b = 3x + 4 são as medidas dos
Grupo de exercícios I - Geometria plana- 1. (G1 - ifce 01) Na figura abaixo, R, S e T são pontos sobre a circunferência de centro O. Se x é o número real, tal que a = 5x e b = 3x + 4 são as medidas dos
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 98/99 1ª P A R T E - MATEMÁTICA
 21 1ª P A R T E - MATEMÁTICA ITEM 01. O produto do MMC entre 30, 60 e 192 pelo MDC entre 144, 180 e 640 pode ser expresso por 2 a x 3 x 5. O valor do expoente a é a.( ) 1 b.( ) 2 c.( ) 4 d.( ) 6 e.( )
21 1ª P A R T E - MATEMÁTICA ITEM 01. O produto do MMC entre 30, 60 e 192 pelo MDC entre 144, 180 e 640 pode ser expresso por 2 a x 3 x 5. O valor do expoente a é a.( ) 1 b.( ) 2 c.( ) 4 d.( ) 6 e.( )
MATEMÁTICA - 3o ciclo Circunferência - ângulos e arcos (9 o ano) Propostas de resolução
 MATEMÁTICA - 3o ciclo Circunferência - ângulos e arcos (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como o trapézio é isósceles, então BC = AD, pelo que também
MATEMÁTICA - 3o ciclo Circunferência - ângulos e arcos (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Como o trapézio é isósceles, então BC = AD, pelo que também
Área das figuras planas
 AS ESPOSTAS ESTÃO NO FINAL DOS EXECÍCIOS. ) Calcule as áreas dos retângulos de base b e altura h nos seguintes casos: a) b = cm e h = 7cm b) b =,dm e h = dm c) b = m e h = m d) b =,m e h =,m ) Determine:
AS ESPOSTAS ESTÃO NO FINAL DOS EXECÍCIOS. ) Calcule as áreas dos retângulos de base b e altura h nos seguintes casos: a) b = cm e h = 7cm b) b =,dm e h = dm c) b = m e h = m d) b =,m e h =,m ) Determine:
Resolução de Questões 9º Ano Áreas Prof. Túlio. Aplicação: Turmas A e C
 Resolução de Questões 9º Ano Áreas Prof. Túlio Aplicação: Turmas A e C 1. Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1m,
Resolução de Questões 9º Ano Áreas Prof. Túlio Aplicação: Turmas A e C 1. Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1m,
MATEMÁTICA. Capítulo 3 LIVRO 2. (I) Áreas das Figuras Planas (II) Áreas de Polígonos Regulares. Páginas: 168 à 188
 MATEMÁTICA LIVRO Capítulo (I) Áreas das Figuras Planas (II) Áreas de Polígonos Regulares Páginas: 68 à 88 Áreas de Figuras Planas toda área é uma medida de superfície [u] unidade padrão [u]² [u] I. ÁREA
MATEMÁTICA LIVRO Capítulo (I) Áreas das Figuras Planas (II) Áreas de Polígonos Regulares Páginas: 68 à 88 Áreas de Figuras Planas toda área é uma medida de superfície [u] unidade padrão [u]² [u] I. ÁREA
A triângulo equilátero = 3.R2. 3. A hexágono = 2. A triângulo equilátero. Letra B
 GEOMETRIA PLANA ÁREAS QUESTÃO 01 QUESTÃO 03 A = 1 + 16/ -1 = 1 QUESTÃO 0 A hexágono = 3.R. 3 A triângulo equilátero = 3.R. 3 A hexágono =. A triângulo equilátero A triângulo equilátero A hexágono = 1 No
GEOMETRIA PLANA ÁREAS QUESTÃO 01 QUESTÃO 03 A = 1 + 16/ -1 = 1 QUESTÃO 0 A hexágono = 3.R. 3 A triângulo equilátero = 3.R. 3 A hexágono =. A triângulo equilátero A triângulo equilátero A hexágono = 1 No
da população têm cabelos pretos e olhos castanhos e que a população que tem cabelos pretos é 10%
 0 Três pessoas resolveram percorrer um trajeto da seguinte maneira: a primeira andaria a metade do percurso mais km, a segunda a metade do que falta mais km e finalmente a terceira que andaria a metade
0 Três pessoas resolveram percorrer um trajeto da seguinte maneira: a primeira andaria a metade do percurso mais km, a segunda a metade do que falta mais km e finalmente a terceira que andaria a metade
FUNDADOR PROF. EDILSON BRASIL SOÁREZ O Colégio que ensina o aluno a estudar. II Simulado de Matemática ITA. ALUNO(A): N o : TURMA:
 FUNDADOR PROF. EDILSON BRASIL SOÁREZ O Colégio que ensina o aluno a estudar Central de Atendimento: 4006.7777 3 o Ensino Médio II Simulado de Matemática ITA ALUNO(A): N o : TURMA: TURNO: MANHÃ DATA: 1/04/007
FUNDADOR PROF. EDILSON BRASIL SOÁREZ O Colégio que ensina o aluno a estudar Central de Atendimento: 4006.7777 3 o Ensino Médio II Simulado de Matemática ITA ALUNO(A): N o : TURMA: TURNO: MANHÃ DATA: 1/04/007
Colégio Militar de Porto Alegre 2/11
 DE ENSINO BÁSICO, TÉCNICO E TECNOLÓGICO 013 Escolha a única resposta certa, assinalando-a com um X nos parênteses à esquerda QUESTÃO 1 O valor de 74 + 43 + 31+ 1+ 13 + 7 + 3 + 1 é igual a (A) 13 (B) 13
DE ENSINO BÁSICO, TÉCNICO E TECNOLÓGICO 013 Escolha a única resposta certa, assinalando-a com um X nos parênteses à esquerda QUESTÃO 1 O valor de 74 + 43 + 31+ 1+ 13 + 7 + 3 + 1 é igual a (A) 13 (B) 13
Prova Vestibular ITA 2000
 Prova Vestibular ITA Versão. ITA - (ITA ) Sejam f, g : R R definidas por f ( ) = e g cos 5 ( ) =. Podemos afirmar que: f é injetora e par e g é ímpar. g é sobrejetora e f é bijetora e g é par e f é ímpar
Prova Vestibular ITA Versão. ITA - (ITA ) Sejam f, g : R R definidas por f ( ) = e g cos 5 ( ) =. Podemos afirmar que: f é injetora e par e g é ímpar. g é sobrejetora e f é bijetora e g é par e f é ímpar
Solução do Simulado PROFMAT/UESC 2012
 Solução do Simulado PROFMAT/UESC 01 (1) Encontre uma fração equivalente a 9/5 cuja soma dos termos é igual a 196: (A) 96/100 (B) 106/90 (C) 116/80 (D) 16/70 (E) 136/60 9 5 = 9 5 14 14 = 16 70 () Um grupo
Solução do Simulado PROFMAT/UESC 01 (1) Encontre uma fração equivalente a 9/5 cuja soma dos termos é igual a 196: (A) 96/100 (B) 106/90 (C) 116/80 (D) 16/70 (E) 136/60 9 5 = 9 5 14 14 = 16 70 () Um grupo
VESTIBULAR 2002 Prova de Matemática
 VESTIBULAR 00 Prova de Matemática Data: 8//00 Horário: 8 às horas Duração: 0 horas e 0 minutos Nº DE INSCRIÇÃO AGUARDE AUTORIZAÇÃO PARA ABRIR ESTE CADERNO DE QUESTÕES INSTRUÇÕES PARA REALIZAÇÃO DA PROVA
VESTIBULAR 00 Prova de Matemática Data: 8//00 Horário: 8 às horas Duração: 0 horas e 0 minutos Nº DE INSCRIÇÃO AGUARDE AUTORIZAÇÃO PARA ABRIR ESTE CADERNO DE QUESTÕES INSTRUÇÕES PARA REALIZAÇÃO DA PROVA
Áreas IME (A) (B) (C) (D) 104 (E) e 2
 Áreas IME 1. (IME 010) Seja ABC um triângulo de lados AB, BC e AC iguais a 6, 8, e 18, respectivamente. Considere o círculo de centro O isncrito nesse triângulo. A distância AO vale: 104 (A) 6 104 (B)
Áreas IME 1. (IME 010) Seja ABC um triângulo de lados AB, BC e AC iguais a 6, 8, e 18, respectivamente. Considere o círculo de centro O isncrito nesse triângulo. A distância AO vale: 104 (A) 6 104 (B)
As cotações dos itens de cada caderno encontram-se no final do respetivo caderno.
 Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Instruções para a realização da Prova Leia com muita atenção
 Nível 3 Instruções para a realização da Prova Leia com muita atenção Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima segunda edição da Olimpíada de Matemática de São José do
Nível 3 Instruções para a realização da Prova Leia com muita atenção Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima segunda edição da Olimpíada de Matemática de São José do
. Calcule a medida do segmento CD. 05. No triângulo retângulo da figura ao lado, BC = 13m
 05. No triângulo retângulo da figura ao lado, = 1m, D = 8m e D = 4m. alcule a medida do segmento D. LIST DE EXERÍIOS GEOMETRI PLN PROF. ROGERINHO 1º Ensino Médio Triângulo retângulo, razões trigonométricas,
05. No triângulo retângulo da figura ao lado, = 1m, D = 8m e D = 4m. alcule a medida do segmento D. LIST DE EXERÍIOS GEOMETRI PLN PROF. ROGERINHO 1º Ensino Médio Triângulo retângulo, razões trigonométricas,
Colégio Naval 2003 (prova verde)
 Colégio Naval 00 (prova verde) 01) Analise as seguintes afirmativas sobre um sistema S se duas equações do primeiro grau com duas incógnitas X e Y. I - S sempre terá ao menos uma solução, se os seus termos
Colégio Naval 00 (prova verde) 01) Analise as seguintes afirmativas sobre um sistema S se duas equações do primeiro grau com duas incógnitas X e Y. I - S sempre terá ao menos uma solução, se os seus termos
Equipe de Matemática MATEMÁTICA
 Aluno (a): Série: 3ª Turma: TUTORIAL 9R Ensino Médio Equipe de Matemática Data: Áreas de Figuras Planas MATEMÁTICA O estudo da área de figuras planas está ligado aos conceitos relacionados à Geometria
Aluno (a): Série: 3ª Turma: TUTORIAL 9R Ensino Médio Equipe de Matemática Data: Áreas de Figuras Planas MATEMÁTICA O estudo da área de figuras planas está ligado aos conceitos relacionados à Geometria
30's Volume 22 Matemática
 30's Volume Matemática www.cursomentor.com 0 de julho de 015 Q1. Um homem de x + 6 5 altura x + 97 m de altura está de pé próximo a um poste de m. Neste 50 5 caso qual a medida da sombra do homem neste
30's Volume Matemática www.cursomentor.com 0 de julho de 015 Q1. Um homem de x + 6 5 altura x + 97 m de altura está de pé próximo a um poste de m. Neste 50 5 caso qual a medida da sombra do homem neste
RECUPERAÇÃO FINAL DE MATEMÁTICA PROFESSOR GILMAR BORNATTO
 1. (Unesp) Seja A = [a Œ] a matriz 2 x 2 real definida por a Œ = 1 se i j e a Œ = -1 se i > j. Calcule A. 2. (Unesp) Seja A=[a Œ] a matriz real 2 x 2 definida por a Œ=1 se i j e a Œ=-1 se i>j. Calcule
1. (Unesp) Seja A = [a Œ] a matriz 2 x 2 real definida por a Œ = 1 se i j e a Œ = -1 se i > j. Calcule A. 2. (Unesp) Seja A=[a Œ] a matriz real 2 x 2 definida por a Œ=1 se i j e a Œ=-1 se i>j. Calcule
ATIVIDADES COM GEOPLANO CIRCULAR
 ATIVIDADES COM GEOPLANO CIRCULAR Observações. O geoplano circular utilizado tem 24 pinos no círculo. Os pinos do geoplano circular são chamados de pontos. Os pontos do círculo são enumerados de 1 até 24
ATIVIDADES COM GEOPLANO CIRCULAR Observações. O geoplano circular utilizado tem 24 pinos no círculo. Os pinos do geoplano circular são chamados de pontos. Os pontos do círculo são enumerados de 1 até 24
TIPO DE PROVA: A. Questão 3. Questão 1. Questão 4. Questão 2. alternativa D. alternativa E. alternativa D. alternativa D
 Questão TIPO DE PROVA: A O algarismo das dezenas do número! é: a) 5 b) 0 c) d) 7 e) A quantidade de zeros com que termina o número n! é igual ao número de fatores 5 presentes em sua fatoração. Na fatoração
Questão TIPO DE PROVA: A O algarismo das dezenas do número! é: a) 5 b) 0 c) d) 7 e) A quantidade de zeros com que termina o número n! é igual ao número de fatores 5 presentes em sua fatoração. Na fatoração
Lista de exercícios 06 Aluno (a): Turma: 9º ano (Ensino fundamental) Professor: Flávio Disciplina: Matemática
 Antes de iniciar a lista de exercícios leia atentamente as seguintes orientações: É fundamental a apresentação de uma lista legível, limpa e organizada. Rasuras podem invalidar a lista. Nas questões que
Antes de iniciar a lista de exercícios leia atentamente as seguintes orientações: É fundamental a apresentação de uma lista legível, limpa e organizada. Rasuras podem invalidar a lista. Nas questões que
COLÉGIO SHALOM Ensino Fundamental II 9º ANO Profº: RONALDO VILAS BOAS COSTA Disciplina: GEOMETRIA 9 B 25 C
 COLÉGIO SHALOM Ensino Fundamental II 9º ANO Profº: RONALDO VILAS BOAS COSTA Disciplina: GEOMETRIA TRABALHO Data: /1/018 Nota: Estudante :. No. 1) O valor de no triângulo retângulo abaio é: a) 10. b) 1.
COLÉGIO SHALOM Ensino Fundamental II 9º ANO Profº: RONALDO VILAS BOAS COSTA Disciplina: GEOMETRIA TRABALHO Data: /1/018 Nota: Estudante :. No. 1) O valor de no triângulo retângulo abaio é: a) 10. b) 1.
LEIA COM ATENÇÃO E SIGA RIGOROSAMENTE ESTAS INSTRUÇÕES
 DEPARTAMENTO DE RECURSOS HUMANOS - DRH SELEÇÃO PÚBLICA PARA FORMAÇÃO DE CADASTRO DE RESERVA DE PROFESSOR SUBSTITUTO PARA A SECRETARIA MUNICIPAL DE EDUCAÇÃO EDITAL 28/2012 PROFESSOR DE MATEMÁTICA LOCAL
DEPARTAMENTO DE RECURSOS HUMANOS - DRH SELEÇÃO PÚBLICA PARA FORMAÇÃO DE CADASTRO DE RESERVA DE PROFESSOR SUBSTITUTO PARA A SECRETARIA MUNICIPAL DE EDUCAÇÃO EDITAL 28/2012 PROFESSOR DE MATEMÁTICA LOCAL
MATEMÁTICA - 3o ciclo Circunferência (9 o ano)
 MTMÁTI - 3o ciclo ircunferência (9 o ano) xercícios de provas nacionais e testes intermédios 1. Na figura seguinte, está representada uma semicircunferência de centro no ponto e diâmetro [] ponto pertence
MTMÁTI - 3o ciclo ircunferência (9 o ano) xercícios de provas nacionais e testes intermédios 1. Na figura seguinte, está representada uma semicircunferência de centro no ponto e diâmetro [] ponto pertence
Exercícios de Revisão 1º Ano Ensino Médio Prof. Osmar
 Exercícios de Revisão 1º no Ensino Médio Prof. Osmar 1.- Sendo = { x Z / 0 x 2 } e = { y Z / 0 x 5}. esboce o gráfico da função f : tal que y = 2 x + 1 e dê seu conjunto imagem. 2.- No gráfico abaixo de
Exercícios de Revisão 1º no Ensino Médio Prof. Osmar 1.- Sendo = { x Z / 0 x 2 } e = { y Z / 0 x 5}. esboce o gráfico da função f : tal que y = 2 x + 1 e dê seu conjunto imagem. 2.- No gráfico abaixo de
