Métodos multi-malhas aplicados à equação de Poisson bidimensional
|
|
|
- Mauro Benke Domingos
- 5 Há anos
- Visualizações:
Transcrição
1 Métodos multi-malhas aplicados à equação de Poisson bidimensional Leticia Braga Berlandi, Analice Costacurta Brandi Departamento de Matemática e Computação Faculdade de Ciências e Tecnologia, UNESP Presidente Prudente - SP, Brasil leticiaberlandi@gmail.com, analice@fct.unesp.br Resumo O presente trabalho consiste em resolver a equação diferencial parcial elíptica de Poisson, onde a condição de contorno do tipo Dirichlet foi considerada para a obtenção da solução numérica do problema bidimensional, considerando um domínio quadrado. O objetivo deste trabalho é analisar a eficiência computacional de métodos multi-malhas (ou multigrid) quando aplicados à resolução de sistemas lineares provenientes do método de diferenças finitas. No processo de resolução da equação diferencial foram utilizados dois métodos iterativos, o esquema Correction Scheme (CS) e o esquema Full Approximation Scheme (FAS). Ambos os métodos foram implementados no software Matlab, onde os resultados obtidos foram comparados com a solução analítica conhecida na literatura. Dessa forma, foi realizada uma comparação dos métodos multigrid CS e FAS para verificar se os métodos numéricos utilizados foram eficientes para a solução desse tipo de problema. Palavras-chave Equação de Poisson; método de diferenças finitas; métodos multigrid; Matlab. I. INTRODUÇÃO Problemas de equilíbrio são aqueles em que o sistema permanece constante em relação ao tempo, também são conhecidos como problemas em regime permanente ou no estado estacionário e geralmente, dão origem a equações elípticas. As mais conhecidas dessas equações são as equações de Poisson e de Laplace, cujas aplicações são as mais variadas como, por exemplo, problemas de pressão, problemas em elasticidade, problemas de camada limite, problemas de vibração em membranas, problemas de difusão [2], dentre outras. O avanço computacional nos últimos anos foi decisivo para o destaque da simulação numérica no estudo desses problemas, aprimorando cada vez mais os métodos numéricos. A discretização de problemas elípticos utilizando o método de diferenças finitas resulta em um sistema de equações lineares que tem uma estrutura bastante peculiar. Em geral, a matriz desse sistema contém apenas alguns poucos elementos não nulos em cada linha, ou seja, é esparsa, exigindo métodos iterativos que se aproveitem dessa estrutura para resolvê-los mais rapidamente [9]. Outra particularidade dos sistemas lineares provenientes da discretização dessas equações é que são, em geral, muito grandes, pois o número de incógnitas é aproximadamente proporcional ao número de pontos da malha. Na simulação de problemas reais uma tal malha conteria ainda um número muito reduzido de pontos para uma boa representação dos fenômenos que se pretende simular, de forma que malhas mais finas são uma necessidade [1]. A grande dificuldade imposta pelo processo de preenchimento da matriz está em não saber, a priori, quais elementos serão modificados. Portanto, deve-se reservar o espaço necessário para armazenar toda a matriz na memória do computador, apesar da maior parte desse espaço ser preenchida com zeros. Os métodos iterativos não têm esse problema, pois requerem somente o resultado da multiplicação da matriz dos coeficientes por um vetor e, portanto, o padrão de zeros da matriz não sofre qualquer modificação ao longo do processo [4]. Este trabalho trata da aplicação de métodos de solução de sistemas de equações lineares para a solução de problemas elípticos, em especial para a equação de Poisson bidimensional, em que o método de diferenças finitas foi utilizado para aproximação da solução dessa equação. Além disso, a implementação do algoritmo foi realizada
2 através do software Matlab, em que uma análise do erro, comparações entre os métodos numéricos e a solução analítica, conhecidas na literatura, foram realizadas. II. FORMULAÇÃO MATEMÁTICA A equação de Poisson bidimensional é uma equação elíptica de segunda ordem dada por ( 2 u x u ) y 2 = f(x, y). (1) O domínio de integração de uma equação elíptica bidimensional é sempre uma área limitada pela fronteira ΩR. As condições de contorno usualmente especificam os valores da função ou os valores de sua derivada normal ao longo do contorno ΩR, ou uma mistura de ambos, que são, respectivamente, as condições de Dirichlet (u é conhecida em ΩR), de Neumann ( u n é conhecida em ΩR) e Robin (αu = β u n conhecida em ΩR). Em particular, considera-se neste trabalho uma região quadrada R = {(x, y) R 2 / a x b, a y b} com condição de contorno u(x, y) = g(x, y) em ΩR. III. FORMULAÇÃO NUMÉRICA O problema em estudo é formulado por uma equação diferencial parcial do tipo estacionária e por condições auxiliares específicas. Considerando o fato de que nem sempre existe solução analítica, faz-se necessária a resolução do problema de modo numérico. Para tanto, o método de diferenças finitas é adotado para a discretização do domínio e das derivadas parciais. O método numérico de diferenças finitas é usado como uma abordagem alternativa para obter a aproximação da solução de uma equação diferencial parcial. A ideia básica desse método é transformar a resolução de uma equação diferencial em um sistema de equações algébricas, substituindo as derivadas por diferenças [5]. O método de diferenças finitas é facilmente implementado computacionalmente, que consiste da discretização do domínio e na substituição das derivadas presentes na equação diferencial por aproximações utilizando apenas os valores numéricos da função, onde a ferramenta básica no cálculo das aproximações das derivadas é a fórmula de Taylor [6]. Conforme já foi dito, o método de diferenças finitas foi implementado através do software Matlab e a primeira etapa para resolução de qualquer método numérico envolvendo equações diferenciais parciais é discretizar a região onde se procura a solução. Para a discretização define-se uma malha, que é um conjunto finito de pontos pertencentes ao domínio, chamados nós da malha [2]. Considera-se a região quadrada R coberta por uma malha, conforme mostra a Fig. 1. Figura 1: Malha de discretização. Enfatiza-se aqui a importância da discretização correta da fronteira e a importância da escolha correta dos métodos de solução para o sistema linear resultante. A discretização de problemas elípticos sempre resulta em um sistema de equações lineares que tem uma estrutura bastante peculiar. Em geral, a matriz do sistema é grande e esparsa, tendo a necessidade de propor métodos iterativos que se utilizem dessa estrutura para resolvê-los mais rapidamente [9]. O sistema linear proveniente da discretização da equação de Poisson pelo método de diferenças finitas pode ser resolvido por métodos multigrid. Estes são os métodos iterativos mais eficientes conhecidos para se resolver sistemas de equações, onde a ideia básica está em usar um conjunto de malhas e executar alternativamente iterações em cada nível de malha para obter soluções aproximadas desta equação em malhas mais grossas [10]. O objetivo dos métodos multigrid é acelerar a convergência para reduzir o tempo da Unidade Central de Processamento (CPU) necessário para resolver sistemas de equações lineares, onde são realizadas iterações na malha mais fina e em cada nível de malha mais grossa são resolvidas apenas equações residuais [8]. Para isto, são usados operadores para transferir informações da malha fina para a malha imediatamente mais grossa (processo de restrição) e da malha grossa para a malha imediatamente mais fina (processo de prolongação). Considerando a sequência com que as diversas malhas são utilizadas no caso unidimensional, as Fig. 2 e 3 ilustram o ciclo V e W, respectivamente. Figura 2: Ciclo V.
3 dessa equação. Dessa forma, para que a solução seja única, deve-se especificar as condições de contorno com a qual se pretende trabalhar em um determinado problema. O método das diferenças finitas consiste de substituir as derivadas parciais presentes na equação diferencial por aproximações por diferenças finitas. Para ilustrar este processo, considera-se a equação de Poisson com condição de contorno tipo Dirichlet dada por Figura 3: Ciclo W. Assim como no caso unidimensional, o método multigrid utilizase de diversas malhas e ciclos para resolver a equação de Poisson bidimensional, conforme ilustra a Fig. 4. { ( ) 2 u = u = 2 u x + 2 u 2 y = f(x, y) com (x, y) R 2, u = g(x, y) com (x, y) ΩR definida no retângulo R = {(x, y) R 2 / 0 x a, 0 y b} sobre a fronteira ΩR desse retângulo. A discretização de uma equação estacionária nos fornece um sistema de equações que pode ser resolvido por meio de métodos diretos e iterativos. Para ilustrar como esta discretização é realizada na prática considera-se (1). Figura 4: Processo de refinamento de malhas. Os sistemas lineares que aparecem em cada malha são resolvidos através de métodos iterativos, os quais têm propriedades para reduzir os erros oscilatórios rapidamente. Sendo assim, neste trabalho são testados os métodos de Jacobi e Gauss-Seidel, conforme são descritos adiante. Além disso, o esquema de correção CS e o esquema de aproximação total FAS foram estudados, implementados e utilizados no presente trabalho. Primeiramente, para aproximar u xx e u yy por diferenças finitas cobre-se a região R com uma malha. Escolhe-se a opção mais óbvia que consiste em traçar linhas paralelas aos eixos coordenados. Os pontos dessa malha serão denotados por (x i, y j ), x i = ih, y j = jk, i = 0, 1,..., N, j = 0,1,...,M, onde h = a N representa o espaçamento na direção x e k = b M representa o espaçamento na direção y. Denota-se por R δ os pontos da malha interiores a R, isto é, R δ = {(x i, y j ), 0 < i < N, 0 < j < M}, e por ΩR δ os pontos da malha que estão sobre a fronteira, ou seja, ΩR δ = {(x i, y j ), (i = 0, N, 0 j M) e (0 i N, j = 0, M)}. Pode-se agora aproximar as derivadas de (1) da seguinte forma: Sabe-se que (1) é válida para todos os pontos de R, então em particular para um ponto genérico de R δ pode-se escrever, A. Modelo Discreto Bidimensional Inicialmente, considera-se R uma região do plano e ΩR sua fronteira. Se = b 2 4ac < 0 na equação a(x, y) 2 u x 2 + 2b 2 u x y + c(x, u ( y) 2 y 2 = d x, y, u, u x, u ), (2) y tem-se uma equação diferencial parcial (EDP) elíptica, para todo ponto (x, y) pertencente a região limitada do plano R. Sabe-se que muitos problemas práticos são governados por (2), com a = c = 1 e b = 0. Fazendo d = f(x, y), obtém-se a equação de Poisson, dada por (1). [u xx (x i, y j ) + u yy (x i, y j )] = f(x i, y j ). (3) Assim, pode-se aproximar as derivadas por: u xx (x i, y j ) = u(x i + h, y j ) 2u(x i, y j ) + u(x i h, y j ) h 2 u yy (x i, y j ) = u(x. i, y j + k) 2u(x i, y j ) + u(x i, y j k) k 2 Substituindo essas aproximações em (3), obtém-se: (4) A Equação (2) possui infinitas soluções pois, sendo linear e tendo como solução u e v, tem-se que w = αu + βv também é solução
4 [ u(xi + h, y j ) 2u(x i, y j ) + u(x i h, y j ) h u(x i, y j + k) 2u(x i, y j ) + u(x i, y j k) k 2 ] = f(xi, y j ). Seguindo a notação utilizada na literatura, denota-se por u (i,j) o valor da solução no ponto (x i, y j ) e por U (i,j) a solução da equação de diferenças: ( Ui+1,j 2U i,j + U i1,j h 2 + U i,j+1 2U i,j U ) i,j1 k 2 = f i,j. (6) Para pontos adjacentes à fronteira, (6) envolve pontos na fronteira que serão obtidos diretamente da condição de Dirichlet, ou seja, u(x i, y j ) = g(x i, y j ), para todo (x i, y j ) ΩR δ. Para simplificar a notação, introduz-se o operador: (5) e B = f(x 1, y 1 ) + g(x0,y1) h 2 f(x 2, y 1 ) + g(x2,y0) k 2 + g(x1,y0) k 2. f(x N1, y 1 ) + g(x N,y 1) h + g(x N1,y 0) 2 k 2, a b c. b a b.. 0. b a b c A = c b a b c b a [ Ui+1,j 2U i,j + U i1,j δ U i,j = h 2 + U i,j+1 2U i,j U ] i,j1 k 2. Na matriz A, os números a, b e c são os coeficientes da discretização de 5 pontos e são dados por: Com essa notação, (6) pode ser escrita como a = 2 h k 2, b = 1 h 2, c = 1 k 2. δ U i,j = f(x i, y j ), (x i, y j ) R δ, (7) sendo que sua condição de contorno é dada por U i,j = g(x i, y j ), para todo (x i, y j ) ΩR δ. (8) A Equação (7) quando aplicada nos pontos internos de R δ, resulta num sistema linear simétrico com (N 1) (M 1) equações. Esperase que resolvendo esse sistema linear, os valores U i,j encontrados sejam uma boa aproximação para u i,j. De fato, será visto que a solução obtida por (7) converge para u i,j, quando a malha for refinada. O sistema linear proveniente de (7) pode ser escrito na forma matricial AU = B onde U = (U 1,1, U 2,1,..., U N1,1, U 1,2, U 2,2,......, U N1,2,..., U 1,M1, U 2,M1,..., U N1,M1 ) T, Os conceitos de métodos explícitos ou implícitos no tempo não são aplicáveis às equações elípticas devido à ausência da integração temporal. Dessa forma, é sempre necessário resolver um sistema de equações lineares e, como a matriz de coeficientes do sistema não é, em geral, tridiagonal, a solução é obtida por métodos iterativos. B. Método de Jacobi O primeiro método iterativo (que já foi descrito como o mais lento para convergir, embora isso realmente dependa da matriz A do sistema) é o algoritmo de Jacobi. Escrevendo o sistema Ax = b na forma a 1j x j = b 1., a nj x j = b n se 0 para todo i, cada x i pode ser isolado na i-ésima equação
5 e escrito na forma x i = 1 b i,j i a ij x j. Isso sugere definir um método iterativo da seguinte forma: suposto x k = (x k 1,, x k n) obtido no passo anterior, obtém-se x k+1 = (x k+1 1,, x k+1 n ) por x k+1 i = 1 b i,j i a ij x k j. (9) No caso da fórmula de cinco pontos para o problema de Poisson com h = k, como a equação para cada ponto (i, j) é dada por u i,j1 u i,j+1 + 4u i,j u i1,j u i+1,j = h 2 f i,j, o método de Jacobi é ou x k+1 = D 1 (Cx k + b), (13) onde C = (D A) é a matriz composta pelos elementos de A fora os elementos da diagonal principal. C. Método de Gauss-Seidel Um método iterativo que converge cerca de duas vezes mais rápido que o método de Jacobi é o método de Gauss-Seidel, onde os valores de x são atualizados dentro de cada iteração, sem esperar pela próxima. Em outras palavras, obtido o valor de x k+1 j, este é usado no lugar de x k j no cálculo seguinte. No sistema Ax = b em que 0 para todo i, como antes isola-se cada x i na i-ésima equação, agora escreve-se x i = 1 b i i1 a ij x j j=i+1 a ij x j. Então define-se u k+1 i,j = 1 ( u k 4 i,j1 + u k i,j+1 + u k i1,j + u k i+1,j + h 2 ) f i,j. (10) No caso especial da equação de Laplace (f(x, y) = 0) com condição de fronteira de Dirichlet não-nula, o método de Jacobi é simplesmente a propriedade do valor médio discreta u k+1 i,j = 1 ( u k 4 i,j1 + u k i,j+1 + u k i1,j + u k ) i+1,j. (11) Em outras palavras, calculados os valores de u em todos os pontos da malha na iteração anterior, o novo valor de u em um ponto interior da malha nesta iteração é calculado através da média dos seus quatro pontos vizinhos. Os valores iniciais de u nos pontos interiores da malha para a primeira iteração (isto é, o chute inicial) podem ser atribuídos arbitrariamente ou através de algum argumento razoável. Por exemplo, pode-se utilizar uma média ponderada dos valores de fronteira para o valor inicial em cada ponto interior da malha, de acordo com a posição do ponto em relação aos pontos das quatro fronteiras discretizadas. Em forma matricial, o algoritmo de Jacobi pode ser descrito da seguinte forma: denotando por D = diag(a 11,, a nn ) a matriz diagonal cujas entradas são as entradas diagonais de A, tem-se que x k+1 i = 1 b i i1 pois os valores x k+1 1,, x k+1 i1 a ij x k+1 j j=i+1 a ij x k j, (14) já foram computados nesta iteração, enquanto que os valores x k i+1,, xk n são fornecidos pela iteração anterior. Por exemplo, no caso da equação de Laplace, pode-se utilizar a fórmula u k+1 i,j = 1 ( u k+1 i,j1 4 + uk i,j+1 + u k+1 i1,j + i+1,j) uk, (15) assumindo que os pontos da malha são percorridos na ordem lexicográfica, de modo que quando calcula-se o valor de u no ponto i, j na iteração k +1, nesta mesma iteração já se calcula os valores de u em i 1, j e em i, j 1, e se usa estes valores para calcular u k+1 i,j ao invés dos valores u k i,j1 e uk i1,j obtidos na iteração anterior. Em forma matricial, o algoritmo de Gauss-Seidel pode ser descrito da seguinte forma: dada uma matriz A, existe uma decomposição x k+1 = D 1 [(D A)x k + b], (12) A = L + D + U, (16)
6 onde D é uma matiz diagonal, L é uma matriz estritamente triangular inferior e U é uma matriz estritamente triangular superior. Então o algoritmo de Gauss-Seidel é definido por ou ou ainda, pode ser escrito como x k+1 = D 1 (b Lx k+1 Ux k ), (17) (L + D)x k+1 = b Ux k, x k+1 = (L + D) 1 (b Ux k ). (18) IV. RESULTADOS NUMÉRICOS Considere a equação de Poisson bidimensional dada por 2 u x u y 2 = 2[(1 6x2 )y 2 (1 y 2 ) + (1 6y 2 )x 2 (1 x 2 )], pertencente ao domínio R = {(x, y) R 2 / 0 x 1, 0 y 1}, cuja solução analítica é dada por (19) Aplicando o método em uma malha intermediária fina, tomados 16 subintervalos nas direções x e y (h = 0, 0625), obtém-se 289 pontos discretos. Isso significa que o sistema linear resultante possui 225 equações. Esse número também representa a dimensão da matriz dos coeficientes, que é pentadiagonal tratando-se do método de diferenças finitas de segunda ordem. Isso indica o quanto a matriz é esparsa, e por isso há a necessidade de resolvê-la por métodos iterativos, que aproveitem essa característica, reduzindo o gasto computacional. Por fim, refinando a malha pela última vez, tem-se uma malha fina (h = 0, 03125), gerando um sistema demasiadamente grande e, ainda, espera-se gerar uma aproximação mais consistente. Neste trabalho foi verificada a eficiência de métodos multigrid e, para tal verificação, foi realizada uma análise do erro máximo absoluto (E max ) cometido na solução do problema com diferentes espaçamentos, para duas e quatro malhas. E ainda, foi considerado o erro máximo menor ou igual a Sabe-se que E max é dado por E max = max 1 i,j N1 u (i,j) U (i,j), (21) onde u (i,j) representa a solução exata do problema, enquanto que U (i,j) a solução aproximada, de acordo com o método numérico utilizado. A distribuição do (E max ) do esquema de correção CS pode ser observada na Tabela I. Tabela I: Comparação do (E max ) cometido em diferentes espaçamentos pelo esquema CS. Espaçamento (h = k) Esquema de correção CS 2 malhas 4 malhas 0,25 0,0030 0,0030 0,125 7,6388e-04 7,6389e-04 0,0625 1,9672e-04 1,9673e-04 0, ,9171e-05 4,9172e-05 u(x, y) = (x 2 x 4 )(y 4 y 2 ). (20) O problema descrito foi simulado para diferentes refinamentos de malha, onde as malhas utilizadas são regulares e se adota aqui, h para descrever o espaçamento. A princípio, inicia-se com uma malha mais grossa e, a partir de então, começa a refiná-la objetivando a analisar o comportamento da solução numérica do problema diante dessas modificações. Inicialmente considera-se uma malha grossa 5 5 (h = 0, 25). Ao refinar a malha pela primeira vez, obtém-se um espaçamento que equivale à metade do espaçamento anterior. Consequentemente, existem mais pontos discretos nos quais a função deve ser avaliada, pois trata-se de uma malha intermediária grossa 9 9 (h = 0, 125). Agora, observa-se através da Tabela II os valores do E max cometido pelo esquema de aproximação total FAS em cada malha computacional utilizada Tabela II: Comparação do (E max ) cometido em diferentes espaçamentos pelo esquema FAS. Espaçamento (h = k) Esquema de aproximação total FAS 2 malhas 4 malhas 0,25 0,0325 0,0030 0,125 0,1250 7,6388e-04 0,0625 0,4731 1,9673e-04 0, ,7927 4,9177e-05 Uma síntese do E max cometido pelos dois esquemas com o método multigrid, em quatro diferentes espaçamentos, é apresentada
7 nas tabelas I e II. Nota-se que o esquema de aproximação total FAS apresenta um erro maior que o esquema de correção CS, para todos os espaçamentos testados utilizando-se duas malhas. Isso decorre do fato de que não é muito efetivo usar somente dois níveis de malha [7], uma vez que para se obter um bom desempenho do método multigrid diversos níveis de malhas devem ser usados [3]. Portanto, o método CS se mostrou eficaz para o problema analisado. Já o método FAS mostrou-se não ser um esquema eficaz quando utilizou-se duas malhas na obtenção da solução numérica do problema. [7] P. J. Roache, Fundamentals of computational fluid dynamics. Socorro, United States: Hermosa Publishers, [8] P. Wesseling, An Introduction to Multigrid Methods. Chichester, England: John Wiley Sons Ltd., [9] R. L. Burden e J. D. Faires, Análise numérica. São Paulo, Brasil: Cengage Learning, [10] W. L. Briggs, V. E. Henson and S. F. McCormick, A Multigrid Tutorial, 2nd ed. Philadelphia, United States: SIAM, V. CONCLUSÕES O presente trabalho teve por objetivo estudar a equação de Poisson, em um domínio bidimensional. O método de diferenças finitas foi utilizado para aproximar as derivadas do problema aqui apresentado e, além disso, foram estudados os esquemas CS e FAS com o método multigrid. Estes foram utilizados no cálculo da solução aproximada do sistema linear obtido através da discretização da equação de Poisson, com condição de contorno do tipo Dirichlet. Para a obtenção de soluções aproximadas, diferentes espaçamentos foram considerados e o esquema de correção CS se mostrou eficaz na solução da equação. Isso decorre do fato de que a solução numérica apresentou resultados bem próximos da solução analítica do problema, resultando em um erro que pode ser considerado desprezível. Além disso, pôde-se constatar que quanto maior o refinamento da malha, melhor a solução numérica do problema analisado. A comparação dos erros cometidos com duas e quatro malhas foi realizada e verificou-se o comportamento dos métodos numéricos para ambos os casos. Porém, sob o ponto de vista de uma melhor aproximação, a solução obtida utilizando-se quatro malhas apresentou um desempenho superior quanto à utilização de duas malhas, pois o erro cometido ao se utilizar duas malhas foi maior do que o erro com quatro malhas. AGRADECIMENTOS Agradecemos à Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) pelo apoio financeiro no desenvolvimento deste trabalho, processo n o 2016/ REFERÊNCIAS [1] E. Kreyszig, Advanced engineering mathematics, 9th ed. Hoboken, United States: John Wiley & Sons, [2] J. A. Cuminato e M. Meneguette, Discretização de equações diferenciais parciais: técnicas de diferenças finitas, 1. ed. Rio de Janeiro, Brasil: SBM, [3] J. C. Tannehill, D. A. Anderson and R. H. Pletcher, Computational fluid mechanics and heat transfer, 2nd ed. Washington, United States: Taylor & Francis, [4] J. Zhao, T. Zhang and R. M. Corless, Convergence of compact finite difference method, Applied mathematics and computation, vol 182, Issue 2, p , [5] M. A. G. Ruggiero e V. L. R. Lopes, Cálculo numérico: aspectos teóricos e computacionais, 2. ed. São Paulo, Brasil: Makron Books, [6] N. B. Franco, Cálculo numérico. São Paulo, Brasil: Pearson Prentice Hall, 2006.
Comparação entre métodos de resolução de sistemas aplicados à discretização da equação de Poisson via diferenças finitas exponencial
 Comparação entre métodos de resolução de sistemas aplicados à discretização da equação de Poisson via diferenças finitas exponencial Beatriz Liara Carreira; Analice Costacurta Brandi Departamento de Matemática
Comparação entre métodos de resolução de sistemas aplicados à discretização da equação de Poisson via diferenças finitas exponencial Beatriz Liara Carreira; Analice Costacurta Brandi Departamento de Matemática
étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO
étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO
Cálculo Numérico BCC760
 Cálculo Numérico BCC760 Resolução de Sistemas de Equações Lineares Simultâneas Departamento de Computação Página da disciplina http://www.decom.ufop.br/bcc760/ 1 Introdução! Definição Uma equação é dita
Cálculo Numérico BCC760 Resolução de Sistemas de Equações Lineares Simultâneas Departamento de Computação Página da disciplina http://www.decom.ufop.br/bcc760/ 1 Introdução! Definição Uma equação é dita
Universidade Federal do Espírito Santo - UFES
 Universidade Federal do Espírito Santo - UFES Centro Universitário Norte do Espírito Santo - CEUNES Departamento de Matemática Aplicada - DMA Prof. Isaac P. Santos - 2018/1 Aula: Métodos Iterativos Para
Universidade Federal do Espírito Santo - UFES Centro Universitário Norte do Espírito Santo - CEUNES Departamento de Matemática Aplicada - DMA Prof. Isaac P. Santos - 2018/1 Aula: Métodos Iterativos Para
Métodos Iterativos para a Solução da Equação de Poisson
 Métodos Iterativos para a Solução da Equação de Poisson Valdirene da Rosa Rocho, Dagoberto Adriano Rizzotto Justo, Programa de Pós-Graduação em Matemática Aplicada, PPGMap, UFRGS, 91509-900, Porto Alegre,
Métodos Iterativos para a Solução da Equação de Poisson Valdirene da Rosa Rocho, Dagoberto Adriano Rizzotto Justo, Programa de Pós-Graduação em Matemática Aplicada, PPGMap, UFRGS, 91509-900, Porto Alegre,
Laboratório de Simulação Matemática. Parte 7 2
 Matemática - RC/UFG Laboratório de Simulação Matemática Parte 7 2 Prof. Thiago Alves de Queiroz 2/2017 2 [Cap. 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Matemática - RC/UFG Laboratório de Simulação Matemática Parte 7 2 Prof. Thiago Alves de Queiroz 2/2017 2 [Cap. 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Modelagem Computacional. Aula 9 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Aula 9 2 Prof. Thiago Alves de Queiroz 2 [Cap. 12] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010.
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Aula 9 2 Prof. Thiago Alves de Queiroz 2 [Cap. 12] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010.
lineares via método de diferenças finitas exponencial de alta ordem
 Solução numérica de problemas elípticos não lineares via método de diferenças finitas exponencial de alta ordem Numerical solution of nonlinear elliptic problems by the exponential finite difference method
Solução numérica de problemas elípticos não lineares via método de diferenças finitas exponencial de alta ordem Numerical solution of nonlinear elliptic problems by the exponential finite difference method
SISTEMAS LINEARES PROF. EDÉZIO
 SOLUÇÕES NUMÉRICAS DE SISTEMAS LINEARES PROF. EDÉZIO Considere o sistema de n equações e n incógnitas: onde E : a x + a x +... + a n x n = b E : a x + a x +... + a n x n = b. =. () E n : a n x + a n x
SOLUÇÕES NUMÉRICAS DE SISTEMAS LINEARES PROF. EDÉZIO Considere o sistema de n equações e n incógnitas: onde E : a x + a x +... + a n x n = b E : a x + a x +... + a n x n = b. =. () E n : a n x + a n x
Análise da ordem de acurácia do erro em soluções numéricas da equação de Poisson
 Análise da ordem de acurácia do erro em soluções numéricas da equação de Poisson Analysis of the order of accuracy of the error in numerical solutions of the Poisson equation ISSN 2316-9664 Volume 10,
Análise da ordem de acurácia do erro em soluções numéricas da equação de Poisson Analysis of the order of accuracy of the error in numerical solutions of the Poisson equation ISSN 2316-9664 Volume 10,
Modelagem Computacional. Parte 8 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Um Comparativo do desempenho dos solvers Gauss- Seidel linha e zebra no método multigrid em problemas de difusão anisotrópica
 Um Comparativo do desempenho dos solvers Gauss- Seidel linha e zebra no método multigrid em problemas de difusão anisotrópica Michely Laís de Oliveira Programa de Pós-Graduação em Métodos Numéricos em
Um Comparativo do desempenho dos solvers Gauss- Seidel linha e zebra no método multigrid em problemas de difusão anisotrópica Michely Laís de Oliveira Programa de Pós-Graduação em Métodos Numéricos em
Agenda do Dia Aula 14 (19/10/15) Sistemas Lineares: Introdução Classificação
 Agenda do Dia Aula 14 (19/10/15) Sistemas Lineares: Introdução Classificação Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares. Um
Agenda do Dia Aula 14 (19/10/15) Sistemas Lineares: Introdução Classificação Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares. Um
Redução do erro de iteração e aceleração do método Multigrid com o uso de extrapoladores
 Redução do erro de iteração e aceleração do método Multigrid com o uso de extrapoladores Márcio A. M. de Anunciação Programa de Pós-Graduação em Métodos Numéricos em Engenharia (PPGMNE), Universidade Federal
Redução do erro de iteração e aceleração do método Multigrid com o uso de extrapoladores Márcio A. M. de Anunciação Programa de Pós-Graduação em Métodos Numéricos em Engenharia (PPGMNE), Universidade Federal
Disciplina: Cálculo Numérico IPRJ/UERJ. Sílvia Mara da Costa Campos Victer. Aula 6 - Solução de Sistema de Equações Algébricas
 Disciplina: Cálculo Numérico IPRJ/UERJ Sílvia Mara da Costa Campos Victer Aula 6 - Solução de Sistema de Equações Algébricas Métodos diretos: 1- Eliminação de Gauss com substituição recuada 2- Decomposição
Disciplina: Cálculo Numérico IPRJ/UERJ Sílvia Mara da Costa Campos Victer Aula 6 - Solução de Sistema de Equações Algébricas Métodos diretos: 1- Eliminação de Gauss com substituição recuada 2- Decomposição
Aula 3 Volumes Finitos
 Universidade Federal do ABC Aula 3 Volumes Finitos EN3224 Dinâmica de Fluidos Computacional Duas metodologias Leis de Conservação Integrais EDPs O Método dos Volumes Finitos (MVF) Leis de Conservação Integrais
Universidade Federal do ABC Aula 3 Volumes Finitos EN3224 Dinâmica de Fluidos Computacional Duas metodologias Leis de Conservação Integrais EDPs O Método dos Volumes Finitos (MVF) Leis de Conservação Integrais
Capítulo 1. INTRODUÇÃO
 Capítulo 1. INTRODUÇÃO A simulação numérica de problemas de engenharia ocupa atualmente uma posição de destaque no cenário mundial de pesquisa e desenvolvimento de novas tecnologias. O crescente interesse,
Capítulo 1. INTRODUÇÃO A simulação numérica de problemas de engenharia ocupa atualmente uma posição de destaque no cenário mundial de pesquisa e desenvolvimento de novas tecnologias. O crescente interesse,
Sistemas de equações lineares
 É um dos modelos mais u3lizados para representar diversos problemas de Engenharia (cálculo estrutural, circuitos elétricos, processos químicos etc.) Conservação da carga: i 1 i 2 i 3 = 0 i 3 i 4 i 5 =
É um dos modelos mais u3lizados para representar diversos problemas de Engenharia (cálculo estrutural, circuitos elétricos, processos químicos etc.) Conservação da carga: i 1 i 2 i 3 = 0 i 3 i 4 i 5 =
Métodos Numéricos - Notas de Aula
 Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares,
Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares,
Métodos iterativos para sistemas lineares.
 Métodos iterativos para sistemas lineares. Alan Costa de Souza 7 de Setembro de 2017 Alan Costa de Souza Métodos iterativos para sistemas lineares. 7 de Setembro de 2017 1 / 46 Introdução. A ideia central
Métodos iterativos para sistemas lineares. Alan Costa de Souza 7 de Setembro de 2017 Alan Costa de Souza Métodos iterativos para sistemas lineares. 7 de Setembro de 2017 1 / 46 Introdução. A ideia central
Laboratório de Simulação Matemática. Parte 6 2
 Matemática - RC/UFG Laboratório de Simulação Matemática Parte 6 2 Prof. Thiago Alves de Queiroz 2/2017 2 [Cap. 6] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Matemática - RC/UFG Laboratório de Simulação Matemática Parte 6 2 Prof. Thiago Alves de Queiroz 2/2017 2 [Cap. 6] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning, 2010. Thiago
Modelagem Computacional. Parte 7 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 7 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 7 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
USO DO MÉTODO MULTIGRID NA RESOLUÇÃO DO PROBLEMA DE DIFUSÃO DE CALOR 2D EM MALHAS ESTRUTURADAS NÃO-ORTOGONAIS
 USO DO MÉTODO MULTIGRID NA RESOLUÇÃO DO PROBLEMA DE DIFUSÃO DE CALOR 2D EM MALHAS ESTRUTURADAS NÃO-ORTOGONAIS Daiane Cristina Zanatta daiaczanatta@gmail.com Universidade Estadual do Centro-Oeste - UNICENTRO,
USO DO MÉTODO MULTIGRID NA RESOLUÇÃO DO PROBLEMA DE DIFUSÃO DE CALOR 2D EM MALHAS ESTRUTURADAS NÃO-ORTOGONAIS Daiane Cristina Zanatta daiaczanatta@gmail.com Universidade Estadual do Centro-Oeste - UNICENTRO,
Resolução de Sistemas Lineares. Ana Paula
 Resolução de Sistemas Lineares Sumário 1 Introdução 2 Alguns Conceitos de Álgebra Linear 3 Sistemas Lineares 4 Métodos Computacionais 5 Sistemas Triangulares 6 Revisão Introdução Introdução Introdução
Resolução de Sistemas Lineares Sumário 1 Introdução 2 Alguns Conceitos de Álgebra Linear 3 Sistemas Lineares 4 Métodos Computacionais 5 Sistemas Triangulares 6 Revisão Introdução Introdução Introdução
UNIVERSIDADE FEDERAL DO ABC
 UNIVERSIDADE FEDERAL DO ABC BC49 Cálculo Numérico - LISTA - sistemas lineares de equações Profs André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda Métodos diretos Analise os sistemas
UNIVERSIDADE FEDERAL DO ABC BC49 Cálculo Numérico - LISTA - sistemas lineares de equações Profs André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda Métodos diretos Analise os sistemas
4 Modelagem Numérica. 4.1 Método das Diferenças Finitas
 4 Modelagem Numérica Para se obter a solução numérica das equações diferenciais que regem o processo de absorção de CO 2,desenvolvido no capitulo anterior, estas precisam ser transformadas em sistemas
4 Modelagem Numérica Para se obter a solução numérica das equações diferenciais que regem o processo de absorção de CO 2,desenvolvido no capitulo anterior, estas precisam ser transformadas em sistemas
Capítulo 4 - Equações Diferenciais às Derivadas Parciais
 Capítulo 4 - Equações Diferenciais às Derivadas Parciais balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Mestrados em Engenharia da Construção Métodos de Aproximação
Capítulo 4 - Equações Diferenciais às Derivadas Parciais balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Mestrados em Engenharia da Construção Métodos de Aproximação
Linearização do Sistema resultante da
 Trabalho apresentado no CMAC-Sul, Curitiba-PR, 2014. Linearização do Sistema resultante da Discretização da Equação de Burgers Tadasi Matsubara Jr Neyva M. Lopes Romeiro Departamento de Matemática, CCE,
Trabalho apresentado no CMAC-Sul, Curitiba-PR, 2014. Linearização do Sistema resultante da Discretização da Equação de Burgers Tadasi Matsubara Jr Neyva M. Lopes Romeiro Departamento de Matemática, CCE,
Geração de aproximações de diferenças finitas em malhas não-uniformes para as EDPs de Laplace e Helmholtz
 Proceeding Series of the Brazilian Society of Applied and Computational Mathematics, Vol. 5, N., 7. Trabalho apresentado no CNMAC, Gramado - RS, 6. Proceeding Series of the Brazilian Society of Computational
Proceeding Series of the Brazilian Society of Applied and Computational Mathematics, Vol. 5, N., 7. Trabalho apresentado no CNMAC, Gramado - RS, 6. Proceeding Series of the Brazilian Society of Computational
Modelagem Computacional. Parte 6 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 6 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 6 e 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 6 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 6 e 7] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
étodos uméricos RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS (Continuação) Prof. Erivelton Geraldo Nepomuceno
 étodos uméricos RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE
étodos uméricos RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE
Sistemas de Equações Lineares
 Capítulo 3 Sistemas de Equações Lineares Um sistema com n equações lineares pode ser escrito na forma : ou na forma matricial onde com a 1,1 x 1 + a 1,2 x 2 + + a x n = b 1 a 2,1 x 1 + a 2,2 x 2 + + a
Capítulo 3 Sistemas de Equações Lineares Um sistema com n equações lineares pode ser escrito na forma : ou na forma matricial onde com a 1,1 x 1 + a 1,2 x 2 + + a x n = b 1 a 2,1 x 1 + a 2,2 x 2 + + a
étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO
étodos uméricos SISTEMAS DE EQUAÇÕES LINEARES (Continuação) Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO
3 o Trabalho de Algoritmos Numéricos II /1 Algoritmos de Avanço no Tempo para problemas Parabólicos Data de entrega:
 3 o Trabalho de Algoritmos Numéricos II - 2017/1 Algoritmos de Avanço no Tempo para problemas Parabólicos Data de entrega: Considerar os algoritmos explícito, implícito e Crank-Nicolson para resolver a
3 o Trabalho de Algoritmos Numéricos II - 2017/1 Algoritmos de Avanço no Tempo para problemas Parabólicos Data de entrega: Considerar os algoritmos explícito, implícito e Crank-Nicolson para resolver a
XXIX CILAMCE November 4 th to 7 th, 2008 Maceió - Brazil
 XXIX CILAMCE November 4 th to 7 th, 008 Maceió - Brazil EFEITO DA ANISOTROPIA FÍSICA SOBRE O MÉTODO MULTIGRID NA SOLUÇÃO DA EQUAÇÃO DE ADVECÇÃO-DIFUSÃO D Roberta Suero robertasuero@demec.ufpr.br Programa
XXIX CILAMCE November 4 th to 7 th, 008 Maceió - Brazil EFEITO DA ANISOTROPIA FÍSICA SOBRE O MÉTODO MULTIGRID NA SOLUÇÃO DA EQUAÇÃO DE ADVECÇÃO-DIFUSÃO D Roberta Suero robertasuero@demec.ufpr.br Programa
Resolução de Sistemas de Equações Lineares
 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Resolução de Sistemas de Equações
1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Resolução de Sistemas de Equações
Comparação entre métodos numéricos computacionais na solução de um problema de valor inicial
 Comparação entre métodos numéricos computacionais na solução de um problema de valor inicial Comparison of computational numerical methods in an initial value problem solution ISSN 2316-9664 Volume 7,
Comparação entre métodos numéricos computacionais na solução de um problema de valor inicial Comparison of computational numerical methods in an initial value problem solution ISSN 2316-9664 Volume 7,
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 13 04/2014 Sistemas de Equações Lineares Parte 3 MÉTODOS ITERATIVOS Cálculo Numérico 3/44 MOTIVAÇÃO Os métodos iterativos
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 13 04/2014 Sistemas de Equações Lineares Parte 3 MÉTODOS ITERATIVOS Cálculo Numérico 3/44 MOTIVAÇÃO Os métodos iterativos
Sistemas Lineares. Métodos Iterativos Estacionários
 -58 Sistemas Lineares Estacionários Lucia Catabriga e Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo -
-58 Sistemas Lineares Estacionários Lucia Catabriga e Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo -
x exp( t 2 )dt f(x) =
 INTERPOLAÇÃO POLINOMIAL 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia Aproximação
INTERPOLAÇÃO POLINOMIAL 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia Aproximação
SME602 - Cálculo Numérico - - Prof. Murilo F. Tomé. Solução Numérica de Sistema Lineares A = MÉTODOS DIRETOS. x y z
 SME602 - Cálculo Numérico - - Prof. Murilo F. Tomé Solução Numérica de Sistema Lineares NORMAS DE VETORES E MATRIZES 1. Dado o vetor v = (, 1, 8, 2) T, calcule v 1, v 2 e v. 2. Dada a matriz: A = 5 7 2
SME602 - Cálculo Numérico - - Prof. Murilo F. Tomé Solução Numérica de Sistema Lineares NORMAS DE VETORES E MATRIZES 1. Dado o vetor v = (, 1, 8, 2) T, calcule v 1, v 2 e v. 2. Dada a matriz: A = 5 7 2
Cálculo Numérico. Resumo e Exercícios P1
 Cálculo Numérico Resumo e Exercícios P1 Fórmulas e Resumo Teórico Parte 1 Aritmética de ponto flutuante Operar com o número de algarismos significativos exigido. Arredondar após cada conta. Método de escalonamento
Cálculo Numérico Resumo e Exercícios P1 Fórmulas e Resumo Teórico Parte 1 Aritmética de ponto flutuante Operar com o número de algarismos significativos exigido. Arredondar após cada conta. Método de escalonamento
INTRODUÇÃO AOS MÉTODOS NUMÉRICOS. Solução de Sistemas Lineares
 INTRODUÇÃO AOS MÉTODOS NUMÉRICOS Solução de Sistemas Lineares Introdução Uma variedade de problemas de engenharia pode ser resolvido através da análise linear; entre eles podemos citar: determinação do
INTRODUÇÃO AOS MÉTODOS NUMÉRICOS Solução de Sistemas Lineares Introdução Uma variedade de problemas de engenharia pode ser resolvido através da análise linear; entre eles podemos citar: determinação do
étodos uméricos ZEROS DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos ZEROS DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA
étodos uméricos ZEROS DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA
A = Utilizando ponto flutuante com 2 algarismos significativos, 2 = 0, x (0)
 MAP 22 - CÁLCULO NUMÉRICO (POLI) Lista de Exercícios sobre Sistemas Lineares : Utilizando o método de eliminação de Gauss, calcule o determinante e a seguir a inversa da matriz abaixo. Efetue todos os
MAP 22 - CÁLCULO NUMÉRICO (POLI) Lista de Exercícios sobre Sistemas Lineares : Utilizando o método de eliminação de Gauss, calcule o determinante e a seguir a inversa da matriz abaixo. Efetue todos os
6 MÉTODO DE ELEMENTOS FINITOS - MEF
 6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
Prof. MSc. David Roza José 1/35
 1/35 Métodos Iterativos Objetivos: Compreender a diferença entre os métodos de Gauss-Seidel e Jacobi; Saber analisar a dominância diagonal e entender o quê significa; Reconhecer como a relaxação pode ser
1/35 Métodos Iterativos Objetivos: Compreender a diferença entre os métodos de Gauss-Seidel e Jacobi; Saber analisar a dominância diagonal e entender o quê significa; Reconhecer como a relaxação pode ser
Setor de Tecnologia - TC Engenharia Ambiental Avaliação 1. Matemática Aplicada II
 Universidade Federal do Paraná Matemática Aplicada II Setor de Tecnologia - TC Engenharia Ambiental 2012-1 Curitiba, 02.05.2012 Avaliação 1 Matemática Aplicada II Tobias Bleninger Departamento de Engenharia
Universidade Federal do Paraná Matemática Aplicada II Setor de Tecnologia - TC Engenharia Ambiental 2012-1 Curitiba, 02.05.2012 Avaliação 1 Matemática Aplicada II Tobias Bleninger Departamento de Engenharia
SME300 - Cálculo Numérico - Turma Elétrica/Automação - Prof. Murilo F. Tomé. Lista 1: Solução Numérica de Sistema Lineares A = MÉTODOS DIRETOS.
 SME300 - Cálculo Numérico - Turma Elétrica/Automação - Prof. Murilo F. Tomé Lista 1: Solução Numérica de Sistema Lineares NORMAS DE VETORES E MATRIZES 1. Dado o vetor v = ( 3, 1, 8, 2) T, calcule v 1,
SME300 - Cálculo Numérico - Turma Elétrica/Automação - Prof. Murilo F. Tomé Lista 1: Solução Numérica de Sistema Lineares NORMAS DE VETORES E MATRIZES 1. Dado o vetor v = ( 3, 1, 8, 2) T, calcule v 1,
0.5 setgray0 0.5 setgray1. Mecânica dos Fluidos Computacional. Aula 5. Leandro Franco de Souza. Leandro Franco de Souza p.
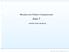 Leandro Franco de Souza lefraso@icmc.usp.br p. 1/1 0.5 setgray0 0.5 setgray1 Mecânica dos Fluidos Computacional Aula 5 Leandro Franco de Souza Leandro Franco de Souza lefraso@icmc.usp.br p. 2/1 Equações
Leandro Franco de Souza lefraso@icmc.usp.br p. 1/1 0.5 setgray0 0.5 setgray1 Mecânica dos Fluidos Computacional Aula 5 Leandro Franco de Souza Leandro Franco de Souza lefraso@icmc.usp.br p. 2/1 Equações
Comparação de Desempenho entre o Método dos Elementos de Contorno com Integração Direta e o Método dos Elementos Finitos em problemas de Poisson
 Trabalho apresentado no III CMAC - SE, Vitória-ES, 2015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Comparação de Desempenho entre o Método dos Elementos de Contorno
Trabalho apresentado no III CMAC - SE, Vitória-ES, 2015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Comparação de Desempenho entre o Método dos Elementos de Contorno
Introdução aos Métodos Numéricos
 Métodos Numéricos para Mecânica dos Fluidos Introdução aos Métodos Numéricos Introdução aos Métodos Numéricos Bibliografia: J. H. Ferziger and M. Peric, 'Computational Methods for Fluid Dynamics', Springer
Métodos Numéricos para Mecânica dos Fluidos Introdução aos Métodos Numéricos Introdução aos Métodos Numéricos Bibliografia: J. H. Ferziger and M. Peric, 'Computational Methods for Fluid Dynamics', Springer
Aula 5 O Método dos Volumes Finitos
 Universidade Federal do ABC Aula 5 O Método dos Volumes Finitos EN3224 Dinâmica de Fluidos Computacional Método dos volumes finitos (MVF) Origens: mecânica estrutural, cálculo das variações para condições
Universidade Federal do ABC Aula 5 O Método dos Volumes Finitos EN3224 Dinâmica de Fluidos Computacional Método dos volumes finitos (MVF) Origens: mecânica estrutural, cálculo das variações para condições
CCI-22 FORMALIZAÇÃO CCI-22 MODOS DE SE OBTER P N (X) Prof. Paulo André CCI - 22 MATEMÁTICA COMPUTACIONAL INTERPOLAÇÃO
 CCI - MATEMÁTICA COMPUTACIONAL INTERPOLAÇÃO Prof. Paulo André ttp://www.comp.ita.br/~pauloac pauloac@ita.br Sala 0 Prédio da Computação -Gregory DEFINIÇÃO Em matemática computacional, interpolar significa
CCI - MATEMÁTICA COMPUTACIONAL INTERPOLAÇÃO Prof. Paulo André ttp://www.comp.ita.br/~pauloac pauloac@ita.br Sala 0 Prédio da Computação -Gregory DEFINIÇÃO Em matemática computacional, interpolar significa
Uma equação linear com n variáveis tem a seguinte forma:
 Edgard Jamhour Uma equação linear com n variáveis tem a seguinte forma: a 1 x 1 + a 2 x 2 +... + a n x n = b onde a 1, a 2,..., a n e b são constantes reais. Um sistema de equações lineares é um conjunto
Edgard Jamhour Uma equação linear com n variáveis tem a seguinte forma: a 1 x 1 + a 2 x 2 +... + a n x n = b onde a 1, a 2,..., a n e b são constantes reais. Um sistema de equações lineares é um conjunto
Fundamentos IV. Sistemas Lineares. Gustavo Vinhal. August 18, Departamento de Computação
 Fundamentos IV Sistemas Lineares Gustavo Vinhal Departamento de Computação August 18, 2016 Métodos iterativos para a solução de sistema lineares Métodos iterativos Um sistema Ax = b pode ser resolvido
Fundamentos IV Sistemas Lineares Gustavo Vinhal Departamento de Computação August 18, 2016 Métodos iterativos para a solução de sistema lineares Métodos iterativos Um sistema Ax = b pode ser resolvido
A solução completa da equação de Poisson depende dos valores do potencial na fronteira do domínio em estudo. Os dois tipos mais comuns de
 4 Solução Numérica da Equação de Poisson Usando SPH 4.1 Equação de Poisson Seja Ω uma região em R 2 limitada por uma superfície fechada S = Ω. Nesta seção, é apresentado um método para resolver a equação
4 Solução Numérica da Equação de Poisson Usando SPH 4.1 Equação de Poisson Seja Ω uma região em R 2 limitada por uma superfície fechada S = Ω. Nesta seção, é apresentado um método para resolver a equação
AVALIAÇÃO DO ENRIQUECIMENTO POLINOMIAL NO MÉTODO DOS ELEMENTOS FINITOS GENERALIZADOS EM ELEMENTOS TRIANGULARES
 AVALIAÇÃO DO ENRIQUECIMENTO POLINOMIAL NO MÉTODO DOS ELEMENTOS FINITOS GENERALIZADOS EM ELEMENTOS TRIANGULARES Neimar A. da Silveira Filho niemarsilveira@ufmg.br Thaiane Simonetti de Oliveira thaianesimo@gmail.com
AVALIAÇÃO DO ENRIQUECIMENTO POLINOMIAL NO MÉTODO DOS ELEMENTOS FINITOS GENERALIZADOS EM ELEMENTOS TRIANGULARES Neimar A. da Silveira Filho niemarsilveira@ufmg.br Thaiane Simonetti de Oliveira thaianesimo@gmail.com
INSTITUTO SUPERIOR TÉCNICO Mestrado Integrado em Engenharia Física Tecnológica Ano Lectivo: 2007/2008 Semestre: 1 o
 INSTITUTO SUPERIOR TÉCNICO Mestrado Integrado em Engenharia Física Tecnológica Ano Lectivo: 27/28 Semestre: o MATEMÁTICA COMPUTACIONAL Exercícios [4 Sendo A M n (C) mostre que: (a) n A 2 A n A 2 ; (b)
INSTITUTO SUPERIOR TÉCNICO Mestrado Integrado em Engenharia Física Tecnológica Ano Lectivo: 27/28 Semestre: o MATEMÁTICA COMPUTACIONAL Exercícios [4 Sendo A M n (C) mostre que: (a) n A 2 A n A 2 ; (b)
Notas de Aula. Diferenciais Parciais Elípticas
 Notas de Aula Métodos Numéricos para Equações Diferenciais Parciais Elípticas Rodney Josué Biezuner Departamento de Matemática Instituto de Ciências Exatas ICEx) Universidade Federal de Minas Gerais UFMG)
Notas de Aula Métodos Numéricos para Equações Diferenciais Parciais Elípticas Rodney Josué Biezuner Departamento de Matemática Instituto de Ciências Exatas ICEx) Universidade Federal de Minas Gerais UFMG)
Sistemas de equações lineares
 DMPA IM UFRGS Cálculo Numérico Índice Sistema de Equações Lineares 1 Sistema de Equações Lineares 2 com pivoteamento parcial 3 Método de Jacobi Método Gauss-Seidel Sistema de Equações Lineares n equações
DMPA IM UFRGS Cálculo Numérico Índice Sistema de Equações Lineares 1 Sistema de Equações Lineares 2 com pivoteamento parcial 3 Método de Jacobi Método Gauss-Seidel Sistema de Equações Lineares n equações
Formulação de volumes finitos para as faces
 Formulação de volumes finitos para as faces Diego Fernando Moro Programa de Pós-Graduação em Engenharia Mecânica Universidade Federal do Paraná Curitiba-PR, Brasil email: difmoro@gmail.com, difmoro@ufpr.br
Formulação de volumes finitos para as faces Diego Fernando Moro Programa de Pós-Graduação em Engenharia Mecânica Universidade Federal do Paraná Curitiba-PR, Brasil email: difmoro@gmail.com, difmoro@ufpr.br
Introdução aos Métodos Numéricos
 Introdução aos Métodos Numéricos Instituto de Computação UFF Departamento de Ciência da Computação Otton Teixeira da Silveira Filho Conteúdo específico Sistemas de Equações Lineares. Métodos Iterativos
Introdução aos Métodos Numéricos Instituto de Computação UFF Departamento de Ciência da Computação Otton Teixeira da Silveira Filho Conteúdo específico Sistemas de Equações Lineares. Métodos Iterativos
A computação aplicada à resolução de sistemas lineares
 Universidade Federal de Campina Grande Centro de Engenharia Elétrica e Informática Departamento de Sistemas e Computação Programa de Educação Tutorial (PET) A computação aplicada à resolução de sistemas
Universidade Federal de Campina Grande Centro de Engenharia Elétrica e Informática Departamento de Sistemas e Computação Programa de Educação Tutorial (PET) A computação aplicada à resolução de sistemas
ESTATÍSTICA COMPUTACIONAL
 ESTATÍSTICA COMPUTACIONAL Ralph dos Santos Silva Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Introdução Solução de equações não lineares
ESTATÍSTICA COMPUTACIONAL Ralph dos Santos Silva Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Introdução Solução de equações não lineares
O teorema do ponto fixo de Banach e algumas aplicações
 O teorema do ponto fixo de Banach e algumas aplicações Andressa Fernanda Ost 1, André Vicente 2 1 Acadêmica do Curso de Matemática - Centro de Ciências Exatas e Tecnológicas - Universidade Estadual do
O teorema do ponto fixo de Banach e algumas aplicações Andressa Fernanda Ost 1, André Vicente 2 1 Acadêmica do Curso de Matemática - Centro de Ciências Exatas e Tecnológicas - Universidade Estadual do
Cálculo Numérico Algoritmos
 Cálculo Numérico Algoritmos Valdenir de Souza Junior Abril de 2007 Sumário 1 Introdução 1 2 Raízes de Equações 1 2.1 Método da Bisseção......................... 2 2.2 Método de Newton-Raphson.....................
Cálculo Numérico Algoritmos Valdenir de Souza Junior Abril de 2007 Sumário 1 Introdução 1 2 Raízes de Equações 1 2.1 Método da Bisseção......................... 2 2.2 Método de Newton-Raphson.....................
Métodos Numéricos C. A. Ismael F. Vaz 1. Escola de Engenharia Universidade do Minho Ano lectivo 2007/2008
 Métodos Numéricos C A. Ismael F. Vaz 1 1 Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho aivaz@dps.uminho.pt Ano lectivo 2007/2008 A. Ismael F. Vaz (UMinho) MN C 2007/2008
Métodos Numéricos C A. Ismael F. Vaz 1 1 Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho aivaz@dps.uminho.pt Ano lectivo 2007/2008 A. Ismael F. Vaz (UMinho) MN C 2007/2008
3 Implementação Computacional
 3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
Aula 4 Otimização e Discretização
 Universidade Federal do ABC Aula 4 Otimização e Discretização EN3224 Dinâmica de Fluidos Computacional Forma adimensional das equações Motivação: às vezes, as equações são normalizadas para: facilitar
Universidade Federal do ABC Aula 4 Otimização e Discretização EN3224 Dinâmica de Fluidos Computacional Forma adimensional das equações Motivação: às vezes, as equações são normalizadas para: facilitar
Trabalho Prático. CI316 Programação Paralela Prof. Daniel Weingaertner
 Trabalho Prático CI316 Programação Paralela Prof. Daniel Weingaertner Equações Diferencias Parciais Método de Jacobi Método de Gaus-Seidel Red-Black Gaus-Seidel Trabalho Prático Equações Diferenciais Parciais
Trabalho Prático CI316 Programação Paralela Prof. Daniel Weingaertner Equações Diferencias Parciais Método de Jacobi Método de Gaus-Seidel Red-Black Gaus-Seidel Trabalho Prático Equações Diferenciais Parciais
Plano de Ensino. Identificação. Câmpus de Bauru. Curso Licenciatura em Matemática. Ênfase. Disciplina A - Cálculo Numérico Computacional
 Curso 1503 - Licenciatura em Matemática Ênfase Identificação Disciplina 0006315A - Cálculo Numérico Computacional Docente(s) Antonio Roberto Balbo Unidade Faculdade de Ciências Departamento Departamento
Curso 1503 - Licenciatura em Matemática Ênfase Identificação Disciplina 0006315A - Cálculo Numérico Computacional Docente(s) Antonio Roberto Balbo Unidade Faculdade de Ciências Departamento Departamento
Matemática Computacional - Exercícios
 Matemática Computacional - Exercícios 1 o semestre de 2007/2008 - Engenharia Biológica Teoria de erros e Representação de números no computador Nos exercícios deste capítulo os números são representados
Matemática Computacional - Exercícios 1 o semestre de 2007/2008 - Engenharia Biológica Teoria de erros e Representação de números no computador Nos exercícios deste capítulo os números são representados
INSTITUTO SUPERIOR TÉCNICO Licenciatura em Engenharia Física Tecnológica Licenciatura em Engenharia e Gestão Industrial Ano Lectivo: 2002/
 INSTITUTO SUPERIOR TÉCNICO Licenciatura em Engenharia Física Tecnológica Licenciatura em Engenharia e Gestão Industrial Ano Lectivo: / ANÁLISE NUMÉRICA Exercícios Considere o sistema linear 6 x 5 y = a)
INSTITUTO SUPERIOR TÉCNICO Licenciatura em Engenharia Física Tecnológica Licenciatura em Engenharia e Gestão Industrial Ano Lectivo: / ANÁLISE NUMÉRICA Exercícios Considere o sistema linear 6 x 5 y = a)
TEA 751: Métodos Numéricos para Engenharia Ambiental RELATÓRIO II
 TEA 751: Métodos Numéricos para Engenharia Ambiental RELATÓRIO II discente: Sara Coelho da Silva docente: Cynara de Lourdes da Nóbrega Cunha PPGMNE: Programa de Pós Graduação em Métodos Numéricos, UFPR.
TEA 751: Métodos Numéricos para Engenharia Ambiental RELATÓRIO II discente: Sara Coelho da Silva docente: Cynara de Lourdes da Nóbrega Cunha PPGMNE: Programa de Pós Graduação em Métodos Numéricos, UFPR.
Figura : Monitoria. Monitoria Cálculo Numérico
 Monitoria Cálculo Numérico 207-02 NOME Email Dia / Horário Local Ana Sofia Nunez de Abreu nunez.asofia@gmail.com Sex. 0-2h D- Luiz Eduardo Xavier luizeduardosxavier@gmail.com Ter, 5-7h Lab Rafael Mendes
Monitoria Cálculo Numérico 207-02 NOME Email Dia / Horário Local Ana Sofia Nunez de Abreu nunez.asofia@gmail.com Sex. 0-2h D- Luiz Eduardo Xavier luizeduardosxavier@gmail.com Ter, 5-7h Lab Rafael Mendes
MAP Primeiro exercício programa Método de Diferenças Finitas para solução de problemas de contorno de equações diferenciais ordinárias
 MAP-2121 - Primeiro exercício programa - 2006 Método de Diferenças Finitas para solução de problemas de contorno de equações diferenciais ordinárias Instruções gerais - Os exercícios computacionais pedidos
MAP-2121 - Primeiro exercício programa - 2006 Método de Diferenças Finitas para solução de problemas de contorno de equações diferenciais ordinárias Instruções gerais - Os exercícios computacionais pedidos
Análise da estabilidade do método explícito para discretização de equações diferenciais parabólicas por meio de diferenças finitas
 Análise da estabilidade do método explícito para discretização de equações diferenciais parabólicas por meio de diferenças finitas Analysis of the stability of the explicit method for discretization of
Análise da estabilidade do método explícito para discretização de equações diferenciais parabólicas por meio de diferenças finitas Analysis of the stability of the explicit method for discretization of
étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno
 étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA
étodos uméricos SOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS ORDINÁRIOAS Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA
Métodos Numéricos I. A. Ismael F. Vaz. Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho
 Métodos Numéricos I A. Ismael F. Vaz Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho aivaz@dps.uminho.pt Engenharia Mecânica Ano lectivo 2007/2008 A. Ismael F. Vaz (UMinho)
Métodos Numéricos I A. Ismael F. Vaz Departamento de Produção e Sistemas Escola de Engenharia Universidade do Minho aivaz@dps.uminho.pt Engenharia Mecânica Ano lectivo 2007/2008 A. Ismael F. Vaz (UMinho)
SME0300 Cálculo Numérico Aula 11
 SME0300 Cálculo Numérico Aula 11 Maria Luísa Bambozzi de Oliveira marialuisa @ icmc. usp. br Sala: 3-241 Página: tidia-ae.usp.br 21 de setembro de 2015 Tópico Anterior Sistemas Lineares: Métodos Exatos:
SME0300 Cálculo Numérico Aula 11 Maria Luísa Bambozzi de Oliveira marialuisa @ icmc. usp. br Sala: 3-241 Página: tidia-ae.usp.br 21 de setembro de 2015 Tópico Anterior Sistemas Lineares: Métodos Exatos:
Universidade de Coimbra Departamento de Engenharia Electrotecnica e Computadores Matemática Computacional
 Ano Lectivo: 2007/2008 Sumários da turma Teórico-Prática [TP1]: Aula: 1 Data: 2008-02-12 Hora de Início: 15:00 Duração: 1h30m Apresentação da Unidade Curricular. Discussão de aspectos relacionados com
Ano Lectivo: 2007/2008 Sumários da turma Teórico-Prática [TP1]: Aula: 1 Data: 2008-02-12 Hora de Início: 15:00 Duração: 1h30m Apresentação da Unidade Curricular. Discussão de aspectos relacionados com
Conceitos fundamentais em uma dimensão Bases
 fundamentais em uma dimensão PME5425 Métodos de Elementos Finitos de Alta Ordem com Aplicações em Mecânica dos Fluidos e Transferência de Calor Prof. Programa de Pós-Graduação em Engenharia Mecânica Escola
fundamentais em uma dimensão PME5425 Métodos de Elementos Finitos de Alta Ordem com Aplicações em Mecânica dos Fluidos e Transferência de Calor Prof. Programa de Pós-Graduação em Engenharia Mecânica Escola
Matemática Computacional - Exercícios
 Matemática Computacional - Exercícios 2 o semestre de 2005/2006 - LEE, LEGI e LERCI Programação em Mathematica 1. Calcule no Mathematica e comente os resultados: (a) 7; (b) 7.0; (c) 14406; (d) cos π 6
Matemática Computacional - Exercícios 2 o semestre de 2005/2006 - LEE, LEGI e LERCI Programação em Mathematica 1. Calcule no Mathematica e comente os resultados: (a) 7; (b) 7.0; (c) 14406; (d) cos π 6
Plano de Ensino. Identificação. Câmpus de Bauru. Curso Engenharia de Produção. Ênfase. Disciplina EM1 - Cálculo Numérico Computacional
 Curso 4402 - Engenharia de Produção Ênfase Identificação Disciplina 0002029EM1 - Cálculo Numérico Computacional Docente(s) Adriana Cristina Cherri Nicola Unidade Faculdade de Ciências Departamento Departamento
Curso 4402 - Engenharia de Produção Ênfase Identificação Disciplina 0002029EM1 - Cálculo Numérico Computacional Docente(s) Adriana Cristina Cherri Nicola Unidade Faculdade de Ciências Departamento Departamento
étodos uméricos INTERPOLAÇÃO, EXTRAPOLAÇÃO, APROXIMAÇÃO E AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno
 étodos uméricos INTERPOLAÇÃO, EXTRAPOLAÇÃO, APROXIMAÇÃO E AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA
étodos uméricos INTERPOLAÇÃO, EXTRAPOLAÇÃO, APROXIMAÇÃO E AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA
Um modelo do Método dos Volumes Finitos com malha não estruturada
 Trabalho apresentado no III CMAC - SE, Vitória-ES, 015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Um modelo do Método dos Volumes Finitos com malha não estruturada
Trabalho apresentado no III CMAC - SE, Vitória-ES, 015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Um modelo do Método dos Volumes Finitos com malha não estruturada
SOLUÇÃO DE UM PROBLEMA UNIDIMENSIONAL DE CONDUÇÃO DE CALOR
 SOLUÇÃO DE UM ROBLEMA UNIDIMENSIONAL DE CONDUÇÃO DE CALOR Marcelo M. Galarça ós Graduação em Engenharia Mecânica Universidade Federal do Rio Grande do Sul ransferência de Calor e Mecânica dos Fluidos Computacional
SOLUÇÃO DE UM ROBLEMA UNIDIMENSIONAL DE CONDUÇÃO DE CALOR Marcelo M. Galarça ós Graduação em Engenharia Mecânica Universidade Federal do Rio Grande do Sul ransferência de Calor e Mecânica dos Fluidos Computacional
Cálculo Numérico. Aula 10 Sistemas de Equações Lineares / Parte 3 Jacobi & Gauss-Seidel. Prof. Guilherme Amorim
 Cálculo Numérico Aula 10 Sistemas de Equações Lineares / Parte 3 Jacobi & Gauss-Seidel Prof. Guilherme Amorim gbca@cin.ufpe.br 2014.1-15/05/2014 Aula passada... Método da Decomposição LU Seja o sistema
Cálculo Numérico Aula 10 Sistemas de Equações Lineares / Parte 3 Jacobi & Gauss-Seidel Prof. Guilherme Amorim gbca@cin.ufpe.br 2014.1-15/05/2014 Aula passada... Método da Decomposição LU Seja o sistema
Resolução de Sistemas Lineares. Ana Paula
 Resolução de Sistemas Lineares Sumário 1 Aula Anterior 2 Decomposição LU 3 Decomposição LU com Pivotamento 4 Revisão Aula Anterior Aula Anterior Aula Anterior Aula Anterior Eliminação de Gauss Transforma
Resolução de Sistemas Lineares Sumário 1 Aula Anterior 2 Decomposição LU 3 Decomposição LU com Pivotamento 4 Revisão Aula Anterior Aula Anterior Aula Anterior Aula Anterior Eliminação de Gauss Transforma
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de orena (EE) Universidade de São Paulo (USP) OM3 - Teoria da Elasticidade Aplicada Parte 4 - Análise Numérica de Tensões e Deformações
Modelagem Computacional. Parte 2 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 2 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 2 e 3] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 2 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 2 e 3] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Capítulo III: Sistemas de equações. III.1 - Condicionamento de sistemas lineares
 EXERCÍCIOS DE MATEMÁTICA COMPUTACIONAL Capítulo III: Sistemas de equações III1 - Condicionamento de sistemas lineares 1 Seja 1 0 0 10 6 e considere o sistema Ax = b, com b = 1 10 6 T, que tem por solução
EXERCÍCIOS DE MATEMÁTICA COMPUTACIONAL Capítulo III: Sistemas de equações III1 - Condicionamento de sistemas lineares 1 Seja 1 0 0 10 6 e considere o sistema Ax = b, com b = 1 10 6 T, que tem por solução
MÉTODO DE ELEMENTOS FINITOS (MEF) -UMA INTRODUÇÃO-
 MÉTODO DE ELEMENTOS FINITOS (MEF) -UMA INTRODUÇÃO- Curso de Transferência de Calor 1 - FEN03-5190 Prof. Gustavo R. Anjos gustavo.anjos@uerj.br 17 e 23 de junho de 2015 EXEMPLOS - VÍDEOS Escoamento de fluido
MÉTODO DE ELEMENTOS FINITOS (MEF) -UMA INTRODUÇÃO- Curso de Transferência de Calor 1 - FEN03-5190 Prof. Gustavo R. Anjos gustavo.anjos@uerj.br 17 e 23 de junho de 2015 EXEMPLOS - VÍDEOS Escoamento de fluido
Autovalores e Autovetores
 Algoritmos Numéricos II / Computação Científica Autovalores e Autovetores Lucia Catabriga 1 1 DI/UFES - Brazil Junho 2016 Introdução Ideia Básica Se multiplicarmos a matriz por um autovetor encontramos
Algoritmos Numéricos II / Computação Científica Autovalores e Autovetores Lucia Catabriga 1 1 DI/UFES - Brazil Junho 2016 Introdução Ideia Básica Se multiplicarmos a matriz por um autovetor encontramos
Gauss-Seidel para Solução de Sistemas com Matrizes Banda Usando Armazenamento Especial
 Universidade Federal do Espírito Santo Departamento de Informática Algoritmos Numéricos 2016/2 Profa. Claudine Badue Trabalho 1 Objetivos Gauss-Seidel para Solução de Sistemas com Matrizes Banda Usando
Universidade Federal do Espírito Santo Departamento de Informática Algoritmos Numéricos 2016/2 Profa. Claudine Badue Trabalho 1 Objetivos Gauss-Seidel para Solução de Sistemas com Matrizes Banda Usando
Efeito de hardware e software sobre o erro de arredondamento em CFD
 Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Efeito de hardware e software sobre o erro de arredondamento em CFD Diego Fernando Moro 1 Programa de Pós Graduação em
Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Efeito de hardware e software sobre o erro de arredondamento em CFD Diego Fernando Moro 1 Programa de Pós Graduação em
Uma breve introdução ao Curso de Computação Científica / Algoritmos Numéricos II
 Uma breve introdução ao Curso de Computação Científica / Algoritmos Numéricos II Lucia Catabriga luciac@inf.ufes.br March 28, 2017 Lucia Catabriga (UFES) ANII e CC DI/PPGI/PPGEM March 28, 2017 1 / 27 Contextualizando
Uma breve introdução ao Curso de Computação Científica / Algoritmos Numéricos II Lucia Catabriga luciac@inf.ufes.br March 28, 2017 Lucia Catabriga (UFES) ANII e CC DI/PPGI/PPGEM March 28, 2017 1 / 27 Contextualizando
O Método de Diferenças Finitas
 1-16 O Método de Diferenças Finitas Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo - UFES, Vitória, ES,
1-16 O Método de Diferenças Finitas Andréa Maria Pedrosa Valli Laboratório de Computação de Alto Desempenho (LCAD) Departamento de Informática Universidade Federal do Espírito Santo - UFES, Vitória, ES,
diferenças finitas. Centro de Ciências Exatas e Tecnológicas da Universidade Estadual do Oeste do Paraná - Cascavel - PR - Brasil
 Solução numérica do problema de interação fluido-estrutura de cavidades acústicas bidimensionais pelo método das diferenças finitas Suzana P. Martos 1, Bruno Belorte 2, Claúdia B. Rizzi 3, Rogério L. Rizzi
Solução numérica do problema de interação fluido-estrutura de cavidades acústicas bidimensionais pelo método das diferenças finitas Suzana P. Martos 1, Bruno Belorte 2, Claúdia B. Rizzi 3, Rogério L. Rizzi
