UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE TECNOLOGIA - ITEC JOÃO CARLOS RODRIGUES DE SOUZA
|
|
|
- Ana de Sintra Ferretti
- 8 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE TECNOLOGIA - ITEC PROGRAMA DE PÓS- GRADUAÇÃO EM ENGENHARIA ELÉTRICA MESTRADO PROFISSIONAL EM ENGENHARIA ELÉTRICA JOÃO CARLOS RODRIGUES DE SOUZA ANÁLISE DE EXPERIMENTOS APLICADA NA MAXIMIZAÇÃO DO RENDIMENTO DA RECICLAGEM DA BORRA DE SOLDA (LEAD FREE): UMA APLICAÇÃO DO PÓ DE SERRA COMO REDUTOR ORGÂNICO DISSERTAÇÃO DE MESTRADO BELÉM - PA 2011
2 i UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE TECNOLOGIA - ITEC PROGRAMA DE PÓS- GRADUAÇÃO EM ENGENHARIA ELÉTRICA MESTRADO PROFISSIONAL EM ENGENHARIA ELÉTRICA ANÁLISE DE EXPERIMENTOS APLICADA NA MAXIMIZAÇÃO DO RENDIMENTO DA RECICLAGEM DA BORRA DE SOLDA (LEAD FREE): UMA APLICAÇÃO DO PÓ DE SERRA COMO REDUTOR ORGÂNICO Dissertação de Mestrado apresentada ao Programa de Pós-Graduação em Engenharia Elétrica do Instituto de Tecnologia, ITEC, da Universidade Federal do Pará como parte dos requisitos necessários para obtenção do Título de Mestre em Engenharia Elétrica com ênfase em Processos Industriais. JOÃO CARLOS RODRIGUES DE SOUZA Orientador: Prof. Dr. José Antonio da Silva Souza - UFPA BELÉM - PA 2011 UNIVERSIDADE FEDERAL DO PARÁ
3 ii INSTITUTO DE TECNOLOGIA - ITEC PROGRAMA DE PÓS- GRADUAÇÃO EM ENGENHARIA ELÉTRICA MESTRADO PROFISSIONAL EM PROCESSOS INDUSTRIAIS JOÃO CARLOS RODRIGUES DE SOUZA TÍTULO: ANÁLISE DE EXPERIMENTOS APLICADA NA MAXIMIZAÇÃO DO RENDIMENTO DA RECICLAGEM DA BORRA DE SOLDA (LEAD FREE): UMA APLICAÇÃO DO PÓ DE SERRA COMO REDUTOR ORGÂNICO DEFESA DE MESTRADO Esta dissertação foi julgada e aprovada para a obtenção do título de Mestre em Engenharia Elétrica na área de Concentração em Processos Industriais do programa de Pós-Graduação Stricto Sensu em Engenharia Elétrica da Universidade Federal do Pará - ITEC UFPA. Belém - PA, / /2011 Prof. Dr. José Antonio da Silva Souza - UFPA Coordenador do CMPPI
4 iii BANCA EXAMINADORA Prof. Dr. José Antonio da Silva Souza - UFPA Orientador Prof. Dr. Célio Augusto Gomes de Souza - UFPA Prof. Dr. Lênio José Guerreiro de Faria - UFPA
5 iv Ficha catalográfica preparada pela Seção de Tratamento da Informação do Serviço de Biblioteca - ITEC / UFPA Instituto de Tecnologia/ Programa de Pós - graduação em Engenharia Elétrica. Mestrado em Processos Industriais Souza, João Carlos Rodrigues Análise de experimentos aplicada na maximização do rendimento da reciclagem da borra de solda (Lead Free): uma aplicação do pó de serra como redutor orgânico / João Carlos Rodrigues de Souza; orientador, José Antonio da Silva Souza. - Belém, 2011 Dissertação (Mestrado) Universidade Federal do Pará. Instituto de Tecnologia / Programa de Pós - graduação em Engenharia Elétrica. Mestrado em Processos Industriais, Experimentos industriais, 2. Análise fatorial, 3.Reciclagem da borra de solda. I. Título CDD XX Ed. XXX.XX
6 v DEDICATÓRIA À minha esposa Marta, companheira de todas as horas, e os meus filhos de ouro Junior e Gabriel, pela compreensão e pelo apoio incondicional que tiveram comigo nas horas mais difíceis dessa jornada, que não seria possível sem o amor de vocês. A vocês meu motivo de orgulho.
7 vi epígrafe O que ouço, esqueço. O que vejo, lembro. Mas o que faço, aprendo. Albert Einstein
8 vii AGRADECIMENTOS Gostaria de agradecer a todos aqueles que de alguma forma contribuíram com a evolução dessa dissertação e que, portanto, merecem meu profundo agradecimento. A Profª. Dra. Marlene Araújo de Faria pelo incentivo e apoio que foram essenciais para estruturar a dissertação do mestrado. Obrigado pelas ligações nos momentos mais difíceis da jornada escolar. Ao prof. Dr. Tavares demonstrando que Controle e Automação de Processos entre outras coisas pode ser implementado com Lógica Fuzzy, e visitou nossa empresa onde foi implantado a reciclagem da borra de solda. Ao prof. Dr. Lênio que me fez despertar para o Planejamento Experimentos e Otimização de Processos. de Meu agradecimento especial ao Professor Doutor José Antonio da Silva Souza, por sua contribuição nesse trabalho. Ao Eng. Jandecy Cabral Leite pela disposição de trazer meios de capacitação educacional para Manaus. Ao especialista Jorge Moriya grande incentivador do uso do pó de serra como redutor orgânico. Aos professores membros da banca de avaliação, pelas críticas construtivas, durante a qualificação, que foram fundamentais no realinhamento do tema. Aos diversos profissionais da Empresa Samsung (Marcos Fernandes, Roberto, Mauro, Daniel, Rui Procópio, Jonathas e David que possibilitaram que esse processo de Reciclagem da borra de solda fosse implementado com sucesso. Aos alunos do Mestrado em Processos Indústrias, pela amizade, trocas de idéias para realização da dissertação. A UFPA/ITEGAM, ao Departamento de pósgraduação, pelo apoio administrativo para que o curso pudesse ter sido realizado da melhor forma possível.
9 viii RESUMO Experimentos são conduzidos por empresas industriais, a fim de melhorar a eficiência e produtividade de produtos e processos de fabricação. O objetivo desta dissertação foi analisar e empregar as técnicas de planejamento e análise de experimentos na melhoria do desempenho do processo de reciclagem da borra de solda, aplicando um redutor orgânico para a remoção do óxido da borra de solda, utilizado por uma indústria do Pólo Industrial de Manaus (PIM) fabricante de produtos eletrônicos, que utiliza solda Lead Free (livre de chumbo) na soldagem dos componentes. A metodologia utilizada foi a pesquisa experimental para ajudar a identificar os parâmetros relevantes do processo de reciclagem da borra de solda, que são: redutor orgânico (pó de serra) e temperatura do tanque. Assim, com este estudo, avaliou-se o processo de implantação da técnica de análise de experimentos na maximização da reciclagem da borra de solda. Este trabalho buscou também, mostrar a necessidade da participação das empresas na preservação do meio ambiente, contribuindo com atividades destinadas a satisfazer as necessidades humanas, sem comprometer a natureza. Conceitos como de desenvolvimento sustentável, pode também atender aos objetivos econômicos. Com o modelo obtido, percebeu-se que, de uma forma geral, os parâmetros de entrada apresentam, isoladamente ou interados, influência significativa na resposta, possibilitando a otimização do processo como um todo, levando-se em consideração aspectos técnicos e resultados financeiros muitos significativos. Palavras- chave: experimentos industriais, análise fatorial, reciclagem da borra de solda. * pó de serra = serragem de madeira.
10 ix ABSTRACT Experiments are conducted by industrial companies in order to improve efficiency and productivity of products and manufacturing processes. The goal of this dissertation is to analyze and employ the techniques of planning and analysis of experiments in improving the performance of the recycling process of solder dross, applying a reducer for removing organic oxide dross solder, used by an industry the Industrial Pole Manaus (PIM) electronics manufacturer, which uses lead free solder soldering of components. The methodology used is experimental research to help identify the relevant parameters of the process of recycling solder dross, which are: reducing organic (sawdust) and temperature of the tank. So with this study, we evaluate the implementation process of technical analysis of experiments in maximizing recycling solder dross. This study also seeks to show the need for participation of companies in preservation of the environment, helping with activities designed to meet human needs without compromising nature. Concepts such as sustainable development, may also meet economic goals. With the model obtained, we noticed that, in general, the input parameters presented in isolation or interest, significant influence on the response, enabling the optimization of the process as a whole, taking into account technical and financial results for many significant Keywords: industrial experiments, factor analysis, solder dross recycling.
11 x SUMÁRIO 1. INTRODUÇÃO CONTEXTUALIZAÇÃO OBJETIVO GERAL DO TRABALHO JUSTIFICATIVAS DO TRABALHO DESENVOLVIMENTO DO TRABALHO E METODOLOGIA DE PESQUISA ESTRUTURA DO TRABALHO TÉCNICAS DE PLANEJAMENTO E ANÁLISE DE EXPERIMENTOS TÉCNICAS DE PLANEJAMENTO NO DESENVOLVIMENTO DE PROJETOS PRINCÍPIOS BÁSICOS DE PLANEJAMENTO E ANÁLISE DE EXPERIMENTOS CONCEITOS GERAIS DE EXPERIMENTAÇÃO PROCESSO PARA CONDUZIR OS EXPERIMENTOS TÉCNICAS DE PLANEJAMENTO E ANÁLISE DE EXPERIMENTOS PLANEJAMENTO FATORIAL PLANEJAMENTO FATORIAL 2 K ANÁLISE DE VARIÂNCIA DOS EFEITOS DO EXPERIMENTO FATORIAL 2 K PLANEJAMENTO FATORIAL FRACIONADO 2 K-P METODOLOGIA DE SUPERFÍCIE DE RESPOSTA EXPERIMENTO FATORIAL 2 K PARA AJUSTAR A SUPERFÍCIE DE RESPOSTA
12 xi ANÁLISE DE VARIÂNCIA DE SUPERFÍCIE DE RESPOSTA: EXPERIMENTO 2 K EXPERIMENTOS INDUSTRIAIS ESTUDO DE UM PROCESSO DE MANUFATURA INDUSTRIAL EMPRESA ESTUDADA PROCESSOS DE SOLDAGEM USANDO SOLDA LEAD FREE DEFINIÇÕES DO OBJETO DE ESTUDO COMO SURGE A OXIDAÇÃO DA SOLDA NO PROCESSO DE SOLDAGEM INFLUÊNCIA DA OXIDAÇÃO EM SOLDAGEM DE PLACAS SOLUÇÃO PARA O PROBLEMA DA GERAÇÃO DA BORRA PLANEJAMENTO DE EXPERIMENTOS SELEÇÃO DOS FATORES DE CONTROLE E OS NÍVEIS DO PROCESSO SELEÇÃO DAS VARIÁVEIS DE SAÍDA DO PROCESSO REALIZAÇÃO DO EXPERIMENTO PLANEJAMENTO MATRIZ DE PLANEJAMENTO EXECUÇÃO PROCESSAMENTO INTERPRETAÇÃO DOS GRÁFICOS DE EFEITOS RESULTADOS RESULTADOS OBTIDO PARA A VARIÁVEL DE SAÍDA (SOLDA) MATRIZ DE EXPERIMENTO COM A (M.S.R) ANÁLISE DE RESÍDUOS... 99
13 xii RESULTADOS DA RECICLAGEM DA BORRA DE SOLDA EM CONCLUSÃO SUGESTÕES DE TRABALHOS FUTUROS ANEXOS REFERÊNCIAS
14 xiii LISTA DE FIGURAS FIGURA 2.1 MODELO GERAL DE UM SISTEMA DE TRANSFORMAÇÃO FIGURA 2.2 PLANO PARA CONDUZIR EXPERIMENTOS FIGURA 2.3 GRÁFICO DE EFEITOS PRINCIPAIS, PLANEJAMENTO FATORIAL FIGURA 2.4 GRÁFICOS DE EFEITOS DE INTERAÇÃO FIGURA 2.5 REGIÕES DE REJEIÇÃO E NÃO REJEIÇÃO PARA UMA DISTRIBUIÇÃO F FIGURA 2.6 SUPERFÍCIE DE RESPOSTA TRIDIMENSIONAL PLANA FIGURA 2.7 SUPERFÍCIE DE RESPOSTA TRIDIMENSIONAL NÃO PLANA61 FIGURA 2.8 PLANEJAMENTO FATORIAL 2 2, COM PONTOS CENTRAIS FIGURA 2.9 REPRESENTAÇÃO GRÁFICA DO PLANEJAMENTO COMPOSTO CENTRAL FIGURA 3.1 ETAPAS DO PROCESSO DE SOLDAGEM POR MÁQUINA...75 FIGURA 3.2 MÁQUINA DE SOLDAGEM POR ONDA (SOLDA LEAD FREE)72 FIGURA 3.3 SISTEMA DE EXAUSTÃO DA ÁREA RECICLAGEM FIGURA 3.4 TANQUE DE RECICLAGEM DA BORRA DE SOLDA FIGURA 3.5 PÓ DE SERRA USADO NA RECICLAGEM DA BORRA FIGURA 3.6 CONTROLADOR DE TEMPERATURA FIGURA 3.7 LINGOTE DE SOLDA FIGURA 3.8 PROBALIDADE NORMAL DOS RESIDUOS (MINITAB) FIGURA 3.9 QUADRO COM AS MÉDIAS DAS OBSERVAÇOES...87 FIGURA 3.10 PROBALIDADE NORMAL DOS EFEITOS (MINITAB) FIGURA 3.11 DIAGRAMA DE PARETO (MINITAB) FIGURA 3.12 EFEITOS PRINCIPAIS (MINITAB)... 94
15 xiv FIGURA 3.13 EFEITOS DE INTERAÇÃO (MINITAB) FIGURA 3.14 GRÁFICO DE CONTORNO DA SOLDA (MINITAB) FIGURA 3.15 GRÁFICO DE SUPERFÍCIE DA SOLDA (MINITAB) FIGURA 3.16 GRÁFICO DE RESÍDUOS (MINITAB) FIGURA 3.17 RESULTADO DA BORRA DE SOLDA (SEM) FIGURA 3.18 RESULTADO DA BORRA DE SOLDA (COM) FIGURA 3.19 RESULTADO DA BORRA DE SOLDA (SEM) FIGURA 3.20 RECICLAGEM DA BORRA AUTOMATIZADA FIGURA 3.21 MISTURA DA BORRA AUTOMATIZADA
16 xv LISTA DE TABELAS TABELA 2.1 MATRIZ DE PLANEJAMENTO TABELA 3.1 PLANEJAMENTO DE EXPERIMENTO
17 xvi LISTA DE QUADROS QUADRO 2.1 VANTAGENS E LIMITAÇÕES DO ROTEIRO EXPERIMENTAL...38 QUADRO 2.2 EXPERIMENTO FATORIAL DE DOIS FATORES, CASO GERAL.40 QUADRO 2.3 EXPERIMENTO FATORIAL QUADRO 2.4 ANÁLISE DE VARIÂNCIA DE SUPERFÍCIE DE RESPOSTA, FATORIAL QUADRO 3.1 FATORES COM DOIS NÍVEIS...84 QUADRO 3.2 PLANEJAMENTO DE EXPERIMENTO QUADRO 3.3 ANÁLISE DE VARIANCIA DA RESPOSTA SOLDA...90 QUADRO 3.4 COEFICIENTES ESTIMADOS DA RESPOSTA SOLDA...90 QUADRO 3.5 EFEITOS ESTIMADOS DA RESPOSTA SOLDA...93 QUADRO 3.6 RESULTADOS DO EXPERIMENTO FATORAL CENTRAL...96 QUADRO 3.7 COEFICIENTES DA EQUAÇÃO QUADRO 3.8 COEFICIENTES DE REGRESSÃO E DESVIO QUADRO 3.9 RESUMO DA RECICLAGEM FEV-JUN QUADRO 3.10 RESUMO DA RECICLAGEM JUN-DEZ
18 xvii LISTA DE ABREVIATURAS E SIGLAS ANOVA Analysis of variance DOE - Design of Experiments equação - Equação gl. - Graus de liberdade PIM Pólo Industrial de Manaus MMA - Ministério do Meio Ambiente MSR - Metodologia de Superfície de Resposta MS - Quadrado médio SS - Soma de quadrados SQ - Soma quadrática das respostas Sn - Estanho Pb - Chumbo
19 xviii LISTA DE SÍMBOLOS ε - erro experimental μ - média geral α - nível de significância α1 - ponto axial do experimento C - graus Celsius a - níveis do fator A b - níveis do fator B y f - média das respostas do experimento fatorial F0 - Estatística estimada com os experimentos industriais g - grama H1 - Hipótese alternativa Ho - Hipótese nula k - número de fatores Kg - quilograma n - número de réplicas nc - número de pontos centrais nf - número de pontos do experimento fatorial utilizado T - soma total de observações xi - fatores experimentais yi - total das observações no i-ésimo nível de um fator くi - coeficientes do polinômio algébrico さ - superfície de resposta
20 19 CAPÍTULO 1 INTRODUÇÃO 1.1 Contextualização O Pólo Industrial de Manaus (PIM) comporta mais de 500 indústrias de alta tecnologia gerando mais de meio milhão de empregos, diretos e indiretos. Prevalecem as de produtos eletrônicos. Uma grande parcela dos componentes eletrônicos são soldados com pasta de solda (processo de refusão) e solda em formato de fio ou barra. Esta liga de solda pode ser Lead Free (livre de chumbo) ou Tin-Lead (Estanho e chumbo Sn/Pb). Ainda, no processo de soldagem que utiliza máquinas de solda por onda, existe a necessidade da limpeza e manutenção periódica dos tanques de solda, através da retirada dos óxidos (borra de solda). Diante do exposto observa-se, que o uso de uma liga Lead Free ou Tin-Lead, para a soldagem dos componentes, gera problemas durante o processo de fabricação na empresa e também após o descarte dos aparelhos em locais inadequados. A problemática dos resíduos torna-se tanto mais complexa quanto maior for o volume de descarte produzido. Através da aplicação de técnicas de tratamento, obtém-se uma redução do volume produzido. Dentre essas técnicas destaca-se a reciclagem, por propiciar diversos benefícios ambientais, sociais e econômicos. A necessidade de se preservar o meio ambiente e maximizar o rendimento da reciclagem dos materiais utilizados atualmente, fazem com que novas tecnologias sejam constantemente desenvolvidas para este fim. No que se refere à indústria eletroeletrônica, além das dificuldades pelo uso de diferentes materiais, tecnologias de fabricação e reparo, obsolescência dos equipamentos entre outros, as dificuldades de recuperar, reaproveitar ou mesmo reciclar produtos avariados ou com tecnologia ultrapassada vêm se dificultando e também se tornando inviável. Além da preocupação com o meio ambiente as empresa precisam de melhorias contínuas em seus processos produtivos, tanto em capacitação de seus
21 20 colaboradores quanto em inovação tecnológica como técnicas de planejamento e análise de experimentos com ajuda de ferramentas computacionais, ex: Minitab. Os conceitos estatísticos assumiram um papel importante nas empresas. Segundo CHEW (1957), estatística é a arte de adquirir conhecimento através da coleta, análise e interpretação de informações. Nas empresas essa ciência é transformada em ferramentas de qualidade (Seis Sigma, Projeto de Experimentos - Design of Experiment, Analise de Variância - ANOVA, Controle Estatístico do Processo - CEP, que podem contribuir na melhoria contínua dos processos produtivos de fabricação e produtos. Nessa conjuntura, o projeto de experimentos apresenta-se como uma das formas para se conseguir as características de competitividade. 1.2 Objetivo geral do trabalho O propósito principal deste trabalho é desenvolver e aperfeiçoar um processo de reciclagem de borra de solda Lead Free que atenda os requisitos de legislação ambiental, custos e qualidade da soda reciclada. Como objetivos específicos, este trabalho buscou: Estudar e compreender os processos produtivos que utilizam solda Lead Free para soldagem dos componentes na placa de circuito impresso dos produtos eletroeletrônicos; Identificar quais são as variáveis no processo de reciclagem que influenciam positivamente para os melhores valores de ajuste desses parâmetros para maximizar o rendimento do processo de reciclagem; Aplicar as técnicas de planejamento e análise de experimentos no processo de reciclagem;
22 21 Avaliar os resultados da solda reciclada em termos de qualidade e retorno financeiro; Contribuir com o processo de reciclagem que usam redutores orgânicos não agressivos ao meio ambiente. 1.3 Justificativa do trabalho Conforme informações extra-oficiais da empresa fabricante de liga de solda, Cookson Electronics o consumo mensal de liga de solda no PIM é de aproximadamente trinta e cinco toneladas, sendo 70% (24,5 toneladas) solda Lead Free e 30% (10,5 toneladas) de liga Tin-Lead. Deste modo, o estudo e aplicação das técnicas de planejamento e análise de experimento no aperfeiçoamento de um processo de reciclagem de borra de solda Lead Free, tornam-se significantes porque a empresa alcançará redução de seus custos de produção. Com isso, ela assegura vantagens competitivas no seu custo industrial, uma vez que a solda Lead Free é um dos insumos mais caros usados na manufatura dos produtos eletroeletrônicos. Ainda, com o projeto contribuise no processo de divulgação das técnicas de planejamento e análise de experimentos nas indústrias do PIM. De acordo com as pesquisas realizadas por KRUGLIANSKAS (1995), as técnicas experimentais são pouco disseminadas nas empresas brasileiras. O trabalho demonstra que apesar do avanço das metodologias de gestão e de melhorias no processo produtivo usadas para incrementar o desempenho operacional e administrativo das organizações, existem deficiências técnicas específicas relacionadas ao desenvolvimento de projetos de produtos e processos de fabricação. De acordo com o autor essas deficiências ocorrem pela falta de conhecimento estatístico, que comumente as chefias, funcionários e engenheiros das empresas enfrentam ao usar ferramentas estatísticas. Quando os dados dos experimentos são analisados estatisticamente, garante-se que o produto será projetado com robustez às variações decorrentes do
23 22 próprio processo de fabricação, meio ambiente e usuário. Além disso, a análise estatística é importante porque uma pequena diferença entre as especificações técnicas de um produto ou nos níveis de ajustagem dos fatores de controle de um processo de fabricação pode significar um número maior de defeitos ou resultados mais satisfatórios podem ser alcançados pelas empresas. 1.4 Desenvolvimento do trabalho e metodologia de pesquisa As teorias e técnicas sobre a metodologia da pesquisa científica conceituam método como o conjunto das atividades sistemáticas e racionais que, com maior segurança e economia, permitem alcançar os objetivos, conhecimentos válidos e verdadeiros, traçando desta forma o caminho a ser seguido, detectando erros e auxiliando as decisões (VERGARA 2004). Segundo Vergara (2004), a metodologia compreende as concepções teóricas de abordagem e o conjunto de técnicas que possibilitam o entendimento, aliados ao potencial do pesquisador. De acordo com Gil (2002), para se atingir os objetivos pretendidos com a investigação são necessários alguns passos: formulação do problema; definição das hipóteses; definição do tipo de pesquisa; coleta de dados; análise dos resultados; revisão final e redação. O conhecimento científico, segundo Togneti (2006), é o resultado da investigação científica, que surge da necessidade de encontrar soluções aos problemas de ordem prática da vida diária e em fornecer explicações sistemáticas capazes de serem testadas e criticadas por meio de provas empíricas e discussões intersubjetivas. Lakatos e Marconi (1995) definem a metodologia científica como uma série de atividades sistemáticas e racionais que busca confiabilidade na solução de problemas e, que não existe ciência sem o emprego deste tipo de modelo. A aplicação da metodologia científica engloba métodos e técnicas de pesquisa como elementos essenciais na aplicação do modelo estudado. Para Lima (2007), os métodos de pesquisa são subdivididos em métodos amplos (trata de questões genéricas e abstratas) e métodos de procedimentos (contém estratégias e
24 23 abordagens de pesquisa). Para se atingir os objetivos pretendidos com a investigação, são necessários à tipificação da pesquisa de acordo com a abordagem quantitativa ou qualitativa. A abordagem quantitativa, também denominada de pesquisa empírica, parte da formulação dedutiva de uma ou mais hipóteses através de pesquisa teórica inicial, confirmando, ou não, estas hipóteses, através de observação empírica. O conhecimento empírico é um conhecimento que se adquire independentemente de estudos, de pesquisas, de reflexões ou de aplicações de método. Esse geralmente é conseguido no percurso da vida, no cotidiano e, muitas vezes, ao acaso, fundamentado apenas em experiências vivenciadas ou transmitidas de pessoas para outras pessoas, fazendo parte das antigas tradições. Esse conhecimento também pode derivar das experiências casuais por meio de erros e acertos, sem a fundamentação dos postulados metodológicos. O primeiro nível dos contatos entre o intelecto e o mundo sensível se faz sentir pelo conhecimento empírico, pois ele se contenta com as imagens superficiais das coisas, com a visão ingênua do contexto exterior, da realidade objetiva. Esse conhecimento, por sua característica, não estabelece relações significativas de suas interpretações, proporcionando uma imagem fragmentária da realidade. As declarações do conhecimento empírico referem-se à vivência imediata sobre os objetos ou fatos observados, e possui grandes limitações. Por ser um conhecimento do dia-a-dia e preso a convicções pessoais, passa a ser, muitas vezes, incoerente e até impreciso. Outras vezes produz crenças arbitrárias com inúmeras interpretações para a complexidade de fatos, o que é respaldado por Koche, (1997) Os trabalhos realizados por HOPPEN et al. (1996), TRIVIÑOS (1992), DANE (1990) e GIL (1988) demonstram que todas as pesquisas ou trabalhos científicos podem ser classificados de acordo com os objetivos propostos, para encontrar a resposta ou a solução de um problema. Em geral, esses autores descrevem três grupos de estudo, exploratórios, descritivos e explicativos (experimentais). Entre os grupos desses estudos, o explicativo é o processo formal que melhor define o método científico utilizado no presente trabalho. Os estudos explicativos são utilizados para identificar os fatores que contribuem ou influenciam a ocorrência de um fenômeno, ou também para
25 24 determinar através da razão, o fundamento das coisas (GIL, 1988). Nesses estudos, vários métodos são utilizados como meio científico de validar ou rejeitar as hipóteses formuladas. Na área de ciências sociais são utilizados os métodos observacional e quase-experimental. Enquanto, que nas áreas de ciências naturais é utilizado o método experimental. Dentro do estudo explicativo o projeto é classificado como uma pesquisa experimental, que consiste...em determinar um objeto de estudo, selecionar as variáveis que seriam capazes de influenciá-lo, definir as formas de controle e de observação dos efeitos que a variável produz no objeto (GIL, 1988). A técnica de coleta das informações utilizada é denominada de Projetos fatoriais com duas ou mais variáveis independentes (REY, 1993; DANE, 1990). Neste caso, experimentos são realizados, para determinar os efeitos principais e as eventuais interações entre as variáveis ou fatores de controle, no meio natural ou no campo de experimentação (experimentos realizados nas próprias empresas). Nesta dissertação todas as etapas desenvolvidas, se enquadram à metodologia de pesquisa experimental (Projeto Fatoriais) descrita na literatura por REY (1993); HOPPEN et al. (1996); DANE (1990) e GIL (1988) e pelos autores ANTONY et al. (1998); WERKEMA & AGUIAR (1996); TAGUCHI (1993) e MONTGOMERY (1991), que estudam as técnicas de planejamento e análise de experimentos. 1.5 Estrutura do trabalho O presente trabalho está estruturado em quatro (4) capítulos. Os três (3) capítulos subseqüentes ao primeiro delineiam o seguinte: O capítulo 2 oferece uma revisão bibliográfica dos conceitos das técnicas de planejamento e análise de experimentos utilizados para o desenvolvimento desta
26 25 dissertação. Bem como, apresenta a metodologia empregada para realizar os experimentos industriais. O capítulo 3 apresenta o planejamento e a análise estatística dos experimentos industriais realizados em uma empresa do PIM. Ao mesmo tempo, são apresentados os processos produtivos de soldagem de placas de circuito impresso e o processos de transformação da borra de solda em solda novamente. O capítulo 4 finaliza a dissertação com uma discussão geral sobre as vantagens e restrições práticas do projeto, bem como oferece algumas sugestões de trabalhos futuros.
27 26 2 TÉCNICAS DE PLANEJAMENTO E ANÁLISE DE EXPERIMENTOS 2.1 Técnicas de planejamento no desenvolvimento de projetos O planejamento de experimentos é creditado a Ronald A. Fisher, que foi responsável durante anos pela estatística e análise de dados na Estação Agrícola Experimental em Londres - Inglaterra. Fisher desenvolveu e usou pela primeira vez a técnica de ANOVA (Analysis of variance) como ferramenta primária para a análise estatística do projeto experimental. De acordo com Montgomery (1991), Fisher foi o inovador da utilização de métodos estatísticos no projeto experimental. Basicamente, a experimentação tem como abordagem principal a quantitativa (Nakano e Fleury, 1996). Apesar de ter suas primeiras publicações na década de 30 e de ser ainda pouco conhecida, vem despertando um grande interesse no meio acadêmico e produtivo, após as idéias apresentadas pelo Dr. Tagushi nos anos 80. Em aplicações na área industrial, destacamos Box e Hunter (1978), Box e Draper (1987) e Mason et al (1989). Observam-se ainda muitos trabalhos que se referem a aplicações na indústria ou não, como por exemplo, Ramirez et al (2001), na área biológica. Na área industrial, podem-se citar diversos, como o de Câmara (1998), voltado para a área química, Antony (2000), com ênfase na melhoria da capabilidade de processos, Albin (2001), na indústria eletrônica, Goodman e Wyld (2001), na indústria mecânica, Galdámez (2002), na área fabril de plásticos. Antony et al (1998) citam o Design of Experiment (DOE) como uma das técnicas estatísticas mais avançadas para melhoria dos processos fabris. Em novas metodologias de melhoria da qualidade, como a Seis Sigmas, a técnica é de fundamental importância para diminuição da dispersão dos processos, conforme descrevem Ingle e Roe (2001). Um das dificuldades mais comuns que um experimentador se depara é a determinação da influência de uma ou mais variáveis de entrada de um processo, que influenciam a variável de saída. Estatisticamente há o interesse de descobrir como a resposta é influenciada por fatores chamados de entrada. O objetivo do
28 27 pesquisador que realiza os experimentos é descobrir esta função, ou pelo menos obter uma aproximação satisfatória para ela. O experimento planejado é um teste ou uma série de testes nos quais se induzem mudanças ou estímulos nas variáveis de entrada (inputs) do processo ou sistema, de tal maneira que seja possível observar e identificar os efeitos nas respostas ou nas variáveis de saída (outputs). O processo ou sistema de transformação é representado pela combinação de máquinas, métodos, pessoas e outros recursos que transformam uma entrada em produtos acabados ou semiacabados, com características ou parâmetros específicos, conforme Figura 2.1. FIGURA MODELO GERAL DE UM SISTEMA DE TRANSFORMAÇÃO Fonte: MONTGOMERY (1991). No âmbito industrial, ordinariamente se objetiva extrair o máximo de informações sobre a influência dos fatores de entrada, que são as variáveis controladas do processo, sobre os fatores de saída (respostas) ou variáveis de interesse, com o menor número possível de observações, visando um menor custo e maior rapidez. Conforme MONTGOMERY (1991), as técnicas de planejamento e análise de experimentos são empregadas essencialmente para aprimorar as características de qualidade dos produtos ou processos de fabricação, reduzir o número de testes e aperfeiçoar o uso de recursos da empresa (matéria prima, componentes, tempo dos
29 28 funcionários, disponibilidade de equipamentos, etc). BUTTON (2001), descreve que esse objetivo geral pode ser dividido em outros objetivos secundários: identificar as variáveis (fatores de controle) do processo que mais influem nos parâmetros de resposta de interesse; atribuir valores às variáveis influentes do processo de modo que a variabilidade da resposta de interesse seja mínima ou que o valor do resultado seja próximo do valor nominal; aplicar valores às variáveis influentes do processo de modo que o efeito das variáveis não controláveis seja reduzido. Conforme SLACK et al. (1997), o projeto de um produto envolve cinco etapas: geração do conceito, triagem, projeto preliminar, avaliação/melhoria e prototipagem/projeto final. Na etapa de geração do conceito, as idéias oriundas de várias fontes (consumidores, concorrência, vendas, departamento de pesquisa e desenvolvimento - P&D, etc.) são transformadas em conceitos. Segundo os autores, conceitos são diferentes de idéias pelo fato de serem declarações transparentes que englobam a idéia e também indicam sua forma, função, objetivo e benefício globais. Na segunda etapa, são verificadas a viabilidade, a aceitabilidade e a vulnerabilidade do conceito. Esses pontos, dependendo da organização, podem ser avaliados por várias funções, tais como marketing, produção e finanças. O projeto preliminar que corresponde à terceira etapa apresenta a especificação dos produtos e processos de fabricação. Na etapa de avaliação e melhoria, o projeto preliminar sofre várias considerações no intuito de se avaliar as melhorias que podem ser feitas antes do lançamento e produção em massa. Finalmente na última etapa, o projeto melhorado é transformado num protótipo passível de teste para então ser finalizado. Os protótipos são produzidos e testados para avaliação do processo produtivo e do produto final. Nesta etapa são realizados exaustivos testes no departamento de Qualidade da empresa objetivando a validação do produto. As etapas do projeto do produto expostas por SLACK et al. (1997), são também economias de estágios de desenvolvimentos de produtos e envolvem as seguintes atividades: definição dos objetivos dos produtos, desenvolvimento do
30 29 produto, projeto do processo de fabricação, a produção, a comercialização (vendas) e o serviço de garantia pós-venda (TAGUCHI, 1993). As técnicas de planejamento de experimentos podem ser utilizadas nas etapas de projeto preliminar, projeto do produto e processo de fabricação e na etapa de avaliação e melhoria. Nessas fases, muitas vezes, torna-se necessário analisar a influência de um ou mais fatores. Quando for avaliado apenas o efeito de um fator nas respostas do produto ou processo de fabricação, recomenda-se utilizar a técnica de planejamento de experimentos completamente aleatorizados ou a técnica de planejamento de experimentos em blocos aleatorizados, descritas por OLIVEIRA (1999), WERKEMA & AGUIAR (1996), MONTGOMERY (1991) e JURAN et al.(1951). Quando se torna importante investigar o efeito provocado nas respostas dos experimentos por dois ou mais fatores de controle e, cada um deles com dois ou mais níveis de regulagens, JURAN et al. (1951) e MONTGOMERY (1991) recomendam o uso de técnicas clássicas de planejamento, como por exemplo: técnica de planejamento fatorial completo, fatorial fracionado ou experimentos com pontos centrais. Outra metodologia que é bastante aplicada na indústria é o método Taguchi. Essa técnica experimental foi desenvolvida, a partir das técnicas clássicas de experimentos, entre os anos de 1950 e 1960 pelo engenheiro japonês G. Taguchi (TAY & BUTLER, 1999). 2.2 Princípios básicos de planejamento e análise de experimentos Experimentos são empregados para resolver problemas de fabricação, decidir entre diferentes processos de manufatura, diferentes conceitos de produto, entender a influência de determinados fatores, etc... Além disso, esta empreitada torna-se cada vez mais importante na medida em que se intensifica a base tecnológica dos produtos e as exigências governamentais e de clientes aumentando a necessidade de emprego de experimentos durante todas as etapas do ciclo de vida do produto.
31 30 Nas indústrias de eletroeletrônicos, os processos produtivos são compostos de vários fatores e níveis de regulagens, que influenciam as características de qualidade dos produtos e um problema comum encontrado pelas empresas ao realizar experimentos, é a necessidade de estudar simultaneamente o efeito desses fatores com diferentes níveis de regulagens. Neste caso, observa-se que o número de testes demandado para a experimentação tende a crescer à medida que a quantidade de fatores aumenta. Isso torna os experimentos industriais inviáveis nas empresas, porque os custos e o tempo de execução são elevados. Muitas vezes a falta de planejamento também contribui para o insucesso de um experimento. Contudo, experimentos industriais são realizados pelas empresas, principalmente, para se resolver os problemas críticos dos processos de fabricação ou do produto e também para aperfeiçoamento dos processos produtivos. Com esses experimentos, busca-se reduzir o número de produtos com defeitos fabricados, responder questões relacionadas aos níveis e parâmetros que influenciam o desempenho do produto final, aumentar a produtividade visando reduzir o custo industrial de manufatura. Um processo produtivo oferece inúmeras possibilidades de melhorias contínuas, tudo isso, motivados com o uso dos experimentos industriais. ANTONY et al. (1998), COLEMAN & MONTGOMERY (1993), MONTGOMERY (1991) e STEINBERG & HUNTER (1984) recomendam que a solução dos problemas pode ser conseguida com mais facilidade quando os experimentos são planejados e as respostas analisadas com métodos ou técnicas estatísticas. A técnica de planejamento de experimentos é utilizada para se definir quais dados, em que quantidade e em que condições devem ser coletados durante um determinado experimento, buscando, basicamente, satisfazer dois grandes objetivos: a maior precisão estatística possível na resposta e o menor custo. Sendo uma técnica de extrema importância para a indústria, pois seu emprego permite resultados mais confiáveis economizando dinheiro e tempo, parâmetros fundamentais em tempos de concorrência acirrada. A sua aplicação no desenvolvimento de novos produtos e processos produtivos é muito importante, onde uma maior qualidade dos resultados dos testes pode levar a um projeto com
32 31 desempenho superior seja em termos de suas características funcionais como também sua durabilidade. Nessa acepção, BARKER (1985) adverte que ao realizar as atividades (definição dos objetivos, parâmetros do produto ou processo de fabricação, seleção dos fatores de controle e variáveis de resposta, seleção da matriz experimental, realização do experimento, análise de dados, interpretação dos resultados e elaboração de relatórios) dos experimentos industriais de forma planejada, as informações obtidas dos produtos ou dos processos de fabricação tornam-se mais confiáveis e, com isso ações de melhoria mais eficientes podem ser tomadas pelos funcionários das empresas. Um fator que tem impulsionado a aplicação industrial do planejamento de experimentos são as ferramentas computacionais de análise estatística e soluções corporativas (para esta dissertação será utilizado a ferramenta computacional MINITAB) que cada vez mais facilitam a realização das análises e manutenção e gerenciamento de dados. Neste sentido a tendência é que tais técnicas tornem-se cada vez mais próximas de aplicações práticas e, portanto, cada vez mais utilizadas Conceitos gerais de experimentação Tem-se a seguir alguns conceitos e termos fundamentais para a aplicação das técnicas de planejamento e análise de experimentos industriais (OLIVEIRA, 1999; WERKEMA & AGUIAR, 1996; MONTGOMERY, 1991; JURAN et al. 1951). Variáveis de resposta: são as variáveis dependentes que sofrem algum efeito nos testes, quando estímulos são introduzidos propositalmente nos fatores que regulam ou ajustam os processos de fabricação. Nos experimentos, podem existir uma ou mais variáveis de resposta (y) que são importantes de se avaliar. Fatores de Controle: estes são os fatores alterados deliberadamente no experimento. O objetivo principal de introduzir estímulos nos fatores de controle é
33 32 avaliar o efeito produzido nas variáveis de resposta e, com isso poder determinar os principais fatores do processo. JURAN et al. (1951) dividem os fatores de controle em quantitativos (quantidade de pó de serra, temperatura, etc.) e qualitativos (diferentes máquinas de soldagens, operadores, etc.). Nos experimentos, os fatores podem ser representados por números arábicos (1, 2, 3...) ou por letras (A, B, C...). Fatores de Ruído: são os fatores, conhecidos ou não, que influenciam nas variáveis de resposta do experimento. Cuidados especiais devem ser tomados na hora de realizar os testes com esses fatores, pois, é importante evitar que os efeitos produzidos pelos fatores de controle, fiquem misturados ou mascarados com os efeitos provocados pelos fatores de ruído. Níveis dos fatores: são as condições de operação dos fatores de controle investigados nos experimentos. Os níveis são identificados por nível baixo (-1) e nível alto (+1). Segundo OLIVEIRA (1999), é comum considerar como nível baixo o menor valor, quando os fatores forem ajustados por níveis quantitativos. Tratamentos: é a combinação dos níveis de fatores de controle, isto significa que cada uma das corridas do experimento representará um tratamento. Efeito principal: é a diferença média observada na reposta quando se muda o nível do fator de controle investigado. Efeito de interação: é a metade da diferença entre os efeitos principais de fator nos níveis de outro fator. Matriz de experimentos: é o plano formal construído para conduzir os experimentos. Nesta matriz são incluídos os fatores de controle, os níveis e tratamentos do experimento. Aleatorização: é o processo de definir a ordem dos tratamentos da matriz experimental, através de sorteios ou por limitações específicas dos testes. Esse conceito também se refere ao processo de alocação do material e equipamento às diferentes condições de experimentação. Aleatorização nos experimentos é realizada para balancear os efeitos produzidos pelos fatores não-controláveis nas respostas analisadas e para se atender aos requisitos dos métodos estatísticos, os quais exigem que os
34 33 componentes do erro experimental sejam variáveis aleatórias independentes (CHEW, 1957). Repetição: é o processo de repetir cada uma das combinações (linhas) da matriz experimental sob as mesmas condições de experimentação. Segundo MONTGOMERY (1991), este conceito permite encontrar uma estimativa do erro experimental, que é utilizado para determinar se as diferenças observadas entre os dados são estatisticamente significativas. Blocos: é a técnica utilizada para controlar e avaliar a variabilidade produzida pelos fatores perturbadores (controláveis ou não-controláveis) dos experimentos. Com esta técnica procura-se criar um experimento (grupo ou unidades experimentais balanceadas) mais homogêneo e aumentar a precisão das respostas que são analisadas. Nas próximas seções será descrito o procedimento experimental usado para realizar a parte prática do estudo descrita no capítulo 3. As etapas desse plano ou método de pesquisa são propostas por diversos autores que estudam as técnicas de planejamento e análise de experimentos (OLIVEIRA, 1999; WERKEMA & AGUIAR, 1996; MONTGOMERY, 1991; MYERS et al. 1989; BOX & DRAPER, 1987; STEINBERG & HUNTER, 1984; JURAN et al. 1951) Processo para conduzir os experimentos É importante estabelecer o planejamento dos testes antes de iniciar qualquer experimentação, WERKEMA & AGUIAR (1996), COLEMAN & MONTGOMERY (1993) e MONTGOMERY (1991) advertem a importância do domínio do problema por todas as pessoas envolvidas e recomendam que durante os experimentos, o processo seja cuidadosamente monitorado, para garantir que tudo seja realizado de acordo com os planos, pois erros no procedimento experimental muito provavelmente anularão os resultados. Vários autores (ANTONY, et al. 1998; HOPPEN, et al. 1996; WERKEMA & AGUIAR, 1996; REY, 1993; COLEMAM & MONTGOMERY, 1993; MONTGOMERY, 1991; DANE, 1990; GIL, 1988) aconselham que durante o processo de experimentação seja feito um plano
35 34 estratégico para coordenar as atividades. A seguir, do procedimento experimental, descrito por esses autores: apresenta-se as atividades 1. Definição dos objetivos do experimento: Nesta fase inicial é importante definir os problemas dos produtos e processos de fabricação, os objetivos do experimento e principalmente, selecionar um time que seja responsável por todas as atividades do processo experimental. WERKEMA & AGUIAR (1996) lembram que as pessoas envolvidas devem ser conscientizadas sobre a importância de analisar cientificamente os fatores que influenciam no produto ou processo de fabricação, enquanto que GUEDES (1996) e COLEMAM & MONTGOMERY (1993) recomendam que brainstorming sejam realizados com as pessoas das áreas de controle da qualidade, manufatura, P&D (Pesquisa e Desenvolvimento) ou qualquer outra que possa contribuir com informações relevantes aos experimentos (publicações, experiências e resultados práticos de outros experimentos). Ao realizar o brainstorming, todas as idéias ou informações coletadas devem ser criticamente examinadas pelo time responsável. Segundo ANTONY ET al. (1998), é natural que as pessoas descrevam vários problemas nos produtos ou processos de fabricação e, neste caso, outras ferramentas como os gráficos de Pareto e o diagrama Causa e Efeitos podem ser utilizadas para se identificar os principais problemas (SMITH, 1998; BOX & BISGAARD, 1987; ISHIKAWA, 1976). 2. Parâmetros do experimento: Esta fase envolve a coleta de informações técnicas do produto ou processo. Neste trabalho, a coleta será sobre o processo de reciclagem da borra de solda Lead Free, na qual, o grupo deve listar todos os fatores de controle, fatores de ruído, os níveis de ajustagem e as variáveis de resposta. Nessa fase, segundo MONTGOMERY (1991), as informações técnicas podem resultar de uma combinação entre o conhecimento prático (experiência) e a compreensão teórica do objeto de estudo.
36 35 3. Seleção dos fatores de controle e das variáveis de resposta: Nesta fase o time deve selecionar os fatores de controle (variáveis independentes), as faixas de variação dos níveis de ajustagem desses fatores e as respostas do experimento (variáveis dependentes), assim como, definir o método de medição dos fatores de controle e a escala numérica que será utilizada para se avaliar as respostas do experimento definidas nas fases anteriores. COLEMAN & MONTGOMERY (1993) recomendam que nesta fase os parâmetros do processo sejam classificados por categorias (grau de influência na resposta, capacidade de se controlar ou capacidade de se medir - precisão). Esse esquema pode ajudar a selecionar e a priorizar os fatores críticos que afetam as respostas do experimento. 4. Seleção da matriz experimental: De acordo com MONTGOMERY (1991), se as três etapas anteriores foram seguidas corretamente, esta quarta etapa será relativamente simples de realizar. Ao selecionar ou construir a matriz experimental, devem ser considerados o número de fatores de controle, o número de níveis e os fatores não controláveis do processo. Ainda, nesta fase são definidas as seqüências das corridas (aleatoriamente), o número de replicas, as restrições dos experimentos e as possíveis interações que possam vir a ocorrer entre os fatores que estão sendo avaliados. Algumas das técnicas de planejamento de experimentos que podem ser utilizadas nesta fase serão descritas nas próximas seções. 5. Realização do experimento: Nesta etapa é importante que o processo seja acompanhado pelo time ou por um responsável, para assegurar-se que todos os procedimentos sejam executados conforme planejado. HOPPEN et al. (1996) ressaltam que, qualquer mudança no momento em que os experimentos são realizados deve ser registrada (datas, ensaios adicionais, alteração na seqüência das corridas, etc.) e recomendam que relatórios sejam apresentados no final da experimentação, visto que, essas informações podem enriquecer os resultados obtidos pela análise de dados e verificar se os experimentos foram corretamente executados pelo responsável.
37 36 Outro aspecto importante que deve ser considerado durante a realização dos experimentos, é o equilíbrio dos recursos de experimentação disponíveis. MONTGOMERY (1991) considera a pesquisa experimental como um processo interativo, ou seja, as informações reunidas da primeira rodada de teste são utilizadas como dados de entrada da segunda rodada e por isso, cuidados devem ser tomados para não esgotar todos os recursos na primeira rodada do experimento. 6. Análise de dados: Nesta etapa podem ser utilizados softwares estatísticos (MINITAB, EXCEL, STATISTICA), nesta dissertação foi usada a ferramenta computacional MINITAB, que ajuda nas técnicas de planejamento e análise de experimentos, com os gráficos lineares e os gráficos de probabilidade normal (WERKEMA & AGUIAR, 1996; MONTGOMERY, 1991). Os conceitos estatísticos são aplicados nos resultados de um experimento, para descrever o comportamento das variáveis de controle, a relação entre elas e para estimar os efeitos produzidos nas respostas observadas. Ainda, a análise estatística permite tomar decisões quanto à aceitar ou rejeitar as hipóteses formuladas na primeira etapa dos experimentos (REY, 1993). 7. Interpretação dos resultados: Ao finalizar a etapa anterior, o time responsável pelo plano de atividades deve extrair as conclusões práticas dos resultados e recomendar as ações de melhorias contínua do processo de manufatura, aperfeiçoamento do processo de teste e validação. Uma prática comum nesta fase é descrever os resultados através de gráficos, especialmente quando são apresentados às pessoas externas ao projeto. Ainda, o grupo deve discutir se as respostas satisfazem as questões experimentais definidas na primeira etapa, ou formular novas questões experimentais, revisando as fases anteriores. 8. Elaboração de relatórios: WERKEMA & AGUIAR (1996) advertem que o trabalho realizado deve ser descrito, identificando-se as limitações práticas e teóricas encontradas, as recomendações para futuros experimentos e as conclusões obtidas. A obtenção
38 37 desse retorno pode ser de grande benefício, para o processo de avaliação do desempenho dos experimentos industriais, como também, para o processo de revisão (YUKIMURA, 1991). Esta etapa é importante porque demonstra que o estudo desenvolvido é um processo contínuo de aprendizado (MONTGOMERY, 1991). Assim, a parte prática desta dissertação é baseada no roteiro apresentado anteriormente. Segundo HAHN (1993), esse plano experimental ajuda a desenvolver e conduzir efetivamente as atividades já definidas e, principalmente, permite maximizar as respostas das questões formuladas pelo time de trabalho. FIGURA PLANO PARA CONDUZIR EXPERIMENTOS Objetivo do experimento Questões experimentais Não Informações técnicas do experimento Seleção dos fatores de controle, níveis de ajustes e as variáveis de resposta Seleção da matriz experimental Interpretação dos resultados respondeu as questões experimentais, novas questões, Realização do Experimento Análise de dados R e a l i m e n t a ç ã o Elaboração de relatórios Fonte: Adaptado de HAALAND & O CONNELL (1993) e ANTONY et al. (1998).
39 38 A metodologia descrita anteriormente, foi utilizada por ANTONY et al. (1998), para realizar experimentos industriais em cinco diferentes processos de fabricação (fabricação de produtos, processo de soldagem, processo produtivo, fabricação de radiografias e fabricação de fios elétricos). Nesse trabalho, são apresentadas as vantagens e as limitações da metodologia, conforme o Quadro 2.1. Quadro VANTAGENS E LIMITAÇÕES DO ROTEIRO EXPERIMENTAL Fonte: ANTONY et al. (1998) VANTAGENS Melhora a comunicação entre as pessoas (engenheiros, gerentes e pesquisadores) que formam a equipe responsável por conduzir os experimentos industriais. Com o uso da metodologia foi possível converter os problemas de processos industriais, em conceitos estatísticos. Com o plano experimental foi possível passar novas informações aos funcionários. Com isso a interpretação dos experimentos industriais foi melhorada. LIMITAÇÕES A metodologia foi desenvolvida para fatores de dois níveis, utilizando-se as técnicas de planejamento fatorial completo. A metodologia foi desenvolvida para características de rendimento de um processo de reciclagem de borra de solda. O rendimento fica limitado pela pelo espaço físico do tanque. Não é necessário um treinamento intensivo dos funcionários da empresa para utilizar as técnicas de planejamento e análise de experimento.informações (relatórios) ficam disponíveis para consultas
40 39 Nas próximas seções serão descritas algumas técnicas de planejamento e análise de experimentos (experimento fatorial, fatorial fracionado de 2 k-p, metodologia de superfície de resposta e análise de variância). Outras formas de planejar e analisar experimentos industriais são descritas por OLIVEIRA (1999), WERKEMA & AGUIAR (1996), MONTGOMERY (1991), MYERS et al. (1989), BARKER (1985), STEINBERG & HUNTER (1984), CHEW (1957) e JURAN et al. (1951). 2.3 Técnicas de Planejamento e Análise de Experimentos Os experimentos industriais devem ser planejados em uma matriz experimental. A construção dessa matriz corresponde a etapa n 4 (quatro) do roteiro para conduzir os ensaios, apresentado anteriormente. O objetivo dessa atividade é garantir que as informações obtidas sejam confiáveis e que os recursos (equipamentos, pessoas, materiais e informações) disponíveis para experimentação sejam bem utilizados (OLIVEIRA, 1999; COLEMAN & MONTGOMERY, 1993; MONTGOMERY, 1991). Nesta fase do projeto experimental, diversas técnicas de planejamento e análise de experimentos podem ser utilizadas, conforme será descrito a seguir Planejamento fatorial Considera-se, ao planejar os experimentos industriais com a técnica fatorial, em que todos os tratamentos da matriz experimental são realizados pelo time responsável por esta atividade (BOX & BISGAARD, 1987). De acordo com BUTTON (2001), o planejamento fatorial é indicado para a fase inicial do procedimento experimental quando há necessidade de se definir os fatores mais importantes e estudar os efeitos sobre a variável resposta escolhida. Ainda, é um modelo de efeitos fixos, isto é, a análise dos efeitos provocados pelos fatores não pode ser transferida para outros níveis que não os analisados no planejamento. Para ilustrar o procedimento dessa técnica considere-se um experimento com dois fatores (A e B), cada um desses parâmetros serão testados com a níveis para o fator A e b níveis
41 Fator A 40 para o fator B. Assim, nesse experimento existem ab combinações de teste. A matriz de planejamento para o experimento fatorial de dois fatores de controle, nos níveis a e b, é representada pelo Quadro 2.2. Essa organização também representa o caso geral do experimento fatorial de dois fatores, para uma reposta (yijk) observada quando o fator A está no i-ésimo nível (i = 1, 2,..., a). É importante ressaltar que as abn observações do experimento devem ser realizadas aleatoriamente (MONTGOMERY, 1991). Quadro EXPERIMENTO FATORIAL DE DOIS FATORES, CASO GERAL Fonte: MONTGOMERY (1991). Fator B Níveis b 1 Y111, Y112,...,Y11n Y121, Y122,...,Y12n Y1b1, Y1b2,...,Y1bn 2 Y211, Y212,...,Y21n Y221, Y222,...,Y22n Y2b1, Y2b2,...,Y2bn : a Ya11, Ya12,...,Ya1n Ya21, Ya22,...,Ya2n Yab1, Yab2,...,Yabn De acordo com DEVOR et al. (1992) e MONTGOMERY (1991), com o experimento organizado dessa forma é possível verificar se: a reposta é alterada significativamente quando muda o nível do fator A; a resposta é alterada significativamente quando muda o nível do fator B; a interação dos fatores (coluna x linha) altera significativamente a resposta. Os autores também definem que o modelo estatístico do planejamento fatorial é dado pela equação (2.1). yijk = μ + τi + βi + (τβ)ij + εijk (2.1) sendo que, μ é a média dos resultados
42 41 τi é o efeito principal do fator A, ßi é o efeito principal do fator B, (τβ)ij é o efeito da interação dos fatores A e B; εijk é o erro experimental Um dos métodos que pode ser utilizado para determinar os coeficientes da equação (2.1) é a Análise de Variância (ANOVA), que também pode ser utilizada para verificar se esses efeitos são significativos nas repostas (apresentada na próxima seção). No planejamento de experimentos fatoriais é comum encontrar experimentos planejados com as técnicas fatoriais com dois, três ou mais níveis. Entretanto, no presente trabalho, não serão abordados os testes executados mais de três níveis, visto que, os experimentos industriais realizados na empresa foram com dois e três níveis. Esse tipo de planejamento e alguns exemplos de como conduzir experimentos industriais com essas técnicas fatoriais são ilustrados por OLIVEIRA (1999); DEVOR et al. (1992); MONTGOMERY (1991) e COCHRAN & COX (1957) Planejamento fatorial 2 k De acordo com JURAN et al. (1951), um experimento fatorial com k fatores, cada um deles com dois (2) níveis, é denominado de experimento fatorial 2 k. O processo experimental dessa técnica consiste em realizar testes com cada uma das combinações da matriz experimental, para em seguida, determinar e interpretar os efeitos principais e de interação dos fatores investigados e assim, poder identificar as melhores condições experimentais do processo de fabricação, neste caso, no processo de reciclagem da borra de solda Lead Free, usando o pó de serra como redutor orgânico. Para ilustrar o procedimento dessa técnica considerou-se um experimento com dois fatores (x1e x2 ), cada um desses parâmetros foi testado com dois níveis (-1, +1). Esse exemplo é apresentado por vários autores que estudam as
43 42 técnicas de planejamento e análise de experimentos (DEVOR et al., 1992; MONTGOMERY, 1991; BOX & BISGAARD, 1987). Assim, a matriz de planejamento para o experimento fatorial 2 2 é representada pela Tabela 2.1. A resposta de cada ensaio ou tratamento é descrita pela coluna yi. É importante ressaltar que a ordem de realização do teste é definida aleatoriamente. TABELA MATRIZ DE PLANEJAMENTO DO EXPERIMENTO FATORIAL 2 2 Fonte: DEVOR et al. (1992) e MONTGOMERY (1991). Fatores controle Teste x1 x2 Ordem Resposta (Yi) y y y y4 O procedimento que pode ser utilizado para construir a matriz genérica do experimento fatorial 2 k é descrito por DEVOR et al. (1992). Na matriz de planejamento as colunas representam o conjunto de fatores investigados (x1, x2, x3, x4..., xk), e as linhas representam os diferentes níveis ou as combinações dos fatores (níveis codificados -1 (mínimo) e +1 (máximo)). 1. Para x1, a coluna será definida pela combinação dos níveis -1, +1, -1, +1, ou seja, o sinal dessa coluna alterna em grupos de 2 0 = Para x2, a coluna será definida pela combinação dos níveis -1, -1, +1, +1, ou seja, o sinal dessa coluna alterna em grupos de 2 1 = O procedimento será igual para x3, x4,..., xk. Para xk, o sinal alterna em grupos de 2 (k-1), ou seja, 2 (k-1) vezes (-1), seguido de 2 (k-1) vezes (+1). DEVOR et al. (1992) definem que esta forma de organizar o experimento é chamada de ordem padrão (standard order). Ainda, ressaltam que com esse arranjo garante-se que todas as colunas da matriz sejam ortogonais entre si. Com esse tipo
44 43 de planejamento é possível determinar os efeitos principais e de interação que as variáveis independentes produzem nas respostas. De acordo com MONTGOMERY (1991), o modelo estatístico do experimento fatorial 2 3 é dado pela equação (2.2). yijk = μ + τi + βj + γk + (τβij) + (τγik) + (βγjk) + (τβγijk) + εijk (2.2) sendo que, μ é a média dos resultados, τi é o efeito principal do fator x1, ßj é o efeito principal do fator x2, γk é o efeito principal do x3, (τßij) é o efeito de interação entre os fatores x1 e x2, (τγik) é o efeito de interação entre os fatores x1 e x3, (βγjk) é o efeito de interação entre os fatores x2 e x3, (τβγijk) é o efeito de interação dos fatores x1, x2 e x3, εijk é o erro experimental. A seguir é apresentado o método generalizado que pode ser utilizado para estimar os efeitos principais e de interação dos fatores. Esse método é descrito por DEVOR et al. (1992) e MONTGOMERY (1991) e também é conhecido como método de sinais (OLIVEIRA, 1999). Os efeitos principais correspondem à mudança da resposta média quando o nível de um fator é alterado de (-1) para (+1), mantendo os outros fatores constantes. O procedimento consiste em multiplicar os resultados da coluna yi pelos valores ± 1 associados a coluna xi da matriz experimental correspondente ao efeito principal que se deseja estimar (Tabela 2.1). Em seguida, os valores obtidos devem ser somados e divididos pela metade do número de ensaios realizados, conforme é ilustrado pela equação (2.3). Ei = Σyi*xi / (N/2) (2.3)
45 44 sendo que Ei será o efeito estimado, N é o número total de observações, Σyi*xi é a soma dos resultados (yi) do experimento multiplicados pela coluna xi. Para determinar o efeito de interação, primeiramente devem ser construídas as colunas das interações da matriz de planejamento. Essas colunas são formadas por meio da multiplicação das colunas dos efeitos principais. Por exemplo, para estimar o efeito de interação E12, serão multiplicadas as colunas dos fatores x1 e x2. Em seguida, os valores ± 1 associados à coluna x1x2 da matriz experimental são utilizados para estimar o efeito de interação, conforme descrito anteriormente pela equação (2.3). No entanto, nesta etapa dos experimentos alguns autores comentam que embora seja simples estimar esses efeitos, muitas vezes é difícil definir qual é realmente o fator de controle que produz uma diferença significativa nas respostas e a maioria das vezes necessita-se usar os gráficos lineares (que representam os efeitos principais e de interação) e de probabilidade normal (DEVOR et. al., 1992; MONTGOMERY, 1991). Nessa fase do procedimento experimental podem ser utilizados diferentes softwares para construir os gráficos (planilha EXCEL, STATISTICA, MINITAB). Os autores recomendam ainda, que para se concluir sobre os efeitos principais e de interação dos fatores é necessário aplicar técnicas de análise de variância (ANOVA). Essa técnica será discutida na próxima seção. Para representar e interpretar graficamente os efeitos principais e de interação é necessário definir duas propriedades, conforme segue (DEVOR et al., 1992). o sinal (±) indica a direção do efeito, isto é, se a resposta aumenta ou decresce com a variação do nível de (-1) para (+1); a magnitude indica a intensidade do efeito. A forma gráfica do efeito principal (Ei) é representada pela Figura 2.3. Esse gráfico linear ilustra a variação média das respostas em função da mudança no nível (-1, +1) de um fator (xi), mantendo os outros fatores constantes (Tabela 2.1).
46 resposta Yi resposta Yi resposta Yi 45 Yi +1 Fator Xi (-1 +1) FIGURA 2.3-GRÁFICO DE EFEITOS PRINCIPAIS, PLANEJAMENTO FATORIAL 2 K Os gráficos dos efeitos de interação descrevem a variação média de um fator em função dos níveis de outros fatores. Por exemplo, a Figura 2.3(a) ilustra que o efeito provocado pela mudança de nível do fator x1 na resposta depende do nível do fator x2, portanto, existe interação entre os fatores x1 e x2. A Figura 2.3(b) demonstra que o efeito provocado pela mudança do nível do fator x1 na resposta é independente do nível do fator x2, portanto não existe interação entre esses fatores. Efeito de interação x1x2 Efeito de interação x1x2 x2= -1 x2= -1 x2= +1 x2= +1 Fator Xi (-1 +1) Fator Xi (-1 +1) (a) (b) FIGURA GRÁFICOS DE EFEITOS DE INTERAÇÃO Outro tipo de gráfico que pode ser utilizado na análise de experimentos é o de probabilidade normal. Esses gráficos são utilizados nas situações onde não é possível repetir um experimento fatorial 2 k, e é importante obter uma estimativa independente do erro experimental para julgar a importância dos efeitos principais e de interação (DEVOR et al., 1992). Esse tipo de erro é proveniente de fatores incontroláveis que produzem uma variação nas repostas ao realizar os ensaios sob condições preestabelecidas (BUTTON, 2001). CRUZ et al. (1997) definem que os erros podem ser classificados em dois grupos, conforme segue:
47 46 erros sistemáticos: são causados por fontes identificáveis. Esse tipo de erro faz com que os resultados experimentais estejam acima ou abaixo do valor real, influenciado a exatidão da medida. Essa flutuação pode ser causada pelo instrumento utilizado para controlar o experimento (ex. relógio, micrômetro, régua, etc.), método de observação, efeitos ambientais ou pelas simplificações do modelo teórico (ex. eliminar um fator importante para o sistema). erros aleatórios: são as flutuações que ocorrem de uma repetição para outra, porém, todos os possíveis resultados estão dentro de um intervalo de valores. Esse tipo de erro afeta a precisão das medidas. Segundo os autores nem sempre podem ser identificadas as fontes que causam o erro aleatório. Entretanto, esse tipo de...erro no experimento pode ser tratado quantitativamente através de métodos estatísticos, de modo que seus efeitos na grandeza física medida podem ser, em geral, determinados. O uso dos gráficos de probabilidade normal é baseado no fato de que os efeitos principais ou de interação que são desprezíveis, se distribuem segundo uma distribuição normal centrada em zero e com variância σ 2, ou seja esses efeitos tendem a se concentrar ao longo de uma reta normal no gráfico. No entanto, se os pontos marcados no gráfico parecem desviar-se de algum modo dessa linha imaginária, existem motivos para acreditar que esses dados obtidos não estão distribuídos de maneira normal, portanto, são efeitos significativos que devem ser analisados com mais detalhes pelo time que realiza os experimentos industriais (LEVINE et al., 1998). DEVOR et al. (1992) recomendam que para garantir a aplicação efetiva desse método, os experimentos fatoriais 2 k devem ser realizados com pelo menos quatro fatores. Apesar de levar isso em consideração, no experimento do processo de reciclagem da borra de solda, foi utilizado apenas dois fatores principais, a saber: temperatura do tanque e quantidade de pó de serra. As principais vantagens da técnica fatorial 2 k é que através da análise dos experimentos pode-se indicar as principais tendências e determinar uma direção promissora para as experimentações subseqüentes (OLIVEIRA, 1999;
48 47 MONTGOMERY, 1991). Ainda, os autores ressaltam que com esse tipo de experimento também é possível quantificar o erro experimental. As limitações atribuídas à técnica de fatorial 2 k são apresentadas a seguir (OLIVEIRA 1999, MONTGOMERY 1991; ABRAHAM et al., 1999). com esse tipo de técnica de planejamento de experimento não é possível obter informações dos fatores em níveis intermediários; em alguns experimentos não é possível realizar réplicas, porque na maioria das vezes os custos de experimentação são elevados, com isso os erros experimentais não podem ser estimados (ANDERSON, 1957); não é suficiente avaliar os efeitos significativos apenas sob o ponto de vista estatístico, mas torna-se necessário avaliá-los também em termos práticos para as empresas; torna-se inviável utilizar a técnica nas empresas quando existe um número grande de fatores; ao utilizar essa técnica existe o risco de construir e planejar experimentos super dimensionados, uma vez que, são considerados vários fatores para realizar os testes. Uma das soluções encontradas para as limitações apresentadas anteriormente, é construir e planejar experimentos industriais utilizando-se a técnica de confundimento (do inglês factorial experiments with design confounded) ou as técnicas de experimentos fatoriais fracionados 2 k-p. A técnica de confundimento é uma técnica de planejamento utilizada para acomodar um experimento fatorial completo em blocos, onde o tamanho do bloco é menor que o número de tratamentos de uma replica (MONTGOMERY, 1991; COCHRAN & COX, 1957). O planejamento experimental com a técnica de fatorial fracionado 2 k-p será abordado com mais detalhes nas próximas seções. Porém nesta dissertação não será utilizada a técnica de fatorial fracionado, por causa da quantidade das variáveis influentes de entrada do experimento serem apenas duas.
49 Análise de variância dos efeitos do experimento fatorial 2 k As técnicas estatísticas de experimentos são utilizadas, principalmente, para analisar, interpretar e apresentar as informações de experimentos planejados. Ainda, são ferramentas que ajudam a melhorar o desempenho industrial dos produtos e processos de fabricação (BOWER, 1997). O princípio básico das técnicas é usar os conceitos matemáticos de estatística e as informações obtidas dos experimentos realizados com os processos de fabricação. Com os dados analisados matematicamente e com os testes planejados corretamente é possível rejeitar ou aceitar as hipóteses formuladas pelo time responsável por conduzir o experimento industrial. BARKER (1985) denomina esse processo de inferência estatística. Antes de descrever as técnicas estatísticas é importante considerar alguns pontos (MONTGOMERY, 1991): geralmente as pessoas das empresas conhecem os problemas dos processos industriais, e sabem do relacionamento que existe entre os parâmetros de controle e as respostas. Esse tipo de conhecimento contribui na fase inicial do processo experimental, com a formulação das hipóteses, e nas conclusões finais do processo, com a análise estatística; recomenda-se que o time responsável pelo experimento não deve usar técnicas estatísticas complexas no início dos testes; os funcionários das empresas devem avaliar se a diferença estatística entre os resultados dos experimentos tem significado prático; as técnicas estatísticas demonstram que as diferenças entre as médias dos experimentos são grandes ou não, mas não diz porque essas diferenças ocorrem; usualmente os experimentos são interativos, com isso deve-se considerar que os primeiros teste na maioria das vezes são realizados para refinar as informações técnicas dos produtos ou dos processos de fabricação. LEVINE et al. (1998), DEVOR et al. (1992) e MONTGOMERY (1991) propõem uma metodologia ou uma série de passos que podem ser utilizados para
50 49 conduzir o teste de hipótese dos experimentos. Alguns conceitos e pontos importantes desse procedimento são abordados a seguir: a. Formulação das hipóteses: ao realizar um experimento industrial o time deve partir de duas hipóteses sobre determinados parâmetros. A primeira é a hipótese nula (Ho). Essa hipótese parte do princípio que não existe nenhuma diferença significativa entre os fatores analisados de uma população e será sempre a hipótese testada no experimento. A segunda é a hipótese alternativa (H1) e parte do princípio que será verdadeira caso a hipótese nula seja considerada falsa. b. Determinar o valor crítico da estatística de teste: ao desenvolver as hipóteses dos experimentos industriais é necessário que seja calculado uma estatística especifica, com base em um determinado resultado da amostra. Tais valores podem ser determinados com o auxilio de softwares estatísticos. LEVINE et al. (1998) e MONTGOMERY (1991) apresentam várias distribuições estatística (tstudent, FFisher, Z-standard, entre outras) que podem ser usadas para se determinar a probabilidade de uma hipótese nula ser verdadeira. É importante ressaltar que para os experimentos industriais realizados nesta dissertação, será utilizada a distribuição F, portanto, alguns pontos importantes desta ferramenta estatística serão abordados posteriormente. Maiores informações sobre as outras distribuições podem ser obtidas na literatura que trata de planejamento e análise de experimentos (LEVINE et al., 1998; DEVOR et al., 1992; MONTGOMERY, 1991). c. Riscos na tomada de decisão por meio da metodologia do teste de hipótese: ao utilizar uma estatística para se concluir sobre o resultado de experimentos industriais podem ser cometidos dois tipos de erros: O primeiro erro (erro tipo I) ocorre se a hipótese nula for rejeitada quando ela é verdadeira e o erro tipo II ocorre quando a hipótese nula não é rejeitada sendo falsa. No entanto, ao realizar os experimentos industriais, o time pode estimar alguns parâmetros que reduzem a probabilidade de errar nas decisões ou chegar a uma conclusão incorreta sobre os fatores que influenciam o sistema investigado, conforme segue (LEVINE et al., 1998):
51 50 d. Nível de significância. A probabilidade de se cometer o erro tipo I é identificada como o nível de significância (α) do teste estatístico. Geralmente, o time pode controlar a probabilidade do erro tipo I decidindo o nível de risco α que estão dispostos a tolerar, em termos de rejeitar a hipótese nula quando ela for verdadeira. Os autores da literatura de planejamento e análise de experimentos recomendam que o time deva selecionar os níveis de α em 0,1 ou menos. Ainda, uma vez selecionado o valor de α é possível determinar o tamanho da região de rejeição da hipótese nula do experimento. Com isso, os valores críticos que dividem as regiões de rejeição e nãorejeição podem ser determinados, conforme apresentado pela Figura 2.5, para a estatística F. Os valores críticos dessa ferramenta são apresentados por LEVINE et al. (1998); DEVOR et al. (1992) e MONTGOMERY (1991). FIGURA REGIÕES DE REJEIÇÃO E NÃO-REJEIÇÃO PARA UMA DISTRIBUIÇÃO F Fonte: LEVINE et al. (1998) e DEVOR et al. (1992). e. O coeficiente de confiança. O complemento da probabilidade de um erro tipo I é denominado de coeficiente de confiança, que é identificado como (1 - α). Quando esse termo é
52 51 multiplicado por 100% passa a simbolizar o nível de confiança do experimento. Com essa estimativa é possível afirmar se a média aritmética da população está contida dentro de um intervalo. MONTGOMERY (1991) destaca que com esse procedimento se garante um valor pequeno para a probabilidade do erro tipo II. Em termos de metodologia de teste... esse coeficiente representa a probabilidade de se concluir que o resultado de um fator que está sendo testado para a hipótese nula seja plausível... (LEVINE et al., 1992). Considerando-se esses fatores, a seguir é descrita a técnica estatística de Análise de Variância, também conhecida como Analysis of Variance (ANOVA). As definições são baseadas nas referências bibliográficas DEVOR et al. (1992) e MONTGOMERY (1991). O texto também foi construído com base nas apostilas preparadas por BUTTON (2001); CARPINETTI (2001) e CRUZ et al. (1997). É importante, destacar que outras técnicas podem ser utilizadas para analisar os experimentos industriais (OLIVEIRA, 1999; WERKEMA & AGUIAR, 1996; MONTGOMERY, 1991). A análise de variância é utilizada para aceitar ou rejeitar, estatisticamente, as hipóteses investigadas com os experimentos industriais. O objetivo dessa técnica é analisar a variação média dos resultados dos testes e demonstrar quais são os fatores que realmente produzem efeitos (principais e de interação) significativos nas respostas de um sistema. Para ilustrar o procedimento considere-se o experimento fatorial com dois fatores, cada um deles com apenas dois níveis. O modelo matemático que define a variação da resposta em função dos fatores de controle é dado pela equação 2.1. Com a análise de variância procura-se identificar se alguns dos coeficientes desse modelo são reflexos do erro experimental ou se realmente são efeitos significativos. Assim, a contribuição de qualquer parâmetro (Ei) no modelo matemático é dado pela soma de quadrados (SS E ), conforme equação (2.4). SS Ei = (Ei) 2 (2.4) 4n sendo que n é o número de observações realizadas.
53 52 Os resultados da ANOVA são geralmente apresentados em um quadro ou tabela, Tais resultados representam a análise do experimento fatorial com dois fatores, cada um deles com dois níveis. O método de análise de variância apresentado anteriormente refere-se ao caso de um planejamento fatorial, com dois fatores, cada um deles com dois níveis. Esse processo pode ser generalizado para o experimento fatorial 2 k. Segundo VIEIRA (1996), a interpretação dos resultados do quadro de ANOVA se apresenta em duas categorias, conforme segue. os parâmetros que possuam razão F0 maior que a estatística F critica, são os fatores que exercem influência sobre o valor da média de resultados. A estatística F, que segue uma distribuição com v1 (numerador) e v2 (denominador) graus de liberdade, para um dado nível de significância α, são retiradas das tabelas apresentadas por vários autores (LEVINE et al., 1998; DEVOR et al., 1992; MONTGOMERY, 1991). É importante ressaltar que o quadro ANOVA é facilmente construído com softwares estatísticos (EXCEL, MINITAB, STATISTICA). Neste experimento foi utilizado o software MINITAB. Além dessa vantagem, na maioria dos programas computacionais está incluído o valor p. Esse valor corresponde à área sob a qual a estatística F é limite da razão F0 calculada. Com esse parâmetro estatístico é possível concluir sobre as hipóteses nulas sem precisar recorrer a uma tabela de valores críticos da distribuição F. Isto é, se o valor p for menor que o nível de significância escolhido α, a hipótese nula é rejeitada. No entanto, a inferência estatística com a ANOVA é um processo que requer alguns cuidados: o time não pode esquecer que um efeito de interação indica que todos os fatores envolvidos (na interação) são significativos, apesar do fato de que seus efeitos principais na ANOVA possam não mostrar a significância; os fatores de ruído a priori não são completamente investigados. Nesse caso outras técnicas com um melhor desempenho podem ser utilizadas (ex. Projeto Robusto) (TAGUCHI, 1993).
54 Planejamento fatorial fracionado 2 k-p Ao realizar experimentos industriais, é comum verificar a necessidade de estudar o efeito de um ou mais fatores de controle ao mesmo tempo (ABRAHAM et al., 1999). A aplicação das técnicas de planejamentos de experimentos fatoriais fracionados 2 k-p, mostra-se como uma das soluções para esse tipo de problema. MONTGOMERY (1991) ressalta que, com essas técnicas, é possível analisar os efeitos sobre uma resposta de interesse, de k fatores com dois níveis cada um, em 2 k-p combinações de testes, realizando-se apenas uma parte (metade do experimento quando p é igual a um, ou um quarto do experimento quando p é igual a dois), do experimento sem comprometer significativamente a precisão das conclusões decorrentes da análise de resultados. Simultaneamente, os custos e o tempo de duração dos ensaios são significativamente reduzidos. Segundo ABRAHAM et al. (1999), quando são utilizadas as técnicas de experimentos fatoriais 2 k-p, o time responsável assume que os efeitos de interação de ordem superior são desprezíveis. Nesse sentido, BOX & LIU (1999) descrevem um estudo sobre as técnicas fatoriais fracionados 2 k-p e ressaltam a eficiência de obter informações confiáveis com esses métodos. MONTGOMERY (1991) ressalta três idéias importantes que justificam a utilização das técnicas de experimentos fatoriais fracionados. A primeira delas é a dispersão dos efeitos. Isto é, quando existem vários fatores de controle, torna-se provável que o processo seja influenciado apenas por alguns efeitos principais e de interação de ordem inferior. A segunda característica é denominada de propriedade de projeção. Neste caso, os experimentos fatoriais fracionados podem ser planejados em matrizes maiores, que podem ser construídas a partir de um subconjunto de fatores significativos. A terceira característica desse tipo de técnica é a experimentação seqüencial. Ocorre quando é possível combinar as corridas de dois ou mais experimentos fatoriais fracionados. A seguir, utilizando-se como base os três princípios abordados anteriormente, são descritos outros aspectos que devem ser considerados ao se construir experimentos industriais com essas técnicas (CARPINETTI, 2000; OLIVEIRA, 1999; DEVOR et al., (1992), MONTGOMERY, 1991; BOX & BISGAARD, 1987):
55 54 Considere-se um estudo com três fatores de controle (1, 2, e 3), com dois níveis cada um. O time responsável por conduzir o experimento determinou que é inviável economicamente realizar as oito combinações (2 3 = 8) da matriz. Porém, é possível realizar um experimento com quatro (metade) observações (2 3/2 = = 4). Esse exemplo é apresentado por MONTGOMERY (1991) e DEVOR et al. (1992). No Quadro 2.3, aparecem todas as combinações possíveis do experimento fatorial completo 2 3. As colunas 12, 13, 23 e 123 foram estimadas pela multiplicação das colunas que contem os fatores 1, 2 e 3. Por conveniência as combinações (linhas da matriz) foram separadas pelos sinais de positivo e negativo da coluna de interação de maior ordem, ou seja, pela interação 123. Essa coluna da matriz é denominada de relação definidora do experimento. Nesse tipo de experimento o time responsável pode optar pela execução das combinações referentes à parte positiva (teste número 1, 2, 3 e 4), o que é mais usual, ou executar a outra parte (corridas 5, 6,7 e 8). No primeiro caso a combinação dos ensaios é representada por I = 123. Se for selecionada a parte negativa, deve-se lembrar que a relação definidora do experimento será I = Quadro EXPERIMENTO FATORIAL 2 3 Fonte:DEVOR et al. (1992). Combinações Efeito fatorial tratamento l Yi y y y y y y y y8 A seguir, com objetivo de ilustrar o processo de planejamento experimental com a técnica fatorial fracionado será utilizada a parte positiva do experimento, apresentado no Quadro 2.3. Nessa matriz são identificadas as seguintes
56 55 combinações lineares para estimar os efeitos principais dos fatores 1, 2 e 3, conforme segue. l1 = ½ ( ) l2 = ½ ( ) l3= ½ ( ) e para os efeitos de interação 12, 13 e 23 se obtém: l12 = ½ ( ) l13 = ½ ( ) l23= ½ ( ) Percebe-se que algumas combinações lineares são iguais (l1 = l23, l2 = l13 e l3 = l12). Quando isso ocorre torna-se impossível identificar claramente quais são os efeitos principais de cada fator porque estão misturados com os efeitos produzidos pela combinação de dois fatores. Nesse caso, MONTGOMERY (1991) e DEVOR et al. (1992) afirmam que na realidade está sendo determinado o efeito das combinações de , e , e está propriedade é conhecida como efeito de confundimento. A estrutura de confundimento de um efeito principal ou de interação em um experimento pode se determinar por meio da multiplicação do efeito com a relação definidora. Por exemplo, a estrutura de confundimento do efeito principal pode ser obtida conforme segue: Para o efeito principal 1; (1) I = (1)123 = 23 O mesmo procedimento é utilizado para estimar 2 = 13 e 3 = 12. Nota-se que não existe confundimento entre os efeitos principais, porém essas informações estão confundidas com os efeitos das interações entre dois fatores. Sendo assim, um aspecto importante que deve ser considerado nos experimentos fatoriais fracionados é a resolução que está sendo utilizada. Segundo MONTGOMERY (1991), a resolução de um planejamento fatorial fracionado está
57 56 relacionada ao padrão de confundimento entre os efeitos dos fatores. O autor recomenda que nos experimentos deve-se utilizar a maior resolução possível, porque com isso é possível desprezar os efeitos de interação de mais alta ordem. A seguir são apresentadas as definições de resolução III, IV e V, que são consideras como as mais importantes e utilizadas ao se construir os experimentos industriais (MONTGOMERY, 1991; STEINBERG & HUNTER, 1984). Resolução III - isto significa que ao menos alguns efeitos principais são confundidos com efeitos de interação de dois fatores; Resolução IV - se um planejamento é de resolução IV isto significa que ao menos alguns efeitos principais serão confundidos com efeitos de interação de três fatores, e ao menos alguns efeitos de interação de dois fatores são confundidos com outros efeitos de interação de dois fatores; Resolução V - se um planejamento é de Resolução V, ao menos alguns dos efeitos principais são confundidos com efeitos de interação de quatro fatores, e os efeitos de interação de dois fatores são confundidos com os efeitos de interação de três fatores. Em alguns casos dependendo do número de fatores que são investigados, uma fração menor de combinações é necessária para realizar os experimentos fatoriais. Por exemplo, o time pode apenas realizar um quarto ( 1/4 ) do experimento fatorial completo. Este tipo de experimento é conhecido como experimento fatorial fracionado 2 k-2. O experimento pode ser construído inicialmente com as combinações de tratamento ou colunas da matriz de um planejamento fatorial com k- 2 fatores. Em seguida, são adicionadas duas colunas com as interações, escolhidas apropriadamente pelo time responsável por conduzir os experimentos, que incluem os primeiros k-2 fatores. Uma característica importante desse experimento é a necessidade de determinar duas colunas geradoras para construir a matriz. Conforme o número de fatores outras frações podem ser utilizadas. Na literatura que estuda as técnicas de planejamento e análise de experimentos industriais estão disponíveis o número de combinações e as estruturas de confundimento para esse tipo de experimento (WU & CHEN, 1992; MONTGOMERY, 1991). Ainda, softwares estatísticos (MINITAB, STATISTICA) podem ser usados
58 57 para construir esse tipo de matriz. Ao mesmo tempo, ressalta-se que a análise estatística e descritiva (gráficos lineares e de probabilidade normal) dos efeitos principais e de interação dos fatores segue os mesmos princípios apresentados anteriormente para um experimento fatorial 2 k. Outras informações podem ser consultadas na literatura que trata de projetos de experimentos (MONTGOMERY, 1991; DEVOR et al., 1992). 2.4 Metodologia de Superfície de Resposta De acordo com TAY & BUTLER (1999) e MYERS et al. (1989), a Metodologia de Superfície de Resposta (MSR ou RSM do inglês Response Surface Methodology), é um conjunto de técnicas de planejamento e análise de experimentos usadas na modelagem matemática de respostas. Esse método foi desenvolvido por George Box, da Universidade de Princeton - Estados Unidos, com a colaboração de outros autores, na década de O estudo foi motivado porque os pesquisadores sentiram a necessidade de utilizar um procedimento para determinar as condições ótimas (ou níveis ótimos) dos fatores de controle que interferem na resposta de um sistema (MYERS et al., 1989). No entanto, a literatura que pesquisa o tema relata que só a partir dos anos 80, a MSR passou a ser aplicada pelas empresas, principalmente a indústria japonesa e americana. Nas fábricas o método pode contribuir na melhoria da qualidade dos produtos ou processos de fabricação, a aumentar a produtividade e a reduzir o tempo de desenvolvimento de produtos, entre outros fatores (GUEDES, 1996). O sucesso alcançado pelas indústrias motivou outros setores a conduzir (planejar) e analisar estatisticamente os experimentos. Entre as áreas que mais utilizam os conceitos pode-se citar: Física, Engenharia, Indústria de alimentos, Ciências sociais (economia, pesquisa operacional e sistemas de simulação) e Biologia (por exemplo, os conceitos podem ser utilizados para determinar o relacionamento que existe entre a estrutura química de um componente e sua reação biológica, assim como, para realizar estudos sobre os efeitos da poluição industrial no meio ambiente) (ELSAYED & CHEN, 1993; MYERS et al., 1989).
59 58 Na maioria dos estudos publicados observa-se que os projetos experimentais desenvolvidos com o método, envolvem a modelagem matemática de apenas uma resposta (Single-Response Analysis) (REDDY et al., 1998). Nesta dissertação foi usado apenas uma variável de resposta, no caso, a solda. Porém, é importante ressaltar que a MSR é um procedimento que pode ser aplicado na modelagem de problemas em que são observadas várias características de qualidade. Esse método também é conhecido como otimização de multi-respostas (multiple-response experimental design) (MYERS & MONTGOMERY, 1995; KHURI & CORNEL, 1987). Destaca-se que um fator importante que facilita o uso da MSR com multi-resposta é o avanço tecnológico dos softwares estatísticos. Com essa evolução também foi possível reduzir os erros nas análises estatísticas dos problemas estudados (TAY & BUTLER, 1999). De acordo BOX & HUNTER (1957) os principais motivos para estudar os problemas de um sistema com a MSR são: necessidade de se conhecer as características da função resposta, que se aproxima das condições reais de operação dos sistemas. Nas empresas do PIM, essas informações podem ser utilizadas para mudar as condições de operação dos processos de fabricação sem aumentar os custos de produção e melhorar o sistema de controle do processo produtivo; determinar quais são as condições dos fatores (x1, x2,..., xk) que determinam o melhor valor para a reposta yi; interesse em identificar o relacionamento que existe entre os parâmetros (que podem ser representados por variáveis quantitativas tipo temperatura, tempo, velocidade, pressão,, etc.) e as respostas. Segundo COCHRAN & COX (1957) a função matemática que descreve a superfície de resposta é dada pela equação (2.5). ŷ = f(x1, x2,..., xk) + ε (2.5) sendo que x1, x2,..., xk são os fatores experimentais e ε é o resíduo ou erro experimental, ou seja, é a dispersão dos resultados em torno da função matemática
60 59 aproximada aos pontos. Na maioria dos problemas analisados com a MSR é desconhecida a função matemática que define o relacionamento entre a resposta e os fatores experimentais. No entanto, na literatura de projetos experimentais algumas funções de resposta (também conhecidas como função objetivo) são descritas e utilizadas por vários autores (RIBEIRO et al., 2000; REDDY et al., 1998; GUEDES, 1996; ELSAYED & CHEN, 1993 e TAGUCHI, 1993). Os aspectos mais importantes que são considerados pelos modelos no procedimento de otimização são: a média e a variância das repetições de cada corrida experimental. A seguir é descrito um dos métodos de otimização que podem ser utilizados para se aproximar da superfície de resposta (MYERS & MONTGOMERY, 1995; KHURI & CORNELL, 1987). No procedimento de otimização, um primeiro passo é identificar uma função matemática que modele a variação das respostas em função da variação dos fatores investigados. Segundo MYERS et al. (1989), os polinômios algébricos são amplamente utilizados para se aproximar da região de resposta. GUEDES (1996), afirma que o grau de aproximação depende essencialmente do grau do polinômio (definido pelo produto de k fatores) e da faixa do intervalo considerado. Geralmente, a primeira função que é utilizada para se aproximar ao conjunto de resultados são os polinômios de primeira ordem, representado pela equação (2.6). Nesse caso, procura-se verificar se a variação da resposta em função dos fatores é bem modelada por uma superfície plana, conforme a Figura 2.6 y = β 0 + β 1 x 1 + β 2 x βkxk + ε (2.6) sendo que β 0, β 1, β 2... β k, representam os coeficientes do polinômio; x1, x2,..., xk são os fatores experimentais e ε é o erro experimental
61 60 FIGURA SUPERFÍCIE DE RESPOSTA TRIDIMENSIONAL PLANA MONTGOMERY (1991) ressalta que se a variação da resposta em função dos fatores é melhor modelada por uma superfície não plana, ou seja, o teste estatístico aponta que o modelo linear não satisfaz as condições de operação do sistema porque existe uma curvatura na superfície de resposta, conforme a Figura 2.7, então a função a ser aproximada ao conjunto de resultados é um polinômio de mais alta ordem, como um modelo de segunda ordem, dado pela equação (2.6). Segundo COCHRAN & COX (1957), esse modelo é o mais utilizado para ajustar a superfície de resposta. (2.6) sendo que β 0, β 1, β 2... β k, representam os coeficientes do polinômio; xi, xj,..., xk são os fatores experimentais e ε é o erro experimental.
62 61 FIGURA SUPERFÍCIE DE RESPOSTA TRIDIMENSIONAL NÃO PLANA Em muitas aplicações da MSR o maior problema enfrentado é na hora de selecionar o planejamento experimental. A seguir são apresentadas algumas propriedades e características dos experimentos fatoriais 2 k que podem ser utilizados na MSR. A classificação das técnicas de experimentos será realizada conforme o grau do polinômio que é utilizado para ajustar a resposta Experimento fatorial 2 k para ajustar a superfície de resposta MYERS & MONTGOMERY (1995) e BOX & HUNTER (1957), advertem que antes de realizar os experimentos é conveniente que os fatores de controle sejam codificados no intervalo (-1, 1). Uma forma de fazer a transformação é dada pela equação (2.7). Essa codificação é utilizada porque facilita a construção dos planejamentos experimentais, remove as unidades de medida dos fatores de controle e a distância ao longo dos eixos. (2.7)
63 62 sendo que ζi representa o nível da variável natural do processo de fabricação, n c é o ponto central utilizado no experimento e Δxi é o valor de escala ou o incremento na variável independente. O planejamento experimental deve determinar os coeficientes de regressão dos polinômios com variância mínima (BOX & HUNTER, 1957). GUEDES (1996) afirma que se os fatores experimentais de uma matriz X são funcionalmente independentes então, a anterior exigência será satisfeita ao selecionar um planejamento que produza a matriz X X diagonal. Nesse caso, os planejamentos ortogonais (uma matriz é dita ortogonal quando os elementos fora da diagonal da matriz X X são todos zero. Isto implica que a soma do produto da matriz X também é zero) e em particular os experimentos fatoriais 2 k e algumas de suas classificações satisfazem está condição. Quando é efetivado um experimento fatorial 2 k, dificilmente o experimentador sabe se a resposta de interesse varia de forma linear ou não linear em função dos fatores, pois apenas existem dois níveis para cada parâmetro. A seguir, algumas técnicas de planejamento que ajudam a resolver esse problema são apresentadas (GUEDES, 1996; MYERS & MONTGOMERY, 1995;MONTGOMERY, 1991; KHURI & CORNELL, 1987). Planejamento para o ajuste de um modelo de primeira ordem: esse tipo de experimento é utilizado quando se deseja aproximar rapidamente da superfície de resposta. A classe de planejamento que satisfaz as condições (principalmente a ortogonalidade e a variação mínima dos coeficientes de regressão) apresentada anteriormente, é o experimento fatorial 2 k, com pontos centrais (nc). Esse método consiste em adicionar um ponto de experimentação no nível x0 (0, 0), intermediário aos níveis (-1, +1), para os fatores xi (i = 1, 2,..., k). Neste caso, assume-se que os k fatores sejam quantitativos. Segundo MONTGOMERY (1991), os pontos centrais são utilizados para conservar a linearidade dos efeitos provocados pelos fatores no
64 63 experimento, assim como, para se estimar os erros experimentais, sem influenciar os efeitos produzidos pelos fatores nas respostas. Para ilustrar a técnica, considere-se um experimento 2 2. Neste caso, as combinações lineares dos níveis dos fatores seriam (-1, -1), (-1, +1), (+1, -1) e (+1, +1), e ainda existem nc observações nos níveis (0, 0), como ilustrado pela Figura 2.8. FIGURA PLANEJAMENTO FATORIAL 2 2, COM PONTOS CENTRAIS Fonte: MONTGOMERY (1991). A ferramenta estatística que é utilizada para testar se existe ou não curvatura na região central será descrita na próxima seção. Se, ao realizar a análise de variância (ANOVA), verifica-se que o modelo de primeira ordem não pode ser utilizado para ajustar a superfície de resposta, o time de experimentadores deve partir para a construção de um modelo de segunda ordem. Em alguns casos novos experimentos devem ser planejados conforme será descrito a seguir. Planejamento para o ajuste de um modelo de segunda ordem: Um planejamento experimental para o modelo de segunda ordem devem conter pelo menos três (3) níveis para cada fator (MONTGOMERY, 1991). Neste caso, a série de experimentos que podem ser utilizados no planejamento da superfície de resposta de segunda ordem são os planejamentos rotáveis (rotatable second design) (BOX & HUNTER, 1957). Um experimento é rotável se a variância da resposta estimada, para algum ponto xi, é em função da distancia do ponto ao centro e não em função da direção (MONTGOMERY, 1991). GUEDES (1996) afirma
65 64 que essa característica define que o contorno de variância da resposta estimada é formado por círculos concêntricos. A classe de planejamento rotável mais usado para ajustar o modelo de segunda ordem é o planejamento composto central. Este planejamento consiste de um 2k fatorial ou fatorial fracionado 2k-p mais 2k pontos axiais e nc pontos centrais (BOX & HUNTER, 1957). Os 2k pontos axiais, são localizados em (±α1, 0, 0,..., 0), (0, ±α1, 0,..., 0), (0, 0, ±α1,..., 0),..., (0, 0, 0,..., ±α1), sendo que α1 é dado pela equação (2.13). α1 = (2k) ¼ (2.8) O ponto axial no planejamento é utilizado para garantir que o experimento seja rotável. Segundo MONTGOMERY (1991) e BOX & DRAPER (1987), com esse ponto é possível estimar os coeficientes da superfície em todas as direções possíveis. Ainda, o valor de α1 depende do número de pontos na porção fatorial do planejamento. Por exemplo, a configuração de um experimento fatorial composto central com dois fatores pode ser visualizada pela Figura 2.9, sendo que o quadrado com círculos sólidos nas arestas representa o fatorial 2 2, o círculo no centro representa o ponto central nc (0, 0), (0, 0),..., (0, 0), e o losango com quadrados nas arestas representa os pontos axiais do experimento fatorial composto central. FIGURA REPRESENTAÇÃO GRÁFICA DO PLANEJAMENTO COMPOSTO CENTRAL Fonte: Adaptado de MONTGOMERY (1991).
66 65 Nota-se que outra propriedade do planejamento composto central é que pode ser controlado pela escolha do número de pontos centrais nc, ou seja, com um número apropriado de pontos centrais o planejamento é ortogonal e pode ser de precisão uniforme. Nesse caso, a variância da resposta estimada na origem é igual para as distâncias unitárias desde a origem (GUEDES, 1996). Outro tipo de planejamento que pode ser utilizado para conduzir os experimentos são os arranjos ortogonais propostos pelo Método Taguchi. Tais matrizes são descritas por TON et al. (1997); ELSAYED & CHEN (1993); REDDY et al. (1998); MYERS et al. (1989) e STEINBERG & HUNTER (1984). Ainda, na literatura observa-se que existem outros algoritmos que podem ser utilizados para construir as matrizes dos experimentos utilizados na otimização de respostas, conforme descritos por YONCHEV (1988) e STEINBERG & HUNTER (1984) Análise de variância de superfície de resposta: experimento 2 k HILL & HUNTER (1966) propõem um procedimento para realizar a análise estatística de superfície de resposta. Essa estratégia é dividida em quatro passos, conforme segue. 1. Executar com bom desempenho os experimentos. Está etapa depende, principalmente, da técnica de planejamento utilizada para conduzir os experimentos, conforme descrito anteriormente. 2. Determinar os coeficientes do modelo matemático de ajustagem. Para estimar os coeficientes (β) dos polinômios de primeira e segunda ordem, vários autores apresentam o método de mínimos quadrados, conforme descrito pela equação (2.9). β = (X X) -1 X y (2.9) sendo que β é a matriz com os coeficientes, X é a matriz com os parâmetros experimentais codificados e y é a resposta experimental.
67 66 3. Checar se o modelo matemático é adequado para ajustar a superfície de resposta. Na análise de superfície de resposta podem ser utilizadas diversas ferramentas estatísticas. As mais comuns são os gráficos de superfície de resposta e a técnica de análise de variância (ANOVA). Os gráficos podem ser utilizados para estudar visualmente o relacionamento que existe entre os fatores e as respostas. Porém, HILL & HUNTER (1966) advertem que essas ferramentas não são exatas para representar o relacionamento. A ANOVA é utilizada para verificar se a variação dos coeficientes (β1, β2,..., βk) do modelo matemático interfere significativamente na modelagem da superfície de resposta. De acordo com MONTGOMERY (1991), a linearidade do modelo matemático pode ser verificada ao estimar a diferença entre a média das respostas para os pontos fatoriais do experimento ( f y ), e a média dos resultados obtidos em nc rodadas no ponto central ( c y ). Se a diferença entre (y y ) f c for pequena, então assume-se que o ponto central está próximo ao plano que contém as respostas do experimento fatorial (a superfície de resposta plana) e portanto não há curvatura no sistema. No entanto, se essa diferença for grande, assume-se que a superfície de resposta na região é não plana (MONTGOMERY, 1991; BOX & HUNTER, 1957). Para testar estatisticamente se existe ou não curvatura na região central, calcula-se a soma quadrática nesse ponto, dada pela equação (2.10). (2.10) sendo que nf é o número de resultados na parte fatorial do experimento e nc é o número de resultados no ponto central. Em seguida, a estatística F é determinada, conforme a equação (2.11).
68 67 (2.11) sendo que σ 2 é uma estimativa do erro experimental (SSE) calculada a partir dos resultados no ponto central (nc), dado pela equação (2.12). (2.12) sendo que y é a média dos resultados no ponto central e yi são as respostas do experimento fatorial. Ainda, antes de assegurar que o modelo matemático pode ser utilizado para ajustar a superfície de resposta, é indispensável realizar uma análise estatística mais completa dos coeficientes do polinômio. A finalidade é verificar se esses termos influenciam significativamente a modelagem da superfície. O processo é decompor a soma total de quadrados, dado pela equação (2.13). SST = SSβ + SSE (2.13) A soma de quadrados dos coeficientes (SSβ) é dada pela equação (2.14). (2.14) sendo que SSiy é a soma de quadrados da i-ésima variável de experimentação, dada pela equação (2.15). (2.15)
69 68 sendo que yj é a resposta experimental, xij é o nível da i-ésima variável e n número de observações. Para aceitar ou rejeitar a hipótese de curvatura ou verificar se o modelo matemático é ajustado à superfície de resposta, será realizado o teste com a estatística F. Geralmente, se o valor de F0 for menor que a estatística critica Fg, k, (c n -1), para um dado nível de significância α, significa que não existe uma curvatura acentuada no plano e, portanto o polinômio pode ser adotado como boa aproximação da superfície de resposta (MONTGOMERY, 1991). Ao mesmo tempo, o teste aponta quais são os fatores mais importantes na modelagem. Geralmente, a análise de variância pode ser resumida no Quadro 2.4. É importante ressaltar que esses resultados podem ser obtidos facilmente por meio de softwares estatísticos (STATISTICA, MINITAB). Além dessa vantagem, na maioria dos programas computacionais está incluído o valor p, conforme descrito anteriormente. Quadro 2.4-ANÁLISE DE VARIÂNCIA DE SUPERFÍCIE DE RESPOSTA, FATORIAL 2 2 Uma vez finalizado que na região de experimentação, a variação da resposta é bem modelada por uma função linear dos fatores, pode-se iniciar um procedimento de busca da melhor condição de operação, ou seja, procura-se
70 69 determinar os níveis dos fatores quantitativos que otimizam a resposta de interesse. Com esse objetivo, novos experimentos são planejados, variando-se os parâmetros na direção que, segundo o modelo matemático, levará a uma mais rápida otimização da resposta. Segundo MONTGOMERY (1991), esse processo pode ser chamado de técnica seqüencial que pode ocorrer de duas maneiras, conforme segue. Se um ponto qualquer da superfície (pode representar as condições atuais de operação de um processo) está distanciado das condições ótimas de operação e é necessário se aproximar ou determinar a região de resposta, a análise da superfície de resposta pode ser interpretada como a ascensão a uma montanha, onde o pico representa a resposta máxima do experimento. Esse método é denominado de máxima pendente em ascensão; Se ocorrer o contrário, ou seja, a aproximação ocorre na forma de descenso, o ponto ótimo será a resposta mínima da superfície, e esse procedimento também é conhecido como método de máxima pendente em descenso. 4. Enfim, a última etapa proposta por HILL & HUNTER (1966) é estudar a superfície de resposta na região de interesse. Essa etapa deve ser realizada depois que se comprova a validade do modelo matemático e tem como objetivo determinar os níveis ótimos do sistema investigado. MONTGOMERY (1991) descreve que uma maneira de localizar o ponto ótimo é por meio da técnica de localização do ponto estacionário e planejamento composto central (descrito anteriormente). O ponto ótimo, se realmente existe no sistema investigado, será definido pelo conjunto de pontos (x1, x2,..., xk) para os quais as derivadas parciais se igualam a zero, conforme a equação (2.16). y / x1 = y / x2 =... = y / xk = 0 (2.16) Esse ponto é denominado de ponto estacionário, que pode representar um ponto máximo de resposta, um ponto mínimo ou um ponto de sela (MONTGOMERY, 1991; BOX & HUNTER, 1957). A solução geral do ponto
71 70 estacionário é obtida quando o modelo de segunda ordem equação(2.6) é escrito em notação matricial, conforme a equação (2.17) (MONTGOMERY, 1991). y = β0 + x b + x Bx (2.17) sendo que, Nessa representação matricial b é um vetor (kx1) dos termos lineares, B é uma matriz simétrica (kxk), cujos elementos da diagonal são coeficientes quadráticos puros (βii) e os elementos fora da diagonal correspondem à metade dos termos de interação (βij, i j) do polinômio algébrico. A derivada da equação (2.17) com relação aos elementos do vetor x é dada pela equação (2.18). y / x = b + 2Bx = 0 (2.18) O ponto estacionário é a solução da equação (2.18), cujo resultado é dado pela equação (2.19). X0 = -½ B -1 b (2.19) MONTGOMERY (1991) adverte que uma vez determinado o ponto estacionário, algumas vezes será necessário caracterizar a superfície de resposta com a vizinhança imediata a esse ponto. Neste caso, os autores propõem que seja realizada uma análise mais formal (análise canônica) na superfície de resposta, conforme será descrito a seguir (MONTGOMERY, 1991; HILL & HUNTER, 1966; BOX & HUNTER, 1957). A seguir, no próximo capítulo são descritos os experimentos industriais que foram planejados e analisados estatisticamente com os conceitos e técnicas apresentadas anteriormente.
72 71 3 EXPERIMENTOS INDUSTRIAIS 3.1 Estudo de um processo de manufatura industrial Os conceitos, técnicas de planejamento e análise de experimentos, expostos no capítulo 2, serão aqui aplicados. A finalidade é apresentar os experimentos industriais realizados para definir os principais parâmetros de controle e os níveis de ajustes de um processo de reciclagem de borra de solda Lead Free. O estudo foi desenvolvido em uma empresa do (PIM), com a participação de seus funcionários, e um consultor (prof. Jorge Moriya) na área de metalurgia de solda, no período de fevereiro de 2010 a Junho de A empresa escolhida foi a mesma onde trabalho (Samsung) como membro do time de Pesquisa e Desenvolvimento (P&D). Mostrou-se interessada e receptiva a desenvolver um trabalho dessa natureza. Assim, nas próximas seções, será apresentada uma breve caracterização da empresa Samsung da Amazônia, os processos de manufatura que são utilizados pela empresa, preparação dos experimentos, os resultados e a análise estatística desses experimentos realizados. 3.2 Empresa estudada No início da fase experimental foram realizadas reuniões para que o time fosse informado da proposta da pesquisa na empresa, para apresentar os conceitos das técnicas de planejamento e análises de experimentos. Contamos com o apoio de um consultor na área de metalurgia de solda que já prestava serviços para a empresa. A Samsung da Amazônia iniciou suas atividades em 1995 com 318 funcionários e, hoje, 16 anos depois, já emprega mais de pessoas. A fábrica desde o início de 2011, em nova planta, está operando com as seguintes linhas: Ar condicionado; Câmera Fotográfica Digital; Celulares; CRT ( TVs de Tubo de Imagem); Discos Rígidos (HDD); DVD e BluRay; LCM ( módulo de cristal liquido); Mini System de som e Home theater; Monitor; Press ( estamparia); SMD-
73 72 PCB ( placas) ; gabinetes Touch of Color TOC e televisores de Led Emissor de Luz ( LED) e Display de Cristal Líquido (LCD). A empresa tem investido em novos equipamentos, na melhoria de suas instalações, no treinamento das pessoas e na melhoria de qualidade dos produtos. Desde 2006 a empresa baniu de seus processos produtivos o uso de substancias perigosas como o chumbo e outros elementos químicos nocivos à saúde humana. Utiliza no processo fabril de soldagem dos componentes, a solda Lead Free. E também possui um laboratório para diversas análises, entre as quais podemos destacar a análise de Espectrometria por Fluorescência de Raios-X, (XRF) que é um método não destrutivo para análise da constituição química de sólidos e líquidos. Empenhada em inovação e produtos que atendam as normas de preservação ambiental, destacam-se como exemplos, o gabinete do televisor ToC que não utiliza pintura spray nociva, o que reduz a quantidade de CO² liberada para a atmosfera durante o processo de produção, não utiliza pulverização de tinta para brilho, com isso, não há compostos orgânicos voláteis perigosos, possibilitando a reciclagem. O televisor consome até 33% menos energia. Outro ponto relevante é que os televisores de LED não necessitam de Lâmpadas Fluorescentes de Catodo Frio (CCFLs) para o Backlight (luz de fundo), elas são completamente livres de mercúrio. Os televisores também não utilizam chumbo na composição da liga de solda, para soldagem dos componentes. Isto significa que o descarte e reciclagem das TVs podem ser feitos de forma mais segura com o mínimo impacto para o meio ambiente. Todas essas mudanças no ambiente de trabalho estão sendo provocadas, principalmente, pelas ações de órgãos governamentais que controlam o impacto ambiental produzido pela transformação de matéria prima (MINISTÉRIO DO MEIO AMBIENTE, 2001), pelas exigências das normas internacionais de qualidade como a ISO 9001 de Qualidade, ISO Meio Ambiente e OHSAS de Saúde e Segurança, pelas necessidades dos clientes e a concorrência de outros fabricantes do setor. E principalmente pelas diretrizes da Matriz que são focadas na preservação do meio ambiente.
74 73 Assim, como resultado de muitos esforços a empresa já é líder de mercados em vários segmentos, um aumento dos índices de competitividade e qualidades com redução drástica de problemas detectados no campo. Ao longo do ano a empresa lançou mais de 100 produtos novos no mercado. E no ano de 2010 foram manufaturados e comercializados mais de 10 milhões de produtos. 3.3 Processos de soldagem dos componentes usando solda Lead Free Um dos processos de soldagem utilizados atualmente é a soldagem por refusão. Usa-se um stencil que é uma folha metálica perfurada onde os furos são feitos exatamente onde estão localizados os terminais de contato dos Componentes de Montagem em Superfície (SMD), com o objetivo de colocar pasta de solda sobre estes pontos da placa de circuito impresso. Os componentes são posicionados e então, a placa vai para um forno com temperatura controlada para o processo de soldagem. Outro processo de soldagem muito utilizado ainda é o processo de soldagem por onda. A soldagem por onda é mais antigo e recebeu uma série de aprimoramentos, mas a essência permanece a mesma. As etapas no processo de soldagem por onda são: Fluxagem; Pré-Aquecimento e Soldagem. A operação de Fluxagem faz o trabalho de limpeza e desoxidação da PCI e componentes para que ocorra uma fixação mecânica e elétrica adequada. Ainda melhora a força de capilaridade da solda. Quando se trata de PCI s com furos metalizados, além de soldar um componente, é necessário que a solda passe pelo furo e preencha o espaço entre o terminal do componente convencional. Para que uma soldagem possa ser executada, é necessário que as superfícies estejam limpas. Se a solda se espalha pela superfície com facilidade, deduz-se que esta superfície se encontra limpa e isenta de sujeiras e óxidos. Pré-Aquecimento, nesta etapa do processo tem as seguintes funções básicas: aquecer a PCI com o objetivo de reduzir o stress térmico durante sua passagem pela máquina de solda por onda; evaporar os solventes presentes no
75 74 fluxo; minimizar a diferença de temperatura na PCI; ativar os fluxos. O fluxo orgânico tem sua ativação na temperatura ambiente, mas se torna mais ativo durante o processo de pré-aquecimento da PCI; promover a subida da solda pelo furo (em componentes de tecnologia convencional) e seu respectivo preenchimento com solda. O controle de pré-aquecimento é o controle de sistemas por Convecção que é mais preciso. A temperatura do fluxo de ar que atinge a PCI é muito próxima à temperatura desejada no produto. O controle deste sistema é realizado rapidamente monitorando a temperatura do fluxo de ar através de termopares que estão instalados em posições específicas e definidos. Soldagem. Após as operações de Fluxagem (onde a PCI recebeu o fluxo que retirou as sujeiras (óleos, graxas, etc.) e as oxidações) e Pré-Aquecimento (onde a PCI e componentes receberam uma carga térmica consistente e dentro de limites que mantiveram sua integridade, onde os componentes do fluxo foram devidamente ativados e o solvente volatilizado), a PCI finalmente vai para a etapa final do processo de soldagem: a onda de solda. A onda de solda é formada por bocais instalados dentro do tanque de solda. A configuração destes bocais vai depender do tipo de PCI que será soldada. A soldagem por onda é um modo conveniente de fixar componentes convencionais e Componentes de Montagem em Superfície (SMD) colados no lado inferior da placa de circuito impresso. No caso dos componentes convencionais, estes são inseridos através dos furos na PCI e são soldados passando pela onda de solda. O mesmo ocorre com os componentes SMD colados no lado inferior da placa.
76 75 Etapas do Processo de Soldagem usando o tanque da máquina de solda. FIGURA 3.1. Etapas do Processo de Soldagem por Máquina
77 76 FIGURA 3.2 máquina de soldagem por onda (solda Lead Free). Acervo do autor 3.4 Definições do objeto de estudo No Capitulo 2, foi mostrado a metodologia experimental, a etapa seguinte será definir os objetivo dos experimentos industriais. Nesta etapa as seguintes informações foram analisadas pelo time: O que fazer com a borra de solda Lead Free gerada na empresa; Propor a realização do processo de Reciclagem na própria empresa; Implantar um redutor orgânico no processo de reciclagem da borra de solda uma vez implantado o processo de reciclagem da borra de solda, usar o planejamento e análise de experimentos para maximizar o rendimento da solda extraída da borra. diariamente são produzidos em média produtos de diversos modelos, o que significa que qualquer problema, ocorrido no processo produtivo, deve ser imediatamente tratado e as causas devidamente esclarecidas;
78 77 se ao aplicar as técnicas de planejamento e análise de experimentos industriais, o uso dos recursos naturais (solda lead Free) serão minimizados e o meio ambiente respeitado e preservado; A figura 3.3 a seguir mostra a área que a empresa liberou para a realização reciclagem da borra de solda Lead Free. O que possibilita a realização dos experimentos planejados sem afetar o processo de manufatura da empresa; FIGURA 3.3 Sistema de exaustão (Visto por trás). Área de Reciclagem. Acervo do autor Assim, o estudo se concentraria na engenharia de processos da empresa, ou seja, o principal objetivo foi melhorar o rendimento da reciclagem da borra de solda. Especificamente, foi selecionado como objeto de estudo o processo de reciclagem da borra de solda que é realizado na própria empresa. Contando que os recursos naturais estão cada vez mais escassos, a empresa percebeu que tudo aquilo que for reciclado internamente, reduz-se o uso desta matéria prima. Ao mesmo tempo com a ajuda de um consultor, decidiu-se implantar o processo de reciclagem internamente, utilizando o pó de serra (que é um subproduto da madeira
79 78 e abundante aqui no estado do Amazonas). Com a implantação deste novo processo de reciclagem, partiu-se para o desafio de utilizar as técnicas de planejamento e análise de experimentos para aperfeiçoar o processo de reciclagem de forma a maximizar o rendimento da solda obtida. 3.5 Como surge a oxidação da solda no processo produtivo de soldagem. A oxidação é um fenômeno natural, onde o oxigênio tem uma enorme capacidade de atuar em todos os elementos químicos da natureza, onde somente os gases nobres não são oxidados pelo oxigênio. A velocidade da oxidação está ligada diretamente aos fatores como: calor, corrente elétrica e ação ultravioleta. Particularmente em soldagem de placas de circuito impresso a oxidação está ligada à ação térmica (calor) devido ao estado do metal (liga de estanho Sn) se encontrar na fase líquida. 3.6 INFLUÊNCIA DA OXIDAÇÃO EM SOLDAGEM DE PLACAS: No processo de soldagem eletrônica, a oxidação dos metais (Me) tem influência nos seguintes aspectos: - Custos: O metal líquido é oxidado, o que obriga a sua retirada e adição de novas ligas, gerando aumento de consumo da solda. A reação química deste fenômeno segue da seguinte forma: Equação 1: O 2 + Me (solda) -----> MeO (óxido1) + ½ O 2 Uma molécula do oxigênio do ar reage com o metal da solda Equação 2: O 2 + MeO (óxido1) MeO 2 (óxido2) + ½ O 2 Outra molécula do oxigênio do ar reage com o óxido1 formando o óxido 2 (outra fase de óxido)
80 79 Os oxigênios que sobram das equações 1 e 2 vão reagir com Me (solda) formando mais óxidos da fase 1 (MeO), que combina com oxigênio vindo do ar formando mais óxidos da fase 2, ou seja, MeO 2 (óxido2). Contudo, a forma mais estável do óxido é da fase 1, ou seja, MeO, e com isso segue a equação 3: MeO 2 (óxido2) MeO (óxido1) + ½ O 2 Ou seja, inicia se a liberação de oxigênio dentro do tanque da máquina de solda, iniciando novamente o ciclo pela equação 1 : O 2 + Me (solda) MeO (óxido1) + ½ O 2 Temos então o ciclo de geração de borra da solda, conseqüentemente aumento de consumo da liga de Sn, aumentando-se o custo de produção. FIGURA 3.4 Tanque de Reciclagem da Borra de Solda. Acervo do autor
81 SOLUÇÃO PARA O PROBLEMA DA GERAÇÃO DA BORRA Solução 1: Uso de nitrogênio, ou seja, com a ausência ou redução da presença de oxigênio as equações descritas acima ocorrem em situação mais lenta, portanto menos borra, porém com exigências de instalações para aprovisionamento de nitrogênio, dutos e canos, máquinas de solda adequadas e preparadas para o uso do nitrogênio, bem como o consumo de nitrogênio. Solução pouco viável economicamente. Solução 2: Uso de redutores orgânicos dos óxidos. Pode-se adotar uma série de redutores para converter o metal oxidado para o retorno do metal ao tanque e assim minimizar o consumo da liga de estanho. Os redutores orgânicos podem ser quaisquer materiais que contenham hidrogênio, os quais quando aquecidos são liberados e em contato com o oxigênio da borra, transformam-se em vapor de água, reduzem o metal oxidado e com isso o metal liberado permanece no tanque. MeO (óxido1) + H + (ácido) Me (solda) + H 2 O (gás) O redutor orgânico a ser utilizado, foi proposto pelo prof. Jorge Moriya, é o pó de serra, um resíduo da madeira, material por sinal, muito abundante na região Amazônica. A geração deste tipo de resíduo (pó de serra) não é pequena. Segundo o engenheiro Flávio Pedrosa Dantas Filho ao iniciar sua pesquisa de mestrado na Faculdade de Engenharia Civil, estimou que uma serraria de porte médio destinada a produzir 2 mil metros cúbicos de madeira serrada por mês, poderia gerar 78 toneladas de serragem. Ao todo, as serrarias do país gerariam em torno de 620 mil toneladas de serragem por ano. Os problemas causados para o meio ambiente são inúmeros, afirma. Um dos principais fatores é a queima que polui o ambiente, gerando gás carbônico, completa. A outra porcentagem, segundo o engenheiro, é descartada no meio ambiente, provocando poluição do solo e água. Assim, o redutor orgânico proposto no processo de reciclagem da borra de solda, contribui com a redução de resíduos sólidos descartados, muitas vezes, no meio ambiente.
82 81 Neste caso o consumo de metal é reduzido pelo reaproveitamento do metal oxidado (borra de solda) reduzindo-se com os ácidos orgânicos presentes no pó de serra. Este processo é conseguido com a reciclagem da borra de solda Lead Free. O pó de serra utilizado na reciclagem é recolhido de uma serraria local, Aqui na empresa o mesmo é armazenado em um recipiente (tambor). Antes do uso na reciclagem o pó de serra é peneirado. Conforme pode ser visto a seguir. FIGURA 3.5 Pó de serra usado na reciclagem da borra. Acervo do autor 3.7 Planejamento de experimentos Seleção dos fatores e os níveis do processo de entrada Os fatores e os níveis do processo de entrada foi amplamente discutido pelo time envolvido no processo de Reciclagem da borra de solda Lead Free. No período de análise do processo de reciclagem, o time identificou vários fatores relacionados ao experimento, conforme descrito a seguir: Composição química da solda;
83 82 Composição da borra de solda; Temperatura ambiente; Energia elétrica ( quadro trifásico de voltagem AC); Operador do processo de reciclagem; Tempo de mexida (mixagem do pó de serra com a borra) Temperatura do tanque; Processo de coleta da borra das máquinas de soldagem; Pó de serra. Entre os fatores mencionados, foram considerados como sendo de ruído ou constantes os seguintes: Composição química da solda; Composição da borra de solda; Temperatura ambiente; Energia elétrica (quadro trifásico de voltagem AC); Operador do processo de reciclagem; Tempo de mexida (mixagem do pó de serra com a borra) Processo de coleta da borra das máquinas de soldagem; Assim, os fatores considerados inteiramente pautados com o resultado desejado e, portanto, estudado durante os experimentos são: Temperatura do tanque, sendo uma das duas variáveis de entrada escolhida. Procurou-se respeitar as especificações técnicas de soldabilidade. Pó de serra. Segunda variável escolhida, o pó de serra, que em uma outra fase anterior do projeto, havia sido implantado como o redutor orgânico Seleção da variável de saída do processo
84 83 Para este trabalho estava muito claro qual seria a variável de resposta do experimento. O objetivo principal da observação da variável resposta é aumentar o rendimento da solda extraída da borra de solda Lead Free. 3.8 Realização do experimento Considerando que os experimentos tenham diferentes objetivos e montagem física, têm algumas ações e regras aplicáveis, praticamente, a todo tipo de experimento. No mínimo um experimento precisa dos seguintes requisitos: Planejamento; Execução; Processamento; Análise e emissão de relatório Planejamento Com o levantamento do problema começa o planejamento da experimentação. Assim, o problema pode ser estabelecido como a procura da maximização do rendimento da reciclagem da borra de solda Lead Free, por meio da análise da influência e comportamento dos fatores: temperatura do tanque e quantidade do pó de serra utilizado. Com o levantamento acima, se fizeram necessárias algumas definições. A escolha da variável de resposta do processo analisado. O alvo de preocupação inicial é o rendimento e a qualidade da solda extraída do processo de reciclagem Matriz de Planejamento Concluída as fases de seleção dos fatores de entrada, definiu-se a variável de saída. Foram considerados dois fatores de entrada e um fator de saída. Em função
85 84 das duas variáveis de entrada foi adotado a realização do experimento fatorial completo 2 2. Com a definição do projeto de experimento, foi necessário mencionar os níveis dos fatores das variáveis de entrada. O nível da variável temperatura do tanque foi determinado, levando-se em conta os parâmetros de temperatura de soldagem da solda Lead Free (ponto de fusão da liga Lead Free e temperatura de soldagem recomendada). O nível da variável pó de serra foi estimado, baseado no processo empírico que havia sido adotado antes no processo de reciclagem. Ou seja, contou-se com a experiência dos operadores que executavam a reciclagem da borra de solda Lead Free. Partindo destas informações, estabeleceu-se os níveis inferior e superior para os fatores, vistos no Quadro 3.1 Fator Nível inferior (-) Nível superior (+) Temperatura do tanque 250ºC 270ºC Pó de serra 0.9 Kg 1.8 Kg Quadro 3.1: Fatores com os níveis. Fonte: acervo do autor Foi usado as escalas e equipamentos listados a seguir: º C unidade para grau Celsius, Kg para unidade de peso, balança e Controlador de Temperatura, modelo TZ4ST Figura 3.6 Controlador de Temperatura. Fonte: Catálogo do fabricante Autonics
86 Execução O principal objetivo de interesse na realização do experimento é descobrir na reciclagem da borra de solda Lead Free, quais combinações entre os níveis das variáveis de entrada que apresentarão o melhor rendimento do metal oxidado, ou seja, em que condição a variável de saída é máxima, resultando em mais solda livre do óxido, permanecendo presente no tanque, após a reciclagem da borra. Inicialmente é acrescentada uma quantidade de solda no tanque para ajudar no processo de derretimento da solda e da borra. Em cada experimento a quantidade de borra utilizada foi de 90 kg. Durante o processo é acrescentado o pó de serra. No final de cada experimento, pesou-se o óxido resultante. E o que vai para a tabela é: 90 kg (borra) óxido = Solda, que permanece no tanque. A etapa posterior é fazer os lingotes com a solda derretida FIGURA 3.7 Lingote de solda. Acervo do autor. Conforme definido anteriormente, foi realizado um experimento fatorial completo com três replicações, geração de uma matriz de 12 combinações. Os dados das variáveis de entrada (Temperatura do tanque e Pó de serra) com seus respectivos níveis são inseridos na planilha. Os dados da variável de saída (solda) após sua coleta realizada do experimento também foi acrescento no MINITAB.
87 86 Conforme vistos na tabela e no quadro a seguir que mostram os valores resultantes do experimento fatorial 2 2, realizado no experimento industrial da reciclagem da borra de solda, Fatores Saída Combinaçoes A B AB Solda (kg) Total Média (l) a b ab Tabela 3.1 Planejamento de experimento 2 2. Fonte: acervo do autor Ordem Ponto Temperatura Pó de Solda Sequencia Blocos padrao Central (ºC) Serra (kg) (kg) ,9 36, ,9 39, ,8 37, ,8 49, ,9 36, ,9 40, ,8 38, ,8 48, ,9 37, ,9 40, ,8 39, ,8 48,4 Quadro 3.2: Matriz de planejamento mostrando o resultado dos testes. Fonte: Acervo do autor Processamento De posse dos dados, foram realizados os primeiros cálculos e gráficos do experimento. A meta foi começar a elaboração das equações e observar o comportamento do processo.
88 87 Figura 3.8. Probabilidade Normal dos Resíduos (Minitab) Foi calculado os efeitos de interesse no planejamento 2 2 que são os efeitos principais A e B e o fator de interação AB. Para este estudo o fator A refere-se a variável de entrada Temperatura e o fator B refere-se a variável de entrada Pó de serra. Para estimar o efeito principal do fator A, deve-se fazer a média das observações do lado direito do quadrado na fig.3.9, estando A no nível alto, e subtrair desse valor a media das observações do lado esquerdo do quadrado, em que A está no nível baixo. b ab B (+) Tratamento A B (1) a + -- b -- + ab + + (-) (1) A a (-) (+) Fig.3.9 Quadrado com as médias das observações Para o cálculo do efeito de A, B e Interação AB deste experimento faz-se:
Gerenciamento de Riscos do Projeto Eventos Adversos
 Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
Projeto de Sistemas I
 Instituto Federal de Educação, Ciência e Tecnologia de São Paulo Projeto de Sistemas I Professora: Kelly de Paula Cunha E-mail:kellypcsoares@ifsp.edu.br Requisitos: base para todo projeto, definindo o
Instituto Federal de Educação, Ciência e Tecnologia de São Paulo Projeto de Sistemas I Professora: Kelly de Paula Cunha E-mail:kellypcsoares@ifsp.edu.br Requisitos: base para todo projeto, definindo o
Roteiro SENAC. Análise de Riscos. Planejamento do Gerenciamento de Riscos. Planejamento do Gerenciamento de Riscos
 SENAC Pós-Graduação em Segurança da Informação: Análise de Riscos Parte 2 Leandro Loss, Dr. Eng. loss@gsigma.ufsc.br http://www.gsigma.ufsc.br/~loss Roteiro Introdução Conceitos básicos Riscos Tipos de
SENAC Pós-Graduação em Segurança da Informação: Análise de Riscos Parte 2 Leandro Loss, Dr. Eng. loss@gsigma.ufsc.br http://www.gsigma.ufsc.br/~loss Roteiro Introdução Conceitos básicos Riscos Tipos de
PÓS GRADUAÇÃO EM CIÊNCIAS DE FLORESTAS TROPICAIS-PG-CFT INSTITUTO NACIONAL DE PESQUISAS DA AMAZÔNIA-INPA. 09/abril de 2014
 PÓS GRADUAÇÃO EM CIÊNCIAS DE FLORESTAS TROPICAIS-PG-CFT INSTITUTO NACIONAL DE PESQUISAS DA AMAZÔNIA-INPA 09/abril de 2014 Considerações Estatísticas para Planejamento e Publicação 1 Circularidade do Método
PÓS GRADUAÇÃO EM CIÊNCIAS DE FLORESTAS TROPICAIS-PG-CFT INSTITUTO NACIONAL DE PESQUISAS DA AMAZÔNIA-INPA 09/abril de 2014 Considerações Estatísticas para Planejamento e Publicação 1 Circularidade do Método
Engenharia de Software
 Universidade São Judas Tadeu Profª Dra. Ana Paula Gonçalves Serra Engenharia de O Processo Uma Visão Genérica Capítulo 2 (até item 2.2. inclusive) Engenharia de - Roger Pressman 6ª edição McGrawHill Capítulo
Universidade São Judas Tadeu Profª Dra. Ana Paula Gonçalves Serra Engenharia de O Processo Uma Visão Genérica Capítulo 2 (até item 2.2. inclusive) Engenharia de - Roger Pressman 6ª edição McGrawHill Capítulo
Módulo 15 Resumo. Módulo I Cultura da Informação
 Módulo 15 Resumo Neste módulo vamos dar uma explanação geral sobre os pontos que foram trabalhados ao longo desta disciplina. Os pontos abordados nesta disciplina foram: Fundamentos teóricos de sistemas
Módulo 15 Resumo Neste módulo vamos dar uma explanação geral sobre os pontos que foram trabalhados ao longo desta disciplina. Os pontos abordados nesta disciplina foram: Fundamentos teóricos de sistemas
CHECK - LIST - ISO 9001:2000
 REQUISITOS ISO 9001: 2000 SIM NÃO 1.2 APLICAÇÃO A organização identificou as exclusões de itens da norma no seu manual da qualidade? As exclusões são relacionadas somente aos requisitos da sessão 7 da
REQUISITOS ISO 9001: 2000 SIM NÃO 1.2 APLICAÇÃO A organização identificou as exclusões de itens da norma no seu manual da qualidade? As exclusões são relacionadas somente aos requisitos da sessão 7 da
Gerenciamento de Projetos Modulo II Ciclo de Vida e Organização do Projeto
 Gerenciamento de Projetos Modulo II Ciclo de Vida e Organização do Projeto Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com PMBoK Organização do Projeto Os projetos e o gerenciamento
Gerenciamento de Projetos Modulo II Ciclo de Vida e Organização do Projeto Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com PMBoK Organização do Projeto Os projetos e o gerenciamento
PLANEJAMENTO EXPERIMENTAL
 PLANEJAMENTO EXPERIMENTAL Técnicas de Pesquisas Experimentais LUIS HENRIQUE STOCCO MARCIO TENÓRIO SANDRA MARCHI Introdução O Planejamento de Experimentos (Design of Experiments, DoE), técnica utilizada
PLANEJAMENTO EXPERIMENTAL Técnicas de Pesquisas Experimentais LUIS HENRIQUE STOCCO MARCIO TENÓRIO SANDRA MARCHI Introdução O Planejamento de Experimentos (Design of Experiments, DoE), técnica utilizada
Extração de Requisitos
 Extração de Requisitos Extração de requisitos é o processo de transformação das idéias que estão na mente dos usuários (a entrada) em um documento formal (saída). Pode se entender também como o processo
Extração de Requisitos Extração de requisitos é o processo de transformação das idéias que estão na mente dos usuários (a entrada) em um documento formal (saída). Pode se entender também como o processo
Pós-Graduação em Gerenciamento de Projetos práticas do PMI
 Pós-Graduação em Gerenciamento de Projetos práticas do PMI Planejamento do Gerenciamento das Comunicações (10) e das Partes Interessadas (13) PLANEJAMENTO 2 PLANEJAMENTO Sem 1 Sem 2 Sem 3 Sem 4 Sem 5 ABRIL
Pós-Graduação em Gerenciamento de Projetos práticas do PMI Planejamento do Gerenciamento das Comunicações (10) e das Partes Interessadas (13) PLANEJAMENTO 2 PLANEJAMENTO Sem 1 Sem 2 Sem 3 Sem 4 Sem 5 ABRIL
Processo de Implementação de um Sistema de Gestão da Qualidade
 3 Processo de Implementação de um Sistema de Gestão da Qualidade Não existe um jeito único de se implementar um sistema da qualidade ISO 9001: 2000. No entanto, independentemente da maneira escolhida,
3 Processo de Implementação de um Sistema de Gestão da Qualidade Não existe um jeito único de se implementar um sistema da qualidade ISO 9001: 2000. No entanto, independentemente da maneira escolhida,
Processos de gerenciamento de projetos em um projeto
 Processos de gerenciamento de projetos em um projeto O gerenciamento de projetos é a aplicação de conhecimentos, habilidades, ferramentas e técnicas às atividades do projeto a fim de cumprir seus requisitos.
Processos de gerenciamento de projetos em um projeto O gerenciamento de projetos é a aplicação de conhecimentos, habilidades, ferramentas e técnicas às atividades do projeto a fim de cumprir seus requisitos.
SISTEMA DE GESTÃO AMBIENTAL ABNT NBR ISO 14001
 SISTEMA DE GESTÃO AMBIENTAL ABNT NBR ISO 14001 Prof. Eduardo Lucena Cavalcante de Amorim INTRODUÇÃO A norma ISO 14001 faz parte de um conjunto mais amplo de normas intitulado ISO série 14000. Este grupo
SISTEMA DE GESTÃO AMBIENTAL ABNT NBR ISO 14001 Prof. Eduardo Lucena Cavalcante de Amorim INTRODUÇÃO A norma ISO 14001 faz parte de um conjunto mais amplo de normas intitulado ISO série 14000. Este grupo
CENTRO DE CIÊNCIAS TECNOLÓGICAS CCT
 UNIVERSIDADE DO ESTADO DE SANTA CATARINA CENTRO DE CIÊNCIAS TECNOLÓGICAS CCT CURSO DE TECNOLOGIA EM SISTEMAS DE INFORMAÇÃO ENGENHARIA DO PRODUTO FABIANO RAMOS DOS SANTOS SERGIO DA COSTA FERREIRA JOELSON
UNIVERSIDADE DO ESTADO DE SANTA CATARINA CENTRO DE CIÊNCIAS TECNOLÓGICAS CCT CURSO DE TECNOLOGIA EM SISTEMAS DE INFORMAÇÃO ENGENHARIA DO PRODUTO FABIANO RAMOS DOS SANTOS SERGIO DA COSTA FERREIRA JOELSON
A IMPORTÂNCIA DA GESTÃO DE CUSTOS NA ELABORAÇÃO DO PREÇO DE VENDA
 553 A IMPORTÂNCIA DA GESTÃO DE CUSTOS NA ELABORAÇÃO DO PREÇO DE VENDA Irene Caires da Silva 1, Tamires Fernanda Costa de Jesus, Tiago Pinheiro 1 Docente da Universidade do Oeste Paulista UNOESTE. 2 Discente
553 A IMPORTÂNCIA DA GESTÃO DE CUSTOS NA ELABORAÇÃO DO PREÇO DE VENDA Irene Caires da Silva 1, Tamires Fernanda Costa de Jesus, Tiago Pinheiro 1 Docente da Universidade do Oeste Paulista UNOESTE. 2 Discente
Texto para Coluna do NRE-POLI na Revista Construção e Mercado Pini Abril 2012
 Texto para Coluna do NRE-POLI na Revista Construção e Mercado Pini Abril 2012 O RISCO DOS DISTRATOS O impacto dos distratos no atual panorama do mercado imobiliário José Eduardo Rodrigues Varandas Júnior
Texto para Coluna do NRE-POLI na Revista Construção e Mercado Pini Abril 2012 O RISCO DOS DISTRATOS O impacto dos distratos no atual panorama do mercado imobiliário José Eduardo Rodrigues Varandas Júnior
Gerenciamento de Projetos Modulo VIII Riscos
 Gerenciamento de Projetos Modulo VIII Riscos Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com Bibliografia* Project Management Institute. Conjunto de Conhecimentos em Gerenciamento
Gerenciamento de Projetos Modulo VIII Riscos Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com Bibliografia* Project Management Institute. Conjunto de Conhecimentos em Gerenciamento
PROCESSO DE DESENVOLVIMENTO DE SOFTWARE. Modelos de Processo de Desenvolvimento de Software
 PROCESSO DE DESENVOLVIMENTO DE SOFTWARE Introdução Modelos de Processo de Desenvolvimento de Software Os modelos de processos de desenvolvimento de software surgiram pela necessidade de dar resposta às
PROCESSO DE DESENVOLVIMENTO DE SOFTWARE Introdução Modelos de Processo de Desenvolvimento de Software Os modelos de processos de desenvolvimento de software surgiram pela necessidade de dar resposta às
PLANOS DE CONTINGÊNCIAS
 PLANOS DE CONTINGÊNCIAS ARAÚJO GOMES Capitão SC PMSC ARAÚJO GOMES defesacivilgomes@yahoo.com.br PLANO DE CONTINGÊNCIA O planejamento para emergências é complexo por suas características intrínsecas. Como
PLANOS DE CONTINGÊNCIAS ARAÚJO GOMES Capitão SC PMSC ARAÚJO GOMES defesacivilgomes@yahoo.com.br PLANO DE CONTINGÊNCIA O planejamento para emergências é complexo por suas características intrínsecas. Como
Na medida em que se cria um produto, o sistema de software, que será usado e mantido, nos aproximamos da engenharia.
 1 Introdução aos Sistemas de Informação 2002 Aula 4 - Desenvolvimento de software e seus paradigmas Paradigmas de Desenvolvimento de Software Pode-se considerar 3 tipos de paradigmas que norteiam a atividade
1 Introdução aos Sistemas de Informação 2002 Aula 4 - Desenvolvimento de software e seus paradigmas Paradigmas de Desenvolvimento de Software Pode-se considerar 3 tipos de paradigmas que norteiam a atividade
Sugestão de Roteiro para Elaboração de Monografia de TCC
 Sugestão de Roteiro para Elaboração de Monografia de TCC Sugerimos, para elaborar a monografia de TCC (Trabalho de Conclusão de Curso), que o aluno leia atentamente essas instruções. Fundamentalmente,
Sugestão de Roteiro para Elaboração de Monografia de TCC Sugerimos, para elaborar a monografia de TCC (Trabalho de Conclusão de Curso), que o aluno leia atentamente essas instruções. Fundamentalmente,
ATENÇÃO. Apresentação
 Apresentação O tema logística reversa vem crescendo em importância entre as empresas desde a regulamentação da Política Nacional de Resíduos Sólidos. Com as novas exigências, as empresas precisam buscar
Apresentação O tema logística reversa vem crescendo em importância entre as empresas desde a regulamentação da Política Nacional de Resíduos Sólidos. Com as novas exigências, as empresas precisam buscar
Gestão do Conhecimento A Chave para o Sucesso Empresarial. José Renato Sátiro Santiago Jr.
 A Chave para o Sucesso Empresarial José Renato Sátiro Santiago Jr. Capítulo 1 O Novo Cenário Corporativo O cenário organizacional, sem dúvida alguma, sofreu muitas alterações nos últimos anos. Estas mudanças
A Chave para o Sucesso Empresarial José Renato Sátiro Santiago Jr. Capítulo 1 O Novo Cenário Corporativo O cenário organizacional, sem dúvida alguma, sofreu muitas alterações nos últimos anos. Estas mudanças
Introdução Visão Geral Processos de gerenciamento de qualidade. Entradas Ferramentas e Técnicas Saídas
 Introdução Visão Geral Processos de gerenciamento de qualidade Entradas Ferramentas e Técnicas Saídas O que é qualidade? Qualidade é a adequação ao uso. É a conformidade às exigências. (ISO International
Introdução Visão Geral Processos de gerenciamento de qualidade Entradas Ferramentas e Técnicas Saídas O que é qualidade? Qualidade é a adequação ao uso. É a conformidade às exigências. (ISO International
Gestão da Qualidade Políticas. Elementos chaves da Qualidade 19/04/2009
 Gestão da Qualidade Políticas Manutenção (corretiva, preventiva, preditiva). Elementos chaves da Qualidade Total satisfação do cliente Priorizar a qualidade Melhoria contínua Participação e comprometimento
Gestão da Qualidade Políticas Manutenção (corretiva, preventiva, preditiva). Elementos chaves da Qualidade Total satisfação do cliente Priorizar a qualidade Melhoria contínua Participação e comprometimento
Prof. Dr. Guanis de Barros Vilela Junior
 Prof. Dr. Guanis de Barros Vilela Junior INTRODUÇÃO O que é pesquisa? Pesquisar significa, de forma bem simples, procurar respostas para indagações propostas. INTRODUÇÃO Minayo (1993, p. 23), vendo por
Prof. Dr. Guanis de Barros Vilela Junior INTRODUÇÃO O que é pesquisa? Pesquisar significa, de forma bem simples, procurar respostas para indagações propostas. INTRODUÇÃO Minayo (1993, p. 23), vendo por
CONCURSO PÚBLICO ANALISTA DE SISTEMA ÊNFASE GOVERNANÇA DE TI ANALISTA DE GESTÃO RESPOSTAS ESPERADAS PRELIMINARES
 CELG DISTRIBUIÇÃO S.A EDITAL N. 1/2014 CONCURSO PÚBLICO ANALISTA DE GESTÃO ANALISTA DE SISTEMA ÊNFASE GOVERNANÇA DE TI RESPOSTAS ESPERADAS PRELIMINARES O Centro de Seleção da Universidade Federal de Goiás
CELG DISTRIBUIÇÃO S.A EDITAL N. 1/2014 CONCURSO PÚBLICO ANALISTA DE GESTÃO ANALISTA DE SISTEMA ÊNFASE GOVERNANÇA DE TI RESPOSTAS ESPERADAS PRELIMINARES O Centro de Seleção da Universidade Federal de Goiás
FUNDAMENTOS PARA A ADMINISTRAÇÃO ESTRATÉGICA
 FUNDAMENTOS PARA A ADMINISTRAÇÃO ESTRATÉGICA Abordagem da estratégia Análise de áreas mais específicas da administração estratégica e examina três das principais áreas funcionais das organizações: marketing,
FUNDAMENTOS PARA A ADMINISTRAÇÃO ESTRATÉGICA Abordagem da estratégia Análise de áreas mais específicas da administração estratégica e examina três das principais áreas funcionais das organizações: marketing,
DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE
 DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE Mariane Alves Gomes da Silva Eliana Zandonade 1. INTRODUÇÃO Um aspecto fundamental de um levantamento
DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE Mariane Alves Gomes da Silva Eliana Zandonade 1. INTRODUÇÃO Um aspecto fundamental de um levantamento
)HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR
 6LPXODomR GH6LVWHPDV )HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR #5,6. Simulador voltado para análise de risco financeiro 3RQWRV IRUWHV Fácil de usar. Funciona integrado a ferramentas já bastante conhecidas,
6LPXODomR GH6LVWHPDV )HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR #5,6. Simulador voltado para análise de risco financeiro 3RQWRV IRUWHV Fácil de usar. Funciona integrado a ferramentas já bastante conhecidas,
QUALIDADE Noções iniciais
 Este segmento do curso é baseado no livro: JURAN, J.M. A qualidade desde o projeto. São Paulo: Thomson, 1992. QUALIDADE Noções iniciais Questões de qualidade e gerenciamento de qualidade são preocupações
Este segmento do curso é baseado no livro: JURAN, J.M. A qualidade desde o projeto. São Paulo: Thomson, 1992. QUALIDADE Noções iniciais Questões de qualidade e gerenciamento de qualidade são preocupações
Universidade de Brasília Faculdade de Economia, Administração, Contabilidade e Ciência da Informação e Documentação Departamento de Ciência da
 Universidade de Brasília Faculdade de Economia, Administração, Contabilidade e Ciência da Informação e Documentação Departamento de Ciência da Informação e Documentação Disciplina: Planejamento e Gestão
Universidade de Brasília Faculdade de Economia, Administração, Contabilidade e Ciência da Informação e Documentação Departamento de Ciência da Informação e Documentação Disciplina: Planejamento e Gestão
Processos Técnicos - Aulas 4 e 5
 Processos Técnicos - Aulas 4 e 5 Trabalho / PEM Tema: Frameworks Públicos Grupo: equipe do TCC Entrega: versão digital, 1ª semana de Abril (de 31/03 a 04/04), no e-mail do professor (rodrigues.yuri@yahoo.com.br)
Processos Técnicos - Aulas 4 e 5 Trabalho / PEM Tema: Frameworks Públicos Grupo: equipe do TCC Entrega: versão digital, 1ª semana de Abril (de 31/03 a 04/04), no e-mail do professor (rodrigues.yuri@yahoo.com.br)
Sistemas de Gestão Ambiental O QUE MUDOU COM A NOVA ISO 14001:2004
 QSP Informe Reservado Nº 41 Dezembro/2004 Sistemas de Gestão O QUE MUDOU COM A NOVA ISO 14001:2004 Material especialmente preparado para os Associados ao QSP. QSP Informe Reservado Nº 41 Dezembro/2004
QSP Informe Reservado Nº 41 Dezembro/2004 Sistemas de Gestão O QUE MUDOU COM A NOVA ISO 14001:2004 Material especialmente preparado para os Associados ao QSP. QSP Informe Reservado Nº 41 Dezembro/2004
Guia de recomendações para implementação de PLM em PME s
 1 Guia de recomendações para implementação de PLM em PME s RESUMO EXECUTIVO Este documento visa informar, de uma forma simples e prática, sobre o que é a gestão do ciclo de vida do Produto (PLM) e quais
1 Guia de recomendações para implementação de PLM em PME s RESUMO EXECUTIVO Este documento visa informar, de uma forma simples e prática, sobre o que é a gestão do ciclo de vida do Produto (PLM) e quais
FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS - FAN CEUNSP SALTO /SP CURSO DE TECNOLOGIA EM MARKETING TRABALHO INTERDISCIPLINAR
 APRESENTAÇÃO DO TI O Trabalho Interdisciplinar é um projeto desenvolvido ao longo dos dois primeiros bimestres do curso. Os alunos tem a oportunidade de visualizar a unidade da estrutura curricular do
APRESENTAÇÃO DO TI O Trabalho Interdisciplinar é um projeto desenvolvido ao longo dos dois primeiros bimestres do curso. Os alunos tem a oportunidade de visualizar a unidade da estrutura curricular do
ISO 9001:2008. Alterações e Adições da nova versão
 ISO 9001:2008 Alterações e Adições da nova versão Notas sobe esta apresentação Esta apresentação contém as principais alterações e adições promovidas pela edição 2008 da norma de sistema de gestão mais
ISO 9001:2008 Alterações e Adições da nova versão Notas sobe esta apresentação Esta apresentação contém as principais alterações e adições promovidas pela edição 2008 da norma de sistema de gestão mais
SISTEMAS DE GESTÃO São Paulo, Janeiro de 2005
 SISTEMAS DE GESTÃO São Paulo, Janeiro de 2005 ÍNDICE Introdução...3 A Necessidade do Gerenciamento e Controle das Informações...3 Benefícios de um Sistema de Gestão da Albi Informática...4 A Ferramenta...5
SISTEMAS DE GESTÃO São Paulo, Janeiro de 2005 ÍNDICE Introdução...3 A Necessidade do Gerenciamento e Controle das Informações...3 Benefícios de um Sistema de Gestão da Albi Informática...4 A Ferramenta...5
MASTER IN PROJECT MANAGEMENT
 MASTER IN PROJECT MANAGEMENT PROJETOS E COMUNICAÇÃO PROF. RICARDO SCHWACH MBA, PMP, COBIT, ITIL Atividade 1 Que modelos em gestão de projetos estão sendo adotados como referência nas organizações? Como
MASTER IN PROJECT MANAGEMENT PROJETOS E COMUNICAÇÃO PROF. RICARDO SCHWACH MBA, PMP, COBIT, ITIL Atividade 1 Que modelos em gestão de projetos estão sendo adotados como referência nas organizações? Como
Profissionais de Alta Performance
 Profissionais de Alta Performance As transformações pelas quais o mundo passa exigem novos posicionamentos em todas as áreas e em especial na educação. A transferência pura simples de dados ou informações
Profissionais de Alta Performance As transformações pelas quais o mundo passa exigem novos posicionamentos em todas as áreas e em especial na educação. A transferência pura simples de dados ou informações
EDITAL SENAI SESI DE INOVAÇÃO. Caráter inovador projeto cujo escopo ainda não possui. Complexidade das tecnologias critério de avaliação que
 ANEXO II Caráter inovador projeto cujo escopo ainda não possui registro em base de patentes brasileira. Também serão considerados caráter inovador para este Edital os registros de patente de domínio público
ANEXO II Caráter inovador projeto cujo escopo ainda não possui registro em base de patentes brasileira. Também serão considerados caráter inovador para este Edital os registros de patente de domínio público
ROTEIRO PARA ELABORAÇÃO DE PROJETOS
 APRESENTAÇÃO ROTEIRO PARA ELABORAÇÃO DE PROJETOS Breve histórico da instituição seguido de diagnóstico e indicadores sobre a temática abrangida pelo projeto, especialmente dados que permitam análise da
APRESENTAÇÃO ROTEIRO PARA ELABORAÇÃO DE PROJETOS Breve histórico da instituição seguido de diagnóstico e indicadores sobre a temática abrangida pelo projeto, especialmente dados que permitam análise da
O que é Administração
 O que é Administração Bem vindo ao curso de administração de empresas. Pretendemos mostrar a você no período que passaremos juntos, alguns conceitos aplicados à administração. Nossa matéria será puramente
O que é Administração Bem vindo ao curso de administração de empresas. Pretendemos mostrar a você no período que passaremos juntos, alguns conceitos aplicados à administração. Nossa matéria será puramente
Governança de TI. ITIL v.2&3. parte 1
 Governança de TI ITIL v.2&3 parte 1 Prof. Luís Fernando Garcia LUIS@GARCIA.PRO.BR ITIL 1 1 ITIL Gerenciamento de Serviços 2 2 Gerenciamento de Serviços Gerenciamento de Serviços 3 3 Gerenciamento de Serviços
Governança de TI ITIL v.2&3 parte 1 Prof. Luís Fernando Garcia LUIS@GARCIA.PRO.BR ITIL 1 1 ITIL Gerenciamento de Serviços 2 2 Gerenciamento de Serviços Gerenciamento de Serviços 3 3 Gerenciamento de Serviços
CRIAÇÃO DA DISCIPLINA SISTEMA DE GESTÃO AMBIENTAL NO CURSO DE ENGENHARIA CIVIL
 CRIAÇÃO DA DISCIPLINA SISTEMA DE GESTÃO AMBIENTAL NO CURSO DE ENGENHARIA CIVIL Elias S. Assayag eassayag@internext.com.br Universidade do Amazonas, Departamento de Hidráulica e Saneamento da Faculdade
CRIAÇÃO DA DISCIPLINA SISTEMA DE GESTÃO AMBIENTAL NO CURSO DE ENGENHARIA CIVIL Elias S. Assayag eassayag@internext.com.br Universidade do Amazonas, Departamento de Hidráulica e Saneamento da Faculdade
MRP II. Planejamento e Controle da Produção 3 professor Muris Lage Junior
 MRP II Introdução A lógica de cálculo das necessidades é conhecida há muito tempo Porém só pode ser utilizada na prática em situações mais complexas a partir dos anos 60 A partir de meados da década de
MRP II Introdução A lógica de cálculo das necessidades é conhecida há muito tempo Porém só pode ser utilizada na prática em situações mais complexas a partir dos anos 60 A partir de meados da década de
2. Função Produção/Operação/Valor Adicionado
 2. Função Produção/Operação/Valor Adicionado Conteúdo 1. Função Produção 3. Administração da Produção 1 Bibliografia Recomenda Livro Texto: Introdução à Administração Eunice Lacava Kwasnicka - Editora
2. Função Produção/Operação/Valor Adicionado Conteúdo 1. Função Produção 3. Administração da Produção 1 Bibliografia Recomenda Livro Texto: Introdução à Administração Eunice Lacava Kwasnicka - Editora
Teoria da Decisão MÉTODOS QUANTITATIVOS DE GESTÃO
 Teoria da Decisão MÉTODOS QUANTITATIVOS DE GESTÃO INTRODUÇÃO Todo problema de decisão envolve julgamento sobre um conjunto conhecido de alternativas; Informações Disponíveis (Dados) Conhecidos com certeza;
Teoria da Decisão MÉTODOS QUANTITATIVOS DE GESTÃO INTRODUÇÃO Todo problema de decisão envolve julgamento sobre um conjunto conhecido de alternativas; Informações Disponíveis (Dados) Conhecidos com certeza;
Capítulo 8 MONITORAMENTO E AVALIAÇÃO
 Capítulo 8 MONITORAMENTO E AVALIAÇÃO 8 MONITORAMENTO E AVALIAÇÃO 8.1 Introdução O processo de monitoramento e avaliação constitui um instrumento para assegurar a interação entre o planejamento e a execução,
Capítulo 8 MONITORAMENTO E AVALIAÇÃO 8 MONITORAMENTO E AVALIAÇÃO 8.1 Introdução O processo de monitoramento e avaliação constitui um instrumento para assegurar a interação entre o planejamento e a execução,
TREINAMENTO SOBRE PRODUTOS PARA VENDEDORES DO VAREJO COMO ESTRATÉGIA PARA MAXIMIZAR AS VENDAS 1. Liane Beatriz Rotili 2, Adriane Fabrício 3.
 TREINAMENTO SOBRE PRODUTOS PARA VENDEDORES DO VAREJO COMO ESTRATÉGIA PARA MAXIMIZAR AS VENDAS 1 Liane Beatriz Rotili 2, Adriane Fabrício 3. 1 Pesquisa realizada no curso de Administração da Unijuí 2 Aluna
TREINAMENTO SOBRE PRODUTOS PARA VENDEDORES DO VAREJO COMO ESTRATÉGIA PARA MAXIMIZAR AS VENDAS 1 Liane Beatriz Rotili 2, Adriane Fabrício 3. 1 Pesquisa realizada no curso de Administração da Unijuí 2 Aluna
SETIS- III Seminário de Tecnologia Inovação e Sustentabilidade 4 e 5 de novembro de 2014.
 A importância da comunicação no gerenciamento de projetos de softwares: reflexões teóricas Lucas Krüger lucas_kruger-@hotmail.com Resumo: Esse artigo objetiva estudar a comunicação entre cliente e desenvolvedor
A importância da comunicação no gerenciamento de projetos de softwares: reflexões teóricas Lucas Krüger lucas_kruger-@hotmail.com Resumo: Esse artigo objetiva estudar a comunicação entre cliente e desenvolvedor
Planejamento - 7. Planejamento do Gerenciamento do Risco Identificação dos riscos. Mauricio Lyra, PMP
 Planejamento - 7 Planejamento do Gerenciamento do Risco Identificação dos riscos 1 O que é risco? Evento que representa uma ameaça ou uma oportunidade em potencial Plano de gerenciamento do risco Especifica
Planejamento - 7 Planejamento do Gerenciamento do Risco Identificação dos riscos 1 O que é risco? Evento que representa uma ameaça ou uma oportunidade em potencial Plano de gerenciamento do risco Especifica
Portaria Inep nº 249, de 02 de junho de 2014. Publicada no Diário Oficial da União em 04 de junho de 2014.
 Portaria Inep nº 249, de 02 de junho de 2014. Publicada no Diário Oficial da União em 04 de junho de 2014. O Presidente do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep),
Portaria Inep nº 249, de 02 de junho de 2014. Publicada no Diário Oficial da União em 04 de junho de 2014. O Presidente do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep),
PROJETOS DE SISTEMA EMBALAGEM COM A ABORDAGEM PLM FIGURA 1: O SISTEMA EMBALAGEM E SEUS COMPONENTES.
 PROJETOS DE SISTEMA EMBALAGEM COM A ABORDAGEM PLM Antonio Cabral Coordenador do curso de Pós-graduação em Engenharia de Embalagem Centro Universitário do Instituto Mauá de Tecnologia acabral@maua.br Projetar
PROJETOS DE SISTEMA EMBALAGEM COM A ABORDAGEM PLM Antonio Cabral Coordenador do curso de Pós-graduação em Engenharia de Embalagem Centro Universitário do Instituto Mauá de Tecnologia acabral@maua.br Projetar
Universidade de Brasília Faculdade de Ciência da Informação Profa. Lillian Alvares
 Universidade de Brasília Faculdade de Ciência da Informação Profa. Lillian Alvares Existem três níveis distintos de planejamento: Planejamento Estratégico Planejamento Tático Planejamento Operacional Alcance
Universidade de Brasília Faculdade de Ciência da Informação Profa. Lillian Alvares Existem três níveis distintos de planejamento: Planejamento Estratégico Planejamento Tático Planejamento Operacional Alcance
Seção 2/E Monitoramento, Avaliação e Aprendizagem
 Seção 2/E Monitoramento, Avaliação e Aprendizagem www.bettercotton.org Orientação Text to go here O documento Monitoramento, Avaliação e Aprendizagem da BCI proporciona uma estrutura para medir as mudanças
Seção 2/E Monitoramento, Avaliação e Aprendizagem www.bettercotton.org Orientação Text to go here O documento Monitoramento, Avaliação e Aprendizagem da BCI proporciona uma estrutura para medir as mudanças
Professor Severino Domingos Júnior Disciplina: Gestão de Compras e Estoques no Varejo
 Professor Severino Domingos Júnior Disciplina: Gestão de Compras e Estoques no Varejo 1) Definições de Previsão de Demanda 2) Mercados 3) Modelo de Previsão 4) Gestão da Demanda 5) Previsão como Processo
Professor Severino Domingos Júnior Disciplina: Gestão de Compras e Estoques no Varejo 1) Definições de Previsão de Demanda 2) Mercados 3) Modelo de Previsão 4) Gestão da Demanda 5) Previsão como Processo
Sistemas de Gestão da Qualidade. Introdução. Engenharia de Produção Gestão Estratégica da Qualidade. Tema Sistemas de Gestão da Qualidade
 Tema Sistemas de Gestão da Qualidade Projeto Curso Disciplina Tema Professor Pós-graduação Engenharia de Produção Gestão Estratégica da Qualidade Sistemas de Gestão da Qualidade Elton Ivan Schneider Introdução
Tema Sistemas de Gestão da Qualidade Projeto Curso Disciplina Tema Professor Pós-graduação Engenharia de Produção Gestão Estratégica da Qualidade Sistemas de Gestão da Qualidade Elton Ivan Schneider Introdução
Análise Estruturada de Sistemas
 Análise Estruturada de Sistemas Capítulo 3 Estudo de Viabilidade Definição das Necessidades Funcionais O propósito desta etapa é produzir um documento formal que contenha uma descrição detalhada da proposta,
Análise Estruturada de Sistemas Capítulo 3 Estudo de Viabilidade Definição das Necessidades Funcionais O propósito desta etapa é produzir um documento formal que contenha uma descrição detalhada da proposta,
CAPÍTULO 1 - CONTABILIDADE E GESTÃO EMPRESARIAL A CONTROLADORIA
 CAPÍTULO 1 - CONTABILIDADE E GESTÃO EMPRESARIAL A CONTROLADORIA Constata-se que o novo arranjo da economia mundial provocado pelo processo de globalização tem afetado as empresas a fim de disponibilizar
CAPÍTULO 1 - CONTABILIDADE E GESTÃO EMPRESARIAL A CONTROLADORIA Constata-se que o novo arranjo da economia mundial provocado pelo processo de globalização tem afetado as empresas a fim de disponibilizar
Proposta de Trabalho para a Disciplina de Introdução à Engenharia de Computação PESQUISADOR DE ENERGIA
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA E INSTITUTO DE INFOMÁTICA ENGENHARIA DE COMPUTAÇÃO INTRODUÇÃO À ENGENHARIA DE COMPUTAÇÃO Bruno Silva Guedes Cartão: 159033 Proposta de Trabalho
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA E INSTITUTO DE INFOMÁTICA ENGENHARIA DE COMPUTAÇÃO INTRODUÇÃO À ENGENHARIA DE COMPUTAÇÃO Bruno Silva Guedes Cartão: 159033 Proposta de Trabalho
Roteiro para a escrita do documento de Especificação de Requisitos de Software (ERS)
 Roteiro para a escrita do documento de Especificação de Requisitos de Software (ERS) Definição Geral: Disciplina de Compiladores Prof. Jorge Bidarra (UNIOESTE) A especificação de requisitos tem como objetivo
Roteiro para a escrita do documento de Especificação de Requisitos de Software (ERS) Definição Geral: Disciplina de Compiladores Prof. Jorge Bidarra (UNIOESTE) A especificação de requisitos tem como objetivo
Gerenciamento de Projetos
 Gerenciamento de Projetos (ref. capítulos 1 a 3 PMBOK) TC045 Gerenciamento de Projetos Sergio Scheer - scheer@ufpr.br O que é Gerenciamento de Projetos? Aplicação de conhecimentos, habilidades, ferramentas
Gerenciamento de Projetos (ref. capítulos 1 a 3 PMBOK) TC045 Gerenciamento de Projetos Sergio Scheer - scheer@ufpr.br O que é Gerenciamento de Projetos? Aplicação de conhecimentos, habilidades, ferramentas
Importância da normalização para as Micro e Pequenas Empresas 1. Normas só são importantes para as grandes empresas...
 APRESENTAÇÃO O incremento da competitividade é um fator decisivo para a maior inserção das Micro e Pequenas Empresas (MPE), em mercados externos cada vez mais globalizados. Internamente, as MPE estão inseridas
APRESENTAÇÃO O incremento da competitividade é um fator decisivo para a maior inserção das Micro e Pequenas Empresas (MPE), em mercados externos cada vez mais globalizados. Internamente, as MPE estão inseridas
UNIDADE 4. Introdução à Metodologia de Desenvolvimento de Sistemas
 UNIDADE 4. Introdução à Metodologia de Desenvolvimento de Sistemas 4.1 Motivação Sistemas de Informação são usados em diversos níveis dentro de uma organização, apoiando a tomada de decisão; Precisam estar
UNIDADE 4. Introdução à Metodologia de Desenvolvimento de Sistemas 4.1 Motivação Sistemas de Informação são usados em diversos níveis dentro de uma organização, apoiando a tomada de decisão; Precisam estar
PLANEJAMENTO OPERACIONAL - MARKETING E PRODUÇÃO MÓDULO 3 O QUE É PLANEJAMENTO DE VENDAS E OPERAÇÕES?
 PLANEJAMENTO OPERACIONAL - MARKETING E PRODUÇÃO MÓDULO 3 O QUE É PLANEJAMENTO DE VENDAS E OPERAÇÕES? Índice 1. O que é planejamento de...3 1.1. Resultados do planejamento de vendas e operações (PVO)...
PLANEJAMENTO OPERACIONAL - MARKETING E PRODUÇÃO MÓDULO 3 O QUE É PLANEJAMENTO DE VENDAS E OPERAÇÕES? Índice 1. O que é planejamento de...3 1.1. Resultados do planejamento de vendas e operações (PVO)...
componente de avaliação de desempenho para sistemas de informação em recursos humanos do SUS
 Informação como suporte à gestão: desenvolvimento de componente de avaliação de desempenho para sistemas de Esta atividade buscou desenvolver instrumentos e ferramentas gerenciais para subsidiar a qualificação
Informação como suporte à gestão: desenvolvimento de componente de avaliação de desempenho para sistemas de Esta atividade buscou desenvolver instrumentos e ferramentas gerenciais para subsidiar a qualificação
Na introdução o aluno deverá explicar o assunto que deseja desenvolver. Situar o tema dentro do contexto geral da sua área de trabalho
 PROJETO DE PESQUISA INTRODUÇÃO (O QUE É O TEMA?) Na introdução o aluno deverá explicar o assunto que deseja desenvolver. Desenvolver genericamente o tema Anunciar a idéia básica Delimitar o foco da pesquisa
PROJETO DE PESQUISA INTRODUÇÃO (O QUE É O TEMA?) Na introdução o aluno deverá explicar o assunto que deseja desenvolver. Desenvolver genericamente o tema Anunciar a idéia básica Delimitar o foco da pesquisa
Estrutura do Trabalho: Fazer um resumo descrevendo o que será visto em cada capítulo do trabalho.
 UNIVERSIDADE ESTADUAL DE MARINGÁ A monografia é um texto escrito contendo o resultado da pesquisa realizada como trabalho de conclusão do curso de especialização. Os itens básicos a constarem da monografia
UNIVERSIDADE ESTADUAL DE MARINGÁ A monografia é um texto escrito contendo o resultado da pesquisa realizada como trabalho de conclusão do curso de especialização. Os itens básicos a constarem da monografia
Desenvolvimento de um software de gerenciamento de projetos para utilização na Web
 Resumo. Desenvolvimento de um software de gerenciamento de projetos para utilização na Web Autor: Danilo Humberto Dias Santos Orientador: Walteno Martins Parreira Júnior Bacharelado em Engenharia da Computação
Resumo. Desenvolvimento de um software de gerenciamento de projetos para utilização na Web Autor: Danilo Humberto Dias Santos Orientador: Walteno Martins Parreira Júnior Bacharelado em Engenharia da Computação
ATIVIDADES DE LINHA E DE ASSESSORIA
 1 ATIVIDADES DE LINHA E DE ASSESSORIA SUMÁRIO Introdução... 01 1. Diferenciação das Atividades de Linha e Assessoria... 02 2. Autoridade de Linha... 03 3. Autoridade de Assessoria... 04 4. A Atuação da
1 ATIVIDADES DE LINHA E DE ASSESSORIA SUMÁRIO Introdução... 01 1. Diferenciação das Atividades de Linha e Assessoria... 02 2. Autoridade de Linha... 03 3. Autoridade de Assessoria... 04 4. A Atuação da
QUALIDADE DE SOFTWARE. Ian Sommerville 2006 Engenharia de Software, 8ª. edição. Capítulo 27 Slide 1
 QUALIDADE DE SOFTWARE Ian Sommerville 2006 Engenharia de Software, 8ª. edição. Capítulo 27 Slide 1 Objetivos Apresentar o processo de gerenciamento de qualidade e as atividades centrais da garantia de
QUALIDADE DE SOFTWARE Ian Sommerville 2006 Engenharia de Software, 8ª. edição. Capítulo 27 Slide 1 Objetivos Apresentar o processo de gerenciamento de qualidade e as atividades centrais da garantia de
RELATÓRIO TREINAMENTO ADP 2013 ETAPA 01: PLANEJAMENTO
 RELATÓRIO TREINAMENTO ADP 2013 ETAPA 01: PLANEJAMENTO 1. Apresentação geral Entre os dias 15 e 18 de Abril de 2013 foram realizados encontros de quatro horas com os servidores e supervisores da Faculdade
RELATÓRIO TREINAMENTO ADP 2013 ETAPA 01: PLANEJAMENTO 1. Apresentação geral Entre os dias 15 e 18 de Abril de 2013 foram realizados encontros de quatro horas com os servidores e supervisores da Faculdade
4 Metodologia da Pesquisa
 79 4 Metodologia da Pesquisa Este capítulo se preocupa em retratar como se enquadra a pesquisa de campo e como foram desenvolvidas as entrevistas incluindo o universo pesquisado e a forma de analisá-las
79 4 Metodologia da Pesquisa Este capítulo se preocupa em retratar como se enquadra a pesquisa de campo e como foram desenvolvidas as entrevistas incluindo o universo pesquisado e a forma de analisá-las
Aspectos Sociais de Informática. Simulação Industrial - SIND
 Aspectos Sociais de Informática Simulação Industrial - SIND Jogos de Empresas Utilizada com sucesso para o treinamento e desenvolvimento gerencial Capacita estudantes e profissionais de competência intelectual
Aspectos Sociais de Informática Simulação Industrial - SIND Jogos de Empresas Utilizada com sucesso para o treinamento e desenvolvimento gerencial Capacita estudantes e profissionais de competência intelectual
ROTEIRO PARA A ELABORAÇÃO DE PROJETOS DE PESQUISA - CEUA
 ROTEIRO PARA A ELABORAÇÃO DE PROJETOS DE PESQUISA - CEUA Estrutura do Projeto de Pesquisa CAPA FOLHA DE ROSTO SUMÁRIO 1. RESUMO 2. PROBLEMA DE PESQUISA OU INTRODUÇÃO 3. REFERENCIAL TEÓRICO (REVISÃO DE
ROTEIRO PARA A ELABORAÇÃO DE PROJETOS DE PESQUISA - CEUA Estrutura do Projeto de Pesquisa CAPA FOLHA DE ROSTO SUMÁRIO 1. RESUMO 2. PROBLEMA DE PESQUISA OU INTRODUÇÃO 3. REFERENCIAL TEÓRICO (REVISÃO DE
Mídias sociais como apoio aos negócios B2C
 Mídias sociais como apoio aos negócios B2C A tecnologia e a informação caminham paralelas à globalização. No mercado atual é simples interagir, aproximar pessoas, expandir e aperfeiçoar os negócios dentro
Mídias sociais como apoio aos negócios B2C A tecnologia e a informação caminham paralelas à globalização. No mercado atual é simples interagir, aproximar pessoas, expandir e aperfeiçoar os negócios dentro
Pesquisa realizada com os participantes do 12º Seminário Nacional de Gestão de Projetos. Apresentação
 Pesquisa realizada com os participantes do de Apresentação O perfil do profissional de Projetos Pesquisa realizada durante o 12 Seminário Nacional de, ocorrido em 2009, traça um importante perfil do profissional
Pesquisa realizada com os participantes do de Apresentação O perfil do profissional de Projetos Pesquisa realizada durante o 12 Seminário Nacional de, ocorrido em 2009, traça um importante perfil do profissional
Profissionalização em GP GPA010 - Gerenciamento do Escopo. Introdução: Proposta do Treinamento: Atividades: Temos nesse Módulo 4 Unidades de Ensino:
 Introdução: Este módulo não é um módulo básico e depende de formação geral em Gerenciamento de Projetos, padrão PMI, sendo aplicado no aprofundamento de conhecimentos dessa área Nesse módulo o participante
Introdução: Este módulo não é um módulo básico e depende de formação geral em Gerenciamento de Projetos, padrão PMI, sendo aplicado no aprofundamento de conhecimentos dessa área Nesse módulo o participante
Gerência de Projetos
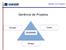 Gerência de Projetos Escopo Custo Qualidade Tempo CONCEITO PROJETOS: são empreendimentos com objetivo específico e ciclo de vida definido Precedem produtos, serviços e processos. São utilizados as funções
Gerência de Projetos Escopo Custo Qualidade Tempo CONCEITO PROJETOS: são empreendimentos com objetivo específico e ciclo de vida definido Precedem produtos, serviços e processos. São utilizados as funções
Gerência da Qualidade
 Gerência da Qualidade Curso de Engenharia de Produção e Transportes PPGEP / UFRGS ENGENHARIA DE PRODUÇÃO Temas Abordados Qualidade Ferramentas da Qualidade 5 Sensos PDCA/MASP Os Recursos Humanos e o TQM
Gerência da Qualidade Curso de Engenharia de Produção e Transportes PPGEP / UFRGS ENGENHARIA DE PRODUÇÃO Temas Abordados Qualidade Ferramentas da Qualidade 5 Sensos PDCA/MASP Os Recursos Humanos e o TQM
Resolução de Exercícios Orientações aos alunos
 2015 Resolução de Exercícios Orientações aos alunos Área de Concentração: EXATAS Disciplina de Concentração: FÍSICA Professores: Gustavo Castro de Oliveira, Reine Agostinho Ribeiro. UBERABA 2015 Colégio
2015 Resolução de Exercícios Orientações aos alunos Área de Concentração: EXATAS Disciplina de Concentração: FÍSICA Professores: Gustavo Castro de Oliveira, Reine Agostinho Ribeiro. UBERABA 2015 Colégio
Práticas de Marketing relacionadas com o sucesso no lançamento de novos produtos
 Práticas de Marketing relacionadas com o sucesso no lançamento de novos produtos Revista de Administração, v. 18, n. 1, Janeiro/Março 1983, p. 44 a 51 Fauze Najib Mattar Entre os vários fatores internos
Práticas de Marketing relacionadas com o sucesso no lançamento de novos produtos Revista de Administração, v. 18, n. 1, Janeiro/Março 1983, p. 44 a 51 Fauze Najib Mattar Entre os vários fatores internos
PLANEJAMENTO DA MANUFATURA
 58 FUNDIÇÃO e SERVIÇOS NOV. 2012 PLANEJAMENTO DA MANUFATURA Otimizando o planejamento de fundidos em uma linha de montagem de motores (II) O texto dá continuidade à análise do uso da simulação na otimização
58 FUNDIÇÃO e SERVIÇOS NOV. 2012 PLANEJAMENTO DA MANUFATURA Otimizando o planejamento de fundidos em uma linha de montagem de motores (II) O texto dá continuidade à análise do uso da simulação na otimização
FLUXOGRAMA DA PESQUISA
 FLUXOGRAMA DA PESQUISA Desde a preparação até a apresentação de um relatório de pesquisa estão envolvidas diferentes etapas. Algumas delas são concomitantes; outras são interpostas. O fluxo que ora se
FLUXOGRAMA DA PESQUISA Desde a preparação até a apresentação de um relatório de pesquisa estão envolvidas diferentes etapas. Algumas delas são concomitantes; outras são interpostas. O fluxo que ora se
Prêmio Inovação UP 2012 Manual de Preenchimento do Formulário
 ORIENTAÇÕES GERAIS Considerando que projeto deverá ser executado de agosto de 2012 a janeiro de 2013, avaliar a viabilidade de execução e finalização no prazo. Para preencher o formulário, observar as
ORIENTAÇÕES GERAIS Considerando que projeto deverá ser executado de agosto de 2012 a janeiro de 2013, avaliar a viabilidade de execução e finalização no prazo. Para preencher o formulário, observar as
F.1 Gerenciamento da integração do projeto
 Transcrição do Anexo F do PMBOK 4ª Edição Resumo das Áreas de Conhecimento em Gerenciamento de Projetos F.1 Gerenciamento da integração do projeto O gerenciamento da integração do projeto inclui os processos
Transcrição do Anexo F do PMBOK 4ª Edição Resumo das Áreas de Conhecimento em Gerenciamento de Projetos F.1 Gerenciamento da integração do projeto O gerenciamento da integração do projeto inclui os processos
PLANEJAMENTO OPERACIONAL: RECURSOS HUMANOS E FINANÇAS MÓDULO 16
 PLANEJAMENTO OPERACIONAL: RECURSOS HUMANOS E FINANÇAS MÓDULO 16 Índice 1. Orçamento Empresarial...3 2. Conceitos gerais e elementos...3 3. Sistema de orçamentos...4 4. Horizonte de planejamento e frequência
PLANEJAMENTO OPERACIONAL: RECURSOS HUMANOS E FINANÇAS MÓDULO 16 Índice 1. Orçamento Empresarial...3 2. Conceitos gerais e elementos...3 3. Sistema de orçamentos...4 4. Horizonte de planejamento e frequência
ISO/IEC 12207: Gerência de Configuração
 ISO/IEC 12207: Gerência de Configuração Durante o processo de desenvolvimento de um software, é produzida uma grande quantidade de itens de informação que podem ser alterados durante o processo Para que
ISO/IEC 12207: Gerência de Configuração Durante o processo de desenvolvimento de um software, é produzida uma grande quantidade de itens de informação que podem ser alterados durante o processo Para que
Metodologia de Gerenciamento de Projetos da Justiça Federal
 Metodologia de Gerenciamento de Projetos da Justiça Federal Histórico de Revisões Data Versão Descrição 30/04/2010 1.0 Versão Inicial 2 Sumário 1. Introdução... 5 2. Público-alvo... 5 3. Conceitos básicos...
Metodologia de Gerenciamento de Projetos da Justiça Federal Histórico de Revisões Data Versão Descrição 30/04/2010 1.0 Versão Inicial 2 Sumário 1. Introdução... 5 2. Público-alvo... 5 3. Conceitos básicos...
Gerenciamento de projetos. cynaracarvalho@yahoo.com.br
 Gerenciamento de projetos cynaracarvalho@yahoo.com.br Projeto 3URMHWR é um empreendimento não repetitivo, caracterizado por uma seqüência clara e lógica de eventos, com início, meio e fim, que se destina
Gerenciamento de projetos cynaracarvalho@yahoo.com.br Projeto 3URMHWR é um empreendimento não repetitivo, caracterizado por uma seqüência clara e lógica de eventos, com início, meio e fim, que se destina
SISTEMAS INTEGRADOS DE GESTÃO PAS 99:2006. Especificação de requisitos comuns de sistemas de gestão como estrutura para a integração
 Coleção Risk Tecnologia SISTEMAS INTEGRADOS DE GESTÃO PAS 99:2006 Especificação de requisitos comuns de sistemas de gestão como estrutura para a integração RESUMO/VISÃO GERAL (visando à fusão ISO 31000
Coleção Risk Tecnologia SISTEMAS INTEGRADOS DE GESTÃO PAS 99:2006 Especificação de requisitos comuns de sistemas de gestão como estrutura para a integração RESUMO/VISÃO GERAL (visando à fusão ISO 31000
Modelagem e Simulação Material 02 Projeto de Simulação
 Modelagem e Simulação Material 02 Projeto de Simulação Prof. Simão Sirineo Toscani Projeto de Simulação Revisão de conceitos básicos Processo de simulação Etapas de projeto Cuidados nos projetos de simulação
Modelagem e Simulação Material 02 Projeto de Simulação Prof. Simão Sirineo Toscani Projeto de Simulação Revisão de conceitos básicos Processo de simulação Etapas de projeto Cuidados nos projetos de simulação
