Regressão Logística Multinível com Estimação de Equações Generalizadas (GEE): Uma Aplicação em Dados Odontológicos
|
|
|
- Afonso Macedo
- 5 Há anos
- Visualizações:
Transcrição
1 Universidade de Brasília Instituto de Exatas Departamento de Estatística Regressão Logística Multinível com Estimação de Equações Generalizadas (GEE): Uma Aplicação em Dados Odontológicos Ludmilla Lorrany Mattos Silva Orientador: Professor Dr. Eduardo Freitas da Silva Brasília 2017
2
3 Ludmilla Lorrany Mattos Silva Regressão Logística Multinível com Estimação de Equações Generalizadas (GEE): Uma Aplicação em Dados Odontológicos Relatório final apresentado à disciplina Trabalho de Conclusão de Curso de graduação em Estatística apresentado ao Departamento de Estatística, Instituto de Exatas, Universidade de Brasília, como parte dos requisitos necessários para o grau de Bacharel em Estatística. Orientador: Professor Dr. Eduardo Freitas da Silva Universidade de Brasília UnB Instituto de Exatas Departamento de Estatística Trabalho de Conclusão de Curso de Graduação Brasília 2017
4
5 Aos meus pais.
6
7 Resumo Quando várias medidas são observadas repetidamente em uma mesma unidade observacional, podemos ter o que se chama de estrutura multinível. Nesta configuração de dados, também conhecida como hierárquica, os indivíduos são independentes ente si, porém existe uma correlação intra-indivíduos. A estimação de equações generalizadas (Generalized Estimating Equations - GEE) é uma técnica capaz de estimar a matriz de correlação intra-indivíduos e assim, produz estimativas não enviesadas para os parâmetros dos modelos de regressão generalizados (Generalized Regression Models - GLM ). Neste trabalho foi realizado um estudo com crianças diagnosticadas com a doença Hipomineralização Molar Incisivo. Foi investigada a associação entre a prevalência de dentes quebrados e a presença de opacidades de coloração escura no esmalte. A análise foi realizada utilizando um modelo logístico multinível com estimação de equações generalizadas. Os resultados obtidos revelam que no nível intra-divíduo, dentes de coloração escura são 7,74 vezes mais suscetíveis a sofrerem fratura, confirmando as expectativas dos especialistas. Palavras-chave: Modelos Lineares Generalizados. Modelos de regressão multinível. Estimação de Equações Generalizadas. Hipomineralização Molar Incisivo
8
9 Sumário Introdução REFERENCIAL TEÓRICO Modelos Lineares Generalizados Regressão Logística Estimação de equações generalizadas (GEEs) Estimação Matriz de correlação de trabalho APLICAÇÃO Introdução Metodologia Análise descritiva Análise bivariada no nível do dente Análise bivariada no nível do indivíduo Modelagem CONCLUSÃO REFERÊNCIAS
10
11 Lista de ilustrações Figura 1 Relação hierárquica Figura 2 Opacidade de coloração branca
12
13 Lista de tabelas Tabela 1 Matrizes de correlação de trabalho Tabela 2 Frequências no nível do dente Tabela 3 Molelos log-lineares Tabela 4 Frequências no nível da criança Tabela 5 Testes qui-quadrado Tabela 6 Estimativas dos parâmetros
14
15 13 Introdução Em estudos na área da pesquisa odontológica, é usual lidar com complexas estruturas de dados. Complicações como medidas correlacionadas devido aninhamento ou cluster, violam as suposições de independência dos modelos tradicionais de regressão e análise de variância. As variáveis que representam os fatores de risco, geralmente são observadas em múltiplos dentes no mesmo paciente. Sendo assim, necessariamente as unidades observacionais são correlacionadas, pois estão agrupadas (aninhadas) em cada indivíduo. Isso gera uma estrutura hierárquica em dois níveis: indivíduo e dente. Figura 1 Relação hierárquica Trata-se de uma correlação que ocorre de forma natural. Afinal, cada grupo de dentes possui características semelhantes, inerentes ao indivíduo a quem pertencem. Por exemplo, são submetidos à mesma dieta, frequência de escovação, exposição à nicotina ou não. Cada nível dessa hierarquia pode apresentar informações estatísticas diferentes sobre os dados. Faz-se assim necessária uma decomposição das variáveis capaz de captar as relações entre-indivíduos e intra-indivíduos (between-subject e within-subject). Estudos que ignoram esta particularidade dos dados tendem a apresentar resultados enviesados, principalmente quando as informações em cada nível divergem. Para a avaliação de dados com esta estrutura de aninhamento, são utilizados os modelos hierárquicos, comumente chamados em várias áreas por modelos multinível. São alternativas flexíveis, que permitem a análise dos efeitos de tratamentos em todos os níveis da hierarquia possibilitando a comparação entre e dentre os indivíduos. Existem duas abordagens principais para modelar dados hierárquicos: os modelos mistos, que combinam fatores fixos e aleatórios, e também a abordagem marginal dos
16 14 Introdução modelos com estimação de equações generalizadas (Generalized Estimating Equations - GEE), que apresenta resultados com precisão satisfatória e alta flexibilidade para modelar a correlação presente nos dados. Neste caso, os efeitos modelados são fixos, calculados de forma que leva em consideração uma estrutura de correlação pré-determinada através da chamada Matriz Auxiliar (Working Matrix). Todo o procedimento será descrito em maiores detalhes na parte metodológica deste trabalho. A abordagem GEE será utilizada no estudo de caso, aplicado por um prisma analítico de suas particularidades, vantagens e desvantagens. Ao longo deste trabalho, será realizada uma revisão objetiva dos Modelos Lineares Generalizados, especificamente os casos que permitem a análise de estruturas multinível. Em seguida, será feita uma aplicação em um conjunto de dados odontológicos de crianças com a doença dentária Hipomineralização Molar Incisivo. Trata-se de um estudo de natureza observacional no qual a variável resposta é binária e portanto, será utilizada uma regressão logística para estimar a razão de chances (Odds Ratio - OR) para a quebra do dente quando existem opacidades no esmalte.
17 15 1 Referencial Teórico Nesta seção, é revisado o arcabouço teórico das técnicas de modelos lineares generalizados que permitem o estudo de dados que apresentam estrutura de correlação. 1.1 Modelos Lineares Generalizados A classe dos modelos lineares generalizados (GLMs) é uma extensão dos modelos lineares tradicionais. Os GLMs permitem a modelagem de uma variável resposta que não necessariamente segue uma distribuição normal. A resposta média da população µ = E(y) é relacionada a um preditor linear através de uma função de ligação não linear g(µ) citehosmer. Desse modo, a dependente y pode seguir qualquer distribuição de probabilidade pertencente à família exponencial. Esta é uma vantagem essencial em muitas áreas que estudam variáveis dicotômicas ou outra resposta não linear. De forma mais detalhada, os GLMs possuem três componentes: Componente Aleatória: é a especificação da distribuição de probabilidade da variável resposta Y. As observações (y 1,..., y n ) geralmente são consideradas independentes. Componente Fixa: é a combinação linear das variáveis explicativas e os parâmetros desconhecidos, denominada preditor linear, é dado por: α + β 1 x β k x k. (1.1) Função de Ligação: função monotônica diferenciável g(.) que relaciona µ = E(Y ) com o preditor linear, isto é, conecta os componentes aleatória e fixa: g(µ) = α + β 1 x β k x k. (1.2) A função de ligação utilizada depende da distribuição de probabilidade da resposta. No caso do estudo abordado neste trabalho, a variável em questão é dicotomizada e segue uma distribuição binomial. A função de ligação (link function) utilizada nesta ocasião é a função logito Regressão Logística A regressão logística é o caso particular dos modelos lineares generalizados em que a variável resposta é categórica com distribuição binomial. Nesse caso, a função de ligação utilizada é a logito:
18 16 Capítulo 1. Referencial Teórico Seja um modelo com variável resposta Y com duas categorias e uma variável explicativa X. Então π(x) será a probabilidade de sucesso de Y quando X = x: Aplicando a transformação Logito: π(x) = exp(β 0 + β 1 x) 1 + exp(β 0 + β 1 x). (1.3) logito(π(x)) = ln π(x) 1 π(x) = β 0 + β 1 x. (1.4) Ou seja, o logaritmo natural da chance de sucesso de Y assume forma linear. Seja a razão de chances (Odds Ratio), tem-se que o efeito multiplicativo na chance de sucesso para cada acréscimo de uma unidade em x é dada por: OR = π(1) 1 π(1) π(0) 1 π(0) = e β 0 +β1 1+e β 0 +β1 1 1+e β 0 +β 1 e β 0 1+e β e β 0 = e β 1. (1.5)
19 1.2. Estimação de equações generalizadas (GEEs) Estimação de equações generalizadas (GEEs) Uma medida de interesse binária y ij é observada repetidamente: são obtidas j = 1,..., n i medidas para o i-ésimo indivíduo i = 1,..., k. Este é um cenário comum no universo da pesquisa. Na odontologia, a necessidade de observar os vários dentes de um indivíduo é o que resulta nesta estrutura de cluster. Em 1986, LIANG e ZEGER (1986) propuseram uma classe de equações de estimação que geram estimativas consistentes para os parâmetros de regressão sob brandas suposições de dependência. As equações estimação generalizadas (GEE), resultam de uma extensão dos modelos lineares generalizados para dados longitudinais. No GEE, dados correlacionados são modelados utilizando o mesmo preditor linear e função de ligação que seriam utilizados no caso independente. Entretanto, a estrutura de covariância das medidas repetidas também é modelada. As associações intra-indivíduos, são consideradas através das matrizes auxiliares de correlação intra-indivíduo, que incorporam a estrutura de dependência diretamente na estimação dos betas. O método GEE ajusta um modelo marginal (population-averaged model), ou seja, um modelo de médias com efeitos fixos. Isso significa que, assim como no modelo de regressão linear generalizado, a interpretação dos parâmetros é relativa à média da população e não a um indivíduo específico. O valor esperado marginal da resposta, E(Y it x it ) = µ it, é relacionado ao preditor linear através da função de ligação g(µ it ) = x itβ, onde β = (β 1, β 2,..., β p ) é o vetor p x 1 dos parâmetros regressivos Estimação Afim de entender o desenvolvimento que leva às equações de estimação generalizadas, vamos primeiramente definir o caso em que as observações repetidas para um indivíduo são independentes. Definindo a anotação utilizada, considere o vetor de respostas observadas no i-ésimo indivíduo Y i = [y i1,..., y ini ] e seja X ij = [x ij1,..., x ijp ] o vetor de p co-variáveis para cada i-ésimo indivíduo i = 1,..., k. Assume-se que a densidade marginal de y it como sendo a família exponencial com parâmetro de dispersão φ: F (y it ) = exp[{y it θ it a(θ it ) + b(y it )}φ], (1.6) sendo que θ it = h(η it ) e η it = x it β. Assim, podemos definir os primeiros dois momentos de
20 18 Capítulo 1. Referencial Teórico y it como sendo: E(y it ) = a (θ it ), (1.7) V ar(y it ) = a (θ it ) φ. (1.8) A seguir, temos a equação escore, que é a derivada da função de verossimilhança. O estimador ˆβ de β é obtido pela solução do escore. U I (β) = K X i i S i = 0, (1.9) i na qual i = diag(dθ it /dη it ) é uma matriz nxn e S i = Y i a i(θ). A generalização da estimação para o caso em que as respostas para um mesmo indivíduo são correlacionadas, consiste em adicionar uma matriz auxiliar que represente a correlação existente nos dados. A estimativa de β permanece consistente e estimativas consistentes de variância podem ser obtidas supondo que a matriz de correlação estimada converge para a matriz auxiliar. Seja a estrutura de correlação intra-indivíduos R i (α) uma matriz n x n de correlação para medidas repetidas ou em estrutura de cluster, sendo α o vetor de parâmetros desconhecidos que especifica a matriz. Então a matriz de covariância de Y i é dada como: V i = φa ˆR(α)A 1 2 1, (1.10) na qual, A i é uma matriz com v(µ ij ) sendo o j-ésimo elemento diagonal. Se R i (α) é de fato a verdadeira matriz de correlação de Y i, então V i é a verdadeira matriz de covariância cov(y i ). Sendo assim, equação de estimação generalizada para estimar o vetor de parâmetros ˆβ é dada por: na qual: S(β) = K i=1 D iv 1 i (Y i µ i (β)) = 0, (1.11) V i é a matriz de covariância de Y i D i = A i i X i = dµ i dβ
21 1.2. Estimação de equações generalizadas (GEEs) 19 A matriz p x n i das derivadas parciais com relação aos parâmetros de regressão para o i-ésimo indivíduo é dada por: D i = dµ i dβ = x i11 g (µ i1 ).... x i1p g (µ i1 )... x ini 1 g (µ ini ). x ini p g (µ ini ) sendo g(µ ij ) = x ijβ e g é a função de ligação. Temos que U i (β, α) = Di T Vi 1 é muito similar à abordagem de quasi-verossimilhança, exceto pelo fato de que V i não é uma função de β apenas, mas de α também. A Equação (1.11) pode ser escrita em termos de β somente, substituindo α por um estimador consistente quando β e φ são conhecidos: ˆα(Y, β, φ) e φ também será estimado por um estimador ˆφ(Y, β). Consequentemente, (2.12) terá a forma: k U i [β, ˆα{β, ˆφ(β)}] = 0, (1.12) i=1 e ˆβ é definido como sendo a solução da Equação 2.13, que é um sistema não linear de β e dos parâmetros R(α) e φ. Como o problema não apresenta forma-fechada, a solução é dada pelo procedimento iterativo de estimação O algorítimo utilizado para ajustar iterativamente o modelo é descrito a seguir: Algoritmo 1: GEE início Determina a estimativa inicial de β assumindo independência. fim para todo i k e j n, até a convergência faça Estima a matriz de trabalho R com base no β atual e a estrutura fim R 0 Calcula a estimativa da covariância ˆR(α)W A V i = φa W Atualiza β β r+1 = β r [ K i=1 δµ i δβ V 1 δµ i i δβ ] 1 [ K i=1 δµ i δβ V 1 i (Y i µ i ) ]
22 20 Capítulo 1. Referencial Teórico Matriz de correlação de trabalho A matriz de correlação é normalmente desconhecida e precisa ser estimada. Sua estimação é feita pelo processo de ajustamento iterativo usando o valor atual do vetor β para calcular os parâmetros de correlação α com base nos resíduos de Pearson definidos por: ɛ ij = y ij µ if v(µij )/w ij. (1.13) O estimador utilizado depende da suposição que se faz sobre a estrutura de correlação das observações. Diversas estruturas de matrizes de correlação de trabalho R 0 são possíveis. A Tabela a seguir detalha algumas estruturas comumente utilizadas e seus estimadores. Tabela 1 Matrizes de correlação de trabalho Estrutura Estimador Fixo Corr(Y ij, Y ik ) = r jk Nesse caso, a matriz de correlação onde r jk é constante { não é estimada 1, j = k Independente Corr(Y ij, Y ik ) = Nesse caso, a matriz de correlação 0, j k não é estimada 1, t = 0 1 M-dependente Corr(Y ij, Y i+t ) = α t, t = 1,..., m ˆα t = ki=1 (K t p)φ j n i ɛ ij ɛ i,j+t 0, t = m K t = k { i=1 (n i t) 1, j = k 1 Permutável Corr(Y ij, Y ik ) = ˆα α, j k t = ki=1 (N p)φ j<k ɛ ij ɛ i,k N = 0.5 k { i=1 n i (n i 1) 1, j = k Não estruturada Corr(Y ij, Y ik ) = ˆα α jk, j k t = 1 ki=1 ɛ (K p)φ ij ɛ i,k Autoregressiva Corr(Y ij, Y i+t ) = α t ˆα t = 1 ki=1 (k 1 p)φ j n i 1 ɛ ij ɛ i,j+1 AR(1) para t = 0, 1, 2,..., n i j K 1 = k i=1 (n i 1) O método GEE é capaz de proporcionar excelentes resultados com estimativas consistentes para os parâmetros de regressão. Entretanto, o desafio da técnica reside na escolha da matriz auxiliar, afinal não é possível saber de antemão qual estrutura é a correta. A escolha apropriada da matriz é de suma importância, pois pode resultar em considerável redução ou eliminação do viés de estimação. A seguir, estão elencadas as características das principais matrizes e os casos em que geralmente são utilizadas. A estrutura Independente é a matriz identidade, assim nenhum coeficiente de correlação é estimado. É usada em ocasiões em que é razoável supor que as múltiplas
23 1.2. Estimação de equações generalizadas (GEEs) 21 medidas na mesma unidade observacional são independentes entre si. A matriz Permutável assume que qualquer par de medidas em um indivíduo possui a mesma correlação. Adequado para problemas de cluster e aninhamento, como crianças de uma mesma escola ou dentes de um indivíduo. É uma opção interessante para pequenas amostras por ser uma estrutura parcimoniosa com apenas um parâmetro α à ser estimado. Em problemas de medidas repetidas, coletadas ao longo do tempo, a correlação intra indivíduo pode ser caracterizada como Autoregressiva, pois tende a diminuir com o passar do tempo. Em alguns estudos longitudinais a redução no nível de correlação pode ser abrupto, assim a matriz AR-1, que é uma autoregressiva de ordem um, se mostra como uma alternativa. A correlação Não Estruturada não possui um padrão, é a opção mais flexível, porém seu número de parâmetros cresce rapidamente e a estimação pode se tornar instável. Para amostras pequenas e desbalanceadas é desejável estruturas mais parcimoniosas.
24
25 23 2 Aplicação Nesta seção, é apresentada uma típica aplicação do modelo logístico para dados hierárquicos, utilizando estimação de equações generalizadas. Consiste em um estudo de caráter observacional com interesse em estimar razões de chances da quebra do dente dado um fator de risco, em portadores da doença Hipomineralização Molar Incisivo (HMI). 2.1 Introdução A Hipomineralização Molar Incisivo (HMI) é um defeito do esmalte que tem origem na fase de desenvolvimento do dente e que atinge os primeiros molares e incisivos permanentes. O MHI é uma patologia que causa porosidade do esmalte, deixando-o com aspecto de giz. Como consequência, o dente fica hipersensibilizado, mais suscetível à careação e a impactos mecânicos, podendo quebrar-se até mesmo com a própria mastigação. A doença pode ser identificada visualmente pela presença de opacidades em pelo menos um dos primeiros molares. As alterações na translucidez do esmalte podem variar de uma coloração esbranquiçada até castanho-amarelada ou marrom, que tende a representar maior severidade do problema. Na Figura a seguir, observamos um exemplo de MHI. Figura 2 Opacidade de coloração branca O fator de risco analisado neste caso é a coloração do esmalte. Fatos estilizados sugerem que a tonalidade mais escurecida do dente está associada a maior chance de quebra em relação aos dentes que possuem cor mais esbranquiçada. O objetivo deste estudo será testar a hipótese de independência entre a frequência de dentes quebrados e as variáveis que indicam a tonalidade da cor, tipo de dente (molar ou incisivo) e sua localização (superior ou inferior).
26 24 Capítulo 2. Aplicação Os dados utilizados neste estudo são uma amostra de 170 estudantes do Distrito Federal, todos portadores da doença HMI, foi extraída de um estudo de prevalência de cárie e MIH realizado em 2013 com crianças de 7 a 12 anos de escolas públicas do Paranoá/DF, realizado para uma pesquisa de doutorado em odontologia. 2.2 Metodologia Inicialmente, é conduzida uma análise descritiva para melhor caracterizar as observações. Para conhecer o nível de associação entre as variáveis, testes bivariados são realizados em ambos os níveis da hierarquia. A análise no nível do indivíduo é feita através de testes qui-quadrado. Ao nível do dente, por sua vez, a análise exige que a correlação intra-indivíduo seja considerada. Para isso, será utilizado o modelo log-linear (CARVALHO et al., 2011). As observações do banco de dados são da forma {Y ij, X ij }, sendo j = 1, 2...J o j-ésimo dente para o i-ésimo indivíduo i = 1, 2...I. A variável resposta Y ij é binária, assim para cada observação ij assume-se Y ij = 1 ou Y ij = 0 e X ij é a co-variável ou fator de risco observado no nível do dente. Os efeitos entre e intra-indivíduos podem ser obtidos separadamente através do modelo logístico multinível. Para isso, cada covariável observada no nível do dente (x ij ) é decomposta em duas componentes. Assim é possível distinguir a informação contida no nível da criança como sendo a média da covariável para os indivíduos ( x i ). E a informação no nível do dente será (x ij x i ) (HOLT; SCOTT, 1982). Esse tipo de modelagem se faz necessária uma vez que os dados apresentam estrutura de agrupamento por indivíduo, ou seja, observações pertencentes a uma mesma criança, tendem a apresentar características semelhantes. A estimação por equações generalizadas (GEE) será utilizada para que o padrão de correlação contido nos dados possa ser considerado no modelo. Na implementação da GEE, o modelo de regressão para a média marginal µ ij = E[y ij x ij, x i ] tem a seguinte forma: g(µ ij ) = α + β entre x i + β intra (x ij x i ), (2.1) na qual g é a função de ligação logito. Note que os coeficientes (α, β entre, β intra ) representam o efeito marginal do fator de risco na média da população. O coeficiente de x i mede o efeito da covariável quando a média para os indivíduos difere em uma unidade. Já o coeficiente de (x ij x i ) reflete o
27 2.2. Metodologia 25 efeito baseado na comparação dentro do cluster, quando a diferença entre os dentes é de uma unidade (MANCL; LEROUX; DEROUENL, 2000). A escolha da matriz auxiliar de correlação intra indivíduos que melhor se ajusta aos dados envolve comparar critérios de informação para modelos com diferentes matrizes. Também é importante a ponderação racional de qual alternativa se adéqua melhor dada a natureza do problema de forma parcimoniosa. Ou seja, a matriz auxiliar deve ser aquela que não exija muitos parâmetros a serem estimados e que também não apresente uma estrutura muito simples. A matriz Permutável satisfaz a essas condições e portanto será a alternativa adotada neste trabalho. Foi utilizado o software SAS (release 9.4) para manipulação do banco de dados, bem como para a aplicação dos modelos descritos utilizando o procedimento PROC GENMOD.
28 26 Capítulo 2. Aplicação 2.3 Análise descritiva Nesta seção apresentamos um panorama geral de como se distribuem as variáveis e como elas se comportam. Foi realizada uma análise descritiva uni e bivariada em ambos os níveis da hierarquia. A base de dados em questão, possui dados de 170 crianças, todas acometidas pela doença HMI. Para cada uma delas foram registradas informações de, em média, 3 dentes nos quais foram identificadas alterações na opacidade. Ao todo, 437 dentes foram analisados. Além do sexo da criança, foram obtidas medidas categóricas no nível do dente: a variável Cor indica se a opacidade presente no dente possui coloração branca ou não branca; Posição classifica o dente como superior ou inferior, enquanto Tipo identifica molares e incisivos. A Tabela 2 apresenta as proporções e porcentagens em que as variáveis ocorrem. Tabela 2 Frequências no nível do dente Frequência Quebra Não Quebra ,85 Quebra 40 9,15 Tipo Incisivo ,35 Molar ,65 Posição Inferior ,65 Superior ,35 Cor Branco ,11 Não Branco ,89 Porcentagem Observa-se que apenas 40 dos 437 dentes analisados sofreram quebra (9,15%), tratase assim de um evento pouco observado. Quanto a coloração, existe um balanceamento maior entre brancos (69%) e não brancos (30,89%). As variáveis de controle Tipo e Posição também sem mostram bem distribuídas. Foram observados 255 (58%) dentes superiores e 182 (41%) inferiores. Quanto ao tipo, 68% são molares e 31% incisivos Análise bivariada no nível do dente A análise bivariada permite verificar de forma exploratória quais variáveis se mostram mais importantes para o modelo. Nesta etapa queremos investigar preliminarmente a relação entre as variáveis independentes e resposta. No nível do dente, a correlação intra-indivíduo deve ser considerada e para isso, é utilizado o modelo log-linear. Utilizando o modelo linear generalizado com distribuição de Poisson e variância robusta, é possível identificar a repetição do indivíduo
29 2.3. Análise descritiva 27 e a correlação entre as observações pertencentes a uma única criança. Desse modo, determinamos o quanto a contagem de dentes quebrados depende dos níveis de cada variável independente. Tabela 3 Molelos log-lineares Porcentagem de quebrados Razão de Chances P-valor Cor Não Branco 19,26 4,26 0,0001 Branco 4,64 Tipo Molar 11, ,0252 Incisivo 5,11 Posição Superior 10,59 1,49 0,3322 Inferior 7,14 A análise bivariada no nível do dente revela que a prevalência de dentes quebrados é associada à coloração (p=0,0001). O dente que apresenta opacidade não branca é 2,94 vezes mais suscetível a sofrer quebra do que os dentes brancos. Segundo o teste, as variáveis Tipo e Posição não apresentam dependência significante ao nível de 0,005%. Embora as variáveis controle Tipo e Posição não tenham apresentado significância quando analisadas no nível do dente, uma análise mais profunda, que inclua a decomposição entre e intra-indivíduos, pode vir a revelar resultados diferentes e portanto, foram incluídas no modelo logístico Análise bivariada no nível do indivíduo Enquanto no nível intra-indivíduos, as características eram observadas no nível do dente, no caso do nível da criança, observamos se há a ocorrência de pelo menos um dente quebrado e se há pelo menos um dente com opacidade não branca. Seguindo esse critério, a Tabela 4 apresenta as frequências de crianças que apresentaram dentes danificados, com opacidade escura e também o sexo. Tabela 4 Frequências no nível da criança Cor Frequência Porcentagem Quebra Quebrados 48 28,24 Não quebrados ,76 Cor Branco Não Branco Sexo Masculino 86 50,59 Feminino 84 49,41 Observa-se que 28,24% (48) das crianças avaliadas apresentaram dentes quebrados, contra 71,76% (122) que não possuíam nenhum dente danificado. A maior parte das
30 28 Capítulo 2. Aplicação crianças possuem pelo menos um dente não branco (60%). A amostra é bem distribuída entre meninos e meninas, 50,59% das crianças são do sexo masculino. No nível da criança, foram realizados testes qui-quadrado de associação entre a ocorrência de dentes quebrados e a coloração. A Tabela 5 apresenta os resultados. Tabela 5 Testes qui-quadrado Porcentagem de quebrados χ 2 P-valor Cor Não Branco 36,27 8,1333 0,0043 Branco 16,18 Sexo Masculino 27,91 0,0093 0,9233 Feminino 28,57 O teste qui-quadrado de associação entre a Quebra e Cor foi significante ao nível de 0,005. Indicando que crianças que apresentaram pelos menos um dente não branco, possui chance 2,94 vezes maior de apresentar pelo menos um dente quebrado. Já variável Sexo, conforme esperado, não se mostrou significantemente relacionada com a prevalecia de dentes quebrados. Assim como as variáveis de controle Tipo e Posição, a covariável Sexo também é incluída no modelo final logístico multivariado. Não foi realizada nenhuma técnica de seleção de variáveis. Todas as características utilizadas neste estudo, foram selecionadas por motivações clínicas e a inclusão no modelo, independe da significância estatística aferida na análise exploratória.
31 2.4. Modelagem Modelagem Levando em consideração todas as peculiaridades do conjunto de dados, a modelagem proposta foi realizada utilizando o modelo logístico multinível. A indicadora de quebra do dente foi utilizada como variável dependente. A coloração do dente é o fator explicativo, mantendo controladas o sexo da criança e as características no nível do dente: posição e tipo. O modelo foi ajustado utilizando o estimação de equações generalizadas (GEE) com matriz de correlação intra indivíduo permutável. Todos os testes foram conduzidos utilizando o procedimento GENMOD no software SAS, com p-valores maiores que 0,05 sendo considerados estatisticamente significantes. O modelo final com as variáveis explicativas e seus coeficientes estimados estão representados a seguir. logito(π ij ) = β 0 + β 1 Cor(entre) + β 2 Cor(intra) + β 3 P osic(entre) +β 4 P osic(intra) + β 5 T ipo(entre) + β 6 T ipo(intra) + β 7 Sexo Através deste modelo, foi testada a hipótese nula de que a quebra do dente e a coloração são independentes. A Tabela 6 apresenta as estimativas obtidas para os parâmetros entre e intra-indivíduos, bem como o erro padrão, a razão de chances e o p-valor. Entre parênteses, está indicado qual é a categoria de referência utilizada em cada variável. Tabela 6 Estimativas dos parâmetros Parâmetro Coeficiente Erro padrão Razão de Chances P-valor Cor-entre (Não branco x Branco) 0,958 0,547 2,607 0,0798 Cor-intra (Não branco x Branco) 2,046 0,558 7,740 0,0002 Posição-entre (Superior x Inferior) 0,391 0,588 1,478 0,5067 Posição-intra (Superior x Inferior) 0,255 0,507 1,291 0,6148 Tipo-entre (Molar x Incisivo) -0,110 0,642 0,896 0,8640 Tipo-intra (Molar x Incisivo) 1,090 0,439 2,975 0,0129 Sexo (Masculino x Feminino) 0,222 0,394 1,249 0,5721 No nível do dente, ou seja, intra-indivíduos, a variável Cor apresentou p-valor significativo (p=0,0002), rejeitando a hipótese nula de independência. Assim, temos evidências para concluir que existe associação entre a cor da opacidade e a chance de quebra. O coeficiente estimado apresenta valoração positiva indicando aumento na chance de quebra associado ao escurecimento do dente. Em termos de razão de chances, o dente que apresenta coloração não-branca tem em média, 7,74 vezes mais chance de se quebrar do que um dente branco. Entretanto, a análise no nível do indivíduo apresenta p-valor não significante, indicando que entre os indivíduos, não se identifica efeito da cor na variável
32 30 Capítulo 2. Aplicação resposta. Nesse ponto, podemos perceber a importância da análise que considera todos os níveis da hierarquia, de outro modo, estimativas equivocadas podem ser obtidas. A variável Tipo do dente apresentou significância ao nível do dente, revelando que dentes molares são mais suscetíveis à quebra, entretanto a diferença é de apenas 0,09%. O sexo da criança e a posição do dente apresentaram apresentaram p-valores não significantes em ambos os níveis da hierarquia. Os resultados obtidos pela modelagem do problema confirmam as hipóteses dos pesquisadores.
33 31 3 Conclusão Na pesquisa odontológica e também em outras áreas, uma variedade de trabalhos tratam de dados hierárquicos, lançando mão de diversas técnicas que permitem o estudo de dados correlacionados. Entretanto, é comum nos depararmos com estudos que implícita ou explicitamente, assumem que as fontes de informação entre e intra-indivíduos produzem a mesma estimativa para os efeitos dos fatores de risco ou tratamento. Geralmente, cada nível da hierarquia revela uma informação sobre os dados, podendo inclusive apresentar resultados divergentes. Nesses casos, negligenciar a decomposição das variáveis em fatores intra e entre-indivíduos pode resultar em estimativas enviesadas, de interpretação incoerente. A utilização da abordagem da estimação de equações generalizadas (GEE), juntamente com a decomposição das covariáveis em fontes de informação nos níveis do dente e do indivíduo, mostrou resultados satisfatórios, corroborando com as expectativas clínicas dos pesquisadores. A análise bivariada em ambos os níveis apontaram associação entre a coloração da opacidade no esmalte e a quebra do dente. Entretanto, a análise multivariada através da regressão logística revelou que essa associação se dá principalmente no nível do dente. O efeito da coloração não branca aumenta, em média, 6,74% a fragilidade do dente. Nenhum efeito se mostrou significante ao nível da criança, confirmando a importância da análise em todos os níveis da hierarquia. Conforme ilustrado neste estudo, covariáveis podem causar efeitos diferentes em cada nível da hierarquia. A pergunta seguinte é por que isso ocorre. Efeitos intra e entreindivíduos podem diferir por viés causado por erros de medida ou confundimento causado por cofatores não observados (PALTA; YAO, 1991). Próximos estudos podem procurar investigar essa questão e ainda trazer uma comparação de métodos.
34
35 33 Referências AGRESTI, A. An Introduction to Categorical Data Analysis. England: John Wiley and Sons INC, Nenhuma citação no texto. BROWN, H.; PRESCOTT, R. Applied Mixed Models in Medicine. United Kingdom: John Wiley and Sons INC, Nenhuma citação no texto. CARVALHO, J. et al. Impact of enamel defects on early caries development in preschool children. Caries Res, v. 45, n. 1, p , Citado na página 24. HOLT, A. J.; SCOTT, D. The effect of two-stage sampling on ordinary least square methods. J Am Stat Assoc, v. 77, p , Citado na página 24. HOSMER, D. W.; LEMESHOW, S. Applied logistic regression. Canada: John Wiley and Sons, ISBN , Nenhuma citação no texto. JOHNSON, R.; WICHERN, D. Applied Multivariate Statistical Analysis. Applied Multivariate Statistical Analysis. New Jersey: Pearson Prentice Hall, Nenhuma citação no texto. LIANG, K.-Y.; ZEGER, S. L. Longitudinal data analysis using generalized linear models. Biometrika, v. 73, p , ISSN Citado na página 17. MANCL, L.; LEROUX, B.; DEROUENL, T. Between-subject and within-subject statistical information in dental research. Journal of Dental Research, n. 79, p , Citado na página 25. PALTA, M.; YAO, T. J. Analysis of longitudinal data with unmeasured confounders. Biometrics, v. 47, n. 2, p , ISSN Citado na página 31.
Exemplos Equações de Estimação Generalizadas
 Exemplos Equações de Estimação Generalizadas Bruno R. dos Santos e Gilberto A. Paula Departamento de Estatística Universidade de São Paulo, Brasil giapaula@ime.usp.br Modelos Lineares Generalizados dos
Exemplos Equações de Estimação Generalizadas Bruno R. dos Santos e Gilberto A. Paula Departamento de Estatística Universidade de São Paulo, Brasil giapaula@ime.usp.br Modelos Lineares Generalizados dos
Disciplina de Modelos Lineares Professora Ariane Ferreira
 Disciplina de Modelos Lineares 2012-2 Regressão Logística Professora Ariane Ferreira O modelo de regressão logístico é semelhante ao modelo de regressão linear. No entanto, no modelo logístico a variável
Disciplina de Modelos Lineares 2012-2 Regressão Logística Professora Ariane Ferreira O modelo de regressão logístico é semelhante ao modelo de regressão linear. No entanto, no modelo logístico a variável
Análise de Dados Longitudinais Aula
 1/35 Análise de Dados Longitudinais Aula 08.08.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/35 Sumário 1 Revisão para dados transversais 2 Como analisar dados longitudinais 3 Perspectiva
1/35 Análise de Dados Longitudinais Aula 08.08.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/35 Sumário 1 Revisão para dados transversais 2 Como analisar dados longitudinais 3 Perspectiva
Modelo marginal de odds proporcionais para dados longitudinais: um estudo de simulação
 Modelo marginal de odds proporcionais para dados longitudinais: um estudo de simulação Nívea B. da Silva 1 Enrico A. Colosimo 2 Leila A. F. Amorim 3 1 Introdução Nos últimos anos muitas metodologias têm
Modelo marginal de odds proporcionais para dados longitudinais: um estudo de simulação Nívea B. da Silva 1 Enrico A. Colosimo 2 Leila A. F. Amorim 3 1 Introdução Nos últimos anos muitas metodologias têm
Modelos Lineares Generalizados
 Modelos Lineares Generalizados Emilly Malveira de Lima Análise de Dados Categóricos Universidade Federal de Minas Gerais - UFMG 10 de Maio de 2018 Emilly Malveira (PGEST-UFMG) 10 de Maio de 2018 1 / 20
Modelos Lineares Generalizados Emilly Malveira de Lima Análise de Dados Categóricos Universidade Federal de Minas Gerais - UFMG 10 de Maio de 2018 Emilly Malveira (PGEST-UFMG) 10 de Maio de 2018 1 / 20
A Importância da Estatística na Pesquisa Científica e na Tomada de Decisão
 A Importância da Estatística na Pesquisa Científica e na Tomada de Decisão Ricardo Alves de Olinda Universidade Estadual da Paraíba - UEPB Centro de Ciências e Tecnologia - CCT Departamento de Estatística
A Importância da Estatística na Pesquisa Científica e na Tomada de Decisão Ricardo Alves de Olinda Universidade Estadual da Paraíba - UEPB Centro de Ciências e Tecnologia - CCT Departamento de Estatística
Regressão de Poisson e parentes próximos
 Janeiro 2012 Família Exponencial Seja Y uma variável aleatória. A distribuição de probabilidade de Y pertence à família exponencial se a sua função densidade de probabilidade é da forma ( ) yθ b(θ) f (y
Janeiro 2012 Família Exponencial Seja Y uma variável aleatória. A distribuição de probabilidade de Y pertence à família exponencial se a sua função densidade de probabilidade é da forma ( ) yθ b(θ) f (y
Modelos Lineares Generalizados - Estimação em Modelos Lineares Generalizados
 Modelos Lineares Generalizados - Estimação em Modelos Lineares Generalizados Erica Castilho Rodrigues 23 de Maio de 207 Introdução 2 3 Vimos como encontrar o EMV usando algoritmos numéricos. Duas possibilidades:
Modelos Lineares Generalizados - Estimação em Modelos Lineares Generalizados Erica Castilho Rodrigues 23 de Maio de 207 Introdução 2 3 Vimos como encontrar o EMV usando algoritmos numéricos. Duas possibilidades:
Análise de Regressão EST036
 Análise de Regressão EST036 Michel Helcias Montoril Instituto de Ciências Exatas Universidade Federal de Juiz de Fora Regressão sem intercepto; Formas alternativas do modelo de regressão Regressão sem
Análise de Regressão EST036 Michel Helcias Montoril Instituto de Ciências Exatas Universidade Federal de Juiz de Fora Regressão sem intercepto; Formas alternativas do modelo de regressão Regressão sem
Quantis residuais. Luziane Franciscon Acadêmica de Estatística Universidade Federal do Paraná
 Quantis residuais Luziane Franciscon Acadêmica de Estatística Universidade Federal do Paraná Orientador: Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Resumo Uma etapa importante
Quantis residuais Luziane Franciscon Acadêmica de Estatística Universidade Federal do Paraná Orientador: Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Resumo Uma etapa importante
Coeficiente de determinação R 2 no modelo de regressão linear normal
 Coeficiente de determinação R 2 no modelo de regressão linear normal Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Curitiba/PR, 81531 990, Brasil email: lucambio@ufpr.br
Coeficiente de determinação R 2 no modelo de regressão linear normal Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Curitiba/PR, 81531 990, Brasil email: lucambio@ufpr.br
Modelos de regressão para dados correlacionados. Cibele Russo
 Modelos de regressão para dados correlacionados Cibele Russo cibele@icmc.usp.br ICMC USP Mini-curso oferecido no Workshop on Probabilistic and Statistical Methods 28 a 30 de janeiro de 2013 Cibele Russo
Modelos de regressão para dados correlacionados Cibele Russo cibele@icmc.usp.br ICMC USP Mini-curso oferecido no Workshop on Probabilistic and Statistical Methods 28 a 30 de janeiro de 2013 Cibele Russo
Modelos Lineares Generalizados - Modelos log-lineares para tabelas de contingência
 Modelos Lineares Generalizados - Modelos log-lineares para tabelas de contingência Erica Castilho Rodrigues 12 de Agosto 3 Vimos como usar Poisson para testar independência em uma Tabela 2x2. Veremos
Modelos Lineares Generalizados - Modelos log-lineares para tabelas de contingência Erica Castilho Rodrigues 12 de Agosto 3 Vimos como usar Poisson para testar independência em uma Tabela 2x2. Veremos
CE062c - GAMLSS. Silva, J.P; Taconeli, C.A. 09 de outubro, Silva, J.P; Taconeli, C.A. CE062c - GAMLSS 09 de outubro, / 42
 CE062c - GAMLSS Silva, J.P; Taconeli, C.A. 09 de outubro, 2018 Silva, J.P; Taconeli, C.A. CE062c - GAMLSS 09 de outubro, 2018 1 / 42 Por que GAMLSS? Silva, J.P; Taconeli, C.A. CE062c - GAMLSS 09 de outubro,
CE062c - GAMLSS Silva, J.P; Taconeli, C.A. 09 de outubro, 2018 Silva, J.P; Taconeli, C.A. CE062c - GAMLSS 09 de outubro, 2018 1 / 42 Por que GAMLSS? Silva, J.P; Taconeli, C.A. CE062c - GAMLSS 09 de outubro,
4 Metodologia. Wt = W 0 exp{(l/k)(1-e-kt)} (8)
 4 Metodologia Serão apresentadas duas formas de se estimar a persistência. A primeira é de forma mais agregada e se utiliza de dados em forma de triângulos de run-off e é conhecida como Chain Ladder, uma
4 Metodologia Serão apresentadas duas formas de se estimar a persistência. A primeira é de forma mais agregada e se utiliza de dados em forma de triângulos de run-off e é conhecida como Chain Ladder, uma
Modelos Lineares Generalizados - Modelos log-lineares para tabelas de contingência
 Modelos Lineares Generalizados - Modelos log-lineares para tabelas de contingência Erica Castilho Rodrigues 12 de Agosto Introdução 3 Vimos como usar Poisson para testar independência em uma Tabela 2x2.
Modelos Lineares Generalizados - Modelos log-lineares para tabelas de contingência Erica Castilho Rodrigues 12 de Agosto Introdução 3 Vimos como usar Poisson para testar independência em uma Tabela 2x2.
4 Modelos Lineares Generalizados
 4 Modelos Lineares Generalizados Neste capítulo, serão apresentados arcabouços teóricos dos modelos lineares generalizados (MLGs) e como casos particulares desses modelos são aplicáveis ao problema da
4 Modelos Lineares Generalizados Neste capítulo, serão apresentados arcabouços teóricos dos modelos lineares generalizados (MLGs) e como casos particulares desses modelos são aplicáveis ao problema da
ANÁLISE E MODELAGEM DE DADOS LONGITUDINAIS NO R
 Revista da Estatística UFOP, Vol II, 2012, ISSN 2237-8111, XI Encontro Mineiro de Estatística - MGEST ANÁLISE E MODELAGEM DE DADOS LONGITUDINAIS NO R Leandro Vitral Andraos 1,2, Marcel de Toledo Vieira
Revista da Estatística UFOP, Vol II, 2012, ISSN 2237-8111, XI Encontro Mineiro de Estatística - MGEST ANÁLISE E MODELAGEM DE DADOS LONGITUDINAIS NO R Leandro Vitral Andraos 1,2, Marcel de Toledo Vieira
variável dependente natureza dicotômica ou binária independentes, tanto podem ser categóricas ou não estimar a probabilidade associada à ocorrência
 REGRESSÃO LOGÍSTICA É uma técnica recomendada para situações em que a variável dependente é de natureza dicotômica ou binária. Quanto às independentes, tanto podem ser categóricas ou não. A regressão logística
REGRESSÃO LOGÍSTICA É uma técnica recomendada para situações em que a variável dependente é de natureza dicotômica ou binária. Quanto às independentes, tanto podem ser categóricas ou não. A regressão logística
Aula 2 Uma breve revisão sobre modelos lineares
 Aula Uma breve revisão sobre modelos lineares Processo de ajuste de um modelo de regressão O ajuste de modelos de regressão tem como principais objetivos descrever relações entre variáveis, estimar e testar
Aula Uma breve revisão sobre modelos lineares Processo de ajuste de um modelo de regressão O ajuste de modelos de regressão tem como principais objetivos descrever relações entre variáveis, estimar e testar
Ralph S. Silva
 ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
Dimensionamento de amostras para regressão logística
 Dimensionamento de amostras para regressão logística Arminda Lucia Siqueira 1 Flávia Komatsuzaki 1 Introdução Regressão logística é hoje padrão de análise para muitos estudos da área da saúde cuja variável
Dimensionamento de amostras para regressão logística Arminda Lucia Siqueira 1 Flávia Komatsuzaki 1 Introdução Regressão logística é hoje padrão de análise para muitos estudos da área da saúde cuja variável
Professora: Cira Souza Pitombo. Disciplina: Aplicações de técnicas de análise de dados
 UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA MESTRADO EM ENGENHARIA AMBIENTAL E URBANA Apresentação do Curso Introdução Professora: Cira Souza Pitombo Disciplina: Aplicações de técnicas de análise
UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA MESTRADO EM ENGENHARIA AMBIENTAL E URBANA Apresentação do Curso Introdução Professora: Cira Souza Pitombo Disciplina: Aplicações de técnicas de análise
Modelos Lineares Generalizados - Componentes do Modelo
 Modelos Lineares Generalizados - Componentes do Modelo Erica Castilho Rodrigues 01 de Abril de 2014 3 Vejamos agora quais as componentes de um Modelo Linear Generalizado. Temos um conjunto de variáveis
Modelos Lineares Generalizados - Componentes do Modelo Erica Castilho Rodrigues 01 de Abril de 2014 3 Vejamos agora quais as componentes de um Modelo Linear Generalizado. Temos um conjunto de variáveis
REGRESSÃO E CORRELAÇÃO
 REGRESSÃO E CORRELAÇÃO A interpretação moderna da regressão A análise de regressão diz respeito ao estudo da dependência de uma variável, a variável dependente, em relação a uma ou mais variáveis explanatórias,
REGRESSÃO E CORRELAÇÃO A interpretação moderna da regressão A análise de regressão diz respeito ao estudo da dependência de uma variável, a variável dependente, em relação a uma ou mais variáveis explanatórias,
4 Modelos de Regressão Dinâmica
 4 Modelos de Regressão Dinâmica Nos modelos de regressão linear (Johnston e Dinardo, 1998) estudados comumente na literatura, supõe-se que os erros gerados pelo modelo possuem algumas características como:
4 Modelos de Regressão Dinâmica Nos modelos de regressão linear (Johnston e Dinardo, 1998) estudados comumente na literatura, supõe-se que os erros gerados pelo modelo possuem algumas características como:
Análise Multivariada Aplicada à Contabilidade
 Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Análise de Dados Longitudinais Modelos de Regressão - Perspecitva Histórica
 1/41 Análise de Dados Longitudinais Modelos de Regressão - Perspecitva Histórica Enrico A. Colosimo/UFMG http://www.est.ufmg.br/ enricoc/ Revisão para Dados Transversais 1 Características Informações amostrais
1/41 Análise de Dados Longitudinais Modelos de Regressão - Perspecitva Histórica Enrico A. Colosimo/UFMG http://www.est.ufmg.br/ enricoc/ Revisão para Dados Transversais 1 Características Informações amostrais
Ajustar Técnica usada na análise dos dados para controlar ou considerar possíveis variáveis de confusão.
 Glossário Ajustar Técnica usada na análise dos dados para controlar ou considerar possíveis variáveis de confusão. Análise de co-variância: Procedimento estatístico utilizado para análise de dados que
Glossário Ajustar Técnica usada na análise dos dados para controlar ou considerar possíveis variáveis de confusão. Análise de co-variância: Procedimento estatístico utilizado para análise de dados que
Modelos Lineares Generalizados - Verificação do Ajuste do Modelo
 1 Modelos Lineares Generalizados - Verificação do Ajuste do Modelo Erica Castilho Rodrigues 9 de Abril de 2015 2 3 Função Deviance Podemos ver o ajuste de um modelo a um conjunto de dados como: uma forma
1 Modelos Lineares Generalizados - Verificação do Ajuste do Modelo Erica Castilho Rodrigues 9 de Abril de 2015 2 3 Função Deviance Podemos ver o ajuste de um modelo a um conjunto de dados como: uma forma
Análise de Regressão Linear Simples e
 Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Análise de Dados Categóricos
 1/43 Análise de Dados Categóricos Modelo de Regressão de Poisson Enrico A. Colosimo/UFMG http://www.est.ufmg.br/ enricoc/ Departamento de Estatística Universidade Federal de Minas Gerais 2/43 Revisão:
1/43 Análise de Dados Categóricos Modelo de Regressão de Poisson Enrico A. Colosimo/UFMG http://www.est.ufmg.br/ enricoc/ Departamento de Estatística Universidade Federal de Minas Gerais 2/43 Revisão:
Fundação Oswaldo Cruz Escola Nacional de Saúde Pública Departamento de Epidemiologia. Estatística espacial. Padrão Pontual
 Fundação Oswaldo Cruz Escola Nacional de Saúde Pública Departamento de Epidemiologia Estatística espacial Padrão Pontual Padrão de Pontos A análise de padrão de pontos, é o tipo mais simples de análise
Fundação Oswaldo Cruz Escola Nacional de Saúde Pública Departamento de Epidemiologia Estatística espacial Padrão Pontual Padrão de Pontos A análise de padrão de pontos, é o tipo mais simples de análise
Quiz Econometria I versão 1
 Obs: muitos itens foram retirados da ANPEC. Quiz Econometria I versão 1 V ou F? QUESTÃO 1 É dada a seguinte função de produção para determinada indústria: ln(y i )=β 0 + β 1 ln( L i )+β 2 ln( K i )+u i,
Obs: muitos itens foram retirados da ANPEC. Quiz Econometria I versão 1 V ou F? QUESTÃO 1 É dada a seguinte função de produção para determinada indústria: ln(y i )=β 0 + β 1 ln( L i )+β 2 ln( K i )+u i,
Ajuste e comparação de modelos para dados grupados e censurados
 Ajuste e comparação de modelos para dados grupados e censurados 1 Introdução José Nilton da Cruz 1 Liciana Vaz de Arruda Silveira 2 José Raimundo de Souza Passos 2 A análise de sobrevivência é um conjunto
Ajuste e comparação de modelos para dados grupados e censurados 1 Introdução José Nilton da Cruz 1 Liciana Vaz de Arruda Silveira 2 José Raimundo de Souza Passos 2 A análise de sobrevivência é um conjunto
Análise de Dados Longitudinais Aula
 1/24 Análise de Dados Longitudinais Aula 31.10.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/24 Sumário 1 Dados Ausentes em Estudos Longitudinais 2 Imputação de Dados 3 Simulações
1/24 Análise de Dados Longitudinais Aula 31.10.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/24 Sumário 1 Dados Ausentes em Estudos Longitudinais 2 Imputação de Dados 3 Simulações
Disciplina de Modelos Lineares
 Disciplina de Modelos Lineares 2012-2 Seleção de Variáveis Professora Ariane Ferreira Em modelos de regressão múltipla é necessário determinar um subconjunto de variáveis independentes que melhor explique
Disciplina de Modelos Lineares 2012-2 Seleção de Variáveis Professora Ariane Ferreira Em modelos de regressão múltipla é necessário determinar um subconjunto de variáveis independentes que melhor explique
Modelos de regressão para dados correlacionados. Cibele Russo
 Modelos de regressão para dados correlacionados Cibele Russo cibele@icmc.usp.br ICMC USP Mini-curso oferecido no Workshop on Probabilistic and Statistical Methods 28 a 30 de janeiro de 2013 Cibele Russo
Modelos de regressão para dados correlacionados Cibele Russo cibele@icmc.usp.br ICMC USP Mini-curso oferecido no Workshop on Probabilistic and Statistical Methods 28 a 30 de janeiro de 2013 Cibele Russo
Esse material foi extraído de Barbetta (2007 cap 13)
 Esse material foi extraído de Barbetta (2007 cap 13) - Predizer valores de uma variável dependente (Y) em função de uma variável independente (X). - Conhecer o quanto variações de X podem afetar Y. Exemplos
Esse material foi extraído de Barbetta (2007 cap 13) - Predizer valores de uma variável dependente (Y) em função de uma variável independente (X). - Conhecer o quanto variações de X podem afetar Y. Exemplos
Utilização de modelos marginais na análise de dados longitudinais irregulares em relação ao tempo
 Utilização de modelos marginais na análise de dados longitudinais irregulares em relação ao tempo César Gonçalves de Lima 1 Michele Barbosa 2 Valdo Rodrigues Herling 3 1. Introdução Dados longitudinais
Utilização de modelos marginais na análise de dados longitudinais irregulares em relação ao tempo César Gonçalves de Lima 1 Michele Barbosa 2 Valdo Rodrigues Herling 3 1. Introdução Dados longitudinais
i j i i Y X X X i j i i i
 Mario de Andrade Lira Junior lira.pro.br\wordpress lira.pro.br\wordpress Diferença Regressão - equação ligando duas ou mais variáveis Correlação medida do grau de ligação entre duas variáveis Usos Regressão
Mario de Andrade Lira Junior lira.pro.br\wordpress lira.pro.br\wordpress Diferença Regressão - equação ligando duas ou mais variáveis Correlação medida do grau de ligação entre duas variáveis Usos Regressão
Modelos Binomial e Poisson
 Objetivos Motivação BIE5781 - Pós-Graduação em Ecologia USP setembro de 2012 Objetivo da Aula Objetivos Motivação Os objetivos dessa aula são: Objetivos Motivação Objetivo da Aula Os objetivos dessa aula
Objetivos Motivação BIE5781 - Pós-Graduação em Ecologia USP setembro de 2012 Objetivo da Aula Objetivos Motivação Os objetivos dessa aula são: Objetivos Motivação Objetivo da Aula Os objetivos dessa aula
Modelo de Regressão Múltipla
 Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Modelo de regressão estável aplicado a econometria
 Modelo de regressão estável aplicado a econometria financeira Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Curitiba/PR, 81531 990, Brasil email: lucambio@ufpr.br 1 Objetivos
Modelo de regressão estável aplicado a econometria financeira Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Curitiba/PR, 81531 990, Brasil email: lucambio@ufpr.br 1 Objetivos
MAE Modelos Lineares Generalizados 2 o semestre 2017
 MAE5763 - Modelos Lineares Generalizados 2 o semestre 2017 Prof. Gilberto A. Paula 3 a Lista de Exercícios 1. Supor y i ind FE(µ, φ i ) com φ i = α + γz i, para i = 1,..., n. Como ca a matriz modelo Z?
MAE5763 - Modelos Lineares Generalizados 2 o semestre 2017 Prof. Gilberto A. Paula 3 a Lista de Exercícios 1. Supor y i ind FE(µ, φ i ) com φ i = α + γz i, para i = 1,..., n. Como ca a matriz modelo Z?
Análise de Dados Longitudinais Aula
 1/20 Análise de Dados Longitudinais Aula 13.08.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/20 Sumário 1 Modelos Marginais 2 3/20 Modelos Marginais Modelos Marginais para Dados
1/20 Análise de Dados Longitudinais Aula 13.08.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/20 Sumário 1 Modelos Marginais 2 3/20 Modelos Marginais Modelos Marginais para Dados
O USO DE MODELOS DE REGRESSÃO LOGÍSTICA PARA AVALIAÇÃO DO PROBLEMA DE EVASÃO DE ALUNOS NO CURSO DE QUÍMICA INDUSTRIAL DA UNUCET-UEG
 O USO DE MODELOS DE REGRESSÃO LOGÍSTICA PARA AVALIAÇÃO DO PROBLEMA DE EVASÃO DE ALUNOS NO CURSO DE QUÍMICA INDUSTRIAL DA UNUCET-UEG Robson de Souza Vieira 1 ; Rogério Silva Pimentel 1 ; Emerson Wruck 2
O USO DE MODELOS DE REGRESSÃO LOGÍSTICA PARA AVALIAÇÃO DO PROBLEMA DE EVASÃO DE ALUNOS NO CURSO DE QUÍMICA INDUSTRIAL DA UNUCET-UEG Robson de Souza Vieira 1 ; Rogério Silva Pimentel 1 ; Emerson Wruck 2
AULA 09 Regressão. Ernesto F. L. Amaral. 17 de setembro de 2012
 1 AULA 09 Regressão Ernesto F. L. Amaral 17 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario F. 2008. Introdução à
1 AULA 09 Regressão Ernesto F. L. Amaral 17 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario F. 2008. Introdução à
Modelagem da estrutura de covariância na análise de medidas repetidas
 Modelagem da estrutura de covariância na análise de medidas repetidas Marisol García Peña Sergio Arciniegas Alarcón Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento
Modelagem da estrutura de covariância na análise de medidas repetidas Marisol García Peña Sergio Arciniegas Alarcón Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento
Relatório GLM - Predição de doênça coronária cardíaca através do modelo de regressão generalizado com resposta Binomial
 UNIVERSIDADE FEDERAL DO PARANÁ Rafael Morciani Alves da Silva Maike Willian Martins dos Santos Mateus Gemelli Ramos Relatório GLM - Predição de doênça coronária cardíaca através do modelo de regressão
UNIVERSIDADE FEDERAL DO PARANÁ Rafael Morciani Alves da Silva Maike Willian Martins dos Santos Mateus Gemelli Ramos Relatório GLM - Predição de doênça coronária cardíaca através do modelo de regressão
CONHECIMENTOS ESPECÍFICOS
 fonte de graus de soma de quadrado variação liberdade quadrados médio teste F regressão 1 1,4 1,4 46,2 resíduo 28 0,8 0,03 total 2,2 A tabela de análise de variância (ANOVA) ilustrada acima resulta de
fonte de graus de soma de quadrado variação liberdade quadrados médio teste F regressão 1 1,4 1,4 46,2 resíduo 28 0,8 0,03 total 2,2 A tabela de análise de variância (ANOVA) ilustrada acima resulta de
Análise de Dados Longitudinais Modelos Lineares Generalizados Longitudinais
 1/55 Análise de Dados Longitudinais Modelos Lineares Generalizados Longitudinais Enrico A. Colosimo-UFMG www.est.ufmg.br/ enricoc 2/55 Respostas Longitudinal Não-Gaussiana 1 Y ij, i = 1,..., N; j = 1,...,
1/55 Análise de Dados Longitudinais Modelos Lineares Generalizados Longitudinais Enrico A. Colosimo-UFMG www.est.ufmg.br/ enricoc 2/55 Respostas Longitudinal Não-Gaussiana 1 Y ij, i = 1,..., N; j = 1,...,
UNIVERSIDADE FEDERAL DO PARANÁ CURSO ESTATÍSTICA DENNIS LEÃO GRR LUAN FIORENTIN GRR
 UNIVERSIDADE FEDERAL DO PARANÁ CURSO ESTATÍSTICA DENNIS LEÃO GRR - 20160239 LUAN FIORENTIN GRR - 20160219 MODELAGEM DE DADOS DE ÓBITOS POR AGRESSÕES NO ESTADO DE SÃO PAULO NO ANO DE 2016 CURITIBA Novembro
UNIVERSIDADE FEDERAL DO PARANÁ CURSO ESTATÍSTICA DENNIS LEÃO GRR - 20160239 LUAN FIORENTIN GRR - 20160219 MODELAGEM DE DADOS DE ÓBITOS POR AGRESSÕES NO ESTADO DE SÃO PAULO NO ANO DE 2016 CURITIBA Novembro
Sumário. CAPÍTULO 1 Conceitos preliminares 1. CAPÍTULO 2 Descrição de dados: análise monovariada 47
 CAPÍTULO 1 Conceitos preliminares 1 Introdução........................................................1 O que é estatística?.................................................. 4 Papel dos microcomputadores.........................................
CAPÍTULO 1 Conceitos preliminares 1 Introdução........................................................1 O que é estatística?.................................................. 4 Papel dos microcomputadores.........................................
Aula inaugural do curso Análise de Regressão
 Aula inaugural do curso Prof a Silvia Nagib Elian Sala 215 - Bloco A Instituto de Matemática e Estatística Universidade de São Paulo Agenda 1. Exemplo 2. Introdução 3. Modelo de regressão linear simples
Aula inaugural do curso Prof a Silvia Nagib Elian Sala 215 - Bloco A Instituto de Matemática e Estatística Universidade de São Paulo Agenda 1. Exemplo 2. Introdução 3. Modelo de regressão linear simples
RESUMO DO CAPÍTULO 3 DO LIVRO DE WOOLDRIDGE ANÁLISE DE REGRESSÃO MÚLTIPLA: ESTIMAÇÃO
 RESUMO DO CAPÍTULO 3 DO LIVRO DE WOOLDRIDGE ANÁLISE DE REGRESSÃO MÚLTIPLA: ESTIMAÇÃO Regressão simples: desvantagem de apenas uma variável independente explicando y mantendo ceteris paribus as demais (ou
RESUMO DO CAPÍTULO 3 DO LIVRO DE WOOLDRIDGE ANÁLISE DE REGRESSÃO MÚLTIPLA: ESTIMAÇÃO Regressão simples: desvantagem de apenas uma variável independente explicando y mantendo ceteris paribus as demais (ou
Avaliação Monte Carlo do teste para comparação de duas matrizes de covariâncias normais na presença de correlação
 Avaliação Monte Carlo do teste para comparação de duas matrizes de covariâncias normais na presença de correlação Vanessa Siqueira Peres da Silva 1 2 Daniel Furtado Ferreira 1 1 Introdução É comum em determinadas
Avaliação Monte Carlo do teste para comparação de duas matrizes de covariâncias normais na presença de correlação Vanessa Siqueira Peres da Silva 1 2 Daniel Furtado Ferreira 1 1 Introdução É comum em determinadas
Dimensionamento de amostras para estudos com variável resposta ordinal
 Dimensionamento de amostras para estudos com variável resposta ordinal Arminda Lucia Siqueira 1 Aloísio Joaquim Freitas Ribeiro 1 Edna Afonso Reis 1 Ilka Afonso Reis 1 1 Introdução Uma situação comum na
Dimensionamento de amostras para estudos com variável resposta ordinal Arminda Lucia Siqueira 1 Aloísio Joaquim Freitas Ribeiro 1 Edna Afonso Reis 1 Ilka Afonso Reis 1 1 Introdução Uma situação comum na
CE071 - Análise de Regressão Linear
 CE071 - Análise de Regressão Linear Cesar Augusto Taconeli 30 de maio, 2018 Cesar Augusto Taconeli CE071 - Análise de Regressão Linear 30 de maio, 2018 1 / 21 Aula 7 - Regressão linear com covariáveis
CE071 - Análise de Regressão Linear Cesar Augusto Taconeli 30 de maio, 2018 Cesar Augusto Taconeli CE071 - Análise de Regressão Linear 30 de maio, 2018 1 / 21 Aula 7 - Regressão linear com covariáveis
diferença não aleatória na distribuição dos fatores de risco entre os dois grupos
 Confundimento erro devido a uma diferença não aleatória na distribuição dos fatores de risco entre os dois grupos. A variável de confundimento está distribuída desigualmente entre os grupos comparados.
Confundimento erro devido a uma diferença não aleatória na distribuição dos fatores de risco entre os dois grupos. A variável de confundimento está distribuída desigualmente entre os grupos comparados.
Alternativas à Regressão Logística para análise de dados
 XVIII Congresso Mundial de Epidemiologia VII Congresso Brasileiro de Epidemiologia EIDEMIOLOGIA NA CONSTRUÇÃO DA SAÚDE ARA TODOS: MÉTODOS ARA UM MUNDO EM TRANSFORMAÇÃO Alternativas à Regressão Logística
XVIII Congresso Mundial de Epidemiologia VII Congresso Brasileiro de Epidemiologia EIDEMIOLOGIA NA CONSTRUÇÃO DA SAÚDE ARA TODOS: MÉTODOS ARA UM MUNDO EM TRANSFORMAÇÃO Alternativas à Regressão Logística
Comparando equações de regressão em dados de saúde
 Comparando equações de regressão em dados de saúde Terezinha Aparecida Guedes*, Ivan Ludgero Ivanqui e Ana Beatriz Tozzo Martins Departamento de Estatística, Universidade Estadual de Maringá, Av Colombo,
Comparando equações de regressão em dados de saúde Terezinha Aparecida Guedes*, Ivan Ludgero Ivanqui e Ana Beatriz Tozzo Martins Departamento de Estatística, Universidade Estadual de Maringá, Av Colombo,
Modelos de Regressão Linear Simples - parte III
 1 Modelos de Regressão Linear Simples - parte III Erica Castilho Rodrigues 20 de Setembro de 2016 2 3 4 A variável X é um bom preditor da resposta Y? Quanto da variação da variável resposta é explicada
1 Modelos de Regressão Linear Simples - parte III Erica Castilho Rodrigues 20 de Setembro de 2016 2 3 4 A variável X é um bom preditor da resposta Y? Quanto da variação da variável resposta é explicada
Meta-análise: comparação de proporções para o caso de duas amostras independentes
 Meta-análise: comparação de proporções para o caso de duas amostras independentes Arminda Lucia Siqueira 1 Edna Afonso Reis 1 Ilka Afonso Reis 1 Luana Sílvia dos Santos 1 Pollyanna Vieira Gomes da Silva
Meta-análise: comparação de proporções para o caso de duas amostras independentes Arminda Lucia Siqueira 1 Edna Afonso Reis 1 Ilka Afonso Reis 1 Luana Sílvia dos Santos 1 Pollyanna Vieira Gomes da Silva
AGA Análise de Dados em Astronomia I 7. Modelagem dos Dados com Máxima Verossimilhança: Modelos Lineares
 1 / 0 AGA 0505- Análise de Dados em Astronomia I 7. Modelagem dos Dados com Máxima Verossimilhança: Modelos Lineares Laerte Sodré Jr. 1o. semestre, 018 modelos modelagem dos dados dado um conjunto de dados,
1 / 0 AGA 0505- Análise de Dados em Astronomia I 7. Modelagem dos Dados com Máxima Verossimilhança: Modelos Lineares Laerte Sodré Jr. 1o. semestre, 018 modelos modelagem dos dados dado um conjunto de dados,
Teste de % de defeituosos para 1 amostra
 DOCUMENTO OFICIAL DO ASSISTENTE DO MINITAB Este documento é de uma série de papéis que explicam a pesquisa conduzida por estatísticos da Minitab para desenvolver os métodos e as verificações de dados usadas
DOCUMENTO OFICIAL DO ASSISTENTE DO MINITAB Este documento é de uma série de papéis que explicam a pesquisa conduzida por estatísticos da Minitab para desenvolver os métodos e as verificações de dados usadas
Ralph S. Silva
 ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S. Silva http://www.im.ufrj.br/ralph/multivariada.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Agradecimentos
ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S. Silva http://www.im.ufrj.br/ralph/multivariada.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Agradecimentos
Modelos para dados de contagem
 O modelo de Poisson Sumário 1 Introdução 2 Regressão de Poisson Taxa de Incidência Inclusão de covariáveis Interpretação dos parâmetros 3 Exemplos 4 Superdispersão Dados de Contagem Podemos estar interessados
O modelo de Poisson Sumário 1 Introdução 2 Regressão de Poisson Taxa de Incidência Inclusão de covariáveis Interpretação dos parâmetros 3 Exemplos 4 Superdispersão Dados de Contagem Podemos estar interessados
MAE Planejamento e Pesquisa II
 MAE0327 - Planejamento e Pesquisa II EXPERIMENTOS/ESTUDOS NÃO-BALANCEADOS COM FATORES FIXOS - PARTE 1 7 de agosto de 2016 Denise A Botter MAE0327 7 de agosto de 2016 1 / 1 PLANEJAMENTO E PESQUISA I Estudos
MAE0327 - Planejamento e Pesquisa II EXPERIMENTOS/ESTUDOS NÃO-BALANCEADOS COM FATORES FIXOS - PARTE 1 7 de agosto de 2016 Denise A Botter MAE0327 7 de agosto de 2016 1 / 1 PLANEJAMENTO E PESQUISA I Estudos
Definição. Os valores assumidos pelos estimadores denomina-se estimativas pontuais ou simplesmente estimativas.
 1. Inferência Estatística Inferência Estatística é o uso da informção (ou experiência ou história) para a redução da incerteza sobre o objeto em estudo. A informação pode ou não ser proveniente de um experimento
1. Inferência Estatística Inferência Estatística é o uso da informção (ou experiência ou história) para a redução da incerteza sobre o objeto em estudo. A informação pode ou não ser proveniente de um experimento
Exemplos Modelos Binomiais de Dose-Resposta
 Exemplos Modelos Binomiais de Dose-Resposta p. 1/14 Exemplos Modelos Binomiais de Dose-Resposta Gilberto A. Paula Departamento de Estatística IME-USP MAE5763 - Modelos Lineares Generalizados 2 o semestre
Exemplos Modelos Binomiais de Dose-Resposta p. 1/14 Exemplos Modelos Binomiais de Dose-Resposta Gilberto A. Paula Departamento de Estatística IME-USP MAE5763 - Modelos Lineares Generalizados 2 o semestre
EAE0325 Econometria II. Professora: Fabiana Fontes Rocha. Gabarito Primeira Lista Teórica de Exercícios
 EAE0325 Econometria II Professora: Fabiana Fontes Rocha Gabarito Primeira Lista Teórica de Exercícios Bloco 1 Assinalar se as afirmativas a seguir são verdadeiras V) ou falsas F) Exercício 1 Sobre o modelo
EAE0325 Econometria II Professora: Fabiana Fontes Rocha Gabarito Primeira Lista Teórica de Exercícios Bloco 1 Assinalar se as afirmativas a seguir são verdadeiras V) ou falsas F) Exercício 1 Sobre o modelo
Modelos Binomial e Poisson
 Objetivos Motivação BIE5781 - Pós-Graduação em Ecologia USP Setembro de 2016 Objetivos Motivação Objetivo da Aula Os objetivos dessa aula são: Objetivos Motivação Objetivo da Aula Os objetivos dessa aula
Objetivos Motivação BIE5781 - Pós-Graduação em Ecologia USP Setembro de 2016 Objetivos Motivação Objetivo da Aula Os objetivos dessa aula são: Objetivos Motivação Objetivo da Aula Os objetivos dessa aula
Testes de Hipóteses para. uma Única Amostra. Objetivos de Aprendizagem. 9.1 Teste de Hipóteses. UFMG-ICEx-EST-027/031 07/06/ :07
 -027/031 07/06/2018 10:07 9 ESQUEMA DO CAPÍTULO 9.1 TESTE DE HIPÓTESES 9.2 TESTES PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA CONHECIDA 9.3 TESTES PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA
-027/031 07/06/2018 10:07 9 ESQUEMA DO CAPÍTULO 9.1 TESTE DE HIPÓTESES 9.2 TESTES PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA CONHECIDA 9.3 TESTES PARA A MÉDIA DE UMA DISTRIBUIÇÃO NORMAL, VARIÂNCIA
Transformações e Ponderação para corrigir violações do modelo
 Transformações e Ponderação para corrigir violações do modelo Diagnóstico na análise de regressão Relembrando suposições Os erros do modelo tem média zero e variância constante. Os erros do modelo tem
Transformações e Ponderação para corrigir violações do modelo Diagnóstico na análise de regressão Relembrando suposições Os erros do modelo tem média zero e variância constante. Os erros do modelo tem
i j i i Y X X X i j 1 i 2 i i
 Mario de Andrade Lira Junior lira.pro.br\wordpress lira.pro.br\wordpress Diferença Regressão - equação ligando duas ou mais variáveis Correlação medida do grau de ligação entre duas variáveis Usos Regressão
Mario de Andrade Lira Junior lira.pro.br\wordpress lira.pro.br\wordpress Diferença Regressão - equação ligando duas ou mais variáveis Correlação medida do grau de ligação entre duas variáveis Usos Regressão
AULAS 21 E 22 Análise de Regressão Múltipla: Estimação
 1 AULAS 21 E 22 Análise de Regressão Múltipla: Estimação Ernesto F. L. Amaral 28 de outubro e 04 de novembro de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Cohen, Ernesto, e Rolando Franco. 2000. Avaliação
1 AULAS 21 E 22 Análise de Regressão Múltipla: Estimação Ernesto F. L. Amaral 28 de outubro e 04 de novembro de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Cohen, Ernesto, e Rolando Franco. 2000. Avaliação
CONHECIMENTOS ESPECÍFICOS
 CONHECIMENTOS ESPECÍFICOS Julgue os itens que se seguem, acerca da estatística descritiva. 51 Na distribuição da quantidade de horas trabalhadas por empregados de certa empresa, é sempre possível determinar
CONHECIMENTOS ESPECÍFICOS Julgue os itens que se seguem, acerca da estatística descritiva. 51 Na distribuição da quantidade de horas trabalhadas por empregados de certa empresa, é sempre possível determinar
IND 1115 Inferência Estatística Aula 6
 Conteúdo IND 5 Inferência Estatística Aula 6 Setembro de 004 A distribuição Lognormal A distribuição Beta e sua relação com a Uniforme(0,) Mônica Barros mbarros.com mbarros.com A distribuição Lognormal
Conteúdo IND 5 Inferência Estatística Aula 6 Setembro de 004 A distribuição Lognormal A distribuição Beta e sua relação com a Uniforme(0,) Mônica Barros mbarros.com mbarros.com A distribuição Lognormal
Stela Adami Vayego Estatística II CE003/DEST/UFPR
 Resumo 1 Teste de hipóteses não paramétricos Os métodos não-paramétricos fazem poucas suposições sobre a natureza das distribuições dos dados. Não exige que as distribuições nas populações sejam normais,
Resumo 1 Teste de hipóteses não paramétricos Os métodos não-paramétricos fazem poucas suposições sobre a natureza das distribuições dos dados. Não exige que as distribuições nas populações sejam normais,
Exemplo Ataques Epilépticos
 Exemplo Ataques Epilépticos Gilberto A. Paula Departamento de Estatística IME-USP, Brasil giapaula@ime.usp.br 2 o Semestre 2015 G. A. Paula (IME-USP) Ataques Epilépticos 2 o Semestre 2015 1 / 20 Ataques
Exemplo Ataques Epilépticos Gilberto A. Paula Departamento de Estatística IME-USP, Brasil giapaula@ime.usp.br 2 o Semestre 2015 G. A. Paula (IME-USP) Ataques Epilépticos 2 o Semestre 2015 1 / 20 Ataques
TESTES DE HIPÓTESES E INTERVALOS DE CONFIANÇA EM MODELOS LINEARES GENERALIZADOS
 TESTES DE HIPÓTESES E INTERVALOS DE CONFIANÇA EM MODELOS LINEARES GENERALIZADOS Antes de apresentar alguns dos testes de hipóteses e intervalos de confiança mais usuais em MLG, segue a definição de modelos
TESTES DE HIPÓTESES E INTERVALOS DE CONFIANÇA EM MODELOS LINEARES GENERALIZADOS Antes de apresentar alguns dos testes de hipóteses e intervalos de confiança mais usuais em MLG, segue a definição de modelos
Modelos de Regressão Linear Simples - parte II
 Modelos de Regressão Linear Simples - parte II Erica Castilho Rodrigues 14 de Outubro de 2013 Erros Comuns que Envolvem a Análise de Correlação 3 Erros Comuns que Envolvem a Análise de Correlação Propriedade
Modelos de Regressão Linear Simples - parte II Erica Castilho Rodrigues 14 de Outubro de 2013 Erros Comuns que Envolvem a Análise de Correlação 3 Erros Comuns que Envolvem a Análise de Correlação Propriedade
Exemplos Regressão Dados Binários
 Exemplos Regressão Dados Binários p. 1/28 Exemplos Regressão Dados Binários Gilberto A. Paula Departamento de Estatística IME-USP MAE5763 - Modelos Lineares Generalizados 2 o semestre de 2011 Exemplos
Exemplos Regressão Dados Binários p. 1/28 Exemplos Regressão Dados Binários Gilberto A. Paula Departamento de Estatística IME-USP MAE5763 - Modelos Lineares Generalizados 2 o semestre de 2011 Exemplos
UM MODELO DE FRAGILIDADE PARA DADOS DISCRETOS DE SOBREVIVÊNCIA. Eduardo Yoshio Nakano 1
 1 UM MODELO DE FRAGILIDADE PARA DADOS DISCRETOS DE SOBREVIVÊNCIA Eduardo Yoshio Nakano 1 1 Professor do Departamento de Estatística da Universidade de Brasília, UnB. RESUMO. Em estudos médicos, o comportamento
1 UM MODELO DE FRAGILIDADE PARA DADOS DISCRETOS DE SOBREVIVÊNCIA Eduardo Yoshio Nakano 1 1 Professor do Departamento de Estatística da Universidade de Brasília, UnB. RESUMO. Em estudos médicos, o comportamento
AULA 11 Heteroscedasticidade
 1 AULA 11 Heteroscedasticidade Ernesto F. L. Amaral 30 de julho de 2012 Análise de Regressão Linear (MQ 2012) www.ernestoamaral.com/mq12reg.html Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
1 AULA 11 Heteroscedasticidade Ernesto F. L. Amaral 30 de julho de 2012 Análise de Regressão Linear (MQ 2012) www.ernestoamaral.com/mq12reg.html Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
2 ou mais fatores são de interesse.
 5. Experimentos Fatoriais 5.1 Definições e Princípios Básicos 2 ou mais fatores são de interesse. Experimentos Fatoriais: em cada replicação do experimento todas as combinações dos níveis de tratamento
5. Experimentos Fatoriais 5.1 Definições e Princípios Básicos 2 ou mais fatores são de interesse. Experimentos Fatoriais: em cada replicação do experimento todas as combinações dos níveis de tratamento
Stela Adami Vayego DEST/UFPR
 Resumo 1 Testes de hipóteses não paramétricos Os métodos não-paramétricos fazem poucas suposições sobre a natureza das distribuições dos dados. Não exige que as distribuições nas populações sejam normais,
Resumo 1 Testes de hipóteses não paramétricos Os métodos não-paramétricos fazem poucas suposições sobre a natureza das distribuições dos dados. Não exige que as distribuições nas populações sejam normais,
Exemplos Modelos de Quase-Verossimilhança
 Exemplos Modelos de Quase-Verossimilhança p. 1/40 Exemplos Modelos de Quase-Verossimilhança Gilberto A. Paula Departamento de Estatística IME-USP MAE5763 - Modelos Lineares Generalizados 2 o semestre de
Exemplos Modelos de Quase-Verossimilhança p. 1/40 Exemplos Modelos de Quase-Verossimilhança Gilberto A. Paula Departamento de Estatística IME-USP MAE5763 - Modelos Lineares Generalizados 2 o semestre de
Testes de Hipóteses. Ricardo Ehlers Departamento de Matemática Aplicada e Estatística Universidade de São Paulo
 Testes de Hipóteses Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Introdução e notação Em geral, intervalos de confiança são a forma mais
Testes de Hipóteses Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Introdução e notação Em geral, intervalos de confiança são a forma mais
AULA 9 - MQO em regressão múltipla: Propriedades Estatísticas (Valor Esperado)
 AULA 9 - MQO em regressão múltipla: Propriedades Estatísticas (Valor Esperado) Susan Schommer Econometria I - IE/UFRJ Valor esperado dos estimadores MQO Nesta aula derivamos o valor esperado dos estimadores
AULA 9 - MQO em regressão múltipla: Propriedades Estatísticas (Valor Esperado) Susan Schommer Econometria I - IE/UFRJ Valor esperado dos estimadores MQO Nesta aula derivamos o valor esperado dos estimadores
INCIDÊNCIA DE DENGUE EM UMA CIDADE DA COSTA MEXICANA: UM ESTUDO PREDITIVO
 Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Estatística INCIDÊNCIA DE DENGUE EM UMA CIDADE DA COSTA MEXICANA: UM ESTUDO PREDITIVO CE225 - Modelos Lineares Generalizados Eduardo
Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Estatística INCIDÊNCIA DE DENGUE EM UMA CIDADE DA COSTA MEXICANA: UM ESTUDO PREDITIVO CE225 - Modelos Lineares Generalizados Eduardo
Testes de Raiz Unitária para Dados em Painel
 Aula 7 Bibliografia: Stata, 2017. help xtunitroot. From Stata/SE 13 (accessed on Oct. 23, 2018). Pesaran, M.H. (2015). Time series and panel data econometrics. Oxford: Oxford University Press. Rafael S.
Aula 7 Bibliografia: Stata, 2017. help xtunitroot. From Stata/SE 13 (accessed on Oct. 23, 2018). Pesaran, M.H. (2015). Time series and panel data econometrics. Oxford: Oxford University Press. Rafael S.
Técnicas computacionais em probabilidade e estatística II
 Técnicas computacionais em probabilidade e estatística II Universidade de São Paulo Instituto de Matemática e Estatística http:www.ime.usp.br/ mbranco AULA 1: Problemas Computacionais em Inferência Estatística.
Técnicas computacionais em probabilidade e estatística II Universidade de São Paulo Instituto de Matemática e Estatística http:www.ime.usp.br/ mbranco AULA 1: Problemas Computacionais em Inferência Estatística.
Análise de regressão linear simples. Diagrama de dispersão
 Introdução Análise de regressão linear simples Departamento de Matemática Escola Superior de Tecnologia de Viseu A análise de regressão estuda o relacionamento entre uma variável chamada a variável dependente
Introdução Análise de regressão linear simples Departamento de Matemática Escola Superior de Tecnologia de Viseu A análise de regressão estuda o relacionamento entre uma variável chamada a variável dependente
Análise Multivariada Aplicada à Contabilidade
 Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Modelo de regressão Beta
 Modelo de regressão Beta Fernando Lucambio Pérez Departamento de Estatística Universidade Federal do Paraná Agosto de 2004 1 Consideremos uma situação em que a variável resposta contínua é restrita ao
Modelo de regressão Beta Fernando Lucambio Pérez Departamento de Estatística Universidade Federal do Paraná Agosto de 2004 1 Consideremos uma situação em que a variável resposta contínua é restrita ao
Capítulo 2. Distribuições de Probabilidade Estimativas de parâmetros e tempos-atéfalha. Flávio Fogliatto
 Capítulo 2 Distribuições de Probabilidade Estimativas de parâmetros e tempos-atéfalha Flávio Fogliatto 1 Ajustes de distribuições Em estudos de confiabilidade, dados são amostrados a partir de uma população
Capítulo 2 Distribuições de Probabilidade Estimativas de parâmetros e tempos-atéfalha Flávio Fogliatto 1 Ajustes de distribuições Em estudos de confiabilidade, dados são amostrados a partir de uma população
1. Avaliação de impacto de programas sociais: por que, para que e quando fazer? (Cap. 1 do livro) 2. Estatística e Planilhas Eletrônicas 3.
 1 1. Avaliação de impacto de programas sociais: por que, para que e quando fazer? (Cap. 1 do livro) 2. Estatística e Planilhas Eletrônicas 3. Modelo de Resultados Potenciais e Aleatorização (Cap. 2 e 3
1 1. Avaliação de impacto de programas sociais: por que, para que e quando fazer? (Cap. 1 do livro) 2. Estatística e Planilhas Eletrônicas 3. Modelo de Resultados Potenciais e Aleatorização (Cap. 2 e 3
Exemplo Placas Dentárias
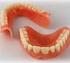 Exemplo Placas Dentárias Gilberto A. Paula Departamento de Estatística IME-USP, Brasil giapaula@ime.usp.br 2 o Semestre 2016 G. A. Paula (IME-USP) Placas Dentárias 2 o Semestre 2016 1 / 20 Placas Dentárias
Exemplo Placas Dentárias Gilberto A. Paula Departamento de Estatística IME-USP, Brasil giapaula@ime.usp.br 2 o Semestre 2016 G. A. Paula (IME-USP) Placas Dentárias 2 o Semestre 2016 1 / 20 Placas Dentárias
