Proposta de teste de avaliação

Transcrição

1 Proposta de teste de avaliação Matemática A. O ANO DE ESOLARIDADE Duração: 90 minutos Data:

2 Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número do item e a letra que identificam a opção escolhida.. A Maria tem um cofre protegido com um código composto por 5 algarismos de a 9. Sabe-se que o primeiro e o último são pares e diferentes entre si. Quantos códigos existem nestas condições? (A) 74 (B) 4 () 4 50 (D) 5. Em qual das opções se apresentam valores de x e p que verificam a igualdade: = x p (A) x = 00 e p = 55 (B) x = 009 e p = 54 () x = 00 e p = 54 (D) x = 009 e p = 5. Uma variável aleatória X tem distribuição normal. Sabe-se que P ( X >00) é inferior a ( < 90) P X. Qual dos seguintes pode ser o valor médio da variável aleatória X? (A) 9 (B) 95 () 9 (D) 0 4. O Sr. José tem carros para alugar. Desses carros oito, são de cor preta e dois de cor cinzenta. Pediram-lhe que escolhesse seis automóveis para levar um grupo de visitantes a passear. Sabendo que X designa a variável número de automóveis de cor cinzenta escolhidos, qual é a distribuição de probabilidades que corresponde à variável X? (A) X (B) X P ( X = x i ) P ( X = x i ) () X 0 (D) X 0 P ( X = x i ) P ( X = x i ) Proposta de teste de avaliação Matemática A,. o ano Página

3 5. onsidere a função g cujo gráfico está representado no referencial ortonormado xoy ao lado e a função f definida em R por x f x = 4. Qual é o valor de ( )( ) f g? (A) (B) 7 () 4 (D) 9 Grupo II Na resposta aos itens deste grupo apresente todos os cálculos que tiver de efetuar e todas as justificações necessárias.. Seja S, conjunto finito, o espaço de resultados associados a uma experiência aleatória. Sejam A e B dois acontecimentos possíveis ( e ) Sabe-se que A S B S. P A + P B = P A B P A B +... Mostre que A e B não são independentes... onsidere a experiência aleatória que consiste no lançamento de dois dados cúbicos equilibrados com as faces numeradas de a e o registo da soma dos números das faces voltadas para cima. Sejam os acontecimentos: A : A soma é um número par B : A soma é um número primo superior a Determine P( A B ). Sugestão: Pode utilizar a igualdade do enunciado. Proposta de teste de avaliação Matemática A,. o ano Página

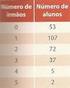
4 . Uma caixa tem duas bolas pretas e uma bola branca. Uma caixa tem três bolas pretas e duas bolas brancas. As bolas são indistinguíveis ao tato... onsidere a experiência aleatória que consiste em retirar, ao acaso, uma bola da caixa e colocá-la na caixa e, posteriormente, retirar uma bola da caixa, observando a sua cor. Sejam os acontecimentos: A : A bola retirada da caixa é preta. B : A bola retirada da caixa é branca. Determine P ( A B ):... utilizando a fórmula da probabilidade condicionada;... recorrendo à Lei de Laplace (sem utilizar a fórmula da probabilidade condicionada)... onsidere agora a experiência que consiste em tirar, ao acaso, uma bola da caixa, observar a cor e repor a bola na caixa. Repete-se esta experiência quatro vezes. Qual a probabilidade de sair bola branca pelo menos três vezes?. Numa escola foi feito um inqúerito sobre o número de alunos que chegaram atrasados à escola num dia de chuva. oncluiu-se que: dos alunos que chegaram atrasados vieram no automóvel dos pais; 4 dos alunos que vieram no automóvel dos pais chegaram atrasados; dos alunos chegaram atrasados. Escolhido um aluno ao acaso qual é a probabilidade de, nesse dia, ter vindo para a escola no automóvel dos pais? Proposta de teste de avaliação Matemática A,. o ano Página 4

5 4. Numa dada faculdade, os alunos podem ingressar no programa Erasmus indo estudar para o estrangeiro durante um certo período de tempo. Relativamente aos alunos que frequentam este programa, sabe-se que: 70% dos estudantes optam por realizar o programa Erasmus num país europeu; 5% dos estudantes que realizam este programa concluem com sucesso todas as unidades curriculares; 0% dos estudantes que não concluem com sucesso todas as unidades curriculares estão a realizar este programa fora da Europa. 4.. O André é um aluno desta faculdade e está no programa Erasmus na Alemanha. Qual é a probabilidade de concluir com sucesso todas as unidades curriculares? Apresente o resultado em forma de percentagem. 4.. Tendo em conta que 00 alunos optaram por utilizar o programa Erasmus, calcule a probabilidade de, escolhendo três destes alunos ao acaso, pelo menos um ter concluído com sucesso todas as unidades curriculares. Apresente o resultado na forma de dízima arredondada às milésimas. 5. Na figura estão representados, num referencial ortonormado xoy, parte do gráfico da função f, de domínio R, definida por f ( x ) = x e o triângulo [ AB ], retângulo em B. Os pontos D e pertencem ao gráfico de f. O ponto D tem abcissa a e o ponto tem abcissa a ( a > 0). Os pontos A e B pertencem ao eixo Oy e têm ordenadas iguais às de D e, respetivamente. Determine o valor de a sabendo que a medida da área do triângulo [ AB ] é igual a a.. Uma das formas de arrefecer um fluído é colocá-lo num tanque bem agitado por um rotor na presença de um líquido arrefecedor. A temperatura da água deste tanque ao longo do tempo, em graus elsius, é dada por: = 55 5( e t ) T t com t em minutos tal que t 0... Determine T ( 0) e lim x + no contexto da situação descrita... Mostre que ( + ) T ( t ) ( + ) T ( t ) T t T t T t e interprete os valores obtidos = +. e Proposta de teste de avaliação Matemática A,. o ano Página 5

6 7. onsidere a função g cuja expressão analítica é k x k g x = Sabendo que x = é um zero de g, determine o valor de k. Nota: No caso de não ter conseguido resolver esta alínea considere na próxima questão k =. 7.. onsidere, num referencial ortonormado xoy : Os pontos A e B pertencem ao gráfico de g e O corresponde à origem do referencial. O ponto A corresponde à interseção do gráfico da função g com a bissetriz dos quadrantes ímpares. O ponto B é um ponto tal que OA = OB. Determine, recorrendo à calculadora gráfica, a medida da área do triângulo [ OAB ]. Na sua resposta deve: Reproduzir, num referencial ortonormado xoy, o gráfico de g no intervalo [, ]. Apresentar o desenho do triângulo [ OAB ]. Indicar as coordenadas do ponto A, com cinco casas decimais. Apresentar a medida da área do triângulo arredondado às centésimas. FIM Grupo I: Questões 4 5 otações otação 40 Grupo II: Questões otação Proposta de teste de avaliação Matemática A,. o ano Página

7 Proposta de resolução Grupo I. Par Par = 74 Resposta: (A) = + + = + = Resposta: (D). Sabe-se que: P ( X ) P ( X ) Se µ = 9 : Se µ = 95 : Se µ = 9 : Se µ = 0: Resposta: (A) > 00 < < 90 µ 90 < 00 µ < Verdade 5 < 5 Falso < Falso < Falso 4. X : 0,, = = 0 ( 0) P X 5 = = 0 ( ) P X 4 = = 0 P X Resposta: (D) Proposta de teste de avaliação Matemática A,. o ano Página 7

8 5. Pelo gráfico, g = 0. ( f g ) f ( g ) f f x = = 0 =? x = 0 4 = 0 4 = x x = x = 4 f 4 = 0 f 0 = 4 x = x = 4 4 Resposta: ().. P ( A) P ( B) P ( A B) P ( A B ) + = + Grupo II P A + P B = P A B P A B + P A + P B = P A B P A B + P ( A) P ( B) P ( A B ) + ( ) + + = P A B P A + P B = P A B + P A + P B P A B P ( A ) + P ( B ) P ( A ) P ( B ) P ( A B ) P ( A B ) = 0 = Sabemos que: A e B são independentes P ( A B) = P ( A) P ( B ). omo P ( A ) > 0 e P ( B ) > 0, então P ( A) P ( B ) > 0, logo ( ) consequentemente, A e B não são independentes. P A B P A P B e, Proposta de teste de avaliação Matemática A,. o ano Página

9 .. P ( A B ) =? P A + P B = P A B P A B = 0 P ( A B ) P ( A B ) = Ou P ( A B ) = P A B = P( A) = = ; P( B) = = P A = 0 ( B) Através do esquema podemos concluir que 4 P A B = =. 9 Assim, A B corresponde à soma igual a P ( A B) ( ) P ( B) = P A B P ( A B) = P ( A) P ( B A ) = = 9 P ( B) = P ( A B) + P ( A B ) = 4 7 = + = + = + = 9 9 Então, P ( A B) P ( A B) 9 4 = = = =. P ( B) P ( A B ) é a probabilidade de a bola retirada da caixa ser preta sabendo que a bola retirada da caixa é branca. Número de casos possíveis: Há duas situações a considerar: a bola retirada da caixa (e introduzida na caixa ) é preta ou é branca:.º Preta retirada da caixa e Branca retirada da caixa.º Branca retirada da caixa e Branca retirada da caixa Há, portanto, + = 7 casos possíveis. Proposta de teste de avaliação Matemática A,. o ano Página 9 A A B B B B

10 Número de casos favoráveis: ( ) P A B De entre os casos possíveis apenas os = 4 da.ª situação são favoráveis. 4 = = Seja X o número de vezes que, nas quatro extrações, sai bola branca. X é uma variável binomial. X B 4, ( ) ( ) ( 4) P X = P X = + P X = = = + = 9 = = 9. Sejam os acontecimentos: A: O aluno chega atrasado : O aluno vem no automóvel dos pais P( A ) = 4 ( ) P A P A = P( ) =? = ( ) = ( ) P A P A P A ( ) = ( ) P A P P A = P( ) P( ) = P( ) = = = 4 Proposta de teste de avaliação Matemática A,. o ano Página 0

11 4.. Sejam os acontecimentos: E: O aluno realiza o programa Erasmus num país europeu. S: O aluno conclui com sucesso todas as unidades curriculares. P( E ) = 0,7 E P( S ) = 0,5 0, 5 S P E S = 0, ( ) P S E ( ) P ( E ) = P S E 0, 5 S 0,4 0, E E E P S = P S = 0,5 = 0,5 P E S = P E S = 0, = 0,4 P E = 0,7 P S E + P S E = 0,7 P S E + P S P E S = 0,7 P( S E ) + 0,5 0,4 = 0,7 P( S E ) = 0,7 0,4 P( S E ) = 0,5 ( E ) P ( E ) P S 0,5 P ( S E ) = = = 0, 0,7 4.. P( S ) 00 = 0,5 00 = = estudantes não concluem com sucesso todas as unidades curriculares. P = , A = AB B a AB = f a f a = B = a A = a a a a = a a a Proposta de teste de avaliação Matemática A,. o ano Página

12 omo A = a, temos a a a = a a a = 0 Seja x = a : ± + 4 x x = 0 x = ± 5 x = x = x = = = a a ( a > 0, R ) a = 0.. T ( e ) 0 = 55 5 = 55 5 = 55 T ( 0) é o valor da temperatura inicial da água que entra no tanque, em graus elsius. t t lim T t = lim 55 5 e = 55 5 lim e = t + t + t + ( + ) = 55 5 e = 55 5 e = = 55 5( 0) = 55 5 = 0 lim T t = 0 significa que, com o decorrer do tempo, a temperatura do fluído tende a estabilizar x + em 0 º (temperatura ambiente)... T ( t ) = 55 5 e = e = 0 + 5e t t t ( t+ ) t t T t + = 0 + 5e = 0 + 5e = e e ( t+ ) t t T t + = 0 + 5e = 0 + 5e = e e ( + ) T ( t ) T ( t ) t t t e e 0 + 5e T t = = t T t e e 0 + 5e t t e e 0 5e t t 5 e e 5e t t e e 0 5e t t 5 e e 5e = = = e t 5 e e (e ) e e + = = = = t 5 e e e = e + = + e Proposta de teste de avaliação Matemática A,. o ano Página

13 7.. g ( x ) k x k = 9 g k 9 k = 0 9 = 0 = k 9 k k + 9 k k = = Logo, k + 9 = k = k =. 7.. g ( x ) x 4 = 9 Depois de se introduzir a função g na calculadora obtém-se o gráfico ao lado. Seja a abcissa de A. A y O h g y = x B x O ponto A tem de coordenadas (, ) a g a e, como OB = OA e a função g é par, então B ( a, g( a) ). Assim, = AB a e a medida da altura h do triângulo [OAB] relativa à base [AB] é = Medida da área do triângulo [ OAB ]: AB h a g ( a) A = = = a g ( a) = a a = a [ OAB] ( g a = a ) Posteriormente, calcula-se a interseção do gráfico da função g com a reta y = h g a. x (bissetriz dos quadrantes ímpares) e obtém-se, com cinco casas decimais, (,577 ;,577) a,577 e A[ ] = a (, 577) 7, 04. OAB A pelo que Assim, a medida da área do triângulo [OAB] é aproximadamente igual a 7,04 u.a. Proposta de teste de avaliação Matemática A,. o ano Página