MATEMÁTICA A - 12o Ano Probabilidades - Probabilidade condicionada Propostas de resolução
|
|
|
- Ricardo Raminhos Guterres
- 6 Há anos
- Visualizações:
Transcrição
1 MATEMÁTICA A - o Ano Probabilidades - Probabilidade condicionada Propostas de resolução Exercícios de exames e testes intermédios. No contexto do problema P ( B A ) é a probabilidade de retirar uma bola branca da caixa C após terem sido lá colocadas duas bolas retiradas da caixa C que não têm a mesma cor. Como é sabido que ocorre o acontecimento A, ou seja, que as bolas retiradas da caixa C não têm a mesma cor, então duas as bolas retiradas da caixa C são uma preta e uma branca. Como a caixa C tem sete bolas antes da realização da experiência, e serão colocadas nesta caixa bolas, a caixa C ficará com 9 bolas, ou seja o número de casos possíveis é 9, pelo que o número de casos favoráveis é 6, porque o valor da probabilidade é : P ( B A ) = = = 6 9 Assim, o número de casos favoráveis é 6, ou seja, existem 6 bolas brancas na caixa C, num total de 9, ou seja, existem bolas pretas na caixa C. Como foram lá colocadas bola preta e bola branca, inicialmente,na caixa C existiam: 6 = 5 bolas brancas = bolas pretas Exame 07, Ép. especial. De acordo com os acontecimentos A e B definidos, e os dados do enunciado, temos que: P ( A B ) = 0,8 P (B A) = Assim, usando as Leis de De Morgan, e o teorema do acontecimento contrário, temos que: P ( A B ) = 0,8 P ( A B ) = 0,8 = 0,8 = 0,8 = 0,8 Usando a definição de probabilidade condiciona, podemos calcular P (A): P (B A) = P (A) = 0,8 P (A) = 0,8 = P (A) P (A) = 0,54 Exame 07, a Fase Página de 4
2 . Considerando a experiência aleatória que consiste em escolher, ao acaso, um aluno da turma, e os acontecimentos: V : O aluno ter olhos verdes R: O aluno é um rapaz Temos que P (V R) = e P (V R) = 4 0 Assim, temos que: P (V R) P (R) = = 0 = 4 P (V R) 0 = 5 4 Ou seja a probabilidade de escolher um aluno da turma e ele ser rapaz, ou seja, a proporção de rapazes relativamente ao total de alunos da turma é. Como existem 0 alunos na turma o número de rapazes 5 da turma é: 40 0 = 5 5 = 8 Resposta: Opção B Exame 07, a Fase 4. No contexto da situação descrita, é a probabilidade de que a primeira bola extraída tenha um número par e que a segunda bola extraída também tenha um número par, ou seja, a probabilidade de que as duas bolas tenham um número par. No caso de a extração ser feita com reposição, para calcular a probabilidade de que a segunda bola tenha um número par, sabendo que a primeira também tem um número par, devemos considerar 8 casos possíveis (as 8 bolas do saco, porque a primeira bola foi reposta), e 4 casos favoráveis (as 4 bolas com um número par, porque como a primeira bola foi reposta, existem 4 números pares), ou seja: P (B A) = 4 8 = No caso de a extração ser feita sem reposição, para calcular a probabilidade de que a segunda bola tenha um número par, sabendo que a primeira também tem um número par, devemos considerar 7 casos possíveis (porque das 8 bolas do saco, foi extraída uma que não foi reposta), e casos favoráveis (porque das 4 bolas com um número par existentes inicialmente, uma foi retirada e não foi reposta), ou seja: P (B A) = 7 Assim, como a probabilidade de que a primeira bola extraída tenha um número par é P (A) =, temos que os valores de são: Com reposição: a = = P (A) P (B A) = = 4 Sem reposição: b = = P (A) P (B A) = 7 = 4 5. Como P ( A B ) = P ( A B ) = P (A B), temos que: Exame 06, Ép. especial P ( A B ) = 0,6 P (A B) = 0,6 P (A B) = 0,6 P (A B) = 0,4 Como P (A B) = P (A) + P (B) = P (A) + P (B) P (A B), temos que: E assim, vem que: Resposta: Opção A = 0, + 0, 0,4 = 0, P (A B) = P (B) = 0, 0, = Exame 06, a Fase Página de 4
3 6. No contexto da situação descrita P (B A) é a probabilidade de que, retirando uma ficha da caixa U e uma ficha da caixa V, o produto dos números das fichas retiradas seja ímpar, sabendo que a soma dos números das fichas retiradas é igual a 0. Como se retira uma bola de cada caixa, o número de casos possíveis é 4 e correspondem a pares de bolas (em que cada uma é retirada de uma caixa) cuja soma é 0, ou seja: (,9); (,8); (,7) e (4,6) De entre estes pares os que correspondem a produtos ímpares são (,9), porque 9 = 9 e (,7), porque 7 = ; (os restantes pares de números, por serem constituídos por números pares resultam num produto par). Assim, existem casos favoráveis, e, recorrendo à Regra de Laplace para o cálculo da probabilidade, e escrevendo o resultado na forma de fração irredutível, vem: P (B A) = 4 = Exame 06, a Fase 7. Como P (A B) = P (B) = P (A B) P (B) vem que: = 6 0 = 60 = 0 Como P (A B) = P (A) + P (B), temos que: Resposta: Opção C P (A B) = = = 0 Exame 06, a Fase 8. Como P (A B) = P (A) + P (B), substituindo os valores conhecidos, podemos calcular P (A): Como P (B A) = Resposta: Opção D 0,7 = P (A) + 0,4 0, 0,7 0,4 + 0, = P (A) 0,5 = P (A), vem que P (A) P (B A) = 0, 0,5 = 5 = 0,4 Exame 05, Ép. especial 9. No contexto da situação descrita P (A B) é a probabilidade de que, retirando ao acaso uma bola do saco, ela seja preta sabendo que tem um número par. Como existem apenas 4 bolas numeradas com números pares (nomeadamente as bolas com os números, 4, 6 e 8), temos que o número de casos possíveis é 4. Destas, apenas as bolas com os números e 4 são pretas (porque As bolas numeradas de a 5 são pretas ), pelo que existem casos favoráveis, e assim, recorrendo à Regra de Laplace para o cálculo da probabilidade, vem: Resposta: Opção B P (A B) = 4 = Exame 05, a Fase Página de 4
4 0. Considerando a experiência aleatória que consiste em escolher, ao acaso, um funcionário da empresa, e os acontecimentos: M: O funcionário ser mulher C: O funcionário residir em Coimbra Temos que P ( C ) = 0,6; P (M) = P ( M ) e P ( C M ) = 0, P (C) = P ( C ) = 0,6 = 0,4 P (M) = P ( M ) P (M) = P (M) P (M)=P(M) P (M) + P (M) = P (M) = P (M) = 0,5 P ( C M ) = P ( M ) P ( C M ) = 0,5 0, = 0,5 P ( M C ) = P ( C ) P ( C M ) = 0,6 0,5 = 0,45 P (M C) = P (M) P ( D ) = 0,5 0,45 = 0,05 M M C 0,05 0,4 C 0,45 0,5 0,6 0,5 0,5 Assim, calculando a probabilidade de o funcionário escolhido ser mulher, sabendo que reside em Coimbra, e escrevendo o resultado na forma de fração irredutível, temos P (M C) = P (M C) P (C) = 0,05 0,4 = 5 40 = 8 Exame 05, a Fase. Considerando a experiência aleatória que consiste em escolher, ao acaso, um aluno nesta turma, e os acontecimentos: R: O aluno ser rapariga D: O aluno está inscrito no desporto escolar Temos que P ( R ) = 0,6; P (D) = 0,8 e P ( D R ) = 0, P (R) = P ( R ) = 0,6 = 0,4 P ( D ) = P (D) = 0,8 = 0, P ( D R ) = P ( R ) P ( D R ) = 0,6 0, = 0, P ( R D ) = P ( D ) P ( D R ) = 0, 0, = 0,08 P (R D) = P (R) P ( R D ) = 0,4 0,08 = 0, R R D 0, 0,8 D 0,08 0, 0, 0,4 0,6 Assim, calculando a probabilidade de um aluno dessa turma, escolhido ao acaso, ser rapariga, sabendo que está inscrito no desporto escolar e, escrevendo o resultado na forma de fração irredutível, temos P (R D) = P (R D) P (D) = 0, 0,8 = 5 Exame 04, Ép. especial Página 4 de 4
5 . Sabemos que P (B A) = P ( B A ) P ( A ) P ( B A ) = P (B A) P ( A ) Como P (A) = 0,4, temos que P ( A ) = P (A) = 0,4 = 0,6 Como P (B A) = 0,8 e P ( A ) = 0,6, temos que P ( B A ) = 0,8 0,6 = 0,48 Como P ( B A ) = P (B \ A) = P (B A), temos que P ( B A ) = P (B) P (B) = P ( B A ) + Como P ( B A ) = 0,48 e = 0,, vem que Resposta: Opção C P (B) = 0,48 + 0, = 0,68 Exame 04, a Fase. De acordo com o enunciado P (A B) é a probabilidade de, lançar o dado o dado duas vezes, e obter um número negativo no primeiro lançamento, sabendo que o produto dos dois números obtidos é positivo. Como sabemos que o produto dos números obtidos é positivo, pode ter resultado da multiplicação de dois números positivos ou de dois números negativos. De acordo com a Regra de Laplace, a probabilidade é calculada pelo quociente do número de casos favoráveis pelo número de casos possíveis, sendo os casos possíveis equiprováveis. Assim, temos que o número de casos possíveis resulta de considerar o produto de dois números negativos ( ) ou dois números positivos ( ), ou seja, um total de + 9 = 0 casos possíveis. Destes, apenas um () caso é favorável, nomeadamente o que corresponde à hipótese do produto positivo ter resultado da multiplicação de dois valores negativos, o que garante que o número saído no primeiro lançamento é negativo. Assim temos que P (A B) = 0 Exame 04, a Fase 4. A probabilidade de o professor escolhido ensinar Matemática, sabendo que é do sexo feminino, pode ser escrita como P ( B A ) e P ( B A ) = P ( B A ) P ( A ) Como A B = A B, então = P (A B) Assim, temos que = 0,9 = 0,08 e que P ( A ) = P (A) = 0,44 = 0,56, logo Resposta: Opção C P ( B A ) = P ( B A ) P ( A ) = P ( ) A B P ( A ) = 0,08 0,56 = 7 Teste Intermédio o ano Página 5 de 4
6 5. Considerando a experiência aleatória que consiste em escolher, ao acaso, um dos dados da coleção, e os acontecimentos: O: O dado escolhido é octaédrico V : O dado escolhido é verde A probabilidade pedida pode ser escrita como P (O V ) Temos que P ( V ) = 0, = 0 ; P ( O ) = P (O) e P ( O V ) = 0, = 0 Como P (O) + P ( O ) =, temos que P (O) + P (O) + P ( O ) = 4 P (O) = P (O) = 4 P (O V ) = P ( V ) P (O V ) = 0 0 = 50 P ( O ) = P (O) = 4 = 4 P ( O V ) = P ( O ) P ( O V ) = 4 50 = 7 00 P (V ) = P ( V ) = 0 = 9 0 P (O V ) = P (V ) P ( O V ) = = 7 00 Assim, calculando a probabilidade de, escolher um dado octaédrico, sabendo que é verde, e escrevendo o resultado na forma de fração irredutível, temos O O V V P (O V ) = P (O V ) P (V ) = = 7 90 Teste Intermédio o ano Considerando a experiência aleatória que consiste em escolher, ao acaso, uma lâmpada produzida nessa empresa, e os acontecimentos: F : A lâmpada escolhida é fluorescente T : A lâmpada escolhida tem a forma tubular Temos que P (F ) = 0,55, P (T F ) = 0,5 e P ( T F ) = 0,9 P ( F ) = P (F ) = 0,55 = 0,45 P (T F ) = P (F ) P (T F ) = 0,55 0,5 = 0,75 P ( T F ) = P (F ) P (T F ) = 0,55 0,75 = 0,75 P ( T F ) = P ( F ) P ( T F ) = 0,45 0,9 = 0,405 P ( T ) = P ( T F ) + P ( T F ) = 0,75 + 0,405 = 0,68 P (T ) = P ( T ) = 0,68 = 0, F F T 0,75 0, T 0,75 0,405 0,68 0,55 0,45 Assim, calculando a probabilidade de, ao escolher, ao acaso, uma lâmpada produzida nessa empresa, ela ser fluorescente, sabendo que tem a forma tubular, e escrevendo o resultado com arredondamento às centésimas, temos P (F T ) = P (F T ) P (T ) = 0,75 0, 0,86 Exame 0, Ép. especial Página 6 de 4
7 7. Pelas leis de De Morgan, e pelo teorema do acontecimento contrário, temos que: P ( A B ) = P ( A B ) = Assim, vem que: P ( A B ) = 5 9 = 5 9 = = 4 9 = = 9 Como P (B A) = P (B A) P (A) P (A) = P (B A) P (B A) ; P (B A) = 9 e P (B A) =, temos que 7 P (A) = P (B A) P (B A) = 9 7 = 7 9 Logo, temos que P ( A ) = P (A) = 7 9 = 9 E que P ( A B ) = = 9 = 7 9 Se repararmos que A B =, ou seja que A e B são acontecimentos incompatíveis (porque não existem números pares iguais ou maiores que ), temos que: P ( A B ) = P ( A ) + P ( B ) P ( A B ) P ( A ) = P ( B ) E assim a probabilidade de sair o número, ou seja ocorrer o acontecimento B, é, P ( B ) = = 5 9 Exame 0, a Fase Considerando a experiência aleatória que consiste em retirar, ao acaso, uma bola da caixa, e os acontecimentos: B: A bola retirada é branca I: A bola retirada tem número ímpar Temos que P ( B ) = 5, P ( I B ) = 0 00 = 5 P ( I B ) = P ( B ) P ( I B ) = 5 5 = P (B) = P ( B ) = 5 = 5 P (I B) = P (B) P (I B) = 5 5 = 6 e P (I B) = = 5 P ( B I ) = P (B) P (B I) = 5 6 = 9 P ( I ) = P ( B I ) + P ( B I ) = 9 + = Assim, calculando a probabilidade de, ao retirar, ao acaso, uma bola da caixa, ela ser preta, sabendo que tem um número par, e escrevendo o resultado na forma de fração irredutível, temos: I I B B 5 P ( B I ) = P ( B I ) P ( I ) = = Página 7 de 4
8 8.. Como a caixa tem n bolas e em cada 5 são pretas, o número de bolas pretas é n 5 Logo, o número de bolas brancas é n 5 Como a extração é feita sem reposição, a probabilidade da primeira bola extraída ser branca é n 5 = e a probabilidade da segunda bola ser branca, sabendo que a primeira também é branca n 5 n é 5 n Assim, usando a probabilidade conhecida podemos escrever e resolver a equação: 5 n 5 n = 7 0 n n = 5 60 n 5 5(n ) = 5 60 n 5 n = n (n 5) = 5(n ) 6n 60 = 5n 5 6n 5n = 60 5 n = Exame 0, a Fase 9. Pelas leis de De Morgan, e usando o teorema do acontecimento contrário temos que P ( A B ) = P ( A B ) =, e assim 5 5 = = 6 6 = 6 Assim, organizando este e os restantes dados do enunciado numa tabela obtemos: P ( B ) = P (B) = 4 = 4 P ( A B ) = P ( B ) P ( A B ) = 4 7 = 48 E assim P (A) = + P ( A B ) = = B B A 6 48 A 4 4 Exame 0, a Fase 0. No contexto da situação descrita, P (B A) representa a probabilidade de que, na extração das bolas do saco, a bola com o número seja a segunda bola retirada, sabendo que bolas com o número 0 não saem em extrações sucessivas. Como existem 4 bolas com o número 0, e sabemos que não saem em extrações sucessivas, significa que entre duas bolas com o número 0 existe sempre uma bola com outro número, e como no total são 7 bolas, significa que as bolas com o número 0 saem em todas as extrações de ordem ímpar, ou seja são as bolas que saem nas a, a, 5 a e 7 a extrações. Desta forma, a bola com o número pode ocupar sair na a, 4 a ou 6 a posições, ficando as restantes ocupadas com as restantes duas posições bolas com as bolas de número. Com o objetivo de usar a Regra de Laplace, podemos considerar casos possíveis, correspondendo às posições de ordem par que a bola pode ocupar na ordenação, uma vez que esta escolha define imediatamente uma sequência em que as bolas com o número 0 não saem em extrações sucessivas. Considerando os casos possíveis, apenas é favorável, precisamente a situação em que a bola saem na a posição. Desta forma, temos que P (B A) = Teste Intermédio o ano Página 8 de 4
9 ... Considerando a experiência aleatória que consiste em escolher ao acaso um aluno da turma, e os acontecimentos: R: O aluno é uma rapariga S: O aluno pretende frequentar um curso na área da saúde Temos que P (R) =, P (S) = 4 e P ( R S ) = 7 P ( S ) = P (S) = 4 = 4 P ( R S ) = P ( S ) P ( R S ) = 4 7 = 8 = 4 P (S R) = P (R) P ( S R ) = 4 = 7 S S R 7 4 R 4 4 Assim, calculando a probabilidade de, ao escolher, ao acaso, um aluno da turma ele pretender frequentar um curso da área de saúde, sabendo que é uma rapariga, e escrevendo o resultado na forma de fração irredutível, temos: P (S R) = P (S R) P (R).. Como o número de rapazes é igual ao número de raparigas, e existem n rapazes, o número total de alunos é n. Ao selecionar dois alunos da turma, a probabilidade de que o primeiro aluno selecionado seja um rapaz é n n = A probabilidade de selecionar um segundo rapaz, sabendo que o primeiro aluno selecionado também é um rapaz, é n n Assim, usando a probabilidade conhecida podemos escrever e resolver a equação: = 7 = 6 7 n n = 54 n n = 6 54 n 54(n ) = 6(n ) 54n 54 = 5n 6 54n 5n = 54 6 n = 8 n = 4 Teste Intermédio o ano Considerando a experiência aleatória que consiste em escolher, ao acaso, um funcionário desta empresa, e os acontecimentos: T : O funcionário aposta no totoloto E: O funcionário aposta no euromilhões Temos que P (E) = 0,8, P (T E) = 0, e P ( T E ) = 0,05 Organizando os dados numa tabela obtemos: P (E) = P (F ) = 0,55 = 0,45 P ( E ) = P (E) = 0,8 = 0, P ( T E ) = P ( E ) P ( T E ) = 0, 0,05 = 0,5 T T E 0, 0,8 E 0,5 0,05 0, 0,5 Assim, a probabilidade de, ao escolher, ao acaso, um funcionário dessa empresa, ele apostar no totoloto é P (T ) = P (T E) + P ( T E ) = 0, + 0,5 = 0,5 Exame 0, Ép. especial Página 9 de 4
10 . Considerando a experiência aleatória que consiste em escolher, ao acaso, um aluno dessa escola, e os acontecimentos: R: O aluno é um rapaz E: O aluno tem excesso de peso Temos que P ( R ) = 0,55, P ( E R ) = 0, e P ( E R ) = 0,4 P ( E R ) = P ( R ) P ( E R ) = 0,55 0, = 0,65 P (R) = P ( R ) = 0,55 = 0,45 P ( E R ) = P (R) P ( E R ) = 0,45 0,4 = 0,8 P (R E) = P (R) P ( E R ) = 0,45 0,8 = 0,7 P (E) = P (R E) + P ( R E ) = 0,7 + 0,65 = 0,45 R R E 0,7 0,65 0,45 E 0,8 0,45 0,55 Assim, calculando a probabilidade de o aluno escolhido ser rapaz, sabendo que tem excesso de peso, e escrevendo o resultado na forma de fração irredutível, temos P (R E) = P (R E) P (E) = 0, 0,45 = 8 9 Exame 0, a Fase 4. Considerando a experiência aleatória que consiste em escolher, ao acaso, um frango do aviário e aplicar o teste para detetar a presença do vírus, e os acontecimentos: I: O frango estar infetado T : O teste dar positivo Temos que P (I) = = 0,, P ( I ) = = 0, P (T I) = 0,96 e P ( T I ) = 0,9 P (I T ) = P (I) P (T I) = 0, 0,96 = 0,096 P ( I T ) = P (I) P (I T ) = 0, 0,096 = 0,004 P ( I T ) = P ( I ) P ( T I ) = 0,9 0,9 = 0,8 P ( T ) = P ( I T ) + P ( I T ) = 0, ,8 = 0,84 I T 0,096 T 0,004 0,8 0,84 I 0, 0,9 Assim, calculando a probabilidade do aluno escolhido frango escolhido não estar infetado, sabendo que teste deu negativo, e escrevendo o resultado na forma de dízima, arredondado às milésimas, temos P ( I T ) = P ( I T ) P ( T ) = 0,8 0,84 0,995 Teste Intermédio o ano.0.0. Considerando a experiência aleatória que consiste em escolher, ao acaso, um aluno da turma, e os acontecimentos: R: O aluno ser uma rapariga I: O ter Inglês O número de raparigas que tem Inglês é 0 4 = 6 Assim, como a turma tem 8 raparigas, o número de raparigas que não tem Inglês é 8 6 = Logo a probabilidade de selecionar um aluno que não tem inglês, de entre o conjunto das raparigas é Resposta: Opção A P ( I R ) = 8 = 9 Exame 0, Prova especial Página 0 de 4
11 6. No contexto da situação descrita, P (J I) é a probabilidade de que ao lançar 4 vezes o tetraedro, a soma dos números registados nos quatro lançamentos seja menor do que 0, sabendo que nos primeiros lançamentos saiu sempre o número dois. Como sabemos que a soma relativa aos primeiros lançamentos é + + = 6, para que a soma dos 4 lançamentos seja inferior a 0, no último lançamento podem sair as faces com os números, um (que resultará na soma 7), dois (soma 8) ou três (soma 9). Assim, usando a Regra de Laplace, para a determinação da probabilidade, temos 4 casos possíveis, correspondentes às faces que podem sair no quarto lançamento, e casos favoráveis, correspondendo às faces que correspondem a uma soma inferior a 0, pelo que P (J I) = 4 Exame 0, Prova especial 7. Considerando a experiência aleatória que consiste em escolher, ao acaso, um jovem inscrito no clube, e os acontecimentos: A: O jovem pratica andebol F : O jovem pratica futebol Sabemos que existem 8 jogadores que jogam apenas futebol e que jogam futebol e andebol, ou seja, o número total de praticantes de futebol é de 8 + = 40 De entre estes, apenas jogam andebol, pelo que a probabilidade de selecionar ao acaso um jovem inscrito, de entre os praticantes de futebol, e ele também jogar andebol é Resposta: Opção B P (A F ) = 40 = 0 Exame 0, Ép. especial 8. Considerando a experiência aleatória que consiste em escolher ao acaso um funcionário da empresa, e os acontecimentos: L: O funcionário é licenciado Q: O funcionário tem idade não inferior a 40 anos Temos que P (L) = = 5, P ( Q L ) = = 4 5 e P ( Q L ) = 0 00 = 0 P ( L Q ) = P (L) P ( Q L ) = = P ( L ) = P (L) = 5 = 5 P ( L Q ) = P ( L ) P ( Q L ) = 5 0 = 50 = P ( Q ) = P ( L Q ) + P ( L Q ) = + = P (L Q) = P (L) P ( L Q ) = 5 = P (Q) = P ( L ) = = Assim, calculando a probabilidade de, ao escolher, ao acaso, um funcionário desta empresa e ele ser licenciado, sabendo que tem uma idade não inferior a 40 anos, e escrevendo o resultado na forma de fração irredutível, temos: P (L Q) = P (L Q) P (Q) = = = 4 Q Q L 5 L 5 Exame 0, a Fase Página de 4
12 9. A igualdade da opção A é válida para acontecimentos contrários, a igualdade da opção B é válida para acontecimentos incompatíveis e a condição da opção C é válida para acontecimentos não equiprováveis. Como A e B são dois acontecimentos independentes, sabemos que P (A) P (B) = P (A B) e assim temos que Resposta: Opção D P (B A) = P (A) = P (A) P (B) P (A) = P (B) Exame 0, a Fase 0. Considerando a experiência aleatória que consiste em seleccionar, ao acaso, um cliente desta companhia aérea, e os acontecimentos: B: O cliente ter comprado um bilhete para Berlim V : O cliente faz a viagem sem perder o voo Temos que P ( V B ) = 5 00 = 0,05, P ( V B ) = 9 0 = 0,9 e P (B) = = 0, P ( V B ) = P (B) P ( V B ) = 0, 0,05 = 0,05 P ( B ) = P (B) = 0, = 0,7 P ( V B ) = P ( B ) P ( V B ) = 0,7 0,9 = 0,644 P ( V B ) = P ( B ) P ( V B ) = 0,7 0,664 = 0,056 B B V 0,644 V 0,05 0,056 0,07 0, 0,7 Assim, calculando a probabilidade de um passageiro desta companhia aérea perder o voo, e escrevendo o resultado na forma de dízima, temos P ( V ) = P ( V B ) + P ( V B ) = 0,05 + 0,056 = 0,07 Exame 0, a Fase. Podemos observar que existem 8 + = 0 alunos do sexo masculino. Destes, apenas têm 8 anos, pelo que a probabilidade de selecionar, ao acaso, de entre os rapazes da turma, um que tenha 8 anos, é Resposta: Opção D P (B A) = 0 = 5 Teste Intermédio o ano Organizando os dados numa tabela obtemos: = P (B) P (A B) = 0, 0, = 0,06 P ( B ) = P (B) = 0, = 0,7 P ( B Q ) = P ( B ) P ( A B ) = 0,7 0,4 = 0,8 P ( A B ) = P ( Q ) P ( A B ) = 0,7 0,8 = 0,4 P (A) = + P ( A B ) = 0,06 + 0,4 = 0,48 A A B 0,06 0, B 0,4 0,8 0,7 0,48 Assim, calculando a probabilidade e escrevendo o resultado na forma de fração irredutível, temos: P (B A) = P (A) = 0,06 0,48 = 8 Teste Intermédio o ano Página de 4
13 . No contexto da situação descrita, P (L J) é a probabilidade de que lançando os dois dados e usando os números indicados pelos dados como coordenadas do ponto Q, este ponto pertença ao terceiro quadrante, sabendo que o número indicado pelo dado A é negativo. Como é sabido que a abcissa do ponto Q é negativa, este ponto pertence ao terceiro quadrante se a ordenada também for negativa, o que ocorre em cada 6 vezes, visto que das 6 faces do dado B, apenas uma tem um número negativo inscrito. Assim, usando a Regra de Laplace, e escrevendo o resultado na forma de fração, temos P (L J) = 6 Exame 00, a Fase 4. Considerando a experiência aleatória que consiste em escolher, ao acaso, um dos alunos da escola, e os acontecimentos: C: O aluno tem computador portátil D: O aluno sabe o nome do diretor Temos que P (C) = 5 ; P ( D ) = e P ( C D ) = P ( C D ) = P ( D ) P (C D) = = 6 P (C D) = P (C) P ( C D ) = 5 6 = 0 P (D) = P ( D ) = D D C C 7 5 Assim, calculando a probabilidade de um aluno dessa escola, escolhido ao acaso, não ter computador portátil e saber o nome do diretor, e escrevendo o resultado na forma de fração irredutível, temos P ( C D ) = P (D) P (C D) = 0 = 7 5 Exame 00, a Fase 5. No contexto da experiência aleatória definida, P (A B) é a probabilidade de que os números sejam iguais, sabendo que a soma dos números saídos nas duas bolas é igual a. Como todas as bolas têm números inteiros e não é possível que a soma de dois números inteiros iguais seja, então é impossível que os números extraídos sejam iguais, sabendo que a soma é, ou seja P (A B) = 0 Teste Intermédio o ano No contexto da experiência aleatória definida, P (A B) é a probabilidade de selecionar um cartão com um número inferior a 0, sabendo que o cartão escolhido tem a forma de um círculo. Como 0 5,48 e, dos números dos 4 cartões com a forma de um círculo, apenas um deles é maior que 0, nomeadamente o 7, então, recorrendo à Regra de Laplace, temos caso possível e 4 casos favoráveis, pelo que Resposta: Opção B P (A B) = 4 Teste Intermédio o ano Página de 4
14 7. Considerando a experiência aleatória que consiste em selecionar, ao acaso um atleta participante no encontro desportivo, e com o objetivo de utilizar a igualdade indicada, e uma vez que sabemos que Metade dos atletas portugueses que participam no encontro são do sexo feminino, podemos definir que P (B A) =, para os acontecimentos: A: O atleta é português B: O atleta é do sexo feminino E assim, para além de P (B A) =, sabemos também que P ( A B ) = = 9 0 e que P ( A ) = P (A) Assim, substituindo em P (A) [P (B A) ] + P ( A B ) = P ( A ), vem: ( ) P (A) + 9 ( = P (A) P (A) ) + P (A) = P (A) = 0 P (A) = 0 P (A) = 5 Como existiam 00 participantes no encontro, e sabemos que o número de portugueses é, temos que o 5 número de atletas portugueses é = 5 5 = 40 Teste Intermédio o ano Considerando a experiência aleatória que na realização dos dois testes no mesmo dia, pelo estudante, e os acontecimentos: T : Ter positiva no primeiro teste T : Ter positiva no segundo teste Temos que P (T ) = 0,7; P (T ) = 0,8 e P ( ) T T = 0, Pelo teorema do acontecimento contrário, vem que P ( ) T = P (T ) = 0,7 = 0, Assim,a probabilidade de o estudante ter negativa no segundo teste, sabendo que teve negativa no primeiro teste, é P ( ) P ( ) T T T T = P ( ) = 0, T 0, = Resposta: Opção C Exame 009, a Fase 9. Como P (A B) = P (A) + P (B) = P (A) + P (B) P (A B), temos que: = 0, + 0,4 0,5 = 0, Logo, a probabilidade de se realizar A, sabendo que B se realiza, é Resposta: Opção D P (A B) = P (B) = 0, 0,4 = Exame 009, a Fase 40. No contexto da situação descrita P ((B C) A) é a probabilidade de a segunda bola retirada da caixa seja amarela e tenha um número par, sabendo que a primeira bola retirada é verde. De acordo com a Regra de Laplace, a probabilidade é calculada pelo quociente do número de casos favoráveis pelo número de casos possíveis, sendo os casos possíveis equiprováveis. Como a caixa tem 0 bolas e sabemos que foi extraída uma bola de cor verde, que não foi resposta, ficaram na caixa 9 bolas, ou seja, existem 9 casos possíveis, para a extração da segunda bola. Como sabemos que a primeira bola extraída é verde, logo tem um número inferior ou igual a 0, pelo que das bolas amarelas que estão na caixa, numeradas de a 0, 5 têm números pares. Logo, o número de casos favoráveis é 5. Desta forma temos que P ((B C) A) = 5 9 Exame 009, a Fase Página 4 de 4
15 4. No contexto da situação descrita, P ( B A ) é a probabilidade de que, ao retirar sucessivamente e sem reposição duas bolas do saco, o número da segunda bola retirada seja par, sabendo que ao número da primeira bola retirada não seja para, isto é, sabendo que o número da primeira bola retirada seja ímpar. Assim, quando se faz a extração da segunda bola, existem no saco 0 bolas (menos uma que as que estavam inicialmente porque a primeira bola não foi reposta), das quais 5 têm um número par (porque sabemos que na primeira extração não foi retirada nenhuma das bolas com número par). Desta forma, recorrendo à Regra de Laplace existem 0 casos possíveis e 5 favoráveis, pelo que P ( B A ) = 5 0 = Teste Intermédio o ano Com o objetivo de usar a fórmula P (A B) P (B) P (A B) = P (A) P (B A), podemos verificar que P (A B) P (B) P (A B) = P (A) P (B A) P (A B) ( P (B) ) = P (A) P (B A) P (A B) P (B) = P (A) P (B A) P (A B) = P (A) P (B A) P (B) Como se pretende calcular a probabilidade de um aluno da turma, escolhido ao acaso, ser praticante de desporto, sabendo que é uma rapariga, vamos definir os acontecimentos: A: O aluno é praticante de desporto B: O aluno é uma rapariga E assim temos que P (A) = 0,6, P (B) = 0,4 e P (B A) = 0,5 Logo, a probabilidade de um aluno da turma, escolhido ao acaso, ser praticante de desporto, sabendo que é uma rapariga, é P (A B) = A que corresponde uma probabilidade de 75% 0,6 0,5 0,4 = 0, 0,4 = 0,75 Teste Intermédio o ano Como na experiência aleatória descrita, foi definido que Se sair o número 5, tira-se uma bola da caixa A, para calcular a probabilidade de a bola retirada ser verde, consideramos apenas o conteúdo da caixa A (duas bolas verdes e uma bola amarela). Assim temos que existem bolas verdes (número de casos favoráveis) num total de bolas (número de casos possíveis), pelo que a probabilidade é de Resposta: Opção D Exame 008, a Fase 44. Se a probabilidade de a bola retirada da caixa B ser azul é igual a, e na caixa B só existem bolas verdes e azuis, então o número de bolas azuis e verde é igual. Como a composição inicial era de bolas verdes e 4 bolas azuis, então a bola retirada da caixa A (e colocada na caixa B) tinha cor verde. Exame 008, a Fase Página 5 de 4
16 45. Sabemos que P (A B) = 5, pelo que, substituindo na igualdade P (A B) = P (A) + P (B), vem que: 5 = P (A) + P (B) 5 + = P (A) + P (B) Como P (A) = P (B), temos que 6 = P (A) + P (B) 6 = P (B) + P (B) 6 = P (B) = 6 P (B) = P (B) Assim, a probabilidade de A acontecer, sabendo que B aconteceu é dada por Resposta: Opção D P (A B) = P (B) = P (B) = P (B) P (B) 0 Teste Intermédio o ano Assumir a ocorrência do acontecimento M, significa que as bolas retiradas da caixa (e colocadas na caixa ) não têm a mesma cor, ou seja, são de cores diferentes. Como na caixa, só existia uma bola de cor verde e as restantes eram azuis, se foram retiradas duas bolas de cores diferentes, sabemos que estas duas bolas eram, uma de cor verde e outra de cor azul. Assim, a caixa passou a ter duas bolas de cor verde e uma de cor azul, pelo que ao retirar uma bola da caixa, temos bolas possíveis, das quais duas são verdes, pelo que, recorrendo à Regra de Laplace, temos P ( V M ) = Resposta: Opção C Teste Intermédio o ano Quando se lançam dois dados numerados de a 6, existem apenas hipóteses de obter uma soma igual a 4 ( +, + e + ). Assim, para calcular a probabilidade de ter saído o mesmo número, em ambos os dados, sabendo que a soma dos números saídos foi quatro, consideramos casos possíveis e apenas favorável ( + ), pelo que, a probabilidade é Resposta: Opção C Exame 007, a Fase 48. Como a extração é feita sem reposição, no final da terceira extração restam bolas no saco. Como sabemos que as primeiras extrações formaram a sucessão de letras TIM, existem apenas duas hipóteses para formar a sucessão das 5 letras: TIMOR e TIMRO, uma vez, que depois de extraída a quarta bola, não existe nenhuma incerteza relativamente à última. Assim, a probabilidade de que, no final do processo, fique formada a palavra TIMOR, sabendo-se que, ao fim da terceira extração, estava formada a sucessão de letras TIM é Resposta: Opção C Exame 007, a Fase 49. Como P (A B) = P (A) + P (B) quaisquer que sejam os acontecimentos A e B, e neste caso, P (A B) = P (A) + P (B), podemos concluir que = 0 Assim, temos que P (A B) = Resposta: Opção A P (B) = 0 P (B) = 0 Teste Intermédio o ano Página 6 de 4
17 50. Sabemos que um número é múltiplo de 0, se for múltiplo de 5 e de simultaneamente; ou seja, no contexto da situação descrita C = A B, pelo que P (C) = Assim, vem que P (A B) = P (B) P (A B) = P (C) P (B) P (B) = Substituindo os valores de P (C) e de P (A B) vem que P (B) = Resposta: Opção B = 5 P (C) P (A B) Teste Intermédio o ano No contexto da situação descrita, P (B A) é a probabilidade de sair bola com número na segunda extração sabendo que a bola saída na primeira extração tinha o mesmo número. Assim, como sabemos que na primeira extração saiu bola com o número, ela foi resposta no saco e foram adicionadas mais 0 bolas com o número, pelo que no saco ficaram = 4 bolas numeradas com o número, 5 com o número e com o número. Desta forma o número de casos possíveis para a extração da segunda bola é de = 0 e o número de casos favoráveis é de 4. Assim, recorrendo à Regra de Laplace temos que P (B A) = 4 0 = 7 0 Teste Intermédio o ano No contexto da situação descrita, P (C D) é a probabilidade de saírem números cujo produto é 6, sabendo que são números iguais. Analogamente, P (D C) é a probabilidade de saírem números iguais, sabendo que o produto desses números é 6. Para determinar P (C D), temos que o número de casos possíveis é 6, porque como um dos dados está numerado de a 6 (e também existem estes números no outro dado), existem 6 pares de números iguais. Destes apenas resulta num produto 6, o que acontece quando ambos os números são quatro (4 4 = 6), e assim, recorrendo à Regra de Laplace temos que P (D C) = 6 Para determinar P (D C), observamos que o número de casos possíveis é, porque como 6 é múltiplo de, 4 e 8, só é possível obter um produto igual a 6 em duas combinações (4 4 = 6 e 8 = 6). Como destas duas apenas uma resulta do produto de números iguais (4 4 = 6), recorrendo à Regra de Laplace temos que P (C D) = Exame 006, Ép. especial 5. Como P (B A) é a probabilidade de, ao selecionar um aluno ao acaso, escolher um rapaz, sabendo que o aluno tem 7 anos, existem 9 casos possíveis, que correspondem ao total de alunos com 7 anos ( + 7 = 9). Como se pretende que o aluno seja um rapaz, o número de casos favoráveis é, que corresponde ao número de rapazes com 7 anos. Assim, recorrendo à Regra de Laplace temos que P (B A) = 9 Exame 006, a Fase 54. No contexto da situação descrita, P (B A) é a probabilidade de que a segunda bola extraída da caixa seja branca, sabendo que a primeira bola extraída é preta. Página 7 de 4
18 Como P (B A) =, então no momento da extração da segunda bola, o número de bolas pretas e brancas, dentro da caixa é igual. Como é sabido que a primeira bola extraída é preta, no momento da extração da segunda bola, ainda estão as 0 bolas brancas na caixa. Assim, como no momento da extração da segunda bola, existem 0 bolas brancas e o mesmo número de bolas pretas, e já tinha sido extraída uma bola preta, sem ter sido reposta, o número de bolas pretas que estão inicialmente na caixa é 0 + = Exame 006, a Fase 55. Considerando a experiência aleatória que consiste em escolher, ao acaso, um dos alunos da turma, e os acontecimentos: A: O aluno pratica andebol B: O aluno pratica basquetebol Temos que P (A) = 0,5, P (B) = 0,7 e P (A B) = (porque todos os alunos da turma praticam pelo menos um dos desportos). Pretendemos determinar o valor de P (B A), que é dado por P (B A) = P (A) Assim, como P (A B) = P (A) + P (B) = P (A) + P (B) P (A B), vem que = 0,5 + 0,7 = 0, e logo, temos que: Resposta: Opção D P (B A) = P (A) = 0, 0,5 = 0,4 Teste Intermédio o ano Considerando a experiência aleatória que consiste em selecionar, ao acaso, um jovem, participante no acampamento, e os acontecimentos: F : O jovem ser uma rapariga N: O jovem ser de nacionalidade portuguesa Temos que P (N) = 4 = 0,, P (F ) = 0,5 e P ( F N ) = 5 = 0,6 P ( F N ) = P (N) P ( F N ) = 0, 0,6 = 0,5 P (N F ) = P (N) P ( F N ) = 0, 0,5 = 0, N N F 0, 0,4 0,5 F 0,5 0, Assim, calculando a probabilidade de o prémio sair a um jovem do sexo feminino que seja de nacionalidade estrangeira, temos P ( N F ) = P (F ) P (N F ) = 0,5 0, = 0,4 a que corresponde um probabilidade de 4 % Teste Intermédio o ano Página 8 de 4
19 57. No contexto da situação descrita, P (B A) é a probabilidade de que a Catarina e o Filipe ficarem sentados ao lado um do outro, sabendo que o Diogo, a Elsa e o Filipe, se sentam em lugares consecutivos, ficando a Elsa no meio. Como sabemos que a Elsa se sentou entre o Diogo e o Filipe, em lugares consecutivos, e a mesa é circular e tem 6 lugares, existem lugares disponíveis - um junto do Filipe, e outros dois (que não estão junto do Filipe). Assim, a Catarina deve sentar-se num dos lugares disponíveis (número de casos possíveis), sendo que em apenas deles, ficará sentada ao lado do Filipe (número de casos favoráveis). Assim, recorrendo à Regra de Laplace, temos que P (B A) = Exame 005, Ép. especial (cód. 45) 58. No contexto da situação descrita P (X Y ) = significa que, de entre as figuras pintadas de preto, metade são quadrados. Assim, o único conjunto que obedece a esta condição é o da opção (B). Podemos observar apenas as figuras pintadas de preto e verificar que na opção (A), temos que P (X Y ) = = na opção (B), temos que P (X Y ) = na opção (C), temos que P (X Y ) = na opção (B), temos que P (X Y ) = = Resposta: Opção B Exame 005, a Fase (cód. 45) 59. Considerando a experiência aleatória que extrair sucessivamente duas bolas da caixa, não repondo a primeira bola na caixa, antes de retirar a segunda, e os acontecimentos: A: a primeira bola retirada é preta B: a segunda bola retirada é branca Temos que P (B A) é a probabilidade de que a segunda bola retirada seja branca, sabendo que a primeira é preta. Como a primeira bola retirada não é reposta, antes da segunda extração existem 7 bolas - pretas e 5 brancas, pelo que, usando a Regra de Laplace, vem que P (B A) = 5 7 Da mesma forma, P ( B A ) é a probabilidade de que a segunda bola retirada seja branca, sabendo que a primeira não é preta, ou seja, é branca. Nestas circunstâncias, o conteúdo da caixa, antes da segunda extração é de bolas pretas e 4 brancas, num total de 7 bolas, pelo que P ( B A ) = 4 7 Logo, como P (B A) P ( B A ) então A e B não são independentes. Exame 004, Ép. especial (cód. 45) 60. No contexto da situação descrita P (B A) é a probabilidade de lançar um dado equilibrado, com as faces numeradas de a 6 e sair um número menor do que 4, sabendo que saiu face par. Como é sabido que saiu face par, o número de casos possíveis é (correspondendo às faces, 4 ou 6). Destes casos apenas é favorável (o ). Assim, recorrendo à Regra de Laplace, temos que P (B A) = Exame 004, a Fase (cód. 45) Página 9 de 4
20 Como o Manuel vai comprar pão em 40% dos dias e a Adelaide nos restantes dias, a Adelaide vai comparar pão em 60% dos dias (00 40 = 60), ou seja, vai comprar pão em mais dias que o Manuel, pelo que é mais provável que o vizinho encontre, na padaria, a Adelaide. 6.. Considerando a experiência aleatória que consiste em selecionar, ao acaso um dia, e os acontecimentos: A: A Adelaide foi comprar pão C: A Adelaide comprou pão de centeio Temos que P (A) = 0,6 e P ( C A ) = 0, e pretendemos calcular P (A C) Como P (C A) = P ( C A ), temos que P (C A) = 0, = 0,8 (ou seja, quando a Adelaide vai comprar pão, compra pão de centeio em 80% das vezes). P (A C) Assim, como P (C A) = P (A C) = P (C A) P (A), pelo que a probabilidade P (A) de que, num dia escolhido ao acaso, seja a Adelaide a ir à padaria e traga pão de centeio é o que corresponde a uma probabilidade de 48% 6. Como P (A B) = P (B) P (B) = P (A C) = 0,8 0,6 = 0,48, vem que P (A B) P (B) = 0, 0, = 0,4 Exame 00, Prova para militares (cód. 45) Como P (A B) = P (A) + P (B) P (A) = P (A B) P (B) + P (A B), temos que Como P ( A ) = P (A), vem que P (A) = 0,8 0,4 + 0, = 0,5 P ( A ) = 0,5 = 0,5 Logo P (A) = 0,5 = P ( A ) Exame 00, a Fase (cód. 45) 6. Considerando a experiência aleatória que consiste em selecionar um português ao acaso, e os acontecimentos: N: Ser Rhésus negativo A: Ter sangue do tipo A Temos que P (N) = 6,5 +, + 0,4 + 6,7 = 4,8% e P (A N) = 6,5% Assim, calculando a probabilidade de escolher um português ao acaso, ele ter sangue do tipo A, sabendo que é Rhésus negativo, é P (A N) P (A N) = = 6,5% P (A) 4,8% 0,44 a que corresponde um probabilidade aproximada de 44% Exame 00, a Fase a chamada (cód. 45) 64. No contexto da situação descrita P (Y X) é a probabilidade de sair bola verde, depois de lançar o dado, escolher a caixa e retirar uma bola da caixa escolhida, sabendo que saiu face par no lançamento do dado. Como sabemos que saiu face para no lançamento do dado, e como não é par, então a bola é retirada da caixa B. Como a caixa B contém seis bolas verdes e uma bola amarela, existem 6 casos favoráveis (número de bolas verdes), e 7 casos possíveis (número de bolas na caixa), pelo que, recorrendo à Regra de Laplace, temos P (Y X) = 6 7 Exame 00, a Fase a chamada (cód. 45) Página 0 de 4
21 65. Como se sabe que a probabilidade de a segunda bola extraída ser preta, sabendo que a primeira bola extraída foi verde, é, então na caixa, antes da segunda extração existem o mesmo número de bolas verdes e pretas. Assim, como antes da primeira extração existiam 6 bolas verdes e uma foi retirada, e a segunda extração é feita sem reposição da primeira bola, então, antes da segunda extração existem 5 bolas verdes. Logo, como antes da segunda extração o número de bolas verdes é igual ao número de bolas pretas, antes da segunda extração, e também inicialmente, o número de bolas pretas na caixa é 5. Resposta: Opção B Exame 00, Prova para militares (cód. 45) 66. No contexto da situação descrita P ((F C ) E ) é a probabilidade de sair uma figura de copas - carta que é simultaneamente figura e do naipe de copas - na segunda extração, sabendo que saiu uma carta de espadas na primeira extração. Assim, como a extração das duas cartas é feita suessivamente e sem reposição, antes da segunda extração existem 5 = 5 cartas, porque a carta retirada não voltou a ser colocada no baralho, ou seja, 5 casos possíveis para a segunda extração. Como sabemos que a primeira carta extraída era uma carta de espadas, todas as figuras de copas continuam no baralho, incluindo as figuras de copas, pelo que o número de casos favoráveis é. Assim, recorrendo à Regra de Laplace, vem que P ((F C ) E ) = 5 Exame 00, a Fase (cód. 45) 67. Como a afirmação só se reporta ao conjunto dos dias em que o João vai de autocarro para a escola, este acontecimento é condicionante da probabilidade referida. Assim, só podemos afirmar que o João chega atrasado à escola em metade das vezes, se considerarmos que foi de autocarro para a escola, ou seja a afirmação Metade dos dias em que vai de autocarro para a escola, o João chega atrasado é equivalente a A probabilidade de o João chegar atrasado à escola, sabendo que foi de autocarro, é 0,5, ou seja, P (B A) = 0,5 Resposta: Opção D Exame 00, a Fase a chamada (cód. 45) 68. Considerando a experiência aleatória que consiste em escolher, aleatoriamente, uma rapariga de Vale do Rei, e os acontecimentos: L: A rapariga tem cabelo louro V : A rapariga tem olhos verdes Temos que P (V ) = 4 ; P (L) = e P (V L) = P ( V ) = P (V ) = 4 = 4 P ( L ) = P (L) = = P (V L) = P (V L) P (L) = = 6 P ( V L ) = P (V ) P (V L) = 4 6 = Assim, calculando a probabilidade de escolher aleatoriamente uma rapariga de Vale do Rei, ela não ser loura nem ter olhos verdes, é P ( V L ) = P ( V ) P ( V L ) = = 8 = 7 V V L 6 L Página de 4
22 Exame 00, a Fase a chamada (cód. 45) 69. Considerando a experiência aleatória que consiste em selecionar, aleatoriamente, um estudante da turma, e os acontecimentos: I: O estudante ter escolhido a disciplina de Inglês A: O estudante ter escolhido a disciplina de Alemão Temos que P (I) = 0,; P (A) = 0,5 e P (A I) = 0, Assim, a probabilidade de um estudante dessa turma, selecionado aleatoriamente, ter escolhido Alemão sabendo que ele escolheu Inglês, é Resposta: Opção C P (A I) = P (A I) P (I) = 0, 0, = 0 = 5 Exame 00, Prova para militares (cód. 45) 70. No contexto da situação descrita P (B A) é a probabilidade de ficarem, na caixa, menos bolas brancas do que pretas, sabendo que sai face 5 no primeiro lançamento do dado. Como sabemos que sai face 5 no primeiro lançamento o conteúdo da caixa, antes do segundo lançamento passou a ser de bola branca, porque se retiraram 5 das 6 que estavam no interior da caixa. Assim, para que fiquem na caixa menos bolas brancas que pretas, devem ser colocadas,, 4, 5 ou 6 bolas pretas, ou seja, existem 5 casos favoráveis em 6 possíveis para o segundo lançamento do dado. Assim, recorrendo à Regra de Laplace, temos que P (B A) = 5 6 Exame 00, Ép. especial (cód. 45) 7. No contexto da situação descrita P (C A B) é a probabilidade de que a comissão seja formada só por raparigas, sabendo que o presidente e o tesoureiro são ambos, raparigas. Como é sabido que o presidente e o tesoureiro são ambos raparigas, então, antes da extração da terceira folha de papel, no saco estão nomes - os iniciais, menos os dois que foram entretanto retirados para a definição dos cargos de presidente e tesoureiro. Assim, antes da terceira extração, existem casos possíveis. Como a turma tem 5 raparigas, e já se sabe que foram selecionadas, restam. Para que a comissão é formada só por raparigas, ou seja, para que ocorra o acontecimento C, na terceira extração deve sair o nome de uma rapariga, ou seja, existem casos favoráveis. Assim, recorrendo à Regra de Lapace, vem que P (C A B) = Exame 00, a Fase (cód. 45) 7. Como P (A B) = P (A) + P (B) P (B) = P (A B) P (A) +, ou seja Como P (A B) = Resposta: Opção C, temos que P (B) P (B) = 0,8 0,6 + 0, = 0, P (A B) = 0, 0, = Exame 00, a Fase a chamada (cód. 45) Página de 4
23 7. Considerando a experiência aleatória que consiste em escolher, aleatoriamente, um dos carros vendidos no stand, e os acontecimentos: A: O automóvel está equipado com alarme A A R: O automóvel está equipado com rádio Temos que P (A R) = 0,5; P ( A R ) R 0,5 = 0, e P (A) = 0,45 R 0, 7.. Pretendemos calcular P ( R A ), e temos que E assim: P ( A ) = P (A) = 0,45 = 0,55 P ( R A ) = P ( A ) P ( A R ) = 0,55 0, = 0,5 0,45 Logo a probabilidade da Marina acertar é de 5% 7.. A probabilidade da Marina ganhar a aposta é P (R A). Calculando o valor da probabilidade e escrevendo o resultado na forma de fração irredutível, temos P (R A) = P (A R) P (A) = 0,5 0,45 = 5 45 = Prova modelo 00 (cód. 45) 74. Considerando a experiência aleatória que consiste em extrair, sucessivamente e sem reposição, duas cartas de um baralho completo e os acontecimentos: E : Sair carta de espadas na primeira extração E : Sair carta de espadas na segunda extração Assim, vem que a probabilidade de pelo menos uma das cartas extraídas não seja do naipe de espadas, é equivalente a considerar que a primeira carta não é de espadas, ou a segunda carta não é de espadas, isto é, P ( E E ) Assim, como P (E ) = 5 = 4 P (E E ) = (na segunda extração restam cartas de espadas num total de 5 cartas) 5 Assim, utilizando a igualdade P ( ) E E = P (E ) P (E E ), e escrevendo o resultado na forma de fração irredutível, vem que P ( ) E E = 4 5 = 6 7 Exame 000, a Fase (cód. 45) 75. Considerando a experiência aleatória que consiste em selecionar, ao acaso, um dos 0 iogurtes desta marca e os acontecimentos: V : O iogurte está dentro do prazo de validade E: O iogurte está estragado Assim, de acordo com o enunciado temos que P (E V ) = 0,005 P ( E V ) = 0,65 Como se pretende calcular a probabilidade de escolher, ao acaso, um dos dez iogurtes ele estar estragado, podemos considerar que o iogurte estragado pode ser um dos 8 iogurtes dentro do prazo, ou então um dos que estão fora do prazo, e a soma das respetivas probabilidades: P (E) = P (V ) P (E V ) + P ( V ) P ( E V ) P (E) = 8 0 0, ,65 = 0,4 0 Exame 000, a Fase a chamada (cód. 45) Página de 4
24 76. Podemos interpretar que se é garantida a ocorrência do acontecimento A, então a probabilidade do próprio acontecimento ocorrer é, ou seja P (A A) = Em alternativa podemos verificar que A A = A, pelo que, recorrendo à definição de probabilidade condicionada, vem P (A A) P (A A) = = P (A) P (A) P (A) = Resposta: Opção B Exame 00, a Fase a chamada (cód. 45) 77. Como P (B B ) é a probabilidade de que a bola retirada em segundo lugar seja branca, sabendo que a que foi retirada em primeiro lugar também era branca, sabemos que o conteúdo da caixa (antes da segunda extração, o conteúdo da caixa era de 4 bolas brancas e 5 bolas pretas. Assim, existem 4 bolas brancas (casos favoráveis), num total de 9 bolas (casos possíveis), pelo que recorrendo à Regra de Laplace temos p = 4 9 Resposta: Opção C Prova modelo 000 (cód. 45) 78. Como é sabido que os dois primeiros lançamentos já foram realizados, e para que os números saídos nos quatro lançamentos sejam diferentes, no terceiro lançamento existem apenas 4 faces que têm números diferentes dos primeiros dois lançamentos, e no quarto lançamento, apenas faces têm números diferentes dos três anteriores, pelo que a probabilidade é: Resposta: Opção D p = = 4 6 Exame 999, a Fase a chamada (cód. 5) 79. Para calcular a probabilidade da segunda bola retirada ser par, sabendo que a primeira também é par, como a primeira bola não foi reposta, temos casos possíveis ( = ) correspondentes às bolas que ainda estão no saco, e 5 casos favoráveis (6 = 5) correspondentes às 5 bolas com o número par que ainda permanecem no saco. Assim, recorrendo à Regra de Laplace, temos que a probabilidade é 5 Resposta: Opção D Exame 998, a Fase (cód. 5)(prog. antigo) Página 4 de 4
MATEMÁTICA A - 12o Ano Probabilidades - Probabilidade condicionada
 MATEMÁTICA A - 12o Ano Probabilidades - Probabilidade condicionada Exercícios de exames e testes intermédios 1. Considere duas caixas, C 1 e C 2. A caixa C 1 tem 12 bolas, das quais cinco são brancas e
MATEMÁTICA A - 12o Ano Probabilidades - Probabilidade condicionada Exercícios de exames e testes intermédios 1. Considere duas caixas, C 1 e C 2. A caixa C 1 tem 12 bolas, das quais cinco são brancas e
Exercícios de exames e provas oficiais
 mata Exercícios de exames e provas oficiais. Seja Ω, o conjunto finito, o espaço de resultados associado a uma experiência aleatória. Sejam A e B dois acontecimentos ( A e B ). A e B são acontecimentos
mata Exercícios de exames e provas oficiais. Seja Ω, o conjunto finito, o espaço de resultados associado a uma experiência aleatória. Sejam A e B dois acontecimentos ( A e B ). A e B são acontecimentos
Exercícios de provas oficiais
 mata Exercícios de provas oficiais. Considere duas caixas, C e C. A caixa C tem bolas, das quais cinco são brancas e as restantes são pretas, A caixa C tem sete bolas, umas brancas e outras pretas. Considere
mata Exercícios de provas oficiais. Considere duas caixas, C e C. A caixa C tem bolas, das quais cinco são brancas e as restantes são pretas, A caixa C tem sete bolas, umas brancas e outras pretas. Considere
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução Exercícios de exames e testes intermédios 1. Como P (B) = 1 P ( B ) = P (B) P (A B) vem que P (B) = 1 0,7
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução Exercícios de exames e testes intermédios 1. Como P (B) = 1 P ( B ) = P (B) P (A B) vem que P (B) = 1 0,7
MATEMÁTICA A - 12o Ano Probabilidades - Cálculo combinatório: Cálculo de Probabilidades Propostas de resolução
 MATEMÁTICA A - 12o Ano Probabilidades - Cálculo combinatório: Cálculo de Probabilidades Propostas de resolução Exercícios de exames e testes intermédios 1. Como são extraídos 4 cartões simultaneamente
MATEMÁTICA A - 12o Ano Probabilidades - Cálculo combinatório: Cálculo de Probabilidades Propostas de resolução Exercícios de exames e testes intermédios 1. Como são extraídos 4 cartões simultaneamente
MATEMÁTICA A - 12o Ano Probabilidades - Cálculo combinatório: Cálculo de Probabilidades Propostas de resolução
 MATEMÁTICA A - 12o Ano Probabilidades - Cálculo combinatório: Cálculo de Probabilidades Propostas de resolução Exercícios de exames e testes intermédios 1. Determinando a probabilidade com recurso à Regra
MATEMÁTICA A - 12o Ano Probabilidades - Cálculo combinatório: Cálculo de Probabilidades Propostas de resolução Exercícios de exames e testes intermédios 1. Determinando a probabilidade com recurso à Regra
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Propostas de resolução
 MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014
 AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014 1. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014 1. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Distribuições de probabilidades
 MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
( ) ( ) Questões tipo exame. O número pedido é: Questões tipo exame Pág Os algarismos 1 e 2 podem ocupar 5 A. posições diferentes.
 Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
Escola Secundária/2,3 da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 2011/12 Distribuição de probabilidades 12.º Ano
 Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
2. Se A e B são acontecimentos incompatíveis, a sua interseção é o conjunto vazio, pelo que
 reparar o Exame 0 06 Matemática ágina 6. nalisemos cada opção: : e não são contrários pois a sua união não é o espaço amostral. Há, ainda, bolas pretas. : e não são contrários pois a sua união não é o
reparar o Exame 0 06 Matemática ágina 6. nalisemos cada opção: : e não são contrários pois a sua união não é o espaço amostral. Há, ainda, bolas pretas. : e não são contrários pois a sua união não é o
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
Mais exercícios de 12.º ano:
 Escola Secundária de Francisco Franco Matemática A (métodos curriculares) 12.º ano Exercícios saídos em testes intermédios e em exames nacionais (desde 2008) PROBABILIDADES 1. Seja o espaço de resultados
Escola Secundária de Francisco Franco Matemática A (métodos curriculares) 12.º ano Exercícios saídos em testes intermédios e em exames nacionais (desde 2008) PROBABILIDADES 1. Seja o espaço de resultados
(Testes intermédios e exames 2010/2011)
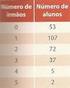
 (Testes intermédios e exames 2010/2011) 211. Os vinte e cinco alunos de uma turma do 12.º ano distribuem-se, por idade e sexo, de acordo com a tabela seguinte. Escolhe-se, ao acaso, um dos vinte e cinco
(Testes intermédios e exames 2010/2011) 211. Os vinte e cinco alunos de uma turma do 12.º ano distribuem-se, por idade e sexo, de acordo com a tabela seguinte. Escolhe-se, ao acaso, um dos vinte e cinco
Proposta de teste de avaliação
 Proposta de teste de avaliação Matemática A 1.º ANO DE ESCOLARIDADE Duração: 90 minutos Data: O teste é constituído por dois grupos, I e II. O Grupo I inclui quatro questões de escolha múltipla. O Grupo
Proposta de teste de avaliação Matemática A 1.º ANO DE ESCOLARIDADE Duração: 90 minutos Data: O teste é constituído por dois grupos, I e II. O Grupo I inclui quatro questões de escolha múltipla. O Grupo
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº1 - Probabilidades - 12º ano Exames
 AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº - Probabilidades - 2º ano Exames 2000-200-2002-2003. Uma caixa contém cinco bolas brancas e cinco bolas pretas, indistinguíveis ao tato. Tiram-se
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº - Probabilidades - 2º ano Exames 2000-200-2002-2003. Uma caixa contém cinco bolas brancas e cinco bolas pretas, indistinguíveis ao tato. Tiram-se
Ficha de trabalho - Combinatória. a) De quantas maneiras distintas se podem colocar os sete sabores no recipiente?
 12º Ano - Matemática A Ficha de trabalho - Combinatória 1. No balcão de uma geladaria existe um recipiente com dez compartimentos, cinco à frente e cinco atrás, para colocar gelado. Em cada compartimento
12º Ano - Matemática A Ficha de trabalho - Combinatória 1. No balcão de uma geladaria existe um recipiente com dez compartimentos, cinco à frente e cinco atrás, para colocar gelado. Em cada compartimento
TEMA 1 COMBINATÓRIA E PROBABILIDADES FICHAS DE TRABALHO 12.º ANO COMPILAÇÃO TEMA 1 COMBINATÓRIA E PROBABILIDADES
 FICHAS DE TRABALHO.º ANO COMPILAÇÃO TEMA COMBINATÓRIA E PROBABILIDADES Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA COMBINATÓRIA E PROBABILIDADES Matemática A.º Ano
FICHAS DE TRABALHO.º ANO COMPILAÇÃO TEMA COMBINATÓRIA E PROBABILIDADES Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA COMBINATÓRIA E PROBABILIDADES Matemática A.º Ano
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº3 - Probabilidades - 12º ano Exames
 AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº3 - Probabilidades - º ano Exames 006-007-00-009-00. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº3 - Probabilidades - º ano Exames 006-007-00-009-00. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
Exercícios de exames e provas oficiais
 mata2 Eercícios de eames e provas oficiais. Uma caia tem seis bolas distinguíveis apenas pela cor: duas azuis e quatro pretas. Considere a eperiência aleatória que consiste em retirar dessa caia, simultaneamente
mata2 Eercícios de eames e provas oficiais. Uma caia tem seis bolas distinguíveis apenas pela cor: duas azuis e quatro pretas. Considere a eperiência aleatória que consiste em retirar dessa caia, simultaneamente
TEMA 1 PROBABILIDADES E COMBINATÓRIA FICHA DE TRABALHO 12.º ANO COMPILAÇÃO TEMA 1 PROBABILIDADES E COMBINATÓRIA
 FICHA DE TRABALHO.º ANO COMPILAÇÃO TEMA 1 PROBABILIDADES E COMBINATÓRIA Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA 1 PROBABILIDADES E COMBINATÓRIA Matemática A.º
FICHA DE TRABALHO.º ANO COMPILAÇÃO TEMA 1 PROBABILIDADES E COMBINATÓRIA Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA 1 PROBABILIDADES E COMBINATÓRIA Matemática A.º
COLEÇÃO DARLAN MOUTINHO VOL. 01 RESOLUÇÕES
 COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 00 - a Fase Proposta de resolução GRUPO I. Como A e B são acontecimentos incompatíveis, temos que A B, ou seja, P A B 0 Como P A B P A + P B P A B P A B + P A B P
Prova Escrita de MATEMÁTICA A - o Ano 00 - a Fase Proposta de resolução GRUPO I. Como A e B são acontecimentos incompatíveis, temos que A B, ou seja, P A B 0 Como P A B P A + P B P A B P A B + P A B P
Prova Escrita de MATEMÁTICA A - 12o Ano Época especial
 Prova Escrita de MATEMÁTICA A - o Ano 0 - Época especial Proposta de resolução GRUPO I. Temos que A e B são acontecimentos incompatíveis, logo P A B 0 Como P A B P B P A B, e P A B 0, vem que: P A B P
Prova Escrita de MATEMÁTICA A - o Ano 0 - Época especial Proposta de resolução GRUPO I. Temos que A e B são acontecimentos incompatíveis, logo P A B 0 Como P A B P B P A B, e P A B 0, vem que: P A B P
Agrupamento de Escolas de Diogo Cão, Vila Real
 Agrupamento de Escolas de Diogo Cão, Vila Real 2015/2016 MATEMÁTICA FICHA DE TRABALHO 7 3º PERÍODO MAIO Nome: Nº Turma: 9º Data: CIRCUNFERÊNCIA 1. Relativamente à fig. 1 indica: 1.1 duas cordas; 1.2 a
Agrupamento de Escolas de Diogo Cão, Vila Real 2015/2016 MATEMÁTICA FICHA DE TRABALHO 7 3º PERÍODO MAIO Nome: Nº Turma: 9º Data: CIRCUNFERÊNCIA 1. Relativamente à fig. 1 indica: 1.1 duas cordas; 1.2 a
12.º Ano de Escolaridade
 gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 12º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema I Probabilidades e Combinatória
 ESOLA SEUNDÁRIA OM 3º ILO D. DINIS º ANO DE ESOLARIDADE DE MATEMÁTIA A Tema I Probabilidades e ombinatória Tarefa nº do plano de trabalho nº 5. onsidere o seguinte problema: Um saco contém doze bolas,
ESOLA SEUNDÁRIA OM 3º ILO D. DINIS º ANO DE ESOLARIDADE DE MATEMÁTIA A Tema I Probabilidades e ombinatória Tarefa nº do plano de trabalho nº 5. onsidere o seguinte problema: Um saco contém doze bolas,
Proposta de teste de avaliação
 Proposta de teste de avaliação Matemática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
Proposta de teste de avaliação Matemática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
Prova Escrita de MATEMÁTICA A - 12o Ano Época especial
 Prova Escrita de MATEMÁTICA A - 1o Ano 01 - Época especial Proposta de resolução GRUPO I 1. Como o primeiro e último algarismo são iguais, o segundo e o penúltimo também, o mesmo acontecendo com o terceiro
Prova Escrita de MATEMÁTICA A - 1o Ano 01 - Época especial Proposta de resolução GRUPO I 1. Como o primeiro e último algarismo são iguais, o segundo e o penúltimo também, o mesmo acontecendo com o terceiro
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 0 - a Fase Proposta de resolução GRUPO I. Temos que P A B) P A) + P B) P A B) P A B) P A) + P B) P A B) Como A e B são independentes, então P A) P B) P A B), pelo
Prova Escrita de MATEMÁTICA A - o Ano 0 - a Fase Proposta de resolução GRUPO I. Temos que P A B) P A) + P B) P A B) P A B) P A) + P B) P A B) Como A e B são independentes, então P A) P B) P A B), pelo
Prova Escrita de MATEMÁTICA A - 12o Ano Época especial
 Prova Escrita de MATEMÁTICA A - o Ano 04 - Época especial Proposta de resolução GRUPO I. Para que os números de cinco algarismos sejam ímpares e tenham 4 algarismo pares, todos os números devem ser pares
Prova Escrita de MATEMÁTICA A - o Ano 04 - Época especial Proposta de resolução GRUPO I. Para que os números de cinco algarismos sejam ímpares e tenham 4 algarismo pares, todos os números devem ser pares
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 12o Ano 2008-1 a Fase Proposta de resolução GRUPO I 1. Como se pretende ordenar 5 elementos amigos) em 5 posições lugares), existem 5 A 5 = P 5 = 5! casos possíveis. Como
Prova Escrita de MATEMÁTICA A - 12o Ano 2008-1 a Fase Proposta de resolução GRUPO I 1. Como se pretende ordenar 5 elementos amigos) em 5 posições lugares), existem 5 A 5 = P 5 = 5! casos possíveis. Como
4 3 10! Resposta pedida: 3! x 4! = 144 Resposta: C
 ágina 80. reparar o Exame 0 07 Matemática A 4 0! 4 x x 0!. Devemos escolher, das oito posições, duas para as letras A: temos 8 formas de o fazer. Das seis posições restantes, uma tem de ser para a letra
ágina 80. reparar o Exame 0 07 Matemática A 4 0! 4 x x 0!. Devemos escolher, das oito posições, duas para as letras A: temos 8 formas de o fazer. Das seis posições restantes, uma tem de ser para a letra
TESTE GLOBAL PROBABILIDADES 12.º ANO
 TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
TESTE GLOBAL PROBABILIDADES 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / DATA: / / DURAÇÃO DO TESTE: 90 MINUTOS VERSÃO 2 Na tua folha de respostas, indica de forma legível a versão do teste. FORMULÁRIO Probabilidades
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 7 - a Fase Proposta de resolução GRUPO I. Como a área do retângulo é igual a 5, designado por x o comprimento de um dos lados e por y o comprimento de um lado adjacente,
Prova Escrita de MATEMÁTICA A - o Ano 7 - a Fase Proposta de resolução GRUPO I. Como a área do retângulo é igual a 5, designado por x o comprimento de um dos lados e por y o comprimento de um lado adjacente,
12.º Ano de Escolaridade
 gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
12.º Ano de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) PROBABILIDADES E COMBINATÓRIA VERSÃO 2
 gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A A 12.º Ano de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) Duração da Prova: 90 minutos 7/Dezembro/2006
gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A A 12.º Ano de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) Duração da Prova: 90 minutos 7/Dezembro/2006
Proposta de Resolução
 Novo Espaço Matemática A 1.º ano Proposta de Teste Intermédio [novembro 014] Proposta de Resolução GRUPO I 1. Seja Ω = { a, b, c, d} o espaço de resultados de uma eperiência aleatória. P ({ a} ) = P ({
Novo Espaço Matemática A 1.º ano Proposta de Teste Intermédio [novembro 014] Proposta de Resolução GRUPO I 1. Seja Ω = { a, b, c, d} o espaço de resultados de uma eperiência aleatória. P ({ a} ) = P ({
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 3
 FIHA de AVALIAÇÃO de MATEMÁTIA A 1.º Ano Versão 3 Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
FIHA de AVALIAÇÃO de MATEMÁTIA A 1.º Ano Versão 3 Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ano 007-1 a Fase Proposta de resolução GRUPO I 1. Calculando o valor do ite, temos: x + 1 1 x + 4 x = x + 4 x ) = 1 4 + ) = 1 4 4 + = 1 0 =. Resolvendo a inequação temos
Prova Escrita de MATEMÁTICA A - 1o Ano 007-1 a Fase Proposta de resolução GRUPO I 1. Calculando o valor do ite, temos: x + 1 1 x + 4 x = x + 4 x ) = 1 4 + ) = 1 4 4 + = 1 0 =. Resolvendo a inequação temos
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ano 009-1 a Fase Proposta de resolução GRUPO I 1. Como existem 4 cartas de cada tipo, existem 4 4 4 4 4 4 = 4 6 sequências do tipo 4 6 7 Dama Rei existem 4 hipóteses
Prova Escrita de MATEMÁTICA A - 1o Ano 009-1 a Fase Proposta de resolução GRUPO I 1. Como existem 4 cartas de cada tipo, existem 4 4 4 4 4 4 = 4 6 sequências do tipo 4 6 7 Dama Rei existem 4 hipóteses
TESTE DE PROBABILIDADES E COMBINATÓRIA 12.º ANO
 TESTE DE PROBABILIDADES E COMBINATÓRIA 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / AVALIAÇÃO: PROFESSOR: ENC. EDUCAÇÃO: DURAÇÃO DO TESTE: 90 MINUTOS O teste é constituído por dois grupos. O Grupo I é constituído
TESTE DE PROBABILIDADES E COMBINATÓRIA 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / AVALIAÇÃO: PROFESSOR: ENC. EDUCAÇÃO: DURAÇÃO DO TESTE: 90 MINUTOS O teste é constituído por dois grupos. O Grupo I é constituído
Noções sobre Probabilidade
 Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 7
 P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 7 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Nas condições do enunciado, o número de triângulos que se podem formar com três dos doze pontos é (dos
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 7 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Nas condições do enunciado, o número de triângulos que se podem formar com três dos doze pontos é (dos
Se o número começar por 2, este algarismo já não pode ser o último
 reparar o Exame 0 0 Matemática A ágina 9. Resposta pedida: x = 09. asos possíveis: 09 asos favoráveis: x x = 9 Resposta pedida: 9 09. asos possíveis: 09 asos favoráveis: Existem x x x + x x x = 0 números
reparar o Exame 0 0 Matemática A ágina 9. Resposta pedida: x = 09. asos possíveis: 09 asos favoráveis: x x = 9 Resposta pedida: 9 09. asos possíveis: 09 asos favoráveis: Existem x x x + x x x = 0 números
Prova Escrita de MATEMÁTICA A - 12o Ano Época especial
 Prova Escrita de MATEMÁTICA A - 2o Ano 20 - Época especial Proposta de resolução GRUPO I. Considerando a eperiência aleatória que consiste em escolher, ao acaso, um jovem inscrito no clube, e os acontecimentos:
Prova Escrita de MATEMÁTICA A - 2o Ano 20 - Época especial Proposta de resolução GRUPO I. Considerando a eperiência aleatória que consiste em escolher, ao acaso, um jovem inscrito no clube, e os acontecimentos:
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ano 011-1 a Fase Proposta de resolução GRUPO I 1. A igualdade da opção A é válida para acontecimentos contrários, a igualdade da opção B é válida para acontecimentos
Prova Escrita de MATEMÁTICA A - 1o Ano 011-1 a Fase Proposta de resolução GRUPO I 1. A igualdade da opção A é válida para acontecimentos contrários, a igualdade da opção B é válida para acontecimentos
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ano 009 - a Fase Proposta de resolução GRUPO I 1. Como a Maria escolheu CD de um conjunto de 9, sem considerar a ordem relevante, existem 9 C pares diferentes que podem
Prova Escrita de MATEMÁTICA A - 1o Ano 009 - a Fase Proposta de resolução GRUPO I 1. Como a Maria escolheu CD de um conjunto de 9, sem considerar a ordem relevante, existem 9 C pares diferentes que podem
ESCOLA SECUNDÁRIA DA RAMADA. Teste de Matemática A. 28 de outubro de º E. Grupo I
 ESCOLA SECUNDÁRIA DA RAMADA Teste de Matemática A 28 de outubro de 206 2º E Versão Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas, são indicadas quatro alternativas,
ESCOLA SECUNDÁRIA DA RAMADA Teste de Matemática A 28 de outubro de 206 2º E Versão Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas, são indicadas quatro alternativas,
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades
 Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 1
 P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 1 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Trata-se de uma permutação com repetições, ou seja, é uma sequência de oito letras em que a letra repete-se
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 1 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Trata-se de uma permutação com repetições, ou seja, é uma sequência de oito letras em que a letra repete-se
FICHA DE TRABALHO N. O 9
 FICHA DE TRABALHO N. O 9 ASSUNTO: Modelos de probabilidade: probabilidade condicional 1. Sejam A e B dois acontecimentos tais que: P (A) = 0,3 e P (B ) = 0,7 Determine P (A B ), sabendo que: 1.1 Os acontecimentos
FICHA DE TRABALHO N. O 9 ASSUNTO: Modelos de probabilidade: probabilidade condicional 1. Sejam A e B dois acontecimentos tais que: P (A) = 0,3 e P (B ) = 0,7 Determine P (A B ), sabendo que: 1.1 Os acontecimentos
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 4
 P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 4 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. O número de casos possíveis é. Para determinar o número de casos possíveis tem que se considerar três
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 4 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. O número de casos possíveis é. Para determinar o número de casos possíveis tem que se considerar três
12.º Ano de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) PROBABILIDADES E COMBINATÓRIA VERSÃO 4
 gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A A 12.º Ano de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) Duração da Prova: 90 minutos 7/Dezembro/2006
gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A A 12.º Ano de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) Duração da Prova: 90 minutos 7/Dezembro/2006
4. Seja A o acontecimento associado a uma experiência aleatória em que o espaço amostral é Quais as igualdades necessariamente falsas?
 mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
1. Num universo S os acontecimentos A e B são incompatíveis.
 12ºANO ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO Matemática B Probabilidades 2007/08 1. Num universo S os acontecimentos A e B são incompatíveis. Sabe-se que: P( B ) = 0,1 e que P( A B ) = 0,6. Determina P(
12ºANO ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO Matemática B Probabilidades 2007/08 1. Num universo S os acontecimentos A e B são incompatíveis. Sabe-se que: P( B ) = 0,1 e que P( A B ) = 0,6. Determina P(
12.º Ano de Escolaridade
 gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
gabinete de avaliação educacional T E S T E I N T E R M É D I O D E M A T E M Á T I C A 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) (Dec.-Lei n.º 286/89, de 29 de Agosto, para alunos
Matemática A RESOLUÇÃO GRUPO I. Teste Intermédio. Versão 1. Duração do Teste: 90 minutos º Ano de Escolaridade. 1.
 Teste Intermédio Matemática A Versão Duração do Teste: 90 minutos 9..0.º Ano de Escolaridade Decreto-Lei n.º 7/00, de de março????????????? RESOLUÇÃO GRUPO I. Resposta (B) Tem-se, a 0+ b + 0,, pelo que
Teste Intermédio Matemática A Versão Duração do Teste: 90 minutos 9..0.º Ano de Escolaridade Decreto-Lei n.º 7/00, de de março????????????? RESOLUÇÃO GRUPO I. Resposta (B) Tem-se, a 0+ b + 0,, pelo que
24 de outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Proposta de resolução da Prova de Matemática A (código 635) 21 de Junho de 2010
 Proposta de resolução da Prova de Matemática A (código 635) 1. Como A e B são acontecimentos incompatíveis, 0 e Ou seja, de acordo com os dados do enunciado, 70% 30% 40% Versão 1: B Versão : C. Como se
Proposta de resolução da Prova de Matemática A (código 635) 1. Como A e B são acontecimentos incompatíveis, 0 e Ou seja, de acordo com os dados do enunciado, 70% 30% 40% Versão 1: B Versão : C. Como se
Tarefa nº_ 1.9 (C) 3 5
 Tarefa nº_ 1.9 MATEMÁTICA Probabilidades e Combinatória Cálculo Combinatório Nome: 12º Ano Data / / 1. Os códigos dos cofres fabricados por uma certa empresa, consistem numa sequência de cinco algarismos
Tarefa nº_ 1.9 MATEMÁTICA Probabilidades e Combinatória Cálculo Combinatório Nome: 12º Ano Data / / 1. Os códigos dos cofres fabricados por uma certa empresa, consistem numa sequência de cinco algarismos
Proposta de teste de avaliação
 Matemática A 1. O ANO DE ESOLARIDADE Duração: 90 minutos Data: aderno 1 (4 min) (é permitido o uso de calculadora) 1. Uma caixa contém seis bolas vermelhas, três bolas brancas e quatro bolas azuis. Tanto
Matemática A 1. O ANO DE ESOLARIDADE Duração: 90 minutos Data: aderno 1 (4 min) (é permitido o uso de calculadora) 1. Uma caixa contém seis bolas vermelhas, três bolas brancas e quatro bolas azuis. Tanto
8 A do total de lançamentos, ou seja, x = 5625 Resposta: C
 Página 7 Preparar o Exame 0 07 Matemática A. x7x 7 Observa que sair primeiro o sabor laranja e depois o sabor morango são casos diferentes x Resposta: D. Repara que se os dois primeiros rebuçados foram
Página 7 Preparar o Exame 0 07 Matemática A. x7x 7 Observa que sair primeiro o sabor laranja e depois o sabor morango são casos diferentes x Resposta: D. Repara que se os dois primeiros rebuçados foram
Noção de fenómeno aleatório e de experiência aleatória
 Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
MATEMÁTICA MÓDULO 4 PROBABILIDADE
 PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
Ficha de Avaliação. Matemática A. Duração do Teste: 90 minutos. 12.º Ano de Escolaridade. Teste de Matemática A 12.º Ano Página 1
 Ficha de Avaliação Matemática A Duração do Teste: 90 minutos 12.º Ano de Escolaridade Teste de Matemática A 12.º Ano Página 1 1. Colocaram-se numa urna 12 bolas, indistinguíveis pelo tato, numeradas de
Ficha de Avaliação Matemática A Duração do Teste: 90 minutos 12.º Ano de Escolaridade Teste de Matemática A 12.º Ano Página 1 1. Colocaram-se numa urna 12 bolas, indistinguíveis pelo tato, numeradas de
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 05 - a Fase Proposta de resolução GRUPO I. Escolhendo os lugares das etremidades para os dois rapazes, eistem hipóteses correspondentes a uma troca entre os rapazes.
Prova Escrita de MATEMÁTICA A - o Ano 05 - a Fase Proposta de resolução GRUPO I. Escolhendo os lugares das etremidades para os dois rapazes, eistem hipóteses correspondentes a uma troca entre os rapazes.
Proposta de teste de avaliação
 Proposta de teste de avaliação Matemática A. O ANO DE ESOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
Proposta de teste de avaliação Matemática A. O ANO DE ESOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
22 de Outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Teste Intermédio 2012
 Teste Intermédio 01 1. Uma escola básica tem duas turmas de 9. ano: a turma e a turma. Os alunos da turma distribuem-se, por idades, de acordo com o seguinte diagrama circular. Idades dos alunos da turma
Teste Intermédio 01 1. Uma escola básica tem duas turmas de 9. ano: a turma e a turma. Os alunos da turma distribuem-se, por idades, de acordo com o seguinte diagrama circular. Idades dos alunos da turma
22 de Outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Prova final de MATEMÁTICA - 3o ciclo Época especial
 Prova final de MTMÁT - 3o ciclo 011 - Época especial Proposta de resolução 1. 1.1. onstruindo uma tabela para identificar todos os pares de pares de bolas que existem, e calculando o produto dos dois números,
Prova final de MTMÁT - 3o ciclo 011 - Época especial Proposta de resolução 1. 1.1. onstruindo uma tabela para identificar todos os pares de pares de bolas que existem, e calculando o produto dos dois números,
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA
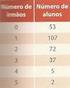 Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS COIMBRA 12º ANO DE ESCOLARIDADE MATEMÁTICA A FICHA DE AVALIAÇÃO 12º A1 Grupo I
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS COIMBRA 1º ANO DE ESCOLARIDADE MATEMÁTICA A FICHA DE AVALIAÇÃO 1º A1 Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS COIMBRA 1º ANO DE ESCOLARIDADE MATEMÁTICA A FICHA DE AVALIAÇÃO 1º A1 Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
Teste de Avaliação de MATEMÁTICA 12º ano
 Teste de Avaliação de MATEMÁTICA º ano º Período de 0/ duração 90 min. Prof. Josué Baptista Turma: e º teste A 4 de Outubro Classificação: Nº Nome GRUPO I O Professor: As cinco questões deste grupo são
Teste de Avaliação de MATEMÁTICA º ano º Período de 0/ duração 90 min. Prof. Josué Baptista Turma: e º teste A 4 de Outubro Classificação: Nº Nome GRUPO I O Professor: As cinco questões deste grupo são
Teste de Avaliação Escrita
 Teste de Avaliação Escrita Duração: 9 minutos 8 de outubro de Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo /4 Matemática 9.º B Nome: N.º Classificação: Fraco (% 9%) Insuficiente (% 49%) Suficiente
Teste de Avaliação Escrita Duração: 9 minutos 8 de outubro de Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo /4 Matemática 9.º B Nome: N.º Classificação: Fraco (% 9%) Insuficiente (% 49%) Suficiente
EXERCÍCIOS REVISIONAIS SOBRE BINÔMIO DE NEWTON SISTEMAS LINEARES PROBABILIDADE 2 ANO
 QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema II Introdução ao Cálculo Diferencial II. TPC nº 9 (entregar em )
 Escola Secundária com º ciclo D. Dinis º Ano de Matemática A Tema II Introdução ao álculo Diferencial II TP nº 9 (entregar em 09-0-0) Grupo I. Uma caixa A contém duas bolas verdes e uma bola amarela. Outra
Escola Secundária com º ciclo D. Dinis º Ano de Matemática A Tema II Introdução ao álculo Diferencial II TP nº 9 (entregar em 09-0-0) Grupo I. Uma caixa A contém duas bolas verdes e uma bola amarela. Outra
Professora: Maria Adriana Batista
 Professora: Maria Adriana Batista 1 Teste Intermédio Dezembro 2005 1. Três raparigas e os respectivos namorados posam para uma fotografia. De quantas maneiras se podem dispor, lado a lado, de modo que
Professora: Maria Adriana Batista 1 Teste Intermédio Dezembro 2005 1. Três raparigas e os respectivos namorados posam para uma fotografia. De quantas maneiras se podem dispor, lado a lado, de modo que
ESCOLA SECUNDÁRIA DE CASQUILHOS
 ESCOLA SECUNDÁRIA DE CASQUILHOS 12º Ano Turma A - C.C.H. de Ciências e Tecnologias - 1ª Teste de Avaliação de Matemática A V1 Duração: 90 min 05 Nov. 09 Prof.: Na folha de respostas, indicar de forma legível
ESCOLA SECUNDÁRIA DE CASQUILHOS 12º Ano Turma A - C.C.H. de Ciências e Tecnologias - 1ª Teste de Avaliação de Matemática A V1 Duração: 90 min 05 Nov. 09 Prof.: Na folha de respostas, indicar de forma legível
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MAEMÁICA A - o Ano 006 - a Fase Proposta de resolução GRUPO I. Como o ponto (0,) pertence ao gráfico de f, temos que f(0) =, e assim vem que: f(0) = a 0 + b = + b = b = b = Como o ponto
Prova Escrita de MAEMÁICA A - o Ano 006 - a Fase Proposta de resolução GRUPO I. Como o ponto (0,) pertence ao gráfico de f, temos que f(0) =, e assim vem que: f(0) = a 0 + b = + b = b = b = Como o ponto
Na resposta a cada um dos itens deste grupo, selecione a única opção correta.
 Exame Nacional exame nacional do ensino secundário Decreto Lei n. 9/0, de de julho Prova Escrita de Matemática A. Ano de Escolaridade Prova 6/.ª Fase Duração da Prova: 0 minutos. Tolerância: 0 minutos
Exame Nacional exame nacional do ensino secundário Decreto Lei n. 9/0, de de julho Prova Escrita de Matemática A. Ano de Escolaridade Prova 6/.ª Fase Duração da Prova: 0 minutos. Tolerância: 0 minutos
Proposta de Resolução do Exame do 12º ano Matemática A (Prova 635) ª Fase. Grupo I. 1. BComo A e B são acontecimentos incompatíveis, 0 e
 Proposta de Resolução do Exame do 1º ano Matemática A (Prova 635) 010-1ª Fase 1. BComo A e B são acontecimentos incompatíveis, 0 e Ou seja, de acordo com c os dados do enunciado, 70% 30% 40% A opção correcta
Proposta de Resolução do Exame do 1º ano Matemática A (Prova 635) 010-1ª Fase 1. BComo A e B são acontecimentos incompatíveis, 0 e Ou seja, de acordo com c os dados do enunciado, 70% 30% 40% A opção correcta
Sumário. 2 Índice Remissivo 12
 i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
1 Definição Clássica de Probabilidade
 Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
DRUIDAS DO SABER CENTRO DE EXPLICAÇÕES. Matemática - 9º Ano
 DRUIDAS DO SABER CENTRO DE EXLICAÇÕES Matemática - 9º Ano Em todas as questões apresenta o teu raciocínio de forma clara, indicando todos os cálculos que tiveres de efectuar e todas as justificações que
DRUIDAS DO SABER CENTRO DE EXLICAÇÕES Matemática - 9º Ano Em todas as questões apresenta o teu raciocínio de forma clara, indicando todos os cálculos que tiveres de efectuar e todas as justificações que
ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO
 ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO Teste 1 Matemática 9.º C Nome: n.º Data: 14/10/2016 Classificação: Professor: Instruções gerais Não é permitido o uso de corretor. É permitido a utilização
ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO Teste 1 Matemática 9.º C Nome: n.º Data: 14/10/2016 Classificação: Professor: Instruções gerais Não é permitido o uso de corretor. É permitido a utilização
3. Probabilidade P(A) =
 7 3. Probabilidade Probabilidade é uma medida numérica da plausibilidade de que um evento ocorrerá. Assim, as probabilidades podem ser usadas como medidas do grau de incerteza e podem ser expressas de
7 3. Probabilidade Probabilidade é uma medida numérica da plausibilidade de que um evento ocorrerá. Assim, as probabilidades podem ser usadas como medidas do grau de incerteza e podem ser expressas de
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Propostas de resolução
 MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Observando que o número de rapazes da turma da Ana é 3+8+2 = 13, e que existem
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Observando que o número de rapazes da turma da Ana é 3+8+2 = 13, e que existem
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 12º ANO DE ESCOLARIDADE DE MATEMÁTICA A. TESTE Nº 1 Grupo I
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A TESTE Nº Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A TESTE Nº Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
Escola Secundária de Lousada. Matemática do 9º ano FT 17 Data: / / 2013 Assunto: Ficha de Preparação para o 3º Teste
 Escola Secundária de Lousada Matemática do 9º ano FT 7 Data: / / 0 Assunto: Ficha de Preparação para o º Teste Apresentação dos Conteúdos e Objetivos para o º Teste de Avaliação de Matemática Data da Realização
Escola Secundária de Lousada Matemática do 9º ano FT 7 Data: / / 0 Assunto: Ficha de Preparação para o º Teste Apresentação dos Conteúdos e Objetivos para o º Teste de Avaliação de Matemática Data da Realização
Prova Escrita de MATEMÁTICA A - 12o Ano Época especial
 Prova Escrita de MATEMÁTICA A - o Ano 07 - Época especial Proposta de resolução GRUPO I. Como o número a formar deve ser maior que 0 000, então para o algarismo das dezenas de milhar existem apenas 3 escolhas
Prova Escrita de MATEMÁTICA A - o Ano 07 - Época especial Proposta de resolução GRUPO I. Como o número a formar deve ser maior que 0 000, então para o algarismo das dezenas de milhar existem apenas 3 escolhas
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ano Versão Nome: N.º Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias. Quando,
