Efeito Hall quântico de vale no grafeno
|
|
|
- Giovanni Regueira Silva
- 8 Há anos
- Visualizações:
Transcrição
1 Universidade de são paulo Instituto de física Departamento de física de materiais Efeito Hall quântico de vale no grafeno Walace de sousa elias Disciplina: teoria quântica de muitos corpos Prof. Dr. Luis gregório dias
2 INTRODUÇÃO O grafeno é uma das formas cristalinas do carbono, assim como o diamante, o grafite, os nanotubos de carbono e fulerenos. É o material mais forte já demonstrado, consistindo em uma folha plana de átomos de carbono densamente compactados em uma grade de duas dimensões. O grafeno de alta qualidade é muito forte, leve, quase transparente, um excelente condutor de calor e eletricidade.
3 A realização experimental do grafeno abriu uma possibilidade fascinante de observações em física da matéria condensada, com um número de efeitos interessantes, antes considerados apenas ocorrer, exclusivamente, em física de partículas. O grafeno exibe alguns fenômenos de transportes não convencionais, dentre eles: Efeito Hall Quântico inteiro anômalo; Condutividade dc σ finita, mesmo na ausência de um campo elétrico externo, E = 0. Possibilidade de observar uma condutividade transversa quantizada.
4 O que é o efeito hall quântico? Em 1879, durante experiências feitas para se medir diretamente o sinal dos portadores de carga em um condutor Edwin H. Hall percebeu um fenômeno peculiar. Edwin Hall descreveu foi o surgimento de regiões com carga negativa e outras com carga positiva no condutor, criando um campo magnético perpendicular ao campo gerado pela corrente principal. Uma manifestação ainda mais marcante de efeitos quânticos nas propriedades de transporte de um gás de elétrons bidimensional foi observada 50 anos mais tarde com a descoberta do efeito Hall quântico inteiro. Esse efeito consiste na quantização da resistência Hall, não mais linear em como previsto classicamente
5 MODELO Os elétrons p do átomo de carbono na rede hexagonal do grafeno são usualmente descritos por férmions sem massa de 4 componentes, sendo cada componente correspondendo a duas sub-redes (A e B) e dois vales (valley) (K e K ). Desconsiderando a interação entre os vales, podemos descrever o sistema como dois férmions de 2 componentes. Assumindo que a interação entre os férmions em 2D seja eletromagnética, isto é, uma interação coulombiana, um modelo para se utilizar será a lagrangeana da Pseudo Eletrodinâmica Quântica (PQED) com
6 A PQED foi proposta por Marino, como uma alternativa para estudar interações entre férmions em sistemas bidimensionais. Em seu trabalho, realizando uma redução dimensional, obteve um modelo para férmions bidimensionais interagindo através de um potencial do tipo Coulomb. Em sistemas bidimensionais, como é o caso do grafeno, é sabido que a interação eletromagnética, descrita pela QED, é do tipo logarítmica. Na PQED, por outro lado, a interação é do tipo coulombiana.
7 FUNÇÃO DE CORRELAÇÃO CORRENTE-CORRENTE Determinamos no limite de ω 0, a condutividade ótica no grafeno utilizando a fórmula de Kubo, que descreve a resposta linear de um campo elétrico externo estático. No formalismo de tempo real, temos onde a função de correlação corrente-corrente contêm apenas os diagramas 1PI. Uma forma mais usada para se obter as funções de correlação, se dá a partir do funcional gerador correspondente.
8 O gerador das funções de correlação conectadas é determinado por O gerador funcional das funções de correlação 1PI é então obtido por uma transformação de Legendre do tipo com A função de correlação corrente-corrente pode ser finalmente obtida, como sendo a segunda derivada do funcional gerador Γ[Ac]:
9 Porém, a expressão anterior nada mais é que a auto energia do campo de gauge A μ, também conhecido como tensor de polarização O propagador livre do campo de gauge é facilmente obtido a partir da lagrangeana e escrito como Portanto, imediatamente relacionamos a função de correlação corrente-corrente com a auto energia de A μ, isto é,
10 O cálculo da auto energia do campo de gauge é bem conhecido em ordens superiores a dois loops para a QED. A contribuição de um loop no espaço euclidiano para um férmion sem massa é o mesmo resultado obtido pela Eletrodinâmica Quântica e dada por A contribuição em ordem de dois loops é exclusiva da PQED e para um férmion simples e sem massa, obtêm-se o seguinte resultado
11 A função de correlação corrente-corrente 1PI será então determinada por Determinada a função de correlação corrente-corrente, façamos física!
12 CONDUTIVIDADE (T = 0, ω 0) A condutividade ótica no limite de T = 0, ω 0 pode ser obtido usando a fórmula de Kubo, isto é, Quando calculamos a função de correlação corrente-corrente neste regime, devemos repassar γ i v F γ i, nos vértices. Dessa forma, as contribuições da auto energia do campo de gauge serão escritas como
13 A função de correlação corrente-corrente será expressa em termos de Π ij, Π 00 e Π i0. Tomando o limite de p 0, na fórmula de Kubo, a única contribuição virá do termo Π ij. A função de correlação é proporcianal ao número de sabor N f, composto pelos spins, e nos valoes K e K, portanto N f = N S + N V. Devemos ter cuidado, no entanto, quando somar as contribuições dos vales K e K. Por razões de simetria, é razoável esperar que ambos os vales irão contribuir de forma idêntica. No entanto, os vales são ligados uns aos outros por time reverso symmetry (TRS) e, consequentemente, a sua contribuição dependerá do fato desta simetria ser espontaneamente quebrada ou não. Quando a simetria de TR preservada, ambos os vales dão claramente contribuições idênticas e N V = 2 ou N V = 4.
14 Na teoria da resposta linear, para cada vale têm-se que sendo E i o campo elétrico externo. A contribuição dos dois vales para a corrente média é dada da seguinte forma, Quando a TRS não é quebrada espontâneamente, a soma das contribuições dos dois vales para a condutividade é dada por
15 No limite em que p 0, a função de correlação e sua versão de tempo reverso são determinados, respectivamente pelas expressões A coordenada p 0 que aparece nas equações acima, deve ser interpretado como a frequência ω na fórmula de Kubo. Utilizando os resultados para a função de correlação e a sua versão de tempo reverso, determina-se que a condutividade possuirá a seguinte estrutura
16 Portanto, encontra-se que para uma fase TR não quebrada, apenas a parte longitudinal contribuirá. Os dois vales contribuirão igualmente e, dessa maneira, N V = 2 ou N f = 4. Finalmente, encontra-se que O limite considerado para a condutividade ótica foi ω k BT ħ e determinaram a correção para interação eletromagnética completa, para o valor não interagente de σ 0 = πe2 2h. σ th xx = 1.76 e2 h σ xx ex = 2.16 e2 h
17 EFEITO HALL QUÂNTICO DE VALLEY O valor médio da corrente de vale é definido como Para K = K, a corrente será nula. A partir da expressão acima, fica claro que Portanto, definimos um limite de frequência zero da condutividade ótica de vale, sendo calculada como
18 A condutividade de vale, portanto, é determinada por com n sendo um número inteiro. A componente longitudinal, por outro lado, será nula. Ou seja, A existência de uma condutividade de vale transversa caracteriza a ocorrência do Efeito Hall Quântico de Vale. É causado pela presença do termo que viola paridade e inversão temporal que surgiu da auto energia ou, equivalentemente, da função de correlação.
19 A condutividade Hall foi determinada exatamente e coincide com aquela obtida no Efeito Hall Quântico usual, apesar da ausência de qualquer campo magnético aplicado. A pesquisa foi publicada no Physical Review X este ano e tem como autores o pesquisador Eduardo Marino e o doutorando Leandro Oliveira do Nascimento, ambos do Instituto de Física da UFRJ (Universidade Federal do Rio de Janeiro), juntamente com Cristiane de Morais Smith, pesquisadora da Universidade de Utrecht, na Holanda, e Van Sérgio Alves, pesquisador da UFPa. Os pesquisadores identificaram o efeito teoricamente ao incluir, pela primeira vez em um modelo do grafeno, a interação eletrodinâmica completa entre os elétrons dos orbitais p do carbono. Também foram determinadas as correções à condutividade dc longitudinal do grafeno devidas a tais interações, estando os resultados em excelente acordo com os experimentos.
20
Diagramas de Feynman para a Matriz S
 Teoria Quântica de Campos I 186 Diagramas de Feynman para a Matriz S ( Nastase 20; Peskin 4.6 ) Agora queremos calcular a matriz S da mesma forma que fizemos para as funções de Green, passando para o quadro
Teoria Quântica de Campos I 186 Diagramas de Feynman para a Matriz S ( Nastase 20; Peskin 4.6 ) Agora queremos calcular a matriz S da mesma forma que fizemos para as funções de Green, passando para o quadro
Violação das simetrias de Lorentz e CPT em teoria de campos
 Violação das simetrias de Lorentz e CPT em teoria de campos Eduardo Passos UAF-UFCG, PNPD/CAPES October 21, 2008 Conteúdo 1 Questões e Motivações 2 Indução do termo tipo Chern-Simons na QED não-massiva
Violação das simetrias de Lorentz e CPT em teoria de campos Eduardo Passos UAF-UFCG, PNPD/CAPES October 21, 2008 Conteúdo 1 Questões e Motivações 2 Indução do termo tipo Chern-Simons na QED não-massiva
Física de Partículas
 [email protected] http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
[email protected] http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
Física de Partículas
 [email protected] http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
[email protected] http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 1 Ricardo D Elia Matheus O que queremos da Física de Partículas? Animação: Scales of the Universe II http://htwins.net/scale2/
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Física Quântica. Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli. Pieter Westera
 Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera [email protected] http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera [email protected] http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Introdução à Magneto-hidrodinâmica
 Introdução à Magneto-hidrodinâmica Gilson Ronchi November, 013 1 Introdução A magneto-hidrodinâmica é o estudo das equações hidrodinâmicas em uidos condutores, em particular, em plasmas. Entre os principais
Introdução à Magneto-hidrodinâmica Gilson Ronchi November, 013 1 Introdução A magneto-hidrodinâmica é o estudo das equações hidrodinâmicas em uidos condutores, em particular, em plasmas. Entre os principais
Problemas de Duas Partículas
 Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
Efeito Hall quântico fracionário
 Efeito Hall quântico fracionário Ricardo Costa de Almeida Instituto de Física Universidade de São Paulo [email protected] 24 de novembro de 2015 Ricardo Costa de Almeida (USP) FQHE 24 de novembro
Efeito Hall quântico fracionário Ricardo Costa de Almeida Instituto de Física Universidade de São Paulo [email protected] 24 de novembro de 2015 Ricardo Costa de Almeida (USP) FQHE 24 de novembro
A equação de Callan-Symanzik
 Teoria Quântica de Campos II 103 A equação de Callan-Symanzik (Peskin 12.2, Ryder 9.4) Embora o tratamento que fizemos para o campo escalar seja bastante claro do ponto de vista físico ele pode se tornar
Teoria Quântica de Campos II 103 A equação de Callan-Symanzik (Peskin 12.2, Ryder 9.4) Embora o tratamento que fizemos para o campo escalar seja bastante claro do ponto de vista físico ele pode se tornar
JORNADA DE FÍSICA TEÓRICA INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a
 JORNADA DE FÍSICA TEÓRICA 2010 INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 23-07-2010 Monday, July 19, 2010 1 CAMPOS CLÁSSICOS, QUÂNTICOS, DE CALIBRE E POR AÍ AFORA JORNADA DE FÍSICA TEÓRICA 2010 Instituto
JORNADA DE FÍSICA TEÓRICA 2010 INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 23-07-2010 Monday, July 19, 2010 1 CAMPOS CLÁSSICOS, QUÂNTICOS, DE CALIBRE E POR AÍ AFORA JORNADA DE FÍSICA TEÓRICA 2010 Instituto
Física Estatística ??? Representação macroscópica. Representação microscópica. sistema U (S, V, N) S (U, V, N)
 Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Eq. de Dirac com campo magnético
 Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das
 Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das frases abaixo descreve corretamente a menor energia possível
Fundamentos de Física Capítulo 39 Mais Ondas de Matéria Questões Múltipla escolha cap. 39 Fundamentos de Física Halliday Resnick Walker 1) Qual das frases abaixo descreve corretamente a menor energia possível
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
Vitor Oguri Departamento de Física Nuclear e Altas Energias Instituto de Física Armando Dias Tavares Universidade do Estado do Rio de Janeiro (UERJ)
 Vitor Oguri Departamento de Física Nuclear e Altas Energias Instituto de Física Armando Dias Tavares Universidade do Estado do Rio de Janeiro (UERJ) Manaus, 28 de julho de 2015 Descrição eletromagnética
Vitor Oguri Departamento de Física Nuclear e Altas Energias Instituto de Física Armando Dias Tavares Universidade do Estado do Rio de Janeiro (UERJ) Manaus, 28 de julho de 2015 Descrição eletromagnética
ENRICO BERTUZZO (DFMA-IFUSP) UMA INTRODUÇÃO À FÍSICA DE PARTÍCULAS
 ENRICO BERTUZZO (DFMA-IFUSP) UMA INTRODUÇÃO À FÍSICA DE PARTÍCULAS PLANO DO CURSO Aula 1- Uma história da Física de Partículas (parte 1: 1897-1936) Aula 2 - Uma história da Física de Partículas (parte
ENRICO BERTUZZO (DFMA-IFUSP) UMA INTRODUÇÃO À FÍSICA DE PARTÍCULAS PLANO DO CURSO Aula 1- Uma história da Física de Partículas (parte 1: 1897-1936) Aula 2 - Uma história da Física de Partículas (parte
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi
 Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
Corrente elétrica. GRANDE revolução tecnológica. Definição de corrente Controle do movimento de cargas
 Definição de corrente Controle do movimento de cargas corrente elétrica{ GANDE revolução tecnológica fi eletrotécnica, eletrônica e microeletrônica (diversidade de aplicações!!) Ex. motores elétricos,
Definição de corrente Controle do movimento de cargas corrente elétrica{ GANDE revolução tecnológica fi eletrotécnica, eletrônica e microeletrônica (diversidade de aplicações!!) Ex. motores elétricos,
1 Regras de Feynman para QED
 1 Regras de Feynman para QED Decaimentos e espalhamentos que geram duas partículas no estado final são descritas da seguinte maneira no CM: Γ = p f 3π M dω 1) s onde s é a energia do centro de massa; e
1 Regras de Feynman para QED Decaimentos e espalhamentos que geram duas partículas no estado final são descritas da seguinte maneira no CM: Γ = p f 3π M dω 1) s onde s é a energia do centro de massa; e
2.2.1 Efeito Hall e Magnetoresistência Condutividade Elétrica AC Corrente Elétrica em um Campo Magnético
 Conteúdo 1 Revisão de Física Moderna 1 1.1 Equação de Schrödinger; Autoestados e Valores Esperados.. 1 1.2 O Poço de Potencial Innito:Quantização da Energia.............................. 7 1.3 O Oscilador
Conteúdo 1 Revisão de Física Moderna 1 1.1 Equação de Schrödinger; Autoestados e Valores Esperados.. 1 1.2 O Poço de Potencial Innito:Quantização da Energia.............................. 7 1.3 O Oscilador
Física Moderna II Aula 08. Marcelo G Munhoz Edifício HEPIC, sala 202, ramal
 Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 [email protected] 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 [email protected] 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Campo Escalar Complexo
 Finalmente consideremos: Teoria Quântica de Campos I 60 operador na representação de Schödinger, basta partir de 59.2 e usar lembrando que: É uma superposição de vários estados de uma partícula (cada um
Finalmente consideremos: Teoria Quântica de Campos I 60 operador na representação de Schödinger, basta partir de 59.2 e usar lembrando que: É uma superposição de vários estados de uma partícula (cada um
Magnetismo e movimento de cargas. Fontes de Campo Magnético. Prof. Cristiano Oliveira Ed. Basilio Jafet sala 202
 Eletricidade e Magnetismo - IME Fontes de Campo Magnético Prof. Cristiano Oliveira Ed. Basilio Jafet sala 202 [email protected] Magnetismo e movimento de cargas Primeira evidência de relação entre magnetismo
Eletricidade e Magnetismo - IME Fontes de Campo Magnético Prof. Cristiano Oliveira Ed. Basilio Jafet sala 202 [email protected] Magnetismo e movimento de cargas Primeira evidência de relação entre magnetismo
Aula-11. (quase) Tudo sobre os átomos
 Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
Liberdade assintótica na cromodinâmica quântica
 Liberdade assintótica na cromodinâmica quântica Emmanuel Gräve de Oliveira Grupo de Fenomenologia de Partículas de Altas Energias Instituto de Física Universidade Federal do Rio Grande do Sul Porto Alegre
Liberdade assintótica na cromodinâmica quântica Emmanuel Gräve de Oliveira Grupo de Fenomenologia de Partículas de Altas Energias Instituto de Física Universidade Federal do Rio Grande do Sul Porto Alegre
Resolução Abreviada. Q R 2 + z 2. V (z) = 1 Q. dv (r) = r. dq R 2 + z 2 = 1
 1º teste Electromagnetismo e Óptica MEEC Resolução Abreviada 14 de Novembro de 217, 2h Duração: 1h3 Docentes: Prof Eduardo V Castro (responsável); Prof António Jorge ilvestre; Prof Hugo Terças; Prof Luís
1º teste Electromagnetismo e Óptica MEEC Resolução Abreviada 14 de Novembro de 217, 2h Duração: 1h3 Docentes: Prof Eduardo V Castro (responsável); Prof António Jorge ilvestre; Prof Hugo Terças; Prof Luís
MATERIAL PARA ESTUDO, FAVOR NÃO DIVULGAR ONLINE, POIS FALTA CITAR VÁRIOS AUTORES QUE FORAM APRESENTAÇÃO.
 MATERIAL PARA ESTUDO, FAVOR NÃO DIVULGAR ONLINE, POIS FALTA CITAR VÁRIOS AUTORES QUE FORAM USADOS NA CONFECÇÃO DESSA APRESENTAÇÃO. Mini-Curso:Introdução aos Isolantes Topológicos. Leandro Oliveira do Nascimento
MATERIAL PARA ESTUDO, FAVOR NÃO DIVULGAR ONLINE, POIS FALTA CITAR VÁRIOS AUTORES QUE FORAM USADOS NA CONFECÇÃO DESSA APRESENTAÇÃO. Mini-Curso:Introdução aos Isolantes Topológicos. Leandro Oliveira do Nascimento
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 11 MOLÉCULAS Primeira Edição junho de 2005 CAPÍTULO 11 MOLÉCULAS ÍNDICE 11-1- Introdução 11.2- Ligação por Tunelamento e a Molécula
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 11 MOLÉCULAS Primeira Edição junho de 2005 CAPÍTULO 11 MOLÉCULAS ÍNDICE 11-1- Introdução 11.2- Ligação por Tunelamento e a Molécula
Marina Nielsen Instituto de Física USP
 Marina Nielsen Instituto de Física USP Marina Nielsen Instituto de Física USP Introdução à QCD: Elementos Invariância de gauge Introdução às Regras de Soma da QCD Partículas Elementares (metade do sec.
Marina Nielsen Instituto de Física USP Marina Nielsen Instituto de Física USP Introdução à QCD: Elementos Invariância de gauge Introdução às Regras de Soma da QCD Partículas Elementares (metade do sec.
3) Quais são os valores possíveis do número quântico magnético de spin? a) -1,- ½,0, ½,1 b) 0 e + ½ c) 1, 0 e +1 d) 0, 1, 2, 3,...
 Fundamentos de Física Capítulo 40 Tudo sobre átomos. Questões Múltipla escolha cap. 40 Fundamentos de Física Halliday Resnick Walker 1) Qual das opções abaixo não é uma propriedade dos átomos? a) Os átomos
Fundamentos de Física Capítulo 40 Tudo sobre átomos. Questões Múltipla escolha cap. 40 Fundamentos de Física Halliday Resnick Walker 1) Qual das opções abaixo não é uma propriedade dos átomos? a) Os átomos
Teoria Clássica de Campos
 Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
Equações de Maxwell e densidades Lagrangiana e Hamiltoniana do eletromagnetismo clássico
 Equações de Maxwell e densidades Lagrangiana e Hamiltoniana do eletromagnetismo clássico André Juan Ferreira Martins de Moraes Resumo Estas notas se baseiam na Seção 1.1 do artigo 1, na qual as equações
Equações de Maxwell e densidades Lagrangiana e Hamiltoniana do eletromagnetismo clássico André Juan Ferreira Martins de Moraes Resumo Estas notas se baseiam na Seção 1.1 do artigo 1, na qual as equações
FÍSICA (ELETROMAGNETISMO) CORRENTE ELÉTRICA E RESISTÊNCIA
 FÍSICA (ELETROMAGNETISMO) CORRENTE ELÉTRICA E RESISTÊNCIA FÍSICA (Eletromagnetismo) Nos capítulos anteriores estudamos as propriedades de cargas em repouso, assunto da eletrostática. A partir deste capítulo
FÍSICA (ELETROMAGNETISMO) CORRENTE ELÉTRICA E RESISTÊNCIA FÍSICA (Eletromagnetismo) Nos capítulos anteriores estudamos as propriedades de cargas em repouso, assunto da eletrostática. A partir deste capítulo
A Estrutura Eletrônica dos Átomos. Prof. Fernando R. Xavier
 A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
A solução de Onsager para o modelo de Ising em 2D: a complexidade do Magnetismo Quântico
 A solução de Onsager para o modelo de Ising em 2D: a complexidade do Magnetismo Quântico Ivan de Paula Miranda Nanomagnetismo Redução do tamanho efeitos quânticos individuais Desenvolvimento de técnicas
A solução de Onsager para o modelo de Ising em 2D: a complexidade do Magnetismo Quântico Ivan de Paula Miranda Nanomagnetismo Redução do tamanho efeitos quânticos individuais Desenvolvimento de técnicas
Física da Matéria Condensada - GFI 04129
 Física da Matéria Condensada - GFI 04129 Antonio T. Costa I semestre, 2007 Programa 1 A estrutura eletrônica de sólidos cristalinos a O que é um sólido cristalino b Comportamento do elétron num sólido
Física da Matéria Condensada - GFI 04129 Antonio T. Costa I semestre, 2007 Programa 1 A estrutura eletrônica de sólidos cristalinos a O que é um sólido cristalino b Comportamento do elétron num sólido
Ronaldo Thibes Universidade Estadual do Sudoeste da Bahia Campus de Itapetinga DCEN Dez 2017
 QFT O que é e porque precisamos Ronaldo Thibes Universidade Estadual do Sudoeste da Bahia Campus de Itapetinga DCEN Dez 2017 Aquecimento Inicial - A teoria da relatividade torna tempo e espaço completamente
QFT O que é e porque precisamos Ronaldo Thibes Universidade Estadual do Sudoeste da Bahia Campus de Itapetinga DCEN Dez 2017 Aquecimento Inicial - A teoria da relatividade torna tempo e espaço completamente
Introdução. O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico.
 Ressonância de Spin Introdução O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico. Nos próximos slides apresentaremos, brevemente, alguns aspectos
Ressonância de Spin Introdução O spin é uma propriedade das partículas elementares, eminentemente quântica, sem equivalente no mundo clássico. Nos próximos slides apresentaremos, brevemente, alguns aspectos
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Física 4. Ótica e Física moderna. Profa. Keli F. Seidel
 Física 4 Ótica e Física moderna Informações Gerais Site https://kelifisica.wordpress.com/utfpr/ https://kelifisica.wordpress.com/utfpr/fisica-3-experimental/ Informações sobre: - plano de ensino; - Datas
Física 4 Ótica e Física moderna Informações Gerais Site https://kelifisica.wordpress.com/utfpr/ https://kelifisica.wordpress.com/utfpr/fisica-3-experimental/ Informações sobre: - plano de ensino; - Datas
estrutura atômica e ligações
 Aula 02 estrutura atômica e ligações ZEA 1038 Ciência e Tecnologia dos Materiais Prof. João Adriano Rossignolo Profa. Eliria M.J.A. Pallone introdução conceitos elementares a estrutura dos átomos a estrutura
Aula 02 estrutura atômica e ligações ZEA 1038 Ciência e Tecnologia dos Materiais Prof. João Adriano Rossignolo Profa. Eliria M.J.A. Pallone introdução conceitos elementares a estrutura dos átomos a estrutura
Equações de Dyson-Schwinger e identidades de Ward
 Teoria Quântica de Campos I 168 Que, em diagramas fica: consigo gerar qualquer diagrama em árvore, mas nunca um loop Isso quer dizer que os diagramas em nível árvore são clássicos (no sentido mais geral
Teoria Quântica de Campos I 168 Que, em diagramas fica: consigo gerar qualquer diagrama em árvore, mas nunca um loop Isso quer dizer que os diagramas em nível árvore são clássicos (no sentido mais geral
Circuitos resistivos alimentados com onda senoidal
 Circuitos resistivos alimentados com onda senoidal 3 3.1 Material resistores de 1 kω e 100 Ω. 3.2 Introdução Nas aulas anteriores estudamos o comportamento de circuitos resistivos com tensão constante.
Circuitos resistivos alimentados com onda senoidal 3 3.1 Material resistores de 1 kω e 100 Ω. 3.2 Introdução Nas aulas anteriores estudamos o comportamento de circuitos resistivos com tensão constante.
Tópico 01: Estudo de circuitos em corrente contínua (CC) Profa.: Ana Vitória de Almeida Macêdo
 Disciplina Eletrotécnica Tópico 01: Estudo de circuitos em corrente contínua (CC) Profa.: Ana Vitória de Almeida Macêdo Conceitos básicos Eletricidade Eletrostática Eletrodinâmica Cargas elétricas em repouso
Disciplina Eletrotécnica Tópico 01: Estudo de circuitos em corrente contínua (CC) Profa.: Ana Vitória de Almeida Macêdo Conceitos básicos Eletricidade Eletrostática Eletrodinâmica Cargas elétricas em repouso
O poço de potencial finito
 O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 4 Ref. Butkov, cap. 8, seção 8.4
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 4 Ref. Butkov, cap. 8, seção 8.4 Equação da Difusão Um problema importante para vários ramos da Física é saber como
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 4 Ref. Butkov, cap. 8, seção 8.4 Equação da Difusão Um problema importante para vários ramos da Física é saber como
n Camadas K L M N...
 Notação Espectroscópica para Configurações Eletrônicas em Átomos. Modelo de Partícula Independente. Podemos obter uma quantidade expressiva importante de informações sobre estados atômicos de sistemas
Notação Espectroscópica para Configurações Eletrônicas em Átomos. Modelo de Partícula Independente. Podemos obter uma quantidade expressiva importante de informações sobre estados atômicos de sistemas
AULA 01 TEORIA ATÔMICA COMPLETA
 AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. QUÍMICA estudo
AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. QUÍMICA estudo
Fundamentos da Eletrostática Aula 05 A Lei de Coulomb e o Campo Elétrico
 A lei de Coulomb Fundamentos da Eletrostática Aula 5 A Lei de Coulomb e o Campo Elétrico Prof. Alex G. Dias Prof. Alysson F. Ferrari Conforme mencionamos anteriormente, trataremos neste curso de distribuções
A lei de Coulomb Fundamentos da Eletrostática Aula 5 A Lei de Coulomb e o Campo Elétrico Prof. Alex G. Dias Prof. Alysson F. Ferrari Conforme mencionamos anteriormente, trataremos neste curso de distribuções
Teoria Quântica de Campos
 Teoria Quântica de Campos I 1 Teoria Quântica de Campos (escopo do curso e um pouco de história) (Weinberg cap 1, Peskin 2.1, Nastase 1) Objetivo: uma teoria Quântica e Relativística (no sentido restrito)
Teoria Quântica de Campos I 1 Teoria Quântica de Campos (escopo do curso e um pouco de história) (Weinberg cap 1, Peskin 2.1, Nastase 1) Objetivo: uma teoria Quântica e Relativística (no sentido restrito)
Equação de Schrödinger em 3D
 Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
(x 1, y 1 ) (x 2, y 2 ) = (x 1 x 2, y 1 y 2 ); e α (x, y) = (x α, y α ), α R.
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-2457 Álgebra Linear para Engenharia I Terceira Lista de Exercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Considere as retas
Bilineares do Campo de Dirac. Analogamente:
 Teoria Quântica de Campos I 133 ( eq. 133.1 ) Analogamente: ( eq. 133.2 ) Bilineares do Campo de Dirac Claramente, qualquer grandeza observável vai ter que ser composta do produto de um número par de campos
Teoria Quântica de Campos I 133 ( eq. 133.1 ) Analogamente: ( eq. 133.2 ) Bilineares do Campo de Dirac Claramente, qualquer grandeza observável vai ter que ser composta do produto de um número par de campos
Sumário. 1 Introdução Álgebra Vetorial Cálculo Vetorial 62
 Sumário 1 Introdução 18 1-1 Linha do Tempo Histórico 19 1-1.1 Eletromagnetismo na Era Clássica 19 1-1.2 Eletromagnetismo na Era Moderna 20 1-2 Dimensões, Unidades e Notação 21 1-3 A Natureza do Eletromagnetismo
Sumário 1 Introdução 18 1-1 Linha do Tempo Histórico 19 1-1.1 Eletromagnetismo na Era Clássica 19 1-1.2 Eletromagnetismo na Era Moderna 20 1-2 Dimensões, Unidades e Notação 21 1-3 A Natureza do Eletromagnetismo
Lista 3 - FIS Relatividade Geral Curvatura, campos de Killing, fluidos, eletromagnetismo.
 Lista 3 - FIS 404 - Relatividade Geral Curvatura, campos de Killing, fluidos, eletromagnetismo. 2 quadrimestre de 2017 - Professor Maurício Richartz Leitura sugerida: Carroll (seções 3.1-3.4,3.6-3.8),
Lista 3 - FIS 404 - Relatividade Geral Curvatura, campos de Killing, fluidos, eletromagnetismo. 2 quadrimestre de 2017 - Professor Maurício Richartz Leitura sugerida: Carroll (seções 3.1-3.4,3.6-3.8),
FÍSICA 3 FCI0105/2016
 FÍSICA 3 FCI0105/2016 SUMÁRIO DO PROGRAMA 1. Cargas, força & campo elétrico 1.1. Carga elétrica, tipos de força e eletrização 1.2. Cargas da matéria: o átomo, quantização e conservação 1.3. Condutores,
FÍSICA 3 FCI0105/2016 SUMÁRIO DO PROGRAMA 1. Cargas, força & campo elétrico 1.1. Carga elétrica, tipos de força e eletrização 1.2. Cargas da matéria: o átomo, quantização e conservação 1.3. Condutores,
h mc 2 =hν mc 2 =hc/ λ
 Louis de Broglie investigou as propriedades ondulatórias da matéria na década de 30. Ele supôs que o e-, em seu movimento ao redor do núcleo, tinha associado a ele um λ. Ele igualou as duas expressões
Louis de Broglie investigou as propriedades ondulatórias da matéria na década de 30. Ele supôs que o e-, em seu movimento ao redor do núcleo, tinha associado a ele um λ. Ele igualou as duas expressões
1.1. IMPORTÂNCIA DOS MATERIAIS
 INTRODUÇÃO AOS MATERIAIS DE ENGENHARIA O material disponibilizado nesta apostila do curso de Ciência dos Materiais objetiva apresentar os fundamentos e a interrelação entre os diferentes níveis de estrutura
INTRODUÇÃO AOS MATERIAIS DE ENGENHARIA O material disponibilizado nesta apostila do curso de Ciência dos Materiais objetiva apresentar os fundamentos e a interrelação entre os diferentes níveis de estrutura
Átomo de Hidrogênio 1
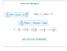 Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Física de Partículas
 [email protected] http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 3 Ricardo D Elia Matheus Construindo o Modelo Padrão da Física de Partículas Onde estamos: sabemos qual teoria usar
[email protected] http://www.ift.unesp.br/users/matheus/ Física de Partículas Parte 3 Ricardo D Elia Matheus Construindo o Modelo Padrão da Física de Partículas Onde estamos: sabemos qual teoria usar
Capítulo 5 - Aplicações das leis de Newton. Hoje reconhecemos 4 forças da natureza. São elas (em ordem crescente de
 Capítulo 5 - Aplicações das leis de Newton Hoje reconhecemos 4 forças da natureza. São elas (em ordem crescente de intensidade) Força Gravitacional Força Fraca Intensidade Força Eletromagnética Força Forte
Capítulo 5 - Aplicações das leis de Newton Hoje reconhecemos 4 forças da natureza. São elas (em ordem crescente de intensidade) Força Gravitacional Força Fraca Intensidade Força Eletromagnética Força Forte
