Eq. de Dirac com campo magnético

Transcrição

1 Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias

2 Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada em campo mag.

3 Partícula em campo magnético O campo magnético não altera a energia cinética do sistema (=> campo elétrico, pois W B =0), contudo altera a direção da velocidade (e do momentum linear): F = q E l +q v B Se E = 0 temos um movimento circular (freq. de cíclotron): ω c = q B m Vamos escrever a hamiltoniana do sistema, ao invés de trabalhar com a Força de Lorentz. H = K + U

4

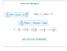
5 Do modelo de Bohr: L = n ħ Então para n = 1, no caso de um elétron no nível fundamental: μ B = e ħ 2 m e (magneton de Bohr) μ B = 0, A m 2 = 5, ev /T Precessão de Larmor: ω L = q B 2 m μ l = μ B ħ L

6 Em termos do potencial eletrostático: De maneira análoga: E l U el U mag = V = q V (r) = B μ Hamiltoniana: U mag = q 2 m B L H = K + U ^H = ^p 2 2 m + ^U (r) + ^U mag

7 Partícula livre carregada em campo E e B E l = A t V ; B = A Neste caso V não é mais eletrostático. E tot = 1 2 m v 2 + qv p tot = m v + q A Usando o princípio da correspondência (clássico quântico): ^H = 1 2 m ^p 2 cin + q ^V ^p tot = i ħ = ^p cin + q ^A

8 ^p cin = i ħ ^ q ^A ^H = 1 2 m ^p 2 cin + q ^V ^H = 1 2 m [ i ħ q A]2 + q ^V Partícula livre e carregada sob influência de campos elétrico e magnético, caso não-relativístico. ^H Ψ = E Ψ p i ħ ; E i ħ t p i ħ q A

9 Elétron livre num campo magnético uniforme Podemos escrever o potencial vetor na forma: tal que: A = (0,B 0 x,0) = B 0 x ^j B = A=B 0 ^k Hamiltoniana (com V = 0, pois E = 0): ^H = 1 2 m [ i ħ q ^A] 2 ^H = 1 2 m [ ^p+e B 0 ^x ^j] 2

10 Lembrando que: ^H = 1 2 m [ ^p 2 + e B 0 ^p ^x ^j + e B 0 ^x ^j ^p + e 2 B 02 ^x 2 ] ^H = 1 2 m [ ^p 2 + e B 0 ^ p y ^x + e B 0 ^x ^p y + e 2 B 02 ^x 2 ] [ x i, p i ] = i ħ δ ij ; [ x, p y ] = 0 ; p y = i ħ t ^H = 1 2 m [ p2 + 2 e B 0 p y x + e 2 B 0 2 x 2 ] Também temos que: d d t ^O = i ħ [ ^H, ^O] + ( ^O t ) Se comuta com H, < O > é cte no tempo, há uma grandeza cujo valor esperado é conservada; também forma uma base com H; autofunções...

11 ^H = 1 2 m [ p 2 x + p 2 y + p 2 z + 2e B 0 p y x + e 2 B 2 0 x 2 ] ^H = 1 2 m [ p 2 x + p 2 z + ( p y + e B 0 x) 2 ] ^H = ħ2 2 m [ 2 x z 2 ( + y + i e B 0 ħ x)2] Fazemos: [ p i, H ] = 1 2m [ 2e B 0 ( p i x p y x p y p i ) + e 2 B 0 2 ( p i x 2 x 2 p i ) ] p i x p y x p y p i = [ p i, x p y ] = x [ p y, p i ] [ x, p i ] p y encontramos que p y e p z comutam com H...

12 Podemos escrever: (i p r Et )/ħ Ψ( x, y, z,t ) = A e Tomando a parte espacial, e escrevendo p i = ħ k i Ψ( x, y, z) = Ψ(x) e i k y y e i k z z Com o hamiltoniano obtido anteriormente: ^H = ħ2 2 m [ 2 x z 2 ( + y + i e B 0 ħ x)2] podemos aplicar em: ^H Ψ = E Ψ obtendo:

13 [ ħ2 2m 2 + ħ 2 x 2 2 2m k y + e B 0 m x ħ k y+ e2 B 2 0 x 2 2m ] Ψ (x) = ( E ħ2 2 k z ) Ψ( x) 2 m a qual podemos escrever como: [ ħ2 2 m 2 x 2 2] + mω 2 c 2 ( x x 0) Ψ (x) = E ' Ψ (x) que tem a forma da equação para o oscilador harmônico quântico (centrado em x 0 ), com frequência ω c sendo: logo: x 0 = ħ k y e B 0 = p y ; ω e B c = e B 0 0 m E '=E n = ( n+ 1 2 ) ħ ω c com n = 0,1,2,3,...

14 Neste caso podemos escrever: E n = p z 2 2m + ( n+ 1 2 ) ħ ω c onde n representa os níveis de Landau. (x 0 não comuta com y, o centro da órbita tem coordenada y que não é bem definida, k y ou p y é limitado pelo sistema)

15 Caso relativístico eq. de Dirac - descreve férmions de spin ½ - energia relativística - quadri-vetores - invariância de Lorentz usando unidades naturais (c = h = 1) E 2 = p 2 c 2 + m 2 c 4 onde: E 2 = p 2 + m 2 p μ = (p 0, p) = ( E/c, p) Através de: ^p i ħ ^ ; ^E i ħ t

16 Novamente usando: obtém-se: ħ 2 2 Ψ t 2 H Ψ = E Ψ = ħ 2 c 2 2 Ψ + m 2 c 4 Ψ que é a equação de Klein-Gordon, sendo posteriormente verificado que descreve partículas de spin 0. Buscando uma equação linear em t, respeitando a energia relativística, Dirac então seguiu por outro caminho. Lembrando que: p μ p μ = m 2 c 2 E 2 = p 2 c 2 + m 2 c 4 Dirac propôs: p μ p μ m 2 c 2 = 0 p μ p μ m 2 c 2 = (β i p i +mc)(γ j p j m c) = 0

17 p μ p μ m 2 c 2 = (β κ p κ +mc)(γ λ p λ mc) = 0 que fica: β κ γ λ p κ p λ m c(β κ γ κ ) p κ m 2 c 2 = 0 Para resultar em: p μ p μ m 2 c 2 = 0 basta determinar. Como não interessam termos lineares em p i, significa: β κ, γ κ β κ = γ κ γ κ γ λ p κ p λ m 2 c 2 = 0 p μ p μ = γ κ γ λ p κ p λ Abrindo a expressão acima, obtemos que os gamas são matrizes 4x4.

18 γ 0 = ( i, γ ) = ( 0 σi σ i 0 ) onde as matrizes de Pauli são dadas por: σ 1 = ( ), σ 2 = ( 0 i i 0 ), σ 3 = ( ) Deste modo, a equação: Pode ser escrita como: (β κ p κ + mc)( γ λ p λ m c) = 0 (γ μ p μ + mc)(γ μ p μ mc) = 0

19 ( de onde obtemos: (γ μ p μ m c) = 0 Voltando a usar a equação de autovalores e autofunções: chegamos em: H Ψ = E Ψ (i ħ γ μ μ m c)ψ = 0 eq. de Dirac sendo agora: Ψ = ψ 1 ψ 2 4) ψ 3 ψ e μ = x μ = ( 1 c t, i)

20 Podemos escrever: p μ p μ q c A μ Na eq. de Dirac, de modo análogo ao efetuado na eq. de Schödinger: [γ μ p μ m c]ψ = 0 resulta em: [ γμ ( p μ q c A μ) mc] Ψ = 0 Em unidades naturais ( c = h = 1, sendo massa e momentum em MeV) ou [ γ μ ( p μ q A μ ) m ] Ψ = 0 [γ μ (i μ q A μ ) m]ψ = 0

21 Eq. de Dirac em campo magnético Na verdade usamos a eq. de Dirac para uma partícula livre com spin ½ e carga elétrica 'q' na presença de um campo magnético. (i ħ γ μ μ m c)ψ = 0 De modo geral (com campo E l e B): agora temos quadri-potencial: e o quadri-momentum: sem campos: A μ = (cv, A ) p μ = ( 1 c (E cv ), p q c A ) p μ = ( E c, p ) p i p i q c A, p 0 p 0 V

22 ( Abrindo a eq. Na ausência de campo elétrico ( A 0 = 0) onde: Ψ = ψ 1 ψ 2 ψ 3 ψ 4) = (u A u B ) Precisamos resolver a eq. de autovalor:

23 Para um campo uniforme na direção z, escolhemos: B = B ^k e em termos do quadri-potencial eletromagnético: Assim: Usando as regras de comutação:

24 obtemos: sendo o último termo: Então: Dando origem a duas equações por causa de σ z As coordenadas x 0 [t], x e z não aparecem explicitamente, suas soluções podem ser escritas como ondas planas. Assim podemos fazer:

25 As duas equação se diferenciam pelos autovalores da matriz σ z, ou seja s = ± 1. Usando regras de comutação para operadores p, podemos escrever as duas equações como: Fazendo uma substituição de variáveis: Então:

26 Reescrevendo: Esta equação possui a mesma forma da equação para o oscilador harmônico quântico. Livro do Eisberg: d 2 F s d ξ 2 + ( β α ξ2 ) F s = 0

27 FIM! Obrigado.

28 Assim, para que a solução exista temos a seguinte condição: e os autovalores da energia passam a ser: Tendo então que analisar os autovalores em função de l e s. Exemplos: p = ħ k, (ħ=c=1 p = k) l = 0 e s = 1 => l = 0 e s = -1 => l = 1 e s = 1 => E = m 2 + p z 2 E = m 2 + p z 2 +2 e B

29 Por causa da degenerescência, podemos escrever a energia de um férmion de spin ½ num campo magnético uniforme em função de um único parâmetro: E = m 2 + p z 2 + 2ν e B onde ν representa os níveis de Landau. Próximo passo: estudar a densidade de estados para um gás de Férmi.

30 FIM! OBRIGADO!!!

31 Alguns Links: /Nu1X19gjnfg/s1600/precesion+en+presencia+de+campo+magnetico.png