CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 1 a FICHA DE EXERCÍCIOS 1 [
|
|
|
- Manuel Azevedo Ferretti
- 6 Há anos
- Visualizações:
Transcrição
1 Instituto Superior Técnico Departamento de Matemática CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT o SEM. 04/5 a FICHA DE EXERCÍCIOS 0. Desigualdades e Módulos. Mostre que:.. R : + < =, 7, +.. R : + = 7,.. R : + =, 7, +.4. R : + > =, 7.5. R : + < =, 5, +.6. R : + = 5,.7. R : + =, 5, +.8. R : + > =, 5.9. R : + < =, +.0. R : + =,.. R : + =,.. R : + > =, +.. R : + < =,, +.4. R : + =,,.5. R : + > =,,.6. R : + =,, +.7. R : + 4 < =,, +.8. R : + 4 =,,.9. R : 4 + > =,,.0. R : 4 + =,, +.. R : 7 < =, 7, +.. R : 7 =, 7,.. R : =, 7,.4. R : > =, 7, +
2 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA. Mostre que:.. R : + = = 5,.. R : + =,.. R : > =, 5, +.4. R : < < =,,.5. R : < 5 =, 5, 7.6. R : > 0 = 0, 5, +.7. R : + + > 0 =,.8. R : 4 < =,.9. R : 4 + > =,, +.0. R : 5 =, 7.. R : 5 + =, 7, +.. R : 4 + > 5 =,, +.. R : 4 < 5 =,.4. R : 5 + =,, R : 5 =, 5.6. R : 4 =, 5.7. R : + 4 =, 5, +.8. R : + > 5 =, 4, +.9. R : < 5 =, 4.0. R : < =,.. R : + > =,, +.. R : 5 4 =, 5.. R : =,, R : 5 < =,.5. R : + 5 > =,, +.6. R : 5 6 =,.7. R : 6 5 > =,, +.8. R : 9 < = 4, 5.9. R : 9 =, 4 5, +.0. R : 4 < 8 = 4, 4.. R : 4 8 =, 4 4, +.. R : 4 7 =, 5.. R : 4 > 7 =, 5, +.4. R : 7 =, 4.5. R : 7 > =, 4, +.6. R : 5 < 9 =, 7.7. R : 5 9 =, 7, +.8. R : 5 < = 4,.9. R : 5 =, 4, R : < + 5 = 8, 5,
3 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA. Mostre que:.. R : + =, 5, +.. R : = =.. R : =,.4. R : 5 =, 4, +.5. R : 6 5 < 8 =,, R : =, 7.7. R : 9 < 8 =, 4, +.8. R : 9 8 = 4,.9. R : =,, +.0. R : 4 > 9 8 =,.. R : 4 < 7 6 =,, +.. R : =,.. R : 7 < 6 =,, +.4. R : 7 6 =,.5. R : =, 7, +.6. R : 5 > 4 9 =, 7.7. R : 5 4 =, 4 6, R : 5 > 4 = 4, R : =,.0. R : > =,, +.. R : =,, +.. R : 9 4 < 6 =,.. R : =,.4. R : + 4 > + 8 =,, +.5. R : 5 + =, 0, +.6. R : 5 < + = 0,.7. R : =, 4.8. R : 4 7 > + =, 4, +.9. R : =, 0, +.0. R : 4 5 < + 4 = 0,.. R : 7 + =, 8.. R : 7 > + =, 8, +.. R : 5 < =, 4.4. R : + = 5,.5. R : 5 < 7 6 =, 4, +.6. R : =, 4.7. R : > 4 9 =,.8. R : 9 4 =,, +.9. R : 5 > 4 =,, R : 5 4 =,
4 4 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA 4. Mostre que: 4.. R : 4 < < 9 =,, 4.. R : 9 ( ) < 5 = 4, 4, R : > 0 0 =,, 4.4. R : > 0 =, 4.5. R : 0 =,, R : > 0 =, 4.7. R : =,, 4.8. R : + = 5 =, R : + < 5 =, R : =, 4 7, + 7 6, R : + 5 < 9 = 6, 7 + 7, R : 4 > =, 7, + 7, R : + 4 = 7,, R : 5 + =, 0, 5, R : < = 5,, R : + 4 > =, 5 5, + 5, R : + 4 =, 5 + 5, R : 5 =,,, R : + 5 < =,, 4.0. R : + 4 > =, 0 0, R : + 4 = 0, 4 0, R : + =, 4, 0, R : + < =, 0, R : 5 + =, 0, 4 5, R : < = 5, 4, R : > =, 0,, R : + =, 0, 4.8. R : + 4 > =,, 0, R : + 4 =, 0, 4.0. R : + 7 =, 5 4,, R : 7 < =, 4, R : 4 =,,, R : 4 < =,, 4.4. R : + > =, 5,, R : + =,, R : > =, 4 5, R : 5 4 =, 0 4, R : =, 5 9, 4.9. R : < 4 =, 5, 9 5, + 5, + 5, +
5 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA 5 5. Mostre que: 5.. R : ( ) = =,,, R : ( ) > =,, +, R : =,,, 5.4. R : =, R : + 4 > + = 5, + 5, 5.6. R : 4 > =, 5, R : =,, R : = 4,, 5.9. R : < =,, R : + < + =, +, 5.. R : > =,, 5.. R : 5 4 > 4 5 =,, 5.. R : =,, 5.4. R : + + =,, 5.5. R : = 5, 5, R : 5 = 5, 5, R : + < + 4 =,, 5.8. R : < 4 =,, 5.9. R : + > + =,, R : =,, R : + + =, 5.. R : < =,, 5.. R : =,,, R : 4 > =,,, R : + + =,,, R : < =,,, R : =,, 4 4, R : 8 > =,, 4 4, R : =, 7 + 7, R : 6 < 4 =, 7 + 7, +
6 6 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA I. Indução Matemática. Demonstre por indução as relações seguintes (entre parentesis, cada relação é escrita usando o símbolo de somatório, cf. eercícios do grupo II). (a) n = n(n + )/ para qualquer n N. ( n = n(n + )/ ) (b) (n ) = n para qualquer n N. ( n ( ) = n ) (c) n = n(n + )(n + )/6 para qualquer n N. ( n = n(n + )(n + )/6 ) (d) n = ( n) para qualquer n N. ( n = ( n ) ) (e) (n ) < n 4 /4 < n para qualquer n N. ( n ( ) < n 4 /4 < n ) (f) / + / + + / n > ( n para qualquer n N tal que n. n / > ) n. Seja P (n) a proposição: n + n + é par para todo o n N. (a) Mostre que se P () é verdadeira para um dado N, então P ( + ) também é verdadeira. (b) Critique a afirmação: Por indução fica provado que P (n) é verdadeira para todo o n N. (c) Prove que n + n + é ímpar para todo o n N.. Seja P (n) a proposição: n = (n + ) /8 para todo o n N. (a) Mostre que se P () é verdadeira para um dado N, então P ( + ) também é verdadeira. (b) Critique a afirmação: Por indução fica provado que P (n) é verdadeira para todo o n N. (c) Modifique P (n), mudando a igualdade para uma desigualdade que seja verdadeira para todo o n N. 4. Mostre a desigualdade de Bernoulli, i.e. ( + ) n + n para qualquer n N e qualquer R tal que.
7 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA 7 II. Símbolo de Somatório Dado n N e uma sequência de números reais a, a,..., a n R, o símbolo de somatório n a define-se por recorrência da seguinte forma: ( n ) a = a se n =, a = a + a n se n >. Resolva os eercícios seguintes com base nesta definição.. Determine os valores numéricos das seguintes somas: (a) (i ) ; (b) ( 4) ; (c) j(j + )(j + ) ; i= (e) j j ; j= (f) j= 7 ( ) ( ) ; (g) 5 n= n(n + ). (d) 4 6 ;. Demonstre as seguintes propriedades do somatório: (a) n (a + b ) = n a + n b (propriedade aditiva); (b) n (c a ) = c n a para qualquer constante c R (homogeneidade); (c) n (a a ) = a n a 0 (propriedade telescópica).. Utilizando os resultados do Eercício I. e as propriedades anteriores do somatório, calcule: (a) 8 (d) ( + ) ; (b) 0 ( + 4. Mostre que para qualquer n N 0 ) ( ) ; (c) ; (e) ( + ) = 0 n n + 5 ( +). ( ) ; pelos seguintes dois métodos distintos: (a) usando indução. (b) observando que = e usando as propriedades do Eercício. (+) + 5. Mostre que para qualquer n N e quaisquer números reais a, b R é válida a igualdade a n b n = (a b) a n b. i=
8 8 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA 6. Mostre que para quaisquer n N e r R com r r = rn+ r =0 pelos seguintes dois métodos distintos: (a) usando indução. (b) aplicando as propriedades do Eercício a ( r) n A que é igual a soma quando r =? Nota: por definição, r 0 =. =0 r. 7. O símbolo n!, designado por n-factorial, define-se por recorrência da seguinte forma: 0! = e n! = n (n )!, para qualquer n N. Observe que n! = n. Dados inteiros 0 n, o coeficiente binomial ( n ) (às vezes também representado por C n ) é definido por ( ) n n! =!(n )!. (a) Mostre que ( ) ( ) n n = n e ( ) n + = ( ) n + ( ) n. Esta última fórmula é a chamada lei do triângulo de Pascal, permitindo o cálculo rápido dos sucessivos coeficientes binomiais. (b) Prove por indução a fórmula do desenvolvimento do binómio de Newton: ( ) n (a + b) n = a b n, para quaisquer a, b R e n N 0. =0 (c) Use a fórmula anterior para estabelecer as igualdades ( ) n ( ) n = n e ( ) = 0, para qualquer n N 0. =0 =0 8. Usando a desigualdade triangular ( + y + y ) e o método de indução, mostre que para todo o n N e quaisquer números reais,..., n R é válida a desigualdade.
9 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA 9 III. Indução e Somatórios Use indução para mostrar que, para qualquer n N: ( + )! = (n + )!. ( )( + ) = n n +. ( ) = n (n + ). ( + ) = n(n + ). ( )( + ) = (n )n(n + 4) ( )( + ) = (n )n(n + ). ( + ) = n n+. ( + ) = n n. ( + ) = = n + n. = n + +. n+ n(n + )(n + 5)..
10 0 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA ( + 5) = n(n + )(n + ). ( + ) = n n+. ( + ) = n n. + ( + ) = (n + ). 5 = + n n. = n + n. ( + ) = (n + ) n+. ( + ) = (n + ) n. ( ) = n + n. ( ) = (n ) +. n ( ) ( + )! ( )! = n (n + )!. = n n!.
11 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA IV. Funções Elementares ) Esboce os gráficos dos polinómios f() = e g() =, assinalando de forma conveniente os seus três pontos de intersecção. ) Esboce os gráficos dos polinómios f() = e g() = +4+, assinalando de forma conveniente os seus dois pontos de intersecção. ) Seja f() = n =0 c um polinómio de grau n N. Prove cada uma das seguintes proposições. (a) Se n e f(0) = 0, então f() = g() com g um polinómio de grau n. (b) Para cada a R, a função p dada por p() = f( + a) é também um polinómio de grau n. (c) Se n e f(a) = 0 para um dado a R, então f() = ( a)h() com h um polinómio de grau n. Sugestão: considere p() = f( + a). (d) Se f() = 0 para (n + ) valores distintos de R, então c = 0, = 0,..., n, e portanto f() = 0, R. (e) Seja g() = m =0 b um polinómio de grau m N, com m n. Se g() = f() para (m + ) valores distintos de R, então m = n, b = c, = 0,..., n, e portanto g() = f(), R. 4) Em cada caso, determine todos os polinómios p de grau satisfazendo as condições dadas. (a) p(0) = p() = p() = (c) p(0) = p() = (b) p(0) = p() =, p() = (d) p(0) = p() 5) Em cada caso, determine todos os polinómios p de grau satisfazendo as condições dadas para qualquer R. (a) p() = p( ) (b) p() = p(+) (c) p() = p() (d) p() = p(+) 6) Considere as seguintes propriedades fundamentais das funções seno, sin : R R, e coseno, cos : R R:. cos(0) = sin(π/) = e cos(π) =.. Para quaisquer, y R tem-se que cos( y) = cos() cos(y) + sin() sin(y).. Para 0 < < π/ tem-se que 0 < cos() < sin() < cos(). Prove a partir delas as seguintes propriedades importantes das funções seno e coseno. Sugestão: Apostol, Vol. I,.5. (a) sin () + cos () =, R. (b) sin(0) = cos(π/) = sin(π) = 0. (c) sin( ) = sin() e cos( ) = cos(), R (i.e. o seno é uma função ímpar e o coseno uma função par). (d) sin( + π/) = cos() e cos( + π/) = sin(), R.
12 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA (e) sin( + π) = sin() e cos( + π) = cos(), R (i.e. o seno e o coseno são funções periódicas). (f) Para quaisquer, y R tem-se que cos( + y) = cos() cos(y) sin() sin(y), sin( + y) = sin() cos(y) + cos() sin(y). (g) Para quaisquer a, b R tem-se que ( ) ( ) a b a + b sin(a) sin(b) = sin cos, ( ) ( ) a b a + b cos(a) cos(b) = sin sin. (h) No intervalo 0, π/, o seno é estritamente crescente e o coseno é estritamente decrescente. 7) Com base nas propriedades das funções seno e coseno listadas no eercício anterior, mostre que: (a) sin() = 0 = π com Z. (b) cos() = 0 = π + π/ com Z. (c) sin( + π) = sin() e cos( + π) = cos(), R. (d) cos() = cos () sin () e sin() = sin() cos(), R. (e) cos() cos(y) = cos( y) + cos( + y),, y R. (f) sin() sin(y) = cos( y) cos( + y),, y R. (g) sin() cos(y) = sin( y) + sin( + y),, y R. (h) Para quaisquer, y R e h 0 tem-se que sin( + h) sin() h cos( + h) cos() h = sin(h/) h/ = sin(h/) h/ cos( + h/), sin( + h/). 8) Considere as funções seno hiperbólico, sinh : R R, e coseno hiperbólico, cosh : R R, definidas por sinh() = e e e cosh() = e + e. Mostre que: (a) cosh () sinh () =, R. (b) sinh(0) = 0 e cosh(0) =. (c) sinh( ) = sinh() e cosh( ) = cosh(), R. (d) para quaisquer, y R tem-se que cosh( + y) = cosh() cosh(y) + sinh() sinh(y), sinh( + y) = sinh() cosh(y) + cosh() sinh(y). (e) cosh() = cosh () + sinh () e sinh() = sinh() cosh(), R. (f) cosh() + sinh() = e e cosh() sinh() = e, R.
13 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA 9) Determine o domínio das funções definidas pelas seguintes epressões. (a) f() = tan cot (b) f() = cos + sin (c) f() = 4 (d) f() = log(log ) (e) f() = log ( + /) (f) f() = log ( /) (g) f() = log ( + ) (h) f() = log ( + ) + V. Limites Elementares ) Calcule os seguintes limites. 4 (a) lim (d) lim 0 ) Usando o caso notável mostre que: (a) lim 0 sin() (d) lim a sin sin a a + (b) lim (c) (e) lim (f) lim 0 + (g) lim 0 sin lim 0 =, = (b) lim 0 sin(5) sin ) Calcule os seguintes limites. (a) lim t 0 sin(tan t) sin(t) (d) lim sin( ) = cos a (e) lim 0 tan() sin (b) lim π (e) lim sin(5) sin() = 5 (c) lim 0 sin(cos ) cos lim + sin = (f) lim 0 (c) lim t π sin(t π) t π = cos = (f) lim 0 cos() 4) Seja D = 0, + \ e considere a função f : D R definida por f() = para D. Calcule lim f(), lim f() e lim f() ) Calcule os limites quando 0 +, 0, + e das seguintes funções definidas em R \ 0. (a) e / (b) sinh(/) (c) cosh(/) (d) e / (e) sinh(/ ) (f) cosh(/ )
14 4 CDI I - LMAC, MEBIOM, MEFT SEM. 04/5 FICHA 6) Calcule os limites quando 0, + e das funções definidas pelas seguintes epressões. (a) sin() ( ) ( ) ( ) + π π (b) cos (c) cos (d) cos + + ( ) ( ) ( ) ( ) π + π + π π (e) sin (f) cos (g) cos (h) cos ( ) ( ) ( ) ( ) + π π π π (i) sin (j) sin () sin (l) cos ( ) ( ) π π (m) sin (n) cos ) Calcule os limites quando 0 + e + das funções definidas pelas seguintes epressões. ( ) ( ) ( ) ( ) (a) log + (b) log (c) log + + (d) log + ( ) ( ) ( ) ( ) + + (e) log + (f) log (g) log (h) log ( ) ( ) ( ) ( ) + (i) log (j) log () log (l) log ) Calcule os limites quando 0 + e + das funções definidas pelas seguintes epressões. (a) e (b) e (g) e (c) e + (d) e (e) e + (f) e + (h) e + (i) e + (j) e + () e + (l) e +
x + 2 > 1 (x 2)(x + 2) x + 2 > e
Instituto Superior Técnico Departamento de Matematica TESTES DE RECUPERAÇÃO DE CDI I O SEM. / DURAÇÃO: H/H VERSÃO A LEMAT, LEAN, MEBIOL, MEQ, MEAMBI E LMAC, MEBIOM, MEFT RESOLUÇÃO. (,5 val.) (a) (,9 val.)
Análise Matemática I 1 o Semestre de 2002/03 LEBM, LEFT, LMAC Exercícios para as aulas práticas
Análise Matemática I o Semestre de 2002/03 LEBM LEFT LMAC Eercícios para as aulas práticas I Elementos de Lógica e Teoria dos Conjuntos (30/9/2002-4/0/2002) (Eercício 2 de [3]) Prove que quaisquer que
CÁLCULO DIFERENCIAL E INTEGRAL I LEIC 1 o Sem. 2009/10 9 a FICHA DE EXERCÍCIOS. 1) Quais dos seguintes integrais são impróprios? Porquê?
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise CÁLCULO DIFERENCIAL E INTEGRAL I LEIC o Sem. 9/ 9 a FICHA DE EXERCÍCIOS I. Integrais Impróprios. ) Quais dos seguintes
Lista 9. (b) π 2 + x (c) π + x (d) 3π 2
Lista 9 Funções Trigonométricas I - Calculando o valor de uma função trigonométrica para um ângulo qualquer reduzindo-a a uma função trigonométrica de um ângulo agudo. 1. Expresse cada uma das expressões
SMA333 8a. Lista - séries de Taylor 07/06/2013
SMA333 8a Lista - séries de Taylor 7/6/213 Definição Para qualquer n = 1, 2, 3,, se uma função f tiver todas as derivadas até ordem n em algum intervalo contendo a como ponto interior, então o polinômio
(j) f(x) = (w) h(x) = x. (y) f(x) = sin(2x) (z) h(x) = 2 sin x. > 0 x 2 4x (g) x + 4 2x 6 (h)
Professora: Elisandra Bär de Figueiredo Lista : Funções - Cálculo Diferencial e Integral I. Determine o domínio e construa o gráco das seguintes funções. A seguir identique como estão relacionados os grácos
Polinómio e série de Taylor
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA II - o Semestre 05/06 Exercícios Suplementares (Eng a Física Tecnológica, Matemática Aplicada e Computação
4 Cálculo Diferencial
4 Cálculo Diferencial 1. (Eercício IV.1 de [1]) Calcule as derivadas das funções: a) tg, b) +cos 1 sen, c) e arctg, d) e log2, e) sen cos tg, f) 2 (1 + log ), g) cos(arcsen ) h) (log ), i) sen 2. 2. Derive:
CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2010/11 2 a FICHA DE EXERCÍCIOS - PARTE 2
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 010/11 a FICHA DE EXERCÍCIOS - PARTE I. Representação gráfica
4 Cálculo Diferencial
4 Cálculo Diferencial 1 (Eercício IV1 de [1]) Calcule as derivadas das funções: a) tg, b) +cos 1 sen, c) e arctg, d) e log, e) sen cos tg, f) (1 + log ), g) cos(arcsen ) h) (log ), i) sen Derive: a) arctg
CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2010/11 3 a FICHA DE EXERCÍCIOS
Instituto Superior Técnico Departamento e Matemática Secção e Álgebra e Análise CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT o SEM. / 3 a FICHA DE EXERCÍCIOS Primitivação é a operação inversa a
Exercícios de Cálculo p. Informática, Ex 1-1 Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar
Eercícios de Cálculo p. Informática, 2006-07 Números Reais. E - Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar o número dado: 7 a) b) 6 7 c) 2.(3) = 2.33 d) 2 3 e)
CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS. k + e 1 x, x > 0 f(x) = x cos 1, x > 0
Instituto Superior Técnico Departamento de Matemática CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS I. Continuidade de Funções. 1) Considere a função f :
g) 2 x2 (2 x ) 2, 6 x i) x 2 x + 2, j) k) log ( 1 l) log ( 2x 2 + 2x 2) + log ( x 2
Números Reais. Simplifique as seguintes epressões (definidas nos respectivos domínios): a), b) + +, c) + + +, d), e) ( ), f) 4 4, g) ( ), h) 3 6, i) +, j) +, k) log ( ) + log ( ), l) log ( + ) + log (
Lista de Férias. 6 Prove a partir da definição de limite que: a) lim. (x + 6) = 9. 1 Encontre uma expressão para a função inversa: b) lim
Lista de Férias Bases Matemáticas/FUV Encontre uma epressão para a função inversa: + 3 a) 5 2 + e b) e c) 2 + 5 d) ln( + 3) 6 Prove a partir da definição de ite que: a) 3 ( + 6) = 9 b) = c) 2 = 4 2 d)
Análise Matemática I 1 o Semestre de 2004/05 LEAero, LEBiom, LEFT e LMAC Exercícios para as aulas práticas
Análise Matemática I o Semestre de 2004/05 LEAero LEBiom LEFT e LMAC Eercícios para as aulas práticas I Elementos de Lógica e Teoria dos Conjuntos (20-24/9/2004) (Eercício 2 de [3]) Prove que quaisquer
Universidade Federal do ABC Centro de Matemática, Computação e Cognição Análise na Reta (2017) Curso de Verão
Lista L1 Preliminares Observações: Universidade Federal do ABC Centro de Matemática, Computação e Cognição Análise na Reta (017) Curso de Verão Esta lista corresponde a um conjunto de exercícios selecionados
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-45 Cálculo Diferencial e Integral I (Escola Politécnica) Terceira Lista de Eercícios - Professor: Equipe de Professores. APLICAÇÕES DE
Revisão do Teorema de Green
Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Aula 3 Propriedades de limites. Limites laterais.
Propriedades de ites. Limites laterais. MÓDULO - AULA 3 Aula 3 Propriedades de ites. Limites laterais. Objetivos Estudar propriedades elementares de ites, tais como: soma, produto, quociente e confronto.
Universidade de Trás-os-Montes e Alto Douro. Biomatemática/ Matemática I FOLHAS PRÁTICAS
Universidade de Trás-os-Montes e Alto Douro Biomatemática/ Matemática I FOLHAS PRÁTICAS Licenciaturas em Arquitectura Paisagista, Biologia e Geologia (ensino) e Biologia (cientíco) Ano lectivo 004/005
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão Lista 2. Sequências de Números Reais
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão 0 Lista Sequências de Números Reais. Dê o termo geral de cada uma das seguintes sequências: a,, 3, 4,... b, 4, 9, 6,... c,,
Gr aficos de Fun c oes Elementares
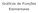Gráficos de Funções Elementares O gráfico de uma f.r.v.r. é uma curva ou uma união de curvas. Para a sua determinação é necessário conhecer o comportamento da função. Entre os vários aspectos da teoria
FEUP - MIEEC - Análise Matemática 1
FEUP - MIEEC - Análise Matemática Resolução da a Chamada - de Janeiro de 9 Respostas a perguntas diferentes em folhas diferentes Justifique cuidadosamente todas as respostas. Não é permitida a utilização
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO. Mestrado Integrado em Engenharia Electrotécnica e de Computadores ANÁLISE MATEMÁTICA 1
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO Mestrado Integrado em Engenharia Electrotécnica e de Computadores ANÁLISE MATEMÁTICA 1 PARTE 1: EXERCÍCIOS DE REVISÃO Maria do Rosário de Pinho e Maria
CÁLCULO DIFERENCIAL E INTEGRAL I (CDI-I) PROVA I 20/03/2013. O desenvolvimento de todos os cálculos deve estar presente na prova.
Universidade do Estado de Santa Catarina Centro de Ciências Tecnológicas - CCT Departamento de Matemática Antônio João Fidélis CÁLCULO DIFERENCIAL E INTEGRAL I (CDI-I) PROVA I 0/03/013 É proibido o uso
Exercícios Complementares 3.4
Eercícios Complementares 3.4 3.4A Falso ou Verdadeiro? Justi que. (a) se jc n j é convergente, então c n n é absolutamente convergente no intervalo [ ; ] ; (b) se uma série de potências é absolutamente
ANÁLISE MATEMÁTICA IV
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
1 Números Complexos e Plano Complexo
UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão Lista 1. Números Naturais
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão 01 Lista 1 Números Naturais 1. Demonstre por indução as seguintes fórmulas: (a) (b) n (j 1) = n (soma dos n primeiros ímpares).
UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática MA12 - Matemática Discreta - PROFMAT Prof.
UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática MA - Matemática Discreta - PROFMAT Prof. Zeca Eidam Lista Números Naturais e o Princípio de Indução. Prove que
a) Represente na forma de um intervalo ou de uma união disjunta de intervalos o domínio D da função definida pela expressão: f(x) = log 1 x 1 )
Instituto Superior Técnico Departamento e Matemática Secção e Álgebra e Análise o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEFT, MEBiom o Sem. 20/2 2//20 Duração: h30mn.,5 val.) a) Represente na
Exercícios sobre Polinômios
uff Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Eercícios sobre Polinômios Prof Saponga Rua Mário Santos Braga
LICENCIATURA EM ENGENHARIA CIVIL FOLHA 2
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL REGIME DIURNO/NOCTURNO - o SEMESTRE - o ANO - 009/00 DISCIPLINA DE ANÁLISE MATEMÁTICA FOLHA. Das figuras abaio esboçadas
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Matemática E Extensivo V. 6
Etensivo V. 6 Eercícios ) a) P() é sempre igual à soma dos coeficientes de P(). b) P() é sempre igual ao termo independente de P(). c) P() é a raiz de P(), pois P() =. ) D a) P() = ³ + 7. ² 7. P() = +
(b) lim. n 3 2. (e) lim
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise CÁLCULO DIFERENCIAL E INTEGRAL I LEGM, LET, MEC o SEM. 008/09 6 a FICHA DE EXERCÍCIOS I. I. Derivação Logarítmica. Calcule
#Desafios SPM. #Probabilidades e Combinatória. Exercício 1. Exercício 2
#Desafios SPM Os #Desafios SPM destinam-se a alunos do 12.º ano que frequentam a disciplina de Matemática A. Pretendem mobilizar, em situações diversificadas, os conhecimentos e as capacidades que adquiriram
CÁLCULO DIFERENCIAL 5-1 Para cada uma das funções apresentadas determine a sua derivada formando
5 a Ficha de eercícios de Cálculo para Informática CÁLCULO DIFERENCIAL 5-1 Para cada uma das funções apresentadas determine a sua derivada formando o quociente f( + h) f() h e tomando o ite quando h tende
Lista 6 Gráficos: Pontos críticos, máximos e mínimos, partes crescentes e decrescentes. L Hôpital. Diferencial. Polinômio de Taylor
Departamento de Computação é Matemática Cálculo I USP- FFCLRP Prof. Rafael A. Rosales 5 de março de 014 Lista 6 Gráficos: Pontos críticos, máimos e mínimos, partes crescentes e decrescentes. L Hôpital.
MAT2453- Cálculo Diferencial e Integral para Engenharia I - POLI 1 o Semestre de a Lista de Exercícios. sen 3 x cos x. x dx 11. sec x dx 15.
MAT45- Cálculo Diferencial e Integral para Engenharia I - POLI o Semestre de - a Lista de Eercícios I - Integrais Indefinidas Calcule as integrais indefinidas abaio: 7 + +.. 7 5. 6. 9. tg. e. tg sec 7..
Polinômios de Legendre
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
MAT2453- Cálculo Diferencial e Integral para Engenharia I - POLI 1o. Semestre de a. Lista de Exercícios. x cos x. x 1+ x 4 dx 12. sec x dx 15.
MAT45- Cálculo Diferencial e Integral para Engenharia I - POLI o. Semestre de - a. Lista de Eercícios I - Integrais Indefinidas Calcule as integrais indefinidas abaio: 7 + +.. e. cos 7 4. tg 7 sen 5. 6.
Fun c oes Trigonom etricas Fun c oes Trigonom etricas ( ) Fun c oes Trigonom etricas Matem atica II 2008/2009
Funções Trigonométricas (13-03-08) Funções periódicas Muitos dos fenómenos correntes têm um comportamento periódico, isto é, um comportamento que se repete em períodos de tempo iguais. Entre outros exemplos
2a. Lista de Exercícios
UFPR - Universidade Federal do Paraná Departamento de Matemática Prof. José Carlos Eidam CM04 - Cálculo I - Turma C - 0/ a. Lista de Eercícios Teoremas do valor intermediário e do valor médio. Seja h()
5 Cálculo Diferencial Primitivação
5 Cálculo Diferencial Primitivação. Determine uma primitiva de cada uma das funções: a) + 3 3, b) + +, c) +, d) 3 3 +, e) 3, f) 5, 3 e g) h) 3 + 4 + e, i) cos + sen, sen() j) sen(), k) + sen, l) cos, m)
Expansões AULA ... META. Apresentar a expansão binomial e multinomial. OBJETIVOS. Ao final da aula o aluno deverá ser capaz de:
Expansões META Apresentar a expansão binomial e multinomial. OBJETIVOS Ao final da aula o aluno deverá ser capaz de: Identificar e utilizar algumas propriedades dos coeficientes binomiais; Expandir produto
MAT 104 Cálculo 1 Prof. Paolo Piccione. Prova
MAT 104 Cálculo 1 Prof. Paolo Piccione Prova 1 26.04.2010 2010122 Nome: RG: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos. Assinale as alternativas corretas na folha de respostas
MAT 104 Cálculo 1 Prof. Paolo Piccione. Prova
MAT 104 Cálculo 1 Prof. Paolo Piccione Prova 1 26.04.2010 2010122 Nome: RG: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos. Assinale as alternativas corretas na folha de respostas
Capítulo 1. Funções e grácos
Capítulo 1 Funções e grácos Denição 1. Sejam X e Y dois subconjuntos não vazios do conjunto dos números reais. Uma função de X em Y ou simplesmente uma função é uma regra, lei ou convenção que associa
13 Fórmula de Taylor
13 Quando estudamos a diferencial vimos que poderíamos calcular o valor aproimado de uma função usando a sua reta tangente. Isto pode ser feito encontrandose a equação da reta tangente a uma função y =
Matemática E Extensivo V. 6
Etensivo V. 6 Eercícios ) a) P() é sempre igual à soma dos coeficientes de P(). b) P() é sempre igual ao termo independente de P(). c) P() é a raiz de P(), pois P() =. a) P() = ³ + 7. ² 7. P() = + 7 7
Teste de Matemática Elementar 2017/II
Universidade Federal de Viçosa Departamento de Matemática Teste de Matemática Elementar 07/II. A frase: Se João joga futebol, então Maria toca violão é equivalente a: João joga futebol se, e somente se,
2a Lista de Exercícios. f (x), se x a g (x), se x < a. x 3 x, x 0, se x = 0. 1, se x 1 x 2 4 x 4, se x 1
UFPR - Universidade Federal do Paraná Setor de Ciências Eatas Departamento de Matemática Prof. José Carlos Eidam MA/PROFMAT - Fundamentos de Cálculo a Lista de Eercícios Derivadas. Sejam f e g funções
Curso de Verão Exemplos para o curso de
Curso de Verão 006 Programa de Pós-Graduação em Matemática Aplicada DCCE - Departamento de Ciência da Computação e Estatística Universidade Estadual Paulista - UNESP Instituto de Biociências, Letras e
Introdução à Trigonometria 1
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Introdução à Trigonometria
Instituto Superior Técnico - 1 o Semestre 2006/2007 Cálculo Diferencial e Integral I LEA-pB, LEM-pB, LEN-pB, LEAN, MEAer e MEMec
Instituto Superior Técnico - o Semestre 006/007 Cálculo Diferencial e Integral I LEA-pB, LEM-pB, LEN-pB, LEAN, MEAer e MEMec a Ficha de eercícios para as aulas práticas 3-4 Novembro de 006. Determine os
Cálculo Diferencial e Integral I
Cálculo Diferencial e Integral I Resolução do Eame / Testes de Recuperação I.. (, val.)determine os ites das seguintes sucessões convergentes (i) u n n + n n e n + n, (ii) v n n + π n Resolução: i) A sucessão
QUESTÕES-AULA 37. (a) O período da função F (x) é T = 3 0 = 3. Dividimos a reta em intervalos da forma:
QUESTÕES-AULA 37 1. Considere a função f(x) = 4 x, 0 x < 3. 3 (a) Construa uma função periódica F (x) definida em todo o R, tal que F (x) = f(x) para todo x [0, 3). (b) Determine o período, a frequência
Integrais indefinidas
Integrais indefinidas que: Sendo f() e F() definidas em um intervalo I R, para todo I, dizemos F é uma antiderivada ou uma primitiva de f, em I, se F () = f() F() = é uma antiderivada (primitiv de f()
Funções Elementares. Sadao Massago. Maio de Alguns conceitos e notações usados neste texto. Soma das funções pares é uma função par.
Funções Elementares Sadao Massago Maio de 0. Apresentação Neste teto, trataremos rapidamente sobre funções elementares. O teto não é material completo do assunto, mas é somente uma nota adicional para
Tópicos de Matemática Elementar
Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Exercícios sobre Trigonometria
Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Curso: MAT 221- CÁLCULO DIFERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008
Curso: MAT 22- CÁLCULO DIFERENCIAL E INTEGRAL IV Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 2008 APRESENTAÇÃO Um objetivo do curso: Um estudo da exponenciação, subdividido nos
7 Derivadas e Diferenciabilidade.
Eercícios de Cálculo p. Informática, 006-07 1 7 Derivadas e Diferenciabilidade. E 7-1 Para cada uma das funções apresentadas determine a sua derivada formando o quociente f( + h) f() h e tomando o ite
Cálculo Diferencial e Integral I
Cálculo Diferencial e Integral I Eame - Parte I - de Julho de 8 LERC, LEGI, LEE, LEIC-T Número: Nome: valores a) valores b) valores 3 4 valores 4 valores 5 a) 3 valores 5 b) 3 valores 6 valores páginas
MATEMÁTICA 3 ( ) A. 17. Sejam f(x) = sen(x) e g(x) = x/2. Associe cada função abaixo ao gráfico que. 2 e g.f 3. O número pedido é = 75
MATEMÁTICA 3 17. Sejam f() sen() e g() /2. Associe cada função abaio ao gráfico que melhor a representa. Para cada associação feita, calcule i k, onde i é o número entre parênteses à direita da função,
Capítulo 6 - Integral Inde nida
Caítulo - Integral Inde nida. Calcule as integrais inde nidas abaio usando integração imediata ou o método da substituição. e d (j) e d d e ( ) (k) d d arctan (l) ( ) d d sec tg (m) d ln d e (n) ( e )
matemática Antes de chegarmos a uma definição precisa deste conceito vamos observar alguns exemplos simples:
Matemática I 1 Limites O conceito de limite é fundamental para o estudo de funções de variável real. Uma das situações em que ele aparece naturalmente é o do estudo do comportamento assintótico de uma
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
1. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R
. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R D x f(x). Uma função é uma regra que associa a cada elemento x D um valor f(x)
Exercícios sobre Trigonometria
Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Séries Potências II. por Abílio Lemos. Universidade Federal de Viçosa. Departamento de Matemática UFV. Aulas de MAT
Séries Potências II por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2018 26 e 28 de setembro de 2018 Se a série de potências c n (x a) n tiver um raio de convergência
Notas de aula: Cálculo e Matemática Aplicados à Notas de aula: Gestão Ambiental
Notas de aula: Cálculo e Matemática Aplicados à Notas de aula: Gestão Ambiental 3 Limites Considere a função f definida por: Qual o domínio dessa função? Se 1, então f () é dada por: (2 + 3)( 1). 1 2 +
Departamento de Matemática da Universidade de Aveiro
Departamento de Matemática da Universidade de Aveiro ANÁLISE MATEMÁTICA II 7/8 Folha 4 - soluções: Séries de Fourier; notação complexa. Vamos mostrar que se f e g são funções periódicas de período T, fg
Matemática Licenciatura - Semestre Curso: Cálculo Diferencial e Integral I Professor: Robson Sousa. Diferenciabilidade.
1 Matemática Licenciatura - Semestre 2010.1 Curso: Cálculo Diferencial e Integral I Professor: Robson Sousa Diferenciabilidade Funções Trigonométricas Inicialmente, observe pela gura que para ângulos 0
Matemática. Lic. em Enologia, 2009/2010
Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Cálculo I IM UFRJ Lista 1: Pré-Cálculo Prof. Marco Cabral Versão Para o Aluno. Tópicos do Pré-Cálculo
Cálculo I IM UFRJ Lista : Pré-Cálculo Prof. Marco Cabral Versão 7.03.05 Para o Aluno O sucesso (ou insucesso) no Cálculo depende do conhecimento de tópicos do ensino médio que chamaremos de pré-cálculo.
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005. Cálculo I. Caderno de Exercícios 4
Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005 Cálculo I Caderno de Eercícios 4 Limites, continuidade e diferenciabilidade de funções; fórmulas de Taylor e MacLaurin; estudo de funções.
Rafael A. Rosales 29 de maio de Diferencial 1. 4 l Hôpital 3. 5 Série de Taylor 3 01.
Departamento de Computação é Matemática Cálculo I USP- FFCLRP Física Médica Rafael A. Rosales 9 de maio de 07 Sumário Diferencial Teorema do Valor Médio 3 Máimos e Mínimos. Gráficos 4 l Hôpital 3 5 Série
Lista 9 - Bases Matemáticas
Lista 9 - Bases Matemáticas Limites - Parte Definição de Limites Verifique se é verdadeiro ou falso: a) x 2 < 0 f (x) 5 < 0, onde 2x + b) x 2 < 0 2 f (x) 5 < 0, onde 2x + c) x < 0 f (x) 3 < 0, onde 4x
AGRUPAMENTO DE ESCOLAS DO CADAVAL
AGRUPAMENTO DE ESCOLAS DO CADAVAL DEPARTAMENTO: PLANIFICAÇÃO ANUAL - ANO LETIVO: DISCIPLINA: Matemática A (12.º ano) Matemática e Ciências Experimentais 2015/2016 UNIDADE Tema 1 - Probabilidades e Combinatória
Onde usar os conhecimentos
VI LOGARIMO Por que aprender Binômio de Newton?... Binômio de Newton é uma ferramenta matemática desenvolvida por Isaac Newton que facilita certos cálculos matemáticos que seriam trabalhosos pelo processo
Binómio de Newton. De modo análogo, podemos calcular as quintas e sextas potências e, de modo geral, obter o
Binómio de Newton Introdução Pelos produtos notáveis, sabemos que (a+b)² = a² + 2ab + b². Se quisermos calcular (a + b)³, podemos escrever: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 Se quisermos calcular,
MAT 111 Cálculo Diferencial e Integral I. Prova 2 14 de Junho de 2012
MAT 111 Cálculo Diferencial e Integral I Prof. Paolo Piccione Prova 2 14 de Junho de 2012 Nome: Número USP: Assinatura: Instruções A duração da prova é de duas horas. Assinale as alternativas corretas
MAT 111 Cálculo Diferencial e Integral I. Prova 2 14 de Junho de 2012
MAT 111 Cálculo Diferencial e Integral I Prof. Paolo Piccione Prova 2 14 de Junho de 2012 Nome: Número USP: Assinatura: Instruções A duração da prova é de duas horas. Assinale as alternativas corretas
Capítulo 1 Números Reais
Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 1 Números Reais Conjuntos Numéricos Conjunto dos naturais: N = {1,, 3, 4,... } Conjunto dos inteiros: Z = {..., 3,, 1, 0, 1,, 3,... } {
MÓDULO 45 TRIGONOMETRIA II. Ciências da Natureza, Matemática e suas Tecnologias MATEMÁTICA. 1. Considere a equação. (3 2 cos 2 x) 1 + tg 2. 6 tg = 0.
Ciências da Natureza, Matemática e suas Tecnologias MATEMÁTICA. Considere a equação TRIGONOMETRIA II ( cos ) + tg MÓDULO 5 tg = 0. a) Determine todas as soluções no intervalo [0, [. b) Para as soluções
Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].
![Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].](/thumbs/100/144026914.jpg "Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].")
Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
CAPITULO I PRIMITIVAS. 1. Generalidades. Primitivação imediata e quase imediata
CAPITULO I PRIMITIVAS. Generalidades. Primitivação imediata e quase imediata Sendo f () uma função real de variável real definida no intervalo não degenerado I, chama-se primitiva de f () em I a qualquer
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 1ª FASE 25 DE JUNHO Grupo I
Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 27-A 500-236 Lisboa Tel.: +35 2 76 36 90 / 2 7 03 77 Fa: +35 2 76 64 24 http://www.apm.pt email: geral@apm.pt PROPOSTA DE RESOLUÇÃO
Índice. Introdução Unidade 1 Probabilidades e Cálculo Combinatório
Índice Introdução... 9 Unidade 1 Probabilidades e Cálculo Combinatório Probabilidades Introdução ao cálculo das probabilidades...12 Experiência...13 Classificação para os acontecimentos. Espaço de acontecimentos...14
Escola Secundária com 3º ciclo D. Dinis 11º Ano de Matemática A Tema I Geometria no Plano e no Espaço II. Ficha de trabalho nº 3.
Escola Secundária com 3º ciclo D. Dinis 11º Ano de Matemática A Tema I Geometria no Plano e no Espaço II Ficha de trabalho nº 3 1. Resolver, da página 80 do seu manual, 1.1. as alíneas a), c) e e) dos
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 1ª FASE 25 DE JUNHO Grupo I
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) ª FASE 25 DE JUNHO 203 Grupo I Questões 2 3 4 5 6 7 8 Versão B D C A D B C A Versão 2 C A B D D C B B Grupo II...
4a. Lista de Exercícios
UFPR - Universidade Federal do Paraná Deparameno de Maemáica Prof. José Carlos Eidam CM4 - Cálculo I - Turma C - / 4a. Lisa de Eercícios Inegrais impróprias. Decida quais inegrais impróprias abaio são
01. Escreva uma equação para a função do primeiro grau f satisfazendo as condições dadas. Represente as funções graficamente.
DEPARTAMENTO DE MATEMÁTICA APLICADA - ICTE Lista 0 Cálculo Diferencial e Integral I Profa.: LIDIANE SARTINI 0. Escreva uma equação para a função do primeiro grau f satisfazendo as condições dadas. Represente