Equação Diferencial Implícita aplicada ao Estudo de Curvas de Rarefação.
|
|
|
- Heloísa Santarém
- 5 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DE MINAS GERAIS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE PÓS-GRADUAÇÃO EM MATEMÁTICA Equação Diferencial Implícita aplicada ao Estudo de Curvas de Rarefação. Fiorella María Rendón García Belo Horizonte - MG 2017
2 UNIVERSIDADE FEDERAL DE MINAS GERAIS INSTITUTO DE CIÊNCIAS EXATAS DEPARTAMENTO DE PÓS-GRADUAÇÃO EM MATEMÁTICA Equação Diferencial Implícita aplicada ao Estudo de Curvas de Rarefação Fiorella María Rendón García Orientador: Cesar de Souza Eschenazi Dissertação apresentada ao Programa de Pós-Graduação em Matemática do Instituto de Ciências Exatas ICEX) da Universidade Federal de Minas Gerais, como requisito parcial para obtenção de título de Mestre em Matemática. Belo Horizonte - MG 2017
3 A meus pais Giovanna e Pedro e minha irmã Angela.
4 Sumário Agradecemientos 2 Introdução 3 Preliminares 5 1 Equações Diferenciais Implícitas O recobrimento duplo de M e o levantamento de campos Redução formal das EDIs Uma redução adicional da EDI Topologia das formas normais Famílias genéricas a 1-parâmetro de EDIs do tipo Morse Redução das EDIs Topologia das formas normais Aplicação Formulação do problema Estudo das configurações Referências Bibliográficas 75
5 Agradecemientos Em primeiro lugar, gostaria de agradecer especialmente a meu orientador Prof. Cesar De Souza Eschenazi. Em particular, quero manifestar o meu apreço ao Cesar que, além de orientador, tem sido um amigo. Eu não tenho palavras para expressar minha sincera gratidão a ele, mas eu me considero afortunado por ter trabalhado com ele. Também sou grata aos membros da minha banca examinadora, Prf. Alberto Berly Sarmiento Vera, Prf. Carlos Maria Carballo, Prf. Jose Antonio Gonçalves Miranda, que comprometeram muito generosamente seu tempo e conhecimento para avaliar a minha disertação. Eu também gostaria de agradecer a meus pais Pedro e Giovanna pelo apoio, mesmo a muitos quilômetros de distância, que tem sido essencial para encontrar forças e continuar lutando pelos meus objetivos. Palavras não podem expressar a imensidão da gratidão que tenho por eles. À minha irmã Angela pela força e confiança. E para uma parte importante para mim, meus amigos Camilo e Manuel, e por quem començou todo Edison. Por último, mas não menos importante, gostaria de agradecer à CAPES pelo apoio financeiro.
6 Introdução Equações diferenciais implícitas aparecem muitos contextos da matemática e existe uma grande literatura sobre o assunto, bem como um grande número de técnicas para estudá-las. Nesta dissertação abordamos as técnicas introduzidas em [1] e [2]. Nosso objetivo é aplicar tais técnicas para reobter a configuração das curvas de rarefação em sistemas quadráticos de duas leis de conservação estudadas em [8], [9] e [10]. No capítulo 1 consideramos equações diferencias implícitas da forma ax, y)dy 2 + 2bx, y)dxdy + cx, y)dx 2 = 0, 1) onde a, b e c são funções suaves que se anulam na origem, na vizinhança de pontos onde a função discriminante x, y) = bx, y) 2 ax, y)cx, y) tem singularidades do tipo Morse. Equações diferenciais implícitas do tipo 1 são também conhecidas como equações diferenciais binárias. Aqui manteremos a nomenclatura Equações diferenciais implícitas EDI). Em pontos onde x, y) > 0 a equação 1) define um par de direções no plano. Para estudar as soluções de 1) considera-se em R 2 RP o conjunto M de pontos x, y, p), com b 2 x, y) + ax, y)cx, y) 0 e p é uma direção definida por 1) no ponto x, y). As configurações topológicas das soluções são classificadas de acordo com os tipos de singularidades que apresentam. No capítulo 2 consideraremos famílias genéricas a 1-parâmetro de equações diferenciais implícitas da forma ax, y, t)dy 2 + 2bx, y, t)dxdy + cx, y, t)dx 2 = 0, foram estudadas em [2] na vizinhança de pontos onde o discriminante b 2 ac = 0 tem uma singularidade do tipo Morse em t = 0, que é o caso acima. Descreve-se então a mudança da configuração da curvas soluções de acordo com a variação do parâmetro. No capítulo 3 aplicaremos as técnicas dos capítulos 1) e 2) no estudo da configuração topológica das curvas de rarefação de um sistema quadrático de duas leis de conservação. As curvas de rarefação são soluções contínuas de um sistema de leis de conservação em uma variável espacial. Consideramos aqui um sistema de duas leis de rarefação U t + F U) x = 0,
7 Introdução 4 onde x R, t > 0, Ux, t) R 2 e as funções de fluxo F : R 2 R 2, F u, v) = fu, v), gu, v)) são funções quadráticas. Mostramos que as curvas de rarefação são as curvas integrais da equação diferencial implícita f v dy) 2 + f u g v )dudv g u du) 2 = 0, que é uma EDI do tipo 1). Terminamos nosso trabalho fazendo de uma breve comparação entre as técnicas introduzidas em [1] e [2] e as técnicas que foram usadas em [9] e [6].
8 Preliminares Definição 0.1. Dada uma equação diferencial de primeira ordem F x, y, dy dx ) = 0 onde F C nas variáveis x, y, p = dy dx, chamamos ponto singular da equação todo ponto de R3 que anula a derivada de F em relação a p, isto é, F p = 0. Na vizinhança de um ponto singular a equação não é solúvel em relação a variável p = dy dx, temos então a seguinte definição. Definição 0.2. Equações diferenciais que apresentam pontos singulares são denominadas de equações diferenciais implícitas, EDI) também conhecidas classicamente como equações diferenciais multiformes. Fora dos pontos singulares, as equações diferenciais implícitas podem ser resolvidas pelas técnicas usuais conhecidas. Observação Neste trabalho supomos que 0 é valor regular para a função F, ou seja, que a superfície definida por F x, y, p) = 0 é uma superfície suave M 2 R 3. A observação acima juntamente com o fato de que p = dy dx, permite-nos por O estudo das EDI não é novo. F x, y, p) = 0 dy pdx = 0 Em [12] René Thom retomou o estudo desse problema considerando o contexto de teoria das Singularidades. O estudo das EDI neste contexto permite que encaremos o problema da seguinte forma: estudar o campo de linhas definido pelo núcleo da 1-forma t = dy pdx sobre a superfície M 2. Geometricamente, esse campo de linhas é definido pela interseção do plano tangente à superfície M 2 com o plano vertical dy pdx = 0. Observação dx, dy não estão sendo encarados como elementos infinitesimais, são interpretados como as componentes dos vetores tangentes à superfície M 2. Ainda deste ponto de vista, os pontos singulares da equação F x, y, p) = 0, que são dados por F p = 0, definem, em geral, uma curva na superfície M 2 definida pelas equações F = 0 e F p = 0. As soluções da equação diferencial original que desejamos estudar são obtidas tomando-se a imagem pela projeção π : M 2 R 2, x, y, p) x, y) das trajetórias do campo de linhas em
9 Preliminares 6 M 2. O campo de linhas definido pelo núcleo da 1-forma t na superfície M 2, é singular nos pontos da superfície M 2 onde o plano tangente e o plano vertical dy pdx = 0 são paralelos, isto é, são os pontos onde os vetores F x, F y, F p ) e p, 1, 0) são paralelos. Segue que F p = 0, o que significa que as singularidades estão sobre a curva singular Γ definida por F = F p = 0 e F x + pf y = 0. Observação Não é difícil mostrar que a imagem das singularidades do campo de linhas pela projeção π são exatamente os pontos onde as soluções da equação são tangentes à curva πγ). Um exemplo particular de uma equação diferencial implícita é a equação de Clairaut, que é uma equação do tipo y = xp + fp); p = dy dx. A superfície F x, y, p) = xp+fp) y = 0 é uma superfície regrada pois para cada p fixo temse a equação de uma reta. A curva singular Γ é dada pela equação F = 0; F p = x + f p) = 0. Como y já está isolado no lado esquerdo, as coordenadas naturais para a superfície M 2 são x e p. O campo de linhas restrito à superfície M 2, nessas coordenadas, se escrevem como x + f p))dp = 0 em cada ponto onde este sistema de coordenadas é válido, o campo de linhas tem o mesmo comportamento que o campo de vetores: ẋ = x + f p) ṗ = 0 Este campo é singular se x + f p) = 0, ou seja, todo ponto da curva Γ é uma singularidade do campo de linhas. Este fato junto com a observação 0.0.3) mostra que a imagem da curva Γ pela projeção π é a envoltória das soluções da equação de Clairaut. As soluções da equação de Clairaut no plano x, p) são as retas p constantes. Por exemplo: fp) = p3 p3 3, ou seja, y = xp 3. Usando x, p como coordenadas para M 2 tem-se que a curva Gamma é dada no plano x, p) pela equação x = p 2. No plano x, p) as soluções são as retas p = cte A curva πγ) projeção no plano x, y) da curva é a parábola semi-cúbica y = ± 2 3 x 3 2 Projeção no plano x, p) Projeção no plano x, y)
10 Preliminares 7 Em [3] L. Dara retoma a questão de estudar as singularidades das equações diferenciais implícitas. O trabalho de Dara pode ser dividido em duas partes: mostra via Teorema de Transversalidade, que as equações diferenciais implícitas apresentam 6 tipos de singularidades genéricas lista de Thom é incompleta). Procura dar modelos das diferentes singularidades genéricas. Destes modelos fornecidos por Dara, enfocaremos apenas 3. Exemplo Dobra simples seguindo com a denominação original do autor) p 2 = x. A superfície F x, y, p) = 0 é dada por p 2 x = 0. A curva singular Γ que é dada pelas equações F = 0. F p = 0 é o eixo y. x p 2 = 0 dy pdx = 0 é natural tomar y, p como coordenadas. Nestas coordenadas o campo de linhas definido pelo núcleo 1-forma t = dy pdx na superfície M 2 se escreve como: dy 2p 2 dp = 0. Que tem o mesmo comportamento que o campo de vetores ẏ = 2p 2 ṗ = 1 cuja solução é a família de curvas y = 2 3 p3 + c como p = ± x, a imagem de curvas soluções pela projeção π é uma família de parabolas semicúbicas y = ± 3 2 x c. Observação Neste caso, usamos a denominação curva de dobra para a curva Γ, uma vez que todos os pontos da curva Γ são singularidades do tipo dobra para a projeção π
11 Preliminares 8 Exemplo Singularidades do tipo dobra-sela y = 2xp + p 2 dy pdx = 0 a superfície F x, y, p) = 0 é a superfície p 2 + 2xp y = 0. A curva singular Γ é dada por 2x + 2p = 0, então x = p. A superfície F é regrada. Pode-se notar ainda que fixando x, y) R 2 a pré-imagem desse ponto pela projeção π pode ter cardinalidade zero, 1 ou 2 pontos conforme y + x 2 seja negativo, zero ou positivo respectivamente. Tomamos x, p como coordenadas para a superfície M 2. Neste sistema de coordenadas, dy pdx = 0 restrita a M 2 se escreve como pdx + 2x + p)dp = 0 que tem o mesmo comportamento que o campo de vetores. ẋ = 2x + p) ṗ = p ) 2 2 Este campo é singular em 0, 0) e esta singularidade é do tipo sela uma vez que det < As variedades invariantes são o eixo x e a reta p = 3 2 x. 1 sela no plano px 1 sela no plano xy A imagem da curva Γ pela projeção π é a parábola y = x 2 Para ver isto ponha p = x na equação define F ). Esta curva é a curva que separa a cardinalidade das pré-imagens dos pontos no plano. A imagem do eixo x pela projeção π é o próprio eixo x e a imagem da reta y = 3 2 x é a parábola y = 3 4 x2. Observação A denominação de dobra-sela dada por Dara justifica-se pelo fato de que as singularidades da projeção π são do tipo dobra e a singularidade do campo de linhas é do tipo sela.
12 Preliminares 9 Exemplo Singularidade do tipo dobra-nó y = p xp De novo a superfície F é regrada, a curva Γ é dada por 2p x = 0, então p = 1 6 x. A pré-imagem de cada ponto x, p) R 2 pode ter cardinalidade 0, 1 ou 2 conforme x y seja negativo, nulo o positivo respectivamente. As coordenadas naturais para M 2 são x e p. Nestas coordenadas o campo de linhas se escreve 2p x)dp 2 3 pdx = 0 que localmente tem o mesmo comportamento do campo de vetores ẋ = 2p x ṗ = 2 3 p ) Este campo tem uma singularidade na origem do tipo nó, uma vez que det = 2 9 > 0. As variedades invariantes são o eixo x e a reta p = 1 6 x A imagem da curva Γ pela projeção π é a curva y = 1 36 x2. A imagem das variedades invariantes são πx, p = 0) = x, y 0) e πx, 1 6 ) = x, 1 12 x2 ). Observação Davidov mostrou posteriormente que estas singularidades são estruturalmente estáveis. 2. Palmeira em [9] usou esta técnica para descrever a configuração dos campos de linhas gerados pelos autoespaços da matriz derivada de uma função F : R 2 R 2 cujas funções coordenadas são polinômios quadráticos. Para este problema, a curva singular F = 0, F p = 0 é a curva onde os autovalores da matriz DF têm multiplicidade algébrica igual a 2 e multiplicidade geométrica igual a 1. A região do plano onde não tem solução da E.D.I. são os pontos onde os autovalores da matriz DF são complexos. A função F considerada é tal que a região onde os autovalores de DF são complexos é limitada. O interesse desse estudo está no fato de que as ondas de rarefação podem ser interpretadas como as curvas integrais do campo de linhas gerados pelos autoespaços da matriz derivada da função de fluxo F do sistema de leis de conservação U t + F U) x = 0, U R n ; x, t R
13 Capítulo 1 Equações Diferenciais Implícitas Neste capítulo nós vamos dar uma classificação local das curvas solução das equações diferenciais implícitas da forma ax, y)dy 2 + 2bx, y)dxdy + cx, y)dx 2 = 0 1) em pontos nos quais a função discriminante b 2 ac tem uma singularidade de Morse. Vamos apresentar uma forma normal para tais equações. 1.1 O recobrimento duplo de M e o levantamento de campos Nesta seção vamos estudar o recobrimento duplo M e os zeros do levantamento do campo na reta projetiva 0 RP 1. Consideramos equações diferenciais implicitas EDIs) do tipo 1) da equação 1) onde a, b, c são funções suaves que se anulam no origem. Em pontos onde b 2 x, y) ax, y)cx, y) > 0 A equação 1) define um par de direções no plano. Uma forma natural de estudar estas equações é fazendo o levantamento do campo de direções bivaluado a um campo de recobrimento duplo associado. Tomamos a carta afim RP 1 com a direção p = dy dx e consideramos localmente em R3 a superfície de recobrimento duplo. M = {x, y, p) : ap 2 + 2bp + c = 0} 2) Denotamos por F x, y, p) a função F x, y, p) = ap 2 + 2bp + c
14 1.1. O RECOBRIMENTO DUPLO DE M E O LEVANTAMENTO DE CAMPOS 11 onde a = a 1 x + a 2 y + O2) b = b 1 x + b 2 y + O2) c = c 1 x + c 2 y + O2) Definição 1.1. Denominamos de curva discriminante da EDI 1) o conjunto = {x, y) : b 2 ac = 0} 3) Proposição A superfície M em 2) é suave numa vizinhança de 0 RP 1 se, e somente se, a função discriminante b 2 ac tem uma singularidade de Morse. 2. A projeção natural π : M R 2 x, y, p) x, y) Prova. é um difeomorfismo local fora de π 1 ). 1. Seja Em x, y) = 0, 0) F p = F p = 2ap + 2b F p = 2a 1 x + a 2 y + O2))p + 2b 1 x + b 2 y + O2)) = 0 Portanto a superfície M não é suave se, e somente se F x 0, 0, p) = a 1p 2 + 2b 1 p + c 1 4) F y 0, 0, p) = a 2p 2 + 2b 2 p + c 2, 5) Se anulam ao mesmo tempo para algum p. Multiplicando-se Eq. 4) por a 2 e a Eq. 5) por a 1 temos o sistema. a 1 a 2 p 2 2a 2 b 1 p a 2 c 1 = 0 a 1 a 2 p 2 + 2a 1 b 2 p + a 1 c 2 = 0, 6)
15 1.1. O RECOBRIMENTO DUPLO DE M E O LEVANTAMENTO DE CAMPOS 12 Resolvendo o sistema para p temos p = a 2c 1 a 1 c 2 ) 2b 2 a 1 b 1 a 2 ) Multiplicando-se a Eq. 4) por b 2 e a Eq. 5) por b 1 obtemos o sistema Resolvendo esse sistema para p obtemos a 1 b 2 p 2 2b 1 b 2 p b 2 c 1 = 0 a 2 b 1 p 2 + 2b 1 b 2 p + b 1 c 2 = 0 p 2 = b 1c 2 b 2 c 1 ) a 1 b 2 a 2 b 1 ) Se consideramos o quadrado da solução do sistema 6) obtemos. A igualdade é válida se, e somente se, a 2 c 1 a 1 c 2 ) 2 4b 2 a 1 b 1 a 2 ) 2 = b 1c 2 b 2 c 1 ) a 1 b 2 a 2 b 1 ) a 2 c 1 a 1 c 2 ) 2 4a 1 b 2 a 2 b 1 )b 1 c 2 b 2 c 1 ) = 0 7) A expansão de Taylor de ordem 2 da função discriminate é a seguinte b 2 ac = b 1 x + b 2 y + O2)) 2 a 1 x + a 2 y + O2))c 1 x + c 2 y + O2)) = b 2 1 c 1 a 1 )x 2 + 2b 1 b 2 c 2 a 1 c 1 a 2 )xy + b 2 2 c 2 a 2 )y 2 + O2) Escrita na forma matricial, a parte quadrática desta função se escreve como b 2 ac = x segue-se que seu determinante é dado por ) b 2 1 y a 1 1c 1 2 2b ) ) 1b 2 a 1 c 2 a 2 c 1 ) x 1 2 2b 1b 2 a 1 c 2 a 2 c 1 ) b 2 2 a 2c 2 y Detb 2 ac) = b 2 1 a 1 c 1 )b 2 2 a 2 c 2 ) 1 4 2b 1b 2 a 1 c 2 a 2 c 1 ) 2 = 1 4 4b2 1a 2 c 2 + 4a 1 b 2 2c 1 4a 1 a 2 c 1 c 2 4b 1 b 2 c 2 a 1 4b 1 b 2 c 1 a 2 + c 2 2a a 1 a 2 c 1 c 2 + c 2 1a 2 2) = 1 ) a 2 c 1 a 1 c 2 ) 2 4b 2 a 1 b 1 a 2 )b 1 c 2 b 2 c 1 ). 4 Assim, Detb 2 ac) = 0 se, e somente se, vale a equação 7). 2. Sabemos que a projeçao π não será um difeomorfismo local em x, y, p) se F p x, y, p) = 0.
16 1.1. O RECOBRIMENTO DUPLO DE M E O LEVANTAMENTO DE CAMPOS 13 Por outro lado temos que π 1 ) = {x, y, p) : πx, y, p) } = {x, y, p) : x, y) } = {x, y, p) : b 2 ac = 0} Assim devemos ter e portanto Que é precisamente o conjunto p = 2b ± 4b 2 4ac 2a = b a F p = 2ap + 2b = 2a b a + 2b = 0 π 1 ) = {x, y, p) : F = F p = 0} Pela proposição 1.1.1) M = {F x, y, p) = ap 2 + 2bp + c = 0} é uma superfície suave, podemos fazer a seguinte construção. Notemos que cada ponto no plano onde b 2 ac > 0 existem duas direções p 1 x, y) e p 2 x, y) que correspondem a dois pontos na superfície M sobre a reta vertical que passa por x, y) ver figura 1.1). Pelo teorema da funçao implícita, temos que localmente duas componentes ou superfícies que projetam-se difeomorficamente sobre o plano x, y). Localmente nos pontos onde b 2 ac > 0, a EDI 1) define as direções p 1 = b + b 2 ac a e p 2 = b b 2 ac que definem os campos vetoriais associados v 1 = 1, p 1 ) e v 2 = 1, p 2 ). a Definição 1.2 Levantamento). O campo vetorial ξ sobre M é dito o levantamento de EDI 1) ou do campo bivaluado determinado se, e somente se d π ξ)x, y, p) é um vetor com direção p. Em outras palavras, deve-se projetar um vetor no plano com a correspondente direção p. Proposição O campo vetorial ξ denotado por: ξ = F p x + pf p y F x + pf y ) p é o levantamento para M do par de direções no plano definido por 1). 2. O campo vetorial ξ tem uma ou três singularidades em 0 RP 1. Estas singularidades são do tipo sela ou nó.
17 1.1. O RECOBRIMENTO DUPLO DE M E O LEVANTAMENTO DE CAMPOS 14 folha 2 RP 1 x, y, p 2 ) p 2 x, y, p 1 ) folha 1 p 1 RP 1 x, y) p 1 p 2 Figura 1.1: Prova. 1. Como ξ é o levantamento do campo bivaluado v = x + p y, isto é, dπξx, y, p)) = vx, y) temos ξ = x + p y + C p. Além disso, como ξ é um campo de vetores em M = F 1 0), ξ é ortogonal a F. F q ξ T q M M Figura 1.2:
18 1.1. O RECOBRIMENTO DUPLO DE M E O LEVANTAMENTO DE CAMPOS 15 A condição de tangência de ξ em M dá ξ. F = F x + p F y + C F p = 0 = F x + pf y + CF p = 0 Como F p 0, C = F x + pf y )/F p Segue-se que ou ainda, ξ = x + p y F x + pf y )/F p p ξx, y, p) = F p x + pf p y F x + pf y ) p 2. Vamos mostrar que as singularidades de ξ estão na reta 0 RP 1, logo a singularidade tem coordenada 0, 0, p), a) 0, 0, p) M, então F 0, 0, p) = 0. b) ξ0, 0, p) = 0, então F p x + pf p y F x + pf y ) p = 0 F p 0, 0, p) = 0 e F x + pf y 0, 0, p) = 0 Vamos estudar F x + pf y = 0 em 0, 0, p). φp) = F x + pf y )0, 0, p) = F x + p F 0, 0, p) y = a 1 p 2 + 2b 1 p + c 1 + pa 2 p 2 + 2b 2 p + c 2 ) = a 2 p 3 + a 1 + 2b 2 )p 2 + 2b 1 + c 2 )p + c 1 Supondo a 2 0 a função cúbica φp) tem uma ou três raízes fora da variedade de codimensão 1 no espaço a i, b 1, c i ) gerado pelos anuladores do discriminante de φ. Agora encontraremos a natureza de cada singularidade de ξ. O ponto 0, 0, p) é singularidade de ξ. Pela proposição 1.1.1) M é suave, assim F x 0, 0, p) 0 ou F y 0, 0, p) 0. Seja p 1 um zero de φ. Supondo que F y 0, 0, p 1 ) 0, M será localmente o gráfico da função y = gx, p). De fato, F x, y, p) = F x, gx, p), p) = 0
19 1.1. O RECOBRIMENTO DUPLO DE M E O LEVANTAMENTO DE CAMPOS 16 Derivando com respeito a x e p obtemos, Seja ξ a projeção de ξ no plano x, p) F x + F y F y g p + F p g x = 0 = 0 ξx, p) = F p x F x + pf y ) p Vamos a escrever o polinômio de Taylor de ordem 1 em torno de 0, p 1 ) ξ = ξ 1 x + ξ 2 p ξ 1 x, p) = α 1 x + α 2 p p 1 ) + O2) ξ 2 x, p) = β 1 x + β 2 p p 1 ) + O2) Assim, ξ = ξ 1 x + ξ 2 p = [α 1 x + α 2 p p 1 ) + O2)] x + [β 1x + β 2 p p 1 ) + O2)] p. Vamos agora obter a expressão de ξ em função de a i, b i, c i ) Para tal procedemos como segue Sejam, ξ = F p x, g, p) x F xx, g, p) + pf y x, g, p)) p α 1 = x ξ 1 = x F px, g, p) ) g = F p ) x + F p ) y 0, p 1 ) x α 2 = p ξ 1 = p F px, g, p) ) g = F p ) y p + F p) p 0, p 1 )
20 1.1. O RECOBRIMENTO DUPLO DE M E O LEVANTAMENTO DE CAMPOS 17 β 1 = x ξ 2 = x F xx, g, p) + pf yx, g, p)) )) g = F x ) x + F y ) x x + p g F y ) x + F y ) y 0, p 1 ) x β 2 = p ξ 2 = p F xx, g, p) + pf y x, g, p)) ) ) g = F x ) y p + F g x) p + p F y ) y p + F y) p + F y 0, p 1 ) 2 ) F α 1 = x p + 2 F g 0, p 1 ) y p x 2 ) F α 2 = p F g 0, p 1 ) y p p 2 F β 1 = x F g 2 x y x + p F x y + 2 F g y 2 x 2 F β 2 = p x + 2 F g y x p + F 2 y + p F p y + 2 F g y 2 p )) 0, p 1 ) )) 0, p 1 ), onde, φp 1 ) = F x + pf y )0, p 1 ) = F g y x + p F y )0, p 1) = F p g ) 0, p 1 ). y x como ψp 1 ) = 0 temos, g x 0, p 1) = p 1, g Assim, [ F p 0, p 1) = y ] 1 F p 0, p 1) = 0 α 1 = ) p a 1p 2 + 2b 1 p + c 1 )0, p 1 ) + p p a 2p 2 + 2b 2 p + c 2 ) 0, p 1 ) = 2a 2 p 2 + b 2 + a 1 )p 1 + b 1 ) α 2 = 0 ) β 2 = p a 1p 2 + 2b 1 p + c 1 0, p 1 ) + a 2 p 2 + 2b 2 p + c 2 ))0, p 1 ) + ) p p a 2p 2 + 2b 2 p + c 2 )) 0, p 1 )) = 3a 2 p a 1 + 2b 2 )p 1 + c 2 + 2b 1 )) = φ p 1 ) Para determinar a natureza das singularidades precisamos conhecer os autovalores da parte linear de ξ, estes são os autovalores da matriz da parte linear de ξ, α 1 p 1 ) = 2a 2 p b 2 + a 1 )p 1 + b 1 ) e φ p 1 ). ) D ξ0, α1 α 2 2a2 p 2 1 p 1 ) = = + b ) 2 + a 1 )p 1 + b 1 ) 0 β 1 β 2 β 1 φ p 1 ) Como p 1 não é uma raiz repetida da função cúbica φ, segue-se que φ p 1 ) 0. Como genericamente α 1 e φ não têm raízes em comum, obtemos que α 1 p 1 ) 0. Assim, as
21 1.2. REDUÇÃO FORMAL DAS EDIS 18 singularidades de ξ são nós ou selas. Existe a posibilidade de que tenha dois ramos de zeros, onde o campo pode acumular todos os pontos com a exceção de uma fibra correspondente a eles. Mais geralmente as singularidades terão sempre autovalores diferentes de zero e que são isolados. Pela expansão de Taylor da função discriminante vemos que os pontos correspondentes 0, 0, p) satisfazem φp) = F x + pf y)0, 0, p) = a 2 p 3 + a 1 + 2b 2 )p 2 + 2b 1 + c 2 )p + c 1 e, certamente, φp) = 0. A condição de que a equação quadrática e a equação cúbica tenham raízes comun, determina uma subvariedade de codimensão 1 do espaço a i, b i, c i ) que corresponde a um autovalor zero. 1.2 Redução formal das EDIs Nesta seção formalizaremos a redução de uma EDI do tipo 1) com a = ±c = y. Proposição Suponha que φ não tem raízes repetidas, e que α 1 p) e φp) não têm raízes em comun, então os termos lineares a, b, c da EDI ady 2 + 2bdxdy + cdx 2 = 0 pode ser reduzida á forma: ydy 2 + 2b 1 x + b 2 y)dxdy ± ydx 2 8) Prova. Começamos reduzindo a parte linear das funções a, b, c. a = a 1 x + a 2 y b = b 1 x + b 2 y c = c 1 x + c 2 y Seja L = a 1 x + a 2 y)dy 2 + 2b 1 x + b 2 y)dxdy + c 1 x + c 2 y)dx 2 Vamos escrever a parte linear com respeito a x, y) na forma matricial L = x ) ) dx 2 c 1 b 1 a 1 y c 2 b 2 a 2dxdy 2 dy 2
22 1.2. REDUÇÃO FORMAL DAS EDIS 19 Por abuso de notação, vamos escrever ) c1 b 1 a 1 L = c 2 b 2 a 2. Considerando a mudança de coordenadas lineares x = αx + βy y = γx + δy Temos dx = αdx + βdy dy = γdx + δdy dx 2 = α 2 dx 2 + 2αβdXdY + β 2 dy 2 dxdy = αγdx 2 + αδ + βγ)dxdy + βδdy 2 dy 2 = γ 2 dx 2 + 2γδdXdY + δ 2 dy 2 x ) y = dx 2 2dxdy = dy 2 = ) ) α γ X Y β δ α 2 2αβ β 2 dx 2 2αγ 2αδ + βγ) 2βδ dxdy γ 2 2γδ δ 2 dy 2 α 2 αβ β 2 dx 2 2αγ αδ + βγ 2βδ 2dXdY γ 2 γδ δ 2 dy 2 Pondo ) α 2 αβ β 2 α γ U =, e W = β δ 2αγ αδ + βγ 2βδ γ 2 γδ δ 2 temos que S = ULW ) ) α 2 αβ β 2 α γ c1 b 1 a 1 = β δ c 2 b 2 a 2αγ αδ + βγ 2βδ 2 γ 2 γδ δ 2
23 1.2. REDUÇÃO FORMAL DAS EDIS 20 Assim nas novas coordenadas X, Y ) a parte linear se escreve como L XY = X ) Y S dx 2 2dXdY dy 2 L XY = AdY 2 + 2BdXdY + CdX 2 com A = A 1 X + A 2 Y B = B 1 X + B 2 Y C = C 1 X + C 2 Y onde A 1 = δ 2 αa 1 + γa 2 ) + 2δβαb 1 + γb 2 ) + β 2 αc 1 + γc 2 ) A 2 = a 2 δ 3 + 2b 2 + a 1 )δ 2 β + 2b 1 + c 2 )δβ 2 + c 1 β 3 B 1 = γδαa 1 + γa 2 ) + αδ + γβ)αb 1 + γb 2 ) + αβαc 1 + γc 2 ) B 2 = γδβa 1 + δa 2 ) + αδ + γβ)βb 1 + δb 2 ) + αββc 1 + δc 2 ) C 1 = a 2 γ 3 + 2b 2 + a 1 )γ 2 α + 2b 1 + c 2 )γα 2 + c 1 α 3 C 2 = γ 2 βa 1 + δa 2 ) + 2γαβb 1 + δb 2 ) + α 2 βc 1 + δc 2 ) Para conseguir nosso objetivo precisamos de uma condição genérica para qualquer mudança de coordenadas α, β, γ, δ) tal que C 1 = 0 e A 1 = 0. Lembrando que a expressão de φ proporciona os zeros cúbicos do levantamento de ξ em 0 RP 1, então A 2 = a 2 δ 3 + 2b 2 + a 1 )δ 2 β + 2b 1 + c 2 )δβ 2 + c 1 β 3 = β 3 δ 3 a 2 β 3 + 2b 2 + a 1 ) δ2 β 2 + 2b 1 + c 2 ) δ ) β + c 1 ) δ = β 3 φ β C 1 = a 2 γ 3 + 2b 2 + a 1 )γ 2 α + 2b 1 + c 2 )γα 2 + c 1 α 3 = α 3 γ 3 a 2 α 3 + 2b 2 + a 1 ) γ2 α 2 + 2b 1 + c 2 ) γ ) α + c 1 γ = α 3 φ α) Como φ tem pelo menos uma raiz, denotamos esta por p 1. Pondo γ = αp 1, temos ) ) γ C 1 = α 3 φ = α 3 αp1 φ = 0 α α
24 1.2. REDUÇÃO FORMAL DAS EDIS 21 Observe que não se pode tomar δ = βp 1, uma vez que a mudança de coordenadas se escreveria como ) ) α γ α αp1 = β δ β βp 1, que tem determinante zero. Substituindo o valor de γ nas expressões de A 1 e C 2 temos: { } A 1 = α δ 2 a 1 + p 1 a 2 ) + 2δβb 1 + p 1 b 2 ) + β 2 c 1 + p 1 c 2 ) } C 2 = α {a 2 1 p b 1 p 1 + c 1 )β + a 2 p b 2 p 1 + c 2 )δ 1. Genericamente temos que C 2 0, pois se C 2 = 0 temos que a 1 p b 1p 1 + c 1 )β + a 2 p b 2p 1 + c 2 )δ = 0. F x 0, 0, p 1 ) = a 1 p b 1 p 1 + c 1 F y0, 0, p 1 ) = a 2 p b 2 p 1 + c 2 Logo, F x 0, 0, p 1 )β + F y 0, 0, p 1 )δ = 0 O que leva a uma contradição pois, F x e F y não se anulam simultaneamente do contrario a função discriminante é degenerada). Vamos supor que F y 0, 0, p 1 ) 0 segue que δ = F x0, 0, p 1 )β F y 0, 0, p 1 ) A mudança de coordenadas ficaria x ) y = X ) ) α γ Y = β δ X ) ) α αp 1 Y β Fx0,0,p 1)β F y0,0,p 1 ) O determinante desta matriz é O que não pode acontecer. αβ F x0, 0, p 1 ) F y 0, 0, p 1 ) αβp 1 = Assim, genericamente para β e δ temos que αβ F y 0, 0, p 1 ) φp 1) = 0 F x β + F y δ 0 2. Genericamente A 1 = 0.
25 substituindo δ = βp 1 A 1 = αβ 2 φp 1 ) = REDUÇÃO FORMAL DAS EDIS 22 De fato, A 1 = 0 se, e somente se, δ 2 a 1 + p 1 a 2 ) + 2δβb 1 + p 1 b 2 ) + β 2 c 1 + p 1 c 2 ) = 0 já que p 1 é raiz de φ. Logo se δ = βp 1, A 1 = 0. A equação tem outra solução para δ = λβ, se estas duas soluções coincidem δ = 2b 2p 1 + b 1 )β ± 4b 2 p 1 + b 1 ) 4a 2 p 1 + a 1 )c 2 p 1 + c 1 ) 2a 2 p 1 + a 1 ) βp 1 = b 2p 1 + b 1 )β a 2 p 1 + a 1 ) p 1 = b 2p 1 + b 1 ) a 2 p 1 + a 1 ) Equivalentemente a 2 p a 1 + b 2 )p 1 + b 1 = 0 α 1 p 1 ) = 2a 2 p b 2 + a 1 )p 1 + b 1 ) = 0 Se p 1 = λ, onde p 1 é uma raiz de φ e α 1. Não é generico, logo podemos assumir que p 1 λ, e δ = λβ anula a A 1 na nova EDI. 3. Genericamente A 2 0 Como A 2 = β 3 φ δ β ), e pela condição de que φ não tem raiz repetida, genericamente para a escolha de β tal que λ não é raiz de φ. Por tanto A 2 0. Por uma nova mudança de escala dada por A 2 = 1,e C 2 = ±1 a equação L = A 2 Y dy 2 + 2B 1 X + B 2 Y )dxdy + C 2 Y dx 2 Pode ser escrita como L = Y dy 2 + 2B 1 X + B 2 Y )dxdy ± Y dx 2 Considerando que a mudança de coordenadas feita foi linear, por abuso de notação vamos substituir X, Y ) x, y) L = ydy 2 + 2b 1 x + b 2 y)dxdy ± ydx 2
26 1.2. REDUÇÃO FORMAL DAS EDIS 23 Observação Destaco aqui que as novas variáveis x e y não são as originais da equação 1) Uma redução adicional da EDI Pela proposição 1.2.1), consideraremos a EDI da forma y + ax, y))dy 2 + 2b 1 x + b 2 y + bx, y))dxdy + ±y + cx, y))dx 2 = 0 9) onde a, b, c são funções suaves sem termos constantes e lineares. Mostraremos que esta EDI pode ser reduzida formalmente, não a uma forma linear, mas a uma forma com os coeficientes de dx 2 e dy 2 lineares. Procederemos como no caso de campos de vetores univaluados seguindo a teoria de Poincaré, de transformar, na classe de série de potências formais, um campo vetorial não ressonante para sua forma linear em um ponto singular por um difeomorfismo formal. Este processo consiste em anular sucessivamente todos os termos de grau k 2) na equação. Suponhamos que neste processo todos os graus são menores ou iguais a k 1 assim temos uma nova EDI com a = a k + Ok + 1) c = c k + Ok + 1) onde a k e c k são polinômios homogêneos de grau k. Consideramos a mudança de coordenadas H k em R 2 dada por x = X + p k y = Y + q k onde p k e q k são polinômios de grau k em X e Y. L = x ) ) dx 2 0 b 1 0 ) dx y ±1 b 2 1 2dxdy cx, 2 + y) bx, y) ax, y) 2dxdy dy 2 dy 2 O difeomorfismo H k dará uma nova EDI, a k x, y) = a k X + p k, Y + q k ) = k a i,k x k i y i i=0 k a i,k X + p k ) k i Y + q k ) i i=0
27 1.2. REDUÇÃO FORMAL DAS EDIS 24 k = a i,k X k i Y i + Ok + 1) i=0 = a k X, Y ) + Ok + 1) dx = dx + p k dx + p k dy dy = dy + q k dx + q k dy dx 2 dxdy = dy 2 dx 2 2dxdy = dy 2 = p + p 2 k p k q k + q k 2 q k p + p 2 k p k 2 q k + 2 q k q k p 2 + p k p k q k 2 q k + 2 q k 1 + q k 21 + q k 2 p k p k + p k + p k 2 q k q k 2 p k p k + 2 p k q k + 2 q k + 2 p k + p k + p k 2 q k q k 2 p k p k 1 + q k + p k 2 q k q k + 2 q k + p k q k + p k q k + q k + p k q k + p k + p k q k q k ) p k p k 2 + p k q k 2 p k 2 p k q k + q k p k q k p k q k p k + q k p k q k + q k dx 2 dxdy dy 2 dx 2 q k ) dxdy 2 dy 2 dx 2 2dXdY 2 dy p W = + p k p k q k 2 q k + 2 q k 2 p k p k 1 + q k + p k 2 q k + p k q k + p k q k + q k + p k q k 2 p k p k q k + 2 p k q k 2 + q k S = X ) ) 0 b 1 0 Y W = ±1 b 2 1 X ) ) S 1 R 1 T 1 Y S 2 R 2 T 2 onde S 1 = 2b 1 q k + q k p k ) R 1 = b q k + p k + p k p k T 1 = 2b 1 + p k q k S 2 = ±1 + 2 p k + p k p k q k + p k q k ) 2 ) + 2b 2 q k + q k p k ) + q k R 2 = ± p k + p k ) + b 21 + q k + p k + p k T 2 = ± p 2 k ) + 2b 2 p k + p k q k ) q k + q k 2 q k + p k 2 q k ) + q k q k + q k
28 1.2. REDUÇÃO FORMAL DAS EDIS 25 Por outro lado ) c b a W = p k q k ) S 1 R 1 T 1 S 2 R 2 T 2 ) = c k + W 1 b + W 2 a k + W 3 ) ) ±q k + SX, Y ) b 1 p k + b 2 q k + RX, Y ) q k + T X, Y ) onde W 1, W 2, W 3, S, R, T têm grau maior que k juntando todos os resultados temos onde ) dx 2 L = ±Y + CX, Y ) BX, Y ) Y + AX, Y ) 2dXdY dy 2 AX, Y ) = 2b 1 X p k + X p k q k ± Y p k BX, Y ) = b 1 X1 + q k + p k + p k + b 2 Y 1 + q k + p k + p k + Y q k q k 2 + 2b 2 Y p k + p k q k + p k q k ) q k + p k q k ) ± Y p k + Y q k + b k + b 1 p k + b 2 q k CX, Y ) = 2b 1 X q k + q k p k ) + 2b 2Y q k + q k q k ) + 2Y q k + Y q 2 k + a k + q k p k + p k ) p k ) ± 2Y p k ± Y p 2 k + Y q 2 k + c k ± q k E os termos de grau k são dados por A k = q k + 2b 1 X + b 2 Y ) p k + 2Y q k + a k 10) C k = ±q k + 2b 1 X + b 2 Y ) q k ± 2Y p k + c k 11) Aqui p k, q k são polinômios homogêneos de ordem k nas variáveis X e Y que podem ser escritas na forma p k = q k = k p i,k X k i Y i i=0 k q i,k X k i Y i i=0 Procurando p k e q k isto é p i,k e q i,k, com 2k + 1) variáveis) de modo que a mudança de
29 1.2. REDUÇÃO FORMAL DAS EDIS 26 coordenadas H k satisfazem as equações 10), 11), então A k = C k = 0 qk + 2b 1 X + b 2 Y ) p k + 2Y ) q k ±q k + 2b 1 X + b 2 Y ) q k ± 2Y p k ) pk M k q k Afirmação: A matriz M k só depende de b 1, b 2, k De fato, da primeira equação k a i,k X k i Y i = i=0 = k q i,k X k i Y i + 2b 1 X + b 2 Y ) i=0 k i=0 +2 = = ak c k ak c k ) ) k ip i,k X k i Y i 1 + 2Y i=1 k 1 q i,k X k i Y i + 2 i + 1)b 1 p i+1,k X k i Y i + 2 k iq i,k X k i Y i i=1 i=0 k iq i,k X k i Y i 1 i=1 k ib 2 p i,k X k i Y i k 1 = q 0,k X k + q k,k Y k + 2b 1 p 1,k X k + 2i + 1)b 1 p i+1,k + ib 2 p i, k + iq i,k )X k i Y i 2kb 2 p k,k Y k + 2kq k,k Y k i=1 i=1 Da segunda equação k c i,k X k i Y i = ± i=0 = ± k i=0 k 1 q i,k X k i Y i + 2b 1 X + b 2 Y ) k i)q i,k X k i 1 Y i k i ±2Y k i)p i,k X k i 1 Y i ±2 k i=0 i=0 i=0 k 1 q i,k X k i Y i + 2 k i)b 1 q i,k X k i Y i + 2 i=0 k k i + 1)p i 1,k X k i Y i i=1 = ±q 0,k X k ± q k,k Y k + 2kb 1 q 0,k X k + 2b 2 q k 1,k Y k k k i + 1)b 2 q i 1,k X k i Y i ±2k + 1)p 0,k X k ± 2p k1,ky k k 1 [ ] ± q i,k + 2k i)b 1 q i,k + k i + 1)b 2 q i 1,k ± p i 1,k )) X k i Y i i=1 Logo, o determinante é um polinômio não nulo em termos de b 1, b 2. Assim, o conjunto de pares b 1, b 2 ) que anulam DetM k ) tem medida zero em R 2 i=1
30 1.3. TOPOLOGIA DAS FORMAS NORMAIS 27 Definição 1.3. O par b 1, b 2 ) é dito ressonante, se existe um inteiro k 2, tal que a matriz M k é singular. Podemos enunciar o seguinte teorema. Proposição Se b 1, b 2 ) é um par não resonante, então a EDI 9) pode ser reduzida por um difeomorfismo formal a ydy 2 + 2b 1 x + b 2 y + bx, y))dxdy ± ydx 2 = 0, onde bx, y) é uma série de potências formal não constante e que não tem termos lineares. Prova. Se o par b 1, b 2 ) é não ressonante, então o sistema linear ) pk M k q k = ak c k ) tem uma única solução. Como o difeomorfismo correspondente H k anula os termos de ordem k em a e c, obtemos o sistema desejado. 1.3 Topologia das formas normais Na seção anterior,mostramos que em geral uma EDI 1) pode ser escrita na forma ydy 2 + 2b 1 x + b 2 y)dxdy ± ydx 2 = 0 Uma EDI desta forma, divide o plano de parâmetros b 1, b 2 ) de acordo com o tipo de singularidade do campo levantado ξ. Primeiro notemos que a mudança de coordenadas x, y) x, y) produz uma EDI equivalente a EDI do tipo 1) dada pelo par b 1, b 2 ). A nova EDI se escreve como L = ydy 2 + 2b 1 x b 2 y)dxdy ± ydx 2. Temos assim uma simetria com respeito ao eixo b 1 no plano b 1, b 2 ). O plano b 1, b 2 ) é separado por três curvas que são os casos especiais quando φ tem raiz dupla, para α 1 e φ tenham uma raiz em comum e a curva não é de Morse, isto é fazendo a prova da primeira proposição resolvemos o sistema 6) quando a superfície M não é suave, obtendo que p = a 2c 1 a 1 c 2 ) 2b 2 a 1 b 1 a 2 ) onde precisamos que b 2a 1 b 1 a 2 0, assim para que a função discriminante não tenha uma singularidade de Morse precisamos de a 1 b 2 a 2 b 1 = Vamos estudar a divisão do espaço de parâmetros b 1, b 2 ) para a EDI do tipo 1) reduzida à equação ydy 2 +2b 1 x+b 2 y)dxdy ydx 2 = 0 como ax, y) = a 1 x+a 2 y, bx, y) = b 1 x+b 2 y,e cx, y) = c 1 x + c 2 y, temos que a 1 = c 1 = 0 e a 2 = c 2 = 1.
31 1.3. TOPOLOGIA DAS FORMAS NORMAIS 28 Lembrando que φp) = a 2 p 3 + 2b 2 + a 1 )p 2 + 2b 1 + c 2 )p + c 1 = p 3 + 2b 2 p 2 + 2b 1 1)p = pp 2 + 2b 2 p + 2b 1 1) a) Uma curva que não é de Morse: b 1 = 0 b) A curva φ tem uma raiz dupla: 2b 1 1 = 0 ou b 1 = 1 2 b ) Assim para 2b 1 1 = 0 obtemos φp) = p 2 p + 2b 2 ) Outro caso é quando o discriminante da parte quadrática é zero, isto é, b 2 2 2b 1 1) = 0, onde b 1 = 1 2 b ) c) As curvas α 1 e φ tem uma raiz em comun: b 1 = 0 α 1 = 2a 2 p 2 + b 2 + a 1 )p + b 1 ) = 2p 2 + b 2 p + b 1 ) Observamos que p = 0 é uma raiz de φ. Logo para que seja uma raiz de α 1, precisamos de b 1 = 0 A figura 1.3) mostra a divisão do plano de parâmetros b 1, b 2 ). b 2 Figura 1.3: R 2 R 3 R 1 R b 1 Vamos analisar o tipo de cada uma das singularidades em cada uma dessas regiões, pela
32 1.3. TOPOLOGIA DAS FORMAS NORMAIS 29 proposição 1.1.2) temos que os autovalores de ξ são α 1 p) e β 2 p), onde α 1 p) = 2p 2 + b 2 p + b 1 ) β 2 p) = 3p 2 + 4b 2 p 1 + 2b 1 ) As raízes de φp) são p 1 = 0, p 2 = b 2 + b 2 2 2b 1 + 1, p 3 = b 2 b 2 2 2b Assim em cada singularidade os autovalores são dados por α 1 p 1 ) = 2b 1 β 2 p 1 ) = 1 2b 1 α 1 p 2 ) = 2 b 2 p 2 b 1 + 1) β 2 p 2 ) = 2 b 2 p 2 2b 1 + 1) α 1 p 3 ) = 2 b 2 p 3 b 1 + 1) β 2 p 3 ) = 2 b 2 p 3 2b 1 + 1) Vamos determinar a natureza das singularidades em cada uma das regiões R i com 1 i 4 a) Na região R 1, b 1 < 0 a 1 ) A singularidade p 1 = 0 é uma sela. De fato, α 1 p 1 ) = 2b 1 < 0, β 2 p 1 ) = 1 2b 1 > 1. Por tanto DetDξp 1 )) < 0. a 2 ) A singularidade p 2 é uma sela. De fato, α 1 p 2 ) > 2b 2 p > 0, β 2 p 2 ) = α 1 p 2 ) 2b 1 ) < 0. Segue-se que DetDξp 2 )) = α 1 p 2 ).β 2 p 2 ) = α b 1 < 0 a 3 ) A singularidade p 3 é uma sela. De fato, procendo-se como no caso p 2 concluimos que p 3 é uma sela. Assim as singularidades na região R 1 são todas do tipo sela. b) Na região R 2, 0 < b 1 < 1/2 com p 3 < p 1 < p 2 e α 1 p 1 )β 2 p 1 ) > 0, por enquanto α 1 β 2 < 0 para p 2 e p 3. α 1 p 1 ) = 2b 1 > 0 β 2 p 1 ) = 1 2b 1 > 0 α 1 p 2 ) = 2 b 2 p 2 b 1 + 1) β 2 p 2 ) = 2 b 2 p 2 2b 1 + 1) = α 1 2b 1 ) Assim, temos em 0 < b 1 < 1/2 duas selas e um nó entre elas. c) Na região R 3, b 1 > 1/2 e b 1 < 1/2b ) c 1 ) A singularidade p 1 = 0 é uma sela. De fato, α 1 p 1 ) = 2b 1 > 0, β 2 p 1 ) = 1 2b 1 < 0. Segue-se que DetDξp 2 )) < 0
33 1.3. TOPOLOGIA DAS FORMAS NORMAIS 30 c 2 ) A singularidade p 2 é um nó. De fato, α 1 p 2 ) = 2 b 2 p 2 b 1 + 1) < b 2 p 2 + 1/2) < 0, β 2 p 2 ) = 2 b 2 p 2 2b 1 + 1) < 2b 2 p 2 < 0. Segue-se que DetDξp 2 )) > 0. c 3 ) A singularidade p 3 é uma sela. De fato, α 1 p 3 ) = 2 b 2 p 2 b 1 + 1) = 2b b 2 b 2 2 2b b 1 + 1) > 2b 1 > 0, β 2 p 3 ) = 2 b 2 p 2 2b 1 + 1) = α 1 + 2b 1 < 0. Segue-se que DetDξp 3 )) < 0. d) Na região R 4, b 1 > 1/2b ). O campo tem uma única singularidade p 1 = 0 que é uma sela. De fato, α 1 p 1 ) = 2b 1 > 0, β 2 p 1 ) = 1 2b 1 < 0. Logo em R 4, p 1 é uma sela. b 2 2 selas +1 nó 3 selas 1 sela b 1 Figura 1.4: Partição do plano b 1, b 2 ) Observação A variação dos parâmetros b 1 e b 2 mostram que ao cruzar as fronteiras das regiões do plano de parâmetros b 1, b 2 ) algumas singularidades mudam de tipo. O comportamento das singularidades sobre as fronteiras das regiões não é genérico e por esse motivo não foram estudados aqui. 2. Vamos estudar a divisão do espaço de parâmetros b 1, b 2 ) para a EDI do tipo 1) reduzida à equação ydy 2 + 2b 1 x + b 2 y)dxdy + ydx 2 = 0 como ax, y) = a 1 x + a 2 y, bx, y) = b 1 x + b 2 y,e cx, y) = c 1 x + c 2 y, temos que a 1 = c 1 = 0 e a 2 = c 2 = 1 Lembrando que φp) = a 2 p 3 + 2b 2 + a 1 )p 2 + 2b 1 + c 2 )p + c 1 = p 3 + 2b 2 p 2 + 2b 1 + 1)p = pp 2 + 2b 2 p + 2b 1 + 1) a) Uma curva que não é de Morse: b 1 = 0
34 1.3. TOPOLOGIA DAS FORMAS NORMAIS 31 b) A curva φ tem uma raiz dupla: 2b = 0 ou b 1 = 1 2 b2 2 1) Assim para 2b = 0 obtemos φp) = p 2 p + 2b 2 ) Outro caso é quando o discriminate da parte quadratica é zero, isto é, b 2 2 2b 1+1) = 0, onde b 1 = 1 2 b2 2 1) c) As curvas α 1 e φ tem uma raiz em comun: b 1 = 0 ou b 1 = ±b 2 1 α 1 = 2a 2 p 2 + b 2 + a 1 )p + b 1 ) = 2p 2 + b 2 p + b 1 ) Observamos que p = 0 é uma raiz de φ. Logo para que seja uma raiz de α 1, é necessário que b 1 = 0, as raízes da parte quadrática de φ, são p = b 2 ± b 2 2 2b 1 1. Logo para que seja uma raiz de α 1 é necessário que b 2 ± b 2 2 2b 1 1) 2 + b 2 b 2 ± b 2 2 2b 1 1) + b 1 = 0, o que dá b 1 + 1) 2 = b 2 2 assim, b 1 = ±b 2 1. R 2 b 2 R 4 R 5 R 8 R 1 1 R 3 R 6 R b 1 Vamos a analisar o tipo de cada uma das singularidades em cada uma dessas regiões. Pela proposição 1.1.2) os autovalores de ξ são dados por α 1 p) e por β 2 p). α 1 p) = 2p 2 + b 2 p + b 1 ) β 2 p) = 3p 2 + 4b 2 p b 1 ) As raízes de φp) são dadas por: p 1 = 0, p 2 = b 2 + b 2 2 2b 1 1, p 3 = b 2 b 2 2 2b 1 1
35 1.3. TOPOLOGIA DAS FORMAS NORMAIS 32 Para cada singularidade temos os seguintes autovalores α 1 p 1 ) = 2b 1 β 2 p 1 ) = 1 2b 1 α 1 p 2 ) = 2b 2 p 2 + b 1 + 1) β 2 p 2 ) = 2b 2 p 2 + 2b 1 + 1) α 1 p 3 ) = 2b 2 p 3 + b 1 + 1) β 2 p 3 ) = 2b 2 p 3 + 2b 1 + 1) Vamos determinar a natureza das singularidades em cada uma das regiões R i, 1 i 8. a) Na região R 1, b 1 < b 2 1 e b 1 < b 2 1 com b 1 < 1 e b 2 > 0 a 1 ) A singularidade p 1 = 0 é uma sela. De fato, α 1 p 1 ) = 2b 1 < 2 < 0, β 2 p 1 ) = 1 2b 1 > 1 > 0. Por tanto DetDξp 1 )) < 0. a 2 ) A singularidade p 2 é uma sela. De fato, p 2 < 0 α 1 p 2 ) > 2b 2 p 2 > 0, β 2 p 2 ) < 2b 2 p 2 < 0. Segue-se que DetDξp 2 )) = α 1 p 2 ).β 2 p 2 ) < 0 a 3 ) A singularidade p 3 é uma sela. De fato, procendo-se como no caso p 2 concluimos que p 3 é uma sela. Assim as singularidades na região R 1 são todas do tipo sela. b) Na região R 2, b 1 > b 2 1, b 1 < b 2 1 com b 1 < 1/2 e b 2 > 0 b 1 ) A singularidade p 1 = 0 é uma sela. De fato, α 1 p 1 ) = 2b 1 < 0, β 2 p 1 ) = 1 2b 1 > 0. Por tanto DetDξp 1 )) < 0. b 2 ) A singularidade p 2 é um nó. De fato, p 2 > 0 α 1 p 2 ) < 2b 2 p 2 + 2b 2 < 0, β 2 p 2 ) < 22b 1 + 1) < 0. Segue-se que DetDξp 2 )) = α 1 p 2 ).β 2 p 2 ) > 0 b 3 ) A singularidade p 3 é uma sela. De fato, p 3 < 0 α 1 p 3 ) > 2b 2 p 2 2b 2 > 0, β 2 p 3 ) < 2b 2 p 2 < 0. Segue-se que DetDξp 3 )) = α 1 p 3 ).β 2 p 3 ) < 0 Assim as singularidades na região R 2 são dois do tipo sela e um nó. c) Na região R 3, b 1 > b 2 1, b 1 > b 2 1 e b 2 > 0 c 1 ) A singularidade p 1 = 0 é uma sela. De fato, α 1 p 1 ) = 2b 1 < 0, β 2 p 1 ) = 1 2b 1 > 0. Por tanto DetDξp 1 )) < 0. c 2 ) A singularidade p 2 é um nó. De fato, p 2 > 0 α 1 p 2 ) < 2b 2 p 2 + 2b 2 < 0, β 2 p 2 ) 22b 1 + 1) < 0. Segue-se que DetDξp 2 )) = α 1 p 2 ).β 2 p 2 ) > 0
36 1.3. TOPOLOGIA DAS FORMAS NORMAIS 33 c 3 ) A singularidade p 3 é um nó. De fato, procendo-se como no caso p 2 concluimos que p 3 é um nó. Assim as singularidades na região R 3 são dois do tipo nó e uma sela. d) Na região R 4, b 1 < b 2 1, e 1/2 < b 1 < 0 d 1 ) A singularidade p 1 = 0 é um nó. De fato, α 1 p 1 ) = 2b 1 < 0, β 2 p 1 ) = 1 2b 1 < 0. Por tanto DetDξp 1 )) > 0. d 2 ) A singularidade p 2 é uma sela. De fato, p 2 < 0 α 1 p 2 ) < 2b 2 p 2 +2b 2 < 0, β 2 p 2 ) > 0. Segue-se que DetDξp 2 )) = α 1 p 2 ).β 2 p 2 ) < 0 d 3 ) A singularidade p 3 é uma sela. De fato, procendo-se como no caso p 2 concluimos que p 3 é uma sela. Assim as singularidades na região R 4 são dois do tipo sela e um nó. e) Na região R 5, b 1 < b 2 1, e b 1 > 0 e 1 ) A singularidade p 1 = 0 é uma sela. De fato, α 1 p 1 ) = 2b 1 > 0, β 2 p 1 ) = 1 2b 1 < 0. Por tanto DetDξp 1 )) < 0. e 2 ) A singularidade p 2 é uma sela. De fato, p 2 < 0 com valores b 1 = 1, e b 2 = 2.5 α 1 p 2 ) < 0, β 2 p 2 ) > 0. Segue-se que DetDξp 2 )) = α 1 p 2 ).β 2 p 2 ) < 0 e 3 ) A singularidade p 3 é uma sela. De fato, procendo-se como no caso p 2 concluimos que p 3 é uma sela. Assim as singularidades na região R 5 são três do tipo sela. f) Na região R 8, b 1 > b 2 1, e b 1 > 0 f 1 ) A singularidade p 1 = 0 é uma sela. De fato, α 1 p 1 ) = 2b 1 > 0, β 2 p 1 ) = 1 2b 1 < 0. Por tanto DetDξp 1 )) < 0. f 2 ) A singularidade p 2 é um nó. De fato, p 2 < 0 com valores b 1 = 1, e b 2 = 1.8 α 1 p 2 ) > 0, β 2 p 2 ) > 0. Segue-se que DetDξp 2 )) = α 1 p 2 ).β 2 p 2 ) > 0 f 3 ) A singularidade p 3 é uma sela. De fato,p 3 < 0 com valores b 1 = 1, e b 2 = 1.8 α 1 p 3 ) > 0, β 2 p 3 ) < 0. Segue-se que DetDξp 3 )) = α 1 p 3 ).β 2 p 3 ) < 0 Assim as singularidades na região R 5 são dois do tipo sela e um nó. g) Na região R 6, b 1 > 1/2b ) e 1/2 < b 1 < 0. O campo tem uma única singularidade p 1 = 0 que é um nó. De fato, α 1 p 1 ) = 2b 1 < 0, β 2 p 1 ) = 1 2b 1 < 0. Logo em R 6, p 1 é um nó. h) Na região R 7, b 1 > 1/2b ) e b 1 > 0. O campo tem uma única singularidade p 1 = 0 que é uma sela. De fato, α 1 p 1 ) = 2b 1 > 0, β 2 p 1 ) = 1 2b 1 < 1 < 0. Logo em R 7, p 1 é uma sela.
37 1.3. TOPOLOGIA DAS FORMAS NORMAIS 34 Figura 1.5: 2 nós+1 sela 2 selas +1 nó b 2 3 selas 2 selas +1 nó 3 selas nó 0 1 sela b 1 2 selas +1 nó 2 selas +1 nó 3 selas A figura 1.5) mostra a distribuição das singularidades no plano b 1, b 2 ) onde: Nas regiões 1 e 5 temos 3 selas. Nas regiões 2, 4 e 8 tem-se 2 selas e 1 nó. Na região 3 tem-se 2 nó e 1 sela. Na região 6 tem-se 1 nó. Na região 7 tem-se 1 sela. Dada uma EDI do tipo 1), suponha que a função discriminante tem uma singularidade de Morse na origem e que φp) não tem raízes duplas ou raiz em comum com α 1 p). Podemos enunciar o teorema. Teorema Com as hipóteses acima, existe um homeomorfismo genérico h : R 2, 0 R 2, 0 que aplica as curvas integrais da EDI original nas curvas integrais de uma das formas normais: I O discriminante é um ponto isolado: a) ydy 2 + 2xdxdy ydx 2 = 0 1 sela, lemon) b) ydy 2 2xdxdy ydx 2 = 0 3 selas, star) c) ydy 2 + 1/2xdxdy ydx 2 = 0 2 selas e 1 nó, monstar) II O discriminante é uma cruz de duas curvas suaves: a) ydy 2 + 2xdxdy + ydx 2 = 0 1 sela) b) ydy 2 1/2xdxdy + ydx 2 = 0 1 nó) c) ydy 2 4xdxdy + ydx 2 = 0 3 selas) d) ydy 2 + 2y x)dxdy + ydx 2 = 0 2 selas+1 nó) e) ydy 2 + 4/3xdxdy + ydx 2 = 0 1 sela+2 nó) O tipo é determinado pelas funções a, b, c. Mais ainda, este homeomorfismo é um difeomorfismo fora de certas direções singulares que passam pelo origem.
38 1.3. TOPOLOGIA DAS FORMAS NORMAIS 35 A importância deste teorema é estabelecer a classificação das curvas integrais de nossa EDI por meio de homeomorfismos. Vamos a obter a configuração das curvas integrais no caso 3 selas Star). Para F = p 2 y 2px y, obtemos suas derivadas parciais F p = 2py 2x, F x = 2p, F y = p 2 1, Resolvemos o sistema F = 0, F p = 0, F x + pf y = 2p + pp 2 1) = pp 2 3) = 0, tem-se 3 singularidades localizadas nos pontos 0, 0), 0, p 1 ), 0, p 2 ); onde, p 1 = 3, p 2 = 3. Para obter as trajetórias do campo de linha no plano p, x) faremos o mesmo processo que em [6] e [9]. Em cada região do plano p, x) onde este sistema de coordenadas está definido, as trajetórias do campo de linha tem o mesmo comportamento que as trajetorias do campo de vetores de ẋ = 2p2 x+2x p 2 1) 2 ṗ = p5 4p 3 +3p p 2 1) 2 Vamos estudar a natureza dessas singularidades. Assim obtemos que ẋ x = 2p2 + 1) p 2 1) 2 ẋ p = 4xpp2 + 3) p 2 1) 3 ṗ x = 0 ṗ p = p p 2 1) 2 a) Para 0, 0) temos que é uma sela. De fato, D ξ0, 0) = 2p2 +1) p 2 1) 2 0 4xpp 2 +3) p 2 1) 3 p 4 +3 p 2 1) 2 ) 2 0 = 0,0) 0 3 b) Para 0, p 1 ) temos que é uma sela. De fato, D ξ0, p 1 ) = 2p2 +1) p 2 1) 2 0 4xpp 2 +3) p 2 1) 3 p 4 +3 p 2 1) 2 = 0, 3) ) = ) c) Para 0, p 2 ) temos que é uma sela. De fato, procendo-se como no caso para p 1 concluimos que 0, p 2 ) é uma sela. Assim, as singularidades para esta forma normal são todas do tipo sela. Nestas coordenadas a curva F = 0, F p = 0 dada por xp) = 0 é a curva de dobra no plano px. Temos então em 0, 0) uma singularidade que tem o eixo x como variedade invariante para o autovalor 3. A outra variedade invariante associada ao autovalor 2 da matriz tem a direção do vetor 5p 2 + 1) 2, p 4 + 3).
39 1.3. TOPOLOGIA DAS FORMAS NORMAIS 36 No plano xy a curva de dobra é um ponto isolado 0, 0). colocamos em evidência y em F = yp 2 2xp y = 0, Chamamos y px a equação onde y px = 2xp p 2 1 Projetando a variedade invariante, eixo x. Fazendo p = 0 na equação y px, e as outras variedades invariantes são fazendo p = p 1,e p = p 2 respectivamente na equação de y px. ypx0 = 0 ypxp 1 = 3x ypxp 2 = 3x Onde a configuração local do campo é dada pela seguinte figura esquerda), e projetada no plano x, y) dá a configuração mostrada na figura seguinte direita). 3 selas no plano px 3 selas no plano xy
40 Capítulo 2 Famílias genéricas a 1-parâmetro de EDIs do tipo Morse No capítulo anterior fizemos a classificação de Equacões Diferenciais Implícitas ax, y)dy 2 + 2bx, y)dxdy + cx, y)dx 2 1) perto de pontos onde a função discriminante b 2 ac tem uma singularidade de Morse. Tais pontos aparecem naturalmente em famílias de equações diferenciais implícitas. Neste capítulo descreveremos como a configuração de curvas de solução muda de acordo com a deformação do parâmetro. 2.1 Redução das EDIs Seja ax, y, t)dy 2 + 2bx, y, t)dxdy + cx, y, t)dx 2 = 0 2) uma família de 1-parâmetro de EDIs do tipo Morse em t = 0. Denotamos por F x, y, t, dx, dy) = 0 a equação acima, e o levantamento da família do campo bivaluado que está determinado por esta equação à uma família de campo vetorial univaluado sobre a hipersuperfície M em R 3 RP 1, dado por M = {x, y, t, p); F x, y, t, p) = ap 2 + 2bp + c = 0} A condição de Morse em t = 0 garante que a superficie M 0 = M t=0 é suave pela Prop1.1.1), e consequentemente todo M é suave. A projeção natural π : M R 2 R x, y, t, p) x, y, t) Para cada ponto x, y, t, p) escolhemos a direção tangente de M que se projeta em linhas que passam por x, y, t) com uma inclinação p no plano t constante. A família de campo de vetores
41 2.1. REDUÇÃO DAS EDIS 38 dada por ξ = F p x + pf p y F x + pf y ) p é um levantamento adequado para a família de campo bivaluado. Espera-se, como no caso para a EDI simples, que a parte linear da equação 2) contenha toda a informação topológica da família de EDIs. Começamos reduzindo a parte linear a uma forma simples. Denotemos por ax, y, t) = a 1 x + a 2 y + l 1 t bx, y, t) = b 1 x + b 2 y + l 2 t cx, y, t) = c 1 x + c 2 y + l 3 t Como no capítulo anterior, supomos aqui que em t = 0 a cúbica φ, φp) = F x + pf y )0, 0, 0, p) = a 2 p 3 + 2b 2 + a 1 )p 2 + 2b 1 + c 2 )p + c 1, que dá os zeros do campo ξ 0 = ξ t=0 não tem raízes repetidas, e que os autovalores da matriz derivada destas singularidades são diferentes de zero. Proposição A família de equações do tipo 2) pode ser reduzida a y + t)dy 2 + 2b 1 x + b 2 y)dxdy ± ydx 2 com um novo par b 1, b 2 ), se a seguinte condição de versalidade é satisfeita a 1 a 2 l 1 b 1 b 2 l 2 0 c 1 c 2 l 3 Prova. Seja L = ax, y, t)dy 2 + 2bx, y, t)dxdy + cx, y, t)dx 2 se a parte linear com respeito a x, y, t) é representada por matrizes da seguinte forma Fazemos a mudança de coordenadas lineares ) c 1 b 1 a 1 dx 2 L x,y,t) = x y t c 2 b 2 a 2 2dxdy l 3 l 2 l 1 dy 2 x = αx + βy y = γx + δy
42 2.1. REDUÇÃO DAS EDIS 39 Sejam U a matriz de mudança de coordenada X, Y ), e W a matriz que representa a mudança das formas quadráticas binárias correspondentes. dx = αdx + βdy dy = γdx + δdy dx 2 = α 2 dx 2 + 2αβdXdY + β 2 dy 2 dxdy = αγdx 2 + αδ + βγ)dxdy + βδdy 2 dy 2 = γ 2 dx 2 + 2γδdXdY + δ 2 dy 2 ) x y t = dx 2 2dxdy = dy 2 = ) α γ 0 X Y t β δ α 2 2αβ β 2 dx 2 2αγ 2αδ + βγ) 2βδ dxdy γ 2 2γδ δ 2 dy 2 α 2 αβ β 2 dx 2 2αγ αδ + βγ 2βδ 2dXdY γ 2 γδ δ 2 dy 2 α γ 0 α 2 αβ β 2 U = β δ 0, W = 2αγ αδ + βγ 2βδ γ 2 γδ δ 2 Assim temos que R = USW α γ 0 c 1 b 1 a 1 α 2 αβ β 2 = β δ 0 c 2 b 2 a 2 2αγ αδ + βγ 2βδ l 3 l 2 l 1 γ 2 γδ δ 2 porém a nova parte linear de L em coordenadas X, Y ) é L X,Y,t) = ) dx 2 X Y t R 2dXdY dy 2 L = AdY 2 + 2BdXdY + CdX 2
43 2.1. REDUÇÃO DAS EDIS 40 com A = A 1 X + A 2 Y + L 1 t B = B 1 X + B 2 Y + L 2 t C = C 1 X + C 2 Y + L 3 t onde A 1 = δ 2 αa 1 + γa 2 ) + 2δβαb 1 + γb 2 ) + β 2 αc 1 + γc 2 ) A 2 = a 2 δ 3 + 2b 2 + a 1 )δ 2 β + 2b 1 + c 2 )δβ 2 + c 1 β 3 B 1 = γδαa 1 + γa 2 ) + αδ + γβ)αb 1 + γb 2 ) + αβαc 1 + γc 2 ) B 2 = γδβa 1 + δa 2 ) + αδ + γβ)βb 1 + δb 2 ) + αββc 1 + δc 2 ) C 1 = a 2 γ 3 + 2b 2 + a 1 )γ 2 α + 2b 1 + c 2 )γα 2 + c 1 α 3 C 2 = γ 2 βa 1 + δa 2 ) + 2γαβb 1 + δb 2 ) + α 2 βc 1 + δc 2 ) L 1 = δ 2 l 1 + 2δβl 2 + β 2 l 3 L 2 = γδl 1 + γβ + δα)l 2 + αβl 3 L 3 = γ 2 l 1 + 2αγl 2 + α 2 l 3 Cálculos diretos fornecem que A 2 = β 3 φ ) δ β γ C 1 = α 3 φ α) onde φp) é a cúbica que dá os zeros do levantamento em t = 0, denotemos por γ = p 1 α como no capítulo anterior seção 1.2)) e δ = λ 0 β. Modificamos a função φ, para obter a seguinte equação quadrática ψλ) = F x + p 1 F y 0, 0, 0, λ) = a 1 λ 2 + 2b 1 λ + c 1 ) + p 1 a 2 λ 2 + 2b 2 λ + c 2 ) = a 2 p 1 + a 1 )λ 2 + 2b 2 p 1 + b 1 )λ + c 2 p 1 + c 1 ) Como p 1 é uma raiz de φ, também é raiz desta nova equação quadrática. De fato, ψp 1 ) = a 2 p b 2 + a 1 )p b 1 + c 2 )p 1 + c 1 = φp 1 ) = 0 Seja λ 0 a outra raiz de ψ, λ 0 p 1 segue que ψλ) = a 2 p 1 + a 1 )λ 2 + 2b 2 p 1 + b 1 )λ + c 2 p 1 + c 1 ) = λ p 1 )[a 2 p 1 + a 1 )λ + 2b 2 p 1 + b 1 ) + a 1 p 1 + a 2 p 2 1]
44 2.1. REDUÇÃO DAS EDIS 41 e portanto Outra forma de se escrever ) 2b2 λ 0 = p a 2 p 1 + a 1 ψλ 0 ) = f 1 λ 0 ) + f 2 λ 0 )p 1 = 0 Onde f 1 p) = a 1 p 2 + 2b 1 p + c 1 f 2 p) = a 2 p 2 + 2b 2 p + c 2 Por outro lado temos que A 1 = C 1 = 0 pela seção 1.2)). Portanto obtemos uma EDI com a parte linear sem termos em X nos coeficientes de dx 2 e dy 2, isto é, L = A 2 Y + L 1 t)dy 2 + 2B 1 X + B 2 Y + L 2 t)dxdy + C 2 Y + L 3 t)dx 2 onde A 2 = β 3 φ ) δ = β 3 φλ 0 ) β C 2 = p 2 1α 2 βa 1 + δa 2 ) + 2p 1 α 2 βb 1 + δb 2 ) + α 2 βc 1 + δc 2 ) = α 2 βa 2 p b 2 p 1 + c 2 )λ 0 + a 1 p b 1 p 1 + c 1 )) L 1 = λ 2 0β 2 l 1 + 2λ 0 β 2 l 2 + β 2 l 3 = β 2 λ 2 0l 1 + 2λ 0 l 2 + l 3 ) L 3 = p 2 1α 2 l 1 + 2α 2 p 1 l 2 + αl 3 = α 2 p 1 l 1 + 2p 1 l 2 + l 3 ) uma nova mudança de coordenadas da forma X, Y, t) x+ut, y+vt, wt ), na forma matricial ) ) X Y t = x y T u v w Leva a parte linear à forma desejada se e só se o determinante da segunda matriz L M é diferente de zero, isto é, B 1 0 e C 2 L 1 A 2 L B B C 2 B 2 A 2 = C 2 B 2 A 2 = L M u v w L 3 L 2 L 1 C 2 v + L 3 w B 1 u + B 2 v + L 2 w A 2 v + L 1 w 1. A condição B 1 0, segue da proposição 1.1.1), uma vez que em t = 0 tem-se uma singularidade do tipo Morse, isto é, B 1 A 2 B 2 A 1 0, e mostramos anteriormente que A 1 = 0 e que genericamente A Para mostrar que a condição C 2 L 1 A 2 L 3 0 é valida, suponhamos C 2 L 1 A 2 L 3 = 0. Provamos no primeiro capítulo que em geral C 2 0, isto é, F x β + F y δ 0 Por outro lado,
45 2.1. REDUÇÃO DAS EDIS 42 F x β + F y δ = βf x + F y δ β ) = βf x + F y λ 0 ) dessa forma temos que C 2 = α 2 βf x p 1 ) + F y p 1 )λ 0 ) 0, pondo gp) = l 1 p 2 + 2l 2 p + l 3 obtemos que L 1 = β 2 gλ 0 ) L 2 = α 2 gp 1 ) Portanto a equação se escreveria como C 2 L 1 A 2 L 3 = α 2 β 3 [f 1 p 1 ) + f 2 p 1 )λ 0 )gλ 0 ) φλ 0 )gp 1 )] = 0 3) Usando f 1 e f 2 temos que φλ 0 ) = f 1 λ 0 ) + f 2 λ 0 )p 1 subtituindo φλ 0 ) na equação 3) obtem-se [f 1 λ 0 ) + f 2 λ 0 )λ 0 ]gp 1 ) = [f 2 p 1 )λ 0 + f 1 p 1 )]gλ 0 ) Resolvendo para λ 0 e lembrando que λ 0 = δ β temos λ 0 = gλ 0)f 1 p 1 ) gp 1 )f 1 λ 0 ) gp 1 )f 2 λ 0 ) gλ 0 )f 2 p 1 ) δ = gλ 0)f 1 p 1 ) gp 1 )f 1 λ 0 ) gp 1 )f 2 λ 0 ) gλ 0 )f 2 p 1 ) β Assim a mudança de coordenadas teria a matriz cujo determinante é α γ 0 α αp 1 0 U = β δ 0 = β gλ 0)f 1 p 1 ) gp 1 )f 1 λ 0 ) gp 1 )f 2 λ 0 ) gλ 0 )f 2 p 1 ) β detu) = αβ gλ 0)f 1 p 1 ) gp 1 )f 1 λ 0 ) p 1 gp 1 )f 2 λ 0 ) + p 1 gλ 0 )f 2 p 1 )) gp 1 )f 2 λ 0 ) gλ 0 )f 2 p 1 ) = αβ gλ 0)f 1 p 1 ) gp 1 )f 1 λ 0 ) p 1 gp 1 )f 2 λ 0 ) gλ 0 )f 1 p 1 ) gp 1 )f 2 λ 0 ) gλ 0 )f 2 p 1 ) f 1 λ 0 ) + p 1 f 2 λ 0 ) = αβgp 1 ) gp 1 )f 2 λ 0 ) gλ 0 )f 2 p 1 ) = 0 o que é uma contradição pois detu) 0 por hipotese. Por uma nova mudança de escala dada por A 2 = 1 e C 2 = ±1 podemos escrever L = ±y + ±v + L 3 w)t )dx 2 + 2B 1 x + B 2 y + B 1 u + B 2 v + L 2 w)t )dxdy + y + v + L 1 w)t )dy 2
46 2.2. TOPOLOGIA DAS FORMAS NORMAIS 43 Lembrando que w e B 1 são diferentes de zero, tomando L 1 = 1 L 3 = 0 u = L 2w B 1 v = 0 A EDI se escreve como, L = y + t)dy 2 + 2B 1 x + B 2 y)dxdy ± ydx 2 Proposição Para quase todos os pares b 1, b 2 ), a família de EDIs cuja parte linear é dada na Prop 2.1.1) pode ser reduzida por um difeomorfismo à y + t)dy 2 + 2b 1 x + b 2 y + bx, y))dxdy ± ydx 2 = 0 onde bx, y) é uma série de potências formal sem termos constantes nem termos lineares. Prova. Segue-se da prova da proposição 1.2.3) junto com a proposição 2.1.1). 2.2 Topologia das formas normais Não podemos aplicar o método do capítulo anterior diretamente para obter um modelo de família de EDIs pelo levantamento de ξ t. Porém estes campos nos fornecem uma boa informação das famílias dos campos bivaluados. De agora em diante, assumiremos que as familias de EDIs satisfazem a condição de versalidade da Proposição 2.1.1). Para nosso primeiro resultado, temos que dado um cone C com a equação x 2 + y 2 z 2 = 0 em R 3, existem dois germes de funções genéricas R 3, 0 R, 0 que preserva o cone C. A menos de difeomorfismo, são as funções g 1 x, y, z) = z e g 2 x, y, z) = x cujos zeros no cone correspondem a um ponto e um par de retas, respectivamente. Proposição O discriminante = {x, y, t); b 2 ac = 0} é um cone, e a projeção ao longo do parâmetro t é uma família genérica de seções deste cone. Prova. Segue-se da mudança de coordenadas da Proposição 2.1.1), onde: ax, y, t) = y + t bx, y, t) = b 1 x + b 2 y cx, y, t) = ±y
47 2.2. TOPOLOGIA DAS FORMAS NORMAIS 44 que b 2 ac = b 1 x + b 2 y) 2 yy + t) Como b 1 0 e b 2 sem restrição, fazemos: b 1 = 1, b 2 = 0 b 2 ac = b 1 x + b 2 y) 2 yy + t) = x 2 yy + t) = x 2 y 2 yt = x 2 y + t 2 )2 ± t2 4 Por uma nova mudança dada por x = x ỹ = y + t 2 t = t 2, obtemos que o discriminante é dado por = x 2 ỹ 2 t 2, que tem a estructura de um cone. Além disso, as seções para t = 0 são preservadas. Observamos que para o caso x 2 + y 2 t 2 a seção de zeros é dada pelo ponto zero e para o caso x 2 y 2 + t 2 a seção de zeros é dada por um par de linhas. Proposição As singularidades do campo levantado ξ se projetam em 1 ou 3 curvas suaves mutuamente transversais através do ponto do cone. As singularidades resultantes da EDI para um t fixo t 0) são do tipo dobra-selas ou dobra-nós. Observação A nomenclatura singularidade do tipo dobra-sela dobra-nó) é como em [3]. Significa que a projeção π : M t R 2, M t superfície associada a EDI, tem uma singularidade
48 2.2. TOPOLOGIA DAS FORMAS NORMAIS 45 do tipo dobra nesse ponto e que este ponto é uma singularidade do tipo sela nó) do campo levantado. Prova. As singularidadeszeros) do campo levantado ξ = F p x + pf p y F x + pf y ) p são dados por F p = F = F x + pf y = 0 Pelo teorema da função implícita, temos que a solução da equação acima tem curvas suaves através da fibra exepcional nos zeros de ξ 0. Assim obtemos 1 ou 3 curvas. Fixando um t, obtemos que um campo levantado ξ t que terá 1 ou 3 zeros. Por continuidade a natureza destes zeros não trocam ao longo das curvas, isto é, os zeros de ξ t são do mesmo tipo selas e nós) do que ξ 0. Seja M t = {x, y, p) : F t x, y, p) = F x, y, t, p) = 0} para t 0 Como a EDI é do tipo Morse em t = 0, a superfície M t é suave. A projeção para t 0, π t : M t R 2 x, y, p) x, y) é uma dobra sobre o discriminante levantado t, uma t seção de ). Afirmação A projeção π t não será uma dobra em F = F p = 0 se e somente se, F pp = 0. Se F = F p = 0 tem-se que F pp = 0. A recíproca é por contradição. Suponhamos que π t é uma dobra para t 0, com F pp = 0, isto é 2 F x, y, t) = 2a = 0 p2 assim sobre a t-seção de se tem que b 2 ac = 0, por tanto b = 0. De fato, ax, y, t) = a 1 x + a 2 y + l 1 t = 0 bx, y, t) = b 1 x + b 2 y + l 2 t = 0 cx, y, t) = c 1 x + c 2 y + l 3 t = 0
49 2.2. TOPOLOGIA DAS FORMAS NORMAIS 46 Escrito na forma matricial a 1 a 2 l 1 x 0 b 1 b 2 l 2 y = 0 c 1 c 2 l 3 t 0 Como assumimos que esta familia de EDI satisfaz a condição de versalidade temos que a única solução desta equação é x, y, t) = 0, 0, 0) o que é uma contradição para t 0. Portanto obtemos que para t 0 se tem que F pp 0. Precisamos mostrar que a involução troca dois pontos de M t, e que estes são projetados sobre a mesma imagem, e esta será ξ t -bom ou seja, os autovetores da parte linear de ξ t avaliados nas singularidades e a tangente ao conjunto crítico de π t são dois a dois distintos. Para simplificar a notação, escrevemos F em lugar de F t. E assumimos que M t é parametrizada por x, gx, p), p). Assim no plano x, p) a tangente de π t ao conjunto crítico F = F p = 0 é dado por w = i j k F x F y F p = F y F pp F p F yp, F p F xp F x F pp, F x F yp F y F xp ) F xp F yp F pp Como F p = 0 temos w = F y F pp, F x F pp, F x F yp F y F xp ) Projetando no plano x, p) tem-se w = F y F pp, F x F yp F y F xp ) Em uma singularidade de ξ t temos F x + pf y = 0. Assim, w = F y F pp, F x F yp F y F xp ) = F y F pp, pf y F yp F y F xp ) = F y F pp, pf yp + F xp )) A tangente é dada ao longo de v = F pp, pf yp + F xp )) 4) Agora projetamos o campo ξ t no plano x, p) e obtemos ξ t = F p x F x + pf y ) p
50 2.2. TOPOLOGIA DAS FORMAS NORMAIS 47 Procedendo como na prova da proposição 1.1.2) temos que a parte linear de ξ t dada por 2 ) F α 1 = x p + 2 F g 0, p) y p x 2 ) F α 2 = p F g 0, p) y p p 2 F β 1 = x F g 2 )) x y x + p F x y + 2 F g y 2 0, p) x 2 F β 2 = p x + 2 F g y x p + F 2 )) y + p F p y + 2 F g y 2 0, p), p onde, 0 = φp) = F x + pf y )0, p) = F g y x + p F F )0, p) = p g ) 0, p) y y x Então, g 0, p) = p x [ g F 0, p) = p y ] 1 F 0, p) = 0 p Porém, α 1 = ) p a 1p 2 + 2b 1 p + c 1 )0, p) + p p a 2p 2 + 2b 2 p + c 2 ) 0, p) = 2a 2 p 2 + b 2 + a 1 )p 1 + b 1 ) = F xp + pf yp α 2 = F pp β 1 = F xx + pf y x + pf yx + pf yy ))0, p) = F xx + 2pF yx + p 2 F yy ) ) β 2 = p a 1p 2 + 2b 1 p + c 1 0, p) + a 2 p 2 + 2b 2 p + c 2 ))0, p) + ) p p a 2p 2 + 2b 2 p + c 2 )) 0, p)) = 3a 2 p a 1 + 2b 2 )p 1 + c 2 + 2b 1 )) = F y + F xp + pf yp ) Assim a matriz da parte linear fica ) F xp + pf yp F pp A = F xx + 2pF yx + p 2 F yy ) F y + F xp + pf yp ) A direção v dada em 4) é um autovetor desta matriz, se e somente se, F pp = 0. De fato, 1. Se v é um autovetor de A associado ao autovalor λ, isto é.
51 2.2. TOPOLOGIA DAS FORMAS NORMAIS 48 Av = λv ou ainda F xp + pf yp F xx + 2pF yx + p 2 F yy ) F y + F xp + pf yp ) F xp + pf yp ) Assim obtemos que F pp = 0 2. Se F pp = 0 temos a nova A A = os autovalores são F pp ) F xp + pf yp 0 F pp F xx + 2pF yx + p 2 F yy ) F y + F xp + pf yp ) ) = λ ) F pp F xp + pf yp ) ) λ 1 = F xp + pf yp λ 2 = F y + F xp + pf yp ) Encontramos o autovetor correspondente para cada autovalor. a) Para λ 1 = F xp + pf yp ) ) ) 0 0 v1 0 = F xx + 2pF yx + p 2 F yy ) F y + 2F xp + 2pF yp ) 0 Assim v = v 1, v 2 ) = F y + 2F xp + 2pF yp, F xx + 2pF yx + p 2 F yy )) b) Para λ 2 = F y + F xp + pf yp ) v 2 ) ) ) 2F xp + 2pF yp 0 v1 0 = F xx + 2pF yx + p 2 F yy ) 0 0 Assim, v 1 = 0 e com v 2 = F xp + pf yp ). Tem-se que v = v 1, v 2 ) = 0, F xp + pf yp )) é o autovetor associado ao autovalor λ 2 Mas isto não pode acontecer para t 0. Pela afirmação anterior ) Portanto obtemos que o autovetor desta matriz e o vetor v são diferentes; assim a involução é ξ t bom. Obtemos nosso resultado, para t 0 todas as singularidades são dobras-selas dobras-nós). v 2
52 2.2. TOPOLOGIA DAS FORMAS NORMAIS 49 Proposição Quando o discriminante 0 = t=0 é um nó, a posição das curvas de zeros e do discriminante 0 no cone depende apenas da parte linear da EDI em t = 0. Observação O discriminante é um nó quando é o cruzamento transversal de dois curvas suaves. Prova. As curvas dos zeros são dadas por F = F p = F x + pf y = 0 onde se utiliza o produto vetorial generalizado como em [11], e se projetam em curvas de R 3 com direções tangentes à origem ao longo de w i. w = F F p F x + pf y ) = F y F tp F t F yp )F px + F y + pf py ), F t F xp F x F tp )F px + F y + pf py ), F x F yp F y F xp )F px + F y + pf py ), F x F yp F t x + pf ty ) F tp F yx + pf yy )) + F y F xp F tx + pf ty ) F tp F xx + pf xy )) F t F xp F yx + pf yy ) F yp F xx + pf xy ))) w i = F y F tp F t F yp, F t F xp F x F tp, F x F yp F y F xp ) para F p = 0, onde as componentes são avaliadas em 0, 0, 0, p i ) com p i sendo zero da função cúbica φ. O vetor w i depende só da parte linear da equação ax, y, t)dy 2 + 2bx, y, t)dxdy + cx, y, t)dx 2 = 0 e pela proposição 2.1.1) podemos tomar a parte linear de a, b, c para obter a forma y + t)dy 2 + 2b 1 x + b 2 y)dxdy + ydx 2 Ou seja as funções a, b, c tem a seguinte forma normal ax, y, t) = y + t, onde {a 1 = 0, a 2 = 1, l 1 = 1} bx, y, t) = b 1 x + b 2 y, onde {l 2 = 0} cx, y, t) = y, onde {c 1 = 0, c 2 = 1, l 3 = 0} Portanto obtemos F t = l 1 p 2 i + 2l 2p i + l 3 = p 2 i F tp = 2p i F x = a 1 p 2 i + 2b 1p i + c 1 = 2b 1 p i F xp = 2b 1 F y = a 2 p 2 i + 2b 2p i + c 2 = p 2 i + 2b 2p i + 1 F yp = 2p i + b 2 ) Substituindo w i = 2b 2 p 2 i + p i, p 2 i b 1, b 1 p 2 1 b 1 )
53 2.2. TOPOLOGIA DAS FORMAS NORMAIS 50 onde p 1 é zero de φp) = p 3 + 2b 2 p 2 + 2b 1 + 1)p. A figura 2.1) i) mostra a partição do plano b 1, b 2 ) de acordo com as diferentes órbitas topológicas da EDI em t = 0. Os detalhes de como foi feito esta figura estão no primeiro capítulo. E encontramos que as configurações dos vetores w i e 0 sobre o cone são as mesmas componentes para cada partição. Pode se notar na Figura 2.2) as posições destas curvas sobre o cone, e para as partições dos zeros de ξ t para t = constante. 2 nós+1 sela 2 selas +1 nó b 2 3 selas 2 selas +1 nó 3 selas nó 0 1 sela b 1 2 selas +1 nó 2 selas +1 nó 3 selas Figura 2.1: i) S S N S S S S N N 3 selas. 2 selas +1 nó. 2 nós+1 sela. Figura 2.2: A partir da figura 2.2) podemos concluir que: As imagens das singularidades x 1, p 1 ) e x 2, p 2 ) do tipo sela pela projeção π estão num mesmo ramo da hipérbole, isto é sobre a mesma linha do cone, enquanto que a imagen da singularidade 0, 0) do tipo sela está no outro ramo, a outra linha do cone. As imagens das singularidades x 1, p 1 ) do tipo sela e x 2, p 2 ) do tipo nó pela projeção π estão num mesmo ramo da hipérbole, enquanto que a imagen da singularidade 0, 0) do tipo sela está no outro ramo. As imagens das singularidades x 1, p 1 ) e x 2, p 2 ) do tipo nó e a singularidade 0, 0) do tipo sela pela projeção π estão num mesmo ramo da hipérbole. Para provar nosso resultado principal precisaremos colar vários modelos locais para curvas integrais. As faixas usadas neste processo de colagem consistem de famílias paralelas de cúspides, isto é, dada pela forma y 3 = x t) 2 com a família de cúspides passando ao longo do eixo x e a cúspide tangente vertical.
54 2.2. TOPOLOGIA DAS FORMAS NORMAIS 51 Primeiro precisamos de um resultado de homogeneidade, que mostra que qualquer duas faixas dessa cúspide são difeomorfas. Lema Seja r um número real qualquer. Então existe um difeomorfismo do plano preservando as curvas da cúspide y 3 = x t) 2 que levam o intervalo [ 1, 1] {0} à [ r, r] {0}. Prova. Seja α um número positivo, e g a aplicação g : R 2 R 2 x, y) gx, y) = α 3 x, α 2 y) onde g é continua e ) α 3 0 Dg = 0 α 2 Assim detdg) = α 5 > 0. Verificando que g é um difeomorfismo. E que também preserva as cúspides α 2 y) 3 = α 3 x t) 2 = α 6 x 2 2α 3 xt + t 2 y 3 = x 2 2 xt α 3 + t2 α 6 = x t ) 2 α 3 e para t = t α 3, tem-se y 3 = x t) 2. De fato g : [ 1, 1] {0} [ α 3, α 3 ] {0}, e com α = r 1 3 se tem o resultado. Agora vamos a enunciar e mostrar nosso resultado principal desta dissertação, o qual diz assim, Teorema Suponha que a família das EDIs é do tipo Morse em t = 0, e que a função cúbica φ não tem raízes repetidas, os zeros de ξ 0 são normais e a família satisfaz a condição de versalidade da proposição 2.1.1). Então a família é topologicamente equivalente a uma das seguintes formas normais. I 0 é um ponto isolado a)y + t)dy 2 + 2xdxdy ydx 2 = 0 b)y + t)dy 2 2xdxdy ydx 2 = 0 c)y + t)dy xdxdy ydx2 = 0 1 sela, lemon) 3 selas, star) 2 selas e 1 nó)
55 2.2. TOPOLOGIA DAS FORMAS NORMAIS 52 II 0 é um cruzamento transversal de dois curvas suaves a)y + t)dy 2 + 2xdxdy + ydx 2 = 0 b)y + t)dy xdxdy + ydx2 = 0 c)y + t)dy 2 4xdxdy + ydx 2 = 0 d)y + t)dy 2 + 2y x)dxdy + ydx 2 = 0 e)y + t)dy xdxdy + ydx2 = 0 1 sela 1 nó 3 selas 2 selas e 1 nó 1 sela e 2 nós A normalização é uma condição técnica sobre os valores dos zeros de um campo vetorial que vale para a maioria dos campos. Prova. Pela proposição 2.2.1) temos que o discriminante da família de EDIs dada pela equação 1) é um cone e como o parâmetro na família muda, obtemos 2 famílias genéricas de seções do cone dependendo se o discriminante 0 é um ponto isolado ou é um nó. 1. No primeiro caso, quando 0 é um ponto isolado, o discriminante t, para t 0 é uma curva suave fechada. Além disso, existem 1 ou 3 zeros no campo ξ t sobre t. A natureza destes zeros dependem só do tipo da EDI em t = 0, e são do tipo dobra-sela ou dobra-nó Prop 2.2.2). Aplicando o resultado de Davydov, encontramos um homeomorfismo tomando as curvas integrais de ξ t nestes zeros para nosso modelo. Usando o Lema 2.2.6) estendemos este homeomorfismo a uma vizinhança de t. Como o campo vetorial ξ 0 tem pontos não singulares fora do origem, podemos fixar o diâmetro da vizinhança de t onde o homeomorfismo é definido. 2. No segundo caso, onde 0 é um nó, temos vários casos para cada tipo de EDI em t = 0, dependendo da possição dos zeros do campo ξ t nas componentes de t a união de dois curvas suaves). Como tínhamos observado na Proposição 2.2.4) que a forma destes zeros são dados sobre t dependem somente do tipo de EDI em t = 0. Assim procedemos igual ao caso onde 0 é um ponto isolado. Vamos obter a configuração das curvas integrais no caso 2 selas e um nó. Para F = y + t)p 2 + 2y x)p + y = 0, obtemos seus derivadas parciais F p = 2py + t) + 2y x), F x = 2p, F y = p 2 + 2p + 1, Resolvemos o sistema F = 0, F p = 0, F x + pf y = 2p + pp 2 + 2p + 1) = pp 2 + 2p 1) = 0, tem-se 3 singularidades localizadas nos pontos 0, 0, 0), x 1, y 1, p 1 ), x 2, y 2, p 2 ); onde p 1 = 2 1, p 2 = 2 1. Onde, p 1 = 2 1 p 2 = 2 1 x 1 = t 2 p 1 + 1) x 2 = t 2 p 2 + 1) y 1 = t 2 p 1 y 2 = t 2 p 2
56 2.2. TOPOLOGIA DAS FORMAS NORMAIS 53 Para obter as trajetórias do campo de linha no plano p, x) faremos o mesmo processo que em [6] e [9]. Em cada região do plano p, x) onde este sistema de coordenadas está definido, as trajetórias do campo de linha tem o mesmo comportamento que as trajetórias do campo de vetores de ẋ = 2p + 2px 2x p + 1)p 2 + 2p + 1) ṗ = p4 + 3p 3 + p 2 p p + 1)p 2 + 2p + 1) Vamos estudar a natureza dessas singularidades ẋ x = 2p 2 p + 1)p 2 + 2p + 1) ẋ p = 22p + 2px 1 4x) p 2 + 2p + 1) 2 ṗ x = 0 ṗ p = p3 + 3p 2 + 5p 1 p + 1)p 2 + 2p + 1) Assim obtemos que para 0, 0) temos que é uma sela. De fato, D ξ0, 0) = 2p 2 p+1)p 2 +2p+1) 0 para x 1, p 1 ) temos que é um nó. De fato, D ξx 1, p 1 ) = 22p+2px 1 4x) p 2 +2p+1) 2 p3 +3p 2 +5p 1 p+1)p 2 +2p+1) 2p 2 p+1)p 2 +2p+1) 0 22p+2px 1 4x) p 2 +2p+1) 2 p3 +3p 2 +5p 1 p+1)p 2 +2p+1) para x 2, p 2 ) temos que é uma sela. De fato, D ξx 2, p 2 ) = 2p 2 p+1)p 2 +2p+1) 0 22p+2px 1 4x) p 2 +2p+1) 2 p3 +3p 2 +5p 1 p+1)p 2 +2p+1) x1,p 1 ) x2,p 2 ) ) 2 0 = 0,0) 2 1 = = ) 1 2) ) 1 + 2) 2 Assim, as singularidades para esta forma normal são dois do tipo sela e um nó. Nestas coordenadas a curva F = 0, F p = 0 dada por xp) = p p 1 é a curva de dobra no plano px. Temos então em 0, 0) uma singularidade que tem ao eixo x como variedade invariante para o autovalor 2. A outra variedade invariante associciada ao autovetor 1 da matriz tem a direção do vetor 2, 3). No plano xy a curva de dobra é um cruzamento transversal de dois curvas xp) = p p 1 yp) = p2 p 2 1 ) )
57 2.2. TOPOLOGIA DAS FORMAS NORMAIS 54 Chamamos ypx a equação onde colocamos em evidência y em F = yp 2 + 2x y)p + y = 0, pp 2xp) ypx = p 2 + 2p + 1 Projetando a variedade invariante, eixo x. Fazendo p = 0 na equação ypx, e as outras variedades invariantes são fazendo p = p 1,e p = p 2 respetivamente na equação de ypx. ypx0 = 0 ypxp 1 = )) 2 1 2x) ypxp 2 = )) x) Onde a configuração local do campo é dada pela seguinte figura esquerda), e projetada no plano x, y) dá a configuração mostrada na figura seguinte direita). 2 selas e 1nó no plano px e t = 1 2 selas e 1 nó no plano xy e t = 1
58 Capítulo 3 Aplicação Neste capítulo aplicaremos as técnicas estudadas nos capítulos 1 e 2 como ferramentas para a obtenção da configuração topológica de um sistema de duas leis de conservação. Dado um sistema de duas leis de conservação U t + F u) x = 0, onde x R; t > 0, Ux, t) R 2 e F : R 2 R 2, F u, v) = fu, v), gu, v)) se considerarmos soluções contínuas invariantes por escala do tipo U x t ), pondo s = x t obtemos dus) ds.ds dt + DF U).dUs) ds e substituindo no sistema ds dx = 0 1) denotando dus) ds = Us) obtemos que o sistema 1) é equivalente DF U) U = s U, ou seja, Us) são os autovetores da matriz derivada da função de fluxo, associados aos autovalores s, nesse sentido, dizemos que as curvas de rarefação são as curvas integrais do campo de linhas gerado pelos autovetores da matriz derivada ) função de fluxo. Se denotamos U por U du =, teremos dv ) ) ) fu f v du du = s, dv ds g u g v Eliminando-se s entre as duas equações que dão as coordenadas dos autovetores de DF teremos f v dv) 2 + f u g v )dudv g u du) 2 = 0, 2) que é uma EDI do tipo 1, ou seja, as curvas de rarefação são as curvas integrais da equação 2). Aqui consideraremos a função de fluxo F : R 2 R 2 com funções coordenadas polinômios homogêneos completos de grau 2. Seguindo [6], após mudança linear de coordenadas mostraremos que é suficiente considerar funções coordenadas da forma: fx, y) = x 2 xy 3) gx, y) = mx 2 + n + 1 y 2, m, n R. 4) 2
59 3.1. FORMULAÇÃO DO PROBLEMA 56 Temos então duas possibilidades: 1) Se m < 0, existem regiões do plano onde os autovalores da matriz DF são complexos, essas regiões são chamadas de região elítica, no problema em questão essas regiões são delimitadas por duas retas que passam pela origem. 2) Se m > 0, estamos no problema do ponto umbílico isolado não há uma região elítica. A configuração das rarefações para o problema 1 com funcões f, g acrescidas de termos lineares foi completamente descrita por Eschenazi em [6]. O acréscimo de termos lineares transformou a região elítica numa região ilimitada cujo bordo é uma hipérbole. A configuração para as funções f, g como em 3) e 4) não foi apresentada. O problema 2, ou seja, estudar a configuração das curvas integrais da equação 2) na vizinhança de um ponto umbílico isolado foi estudado por Gutierrez-Sotomayor em [7] do ponto de vista de sistemas dinâmicos e por Shaeffer-Shearer em [10] do ponto de vista de leis de conservação. Em [10], por outro caminho, os autores reobtiveram os resultados de [7]. O acréscimo de termos lineares transformou o ponto umbílico isolado numa região elítica limitada cujo bordo é uma elipse. 3.1 Formulação do problema Nesta seção mostramos que a equação diferencial sobre a superficie M 2 pode ter uma ou 3 singularidades. Usando as técnicas desenvolvidas nos capítulos 1 e 2 determinamos a natureza dessas singularidades e descrevemos como obter as configurações das curvas de rarefação curvas integrais dos campos de linhas gerados pelos autoespaços da matriz DF ) no espaço de estados. Consideramos fx, y) = ax 2 +bxy +cy 2, gx, y) = a x 2 + b xy + c y 2, a proposição abaixo mostra que existe uma mudança de coordenadas linear que reduz o número de parâmetros da função F de 6 para 2. Proposição ) Seja ) F : R 2 R 2 definida por F x, y) = fx, y), gx, y)) e denotemos x x por X =, Y =. Existe uma mudança de coordenadas linear, P, tal que nas novas y y coordenadas as funções f, g se escrevem como: onde m, n R. fx, y ) = x ) 2 + x y gx, y ) = mx ) 2 + n + 1 y ) 2 2
60 3.1. FORMULAÇÃO DO PROBLEMA 57 Prova. Queremos escrever X = P Y, onde P = Se escrevemos: Temos que Q = Q = ) α γ β δ ) a b 2 b 2 c a ) b 2 b 2 c X F X) = X T QX, X T Q X) E desta forma usando que X = P Y,obtemos ) Y Y = P 1 X P 1 T P T QP Y Y T P T Q P Y isto é, as novas f, g são dadas por Escrevendo, como ) fx, y ) gx, y ) = F Y ) ) Y = P 1 T P T QP Y Y T P T Q P Y ) ) 1 δ γ Y T P T QP Y = αδ γβ β α Y T P T Q P Y ) 1 Y T P T δq γq )P Y = αδ γβ Y T P T αq βq)p Y ) Y P 1 T P T QP Y Y T P T Q P Y ) A B Y T 2 Y B 2 C ) A B Y T 2 Y B 2 C
61 3.1. FORMULAÇÃO DO PROBLEMA 58 temos A = B = C = A = B = C = 1 α 2 aδ a γ) + αβbδ b γ) + β 2 cδ c γ) ) αδ βγ 1 2a b )αγδ 2a αγ 2 + bαδ 2 + b 2c )βγδ b βγ 2 + 2cβδ 2) αδ βγ 1 cδ 3 + b c )δ 2 γ + a b )δγ 2 a γ 3) αδ βγ 1 a α 3 + b a)α 2 β + c b)αβ 2 cβ 3) αδ βγ 1 b 2a)αβ + 2a α 2 γ bβ 2 γ + 2c b)αβδ + b α 2 δ 2cβ 2 δ ) αδ βγ 1 aβγ 2 + a αγ bβγδ + b αγδ cβδ 2 + c αδ 2) αδ βγ 1. Genericamente temos que C = 0, pois se C 0, cδ 3 + b c )δ 2 γ + a b )δγ 2 a γ 3) 0 podemos escolher δ γ como sendo uma raiz da equação ψx) = cx 3 + b c )x 2 + a b )x a = 0 Assim, C = = = 1 cδ 3 + b c )δ 2 γ + a b )δγ 2 a γ 3) αδ βγ γ 3 c δ3 αδ βγ γ 3 + b c ) δ2 γ 3 γ + a b ) δ ) γ 3 γ2 a γ3 γ 3 γ 3 ) δ αδ βγ ψ = 0 γ 2. Tomamos α, β tal que αδ βγ 0 Temos agora. fx, y) = Ax 2 + Bxy gx, y) = A x 2 + B xy + C y 2 Fazemos uma nova mudança de variáveis com ) α 0 P = β δ
62 3.1. FORMULAÇÃO DO PROBLEMA 59 obtemos : A 1 = α A + β B B 1 = Bδ C 1 = 0 A 1 = A α ) 2 + B A)α β + C B)β ) 2 δ B 1 = 2C B)β + B α C 1 = C δ 1. Genericamente B 1 = 0, isto é, 2C B)β + B α = 0 β B α = B 2C esta escolha é sempre possível uma vez que a escolha δ γ B 2C 0 e o fato αδ βγ 0 implica que 2. Temos A 1 = α A + BB B 2C α A 1 = α A + β B = α A + Bβ ) α = α A + BB B 2C ) Fazemos α = B 2C BB + AB 2AC tem-se A 1 = 1 3. Temos B 1 = 1, escolha dada por δ = 1 B ) 4. A 1 A = B + B A B 2C B + C B B ) 2 α ) 2 B 2C ) 2 A 1 = A α ) 2 + B A)α β + C B)β ) 2 δ = A α ) 2 δ + B A)β α ) 2 δ α + C B)β ) 2 α ) 2 δ α ) 2 = α ) 2 ) δ A + B A B 2C B + C B B 2C ) 2 B ) 2 = Bα ) 2 A + B A B 2C B + C B B 2C ) 2 B ) 2 )
63 3.1. FORMULAÇÃO DO PROBLEMA Para C 1 = C B, pela escolha de δ C 1 = C δ = C B Segue-se que as novas funções f, g se escrevem como: fx, y) = A 1 x 2 + B 1 xy + C 1 y 2 = x 2 + xy gx, y) = A 1x 2 + B 1xy + C 1y 2 = mx 2 + n + 1 y 2 2 Onde m, n R. Os autoespaços da matriz DF são dados pela equação ) ) ) fx f y dx dx = s dy dy g x g y Eliminando-se s entre essas duas equações obtemos ) dy 2 f y + f x g y ) dy dx dx g x = 0 f y dy 2 + f x g y )dxdy g x dx 2 = 0 Aqui dx e dy representam a primeira e a segunda coordenada de um autovetor de DF, respectivamente. Substituindo as derivadas parciais envolvidas, a equação se escreve como: xdy 2 + 2x ny)dxdy 2mxdx 2 = 0 5) que é uma equação diferencial implícita do tipo estudado no capítulo 1 ax, y)dy 2 + 2bx, y)dxdy + cx, y)dx 2 = 0, onde, ax, y) = a 1 x + a 2 y = x bx, y) = b 1 x + b 2 y = x n 2 y cx, y) = c 1 x + c 2 y = 2mx Seja Lx, y) = a 1 x + a 2 y)dy 2 + 2b 1 x + b 2 y)dxdy + c 1 x + c 2 y)dx 2
64 3.2. ESTUDO DAS CONFIGURAÇÕES 61 Escrevendo a parte linear com respeito a x, y) na forma matricial temos Lx, y) = x Vamos considerar a mudança linear de coordenadas ) ) dx 2 2m 1 1 y 0 n 2 0 2dxdy dy 2 x = αy y = βx Substituindo x e y na expressão de Lx, y) obtemos L X,Y ) = 2mY dy 2 + nx 2Y )dxdy Y dx 2. Estamos interessados em estudar o problema considerando as funções f, g acrescidas de termos lineares, isto é, estudaremos os campos de linhas gerados pelos autoespaços da matriz derivada da função F : R 2 R 2 x, y) F x, y) = fx, y), gx, y)) onde fx, y) = x 2 + xy + d 1 x + e 1 y gx, y) = mx 2 + n + 1 y 2 + d 2 x + e 2 y 2 Cálculos semelhantes aos desenvolvidos no capítulo 2 dão que L X,Y,t) = 2mY + t)dy 2 + 2Y nx)dxdy + Y dx 2 6) 3.2 Estudo das configurações Nesta seção obteremos as cofigurações das curvas integrais de algumas das EDI estudadas na seção anterior. Para a obtenção das configurações usamos a mesma técnica de [6] e [9]. Conforme estudado no capítulo 2, o espaço de parâmetros m, n) é separada por três curvas. 1. Uma curva que não é de Morse. 2. A curva φ tem uma raiz dupla. 3. A curva onde α 1 e φ tem uma raiz em comun.
65 3.2. ESTUDO DAS CONFIGURAÇÕES 62 Devemos considerar dois casos: m > 0 e m < 0. Queremos estudar a equação 2my + t)dy 2 + nx 2y)dxdy ydx 2 = 0. Fazendo a correspondência entre os coeficientes da equação considerada no capítulo 2 com esta temos a 1 = c 1 = 0, a 2 = 2m, b 1 = n 2, b 2 = 1, c 2 = 1. Usando esta correspondência na expressão de φp) temos que para esta equação φp) = p2mp 2 2p + n 1). Vamos determinar as curvas que separam regiões com diferentes tipos de sigularidades no espaço de parâmetros. Para isso faremos uso das técnicas descritas nos capítulos 1 e 2 para a EDI que consideramos as três curvas especiais de nosso interesse: a) Para que a curva não seja de Morse devemos ter 2mn = 0 o que dá n = 0 uma vez que m 0. b) A curva φ tem uma raiz dupla: n = 1 ou m = 1 2n 1) De fato, como uma raiz é p = 0 para que seja dupla, precisamos de n 1 = 0 O outro caso é quando o discriminante da parte quadrática é zero, isto é, c) As curvas α 1 e φ têm uma raiz em comun: Lembrando que 4 42m)n 1) = 0 m = 1 2n 1) α 1 p) = 2a 2 p 2 + b 2 + a 1 )p + b 1 ) = 4mp 2 2p + n 1 Observamos que como p = 0 é uma raiz de φ, e como α 1 0) = n, segue-se que n = 0. 2 Para m < 0, n = 2 ± 2m m Se tem que ± 1 2m são raízes de φp) e de α 1 p), onde obtemos que n = 2 ± A divisão do espaço de parâmetros é mostrado na figura 3.1) 2m m.
66 3.2. ESTUDO DAS CONFIGURAÇÕES 63 Figura 3.1: Separação do plano de parâmetros Considerando o discriminante, o campo de linhas terá mais duas singularidades se 1 2mn 1) > 0 e só terá uma singularidade se 1 2mn 1) < 0 o que corresponde às regiões sombreadas na figura 3.1). Seja p i com i = 0, 1, 2 raízes de φp), onde p 0 = 0 os autovalores α 1 p), β 2 p) são dados por: p 1 = mn 1) 2m p 2 = 1 1 2mn 1) 2m α 1 = 4mp 2 2p + n β 2 = 6mp 2 + 4p + 1 n segue que a matriz D ξ0, p 0 ) é dada por ) ) D ξ0, α1 0 n 0 p 0 ) = = β 1 β 2 β 1 1 n Assim podemos concluir que a singularidade p 0 é do tipo nó se 0 < n < 1 sela se n < 0 ou n > 1
67 3.2. ESTUDO DAS CONFIGURAÇÕES 64 Cálculos diretos mostram que α 1 p 1 ) = mn + 2m nm + 2m, m α 1 p 2 ) = 1 1 2mn + 2m 2nm + 2m, m β 1 p 1 ) = 1 1 2mn + 2m + 2nm 2m, m β 1 p 2 ) = mn + 2m + 2nm 2m. m Vamos analisar o tipo de cada uma das singularidades em cada uma destas regiões 1. Começamos com o caso m > 0, o sinal do denomiador é positivo, somente se analisará o sinal de cada numerador. Fazendo part 1 = 1 mn + 2m) 2, part 2 = 1 2mn + 2m, part 3 = 1 2mn + 2m) 2 sinalα 1 p 1 )) = mn + 2m nm + 2m, sinalα 1 p 2 )) = 1 1 2mn + 2m 2nm + 2m = part 1 part 2 ) = part 1 part 2 ) = m 2 n 2 4m 2 n + 4m 2 + 2m, sinalβ 2 p 1 )) = 1 1 2mn + 2m + 2nm 2m, sinalβ 2 p 2 )) = mn + 2m + 2nm 2m = part 2 part 3 ) = part 2 part 3 ) = 4m 2 n 2 + 8m 2 n 4m 2 + 2mn 2m. Figura 3.2: m > 0 a) Na região R 1, n < 0 as três singularidades são tipo sela. De fato, a singularidade p 0 é uma sela, para p 1, sinalα 1 p 1 )) > mn + 2m + 2m > 0 e sinalβ 2 p 1 )) < 1 1 2mn + 2m 2m < 0, segue-se que a singularidade p 1 é do tipo sela, e para
68 3.2. ESTUDO DAS CONFIGURAÇÕES 65 p 2 sinalα 1 p 2 )) > 4m 2 + 2m > 0 e sinalβ 2 p 2 )) < 4m 2 + 2mn 2m < 0 segue-se a singularidade p 2 é do tipo sela. b) Na região R 2, 0 < n < 1 as duas singularidades são tipo sela e a outra um nó. De fato, a singularidade p 0 é um nó. para p 1, sinalα 1 p 1 )) > mn + 2m + m > 0 e sinalβ 2 p 1 )) < 1 1 2mn + 2m m 2m = 1 2mn + 2m < 0, segue-se que a singularidade p 1 é do tipo sela, e para p 2 sinalα 1 p 2 )) > 4m 2 n + 4m 2 + 2m = 4m 2 1 m) + 2m > 0 sinalβ 2 p 2 )) < 0 uma vez que essa função é positiva para 1 21 m) < m < 0 e estamos no caso m > 0, segue-se que p 2 é do tipo sela. c) Na região R 3, 1 < n < 1 2m + 1 as duas singularidades são tipo nó e a outra uma sela. De fato, a singularidade p 0 é sela. Para analisar a natureza das singularidades p 1 e p 2 usaremos que n < 1 2m + 1 para p 1, sinalα 1 p 1 )) > m) 1 2mn + 2m + 2 2m > 0 e sinalβ 2 p 1 )) < 1 1 2mn + 2m + 2m + 1) 2m < 0, segue-se que a singularidade p 1 é do tipo sela, e para p 2 sinalα 1 p 2 )) > 2m + 4m 2 + 4m 2 + 2m > 8m 2 > 0 e sinalβ 2 p 2 )) > 0 é positivo somente entre suas raízes. segue-se a singularidade p 2 é do tipo nó. d) Na região R 4, n > 1 2m + 1. Para p 0 temos uma sela, e como 1 2mn 1) < 0, só se tem uma singularidade. A figura 3.3) mostra a distribução das singularidades no semi plano m > 0 Figura 3.3: Distribução das singularidades para m > 0 2. Vamos considerar o caso m < 0 Vamos a analisar o tipo de cada uma das singularidades em cada uma dessas regiões. Para o caso m < 0, o sinal do denominador é negativo, assim o sinal do autovalor será contrário ao sinal do numerador. Fazendo part 1 = 1 mn + 2m) 2, part 2 = 1 2mn + 2m, part 3 = 1 2mn + 2m) 2
69 3.2. ESTUDO DAS CONFIGURAÇÕES 66 sinalα 1 p 1 )) = 1 1 2mn + 2m + nm 2m sinalα 1 p 2 )) = m 2 n 2 + 4m 2 n 4m 2 2m, sinalβ 2 p 1 )) = mn + 2m 2nm + 2m, sinalβ 2 p 2 )) = 4m 2 n 2 8m 2 n + 4m 2 2mn + 2m. Figura 3.4: m < 0 a) Na região R 1, onde m < n < 0 existe somente uma singularidade em p 0, e esta é uma sela. b) Na região R 2, onde m < n, n > 0 existe somente uma singularidade em p 0, e esta é um nó. c) Na região R 3, onde 2 + 2m m < n < 1. Existem 3 singularidades 1 nó e 2 selas. A singularidade p 0 é um nó, para p 1, e para 1 2 < m < 0 sinalα 1p 1 )) < 1 1 2mn + 2m + m 1 2 2m < 0 e para m 1 2 tem-se sinalα 1p 1 )) < 1 1 2mn + 2m + 2m + 2m 2m < 0 logo sinalβ2 p 1 )) > 0, segue-se que a singularidade p 1 é do tipo sela, e para a singularidade p 2 sinalα 1 p 2 )) = 2m1 2mn 2m) m 2 n 2 > 0 e sinalβ 2 p 2 )) < 4m 2 8m 2 4m + 4m 2 2m + 2m < 0 segue-se a singularidade p 2 é do tipo sela. d) Na região R 4, onde 0 < n < 2 + sela. 2m m e n < 1 existem 3 singularidades 2 nós e 1 A singularidade p 0 é um nó. para p 1, tem-se 1 2 < m < 0, sinalα 1p 1 )) < 1 1 2mn + 2m < 0 e logo sinalβ 2 p 1 )) > 0, segue-se que a singularidade p 1 é do tipo sela, e para a singularidade p 2 sinalα 1 p 2 )) < 0 para m > 1/4 o sinalβ 2 p 2 )) < 4m 1 < 0 e para m < 1/4 sinalβ 2 p 2 )) < 8m 2 n 2mn < 0 segue-se a singularidade p 2 é do tipo nó. e) Na região R 5, onde 1 < n < 2 + 2m m existem 3 singularidades 2 nó e 1 sela. A singularidade p 0 uma sela, para p 1, sinalα 1 p 1 )) > 1 1 2mn + 2m + 2m > 0 logo sinalβ2 p 1 )) > 0, segue-se que a singularidade p 1 é do tipo nó, e
70 3.2. ESTUDO DAS CONFIGURAÇÕES 67 para a singularidade p 2 sinalα 1 p 2 )) < 0 e com m < 2 sinalβ 2 p 2 )) > 4m 1 > 0 segue-se a singularidade p 2 é do tipo sela. f) Na região R 6, onde 2 + selas. 2m m < n < 2 2m m, existem 3 singularidades 1 nó e 2 Temos em p 0 uma sela, para p 1, sinalα 1 p 1 )) < 1 1 2mn + 2m+2m+ 2m 2m < 0 logo sinalβ 2 p 1 )) > 0, segue-se que a singularidade p 1 é do tipo sela, e para a singularidade p 2 sinalα 1 p 2 )) > 2 2m) 2 +8m 2 4m 2m 4m 2 2m > 0 e sinalβ 2 p 2 )) > 4m 2 8m 2 4m + 4m 2 2m + 2m > 0 segue-se a singularidade p 2 é do tipo nó. g) Na região R 7, onde n > 2 2m m com n > 1, existem 3 sigularidades do tipo sela, para p 1, sinalα 1 p 1 )) < 1 1 2mn + 2m + 2m + 2m 2m < 0, sinalβ 2 p 1 )) > 0, segue-se que a singularidade p 1 é do tipo sela, e para a singularidade p 2 sinalα 1 p 2 )) < 2 2m) 2 + 8m 2 4m 2m 4m 2 2m < 0 e sinalβ 2 p 2 )) > 4m 2 8m 2 4m + 4m 2 2m + 2m > 0 segue-se a singularidade p 2 é do tipo sela. A figura 3.5) mostra a distribuição das singularidades no semi plano m < 0. Figura 3.5: m < 0 A figura 3.6) mostra a distribuição das singularidades de todo o plano, juntando a natureza para m < 0 e m > 0.
71 3.2. ESTUDO DAS CONFIGURAÇÕES 68 Figura 3.6: Natureza para m, n Proposição Suponha que a EDI 6) é do tipo Morse, que a função cúbica φp) não tem raízes duplas, e que φp), α 1 p) não têm raízes em comum, então a EDI é topologicamente equivalente à seguinte forma normal. 2my + t)dy 2 + nx 2y)dxdy ydx 2 = 0 I- 0 é um ponto isolado: m > 0 a) 1 sela, 1 2m + 1 < n b) 3 selas, n < 0 c) 2 selas +1 nó, 0 < n < 1ou 1 < n < 1 2m + 1 II- 0 é um cruzamento transversal de duas retas suaves: m < 0 a) 1 sela 1 2m + 1 < n < 0 b) 1 nó 1 2m + 1 < n, n > 0 c) 3 selas 2 2m m < n, n > 1 d) 2 selas e 1 nó 2 + 2m m < n < 1 e) 1 sela e 2 nós 0 < n < 2 + d 2m m 2m ou 1 < n < 2 + m Para obter as trajetórias do campo de linha no plano p, x) faremos o mesmo processo que em [6] e [9]. Em cada região do plano p, x) onde este sistema de coordenadas está definido, as trajetórias do campo de linhas tem o mesmo comportamento que as trajetórias do campo de vetores de ẋ = 2mnp2 x 2p 2 t + nx 2pt 2mp 2 2p 1) 2 ṗ = 4m2 p 5 2mnp 3 + 8mp 4 + 4mp 3 + 2np 2 4p 3 + np 4p 2 p 2mp 2 2p 1) 2
72 3.2. ESTUDO DAS CONFIGURAÇÕES 69 Nestas coordenadas a curva F = 0, F p = 0 se escreve como 2ptp + 1) xp) = n2mp 2 + 1) A curva xp) é a curva de dobra no plano px. Temos então em 0, 0) uma singularidade que tem o eixo x como variedade invariante para o autovalor n 1. A outra variedade invariante associada ao autovalor n da matriz tem a direção do vetor 1 2n, 2t). No plano xy a curva de dobra tem equações paramétricas 2ptp + 1) xp) = n2mp 2 + 1) p 2 yp) = 2mp Projetando a variedade invariante, eixo x. Fazendo p = 0 na equação y px pnx pt) y px = 2mp 2 2p 1 Quando o campo tem somente uma singularidade, isto é, 1 + 2m < 0 e 1 2mn 1) < 0. Temos as duas possibilidades: para m > 0 e m < m > 0 1 sela Fazemos os calculos para m = 1, n = 2, e para o parâmetro t = 1. 1 sela no plano px 1 sela no plano xy A configuração local do campo no plano px é dada pela figura à esquerda que projetada no plano x, y) dá a configuração mostrada na figura à direita. 2. m < 0 a) 1 nó, se 0 < n < 1 Fazemos os cálculos para m = 1, n = 1/3 e o parâmetro t = 1.
73 3.2. ESTUDO DAS CONFIGURAÇÕES 70 1 nó no plano px 1 nó no plano xy A configuração local do campo no plano px é dada pela figura à esquerda que projetada no plano x, y) dá a configuração mostrada na figura à direita. Vamos a considerar agora 1 + 2m < 0 e 1 2mn 1) > 0, isto é, consideraremos o caso em que o campo tem 3 singularidades localizadas nos pontos 0, 0), x 1, p 1 ), x 2, p 2 ). Onde, p 1 = mn 1) 2m x 1 = t2mp 1+2p 1 n+1) mn2p 1 n+2) t2p 1 n+1) y 1 = 1 2 m2p 1 n+2) y 2 = 1 2 p 2 = 1 1 2mn 1) 2m x 2 = t2mp 2+2p 2 n+1) mn2p 2 n+2) t2p 2 n+1) m2p 2 n+2) As outras variedades invariantes são obtidas fazendo p = p 1,e p = p 2, respectivamente, na equação de ypx. y pxp1 = mn + 2m + 1) 2mnx + 2mn + 2m ) 4 m 2 n y pxp2 = mn + 2m + 1)2mnx + 2mn + 2m + 1 1) 4 m 2 n Temos as duas possibilidades: para m > 0,m < m > 0 a) 3 selas Fazemos os cálculos com m = 1/4, n = 2 e com o parâmetro t = 1. Obtemos que as variedades invariantes são: y px0 = 0 y pxp1 = ) x) y pxp2 = ) x)
74 3.2. ESTUDO DAS CONFIGURAÇÕES 71 3 selas no plano px 3 selas no plano xy A configuração local do campo no plano px é dada pela figura à esquerda que projetada no plano x, y) dá a configuração mostrada na figura à direita. b) 2 selas e 1 nó Fazemos os cálculos com m = 1/4, n = 2 e com o parâmetro t = 3. Obtemos que as variedades invariantes são: y px0 = 0 y pxp 1 = ) x) y pxp 2 = ) x) 2 selas e 1 nó no plano px 2 selas e 1 nó no plano xy 2. m < 0 A configuração local do campo no plano px é dada pela figura à esquerda que projetada no plano x, y) dá a configuração mostrada na figura à direita. a) 3 selas, se n > 2 2m m com n > 1. Fazemos os calculos com m = 3, n = 3 e com o parâmetro t = 1.
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
A primeira coisa a fazer é saber quais são as equações das curvas quando elas já se encontram na melhor
 Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Ga no plano 1. GA no plano. Prof. Fernando Carneiro Rio de Janeiro, Outubro de u v = aa + bb.
 Ga no plano 1 GA no plano Prof. Fernando Carneiro Rio de Janeiro, Outubro de 015 1 Introdução Estudaremos as retas no plano euclidiano bidimensional e uma interessante aplicação, que recebe o nome de programação
Ga no plano 1 GA no plano Prof. Fernando Carneiro Rio de Janeiro, Outubro de 015 1 Introdução Estudaremos as retas no plano euclidiano bidimensional e uma interessante aplicação, que recebe o nome de programação
1 Equações Diferenciais Ordinárias: Sistemas de Equações
 Equações Diferenciais Ordinárias: Sistemas de Equações O sistema geral de duas equações diferenciais pode ser escrito como: ẋ = F x,y,t ẏ = Gx,y,t Uma Solução de é um par x t e y t de funções de t tais
Equações Diferenciais Ordinárias: Sistemas de Equações O sistema geral de duas equações diferenciais pode ser escrito como: ẋ = F x,y,t ẏ = Gx,y,t Uma Solução de é um par x t e y t de funções de t tais
DERIVADAS PARCIAIS. y = lim
 DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
Geometria Analítica - Aula
 Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Geometria Analítica - Aula 19 246 IM-UFF K. Frensel - J. Delgado Aula 20 Vamos analisar a equação Ax 2 + Cy 2 + Dx + Ey + F = 0 nos casos em que exatamente um dos coeficientes A ou C é nulo. 1. Parábola
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 2018
 GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Interbits SuperPro Web
 1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
Teoremas e Propriedades Operatórias
 Capítulo 10 Teoremas e Propriedades Operatórias Como vimos no capítulo anterior, mesmo que nossa habilidade no cálculo de ites seja bastante boa, utilizar diretamente a definição para calcular derivadas
Capítulo 10 Teoremas e Propriedades Operatórias Como vimos no capítulo anterior, mesmo que nossa habilidade no cálculo de ites seja bastante boa, utilizar diretamente a definição para calcular derivadas
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
Singularidades Estáveis de Curvas e Superfícies
 Singularidades Estáveis de Curvas e Superfícies Aluno: Igor Albuquerque Araujo Orientador: Marcos Craizer Introdução Em matemática, a teoria das singularidades estuda e classifica os germes de aplicações
Singularidades Estáveis de Curvas e Superfícies Aluno: Igor Albuquerque Araujo Orientador: Marcos Craizer Introdução Em matemática, a teoria das singularidades estuda e classifica os germes de aplicações
= f(0) D2 f 0 (x, x) + o( x 2 )
 6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
6 a aula, 26-04-2007 Formas Quadráticas Suponhamos que 0 é um ponto crítico duma função suave f : U R definida sobre um aberto U R n. O desenvolvimento de Taylor de segunda ordem da função f em 0 permite-nos
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática
 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 3 a Lista MAT 146 - Cálculo I 218/I APLICAÇÃO DE DERIVADAS: OTIMIZAÇÃO Otimização é outra aplicação de derivadas. Em
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 3 a Lista MAT 146 - Cálculo I 218/I APLICAÇÃO DE DERIVADAS: OTIMIZAÇÃO Otimização é outra aplicação de derivadas. Em
Matemática 2. Teste Final. Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
 Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
2.1 Mudança de variáveis em integral dupla
 ! "! # $! % & #! ' ( $ Objetivos. Os objetivos desta Aula são: apresentar a ideia de mudança de variáveis no plano para calcular integrais duplas; usar as coordenadas polares para calcular a integral dupla
! "! # $! % & #! ' ( $ Objetivos. Os objetivos desta Aula são: apresentar a ideia de mudança de variáveis no plano para calcular integrais duplas; usar as coordenadas polares para calcular a integral dupla
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
CM005 Álgebra Linear Lista 3
 CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
CM005 Álgebra Linear Lista 3 Alberto Ramos Seja T : V V uma transformação linear. Se temos que T v = λv, v 0, para λ K. Dizemos que λ é um autovalor de T e v autovetor de T associado a λ. Observe que λ
Aula 3 A Reta e a Dependência Linear
 MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
MÓDULO 1 - AULA 3 Aula 3 A Reta e a Dependência Linear Objetivos Determinar a equação paramétrica de uma reta no plano. Compreender o paralelismo entre retas e vetores. Entender a noção de dependência
Marcelo M. Santos DM-IMECC-UNICAMP msantos/
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Nota: Turma: MA 327 Álgebra Linear. Terceira Prova. Boa Prova! Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática. Notas de Aulas de
 Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão e B =
 3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
3 a Lista de Exercícios de Introdução à Álgebra Linear IMPA - Verão 2008. (a) Ache os auto-valores e auto-vetores de A = 3 4 2 0 2 0 0 0 e B = 0 0 2 0 2 0 2 0 0 (b) Mostre que λ + λ 2 + λ 3 é igual ao
Apostila Minicurso SEMAT XXVII
 Apostila Minicurso SEMAT XXVII Título do Minicurso: Estrutura algébrica dos germes de funções Autores: Amanda Monteiro, Daniel Silva costa Ferreira e Plínio Gabriel Sicuti Orientadora: Prof a. Dr a. Michelle
Apostila Minicurso SEMAT XXVII Título do Minicurso: Estrutura algébrica dos germes de funções Autores: Amanda Monteiro, Daniel Silva costa Ferreira e Plínio Gabriel Sicuti Orientadora: Prof a. Dr a. Michelle
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de T ( p(x) ) = p(x + 1) p(x), (a) 8, (b) 5, (c) 0, (d) 3, (e) 4.
 MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
Singularidades de Equações Diferenciais Implícitas.
 Universidade Federal da Paraíba Centro de Ciências Exatas e da Natureza Programa de Pós-Graduação em Matemática Curso de Mestrado em Matemática Singularidades de Equações Diferenciais Implícitas. Por Francisco
Universidade Federal da Paraíba Centro de Ciências Exatas e da Natureza Programa de Pós-Graduação em Matemática Curso de Mestrado em Matemática Singularidades de Equações Diferenciais Implícitas. Por Francisco
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4 O problema de Sturm-Liouville A separação de variáveis da equação de Helmholtz,
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 7 Ref. Butkov, cap. 9, seções 9.3 e 9.4 O problema de Sturm-Liouville A separação de variáveis da equação de Helmholtz,
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 17 Superfícies quádricas - parabolóides
 Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Introdução às Equações Diferenciais e Ordinárias
 Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
TÓPICO. Fundamentos da Matemática II APLICAÇÕES NA GEOMETRIA ANALÍTICA. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 APLICAÇÕES NA GEOMETRIA ANALÍTICA 4 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 4.1 Geometria Analítica e as Coordenadas Cartesianas 4.2 Superfícies 4.2.1 Superfícies planas 4.2.2 Superfícies
APLICAÇÕES NA GEOMETRIA ANALÍTICA 4 Gil da Costa Marques TÓPICO Fundamentos da Matemática II 4.1 Geometria Analítica e as Coordenadas Cartesianas 4.2 Superfícies 4.2.1 Superfícies planas 4.2.2 Superfícies
O Plano no Espaço. Sumário
 17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
Equações não lineares
 DMPA IME UFRGS Cálculo Numérico Índice Raizes de polinômios 1 Raizes de polinômios 2 raizes de polinômios As equações não lineares constituídas por polinômios de grau n N com coeficientes complexos a n,a
DMPA IME UFRGS Cálculo Numérico Índice Raizes de polinômios 1 Raizes de polinômios 2 raizes de polinômios As equações não lineares constituídas por polinômios de grau n N com coeficientes complexos a n,a
Exponencial de uma matriz
 Exponencial de uma matriz Ulysses Sodré Londrina-PR, 21 de Agosto de 2001; Arquivo: expa.tex Conteúdo 1 Introdução à exponencial de uma matriz 2 2 Polinômio característico, autovalores e autovetores 2
Exponencial de uma matriz Ulysses Sodré Londrina-PR, 21 de Agosto de 2001; Arquivo: expa.tex Conteúdo 1 Introdução à exponencial de uma matriz 2 2 Polinômio característico, autovalores e autovetores 2
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 2015
 MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
P4 de Álgebra Linear I de junho de 2005 Gabarito
 P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
Curso: Engenharia Ambiental. Disciplina: Equações Diferenciais Ordinárias. Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2
 Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
Teoria Escalar da Difração
 Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
Teoria Escalar da Difração Em óptica geométrica, o comprimento de onda da luz é desprezível e os raios de luz não contornam obstáculos, mas propagam-se sempre em linha reta. A difração acontece quando
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
Renato Martins Assunção
 Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Nota: Turma: MA 327 Álgebra Linear. Segunda Prova. Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 2006 Segunda Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Questão 1. A matriz de mudança da base ordenada
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 2006 Segunda Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Questão 1. A matriz de mudança da base ordenada
Retas e círculos, posições relativas e distância de um ponto a uma reta
 Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Capítulo 3 Retas e círculos, posições relativas e distância de um ponto a uma reta Nesta aula vamos caracterizar de forma algébrica a posição relativa de duas retas no plano e de uma reta e de um círculo
Multiplicidade de Equações Diferenciais Parciais de Primeira Ordem
 Universidade Federal da Paraíba Centro de Ciências Exatas e da Natureza Departamento de Matemática Programa de Pós-Graduação em Matemática Multiplicidade de Equações Diferenciais Parciais de Primeira Ordem
Universidade Federal da Paraíba Centro de Ciências Exatas e da Natureza Departamento de Matemática Programa de Pós-Graduação em Matemática Multiplicidade de Equações Diferenciais Parciais de Primeira Ordem
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais
 Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais Reginaldo J Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 16 de novembro
Teorema da Triangularização de Schur e Diagonalização de Matrizes Normais Reginaldo J Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 16 de novembro
Aula 1 Autovetores e Autovalores de Matrizes Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17
 Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
Sumário Aula 1 Autovetores e Autovalores de Matrizes.......... 8 Aula 2 Autovetores e Autovalores de Matrizes Casos Especiais 17 Aula 3 Polinômio Característico................. 25 Aula 4 Cálculo de Autovalores
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Curvas Planas em Coordenadas Polares
 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
21 e 22. Superfícies Quádricas. Sumário
 21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
dosteoremasdepascaledepappus
 Uma demonstração algébrica dosteoremasdepascaledepappus Um dos teoremas mais bonitos da Matemática é o teorema de Pascal: Teorema de Pascal Dados seis pontos A, B, C, D, E e F sobre uma circunferência,
Uma demonstração algébrica dosteoremasdepascaledepappus Um dos teoremas mais bonitos da Matemática é o teorema de Pascal: Teorema de Pascal Dados seis pontos A, B, C, D, E e F sobre uma circunferência,
Álgebra Linear
 Álgebra Linear - 0191 Lista 3 - Dependência e Independência Linear Bases e Soma Direta 1) Exiba três vetores u v w R 3 com as seguintes propriedades: nenhum deles é múltiplo do outro nenhuma das coordenadas
Álgebra Linear - 0191 Lista 3 - Dependência e Independência Linear Bases e Soma Direta 1) Exiba três vetores u v w R 3 com as seguintes propriedades: nenhum deles é múltiplo do outro nenhuma das coordenadas
Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016
 Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016 Questão 1: (2 pontos) x (a) (0.4 ponto) Calcule o ite: 2 + 3 2. x 1 x 1 ( πx + 5 ) (b) (0.4 ponto) Calcule o ite:
Instituto de Matemática - IM/UFRJ Cálculo I - MAC118 1 a Prova - Gabarito - 13/10/2016 Questão 1: (2 pontos) x (a) (0.4 ponto) Calcule o ite: 2 + 3 2. x 1 x 1 ( πx + 5 ) (b) (0.4 ponto) Calcule o ite:
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Campos hamiltonianos e primeiro grupo de cohomologia de De Rham.
 Campos hamiltonianos e primeiro grupo de cohomologia de De Rham. Ronaldo J. S. Ferreira e Fabiano B. da Silva 18 de novembro de 2015 Resumo Neste trabalho vamos explorar quando um campo vetorial simplético
Campos hamiltonianos e primeiro grupo de cohomologia de De Rham. Ronaldo J. S. Ferreira e Fabiano B. da Silva 18 de novembro de 2015 Resumo Neste trabalho vamos explorar quando um campo vetorial simplético
MATEMÁTICA I FUNÇÕES. Profa. Dra. Amanda L. P. M. Perticarrari
 MATEMÁTICA I FUNÇÕES Profa. Dra. Amanda L. P. M. Perticarrari amanda.perticarrari@unesp.br Conteúdo Função Variáveis Traçando Gráficos Domínio e Imagem Família de Funções Funções Polinomiais Funções Exponenciais
MATEMÁTICA I FUNÇÕES Profa. Dra. Amanda L. P. M. Perticarrari amanda.perticarrari@unesp.br Conteúdo Função Variáveis Traçando Gráficos Domínio e Imagem Família de Funções Funções Polinomiais Funções Exponenciais
Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas. A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa
 MA33 - Introdução à Álgebra Linear Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto
MA33 - Introdução à Álgebra Linear Unidade 22 - Teorema espectral para operadores simétricos, reconhecimento de cônicas A. Hefez e C. S. Fernandez Resumo elaborado por Paulo Sousa PROFMAT - SBM 10 de agosto
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo. Módulo I: Cálculo Diferencial e Integral Funções de Duas ou Mais Variáveis
 Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo Módulo I: Cálculo Diferencial e Integral Funções de Duas ou Mais Variáveis Professora Renata Alcarde Sermarini Notas de aula do
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo Módulo I: Cálculo Diferencial e Integral Funções de Duas ou Mais Variáveis Professora Renata Alcarde Sermarini Notas de aula do
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES
 47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
47 6. FUNÇÃO QUADRÁTICA 6.1. CONSIDERAÇÕES PRELIMINARES Na figura abaixo, seja a reta r e o ponto F de um determinado plano, tal que F não pertence a r. Consideremos as seguintes questões: Podemos obter,
17.1 multiplicidade de um ponto da curva
 Aula 17 multiplicidades de interseção (Anterior: C é fecho algébrico de R ) Voltamos ao estudo de curvas planas O assunto agora diz respeito à compreensão das multiplicidades O exemplo modelo bem conhecido
Aula 17 multiplicidades de interseção (Anterior: C é fecho algébrico de R ) Voltamos ao estudo de curvas planas O assunto agora diz respeito à compreensão das multiplicidades O exemplo modelo bem conhecido
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então
 Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
Derivadas direcionais Definição (Derivadas segundo um vector): f : Dom(f) R n R e P 0 int(dom(f)) então Seja D v f(p 0 ) = lim λ 0 f(p 0 + λ v) f(p 0 ) λ v representa a derivada direcional de f segundo
CÔNICAS - MAT CÁLCULO II - Bacharelado Química - Diurno 2 o SEMESTRE de 2009 Professor Oswaldo Rio Branco ELIPSE
 CÔNICAS - MAT 2127 - CÁLCULO II - Bacharelado Química - Diurno 2 o SEMESTRE de 2009 Professor Oswaldo Rio Branco No plano euclidiano consideremos F 1 e F 2 dois pontos (focos) distintos. ELIPSE (1) Se
CÔNICAS - MAT 2127 - CÁLCULO II - Bacharelado Química - Diurno 2 o SEMESTRE de 2009 Professor Oswaldo Rio Branco No plano euclidiano consideremos F 1 e F 2 dois pontos (focos) distintos. ELIPSE (1) Se
Objetivos. Expressar o vértice da parábola em termos do discriminante e dos
 MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
Resumo: Nestas notas faremos um breve estudo sobre as principais propriedades. mínimos, gráficos e algumas aplicações simples.
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Os números reais. Capítulo O conjunto I
 Capítulo 4 Os números reais De todos os conjuntos numéricos que estudamos agora, a transição de um para outro sempre era construída de forma elementar A passagem do conjunto dos números racionais aos reais
Capítulo 4 Os números reais De todos os conjuntos numéricos que estudamos agora, a transição de um para outro sempre era construída de forma elementar A passagem do conjunto dos números racionais aos reais
23 e 24. Forma Quadrática e Equação do Segundo Grau em R 3. Sumário
 23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
23 e 24 Forma Quadrática e Equação do Segundo Grau em R 3 Sumário 23.1 Introdução....................... 2 23.2 Autovalores e Autovetores de uma matriz 3 3.. 2 23.3 Mudança de Coordenadas no Espaço........
Técnicas de. Integração
 Técnicas de Capítulo 7 Integração TÉCNICAS DE INTEGRAÇÃO 7.4 Integração de Funções Racionais por Frações Parciais Nessa seção, vamos aprender como integrar funções racionais reduzindo-as a uma soma de
Técnicas de Capítulo 7 Integração TÉCNICAS DE INTEGRAÇÃO 7.4 Integração de Funções Racionais por Frações Parciais Nessa seção, vamos aprender como integrar funções racionais reduzindo-as a uma soma de
1 Diferenciabilidade e derivadas direcionais
 UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
UFPR - Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Matemática CM048 - Cálculo II - Matemática Diurno Prof. Zeca Eidam Nosso objetivo nestas notas é provar alguns resultados
Geometria Analítica - Aula
 Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Tensores (Parte 1) 15 de abril de Primeira aula sobre tensores para a disciplina de CVT 2019Q1
 Tensores (Parte 1) 15 de abril de 2019 Primeira aula sobre tensores para a disciplina de CVT 2019Q1 Introdução Procuramos generalizar a ideia de escalares e vetores introduzindo esse novo conceito que
Tensores (Parte 1) 15 de abril de 2019 Primeira aula sobre tensores para a disciplina de CVT 2019Q1 Introdução Procuramos generalizar a ideia de escalares e vetores introduzindo esse novo conceito que
12 AULA. ciáveis LIVRO. META Estudar derivadas de funções de duas variáveis a valores reais.
 1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS
 EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS PEDRO ALADAR TONELLI 1. Introdução Nosso objetivo é apresentar de uma forma simples o procedimento para achar soluções de uma equação relacional fuzzy para
EQUAÇÕES RELACIONAIS FUZZY E COMO RESOLVÊ-LAS PEDRO ALADAR TONELLI 1. Introdução Nosso objetivo é apresentar de uma forma simples o procedimento para achar soluções de uma equação relacional fuzzy para
Resumo: Nestas notas faremos um breve estudo sobre as principais propriedades. mínimos, gráficos e algumas aplicações simples.
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Equação quadrática Prof. Doherty
Projecto Delfos: Escola de Matemática Para Jovens 1 FICHA DE TRABALHO
 Projecto Delfos: Escola de Matemática Para Jovens 1 Uma função, f, é uma aplicação de um conjunto, D, que designamos por domínio, para um conjunto, C, designado por contra-domínio, segundo uma lei, f(x),
Projecto Delfos: Escola de Matemática Para Jovens 1 Uma função, f, é uma aplicação de um conjunto, D, que designamos por domínio, para um conjunto, C, designado por contra-domínio, segundo uma lei, f(x),
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
G2 de Álgebra Linear I
 G2 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Suponha
G2 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Suponha
Exercícios de Mínimos Quadrados
 INSTITUTO DE CIÊNCIAS MATEMÁTICAS E DE COMPUTAÇÃO DEPARTAMENTO DE MATEMÁTICA APLICADA E ESTATÍSTICA Exercícios de Mínimos Quadrados 1 Provar que a matriz de mínimos quadrados é denida positiva, isto é,
INSTITUTO DE CIÊNCIAS MATEMÁTICAS E DE COMPUTAÇÃO DEPARTAMENTO DE MATEMÁTICA APLICADA E ESTATÍSTICA Exercícios de Mínimos Quadrados 1 Provar que a matriz de mínimos quadrados é denida positiva, isto é,
Capítulo 2. f : A B. elementos A com elementos de B ilustradas nos seguintes diagramas.
 Capítulo 2 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Capítulo 2 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Campos de Vetores sem Curvas Algébricas Tangentes
 Campos de Vetores sem Curvas Algébricas Tangentes Um Enfoque Computacional S. C. Coutinho UFRJ Colóquio 2005 p. 1/44 Campos de vetores Um campo de vetores polinomial no plano C 2 é uma aplicação Φ : C
Campos de Vetores sem Curvas Algébricas Tangentes Um Enfoque Computacional S. C. Coutinho UFRJ Colóquio 2005 p. 1/44 Campos de vetores Um campo de vetores polinomial no plano C 2 é uma aplicação Φ : C
Prova tipo A. Gabarito. Data: 8 de outubro de ) Decida se cada afirmação a seguir é verdadeira ou falsa. 1.a) Considere os vetores de R 3
 Prova tipo A P2 de Álgebra Linear I 2004.2 Data: 8 de outubro de 2004. Gabarito Decida se cada afirmação a seguir é verdadeira ou falsa..a Considere os vetores de R 3 v = (, 0,, v 2 = (2,, a, v 3 = (3,,
Prova tipo A P2 de Álgebra Linear I 2004.2 Data: 8 de outubro de 2004. Gabarito Decida se cada afirmação a seguir é verdadeira ou falsa..a Considere os vetores de R 3 v = (, 0,, v 2 = (2,, a, v 3 = (3,,
Capítulo 2. f : A B. 3. A regra em (3) não define uma função de A em B porque 4 A está associado a mais de um. elemento de B.
 Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 2 Funções 2.1 Definição Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento
Departamento de Matemática Disciplina MAT154 - Cálculo 1 Capítulo 2 Funções 2.1 Definição Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento
Capítulo 5. Operadores Auto-adjuntos. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
Capítulo 5 Operadores Auto-adjuntos Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 5: Operadores Auto-adjuntos
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
ORDINÁRIAS. Víctor Arturo Martínez León
 INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
GAAL - Exame Especial - 12/julho/2013. Questão 1: Considere os pontos A = (1, 2, 3), B = (2, 3, 1), C = (3, 1, 2) e D = (2, 2, 1).
 GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
Aula 16. Máximos e Mínimos Locais
 Aula 16 Máximos e Mínimos Locais Seja f, y) uma função de 2 variáveis diferenciável em R 2 (ou num domínio aberto). Para estudar a função f, y), começamos por identificar os pontos de Máximo local e Mínimo
Aula 16 Máximos e Mínimos Locais Seja f, y) uma função de 2 variáveis diferenciável em R 2 (ou num domínio aberto). Para estudar a função f, y), começamos por identificar os pontos de Máximo local e Mínimo
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
Cúbicas Reversas e Redes de Quádricas
 Cúbicas Reversas e Redes de Quádricas I. Vainsencher M.A.G. Zarzar 1999 Uma cúbica reversa é a imagem da aplicação P 1 [t, u] [t 3, t 2 u, tu 2, u 3 ] P 3, para uma escolha adequada de coordenadas homogêneas
Cúbicas Reversas e Redes de Quádricas I. Vainsencher M.A.G. Zarzar 1999 Uma cúbica reversa é a imagem da aplicação P 1 [t, u] [t 3, t 2 u, tu 2, u 3 ] P 3, para uma escolha adequada de coordenadas homogêneas
Autovalores e Autovetores Determinante de. Motivando com Geometria Definição Calculando Diagonalização Teorema Espectral:
 Lema (determinante de matriz ) A B A 0 Suponha que M = ou M =, com A e D 0 D C D matrizes quadradas Então det(m) = det(a) det(d) A B Considere M =, com A, B, C e D matrizes C D quadradas De forma geral,
Lema (determinante de matriz ) A B A 0 Suponha que M = ou M =, com A e D 0 D C D matrizes quadradas Então det(m) = det(a) det(d) A B Considere M =, com A, B, C e D matrizes C D quadradas De forma geral,
1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y 2 = 0. (x 3) 2 + (y + 4) 2 =
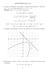 QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
QUESTÕES-AULA 18 1. A partir da definição, determinar a equação da parábola P, cujo foco é F = (3, 4) e cuja diretriz é L : x + y = 0. Solução Seja P = (x, y) R. Temos que P P d(p, F ) = d(p, L) (x 3)
Máximos e mínimos (continuação)
 UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 3 Assunto: Máximos e mínimos Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos (continuação) Sejam f
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 3 Assunto: Máximos e mínimos Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos (continuação) Sejam f
Cálculo 2. Guia de Estudos P1
 Cálculo 2 Guia de Estudos P1 Resuminho Teórico e Fórmulas Parte 1 Cônicas Conceito: Cônicas são formas desenhadas em duas dimensões, considerando apenas os eixos x (horizontal) e y (vertical). Tipos de
Cálculo 2 Guia de Estudos P1 Resuminho Teórico e Fórmulas Parte 1 Cônicas Conceito: Cônicas são formas desenhadas em duas dimensões, considerando apenas os eixos x (horizontal) e y (vertical). Tipos de
Funções de Uma Variável - 1 a Avaliação - Turma B3 31 de outubro de Prof. Armando Caputi
 Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função f(x) = arctan x x + 1 (justifique) e a equação da reta tangente ao seu gráfico
Funções de Uma Variável - 1 a Avaliação - Turma B 1 de outubro de 017 - Prof. Armando Caputi 1 Determine o domínio da função f(x) = arctan x x + 1 (justifique) e a equação da reta tangente ao seu gráfico
