1º Teste Computação Gráfica
|
|
|
- Raquel Martini Back
- 8 Há anos
- Visualizações:
Transcrição
1 1º Teste Computação Gráfica LEIC-Alameda/LEIC-Tagus/LERCI Prof. Mário Rui Gomes Prof. João Brisson Lopes de Abril de 4 Nº Nome: Responda às questões seguintes justificando adequadamente todas as respostas. O Teste tem uma duração de 1h3m. Todas as páginas devem ter o nº mecanográfico. I 1. A arquitectura lógica de uma aplicação gráfica interactiva baseia-se nos conceitos de eventos e de subscrição de serviços. Relacione estes dois conceitos com o fluxo de execução da aplicação. A arquitectura lógica de uma aplicação gráfica interactiva baseia-se no conceito de evento, definido como uma ocorrência na vida da aplicação e no conceito de subscrição de um serviço a ser efectuado pela aplicação. Assim, quando a aplicação é executada mostra em primeiro lugar toda a sua interface gráfica (botões, menus, ícones, etc.) assim como uma Vista inicial do Modelo. Seguidamente, efectua-se a subscrição dos serviços disponíveis (criar círculo, alterar atributo, agrupar objectos, etc.). O mecanismo de subscrição consiste em associar um ou mais tipos de eventos (premir uma tecla, escolher uma opção de um menu, etc.) a um serviço. O denominado ciclo principal de uma aplicação gráfica interactiva consiste numa espera activa de ocorrência de eventos. Quando ocorre um evento, é analisado o seu tipo e é executado o respectivo serviço, sendo redesenhada a Vista sobre o Modelo que poderá ter sido editado. Normalmente existe um tipo de evento que está associado ao serviço de sair, o qual armazena o Modelo e termina a execução do processo.
2 . Considere a transformação D que produz a forma representada na Figura a partir do quadrado representado na Figura 1. Figura 1 Figura Indique que transformações elementares compõem essa transformação, por que ordem são aplicadas e quais as matrizes correspondentes. Uma translação de (-,-1), seguida de uma rotação de 45º e de uma translação de (,). 1 T 1(, 1) = cos(45º) R(45º) = sin(45º ) 1 T (,) = sin(45º ) cos(45º) = Além da modelação por instanciação de primitivas, existe outro tipo de modelação que também emprega primitivas? Em caso afirmativo, indique quais as diferenças. Sim, existe a modelação por decomposição em células em que existem formas primitivas livremente escaláveis e posicionáveis que, adaptadas à forma dos objectos a modelar, modelam os objectos. No caso da modelação por instanciação de primitivas, estas são objectos que, embora posicionáveis, não apresentam a liberdade de escalamento livre pois as suas dimensões encontram-se restringidas pelos valores dos parâmetros das primitivas e da sua correspondência com as respectivas dimensões. 4. Que diferenças existem entre as malhas poligonais de lista explícita, as malhas de lista de vértices e as malhas de lista de arestas? Dê um exemplo de uma operação que seja fácil num destes tipos e muito difícil noutro. Nas malhas de lista explícita, cada polígono dispõe de uma lista de vértices própria, que não partilha com quaisquer outros polígonos, e em que cada vértice está representado /8
3 pelas suas coordenadas. Na malha por lista de vértices, existe uma lista de vértices geral e cada polígono possui uma lista de referências para os vértices que o constituem. Finalmente, na lista de arestas, existem a lista de arestas e a lista de vértices. Cada polígono possui uma lista de referências para as arestas que o constituem e cada aresta tem duas referências aos respectivos vértices e uma lista de referências para os polígonos de que faz parte. A alteração das coordenadas de um vértice é muito difícil com a lista explícita, pois é necessário determinar quais os polígonos a que pertence para que as suas coordenadas possam ser alteradas. O mesmo não se passa com a modelação por lista de vértices dado que basta alterar um único vértice sem ter que procurar as suas cópias. II 1. A seguinte figura apresenta um cubo assim como o plano de projecção para realizar a vista do cubo em perspectiva. Quantos pontos de fuga caracterizam esta projecção perspectiva? Justifique a resposta e apresente uma vista do cubo em que estes pontos de fuga estejam visíveis. y Plano de projecçao x z Intersecçao eixos/plano Na projecção perspectiva, um qualquer conjunto de linhas paralelas que não sejam paralelas ao plano de projecção converge num ponto de fuga. Neste caso, o cubo apresenta 3 conjuntos de linhas paralelas independentes que não são paralelas ao plano de projecção logo existem 3 pontos de fuga. Como se pode verificar o plano de projecção intersecta os três eixos e não é paralelo a nenhuma das faces do cubo. A figura apresenta a localização destes pontos de fuga na imagem do cubo. 3/8
4 Ponto de fuga Centro de Projecção. Apresente (dois) tipos de projecções paralelas e, para cada uma delas, caracterize a relação entre a normal ao plano de projecção (NPP) e os eixos do mundo assim como a relação entre a normal ao plano de projecção (NPP) e a direcção de projecção (DP) Projecções Ortogonais: NPP paralela a um dos eixos e DP paralela a NPP. Projecção Axiometrica: NPP não é paralela a qualquer um dos eixos e DP é perpendicular a NPP. Projecção Obliqua: NPP paralela a um eixo e DP nem é paralela nem perpendicular a NPP. 3. Aplique o algoritmo de Cohen-Sutherland ao recorte do segmento de recta AB com coordenadas (1, -1) e (1, 3) pelo rectângulo de recorte com coordenadas do vértice inferior esquerdo (, ) e do vértice superior direito (, 1), calculando os códigos e descrevendo o critério de escolha das arestas de recorte. Em primeiro lugar calculam-se os códigos dos vértices A e B os quais são, respectivamente, 1 e 1, convencionando que a sequência de bits corresponde aos limites x máximo, x mínimo, y máximo e y mínimo. Efectuando a operação de AND bit a bit dos dois códigos, obtém-se o valor, pelo que será necessário subdividir o segmento de recta no ponto de intersecção com a recta sobre a qual assenta uma das arestas do rectângulo de recorte. O bit a 1 do primeiro vértice, A, indica que se deve realizar o recorte contra o limite inferior do rectângulo de recorte. Daqui resulta, como ponto de intersecção, o vértice A (1, ) que tem como código o valor. Efectuando-se a operação de AND deste ponto com B, continua a ser necessário efectuar a subdivisão do segmento de recta A B, através do cálculo de uma nova intersecção com a recta sobre a qual assenta uma das restantes arestas do rectângulo de recorte. Como o 1º vértice, A agora tem código (não tem qualquer bit a 1) utiliza-se o 1º bit a 1 do segundo vértice, B, para escolher a aresta com a qual será efectuado o cálculo do ponto de intersecção. Neste caso é o limite superior do rectângulo de recorte e daqui resulta o vértice B (1, ) o qual tem, como código. 4/8
5 Assim obtém-se um segmento de recta recortado, A B, com ambos os vértices com código, o qual é virtualmente aceite. 4. Considere o algoritmo de Cyrus-Beck aplicado aos dois segmentos de recta da figura. Classifique os tipos de pontos de cada intersecção com as rectas que suportam cada uma das arestas do rectângulo de recorte e utilize essa informação para explicar por que é que o segmento de recta AB é rejeitado e o segmento CD é aceite, após recorte. B D A C Consideraremos que, em AB, o valor do parâmetro t cresce de para 1 de A para B e, em CD, de C para D. Considerando então a recta inferior do rectângulo de recorte, como o início de ambos os segmentos se encontram no subespaço inferior, ambas as intersecções dos segmentos com esta recta são pontos classificados como PE, Potencial Entrada. Considerando a recta superior, ambos os pontos de intersecção da recta com os segmentos são PS, Potencial Saída. Para a aresta esquerda ambos os pontos são PE, Potencial Entrada, e, para a aresta direita, ambos os pontos são PS, Potencial Saída. Assim resulta que as intersecções do segmento de recta AB, ordenados pelo parâmetro t, serão, PE, PS, PE, PS e as do segmento CD são PE, PE, PS, PS. Como no primeiro caso o t maior entre os de PE é maior que o menor t dos PS, teremos a situação em que o segmento de recta é rejeitado. Para o segmento CD, o maior t dos PE é inferior ao menor t dos PE, devendo o segmento ser aceite entre estes dois pontos. III 1. A representação de segmentos de recta num dispositivo de quadrículas requer a utilização de algoritmos de rasterização. Enumere três algoritmos para realizar a rasterização, indicando, resumidamente, em que medida estes três algoritmos diferem entre si. 1 - Algoritmo imediato Algoritmo incremental básico 5/8
6 3 Algoritmo de Bresenham Os três algoritmos diferem principalmente na precisão dos resultados e na velocidade de execução (carga computacional). Estas diferenças devem-se ao tipo de aritmética usada. Os algoritmos imediato e o incremental usam aritmética real e arredondamentos, enquanto o algoritmo de Bresenham usa aritmética inteira.. Considere o polígono da figura seguinte. a) Assumindo que está a usar o algoritmo de Preenchimento por Varrimento (scan-line), preencha a Tabela de Lados inicial. b) Apresente agora a Tabela de Lados Activos em duas situações diferentes, uma assumindo que a linha de varrimento está na posição y=3 e outra em y=6. a) A tabela de lados tem as seguintes entradas não nulas: TL[1] = [(AD, Ymax=3, X(Ymin)=5, 1/m = -), (CD, Ymax=5, X(Ymin)=5, 1/m = 1/4)] TL[3] = [(AB, Ymax=7, X(Ymin)=1, 1/m = 3/4)] TL[5] = [(BC, Ymax=7, X(Ymin)=6, 1/m = -1)] b) TLA[3]=[(AB, Ymax=7, X=1, 1/m = 3/4), (CD, Ymax=5, X=5,5, 1/m = 1/4)] TLA[6]=[(AB, Ymax=7, X=13/4, 1/m = 3/4), (BC, Ymax=7, X=5, 1/m = -1)] 3. Defina o nó VRML PointLight e descreva 4 dos seus campos. O nó VRML PointLight é uma luz pontual que irradia em todas as direcções a partir de um ponto, que é a sua localização no espaço. Os campos do nó PointLight são: attenuation: atenuação da luz com a distância; ambientitensity: a contribuição para a luz ambiente geral da cena; color: a cor da luz emitida; intensity: o brilho da luz (intensidade da luz emitida); location: localização da luz no mundo; on: liga e desliga a luz; radius: distância máxima afectada pela luz. 6/8
7 4. Considere o nó VRML Transform e a imagem seguinte: Quais das seguintes alternativas produz a imagem apresentada? Justifique. Alternativa A DEF TransfA Transform { translation children [ DEF Caixa Shape { geometry Box { size 1 1 appearance Appearance { material Material { diffusecolor 1 ] Transform { rotation children USE TransfA Alternativa B DEF TransfB Transform { translation rotation children [ DEF Caixa Shape { geometry Box { size 1 1 appearance Appearance { material Material { diffusecolor 1 ] Transform { translation children USE Caixa A alternativa A define um nó (TransfA) em que, a um paralelepípedo centrado na origem e orientado segundo o eixo dos XX, é aplicada uma translação segundo X de unidades. A seguir, uma cópia deste nó é rodada de +9º em torno do eixo dos ZZ, o que corresponde à figura. A alternativa B define um nó (Caixa) contendo um paralelepípedo centrado na origem e com o maior eixo segundo X. A este nó é primeiro aplicada uma rotação de +9º e só depois uma translação de unidades segundo X, porque a ordem das transformações de um único nó Transform é esta. O paralelepípedo fica na posição pretendida encontra-se 7/8
8 na posição pretendida mas com o eixo principal segundo Z, o que não corresponde à figura. Assim, a alternativa correcta é a alternativa A. Cotação I II III 1. 1,5 1. 1,5 1,5 3. 1,5 1,5 4. 1,5 Total 6,5 7 6,5 8/8
1º Exame/2º Teste Computação Gráfica
 1º Exame/2º Teste Computação Gráfica LEIC-Alameda/LEIC-Tagus/LERCI Prof. Mário Rui Gomes Prof. João Brisson Lopes 19 de Junho de 2004 Nº Nome: Deve escrever o seu nº em todas as páginas. Responda às questões
1º Exame/2º Teste Computação Gráfica LEIC-Alameda/LEIC-Tagus/LERCI Prof. Mário Rui Gomes Prof. João Brisson Lopes 19 de Junho de 2004 Nº Nome: Deve escrever o seu nº em todas as páginas. Responda às questões
Exame Tipo Computação Gráfica
 Exame Tipo Computação Gráfica LEIC-T Prof. Mário Rui Gomes Nº Nome: Antes de começar: Identifique todas as folhas com o seu número. Responda às questões seguintes justificando adequadamente todas as respostas.
Exame Tipo Computação Gráfica LEIC-T Prof. Mário Rui Gomes Nº Nome: Antes de começar: Identifique todas as folhas com o seu número. Responda às questões seguintes justificando adequadamente todas as respostas.
2º Exame de Computação Gráfica
 2º Exame de Computação Gráfica LEIC/LESIM/LCI Prof. Mário Rui Gomes Prof. João Brisson Lopes 26 de Julho de 2003 Nº Nome: Responda às questões seguintes justificando adequadamente todas as respostas. O
2º Exame de Computação Gráfica LEIC/LESIM/LCI Prof. Mário Rui Gomes Prof. João Brisson Lopes 26 de Julho de 2003 Nº Nome: Responda às questões seguintes justificando adequadamente todas as respostas. O
de Recta e Polígonos
 Mário Rui Gomes Computação Gráfica 1 Recorte de Segmentos de Recta e Polígonos 1.1 Introdução Relembrando os andares do pipeline de visualização, podemos verificar que no andar anterior foi efectuada a
Mário Rui Gomes Computação Gráfica 1 Recorte de Segmentos de Recta e Polígonos 1.1 Introdução Relembrando os andares do pipeline de visualização, podemos verificar que no andar anterior foi efectuada a
RECORTE (CLIPPING) por janelas rectangulares
 RECORTE (CLIPPING) por janelas rectangulares y max y min x min x max i. PONTOS P(x,y) é visível se não for exterior à janela x x max x x min y y max y y min ii. LINHAS (segmentos de recta) PQ é visível
RECORTE (CLIPPING) por janelas rectangulares y max y min x min x max i. PONTOS P(x,y) é visível se não for exterior à janela x x max x x min y y max y y min ii. LINHAS (segmentos de recta) PQ é visível
Modelação de Sólidos. Sistemas Gráficos/ Computação Gráfica e Interfaces FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO
 Modelação de Sólidos Sistemas Gráficos/ Computação Gráfica e Interfaces 1 Modelação de Sólidos Em 2D um conjunto de segmentos de recta ou curvas não formam necessariamente uma área fechada. Em 3D uma colecção
Modelação de Sólidos Sistemas Gráficos/ Computação Gráfica e Interfaces 1 Modelação de Sólidos Em 2D um conjunto de segmentos de recta ou curvas não formam necessariamente uma área fechada. Em 3D uma colecção
Visualização 2D: - Transformação window to viewport - Clipping
 Visualização 2D: - Transformação window to viewport - Clipping Sistemas Gráficos/ Computação Gráfica e Interfaces 1 Transformação de Visualização (window to viewport) Objectivo: obter uma matriz de transformação
Visualização 2D: - Transformação window to viewport - Clipping Sistemas Gráficos/ Computação Gráfica e Interfaces 1 Transformação de Visualização (window to viewport) Objectivo: obter uma matriz de transformação
Transformações de Visualização 2D: Clipping. Antonio L. Bajuelos Departamento de Matemática Universidade de Aveiro
 Transformações de Visualização 2D: Clipping Antonio L. Bajuelos Departamento de Matemática Universidade de Aveiro 1 Clipping (recorte) Qualquer procedimento que identifica porções de uma figura que estão
Transformações de Visualização 2D: Clipping Antonio L. Bajuelos Departamento de Matemática Universidade de Aveiro 1 Clipping (recorte) Qualquer procedimento que identifica porções de uma figura que estão
GDC I AULA TEÓRICA 07
 GDC I AULA TEÓRICA 07 Perspectiva linear de quadro plano: - Determinação de pontos de fuga de direcções de figuras planas contidas em orientações (dadas) ortogonais e oblíquas ao quadro. - O rebatimento
GDC I AULA TEÓRICA 07 Perspectiva linear de quadro plano: - Determinação de pontos de fuga de direcções de figuras planas contidas em orientações (dadas) ortogonais e oblíquas ao quadro. - O rebatimento
António Costa. Paulo Roma Cavalcanti
 Introdução à Computação Gráfica Preâmbulo Adaptação: Autoria: João Paulo Pereira António Costa Claudio Esperança Paulo Roma Cavalcanti Computação Gráfica Modelos Matemáticos Análise (reconhecimento de
Introdução à Computação Gráfica Preâmbulo Adaptação: Autoria: João Paulo Pereira António Costa Claudio Esperança Paulo Roma Cavalcanti Computação Gráfica Modelos Matemáticos Análise (reconhecimento de
Pipeline de Visualização 2D
 Pipeline de Visualização 2D André Tavares da Silva [email protected] Capítulo 2 do Foley Requisitos de matemática para CG Vetores e pontos Matrizes Transformações geométricas Pontos e espaços afim Representação
Pipeline de Visualização 2D André Tavares da Silva [email protected] Capítulo 2 do Foley Requisitos de matemática para CG Vetores e pontos Matrizes Transformações geométricas Pontos e espaços afim Representação
exercícios de perspectiva linear
 G E O M E T R I A D E S C R I T I V A E C O N C E P T U A L I exercícios de perspectiva linear MESTRADOS INTEGRADOS EM ARQUITECTURA e LICENCIATURA EM DESIGN - FA/UTL - 2010/2011 Prof.Aux. António Lima
G E O M E T R I A D E S C R I T I V A E C O N C E P T U A L I exercícios de perspectiva linear MESTRADOS INTEGRADOS EM ARQUITECTURA e LICENCIATURA EM DESIGN - FA/UTL - 2010/2011 Prof.Aux. António Lima
UARCA-E.U.A.C. Escola Universitária de Artes de Coimbra
 GDI - Geometria Descritiva I Exercícios práticos para preparação da frequência de semestre. Objectivos: Estes exercício-tipo, pretendem por um lado apresentar uma minuta, uma definição de exercício-tipo
GDI - Geometria Descritiva I Exercícios práticos para preparação da frequência de semestre. Objectivos: Estes exercício-tipo, pretendem por um lado apresentar uma minuta, uma definição de exercício-tipo
Instituto de Computação Bacharelado em Ciência da Computação Disciplina: Computação Gráfica Primeira lista de exercícios
 Instituto de Computação Bacharelado em Ciência da Computação Disciplina: Computação Gráfica Primeira lista de exercícios - 2013.1 Conceitos fundamentais 1) A Computação Gráfica é dividida em diversas sub-áreas.
Instituto de Computação Bacharelado em Ciência da Computação Disciplina: Computação Gráfica Primeira lista de exercícios - 2013.1 Conceitos fundamentais 1) A Computação Gráfica é dividida em diversas sub-áreas.
Escola Secundária com 3º Ciclo D. Dinis. Ficha de Apoio nº2
 Escola Secundária com 3º Ciclo D. Dinis Ano Lectivo 2008 /2009 Matemática B Ano 10º Turma D 1. Observe a figura. 1.1.Indique as coordenadas dos pontos A, B, C, A, B e C. 1.2. Descreva a transformação geométrica
Escola Secundária com 3º Ciclo D. Dinis Ano Lectivo 2008 /2009 Matemática B Ano 10º Turma D 1. Observe a figura. 1.1.Indique as coordenadas dos pontos A, B, C, A, B e C. 1.2. Descreva a transformação geométrica
Computação Gráfica - 09
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 9 [email protected] www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav Objetos
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 9 [email protected] www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav Objetos
Visibilidade. Apontamentos CG + Edward Angel, Sec Instituto Superior Técnico Computação Gráfica 2009/2010
 Visibilidade Apontamentos CG + Edward Angel, Sec. 7.11 Instituto Superior Técnico Computação Gráfica 2009/2010 1 Na últimas aulas Rasterização Discretização de linhas Preenchimento de polígonos Aliasing
Visibilidade Apontamentos CG + Edward Angel, Sec. 7.11 Instituto Superior Técnico Computação Gráfica 2009/2010 1 Na últimas aulas Rasterização Discretização de linhas Preenchimento de polígonos Aliasing
Preparação para o Teste de Maio 2012 (GEOMETRIA)
 Nº8 Matemática: ºA Preparação para o Teste de Maio (GEOMETIA) Grupo I. Num referencial o.n. Oy, considera um ponto A pertencente ao semieio positivo O e um ponto B pertencente ao semieio positivo Oy. Quais
Nº8 Matemática: ºA Preparação para o Teste de Maio (GEOMETIA) Grupo I. Num referencial o.n. Oy, considera um ponto A pertencente ao semieio positivo O e um ponto B pertencente ao semieio positivo Oy. Quais
GDC I AULA TEÓRICA 3
 GDC I AULA TEÓRICA 3 O Sistema axonométrico: - O caso geral da axonometria ortogonal: o triângulo fundamental e o rebatimento dos planos coordenados. - Subsistemas axonométricos ortogonais: trimetria ou
GDC I AULA TEÓRICA 3 O Sistema axonométrico: - O caso geral da axonometria ortogonal: o triângulo fundamental e o rebatimento dos planos coordenados. - Subsistemas axonométricos ortogonais: trimetria ou
Introdução à Computação Gráfica
 Introdução à Computação Gráfica Desenho de Construção Naval Manuel Ventura Instituto Superior Técnico Secção Autónoma de Engenharia Naval 27 Sumário Entidades Geométricas Transformações Geométricas 2D
Introdução à Computação Gráfica Desenho de Construção Naval Manuel Ventura Instituto Superior Técnico Secção Autónoma de Engenharia Naval 27 Sumário Entidades Geométricas Transformações Geométricas 2D
O Problema de Visibilidade. Computação Gráfica Recorte. Onde Acontece? O que é Recorte? Renato Ferreira
 O Problema de Visibilidade Computação Gráfica Recorte Renato Ferreira Numa cena tri-dimensional, normalmente não é possível ver todas as superfícies de todos os objetos Queremos descartar objetos ou partes
O Problema de Visibilidade Computação Gráfica Recorte Renato Ferreira Numa cena tri-dimensional, normalmente não é possível ver todas as superfícies de todos os objetos Queremos descartar objetos ou partes
EXERCÍCIOS RESOLVIDOS - COTADAS - Ano lectivo 2010/2011
 EXERCÍCIOS RESOLVIDOS - COTADAS - Ano lectivo 2010/2011 Este documento contém um conjunto de exercícios resolvidos sobre o tema das projecções cotadas. Os exercícios foram retirados de provas de frequências
EXERCÍCIOS RESOLVIDOS - COTADAS - Ano lectivo 2010/2011 Este documento contém um conjunto de exercícios resolvidos sobre o tema das projecções cotadas. Os exercícios foram retirados de provas de frequências
Triangulação Mapeamento em Viewport Modelação Geométrica
 Triangulação Mapeamento em Viewport Modelação Geométrica Apontamentos CG + Edward Angel, Cap Instituto Superior Técnico Computação Gráfica 29/2 Na última aula... Iluminação e Reflexão Modelo de Iluminação
Triangulação Mapeamento em Viewport Modelação Geométrica Apontamentos CG + Edward Angel, Cap Instituto Superior Técnico Computação Gráfica 29/2 Na última aula... Iluminação e Reflexão Modelo de Iluminação
Sumário COMPUTAÇÃO GRÁFICA E INTERFACES. Modelos e modelagem. Modelos e modelagem. Transformações Geométricas e Visualização 2D
 Sumário COMPUTAÇÃO GRÁFICA E INTERFACES Transformações Geométricas e Visualização D Transformações geométricas Pipeline de visualização D Transformação de coordenadas Window-Viewport Recorte (Clipping)
Sumário COMPUTAÇÃO GRÁFICA E INTERFACES Transformações Geométricas e Visualização D Transformações geométricas Pipeline de visualização D Transformação de coordenadas Window-Viewport Recorte (Clipping)
TI-NSPIRE NA GEOMETRIA
 TI-NSPIRE NA GEOMETRIA Raul Aparício Gonçalves Maio 2010 Índice Introdução ----------------------------------------------------------------------------------------- -------- 02 Como construir pontos, segmentos
TI-NSPIRE NA GEOMETRIA Raul Aparício Gonçalves Maio 2010 Índice Introdução ----------------------------------------------------------------------------------------- -------- 02 Como construir pontos, segmentos
EXAME NACIONAL DO ENSINO SECUNDÁRIO
 EXAME NACIONAL DO ENSINO SECUNDÁRIO 10.º/11.º ou 11.º/12.º Anos de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) PROVA 708/6 Págs. Duração da prova: 150 minutos 2007 1.ª FASE PROVA PRÁTICA DE
EXAME NACIONAL DO ENSINO SECUNDÁRIO 10.º/11.º ou 11.º/12.º Anos de Escolaridade (Decreto-Lei n.º 74/2004, de 26 de Março) PROVA 708/6 Págs. Duração da prova: 150 minutos 2007 1.ª FASE PROVA PRÁTICA DE
EXAME NACIONAL DO ENSINO SECUNDÁRIO
 EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) PROVA 408/4 Págs. Duração da prova: 150 minutos 2007 1.ª FASE PROVA PRÁTICA DE DESENHO E GEOMETRIA
EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) PROVA 408/4 Págs. Duração da prova: 150 minutos 2007 1.ª FASE PROVA PRÁTICA DE DESENHO E GEOMETRIA
Remoção de Faces Traseiras Recorte
 Remoção de Faces Traseiras Recorte Edward Angel, Cap. 7 Instituto Superior Técnico Computação Gráfica 2009/2010 1 Na última aula... Câmara Virtual Simples Transformação de Visualização Volumes canónicos
Remoção de Faces Traseiras Recorte Edward Angel, Cap. 7 Instituto Superior Técnico Computação Gráfica 2009/2010 1 Na última aula... Câmara Virtual Simples Transformação de Visualização Volumes canónicos
TEMA 3 GEOMETRIA FICHAS DE TRABALHO 10.º ANO COMPILAÇÃO TEMA 3 GEOMETRIA. Jorge Penalva José Carlos Pereira Vítor Pereira MathSuccess
 FICHAS DE TRAALHO 10.º ANO COMPILAÇÃO TEMA 3 GEOMETRIA Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA 3 GEOMETRIA 016 017 Matemática A 10.º Ano Fichas de Trabalho Compilação
FICHAS DE TRAALHO 10.º ANO COMPILAÇÃO TEMA 3 GEOMETRIA Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA 3 GEOMETRIA 016 017 Matemática A 10.º Ano Fichas de Trabalho Compilação
Tarefa nº_ 2.2. (A) Um ponto (B) Uma reta (C) Um plano (D) Nenhuma das anteriores
 Tarefa nº_. MATEMÁTICA Geometria Nome: 11º Ano Data / / 1. Num referencial o.n. Oxyz, qual das seguintes condições define uma recta paralela ao eixo Oz? (A) x = y = 1 (C) z = 1 (B) (x, y, z) = (1,,0) +
Tarefa nº_. MATEMÁTICA Geometria Nome: 11º Ano Data / / 1. Num referencial o.n. Oxyz, qual das seguintes condições define uma recta paralela ao eixo Oz? (A) x = y = 1 (C) z = 1 (B) (x, y, z) = (1,,0) +
Lista 6: transformações lineares.
 Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Canguru sem fronteiras 2007
 Canguru sem fronteiras 2007 Duração: 1h15mn Destinatários: alunos do 9 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30
Canguru sem fronteiras 2007 Duração: 1h15mn Destinatários: alunos do 9 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30
2º Exame Computação Gráfica
 2º Exame Computação Gráfica LEIC-T Prof. Mário Rui Gomes 17 de Julho 2007 Nº Nome: Antes de começar: Identifique todas as folhas com o seu número. Responda às questões seguintes justificando adequadamente
2º Exame Computação Gráfica LEIC-T Prof. Mário Rui Gomes 17 de Julho 2007 Nº Nome: Antes de começar: Identifique todas as folhas com o seu número. Responda às questões seguintes justificando adequadamente
Prof. Fernando V. Paulovich 3 de agosto de SCC Computação Gráca
 Dispositivos de Saída e SCC0250 - Computação Gráca Prof. Fernando V. Paulovich http://www.icmc.usp.br/~paulovic [email protected] Instituto de Ciências Matemáticas e de Computação (ICMC) Universidade
Dispositivos de Saída e SCC0250 - Computação Gráca Prof. Fernando V. Paulovich http://www.icmc.usp.br/~paulovic [email protected] Instituto de Ciências Matemáticas e de Computação (ICMC) Universidade
Atividade 1. Construindo um prisma
 Atividade 1. Construindo um prisma 1- Clique em Unidades = Poliedro = Prisma (ver Figura 3). Abre-se uma janela na qual você pode escolher o número de lados do polígono (regular), o comprimento de cada
Atividade 1. Construindo um prisma 1- Clique em Unidades = Poliedro = Prisma (ver Figura 3). Abre-se uma janela na qual você pode escolher o número de lados do polígono (regular), o comprimento de cada
Algoritmos geométricos
 Algoritmos geométricos introdução a conceitos básicos de geometria computacional que serão abordados de forma mais avançada na disciplina Computação Gráfica disciplina de computação gráfica arquitetura
Algoritmos geométricos introdução a conceitos básicos de geometria computacional que serão abordados de forma mais avançada na disciplina Computação Gráfica disciplina de computação gráfica arquitetura
SÓLIDOS DE BASE(S) HORIZONTAL(AIS) OU FRONTAL(AIS)
 SÓLIDOS DE BASE(S) HORIZONTAL(AIS) OU FRONTAL(AIS) 56. Exame de 1998 Prova Modelo (código 109) Represente, no sistema de dupla projecção ortogonal, dois segmentos de recta concorrentes, [AE] e [AI]. Os
SÓLIDOS DE BASE(S) HORIZONTAL(AIS) OU FRONTAL(AIS) 56. Exame de 1998 Prova Modelo (código 109) Represente, no sistema de dupla projecção ortogonal, dois segmentos de recta concorrentes, [AE] e [AI]. Os
Prova Prática de Geometria Descritiva A
 EXAME FINAL NACIONAL DO ENSINO SECUNDÁRIO Prova Prática de Geometria Descritiva A 11.º Ano de Escolaridade Decreto-Lei n.º 139/2012, de 5 de julho Prova 708/1.ª Fase 3 Páginas Duração da Prova: 150 minutos.
EXAME FINAL NACIONAL DO ENSINO SECUNDÁRIO Prova Prática de Geometria Descritiva A 11.º Ano de Escolaridade Decreto-Lei n.º 139/2012, de 5 de julho Prova 708/1.ª Fase 3 Páginas Duração da Prova: 150 minutos.
4.4 Secções planas de superfícies e sólidos
 4.4 Secções planas de superfícies e sólidos Geometria Descritiva 2006/2007 e sólidos Quando um plano intersecta uma superfície geométrica determina sobre ela uma linha plana que pertence à superfície A
4.4 Secções planas de superfícies e sólidos Geometria Descritiva 2006/2007 e sólidos Quando um plano intersecta uma superfície geométrica determina sobre ela uma linha plana que pertence à superfície A
TESTE DE AVALIAÇÃO MATEMÁTICA A. Versão A
 E S C O L A S E C U N D Á R I A A F O N S O L O P E S V I E I R A Escola Secundária Afonso Lopes Vieira TESTE DE AVALIAÇÃO MATEMÁTICA A Nome:... Data: //9 Duração da prova 9 min Nº:... º Ano Turma A Versão
E S C O L A S E C U N D Á R I A A F O N S O L O P E S V I E I R A Escola Secundária Afonso Lopes Vieira TESTE DE AVALIAÇÃO MATEMÁTICA A Nome:... Data: //9 Duração da prova 9 min Nº:... º Ano Turma A Versão
FACULDADE DE ARQUITECTURA DA UNIVERSIDADE TÉCNICA DE LISBOA ÁREA CIENTÍFICA DE DESENHO E COMUNICAÇÃO GRUPO DE DISCIPLINAS DE GEOMETRIA
 FACULDADE DE ARQUITECTURA DA UNIVERSIDADE TÉCNICA DE LISBOA ÁREA CIENTÍFICA DE DESENHO E COMUNICAÇÃO GRUPO DE DISCIPLINAS DE GEOMETRIA MÚLTIPLA PROJECÇÃO ORTOGONAL (exercícios resolvidos) 2006 EXERCÍCIOS
FACULDADE DE ARQUITECTURA DA UNIVERSIDADE TÉCNICA DE LISBOA ÁREA CIENTÍFICA DE DESENHO E COMUNICAÇÃO GRUPO DE DISCIPLINAS DE GEOMETRIA MÚLTIPLA PROJECÇÃO ORTOGONAL (exercícios resolvidos) 2006 EXERCÍCIOS
CG 2013/2014 Primeiro Teste LEIC Alameda/Taguspark
 Computação Gráfica Licenciatura em Engenharia Informática e de Computadores Alameda / Taguspark Primeiro Teste 6 de Outubro de 013 O teste tem a duração de 1h00, tolerância incluída. Responda às questões
Computação Gráfica Licenciatura em Engenharia Informática e de Computadores Alameda / Taguspark Primeiro Teste 6 de Outubro de 013 O teste tem a duração de 1h00, tolerância incluída. Responda às questões
Computação Gráfica. Representação e Modelagem
 Computação Gráfica Representação e Modelagem Professora: Sheila Cáceres Baseado nos slides da Prof. Soraia Musse Modelagem Área da Computação Gráfica que estuda a criação de modelos dos objetos reais.
Computação Gráfica Representação e Modelagem Professora: Sheila Cáceres Baseado nos slides da Prof. Soraia Musse Modelagem Área da Computação Gráfica que estuda a criação de modelos dos objetos reais.
Fundamentos da Computação Gráfica Lista de Exercícios Marcelo Gattass TeCGraf/Departamento de Informática/PUC-Rio 19jun2003
 Fundamentos da Computação Gráfica Lista de Exercícios Marcelo Gattass TeCGraf/Departamento de Informática/PUC-Rio 19jun2003 I. Introdução 1) Qual a diferença entre Processamento de Imagens, Visão Computacional
Fundamentos da Computação Gráfica Lista de Exercícios Marcelo Gattass TeCGraf/Departamento de Informática/PUC-Rio 19jun2003 I. Introdução 1) Qual a diferença entre Processamento de Imagens, Visão Computacional
Sumário. Educação Matemática: Oficinas Didáticas com GeoGebra 2012
 Sumário A Interface do GeoGebra...2 O menu do GeoGebra...3 Ferramentas de construção...4 LIÇÃO 1: Polígonos e ângulos...7 LIÇÃO 2: Retas perpendiculares e paralelas...11 LIÇÃO 3: Construindo gráficos...18
Sumário A Interface do GeoGebra...2 O menu do GeoGebra...3 Ferramentas de construção...4 LIÇÃO 1: Polígonos e ângulos...7 LIÇÃO 2: Retas perpendiculares e paralelas...11 LIÇÃO 3: Construindo gráficos...18
EXERCÍCIOS RESOLVIDOS - SUPERFÍCIES - Ano lectivo 2010/2011
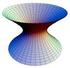 EXERCÍCIOS RESOLVIDOS - SUPERFÍCIES - Ano lectivo 2010/2011 Este documento contém um conjunto de exercícios resolvidos sobre o tema das superfícies. Os exercícios foram retirados de provas de frequências
EXERCÍCIOS RESOLVIDOS - SUPERFÍCIES - Ano lectivo 2010/2011 Este documento contém um conjunto de exercícios resolvidos sobre o tema das superfícies. Os exercícios foram retirados de provas de frequências
❷ Uma recta e um ponto exterior à recta definem um e um só plano.
 Uma resolução da Ficha de Trabalho (10.º Ano) POSIÇÕES RELATIVAS, PERSPECTIVAS, CORTES. 1. FORMAS DE DEFINIR UM PLANO: ❶ Três pontos não colineares definem um e um só plano. ❷ Uma recta e um ponto exterior
Uma resolução da Ficha de Trabalho (10.º Ano) POSIÇÕES RELATIVAS, PERSPECTIVAS, CORTES. 1. FORMAS DE DEFINIR UM PLANO: ❶ Três pontos não colineares definem um e um só plano. ❷ Uma recta e um ponto exterior
4. Superfícies e sólidos geométricos
 4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
9.º Ano. Escola EB 2,3 de Ribeirão (Sede) ANO LECTIVO 2009/2010
 Escola EB,3 de Ribeirão (Sede) ANO LECTIVO 009/010 Ficha Trabalho Circunferência, Trigonometria, Áreas e Volumes, Equações do º grau Maio 010 Nome: 1ª PARTE N.º: Turma: 9.º Ano 1. Observa a seguinte figura:
Escola EB,3 de Ribeirão (Sede) ANO LECTIVO 009/010 Ficha Trabalho Circunferência, Trigonometria, Áreas e Volumes, Equações do º grau Maio 010 Nome: 1ª PARTE N.º: Turma: 9.º Ano 1. Observa a seguinte figura:
Pipeline de Visualização 3D
 Pipeline de Visualização 3D André Tavares da Silva [email protected] Capítulo 5 de Foley Capítulo 2 de Azevedo e Conci Processo de Visualização https://www.youtube.com/watch?v=ogqam2mykng Processo de
Pipeline de Visualização 3D André Tavares da Silva [email protected] Capítulo 5 de Foley Capítulo 2 de Azevedo e Conci Processo de Visualização https://www.youtube.com/watch?v=ogqam2mykng Processo de
ESCOLA SECUNDÁRIA FERREIRA DIAS
 ESCOLA SECUNDÁRIA FERREIRA DIAS ENSINO RECORRENTE DE NÍVEL SECUNDÁRIO POR MÓDULOS CAPITALIZÁVEIS CURSO DE CIÊNCIAS E TECNOLOGIAS DISCIPLINA : MATEMÁTICA A ANO: 10.º - CONJUNTO DOS MÓDULOS 1-2-3 DURAÇÃO
ESCOLA SECUNDÁRIA FERREIRA DIAS ENSINO RECORRENTE DE NÍVEL SECUNDÁRIO POR MÓDULOS CAPITALIZÁVEIS CURSO DE CIÊNCIAS E TECNOLOGIAS DISCIPLINA : MATEMÁTICA A ANO: 10.º - CONJUNTO DOS MÓDULOS 1-2-3 DURAÇÃO
A terceira dimensão. Modelagem tridimensional Elaboração tridimensional Realidade virtual
 A terceira dimensão A terceira dimensão Modelagem tridimensional Elaboração tridimensional Realidade virtual 2 Modelagem tridimensional Métodos de representação tridimensional: modelos geométricos; superfícies
A terceira dimensão A terceira dimensão Modelagem tridimensional Elaboração tridimensional Realidade virtual 2 Modelagem tridimensional Métodos de representação tridimensional: modelos geométricos; superfícies
Algoritmos de Recorte em 2D
 Algoritmos de Recorte em 2D Computação Gráfica DCC065 Prof. Rodrigo Luis de Souza da Silva, D.Sc. Sumário Conceito de Recorte (Clipping) Introdução Algoritmo simples (Força Bruta) Algoritmo de Cohen-Sutherland
Algoritmos de Recorte em 2D Computação Gráfica DCC065 Prof. Rodrigo Luis de Souza da Silva, D.Sc. Sumário Conceito de Recorte (Clipping) Introdução Algoritmo simples (Força Bruta) Algoritmo de Cohen-Sutherland
MATEMÁTICA A - 12o Ano N o s Complexos - Conjuntos e condições
 MATEMÁTICA A - 1o Ano N o s Complexos - Conjuntos e condições Exercícios de exames e testes intermédios 1. Na figura ao lado, está representado, no plano complexo, um quadrado cujo centro coincide com
MATEMÁTICA A - 1o Ano N o s Complexos - Conjuntos e condições Exercícios de exames e testes intermédios 1. Na figura ao lado, está representado, no plano complexo, um quadrado cujo centro coincide com
Cosmo Worlds. truques & dicas. cosmo Worlds. José Carlos Miranda 1
 truques & dicas cosmo Worlds José Carlos Miranda 1 Nocões Básicas Criar primitivas gráficas? Transformações Geométricas 1. Criar um objecto Create Box 2. Aplicar transformações geométricas aos objectos
truques & dicas cosmo Worlds José Carlos Miranda 1 Nocões Básicas Criar primitivas gráficas? Transformações Geométricas 1. Criar um objecto Create Box 2. Aplicar transformações geométricas aos objectos
UNIVERSIDADE FEDERAL FLUMINENSE Pedro Martins Menezes. Um estudo dos estágios dos pipelines gráficos
 UNIVERSIDADE FEDERAL FLUMINENSE Pedro Martins Menezes Um estudo dos estágios dos pipelines gráficos Niterói 2008 Pedro Martins Menezes Um estudo dos estágios dos pipelines gráficos Trabalho de Conclusão
UNIVERSIDADE FEDERAL FLUMINENSE Pedro Martins Menezes Um estudo dos estágios dos pipelines gráficos Niterói 2008 Pedro Martins Menezes Um estudo dos estágios dos pipelines gráficos Trabalho de Conclusão
Escola Secundária de Francisco Franco Matemática 12.º ano Números Complexos - Exercícios saídos em (Exames Nacionais 2000)
 Mais exercícios de.º ano: www.prof000.pt/users/roliveira0/ano.htm Escola Secundária de Francisco Franco Matemática.º ano Números Complexos - Exercícios saídos em (Exames Nacionais 000). Seja C o conjunto
Mais exercícios de.º ano: www.prof000.pt/users/roliveira0/ano.htm Escola Secundária de Francisco Franco Matemática.º ano Números Complexos - Exercícios saídos em (Exames Nacionais 000). Seja C o conjunto
EXERCÍCIOS DE AULA - 01
 EXERCÍCIOS DE AULA - 01 Representação de objectos em axonometria normalizada FA.ULisboa Ano lectivo 2017/2018 1º semestre Professor Luís Mateus ([email protected]) Notas: 1) Resolva os exercícios
EXERCÍCIOS DE AULA - 01 Representação de objectos em axonometria normalizada FA.ULisboa Ano lectivo 2017/2018 1º semestre Professor Luís Mateus ([email protected]) Notas: 1) Resolva os exercícios
A terceira dimensão. A terceira dimensão. Modelagem tridimensional. A terceira dimensão Wilson de Pádua Paula Filho
 A terceira dimensão A terceira dimensão Realidade virtual Métodos de representação tridimensional: modelos geométricos; superfícies poligonais; superfícies curvas; representações de varredura; geometria
A terceira dimensão A terceira dimensão Realidade virtual Métodos de representação tridimensional: modelos geométricos; superfícies poligonais; superfícies curvas; representações de varredura; geometria
Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria III Equação do plano e equação da reta no espaço
 Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria III Equação do plano e equação da reta no espaço º Ano Plano definido por um ponto e um vetor normal : um Seja A x um ponto
Escola Secundária de Alberto Sampaio Ficha Formativa de Matemática A Geometria III Equação do plano e equação da reta no espaço º Ano Plano definido por um ponto e um vetor normal : um Seja A x um ponto
FA.ULisboa Secção de Desenho, Geometria e Computação 2016 / º ano Mestrado Integrado em Arquitectura - Urbanismo (C) GDC I
 FA.ULisboa Secção de Desenho, Geometria e Computação 2016 / 2017 1º ano Mestrado Integrado em Arquitectura - Urbanismo (C) GDC I rova de frequência (2ª parte erspectiva) 20 de Dezembro de 2016 9h00m Esta
FA.ULisboa Secção de Desenho, Geometria e Computação 2016 / 2017 1º ano Mestrado Integrado em Arquitectura - Urbanismo (C) GDC I rova de frequência (2ª parte erspectiva) 20 de Dezembro de 2016 9h00m Esta
Exame Nacional de a chamada
 1. O Miguel vê televisão, na sala de estar, sentado a 3 m do televisor. Na figura abaixo, está desenhada a planta dessa sala, à escala de 1:0. O ponto A representa o local onde o Miguel se senta para ver
1. O Miguel vê televisão, na sala de estar, sentado a 3 m do televisor. Na figura abaixo, está desenhada a planta dessa sala, à escala de 1:0. O ponto A representa o local onde o Miguel se senta para ver
AGRUPAMENTO DE ESCOLAS DE SAMORA CORREIA ESCOLA BÁSICA PROF. JOÃO FERNANDES PRATAS ESCOLA BÁSICA DE PORTO ALTO
 AGRUPAMENTO DE ESCOLAS DE SAMORA CORREIA ESCOLA BÁSICA PROF. JOÃO FERNANDES PRATAS ESCOLA BÁSICA DE PORTO ALTO Prova Extraordinária de Avaliação Matemática 2º Ciclo - 6.º Ano de Escolaridade Despacho Normativo
AGRUPAMENTO DE ESCOLAS DE SAMORA CORREIA ESCOLA BÁSICA PROF. JOÃO FERNANDES PRATAS ESCOLA BÁSICA DE PORTO ALTO Prova Extraordinária de Avaliação Matemática 2º Ciclo - 6.º Ano de Escolaridade Despacho Normativo
Escola Básica Integrada c/ Jardim de Infância da Malagueira SÍNTESE DO TÓPICO ISOMETRIAS. rotaçã
 Escola Básica Integrada c/ Jardim de Infância da Malagueira Ficha informativa nº9 Matemática Nome: Nº: Ano: 8º Turma: Data: 11 SÍNTESE DO TÓPICO ISOMETRIAS ISOMETRIAS I - Transformações geométricas: reflexão,
Escola Básica Integrada c/ Jardim de Infância da Malagueira Ficha informativa nº9 Matemática Nome: Nº: Ano: 8º Turma: Data: 11 SÍNTESE DO TÓPICO ISOMETRIAS ISOMETRIAS I - Transformações geométricas: reflexão,
Transformações Geométricas Grafos de Cena
 Transformações Geométricas Grafos de Cena Edward Angel, Cap. 4 Instituto Superior Técnico Computação Gráfica 2009/2010 1 Na última aula... Transformações Geométricas Translação Escala Rotação Espaço Homogéneo
Transformações Geométricas Grafos de Cena Edward Angel, Cap. 4 Instituto Superior Técnico Computação Gráfica 2009/2010 1 Na última aula... Transformações Geométricas Translação Escala Rotação Espaço Homogéneo
2 Igualdade e Operações com pares ordenados. 1 Conjunto R 2. 3 Vetores. 2.1 Igualdade. 1.2 Coordenadas Cartesianas no Plano
 1 Conjunto R 1.1 Definição VETORES NO PLANO Representamos por R o conjunto de todos os pares ordenados de números reais, ou seja: R = {(x, y) x R y R} 1. Coordenadas Cartesianas no Plano Em um plano α,
1 Conjunto R 1.1 Definição VETORES NO PLANO Representamos por R o conjunto de todos os pares ordenados de números reais, ou seja: R = {(x, y) x R y R} 1. Coordenadas Cartesianas no Plano Em um plano α,
Transformações 3D. Soraia Raupp Musse
 Transformações 3D Soraia Raupp Musse 1 Transformações 3D Translação gltranslatef(dx, dy, dz) T(dx, dy, dz): 1 1 1 dz dy dx 2 Escala glscalef(sx, Sy, Sz) S(Sx, Sy, Sz): 1 1 Sz Sy Sx Transformações 3D Rotação
Transformações 3D Soraia Raupp Musse 1 Transformações 3D Translação gltranslatef(dx, dy, dz) T(dx, dy, dz): 1 1 1 dz dy dx 2 Escala glscalef(sx, Sy, Sz) S(Sx, Sy, Sz): 1 1 Sz Sy Sx Transformações 3D Rotação
>> EXERCÍCIOS SEMANA 11 (26/11 a 30/11)
 >> EXERCÍCIOS SEMANA 11 (26/11 a 30/11) Problema 1: Considere o problema 1 da semana 9. Determine o reflexo da pirâmide produzido pelo plano frontal passante pelos pontos A e B. Resolução: Ver figura do
>> EXERCÍCIOS SEMANA 11 (26/11 a 30/11) Problema 1: Considere o problema 1 da semana 9. Determine o reflexo da pirâmide produzido pelo plano frontal passante pelos pontos A e B. Resolução: Ver figura do
GDC I AULA TEÓRICA 08
 GDC I AULA TEÓRICA 08 Perspectiva linear de quadro plano: - Aplicação do teorema de Thales para a divisão de segmentos em partes iguais. - A noção de ponto de nascença de uma recta (traço no quadro) e
GDC I AULA TEÓRICA 08 Perspectiva linear de quadro plano: - Aplicação do teorema de Thales para a divisão de segmentos em partes iguais. - A noção de ponto de nascença de uma recta (traço no quadro) e
1º Teste Computação Gráfica
 1º Teste Computação Gráfica LEIC-Tagus/LERCI Prof. Mário Rui Gomes Prof. João Brisson Lopes 23 de Abril de 25 Nº Nome: Responda às questões seguintes justificando adequadamente todas as respostas. O Teste
1º Teste Computação Gráfica LEIC-Tagus/LERCI Prof. Mário Rui Gomes Prof. João Brisson Lopes 23 de Abril de 25 Nº Nome: Responda às questões seguintes justificando adequadamente todas as respostas. O Teste
Escola Secundária com 3ºCEB de Lousada Ficha de Trabalho de Matemática do 9º ano 2011 Assunto: Preparação para o Exame Nacional
 Escola Secundária com 3ºCEB de Lousada Ficha de Trabalho de Matemática do 9º ano 011 Assunto: Preparação para o Exame Nacional 1. Copia o triângulo [ ABC ] para o teu caderno. Desenha o triângulo [ A '
Escola Secundária com 3ºCEB de Lousada Ficha de Trabalho de Matemática do 9º ano 011 Assunto: Preparação para o Exame Nacional 1. Copia o triângulo [ ABC ] para o teu caderno. Desenha o triângulo [ A '
ORDEM. Periocidade. SÓLIDO CRISTALINO OU CRISTAL agregado ordenado e periódico de átomos, moléculas ou iões, formando uma estrutura cristalina regular
 Capítulo I ESTRUTURA CRISTALINA DE SÓLIDOS ORDEM curto alcance médio alcance longo alcance Periocidade unidimensional bidimensional tridimensional SÓLIDO CRISTALINO OU CRISTAL agregado ordenado e periódico
Capítulo I ESTRUTURA CRISTALINA DE SÓLIDOS ORDEM curto alcance médio alcance longo alcance Periocidade unidimensional bidimensional tridimensional SÓLIDO CRISTALINO OU CRISTAL agregado ordenado e periódico
CG 2015/2016 Segundo Teste LEIC Alameda/Taguspark. Segundo Teste. 18 de Novembro de 2015
 CG 015/016 Segundo Teste LEIC Alameda/Taguspark Computação Gráfica Licenciatura em Engenharia Informática e de Computadores Alameda / Taguspark Segundo Teste 18 de Novembro de 015 O teste tem a duração
CG 015/016 Segundo Teste LEIC Alameda/Taguspark Computação Gráfica Licenciatura em Engenharia Informática e de Computadores Alameda / Taguspark Segundo Teste 18 de Novembro de 015 O teste tem a duração
GEOMETRIA MÉTRICA ESPACIAL
 GEOMETRIA MÉTRICA ESPACIAL .. PARALELEPÍPEDOS RETÂNGULOS Um paralelepípedo retângulo é um prisma reto cujas bases são retângulos. AB CD A' B' C' D' a BC AD B' C' A' D' b COMPRIMENTO LARGURA AA' BB' CC'
GEOMETRIA MÉTRICA ESPACIAL .. PARALELEPÍPEDOS RETÂNGULOS Um paralelepípedo retângulo é um prisma reto cujas bases são retângulos. AB CD A' B' C' D' a BC AD B' C' A' D' b COMPRIMENTO LARGURA AA' BB' CC'
Prova Prática de Geometria Descritiva A
 EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 74/2004, de 26 de Março Prova Prática de Geometria Descritiva A 11.º/12.º Anos de Escolaridade Prova 708/1.ª Fase 6 Páginas Duração da Prova: 150 minutos.
EXAME NACIONAL DO ENSINO SECUNDÁRIO Decreto-Lei n.º 74/2004, de 26 de Março Prova Prática de Geometria Descritiva A 11.º/12.º Anos de Escolaridade Prova 708/1.ª Fase 6 Páginas Duração da Prova: 150 minutos.
EXAME NACIONAL DO ENSINO SECUNDÁRIO
 PROVA 435/9 Págs. EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) Cursos Gerais e Cursos Tecnológicos Duração da prova: 120 minutos Época Especial
PROVA 435/9 Págs. EXAME NACIONAL DO ENSINO SECUNDÁRIO 12.º Ano de Escolaridade (Decreto-Lei n.º 286/89, de 29 de Agosto) Cursos Gerais e Cursos Tecnológicos Duração da prova: 120 minutos Época Especial
Aula Exemplos e aplicações. Exemplo 1. Nesta aula apresentamos uma série de exemplos e aplicações dos conceitos vistos.
 Aula 16 Nesta aula apresentamos uma série de exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações Exemplo 1 Considere os pontos A = (1, 2, 2), B = (2, 4, 3), C = ( 1, 4, 2), D = (7, 1,
Aula 16 Nesta aula apresentamos uma série de exemplos e aplicações dos conceitos vistos. 1. Exemplos e aplicações Exemplo 1 Considere os pontos A = (1, 2, 2), B = (2, 4, 3), C = ( 1, 4, 2), D = (7, 1,
a1q1: Seja ABCDEF GH um cubo de aresta unitária de E 3 e considere o espaço V 3 orientado pela base { CD, CB, CH}. Então podemos afirmar que: a)
 1 a1q1: Seja ABCDEF GH um cubo de aresta unitária de E 3 e considere o espaço V 3 orientado pela base { CD, CB, CH}. Então podemos afirmar que: a) EB ED = GA b) EB ED = AG c) EB ED = EH d) EB ED = EA e)
1 a1q1: Seja ABCDEF GH um cubo de aresta unitária de E 3 e considere o espaço V 3 orientado pela base { CD, CB, CH}. Então podemos afirmar que: a) EB ED = GA b) EB ED = AG c) EB ED = EH d) EB ED = EA e)
Algoritmos de Preenchimento de Regiões
 Sistemas Gráficos/ Computação Gráfica e Interfaces 1 Classificação dos algoritmos: Preenchimento segundo contorno existente Por difusão [flood-fill]: a. Limitado por contorno b. Limitado por interior de
Sistemas Gráficos/ Computação Gráfica e Interfaces 1 Classificação dos algoritmos: Preenchimento segundo contorno existente Por difusão [flood-fill]: a. Limitado por contorno b. Limitado por interior de
Poliedros 1 ARESTAS FACES VERTICES. Figura 1.1: Elementos de um poliedro
 Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
 Escola Básica de Ribeirão (Sede) ANO LETIVO 2011/2012 Ficha de Trabalho Abril 2012 Nome: N.º: Turma: Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Circunferência
Escola Básica de Ribeirão (Sede) ANO LETIVO 2011/2012 Ficha de Trabalho Abril 2012 Nome: N.º: Turma: Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Circunferência
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A TEMA 1 GEOMETRIA NO PLANO E NO ESPAÇO I. TPC nº 7 entregar no dia
 Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A TEMA 1 GEOMETRIA NO PLANO E NO ESPAÇO I TPC nº 7 entregar no dia 4 0 013 1. O cubo da figura tem as faces paralelas aos planos coordenados
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A TEMA 1 GEOMETRIA NO PLANO E NO ESPAÇO I TPC nº 7 entregar no dia 4 0 013 1. O cubo da figura tem as faces paralelas aos planos coordenados
Escola Secundária com 3º ciclo D. Dinis. 10º Ano de Matemática A. Geometria no Plano e no Espaço I
 Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Geometria no Plano e no Espaço I Trabalho de casa nº 7 GRUPO I 1. Num certo prisma, cada uma das bases tem n vértices. Quantas faces e quantas
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A Geometria no Plano e no Espaço I Trabalho de casa nº 7 GRUPO I 1. Num certo prisma, cada uma das bases tem n vértices. Quantas faces e quantas
