AULA 2 CONDUÇÃO DE CALOR
|
|
|
- Neuza Lopes Peixoto
- 8 Há anos
- Visualizações:
Transcrição
1 Noas de aula de PME 36 Pocessos de ansfeência de Calo 0 AULA CONDUÇÃO DE CALOR CONDUÇÃO DE CALOR Conduibilidade ou Conduividade éica Da Lei de Fouie da condução de calo e-se ue o fluo de calo é dieaene popocional ao gadiene de epeauas de acodo co a seguine epessão: onde A é a áea pependicula à dieção do fluo de calo e é a conduividade éica do aeial. A As unidades no SI da conduividade éica do aeial são: o C A o C ou. K Sendo: : popiedade (de anspoe) do aeial ue pode se facilene deeinada de foa epeienal. Valoes abelados de divesos aeiais se encona na seção de apêndice do livo eo. Eeplo de epeieno laboaoial paa obenção de hp:// José R. Siões Moeia aualiação Agoso/04
2 Noas de aula de PME 36 Pocessos de ansfeência de Calo No epeieno indicado ua coene eléica é fonecida à esisência eléica enolada e ono da hase do basão. O calo geado po efeio joule vai se conduido deno da hase paa foa do basão (lado dieio). Mediane a insalação de sensoes de epeaua (eopaes p. e.) pode-se levana o pefil da disibuição de epeauas coo auele indicado no gáfico acia. Esiaene falando esse pefil epeaua é linea coo vai se ve adiane. Po ouo lado o fluo de calo fonecido é a pópia poência eléica R I U I. Sendo a seção ansvesal A conhecida enão da lei de Fouie deeina-se a conduividade éica do aeial da hase. Nese caso. A U aspeco ipoane da condução de calo é ue o ecaniso da condução de calo é difeene dependendo do esado físico e da nauea do aeial. Abaio indica-se os ecanisos físicos de anspoe de acodo co o esado físico. ases O choue olecula peie a oca de enegia cinéica das oléculas ais enegéicas paa as enos enegéicas. A enegia cinéica esá elacionada co a epeaua absolua do gás. Quano aio a epeaua aio o ovieno olecula aio o núeo de choues e poano ais apidaene a enegia éica flui. Pode-se osa ue. Paa alguns gases a pessão odeada é só função de. Assi os dados abelados paa ua dada epeaua e pessão pode se usados paa oua pessão desde ue seja à esa epeaua. Isso não é valido póio do pono ciico. Líuidos Qualiaivaene o ecaniso físico de anspoe de calo po condução nos líuidos é o eso ue o dos gases. Eneano a siuação é consideavelene ais coplea devido à eno obilidade das oléculas. hp:// José R. Siões Moeia aualiação Agoso/04
3 Noas de aula de PME 36 Pocessos de ansfeência de Calo Sólidos Duas aneias básicas ege a ansfeência de calo po condução e sólidos: vibação da ede cisalina e anspoe po eléons lives. O segundo odo é o ais efeivo e é o pepondeane e aeiais eálicos. Iso eplica poue e geal bons conduoes de eleicidade abé são bons conduoes de calo. A ansfeência de calo e isolanes se dá po eio da vibação da ede cisalina ue é enos eficiene. O gáfico abaio ilusa ualiaivaene as odens de gandea da conduibilidade éica dos aeiais. Noa-se ue e geal a conduibilidade aueno de gases paa líuidos e sólidos e ue os eais puos são os de aio conduividade éica. EQUAÇÃO ERAL DA CONDUÇÃO DE CALOR EM COORDENADAS CARESIANAS Balanço de enegia e u volue de conole eleena hp:// José R. Siões Moeia aualiação Agoso/04
4 J / g oc Noas de aula de PME 36 Pocessos de ansfeência de Calo 3 BALANÇO DE ENERIA (ª LEI) Fluo de aa de aa epoal Fluo de calo calo de vaiação calo ue ue ena no + geada = da enegia + deia o ue V.C. no V.C. Inena no V.C. V.C. (I) (II) (III) (IV) Seja os eos: (I) Fluo de calo ue ena no V.C. Dieção d d Dieção d d - da Dieção d d (II) aa de calo geado E onde: d d d g = aa de calo geado na unidade de volue. (III) aa epoal de vaiação da enegia inena 3 E a U u d d d c onde: c = calo específico; = assa eleena do V.C. e a densidade. (IV) Fluo de calo ue deia o V.C. epansão e seie de alo: Dieção d d d 0( d ) Dieção d d hp:// José R. Siões Moeia aualiação Agoso/04
5 Noas de aula de PME 36 Pocessos de ansfeência de Calo hp:// José R. Siões Moeia aualiação Agoso/04 4 Dieção d d Enão junando os eos (I) + (II) = (III) + (IV) ve: d d d cddd ddd + ode supeio siplificando os eos e ve: d d d cddd ddd e subsiuindo a Lei de Fouie paa os eos de fluo de calo ddd ddd ddd cddd ddd Eliinando o volue de conole eleena ddd eos finalene: Essa é a euação geal da condução de calo. Não eise ua solução geal analíica paa a esa poue se aa de u poblea ue depende das condições inicial e de conono. Po isso ela é gealene esolvida paa divesos casos ue depende da geoeia do poblea do ipo (egie peanene) e das condições iniciais e de conono. Evideneene pocua-se ua solução do ipo: ) (. A segui são apesenados alguns casos básicos. Casos: A) Conduividade éica unifoe (aeial isoópico) e consane (independe de ) g " ' c
6 Noas de aula de PME 36 Pocessos de ansfeência de Calo hp:// José R. Siões Moeia aualiação Agoso/04 5 onde = c é conhecida coo difusibilidade ou difusividade éica cuja unidade no SI é: s s s J K g J g K c ² ² 3 Essa euação ainda pode se escia e noação ais sinéica da seguine foa: onde: é o opeado aeáico chaado de Laplaciano no sisea caesiano de coodenadas. Esa úlia foa de esceve a euação da condução de calo é pefeível pois eboa ela enha sido deduida paa o sisea caesiano de coodenadas ela é independe do sisea de coodenadas adoado. Caso haja ineesse e usa ouos siseas de coodenadas basa subsiui o Laplaciano do sisea de ineesse coo eeplificado abaio - Cilíndico: - Esféico: sen sen sen B) Se geação de calo e unifoe e consane 0 (E. de Fouie) C) Regie peanene (ou esacionáio) e unifoe e consane 0 (E. de Poisson) D) Regie peanene e consane e unifoe (E. de Laplace) 0 0
AS EQUAÇÕES DE MAXWELL E AS ONDAS ELETROMAGNÉTICAS
 A QUAÇÕ D MAXWLL A ONDA LTROMAGNÉTICA 1.1 A QUAÇÕ D MAXWLL Todos os poblemas de eleicidade e magneismo podem se esolvidos a pai das equações de Mawell: v 1. Lei de Gauss: φ. nda ˆ. Lei de Gauss paa o magneismo:
A QUAÇÕ D MAXWLL A ONDA LTROMAGNÉTICA 1.1 A QUAÇÕ D MAXWLL Todos os poblemas de eleicidade e magneismo podem se esolvidos a pai das equações de Mawell: v 1. Lei de Gauss: φ. nda ˆ. Lei de Gauss paa o magneismo:
Exercícios propostos
 Eecícios poposos 01 Esceva uma equação da ea nos casos a segui a) passa pelo pono P(, 1,) e em a dieção do veo u (,1,1 ) b) passa pelos ponos A(1,, 1) e B(0,,) 0 Veifique, em cada um dos iens abaio, se
Eecícios poposos 01 Esceva uma equação da ea nos casos a segui a) passa pelo pono P(, 1,) e em a dieção do veo u (,1,1 ) b) passa pelos ponos A(1,, 1) e B(0,,) 0 Veifique, em cada um dos iens abaio, se
Princípios de conservação e Equação de Evolução
 Pincípios de consevação e Equação de Evolução Os pincípios fundamenais da Mecânica aplicam-se a copos maeiais e po isso em fluidos aplicam-se a uma poção de fluido e não a um volume fixo do espaço. Ese
Pincípios de consevação e Equação de Evolução Os pincípios fundamenais da Mecânica aplicam-se a copos maeiais e po isso em fluidos aplicam-se a uma poção de fluido e não a um volume fixo do espaço. Ese
Aula 2 de Fenômemo de transporte II. Cálculo de condução Parede Plana Parede Cilíndrica Parede esférica
 Aula 2 de Fenômemo de tanspote II Cálculo de condução Paede Plana Paede Cilíndica Paede esféica Cálculo de condução Vamos estuda e desenvolve as equações da condução em nível básico paa egime pemanente,
Aula 2 de Fenômemo de tanspote II Cálculo de condução Paede Plana Paede Cilíndica Paede esféica Cálculo de condução Vamos estuda e desenvolve as equações da condução em nível básico paa egime pemanente,
SISTEMA DE COORDENADAS
 ELETROMAGNETISMO I 1 0 ANÁLISE VETORIAL Este capítulo ofeece uma ecapitulação aos conhecimentos de álgeba vetoial, já vistos em outos cusos. Estando po isto numeado com o eo, não fa pate de fato dos nossos
ELETROMAGNETISMO I 1 0 ANÁLISE VETORIAL Este capítulo ofeece uma ecapitulação aos conhecimentos de álgeba vetoial, já vistos em outos cusos. Estando po isto numeado com o eo, não fa pate de fato dos nossos
carga da esfera: Q. figura 1 Consideramos uma superfície Gaussiana interna e outra superfície externa á esfera.
 Detemine o módulo do campo elético em todo o espaço geado po uma esfea maciça caegada com uma caga distibuída unifomemente pelo seu volume. Dados do poblema caga da esfea:. Esuema do poblema Vamos assumi
Detemine o módulo do campo elético em todo o espaço geado po uma esfea maciça caegada com uma caga distibuída unifomemente pelo seu volume. Dados do poblema caga da esfea:. Esuema do poblema Vamos assumi
Introdução à Análise Diferencial dos Movimentos dos Fluidos
 Inodção à Análise Difeencial dos Moimenos dos Flidos Eqação de conseação de massa (coninidade) Definições ailiaes: Fnção coene Deiada maeial Aceleação Roação de flidos Eqação de Conseação de Qanidade de
Inodção à Análise Difeencial dos Moimenos dos Flidos Eqação de conseação de massa (coninidade) Definições ailiaes: Fnção coene Deiada maeial Aceleação Roação de flidos Eqação de Conseação de Qanidade de
Condução Unidimensional em Regime Permanente
 Condução Unidimensional em Regime Pemanente Num sistema unidimensional os gadientes de tempeatua existem somente ao longo de uma única coodenada, e a tansfeência de calo ocoe exclusivamente nesta dieção.
Condução Unidimensional em Regime Pemanente Num sistema unidimensional os gadientes de tempeatua existem somente ao longo de uma única coodenada, e a tansfeência de calo ocoe exclusivamente nesta dieção.
Aula 2 de Fenômemo de transporte II. Cálculo de condução Parede Plana Parede Cilíndrica Parede esférica
 Aula 2 de Fenômemo de tanspote II Cálculo de condução Paede Plana Paede Cilíndica Paede esféica Cálculo de condução Vamos estuda e desenvolve as equações da condução em nível básico paa egime pemanente,
Aula 2 de Fenômemo de tanspote II Cálculo de condução Paede Plana Paede Cilíndica Paede esféica Cálculo de condução Vamos estuda e desenvolve as equações da condução em nível básico paa egime pemanente,
Dinâmica Estocástica Aula 6
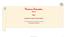 Dinâica Esocásica Aula 6 016 (coninuação) 1) Deslocaeno quadráico édio ) Energia & Poência 1 dv v F() (1) Equação de ovieno da parícula (ovieno e ua diensão) assa da parícula v velocidade da parícula coeficiene
Dinâica Esocásica Aula 6 016 (coninuação) 1) Deslocaeno quadráico édio ) Energia & Poência 1 dv v F() (1) Equação de ovieno da parícula (ovieno e ua diensão) assa da parícula v velocidade da parícula coeficiene
ENGENHARIA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA 2ª LISTA DE EXERCÍCIOS. (Atualizada em abril de 2009)
 ENGENHARIA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Pofesso : Humbeo Anônio Baun d Azevedo ª LISTA DE EXERCÍCIOS (Aualizada em abil de 009 1 Dados A (1, 0, -1, B (, 1,, C (1, 3, 4 e D (-3, 0, 4 Deemina: a
ENGENHARIA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Pofesso : Humbeo Anônio Baun d Azevedo ª LISTA DE EXERCÍCIOS (Aualizada em abil de 009 1 Dados A (1, 0, -1, B (, 1,, C (1, 3, 4 e D (-3, 0, 4 Deemina: a
carga da esfera: Q densidade volumétrica de carga: ρ = r.
 Detemine o módulo do campo elético em todo o espaço geado po uma esfea maciça caegada com uma caga distibuída com uma densidade volumética de caga dada po ρ =, onde α é uma constante ue tona a expessão
Detemine o módulo do campo elético em todo o espaço geado po uma esfea maciça caegada com uma caga distibuída com uma densidade volumética de caga dada po ρ =, onde α é uma constante ue tona a expessão
a) Qual é a energia potencial gravitacional, em relação à superfície da água, de um piloto de 60kg, quando elevado a 10 metros de altura?
 1. (Espcex (Aan) 17) U cubo de assa 4 kg está inicialente e epouso sobe u plano hoizontal se atito. Duante 3 s, aplica-se sobe o cubo ua foça constante, hoizontal e pependicula no cento de ua de suas faces,
1. (Espcex (Aan) 17) U cubo de assa 4 kg está inicialente e epouso sobe u plano hoizontal se atito. Duante 3 s, aplica-se sobe o cubo ua foça constante, hoizontal e pependicula no cento de ua de suas faces,
Seção 24: Laplaciano em Coordenadas Esféricas
 Seção 4: Laplaciano em Coodenadas Esféicas Paa o leito inteessado, na pimeia seção deduimos a expessão do laplaciano em coodenadas esféicas. O leito ue estive disposto a aceita sem demonstação pode dietamente
Seção 4: Laplaciano em Coodenadas Esféicas Paa o leito inteessado, na pimeia seção deduimos a expessão do laplaciano em coodenadas esféicas. O leito ue estive disposto a aceita sem demonstação pode dietamente
do sistema. A aceleração do centro de massa é dada pela razão entre a resultante das forças externas ao sistema e a massa total do sistema:
 Colisões.F.B, 004 Física 004/ tua IFA AULA 3 Objetio: discuti a obseação de colisões no efeencial do cento de assa Assuntos:a passage da descição no efeencial do laboatóio paa o efeencial do cento de assa;
Colisões.F.B, 004 Física 004/ tua IFA AULA 3 Objetio: discuti a obseação de colisões no efeencial do cento de assa Assuntos:a passage da descição no efeencial do laboatóio paa o efeencial do cento de assa;
Movimentos bi e tridimensional 35 TRIDIMENSIONAL
 Moimenos bi e idimensional 35 3 MOVIMENTOS BI E TRIDIMENSIONAL 3.1 Inodução O moimeno unidimensional que imos no capíulo aneio é um caso paicula de uma classe mais ampla de moimenos que ocoem em duas ou
Moimenos bi e idimensional 35 3 MOVIMENTOS BI E TRIDIMENSIONAL 3.1 Inodução O moimeno unidimensional que imos no capíulo aneio é um caso paicula de uma classe mais ampla de moimenos que ocoem em duas ou
CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS
 CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS. Moivaçõe Como vio o Regulado de Eado maném o iema em uma deeminada condição de egime pemanene, ou eja, ena mane o eado em uma dada condição eacionáia.
CONTROLE POR REALIMENTAÇÃO DOS ESTADOS SISTEMAS SERVOS. Moivaçõe Como vio o Regulado de Eado maném o iema em uma deeminada condição de egime pemanene, ou eja, ena mane o eado em uma dada condição eacionáia.
Campo magnético criado por uma corrente eléctrica e Lei de Faraday
 Campo magnéico ciado po uma coene elécica e Lei de Faaday 1.Objecivos (Rev. -007/008) 1) Esudo do campo magnéico de um conjuno de espias (bobine) pecoidas po uma coene elécica. ) Esudo da lei de indução
Campo magnéico ciado po uma coene elécica e Lei de Faaday 1.Objecivos (Rev. -007/008) 1) Esudo do campo magnéico de um conjuno de espias (bobine) pecoidas po uma coene elécica. ) Esudo da lei de indução
carga da esfera: Q densidade volumétrica de carga: ρ = r.
 Detemine o módulo do campo elético em todo o espaço geado po uma esfea maciça caegada com uma caga Q distibuída com uma densidade volumética de caga dada po ρ =, onde α é uma constante ue tona a expessão
Detemine o módulo do campo elético em todo o espaço geado po uma esfea maciça caegada com uma caga Q distibuída com uma densidade volumética de caga dada po ρ =, onde α é uma constante ue tona a expessão
AULA 23 FATORES DE FORMA DE RADIAÇÃO TÉRMICA
 Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
RESOLUÇÃO 1 A AVALIAÇÃO UNIDADE I COLÉGIO ANCHIETA-BA RESOLUÇÃO: PROFA. MARIA ANTÔNIA C. GOUVEIA
 RESOLUÇÃO VLIÇÃO UNIDDE I - OLÉGIO NHIET- PROF MRI NTÔNI GOUVEI ELORÇÃO e PESQUIS: PROF DRINO RIÉ e WLTER PORTO Questão ) figua abaio epesenta u galpão foado po u paalelepípedo etângulo e u seicilindo
RESOLUÇÃO VLIÇÃO UNIDDE I - OLÉGIO NHIET- PROF MRI NTÔNI GOUVEI ELORÇÃO e PESQUIS: PROF DRINO RIÉ e WLTER PORTO Questão ) figua abaio epesenta u galpão foado po u paalelepípedo etângulo e u seicilindo
O sistema constituído por um número infinito de partículas é vulgarmente designado por sólido.
 Capíulo CINEMÁTIC DE UM SISTEM DE PRTÍCULS. INTRODUÇÃO Po sisema de paículas, ou sisema de ponos maeiais, designa-se um conjuno finio ou infinio de paículas, de al modo que a disância ene qualque dos seus
Capíulo CINEMÁTIC DE UM SISTEM DE PRTÍCULS. INTRODUÇÃO Po sisema de paículas, ou sisema de ponos maeiais, designa-se um conjuno finio ou infinio de paículas, de al modo que a disância ene qualque dos seus
Antenas. Parâmetros fundamentais das antenas - 1 Diagrama de radiação
 aâmeos fundamenais das anenas - iaama de adiação O diaama de adiação é definido como a função maemáica ou a epesenação áfica das popiedades de adiação da anena em função das coodenadas espaciais. Uma anena
aâmeos fundamenais das anenas - iaama de adiação O diaama de adiação é definido como a função maemáica ou a epesenação áfica das popiedades de adiação da anena em função das coodenadas espaciais. Uma anena
setor 1214 Aulas 35 e 36
 seto 114 1140509 1140509-SP Aulas 35 e 36 LANÇAMENTO HORIZONTAL E OBLÍQUO O oviento de u copo lançado hoizontalente no vácuo (ou e cicunstâncias tais que a esistência do a possa se despezada) é a coposição
seto 114 1140509 1140509-SP Aulas 35 e 36 LANÇAMENTO HORIZONTAL E OBLÍQUO O oviento de u copo lançado hoizontalente no vácuo (ou e cicunstâncias tais que a esistência do a possa se despezada) é a coposição
DIVERGÊNCIA DO FLUXO ELÉTRICO E TEOREMA DA DIVERGÊNCIA
 ELETROMAGNETIMO I 18 DIVERGÊNCIA DO FLUXO ELÉTRICO E TEOREMA DA DIVERGÊNCIA.1 - A LEI DE GAU APLICADA A UM ELEMENTO DIFERENCIAL DE VOLUME Vimos que a Lei de Gauss pemite estuda o compotamento do campo
ELETROMAGNETIMO I 18 DIVERGÊNCIA DO FLUXO ELÉTRICO E TEOREMA DA DIVERGÊNCIA.1 - A LEI DE GAU APLICADA A UM ELEMENTO DIFERENCIAL DE VOLUME Vimos que a Lei de Gauss pemite estuda o compotamento do campo
Aula 6: Aplicações da Lei de Gauss
 Univesidade Fedeal do Paaná eto de Ciências xatas Depatamento de Física Física III Pof. D. Ricado Luiz Viana Refeências bibliogáficas: H. 25-7, 25-9, 25-1, 25-11. 2-5 T. 19- Aula 6: Aplicações da Lei de
Univesidade Fedeal do Paaná eto de Ciências xatas Depatamento de Física Física III Pof. D. Ricado Luiz Viana Refeências bibliogáficas: H. 25-7, 25-9, 25-1, 25-11. 2-5 T. 19- Aula 6: Aplicações da Lei de
2.3 - Desenvolvimento do Potencial Gravitacional em Série de Harmônicos Esféricos
 . - Desevovieto do otecia avitacioa e Séie de Haôicos Esféicos O potecia gavitacioa de u copo que te distibuição de assa hoogêea e foa geoética sipes, e gea, aite ua epesetação ateática eata. Mas o potecia
. - Desevovieto do otecia avitacioa e Séie de Haôicos Esféicos O potecia gavitacioa de u copo que te distibuição de assa hoogêea e foa geoética sipes, e gea, aite ua epesetação ateática eata. Mas o potecia
UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA ANDERSON HOFFMANN
 UIVERSIDADE FEDERAL DE SATA CATARIA CETRO DE CIÊCIAS FÍSICAS E MATEMÁTICAS DEPARTAMETO DE MATEMÁTICA ADERSO HOFFMA UMA ITRODUÇÃO AO PROBLEMA DE -CORPOS Floianópolis, 8 de novembo de 9 AGRADECIMETOS A
UIVERSIDADE FEDERAL DE SATA CATARIA CETRO DE CIÊCIAS FÍSICAS E MATEMÁTICAS DEPARTAMETO DE MATEMÁTICA ADERSO HOFFMA UMA ITRODUÇÃO AO PROBLEMA DE -CORPOS Floianópolis, 8 de novembo de 9 AGRADECIMETOS A
Exercícios e outras práticas sobre as aplicações da Termodinâmica Química 1 a parte
 5 Capítulo Capítulo Execícios e outas páticas sobe as aplicações da emodinâmica Química 1 a pate Só queo sabe do que pode da ceto Não tenho tempo a pede. (leta da música Go Back, cantada pelo gupo itãs.
5 Capítulo Capítulo Execícios e outas páticas sobe as aplicações da emodinâmica Química 1 a pate Só queo sabe do que pode da ceto Não tenho tempo a pede. (leta da música Go Back, cantada pelo gupo itãs.
Cap.2 - Mecanica do Sistema Solar II: Leis de Kepler do movimento planetário
 Cap. - Mecanica do Sistea Sola II: Leis de Keple do oviento planetáio Johannes Keple Tycho Bahe Mateático e Astônoo Aleão 57-630 Astônoo Dinaaquês 546-60 = Cicunfeência achatada = Elipse Lei das Elipses
Cap. - Mecanica do Sistea Sola II: Leis de Keple do oviento planetáio Johannes Keple Tycho Bahe Mateático e Astônoo Aleão 57-630 Astônoo Dinaaquês 546-60 = Cicunfeência achatada = Elipse Lei das Elipses
a) A energia potencial em função da posição pode ser representada graficamente como
 Solução da questão de Mecânica uântica Mestado a) A enegia potencial em função da posição pode se epesentada gaficamente como V(x) I II III L x paa x < (egião I) V (x) = paa < x < L (egião II) paa x >
Solução da questão de Mecânica uântica Mestado a) A enegia potencial em função da posição pode se epesentada gaficamente como V(x) I II III L x paa x < (egião I) V (x) = paa < x < L (egião II) paa x >
3. Elementos de Sistemas Elétricos de Potência
 Sisteas Eléticos de otência. Eleentos de Sisteas Eléticos de otência.. ndutância e Reatância ndutiva das inhas de Tansissão ofesso:. Raphael Augusto de Souza Benedito E-ail:[email protected] disponível
Sisteas Eléticos de otência. Eleentos de Sisteas Eléticos de otência.. ndutância e Reatância ndutiva das inhas de Tansissão ofesso:. Raphael Augusto de Souza Benedito E-ail:[email protected] disponível
Faculdade de Engenharia. Antenas e Radiação OE - MIEEC 2014/2015
 Faculdad d ngnhaia Annas adiação O - MIC /5 Annas adiaçao Faculdad d ngnhaia dipolos lnas dipolo lécico dipolo agnéico diagaas d adiação paâos caacísi d annas annas linas finas aggados d annas Annas Faculdad
Faculdad d ngnhaia Annas adiação O - MIC /5 Annas adiaçao Faculdad d ngnhaia dipolos lnas dipolo lécico dipolo agnéico diagaas d adiação paâos caacísi d annas annas linas finas aggados d annas Annas Faculdad
Lei de Ampère. (corrente I ) Foi visto: carga elétrica com v pode sentir força magnética se existir B e se B não é // a v
 Lei de Ampèe Foi visto: caga elética com v pode senti foça magnética se existi B e se B não é // a v F q v B m campos magnéticos B são geados po cagas em movimento (coente ) Agoa: esultados qualitativos
Lei de Ampèe Foi visto: caga elética com v pode senti foça magnética se existi B e se B não é // a v F q v B m campos magnéticos B são geados po cagas em movimento (coente ) Agoa: esultados qualitativos
Análise de uma Fila Única
 Aálise de ua Fila Úica The A of oue Syses Pefoace Aalysis Ra Jai a. 3 Fila Úica O odelo de filas ais siles coé aeas ua fila Pode se usado aa aalisa ecusos idividuais e siseas de couação Muias filas ode
Aálise de ua Fila Úica The A of oue Syses Pefoace Aalysis Ra Jai a. 3 Fila Úica O odelo de filas ais siles coé aeas ua fila Pode se usado aa aalisa ecusos idividuais e siseas de couação Muias filas ode
Buracos Negros. Óscar Dias 4ª EAG. 1. BNs em Relatividade Geral. Universidade de Barcelona & Centro de Física do Porto (Univ.
 Buacos Negos 1. BNs em Relatividade Geal Ósca Dias Univesidade de Bacelona & Cento de Física do Poto (Univ. Poto) 4ª EAG v < v Conceito Newtoniano de Buaco Nego Tudo o que sobe cai de seguida... se esc
Buacos Negos 1. BNs em Relatividade Geal Ósca Dias Univesidade de Bacelona & Cento de Física do Poto (Univ. Poto) 4ª EAG v < v Conceito Newtoniano de Buaco Nego Tudo o que sobe cai de seguida... se esc
PUC-RIO CB-CTC. P2 DE ELETROMAGNETISMO segunda-feira GABARITO. Nome : Assinatura: Matrícula: Turma:
 PUC-RIO CB-CTC P2 DE ELETROMAGNETISMO 16.05.11 segunda-feia GABARITO Nome : Assinatua: Matícula: Tuma: NÃO SERÃO ACEITAS RESPOSTAS SEM JUSTIFICATIVAS E CÁLCULOS EXPLÍCITOS. Não é pemitido destaca folhas
PUC-RIO CB-CTC P2 DE ELETROMAGNETISMO 16.05.11 segunda-feia GABARITO Nome : Assinatua: Matícula: Tuma: NÃO SERÃO ACEITAS RESPOSTAS SEM JUSTIFICATIVAS E CÁLCULOS EXPLÍCITOS. Não é pemitido destaca folhas
8.2 Indução eletromagnética e a lei das malhas
 8. Indução eleomagnéica e a lei das malhas Vimos na úlima seção que a lei das malhas na foma E dl = não vale na pesença de campos magnéicos empoalmene vaiáveis. Iso não é nenhuma agédia, é fácil consea
8. Indução eleomagnéica e a lei das malhas Vimos na úlima seção que a lei das malhas na foma E dl = não vale na pesença de campos magnéicos empoalmene vaiáveis. Iso não é nenhuma agédia, é fácil consea
F-328 Física Geral III
 F-328 Física Geal III Aula exploatóia Cap. 23 UNICAMP IFGW 1 Ponto essencial O fluxo de água atavessando uma supefície fechada depende somente das toneias no inteio dela. 2 3 1 4 O fluxo elético atavessando
F-328 Física Geal III Aula exploatóia Cap. 23 UNICAMP IFGW 1 Ponto essencial O fluxo de água atavessando uma supefície fechada depende somente das toneias no inteio dela. 2 3 1 4 O fluxo elético atavessando
Escola Básica e Secundária Dr. Ângelo Augusto da Silva
 Escola Básica e Secdáia D. Âgelo Agsto da Silva Teste de MATEMÁTICA A.º Ao Dação: 90 itos Maço/ 06 Noe N.º T: Classificação Pof. (Lís Abe).ª PARTE Paa cada a das segites qestões de escolha últipla, selecioe
Escola Básica e Secdáia D. Âgelo Agsto da Silva Teste de MATEMÁTICA A.º Ao Dação: 90 itos Maço/ 06 Noe N.º T: Classificação Pof. (Lís Abe).ª PARTE Paa cada a das segites qestões de escolha últipla, selecioe
MECÂNICA DOS MEIOS CONTÍNUOS. Exercícios
 MECÂNICA DO MEIO CONTÍNUO Execícios Mecânica dos Fluidos 1 Considee um fluido ideal em epouso num campo gavítico constante, g = g abendo que p( z = 0 ) = p a, detemine a distibuição das pessões nos casos
MECÂNICA DO MEIO CONTÍNUO Execícios Mecânica dos Fluidos 1 Considee um fluido ideal em epouso num campo gavítico constante, g = g abendo que p( z = 0 ) = p a, detemine a distibuição das pessões nos casos
1. Mecanica do Sistema Solar (II): Leis de Kepler do movimento planetário
 . Mecanica do Sistea Sola (II): Leis de Keple do oviento planetáio Astonoy: A Beginne s Guide to the Univese, E. Chaisson & S. McMillan (Caps. 0 e ) Intoductoy Astonoy & Astophysics, M. Zeilek, S. A. Gegoy
. Mecanica do Sistea Sola (II): Leis de Keple do oviento planetáio Astonoy: A Beginne s Guide to the Univese, E. Chaisson & S. McMillan (Caps. 0 e ) Intoductoy Astonoy & Astophysics, M. Zeilek, S. A. Gegoy
AULA 8 CONDUÇÃO DE CALOR EM REGIME TRANSITÓRIO SISTEMA CONCENTRADO
 Noas de aula de PME 3361 Processos de Transferência de Calor 57 AULA 8 CONDUÇÃO DE CALOR EM REGIME TRANSITÓRIO SISTEMA CONCENTRADO Inrodução Quando um corpo ou sisema a uma dada emperaura é bruscamene
Noas de aula de PME 3361 Processos de Transferência de Calor 57 AULA 8 CONDUÇÃO DE CALOR EM REGIME TRANSITÓRIO SISTEMA CONCENTRADO Inrodução Quando um corpo ou sisema a uma dada emperaura é bruscamene
Cap. 3: ROI do Governo e as Contas Públicas 1GE211: MACROECONOMIA II
 Cap. 3: ROI do oveno e as Conas Públicas E: MACROECONOMIA II Equipa de Macoeconomia II, 04/05 Capíulo 3. Resição Oçamenal Ineempoal do oveno e as Conas Públicas 3.. Facos sobe as Conas Públicas na Economia
Cap. 3: ROI do oveno e as Conas Públicas E: MACROECONOMIA II Equipa de Macoeconomia II, 04/05 Capíulo 3. Resição Oçamenal Ineempoal do oveno e as Conas Públicas 3.. Facos sobe as Conas Públicas na Economia
O gráfico que é uma reta
 O gráfico que é uma rea A UUL AL A Agora que já conhecemos melhor o plano caresiano e o gráfico de algumas relações enre e, volemos ao eemplo da aula 8, onde = + e cujo gráfico é uma rea. Queremos saber
O gráfico que é uma rea A UUL AL A Agora que já conhecemos melhor o plano caresiano e o gráfico de algumas relações enre e, volemos ao eemplo da aula 8, onde = + e cujo gráfico é uma rea. Queremos saber
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 14. A equação de Schrödinger em 3D: átomo de hidrogénio (parte 2)
 UFABC - Física Quântica - Cuso 2017.3 Pof. Gemán Lugones Aula 14 A equação de Schödinge em 3D: átomo de hidogénio (pate 2) 1 Equação paa a função adial R() A equação paa a pate adial da função de onda
UFABC - Física Quântica - Cuso 2017.3 Pof. Gemán Lugones Aula 14 A equação de Schödinge em 3D: átomo de hidogénio (pate 2) 1 Equação paa a função adial R() A equação paa a pate adial da função de onda
Voo Nivelado - Avião a Hélice
 - Avião a Hélice 763 º Ano da icenciaura em ngenharia Aeronáuica edro. Gamboa - 008. oo de ruzeiro De modo a prosseguir o esudo analíico do desempenho, é conveniene separar as aeronaves por ipo de moor
- Avião a Hélice 763 º Ano da icenciaura em ngenharia Aeronáuica edro. Gamboa - 008. oo de ruzeiro De modo a prosseguir o esudo analíico do desempenho, é conveniene separar as aeronaves por ipo de moor
Exercícios Resolvidos Astronomia (Gravitação Universal)
 Execícios Resolvios Astonoia (Gavitação Univesal) 0 - Cite as leis e Keple o oviento os copos celestes I "As óbitas que os planetas esceve ao eo o Sol são elípticas, co o Sol ocupano u os focos a elipse"
Execícios Resolvios Astonoia (Gavitação Univesal) 0 - Cite as leis e Keple o oviento os copos celestes I "As óbitas que os planetas esceve ao eo o Sol são elípticas, co o Sol ocupano u os focos a elipse"
CÁLCULO DIFERENCIAL E INTEGRAL II 014.2
 CÁLCULO IFERENCIAL E INTEGRAL II Obsevações: ) Todos os eecícios popostos devem se esolvidos e entegue no dia de feveeio de 5 Integais uplas Integais uplas Seja z f( uma função definida em uma egião do
CÁLCULO IFERENCIAL E INTEGRAL II Obsevações: ) Todos os eecícios popostos devem se esolvidos e entegue no dia de feveeio de 5 Integais uplas Integais uplas Seja z f( uma função definida em uma egião do
