CRM e Prospecção de Dados
|
|
|
- Maria Laura Gil Wagner
- 10 Há anos
- Visualizações:
Transcrição
1 CRM e Prospecção de Dados Marília Antunes aula de 4 de Maio 09 5 Modelos preditivos para classificação (continuação) 5.6 Modelos naive Bayes - classificador bayesiano simples O método ganha a designação de classificador bayesiano simples ou ingénuo (naif ) por partir do pressuposto simplificador de existência de independência condicional das variáveis dada a classe. Isto é, assenta na validade da seguinte igualdade: p(x c k ) = p(x 1,...,x p c k ) = p p(x j c k ), 1 k m. (1) Usando o teorema de Bayes, a probabilidade a posteri de uma dada classe condicional à observação do vector x é dada por p(c k x) = p(x c k)p(c k ) m l=1 p(x c k)p(c l ). (2) Se, mais uma vez, a regra de classificação dado um objecto (representado por um vector x) consistir em classificá-lo na classe que apresentar o maior valor da probabilidade a posteriori, bastará, para tal, atender ao valor no numerador da expressão anterior: p(c k x) p(x c k )p(c k ) p = p(c k ) p(x j c k ), 1 k m. (3) 1
2 CRM e Prospecção de Dados 2008/09 M. Antunes, DEIO-FCUL 2 Consideremos o caso em que existem apenas duas classes, c 1 e c 2. À razão das probabilidades p(c 1 x) p(c 2 x) chama-se chance da classe c 1 dado x e representa a relação entre as probabilidades a posteriori das classes c 1 e c 2. Exemplo 1. Se p(c 1 x) p(c 2 = 1.2, conclui-se que, para um objecto com um vector x) de medições x, a probabilidade deste pertencer à classe c 1 é superior em 20% à probabilidade de pertencer à classe c 2. Analogamente se poderá dizer que a probabilidade de pertencer à classe c 2 é 17% menor do que a probabilidade de pertencer à classe c 1, já que 1 = Tomando o logaritmo da chance obtém-se log p(c 1 x) p(c 2 x) = log p(c 1) p(c 2 ) + p log p(x j c 1 ) p(x j c 2 ). (4) Portanto, o logaritmo da chance de um objecto caracterizado por x pertencer à classe c 1 é dado pela soma da contribuição da priori e das contribuições de cada uma das variáveis, todas em termos separados da soma. Esta forma aditiva tem utilidade no sentido de permitir uma interpretação de cada termo. Note-se que observando o sinal de log p(x j c 1 ) p(x j c 2 se obtém a informação sobre ) qual das classes, c 1 ou c 2, com maior probabilidade produziria o valor observado para a j ésima variável, x j e, portanto, se o valor observado x j está a contribuir para que a classificação de x penda para a classe c 1 ou para a classe c 2. No caso de x j ser o valor de uma variável contínua, o pressuposto de independência condicional continua a ser válido. Nesse caso, p(x j c k ) representa a função de densidade de probabilidade, tomando-se o produto dos valores destas funções no cálculo das probabilidades a posteriori. As funções de densidade de probabilidade são estimadas da forma usual: adoptando-se um modelo paramétrico (como a distribuição normal, por exemplo), uma solução paramétrica mais flexível como uma mistura ou uma solução não paramétrica como o estimador kernel. Se os objectos forem caracterizados por variáveis quantitativas e categóricas, a expressão da probabilidade a posteriori envolverá o produto de funções de densidade de probabilidade e de funções de probabilidade das variáveis categóricas condicionais à classe. Estas últimas serão estimadas pelas frequências observadas nas classes considerando o conjunto de treino. Regra de classificação: Dado um novo objecto caracterizado por um vector x, este é classificado no grupo que apresentar maior valor para a probabilidade a posteriori.
3 CRM e Prospecção de Dados 2008/09 M. Antunes, DEIO-FCUL 3 Exemplo 2. Consideremos novamente os dados relativos a condições climatéricas e ao desfecho relativamente à realização de partidas de ténis: 1 sol quente alta fraco não 2 sol quente alta forte não 3 nublado quente alta fraco sim 4 chuva moderado alta fraco sim 5 chuva frio normal fraco sim 6 chuva frio normal forte não 7 nublado frio normal forte sim 8 sol moderado alta fraco não 9 sol frio normal fraco sim 10 chuva moderado normal fraco sim 11 sol moderado normal forte sim 12 nublado moderado alta forte sim 13 nublado quente normal fraco sim 14 chuva moderado alta forte não O objectivo é prever o desfecho de uma situação x =(Tempo,Temperatura,Humidade,Vento)=(sol,frio,normal,forte). Comecemos por separar os dados do conjunto de treino pelas classes relativas ao desfecho, c 1 =(Joga=N~ao) e c 2 =(Joga=Sim): e 1 sol quente alta fraco não 2 sol quente alta forte não 6 chuva frio normal forte não 8 sol moderado alta fraco não 14 chuva moderado alta forte não
4 CRM e Prospecção de Dados 2008/09 M. Antunes, DEIO-FCUL 4 3 nublado quente alta fraco sim 4 chuva moderado alta fraco sim 5 chuva frio normal fraco sim 7 nublado frio normal forte sim 9 sol frio normal fraco sim 10 chuva moderado normal fraco sim 11 sol moderado normal forte sim 12 nublado moderado alta forte sim 13 nublado quente normal fraco sim A partir daqui, estimam-se facilmente as probabilidades p(c k ) e p(x j c k ), para k = 1, 2 e j = 1,..., 4 : p(c 1 ) = 5 14, p(c 2) = 9 14 p(sol c 1 ) = 3 5, p(sol c 2) = 2 9 p(frio c 1 ) = 1 5, p(frio c 2) = 3 9 p(normal c 1 ) = 1 5, p(normal c 2) = 6 9 p(forte c 1 ) = 3 5, p(forte c 2) = 3 9 donde se obtém p(c 1 ) 4 p(x j c 1 ) = = e p(c 2 ) 4 p(x j c 2 ) = = A conclusão é que a nova observação deverá ser classificada na classe c 2 ou seja, perante as condições x =(sol,frio,normal,forte), a previsão de desfecho é Joga=sim. Calculemos os termos envolvidos no logaritmo da chance de uma observação caracterizada por x =(sol,frio,normal,forte): log p(c 1 x) p(c 2 x) = log p(c 1) p p(c 2 ) + log p(x j c 1 ) p(x j c 2 ) = Esta igualdade permite-nos afirmar o seguinte (com base no grupo de treino): a conjunção das condições é mais favorável ao desfecho Joga=sim;
5 CRM e Prospecção de Dados 2008/09 M. Antunes, DEIO-FCUL 5 a informação sobre o desfecho de situações do passado (grupo de treino) é mais favorável ao desfecho Joga=sim; Tempo=sol é mais favorável ao desfecho Joga=n~ao; Temperatura=frio é mais favorável ao desfecho Joga=sim; Humidade=normal é mais favorável ao desfecho Joga=sim; Vento=forte é mais favorável ao desfecho Joga=n~ao. 5.7 Modelo de regressão linear Leitura recomendada: Capítulo 10 de Principles of Data Mining. Hand, David J.; Mannila, Heikki; Smyth, Padhraic. (Fotocópias disponíveis na reprografia do departamento.)
CRM e Prospecção de Dados
 CRM e Prospecção de Dados Marília Antunes aula de 6 Abril 09 5 Modelos preditivos para classificação 5. Introdução Os modelos descritivos, tal como apresentados atrás, limitam-se à sumarização dos dados
CRM e Prospecção de Dados Marília Antunes aula de 6 Abril 09 5 Modelos preditivos para classificação 5. Introdução Os modelos descritivos, tal como apresentados atrás, limitam-se à sumarização dos dados
CRM e Prospecção de Dados
 CRM e Prospecção de Dados Marília Antunes aula de 11 de Maio 09 6 Modelos de regressão 6.1 Introdução No capítulo anterior foram apresentados alguns modelos preditivos em que a variável resposta (a variável
CRM e Prospecção de Dados Marília Antunes aula de 11 de Maio 09 6 Modelos de regressão 6.1 Introdução No capítulo anterior foram apresentados alguns modelos preditivos em que a variável resposta (a variável
CRM e Prospecção de Dados
 CRM e Prospecção de Dados Marília Antunes aula de 18 de Maio 09 6 Modelos de regressão (continuação) 6.1 Interpretação do modelo ajustado Os coeficientes do modelo de regressão múltipla podem ser interpretados
CRM e Prospecção de Dados Marília Antunes aula de 18 de Maio 09 6 Modelos de regressão (continuação) 6.1 Interpretação do modelo ajustado Os coeficientes do modelo de regressão múltipla podem ser interpretados
O Processo de KDD. Data Mining SUMÁRIO - AULA1. O processo de KDD. Interpretação e Avaliação. Seleção e Pré-processamento. Consolidação de dados
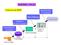 SUMÁRIO - AULA1 O Processo de KDD O processo de KDD Interpretação e Avaliação Consolidação de dados Seleção e Pré-processamento Warehouse Data Mining Dados Preparados p(x)=0.02 Padrões & Modelos Conhecimento
SUMÁRIO - AULA1 O Processo de KDD O processo de KDD Interpretação e Avaliação Consolidação de dados Seleção e Pré-processamento Warehouse Data Mining Dados Preparados p(x)=0.02 Padrões & Modelos Conhecimento
Aula 5 - Matemática (Gestão e Marketing)
 ISCTE, Escola de Gestão Aula 5 - Matemática (Gestão e Marketing) Diana Aldea Mendes 29 de Outubro de 2008 Espaços Vectoriais Definição (vector): Chama-se vector edesigna-sepor v um objecto matemático caracterizado
ISCTE, Escola de Gestão Aula 5 - Matemática (Gestão e Marketing) Diana Aldea Mendes 29 de Outubro de 2008 Espaços Vectoriais Definição (vector): Chama-se vector edesigna-sepor v um objecto matemático caracterizado
Lógica e Raciocínio. Decisão sob Risco Probabilidade. Universidade da Madeira. http://dme.uma.pt/edu/ler/
 Lógica e Raciocínio Universidade da Madeira http://dme.uma.pt/edu/ler/ Decisão sob Risco Probabilidade 1 Probabilidade Em decisões sob ignorância a probabilidade dos diferentes resultados e consequências
Lógica e Raciocínio Universidade da Madeira http://dme.uma.pt/edu/ler/ Decisão sob Risco Probabilidade 1 Probabilidade Em decisões sob ignorância a probabilidade dos diferentes resultados e consequências
CRM e Prospecção de Dados
 CRM e Prospecção de Dados Marília Antunes aula de 2 Março 09 1 Introdução à Prospecção de Dados 1.1 Introdução O progresso da tecnologia que permite a aquisição de dados e seu armazenamento resultaram
CRM e Prospecção de Dados Marília Antunes aula de 2 Março 09 1 Introdução à Prospecção de Dados 1.1 Introdução O progresso da tecnologia que permite a aquisição de dados e seu armazenamento resultaram
Lista de Exercícios Tratamento de Incerteza baseado em Probabilidade
 Lista de Exercícios Tratamento de Incerteza baseado em Probabilidade 1) Explique o termo probabilidade subjetiva no contexto de um agente que raciocina sobre incerteza baseando em probabilidade. 2) Explique
Lista de Exercícios Tratamento de Incerteza baseado em Probabilidade 1) Explique o termo probabilidade subjetiva no contexto de um agente que raciocina sobre incerteza baseando em probabilidade. 2) Explique
A MATEMÁTICA NO ENSINO SUPERIOR POLICIAL 1
 A MATEMÁTICA NO ENSINO SUPERIOR POLICIAL 1 A IMPORTÂNCIA DA MATEMÁTICA O desenvolvimento das sociedades tem sido também materializado por um progresso acentuado no plano científico e nos diversos domínios
A MATEMÁTICA NO ENSINO SUPERIOR POLICIAL 1 A IMPORTÂNCIA DA MATEMÁTICA O desenvolvimento das sociedades tem sido também materializado por um progresso acentuado no plano científico e nos diversos domínios
GERAÇÃO DE VIAGENS. 1.Introdução
 GERAÇÃO DE VIAGENS 1.Introdução Etapa de geração de viagens do processo de planejamento dos transportes está relacionada com a previsão dos tipos de viagens de pessoas ou veículos. Geralmente em zonas
GERAÇÃO DE VIAGENS 1.Introdução Etapa de geração de viagens do processo de planejamento dos transportes está relacionada com a previsão dos tipos de viagens de pessoas ou veículos. Geralmente em zonas
Gerenciamento de Riscos do Projeto Eventos Adversos
 Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
Universidade Tecnológica Federal do Paraná UTFPR Programa de Pós-Graduação em Computação Aplicada Disciplina de Mineração de Dados
 Universidade Tecnológica Federal do Paraná UTFPR Programa de Pós-Graduação em Computação Aplicada Disciplina de Mineração de Dados Prof. Celso Kaestner Poker Hand Data Set Aluno: Joyce Schaidt Versão:
Universidade Tecnológica Federal do Paraná UTFPR Programa de Pós-Graduação em Computação Aplicada Disciplina de Mineração de Dados Prof. Celso Kaestner Poker Hand Data Set Aluno: Joyce Schaidt Versão:
ESCOLA SECUNDÁRIA MANUEL DA FONSECA, SANTIAGO DO CACÉM GRUPO DISCIPLINAR: 500 Matemática Aplicada às Ciências Sociais
 ANO: 11º ANO LECTIVO : 008/009 p.1/7 CONTEÚDOS MODELOS MATEMÁTICOS COMPETÊNCIAS A DESENVOLVER - Compreender a importância dos modelos matemáticos na resolução de problemas de problemas concretos. Nº. AULAS
ANO: 11º ANO LECTIVO : 008/009 p.1/7 CONTEÚDOS MODELOS MATEMÁTICOS COMPETÊNCIAS A DESENVOLVER - Compreender a importância dos modelos matemáticos na resolução de problemas de problemas concretos. Nº. AULAS
Conceitos Fundamentais
 Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
Algoritmos Indutores de Árvores de
 Algoritmos Indutores de Árvores de Decisão Fabrício J. Barth Sistemas Inteligentes Análise e Desenvolvimento de Sistemas Faculdades de Tecnologia Bandeirantes Abril de 2013 Problema: Diagnóstico para uso
Algoritmos Indutores de Árvores de Decisão Fabrício J. Barth Sistemas Inteligentes Análise e Desenvolvimento de Sistemas Faculdades de Tecnologia Bandeirantes Abril de 2013 Problema: Diagnóstico para uso
INF 1771 Inteligência Artificial
 Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 12 Aprendizado de Máquina Agentes Vistos Anteriormente Agentes baseados em busca: Busca cega Busca heurística Busca local
Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 12 Aprendizado de Máquina Agentes Vistos Anteriormente Agentes baseados em busca: Busca cega Busca heurística Busca local
 MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
Análise bioestatística em fumantes dinamarqueses associado
 Análise bioestatística em fumantes dinamarqueses associado à câncer de esôfago Bárbara Camboim Lopes de Figueirêdo 1 Gustavo Henrique Esteves 2 1 Introdução A Bioestatística surgiu em 1894 quando Karl
Análise bioestatística em fumantes dinamarqueses associado à câncer de esôfago Bárbara Camboim Lopes de Figueirêdo 1 Gustavo Henrique Esteves 2 1 Introdução A Bioestatística surgiu em 1894 quando Karl
Definição. A expressão M(x,y) dx + N(x,y)dy é chamada de diferencial exata se existe uma função f(x,y) tal que f x (x,y)=m(x,y) e f y (x,y)=n(x,y).
 PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
Vetores Aleatórios, correlação e conjuntas
 Vetores Aleatórios, correlação e conjuntas Cláudio Tadeu Cristino 1 1 Universidade Federal Rural de Pernambuco, Recife, Brasil Segundo Semestre, 2013 C.T.Cristino (DEINFO-UFRPE) Vetores Aleatórios 2013.2
Vetores Aleatórios, correlação e conjuntas Cláudio Tadeu Cristino 1 1 Universidade Federal Rural de Pernambuco, Recife, Brasil Segundo Semestre, 2013 C.T.Cristino (DEINFO-UFRPE) Vetores Aleatórios 2013.2
A ideia de coordenatização (2/2)
 8 a : aula (1h) 12/10/2010 a ideia de coordenatização (2/2) 8-1 Instituto Superior Técnico 2010/11 1 o semestre Álgebra Linear 1 o ano das Lics. em Engenharia Informática e de Computadores A ideia de coordenatização
8 a : aula (1h) 12/10/2010 a ideia de coordenatização (2/2) 8-1 Instituto Superior Técnico 2010/11 1 o semestre Álgebra Linear 1 o ano das Lics. em Engenharia Informática e de Computadores A ideia de coordenatização
ASSOCIAÇÃO ENTRE PRESENÇA DE CÂNCER DE ESÔFAGO COMPARADA COM HÁBITO DE FUMAR E IDADE EM INDIVÍDUOS DA DINAMARCA
 ASSOCIAÇÃO ENTRE PRESENÇA DE CÂNCER DE ESÔFAGO COMPARADA COM HÁBITO DE FUMAR E IDADE EM INDIVÍDUOS DA DINAMARCA Bárbara Camboim Lopes de FIGUEIRÊDO 1, Gustavo Henrique ESTEVES 2 1 Departamento de Estatística
ASSOCIAÇÃO ENTRE PRESENÇA DE CÂNCER DE ESÔFAGO COMPARADA COM HÁBITO DE FUMAR E IDADE EM INDIVÍDUOS DA DINAMARCA Bárbara Camboim Lopes de FIGUEIRÊDO 1, Gustavo Henrique ESTEVES 2 1 Departamento de Estatística
Introdução à genética quantitativa usando os recursos do R
 Introdução à genética quantitativa usando os recursos do R Marisa R. Cantarino 1 Julia M. P. Soler (orientadora) 2 1 Introdução Um dos principais desafios da pesquisa genética atualmente é estabelecer
Introdução à genética quantitativa usando os recursos do R Marisa R. Cantarino 1 Julia M. P. Soler (orientadora) 2 1 Introdução Um dos principais desafios da pesquisa genética atualmente é estabelecer
Inferências Geográfica: Inferência Bayesiana Processo Analítico Hierárquico Classificação contínua
 Inferências Geográfica: Inferência Bayesiana Processo Analítico Hierárquico Classificação contínua Análise Multi-Critério Classificação continua (Lógica Fuzzy) Técnica AHP (Processo Analítico Hierárquico)
Inferências Geográfica: Inferência Bayesiana Processo Analítico Hierárquico Classificação contínua Análise Multi-Critério Classificação continua (Lógica Fuzzy) Técnica AHP (Processo Analítico Hierárquico)
TÉCNICAS EXPERIMENTAIS APLICADAS EM CIÊNCIA DO SOLO
 1 TÉCNICAS EXPERIMENTAIS APLICADAS EM CIÊNCIA DO SOLO Mario de Andrade Lira Junior www.lira.pro.br direitos autorais. INTRODUÇÃO À ANÁLISE MULTIVARIADA Apenas uma breve apresentação Para não dizerem que
1 TÉCNICAS EXPERIMENTAIS APLICADAS EM CIÊNCIA DO SOLO Mario de Andrade Lira Junior www.lira.pro.br direitos autorais. INTRODUÇÃO À ANÁLISE MULTIVARIADA Apenas uma breve apresentação Para não dizerem que
Aula 05 Raciocínio Lógico p/ INSS - Técnico do Seguro Social - Com Videoaulas
 Aula 05 Raciocínio Lógico p/ INSS - Técnico do Seguro Social - Com Videoaulas Professor: Arthur Lima AULA 05: RESUMO Caro aluno, Para finalizar nosso curso, preparei um resumo de toda a teoria vista nas
Aula 05 Raciocínio Lógico p/ INSS - Técnico do Seguro Social - Com Videoaulas Professor: Arthur Lima AULA 05: RESUMO Caro aluno, Para finalizar nosso curso, preparei um resumo de toda a teoria vista nas
Instrução de Trabalho Registro de chamado no sistema OCOMON
 Aprovado por Comitê da Qualidade Analisado Chefe do Departamento de Atendimento ao Usuário criticamente por 1. OBJETIVOS Orientar os atendentes que usam o sistema de controle e registro de ocorrências
Aprovado por Comitê da Qualidade Analisado Chefe do Departamento de Atendimento ao Usuário criticamente por 1. OBJETIVOS Orientar os atendentes que usam o sistema de controle e registro de ocorrências
4.2 Modelação da estrutura interna
 4.2 Modelação da estrutura interna AST434: C4-25/83 Para calcular a estrutura interna de uma estrela como o Sol é necessário descrever como o gás que o compõe se comporta. Assim, determinar a estrutura
4.2 Modelação da estrutura interna AST434: C4-25/83 Para calcular a estrutura interna de uma estrela como o Sol é necessário descrever como o gás que o compõe se comporta. Assim, determinar a estrutura
Cláudio Tadeu Cristino 1. Julho, 2014
 Inferência Estatística Estimação Cláudio Tadeu Cristino 1 1 Universidade Federal de Pernambuco, Recife, Brasil Mestrado em Nutrição, Atividade Física e Plasticidade Fenotípica Julho, 2014 C.T.Cristino
Inferência Estatística Estimação Cláudio Tadeu Cristino 1 1 Universidade Federal de Pernambuco, Recife, Brasil Mestrado em Nutrição, Atividade Física e Plasticidade Fenotípica Julho, 2014 C.T.Cristino
Auto-energia do elétron
 Teoria Quântica de Campos II 116 É possível mostrar que este cancelamento ocorre para todas as ordens de perturbação (Peskin sec 6.5), neste caso a seção de choque medida é: Auto-energia do elétron (Peskin
Teoria Quântica de Campos II 116 É possível mostrar que este cancelamento ocorre para todas as ordens de perturbação (Peskin sec 6.5), neste caso a seção de choque medida é: Auto-energia do elétron (Peskin
ESPAÇOS QUOCIENTES DANIEL SMANIA. [x] := {y X t.q. x y}.
![ESPAÇOS QUOCIENTES DANIEL SMANIA. [x] := {y X t.q. x y}. ESPAÇOS QUOCIENTES DANIEL SMANIA. [x] := {y X t.q. x y}.](/thumbs/20/415204.jpg) ESPAÇOS QUOCIENTES DANIEL SMANIA 1. Relações de equivalência Seja uma relação de equivalência sobre um conjunto X, isto é, uma rel ção binária que satisfaz as seguintes propriedades i. (Prop. Reflexiva.)
ESPAÇOS QUOCIENTES DANIEL SMANIA 1. Relações de equivalência Seja uma relação de equivalência sobre um conjunto X, isto é, uma rel ção binária que satisfaz as seguintes propriedades i. (Prop. Reflexiva.)
4. Curvas planas. T = κn, N = κt, B = 0.
 4. CURVAS PLANAS 35 4. Curvas planas Nesta secção veremos que no caso planar é possível refinar a definição de curvatura, de modo a dar-lhe uma interpretação geométrica interessante. Provaremos ainda o
4. CURVAS PLANAS 35 4. Curvas planas Nesta secção veremos que no caso planar é possível refinar a definição de curvatura, de modo a dar-lhe uma interpretação geométrica interessante. Provaremos ainda o
Universidade Federal do Paraná Departamento de Informática. Reconhecimento de Padrões. Revisão de Probabilidade e Estatística
 Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões Revisão de Probabilidade e Estatística Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Conceitos Básicos Estamos
Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões Revisão de Probabilidade e Estatística Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Conceitos Básicos Estamos
RECOMENDAÇÃO N.º 6/ B / 2004 [art.º 20.º, n.º 1, alínea b), da Lei n.º 9/91, de 9 de Abril]
![RECOMENDAÇÃO N.º 6/ B / 2004 [art.º 20.º, n.º 1, alínea b), da Lei n.º 9/91, de 9 de Abril] RECOMENDAÇÃO N.º 6/ B / 2004 [art.º 20.º, n.º 1, alínea b), da Lei n.º 9/91, de 9 de Abril]](/thumbs/27/11688934.jpg) Número: 6/B/2004 Data: 25-03-2004 Entidade visada: Secretária de Estado da Administração Pública Assunto: Curso de Estudos Avançados em Gestão Pública. Promoção a técnico superior de 1.ª classe. Processo:
Número: 6/B/2004 Data: 25-03-2004 Entidade visada: Secretária de Estado da Administração Pública Assunto: Curso de Estudos Avançados em Gestão Pública. Promoção a técnico superior de 1.ª classe. Processo:
CRM e Prospecção de Dados
 CRM e Prospecção de Dados Marília Antunes aula de 9 Março 09 2 Dados e medição 2.1 Introdução O objectivo a que nos propomos é o de descobrir relações existentes no mundo real a partir de dados que o descrevem.
CRM e Prospecção de Dados Marília Antunes aula de 9 Março 09 2 Dados e medição 2.1 Introdução O objectivo a que nos propomos é o de descobrir relações existentes no mundo real a partir de dados que o descrevem.
Reconhecimento de Padrões
 Engenharia Informática (ramos de Gestão e Industrial) Departamento de Sistemas e Informação Reconhecimento de Padrões Projecto Final 2004/2005 Realizado por: Prof. João Ascenso. Departamento de Sistemas
Engenharia Informática (ramos de Gestão e Industrial) Departamento de Sistemas e Informação Reconhecimento de Padrões Projecto Final 2004/2005 Realizado por: Prof. João Ascenso. Departamento de Sistemas
COMENTÁRIO AFRM/RS 2012 ESTATÍSTICA Prof. Sérgio Altenfelder
 Comentário Geral: Prova muito difícil, muito fora dos padrões das provas do TCE administração e Economia, praticamente só caiu teoria. Existem três questões (4, 45 e 47) que devem ser anuladas, por tratarem
Comentário Geral: Prova muito difícil, muito fora dos padrões das provas do TCE administração e Economia, praticamente só caiu teoria. Existem três questões (4, 45 e 47) que devem ser anuladas, por tratarem
Esmiuçando o Teorema de Bayes e fazendo exercícios
 PROAILIDADES Esmiuçando o Teorema de ayes e fazendo exercícios ERTOLO Lembrando as Aulas Anteriores Probabilidade Condicional: Teorema do Produto: Se os eventos e E 1 forem INDEPENDENTES: 11/09/2012 ertolo
PROAILIDADES Esmiuçando o Teorema de ayes e fazendo exercícios ERTOLO Lembrando as Aulas Anteriores Probabilidade Condicional: Teorema do Produto: Se os eventos e E 1 forem INDEPENDENTES: 11/09/2012 ertolo
PLANIFICAÇÃO ANUAL. MACS Matemática Aplicada às Ciências Sociais. Curso de Línguas e Humanidades 2º ANO (11º ANO)
 PLANIFICAÇÃO ANUAL MACS Matemática Aplicada às Ciências Sociais Curso de Línguas e Humanidades º ANO (º ANO) Ano Lectivo 0/05 Planificação º Ano - MACS º Período Número de Aulas Previstas 0 Apresentação
PLANIFICAÇÃO ANUAL MACS Matemática Aplicada às Ciências Sociais Curso de Línguas e Humanidades º ANO (º ANO) Ano Lectivo 0/05 Planificação º Ano - MACS º Período Número de Aulas Previstas 0 Apresentação
Exercícios Resolvidos sobre probabilidade total e Teorema de Bayes
 Exercícios Resolvidos sobre probabilidade total e Teorema de Bayes Para ampliar sua compreensão sobre probabilidade total e Teorema de Bayes, estude este conjunto de exercícios resolvidos sobre o tema.
Exercícios Resolvidos sobre probabilidade total e Teorema de Bayes Para ampliar sua compreensão sobre probabilidade total e Teorema de Bayes, estude este conjunto de exercícios resolvidos sobre o tema.
SAD orientado a MODELO
 Universidade do Contestado Campus Concórdia Curso de Sistemas de Informação Prof.: Maico Petry SAD orientado a MODELO DISCIPLINA: Sistemas de Apoio a Decisão SAD Orientado a Modelo De acordo com ALTER
Universidade do Contestado Campus Concórdia Curso de Sistemas de Informação Prof.: Maico Petry SAD orientado a MODELO DISCIPLINA: Sistemas de Apoio a Decisão SAD Orientado a Modelo De acordo com ALTER
Aprendizado Bayesiano. Disciplina: Agentes Adaptativos e Cognitivos
 Aprendizado Bayesiano Disciplina: Agentes Adaptativos e Cognitivos Conhecimento com Incerteza Exemplo: sistema de diagnóstico odontológico Regra de diagnóstico " p sintoma (p,dor de dente) doença (p,cárie)
Aprendizado Bayesiano Disciplina: Agentes Adaptativos e Cognitivos Conhecimento com Incerteza Exemplo: sistema de diagnóstico odontológico Regra de diagnóstico " p sintoma (p,dor de dente) doença (p,cárie)
Resoluções comentadas das questões de Estatística da prova para. ANALISTA DE GERENCIAMENTO DE PROJETOS E METAS da PREFEITURA/RJ
 Resoluções comentadas das questões de Estatística da prova para ANALISTA DE GERENCIAMENTO DE PROJETOS E METAS da PREFEITURA/RJ Realizada pela Fundação João Goulart em 06/10/2013 41. A idade média de todos
Resoluções comentadas das questões de Estatística da prova para ANALISTA DE GERENCIAMENTO DE PROJETOS E METAS da PREFEITURA/RJ Realizada pela Fundação João Goulart em 06/10/2013 41. A idade média de todos
O degrau de potencial. Caso II: energia maior que o degrau
 O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
Aula 8 Circuitos Integrados
 INTRODUÇÃO À ENGENHRI DE COMPUTÇÃO PONTIFÍCI UNIVERSIDDE CTÓLIC DO RIO GRNDE DO SUL FCULDDE DE ENGENHRI ula Circuitos Integrados Introdução Portas Lógicas em Circuitos Integrados Implementação de Funções
INTRODUÇÃO À ENGENHRI DE COMPUTÇÃO PONTIFÍCI UNIVERSIDDE CTÓLIC DO RIO GRNDE DO SUL FCULDDE DE ENGENHRI ula Circuitos Integrados Introdução Portas Lógicas em Circuitos Integrados Implementação de Funções
Curso Satélite de. Matemática. Sessão n.º 2. Universidade Portucalense
 Curso Satélite de Matemática Sessão n.º 2 Universidade Portucalense Funções reais de variável real Deinição e generalidades Uma unção é uma correspondência que a qualquer elemento de um conjunto D az corresponder
Curso Satélite de Matemática Sessão n.º 2 Universidade Portucalense Funções reais de variável real Deinição e generalidades Uma unção é uma correspondência que a qualquer elemento de um conjunto D az corresponder
Métodos de Monte Carlo
 Departamento de Estatística - UFJF Outubro e Novembro de 2014 são métodos de simulação São utilizados quando não temos uma forma fechada para resolver o problema Muito populares em Estatística, Matemática,
Departamento de Estatística - UFJF Outubro e Novembro de 2014 são métodos de simulação São utilizados quando não temos uma forma fechada para resolver o problema Muito populares em Estatística, Matemática,
Vamos Jogar no Totoloto?
 Vamos Jogar no Totoloto? N CRISTIN BICO MTOS CRL HENRIQUES Departamento de Matemática, Escola Superior de Tecnologia de Viseu Tendo como objectivo despertar o interesse dos alunos pelo cálculo de probabilidades,
Vamos Jogar no Totoloto? N CRISTIN BICO MTOS CRL HENRIQUES Departamento de Matemática, Escola Superior de Tecnologia de Viseu Tendo como objectivo despertar o interesse dos alunos pelo cálculo de probabilidades,
1 Módulo ou norma de um vetor
 Álgebra Linear I - Aula 3-2005.2 Roteiro 1 Módulo ou norma de um vetor A norma ou módulo do vetor ū = (u 1, u 2, u 3 ) de R 3 é ū = u 2 1 + u2 2 + u2 3. Geometricamente a fórmula significa que o módulo
Álgebra Linear I - Aula 3-2005.2 Roteiro 1 Módulo ou norma de um vetor A norma ou módulo do vetor ū = (u 1, u 2, u 3 ) de R 3 é ū = u 2 1 + u2 2 + u2 3. Geometricamente a fórmula significa que o módulo
ficha 3 espaços lineares
 Exercícios de Álgebra Linear ficha 3 espaços lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 3 Notação Sendo
Exercícios de Álgebra Linear ficha 3 espaços lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 3 Notação Sendo
TIC Unidade 2 Base de Dados. Informação é todo o conjunto de dados devidamente ordenados e organizados de forma a terem significado.
 Conceitos relativos à Informação 1. Informação O que á a informação? Informação é todo o conjunto de dados devidamente ordenados e organizados de forma a terem significado. 2. Dados Em informática designa-se
Conceitos relativos à Informação 1. Informação O que á a informação? Informação é todo o conjunto de dados devidamente ordenados e organizados de forma a terem significado. 2. Dados Em informática designa-se
Computabilidade 2012/2013. Sabine Broda Departamento de Ciência de Computadores Faculdade de Ciências da Universidade do Porto
 Computabilidade 2012/2013 Sabine Broda Departamento de Ciência de Computadores Faculdade de Ciências da Universidade do Porto Capítulo 1 Computabilidade 1.1 A noção de computabilidade Um processo de computação
Computabilidade 2012/2013 Sabine Broda Departamento de Ciência de Computadores Faculdade de Ciências da Universidade do Porto Capítulo 1 Computabilidade 1.1 A noção de computabilidade Um processo de computação
I.3 Indução de Árvores de Decisão
 I.3 Indução de Árvores de Decisão Nesta seção serão apresentados alguns conceitos básicos da técnica de indução de árvores de decisão a partir de um exemplo sobre o efeito dos raios solares sobre algumas
I.3 Indução de Árvores de Decisão Nesta seção serão apresentados alguns conceitos básicos da técnica de indução de árvores de decisão a partir de um exemplo sobre o efeito dos raios solares sobre algumas
PROPOSTA DE RESOLUÇÃO DO EXAME NACIONAL DE MACS (PROVA 835) 2ªFASE
 PROPOSTA DE RESOLUÇÃO DO EXAME NACIONAL DE MACS (PROVA 835) 2ªFASE 1. 1.1. Aplicando o método de Hondt: Efetuando-se as divisões do número de votos de cada partido por 1, 2, 3, 4, 5 e 6, obtêm-se os seguintes
PROPOSTA DE RESOLUÇÃO DO EXAME NACIONAL DE MACS (PROVA 835) 2ªFASE 1. 1.1. Aplicando o método de Hondt: Efetuando-se as divisões do número de votos de cada partido por 1, 2, 3, 4, 5 e 6, obtêm-se os seguintes
Data Mining II Modelos Preditivos
 Data Mining II Modelos Preditivos Prof. Doutor Victor Lobo Mestre André Melo Mestrado em Estatística e Gestão de Informação Objectivo desta disciplina Fazer previsões a partir de dados. Conhecer os principais
Data Mining II Modelos Preditivos Prof. Doutor Victor Lobo Mestre André Melo Mestrado em Estatística e Gestão de Informação Objectivo desta disciplina Fazer previsões a partir de dados. Conhecer os principais
CONCURSO PETROBRAS DRAFT. Pesquisa Operacional, TI, Probabilidade e Estatística. Questões Resolvidas. Produzido por Exatas Concursos www.exatas.com.
 CONCURSO PETROBRAS ENGENHEIRO(A) DE PRODUÇÃO JÚNIOR ENGENHEIRO(A) JÚNIOR - ÁREA: PRODUÇÃO Pesquisa Operacional, TI, Probabilidade e Estatística Questões Resolvidas QUESTÕES RETIRADAS DE PROVAS DA BANCA
CONCURSO PETROBRAS ENGENHEIRO(A) DE PRODUÇÃO JÚNIOR ENGENHEIRO(A) JÚNIOR - ÁREA: PRODUÇÃO Pesquisa Operacional, TI, Probabilidade e Estatística Questões Resolvidas QUESTÕES RETIRADAS DE PROVAS DA BANCA
Momentos de uma variável aleatória
 Momentos de uma variável aleatória O cálculo de E[X] (valor médio de X) e E[X 2 ] (que intervém na variância), pode ser generalizado pensando em E[X k ] com k IN. Definição: Dada uma v.a. X, chama-se momento
Momentos de uma variável aleatória O cálculo de E[X] (valor médio de X) e E[X 2 ] (que intervém na variância), pode ser generalizado pensando em E[X k ] com k IN. Definição: Dada uma v.a. X, chama-se momento
Matemática Aplicada às Ciências Sociais
 Prova de Exame Nacional de Matemática Aplicada às Ciências Sociais Prova 835 2011 10.º e 11.º Anos de Escolaridade Decreto-Lei n.º 74/2004, de 26 de Março Para: Direcção-Geral de Inovação e de Desenvolvimento
Prova de Exame Nacional de Matemática Aplicada às Ciências Sociais Prova 835 2011 10.º e 11.º Anos de Escolaridade Decreto-Lei n.º 74/2004, de 26 de Março Para: Direcção-Geral de Inovação e de Desenvolvimento
INSTITUTO TECNOLÓGICO
 PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
X.0 Sucessões de números reais 1
 «Tal como a tecnologia requer as tøcnicas da matemætica aplicada, tambøm a matemætica aplicada requer as teorias do nœcleo central da matemætica pura. Da l gica matemætica topologia algøbrica, da teoria
«Tal como a tecnologia requer as tøcnicas da matemætica aplicada, tambøm a matemætica aplicada requer as teorias do nœcleo central da matemætica pura. Da l gica matemætica topologia algøbrica, da teoria
Aula 1: Introdução à Probabilidade
 Aula 1: Introdução à Probabilidade Prof. Leandro Chaves Rêgo Programa de Pós-Graduação em Engenharia de Produção - UFPE Recife, 07 de Março de 2012 Experimento Aleatório Um experimento é qualquer processo
Aula 1: Introdução à Probabilidade Prof. Leandro Chaves Rêgo Programa de Pós-Graduação em Engenharia de Produção - UFPE Recife, 07 de Março de 2012 Experimento Aleatório Um experimento é qualquer processo
Pré processamento de dados II. Mineração de Dados 2012
 Pré processamento de dados II Mineração de Dados 2012 Luís Rato Universidade de Évora, 2012 Mineração de dados / Data Mining 1 Redução de dimensionalidade Objetivo: Evitar excesso de dimensionalidade Reduzir
Pré processamento de dados II Mineração de Dados 2012 Luís Rato Universidade de Évora, 2012 Mineração de dados / Data Mining 1 Redução de dimensionalidade Objetivo: Evitar excesso de dimensionalidade Reduzir
 Termos Técnicos Ácidos Classe de substâncias que têm ph igual ou maior que 1 e menor que 7. Exemplo: sumo do limão. Átomos Todos os materiais são formados por pequenas partículas. Estas partículas chamam-se
Termos Técnicos Ácidos Classe de substâncias que têm ph igual ou maior que 1 e menor que 7. Exemplo: sumo do limão. Átomos Todos os materiais são formados por pequenas partículas. Estas partículas chamam-se
Introdução a Datamining (previsão e agrupamento)
 E o que fazer depois de ter os dados organizados? Introdução a Datamining (previsão e agrupamento) Victor Lobo Mestrado em Estatística e Gestão de Informação Ideias base Aprender com o passado Inferir
E o que fazer depois de ter os dados organizados? Introdução a Datamining (previsão e agrupamento) Victor Lobo Mestrado em Estatística e Gestão de Informação Ideias base Aprender com o passado Inferir
Unidade 11 - Probabilidade. Probabilidade Empírica Probabilidade Teórica
 Unidade 11 - Probabilidade Probabilidade Empírica Probabilidade Teórica Probabilidade Empírica Existem probabilidade que são baseadas apenas uma experiência de fatos, sem necessariamente apresentar uma
Unidade 11 - Probabilidade Probabilidade Empírica Probabilidade Teórica Probabilidade Empírica Existem probabilidade que são baseadas apenas uma experiência de fatos, sem necessariamente apresentar uma
a 1 x 1 +... + a n x n = b,
 Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
PROBABILIDADE Prof. Adriano Mendonça Souza, Dr.
 PROBABILIDADE Prof. Adriano Mendonça Souza, Dr. Departamento de Estatística - PPGEMQ / PPGEP - UFSM - O intelecto faz pouco na estrada que leva à descoberta, acontece um salto na consciência, chameo de
PROBABILIDADE Prof. Adriano Mendonça Souza, Dr. Departamento de Estatística - PPGEMQ / PPGEP - UFSM - O intelecto faz pouco na estrada que leva à descoberta, acontece um salto na consciência, chameo de
Parece claro que há uma, e uma só, conclusão a tirar destas proposições. Esa conclusão é:
 Argumentos Dedutivos e Indutivos Paulo Andrade Ruas Introdução Em geral, quando se quer explicar que géneros de argumentos existem, começa-se por distinguir os argumentos dedutivos dos não dedutivos. A
Argumentos Dedutivos e Indutivos Paulo Andrade Ruas Introdução Em geral, quando se quer explicar que géneros de argumentos existem, começa-se por distinguir os argumentos dedutivos dos não dedutivos. A
Processos Estocásticos
 Processos Estocásticos Segunda Lista de Exercícios 01 de julho de 2013 1 Uma indústria fabrica peças, das quais 1 5 são defeituosas. Dois compradores, A e B, classificam os lotes de peças adquiridos em
Processos Estocásticos Segunda Lista de Exercícios 01 de julho de 2013 1 Uma indústria fabrica peças, das quais 1 5 são defeituosas. Dois compradores, A e B, classificam os lotes de peças adquiridos em
Propagação de distribuições pelo método de Monte Carlo
 Sumário Propagação de distribuições pelo método de Monte Carlo João Alves e Sousa Avaliação de incertezas pelo GUM Propagação de distribuições O método de Monte Carlo Aplicação a modelos de medição por
Sumário Propagação de distribuições pelo método de Monte Carlo João Alves e Sousa Avaliação de incertezas pelo GUM Propagação de distribuições O método de Monte Carlo Aplicação a modelos de medição por
ActivALEA. active e actualize a sua literacia
 ActivALEA active e actualize a sua literacia N.º 25 HIISTOGRAMA Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL [email protected] Emília Oliveira Escola
ActivALEA active e actualize a sua literacia N.º 25 HIISTOGRAMA Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL [email protected] Emília Oliveira Escola
Testes (Não) Paramétricos
 Armando B. Mendes, DM, UAç 09--006 ANOVA: Objectivos Verificar as condições de aplicabilidade de testes de comparação de médias; Utilizar ANOVA a um factor, a dois factores e mais de dois factores e interpretar
Armando B. Mendes, DM, UAç 09--006 ANOVA: Objectivos Verificar as condições de aplicabilidade de testes de comparação de médias; Utilizar ANOVA a um factor, a dois factores e mais de dois factores e interpretar
Desta propriedade, caminhando no sentido inverso, retira-se a regra de primitivação por partes, que se apresenta no seguinte. f g = fg fg.
 HÉLIO BERNARDO LOPES Resumo. Epõem-se neste teto os fundamentos do método de primitivação por partes, que se estuda nas disciplinas de Análise Matemática de muitos dos cursos de licenciatura de natureza
HÉLIO BERNARDO LOPES Resumo. Epõem-se neste teto os fundamentos do método de primitivação por partes, que se estuda nas disciplinas de Análise Matemática de muitos dos cursos de licenciatura de natureza
Testes de Ajustamento (testes da bondade do ajustamento)
 Testes de Ajustamento (testes da bondade do ajustamento) Os testes de ajustamento servem para testar a hipótese de que uma determinada amostra aleatória tenha sido extraída de uma população com distribuição
Testes de Ajustamento (testes da bondade do ajustamento) Os testes de ajustamento servem para testar a hipótese de que uma determinada amostra aleatória tenha sido extraída de uma população com distribuição
2 Independência e dependência das taxas de juro
 1 Incerteza e juro aleatório Considere-se o intervalo [0, n], o tempo medido em anos, e a partição [0, 1], (1, 2],..., (n 1, 1] e suponha-se que no início do ano t são aplicadas C t unidades de capital,
1 Incerteza e juro aleatório Considere-se o intervalo [0, n], o tempo medido em anos, e a partição [0, 1], (1, 2],..., (n 1, 1] e suponha-se que no início do ano t são aplicadas C t unidades de capital,
Os elementos de circuito que estudámos até agora foram elementos lineares. Ou seja, se duplicamos a ddp aos terminais de um
 O Díodo Os elementos de circuito que estudámos até agora foram elementos lineares. Ou seja, se duplicamos a ddp aos terminais de um componente, a intensidade da corrente eléctrica que o percorre também
O Díodo Os elementos de circuito que estudámos até agora foram elementos lineares. Ou seja, se duplicamos a ddp aos terminais de um componente, a intensidade da corrente eléctrica que o percorre também
[ \ x Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \.
 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV Å 1Ro}HV *HUDLV Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \. [\ [\ É fácil verificar
&DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV Å 1Ro}HV *HUDLV Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \. [\ [\ É fácil verificar
Exercícios 1. Determinar x de modo que a matriz
 setor 08 080509 080509-SP Aula 35 MATRIZ INVERSA Uma matriz quadrada A de ordem n diz-se invertível, ou não singular, se, e somente se, existir uma matriz que indicamos por A, tal que: A A = A A = I n
setor 08 080509 080509-SP Aula 35 MATRIZ INVERSA Uma matriz quadrada A de ordem n diz-se invertível, ou não singular, se, e somente se, existir uma matriz que indicamos por A, tal que: A A = A A = I n
Extração de Árvores de Decisão com a Ferramenta de Data Mining Weka
 Extração de Árvores de Decisão com a Ferramenta de Data Mining Weka 1 Introdução A mineração de dados (data mining) pode ser definida como o processo automático de descoberta de conhecimento em bases de
Extração de Árvores de Decisão com a Ferramenta de Data Mining Weka 1 Introdução A mineração de dados (data mining) pode ser definida como o processo automático de descoberta de conhecimento em bases de
Associação de Professores de Matemática PROPOSTA DE RESOLUÇÃO DO EXAME DE MATEMÁTICA APLICADA ÀS CIÊNCIAS SOCIAIS (PROVA 835) 2013 1ªFASE.
 Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 27-A 1500-236 Lisboa Tel.: +351 21 716 36 90 / 21 711 03 77 Fax: +351 21 716 64 24 http://www.apm.pt email: [email protected] PROPOSTA
Associação de Professores de Matemática Contactos: Rua Dr. João Couto, n.º 27-A 1500-236 Lisboa Tel.: +351 21 716 36 90 / 21 711 03 77 Fax: +351 21 716 64 24 http://www.apm.pt email: [email protected] PROPOSTA
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE
 INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
2. O número de vectores da base de L construída na alínea anterior é a soma do número de vectores das bases de M e N.
 2.4. PROJECÇÕES 2. dim(l)=dim(m)+dim(n) Demonstração. Se L=M N, qualquer vector x L se pode escrever de forma única como a soma de um vector x M M e outro vector x N N. 1. Dada uma base de M, x M pode
2.4. PROJECÇÕES 2. dim(l)=dim(m)+dim(n) Demonstração. Se L=M N, qualquer vector x L se pode escrever de forma única como a soma de um vector x M M e outro vector x N N. 1. Dada uma base de M, x M pode
O caso estacionário em uma dimensão
 O caso estacionário em uma dimensão A U L A 6 Meta da aula Aplicar o formalismo quântico no caso de o potencial ser independente do tempo. objetivos verificar que, no caso de o potencial ser independente
O caso estacionário em uma dimensão A U L A 6 Meta da aula Aplicar o formalismo quântico no caso de o potencial ser independente do tempo. objetivos verificar que, no caso de o potencial ser independente
Clima e sociedade: Rumo a um uso mais eficaz das informações de clima e tempo no Ceará
 Clima e sociedade: Rumo a um uso mais eficaz das informações de clima e tempo no Ceará FUNCEME / IRI-Univ. Columbia / Univ. Arizona Janeiro de 2006 Renzo Taddei IRI-Univ. Columbia Terra em transe 2005
Clima e sociedade: Rumo a um uso mais eficaz das informações de clima e tempo no Ceará FUNCEME / IRI-Univ. Columbia / Univ. Arizona Janeiro de 2006 Renzo Taddei IRI-Univ. Columbia Terra em transe 2005
Álgebra A - Aula 11 RSA
 Álgebra A - Aula 11 RSA Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Criptografia RSA- pré-codificação Converter a mensagem em uma seqüência de números pré-codificação.
Álgebra A - Aula 11 RSA Elaine Pimentel Departamento de Matemática, UFMG, Brazil 2 o Semestre - 2010 Criptografia RSA- pré-codificação Converter a mensagem em uma seqüência de números pré-codificação.
Os juros podem ser capitalizados segundo dois regimes: simples ou compostos.
 1/7 3. Modelos de capitalização simples 4. Modelos de capitalização composta Conceitos básicos A Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de investimentos ou financiamentos
1/7 3. Modelos de capitalização simples 4. Modelos de capitalização composta Conceitos básicos A Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de investimentos ou financiamentos
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/15 Cursos: LEGM, MEC. Michael Paluch
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/15 Cursos: LEGM, MEC Michael Paluch Avaliação 1. Avaliação Contínua a) 1 Teste dia 11 de abril de 2015 duração 90 minutes (40% de nota final)
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/15 Cursos: LEGM, MEC Michael Paluch Avaliação 1. Avaliação Contínua a) 1 Teste dia 11 de abril de 2015 duração 90 minutes (40% de nota final)
Sistemas Distribuídos: Princípios e Algoritmos Introdução à Análise de Complexidade de Algoritmos
 Sistemas Distribuídos: Princípios e Algoritmos Introdução à Análise de Complexidade de Algoritmos Francisco José da Silva e Silva Laboratório de Sistemas Distribuídos (LSD) Departamento de Informática
Sistemas Distribuídos: Princípios e Algoritmos Introdução à Análise de Complexidade de Algoritmos Francisco José da Silva e Silva Laboratório de Sistemas Distribuídos (LSD) Departamento de Informática
Investigação Operacional- 2009/10 - Programas Lineares 3 PROGRAMAS LINEARES
 Investigação Operacional- 2009/10 - Programas Lineares 3 PROGRAMAS LINEARES Formulação A programação linear lida com problemas nos quais uma função objectivo linear deve ser optimizada (maximizada ou minimizada)
Investigação Operacional- 2009/10 - Programas Lineares 3 PROGRAMAS LINEARES Formulação A programação linear lida com problemas nos quais uma função objectivo linear deve ser optimizada (maximizada ou minimizada)
INTRODUÇÃO AOS MÉTODOS FACTORIAIS
 Capítulo II INTRODUÇÃO AOS MÉTODOS FACTORIAIS A Análise Factorial de Correspondências é uma técnica simples do ponto de vista matemático e computacional. Porém, devido ao elevado suporte geométrico desta
Capítulo II INTRODUÇÃO AOS MÉTODOS FACTORIAIS A Análise Factorial de Correspondências é uma técnica simples do ponto de vista matemático e computacional. Porém, devido ao elevado suporte geométrico desta
AVALIAÇÃO DO MESTRADO EM EDUCAÇÃO ESPECIAL
 AVALIAÇÃO DO MESTRADO EM EDUCAÇÃO ESPECIAL Outubro 2009 ÍNDICE 1. Introdução 3 2. População e Amostra 3 3. Apresentação de Resultados 4 3.1. Opinião dos alunos do Mestrado em Educação Especial sobre a
AVALIAÇÃO DO MESTRADO EM EDUCAÇÃO ESPECIAL Outubro 2009 ÍNDICE 1. Introdução 3 2. População e Amostra 3 3. Apresentação de Resultados 4 3.1. Opinião dos alunos do Mestrado em Educação Especial sobre a
Artigo 4.º Regime excecional de avaliação
 Associação Sindical de Docentes e investigadores Exmo. Senhor Professor Doutor Luís Curral Diretor da Faculdade de Psicologia da Universidade de Lisboa N/Refª:Dir:AV/0790/15 03-08-2015 Assunto: Posição
Associação Sindical de Docentes e investigadores Exmo. Senhor Professor Doutor Luís Curral Diretor da Faculdade de Psicologia da Universidade de Lisboa N/Refª:Dir:AV/0790/15 03-08-2015 Assunto: Posição
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Regulamento de Estágios
 Programa de Inserção Profissional Regulamento de Estágios Faculdade de Ciências Humanas Nos últimos anos, o ensino universitário tem vindo a integrar nos percursos formativos a realização de estágios curriculares
Programa de Inserção Profissional Regulamento de Estágios Faculdade de Ciências Humanas Nos últimos anos, o ensino universitário tem vindo a integrar nos percursos formativos a realização de estágios curriculares
Matemática Discreta para Computação e Informática
 Matemática Discreta para Computação e Informática P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Computação e Informática
Matemática Discreta para Computação e Informática P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Computação e Informática
Gerenciamento de Projeto: Criando o Termo de Abertura III. Prof. Msc Ricardo Britto DIE-UFPI [email protected]
 Gerenciamento de Projeto: Criando o Termo de Abertura III Prof. Msc Ricardo Britto DIE-UFPI [email protected] Sumário Desenvolvendo o Termo de Abertura do Projeto. Identificando as Partes Interessadas
Gerenciamento de Projeto: Criando o Termo de Abertura III Prof. Msc Ricardo Britto DIE-UFPI [email protected] Sumário Desenvolvendo o Termo de Abertura do Projeto. Identificando as Partes Interessadas
Introdução. Existem situações nas quais há interesse em estudar o comportamento conjunto de uma ou mais variáveis;
 UNIVERSIDADE FEDERAL DA PARAÍBA Correlação e Regressão Luiz Medeiros de Araujo Lima Filho Departamento de Estatística Introdução Eistem situações nas quais há interesse em estudar o comportamento conjunto
UNIVERSIDADE FEDERAL DA PARAÍBA Correlação e Regressão Luiz Medeiros de Araujo Lima Filho Departamento de Estatística Introdução Eistem situações nas quais há interesse em estudar o comportamento conjunto
