SUPERFÍCIE ESFÉRICA I
|
|
|
- Wilson Marinho Ferreira
- 9 Há anos
- Visualizações:
Transcrição
1 Pedro M. Fialho de Sousa Professor Associado SUPERFÍCIE ESFÉRICA I DUPLA PROJECÇÃO ORTOGONAL FACULDADE DE ARQUITECTURA-UTL Departamento de Arquitectura Secção de Desenho/Geometria/CAD Janeiro de /19
2 NOTA: No texto e nas figuras utilizou-se a nomenclatura convencional para a designação de pontos (letras latinas maiúsculas), linhas rectas (letras latinas minúsculas) e curvas (letras latinas minúsculas dentro de um parêntesis recto), planos (letras gregas minúsculas) e superfícies curvas (letras gregas minúsculas, dentro de um parêntesis recto). Em algumas figuras nâo estão representados ou designados alguns dos seus componentes geométricos Tal deve-se ao facto, facilmente compreensível, de que a sua representação não ser necessária para a respectiva resolução, tornando assim a leitura de resolução gráfica mais clara. Também não estão pormenorizadarnente expressas justificações que tenham por base conceitos ou traçados cujo conhecimento tenha sido adquirido em níveis de ensino anteriores ou em capítulos próprios anteriormente estudados. Assim, sempre que tal se verifique, faz-se somente referência ao conceito justificativo. Na representação da superfície esférica considerou-se sempre o eixo em posição vertical. Nos textos explicativos e sempre que as operações conducentes a traçados sejam iguais a anteriormente efectuadas, remeter-se-ão para elas para evitar repetições sem interesse objectivo. Nas aplicações respeitantes a planos tangentes à superfície e respectivos pontos de tangência, usaremos esta designação, como liberdade de linguagem, sem prejuízo da noção de que estes planos são osculantes e que o ponto de contacto com a superfície é o ponto de osculação. 2/19
3 SUPERFÍCIE ESFÉRICA 1. DEFINIÇÃO E REPRESENTAÇÃO Uma Superfície Esférica é uma superfície de 2 a ordem 1, de revolução, limitada e fechada, gerada por uma circunferência que roda em torno de um dos diâmetros. A recta de suporte do segmento do diâmetro considerado, constitui o EIXO da superfície. A superfície esférica é representada no SDPO pelas projecções dos seus contornos aparentes. Assim a sua projecção vertical é uma circunferência correspondente à projecção vertical do seu contorno aparente verical e a projecção horizontal é também uma circunferência correspondente à projecção horizontal do contorno aparente horizontal da superfície. 2. PONTOS E LINHAS NOTÁVEIS DA SUPERFÍCIE ESFÉRICA (fig. l) Enunciam-se os pontos e linhas fundamentais para a resolução dos problemas suscitados pela superfície esférica. Em ponto próprio e na sequência imediata deste, apresentam-se algumas definições relativas a esta superfície e ao sólido seu derivado, a esfera, que se consideram úteis para a compreenção global da forma geométrica em em geral. As circunferências existentes numa superfície esférica são de dois tipos: Círculos Máximos, se os seus raios forem iguais ao raio da superfície e Círculos Menores quando os seus raios forem menores do que o raio da superfície. Os pontos P e P1, onde o eixo encontra a superfície, denominam-se Polos. Os círculos máximos que conteem os polos denominam-se Meridianos. O círculo máximo complanar com o centro da superfície e que é perpendicular ao eixo, denomina-se Equador e qualquer círculo menor, também perpendicular ao eixo, denomina-se Paralelo. fig.1 ' O número de ordem de uma superfície é dado pelo número máximo de pontos que uma recta encontra essa superfície. 3/19
4 2.1. Partes da esfera e da superfície esférica. Segmento Esférico (fig. 2): Designa cada uma das duas partes da esfera resultantes da intersecção de um plano. Se o plano secante passar pelo centro da esfera, os dois segmentos esféricos são iguais e cada um deles chama-se semi-esfera ou hemisfério. Os segmentos esféricos são sólidos de revolução e cada um denomina-se segmento esférico de uma base. Calote Esférica (fig. 3): Chama-se calote esférica (ou zona de uma base) a uma das duas partes da superfície esférica determinadas por um plano secante. A calote esférica é, portanto, a parte curva da superfície de um segmento esférico de uma base. Zona Esférica (fig. 4): E a parte da superfície esférica compreendida entre dois planos paralelos que intersectam a superfície. A parte da esfera que lhe correspondente designa-se zona de duas bases. Sector Esférico (figs. 5a e 5b): É o sólido gerado por um sector circular, numa rotação completa em tomo de um eixo situado no seu plano, mas que não atravessa esse sector. Cunha Esférica (fíg. 6): É a parte da esfera compreendida entre entre dois semi-planos cuja origem comum é um diâmetro (ou o eixo). A superfície curva da cunha esférica designa-se lúnula esférica ou fuso esférico. Angulo de um fuso: E o ângulo diedro formado pelos planos dos círculos máximos que limitam o fuso. Camada Esférica: É o sólido limitado por duas superfícies esféricas concêntricas. A diferença dos dois raios denomina-se espessura da camada. fig.2 fig. 3 fig. 4 fig. 5a fig. 5b fig. 6 Teorema l: Qualquer ponto da superfície esférica fica definido pelo cruzamento de dois círculos que passam por esse ponto. Teorema 2: Para que um ponto pertença à superfície esférica tem de pertencer a uma linha da superfície (normalmente um dos círculos). 4/19
5 2.2. Aplicação Dada uma das projecções de um ponto da superfície esférica, determinar a outra projecção: Sejam dados, fig. 7, a superfície esférica [e], que se considera de eixo vertical, com centro em C, e P" a projecção vertical do ponto P da superfície. Pelo teorema 2 considera-se o ponto P como pertencente ao paralelo [p], naturalmente de nível, contido no plano a. Assim [p"] terá de conter P"; determinando [p'] (cujo centro é C'), sobre este localizar-se-à P'. Note-se que podem existir dois pontos como solução (não representado o segundo), situados no mesmo segmento de topo. Se fosse dada a projecção horizontal do ponto P, a determinação da respectiva projecção vertical far-se-ia por meio de um raciocínio idêntico, a partir da projecção horizontal do paralelo que contivesse a projecção horizontal do ponto. fíg.7 5/19
6 3. CONCORDÂNCIAS Teorema 3: Duas superfícies são concordantes quando admitem planos tangentes comuns em todos os pontos da linha de concordância. (fig. 8). A superfície esférica admite como superfícies concordantes, as superfícies cónica e cilíndrica Teorema 4: Uma superfície cónica concorda com um superfície esférica segundo um círculo menor, que é directriz da primeira. Corolário: Se a superfície cónica for concordante segundo um paralelo da superfície esférica, o seu vértice localiza-se no eixo da superfície esférica. Teorema 5: Uma superfície cilíndrica é concordante com uma superfície esférica segundo um círculo máximo. Corolário: Se as geratrizes da superfície cilíndrica de concordância tiverem uma direcção paralela ao eixo da superfície esférica, as duas superfícies concordam segundo o equador da superfície esférica. fig SECÇÃO PLANA DA SUPERFÍCIE ESFÉRICA. A secção plana de uma superfície esférica é sempre uma circunferência que se projecta segundo uma linha curva, fechada, de tipologia (circunferência ou elipse), dependente da posição do plano secante relativamente aos planos de projecção. Se o plano secante for oblíquo, ambas as projecções da secção são elipses; se o plano for simplesmente projectante (de topo ou vertical), a projecção da secção coincidente com o traço oblíquo, relativamente a LT, é um segmento de recta e a outra é uma elipse. Se o plano 6/19
7 secante for de nível ou de frente a projecção da secção coincidente com o traço respectivo é um segmento de recta e a outra é uma circunferência. Se o plano secante for duplamente projectante (de perfil), ambas as projecções da secção são segmentos de recta, coincidentes com os traços do plano. 5. INTERSECÇÃO DE UMA RECTA COM A SUPERFÍCIE ESFÉRICA. Para determinar os traços de uma recta numa superfície esférica, aplica-se aregra geral para a determinação do/s traço/s de uma recta numa superfície qualquer: 1º Faz-se passar pela recta um plano auxiliar. 2º Determina-se a linha de intersecção deste plano com a superfície. 3º O/s pontos de cruzamento da recta com esta linha de intersecção é/são o/s ponto/s pretendido/s. Nota: No caso da superfície ser esférica, e excluindo os planos secantes de nível e de frente as secções têm pelo menos uma das projecções elíptica, que sendo uma curva de erro deverá ser evitada a sua utilização, recorrendo a um dos Métodos Auxiliares (Rotações, Rebatimentos ou Mudança de Planos), para a colocação da secção numa posição de leitura e de traçado mais convenientes, isto é de nível ou de frente, para que uma das projecções seja uma circunferência. 6. PLANOS TANGENTES À SUPERFÍCIE ESFÉRICA. Norma: O plano tangente a uma superfície esférica num ponto desta, deverá ser sempre definido pelas duas rectas tangentes à superfície esférica, que se cruzem nesse ponto Plano tangente à superfície esférica num ponto desta. 1 Método - uso do Teorema l: Para a marcação do ponto dado A (fig 9), marca-se o paralelo [p] que o irá conter. Marca-se em seguida, o círculo menor de frente 2 que também contenha A. O plano tangente pretendido ficará definido pelas tangentes t e t1 aos dois círculos, no ponto A. Como facilmente se compreende, a tangente t é de nível e a t1 é de frente, por serem estas as posições dos respectivos círculos de tangência. 2 Pode ser utilizado qualquer circulo que contenha o ponto, mas a opção por um círculo de frente toma aqui, obviamente, o traçado mais simples e racional. 7/19
8 fig. 9 2 Método - uso da superfície cónica concordante: Consideram-se o paralelo e o meridiano que contêm o ponto dado T. O plano tangente q pretendido fica definido pelas tangentes, t e t1. a estes dois círculos, no ponto T. Seja dada, fig.10, a superfície esférica [e] de eixo vertical e considere-se o ponto T como ponto de tangência pretendido, pertencente ao paralelo [p]. A tangente t ao paralelo, no ponto T. é de nível e de traçado imediato. A tangente t1 ao meridiano seria de traçado imediato pouco rigoroso uma vez que aquele é vertical e a sua projecção vertical é, nestas circunstâncias, uma elipse. Para contornar esta situação marca-se uma superfície cónica de concordância com a esférica segundo o paralelo [p], cujo vértice V (ver corolário do teorema 4) é determinado pelo cruzamento do eixo da superfície esférica com uma geratriz g, de frente, da superfície cónica; esta geratriz é tangente ao meridiano de frente (contorno aparente vertical) no ponto extremo A da projecção vertical do paralelo. Qualquer geratriz desta superfície cónica é tangente à superfície esférica e consequentemente ao meridiano que contenha qualquer ponto do paralelo. Assim a recta tangente t1 é simultaneamente geratriz da superfície cónica e a tangente ao meridiano que passa por T, ficando definida pelos pontos V e T. 8/19
9 fíg Plano tangente à superfície esférica, contendo um ponto exterior à superfície. O número de planos que satisfazem a condição é infinito. O lugar geométrico destes planos é uma superfície cónica, concordante com a esférica, cujo vértice é o ponto dado (fig.11). O problema é assim indeterminado se não forem estabelecidas condicionantes. Antes de estabelecer qualquer condição observe-se ainda na mesma figura que só podem existir planos nas condições pretendidas, compreendidos entre dois paralelos [p] e [p1], denominados paralelos limite. fig. 11 9/19
10 Vejamos como se podem determinar estes paralelos limite. Sejam dados (fig. 12) a superfície esférica [ε], de centro C, eixo vertical e o ponto exterior P. Se determinarmos as rectas tangentes à superfície esférica, em pontos do meridiano [m] que exista no mesmo plano do ponto P, pelos respectivos pontos de tangência passam os paralelos limite. Conforme a fig. 13, roda-se o ponto P em torno do eixo da superfície, até se situar no plano de frente que contém o centro C. O meridiano que era vertical fica agora de frente, coincidente com o contorno aparente vertical da superfície esférica. Assim tirando por P"r as tangentes t"r e t"lr a [m"r] obtêm-se T"r e T"lr por onde passam as projecções verticais dos paralelos limites, uma vez que a rotação tendo sido feita em tomo de um eixo vertical, os arcos descritos são de nível. Conhecendo as projecções verticais dos paralelos é imediata a determinação das respectivas projecções horizontais. fig. 12 fig. 13 Regressemos à determinação dos planos tangentes à superfície esférica contendo o ponto exterior P. 1 Método: Utilização da superfície cónica concordante com vértice no ponto P: 10/19
11 Considera-se (fig.14) um plano p que contenha o ponto P e o centro C da superfície esférica. Este plano seccionará a superfície segundo um círculo máximo [c] ; as rectas tangentes t e t1 a este círculo tiradas pelo ponto P não são mais do que as geratrizes da secção produzida por p na superfície cónica concordante. Os pontos de tangência T e Tl serão os pontos de contacto dos planos tangentes pretendidos; existirão assim dois planos tangentes e cada um ficará definido pela tangente determinada e pela tangente (de nível) ao paralelo (não representado) que contenha o ponto de tangência. fig. 14 Para a resolução gráfica (fig. 15), considera-se o plano projectante vertical p que contenha C e P, como o plano secante, cuja secção produzida na superfície esférica é o círculo [c]. Este círculo estando de topo tem como projecção horizontal uma elipse (não representada) o que não permite um traçado rigoroso das tangentes. Rodando o plano em torno do eixo de topo e, que contenha C, até uma posição de nível, a secção [cr] fica coincidente com o equador da superfície esférica e o ponto P adquire a posição Pr. Por P'r tira-se a tangente t'r a [c'r] obtendo-se o ponto de tangência T'r cuja projecção vertical T"r se localiza em [c"r]; desfazendo a rotação, para a posição inicial, obtem-se T T'.T" ficando a tangente t P.T. A tangente t1 ao paralelo (não representado por não ser necessário o seu traçado) é de nível, logo a sua projeção vertical t"l contem T" e a projecção horizontal, t l, contem T e é perpendicular à projecção horizontal do raio da superfície esférica definida pelo segmento C'T'. 11/19
12 fig Método - Uso da superfície cónica concordante, com vértice no eixo da superfície esférica: Aplica-se este método quando se põe como condição que os pontos de tangência pertençam a um paralelo determinado, localizado, naturalmente, entre os paralelos limite, o que deixa pressupor que se deverá determinar previamente estes e "a posteriori" localizar o paralelo pretendido entre aqueles. Se o paralelo pretendido se localiza entre os planos limite existem duas soluções para o problema, se coincidir com um qualquer deles existirá uma única solução, se se localizar fora da zona compreendida entre os paralelos limite o problema não tem qualquer solução. Seja dada a superfície esférica [e] e fixado o paralelo [p] (fig.16) 3. Faz-se concordar com a superfície esférica dada uma superfície cónica cuja linha de concordância é o paralelo [p], sendo este, assim, a directiz da superfície cónica. O problema fíca transformado (Teorema 3) na determinação do plano tangente (note-se que há dois) à superfície cónica, passando pelo ponto P. 12/19
13 fíg Para simplificação da leitura da figura não se encontram representados os paralelos limite. Para a resolução gráfica (fig. 17) determina-se o vértice V da superfície cónica utilizando o mesmo traçado que foi aplicado em 6.1., 2 método: marca-se a recta a definida por V e P; em seguida determina-se o traço A desta recta, no plano α do paralelo. Por este ponto A tirar-se-iam as tangentes ao paralelo, estando na figura só representada uma delas, t, que lhe é tangente no ponto T, que com V define r em situação de resolução em tudo igual à utilizada na mesma aplicação atrás referida. fig.17 13/19
14 6.3. Plano tangente à superfície esférica, paralelo a uma recta exterior à superfície. Facilmente se compreende que o problema tem infinitas soluções pois de facto existe um número infinito de planos ( - 1, onde a excepção será o que contem a recta) que satisfazem a condição, cujo lugar geométrico é uma superfície cilíndrica de concordância com a esférica, cujas geractrizes são paralelas à recta dada (fig. 18). O lugar geométrico dos pontos de contacto desses planos tangentes, com a superfície esférica, é a circunferência limite do círculo máximo [m] que existe num plano p que contém o centro da superfície esférica e é perpendicular à recta dada r. Note-se que este círculo máximo existe numa zona esférica limitada pêlos paralelos limite [p] e [p1]. Vejamos como se podem determinar estes paralelos limite 4. Considere-se o plano definido pela recta exterior dada e pelo centro de superfície esférica, que a seccionará segundo um círculo máximo. As rectas tangentes a este círculo e paralelas à recta dada, definem os pontos de tangência que contêm, cada um deles, um dos paralelos limite. fig Não se apresenta a resolução gráfica, sugerindo a sua execução como exercício complementar. 1 Método - Plano tangente num ponto qualquer da linha de concordância [m]. Sejam dados a superfície esférica [e], de centro C, e a recta exterior r (fig. 19). Determinam-se os traços, hp e Vp, nos planos de projecção 5 do plano p que contem C e é perpendicular a r, utilizando uma recta de frente f de p, que passa por C, sendo, naturalmente, f perpendicular a r". Considera-se um paralelo [p] qualquer onde irá existir o ponto de tangência do plano 14/19
15 tangente. Determina-se a recta n (de nível) de intersecção entre o plano d do paralelo e o plano dado p. Esta recta cruzará o paralelo em dois pontos, dos quais só um. T T';T", está representado e que será o ponto de tangência do plano. O plano tangente ficará definido pela tangente t (de nível) ao paralelo, no ponto T. e pela recta a paralela à recta dada r tambem contendo T. fig Utiliza-se aqui a Linha de Terra para facilitar o traçado e arespectiva leitura. Sem tal ter-se-ia de definir o plano secante π por duas rectas (a de nível e a de frente) concorrentes no centro C da superfície esférica o que iria somente complicar o traçado da resolução. Como puro exercício académico pode-se sugerir a resolução por esta via. 2 Método - Uso da superfície cónica de concordância com a superfície esférica, com vértice no eixo da segunda. Este método utiliza-se quando o ponto de tangência pertence a um paralelo determinado. Considere-se a superfície esférica [e], a recta exterior r e fixemos o paralelo [p] (fig. 20). Se colocarmos a superfície cónica [p] de concordância segundo o paralelo, que lhe serve de directriz e com vértice no ponto V, o problema fica transformado na determinação do plano tangente (existem dois planos) à superfície cónica, de directriz [p] e vértice V, paralelo à recta r cujo traçado já se conhece. 15/19
16 fig. 20 Para o traçado gráfico (fig. 21), considere-se a superfície esférica [e] e fixemos o seu paralelo [p] onde pretendemos que exista o ponto de tangência. Determinando a superfície cónica concordante com a esférica, segundo o paralelo definido, utilizando o mesmo processo aplicado em 6.1., 2 método: faz-se passar por V um recta a paralela à recta dada r; determina-se o traço I I';I" da recta a no plano a do paralelo. A determinação das rectas tangentes, t e t1, que definem o plano tangente e que concorrem no ponto de tangência T, é feita pelo mesmo processo aplicado em 6.2, 2 método. fig /19
17 6.4. Plano tangente à superfície esférica, paralelo a um plano dado. Considerando (fig. 22) a superfície esférica [e] e o plano a, existem dois planos, p e d, que são paralelos a a e tangentes à superfície esférica, em dois pontos E e S, que são os pontos de intersecção da superfície esférica com uma recta r que contém o centro C da superfície e é perpendicular ao plano a. fig. 22 Para a resolução gráfica (fig. 23), faz-se passar pelo centro C da superfície uma recta r perpendicular ao plano dado a, ficando r' ^ ha e r" ^ va 6 e determinam-se os pontos E e S de intersecção de r com a superfície esférica, aplicando a regra geral para a determinação do traço (ou dos traços) de uma recta numa superfície qualquer (ver ponto 5.), começando por conduzir por r um plano auxiliar w, aqui projectante vertical. Este plano seccionará a superfície esférica segundo um círculo máximo [m], cuja representação se omite por desnecessária; bastará reconhecer que [m"] estará sobre va e [m'] é uma elipse de traçado não rigoroso e este traçado, como se verá, não tem interesse para a resolução do problema. Utilizando um raciocínio idêntico aplicado em 6.2., 1 Método: roda-se o plano w para uma posição de nível, em tomo de um eixo de topo (t) que contenha C. A secção [m] virá a coincidir com o equador da superfície esférica e a recta tomará a posição de nível rr. Onde r'r cruza o equador (secção [m] rodada) localizam-se as projecções horizontais rodadas dos pontos pretendidos, E'r e S'r, dos quais não é necessário a representação das respectivas projecções verticais. Invertendo as rotações de E'r e de S'r para r 7 inicial, obtêm-se as projecções horizontais. E' e S' sobre r', cujas projecções verticais E" e S" se localizam sobre r". Na figura só está representado um dos planos tangentes, o que o é no ponto E, e que fica definido por duas rectas, n e f, concorrentes nesse mesmo ponto (recorde-se a condição de 17/19
18 paralelismo entre dois planos), sendo n de nível e paralela a ha (note-se que esta recta é também a tangente ao paralelo que contem E) e f de frente paralela a va. 6 Define-se aqui o plano a pelos seus traços nos planos de projecção, para evitar traçados de expressão linear complexa, que existiriam se o plano fosse definido por rectas, sem ganho de compreensão metodológica. Sugere-se, como puro exercício académico, a resolução utilizando a definição do plano referida. fig Plano tangente à superfície esférica, contendo uma recta exterior á superfície. Conforme se pode reconhecer (fie. 24) o problema tem duas soluções. Existem dois planos, a e p, que passando pela recta r (note-se que r é a recta de intersecção dos dois planos), são tangentes à superfície esférica nos pontos T e Tl existentes num círculo máximo [m]. Este círculo máximo existe num plano d que é perpendicular à recta r. Os pontos T e Tl são os pontos de tangência das rectas, t e t1 respectivamente, tangentes à superfície esférica tiradas pelo ponto I. de intersecção de r com d. fig.24 18/19
19 Para a resolução gráfica (fig. 25), considerem-se dados a superfície esférica [e] e a recta r, numa posição de frente 7. Marca-se o plano d contendo C e perpendicular a r (d é, portanto, um plano de topo, sendo vδ r") e determina-se o traço I de r em d, que é imediato visto d ser projectante vertical. Considerando um eixo de topo contendo C e rodando d até uma posição de nível, a sequência operativa é em tudo igual à aplicada no ponto 6.2., 1 Método. No final os plano tangentes pretendidos ficam definidos pelas rectas tangentes t e t1 e pela recta dada r. Sugerese a execução dos traçados para definição dos planos tangentes de acordo com a Norma enunciada no ponto 6. fig.25 7 Usa-se uma recta de frente para tornar o traçado mais explicito. A opção por outra recta qualquer, naturalmente possível, obrigaria à execução de um traçado mais complexo, obrigando ainda, na sequência, à aplicação de um qualquer método gráfico auxiliar sobre planos oblíquos. Para comprovação desta complexidade do traçado pode-se sugerir, sem que a sequência operativa se altere, a sua execução, como puro exercício académico. 19/19
GEOMETRIA DESCRITIVA A (Bloco I)
 ACTIVIDADES LECTIVAS 1º Período 2º Período 3º Período para o ano lectivo Apresentação 2 ----- ----- 2 x 45 minutos Avaliação 3 Testes 3 Testes 2 Testes 16 x 45 minutos Auto-avaliação 2 2 2 6 x 45 minutos
ACTIVIDADES LECTIVAS 1º Período 2º Período 3º Período para o ano lectivo Apresentação 2 ----- ----- 2 x 45 minutos Avaliação 3 Testes 3 Testes 2 Testes 16 x 45 minutos Auto-avaliação 2 2 2 6 x 45 minutos
Representação de sólidos
 110 Representação de sólidos Pirâmides e prismas regulares com base(s) contida(s) em planos verticais ou de topo Desenhe as projecções de uma pirâmide quadrangular regular, situada no 1. diedro e com a
110 Representação de sólidos Pirâmides e prismas regulares com base(s) contida(s) em planos verticais ou de topo Desenhe as projecções de uma pirâmide quadrangular regular, situada no 1. diedro e com a
RETA. Sumário: Manual de Geometria Descritiva - António Galrinho Reta - 1
 2 RETA O alfabeto da reta é o conjunto das posições genéricas que uma reta pode ter em relação aos planos de projeção. Neste capítulo apresentam-se essas posições, assim como posições particulares que
2 RETA O alfabeto da reta é o conjunto das posições genéricas que uma reta pode ter em relação aos planos de projeção. Neste capítulo apresentam-se essas posições, assim como posições particulares que
18/06/2013. Professora: Sandra Tieppo UNIOESTE Cascavel
 18/06/01 Professora: Sandra Tieppo UNIOESTE Cascavel 1 Superfícies geradas por uma geratriz (g) que passa por um ponto dado V (vértice) e percorre os pontos de uma linha dada d (diretriz), V d. Se a diretriz
18/06/01 Professora: Sandra Tieppo UNIOESTE Cascavel 1 Superfícies geradas por uma geratriz (g) que passa por um ponto dado V (vértice) e percorre os pontos de uma linha dada d (diretriz), V d. Se a diretriz
SOMBRAS II. Sumário: Manual de Geometria Descritiva - António Galrinho Sombras II - 1
 14 SOMBRAS II Neste capítulo mostra-se como se determinam sombras próprias e projetadas de sólidos sobre os planos de projeção, nomeadamente de pirâmides, prismas, cones e cilindros. Sumário: 2. Sombras
14 SOMBRAS II Neste capítulo mostra-se como se determinam sombras próprias e projetadas de sólidos sobre os planos de projeção, nomeadamente de pirâmides, prismas, cones e cilindros. Sumário: 2. Sombras
Geometria Descritiva Representação do Plano
 Geometria Descritiva Representação do Plano Um plano pode ser determinado por uma das quatro possibilidades: - três pontos não alinhados; (1) - uma recta e um ponto exterior; (2) - duas rectas concorrentes;
Geometria Descritiva Representação do Plano Um plano pode ser determinado por uma das quatro possibilidades: - três pontos não alinhados; (1) - uma recta e um ponto exterior; (2) - duas rectas concorrentes;
GDC I AULA TEÓRICA 06
 GDC I AULA TEÓRICA 06 Perspectiva linear de quadro plano. - Análise de desenhos de perspectiva executados à mão levantada e de imagens fotográficas (perspectivas de 1, 2 e 3 pontos de fuga; noção de sombra
GDC I AULA TEÓRICA 06 Perspectiva linear de quadro plano. - Análise de desenhos de perspectiva executados à mão levantada e de imagens fotográficas (perspectivas de 1, 2 e 3 pontos de fuga; noção de sombra
Manual de. Geometria Descritiva. António Galrinho
 Manual de Geometria Descritiva António Galrinho FICHA TÉCNICA Título Manual de Geometria Descritiva Autor António Galrinho Grafismo Do autor Edição 1ª - 2010 APRESENTAÇÃO Este livro apresenta uma compilação
Manual de Geometria Descritiva António Galrinho FICHA TÉCNICA Título Manual de Geometria Descritiva Autor António Galrinho Grafismo Do autor Edição 1ª - 2010 APRESENTAÇÃO Este livro apresenta uma compilação
Escola Secundária/3 da Sé-Lamego Ficha de Trabalho de Matemática Ano Lectivo 2003/04 Geometria 2 - Revisões 11.º Ano
 Escola Secundária/ da Sé-Lamego Ficha de Trabalho de Matemática no Lectivo 00/0 Geometria - Revisões º no Nome: Nº: Turma: região do espaço definida, num referencial ortonormado, por + + = é: [] a circunferência
Escola Secundária/ da Sé-Lamego Ficha de Trabalho de Matemática no Lectivo 00/0 Geometria - Revisões º no Nome: Nº: Turma: região do espaço definida, num referencial ortonormado, por + + = é: [] a circunferência
GEOMETRIA DESCRITIVA... o que é e para que serve!
 GEOMETRIA DESCRITIVA... o que é e para que serve! Desde sempre, o homem, na sua necessidade de comunicação, procurou encontrar um meio de representar as formas dos objectos que o rodeavam. Assim, Gaspar
GEOMETRIA DESCRITIVA... o que é e para que serve! Desde sempre, o homem, na sua necessidade de comunicação, procurou encontrar um meio de representar as formas dos objectos que o rodeavam. Assim, Gaspar
PONTO E SEGMENTO DE RETA
 1 PONTO E SEGMENTO DE RETA Neste capítulo aborda-se essencialmente o Ponto, elemento geométrico mais simples. Resultado da união de dois pontos, aborda-se também o Segmento de Reta. Com esses elementos
1 PONTO E SEGMENTO DE RETA Neste capítulo aborda-se essencialmente o Ponto, elemento geométrico mais simples. Resultado da união de dois pontos, aborda-se também o Segmento de Reta. Com esses elementos
PLANO. Sumário: Manual de Geometria Descritiva - António Galrinho Plano - 1
 3 PLANO O alfabeto do plano é o conjunto das posições genéricas que um plano pode ter em relação aos planos de projeção. Neste capítulo apresentam-se essas posições, assim como posições particulares que
3 PLANO O alfabeto do plano é o conjunto das posições genéricas que um plano pode ter em relação aos planos de projeção. Neste capítulo apresentam-se essas posições, assim como posições particulares que
Geometria Espacial. Revisão geral
 Geometria Espacial Revisão geral Considere o poliedro cujos vértices são os pontos médios das arestas de um cubo. O número de faces triangulares e o número de faces quadradas desse poliedro são, respectivamente:
Geometria Espacial Revisão geral Considere o poliedro cujos vértices são os pontos médios das arestas de um cubo. O número de faces triangulares e o número de faces quadradas desse poliedro são, respectivamente:
UNESP DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD. Parte 6/5: Prof. Víctor O. Gamarra Rosado
 UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 6/5: 14. Perspectivas Prof. Víctor O. Gamarra Rosado
UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 6/5: 14. Perspectivas Prof. Víctor O. Gamarra Rosado
4.4 Secções planas de superfícies e sólidos
 4.4 Secções planas de superfícies e sólidos Geometria Descritiva 2006/2007 e sólidos Quando um plano intersecta uma superfície geométrica determina sobre ela uma linha plana que pertence à superfície A
4.4 Secções planas de superfícies e sólidos Geometria Descritiva 2006/2007 e sólidos Quando um plano intersecta uma superfície geométrica determina sobre ela uma linha plana que pertence à superfície A
Proposta de resolução da Prova de Matemática A (código 635) 2ª fase. 19 de Julho de 2010
 Proposta de resolução da Prova de Matemática A (código 65) ª fase 9 de Julho de 00 Grupo I. Como só existem bolas de dois tipos na caixa e a probabilidade de sair bola azul é, existem tantas bolas roxas
Proposta de resolução da Prova de Matemática A (código 65) ª fase 9 de Julho de 00 Grupo I. Como só existem bolas de dois tipos na caixa e a probabilidade de sair bola azul é, existem tantas bolas roxas
Construções Geométricas Usuais
 Construções Geométricas Usuais Rectas. Ângulos. Circunferência e círculo. Tangentes a circunferências. Polígonos. Rectas Duas rectas dizem-se perpendiculares quando dividem o espaço em quatro partes iguais,
Construções Geométricas Usuais Rectas. Ângulos. Circunferência e círculo. Tangentes a circunferências. Polígonos. Rectas Duas rectas dizem-se perpendiculares quando dividem o espaço em quatro partes iguais,
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1. Coordenadas UTM
 UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1 Coordenadas UTM Recife, 2014 Modelo Plano Considera a porção da Terra em estudo com sendo plana. É a simplificação
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP LABTOP Topografia 1 Coordenadas UTM Recife, 2014 Modelo Plano Considera a porção da Terra em estudo com sendo plana. É a simplificação
MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos
 MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos 1 Seja um número real. Considere, num referencial o.n., a reta e o plano definidos, respetivamente, por e Sabe-se
MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos 1 Seja um número real. Considere, num referencial o.n., a reta e o plano definidos, respetivamente, por e Sabe-se
P 3 ) Por dois pontos distintos passa uma única reta. P 4 ) Um ponto qualquer de uma reta divide-a em duas semi-retas.
 Geometria Espacial Conceitos primitivos São conceitos primitivos ( e, portanto, aceitos sem definição) na Geometria espacial os conceitos de ponto, reta e plano. Habitualmente, usamos a seguinte notação:
Geometria Espacial Conceitos primitivos São conceitos primitivos ( e, portanto, aceitos sem definição) na Geometria espacial os conceitos de ponto, reta e plano. Habitualmente, usamos a seguinte notação:
Desenho Técnico e Geometria Descritiva Construções Geométricas. Construções Geométricas
 Desenho Técnico e Geometria Descritiva Prof. Luiz Antonio do Nascimento Engenharia Ambiental 2º Semestre Bissetriz - é a reta que divide um ângulo qualquer em dois ângulos iguais, partindo do vértice deste
Desenho Técnico e Geometria Descritiva Prof. Luiz Antonio do Nascimento Engenharia Ambiental 2º Semestre Bissetriz - é a reta que divide um ângulo qualquer em dois ângulos iguais, partindo do vértice deste
Projeto Rumo ao ITA Exercícios estilo IME
 PROGRAMA IME ESPECIAL 1991 GEOMETRIA ESPACIAL PROF PAULO ROBERTO 01 (IME-64) Um cone circular reto, de raio da base igual a R e altura h, está circunscrito a 1 1 uma esfera de raio r Provar que = rh r
PROGRAMA IME ESPECIAL 1991 GEOMETRIA ESPACIAL PROF PAULO ROBERTO 01 (IME-64) Um cone circular reto, de raio da base igual a R e altura h, está circunscrito a 1 1 uma esfera de raio r Provar que = rh r
MÓDULO 2 ÓPTICA E ONDAS Ronaldo Filho e Rhafael Roger
 ELEMENTOS DOS ESPELHOS Os elementos geométricos que caracterizam um espelho esférico são: CAPÍTULO 03 ESPELHOS ESFÉRICOS Seccionando-se uma esfera por um plano, ela ficará dividida em duas partes ou Calotas
ELEMENTOS DOS ESPELHOS Os elementos geométricos que caracterizam um espelho esférico são: CAPÍTULO 03 ESPELHOS ESFÉRICOS Seccionando-se uma esfera por um plano, ela ficará dividida em duas partes ou Calotas
20 TANGÊNCIA E CONCORDÂNCIA 20.1 PROPRIEDADES DE TANGÊNCIA
 144 20 TNGÊNI E ONORDÂNI 20.1 PROPRIEDDES DE TNGÊNI Definições: 1) tangente a uma curva é uma reta que tem um só ponto em comum com esta curva. 2) Duas curvas são tangentes num ponto dado T, quando as
144 20 TNGÊNI E ONORDÂNI 20.1 PROPRIEDDES DE TNGÊNI Definições: 1) tangente a uma curva é uma reta que tem um só ponto em comum com esta curva. 2) Duas curvas são tangentes num ponto dado T, quando as
Escola Secundária Gabriel Pereira. Nome: N.º: Ano Turma
 Escola Secundária Gabriel Pereira FICHA DE EXERCÍCIOS Nº MATEMÁTICA A Rectas e Planos Nome: Nº: Ano Turma 1) Determina uma equação vectorial e cartesianas da recta que passa em A,1, 4 11) paralela ao vector
Escola Secundária Gabriel Pereira FICHA DE EXERCÍCIOS Nº MATEMÁTICA A Rectas e Planos Nome: Nº: Ano Turma 1) Determina uma equação vectorial e cartesianas da recta que passa em A,1, 4 11) paralela ao vector
SOMBRAS I. Sumário: Manual de Geometria Descritiva - António Galrinho Sombras - 1
 13 SOMBRAS I Neste capítulo mostra-se como se determinam sombras de figuras planas sobre os planos de projecção, nomeadamente pontos, segmentos de recta, rectas, polígonos e circunferências. Sumário: 2.
13 SOMBRAS I Neste capítulo mostra-se como se determinam sombras de figuras planas sobre os planos de projecção, nomeadamente pontos, segmentos de recta, rectas, polígonos e circunferências. Sumário: 2.
Matemática Fascículo 07 Manoel Benedito Rodrigues
 Matemática Fascículo 07 Manoel Benedito Rodrigues Índice Geometria Resumo Teórico...1 Exercícios...4 Dicas...5 Resoluções...7 Geometria Resumo Teórico 1. O volume de um prisma eodeumcilindro (retos ou
Matemática Fascículo 07 Manoel Benedito Rodrigues Índice Geometria Resumo Teórico...1 Exercícios...4 Dicas...5 Resoluções...7 Geometria Resumo Teórico 1. O volume de um prisma eodeumcilindro (retos ou
3.5 Posições relativas
 3.5 Posições relativas Geometria Descritiva 2006/2007 Paralelismo Paralelismo de duas rectas É condição necessária e suficiente para que duas rectas, não de perfil, sejam paralelas que as suas projecções
3.5 Posições relativas Geometria Descritiva 2006/2007 Paralelismo Paralelismo de duas rectas É condição necessária e suficiente para que duas rectas, não de perfil, sejam paralelas que as suas projecções
ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / Nome ; Ano/Turma ; N.º
 EDUCAÇÃO VISUAL ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / APONTAMENTOS DE GEOMETRIA Nome ; Ano/Turma ; N.º 1 - O PONTO - ao colocares o bico do teu lápis no papel obténs um ponto. O
EDUCAÇÃO VISUAL ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / APONTAMENTOS DE GEOMETRIA Nome ; Ano/Turma ; N.º 1 - O PONTO - ao colocares o bico do teu lápis no papel obténs um ponto. O
Projeto Jovem Nota 10 Geometria Analítica Circunferência Lista 3 Professor Marco Costa
 1 1. (Fgv 97) Uma empresa produz apenas dois produtos A e B, cujas quantidades anuais (em toneladas) são respectivamente x e y. Sabe-se que x e y satisfazem a relação: x + y + 2x + 2y - 23 = 0 a) esboçar
1 1. (Fgv 97) Uma empresa produz apenas dois produtos A e B, cujas quantidades anuais (em toneladas) são respectivamente x e y. Sabe-se que x e y satisfazem a relação: x + y + 2x + 2y - 23 = 0 a) esboçar
CARTOGRAFIA SISTEMÁTICA
 CARTOGRAFIA SISTEMÁTICA PROJEÇÃO Universal Transversa de Mercator (UTM) COORDENADAS UTM Elaborado por: Andréia Medinilha Pancher e Maria Isabel Castreghini de Freitas SISTEMA DE PROJEÇÃO UNIVERSAL TRANSVERSA
CARTOGRAFIA SISTEMÁTICA PROJEÇÃO Universal Transversa de Mercator (UTM) COORDENADAS UTM Elaborado por: Andréia Medinilha Pancher e Maria Isabel Castreghini de Freitas SISTEMA DE PROJEÇÃO UNIVERSAL TRANSVERSA
CIRCUNFERÊNCIA. Centro Diâmetro Secante Corda Tangente Ponto de tangência Normal Raio Distância do ponto P à circunferência. O AB s CD t T s AB 2
 CIRCUNFERÊNCIA ELEMENTOS DA CIRCUNFERÊNCIA N t T C A B D X s p Centro Diâmetro Secante Corda Tangente Ponto de tangência Normal Raio Distância do ponto P à circunferência O AB s CD t T s AB 2 PX / Algumas
CIRCUNFERÊNCIA ELEMENTOS DA CIRCUNFERÊNCIA N t T C A B D X s p Centro Diâmetro Secante Corda Tangente Ponto de tangência Normal Raio Distância do ponto P à circunferência O AB s CD t T s AB 2 PX / Algumas
3. Representação diédrica de pontos, rectas e planos
 3. Representação diédrica de pontos, rectas e planos Geometria Descritiva 2006/2007 Geometria de Monge Utilizam-se simultaneamente dois sistemas de projecção paralela ortogonal. Os planos de projecção
3. Representação diédrica de pontos, rectas e planos Geometria Descritiva 2006/2007 Geometria de Monge Utilizam-se simultaneamente dois sistemas de projecção paralela ortogonal. Os planos de projecção
Metrologia Professor: Leonardo Leódido
 Metrologia Professor: Leonardo Leódido Sumário Definição Conceitos Básicos Classificação de Forma de Orientação de Posição Definição Tolerância pode ser definida como um intervalo limite no qual as imperfeições
Metrologia Professor: Leonardo Leódido Sumário Definição Conceitos Básicos Classificação de Forma de Orientação de Posição Definição Tolerância pode ser definida como um intervalo limite no qual as imperfeições
Escalas ESCALAS COTAGEM
 Escalas Antes de representar objectos, modelos, peças, etc. Deve-se estudar o seu tamanho real. Tamanho real é a grandeza que as coisas têm na realidade. Existem coisas que podem ser representadas no papel
Escalas Antes de representar objectos, modelos, peças, etc. Deve-se estudar o seu tamanho real. Tamanho real é a grandeza que as coisas têm na realidade. Existem coisas que podem ser representadas no papel
DESENHO TÉCNICO I. Prof. Peterson Jaeger. APOSTILA Versão 2013
 APOSTILA Versão 2013 Prof. Peterson Jaeger 1. Folhas 2. Régua paralela e esquadros 3. Distinção de traços 4. Uso do compasso 5. Construções geométricas básicas 6. Tangentes e concordantes 7. Caligrafia
APOSTILA Versão 2013 Prof. Peterson Jaeger 1. Folhas 2. Régua paralela e esquadros 3. Distinção de traços 4. Uso do compasso 5. Construções geométricas básicas 6. Tangentes e concordantes 7. Caligrafia
Assunto: Estudo do ponto
 Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
Aula de Matemática. Semana do período zero Turma 2 28/03/13 Prof. Silvânia Alves de Carvalho Cursinho TRIU Barão Geraldo Campinas /SP
 Aula de Matemática Semana do período zero Turma 2 28/03/13 Prof. Silvânia Alves de Carvalho Cursinho TRIU Barão Geraldo Campinas /SP Cursinho TRIU -Matemática Ementa Geometria plana Congruência de figuras
Aula de Matemática Semana do período zero Turma 2 28/03/13 Prof. Silvânia Alves de Carvalho Cursinho TRIU Barão Geraldo Campinas /SP Cursinho TRIU -Matemática Ementa Geometria plana Congruência de figuras
GEOMETRIA ANALÍTICA II
 Conteúdo 1 O PLANO 3 1.1 Equação Geral do Plano............................ 3 1.2 Determinação de um Plano........................... 7 1.3 Equação Paramétrica do Plano........................ 11 1.4 Ângulo
Conteúdo 1 O PLANO 3 1.1 Equação Geral do Plano............................ 3 1.2 Determinação de um Plano........................... 7 1.3 Equação Paramétrica do Plano........................ 11 1.4 Ângulo
SÓLIDOS II. Sumário: Manual de Geometria Descritiva - António Galrinho Sólidos II - 1
 8 SÓLIDOS II Neste capítulo mostra-se como se determinam secções provocadas por diferentes tipos de planos, em pirâmides, prismas, cones, cilindros e na esfera. Mostra-se também como se efectuam as truncagens
8 SÓLIDOS II Neste capítulo mostra-se como se determinam secções provocadas por diferentes tipos de planos, em pirâmides, prismas, cones, cilindros e na esfera. Mostra-se também como se efectuam as truncagens
Percepção Espacial e Geometria Descritiva. Prof. Carlos Kleber
 Percepção Espacial e Geometria Descritiva Prof. Carlos Kleber [email protected] 7 de abril de 2009 Capítulo 1 Introdução O universo é essencialmente tridimensonal. Mas nossa percepção é bidimensional:
Percepção Espacial e Geometria Descritiva Prof. Carlos Kleber [email protected] 7 de abril de 2009 Capítulo 1 Introdução O universo é essencialmente tridimensonal. Mas nossa percepção é bidimensional:
13 PARALELISMO SOLUÇÕES DOS EXERCÍCIOS PROPOSTOS
 SOLUÇÕES DOS EXERCÍCIOS PROPOSTOS NOTA: Se bem que os dados métricos dos enunciados estejam em centímetros, as soluções apresentadas a partir da página seguinte não consideraram o centímetro como unidade.
SOLUÇÕES DOS EXERCÍCIOS PROPOSTOS NOTA: Se bem que os dados métricos dos enunciados estejam em centímetros, as soluções apresentadas a partir da página seguinte não consideraram o centímetro como unidade.
Matemática Básica Intervalos
 Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Escola Secundária com 3º ciclo D. Dinis 11º Ano de Matemática A Tema II Introdução ao Cálculo Diferencial I Funções Racionais e com Radicais
 Escola Secundária com 3º ciclo D. Dinis 11º Ano de Matemática A Tema II Introdução ao Cálculo Diferencial I Funções Racionais e com Radicais Taxa de Variação e Derivada TPC nº 6 (entregar no dia 14 01
Escola Secundária com 3º ciclo D. Dinis 11º Ano de Matemática A Tema II Introdução ao Cálculo Diferencial I Funções Racionais e com Radicais Taxa de Variação e Derivada TPC nº 6 (entregar no dia 14 01
FEUP-DEMEGI-SDI Desenho Técnico APL-1.1. Mestrado Integrado em Engenharia Mecânica DESENHO TÉCNICO. (1º ano)
 FEUP-DEMEGI-SDI Desenho Técnico APL-1.1 Mestrado Integrado em Engenharia Mecânica DESENHO TÉCNICO (1º ano) (Introdução aos Sistemas e Componentes Mecânicos Normalizados de utilização corrente) Aulas Práticas
FEUP-DEMEGI-SDI Desenho Técnico APL-1.1 Mestrado Integrado em Engenharia Mecânica DESENHO TÉCNICO (1º ano) (Introdução aos Sistemas e Componentes Mecânicos Normalizados de utilização corrente) Aulas Práticas
Prova Escrita de MATEMÁTICA A - 12o Ano 2015-2 a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 205-2 a Fase Proposta de resolução GRUPO I. O valor médio da variável aleatória X é: µ a + 2 2a + 0, Como, numa distribuição de probabilidades de uma variável aleatória,
Prova Escrita de MATEMÁTICA A - o Ano 205-2 a Fase Proposta de resolução GRUPO I. O valor médio da variável aleatória X é: µ a + 2 2a + 0, Como, numa distribuição de probabilidades de uma variável aleatória,
3. (Uerj 98) a) Calcule o comprimento da corda AB, do círculo original, em função de R e m.
 1. (Unicamp 91) Uma esfera de raio 1 é apoiada no plano xy de modo que seu pólo sul toque a origem desse plano. Tomando a reta que liga o pólo norte dessa esfera a qualquer outro ponto da esfera, chamamos
1. (Unicamp 91) Uma esfera de raio 1 é apoiada no plano xy de modo que seu pólo sul toque a origem desse plano. Tomando a reta que liga o pólo norte dessa esfera a qualquer outro ponto da esfera, chamamos
Aula 01 Introdução à Geometria Espacial Geometria Espacial
 Aula 01 Introdução à 1) Introdução à Geometria Plana Axioma São verdades matemáticas aceitas sem a necessidade de demonstração. 1 1.1) Axioma da Existência Existem infinitos pontos em uma reta (e fora
Aula 01 Introdução à 1) Introdução à Geometria Plana Axioma São verdades matemáticas aceitas sem a necessidade de demonstração. 1 1.1) Axioma da Existência Existem infinitos pontos em uma reta (e fora
Capítulo 7. 1. Bissetrizes de duas retas concorrentes. Proposição 1
 Capítulo 7 Na aula anterior definimos o produto interno entre dois vetores e vimos como determinar a equação de uma reta no plano de diversas formas. Nesta aula, vamos determinar as bissetrizes de duas
Capítulo 7 Na aula anterior definimos o produto interno entre dois vetores e vimos como determinar a equação de uma reta no plano de diversas formas. Nesta aula, vamos determinar as bissetrizes de duas
Capítulo 4. Retas e Planos. 4.1 A reta
 Capítulo 4 Retas e Planos Neste capítulo veremos como utilizar a teoria dos vetores para caracterizar retas e planos, a saber, suas equações, posições relativas, ângulos e distâncias. 4.1 A reta Sejam
Capítulo 4 Retas e Planos Neste capítulo veremos como utilizar a teoria dos vetores para caracterizar retas e planos, a saber, suas equações, posições relativas, ângulos e distâncias. 4.1 A reta Sejam
INSTITUTO DE APLICAÇÃO FERNANDO RODRIGUES DA SILVEIRA 2ª SÉRIE DO ENSINO MÉDIO PROF. ILYDIO PEREIRA DE SÁ
 INSTITUTO E PLIÇÃO FERNNO RORIGUES SILVEIR 2ª SÉRIE O ENSINO MÉIO PROF. ILYIO PEREIR E SÁ Geometria Espacial: Elementos iniciais de Geometria Espacial Introdução: Geometria espacial (euclidiana) funciona
INSTITUTO E PLIÇÃO FERNNO RORIGUES SILVEIR 2ª SÉRIE O ENSINO MÉIO PROF. ILYIO PEREIR E SÁ Geometria Espacial: Elementos iniciais de Geometria Espacial Introdução: Geometria espacial (euclidiana) funciona
Universidade Ibirapuera Arquitetura e Urbanismo Conforto Ambiental: Insolação e Iluminação MÓDULO 2: ILUMINAÇÃO NATURAL
 Universidade Ibirapuera Arquitetura e Urbanismo Conforto Ambiental: Insolação e Iluminação MÓDULO : INSOLAÇÃO MÓDULO : ILUMINAÇÃO NATURAL MÓDULO : ILUMINAÇÃO DE INTERIORES Docente: Claudete Gebara J. Callegaro
Universidade Ibirapuera Arquitetura e Urbanismo Conforto Ambiental: Insolação e Iluminação MÓDULO : INSOLAÇÃO MÓDULO : ILUMINAÇÃO NATURAL MÓDULO : ILUMINAÇÃO DE INTERIORES Docente: Claudete Gebara J. Callegaro
Capítulo 6 ESCALAS E DIMENSIONAMENTO
 Capítulo 6 ESCALAS E DIMENSIONAMENTO Introdução Ainda que o principal objetivo deste livro seja preparar para a leitura e interpretação de desenho técnico, é necessário abordar os princípios básicos de
Capítulo 6 ESCALAS E DIMENSIONAMENTO Introdução Ainda que o principal objetivo deste livro seja preparar para a leitura e interpretação de desenho técnico, é necessário abordar os princípios básicos de
4. Superfícies e sólidos geométricos
 4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
UNIVERSIDADE VALE DO RIO DOCE
 UNIVERSIDADE VALE DO RIO DOCE DISCIPLINA: GEOMETRIA DESCRITIVA FAENGE FACULDADE DE ENGENHARIA CURSOS - ENGENHARIA CIVIL - ENGENHARIA CIVIL E AMBIENTAL 1 SUMÁRIO - Apresentação Pag 3 - Noções de Projeções
UNIVERSIDADE VALE DO RIO DOCE DISCIPLINA: GEOMETRIA DESCRITIVA FAENGE FACULDADE DE ENGENHARIA CURSOS - ENGENHARIA CIVIL - ENGENHARIA CIVIL E AMBIENTAL 1 SUMÁRIO - Apresentação Pag 3 - Noções de Projeções
Capítulo 5 VISTAS EM CORTE
 apítulo 5 VISTS EM ORTE Definição Quando a peça a ser desenhada possuir muitos detalhes internos, detalhes invisíveis, as projeções ortogonais terão muitas linhas tracejadas e poderão dificultar a interpretação
apítulo 5 VISTS EM ORTE Definição Quando a peça a ser desenhada possuir muitos detalhes internos, detalhes invisíveis, as projeções ortogonais terão muitas linhas tracejadas e poderão dificultar a interpretação
Ficha de Trabalho nº11
 Ano lectivo 011/01 Matemática A 11º Ano / Curso de Ciências e Tecnologias Tema: Geometria Ficha de Trabalho nº11 Geometria no Espaço 1. Observa a figura onde está representado um cone recto cuja base pertence
Ano lectivo 011/01 Matemática A 11º Ano / Curso de Ciências e Tecnologias Tema: Geometria Ficha de Trabalho nº11 Geometria no Espaço 1. Observa a figura onde está representado um cone recto cuja base pertence
Aula 9. Superfícies de Revolução. Seja C uma curva e r uma reta contidas num plano π.
 Aula 9 Superfícies de Revolução Seja C uma curva e r uma reta contidas num plano π. Fig. 1: Superfície de revolução S, geratriz C e eixo r contidos no plano π A superfície de revolução S de geratriz C
Aula 9 Superfícies de Revolução Seja C uma curva e r uma reta contidas num plano π. Fig. 1: Superfície de revolução S, geratriz C e eixo r contidos no plano π A superfície de revolução S de geratriz C
1 Noções Primitivas MAT175 - GEOMETRIA ESPACIAL MAT175 - GEOMETRIA ESPACIAL
 MAT175 - GEOMETRIA ESPACIAL Bibliografia: [1] Fundamentos de Matemática Elementar, 10: Geometria Espacial, posição e métrica. Osvaldo Dolce e José Nicolau Pompeo. 6. ed., São Paulo, Atual, 2005. [2] A
MAT175 - GEOMETRIA ESPACIAL Bibliografia: [1] Fundamentos de Matemática Elementar, 10: Geometria Espacial, posição e métrica. Osvaldo Dolce e José Nicolau Pompeo. 6. ed., São Paulo, Atual, 2005. [2] A
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA
 UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA TEXTO: CÍRCULO TRIGONOMÉTRICO AUTORES: Mayara Brito (estagiária da BOM) André Brito (estagiário da BOM) ORIENTADOR:
UNIVERSIDADE FEDERAL DO PARÁ BIBLIOTECA DE OBJETOS MATEMÁTICOS COORDENADOR: Dr. MARCIO LIMA TEXTO: CÍRCULO TRIGONOMÉTRICO AUTORES: Mayara Brito (estagiária da BOM) André Brito (estagiário da BOM) ORIENTADOR:
Matemática A. Versão 1. Na sua folha de respostas, indique de forma legível a versão do teste. Teste Intermédio de Matemática A.
 Teste Intermédio de Matemática A Versão 1 Teste Intermédio Matemática A Versão 1 Duração do Teste: 90 minutos 7.01.011 11.º Ano de Escolaridade Decreto-Lei n.º 74/004, de 6 de Março Na sua folha de respostas,
Teste Intermédio de Matemática A Versão 1 Teste Intermédio Matemática A Versão 1 Duração do Teste: 90 minutos 7.01.011 11.º Ano de Escolaridade Decreto-Lei n.º 74/004, de 6 de Março Na sua folha de respostas,
SÓLIDOS I. Sumário: Manual de Geometria Descritiva - António Galrinho Sólidos I - 1
 7 SÓLIDOS I Neste capítulo mostra-se como se representam pirâmides, prismas, cones e cilindros em diferentes circunstâncias, recorrendo ou não a processos auiliares. Mostra-se também como se traçam e determinam
7 SÓLIDOS I Neste capítulo mostra-se como se representam pirâmides, prismas, cones e cilindros em diferentes circunstâncias, recorrendo ou não a processos auiliares. Mostra-se também como se traçam e determinam
. B(x 2, y 2 ). A(x 1, y 1 )
 Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
Universidade Lusíada (Vila Nova de Famalicão) MATEMÁTICA. Regente da unidade curricular: Manuel Arménio Almeida (Eng. Civil )
 Universidade Lusíada (Vila Nova de Famalicão) Faculdade de Arquitectura e Artes Licenciatura em Arquitectura MATEMÁTICA Regente da unidade curricular: Manuel Arménio Almeida (Eng. Civil ) Unidade curricular
Universidade Lusíada (Vila Nova de Famalicão) Faculdade de Arquitectura e Artes Licenciatura em Arquitectura MATEMÁTICA Regente da unidade curricular: Manuel Arménio Almeida (Eng. Civil ) Unidade curricular
LOCALIZANDO PONTOS ATRAVÉS DE COORDENADAS GEOGRÁFICAS
 CONHECENDO A CARTOGRAFIA E OS MAPAS Segundo a Associação Brasileira de Normas Técnicas (ABNT), Cartografia é definida como: "A arte do levantamento, construção e edição de mapas e cartas de qualquer natureza..
CONHECENDO A CARTOGRAFIA E OS MAPAS Segundo a Associação Brasileira de Normas Técnicas (ABNT), Cartografia é definida como: "A arte do levantamento, construção e edição de mapas e cartas de qualquer natureza..
(1, 6) é também uma solução da equação, pois 3 1 + 2 6 = 15, isto é, 15 = 15. ( 23,
 Sistemas de equações lineares generalidades e notação matricial Definição Designa-se por equação linear sobre R a uma expressão do tipo com a 1, a 2,... a n, b R. a 1 x 1 + a 2 x 2 +... + a n x n = b (1)
Sistemas de equações lineares generalidades e notação matricial Definição Designa-se por equação linear sobre R a uma expressão do tipo com a 1, a 2,... a n, b R. a 1 x 1 + a 2 x 2 +... + a n x n = b (1)
CARTOGRAFIA LINHA DE APOIO
 COMEÇO DE CONVERSA PROF. Wagner Atallah CARTOGRAFIA LINHA DE APOIO Chegar a um lugar desconhecido utilizando um mapa requer uma série de conhecimentos que só são adquiridos num processo de alfabetização
COMEÇO DE CONVERSA PROF. Wagner Atallah CARTOGRAFIA LINHA DE APOIO Chegar a um lugar desconhecido utilizando um mapa requer uma série de conhecimentos que só são adquiridos num processo de alfabetização
REGRAS GERAIS DE GEOMETRIA DESCRITIVAII 2010
 1 Isabel coelho 20. SECÇÕES PLANAS 20.1 Secções planas em poliedros 20.1.2 Secções planas produzidas por planos paralelos aos planos das bases A figura da secção será paralela à figura da base. Identificar
1 Isabel coelho 20. SECÇÕES PLANAS 20.1 Secções planas em poliedros 20.1.2 Secções planas produzidas por planos paralelos aos planos das bases A figura da secção será paralela à figura da base. Identificar
Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas
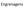 Engrenagens Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas alavancas. Classificação das Engrenagens As engrenagens
Engrenagens Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas alavancas. Classificação das Engrenagens As engrenagens
DESENHO TÉCNICO ( AULA 03)
 Sólidos Geométricos DESENHO TÉCNICO ( AULA 03) Você já sabe que todos os pontos de uma figura plana localizam-se no mesmo plano. Quando uma figura geométrica tem pontos situados em diferentes planos, temos
Sólidos Geométricos DESENHO TÉCNICO ( AULA 03) Você já sabe que todos os pontos de uma figura plana localizam-se no mesmo plano. Quando uma figura geométrica tem pontos situados em diferentes planos, temos
EXERCÍCIOS RESOLVIDOS ESTUDO DA RETA
 1 EXERCÍCIOS RESOLVIDOS ESTUDO DA RETA 1. SEJA O CUBO DADO NA FIGURA ABAIXO CUJOS VÉRTICES AB PERTENCEM À LT. PERGUNTA-SE: A) QUE TIPO DE RETAS PASSA PELAS ARESTAS EF, EC, EG. B) QUE TIPO DE RETAS PASSA
1 EXERCÍCIOS RESOLVIDOS ESTUDO DA RETA 1. SEJA O CUBO DADO NA FIGURA ABAIXO CUJOS VÉRTICES AB PERTENCEM À LT. PERGUNTA-SE: A) QUE TIPO DE RETAS PASSA PELAS ARESTAS EF, EC, EG. B) QUE TIPO DE RETAS PASSA
Características das Figuras Geométricas Espaciais
 Características das Figuras Geométricas Espaciais Introdução A Geometria espacial (euclidiana) funciona como uma ampliação da Geometria plana e trata dos métodos apropriados para o estudo de objetos espaciais,
Características das Figuras Geométricas Espaciais Introdução A Geometria espacial (euclidiana) funciona como uma ampliação da Geometria plana e trata dos métodos apropriados para o estudo de objetos espaciais,
No arquivo Exames e Provas podem ser consultados itens e critérios de classificação de provas desta disciplina.
 INFORMAÇÃO-PROVA GEOMETRIA DESCRITIVA A Novembro de 2016 Prova 708 11.º Ano de Escolaridade (Decreto-Lei n.º 139/2012, de 5 de julho) O presente documento divulga informação relativa à prova de exame final
INFORMAÇÃO-PROVA GEOMETRIA DESCRITIVA A Novembro de 2016 Prova 708 11.º Ano de Escolaridade (Decreto-Lei n.º 139/2012, de 5 de julho) O presente documento divulga informação relativa à prova de exame final
Projeto Jovem Nota 10 Geometria Analítica Circunferência Lista 1 Professor Marco Costa
 1 1. (Fgv 2005) No plano cartesiano, considere o feixe de paralelas 2x + y = c em que c Æ R. a) Qual a reta do feixe com maior coeficiente linear que intercepta a região determinada pelas inequações: ýx
1 1. (Fgv 2005) No plano cartesiano, considere o feixe de paralelas 2x + y = c em que c Æ R. a) Qual a reta do feixe com maior coeficiente linear que intercepta a região determinada pelas inequações: ýx
TOPOGRAFIA. Poligonais
 TOPOGRAFIA Poligonais COORDENADAS RECTANGULARES Quando se pretende representar numa superfície plana zonas extensas da superfície terrestre, é necessário adoptar sistemas de representação plana do elipsóide,
TOPOGRAFIA Poligonais COORDENADAS RECTANGULARES Quando se pretende representar numa superfície plana zonas extensas da superfície terrestre, é necessário adoptar sistemas de representação plana do elipsóide,
MATEMÁTICA 32,2 30. 0 2 4 5 6 8 10 x
 MATEMÁTICA 01. O preço pago por uma corrida de táxi normal consiste de uma quantia fixa de R$ 3,50, a bandeirada, adicionada de R$ 0,25 por cada 100 m percorridos, enquanto o preço pago por uma corrida
MATEMÁTICA 01. O preço pago por uma corrida de táxi normal consiste de uma quantia fixa de R$ 3,50, a bandeirada, adicionada de R$ 0,25 por cada 100 m percorridos, enquanto o preço pago por uma corrida
Para cada partícula num pequeno intervalo de tempo t a percorre um arco s i dado por. s i = v i t
 Capítulo 1 Cinemática dos corpos rígidos O movimento de rotação apresenta algumas peculiaridades que precisam ser entendidas. Tem equações horárias, que descrevem o movimento, semelhantes ao movimento
Capítulo 1 Cinemática dos corpos rígidos O movimento de rotação apresenta algumas peculiaridades que precisam ser entendidas. Tem equações horárias, que descrevem o movimento, semelhantes ao movimento
[ Elaborado por Rosário Laureano ] Análise Matemática II
![[ Elaborado por Rosário Laureano ] Análise Matemática II [ Elaborado por Rosário Laureano ] Análise Matemática II](/thumbs/41/22403750.jpg) [ Elaborado por ] Análise Matemática II Considere a função f(x,y)=x^3+y^3-3*x-3*y. Designamos por z as imagens por f de cada par (x,y), ou seja, z=f(x,y). Na figura à esquerda são visíveis o gráfico de
[ Elaborado por ] Análise Matemática II Considere a função f(x,y)=x^3+y^3-3*x-3*y. Designamos por z as imagens por f de cada par (x,y), ou seja, z=f(x,y). Na figura à esquerda são visíveis o gráfico de
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE. Professor: João Carmo
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo INTRODUÇÃO O traçado de linhas retas PERPENDICULARES, PARALELAS e OBLÍQUAS é feito com o auxílio de esquadros,
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo INTRODUÇÃO O traçado de linhas retas PERPENDICULARES, PARALELAS e OBLÍQUAS é feito com o auxílio de esquadros,
Os eixo x e y dividem a circunferência em quatro partes congruentes chamadas quadrantes, numeradas de 1 a 4 conforme figura abaixo:
 Circunferência Trigonométrica É uma circunferência de raio unitário orientada de tal forma que o sentido positivo é o sentido anti-horário. Associamos a circunferência (ou ciclo) trigonométrico um sistema
Circunferência Trigonométrica É uma circunferência de raio unitário orientada de tal forma que o sentido positivo é o sentido anti-horário. Associamos a circunferência (ou ciclo) trigonométrico um sistema
FIGURAS DE LISSAJOUS
 FIGURAS DE LISSAJOUS OBJETIVOS: a) medir a diferença de fase entre dois sinais alternados e senoidais b) observar experimentalmente, as figuras de Lissajous c) comparar a frequência entre dois sinais alternados
FIGURAS DE LISSAJOUS OBJETIVOS: a) medir a diferença de fase entre dois sinais alternados e senoidais b) observar experimentalmente, as figuras de Lissajous c) comparar a frequência entre dois sinais alternados
NOTAÇÕES. : distância do ponto P à reta r : segmento de extremidades nos pontos A e B
 R C i z Rez) Imz) det A tr A : conjunto dos números reais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : parte real do número z C : parte imaginária do número z C
R C i z Rez) Imz) det A tr A : conjunto dos números reais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : parte real do número z C : parte imaginária do número z C
1 Teoria de conjuntos e lógica
 1 Teoria de conjuntos e lógica Estes breves apontamentos dizem respeito à parte do programa dedicada à teoria de conjuntos e à lógica matemática. Embora concebidos sem grandes formalismos e com poucas
1 Teoria de conjuntos e lógica Estes breves apontamentos dizem respeito à parte do programa dedicada à teoria de conjuntos e à lógica matemática. Embora concebidos sem grandes formalismos e com poucas
ABCD ADEF 810. é a corda da circunferência contida no eixo Oy. é uma corda da circunferência, paralela ao eixo Ox
 Ficha de Trabalho n.º 3 página.1. Mostre que o ponto C tem coordenadas ( 09, ) e que o ponto D tem coordenadas ( 8, 9 )... Determine uma equação da mediatriz do segmento AD. Apresente a sua resposta na
Ficha de Trabalho n.º 3 página.1. Mostre que o ponto C tem coordenadas ( 09, ) e que o ponto D tem coordenadas ( 8, 9 )... Determine uma equação da mediatriz do segmento AD. Apresente a sua resposta na
1 PONTOS NOTÁVEIS. 1.1 Baricentro. 1.3 Circuncentro. 1.2 Incentro. Matemática 2 Pedro Paulo
 Matemática 2 Pedro Paulo GEOMETRIA PLANA VIII 1 PONTOS NOTÁVEIS 1.1 Baricentro O baricentro é o encontro das medianas de um triângulo. Na figura abaixo, é o ponto médio do lado, é o ponto médio do lado
Matemática 2 Pedro Paulo GEOMETRIA PLANA VIII 1 PONTOS NOTÁVEIS 1.1 Baricentro O baricentro é o encontro das medianas de um triângulo. Na figura abaixo, é o ponto médio do lado, é o ponto médio do lado
Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas:
 * 16/03/16 Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas: * *Definição *Um espelho plano é aquele em que a superfície
* 16/03/16 Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas: * *Definição *Um espelho plano é aquele em que a superfície
Tópico 2. Funções elementares
 Tópico. Funções elementares.6 Funções trigonométricas A trigonometria (do grego trigonon triângulo + metron medida ) é um ramo da matemática que estuda os triângulos, particularmente triângulos em um plano
Tópico. Funções elementares.6 Funções trigonométricas A trigonometria (do grego trigonon triângulo + metron medida ) é um ramo da matemática que estuda os triângulos, particularmente triângulos em um plano
1.1 UFPR 2014. Rumo Curso Pré Vestibular Assistencial - RCPVA Disciplina: Matemática Professor: Vinícius Nicolau 04 de Novembro de 2014
 Sumário 1 Questões de Vestibular 1 1.1 UFPR 2014.................................... 1 1.1.1 Questão 1................................. 1 1.1.2 Questão 2................................. 2 1.1.3 Questão
Sumário 1 Questões de Vestibular 1 1.1 UFPR 2014.................................... 1 1.1.1 Questão 1................................. 1 1.1.2 Questão 2................................. 2 1.1.3 Questão
1 - RECORDANDO 2 - CENTRO NA ORIGEM 3 - EQUAÇÃO GERAL DA CIRCUNFERÊNCIA. Exercício Resolvido 2: Exercício Resolvido 1: Frente I
 Matemática Frente I CAPÍTULO 22 EQUAÇÕES DA CIRCUNFERÊNCIA 1 - RECORDANDO Até agora, o nosso foco principal foi as retas: calculamos as equações geral e reduzida de uma reta, a interseção entre duas retas,
Matemática Frente I CAPÍTULO 22 EQUAÇÕES DA CIRCUNFERÊNCIA 1 - RECORDANDO Até agora, o nosso foco principal foi as retas: calculamos as equações geral e reduzida de uma reta, a interseção entre duas retas,
Figuras geométricas. Se olhar ao seu redor, você verá que os objetos. Acesse: Nossa aula. Figuras geométricas elementares
 A UU L AL A Figuras geométricas Se olhar ao seu redor, você verá que os objetos têm forma, tamanho e outras características próprias. As figuras geométricas foram criadas a partir da observação das formas
A UU L AL A Figuras geométricas Se olhar ao seu redor, você verá que os objetos têm forma, tamanho e outras características próprias. As figuras geométricas foram criadas a partir da observação das formas
Intersecção de duas rectas
 3.6. Intersecções Geometria Descritiva 2006/2007 Intersecção de duas rectas É condição necessária e suficiente para que duas rectas sejam concorrentes que as suas projecções homónimas se intersectem sobre
3.6. Intersecções Geometria Descritiva 2006/2007 Intersecção de duas rectas É condição necessária e suficiente para que duas rectas sejam concorrentes que as suas projecções homónimas se intersectem sobre
Apontamentos de matemática 5.º ano - Múltiplos e divisores
 Múltiplos e divisores (revisão do 1.º ciclo) Os múltiplos de um número inteiro obtêm-se multiplicando esse número pela sequência dos números inteiros. Exemplos: Alguns múltiplos de 6 são: 0, 6, 12, 18,
Múltiplos e divisores (revisão do 1.º ciclo) Os múltiplos de um número inteiro obtêm-se multiplicando esse número pela sequência dos números inteiros. Exemplos: Alguns múltiplos de 6 são: 0, 6, 12, 18,
= i= Com a aplicação ou uso da primeira expressão obtém-se 18,50m 2. Area=(1*(1 5 )+ 3*(2 6)+ 5*(5 5)+ 7*(6-4) + 9*(5-2)+4*(4-1)+3*(2-2))/2= 18,50m 2.
 4.8.5 Avaliação de Área na Projeção UTM O valor numérico da área de um limite determinado por um conjunto de pontos unidos entre si por segmentos de linha reta sucessivos que não se cruzam pode ser calculado
4.8.5 Avaliação de Área na Projeção UTM O valor numérico da área de um limite determinado por um conjunto de pontos unidos entre si por segmentos de linha reta sucessivos que não se cruzam pode ser calculado
GEOMETRIA. 1 Definições. 2 Notações
 GEOMETRIA 1 Definições Mediatriz (de um segmento): conjunto de pontos que estão à mesma distância de dois pontos unidos por um segmento de recta. É uma recta e é perpendicular a este segmento no seu ponto
GEOMETRIA 1 Definições Mediatriz (de um segmento): conjunto de pontos que estão à mesma distância de dois pontos unidos por um segmento de recta. É uma recta e é perpendicular a este segmento no seu ponto
, 10 4. pertence ao conjunto dado? Justifica a resposta e apresenta todos os cálculos que efetuares.
 Teste de Avaliação Escrita Duração: 90 minutos 9 de maio de 0 Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo 0/0 Matemática 9.º B Nome: N.º Classificação: Fraco (0% 9%) Insuficiente (0% 9%) Suficiente
Teste de Avaliação Escrita Duração: 90 minutos 9 de maio de 0 Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo 0/0 Matemática 9.º B Nome: N.º Classificação: Fraco (0% 9%) Insuficiente (0% 9%) Suficiente
O Plano. Equação Geral do Plano:
 O Plano Equação Geral do Plano: Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = (a, b, c), n 0, um vetor normal (ortogonal) ao plano (figura ao lado). Como n π, n é ortogonal a todo vetor
O Plano Equação Geral do Plano: Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = (a, b, c), n 0, um vetor normal (ortogonal) ao plano (figura ao lado). Como n π, n é ortogonal a todo vetor
Estática do Ponto Material e do Corpo Rígido
 CAPÍTULO I Estática do Ponto Material e do Corpo Rígido SEMESTRE VERÃO 2004/2005 Maria Idália Gomes 1/7 Capitulo I Estática do Ponto Material e do Corpo Rígido Este capítulo tem por objectivo a familiarização
CAPÍTULO I Estática do Ponto Material e do Corpo Rígido SEMESTRE VERÃO 2004/2005 Maria Idália Gomes 1/7 Capitulo I Estática do Ponto Material e do Corpo Rígido Este capítulo tem por objectivo a familiarização
PROPRIEDADES DOS FLUÍDOS
 NATAÇÃO I Fundamentos do Desporto PROPRIEDADES DOS FLUÍDOS Fluidez e noção de fluxo Compressibilidade e incompressibilidade Massa específica, peso volúmico e densidade Viscosidade, fluidos reais e fluidos
NATAÇÃO I Fundamentos do Desporto PROPRIEDADES DOS FLUÍDOS Fluidez e noção de fluxo Compressibilidade e incompressibilidade Massa específica, peso volúmico e densidade Viscosidade, fluidos reais e fluidos
TEORIA 5: EQUAÇÕES E SISTEMAS DO 1º GRAU MATEMÁTICA BÁSICA
 TEORIA 5: EQUAÇÕES E SISTEMAS DO 1º GRAU MATEMÁTICA BÁSICA Nome: Turma: Data / / Prof: Walnice Brandão Machado Equações de primeiro grau Introdução Equação é toda sentença matemática aberta que exprime
TEORIA 5: EQUAÇÕES E SISTEMAS DO 1º GRAU MATEMÁTICA BÁSICA Nome: Turma: Data / / Prof: Walnice Brandão Machado Equações de primeiro grau Introdução Equação é toda sentença matemática aberta que exprime
5. Derivada. Definição: Se uma função f é definida em um intervalo aberto contendo x 0, então a derivada de f
 5 Derivada O conceito de derivada está intimamente relacionado à taa de variação instantânea de uma função, o qual está presente no cotidiano das pessoas, através, por eemplo, da determinação da taa de
5 Derivada O conceito de derivada está intimamente relacionado à taa de variação instantânea de uma função, o qual está presente no cotidiano das pessoas, através, por eemplo, da determinação da taa de
