Estática do Ponto Material e do Corpo Rígido
|
|
|
- Bernadete Gusmão Barreiro
- 9 Há anos
- Visualizações:
Transcrição
1 CAPÍTULO I Estática do Ponto Material e do Corpo Rígido SEMESTRE VERÃO 2004/2005 Maria Idália Gomes 1/7
2 Capitulo I Estática do Ponto Material e do Corpo Rígido Este capítulo tem por objectivo a familiarização dos alunos com o conceito de FORÇA (resultado da interacção entre corpos) para a compreensão da estática do ponto material e do corpo rígido. Ponto material A estática do ponto material engloba a composição e decomposição das forças (representadas por vectores fixos) que nele actuam, isto é, passa pela definição de sistemas de forças equivalentes - sistemas que produzem o mesmo feito no ponto material. Quando o sistema de forças é substituído por uma única força esta é designada por resultante. Quando a resultante de todas as forças que actuam sobre o ponto material é zero, o ponto material está em equilíbrio. Para um sistema de forças no plano, a via a utilizar tanto pode ser a gráfica como a analítica mas, sendo as forças espaciais então a via a seguir é a analítica. Quando um sistema é constituído por três ou mais forças é mais conveniente trabalhar com as suas componentes cartesianas. Apresentam-se de seguida oito exemplos de aplicação. Qual o ângulo θ para que a resultante das duas forças tenha intensidade de 1200N? Nestas condições qual o ângulo que a resultante faz com a horizontal? Composição de forças no plano. Decompor a força de 4 kn em componentes, uma na direcção AB e a outra na BC. Decomposição de uma força em duas componentes de direcção conhecida. Maria Idália Gomes 2/7
3 Deseja-se retirar o grampo, cravado na madeira, movendo-o na direcção do seu eixo horizontal. Um obstáculo impede o acesso directo, de modo que vão ser aplicadas duas forças, uma de 2,0 kn e outra F, através de cabos conforme a figura. Calcular a intensidade de F e da resultante das forças F e 2,0 kn. Composição de forças no plano. Determinar a resultante das forças expressa como vector, usando os vectores unitários nas direcções x e y. Composição de forças expressas nas suas componentes cartesianas. Resolução analítica. Determinar as tracções nos cabos AB e BC. Equilíbrio de forças no plano. Os cabos AB e AC estão atados no ponto A e sujeitos a uma carga vertical de 530N. Determinar o intervalo de valores de F para os quais os dois cabos permanecem esticados. Equilíbrio de forças no plano. Maria Idália Gomes 3/7
4 Determinar a resultante das forças. Composição de forças no espaço. Calcular a tracção em cada um dos três cabos que suportam a placa quadrada de aço com 1800 kg na posição horizontal. Equilíbrio de forças no espaço. Corpo rígido As forças que actuam um corpo rígido são externas e internas. As forças externas representam a acção de outros corpos e são responsáveis pelo seu movimento ou asseguram a sua permanência em repouso. As forças internas mantêm unidas os pontos materiais que formam o corpo. Se o corpo for constituído por diversas partes, as forças que as mantêm unidas são também forças internas. Neste capítulo apenas se consideram as forças exteriores. Cada força tende a deslocar o corpo na direcção da sua aplicação e tende também a rodá-lo em torno de um qualquer eixo que não intercepte nem seja paralelo à sua linha de acção. Assim, se as forças externas que actuam um corpo rígido não forem anuladas são capazes de comunicar ao corpo um movimento de translação, de rotação ou ambos. O efeito de uma força exterior sobre um corpo rígido não se altera se a força se deslocar ao longo da sua recta suporte, assim, duas forças com igual intensidade, igual sentido e a mesma linha de acção, são equivalentes. Maria Idália Gomes 4/7
5 Dois sistemas de forças são equivalentes se provocarem o mesmo efeito de translação e rotação, isto é, se for igual a sua redução num mesmo ponto. Qualquer sistema de forças pode ser reduzido a um sistema constituído por uma força (R) e um momento(m o ) aplicados a um ponto O. Os casos possíveis da redução de um sistema de forças são: o sistema está em equilíbrio se R = 0 e M o = 0; o sistema é equivalente a um binário M o se R = 0 e M o 0; o sistema é equivalente a uma única força R se R 0 e M o = 0 e R passa pelo ponto O ou R 0 e M o 0 e R M o (produto interno dos vectores é nulo). E R passa pelo ponto P(x,y,z) tal que (P-O) ^ R = Mo; O sistema de forças é equivalente a uma única força sempre que as forças são concorrentes num mesmo ponto, são paralelas entre si ou são coplanares. o sistema é equivalente a um torsor R e M R se R 0 e M o 0 e R não é a M o (produto interno dos vectores não é nulo). M R é a componente de M o com a direcção de R e a recta suporte do torsor passa pelo ponto P(x,y,z) tal que M o = M R +(P-O) ^ R. Maria Idália Gomes 5/7
6 Apresentam-se de seguida sete exemplos de aplicação. A força de 3 kn passa pelos pontos A (2,-1, 3) e B (-3, 0, 1) e tem sentido de A para B. Calcule o seu momento em torno do ponto C (1, 1, -2). Momento de uma força relativamente a um ponto. Calcule o momento da força de 20 kn em torno do ponto O. Momento de uma força relativamente a um ponto. A força e o binário devem ser substituídos por uma única força equivalente. Com F = 2Q determine o valor do ângulo α para que a força equivalente passe pelo ponto C. Momento de um binário. Quatro forças estão aplicadas à placa. Determine gráfica e analiticamente: a) a resultante das forças; b) outras três forças equivalentes que passem pelos pontos AB, AC e BE. Redução de um sistema de forças coplanares a uma única força. Decomposição e uma força em três direcções não concorrentes num ponto. Determinar a resultante das quatro cargas que actuam a laje. Redução de um sistema de forças paralelas a uma única força. Maria Idália Gomes 6/7
7 Reduza o sistema das quatro forças a = 34 kn, b = 25 kn, c = 24 kn e d = 6 kn: a) ao ponto A; b) ao ponto B; c) a um torsor. Redução de um sistema de forças no espaço a um ponto e a um torsor. A tabuleta rectangular homogénea tem 100 kg de massa, está ligada à parede nos pontos C e D e mantém-se na posição mostrada através dos fios. C é uma rótula e em D a tabuleta apenas recebe apoio na direcção y. Calcule a tracção nos fios e as forças reactivas em C e D. Equilíbrio do corpo rígido Maria Idália Gomes 7/7
Equilíbrio de um corpo rígido
 Equilíbrio de um corpo rígido Objetivos da aula: Desenvolver as equações de equilíbrio para um corpo rígido. Introduzir o conceito do diagrama de corpo livre para um corpo rígido. Mostrar como resolver
Equilíbrio de um corpo rígido Objetivos da aula: Desenvolver as equações de equilíbrio para um corpo rígido. Introduzir o conceito do diagrama de corpo livre para um corpo rígido. Mostrar como resolver
Equilíbrio de uma Partícula
 Apostila de Resistência dos Materiais I Parte 2 Profª Eliane Alves Pereira Turma: Engenharia Civil Equilíbrio de uma Partícula Condição de Equilíbrio do Ponto Material Um ponto material encontra-se em
Apostila de Resistência dos Materiais I Parte 2 Profª Eliane Alves Pereira Turma: Engenharia Civil Equilíbrio de uma Partícula Condição de Equilíbrio do Ponto Material Um ponto material encontra-se em
Prof. Michel Sadalla Filho
 MECÂNICA APLICADA Prof. Michel Sadalla Filho MOMENTO DE UMA FORÇA + EQUILÍBRIO DE UMA BARRA (No Plano XY) Referência HIBBELER, R. C. Mecânica Estática. 10 ed. São Paulo: Pearson Education do Brasil, 2005,
MECÂNICA APLICADA Prof. Michel Sadalla Filho MOMENTO DE UMA FORÇA + EQUILÍBRIO DE UMA BARRA (No Plano XY) Referência HIBBELER, R. C. Mecânica Estática. 10 ed. São Paulo: Pearson Education do Brasil, 2005,
Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/
 Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/ Estrutura Sistema qualquer de elementos ligados, construído para suportar ou transferir
Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/ Estrutura Sistema qualquer de elementos ligados, construído para suportar ou transferir
Faculdades Oswaldo Cruz ESQ (Física I Profº Ito Lista de Torque)
 1. Um ponto material está parado sobre uma prancha rígida horizontal, de massa desprezível, apoiada nas extremidades. O comprimento da prancha é de 3,0 m. O peso do ponto material é de 60 N e este está
1. Um ponto material está parado sobre uma prancha rígida horizontal, de massa desprezível, apoiada nas extremidades. O comprimento da prancha é de 3,0 m. O peso do ponto material é de 60 N e este está
EQUILÍBRIO DA PARTÍCULA
 Questão 1 - As cordas A, B e C mostradas na figura a seguir têm massa desprezível e são inextensíveis. As cordas A e B estão presas no teto horizontal e se unem à corda C no ponto P. A corda C tem preso
Questão 1 - As cordas A, B e C mostradas na figura a seguir têm massa desprezível e são inextensíveis. As cordas A e B estão presas no teto horizontal e se unem à corda C no ponto P. A corda C tem preso
Mecânica Geral. Aula 05 - Equilíbrio e Reação de Apoio
 Aula 05 - Equilíbrio e Reação de Apoio 1 - Equilíbrio de um Ponto Material (Revisão) Condição de equilíbrio de um Ponto Material Y F 0 F X 0 e F 0 Exemplo 01 - Determine a tensão nos cabos AB e AD para
Aula 05 - Equilíbrio e Reação de Apoio 1 - Equilíbrio de um Ponto Material (Revisão) Condição de equilíbrio de um Ponto Material Y F 0 F X 0 e F 0 Exemplo 01 - Determine a tensão nos cabos AB e AD para
PLANO INCLINADO. a. a aceleração com que o bloco desce o plano; b. a intensidade da reação normal sobre o bloco;
 PLANO INCLINADO 1. Um corpo de massa m = 10kg está apoiado num plano inclinado de 30 em relação à horizontal, sem atrito, e é abandonado no ponto A, distante 20m do solo. Supondo a aceleração da gravidade
PLANO INCLINADO 1. Um corpo de massa m = 10kg está apoiado num plano inclinado de 30 em relação à horizontal, sem atrito, e é abandonado no ponto A, distante 20m do solo. Supondo a aceleração da gravidade
. B(x 2, y 2 ). A(x 1, y 1 )
 Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
MECÂNICA - DINÂMICA APLICAÇÃO DAS LEIS DE NEWTON BLOCOS
 1 MECÂNICA - DINÂMICA APLICAÇÃO DAS LEIS DE NEWTON BLOCOS 1. (Ufrj) Dois blocos de massa igual a 4kg e 2kg, respectivamente, estão presos entre si por um fio inextensível e de massa desprezível. Deseja-se
1 MECÂNICA - DINÂMICA APLICAÇÃO DAS LEIS DE NEWTON BLOCOS 1. (Ufrj) Dois blocos de massa igual a 4kg e 2kg, respectivamente, estão presos entre si por um fio inextensível e de massa desprezível. Deseja-se
aplicada no outro bloco exceder o valor calculado na alínea 4.1? R: 16 N; 2 ms -2 ; 1 ms -2
 Engenharia Electrotécnica e de Computadores Exercícios de Física Ficha 6 Dinâmica do Ponto Material Capítulo 3 no lectivo 2010-2011 Conhecimentos e capacidades a adquirir pelo aluno plicação dos conceitos
Engenharia Electrotécnica e de Computadores Exercícios de Física Ficha 6 Dinâmica do Ponto Material Capítulo 3 no lectivo 2010-2011 Conhecimentos e capacidades a adquirir pelo aluno plicação dos conceitos
14-11-2013. Adaptado de Serway & Jewett Marília Peres 2013. Marília Peres
 Adaptado de Serway & Jewett Marília Peres 2013 2 1 Se a aceleração de um objecto é zero, podemos dizer que equilíbrio. di er q e este se encontra em eq ilíbrio Matematicamente, é equivalente a dizer que
Adaptado de Serway & Jewett Marília Peres 2013 2 1 Se a aceleração de um objecto é zero, podemos dizer que equilíbrio. di er q e este se encontra em eq ilíbrio Matematicamente, é equivalente a dizer que
Parte da Física que estuda o comportamento de sistemas físicos sujeitos a forças. Figura 5.1: Exemplo de equilíbrio estático. ~F i = ~0 (5.
 Capítulo 5 Mecânica Parte da Física que estuda o comportamento de sistemas físicos sujeitos a forças. 5.1 Estática Ramo da mecânica que estuda as forças actuantes num sistema mecânico em equilíbrio (todos
Capítulo 5 Mecânica Parte da Física que estuda o comportamento de sistemas físicos sujeitos a forças. 5.1 Estática Ramo da mecânica que estuda as forças actuantes num sistema mecânico em equilíbrio (todos
Mecânica dos Sólidos - Colecção de Problemas Resolvidos. 2º ano da Licenciatura em Engenharia Civil
 ALVARO F. M. AZEVEDO Mecânica dos Sólidos - Colecção de Problemas Resolvidos 2º ano da Licenciatura em Engenharia Civil Faculdade de Engenharia da Universidade do Porto - Portugal 1993 Faculdade de Engenharia
ALVARO F. M. AZEVEDO Mecânica dos Sólidos - Colecção de Problemas Resolvidos 2º ano da Licenciatura em Engenharia Civil Faculdade de Engenharia da Universidade do Porto - Portugal 1993 Faculdade de Engenharia
NOME: Matrícula: Turma: Prof. : Importante: i. Nas cinco páginas seguintes contém problemas para serem resolvidos e entregues.
 Lista 12: Equilíbrio do Corpo Rígido NOME: Matrícula: Turma: Prof. : Importante: i. Nas cinco páginas seguintes contém problemas para serem resolvidos e entregues. ii. Ler os enunciados com atenção. iii.
Lista 12: Equilíbrio do Corpo Rígido NOME: Matrícula: Turma: Prof. : Importante: i. Nas cinco páginas seguintes contém problemas para serem resolvidos e entregues. ii. Ler os enunciados com atenção. iii.
LISTA DE EXERCÍCIOS DE FÍSICA
 LISTA DE EXERCÍCIOS DE FÍSICA / /2012 ALUNO: N.º TURMA 01. Em um jogo de basebol, o rebatedor aplica uma força de contato do taco com a bola. Com a tecnologia atual, é possível medir a força média aplicada
LISTA DE EXERCÍCIOS DE FÍSICA / /2012 ALUNO: N.º TURMA 01. Em um jogo de basebol, o rebatedor aplica uma força de contato do taco com a bola. Com a tecnologia atual, é possível medir a força média aplicada
FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO
 FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO Fixação 1) O bloco da figura, de peso P = 50N, é arrastado ao longo do plano horizontal pela força F de intensidade F = 100N. A força de
FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO Fixação 1) O bloco da figura, de peso P = 50N, é arrastado ao longo do plano horizontal pela força F de intensidade F = 100N. A força de
O Plano. Equação Geral do Plano:
 O Plano Equação Geral do Plano: Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = (a, b, c), n 0, um vetor normal (ortogonal) ao plano (figura ao lado). Como n π, n é ortogonal a todo vetor
O Plano Equação Geral do Plano: Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = (a, b, c), n 0, um vetor normal (ortogonal) ao plano (figura ao lado). Como n π, n é ortogonal a todo vetor
Física Professor Fernando 2ª série / 1º trimestre
 Física Professor Fernando 2ª série / 1º trimestre Questão 01) Em um parque de diversão, Carlos e Isabela brincam em uma gangorra que dispõe de dois lugares possíveis de se sentar nas suas extremidades.
Física Professor Fernando 2ª série / 1º trimestre Questão 01) Em um parque de diversão, Carlos e Isabela brincam em uma gangorra que dispõe de dois lugares possíveis de se sentar nas suas extremidades.
Física Experimental - Mecânica - Conjunto para mecânica com painel multiuso - EQ032G.
 Índice Remissivo... 4 Abertura... 6 Guarantee / Garantia... 7 Certificado de Garantia Internacional... 7 As instruções identificadas no canto superior direito da página pelos números que se iniciam pelos
Índice Remissivo... 4 Abertura... 6 Guarantee / Garantia... 7 Certificado de Garantia Internacional... 7 As instruções identificadas no canto superior direito da página pelos números que se iniciam pelos
Capítulo TRABALHO E ENERGIA
 Capítulo 6 TRABALHO E ENERGIA A B C DISCIPLINA DE FÍSICA CAPÍTULO 6 - TRABALHO E ENERGIA 6.1 Um bloco, com 20kg de massa, sobe uma rampa com 15º de inclinação e percorre 55,375 metros até parar. Os coeficientes
Capítulo 6 TRABALHO E ENERGIA A B C DISCIPLINA DE FÍSICA CAPÍTULO 6 - TRABALHO E ENERGIA 6.1 Um bloco, com 20kg de massa, sobe uma rampa com 15º de inclinação e percorre 55,375 metros até parar. Os coeficientes
1ª lei de Newton (Lei da Inércia)
 1ª lei de Newton (Lei da Inércia) Inércia: Por si só, um corpo não é capaz de alterar o seu estado de repouso ou de movimento rectilíneo e uniforme. A inércia de um corpo é uma medida da oposição que o
1ª lei de Newton (Lei da Inércia) Inércia: Por si só, um corpo não é capaz de alterar o seu estado de repouso ou de movimento rectilíneo e uniforme. A inércia de um corpo é uma medida da oposição que o
Resistência dos Materiais
 Aula 4 Deformações e Propriedades Mecânicas dos Materiais Tópicos Abordados Nesta Aula Estudo de Deformações, Normal e por Cisalhamento. Propriedades Mecânicas dos Materiais. Coeficiente de Poisson. Deformação
Aula 4 Deformações e Propriedades Mecânicas dos Materiais Tópicos Abordados Nesta Aula Estudo de Deformações, Normal e por Cisalhamento. Propriedades Mecânicas dos Materiais. Coeficiente de Poisson. Deformação
ESCOLA BÁSICA 2,3 MARTIM DE FREITAS NÚCLEO DE ESTÁGIO DE MATEMÁTICA ANO LETIVO 2011/2012
 Escola Martim de Freitas ESCOLA BÁSICA 2,3 MARTIM DE FREITAS NÚCLEO DE ESTÁGIO DE MATEMÁTICA ANO LETIVO 2011/2012 Disciplina de Matemática Tópico: Isometrias Ficha de Trabalho n.º 1 Data: 20 / 10 / 2011
Escola Martim de Freitas ESCOLA BÁSICA 2,3 MARTIM DE FREITAS NÚCLEO DE ESTÁGIO DE MATEMÁTICA ANO LETIVO 2011/2012 Disciplina de Matemática Tópico: Isometrias Ficha de Trabalho n.º 1 Data: 20 / 10 / 2011
CINEMÁTICA DO PONTO MATERIAL
 1.0 Conceitos CINEMÁTICA DO PONTO MATERIAL Cinemática é a parte da Mecânica que descreve os movimentos. Ponto material é um corpo móvel cujas dimensões não interferem no estudo em questão. Trajetória é
1.0 Conceitos CINEMÁTICA DO PONTO MATERIAL Cinemática é a parte da Mecânica que descreve os movimentos. Ponto material é um corpo móvel cujas dimensões não interferem no estudo em questão. Trajetória é
ROLAMENTO, TORQUE E MOMENTUM ANGULAR Física Geral I (1108030) - Capítulo 08
 ROLAMENTO, TORQUE E MOMENTUM ANGULAR Física Geral I (1108030) - Capítulo 08 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 21 Sumário Rolamento Rolamento como rotação e translação combinados e como uma
ROLAMENTO, TORQUE E MOMENTUM ANGULAR Física Geral I (1108030) - Capítulo 08 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 21 Sumário Rolamento Rolamento como rotação e translação combinados e como uma
FÍSICA - 1 o ANO MÓDULO 10 EQUILÍBRIO DE CORPOS EXTENSOS
 FÍSICA - 1 o ANO MÓDULO 10 EQUILÍBRIO DE CORPOS EXTENSOS F d M 0 F = Fd O + - A C α B Q F at T N α P B P Q F at T T sen α N A T cos α α B P B PQ Como pode cair no enem? Desde muito cedo, bem antes do início
FÍSICA - 1 o ANO MÓDULO 10 EQUILÍBRIO DE CORPOS EXTENSOS F d M 0 F = Fd O + - A C α B Q F at T N α P B P Q F at T T sen α N A T cos α α B P B PQ Como pode cair no enem? Desde muito cedo, bem antes do início
Mecânica Geral. Aula 04 Carregamento, Vínculo e Momento de uma força
 Aula 04 Carregamento, Vínculo e Momento de uma força 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
Aula 04 Carregamento, Vínculo e Momento de uma força 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
(Séries de Problemas) Paulo Vargas Moniz Universidade da Beira Interior Departamento de Fisica
 . Mecânica Clássica (Séries de Problemas) Paulo Vargas Moniz Universidade da Beira Interior Departamento de Fisica 1 1 a Serie 1. Considera um bloco B de massa m deslizando sobre um plano inclinado PI
. Mecânica Clássica (Séries de Problemas) Paulo Vargas Moniz Universidade da Beira Interior Departamento de Fisica 1 1 a Serie 1. Considera um bloco B de massa m deslizando sobre um plano inclinado PI
Introdução aos Sistemas Estruturais
 Introdução aos Sistemas Estruturais Noções de Mecânica Estrutural Estuda o comportamento das estruturas frente aos esforços externos. Por definição estrutura é qualquer corpo sólido capaz de oferecer resistência
Introdução aos Sistemas Estruturais Noções de Mecânica Estrutural Estuda o comportamento das estruturas frente aos esforços externos. Por definição estrutura é qualquer corpo sólido capaz de oferecer resistência
1 Noções Primitivas MAT175 - GEOMETRIA ESPACIAL MAT175 - GEOMETRIA ESPACIAL
 MAT175 - GEOMETRIA ESPACIAL Bibliografia: [1] Fundamentos de Matemática Elementar, 10: Geometria Espacial, posição e métrica. Osvaldo Dolce e José Nicolau Pompeo. 6. ed., São Paulo, Atual, 2005. [2] A
MAT175 - GEOMETRIA ESPACIAL Bibliografia: [1] Fundamentos de Matemática Elementar, 10: Geometria Espacial, posição e métrica. Osvaldo Dolce e José Nicolau Pompeo. 6. ed., São Paulo, Atual, 2005. [2] A
Se a força de tração de cálculo for 110 kn, a área do tirante, em cm 2 é A) 5,0. B) 4,5. C) 3,0. D) 2,5. E) 7,5.
 25.(TRT-18/FCC/2013) Uma barra de aço especial, de seção circular com extremidades rosqueadas é utilizada como tirante em uma estrutura metálica. O aço apresenta f y = 242 MPa e f u = 396 MPa. Dados: Coeficientes
25.(TRT-18/FCC/2013) Uma barra de aço especial, de seção circular com extremidades rosqueadas é utilizada como tirante em uma estrutura metálica. O aço apresenta f y = 242 MPa e f u = 396 MPa. Dados: Coeficientes
FESP Faculdade de Engenharia São Paulo. CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Duração: 85 minutos
 FESP Faculdade de Engenharia São Paulo Avaliação: S1 Data: 16/jun/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Duração: 85 minutos Nome: Matrícula ORIENTAÇÕES PARA PROVA a b c
FESP Faculdade de Engenharia São Paulo Avaliação: S1 Data: 16/jun/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Duração: 85 minutos Nome: Matrícula ORIENTAÇÕES PARA PROVA a b c
Capítulo 4. Retas e Planos. 4.1 A reta
 Capítulo 4 Retas e Planos Neste capítulo veremos como utilizar a teoria dos vetores para caracterizar retas e planos, a saber, suas equações, posições relativas, ângulos e distâncias. 4.1 A reta Sejam
Capítulo 4 Retas e Planos Neste capítulo veremos como utilizar a teoria dos vetores para caracterizar retas e planos, a saber, suas equações, posições relativas, ângulos e distâncias. 4.1 A reta Sejam
TRELIÇAS ISOSTÁTICAS
 86 TRELIÇAS ISOSTÁTICAS I. DEFINIÇÃO: Treliça ideal é um sistema reticulado indeformável cujas barras possuem todas as suas extremidades rotuladas e cujas cargas estão aplicadas nestas rótulas. Obs 1 :
86 TRELIÇAS ISOSTÁTICAS I. DEFINIÇÃO: Treliça ideal é um sistema reticulado indeformável cujas barras possuem todas as suas extremidades rotuladas e cujas cargas estão aplicadas nestas rótulas. Obs 1 :
Centro de gravidade de um corpo é o ponto onde podemos supor que seu peso esteja aplicado.
 Apostila de Revisão n 4 DISCIPLINA: Física NOME: N O : TURMA: 2M311 PROFESSOR: Glênon Dutra DATA: Mecânica - 4. Corpo Rígido 4.1. Torque análise semiquantitativa, na Primeira Etapa, e quantitativa, na
Apostila de Revisão n 4 DISCIPLINA: Física NOME: N O : TURMA: 2M311 PROFESSOR: Glênon Dutra DATA: Mecânica - 4. Corpo Rígido 4.1. Torque análise semiquantitativa, na Primeira Etapa, e quantitativa, na
Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da massa específica do meio µ, de acordo com a expressão:
 PROVA DE FÍSICA DO VESTIBULAR 96/97 DO INSTITUTO MILITAR DE ENGENHARIA (03/12/96) 1 a Questão: Valor : 1,0 Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da
PROVA DE FÍSICA DO VESTIBULAR 96/97 DO INSTITUTO MILITAR DE ENGENHARIA (03/12/96) 1 a Questão: Valor : 1,0 Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da
a) P 1 = 1,5 Kg P 2 = 1,5 Kg; b) P 1 = 1,5 Kg P 2 = kg c) P 1 = 3,0 Kg P 2 = kg d) P 1 = 2,0 Kg P 2 = 4,0 Kg; e) P 1 = Kg P 2 = kg Resposta: B
 1. (ITA - 1968) Na situação abaixo, o bloco 3 de massa igual a 6,0 kg está na eminência de deslizar. Supondo as cordas inextensíveis e sem massa e as roldanas também sem massa e sem atrito, quais são as
1. (ITA - 1968) Na situação abaixo, o bloco 3 de massa igual a 6,0 kg está na eminência de deslizar. Supondo as cordas inextensíveis e sem massa e as roldanas também sem massa e sem atrito, quais são as
ENG1200 Mecânica Geral Lista de Exercícios 1 Equilíbrio da Partícula
 ENG1200 Mecânica Geral 2013.2 Lista de Exercícios 1 Equilíbrio da Partícula Questão 1 - Prova P1 2013.1 Determine o máximo valor da força P que pode ser aplicada na estrutura abaixo, sabendo que no tripé
ENG1200 Mecânica Geral 2013.2 Lista de Exercícios 1 Equilíbrio da Partícula Questão 1 - Prova P1 2013.1 Determine o máximo valor da força P que pode ser aplicada na estrutura abaixo, sabendo que no tripé
aplicada à força sentida por uma carga q 0, devida à N cargas q 1 q 2 q n
 Eletricidade O Campo eléctrico Consideremos a equação aplicada à força sentida por uma carga q 0, devida à N cargas q 1 q 2 q n onde é a distância desde a carga até o ponto do espaço onde se encontra a
Eletricidade O Campo eléctrico Consideremos a equação aplicada à força sentida por uma carga q 0, devida à N cargas q 1 q 2 q n onde é a distância desde a carga até o ponto do espaço onde se encontra a
Lista de Exercícios - Aula 02 Aplicações das Leis de Newton
 Lista de Exercícios - Aula 02 Aplicações das Leis de Newton 1 - Equilíbrio Estático 1 - Um garoto, apoiando-se em uma bengala, encontra-se em cima de uma balança que marca 40 Kg. Se o garoto empurrar fortemente
Lista de Exercícios - Aula 02 Aplicações das Leis de Newton 1 - Equilíbrio Estático 1 - Um garoto, apoiando-se em uma bengala, encontra-se em cima de uma balança que marca 40 Kg. Se o garoto empurrar fortemente
Para cada partícula num pequeno intervalo de tempo t a percorre um arco s i dado por. s i = v i t
 Capítulo 1 Cinemática dos corpos rígidos O movimento de rotação apresenta algumas peculiaridades que precisam ser entendidas. Tem equações horárias, que descrevem o movimento, semelhantes ao movimento
Capítulo 1 Cinemática dos corpos rígidos O movimento de rotação apresenta algumas peculiaridades que precisam ser entendidas. Tem equações horárias, que descrevem o movimento, semelhantes ao movimento
A unidade de freqüência é chamada hertz e simbolizada por Hz: 1 Hz = 1 / s.
 Movimento Circular Uniforme Um movimento circular uniforme (MCU) pode ser associado, com boa aproximação, ao movimento de um planeta ao redor do Sol, num referencial fixo no Sol, ou ao movimento da Lua
Movimento Circular Uniforme Um movimento circular uniforme (MCU) pode ser associado, com boa aproximação, ao movimento de um planeta ao redor do Sol, num referencial fixo no Sol, ou ao movimento da Lua
Geometria Diferencial de Curvas Espaciais
 Geometria Diferencial de Curvas Espaciais 1 Aceleração tangencial e centrípeta Fernando Deeke Sasse Departamento de Matemática CCT UDESC Mostremos que a aceleração de uma partícula viajando ao longo de
Geometria Diferencial de Curvas Espaciais 1 Aceleração tangencial e centrípeta Fernando Deeke Sasse Departamento de Matemática CCT UDESC Mostremos que a aceleração de uma partícula viajando ao longo de
UNIVERSITÁRIO DE SINOP CURSO DE ENGENHARIA CIVIL
 Exercícios propostos: aulas 01 e 02 GOVERNO DO ESTADO DE MATO GROSSO GA - LISTA DE EXERCÍCIOS 001 1. Calcular o perímetro do triângulo ABC, sendo dado A = (2, 1), B = (-1, 3) e C = (4, -2). 2. Provar que
Exercícios propostos: aulas 01 e 02 GOVERNO DO ESTADO DE MATO GROSSO GA - LISTA DE EXERCÍCIOS 001 1. Calcular o perímetro do triângulo ABC, sendo dado A = (2, 1), B = (-1, 3) e C = (4, -2). 2. Provar que
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I
 LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a. Se AB tiver diâmetro de 10 mm
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a. Se AB tiver diâmetro de 10 mm
Departamento de Matemática da Universidade de Coimbra Álgebra Linear e Geometria Analítica Engenharia Civil Ano lectivo 2005/2006 Folha 1.
 Departamento de Matemática da Universidade de Coimbra Álgebra Linear e Geometria Analítica Engenharia Civil Ano lectivo 2005/2006 Folha 1 Matrizes 1 Considere as matrizes A = 1 2 3 2 3 1 3 1 2 Calcule
Departamento de Matemática da Universidade de Coimbra Álgebra Linear e Geometria Analítica Engenharia Civil Ano lectivo 2005/2006 Folha 1 Matrizes 1 Considere as matrizes A = 1 2 3 2 3 1 3 1 2 Calcule
LISTA DE EXERCÍCIOS DE GEOMETRIA ANALÍTICA. 01) Dados os vetores e, determine o valor da expressão vetorial. Resp: A=51
 1 LISTA DE EXERCÍCIOS DE GEOMETRIA ANALÍTICA 01) Dados os vetores e, determine o valor da expressão vetorial. A=51 02) Decomponha o vetor em dois vetores tais que e, com. 03) Dados os vetores, determine
1 LISTA DE EXERCÍCIOS DE GEOMETRIA ANALÍTICA 01) Dados os vetores e, determine o valor da expressão vetorial. A=51 02) Decomponha o vetor em dois vetores tais que e, com. 03) Dados os vetores, determine
Reflexão e Refracção (7)ë
 Arco -Íris Reflexão e Refracção (7)ë O índice de refracção do meio (por ex. água) depende ligeiramente do comprimento de onda da luz Resulta daí a separação das cores no arco-íris! 10 Arco -Íris (cont.)ë
Arco -Íris Reflexão e Refracção (7)ë O índice de refracção do meio (por ex. água) depende ligeiramente do comprimento de onda da luz Resulta daí a separação das cores no arco-íris! 10 Arco -Íris (cont.)ë
Capítulo CORPOS RÍGIDOS E SISTEMAS EQUIVALENTES DE FORÇAS
 Capítulo 3 CORPOS RÍGIDOS E SISTEMAS EQUIVALENTES DE FORÇAS 3.1 Determine o momento da força em relação a B: 3.1.1 Sem decompor a força. 3.1.2 Decompondo a força em componente horizontal e vertical. 3.2
Capítulo 3 CORPOS RÍGIDOS E SISTEMAS EQUIVALENTES DE FORÇAS 3.1 Determine o momento da força em relação a B: 3.1.1 Sem decompor a força. 3.1.2 Decompondo a força em componente horizontal e vertical. 3.2
MECÂNICA DOS SÓLIDOS
 MECÂNICA DOS SÓLIDOS Cláudio Messias da Silva O principal objetivo de um curso básico de mecânica deveria se o de desenvolver no estudante de engenharia a habilidade de analisar um dado problema, de maneira
MECÂNICA DOS SÓLIDOS Cláudio Messias da Silva O principal objetivo de um curso básico de mecânica deveria se o de desenvolver no estudante de engenharia a habilidade de analisar um dado problema, de maneira
1.10 Sistemas de coordenadas cartesianas
 7 0 Sistemas de coordenadas cartesianas Definição : Um sistema de coordenadas cartesianas no espaço é um v v conjunto formado por um ponto e uma base { } v3 Indicamos um sistema de coordenadas cartesianas
7 0 Sistemas de coordenadas cartesianas Definição : Um sistema de coordenadas cartesianas no espaço é um v v conjunto formado por um ponto e uma base { } v3 Indicamos um sistema de coordenadas cartesianas
Matemática Básica Intervalos
 Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
ESTÁTICA DO PONTO MATERIAL
 ESTÁTICA DO PONTO MATERIAL 0) CFTMG- As figuras e a seguir representam, respectivamente, todas as forças, constantes e coplanares, que atuam sobre uma partícula e o diagrama da soma vetorial destas forças.
ESTÁTICA DO PONTO MATERIAL 0) CFTMG- As figuras e a seguir representam, respectivamente, todas as forças, constantes e coplanares, que atuam sobre uma partícula e o diagrama da soma vetorial destas forças.
Equações paramétricas da Reta
 39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
Capítulo 2 - Determinantes
 Capítulo 2 - Determinantes Carlos Balsa [email protected] Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/ 19 DeMat-ESTiG Sumário
Capítulo 2 - Determinantes Carlos Balsa [email protected] Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2011/2012 Matemática I 1/ 19 DeMat-ESTiG Sumário
EXERCÍCIOS DE REVISÃO MATEMÁTICA II GEOMETRIA ANALÍTICA PLANA (Ponto, reta e circunferência)
 EXERCÍCIOS DE REVISÃO MATEMÁTICA II GEOMETRIA ANALÍTICA PLANA (Ponto, reta e circunferência) ************************************************************************************* 1) (U.F.PA) Se a distância
EXERCÍCIOS DE REVISÃO MATEMÁTICA II GEOMETRIA ANALÍTICA PLANA (Ponto, reta e circunferência) ************************************************************************************* 1) (U.F.PA) Se a distância
Resolução do exemplo 8.6a - pág 61 Apresente, analítica e geometricamente, a solução dos seguintes sistemas lineares.
 Solução dos Exercícios de ALGA 2ª Avaliação EXEMPLO 8., pág. 61- Uma reta L passa pelos pontos P 0 (, -2, 1) e P 1 (5, 1, 0). Determine as equações paramétricas, vetorial e simétrica dessa reta. Determine
Solução dos Exercícios de ALGA 2ª Avaliação EXEMPLO 8., pág. 61- Uma reta L passa pelos pontos P 0 (, -2, 1) e P 1 (5, 1, 0). Determine as equações paramétricas, vetorial e simétrica dessa reta. Determine
Escola Secundária Dom Manuel Martins
 Escola Secundária Dom Manuel Martins Setúbal 1ª Ficha Avaliação FÍSICA ANO LECTIVO 005 / 006 1º ANO N. º NOME: TURMA: CLASSIFICAÇÃO Um automóvel em movimento, descreve uma trajectória que se apresenta
Escola Secundária Dom Manuel Martins Setúbal 1ª Ficha Avaliação FÍSICA ANO LECTIVO 005 / 006 1º ANO N. º NOME: TURMA: CLASSIFICAÇÃO Um automóvel em movimento, descreve uma trajectória que se apresenta
Geometria Descritiva Representação do Plano
 Geometria Descritiva Representação do Plano Um plano pode ser determinado por uma das quatro possibilidades: - três pontos não alinhados; (1) - uma recta e um ponto exterior; (2) - duas rectas concorrentes;
Geometria Descritiva Representação do Plano Um plano pode ser determinado por uma das quatro possibilidades: - três pontos não alinhados; (1) - uma recta e um ponto exterior; (2) - duas rectas concorrentes;
Assunto: Estudo do ponto
 Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
Assunto: Estudo do ponto 1) Sabendo que P(m+1;-3m-4) pertence ao 3º quadrante, determine os possíveis valores de m. resp: -4/3
GEOMETRIA ANALÍTICA II
 Conteúdo 1 O PLANO 3 1.1 Equação Geral do Plano............................ 3 1.2 Determinação de um Plano........................... 7 1.3 Equação Paramétrica do Plano........................ 11 1.4 Ângulo
Conteúdo 1 O PLANO 3 1.1 Equação Geral do Plano............................ 3 1.2 Determinação de um Plano........................... 7 1.3 Equação Paramétrica do Plano........................ 11 1.4 Ângulo
GDC I AULA TEÓRICA 06
 GDC I AULA TEÓRICA 06 Perspectiva linear de quadro plano. - Análise de desenhos de perspectiva executados à mão levantada e de imagens fotográficas (perspectivas de 1, 2 e 3 pontos de fuga; noção de sombra
GDC I AULA TEÓRICA 06 Perspectiva linear de quadro plano. - Análise de desenhos de perspectiva executados à mão levantada e de imagens fotográficas (perspectivas de 1, 2 e 3 pontos de fuga; noção de sombra
Projeto Rumo ao ITA Exercícios estilo IME
 PROGRAMA IME ESPECIAL 1991 GEOMETRIA ESPACIAL PROF PAULO ROBERTO 01 (IME-64) Um cone circular reto, de raio da base igual a R e altura h, está circunscrito a 1 1 uma esfera de raio r Provar que = rh r
PROGRAMA IME ESPECIAL 1991 GEOMETRIA ESPACIAL PROF PAULO ROBERTO 01 (IME-64) Um cone circular reto, de raio da base igual a R e altura h, está circunscrito a 1 1 uma esfera de raio r Provar que = rh r
Aula 2 Vetores de força
 Aula 2 Vetores de força slide 1 Escalares e vetores Um escalar é qualquer quantidade física positiva ou negativa que pode ser completamente especificada por sua intensidade. Exemplos de quantidades escalares:
Aula 2 Vetores de força slide 1 Escalares e vetores Um escalar é qualquer quantidade física positiva ou negativa que pode ser completamente especificada por sua intensidade. Exemplos de quantidades escalares:
Física I 2010/2011. Aula12 Centro de Massa e Momento Linear II
 Física I 2010/2011 Aula12 Centro de Massa e Momento Linear II Sumário Colisões Momento linear e energia cinética em colisões Colisões inelásticas a uma dimensão Colisões elásticas a uma dimensão Colisões
Física I 2010/2011 Aula12 Centro de Massa e Momento Linear II Sumário Colisões Momento linear e energia cinética em colisões Colisões inelásticas a uma dimensão Colisões elásticas a uma dimensão Colisões
(1, 6) é também uma solução da equação, pois 3 1 + 2 6 = 15, isto é, 15 = 15. ( 23,
 Sistemas de equações lineares generalidades e notação matricial Definição Designa-se por equação linear sobre R a uma expressão do tipo com a 1, a 2,... a n, b R. a 1 x 1 + a 2 x 2 +... + a n x n = b (1)
Sistemas de equações lineares generalidades e notação matricial Definição Designa-se por equação linear sobre R a uma expressão do tipo com a 1, a 2,... a n, b R. a 1 x 1 + a 2 x 2 +... + a n x n = b (1)
Aula 2 - Revisão. Claudemir Claudino 2014 1 Semestre
 Aula 2 - Revisão I Parte Revisão de Conceitos Básicos da Matemática aplicada à Resistência dos Materiais I: Relações Trigonométricas, Áreas, Volumes, Limite, Derivada, Integral, Vetores. II Parte Revisão
Aula 2 - Revisão I Parte Revisão de Conceitos Básicos da Matemática aplicada à Resistência dos Materiais I: Relações Trigonométricas, Áreas, Volumes, Limite, Derivada, Integral, Vetores. II Parte Revisão
ALGA - Eng.Civil - ISE - 2009/2010 - Matrizes 1. Matrizes
 ALGA - Eng.Civil - ISE - 00/010 - Matrizes 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n (m vezes n ou m por n) a uma aplicação A : f1; ; :::; mg f1; ; :::; ng R:
ALGA - Eng.Civil - ISE - 00/010 - Matrizes 1 Matrizes Introdução Se m e n são números naturais, chama-se matriz real de tipo m n (m vezes n ou m por n) a uma aplicação A : f1; ; :::; mg f1; ; :::; ng R:
ESTÁTICA DO PONTO MATERIAL EXERCÍCIOS
 ESTÁTICA DO PONTO MATERIAL EXERCÍCIOS 1. Quando um homem está deitado numa rede (de massa desprezível), as forças que esta aplica na parede formam um angulo de 30 com a horizontal, e a intensidade de cada
ESTÁTICA DO PONTO MATERIAL EXERCÍCIOS 1. Quando um homem está deitado numa rede (de massa desprezível), as forças que esta aplica na parede formam um angulo de 30 com a horizontal, e a intensidade de cada
Projeto Jovem Nota 10 Geometria Analítica Circunferência Lista 3 Professor Marco Costa
 1 1. (Fgv 97) Uma empresa produz apenas dois produtos A e B, cujas quantidades anuais (em toneladas) são respectivamente x e y. Sabe-se que x e y satisfazem a relação: x + y + 2x + 2y - 23 = 0 a) esboçar
1 1. (Fgv 97) Uma empresa produz apenas dois produtos A e B, cujas quantidades anuais (em toneladas) são respectivamente x e y. Sabe-se que x e y satisfazem a relação: x + y + 2x + 2y - 23 = 0 a) esboçar
ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU
 INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU Departamento Matemática Disciplina Matemática I Curso Gestão de Empresas Ano 1 o Ano Lectivo 2007/2008 Semestre 1 o Apontamentos Teóricos:
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA DE VISEU Departamento Matemática Disciplina Matemática I Curso Gestão de Empresas Ano 1 o Ano Lectivo 2007/2008 Semestre 1 o Apontamentos Teóricos:
Professor: José Junio Lopes
 Aula 2 - Tensão/Tensão Normal e de Cisalhamento Média; Tensões Admissíveis. A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a.
Aula 2 - Tensão/Tensão Normal e de Cisalhamento Média; Tensões Admissíveis. A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a.
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Universidade Fernando Pessoa Faculdade de Ciências e Tecnologia 1. Calcule: Capítulo I - Matrizes e Sistemas de Equações Lineares EXERCÍCIOS 1 3 4 3 5 6 1 a + 0 5 1
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Universidade Fernando Pessoa Faculdade de Ciências e Tecnologia 1. Calcule: Capítulo I - Matrizes e Sistemas de Equações Lineares EXERCÍCIOS 1 3 4 3 5 6 1 a + 0 5 1
AÇÃO FORMATIVA EM PRODUÇÃO AUDIOVISUAL
 AÇÃO FORMATIVA EM PRODUÇÃO AUDIOVISUAL Fotograma Um Fotograma é cada uma das imagens fotográficas estáticas captadas pelo equipamento de filmagem, as quais, projetadas em uma certa velocidade, produzem
AÇÃO FORMATIVA EM PRODUÇÃO AUDIOVISUAL Fotograma Um Fotograma é cada uma das imagens fotográficas estáticas captadas pelo equipamento de filmagem, as quais, projetadas em uma certa velocidade, produzem
Tema de Física Eletrostática Força elétrica e campo elétrico Prof. Alex S. Vieira
 Tema de Física Eletrostática Força elétrica e campo elétrico 1) Se, após o contato e posterior separação, F 2 é o módulo da força coulombiana entre X e Y, podese afirmar corretamente que o quociente F
Tema de Física Eletrostática Força elétrica e campo elétrico 1) Se, após o contato e posterior separação, F 2 é o módulo da força coulombiana entre X e Y, podese afirmar corretamente que o quociente F
ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 2013 RECUPERAÇÃO ESTUDOS INDENPENDENTES
 ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 2013 RECUPERAÇÃO ESTUDOS INDENPENDENTES Nome Nº Turma 3 EJAS Data / / Nota Disciplina Matemática Prof. Elaine e Naísa Valor 30 Instruções: TRABALHO DE
ESCOLA ESTADUAL DR. JOSÉ MARQUES DE OLIVEIRA - ANO 2013 RECUPERAÇÃO ESTUDOS INDENPENDENTES Nome Nº Turma 3 EJAS Data / / Nota Disciplina Matemática Prof. Elaine e Naísa Valor 30 Instruções: TRABALHO DE
Propriedade: Num trapézio isósceles os ângulos de uma mesma base são iguais e as diagonais são também iguais.
 125 19 QUADRILÁTEROS Propriedades 1) Num quadrilátero qualquer ABCD a soma dos ângulos internos é 1800. 2) Um quadrilátero ABCD é inscritível quando seus vértices pertence a uma mesma circunferência. 3)
125 19 QUADRILÁTEROS Propriedades 1) Num quadrilátero qualquer ABCD a soma dos ângulos internos é 1800. 2) Um quadrilátero ABCD é inscritível quando seus vértices pertence a uma mesma circunferência. 3)
TOPOGRAFIA. Poligonais
 TOPOGRAFIA Poligonais COORDENADAS RECTANGULARES Quando se pretende representar numa superfície plana zonas extensas da superfície terrestre, é necessário adoptar sistemas de representação plana do elipsóide,
TOPOGRAFIA Poligonais COORDENADAS RECTANGULARES Quando se pretende representar numa superfície plana zonas extensas da superfície terrestre, é necessário adoptar sistemas de representação plana do elipsóide,
FIGURAS DE LISSAJOUS
 FIGURAS DE LISSAJOUS OBJETIVOS: a) medir a diferença de fase entre dois sinais alternados e senoidais b) observar experimentalmente, as figuras de Lissajous c) comparar a frequência entre dois sinais alternados
FIGURAS DE LISSAJOUS OBJETIVOS: a) medir a diferença de fase entre dois sinais alternados e senoidais b) observar experimentalmente, as figuras de Lissajous c) comparar a frequência entre dois sinais alternados
Exercícios Aulas Práticas 2004/2005
 Exercícios Aulas Práticas 2004/2005 Manuel Teixeira Brás César Mário Nuno Moreira Matos Valente 1/17 2/17 Tema: Corpos Rígidos: Sistemas Equivalentes de Forças 7 - Uma força de 150 N é aplicada à alavanca
Exercícios Aulas Práticas 2004/2005 Manuel Teixeira Brás César Mário Nuno Moreira Matos Valente 1/17 2/17 Tema: Corpos Rígidos: Sistemas Equivalentes de Forças 7 - Uma força de 150 N é aplicada à alavanca
O sistema de cofragem para oaredes e pilares
 O sistema de cofragem para oaredes e pilares Sistema de módulos adaptável a cada obra Stem ofrece soluções de cofragem para paredes de qualquer dimensão e forma, acoplando os seus paineis no sentido vertical
O sistema de cofragem para oaredes e pilares Sistema de módulos adaptável a cada obra Stem ofrece soluções de cofragem para paredes de qualquer dimensão e forma, acoplando os seus paineis no sentido vertical
Exercícios: Espelhos planos. 1-(PUC-CAMPINAS-SP) Um pincel de raios paralelos quando refletido por um espelho plano: a) conserva-se paralelo
 Exercícios: Espelhos planos. 1-(PUC-CAMPINAS-SP) Um pincel de raios paralelos quando refletido por um espelho plano: a) conserva-se paralelo d) converge b) diverge e) nenhuma das anteriores c) é difundido
Exercícios: Espelhos planos. 1-(PUC-CAMPINAS-SP) Um pincel de raios paralelos quando refletido por um espelho plano: a) conserva-se paralelo d) converge b) diverge e) nenhuma das anteriores c) é difundido
A) -5,5i - 4,3j - 8,8k B) -19,5i - 16,7j - 14,9k. 5,3i - 1,2j + 4,3k. 0,5i + 6,0j - 4,5k. 9,5i - 6,1j - 4,0k
 Page 1 of 13 Exercício 1 Exercício 2 Exercício 3 Exercício 4 Exercício 5 Exercício 6 Exercício 7 Exercício 8 Exercício 9 Exercício 10 Exercício 11 Exercício 12 Exercício 13 Exercício 14 Exercício 15 Exercício
Page 1 of 13 Exercício 1 Exercício 2 Exercício 3 Exercício 4 Exercício 5 Exercício 6 Exercício 7 Exercício 8 Exercício 9 Exercício 10 Exercício 11 Exercício 12 Exercício 13 Exercício 14 Exercício 15 Exercício
Exercícios de Mecânica - Área 3
 1) O bloco de peso 10lb tem uma velocidade inicial de 12 pés/s sobre um plano liso. Uma força F = (3,5t) lb onde t é dado em segundos, age sobre o bloco durante 3s. Determine a velocidade final do bloco
1) O bloco de peso 10lb tem uma velocidade inicial de 12 pés/s sobre um plano liso. Uma força F = (3,5t) lb onde t é dado em segundos, age sobre o bloco durante 3s. Determine a velocidade final do bloco
Matrizes. matriz de 2 linhas e 2 colunas. matriz de 3 linhas e 3 colunas. matriz de 3 linhas e 1 coluna. matriz de 1 linha e 4 colunas.
 Definição Uma matriz do tipo m n (lê-se m por n), com m e n, sendo m e n números inteiros, é uma tabela formada por m n elementos dispostos em m linhas e n colunas. Estes elementos podem estar entre parênteses
Definição Uma matriz do tipo m n (lê-se m por n), com m e n, sendo m e n números inteiros, é uma tabela formada por m n elementos dispostos em m linhas e n colunas. Estes elementos podem estar entre parênteses
, 10 4. pertence ao conjunto dado? Justifica a resposta e apresenta todos os cálculos que efetuares.
 Teste de Avaliação Escrita Duração: 90 minutos 9 de maio de 0 Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo 0/0 Matemática 9.º B Nome: N.º Classificação: Fraco (0% 9%) Insuficiente (0% 9%) Suficiente
Teste de Avaliação Escrita Duração: 90 minutos 9 de maio de 0 Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo 0/0 Matemática 9.º B Nome: N.º Classificação: Fraco (0% 9%) Insuficiente (0% 9%) Suficiente
Óptica Geométrica 9º EF
 Óptica Geométrica 9º EF Fonte de luz Estrelas Lâmpada acesa Lua Lâmpada apagada Fonte Primária Fonte Secundária Classificação de fontes de luz Quanto a emissão a) Fonte Primária (luminoso): produz a luz
Óptica Geométrica 9º EF Fonte de luz Estrelas Lâmpada acesa Lua Lâmpada apagada Fonte Primária Fonte Secundária Classificação de fontes de luz Quanto a emissão a) Fonte Primária (luminoso): produz a luz
Aprimorando os Conhecimentos de Mecânica Lista 6 Vetores II
 Aprimorando os Conhecimentos de Mecânica Lista 6 Vetores II O texto seguinte refere-se às questões 1 e 2. O Atol das Rocas, localizado em mar territorial brasileiro (aproximadamente 267km da cidade de
Aprimorando os Conhecimentos de Mecânica Lista 6 Vetores II O texto seguinte refere-se às questões 1 e 2. O Atol das Rocas, localizado em mar territorial brasileiro (aproximadamente 267km da cidade de
FÍSICA - 1 o ANO MÓDULO 30 QUANTIDADE DE MOVIMENTO E IMPULSÃO REVISÃO
 FÍSICA - 1 o ANO MÓDULO 30 QUANTIDADE DE MOVIMENTO E IMPULSÃO REVISÃO Como pode cair no enem? Quando uma fábrica lança um modelo novo de automóvel é necessário que muitos testes sejam feitos para garantir
FÍSICA - 1 o ANO MÓDULO 30 QUANTIDADE DE MOVIMENTO E IMPULSÃO REVISÃO Como pode cair no enem? Quando uma fábrica lança um modelo novo de automóvel é necessário que muitos testes sejam feitos para garantir
ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / Nome ; Ano/Turma ; N.º
 EDUCAÇÃO VISUAL ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / APONTAMENTOS DE GEOMETRIA Nome ; Ano/Turma ; N.º 1 - O PONTO - ao colocares o bico do teu lápis no papel obténs um ponto. O
EDUCAÇÃO VISUAL ESCOLA BÁSICA INTEGRADA DE MANIQUE DO INTENDENTE Ano Letivo / APONTAMENTOS DE GEOMETRIA Nome ; Ano/Turma ; N.º 1 - O PONTO - ao colocares o bico do teu lápis no papel obténs um ponto. O
Álgebra Linear I - Aula 20
 Álgebra Linear I - Aula 0 1 Matriz de Mudança de Base Bases Ortonormais 3 Matrizes Ortogonais 1 Matriz de Mudança de Base Os próximos problemas que estudaremos são os seguintes (na verdade são o mesmo
Álgebra Linear I - Aula 0 1 Matriz de Mudança de Base Bases Ortonormais 3 Matrizes Ortogonais 1 Matriz de Mudança de Base Os próximos problemas que estudaremos são os seguintes (na verdade são o mesmo
Equilíbrio de Corpos Extensos
 Equilíbrio de Corpos Extensos 1. (G1 - ifsp 2013) Em um parque de diversão, Carlos e Isabela brincam em uma gangorra que dispõe de dois lugares possíveis de se sentar nas suas extremidades. As distâncias
Equilíbrio de Corpos Extensos 1. (G1 - ifsp 2013) Em um parque de diversão, Carlos e Isabela brincam em uma gangorra que dispõe de dois lugares possíveis de se sentar nas suas extremidades. As distâncias
1ª Lista de exercícios Resistência dos Materiais IV Prof. Luciano Lima (Retirada do livro Resistência dos materiais, Beer & Russel, 3ª edição)
 11.3 Duas barras rígidas AC e BC são conectadas a uma mola de constante k, como mostrado. Sabendo-se que a mola pode atuar tanto à tração quanto à compressão, determinar a carga crítica P cr para o sistema.
11.3 Duas barras rígidas AC e BC são conectadas a uma mola de constante k, como mostrado. Sabendo-se que a mola pode atuar tanto à tração quanto à compressão, determinar a carga crítica P cr para o sistema.
Trabalho 4 - Traçado de linhas equipotenciais e linhas de força.
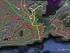 Trabalho 4 - Traçado de linhas euipotenciais e linhas de força. Objectivo:Obtenção e análise de curvas euipotenciais numa superfície a duas dimensões, para duas distribuições de carga. Pretende-se ainda
Trabalho 4 - Traçado de linhas euipotenciais e linhas de força. Objectivo:Obtenção e análise de curvas euipotenciais numa superfície a duas dimensões, para duas distribuições de carga. Pretende-se ainda
Definição de determinantes de primeira e segunda ordens. Seja A uma matriz quadrada. Representa-se o determinante de A por det(a) ou A.
 Determinantes A cada matriz quadrada de números reais, pode associar-se um número real, que se designa por determinante da matriz Definição de determinantes de primeira e segunda ordens Seja A uma matriz
Determinantes A cada matriz quadrada de números reais, pode associar-se um número real, que se designa por determinante da matriz Definição de determinantes de primeira e segunda ordens Seja A uma matriz
Capítulo 7. 1. Bissetrizes de duas retas concorrentes. Proposição 1
 Capítulo 7 Na aula anterior definimos o produto interno entre dois vetores e vimos como determinar a equação de uma reta no plano de diversas formas. Nesta aula, vamos determinar as bissetrizes de duas
Capítulo 7 Na aula anterior definimos o produto interno entre dois vetores e vimos como determinar a equação de uma reta no plano de diversas formas. Nesta aula, vamos determinar as bissetrizes de duas
MOVIMENTO CIRCULAR UNIFORME Força centrípeta
 Departamento de Física da Faculdade de Ciências da Universidade de Lisboa T1 FÍSICA EXPERIMENTAL I - 2007/2008 MOVIMENTO CIRCULAR UNIFORME Força centrípeta 1. Objectivos Verificar a relação entre a força
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa T1 FÍSICA EXPERIMENTAL I - 2007/2008 MOVIMENTO CIRCULAR UNIFORME Força centrípeta 1. Objectivos Verificar a relação entre a força
Aplicações de integração. Cálculo 2 Prof. Aline Paliga
 Aplicações de integração Cálculo Prof. Aline Paliga Áreas entre curvas Nós já definimos e calculamos áreas de regiões que estão sob os gráficos de funções. Aqui nós estamos usando integrais para encontrar
Aplicações de integração Cálculo Prof. Aline Paliga Áreas entre curvas Nós já definimos e calculamos áreas de regiões que estão sob os gráficos de funções. Aqui nós estamos usando integrais para encontrar
Matrizes e Sistemas Lineares. Professor: Juliano de Bem Francisco. Departamento de Matemática Universidade Federal de Santa Catarina.
 e Aula Zero - Álgebra Linear Professor: Juliano de Bem Francisco Departamento de Matemática Universidade Federal de Santa Catarina agosto de 2011 Outline e e Part I - Definição: e Consideremos o conjunto
e Aula Zero - Álgebra Linear Professor: Juliano de Bem Francisco Departamento de Matemática Universidade Federal de Santa Catarina agosto de 2011 Outline e e Part I - Definição: e Consideremos o conjunto
