Uma Fundamentação Intervalar Aplicada à Morfologia Matemática
|
|
|
- Sebastiana Sequeira Duarte
- 5 Há anos
- Visualizações:
Transcrição
1 Universidade Federal do Rio Grande do Norte Centro de Tecnologia Programa de Pós-Graduação em Engenharia Elétrica e de Computação Departamento de Computação e Automação Uma Fundamentação Intervalar Aplicada à Morfologia Matemática Doutorando: Marcia Maria de Castro Cruz Natal/RN - Brasil Setembro de 2008
2 Marcia Maria de Castro Cruz Uma Fundamentação Intervalar Aplicada à Morfologia Matemática Orientadores: Prof. Dr. Adrião Duarte Dória Neto Prof. Dr. Regivan Hugo Nunes Santiago Tese submetida ao programa de Pós-Graduação em Engenharia Elétrica e de Computação da Universidade Federal do Rio Grande do Norte como parte dos requisitos para obtenção do grau de DOUTOR em CIÊNCIAS. Natal/RN- Brasil Setembro de 2008
3 i Catalogação da publicação na fonte. UFRN / Biblioteca Central Zila Seção de Processos Técnicos Mamede Cruz, Marcia Uma Fundamentação Intervalar Aplicada à Morfologia Matemática / Marcia Maria de Castro Cruz. Natal: xviii. 109p. Orientador: Prof. Dr. Adrião Duarte Dória Neto Orientador: Prof. Dr. Regivan Hugo Nunes Santiago Tese (Doutorado) - Universidade Federal do Rio Grande do Norte. Centro de Tecnologia. Programa de Pós-Graduação em Engenharia Elétrica. 1. Processamento de Imagens Intervalares 2. Morfologia Matemática 3. Matemática Intervalar 4. Incerteza 5. Reticulados Completo 6. Imagens Indefinidas 7. Dilatação 8. Erosão RN/UF/BCZM
4 UMA FUNDAMENTAÇÃO INTERVALAR APLICADA À MORFOLOGIA MATEMÁTICA Marcia Maria de Castro Cruz Tese apresentada à Coordenação do Curso de Pós-Graduação em Engenharia Elétrica e de Computação da Universidade Federal do Rio Grande do Norte como requisito parcial à obtenção do grau de Doutor em Ciências. Aprovada, em 05 de Setembro de 2008, pela Comissão Examinadora formada com os seguintes membros: Composição da Banca Examinadora: Adrião Duarte Dória Neto: UFRN, (Doutor), Orientador Graçaliz Pereira Dimuro: UCPEL, (Doutor), Examinador Benjamín René Callejas Bedregal: UFRN, (Doutor), Examinador Aarão Lyra, (Doutor), Examinador: UnP Ronei Marcos de Moraes: UFPB, (Doutor), Examinador Natal/RN - Brasil Setembro de 2008
5 DEDICATÓRIA i Ao meu esposo e filhos, Rubens, Janaina e Izan, que sem a confiança, paciência e o companherismo deles, não teria tido oportunidade de galgar este grau.
6 AGRADECIMENTOS ii Agradecimentos Após esta difícil jornada, quero agradecer a todos aqueles que, de diferentes formas, contribuíram para a realização desse trabalho. Na impossibilidade de citar todos os nomes, destaco alguns, na certeza de que sou grato a todos que direta ou indiretamente contribuíram para o sucesso deste trabalho. A Deus, o ser SUPREMO do universo, presente em todos os momentos. Aos meus amados esposo e filhos (em ordem hereditária), Rubens Leão de Andrade, Janaina de Castro Leão e Izan de Castro leão pelo estímulo, carinho, amor e apoio na concretização deste trabalho. Em especial, um profundo agradecimento ao meu filho Izan que, por muitas vezes me ajudou em vários aspectos desta tese, tais como obtenção de algumas imagens. A minha mãe, que mesmo de longe sempre torceu pelo meu sucesso em tudo que faço, em especial para esse trabalho. Ao meus irmão Jadilson Rubens, que foi um dos maiores incentivadores da minha vida acadêmica. Também as minhas irmãs, Rita de Cássia e Regina Celi pela amizade. Um especial agradecimento a minha querida avó Francisca Amélia (codinome Yayá), que já não está mais entre nós, mas que foi uma das pessoas mais importantes da minha vida. Se não fosse por ela, certamente não chegaria onde eu cheguei, pois foi ela uma das maiores incentivadoras da minha vida estudantil e acadêmica. Aos professores, orientador e co-orientadores, Adrião Duarte Dória Neto, Regivan Hugo Nunes Santiago e Benjamín Rene Callejas Bedregal, pela tão competente orientação, a minha admiração e agradecimento pelo apoio constante, pela confiança, amizade e, principalmente pelo incentivo dedicado durante todo o decorrer desta jornada.
7 AGRADECIMENTOS iii Meu agradecimento especialmente para o porfessor Regivan que me orientou no meu curso de mestrado e aceitou mais uma vez o desafio de me orientar em um curso de maior responsabilidade que é o doutorado. Graças as suas sugestões e críticas, algumas vezes duras, ele conseguiu me mostrar o caminho de aprimoramento dos meus limitados conhecimentos científicos, na área de matemática aplicada. Ao Professor adrião, também devo externar meu profundo reconhecimento pela credibilidade em mim depositada. Também agradeço de coração ao professor Benjamím que aceitou me ajudar em momentos difíceis durante o desenvolvimento desse trabalho e foi de extrema importância para a finalização deste trabalho. A todos vocês, os meus mais sinceros agradecimentos. Aos Professores do DCA, LECA e DIMAp, pelas significativas contribuições que enriqueceram este estudo. Em especial ao professor José Alfredo Costa, que além dos seus ensinamentos como professor, participou de outras atividades tal como a colaboração conjunta de um trabalho em um importante congresso nacional de matemática aplicada, o CNMAC. Ao Prof. Dr. Junior Barrera, da USP de São Paulo, pelas importantes sugestões e pela grande atenção que me teve quando necessitei da ajuda de seus conhecimentos. Aos funcionários da secretaria do Departamento de Matemática, Helio Meira e Nízia Maria Lima, bem como, da secretaria da coordenação do PPGEE, que sempre me atenderam com bastante presteza quando necessitei de seus serviços.
8 Sumário Lista de figuras Resumo Abstract vii xii xiii 1 Introdução 1 2 Uma Abordagem da Morfologia Matemática Clássica Morfologia matemática para imagens binária Conceitos básicos da teoria dos conjuntos As operações de Minkowski Os operadores elementares da morfologia matemática Outros operadores morfológicos Algumas importantes aplicações das operações morfológicas binárias Abordagem algébrica dos operadores morfológicos como reticulado completo Análise binária e reticulados Álgebra de Boole das funções binárias Relação de ordem e reticulados A estrutura dos operadores elementares da morfologia matemática sobre {0,1} E Morfologia matemática para imagens em níveis de cinza iv
9 SUMÁRIO v Os operadores elementares da morfologia matemática para imagens em tons de cinza Outros operadores morfológicos Uma Abordagem da Matemática Intervalar Introdução Análise intervalar Definições básicas Aritmética intervalar Propriedades da aritmética intervalar Relações de ordem Processamento de Imagens Digitais Intervalares Introdução Definições Operações lógicas-aritméticas entre pixels intervalares Morfologia para imagens binárias intervalares Construção do espaço algébrico Ω Imagens binárias contendo incertezas Operações básicas Operações derivadas Morfologia sobre imagens binárias intervalares Operadores sobre imagens binárias intervalares Translação, reflexão e invariança por translação Operações de Minkowiski Conclusão do capítulo Um Modelo Intervalar para Imagens em Níveis de Cinza Construção do espaço algébrico para imagens intervalares em escala de cinzas O reticulado completo das imagens sobre Ω N Imagens intervalares em escala de cinzas
10 SUMÁRIO vi 6.3 Operações morfológicas para imagens intervalars em níveis de cinza Operações básicas Dilatação e erosão para imagens intervalares em níveis de cinzas Outros operadores morfológicos Potenciais aplicações Consclusão sobre o capítulo Considerações Finais Principais contribuições Na matemática intervalar Na morfologia matemática Perspectivas Conclusão final Trabalhos Aceitos e submetidos em Eventos Científicos e Revistas Científicas
11 Lista de Figuras 2.1 Operações de translação e reflexão Operações de soma e subtração de Minkowski Exemplo de elementos estruturante em uma imagem binária Efeitos da dilatação e da erosão em uma imagem binária Efeitos da operação de abertura em uma imagem binária Efeitos da operação de fechamento em uma imagem binária Exemplo de uma operação de gradiente morfológico em imagem binária Exemplo de filtragem morfológica em uma imagem binária Exemplo de uma operação hit-or-miss Exemplo de uma operação de extração de contorno em uma imagem binária Exemplo de esqueletos binários Uma imagem binária Gráfico de uma função binária Representação de uma imagem binária Imagem da Lena e os efeitos causados pelos operadores de dilatação e erosão N Z Q R IR Par ordenado intervalar Representação geométrica da interseção em R Representação geométrica da união em R Imagem média da Lena disjunta com uma imagem constante Imagem média da Lena conjunta com uma imagem constante vii
12 LISTA DE FIGURAS viii 4.3 Imagem da Lena original e negativa Imagem Binarizada Operações básicas e algumas operações derivadas sobre imagens binárias intervalares Operações Morfológicas para imagens binárias intervalares intervalares Imagens apresentando um processo de segmentação em uma mama com suspeito de nódulo canceroso. (a) Imagem original, (b) imagem binarizada e (c) imagem segmentada com o nódulo destacado Estrutura do reticulado Ω N Uma função intervalar com uma translação horizontal Uma função intervalar com uma translação vertical Uma função intervalar com uma translação morfológica Imagem representada por uma função F e por uma função estrurante G Dilatação intervalar de F pela função estrurante G Erosão intervalar de F pela função estrurante G
13 ix Lista de Símbolos N N N + Z Q R R + R n IR IN x i a i j Conjunto dos números naturais Para todo Existe Conjunto dos números naturais Conjunto dos números naturais positivos Conjunto dos números inteiros Conjunto dos números racionais Conjunto dos números reais Conjunto dos números reais positivos Conjunto dos números reais no espaço n Conjunto dos intervalos reais Conjunto dos intervalos naturais Elemento x da posição i de uma sequência Elemento de uma matriz na posição i relativo a linha e j relativo a coluna A = [a 1,a 2 ] Intervalo de extremos a 1 e a 2 A = (a 1,a 2 ) Par ordenado A de abscissa a 1 e ordenada a 2 max{x} Maior elemento do conjunto X min{x} Menor elemento do conjunto X (F) Supremo de uma função (F) ínfimo de uma função
14 LISTA DE SÍMBOLOS x Subconjunto, contém ou igual Relação de ordem do domínio contínuo real Pertence Não pertence União Interseção A B União convexa Menor ou igual Maior ou igual KM dist Menor ou igual na ordem de Kulisch-Miranker menor ou igual na ordem parcial em C Menor ou igual na ordem da aproximação Distância entre intervalos A Módulo do intervalo A diam Diâmetro de um intervalo med Ponto médio de um intervalo R Relação binária entre intervalos f : R R Função f cujo domínio e contra-domínio é conjunto dos números reais F : IR IR Função intervalar F cujo domínio e contra-domínio é o conjunto dos intervalos reais
15 LISTA DE SÍMBOLOS xi I md Ω Ω N Ω E Ω E N Imagem média Disjunção Conjunção Conjunto de valores Conjunto finito de valores intervalares Conjunto das funções que representam imagens binárias intervalares Conjunto das funções que representam imagens intervalares em níveis de cinza Operador de dilatação Operador de erosão + Soma limitada Diferença limitada Maior elemento Menor elemento
16 RESUMO xii Resumo Este trabalho apresenta uma abordagem intervalar para lidar com imagens que contêm incertezas, bem como tratar essas incertezas através de operações morfológicas. Foram apresentado dois modelos intervalares. Para o primeiro, é introduzido um espaço algébrico com três valores que foi construído com base na lógica tri-valorada de Lukasiewiecz. Com essa estrutura algébrica, introduz-se a teoria das imagens binárias intervalares, que estende o modelo clássico binário, com a inclusão da informação de incerteza. A mesma pode ser aplicada para representar imagens binárias com incerteza em certos pixels, que foi originada, por exemplo, durante o processo da aquisição da imagem. A estrutura reticular dessas imagens permite a definição de operadores morfológicos, onde as incertezas são tratadas localmente. O segundo modelo, estende o modelo clássico para imagens em níveis de cinza, onde as funções que representam essas imagens são mapeadas em um conjunto finito de valores intervalares. A estrutura algébrica desse conjunto pertence a classe dos reticulados completos, o que permite a definição dos operadores elementares da morfologia matemática, dilatação e erosão para essas imagens. Dessa forma, fica estabelecida uma teoria intervalar aplicada à morfologia matemática para tratar problemas de incertezas em imagens.
17 ABSTRACT xiii Abstract This work present a interval approach to deal with images with that contain uncertainties, as well, as treating these uncertainties through morphologic operations. Had been presented two intervals models. For the first, is introduced an algebraic space with three values, that was constructed based in the tri-valorada logic of Lukasiewiecz. With this algebraic structure, the theory of the interval binary images, that extends the classic binary model with the inclusion of the uncertainty information, was introduced. The same one can be applied to represent certain binary images with uncertainty in pixels, that it was originated, for example, during the process of the acquisition of the image. The lattice structure of these images, allow the definition of the morphologic operators, where the uncertainties are treated locally. The second model, extend the classic model to the images in gray levels, where the functions that represent these images are mapping in a finite set of interval values. The algebraic structure belong the complete lattices class, what also it allow the definition of the elementary operators of the mathematical morphology, dilation and erosion for this images. Thus, it is established a interval theory applied to the mathematical morphology to deal with problems of uncertainties in images.
18 Capítulo 1 Introdução A área de processamento de imagens digitais está evoluindo continuamente, e a cada dia surgem novas técnicas cada vez mais sofisticadas para a análise de imagens digitais. Estudos mais avançados desta área inicialmente foram direcionados para o processamento de imagens espaciais, porém as pesquisas foram se estendendo e hoje atinge as mais diversas áreas do mundo científico. Durante os últimos anos tem havido um aumento crescente no nível de interesse desta área, voltada para morfologia matemática, redes neurais, lógica fuzzy entre outras. Alguns trabalhos de processamento de imagens, entre livros e artigos que serviram de fontes de pesquisa nesse trabalho, podem ser encontrados em [20, 35, 45, 57] Uma das questões ao longo dos anos, que tem sido aprimorada no processamento de imagens digitais, são a ocorrência de erros decorrentes de alguma(s) etapas do processo de análise de imagens. Várias metodologias vem sendo usadas para o controle desses erros, uma delas é através da teoria fuzzy que de um modo geral lida com esse tipo de problema. Existe uma ampla literatura que aborda a teoria fuzzy e o processamento de imagens, incluindo morfologia matemática. Algumas dessas abordagens podem ser encontradas em([16, 22]). Outras são através de wavelets ([23]) e também de modelos de distribuição probabilístico tal como, processo estocástico [39, 70]. Podemos citar por exemplo, um estudo relativo à avaliação de imagens para diagnósticos específicos, como no caso de uma imagem médica ou simplesmente uma região em um mapa onde existe a necessidade de exatidão, uma vez que certeza é um fator fundamental nestes casos. Os diversos trabalhos nesta área têm como objetivo a melhoria da informação visual para a interpretação do 1
19 CAPÍTULO 1. INTRODUÇÃO 2 especialista, bem como, para o melhor processamento de dados de cenas para a percepção automática através de máquinas. O processamento de imagens digitais envolve operações computacionais que capturam uma imagem real e a discretiza espacialmente em uma matriz de pixel. Os erros numéricos ocorrem com facilidade, uma vez que, diversos fatores influenciam na aquisição da imagem como a iluminação, reflectância dos objetos e capacidade limitada ao aparelho de captura. As imagens intervalares possibilitam um controle maior da informação. Alguns trabalhos destacam-se na área de processamento de imagens digitais, dentre eles citamse [32, 34, 52, 69], nos quais constatou-se que foram realizadas importantes abordagens e algumas aplicações para a processamento de imagens digitais usando a lógica fuzzy, redes neurais e morfologia fuzzy. Pode-se citar por exemplo, o desenvolvimento de filtros fuzzy e a extensão de algumas redes neurais para a utilização da lógica fuzzy em aplicações em clusterização de imagens [52]. Algumas aplicações da lógica fuzzy utilizadas no processamento de imagens digitais incluindo morfologia matemática podem ser vistas em [53] e [1]. Outras referências sobre a teoria fuzzy podem ser encontradas em [10, 42, 49, 69]. A morfologia matemática é uma das áreas de destaque do processamento de imagens com inúmeras práticas de análise de imagens, tais como: filtragens de ruídos, reconhecimento e classificação de padrões, segmentação, reconstrução, extração de objetos de interesse, etc. Introduzida na década de 60 por Jean Serra e George Matheron na Ècole Nationale Superiéure des Mines de Paris [46? ], através da morfologia matemática é possível se fazer transformações entre reticulados completos, os quais são chamados de operadores morfológicos. Inicialmente foi construída para imagens binárias com base na teoria dos conjuntos onde foram introduzidos os operadores elementares dilatação e erosão. Alguns anos depois, na década de 80, Serra e Matheron, pecebendo uma série de características interessantes destes operadores, formalizaram a teoria para o dominio dos reticulados completos. Essa formalização levou a ampliação e generalização da área para imagens em escala de cinzas e depois também para imagens a cores. Importantes trabalhos sobre morfologia matemática que apresentam abordagens teóricas, modelos e importantes aplicações, podem ser vistos em [24, 25, 41, 63]. A matemática intervalar é uma teoria originada na década de 60 [60] com o objetivo
20 CAPÍTULO 1. INTRODUÇÃO 3 de tratar questões de exatidão e eficiência que surgem na prática da computação científica e na resolução de problemas numéricos. Moore apresentou uma arimetica para intervalos, com base na aritmética dos reais. A matemática intervalar se apresenta como uma ferramenta poderosa para a análise e controle de erros em computação científica. Pela sua natureza de tratar os números não mais como entes pontuais, mas como intervalos que encapsulam estes números, é possível, de uma forma segura, armazenar os dados físicos através de uma medida provável e um possível porcentual de erro associado. Isto faz com que, ao final do processo matemático-computacional, se tenha uma estimativa da influência destes erros de entrada no resultado final obtido. Existem um número significativo de trabalhos desenvolvidos nesta área, dentre eles pode-se citar: [12, 13, 17, 51, 56] Atualmente, a matemática intervalar ultrapassou as fronteiras das aplicações numéricas, sendo muito utilizada para aplicações no tratamento e modelagem da incerteza em computação, no processamento de informações fuzzy, na teoria de controle, na inteligência artificial, representação do conhecimento, redes, computação gráfica, processamento de imagens e diversas outras aplicações em ciência e tecnologia que lidam com dados incertos. [38, 59]. Pode-se dizer que a computação intervalar tem sido bem sucedida em aplicações em áreas como engenharia elétrica, física, engenharia química, localização de depósitos de minerais e petróleo, estimação de erros em sistemas de laser, engenharia da computação, no controle da mobilidade de robôs, cálculo da relação profundidade-pressão em reservatórios, modelagem geométrica e Sistema multiresolucional. Pode-se citar, por exemplo, trabalhos recentes tais como, o desenvolvido por Grigoletti e Dimuro em [55] que apresentou um software para a análise de circuitos elétricos baseado na filosofia de software livre e na Matemática Intervalar. Este é capaz de automaticamente avaliar a influência das tolerâncias dos valores nominais dos resistores sobre as tensões nodais do circuito elétrico. Neste trabalho, será apresentada uma fundamentação matemática para lidar com incertezas em imagens, bem como tratar essas incertezas através de operações morfológicas. Para essa abordagem, serão introduzidos dois modelos intervalares. Para o primeiro modelo, foi introduzido um espaço algébrico representado por um conjunto de três valores construído com base na lógica tri-valorada de Lukasiewiecz. Com essa
21 CAPÍTULO 1. INTRODUÇÃO 4 estrutura algébrica, introduz-se a teoria das imagens binárias intervalares, que estende o modelo clássico binário, com a inclusão da informação de incerteza. A estrutura reticular dessas imagens permitiu definir os operadores morfológicos, onde as incertezas são tratadas localmente. O segundo modelo, estende o modelo clássico de imagens em níveis de cinza, onde as funções que representam essas imagens são mapeadas em um conjunto finito de valores intervalares. A estrutura algébrica desse conjunto pertence a classe dos reticulados [37], o que também permitiu definir os operadores elementares da morfologia matemática, dilatação e erosão. A teoria, será baseada na matemática intervalar, ou seja, apresenta-se uma generalização da teoria da morfologia clássica para a teoria intervalar, onde ao invés de lidar com imagens de valores pontuais (pixels), lida-se com valores (pixels) intervalares. Dessa forma, será mostrado que, os modelos intervalares apresentados, satisfazem as propriedades fundamentais para a introdução dos operadores morfológicas nessa ótica. O principal objetivo do uso de intervalos será lidar com questões de incertezas em pixels de imagens. Esses problemas em geral ocorrem principalmente por causa dos erros durante a aquisição ou processo de discretização da imagem original (contínua) para a imagem digital (discreta). Tais erros, na maioria das vezes, conduzem a incertezas com relação à intensidade do brilho de pixels da imagem levando a importantes perdas de informações. Como trabalhos mais recentes, algumas pesquisas foram feitas envolvendo matemática intervalar e processamento de imagens. Kearfott e Kreinovch em [33] apresentam uma abordagem sobre o uso de métodos intervalares em sistemas de multiresolução. Naquele trabalho é mostrado que a estimativa do erro quando são tomadas aproximações de imagens de baixa resolução podem ser controladas por métodos intervalares. Uma outra importante contribuição nessa linha pode ser encontrada em [4] onde Lyra, desenvolve "Uma Fundamentação Matemática para o Processamento de Imagens Digitais Intervalares". Nesta discertação, apresentam-se diversos conceitos fundamentais da área de processamento de imagens, dentro da ótica intervalar, inclusive como captar uma imagem digital intervalar a partir de uma imagem real. Um dos mais recentes trabalhos nessa direção, foi desenvolvido por Takahashi et all em [6], que apresentou uma aplicação
22 CAPÍTULO 1. INTRODUÇÃO 5 de um método de segmentação de imagens em mamas densas, usando imagens digitais intervalares. Para lidar com problemas de incerteza pesquisadores da área de morfologia matemática tem feito uso de métodos através da teoria fuzzy. Existem diversas abordagens sobre essa teoria em operações morfológicas [10, 29]. Esse trabalho tem similaridade com a teoria fuzzy, pois também lida com indecisões ou imprecisões em determinadas regiões de uma imagem. Tanto a teoria fuzzy, quanto a teoria intervalar, são ferramentas usadas para tratar as incertezas e otimização de erros computacionais. Entretanto, esta é a primeira abordagem que relaciona as duas áreas: morfolologia matemática e matemática intervalar e, obviamente o objetivo é introduzir um modelo intervalar que permita estimar erros com a melhor precisão possível. As imagens intervalares possibilitam um controle maior da informação, subsidiando melhor ao especialista nas tomadas de decisões, por exemplo, buscar em uma imagem intervalar de um mamograma regiões fundamentais, como uma área suspeita de existência de nódulo canceroso. Neste caso, o especialista vai poder obter informações (intervalares), visualizar e decidir, de forma que garanta um diagnóstico mais preciso sobre o grau gravidade do caso. A contribuição científica desse trabalho é oferecer uma abordagem teórica ao mundo científico em que são integradas duas importantes áreas: Morfologia Matemática e Matemática Intervalar, que permita tratar com problemas das incertezas que frequentemente aparecem no tratamento de imagens. Será oferecido então, mais uma ferramenta de controle de erros computacionais, abrindo caminho para o estudo prático dos novos modelos, bem como, a obtenção de um maior controle nas variações decorrentes de fatores que levam as incertezas. Será dado ênfase aos conceitos oriundos da matemática intervalar, herdando a característica desta abordagem, que é o controle do erro computacional, que poderá advir de ruídos, do processo de aquisição, digitalização, bem como, processos de filtragens, processos de segmentação, ou de algum outro que são utilizados no processamento de imagens morflogicamente. Esta discertação está dividida em sete capítulos descritos a seguir: Capítulo 1. Introdução. Capítulo 2. Uma abordagem da morfologia matemática clássica: Neste capítulo,
23 CAPÍTULO 1. INTRODUÇÃO 6 serão apresentados os principais conceitos clássicos dessa teoria, tanto para as imagens binárias quanto para imagens em tons de cinza, apresentando inclusive algumas técnicas e aplicações usando os operadores morfológicos. Capítulo 3. Uma abordagem da matemática intervalar: Para esse capítulo, serão apresentados os principais conceitos da matemática intervalar que nortearão o desenvolvimento desta tese, tais como a arimética de Moore e algumas propriedades algébricas desta teoria que serão de fundamental importância no desenvolvimento do modelo aqui proposto. Capítulo 4. O processamento de imagens digitais intervalares: Aqui, apresenta-se uma noção da abordagem feita por Lyra (e colaboradores), onde ele introduz uma abordagem matemática de conceitos fundamentais do processamento de imagens que foram redefinidos sob uma nova visão: a visão intervalar. Capítulo 5. Um modelo intervalar para lidar com incertezas entre dois pixels de imagens: Neste capítulo, será introduzido o primeiro resultado modelo intervalar para um conjuto de três elementos, com o objetivo de lidar localmente com as questões de incertezas em imagens. Capítulo 6. Um modelo intervalar para imagens em escala de cinzas: Neste capítulo, apresenta-se uma abordagem mais geral, que estende o modelo apresentado no Capítulo 5. Em outras palavras, introduz-se uma teoria intervalar para lidar com questões de incertezas, em um sentido mais amplo no caso de tons de cinza, ou seja, considera-se um conjunto que engloba valores de tons de cinza para conjuntos finitos. Capítulo 7. Considerações finais.
24 Capítulo 2 Uma Abordagem da Morfologia Matemática Clássica Uma forma elegante de resolver problemas de processamento de imagens é através da utilização de uma base teórica consistente. Uma destas teorias é a morfologia matemática. Esta teoria diz que é possível fazer transformações entre reticulados completos, os quais são chamados de operadores morfológicos. Na morfologia matemática existem quatro classes básicas de operadores: dilatação, erosão, anti-dilatação e anti-erosão, chamadas de operadores elementares. Banon e Barrera em [36] provaram que todos os operadores morfológicos, no caso binário, invariantes por translação podem ser obtidos a partir de combinações de operadores elementares juntamente com as operações de união e intersecção. Usando estes operadores elementares é possível construir uma linguagem formal, a linguagem morfológica, e sua implementação é chamada máquina morfológica. Um exemplo de uma máquina morfológica é a MMach ([25]). Neste capítulo apresentaremos alguns conceitos básicos da morfologia matemática clássica. Morfologia Matemática pode ser descrita como uma ferramenta para extração de componentes de uma imagem digital que sejam úteis na representação e descrição da forma de uma região, como por exemplo, detecção de bordas. Outro aspecto do uso das técnicas morfológicas está no pré e pós processamento de imagens, como filtragem. As operações morfológicas elementares, a dilatação e a erosão, foram introduzidos a partir das noções de soma e subtração de Minkowski. Inicialmente as transformações foram produzidas para imagens binárias (i.e. cujos pixels podem tomar apenas os valores 0 7
25 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA8 ou 1) pelas dilatações e erosões e dependem de padrões predefinidos que são chamados elementos estruturantes, que as sondam localmente. Na dilatação, verifica-se quando o elemento estruturante toca o objeto (i.e., os pixels da imagem binária que têm o valor 1) e na erosão, quando ele está contido. De acordo com a definição desses operadores, obtem-se como resultado, uma imagem transformada. As bases teóricas da morfologia matemática para subconjuntos foram formalizadas pelos próprios Serra e Matheron, que estudando as dilatações e erosões, descobriram uma coleção de propriedades e chegaram a um resultado bastante interessante: "qualquer operador invariante por translação e isotônico ou crescente (i.e., que preserva a relação de inclusão) pode ser decomposto como um supremo de erosões ou ínfimo de dilatações. Em outros palavras, as dilatações e erosões são os elementos fundamentais para construir uma ampla classe de operadores". A morfologia matemática tem se mostrado útil na extração de componentes da imagem na representação e descrição da forma da região, tais como: extração do contorno, esqueletos morfológicos, fecho convexo, filtragem morfológica, afinamento, espessamento, etc. Conjuntos em morfologia matemática representam objetos em uma imagem. O elemento do conjunto é a coordenada (x,y) do pixel que pertence ao objeto do espaço discreto Z 2. A Morfologia matemática consiste em extrair informações relativas à geometria e à topologia de um conjunto desconhecido de uma imagem, a partir de transformações de formas, realizadas através dos operadores dilatação e erosão. A dilatação faz com que os objetos dilatem ou aumentem de tamanho. A erosão faz com que eles encolham. A quantidade e maneira como eles aumentam ou encolhem depende da escolha do "elemento estruturante". No caso das imagens binárias, a morfologia matemática pode ser definida como sendo um conjunto básico de operações que são utilizadas para transformar a estrutura geométrica de uma imagem. 2.1 Morfologia matemática para imagens binária Nesta seção apresentaremos os principais conceitos da morfologia matemática para imagens binárias, iniciando com algumas definições básicas da teoria dos conjuntos.
26 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA Conceitos básicos da teoria dos conjuntos Sejam A e B dois conjuntos, cujos componentes são pares ordenados dados por a = (a 1,a 2 ) e b = (b 1,b 2 ), respectivamente. A somaé dada por: A + B = (a 1 + b 1,a 2 + b 2 ) A diferença é dada por A B = (a 1 b 1,a 2 b 2 ). A translação de A por x = (x 1,x 2 ), é definida como: (A) x = {c c = a + x, a A} A reflexão é definida por B = {x x = b, a B} O complemento do conjunto A é definida por: A c = {x x A} A Figura 2.1 mostra duas importantes operações básicas sobre conjuntos que serão utilizada nesse trabalho. Figura 2.1: Operações de translação e reflexão As operações de Minkowski A adição de Minkowski baseada na teoria dos conjuntos foi proposta por Minkowski (1903) para caracterizar medidas integrais de certos conjuntos esparsos. A adição de Minkowski pode ser definida como a seguir [25]. Seja E o conjunto de pares ordenados tal que E = Z Z e Sejam A e B dois subconjuntos de E. A soma de Minkowski é definida por: A + B = {x E a A, b B x = a + b} (2.1.1)
27 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA10 Ou equivalentemente A B = b B(A + {b}) (2.1.2) E a subtração de Minkowski é definida por: A B = {x E b B, a A : x = a b} (2.1.3) Ou equivalentemente A B = b B(A {b}) (2.1.4) A Figura 2.2 (extraída de [25]) mostra exemplos da soma e subtração de Minkowski respectivamente. Figura 2.2: Operações de soma e subtração de Minkowski Os operadores elementares da morfologia matemática As transformações sobre imagens binárias, fazendo uso das dilatações e erosões dependem de padrões predefinidos (forma e tamanho), denominados elementos estruturantes, que são comparados ao conjunto desconhecido da imagem. O resultado desta transformação permite avaliar tal conjunto. O elemento estruturante é um conjunto pre-definido. O seu formato e tamanho possibilitam testar e quantificar de que maneira ele está ou não está contido na imagem. Na Figura 2.3 tem-se um exemplos de elementos estruturantes em imagem binária. Marcando os resultados das posições onde o elemento estruturante inclui-se na imagem, temos uma primeira resposta sobre a estrutura geométrica dessa imagem. Mudando o elemento estruturante, tem-se outras respostas
28 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA11 sobre a estrutura geométrica da imagem. O tipo e a natureza da informação extraída depende necessariamente do tipo do elemento estruturante e do tipo da imagem estudada. Por exemplo, a natureza bordas quadradas e desejamos obter bordas arredondadas. Nesse caso, escolhe-se um elemento estruturante na forma circular. Figura 2.3: Exemplo de elementos estruturante em uma imagem binária Seja E = Z Z, uma grade definida no espaço Euclidiano bidimensional e A e B subconjuntos de E, a operação de dilatação é definida por A B = {x B x A φ} (2.1.5) Ou A B = {x [ B x A] A} (2.1.6) A erosão é definida por A B = {x (B) x A} (2.1.7) Em termos da soma e subtração de Minkowski, as operações de dilatação e erosão são definidas respectivamente por A B = {x E x = a + b,a A,b B} (2.1.8) A B = {x E x + b A b B} (2.1.9) Ou equivalentemente por A B = b B(A + {b}) (2.1.10) A B = b B(A {b}) (2.1.11) Os principais efeitos da dilatação e da erosão são: a dilatação expande uma imagem, enquanto a erosão a encolhe, como mostra a Figura 2.4
29 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA12 Figura 2.4: Efeitos da dilatação e da erosão em uma imagem binária Outros operadores morfológicos Os operadores dilatação e erosão, aplicados isoladamente, são transformações que nem sempre evidenciam características das imagens, mas permitem construir algumas funções muito interessantes, como por exemplo, o fechamento, a abertura, o gradiente morfológico entre outros. Abertura É uma operação que consiste em aplicar-se uma erosão seguida de dilatação. A abertura de um conjunto, denotada A B, é definida como: A B = (A B) B (2.1.12) A operação de abertura tem como principais efeitos: Separar objetos muito próximos em uma imagem, ou seja, criar espaços (aberturas) entre objetos na imagem; Eliminar ruídos (pixels negros aleatoriamente espalhados em toda a imagem); Regularizar os contornos e eliminar pequenas "ilhas"e "cabos"estreitos de uma imagem binária; A Figura 2.5 apresenta um exemplo de um procedimento de abertura em uma imagem binária. Note que, o objetivo é eliminar um cabo estreito para separar a imagem em duas partes. Além disso, como o elemento estruturante tem a forma circular, o resultado é uma imagem com as bordas arredondadas. A figura é descrita do seguinte modo: (a) imagem original; (b) Aplicação da erosão com elemento estrurante circular; (c) Imagem resultante da erosão; (d) Aplicação da dilatação sob a imagem (c), com o mesmo elemento estruturante; (e) Imagem resultante obtida por abertura.
30 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA13 Figura 2.5: Efeitos da operação de abertura em uma imagem binária Fechamento É uma operação que consiste em aplicar-se uma dilatação seguida por erosão. fechamento, é definido como: O A B = (A B) B (2.1.13) A operação de fechamento tem como principais efeitos: Eliminar espaços entre objetos em uma imagem; Eliminar falhas dentro dos objetos da imagem (pixels brancos em um objeto negro, por exemplo); Suavizar as bordas de um objeto na imagem. Suprimir pequenos "lagos"e "canais"estreitos em uma imagem Utilizando-se a mesma imagem e o mesmo elemento estruturante do exemplo anterior, a Figura 2.6 mostra uma operação de fechamento, no caso, o objetivo é a eliminação de uma fenda. A figura é descrita do seguinte modo: (a) imagem original; (b) Aplicação da dilatação; (c) Imagem resultante da dilatação; (d) Aplicação da erosão sob a imagem (c); (e) Imagem resultante obtida por fechamento. Gradiente Morfológico O gradiente morfológico é uma operação frequentemente utilizada para obtenção de
31 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA14 Figura 2.6: Efeitos da operação de fechamento em uma imagem binária contorno de objetos em figuras binárias e realçar o contorno de objetos em imagens em tons de cinza. Essa operação é composta de três operações: erosão, dilatação e subtração e é definido como sendo a diferença entre a dilatação e a erosão. Grad(A) = (A B) (A B) (2.1.14) A Figura 2.7 mostra um exemplo Figura 2.7: Exemplo de uma operação de gradiente morfológico em imagem binária Filtros Morfológicos Exploram propriedades geométricas dos sinais. As máscaras são os elementos estruturantes que apresentam valores 0 ou 1 na matriz que correspondem ao pixel considerado. Os filtros morfológicos básicos são: filtro da mediana, erosão e dilatação. O processo de filtragem são sequências de operações de abertura e fechamento. A Figura 2.8 apresenta um exemplo de filtragem morfológica para imagem binária usando operadores de abertura e fechamento. Operador Hit-or-Miss
32 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA15 Figura 2.8: Exemplo de filtragem morfológica em uma imagem binária É possível combinar erosão e dilatação para produzir um operador que tem uma ação como esta: acerto e erro (folga). O operador leva dois elementos, o primeiro é o acerto e o outro é o erro. O operador é definido por A B = (A B 1 ) (A c B 2 ) (2.1.15) onde A é a imagem original e B 1 e B 2 são os elementos estrurantes. A Figura 2.9 mostra uma aplicação do operador hit-or-miss. Figura 2.9: Exemplo de uma operação hit-or-miss Extração de Fronteiras A fronteira de um conjunto A, denotado β(a) pode ser obtida como segue β(a) = A (A B) (2.1.16) A figura 2.10 mostra um exemplo de uma extração de bordas.
33 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA16 Figura 2.10: Exemplo de uma operação de extração de contorno em uma imagem binária Algumas importantes aplicações das operações morfológicas binárias A principal aplicação de morfologia, no caso de imagens binárias, é a extração de componentes da imagem que sejam úteis na representação e na descrição de formas. Algoritmos que fazem o afinamento, o espessamento, a extração de fronteiras e o esqueleto de uma região, entre outros, são bastante úteis nesse expediente. O afinamento visa remover os pixels de um grupo de componentes conectados, até restar apenas um estreito conjunto. Pode ser definido em função da transformada Hit-or-miss. Outra importante aplicação para a representação estrutural da forma de um objeto consiste na obtenção do seu esqueleto através do algoritmo de afinamento. Em vez de bordas pode-se extrair seu eixo medial, que são linhas finas que condensam a informação original enquanto se tenta preservar a homotopia dos objetos. Esse processo é bastante utilizado em problemas de inspeção automática de circuitos impressos, e também bastante útil na segmentação morfológica. Existem duas formas de esqueletização. Lantuejoul ([19]) definiu um tipo particular de esqueleto, usando transformações da morfologia matemática, para aplicações na compressão de dados, com a intenção de que o objeto original pudesse ser reconstruído a partir do seu esqueleto. Este tipo de esqueleto também tem aplicações úteis para a representação e o reconhecimento de objetos. O esqueleto pode ser definido como uma sucessão de operações de erosão dados por n S(A) = S k (A) (2.1.17) k=0
34 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA17 Onde S k (A) é dado por S k (A) = (A kb) (A kb) B (2.1.18) onde k = 1,2,...n. A Figura 2.11, mostra um exemplo de esqueleto binário. Figura 2.11: Exemplo de esqueletos binários 2.2 Abordagem algébrica dos operadores morfológicos como reticulado completo Nesta seção será feita uma abordagem algébrica dos operadores morfológicos como reticulado completo, que foi desenvolvida por Banon e Barrera em [25]. A estrutura algébrica desses operadores morfológicos como reticulados, foi introduzida no início da década de 80 pelos criadores Matheron e Serra que, a partir daí mudaram os rumos da teoria. Antes de apresentar a estrutura dos reticulados e dos operadores morfológicos nesse domínio, será feita uma breve introdução de análise das imagens binárias Análise binária e reticulados Seja E um conjunto não vazio. As imagens binárias podem ser representadas por subconjuntos, ou equivalentemente, por funções binárias. Seja X um subconjunto de E e (E) a coleção de todos os subconjuntos de E, então, X (E). A figura 2.12 mostra a representação de uma imagem binária em uma grade E (ou conjunto de pixels).
35 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA18 Figura 2.12: Uma imagem binária Definição Uma função binária é definida e denotada por f : E {0,1}, isto é, para cada valor de E a função toma valor 0 ou 1. Sendo {0,1} E o conjunto de todas as funções binárias, então f {0,1} E. A Figura 2.13 mostra o gráfico de uma função binária. Observe que o gráfico é formado pelo conjunto de pontos da forma (x, f (x)). Figura 2.13: Gráfico de uma função binária Observe tambem na Figura 2.13 que a representação por uma função binária a imagem, é assimilada à função binária que toma o valor 0, nos elementos x de E que representam a posição dos pixels pretos e o valor 1, nos elementos x de E que representam a posição dos pixels brancos. A função binária f é chamada de imagem e para todo x em E, o par (x, f (x)) é chamado de pixel da imagem f, x é a posição do pixel e f (x) é seu valor. A Figura 2.14, mostra a representação de uma imagem binária Álgebra de Boole das funções binárias As operações sobre as imagens binárias são aquelas que derivam das operações usuais sobre subconjuntos ou funções binárias. Com estas operações, as imagens têm uma
36 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA19 Figura 2.14: Representação de uma imagem binária estrutura de Álgebra de Boole. Seja {0,1} E o conjunto das funções binárias. {0,1} E,,,, onde, e são as operações de união, interseção e complemento respectivamente, dadas por: ( f 1 f 2 )(x) = f 1 (x) f 2 (x) (2.2.1) ( f 1 f 2 )(x) = f 1 (x) f 2 (x) (2.2.2) ( f )(x) = f (x) (2.2.3) forma uma álgebra de Boole, Extensão das operações de união e interseção das funções Binárias A união e a interseção de uma família dos elementos f i é o elemento de {0,1} E definido respectivamente por 1, se i I, f i (x) = 1 ( f i ) i I (x) = 0, caso contrário 1, se i I, f i (x) = 1 ( f i ) i I (x) = 0, caso contrário (2.2.4) (2.2.5) Se I for vazio então f i (x) 0 e f i (x) 1, x E Relação de ordem e reticulados Um dos conceitos importantes da Morfologia matemática é o de relação de ordem parcial. Nesta seção, será apresentado esse conceito para funções binárias, utilizando-se a relação menor ou igual. [25]
37 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA20 Relação de ordem O conjunto {0,1} E das funções binárias definidas em E provido da relação de ordem "menor que"forma um conjunto parcialmente ordenado, denotado ({0,1} E, ), ou seja satisfaz os três axiomas: (prova em [25], pp 22) f (x) f (x) (reflexividade) f (x) g(x) e g(x) f (x) f (x) = g(x) (anti-simetria) f (x) g(x) e g(x) h(x) f (x) h(x) (transitividade) Reticulados Muitos conjuntos parcialmente ordenados gozam da propriedade de conterem o ínfimo e o supremo de um par qualquer de elementos do sistema. Os reticulados por exemplo é um deles. Essa característica dos reticulados nos permite usá-las em teorias tanto algébrica como lógicas. Definição Seja (L, ) uma ordem parcial e, L tal que x e x, para todo x L. L diz-se um reticulado se para todo x,y L o conjunto x,y tem ínfimo e supremo em L denotados por x y e x y, respectivamente. Se além disso, L satisfaz as igualdades x (y z) = (x y) (x z) e x (y z) = (x y) (x z) é dito distributivo. Exemplo O conjunto de todas as funções reais de variável real definidos num intervalo a x b, parcialmente ordenados pela relação f g, se e somente se f (x) g(x) para todo x [a,b] é um reticulado. O supremo é a função definida por ( f g)(x) = max{ f (x),g(x)} e o ínfimo é a função definida por ( f g)(x) = min{ f (x),g(x)} O conjunto de todos os subespaços de um espaço vetorial parcialmente ordenado pela relação de inclusão é um reticulado. O ínfimo é a interseção e o supremo é o subespaço gerado pela união.
38 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA21 Seja a coleção dos subconjuntos de X, ( ou o conjunto das partes de X). Então ( (X),, ) é um reticulado distributivo, onde e. Definição (Reticulado Completo) Seja (L,, ) um reticulado. L diz-se um reticulado completo se todo subconjunto X L tem supremo e tem ínfimo, denotados por X e X (ou supx e in f X ), respectivamente. Podemos dizer que um reticulado completo é uma estrutura do tipo (L,,,, ), onde,, e são definidos acima. L diz-se distributivo se ( X) Y = x y x X,Y Y e ( X) Y = x y x X,y Y e ( X) Y = x y x X,y Y. Em particular L deve satisfazer as equações de distributividade com relação as operações e. Exemplo A estrutura ( (X),, ) é um reticulado completo distributivo, Reticulado das funções binárias O conjunto parcialmente ordenado ({0,1} E, ) das funções binárias definidas em E, provido das operações de união e interseção, forma um reticulado completo. Em outros termos, para todo conjunto de indices I, estas operações verificam os dois axiomas abaixo. Para toda família ( f i ) i I em ({0,1} E temos que ( f i ) i I = supf i (2.2.8) onde ( f i ) i I = in f F i (2.2.9) F i = { f {0,1} E i I, f i = f } (2.2.10) A estrutura dos operadores elementares da morfologia matemática sobre {0,1} E A Morfologia Matemática estuda a decomposição de operadores entre reticulados completos em termos de quatro classes de operadores: as dilatações, as erosões, as antidilatações e as anti-erosões. Estes operadores, chamados de elementares, têm um papel fundamental porque a partir deles é possível construir uma série de outros operadores.
39 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA22 No que segue, será introduzido conceitos fundamentais sobre operadores definidos na classe pertencente ao conjunto das funções {0,1} E. Todos esses conceitos tiveram com base o trabalho desenvolvido por Banon e Barrera em [25]. Por questão de simplificação notacional, daqui para a frente o símbolo T será usado sempre que necessário ao invés de {0,1} E. Definição (extensividade e anti-extensividade): Um operador ψ sobre T é extensivo se, e somente se, para todo f T, f ψ( f ) e anti-extensivo, se ψ( f ) f Definição (idempotência): Um operador unário ψ sobre T é idempotente do tipo 1 ou de fecho se, para todo f T, ψ(ψ( f )) = ψ( f ) e idempotente do tipo 2 ou simplesmente indempotente, se, para todo f T, ψ(ψ( f )) = f Definição (Operador isotônico): Um operdor ψ sobre T diz-se isotônico (ou crescente) se e somente se, f,g T f g ψ( f ) ψ(g) Definição (Operador antitônico): Um operdor ψ sobre T diz-se antitônico (ou decrescente) se e somente se, f,g T f g ψ(g) ψ( f ) A proposição a seguir mostra definições equivalentes de um operador isotônico. Proposição Seja ψ [T T ], então para toda família de imagens { f i }, as tres proposições são equivalentes: (1) ψ é isotônico; (2) Para toda família de imagens { f i } T, supψ({ f i }) ψ({sup f i }) (3) Para toda família de imagens { f i } T, ψ({in f f i }) in f ψ({ f i } A prova dessa proposição pode ser encontrada em [25], pp 33. A proposição a seguir apresenta definições equivalentes de um operador antitônico. Proposição Seja ψ [T T ], então para toda família de imagens { f i }, as três proposições são equivalentes:
40 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA23 (1) ψ é antitônico; (2) Para toda família de imagens { f i } T, ψ(sup{ f i }) supψ({ f i }) (3) Para toda família de imagens { f i } T, (ψ({in f f i }) ψin f ({ f i }) A prova é análoga a da proposição anterior ([25], pp 33). No que segue apresentaremos as definições das quatro classes fundamentais dos operadores elementares da morfologia matemática que são: dilatações, erosões, antidilatações e anti-erosões Definição (dilatação) Um operador ψ sobre T é uma dilatação se, para toda família de imagens { f i } T ψ(sup{ f i }) = supψ({ f i }) Uma erosão se e somente se, para toda família de imagens { f i } T ψ(in f { f i }) = in f ψ({ f i }) é uma anti-dilatação se e somente se, para toda família de imagens { f i } T ψ(sup{ f i }) = in f ψ({ f i }) Uma anti-erosãose e somente se, para toda família de imagens ternárias { f i } T ψ(in f { f i }) = supψ({ f i }) Proposição (isotonia das dilatações e erosões) as dilatações e erosões são isotônicas. A prova dessa proposição pode ser encontrada em [25]. Definição (relação de ordem dos operadores) Dado dois operadores ψ, ϕ [T T ] e f T, define-se a seguinte relação. ψ ϕ se para todo x E e f T ψ( f (x)) ϕ( f (x)) i.e, [T T ], torna-se uma ordem parcial. Proposição (reticulado do conjunto de operadores) O conjunto [T T ], é um reticulado completo.
41 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA24 Prova O conjunto T T = [T T ] dos operadores sobre T provido da relação forma um conjunto parcialmente ordenado. Este conjunto munido das operações de supremo e de ínfimo estendidas às famílias de operadores forma também um reticulado completo (por herança do reticulado do conjunto das funções binárias). Em outras palavras, para todo conjunto de índices I, estas operações verificam que, para toda família (Ψ i ) i I de operadores sobre T i I Ψ i ( f ) = supψ i ( f ) i I Ψ i ( f ) = in f Ψ i ( f ) Onde Ψ I é a imagem de I através da família (Ψ i ) i I, i.e., Ψ I = {Ψ T T I, ({) = ({)} A condição para um subconjunto de um reticulado completo ser um reticulado completo, é que ele seja superiormente ou inferiormente fechado sobre o reticulado. Segundo Banon e Barrera em [25], o conjunto das dilatações das erosões é superiormente (inferiormente) fechado de [T T ], portanto o conjunto das dilatações (erosões) provido da ordem é reticulado completo. 2.3 Morfologia matemática para imagens em níveis de cinza Na década de 80, a descoberta dos operadores morfológicos no domínio dos reticulados completos, foi o primeiro passo para a extensão da morfologia matemática em níveis de cinza. O uso de tons de cinza introduz complicação maior, tanto do ponto de vista conceitual como nas implementações. Um pixel pode agora ter qualquer valor inteiro, assim a facilidade de considerar a imagem como um conjunto desaparece. Algumas abordagens sobre a teoria da morfologia matemática para imagens em tons de cinza podem ser encontradas em [40, 44]
42 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA Os operadores elementares da morfologia matemática para imagens em tons de cinza Da mesma forma que imagens binária, os operadores elementares da morfologia matemática para o caso de imagens em níveis de cinza, a dilatação e erosão são definidos dualmente. No caso binário, apresentou-se a estrutura algébrica dos operadores morfológicos como reticulados completos, definidos de acordo com a álgebra das operações de Minkowiski e representados em uma grade do espaço Euclidiano bidimensional. Para o caso de tons de cinza, estes operadores possuem uma estrutura algébrica similar, estendido para o espaço euclidiano n-dimensional, satisfazendo também as características de um reticulado completo. Além disso satisfazem a várias propriedades correspondentes ao caso binário, tais como comutatividade, associatividade e distributividade. Nesta seção, apresentam-se as definições básicas dos operadores dilatação e erosão e alguns dos principais operadores morfológicos tais como, abertura, fechamento, gradiente morfológico, filtros sequenciais e transformada top-hat. Antes de definir estes operadores, necessita-se apresentar algumas definições básicas. Vale salientar que os resultados e definições apresentados nesta seção são baseados nas definições clássicas para o caso de imagens pontuais. ([27]) Na morfologia clássica, os modelos para imagens em tons de cinza são representados matematicamente pelo mapeamento f : E L onde L é um reticulado completo. L é definido por um conjunto de valores de tons de cinza que pode ser dado por R = R {,+ } ou Z = Z {,+ }. Também L pode ser dado como sendo o intervalo [0,1] ou o conjunto finito {0,1,...N}, para algum N Definição Dados duas funções f,g L. As operações de supremo e de ínfimo entre f e g, são definidas respectivamente por: ( f g)(x) = f (x) g(x) (2.3.1) ( f g)(x) = f (x) g(x) (2.3.2)
43 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA26 Definição (Translação) Seja f : E L, x,u E e v L, a translação horizontal de f por u, f u : E L é definida por f u (x) = f (x u) e the translação vertical de f x by v L is defined by ( f + v)(x) = f (x) + v. Quando ambas as operações são aplicadas juntas, obtemos a translação morfológica dada por ( f u + v)(x) = f (x u) + v (2.3.3) Definição Dado uma imagem g e x E, A reflexão de g é definida por ĝ(x) = g( x) Definição (Operações de Minkowiski) Dada dois sinais f, g L. diferença Minkowski são definidas respectivamente por: A soma e a f g = u E{ f u ĝ(u)} (2.3.4) f g = u E{ f u + g(u)} (2.3.5) Definição Dada duas imagens em níveis de cinzas f e g, então ε g ( f )(x) = u E[ f (x u) ĝ(u)] (2.3.6) g ( f )(x) = u E[ f (x u) + g(u)] (2.3.7) ε g ( f ) = ( f g)(x) e g ( f ) = ( f g)(x) são uma erosão e uma dilatação, respectivamente. g é chamada de função aditiva estruturante Efeitos gerais causados pelos operadores dilatação e erosão No caso da dilatação, se todos os valores da função estruturante são positivos, a imagem de saída aumenta a luminosidade, em consequência, detalhes escuros ou são reduzidos ou são eliminados, dependendo de como os seus valores e formas estão relacionados om o elemento estruturante usado para a dilatação No caso da erosão, se todos os elementos da função estruturante são positivos, a imagem de saída fica mais escura, consequentemente os detalhes claros na imagem de entrada ficam menores do que o elemento estruturante é reduzido. O grau de redução é determinado pelos níveis de cinza dos vizinhos e pela forma e amplitude do elemento estruturante. A Figura 2.15 mostra imagens da Lena e os efeitos da dilatação e da erosão no caso de imagens em níveis de cinza. Observe que a dilatação em relação a imagem original, fica mais clara, enquanto que a erosão torna a imagem mais escura.
44 CAPÍTULO 2. UMA ABORDAGEM DA MORFOLOGIA MATEMÁTICA CLÁSSICA27 Figura 2.15: Imagem da Lena e os efeitos causados pelos operadores de dilatação e erosão Outros operadores morfológicos Tal como o caso binário, podemos definir outras operações morfológicas para imagens em tons de cinza onde as mais básicas são a abertura e o fechamento. Estas operações são consideradas os filtros básicos da morfologia matemática e são definidas respectivamente por: f g = ( f g) g (2.3.8) f g = ( f g) g (2.3.9) Para extrair contornos da imagem em geral é utilizado a operação de gradiente morfológico. Esta operação envolve três operações: dilatação, erosão e subtração e é definida por: Grad( f,g)(x) = ( f g)(x) ( f G)(x) (2.3.10) Uma outra importante operação em imagens em tons de cinza é a transformada top hat ou chapéu mexicano. O objetivo principal dessa operação é extrair componentes com baixo contraste em relaçao ao fundo. É importante por exemplo, para realçar detalhes da imagem na presença de sombra. Esses filtros podem ser definidos de dois modos: claro e escuro e são dados respectivamente pelas equações: H(F) + (x) = f (x) ( f g)(x) (2.3.11) H(F) (x) = ( f g)(x) f (x) (2.3.12) O próximo capítulo, apresenta suscitamente a Matemática Intervalar e os conceitos necessários para o desenvolvimento dessa discertação.
45 Capítulo 3 Uma Abordagem da Matemática Intervalar 3.1 Introdução A matemática intervalar busca dar suporte para resolver problemas em dois aspectos fundamentais da computação científica: Um deles é na criação de um modelo computacional que reflita com exatidão o controle e análise dos erros que ocorrem no processo computacional; o outro é na escolha de técnicas de programação adequadas para desenvolvimento de softwares científicos buscando no final do processo matemáticocomputacional, uma boa estimativa da evidência dos erros de entrada. Na literatura existem diferentes abordagens para a computabilidade nos números reais, mas, uma importante diferença entre estas abordagens está na maneira como é representado o número real [64]. A aritmética intervalar permite o cálculo de extremos seguros para as soluções de um problema. Operações aritméticas com máxima precisão são necessárias para se ter uma aritmética de alta exatidão. Elas são definidas de forma que só um arredondamento é aplicado nas operações aritméticas básicas, resultando que o valor calculado e o valor exato diferem por apenas um arredondamento. Uma aplicação da aritmética intervalar poderá levar a extremos confiáveis [55]. O uso desta aritmética, aliada a um controle rígido dos algoritmos, é objeto do atual estado da arte nesta área. Nesta 28
46 CAPÍTULO 3. UMA ABORDAGEM DA MATEMÁTICA INTERVALAR 29 seção serão apresentados alguns conceitos da aritmética intervalar, fundamentais para o desenvolvimento dos principais resultados dessa tese. 3.2 Análise intervalar A qualidade do resultado em computação científica depende do conhecimento e controle dos erros na computação. Algoritmos convencionais, chamados algoritmos pontuais, computam uma resposta e, algumas vezes, uma estimativa do erro. No entanto, o usuário não pode conseguir uma resposta exata sem o auxílio de uma análise rigorosa dos erros, o qual é extensa, dispendiosa e nem sempre viável [7]. Desta forma, a obtenção de uma solução numérica para um problema real, aplicando os métodos numéricos tradicionais, geralmente conduz a aproximação dos resultados. Por outro lado, técnicas intervalares podem ser programadas em computadores de tal modo que a computação possua uma rigorosa e completa análise do erro no resultado. Muitas vezes, para melhor compreender como se comporta globalmente o erro durante a evolução dos cálculos numéricos, torna-se necessário identificar qual a sua origem ou fonte. 3.3 Definições básicas Nesta seção apresentam-se algumas definições básicas da aritmética intervalar que foi introduzida por Moore e Sunaga paralelamente [60, 66]. Essas definições serão importantes para esse trabalho, porque nos Capítulos 5 e 6 serão apresentados dois modelos intervalares em imagens aplicada a morfologia matemática. A estrutura algébrica desses modelos, requerem algumas vezes operações intervalares entre elementos de conjuntos. Definição Intervalo de Números Reais Seja R o conjunto dos números reais, e sejam x 1,x 2 R tais que x 1 x 2 Então, o conjunto {x R x 1 x x 2 } é um intervalo de números reais ou simplesmente um intervalo, e será denotado por [x 1,x 2 ]. Definição Conjunto dos Intervalos de Números Reais
47 CAPÍTULO 3. UMA ABORDAGEM DA MATEMÁTICA INTERVALAR 30 Denota-se por IR o conjunto de todos os intervalos de números reais, isto é, IR = {[x 1,x 2 ] x 1,x 2 R e x 1 x 2 } Os pontos do conjunto dos intervalos de números reais serão denotados usualmente por letras latinas maiúsculas. Neste trabalho, os intervalos são usados com a finalidade de aproximar valores imprecisos. Neste sentido, não será utilizado a forma tradicional de representação geométrica, visto que, neste caso, associando-se a cada extremo do intervalo um eixo cartesiano, constrói-se uma representação cartesiana, enquanto que aqui, o intervalo está associado a um ponto real impreciso no mesmo eixo. Todo número real x R pode ser visto como um intervalo de IR. Para tanto, basta identificar os pontos x R com os intervalos pontuais X = [x,x], onde X IR. Estes intervalos também são chamados de intervalos degenerados ou intervalos pontuais. Assim vale a seguinte cadeia de inclusões: Figura 3.1: N Z Q R IR Vendo cada intervalo da reta como um conjunto, a noção de igualdade entre dois intervalos é dada pela noção de igualdade entre conjuntos, ou seja, A = B x A x B e x B x A Definição Igualdade entre Intervalos Sejam A = [a 1,a 2 ] e B = [b 1,b 2 ] dois intervalos de IR. Diz-se que A = B se, e somente se,
48 CAPÍTULO 3. UMA ABORDAGEM DA MATEMÁTICA INTERVALAR 31 a 1 = b 1 e a 2 = b 2 Definição Região Intervalar Uma região intervalar é uma porção contida em R n cujos limites são bem definidos e variáveis. Definição Par Ordenado Intervalar Sejam os intervalos A = [a 1,a 2 ] e B = [b 1,b 2 ]. Definimos Par ordenado (A;B) à região intervalar ([a 1,a 2 ];[b 1,b 2 ]) em que os intervalos A e B são denominados respectivamente abscissa intervalar e ordenada intervalar. Geometricamente, um par ordenado intervalar é visto como uma região intervalar no plano, conforme podemos ver na figura 3.2. Figura 3.2: Par ordenado intervalar Aritmética intervalar Apresentaremos agora um estudo das definições básicas de matemática intervalar, segundo a aritmética de Moore. [8, 54, 61].
49 CAPÍTULO 3. UMA ABORDAGEM DA MATEMÁTICA INTERVALAR 32 Aritmética intervalar clássica Consideremos os intervalos X = [x 1,x 2 ] e Y = [y 1,y 2 ], então: 1. X +Y = [x 1,x 2 ] + [y 1,y 2 ] = [x 1 + y 1,x 2 + y 2 ] 2. X Y = [x 1,x 2 ] [y 1,y 2 ] = [x 1 y 2,x 2 y 1 ] 3. X Y = [x 1,x 2 ] [y 1,y 2 ] = [min{x 1 y 1,x 1 y 2,x 2 y 1,x 2 y 2 },max{x 1 y 1,x 1 y 2,x 2 y 1,x 2 y 2 }] [ ] 1 4. X = 1x2, 1 se x x1 1 > 0 ou x 2 < 0 [ ] 5. X Y = X Y 1 = [x 1,x 2 ] 1y2, 1, se 0 Y y1 Operações de reais com intervalos: Sejam a R e X = [a 1,a 2 ]. Valem: 1. a + X = [a,a] + [a 1,a 2 ] = [a + a 1,a + a 2 ] 2. a X = [a,a] [a 1,a 2 ] = [a a 2,a a 1 ] 3. a X = a [a 1,a 2 ] = [a a 1,a a 2 ] 4. X a = [a 1,a 2 ] a = [ a 1 a, a 2 a ], para a 0 Nota-se que a imagem de cada uma das operações intervalares básicas é uma extensão exata da operação real correspondente. Teorema Sejam os intervalos X = [x 1,x 2 ] e Y = [y 1,y 2 ], então: 1. X +Y = {r + s r X e s Y } 2. X Y = {r s r X e s Y } 3. X Y = [x 1,x 2 ] [y 1,y 2 ] = {r s r X e s Y } 5. X Y = {r s r X e s Y }, se 0 Y Prova A prova deste teorema pode ser vista em [66].
50 CAPÍTULO 3. UMA ABORDAGEM DA MATEMÁTICA INTERVALAR 33 Se a expressão intervalar for composta, não haverá necessariamente uma correspondência exata de tais operações. Por exemplo, se f (x) = x 2 x, for estendida com elementos intervalares, temos F(X) = X 2 X ou F(X) = X(X 1). Neste caso, têm resultados diferentes, porém inclusos, ou seja, para X = [0,1], temos: F(X) = X 2 X = [0,1] 2 [0,1] = [0,1] + [ 1,0] = [ 1,1] F(X) = X(X 1) = [0,1] ([0,1] [1,1]) = [0,1] [ 1,0] = [ 1,0] Portanto, [ 1,1] [ 1,0], mas [ 1,0] [ 1,1] Propriedades da aritmética intervalar Teorema A aritmética intervalar é subdistributiva no sentido que, se X,Y e Z são intervalos, então X(Y + Z) XY + XZ [61]. Assim, embora adição e multiplicação de intervalos sejam comutativas e associativas, não mantém a lei da distributividade. Além disso, embora os intervalos pontuais [0, 0] e [1, 1] sejam identidades aditiva e multiplicativa, respectivamente, não existe inversos aditivos e multiplicativos, isto é: [1,2] [1,2] = [1,2] + [ 2, 1] = [ 1,1] [1,2] [1,2] = [1,2] [ 1 2,1 ] = [ 1 2,2 ] (α β) A = (α β) [a 1,a 2 ] = [(α β) a 2,(α β) a 1 ] para α β < 0 = [α β a 2,α β a 1 ] = α [β a 1,β a 2 ] para β 0 (inverteremos a posição de α por β, caso contrário) = α (β [a 1,a 2 ]) = α (β A). Definição Interseção entre dois Intervalos Sejam A = [a 1,a 2 ] e B = [b 1,b 2 ] dois intervalos. se max{a 1,b 1 } min{a 2,b 2 }, definese a interseção dos intervalos A e B como sendo o intervalo A B = [max{a 1,b 1 },min{a 2,b 2 }],
51 CAPÍTULO 3. UMA ABORDAGEM DA MATEMÁTICA INTERVALAR 34. Exemplo [2,5] [3,8] = [max{2,3},min{5,8}] = [3,5] 2. [3,8] [ 1,10] = [max{3, 1},min{8,10}] = [3,8] 3. [ 3,2] [2,5] = [max{ 3,2},min{2,5}] = [2,2] A Figura 3.3 dá a interpretação geométrica da operação de interseção de intervalos na reta real: Figura 3.3: Representação geométrica da interseção em R Teorema Propriedade da interseção Sejam A,B,C,D IR. Se A C, B D e, se A B está definido, então C D está definido e: A B C D A prova deste teorema pode ser vista em [54] Exemplo Sejam A = [3,5],B = [ 1,4],C = [2,8] e D = [ 1,6]. Assim, A C e B D, então, A B = [3,4], C D = [2,6] e [3,4] [2,6]. Definição União entre dois Intervalos Sejam A = [a 1,a 2 ] e B = [b 1,b 2 ] dois intervalos tais que A B está definido. Define-se a união dos intervalos A e B como sendo o intervalo: A B = [min{a 1,b 1 },max{a 2,b 2 }]
52 CAPÍTULO 3. UMA ABORDAGEM DA MATEMÁTICA INTERVALAR 35 Exemplo [2,5] [3,8] = [min{2,3},max{5,8}] = [2,8]; 2. [3,8] [ 1,10] = [min{3, 1},max{8,10}] = [ 1,10]; 3. [ 3,2] [2,5] = [min{ 3,2},max{2,5}] = [ 3,5]; 4. [ 3,2] [3,8] = não está definido. A figura 3.4 dá a interpretação geométrica da operação de união de intervalos na reta real: Figura 3.4: Representação geométrica da união em R Relações de ordem É possível definir muitas relações de ordem paciais, sobre IR. Dentre elas podemos destacar: Definição Ordem de Inclusão Sejam X = [r,s] e Y = [t,u]. Então, X é menor ou igual a Y, representado por X Y, se t r e s u. Kulisch e Miranker [68], definiram a seguinte ordem: Definição Ordem de Kulisch-Miranker Seja X = [r,s] e Y = [t,u]. Então X é menor ou igual a Y, representado por X KM Y, se r t e s u. O próximo capítulo, apresenta alguns conceitos do Processamento de Imagens Digitais Intervalares e que servirão para a compreensão do que seja um modelo de imagem intervalar.
53 Capítulo 4 Processamento de Imagens Digitais Intervalares 4.1 Introdução Nesta seção serão apresentados alguns conceitos de imagens digitais intervalares que foram introduzidas por Lyra em [4]. Considera-se que os conceitos apresentados neste capítulo, são importantes porque no capítulo 6 será introduzido um modelo intervalar para imagens em níveis de cinza e que foi desenvolvido sobre esse tipo de imagens. Uma imagem intervalar refere-se a uma função luminosa bidimensional, denotada por F(x,y), em que um intervalo assume a amplitude de F nas coordenadas espaciais (x,y) dando a intensidade (brilho) da imagem naquele ponto em relação a um coeficiente de tolerância que determina a diferença entre o limite superior e inferior do intervalo. Da mesma forma que as imagens digitais, para ser adequada para o processamento computacional, a imagem precisa ser digitalizada tanto espacialmente quanto em amplitude. A digitalização das coordenadas espaciais (x, y) é denominada amostragem da imagem e a quantização em níveis de cinza ocorre de forma contínua, em um intervalo diminuindo a perda neste processo de discretização. O objetivo do modelo intervalar para imagens digitais desenvolvido por Lyra, foi definir uma imagem intervalar em que, através de software/hardware, seja convertido o valor de cada pixel digitalizado em um intervalo. A diferença entre o limite superior e o inferior, dependerá da relação com que o pixel 36
54 CAPÍTULO 4. PROCESSAMENTO DE IMAGENS DIGITAIS INTERVALARES 37 analisado terá com a imagem. Em uma região indefinida por exemplo, esta diferença será maior que em uma região definida. Alguns trabalhos de métodos intervalares aplicados ao processamento de imagens podem ser encontrados em [3, 15, 28, 30] 4.2 Definições Definição Imagem Digital Intervalar e Pixel Intervalar Seja A = a i j uma matriz intervalar de ordem m n. A é uma imagem digital intervalar, discretizada espacialmente e em tons de cinza, se ela for obtida através de um dispositivo de aquisição de imagens e digitalizado por um digitalizador intervalar ou obtido através de um dispositivo de aquisição intervalar e, de alguma forma, digitalizado. A definição merece um detalhamento. Existem duas formas de geração da matriz intervalar, consequentemente da imagem digital intervalar. A primeira é feita no momento da aquisição da imagem, através da regulagem do dispositivo de aquisição, ou através de modificações ambientais. Por exemplo, existem n regulagens que pode ser efetuadas em uma câmera fotográfica digital para a obtenção de uma imagem, bem como, o ambiente poderá sofrer variação de luminosidade, umidade, etc. Estas modificações contribuirão para a aquisição de uma imagem intervalar, onde a imagem ótima estará contida. Uma outra forma de análise da imagem intervalar será quando aplicada sob um objeto em movimento. Sobre está ótica a imagem intervalar terá mais informações sobre a imagem, como: deslocamento, modificações, definições de formas, etc. Uma outra forma de se trabalhar a imagem digital intervalar é na digitalização, em que a construção da matriz intervalar se baseia na matriz de pixels da imagem clássica, sendo analisada a vinhança e conectividade de cada pixel ou seja, cada a i j IR, denominado pixel intervalar, será um intervalo que definirá a intensidade intervalar luminosa deste pixel intervalar na posição i, j da imagem discretizada, tomando como critério a vizinhança. Definição Imagem Digital Binária Intervalar Seja A = a i j uma imagem intervalar. A é uma imagem binária intervalar se cada intervalo a i j for um intervalo degenerado e igual a [0,0] ou [1,1].
55 CAPÍTULO 4. PROCESSAMENTO DE IMAGENS DIGITAIS INTERVALARES 38 A definição de métrica está relacionada com a região espacial ocupada pelos pixels. Esta métrica obedece às propriedades tradicionais. Quanto ao intervalo de tons de cinzas, cada pixel representa uma informação da imagem. Foi definido a relação entre os pixels com uma quasi-métrica, para este caso específico, utilizando a quasi-métrica definida por Acióly e Bedregal que se adequa também à estrutura intervalar [9]. Sejam I p = [p 1, p 2 ] e I q = [q 1,q 2 ] as intensidades intervalares dos pixels p(x,y) e p(u, v), respectivamente. A distância de Moore [61] entre estas intensidades intervalares é dada pela função D(I p,i q ) = Max( p 1 q 1, p 2 q 2 ). Já a distância de Acióly e Bedregal [9] é dada pela função Q(I p,i q ) = 0 se q 1 p 1 p 2 q 2 e Q(I p,i q ) = Max(q 1 p 1, p 2 q 2,0), caso contrário. A distância de Moore [61] satisfaz a noção clássica de métrica [43] já a de Acióly-Bedregal [9] satisfaz a noção de quasi-métrica [47]. 4.3 Operações lógicas-aritméticas entre pixels intervalares As operações aritméticas em imagens inteiras intervalares são aplicadas pixel a pixel. Elas envolvem apenas uma posição espacial de pixel intervalar por vez, de modo que são feitas no local, ou seja, o resultado da operação aritmética feita na posição (x,y) é armazenado naquela posição. Em alguns momentos é apresentado apenas uma das infinitas imagens considera-se a imagem intervalar como um conjunto infinito de imagens devido a cada pixel intervalar ser contínuo contidas em uma imagem intervalar para servir de referência e esta será denominada imagem média. Definição Imagem Média Seja A = a i j uma matriz, onde a i j = [a i j,a i j ] de ordem m n. A imagem média de A, é uma matriz I md = I i j de ordem m n, tal que: I md = a i j+a i j 2 para todo i, j N. A seguir, serão definidas algumas operações aritméticas e lógicas entre pixels intervalares. Para estas definições, é considerado o intervalo degenerado K = [k, k] onde
56 CAPÍTULO 4. PROCESSAMENTO DE IMAGENS DIGITAIS INTERVALARES 39 k R é a maior intensidade possível de uma imagem. Sejam p(x,y) e q(x,y) pixels intervalares tal que p(x,y) = [p i, p s ] e q(x,y) = [q i,q s ], respectivamente, então: Definição Soma entre pixels intervalares A soma, s(x,y) = p(x,y)+q(x,y), é um pixel intervalar, igual à soma das intensidades dos pixels intervalares respeitado o limite superior de intensidade, isto é: s(x,y) = [min(p i + q i,k),min(p s + q s,k)] Definição Subtração entre pixels intervalares A diferença, m(x,y) = p(x,y) q(x,y), é um pixel intervalar, igual à diferença das intensidades dos pixels intervalares respeitado o limite inferior de intensidade, isto é: m(x,y) = [max(p i q s,0),max(p s q i,0)] Definição Produto entre pixels intervalares O produto, t(x,y) = p(x,y) q(x,y), é um pixel intervalar, igual ao produto das intensidades dos pixels intervalares respeitado o limite superior de intensidade, isto é: t(x,y) = [min(p i q i,k),min(p s q s,k)] Definição Divisão entre pixels intervalares A divisão, d(x,y) = p(x,y) q(x,y), é um pixel intervalar, igual ao quociente das intensidades dos pixels intervalares, isto é: d(x,y) = [max( p i q i ),max( p s q s )],q i,q s 0 Definição Soma entre imagens intervalares Sejam as matrizes de pixels intervalares A = a i j e B = b i j de ordem m n. A soma entre estas imagens é a matriz intervalar S = s i j de ordem m n, construída pixel a pixel tal que, para cada a i j A e b i j B: s i j = a i j + b i j
57 CAPÍTULO 4. PROCESSAMENTO DE IMAGENS DIGITAIS INTERVALARES 40 Definição Subtração entre imagens intervalares Sejam as matrizes de pixels intervalares A = a i j e B = b i j de ordem m n. A subtração entre estas imagens é a matriz intervalar M = m i j de ordem m n, construída pixel a pixel tal que, para cada a i j A e b i j B: m i j = a i j b i j Definição Multiplicação entre imagens intervalares Sejam as matrizes de pixels intervalares A = a i j e B = b i j de ordem m n. O produto entre estas imagens é a matriz intervalar K = k i j de ordem m n, construída pixel a pixel tal que, para cada a i j A e b i j B: k i j = a i j b i j Definição Divisão entre imagens intervalares Sejam as matrizes de pixels intervalar A = a i j e B = b i j de ordem m n. O quociente entre estas imagens é a matriz intervalar D = d i j de ordem m n, construída pixel a pixel tal que, para cada a i j A e b i j B: d i j = a i j b i j,0 b i j As operações lógicas tradicionais definidas sob uma imagem digital intervalar binária, dar-se-ão da mesma forma que quando utilizadas nas imagens tradicionais por utilizar apenas a informação sob ponto de vista espacial. Os resultados obtidos também serão similares uma vez que, ao definir a imagem intervalar, mante-se a posição espacial de cada pixel intervalar, modificando apenas a forma de apresentação de seus tons de cinza que são definidos agora como intervalo. Definição Disjunção de imagens intervalares Sejam A = [a i j ] e B = [b i j ] imagens intervalares de ordem m n. A disjunção destas imagens é a matriz C = c i j de ordem m n, construída pixel a pixel escolhendo aquele de intensidade maior. Isto é, A B = C, onde c i j = sup[a i j,b i j ], para todo i, j. A operação de disjunção pode ser vista na Figura 4.1 (extraída de [4]).
58 CAPÍTULO 4. PROCESSAMENTO DE IMAGENS DIGITAIS INTERVALARES 41 Figura 4.1: Imagem média da Lena disjunta com uma imagem constante. Definição Conjunção de imagens intervalares Seja A = a i j e B = b i j imagens intervalares de ordem m n. A conjunção destas imagens é a matriz C = c i j de ordem m n, construída pixel a pixel escolhendo aquele de intensidade menor. Isto é, A B = C, onde c i j = in f [a i j,b i j ], para todo i, j. A operação de conjunção pode ser vista na Figura 4.2 extraída de ([4]). Figura 4.2: Imagem média da Lena conjunta com uma imagem constante. Definição Negação de imagens intervalares Sejam A = a i j e K = k i j imagens intervalares de ordem m n, onde k i j = K. A negação de A é a matriz A = a i j de ordem m n, construída pixel a pixel escolhendo o complemento com respeito a K. Isto é, A = K A. Assim a i j = k i j a i j, para todo i, j. A operação de complemento ou negativo pode ser vista na Figura 4.3. A abordagem aqui apresentada teve como base o trabalho desenvolvido por Lyra, em [4]. Lyra desenvolveu importantes fundamentos do processamento digital de imagens onde pela primeira vez vários aspectos dessa teoria foi apresentado sob a ótica intervalar. Em seu trabalho ele apresentou importantes conceitos de análise de imagens tais
59 CAPÍTULO 4. PROCESSAMENTO DE IMAGENS DIGITAIS INTERVALARES 42 Figura 4.3: Imagem da Lena original e negativa. como imagens representadas por matriz de pixels na forma intervalar, operações entre pixels intervalar, convolução intervalar, transformada de Fourier intervalar entre outros conceitos. Os dois capítulos a seguir, desenvolvem a proposta desse trabalho. O capítulo 5 propõe um modelo para imagens binárias que contenha incertezas. Já o capítulo 6, extende o capítulo 5, propondo um modelo para imagens em níveis de cinza que apresentam incertezas.
60 Capítulo 5 Morfologia para imagens binárias intervalares Transformar uma imagem em níveis de cinza em uma imagem binária, processo chamado de binarização ou limiarização, é provavelmente, uma das técnicas mais utilizada em várias aplicações, incluindo segmentação de imagens. Isto porque se faz uso freqüente de processos de reconhecimento de caracteres que necessitam de imagens binárias. Toda técnica de binarização, busca particionar uma imagem em duas classes C1 e C2, a partir de um limiar L. De forma ideal, o limiar L situa-se em um determinado ponto da imagem, onde uma das regiões, digamos C1 representa a região onde fica os pixels pretos e C2 onde ficam os pixels brancos. A escolha do limiar é importante porque dela vai resultar uma imagem com mais ou menos pixels brancos. Em um processo que busca selecionar um objeto de uma imagem, por exemplo, a técnica frequentemente utilizada é a binarização. Esse processo, em geral é feito durante uma segmentação de imagens ([67]). A figura 5.1, extraída de [67] mostra uma imagem em tons de cinza e sua respectiva binarização. A imagem original é parte de uma mama densa. A morfologia matemática se apresenta como uma ferramenta que melhor se adequa ao processo de binarização, por ser uma abordagem não linear e por processar da mesma maneira imagens em níveis de cinza e binárias. Alguns tipos de técnicas, apesar da simplicidade do processo, dependendo da qualidade do original, não apresenta bons resultados, isso porque pode haver "buracos"nas linhas, borda rompida na região limite ou região "estranha"de pixels. O modelo que será apresentado a seguir, poderá ser usado para 43
61 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 44 tratar esse tipo de problema, que serão considerados como incertezas que aparecem no processo da binarização e que em geral ocorrem próximo ao limiar. Técnicas intervalares apresentam-se como boas ferramentas para lidar com problemas dessa natureza e as incertezas oriundas do processo de binarização serão codificados em um intervalo, a saber, o intervalo [0, 1]. Em outras palavras, as imagens oriundas de processos de binarização, terão pixels com valores [0,0], [0,1] e [1,1], onde [0,1], será o valor de incerteza. Figura 5.1: Imagem Binarizada Este capítulo, apresenta então um modelo intervalar binário, onde a representação intervalar significa a presença de incerteza entre valores exatos do conjunto binário {0,1}. Para isso, será introduzido o conjunto de pixels Ω = {[0,0][0,1],[1,1]}, onde como mencionado [0, 1] representa a informação de incerteza. O conjunto Ω e suas propriedades algébricas, serão aqui estudadas, e sobre este conjunto serão definidas as operações morfológicas elementares de dilatação e erosão. Neste capítulo demontrase ainda que, tanto Ω quanto a classe das operações morfológicas sobre Ω formam um reticulado completo. Uma outra contribuição deste capítulo, é demonstrar que a estrutura algébrica de Ω, diferentemente do caso binário, não constitui uma álgebra Booleana, mas uma estrutura algébrica mais fraca chamada álgebra pseudo Booleana. Em outras palavras, a introdução de um valor de incerteza no universo dos pixels binários afeta (enfraquece) a estrutura algébrica da álgebra dos pixels binários {0, 1}. Assim, o conceito de imagens binárias, é generalizado permitindo o mapeamento de uma coordenada no valor de incerteza representada pelo intervalo [0,1], ou seja, o modelo será capaz de expressar as incertezas nas respectivas coordenadas. Ou ainda, a coordenada de valor [0, 0] representa a cor
62 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 45 preta, a coordenada de valor [1,1] representa a cor branca, e o valor [0,1] representa a indefinição. 5.1 Construção do espaço algébrico Ω Esta seção apresentará a estrutura algébrica do conjunto de pixels Ω, citado anteriormente. De forma a tornar o texto autocontido, sempre que for necessário serão apresentados resultados conhecidos da literatura. Proposição Toda cadeia P é um reticulado distributivo; i.e. um reticulado onde para quaisquer elementos x, y, z valem as seguintes propriedades: (I) x (y z) = (x y) (x z) e (II) x (y z) = (x y) (x z) Prova Seja P uma cadeia, então dados x,y P, como x y ou y x, então x y,x y P. Logo P é um reticulado. Dados x,y,z P, como P é uma cadeia, então tem-se dois casos: (1) y,z x e (2) x y ou x z. No Caso (1), y,z x, então y z x. Logo, (x y) (x z) hip = y z, e x (y z) = y z. Ou seja, x (y z) = (x y) (x z). No Caso (2) x y ou x z. Caso x y, como y,z y z, então x y z, i.e. x (y z) = x. Mas (x y) (x z) = x (x z) e por absorção x (x z) = x. Portanto, x (y z) = (x y) (x z). Caso x z, então como y,z y z, então x y z e x (y z) = x. Além disso, (x y) (x z) = (x y) x = x. Logo, x (y z) = (x y) (x z). Portanto, em todos os casos x (y z) = (x y) (x z). A proposição x (y z) = (x y) (x z) sai por dualidade. Corolário O conjunto dos números reais, R, é um reticulado distributivo; onde (1) min(a, max(b, c)) = max(min(a, b), min(a, c)) e (2) max(a, min(b, c) = min(max(a, b), max(a, c)). Prova Dados a,b,c R, como se tem uma quantidade finita de elementos e R é uma cadeia, então a operação de supremo e de ínfimo são respectivamente as conhecidas
63 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 46 [1, 1] [0, 0] [0, 1] [1,1] [1,1] [1,1] [1,1] [0,0] [1,1] [0,0] [0,1] [0,1] [1,1] [0,1] [0,1] [1, 1] [0, 0] [0, 1] [1,1] [1,1] [0,0] [0,1] [0,0] [0,0] [0,0] [0,0] [0,1] [0,1] [0,0] [0,1] Tabela 5.1: Operações binárias e sobre Ω operações de máximo e de mínimo. Definição Seja Ω = {[0,0],[0,1],[1,1]}, onde [0,0] [0,1] [1,1]. Sobre Ω definese as operações e de acordo com a Tabela 5.1. Proposição A estrutura Ω,,,[0, 0],[1, 1] forma um reticulado completo, onde as operações e são as operações de supremo e ínfimo respectivamente. Prova Como Ω é uma cadeia finita, então ele é um reticulado completo, e claramente e, definidas na tabela 5.1, são suas operações de supremo e ínfimo respectivamente, pois quaisquer dois elementos x e y do conjunto Ω, tem-se que x y x,y e x,y x y, o que pode ser verificado na tabela 5.1. Corolário O conjunto Ω é um reticulado completo distributivo. Prova Direto das proposições e No que segue, apresentam-se algumas definições de complemento e pseudocomplemeto [31]. Definição Seja L um reticulado contendo o elemento zero ( ). Sejam a e b elementos do reticulado L. Um elemento c L é dito ser o -complemento de a em L, se c é o maior elemento tal que a c =. Supondo que o reticulado L tenha o elemento unidade ( ), um elemento c é dito ser o -complemento de a em L se c é o menor elemento tal que a c =.
64 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 47 Segue da definição que o -complemento ( -complemento) de a, se existe, é unicamente determinado por a. As noções de -complemento e -complemento são duais. Se um elemento a L tem simultaneamente o -complemento c 1 e -complemento c 2, então, c 1 e c 2 não são necessariamente iguais. Por exemplo, se o reticulado L for distributivo então c 1 c 2, pois c 1 = c 1 = c 1 (a c 2 ) = (c 1 a) (c 1 c 2 ) = (c 1 c 2 ) = c 1 c 2. Definição Um elemento c L é dito ser o complemeto de um elemento a L, se c é simultâneamente o -complemento e -complemento de a. Então a c = e a c = Definição O pseudo complemento de a relativo b, quando existe, é denotado por a b. Um reticulado é dito ser relativamente pseudo-complementado, se a b existe, para quaisquer par de elementos a,b L [62]. Corolário Por definição, para todo x L, x a b se e somente se a x b (5.1.1) Observe que "Todo reticulado relativamente pseudo-complementado tem maior elemento ; entretanto, em geral não tem menor elemento [62], pp 53" Definição Um reticulado relativamente pseudo-complementado que possui menor elemento " "é chamado álgebra pseudo-booleana [62], pp 58. Definição Dado Ω = {[0, 0],[0, 1],[1, 1]}, as tabelas 5.2 e 5.3 definem respectivamente, as operações de pseudo-complemento relativo: "a b; -complemeto: " a"; -complemento: "a"; e negação: " a". Observe que a diferença entre as operações a, ā e a reside no tratamento da incerteza [0, 1]. Observe ainda que a tabela 5.3 foi obtida do seguinte modo: se
65 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 48 [0, 1] [0, 1] [1, 1] [0,0] [0,0] [0,0] [0,0] [0,1] [0,0] [1,1] [1,1] [1,1] [0,0] [0,1] [1,1] Tabela 5.2: Operação de complemento relativo [0, 0] [0, 1] [1, 1] [1,1] [0,0] [0,0] [0, 0] [0, 1] [1, 1] [1,1] [0,1] [0,0] [0, 0] [0, 1] [1, 1] [1,1] [1,1] [0,0] Tabela 5.3: Operações de pseudo-complemento, -complemento e negação sobre Ω a = b = [0,0], o maior elemento que satisfaz a definição a c b é c = [1,1], pois [0,0] [0,0] = [0,0]; [0,0] [1,1] = [0,0] e [0,0] [0,1] = [0,0]. Os outros elementos são calculados de modo análogo (veja [62], pp 54). Proposição A estrutura Ω,,,[1, 1],[0, 0] forma um reticulado completo distributivo com pseudo-complemento relativo. Prova Pelo corolário 5.1.5, Ω é um reticulado completo distributivo. A Tabela 5.2 define as operações de pseudo complemento relativo sobre Ω. Corolário A estrutura Ω,,,,, é uma álgebra psedo-booleana com - complemento. Prova Ω,,, é uma álgebra relativamente pseudo-complementado cujo menor elemento [0, 0], então Ω é uma álgebra pseudo-booleana. Adicionalmente, a estrutura possui a operação de -complemento "a"definida na Tabela 5.3. Definição Uma operação f : Ω Ω chama-se reversão, sempre que f ([0, 0]) = [1,1] e f ([1,1]) = [0,0].
66 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 49 Existem três operações de reversão sobre Ω que são descritas na tabela 5.3. Observe que elas se diferenciam apenas quando o argumento é o elemento indefinido [0, 1]. Isso significa que essas operações coincidem com o complemento no caso binário, portanto qualquer operação morfológica que envolve o complemento no caso binário, irá possuir três versões para o caso do conjunto Ω aqui proposto, a saber, uma versão pra cada operador de reversão. A álgebra pseudo Booleana Ω munida das operações,,, constitui o espaço de pixels intervalares dotados do valor de incerteza [0,1]. No que segue, apresenta-se a estrutura algébrica das imagens cujos pixels são valorados no conjunto Ω. 5.2 Imagens binárias contendo incertezas Esta seção, apresenta a álgebra das imagens cujos pixels são valorados no conjunto Ω apresentado na seção anterior. As imagens serão funções da forma f : E Ω, onde E é um conjunto de coordenadas E = Z Z. Tais funções representam as imagens binárias contendo informação de incertezas e serão chamadas de imagens binárias intervalares. Nesta seção definem-se essas imagens e estudam-se suas propriedades algébricas Operações básicas Definição Chama-se imagem binária intervalar uma função f : E Ω, onde Ω = {[0,0],[0,1],[1,1]}. O conjunto de todas essas imagens é denotado por Ω E. Definição Dado o conjunto Ω E e f,g Ω E, Podemos estabelecer a seguinte relação de ordem sobre Ω E : f g se e somente se, para todo x E, f (x) g(x). Lema As funções, : E Ω, tal que (x) = [1,1] e (x) = [0,0] para todo x E são, respectivamente o maior e o menor elemento Ω E. Prova Seja f Ω E, então para qualquer x E, (x) = [0,0] f (x) [1,1] = (x). Assim, f, para todo f Ω E.
67 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 50 Definição Dada uma família não vazia de imagens binárias intervalares, { f i } i I, definimos as seguintes operações: { fi } i I (x) = { fi } i I (x) = [1,1], se i I, f i (x) = [1,1] [0,0], se i I, f i (x) = [0,0] [0,1], caso contrário [1,1], se i I, f i (x) = [1,1] [0,0], se i I, f i (x) = [0,0] [0,1], caso contrário (5.2.1) (5.2.2) Proposição Dada uma família não vazia f I = { f i } i I Ω E, f I é o supremo de { f i } i I. Prova (a) Primeiro vamos mostrar que f I majora f I. Sejam f I = { f i } i I Ω E e x E. Caso 1. j I tal que f j (x) = [1,1] então, f I (x) = [1,1] f h (x) para todo h I. Caso 2. j I, f j (x) = [0,0] então f I (x) = [0,0] f h (x) = [0,0] para todo h I. Caso 3. k I tal que f k (x) = [0,1] e j I, f j (x) [1,1], então por definição fi (x) = [0,1]. Como j I, f j (x) 1, então f I (x) = [0,1] f h (x), h I. Portanto, em todos os casos f I (x) f h (x) para todo h I. Como x é arbitrário, então para todo x e para todo h I, f I (x) f h (x), o que, por definição significa que fi f h, h I (b) Vamos mostrar agora que f I é o menor majorante de { f i } i I. Seja g um majorante (limitante superior) de f I, por definição x E, j I, f j (x) g(x). Caso 1. se existir k I tal que f k (x) = [1,1], então necessariamente g(x) = [1,1]. Logo por definição, j I, f j (x) [1,1] = f I (x) [1,1] = g(x). Caso 2. k I, f k (x) = [0,0] então g(x) = [0,0],g(x) = [0,1] ou g(x) = [1,1], mas por definição f I (x) = [0,0] g(x).
68 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 51 Caso 3. k I, f k (x) = [0,1] e m I, f m (x) [1,1] então g(x) = [0,1] ou g(x) = [1,1]. Por definição f I (x) = [0,1]. Logo m I, f m (x) f I (x) g(x). Como x é arbitrário, então j I, x E, f j (x) f I (x) g(x); ou seja j I, f j f I g. Logo f I é o menor majorante de { f i } i I. Proposição Dada uma família não vazia f I = { f i } i I Ω E, f I é o ínfimo de { f i } i I. Prova A prova do ínfimo é análoga ao caso do supremo dada na proposição anterior. Lema As funções, Ω E são, respectivamente, o ínfimo e o supremo da família vazia. Prova De fato, do lema 5.2.3, e são os elementos máximos e mínimos de Ω E. De acordo com [21] pp Se f I = /0 então in f f I = e sup f I =. Proposição A estrutura Ω E,,,, é um reticulado completo. Prova Direto das proposições e e do lema Definição Dado f,g Ω E e x E, define-se ( f g) : E Ω por ( f g)(x) = ( f (x) g(x)). Corolário Ω E é um reticulado relativamente pseudo-complementado. Prova Dado f,g Ω E e o conjunto C = {h Ω E f h g}, então, por definição, para todo h C e x E, f (x) h(x) g(x). Como, Ω é um reticulado relativamente pseudo-complementado, para todo x, f (x) g(x) = ( f g)(x) é o maior elemento k tal que f (x) k g(x); ou seja, ( f g) é o maior elemento de C.
69 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 52 Proposição A estrutura Ω E,,, é uma álgebra pseudo-booleana. Prova Direto do lema e do corolário Corolário (Pseudo-complemento sobre Ω E ) Dado f Ω E, o pseudocomplemento de f, denotado por f, é dado pela expressão f = ( f ), onde Ω E é a função previamente definida (x) = [0,0]. Corolário Dado x E e f Ω E, então Se f (x) = [1,1] então f (x) = [0,0]; Se f (x) = [0,0] então f (x) = [1,1]; Se f (x) = [0,1] então f (x) = [0,0]. Prova Caso f (x) = [1,1], então f (x) = [1,1] = [1,1] [0,0] = [0,0]. Caso f (x) = [0,0], então f (x) = [0,0] = [0,0] [0,0] = [1,1]. Caso f (x) = [0,1], então f (x) = [0,1] = [0.1] [0,0] = [0,0]. Proposição Dado f Ω E, a função f, definida por f (x) = f (x) é o - complemento de f. Prova Dado f Ω E e o conjunto C = {h Ω E f h = [1,1]}. então, para qualquer x E, f (x) é o menor elemento h tal que f (x) h = [1,1]. Assim, f é o menor elemento de C. Corolário Dado x E e f Ω E, Se f (x) = [1,1] então f (x) = [0,0]. Se f (x) = [0,0] então f (x) = [1,1]. Se f (x) = [0,1] então f (x) = [1,1].
70 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 53 Prova Caso f (x) = [1,1], então f (x) = [1,1] = [0,0]. Caso f (x) = [0,0], então f (x) = [0,0] = [1,1]. Caso f (x) = [0,1], então f (x) = [0,1] = [1,1]. Corolário Ω E,,,,,,,, é uma álgebra pseudo-booleana com - complemento, mas, não é uma álgebra Booleana. Prova As operações de pseudo-complemento e -complemento não coincidem (veja os corolários e ). Definição Dado f Ω E, a negação de f, f, é definida por: f (x) = [1,1], se f (x) = [0,0] [0,0], se f (x) = [1,1] [0,1], se f (x) = [0,1] (5.2.3) Definição Uma operação ρ : Ω E Ω E, é dita operação de reversão, quando para qualquer f,g Ω E, se f (x) = [0,0] e g(x) = [1,1], então ρ( f )(x) = [1,1] e ρ(g)(x) = [0,0]. Corolário As operações f, f e f são operações de reversão sobre Ω E. 5.3 Operações derivadas As reversões f, f e f induzem três versões de qualquer operação que seja definida a partir de complementação em imagens binárias. Por exemplo, pode-se definir três operadores XOR, um para cada reversão. Semelhantemente, o mesmo acontecerá para as NAND,NOR e as operações morfológicas. Definição Dados f,g Ω E, obtém-se as seguintes operações derivadas: NAND ( f,g) = f g;
71 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 54 NAND ( f,g) = f g; NAND( f,g) = f g; NOR ( f,g) = f g; NOR ( f,g) = f g; NOR( f,g) = f g; XOR ( f,g) = ( f g) (g f ); XOR ( f,g) = ( f g) (g f ); XOR( f,g) = ( f g) (g f ). Observação As definições das operações de NAND, NOR e XOR descritas acima, não são as únicas. Existem outras formas de definir essas operações. No caso da XOR por exemplo, pode-se definir como XOR( f,g) = ( f g) ( f g). Na Figura 5.2 apresentam-se algumas operações básicas entre duas imagens binárias intervalares f e g. A Figura mostra também algumas operações derivadas. Observe que "i = [0, 1]"significa "elemento indefinido". 5.4 Morfologia sobre imagens binárias intervalares Nesta seção apresenta-se as operações morfológicas básicas que serão definidas sobre Ω E. A principal motivação será a investigação das tranformações geométricas das imagens que possuem valores que representam incertezas em alguma coordenada. O modelo construído previamente, será utilizado agora para definir os operadores morfológicos do ponto de vista das imagens binárias intervalares. Antes porém, serão apresentados conceitos fundamentais dos operadores que serão aplicados sobre essas imagens. Por questão de simplificação, daqui por diante o símbolo T será usado sempre que necessário no lugar de Ω E.
72 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 55 Figura 5.2: Operações básicas e algumas operações derivadas sobre imagens binárias intervalares Operadores sobre imagens binárias intervalares Definição (Operador m-ário) Um operador m-ário sobre T (i.e., sobre Ω E ) é uma função ϕ : T m T. Por exemplo, as operações, e são operadores unários sobre T, enquanto que as operações, e são operadores binários sobre T. O conjunto de todos os operadores m-ários sobre T será denotado por [T m T ]. No caso particular
73 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 56 de m = 1, pode-se usar a seguinte representação T T = [T T ] Definição Um operador unário ψ sobre T é uma dilatação, se e somente se, para toda família de imagens { f i } T, ψ(sup{ f i }) = supψ({ f i }). Ele é uma erosão, se e somente se, para toda família de imagens { f i } T, ψ(inf{ f i }) = infψ({ f i }). Ele é uma anti-dilatação se e somente se, para toda família de imagens { f i } T, ψ(sup{ f i }) = infψ({ f i }). Por fim, ele é uma anti-erosão, se e somente se, para toda família de imagens { f i } T, ψ(inf{ f i }) = supψ({ f i }) [25], pp 34. Notações: No que segue, introduz-se alguns símbolos utilizados em morfologia. : Conjunto das dilatações. : Conjunto das erosões. a : Conjunto das anti-dilatações. a : Conjunto das anti-erosões. δ : Operador de dilatação; i.e. δ ε : Operador de erosão; i.e. ε δ a : Operador de anti-dilatação; i.e.δ a a ε a : Operador de anti-erosão - i.e. ε a a Essas operações podem ser caracterizadas através de funções f : E T. Considere, por enquanto, somente as dilatações. Neste caso, a cada dilatação δ : T T, estará associada à uma função a δ : E T. Mas antes disso, será feita uma consideração a respeito da caracterização de função como conjunto unitário. Proposição Uma vez que T é um reticulado completo, então o conjunto dos operadores unários sobre T, [T T ], munido da seguinte relação de ordem parcial:para todo f : E Ω, ϕ 1,ϕ 2 [T T ], ϕ 1 ϕ 2 ϕ 1 ( f ) ϕ 2 ( f ) (5.4.1) é um reticulado ompleto. Prova Como T é um reticulado completo, defina sobre [T T ] a ordem parcial do enunciado. [T T ] possui maior e menor elemento. Com efeito, o operador θ( f ) =
74 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 57 : E Ω é o maior operador em [T T ], pois para qualquer ϕ [T T ], ϕ( f ) = θ( f ). Semelhantemente, o operador β( f ) = é o menor operador. Isso significa que existe o supremo e ínfimo da família vazia. Dada uma família não vazia de operadores Γ [T T ], o operador Γ, definido por Γ( f ) = sup{ϕ( f ) : ϕ Γ} é um majorante de Γ, pois para todo g Γ e f T, g( f ) sup{ϕ( f ) : ϕ Γ} = Γ( f ). Γ é o menor dos majorantes, pois dado um majorante h, então por definição, para todo g Γ, g h, ou seja para todo f T,g( f ) h( f ), mas g( f ) sup{ϕ( f ) : ϕ Γ} h( f ). Logo, g( f ) Γ( f ) h( f ). Portanto Γ é o menor dos majorantes de Γ. Dualmente, demonstra-se que infγ [T T ]. Corolário Dados ϕ 1,ϕ 2 [T T ], (ϕ 1 ϕ 2 )( f ) = ϕ 1 ( f ) ϕ 2 ( f ) e (ϕ 1 ϕ 2 )( f ) = ϕ 1 ( f ) ϕ 2 ( f ). Definição Dada a função identidade id : [T T ], onde id( f ) = f, e um operador ϕ [T T ], ϕ chama-se extensivo, se e somente se, id ϕ, e anti-extensivo se ϕ id Definição Dados dois operadores ϕ 1,ϕ 2 [T T ], a composição de ϕ 1 com ϕ 2, denotada por (ϕ 1 ϕ 2 ) ou (ϕ 1 ϕ 2 ) é definida por (ϕ 1 ϕ 2 )( f ) = ϕ 1 (ϕ 2 ( f )) Definição Um operador ρ : [T T ] chama-se isotônico, sempre que para qualquer pares de operadores ϕ 1,ϕ 2 [T T ], ϕ 1 ϕ 2 implica que ρ(ϕ 1 ) ρ(ϕ 2 ). ρ chama-se antitônico sempre que para qualquer par de operadores ϕ 1,ϕ 2 [T T ], ϕ 1 ϕ 2 implica ρ(ϕ 1 ) ρ(ϕ 2 ). Proposição O conjunto das dilatações ( das erosões) é superiormente (inferiormente) fechado. Prova Para todo Ψ, { f i } T e para todo f k { f i } tem-se que (supψ)(sup({ f i }) = ( ϕ Ψ)(sup{ f i }) = ϕ Ψ ϕ(sup{ f i }) = ϕ Ψ supϕ({ f i }) = ϕ Ψ f k { f i } ϕ( f k ) = f k { f i } ϕ( f k ) ϕ Ψ = f k { f i }(supψ)( f k ) = sup(supψ)({ f i }). O que prova que supψ e portanto, é superiormente fechado. O caso das erosões é análogo.
75 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 58 Corolário Os subconjuntos e são reticulados completos. Prova Como e são subconjuntos do reticulado [T T ], de acordo com a proposição então eles são reticulados completos Translação, reflexão e invariança por translação Será introduzido agora, a noção de translação e de transposição para o caso das imagens binárias intervalares. Alguns resultados aqui apresentados tiveram como base o caso binário descrito por Banon e Barrera em [25]. No caso binário, em [25], é utilizado a noção de adição módulo n, cujo objetivo é tratar o domínio de entrada dos sinais digitais como um intervalo finito e cuja estrutura é a de um grupo Abeliano. Observando que, embora nossa estrutura algébrica seja diferente da clássica binária, o domínio utilizado também é definido em uma grade E representado no espaço Euclidiano bidimensional. Dessa forma, os valores correspondentes a um ponto p = (x, y) tomados na função f (p) serão os mesmos considerados no caso binário. Para definirmos as operações de translação, no caso das imagens binária intervalares, tomou-se como base as definições de imagens k-níveis ou multi-scala (níveis de cinza), uma vez que essas imagens podem ser consideradas como um caso particular de imagens em níveis de cinza, k = 3 ( veja [27, 40, 46]). Definição (Translação em imagens binárias intervalares) Seja A um conjunto de coordenadas de E e f A uma imagem binária intervalar. A translação de f A por um elemento u E é a função f A+u : E Ω, onde: f A+u (x) = f A (x u) Definição (Reflexão) Dada uma imagem binária intervalar f A e x E, a reflexão é definida por f A (x) = f A ( x) Definição (Invariança por translação) Seja E um grupo Abeliano. Seja f : E Ω. Seja Ψ um operador sobre [T T ]. Diz-se que Ψ é invariante por translação se somente se, para todo valor u de E, [25], pp 59 Ψ( f A+u (x)) = (Ψ( f (x))) A+u
76 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 59 Proposição (Propriedades do translado): Seja E, +, 0 um grupo abeliano e f A, f B : E Ω. Sejam u,v E, então 1. f A+0 = f A 2. f (A+u)+v = f A+(u+v) 3. f A f B f A+u f B+u Prova 1. f A+0 (x) = f A (x 0) = f A (x) 2. f (A+u)+v (x) = f A+u (x v) = f A ((x v) u) = f A (x (u + v)) = f A+(u+v) (x) 3. ( ) f A f B f A (x u) f B (x u) f A+u (x) f B+u (x) f A+u f B+u ( ) f A+u f B+u f (A+u)+( u) f (B+u)+( u) f A+(u+( u)) f B+(u+( u)) f A+0 f B+0 f A f B Proposição (Propriedades da reflexão) Seja E um grupo Abeliano e sejam x E. Para todo f A e f B 1 f A (x) = f A (x); 2 f A (x) f B (x) f A (x) f B (x) Prova (1) f A (x) = [ f A ( (x)) = [ f A ( ( (x))] = f A (x) (2) f A (x) f B (x) f A+(x+x) (x) f B+(x+x) (x) f A+x (x x) f B+x (x x) f A+x (0) f B+x (0)
77 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 60 f A (0 x) f B (0 x) f A ( x) f B ( x) f A (x) f B (x) (2) f A (x) f B (x) f A ( (x)) f B ( (x)) f A( x x) ( x) f B( x x) ( x) f A+( x) (x x) f B+( x) (x x) f A+( x) (0) f B+( x) (0) f A (0 + x) f B (0 + x) f A (x) f B (x) Operações de Minkowiski Na seção anterior, foram introduzidas as operações de translação e reflexão de imagens binárias intervalares e a classe dos operadores invariantes por translação para esse tipo de imagem. Nesta seção, serão introduzidas as operações de Minkowski e na sequência serão descritas os operadores elementares da morfologia matemática em termos dessas operações. As operações de Minkowski foram baseadas na teoria dos conjuntos e constituem os blocos de construção básicos para os operadores elementares da morfologia matemática, denominados dilatação e erosão. No caso das imagens binárias intervalares, as operações de adição e subtração de Minkowski são definidas como segue. Definição (Soma e diferença de Minkowisky) Dada uma imagem binária intervalar f A, e B um conjunto de coordenadas não nulas dado por B = {u E : f B (u) [0,0]}. A soma e a diferença de Minkowiski são definidas repectivamente por: f A B = f A+u = { f A+u : u B} (5.4.2) u B f A B = f A u = { f A u : u B} (5.4.3) u B Definição (Dilatação e erosão para imagens binárias intervalares) SejamE,,+,0 um grupo abeliano de coordenadas, f A uma imagem binária intervalar
78 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 61 e B E o conjunto de todas as coordenadas não nulas de f B tal que 0 B. Então, os operadores dilatação δ B ( f A ) e erosão ε B ( f A ), são dados respectivamente por: δ B ( f A )(x) = f A B (x) = f A (x u) = { f A (x u) : u B} (5.4.4) u B ε B ( f A )(x) = f A B (x) = f A (x u) = { f A (x u) : u B} (5.4.5) u B Proposição As funções δ B,ε B : T T satisfazem a definição Prova δ B ({ f i } i I )(x) = δ B ({ f A : f A { f i } i I })(x) = {δ B ( f A ) : f A { f i } i I }(x) = {δ B ( f A )(x) : f A { f i } i I }, Já que, para todo f,g Ω E, f g(x) = f (x) g(x) = { { f A+u : u B}(x) : f A { f i } i I }, pela definição = { { f A+u (x) : u B} : f A { f i } i I } já que h g(x) = h(x) g(x) = { { f A (x u) : u B} : f A { f i } i I }, Pela definição = { { f A (x u) : f A { f i } i I } : u B} (por associatividade e comutatividade de ). Além disso, fazendo h A = { f i } i I, δ B (h A )(x) = h A B (x) = u B{h A+u }(x) = {h A+u : u B}(x) = {h A+u (x) : u B} = {h A (x u) : u B} = { { f i } i I (x u) : u B} = { { f A : f A { f i } i I }(x u) : u B} = { { f A (x u) : f A { f i } i I } : u B}. Portanto, para todo x, δb ({ f i } i I )(x) = δ B ( { f i } i I )(x); i.e., δb ({ f i } i I ) = δ B ( { f i } i I ). Por dualidade, provamos a erosão. Assim como combinam-se funções booleanas primitivas para definir circuitos complexos, pode-se combinar as operações de soma e diferença de Minkowski para obterse operações morfológicas mais complexas. Dentre essas operações, as mais importantes são as de abertura e fechamento, que são fundamentais em aplicações como filtragens de ruídos entre outras aplicações para o tratamento de imagens.
79 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 62 Definição (Operadores de abertura e fechamento) Sejam f A uma imagem binária intervalar e B um subconjunto de coordenadas não nulas de E tal que 0 B. Chama-se abertura da imagem f A à operação: f A B = f (A B) B Chama-se fechamento da imagem f A à operação: f A B = f (A B) B Outro operador frequentemente usado em morfologia matemática é o gradiente morfológico. Essa operação tem como principal objetivo extrair contorno de objetos de uma imagem e é composta de três operações básicas da morfologia: a dilação, erosão e a subtração, sendo definida do seguinte modo: Grad( f ) = f A B f A B Como a operação de subtração de imagens envolve complementação, então, no caso das imagens binárias intervalares, obtém-se três operações de gradiente, uma para cada operação de reversão. A seguir, será apresentado um exemplo para ilustrar as operações sob imagens binárias intervalares. Exemplo Sejam as imagens da figura 5.2. Dados os conjunto de coordenadas A = {(1,1),(1,2),(2,1)(2,2)} e B = {(0,0),(0,1)}, tem-se: Cálculo da dilatação Primeiro passo: Obter a soma das coordendas do conjunto A com cada elemento do conjunto B. A + (0,0) = {(1,1),(1,2),(2,1)(2,2)} A + (0,1) = {(1,2),(1,3),(2,2)(2,3)} Segundo passo: Calcular b B f A+b f A+(0,0) (1,1) = f A (1,1) = [1,1]
80 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 63 f A+(0,0) (1,2) = f A (1,2) = [1,1] f A+(0,0) (2,1) = f A (2,1) = [0,1] f A+(0,0) (2,2) = f A (2,2) = [1,1] f A+(0,1) (1,2) = f A (1,1) = [1,1] f A+(0,1) (1,3) = f A (1,2) = [1,1] f A+(0,1) (2,2) = f A (2,1) = [0,1] f A+(0,1) (2,3) = f A (2,2) = [1,1] O resultado da dilatação, f A B = b B f A+b é mostrado na figura 5.3 (c). Para o cálculo da erosão, devemos seguir os seguintes passos: Primeiro passo: Obter a diferença das coordendas do conjunto A com cada elemento do conjunto B. A (0,0) = A = {(1,1),(1,2),(2,1)(2,2)} A (0,1) = A = {(1,0),(1,1),(2,0)(2,1)} Segundo passo: Calcular f A b para cada valor transladado. f A (0,0) (1,1) = f A (1,1) = [1,1] f A (0,0) (1,2) = f A (1,2) = [1,1] f A (0,0) (2,1) = f A (2,1) = [0,1] f A (0,0) (2,2) = f A (2,2) = [1,1] f A (0,1) (1,0) = f A (1,1) = [1,1] f A (0,1) (1,1) = f A (1,2) = [1,1] f A (0,1) (2,0) = f A (2,1) = [0,1] f A (0,1) (2,1) = f A (2,2) = [1,1] O resultado f A B = b B f A b pode ser visto na Figura 5.3 (d). A Figura 5.3, apresenta também as imagens das operações de abertura (e), fechamento (f) e as três versões da operação de gradiente morfológico obtidas a partir de f A e f B. Observação Como as operações acima estendem as operações binárias clássicas,
81 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 64 Figura 5.3: Operações Morfológicas para imagens binárias intervalares intervalares então quando a imagem não possuir pixels com valores indefinidos essas operações funcionarão como no caso binário, pois as operações de reversão não terão que lidar com indefinições e se comportam como a operação de complemento Conclusão do capítulo Neste capítulo, foi visto que o conjunto das imagens binárias intervalares não constitui uma álgebra booleana, como é o caso das imagens binárias. Entretanto, mostrou-se que a álgebra que modela a inclusão de pixels com valores indefinidos, é uma álgebra pseudo-booleana. Foram apresentadas as operações usuais desta álgebra para as funções binárias intervalares, tais como operações de supremo e ínfimo, a operação de pseudocomplemento relativo e três operações de reversão: negação, pseudo complemento e o -complemento. Segundo a noção proposta de reversão, a definição de complementação em imagens
82 CAPÍTULO 5. MORFOLOGIA PARA IMAGENS BINÁRIAS INTERVALARES 65 binárias é uma operação de reversão. Com a introdução da noção de pixel com valores indefinido obteve-se mais de uma operação de reversão, que se diferenciam apenas no tratamento do valor indefinido. Obviamente como a indefinição não ocorre no caso binário, todas elas coincidem com a complementação. Pode-se interpretar os tipos de reversão acima da seguinte maneira: Tanto o pseudo quanto o -complemento são operações ad-hoc que são acionadas diante da indefinição, ao passo que a negação deixa ao usuário (humano ou não) decidir a indefinição detectada.
83 Capítulo 6 Um Modelo Intervalar para Imagens em Níveis de Cinza Uma das técnicas mais utilizadas em processamento de imagens digitais é a segmentação. Segmentação é um processo de divisão de uma imagem em múltiplas regiões (conjunto de pixels) e é tipicamente usada para localizar objetos e limites (linhas, curvas, etc.) em imagens. O resultado da segmentação de uma imagem é um conjunto de regiões que coletivamente cobre a imagem inteira, ou um conjunto de contornos extraído da imagem (detecção de bordas). Algumas aplicações práticas de segmentação de imagens são: imagens médicas (localização de tumores ou outras patologias e diagnósticos), localização de objetos em images de satélites (ruas, florestas, etc.), reconhecimento de faces, impressões digitais, etc. Localizar um objeto em uma imagem pode ser uma tarefa difícil. No processo de segmentação, delinear a região do objeto a ser detectado, principalmente se o objeto está localizado em uma região onde existem a presença de incertezas, necessita de um bom mecanismo de controle dos erros que conduzem à incertezas. No caso de imagens médicas, por exemplo, algumas vezes essa técnica é empregada para diagnosticar doenças como o câncer [67]. A figura 6.1 extraída de [67] mostra uma imagem de uma mama e uma segmentação dessa imagem para destacar um nódulo canceroso. Observe que, destacar o nódulo não é uma tarefa fácil devido as incertezas existentes em torno deste. Algumas aplicações de métodos de segmentação de imagens podem ser encontrados em [11, 26, 48]. Um recente trabalho sobre segmentação usando morfologia matemática e 66
84 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA67 conjuntos fuzzy, pode ser visto em [2]. Figura 6.1: Imagens apresentando um processo de segmentação em uma mama com suspeito de nódulo canceroso. (a) Imagem original, (b) imagem binarizada e (c) imagem segmentada com o nódulo destacado. O modelo que será apresentado neste capítulo é uma alternativa para processos de segmentação. Acredita-se que o uso de um modelo intervalar junto com operações morfológicas permitirá, além de detectar as incertezas, localizar mais facilmente as regiões imprecisas e desse modo ter um maior controle dos erros dentro de limites confiáveis. Neste capítulo apresenta-se um modelo intervalar para lidar com incertezas em imagens em níveis de cinza e aplicado à morfologia matemática. A principal meta é então construir uma estrutura algébrica intervalar no qual seja possível definir os operadores morfológicos elementares. De um modo geral, modelos intervalares tem como objetivo lidar com erros computacionais, e no caso de imagens, esses erros geralmente conduzem a informações incertas. Para lidar com as incertezas, algumas vezes é necessário fazer uso de algum mecanismo de controle. Existem diversos mecanismos. Por exemplo, a lógica fuzzy que é bastante utlizada em várias áreas incluindo morfologia matemática. A matemática intervalar também tem grandes aplicações em situações práticas que exigem controle de erros computacionais. No caso de procesamento digitais de imagens, essa teoria já vem sendo aplicada em alguns trabalhos recentes como em [4, 6]. Grandes aplicações da morfologia matemática são realizadas nas mais diversas áreas. Existe uma grande concentração de uso de metodologias buscando tratar com questões de incertezas através de operadores morfológicos. Os mais conhecidos métodos são
85 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA68 através da teoria dos conjuntos fuzzy (morfologia fuzzy) [32, 65], waveletes [14] e modelos de distribuição probabilístico, tal como processos estocásticos. Os mais recentes trabalhos neste contexto, usam as teorias: fuzzy e matemática intervalar (morfologia fuzzy intervalar) [50]. Aqui oferemos uma ferramenta que faz uso somente da teoria intervalar (morfologia intervalar) [58]. Uma das técnicas bastante utilizada na morfologia matemática é filtragens de imagens corrompidas por ruídos. Para isso, às vezes são necessárias várias sequências de operação morfológicas (filtros sequênciais). No caso de imagens em tons de cinza, essas tranformações, na maioria das vezes são perceptíveis pela intensidade do brilho (regiões mais clara ou mais escura em relação a imagem original). Em geral, o objetivo é a eliminação ou modificação de tons nas regiões onde existe a necessidade do efeito que deverá ser causado por algumas operações morfológicas. Todo esse processo envolve técnicas que são tratadas por sistemas computacionais e que, por este motivo frequentemente há ocorrência de erros que conduzem as incertezas em alguns pixels. No Capítulo 5 foi desenvolvido um modelo para lidar com incertezas em imagens binárias com informação de incerteza. Foi considerado um conjunto intervalar com três elementos, onde um deles representa uma indefinição. No capítulo anterior a incerteza entre os valores 0 e 1 foi representada pelo intervalo degenerado [0, 1]. Este capítulo generaliza a idéia de um intervalo não degenerado [l, L] ser a representação da incerteza de um valor de pixel em uma coordenada, desta vez para tons de cinza; ou seja, para N valores. Neste caso, um intervalo degenerado [l, L] reprepresentará a incerteza do real valor do pixel que varia entre l e L, onde l L N. A representação da incerteza em imagens em níveis de cinza como um intervalo [l,l] pode ser aplicada, por exemplo, em sequências de imagens obtidas de uma mesma cena e na mesma posição, que geram portanto, incerteza em relação ao "verdadeiro"valor do pixel. As incertezas são representadas através de intervalos de confiança e faz uso da aritmética intervalar para realizar as operações necessárias. Em geral a teoria intervalar fornece um mecanismo para representar e manipular algum tipo de incerteza, principalmente originadas por disceminação de dados contínuos e propagação destas incertezas.
86 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA Construção do espaço algébrico para imagens intervalares em escala de cinzas Nesta seção, será introduzida a estrutura algébrica intervalar que modelará as funções que representam as imagens em níveis de cinza e onde um pixel terá a forma de um intervalo. Definição Seja n N e IN = {[a,b] N : [a,b IR]}. Define-se Ω N como sendo o conjunto dado por Ω N = {[x,y] IN : x y n}. Um intervalo da forma [a,a] é chamado intervalo degenerado. Aqui, um intervalo X Ω N será denotado por X = [x,x]. Observação Observe que Ω N = {X IN : O X N} onde O = [0,0] e N = [n,n]. A ordem, " ", utilizada será a ordem de Kulisch-Miranker que foi definida no capítulo 3. Observação A relação de ordem de Kulisch e Miranker é uma ordem usual em abordagens de matemática intervalar, porém existem outras ordens, tais como a ordem de inclusão que é dada por: X Y x y e y x. Escolheu-se a ordem Kulisch e Miranker, por generalizar o caso pontual, no sentido que, quando considera-se intervalos degenerado, esta coincide com o caso pontual. Lema Ω N possui menor e maior elementos; a saber O e N respectivamente. Prova Dado X Ω N, onde X = [x,y], com [0,0] Ω N, [0,0] [x,y], pois 0 x e 0 y. Com [n,n] Ω N, então [x,y] [n,n], pois x n e y n. A Figura 6.2 representa a estrutura do reticulado Ω N. É possível observar que esta estrutura é uma cadeia finita; lembrando que, um intervalos da forma [x,y] com x y representa uma incerteza. Definição Dado X,Y Ω N tal que X = [x,x] e Y = [y,y], então, define-se as seguintes operações: X Y = [max(x,y),max(x,y)] (6.1.1)
87 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA70 Figura 6.2: Estrutura do reticulado Ω N X Y = [min(x,y),min(x,y)] (6.1.2) Proposição Ω N é um reticulado completo. Prova Ω N é um reticulado completo com as operações de supremo e ínfimo e de acordo com a definição Seja S Ω N, se S = /0, então S = O e S = N. Portanto, se S = /0 então S Ω N e S Ω N. Caso S /0, seja µ 1 (S) = {x N : y N,[x,y] S} e µ 2 (S) = {v N : u N,[u,v] S}. Como, µ 1 (S) e µ 2 (S) são superiormente e inferiormente limitadas, então existe o supremo e o ínfimo de µ 1 (S) e de µ 2 (S), denotada por µ 1 (S), µ 1 (S), µ 2 (S) e µ 2 (S) respectivamente. Desse modo, claramente S = [ µ1 (S), µ 2 (S] e S = [ µ 1 (S), µ 2 (S)]. Proposição Ω N é um reticulado distributivo. Prova Dados X,Y,Z Ω N, onde X = [x,x], Y = [y,y] e Z = [z,z], então: (1) X (Y Z) = (X Y ) (X Z) (2) X (Y Z) = (X Y ) (X Z) Assim: (1) X (Y Z) = [x,x] ([y,y] [z,z]) = [x,x] [max(y,z),max(y,z)] = [min(x, max(y, z)), min(x, max(y, z))] = [max(min(x, y), min(x, z)), max(min(x, y), min(x, z))] = [min(x,y),min(x,y)] [min(x,z),min(x,z)]
88 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA71 = ([x,x] [y,y]) ([x,x] [z,z]) = (X Y ) (X Z) (2) Análogo ao item 1 A seguir, será apresentado o complemento intervalar para imagem em níveis de cinzas (veja [18]). Definição Seja Ω N,,O,N um reticulado completo. Uma operação C : Ω N Ω N é um complemento se satisfaz as seguintes propriedades: 1. C(O) = N e C(N) = O 2. X Y C(X) C(Y ), X,Y Ω N 3. se, além disso C(C(X)) = X então C é chamado de complemento forte por: De acordo com a aritmética intervalar de Moore em [60] a subtração intervalar é dada Isso leva a seguinte definição de complemento X Y = [x y,x y] (6.1.3) Definição Sendo X = [x,x] Ω N tome : Ω N Ω N por X = [n,n] [x,x] = [n x,n x] (6.1.4) Corolário Para X = [x, x], então X = [ x, x] (6.1.5) onde x = n x e x = n x Proposição A função : Ω N Ω N é um complemento forte. Prova 1. [0,0] = [n 0,n 0] = [n,n] e [n,n] = [n n,n n] = [0,0] [0,0] = [n 0,n 0] = [n,n]
89 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA72 and [n,n] = [n n,n n] = [0,0] 2. Seja X=[x,x] e Y = [y,y] X Y x y e x y N X N Y n x n y e n x n y [n x,n x] [n y,n y] X Y 3. (N X) = N (N X) = N + ( N X) = N + ( N) + X = 0 + X = X, desde que N é degenerado. Antes de introduzir as imagens intervalares em escala de cinzas, será definida uma classe especial de operações de soma e diferença entre dois elementos do conjunto Ω N. Este conceito é baseado no caso pontual desenvolvido por Heijmans em [40], sendo importante porque as funções que modelam as imagens intervalares em tons de cinza serão definidas sobre um conjunto finito de Ω N. Definição Sejam IZ = {[a, b] Z : [a, b] IR}, munido da aritmética de Moore e V = [v,v] IZ, O = [0,0] e N = [n,n]. A operação T T V sobre Ω N é definida por O, se T = O ou T +V O [0,t + v] se T > O e t + v 0 T +V, se T > O e O T +V N T V = N, se T > O e T +V > N [0,n] se T > O e [0,n] T +V [t + v,n] if T > O e t + v N E a operação T T V sobre Ω N é definida por [0,t v] se T < N e O T V [t v,n] se T < N e N T V T V = O, se T < N e T V O T V, se T < N e O T V N N, se T = N ou T V > N (6.1.6) (6.1.7)
90 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA73 Proposição Seja A,B Ω N, então A B = [A B,A B] (6.1.8) e A B = [A B,A B] (6.1.9) Prova Direto da definição Observação A definição para o caso pontual, (veja [40, pp 14]), é dada do seguinte modo: Seja v Z, define-se t v e t v por 0, se t = 0 ou t > 0 e t + v 0 t v = t + v, se t > 0 e 0 t + v n n se t > 0 e t + v n 0, se t = 0 ou t < n e t v 0 t v = t v, se t < n e 0 t v n n, se t = n ou t v > n (6.1.10) (6.1.11) 6.2 O reticulado completo das imagens sobre Ω N As funções F : E Ω N modelam imagens em tons de cinza e serão usadas para definir os operadores morfológicos que serão introduzidos na próxima seção. Observando que Ω N é o reticulado apresentado na seção anterior e E representa um conjunto finito de coordenadas que é considerado como um grupo Abeliano. De um modo geral considerase E = Z Z. Nesta seção serão definidas tais funções e estudadas suas propriedades algébricas. Um sinal digital em escala de cinza é em geral definido sobre um subconjunto de números inteiros. Se x E, então F(x) denota um valor do sinal em x. Nesta seção serão introduzidas as funções intervalares para imagens em escala de cinzas e que modelarão as incertezas entre pixels dessas imagens.
91 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA74 Por exemplo, suponha que, em uma determinada posição do espaço, o valor retornado pela função corresponde a 15, e na seqüência de imagens, na mesma posição, esse valor varia entre 13 e 16. Observa-se aí a existência de uma incerteza. Neste caso, considerase uma imagem intervalar em que para essa posição teremos o intervalo [13,16]. Esse intervalo corresponde ao menor e maior valor obtido na sequência garantindo que o valor exato do tom pertence a ele. Em [4], Lyra define uma imagem digital intervalar como sendo uma matriz A, de ordem m x n que representa uma imagem espacialmente discretizada, obtida através de um dispositivo de aquisição de imagens e digitalizada por um digitalizador intervalar que transforma cada pixel da imagem em um intervalo. Alguns pixels serão representados por intervalos degenerados, por exemplo, [12,12], outros serão representados por intervalos contendo um menor e um maior valor em suas extremidades e que representam os pixels indefinidos, como por exemplo, [11,16]. Cada a i, j em A é denominado pixel intervalar, porque é um intervalo que define a variação I da intensidade luminosa deste pixel intervalar Imagens intervalares em escala de cinzas De acordo com Lyra et all [4], um dos caminhos para gerar uma imagem digital intervalar, é feito no momento da aquisição, através da regulagem do dispositivo de aquisição ou modificações ambientais. Estas modificações podem ocorrer devido a alguns fatores como por exemplo, luminosidade, humidade, etc. Certamente, estas modificações contribuem para a geração de uma imagem intervalar onde a imagem ótima deverá estar contida. A seguir, serão apresentada, as imagens em escala de cinzas, como funções mapeadas no reticulado Ω N. Definição Seja E = Z Z. Uma imagem intervalar em escala de cinzas cuja posição do pixel é correspondente a valores intervalares, é definida pelo mapeamento F : E Ω N. O conjunto de todas as funções que representam as imagens em escala de cinzas será denotado por Ω E N. Desde que Ω N é um reticulado completo, então Ω E N é também um reticulado completo
92 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA75 com ordem parcial e operações de supremo e ínfimo descritas nas definições e a seguir. Definição Dadas F,G Ω E N, a seguinte relação de ordem é definida sobre ΩE N : F G F(x) G(x), x E, i.e, Ω E N, torna-se uma ordem parcial. Proposição Ω E N, é uma ordem parcial satisfazendo as seguintes propriedades: F F (Reflexividade); Se F G e G F, então F = G (Anti-simetria); Se F G e G H, então F H (Transitividade) Prova Desde que Ω N, é uma ordem parcial (veja a estrutura representada na figura 6.2), por herança, Ω E N, também é uma ordem parcial. Operações Básicas Definição (Operações de supremo e ínfimo) Seja I um conjunto de índices. Dada uma família não vazia de funções intervalares F I = {F i } i I e X Ω N. Sejam π 1 ([a,b]) = a e Π 1 (X) = {π 1 (x i ) : x i X}, π 2 ([a,b]) = b, e Π 2 (X) = {π 2 (x i ) : x i X}. Define-se as seguintes operações: {Fi } i I (x) = [ Π 1 {F i (x)} i I, Π 2 {F i (x)} i I ] (6.2.1) {Fi } i I (x) = [ Π 1 {F i (x)} i I, Π 2 {F i (x) i I }] (6.2.2) Proposição Dada qualquer família não vazia {F i } i I Ω E N, então, {F i } i I (x) e {Fi } i I (x) é uma operação de supremo e de ínfimo respectivamente. Prova Primeiro mostra-se que x E, {F i }(x) é um marjorante de {F i (x)}. Como para cada x, π 1 F i (x) supπ 1 F i (x) e π 2 F i (x) supπ 2 F i (x), então {F i } é um marjorante de {F i }.
93 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA76 Agora mostra-se que {F i } é dos menor dos marjorantes de {F i }. Seja G outro marjorante de {F i }. Por definição x E,F i (x) G(x). Então, x, π 1 F i (x) π 1 G(x) e π 2 F i (x) π 2 G(X). Então, supπ 1 F i (x) π 1 G(x) e supπ 2 F i (x) π 1 G(x). Portanto {F i } i I (x) G(x), x E. desse modo, {F i }(x) é uma operação de supremo. A prova da operação de infimo é análoga. Lema As funções N,O : E Ω E N, tal que N(x) = [n,n] e O(x) = [0,0] para todo x E são, respectivamente, o maior e o menor elemento de Ω E N. Prova Seja F Ω E N. Então, para qualquer x E, O(x) = [0,0] F(x) [n,n] = N(x). Assim, O F N, para toda função F Ω E N. Corolário Se I = /0 então, as funções constantes 0 e N são respectivamente o supremo e o infimo de F I. Prova Direto do lema Teorema Ω E N,,N,O, onde " "é uma ordem parcial, é um reticulado completo Prova Direto da definição e da proposição Ω E N tem operação de complemento dada como segue. Definição Seja F Ω E N então, a negação : ΩE N ΩE N é definida por ( F)(X) = F(X) (6.2.3) Desse modo, se F Ω E N e F(X) = [x,x] então F(X) = [n x,n x] Proposição é um complemento forte.
94 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA77 Prova 1. (0) = N e (N) = 0 a) (0)(x) de f = [n 0,n 0] = [n,n] = N b) (N)(x) de f = [n n,n n] = [0,0] = 0 2. Supondo X Y, então x y e x y, então n y n x e n y n x n x n y e n x n y [n x,n x] [n y,n y] X Y 3. F(X) = ([n x,n x]) = [n n + x,n n + x] = [x,x] Portanto, F(x) = F(x) Corolário A ordem parcial (Ω E N, ) é um reticulado completo com sendo um complemento forte. Prova Direto das proposições e Existem vários outros complementos fortes que podem ser definidos sobre Ω E N, porém considera-se o complemento acima por sua simplicidade e naturalidade. Na próxima seção será apresentada a extensão das operações morfológicas para Ω E N. 6.3 Operações morfológicas para imagens intervalars em níveis de cinza O modelo morfológico aplicado a de problemas de análise de imagem está baseado na extração de informações de imagens a partir de transformações de formas, conforme foi dito no início desta discertação. Proposta por Matheron e Serra, as dilatações e erosões são usadas para a criação de transformações mais sofisticadas. Essas transformações por sua vez, levaram a vários resultados importantes do ponto de vista de análise de imagens,
95 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA78 dentre eles, pode-se citar os filtros morfológicos, o preenchimento de buracos, extração de contornos e reconhecimento de padrões. A construção de sistemas morfológicos, geralmente, é implementada a partir da concepção do problema e pela escolha dos operadores mais adequados à solução em questão. Um dos maiores problemas para a adequação de operadores é observado na especificação dos elementos estruturantes. Uma possível solução para este problema é a criação de um mecanismo capaz de encontrar as funções aditivas estruturantes adequadas, de forma a realizar a transformação desejada. No caso da abordagem intervalar, vale salientar que serão necessárias algumas restrições para a função estruturante intervalar escolhida. Será necessário impor algumas condições, uma vez que estaremos tratando com conjuntos intervalares finitos e funções mapeadas nesses conjuntos. Isso será possível, porque as transformações utilizadas em morfologia matemática podem ser aplicadas a conjuntos de dimensão qualquer, tais como o N-espaço Euclidiano, ou o espaço das N-uplas de inteiros. A extensão da morfologia matemática para reticulados completos arbitrários, por Serra [46], resultou em diferentes pontos de vista com respeito a imagens em níveis de cinza. De acordo com Banon e Barrera em [24], a idéia central da morfologia matemática é a decomposição dos mapeamentos entre reticulados completos em termos dos operadores elementares: erosão e dilatação. Nesta seção, será estendida a teoria da morfologia em níveis de cinza desenvolvida para o caso pontual, por Heijmans em [40] para mapeamentos entre reticulados intervalares. Nesta seção serão introduzidos alguns conceitos básicos da morfologia matemática, bem como os operadores morfológicos intervalares para imagens em níveis de cinza. Observe que algumas operações são diferentes das operações para o caso tradicional, pois serão operações entre intervalos, cujas propriedades algébricas algumas vezes se diferenciam do caso real.
96 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA Operações básicas Definição Dadas duas funções intervalares F,G Ω E N. As operações de supremo e de ínfimo entre F e G, são definidas repectivamente por: (F G)(x) = F(x) G(x) (6.3.1) (F G)(x) = F(x) G(x) (6.3.2) Assim, se F(x) = [a, b] e G(x) = [c, d], então (F G)(x) = [max(a,c),max(b,d)] e (F G)(x) = [min(a,c),min(b,d)] Exemplo F(x) = [2,8] and G(x) = [3,7] (F G)(x) = [max(2,3),max(8,7)] = [3,8] (F G)(x) = [min(2,3),min(8,7)] = [2,7] Dilatação e erosão para imagens intervalares em níveis de cinzas Para definir os operadores morfológicos necessita-se introduzir os conceitos de translação, soma e diferença de Minkowiski Definição (Translação horizontal) Dada uma imagem intervalar F : E Ω N, u E. A translação horizontal de F por u, é a função intervalar F u : E Ω N definida por F u (x) = F(x u) (6.3.4) A Figura 6.3 apresenta um gráfico de uma função intervalar com uma translação horizontal. Definição (Translação vertical) Dada uma imagem intervalar F : E Ω N, e V Ω N. A translação vertical de F x por V é definida por (F +V )(x) = F(x) V (6.3.5)
97 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA80 Figura 6.3: Uma função intervalar com uma translação horizontal. A Figura 6.4 apresenta um gráfico de uma função intervalar com uma translação vertical. Figura 6.4: Uma função intervalar com uma translação vertical. Quando ambas as translações são aplicadas juntas, morfológica intervalar dada por obtém-se uma translação (F u +V )(x) = F(x u) V (6.3.6) A Figura 6.5 apresenta um gráfico de uma função intervalar com uma translação morfólogica. Definição (Reflexão) Dada uma imagem intervalar G Ω E N G é definida por Ĝ(x) = G( x) e x E, a reflexão de
98 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA81 Figura 6.5: Uma função intervalar com uma translação morfológica. Observação F u (x) = F(x + u) Proposição Seja F : E Ω N então, existe F,F : E L tal que, F(u) = [F(u), F(u)]. Em outras palavras, a função intervalar F pode ter uma forma intervalar, onde as extremidades são funções que pertencem ao caso pontual. Prova Seja F(u) = π 1 (F(u)) e F(u) = π 2 (F(u)), onde π 1 eπ 2 são definidas de acordo com a definição 6.2.4, então F(u) = [π 1 (F(u)),π 2 (F(u))] = [F(u),F(u)] Corolário F u (x) = [F u (x),f u (x)] Prova De fato, temos que, F u (x) = F(x u) = [F(x u),f(x u)] = [F u (x),f u (x)] Ou seja F u = F u e F u = F u Definição (Soma e diferença de Minkowiski) Dada duas imagens intervalares F,G Ω E N. A soma e a diferença Minkowski são definidas respectivamente por: F G = u dom(g) (F u Ĝ(u)) (6.3.7)
99 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA82 F G = (F u G(u)) (6.3.8) u dom(g) Definição Um operador ψ sobre Ω E N é uma dilatação se, para toda família de imagens {F i } Ω E N, ψ( {F i }) = ψ({f i }). Dualmente, é uma erosão, se ψ( {F i }) = ψ({fi }). Observação Em geral a dilatação e a erosão são operações descritas do seguinte modo: Dado duas funções F e G, então G (F)(x) = (F G)(x) = [F(x u) G(u)] (6.3.9) u dom(g) ε G (F)(x) = (F G)(x) = [F(x u) Ĝ(u)] (6.3.10) u dom(g) ε G (F) e G (F) são uma erosão e uma dilatação, respectivamente. G é chamada de função estruturante aditiva. Como Ĝ(x) = G( x), logo, para o caso da erosão, pode-se escrever a equação por (6.3.10) por ε G (F)(x) = (F G)(x) = [F(x + u) G(u)] (6.3.11) u dom(g) Note ainda que as operações descritas acima são utilizadas considerando um domínio finito e somente podem ser utilizadas sob certas condições conforme será visto nesta seção. A seguir, apresentam-se alguns conceitos importantes e resultados tais como, H-operador e relação de adjunção. Esses resultados, foram baseados no caso pontual desenvolvido por Heijmans em [40]. Além disso, de acordo com a definição 6.2.4, uma forma equivalente para definir as operações de dilatação e erosão para o caso intervalar, é dada como segue. Sejam F,G Ω E N. Sejam P u(x) = F(x u) G(u) e Q u (x) = F(x u) Ĝ(u), então por definição a dilatação e a erosão podem ser escrita também por [ Π1 G (F)(x) = (F G)(x) = {P u (x)} u E, ] Π 2 {P u (x)} u E [ Π1 ε G (F)(x) = (F G)(x) = {Q u (x)} u E, ] Π 2 {Q u (x)} u E (6.3.12) (6.3.13)
100 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA83 onde Π 1 e Π 2 são definidas de acordo com a definição No que segue, apresentaremos um teorema que caracteriza as operações de dilatação e erosão para o caso intervalar. Teorema (Teorema da representação intervalar dos operadores morfológicos) Pode-se introduzir uma caracterização alternativa para dilatação e erosão intervalares que é descrita pelas equações (F G)(x) = [(F G)(x),(F G)(x)] (6.3.14) (F G)(x) = [(F G)(x),(F G)(x)] (6.3.15) Prova Primeiro mostra-se que, (F G)(x) = (F G)(x). Tem-se que, (F G)(x) = Π 1 (F G(x)) = Π 1 ( u E F u (x) G(u)) = = Π 1 [ u E Π 1 (F u (x) G(u)), u E Π 2 (F u (x) G(u))], equação = u E Π 1 (F u (x) G(u)) = u E Π 1 [(F u (x) G(u),(F u (x) G(u)] equação = u E(F u (x) G(u)) = u E(F u (x) G(u)) = u E(F u (x) G(u)), corolário = (F G(x)), caso Pontual. Analogamente, (F G)(x) = (F G)(x) (6.3.16) A demonstração para o caso da erosão, é análoga. Na morfologia clássica, o conceito geral de adjunção é dado por: Definição (Adjunção) Sejam M,N dois reticulados completos, tal que ε : M N e δ : N M. O par (ε,δ) é chamado uma adjunção entre M e N se δ(y ) X Y ε(x) [40].
101 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA84 De acordo com Heijmans, em [40], o par (ε G (F), G (F)) é uma adjunção sobre um reticulado M se e somente se, para todo x,y E, existe uma adjunção (ε y,x,δ x,y ) sobre M tal que (F)(y) = δ x,y (F(x)) (6.3.17) x E ε(f)(x) = ε y,x (F(y)) (6.3.18) x E Na morfologia clássica, quando se toma somente a translação horizontal (invariante por tranlação), o operador é chamado de H-operador. Assim, para H-operador, temos que F u (x) = F(x u) e Ψ(F u ) = [Ψ(F) u ]. O mapeamento consiste em F F u. Note que, se Ψ é invariante sob a translação vertical, então Ψ(F + v) = Ψ(F) + v. Este operador Ψ é chamado de um T-operador. Neste caso, consiste em um mapeamento F F + v. Definição Um mapeamento δ : Ω N Ω N é uma dilatação intervalar se δ([0,0]) = [0,0] e δ é não decrescente. A adjunção erosão intervalar é dada por: ε(t ) = max{s δ(s) = T } (6.3.19) Onde o máximo do conjunto vazio é definido para ser O. Toda H-adjunção (ε, ) sobre Ω E N é definida por Definição Seja u E. Se δ u e ε u é uma dilatação intervalar e uma erosão intervalar respectivamente sobre Ω N. As funções operadores e ε são dadas por (F)(y) = u E δ u (F(y u)) (6.3.20) ε(f)(x) = u E ε u (F(x + u)) (6.3.21) definem uma H-dilatação e H-erosão respectivamente e o par (ε u,δ u ) forma uma adjunção sobre Ω N para todo u E. A seguir, apresentam-se alguns resultados que dependem da classe especial de operações de soma e diferença definidas pelas equações (6.1.6) e (6.1.7).
102 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA85 Lema O par (ε,δ) tal como ε(t ) = T V e δ(t ) = T V define uma adjunção sobre Ω N Para todo V IZ. Prova Esta prova é consequência da definição , da proposição Na seção 6.1 foi definida uma classe especial de operações de soma e diferença para o caso intervalar em conjuntos finitos, e que podem ser descritos por: Sendo Ω N = {[0,0],...,[n,n]} com n N e N = [n,n] IN. Para T Ω N e V IZ logo, T T V e T T V sobre Ω N são operações descritas como na definição Coonsiderando a função estruturante G e tomando-se ε u (T ) = T G(u) e δ u (T ) = T G(u), combinando a definição e o lema , então, T = F(y u) δ u (F(y u)) = F(y u) G(u), e T = F(x + u) ε u (F(x + u)) = F(x + u) G(u). Portanto ε G (F)(x) = u E[F(x + u) G(u)] e G (F)(x) = u E[F(x u) G(u)] Proposição A dilatação e a erosão satisfazem respectivamente (F V ) = (F) V (6.3.22) ε(f V ) = ε(f) V (6.3.23) Prova De acordo com as equações (6.3.14) e (6.3.15), descritas 6.3.9, tem-se que: (F V ) = (F V )(x) = [(F V )(x),(f V )] = [ (F V )(x), (F V )(x)] = (F V ), (F V )] onde ([40, Eq 11.3]) (F V ) = (F) V e (F V ) = (F) V O caso da erosão é análogo. A proposição a seguir mostra que, as equações (6.3.9) e (6.3.10), sob certas condições, são satisfeitas para o caso finito intervalar. Proposição Seja uma H-dilatação sobre Ω E N satisfazendo (F V ) = (F) V para F Ω E N e V O, onde O = [0,0], então, existe uma função intervalar não negativa,
103 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA86 G com dom(g) E, tal que é dada pela equação (6.3.9). Analogamente, se ε é uma H- erosão sobre Ω E N satisfazendo ε(f V ) = ε(f) V para F Ω E N e V O, existe uma função intervalar não negativa G com dom(g) E, tal que ε é dada pela equação (6.3.10). Prova Primeiro, para qualquer V Ω N considera-se a função dada por V, se x = 0 f 0,V (x) = [0,0], caso contrário (6.3.24) Quando V = [1,1], f 0,V é chamada de função impulso. Definimos G por G(x) = ( f 0,[1,1] )(x) [1,1] (6.3.25) Logo, dom(g) = {x ( f 0,[1,1] )(x) [1,1]} (6.3.26) Note que, G(x) [0,0], x dom(g). Desde que, qualquer função intervalar pode ser escrita como F = u E f u,f(u), é suficiente mostrar que ( f u,v ) = f u,v G, para cada u E e V Ω N. Observando que, por causa da invariança da translação horizontal, podemos restringir para o caso u = 0. O resultado é trivial para V = [0,0], desde que f 0,[0,0] (x) = [0,0]. Isto é verdade porque, [0,0] G(x) = [0,0]. Por outro lado, ( f 0,[0,0] )(x) = u E δ u ( f 0,[0,0] (x u)) Definição = δ u ([0,0]) = [0,0] Definição = f 0,[0,0] (x) G(x) Será mostrado que ( f 0,V ) = f 0,V G para V = [0,1],...[n,n]. Primeiro considera-se a seguinte igualdade: ( f 0,V ) = ( f 0,[1,1] (V [1,1])) (6.3.27) Dois casos serão analizados, quando x = 0 e x 0. Se x = 0 tem-se que, f 0,[1,1] (x) (V [1,1]) = [1,1] V [1,1] = V = f 0,V (x) Se x 0 tem-se que, f 0,[1,1] (x) V [1,1] = [0,0] V [1,1] = [0,0] = f 0,V (x). Pela proposição , ( f 0,V V [1,1]) = ( f 0,[1,1] ) (V [1,1]) = V.
104 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA87 Logo, ( f 0,V ) = ( f 0,[1,1] ) (V [1,1]). Se x dom(g) então, pela equação (6.3.25), ( f 0,[1,1] )(x) = G(x) + [1,1], logo, ( f 0,V )(x) = ( f 0,[1,1] )(x) (V [1,1]) = (G(x) + [1,1]) (V [1,1]). Se x Dom(G), então ( f 0,[1,1] )(x) [1,1]. Neste caso, tem-se duas alternativas: a) ( f 0,[1,1] )(x) = [0,0] ou b) ( f 0,[1,1] )(x) = [0,1]. Mas, pela equação (6.3.20), ( f 0,[1,1] )(x) = u E δ u ( f 0,[1,1] (x u)) = δ x ([1,1]) u E {x} δ u ([0,0]) = δ x ([1,1]) [0,0] = δ x ([1,1]) [0,0]. Logo, de a) e b), ( f 0,[1,1] )(x) = [0,1]. Assim, (G(x) + [1,1]) (V [1,1]), se x dom(g) ( f 0,V )(x) = [0,1], caso contrário (6.3.28) Desde que, (G(x) + [1,1]) (V [1,1]) = V G(x) se V [0,0], e G(x) [0,0], i.e., x dom(g), então, considera-se dois casos: Caso V = [0,1] (G(x) + [1,1]) ([0,1] [1,1]) = (G(x) + [1,1]) [ 1,0] = G(x) + [0,1] = G(x) +V = V + G(x) = V G(x) Caso V > [0,1] (G(x) + [1,1]) (V [1,1]) = (G(x) + [1,1]) (V [1,1]) = G(x) + V = V + G(x) = V G(x). Assim, ( f 0,V )(x) = V G(x) para todo x Dom(G). Por outro lado, pela equação (6.3.9) ( f 0,V G)(x) = (V G(x)), se x dom(g) ( f 0,V (x u) G(u)) = [0,0], caso contrário u dom(g) (6.3.29) Então ( f 0,V )(x) = ( f 0,V G)(x) se x dom(g). A prova do caso da erosão é análoga. Corolário O par (ε, ) onde ε e é definido como a definição é uma H- adjunção sobre Ω E N.
105 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA88 Prova Direto do lema e proposição No que segue, será apresentado um exemplo de uma imagem intervalar descrita em uma grade E = 7 7, bem como as operações de dilatação e erosão sobre essa imagem, por uma função estruturante G pré-definida. Exemplo Seja E uma grade de dimensão 7 7 e seja F Ω E N tal que F = [F,F]. Supondo que uma sequência de imagens obtidas pela mesmo posição e representadas pelo conjunto de pares ordenados dados por {(0,0),(1,5),(2,3),(3,4),(4,2),(5,5),(6,6)}. Para cada posição, tem-se um valor que algumas vezes apresenta incerteza. De acordo com a definição de imagem intervalar, toma-se para cada F, o menor elemento e para F, o maior elemento. Tem-se que: F(0,0) = 1 e F(0,0) = 3, F(1,5) = 4 e F(1,5) = 6, F(2,3) = 2 e F(2,3) = 4, F(3,4) = 0 e F(3,4) = 2, F(4,2) = 5 e F(4,2) = 5, F(5,5) = 6 e F(5,5) = 7, F(6,6) = 6 e F(6,6) = 8. Nesse caminho, é formada uma função intervalar F : E Ω 8 ou em ordem, Im(F) = {[0,2],[1,3],[2,4],[4,6],[5,5],[6,7],[6,8]} Considerando G como uma função estruturante e tomando G = G. Seja u Z tal que, u = {u 1,u 2,u 3 }, onde u 1 = (0,0), u 2 = (0,2) e u 3 = (1,2). A Figura 6.6 representa a imagem intervalar F e a função estruturante G para G(u 1 ) = [2,2], G(u 2 ) = [1,1] e G(u 3 ) = [3,3]. Para calcular a dilatação, primeiro calcula-se todas as translações horizontais da função F, para cada u i, i = 1,2,3. Em seguida, calcula-se F(x u) G(u), x E e finalmente aplica-se o supremo, i.e., calcula-se [F(x u) G(u)]. Translação de F por u 1 F u1 (0,0) = F((0,0) (0,0)) = F(0,0) = [1,3] F u1 (1,5) = F((1,5) (0,0)) = F(1,5) = [4,6] F u1 (2,3) = F((2,3) (0,0)) = F(2,3) = [2,4] F u1 (3,4) = F((3,4) (0,0)) = F(3,4) = [0,2] F u1 (4,2) = F((4,2) (0,0)) = F(4,2) = [5,5] F u1 (5,5) = F((5,5) (0,0)) = F(5,5) = [6,7] F u1 (6,6) = F((6,6) (0,0)) = F(6,6) = [6,8]
106 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA89 Figura 6.6: Imagem representada por uma função F e por uma função estrurante G Translação de F por u 2 F u2 (0,2) = F((0,2) (0,2)) = F(0,0) = [1,3] F u2 (1,7) = F((1,7) (0,2)) = F(1,5) = [4,6] F u2 (2,5) = F((2,5) (0,2)) = F(2,3) = [2,4] F u2 (3,6) = F((3,6) (0,2)) = F(3,4) = [0,2] F u2 (4,4) = F((4,4) (0,2)) = F(4,2) = [5,5] F u2 (5,7) = F((5,7) (0,2)) = F(5,5) = [6,7] F u2 (6,8) = F((6,8) (0,2)) = F(6,6) = [6,8] Translação de F por u 3 F u3 (1,2) = F((1,2) (1,2)) = F(0,0) = [1,3] F u3 (2,7) = F((2,7) (1,2)) = F(1,5) = [4,6] F u3 (3,5) = F((3,5) (1,2)) = F(2,3) = [2,4] F u3 (4,6) = F((4,6) (1,2)) = F(3,4) = [0,2] F u3 (5,4) = F((5,4) (1,2)) = F(4,2) = [5,5] F u3 (6,7) = F((6,7) (1,2)) = F(5,5) = [6,7] F u3 (7,8) = F((7,8) (1,2)) = F(6,6) = [6,8] Note que, nas posições (6,8) e (7,8) toma- e(6,7) e (7,7)
107 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA90 As novas posições são dadas pelo conjunto {(0,0),(1,5),(2,3),(3,4),(4,2),(5,5),(6,6),(0,2),(1,7),(2,5),(3,6),(4,4),(5,7), (6,7),(1,2),(2,7),(3,5),(4,6),(5,4),(6,7),(7,7)} Em seguida, calcula-se a soma de Minkowiski, F(x u) G(u). F(0,0) G(0,0) = [1,3] [2,2] = [3,5] F(1,5) G(0,0) = [4,6] [2,2] = [6,8] F(2,3) G(0,0) = [2,4] [2,2] = [4,6] F(3,4) G(0,0) = [0,2] [2,2] = [2,4] F(4,2) G(0,0) = [5,5] [2,2] = [7,7] F(5,5) G(0,0) = [6,8] [2,2] = [8,8] F(6,6) G(0,0) = [7,7] [2,2] = [8,8] F(0,0) G(0,2) = [1,3] [1,1] = [2,4] F(1,5) G(0,2) = [4,6] [1,1] = [5,7] F(2,3) G(0,2) = [3,3] [1,1] = [4,4] F(3,4) G(0,2) = [4,4] [1,1] = [6,6] F(4,2) G(0,2) = [5,5] [1,1] = [7,7] F(5,5) G(0,2) = [6,8] [1,1] = [8,8] F(6,6) G(0,2) = [7,7] [1,1] = [8,8] F(0,0) G(1,0) = [1,3] [4,4] = [5,5] F(1,5) G(1,0) = [4,6] [4,4] = [8,8] F(2,3) G(1,0) = [3,3] [4,4] = [7,7] F(3,4) G(1,0) = [4,4] [4,4] = [8.8] F(4,2) G(1,0) = [5,5] [4,4] = [8,8] F(5,5) G(1,0) = [6,8] [4,4] = [8,8] F(6,6) G(1,0) = [7,7] [4,4] = [8,8] Finalmente, para cada posição, x, calcula-se [F(x u) G(u)]. Assim, obtém-se a
108 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA91 dilatação intervalar (F G) que é representada na figura 6.7. Figura 6.7: Dilatação intervalar de F pela função estrurante G Para a erosão, calculamos F(x + u) G(u), como segue. F u1 (0,0) = F((0,0) + (0,0)) = F(0,0) = [1,3] F u1 (1,5) = F((1,5) + (0,0)) = F(1,5) = [4,6] F u1 (2,3) = F((2,3) + (0,0)) = F(2,3) = [2,4] F u1 (3,4) = F((3,4) + (0,0)) = F(3,4) = [0,2] F u1 (4,2) = F((4,2) + (0,0)) = F(4,2) = [5,5] F u1 (5,5) = F((5,5) + (0,0)) = F(5,5) = [6,8] F u1 (6,6) = F((6,6) + (0,0)) = F(6,6) = [7,7] F u2 (0, 2) = F((0, 2) + (0,2)) = F(0,0) = [1,3] F u2 (1,3) = F((1,3) + (0,2)) = F(1,5) = [4,6] F u2 (2,1) = F((2,1) + (0,2)) = F(2,3) = [2,4] F u2 (3,2) = F((3,2) + (0,2)) = F(3,4) = [0,2] F u2 (4,0) = F((4,0) + (0,2)) = F(4,2) = [5,5] F u2 (5,3) = F((5,3) + (0,2)) = F(5,5) = [6,8] F u2 (6,4) = F((6,4) + (0,2)) = F(6,6) = [7,7] F u3 ( 1, 2) = F(( 1, 2) + (1,2)) = F(0,0) = [1,3] F u3 (0,3) = F((0,3) + (1,2)) = F(1,5) = [4,6]
109 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA92 F u3 (1,1) = F((1,1) + (1,2)) = F(2,3) = [2,4] F u3 (2,2) = F((2,2) + (1,2)) = F(3,4) = [0,2] F u3 (3,0) = F((3,0) + (1,2)) = F(4,2) = [5,5] F u3 (4,3) = F((4,3) + (1,2)) = F(5,5) = [6,8] F u3 (5,4) = F((5,4) + (1,2)) = F(6,6) = [7,7] Note que, nas posições (0, 2) e ( 1, 2) toma-se (0,0) e (0,0). Em seguida, calcula-se a diferença Minkowiski F(x + u) G(u). F(0,0) G(0,0) = [1,3] [2,2] = [ 1,1] = [0,1] F(1,5) G(0,0) = [4,6] [2,2] = [2,4] F(2,3) G(0,0) = [2,4] [2,2] = [0,2] F(3,4) G(0,0) = [0,2] [2,2] = [ 2,0] = [0,0] F(4,2) G(0,0) = [5,5] [2,2] = [3,3] F(5,5) G(0,0) = [6,8] [2,2] = [4,6] F(6,6) G(0,0) = [7,7] [2,2] = [5,5] F(0,0) G(0,2) = [1,3] [1,1] = [0,2] F(1,5) G(0,2) = [4,6] [1,1] = [3,5] F(2,3) G(0,2) = [2,4] [1,1] = [2,2] F(3,4) G(0,2) = [4,4] [1,1] = [3,3] F(4,2) G(0,2) = [5,5] [1,1] = [4,4] F(5,5) G(0,2) = [6,8] [1,1] = [5,7] F(6,6) G(0,2) = [7,7] [1,1] = [6,6] F(0,0) G(1,0) = [1,3] [4,4] = [ 3,1] = [0,1] F(1,5) G(1,0) = [4,6] [4,4] = 0,2] F(2,3) G(1,0) = [2,4] [4,4] = [ 2,0] = [0,0] F(3,4) G(1,0) = [4,4] [4,4] = [0,0] F(4,2) G(1,0) = [5,5] [4,4] = [1,1] F(5,5) G(1,0) = [6,8] [4,4] = [2,4]
110 CAPÍTULO 6. UM MODELO INTERVALAR PARA IMAGENS EM NÍVEIS DE CINZA93 F(6,6) G(1,0) = [7,7] [4,4] = [3,3] Para a operação de erosão, calcula-se, para cada posição x, (F G)(x) = u E[F(x+ u) G(u)]. A figura 6.8 mostra a erosão intervalar obtida pelas translações da função estruturante G sobre a imagem intervalar F : E Ω 8. Figura 6.8: Erosão intervalar de F pela função estrurante G Note que, os pixels mais escuros estão representados à direita da imagem intervalar e os mais claros, à esquerda. Observação No exemplo foi possível observar que, a imagem intervalar difere pelo tom de cinza. Quando os tons são diferentes èsquerda e à direita da imagem, na mesma posição, significa que, nesta posição existe uma incerteza. Uma importante propriedade algébrica dos operadores elementares da morfologia matemática é a relação da dualidade entre erosão e dilatação (F G) = F Ĝ. será mostrado que essa propriedade também vale para o caso intervalar. Proposição Sejam F e G duas imagens em intervalares em escala de cinzas, então (F G) = F G (6.3.31) Prova F G = u E{ F u (x) Ĝ(x)} = u E{([L,L] F u (x)) Ĝ(x)} definição = u E{([L,L] [F u (x),f u (x)]) Ĝ(x)}, corolário 6.3.6
Índice. Base de uma subcoleção sup fechada, 110 Bissetor condicional de ordem n, 207 Borda externa, 174 interna, 174 Borda 4 de um subconjunto, 145
 Índice A Aberto morfológico segundo uma morfologia, 131 relativo a uma abertura, 108 topológico segundo uma topologia, 132 Abertura, 100 128 convexa, 183 curva, 184 genérica, 184 morfológica, 110 i.t.,
Índice A Aberto morfológico segundo uma morfologia, 131 relativo a uma abertura, 108 topológico segundo uma topologia, 132 Abertura, 100 128 convexa, 183 curva, 184 genérica, 184 morfológica, 110 i.t.,
Em Direção a Morfologia Matemática para Imagens Binárias
 Em Direção a Morfologia Matemática para Imagens Binárias com Informação de Indefinição Marcia M. C. Cruz, Regivan H. N. Santiago, Depto de Matemática e Depto de Informática e Matemática Aplicada, UFRN
Em Direção a Morfologia Matemática para Imagens Binárias com Informação de Indefinição Marcia M. C. Cruz, Regivan H. N. Santiago, Depto de Matemática e Depto de Informática e Matemática Aplicada, UFRN
MORFOLOGIA MATEMÁTICA
 MORFOLOGIA MATEMÁTICA Morfologia Na Biologia área que trata com a forma e a estrutura de plantas e animais Processamento de Imagens Ferramenta para extração de componentes de imagens que sejam úteis na
MORFOLOGIA MATEMÁTICA Morfologia Na Biologia área que trata com a forma e a estrutura de plantas e animais Processamento de Imagens Ferramenta para extração de componentes de imagens que sejam úteis na
Operadores Morfológicos
 Capítulo 2 Operadores Morfológicos Uma forma elegante de resolver problemas de processamento de imagens é através da utilização de uma base teórica consistente. Uma destas teorias é a morfologia matemática
Capítulo 2 Operadores Morfológicos Uma forma elegante de resolver problemas de processamento de imagens é através da utilização de uma base teórica consistente. Uma destas teorias é a morfologia matemática
Morfologia Matemática. Guillermo Cámara-Chávez
 Morfologia Matemática Guillermo Cámara-Chávez Morfologia Matemática Foi desenvolvida inicialmente por Georges Matheron e Jean Serra na década de 60 Baseada na Teoria dos Conjuntos Originalmente desenvolvida
Morfologia Matemática Guillermo Cámara-Chávez Morfologia Matemática Foi desenvolvida inicialmente por Georges Matheron e Jean Serra na década de 60 Baseada na Teoria dos Conjuntos Originalmente desenvolvida
Mathematical Morphology An Overview
 Universidade Federal Fluminense Instituto de Computação Mathematical Morphology An Overview Jacó Júlio de Souza Costa jacojulio@gmail.com jacojulio@id.uff.br March 29, 2019 Sumário 1 Definição do Tema
Universidade Federal Fluminense Instituto de Computação Mathematical Morphology An Overview Jacó Júlio de Souza Costa jacojulio@gmail.com jacojulio@id.uff.br March 29, 2019 Sumário 1 Definição do Tema
Bases da Morfologia Matemática para análise de imagens binárias
 MINISTÉRIO DA CIÊNCIA E TECNOLOGIA INSTITUTO NACIONAL DE PESQUISAS ESPACIAIS INPE 6779 RPQ/682 Bases da Morfologia Matemática para análise de imagens binárias 2 a Edição Gerald Jean Francis Banon e Junior
MINISTÉRIO DA CIÊNCIA E TECNOLOGIA INSTITUTO NACIONAL DE PESQUISAS ESPACIAIS INPE 6779 RPQ/682 Bases da Morfologia Matemática para análise de imagens binárias 2 a Edição Gerald Jean Francis Banon e Junior
Morfologia Matemática: algumas aplicações. Rosana Gomes Bernardo Universidade Federal Fluminense
 Morfologia Matemática: algumas aplicações Rosana Gomes Bernardo Universidade Federal Fluminense Introdução Aplicações Motivadoras - Consumo de Gás Natural Roteiro - Placas de Veículos Referências - Cartografia
Morfologia Matemática: algumas aplicações Rosana Gomes Bernardo Universidade Federal Fluminense Introdução Aplicações Motivadoras - Consumo de Gás Natural Roteiro - Placas de Veículos Referências - Cartografia
Alunos: Caio Santos Renato Miceli
 rangel@dscufcgedubr/ rangeldequeirop@yahoocombr Alunos: Caio Santos Renato Miceli UNIVERSIDADE FEDERAL DE CAMPINA GRANDE UFCG Av Aprígio Veloso, S/N Bodocongó CEP: 58109-190 Campina Grande PB www.ufcg.edu.br/
rangel@dscufcgedubr/ rangeldequeirop@yahoocombr Alunos: Caio Santos Renato Miceli UNIVERSIDADE FEDERAL DE CAMPINA GRANDE UFCG Av Aprígio Veloso, S/N Bodocongó CEP: 58109-190 Campina Grande PB www.ufcg.edu.br/
Aula 4: Morfologia de Imagens
 SEL 5886 - VISÃO COMPUTACIONAL Aula 4: Morfologia de Imagens Prof. Dr. Marcelo Andrade da Costa Vieira Colaboração: Dr. Bruno R. N. Matheus Morfologia Morfologia matemática: Ferramenta para extração de
SEL 5886 - VISÃO COMPUTACIONAL Aula 4: Morfologia de Imagens Prof. Dr. Marcelo Andrade da Costa Vieira Colaboração: Dr. Bruno R. N. Matheus Morfologia Morfologia matemática: Ferramenta para extração de
Processamento de Imagens
 Processamento de Imagens Morfologia Matemática Binária Prof. Luiz Eduardo S. Oliveira Universidade Federal do Paraná Departamento de Informática http://web.inf.ufpr.br/luizoliveira Luiz S. Oliveira (UFPR)
Processamento de Imagens Morfologia Matemática Binária Prof. Luiz Eduardo S. Oliveira Universidade Federal do Paraná Departamento de Informática http://web.inf.ufpr.br/luizoliveira Luiz S. Oliveira (UFPR)
Capítulo 3. Operadores sobre subconjuntos. 3.1 Operadores
 Capítulo 3 Operadores sobre subconjuntos No capítulo anterior foram definidas vários mapeamentos, chamados de operações, envolvendo subconjuntos ou funções binárias. Neste capítulo, vamos introduzir outros
Capítulo 3 Operadores sobre subconjuntos No capítulo anterior foram definidas vários mapeamentos, chamados de operações, envolvendo subconjuntos ou funções binárias. Neste capítulo, vamos introduzir outros
Processamento Digital de Imagens
 Ciência da Computação Processamento Digital de Imagens Tópicos Detecção de Pontos Isolados Detecção de Linhas Prof. Sergio Ribeiro 2 Operações lógicas e aritméticas orientadas a vizinhança utilizam o conceito
Ciência da Computação Processamento Digital de Imagens Tópicos Detecção de Pontos Isolados Detecção de Linhas Prof. Sergio Ribeiro 2 Operações lógicas e aritméticas orientadas a vizinhança utilizam o conceito
Processamento Digital de Imagens. Análise de Imagens
 Processamento Digital de Imagens Análise de Imagens Eduardo A. B. da Silva Programa de Engenharia Elétrica - COPPE/UFRJ Laboratório de Sinais, Multimídia e Telecomunicações eduardo@smt.ufrj.br Sergio L.
Processamento Digital de Imagens Análise de Imagens Eduardo A. B. da Silva Programa de Engenharia Elétrica - COPPE/UFRJ Laboratório de Sinais, Multimídia e Telecomunicações eduardo@smt.ufrj.br Sergio L.
Capítulo 6. Aberturas e fechamentos. 6.1 Aberturas e fechamentos algébricos
 Capítulo 6 Aberturas e fechamentos Neste capítulo vamos introduzir duas novas classes de operadores: a abertura e o fechamento, que ocupam um papel fundamental na área dos filtros morfológicos [Serra88].
Capítulo 6 Aberturas e fechamentos Neste capítulo vamos introduzir duas novas classes de operadores: a abertura e o fechamento, que ocupam um papel fundamental na área dos filtros morfológicos [Serra88].
UMA VISÃO SOBRE O PROCESSAMENTO DE IMAGENS. Rogério Vargas DCET UESC Home page: rogerio.in
 UMA VISÃO SOBRE O PROCESSAMENTO DE IMAGENS Rogério Vargas DCET UESC Home page: rogerio.in Exemplo de aplicações: automação e visão artificial reconhecimento de caracteres análise de cromossomos veículos
UMA VISÃO SOBRE O PROCESSAMENTO DE IMAGENS Rogério Vargas DCET UESC Home page: rogerio.in Exemplo de aplicações: automação e visão artificial reconhecimento de caracteres análise de cromossomos veículos
Incertezas na Computação Científica: Abordagens via Matemática Intervalar e Teoria Fuzzy
 Incertezas na Computação Científica: Abordagens via Matemática Intervalar e Teoria Fuzzy Rogério Vargas Dr. Luciano Vitoria Barboza, orientador Dra. Graçaliz Pereira Dimuro, co-orientadora Pelotas-RS,
Incertezas na Computação Científica: Abordagens via Matemática Intervalar e Teoria Fuzzy Rogério Vargas Dr. Luciano Vitoria Barboza, orientador Dra. Graçaliz Pereira Dimuro, co-orientadora Pelotas-RS,
Processamento Digital de Imagens
 Ciência da Computação Processamento Digital de Imagens Propriedades de Imagem Digital Prof. Sergio Ribeiro Tópicos Propriedades de uma Imagem Digital Vizinhança Conectividade Operações Lógicas e Aritméticas
Ciência da Computação Processamento Digital de Imagens Propriedades de Imagem Digital Prof. Sergio Ribeiro Tópicos Propriedades de uma Imagem Digital Vizinhança Conectividade Operações Lógicas e Aritméticas
Processamento Digital de Imagens
 Ciência da Computação Processamento Digital de Imagens Propriedades de Imagem Digital Prof. Sergio Ribeiro Tópicos Propriedades de uma Imagem Digital Vizinhança e Aritméticas Efeitos de em Pixel a Pixel
Ciência da Computação Processamento Digital de Imagens Propriedades de Imagem Digital Prof. Sergio Ribeiro Tópicos Propriedades de uma Imagem Digital Vizinhança e Aritméticas Efeitos de em Pixel a Pixel
Morfologia Matemática em Imagens
 Processamento e nálise de Imagens Médicas Morfologia Matemática em Imagens Prof. Luiz Otavio Murta Jr. FMB Departamento de Computação e Matemática (FFCLRP/USP) Principais Tópicos Introdução Morfologia
Processamento e nálise de Imagens Médicas Morfologia Matemática em Imagens Prof. Luiz Otavio Murta Jr. FMB Departamento de Computação e Matemática (FFCLRP/USP) Principais Tópicos Introdução Morfologia
Processamento Digital de Imagens
 Ciência da Computação Processamento Digital de Imagens Prof. Sergio Ribeiro Tópicos Introdução Espectro Eletromagnético Aquisição e Digitalização de Imagens Efeitos da Digitalização Digitalização Sensoriamento
Ciência da Computação Processamento Digital de Imagens Prof. Sergio Ribeiro Tópicos Introdução Espectro Eletromagnético Aquisição e Digitalização de Imagens Efeitos da Digitalização Digitalização Sensoriamento
Processamento Digital de Imagens
 1 Ciência da Computação Processamento Digital de Imagens Prof. Sergio Ribeiro Tópicos Introdução Espectro Eletromagnético Aquisição e de Imagens Sensoriamento Remoto 2 Introdução Espectro Eletromagnético
1 Ciência da Computação Processamento Digital de Imagens Prof. Sergio Ribeiro Tópicos Introdução Espectro Eletromagnético Aquisição e de Imagens Sensoriamento Remoto 2 Introdução Espectro Eletromagnético
Processamento de Imagens Digitais
 Processamento de Imagens Digitais Antonio Cesar Germano Martins 2º semestre de 2018 Apresentações Nascido em Sorocaba. Graduado em Bacharelado em Física pela UNICAMP em 1989, tendo participado de pesquisas
Processamento de Imagens Digitais Antonio Cesar Germano Martins 2º semestre de 2018 Apresentações Nascido em Sorocaba. Graduado em Bacharelado em Física pela UNICAMP em 1989, tendo participado de pesquisas
Visão Computacional. Alessandro L. Koerich. Programa de Pós-Graduação em Engenharia Elétrica Universidade Federal do Paraná (UFPR)
 Visão Computacional Alessandro L. Koerich Programa de Pós-Graduação em Engenharia Elétrica Universidade Federal do Paraná (UFPR) Processamento da Informação Capturei uma Imagem! E agora? Assumindo que
Visão Computacional Alessandro L. Koerich Programa de Pós-Graduação em Engenharia Elétrica Universidade Federal do Paraná (UFPR) Processamento da Informação Capturei uma Imagem! E agora? Assumindo que
UNIVERSIDADE ESTADUAL DO OESTE DO PARANÁ UNIOESTE CAMPUS UNIVERSITÁRIO DE CASCAVEL CURSO DE CIÊNCIA DA COMPUTAÇÃO LISTA DE EXERCÍCIOS
 UNIVERSIDADE ESTADUAL DO OESTE DO PARANÁ UNIOESTE CAMPUS UNIVERSITÁRIO DE CASCAVEL CURSO DE CIÊNCIA DA COMPUTAÇÃO Disciplina: Processamento de Imagens Digitais Prof o : Adair Santa Catarina 1 Considerando
UNIVERSIDADE ESTADUAL DO OESTE DO PARANÁ UNIOESTE CAMPUS UNIVERSITÁRIO DE CASCAVEL CURSO DE CIÊNCIA DA COMPUTAÇÃO Disciplina: Processamento de Imagens Digitais Prof o : Adair Santa Catarina 1 Considerando
Processamento de Imagem. Relaçionamentos entre pixels e Operações Aritméticas e Lógicas Professora Sheila Cáceres
 Processamento de Imagem Relaçionamentos entre pixels e Operações Aritméticas e Lógicas Professora Sheila Cáceres Relacionamentos básicos entre elementos de uma imagem Vizinhança Conectividade Adjacência
Processamento de Imagem Relaçionamentos entre pixels e Operações Aritméticas e Lógicas Professora Sheila Cáceres Relacionamentos básicos entre elementos de uma imagem Vizinhança Conectividade Adjacência
Aula 9 Representação e Descrição. Profa. Fátima Nunes AULA 9 / 1. Profa. Fátima L. S. Nunes
 Fundamentos de Processamento Gráfico Aula 9 Representação e Descrição Profa. Fátima Nunes AULA 9 / 1 Reconhecimento de padrões AULA 9 / 2 Após a segmentação dar significado aos objetos extraídos da cena.
Fundamentos de Processamento Gráfico Aula 9 Representação e Descrição Profa. Fátima Nunes AULA 9 / 1 Reconhecimento de padrões AULA 9 / 2 Após a segmentação dar significado aos objetos extraídos da cena.
Aula 7 - Representação e Descrição de Estruturas Bi-dimensionais. Prof. Adilson Gonzaga
 Aula 7 - Representação e Descrição de Estruturas Bi-dimensionais Prof. Adilson Gonzaga 1 Introdução Objetos ou Segmentos são representados como uma coleção de pixels em uma imagem. Para o reconhecimento
Aula 7 - Representação e Descrição de Estruturas Bi-dimensionais Prof. Adilson Gonzaga 1 Introdução Objetos ou Segmentos são representados como uma coleção de pixels em uma imagem. Para o reconhecimento
Seminários de pesquisa do DAINF Transformações de imagens baseadas em morfologia
 Universidade Tecnológica Federal do Paraná - UTFPR Departamento Acadêmico de Informática - DAINF Seminários de pesquisa do DAINF Transformações de imagens baseadas em morfologia matemática e aplicações
Universidade Tecnológica Federal do Paraná - UTFPR Departamento Acadêmico de Informática - DAINF Seminários de pesquisa do DAINF Transformações de imagens baseadas em morfologia matemática e aplicações
Restauração de imagens NOAA por Morfologia Matemática
 Restauração de imagens NOAA por Morfologia Matemática GERALD JEAN FRANCIS BANON 1 ANA LÚCIA BEZERRA CANDEIAS 1 1 DPI/INPE Divisão de Processamento de Imagens / Instituto Nacional de Pesquisas Espacias
Restauração de imagens NOAA por Morfologia Matemática GERALD JEAN FRANCIS BANON 1 ANA LÚCIA BEZERRA CANDEIAS 1 1 DPI/INPE Divisão de Processamento de Imagens / Instituto Nacional de Pesquisas Espacias
Uma Extensão Intervalar do Algoritmo Fuzzy C-Means
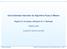 Uma Extensão Intervalar do Algoritmo Fuzzy C-Means Rogério R. de Vargas e Benjamín R. C. Bedregal CNMAC 2009 Cuiabá-MT, Setembro de 2009 Vargas e Bedregal PPgSC/ Universidade Federal do Rio Grande do Norte
Uma Extensão Intervalar do Algoritmo Fuzzy C-Means Rogério R. de Vargas e Benjamín R. C. Bedregal CNMAC 2009 Cuiabá-MT, Setembro de 2009 Vargas e Bedregal PPgSC/ Universidade Federal do Rio Grande do Norte
Exemplos de aplicação de álgebra booleana
 Exemplos de aplicação de álgebra booleana Como já vimos, o conjunto P(S) juntamente com as operações de união, intersecção e complemento de conjuntos forma uma álgebra booleana. Cálculo proposicional é
Exemplos de aplicação de álgebra booleana Como já vimos, o conjunto P(S) juntamente com as operações de união, intersecção e complemento de conjuntos forma uma álgebra booleana. Cálculo proposicional é
Rogério Vargas. Pelotas, 29 de Fevereiro de Rogério Vargas PPGInf / Universidade Católica de Pelotas slide 1
 Técnicas Matemático-Computacionais para o Tratamento de Incertezas Aplicadas ao Problema do Fluxo de Potência em Sistemas de Transmissão de Energia Elétrica Rogério Vargas orientador: Luciano Barboza co-orientadora:
Técnicas Matemático-Computacionais para o Tratamento de Incertezas Aplicadas ao Problema do Fluxo de Potência em Sistemas de Transmissão de Energia Elétrica Rogério Vargas orientador: Luciano Barboza co-orientadora:
DEFEITOS EM IMAGENS RADIOGRÁFICAS DE JUNTAS SOLDADAS EM TUBULAÇÕES: SEGMENTAÇÃO E EXTRAÇÃO DE DEFEITOS
 DEFEITOS EM IMAGENS RADIOGRÁFICAS DE JUNTAS SOLDADAS EM TUBULAÇÕES: SEGMENTAÇÃO E EXTRAÇÃO DE DEFEITOS * Aluno do curso Tecnologia em Sistemas de Telecomunicações da UTFPR jvrsschaid@gmail.com ** Aluno
DEFEITOS EM IMAGENS RADIOGRÁFICAS DE JUNTAS SOLDADAS EM TUBULAÇÕES: SEGMENTAÇÃO E EXTRAÇÃO DE DEFEITOS * Aluno do curso Tecnologia em Sistemas de Telecomunicações da UTFPR jvrsschaid@gmail.com ** Aluno
Universidade Federal de Pernambuco Graduação em Engenharia da Computação Centro de Informática
 Universidade Federal de Pernambuco Graduação em Engenharia da Computação Centro de Informática DETECÇÃO DE BORDAS DE IMAGENS UTILIZANDO ELEMENTOS DE MORFOLOGIA MATEMÁTICA PROPOSTA DE TRABALHO DE GRADUAÇÃO
Universidade Federal de Pernambuco Graduação em Engenharia da Computação Centro de Informática DETECÇÃO DE BORDAS DE IMAGENS UTILIZANDO ELEMENTOS DE MORFOLOGIA MATEMÁTICA PROPOSTA DE TRABALHO DE GRADUAÇÃO
Operadores invariantes por translação
 Capítulo 4 Operadores invariantes por translação As funções estruturantes do capítulo anterior podem ser vistas como uma maneira de definir uma noção de vizinhança para os pontos do conjunto E. Por exemplo,
Capítulo 4 Operadores invariantes por translação As funções estruturantes do capítulo anterior podem ser vistas como uma maneira de definir uma noção de vizinhança para os pontos do conjunto E. Por exemplo,
2 Conceitos básicos de topologia
 2 Conceitos básicos de topologia Neste Capítulo são introduzidos alguns conceitos básicos de topologia combinatória e da Teoria das Alças que formam a base teórica do presente trabalho. 2.1 Topologia combinatória
2 Conceitos básicos de topologia Neste Capítulo são introduzidos alguns conceitos básicos de topologia combinatória e da Teoria das Alças que formam a base teórica do presente trabalho. 2.1 Topologia combinatória
Universidade Federal do Rio de Janeiro - IM/DCC & NCE
 Universidade Federal do Rio de Janeiro - IM/DCC & NCE Processamento de Imagens Segmentação Antonio G. Thomé thome@nce.ufrj.br Sala AEP/133 Conceituação Segmentação é uma tarefa básica no processo de análise
Universidade Federal do Rio de Janeiro - IM/DCC & NCE Processamento de Imagens Segmentação Antonio G. Thomé thome@nce.ufrj.br Sala AEP/133 Conceituação Segmentação é uma tarefa básica no processo de análise
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
CÓDIGO DE VIZINHANÇA APLICADO EM OPERADORES DE MORFOLOGIA MATEMÁTICA
 Universidade Federal de Pernambuco Graduação em Ciência da Computação Centro de Informática CÓDIGO DE VIZINHANÇA APLICADO EM OPERADORES DE MORFOLOGIA MATEMÁTICA Trabalho de Graduação Aluno: Paulo Roberto
Universidade Federal de Pernambuco Graduação em Ciência da Computação Centro de Informática CÓDIGO DE VIZINHANÇA APLICADO EM OPERADORES DE MORFOLOGIA MATEMÁTICA Trabalho de Graduação Aluno: Paulo Roberto
Processamento de Imagens
 Processamento de Imagens Prof. Julio Arakaki Ciência da Computação 1 Imagem Digital Full Color Image (Matriz de Pixels) RGB (24 bits): Red (8 bits) Green (8 bits) Blue (8 bits) 2 Imagem Digital Um modelo
Processamento de Imagens Prof. Julio Arakaki Ciência da Computação 1 Imagem Digital Full Color Image (Matriz de Pixels) RGB (24 bits): Red (8 bits) Green (8 bits) Blue (8 bits) 2 Imagem Digital Um modelo
CÁLCULO I. 1 Número Reais. Objetivos da Aula
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida EMENTA: Conceitos introdutórios de limite, limites trigonométricos, funções contínuas, derivada e aplicações. Noções introdutórias sobre a integral
Processamento digital de imagens
 Processamento digital de imagens Agostinho Brito Departamento de Engenharia da Computação e Automação Universidade Federal do Rio Grande do Norte 6 de outubro de 2016 Segmentação de imagens A segmentação
Processamento digital de imagens Agostinho Brito Departamento de Engenharia da Computação e Automação Universidade Federal do Rio Grande do Norte 6 de outubro de 2016 Segmentação de imagens A segmentação
Processamento de Imagens: fundamentos. Julio C. S. Jacques Junior
 Processamento de Imagens: fundamentos Julio C. S. Jacques Junior juliojj@gmail.com Fronteiras do Processamento de Imagens Processamento de dados Dados / Informação Visão Computacional Computação Gráfica
Processamento de Imagens: fundamentos Julio C. S. Jacques Junior juliojj@gmail.com Fronteiras do Processamento de Imagens Processamento de dados Dados / Informação Visão Computacional Computação Gráfica
CAPÍTULO 3 ANÁLISE DE IMAGENS DE SENSORIAMENTO REMOTO
 44 45 CAPÍTULO 3 ANÁLISE DE IMAGENS DE SENSORIAMENTO REMOTO 3. INTRODUÇÃO O olho humano é um sensor muito sofisticado e detecta muito bem as informações provenientes de uma imagem. Estas informações são
44 45 CAPÍTULO 3 ANÁLISE DE IMAGENS DE SENSORIAMENTO REMOTO 3. INTRODUÇÃO O olho humano é um sensor muito sofisticado e detecta muito bem as informações provenientes de uma imagem. Estas informações são
4 Detecção de Silhueta
 4 Detecção de Silhueta No decorrer deste capítulo é proposto um modelo de detecção da silhueta da mão capaz de lidar com os erros da segmentação e ruídos na sua morfologia. Num primeiro passo são considerados
4 Detecção de Silhueta No decorrer deste capítulo é proposto um modelo de detecção da silhueta da mão capaz de lidar com os erros da segmentação e ruídos na sua morfologia. Num primeiro passo são considerados
RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03
 RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03 PEDRO A. TONELLI 1. Introdução: o esqueleto do espírito E ainda mais remoto que o tempo em que as coisas não tinham nome, é o tempo em que as coisas nem existiam,
RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03 PEDRO A. TONELLI 1. Introdução: o esqueleto do espírito E ainda mais remoto que o tempo em que as coisas não tinham nome, é o tempo em que as coisas nem existiam,
1 1 1 *1/ *1/ *1/49
 O que é filtragem? As técnicas de filtragem são transformações da imagem pixel a pixel, que não dependem apenas do nível de cinza de um determinado pixel, mas também do valor dos níveis de cinza dos pixels
O que é filtragem? As técnicas de filtragem são transformações da imagem pixel a pixel, que não dependem apenas do nível de cinza de um determinado pixel, mas também do valor dos níveis de cinza dos pixels
Programa. 4. Conceitos teóricos e notação. Computação Fuzzy - PCS 5711 (capítulo 4 - Parte c)
 Computação Fuzzy - PCS 57 (capítulo 4 - Parte c) Pós-Graduação: área de Sistemas Digitais (34) Professor Marco Túlio Carvalho de ndrade PCS - Depto. de Enga. de Computação e Sistemas Digitais - EPUSP Programa.
Computação Fuzzy - PCS 57 (capítulo 4 - Parte c) Pós-Graduação: área de Sistemas Digitais (34) Professor Marco Túlio Carvalho de ndrade PCS - Depto. de Enga. de Computação e Sistemas Digitais - EPUSP Programa.
Cálculo Numérico IPRJ/UERJ. Sílvia Mara da Costa Campos Victer ÍNDICE. Aula 1- Introdução. Representação de números. Conversão de números
 Cálculo Numérico IPRJ/UERJ Sílvia Mara da Costa Campos Victer ÍNDICE Aula 1- Introdução Representação de números Conversão de números Aritmética de ponto flutuante Erros em máquinas digitais Aula 1 - Introdução
Cálculo Numérico IPRJ/UERJ Sílvia Mara da Costa Campos Victer ÍNDICE Aula 1- Introdução Representação de números Conversão de números Aritmética de ponto flutuante Erros em máquinas digitais Aula 1 - Introdução
CONSTRUÇÃO AUTOMÁTICA DE OPERADORES MORFOLÓGICOS UTILIZANDO PROGRAMAÇÃO GENÉTICA.
 CONSTRUÇÃO AUTOMÁTICA DE OPERADORES MORFOLÓGICOS UTILIZANDO PROGRAMAÇÃO GENÉTICA. Emerson Carlos Pedrino * e-mail: ecpedrin@sel.eesc.sc.usp.br Valentin Obac Roda ** e-mail: valentin@sel.eesc.sc.usp.br
CONSTRUÇÃO AUTOMÁTICA DE OPERADORES MORFOLÓGICOS UTILIZANDO PROGRAMAÇÃO GENÉTICA. Emerson Carlos Pedrino * e-mail: ecpedrin@sel.eesc.sc.usp.br Valentin Obac Roda ** e-mail: valentin@sel.eesc.sc.usp.br
Cálculo Diferencial e Integral Química Notas de Aula
 Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Cálculo Diferencial e Integral Química Notas de Aula João Roberto Gerônimo 1 1 Professor Associado do Departamento de Matemática da UEM. E-mail: jrgeronimo@uem.br. ÍNDICE 1. INTRODUÇÃO Esta notas de aula
Resumo. Parte 2 Introdução à Teoria da Probabilidade. Ramiro Brito Willmersdorf Introdução.
 Parte 2 Introdução à Teoria da Probabilidade Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2011.2 Resumo 1 Introdução 2 Espaço
Parte 2 Introdução à Teoria da Probabilidade Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2011.2 Resumo 1 Introdução 2 Espaço
PMR2560 Visão Computacional Detecção de bordas. Prof. Eduardo L. L. Cabral
 PMR56 Visão Computacional Detecção de bordas Prof. Eduardo L. L. Cabral Objetivos Processamento de imagens: Características; Detecção de bordas. Características Tipos de características: Bordas; Cantos;
PMR56 Visão Computacional Detecção de bordas Prof. Eduardo L. L. Cabral Objetivos Processamento de imagens: Características; Detecção de bordas. Características Tipos de características: Bordas; Cantos;
PROCESSAMENTO DE IMAGENS DIGITAIS. Universidade Estadual de Maringá
 PROCESSAMENTO DE IMAGENS DIGITAIS Airton Marco Polidorio ampolido@din.uem.br Universidade Estadual de Maringá PROCESSAMENTO DE IMAGENS DIGITAIS Introdução Realce Convolução Segmentação Reconhecimento de
PROCESSAMENTO DE IMAGENS DIGITAIS Airton Marco Polidorio ampolido@din.uem.br Universidade Estadual de Maringá PROCESSAMENTO DE IMAGENS DIGITAIS Introdução Realce Convolução Segmentação Reconhecimento de
Tratamento da Imagem Transformações (cont.)
 Universidade Federal do Rio de Janeiro - IM/DCC & NCE Tratamento da Imagem Transformações (cont.) Antonio G. Thomé thome@nce.ufrj.br Sala AEP/33 Transformações Geométricas 3 Transformações Geométricas
Universidade Federal do Rio de Janeiro - IM/DCC & NCE Tratamento da Imagem Transformações (cont.) Antonio G. Thomé thome@nce.ufrj.br Sala AEP/33 Transformações Geométricas 3 Transformações Geométricas
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA. Medida e Probabilidade
 UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
Extração de Redes de Drenagem em Imagens Orbitais Utilizando a Teoria da Morfologia Matemática
 Extração de Redes de Drenagem em Imagens Orbitais Utilizando a Teoria da Morfologia Matemática Aline Sayuri Ishikawa Paulo Henrique Amorim da Silva Erivaldo Antônio da Silva UNESP- Depto. de Cartografia
Extração de Redes de Drenagem em Imagens Orbitais Utilizando a Teoria da Morfologia Matemática Aline Sayuri Ishikawa Paulo Henrique Amorim da Silva Erivaldo Antônio da Silva UNESP- Depto. de Cartografia
Notas de aula de MAC0329 Álgebra Booleana e Aplicações
 Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
PROCESSAMENTO DIGITAL DE IMAGENS
 UNIVERSIDADE DE SÃO PAULO ESCOLA SUPERIOR DE AGRICULTURA LUIZ DE QUEIROZ DEPARTAMENTO DE ENGENHARIA DE BIOSSISTEMAS DISCIPLINA: LEB450 TOPOGRAFIA E GEOPROCESSAMENTO II PROF. DR. CARLOS ALBERTO VETTORAZZI
UNIVERSIDADE DE SÃO PAULO ESCOLA SUPERIOR DE AGRICULTURA LUIZ DE QUEIROZ DEPARTAMENTO DE ENGENHARIA DE BIOSSISTEMAS DISCIPLINA: LEB450 TOPOGRAFIA E GEOPROCESSAMENTO II PROF. DR. CARLOS ALBERTO VETTORAZZI
Exemplos. Propagação (Reconstrução)
 Processamento de Imagens Médicas Morfologia Matemática em Imagens Prof. Luiz Otavio Murta Jr. Informática Biomédica Depto. de Física e Matemática (FFCLRP/USP) Propagação (Reconstrução) lgoritmos Baseados
Processamento de Imagens Médicas Morfologia Matemática em Imagens Prof. Luiz Otavio Murta Jr. Informática Biomédica Depto. de Física e Matemática (FFCLRP/USP) Propagação (Reconstrução) lgoritmos Baseados
Rastreamento de Objetos Baseado em Grafos. Casamento Inexato entre Grafos Relacionais com Atributos
 Rastreamento de Objetos Baseado em Casamento Inexato entre Grafos Relacionais com Atributos Exame de Qualificação de Mestrado Ana Beatriz Vicentim Graciano Orientador: Roberto M. Cesar Jr. Colaboradora:
Rastreamento de Objetos Baseado em Casamento Inexato entre Grafos Relacionais com Atributos Exame de Qualificação de Mestrado Ana Beatriz Vicentim Graciano Orientador: Roberto M. Cesar Jr. Colaboradora:
Curso de Matemática Aplicada.
 Aula 1 p.1/25 Curso de Matemática Aplicada. Margarete Oliveira Domingues PGMET/INPE Sistema de números reais e complexos Aula 1 p.2/25 Aula 1 p.3/25 Conjuntos Conjunto, classe e coleção de objetos possuindo
Aula 1 p.1/25 Curso de Matemática Aplicada. Margarete Oliveira Domingues PGMET/INPE Sistema de números reais e complexos Aula 1 p.2/25 Aula 1 p.3/25 Conjuntos Conjunto, classe e coleção de objetos possuindo
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Cálculo Diferencial e Integral I Texto de apoio às aulas. Amélia Bastos, António Bravo Dezembro 2010 Capítulo 1 Números reais As propriedades do conjunto dos números reais têm por base um conjunto restrito
Tratamento da Imagem Transformações (cont.)
 Universidade Federal do Rio de Janeiro - IM/DCC & NCE Tratamento da Imagem Transformações (cont.) Antonio G. Thomé thome@nce.ufrj.br Sala AEP/133 Tratamento de Imagens - Sumário Detalhado Objetivos Alguns
Universidade Federal do Rio de Janeiro - IM/DCC & NCE Tratamento da Imagem Transformações (cont.) Antonio G. Thomé thome@nce.ufrj.br Sala AEP/133 Tratamento de Imagens - Sumário Detalhado Objetivos Alguns
Universidade Federal do Paraná Departamento de Informática. Reconhecimento de Padrões. Extração de Características
 Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões Extração de Características Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Objetivos Entender os conceitos de
Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões Extração de Características Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Objetivos Entender os conceitos de
Morfologia Matemática? Mathematical morphology (MM) : what is it?
 Morfologia Matemática? Mathematical morphology (MM) : what is it? Que qué isso? Combining methods from set theory, topology, and discrete mathematics, mathematical morphology provides a powerful approach
Morfologia Matemática? Mathematical morphology (MM) : what is it? Que qué isso? Combining methods from set theory, topology, and discrete mathematics, mathematical morphology provides a powerful approach
PMR2560 Visão Computacional Processamento morfológico. Prof. Eduardo L. L. Cabral
 PMR256 Visão Computacional Processamento morfológico Prof. Eduardo L. L. Cabral Objetivos Processamento de imagens: Algumas operações de processamento morfológico de imagens; Imagens binárias; Imagens
PMR256 Visão Computacional Processamento morfológico Prof. Eduardo L. L. Cabral Objetivos Processamento de imagens: Algumas operações de processamento morfológico de imagens; Imagens binárias; Imagens
Representação esquemática de estruturas de dados
 UNIVERSIDADE DE SÃO PAULO - USP Instituto de Química de São Carlos - IQSC Grupo de Química Medicinal do IQSC/USP 1 Representação esquemática de estruturas de dados 2 1 Tipos de variáveis Contínua Concentração,
UNIVERSIDADE DE SÃO PAULO - USP Instituto de Química de São Carlos - IQSC Grupo de Química Medicinal do IQSC/USP 1 Representação esquemática de estruturas de dados 2 1 Tipos de variáveis Contínua Concentração,
RECONSTRUÇÃO MORFOLÓGICA POR DILATAÇÕES CONDICIONAIS PARA DETECÇÃO DE FEIÇÕES EM IMAGENS DIGITAIS
 RECONSTRUÇÃO MORFOLÓGICA POR DILATAÇÕES CONDICIONAIS PARA DETECÇÃO DE FEIÇÕES EM IMAGENS DIGITAIS Thiago Statella 1, Erivaldo Antônio da Silva 2 Resumo: Este trabalho apresenta os resultados obtidos pela
RECONSTRUÇÃO MORFOLÓGICA POR DILATAÇÕES CONDICIONAIS PARA DETECÇÃO DE FEIÇÕES EM IMAGENS DIGITAIS Thiago Statella 1, Erivaldo Antônio da Silva 2 Resumo: Este trabalho apresenta os resultados obtidos pela
Sistemas especialistas Fuzzy
 Sistemas Fuzzy Sistemas especialistas Fuzzy Especialistas Senso comum para resolver problemas Impreciso, inconsistente, incompleto, vago Embora o transformador esteja um pouco carregado, pode-se usá-lo
Sistemas Fuzzy Sistemas especialistas Fuzzy Especialistas Senso comum para resolver problemas Impreciso, inconsistente, incompleto, vago Embora o transformador esteja um pouco carregado, pode-se usá-lo
A = B, isto é, todo elemento de A é também um elemento de B e todo elemento de B é também um elemento de A, ou usando o item anterior, A B e B A.
 Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
INTRODUÇÃO AO PROCESSAMENTO DIGITAL DE IMAGENS SENSORIAMENTO REMOTO
 INTRODUÇÃO AO PROCESSAMENTO DIGITAL DE IMAGENS SENSORIAMENTO REMOTO PROCESSAMENTO DE IMAGENS Introdução Conceitos básicos Pré-processamento Realce Classificação PROCESSAMENTO DE IMAGENS Extração de Informações
INTRODUÇÃO AO PROCESSAMENTO DIGITAL DE IMAGENS SENSORIAMENTO REMOTO PROCESSAMENTO DE IMAGENS Introdução Conceitos básicos Pré-processamento Realce Classificação PROCESSAMENTO DE IMAGENS Extração de Informações
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO Álgebra de Boole Disciplina: Lógica Professora Dr.ª: Donizete
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO Álgebra de Boole Disciplina: Lógica Professora Dr.ª: Donizete
INTRODUÇÃO À TEORIA DOS CONJUNTOS
 1 INTRODUÇÃO À TEORIA DOS CONJUNTOS Gil da Costa Marques 1.1 Introdução 1.2 Conceitos básicos 1.3 Subconjuntos e intervalos 1.4 O conjunto dos números reais 1.4.1 A relação de ordem em 1.5 Intervalos 1.5.1
1 INTRODUÇÃO À TEORIA DOS CONJUNTOS Gil da Costa Marques 1.1 Introdução 1.2 Conceitos básicos 1.3 Subconjuntos e intervalos 1.4 O conjunto dos números reais 1.4.1 A relação de ordem em 1.5 Intervalos 1.5.1
Implementação dos Algoritmos e Resultados
 Capítulo 6 Implementação dos Algoritmos e Resultados 6.1 Considerações Iniciais Diversas situações foram exploradas neste trabalho visando analisar qual seria a wavelet mais adequada para sistemas de extração
Capítulo 6 Implementação dos Algoritmos e Resultados 6.1 Considerações Iniciais Diversas situações foram exploradas neste trabalho visando analisar qual seria a wavelet mais adequada para sistemas de extração
Processamento de Imagens Marcia A. S. Bissaco
 Engenharia Biomédica Processamento de Imagens Marcia A. S. Bissaco 1 Exemplos filtros Média Mediana Passa_B Passa_A Borda_H Borda_V Sobel_Y Sobel_X Oliveira, Henrique J. Quintino (UMC-SP), 2 Media Mediana
Engenharia Biomédica Processamento de Imagens Marcia A. S. Bissaco 1 Exemplos filtros Média Mediana Passa_B Passa_A Borda_H Borda_V Sobel_Y Sobel_X Oliveira, Henrique J. Quintino (UMC-SP), 2 Media Mediana
SEL-0339 Introdução à Visão Computacional. Aula 5 Segmentação de Imagens
 Departamento de Engenharia Elétrica - EESC-USP SEL-0339 Introdução à Visão Computacional Aula 5 Segmentação de Imagens Prof. Dr. Marcelo Andrade da Costa Vieira Prof. Dr. Adilson Gonzaga Segmentação de
Departamento de Engenharia Elétrica - EESC-USP SEL-0339 Introdução à Visão Computacional Aula 5 Segmentação de Imagens Prof. Dr. Marcelo Andrade da Costa Vieira Prof. Dr. Adilson Gonzaga Segmentação de
PMR2560 Visão Computacional Detecção de cores e blobs. Prof. Eduardo L. L. Cabral
 PMR2560 Visão Computacional Detecção de cores e blobs Prof. Eduardo L. L. Cabral Objetivos Detecção de cores; Detecção de blobs. Detecção de cores Cores são facilmente identificadas nas imagens. Cor a
PMR2560 Visão Computacional Detecção de cores e blobs Prof. Eduardo L. L. Cabral Objetivos Detecção de cores; Detecção de blobs. Detecção de cores Cores são facilmente identificadas nas imagens. Cor a
Análise Intervalar de Circuitos Elétricos
 Análise Intervalar de Circuitos Elétricos Pablo S. Grigoletti 1, Graçaliz P. Dimuro 1, Luciano V. Barboza 2,3, Renata H.S. Reiser 1 1 Escola de Informática, Universidade Católica de Pelotas, 2 Escola de
Análise Intervalar de Circuitos Elétricos Pablo S. Grigoletti 1, Graçaliz P. Dimuro 1, Luciano V. Barboza 2,3, Renata H.S. Reiser 1 1 Escola de Informática, Universidade Católica de Pelotas, 2 Escola de
Processamento de Imagem. Prof. MSc. André Yoshimi Kusumoto
 Processamento de Imagem Prof. MSc. André Yoshimi Kusumoto andrekusumoto.unip@gmail.com Filtragem de Imagens A utilização de filtros tem como objetivo melhorar a qualidade das imagens através da: ampliação
Processamento de Imagem Prof. MSc. André Yoshimi Kusumoto andrekusumoto.unip@gmail.com Filtragem de Imagens A utilização de filtros tem como objetivo melhorar a qualidade das imagens através da: ampliação
Dr. Sylvio Barbon Junior. Departamento de Computação - UEL. 1 o Semestre de 2015
 Introdução a Computação Gráfica [5COP100] Dr. Sylvio Barbon Junior Departamento de Computação - UEL 1 o Semestre de 2015 Assunto Aula 8 Descritores de Imagens Digitais 2 of 47 Sumário Descritores e Reconhecimento
Introdução a Computação Gráfica [5COP100] Dr. Sylvio Barbon Junior Departamento de Computação - UEL 1 o Semestre de 2015 Assunto Aula 8 Descritores de Imagens Digitais 2 of 47 Sumário Descritores e Reconhecimento
Filtros e Morfologia. Prof. Dr. Geraldo Braz Junior
 Filtros e Morfologia Prof. Dr. Geraldo Braz Junior Filtragem Operações que visam extrair informações importantes da imagem CaracterísAcas Cantos, bordas, agrupamentos Melhoramento rearada de ruídos, aumento
Filtros e Morfologia Prof. Dr. Geraldo Braz Junior Filtragem Operações que visam extrair informações importantes da imagem CaracterísAcas Cantos, bordas, agrupamentos Melhoramento rearada de ruídos, aumento
Universidade Federal de Sergipe Departamento de Matemática. Imagem* Profª. Maria Andrade. *Parte desta apresentação foi do Prof. Thales Vieira.
 Universidade Federal de Sergipe Departamento de Matemática Imagem* Profª. Maria Andrade *Parte desta apresentação foi do Prof. Thales Vieira. 2016 O que é uma imagem digital? Imagem no universo físico
Universidade Federal de Sergipe Departamento de Matemática Imagem* Profª. Maria Andrade *Parte desta apresentação foi do Prof. Thales Vieira. 2016 O que é uma imagem digital? Imagem no universo físico
Preliminares de Cálculo
 Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
Representação e erros numéricos
 Representação e erros numéricos Marina Andretta ICMC-USP 29 de fevereiro de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - cálculo numérico
Representação e erros numéricos Marina Andretta ICMC-USP 29 de fevereiro de 2012 Baseado no livro Análise Numérica, de R. L. Burden e J. D. Faires. Marina Andretta (ICMC-USP) sme0500 - cálculo numérico
Metodologia Aplicada a Computação.
 Metodologia Aplicada a Computação gaudenciothais@gmail.com Pré-processamento de dados Técnicas utilizadas para melhorar a qualidade dos dados; Eliminam ou minimizam os problemas como ruídos, valores incorretos,
Metodologia Aplicada a Computação gaudenciothais@gmail.com Pré-processamento de dados Técnicas utilizadas para melhorar a qualidade dos dados; Eliminam ou minimizam os problemas como ruídos, valores incorretos,
Fabio Augusto Camargo
 Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
Universidade Federal de São Carlos Centro de Ciências Exatas e de Tecnologia Departamento de Matemática Introdução à Topologia Autor: Fabio Augusto Camargo Orientador: Prof. Dr. Márcio de Jesus Soares
Processamento Digital de Imagens Aula 02
 exatasfepi.com.br Processamento Digital de Imagens Aula 02 André Luís Duarte O que adquire entendimento ama a sua alma; o que cultiva a inteligência achará o bem. Provérbios 19:8 Processamento Digital
exatasfepi.com.br Processamento Digital de Imagens Aula 02 André Luís Duarte O que adquire entendimento ama a sua alma; o que cultiva a inteligência achará o bem. Provérbios 19:8 Processamento Digital
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA PLANIFICAÇÃO ANUAL 7.
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA PLANIFICAÇÃO ANUAL 7.º ANO ANO LECTIVO 2009/2010 DOMÍNIO TEMÁTICO: NÚMEROS E CÁLCULO 1.º PERÍODO
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS MATEMÁTICA PLANIFICAÇÃO ANUAL 7.º ANO ANO LECTIVO 2009/2010 DOMÍNIO TEMÁTICO: NÚMEROS E CÁLCULO 1.º PERÍODO
Capítulo 3. Álgebra de Bool
 Capítulo 3 Álgebra de Bool Adaptado dos transparentes das autoras do livro The Essentials of Computer Organization and Architecture Objectivos Compreender a relação entre lógica Booleana e os circuitos
Capítulo 3 Álgebra de Bool Adaptado dos transparentes das autoras do livro The Essentials of Computer Organization and Architecture Objectivos Compreender a relação entre lógica Booleana e os circuitos
Símbolo Nome lê-se como Categoria = 10 significa que se se somar 4 a 6, a soma, ou resultado, é 10.
 Símbolo Nome lê-se como Categoria adição mais aritmética + 4 + 6 = 10 significa que se se somar 4 a 6, a soma, ou resultado, é 10. Exemplo: 43 + 65 = 108; 2 + 7 = 9 subtração menos aritmética - 9-4 = 5
Símbolo Nome lê-se como Categoria adição mais aritmética + 4 + 6 = 10 significa que se se somar 4 a 6, a soma, ou resultado, é 10. Exemplo: 43 + 65 = 108; 2 + 7 = 9 subtração menos aritmética - 9-4 = 5
Descritores de Imagem (introdução)
 Descritores de Imagem (introdução) André Tavares da Silva andre.silva@udesc.br Roteiro da aula Definição de descritor de imagem Extração de Característica Tipos Geral x Específico Global (cor, textura,
Descritores de Imagem (introdução) André Tavares da Silva andre.silva@udesc.br Roteiro da aula Definição de descritor de imagem Extração de Característica Tipos Geral x Específico Global (cor, textura,
Números Reais. Gláucio Terra. Departamento de Matemática IME - USP. Números Reais p. 1/2
 Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
Números Reais Gláucio Terra glaucio@ime.usp.br Departamento de Matemática IME - USP Números Reais p. 1/2 Corpos DEFINIÇÃO Seja K um conjunto munido de duas operações, denotadas por + e. Diz-se que (K,
2 Medida de Incertezas: Fundamentos
 2 Medida de Incertezas: Fundamentos 2. Introdução O resultado de um processo de medição fornece uma determinada informação que usualmente é chamada de conhecimento. A fim de quantificar quão completo é
2 Medida de Incertezas: Fundamentos 2. Introdução O resultado de um processo de medição fornece uma determinada informação que usualmente é chamada de conhecimento. A fim de quantificar quão completo é
Processamento digital de imagens
 Processamento digital de imagens Agostinho Brito Departamento de Engenharia da Computação e Automação Universidade Federal do Rio Grande do Norte 3 de março de 2016 Transformação e filtragem de imagens
Processamento digital de imagens Agostinho Brito Departamento de Engenharia da Computação e Automação Universidade Federal do Rio Grande do Norte 3 de março de 2016 Transformação e filtragem de imagens
n. 25 DIAGRAMAS DE VENN
 n. 25 DIAGRAMAS DE VENN Foi o matemático inglês John Venn (1834-1923) que criou os diagramas, com o intuito de facilitar a compreensão na relação de união e intersecção entre conjuntos. John Venn desenvolveu
n. 25 DIAGRAMAS DE VENN Foi o matemático inglês John Venn (1834-1923) que criou os diagramas, com o intuito de facilitar a compreensão na relação de união e intersecção entre conjuntos. John Venn desenvolveu
Geometria Computacional
 Geometria Computacional Claudio Esperança Paulo Roma Cavalcanti Estrutura do Curso Aspectos teóricos e práticos Construção e análise de algoritmos e estruturas de dados para a solucionar problemas geométricos
Geometria Computacional Claudio Esperança Paulo Roma Cavalcanti Estrutura do Curso Aspectos teóricos e práticos Construção e análise de algoritmos e estruturas de dados para a solucionar problemas geométricos
Respostas do Teste de Analise de Imagens :
 Respostas do Teste de Analise de Imagens - 2004: 1Diga com suas palavras o que é: (Valor total da questão: 12) Filtragem passa alta (valor deste item até 0,3) - importante falar que apesar do nome ser
Respostas do Teste de Analise de Imagens - 2004: 1Diga com suas palavras o que é: (Valor total da questão: 12) Filtragem passa alta (valor deste item até 0,3) - importante falar que apesar do nome ser
T4 Processamento de Imagem
 T4 Processamento de Imagem Proc. Sinal e Imagem Mestrado em Informática Médica Hélder Filipe Pinto de Oliveira Resumo 1. Manipulação ponto a ponto 2. Conetividade 3. Filtros espaciais 4. Extração de estruturas
T4 Processamento de Imagem Proc. Sinal e Imagem Mestrado em Informática Médica Hélder Filipe Pinto de Oliveira Resumo 1. Manipulação ponto a ponto 2. Conetividade 3. Filtros espaciais 4. Extração de estruturas
