Gases quânticos sem interação
|
|
|
- Adriana Belo Rodrigues
- 7 Há anos
- Visualizações:
Transcrição
1 UFABC - Mecânica Estatística Curso Prof. Germán Lugones CAPÍTULO 6 Gases quânticos sem interação!1
2 Regime clássico e regime quântico Para um gás ideal clássico em equilíbrio térmico a uma temperatura T, a energia média de uma partícula é E=(3/2)kT e o comprimento de onda de de Broglie é B = h p = Por outro lado, o comprimento de onda térmico = h p 2mE = h p 2 mkt. h p 3mkT. é da mesma ordem de grandeza que! B. Por isso, tanto! quanto! B dão uma ideia da ``extensão espacial'' ou tamanho de uma partícula do gás. Para grandes temperaturas as partículas se tornam localizadas e tendem a ter um comportamento clássico. A baixas temperaturas as partículas ficam mais deslocalizadas" e se a densidade for grande o suficiente podemos ter um overlapping entre as suas funções de onda.!2
3 A distância média entre partículas pode ser estimada por d = v 1/3 = n 1/3 onde n=n/v é o número de partículas por unidade de volume, e v 1/n é o volume específico (volume ocupado por uma partícula do gás). A relação entre as grandezas d e! permite identificar os regimes clássico e quântico: Regime clássico. O tamanho das partículas é muito menor que a separação entre as mesmas, i.e.,! n -1/3, logo, 3 n 1!3
4 Regime quântico. O tamanho das partículas é da ordem ou maior que a separação entre as mesmas, i.e.,! n -1/3, logo, 3 n & 1!4
5 Bósons e Férmions Consideremos um gás quântico composto por N partículas livres sem spin (bósons ou férmions). Atenção! Obviamente, não existem férmions sem spin na natureza. O conceito de férmions sem spin indica apenas que temos partículas que verificam o principio de exclusão de Pauli, e que o número de partículas possível em cada nível de energia é 0 ou 1. Para descrever férmions reais, basta introduzir um fator de degenerescência que leve em consideração o número de partículas permitido em cada nível de energia. Como as partículas são não-interagentes, o Hamiltoniano do sistema de N partículas é a soma de N Hamiltonianos de uma partícula, Ĥ(q, p) = NX ĥ i (q i,p i ) onde os operadores ĥ i são formalmente idênticos, e diferem apenas nas coordenadas e momentos q i, p i.!5 i=1
6 A equação de Schrödinger independente do tempo para esse sistema é onde " E (q) são as autofunções de energia e E os correspondentes autovalores. Pela forma do hamiltoniano, um estado estacionário do sistema de N partículas pode ser descrito em função dos autoestados do hamiltoniano de uma partícula. A função de onda tem a forma Y NY E(q) = i (q i ), Eq. (*) e os autovalores ficam da forma Ĥ(q, p) E (q) =E E (q) onde φ ε i e εi são as autofunções e autovalores do hamiltoniano de uma partícula, i.e. ĥ i φ # i(q i ) = ε i φ # i(q i ).!6 i=1 XE = NX i, i=1
7 Adicionalmente, devemos levar em consideração a indistinguibilidade das partículas: Todos os microestados resultantes das permutações de N partículas devem ser considerados como um único estado. Por isso, a função de onda de um sistema de N partículas deve ser simétrica ou anti-simétrica pela troca das coordenadas de qualquer par de partículas (i.e ao fazermos ""* obteremos a mesma densidade de probabilidade). As partículas que são descritas por uma função de onda simétrica são denominadas bósons e as descritas por uma função de onda anti-simétrica são denominadas férmions.!7
8 Portanto, a função de onda apresentada anteriormente [na Eq. (*)] deve ser simetrizada ou anti-simetrizada em relação às coordenadas q i, ou, equivalentemente, em relação aos índices i. A função de onda resultante é da forma onde P é um operador que permuta os índices da funções de onda de uma partícula. X A soma deve ser realizada sobre as N! permutações possíveis. O fator $ P é E(q 1,...,q N )= 1 p N! X P P P [ 1 (q 1 )... N (q N )], P = 1 (para bósons), ( 1 se P é uma permutação par P = 1 se P é uma permutação impar (para férmions).!8
9 No caso dos férmions, a função de onda adota a forma do determinante de Slater E(q 1,...,q N )= p 1 2 (q 1 ) 2 (q 2 )... 2 (q N ) N! (q 1) 1(q 2)... 1(q N) N (q 1 ) N (q 2 )... N (q N ). Note que cada fila contém sempre a mesma função de onda de uma partícula, enquanto cada coluna contém o mesmo argumento na função de onda de uma partícula. A partir desta expressão, fica evidente que a função de onda " E é identicamente nula se duas funções de onda de uma partícula forem iguais, já que o determinante teria duas filas idênticas. Este é o princípio de exclusão de Pauli.!9
10 Base de Fock Construiremos um formalismo que nos permitirá levar em conta o princípio de Pauli sem precisar rotular as partículas indistinguíveis. O Hamiltoniano de partículas não-interagentes no espaço de Hilbert de N partículas, E H (N), tem a forma de de uma soma de operadores idênticos que se referem respectivamente às partículas i = 1,2,...,N. N!10
11 <latexit sha1_base64="ojhefi3tz9zi46of31lo9wbklxm=">aaacjhicbvdlsgmxfm34rpu16tjnsah1u6yiqgchkejxpyk1hu47znjmg5rjdelgkgf+xo2/4saffrdu/bbtx6k2hggczjmxm3v8mfgphofbwlldw9/yzgxlt3d29/btg8mngsuckzqowcsappkeuu7qiipgmregkpqzafidu7hfeczc0og/qmfm2ihqcrpqjjsrpptguxgxej96upjcwikut3trzblp6wrjstvaptxqwxtobzs6xz1lowfnniizavwmxrnjgrlqnj1yuxfoqsivzkjkvtgjvvsjoshmjm26isqxwgpuiy1doqqjbovjlsk8nuoxbpewjys4uecnnaqlhia+syzi9ewinxb/81qjcq7amvi4uytj6aigyvbfcfwz7fjbsgjdqxaw1pwv4j4sccttbnauufw8eznuzwvxbefhile+nbwracfgborbevycmqiagqgddf7ag/gai+vverc+ra9pdmwazrybp7b+fghfx6rn</latexit> Para evitar as complicações devidas à simetrização ou antissimetrização das funções de onda, trabalharemos no espaço de Fock deixando o número de partículas N arbitrário. Lembremos que estamos lidando com o espaço de Fock 1M E H = N=0 E (N) H que é a soma direta de espaços de Hilbert de N partículas indistinguíveis (bósons ou férmions). Usaremos a mesma notação para esses dois tipos de partículas, mesmo que os espaços correspondentes não sejam equivalentes (exceto no caso N 2).!11
12 Single-Particle States: We start from the Hilbert space E (1) H of the single-particle states. In contrast to the complete Fock space, this space has the same structure for fermions as for bosons: the nature of the particles does not manifest itself until there are several particles present. We choose for the base {% i } of the space E H (1) the set of eigenvectors of the single-particle Hamiltonian ĥ. We indicate the set of quantum numbers which characterize each of these vectors by % i, and the value of the corresponding energy eigenvalue by & i.!12
13 Estados de Partículas Individuais:: Analisemos o espaço de Hilbert E H (1) dos estados de uma única partícula. Em contraste com o espaço Fock completo, este espaço tem a mesma estrutura para férmions e bósons: a natureza das partículas não se manifesta até que haja várias partículas presentes. Para a base {% i } do espaço E (1) H escolhemos o conjunto de autovetores do Hamiltoniano ĥ de uma única partícula. Cada um dos elementos da base tem associado um conjunto de números quânticos. O autovalor de energia correspondente é & i.!13
14 Números de ocupação: Para descrever um estado de N bósons ou de N férmions adotamos a seguinte estratégia. - vamos olhar para o conjunto de estados de uma partícula {% 1, % 2, % 3,,% } e especificar qual deles está ocupado e qual deles está vazio. - isto definirá para cada estado de uma partícula, % i, um número de ocupação n i, que pode ser zero. Descrição do vácuo: O vácuo é um estado (único) do espaço de Hilbert de zero partículas E H (0). No formalismo de números de ocupação, ele é descrito como o estado no qual todos os n i são nulos.!14
15 Descrição de estados de uma única partícula: Como descrevemos os estados de uma partícula, pertencentes ao espaço de Hilbert E H (1)? Para expressar que a partícula está no estado q, usamos a seguinte linguagem: - dizemos que o número de ocupação n i do estado % i é igual a 1 e que os números de ocupação n j dos outros estados % j (j i) são todos zero. - Cada estado de uma partícula da base {%} será então denotado por um conjunto de números de ocupação {n i } que são todos iguais a 0, exceto um deles que é igual a 1. Portanto, o ket % i que representa a partícula no estado % i, é escrito como: 0, 0,, {n q }=1, 0, 0, 0 onde organizamos os estados de uma única partícula, % i, em uma ordem padrão e onde os números de ocupação são escritos nessa ordem padrão.!15
16 <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="nis/6i/7rtigldqyqk+/ek2acvi=">aaacmxicbvdns8mwhe39npor6tflcajbwdeoqy9dlztocb/q1pfm6rawtdvjhvh6l3nxpxevoyji1x/cdotbnx+epn57p5lf82ngpbksmbg2vrg5tv3ake/u7r8cmkfhxrklapmojlgk+j6shngqdbrvjprjqrd3gen5k9vc7z0riwku3qtptdyorienkezkswoz5qyc4dtoulc+cpu2sgw6bjymvbsg8/shdwnbocmqjrq8wjkkjla8gvmx6tyccjxybamaau2b+eooi5xweirmkjsobcxks5fqfdosld1ekhjhcrorr9mqcsk9dl5xbs+1morbjpqjfzyrvydsxkwccl8novjjuezl4n+ek6jg2ktpgcekhhjxujawqcky1wehvbcs2fqthaxvf4v4jhsfspdc1ixyyyuvkm6jblt1++6y0rwp6iibu3agqsagv6ajwqanogcdz/ag3sgh8wlmje/jaxfdm4qze/ahxvcpmdaohq==</latexit> <latexit sha1_base64="nis/6i/7rtigldqyqk+/ek2acvi=">aaacmxicbvdns8mwhe39npor6tflcajbwdeoqy9dlztocb/q1pfm6rawtdvjhvh6l3nxpxevoyji1x/cdotbnx+epn57p5lf82ngpbksmbg2vrg5tv3ake/u7r8cmkfhxrklapmojlgk+j6shngqdbrvjprjqrd3gen5k9vc7z0riwku3qtptdyorienkezkswoz5qyc4dtoulc+cpu2sgw6bjymvbsg8/shdwnbocmqjrq8wjkkjla8gvmx6tyccjxybamaau2b+eooi5xweirmkjsobcxks5fqfdosld1ekhjhcrorr9mqcsk9dl5xbs+1morbjpqjfzyrvydsxkwccl8novjjuezl4n+ek6jg2ktpgcekhhjxujawqcky1wehvbcs2fqthaxvf4v4jhsfspdc1ixyyyuvkm6jblt1++6y0rwp6iibu3agqsagv6ajwqanogcdz/ag3sgh8wlmje/jaxfdm4qze/ahxvcpmdaohq==</latexit> <latexit sha1_base64="nis/6i/7rtigldqyqk+/ek2acvi=">aaacmxicbvdns8mwhe39npor6tflcajbwdeoqy9dlztocb/q1pfm6rawtdvjhvh6l3nxpxevoyji1x/cdotbnx+epn57p5lf82ngpbksmbg2vrg5tv3ake/u7r8cmkfhxrklapmojlgk+j6shngqdbrvjprjqrd3gen5k9vc7z0riwku3qtptdyorienkezkswoz5qyc4dtoulc+cpu2sgw6bjymvbsg8/shdwnbocmqjrq8wjkkjla8gvmx6tyccjxybamaau2b+eooi5xweirmkjsobcxks5fqfdosld1ekhjhcrorr9mqcsk9dl5xbs+1morbjpqjfzyrvydsxkwccl8novjjuezl4n+ek6jg2ktpgcekhhjxujawqcky1wehvbcs2fqthaxvf4v4jhsfspdc1ixyyyuvkm6jblt1++6y0rwp6iibu3agqsagv6ajwqanogcdz/ag3sgh8wlmje/jaxfdm4qze/ahxvcpmdaohq==</latexit> <latexit sha1_base64="nis/6i/7rtigldqyqk+/ek2acvi=">aaacmxicbvdns8mwhe39npor6tflcajbwdeoqy9dlztocb/q1pfm6rawtdvjhvh6l3nxpxevoyji1x/cdotbnx+epn57p5lf82ngpbksmbg2vrg5tv3ake/u7r8cmkfhxrklapmojlgk+j6shngqdbrvjprjqrd3gen5k9vc7z0riwku3qtptdyorienkezkswoz5qyc4dtoulc+cpu2sgw6bjymvbsg8/shdwnbocmqjrq8wjkkjla8gvmx6tyccjxybamaau2b+eooi5xweirmkjsobcxks5fqfdosld1ekhjhcrorr9mqcsk9dl5xbs+1morbjpqjfzyrvydsxkwccl8novjjuezl4n+ek6jg2ktpgcekhhjxujawqcky1wehvbcs2fqthaxvf4v4jhsfspdc1ixyyyuvkm6jblt1++6y0rwp6iibu3agqsagv6ajwqanogcdz/ag3sgh8wlmje/jaxfdm4qze/ahxvcpmdaohq==</latexit> Descrição de estados de duas partículas: Os estados de duas partículas pertencem ao espaço de Hilbert E H (2). Para partículas não interagentes, o Hamiltoniano é da forma: Ĥ (2) = ĥ 1 + ĥ 2 Se desconsiderarmos a indistinguibilidade, as autofunções de Ĥ (2) são simplesmente o produto de duas funções, %(1) para a partícula 1 e %'(2) para a partícula 2, e a energia é & + &. No caso de férmions, o espaço de Hilbert E H (2) é o espaço de Hilbert das funções anti-simétricas. A função de onda tem a forma 1 p 2 [ (1) 0 (2) 0 (1) (2)] e é representada por 0,, 0,n =1, 0,, 0,n 0 =1, 0, i!16
17 <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="oemftyr9kccbngkma9tterokmxw=">aaaco3icbvdlsgmxfm34rpvvdekmwaqxpcyiobuh6mzlffuati2z9e4bmskmsuyo4/yxg3/cnrs3lhrx6950wkhbxkg4oedcbu7xis6utu0xa2fxaxllnbewx9/y3nou7ozwvrhlcjua8la2pakamwe1ztshzisbbb6hhje4homne5ckhejwdynob6qnmm8o0ybqfg4esf3clu2gwpvguhqsn+qz9nzjnnoko3nlfkd66xlbscuj6hhanulrlttz4vngteartarakty73zdgaqhnovgq5dirbideaky5phk3vharoia9abkosacqnws7p/jqmf3sh9icoxhg/u1iskdumpcmmyc6r6a1etlpa8xap2sntesxbkhhg/yyyx3iuzc4yyrqzycgecqz+sumfsij1sbuvanbmv55ftspy45ddq5pipwlsrw5ti8o0bfy0cmqocturtve0sn6re/ow3qy3qxp62tsxbampxvox1nfp03dqiy=</latexit> <latexit sha1_base64="eny1f5yynu0bilbv8dkpkznfmek=">aaacmxicbvdns8mwhe39npor6tflcagbwmihomehlx0nua9o60izdatl2pqkwij9l7z4n4ixhrtx6j9huvwgmw9chu+9h8nv+tgjulnwzfhb39jc2i7tlhf39g8ozapjrowsgukhrywsfr9jwmhioooqrvqxiij7jpt8yw3u956ikdqk79u0jh5ho5agfcolpyhzcgobcgpnqssfhuobwqydnx7tql2d+f2qurggngtvrg1elelfrlvewkxydwsouersglragfbafhwheu44crvmserhtmllpugoihnjym4isyzwbi2io2miojfeot84g+dagcigevqecs7v3xmp4ljoua+thkmxxpzy8t/psvrw7au0jbnfqrx4kegyvbhm64ndkghwbkojwolqv0i8rrpcpusu6xls5zvxsbdrt626fxdzad4udztaktgdvwcdk9aeldaghydbm3gd7+ddedfmxqfxtyiugcxmcfgd4/shlpqogw==</latexit> <latexit sha1_base64="eny1f5yynu0bilbv8dkpkznfmek=">aaacmxicbvdns8mwhe39npor6tflcagbwmihomehlx0nua9o60izdatl2pqkwij9l7z4n4ixhrtx6j9huvwgmw9chu+9h8nv+tgjulnwzfhb39jc2i7tlhf39g8ozapjrowsgukhrywsfr9jwmhioooqrvqxiij7jpt8yw3u956ikdqk79u0jh5ho5agfcolpyhzcgobcgpnqssfhuobwqydnx7tql2d+f2qurggngtvrg1elelfrlvewkxydwsouersglragfbafhwheu44crvmserhtmllpugoihnjym4isyzwbi2io2miojfeot84g+dagcigevqecs7v3xmp4ljoua+thkmxxpzy8t/psvrw7au0jbnfqrx4kegyvbhm64ndkghwbkojwolqv0i8rrpcpusu6xls5zvxsbdrt626fxdzad4udztaktgdvwcdk9aeldaghydbm3gd7+ddedfmxqfxtyiugcxmcfgd4/shlpqogw==</latexit> <latexit sha1_base64="eny1f5yynu0bilbv8dkpkznfmek=">aaacmxicbvdns8mwhe39npor6tflcagbwmihomehlx0nua9o60izdatl2pqkwij9l7z4n4ixhrtx6j9huvwgmw9chu+9h8nv+tgjulnwzfhb39jc2i7tlhf39g8ozapjrowsgukhrywsfr9jwmhioooqrvqxiij7jpt8yw3u956ikdqk79u0jh5ho5agfcolpyhzcgobcgpnqssfhuobwqydnx7tql2d+f2qurggngtvrg1elelfrlvewkxydwsouersglragfbafhwheu44crvmserhtmllpugoihnjym4isyzwbi2io2miojfeot84g+dagcigevqecs7v3xmp4ljoua+thkmxxpzy8t/psvrw7au0jbnfqrx4kegyvbhm64ndkghwbkojwolqv0i8rrpcpusu6xls5zvxsbdrt626fxdzad4udztaktgdvwcdk9aeldaghydbm3gd7+ddedfmxqfxtyiugcxmcfgd4/shlpqogw==</latexit> <latexit sha1_base64="eny1f5yynu0bilbv8dkpkznfmek=">aaacmxicbvdns8mwhe39npor6tflcagbwmihomehlx0nua9o60izdatl2pqkwij9l7z4n4ixhrtx6j9huvwgmw9chu+9h8nv+tgjulnwzfhb39jc2i7tlhf39g8ozapjrowsgukhrywsfr9jwmhioooqrvqxiij7jpt8yw3u956ikdqk79u0jh5ho5agfcolpyhzcgobcgpnqssfhuobwqydnx7tql2d+f2qurggngtvrg1elelfrlvewkxydwsouersglragfbafhwheu44crvmserhtmllpugoihnjym4isyzwbi2io2miojfeot84g+dagcigevqecs7v3xmp4ljoua+thkmxxpzy8t/psvrw7au0jbnfqrx4kegyvbhm64ndkghwbkojwolqv0i8rrpcpusu6xls5zvxsbdrt626fxdzad4udztaktgdvwcdk9aeldaghydbm3gd7+ddedfmxqfxtyiugcxmcfgd4/shlpqogw==</latexit> No caso de bósons, o espaço de Hilbert E H (2) é o espaço de Hilbert das funções simétricas. A função de onda tem a forma 1 p 2 [ (1) 0 (2) + 0 (1) (2)] e é representada por 0,, 0,n =1, 0,, 0,n 0 =1, 0, i O uso da mesma notação para o estado antissimétrico e para o estado simétrico não deve levar a qualquer confusão, desde que deixemos claro desde o início se estamos lidando com férmions ou com bósons.!17
18 <latexit sha1_base64="lal/jaopfft/9xz5h1p4irigbfu=">aaacghicbzbns8mwgmdtx+d8q3r0ehychzhbiehfghrxomg9wfpkmqzbwjqwjbvg3cfw4lfx4kerr7v5buy7hntzgcav///zkdx/p2fuksv6nlzw19y3nitb1e2d3b198+cwk+nuynlbmytf30esmmpjr1hfsd8rbeu+iz1/fjv7vuciji35g5okxi3qknoqyqs05jnnt9cqqwchszl1hlmxocmitq+bxbw0ocmqhzicpbnmnayi4dlyjdraww3pndlbjnoiciuzknjgw4lymyquxyxmq04qsylwga3jqcnhezfuviw2hadacwayc324gox6eyjdkzstynedevijuejl4n/eifxhlztrnqskcdx/kewzvdhmu4ibfqqrntgaskd6rxcpkeby6syrogr7cevl6dybttww7y9qrzsyjgo4bifgdnjgertahwiddsdggbycd/bhvbhvxqfxnw9dmcqzi/cnjnkpxcydiq==</latexit> <latexit sha1_base64="lal/jaopfft/9xz5h1p4irigbfu=">aaacghicbzbns8mwgmdtx+d8q3r0ehychzhbiehfghrxomg9wfpkmqzbwjqwjbvg3cfw4lfx4kerr7v5buy7hntzgcav///zkdx/p2fuksv6nlzw19y3nitb1e2d3b198+cwk+nuynlbmytf30esmmpjr1hfsd8rbeu+iz1/fjv7vuciji35g5okxi3qknoqyqs05jnnt9cqqwchszl1hlmxocmitq+bxbw0ocmqhzicpbnmnayi4dlyjdraww3pndlbjnoiciuzknjgw4lymyquxyxmq04qsylwga3jqcnhezfuviw2hadacwayc324gox6eyjdkzstynedevijuejl4n/eifxhlztrnqskcdx/kewzvdhmu4ibfqqrntgaskd6rxcpkeby6syrogr7cevl6dybttww7y9qrzsyjgo4bifgdnjgertahwiddsdggbycd/bhvbhvxqfxnw9dmcqzi/cnjnkpxcydiq==</latexit> <latexit sha1_base64="lal/jaopfft/9xz5h1p4irigbfu=">aaacghicbzbns8mwgmdtx+d8q3r0ehychzhbiehfghrxomg9wfpkmqzbwjqwjbvg3cfw4lfx4kerr7v5buy7hntzgcav///zkdx/p2fuksv6nlzw19y3nitb1e2d3b198+cwk+nuynlbmytf30esmmpjr1hfsd8rbeu+iz1/fjv7vuciji35g5okxi3qknoqyqs05jnnt9cqqwchszl1hlmxocmitq+bxbw0ocmqhzicpbnmnayi4dlyjdraww3pndlbjnoiciuzknjgw4lymyquxyxmq04qsylwga3jqcnhezfuviw2hadacwayc324gox6eyjdkzstynedevijuejl4n/eifxhlztrnqskcdx/kewzvdhmu4ibfqqrntgaskd6rxcpkeby6syrogr7cevl6dybttww7y9qrzsyjgo4bifgdnjgertahwiddsdggbycd/bhvbhvxqfxnw9dmcqzi/cnjnkpxcydiq==</latexit> <latexit sha1_base64="lal/jaopfft/9xz5h1p4irigbfu=">aaacghicbzbns8mwgmdtx+d8q3r0ehychzhbiehfghrxomg9wfpkmqzbwjqwjbvg3cfw4lfx4kerr7v5buy7hntzgcav///zkdx/p2fuksv6nlzw19y3nitb1e2d3b198+cwk+nuynlbmytf30esmmpjr1hfsd8rbeu+iz1/fjv7vuciji35g5okxi3qknoqyqs05jnnt9cqqwchszl1hlmxocmitq+bxbw0ocmqhzicpbnmnayi4dlyjdraww3pndlbjnoiciuzknjgw4lymyquxyxmq04qsylwga3jqcnhezfuviw2hadacwayc324gox6eyjdkzstynedevijuejl4n/eifxhlztrnqskcdx/kewzvdhmu4ibfqqrntgaskd6rxcpkeby6syrogr7cevl6dybttww7y9qrzsyjgo4bifgdnjgertahwiddsdggbycd/bhvbhvxqfxnw9dmcqzi/cnjnkpxcydiq==</latexit> <latexit sha1_base64="ajby9qq/zoqzvj7zqxpgmnqp8oc=">aaab+xicbvbns8naej3ur1q/oh69lbahvzskchosevfywbsfnptndtmu3wzc7qzqqv+jfw+kepwfeppfue1z0nyhwzzem2fnx5bwprtjffulre2d3b3yfuxg8oj4xd4966g4lyr6joax7avyuc4e9tttnpyssxeucnonpvdlvzujurfypol5qv0ijwulgchasepbhiqtvnprko/nohravafh5ecbxc1ifqq0h/bxybstnkjce46v6rtoov0ms80ip4vkifu0wwskx7rvqmarvx6wx75av0yzotcwporgufp7i8oruvmomjmr1ho17i3f/7x+qsnbp2mistuvzpvqmhkky7smay2ypetzusgysgzurwscjsbahfuxibjrx94knwbddrru43w1dvfeuyyluiqauhadlxiannhayabp8apvvma9wo/wx2q0zbu75/ah1ucpyp6ryg==</latexit> <latexit sha1_base64="ajby9qq/zoqzvj7zqxpgmnqp8oc=">aaab+xicbvbns8naej3ur1q/oh69lbahvzskchosevfywbsfnptndtmu3wzc7qzqqv+jfw+kepwfeppfue1z0nyhwzzem2fnx5bwprtjffulre2d3b3yfuxg8oj4xd4966g4lyr6joax7avyuc4e9tttnpyssxeucnonpvdlvzujurfypol5qv0ijwulgchasepbhiqtvnprko/nohravafh5ecbxc1ifqq0h/bxybstnkjce46v6rtoov0ms80ip4vkifu0wwskx7rvqmarvx6wx75av0yzotcwporgufp7i8oruvmomjmr1ho17i3f/7x+qsnbp2mistuvzpvqmhkky7smay2ypetzusgysgzurwscjsbahfuxibjrx94knwbddrru43w1dvfeuyyluiqauhadlxiannhayabp8apvvma9wo/wx2q0zbu75/ah1ucpyp6ryg==</latexit> <latexit sha1_base64="ajby9qq/zoqzvj7zqxpgmnqp8oc=">aaab+xicbvbns8naej3ur1q/oh69lbahvzskchosevfywbsfnptndtmu3wzc7qzqqv+jfw+kepwfeppfue1z0nyhwzzem2fnx5bwprtjffulre2d3b3yfuxg8oj4xd4966g4lyr6joax7avyuc4e9tttnpyssxeucnonpvdlvzujurfypol5qv0ijwulgchasepbhiqtvnprko/nohravafh5ecbxc1ifqq0h/bxybstnkjce46v6rtoov0ms80ip4vkifu0wwskx7rvqmarvx6wx75av0yzotcwporgufp7i8oruvmomjmr1ho17i3f/7x+qsnbp2mistuvzpvqmhkky7smay2ypetzusgysgzurwscjsbahfuxibjrx94knwbddrru43w1dvfeuyyluiqauhadlxiannhayabp8apvvma9wo/wx2q0zbu75/ah1ucpyp6ryg==</latexit> <latexit sha1_base64="ajby9qq/zoqzvj7zqxpgmnqp8oc=">aaab+xicbvbns8naej3ur1q/oh69lbahvzskchosevfywbsfnptndtmu3wzc7qzqqv+jfw+kepwfeppfue1z0nyhwzzem2fnx5bwprtjffulre2d3b3yfuxg8oj4xd4966g4lyr6joax7avyuc4e9tttnpyssxeucnonpvdlvzujurfypol5qv0ijwulgchasepbhiqtvnprko/nohravafh5ecbxc1ifqq0h/bxybstnkjce46v6rtoov0ms80ip4vkifu0wwskx7rvqmarvx6wx75av0yzotcwporgufp7i8oruvmomjmr1ho17i3f/7x+qsnbp2mistuvzpvqmhkky7smay2ypetzusgysgzurwscjsbahfuxibjrx94knwbddrru43w1dvfeuyyluiqauhadlxiannhayabp8apvvma9wo/wx2q0zbu75/ah1ucpyp6ryg==</latexit> No caso de dois bósons, existe ainda a possibilidade de colocar as duas partículas no mesmo estado %. A função de onda tem a forma e é representada por (1) (2) 0,, 0,n =2, 0, i!18
19 <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> Podemos estender facilmente esses argumentos a um número de partículas arbitrário. Para N férmions, cada microestado pode estar ocupado por, no máximo, uma partícula, devido ao princípio de exclusão de Pauli. Assim, um estado qualquer tem a forma: n 1,,n i, i onde os números de ocupação podem adotar apenas os valores 0 ou 1. O número de partículas do sistema é dado por: N = X i n i e a energia da configuração caracterizada por {n i } é: E = X i n i i!19
20 <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> Para N bósons, cada microestado pode estar ocupado por mais de uma partícula. Assim, um estado qualquer tem a forma: n 1,,n i, i onde os números de ocupação podem adotar qualquer valor inteiro (ou zero): n i = 0, 1, 2,.. O número de partículas do sistema é dado por: N = X i n i e a energia da configuração caracterizada por {n i } é: E = X i n i i!20
21 <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="uygffwnssq7n0o/wty0c8o6og+w=">aaacexicbvc7tsmwfhv4lvikmljyvegdqipbsdbwsdawit6knoocx2mtok5k3ybvob/awq+wmiaqkxsbf4pbzocwi1k+pudexd8tpijrcjxva2v1bx1js7rv3t7z3du3dw7boskuzs2aier1a6kz4jk1ging3vqxegecdylr9dtv3doleslvyjwylyydysnocrjjt6spwppudfdpmicuyfpk+ctchyl7isibyni3k07dmqeve7cgfvsg6dtf/tchwcwkueg07rlocl5ofhaq2ktczzrlcr2raeszkknmtjfpnprgu6oeoequorlwtp3dkzny63ecmmqywfavelpxp6+xqxtp5vymgtbj54oitgbi8dqehhlfkiixiyqqbv6k6zaoqsgewdyhuisrl5p2wd116u7teavxvcrrqsfobfwriy5qa92gjmohih7rm3pfb9at9wk9wx/z0hwr6dlcf2b9/gazypto</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="hozyrwkcbeehlcierokqmr3q34g=">aaacbhicbvbns8naen3ur1q/oh57wsycp5kiobehkilhcvydmha220m7dlmjuxuhhb68+fe8efdeqz/cm//gbzudtj4yelw3w8y8movmacf5tkorq2vrg+xnytb2zu6evx/qvkkmkbrowhpzdykczgs0nnmcuqkeeoccouhoeup3hkaqloh7pu7bj8lasihroo0u2nubfik9lcvbzizybax7kcrgjcccu+bunrnwmnelukmfmoh95futmsugnoveqz7rpnrpidsmcphuvexbsuiidkbnqcaxkd+fpthbx0bp4yirpotgm/x3re5ipczxadpjoodq0zuk/3m9tecxfs5emmkqdl4oyjjwcz4mgvtmatv8baihkplbmr0ssag2uvvmco7iy8ukfvp3nbp7d1zrxbvxlfevhaet5kjz1ec3qilaikjh9ixe0zv1zl1y79bhvlvkftoh6a+szx+z7zea</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> <latexit sha1_base64="kndihhn++n12j0ubaagokp5dgc8=">aaab+xicbvbns8naej3ur1q/oh69lbbbu0le0itq9ojjktgpaepybdft0t1n2n0usug/8ejbea/+e2/+g7dtdtr6yodx3gwz86kum20879spra1vbg6vtys7u3v7b+7huusnmsk0srkeqe6enevm0qzhhtnoqigweaftahq389tjqjrl5jozpdqqecbzzag2vgpd9whdoj7orjizkzihc92qv/pmqkvel0gvcjrc96vxt0gmqdsey627vpeaimfkmmlptnllne0xgeeb7voqsaa6yoext9gzvfootpqtadbc/t2ry6h1res2u2az1mvetpzp62ymvg5yjtpmuekwi+kmi5ogwqyozxqlhk8swuqxeysiq6wwmtasig3bx355lbquar5x8x8vq/xbio4ynmapnimpv1che2haewim4rle4c3jnrfn3flytjacyuyy/sd5/afqqzld</latexit> Para N bósons, cada microestado pode estar ocupado por mais de uma partícula. Assim, um estado qualquer tem a forma: n 1,,n i, i onde os números de ocupação podem adotar qualquer valor inteiro (ou zero): n i = 0, 1, 2,.. O número de partículas do sistema é dado por: N = X i n i e a energia da configuração caracterizada por {n i } é: E = X i n i i!21
22 Partindo dos estados de uma partícula no espaço de Hilbert E H (1), conseguimos construir uma base completa para o espaço de Fock de estados com um número arbitrário de partículas E H = E H (0) E H (1) E H (2) E H (3) +. em dois casos diferentes: quando as funções de onda devem ser antisimétricas (férmions) ou quando devem ser simétricas (bósons). Cada estado desta base, é caracterizado através dos números quânticos n i (números de ocupação), cada um dos quais pode assumir os valores 0,1 para férmions, ou 0,1,2,... para bósons. A base é chamada base de Fock associada à base {% i } dos estados de uma única partícula.!22
23 Segunda quantização: A construção da base de Fock, a partir do espaço dos estados de um única partícula, é chamada de segunda quantização. Este nome é justificado pela existência de dois níveis de números quânticos, que são diferentes em caráter e no papel que desempenham: - Os vetores da base {% i } do espaço de Hilbert E H (1) dos estados de uma única partícula são caracterizados por certos números quânticos % de uma partícula (por exemplo m x, m y, m z = 1, 2,. para uma partícula livre numa caixa). - Quando mudamos para o espaço de Fock E H com um número arbitrário de bósons ou férmions, temos um novo conjunto de números quânticos que caracterizam os elementos da base de Fock os números de ocupação {n i }. Na representação de Fock, não é mais necessário considerar os números % como números quânticos; eles passam a desempenhar o papel de índices dos números de ocupação n.!23
24 <latexit sha1_base64="szdelcfniymslk7wo7c50t1yq0e=">aaadp3icjvlpaxnbfj5df9x4o6kevtwawirgscucxosibhoqltrtibox2clsmnr2dpl5k4tn/mde/be8efxiqrgv3pwkszstfr8mfpo9773vzy84v9jiehzy/gvxb9y8txg7cefuvfubza0hpzyrdbc9nqnm9gnmhzja9fciev3ccjbgspzf52/m+bn3wliz6roc5mkysrgwieqmhrvtet3al7alr4cmdccmlu9mrzvice+8lz8cjquykomeirxu8kqmafru5gfvatvypmhhrglqw6rrqaowdzspmrtqbh2vvooep04kvde9vgkukszgf32hgtlvxdxisxtkgzu7vwc7hg61gsft1ty6azboyoyuq06rht32paf/riyaraatlaiug7aglvlhudt8seczl1khkstm7samchywzkdkslqnwlirm37oxmlgogapsmny8f4v7dhmbelm3niic/bpipkl1k7t2cnnj2wv5ubk33kdapoxw1lqvech+diokrrgbvppbcnpbec1dybxi92swcfmmi7uyzxcjyqxj3wznd7rheenph7e2n9dx8cgeus2yr4jyquytw7ieekr7r33pntfvw/+b/+l/93/szt6xl3zkkyf//mxnxmaaq==</latexit> <latexit sha1_base64="szdelcfniymslk7wo7c50t1yq0e=">aaadp3icjvlpaxnbfj5df9x4o6kevtwawirgscucxosibhoqltrtibox2clsmnr2dpl5k4tn/mde/be8efxiqrgv3pwkszstfr8mfpo9773vzy84v9jiehzy/gvxb9y8txg7cefuvfubza0hpzyrdbc9nqnm9gnmhzja9fciev3ccjbgspzf52/m+bn3wliz6roc5mkysrgwieqmhrvtet3al7alr4cmdccmlu9mrzvice+8lz8cjquykomeirxu8kqmafru5gfvatvypmhhrglqw6rrqaowdzspmrtqbh2vvooep04kvde9vgkukszgf32hgtlvxdxisxtkgzu7vwc7hg61gsft1ty6azboyoyuq06rht32paf/riyaraatlaiug7aglvlhudt8seczl1khkstm7samchywzkdkslqnwlirm37oxmlgogapsmny8f4v7dhmbelm3niic/bpipkl1k7t2cnnj2wv5ubk33kdapoxw1lqvech+diokrrgbvppbcnpbec1dybxi92swcfmmi7uyzxcjyqxj3wznd7rheenph7e2n9dx8cgeus2yr4jyquytw7ieekr7r33pntfvw/+b/+l/93/szt6xl3zkkyf//mxnxmaaq==</latexit> <latexit sha1_base64="szdelcfniymslk7wo7c50t1yq0e=">aaadp3icjvlpaxnbfj5df9x4o6kevtwawirgscucxosibhoqltrtibox2clsmnr2dpl5k4tn/mde/be8efxiqrgv3pwkszstfr8mfpo9773vzy84v9jiehzy/gvxb9y8txg7cefuvfubza0hpzyrdbc9nqnm9gnmhzja9fciev3ccjbgspzf52/m+bn3wliz6roc5mkysrgwieqmhrvtet3al7alr4cmdccmlu9mrzvice+8lz8cjquykomeirxu8kqmafru5gfvatvypmhhrglqw6rrqaowdzspmrtqbh2vvooep04kvde9vgkukszgf32hgtlvxdxisxtkgzu7vwc7hg61gsft1ty6azboyoyuq06rht32paf/riyaraatlaiug7aglvlhudt8seczl1khkstm7samchywzkdkslqnwlirm37oxmlgogapsmny8f4v7dhmbelm3niic/bpipkl1k7t2cnnj2wv5ubk33kdapoxw1lqvech+diokrrgbvppbcnpbec1dybxi92swcfmmi7uyzxcjyqxj3wznd7rheenph7e2n9dx8cgeus2yr4jyquytw7ieekr7r33pntfvw/+b/+l/93/szt6xl3zkkyf//mxnxmaaq==</latexit> <latexit sha1_base64="szdelcfniymslk7wo7c50t1yq0e=">aaadp3icjvlpaxnbfj5df9x4o6kevtwawirgscucxosibhoqltrtibox2clsmnr2dpl5k4tn/mde/be8efxiqrgv3pwkszstfr8mfpo9773vzy84v9jiehzy/gvxb9y8txg7cefuvfubza0hpzyrdbc9nqnm9gnmhzja9fciev3ccjbgspzf52/m+bn3wliz6roc5mkysrgwieqmhrvtet3al7alr4cmdccmlu9mrzvice+8lz8cjquykomeirxu8kqmafru5gfvatvypmhhrglqw6rrqaowdzspmrtqbh2vvooep04kvde9vgkukszgf32hgtlvxdxisxtkgzu7vwc7hg61gsft1ty6azboyoyuq06rht32paf/riyaraatlaiug7aglvlhudt8seczl1khkstm7samchywzkdkslqnwlirm37oxmlgogapsmny8f4v7dhmbelm3niic/bpipkl1k7t2cnnj2wv5ubk33kdapoxw1lqvech+diokrrgbvppbcnpbec1dybxi92swcfmmi7uyzxcjyqxj3wznd7rheenph7e2n9dx8cgeus2yr4jyquytw7ieekr7r33pntfvw/+b/+l/93/szt6xl3zkkyf//mxnxmaaq==</latexit> <latexit sha1_base64="shiqp+6shsy5p2ku0w4z1udpypy=">aaadghictvjnaxrbeo0zv+l6tdgjl8jfeyzljajjrqik4ekiumnc9jr09nzsmnt3dn01wjkzn+hfv+lfgyjec/pf2ls7b5my8glrdy9xr6qrqiuvtpkujl+i+nllk1evbvzv3bh56/ad/ubdfv/wtujilrp041x41mriibrphfcohck1hurhr5b+g4/ovcrte1puodviblwhpkbazzvrki8vpiixanzxjmtslm4bl7ospgybzrqubegltg0clexci1wkoqb80dwfnimjea1posrndw9bol4odlhb5+w89x8kwwvtwlhysoewvtinausegf6hirp+ibkmk4pzio3aghw2l/vp+kyutuflugvvj2ls0bqrjptu2pz47bes8kjmcrkgfqb9tfl9baspazodonthwoiv+2dei4z3c5mhprf06m/6lutffjoaip1po2xve1q5fqionvajyy2bmxioss8cenkpucviq+geplblvtce9gzl58h+s2gadnn3zwe7l7txbld77af7zfk2zxbzg7bhrkxgn6iv0bfoe/w5/hr/ih+upxhuxdxjpyw++q2wfvyl</latexit> <latexit sha1_base64="shiqp+6shsy5p2ku0w4z1udpypy=">aaadghictvjnaxrbeo0zv+l6tdgjl8jfeyzljajjrqik4ekiumnc9jr09nzsmnt3dn01wjkzn+hfv+lfgyjec/pf2ls7b5my8glrdy9xr6qrqiuvtpkujl+i+nllk1evbvzv3bh56/ad/ubdfv/wtujilrp041x41mriibrphfcohck1hurhr5b+g4/ovcrte1puodviblwhpkbazzvrki8vpiixanzxjmtslm4bl7ospgybzrqubegltg0clexci1wkoqb80dwfnimjea1posrndw9bol4odlhb5+w89x8kwwvtwlhysoewvtinausegf6hirp+ibkmk4pzio3aghw2l/vp+kyutuflugvvj2ls0bqrjptu2pz47bes8kjmcrkgfqb9tfl9baspazodonthwoiv+2dei4z3c5mhprf06m/6lutffjoaip1po2xve1q5fqionvajyy2bmxioss8cenkpucviq+geplblvtce9gzl58h+s2gadnn3zwe7l7txbld77af7zfk2zxbzg7bhrkxgn6iv0bfoe/w5/hr/ih+upxhuxdxjpyw++q2wfvyl</latexit> <latexit sha1_base64="shiqp+6shsy5p2ku0w4z1udpypy=">aaadghictvjnaxrbeo0zv+l6tdgjl8jfeyzljajjrqik4ekiumnc9jr09nzsmnt3dn01wjkzn+hfv+lfgyjec/pf2ls7b5my8glrdy9xr6qrqiuvtpkujl+i+nllk1evbvzv3bh56/ad/ubdfv/wtujilrp041x41mriibrphfcohck1hurhr5b+g4/ovcrte1puodviblwhpkbazzvrki8vpiixanzxjmtslm4bl7ospgybzrqubegltg0clexci1wkoqb80dwfnimjea1posrndw9bol4odlhb5+w89x8kwwvtwlhysoewvtinausegf6hirp+ibkmk4pzio3aghw2l/vp+kyutuflugvvj2ls0bqrjptu2pz47bes8kjmcrkgfqb9tfl9baspazodonthwoiv+2dei4z3c5mhprf06m/6lutffjoaip1po2xve1q5fqionvajyy2bmxioss8cenkpucviq+geplblvtce9gzl58h+s2gadnn3zwe7l7txbld77af7zfk2zxbzg7bhrkxgn6iv0bfoe/w5/hr/ih+upxhuxdxjpyw++q2wfvyl</latexit> <latexit sha1_base64="shiqp+6shsy5p2ku0w4z1udpypy=">aaadghictvjnaxrbeo0zv+l6tdgjl8jfeyzljajjrqik4ekiumnc9jr09nzsmnt3dn01wjkzn+hfv+lfgyjec/pf2ls7b5my8glrdy9xr6qrqiuvtpkujl+i+nllk1evbvzv3bh56/ad/ubdfv/wtujilrp041x41mriibrphfcohck1hurhr5b+g4/ovcrte1puodviblwhpkbazzvrki8vpiixanzxjmtslm4bl7ospgybzrqubegltg0clexci1wkoqb80dwfnimjea1posrndw9bol4odlhb5+w89x8kwwvtwlhysoewvtinausegf6hirp+ibkmk4pzio3aghw2l/vp+kyutuflugvvj2ls0bqrjptu2pz47bes8kjmcrkgfqb9tfl9baspazodonthwoiv+2dei4z3c5mhprf06m/6lutffjoaip1po2xve1q5fqionvajyy2bmxioss8cenkpucviq+geplblvtce9gzl58h+s2gadnn3zwe7l7txbld77af7zfk2zxbzg7bhrkxgn6iv0bfoe/w5/hr/ih+upxhuxdxjpyw++q2wfvyl</latexit> Função de partição grande canônica Calcularemos a função de partição grande canônica na base de Fock: Ĥ+ µ =Tr e ˆN = X Ĥ+ µ hn 1,,n 1 e ˆN n 1,,n 1 i n 1,,n 1 Como os estados da base são autoestados do hamiltoniano Ĥ e do operador número N, ˆ ambos operadores podem ser substituídos por seus autovalores E = i & i n i e N= i n i respectivamente: = X hn 1,,n 1 e n 1,,n 1 = X hn 1,,n 1 e n 1,,n 1 E+ µn n 1,,n 1 i P i in i + µ P i n i n 1,,n 1 i!24
25 <latexit sha1_base64="thfifhyxlcspar2+msgqetdleg8=">aaae/xicvvrba9rafj420db10q199oxgomyhloki9uuo+ujjbbddykrhmjvzhtqzhjmjskbbv+kld4r46v/wzx/jzde9bltdhiohaifn8n3fmvucc66n5/1ewxxcw7fx1u+07t67/2cjvfnwqgefoqxpm5gpquw0e1yyvufgsegugeljwq7j4zd1/vadu5pn8r2z5cxmyujyhfnibcjadlbwgmnteawadzfgpyz8hcb0mbknoycjenozmelv2qjb5egwuk7kbnhroyphedwdhdndoitzrrmwzbxslc22bqspkzi5dgewmhfh3ppxyncusqfvucv8r9lomlfgiqmmapbw1wx8ndbhkqxl9wh/t7smwf9i4fenyeubz6zfhhfxg0611mddc8k3udf9255teq48dwjurr8ha7widsfrevodq47fob3u2h7u/owhgs1sjg0vrova93itlkqztgwrwrjqlcf0mixyyf1juqbdcnp7k3hii0nimmu/awaavdhrkltrsrrbypsysb6cq4olckfhkpdhywvegcbpjcgpbjgm6qcahlwxasteooqqbruchrnfqleprr0i/uwrrzohz3u+1/pfvejsvw6wyx09qo9rf/lof+2ht2gf9rf1pjqfna/on/et+8x97v6yla6und1bam7cn38arekayq==</latexit> <latexit sha1_base64="thfifhyxlcspar2+msgqetdleg8=">aaae/xicvvrba9rafj420db10q199oxgomyhloki9uuo+ujjbbddykrhmjvzhtqzhjmjskbbv+kld4r46v/wzx/jzde9bltdhiohaifn8n3fmvucc66n5/1ewxxcw7fx1u+07t67/2cjvfnwqgefoqxpm5gpquw0e1yyvufgsegugeljwq7j4zd1/vadu5pn8r2z5cxmyujyhfnibcjadlbwgmnteawadzfgpyz8hcb0mbknoycjenozmelv2qjb5egwuk7kbnhroyphedwdhdndoitzrrmwzbxslc22bqspkzi5dgewmhfh3ppxyncusqfvucv8r9lomlfgiqmmapbw1wx8ndbhkqxl9wh/t7smwf9i4fenyeubz6zfhhfxg0611mddc8k3udf9255teq48dwjurr8ha7widsfrevodq47fob3u2h7u/owhgs1sjg0vrova93itlkqztgwrwrjqlcf0mixyyf1juqbdcnp7k3hii0nimmu/awaavdhrkltrsrrbypsysb6cq4olckfhkpdhywvegcbpjcgpbjgm6qcahlwxasteooqqbruchrnfqleprr0i/uwrrzohz3u+1/pfvejsvw6wyx09qo9rf/lof+2ht2gf9rf1pjqfna/on/et+8x97v6yla6und1bam7cn38arekayq==</latexit> <latexit sha1_base64="thfifhyxlcspar2+msgqetdleg8=">aaae/xicvvrba9rafj420db10q199oxgomyhloki9uuo+ujjbbddykrhmjvzhtqzhjmjskbbv+kld4r46v/wzx/jzde9bltdhiohaifn8n3fmvucc66n5/1ewxxcw7fx1u+07t67/2cjvfnwqgefoqxpm5gpquw0e1yyvufgsegugeljwq7j4zd1/vadu5pn8r2z5cxmyujyhfnibcjadlbwgmnteawadzfgpyz8hcb0mbknoycjenozmelv2qjb5egwuk7kbnhroyphedwdhdndoitzrrmwzbxslc22bqspkzi5dgewmhfh3ppxyncusqfvucv8r9lomlfgiqmmapbw1wx8ndbhkqxl9wh/t7smwf9i4fenyeubz6zfhhfxg0611mddc8k3udf9255teq48dwjurr8ha7widsfrevodq47fob3u2h7u/owhgs1sjg0vrova93itlkqztgwrwrjqlcf0mixyyf1juqbdcnp7k3hii0nimmu/awaavdhrkltrsrrbypsysb6cq4olckfhkpdhywvegcbpjcgpbjgm6qcahlwxasteooqqbruchrnfqleprr0i/uwrrzohz3u+1/pfvejsvw6wyx09qo9rf/lof+2ht2gf9rf1pjqfna/on/et+8x97v6yla6und1bam7cn38arekayq==</latexit> <latexit sha1_base64="thfifhyxlcspar2+msgqetdleg8=">aaae/xicvvrba9rafj420db10q199oxgomyhloki9uuo+ujjbbddykrhmjvzhtqzhjmjskbbv+kld4r46v/wzx/jzde9bltdhiohaifn8n3fmvucc66n5/1ewxxcw7fx1u+07t67/2cjvfnwqgefoqxpm5gpquw0e1yyvufgsegugeljwq7j4zd1/vadu5pn8r2z5cxmyujyhfnibcjadlbwgmnteawadzfgpyz8hcb0mbknoycjenozmelv2qjb5egwuk7kbnhroyphedwdhdndoitzrrmwzbxslc22bqspkzi5dgewmhfh3ppxyncusqfvucv8r9lomlfgiqmmapbw1wx8ndbhkqxl9wh/t7smwf9i4fenyeubz6zfhhfxg0611mddc8k3udf9255teq48dwjurr8ha7widsfrevodq47fob3u2h7u/owhgs1sjg0vrova93itlkqztgwrwrjqlcf0mixyyf1juqbdcnp7k3hii0nimmu/awaavdhrkltrsrrbypsysb6cq4olckfhkpdhywvegcbpjcgpbjgm6qcahlwxasteooqqbruchrnfqleprr0i/uwrrzohz3u+1/pfvejsvw6wyx09qo9rf/lof+2ht2gf9rf1pjqfna/on/et+8x97v6yla6und1bam7cn38arekayq==</latexit> Agora, a exponencial é um número e pode ser escrita como um produto de exponenciais: = X P hn 1,,n 1 e i [ ( i µ)n i ] n 1,,n 1 i n 1,,n 1 = X Y hn 1,,n 1 e [ ( i µ)n i ] n 1,,n 1 i n 1,,n 1 = X Y h i n i ( e i µ) n 1,,n 1 = X i h e ( 1 µ) i n 1 h e ( 1 µ) i n 1 n 1,,n 1 = X n 1 he ( 1 µ) i n 1! X h e ( 1 µ) i n 1! n 1!25
26 <latexit sha1_base64="aqjkqs6f6idhnd+ff7eueanarcs=">aaadfxicjvjda9swffxsfxtzv7o97uwy0jfsbbdgoh0plo1ljx0sbsbyjszliagsg0kubonfsx+2t/2vvwxy6kdnljelgqnzp86ruhehhbfb8kvn+q8epnq896t/9nnzfy8h+68utf5qxqcsl7mexdrwkrsfwmelnxwa0yyw/dk+/tlkl2+4nijx3+2q4gfgf0qkglhrqgi/94pmblyduwaiewphqeyzrzwk8glwigto+tnwqwqogmtcuhgrxhgh3qdccfk5hhqifoulda+a3s1tdiqlutxd4rurkrwrutx4r8sm9l6ltfkoiok3z2kfmxyaxa13zta9o1rqihc6tyibsimnsw0jggydsbao2aa4bupuxnk0+emsnjuzv5zjaswcb4unk6qtyjlxfviaxlb2trd87qcigtdhtd6egg4ck0caa3euhtv7t6oimtgrlhavgbvl08015h25ewntk7asqigtv+xwkc0l2byavyream6sxdlamrbok7al1zrzt7b99wm4++rtcpfxgomj/vzpepa5/y499aa9rsoe0te6q1/rozoi1vvtgtf23nt//ap/0j/clnq9tuc1+if8479jia9g</latexit> <latexit sha1_base64="aqjkqs6f6idhnd+ff7eueanarcs=">aaadfxicjvjda9swffxsfxtzv7o97uwy0jfsbbdgoh0plo1ljx0sbsbyjszliagsg0kubonfsx+2t/2vvwxy6kdnljelgqnzp86ruhehhbfb8kvn+q8epnq896t/9nnzfy8h+68utf5qxqcsl7mexdrwkrsfwmelnxwa0yyw/dk+/tlkl2+4nijx3+2q4gfgf0qkglhrqgi/94pmblyduwaiewphqeyzrzwk8glwigto+tnwqwqogmtcuhgrxhgh3qdccfk5hhqifoulda+a3s1tdiqlutxd4rurkrwrutx4r8sm9l6ltfkoiok3z2kfmxyaxa13zta9o1rqihc6tyibsimnsw0jggydsbao2aa4bupuxnk0+emsnjuzv5zjaswcb4unk6qtyjlxfviaxlb2trd87qcigtdhtd6egg4ck0caa3euhtv7t6oimtgrlhavgbvl08015h25ewntk7asqigtv+xwkc0l2byavyream6sxdlamrbok7al1zrzt7b99wm4++rtcpfxgomj/vzpepa5/y499aa9rsoe0te6q1/rozoi1vvtgtf23nt//ap/0j/clnq9tuc1+if8479jia9g</latexit> <latexit sha1_base64="aqjkqs6f6idhnd+ff7eueanarcs=">aaadfxicjvjda9swffxsfxtzv7o97uwy0jfsbbdgoh0plo1ljx0sbsbyjszliagsg0kubonfsx+2t/2vvwxy6kdnljelgqnzp86ruhehhbfb8kvn+q8epnq896t/9nnzfy8h+68utf5qxqcsl7mexdrwkrsfwmelnxwa0yyw/dk+/tlkl2+4nijx3+2q4gfgf0qkglhrqgi/94pmblyduwaiewphqeyzrzwk8glwigto+tnwqwqogmtcuhgrxhgh3qdccfk5hhqifoulda+a3s1tdiqlutxd4rurkrwrutx4r8sm9l6ltfkoiok3z2kfmxyaxa13zta9o1rqihc6tyibsimnsw0jggydsbao2aa4bupuxnk0+emsnjuzv5zjaswcb4unk6qtyjlxfviaxlb2trd87qcigtdhtd6egg4ck0caa3euhtv7t6oimtgrlhavgbvl08015h25ewntk7asqigtv+xwkc0l2byavyream6sxdlamrbok7al1zrzt7b99wm4++rtcpfxgomj/vzpepa5/y499aa9rsoe0te6q1/rozoi1vvtgtf23nt//ap/0j/clnq9tuc1+if8479jia9g</latexit> <latexit sha1_base64="aqjkqs6f6idhnd+ff7eueanarcs=">aaadfxicjvjda9swffxsfxtzv7o97uwy0jfsbbdgoh0plo1ljx0sbsbyjszliagsg0kubonfsx+2t/2vvwxy6kdnljelgqnzp86ruhehhbfb8kvn+q8epnq896t/9nnzfy8h+68utf5qxqcsl7mexdrwkrsfwmelnxwa0yyw/dk+/tlkl2+4nijx3+2q4gfgf0qkglhrqgi/94pmblyduwaiewphqeyzrzwk8glwigto+tnwqwqogmtcuhgrxhgh3qdccfk5hhqifoulda+a3s1tdiqlutxd4rurkrwrutx4r8sm9l6ltfkoiok3z2kfmxyaxa13zta9o1rqihc6tyibsimnsw0jggydsbao2aa4bupuxnk0+emsnjuzv5zjaswcb4unk6qtyjlxfviaxlb2trd87qcigtdhtd6egg4ck0caa3euhtv7t6oimtgrlhavgbvl08015h25ewntk7asqigtv+xwkc0l2byavyream6sxdlamrbok7al1zrzt7b99wm4++rtcpfxgomj/vzpepa5/y499aa9rsoe0te6q1/rozoi1vvtgtf23nt//ap/0j/clnq9tuc1+if8479jia9g</latexit> <latexit sha1_base64="s9xjhlhnsgpcto0wrxcyblw73ho=">aaack3icbvdlsgnbejz1gemr6tfly1aumeykobdb4swjgtfanobzsw8yoptgpleis/7hi7/iqq8+8op/oik5+coykkqq6ekkuiunue6rmzy+mtk1xzgpzs7nlyywlpyvtjjpgtwrqetxa25qyrhrjelhpdxio0dhzxb9ppavb1abmctn1euxgffolempofmpvar6dqkbcah+qpn2swkarzcktfbgg+aw8cqhhfadja4+pkyqo2zjffc17hrpc1qlsltxh4c/xburmhvhtfv69nujyckmsshutmnzu2rmxjmucvtfpzoycnhno9iwnoyrmmy+vlup61zpq5ho+2kcofp9iuermb0osmmiu9f89gbif14jo/cgmcs4zqhj8buozbrqaopioc01cli9s7jq0v4vrjdrlsjww7qlel9p/ksudiuew/ho9sph1vedbbbk1tgm89g+o2in7jtvmgb37ie9sxfn3nly3pz3r+iym5pzyt/gfhwcrfgjfg==</latexit> <latexit sha1_base64="s9xjhlhnsgpcto0wrxcyblw73ho=">aaack3icbvdlsgnbejz1gemr6tfly1aumeykobdb4swjgtfanobzsw8yoptgpleis/7hi7/iqq8+8op/oik5+coykkqq6ekkuiunue6rmzy+mtk1xzgpzs7nlyywlpyvtjjpgtwrqetxa25qyrhrjelhpdxio0dhzxb9ppavb1abmctn1euxgffolempofmpvar6dqkbcah+qpn2swkarzcktfbgg+aw8cqhhfadja4+pkyqo2zjffc17hrpc1qlsltxh4c/xburmhvhtfv69nujyckmsshutmnzu2rmxjmucvtfpzoycnhno9iwnoyrmmy+vlup61zpq5ho+2kcofp9iuermb0osmmiu9f89gbif14jo/cgmcs4zqhj8buozbrqaopioc01cli9s7jq0v4vrjdrlsjww7qlel9p/ksudiuew/ho9sph1vedbbbk1tgm89g+o2in7jtvmgb37ie9sxfn3nly3pz3r+iym5pzyt/gfhwcrfgjfg==</latexit> <latexit sha1_base64="s9xjhlhnsgpcto0wrxcyblw73ho=">aaack3icbvdlsgnbejz1gemr6tfly1aumeykobdb4swjgtfanobzsw8yoptgpleis/7hi7/iqq8+8op/oik5+coykkqq6ekkuiunue6rmzy+mtk1xzgpzs7nlyywlpyvtjjpgtwrqetxa25qyrhrjelhpdxio0dhzxb9ppavb1abmctn1euxgffolempofmpvar6dqkbcah+qpn2swkarzcktfbgg+aw8cqhhfadja4+pkyqo2zjffc17hrpc1qlsltxh4c/xburmhvhtfv69nujyckmsshutmnzu2rmxjmucvtfpzoycnhno9iwnoyrmmy+vlup61zpq5ho+2kcofp9iuermb0osmmiu9f89gbif14jo/cgmcs4zqhj8buozbrqaopioc01cli9s7jq0v4vrjdrlsjww7qlel9p/ksudiuew/ho9sph1vedbbbk1tgm89g+o2in7jtvmgb37ie9sxfn3nly3pz3r+iym5pzyt/gfhwcrfgjfg==</latexit> <latexit sha1_base64="s9xjhlhnsgpcto0wrxcyblw73ho=">aaack3icbvdlsgnbejz1gemr6tfly1aumeykobdb4swjgtfanobzsw8yoptgpleis/7hi7/iqq8+8op/oik5+coykkqq6ekkuiunue6rmzy+mtk1xzgpzs7nlyywlpyvtjjpgtwrqetxa25qyrhrjelhpdxio0dhzxb9ppavb1abmctn1euxgffolempofmpvar6dqkbcah+qpn2swkarzcktfbgg+aw8cqhhfadja4+pkyqo2zjffc17hrpc1qlsltxh4c/xburmhvhtfv69nujyckmsshutmnzu2rmxjmucvtfpzoycnhno9iwnoyrmmy+vlup61zpq5ho+2kcofp9iuermb0osmmiu9f89gbif14jo/cgmcs4zqhj8buozbrqaopioc01cli9s7jq0v4vrjdrlsjww7qlel9p/ksudiuew/ho9sph1vedbbbk1tgm89g+o2in7jtvmgb37ie9sxfn3nly3pz3r+iym5pzyt/gfhwcrfgjfg==</latexit> No caso de férmions, temos ni = 0, 1, logo = X n 1 =0,1 h e ( 1 µ) i n 1! ( = 1+e 1 µ) = Y ( 1+e i µ) i 1+e X n 1 =0,1 ( 1 µ) h e ( 1 µ) i n 1! A expressão anterior pode ser escrita na forma: = Y i 1+ze i onde z=exp('() é a fugacidade do sistema.!26
27 <latexit sha1_base64="dg7wdj9sgozf+tqnh6mebvp6tea=">aaac3hicfvjlbxmxepyurxjeay5crksgvcrrlkiql0ovxdgwibrb8sbyorojva93zc9wilyrfw4gxjufxo3fwr/am26kkhzgsvz5m8c3hjsttxiurb+c8nr1gzdv7dzu3ll77/6d7snhx66ormshlhrhr6lwqjxbisnsocotijzvejkevm38j2donsrmb1qwmoriblsmpcbptbu/+ujbczga4boz6gn3vt6tztq+ipbipebyvpdzuzizlvfqxo0bjzw8aj4icehzlj3svl7cchm1cyvgvs0xleyawpvtbltvw6xuy/9d87+sm9wrltfocw3wzrtbiwbr2uayifvqy60dtbs/+ayqvy6gpbbojeoopkqwlptuuorwymep5kmy49hdi3j0sb1+nbu888wmssl6zqjw7mwmwutolfpur+acfm7b15bx+cyvza+twpmyijtyxcirnfabzuvdtfmupjcecgmv7xxkqlghyf+hzgjx9puvg+oxgzgaxo9f9q7ftopyyu/yu9znmdtnh+wdo2jdjoopwafgs/a1nisfw2/h9/pqmghzhro/lpzxb5jx4gq=</latexit> <latexit sha1_base64="dg7wdj9sgozf+tqnh6mebvp6tea=">aaac3hicfvjlbxmxepyurxjeay5crksgvcrrlkiql0ovxdgwibrb8sbyorojva93zc9wilyrfw4gxjufxo3fwr/am26kkhzgsvz5m8c3hjsttxiurb+c8nr1gzdv7dzu3ll77/6d7snhx66ormshlhrhr6lwqjxbisnsocotijzvejkevm38j2donsrmb1qwmoriblsmpcbptbu/+ujbczga4boz6gn3vt6tztq+ipbipebyvpdzuzizlvfqxo0bjzw8aj4icehzlj3svl7cchm1cyvgvs0xleyawpvtbltvw6xuy/9d87+sm9wrltfocw3wzrtbiwbr2uayifvqy60dtbs/+ayqvy6gpbbojeoopkqwlptuuorwymep5kmy49hdi3j0sb1+nbu888wmssl6zqjw7mwmwutolfpur+acfm7b15bx+cyvza+twpmyijtyxcirnfabzuvdtfmupjcecgmv7xxkqlghyf+hzgjx9puvg+oxgzgaxo9f9q7ftopyyu/yu9znmdtnh+wdo2jdjoopwafgs/a1nisfw2/h9/pqmghzhro/lpzxb5jx4gq=</latexit> <latexit sha1_base64="dg7wdj9sgozf+tqnh6mebvp6tea=">aaac3hicfvjlbxmxepyurxjeay5crksgvcrrlkiql0ovxdgwibrb8sbyorojva93zc9wilyrfw4gxjufxo3fwr/am26kkhzgsvz5m8c3hjsttxiurb+c8nr1gzdv7dzu3ll77/6d7snhx66ormshlhrhr6lwqjxbisnsocotijzvejkevm38j2donsrmb1qwmoriblsmpcbptbu/+ujbczga4boz6gn3vt6tztq+ipbipebyvpdzuzizlvfqxo0bjzw8aj4icehzlj3svl7cchm1cyvgvs0xleyawpvtbltvw6xuy/9d87+sm9wrltfocw3wzrtbiwbr2uayifvqy60dtbs/+ayqvy6gpbbojeoopkqwlptuuorwymep5kmy49hdi3j0sb1+nbu888wmssl6zqjw7mwmwutolfpur+acfm7b15bx+cyvza+twpmyijtyxcirnfabzuvdtfmupjcecgmv7xxkqlghyf+hzgjx9puvg+oxgzgaxo9f9q7ftopyyu/yu9znmdtnh+wdo2jdjoopwafgs/a1nisfw2/h9/pqmghzhro/lpzxb5jx4gq=</latexit> <latexit sha1_base64="dg7wdj9sgozf+tqnh6mebvp6tea=">aaac3hicfvjlbxmxepyurxjeay5crksgvcrrlkiql0ovxdgwibrb8sbyorojva93zc9wilyrfw4gxjufxo3fwr/am26kkhzgsvz5m8c3hjsttxiurb+c8nr1gzdv7dzu3ll77/6d7snhx66ormshlhrhr6lwqjxbisnsocotijzvejkevm38j2donsrmb1qwmoriblsmpcbptbu/+ujbczga4boz6gn3vt6tztq+ipbipebyvpdzuzizlvfqxo0bjzw8aj4icehzlj3svl7cchm1cyvgvs0xleyawpvtbltvw6xuy/9d87+sm9wrltfocw3wzrtbiwbr2uayifvqy60dtbs/+ayqvy6gpbbojeoopkqwlptuuorwymep5kmy49hdi3j0sb1+nbu888wmssl6zqjw7mwmwutolfpur+acfm7b15bx+cyvza+twpmyijtyxcirnfabzuvdtfmupjcecgmv7xxkqlghyf+hzgjx9puvg+oxgzgaxo9f9q7ftopyyu/yu9znmdtnh+wdo2jdjoopwafgs/a1nisfw2/h9/pqmghzhro/lpzxb5jx4gq=</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="hp+6lruf2d3tzaldqaqqvekmxyw=">aaab2xicbzdnsgmxfixv1l86vq1rn8eiucozbnqpuhfzwbzco5rm5k4bmskmyr2hdh0bf25efc93vo3pz0jbdwq+zknivscullqubn9ebwd3b/+gfugfnfzjk9nmo2fz0gjsilzl5jnmfpxu2cvjcp8lgzylffbj6f0i77+gstlxtzqrmmr4wmtuck7o6oyaraadlmw2ivxdc9yanb+gss7kddujxa0dhefbucunsafw7g9liwuxuz7ggupnm7rrtrxzzi6dk7a0n+5oykv394ukz9bostjdzdhn7ga2mp/lbiwlt1eldvesarh6kc0vo5wtdmajnchizrxwyasblykjn1yqa8z3hysbg29d77odbu3wmya6nmmfxeein3ahd9cblghi4bxevyn35n2suqp569lo4i+8zx84xio4</latexit> <latexit sha1_base64="zyqkmoywjavudqf6+yljgikwjka=">aaac9hicjvjnbxmxepvu+sih0lqsjy4jklaqrltmahckjc4ci0tashgivn7zxkr3q/ysulj2wf/h0kmr4rdw49/g3uyinbfibetpb/yex2phpdgoouhxeo7cuhnr9u6d3t29e/f3+wd7p66ormkrkkxhx7f0ahsoi9jkcfxalfls8cw+f9pmzz6idbri39oyxgkm57lotzlkqdlb8ecmntybvyampjqakvqpat7uwoepah6o4rmigencqgdptpey3njzdqynh8lq+ykoqaikilfp0xlt96mfzlnanlvtrk8rq7rfmtpg479k03+8/pyx/to6w5q+fc76r9ew6gi2av+bi7akk1n/p0gkvwwykzlsuqmpsprw0pjwbpueqbywup3lou48zgwgblp379fay88kkbbwr5ygy9cvtcycw2ax35ljwrjruzbclptull6c1jovk8jcxr2uvgaogpyzqkitkjjld6sy2tckaif9l8h/mz5var9+5u1w+nzioyf/f7fd9pa9ygpg2qv2mr1lj2zevpa5+bpcbt/cl+ff+p2qxwgw6tsh+yvch78bdirjbg==</latexit> <latexit sha1_base64="zyqkmoywjavudqf6+yljgikwjka=">aaac9hicjvjnbxmxepvu+sih0lqsjy4jklaqrltmahckjc4ci0tashgivn7zxkr3q/ysulj2wf/h0kmr4rdw49/g3uyinbfibetpb/yex2phpdgoouhxeo7cuhnr9u6d3t29e/f3+wd7p66ormkrkkxhx7f0ahsoi9jkcfxalfls8cw+f9pmzz6idbri39oyxgkm57lotzlkqdlb8ecmntybvyampjqakvqpat7uwoepah6o4rmigencqgdptpey3njzdqynh8lq+ykoqaikilfp0xlt96mfzlnanlvtrk8rq7rfmtpg479k03+8/pyx/to6w5q+fc76r9ew6gi2av+bi7akk1n/p0gkvwwykzlsuqmpsprw0pjwbpueqbywup3lou48zgwgblp379fay88kkbbwr5ygy9cvtcycw2ax35ljwrjruzbclptull6c1jovk8jcxr2uvgaogpyzqkitkjjld6sy2tckaif9l8h/mz5var9+5u1w+nzioyf/f7fd9pa9ygpg2qv2mr1lj2zevpa5+bpcbt/cl+ff+p2qxwgw6tsh+yvch78bdirjbg==</latexit> <latexit sha1_base64="owxkbjmh0e+2u3zm0imaxqewdc8=">aaac/3icjvjnj9mwehxc11k+uiboxezuok4qvciflkgruhbcjlpbqs6v40xaax0nsidijetax+hcays48je48w9wspuo2woxtqwnn37p47gtuithufqrcc9cvht5yt7v3rxrn27e6u/fpnzfzswozaelo0meq60mjkmrxklpuesjxppk9gwbp3mh1qncvkfvibnclizklbtkqfl+cjdpfdye58a1zjqenlkh67ipiyzhapi2hsfaeyqbq46lu9rl4pblqwno/obwlzz0afymbbltn85ot0/nlclo1ey0472urniw6vybj/8qtf3x8vnf+vebdhv6vjjvd6jr1avsg3gnbmwdr/p+t54wssrrkntcuwkcltsrhsulnty9xjkshtwvc5x6aesoblz379faa8+kkbxwl0pqszukwutorfle78wfld35xevuyk0ryp7namxkitdis4oysgmv0h4gsjvfsxrlgzbw+vpbloxvevkv0/nnim9ferscpxnf0sh+hq0ox6zbscfusftsygl2lb2yv+yijzkmpgsfgi/b1/bj+dn8fn4/2xoga80d9leep34dufbk1q==</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> <latexit sha1_base64="odbveaixsecxfinj1+r1bzjiapw=">aaac/3icjvjnbxmxepvu+sjhoymie5cresgvitpfleccvmgfy5figykokdc7m1j1fsierrswpfsvcohqcnhlb3dj3+ddrii0ewjss09v/j7hy0efvpac4jfnb127fupm9q3o7tt37+10d+8f2bw0eocy17kzrckivhkoszhguwfqpjhg4+jkbzm/pkvjvz59oewbk1tmmpuokchr013vir8peaqvgwtmqa88mujwyv1bcm8a8gmfz4fhsal6haurtjofdzewe1c7wy2azwkpuixzsus+rdfmn4qrlkffvdgod9qycpphuwuu/qs09cflzx/pp606rogb4btbcwzbg7aowixoswuctrs/ezzlmswmpbbwjsogoekldcmpse7w0mih5imy4djbtkroj1x7fju8cuwmsw7cyghadlvridtarrq5namgub2aa8hnuxfjyatjpbkijmzk5ufjqyfyad4dxmqgjl1wqeijxk0g58j1idyx6bgmhfevva6oxgzcybc+3+8dvfm2y5s9yo9zn4xsjttg79ghgzlpffa+eofehx/mf/w/+d8vt/reuvoa/rx+j99tnutz</latexit> No caso de bósons, o número de ocupação pode ser qualquer valor inteiro, n i = 0, 1,, portanto temos: X i! n 1 X i! n 1 ( 1 µ) ( 1 µ) = n 1 =0,1,,1 h e n 1 =0,1,,1 h e Logo, se a grandeza exp[ '(&i - ()] for menor do que 1 para todo i, teremos um conjunto de séries geométricas. Usando n q n = (1 q) 1 com q < 1, obtemos: = = Y i 1 1+e ( 1 µ) 1 1+e ( i µ) = Y i 1 1+e ( 1 µ) 1 1+ze i!27
28 No caso de bósons deve verificar-se exp[ '(&i - ()]<1 ou equivalentemente ze -'ε i < 1 para todo i, para que - não fique divergente. A condição exp[ '(&i - ()] <1 implica '(&i - () >0, portanto: ( < &i Isto é, o potencial químico deve ser menor que qualquer um dos autovalores de energia de uma única partícula. Ou seja, o para bósons o potencial químico deve ser menor que a energia do estado fundamental de uma única partícula: ( < &0 Em muitos casos temos &0=0, e portanto, ( < 0. Se essa condição não se verifica, a função de partição ficará divergente, não podendo representar um sistema físico.!28
29 De forma unificada, podemos escrever a função de partição macrocanônica para um gás ideal quântico como (z,v,t) = Y i (1 ± ze i ) ±1, onde o sinal (+) corresponde a férmions e o sinal ( ) a bósons.!29
30 <latexit sha1_base64="7jmdibjdcnbhauiai03qucn2uuu=">aaacw3ichvfda9swfjw9ry77aly97uwysjfce+wx2f4kowowt2wquieodbjynqpltpdkqmr8j/u2/zrjaabbg9gfocm5954r3ztqkaylol9b+odho8dpdp52nj1/8fkw++p1ysvkcjzyupzmljkluhq4dcjjngmdtkusz9l8a6ufxakxoiwmbqnxodi6ejngzhlq2f1nfyhcs/7vmsthmdmcd3acaxhd4m8y5bogsga6e7czlhzozhivx0lt55nmw7iv8zbvplwtbfrjdxvcaz7xa5qiy0brwyh9s0rzdf63atzs79bqrz+tlldqbf9jt+z2omg0dbgp4h3okv2ml91ruip5pbbwxdjr53gk3ajmxgkusenqyqjmpgdrnhtymiv2uw930mb7z6wgk40/hymt+3dfzzs1g5x6tmxchb2rteq+bv657muifowuhbb8plfwsxaltaufltdindx4wlgr/q3al5ifnvnr7/ghxhe/fb8kh4dxnix/fuqntnfjocbvytvsjzh5tebkoxmtkehbkmicmtdhtzaptehuusngv/og/bnh8wcsec/k</latexit> <latexit sha1_base64="7jmdibjdcnbhauiai03qucn2uuu=">aaacw3ichvfda9swfjw9ry77aly97uwysjfce+wx2f4kowowt2wquieodbjynqpltpdkqmr8j/u2/zrjaabbg9gfocm5954r3ztqkaylol9b+odho8dpdp52nj1/8fkw++p1ysvkcjzyupzmljkluhq4dcjjngmdtkusz9l8a6ufxakxoiwmbqnxodi6ejngzhlq2f1nfyhcs/7vmsthmdmcd3acaxhd4m8y5bogsga6e7czlhzozhivx0lt55nmw7iv8zbvplwtbfrjdxvcaz7xa5qiy0brwyh9s0rzdf63atzs79bqrz+tlldqbf9jt+z2omg0dbgp4h3okv2ml91ruip5pbbwxdjr53gk3ajmxgkusenqyqjmpgdrnhtymiv2uw930mb7z6wgk40/hymt+3dfzzs1g5x6tmxchb2rteq+bv657muifowuhbb8plfwsxaltaufltdindx4wlgr/q3al5ifnvnr7/ghxhe/fb8kh4dxnix/fuqntnfjocbvytvsjzh5tebkoxmtkehbkmicmtdhtzaptehuusngv/og/bnh8wcsec/k</latexit> <latexit sha1_base64="7jmdibjdcnbhauiai03qucn2uuu=">aaacw3ichvfda9swfjw9ry77aly97uwysjfce+wx2f4kowowt2wquieodbjynqpltpdkqmr8j/u2/zrjaabbg9gfocm5954r3ztqkaylol9b+odho8dpdp52nj1/8fkw++p1ysvkcjzyupzmljkluhq4dcjjngmdtkusz9l8a6ufxakxoiwmbqnxodi6ejngzhlq2f1nfyhcs/7vmsthmdmcd3acaxhd4m8y5bogsga6e7czlhzozhivx0lt55nmw7iv8zbvplwtbfrjdxvcaz7xa5qiy0brwyh9s0rzdf63atzs79bqrz+tlldqbf9jt+z2omg0dbgp4h3okv2ml91ruip5pbbwxdjr53gk3ajmxgkusenqyqjmpgdrnhtymiv2uw930mb7z6wgk40/hymt+3dfzzs1g5x6tmxchb2rteq+bv657muifowuhbb8plfwsxaltaufltdindx4wlgr/q3al5ifnvnr7/ghxhe/fb8kh4dxnix/fuqntnfjocbvytvsjzh5tebkoxmtkehbkmicmtdhtzaptehuusngv/og/bnh8wcsec/k</latexit> <latexit sha1_base64="7jmdibjdcnbhauiai03qucn2uuu=">aaacw3ichvfda9swfjw9ry77aly97uwysjfce+wx2f4kowowt2wquieodbjynqpltpdkqmr8j/u2/zrjaabbg9gfocm5954r3ztqkaylol9b+odho8dpdp52nj1/8fkw++p1ysvkcjzyupzmljkluhq4dcjjngmdtkusz9l8a6ufxakxoiwmbqnxodi6ejngzhlq2f1nfyhcs/7vmsthmdmcd3acaxhd4m8y5bogsga6e7czlhzozhivx0lt55nmw7iv8zbvplwtbfrjdxvcaz7xa5qiy0brwyh9s0rzdf63atzs79bqrz+tlldqbf9jt+z2omg0dbgp4h3okv2ml91ruip5pbbwxdjr53gk3ajmxgkusenqyqjmpgdrnhtymiv2uw930mb7z6wgk40/hymt+3dfzzs1g5x6tmxchb2rteq+bv657muifowuhbb8plfwsxaltaufltdindx4wlgr/q3al5ifnvnr7/ghxhe/fb8kh4dxnix/fuqntnfjocbvytvsjzh5tebkoxmtkehbkmicmtdhtzaptehuusngv/og/bnh8wcsec/k</latexit> Termodinâmica do gás ideal quântico Para estabelecer a conexão com a Termodinâmica, usamos (z,v,t) = PV = kt ln (z,v,t) PV kt = kt ln (z,v,t) =kt ln Y i PV kt = ±kt X i ln(1 ± ze X i ) (1 ± ze i ) ±1 Esta expressão pode ser escrita de forma genérica como PV kt =ln (z,v,t) =1 a X ln(1 + aze i i ), onde a = ( 8 1 > para bósons +1 para férmions!30
31 A partir de Ξ podemos obter o número médio de partículas N N = hni ln V,T P = z a X i Lembrando que N = i n i podemos identificar o número de ocupação P médio n i de cada nível de energia como ae i 1+aze i = X i 1 z 1 e i + a. hn i i = 1 z 1 e i + a. Finalmente, a energia interna U é dada por U = ln z,v = X i 1 a az i e i 1+aze i = X i que, como era de esperar, ficou da forma U = i ε i n i. P i z 1 e i + a!31
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Átomos polieletrónicos
 Átomos polieletrónicos Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 2/12/2013 5/11/2013, Aula 8 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Átomo de hidrogénio O Hamiltoniano
Átomos polieletrónicos Química Teórica e Estrutural P.J.S.B. Caridade & U. Miranda 2/12/2013 5/11/2013, Aula 8 Química Teórica & Estrutural (2013) Caridade & Ulises 1 Átomo de hidrogénio O Hamiltoniano
Representação grande
 Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
Capítulo 5 Representação grande canônica 5.1 Introdução Distribuição de probabilidades Vimos no Capítulo 1 que um sistema constituído por partículas que interagem por meio de forças conservativas em contato
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
O Método de Hartree-Fock
 O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
Átomo de Hélio. Tiago Santiago. 2 de novembro de Resumo
 Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
Física estatística MEFT, IST. Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
 Física estatística Gases ideais nas estatísticas quânticas: conjunto microcanónico MEFT, IST Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
Física estatística Gases ideais nas estatísticas quânticas: conjunto microcanónico MEFT, IST Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write.
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
A eq. de Schrödinger em coordenadas esféricas A autofunção espacial, ψ, e a energia, E, são determinadas pela solução da equação independente do tempo: Separação de variáveis Solução do tipo: Que leva
Rotação de Wick para o tempo Euclideano
 Teoria Quântica de Campos I 81 só temos a parte de aniquilação no futuro livre é autovalor de Como verificamos que isto é o mesmo que as condições 75.1. O que ganhamos fazendo de novo este caminho? Para
Teoria Quântica de Campos I 81 só temos a parte de aniquilação no futuro livre é autovalor de Como verificamos que isto é o mesmo que as condições 75.1. O que ganhamos fazendo de novo este caminho? Para
A eq. de Schrödinger em coordenadas esféricas
 A eq. de Schrödinger em coordenadas esféricas Equação de Schrödinger em 3D: 2 = 1 r 2 # % r $ r2 r & (+ ' 1 r 2 senθ # θ senθ & % (+ $ θ ' 1 r 2 sen 2 θ 2 φ 2 Podemos, então, escrever a eq. de Schrödinger
A eq. de Schrödinger em coordenadas esféricas Equação de Schrödinger em 3D: 2 = 1 r 2 # % r $ r2 r & (+ ' 1 r 2 senθ # θ senθ & % (+ $ θ ' 1 r 2 sen 2 θ 2 φ 2 Podemos, então, escrever a eq. de Schrödinger
Física Estatística ??? Representação macroscópica. Representação microscópica. sistema U (S, V, N) S (U, V, N)
 Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Física Estatística sistema Representação macroscópica U (S, V, N) S (U, V, N) Representação microscópica??? Física Estatística - Prof. Paulo Suzuki 1 Física Estatística Formalismo microcanônico S (U, V,
Ensemble Grande Canônico
 UFABC - NANHT3036-15SA - Mecânica Estatística Curso 017. Prof. Germán Lugones CAPÍTULO 5 Ensemble Grande Canônico 1 Sistema em contato com um reservatório Vamos procurar um ensemble que seja apropriado
UFABC - NANHT3036-15SA - Mecânica Estatística Curso 017. Prof. Germán Lugones CAPÍTULO 5 Ensemble Grande Canônico 1 Sistema em contato com um reservatório Vamos procurar um ensemble que seja apropriado
Não serão aceitas respostas sem justificativa:
 Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Primeira Prova de Conceitos de Mecânica Quântica -(,5) Uma partícula de massa m encontra-se no estado ψ(x,t)= A exp[ω(mx /ħ+it)], onde A e a são constantes reais e positivas. a- Normalize ψ(x,t); b- Calcule
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Teoria Clássica de Campos
 Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
Teoria Quântica de Campos I 7 No passo (1) o que estamos fazendo é quantizar (transformar em operadores) uma função definida em todo espaço (um campo) e cuja equação de movimento CLÁSSICA é de Dirac ou
Partícula na Caixa. Química Quântica Prof a. Dr a. Carla Dalmolin
 Partícula na Caixa Química Quântica Prof a. Dr a. Carla Dalmolin Caixa unidimensional Caixa tridimensional Degenerescência Partícula no anel (mov. de rotação) Partícula na Caixa Partícula numa caixa unidimensional
Partícula na Caixa Química Quântica Prof a. Dr a. Carla Dalmolin Caixa unidimensional Caixa tridimensional Degenerescência Partícula no anel (mov. de rotação) Partícula na Caixa Partícula numa caixa unidimensional
Equação de Schrödinger em 3D
 Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 10 ÁTOMOS COMPLEXOS Primeira Edição junho de 2005 CAPÍTULO 10 ÁTOMOS COMPLEXOS ÍNDICE 10-1- Introdução 10.2- Átomos com mais de um
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 10 ÁTOMOS COMPLEXOS Primeira Edição junho de 2005 CAPÍTULO 10 ÁTOMOS COMPLEXOS ÍNDICE 10-1- Introdução 10.2- Átomos com mais de um
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
Exame Unificado das Pós-graduações em Física EUF
 Exame Unificado das Pós-graduações em Física EUF º Semestre/01 Parte 1 4/04/01 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova constitui
Exame Unificado das Pós-graduações em Física EUF º Semestre/01 Parte 1 4/04/01 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova constitui
( eq. 12.1) No caso de um campo com várias componentes, se a transformação for linear em φ, podemos escrever:
 Temos então a corrente conservada: Teoria Quântica de Campos I 12 ( eq. 12.1) No caso de um campo com várias componentes, se a transformação for linear em φ, podemos escrever: De forma que : ( eq. 12.2)
Temos então a corrente conservada: Teoria Quântica de Campos I 12 ( eq. 12.1) No caso de um campo com várias componentes, se a transformação for linear em φ, podemos escrever: De forma que : ( eq. 12.2)
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi
 Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
Mecânica Clássica 1 - Lista de natal - Ho Ho Ho Professor: Gabriel T. Landi O campo vetorial 1 Aquecimento: quadri-potencial e os campos elétrico e magnético O objeto fundamental do eletromagnetismo é
Os Postulados da Mecânica Quântica
 Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná [email protected] Postulados Introdução Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o
Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná [email protected] Postulados Introdução Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o
Momento Angular. 8.1 Álgebra do Momento Angular
 Capítulo 8 Momento Angular Neste capítulo vamos estudar os autovalores e autovetores do momento angular. Este problema também pode ser analisado com o uso do método de operadores, o que faremos na primeira
Capítulo 8 Momento Angular Neste capítulo vamos estudar os autovalores e autovetores do momento angular. Este problema também pode ser analisado com o uso do método de operadores, o que faremos na primeira
Teoria Quântica de Campos
 Teoria Quântica de Campos I 1 Teoria Quântica de Campos (escopo do curso e um pouco de história) (Weinberg cap 1, Peskin 2.1, Nastase 1) Objetivo: uma teoria Quântica e Relativística (no sentido restrito)
Teoria Quântica de Campos I 1 Teoria Quântica de Campos (escopo do curso e um pouco de história) (Weinberg cap 1, Peskin 2.1, Nastase 1) Objetivo: uma teoria Quântica e Relativística (no sentido restrito)
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Aproximação de Hartree-Fock A maior preocupação da química quântica é encontrar e descrever
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Aproximação de Hartree-Fock A maior preocupação da química quântica é encontrar e descrever
Fundamentos de Química Quântica
 Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Aula 3 Professora: Melissa Soares Caetano Átomo de Hidrogênio Um núcleo
Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Aula 3 Professora: Melissa Soares Caetano Átomo de Hidrogênio Um núcleo
Rotor quântico. Quanticamente o rotor é descrito por uma função de onda, tal que: l A função de onda do estado estacionário é dada por:
 Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Rotor quântico Vamos tratar o caso da rotação de um corpo rígido, que corresponde a 2 massas pontuais, ligadas por uma barra rígida e sem massa. Consideremos rotação livre em torno de um eixo perpendicular
Eq. de Dirac com campo magnético
 Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Eq. de Dirac com campo magnético Rafael Cavagnoli GAME: Grupo de Médias e Altas Energias Eletromagnetismo clássico Eq. de Schrödinger Partícula carregada em campo mag. Eq. de Dirac Partícula carregada
Problemas de Duas Partículas
 Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
Quantização por Integrais de Trajetória:
 Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
JORNADA DE FÍSICA TEÓRICA INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a
 JORNADA DE FÍSICA TEÓRICA 2010 INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 23-07-2010 Monday, July 19, 2010 1 CAMPOS CLÁSSICOS, QUÂNTICOS, DE CALIBRE E POR AÍ AFORA JORNADA DE FÍSICA TEÓRICA 2010 Instituto
JORNADA DE FÍSICA TEÓRICA 2010 INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 23-07-2010 Monday, July 19, 2010 1 CAMPOS CLÁSSICOS, QUÂNTICOS, DE CALIBRE E POR AÍ AFORA JORNADA DE FÍSICA TEÓRICA 2010 Instituto
Quantização de um campo fermiônico
 Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Teoria Quântica de Campos II 54 p linhas ( eq. 54.1 ) Um exemplo trivial seria: Quantização de um campo fermiônico (Nastase 12 e 13; Peskin 3.1-3.4 [campo clássico], 3.5 [quant. canônica], 9.5 [quant.
Exame de Ingresso na Pós-graduação
 Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 09 de Junho de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3 (três)
Exame de Ingresso na Pós-graduação Instituto de Física - UFF Profissional - 09 de Junho de 009 Resolva 6 (seis) questões, com pelo menos uma questão de cada uma das seções. A duração da prova é de 3 (três)
Ronaldo Thibes Universidade Estadual do Sudoeste da Bahia Campus de Itapetinga DCEN Dez 2017
 QFT O que é e porque precisamos Ronaldo Thibes Universidade Estadual do Sudoeste da Bahia Campus de Itapetinga DCEN Dez 2017 Aquecimento Inicial - A teoria da relatividade torna tempo e espaço completamente
QFT O que é e porque precisamos Ronaldo Thibes Universidade Estadual do Sudoeste da Bahia Campus de Itapetinga DCEN Dez 2017 Aquecimento Inicial - A teoria da relatividade torna tempo e espaço completamente
Teoria de bandas nos sólidos
 Teoria de bandas nos sólidos Situação: átomos idênticos, distantes níveis de energia desse sistema têm degenerescência de troca dupla. A parte espacial da autofunção eletrônica pode ser uma combinação
Teoria de bandas nos sólidos Situação: átomos idênticos, distantes níveis de energia desse sistema têm degenerescência de troca dupla. A parte espacial da autofunção eletrônica pode ser uma combinação
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS DE UM ELÉTRON Primeira Edição junho de 2005 CAPÍTULO 08 ÁTOMOS DE UM ELÉTRON ÍNDICE 8.1- Introdução 8.2- Força Central 8.3- Equação
Terceira série de exercícios Mecânica Estatística - IFUSP - 13/9/ ensemble canônico -
 Terceira série de exercícios Mecânica Estatística - IFUSP - 3/9/00 - ensemble canônico - We consider especially ensembles of systems in which the index (or logarithm) of probability of phase is a linear
Terceira série de exercícios Mecânica Estatística - IFUSP - 3/9/00 - ensemble canônico - We consider especially ensembles of systems in which the index (or logarithm) of probability of phase is a linear
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 11. Soluções da equação de Schrödinger: potencial degrau
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 11 Soluções da equação de Schrödinger: potencial degrau 1 Partícula em presença de um potencial degrau Imaginemos um potencial com o perfil
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 11 Soluções da equação de Schrödinger: potencial degrau 1 Partícula em presença de um potencial degrau Imaginemos um potencial com o perfil
Exame Unificado EUF. 2º Semestre/2013 Parte 1 23/04/2013
 Exame Unificado das Pós-graduações em Física EUF º Semestre/013 Parte 1 3/04/013 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova constitui
Exame Unificado das Pós-graduações em Física EUF º Semestre/013 Parte 1 3/04/013 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova constitui
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 2017 04 de abril de 2017 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código.
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 2017 04 de abril de 2017 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código.
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS Edição de agosto de 2008 CAPÍTULO 8 ÁTOMOS MONOELETRÔNICOS ÍNDICE 8.1- Introdução 8.2- Problema da Força Central
Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi
 Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi (2016-2) Sólido cristalino Num modelo para um sólido cristalino podemos supor que os N átomos sejam equivalentes a 3N osciladores harmônicos
Mecânica Estatística - Exercícios do EUF Professor: Gabriel T. Landi (2016-2) Sólido cristalino Num modelo para um sólido cristalino podemos supor que os N átomos sejam equivalentes a 3N osciladores harmônicos
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 9. Soluções da equação de Schrödinger: partícula numa caixa infinita
 UFAB - Física Quântica - urso 017.3 Prof. Germán Lugones Aula 9 Soluções da equação de Schrödinger: partícula numa caixa infinita 1 Dada uma função de energia potencial V(x) que representa um certo sistema,
UFAB - Física Quântica - urso 017.3 Prof. Germán Lugones Aula 9 Soluções da equação de Schrödinger: partícula numa caixa infinita 1 Dada uma função de energia potencial V(x) que representa um certo sistema,
O spin do elétron. Vimos, na aula 2, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com 2 valores, com propriedades de momento angular.
 O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
O spin do elétron Vimos, na aula, que Goudsmit e Uhlenbeck propõem uma variável, quantizada, com valores, com propriedades de momento angular. Analogia com o momento angular orbital e e com e foram observadas
A Estrutura Eletrônica dos Átomos. Prof. Fernando R. Xavier
 A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
- identificar operadores ortogonais e unitários e conhecer as suas propriedades;
 DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
Aula 17 Tudo sobre os Átomos
 Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
Aula 17 Tudo sobre os Átomos Física 4 Ref. Halliday Volume4 Sumário Algumas propriedades dos átomos; O spin do elétron; Momento Angular e momento magnético; O experimento de Stern-Gerlach; O princípio
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 015 14 outubro 014 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código (EUFxxx).
EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 015 14 outubro 014 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código (EUFxxx).
Campo Escalar Complexo
 Finalmente consideremos: Teoria Quântica de Campos I 60 operador na representação de Schödinger, basta partir de 59.2 e usar lembrando que: É uma superposição de vários estados de uma partícula (cada um
Finalmente consideremos: Teoria Quântica de Campos I 60 operador na representação de Schödinger, basta partir de 59.2 e usar lembrando que: É uma superposição de vários estados de uma partícula (cada um
UFABC - Física Quântica - Curso Prof. Germán Lugones. Aula 8. A equação de Schrödinger
 UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
UFABC - Física Quântica - Curso 2017.3 Prof. Germán Lugones Aula 8 A equação de Schrödinger 1 A equação de Schrödinger Na primeira parte do curso, introduzimos a dualidade onda-partícula. Usando as relações
Introdução à Física Atômica e Molecular
 4005 Introdução à Física Atômica e Molecular Átomos Multieletrônicos Referências: D. Vianna, A. Fazzio e S. Canuto, Teoria Quântica de Moléculas e Sólidos. P. Atkins e R. Friedman, Molecular Quantum Mechanics,
4005 Introdução à Física Atômica e Molecular Átomos Multieletrônicos Referências: D. Vianna, A. Fazzio e S. Canuto, Teoria Quântica de Moléculas e Sólidos. P. Atkins e R. Friedman, Molecular Quantum Mechanics,
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica
 CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica 1 Introdução. Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o livro texto. Antes iremos fazer um paralelo entre
CF372 Mecânica Quântica I Os Postulados da Mecânica Quântica 1 Introdução. Vamos apresentar nestas notas os postulados da mecânica quântica de acordo com o livro texto. Antes iremos fazer um paralelo entre
Exame Unificado EUF. 1º Semestre/2013 Parte 1 16/10/2012
 Exame Unificado das Pós-graduações em Física EUF 1º Semestre/2013 Parte 1 16/10/2012 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
Exame Unificado das Pós-graduações em Física EUF 1º Semestre/2013 Parte 1 16/10/2012 Instruções: NÃO ESCREVA O SEU NOME NA PROVA. Ela deverá ser identificada apenas através do código (EUFxxx). Esta prova
Como Entender a Física Quântica em 8 Passos! Passos
 Como Entender a Física Quântica em 8 Passos! A física quântica (também chamada de teoria quântica ou mecânica quântica) é um ramo da física que permite uma descrição do comportamento e interação da matéria
Como Entender a Física Quântica em 8 Passos! A física quântica (também chamada de teoria quântica ou mecânica quântica) é um ramo da física que permite uma descrição do comportamento e interação da matéria
I. SISTEMA DE PARTÍCULAS IDÊNTICAS E SEGUNDA QUÂNTIZAÇÃO. A. Permutação de Partículas
 I. SISTEMA DE PARTÍCULAS IDÊNTICAS E SEGUNDA QUÂNTIZAÇÃO A. Permutação de Partículas Vamos considerar um sistema formado de 2 elétrons. Na Mecânica Quântica, surge uma nova situação quando tratar mais
I. SISTEMA DE PARTÍCULAS IDÊNTICAS E SEGUNDA QUÂNTIZAÇÃO A. Permutação de Partículas Vamos considerar um sistema formado de 2 elétrons. Na Mecânica Quântica, surge uma nova situação quando tratar mais
Física Moderna II Aula 08. Marcelo G Munhoz Edifício HEPIC, sala 202, ramal
 Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 [email protected] 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Física Moderna II Aula 08 Marcelo G Munhoz Edifício HEPIC, sala 202, ramal 916940 [email protected] 1 Física Moderna II Particle Physics Education CD-ROM 1999 CERN Sólidos Átomos de 1 e - Núcleo Atômico
Quantização por Integrais de Trajetória:
 Quantização por Integrais de Trajetória: O Oscilador Harmônico Teoria Quântica de Campos II 1 (Peskin cap 9, Ramond 2, Nastase 2) Além da imposição de relações de comutação, existe uma outra forma de quantizar
Quantização por Integrais de Trajetória: O Oscilador Harmônico Teoria Quântica de Campos II 1 (Peskin cap 9, Ramond 2, Nastase 2) Além da imposição de relações de comutação, existe uma outra forma de quantizar
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 [email protected] www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Teorema de Hohenberg-Kohn
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 [email protected] www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Teorema de Hohenberg-Kohn
Representações e Fenomenologia. Soluções (Clássicas) da Equação de Dirac
 Teoria Quântica de Campos I 113 Representações e Fenomenologia Qual destas representações descreve os férmions na natureza? A resposta depende de qual partícula você quer descrever. Para começar note que:
Teoria Quântica de Campos I 113 Representações e Fenomenologia Qual destas representações descreve os férmions na natureza? A resposta depende de qual partícula você quer descrever. Para começar note que:
PROPRIEDADES TERMODINÂMICAS DO MODELO DE ISING BIDIMENSIONAL VIA MONTE CARLO
 EXATAS E DA TERRA PROPRIEDADES TERMODINÂMICAS DO MODELO DE ISING BIDIMENSIONAL VIA MONTE CARLO FRANCELINO, Isabella Grinberg. Estudante do Curso de Engenharia Física- ILACVN UNILA; E-mail: [email protected];
EXATAS E DA TERRA PROPRIEDADES TERMODINÂMICAS DO MODELO DE ISING BIDIMENSIONAL VIA MONTE CARLO FRANCELINO, Isabella Grinberg. Estudante do Curso de Engenharia Física- ILACVN UNILA; E-mail: [email protected];
Quantização por Integrais de Trajetória:
 Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
Teoria Quântica de Campos I 14 Representações Fermiônicas: é possível mostrar que existem representações impossíveis de se obter através do simples produto de Λ s. Em especial o objeto: ( eq. 14.1 ) Matrizes
Regras de Feynman para uma teoria Bosônica em geral
 Teoria Quântica de Campos I 106 mente pois tratamos os estados iniciais e finais com mais detalhe (ainda que de forma heurística), como ondas planas. Veremos que na versão final da história, quando estivermos
Teoria Quântica de Campos I 106 mente pois tratamos os estados iniciais e finais com mais detalhe (ainda que de forma heurística), como ondas planas. Veremos que na versão final da história, quando estivermos
Mecânica Quântica I. Slides 1. Ano lectivo 2008/2009 Semestre ímpar Docente: Alfred Stadler. Departamento de Física da Universidade de Évora
 Mecânica Quântica I Ano lectivo 2008/2009 Semestre ímpar Docente: Alfred Stadler Slides 1 Departamento de Física da Universidade de Évora A equação de Schrödinger Comparação de descrição clássica e quântica:
Mecânica Quântica I Ano lectivo 2008/2009 Semestre ímpar Docente: Alfred Stadler Slides 1 Departamento de Física da Universidade de Évora A equação de Schrödinger Comparação de descrição clássica e quântica:
Regras de Feynman para uma teoria Bosônica em geral
 Teoria Quântica de Campos I 106 mente pois tratamos os estados iniciais e finais com mais detalhe (ainda que de forma heurística), como ondas planas. Veremos que na versão final da história, quando estivermos
Teoria Quântica de Campos I 106 mente pois tratamos os estados iniciais e finais com mais detalhe (ainda que de forma heurística), como ondas planas. Veremos que na versão final da história, quando estivermos
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Átomo de Hidrogênio 1
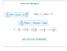 Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Física estatística. Teoria cinética dos gases MEFT, IST
 Física estatística Teoria cinética dos gases MEFT, IST Life is a series of collisions with the future; it is not the sum of what we have been, but what we yearn to be. Jose Ortega y Gasset (1883-1955)
Física estatística Teoria cinética dos gases MEFT, IST Life is a series of collisions with the future; it is not the sum of what we have been, but what we yearn to be. Jose Ortega y Gasset (1883-1955)
Teoria de Bandas 1 Elétrons Livres. CF086 - Introdução a Física do Estado Sólido 1
 Teoria de Bandas 1 Elétrons Livres CF086 - Introdução a Física do Estado Sólido 1 Introdução Para iniciar a investigação da contribuição eletrônica para as propriedades físicas relevantes, vamos considerar
Teoria de Bandas 1 Elétrons Livres CF086 - Introdução a Física do Estado Sólido 1 Introdução Para iniciar a investigação da contribuição eletrônica para as propriedades físicas relevantes, vamos considerar
