Física de Partículas
|
|
|
- Giovanni Marques Wagner
- 8 Há anos
- Visualizações:
Transcrição
1 Física de Partículas Parte 2 Ricardo D Elia Matheus
2 Construindo Lagrangeanas Onde estamos: vimos que a estrutura teórica adequada para descrever a física de partículas é a da Teoria Quântica de Campos (relativística) TQC Vimos também que toda informação física sobre um sistema pode ser codificada em uma Lagrangeana é ela que consiste no modelo que estudarei. Uma vez que temos uma em mãos existe uma prescrição clara de como obter observáveis físicos (pelo menos no regime perturbativo) A questão que se impõe é: em que estão baseadas estas Lagrangeanas?
3 Construindo Lagrangeanas Elementos principais: Graus de liberdade rigorosamente temos infinitos, mas muitas vezes este termo é usado para se referir a quais são os campos relevantes. Invariância de Lorentz: Outras simetrias Renormalizabilidade
4 Simetrias Desempenham um papel importante em qualquer ramo da física. Muitas vezes identificar simetrias é crítico para que um problema possa ser resolvido.
5 Simetrias Mas vai além disso, dada a ação: E dada uma transformação contínua dos campos: esta será uma simetria se as equações de movimento não mudarem, ou seja:
6 Simetrias Mas vai além disso, dada a ação: E dada uma transformação contínua dos campos: esta será uma simetria se as equações de movimento não mudarem, ou seja: Teorema de Noether Eq. de continuidade Corrente conservada A. Noether
7 Simetrias Teor. Gauss Superfície Grande
8 Simetrias Exemplos: Invariância por translação no espaço Invariância por translação no tempo Noether Conservação de Momento Conservação de Energia não depende de x m Invariância por rotações Conservação de Momento Angular Subgrupo das transf. De Lorentz Todas transformações de coordenadas, e as transformações dos campos?
9 Simetrias Escalar Complexo: Transformação de Fase Global Teoria de Grupos: U(1)
10 Simetrias Escalar Complexo: Transformação de Fase Global Teoria de Grupos: U(1) Noether Somente para campos complexos! Veremos em breve que: - carga elétrica - Densidade de corrente EM
11 Simetrias Outro caso em que as simetrias são úteis ocorre quando podemos agrupar partículas de propriedades (aproximadamente) iguais Ex: nucleon m = m p = m n
12 Simetrias Outro caso em que as simetrias são úteis ocorre quando podemos agrupar partículas de propriedades (aproximadamente) iguais Ex: nucleon Neste caso o sistema é invariante por transformações: Teoria de Grupos: SU(2) Simetria de Isospin Matrizes de Pauli
13 Simetrias Outro caso em que as simetrias são úteis ocorre quando podemos agrupar partículas de propriedades (aproximadamente) iguais Ex: nucleon De fato a força nuclear preserva esta simetria de isospin e se origina do termo de interação de Yukawa: Spinor Escalar H. Yukawa
14 Simetrias Outro caso em que as simetrias são úteis ocorre quando podemos agrupar partículas de propriedades (aproximadamente) iguais Ex: nucleon De fato a força nuclear preserva esta simetria de isospin e se origina do termo de interação de Yukawa: Pions H. Yukawa C. Lattes (& C. Powel) G. Occhialini
15 Simetrias Outro caso em que as simetrias são úteis ocorre quando podemos agrupar partículas de propriedades (aproximadamente) iguais Ex: nucleon De fato a força nuclear preserva esta simetria de isospin e se origina do termo de interação de Yukawa: A escolha por um modelo que conserva isospin não foi arbitrária, mas sim baseada em observações:
16 Simetrias: Globais vs. Locais Transformação de Fase Global Transformação de Calibre (ou Gauge) da Primeira Espécie Consiste em uma rotação no plano complexo de f (ou, equivalentemente, uma mudança no referencial que estabelece o ângulo zero )
17 Simetrias: Globais vs. Locais Transformação de Fase Global Transformação de Calibre (ou Gauge) da Primeira Espécie Consiste em uma rotação no plano complexo de f De fato, fazemos uma rotação do mesmo ângulo em todos os pontos do espaço tempo. Estamos assumindo que faz sentido comparar estes ângulos em pontos distantes. Isso é um problema? Não, pois esta fase não é um observável físico (o mesmo raciocínio aplicado a observáveis tais como simultaneidade ou direções no espaço gera problemas com a relatividade)
18 Simetrias: Globais vs. Locais Ainda assim, podemos não assumir isso e considerar uma transformação mais geral: uma mudança de fase arbitrária para cada ponto do espaço. Transformação de Fase Global Transformação de Calibre (ou Gauge) da Primeira Espécie
19 Simetrias: Globais vs. Locais Ainda assim, podemos não assumir isso e considerar uma transformação mais geral: uma mudança de fase arbitrária para cada ponto do espaço. a(x) um função bem comportada de x m A transformação global pode ser obtida da local simplesmente se a(x) = constante Transformação de Fase Local Transformação de Calibre (ou Gauge) da Segunda Espécie
20 Simetrias: Globais vs. Locais O mesmo pode ser feito para simetrias com grupos maiores: SU(N) Global SU(N) Local ou de Gauge ps: no jargão atual de física de partículas raramente se diz gauge global ou espécie. Em geral simetria de gauge quer dizer simetria local. Quais são as consequências de exigir da minha Lagrangeana uma simetria de gauge?
21 Simetria U(1) Local Escalar Complexo: U(1):
22 Simetria U(1) Local Escalar Complexo: U(1): Termo de massa OK!
23 Simetria U(1) Local Escalar Complexo: U(1): Termo de massa OK! Termo Cinético!?
24 Simetria U(1) Local Escalar Complexo: U(1): Termo de massa Termo Cinético OK! Esta Lagrangeana não é invariante pela simetria local. Mas... existe alguma que seria?
25 Simetria U(1) Local Fica mais fácil ver o que está faltando no caso de spinores de Dirac. No caso escalar o que ocorreu foi: Spinorial: Escalar Complexo: No caso spinorial ocorre um problema idêntico:
26 Simetria U(1) Local Fica mais fácil ver o que está faltando no caso de spinores de Dirac. No caso escalar o que ocorreu foi: Spinorial: Escalar Complexo: No caso spinorial ocorre um problema idêntico: Precisamos adicionar um novo termo à Lagrangeana, um que se transforme assim: (no caso escalar a transformação da corrente não era tão simples, mas a conclusão final é a mesma)
27 Simetria U(1) Local Fica mais fácil ver o que está faltando no caso de spinores de Dirac. No caso escalar o que ocorreu foi: Spinorial: Escalar Complexo: No caso spinorial ocorre um problema idêntico: Precisamos adicionar um novo termo à Lagrangeana, um que se transforme assim: OK! U(1) local restaurado!
28 Simetria U(1) Local A conclusão é que, para restaurar a simetria de gauge, foi preciso introduzir um termo de interação com um campo vetorial na Lagrangeana: Constante de acoplamento
29 Simetria U(1) Local A conclusão é que, para restaurar a simetria de gauge, foi preciso introduzir um termo de interação com um campo vetorial na Lagrangeana: Constante de acoplamento As propriedades do novo campo vetorial são dadas pela sua transformação: U(1): Proca
30 Simetria U(1) Local A conclusão é que, para restaurar a simetria de gauge, foi preciso introduzir um termo de interação com um campo vetorial na Lagrangeana: Constante de acoplamento As propriedades do novo campo vetorial são dadas pela sua transformação: U(1): Proca m = 0 Satisfaz as equações de Maxwell
31 Simetria U(1) Local Enfim: Bóson vetorial sem massa que satisfaz as equações de Maxwell Ele se acopla com partículas de spin ½ com intensidade controlada pela constante de acoplamento c 1 Podemos escrever a Lagrangeana final na forma: Derivada covariante:
32 Simetria U(1) Local Enfim: Bóson vetorial sem massa que satisfaz as equações de Maxwell Ele se acopla com partículas de spin ½ com intensidade controlada pela constante de acoplamento c 1 Podemos escrever a Lagrangeana final na forma: Derivada covariante: Uma versão 4D da substituição mínima do EM
33 Simetria U(1) Local Enfim: Bóson vetorial sem massa que satisfaz as equações de Maxwell Ele se acopla com partículas de spin ½ com intensidade controlada pela constante de acoplamento c 1 Podemos escrever a Lagrangeana final na forma: Derivada covariante: Uma versão 4D da substituição mínima do EM Transformações De Gauge do EM
34 Simetria U(1) Local Enfim: Bóson vetorial sem massa que satisfaz as equações de Maxwell Ele se acopla com partículas de spin ½ com intensidade controlada pela constante de acoplamento c 1 Podemos escrever a Lagrangeana final na forma: Derivada covariante: Uma versão 4D da substituição mínima do EM Transf. De Gauge do EM É o foton! É a carga elétrica do férmion em questão
35 Simetria U(1) Local A existência do fóton e a QED são consequências diretas da simetria de gauge! IMPORTANTE: O fóton é um bóson de gauge Os bósons de gauge não podem ter termos de massa! A carga aparece ao mesmo tempo com quantidade conservada ( j 0 dv) e como constante de acoplamento isto sempre acontece quando uma quantidade conservada Q está associada a uma simetria de gauge
36 Elétron vs. Fóton Sobre essa ótica, fica mais clara a relação entre matéria, radiação e interação Férmions são mais sólidos que os bósons além do princípio de exclusão de Pauli, há simetrias de conservação de número associada a eles.
37 Elétron vs. Fóton Sobre essa ótica, fica mais clara a relação entre matéria, radiação e interação Férmions são mais sólidos que os bósons além do princípio de exclusão de Pauli, há simetrias de conservação de número associada a eles.
38 Elétron vs. Fóton Sobre essa ótica, fica mais clara a relação entre matéria, radiação e interação Férmions são mais sólidos que os bósons além do princípio de exclusão de Pauli, há simetrias de conservação de número associada a eles.
39 Elétron vs. Fóton Sobre essa ótica, fica mais clara a relação entre matéria, radiação e interação Férmions são mais sólidos que os bósons além do princípio de exclusão de Pauli, há simetrias de conservação de número associada a eles. As interações em nível árvore são intermediadas por bósons. Os bósons de gauge são consequência da simetria dos férmions Nível árvore Loop
40 Campo Escalar Complexo Escalar Complexo:
41 Campo Escalar Complexo Escalar Complexo: Invariante de U(1) local
42 Campo Escalar Complexo Escalar Complexo: Invariante de U(1) local Esse modelo é conhecido por QED Escalar. Note que um campo escalar real não tem essa simetria f real f complexo Partículas neutras Partículas carregadas
43 Teoria de Gauge SU(N) SU(2): SU(3): SU(N): Estas simetrias pertencem a grupos não-abelianos com N 2-1 geradores. Os férmions estarão agrupados em multipletos que se transformam em alguma representação deste grupo: Rep. Fundamental: n = N Rep. Adjunta: n = N 2-1 Spin: SU(2) Partícula de Spin ½ Fundamental (2 componentes) Partícula de Spin 1 Adjunta (3 componentes)
44 Teoria de Gauge SU(N) A invariância local agora exige mais campos de gauge: Aparece um bóson de gauge para cada gerador Constante de acoplamento
45 Teoria de Gauge SU(N) A invariância local agora exige mais campos de gauge: Aparece um bóson de gauge para cada gerador A Lagrangeana invariante se parece muito com a da QED: Com o tensor F mn definido da seguinte forma: Novidade Cte. De Estrutura
46 Teoria de Gauge SU(N) A invariância local agora exige mais campos de gauge: Aparece um bóson de gauge para cada gerador A Lagrangeana invariante se parece muito com a da QED: Yang-Mills C.N. Yang R. Mills
47 O que muda? Teoria de Gauge SU(N) C.N. Yang R. Mills Auto-interações: os bósons de gauge são carregados
48 Construindo o Modelo Padrão da Física de Partículas Sec XIX (não tão completa)
49 Construindo o Modelo Padrão da Física de Partículas Sec XX Exp.: 1932 a... Teor.: 1920 a... Thompson Rutherford Bohr Chadwick
50 Construindo o Modelo Padrão da Física de Partículas Sec XX? Exp.: 1932 a... Teor.: 1920 a... Anderson
51 Construindo o Modelo Padrão da Física de Partículas Sec XX Méson f Exp.: 1932 a... Teor.: 1920 a 1935 Massa do Méson: cerca de 100 MeV Anderson Yukawa
52 Construindo o Modelo Padrão da Física de Partículas Sec XX Méson f Exp.: 1932 a... Teor.: 1920 a 1935 m m = 105 MeV (foi confundido com o méson de Yukawa por algum tempo) Anderson , 1936 Yukawa Neddermeyer
53 Construindo o Modelo Padrão da Física de Partículas Sec XX Méson (1950) Exp.: 1932 a 1947 Teor.: 1920 a 1935 m p+ = 140 MeV m p0 = 135 MeV Anderson , 1936 Yukawa Neddermeyer Lattes Occhialini
54 Construindo o Modelo Padrão da Física de Partículas Sec XX Méson (1950) A simplicidade não durou : Kaon (~500 MeV) 1947: Λ 0 (~1.1 GeV) Exp.: 1932 a 1947 Teor.: 1920 a 1935
55 Construindo o Modelo Padrão da Física de Partículas (1950) Méson Exp.: 1932 a 1947 Teor.: 1920 a 1935 Mais e mais partículas subatômicas descobertas...
56 Construindo o Modelo Padrão da Física de Partículas (1950) Méson Exp.: 1932 a 1947 Teor.: 1920 a : Kaon 1947: Λ 0 "Had I foreseen that, I would have gone into botany W. Pauli
57 Os Hádrons e a QCD A situação era bem complicada no setor dos hadrons: as partículas que interagiam fortemente:
58 Os Hádrons e a QCD A situação era bem complicada no setor dos hadrons: as partículas que interagiam fortemente: Um padrão foi lentamente emergindo: Spin ½ Spin 3/2 Nishijima Estranheza S Gell-Mann
59 Os Hádrons e a QCD A situação era bem complicada no setor dos hadrons: as partículas que interagiam fortemente: Um padrão foi lentamente emergindo: Spin 0 Spin 1 Nishijima Estranheza S Gell-Mann
60 Os Hádrons e a QCD Zweig "Three quarks for Muster Mark!"
61 Os Hádrons e a QCD Zweig "Three quarks for Muster Mark!" Mecanismo GIM u,d,s,c - Sabores Glashow Iliopoulos Maiani
62 Os Hádrons e a QCD Spin 3/2 S = 0 Q = 2
63 Os Hádrons e a QCD Spin 3/2 S = 0 Q = 2 1/2 1/2 1/2 L = 0 (estado fundamental) Problema de estatística
64 Os Hádrons e a QCD Spin 3/2 S = 0 Q = 2 1/2 1/2 1/2 L = 0 (estado fundamental) Problema de estatística Cor
65 Os Hádrons e a QCD... Quarks se transformam na rep.fundamental de SU(3) Nambu Han Greenberg
66 Os Hádrons e a QCD... Local Nambu Han Greenberg Oito bósons de Gauge, os Gluons
67 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): Acoplamento Forte Toda a riqueza de estados observados no espectro hadrônico vem de um conjunto pequeno de férmions simétricos por SU(3) local. A interação entre hádrons, feita por píons (bósons escalares colocados a mão ) agora na mais é que um efeito coletivo da QCD. Tanto os píons quanto os nucleons são feito de quarks (pense em dois átomos neutros se ligam, ex: H 2 )
68 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): S. Bethke, Nucl. Phys. Proc. Suppl. 135, 345 (2004)
69 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): a s fica enorme para baixas energias. Estados que carreguem cor são ligados fortemente, somente combinações brancas escapam. Chamamos isso de Confinamento. Bárions: 3 quarks Mésons: quark-antiquark
70 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): a s fica enorme para baixas energias. Estados que carreguem cor são ligados fortemente, somente combinações brancas escapam. Chamamos isso de Confinamento. Bárions: 3 quarks Mésons: quark-antiquark Por isso não vemos cargas fracionárias Se tentamos separar cargas de cor, temos que investir tanta energia que produzimos mais partículas: resultam em jatos (observados em exp.)
71 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): a s fica enorme para baixas energias. Estados que carreguem cor são ligados fortemente, somente combinações brancas escapam. Chamamos isso de Confinamento. Bárions: 3 quarks Mésons: quark-antiquark Por isso não vemos cargas fracionárias Se tentamos separar cargas de cor, temos que investir tanta energia que produzimos mais partículas: resultam em jatos (observados em exp.) Mas... e a teoria de perturbação!?!?
72 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): Para altas energias o valor da constante cai rapidamente, nesta escala a QCD funciona perfeitamente. Chamamos isso de liberdade assintótica. Isso torna a QCD útil! Wilczek Politzer Gross
73 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): A origem e a dinâmica do confinamento ainda não são quantitativamente bem compreendidas. Como podemos tratar teorias no regime não perturbativo? Ex: porque não temos estados com mais quarks (4, 5,...)? Poderemos calcular a massa dos hádrons exatamente?
74 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): A origem e a dinâmica do confinamento ainda não são quantitativamente bem compreendidas. Como podemos tratar teorias no regime não perturbativo? X(3872)?
75 Os Hádrons e a QCD A Cromodinâmica Quântica (QCD): A origem e a dinâmica do confinamento ainda não são quantitativamente bem compreendidas. Como podemos tratar teorias no regime não perturbativo? X(3872)? Essa é a área de trabalho de alguns professores do IFT...
76 Construindo o Modelo Padrão da O que temos: Física de Partículas SU(3) c U(1) EM SU(3) c U(1) EM
77 Construindo o Modelo Padrão da O que temos: Física de Partículas Quarks U(1) EM SU(3) c Leptons
78 Construindo o Modelo Padrão da O que temos: Física de Partículas M.L. Perl (1975)
79 Construindo o Modelo Padrão da O que temos: Física de Partículas Kobayashi Maskawa Violação de CP
80 Construindo o Modelo Padrão da Física de Partículas O que temos: (1995) (1977) Lederman E288 O (parcialmente) culpado por ouvirmos tanto partícula de deus
81 Cenas dos próximos capítulos Base teórica: Teoria Quântica de Campos Construindo Lagrangenas, uma questão de simetria Simetrias locais e seu papel especial Relação entre matéria, radiação e interação Construindo um Modelo para a física de partículas - quando as simetrias quebram As interações nucleares fortes As interações nucleares fracas A interação eletrofraca O Modelo Padrão da Física de Partículas Problemas do modelo padrão
Momento Magnético Anômalo
 Momento Magnético Anômalo Na teoria relativística do elétron de Dirac, podemos obter a equação que descreve um elétron em um campo eletromagnético partindo da equação para um elétron livre, e introduzindo
Momento Magnético Anômalo Na teoria relativística do elétron de Dirac, podemos obter a equação que descreve um elétron em um campo eletromagnético partindo da equação para um elétron livre, e introduzindo
Ondas EM no Espaço Livre (Vácuo)
 Secretaria de Educação Profissional e Tecnológica Instituto Federal de Santa Catarina Campus São José Área de Telecomunicações ELM20704 Eletromagnetismo Professor: Bruno Fontana da Silva 2014-1 Ondas EM
Secretaria de Educação Profissional e Tecnológica Instituto Federal de Santa Catarina Campus São José Área de Telecomunicações ELM20704 Eletromagnetismo Professor: Bruno Fontana da Silva 2014-1 Ondas EM
UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA DEPARTAMENTO DE ENGENHARIA QUÍMICA ENG 008 Fenômenos de Transporte I A Profª Fátima Lopes
 Equações básicas Uma análise de qualquer problema em Mecânica dos Fluidos, necessariamente se inicia, quer diretamente ou indiretamente, com a definição das leis básicas que governam o movimento do fluido.
Equações básicas Uma análise de qualquer problema em Mecânica dos Fluidos, necessariamente se inicia, quer diretamente ou indiretamente, com a definição das leis básicas que governam o movimento do fluido.
Sejam P1(x1,y1) e P2(x2,y2) pontos pertencentes ao plano. A equação da reta pode ser expressa como: ou
 Sejam P1(x1,y1) e P2(x2,y2) pontos pertencentes ao plano. A equação da reta pode ser expressa como: ou y = ax + b ax y = b Desta forma, para encontrarmos a equação da reta que passa por entre esses dois
Sejam P1(x1,y1) e P2(x2,y2) pontos pertencentes ao plano. A equação da reta pode ser expressa como: ou y = ax + b ax y = b Desta forma, para encontrarmos a equação da reta que passa por entre esses dois
Lei de Gauss. 2.1 Fluxo Elétrico. O fluxo Φ E de um campo vetorial E constante perpendicular Φ E = EA (2.1)
 Capítulo 2 Lei de Gauss 2.1 Fluxo Elétrico O fluxo Φ E de um campo vetorial E constante perpendicular a uma superfície é definido como Φ E = E (2.1) Fluxo mede o quanto o campo atravessa a superfície.
Capítulo 2 Lei de Gauss 2.1 Fluxo Elétrico O fluxo Φ E de um campo vetorial E constante perpendicular a uma superfície é definido como Φ E = E (2.1) Fluxo mede o quanto o campo atravessa a superfície.
Universidade Federal de Goiás Campus Catalão Departamento de Matemática
 Universidade Federal de Goiás Campus Catalão Departamento de Matemática Disciplina: Álgebra Linear Professor: André Luiz Galdino Aluno(a): 4 a Lista de Exercícios 1. Podemos entender transformações lineares
Universidade Federal de Goiás Campus Catalão Departamento de Matemática Disciplina: Álgebra Linear Professor: André Luiz Galdino Aluno(a): 4 a Lista de Exercícios 1. Podemos entender transformações lineares
Aula 5. Uma partícula evolui na reta. A trajetória é uma função que dá a sua posição em função do tempo:
 Aula 5 5. Funções O conceito de função será o principal assunto tratado neste curso. Neste capítulo daremos algumas definições elementares, e consideraremos algumas das funções mais usadas na prática,
Aula 5 5. Funções O conceito de função será o principal assunto tratado neste curso. Neste capítulo daremos algumas definições elementares, e consideraremos algumas das funções mais usadas na prática,
7. A importância do aterramento na Qualidade da Energia.
 7. A importância do aterramento na Qualidade da Energia. Em primeiro lugar é preciso esclarecer o que significa e para que serve o aterramento do sistema elétrico. Ao contrário do que é usual considerar,
7. A importância do aterramento na Qualidade da Energia. Em primeiro lugar é preciso esclarecer o que significa e para que serve o aterramento do sistema elétrico. Ao contrário do que é usual considerar,
O Modelo Padrão. Muito aprendizado não nos ensina a compreender. Heráclito, "`O Obscuro"', 540AC-480AC
 O Modelo Padrão Marina von Steinkirch Instituto de Física da USP O Modelo Padrão é o modelo das interações fundamentais, que descreve três das quatro forças conhecidas, ou seja, a interação eletromagnética,
O Modelo Padrão Marina von Steinkirch Instituto de Física da USP O Modelo Padrão é o modelo das interações fundamentais, que descreve três das quatro forças conhecidas, ou seja, a interação eletromagnética,
Álgebra Linear Aplicada à Compressão de Imagens. Universidade de Lisboa Instituto Superior Técnico. Mestrado em Engenharia Aeroespacial
 Álgebra Linear Aplicada à Compressão de Imagens Universidade de Lisboa Instituto Superior Técnico Uma Breve Introdução Mestrado em Engenharia Aeroespacial Marília Matos Nº 80889 2014/2015 - Professor Paulo
Álgebra Linear Aplicada à Compressão de Imagens Universidade de Lisboa Instituto Superior Técnico Uma Breve Introdução Mestrado em Engenharia Aeroespacial Marília Matos Nº 80889 2014/2015 - Professor Paulo
Primeira Lista de Exercícios de Métodos Numéricos II Primeiro semestre de 2015
 Primeira Lista de Exercícios de Métodos Numéricos II Primeiro semestre de 015 Introdução Antes de apresentar a lista, introduzirei alguns problemas já vistos em sala de aula para orientar e facilitar a
Primeira Lista de Exercícios de Métodos Numéricos II Primeiro semestre de 015 Introdução Antes de apresentar a lista, introduzirei alguns problemas já vistos em sala de aula para orientar e facilitar a
Seu pé direito nas melhores Faculdades
 10 Insper 01/11/009 Seu pé direito nas melhores Faculdades análise quantitativa 40. No campeonato brasileiro de futebol, cada equipe realiza 38 jogos, recebendo, em cada partida, 3 pontos em caso de vitória,
10 Insper 01/11/009 Seu pé direito nas melhores Faculdades análise quantitativa 40. No campeonato brasileiro de futebol, cada equipe realiza 38 jogos, recebendo, em cada partida, 3 pontos em caso de vitória,
ÁLGEBRA LINEAR. Transformações Lineares. Prof. Susie C. Keller
 ÁLGEBRA LINEAR Transformações Lineares Prof. Susie C. Keller É um tipo especial de função (aplicação), onde o domínio e o contradomínio são espaços vetoriais. Tanto a variável independente quanto a variável
ÁLGEBRA LINEAR Transformações Lineares Prof. Susie C. Keller É um tipo especial de função (aplicação), onde o domínio e o contradomínio são espaços vetoriais. Tanto a variável independente quanto a variável
EGEA ESAPL - IPVC. Resolução de Problemas de Programação Linear, com recurso ao Excel
 EGEA ESAPL - IPVC Resolução de Problemas de Programação Linear, com recurso ao Excel Os Suplementos do Excel Em primeiro lugar deverá certificar-se que tem o Excel preparado para resolver problemas de
EGEA ESAPL - IPVC Resolução de Problemas de Programação Linear, com recurso ao Excel Os Suplementos do Excel Em primeiro lugar deverá certificar-se que tem o Excel preparado para resolver problemas de
Inteligência Artificial
 Inteligência Artificial Aula 7 Programação Genética M.e Guylerme Velasco Programação Genética De que modo computadores podem resolver problemas, sem que tenham que ser explicitamente programados para isso?
Inteligência Artificial Aula 7 Programação Genética M.e Guylerme Velasco Programação Genética De que modo computadores podem resolver problemas, sem que tenham que ser explicitamente programados para isso?
Universidade Federal de Goiás Instituto de Física. Ademar Paulo Júnior
 Universidade Federal de Goiás Instituto de Física Ademar Paulo Júnior Interações efetivas entre quarks a baixas energias a partir da Cromodinâmica Quântica considerando o condensado de quark-antiquark
Universidade Federal de Goiás Instituto de Física Ademar Paulo Júnior Interações efetivas entre quarks a baixas energias a partir da Cromodinâmica Quântica considerando o condensado de quark-antiquark
1PI. Auto-energia do fóton. e a condição em F1 para qualquer ordem de perturbação se torna:
 e a condição em F1 para qualquer ordem de perturbação se torna: Teoria Quântica de Campos II 124 Felizmente, podemos provar que isto é verdade usando as relações de Ward-Takahashi: ( eq 99.1 ) Como uma
e a condição em F1 para qualquer ordem de perturbação se torna: Teoria Quântica de Campos II 124 Felizmente, podemos provar que isto é verdade usando as relações de Ward-Takahashi: ( eq 99.1 ) Como uma
A nuvem mesônica e os fatores de forma estranhos do próton
 Universidade de São Paulo Instituto de Física A nuvem mesônica e os fatores de forma estranhos do próton Daniela Morales Tolentino Leite Orientadora: Profa. Dra. Marina Nielsen Dissertação apresentada
Universidade de São Paulo Instituto de Física A nuvem mesônica e os fatores de forma estranhos do próton Daniela Morales Tolentino Leite Orientadora: Profa. Dra. Marina Nielsen Dissertação apresentada
3.2.7. Diagrama de Impedâncias e Matriz de Admitância de um Sistema Elétrico
 Sistemas Elétricos de Potência 3.2.7. Diagrama de Impedâncias e Matriz de Admitância de um Sistema Elétrico Professor: Dr. Raphael Augusto de Souza Benedito E-mail:[email protected] disponível
Sistemas Elétricos de Potência 3.2.7. Diagrama de Impedâncias e Matriz de Admitância de um Sistema Elétrico Professor: Dr. Raphael Augusto de Souza Benedito E-mail:[email protected] disponível
A Estatística e a Engenharia
 Causarum Cognitio - Stanza della Segnatura, Palácio do Vaticano 1 Uma definição de engenharia: Um engenheiro é alguém que resolve problemas que interessam à sociedade pela aplicação eficiente de princípios
Causarum Cognitio - Stanza della Segnatura, Palácio do Vaticano 1 Uma definição de engenharia: Um engenheiro é alguém que resolve problemas que interessam à sociedade pela aplicação eficiente de princípios
Equações paramétricas da Reta
 39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Produtos Notáveis; Equações; Inequações; Função; Função Afim; Paridade;
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Produtos Notáveis; Equações; Inequações; Função; Função Afim; Paridade;
Probabilidade. Luiz Carlos Terra
 Luiz Carlos Terra Nesta aula, você conhecerá os conceitos básicos de probabilidade que é a base de toda inferência estatística, ou seja, a estimativa de parâmetros populacionais com base em dados amostrais.
Luiz Carlos Terra Nesta aula, você conhecerá os conceitos básicos de probabilidade que é a base de toda inferência estatística, ou seja, a estimativa de parâmetros populacionais com base em dados amostrais.
NOTA SOBRE A TEORIA DA ESTABILIDADE DO EQUILÍBRIO EM MERCADOS MÚLTIPLOS: JOHN HICKS
 NOTA SOBRE A TEORIA DA ESTABILIDADE DO EQUILÍBRIO EM MERCADOS MÚLTIPLOS: JOHN HICKS Tácito Augusto Farias* RESUMO Esta nota trata das principais contribuições conceituais de um importante economista do
NOTA SOBRE A TEORIA DA ESTABILIDADE DO EQUILÍBRIO EM MERCADOS MÚLTIPLOS: JOHN HICKS Tácito Augusto Farias* RESUMO Esta nota trata das principais contribuições conceituais de um importante economista do
AULA 07 Distribuições Discretas de Probabilidade
 1 AULA 07 Distribuições Discretas de Probabilidade Ernesto F. L. Amaral 31 de agosto de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
1 AULA 07 Distribuições Discretas de Probabilidade Ernesto F. L. Amaral 31 de agosto de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
FACULDADE DE CIÊNCIAS E TECNOLOGIA. Redes de Telecomunicações (2006/2007)
 FACULDADE DE CIÊNCIAS E TECNOLOGIA Redes de Telecomunicações (2006/2007) Engª de Sistemas e Informática Trabalho nº4 (1ª aula) Título: Modelação de tráfego utilizando o modelo de Poisson Fundamentos teóricos
FACULDADE DE CIÊNCIAS E TECNOLOGIA Redes de Telecomunicações (2006/2007) Engª de Sistemas e Informática Trabalho nº4 (1ª aula) Título: Modelação de tráfego utilizando o modelo de Poisson Fundamentos teóricos
Uso de escalas logaritmicas e linearização
 Uso de escalas logaritmicas e linearização Notas: Rodrigo Ramos 1 o. sem. 2015 Versão 1.0 Obs: Esse é um texto de matemática, você deve acompanhá-lo com atenção, com lápis e papel, e ir fazendo as coisas
Uso de escalas logaritmicas e linearização Notas: Rodrigo Ramos 1 o. sem. 2015 Versão 1.0 Obs: Esse é um texto de matemática, você deve acompanhá-lo com atenção, com lápis e papel, e ir fazendo as coisas
O exemplo mais simples do uso do método das imagens 1
 arxiv:1405.2903v1 [physics.class-ph] 11 May 2014 O exemplo mais simples do uso do método das imagens 1 The simplest example of the use of the method of images Antonio S. de Castro 2 Departamento de Física
arxiv:1405.2903v1 [physics.class-ph] 11 May 2014 O exemplo mais simples do uso do método das imagens 1 The simplest example of the use of the method of images Antonio S. de Castro 2 Departamento de Física
FÍSICA. A) 2 J B) 6 J C) 8 J D) 10 J E) Zero. A) 6,2x10 6 metros. B) 4,8x10 1 metros. C) 2,4x10 3 metros. D) 2,1x10 9 metros. E) 4,3x10 6 metros.
 FÍSICA 16) Numa tempestade, ouve-se o trovão 7,0 segundos após a visualização do relâmpago. Sabendo que a velocidade da luz é de 3,0x10 8 m/s e que a velocidade do som é de 3,4x10 2 m/s, é possível afirmar
FÍSICA 16) Numa tempestade, ouve-se o trovão 7,0 segundos após a visualização do relâmpago. Sabendo que a velocidade da luz é de 3,0x10 8 m/s e que a velocidade do som é de 3,4x10 2 m/s, é possível afirmar
EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros exercícios)
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros eercícios) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Eercícios
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros eercícios) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Eercícios
Cinemática Bidimensional
 Cinemática Bidimensional INTRODUÇÃO Após estudar cinemática unidimensional, vamos dar uma perspectiva mais vetorial a tudo isso que a gente viu, abrangendo mais de uma dimensão. Vamos ver algumas aplicações
Cinemática Bidimensional INTRODUÇÃO Após estudar cinemática unidimensional, vamos dar uma perspectiva mais vetorial a tudo isso que a gente viu, abrangendo mais de uma dimensão. Vamos ver algumas aplicações
Módulo de Equações do Segundo Grau. Equações do Segundo Grau: Resultados Básicos. Nono Ano
 Módulo de Equações do Segundo Grau Equações do Segundo Grau: Resultados Básicos. Nono Ano Equações do o grau: Resultados Básicos. 1 Exercícios Introdutórios Exercício 1. A equação ax + bx + c = 0, com
Módulo de Equações do Segundo Grau Equações do Segundo Grau: Resultados Básicos. Nono Ano Equações do o grau: Resultados Básicos. 1 Exercícios Introdutórios Exercício 1. A equação ax + bx + c = 0, com
3 Reações Proibidas por Spin
 3 Reações Proibidas por Spin Em reações químicas, elétrons ligantes são redistribuídos quando ligações químicas são quebradas e formadas. Quando alguns dos elétrons dos reagentes ou dos produtos são desemparelhados,
3 Reações Proibidas por Spin Em reações químicas, elétrons ligantes são redistribuídos quando ligações químicas são quebradas e formadas. Quando alguns dos elétrons dos reagentes ou dos produtos são desemparelhados,
DISTRIBUIÇÕES ESPECIAIS DE PROBABILIDADE DISCRETAS
 VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADES 1 1. VARIÁVEIS ALEATÓRIAS Muitas situações cotidianas podem ser usadas como experimento que dão resultados correspondentes a algum valor, e tais situações
VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADES 1 1. VARIÁVEIS ALEATÓRIAS Muitas situações cotidianas podem ser usadas como experimento que dão resultados correspondentes a algum valor, e tais situações
Os eixo x e y dividem a circunferência em quatro partes congruentes chamadas quadrantes, numeradas de 1 a 4 conforme figura abaixo:
 Circunferência Trigonométrica É uma circunferência de raio unitário orientada de tal forma que o sentido positivo é o sentido anti-horário. Associamos a circunferência (ou ciclo) trigonométrico um sistema
Circunferência Trigonométrica É uma circunferência de raio unitário orientada de tal forma que o sentido positivo é o sentido anti-horário. Associamos a circunferência (ou ciclo) trigonométrico um sistema
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 7
 Potencial Elétrico Quando estudamos campo elétrico nas aulas passadas, vimos que ele pode ser definido em termos da força elétrica que uma carga q exerce sobre uma carga de prova q 0. Essa força é, pela
Potencial Elétrico Quando estudamos campo elétrico nas aulas passadas, vimos que ele pode ser definido em termos da força elétrica que uma carga q exerce sobre uma carga de prova q 0. Essa força é, pela
2 Limites e Derivadas. Copyright Cengage Learning. Todos os direitos reservados.
 2 Limites e Derivadas Copyright Cengage Learning. Todos os direitos reservados. 2.7 Derivadas e Taxas de Variação Copyright Cengage Learning. Todos os direitos reservados. Derivadas e Taxas de Variação
2 Limites e Derivadas Copyright Cengage Learning. Todos os direitos reservados. 2.7 Derivadas e Taxas de Variação Copyright Cengage Learning. Todos os direitos reservados. Derivadas e Taxas de Variação
UM JOGO BINOMIAL 1. INTRODUÇÃO
 1. INTRODUÇÃO UM JOGO BINOMIAL São muitos os casos de aplicação, no cotidiano de cada um de nós, dos conceitos de probabilidade. Afinal, o mundo é probabilístico, não determinístico; a natureza acontece
1. INTRODUÇÃO UM JOGO BINOMIAL São muitos os casos de aplicação, no cotidiano de cada um de nós, dos conceitos de probabilidade. Afinal, o mundo é probabilístico, não determinístico; a natureza acontece
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS
 Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS Dois ou mais eventos são mutuamente exclusivos, ou disjuntos, se os mesmos não podem ocorrer simultaneamente. Isto é, a ocorrência de um
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS Dois ou mais eventos são mutuamente exclusivos, ou disjuntos, se os mesmos não podem ocorrer simultaneamente. Isto é, a ocorrência de um
WWW.RENOVAVEIS.TECNOPT.COM
 Energia produzida Para a industria eólica é muito importante a discrição da variação da velocidade do vento. Os projetistas de turbinas necessitam da informação para otimizar o desenho de seus geradores,
Energia produzida Para a industria eólica é muito importante a discrição da variação da velocidade do vento. Os projetistas de turbinas necessitam da informação para otimizar o desenho de seus geradores,
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL
 I. O ZOO das Partículas Elementares. Origem das Partículas Elementares. O Modelo Padrão e a Origem das Partículas e das Forças Fundamentais. O Modelo Padrão é a teoria que explica a origem das partículas
I. O ZOO das Partículas Elementares. Origem das Partículas Elementares. O Modelo Padrão e a Origem das Partículas e das Forças Fundamentais. O Modelo Padrão é a teoria que explica a origem das partículas
UNESP - Faculdade de Engenharia de Guaratinguetá 1
 ANÁLISE GRÁFICA UNESP - Faculdade de Engenharia de Guaratinguetá 0.. Introdução Neste capítulo abordaremos princípios de gráficos lineares e logarítmicos e seu uso em análise de dados. Esta análise possibilitará
ANÁLISE GRÁFICA UNESP - Faculdade de Engenharia de Guaratinguetá 0.. Introdução Neste capítulo abordaremos princípios de gráficos lineares e logarítmicos e seu uso em análise de dados. Esta análise possibilitará
I. Conjunto Elemento Pertinência
 TEORI DOS CONJUNTOS I. Conjunto Elemento Pertinência Conjunto, elemento e pertinência são três noções aceitas sem definição, ou seja, são noções primitivas. idéia de conjunto é praticamente a mesma que
TEORI DOS CONJUNTOS I. Conjunto Elemento Pertinência Conjunto, elemento e pertinência são três noções aceitas sem definição, ou seja, são noções primitivas. idéia de conjunto é praticamente a mesma que
Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios
 Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios O Método Intuitivo de elaboração de circuitos: As técnicas de elaboração de circuitos eletropneumáticos fazem parte
Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios O Método Intuitivo de elaboração de circuitos: As técnicas de elaboração de circuitos eletropneumáticos fazem parte
O Cálculo λ sem Tipos
 Capítulo 2 O Cálculo λ sem Tipos 21 Síntaxe e Redução Por volta de 1930 o cálculo lambda sem tipos foi introduzido como uma fundação para a lógica e a matemática Embora este objectivo não tenha sido cumprido
Capítulo 2 O Cálculo λ sem Tipos 21 Síntaxe e Redução Por volta de 1930 o cálculo lambda sem tipos foi introduzido como uma fundação para a lógica e a matemática Embora este objectivo não tenha sido cumprido
ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA (UFCG- CUITÉ)
 P L A N O S PARALELOS AOS EIXOS E AOS PLANOS COORDENADOS Casos Particulares A equação ax + by + cz = d na qual a, b e c não são nulos, é a equação de um plano π, sendo v = ( a, b, c) um vetor normal a
P L A N O S PARALELOS AOS EIXOS E AOS PLANOS COORDENADOS Casos Particulares A equação ax + by + cz = d na qual a, b e c não são nulos, é a equação de um plano π, sendo v = ( a, b, c) um vetor normal a
Trabalho 4 - Traçado de linhas equipotenciais e linhas de força.
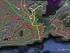 Trabalho 4 - Traçado de linhas euipotenciais e linhas de força. Objectivo:Obtenção e análise de curvas euipotenciais numa superfície a duas dimensões, para duas distribuições de carga. Pretende-se ainda
Trabalho 4 - Traçado de linhas euipotenciais e linhas de força. Objectivo:Obtenção e análise de curvas euipotenciais numa superfície a duas dimensões, para duas distribuições de carga. Pretende-se ainda
A Teoria de Cordas e a Unificação das Forças da Natureza p. 1
 A Teoria de Cordas e a Unificação das Forças da Natureza Victor O. Rivelles Instituto de Física Universidade de São Paulo [email protected] 40 Anos da Sociedade Brasileira de Física, 02-03/10/2006
A Teoria de Cordas e a Unificação das Forças da Natureza Victor O. Rivelles Instituto de Física Universidade de São Paulo [email protected] 40 Anos da Sociedade Brasileira de Física, 02-03/10/2006
Resolução de sistemas de equações lineares: Método de eliminação de Gauss
 Resolução de sistemas de equações lineares: Método de eliminação de Gauss Marina Andretta ICMC-USP 21 de março de 2012 Baseado no livro Análise Numérica, de R L Burden e J D Faires Marina Andretta (ICMC-USP)
Resolução de sistemas de equações lineares: Método de eliminação de Gauss Marina Andretta ICMC-USP 21 de março de 2012 Baseado no livro Análise Numérica, de R L Burden e J D Faires Marina Andretta (ICMC-USP)
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP [email protected].
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP [email protected] Sistemas Lienares 1 Sistemas e Matrizes 2 Operações Elementares e
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP [email protected] Sistemas Lienares 1 Sistemas e Matrizes 2 Operações Elementares e
4.4 Limite e continuidade
 4.4 Limite e continuidade Noções Topológicas em R : Dados dois pontos quaisquer (x 1, y 1 ) e (x, y ) de R indicaremos a distância entre eles por då(x 1, y 1 ), (x, y )è=(x 1 x ) + (y 1 y ). Definição
4.4 Limite e continuidade Noções Topológicas em R : Dados dois pontos quaisquer (x 1, y 1 ) e (x, y ) de R indicaremos a distância entre eles por då(x 1, y 1 ), (x, y )è=(x 1 x ) + (y 1 y ). Definição
ActivALEA. ative e atualize a sua literacia
 ActivALEA ative e atualize a sua literacia N.º 26 A FREQUÊNCIIA RELATIIVA PARA ESTIIMAR A PROBABIILIIDADE Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL
ActivALEA ative e atualize a sua literacia N.º 26 A FREQUÊNCIIA RELATIIVA PARA ESTIIMAR A PROBABIILIIDADE Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL
O circuito RLC. 1. Introdução
 O circuito C Na natureza são inúmeros os fenómenos que envolvem oscilações. Um exemplo comum é o pêndulo de um relógio, que se move periódicamente (ou seja, de repetindo o seu movimento ao fim de um intervalo
O circuito C Na natureza são inúmeros os fenómenos que envolvem oscilações. Um exemplo comum é o pêndulo de um relógio, que se move periódicamente (ou seja, de repetindo o seu movimento ao fim de um intervalo
Corrente elétrica, potência, resistores e leis de Ohm
 Corrente elétrica, potência, resistores e leis de Ohm Corrente elétrica Num condutor metálico em equilíbrio eletrostático, o movimento dos elétrons livres é desordenado. Em destaque, a representação de
Corrente elétrica, potência, resistores e leis de Ohm Corrente elétrica Num condutor metálico em equilíbrio eletrostático, o movimento dos elétrons livres é desordenado. Em destaque, a representação de
1-Eletricidade básica
 SENAI 1 1-Eletricidade básica 1.1 - Grandezas Elétricas: 1.1 - Carga Elétrica, Tensão Elétrica, Corrente Elétrica, Resistência Elétrica; 1.2 - Leis de Ohm: 1.2.1-1 a Lei de Ohm 1.2.2 múltiplos e submúltiplos
SENAI 1 1-Eletricidade básica 1.1 - Grandezas Elétricas: 1.1 - Carga Elétrica, Tensão Elétrica, Corrente Elétrica, Resistência Elétrica; 1.2 - Leis de Ohm: 1.2.1-1 a Lei de Ohm 1.2.2 múltiplos e submúltiplos
2 Conceitos Básicos. onde essa matriz expressa a aproximação linear local do campo. Definição 2.2 O campo vetorial v gera um fluxo φ : U R 2 R
 2 Conceitos Básicos Neste capítulo são apresentados alguns conceitos importantes e necessários para o desenvolvimento do trabalho. São apresentadas as definições de campo vetorial, fluxo e linhas de fluxo.
2 Conceitos Básicos Neste capítulo são apresentados alguns conceitos importantes e necessários para o desenvolvimento do trabalho. São apresentadas as definições de campo vetorial, fluxo e linhas de fluxo.
Guia Sudoe - Para a elaboração e gestão de projetos Versão Portuguesa Ficha 7.0 Auxílio estatal
 Guia Sudoe - Para a elaboração e gestão de projetos Versão Portuguesa Ficha 7.0 Auxílio estatal 2 Ficha 7.0 Auxílio estatal Índice 1 Princípio... 5 2 Definição do conceito de auxílios estatais... 6 3 Quem
Guia Sudoe - Para a elaboração e gestão de projetos Versão Portuguesa Ficha 7.0 Auxílio estatal 2 Ficha 7.0 Auxílio estatal Índice 1 Princípio... 5 2 Definição do conceito de auxílios estatais... 6 3 Quem
ASPECTOS CONSTRUTIVOS DE ROBÔS
 ASPECTOS CONSTRUTIVOS DE ROBÔS Tipos de robôs Classificação de robôs Definições importantes: O arranjo das hastes e juntas em um braço manipulador tem um importante efeito nos graus de liberdade da ferramenta
ASPECTOS CONSTRUTIVOS DE ROBÔS Tipos de robôs Classificação de robôs Definições importantes: O arranjo das hastes e juntas em um braço manipulador tem um importante efeito nos graus de liberdade da ferramenta
Sistemática dos seres vivos
 Sistemática dos seres vivos O mundo vivo é constituído por uma enorme variedade de organismos. Para estudar e compreender tamanha variedade, idd foi necessário agrupar os organismos de acordo com as suas
Sistemática dos seres vivos O mundo vivo é constituído por uma enorme variedade de organismos. Para estudar e compreender tamanha variedade, idd foi necessário agrupar os organismos de acordo com as suas
PROF.: PAULO GOMES MATÉRIA: STR1 MOURA LACERDA
 PROF.: PAULO GOMES MATÉRIA: STR1 MOURA LACERDA TEORIA Princípios básicos de transmissão a. Sinais de radiofreqüência (RF) Possuem freqüências acima de 100 KHz e são usados pelas emissoras para transportar
PROF.: PAULO GOMES MATÉRIA: STR1 MOURA LACERDA TEORIA Princípios básicos de transmissão a. Sinais de radiofreqüência (RF) Possuem freqüências acima de 100 KHz e são usados pelas emissoras para transportar
Árvores. ! utilizada em muitas aplicações. ! modela uma hierarquia entre elementos. ! O conceito de árvores está diretamente ligado à recursão
 Árvores 1 Árvores! utilizada em muitas aplicações! modela uma hierarquia entre elementos! árvore genealógica! diagrama hierárquico de uma organização! modelagem de algoritmos! O conceito de árvores está
Árvores 1 Árvores! utilizada em muitas aplicações! modela uma hierarquia entre elementos! árvore genealógica! diagrama hierárquico de uma organização! modelagem de algoritmos! O conceito de árvores está
PODER JUDICIÁRIO JUSTIÇA DO TRABALHO CONSELHO SUPERIOR DA JUSTIÇA DO TRABALHO
 CONSELHO SUPERIOR DA RELATÓRIO DE DIAGNÓSTICO DA QUALIDADE NO USO DO SISTEMA PROCESSO JUDICIAL ELETRÔNICO DA Fase 1 (magistrados e servidores da Justiça do Trabalho) Secretaria de Tecnologia da Informação
CONSELHO SUPERIOR DA RELATÓRIO DE DIAGNÓSTICO DA QUALIDADE NO USO DO SISTEMA PROCESSO JUDICIAL ELETRÔNICO DA Fase 1 (magistrados e servidores da Justiça do Trabalho) Secretaria de Tecnologia da Informação
Acionamento de Motores: PWM e Ponte H
 Warthog Robotics USP São Carlos www.warthog.sc.usp.br [email protected] Acionamento de Motores: PWM e Ponte H Por Gustavo C. Oliveira, Membro da Divisão de Controle (2014) 1 Introdução Motores são máquinas
Warthog Robotics USP São Carlos www.warthog.sc.usp.br [email protected] Acionamento de Motores: PWM e Ponte H Por Gustavo C. Oliveira, Membro da Divisão de Controle (2014) 1 Introdução Motores são máquinas
Tópicos Especiais em Educação
 Tópicos Especiais em Educação Física II Unidade I -Cognição - Prof. Esp. Jorge Duarte Cognição Um dos objetivos do sistema de ensino é promover o desenvolvimento cognitivo da criança. Esse desenvolvimento
Tópicos Especiais em Educação Física II Unidade I -Cognição - Prof. Esp. Jorge Duarte Cognição Um dos objetivos do sistema de ensino é promover o desenvolvimento cognitivo da criança. Esse desenvolvimento
UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA
 UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA PARTÍCULAS ELEMENTARES: A PROCURA DAS PARTÍCULAS W E Z. Aluno: Reinaldo Augusto da Costa Bianchi. Professor: Gil da Costa Marques. São Paulo, 1992. Esta ilustração
UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA PARTÍCULAS ELEMENTARES: A PROCURA DAS PARTÍCULAS W E Z. Aluno: Reinaldo Augusto da Costa Bianchi. Professor: Gil da Costa Marques. São Paulo, 1992. Esta ilustração
AGRUPAMENTO DE ESCOLAS DE PÓVOA DE LANHOSO - 150915
 INFORMAÇÃO - PROVA DE EQUIVALÊNCIA À FREQUÊNCIA INGLÊS Abril 2016 2016 367 Prova 11º Ano de escolaridade (Decreto-Lei nº 139/2012, de 05 de julho) O presente documento divulga informação relativa à prova
INFORMAÇÃO - PROVA DE EQUIVALÊNCIA À FREQUÊNCIA INGLÊS Abril 2016 2016 367 Prova 11º Ano de escolaridade (Decreto-Lei nº 139/2012, de 05 de julho) O presente documento divulga informação relativa à prova
2 Conceitos de transmissão de dados
 2 Conceitos de transmissão de dados 2 Conceitos de transmissão de dados /24 2. Características dos sinais digitais 2. Características dos sinais digitais 2/24 Características dos sinais digitais Sinal
2 Conceitos de transmissão de dados 2 Conceitos de transmissão de dados /24 2. Características dos sinais digitais 2. Características dos sinais digitais 2/24 Características dos sinais digitais Sinal
Aula 15 Amplificadores Operacionais (pág. 453 a 459)
 Aula 15 Amplificadores Operacionais (pág. 453 a 459) Prof. Dr. Aparecido Nicolett PUC-SP Slide 1 Considerações gerais: Amplificadores Operacionais são amplificadores diferencias com ganho muito alto, impedância
Aula 15 Amplificadores Operacionais (pág. 453 a 459) Prof. Dr. Aparecido Nicolett PUC-SP Slide 1 Considerações gerais: Amplificadores Operacionais são amplificadores diferencias com ganho muito alto, impedância
FÍSICA EXPERIMENTAL 3001
 FÍSICA EXPERIMENTAL 3001 EXPERIÊNCIA 1 CIRCUITO RLC EM CORRENTE ALTERNADA 1. OBJETIOS 1.1. Objetivo Geral Apresentar aos acadêmicos um circuito elétrico ressonante, o qual apresenta um máximo de corrente
FÍSICA EXPERIMENTAL 3001 EXPERIÊNCIA 1 CIRCUITO RLC EM CORRENTE ALTERNADA 1. OBJETIOS 1.1. Objetivo Geral Apresentar aos acadêmicos um circuito elétrico ressonante, o qual apresenta um máximo de corrente
1. Verifique se são operadores lineares no espaço P n (R): (a) F: P n (R) P n (R) tal que F(f(t)) = tf (t), f(t) P n (R).
 UNIVERSIDADE ESTADUAL DE SANTA CRUZ - UESC DEPARTAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET ÁLGEBRA LINEAR ASSUNTO: TRANSFORMAÇÕES LINEARES EXERCÍCIOS RESOLVIDOS 1. Verifique se são operadores lineares
UNIVERSIDADE ESTADUAL DE SANTA CRUZ - UESC DEPARTAMENTO DE CIÊNCIAS EXATAS E TECNOLÓGICAS - DCET ÁLGEBRA LINEAR ASSUNTO: TRANSFORMAÇÕES LINEARES EXERCÍCIOS RESOLVIDOS 1. Verifique se são operadores lineares
O papel do Professor como mediador 1
 O papel do Professor como mediador 1 Uma qualidade importante da profissão do professor na escola, na práxis de sala de aula, tem a ver com a necessidade de integrar o total das competências e exigências
O papel do Professor como mediador 1 Uma qualidade importante da profissão do professor na escola, na práxis de sala de aula, tem a ver com a necessidade de integrar o total das competências e exigências
Como rodar a regressão no gretl. Usando o Console para calcular elasticidade. Elasticidade. Usando o Console para calcular predição
 Como rodar a regressão no gretl Alguns tópicos do gretl Usando o console: Comando: ols y const 3 Estima uma função linear usando o método de Mínimos Quadrados Ordinários. Elasticidade Intuição: resposta
Como rodar a regressão no gretl Alguns tópicos do gretl Usando o console: Comando: ols y const 3 Estima uma função linear usando o método de Mínimos Quadrados Ordinários. Elasticidade Intuição: resposta
Programação Linear - Parte 4
 Mestrado em Modelagem e Otimização - CAC/UFG Programação Linear - Parte 4 Profs. Thiago Alves de Queiroz Muris Lage Júnior 1/2014 Thiago Queiroz (DM) Parte 4 1/2014 1 / 18 Solução Inicial O método simplex
Mestrado em Modelagem e Otimização - CAC/UFG Programação Linear - Parte 4 Profs. Thiago Alves de Queiroz Muris Lage Júnior 1/2014 Thiago Queiroz (DM) Parte 4 1/2014 1 / 18 Solução Inicial O método simplex
Usando potências de 10
 Usando potências de 10 A UUL AL A Nesta aula, vamos ver que todo número positivo pode ser escrito como uma potência de base 10. Por exemplo, vamos aprender que o número 15 pode ser escrito como 10 1,176.
Usando potências de 10 A UUL AL A Nesta aula, vamos ver que todo número positivo pode ser escrito como uma potência de base 10. Por exemplo, vamos aprender que o número 15 pode ser escrito como 10 1,176.
DIMENSÕES DE PESQUISA EM ENGENHARIA DE SOFTWARE
 ESPECIAL Engenharia de Software DIMENSÕES DE PESQUISA EM ENGENHARIA DE SOFTWARE por Paulo Borba DECISÕES IMPORTANTES A SEREM TOMADAS NOS PROJETOS E NA CARREIRA DE UM PESQUISADOR EM ENGENHARIA DE SOFTWARE.
ESPECIAL Engenharia de Software DIMENSÕES DE PESQUISA EM ENGENHARIA DE SOFTWARE por Paulo Borba DECISÕES IMPORTANTES A SEREM TOMADAS NOS PROJETOS E NA CARREIRA DE UM PESQUISADOR EM ENGENHARIA DE SOFTWARE.
Teste de hipótese em modelos normais lineares: ANOVA
 Teste de hipótese em modelos normais lineares: ANOVA Prof Caio Azevedo Prof Caio Azevedo Exemplo 1 No primeiro modelo, o interesse primário, de certa forma, é testar se a carga não contribui para explicar
Teste de hipótese em modelos normais lineares: ANOVA Prof Caio Azevedo Prof Caio Azevedo Exemplo 1 No primeiro modelo, o interesse primário, de certa forma, é testar se a carga não contribui para explicar
A uma plataforma online de gestão de condomínios permite gerir de forma fácil e simples a atividade do seu condomínio.
 PLATAFORMA DE GESTÃO A uma plataforma online de gestão de condomínios permite gerir de forma fácil e simples a atividade do seu condomínio. Principais funcionalidades Possui uma série de funcionalidades
PLATAFORMA DE GESTÃO A uma plataforma online de gestão de condomínios permite gerir de forma fácil e simples a atividade do seu condomínio. Principais funcionalidades Possui uma série de funcionalidades
Processamento Digital de Sinais. Conversão A/D e D/A. Prof. Dr. Carlos Alberto Ynoguti
 Processamento Digital de Sinais Conversão A/D e D/A Prof. Dr. Carlos Alberto Ynoguti Introdução A maioria dos sinais encontrados na natureza é contínua Para processá los digitalmente, devemos: Converter
Processamento Digital de Sinais Conversão A/D e D/A Prof. Dr. Carlos Alberto Ynoguti Introdução A maioria dos sinais encontrados na natureza é contínua Para processá los digitalmente, devemos: Converter
Backup. José Antônio da Cunha CEFET-RN
 José Antônio da Cunha CEFET-RN Introdução Sendo as informações o bem mais valioso da empresa e estando estas informações armazenadas nos bancos de dados da empresa, é de fundamental importância que tenhamos
José Antônio da Cunha CEFET-RN Introdução Sendo as informações o bem mais valioso da empresa e estando estas informações armazenadas nos bancos de dados da empresa, é de fundamental importância que tenhamos
Física Experimental III
 Física Experimental III Unidade 4: Circuitos simples em corrente alternada: Generalidades e circuitos resistivos http://www.if.ufrj.br/~fisexp3 agosto/26 Na Unidade anterior estudamos o comportamento de
Física Experimental III Unidade 4: Circuitos simples em corrente alternada: Generalidades e circuitos resistivos http://www.if.ufrj.br/~fisexp3 agosto/26 Na Unidade anterior estudamos o comportamento de
ESTRUTURA DOS MATERIAIS CERÂMICOS
 ESTRUTURA DOS MATERIAIS CERÂMICOS Os sólidos são caracterizados por uma associação muito próxima de átomos, em geral representados por esferas rígidas, em contato uns com os outros e mantidos juntos por
ESTRUTURA DOS MATERIAIS CERÂMICOS Os sólidos são caracterizados por uma associação muito próxima de átomos, em geral representados por esferas rígidas, em contato uns com os outros e mantidos juntos por
ECONOMIA INTERNACIONAL: NOTAS DE AULA
 ECONOMIA INTERNACIONAL: NOTAS DE AULA Versão: 2015/2 2 PARIDADE DE JUROS E CÂMBIO Uma análise mais completa deste tópico está disponível no capítulo 6 de Eun e Resnick (2011). 2.1 Preliminares Seja n o
ECONOMIA INTERNACIONAL: NOTAS DE AULA Versão: 2015/2 2 PARIDADE DE JUROS E CÂMBIO Uma análise mais completa deste tópico está disponível no capítulo 6 de Eun e Resnick (2011). 2.1 Preliminares Seja n o
Relatório do Experimento 1 Sistema Massa - Mola. Fernando Henrique Ferraz Pereira da Rosa
 FEP0111 - Física I Relatório do Experimento 1 Sistema Massa - Mola Fernando Henrique Ferraz Pereira da Rosa 4 de novembro de 2005 Sumário 1 Introdução 2 2 Objetivos 2 3 Procedimento experimental 2 3.1
FEP0111 - Física I Relatório do Experimento 1 Sistema Massa - Mola Fernando Henrique Ferraz Pereira da Rosa 4 de novembro de 2005 Sumário 1 Introdução 2 2 Objetivos 2 3 Procedimento experimental 2 3.1
[RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013
![[RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013 [RESOLUÇÃO] Economia I; 2012/2013 (2º semestre) Prova da Época Recurso 3 de Julho de 2013](/thumbs/39/19161564.jpg) Economia I; 01/013 (º semestre) Prova da Época Recurso 3 de Julho de 013 [RESOLUÇÃO] Distribuição das respostas correctas às perguntas da Parte A (6 valores) nas suas três variantes: ER A B C P1 P P3 P4
Economia I; 01/013 (º semestre) Prova da Época Recurso 3 de Julho de 013 [RESOLUÇÃO] Distribuição das respostas correctas às perguntas da Parte A (6 valores) nas suas três variantes: ER A B C P1 P P3 P4
Métodos Formais. Agenda. Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções. Relações e Funções
 Métodos Formais Relações e Funções por Mauro Silva Agenda Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções MF - Relações e Funções 2 1 Relações Binárias Definição
Métodos Formais Relações e Funções por Mauro Silva Agenda Relações Binárias Relações e Banco de Dados Operações nas Relações Resumo Relações Funções MF - Relações e Funções 2 1 Relações Binárias Definição
Probabilidade e Estatística
 Probabilidade e Estatística TESTES DE HIPÓTESES (ou Testes de Significância) Estimação e Teste de Hipóteses Estimação e teste de hipóteses (ou significância) são os aspectos principais da Inferência Estatística
Probabilidade e Estatística TESTES DE HIPÓTESES (ou Testes de Significância) Estimação e Teste de Hipóteses Estimação e teste de hipóteses (ou significância) são os aspectos principais da Inferência Estatística
Códigos de bloco. Instituto Federal de Santa Catarina Curso superior de tecnologia em sistemas de telecomunicação Comunicações móveis 2
 Instituto Federal de Santa Catarina Curso superior de tecnologia em sistemas de telecomunicação Comunicações móveis 2 Códigos de bloco Prof. Diego da Silva de Medeiros São José, maio de 2012 Codificação
Instituto Federal de Santa Catarina Curso superior de tecnologia em sistemas de telecomunicação Comunicações móveis 2 Códigos de bloco Prof. Diego da Silva de Medeiros São José, maio de 2012 Codificação
Energia nuclear e segurança no Brasil. Renata Camargo Coordenador de Políticas Públicas
 Energia nuclear e segurança no Brasil Renata Camargo Coordenador de Políticas Públicas É uma energia cara: Nuclear = R$ 150 a 160 MWh (custo médio) Eólica = R$ 100 MWh Hidrelétrica = R$ 80 MWh Não é segura:
Energia nuclear e segurança no Brasil Renata Camargo Coordenador de Políticas Públicas É uma energia cara: Nuclear = R$ 150 a 160 MWh (custo médio) Eólica = R$ 100 MWh Hidrelétrica = R$ 80 MWh Não é segura:
Pelo que foi exposto no teorema de Carnot, obteve-se a seguinte relação:
 16. Escala Absoluta Termodinâmica Kelvin propôs uma escala de temperatura que foi baseada na máquina de Carnot. Segundo o resultado (II) na seção do ciclo de Carnot, temos que: O ponto triplo da água foi
16. Escala Absoluta Termodinâmica Kelvin propôs uma escala de temperatura que foi baseada na máquina de Carnot. Segundo o resultado (II) na seção do ciclo de Carnot, temos que: O ponto triplo da água foi
Figura 4.1: Diagrama de representação de uma função de 2 variáveis
 1 4.1 Funções de 2 Variáveis Em Cálculo I trabalhamos com funções de uma variável y = f(x). Agora trabalharemos com funções de várias variáveis. Estas funções aparecem naturalmente na natureza, na economia
1 4.1 Funções de 2 Variáveis Em Cálculo I trabalhamos com funções de uma variável y = f(x). Agora trabalharemos com funções de várias variáveis. Estas funções aparecem naturalmente na natureza, na economia
Prof. Neckel FÍSICA 1 PROVA 1 TEMA 2 PARTE 1 PROF. NECKEL POSIÇÃO. Sistema de Coordenadas Nome do sistema Unidade do sistema 22/02/2016.
 FÍSICA 1 PROVA 1 TEMA 2 PARTE 1 PROF. NECKEL Cinemática 1D POSIÇÃO Sistema de Coordenadas Nome do sistema Unidade do sistema Reta numérica real com origem Crescimento para direita, decrescimento para esquerda
FÍSICA 1 PROVA 1 TEMA 2 PARTE 1 PROF. NECKEL Cinemática 1D POSIÇÃO Sistema de Coordenadas Nome do sistema Unidade do sistema Reta numérica real com origem Crescimento para direita, decrescimento para esquerda
(Séries de Problemas) Paulo Vargas Moniz Universidade da Beira Interior Departamento de Fisica
 . Mecânica Clássica (Séries de Problemas) Paulo Vargas Moniz Universidade da Beira Interior Departamento de Fisica 1 1 a Serie 1. Considera um bloco B de massa m deslizando sobre um plano inclinado PI
. Mecânica Clássica (Séries de Problemas) Paulo Vargas Moniz Universidade da Beira Interior Departamento de Fisica 1 1 a Serie 1. Considera um bloco B de massa m deslizando sobre um plano inclinado PI
Resolução Comentada Fuvest - 1ª fase 2014
 Resolução Comentada Fuvest - 1ª fase 2014 01 - Em uma competição de salto em distância, um atleta de 70kg tem, imediatamente antes do salto, uma velocidade na direção horizontal de módulo 10m/s. Ao saltar,
Resolução Comentada Fuvest - 1ª fase 2014 01 - Em uma competição de salto em distância, um atleta de 70kg tem, imediatamente antes do salto, uma velocidade na direção horizontal de módulo 10m/s. Ao saltar,
ENGENHARIA DE SOFTWARE
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Curso Técnico em Informática : ENGENHARIA DE SOFTWARE Prof.: Clayton Maciel Costa [email protected] Um conjunto estruturado
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Curso Técnico em Informática : ENGENHARIA DE SOFTWARE Prof.: Clayton Maciel Costa [email protected] Um conjunto estruturado
Métodos de Estudo & Investigação Científica. Elaborando um projeto de pesquisa
 Elaborando um projeto de pesquisa A pesquisa é a realização concreta de uma investigação planeada, desenvolvido e redigida de acordo com as normas das metodologias consagradas pela ciência; Requerida quando
Elaborando um projeto de pesquisa A pesquisa é a realização concreta de uma investigação planeada, desenvolvido e redigida de acordo com as normas das metodologias consagradas pela ciência; Requerida quando
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR. Prof. Angelo Augusto Frozza, M.Sc.
 PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 2 do livro de Taha (2008): Introdução O modelo de PL de duas variáveis Propriedades
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 2 do livro de Taha (2008): Introdução O modelo de PL de duas variáveis Propriedades
