PRINCÍPIOS DE GEOMETRIA PROJETIVA COM APLICAÇÕES EM VISÃO COMPUTACIONAL
|
|
|
- Irene de Sá Bento
- 7 Há anos
- Visualizações:
Transcrição
1 PRINCÍPIOS DE GEOMETRIA PROJETIVA COM APLICAÇÕES EM VISÃO COMPUTACIONAL Aluno: André Phillip Franco Orientador: Marcos Craizer Introdução A Geometria Projetiva surgiu com a dificuldade que os artistas do Renascimento encontravam em dar aos quadros que pintavam uma forma real dos objetos, de modo que qualquer pessoa identificasse sem dificuldades o que estava longe e o que estava perto. Motivados pelo desafio, eles estudaram as leis que determinam a construção dessas projeções criando a teoria fundamental da perspectiva geométrica, que depois foi expandida por um grupo de matemáticos franceses liderados por Gérard Desargues 1. Já a Geometria Computacional é o ramo da ciência da computação que estuda as técnicas e algoritmos para resolução computacional de problemas geométricos. Emergiu em meados de 1970, quando houve um grande progresso da computação gráfica e robótica, para as quais é essencial resolver problemas geométricos de forma eficiente, isto é, utilizando o menor número possível de operações simples sobre os elementos geométricos. Em conjunto, as duas disciplinas contribuem para melhoria de inúmeras aplicações em diferentes áreas como Processamento de Imagens, Visão Computacional, Sistemas de Informações Geográfica (SIGs), entre outras. Atualmente, um desafio para pesquisadores da área envolve a criação de um algoritmo computacional que consiga avaliar os objetos geométricos de forma que o seu reconhecimento não dependa do ponto de vista do usuário. Isto significa criar um algoritmo que reconhça uma pessoa de costas através de uma foto tirada de frente. Objetivos Estudar os fundamentos básicos da geometria projetiva, sua representação e manipulação no computador através do desenvolvimento de um algoritmo computacional em C que permita uma maior compreensão visual do tratamento dos elementos geométricos sobre a ótica projetiva. Conceitos Básicos Ao trabalhar com geometria computacional enfrentamos algumas desvantagens quando usamos coordenadas cartesianas. Se por um lado elas são bastantes conhecidas, por outro a manipulação de problemas que exigem o conceito de pontos no infinito tornam-se difíceis, o que nos obriga a tratar separadamente muitos casos particulares. Por esse motivo, é mais conveniente trabalhar com coordenadas homogêneas, uma representação mais sofisticada. Basicamente, temos que se (X, Y) são coordenadas cartesianas de um ponto, suas coordenadas homogêneas são uma tripla de números reais [w, x, y] tais que X = x/w e 1 Gérard Desargues, , Matemático, engenheiro militar e arquiteto francês de Lyon, considerado um dos fundadores da moderna geometria com sua conceituação de Geometria Projetiva. Mudou-se para Paris onde entrou para o círculo dos mais importantes matemáticos de sua era. Desargues publicou um tratado original sobre seções cônicas, aproveitando idéias de projeção, mas esse trabalho foi ignorado eesquecido pelos matemáticos da época e todas as publicações desapareceram. De pouco sucesso como autor matemático, hoje é reconhecido mundialmente pela importância de seus estudos.
2 Y = y/w. Onde w é chamado de peso. Quando temos uma tripla cujo peso é zero, temos um ponto no infinito. Em coordenadas homogêneas uma reta é definid por três coeficientes homogêneos representados por W, X,Y, onde p = [w, x, y] pertence a reta se W w X x Y y = 0. Outro conceito importante trata do sentido do vetor, isto é, dizemos que as triplas [w, x, y] e [ w, x, y] não são pontos iguais, mas um é o antipodal do outro, isto é, [w, x, y] = [ w, x, y]. Assim, introduzimos os conceitos de Além (quando w > 0) e Aquém (w < 0)[1]. Com isso, podemos definir duas premissas: Dois pontos não antipodais determinam uma reta no Aquém e outra no Além. Dualmente, retas não antipodais se interceptam em dois pontos antipodais. No caso de retas paralelas, esses pontos estarão no infinito. O Modelo Esférico Ao usarmos coordenadas homogêneas estamos tratando de um conjunto de pontos do espaço T denominado Plano Projetivo Orientado. Ele é representado por todas as triplas de números reais [w, x, y], exceto a tripla [0, 0, 0] (imprópria). Geometricamente, podemos visualizar o espaço T através do seu Modelo Esférico, que consiste em uma esfera unitária centrada na origem, onde seu hemisfério w > 0 é o Aquém, o hemisfério w < 0 é o Além, para o círculo em w = 0 temos o Infinito e uma reta corresponde a um círculo unitário que passa pela origem. Um ponto p = [w,x,y] em coordenadas homogêneas é representado no espaço T pela projeção do ponto (x,y,w) em coordenadas cartesianas sobre a esfera. Em Geometria Projetiva Orientada pontos são semi-retas que partem da origem: p = x, y,w x y w O Programa Implementado em C, utilizando as bibliotecas do OpenGL para gráficos e GLUI para interface, o Programa de Visualização Geométrica no Plano Projetivo Orientado constitui-se em uma plataforma que possibilita a visualização de cônicas, cálculo de intercessões, colinearidade e outros, visando o entendimento dos fundamentos da geometria projetiva. Ao iniciar o programa, é aberta uma tela inicial onde aparecem os comandos básicos (zoom, luzes, etc.) e uma esfera unitária representando o Modelo Esférico. Em um menu de opções, encontram-se dez programas diferentes. Uma vez selecionada a opção desejada, uma janela auxiliar é aberta onde o usuário digita os dados de entrada. Da mesma forma, são exibidas as saídas numérica e escrita em uma outra janela auxiliar, enquanto o desenho referente é esboçado na tela. A seguir, são listadas as opções e suas respectivas explicações. De fato, em Geometria Projetiva considera-se que [w, x, y] e [ w, x, y] são pontos iguais. Porém, neste projeto trabalharemos com a Geometria Projetiva Orientada, onde usamos os conceitos de Aquém e Além. Assim, [w, x, y] = [ w, x, y].
3 Figura 1 O Programa de Visualização Geométrica no Plano Projetivo Orientado Opção 1 Verificar se um ponto p pertence a reta r Ao selecionar a primeira opção do programa, uma janela auxiliar é aberta à direita da tela principal. O usuário digita os coeficientes da reta e em seguida as coordenadas homogêneas do ponto que ele deseja avaliar. Ao clicar no botão Verificar o programa exibe a resposta na janela de saída e ao marcar o Checkbox Desenha Reta / Ponto, é possível visualizar no Modelo Esférico a reta e o ponto digitados. Para verificar se o ponto pertence a reta, usamos: W w X x Y y = 0. Para o esboço da reta, tanto nesta opção quanto em qualquer outra neste programa, inicialmente normalizamos os vetores v1 = X,W,0 e v = Y,0,W com os coeficientes digitados e calculamos o ângulo entre eles, onde: X,W,0,0,W = arccos Y X W Y W Em seguida, usando o comando glvertex3f da biblioteca gráfica OpenGL, plotamos ponto a ponto, variando t de 0 a π: [ cos θ cos t sin t sin θ W t,cos t sin X +W sin θ W X,cos t sin t Y +W sin t X +W sin θ Y Y +W ]
4 Opção Obter os pontos no infinito da reta W,X,Y Apesar de simples, a operação para obter os pontos no infinito de uma reta é muito importante. Este novo conceito nos permite saber com menos esforço se duas ou mais retas são paralelas, o que é bastante útil em casos de retas quase paralelas. Nesta opção do programa, o usuário entra com os coeficientes da reta que deseja obter os pontos no infinito. Os pontos são impressos na janela de saída ao pressionar Obter os pontos no infinito. Ao selecionar o Checkbox Desenha Pontos é possível visualizar os dois pontos no Modelo Esférico. (Dica: Habilite o Checkbox Mostrar Infinito e troque a opção no Radio Button para Sem Esfera.) Lembrando que os pontos no infinito são dados pelas triplas cujo peso w = 0, temos que os dois pontos no infinito da reta W,X,Y, são respectivamente: Ponto1 = [0,Y, X ] e Ponto = [0, Y, X ] Para plotar os dois pontos, inicialmente os normalizamos e em seguida usamos o comando glvertex3f da biblioteca gráfica OpenGL. Opção 3 Verificar se duas retas são paralelas Diferente da geometria euclidiana clássica, onde duas retas paralelas nunca se encontram, na geometria projetiva o conceito de infinito nos permite afirmar que esta propriedade não é mais válida. Isto é, duas retas paralelas se encontram no infinito, em dois pontos distintos. Figura Duas retas paralelas no Modelo Esférico.
5 Usando o algoritmo da segunda opção do programa, encontramos os dois pontos no infinito das duas retas digitadas pelo usuário. Se ambos os pontos no infinito de uma das retas forem iguais aos pontos no infinito da outra, dizemos que estas retas são paralelas. Caso contrário, temos duas retas não paralelas. A resposta correspondente é impressa na janela de saída ao pressionar o botão Verificar. O usuário pode habilitar o Checkbox Mostrar Infinito e verificar visualmente que só as retas (círculos unitários no Modelo Esférico) paralelas se interceptam sobre a linha do infinito (w = 0). Opção 4 Obter o ponto que um segmento p0p1 corta uma reta m Uma operação bastante útil em geometria computacional e geometria gráfica é determinar o ponto onde um segmento p0p1 cruza uma determinada linha m. Inicialmente verificamos se os pontos p 0 =[ w 0,x 0,y 0 ] e p 1 = [ w 1,x 1,y 1 ] digitados pelo usuário, estão ou não no mesmo lado da reta m = W, X,Y. Para isto, avaliamos 0 e α 1 [1]: α 0 =W w 0 +X x 0 +Y y 0 α 1 =W w 1 +X x 1 +Y y 1 Onde o segmento p0p1 só cruza a linha m se, e somente se, α 0 e α 1 têm sinais opostos ou um deles é nulo. Quando o segmento p0p1 cruza a linha m, o ponto de interseção é dado por: p = [ α 1 w 0 α 0 w 1, α 1 x 0 α 0 x 1, α 1 y 0 α 0 y 1 ] Ao pressionar Verificar é impresso na janela de saída a resposta. Se o segmento p0p1 cruza a linha m, o programa imprime o ponto onde ocorre a interseção. Para visualizar o segmento e a linha, selecione o Checkbox Desenha Reta / Segmento. Figura 3 - O segmento p0p1 cortando a reta m.
6 Opção 5 Determinar uma reta que passa por dois pontos Na quinta opção do programa, o usuário digita dois pontos, p 0 =[ w 0,x 0,y 0 ] e p 1 =[ w 1,x 1,y 1 ], sobre os quais deseja traçar uma reta. Como destacado anteriormente, na geometria projetiva temos que sobre dois pontos não antipodais passam duas retas coincidentes com orientações opostas. Isto é, uma no Aquém e outra no Além, onde uma reta é antipodal a outra. Neste programa apenas uma das retas é esboçada no Modelo Esférico. Para deduzir os coeficientes das retas que passam por p 0 e p 1, inicialmente iremos estabelecer a condição de colinariedade entre eles e um terceiro ponto genérico p g =[ w g,x g,y g ]. Três pontos são colineares se o determinante entre eles é zero: w 0 x0 y0 w 1 x 1 y 1 w g x g y g = 0 Expandindo este determinante pela última linha obtemos uma das duas retas: p 0 p 1 = x 0 y 0 x 1 y 1, w 0 y 0 w 1 y 1, w 0 x 0 w 1 x 1 = x 0 y 1 x 1 y 0, w 0 y 1 w 1 y 0, w 0 x 1 w 1 x 0 A outra reta é a sua antipodal, dada por p 0 p1. Finalmente, ao pressionar Desenha Reta / Pontos são esboçados os dois pontos e a reta que passa por eles. (Dica: Habilite o Checkbox Desenha Retas / Pontos e experimente mudar as coordenadas de um dos pontos e em seguida, pressione Determinar Reta.) Opção 6 Obter os pontos de interseção entre duas retas Destacando o conceito da Dualidade, a opção seis explora a simetria existente entre as fórmulas que tratam de pontos e retas na geometria projetiva. Esta simetria pode ser verificada pela semelhança das fórmulas usadas na opção cinco e seis. A Dualidade entre pontos e retas do plano projetivo é um princípio importante pois ela nos permite traduzir diversas fórmulas geométricas que envolvem pontos em outras fórmulas que envolvem linhas, e vice-versa. Isto facilita o desenvolvimento e programação de algoritmos geométricos à medida que o tempo de desenvolvimento fica substancialmente reduzido. Para encontrar o ponto de interseção de duas retas, usamos uma fórmula análoga à usada na quinta opção: p 0 p 1 = [ X 0 Y 0 X 1 Y 1, W 0 Y 0 W 1 Y 1, W 0 X 0 W 1 X 1 ] = [ X 0 Y 1 X 1 Y 0, W 0 Y 1 W 1 Y 0, W 0 X 1 W 1 X 0 ] Ao pressionar o botão Verificar, os dois pontos de interseção são impressos na janela de saída.
7 Opção 7 Desenho de segmento dado dois pontos Com o objetivo de visualizar segmentos no plano projetivo orientado, nesta opção o usuário digita os dois pontos pelos quais será traçado um segmento. Ao selecionar o Checkbox Desenha Segmento, o esboço é feito sobre a esfera unitária. Para o esboço do segmento, normalizamos os dois pontos digitados e calculamos o ângulo 7 entre eles utilizando a fórmula descrita na primeira opção do programa. Em seguida, usando o comando glvertex3f do OpenGL, plotamos ponto a ponto o segmento, variando t de 0 a 7. Opção 8 Determinar em que lado de uma reta está um ponto Determinar o lado de uma reta que contém um ponto é outra operação muito importante para algoritmos geométricos. Nesta opção introduzimos o conceito de lados da reta [1], isto é, os pontos [w, x, y] que não estão sobre a reta r = W, X,Y podem estar em seu lado positivo ou em seu lado negativo. Figura 4 - O ponto p no lado positivo da reta r. Para avaliar o lado da reta que contém um ponto, avaliamos o sinal da expressão W w X x Y y, isto é, realizamos o teste de ponto contra reta: r p = sgn W w X x Y y Onde r = W, X,Y e p = [w,x,y] são respectivamente os coeficientes da reta e o ponto digitados pelo usuário. Assim, se r p 0 temos um ponto no lado negativo da reta. Entretanto, se r p 0 temos um ponto no lado positivo da reta. Uma vez digitados os coeficientes e o ponto, ao pressionar o botão Verificar é realizado o teste de ponto contra reta e o lado da reta que contém o ponto é impresso na janela de saída. Para visualizá-los, selecione o Checkbox Desenha Reta / Ponto.
8 Opção 9 Determinar a equação da cônica que passa por cinco pontos Complemento de nosso estudo da geometria projetiva, as opções nove e dez tem como objetivo explorar a teoria projetiva das cônicas e as aplicações destas teorias em problemas de ajuste de curvas. Usamos a geometria projetiva para trabalhar com as cônicas pois desta forma as cônicas são visualmente mais fáceis de serem caracterizadas. Em resumo, temos que cônica é o conjunto de todos os pontos p = [x,y,z] no plano projetivo que satisfazem a equação homogênea do segundo grau (forma quadrática): A x B y C z D x y E x y F y z = 0 Toda forma quadrática pode ser representada pelo produto p Q p T, onde p = [x, y, z ] e Q é uma matriz simétrica 3 3 chamada matriz associada da cônica: 1 A D 1 E 1 Q = D B 1 F 1 E 1 F C As cônicas podem ser classificadas em degeneradas ou não degeneradas. Dizemos que uma cônica projetiva é degenerada se for um par de retas, uma reta, um ponto ou o vazio. Já uma cônica não degenerada não possui retas ou pontos isolados em seu gráfico, podendo ser um círculo, uma elipse, parábola ou hipérbole. Nesta opção do programa, exploramos uma das aplicações da geometria projetiva em cônicas. Nosso objetivo é obter a equação de uma cônica que passa por quaisquer cinco pontos P 1 [w 1, x 1, y 1 ], P [w, x, y ], P 3 [w 3, x 3, y 3 ], P 4 [w 4, x 4, y 4 ], P 5 [ w 5, x 5, y 5 ], sendo que quatro destes pontos não podem ser colineares. Se três destes pontos forem colineares, a cônica será degenerada. Caso contrário, ela será não degenerada. O usuário digita os cinco pontos 3 e ao pressionar Obter Equação da Cônica é impresso na janela de saída, a equação da cônica que passa por estes cinco pontos. Para classificar e esboçar a cônica, devemos avaliar qual é a equação da cônica que passa pelos cinco pontos. Inicialmente encontramos os coeficientes da equação quadrática, calculando o determinante da matriz: x x 1 x x 3 x 4 x 5 y z x y x z y z y 1 z 1 x 1 y 1 x 1 z 1 y 1 z 1 y z y 3 z 3 y 4 z 4 y 5 z 5 x y x z y z 0 x 3 y 3 x 3 z 3 y 3 z 3 x 4 y 4 x 4 z 4 y 4 z 4 x 5 y 5 x 5 z 5 y 5 z 5 = Em seguida, devemos classificar a cônica. Para tanto, a reescrevemos na forma matricial e encontramos uma matriz diagonal R = M Q M T usando a Decomposição LU, 3 Verificou-se erros numéricos em alguns casos, devidos basicamente ao fato de que os pontos dados não estavam em posição geral.
9 cujos elementos da diagonal principal (pivôs) caracterizam a cônica. As possíveis formas da matriz R são: (a) (b) (c) (d) (e) (f) Onde (a) representa uma cônica sem pontos, (b) representa um ponto, (c) representa um par de retas, (d) uma reta. Estas são as formas matriciais reduzidas das cônicas degeneradas. Já em (e) temos a forma matricial reduzida de uma cônica não degenerada, isto é, todas as figuras projetivamente equivalentes ao círculo unitário. Para maiores detalhes, ver []. Se a cônica for degenerada o programa exibe um aviso na janela de saída e a cônica não é, portanto, esboçada. Entretanto, se a cônica for não degenerada, os cinco pontos e a cônica que passa por eles são esboçados. Observamos que também é desenhada a cônica antipodal Figura 5 - Os cincos pontos e a cônica que passa por eles. Opção 10 Desenho de cônicas Nesta opção, em continuação do nosso estudo de cônicas, fica claro a vantagem de se usar os conceitos da geometria projetiva, em especial o conceito de infinito, no tratamento de cônicas. Graças ao Modelo Esférico e aos fundamentos expostos na opção nove, somos capazes de caracterizar visualmente uma cônica dada sua forma matricial.
10 Uma vez digitados os elementos a 11, a 1, a 13, a 1, a, a 31 (lembrando que toda matriz associada é simétrica), conseguimos classificar a cônica pelo número de vezes que ela intercepta o infinito. Veja: Tabela de Classificação de Cônicas Figura Geométrica Elipse Hipérbole Parábola Característica Visual Não intercepta o Infinito Intercepta o Infinito em dois pontos Tangência o Infinito em um ponto Figura 6 - O esboço de uma cônica que intercepta o infinito em dois pontos. Trata-se de uma Hipérbole. Conclusão Motivados pela dificuldade de visualizar os conceitos fundamentais da Geometria Projetiva, constatamos a necessidade de criar um programa computacional com uma interface objetiva e fácil de usar, que fosse capaz de ajudar na compreensão desta geometria. Relacionamos com a Geometria Euclidiana clássica, o que nos permitiu entender e interpretar as noções de infinito, dualidade e interseções entre retas. Além disso, observamos as vantagens dos conceitos geométricos sobre a ótica projetiva na elaboração do algoritmo do programa, dada a sua capacidade de tornar os cálculos mais robustos.
11 Agradecimentos Os autores gostariam de agradecer aos professores Thomas Lewiner e Sinésio Pesco e ao aluno de doutorado Marcos Lage da Pontifícia Universidade Católica pela constante ajuda no decorrer do desenvolvimento deste trabalho. E o aluno gostaria de agradecer a PUC-Rio pelo apoio recebido através da bolsa TEPP. Referências [1] - STOLFI, J. & RESENDE P. Fundamentos de Geometria Computacional. IX Escola de Computação, Recife, Julho [] - PENNA, M. A. & PATTERSON R. R. Projective Geometry and Its Applications to Computer Graphics. Prentice-Hall, 1986.
Notas de Aula - Fascículo 02 Dualidade e Geometria Projetiva Tridimensional
 Tópicos em Computação Gráfica Notas de Aula - Fascículo 02 Dualidade e Geometria Projetiva Tridimensional Jorge Stolfi c 2009 Jorge Stolfi - Universidade Estadual de Campinas. É permitida a reprodução
Tópicos em Computação Gráfica Notas de Aula - Fascículo 02 Dualidade e Geometria Projetiva Tridimensional Jorge Stolfi c 2009 Jorge Stolfi - Universidade Estadual de Campinas. É permitida a reprodução
Instituto Tecnológico de Aeronáutica. Prof. Carlos Henrique Q. Forster Sala 121 IEC. ramal 5981
 CC Visão Computacional Geometria Projetiva Instituto ecnológico de Aeronáutica Prof. Carlos Henrique Q. Forster Sala IEC ramal 598 ópicos da aula Rotação em D, Escala e Refleo Deformação do quadrado unitário
CC Visão Computacional Geometria Projetiva Instituto ecnológico de Aeronáutica Prof. Carlos Henrique Q. Forster Sala IEC ramal 598 ópicos da aula Rotação em D, Escala e Refleo Deformação do quadrado unitário
MAT Poli Roteiro de Estudos sobre as Cônicas
 MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
MAT25 - Poli - 2003 Roteiro de Estudos sobre as Cônicas Martha Salerno Monteiro Departamento de Matemática IME-USP Uma equação quadrática em duas variáveis é uma equação da forma a + by 2 + cxy + dx +
Lista 3: Geometria Analítica
 Lista 3: Geometria Analítica A. Ramos 25 de abril de 2017 Lista em constante atualização. 1. Equação da reta e do plano; 2. Ângulo entre retas e entre planos. Resumo Equação da reta Equação vetorial. Uma
Lista 3: Geometria Analítica A. Ramos 25 de abril de 2017 Lista em constante atualização. 1. Equação da reta e do plano; 2. Ângulo entre retas e entre planos. Resumo Equação da reta Equação vetorial. Uma
Processamento de Imagens CPS755
 Processamento de Imagens CPS755 aula 01 - geometria projetiva e transformações 2D Antonio Oliveira Ricardo Marroquim 1 / 44 laboratório de processamento de imagens tópicos geometria projetiva transformações
Processamento de Imagens CPS755 aula 01 - geometria projetiva e transformações 2D Antonio Oliveira Ricardo Marroquim 1 / 44 laboratório de processamento de imagens tópicos geometria projetiva transformações
Material Teórico - Sistemas Lineares e Geometria Anaĺıtica. Sistemas com três variáveis - Parte 1. Terceiro Ano do Ensino Médio
 Material Teórico - Sistemas Lineares e Geometria Anaĺıtica Sistemas com três variáveis - Parte 1 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto
Material Teórico - Sistemas Lineares e Geometria Anaĺıtica Sistemas com três variáveis - Parte 1 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
Reconstrução Geométrica a Partir de Imagens TIC /TCC
 Reconstrução Geométrica a Partir de Imagens TIC-00.243/TCC-00.241 Aula 5 Conteúdo Geometria Projetiva 3D Professor Leandro Augusto Frata Fernandes laffernandes@ic.uff.br Material disponível em http://www.ic.uff.br/~laffernandes/teaching/2014.2/tic-00.243
Reconstrução Geométrica a Partir de Imagens TIC-00.243/TCC-00.241 Aula 5 Conteúdo Geometria Projetiva 3D Professor Leandro Augusto Frata Fernandes laffernandes@ic.uff.br Material disponível em http://www.ic.uff.br/~laffernandes/teaching/2014.2/tic-00.243
54 CAPÍTULO 2. GEOMETRIA ANALÍTICA ( ) =
 54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
54 CAPÍTULO. GEOMETRIA ANALÍTICA.5 Cônicas O grá co da equação + + + + + = 0 (.4) onde,,,, e são constantes com, e, não todos nulos, é uma cônica. A equação (.4) é chamada de equação geral do grau em e
A primeira coisa a fazer é saber quais são as equações das curvas quando elas já se encontram na melhor
 Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
Identificação de Cônicas Uma equação do segundo grau ax + bxy + cy + dx + ey + f = 0 define de maneira implícita uma curva no plano xy: o conjunto dos pontos (x, y) que satisfazem a equação. Por exemplo,
21 e 22. Superfícies Quádricas. Sumário
 21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
21 e 22 Superfícies uádricas Sumário 21.1 Introdução....................... 2 21.2 Elipsoide........................ 3 21.3 Hiperboloide de uma Folha.............. 4 21.4 Hiperboloide de duas folhas..............
Material Teórico - Módulo de Geometria Anaĺıtica 1. Terceiro Ano - Médio. Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M.
 Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Portal da OBMEP. Material Teórico - Módulo de Geometria Anaĺıtica 1. Terceiro Ano - Médio
 Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Jorge M. V. Capela, Marisa V. Capela. Araraquara, SP
 Cônicas e Equações Quadráticas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Parábolas 2 3 4 5 Introdução Parábolas Parábolas
Cônicas e Equações Quadráticas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Parábolas 2 3 4 5 Introdução Parábolas Parábolas
Sumário. VII Geometria Analítica Jorge Delgado Katia Frensel Lhaylla Crissaff
 1 Coordenadas no plano 1 1.1 Introdução........................................ 2 1.2 Coordenada e distância na reta............................ 3 1.3 Coordenadas no plano.................................
1 Coordenadas no plano 1 1.1 Introdução........................................ 2 1.2 Coordenada e distância na reta............................ 3 1.3 Coordenadas no plano.................................
Ga no plano 1. GA no plano. Prof. Fernando Carneiro Rio de Janeiro, Outubro de u v = aa + bb.
 Ga no plano 1 GA no plano Prof. Fernando Carneiro Rio de Janeiro, Outubro de 015 1 Introdução Estudaremos as retas no plano euclidiano bidimensional e uma interessante aplicação, que recebe o nome de programação
Ga no plano 1 GA no plano Prof. Fernando Carneiro Rio de Janeiro, Outubro de 015 1 Introdução Estudaremos as retas no plano euclidiano bidimensional e uma interessante aplicação, que recebe o nome de programação
MAT Poli Cônicas - Parte I
 MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
MAT2454 - Poli - 2011 Cônicas - Parte I Uma equação quadrática em duas variáveis, x e y, é uma equação da forma ax 2 +by 2 +cxy +dx+ey +f = 0, em que pelo menos um doscoeficientes a, b oucénão nulo 1.
Dizemos que uma superfície é um cilindro se na equação cartesiana da superfície há uma variável que não aparece.
 Aula 9 Cilindros e Quádricas Cilindros Dizemos que uma superfície é um cilindro se na equação cartesiana da superfície há uma variável que não aparece. Exemplo 1. x 2 + y 2 = 1 No espaço, o conjunto de
Aula 9 Cilindros e Quádricas Cilindros Dizemos que uma superfície é um cilindro se na equação cartesiana da superfície há uma variável que não aparece. Exemplo 1. x 2 + y 2 = 1 No espaço, o conjunto de
Capítulo 3 - Geometria Analítica
 1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
1. Gráficos de Equações Capítulo 3 - Geometria Analítica Conceito:O gráfico de uma equação é o conjunto de todos os pontos e somente estes pontos, cujas coordenadas satisfazem a equação. Assim, o gráfico
AGRUPAMENTO DE ESCOLAS
 AGRUPAMENTO DE ESCOLAS De CASTRO DAIRE Escola Secundária de Castro Daire Grupo de Recrutamento 00 MATEMÁTICA Ano letivo 202/203 Planificação Anual Disciplina: Matemática A Ano: 0º Carga horária semanal:
AGRUPAMENTO DE ESCOLAS De CASTRO DAIRE Escola Secundária de Castro Daire Grupo de Recrutamento 00 MATEMÁTICA Ano letivo 202/203 Planificação Anual Disciplina: Matemática A Ano: 0º Carga horária semanal:
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Aula 10 Regiões e inequações no plano
 MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
MÓDULO 1 - AULA 10 Aula 10 Regiões e inequações no plano Objetivos Resolver inequações do segundo grau. Analisar sistemas envolvendo inequações do primeiro e segundo graus. Resolver inequações modulares
Geometria Computacional
 Geometria Computacional Claudio Esperança Paulo Roma Cavalcanti Estrutura do Curso Aspectos teóricos e práticos Construção e análise de algoritmos e estruturas de dados para a solucionar problemas geométricos
Geometria Computacional Claudio Esperança Paulo Roma Cavalcanti Estrutura do Curso Aspectos teóricos e práticos Construção e análise de algoritmos e estruturas de dados para a solucionar problemas geométricos
Preliminares de Cálculo
 Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
Preliminares de Cálculo Profs. Ulysses Sodré e Olivio Augusto Weber Londrina, 21 de Fevereiro de 2008, arquivo: precalc.tex... Conteúdo 1 Números reais 2 1.1 Algumas propriedades do corpo R dos números
Vectores e Geometria Analítica
 Capítulo 1 Vectores e Geometria Analítica 1.1 Vectores em R 2 e R 3. Exercício 1.1.1 Determine um vector unitário que tenha a mesma direcção e sentido que o vector u e outro que que tenha sentido contrário
Capítulo 1 Vectores e Geometria Analítica 1.1 Vectores em R 2 e R 3. Exercício 1.1.1 Determine um vector unitário que tenha a mesma direcção e sentido que o vector u e outro que que tenha sentido contrário
Aula 31 Funções vetoriais de uma variável real
 MÓDULO 3 - AULA 31 Aula 31 Funções vetoriais de uma variável real Objetivos Conhecer as definições básicas de funções vetoriais de uma variável real. Aprender a parametrizar curvas simples. Introdução
MÓDULO 3 - AULA 31 Aula 31 Funções vetoriais de uma variável real Objetivos Conhecer as definições básicas de funções vetoriais de uma variável real. Aprender a parametrizar curvas simples. Introdução
Exercícios de Geometria Analítica - Prof. Ademir
 Exercícios de Geometria nalítica - Prof. demir Vetores 1. onsidere o triângulo, onde = (1, 1, 1), = (2, 1, 0) e = (3, 2, 3). Verifique que este triângulo é retângulo, diga qual vértice contém o ângulo
Exercícios de Geometria nalítica - Prof. demir Vetores 1. onsidere o triângulo, onde = (1, 1, 1), = (2, 1, 0) e = (3, 2, 3). Verifique que este triângulo é retângulo, diga qual vértice contém o ângulo
6.1 equações canônicas de círculos e esferas
 6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
6 C Í R C U LO S E E S F E R A S 6.1 equações canônicas de círculos e esferas Um círculo é o conjunto de pontos no plano que estão a uma certa distância r de um ponto dado (a, b). Desta forma temos que
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Equações da reta no plano
 3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
3 Equações da reta no plano Sumário 3.1 Introdução....................... 2 3.2 Equação paramétrica da reta............. 2 3.3 Equação cartesiana da reta.............. 7 3.4 Equação am ou reduzida da reta..........
Aula 17 Superfícies quádricas - parabolóides
 Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Reconstrução Geométrica a Partir de Imagens TIC /TCC
 Reconstrução Geométrica a Partir de Imagens TIC-00.243/TCC-00.241 Aulas 2 e 3 Conteúdo Geometria Projetiva 2D Professor Leandro Augusto Frata Fernandes laffernandes@ic.uff.br Material disponível em http://www.ic.uff.br/~laffernandes/teaching/2014.2/tic-00.243
Reconstrução Geométrica a Partir de Imagens TIC-00.243/TCC-00.241 Aulas 2 e 3 Conteúdo Geometria Projetiva 2D Professor Leandro Augusto Frata Fernandes laffernandes@ic.uff.br Material disponível em http://www.ic.uff.br/~laffernandes/teaching/2014.2/tic-00.243
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 2018
 GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
SEÇÕES CÔNICAS. Figura 1
 INSTITUTO DE MATEMÁTICA UFBA DISCIPLINA: MATEMÁTICA BÁSICA II - SEM. 004.1 PROF. GRAÇA LUZIA DOMINGUEZ SANTOS SEÇÕES CÔNICAS Sejam duas retas e e r concorrentes em O, tal que o ângulo α entre e e r é diferente
INSTITUTO DE MATEMÁTICA UFBA DISCIPLINA: MATEMÁTICA BÁSICA II - SEM. 004.1 PROF. GRAÇA LUZIA DOMINGUEZ SANTOS SEÇÕES CÔNICAS Sejam duas retas e e r concorrentes em O, tal que o ângulo α entre e e r é diferente
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
0 < c < a ; d(f 1, F 2 ) = 2c
 Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Capítulo 14 Elipse Nosso objetivo, neste e nos próximos capítulos, é estudar a equação geral do segundo grau em duas variáveis: Ax + Bxy + Cy + Dx + Ey + F = 0, onde A 0 ou B 0 ou C 0 Para isso, deniremos,
Aula Exemplos diversos. Exemplo 1
 Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
Aula 3 1. Exemplos diversos Exemplo 1 Determine a equação da hipérbole equilátera, H, que passa pelo ponto Q = ( 1, ) e tem os eixos coordenados como assíntotas. Como as assíntotas da hipérbole são os
(b) { (ρ, θ);1 ρ 2 e π θ } 3π. 5. Representar graficamente
 Universidade Federal de Uberlândia Faculdade de Matemática isciplina : Geometria nalítica (GM003) ssunto: sistemas de coordenadas; vetores: operações com vetores, produto escalar, produto vetorial, produto
Universidade Federal de Uberlândia Faculdade de Matemática isciplina : Geometria nalítica (GM003) ssunto: sistemas de coordenadas; vetores: operações com vetores, produto escalar, produto vetorial, produto
Reconstrução Geométrica a Partir de Imagens TIC
 Reconstrução Geométrica a Partir de Imagens TIC-10.073 Aulas 2 e 3 Conteúdo Geometria Projetiva 2D Professor Leandro Augusto Frata Fernandes laffernandes@ic.uff.br Material disponível em http://www.ic.uff.br/~laffernandes/teaching/2016.1/tic-10.073
Reconstrução Geométrica a Partir de Imagens TIC-10.073 Aulas 2 e 3 Conteúdo Geometria Projetiva 2D Professor Leandro Augusto Frata Fernandes laffernandes@ic.uff.br Material disponível em http://www.ic.uff.br/~laffernandes/teaching/2016.1/tic-10.073
Aula Distância entre duas retas paralelas no espaço. Definição 1. Exemplo 1
 Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
Aula 1 Sejam r 1 = P 1 + t v 1 t R} e r 2 = P 2 + t v 2 t R} duas retas no espaço. Se r 1 r 2, sabemos que r 1 e r 2 são concorrentes (isto é r 1 r 2 ) ou não se intersectam. Quando a segunda possibilidade
A B C A 1 B 1 C 1 A 2 B 2 C 2 é zero (exceto o caso em que as tres retas são paralelas).
 MAT 105- Lista de Exercícios 1. Prolongue o segmento com extremos em (1, -5) e (3, 1) de um comprimento de (10) unidades. Determine as coordenadas dos novos extremos. 2. Determine o centro e o raio da
MAT 105- Lista de Exercícios 1. Prolongue o segmento com extremos em (1, -5) e (3, 1) de um comprimento de (10) unidades. Determine as coordenadas dos novos extremos. 2. Determine o centro e o raio da
1 Geometria Analítica Plana
 UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
UNIVERSIDADE ESTADUAL DO PARANÁ CAMPUS DE CAMPO MOURÃO Curso: Matemática, 1º ano Disciplina: Geometria Analítica e Álgebra Linear Professora: Gislaine Aparecida Periçaro 1 Geometria Analítica Plana A Geometria
Equações paramétricas das cônicas
 Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano
 Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano Americo Cunha Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro Regiões no Plano
Descrevendo Regiões no Plano Cartesiano e no Espaço Euclidiano Americo Cunha Débora Mondaini Ricardo Sá Earp Departamento de Matemática Pontifícia Universidade Católica do Rio de Janeiro Regiões no Plano
UNIVERSIDADE FEDERAL DE ALAGOAS INSTITUTO DE MATEMÁTICA Aluno(a): Professor(a): Curso:
 5 Geometria Analítica - a Avaliação - 6 de setembro de 0 Justique todas as suas respostas.. Dados os vetores u = (, ) e v = (, ), determine os vetores m e n tais que: { m n = u, v u + v m + n = P roj u
5 Geometria Analítica - a Avaliação - 6 de setembro de 0 Justique todas as suas respostas.. Dados os vetores u = (, ) e v = (, ), determine os vetores m e n tais que: { m n = u, v u + v m + n = P roj u
7. Determine a equação da parábola que passa pelos pontos P (0, 6), Q(3, 0) e R(4, 10).
 Lista 3: Cônicas - Engenharia Mecânica Professora Elisandra Bär de Figueiredo 1. Determine a equação do conjunto de pontos P (x, y) que são equidistantes da reta x = e do ponto (0, ). A seguir construa
Lista 3: Cônicas - Engenharia Mecânica Professora Elisandra Bär de Figueiredo 1. Determine a equação do conjunto de pontos P (x, y) que são equidistantes da reta x = e do ponto (0, ). A seguir construa
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
Marcelo M. Santos DM-IMECC-UNICAMP msantos/
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Geometria Analítica - Aula
 Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
Geometria Analítica - Aula 18 228 IM-UFF K. Frensel - J. Delgado Aula 19 Continuamos com o nosso estudo da equação Ax 2 + Cy 2 + Dx + Ey + F = 0 1. Hipérbole Definição 1 Uma hipérbole, H, de focos F 1
DIRETORIA DE PESQUISA E PÓS-GRADUAÇÃO PROJETO: TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO E APRENDIZAGEM DE MATEMÁTICA
 DIRETORIA DE PESQUISA E PÓS-GRADUAÇÃO PROJETO: TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO E APRENDIZAGEM DE MATEMÁTICA NOME: DATA: / / Software GeoGebra 5.0 versão desktop 1ª Parte Conhecendo
DIRETORIA DE PESQUISA E PÓS-GRADUAÇÃO PROJETO: TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO E APRENDIZAGEM DE MATEMÁTICA NOME: DATA: / / Software GeoGebra 5.0 versão desktop 1ª Parte Conhecendo
Departamento de Matemática
 Computação Gráfica - Evolução de Curvas e Superfícies Aluno: Vinícius Segura Orientador: Sinésio Pesco Introdução Nas últimas décadas atravessamos uma verdadeira revolução tecnológica, devido ao avanço
Computação Gráfica - Evolução de Curvas e Superfícies Aluno: Vinícius Segura Orientador: Sinésio Pesco Introdução Nas últimas décadas atravessamos uma verdadeira revolução tecnológica, devido ao avanço
Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA
 Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA 4. Geometria Analítica 4.1. Introdução Geometria Analítica é a parte da Matemática,
Instituto Federal de Educação, Ciência e Tecnologia Rio Grande do Sul Campus Rio Grande CAPÍTULO 4 GEOMETRIA ANALÍTICA 4. Geometria Analítica 4.1. Introdução Geometria Analítica é a parte da Matemática,
Em matemática definimos e estudamos conjuntos de números, pontos, retas curvas, funções etc.
 INTRODUÇÃO Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 02 - Introdução, Plano Cartesiano, Pontos e Retas
INTRODUÇÃO Curso de Geometria Analítica Abrangência: Graduação em Engenharia e Matemática Professor Responsável: Anastassios H. Kambourakis Resumo Teórico 02 - Introdução, Plano Cartesiano, Pontos e Retas
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 2. Retas no plano. 1. Retas verticais e não-verticais. Definição 1
 Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Capítulo 2 Retas no plano O objetivo desta aula é determinar a equação algébrica que representa uma reta no plano. Para isso, vamos analisar separadamente dois tipos de reta: reta vertical e reta não-vertical.
Geometria Analítica Exercícios Cônicas em posição geral
 Geometria Analítica Exercícios Cônicas em posição geral Cleide Martins DMat - UFPE Turmas E1 e E3 Cleide Martins (DMat - UFPE) Soluções Turmas E1 e E3 1 / 16 Resolução dos exercícios da aula 15 Classique
Geometria Analítica Exercícios Cônicas em posição geral Cleide Martins DMat - UFPE Turmas E1 e E3 Cleide Martins (DMat - UFPE) Soluções Turmas E1 e E3 1 / 16 Resolução dos exercícios da aula 15 Classique
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (10º Ano) METAS CURRICULARES/CONTEÚDOS... 2º Período(4 de janeiro a 18 de março)
 DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (10º Ano) METAS CURRICULARES/CONTEÚDOS... 2º Período(4 de janeiro a 18 de março) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (10º Ano) METAS CURRICULARES/CONTEÚDOS... 2º Período(4 de janeiro a 18 de março) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
GEOMETRIA ANALÍTICA 2017
 GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
GEOMETRIA ANALÍTICA 2017 Tópicos a serem estudados 1) O ponto (Noções iniciais - Reta orientada ou eixo Razão de segmentos Noções Simetria Plano Cartesiano Abcissas e Ordenadas Ponto Médio Baricentro -
UECEVEST - ESPECÍFICA Professor: Rikardo Rodrigues
 UECEVEST - ESPECÍFICA Professor: Rikardo Rodrigues 01) (UECE 2017.2) Seja YOZ um triângulo cuja medida da altura OH relativa ao lado YZ é igual a 6 m. Se as medidas dos segmentos YH e HZ determinados por
UECEVEST - ESPECÍFICA Professor: Rikardo Rodrigues 01) (UECE 2017.2) Seja YOZ um triângulo cuja medida da altura OH relativa ao lado YZ é igual a 6 m. Se as medidas dos segmentos YH e HZ determinados por
O Plano no Espaço. Sumário
 17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
17 Sumário 17.1 Introdução....................... 2 17.2 Equações paramétricas do plano no espaço..... 2 17.3 Equação cartesiana do plano............. 15 17.4 Exercícios........................ 21 1 Unidade
Aula 4. Coordenadas polares. Definição 1. Observação 1
 Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Curvas Planas em Coordenadas Polares
 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
CÔNICAS - MAT Complementos de Matemática para Contabilidade FEAUSP - Diurno 2 o semestre de 2015 Professor Oswaldo Rio Branco de Oliveira ELIPSE
 CÔNICAS - MAT 103 - Complementos de Matemática para Contabilidade FEAUSP - Diurno 2 o semestre de 2015 Professor Oswaldo Rio Branco de Oliveira No plano euclidiano consideremos dois pontos (focos) distintos
CÔNICAS - MAT 103 - Complementos de Matemática para Contabilidade FEAUSP - Diurno 2 o semestre de 2015 Professor Oswaldo Rio Branco de Oliveira No plano euclidiano consideremos dois pontos (focos) distintos
Álgebra Linear e Geometria Anaĺıtica. Cónicas e Quádricas
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 6 Cónicas e Quádricas Equação geral de uma cónica [6 01] As cónicas são curvas
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 6 Cónicas e Quádricas Equação geral de uma cónica [6 01] As cónicas são curvas
Superfícies e Curvas no Espaço
 Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Superfícies e Curvas no Espaço Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de deembro de 2001 1 Quádricas Nesta
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Aula 19 Elipse - continuação
 MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
MÓDULO 1 - AULA 19 Aula 19 Elipse - continuação Objetivos Desenhar a elipse com compasso e régua com escala. Determinar a equação reduzida da elipse no sistema de coordenadas com origem no ponto médio
Geometria Analítica? Onde usar os conhecimentos. os sobre Geometria Analítica?
 X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
X GEOMETRIA ANALÍTICA Por que aprender Geometria Analítica?... A Geometria Analítica estabelece relações entre a álgebra e a geometria por meio de equações e inequações. Isso permite transformar questões
P2 de Álgebra Linear I Data: 10 de outubro de Gabarito
 P2 de Álgebra Linear I 2005.2 Data: 10 de outubro de 2005. Gabarito 1 Decida se cada afirmação a seguir é verdadeira ou falsa. Itens V F N 1.a F 1.b V 1.c V 1.d F 1.e V 1.a Considere duas bases β e γ de
P2 de Álgebra Linear I 2005.2 Data: 10 de outubro de 2005. Gabarito 1 Decida se cada afirmação a seguir é verdadeira ou falsa. Itens V F N 1.a F 1.b V 1.c V 1.d F 1.e V 1.a Considere duas bases β e γ de
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
CÁLCULO L1 NOTAS DA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula discutiremos como obter as equações das retas tangentes a uma curva planar que é o gráfico de uma função. 1. Introdução
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
1. Seja θ = ang (r, s). Calcule sen θ nos casos (a) e (b) e cos θ nos casos (c) e (d): = z 3 e s : { 3x + y 5z = 0 x 2y + 3z = 1
 14 a lista de exercícios - SMA0300 - Geometria Analítica Estágio PAE - Alex C. Rezende Medida angular, distância, mudança de coordenadas, cônicas e quádricas 1. Seja θ = ang (r, s). Calcule sen θ nos casos
14 a lista de exercícios - SMA0300 - Geometria Analítica Estágio PAE - Alex C. Rezende Medida angular, distância, mudança de coordenadas, cônicas e quádricas 1. Seja θ = ang (r, s). Calcule sen θ nos casos
Resolvendo inequações: expressões com desigualdades (encontrar os valores que satisfazem a expressão)
 R é ordenado: Se a, b, c R i) a < b se e somente se b a > 0 (a diferença do maior com o menor será positiva) ii) se a > 0 e b > 0 então a + b > 0 (a soma de dois números positivos é positiva) iii) se a
R é ordenado: Se a, b, c R i) a < b se e somente se b a > 0 (a diferença do maior com o menor será positiva) ii) se a > 0 e b > 0 então a + b > 0 (a soma de dois números positivos é positiva) iii) se a
Geometria Analítica. Estudo do Plano. Prof Marcelo Maraschin de Souza
 Geometria Analítica Estudo do Plano Prof Marcelo Maraschin de Souza Plano Equação Geral do Plano Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = a, b, c, n 0, um vetor normal (ortogonal)
Geometria Analítica Estudo do Plano Prof Marcelo Maraschin de Souza Plano Equação Geral do Plano Seja A(x 1, y 1, z 1 ) um ponto pertencente a um plano π e n = a, b, c, n 0, um vetor normal (ortogonal)
MÓDULO 1 - AULA 21. Objetivos
 Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
Aula 1 Hipérbole - continuação Objetivos Aprender a desenhar a hipérbole com compasso e régua com escala. Determinar a equação reduzida da hipérbole no sistema de coordenadas com origem no ponto médio
SECÇÕES CÔNICAS E SUPERFÍCIES QUÁDRICAS Prof. Vasco Ricardo Aquino da Silva
 SECÇÕES CÔNICAS E SUPERFÍCIES QUÁDRICAS Prof. Vasco Ricardo Aquino da Silva SECÇÕES CÔNICAS Usando o programa winplot visualize as cônicas disponíveis em nosso AVA Moodle. 1. Elementos da Elipse: F1, F2:
SECÇÕES CÔNICAS E SUPERFÍCIES QUÁDRICAS Prof. Vasco Ricardo Aquino da Silva SECÇÕES CÔNICAS Usando o programa winplot visualize as cônicas disponíveis em nosso AVA Moodle. 1. Elementos da Elipse: F1, F2:
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
1 Cônicas Não Degeneradas
 Seções Cônicas Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de dezembro de 2001 Estudaremos as (seções) cônicas,
Seções Cônicas Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi regi@mat.ufmg.br 11 de dezembro de 2001 Estudaremos as (seções) cônicas,
Geometria Analítica l - MAT Lista 6 Profa. Lhaylla Crissaff
 Geometria Analítica l - MAT 0016 Lista 6 Profa. Lhaylla Crissaff 1. Encontre as equações paramétricas e cartesiana do plano π que passa pelos pontos A = (1, 0, ), B = (1,, 3) e C = (0, 1, ).. Prove que
Geometria Analítica l - MAT 0016 Lista 6 Profa. Lhaylla Crissaff 1. Encontre as equações paramétricas e cartesiana do plano π que passa pelos pontos A = (1, 0, ), B = (1,, 3) e C = (0, 1, ).. Prove que
Em todas as questões, está fixado um sistema ortogonal (O, i, j, k) com base ( i, j, k) positiva.
 1 Em todas as questões, está fixado um sistema ortogonal (O, i, j, k) com base ( i, j, k) positiva a1q1: Sejam r uma reta, A e B dois pontos distintos não pertencentes a r Seja L o lugar geométrico dos
1 Em todas as questões, está fixado um sistema ortogonal (O, i, j, k) com base ( i, j, k) positiva a1q1: Sejam r uma reta, A e B dois pontos distintos não pertencentes a r Seja L o lugar geométrico dos
Portal OBMEP. Material Teórico - Módulo Cônicas. Terceiro Ano do Ensino Médio
 Material Teórico - Módulo Cônicas Parábolas Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução ω Nesta aula vamos revisar o conceito
Material Teórico - Módulo Cônicas Parábolas Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução ω Nesta aula vamos revisar o conceito
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III
 UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
UNIVERSIDADE FEDERAL DE VIÇOSA DEPARTAMENTO DE MATEMÁTICA LISTA DE EXERCÍCIOS DE MAT243-CÁLCULO III Capítulo 1 Vetores no Rn 1. Sejam u e v vetores tais que e u v = 2 e v = 1. Calcule v u v. 2. Sejam u
4. Tensores cartesianos em 3D simétricos
 4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
INSTITUTO FEDERAL DE BRASILIA 4ª Lista. Nome: DATA: 09/11/2016
 INSTITUTO FEDERAL DE BRASILIA 4ª Lista MATEMÁTICA GEOMETRIA ANALÍTICA Nome: DATA: 09/11/016 Alexandre Uma elipse tem centro na origem e o eixo maior coincide com o eixo Y. Um dos focos é 1 F1 0, 3 e a
INSTITUTO FEDERAL DE BRASILIA 4ª Lista MATEMÁTICA GEOMETRIA ANALÍTICA Nome: DATA: 09/11/016 Alexandre Uma elipse tem centro na origem e o eixo maior coincide com o eixo Y. Um dos focos é 1 F1 0, 3 e a
Processamento de Imagens CPS755
 Processamento de Imagens CPS755 aula 03 - visualizando a planar Antonio Oliveira Ricardo Marroquim 1 / 40 laboratório de processamento de imagens tópicos visualizando a planar discussão dos primeiros 2
Processamento de Imagens CPS755 aula 03 - visualizando a planar Antonio Oliveira Ricardo Marroquim 1 / 40 laboratório de processamento de imagens tópicos visualizando a planar discussão dos primeiros 2
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Introdução ao Processamento e Síntese de imagens -Linhas e superfícies escondidas
 Introdução ao Processamento e Síntese de imagens -Linhas e superfícies escondidas Júlio Kiyoshi Hasegawa 26 Fontes: Rogers, D. F. Procedural Elements for Computer Graphics Introdução Linhas e superfícies
Introdução ao Processamento e Síntese de imagens -Linhas e superfícies escondidas Júlio Kiyoshi Hasegawa 26 Fontes: Rogers, D. F. Procedural Elements for Computer Graphics Introdução Linhas e superfícies
2 - VETORES. Geométricamente, vetores são representados por segmentos orientados no plano ou no espaço. Figura 1: Vetor
 2 - VETORES Geométricamente, vetores são representados por segmentos orientados no plano ou no espaço. Figura 1: Vetor Segmentos orientados com mesma direção, mesmo sentido e mesmo comprimento representam
2 - VETORES Geométricamente, vetores são representados por segmentos orientados no plano ou no espaço. Figura 1: Vetor Segmentos orientados com mesma direção, mesmo sentido e mesmo comprimento representam
GEOGEBRA GUIA RÁPIDO. Na janela inicial temos a barra de ferramentas:
 GeoGebra: Guia Rápido GEOGEBRA GUIA RÁPIDO O GeoGebra é um programa educativo de Geometria Dinâmica que permite construir, de modo simples e rápido, pontos, segmentos de reta, retas, polígonos, circunferências,
GeoGebra: Guia Rápido GEOGEBRA GUIA RÁPIDO O GeoGebra é um programa educativo de Geometria Dinâmica que permite construir, de modo simples e rápido, pontos, segmentos de reta, retas, polígonos, circunferências,
Prof. Rafael Saraiva Campos CEFET/RJ UnED Nova Iguaçu 2011
 Introdução à Geometria Descritiva Aula 01 Prof. Rafael Saraiva Campos CEFET/RJ UnED Nova Iguaçu 2011 Resumo O que é Geometria Descritiva? Projeção Ortogonal de um Ponto Método da Dupla Projeção de Monge
Introdução à Geometria Descritiva Aula 01 Prof. Rafael Saraiva Campos CEFET/RJ UnED Nova Iguaçu 2011 Resumo O que é Geometria Descritiva? Projeção Ortogonal de um Ponto Método da Dupla Projeção de Monge
Material by: Caio Guimarães (Equipe Rumoaoita.com) Referência: cadernos de aula: Professor Eduardo Wagner
 Material by: Caio Guimarães (Equipe Rumoaoita.com) Referência: cadernos de aula: Professor Eduardo Wagner 3 - Parábolas Definição 1.1: Dados um ponto no plano F e uma reta d no plano, é denominada Parábola
Material by: Caio Guimarães (Equipe Rumoaoita.com) Referência: cadernos de aula: Professor Eduardo Wagner 3 - Parábolas Definição 1.1: Dados um ponto no plano F e uma reta d no plano, é denominada Parábola
Com o auxílio do software vamos verificar se os pontos A(4, 7) e B(3, 5) pertencem à reta r do exemplo acima. Procedimentos para o uso do Winplot:
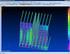 Retas Equações de uma reta com o software Winplot Equação geral Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(x A, y A ) e
Retas Equações de uma reta com o software Winplot Equação geral Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos. Dada uma reta r, sendo A(x A, y A ) e
Cálculo a Várias Variáveis I - MAT Cronograma para P2: aulas teóricas (segundas e quartas)
 Cálculo a Várias Variáveis I - MAT 116 0141 Cronograma para P: aulas teóricas (segundas e quartas) Aula 10 4 de março (segunda) Aula 11 6 de março (quarta) Referências: Cálculo Vol James Stewart Seções
Cálculo a Várias Variáveis I - MAT 116 0141 Cronograma para P: aulas teóricas (segundas e quartas) Aula 10 4 de março (segunda) Aula 11 6 de março (quarta) Referências: Cálculo Vol James Stewart Seções
Capítulo Coordenadas no Espaço. Seja E o espaço da Geometria Euclidiana tri-dimensional.
 Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Plotar Gráficos com Recursos Computacionais
 Plotar 1 Gráficos com Recursos Computacionais Plotar (esboçar) o gráfico de uma função nem sempre é uma tarefa fácil. Para facilitar nosso trabalho, podemos utilizar softwares matemáticos especialmente
Plotar 1 Gráficos com Recursos Computacionais Plotar (esboçar) o gráfico de uma função nem sempre é uma tarefa fácil. Para facilitar nosso trabalho, podemos utilizar softwares matemáticos especialmente
P L A N I F I C A Ç Ã O A N U A L
 P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: 500 - MATEMÁTICA DISCIPLINA: MATEMÁTICA A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias
P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: 500 - MATEMÁTICA DISCIPLINA: MATEMÁTICA A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias
3D no OpenGL. Visualização e Transformações Perspectiva. Transformações do Modelview. Processo
 Visualização e Transformações Perspectiva 3D no OpenGL Para gerar imagens de um objeto 3D, é necessário compreender transformações perspectiva Foley & van Dam - Cap. 6 Notas de aula do Prof. Mount: aulas
Visualização e Transformações Perspectiva 3D no OpenGL Para gerar imagens de um objeto 3D, é necessário compreender transformações perspectiva Foley & van Dam - Cap. 6 Notas de aula do Prof. Mount: aulas
