Prof. Márcio Nascimento. 3 de setembro de 2014
|
|
|
- Ana Luísa Bicalho Medina
- 9 Há anos
- Visualizações:
Transcrição
1 Ângulos Prof. Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática Básica II de setembro de / 23
2 Sumário 1 Ângulo 2 2 / 23
3 Sumário 1 Ângulo 2 3 / 23
4 Ângulo Ângulo: palavra que origina do Latim angulum (esquina, canto). 4 / 23
5 Ângulo Ângulo: palavra que origina do Latim angulum (esquina, canto). é a figura formada por duas semi-retas de mesma origem. 4 / 23
6 Ângulo Ângulo: palavra que origina do Latim angulum (esquina, canto). é a figura formada por duas semi-retas de mesma origem. Notação: AÔB ou BÔA 4 / 23
7 Ângulo Ângulo: palavra que origina do Latim angulum (esquina, canto). é a figura formada por duas semi-retas de mesma origem. Notação: AÔB ou BÔA OA e OB: lados do ângulo. 4 / 23
8 Ângulo Geralmente são usadas letras gregas ou letras de forma para representar um ângulo 5 / 23
9 Ângulo Geralmente são usadas letras gregas ou letras de forma para representar um ângulo α = AÔB = Ô = O 5 / 23
10 Ângulo Alguns ângulos recebem nome especial 6 / 23
11 Ângulo Alguns ângulos recebem nome especial Ângulo raso: Quando as semirretas têm a mesma direção mas sentido oposto. 6 / 23
12 Ângulo Alguns ângulos recebem nome especial Ângulo raso: Quando as semirretas têm a mesma direção mas sentido oposto. Ângulo nulo: Quando as semirretas têm a mesma direção e sentido. 6 / 23
13 Ângulo Ângulo reto: Quando as semirretas são perpendiculares. 7 / 23
14 Ângulo Ângulo agudo: Quando o ângulo formado é menor que um ângulo reto. 8 / 23
15 Ângulo Ângulo obtuso: Quando o ângulo formado é menor que um ângulo raso e maior que um ângulo reto. 9 / 23
16 Ângulo Ângulos Complementares: ângulos que quando justapostos formam um ângulo reto. 10 / 23
17 Ângulo Ângulos Suplementares: ângulos que quando justapostos formam um ângulo raso. 11 / 23
18 Sumário 1 Ângulo 2 12 / 23
19 13 / 23
20 Imagine várias semirretas partindo de um mesmo ponto, como mostra a figura ao lado. 13 / 23
21 Imagine várias semirretas partindo de um mesmo ponto, como mostra a figura ao lado. Considere que o ângulo determinado por quaisquer duas semirretas consecutivas é sempre o mesmo. 13 / 23
22 Imagine várias semirretas partindo de um mesmo ponto, como mostra a figura ao lado. Considere que o ângulo determinado por quaisquer duas semirretas consecutivas é sempre o mesmo. Se tivermos 360 semirretas, teremos 360 ângulos iguais. Cada um deles será chamado grau. 13 / 23
23 Imagine várias semirretas partindo de um mesmo ponto, como mostra a figura ao lado. Considere que o ângulo determinado por quaisquer duas semirretas consecutivas é sempre o mesmo. Se tivermos 360 semirretas, teremos 360 ângulos iguais. Cada um deles será chamado grau. Notação: / 23
24 14 / 23
25 Exemplo: De um mesmo ponto, partem 120 semirretas determinando ângulos iguais entre si. Qual a medida, em graus, de cada ângulo? 14 / 23
26 Exemplo: De um mesmo ponto, partem 120 semirretas determinando ângulos iguais entre si. Qual a medida, em graus, de cada ângulo? Resposta: / 23
27 15 / 23
28 A fração de 1/60 de um grau é 1 0 chamada minuto. Notação: 60 = 1 15 / 23
29 A fração de 1/60 de um grau é 1 0 chamada minuto. Notação: 60 = 1 E a fração de 1/60 de um minuto, é chamada segundo. Notação 1 60 = 1 15 / 23
30 Exemplo: Considere um círculo de raio R. De seu centro O, partem 175 semirretas determinando ângulos iguais entre si. 16 / 23
31 Exemplo: Considere um círculo de raio R. De seu centro O, partem 175 semirretas determinando ângulos iguais entre si. Qual a medida em graus de cada ângulo? Qual a medida em minutos de cada ângulo? Qual a medida em segundos de cada ângulo? 16 / 23
32 Exemplo: Considere um círculo de raio R. De seu centro O, partem 175 semirretas determinando ângulos iguais entre si. Qual a medida em graus de cada ângulo? Aproxidamente 2, 06 0 Qual a medida em minutos de cada ângulo? Qual a medida em segundos de cada ângulo? 16 / 23
33 Exemplo: Considere um círculo de raio R. De seu centro O, partem 175 semirretas determinando ângulos iguais entre si. Qual a medida em graus de cada ângulo? Aproxidamente 2, 06 0 Qual a medida em minutos de cada ângulo? Aproximadamente 123, 43 Qual a medida em segundos de cada ângulo? 16 / 23
34 Exemplo: Considere um círculo de raio R. De seu centro O, partem 175 semirretas determinando ângulos iguais entre si. Qual a medida em graus de cada ângulo? Aproxidamente 2, 06 0 Qual a medida em minutos de cada ângulo? Aproximadamente 123, 43 Qual a medida em segundos de cada ângulo? Aproximadamente 7405, / 23
35 Observação: Em vez da notação decimal, algumas vezes é interessante usar graus, minutos e segundos na mesma representação 17 / 23
36 Observação: Em vez da notação decimal, algumas vezes é interessante usar graus, minutos e segundos na mesma representação 2, 5 0 = , 5 0 = (0, 5).60 = / 23
37 Observação: Em vez da notação decimal, algumas vezes é interessante usar graus, minutos e segundos na mesma representação 2, 5 0 = , 5 0 = (0, 5).60 = , 12 0 = , 12 0 = (0, 12).60 = , 2 = , 2 = , 2(60 ) = / 23
38 Exemplo: Dados os ângulos A = 124, e B = 75, 765 0, 18 / 23
39 Exemplo: Dados os ângulos A = 124, e B = 75, 765 0, Converta A e B para a notação grau/minuto/segundo Expresse A + B, A B na notação grau/minuto/segundo 18 / 23
40 Exemplo: Dados os ângulos A = 124, e B = 75, 765 0, Converta A e B para a notação grau/minuto/segundo A = e B = Expresse A + B, A B na notação grau/minuto/segundo 18 / 23
41 Exemplo: Dados os ângulos A = 124, e B = 75, 765 0, Converta A e B para a notação grau/minuto/segundo A = e B = Expresse A + B, A B na notação grau/minuto/segundo A + B = 200, = e A B = 48, = / 23
42 Exemplo: Dados os ângulos A = e B = , determine: 19 / 23
43 Exemplo: Dados os ângulos A = e B = , determine: A + B A B A 2 + B 3 19 / 23
44 Exemplo: Dados os ângulos A = e B = , determine: A + B A B A 2 + B 3 19 / 23
45 Exemplo: Dados os ângulos A = e B = , determine: A + B A B A 2 + B 3 19 / 23
46 Exemplo: Dados os ângulos A = e B = , determine: A + B A B A 2 + B 3 Aproximadamente / 23
47 Exemplo: Dados os ângulos A = e B = , 20 / 23
48 Exemplo: Dados os ângulos A = e B = , Converta A e B para a notação decimal Expresse A + B, A B na notação decimal 20 / 23
49 Exemplo: Dados os ângulos A = e B = , Converta A e B para a notação decimal A é aproximadamente 42, 46 0 e B é aproximadamente 27, 54 0 Expresse A + B, A B na notação decimal 20 / 23
50 Exemplo: Dados os ângulos A = e B = , Converta A e B para a notação decimal A é aproximadamente 42, 46 0 e B é aproximadamente 27, 54 0 Expresse A + B, A B na notação decimal A + B = 69, 99 0 e A B = 14, / 23
51 Exemplo: Um relógio marca 2 : 25. Qual o menor ângulo entre os ponteiros de horas e minutos? 21 / 23
52 Exemplo: Um relógio marca 2 : 25. Qual o menor ângulo entre os ponteiros de horas e minutos? Lembre que a cada 60 minutos, o ponteiro maior percorre e o menor, / 23
53 Exemplo: Um relógio marca 2 : 25. Qual o menor ângulo entre os ponteiros de horas e minutos? Lembre que a cada 60 minutos, o ponteiro maior percorre e o menor, Portanto, em 1 minuto, o ponteiro maior percorre 6 0 e o menor 0, / 23
54 Exemplo: Um relógio marca 2 : 25. Qual o menor ângulo entre os ponteiros de horas e minutos? Lembre que a cada 60 minutos, o ponteiro maior percorre e o menor, Portanto, em 1 minuto, o ponteiro maior percorre 6 0 e o menor 0, 5 0. Daí, às 2:25, o ponteiro maior terá percorrido (a partir do 12) = e o menor, 25 0, 5 0 = 12, / 23
55 Exemplo: Um relógio marca 2 : 25. Qual o menor ângulo entre os ponteiros de horas e minutos? Lembre que a cada 60 minutos, o ponteiro maior percorre e o menor, Portanto, em 1 minuto, o ponteiro maior percorre 6 0 e o menor 0, 5 0. Daí, às 2:25, o ponteiro maior terá percorrido (a partir do 12) = e o menor, 25 0, 5 0 = 12, 5 0. Se o ponteiro das horas permanecesse fixo, o menor ângulo seria de = 90 0, mas como o ponteiro menor se movimentou 12, 5 0, segue que o ângulo procurado é de 77, / 23
56 Exemplo: Determine o menor ângulo entre os ponteiros de um relógio às: 22 / 23
57 Exemplo: Determine o menor ângulo entre os ponteiros de um relógio às: 15:35 18:10 16:20 12:33 22 / 23
58 Exemplo: Determine o menor ângulo entre os ponteiros de um relógio às: 15:35 102, :10 16:20 12:33 22 / 23
59 Exemplo: Determine o menor ângulo entre os ponteiros de um relógio às: 15:35 102, : :20 12:33 22 / 23
60 Exemplo: Determine o menor ângulo entre os ponteiros de um relógio às: 15:35 102, : : :33 22 / 23
61 Exemplo: Determine o menor ângulo entre os ponteiros de um relógio às: 15:35 102, : : :33 178, / 23
62 Origem das palavras Grau: origem do latim - gradu - que significa degrau. 23 / 23
63 Origem das palavras Grau: origem do latim - gradu - que significa degrau. Minuto: primeiras menores partes - partes minutae primae 23 / 23
64 Origem das palavras Grau: origem do latim - gradu - que significa degrau. Minuto: primeiras menores partes - partes minutae primae Segundo: segundas menores partes - partes minutae secundae 23 / 23
Matemática Básica II - Trigonometria Nota 01 - Ângulo e a Unidade de medida Grau
 Matemática Básica II - Trigonometria Nota 01 - Ângulo e a Unidade de medida Grau Márcio Nascimento da Silva Universidade Estadual Vale do caraú - UV Curso de Licenciatura em Matemática [email protected]
Matemática Básica II - Trigonometria Nota 01 - Ângulo e a Unidade de medida Grau Márcio Nascimento da Silva Universidade Estadual Vale do caraú - UV Curso de Licenciatura em Matemática [email protected]
Aula 33.1 Conteúdo: Ângulos: conceito e classificação dos ângulos; Relação entre ângulos FORTALECENDO SABERES CONTEÚDO E HABILIDADES
 CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO DO DIA Aula 33.1 Conteúdo: Ângulos: conceito e classificação dos ângulos; Relação entre ângulos 2 CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO
CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO DO DIA Aula 33.1 Conteúdo: Ângulos: conceito e classificação dos ângulos; Relação entre ângulos 2 CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO
MATEMÁTICA 3 GEOMETRIA PLANA Professor Renato Madeira
 MATEMÁTICA 3 GEOMETRIA PLANA Professor Renato Madeira MÓDULO 1 Fundamentos de Geometria Euclidiana Plana e Ângulos SUMÁRIO 1. Fundamentos 1.1. Postulados principais 1.2. Determinação do plano 1.3. Posições
MATEMÁTICA 3 GEOMETRIA PLANA Professor Renato Madeira MÓDULO 1 Fundamentos de Geometria Euclidiana Plana e Ângulos SUMÁRIO 1. Fundamentos 1.1. Postulados principais 1.2. Determinação do plano 1.3. Posições
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE. Professor: João Carmo
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo INTRODUÇÃO Os ângulos são formados por duas semi-retas que têm a mesma origem O. OBS.: o ângulo é denominado
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo INTRODUÇÃO Os ângulos são formados por duas semi-retas que têm a mesma origem O. OBS.: o ângulo é denominado
Triângulos e quadriláteros - o triângulo, formado por três segmentos (3 lados); - o quadrilátero, formado por quatro segmentos (4 lados).
 CONSTRUINDO O PENSAMENTO GEOMÉTRICO O plano e as figuras planas Muito do que está à nossa volta nos dá a idéia de plano, como a superfície de uma folha de papel ou de uma chapa de aço. Para resolver problemas
CONSTRUINDO O PENSAMENTO GEOMÉTRICO O plano e as figuras planas Muito do que está à nossa volta nos dá a idéia de plano, como a superfície de uma folha de papel ou de uma chapa de aço. Para resolver problemas
Conceitos básicos de Geometria:
 Conceitos básicos de Geometria: Os conceitos de ponto, reta e plano não são definidos. Compreendemos estes conceitos a partir de um entendimento comum utilizado cotidianamente dentro e fora do ambiente
Conceitos básicos de Geometria: Os conceitos de ponto, reta e plano não são definidos. Compreendemos estes conceitos a partir de um entendimento comum utilizado cotidianamente dentro e fora do ambiente
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Ângulos - Parte 1. Oitavo Ano
 Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 1 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha 1 Ângulos Uma região R do plano é convexa
Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 1 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha 1 Ângulos Uma região R do plano é convexa
Introdução à Geometria Plana. Professor: Antonio Carlos Barros
 Introdução à Geometria Plana Professor: Antonio Carlos Barros Entes Primitivos São os elementos matemáticos que não possuem definição. Ponto nomeado por letra Latina maiúscula. Reta nomeado por letra Latina
Introdução à Geometria Plana Professor: Antonio Carlos Barros Entes Primitivos São os elementos matemáticos que não possuem definição. Ponto nomeado por letra Latina maiúscula. Reta nomeado por letra Latina
7º ANO ENSINO FUNDAMENTAL Matemática. 1º Trimestre 45 questões 26 de abril (Sexta-feira)
 7º ANO ENSINO FUNDAMENTAL Matemática S4 1º Trimestre 45 questões 26 de abril (Sexta-feira) 2019 SIMULADO OBJETIVO 7º ANO 1º TRIMESTRE MATEMÁTICA 1 A situação que representa um número positivo é: a) Há
7º ANO ENSINO FUNDAMENTAL Matemática S4 1º Trimestre 45 questões 26 de abril (Sexta-feira) 2019 SIMULADO OBJETIVO 7º ANO 1º TRIMESTRE MATEMÁTICA 1 A situação que representa um número positivo é: a) Há
Preparação para a Prova Final de Matemática 2.º Ciclo do Ensino Básico Olá, Matemática! 6.º Ano
 Geometria Figuras no plano Retas, semirretas e segmentos de reta Ângulos: amplitude e medição Polígonos: propriedades e classificação Círculo e circunferência: propriedades e construção Reflexão, rotação
Geometria Figuras no plano Retas, semirretas e segmentos de reta Ângulos: amplitude e medição Polígonos: propriedades e classificação Círculo e circunferência: propriedades e construção Reflexão, rotação
Lista de exercícios Aluno (a): Turma: 7º ano (Ensino Fundamental) Professor(a): Denise Santos Disciplina: Matemática
 Lista de exercícios Aluno (a): Turma: 7º ano (Ensino Fundamental) Professor(a): Denise Santos Disciplina: Matemática No Anhanguera você é + Enem Antes de iniciar a lista de exercícios leia atentamente
Lista de exercícios Aluno (a): Turma: 7º ano (Ensino Fundamental) Professor(a): Denise Santos Disciplina: Matemática No Anhanguera você é + Enem Antes de iniciar a lista de exercícios leia atentamente
Trigonometria no Triângulo Retângulo
 Trigonometria no Triângulo Retângulo Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina:
Trigonometria no Triângulo Retângulo Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina:
Radianos. Prof. Márcio Nascimento.
 Radianos Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática Básica II
Radianos Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática Básica II
MATEMÁTICA, 6º Ano do Ensino Fundamental Medidas de ângulos. O que me vem à cabeça quando visualizo a palavra ÂNGULO?
 O que me vem à cabeça quando visualizo a palavra ÂNGULO? Afinal, o que é um ângulo? É o nome que se dá à abertura formada por duas semirretas que partem de um mesmo ponto. Essas semirretas são os lados
O que me vem à cabeça quando visualizo a palavra ÂNGULO? Afinal, o que é um ângulo? É o nome que se dá à abertura formada por duas semirretas que partem de um mesmo ponto. Essas semirretas são os lados
Figura 1 Sala de aula Fonte: Microsoft Office
 ÂNGULOS CONTEÚDOS Ângulos Classificação de um ângulo Ângulos complementares e suplementares Ângulos adjacentes Bissetriz de um ângulo AMPLIANDO SEUS CONHECIMENTOS A ideia de ângulo está presente nas mais
ÂNGULOS CONTEÚDOS Ângulos Classificação de um ângulo Ângulos complementares e suplementares Ângulos adjacentes Bissetriz de um ângulo AMPLIANDO SEUS CONHECIMENTOS A ideia de ângulo está presente nas mais
Atividade complementar I BIMESTRE Ângulos I a Parte
 Aluno(a) Turma N o Série 7 0 Ano Ensino Fundamental II Data / / Disciplina MATEMÁTICA Professores Luís Eduardo / George Atividade complementar I BIMESTRE Ângulos I a Parte 01. Escreva a definição de cada
Aluno(a) Turma N o Série 7 0 Ano Ensino Fundamental II Data / / Disciplina MATEMÁTICA Professores Luís Eduardo / George Atividade complementar I BIMESTRE Ângulos I a Parte 01. Escreva a definição de cada
META Introduzir os axiomas de medição de segmentos e ângulos. OBJETIVOS Determinar o comprimento de um segmento e a distância entre
 META Introduzir os axiomas de medição de segmentos e ângulos. AULA OBJETIVOS Determinar o comprimento de um segmento e a distância entre dois pontos. Determinar a medida de um ângulo Determinar propriedades
META Introduzir os axiomas de medição de segmentos e ângulos. AULA OBJETIVOS Determinar o comprimento de um segmento e a distância entre dois pontos. Determinar a medida de um ângulo Determinar propriedades
Nome: Nº: Disciplina: Matemática. Professor: Sandro Dias Martins CONTEÚDO DE MATEMÁTICA (ÂNGULOS)
 Nota: Nome: Nº: Disciplina: Matemática Professor: Sandro Dias Martins Turma: Data: / / 20 CONTEÚDO DE MATEMÁTICA (ÂNGULOS) O ÂNGULO E SEUS ELEMENTOS Duas semi-retas que não estejam contidas na mesma reta,
Nota: Nome: Nº: Disciplina: Matemática Professor: Sandro Dias Martins Turma: Data: / / 20 CONTEÚDO DE MATEMÁTICA (ÂNGULOS) O ÂNGULO E SEUS ELEMENTOS Duas semi-retas que não estejam contidas na mesma reta,
Revisão de Círculos. Geometria Básica Profa Lhaylla Crissaff
 Revisão de Círculos Geometria Básica Profa Lhaylla Crissaff 2017.2 1 Definição Circunferência é uma figura geométrica formada por todos os pontos que estão a uma mesma distância de um ponto fixado no plano.
Revisão de Círculos Geometria Básica Profa Lhaylla Crissaff 2017.2 1 Definição Circunferência é uma figura geométrica formada por todos os pontos que estão a uma mesma distância de um ponto fixado no plano.
ÂNGULOS. Dados dois pontos distintos, a reunião do conjunto desses dois pontos com o conjunto dos pontos que estão entre eles é o segmento de reta.
 ÂNGULOS 1 CONSIDERAÇÕES PRELIMINARES 1.1 Notação de ponto, reta e plano: a) Letras: Ponto: letras maiúsculas: A, B, C,... Reta: letras minúsculas: a,b,c... Plano: letras gregas minúsculas: α, β, γ,...
ÂNGULOS 1 CONSIDERAÇÕES PRELIMINARES 1.1 Notação de ponto, reta e plano: a) Letras: Ponto: letras maiúsculas: A, B, C,... Reta: letras minúsculas: a,b,c... Plano: letras gregas minúsculas: α, β, γ,...
Curso: Engenharia Disciplina: Desenho Técnico Prof.ª Me. Aline Ribeiro CONSTRUÇÕES GEOMÉTRICAS 1. DESENHO GEOMÉTRICO
 1 Curso: Engenharia Disciplina: Desenho Técnico Prof.ª Me. Aline Ribeiro CONSTRUÇÕES GEOMÉTRICAS 1. DESENHO GEOMÉTRICO 1.1. O que é desenho geométrico Desenho Geométrico é o conjunto de técnicas utilizadas
1 Curso: Engenharia Disciplina: Desenho Técnico Prof.ª Me. Aline Ribeiro CONSTRUÇÕES GEOMÉTRICAS 1. DESENHO GEOMÉTRICO 1.1. O que é desenho geométrico Desenho Geométrico é o conjunto de técnicas utilizadas
RETAS E CIRCUNFERÊNCIAS
 RETAS E CIRCUNFERÊNCIAS Diâmetro Corda que passa pelo centro da circunferência [EF] e [GH] Raio Segmento de reta que une o centro a um ponto da circunferência [OD] [AB], [IJ], [GH], são cordas - segmentos
RETAS E CIRCUNFERÊNCIAS Diâmetro Corda que passa pelo centro da circunferência [EF] e [GH] Raio Segmento de reta que une o centro a um ponto da circunferência [OD] [AB], [IJ], [GH], são cordas - segmentos
Segue, abaixo, o Roteiro de Estudo para a Verificação Global 2 (VG2), que acontecerá no dia 03 de abril de º Olímpico Matemática I
 6º Olímpico Matemática I Sistema de numeração romano. Situações problema com as seis operações com números naturais (adição, subtração, multiplicação, divisão, potenciação e radiciação). Expressões numéricas
6º Olímpico Matemática I Sistema de numeração romano. Situações problema com as seis operações com números naturais (adição, subtração, multiplicação, divisão, potenciação e radiciação). Expressões numéricas
PLANIFICAÇÃO MENSAL DE MATEMÁTICA
 AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA- Cantanhede DEPARTAMENTO CURRICULAR DO 1.º CICLO 4.º ANO DE ESCOLARIDADE PLANIFICAÇÃO MENSAL DE MATEMÁTICA Metas (objectivos) / Descritores de desempenho setembro
AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA- Cantanhede DEPARTAMENTO CURRICULAR DO 1.º CICLO 4.º ANO DE ESCOLARIDADE PLANIFICAÇÃO MENSAL DE MATEMÁTICA Metas (objectivos) / Descritores de desempenho setembro
TEMA / CONTEÚDOS OBJETIVOS / DESCRITORES DE DESEMPENHO AVALIAÇÃO GESTÃO DO TEMPO Contar até ao bilião (mil milhões).
 Números naturais Relações numéricas Operações com números naturais Adição Subtração Números naturais Múltiplos e divisores Operações com números naturais Multiplicação Regularidades Sequências ANO LETIVO
Números naturais Relações numéricas Operações com números naturais Adição Subtração Números naturais Múltiplos e divisores Operações com números naturais Multiplicação Regularidades Sequências ANO LETIVO
PLANIFICAÇÃO ANUAL DE MATEMÁTICA
 AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA- Cantanhede DEPARTAMENTO CURRICULAR DO 1.º CICLO 4.º ANO DE ESCOLARIDADE PLANIFICAÇÃO ANUAL DE MATEMÁTICA Domínios Subdomínios / Conteúdos programáticos METAS
AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA- Cantanhede DEPARTAMENTO CURRICULAR DO 1.º CICLO 4.º ANO DE ESCOLARIDADE PLANIFICAÇÃO ANUAL DE MATEMÁTICA Domínios Subdomínios / Conteúdos programáticos METAS
Matriz Curricular 1º Ciclo 4.ºAno / 2016 Ano de Escolaridade: 4.º Ano Matemática
 Ano Letivo: 2015 / 2016 Ano de Escolaridade: 4.º Ano Matemática Nº total de dias letivos 164 dias Nº de dias letivos - 1.º período - 64 dias - 2.º período - 52 dias - 3.º período - 48 dias Nº Total de
Ano Letivo: 2015 / 2016 Ano de Escolaridade: 4.º Ano Matemática Nº total de dias letivos 164 dias Nº de dias letivos - 1.º período - 64 dias - 2.º período - 52 dias - 3.º período - 48 dias Nº Total de
Radianos e Graus. Prof. Márcio Nascimento.
 Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática Básica II - 2015.1
Prof. Márcio Nascimento [email protected] Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Matemática Básica II - 2015.1
PLANIFICAÇÃO ANUAL 2015/ º Ano Matemática. METAS Domínios/Conteúdos Objetivos Descritores de Desempenho
 METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Número e Operações - Números naturais 1. Contar 1.1. Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de
METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Número e Operações - Números naturais 1. Contar 1.1. Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de
MMC, MDC, TRATAMENTO DA INFORMAÇÃO E GEOMETRIA. Profª Gerlaine Alves
 MMC, MDC, TRATAMENTO DA INFORMAÇÃO E GEOMETRIA Profª Gerlaine Alves Múltiplos e Divisores Divisores: dizemos que um número é divisor do outro número quando a divisão for exata, ou seja, quando o resto
MMC, MDC, TRATAMENTO DA INFORMAÇÃO E GEOMETRIA Profª Gerlaine Alves Múltiplos e Divisores Divisores: dizemos que um número é divisor do outro número quando a divisão for exata, ou seja, quando o resto
4 º Ano Matemática. METAS Domínios/Conteúdos Objetivos Descritores de Desempenho
 METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Ao longo do ano Números e Operações 3. Resolver problemas 3.1. Resolver problemas de vários passos envolvendo as quatro operações. setembro/
METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Ao longo do ano Números e Operações 3. Resolver problemas 3.1. Resolver problemas de vários passos envolvendo as quatro operações. setembro/
CRITÉRIOS DE AVALIAÇÃO 1º CICLO 4.º ANO DE ESCOLARIDADE MATEMÁTICA
 ANO LETIVO 0/06 CRITÉRIOS DE AVALIAÇÃO º CICLO.º ANO DE ESCOLARIDADE MATEMÁTICA Números e Operações Números naturais Contar Reconhece, sem falhas, que se poderia prosseguir a contagem indefinidamente introduzindo
ANO LETIVO 0/06 CRITÉRIOS DE AVALIAÇÃO º CICLO.º ANO DE ESCOLARIDADE MATEMÁTICA Números e Operações Números naturais Contar Reconhece, sem falhas, que se poderia prosseguir a contagem indefinidamente introduzindo
4. Saber a relação entre o número de lados e diagonais em polígonos convexos.
 Objetivos da aula 1 Saber usar o ângulo externo de um polígono 2 Saber que ângulos alternos internos têm a mesma medida 3 Saber calcular a soma dos ângulos internos de um polígono 4 Saber a relação entre
Objetivos da aula 1 Saber usar o ângulo externo de um polígono 2 Saber que ângulos alternos internos têm a mesma medida 3 Saber calcular a soma dos ângulos internos de um polígono 4 Saber a relação entre
Planificação Anual Departamento 1.º Ciclo
 Modelo Dep-01 Agrupamento de Escolas do Castêlo da Maia Planificação Anual Departamento 1.º Ciclo Ano 4º Ano letivo 2013.2014 Disciplina: Matemática Turmas: 4º ano Professores: todos os docentes do 4º
Modelo Dep-01 Agrupamento de Escolas do Castêlo da Maia Planificação Anual Departamento 1.º Ciclo Ano 4º Ano letivo 2013.2014 Disciplina: Matemática Turmas: 4º ano Professores: todos os docentes do 4º
PLANIFICAÇÃO MENSAL/ANUAL Matemática 4.ºano
 PLANIFICAÇÃO MENSAL/ANUAL Matemática 4.ºano MATEMÁTICA 4.º ANO DE ESCOLARIDADE Domínio/ Subdomínio Números Naturais Operações com números naturais Números racionais não negativos Metas a atingir Contar
PLANIFICAÇÃO MENSAL/ANUAL Matemática 4.ºano MATEMÁTICA 4.º ANO DE ESCOLARIDADE Domínio/ Subdomínio Números Naturais Operações com números naturais Números racionais não negativos Metas a atingir Contar
Ensino Fundamental II 8º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO
 COLÉGIO SHALOM 65 Ensino Fundamental II 8º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO TRABALHO DE RECUPERAÇÃO 1) Use a malha quadriculada a seguir para elaborar
COLÉGIO SHALOM 65 Ensino Fundamental II 8º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO TRABALHO DE RECUPERAÇÃO 1) Use a malha quadriculada a seguir para elaborar
1º Período MATEMÁTICA 4.º ANO. setembro. Domínios Conteúdos programáticos Objetivos/Descritores de desempenho
 1º Período setembro Números e Operações Dezenas e centenas de milhar. Resolução de problemas. Rever a matéria do ano anterior Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo
1º Período setembro Números e Operações Dezenas e centenas de milhar. Resolução de problemas. Rever a matéria do ano anterior Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo
Matemática. Nesta aula iremos aprender as. 1 Ponto, reta e plano. 2 Posições relativas de duas retas
 Matemática Aula 5 Geometria Plana Alexandre Alborghetti Londero Nesta aula iremos aprender as noções básicas de Geometria Plana. 1 Ponto, reta e plano Estes elementos primitivos da geometria euclidiana
Matemática Aula 5 Geometria Plana Alexandre Alborghetti Londero Nesta aula iremos aprender as noções básicas de Geometria Plana. 1 Ponto, reta e plano Estes elementos primitivos da geometria euclidiana
Angulo reto, agudo, obtuso - Medida ,...,,...
 IV. Angulo reto, agudo, obtuso - Medida 39. Angulo suplementar adjacente - - - - Dado o angulo AOB, a semi-reta OC oposta a semi-reta OA e a semi-reta OB determinam um angulo BOC que se Chama iingulo suplementar
IV. Angulo reto, agudo, obtuso - Medida 39. Angulo suplementar adjacente - - - - Dado o angulo AOB, a semi-reta OC oposta a semi-reta OA e a semi-reta OB determinam um angulo BOC que se Chama iingulo suplementar
- Plano Anual 4º Ano de Escolaridade -
 Números e Operações TEM A - Plano Anual 4º Ano de Escolaridade - Matemática Domínios de Referência Contar 1.Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de construção
Números e Operações TEM A - Plano Anual 4º Ano de Escolaridade - Matemática Domínios de Referência Contar 1.Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de construção
Graus e Radianos. Dinâmica 7. Professor. 1ª Série 4º Bimestre. DISCIPLINA Série CAMPO CONCEITO DINÂMICA CURRÍCULO MÍNIMO
 Reforço escolar M ate mática Graus e Radianos Dinâmica 7 1ª Série 4º Bimestre DISCIPLINA Série CAMPO CONCEITO Matemática 1a do Ensino Médio Geométrico DINÂMICA Graus e Radianos. Trigonometria da Circunferência
Reforço escolar M ate mática Graus e Radianos Dinâmica 7 1ª Série 4º Bimestre DISCIPLINA Série CAMPO CONCEITO Matemática 1a do Ensino Médio Geométrico DINÂMICA Graus e Radianos. Trigonometria da Circunferência
P L A N I F I C A Ç Ã O A N U A L
 P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: 1.º Ciclo DISCIPLINA: Matemática ANO DE ESCOLARIDADE: 4.º ANO LETIVO: 2017/2018 MANUAL: Projeto Desafios / Matemática 4.º ano Revisões Números e Operações
P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: 1.º Ciclo DISCIPLINA: Matemática ANO DE ESCOLARIDADE: 4.º ANO LETIVO: 2017/2018 MANUAL: Projeto Desafios / Matemática 4.º ano Revisões Números e Operações
SIMULADO OBJETIVO S4
 SIMULADO OBJETIVO S4 7º ano - Ensino Fundamental 1º Trimestre Matemática Dia: 05/05 - Sábado Nome completo: Turma: Unidade: 018 ORIENTAÇÕES PARA APLICAÇÃO DA PROVA OBJETIVA - 1º TRI 1 A prova terá duração
SIMULADO OBJETIVO S4 7º ano - Ensino Fundamental 1º Trimestre Matemática Dia: 05/05 - Sábado Nome completo: Turma: Unidade: 018 ORIENTAÇÕES PARA APLICAÇÃO DA PROVA OBJETIVA - 1º TRI 1 A prova terá duração
Domínio: Geometria. CONSELHO de DOCENTES 1.º Ciclo Página 1
 Domínio: Geometria Subdomínio/Conteúdos Localização e orientação no espaço - Ângulo formado por duas direções; vértice de um ângulo; - Ângulos com a mesma amplitude; - A meia volta e o quarto de volta
Domínio: Geometria Subdomínio/Conteúdos Localização e orientação no espaço - Ângulo formado por duas direções; vértice de um ângulo; - Ângulos com a mesma amplitude; - A meia volta e o quarto de volta
Exemplo Aplicando a proporcionalidade existente no Teorema de Tales, determine o valor dos segmentos AB e BC na ilustração a seguir:
 GEOMETRIA PLANA TEOREMA DE TALES O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: Se duas retas transversais são cortadas por um feixe de retas paralelas, então a razão entre
GEOMETRIA PLANA TEOREMA DE TALES O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: Se duas retas transversais são cortadas por um feixe de retas paralelas, então a razão entre
Axiomas de Incidência Axiomas de Ordem Axiomas de Congruência Axioma das paralelas Axiomas de Continuidade
 1 GEOMETRIA PLANA Atualizado em 04/08/2008 www.mat.ufmg.br/~jorge Bibliografia 1. Pogorélov, A.V. Geometria Elemental Editora Mir. 2. Dolce, Osvaldo e Nicolau, Pompeu Geometria Plana Volume 9 da Coleção
1 GEOMETRIA PLANA Atualizado em 04/08/2008 www.mat.ufmg.br/~jorge Bibliografia 1. Pogorélov, A.V. Geometria Elemental Editora Mir. 2. Dolce, Osvaldo e Nicolau, Pompeu Geometria Plana Volume 9 da Coleção
GEOMETRIA. Esse quadradinho no ângulo O significa que é um ângulo reto e sua medida equivale a 90 graus.
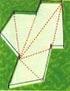 GEOMETRIA Ângulos É a abertura existente entre duas semi-retas que tem a mesma origem. Ângulo reto é formado por duas semi-retas perpendiculares, ou seja, uma horizontal e uma vertical sendo o ponto de
GEOMETRIA Ângulos É a abertura existente entre duas semi-retas que tem a mesma origem. Ângulo reto é formado por duas semi-retas perpendiculares, ou seja, uma horizontal e uma vertical sendo o ponto de
Código da Disciplina CCE0985. Aula 3.
 Código da Disciplina CCE0985 Aula 3 e-mail:[email protected] http://cleliamonasterio.blogspot.com/ O que é geometria? Palavra de origem grega: GEO (terra) METRIA (medida). Há 5.000 anos, era
Código da Disciplina CCE0985 Aula 3 e-mail:[email protected] http://cleliamonasterio.blogspot.com/ O que é geometria? Palavra de origem grega: GEO (terra) METRIA (medida). Há 5.000 anos, era
sen(α)=-sen(360-α) cos(α)=cos(360-α) sen(α)=cos(90-α) cos(α)=sen(90-α) α α sen(α)=-sen(180+α) cos(α)=-cos(180+α) Prof. Gabriel Cremona Parma
 Prof. Gabriel Cremona Parma = = = á í. = = = á í. = TA= = Raio do círculo trigonométrico sempre o raio unitário (igual á uma unidade). X X X tan(x) Simulação online das Funções Trigonométricas: http://alexsanderam.brinkster.net/geogebra/.html
Prof. Gabriel Cremona Parma = = = á í. = = = á í. = TA= = Raio do círculo trigonométrico sempre o raio unitário (igual á uma unidade). X X X tan(x) Simulação online das Funções Trigonométricas: http://alexsanderam.brinkster.net/geogebra/.html
PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO
 PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO Domínios Subdomínios Objetivos Descritores/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Tratamento dados de Representar e interpretar dados e situações
PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO Domínios Subdomínios Objetivos Descritores/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Tratamento dados de Representar e interpretar dados e situações
Agrupamento de Escolas de Sátão, Matemática 4º ano, Planificação Anual PLANIFICAÇÃO ANUAL
 Agrupamento de Escolas de Sátão, Matemática 4º ano, Planificação Anual DOMÍNIOS/ Subdomínios NÚMEROS E OPERAÇÕES Números naturais CONTEÚDOS (Programa) Extensão das regras de construção dos numerais decimais
Agrupamento de Escolas de Sátão, Matemática 4º ano, Planificação Anual DOMÍNIOS/ Subdomínios NÚMEROS E OPERAÇÕES Números naturais CONTEÚDOS (Programa) Extensão das regras de construção dos numerais decimais
Módulo de Elementos básicos de geometria plana. Oitavo Ano
 Módulo de Elementos básicos de geometria plana Ângulos Oitavo Ano Ângulos 1 Exercícios Introdutórios Exercício 1. No desenho abaixo, OC é bissetriz do ângulo AOB. Se AOC = x 5 e COB = x + 3, quanto vale
Módulo de Elementos básicos de geometria plana Ângulos Oitavo Ano Ângulos 1 Exercícios Introdutórios Exercício 1. No desenho abaixo, OC é bissetriz do ângulo AOB. Se AOC = x 5 e COB = x + 3, quanto vale
TRABALHO SOBRE ÂNGULOS E POLÍGONOS - 8º ANO- ENSINO FUNDAMENTAL VALOR: 4,0 PONTOS INSTRUÇÕES - LEIA COM MUITA ATENÇÃO
 TRABALHO SOBRE ÂNGULOS E POLÍGONOS - 8º ANO- ENSINO FUNDAMENTAL - 2014 - VALOR: 4,0 PONTOS INSTRUÇÕES - LEIA COM MUITA ATENÇÃO - O envio das respostas será aceito até: 16/04/2014, às 23h59min. Faça seu
TRABALHO SOBRE ÂNGULOS E POLÍGONOS - 8º ANO- ENSINO FUNDAMENTAL - 2014 - VALOR: 4,0 PONTOS INSTRUÇÕES - LEIA COM MUITA ATENÇÃO - O envio das respostas será aceito até: 16/04/2014, às 23h59min. Faça seu
Agrupamento de Escolas Dr. Vieira de Carvalho P L A N I F I C A Ç Ã O A N U A L D E M A T E M Á T I C A
 Agrupamento de Escolas Dr. Vieira de Carvalho P L A N I F I C A Ç Ã O A N U A L D E M A T E M Á T I C A ANO LETIVO 2016/2017 1º Período Domínios Subdomínios / Conteúdos Números e Operações Números naturais
Agrupamento de Escolas Dr. Vieira de Carvalho P L A N I F I C A Ç Ã O A N U A L D E M A T E M Á T I C A ANO LETIVO 2016/2017 1º Período Domínios Subdomínios / Conteúdos Números e Operações Números naturais
ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO. 1- Ângulos Definição: Chama-se ângulo à porção de plano limitada por duas semirretas com a mesma origem.
 ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO 1ª Ficha Informativa MATEMÁTICA - A 10º Ano 2012/2013 1- Ângulos Definição: Chama-se ângulo à porção de plano limitada por duas semirretas com a mesma origem. Definição:
ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO 1ª Ficha Informativa MATEMÁTICA - A 10º Ano 2012/2013 1- Ângulos Definição: Chama-se ângulo à porção de plano limitada por duas semirretas com a mesma origem. Definição:
TRIGONOMETRIA. AO VIVO MATEMÁTICA Professor Haroldo Filho 02 de fevereiro, AS FUNÇÕES TRIGONOMÉTRICAS DO ÂNGULO AGUDO OA OA OA OA OA OA
 TRIGONOMETRIA 1. AS FUNÇÕES TRIGONOMÉTRICAS DO ÂNGULO AGUDO Considere um ângulo agudo = AÔB, e tracemos a partir dos pontos A, A 1, A etc. da semirreta AO, perpendiculares à semirreta OB. AB A1B1 AB OAB
TRIGONOMETRIA 1. AS FUNÇÕES TRIGONOMÉTRICAS DO ÂNGULO AGUDO Considere um ângulo agudo = AÔB, e tracemos a partir dos pontos A, A 1, A etc. da semirreta AO, perpendiculares à semirreta OB. AB A1B1 AB OAB
Atividade 1 Retrato Falado
 espaço e forma Atividade 1 Retrato Falado 1º momento: Leitura É importante saber o nome das coisas. Ou, pelo menos, saber comunicar o que você quer. Imagine-se entrando numa loja para comprar um um como
espaço e forma Atividade 1 Retrato Falado 1º momento: Leitura É importante saber o nome das coisas. Ou, pelo menos, saber comunicar o que você quer. Imagine-se entrando numa loja para comprar um um como
CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES
 CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES CÍRCULO E CIRCUNFERÊNCIA Circunferência: é uma linha. Exemplos: argola, roda de bicicleta... Círculo: é uma superfície. Exemplos: moeda, mesa redonda... CIRCUNFERÊNCIA
CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES CÍRCULO E CIRCUNFERÊNCIA Circunferência: é uma linha. Exemplos: argola, roda de bicicleta... Círculo: é uma superfície. Exemplos: moeda, mesa redonda... CIRCUNFERÊNCIA
Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015
 Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015 Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Números e Operações Números Naturais Extensão
Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015 Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Números e Operações Números Naturais Extensão
GEOMETRIA ÂNGULOS. Ângulos
 O ÂNGULO E OS SEUS ELEMENTOS Ângulos Duas semi-retas que não estejam contidas na mesma reta, e que tenham a mesma origem, dividem o plano em duas regiões: uma convexa e outra não-convexa. Cada uma dessas
O ÂNGULO E OS SEUS ELEMENTOS Ângulos Duas semi-retas que não estejam contidas na mesma reta, e que tenham a mesma origem, dividem o plano em duas regiões: uma convexa e outra não-convexa. Cada uma dessas
CONSTRUÇÕES GEOMÉTRICAS FUNDAMENTAIS
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPARTAMENTO DE EXPRESSÃO GRÁFICA CONSTRUÇÕES GEOMÉTRICAS FUNDAMENTAIS 2 1 NOÇÕES DE GEOMETRIA PLANA 1.1 GEOMETRIA A necessidade de medir terras
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPARTAMENTO DE EXPRESSÃO GRÁFICA CONSTRUÇÕES GEOMÉTRICAS FUNDAMENTAIS 2 1 NOÇÕES DE GEOMETRIA PLANA 1.1 GEOMETRIA A necessidade de medir terras
Objetivos da aula. 1. Saber usar o ângulo externo de um polígono. 2. Saber que ângulos alternos internos têm a mesma medida.
 Objetivos da aula 1 Saber usar o ângulo externo de um polígono 2 Saber que ângulos alternos internos têm a mesma medida 3 Saber calcular a soma dos ângulos internos de um polígono 4 Saber a relação entre
Objetivos da aula 1 Saber usar o ângulo externo de um polígono 2 Saber que ângulos alternos internos têm a mesma medida 3 Saber calcular a soma dos ângulos internos de um polígono 4 Saber a relação entre
Introdução ALGUNS CUIDADOS ESPECIAIS
 Introdução ALGUNS CUIDADOS ESPECIAIS Ao trabalhar com questões de Geometria Plana, é importante que você não incorra em determinados erros muito comuns. Vamos destacar dois deles. NUNCA PARTICULARIZE UMA
Introdução ALGUNS CUIDADOS ESPECIAIS Ao trabalhar com questões de Geometria Plana, é importante que você não incorra em determinados erros muito comuns. Vamos destacar dois deles. NUNCA PARTICULARIZE UMA
ÂNGULOS. Ângulos no círculo
 ÂNGULOS Ângulos no círculo A circunferência:. Diâmetro Semicircunferên cia Diâmetro - é o segmento de recta que une 2 pontos da circunferência passando pelo centro. Raio - é o segmento de recta que une
ÂNGULOS Ângulos no círculo A circunferência:. Diâmetro Semicircunferên cia Diâmetro - é o segmento de recta que une 2 pontos da circunferência passando pelo centro. Raio - é o segmento de recta que une
Material Teórico - Elementos Básicos de Geometria Plana - Parte 3. Oitavo Ano
 Material Teórico - Elementos ásicos de Geometria Plana - Parte 3 Número π e o Comprimento do Círculo itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha M. Neto Portal da MEP 1 número
Material Teórico - Elementos ásicos de Geometria Plana - Parte 3 Número π e o Comprimento do Círculo itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha M. Neto Portal da MEP 1 número
Plano Curricular de Matemática 4.º Ano - Ano Letivo 2016/2017
 4.º Ano - Ano Letivo 2016/2017 1.º Período - Números naturais Números e operações Contar Estender as regras de construção dos numerais decimais para classes de grandeza indefinida; Conhecer os diferentes
4.º Ano - Ano Letivo 2016/2017 1.º Período - Números naturais Números e operações Contar Estender as regras de construção dos numerais decimais para classes de grandeza indefinida; Conhecer os diferentes
ÂNGULOS e PARALELISMO
 Hewlett-Packard e PARALELISMO Aulas 01 e 02 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Sumário... 1 DEFINIÇÃO DE ÂNGULO... 1 CONGRUENTES ( )... 1 MEDIDA DE ÂNGULO... 1 SUBDIVISÕES DO GRAU... 1 EXERCÍCIOS
Hewlett-Packard e PARALELISMO Aulas 01 e 02 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Sumário... 1 DEFINIÇÃO DE ÂNGULO... 1 CONGRUENTES ( )... 1 MEDIDA DE ÂNGULO... 1 SUBDIVISÕES DO GRAU... 1 EXERCÍCIOS
Ângulos nos triângulos Teorema angular de Tales: a soma dos ângulos internos de qualquer triângulo é igual a 180º. a a + b + c = 180º
 RANILDO LOPES Ângulos nos triângulos Teorema angular de Tales: a soma dos ângulos internos de qualquer triângulo é igual a 180º. b a c a + b + c = 180º Teorema do ângulo externo: em qualquer triângulo,
RANILDO LOPES Ângulos nos triângulos Teorema angular de Tales: a soma dos ângulos internos de qualquer triângulo é igual a 180º. b a c a + b + c = 180º Teorema do ângulo externo: em qualquer triângulo,
Os ângulos estão sempre presentes em nossa vida e quase não nos damos conta disso. Quer ver?
 Se você observar um ângulo de 20 (20 graus) por uma lente que aumenta quatro vezes um objeto, qual será a amplitude (ou abertura) do ângulo visto por você através da lente? Um avião parte de uma cidade
Se você observar um ângulo de 20 (20 graus) por uma lente que aumenta quatro vezes um objeto, qual será a amplitude (ou abertura) do ângulo visto por você através da lente? Um avião parte de uma cidade
EMEF PROFESSORA MARIA MARGARIDA ZAMBON BENINI PIBID. Plano de aula 4 Abril de Ângulos
 EMEF PROFESSORA MARIA MARGARIDA ZAMBON BENINI PIBID Plano de aula 4 Abril de 2015 Ângulos Bolsistas: Mévelin Maus, Patrícia Lombelo, Natacha Subtil. Supervisora: Marlete Basso Roman Disciplina: Matemática
EMEF PROFESSORA MARIA MARGARIDA ZAMBON BENINI PIBID Plano de aula 4 Abril de 2015 Ângulos Bolsistas: Mévelin Maus, Patrícia Lombelo, Natacha Subtil. Supervisora: Marlete Basso Roman Disciplina: Matemática
Retas, semirretas e segmentos de reta. Ângulos, paralelismo e perpendicularidade. Critérios de igualdade de triângulos. Ângulos: amplitude e medição
 GEOMETRIA E MEDIDA Retas, semirretas e segmentos de reta Ângulos, paralelismo e perpendicularidade Triângulos e quadriláteros Critérios de igualdade de triângulos Ângulos: amplitude e medição Unidades
GEOMETRIA E MEDIDA Retas, semirretas e segmentos de reta Ângulos, paralelismo e perpendicularidade Triângulos e quadriláteros Critérios de igualdade de triângulos Ângulos: amplitude e medição Unidades
AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE 1º Ciclo - Grupo 110. Planificação Anual /Critérios de avaliação
 AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE 1º Ciclo - Grupo 110 Planificação Anual /Critérios de Disciplina: Matemática 4.º ano 2014/2015 Domínio (Unidade/ tema) Subdomínio/Conteúdos Metas
AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE 1º Ciclo - Grupo 110 Planificação Anual /Critérios de Disciplina: Matemática 4.º ano 2014/2015 Domínio (Unidade/ tema) Subdomínio/Conteúdos Metas
Ângulo é a abertura que duas semi-reta faz. Observe a figura:
 A geometria plana estuda a geometria no plano, ou seja, em uma coisa plana, imagine um desenho em uma folha de papel ou no chão. Resumindo, a geometria plana tem o objetivo de estudar as figuras geométricas
A geometria plana estuda a geometria no plano, ou seja, em uma coisa plana, imagine um desenho em uma folha de papel ou no chão. Resumindo, a geometria plana tem o objetivo de estudar as figuras geométricas
Estudo da Geometria Euclidiana Plana
 Instituto Municipal de Ensino Superior de Catanduva SP Curso de Licenciatura em Matemática 2º ano Prática de Ensino da Matemática II Prof. M.Sc. Fabricio Eduardo Ferreira [email protected] Estudo da Geometria
Instituto Municipal de Ensino Superior de Catanduva SP Curso de Licenciatura em Matemática 2º ano Prática de Ensino da Matemática II Prof. M.Sc. Fabricio Eduardo Ferreira [email protected] Estudo da Geometria
Matemática GEOMETRIA PLANA. Professor Dudan
 Matemática GEOMETRIA PLANA Professor Dudan Ângulos Geometria Plana Ângulo é a região de um plano concebida pelo encontro de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo. A
Matemática GEOMETRIA PLANA Professor Dudan Ângulos Geometria Plana Ângulo é a região de um plano concebida pelo encontro de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo. A
Informação - Ficha de Avaliação Global de Matemática 4.º ano. 1.º Ciclo do Ensino Básico maio de 2016
 Agrupamento de Escolas de Marrazes Cód. 1609 Informação - Ficha de Avaliação Global de Matemática.º ano 1.º Ciclo do Ensino Básico maio de 016 O presente documento divulga informação relativa à ficha de
Agrupamento de Escolas de Marrazes Cód. 1609 Informação - Ficha de Avaliação Global de Matemática.º ano 1.º Ciclo do Ensino Básico maio de 016 O presente documento divulga informação relativa à ficha de
um saquinho com rebuçados e gomas. Se ela colocar em cada saquinho 5 rebuçados e 3 gomas, quantas guloseimas ela vai precisar?
 FICHA DE AVALIAÇÃO DE MATEMÁTICA 5.º ANO Olá, Matemática! 5.º Ano Nome: Ano / Turma: N.º: Data: - - ANO LETIVO 2013-2014 Avaliação O Professor Enc. de Educação 1. Com os algarismos 6, 3 e 0 forma um número
FICHA DE AVALIAÇÃO DE MATEMÁTICA 5.º ANO Olá, Matemática! 5.º Ano Nome: Ano / Turma: N.º: Data: - - ANO LETIVO 2013-2014 Avaliação O Professor Enc. de Educação 1. Com os algarismos 6, 3 e 0 forma um número
DOMÍNIO/SUBDOMÍNIO OBJETIVOS GERAIS DESCRITORES DE DESEMPENHO CONTEÚDOS 1ºPeríodo
 DISCIPLINA: Matemática ANO DE ESCOLARIDADE: 5º Ano 2016/2017 METAS CURRICULARES PROGRAMA DOMÍNIO/SUBDOMÍNIO OBJETIVOS GERAIS DESCRITORES DE DESEMPENHO CONTEÚDOS 1ºPeríodo Álgebra - Expressões algébricas
DISCIPLINA: Matemática ANO DE ESCOLARIDADE: 5º Ano 2016/2017 METAS CURRICULARES PROGRAMA DOMÍNIO/SUBDOMÍNIO OBJETIVOS GERAIS DESCRITORES DE DESEMPENHO CONTEÚDOS 1ºPeríodo Álgebra - Expressões algébricas
1. Converta para a forma decimal: (a) (b) (c) (d) (e)
 UNIVERSIDADE ESTADUAL VALE DO ACARAÚ Coordenação de Matemática 1 a Lista de Exercícios - Ângulos Matemática Básica II - 2015.1 Professor Márcio Nascimento Fontes: Practice Makes Perfect - Trigonometry
UNIVERSIDADE ESTADUAL VALE DO ACARAÚ Coordenação de Matemática 1 a Lista de Exercícios - Ângulos Matemática Básica II - 2015.1 Professor Márcio Nascimento Fontes: Practice Makes Perfect - Trigonometry
PRÉ-VESTIBULINHO MATEMÁTICA. Leonardo Garibaldi Rigon Luís Otávio Lima Rochel
 PRÉ-VESTIBULINHO MATEMÁTICA Leonardo Garibaldi Rigon Luís Otávio Lima Rochel Setembro/2012 MATEMÁTICA FRAÇÃO Algumas vezes, a/b é uma número natural. Outras vezes, isso não acontece. Neste caso, qual é
PRÉ-VESTIBULINHO MATEMÁTICA Leonardo Garibaldi Rigon Luís Otávio Lima Rochel Setembro/2012 MATEMÁTICA FRAÇÃO Algumas vezes, a/b é uma número natural. Outras vezes, isso não acontece. Neste caso, qual é
MULTIPLOS; DIVISORES; TRATAMENTO DA INFORMAÇÃO E GEOMETRIA PROFª GERLAINE ALVES
 MULTIPLOS; DIVISORES; TRATAMENTO DA INFORMAÇÃO E GEOMETRIA PROFª GERLAINE ALVES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E
MULTIPLOS; DIVISORES; TRATAMENTO DA INFORMAÇÃO E GEOMETRIA PROFª GERLAINE ALVES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E DIVISORES MULTIPLOS E
LISTA DE EXERCÍCIOS MAT GEOMETRIA E DESENHO GEOMÉTRICO I
 LISTA DE EXERCÍCIOS MAT 230 - GEOMETRIA E DESENHO GEOMÉTRICO I 1. Numa geometria de incidência, o plano tem 5 pontos. Quantas retas tem este plano? A resposta é única? 2. Exibir um plano de incidência
LISTA DE EXERCÍCIOS MAT 230 - GEOMETRIA E DESENHO GEOMÉTRICO I 1. Numa geometria de incidência, o plano tem 5 pontos. Quantas retas tem este plano? A resposta é única? 2. Exibir um plano de incidência
COLÉGIO MARQUES RODRIGUES - SIMULADO
 COLÉGIO MRQUES RODRIGUES - SIMULDO PROFESSOR HENRIQUE LEL DISCIPLIN MTEMÁTIC SIMULDO: P5 Estrada da Água Branca, 2551 Realengo RJ Tel: (21) 3462-7520 www.colegiomr.com.br LUNO TURM 801 Questão 1 Qual dos
COLÉGIO MRQUES RODRIGUES - SIMULDO PROFESSOR HENRIQUE LEL DISCIPLIN MTEMÁTIC SIMULDO: P5 Estrada da Água Branca, 2551 Realengo RJ Tel: (21) 3462-7520 www.colegiomr.com.br LUNO TURM 801 Questão 1 Qual dos
À descoberta das retas, semirretas e segmentos de retas
 À descoberta das retas, semirretas e segmentos de retas RETAS NÃO TÊM PRINCIPIO NEM FIM Uma reta pode representar-se de duas formas: através de uma letra minúscula, s (reta s) através de duas letras maiúsculas,
À descoberta das retas, semirretas e segmentos de retas RETAS NÃO TÊM PRINCIPIO NEM FIM Uma reta pode representar-se de duas formas: através de uma letra minúscula, s (reta s) através de duas letras maiúsculas,
Geometria. Uma breve introdução
 Geometria Uma breve introdução Etimologia Geometria, em grego antigo γεωμετρία, geo- "terra", -metria "medida Origem (lazer ou necessidade?) Geometria Euclidiana Euclides de Alexandria, matemático grego
Geometria Uma breve introdução Etimologia Geometria, em grego antigo γεωμετρία, geo- "terra", -metria "medida Origem (lazer ou necessidade?) Geometria Euclidiana Euclides de Alexandria, matemático grego
Ângulo entre ponteiros do relógio 2016
 Ângulo entre ponteiros do relógio 2016 Exemplos: Calcule o valor do menor ângulo entre os ponteiros dos relógios. a) 4h b) 4h 10min c) 4h 12 min www.nsaulasparticulares.com.br Página 1 de 9 d) 4h 38 min
Ângulo entre ponteiros do relógio 2016 Exemplos: Calcule o valor do menor ângulo entre os ponteiros dos relógios. a) 4h b) 4h 10min c) 4h 12 min www.nsaulasparticulares.com.br Página 1 de 9 d) 4h 38 min
1º Período (15 de Setembro a 16 de Dezembro) 39 blocos = 78 aulas
 ESCOLA E B 2,3/S MIGUEL LEITÃO DE ANDRADA - AGRUPAMENTO DE ESCOLAS DE PEDRÓGÃO GRANDE DEPARTAMENTO DAS CIÊNCIAS EXATAS E TECNOLOGIAS 2016/2017 PLANIFICAÇÃO DE MATEMÁTICA 5 ºANO 1º Período 2º Período 3º
ESCOLA E B 2,3/S MIGUEL LEITÃO DE ANDRADA - AGRUPAMENTO DE ESCOLAS DE PEDRÓGÃO GRANDE DEPARTAMENTO DAS CIÊNCIAS EXATAS E TECNOLOGIAS 2016/2017 PLANIFICAÇÃO DE MATEMÁTICA 5 ºANO 1º Período 2º Período 3º
A1R. Matemática - Linhas e ângulos. Matemática - Linhas e ângulos. 1. Define os conceitos de: Reta. Semirreta. Segmento de reta.
 A1 Define os conceitos de: Reta Semirreta Segmento de reta A1R Reta É uma linha que não tem princípio nem fim. Semirreta É uma linha que tem princípio e não tem fim. Segmento de reta É uma linha que tem
A1 Define os conceitos de: Reta Semirreta Segmento de reta A1R Reta É uma linha que não tem princípio nem fim. Semirreta É uma linha que tem princípio e não tem fim. Segmento de reta É uma linha que tem
AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 4.º ANO DE ESCOLARIDADE
 Domínio/ NO4/ Números naturais NO4/ Números racionais não negativos AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 4.º ANO DE ESCOLARIDADE - 2016-2017 1. Contar 1. Reconhecer
Domínio/ NO4/ Números naturais NO4/ Números racionais não negativos AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 4.º ANO DE ESCOLARIDADE - 2016-2017 1. Contar 1. Reconhecer
Geometria Espacial Curso de Licenciatura em Matemática parte II. Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR
 Geometria Espacial Curso de Licenciatura em Matemática parte II Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR - 2014 1. Paralelismo de Retas L20 Postulado das Paralelas ( de Euclides )
Geometria Espacial Curso de Licenciatura em Matemática parte II Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR - 2014 1. Paralelismo de Retas L20 Postulado das Paralelas ( de Euclides )
O que é ângulo. Ângulo é a figura formada por duas semiretas. origem. Essas semiretas são os lados do ângulo e a origem comum é o vértice de ângulo.
 ÂNGULOS O que é ângulo. Ângulo é a figura formada por duas semiretas com a mesma origem. Essas semiretas são os lados do ângulo e a origem comum é o vértice de ângulo. Uma notação bastante usada hoje
ÂNGULOS O que é ângulo. Ângulo é a figura formada por duas semiretas com a mesma origem. Essas semiretas são os lados do ângulo e a origem comum é o vértice de ângulo. Uma notação bastante usada hoje
