As Transformações de Lorentz
|
|
|
- Maria do Pilar Irene Marinho Ramires
- 9 Há anos
- Visualizações:
Transcrição
1 As Transformações de Lorentz Michael Fowler Universidade de Virgínia, Departamento de Física Problemas com as transformações de Galileu A mecânica Newtoniana não se altera perante as transformações de Galileu, no que diz respeito a dois referenciais inerciais em movimento e com velocidade relativa v na direção x, Contudo, nestas transformações assume-se que o tempo é um conceito universal e bem definido, ou seja, é o mesmo em todo o lado, e todos os observadores estão de acordo quanto à contagem do tempo. Contudo, e uma vez aceite o postulado básico da relatividade restrita, que refere que as leis da física, incluindo as equações de Maxwell, são as mesmas em qualquer referencial inercial, e consequentemente a velocidade da luz tem o mesmo valor em qualquer referencial inercial, os observadores colocados em diferentes referenciais não estarão de acordo quanto à sincronia dos relógios, sempre que estes se encontrem a determinada distância um do outro. Para além disso, as dimensões dos objetos em movimento são comprimidas na direção do movimento pelo efeito da contração de Lorentz-Fitzgerald. É óbvio que as equações anteriores são demasiado simples! Devemos pensar cuidadosamente sobre a medição do tempo e do espaço, e construir novas equações de transformação que estejam de acordo com a relatividade restrita. O objetivo deste texto é levar-nos a encontrar um conjunto de equações análogas às anteriores, onde, num dado referencial S, as coordenadas (x, y, z, t) de determinado evento, como por exemplo a explosão de uma bomba, sejam função das coordenadas (x, y, z, t ) do mesmo evento mas medidas num referencial paralelo S que se encontra em movimento, com velocidade v, ao longo do eixo x do referencial S. Os observadores O, na origem do referencial S, e O, na origem do referencial S, sincronizam os seus relógios a t = t = 0 no momento em que passam um pelo outro, ou seja, quando os dois referenciais coincidem. Para determinar o instante de tempo t em que ocorre a explosão da bomba no referencial S, o observador O pode determinar a distância do ponto (x, y, z ) à origem, e seguidamente determinar quanto tempo levaria a luz da explosão a chegar à origem do referencial S e, portanto, ao observador O. Uma abordagem mais direta (e que pode ser útil quando temos em consideração transformações entre diferentes referenciais) é imaginar que o observador O possui uma enorme quantidade de ajudantes, todos munidos de relógios sincronizados utilizando para isso lâmpadas flash e relógios munidos de fotocélulas 1. Assim, o evento a explosão da bomba ocorrerá próximo de um dos relógios, e esse relógio determinará o tempo t em que o evento ocorre, para evitar ter que determinar o tempo que a luz demora desde o local da explosão até ao observador. No referencial S, o observador O e a sua equipa de ajudantes possuem relógios ao longo do eixo x, todos sincronizados: Pense agora como este conjunto de relógios será visto pelo observador O que se encontra no referencial S. Em primeiro lugar, e uma vez que se movem com velocidade v, os relógios medirão a passagem do tempo mais lentamente devido à dilatação do tempo, de acordo com o fator de, em comparação com os relógios idênticos do observador O. Em segundo lugar, os relógios não estarão sincronizados entre si. Se os relógios se encontrarem a uma distância L uns dos outros, distância essa determinada pelo observador O, em dois relógios sucessivos, o da direita (tendo em conta que o movimento ocorre no sentido da esquerda para a direita) estará atrasado, tal como observado por O. 1 N. do T.: Sobre o método para sincronizar relógios referido, ver o texto Relatividade Restrita Sincronizar Relógios, também publicado no portal Casa das Ciências. 1
2 Devemos ter em conta que esta dessincronização, observada a partir de outro referencial, ocorre apenas se houver afastamento entre os relógios na direção em que ocorre o movimento. Considere dois relógios a determinada distância um do outro, ao longo do eixo z do referencial S. Se ambos forem sincronizados pelo mesmo método utilizado anteriormente, torna-se claro que quando observados a partir do referencial S a luz percorre a mesma distância para chegar a cada um dos dois relógios, e por isso estes continuarão sincronizados (embora dessincronizados com os restantes relógios dispostos ao longo da direção do movimento devido ao fator de dilatação do tempo). Derivar as Transformações de Lorentz Suponhamos que o observador O e a sua equipa observam a pequena bomba a explodir em S nas coordenadas (x, 0, 0, t ). Vamos agora encontrar as coordenadas (x, y, z, t) do evento, tal como observadas por O no referencial S (tal como anteriormente, S move-se em relação a S com velocidade v constante e ao longo da direção x). Por outras palavras, devemos proceder à derivação das transformações de Lorentz que são apenas as equações das quatro coordenadas do evento num referencial inercial em função das coordenadas do mesmo evento noutro referencial inercial diferente do primeiro. Consideremos que y e z têm valor zero, uma vez que não ocorre contração de Lorentz-Fitzgerald perpendicular à direção do movimento, e por isso y = y e z = z. Em primeiro lugar, consideremos o instante em que a bomba explode tal como determinado pelo observador O. O observador O e a sua equipa determinaram que a explosão ocorreu no instante t, tal como medido pelo relógio que se encontrava no local da explosão, em x. Em seguida, e tal como observado por O a partir do referencial S, o relógio de O que se encontra na posição x não se encontra sincronizado com o relógio na origem do referencial S. Quando a bomba explode e o relógio na posição x marca o instante t, para o observador O o relógio de O que se encontra na origem do referencial S marca o instante. Que instante marcará o relógio do observador O? Lembre-se que os observadores O e O sincronizaram os relógios que se encontram sobre a origem dos referenciais no momento em que os referenciais coincidiram, sendo esse o instante t = t = 0. Consequentemente, e devido ao fator de dilatação do tempo, O observou o relógio de O a contar mais lentamente o tempo. Assim sendo, quando no instante da explosão, O observa que o relógio de O na origem do referencial S marca o instante tempo apresentado pelo seu relógio é dado por:, notará que no seu referencial, o pois deve ser tido em conta o fator de dilatação temporal. Esta é a primeira das transformações de Lorentz. Em segundo lugar, onde se encontra O quando observa a explosão? Uma vez que a explosão ocorre no instante t após O passar por O, O está vt metros à frente de O no instante t. A explosão ocorre x metros à frente de O, tal como determinado por O, mas é claro que para O essa distância surge contraída para, uma vez que se encontra sobre um referencial em movimento. Assim, O observa a ocorrência da explosão no ponto x, dado por Podemos reescrever a equação anterior para obter o valor de x como função de x e t, ao substituir t pela primeira transformação de Lorentz: Encontramos assim as transformações de Lorentz que expressam as coordenadas (x, y, z, t) de um evento num referencial S em função das coordenadas (x, y, z, t ) do mesmo evento num referencial S : 2
3 Repare que na derivação anterior nada depende do sentido do movimento do referencial S em relação a S e por isso, na transformação inversa (de (x, y, z, t) para (x, y, z, t )) utilizam-se exatamente as mesmas equações anteriores, com v substituído por v. Esferas de luz Considere agora o seguinte cenário: suponha que quando O passa por O (o instante em que ambos concordam quanto à sincronia dos relógios e em que t = t = 0), O emite um flash de luz brilhante que, segundo observa, ilumina uma zona esférica em expansão e com centro no próprio observador O (imagine que é um dia de algum nevoeiro, e que O consegue observar a propagação da luz a partir da fonte luminosa). No instante de tempo t, O (ou, para ser mais preciso, os ajudantes que constituem a sua equipa e que se encontram no mesmo referencial inercial) observa uma esfera de luz de raio ct, ou seja, observa iluminados todos os pontos (x, y, z, t ) da superfície Questão: como será que O e a sua equipa de ajudantes que se encontra em repouso e distribuída ao logo do referencial S observam a propagação e expansão desta luz? Para responder a esta questão, repare que a equação anterior e que diz respeito aos pontos de máximo afastamento da luz em relação à fonte em determinado instante t, tal como observada no referencial S pode ser escrita da seguinte forma: e pode ser imaginada como uma superfície num espaço a quatro dimensões (x, y, z, t ), e que contém todos os eventos de luz emitidos. Para encontrar a superfície correspondente a estes eventos de luz no espaço a quatro dimensões (x, y, z, t), é necessário utilizar as transformações de Lorentz para passar de um conjunto de variáveis, (x, y, z, t ), para o outro, (x, y, z, t): 2 2 N. do T.: Repare que nestas equações a velocidade surge como v, uma vez que a transformação é a inversa da considerada anteriormente, ou seja, neste caso a transformação é de (x, y, z, t ) para (x, y, z, t). 3
4 Ao substituir (x, y, z, t ) por (x, y, z, t) na equação a superfície resultante em (x, y, z, t) é: Isto significa que no instante de tempo t, O e a sua equipa de ajudantes no referencial S dirão que a luz se expandiu até originar uma superfície esférica de centro em O. Como podem O e O, que se afastam um do outro, estar ambos possivelmente corretos ao afirmar que em dado instante a luz emitida se expandiu até originar uma superfície esférica, tendo essa superfície centro em O, segundo o ponto de vista de O, e centro em O, segundo o ponto de vista de O? Imagine a esfera de luz tal como O a vê no instante t, O observa uma esfera de raio r, em particular vê a luz atingir os pontos +r e r no eixo x. Mas do ponto de vista de O, a esfera de luz em expansão não chega a +r ao mesmo tempo que chega a r! (É novamente a mesma questão já levantada anteriormente sobre a sincronia do conjunto de relógios dispostos ao longo da direção do movimento.) É por isso que O não consegue observar a superfície esférica observada por O : a chegada da luz à superfície esférica de raio r e centrada em O no instante de tempo t corresponde, no referencial S, a um contínuo de diferentes eventos que ocorrem em instantes de tempo diferentes. Invariância de Lorentz Para um evento (x, y, z, t ) e para o qual as coordenadas do mesmo evento (x, y, z, t) medidas no referencial S satisfazem também Diz-se que a quantidade é uma invariância de Lorentz: não varia de um referencial para outro. Podemos ter em conta um analogia simples e bidimensional a esta invariância, ao considerar dois conjuntos de eixos, Oxy e Ox y, ambos com a mesma origem, mas sendo Ox inclinado face a Ox, de modo que os eixos são semelhantes, mas o segundo resulta da rotação do primeiro. O ponto P, de coordenadas (x, y) no eixo Oxy, tem coordenadas (x, y ) no eixo Ox y. O quadrado da distância de P à origem comum O é dado por e também por, e por isso para a transformação das coordenadas (x, y) em (x, y ), é invariante. De modo semelhante, se um ponto P 1 tem de coordenadas (x 1, y 1 ) e (x 1, y 1 ) e outro ponto, P 2, tem de coordenadas (x 2, y 2 ) e (x 2, y 2 ), então ambos os pontos estão à mesma distância um do outro, qualquer que seja o referencial considerado, e por isso: ( ) ( ) ( ) ( ) Este ponto é particularmente óbvio: a distância entre dois pontos sobre um plano não pode depender da inclinação do sistema de eixos. A analogia de Lorentz, ignorando as coordenadas y e z, pode ser escrita da seguinte forma: ( ) ( ) ( ) ( ) 4
5 onde s corresponde a uma medida da distância entre os dois eventos (x 1, t 1 ) e (x 2, t 2 ). A este s dá-se por vezes o nome de intervalo espaço-tempo. A grande diferença face ao exemplo bidimensional está no facto de s 2 poder ser positivo ou negativo. Para s 2 negativo, se considerarmos s como a raiz quadrada de s 2, a distância obtida terá valor imaginário e por isso devemos analisar cuidadosamente o caso. Tal como veremos adiante, é muito claro o que deve ser feito em qualquer caso particular casos em que os eventos ocorram em posições diferentes (separação espacial) e instantes diferentes (separação temporal) são mais facilmente analisados quando separados, pelo menos numa primeira abordagem. Considere em primeiro lugar dois eventos simultâneos no referencial S de modo que t 1 = t 2. Estes eventos não ocorrerão simultaneamente no referencial S, mas satisfazem a condição: ( ) ( ) Neste caso os eventos ocorrem com separação espacial. Isso significa que ocorrem suficientemente afastados para que um feixe de luz não tenha tempo para chegar de um a outro, e portanto nenhum destes eventos é a causa do outro. A sequência de eventos pode ser diferente para diferentes referenciais quando estes ocorrem com separação espacial. Considere o exemplo de dois relógios colocados na primeira e na última carruagem de um comboio em movimento com velocidade v e ativados por um flash de luz que parte de uma lâmpada localizada exatamente no meio dos relógios. Analisada a cena a partir do solo, o relógio da última carruagem inicia a contagem do tempo antes do relógio da primeira carruagem. Agora imagine que observa toda a cena a partir de um comboio ainda mais rápido e que ultrapassa o anterior o relógio na primeira carruagem será o primeiro a iniciar a contagem do tempo. O importante neste exemplo é saber que apesar de ambos os eventos ocorrerem numa ordem diferente quando vistos de diferentes referenciais, nenhum deles está dependente do outro, não são a causa um do outro. Considere agora dois eventos que ocorrem no mesmo local no referencial S, mas em diferentes instantes de tempo, (x 1, t 1 ) e (x 2, t 2 ). Assim, no referencial S: ( ) ( ) ( ) Estes eventos ocorrem com separação temporal. Não há nenhum referencial para o qual os eventos ocorram simultaneamente. Eventos de causa e efeito ocorrem com separação temporal. O cone de luz Vamos tentar visualizar, no espaço a quatro dimensões, a superfície esférica descrita pela luz proveniente de um único flash, Pode ajudar pensar numa situação mais simples, como por exemplo uma onda que se propaga à superfície de um lago, quando deixamos cair uma pedra. Se considerarmos c como a velocidade de propagação da onda, é fácil concluir que no instante t após o início da propagação a frente de onda é dada por Pense agora na expansão da frente de onda como se fosse uma superfície no espaço tridimensional (x, y, t). O plano correspondente ao tempo, t, corta esta superfície originando um círculo de raio ct. Isso significa que a superfície é um cone com o vértice na origem. A superfície resultante do flash de luz no espaço a quatro dimensões (x, y, z, t) não é tão fácil de visualizar, mas a situação é análoga à anterior: o plano correspondente ao tempo, t, corta a superfície numa esfera e não num círculo como anteriormente. Esta superfície é designada de cone de luz. Foi dito anteriormente que a separação do ponto P (x, y, z, t) da origem é uma separação espacial se e temporal se. Diz-se que é uma separação do tipo luz se. A separação entre pontos no cone de luz e a origem é do tipo luz. Para ser mais preciso, os pontos correspondentes ao flash de luz emitido a partir da origem no instante t = 0 correspondem ao cone de luz do futuro. Uma vez que a equação depende de t 2, há uma solução para t negativo, o cone de luz do passado, que corresponde à reflexão do cone de luz do futuro no plano t = 0. Possíveis ligações causais são como se segue: um evento que ocorra na origem (0, 0, 0, 0) pode provocar um evento no cone de luz do futuro: o futuro tal como é visto a partir da origem. Eventos que ocorram no cone de luz do passado 5
6 no passado podem provocar eventos na origem. Não há nenhuma ligação causal entre um evento na origem e um evento fora dos cones de luz, já que nesse caso a separação será espacial: fora do cone de luz, o evento ocorre noutro local tal como visto da origem. Michael Fowler, Universidade de Virgínia Casa das Ciências 2013 Tradução/Adaptação de Nuno Machado e Manuel Silva Pinto 6
Graça Ventura Adaptado por Marília Peres
 Física 12º ano Novo Programa Relatividade einsteiniana Graça Ventura Adaptado por Marília Peres Memórias de Einstein... O que aconteceria se alguém cavalgasse um raio luminoso?... Seria capaz de ver a
Física 12º ano Novo Programa Relatividade einsteiniana Graça Ventura Adaptado por Marília Peres Memórias de Einstein... O que aconteceria se alguém cavalgasse um raio luminoso?... Seria capaz de ver a
CINEMÁTICA DO PONTO MATERIAL
 1.0 Conceitos CINEMÁTICA DO PONTO MATERIAL Cinemática é a parte da Mecânica que descreve os movimentos. Ponto material é um corpo móvel cujas dimensões não interferem no estudo em questão. Trajetória é
1.0 Conceitos CINEMÁTICA DO PONTO MATERIAL Cinemática é a parte da Mecânica que descreve os movimentos. Ponto material é um corpo móvel cujas dimensões não interferem no estudo em questão. Trajetória é
ESCOLA BÁSICA E SECUNDÁRIA ARTUR GONÇALVES. FICHA DE TRABALHO DE FÍSICA E QUÍMICA A 11º Ano
 Agrupamento de Escolas AR T U R G O N Ç AL V E S ESCOLA BÁSICA E SECUNDÁRIA ARTUR GONÇALVES FICHA DE TRABALHO DE FÍSICA E QUÍMICA A 11º Ano Assunto: Viagens com GPS 1. Classifica cada uma das afirmações
Agrupamento de Escolas AR T U R G O N Ç AL V E S ESCOLA BÁSICA E SECUNDÁRIA ARTUR GONÇALVES FICHA DE TRABALHO DE FÍSICA E QUÍMICA A 11º Ano Assunto: Viagens com GPS 1. Classifica cada uma das afirmações
1o) constância da inclinação do eixo de rotação da Terra. 2o) movimento de translação da Terra ao redor do Sol.
 Estações do Ano Aluno: Ricardo Augusto Viana de Lacerda Curso de Especialização em Astronomia (2009)-USP_leste Texto adaptado da Oficina de Astronomia do Prof. Dr. João Batista Garcia Canalle. a) A lâmpada
Estações do Ano Aluno: Ricardo Augusto Viana de Lacerda Curso de Especialização em Astronomia (2009)-USP_leste Texto adaptado da Oficina de Astronomia do Prof. Dr. João Batista Garcia Canalle. a) A lâmpada
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 14
 Ondas 5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Introdução: elementos básicos sobre ondas De maneira geral, uma onda é qualquer sinal que se transmite de um ponto a outro
Ondas 5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Introdução: elementos básicos sobre ondas De maneira geral, uma onda é qualquer sinal que se transmite de um ponto a outro
Relatividade conteúdos de 5 a 6
 Relatividade conteúdos de 5 a 6 Conteúdo 5 A teoria da Relatividade Restrita Conteúdo 6- A relatividade da simultaneidade e as transformações de Lorentz A origem da teoria Alguns autores estabelecem a
Relatividade conteúdos de 5 a 6 Conteúdo 5 A teoria da Relatividade Restrita Conteúdo 6- A relatividade da simultaneidade e as transformações de Lorentz A origem da teoria Alguns autores estabelecem a
Dependência 1ª série 2016. Conteúdo programático. 1- Cinemática. Cronograma de Avaliação
 Dependência 1ª série 2016 Conteúdo programático 1- Cinemática 1.1 Movimento Uniforme 1.2 - Movimento Uniformemente Variado 1.3 Cinemática Vetorial 2 Dinâmica 2.1 Princípios Fundamentais da dinâmica 2.2
Dependência 1ª série 2016 Conteúdo programático 1- Cinemática 1.1 Movimento Uniforme 1.2 - Movimento Uniformemente Variado 1.3 Cinemática Vetorial 2 Dinâmica 2.1 Princípios Fundamentais da dinâmica 2.2
SOLUÇÕES N2 2015. item a) O maior dos quatro retângulos tem lados de medida 30 4 = 26 cm e 20 7 = 13 cm. Logo, sua área é 26 x 13= 338 cm 2.
 Solução da prova da 1 a fase OBMEP 2015 Nível 1 1 SOLUÇÕES N2 2015 N2Q1 Solução O maior dos quatro retângulos tem lados de medida 30 4 = 26 cm e 20 7 = 13 cm. Logo, sua área é 26 x 13= 338 cm 2. Com um
Solução da prova da 1 a fase OBMEP 2015 Nível 1 1 SOLUÇÕES N2 2015 N2Q1 Solução O maior dos quatro retângulos tem lados de medida 30 4 = 26 cm e 20 7 = 13 cm. Logo, sua área é 26 x 13= 338 cm 2. Com um
ASSOCIAÇÃO DE INSTRUMENTOS ÓTICOS
 ASSOCIAÇÃO DE INSTRUMENTOS ÓTICOS Neste artigo, a Equipe SEI aborda um assunto que é bastante cobrado nos concursos militares: a associação de instrumentos óticos. Você encontrará um resumo teórico, dois
ASSOCIAÇÃO DE INSTRUMENTOS ÓTICOS Neste artigo, a Equipe SEI aborda um assunto que é bastante cobrado nos concursos militares: a associação de instrumentos óticos. Você encontrará um resumo teórico, dois
Vestibular Comentado - UVA/2011.1
 Vestibular Comentado - UVA/011.1 FÍSICA Comentários: Profs.... 11. Um atirador ouve o ruído de uma bala atingindo seu alvo 3s após o disparo da arma. A velocidade de disparo da bala é 680 m/s e a do som
Vestibular Comentado - UVA/011.1 FÍSICA Comentários: Profs.... 11. Um atirador ouve o ruído de uma bala atingindo seu alvo 3s após o disparo da arma. A velocidade de disparo da bala é 680 m/s e a do som
Tema de Física Eletrostática Força elétrica e campo elétrico Prof. Alex S. Vieira
 Tema de Física Eletrostática Força elétrica e campo elétrico 1) Se, após o contato e posterior separação, F 2 é o módulo da força coulombiana entre X e Y, podese afirmar corretamente que o quociente F
Tema de Física Eletrostática Força elétrica e campo elétrico 1) Se, após o contato e posterior separação, F 2 é o módulo da força coulombiana entre X e Y, podese afirmar corretamente que o quociente F
2 Limites e Derivadas. Copyright Cengage Learning. Todos os direitos reservados.
 2 Limites e Derivadas Copyright Cengage Learning. Todos os direitos reservados. 2.7 Derivadas e Taxas de Variação Copyright Cengage Learning. Todos os direitos reservados. Derivadas e Taxas de Variação
2 Limites e Derivadas Copyright Cengage Learning. Todos os direitos reservados. 2.7 Derivadas e Taxas de Variação Copyright Cengage Learning. Todos os direitos reservados. Derivadas e Taxas de Variação
2 Com base na situação apresentada no exercício número 1, reescreva as afirmativas incorretas, fazendo as correções necessárias, justificando-as.
 EXERCÍCIOS CONCEITOS BÁSICOS DE CINEMÁTICA 9ºANO 3ºBIMESTRE 1-Uma pessoa (A), parada ao lado da via férrea, observa uma locomotiva passar sem vagões. Ela vê o maquinista (B) e uma lâmpada (C) acessa dentro
EXERCÍCIOS CONCEITOS BÁSICOS DE CINEMÁTICA 9ºANO 3ºBIMESTRE 1-Uma pessoa (A), parada ao lado da via férrea, observa uma locomotiva passar sem vagões. Ela vê o maquinista (B) e uma lâmpada (C) acessa dentro
MECÂNICA RELATIVISTA PARTE II
 Aula 2 MECÂNICA RELATIVISTA PARTE II META Dar continuidade ao estudo do movimento relativo a partir das transformadas de Lorentz; detalhando-a e observando a genial interpretação dada por Einstein àquelas
Aula 2 MECÂNICA RELATIVISTA PARTE II META Dar continuidade ao estudo do movimento relativo a partir das transformadas de Lorentz; detalhando-a e observando a genial interpretação dada por Einstein àquelas
3.1. Terra e Sistema Solar (2)
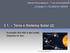 1 Ciências Físico-químicas - 7º ano de escolaridade Unidade 3 PLANETA TERRA (2) Sucessão dos dias e das noites Estações do ano Ciências Físico- Químicas 7º Ano de Escolaridade Docente: Marília Silva Soares
1 Ciências Físico-químicas - 7º ano de escolaridade Unidade 3 PLANETA TERRA (2) Sucessão dos dias e das noites Estações do ano Ciências Físico- Químicas 7º Ano de Escolaridade Docente: Marília Silva Soares
01. (UECE-1996) Um menino, parado em relação ao solo, vê sua imagem em um espelho plano E colocado à parede traseira de um ônibus.
 Óptica Geométrica 3 o Ano - Lista exercícios sobre espelhos planos 01. (UECE-1996) Um menino, parado em relação ao solo, vê sua imagem em um espelho plano E colocado à parede traseira de um ônibus. Se
Óptica Geométrica 3 o Ano - Lista exercícios sobre espelhos planos 01. (UECE-1996) Um menino, parado em relação ao solo, vê sua imagem em um espelho plano E colocado à parede traseira de um ônibus. Se
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 16
 A Equação de Onda em Uma Dimensão Ondas transversais em uma corda esticada Já vimos no estudo sobre oscilações que os físicos gostam de usar modelos simples como protótipos de certos comportamentos básicos
A Equação de Onda em Uma Dimensão Ondas transversais em uma corda esticada Já vimos no estudo sobre oscilações que os físicos gostam de usar modelos simples como protótipos de certos comportamentos básicos
Metrologia Professor: Leonardo Leódido
 Metrologia Professor: Leonardo Leódido Sumário Definição Conceitos Básicos Classificação de Forma de Orientação de Posição Definição Tolerância pode ser definida como um intervalo limite no qual as imperfeições
Metrologia Professor: Leonardo Leódido Sumário Definição Conceitos Básicos Classificação de Forma de Orientação de Posição Definição Tolerância pode ser definida como um intervalo limite no qual as imperfeições
3º Ano do Ensino Médio. Aula nº09 Prof. Paulo Henrique
 Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº09 Prof. Paulo Henrique Assunto: Funções do Segundo Grau 1. Conceitos básicos Definição: É uma função que segue a lei: onde, Tipos
Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº09 Prof. Paulo Henrique Assunto: Funções do Segundo Grau 1. Conceitos básicos Definição: É uma função que segue a lei: onde, Tipos
ESTUDO DE UM MOVIMENTO 519EE TEORIA
 1 TEORIA 1. INTRODUÇÃO Observe a seguinte sequência de fotos: Figura 1: Exemplos de vários tipos de movimento. O que tem a ver as situações do dia a dia ilustradas na figura 1 acima com os conceitos da
1 TEORIA 1. INTRODUÇÃO Observe a seguinte sequência de fotos: Figura 1: Exemplos de vários tipos de movimento. O que tem a ver as situações do dia a dia ilustradas na figura 1 acima com os conceitos da
FICHA DE ATIVIDADE - FÍSICA: MRU E MRV
 Alexandre Santos (Xandão) 9º FICHA DE ATIVIDADE - FÍSICA: MRU E MRV 1 Assinale na coluna I as afirmativas verdadeiras e, na coluna II as falsas. A velocidade da partícula varia de acordo com o gráfico
Alexandre Santos (Xandão) 9º FICHA DE ATIVIDADE - FÍSICA: MRU E MRV 1 Assinale na coluna I as afirmativas verdadeiras e, na coluna II as falsas. A velocidade da partícula varia de acordo com o gráfico
Aula 9. Superfícies de Revolução. Seja C uma curva e r uma reta contidas num plano π.
 Aula 9 Superfícies de Revolução Seja C uma curva e r uma reta contidas num plano π. Fig. 1: Superfície de revolução S, geratriz C e eixo r contidos no plano π A superfície de revolução S de geratriz C
Aula 9 Superfícies de Revolução Seja C uma curva e r uma reta contidas num plano π. Fig. 1: Superfície de revolução S, geratriz C e eixo r contidos no plano π A superfície de revolução S de geratriz C
Equações paramétricas da Reta
 39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
39 6.Retas e Planos Equações de Retas e Planos Equações da Reta Vamos supor que uma reta r é paralela a um vetor V = a, b, c) não nulo e que passa por um ponto P = x, y, z ). Um ponto P = x, pertence a
Por que as antenas são parabólicas?
 Por que as antenas são parabólicas? Adaptado do artigo de Eduardo Wagner A palavra parábola está, para os estudantes do ensino médio, associada ao gráfico da função polinomial do segundo grau. Embora quase
Por que as antenas são parabólicas? Adaptado do artigo de Eduardo Wagner A palavra parábola está, para os estudantes do ensino médio, associada ao gráfico da função polinomial do segundo grau. Embora quase
CONTEÚDO CIÊNCIAS REVISÃO 1 REVISÃO 2 REVISÃO 3 E HABILIDADES. Conteúdo: - Movimento, velocidade e aceleração - Força, ótica e som
 CIÊNCIAS Conteúdo: - Movimento, velocidade e aceleração - Força, ótica e som Habilidades: - Relembrar os conceitos de movimento, velocidade e aceleração, bem como sua exemplificação no dia a dia. - Destacar
CIÊNCIAS Conteúdo: - Movimento, velocidade e aceleração - Força, ótica e som Habilidades: - Relembrar os conceitos de movimento, velocidade e aceleração, bem como sua exemplificação no dia a dia. - Destacar
Capítulo 4. Retas e Planos. 4.1 A reta
 Capítulo 4 Retas e Planos Neste capítulo veremos como utilizar a teoria dos vetores para caracterizar retas e planos, a saber, suas equações, posições relativas, ângulos e distâncias. 4.1 A reta Sejam
Capítulo 4 Retas e Planos Neste capítulo veremos como utilizar a teoria dos vetores para caracterizar retas e planos, a saber, suas equações, posições relativas, ângulos e distâncias. 4.1 A reta Sejam
21- EXERCÍCIOS FUNÇÕES DO SEGUNDO GRAU
 1 21- EXERCÍCIOS FUNÇÕES DO SEGUNDO GRAU 1. O gráfico do trinômio y = ax 2 + bx + c. Qual a afirmativa errada? a) se a > 0 a parábola possui concavidade para cima b) se b 2 4ac > 0 o trinômio possui duas
1 21- EXERCÍCIOS FUNÇÕES DO SEGUNDO GRAU 1. O gráfico do trinômio y = ax 2 + bx + c. Qual a afirmativa errada? a) se a > 0 a parábola possui concavidade para cima b) se b 2 4ac > 0 o trinômio possui duas
Centro de gravidade de um corpo é o ponto onde podemos supor que seu peso esteja aplicado.
 Apostila de Revisão n 4 DISCIPLINA: Física NOME: N O : TURMA: 2M311 PROFESSOR: Glênon Dutra DATA: Mecânica - 4. Corpo Rígido 4.1. Torque análise semiquantitativa, na Primeira Etapa, e quantitativa, na
Apostila de Revisão n 4 DISCIPLINA: Física NOME: N O : TURMA: 2M311 PROFESSOR: Glênon Dutra DATA: Mecânica - 4. Corpo Rígido 4.1. Torque análise semiquantitativa, na Primeira Etapa, e quantitativa, na
TECNÓLOGO EM CONSTRUÇÃO CIVIL. Aula 6 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega
 1 TECNÓLOGO EM CONSTRUÇÃO CIVIL Aula 6 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega FUNÇÃO POLINOMIAL DO 2º GRAU 2 Uma função polinomial do 2º grau (ou simplesmente, função do 2º grau) é uma
1 TECNÓLOGO EM CONSTRUÇÃO CIVIL Aula 6 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega FUNÇÃO POLINOMIAL DO 2º GRAU 2 Uma função polinomial do 2º grau (ou simplesmente, função do 2º grau) é uma
Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da massa específica do meio µ, de acordo com a expressão:
 PROVA DE FÍSICA DO VESTIBULAR 96/97 DO INSTITUTO MILITAR DE ENGENHARIA (03/12/96) 1 a Questão: Valor : 1,0 Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da
PROVA DE FÍSICA DO VESTIBULAR 96/97 DO INSTITUTO MILITAR DE ENGENHARIA (03/12/96) 1 a Questão: Valor : 1,0 Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da
MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos
 MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos 1 Seja um número real. Considere, num referencial o.n., a reta e o plano definidos, respetivamente, por e Sabe-se
MATEMÁTICA (11º ano) Exercícios de Exames e Testes Intermédios Equações de retas e planos 1 Seja um número real. Considere, num referencial o.n., a reta e o plano definidos, respetivamente, por e Sabe-se
Movimento uniformemente variado. Capítulo 4 (MUV)
 Movimento uniformemente variado Capítulo 4 (MUV) Movimento uniformemente variado MUV aceleração escalar (α) é constante e não nula. O quociente α = v t é constante e não nulo. Função horária da velocidade
Movimento uniformemente variado Capítulo 4 (MUV) Movimento uniformemente variado MUV aceleração escalar (α) é constante e não nula. O quociente α = v t é constante e não nulo. Função horária da velocidade
Análise de Regressão. Notas de Aula
 Análise de Regressão Notas de Aula 2 Modelos de Regressão Modelos de regressão são modelos matemáticos que relacionam o comportamento de uma variável Y com outra X. Quando a função f que relaciona duas
Análise de Regressão Notas de Aula 2 Modelos de Regressão Modelos de regressão são modelos matemáticos que relacionam o comportamento de uma variável Y com outra X. Quando a função f que relaciona duas
ÁLGEBRA. Aula 1 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega. Maria Auxiliadora
 1 ÁLGEBRA Aula 1 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega Maria Auxiliadora FUNÇÃO POLINOMIAL DO 2º GRAU 2 Uma função polinomial do 2º grau (ou simplesmente, função do 2º grau) é uma relação
1 ÁLGEBRA Aula 1 _ Função Polinomial do 2º Grau Professor Luciano Nóbrega Maria Auxiliadora FUNÇÃO POLINOMIAL DO 2º GRAU 2 Uma função polinomial do 2º grau (ou simplesmente, função do 2º grau) é uma relação
MÓDULO 2 ÓPTICA E ONDAS Ronaldo Filho e Rhafael Roger
 ELEMENTOS DOS ESPELHOS Os elementos geométricos que caracterizam um espelho esférico são: CAPÍTULO 03 ESPELHOS ESFÉRICOS Seccionando-se uma esfera por um plano, ela ficará dividida em duas partes ou Calotas
ELEMENTOS DOS ESPELHOS Os elementos geométricos que caracterizam um espelho esférico são: CAPÍTULO 03 ESPELHOS ESFÉRICOS Seccionando-se uma esfera por um plano, ela ficará dividida em duas partes ou Calotas
Erros e Incertezas. Rafael Alves Batista Instituto de Física Gleb Wataghin Universidade Estadual de Campinas (Dated: 10 de Julho de 2011.
 Rafael Alves Batista Instituto de Física Gleb Wataghin Universidade Estadual de Campinas (Dated: 10 de Julho de 2011.) I. INTRODUÇÃO Quando se faz um experimento, deseja-se comparar o resultado obtido
Rafael Alves Batista Instituto de Física Gleb Wataghin Universidade Estadual de Campinas (Dated: 10 de Julho de 2011.) I. INTRODUÇÃO Quando se faz um experimento, deseja-se comparar o resultado obtido
Novo Espaço Matemática A 11.º ano Proposta de Teste Intermédio [Novembro 2015]
![Novo Espaço Matemática A 11.º ano Proposta de Teste Intermédio [Novembro 2015] Novo Espaço Matemática A 11.º ano Proposta de Teste Intermédio [Novembro 2015]](/thumbs/40/20919837.jpg) Proposta de Teste Intermédio [Novembro 05] Nome: Ano / Turma: N.º: Data: - - Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado. Para cada resposta, identifica
Proposta de Teste Intermédio [Novembro 05] Nome: Ano / Turma: N.º: Data: - - Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado. Para cada resposta, identifica
Prof. Neckel FÍSICA 1 PROVA 1 TEMA 2 PARTE 1 PROF. NECKEL POSIÇÃO. Sistema de Coordenadas Nome do sistema Unidade do sistema 22/02/2016.
 FÍSICA 1 PROVA 1 TEMA 2 PARTE 1 PROF. NECKEL Cinemática 1D POSIÇÃO Sistema de Coordenadas Nome do sistema Unidade do sistema Reta numérica real com origem Crescimento para direita, decrescimento para esquerda
FÍSICA 1 PROVA 1 TEMA 2 PARTE 1 PROF. NECKEL Cinemática 1D POSIÇÃO Sistema de Coordenadas Nome do sistema Unidade do sistema Reta numérica real com origem Crescimento para direita, decrescimento para esquerda
Teoria da Relatividade Especial
 Teoria da Relatividade Especial Galileu, século XVI XVII: estudo do movimento dos corpos, princípio de inércia, conceito de referencial inercial, estudo de corpos celestes, heliocentrismo, método científico.
Teoria da Relatividade Especial Galileu, século XVI XVII: estudo do movimento dos corpos, princípio de inércia, conceito de referencial inercial, estudo de corpos celestes, heliocentrismo, método científico.
PROVA PARA OS ALUNOS DE 2º ANO DO ENSINO MÉDIO. 4 cm
 PROVA PARA OS ALUNOS DE º ANO DO ENSINO MÉDIO 1ª Questão: Um cálice com a forma de um cone contém V cm de uma bebida. Uma cereja de forma esférica com diâmetro de cm é colocada dentro do cálice. Supondo
PROVA PARA OS ALUNOS DE º ANO DO ENSINO MÉDIO 1ª Questão: Um cálice com a forma de um cone contém V cm de uma bebida. Uma cereja de forma esférica com diâmetro de cm é colocada dentro do cálice. Supondo
Movimento nos céus: Estrelas, Sol, Lua e Planetas
 Movimento nos céus: Estrelas, Sol, Lua e Planetas Michael Fowler Universidade de Virgínia, Departamento de Física Introdução O propósito deste texto é o de rever os diferentes movimentos dos astros visíveis
Movimento nos céus: Estrelas, Sol, Lua e Planetas Michael Fowler Universidade de Virgínia, Departamento de Física Introdução O propósito deste texto é o de rever os diferentes movimentos dos astros visíveis
LISTA ELETROSTÁTICA 3ª SÉRIE
 1. (Pucrj 013) Duas cargas pontuais q1 3,0 μc e q 6,0 μc são colocadas a uma distância de 1,0 m entre si. Calcule a distância, em metros, entre a carga q 1 e a posição, situada entre as cargas, onde o
1. (Pucrj 013) Duas cargas pontuais q1 3,0 μc e q 6,0 μc são colocadas a uma distância de 1,0 m entre si. Calcule a distância, em metros, entre a carga q 1 e a posição, situada entre as cargas, onde o
. B(x 2, y 2 ). A(x 1, y 1 )
 Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
Estudo da Reta no R 2 Condição de alinhamento de três pontos: Sabemos que por dois pontos distintos passa uma única reta, ou seja, dados A(x 1, y 1 ) e B(x 2, y 2 ), eles estão sempre alinhados. y. B(x
Solução da prova da 2a fase OBMEP 2014 Nível 2. Questão 1. item a)
 Questão 1 Cada nova pilha tem dois cubinhos a mais em sua base. Assim, como a terceira pilha tem 5 cubinhos em sua base, a quarta pilha tem 5 + 2 = 7 cubinhos e a quinta pilha tem 7 + 2 = 9 cubinhos em
Questão 1 Cada nova pilha tem dois cubinhos a mais em sua base. Assim, como a terceira pilha tem 5 cubinhos em sua base, a quarta pilha tem 5 + 2 = 7 cubinhos e a quinta pilha tem 7 + 2 = 9 cubinhos em
COMUNICAÇÃO DE INFORMAÇÃO A CURTAS DISTÂNCIAS
 LOGO FQA COMUNICAÇÃO DE INFORMAÇÃO A CURTAS DISTÂNCIAS Propagação de um sinal Energia e velocidade de propagação (modelo ondulatório) Transmissão de sinais Sinal - é qualquer espécie de perturbação que
LOGO FQA COMUNICAÇÃO DE INFORMAÇÃO A CURTAS DISTÂNCIAS Propagação de um sinal Energia e velocidade de propagação (modelo ondulatório) Transmissão de sinais Sinal - é qualquer espécie de perturbação que
Planificação do 2º Período
 Direção-Geral dos Estabelecimentos Escolares Direção de Serviços da Região Centro Planificação do 2º Período Disciplina: Matemática A Grupo: 500 Ano: 10º Número de blocos de 45 minutos previstos: 0 Ano
Direção-Geral dos Estabelecimentos Escolares Direção de Serviços da Região Centro Planificação do 2º Período Disciplina: Matemática A Grupo: 500 Ano: 10º Número de blocos de 45 minutos previstos: 0 Ano
Matemática Básica Intervalos
 Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
Matemática Básica Intervalos 03 1. Intervalos Intervalos são conjuntos infinitos de números reais. Geometricamente correspondem a segmentos de reta sobre um eixo coordenado. Por exemplo, dados dois números
6.2. Volumes. Nesta seção aprenderemos a usar a integração para encontrar o volume de um sólido. APLICAÇÕES DE INTEGRAÇÃO
 APLICAÇÕES DE INTEGRAÇÃO 6.2 Volumes Nesta seção aprenderemos a usar a integração para encontrar o volume de um sólido. SÓLIDOS IRREGULARES Começamos interceptando S com um plano e obtemos uma região plana
APLICAÇÕES DE INTEGRAÇÃO 6.2 Volumes Nesta seção aprenderemos a usar a integração para encontrar o volume de um sólido. SÓLIDOS IRREGULARES Começamos interceptando S com um plano e obtemos uma região plana
FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO
 FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO Fixação 1) O bloco da figura, de peso P = 50N, é arrastado ao longo do plano horizontal pela força F de intensidade F = 100N. A força de
FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO Fixação 1) O bloco da figura, de peso P = 50N, é arrastado ao longo do plano horizontal pela força F de intensidade F = 100N. A força de
Atividade de Recuperação- Física
 Atividade de Recuperação- Física 1º Ano- 1º Trimestre Prof. Sérgio Faro Orientação: Refazer os exemplos seguintes no caderno e resolver os demais exercícios. Anotar eventuais dúvidas para esclarecimento
Atividade de Recuperação- Física 1º Ano- 1º Trimestre Prof. Sérgio Faro Orientação: Refazer os exemplos seguintes no caderno e resolver os demais exercícios. Anotar eventuais dúvidas para esclarecimento
A unidade de freqüência é chamada hertz e simbolizada por Hz: 1 Hz = 1 / s.
 Movimento Circular Uniforme Um movimento circular uniforme (MCU) pode ser associado, com boa aproximação, ao movimento de um planeta ao redor do Sol, num referencial fixo no Sol, ou ao movimento da Lua
Movimento Circular Uniforme Um movimento circular uniforme (MCU) pode ser associado, com boa aproximação, ao movimento de um planeta ao redor do Sol, num referencial fixo no Sol, ou ao movimento da Lua
2. Analise o esquema abaixo referente a um espelho plano. A imagem do objeto que será vista pelo observador localiza-se no ponto: a) 1 b) 2 c) 3 d) 4
 1. Considere um objeto formado por uma combinação de um quadrado de aresta a cujos vértices são centros geométricos de círculos e quadrados menores, como mostra a figura abaixo. Colocando-se um espelho
1. Considere um objeto formado por uma combinação de um quadrado de aresta a cujos vértices são centros geométricos de círculos e quadrados menores, como mostra a figura abaixo. Colocando-se um espelho
Dinâmica de um Sistema de Partículas
 Dinâmica de um Sistema de Partículas Dra. Diana Andrade, Dra. Ângela Krabbe, Dr. Caius Lucius Selhorst & Dr. Sérgio Pilling 2.1 O que é Física? Capítulo 2 Movimento Retilíneo A palavra Física vem do grego
Dinâmica de um Sistema de Partículas Dra. Diana Andrade, Dra. Ângela Krabbe, Dr. Caius Lucius Selhorst & Dr. Sérgio Pilling 2.1 O que é Física? Capítulo 2 Movimento Retilíneo A palavra Física vem do grego
ROLAMENTO, TORQUE E MOMENTUM ANGULAR Física Geral I (1108030) - Capítulo 08
 ROLAMENTO, TORQUE E MOMENTUM ANGULAR Física Geral I (1108030) - Capítulo 08 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 21 Sumário Rolamento Rolamento como rotação e translação combinados e como uma
ROLAMENTO, TORQUE E MOMENTUM ANGULAR Física Geral I (1108030) - Capítulo 08 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 21 Sumário Rolamento Rolamento como rotação e translação combinados e como uma
APLICANDO OS CONCEITOS DE VELOCIDADE.
 APLICANDO OS CONCEITOS DE VELOCIDADE. OBJETIVO: Resolver problemas simples utilizando o conceito de velocidade média (v = distância percorrida dividida pelo intervalo de tempo transcorrido no percurso),
APLICANDO OS CONCEITOS DE VELOCIDADE. OBJETIVO: Resolver problemas simples utilizando o conceito de velocidade média (v = distância percorrida dividida pelo intervalo de tempo transcorrido no percurso),
1.1 UFPR 2014. Rumo Curso Pré Vestibular Assistencial - RCPVA Disciplina: Matemática Professor: Vinícius Nicolau 04 de Novembro de 2014
 Sumário 1 Questões de Vestibular 1 1.1 UFPR 2014.................................... 1 1.1.1 Questão 1................................. 1 1.1.2 Questão 2................................. 2 1.1.3 Questão
Sumário 1 Questões de Vestibular 1 1.1 UFPR 2014.................................... 1 1.1.1 Questão 1................................. 1 1.1.2 Questão 2................................. 2 1.1.3 Questão
Aula 18. Teoria da Relatividade Restrita (1905) Física Geral IV - FIS503. Parte I
 Aula 18 Teoria da Relatividade Restrita (1905) Parte I Física Geral IV - FIS503 1 Documentário - National Geographic Nesta aula: Relatividade das velocidades Próxima aula: Efeito Doppler da Luz Momento
Aula 18 Teoria da Relatividade Restrita (1905) Parte I Física Geral IV - FIS503 1 Documentário - National Geographic Nesta aula: Relatividade das velocidades Próxima aula: Efeito Doppler da Luz Momento
Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas
 Engrenagens Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas alavancas. Classificação das Engrenagens As engrenagens
Engrenagens Engrenagens são elementos de máquinas que transmitem o movimento por meio de sucessivos engates de dentes, onde os dentes atuam como pequenas alavancas. Classificação das Engrenagens As engrenagens
Sala de Estudos FÍSICA - Lucas 3 trimestre Ensino Médio 1º ano classe: Prof.LUCAS Nome: nº
 Sala de Estudos FÍSICA - Lucas 3 trimestre Ensino Médio 1º ano classe: Prof.LUCAS Nome: nº Sala de Estudos: Lentes: Estudo Analítico de Gauss Mecânica: Queda Livre e Lançamento Vertical 1. (Unicamp 2013)
Sala de Estudos FÍSICA - Lucas 3 trimestre Ensino Médio 1º ano classe: Prof.LUCAS Nome: nº Sala de Estudos: Lentes: Estudo Analítico de Gauss Mecânica: Queda Livre e Lançamento Vertical 1. (Unicamp 2013)
Resolução do exemplo 8.6a - pág 61 Apresente, analítica e geometricamente, a solução dos seguintes sistemas lineares.
 Solução dos Exercícios de ALGA 2ª Avaliação EXEMPLO 8., pág. 61- Uma reta L passa pelos pontos P 0 (, -2, 1) e P 1 (5, 1, 0). Determine as equações paramétricas, vetorial e simétrica dessa reta. Determine
Solução dos Exercícios de ALGA 2ª Avaliação EXEMPLO 8., pág. 61- Uma reta L passa pelos pontos P 0 (, -2, 1) e P 1 (5, 1, 0). Determine as equações paramétricas, vetorial e simétrica dessa reta. Determine
ESTUDO DE UM CIRCUITO RC COMO FILTRO
 Departamento de Física da Faculdade de Ciências da Universidade de Lisboa T6 Física Experimental I - 2007/08 ESTUDO DE UM CIRCUITO RC COMO FILTRO 1. Objectivo Estudo do funcionamento, em regime estacionário,
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa T6 Física Experimental I - 2007/08 ESTUDO DE UM CIRCUITO RC COMO FILTRO 1. Objectivo Estudo do funcionamento, em regime estacionário,
Prova Escrita de MATEMÁTICA A - 12o Ano 2015-2 a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 205-2 a Fase Proposta de resolução GRUPO I. O valor médio da variável aleatória X é: µ a + 2 2a + 0, Como, numa distribuição de probabilidades de uma variável aleatória,
Prova Escrita de MATEMÁTICA A - o Ano 205-2 a Fase Proposta de resolução GRUPO I. O valor médio da variável aleatória X é: µ a + 2 2a + 0, Como, numa distribuição de probabilidades de uma variável aleatória,
- Cálculo 1 - Limites -
 - Cálculo - Limites -. Calcule, se eistirem, os seguintes ites: (a) ( 3 3); (b) 4 8; 3 + + 3 (c) + 5 (d) 3 (e) 3. Faça o esboço do gráfico de f() = entre 4 f() e f(4)? 3. Seja f a função definida por f()
- Cálculo - Limites -. Calcule, se eistirem, os seguintes ites: (a) ( 3 3); (b) 4 8; 3 + + 3 (c) + 5 (d) 3 (e) 3. Faça o esboço do gráfico de f() = entre 4 f() e f(4)? 3. Seja f a função definida por f()
Física e Química A Bloco II Teste Sumativo 1 A - 08/11/2011
 E s c o l a S e c u n d á r i a d e A l c á c e r d o S a l Ano letivo 2011/2012 Física e Química A Bloco II Teste Sumativo 1 A - 08/11/2011 1. O GPS é um sistema de navegação à escala global que, em qualquer
E s c o l a S e c u n d á r i a d e A l c á c e r d o S a l Ano letivo 2011/2012 Física e Química A Bloco II Teste Sumativo 1 A - 08/11/2011 1. O GPS é um sistema de navegação à escala global que, em qualquer
Equilíbrio de um corpo rígido
 Equilíbrio de um corpo rígido Objetivos da aula: Desenvolver as equações de equilíbrio para um corpo rígido. Introduzir o conceito do diagrama de corpo livre para um corpo rígido. Mostrar como resolver
Equilíbrio de um corpo rígido Objetivos da aula: Desenvolver as equações de equilíbrio para um corpo rígido. Introduzir o conceito do diagrama de corpo livre para um corpo rígido. Mostrar como resolver
Óptica Geométrica 9º EF
 Óptica Geométrica 9º EF Fonte de luz Estrelas Lâmpada acesa Lua Lâmpada apagada Fonte Primária Fonte Secundária Classificação de fontes de luz Quanto a emissão a) Fonte Primária (luminoso): produz a luz
Óptica Geométrica 9º EF Fonte de luz Estrelas Lâmpada acesa Lua Lâmpada apagada Fonte Primária Fonte Secundária Classificação de fontes de luz Quanto a emissão a) Fonte Primária (luminoso): produz a luz
Geometria Diferencial de Curvas Espaciais
 Geometria Diferencial de Curvas Espaciais 1 Aceleração tangencial e centrípeta Fernando Deeke Sasse Departamento de Matemática CCT UDESC Mostremos que a aceleração de uma partícula viajando ao longo de
Geometria Diferencial de Curvas Espaciais 1 Aceleração tangencial e centrípeta Fernando Deeke Sasse Departamento de Matemática CCT UDESC Mostremos que a aceleração de uma partícula viajando ao longo de
Aula 10 Relatividade. Física 4 Ref. Halliday Volume4. Profa. Keli F. Seidel
 Aula 10 Relatividade Física 4 Ref. Halliday Volume4 ...RELATIVIDADE RESTRITA Sumário A relatividade das distâncias Contração do Espaço Transformada de Lorenz A transformação das velocidades Relembrando...
Aula 10 Relatividade Física 4 Ref. Halliday Volume4 ...RELATIVIDADE RESTRITA Sumário A relatividade das distâncias Contração do Espaço Transformada de Lorenz A transformação das velocidades Relembrando...
NOTAÇÕES. : distância do ponto P à reta r : segmento de extremidades nos pontos A e B
 R C i z Rez) Imz) det A tr A : conjunto dos números reais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : parte real do número z C : parte imaginária do número z C
R C i z Rez) Imz) det A tr A : conjunto dos números reais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : parte real do número z C : parte imaginária do número z C
alocação de custo têm que ser feita de maneira estimada e muitas vezes arbitrária (como o aluguel, a supervisão, as chefias, etc.
 Professor José Alves Aula pocii Aula 3,4 Custeio por Absorção Custeio significa apropriação de custos. Métodos de Custeio é a forma como são apropriados os custos aos produtos. Assim, existe Custeio por
Professor José Alves Aula pocii Aula 3,4 Custeio por Absorção Custeio significa apropriação de custos. Métodos de Custeio é a forma como são apropriados os custos aos produtos. Assim, existe Custeio por
Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas:
 * 16/03/16 Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas: * *Definição *Um espelho plano é aquele em que a superfície
* 16/03/16 Um espelho é uma superfície muito lisa e que permita alto índice de reflexão da luz que incide sobre ele. Espelhos possuem formas variadas: * *Definição *Um espelho plano é aquele em que a superfície
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 7
 Potencial Elétrico Quando estudamos campo elétrico nas aulas passadas, vimos que ele pode ser definido em termos da força elétrica que uma carga q exerce sobre uma carga de prova q 0. Essa força é, pela
Potencial Elétrico Quando estudamos campo elétrico nas aulas passadas, vimos que ele pode ser definido em termos da força elétrica que uma carga q exerce sobre uma carga de prova q 0. Essa força é, pela
Aula de Exercícios Recuperação Paralela (Leis de Newton)
 Aula de Exercícios Recuperação Paralela (Leis de Newton) Exercício 1. (TAUBATÉ) Um automóvel viaja com velocidade constante de 72km/h em trecho retilíneo de estrada. Pode-se afirmar que a resultante das
Aula de Exercícios Recuperação Paralela (Leis de Newton) Exercício 1. (TAUBATÉ) Um automóvel viaja com velocidade constante de 72km/h em trecho retilíneo de estrada. Pode-se afirmar que a resultante das
DEEC Área Científica de Telecomunicações Instituto Superior Técnico. Propagação & Antenas Prof. Carlos R. Paiva SOBRE O CONCEITO DE SIMULTANEIDADE
 3 DEEC Área Científica de Telecomunicações Instituto Superior Técnico Propagação & ntenas Prof Carlos R Paiva SORE O CONCEITO DE SIUTNEIDDE Consideremos uma vagão de comboio que se desloca, em relação
3 DEEC Área Científica de Telecomunicações Instituto Superior Técnico Propagação & ntenas Prof Carlos R Paiva SORE O CONCEITO DE SIUTNEIDDE Consideremos uma vagão de comboio que se desloca, em relação
Capítulo TRABALHO E ENERGIA
 Capítulo 6 TRABALHO E ENERGIA A B C DISCIPLINA DE FÍSICA CAPÍTULO 6 - TRABALHO E ENERGIA 6.1 Um bloco, com 20kg de massa, sobe uma rampa com 15º de inclinação e percorre 55,375 metros até parar. Os coeficientes
Capítulo 6 TRABALHO E ENERGIA A B C DISCIPLINA DE FÍSICA CAPÍTULO 6 - TRABALHO E ENERGIA 6.1 Um bloco, com 20kg de massa, sobe uma rampa com 15º de inclinação e percorre 55,375 metros até parar. Os coeficientes
OS SERES VIVOS DO AMBIENTE PRÓXIMO
 OS SERES VIVOS DO AMBIENTE PRÓXIMO Comparo e classifico as plantas segundo alguns critérios. Desde sempre o homem tomou consciência da variedade de plantas que o rodeavam e sentiu necessidade de as reunir
OS SERES VIVOS DO AMBIENTE PRÓXIMO Comparo e classifico as plantas segundo alguns critérios. Desde sempre o homem tomou consciência da variedade de plantas que o rodeavam e sentiu necessidade de as reunir
Problemas de Mecânica e Ondas 8
 Problemas de Mecânica e Ondas 8 P 8.1. ( Introdução à Física, J. Dias de Deus et. al. ) a) A figura representa uma onda aproximadamente sinusoidal no mar e uma boia para prender um barco, que efectua 10
Problemas de Mecânica e Ondas 8 P 8.1. ( Introdução à Física, J. Dias de Deus et. al. ) a) A figura representa uma onda aproximadamente sinusoidal no mar e uma boia para prender um barco, que efectua 10
ÁLGEBRA VETORIAL E GEOMETRIA ANALÍTICA (UFCG- CUITÉ)
 P L A N O S PARALELOS AOS EIXOS E AOS PLANOS COORDENADOS Casos Particulares A equação ax + by + cz = d na qual a, b e c não são nulos, é a equação de um plano π, sendo v = ( a, b, c) um vetor normal a
P L A N O S PARALELOS AOS EIXOS E AOS PLANOS COORDENADOS Casos Particulares A equação ax + by + cz = d na qual a, b e c não são nulos, é a equação de um plano π, sendo v = ( a, b, c) um vetor normal a
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Definições Comunicações sem fio utilizam-se de ondas eletromagnéticas para o envio de sinais através de longas distâncias.
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Definições Comunicações sem fio utilizam-se de ondas eletromagnéticas para o envio de sinais através de longas distâncias.
Professor (a): Pedro Paulo S. Arrais Aluno (a): Série: 1ª Data: / / 2016. LISTA DE FÍSICA I
 Ensino Médio Unid. São Judas Tadeu Professor (a): Pedro Paulo S. Arrais Aluno (a): Série: 1ª Data: / / 2016. LISTA DE FÍSICA I Orientações: - A lista deverá ser respondida na própria folha impressa ou
Ensino Médio Unid. São Judas Tadeu Professor (a): Pedro Paulo S. Arrais Aluno (a): Série: 1ª Data: / / 2016. LISTA DE FÍSICA I Orientações: - A lista deverá ser respondida na própria folha impressa ou
Escola Secundária de Alcochete. 11.º Ano Matemática A Geometria no Plano e no Espaço II
 Escola Secundária de Alcochete 11.º Ano Matemática A Geometria no Plano e no Espaço II Equações Trigonométricas O que são? São equações que envolvem o uso de funções trigonométricas. Mas... Ainda não se
Escola Secundária de Alcochete 11.º Ano Matemática A Geometria no Plano e no Espaço II Equações Trigonométricas O que são? São equações que envolvem o uso de funções trigonométricas. Mas... Ainda não se
LOCALIZANDO PONTOS ATRAVÉS DE COORDENADAS GEOGRÁFICAS
 CONHECENDO A CARTOGRAFIA E OS MAPAS Segundo a Associação Brasileira de Normas Técnicas (ABNT), Cartografia é definida como: "A arte do levantamento, construção e edição de mapas e cartas de qualquer natureza..
CONHECENDO A CARTOGRAFIA E OS MAPAS Segundo a Associação Brasileira de Normas Técnicas (ABNT), Cartografia é definida como: "A arte do levantamento, construção e edição de mapas e cartas de qualquer natureza..
* Coordenadas Geográficas Movimento de rotação 6ºANO Cap 2 pg 23
 * Coordenadas Geográficas Movimento de rotação 6ºANO Cap 2 pg 23 Nosso planeta abrange uma área de aproximadamente 510 milhões de quilômetros quadrados. A título de comparação, o Brasil representa apenas
* Coordenadas Geográficas Movimento de rotação 6ºANO Cap 2 pg 23 Nosso planeta abrange uma área de aproximadamente 510 milhões de quilômetros quadrados. A título de comparação, o Brasil representa apenas
Mecânica Geral. Aula 04 Carregamento, Vínculo e Momento de uma força
 Aula 04 Carregamento, Vínculo e Momento de uma força 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
Aula 04 Carregamento, Vínculo e Momento de uma força 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
Lista de Exercícios Critérios de Divisibilidade
 Nota: Os exercícios desta aula são referentes ao seguinte vídeo Matemática Zero 2.0 - Aula 10 - Critérios de - (parte 1 de 2) Endereço: https://www.youtube.com/watch?v=1f1qlke27me Gabaritos nas últimas
Nota: Os exercícios desta aula são referentes ao seguinte vídeo Matemática Zero 2.0 - Aula 10 - Critérios de - (parte 1 de 2) Endereço: https://www.youtube.com/watch?v=1f1qlke27me Gabaritos nas últimas
MODELO 1 RESOLUÇÃO RESOLUÇÃO V1 V2 T2 330 K = V2 = V1 V1 V2 = 1,1.V1 T1 T2 T1 300 K
 MODELO 1 1) Suponha que um gás ideal tenha sofrido uma transformação isobárica, na qual sua temperatura varia de 27 C para 57 C. Qual seria a porcentagem de variação que o volume do gás iria experimentar?
MODELO 1 1) Suponha que um gás ideal tenha sofrido uma transformação isobárica, na qual sua temperatura varia de 27 C para 57 C. Qual seria a porcentagem de variação que o volume do gás iria experimentar?
Aula 1 Óptica geométrica, propagação retilínea e refração da luz
 Aula 1 Óptica geométrica, propagação retilínea e refração da luz 1 Último bimestre Definição de corrente elétrica: Leis de Ohm e potência elétrica: i Carga totalque passa por A Intervalo de tempo V R.
Aula 1 Óptica geométrica, propagação retilínea e refração da luz 1 Último bimestre Definição de corrente elétrica: Leis de Ohm e potência elétrica: i Carga totalque passa por A Intervalo de tempo V R.
FÍSICA - Tomás ESPELHOS PLANOS ÓPTICA
 CONCEITOS BÁSICOS LUZ Energia radiante que se propaga no espaço através de ondas eletromagnéticas e que sensibiliza nossa visão. C = 300.000km/s = 3.10 8 m/s Raio de luz - Segmento de reta que representa
CONCEITOS BÁSICOS LUZ Energia radiante que se propaga no espaço através de ondas eletromagnéticas e que sensibiliza nossa visão. C = 300.000km/s = 3.10 8 m/s Raio de luz - Segmento de reta que representa
4.1 Experimento 1: Cuba Eletrostática: Carga, Campo e Potenciais Elétricos
 14 4. Roteiros da Primeira Sequência 4.1 Experimento 1: Cuba Eletrostática: Carga, Campo e Potenciais Elétricos 4.1.1 Objetivos Fundamentar o conceito de carga elétrica. Trabalhar com os conceitos de campo
14 4. Roteiros da Primeira Sequência 4.1 Experimento 1: Cuba Eletrostática: Carga, Campo e Potenciais Elétricos 4.1.1 Objetivos Fundamentar o conceito de carga elétrica. Trabalhar com os conceitos de campo
Cônicas. 2. (Fuvest 2014) Considere a circunferência λ de equação cartesiana parábola α de equação. x y 4y 0 e a. y 4 x.
 Cônicas 1. (Espcex (Aman) 014) Sobre a curva 9x + 5y 6x + 50y 164 = 0, assinale a alternativa correta. a) Seu centro é (,1). b) A medida do seu eixo maior é 5. c) A medida do seu eixo menor é 9. d) A distância
Cônicas 1. (Espcex (Aman) 014) Sobre a curva 9x + 5y 6x + 50y 164 = 0, assinale a alternativa correta. a) Seu centro é (,1). b) A medida do seu eixo maior é 5. c) A medida do seu eixo menor é 9. d) A distância
5. Derivada. Definição: Se uma função f é definida em um intervalo aberto contendo x 0, então a derivada de f
 5 Derivada O conceito de derivada está intimamente relacionado à taa de variação instantânea de uma função, o qual está presente no cotidiano das pessoas, através, por eemplo, da determinação da taa de
5 Derivada O conceito de derivada está intimamente relacionado à taa de variação instantânea de uma função, o qual está presente no cotidiano das pessoas, através, por eemplo, da determinação da taa de
AV2 - MA 12-2011 UMA SOLUÇÃO
 Questão 1. Considere os caminhos no plano iniciados no ponto (0, 0) com deslocamentos paralelos aos eixos coordenados, sempre de uma unidade e no sentido positivo dos eixos x e y (não se descarta a possibilidade
Questão 1. Considere os caminhos no plano iniciados no ponto (0, 0) com deslocamentos paralelos aos eixos coordenados, sempre de uma unidade e no sentido positivo dos eixos x e y (não se descarta a possibilidade
UNESP DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD. Parte 6/5: Prof. Víctor O. Gamarra Rosado
 UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 6/5: 14. Perspectivas Prof. Víctor O. Gamarra Rosado
UNESP UNIVERSIDADE ESTADUAL PAULISTA FACULDADE DE ENGENHARIA CAMPUS DE GUARATINGUETÁ DESENHO TÉCNICO: Fundamentos Teóricos e Introdução ao CAD Parte 6/5: 14. Perspectivas Prof. Víctor O. Gamarra Rosado
LISTA DE EXERCÍCIO REFLEXÃO DA LUZ
 GOVERNO DO ESTADO DE PERNAMBUCO GRÉ MATA NORTE UNIVERSIDADE DE PERNAMBUCO CAMPUS MATA NORTE ESCOLA DE APLICAÇÃO PROFESSOR CHAVES LISTA DE EXERCÍCIO REFLEXÃO DA LUZ ALUNO(A): Nº NAZARÉ DA MATA, DE DE 2015
GOVERNO DO ESTADO DE PERNAMBUCO GRÉ MATA NORTE UNIVERSIDADE DE PERNAMBUCO CAMPUS MATA NORTE ESCOLA DE APLICAÇÃO PROFESSOR CHAVES LISTA DE EXERCÍCIO REFLEXÃO DA LUZ ALUNO(A): Nº NAZARÉ DA MATA, DE DE 2015
Aula 4 Função do 2º Grau
 1 Tecnólogo em Construção de Edifícios Aula 4 Função do 2º Grau Professor Luciano Nóbrega GABARITO 46) f(x) = x 2 + x + 1 www.professorlucianonobrega.wordpress.com 2 FUNÇÃO POLINOMIAL DO 2º GRAU Uma função
1 Tecnólogo em Construção de Edifícios Aula 4 Função do 2º Grau Professor Luciano Nóbrega GABARITO 46) f(x) = x 2 + x + 1 www.professorlucianonobrega.wordpress.com 2 FUNÇÃO POLINOMIAL DO 2º GRAU Uma função
Aula 01: Grandezas Físicas; Sistemas de Unidades; Vetores
 Aula 01: Grandezas Físicas; Sistemas de Unidades; Vetores Tópico 01: Grandezas Físicas - Introdução Caro aluno, quantas vezes você já ouviu alguém falar que Física e Matemática é tudo a mesma coisa? Que
Aula 01: Grandezas Físicas; Sistemas de Unidades; Vetores Tópico 01: Grandezas Físicas - Introdução Caro aluno, quantas vezes você já ouviu alguém falar que Física e Matemática é tudo a mesma coisa? Que
PERSPECTIVA ISOMÉTRICA
 PERSPECTIVA ISOMÉTRICA Aluna: Patricia Carvalho Souza Orientadora: Anna Virgínia Machado Roteiro Perspectiva o Tipos de Perspectiva Perspectiva Axonométrica o Linhas Isométricas e Não Isométricas Papel
PERSPECTIVA ISOMÉTRICA Aluna: Patricia Carvalho Souza Orientadora: Anna Virgínia Machado Roteiro Perspectiva o Tipos de Perspectiva Perspectiva Axonométrica o Linhas Isométricas e Não Isométricas Papel
MATRIZ - FORMAÇÃO E IGUALDADE
 MATRIZ - FORMAÇÃO E IGUALDADE 1. Seja X = (x ij ) uma matriz quadrada de ordem 2, onde i + j para i = j ;1 - j para i > j e 1 se i < j. A soma dos seus elementos é igual a: 2. Se M = ( a ij ) 3x2 é uma
MATRIZ - FORMAÇÃO E IGUALDADE 1. Seja X = (x ij ) uma matriz quadrada de ordem 2, onde i + j para i = j ;1 - j para i > j e 1 se i < j. A soma dos seus elementos é igual a: 2. Se M = ( a ij ) 3x2 é uma
Unidade 13 Introdução à Dinâmica Impulsiva. Introdução Quantidade de Movimento Impulso Teorema do Impulso
 Unidade 13 Introdução à Dinâmica Impulsiva Introdução Quantidade de Movimento Impulso Teorema do Impulso Introdução Em um acidente automobilístico, nem sempre é fácil descobrir quem foi o culpado. Por
Unidade 13 Introdução à Dinâmica Impulsiva Introdução Quantidade de Movimento Impulso Teorema do Impulso Introdução Em um acidente automobilístico, nem sempre é fácil descobrir quem foi o culpado. Por
