|
|
|
- Stéphanie Salvado Jardim
- 10 Há anos
- Visualizações:
Transcrição
1 Professor Victor Eduardo Disciplina Matemática Lista nº 2 Assuntos Função - Modelo UERJ e Exercícios Complementares 1 - (Uerj 2002) Sabedoria egípcia Há mais de anos os egípcios observaram que a sombra no chão provocada pela incidência dos raios solares de um gnômon (um tipo de vareta) variava de tamanho e de direção. Com medidas feitas sempre ao meio dia, notaram que a sombra, com o passar dos dias, aumentava de tamanho. Depois de chegar a um comprimento máximo, ela recuava até perto da vareta. As sombras mais longas coincidiam com dias frios. E as mais curtas, com dias quentes. (Adaptado de Revista "Galileu", janeiro de 2001.) Molecular da Célula." Porto Alegre: Artes Médicas, 1997.) Admita que, a partir dos cinquenta anos, a perda da massa óssea ocorra de forma linear conforme mostra o gráfico abaixo. (Adaptado de "Galileu", janeiro de 1999.) Um estudante fez uma experiência semelhante à descrita no texto, utilizando uma vareta OA de 2 metros de comprimento. No início do inverno, mediu o comprimento da sombra OB, encontrando 8 metros. Utilizou, para representar sua experiência, um sistema de coordenadas cartesianas, no qual o eixo das ordenadas (y) e o eixo das abscissas (x) continham, respectivamente, os segmentos de reta que representavam a vareta e a sombra que ela determinava no chão. Esse estudante pôde, assim, escrever a seguinte equação da reta que contém o segmento AB: a) y = 8-4x b) x = 6-3y c) x = 8-4y d) y = 6-3x 2 - (Uerj 2001) O balanço de cálcio é a diferença entre a quantidade de cálcio ingerida e a quantidade excretada na urina e nas fezes. É usualmente positivo durante o crescimento e a gravidez e negativo na menopausa, quando pode ocorrer a osteoporose, uma doença caracterizada pela diminuição da absorção de cálcio pelo organismo. A baixa concentração de íon cálcio (Ca ++ ) no sangue estimula as glândulas paratireoides a produzirem hormônio paratireoideo (HP). Nesta situação, o hormônio pode promover a remoção de cálcio dos ossos, aumentar sua absorção pelo intestino e reduzir sua excreção pelos rins. (Adaptado de ALBERTS, B. et al., "Urologia Aos 60 e aos 80 anos, as mulheres têm, respectivamente, 90% e 70% da massa óssea que tinham aos 30 anos. O percentual de massa óssea que as mulheres já perderam aos 76 anos, em relação à massa aos 30 anos, é igual a: a) 14 b) 18 c) 22 d) (Uerj 2001) O gráfico abaixo representa o consumo de oxigênio de uma pessoa que se exercita, em condições aeróbicas, numa bicicleta ergométrica. Considere que o organismo libera, em média, 4,8 kcal para cada litro de oxigênio absorvido. A energia liberada no período entre 5 e 15 minutos, em kcal, é: a) 48,0 b) 52,4 c) 67,2 d) 93,6
2 4. (Ufrj 2011) Um ponto P desloca-se sobre uma reta numerada, e sua posição (em metros) em relação à origem é dada, em função do tempo t (em segundos), por P(t) = 2(1 t) + 8t. Não, pois a melhor opção para este cliente seria a opção III. 7. (Uff 2011) Os gráficos I, II e III, a seguir, esboçados em uma mesma escala, ilustram modelos teóricos que descrevem a população de três espécies de pássaros ao longo do tempo. a) Determine a posição do ponto P no instante inicial (t = 0). 2 b) Determine a medida do segmento de reta correspondente ao conjunto dos pontos obtidos pela 3 variação de t no intervalo 0, (Uff 2004) Um grande poluente produzido pela queima de combustíveis fósseis é o SO 2 (dióxido de enxofre). Uma pesquisa realizada na Noruega e publicada na revista "Science" em 1972 concluiu que o número (N) de mortes por semana, causadas pela inalação de SO 2, estava relacionado com a concentração média (C), em mg/m 3, do SO 2 conforme o gráfico a seguir: os pontos (C, N) dessa relação estão sobre o segmento de reta da figura. Com base nos dados apresentados, a relação entre N e C (100 C 700) pode ser dada por: a) N = C b) N = ,03 C c) N = ,03 C d) N = C e) N = C 6. (Ufrj 2004) Um vídeo-clube propõe a seus clientes três opções de pagamento: Opção I: R$ 40,00 de taxa de adesão anual, mais R$ 1,20 por DVD alugado. Opção II: R$ 20,00 de taxa de adesão anual, mais R$ 2,00 por DVD alugado. Opção III: R$ 3,00 por DVD alugado, sem taxa de adesão. Um cliente escolheu a opção II e gastou R$ 56,00 no ano. Esse cliente escolheu a melhor opção de pagamento para o seu caso? Justifique sua resposta. Sabe-se que a população da espécie A aumenta 20% ao ano, que a população da espécie B aumenta 100 pássaros ao ano e que a população da espécie C permanece estável ao longo dos anos. Assim, a evolução das populações das espécies A, B e C, ao longo do tempo, correspondem, respectivamente, aos gráficos a) I, III e II. b) II, I e III. c) II, III e I. d) III, I e II. e) III, II e I. 8. (Ufrrj 2007) O técnico de um atleta passa a seguinte série de exercícios: caminhar meia hora a 3 km/h; correr 12 km, a uma velocidade constante, em 1 hora; nadar durante 1 hora; andar 9 km de bicicleta, a uma velocidade constante, em meia hora. Baseando-se na tabela a seguir, quantas calorias o atleta queima na série de exercícios? a) 1546 calorias. b) 1846 calorias. c) 1356 calorias. d) 1962 calorias. e) 1761 calorias.
3 9. (Uff 2007) Segundo o geógrafo brasileiro Elmo da Silva Amador, as descargas líquidas médias mensais afluentes na Baía de Guanabara são como dadas na tabela: Com base nos dados da tabela, pode-se afirmar que: a) a descarga líquida média mensal dos afluentes rio Macacu e rio Caceribu correspondem a mais de 90% da descarga líquida média mensal de todos os afluentes na Baía de Guanabara; b) os afluentes rio Macacu e rio Saracuruna são responsáveis por mais de 50% da descarga líquida média mensal de todos os afluentes na Baía de Guanabara; c) a descarga líquida média mensal do rio Macacu corresponde a 25% da descarga líquida média mensal de todos os afluentes na Baía de Guanabara; d) a descarga líquida média mensal de todos os afluentes na Baía de Guanabara é menor do que 500 litros por segundo; e) a descarga líquida média mensal das áreas urbanizadas na Baía de Guanabara é superior a litros por segundo. 10. (Uff 2006) No Brasil, são produzidas milhares de toneladas de lixo por dia. Segundo a Pesquisa Nacional de Saneamento Básico, realizada pelo IBGE em 2000, o destino final do lixo, em cada região do país, estava distribuído da seguinte forma: Sabe-se ainda, pela mesma fonte, que a produção diária de lixo (em toneladas), por região, era a seguinte: REGIÃO - TOTAL (toneladas por dia) Nordeste Sul Sudeste Centro-Oeste Norte Gráficos e tabelas construídos com base nas fontes do PNSB 2000/IBGE Com base nesses dados, pode-se afirmar que, em 2000, a quantidade, em toneladas por dia, de lixo depositada a) em lixões na região Sudeste era menor do que a quantidade depositada em lixões na região Norte. b) em lixões na região Nordeste era maior do que a quantidade depositada em lixões na região Norte. c) em estações de compostagem ou de triagem na região Sul era maior do que a quantidade depositada em estações de compostagem ou de triagem na região Sudeste. d) em aterros sanitários na região Nordeste era maior do que a quantidade depositada em aterros sanitários na região Sudeste. e) em aterros controlados na região Sul era menor do que a quantidade depositada em aterros controlados na região Norte. 11. (Ufrj 2006) Dois estados produzem trigo e soja. Os gráficos a seguir representam a produção relativa de grãos de cada um desses estados. a) A produção de trigo do estado A corresponde a que porcentagem da produção de grãos do estado? b) É possível afirmar, a partir dos gráficos, que a produção total de trigo do estado A é maior do que a do estado B? Justifique sua resposta. 12. (Uff 2005) Segundo a Organização das Nações Unidas (ONU), o mundo não conseguirá atingir a meta de reduzir a fome pela metade em Nem mesmo em 2030 esse objetivo poderá ser alcançado. O gráfico a seguir mostra o número, em milhões, de pessoas com fome em cinco regiões do mundo, em diferentes anos (1992, 1999, 2015 e 2030), segundo dados
4 e estimativas da ONU. 14. (Uff 2000) O gráfico da função f está representado na figura: Com base nos dados fornecidos pelo gráfico, pode-se afirmar que: a) em 2030, haverá mais de 700 milhões de pessoas com fome nas regiões destacadas no gráfico; b) em cada região destacada no gráfico, o número de pessoas com fome em 2030 será menor do que em 1992; c) em cada região destacada no gráfico, o número de pessoas com fome em 2030 será menor do que em 2015; d) em cada região destacada no gráfico, o número de pessoas com fome em 2015 será menor do que em 1999; e) em 2030, o número de pessoas com fome no Sul da África será maior do que três vezes o número de pessoas com fome no Sul da Ásia. 13. (Uff 2002) A partir dos dados fornecidos pelo gráfico a seguir, calculou-se a diferença entre a entrada e a saída de capitais nos países em desenvolvimento. Identifique a opção que pode representar, graficamente, a evolução dessa diferença. Sobre a função f é FALSO afirmar que: a) f(1) + f(2) = f(3) b) f(2) = f(7) c) f(3) = 3f(1) d) f(4) - f(3) = f(1) e) f(2) + f(3) = f(5) 15.(Uff 2011) Diz-se que uma família vive na pobreza extrema se sua renda mensal por pessoa é de, no máximo, 25% do salário mínimo nacional. Segundo levantamento do Instituto de Pesquisa Econômica Aplicada (Ipea), mais de treze milhões de brasileiros saíram da pobreza extrema entre 1995 e No entanto, a diminuição generalizada nas taxas de pobreza extrema nesse período não ocorreu de forma uniforme entre as grandes regiões geográficas do país, conforme ilustra o gráfico a seguir. SAÍDA E ENTRADA DE CAPITAIS NOS PAÍSES EM DESENVOLVIMENTO (Fonte: global Development Finance, Banco Mundial e OCDE (Organização para Cooperação e Desenvolvimento Econômico) Tendo em vista o gráfico, verifica-se que a taxa nacional de pobreza extrema caiu 49,8%, passando de 20,9% para 10,5%. Pode-se concluir, então, que a região em que a taxa de pobreza extrema (em %) caiu mais de 50% foi a) a região Norte. b) a região Sudeste. c) a região Nordeste. d) a região Centro-Oeste. e) a região Sul.
5 GABARITO 1-C 2-D 3-C 4- a) 2 b) 9 5-b 6- Não, pois a melhor opção para este cliente seria a opção III. 7- E 8- E 9- E 10 - B 11 - a)80% 12 - C 13 - B 14 E 15 - E
1. Um corpo arremessado tem sua trajetória representada pelo gráfico de uma parábola, conforme a figura a seguir.
 1. Um corpo arremessado tem sua trajetória representada pelo gráfico de uma parábola, conforme a figura a seguir. Nessa trajetória, a altura máxima, em metros, atingida pelo corpo foi de a) 0,52m. b) 0,64m.
1. Um corpo arremessado tem sua trajetória representada pelo gráfico de uma parábola, conforme a figura a seguir. Nessa trajetória, a altura máxima, em metros, atingida pelo corpo foi de a) 0,52m. b) 0,64m.
BIOLOGIA - 3 o ANO MÓDULO 18 SISTEMA ENDÓCRINO PARTE 1
 BIOLOGIA - 3 o ANO MÓDULO 18 SISTEMA ENDÓCRINO PARTE 1 Paratireoides Tireoide Hipófise Timo Pâncreas Cápsulas suprarrenais ilhotas pancreáticas Testículos (no homem) Ovários (na mulher) glândula tireoide
BIOLOGIA - 3 o ANO MÓDULO 18 SISTEMA ENDÓCRINO PARTE 1 Paratireoides Tireoide Hipófise Timo Pâncreas Cápsulas suprarrenais ilhotas pancreáticas Testículos (no homem) Ovários (na mulher) glândula tireoide
CAPÍTULO 2 FUNÇÕES 1. INTRODUÇÃO. y = 0,80.x. 2. DEFINIÇÃO DE FUNÇÃO DE A EM B ( f: A B) 4. GRÁFICO DE UMA FUNÇÃO
 CAPÍTULO 2 FUNÇÕES 1. INTRODUÇÃO Muitas grandezas com as quais lidamos no nosso cotidiano dependem uma da outra, isto é, a variação de uma delas tem como conseqüência a variação da outra. Exemplo 1: Tio
CAPÍTULO 2 FUNÇÕES 1. INTRODUÇÃO Muitas grandezas com as quais lidamos no nosso cotidiano dependem uma da outra, isto é, a variação de uma delas tem como conseqüência a variação da outra. Exemplo 1: Tio
A razão entre a medida da aresta do cubo e a medida do diâmetro da esfera a ele circunscrita, é: (B) (C) (D)
 CIÊNCIAS DA NATUREZA, CIÊNCIAS MATEMÁTICA DA NATUREZA, MATEMÁTICA E SUAS TECNOLOGIAS E SUAS Questão 29 (Galileu Galilei) Com base neste conhecimento, Galileu, antes mesmo de realizar seu famoso experimento
CIÊNCIAS DA NATUREZA, CIÊNCIAS MATEMÁTICA DA NATUREZA, MATEMÁTICA E SUAS TECNOLOGIAS E SUAS Questão 29 (Galileu Galilei) Com base neste conhecimento, Galileu, antes mesmo de realizar seu famoso experimento
NOME: Nº. ASSUNTO: Recuperação Final - 1a.lista de exercícios VALOR: 13,0 NOTA:
 NOME: Nº 1 o ano do Ensino Médio TURMA: Data: 11/ 12/ 12 DISCIPLINA: Física PROF. : Petrônio L. de Freitas ASSUNTO: Recuperação Final - 1a.lista de exercícios VALOR: 13,0 NOTA: INSTRUÇÕES (Leia com atenção!)
NOME: Nº 1 o ano do Ensino Médio TURMA: Data: 11/ 12/ 12 DISCIPLINA: Física PROF. : Petrônio L. de Freitas ASSUNTO: Recuperação Final - 1a.lista de exercícios VALOR: 13,0 NOTA: INSTRUÇÕES (Leia com atenção!)
Aluno (a): 1) O intervalo A de números reais é representado geometricamente da seguinte maneira:
 Educa teu filho no caminho que deve andar, e quando grande não se desviará dele Prov.22.6 Bateria de Exercícios Data: 24/03/2016 Turma: 1º Ano Área II Aluno (a): Prezado aluno caso prefira responder na
Educa teu filho no caminho que deve andar, e quando grande não se desviará dele Prov.22.6 Bateria de Exercícios Data: 24/03/2016 Turma: 1º Ano Área II Aluno (a): Prezado aluno caso prefira responder na
Vestibulando Web Page www.vestibulandoweb.com.br
 1. (Ufv 2000) Um aluno, sentado na carteira da sala, observa os colegas, também sentados nas respectivas carteiras, bem como um mosquito que voa perseguindo o professor que fiscaliza a prova da turma.
1. (Ufv 2000) Um aluno, sentado na carteira da sala, observa os colegas, também sentados nas respectivas carteiras, bem como um mosquito que voa perseguindo o professor que fiscaliza a prova da turma.
FÍSICA - 3 o ANO MÓDULO 13 CINEMÁTICA VETORIAL E COMPOSIÇÃO DE MOVIMENTOS
 FÍSICA - 3 o ANO MÓDULO 13 CINEMÁTICA VETORIAL E COMPOSIÇÃO DE MOVIMENTOS Como pode cair no enem (UERJ) Pardal é a denominação popular do dispositivo óptico-eletrônico utilizado para fotografar veículos
FÍSICA - 3 o ANO MÓDULO 13 CINEMÁTICA VETORIAL E COMPOSIÇÃO DE MOVIMENTOS Como pode cair no enem (UERJ) Pardal é a denominação popular do dispositivo óptico-eletrônico utilizado para fotografar veículos
b) a 0 e 0 d) a 0 e 0
 IFRN - INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN PROFESSOR: MARCELO SILVA MATEMÁTICA FUNÇÃO DO º GRAU 1. Um grupo de pessoas gastou R$ 10,00 em uma lanchonete. Quando foram pagar a conta,
IFRN - INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN PROFESSOR: MARCELO SILVA MATEMÁTICA FUNÇÃO DO º GRAU 1. Um grupo de pessoas gastou R$ 10,00 em uma lanchonete. Quando foram pagar a conta,
Nome: N.º: endereço: data: Telefone: E-mail: PARA QUEM CURSA O 9 Ọ ANO EM 2014. Disciplina: MaTeMÁTiCa
 Nome: N.º: endereço: data: Telefone: E-mail: Colégio PARA QUEM CURSA O 9 Ọ ANO EM 04 Disciplina: MaTeMÁTiCa Prova: desafio nota: QUESTÃO 6 A soma das medidas dos catetos de um triângulo retângulo é 8cm
Nome: N.º: endereço: data: Telefone: E-mail: Colégio PARA QUEM CURSA O 9 Ọ ANO EM 04 Disciplina: MaTeMÁTiCa Prova: desafio nota: QUESTÃO 6 A soma das medidas dos catetos de um triângulo retângulo é 8cm
PROVA DO VESTIBULAR ESAMC-2003-1 RESOLUÇÃO E COMENTÁRIO DA PROFA. MARIA ANTÔNIA GOUVEIA M A T E M Á T I C A
 PROVA DO VESTIBULAR ESAMC-- RESOLUÇÃO E COMENTÁRIO DA PROFA. MARIA ANTÔNIA GOUVEIA M A T E M Á T I C A Q. O valor da epressão para = é : A, B, C, D, E, ( (,..., ( ( RESPOSTA: Alternativa A. Q. Sejam A
PROVA DO VESTIBULAR ESAMC-- RESOLUÇÃO E COMENTÁRIO DA PROFA. MARIA ANTÔNIA GOUVEIA M A T E M Á T I C A Q. O valor da epressão para = é : A, B, C, D, E, ( (,..., ( ( RESPOSTA: Alternativa A. Q. Sejam A
(J/gºC) Água 4,19 Petróleo 2,09 Glicerin a 2,43. Leite 3,93 Mercúri o 0,14. a) a água. b) o petróleo. c) a glicerina. d) o leite.
 COLÉGIO PEDRO II PRÓ-REITORIA DE PÓS-GRADUAÇÃO, PESQUISA, EXTENSÃO E CULTURA PROGRAMA DE RESIDÊNCIA DOCENTE RESIDENTE DOCENTE: Marcia Cristina de Souza Meneguite Lopes MATRÍCULA: P4112515 INSCRIÇÃO: PRD.FIS.0006/15
COLÉGIO PEDRO II PRÓ-REITORIA DE PÓS-GRADUAÇÃO, PESQUISA, EXTENSÃO E CULTURA PROGRAMA DE RESIDÊNCIA DOCENTE RESIDENTE DOCENTE: Marcia Cristina de Souza Meneguite Lopes MATRÍCULA: P4112515 INSCRIÇÃO: PRD.FIS.0006/15
DATA: 17/12/2015 VALOR: 20,0 NOTA: NOME COMPLETO:
 DISCIPLINA: FÍSICA PROFESSORES: Erich/ André NOME COMPLETO: I N S T R U Ç Õ E S DATA: 17/12/2015 VALOR: 20,0 NOTA: ASSUNTO: TRABALHO DE RECUPERAÇÃO FINAL SÉRIE: 1 a EM Circule a sua turma: Funcionários:
DISCIPLINA: FÍSICA PROFESSORES: Erich/ André NOME COMPLETO: I N S T R U Ç Õ E S DATA: 17/12/2015 VALOR: 20,0 NOTA: ASSUNTO: TRABALHO DE RECUPERAÇÃO FINAL SÉRIE: 1 a EM Circule a sua turma: Funcionários:
muito gás carbônico, gás de enxofre e monóxido de carbono. extremamente perigoso, pois ocupa o lugar do oxigênio no corpo. Conforme a concentração
 A UU L AL A Respiração A poluição do ar é um dos problemas ambientais que mais preocupam os governos de vários países e a população em geral. A queima intensiva de combustíveis gasolina, óleo e carvão,
A UU L AL A Respiração A poluição do ar é um dos problemas ambientais que mais preocupam os governos de vários países e a população em geral. A queima intensiva de combustíveis gasolina, óleo e carvão,
Respostas - Exercícios de rotação e translação
 Respostas - Exercícios de rotação e translação 1) "Durante a minha vida inteira me fiz essas perguntas: Existe vida além da Terra? Se existe, como se parece? De que é feita? Os seres de outros mundos se
Respostas - Exercícios de rotação e translação 1) "Durante a minha vida inteira me fiz essas perguntas: Existe vida além da Terra? Se existe, como se parece? De que é feita? Os seres de outros mundos se
MATEMÁTICA TIPO A GABARITO: VFFVF. Solução: é a parábola com foco no ponto (0, 3) e reta diretriz y = -3.
 1 MATEMÁTICA TIPO A 01. Seja o conjunto de pontos do plano cartesiano, cuja distância ao ponto é igual à distância da reta com equação. Analise as afirmações a seguir. 0-0) é a parábola com foco no ponto
1 MATEMÁTICA TIPO A 01. Seja o conjunto de pontos do plano cartesiano, cuja distância ao ponto é igual à distância da reta com equação. Analise as afirmações a seguir. 0-0) é a parábola com foco no ponto
, então. a) 0. c) log 3. c) 1 d) log 4. a) 2 b) c) d) 6. 9-(UECE) Se 6 igual a: a) 36 b) 45 c) 54 d) 81. , então. a) log 20 log 2. a) 3 b) 2 c) 1 d) 0
 LOGARITMOS Professor Clístenes Cunha -(CESGRANRIO-RJ) Se 5 0 a solução vale: a) 5 c) 7/ 0 -(PUC-MG) A soma das raízes da equação 5 a) c) -(CESGRANRIO-RJ) O valor de a) / / c) / / -(UEL-PR) Se 5 7 é igual
LOGARITMOS Professor Clístenes Cunha -(CESGRANRIO-RJ) Se 5 0 a solução vale: a) 5 c) 7/ 0 -(PUC-MG) A soma das raízes da equação 5 a) c) -(CESGRANRIO-RJ) O valor de a) / / c) / / -(UEL-PR) Se 5 7 é igual
FUNÇÃO DE 1º GRAU. = mx + n, sendo m e n números reais. Questão 01 Dadas as funções f de IR em IR, identifique com um X, aquelas que são do 1º grau.
 FUNÇÃO DE 1º GRAU Veremos, a partir daqui algumas funções elementares, a primeira delas é a função de 1º grau, que estabelece uma relação de proporcionalidade. Podemos então, definir a função de 1º grau
FUNÇÃO DE 1º GRAU Veremos, a partir daqui algumas funções elementares, a primeira delas é a função de 1º grau, que estabelece uma relação de proporcionalidade. Podemos então, definir a função de 1º grau
Matemática para Concursos - Provas Gabaritadas. André Luiz Brandão
 Matemática para Concursos - Provas Gabaritadas André Luiz Brandão CopyMarket.com Todos os direitos reservados. Nenhuma parte desta publicação poderá ser reproduzida sem a autorização da Editora. Título:
Matemática para Concursos - Provas Gabaritadas André Luiz Brandão CopyMarket.com Todos os direitos reservados. Nenhuma parte desta publicação poderá ser reproduzida sem a autorização da Editora. Título:
1)Faça a representação gráfica das seguintes funções do primeiro grau: a)y = - x + 3 b)f(x) = - 3x + 5 c)y = x + 2 d)y = x + 3
 Função do Primeiro Grau 1)Faça a representação gráfica das seguintes funções do primeiro grau: a)y = - x + 3 b)f(x) = - 3x + 5 c)y = x + 2 d)y = x + 3 2)Uma função polinomial do 1 o grau y = f(x) é tal
Função do Primeiro Grau 1)Faça a representação gráfica das seguintes funções do primeiro grau: a)y = - x + 3 b)f(x) = - 3x + 5 c)y = x + 2 d)y = x + 3 2)Uma função polinomial do 1 o grau y = f(x) é tal
Gráficos Cinemáticos (2) v (m/s) (1)
 Gráficos Cinemáticos 1- Na figura estão representados os diagramas de velocidade de dois móveis em função do tempo. Esses móveis partem de um mesmo ponto, a partir do repouso, e percorrem a mesma trajetória
Gráficos Cinemáticos 1- Na figura estão representados os diagramas de velocidade de dois móveis em função do tempo. Esses móveis partem de um mesmo ponto, a partir do repouso, e percorrem a mesma trajetória
Supondo que se mantém constante o ritmo de desenvolvimento da população de vírus, qual o número de vírus após uma hora?
 Lista prova parcial 4º bimestre. 1. (Upf 01) Num laboratório está sendo realizado um estudo sobre a evolução de uma população de vírus. A seguinte sequência de figuras representa os três primeiros minutos
Lista prova parcial 4º bimestre. 1. (Upf 01) Num laboratório está sendo realizado um estudo sobre a evolução de uma população de vírus. A seguinte sequência de figuras representa os três primeiros minutos
Física. Questão 1. Questão 2. Avaliação: Aluno: Data: Ano: Turma: Professor:
 Avaliação: Aluno: Data: Ano: Turma: Professor: Física Questão 1 (Unirio 2000) Um aluno pegou um fina placa metálica e nela recortou um disco de raio r. Em seguida, fez um anel também de raio r com um fio
Avaliação: Aluno: Data: Ano: Turma: Professor: Física Questão 1 (Unirio 2000) Um aluno pegou um fina placa metálica e nela recortou um disco de raio r. Em seguida, fez um anel também de raio r com um fio
2. (G1 - ifsp 2012) Em um trecho retilíneo de estrada, dois veículos, A e B, mantêm velocidades constantes. 54 km/h
 MU 1. (Uerj 2013) Um motorista dirige um automóvel em um trecho plano de um viaduto. O movimento é retilíneo e uniforme. A intervalos regulares de 9 segundos, o motorista percebe a passagem do automóvel
MU 1. (Uerj 2013) Um motorista dirige um automóvel em um trecho plano de um viaduto. O movimento é retilíneo e uniforme. A intervalos regulares de 9 segundos, o motorista percebe a passagem do automóvel
Nível 3 IV FAPMAT 28/10/2007
 1 Nível 3 IV FAPMAT 8/10/007 1. A figura abaixo representa a área de um paralelepípedo planificado. A que intervalo de valores, x deve pertencer de modo que a área da planificação seja maior que 184cm
1 Nível 3 IV FAPMAT 8/10/007 1. A figura abaixo representa a área de um paralelepípedo planificado. A que intervalo de valores, x deve pertencer de modo que a área da planificação seja maior que 184cm
Pesquisa Nacional por Amostra de Domicílios - Síntese
 2014 Pesquisa Nacional por Amostra de Domicílios - Síntese Dieese Subseção Força Sindical 19/09/2014 PESQUISA NACIONAL POR AMOSTRA DE DOMICILIOS - PNAD 2013 Síntese dos Indicadores POPULAÇÃO A Pesquisa
2014 Pesquisa Nacional por Amostra de Domicílios - Síntese Dieese Subseção Força Sindical 19/09/2014 PESQUISA NACIONAL POR AMOSTRA DE DOMICILIOS - PNAD 2013 Síntese dos Indicadores POPULAÇÃO A Pesquisa
FÍSICA - 1 o ANO MÓDULO 17 LANÇAMENTO VERTICAL E QUEDA LIVRE
 FÍSICA - 1 o ANO MÓDULO 17 LANÇAMENTO VERTICAL E QUEDA LIVRE Como pode cair no enem? celeração de 5 g (ou 50 m/s²), ocorrendo o enrijecimento dos músculos devido a força que o sangue exerce na volta
FÍSICA - 1 o ANO MÓDULO 17 LANÇAMENTO VERTICAL E QUEDA LIVRE Como pode cair no enem? celeração de 5 g (ou 50 m/s²), ocorrendo o enrijecimento dos músculos devido a força que o sangue exerce na volta
Aula 5 - Parte 1: Funções. Exercícios Propostos
 Aula 5 - Parte 1: Funções Exercícios Propostos 1 Construção de Funções: a) Um grupo de amigos deseja alugar uma van, por um dia, para um passeio, ao custo de R$300,00. Um levantamento preliminar indicou
Aula 5 - Parte 1: Funções Exercícios Propostos 1 Construção de Funções: a) Um grupo de amigos deseja alugar uma van, por um dia, para um passeio, ao custo de R$300,00. Um levantamento preliminar indicou
Matemática. O coeficiente angular dado pelo 3º e 4º pontos é igual ao coeficiente angular dado pelo 1º e 3º. Portanto:
 Matemática O gráfico de uma função polinomial do primeiro grau passa pelos pontos de coordenadas ( x, y) dados abaixo x y 0 5 m 8 6 4 7 k Podemos concluir que o valor de k m é: A 5,5 B 6,5 C 7,5 D 8,5
Matemática O gráfico de uma função polinomial do primeiro grau passa pelos pontos de coordenadas ( x, y) dados abaixo x y 0 5 m 8 6 4 7 k Podemos concluir que o valor de k m é: A 5,5 B 6,5 C 7,5 D 8,5
CPV especializado na ESPM ESPM Resolvida Prova E 10/novembro/2013
 CPV especializado na ESPM ESPM Resolvida Prova E 0/novembro/03 Matemática. As soluções da equação x + 3 x = 3x + são dois números: x + 3 a) primos b) positivos c) negativos d) pares e) ímpares x + 3 x
CPV especializado na ESPM ESPM Resolvida Prova E 0/novembro/03 Matemática. As soluções da equação x + 3 x = 3x + são dois números: x + 3 a) primos b) positivos c) negativos d) pares e) ímpares x + 3 x
ESTUDO GRÁFICO DOS MOVIMENTOS. Gráfico posição x tempo (x x t)
 ESTUDO GRÁFICO DOS MOVIMENTOS No estudo do movimento é bastante útil o emprego de gráficos. A descrição de um movimento a partir da utilização dos gráficos (posição x tempo; velocidade x tempo e aceleração
ESTUDO GRÁFICO DOS MOVIMENTOS No estudo do movimento é bastante útil o emprego de gráficos. A descrição de um movimento a partir da utilização dos gráficos (posição x tempo; velocidade x tempo e aceleração
Problemas de função do 1º grau
 Problemas de função do º grau. (Ucs 204) O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor total, em reais, das vendas que ele efetuar durante o mês. Em um mês em que suas vendas
Problemas de função do º grau. (Ucs 204) O salário mensal de um vendedor é de R$ 750,00 fixos mais 2,5% sobre o valor total, em reais, das vendas que ele efetuar durante o mês. Em um mês em que suas vendas
Undécima lista de exercícios. Função exponencial e função logarítmica.
 MA091 Matemática básica Verão de 01 Undécima lista de exercícios Função exponencial e função logarítmica 1 Você pegou um empréstimo bancário de R$ 500,00, a uma taxa de 5% ao mês a) Escreva a função que
MA091 Matemática básica Verão de 01 Undécima lista de exercícios Função exponencial e função logarítmica 1 Você pegou um empréstimo bancário de R$ 500,00, a uma taxa de 5% ao mês a) Escreva a função que
Exercícios complementares envolvendo a equação de Torricelli
 01. (Vunesp-SP) Um veículo está rodando à velocidade de 36 km/h numa estrada reta e horizontal, quando o motorista aciona o freio. Supondo que a velocidade do veículo se reduz uniformemente à razão de
01. (Vunesp-SP) Um veículo está rodando à velocidade de 36 km/h numa estrada reta e horizontal, quando o motorista aciona o freio. Supondo que a velocidade do veículo se reduz uniformemente à razão de
Velocidade Média Velocidade Instantânea Unidade de Grandeza Aceleração vetorial Aceleração tangencial Unidade de aceleração Aceleração centrípeta
 Velocidade Média Velocidade Instantânea Unidade de Grandeza Aceleração vetorial Aceleração tangencial Unidade de aceleração Aceleração centrípeta Classificação dos movimentos Introdução Velocidade Média
Velocidade Média Velocidade Instantânea Unidade de Grandeza Aceleração vetorial Aceleração tangencial Unidade de aceleração Aceleração centrípeta Classificação dos movimentos Introdução Velocidade Média
UFMS - PRÓ ENEM Matemática Estatística e Médias
 1. (Ufsm 01) O Brasil é o quarto produtor mundial de alimentos, produzindo mais do que o necessário para alimentar sua população. Entretanto, grande parte da produção é desperdiçada. O gráfico mostra o
1. (Ufsm 01) O Brasil é o quarto produtor mundial de alimentos, produzindo mais do que o necessário para alimentar sua população. Entretanto, grande parte da produção é desperdiçada. O gráfico mostra o
Faculdade Sagrada Família
 AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
1. (Fgv 2005) a) Mostre que existem infinitas triplas ordenadas (x,y,z) de números que
 SISTEMAS LINEARES 2 1. (Fgv 2005) a) Mostre que existem infinitas triplas ordenadas (x,y,z) de números que satisfazem a equação matricial: b) Resolva o sistema linear abaixo, nas incógnitas x e y, usando
SISTEMAS LINEARES 2 1. (Fgv 2005) a) Mostre que existem infinitas triplas ordenadas (x,y,z) de números que satisfazem a equação matricial: b) Resolva o sistema linear abaixo, nas incógnitas x e y, usando
Estime, em MJ, a energia cinética do conjunto, no instante em que o navio se desloca com velocidade igual a 108 km h.
 1. (Uerj 016) No solo da floresta amazônica, são encontradas partículas ricas em 1 fósforo, trazidas pelos ventos, com velocidade constante de 0,1m s, desde o deserto do Saara. Admita que uma das partículas
1. (Uerj 016) No solo da floresta amazônica, são encontradas partículas ricas em 1 fósforo, trazidas pelos ventos, com velocidade constante de 0,1m s, desde o deserto do Saara. Admita que uma das partículas
RESOLUÇÃO PROVA TJ PR
 PROVA TJ PR Questão 6 Três amigas estavam de férias em três cidades diferentes. Com base nas informações abaixo, descubra o nome do lugar e o número do quarto de hotel em que Ana, Claudia e Vanessa estavam
PROVA TJ PR Questão 6 Três amigas estavam de férias em três cidades diferentes. Com base nas informações abaixo, descubra o nome do lugar e o número do quarto de hotel em que Ana, Claudia e Vanessa estavam
Analise este mapa topográfico, em que está representada uma paisagem serrana de Minas Gerais:
 QUESTÃO 01 2 Analise este mapa topográfico, em que está representada uma paisagem serrana de Minas Gerais: Um grupo de turistas, hospedado na pousada localizada nesse mapa, realizou uma caminhada ecológica
QUESTÃO 01 2 Analise este mapa topográfico, em que está representada uma paisagem serrana de Minas Gerais: Um grupo de turistas, hospedado na pousada localizada nesse mapa, realizou uma caminhada ecológica
Olimpíada Brasileira de Física 2001 2ª Fase
 Olimpíada Brasileira de Física 2001 2ª Fase Gabarito dos Exames para o 1º e 2º Anos 1ª QUESTÃO Movimento Retilíneo Uniforme Em um MRU a posição s(t) do móvel é dada por s(t) = s 0 + vt, onde s 0 é a posição
Olimpíada Brasileira de Física 2001 2ª Fase Gabarito dos Exames para o 1º e 2º Anos 1ª QUESTÃO Movimento Retilíneo Uniforme Em um MRU a posição s(t) do móvel é dada por s(t) = s 0 + vt, onde s 0 é a posição
MATEMÁTICA ESTATÍSTICA
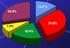 MATEMÁTICA ESTATÍSTICA 1. U.Católica-DF Com base nas informações do texto e da tabela a seguir, julgue as afirmativas que se seguem com V ou F, conforme sejam Verdadeiras ou Falsas. Para uma vida moderna
MATEMÁTICA ESTATÍSTICA 1. U.Católica-DF Com base nas informações do texto e da tabela a seguir, julgue as afirmativas que se seguem com V ou F, conforme sejam Verdadeiras ou Falsas. Para uma vida moderna
TIPO-A FÍSICA. x v média. t t. x x
 12 FÍSICA Aceleração da gravidade, g = 10 m/s 2 Constante gravitacional, G = 7 x 10-11 N.m 2 /kg 2 Massa da Terra, M = 6 x 10 24 kg Velocidade da luz no vácuo, c = 300.000 km/s 01. Em 2013, os experimentos
12 FÍSICA Aceleração da gravidade, g = 10 m/s 2 Constante gravitacional, G = 7 x 10-11 N.m 2 /kg 2 Massa da Terra, M = 6 x 10 24 kg Velocidade da luz no vácuo, c = 300.000 km/s 01. Em 2013, os experimentos
Aluno(a): Nº. Professor: Fabrízio Gentil Série: 2 o ano Disciplina: Física - Calorimetria. Pré Universitário Uni-Anhanguera
 Lista de Exercícios Pré Universitário Uni-Anhanguera Aluno(a): Nº. Professor: Fabrízio Gentil Série: 2 o ano Disciplina: Física - Calorimetria 01 - (MACK SP) Um estudante no laboratório de física, por
Lista de Exercícios Pré Universitário Uni-Anhanguera Aluno(a): Nº. Professor: Fabrízio Gentil Série: 2 o ano Disciplina: Física - Calorimetria 01 - (MACK SP) Um estudante no laboratório de física, por
Resolução Comentada UFTM - VESTIBULAR DE INVERNO 2013
 Resolução Comentada UFTM - VESTIBULAR DE INVERNO 2013 01 - A figura mostra uma série de fotografias estroboscópicas de duas esferas, A e B, de massas diferentes. A esfera A foi abandonada em queda livre
Resolução Comentada UFTM - VESTIBULAR DE INVERNO 2013 01 - A figura mostra uma série de fotografias estroboscópicas de duas esferas, A e B, de massas diferentes. A esfera A foi abandonada em queda livre
Soluções das Questões de Física da Universidade do Estado do Rio de Janeiro UERJ
 Soluções das Questões de Física da Universidade do Estado do Rio de Janeiro UERJ º Exame de Qualificação 011 Questão 6 Vestibular 011 No interior de um avião que se desloca horizontalmente em relação ao
Soluções das Questões de Física da Universidade do Estado do Rio de Janeiro UERJ º Exame de Qualificação 011 Questão 6 Vestibular 011 No interior de um avião que se desloca horizontalmente em relação ao
Prof. Rogério Porto. Assunto: Cinemática em uma Dimensão II
 Questões COVEST Física Mecânica Prof. Rogério Porto Assunto: Cinemática em uma Dimensão II 1. Um carro está viajando numa estrada retilínea com velocidade de 72 km/h. Vendo adiante um congestionamento
Questões COVEST Física Mecânica Prof. Rogério Porto Assunto: Cinemática em uma Dimensão II 1. Um carro está viajando numa estrada retilínea com velocidade de 72 km/h. Vendo adiante um congestionamento
FGV-EAESP PROVA DE RACIOCÍNIO MATEMÁTICO CURSO DE GRADUAÇÃO AGOSTO/2004
 QUESTÃO 1. Numa cidade do interior do estado de São Paulo, uma prévia eleitoral entre 2.000 filiados revelou as seguintes informações a respeito de três candidatos A, B, e C, do Partido da Esperança (PE)
QUESTÃO 1. Numa cidade do interior do estado de São Paulo, uma prévia eleitoral entre 2.000 filiados revelou as seguintes informações a respeito de três candidatos A, B, e C, do Partido da Esperança (PE)
Potência elétrica. 06/05/2011 profpeixinho.orgfree.com pag.1
 1. (Unicamp) Um aluno necessita de um resistor que, ligado a uma tomada de 220 V, gere 2200 W de potência térmica. Ele constrói o resistor usando fio de constante N. 30 com área de seção transversal de
1. (Unicamp) Um aluno necessita de um resistor que, ligado a uma tomada de 220 V, gere 2200 W de potência térmica. Ele constrói o resistor usando fio de constante N. 30 com área de seção transversal de
FÍSICA - 1 o ANO MÓDULO 16 GRÁFICOS DA CINEMÁTICA REVISÃO
 FÍSICA - 1 o ANO MÓDULO 16 GRÁFICOS DA CINEMÁTICA REVISÃO Como pode cair no enem? O estudo dos movimentos (Uniforme e Uniformemente Variado) é a aplicação física do estudo das funções em Matemática. As
FÍSICA - 1 o ANO MÓDULO 16 GRÁFICOS DA CINEMÁTICA REVISÃO Como pode cair no enem? O estudo dos movimentos (Uniforme e Uniformemente Variado) é a aplicação física do estudo das funções em Matemática. As
Agrupamento de Escolas Anselmo de Andrade Avaliação Sumativa - Ciências Físico - Químicas 11.º Ano - Ano Lectivo 09/10
 Agrupamento de Escolas Anselmo de Andrade Avaliação Sumativa - Ciências Físico - Químicas 11.º Ano - Ano ectivo 09/10 Duração da Actividade: 90 minutos Data: 04/ 12 / 09 Responda com clareza às questões
Agrupamento de Escolas Anselmo de Andrade Avaliação Sumativa - Ciências Físico - Químicas 11.º Ano - Ano ectivo 09/10 Duração da Actividade: 90 minutos Data: 04/ 12 / 09 Responda com clareza às questões
Valor da cesta básica diminui em 15 cidades
 1 São Paulo, 04 de setembro de 2015. NOTA à IMPRENSA Valor da cesta básica diminui em 15 cidades Das 18 cidades em que o DIEESE - Departamento Intersindical de Estatística e Estudos Socioeconômicos - realiza
1 São Paulo, 04 de setembro de 2015. NOTA à IMPRENSA Valor da cesta básica diminui em 15 cidades Das 18 cidades em que o DIEESE - Departamento Intersindical de Estatística e Estudos Socioeconômicos - realiza
MATEMÁTICA. y Q. (a,b)
 MATEMÁTICA 1. Sejam (a, b), com a e b positivos, as coordenadas de um ponto no plano cartesiano, e r a reta com inclinação m
MATEMÁTICA 1. Sejam (a, b), com a e b positivos, as coordenadas de um ponto no plano cartesiano, e r a reta com inclinação m
Apresentação de Dados em Tabelas e Gráficos
 Apresentação de Dados em Tabelas e Gráficos Os dados devem ser apresentados em tabelas construídas de acordo com as normas técnicas ditadas pela Fundação Instituto Brasileiro de Geografia e Estatística
Apresentação de Dados em Tabelas e Gráficos Os dados devem ser apresentados em tabelas construídas de acordo com as normas técnicas ditadas pela Fundação Instituto Brasileiro de Geografia e Estatística
3) Uma mola de constante elástica k = 400 N/m é comprimida de 5 cm. Determinar a sua energia potencial elástica.
 Lista para a Terceira U.L. Trabalho e Energia 1) Um corpo de massa 4 kg encontra-se a uma altura de 16 m do solo. Admitindo o solo como nível de referência e supondo g = 10 m/s 2, calcular sua energia
Lista para a Terceira U.L. Trabalho e Energia 1) Um corpo de massa 4 kg encontra-se a uma altura de 16 m do solo. Admitindo o solo como nível de referência e supondo g = 10 m/s 2, calcular sua energia
PROVA RESOLVIDA E COMENTADA DO BANCO DO BRASIL - 2010 - FCC MATEMÁTICA E RACIOCÍNIO LÓGICO.
 PROVA RESOLVIDA E COMENTADA DO BANCO DO BRASIL - 2010 - FCC MATEMÁTICA E RACIOCÍNIO LÓGICO. Professor Joselias - http://professorjoselias.blogspot.com/. MATEMÁTICA 16. Segundo a Associação Brasileira de
PROVA RESOLVIDA E COMENTADA DO BANCO DO BRASIL - 2010 - FCC MATEMÁTICA E RACIOCÍNIO LÓGICO. Professor Joselias - http://professorjoselias.blogspot.com/. MATEMÁTICA 16. Segundo a Associação Brasileira de
(c) 2a = b. (c) {10,..., 29}
 11 Atividade extra UNIDADE CONJUTOS Fascículo 4 Matemática Unidade 11 Conjuntos Exercı cio 11.1 Sejam os conjuntos A = {a, 7, 0} e B = {0, 1, b}, tal que os conjuntos A e B sejam iguais. Qual é a relação
11 Atividade extra UNIDADE CONJUTOS Fascículo 4 Matemática Unidade 11 Conjuntos Exercı cio 11.1 Sejam os conjuntos A = {a, 7, 0} e B = {0, 1, b}, tal que os conjuntos A e B sejam iguais. Qual é a relação
Saneamento básico e seus impactos na sociedade
 UNIVERSIDADE REGIONAL DO CARIRI URCA CENTRO DE CIÊNCIAS E TECNOLOGIA - CCT DEPARTAMENTO DE CONSTRUÇÂO CIVIL Saneamento básico e seus impactos na sociedade JUAZEIRO DO NORTE OUTUBRO 2012 FRANCISCO TAVARES
UNIVERSIDADE REGIONAL DO CARIRI URCA CENTRO DE CIÊNCIAS E TECNOLOGIA - CCT DEPARTAMENTO DE CONSTRUÇÂO CIVIL Saneamento básico e seus impactos na sociedade JUAZEIRO DO NORTE OUTUBRO 2012 FRANCISCO TAVARES
sendo as componentes dadas em unidades arbitrárias. Determine: a) o vetor vetores, b) o produto escalar e c) o produto vetorial.
 INSTITUTO DE FÍSICA DA UFRGS 1 a Lista de FIS01038 Prof. Thomas Braun Vetores 1. Três vetores coplanares são expressos, em relação a um sistema de referência ortogonal, como: sendo as componentes dadas
INSTITUTO DE FÍSICA DA UFRGS 1 a Lista de FIS01038 Prof. Thomas Braun Vetores 1. Três vetores coplanares são expressos, em relação a um sistema de referência ortogonal, como: sendo as componentes dadas
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO INDIVIDUAL DE ESTUDO ESTUDOS INDEPENDENTES RESOLUÇÃO SEE Nº 2.197, DE 26 DE OUTUBRO DE 2012
 ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO INDIVIDUAL DE ESTUDO ESTUDOS INDEPENDENTES RESOLUÇÃO SEE Nº 2.197, DE 26 DE OUTUBRO DE 2012 ANO 2013 PROFESSOR (a) Ana Paula Cintra de Carvalho DISCIPLINA
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO INDIVIDUAL DE ESTUDO ESTUDOS INDEPENDENTES RESOLUÇÃO SEE Nº 2.197, DE 26 DE OUTUBRO DE 2012 ANO 2013 PROFESSOR (a) Ana Paula Cintra de Carvalho DISCIPLINA
Resolução de Curso Básico de Física de H. Moysés Nussenzveig Capítulo 08 - Vol. 2
 HTTP://COMSIZO.BLOGSPOT.COM/ Resolução de Curso Básico de Física de H. Moysés Nussenzveig Capítulo 08 - Vol. 2 Engenharia Física 09 Universidade Federal de São Carlos 10/31/2009 *Conseguimos algumas resoluções
HTTP://COMSIZO.BLOGSPOT.COM/ Resolução de Curso Básico de Física de H. Moysés Nussenzveig Capítulo 08 - Vol. 2 Engenharia Física 09 Universidade Federal de São Carlos 10/31/2009 *Conseguimos algumas resoluções
17- EXERCÍCIOS PROPORÇÕES E REGRA DE TRÊS
 1 17- EXERCÍCIOS PROPORÇÕES E REGRA DE TRÊS 1 - (PUCSP) Um mapa está na escala de 1 para 20.000.Qual o valor real de uma distância representada no mapa por um segmento de 5cm? a) 100m b) 250m c) 1Km d)
1 17- EXERCÍCIOS PROPORÇÕES E REGRA DE TRÊS 1 - (PUCSP) Um mapa está na escala de 1 para 20.000.Qual o valor real de uma distância representada no mapa por um segmento de 5cm? a) 100m b) 250m c) 1Km d)
CPV 82% de aprovação dos nossos alunos na ESPM
 CPV 8% de aprovação dos nossos alunos na ESPM ESPM Resolvida Prova E 11/novembro/01 MATEMÁTICA 1. A distribuição dos n moradores de um pequeno prédio de 4 5 apartamentos é dada pela matriz 1 y, 6 y + 1
CPV 8% de aprovação dos nossos alunos na ESPM ESPM Resolvida Prova E 11/novembro/01 MATEMÁTICA 1. A distribuição dos n moradores de um pequeno prédio de 4 5 apartamentos é dada pela matriz 1 y, 6 y + 1
Lançamento Horizontal
 Lançamento Horizontal 1. (Ufsm 2013) Um trem de passageiros passa em frente a uma estação, com velocidade constante em relação a um referencial fixo no solo. Nesse instante, um passageiro deixa cair sua
Lançamento Horizontal 1. (Ufsm 2013) Um trem de passageiros passa em frente a uma estação, com velocidade constante em relação a um referencial fixo no solo. Nesse instante, um passageiro deixa cair sua
Caracterização do território
 Perfil do Município de Alto Boa Vista, MT 01/08/2013 - Pág 1 de 14 Caracterização do território Área 2248,35 km² IDHM 2010 0,651 Faixa do IDHM Médio (IDHM entre 0,6 e 0,699) (Censo 2010) 5247 hab. Densidade
Perfil do Município de Alto Boa Vista, MT 01/08/2013 - Pág 1 de 14 Caracterização do território Área 2248,35 km² IDHM 2010 0,651 Faixa do IDHM Médio (IDHM entre 0,6 e 0,699) (Censo 2010) 5247 hab. Densidade
Ciclos Biogeoquímicos
 Os organismos retiram constantemente da natureza os elementos químicos de que necessitam, mas esses elementos sempre retornam ao ambiente. O processo contínuo de retirada e de devolução de elementos químicos
Os organismos retiram constantemente da natureza os elementos químicos de que necessitam, mas esses elementos sempre retornam ao ambiente. O processo contínuo de retirada e de devolução de elementos químicos
Física. Questão 1. Avaliação: Aluno: Data: Ano: Turma: Professor:
 Avaliação: Aluno: Data: Ano: Turma: Professor: Física Questão 1 No setor de testes de velocidade de uma fábrica de automóveis, obteve-se o seguinte gráfico para o desempenho de um modelo novo: Com relação
Avaliação: Aluno: Data: Ano: Turma: Professor: Física Questão 1 No setor de testes de velocidade de uma fábrica de automóveis, obteve-se o seguinte gráfico para o desempenho de um modelo novo: Com relação
FÍSICA. Prof. Fracalossi
 FÍSICA Prof. Fracalossi 1. O cérebro humano demora cerca de 0,6 segundos para responder a um estímulo. Por exemplo, se um motorista decide parar o carro, levará no mínimo esse tempo de resposta para acionar
FÍSICA Prof. Fracalossi 1. O cérebro humano demora cerca de 0,6 segundos para responder a um estímulo. Por exemplo, se um motorista decide parar o carro, levará no mínimo esse tempo de resposta para acionar
FUNÇÕES E INEQUAÇÕES
 UNIVERSIDADE FEDERAL DO PARANÁ PROGRAMA INSTITUCIONAL DE BOLSAS DE INICIAÇÃO À DOCÊNCIA ANDRÉIA SCHMIDT GEHHANNY ASSIS JAQUELINI ROCHA SIMÃO LARISSA VANESSA DOMINGUES FUNÇÕES E INEQUAÇÕES CURITIBA 2012
UNIVERSIDADE FEDERAL DO PARANÁ PROGRAMA INSTITUCIONAL DE BOLSAS DE INICIAÇÃO À DOCÊNCIA ANDRÉIA SCHMIDT GEHHANNY ASSIS JAQUELINI ROCHA SIMÃO LARISSA VANESSA DOMINGUES FUNÇÕES E INEQUAÇÕES CURITIBA 2012
PROVA DE MATEMÁTICA DA UFBA VESTIBULAR 2011 1 a Fase. RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UFBA VESTIBULAR a Fase Profa. Maria Antônia Gouveia. Questão. Considerando-se as funções f: R R e g: R R definidas por f(x) = x e g(x) = log(x² + ), é correto afirmar: () A função
PROVA DE MATEMÁTICA DA UFBA VESTIBULAR a Fase Profa. Maria Antônia Gouveia. Questão. Considerando-se as funções f: R R e g: R R definidas por f(x) = x e g(x) = log(x² + ), é correto afirmar: () A função
Não é permitido o uso de corrector. Em caso de engano, deve riscar, de forma inequívoca, aquilo que pretende que não seja classificado.
 Teste Intermédio de Matemática B 2010 Teste Intermédio Matemática B Duração do Teste: 90 minutos 13.04.2010 10.º Ano de Escolaridade Decreto-Lei n.º 74/2004, de 26 de Março Utilize apenas caneta ou esferográfica
Teste Intermédio de Matemática B 2010 Teste Intermédio Matemática B Duração do Teste: 90 minutos 13.04.2010 10.º Ano de Escolaridade Decreto-Lei n.º 74/2004, de 26 de Março Utilize apenas caneta ou esferográfica
Matemática, Raciocínio Lógico e suas Tecnologias
 Matemática, Raciocínio Lógico e suas Tecnologias 21. (UFAL 2008) Uma copiadora pratica os preços expressos na tabela a seguir: Número de cópias Preço unitário (em reais) 1 a 10 0,20 11 a 50 0,15 51 a 200
Matemática, Raciocínio Lógico e suas Tecnologias 21. (UFAL 2008) Uma copiadora pratica os preços expressos na tabela a seguir: Número de cópias Preço unitário (em reais) 1 a 10 0,20 11 a 50 0,15 51 a 200
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Edição 38 (Março/2014)
 Edição 38 (Março/2014) Cenário Econômico: A atividade do comércio varejista registrou crescimento de 6,1% em fevereiro ante o mesmo período do ano anterior, na terceira aceleração consecutiva do resultado
Edição 38 (Março/2014) Cenário Econômico: A atividade do comércio varejista registrou crescimento de 6,1% em fevereiro ante o mesmo período do ano anterior, na terceira aceleração consecutiva do resultado
Professor(a): Série: 1ª EM. Turma: Bateria de Exercícios de Física
 Nome: nº Professor(a): Série: 1ª EM. Turma: Data: / /2013 Sem limite para crescer Bateria de Exercícios de Física 3º Trimestre 1- A casa de Dona Maria fica no alto de uma ladeira. O desnível entre sua
Nome: nº Professor(a): Série: 1ª EM. Turma: Data: / /2013 Sem limite para crescer Bateria de Exercícios de Física 3º Trimestre 1- A casa de Dona Maria fica no alto de uma ladeira. O desnível entre sua
CINEMÁTICA VETORIAL. Observe a trajetória a seguir com origem O.Pode-se considerar P a posição de certo ponto material, em um instante t.
 CINEMÁTICA VETORIAL Na cinemática escalar, estudamos a descrição de um movimento através de grandezas escalares. Agora, veremos como obter e correlacionar as grandezas vetoriais descritivas de um movimento,
CINEMÁTICA VETORIAL Na cinemática escalar, estudamos a descrição de um movimento através de grandezas escalares. Agora, veremos como obter e correlacionar as grandezas vetoriais descritivas de um movimento,
Problemas do 1º grau 2016
 Problemas do º grau 06. (Unicamp 06) O gráfico abaixo exibe o lucro líquido (em milhares de reais) de tręs pequenas empresas A, B e C, nos anos de 03 e 04. Com relaçăo ao lucro líquido, podemos afirmar
Problemas do º grau 06. (Unicamp 06) O gráfico abaixo exibe o lucro líquido (em milhares de reais) de tręs pequenas empresas A, B e C, nos anos de 03 e 04. Com relaçăo ao lucro líquido, podemos afirmar
Direitos do Consumidor. Série Matemática na Escola
 Direitos do Consumidor Série Matemática na Escola Objetivos 1. Introduzir o conceito de função afim; 2. Aplicar o conceito de função afim na resolução de um problema simples. Direitos do consumidor Série
Direitos do Consumidor Série Matemática na Escola Objetivos 1. Introduzir o conceito de função afim; 2. Aplicar o conceito de função afim na resolução de um problema simples. Direitos do consumidor Série
Velocidade Média. Se um
 Velocidade Média 1. (Unicamp 2013) Para fins de registros de recordes mundiais, nas provas de 100 metros rasos não são consideradas as marcas em competições em que houver vento favorável (mesmo sentido
Velocidade Média 1. (Unicamp 2013) Para fins de registros de recordes mundiais, nas provas de 100 metros rasos não são consideradas as marcas em competições em que houver vento favorável (mesmo sentido
Caracterização do território
 Perfil do Município de Santos, SP 30/07/2013 - Pág 1 de 14 Caracterização do território Área 281,35 km² IDHM 2010 0,840 Faixa do IDHM Muito Alto (IDHM entre 0,8 e 1) (Censo 2010) 419400 hab. Densidade
Perfil do Município de Santos, SP 30/07/2013 - Pág 1 de 14 Caracterização do território Área 281,35 km² IDHM 2010 0,840 Faixa do IDHM Muito Alto (IDHM entre 0,8 e 1) (Censo 2010) 419400 hab. Densidade
ANEXO MODELO DE DIAGNÓSTICO
 ANEXO MODELO DE DIAGNÓSTICO OBJETIVO DO DIAGNÓSTICO: Este modelo de diagnóstico contém alguns itens que poderão ser complementados com outras informações e tem o objetivo de possibilitar ao município a
ANEXO MODELO DE DIAGNÓSTICO OBJETIVO DO DIAGNÓSTICO: Este modelo de diagnóstico contém alguns itens que poderão ser complementados com outras informações e tem o objetivo de possibilitar ao município a
Instituto de Educação Infantil e Juvenil Verão, 2014. Londrina, de. Nome: Turma: Tempo: início: término: total: MUDANÇAS CLIMÁTICAS
 Instituto de Educação Infantil e Juvenil Verão, 2014. Londrina, de. Nome: Turma: Tempo: início: término: total: Edição III MMXIV Fase 3 - parte 2 MUDANÇAS CLIMÁTICAS Grupo B Questão 1 Observe que a sequência
Instituto de Educação Infantil e Juvenil Verão, 2014. Londrina, de. Nome: Turma: Tempo: início: término: total: Edição III MMXIV Fase 3 - parte 2 MUDANÇAS CLIMÁTICAS Grupo B Questão 1 Observe que a sequência
Os gráficos estão na vida
 Os gráficos estão na vida A UUL AL A Nas Aulas 8, 9 e 28 deste curso você já se familiarizou com o estudo de gráficos. A Aula 8 introduziu essa importante ferramenta da Matemática. A Aula 9 foi dedicada
Os gráficos estão na vida A UUL AL A Nas Aulas 8, 9 e 28 deste curso você já se familiarizou com o estudo de gráficos. A Aula 8 introduziu essa importante ferramenta da Matemática. A Aula 9 foi dedicada
Estudo de funções parte 2
 Módulo 2 Unidade 3 Estudo de funções parte 2 Para início de conversa... Taxa de desemprego no Brasil cai a 5,8% em maio A taxa de desempregados no Brasil caiu para 5,8% em maio, depois de registrar 6%
Módulo 2 Unidade 3 Estudo de funções parte 2 Para início de conversa... Taxa de desemprego no Brasil cai a 5,8% em maio A taxa de desempregados no Brasil caiu para 5,8% em maio, depois de registrar 6%
Lista de exercícios: Funções de 1ºgrau Problemas Gerais Prof ºFernandinho. Questões:
 Lista de exercícios: Funções de 1ºgrau Problemas Gerais Prof ºFernandinho Questões: 01.(UNESP) Apresentamos a seguir o gráfico do volume do álcool em função de sua massa, a uma temperatura fixa de 0 C.
Lista de exercícios: Funções de 1ºgrau Problemas Gerais Prof ºFernandinho Questões: 01.(UNESP) Apresentamos a seguir o gráfico do volume do álcool em função de sua massa, a uma temperatura fixa de 0 C.
Lista de Exercício 3 MUV
 Nome: Curso: Disciplina: FÍSICA I / MECÂNICA CLÁSSICA Lista de Exercício 3 MUV 1) Um móvel, cujo espaço inicial é S0 8m, se desloca a favor da trajetória, em movimento acelerado, com velocidade inicial
Nome: Curso: Disciplina: FÍSICA I / MECÂNICA CLÁSSICA Lista de Exercício 3 MUV 1) Um móvel, cujo espaço inicial é S0 8m, se desloca a favor da trajetória, em movimento acelerado, com velocidade inicial
Lista de exercícios comitê. (Professor BOB)
 Lista de exercícios comitê (Professor BOB) 1. (Fuvest) Dois carros, A e B, movem-se no mesmo sentido, em uma estrada reta, com velocidades constantes VÛ=l00km/h e V½=80km/h, respectivamente. a) Qual é,
Lista de exercícios comitê (Professor BOB) 1. (Fuvest) Dois carros, A e B, movem-se no mesmo sentido, em uma estrada reta, com velocidades constantes VÛ=l00km/h e V½=80km/h, respectivamente. a) Qual é,
Matemática 1. 20. Abaixo temos um extrato bancário simplificado do mês de novembro.
 Matemática 1 17. Uma revista semanal de larga circulação apresentou matéria contendo o seguinte texto: O governo destinou 400.000 reais para a vacinação de 25 milhões de cabeças de gado, ou seja, um centavo
Matemática 1 17. Uma revista semanal de larga circulação apresentou matéria contendo o seguinte texto: O governo destinou 400.000 reais para a vacinação de 25 milhões de cabeças de gado, ou seja, um centavo
4. A FUNÇÃO AFIM. Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares
 38 4. A FUNÇÃO AFIM Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares 1) A função identidade fr : Rdefinida por f(x) = x para todo
38 4. A FUNÇÃO AFIM Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares 1) A função identidade fr : Rdefinida por f(x) = x para todo
(Testes intermédios e exames 2005/2006)
 158. Indique o conjunto dos números reais que são soluções da inequação log 3 (1 ) 1 (A) [,1[ (B) [ 1,[ (C) ], ] (D) [, [ 159. Na figura abaio estão representadas, em referencial o. n. Oy: parte do gráfico
158. Indique o conjunto dos números reais que são soluções da inequação log 3 (1 ) 1 (A) [,1[ (B) [ 1,[ (C) ], ] (D) [, [ 159. Na figura abaio estão representadas, em referencial o. n. Oy: parte do gráfico
Questão 02 (UFJF MG/2012) Considere as afirmativas abaixo envolvendo as funções f (x) = sen(x), g(x) = x 2 3x + 2 e h(x) = e x.
 SECRETARIA DE SEGURANÇA PÚBLICA/SECRETARIA DE EDUCAÇÃO POLÍCIA MILITAR DO ESTADO DE GOIÁS COMANDO DE ENSINO POLICIAL MILITAR COLÉGIO DA POLÍCIA MILITAR SARGENTO NADER ALVES DOS SANTOS SÉRIE/ANO: ª Série
SECRETARIA DE SEGURANÇA PÚBLICA/SECRETARIA DE EDUCAÇÃO POLÍCIA MILITAR DO ESTADO DE GOIÁS COMANDO DE ENSINO POLICIAL MILITAR COLÉGIO DA POLÍCIA MILITAR SARGENTO NADER ALVES DOS SANTOS SÉRIE/ANO: ª Série
(S.I.) = 10 + 6 3) (FP) O
 Lista Cinemática 1) (FP) Um motorista pretende realizar uma viagem com velocidade média de 90 km/h. A primeira terça parte do percurso é realizada à 50km/h e os próximos 3/5 do restante é realizado à 80
Lista Cinemática 1) (FP) Um motorista pretende realizar uma viagem com velocidade média de 90 km/h. A primeira terça parte do percurso é realizada à 50km/h e os próximos 3/5 do restante é realizado à 80
AVALIAÇÃO DIAGNÓSTICA - 2008 9º ANO UME. Nome. 9º ano N. Professores: LEITURA USAR MENOS ÁGUA
 AVALIAÇÃO DIAGNÓSTICA - 2008 9º ANO UME Nome 9º ano N. Professores: LEITURA Leia o texto e responda às questões 1, 2 e 3. USAR MENOS ÁGUA Hoje em dia, metade da população mundial - mais de 3 bilhões de
AVALIAÇÃO DIAGNÓSTICA - 2008 9º ANO UME Nome 9º ano N. Professores: LEITURA Leia o texto e responda às questões 1, 2 e 3. USAR MENOS ÁGUA Hoje em dia, metade da população mundial - mais de 3 bilhões de
a) 2 b) 3 c) 5 d) 6 e) 9
 Estatística Professor Clístenes Cunha -(UFSCar SP-07) Em uma pesquisa, foram consultados 600 consumidores sobre sua satisfação em relação a uma certa marca de sabão em pó. Cada consumidor deu uma nota
Estatística Professor Clístenes Cunha -(UFSCar SP-07) Em uma pesquisa, foram consultados 600 consumidores sobre sua satisfação em relação a uma certa marca de sabão em pó. Cada consumidor deu uma nota
Dimensão social. Habitação
 Dimensão social Habitação Indicadores de desenvolvimento sustentável - Brasil 2004 235 39 Adequação de moradia Este indicador expressa as condições de moradia através da proporção de domicílios com condições
Dimensão social Habitação Indicadores de desenvolvimento sustentável - Brasil 2004 235 39 Adequação de moradia Este indicador expressa as condições de moradia através da proporção de domicílios com condições
FICHA DE TRABALHO DERIVADAS I PARTE. 1. Uma função f tem derivadas finitas à direita e à esquerda de x = 0. Então:
 FICHA DE TRABALHO DERIVADAS I PARTE. Uma função f tem derivadas finitas à direita e à esquerda de = 0. Então: (A) f tem necessariamente derivada finita em = 0; (B) f não tem com certeza derivada finita
FICHA DE TRABALHO DERIVADAS I PARTE. Uma função f tem derivadas finitas à direita e à esquerda de = 0. Então: (A) f tem necessariamente derivada finita em = 0; (B) f não tem com certeza derivada finita
ESCOLA DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA PROF. CARLINHOS NOME: N O :
 ESCOLA DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES PROF. CARLINHOS NOME: N O : 1 FUNÇÃO IDÉIA INTUITIVA DE FUNÇÃO O conceito de função é um dos mais importantes da matemática.
ESCOLA DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES PROF. CARLINHOS NOME: N O : 1 FUNÇÃO IDÉIA INTUITIVA DE FUNÇÃO O conceito de função é um dos mais importantes da matemática.
Curvas em coordenadas polares
 1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
Caracterização do território
 Perfil do Município de Areado, MG 29/07/2013 - Pág 1 de 14 Caracterização do território Área 282,6 km² IDHM 2010 0,727 Faixa do IDHM Alto (IDHM entre 0,700 e 0,799) (Censo 2010) 13731 hab. Densidade demográfica
Perfil do Município de Areado, MG 29/07/2013 - Pág 1 de 14 Caracterização do território Área 282,6 km² IDHM 2010 0,727 Faixa do IDHM Alto (IDHM entre 0,700 e 0,799) (Censo 2010) 13731 hab. Densidade demográfica
