NOTAS DE AULA DA DISCIPLINA CE076
|
|
|
- Joana Paixão Lemos
- 5 Há anos
- Visualizações:
Transcrição
1 7. ANÁISE DE CORREAÇÃO CANÔNICA 7. INTRODUÇÃO A Análise de Correlação Canônica foi desenvolvida por Hotelling (935) com obetivo de Identificar e quantificar as associações ou relações entre dois conuntos de variáveis. Eemplos: Um pesquisador educacional desea determinar a relação entre três medidas de habilidade escolar com cinco medidas de sucesso na escola. Um sociólogo desea investigar a relação entre dois preditores de mobilidade social baseado em entrevistas, com a mobilidade social atual medida por quatro diferentes indicadores. (3) Um pesquisador médico desea estudar a relação entre vários fatores de risco para o desenvolvimento de um grupo de sintomas. (4) Um pesquisador da área de comportamento desea estudar a relação entre a natureza do trabalho e a satisfação do trabalhador em um grande grupo de eecutivos. Desenvolvimento: Determinar o par de combinações lineares com maior correlação. Determinar outro par de combinações lineares com maior correlação sendo não correlacionado com o par determinado inicialmente. (3) O procedimento continua. Denominações: Variáveis Canônicas: são os pares de combinações lineares. Correlações Canônicas: são as correlações entres esses pares de combinações lineares. 7. CORREAÇÃO CANÔNICA POPUACIONA Considere: O primeiro grupo de p variáveis dado pelo vetor aleatório (p): O segundo grupo de q variáveis dado pelo vetor aleatório (q): (3) Os dois grupos tais que: p q. (4) Para os dois vetores aleatórios e tem-se que: E( ) µ e Cov( ) Σ E( ) µ e Cov( ) Σ Cov(, ) Σ Σ Página
2 (5) Considerando e conuntamente (p+ q) M ( ) p M ( ) q com média (p E( ) µ µ E( ) + q) E( ) µ e matriz covariância Σ (p+ q) (p+ q) Σ (p p) E ( µ)( µ )' Σ (q p) Σ (p q) Σ (q q) (6) As covariâncias entre os pares de variáveis dos diferentes conuntos uma variável de e outra de são contempladas em Σ ou Σ. Isto é, os p.q elementos de Σ medem a associação entre os dois conuntos. Quando p e q são relativamente grandes, a interpretação dos elementos de Σ conuntamente é impraticável, sendo então introduzidas as combinações lineares que permitirão as interpretações deseadas. (7) Considere as combinações lineares: U a e V b, então: V(U) Cov(U,V) a'cov( ) a a' Σ a, V(V) b'cov( ) b b' Σ b e a'cov(, ) b a' Σ b. Devemos encontrar os coeficientes a e b tais que: a' Σ b Corr(U,V) (7.) sea maior possível. a' Σ a b' Σ b (8) Define-se: - o primeiro par de variáveis canônicas como o par de combinações lineares U e V tendo variâncias unitárias, que maimiza a correlação acima (7.); - O segundo par de variáveis canônicas como o par de combinações lineares U e V tendo variâncias unitárias, que maimizam a correlação (7.) entre todas aquelas que são não-correlacionadas com o primeiro par de variáveis canônicas; Página
3 - Na -ésima etapa: o -ésimo par de variáveis canônicas como o par de combinações lineares U e V tendo variâncias unitárias, que maimizam a correlação (7.) entre todas aquelas que são não-correlacionadas com os - primeiros pares de variáveis canônicas. A correlação entre o -ésimo par de variáveis canônicas é chamada de -ésima correlação canônica. Resultado. Suponha p q e seam os vetores aleatórios e tendo Cov( ) Σ, ( p p) Cov( ) Σ ( q q) e Cov(, ) Σ. ( p q) Considere as combinações lineares U a e V b. Então ma a,b Corr(U,V) ρ* é satisfeita pela combinação linear (primeiro par de variável canônica) U a ' e ' Σ / e V b' f ' Σ/ O -ésimo par de variáveis canônicas,, 3,..., p, U a' e ' Σ/ e V b' f ' Σ/ Maimiza Corr(U,V ) ρ* entre aquelas combinações lineares não-correlacionadas com as precedentes,,..., - variáveis canônicas. Aqui * ρ ρ*... ρ * p são os autovalores de Σ / Σ Σ Σ Σ / e e, e,..., e p são os (p ) autovetores associados. (As quantidades ρ *, * ρ,..., ρ* p são também os p autovalores da matriz Σ / Σ Σ Σ Σ / com os correspondentes q autovetores f, f,..., f p. Cada f i é proporcional a Σ / Σ Σ / e ). i As variáveis canônicas têm as propriedades: Para, l,,..., p. Cov(U,U l ) Corr(U,U l ) 0, l Cov(V,V l ) Corr(V,V l ) 0, l Cov(U,V l ) Corr(U,V l ) 0, l Página 3
4 (9) Para variáveis padronizadas: [,,..., ( ) p ]' e [,,..., ]' q, as variáveis canônicas são da forma: U a' e ' / ρ e V b' f ' ρ/ onde: Cov( ) ρ, Cov( ) ρ, Cov(, ) ρ ρ' e e e f são os autovetores de ρ / ρ ρ ρ ρ / e ρ /ρ ρ ρ ρ /, respectivamente. As correlações canônicas ρ* satisfazem Corr(U,V ) ρ*,,,..., p onde: ρ* * ρ... ρ * p são os autovalores não-nulos da matriz ρ / ρ ρ ρ ρ / (ou, equivalentemente, da ρ / ρ ρ ρ ρ / ). 7.3 VARIÁVEIS CANÔNICAS AMOSTRAIS E CORREAÇÕES CANÔNICAS AMOSTRAIS Uma amostra aleatória de n observações das variáveis : p e : q pode ser resumida em uma matriz de dados n (p+q): M n M n M n p p M ( ) np M n M n q q M ) ( nq Página 4
5 onde Os vetores de médias amostrais podem ser resumidos como (p+ onde: n e n q) n n A matriz covariância amostral pode ser representada como S (p p) S (p+ q) (p+ q) S (q p) S (p q) S (q q) onde n S ( () () )( (l) (l) )',, l, l n As combinações lineares: Û a' ˆ e Vˆ b' ˆ têm correlação amostral: aˆ's bˆ r (7.) Û,Vˆ aˆ's aˆ b ˆ'S bˆ O primeiro par variáveis canônicas amostral é o par de combinações lineares Û tendo variância amostral unitária que maimiza a razão (7.).,Vˆ Em geral: o -ésimo par de variáveis canônicas é a combinação linear Û,Vˆ tendo variância amostral que maimiza a razão (9.) entre aquelas combinações lineares não-correlacionadas com as - variáveis amostrais canônicas anteriores. A correlação canônica amostral entre Û e Vˆ é chamada de -ésima correlação canônica amostral. Página 5
6 Resultado. Seam ρˆ * ρˆ *... ρˆ * p os p autovalores ordenados de S / S S S S/ com os correspondentes autovetores eˆ,eˆ, K,eˆ p, onde p q. Seam fˆ,fˆ. K,fˆ q os autovetores de S / S S S S/. O -ésima par da variável canônica amostral é Û aˆ' eˆ' S/ e Vˆ bˆ ' f ˆ ' S/ onde e são os valores das variáveis e para um eperimento particular. O primeiro par de variável canônica amostral tem correlação amostral máima Para o -ésimo par r Û Vˆ ρˆ *. r Û Vˆ ρˆ* e essa correlação é a maior possível entre as combinações lineares não correlacionadas com as precedentes - variáveis canônicas amostrais. As quantidades ρˆ *, ρˆ *,..., ρˆ * p são as correlações canônicas amostrais. 7.4 INTERPRETAÇÕES DAS VARIÁVEIS CANÔNICAS AMOSTRAIS A interpretação de Û e Vˆ pode ser auiliada pelo cálculo das correlações entre as variáveis canônicas e as variáveis nos conunto e. Definindo as matrizes [ˆ ˆ ˆ ]' ( p  a,a p), K,a p ; Bˆ [ˆ b,bˆ, K,bˆ ]' ( q q) q cuas linhas são os vetores coeficientes das variáveis canônicas amostrais, então: ˆ  (p U ) ; ˆ Bˆ (q V ) e podemos definir (7.4.) sendo R matriz das correlações amostrais de Û com U ˆ, R matriz das correlações amostrais de Vˆ com V ˆ, R matriz das correlações amostrais de Û com U ˆ, R matriz das correlações amostrais de Vˆ com V ˆ, Página 6
7 R U, ˆ R V, ˆ R U, ˆ R V, ˆ ÂS D/ Bˆ S D/ ÂS D/ Bˆ S D/ onde: D / é a matriz diagonal (p p) cuo i-ésimo elemento diagonal amostral / corresponde a V( ) e D / i é a matriz diagonal (q q) cuo i-ésimo / elemento diagonal amostral corresponde a V( ). i Se as observações são padronizadas, a matriz de dados torna-se z z M z n com z z z e as variáveis canônicas amostrais tornam-se iguais a Û Â ÂD/ z z z (p ) e Vˆ Bˆ Bˆ D / z z z (q ) As correlações canônicas amostrais não são afetadas pela padronização. As correlações dadas em (7.4.) permanecem inalteradas e podem ser calculadas, para as observações padronizadas, substituindo-se  por Â, Bˆ por Bˆ e R por S. Note que z z D / I e D/ I para as observações padronizadas. (p p) (q q) Página 7
8 Eemplo. Suponha que [ ] padronizadas. Sea ] e ] [ [ e são variáveis ρ Cov( ) ρ.0 ρ 0.4 ρ Calcule os pares de variáveis canônicas e as correlações correspondentes. SOUÇÃO: primeiro par de variáveis canônicas é dado por: U 0, ,77 V 0, ,737 - A correlação entre as variáveis canônicas do 0. par é: 0,5458 0,74 indicando uma forte associação entre os dois conuntos de variáveis, note que o primeiro par é sempre o mais importante; - A correlação entre as variáveis canônicas do 0. par é: 0,0009 0,03 indicando uma fraca associação entre os dois conuntos de variáveis; - As correlações entre as variáveis originais do primeiro conunto, [ ] com a variável canônica U são [0,97 0,6] e as correlações entre as variáveis originais do segundo conunto, [ ] com a segunda variável canônica são [0,69 0,85]. Isto indica que as variáveis e são mais importantes do que as outras. Da mesma forma pode-se ter as correlações de U com as variáveis de que são: [0,5 0,63] e de V com que são: [0,7 0,46]. Eemplo. Como parte de um grande estudo dos efeitos da estrutura organizacional sobre a satisfação no trabalho, Dunham investigou até que ponto as medidas de satisfação no trabalho estão relacionadas com as características do trabalho. Usando como instrumento de pesquisa a entrevista, Dunham obteve as medidas de p 5 variáveis relacionadas com as características do trabalho e q 7 variáveis relacionadas com a satisfação no trabalho para n 784 eecutivos de uma grande corporação ligada a merchandizing. As medidas de satisfação no trabalho estão associadas com as características do trabalho? A resposta deve ter implicações no replaneamento do trabalho. As variáveis originais características do trabalho,, e satisfação no trabalho,, foram definidas como: Página 8
9 treinamento função impor tan te 3 tarefas variadas 4 identificação com a tarefa 5 autonomia satisfação com o supervisor satisfação com o futuro da carreira 3 satisfação financeira 4 satisfação com a carga de trabalho 5 identificação com a companhia 6 satisfação com o tipo de trabalho ( ) satisfação geral 7 As respostas para as variáveis e foram obtidas em uma escala que foi padronizada. A matriz de correlação amostral baseada nas 784 respostas é: R R R R R O min(p,q) min(5, 7) 5 correlações canônicas amostrais e coeficientes das variáveis canônicas amostrais estão na tabela seguinte: Página 9
10 Assim, o primeiro par de variável canônica amostral é dado por Û 0.4z + 0.z + 0.7z 0.0z z 5 Vˆ 0.4z + 0.z 0.03z + 0.0z + 0.9z com correlação canônica amostral ρ ˆ * z 6 0.z 7 CORREAÇÕES AMOSTRAIS ENTRE AS VARIÁVEIS ORIGINAIS E AS VARIÁVEIS CANÔNICAS Variável Û Variáveis canônicas amostrais Vˆ Variável Û.Treinamento Satisfação com o supervisor. Função Satisfação com importante o futuro da 3.Tarefas variadas 4.Identificação com a tarefa carreira Satisfação financeira Satisfação com a carga de trabalho 5.Autonomia Identificação com a companhia 6.Satisfação com o tipo de trabalho 7.Satisfação geral Variáveis canônicas amostrais Vˆ As cinco variáveis das características do trabalho têm aproimadamente mesmas correlações com a primeira variável canônica. Essa variável pode ser interpretada como uma variável índice das características do trabalho. O outro membro do primeiro par de variável canônica, Vˆ, dá a impressão de representar, primeiramente, satisfação com o supervisor, satisfação com o futuro da carreira, identificação com a companhia e satisfação com o tipo de trabalho. Como essas variáveis sugerem, parece considerar o índice de satisfação no trabalho-identificação com a companhia. A correlação amostral entre os dois índices Û e Vˆ é ρ ˆ * Û Vˆ, Página 0
11 As proporções das variâncias total (padronizada) amostral eplicada pelas r primeiras variáveis canônicas são: r p No primeiro conunto por Û,Û,,Û K r r ) i Û i z( p r q r No segundo conunto por Vˆ,Vˆ,,Vˆ K r i z ( ) Vˆ i q Essas medidas descritivas proporcionam indicações de como as variáveis canônicas representam seus respectivos conuntos. Para o eemplo : No primeiro conunto por Û 5 r (0.83) + (0.74) + + (0.85) K Û z 5 No segundo conunto por 7 Vˆ 7 r (0.75) (0.65) + + K + (0.50) Vˆ z 7 A primeira variável canônica amostral, 0.37 Û, do conunto de características do trabalho é responsável por 58% da variação total desse conunto. A primeira variável canônica,, do conunto de satisfação com o trabalho eplica 37% do total desse Vˆ conunto amostral. Podemos inferir que que Vˆ é no seu. Û é mais representativa no seu conunto do Página
Exemplo 1: Variáveis padronizadas Z t = ( Z 1 (1), Z 2 (1), Z 1 (2), Z 2 Z 1 (1) Z (1) = Z (2) = Z 2. Matriz de correlações:
 Exemplo : Variáveis padronizadas t = (,,, ) = = Matriz de correlações: Ρ Ρ Ρ Ρ Ρ.0 0.4 0.5 0.6 0.4.0 0.3 0.4 0.5 0.3.0 0. 0.6 0.4 0..0 De onde se obtém: /.068 0.9.047 0.083 Ρ Ρ 0.9.068 0.083.047 Ρ / /
Exemplo : Variáveis padronizadas t = (,,, ) = = Matriz de correlações: Ρ Ρ Ρ Ρ Ρ.0 0.4 0.5 0.6 0.4.0 0.3 0.4 0.5 0.3.0 0. 0.6 0.4 0..0 De onde se obtém: /.068 0.9.047 0.083 Ρ Ρ 0.9.068 0.083.047 Ρ / /
GPDI Grupo de Profissionais de Dados e Inteligência
 GPDI Grupo de Profissionais de Dados e Inteligência Estatística e sua relação de dados Uma aplicação na redução da dimensionalidade em matrizes de dados Grupo de Profissionais de Dados e Inteligência Quem
GPDI Grupo de Profissionais de Dados e Inteligência Estatística e sua relação de dados Uma aplicação na redução da dimensionalidade em matrizes de dados Grupo de Profissionais de Dados e Inteligência Quem
G3 de Álgebra Linear I
 G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
ANÁLISE DE COMPONENTES PRINCIPAIS/PCA ou ACP
 Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Técnicas Multivariadas em Saúde. Vetores Aleatórios. Métodos Multivariados em Saúde Roteiro. Definições Principais. Vetores aleatórios:
 Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
Ralph S. Silva
 ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
Estatística: Aplicação ao Sensoriamento Remoto SER ANO Componentes Principais
 Estatística: Aplicação ao Sensoriamento Remoto SER 4 - ANO 9 Componentes Principais Camilo Daleles Rennó camilorenno@inpebr http://wwwdpiinpebr/~camilo/estatistica/ Associação entre Variáveis r = < r
Estatística: Aplicação ao Sensoriamento Remoto SER 4 - ANO 9 Componentes Principais Camilo Daleles Rennó camilorenno@inpebr http://wwwdpiinpebr/~camilo/estatistica/ Associação entre Variáveis r = < r
Multicolinariedade e Autocorrelação
 Multicolinariedade e Autocorrelação Introdução Em regressão múltipla, se não existe relação linear entre as variáveis preditoras, as variáveis são ortogonais. Na maioria das aplicações os regressores não
Multicolinariedade e Autocorrelação Introdução Em regressão múltipla, se não existe relação linear entre as variáveis preditoras, as variáveis são ortogonais. Na maioria das aplicações os regressores não
Análise Fatorial e Componentes Principais Aplicadas na Engenharia de Avaliações
 Análise Fatorial e Componentes Principais Aplicadas na Engenharia de Avaliações Diogo de Carvalho Bezerra Universidade Federal de Pernambuco Núcleo de Gestão e-mail:dicbezerra@hotmail.com SOBREA Sociedade
Análise Fatorial e Componentes Principais Aplicadas na Engenharia de Avaliações Diogo de Carvalho Bezerra Universidade Federal de Pernambuco Núcleo de Gestão e-mail:dicbezerra@hotmail.com SOBREA Sociedade
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
8. Análise em Componentes Principais - ACP
 8. Análise em Componentes Principais - ACP 8.1 Introdução O propósito principal da ACP é substituir as variáveis originais por um número menor de variáveis que são função das variáveis originais. A ACP
8. Análise em Componentes Principais - ACP 8.1 Introdução O propósito principal da ACP é substituir as variáveis originais por um número menor de variáveis que são função das variáveis originais. A ACP
Análise de Regressão Linear Múltipla III
 Análise de Regressão Linear Múltipla III Aula 6 Hei et al., 4 Capítulo 3 Suposições e Propriedades Suposições e Propriedades MLR. O modelo de regressão é linear nos parâmetros O modelo na população pode
Análise de Regressão Linear Múltipla III Aula 6 Hei et al., 4 Capítulo 3 Suposições e Propriedades Suposições e Propriedades MLR. O modelo de regressão é linear nos parâmetros O modelo na população pode
Segunda Lista de Exercícios Cálculo de Probabilidades II Prof. Michel H. Montoril
 Exercício 1. Uma urna contém 4 bolas numeradas: {1, 2, 2, 3}. Retira-se dessa urna duas bolas aleatoriamente e sem reposição. Sejam 1 : O número da primeira bola escolhida; 2 : O número da segunda bola
Exercício 1. Uma urna contém 4 bolas numeradas: {1, 2, 2, 3}. Retira-se dessa urna duas bolas aleatoriamente e sem reposição. Sejam 1 : O número da primeira bola escolhida; 2 : O número da segunda bola
Mestrado Profissional em Administração. Disciplina: Análise Multivariada Professor: Hedibert Freitas Lopes 1º trimestre de 2015
 Mestrado Profissional em Administração Disciplina: Análise Multivariada Professor: Hedibert Freitas Lopes 1º trimestre de 015 Decomposição Espectral Autovalores e autovetores MANLY, Cap. Objetivo e Definição
Mestrado Profissional em Administração Disciplina: Análise Multivariada Professor: Hedibert Freitas Lopes 1º trimestre de 015 Decomposição Espectral Autovalores e autovetores MANLY, Cap. Objetivo e Definição
Técnicas Multivariadas em Saúde
 Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
ANÁLISE DE CORRELAÇÕES CANÓNICAS. Identificar e quantificar a associação entre dois conjuntos de variáveis.
 OBJECTIVO Identificar e quantificar a associação entre dois conjuntos de variáveis. Identificar duas combinações lineares das variáveis, num e noutro conjunto, que tenham a maior correlação possível. Identificar
OBJECTIVO Identificar e quantificar a associação entre dois conjuntos de variáveis. Identificar duas combinações lineares das variáveis, num e noutro conjunto, que tenham a maior correlação possível. Identificar
Comunicaçõ. ções Digitais II. Texto original por Prof. Dr. Ivan Roberto Santana Casella
 PTC-43 Comunicaçõ ções Digitais II Texto original por Prof. Dr. Ivan Roberto Santana Casella Representaçã ção o Geométrica de Sinais A modulação digital envolve a escolha de um sinal específico s i (t)
PTC-43 Comunicaçõ ções Digitais II Texto original por Prof. Dr. Ivan Roberto Santana Casella Representaçã ção o Geométrica de Sinais A modulação digital envolve a escolha de um sinal específico s i (t)
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
G4 de Álgebra Linear I 20122 Gabarito 7 de Dezembro de 2012 1 Considere a transformação linear T : R 3 R 3 definida por: T ( v = ( v (1, 1, 2 (0, 1, 1 a Determine a matriz [T ] ε da transformação linear
Estudo dirigido de Análise Multivariada
 Estudo dirigido de Análise Multivariada Conceitos Iniciais De um modo geral, os métodos estatísticos de análise multivariada são aplicados para analisar múltiplas medidas sobre cada indivíduo ou objeto
Estudo dirigido de Análise Multivariada Conceitos Iniciais De um modo geral, os métodos estatísticos de análise multivariada são aplicados para analisar múltiplas medidas sobre cada indivíduo ou objeto
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
Influência dos Fatores Sociais e Econômicos no Acesso do Aluno à Universidade
 barbosa, Artigo sgb; Original fernandes, / Original Article cr Influência dos Fatores Sociais e Econômicos no Acesso do Aluno à Universidade Influence of Social and Economic Factors in Student Access to
barbosa, Artigo sgb; Original fernandes, / Original Article cr Influência dos Fatores Sociais e Econômicos no Acesso do Aluno à Universidade Influence of Social and Economic Factors in Student Access to
Aula 2 Uma breve revisão sobre modelos lineares
 Aula Uma breve revisão sobre modelos lineares Processo de ajuste de um modelo de regressão O ajuste de modelos de regressão tem como principais objetivos descrever relações entre variáveis, estimar e testar
Aula Uma breve revisão sobre modelos lineares Processo de ajuste de um modelo de regressão O ajuste de modelos de regressão tem como principais objetivos descrever relações entre variáveis, estimar e testar
ANÁLISE DE COMPONENTES PRINCIPAIS/PCA ou ACP
 Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Procedimento para a determinação de novas variáveis (componentes) que expliquem a maior variabilidade possível existente em uma matriz de dados multidimensionais. ANÁLISE DE COMPONENTES PRINCIPAIS/PCA
Ralph S. Silva
 ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S. Silva http://www.im.ufrj.br/ralph/multivariada.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Agradecimentos
ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S. Silva http://www.im.ufrj.br/ralph/multivariada.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Agradecimentos
2 Processo de Agrupamentos
 20 2 Processo de Agrupamentos A análise de agrupamentos pode ser definida como o processo de determinação de k grupos em um conjunto de dados. Para entender o que isso significa, observe-se a Figura. Y
20 2 Processo de Agrupamentos A análise de agrupamentos pode ser definida como o processo de determinação de k grupos em um conjunto de dados. Para entender o que isso significa, observe-se a Figura. Y
Álgebra Linear I - Aula Matriz de uma transformação linear em uma base. Exemplo e motivação
 Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Álgebra Linear I - Aula 19 1. Matriz de uma transformação linear em uma base. Exemplo e motivação 2. Matriz de uma transformação linear T na base β 1 Matriz de uma transformação linear em uma base. Exemplo
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
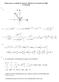 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
Análise de Regressão Linear Simples e
 Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Redes de Computadores sem Fio
 Redes de Computadores sem Fio Prof. Marcelo Gonçalves Rubinstein Programa de Pós-Graduação em Engenharia Eletrônica Faculdade de Engenharia Universidade do Estado do Rio de Janeiro Programa Introdução
Redes de Computadores sem Fio Prof. Marcelo Gonçalves Rubinstein Programa de Pós-Graduação em Engenharia Eletrônica Faculdade de Engenharia Universidade do Estado do Rio de Janeiro Programa Introdução
29 e 30 de julho de 2013
 Programa de Pós-Graduação em Estatística e Experimentação Agronômica ESALQ/USP 29 e 30 de julho de 2013 Dia 2 - Conteúdo 1 2 3 Dados multivariados Estrutura: n observações tomadas de p variáveis resposta.
Programa de Pós-Graduação em Estatística e Experimentação Agronômica ESALQ/USP 29 e 30 de julho de 2013 Dia 2 - Conteúdo 1 2 3 Dados multivariados Estrutura: n observações tomadas de p variáveis resposta.
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
Avaliação Monte Carlo do teste para comparação de duas matrizes de covariâncias normais na presença de correlação
 Avaliação Monte Carlo do teste para comparação de duas matrizes de covariâncias normais na presença de correlação Vanessa Siqueira Peres da Silva 1 2 Daniel Furtado Ferreira 1 1 Introdução É comum em determinadas
Avaliação Monte Carlo do teste para comparação de duas matrizes de covariâncias normais na presença de correlação Vanessa Siqueira Peres da Silva 1 2 Daniel Furtado Ferreira 1 1 Introdução É comum em determinadas
Diagonalização de Operadores. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes.
 Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V
Teorema Autovetores associados a autovalores distintos de um operador linear T : V V são linearmente independentes. Teorema Autovetores associados a autovalores distintos de um operador linear T : V V
Modelo de Regressão Múltipla
 Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Sensoriamento Remoto II
 Sensoriamento Remoto II Componentes principais Revisão de matemática Análise de componentes principais em SR UFPR Departamento de Geomática Prof. Jorge Centeno 2016 copyright@ centenet Revisão matemática
Sensoriamento Remoto II Componentes principais Revisão de matemática Análise de componentes principais em SR UFPR Departamento de Geomática Prof. Jorge Centeno 2016 copyright@ centenet Revisão matemática
Técnicas Multivariadas em Saúde
 Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
Roteiro Técnicas Multivariadas em Saúde Lupércio França Bessegato Dep. Estatística/UFJF 1. Introdução 2. Distribuições de Probabilidade Multivariadas 3. Representação de Dados Multivariados 4. Testes de
INFERÊNCIA EM MODELOS LINEARES GENERALIZADOS ANÁLISE DE DEVIANCE
 INFERÊNCIA EM MODELOS LINEARES GENERALIZADOS ANÁLISE DE DEVIANCE A análise de deviance é uma generalização, para modelos lineares generalizados, da análise de variância. No caso de modelos lineares, utiliza-se
INFERÊNCIA EM MODELOS LINEARES GENERALIZADOS ANÁLISE DE DEVIANCE A análise de deviance é uma generalização, para modelos lineares generalizados, da análise de variância. No caso de modelos lineares, utiliza-se
Seminário de Análise Multivariada
 Seminário de Análise Multivariada Capítulo 1 - Introdução Conteúdo 1 Introdução 1 11 Aplicações de Técnicas Multivariadas 2 12 Organização de Dados 3 121 Arranjos 3 122 Exemplo 11 - Seleção de recibos
Seminário de Análise Multivariada Capítulo 1 - Introdução Conteúdo 1 Introdução 1 11 Aplicações de Técnicas Multivariadas 2 12 Organização de Dados 3 121 Arranjos 3 122 Exemplo 11 - Seleção de recibos
Estatística CORRELAÇÃO E REGRESSÃO LINEAR. Prof. Walter Sousa
 Estatística CORRELAÇÃO E REGRESSÃO LINEAR Prof. Walter Sousa CORRELAÇÃO LINEAR A CORRELAÇÃO mede a força, a intensidade ou grau de relacionamento entre duas ou mais variáveis. Exemplo: Os dados a seguir
Estatística CORRELAÇÃO E REGRESSÃO LINEAR Prof. Walter Sousa CORRELAÇÃO LINEAR A CORRELAÇÃO mede a força, a intensidade ou grau de relacionamento entre duas ou mais variáveis. Exemplo: Os dados a seguir
3 3. Variáveis Aleatórias
 ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
Introdução. São duas técnicas estreitamente relacionadas, que visa estimar uma relação que possa existir entre duas variáveis na população.
 UNIVERSIDADE FEDERAL DA PARAÍBA Correlação e Regressão Luiz Medeiros de Araujo Lima Filho Departamento de Estatística Introdução São duas técnicas estreitamente relacionadas, que visa estimar uma relação
UNIVERSIDADE FEDERAL DA PARAÍBA Correlação e Regressão Luiz Medeiros de Araujo Lima Filho Departamento de Estatística Introdução São duas técnicas estreitamente relacionadas, que visa estimar uma relação
MOQ-13 PROBABILIDADE E ESTATÍSTICA. Professor: Rodrigo A. Scarpel
 MOQ-13 PROBABILIDADE E ESTATÍSTICA Professor: Rodrigo A. Scarpel rodrigo@ita.br www.mec.ita.br/~rodrigo Programa do curso: Semanas 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 e 16 Introdução à probabilidade (eventos,
MOQ-13 PROBABILIDADE E ESTATÍSTICA Professor: Rodrigo A. Scarpel rodrigo@ita.br www.mec.ita.br/~rodrigo Programa do curso: Semanas 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 e 16 Introdução à probabilidade (eventos,
Análise de regressão linear simples. Diagrama de dispersão
 Introdução Análise de regressão linear simples Departamento de Matemática Escola Superior de Tecnologia de Viseu A análise de regressão estuda o relacionamento entre uma variável chamada a variável dependente
Introdução Análise de regressão linear simples Departamento de Matemática Escola Superior de Tecnologia de Viseu A análise de regressão estuda o relacionamento entre uma variável chamada a variável dependente
Álgebra Linear I - Aula Matrizes simultaneamente ortogonais e simétricas
 Álgebra Linear I - Aula 22 1. Matrizes 2 2 ortogonais e simétricas. 2. Projeções ortogonais. 3. Matrizes ortogonais e simétricas 3 3. Roteiro 1 Matrizes simultaneamente ortogonais e simétricas 2 2 Propriedade
Álgebra Linear I - Aula 22 1. Matrizes 2 2 ortogonais e simétricas. 2. Projeções ortogonais. 3. Matrizes ortogonais e simétricas 3 3. Roteiro 1 Matrizes simultaneamente ortogonais e simétricas 2 2 Propriedade
ESTATÍSTICA NÃO-PARAMÉTRICA Aula 5
 ESTATÍSTICA NÃO-PARAMÉTRICA Aula Prof. Dr. Edmilson Rodrigues Pinto Faculdade de Matemática - UFU edmilson@famat.ufu.br Caso de amostras relacionadas O obetivo principal desses testes é comprovar a hipótese
ESTATÍSTICA NÃO-PARAMÉTRICA Aula Prof. Dr. Edmilson Rodrigues Pinto Faculdade de Matemática - UFU edmilson@famat.ufu.br Caso de amostras relacionadas O obetivo principal desses testes é comprovar a hipótese
MOQ 13 PROBABILIDADE E ESTATÍSTICA. Professor: Rodrigo A. Scarpel
 MOQ 3 PROBABILIDADE E ESTATÍSTICA Professor: Rodrigo A. Scarpel rodrigo@ita.br www.mec.ita.br/~rodrigo Programa do curso: Semanas 2 3 4 5 6 7 8 9 0 2 3 4 5 e 6 Introdução à probabilidade (eventos, espaço
MOQ 3 PROBABILIDADE E ESTATÍSTICA Professor: Rodrigo A. Scarpel rodrigo@ita.br www.mec.ita.br/~rodrigo Programa do curso: Semanas 2 3 4 5 6 7 8 9 0 2 3 4 5 e 6 Introdução à probabilidade (eventos, espaço
Estatística Aplicada à Administração II. Tópico. Análise de Componentes Principais
 Estatística Aplicada à Administração II Tópico Análise de Componentes Principais Bibliografia: R.A. Johnson, Applied Multivariate Statistical Analysis, Prentice Hall, 99 Análise de Componentes Principais
Estatística Aplicada à Administração II Tópico Análise de Componentes Principais Bibliografia: R.A. Johnson, Applied Multivariate Statistical Analysis, Prentice Hall, 99 Análise de Componentes Principais
P4 de Álgebra Linear I de junho de 2005 Gabarito
 P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Algebra Linear. 1. Revisitando autovalores e autovetores. 2. Forma Diagonal e Forma de Jordan. 2.1 Autovalores distintos. 2.2 Autovalores complexos
 Algebra Linear 1. Revisitando autovalores e autovetores 2. Forma Diagonal e Forma de Jordan 2.1 Autovalores distintos 2.2 Autovalores complexos 2.3 Nem todos autovalores distintos 3. Autovalores e autovetores
Algebra Linear 1. Revisitando autovalores e autovetores 2. Forma Diagonal e Forma de Jordan 2.1 Autovalores distintos 2.2 Autovalores complexos 2.3 Nem todos autovalores distintos 3. Autovalores e autovetores
5 Análise de Sensibilidade
 MAC-35 - Programação Linear Primeiro semestre de 00 Prof. Marcelo Queiroz http://www.ime.usp.br/~mqz Notas de Aula 5 Análise de Sensibilidade Neste capítulo consideramos o problema de programação linear
MAC-35 - Programação Linear Primeiro semestre de 00 Prof. Marcelo Queiroz http://www.ime.usp.br/~mqz Notas de Aula 5 Análise de Sensibilidade Neste capítulo consideramos o problema de programação linear
MBA em Finanças e Controladoria. Disciplina: Avaliação de Empresas Valuation Tópico 06 Risco e Retorno
 MBA em Finanças e Controladoria Disciplina: Avaliação de Empresas Valuation Tópico 06 Risco e Retorno Obetivos do Tópico 06 5h Obetivo Entender os fundamentos de risco e retorno Obetivos de aprendizagem
MBA em Finanças e Controladoria Disciplina: Avaliação de Empresas Valuation Tópico 06 Risco e Retorno Obetivos do Tópico 06 5h Obetivo Entender os fundamentos de risco e retorno Obetivos de aprendizagem
Álgebra Linear I - Aula 20
 Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Revisões de Matemática e Estatística
 Revisões de Matemática e Estatística Joaquim J.S. Ramalho Contents 1 Operadores matemáticos 2 1.1 Somatório........................................ 2 1.2 Duplo somatório....................................
Revisões de Matemática e Estatística Joaquim J.S. Ramalho Contents 1 Operadores matemáticos 2 1.1 Somatório........................................ 2 1.2 Duplo somatório....................................
GAAL - Terceira Prova - 15/junho/2013. Questão 1: Analise se a afirmação abaixo é falsa ou verdadeira:
 GAAL - Terceira Prova - /junho/3 SOLUÇÕES Questão : Analise se a afirmação abaio é falsa ou verdadeira: [ A matriz A é diagonalizável SOLUÇÃO: Sabemos que uma matriz n n é diagonalizável se ela possuir
GAAL - Terceira Prova - /junho/3 SOLUÇÕES Questão : Analise se a afirmação abaio é falsa ou verdadeira: [ A matriz A é diagonalizável SOLUÇÃO: Sabemos que uma matriz n n é diagonalizável se ela possuir
Definição Há correlação entre duas variáveis quando os valores de uma variável estão relacionados, de alguma maneira, com os valores da outra variável
 Correlação Definição Há correlação entre duas variáveis quando os valores de uma variável estão relacionados, de alguma maneira, com os valores da outra variável Exemplos Perímetro de um quadrado e o tamanho
Correlação Definição Há correlação entre duas variáveis quando os valores de uma variável estão relacionados, de alguma maneira, com os valores da outra variável Exemplos Perímetro de um quadrado e o tamanho
Álgebra Linear I - Aula 22
 Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Universidade Federal do Paraná Departamento de Informática. Reconhecimento de Padrões PCA. Luiz Eduardo S. Oliveira, Ph.D.
 Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões PCA Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Objetivos Introduzir os conceitos de PCA e suas aplicações
Universidade Federal do Paraná Departamento de Informática Reconhecimento de Padrões PCA Luiz Eduardo S. Oliveira, Ph.D. http://lesoliveira.net Objetivos Introduzir os conceitos de PCA e suas aplicações
Estatística Descritiva
 C E N T R O D E M A T E M Á T I C A, C O M P U T A Ç Ã O E C O G N I Ç Ã O UFABC Estatística Descritiva Centro de Matemática, Computação e Cognição March 17, 2013 Slide 1/52 1 Definições Básicas Estatística
C E N T R O D E M A T E M Á T I C A, C O M P U T A Ç Ã O E C O G N I Ç Ã O UFABC Estatística Descritiva Centro de Matemática, Computação e Cognição March 17, 2013 Slide 1/52 1 Definições Básicas Estatística
CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II. q exp( q 2 ) ( 2 π. 2 (2q 2 1) exp( q 2 )
 CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II 1) Dadas as funções ψ 1 (q) e ψ 2 (q), definidas no intervalo < q < + : ψ 1 (q) = ( 2 π ) 1/2 q exp( q 2 ) Calcule: a) (ψ 1, ψ 2 ); b)
CF372 Mecânica Quântica I Segunda Lista de Exercícios - Capítulo II 1) Dadas as funções ψ 1 (q) e ψ 2 (q), definidas no intervalo < q < + : ψ 1 (q) = ( 2 π ) 1/2 q exp( q 2 ) Calcule: a) (ψ 1, ψ 2 ); b)
)XQGDPHQWRVGHSUREDELOLGDGHHHVWDWtVWLFD
 )XQGDPHQWRVGHUREDELOLGDGHHHVWDWtVWLFD,QWURGXomR A história da estatística pode ser dividida em três fases. De acordo com PEANHA (00), a estatística inicialmente não mantinha nenhuma relação com a probabilidade,
)XQGDPHQWRVGHUREDELOLGDGHHHVWDWtVWLFD,QWURGXomR A história da estatística pode ser dividida em três fases. De acordo com PEANHA (00), a estatística inicialmente não mantinha nenhuma relação com a probabilidade,
Departamento de Estatística
 Departamento de Estatística Universidade Federal de São Carlos José Carlos Fogo São Carlos Julho de 207 Sumário Vetores Definição Representação gráfica no R 2 2 2 Propriedades algébricas 2 2 Vetores especiais
Departamento de Estatística Universidade Federal de São Carlos José Carlos Fogo São Carlos Julho de 207 Sumário Vetores Definição Representação gráfica no R 2 2 2 Propriedades algébricas 2 2 Vetores especiais
Motivação. VA n-dimensional. Distribuições Multivariadas VADB
 Motivação Em muitas situações precisamos lidar com duas ou mais variáveis aleatórias ao mesmo tempo. Por exemplo o comprimento e a largura de uma Prof. Lorí Viali, Dr. viali@mat.ufgrs.br http://www.mat.ufrgsbr/~viali/
Motivação Em muitas situações precisamos lidar com duas ou mais variáveis aleatórias ao mesmo tempo. Por exemplo o comprimento e a largura de uma Prof. Lorí Viali, Dr. viali@mat.ufgrs.br http://www.mat.ufrgsbr/~viali/
Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc..
 Introdução a vetor Professor Fiore O que são grandezas? Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc.. O que são
Introdução a vetor Professor Fiore O que são grandezas? Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc.. O que são
P4 de Álgebra Linear I
 P4 de Álgebra Linear I 2008.2 Data: 28 de Novembro de 2008. Gabarito. 1) (Enunciado da prova tipo A) a) Considere o plano π: x + 2 y + z = 0. Determine a equação cartesiana de um plano ρ tal que a distância
P4 de Álgebra Linear I 2008.2 Data: 28 de Novembro de 2008. Gabarito. 1) (Enunciado da prova tipo A) a) Considere o plano π: x + 2 y + z = 0. Determine a equação cartesiana de um plano ρ tal que a distância
Álgebra Linear I - Aula 19
 Álgebra Linear I - Aula 19 1. Matrizes diagonalizáveis. 2. Matrizes diagonalizáveis. Exemplos. 3. Forma diagonal de uma matriz diagonalizável. 1 Matrizes diagonalizáveis Uma matriz quadrada T = a 1,1 a
Álgebra Linear I - Aula 19 1. Matrizes diagonalizáveis. 2. Matrizes diagonalizáveis. Exemplos. 3. Forma diagonal de uma matriz diagonalizável. 1 Matrizes diagonalizáveis Uma matriz quadrada T = a 1,1 a
Estatística 1. Resumo Teórico
 Estatística 1 Resumo Teórico Conceitos do Curso 1. Tipos de Variáveis e Representações Gráficas a. Tipos de Variáveis b. Distribuição de Frequências c. Histograma 2. Estatística Descritiva Medidas Estatísticas
Estatística 1 Resumo Teórico Conceitos do Curso 1. Tipos de Variáveis e Representações Gráficas a. Tipos de Variáveis b. Distribuição de Frequências c. Histograma 2. Estatística Descritiva Medidas Estatísticas
VERIFICAÇÃO DA ADEQUAÇÃO DO MODELO DE ANÁLISE DE VARIÂNCIA ANÁLISE DE RESÍDUOS
 VERIFICAÇÃO DA ADEQUAÇÃO DO MODELO DE ANÁLISE DE VARIÂNCIA ANÁLISE DE RESÍDUOS Conforme foi apresentado anteriormente, o modelo de análise de variância assume que as observações são independentes e normalmente
VERIFICAÇÃO DA ADEQUAÇÃO DO MODELO DE ANÁLISE DE VARIÂNCIA ANÁLISE DE RESÍDUOS Conforme foi apresentado anteriormente, o modelo de análise de variância assume que as observações são independentes e normalmente
PESQUISA EM MERCADO DE CAPITAIS. Prof. Patricia Maria Bortolon, D. Sc.
 PESQUISA EM MERCADO DE CAPITAIS Prof. Patricia Maria Bortolon, D. Sc. Cap. 4 Características do Conjunto de Oportunidades em Condições de Risco ELTO, E.; GRUBER, M.; BROW, S., GOETZMA, W. Moderna Teoria
PESQUISA EM MERCADO DE CAPITAIS Prof. Patricia Maria Bortolon, D. Sc. Cap. 4 Características do Conjunto de Oportunidades em Condições de Risco ELTO, E.; GRUBER, M.; BROW, S., GOETZMA, W. Moderna Teoria
Capítulo 4 Inferência Estatística
 Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a diferença de
Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a diferença de
MOQ-12: PROBABILIDADES E PROCESSOS ESTOCÁSTICOS. VA s e Distribuições
 Motivação: MOQ-2: PROBABILIDADES E PROCESSOS ESTOCÁSTICOS VA s e Distribuições Definimos anteriormente Espaço de Probabilidades como sendo a tripla (W,, P(.)), em que, dado um eperimento, W representa
Motivação: MOQ-2: PROBABILIDADES E PROCESSOS ESTOCÁSTICOS VA s e Distribuições Definimos anteriormente Espaço de Probabilidades como sendo a tripla (W,, P(.)), em que, dado um eperimento, W representa
SCC0173 Mineração de Dados Biológicos
 SCC073 Mineração de Dados Biológicos Análise Exploratória de Dados Parte A: Revisão de Estatística Descritiva Elementar Prof. Ricardo J. G. B. Campello SCC / ICMC / USP Tópicos Análise Exploratória de
SCC073 Mineração de Dados Biológicos Análise Exploratória de Dados Parte A: Revisão de Estatística Descritiva Elementar Prof. Ricardo J. G. B. Campello SCC / ICMC / USP Tópicos Análise Exploratória de
ANÁLISE DOS RESÍDUOS. Na análise de regressão linear, assumimos que os erros E 1, E 2,, E n satisfazem os seguintes pressupostos:
 ANÁLISE DOS RESÍDUOS Na análise de regressão linear, assumimos que os erros E 1, E 2,, E n satisfazem os seguintes pressupostos: seguem uma distribuição normal; têm média zero; têm variância σ 2 constante
ANÁLISE DOS RESÍDUOS Na análise de regressão linear, assumimos que os erros E 1, E 2,, E n satisfazem os seguintes pressupostos: seguem uma distribuição normal; têm média zero; têm variância σ 2 constante
Módulo 1 FUNDAMENTOS DE ESTATÍSTICA
 Módulo 1 FUNDAMENTOS DE ESTATÍSTICA Medidas de posição central Média As medidas de posição central buscam representar uma série de dados. Por exemplo: em média na Suiça cada pessoa come 9Kg de chocolate
Módulo 1 FUNDAMENTOS DE ESTATÍSTICA Medidas de posição central Média As medidas de posição central buscam representar uma série de dados. Por exemplo: em média na Suiça cada pessoa come 9Kg de chocolate
Autovalores e Autovetores
 Algoritmos Numéricos II / Computação Científica Autovalores e Autovetores Lucia Catabriga 1 1 DI/UFES - Brazil Junho 2016 Introdução Ideia Básica Se multiplicarmos a matriz por um autovetor encontramos
Algoritmos Numéricos II / Computação Científica Autovalores e Autovetores Lucia Catabriga 1 1 DI/UFES - Brazil Junho 2016 Introdução Ideia Básica Se multiplicarmos a matriz por um autovetor encontramos
P3 de Álgebra Linear I
 P3 de Álgebra Linear I 2012.2 1 de dezembro de 2012. Gabarito 1) Considere a transformação linear T : R 3 R 3 cuja matriz na base canônica é : 31 2 5 [T ] ε = 2 34 10 5 10 55 Sabendo que todos os vetores
P3 de Álgebra Linear I 2012.2 1 de dezembro de 2012. Gabarito 1) Considere a transformação linear T : R 3 R 3 cuja matriz na base canônica é : 31 2 5 [T ] ε = 2 34 10 5 10 55 Sabendo que todos os vetores
Econometria II. Notas de bolso! Propriedades da E(.), Var(.) e Cov(.) Temos que (a,b) são constantes e (X,Y) são variáveis aleatórias.
 Eco 2 monitoria Leandro Anazawa Econometria II Notas de bolso! Propriedades da E(.), Var(.) e Cov(.) Temos que (a,b) são constantes e (X,Y) são variáveis aleatórias. E(a) = a E(aX) = ae(x) E(a + bx) =
Eco 2 monitoria Leandro Anazawa Econometria II Notas de bolso! Propriedades da E(.), Var(.) e Cov(.) Temos que (a,b) são constantes e (X,Y) são variáveis aleatórias. E(a) = a E(aX) = ae(x) E(a + bx) =
Séries Temporais e Modelos Dinâmicos. Econometria. Marcelo C. Medeiros. Aula 12
 em Econometria Departamento de Economia Pontifícia Universidade Católica do Rio de Janeiro Aula 12 Regressão com Variáveis Não-Estacionárias Considere três processos estocásticos definidos pelas seguintes
em Econometria Departamento de Economia Pontifícia Universidade Católica do Rio de Janeiro Aula 12 Regressão com Variáveis Não-Estacionárias Considere três processos estocásticos definidos pelas seguintes
Preparatório CEA. Módulo 6 Fundamentos de Estatística
 Preparatório CEA Módulo 6 Fundamentos de Estatística Medidas de posição central Média As medidas de posição central buscam representar uma série de dados. Por exemplo: em média na Suiça cada pessoa come
Preparatório CEA Módulo 6 Fundamentos de Estatística Medidas de posição central Média As medidas de posição central buscam representar uma série de dados. Por exemplo: em média na Suiça cada pessoa come
TESTES DE HIPÓTESES E INTERVALOS DE CONFIANÇA EM MODELOS LINEARES GENERALIZADOS
 TESTES DE HIPÓTESES E INTERVALOS DE CONFIANÇA EM MODELOS LINEARES GENERALIZADOS Antes de apresentar alguns dos testes de hipóteses e intervalos de confiança mais usuais em MLG, segue a definição de modelos
TESTES DE HIPÓTESES E INTERVALOS DE CONFIANÇA EM MODELOS LINEARES GENERALIZADOS Antes de apresentar alguns dos testes de hipóteses e intervalos de confiança mais usuais em MLG, segue a definição de modelos
Capítulo 3: Elementos de Estatística e Probabilidades aplicados à Hidrologia
 Departamento de Engenharia Civil Prof. Dr. Doalcey Antunes Ramos Capítulo 3: Elementos de Estatística e Probabilidades aplicados à Hidrologia 3.1 - Objetivos Séries de variáveis hidrológicas como precipitações,
Departamento de Engenharia Civil Prof. Dr. Doalcey Antunes Ramos Capítulo 3: Elementos de Estatística e Probabilidades aplicados à Hidrologia 3.1 - Objetivos Séries de variáveis hidrológicas como precipitações,
Probabilidade e Estatística
 Probabilidade e Estatística Aula 6 - Distribuições Contínuas (Parte 01) Leitura obrigatória: Devore, Capítulo 4 Cap 6-1 Objetivos Nesta aula, vamos aprender: Representações de uma v. a. contínua: função
Probabilidade e Estatística Aula 6 - Distribuições Contínuas (Parte 01) Leitura obrigatória: Devore, Capítulo 4 Cap 6-1 Objetivos Nesta aula, vamos aprender: Representações de uma v. a. contínua: função
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 1
 FUNDAMENTOS DE SISTEMAS LINEARES PARTE 1 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Revisão O que é um corpo (campo)? O que é um espaço
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 1 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Revisão O que é um corpo (campo)? O que é um espaço
Gabarito P2. Álgebra Linear I ) Decida se cada afirmação a seguir é verdadeira ou falsa.
 Gabarito P2 Álgebra Linear I 2008.2 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Se { v 1, v 2 } é um conjunto de vetores linearmente dependente então se verifica v 1 = σ v 2 para algum
Gabarito P2 Álgebra Linear I 2008.2 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Se { v 1, v 2 } é um conjunto de vetores linearmente dependente então se verifica v 1 = σ v 2 para algum
Stela Adami Vayego DEST/UFPR
 Resumo 5 - Análise Bivariada (Bidimensional) 5.1. Introdução O principal objetivo das análises nessa situação é explorar relações (similaridades) entre duas variáveis. A distribuição conjunta das freqüências
Resumo 5 - Análise Bivariada (Bidimensional) 5.1. Introdução O principal objetivo das análises nessa situação é explorar relações (similaridades) entre duas variáveis. A distribuição conjunta das freqüências
5. Seja A uma matriz qualquer. Assinale a afirmativa
 UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
5 Análise dos resultados
 5 Análise dos resultados Os dados foram analisados utilizando o software SPSS (Statistical Package for Social Sciences) base 18.0. Para Cooper e Schindler (2003) a análise de dados envolve a redução de
5 Análise dos resultados Os dados foram analisados utilizando o software SPSS (Statistical Package for Social Sciences) base 18.0. Para Cooper e Schindler (2003) a análise de dados envolve a redução de
Risco de Carteira. O Desvio Padrão de uma carteira constituída por dois ativos (X e Y) pode ser obtido a partir de:
 1 Risco de Carteira O risco de uma carteira depende não somente do risco de cada elemento que a compõe e de sua participação no investimento total, mas também da forma como seus componentes se relacionam
1 Risco de Carteira O risco de uma carteira depende não somente do risco de cada elemento que a compõe e de sua participação no investimento total, mas também da forma como seus componentes se relacionam
Transformação dos dados. Analise de Componentes Principais - PCA
 Transformação dos dados Tratamento nos dados Redução de Dimensionalidade Dados centrados na média e variância xm = /n Σ i=n x i x i = ( x i - xm)/σ (centrados na média) Escalamento ela variância ( quando
Transformação dos dados Tratamento nos dados Redução de Dimensionalidade Dados centrados na média e variância xm = /n Σ i=n x i x i = ( x i - xm)/σ (centrados na média) Escalamento ela variância ( quando
1 Vetores no Plano e no Espaço
 1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
1 Vetores no Plano e no Espaço Definimos as componentes de um vetor no espaço de forma análoga a que fizemos com vetores no plano. Vamos inicialmente introduzir um sistema de coordenadas retangulares no
(a) (1,5) Obtenha os autovalores e autovetores de L. (b) (1,0) A matriz de L em relação à base canônica de M 2 2 é diagonalizável? Explique.
 Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Técnicas Computacionais em Probabilidade e Estatística I
 c Técnicas Computacionais em Probabilidade e Estatística I Aula Chang Chiann MAE 5704- IME/SP º Sem/008 Slide c chang; /4/008 Simulação Estática Obetivo: Em análise estatística de dados, modelos estocásticos
c Técnicas Computacionais em Probabilidade e Estatística I Aula Chang Chiann MAE 5704- IME/SP º Sem/008 Slide c chang; /4/008 Simulação Estática Obetivo: Em análise estatística de dados, modelos estocásticos
Álgebra Linear I - Lista 11. Autovalores e autovetores. Respostas. 1) Calcule os autovalores e autovetores das matrizes abaixo.
 Álgebra Linear I - Lista 11 Autovalores e autovetores Respostas 1 Calcule os autovalores e autovetores das matrizes abaixo. (a ( 4 1 1, (b ( 1 1, (c ( 5 6 3 4, (d 1 1 3 1 6 6, (e 3 5 1, (f 1 1 1 1 1 1
Álgebra Linear I - Lista 11 Autovalores e autovetores Respostas 1 Calcule os autovalores e autovetores das matrizes abaixo. (a ( 4 1 1, (b ( 1 1, (c ( 5 6 3 4, (d 1 1 3 1 6 6, (e 3 5 1, (f 1 1 1 1 1 1
Distância Estatística
 Distância Estatística Renato Assunção 0/05/03 Pressão sistólica A pressão sistólica mede a força do sangue nas artérias, à medida que o coração contrai para impulsionar o sangue através do corpo. Se alta
Distância Estatística Renato Assunção 0/05/03 Pressão sistólica A pressão sistólica mede a força do sangue nas artérias, à medida que o coração contrai para impulsionar o sangue através do corpo. Se alta
Análise Fatorial. Matriz R de coeficientes de correlação: Não confundir análise de componentes principais com análise fatorial!
 Análise Fatorial 1 Na análise fatorial as variáveis y1, y,..., Yp, são combinações lineares de umas poucas variáveis F1, F,..., Fm (m
Análise Fatorial 1 Na análise fatorial as variáveis y1, y,..., Yp, são combinações lineares de umas poucas variáveis F1, F,..., Fm (m
Álgebra Linear I - Lista 12. Matrizes semelhantes. Diagonalização. Respostas
 Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
Exercícios. Finanças Benjamin M. Tabak
 Exercícios Finanças Benjamin M. Tabak ESAF BACEN - 2002 Uma carteira de ações é formada pelos seguintes ativos: Ações Retorno esperado Desvio Padrão Beta A 18% 16% 1,10 B 22% 15% 0,90 Também se sabe que
Exercícios Finanças Benjamin M. Tabak ESAF BACEN - 2002 Uma carteira de ações é formada pelos seguintes ativos: Ações Retorno esperado Desvio Padrão Beta A 18% 16% 1,10 B 22% 15% 0,90 Também se sabe que
PREVISÃO. Prever o que irá. acontecer. boas decisões com impacto no futuro. Informação disponível. -quantitativa: dados.
 PREVISÃO O problema: usar a informação disponível para tomar boas decisões com impacto no futuro Informação disponível -qualitativa Prever o que irá acontecer -quantitativa: dados t DEI/FCTUC/PGP/00 1
PREVISÃO O problema: usar a informação disponível para tomar boas decisões com impacto no futuro Informação disponível -qualitativa Prever o que irá acontecer -quantitativa: dados t DEI/FCTUC/PGP/00 1
Bioestatística e Computação I
 Bioestatística e Computação I Distribuição Amostral da Média Maria Virginia P Dutra Eloane G Ramos Vania Matos Fonseca Variável aleatória numérica parâmetros desconhecidos média desvio padrão estimativa
Bioestatística e Computação I Distribuição Amostral da Média Maria Virginia P Dutra Eloane G Ramos Vania Matos Fonseca Variável aleatória numérica parâmetros desconhecidos média desvio padrão estimativa
