Redes Bayesianas: o que são, para que servem, algoritmos e exemplos de aplicações.
|
|
|
- Amélia Sabrosa Sacramento
- 7 Há anos
- Visualizações:
Transcrição
1 Redes Bayesianas: o que são, para que servem, algoritmos e exemplos de aplicações. ROBERTO LIGEIRO MARQUES 1 INÊS DUTRA 1 1 Coppe Sistemas UFRJ {ligeiro,ines}@cos.ufrj.br Resumo: Redes bayesianas são grafos acíclicos dirigidos que representam dependências entre variáveis em um modelo probabilístico. Esta abordagem representa uma boa estratégia para lidar com problemas que tratam incertezas, onde conclusões não podem ser construídas apenas do conhecimento prévio a respeito do problema. O presente trabalho aborda algumas questões básicas a respeito de modelos probabilísticos, teoria de grafos e sua representação em redes bayesianas. Palavras Chaves: redes bayesianas, IA, DAG, probabilidade condicional. 1 Introdução A inteligência tem sido matéria de estudo dos seres humanos por mais de 2000 anos 1. O sonho do desenvolvimento de uma máquina pensante tem sido fonte de pesquisa desde o desenvolvimento das primeiras máquinas computadas, em meados dos anos A união destas duas áreas de pesquisa deu origem à disciplina chamada, Inteligência Artificial. Atualmente, estudos em inteligência artificial podem ser divididos em duas grandes áreas: o desenvolvimento de sistemas que agem como humanos (robôs) e o desenvolvimento de sistemas que agem racionalmente. Dentro do contexto dos sistemas que agem racionalmente, duas abordagens principais podem ser utilizadas: raciocínio lógico e raciocínio probabilístico. O raciocínio lógico pondera sobre o conhecimento prévio a respeito do problema e, sobre esta base de conhecimento retira suas conclusões. Esta abordagem, apesar de poderosa, pode não ser útil em situações onde não se conhece previamente todo o escopo do problema, para estes casos, o raciocínio probabilístico surge como uma boa opção. Um sistema que possa atuar em situações de incerteza deve ser capaz de atribuir níveis de confiabilidade para todas as sentenças em sua base de conhecimento, e ainda, estabelecer relações entre as sentenças. Redes bayesianas oferecem uma abordagem para o raciocínio probabilístico que engloba teoria de grafos, para o estabelecimento das relações entre sentenças e ainda, teoria de probabilidades, para a atribuição de níveis de confiabilidade 3. A década de 90 marcou o início da maior parte das pesquisas realizadas a respeito das redes Bayesianas. Desde esta época, as redes Bayseanas vêem sendo utilizadas para a solução de vários 1 Desde 463 BC, iniciando com os filósofos gregos Platão, Aristóteles e Sócrates. 2 O primeiro trabalho de IA reconhecido foi: McCulloch e Pitts, Uma alternativa a esta abordagem seria o uso de níveis de verdade de uma sentença (em contrapartida a níveis de confiabilidade) - lógica fuzzy.
2 tipos de problemas em diversas áreas, como por exemplo: diagnóstico médico (Heckerman 1990, Franklin 1989), aprendizado de mapas (Dean 1990), interpretação de linguagem (Goldman 1989), visão (Levitt, 1989). O restante deste trabalho está organizado da seguinte forma: a próxima sessão apresenta algumas questões a respeito de probabilidades, a sessão 3 introduz algumas questões a respeito das redes Bayesinas, suas características e métodos para construção de redes. A sessão 4 demonstra um algoritmo para realização de inferências em redes Bayesinas, em seguida, as sessões 5 e 6 apresentam, respectivamente, alguns exemplos de aplicações e a conclusão do trabalho. 2 Raciocinando sob incertezas A principal vantagem de raciocínio probabilístico sobre raciocínio lógico é fato de que agentes podem tomar decisões racionais mesmo quando não existe informação suficiente para se provar que uma ação funcionará [1]. Alguns fatores podem condicionar a falta de informação em uma base de conhecimento, os principais são: Impossibilidade: Em alguns casos, o trabalho exigido para a inserção de todos os antecedentes ou conseqüentes que configurem uma base de conhecimento onde quaisquer inferências a respeito do domínio do problema podem ser efetuadas, pode ser muito oneroso. Ignorância Teórica: Em alguns casos não se possui o conhecimento de todo domínio do problema. Lidar com falta de informação significa lidar com incertezas. Nestes ambientes é necessário utilizar conectivos que manipulem níveis de certeza e não apenas valores booleanos, verdadeiro (1) e falso (0). Assim, seria possível, por exemplo, tratar uma expressão do tipo: Eu tenho probabilidade 0.8 fazer um bom trabalho de IA ou A probabilidade de um trabalho de IA ser bom é 0.5 ou A probabilidade de um bom trabalho de IA tirar A é 0.9. Com isto, uma possível questão seria: Quais são as minhas chances tirar A?. Para responder a questão é necessário se estabelecer uma regra que combine as três probabilidades. Em outras palavras, é necessário uma função que retorne um valor dadas as probabilidades, 0.8, 0.5 e 0.9. Comparativamente poderíamos dizer que lógica probabilística estende lógica proposicional, no sentido que, probabilidade 1 representa verdadeiro e probabilidade 0 representa falso. Para caracterização de situações de incerteza podemos utilizar grafos representando relações causais entre eventos. Como exemplo, considere o seguinte domínio: Pela manha meu carro não irá funcionar. Eu posso ouvir a ignição, mas nada acontece. Podem existir várias razões para o problema. O rádio funciona, então a bateria está boa. A causa mais provável é que a gasolina tenha sido roubada durante a noite ou que a mangueira esteja entupida. Também pode ser que seja o carburador sujo, um vazamento na ignição ou algo mais sério. Para descobrir primeiro eu verifico o medidor de gasolina. Ele indica ½ tanque, então eu decido limpar a mangueira da gasolina. A problema anterior pode ser representado, de forma simplificada, pelos seguintes eventos: {sim,não} Gasolina?, {sim,não} Mangueira limpa?, {cheio, ½, vazio} Medidor, {sim,não} Funcionado. Em outras palavras, os eventos são agrupados em variáveis que podem assumir alguns estados. Nós sabemos que o estado Gasolina? e o estado Mangueira entupida? possuem impacto direto no estado Funcionando, assim como Gasolina? tem impacto em Medidor. Estas informações podem ser representadas como apresenta a figura1. Na figura também estão 2
3 representadas as direções do impacto da variável. Neste caso, a maior certeza em uma causa, é movida na direção positiva. Gasolina? Mangueira limpa? Medidor Funcionando? Figura1. Rede de causalidade. O grafo da figura1 possibilita a realização de algumas conclusões. Obviamente, se eu sei que a mangueira está entupida (probabilidade 1), então a certeza do não funcionamento do carro aumenta. Entretanto, minha situação é oposta. Eu sei que o carro não funciona e desejo encontrar o motivo. A suspeita de que a gasolina pode ter sido roubada aumenta a expectativa de que o medidor esteja indicando vazio. Lendo a informação do Medidor = ½, diminui as expectativas de que o estado Gasolina seja a fonte do problema, guiando a aresta Gasolina/Funcionamento na direção negativa. Uma vez que a expectativa do problema ter sido causado pela falta de gasolina diminui, cresce a expectativa sobre o estado Mangueira limpa?. Neste instante é possível se concluir o seguinte: O problema não parece ser a Gasolina, então muito provavelmente deve ser a Mangueira. Para fazer estas escolhas, um agente deve inicialmente possuir preferências entre possíveis efeitos das ações a serem tomadas. Preferências são representadas por utilidades (utility indicação do nível de utilidade que possui um estado) combinadas com probabilidades, resultando na chamada: teoria de decisão. Teoria de Decisão = teoria de probabilidades + teoria de utilidade A idéia fundamental em teoria de decisão é: um agente é racional se e somente se ele escolhe a ação que permite a maior expectativa de utilidade, ponderada pelos efeitos de todas as possíveis ações, ou princípio da Máxima expectativa de Utilidade (MEU). O algoritmo para um agente que utilize Teoria de Decisão seria: Função RP-Agente(percepção) retorna ação { Estático: conjunto de sentenças probabilísticas a respeito do problema. } Calcula novas probabilidades para o estado atual baseado na evidência disponível incluindo a percepção atual e a ação anterior. Calcula as probabilidades para as possíveis ações, dado a descrição das ações e as probabilidades atuais. Seleciona a ação com a maior expectativa. Retona ação. A próxima sessão apresenta algumas questões a respeito do calculo de probabilidades. 3
4 2.1 Cálculo de probabilidades Axioma base: (probabilidade incondicional) A probabilidade P(a) de um evento a é um número dentro do intervalo [0,1]. i. P(a) = 1 sss a é certo. ii. Se a e b são mutuamente exclusivos, então: P(a b) = P(a) + P(b) Por exemplo, considerando que Cárie denota a proposição de que um paciente em particular tenha cárie, então: P(Cárie) = 0.1, significa dizer que, na ausência de outra informação, o sistema assinalará a probabilidade 0.1 ao evento ter cárie. Proposições podem também incluir igualdades envolvendo variáveis aleatórias. Por exemplo, caso estejamos interessados em uma variável aleatória, Tempo, poderíamos considerar: a. P(Tempo = Ensolarado) = 0.7 b. P(Tempo = Chuvoso) = 0.2 c. P(Tempo = Nublado) = 0.1 Em alguns casos, podemos nos referir apenas a variável Tempo, como um vetor de probabilidades P(Tempo) = <0.7,0.2,0.1> 4. E ainda, proposições podem assumir o domínio booleano <verdadeiro,falso>, neste caso, a expressão P(Cárie) pode ser vista como P(Cárie = verdadeiro) e, analogamente, P( Cárie) = P(Cárie = falso). Para expressar todas as combinações de valores de duas probabilidades podemos utilizar P(Tempo,Cárie), que pode ser vista como uma tabela de probabilidades conjunta (joint probabilities) de TempoΛCárie, de 3 x 2 posições. Probabilidade condicional: Probabilidade condicional P(a b) = x, pode ser interpretada como: Dado o evento b, a probabilidade do evento a é x. i. Regra fundamental: P(a b) = P(a,b)/P(b), ou P(a b)p(b) = P(a,b). Onde P(a,b) é a probabilidade do evento conjunto do evento a Λ b. Por exemplo, P(Cárie Dor) = 0.8, indica que caso um paciente esteja com dor (de dente) e nenhuma outra informação esteja disponível, então, a probabilidade de o paciente ter uma cárie é de 0.8. É importante ressaltar que P(A B) pode ser utilizado apenas quando toda informação disponível é B. Uma vez que outra variável C é conhecida, deve-se reconsiderar para P(A B Λ C). ii. iii. P(a,b)=P(b,c), então de i, chegamos em P(a b)p(b) = P(b a)p(a), que resulta em: P(b a) = P(a b)p(b)/p(a), chamada Regra de Bayes. Em alguns casos podemos estar interessados em uma probabilidade segundo uma evidencia e, neste caso, aplica-se: P(a b,e)p(b e) = P(a,b e) 4 Variáveis vetor serão representadas por letras maiúsculas: A, P(A), etc. 4
5 Em geral, se estamos interessados em uma proposição A, e temos o conhecimento da evidencia B, devemos calcular P(A B). Em alguns casos este valor não esta disponível na base de conhecimento e, portanto, devemos utilizar algum método de inferência para obtê-lo. Conjunção de Probabilidades Seja X uma variável aleatória com n estados, x 1,..., x n, e P(X) a distribuição de probabilidades para estes estados, P(X) = (a 1,..., a n ); a i 0; a i = 1, onde a i é a probabilidade de X estar no estado a i, P(X=a i ). Se a variável Y possui os estados b 1,...b m, então P(X Y) representa uma tabela n x m contendo os valores P(a i b i ). Por exemplo: b 1 b 2 b 3 a a Tabela1. P(X Y) A conjunção de probabilidades para as variáveis A e B, ou P(A,B), é também uma tabela n x m, representada pela probabilidade de cada configuração (a,, b i ). Aplicando a regra P(A B)=P(A,B)/P(B), para as variáveis X e Y e a tabela1, teríamos: (considerando P(Y) = <0.4,0.4,0.2>) b 1 b 2 b 3 a a Tabela2. P(X,Y) A probabilidade P(X) pode ser então calculada a partir da tabela2, calculando-se: P(ai)= Pa,b i. Este cálculo é chamado marginalização de B em P(A,B). O resultado para a tabela2 será: P(X) = <0.4,0.6>. E ainda, aplicando a regra de Bayes sob a tabela1, obteríamos P(Y X). a 1 a 2 B B B Tabela3. P(Y X) Considerando uma situação real, podemos imaginar um problema contendo centenas ou milhares de variáveis. Considerando o uso apenas de variáveis que assumam valores boolenos, teríamos a necessidade do cálculo de 2 n entradas para a tabela de conjunção de probabilidades do sistema. Ou seja, um crescimento exponencial em relação ao número de variáveis. O que pode se 5
6 tornar algo infactível de se computar. Entretanto, sendo possível a computação de todos os valores, o sistema será capaz de obter qualquer probabilidade que se esteja interessado Aplicando a Regra de Bayes Para aplicação da regra de Bayes precisamos de três termos: uma probabilidade condicional e duas incondicionais. Vamos considerar um exemplo de diagnostico médico: um médico sabe que a meningite causa torcicolo em 50% dos casos. Porém, o médico também conhece algumas probabilidades incondicionais que dizem que, um caso de meningite atinge 1/50000 pessoas e, a probabilidade de alguém ter torcicolo é de 1/20. 5 Considere T e M, respectivamente, como a probabilidade incondicional de um paciente ter torcicolo e a probabilidade incondicional de um paciente ter meningite. Assim: P(T M) = 0.5 (probabilidade de ter torcicolo tendo meningite) P(M) = 1/50000 P(T) = 1/20 Aplicando a rede de Bayes: P(M T) = (P(T M)P(M))/P(T) = (0.5 x 1/50000)/(1/20) = Ou seja, é esperado que apenas 1 em 5000 pacientes com torcicolo tenha meningite. Note que mesmo tendo torcicolo uma alta probabilidade nos casos de meningite (0.5), a probabilidade de um paciente ter meningite continua pequena, devido ao fato de a probabilidade incondicional de torcicolo ser muito maior que a probabilidade de meningite. Uma argumentação válida surge do fato de que o médico poderia também possuir a probabilidade incondicional P(M T), a partir de amostras de seu universo de pacientes, da mesma forma que P(T M), evitando o cálculo realizado anteriormente. Porém, imagine que um surto de meningite aflija o universo de pacientes do médico em questão, aumentando o valor de P(M). Caso P(M T) tenha sido calculado estatisticamente a partir de observações em seus pacientes, o médico não terá nenhuma idéia de como este valor será atualizado (visto que P(M) aumentou). Entretanto, caso tenha realizado o cálculo de P(M T) em relação aos outros três valores (como demonstrado) o médico verificará que P(M T) crescerá proporcionalmente em relação a P(M). Considere agora que um paciente pode estar com problema de coluna C, dado que está com torcicolo: P(C T) = (P(T C)P(C))/P(T). Utilizando P(M T) podemos calcular a probabilidade relativa de C em M dado T, ou, em outras palavras, a marginalização de M e C. Considerando que P(T C) = 0.8 e P(C) = 1/1000. Então: P(M T)/P(C T) = (P(T M)P(M))/(P(T/C)P(C)) = (0.5 x 1/50000)/(0.8 x 1/1000) = 1/80 Isto é, Problema de coluna C é 80 vezes mais comum que meningite M, dado torcicolo. 3 Redes Bayesianas 5 Exemplo extraído de [6]. 6
7 Matematicamente, uma Rede Bayesiana é uma representação compacta de uma tabela de conjunção de probabilidades do universo do problema. Por outro lado, do ponto de vista de um especialista, Redes Bayesianas constituem um modelo gráfico que representa de forma simples 6 as relações de causalidade das variáveis de um sistema. Uma Rede Bayesiana consiste do seguinte: Um conjunto de variáveis e um conjunto de arcos ligando as variáveis. Cada variável possui um conjunto limitado de estados mutuamente exclusivos. As variáveis e arcos formam um grafo dirigido sem ciclos (DAG). Para cada variável A que possui como pais B 1,..., B n, existe uma tabela P(A B 1,..., B n ). Repare que, caso A não possua um pai, a tabela de probabilidades é reduzida para uma probabilidade incondicional P(A) 7.Uma vez definida a topologia da rede, basta especificar as probabilidades dos nós que participam em dependências diretas, e utilizar estas para computar as demais probabilidades que se deseje. Considere o domínio1 como exemplo 8 : Você possui um novo alarme contra ladrões em casa. Este alarme é muito confiável na detecção de ladrões, entretanto, ele também pode disparar caso ocorra um terremoto. Você tem dois vizinhos, João e Maria, os quais prometeram telefonar-lhe no trabalho caso o alarme dispare. João sempre liga quando ouve o alarme, entretanto, algumas vezes confunde o alarme com o telefone e também liga nestes casos. Maria, por outro lado, gosta de ouvir música alta e às vezes não escuta o alarme. Este domínio pode ser representado como apresenta a figura2. Ladrão Terremoto Alarme JoãoLig MariaLig Figura2. Rede Bayesiana domínio1. Repare que a rede não possui nós indicando que Maria está ouvindo música, ou que o telefone está tocando e atrapalhando o entendimento de João. Estes fatos estão implícitos, associados à incerteza relacionada pelos arcos Alarme JoãoLig e MariaLig, pois, poderia ser muito dispendioso (ou até mesmo impossível) se obter tais probabilidades, ou ainda, tais informações poderiam não ser relevantes. Assim, as probabilidades devem resumir as condições 6 O que não significa dizer que as relações sejam simples. 7 Ou, o caso particular P(A ). 8 Exemplo extraído de [6]. 7
8 em que o alarme pode falhar (falta de bateria, campainha estragada, etc) e ainda, as condições em que João e Maria podem falhar (não estava presente, não ouviu o alarme, estava de mau-humor, etc). Desta forma, o sistema pode lidar com uma vasta gama de possibilidades, ao menos de forma aproximada. Uma vez definida a topologia, é necessário se definir a tabela de probabilidades condicionais (CPT) para cada nó. Cada linha na tabela contém a probabilidade condicional para cada caso condicional dos nós pais. Um caso condicional é uma possível combinação dos valores para os nós pais. Por exemplo, para a variável aleatória Alarme temos: Ladrão Terremoto P(Alarme Ladrão,Terremoto) Verdadeiro Falso Verdadeiro Verdadeiro Verdadeiro Falso Falso Verdadeiro Falso Falso Tabela4. CPT Alarme. A figura3 apresenta a Rede Bayesiana para o domínio1 e suas probabilidades condicionais. L P(L) V.001 Ladrão Terremoto T P(T) V.002 J P(J) V.90 F.05 JoãoLig L T P(A) V V.95 Alarme V F.95 F V.29 F F.001 M P(M) V.70 F.01 MariaLig Figura3. Rede Bayesiana e probabilidades, domínio Representando a distribuição da de conjunção de probabilidades Todas as entradas da tabela de conjunção de probabilidades podem ser calculadas a partir das informações disponíveis em uma rede Bayesiana. Uma tabela de conjunção de probabilidades representa a descrição completa de um domínio. Cada entrada da tabela de conjunção de 8
9 probabilidades pode ser calculada a partir da conjunção das variáveis atribuídas aos devidos valores, P(X 1 =x 1... X n = x n ), ou P(x 1,..., x n ). O valor de uma entrada é então dado por: P(x 1,..., x n ) = Π P(x i Pais(X i )) para 0 i n (3.1) Assim, cada entrada da tabela é representada pelo produto dos elementos apropriados das tabelas de probabilidades condicionais (CPT). As CPTs constituem então uma representação distribuída da tabela de conjunção de probabilidades do problema. Como exemplo, considere que se deseja calcular a probabilidade do alarme ter tocado, mas, nem um ladrão nem um terremoto aconteceram, e ambos, João em Maria ligaram, ou P(J M A L T). P(J M A L T) = P(J A)P( M A)P(A L T)P( L ) P( T ) = 0.9 x 0.7 x x x = Método para construção de uma rede Bayesiana A construção de uma rede Bayesiana exige que certos cuidados sejam tomados de forma a permitir que a tabela conjunção de probabilidades resultante seja uma boa representação do problema. Para sua construção utilizaremos como base a equação (3.1). P(x 1,..., x n ) = Π P(x i Pais(X i )) para 0 i n, será reescrita para: P(x 1,..., x n ) = P(x n x n-1,... x 1 ) P(x n-1,... x 1 ) Este processo será repetido, reduzindo cada conjunção de probabilidades em uma probabilidade condicional e uma conjunção menor. P(x 1,..., x n ) = P(x n x n-1,... x 1 ) P(x n-1 x n-2,... x 1 )... P(x 2 x 1 ) P(x 1 ) = Π P(x i xi -1,... x 1 ) para 0 i n Comparando esta equação com (3.1), observamos que a especificação de uma tabela de conjunção de probabilidades é equivalente com a declaração geral: P(X i X i -1,..., X 1 ) = P(X i Pais(X i )) para Pais(X i ) { xi -1,... x 1 } (3.2) Esta equação expressa que, uma rede Bayesiana é a representação correta de um domínio se e somente se, cada nó é condicionalmente independente de seus predecessores, dado seu pai. Portanto, para se construir uma rede cuja estrutura represente devidamente o domínio do problema, é necessário que para todo nó da rede esta propriedade seja atendida. Intuitivamente, os pais de um nó X i devem conter todos os nós X 1,..., X i-1 que influenciem diretamente X i. Assim, é possível, por exemplo, determinar que a seguinte igualdade é verdadeira: 9
10 P(MariaLig JoaoLig,Alarme,Terremoto,Ladrão) = P(MariaLig Alarme) Então, um procedimento geral para construção de redes Bayesianas seria: 1. Escolha um conjunto de variáveis X i que descrevam o domínio. 2. Escolha uma ordem para as variáveis. 3. Enquanto existir variáveis: a. Escolha uma variável X i e adicione um nó na rede. b. Determine os nós Pais(X i ) dentre os nós que já estejam na rede e que satisfaçam a equação (3.2). c. Defina a tabela de probabilidades condicionais para X i. O fato de que cada nó é conectado aos nós mais antigos na rede garante que o grafo será sempre acíclico. 3.3 Compactação e ordenação de nós As Redes Bayesianas, em geral, representam tabelas conjunção de probabilidades de um domínio de forma compacta. Esta característica decorre do fato de que as redes Bayesianas possuem uma propriedade geral chamada, localidade estrutural. Nos sistemas com localidade estrutural, cada subcomponente interage diretamente apenas com uma parte do restante do sistema (demais subcomponentes). No caso das redes Bayesianas, é razoável de se supor que, na maioria dos casos, cada variável aleatória é diretamente influenciada por no máximo k outras variáveis. Suponhamos, por questões de simplicidade, que as variáveis aleatórias possam assumir apenas valores booleanos, neste caso, a quantidade de informação necessária para se especificar uma determinada tabela de probabilidades condicionais será no máximo 2 k números, em contraste com uma tabela de conjunção de probabilidades, 2 n. Apenas como um exemplo do poder se compactação, suponhamos uma rede com 20 nós (n = 20), cada nó com no máximo 5 pais (k = 5), uma rede Bayesiana necessitaria de 640 números, enquanto uma tabela joint mais de 1 milhão. Entretanto, existem domínios que requerem que cada nó seja influenciado por todos os outros grafo fortemente conexo. Nestes casos, a especificação de uma tabela de conjunção de probabilidades requer a mesma quantidade de informação que uma rede Bayesiana. Porém, na prática, a maioria dos problemas podem ser simplificados de forma a se garantir que a rede não seja conexa, sem perda de informação útil. Por exemplo, para o problema proposto em domínio1, poder-se-ia imaginar que na ocorrência de um terremoto, João e Maria não telefonariam, mesmo ouvindo o alarme, visto que saberiam que a causa foi o próprio terremoto. Neste caso, duas arestas seriam inserias ligando Terremoto a JoãoLig e Terremoto a Maria, aumentando o número de CPTs. Esta nova abordagem deveria então ser avaliada considerando-se o custo da informação adicional inserida em relação à relevância da mesma. Mesmo em domínios localmente estruturados, construir uma rede localmente estruturada não é um trabalho trivial. Pois, cada variável deve ser diretamente influenciada por apenas k (k n) outras e, a topologia deve realmente representar o domínio. Alguns métodos podem ser utilizados, porém, não garantem a construção correta da árvore, uma abordagem possível seria: 10
11 incluir inicialmente as raízes, em seguida os nós influenciados por nós do nível anterior, e assim sucessivamente até a inserção das folhas (não possuem influência sobre nenhum nó). Assim, a ordem de inserção dos nós pode influenciar no desempenho da rede. Considere o exemplo para o dominio1, a inserção poderia seguir a seguinte ordem: MariaLig: raiz. JoãoLig: Se Maria ligou, então, provavelmente, o alarme tocou. Neste caso, MariaLig influencia JoaoLig. Portanto, MariaLig é pai de JoaoLig. Alarme: Claramente, se ambos ligaram, provavelmente o alarme tocou. Portanto, Alarme é influenciado por JoãoLig e MariaLig. Ladrão: Influenciado apenas por Alarme. Terremoto: Se o alarme tocou, provavelmente, um terremoto pode ser acontecido. Entretanto, se existe um Ladrão, então as chances de um terremoto diminuem. Neste caso, Terremoto é influenciado por Ladrão e Alarme. A rede resultante (figura4) possui mais arcos em relação à rede original, o que significa que mais tabelas devem ser especificadas. E ainda, pode-se notar que alguns arcos representam situações pouco naturais e, por conseqüência, de difícil especificação, como, por exemplo, a probabilidade de um Terremoto dado Ladrão e Alarme. MariaLig JoãoLig Alarme Ladrão Terremoto Figura4. Rede Bayesiana domínio Tabelas de probabilidades condicionais Tabelas de probabilidades condicionais tendem a ter um grande número de entradas, mesmo para nós com um número pequeno de pais. Preencher estes valores pode ser algo que requeira muita experiência, caso a relação entre nós pais e nós filhos seja completamente arbitrária. Entretanto, na maioria dos casos, esta relação pode ser bem adaptada a algum padrão, o que pode facilitar o trabalho. Estes casos são chamados distribuições canônicas. O caso mais simples é o representado por nós determinísticos. Um nó determinístico tem o seu valor explicitamente determinado a partir dos pais, sem incerteza. Por exemplo, relação entre nós pais Brasileiro, Peruano e Boliviano, e o nó filho SulAmericano é determinado especificamente pela disjunção dos pais. 11
12 Relações com incerteza podem geralmente ser caracterizados como relações com ruídos (noisy logical relatioships). A relação com ruído padrão é chamada ruído-ou (noisy-or), uma generalização da relação lógica OU. Em lógica proposicional pode-se dizer que o estado Febre é verdadeiro se e somente se Gripe, Resfriado ou Malaria é verdadeiro. A relação ruído-ou adiciona um nível de incerteza à relação OU, considerando três suposições: (a) Cada causa possui uma chance independente de causar o efeito, (b) todas as possibilidades estão listadas, (c) a inibição de uma causa é independente da inibição das demais. Considere o exemplo, P(Febre Gripe) = 0,4, P(Febre Resfriado) = 0.8 e P(Febre Malaria) = 0.9, para estes valores os parâmetros de ruído serão respectivamente 0.6, 0.2, 0.1. Se nenhum nó pai é verdadeiro, então o nó filho é falso com 100% de chance. Se apenas um (1) pai é verdadeiro, então a probabilidade do nó filho ser falso é igual ao ruído do nó pai verdadeiro (ou o produto do ruído dos pais, caso exista mais de um verdadeiro). A tabela abaixo apresenta o resultado para o exemplo. Gripe Resfriado Malária P(Febre) P( Febre) F F F F F V F V F F V V = 0.2 x 0.1 V F F V F V = 0.6 x 0.1 V V F = 0.6 x 0.2 V V V = 0.6 x 0.2 x 0.1 Tabela5. ruído-ou. 3.5 Independência condicional em redes Bayesianas Conforme demonstrado anteriormente, uma nó em uma rede Bayesiana possui independência condicional em relação a seus predecessores na rede dado o nó pai. Entretanto, para que possamos utilizar algum método de inferência em uma rede é necessário que possamos dizer mais a respeito das relações entre os nós de uma rede. Por exemplo, é necessário saber se um conjunto de nós X é independente de outro conjunto Y, dado que um conjunto de evidências E 9, ou, em outras palavras, é preciso saber se X é d-separado de Y. Se todo caminho não dirigido entre um nó em X e um nó em Y é d-separado por E, então X e Y são condicionalmente independentes dada a evidência E. Um conjunto de nós E d-separa dois conjuntos de nós X e Y, se todo o caminho não dirigido de um nó em X para um nó em Y é bloqueado dado E. Um caminho é bloqueado por um conjunto de nós E se existe um nó Z no que garante algumas das três condições: 1. Z está em E e Z possui um arco de entrada e um arco de saída no caminho. 9 Evidência em uma variável é uma declaração de uma certeza de seus estados. Se uma variável é instanciada, ela é chamada hard evident. 12
13 2. Z esta em E e Z possui dois arcos de saída no caminho não dirigido. 3. Z e nenhum de seus descentes não estão em E e ambos os arcos no caminho não dirigido são de chegada em Z. A figura5 demonstra os três casos. E X Y Figura5. Casos gerais, nós X e Y d-separados. A próxima sessão discute algumas questões a respeito de inferências em redes Bayesinas. 4 Inferência em Redes Bayesianas A tarefa básica de uma inferência probabilística é computar a distribuição de probabilidades posterior para um conjunto de variáveis de consulta (query variables), dada uma hard evidence, ou seja, o sistema computa P(Query Evidence). Para o exemplo proposto em dominio1, Ladrão constitui uma boa variável de consulta e JoãoLig, MariaLig seriam boas variáveis de evidência (hard evidence). O exemplo abaixo apresenta uma rede Bayesiana formada pelas seguintes variáveis Cloudy (TempoNublado), Sprinklet (Regador), Rain (Chuva) e WetGrass (GramaMolhada) 10. Uma inferência possível seria: Dado que temos a evidência de que a grama está molhada, qual a probabilidade de ter chovido, ou do regador estar ligado? 10 Exemplo extraído de [4]. 13
14 P(C=F) P(C=T) Cloudy Sprinkler Rain C P (S=F) P(S=T) F T C P(R=F) P(R=T) F T S R (W=F) P(W=T) F F TF FT TT WetGrass Figura6. Rede Bayesiana Exemplo de inferência. Neste caso, apesar de S e R serem independentes, tornam-se dependentes dado que W a evidência, é filho de ambos, ou seja, não S e R não são d-separados. Assim, para o calculo de P(S W) deve-se considerar P(R) e vice-versa. A equação seria (1 = T e 0 = V): P(S=1 W=1) = P(S=1,W=1)/P(W=1) = Σ c,r (P(C=c i, S=1,R= r i, W=1)/P(W=1)) = / P(R=1 W=1) = P(R=1,W=1)/P(W=1) = Σ c,s (P(C = c i, S = s i,r =1, W=1)/P(W=1)) = / Onde (W = 1): P(W=1) = Σ c,r,s P(C = c i, S = s i,r = r i, W=1) = Repare que para o cálculo de P(S=1 W=1), considera-se os estados possíveis de C e R (somatório). Assim, pode-se concluir que, dado que a grama está molhada, W =1, a probabilidade de ter chovido, P(R=1 W=1) = / = é maior que a probabilidade de o regador ter sido ligado P(S=1 W=1) = / =
15 Inferências podem ser realizadas sobre redes Bayesianas para: Diagnósticos: Dos efeitos para as causas. Dado JoaoLig, P(Ladrão JoaoLig) Causas: De causas para efeitos. Dado Ladrão, P(JoaoLig Ladrão) Intercausais: Entre causas de um efeito comum. Dado Alarme, P( Ladrão Alarme) e dado Terremoto, P( Ladrão Alarme,Terremoto). Q E Q E E Q Diagnóstico Causa Intercausal Figura7. Tipos de Inferências E, além de consultas a partir de evidências, redes Bayesianas podem ser utilizadas para: Tomar decisões baseadas em probabilidades. Decidir quais evidências adicionais devem ser observadas a fim de se obter informações úteis do sistema. Analisar o sistema a fim de buscar os aspectos do modelo que possuem maior impacto sob as variáveis de consulta. Explicar os resultados de uma inferência probabilística ao usuário. 4.1 Algoritmo para resolução inferências Conforme demonstrado, a computação básica de um método de inferência sobre uma rede Bayeasiana requer o cálculo de todos os nós da rede (sua probabilidade condicional) dado que uma evidência foi observada. Isto implica dizer que, em geral, uma inferência probabilística realizada em uma rede Bayesiana será NP-hard. Este fato é diretamente proporcional a forma como o problema foi modelado, em outras palavras, em algumas situações, uma rede com apenas dezenas de nós pode necessitar de um tempo computacional muito grande (às vezes inviável), enquanto uma rede contendo milhares de nós pode levar apenas alguns instantes. Entretanto, para uma classe restrita de redes, inferências probabilísticas podem ser realizadas em tempo linear. Esta classe é conhecida por: redes simplesmente conexas. Uma rede 15
16 simplesmente conexa é aquela onde, para qualquer dois nós i,j da rede existe apenas um caminho não dirigido entre i e j. A figura abaixo apresenta uma representação genérica de rede simplesmente conexa. Um nó X possui um conjunto U de pais, U = U 1,... U m, e filhos Y = Y 1,... Y n. Cada filho e cada pai está representado dentro de uma caixa contendo todos os seus nós descendentes e ancestrais, exceto em relação a X, ou seja, todas as caixas são disjuntas e não possuem nenhum arco ligando-as. E + x U 1 U m X E - x Z 1j Z nj Y 1 Y n Figura8. Rede simplesmente conexa genérica O algoritmo assume que X é a variável de consulta, e existe um conjunto de variáveis de evidência E (X E). Para o funcionamento do algoritmo é necessário também que as disjunções E - x, E + x, sejam definidas. E + x é o suporte de causa de X. Variáveis de evidência acima de X estão conectadas a X por estes pais. E - x é o suporte de evidência de X. Variáveis de evidência abaixo de X estão conectadas a X por estes filhos. A estratégia geral é a seguinte: 1. Expressar P(X E) em relação a E - x, E + x. 2. Computar a contribuição de E + x através de seus efeitos em Pais(X), e então transportar tais efeitos para X. 16
17 3. Computar a contribuição de E - x através de seus efeitos em Filhos(X), e então transportar tais efeitos para X. Note que computar os efeitos nos filhos de X é uma recursão do problema de computar os efeitos em X. A execução do algoritmo envolve chamadas recursivas a partir de X por todos seus arcos. A recursão termina em nós de evidência, raízes e folhas da árvore. Cada chamada recursiva exclui o nó que a chamou, desta forma, a árvore é coberta apenas uma vez. Portanto o algoritmo é linear no número de nós da rede. O algoritmo está representado abaixo 11. Função Belif-Net-Ask(X) retorna(distribuição de probabilidades sobre X) { Entrada: X, a variável aleatória Suport-Except(X,NULL) } Função Suport-Except(X, V) retorna(p(x E)) { se Evidencia(X) retorna ponto de distribuição observado para X senão Calcula P(E - X) = Evidence-Except(X,V) x U = Pais(X) se U == vazio retorna P(E - X)P(X) x senão para cada U i em U Calcule e armazene P(U i E ui ) = Suport-Except(U i,x) retorna P(E - X) ΣP(X u) ΠP(U E ) x i ui } Função Evidence-Except(X, V) retorna P(E - X) x { Y = Filhos[X] - V se Y == vazio retorna uma distribuição uniforme senão para cada Y i em Y Calcula P(E - y ) = Evidence-Except(Y,NULL) yi i i Z i = Pais[Yi] - X para cada Z ij em Z i Calcule e armazene P(Z ij E zij ) = Suport-Except(Z ij,y i ) } retorna ΠΣP(E - yi Y i )ΣP(Y i X,z i )ΠP(z ij E zij ) Vale lembrar que o algoritmo apenas funciona devido à característica da árvore de ser simplesmente conexa, caso contrário, ou uma mesma evidência seria contada mais de uma vez, ou o algoritmo poderia não terminar. 11 Algoritmo extraído de [6]. 17
18 Para demonstração matemática 12 definida abaixo. do algoritmo, considere a árvore simplesmente conexa Figura9. Rede Bayesiana. Inferência P(e a,b,c,d). Suponha que desejamos calcular a probabilidade de e dadas as evidências a,b,c,d. Es evidências são inicialmente divididas em dois conjuntos, [a,b], nós que estão acima de e e [c,d], nós que estão abaixo de e. O objetivo é se quebrar o problema P(e a,b,c,d), em dois subproblemas. Inicialmente aplicamos a rede de Bayes: P(e a,b,c,d) = P(e)P(a,b,c,d e)/p(a,b,c,d) O segundo termo do numerador pode ser quebrado; P(e a,b,c,d) = P(e) P(a,b e)p(c,d a,b,e)/p(a,b,c,d) Note que P(c,d a,b,e) = P(c,d e), pois e separa a e b de c e d. Substituindo este termo no ultimo termo do numerador e condicionando o denominador em a e b, teremos: P(e a,b,c,d) = P(e) P(a,b e) P(c,d e)/p(a,b) P(c,d a,b) Os fatores podem ser alterados para: P(e a,b,c,d) = (P(e) P(a,b e) /P(a,b)) P(c,d e) P(c,d a,b) Aplicando a regra de Bayes de forma reversa sobre o primeiro termo, teremos: P(e a,b,c,d) = (P(e a,b) P(c,d e))(1/p(c,d ab)) 12 Extraído de [1]. 18
19 Com esta equação obtemos o resultado desejado, o primeiro termo possui apenas variáveis que estão acima de e e o segundo, apenas variáveis que estão abaixo. O último termo envolve ambas as variáveis, mas, na realidade não precisa ser calculado. Basta, resolver esta equação para todos os valores de e, o último termo permanece inalterado, e pode ser marginalizado Inferência em Redes Bayesianas Multiconectadas Um grafo multiconectado é aquele para o qual dois nós são ligados por mais de um caminho não dirigido, ou, um nó possui duas ou mais causas, e estas causas compartilham um ancestral comum (figura6). Conforme já mencionado, o cálculo de inferências sob redes multiconectadas é um problema NP-hard, entretanto, algumas abordagens são propostas de forma se possibilitar estes cálculos em tempo polinomial. Existem três classes de algoritmos para inferência em redes multiconectadas, cada um com uma área de aplicação definida: Clustering Este método transforma probabilisticamente (não topologicamente) a rede em uma rede simplesmente conexa. Conditioning Este método faz uma transformação na rede instanciando variáveis em valores definidos, e então, e então produz uma rede simplesmente conexa para cada variável instanciada. Stochastic simulation Este método usa a rede para gerar um grande número de modelos concretos de um domínio. A partir destes modelos o algoritmo calcula uma aproximação de uma inferência. Métodos de Clustering Considere o exemplo da figura6. Uma forma de obter desta rede em uma rede simplesmente conexa seria a combinação das variáveis Sprinkler e Rain, em um mega nó chamado Sprinkler+Rain, conforme mostra a figura10. Repare que duas variáveis booleanas são substituídas por um nó que possui as quatro probabilidades, TT, TF, FT e FF (a probabilidade dos demais nós da rede permanecem inalteradas). O mega nó obtido possui apenas um pai, a variável booleana Cloudy. Uma vez que a rede foi convertida para uma rede simplesmente conexa, o algoritmo apresentado anteriormente pode ser aplicado. Apesar da técnica permitir a aplicação de um algoritmo de inferência de tempo linear, a característica NP-hard não deixa de existir. No pior caso, o tamanho da rede pode crescer exponencialmente, tendo em vista que o método envolve o produto de tabelas de probabilidade incondicional. O problema passa então a depender da escolha de um bom método para junção de nós. 13 Ver sessão
20 P(C=F) P(C=T) Cloudy Spr+Rain C TT TF FT FF F T S R (W=F) P(W=T) F F TF FT TT WetGrass Figura10. Clustering de nós. Métodos de Cutset conditioning O método Cutset conditioning utiliza uma idéia oposta em relação a anterior. Seu propósito é transformar uma rede em diversas redes mais simples. Cada uma destas redes possui uma ou mais variáveis instanciadas em um valor definido. Assim, P(X E) é computado como uma média ponderada sobre os valores extraídos de cada uma das redes. O conjunto de variáveis que podem ser instanciadas para permitir que uma rede simplesmente conexa seja obtida é chamado cutset. Para o exemplo anterior, o cutset seria apenas a variável Cloudy, como seu valor é booleano, apenas duas árvores são geradas, conforme mostra a figura abaixo. +Cloud +Cloud -Cloudy -Cloudy Spr Rain Spr Rain WetGrass WetGrass Figura1. Cut set conditioning. De forma geral, o número resultante de novas árvores é exponencial em relação ao número de nós, o que significa dizer que, uma boa estratégia para definição de cutsets deve ser utilizada. 20
21 Métodos Stochastic simulation Neste método, simulações sobre a rede são repetidamente executadas permitindo que informações estatísticas sejam extraídas para as probabilidades que se deseja. Em cada rodada da simulação, um valor aleatório é atribuído a cada nó raiz da rede, a escolha é ponderada pela probabilidade incondicional do nó. Para P(Cloudy) = 0.5, do exemplo anterior, Cloudy = True deve ser escolhido metade das vezes, e Cloudy = False, a outra metade. Uma vez escolhido o valor de Cloudy, os valores de Sprinkler e Rain podem são também escolhidos aleatoriamente. Finalmente, o mesmo pode ser realizado para WetGrass, e a primeiro rodada termina. Para se estimar o valor de P(WetGrass Cloudy), ou uma probabilidade qualquer P(X E), o procedimento anterior deve ser repito várias vezes, e então se calcula a razão do número de vezes em que P(Cloudy) e P(WetGrass) foram verdadeiros, pelo número de vezes que apenas Cloudy foi verdadeiro. Este valor tende a se aproximar do valor exato, na medida em que o número de simulações aumenta. 5 Aplicações Redes Bayesianas têm sido utilizadas em diversos tipos de aplicações, entretanto, seu principal foco tem sido a área de diagnósticos, principalmente, diagnósticos médicos. A seguir serão apresentados alguns projetos. Pathfinder, Heckerman Stanford Sistema para diagnósticos de problemas nas glândulas linfáticas. O sistema trata mais de 60 enfermidades sob as probabilidades de mais de 100 causas (sintomas e resultados de testes médicos). Map Learning, Ken Basye Brown University Este projeto combina problemas de diagnostico e teoria de decisão. Um robô deve percorrer um labirinto, procurando aprender os caminhos percorridos e, ao mesmo tempo, explorar caminhos desconhecidos. O robô deve ponderar entre seguir um caminho conhecido até seu objetivo e a tentativa de se descobrir um novo caminho. AutoClass, NASA s Ames Research Center, Sistema de exploração e aquisição de conhecimento espacial. Este projeto está desenvolvendo uma rede bayesiana que permita a interpolação automática de dados espaciais oriundos de diferentes observatórios e planetários espalhados pelo mundo. Lumiere, Microsoft Research, 1998 O projeto pretende criar um sistema que possa automaticamente e inteligentemente interagir com outros sistemas, antecipando os objetivos e necessidades dos usuários. 21
22 6 Conclusões Redes bayesianas constituem uma forma natural para representação de informações condicionalmente independentes. E ainda, possibilitam a representação compacta de uma tabela de conjunção de probabilidades. Em outras palavras, redes bayesinas, oferecem uma boa solução a problemas onde conclusões não podem ser obtidas apenas do domínio do problema, onde, o uso de probabilidades é exigido. Inferências sobre redes bayesinas podem ser executadas em tempo linear, porém, para a maioria das topologias de rede, inferências possuem complexidade NP-hard. Algumas técnicas podem ser aplicadas para se obter tempo linear, mesmo em topologias que impossibilitariam este fato, entretanto, este ainda é um dos grandes desafios ao se desenvolver uma rede. 7 Referências Bibliográficas [1] Charniak, Eugene. Bayesians Networks without Tears. IA Magazine, [2] Darwiche, Adan & Huang, Cecil. Inference in Belief Networks: A procedural guide. International Journal of Approximate Reasoning, [3] Jensen, V. Finn. Bayesian Networks and Decision Graphs. Springer- Verlag,2001. [4] Murphyk, P. Kevin. A Brief Introduction to Graphical Models and Bayesian Networks. [5] Niedermayer, Daryle. An Introduction to Bayesian Networks and their Contemporary Applications [6] Russel, J. Stuart & Norvig, Peter. Artifical Intelligence: A modern Approach.Prentice Hall , ,
Redes Bayesianas: o que são, para que servem, algoritmos e exemplos de aplicações. Inteligência Artificial Profa.: Inês Dutra Roberto Ligeiro
 Redes Bayesianas: o que são, para que servem, algoritmos e exemplos de aplicações. Inteligência Artificial Profa.: Inês Dutra Roberto Ligeiro Resumo Introdução. Raciocinando sobre incertezas. Cálculo de
Redes Bayesianas: o que são, para que servem, algoritmos e exemplos de aplicações. Inteligência Artificial Profa.: Inês Dutra Roberto Ligeiro Resumo Introdução. Raciocinando sobre incertezas. Cálculo de
Redes Bayesianas. Disciplina: Inteligência Artificial Prof.: Cedric Luiz de Carvalho
 Redes Bayesianas Disciplina: Inteligência Artificial Prof.: Cedric Luiz de Carvalho Introdução Tópicos Especificação e topologia das Redes Bayesianas Semântica Construção Tipos de Inferência Conclusões
Redes Bayesianas Disciplina: Inteligência Artificial Prof.: Cedric Luiz de Carvalho Introdução Tópicos Especificação e topologia das Redes Bayesianas Semântica Construção Tipos de Inferência Conclusões
Independência Regra de Bayes Redes Bayesianas
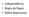 Independência Regra de Bayes Redes Bayesianas Inferência Probabilística Evidência observada: dor. Qual é a probabilidade de cárie dado que foi observado dor? P cárie dor = P(cárie dor) P(dor = 0,6 Independência
Independência Regra de Bayes Redes Bayesianas Inferência Probabilística Evidência observada: dor. Qual é a probabilidade de cárie dado que foi observado dor? P cárie dor = P(cárie dor) P(dor = 0,6 Independência
Inteligência Artificial. Raimundo Osvaldo Vieira [DECOMP IFMA Campus Monte Castelo]
![Inteligência Artificial. Raimundo Osvaldo Vieira [DECOMP IFMA Campus Monte Castelo] Inteligência Artificial. Raimundo Osvaldo Vieira [DECOMP IFMA Campus Monte Castelo]](/thumbs/76/74120787.jpg) Inteligência Artificial Raimundo Osvaldo Vieira [DECOMP IFMA Campus Monte Castelo] Abordagem Estocástica para a Incerteza: Redes Bayesianas Usando a teoria das probabilidades, podemos determinar, frequentemente
Inteligência Artificial Raimundo Osvaldo Vieira [DECOMP IFMA Campus Monte Castelo] Abordagem Estocástica para a Incerteza: Redes Bayesianas Usando a teoria das probabilidades, podemos determinar, frequentemente
lnteligência Artificial Raciocínio Probabilístico - Introdução a Redes Bayesianas
 lnteligência Artificial Raciocínio Probabilístico - Introdução a Redes Bayesianas Referências Adicionais Russel e Norvig cap. 14 e 15 Pearl, Judea. Probabilistic Reasoning in Intelligent Systems: Network
lnteligência Artificial Raciocínio Probabilístico - Introdução a Redes Bayesianas Referências Adicionais Russel e Norvig cap. 14 e 15 Pearl, Judea. Probabilistic Reasoning in Intelligent Systems: Network
Introdução ao tema das Redes Bayesianas
 Introdução ao tema das Redes Bayesianas Seminário de Modelação Cátia Azevedo 25/01/2013 Índice Introdução Redes Bayesianas Aprendizagem Bayesiana Teorema de Bayes Distribuição de probabilidade conjunta
Introdução ao tema das Redes Bayesianas Seminário de Modelação Cátia Azevedo 25/01/2013 Índice Introdução Redes Bayesianas Aprendizagem Bayesiana Teorema de Bayes Distribuição de probabilidade conjunta
Redes Bayesianas. Introdução. Teoria da Probabilidade. Manipulação de Conhecimento Incerto
 Introdução M. Sc. Luiz Alberto lasf.bel@gmail.com As (RBs) são modelos gráficos que codificam relacionamentos probabilísticos entre variáveis de interesse As principais motivações para o estudo e uso de
Introdução M. Sc. Luiz Alberto lasf.bel@gmail.com As (RBs) são modelos gráficos que codificam relacionamentos probabilísticos entre variáveis de interesse As principais motivações para o estudo e uso de
INF 1771 Inteligência Artificial
 INF 1771 Inteligência Artificial Aula 15 Incerteza Edirlei Soares de Lima Agentes Vistos Anteriormente Agentes baseados em busca: Busca cega Busca heurística Busca local Agentes
INF 1771 Inteligência Artificial Aula 15 Incerteza Edirlei Soares de Lima Agentes Vistos Anteriormente Agentes baseados em busca: Busca cega Busca heurística Busca local Agentes
Inferência em Redes de Crenças Sejam Z i pais de Y i e z i, um conj de valores para Z i. e E Y i X
 Sistemas Inteligentes, 11-12 1 Inferência em Redes de Crenças Sejam Z i pais de Y i e z i, um conj de valores para Z i. P(E X X) = i P(E Y i X X) P(E X X) = i y i z i P(E Yi X X,y i,z i )P(y i,z i X) Decompondo
Sistemas Inteligentes, 11-12 1 Inferência em Redes de Crenças Sejam Z i pais de Y i e z i, um conj de valores para Z i. P(E X X) = i P(E Y i X X) P(E X X) = i y i z i P(E Yi X X,y i,z i )P(y i,z i X) Decompondo
Sistemas Inteligentes, Apoio à Decisão: Lidando com Incertezas
 Sistemas Inteligentes, 12-13 1 Apoio à Decisão: Lidando com Incertezas Sistemas Inteligentes, 12-13 2 Incerteza Falta de informação suficiente. Conhecimento não completo ou não correto. Planos condicionais
Sistemas Inteligentes, 12-13 1 Apoio à Decisão: Lidando com Incertezas Sistemas Inteligentes, 12-13 2 Incerteza Falta de informação suficiente. Conhecimento não completo ou não correto. Planos condicionais
Aprendizagem de Máquina
 Aprendizagem de Máquina Modelos gráficos probabilísticos Redes bayesianas Modelos gráficos probabilísticos Os modelos gráficos probabilísticos utilizam representações diagramáticas das distribuições de
Aprendizagem de Máquina Modelos gráficos probabilísticos Redes bayesianas Modelos gráficos probabilísticos Os modelos gráficos probabilísticos utilizam representações diagramáticas das distribuições de
Redes Bayesianas. Prof. Júlio Cesar Nievola PPGIa Escola Politécnica PUCPR
 Redes Bayesianas Prof. Júlio Cesar Nievola PPGIa Escola Politécnica PUCPR Raciocínio com Incerteza Incerteza: qualidade ou estado de não ser conhecido com certeza Fontes de incerteza: Ignorância: qual
Redes Bayesianas Prof. Júlio Cesar Nievola PPGIa Escola Politécnica PUCPR Raciocínio com Incerteza Incerteza: qualidade ou estado de não ser conhecido com certeza Fontes de incerteza: Ignorância: qual
PIP/CA - Programa Interdisciplinar de Pós-Graduação Mestrado em Computação Aplicada da UNISINOS. 2000/1-2o. Trimestre - AULA 05 / FSO
 PIP/CA - Programa Interdisciplinar de Pós-Graduação Mestrado em Computação Aplicada da UNISINOS 2000/1-2o. Trimestre - AULA 05 / FSO INTELIGÊNCIA ARTIFICIAL & SISTEMAS INTELIGENTES Professores Responsáveis:
PIP/CA - Programa Interdisciplinar de Pós-Graduação Mestrado em Computação Aplicada da UNISINOS 2000/1-2o. Trimestre - AULA 05 / FSO INTELIGÊNCIA ARTIFICIAL & SISTEMAS INTELIGENTES Professores Responsáveis:
INTELIGÊNCIA ARTIFICIAL
 Figura: Capa do Livro Russell, S., Norvig, P. Artificial Intelligence A Modern Approach, Pearson, 2009. Universidade Federal de Campina Grande Unidade Acadêmica de Sistemas e Computação Curso de Pós-Graduação
Figura: Capa do Livro Russell, S., Norvig, P. Artificial Intelligence A Modern Approach, Pearson, 2009. Universidade Federal de Campina Grande Unidade Acadêmica de Sistemas e Computação Curso de Pós-Graduação
Raciocínio Probabilístico. Inteligência Artificial. Exemplo. Redes Bayesianas. Exemplo. Exemplo 11/16/2010
 Inteligência Artificial Raciocínio Probabilístico Aula 9 Profª Bianca Zadrozny http://www.ic.uff.br/~bianca/ia-pos Capítulo 14 Russell & Norvig Seções 14.1 a 14.4 2 Redes Bayesianas Estrutura de dados
Inteligência Artificial Raciocínio Probabilístico Aula 9 Profª Bianca Zadrozny http://www.ic.uff.br/~bianca/ia-pos Capítulo 14 Russell & Norvig Seções 14.1 a 14.4 2 Redes Bayesianas Estrutura de dados
Inteligência Artificial Prof. Marcos Quinet Pólo Universitário de Rio das Ostras PURO Universidade Federal Fluminense UFF
 Inteligência Artificial Prof. Marcos Quinet Pólo Universitário de Rio das Ostras PURO Universidade Federal Fluminense UFF No capítulo anterior... Agentes lógicos; Inferência lógica; Introdução ao PROLOG.
Inteligência Artificial Prof. Marcos Quinet Pólo Universitário de Rio das Ostras PURO Universidade Federal Fluminense UFF No capítulo anterior... Agentes lógicos; Inferência lógica; Introdução ao PROLOG.
Conhecimento Incerto
 Conhecimento Incerto Profa. Josiane M. P. erreira exto base: Stuart Russel e Peter Norving - Inteligência Artificial - cap 13. David Poole, Alan Mackworth e Randy Goebel - Computational Intelligence A
Conhecimento Incerto Profa. Josiane M. P. erreira exto base: Stuart Russel e Peter Norving - Inteligência Artificial - cap 13. David Poole, Alan Mackworth e Randy Goebel - Computational Intelligence A
Aprendizado de Máquina (Machine Learning)
 Ciência da Computação Aprendizado de Máquina (Machine Learning) Aula 10 Classificação com Naïve Bayes Max Pereira Raciocínio Probabilístico A notação tradicional para criar e analisar sentenças lógicas
Ciência da Computação Aprendizado de Máquina (Machine Learning) Aula 10 Classificação com Naïve Bayes Max Pereira Raciocínio Probabilístico A notação tradicional para criar e analisar sentenças lógicas
Sistemas Inteligentes. Incerteza
 Sistemas Inteligentes Incerteza Incerteza Seja a ação A t = sair para o aeroporto t minutos antes do vôo. A t me levará ao aeroporto a tempo? Dificuldades de saber o resultado da ação: Estados parcialmente
Sistemas Inteligentes Incerteza Incerteza Seja a ação A t = sair para o aeroporto t minutos antes do vôo. A t me levará ao aeroporto a tempo? Dificuldades de saber o resultado da ação: Estados parcialmente
Artificial Intelligence, 14-15 1
 Artificial Intelligence, 14-15 1 Cap. 14: Incerteza Falta de informação suficiente. Conhecimento não completo ou não correto. Planos condicionais podem lidar com incerteza de forma limitada. Ex: Plano
Artificial Intelligence, 14-15 1 Cap. 14: Incerteza Falta de informação suficiente. Conhecimento não completo ou não correto. Planos condicionais podem lidar com incerteza de forma limitada. Ex: Plano
Probabilidade. É o conjunto de todos os possíveis resultados de um experimento aleatório.
 Probabilidade Introdução O trabalho estatístico se desenvolve a partir da observação de determinados fenômenos e emprega dados numéricos relacionados aos mesmos, para tirar conclusões que permitam conhecê-los
Probabilidade Introdução O trabalho estatístico se desenvolve a partir da observação de determinados fenômenos e emprega dados numéricos relacionados aos mesmos, para tirar conclusões que permitam conhecê-los
Roteiro. Raciocínio Probabilístico. Sistemas Inteligentes. PARTE I - Introdução. Incerteza. Incerteza. Parte I. Parte II. Parte III.
 Roteiro Raciocínio Probabilístico EA072 Inteligência Artificial em Aplicações Industriais Parte I Introdução Parte II Fundamentos da teoria da probabilidade Parte III Redes Parte IV Aprendizado em redes
Roteiro Raciocínio Probabilístico EA072 Inteligência Artificial em Aplicações Industriais Parte I Introdução Parte II Fundamentos da teoria da probabilidade Parte III Redes Parte IV Aprendizado em redes
Inteligência Artificial. Conceitos Gerais
 Inteligência Artificial Conceitos Gerais Inteligência Artificial - IA IA é um campo de estudo multidisciplinar e interdisciplinar, que se apóia no conhecimento e evolução de outras áreas do conhecimento.
Inteligência Artificial Conceitos Gerais Inteligência Artificial - IA IA é um campo de estudo multidisciplinar e interdisciplinar, que se apóia no conhecimento e evolução de outras áreas do conhecimento.
3 Aprendizado por reforço
 3 Aprendizado por reforço Aprendizado por reforço é um ramo estudado em estatística, psicologia, neurociência e ciência da computação. Atraiu o interesse de pesquisadores ligados a aprendizado de máquina
3 Aprendizado por reforço Aprendizado por reforço é um ramo estudado em estatística, psicologia, neurociência e ciência da computação. Atraiu o interesse de pesquisadores ligados a aprendizado de máquina
Probabilidades. Wagner H. Bonat Elias T. Krainski Fernando P. Mayer
 Probabilidades Wagner H. Bonat Elias T. Krainski Fernando P. Mayer Universidade Federal do Paraná Departamento de Estatística Laboratório de Estatística e Geoinformação 06/03/2018 WB, EK, FM ( LEG/DEST/UFPR
Probabilidades Wagner H. Bonat Elias T. Krainski Fernando P. Mayer Universidade Federal do Paraná Departamento de Estatística Laboratório de Estatística e Geoinformação 06/03/2018 WB, EK, FM ( LEG/DEST/UFPR
Inteligência Artificial
 UFRGS 2 Inteligência Artificial Técnicas de Mineração de Dados Árvores de Decisão Regras de Associação Árvores de Decisão As árvores de decisão (AD) são ferramentas poderosas para classificação cuja maior
UFRGS 2 Inteligência Artificial Técnicas de Mineração de Dados Árvores de Decisão Regras de Associação Árvores de Decisão As árvores de decisão (AD) são ferramentas poderosas para classificação cuja maior
Inteligência Artificial
 Universidade Federal de Campina Grande Unidade Acadêmica de Sistemas e Computação Curso de Pós-Graduação em Ciência da Computação Inteligência Artificial Representação do Conhecimento (Parte I) Prof. a
Universidade Federal de Campina Grande Unidade Acadêmica de Sistemas e Computação Curso de Pós-Graduação em Ciência da Computação Inteligência Artificial Representação do Conhecimento (Parte I) Prof. a
Conhecimento e Raciocínio Agente Lógicos Capítulo 7. Leliane Nunes de Barros
 Conhecimento e Raciocínio Agente Lógicos Capítulo 7 Leliane Nunes de Barros leliane@ime.usp.br Agentes Lógicos Agentes que podem formar representações do mundo, usar um processo de inferência para derivar
Conhecimento e Raciocínio Agente Lógicos Capítulo 7 Leliane Nunes de Barros leliane@ime.usp.br Agentes Lógicos Agentes que podem formar representações do mundo, usar um processo de inferência para derivar
Sistemas Inteligentes
 Sistemas Inteligentes Aula 21/10 Agentes Lógicos Agente Baseado em Conhecimento Agentes Baseados em Conhecimento ou Agentes Lógicos. Podem lidar mais facilmente com ambientes parcialmente observáveis.
Sistemas Inteligentes Aula 21/10 Agentes Lógicos Agente Baseado em Conhecimento Agentes Baseados em Conhecimento ou Agentes Lógicos. Podem lidar mais facilmente com ambientes parcialmente observáveis.
Problemas Intratáveis ou computação eficiente X computação ineficiente
 Problemas Intratáveis ou computação eficiente X computação ineficiente Problemas Tratáveis Os problemas que podem ser resolvidos em tempo polinomial em um computador típico são exatamente os mesmos problemas
Problemas Intratáveis ou computação eficiente X computação ineficiente Problemas Tratáveis Os problemas que podem ser resolvidos em tempo polinomial em um computador típico são exatamente os mesmos problemas
DISTRIBUIÇÃO NORMAL DISTRIBUIÇÕES DE PROBABILIDADE CONJUNTAS ROTEIRO DISTRIBUIÇÃO NORMAL
 ROTEIRO DISTRIBUIÇÕES DE PROBABILIDADE CONJUNTAS 1. Distribuições conjuntas 2. Independência 3. Confiabilidade 4. Combinações lineares de variáveis aleatórias 5. Referências DISTRIBUIÇÃO NORMAL Definição:
ROTEIRO DISTRIBUIÇÕES DE PROBABILIDADE CONJUNTAS 1. Distribuições conjuntas 2. Independência 3. Confiabilidade 4. Combinações lineares de variáveis aleatórias 5. Referências DISTRIBUIÇÃO NORMAL Definição:
Aprendizado Bayesiano Anteriormente...
 Aprendizado Bayesiano Anteriormente... Conceito de Probabilidade Condicional É a probabilidade de um evento A dada a ocorrência de um evento B Universidade de São Paulo Instituto de Ciências Matemáticas
Aprendizado Bayesiano Anteriormente... Conceito de Probabilidade Condicional É a probabilidade de um evento A dada a ocorrência de um evento B Universidade de São Paulo Instituto de Ciências Matemáticas
Teoria das Probabilidades
 08/06/07 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto
08/06/07 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto
Aprendizado Bayesiano
 Aprendizado Bayesiano Marcelo K. Albertini 3 de Julho de 2014 2/1 Conteúdo Aprendizado Naive Bayes Exemplo: classificação de texto Redes Bayesiana Algoritmo EM Regressão probabiĺıstica 3/1 Classificador
Aprendizado Bayesiano Marcelo K. Albertini 3 de Julho de 2014 2/1 Conteúdo Aprendizado Naive Bayes Exemplo: classificação de texto Redes Bayesiana Algoritmo EM Regressão probabiĺıstica 3/1 Classificador
IA: Tratamento de Incertezas - Probabilidades
 IA: - Probabilidades Professor: Paulo Gurgel Pinheiro MC906A - Inteligência Articial Instituto de Computação Universidade Estadual de Campinas - UNICAMP 14 de Setembro de 2010 1 / 62 http://www.ic.unicamp.br/
IA: - Probabilidades Professor: Paulo Gurgel Pinheiro MC906A - Inteligência Articial Instituto de Computação Universidade Estadual de Campinas - UNICAMP 14 de Setembro de 2010 1 / 62 http://www.ic.unicamp.br/
PERT PERT PERT PERT PERT PERT. O CPM assume que as estimativas de tempo para um projeto são certas (determinísticas);
 O CPM assume que as estimativas de tempo para um projeto são certas (determinísticas); A duração de cada atividade na prática, contudo, pode ser diferente daquela prevista no projeto; Existem muitos fatores
O CPM assume que as estimativas de tempo para um projeto são certas (determinísticas); A duração de cada atividade na prática, contudo, pode ser diferente daquela prevista no projeto; Existem muitos fatores
Cap. 8 - Variáveis Aleatórias
 Variáveis Aleatórias Discretas: A de Poisson e Outras ESQUEMA DO CAPÍTULO 8.1 A DISTRIBUIÇÃO DE POISSON 8.2 A DISTRIBUIÇÃO DE POISSON COMO APROXIMAÇÃO DA DISTRIBUIÇÃO BINOMIAL 8.3 O PROCESSO DE POISSON
Variáveis Aleatórias Discretas: A de Poisson e Outras ESQUEMA DO CAPÍTULO 8.1 A DISTRIBUIÇÃO DE POISSON 8.2 A DISTRIBUIÇÃO DE POISSON COMO APROXIMAÇÃO DA DISTRIBUIÇÃO BINOMIAL 8.3 O PROCESSO DE POISSON
Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine)
 Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine) Statistics for Managers Using Microsoft Excel, 5e 2008 Pearson Prentice-Hall, Inc. Chap 6-1 Objetivos: Neste capítulo, você aprenderá:
Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine) Statistics for Managers Using Microsoft Excel, 5e 2008 Pearson Prentice-Hall, Inc. Chap 6-1 Objetivos: Neste capítulo, você aprenderá:
3 a Lista de PE Solução
 Universidade de Brasília Departamento de Estatística 3 a Lista de PE Solução. Se X representa o ganho do jogador, então os possíveis valores para X são,, 0, e 4. Esses valores são, respectivamente, correspondentes
Universidade de Brasília Departamento de Estatística 3 a Lista de PE Solução. Se X representa o ganho do jogador, então os possíveis valores para X são,, 0, e 4. Esses valores são, respectivamente, correspondentes
Tabela 1 - Minitermos e Maxtermos para uma função de 3 variáveis.
 Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 FORMAS CANÔNICAS A lógica estruturada é baseada na capacidade de escrever equações booleanas de maneira
Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 FORMAS CANÔNICAS A lógica estruturada é baseada na capacidade de escrever equações booleanas de maneira
Incerteza. Capítulo 13 Russell & Norvig Seções 13.1 a 13.4
 Incerteza Capítulo 13 Russell & Norvig Seções 13.1 a 13.4 Incerteza Seja a ação A t = sair para o aeroporto t minutos antes do vôo. A t me levará ao aeroporto a tempo? Dificuldades de saber o resultado
Incerteza Capítulo 13 Russell & Norvig Seções 13.1 a 13.4 Incerteza Seja a ação A t = sair para o aeroporto t minutos antes do vôo. A t me levará ao aeroporto a tempo? Dificuldades de saber o resultado
Problemas de otimização
 Problemas de otimização Problemas de decisão: Existe uma solução satisfazendo certa propriedade? Resultado: sim ou não Problemas de otimização: Entre todas as soluções satisfazendo determinada propriedade,
Problemas de otimização Problemas de decisão: Existe uma solução satisfazendo certa propriedade? Resultado: sim ou não Problemas de otimização: Entre todas as soluções satisfazendo determinada propriedade,
1 Classificadores Bayseanos Simples
 Aula 12 - Classificadores Bayseanos Curso de Data Mining Sandra de Amo Classificadores Bayseanos são classificadores estatísticos que classificam um objeto numa determinada classe baseando-se na probabilidade
Aula 12 - Classificadores Bayseanos Curso de Data Mining Sandra de Amo Classificadores Bayseanos são classificadores estatísticos que classificam um objeto numa determinada classe baseando-se na probabilidade
Estatística Aplicada. Árvore de Decisão. Prof. Carlos Alberto Stechhahn PARTE II. Administração. p(a/b) = n(a B)/ n(b)
 Estatística Aplicada Administração p(a/b) = n(a B)/ n(b) PARTE II Árvore de Decisão Prof. Carlos Alberto Stechhahn 2014 1. Probabilidade Condicional - Aplicações Considere que desejamos calcular a probabilidade
Estatística Aplicada Administração p(a/b) = n(a B)/ n(b) PARTE II Árvore de Decisão Prof. Carlos Alberto Stechhahn 2014 1. Probabilidade Condicional - Aplicações Considere que desejamos calcular a probabilidade
Renato Assunção - DCC, UFMG. 01 de Setembro de Considere a BN da Figura 1. Suponha que cada uma das variáveis no DAG seja uma v.a.
 a Prova - PGM Renato Assunção - DCC, UFMG 0 de Setembro de 206. Considere a BN da Figura. Suponha que cada uma das variáveis no DAG seja uma v.a. aleatória binária. Figure : Uma BN sem nome. Todas as variáveis
a Prova - PGM Renato Assunção - DCC, UFMG 0 de Setembro de 206. Considere a BN da Figura. Suponha que cada uma das variáveis no DAG seja uma v.a. aleatória binária. Figure : Uma BN sem nome. Todas as variáveis
MC102 Aula 26. Instituto de Computação Unicamp. 17 de Novembro de 2016
 MC102 Aula 26 Recursão Instituto de Computação Unicamp 17 de Novembro de 2016 Roteiro 1 Recursão Indução 2 Recursão 3 Fatorial 4 O que acontece na memória 5 Recursão Iteração 6 Soma em um Vetor 7 Números
MC102 Aula 26 Recursão Instituto de Computação Unicamp 17 de Novembro de 2016 Roteiro 1 Recursão Indução 2 Recursão 3 Fatorial 4 O que acontece na memória 5 Recursão Iteração 6 Soma em um Vetor 7 Números
Sumário. 2 Índice Remissivo 12
 i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
Afirmações Matemáticas
 Afirmações Matemáticas Na aula passada, vimos que o objetivo desta disciplina é estudar estruturas matemáticas, afirmações sobre elas e como provar essas afirmações. Já falamos das estruturas principais,
Afirmações Matemáticas Na aula passada, vimos que o objetivo desta disciplina é estudar estruturas matemáticas, afirmações sobre elas e como provar essas afirmações. Já falamos das estruturas principais,
A análise de séries temporais é uma área da estatística dedicada ao estudo de dados orientados no tempo (MONTGOMERY, 2004).
 3 Séries temporais A análise de séries temporais é uma área da estatística dedicada ao estudo de dados orientados no tempo (MONTGOMERY, 2004). 3.1. Princípios fundamentais Conforme Box et al. (1994), uma
3 Séries temporais A análise de séries temporais é uma área da estatística dedicada ao estudo de dados orientados no tempo (MONTGOMERY, 2004). 3.1. Princípios fundamentais Conforme Box et al. (1994), uma
Probabilidade Aula 03
 0303200 Probabilidade Aula 03 Magno T. M. Silva Escola Politécnica da USP Março de 2017 Sumário Teorema de Bayes 2.5 Independência Teorema de Bayes Sejam A 1,,A k uma partição de S (eventos disjuntos)
0303200 Probabilidade Aula 03 Magno T. M. Silva Escola Politécnica da USP Março de 2017 Sumário Teorema de Bayes 2.5 Independência Teorema de Bayes Sejam A 1,,A k uma partição de S (eventos disjuntos)
Conceitos Básicos, Básicos,Básicos de Probabilidade
 Conceitos Básicos, Básicos,Básicos de Probabilidade Espaço Amostral Base da Teoria de Probabilidades Experimentos são realizados resultados NÃO conhecidos previamente Experimento aleatório Exemplos: Determinar
Conceitos Básicos, Básicos,Básicos de Probabilidade Espaço Amostral Base da Teoria de Probabilidades Experimentos são realizados resultados NÃO conhecidos previamente Experimento aleatório Exemplos: Determinar
Teoria das Probabilidades
 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica 08:8 ESTATÍSTICA APLICADA I - Teoria das
Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica 08:8 ESTATÍSTICA APLICADA I - Teoria das
Teoria da Computação. Complexidade computacional classes de problemas
 Teoria da Computação Complexidade computacional classes de problemas 1 Universo de problemas Problemas indecidíveis ou não-computáveis Não admitem algoritmos Problemas intratáveis Não admitem algoritmos
Teoria da Computação Complexidade computacional classes de problemas 1 Universo de problemas Problemas indecidíveis ou não-computáveis Não admitem algoritmos Problemas intratáveis Não admitem algoritmos
Fundamentos de Lógica Matemática
 Webconferência 5-22/03/2012 Prova por resolução Prof. L. M. Levada http://www.dc.ufscar.br/ alexandre Departamento de Computação (DC) Universidade Federal de São Carlos (UFSCar) 2012/1 Introdução É possível
Webconferência 5-22/03/2012 Prova por resolução Prof. L. M. Levada http://www.dc.ufscar.br/ alexandre Departamento de Computação (DC) Universidade Federal de São Carlos (UFSCar) 2012/1 Introdução É possível
INF 1771 Inteligência Artificial
 Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 23 Redes Bayesianas Vantagens e Desvantagens da Probabilidade Possui uma boa fundamentação formal. Permite encontrar
Edirlei Soares de Lima INF 1771 Inteligência Artificial Aula 23 Redes Bayesianas Vantagens e Desvantagens da Probabilidade Possui uma boa fundamentação formal. Permite encontrar
Probabilidade - aula II
 2012/02 1 Interpretações de Probabilidade 2 3 Amostras Aleatórias e Objetivos Ao final deste capítulo você deve ser capaz de: Calcular probabilidades de eventos conjuntos. Interpretar e calcular probabilidades
2012/02 1 Interpretações de Probabilidade 2 3 Amostras Aleatórias e Objetivos Ao final deste capítulo você deve ser capaz de: Calcular probabilidades de eventos conjuntos. Interpretar e calcular probabilidades
Inteligência Artificial Escola de Verão Laboratório Associado de Computação e Matemática Aplicada LAC
 Inteligência Artificial Escola de Verão 2008 Laboratório Associado de Computação e Matemática Aplicada LAC www.lac.inpe.br/~demisio/ia_lac.html Sistemas Especialistas e Representação do Conhecimento Sistema
Inteligência Artificial Escola de Verão 2008 Laboratório Associado de Computação e Matemática Aplicada LAC www.lac.inpe.br/~demisio/ia_lac.html Sistemas Especialistas e Representação do Conhecimento Sistema
Seminário de Robótica Bruno de Abreu Silva
 Seminário de Robótica Bruno de Abreu Silva 1 Introdução Conceitos gerais Métodos de planejamento de rotas 2 Dadas as configurações inicial e final de um robô, descobrir uma sequência de movimentos a ser
Seminário de Robótica Bruno de Abreu Silva 1 Introdução Conceitos gerais Métodos de planejamento de rotas 2 Dadas as configurações inicial e final de um robô, descobrir uma sequência de movimentos a ser
2 Definição do Problema
 Definição do Problema. Formulação Matemática O problema do Fluxo Máximo entre todos os pares de nós surge no contexto de redes, estas representadas por grafos, e deriva-se do problema singular de fluxo
Definição do Problema. Formulação Matemática O problema do Fluxo Máximo entre todos os pares de nós surge no contexto de redes, estas representadas por grafos, e deriva-se do problema singular de fluxo
Técnicas de Inteligência Artificial
 Universidade do Sul de Santa Catarina Ciência da Computação Técnicas de Inteligência Artificial Aula 02 Representação do Conhecimento Prof. Max Pereira Para que um computador possa solucionar um problema
Universidade do Sul de Santa Catarina Ciência da Computação Técnicas de Inteligência Artificial Aula 02 Representação do Conhecimento Prof. Max Pereira Para que um computador possa solucionar um problema
Cálculo proposicional
 O estudo da lógica é a análise de métodos de raciocínio. No estudo desses métodos, a lógica esta interessada principalmente na forma e não no conteúdo dos argumentos. Lógica: conhecimento das formas gerais
O estudo da lógica é a análise de métodos de raciocínio. No estudo desses métodos, a lógica esta interessada principalmente na forma e não no conteúdo dos argumentos. Lógica: conhecimento das formas gerais
Árvores de decisão. Marcelo K. Albertini. 17 de Agosto de 2015
 Árvores de decisão Marcelo K. Albertini 17 de Agosto de 2015 2/31 Árvores de Decisão Nós internos testam o valor de um atributo individual ramificam de acordo com os resultados do teste Nós folhas especificam
Árvores de decisão Marcelo K. Albertini 17 de Agosto de 2015 2/31 Árvores de Decisão Nós internos testam o valor de um atributo individual ramificam de acordo com os resultados do teste Nós folhas especificam
CEFET/RJ Inteligência Artificial (2018.1) Prof. Eduardo Bezerra Lista de exercícios 05
 . CEFET/RJ Inteligência Artificial (2018.1) Prof. Eduardo Bezerra (ebezerra@cefet-rj.br) Lista de exercícios 05 Créditos: essa lista de exercícios contém a tradução dos exercícios retirados do livro texto
. CEFET/RJ Inteligência Artificial (2018.1) Prof. Eduardo Bezerra (ebezerra@cefet-rj.br) Lista de exercícios 05 Créditos: essa lista de exercícios contém a tradução dos exercícios retirados do livro texto
Probabilidade. Ricardo Ehlers Departamento de Matemática Aplicada e Estatística Universidade de São Paulo
 Probabilidade Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Experimento aleatório Definição. Qualquer experimento cujo resultado não pode
Probabilidade Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Experimento aleatório Definição. Qualquer experimento cujo resultado não pode
Introdução ao Curso. Área de Teoria DCC/UFMG 2019/01. Introdução à Lógica Computacional Introdução ao Curso Área de Teoria DCC/UFMG /01 1 / 22
 Introdução ao Curso Área de Teoria DCC/UFMG Introdução à Lógica Computacional 2019/01 Introdução à Lógica Computacional Introdução ao Curso Área de Teoria DCC/UFMG - 2019/01 1 / 22 Introdução: O que é
Introdução ao Curso Área de Teoria DCC/UFMG Introdução à Lógica Computacional 2019/01 Introdução à Lógica Computacional Introdução ao Curso Área de Teoria DCC/UFMG - 2019/01 1 / 22 Introdução: O que é
INF 1771 Inteligência Artificial
 INF 1771 Inteligência Artificial Aula 07 Agentes Lógicos Edirlei Soares de Lima Introdução Humanos possuem conhecimento e raciocinam sobre este conhecimento. Exemplo: João jogou
INF 1771 Inteligência Artificial Aula 07 Agentes Lógicos Edirlei Soares de Lima Introdução Humanos possuem conhecimento e raciocinam sobre este conhecimento. Exemplo: João jogou
DISTRIBUIÇÕES DE PROBABILIDADE CONJUNTAS DISTRIBUIÇÕES CONJUNTAS ROTEIRO DISTRIBUIÇÃO CONJUNTA
 ROTEIRO DISTRIBUIÇÕES DE PROBABILIDADE CONJUNTAS 1. Distribuições conjuntas 2. Independência 3. Confiabilidade 4. Combinações lineares de variáveis aleatórias 5. Referências DISTRIBUIÇÃO CONJUNTA Em muitos
ROTEIRO DISTRIBUIÇÕES DE PROBABILIDADE CONJUNTAS 1. Distribuições conjuntas 2. Independência 3. Confiabilidade 4. Combinações lineares de variáveis aleatórias 5. Referências DISTRIBUIÇÃO CONJUNTA Em muitos
Conhecimento e Raciocínio Lógica Proposicional
 Conhecimento e Raciocínio Lógica Proposicional Agente Baseado em Conhecimento ou Sistema Baseado em Conhecimento Representa conhecimento sobre o mundo em uma linguagem formal (KB) Raciocina sobre o mundo
Conhecimento e Raciocínio Lógica Proposicional Agente Baseado em Conhecimento ou Sistema Baseado em Conhecimento Representa conhecimento sobre o mundo em uma linguagem formal (KB) Raciocina sobre o mundo
Funções Geradoras de Variáveis Aleatórias. Simulação Discreta de Sistemas - Prof. Paulo Freitas - UFSC/CTC/INE
 Funções Geradoras de Variáveis Aleatórias 1 Funções Geradoras de Variáveis Aleatórias Nos programas de simulação existe um GNA e inúmeras outras funções matemáticas descritas como Funções Geradoras de
Funções Geradoras de Variáveis Aleatórias 1 Funções Geradoras de Variáveis Aleatórias Nos programas de simulação existe um GNA e inúmeras outras funções matemáticas descritas como Funções Geradoras de
Geração de cenários de energia renovável correlacionados com hidrologia: uma abordagem bayesiana multivariada.
 Geração de cenários de energia renovável correlacionados com hidrologia: uma abordagem bayesiana multivariada [alessandro@psr-inc.com] Conteúdo Introdução Estimação não paramétrica (Kernel density) Transformação
Geração de cenários de energia renovável correlacionados com hidrologia: uma abordagem bayesiana multivariada [alessandro@psr-inc.com] Conteúdo Introdução Estimação não paramétrica (Kernel density) Transformação
Aprendizado de Máquina. Conteudo. Terminologia. Notes. Notes. Notes. Notes. Aprendizagem Bayesiana. Luiz Eduardo S. Oliveira
 Aprendizado de Máquina Aprendizagem Bayesiana Luiz Eduardo S. Oliveira Universidade Federal do Paraná Departamento de Informática http://lesoliveira.net Luiz S. Oliveira (UFPR) Aprendizado de Máquina 1
Aprendizado de Máquina Aprendizagem Bayesiana Luiz Eduardo S. Oliveira Universidade Federal do Paraná Departamento de Informática http://lesoliveira.net Luiz S. Oliveira (UFPR) Aprendizado de Máquina 1
Processos Estocásticos
 Processos Estocásticos Quarta Lista de Exercícios 12 de fevereiro de 2014 1 Sejam X e Y duas VAs que só podem assumir os valores 1 ou -1 e seja p(x, y) = P (X = x, Y = y), x, y { 1, 1} a função de probabilidade
Processos Estocásticos Quarta Lista de Exercícios 12 de fevereiro de 2014 1 Sejam X e Y duas VAs que só podem assumir os valores 1 ou -1 e seja p(x, y) = P (X = x, Y = y), x, y { 1, 1} a função de probabilidade
Inteligência Artificial. Sistemas Baseados em Conhecimento. Representação de Conhecimento (continuação)
 Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação http://www.inf.unioeste.br/~claudia/ia2018.html Inteligência Artificial Sistemas Baseados em Conhecimento Representação
Universidade Estadual do Oeste do Paraná Curso de Bacharelado em Ciência da Computação http://www.inf.unioeste.br/~claudia/ia2018.html Inteligência Artificial Sistemas Baseados em Conhecimento Representação
Probabilidade. Ricardo Ehlers Departamento de Matemática Aplicada e Estatística Universidade de São Paulo
 Probabilidade Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Introdução Experimento aleatório Definição Qualquer experimento cujo resultado
Probabilidade Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Introdução Experimento aleatório Definição Qualquer experimento cujo resultado
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/30 3 - INDUÇÃO E RECURSÃO 3.1) Indução Matemática 3.2)
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/30 3 - INDUÇÃO E RECURSÃO 3.1) Indução Matemática 3.2)
Classificadores. André Tavares da Silva.
 Classificadores André Tavares da Silva andre.silva@udesc.br Reconhecimento de padrões (etapas) Obtenção dos dados (imagens, vídeos, sinais) Pré-processamento Segmentação Extração de características Obs.:
Classificadores André Tavares da Silva andre.silva@udesc.br Reconhecimento de padrões (etapas) Obtenção dos dados (imagens, vídeos, sinais) Pré-processamento Segmentação Extração de características Obs.:
2 Medida de Incertezas: Fundamentos
 2 Medida de Incertezas: Fundamentos 2. Introdução O resultado de um processo de medição fornece uma determinada informação que usualmente é chamada de conhecimento. A fim de quantificar quão completo é
2 Medida de Incertezas: Fundamentos 2. Introdução O resultado de um processo de medição fornece uma determinada informação que usualmente é chamada de conhecimento. A fim de quantificar quão completo é
relógio apenas uma vez mediante ao pagamento de uma pequena taxa. Ao encontrarem algum defeito os consumidores devem devolver o relógio pagando
 Capítulo 10 Introdução à Teoria de Decisão 10.1 Introdução Na situação geral de decisão temos várias alternativas bem definidas e procuramos pela melhor ação dado o problema que temos em mãos. Além disso
Capítulo 10 Introdução à Teoria de Decisão 10.1 Introdução Na situação geral de decisão temos várias alternativas bem definidas e procuramos pela melhor ação dado o problema que temos em mãos. Além disso
CLASSIFICADORES BAEYSIANOS
 CLASSIFICADORES BAEYSIANOS Teorema de Bayes 2 Frequentemente, uma informação é apresentada na forma de probabilidade condicional Probabilidade de um evento ocorrer dada uma condição Probabilidade de um
CLASSIFICADORES BAEYSIANOS Teorema de Bayes 2 Frequentemente, uma informação é apresentada na forma de probabilidade condicional Probabilidade de um evento ocorrer dada uma condição Probabilidade de um
Dedução Natural e Sistema Axiomático Pa(Capítulo 6)
 Dedução Natural e Sistema Axiomático Pa(Capítulo 6) LÓGICA APLICADA A COMPUTAÇÃO Professor: Rosalvo Ferreira de Oliveira Neto Estrutura 1. Definições 2. Dedução Natural 3. Sistemas axiomático Pa 4. Lista
Dedução Natural e Sistema Axiomático Pa(Capítulo 6) LÓGICA APLICADA A COMPUTAÇÃO Professor: Rosalvo Ferreira de Oliveira Neto Estrutura 1. Definições 2. Dedução Natural 3. Sistemas axiomático Pa 4. Lista
Árvores. Thiago Martins, Fabio Gagliardi Cozman. PMR2300 / PMR3201 Escola Politécnica da Universidade de São Paulo
 PMR2300 / PMR3201 Escola Politécnica da Universidade de São Paulo Árvore: estrutura composta por nós e arestas entre nós. As arestas são direcionadas ( setas ) e: um nó (e apenas um) é a raiz; todo nó
PMR2300 / PMR3201 Escola Politécnica da Universidade de São Paulo Árvore: estrutura composta por nós e arestas entre nós. As arestas são direcionadas ( setas ) e: um nó (e apenas um) é a raiz; todo nó
1 a Prova - PGM - 14/09/2017
 a Prova - PGM - 4/09/207 Renato Assunção - DCC, UFMG. Sejam A, B e C três eventos de Σ, todos eles com probabilidade positiva (isto e, P(A) > 0, > 0 e P(C) > 0). Mostre que P(A B C) = P(A B C)P(B C)P(C).
a Prova - PGM - 4/09/207 Renato Assunção - DCC, UFMG. Sejam A, B e C três eventos de Σ, todos eles com probabilidade positiva (isto e, P(A) > 0, > 0 e P(C) > 0). Mostre que P(A B C) = P(A B C)P(B C)P(C).
Expert SINTA. Fatores de confiança
 Fatores de confiança Expert SINTA No exemplo dado no slide 87, as variáveis recebiam apenas valores determinísticos ( sim e não ). Porém, é comum que não queiramos determinar com exatidão o valor que cada
Fatores de confiança Expert SINTA No exemplo dado no slide 87, as variáveis recebiam apenas valores determinísticos ( sim e não ). Porém, é comum que não queiramos determinar com exatidão o valor que cada
CEFET/RJ Disciplina: Inteligência Artificial Professor: Eduardo Bezerra Lista de exercícios 02
 . CEFET/RJ Disciplina: Inteligência Artificial Professor: Eduardo Bezerra Lista de exercícios 02 Créditos: alguns itens desta lista são adaptados do material da disciplina CS188 - Artificial Intelligence
. CEFET/RJ Disciplina: Inteligência Artificial Professor: Eduardo Bezerra Lista de exercícios 02 Créditos: alguns itens desta lista são adaptados do material da disciplina CS188 - Artificial Intelligence
MD Lógica de Proposições Quantificadas Cálculo de Predicados 1
 Lógica de Proposições Quantificadas Cálculo de Predicados Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br http://www.dcc.ufmg.br/~loureiro MD Lógica de Proposições Quantificadas Cálculo de Predicados
Lógica de Proposições Quantificadas Cálculo de Predicados Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br http://www.dcc.ufmg.br/~loureiro MD Lógica de Proposições Quantificadas Cálculo de Predicados
Matemática Discreta - 01
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 01 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta - 01 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Aprendizado de Máquina (Machine Learning)
 Ciência da Computação (Machine Learning) Aula 01 Motivação, áreas de aplicação e fundamentos Max Pereira Nem todo conhecimento tem o mesmo valor. O que torna determinado conhecimento mais importante que
Ciência da Computação (Machine Learning) Aula 01 Motivação, áreas de aplicação e fundamentos Max Pereira Nem todo conhecimento tem o mesmo valor. O que torna determinado conhecimento mais importante que
Gabarito P2. Álgebra Linear I ) Decida se cada afirmação a seguir é verdadeira ou falsa.
 Gabarito P2 Álgebra Linear I 2008.2 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Se { v 1, v 2 } é um conjunto de vetores linearmente dependente então se verifica v 1 = σ v 2 para algum
Gabarito P2 Álgebra Linear I 2008.2 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Se { v 1, v 2 } é um conjunto de vetores linearmente dependente então se verifica v 1 = σ v 2 para algum
Inferência Estatistica
 Inferência Estatistica Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Modelos e Inferência Um modelo é uma simplificação da realidade (e alguns
Inferência Estatistica Ricardo Ehlers ehlers@icmc.usp.br Departamento de Matemática Aplicada e Estatística Universidade de São Paulo Modelos e Inferência Um modelo é uma simplificação da realidade (e alguns
Teoria das Probabilidades
 Teoria das Prof. Eduardo Bezerra (CEFET/RJ) 23 de fevereiro de 2018 Eduardo Bezerra (CEFET/RJ) Teoria das 2018.1 1 / 54 Roteiro Experimento aleatório, espaço amostral, evento 1 Experimento aleatório, espaço
Teoria das Prof. Eduardo Bezerra (CEFET/RJ) 23 de fevereiro de 2018 Eduardo Bezerra (CEFET/RJ) Teoria das 2018.1 1 / 54 Roteiro Experimento aleatório, espaço amostral, evento 1 Experimento aleatório, espaço
Probabilidade - aula II
 25 de Março de 2014 Interpretações de Probabilidade Amostras Aleatórias e Objetivos Ao final deste capítulo você deve ser capaz de: Calcular probabilidades de eventos conjuntos. Interpretar e calcular
25 de Março de 2014 Interpretações de Probabilidade Amostras Aleatórias e Objetivos Ao final deste capítulo você deve ser capaz de: Calcular probabilidades de eventos conjuntos. Interpretar e calcular
P(A i ) (n 1) i=1. Sorteia-se um homem desse grupo. Qual é a probabilidade de que seja paulista recém-formado, mas não pediatra?
 GET0089 Probabilidade I Aula de exercícios - 4/08/08 Profa. Ana Maria Lima de Farias. Prove, por indução, a desigualdade de Bonferroni. Se A, A,..., A n são eventos de um espaço de probabilidade (Ω, F,
GET0089 Probabilidade I Aula de exercícios - 4/08/08 Profa. Ana Maria Lima de Farias. Prove, por indução, a desigualdade de Bonferroni. Se A, A,..., A n são eventos de um espaço de probabilidade (Ω, F,
CE Estatística I
 CE 002 - Estatística I Agronomia - Turma B Professor Walmes Marques Zeviani Laboratório de Estatística e Geoinformação Departamento de Estatística Universidade Federal do Paraná 1º semestre de 2012 Zeviani,
CE 002 - Estatística I Agronomia - Turma B Professor Walmes Marques Zeviani Laboratório de Estatística e Geoinformação Departamento de Estatística Universidade Federal do Paraná 1º semestre de 2012 Zeviani,
Estatística I Aula 8. Prof.: Patricia Maria Bortolon, D. Sc.
 Estatística I Aula 8 Prof.: Patricia Maria Bortolon, D. Sc. MODELOS PROBABILÍSTICOS MAIS COMUNS VARIÁVEIS ALEATÓRIAS CONTÍNUAS Lembram o que vimos sobre V.A. contínua na Aula 6? Definição: uma variável
Estatística I Aula 8 Prof.: Patricia Maria Bortolon, D. Sc. MODELOS PROBABILÍSTICOS MAIS COMUNS VARIÁVEIS ALEATÓRIAS CONTÍNUAS Lembram o que vimos sobre V.A. contínua na Aula 6? Definição: uma variável
Projeto e Análise de Algoritmos NP Completude. Prof. Humberto Brandão
 Projeto e Análise de Algoritmos NP Completude Prof. Humberto Brandão humberto@bcc.unifal-mg.edu.br Universidade Federal de Alfenas versão da aula: 0.4 Introdução Problemas intratáveis ou difíceis são comuns
Projeto e Análise de Algoritmos NP Completude Prof. Humberto Brandão humberto@bcc.unifal-mg.edu.br Universidade Federal de Alfenas versão da aula: 0.4 Introdução Problemas intratáveis ou difíceis são comuns
CAPÍTULO 4 PROBABILIDADE PROBABILIDADE PPGEP Espaço Amostral e Eventos Espaço Amostral e Eventos UFRGS. Probabilidade.
 PROBABILIDADE CAPÍTULO 4 PROBABILIDADE UFRGS A Teoria das s estuda os fenômenos aleatórios. Fenômeno Aleatório: são os fenômenos cujo resultado não pode ser previsto exatamente. Se o fenômeno se repetir,
PROBABILIDADE CAPÍTULO 4 PROBABILIDADE UFRGS A Teoria das s estuda os fenômenos aleatórios. Fenômeno Aleatório: são os fenômenos cujo resultado não pode ser previsto exatamente. Se o fenômeno se repetir,
Análise Multivariada
 Análise Multivariada Aula 6.2: Análise Comparativa Qualitativa (QCA) Prof. Admir Antonio Betarelli Junior Juiz de Fora QCA É uma abordagem analítica para dados multivariados. Procura tratar qualitativamente
Análise Multivariada Aula 6.2: Análise Comparativa Qualitativa (QCA) Prof. Admir Antonio Betarelli Junior Juiz de Fora QCA É uma abordagem analítica para dados multivariados. Procura tratar qualitativamente
Mercados de Emparelhamento
 Mercados de Emparelhamento Redes Sociais e Econômicas Prof. André Vignatti Mercados de Emparelhamento Mercados - interação econômica entre pessoas numa rede estruturada Mercados de Emparelhamento modelam:
Mercados de Emparelhamento Redes Sociais e Econômicas Prof. André Vignatti Mercados de Emparelhamento Mercados - interação econômica entre pessoas numa rede estruturada Mercados de Emparelhamento modelam:
