3.1 Politopos convexos De uma maneira não muito difícil de conceituar, politopos são basicamente conhecidos como o termo geral da sequência
|
|
|
- Mirella Rios di Castro
- 6 Há anos
- Visualizações:
Transcrição
1 3 Politopos Os politopos são generalizações dos conceitos conhecidos de polígonos e poliedros. Estas figuras têm relação com os sistemas de raízes estudados nos capítulos anteriores e neste capítulo, o nosso objetivo é estudarmos os chamados Politopos de Gosset. 3. Politopos convexos De uma maneira não muito difícil de conceituar, politopos são basicamente conhecidos como o termo geral da sequência ponto, segmento, polígono, poliedro,... Isto é, um politopo na segunda dimensão é meramente um polígono, enquanto na terceira dimensão é um poliedro. E por analogia podemos perceber outras propriedades, como dois pontos formam um segmento de reta, quatro segmentos de reta formam um quadrado, seis quadrados formam um cubo e etc. Definição 3. X R n é convexo, se e somente se, para todos x, y X e para todo s [0, ], Definição 3.2 Seja X R n. sx + ( s)y X Fecho convexo (X) = { s i x i ; x i X, s i [0, ], s i = } Definição 3.3 Um politopo convexo (em R n ) é o fecho convexo de um conjunto finito (sem perda, os vértices). Proposição 3.. Um politopo convexo é uma interseção de finitos semiespaços; 2. Uma interseção de finitos semi-espaços que seja limitada é um politopo convexo.
2 Politopos de Gosset e os grupos de Coxeter E n 2 Definição 3.5 A dimensão de um politopo X é a dimensão do espaço transladado gerado por X. Definição 3.6 A interseção de um politopo de dimensão n com um semiplano é uma face do politopo se tiver dimensão menor do que n. Seguindo a definição acima, podemos dizer que um vértice é uma face de dimensão 0, enquanto uma aresta é uma face de dimensão. Seja X R n um politopo de dimensão n. O grupo das simetrias de X é o grupo das isometrias ϕ : R n R n com ϕ(x) = X. Note que uma isometria ϕ é da forma ϕv = Qv + v 0, onde v 0 R n, Q O(n). O grupo das isometrias de um politopo convexo é sempre finito, contido no grupo das permutações dos vértices. Definição 3.7 Um politopo convexo de dimensão n 2 é regular se:. o grupo das simetrias age transitivamente sobre os vértices; 2. as faces de dimensão n são regulares; 3. o grupo das simetrias age transitivamente sobre as faces de dimensão n. Note que esta definição é recursiva. Um politopo convexo de dimensão n = é um segmento e é regular (por definição). Definição 3.8 Um politopo convexo de dimensão n é semi-regular se:. o grupo das simetrias age transitivamente sobre os vértice; 2. as faces de dimensão n são regulares; Figura 3.: Politopo regular; politopo semi-regular; politopo convexo com faces regulares que não é semiregular.
3 Politopos de Gosset e os grupos de Coxeter E n 3 Definição 3.9 Um simplexo, α n, é o fecho convexo de e 0, e,, e n R n Figura 3.2: Simplexos Em outras palavras, se chamarmos de α 0, o espaço de dimensão nula, isto é, um ponto. Se ligarmos um outro ponto a α 0, obteremos um segmento de reta, α. Se ligarmos um terceiro ponto a α (fora da reta a que pertence este segmento), obtemos um triângulo, α 2. Já se ligarmos um quarto ponto a α 2 (fora do plano que o contém), obteremos um tetraedro, α 3. E de forma análoga, se ligarmos um quinto ponto a α 3 (que não pertença ao espaço de dimensão três que o contém), então obteremos um pentatopo α. Definição 3.0 Um hiper-octaedro, β n, é o fecho convexo de ±e 0, ±e,, ±e n R n. 2 Figura 3.3: Hiper-octaedros 3 Note que o octaedro β 3 é uma dipirâmide com base β 2. Mais geralmente, β n será sempre uma dipirâmide com base β n. Definição 3. Dois vértices de um politopo são vizinhos se pertencem a uma mesma aresta. Definição 3.2 Seja X um politopo convexo de dimensão n, e v um vértice de X. A figura de vértice (de X em v) é o fecho convexo dos vértices de X vizinhos de v, desde que este fecho tenha dimensão n.
4 Politopos de Gosset e os grupos de Coxeter E n Figura 3.: Figura de vértice do cubo Observação 3.3 Não precisaremos aqui definir figuras de vértice de forma mais geral. Observação 3. Todas as figuras de vértice de um politopo semiregular são isométricas (iguais). 3.2 Politopos de Gosset Thorald Gosset nasceu em 869. Segundo Harold S.M. Coxeter, ele se formou em direito após anos de muito estudo, mas sem clientes, dedicou seu tempo a estudar quais figuras regulares existiam em dimensões mais altas. Após redescobrir todas elas, ele começou a enumerar as figuras semiregulares. Definição 3.5 O prisma triangular da figura 3. é o politopo de Gosset G 3. G n é um politopo semiregular com faces de dimensão n iguais a α n ou β n e figura de vértice G n. Proposição 3.6 Existem (únicos) politopos de Gosset G n, n = 3,, 5, 6, 7, 8. Podemos a partir de G 3 montar G e assim por diante. O politopo G também é chamado de Tetroctaedro, por ser formado por tetraedros e octaedros e sua construção de pode ser feita da seguinte maneira: Considere o hipertetraedro α contido em R 5 com vértices (, 0, 0, 0, 0), (0,, 0, 0, 0), (0, 0,, 0, 0),(0, 0,0,,0), (0, 0, 0, 0, ). Os vértices das faces α 3 e β 3 de G são os pontos médios das arestas de α. Escolhendo um desses vértices, digamos (0,, 0, 0, 0), a face α 3 é o fecho convexo dos pontos médios das arestas adjacentes a esse vértice, isto é, os pontos A, A 2, A 3 e A formam o tetraedro correspondente a face α 3. A face β 3 é formada pelo fecho convexo dos 6 pontos médios restantes das arestas adjacentes, isto é, B, B 2, B 3, B, B 5 e B 6 formam o hiper-octaedro correspondente a face β 3.
5 Politopos de Gosset e os grupos de Coxeter E n 5 Podemos ainda obter informações sobre as faces do tipo α n e β n. Isto é, como G tem 0 vértices e cada um deles é adjacente a dois α 3, temos 20 faces α 3 contadas com multiplicidade. Mas cada α 3 possui vértices, e portanto, G tem 20 = 5 faces α 3. Além disso, cada vértice é adjacente a três faces β 3, resultando em 30 faces contadas com multiplicidade, sendo que cada β 3 possui 6 vértices. Logo, G tem 30 6 = 5 faces β 3. (,0,0,0,0) A (0,,0,0,0) (/2,0,0,0,/2) B B A A 2 B5 A 3 (0,0,0,0,) B 6 (0,0,,0,0) B 2 B 3 (0,0,0,,0) Figura 3.5: Construção das faces α 3 e β 3 de G O politopo de Gosset de quinta dimensão, G 5, que também é conhecido como Demipenteract, que quer dizer metade do hiper-cubo de dimensão 5, é construído tomando-se os vértices alternados do hiper-cubo em R 5 que tem 32 pontos da forma (±, ±, ±, ±, ±). Assim os vértices de G 5 são os 6 vértices com número par de sinais menos. Assim, como G 5 tem 6 vértices e cada um deles é adjacente a cinco α, temos 80 faces α contadas com multiplicidade. Mas cada α possui 5 vértices, e portanto, G 5 tem 80 5 = 6 faces α. E cada vértice é adjacente a cinco faces β, resultando em 80 faces contadas com multiplicidade, sendo que cada β possui 8 vértices. Logo, G 5 tem 80 0 = 0 faces β. 3.3 Os politopos de Gosset G 8, G 7 e G 6 Neste trabalho preferimos usar as construções dos outros capítulos para chegar diretamente em G 8. No capítulo anterior vimos que o reticulado E 8 possui 20 vetores em seu sistema de raízes, isto é, são 20 vetores de norma mínima e estes vetores
6 Politopos de Gosset e os grupos de Coxeter E n 6 são justamente os que descrevem os vértices de G 8. Considere a versão par do o sistema de coordenadas do reticulado E 8. E 8 = {x R 8 ; x i Z ou x i Z + 2, x i 0 (mod 2)} E considere cada um dos 20 vetores de norma mínima deste reticulado como um vértice de um politopo. Escolhendo um dos vértices, como por exemplo (,,,,,,, ) e calculando quais são os vértices cuja distância é mínima, isto é, igual a 2, podemos perceber que ele tem 28 vizinhos da forma (,, 0, 0, 0, 0, 0, 0) e 28 vizinhos da forma ( 2, 2, 2, 2, 2, 2, 2, 2 ), permutando as 8 coordenadas, resultando em 56 vizinhos. Deste modo podemos construir a seguinte figura: (½, ½,½,½,½,½,½,½) 28 vértices do tipo (,,0,0,0,0,0,0) + 28 vértices do tipo (½,½,½,½,½,½,-½,-½) = 56 vértices 56 vértices do tipo (,-,0,0,0,0,0,0) + 70 vértices do tipo (½,½,½,½,-½,-½,-½,-½) = 26 vértices 28 vértices do tipo (-,-,0,0,0,0,0,0) + 28 vértices do tipo (½,½,½,½,½,½,-½,-½) = 56 vértices (-½,-½,-½,-½,-½,-½,-½,-½) Figura 3.6: Politopo com 20 vértices Isto quer dizer que a figura de vértice deste politopo é um politopo de 56 vértices, em que cada um desses vértices tem 27 vizinhos. E desta forma obtemos as seguintes figuras, que representam uma sequência de figuras de vértice de cada politopo.
7 Politopos de Gosset e os grupos de Coxeter E n 7 vértice vértice 27 vértices 6 vértices 27 vértices 0 vértices vértice Politopo com 56 vértices Politopo com 27 vértices vértice vértice 0 vértices 6 vértices 5 vértices 3 vértices Politopo com 6 vértices Politopo com 0 vértices vértice 3 vértices 2 vértices Politopo com 6 vértices Politopo de Gosset de dim 3 Figura 3.7: Politopos de 56, 27, 6, 0 e 6 vértices O último politopo é o G 3, isto é, um prisma de base triangular, pois ao redor de cada face de codimensão 3 vemos um α e 2β s. Ou seja, em cada um dos 6 vértices deste politopo temos um triângulo e dois quadrados.
8 Politopos de Gosset e os grupos de Coxeter E n 8 Logo, G, G 5, G 6, G 7 e G 8 são os politopos de Gosset de 0, 6, 27, 56 e 20 vértices respectivamente. E assim, obtemos os seguintes resultados na tabela a seguir: Dimensão Vértices Faces α n Faces β n G 8 tem como grupo de simetria o grupo de Coxeter E 8 e sendo assim, este é o último politopo de dimensão finita da família dos politopos de Gosset. Coxeter usa a notação 2 por causa das bifurcações do diagrama de Coxeter- Dynkin. Vimos na seção anterior que G 8 é um politopo semiregular de 20 vértices que pertence a oitava dimensão, cujos vértices são os vetores de norma mínima do reticulado E 8. Além disso, vimos também que cada vértice deste politopo tem vizinhos, o que nos diz que G 8 tem = 6720 arestas, isto é, faces de 2 dimensão. Podemos estudar as faces de dimensão 2 fazendo a seguinte projeção: p : R 8 R 2 (3-) (x,...,x 8 ) (x x 8, x + x 2 ) (3-2)
9 Politopos de Gosset e os grupos de Coxeter E n 9 (0,2) (-3,) (-,) (,) (3,) (0,-2) (0,0) (2,0) (-3,-) (-,-) (,-) (3,-) (0,-2) Figura 3.8: Projeção em R 2 A partir daí, podemos observar que: a coordenada (, ) representa 2 vértices do tipo (, 0;, 0, 0, 0, 0, 0) e 5 do tipo (, ;,,,, , 2 ), resultando em 27 vértices; 2 a coordenada (2, 0) representa 5 vértices do tipo (0, 0;,, 0, 0, 0, 0) e 2 do tipo (, 2 ; 2,,,,, ), resultando em 27 vértices; Assim, como o vértice (, ) é vizinho comum a (0, 2) e (3, ), cada aresta de G 8 tem 27 faces de dimensão igual a 2 e isso resulta em = faces de dimensão 2. Além disso pode-se dizer que: Cada face de dimensão 2 é adjacente a 6 faces de dimensão 3, o que resulta em = 2920 faces de dimensão 3; cada face de dimensão 3 é adjacente a 0 faces de dimensão, o que resulta em = 8380 faces de dimensão ; 5 cada face de dimensão é adjacente a 6 faces de dimensão 5, o que resulta em = 8380 faces de dimensão 5; 6
10 Politopos de Gosset e os grupos de Coxeter E n 50 As faces de dimensão 6 são sempre simplexos, mas de dois tipos: αβ e ββ. Isto é, analogamente em dimensão mais baixa temos: Figura 3.9: G 3 Assim, cada face de dimensão 5 é adjacente a 3 faces de dimensão 6, uma do tipo αβ e duas do tipo ββ, o que resulta em 8380 = 6920 faces 7 αβ de dimensão 6 e = 3820 faces ββ de dimensão 6. 7 E para finalizar, como cada vértice de G 8 é adjacente a 576 α 6, então temos = 7280 faces α 7 e como cada vértice também é adjacente a β 6, então temos = 260 faces β 7. Podemos obter uma projeção como abaixo, na qual levamos as 8 coordenadas de cada um dos 20 vértices nas suas três primeiras coordenadas, isto é, p : R 8 R 3 (3-3) (x,..., x 8 ) (x, x 2, x 3 ) (3-)
11 Politopos de Gosset e os grupos de Coxeter E n 5 Figura 3.0: Projeção de G 8 em R 3 O politopo de Gosset G 7, também chamado por Coxeter de 3 2, é formado pela figura de vértice do politopo G 8. Isto é, G 7 é um politopo semiregular com 56 vértices e podemos construí-lo como na figura 3.5, escolhido o vértice (,,,,,,, ) de G , os vizinhos deste são os vértices de G 8 que estão a uma distância igual a 2. Assim, G 7, neste caso, é formado pelo fecho convexo de 28 vértices do tipo (,, 0, 0, 0, 0, 0, 0) 28 vértices do tipo (,,,,,, , 2 ) 2 O politopo G 7 também pode ser construído como o fecho convexo dos vizinhos de um buraco do reticulado E 7. Como já vimos no capítulo anterior, E 7 tem 26 vetores de norma mínima que formam os vértices de um politopo que não é semiregular.
12 Politopos de Gosset e os grupos de Coxeter E n 52 Por exemplo, tome o ponto ( 3, 3,,,,,, ). Os pontos que estão 3 a uma distância igual a são: 2 (0, 0, 0, 0, 0, 0, 0, 0); (, 0;, 0, 0, 0, 0, 0), que permutados somam 2 pontos; (, ;,, 0, 0, 0, 0), que permutados somam 5 pontos; (, 2 ; 2, 2,,,, ), que permutados somam 5 pontos; ( 3, 2 ; 2,,,,, ), que permutados somam 5 pontos; ( 3 2, 2, 2, 2, 2, 2, 2, 2 ). O politopo G 6, também chamado por Coxeter de 2 2, é a figura de vértice do politopo G 7. Ou seja, G 6 é um politopo semiregular com 27 vértices. As tabelas abaixo nos mostram como são as faces de G 7 e de G 6. Dimensão Faces de G 7 56 α α 032 α α α 206 αβ 576 α ββ 26 β 6 Dimensão Faces de G 6 27 α 0 26 α 720 α α 3 26 αβ 72 α 5 32 ββ 27 β 5
13 Politopos de Gosset e os grupos de Coxeter E n Projeções Ortogonais Construção da projeção ortogonal de G 8 será feita com detalhes, já as demais serão omitidas, já que são feitas de forma análoga. Figura 3.: Projeção ortogonal de G 8 em R 2
14 Politopos de Gosset e os grupos de Coxeter E n 5 Para a construção desta projeção tome uma base do reticulado E 8 formada pelos vetores v = (,, 0, 0, 0, 0, 0, 0), v 2 = (0,,, 0, 0, 0, 0, 0), v 3 = (0, 0,,, 0, 0, 0, 0), v = (0, 0, 0,,, 0, 0, 0), v 5 = (0, 0, 0, 0,,, 0, 0), v 6 = (0, 0, 0, 0, 0,,, 0), v 7 = (0, 0, 0, 0, 0, 0,, ), v 8 = ( 2, 2, 2, 2, 2, 2, 2, 2 ) Seja x = (x, x 2, x 3, x, x 5, x 6, x 7, x 8 ) um vetor de R 8. A reflexão com respeito ao vetor v é dada por Rv = x 2 v,x v,v v = x 2 x x 3 x x 5 x 6 x 7 Esta reflexão é associada a matriz A = x De maneira análoga obtemos as outras 7 matrizes, sendo elas como em A mas com permutações das colunas i com i +, onde 2 i 7. E a última matriz de reflexão como abaixo: A 8 =
15 Politopos de Gosset e os grupos de Coxeter E n 55 igual a O elemento de Coxeter, que é o produto destas 8 matrizes de reflexão, é 3 3 M = cujo número de Coxeter, que é a ordem do elemento de Coxeter, é igual a 30, já que M 30 = I 8, onde I 8 é a matriz identidade de ordem 8. O polinômio característico de M é p(t) = t 8 + t 7 t 5 t t 3 + t + e com ajuda do software Maple encontramos 8 autovalores complexos e seus autovetores associados. Escolhendo um dos autovetores, chamaremos de u o vetor de R 8 cujas coordenadas são formadas pelas partes reais das oito coordenadas do autovetor escolhido e chamaremos de w o vetor de R 8 cujas coordenadas são formadas pelas partes imaginárias das oito coordenadas do mesmo autovetor. Temos assim u = e w = A seguir, ortogonalizamos os vetores u e w. Assim, defina agora un := u u, u wt := w un, w un wt wn := wt, wt
16 Politopos de Gosset e os grupos de Coxeter E n 56 Sejam α i, i =,..., 20, os vértices de G 8, os pontos da projeção em R 2 são da forma p i = (a i, b i ), onde a i = un, α i e b i = wn, α i. Logo, a figura 3. nos mostra os 20 de pontos G 8 R 8 em R 2 desta projeção, onde ligamos os pontos cuja distância entre eles em R 8 é mínima, isto é, igual a 2, e as cores são determinadas pelas normas dos vetores em R 2.
17 Politopos de Gosset e os grupos de Coxeter E n 57 Abaixo está a projeção ortogonal do politopo formado pelos 26 vértices do reticulado E 7. Figura 3.2: Projeção ortogonal de E 7 em R 2
18 Politopos de Gosset e os grupos de Coxeter E n 58 A figura abaixo mostram dois círculos com 27 pontos projetados mais dois pontos projetados no centro totalizando os 56 vértices de G 7. Figura 3.3: Projeção ortogonal de G 7 em R 2
19 Politopos de Gosset e os grupos de Coxeter E n 59 Abaixo está a projeção ortogonal do politopo formado pelos 72 vértices do reticulado E 6. Figura 3.: Projeção ortogonal de E 6 em R 2
20 Politopos de Gosset e os grupos de Coxeter E n 60 A figura abaixo mostram dois círculos com 2 pontos projetados mais três pontos projetados no centro totalizando os 27 vértices de G 6. Figura 3.5: Projeção ortogonal de G 6 em R 2
21 Politopos de Gosset e os grupos de Coxeter E n 6 Figura 3.6: Projeção ortogonal de G 5 em R 2
22 Politopos de Gosset e os grupos de Coxeter E n 62 Figura 3.7: Projeção ortogonal de G em R 2 As projeções ortogonais de E 7 e E 6 foram feitas de forma análoga a projeção feita para G 8. Para as projeções ortogonais de G 7, G 6, G 5 e G usamos o mesmo elemento de Coxeter que usado em E 7, E 6, D 5 e A respectivamente.
Poliedros 1 ARESTAS FACES VERTICES. Figura 1.1: Elementos de um poliedro
 Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
Ângulos entre retas Retas e Planos Perpendiculares. Walcy Santos
 Ângulos entre retas Retas e Planos Perpendiculares Walcy Santos Ângulo entre duas retas A idéia do ângulo entre duas retas será adaptado do conceito que temos na Geometria Plana. Se duas retas são concorrentes
Ângulos entre retas Retas e Planos Perpendiculares Walcy Santos Ângulo entre duas retas A idéia do ângulo entre duas retas será adaptado do conceito que temos na Geometria Plana. Se duas retas são concorrentes
GEOMETRIA MÉTRICA ESPACIAL
 GEOMETRIA MÉTRICA ESPACIAL .. PARALELEPÍPEDOS RETÂNGULOS Um paralelepípedo retângulo é um prisma reto cujas bases são retângulos. AB CD A' B' C' D' a BC AD B' C' A' D' b COMPRIMENTO LARGURA AA' BB' CC'
GEOMETRIA MÉTRICA ESPACIAL .. PARALELEPÍPEDOS RETÂNGULOS Um paralelepípedo retângulo é um prisma reto cujas bases são retângulos. AB CD A' B' C' D' a BC AD B' C' A' D' b COMPRIMENTO LARGURA AA' BB' CC'
U. E. PROF. EDGAR TITO - Turma: 2º ano A Prof. Ranildo Lopes Obrigado pela preferência de nossa ESCOLA!
 1 U. E. PROF. EDGAR TITO - Turma: 2º ano A Prof. Ranildo Lopes Obrigado pela preferência de nossa ESCOLA! http://ueedgartito.wordpress.com RESUMO DE GEOMETRIA ESPACIAL São conceitos primitivos ( e, portanto,
1 U. E. PROF. EDGAR TITO - Turma: 2º ano A Prof. Ranildo Lopes Obrigado pela preferência de nossa ESCOLA! http://ueedgartito.wordpress.com RESUMO DE GEOMETRIA ESPACIAL São conceitos primitivos ( e, portanto,
Sólidos Geométricos, Poliedros e Volume Prof. Lhaylla Crissaff
 Sólidos Geométricos, Poliedros e Volume 2017.1 Prof. Lhaylla Crissaff www.professores.uff.br/lhaylla Sólidos Geométricos Prisma Pirâmide Cilindro Cone Esfera Prisma Ex.: P é um pentágono. Prisma Prisma
Sólidos Geométricos, Poliedros e Volume 2017.1 Prof. Lhaylla Crissaff www.professores.uff.br/lhaylla Sólidos Geométricos Prisma Pirâmide Cilindro Cone Esfera Prisma Ex.: P é um pentágono. Prisma Prisma
Poliedros Teoria. Superfície Poliédrica é um conjunto finito de polígonos planos cuja disposição no espaço satisfaz as seguintes propriedades:
 Poliedros Teoria Superfície Poliédrica é um conjunto finito de polígonos planos cuja disposição no espaço satisfaz as seguintes propriedades: P1. Todo polígono da Superfície Poliédrica possui algum lado
Poliedros Teoria Superfície Poliédrica é um conjunto finito de polígonos planos cuja disposição no espaço satisfaz as seguintes propriedades: P1. Todo polígono da Superfície Poliédrica possui algum lado
Geometria Computacional
 GeoComp 2014 p. 1/29 Geometria Computacional Cristina G. Fernandes Departamento de Ciência da Computação do IME-USP http://www.ime.usp.br/ cris/ segundo semestre de 2014 GeoComp 2014 p. 2/29 Poliedros
GeoComp 2014 p. 1/29 Geometria Computacional Cristina G. Fernandes Departamento de Ciência da Computação do IME-USP http://www.ime.usp.br/ cris/ segundo semestre de 2014 GeoComp 2014 p. 2/29 Poliedros
Aula 31.1 Conteúdo: Fundamentos da Geometria: Ponto, Reta e Plano. FORTALECENDO SABERES CONTEÚDO E HABILIDADES DINÂMICA LOCAL INTERATIVA MATEMÁTICA
 CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO DO DIA Aula 31.1 Conteúdo: Fundamentos da Geometria: Ponto, Reta e Plano. 2 CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO DO DIA Habilidades: Identificar
CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO DO DIA Aula 31.1 Conteúdo: Fundamentos da Geometria: Ponto, Reta e Plano. 2 CONTEÚDO E HABILIDADES FORTALECENDO SABERES DESAFIO DO DIA Habilidades: Identificar
Módulo Geometria Espacial II - volumes e áreas de prismas e pirâmides. 3 ano/e.m.
 Módulo Geometria Espacial II - volumes e áreas de prismas e pirâmides Pirâmide ano/em Pirâmide Geometria Espacial II - volumes e áreas de prismas e pirâmides 1 Exercícios Introdutórios Exercício 1 Determine
Módulo Geometria Espacial II - volumes e áreas de prismas e pirâmides Pirâmide ano/em Pirâmide Geometria Espacial II - volumes e áreas de prismas e pirâmides 1 Exercícios Introdutórios Exercício 1 Determine
Soluções do Capítulo 8 (Volume 2)
 Soluções do Capítulo 8 (Volume 2) 1. Não. Basta considerar duas retas concorrentes s e t em um plano perpendicular a uma reta r. As retas s e t são ambas ortogonais a r, mas não são paralelas entre si.
Soluções do Capítulo 8 (Volume 2) 1. Não. Basta considerar duas retas concorrentes s e t em um plano perpendicular a uma reta r. As retas s e t são ambas ortogonais a r, mas não são paralelas entre si.
POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados.
 POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados. Toda figura geométrica espacial de três dimensões (comprimento, largura e altura), formada por POLÍGONOS (figura plana composta de n lados) é chamada
POLIEDROS: POLI = Muitos E EDROS = Lados Muitos lados. Toda figura geométrica espacial de três dimensões (comprimento, largura e altura), formada por POLÍGONOS (figura plana composta de n lados) é chamada
Aula 3 Vetores no espaço
 MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
MÓDULO 1 - AULA 3 Aula 3 Vetores no espaço Objetivos Ampliar a noção de vetor para o espaço. Rever as operações com vetores e sua representação em relação a um sistema ortogonal de coordenadas cartesianas.
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Colégio Adventista Portão EIEFM MATEMÁTICA Poliedros 2º Ano APROFUNDAMENTO/REFORÇO
 Colégio Adventista Portão EIEFM MATEMÁTICA Poliedros 2º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre/2013 Aluno(a): Número: Turma: 1) Coloque V ou F, conforme
Colégio Adventista Portão EIEFM MATEMÁTICA Poliedros 2º Ano APROFUNDAMENTO/REFORÇO Professor: Hermes Jardim Disciplina: Matemática Lista 1 1º Bimestre/2013 Aluno(a): Número: Turma: 1) Coloque V ou F, conforme
Geometria Euclidiana Espacial e Introdução à Geometria Descritiva
 UNIVERSIDDE ESTDUL PULIST DEPRTMENTO DE MTEMÁTIC Geometria Euclidiana Espacial e Introdução à Geometria Descritiva Material em preparação!! Última atualização: 28.04.2008 Luciana F. Martins e Neuza K.
UNIVERSIDDE ESTDUL PULIST DEPRTMENTO DE MTEMÁTIC Geometria Euclidiana Espacial e Introdução à Geometria Descritiva Material em preparação!! Última atualização: 28.04.2008 Luciana F. Martins e Neuza K.
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
Poliedross. ANOTAÇÕES EM AULA Capítulo 23 Poliedros 1.5 CONEXÕES COM A MATEMÁTICA
 Poliedross 1.5 Superfície poliédrica fechada Uma superfície poliédrica fechada é composta de um número finito (quatro ou mais) de superfícies poligonais planas, de modo que cada lado de uma dessas superfícies
Poliedross 1.5 Superfície poliédrica fechada Uma superfície poliédrica fechada é composta de um número finito (quatro ou mais) de superfícies poligonais planas, de modo que cada lado de uma dessas superfícies
Geometria Descritiva. Revisão: Polígonos regulares/irregulares. Linhas e Pontos pertencentes a Faces/Arestas de Poliedros
 Geometria Descritiva Revisão: Polígonos regulares/irregulares Linhas e Pontos pertencentes a Faces/Arestas de Poliedros - Os Poliedros em estudo em GD podem ser: regulares (cujas fases são polígonos regulares,
Geometria Descritiva Revisão: Polígonos regulares/irregulares Linhas e Pontos pertencentes a Faces/Arestas de Poliedros - Os Poliedros em estudo em GD podem ser: regulares (cujas fases são polígonos regulares,
MA13 Geometria I Avaliação
 13 eometria I valiação 011 abarito Questão 1 (,0) figura abaixo mostra um triângulo equilátero e suas circunferências inscrita e circunscrita. circunferência menor tem raio 1. alcule a área da região sombreada.
13 eometria I valiação 011 abarito Questão 1 (,0) figura abaixo mostra um triângulo equilátero e suas circunferências inscrita e circunscrita. circunferência menor tem raio 1. alcule a área da região sombreada.
Aula 26 Poliedros. Objetivos. Identificar poliedros. Aplicar o Teorema de Euler
 MÓDULO 2 - AULA 26 Aula 26 Poliedros Objetivos Identificar poliedros Aplicar o Teorema de Euler Introdução Nesta aula estudaremos outros exemplos de figuras no espaço: os poliedros Começaremos com a definição
MÓDULO 2 - AULA 26 Aula 26 Poliedros Objetivos Identificar poliedros Aplicar o Teorema de Euler Introdução Nesta aula estudaremos outros exemplos de figuras no espaço: os poliedros Começaremos com a definição
NOTAÇÕES. R : conjunto dos números reais C : conjunto dos números complexos
 NOTAÇÕES R : conjunto dos números reais C : conjunto dos números complexos i : unidade imaginária: i = 1 z : módulo do número z C Re(z) : parte real do número z C Im(z) : parte imaginária do número z C
NOTAÇÕES R : conjunto dos números reais C : conjunto dos números complexos i : unidade imaginária: i = 1 z : módulo do número z C Re(z) : parte real do número z C Im(z) : parte imaginária do número z C
Equação Geral do Segundo Grau em R 2
 8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
8 Equação Geral do Segundo Grau em R Sumário 8.1 Introdução....................... 8. Autovalores e autovetores de uma matriz real 8.3 Rotação dos Eixos Coordenados........... 5 8.4 Formas Quadráticas..................
Pirâmides: Neste momento, continuaremos a estudar a geometria espacial dos sólidos geométricos, enfatizando agora as pirâmides.
 Pirâmides: Neste momento, continuaremos a estudar a geometria espacial dos sólidos geométricos, enfatizando agora as pirâmides. A seguir, algumas representações de pirâmides: Essa forma espacial é bastante
Pirâmides: Neste momento, continuaremos a estudar a geometria espacial dos sólidos geométricos, enfatizando agora as pirâmides. A seguir, algumas representações de pirâmides: Essa forma espacial é bastante
Distância Ângulos Esfera Poliedros
 Distância e Ângulos Vamos supor, como na geometria plana, que nossa geometria possui uma função distância, isto é, uma função que a cada par de pontos A e B associa um número real d(a, B) que satisfaz:
Distância e Ângulos Vamos supor, como na geometria plana, que nossa geometria possui uma função distância, isto é, uma função que a cada par de pontos A e B associa um número real d(a, B) que satisfaz:
Geometria Euclidiana II
 Geometria Euclidiana II Professor Fabrício Oliveira Universidade Federal Rural do Semiárido 17 de outubro de 2010 O nosso curso Tópicos abordados Poliedros Convexos O nosso curso Tópicos abordados Poliedros
Geometria Euclidiana II Professor Fabrício Oliveira Universidade Federal Rural do Semiárido 17 de outubro de 2010 O nosso curso Tópicos abordados Poliedros Convexos O nosso curso Tópicos abordados Poliedros
GEOMETRIA MÉTRICA. As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases.
 GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
Lista 11. Geometria, Coleção Profmat, SBM. Problemas selecionados das seções 7.2 (pág. 311) e 7.3 (pág. 329).
 MA13 Exercícios das Unidades 17 e 18 2014 Lista 11 Geometria, Coleção Profmat, SBM. Problemas selecionados das seções 7.2 (pág. 311) e 7.3 (pág. 329). 1) Sejam dados um ponto A e um plano α com A α. Prove
MA13 Exercícios das Unidades 17 e 18 2014 Lista 11 Geometria, Coleção Profmat, SBM. Problemas selecionados das seções 7.2 (pág. 311) e 7.3 (pág. 329). 1) Sejam dados um ponto A e um plano α com A α. Prove
V = 12 A = 18 F = = 2 V=8 A=12 F= = 2
 Por: Belchior, Ismaigna e Jannine Relação de Euler Em todo poliedro convexo é válida a relação seguinte: V - A + F = 2 em que V é o número de vértices, A é o número de arestas e F, o número de faces. Observe
Por: Belchior, Ismaigna e Jannine Relação de Euler Em todo poliedro convexo é válida a relação seguinte: V - A + F = 2 em que V é o número de vértices, A é o número de arestas e F, o número de faces. Observe
Curvas Planas em Coordenadas Polares
 Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Curvas Planas em Coordenadas Polares Sumário. Coordenadas Polares.................... Relações entre coordenadas polares e coordenadas cartesianas...................... 6. Exercícios........................
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
MATEMÁTICA MÓDULO 16 CONE E CILINDRO. Professor Haroldo Filho
 MATEMÁTICA Professor Haroldo Filho MÓDULO 16 CONE E CILINDRO 1. CILINDRO CIRCULAR Considere dois planos paralelos, α e β, seja R um círculo no plano α, seja s uma reta secante aos dois planos que não intersecta
MATEMÁTICA Professor Haroldo Filho MÓDULO 16 CONE E CILINDRO 1. CILINDRO CIRCULAR Considere dois planos paralelos, α e β, seja R um círculo no plano α, seja s uma reta secante aos dois planos que não intersecta
Unidade 9 Geometria Espacial. Poliedros Volume de sólidos geométricos Princípio de Cavalieri
 Unidade 9 Geometria Espacial Poliedros Volume de sólidos geométricos Princípio de Cavalieri Poliedros palavra poliedro tem sua origem no idioma grego (poly significa, muitos, e hedra, faces). Poliedro
Unidade 9 Geometria Espacial Poliedros Volume de sólidos geométricos Princípio de Cavalieri Poliedros palavra poliedro tem sua origem no idioma grego (poly significa, muitos, e hedra, faces). Poliedro
1.- Escrevendo como uma potência de base 2 cada um dos números : A= ( 2 3 ) 7 ; B = e C = escreva-os em ordem decrescente:
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 2014 1ª. SÉRIE 1.- Escrevendo como uma potência de base 2 cada um dos números : A= ( 2 3 ) 7 ; B = e C = escreva-os em ordem decrescente: 2.-Ao fazer uma
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 2014 1ª. SÉRIE 1.- Escrevendo como uma potência de base 2 cada um dos números : A= ( 2 3 ) 7 ; B = e C = escreva-os em ordem decrescente: 2.-Ao fazer uma
1 Matrizes Ortogonais
 Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
Álgebra Linear I - Aula 19-2005.1 Roteiro 1 Matrizes Ortogonais 1.1 Bases ortogonais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de vetores distintos
Geometria analítica - Programação linear
 Ga - Programação linear 1 Geometria analítica - Programação linear Período de 014.1 - Prof. Fernando Carneiro Rio de Janeiro, Junho de 014 1 Introdução Estudaremos as retas no plano euclidiano bidimensional
Ga - Programação linear 1 Geometria analítica - Programação linear Período de 014.1 - Prof. Fernando Carneiro Rio de Janeiro, Junho de 014 1 Introdução Estudaremos as retas no plano euclidiano bidimensional
Figuras Geométricas planas e espaciais. Rafael Carvalho
 Figuras Geométricas planas e espaciais Rafael Carvalho Figuras geométricas planas Na geometria plana vamos então nos atentar ao método de cálculo da área das figuras geométricas planas. Sendo elas os polígonos,
Figuras Geométricas planas e espaciais Rafael Carvalho Figuras geométricas planas Na geometria plana vamos então nos atentar ao método de cálculo da área das figuras geométricas planas. Sendo elas os polígonos,
0 1. Assinale a alternativa verdadeira Q1. Seja A = (d) Os autovalores de A 101 são i e i. (c) Os autovalores de A 101 são 1 e 1.
 Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
Nesta prova, se V é um espaço vetorial, o vetor nulo de V será denotado por 0 V. Se u 1,...,u n forem vetores de V, o subespaço de V gerado por {u 1,...,u n } será denotado por [u 1,...,u n ]. O operador
NDMAT Núcleo de Desenvolvimentos Matemáticos
 01) Determine o número de vértices de um poliedro convexo que tem 3 faces triangulares, 1 face quadrangular, 1 pentagonal e 2 hexagonais. 07) Um poliedro de sete vértices tem cinco ângulos tetraédricos
01) Determine o número de vértices de um poliedro convexo que tem 3 faces triangulares, 1 face quadrangular, 1 pentagonal e 2 hexagonais. 07) Um poliedro de sete vértices tem cinco ângulos tetraédricos
1. Quantos são os planos determinados por 4 pontos não coplanares?justifique.
 Universidade Federal de Uberlândia Faculdade de Matemática Disciplina: Geometria euclidiana espacial (GMA010) Assunto: Paralelisno e Perpendicularismo; Distância e Ângulos no Espaço. Prof. Sato 1 a Lista
Universidade Federal de Uberlândia Faculdade de Matemática Disciplina: Geometria euclidiana espacial (GMA010) Assunto: Paralelisno e Perpendicularismo; Distância e Ângulos no Espaço. Prof. Sato 1 a Lista
APOSTILA GEOMETRIA DESCRITIVA
 APOSTILA GEOMETRIA DESCRITIVA 1 GEOMETRIA MÉTRICA E ESPACIAL 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 SISTEMAS DE PROJEÇÃO Conforme o que foi exposto anteriormente, o estudo da Geometria Descritiva está
APOSTILA GEOMETRIA DESCRITIVA 1 GEOMETRIA MÉTRICA E ESPACIAL 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 SISTEMAS DE PROJEÇÃO Conforme o que foi exposto anteriormente, o estudo da Geometria Descritiva está
Equações paramétricas das cônicas
 Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
Aula 1 Equações paramétricas das cônicas Ao estudarmos as retas no plano, vimos que a reta r que passa por dois pontos distintos P 1 = x 1, y 1 ) e P = x, y ) é dada pelas seguintes equações paramétricas:
A afirmação (ii) está errada. A afirmação correta seria "Uma função cuja derivada é positiva em um intervalo é crescente nesse intervalo.
 Questão nº 1 A afirmação (i) "A função f(x) = tg x... f' (x) = sec x" está correta. A afirmação (ii) está errada. A afirmação correta seria "Uma função cuja derivada é positiva em um intervalo é crescente
Questão nº 1 A afirmação (i) "A função f(x) = tg x... f' (x) = sec x" está correta. A afirmação (ii) está errada. A afirmação correta seria "Uma função cuja derivada é positiva em um intervalo é crescente
1 POLIEDROS 2 ELEMENTOS 4 POLIEDROS REGULARES 3 CLASSIFICAÇÃO. 3.2 Quanto ao número de faces. 4.1 Tetraedro regular. 3.
 Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
 Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Álgebra Linear I - Aula 9. Roteiro
 Álgebra Linear I - Aula 9 1. Distância de um ponto a uma reta. 2. Distância de um ponto a um plano. 3. Distância entre uma reta e um plano. 4. Distância entre dois planos. oteiro 1 Distância de um ponto
Álgebra Linear I - Aula 9 1. Distância de um ponto a uma reta. 2. Distância de um ponto a um plano. 3. Distância entre uma reta e um plano. 4. Distância entre dois planos. oteiro 1 Distância de um ponto
Apostila de Geometria Descritiva. Anderson Mayrink da Cunha GGM - IME - UFF
 Apostila de Geometria Descritiva Anderson Mayrink da Cunha GGM - IME - UFF Novembro de 2013 Sumário Sumário i 1 Poliedros e sua Representação 1 1.1 Tipos de Poliedros.............................. 1 1.1.1
Apostila de Geometria Descritiva Anderson Mayrink da Cunha GGM - IME - UFF Novembro de 2013 Sumário Sumário i 1 Poliedros e sua Representação 1 1.1 Tipos de Poliedros.............................. 1 1.1.1
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
a1q1: Seja ABCDEF GH um cubo de aresta unitária de E 3 e considere o espaço V 3 orientado pela base { CD, CB, CH}. Então podemos afirmar que: a)
 1 a1q1: Seja ABCDEF GH um cubo de aresta unitária de E 3 e considere o espaço V 3 orientado pela base { CD, CB, CH}. Então podemos afirmar que: a) EB ED = GA b) EB ED = AG c) EB ED = EH d) EB ED = EA e)
1 a1q1: Seja ABCDEF GH um cubo de aresta unitária de E 3 e considere o espaço V 3 orientado pela base { CD, CB, CH}. Então podemos afirmar que: a) EB ED = GA b) EB ED = AG c) EB ED = EH d) EB ED = EA e)
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
ESTUDANDO POLIEDROS COM AUXÍLIO DE SOFTWARE EDUCACIONAL
 ESTUDANDO POLIEDROS COM AUXÍLIO DE SOFTWARE EDUCACIONAL Gilmara Teixeira Barcelos - Centro Federal de Educação Tecnológica de Campos (CEFET- Campos) - gilmarab@cefetcampos.br Silvia Cristina Freitas Batista
ESTUDANDO POLIEDROS COM AUXÍLIO DE SOFTWARE EDUCACIONAL Gilmara Teixeira Barcelos - Centro Federal de Educação Tecnológica de Campos (CEFET- Campos) - gilmarab@cefetcampos.br Silvia Cristina Freitas Batista
2 ÁREAS E VOLUME DO TETRAEDRO REGULAR 1 TETRAEDRO REGULAR. 2.1 Área lateral. 2.2 Área da base. 2.3 Área total. 2.4 Volume
 Matemática Pedro Paulo GEOMETRIA ESPACIAL VI são 1 TETRAEDRO REGULAR É uma piramide regular triangular, cujas faces triângulos equiláteros de lado 2 ÁREAS E VOLUME DO TETRAEDRO REGULAR 2.1 Área lateral
Matemática Pedro Paulo GEOMETRIA ESPACIAL VI são 1 TETRAEDRO REGULAR É uma piramide regular triangular, cujas faces triângulos equiláteros de lado 2 ÁREAS E VOLUME DO TETRAEDRO REGULAR 2.1 Área lateral
G1 de Álgebra Linear I Gabarito
 G1 de Álgebra Linear I 2013.1 6 de Abril de 2013. Gabarito 1) Considere o triângulo ABC de vértices A, B e C. Suponha que: (i) o vértice B do triângulo pertence às retas de equações paramétricas r : (
G1 de Álgebra Linear I 2013.1 6 de Abril de 2013. Gabarito 1) Considere o triângulo ABC de vértices A, B e C. Suponha que: (i) o vértice B do triângulo pertence às retas de equações paramétricas r : (
LISTA DE EXERCÍCIOS COMPLEMENTAR 1ª PROVA
 MINISTÉRI DA EDUCAÇÃ UNIVERSIDADE FEDERAL D PARANÁ SETR DE CIÊNCIAS EXATAS DEPARTAMENT DE EXPRESSÃ GRÁFICA Professora Elen Andrea Janzen Lor Representação de Retas LISTA DE EXERCÍCIS CMPLEMENTAR 1ª PRVA
MINISTÉRI DA EDUCAÇÃ UNIVERSIDADE FEDERAL D PARANÁ SETR DE CIÊNCIAS EXATAS DEPARTAMENT DE EXPRESSÃ GRÁFICA Professora Elen Andrea Janzen Lor Representação de Retas LISTA DE EXERCÍCIS CMPLEMENTAR 1ª PRVA
a) 6% b) 7% c) 70% d) 600% e) 700%
 - MATEMÁTICA 01) Supondo-se que o número de vagas em um concurso vestibular aumentou 5% e que o número de candidatos aumentou 35%, o número de candidatos por vaga para esse curso aumentou: a) 8% b) 9%
- MATEMÁTICA 01) Supondo-se que o número de vagas em um concurso vestibular aumentou 5% e que o número de candidatos aumentou 35%, o número de candidatos por vaga para esse curso aumentou: a) 8% b) 9%
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Exercícios de Matemática Poliedros
 Exercícios de Matemática Poliedros 3. (Unitau) Se dobrarmos convenientemente as linhas tracejadas das figuras a seguir, obteremos três modelos de figuras espaciais cujos nomes são: 1. (Uerj) O poliedro
Exercícios de Matemática Poliedros 3. (Unitau) Se dobrarmos convenientemente as linhas tracejadas das figuras a seguir, obteremos três modelos de figuras espaciais cujos nomes são: 1. (Uerj) O poliedro
Aulas 6 / 05 de setembro
 Gabriel Coutinho DCC5 - Pesquisa Operacional - 7. Simplex Ei-lo. Aulas 6 / 5 de setembro Método Simplex Input: Uma PL e uma base viável de colunas B. Output: Uma solução ótima, ou um certificado de que
Gabriel Coutinho DCC5 - Pesquisa Operacional - 7. Simplex Ei-lo. Aulas 6 / 5 de setembro Método Simplex Input: Uma PL e uma base viável de colunas B. Output: Uma solução ótima, ou um certificado de que
Matemática. 3-3) As diagonais do cubo medem x / ) As diagonais da face do cubo medem 2 y 1/3. Resposta: VFFVV.
 Matemática 01. Seja x a área total da superfície de um cubo, e y, o volume do mesmo cubo. Analise as afirmações a seguir, considerando essas informações. 0-0) Se x = 54 então y = 27. 1-1) 6y = x 3 2-2)
Matemática 01. Seja x a área total da superfície de um cubo, e y, o volume do mesmo cubo. Analise as afirmações a seguir, considerando essas informações. 0-0) Se x = 54 então y = 27. 1-1) 6y = x 3 2-2)
Capítulo Coordenadas no Espaço. Seja E o espaço da Geometria Euclidiana tri-dimensional.
 Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
Capítulo 9 1. Coordenadas no Espaço Seja E o espaço da Geometria Euclidiana tri-dimensional. Um sistema de eixos ortogonais OXY Z em E consiste de três eixos ortogonais entre si OX, OY e OZ com a mesma
O origami no ensino da Matemática
 O origami no ensino da Matemática A construção de um origami parte sempre da dobragem de uma folha de papel num quadrado perfeito. Ao voltarmos a dobrar este quadrado podemos obter triângulos e outros
O origami no ensino da Matemática A construção de um origami parte sempre da dobragem de uma folha de papel num quadrado perfeito. Ao voltarmos a dobrar este quadrado podemos obter triângulos e outros
GEOMETRIA ESPACIAL TETRAEDRO HEXAEDRO OCTAEDRO DODECAEDRO ICOSAEDRO REGULARES RETO POLIEDROS OBLÍQUO PRISMA REGULAR IRREGULARES RETA OBLÍQUA PIRÂMIDE
 GEOMETRIA ESPACIAL SÓLIDOS GEOMÉTRICOS POLIEDROS REGULARES SÓLIDOS DE REVOLUÇÃO IRREGULARES CONE TETRAEDRO HEXAEDRO OCTAEDRO DODECAEDRO ICOSAEDRO ESFERA CILINDRO PRISMA PIRÂMIDE RETO OBLÍQUO RETO RETO
GEOMETRIA ESPACIAL SÓLIDOS GEOMÉTRICOS POLIEDROS REGULARES SÓLIDOS DE REVOLUÇÃO IRREGULARES CONE TETRAEDRO HEXAEDRO OCTAEDRO DODECAEDRO ICOSAEDRO ESFERA CILINDRO PRISMA PIRÂMIDE RETO OBLÍQUO RETO RETO
UNITAU APOSTILA PIRÂMIDES PROF. CARLINHOS
 ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA PIRÂMIDES PROF. CARLINHOS NOME DO ALUNO: Nº TURMA: blog.portalpositivo.com.br 1 PIRÂMIDES Pirâmide é o poliedro convexo tal que uma face é um
ESCOLA DE APLICAÇÃO DR. ALFREDO JOSÉ BALBI UNITAU APOSTILA PIRÂMIDES PROF. CARLINHOS NOME DO ALUNO: Nº TURMA: blog.portalpositivo.com.br 1 PIRÂMIDES Pirâmide é o poliedro convexo tal que uma face é um
3. Obter a equação do plano que contém os pontos A = (3, 0, 1), B = (2, 1, 1) e C = (3, 2, 2).
 Lista II: Retas, Planos e Distâncias Professora: Ivanete Zuchi Siple. Equação geral do plano que contém o ponto A = (,, ) e é paralelo aos vetores u = (,, ) e v = (,, ).. Achar a equação do plano que passa
Lista II: Retas, Planos e Distâncias Professora: Ivanete Zuchi Siple. Equação geral do plano que contém o ponto A = (,, ) e é paralelo aos vetores u = (,, ) e v = (,, ).. Achar a equação do plano que passa
Questão 2. Questão 1. Questão 3. alternativa D. alternativa D. alternativa B
 NOTAÇÕES C: conjunto dos números compleos. Q: conjunto dos números racionais. R: conjunto dos números reais. Z: conjunto dos números inteiros. N {0,,,,...}. N {,,,...}. 0: conjunto vazio. A \ B { A; B}.
NOTAÇÕES C: conjunto dos números compleos. Q: conjunto dos números racionais. R: conjunto dos números reais. Z: conjunto dos números inteiros. N {0,,,,...}. N {,,,...}. 0: conjunto vazio. A \ B { A; B}.
Projeções de entidades geométricas elementares condicionadas por relações de pertença (incidência) 8
 Índice Item Representação diédrica Projeções de entidades geométricas elementares condicionadas por relações de pertença (incidência) 8 Reta e plano 8 Ponto pertencente a uma reta 8 Traços de uma reta
Índice Item Representação diédrica Projeções de entidades geométricas elementares condicionadas por relações de pertença (incidência) 8 Reta e plano 8 Ponto pertencente a uma reta 8 Traços de uma reta
DO ENSINO MÉDIO. ELABORAÇÃO: PROFESSOR OCTAMAR MARQUES. RESOLUÇÃO: PROFESSORA MARIA ANTÔNIA GOUVEIA.
 RESOLUÇÃO DA AVALIAÇÃO FINAL DE MATEMÁTICA APLICADA EM 008 NO COLÉGIO ANCHIETA-BA, AOS ALUNOS DA a SÉRIE DO ENSINO MÉDIO. ELABORAÇÃO: PROFESSOR OCTAMAR MARQUES. PROFESSORA MARIA ANTÔNIA GOUVEIA. 0. D C
RESOLUÇÃO DA AVALIAÇÃO FINAL DE MATEMÁTICA APLICADA EM 008 NO COLÉGIO ANCHIETA-BA, AOS ALUNOS DA a SÉRIE DO ENSINO MÉDIO. ELABORAÇÃO: PROFESSOR OCTAMAR MARQUES. PROFESSORA MARIA ANTÔNIA GOUVEIA. 0. D C
Álgebra Linear I - Aula Propriedades dos autovetores e autovalores
 Álgebra Linear I - Aula 17 1. Propriedades dos autovetores e autovalores. 2. Matrizes semelhantes. 1 Propriedades dos autovetores e autovalores Propriedade 1: Sejam λ e β autovalores diferentes de T e
Álgebra Linear I - Aula 17 1. Propriedades dos autovetores e autovalores. 2. Matrizes semelhantes. 1 Propriedades dos autovetores e autovalores Propriedade 1: Sejam λ e β autovalores diferentes de T e
Aula 19 Operadores ortogonais
 Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
OS PRISMAS. 1) Definição e Elementos :
 1 OS PRISMAS 1) Definição e Elementos : Dados dois planos paralelos α e β, um polígono contido em um desses planos e um reta r, que intercepta esses planos, chamamos de PRISMA o conjunto de todos os segmentos
1 OS PRISMAS 1) Definição e Elementos : Dados dois planos paralelos α e β, um polígono contido em um desses planos e um reta r, que intercepta esses planos, chamamos de PRISMA o conjunto de todos os segmentos
Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos. Poliedros - parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos Poliedros - parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha 1 Poliedros Figuras como o paralelepípedo
Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos Poliedros - parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha 1 Poliedros Figuras como o paralelepípedo
Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos. Poliedros - parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos Poliedros - parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha 1 Poliedros Figuras como o paralelepípedo
Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos Poliedros - parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha 1 Poliedros Figuras como o paralelepípedo
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
AVF - MA Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL AVF - MA13-016.1 - Gabarito Questão 01 [,00 pts ] Em um triângulo ABC de perímetro 9, o lado BC mede 3 e a distância entre os pés das bissetrizes interna
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL AVF - MA13-016.1 - Gabarito Questão 01 [,00 pts ] Em um triângulo ABC de perímetro 9, o lado BC mede 3 e a distância entre os pés das bissetrizes interna
Universidade Federal do Rio de Janeiro INSTITUTO DE MATEMÁTICA Departamento de Métodos Matemáticos
 Universidade Federal do Rio de Janeiro INSTITUTO DE MATEMÁTICA Departamento de Métodos Matemáticos Gabarito da 1 a Prova de Geometria I - Matemática - Monica 08/05/2013 1 a Questão: (3 pontos) Dê uma prova
Universidade Federal do Rio de Janeiro INSTITUTO DE MATEMÁTICA Departamento de Métodos Matemáticos Gabarito da 1 a Prova de Geometria I - Matemática - Monica 08/05/2013 1 a Questão: (3 pontos) Dê uma prova
O MÉTODO DAS DUPLAS PROJEÇÕES ORTOGONAIS
 Expressão Gráfica II Geometria Descritiva Engenharia Civil - 2014 13 MÉTD DAS DUPLAS PRJEÇÕES RTGNAIS PARTE I REPRESENTAÇÃ D PNT 1. Planos fundamentais de referência (PFR) Consideremos π e π dois planos
Expressão Gráfica II Geometria Descritiva Engenharia Civil - 2014 13 MÉTD DAS DUPLAS PRJEÇÕES RTGNAIS PARTE I REPRESENTAÇÃ D PNT 1. Planos fundamentais de referência (PFR) Consideremos π e π dois planos
[ ] EXEMPLOS: Muitas vezes precisamos montar uma Matriz a partir de uma lei geral. Analise os exemplos a seguir:
![[ ] EXEMPLOS: Muitas vezes precisamos montar uma Matriz a partir de uma lei geral. Analise os exemplos a seguir: [ ] EXEMPLOS: Muitas vezes precisamos montar uma Matriz a partir de uma lei geral. Analise os exemplos a seguir:](/thumbs/52/30426431.jpg) MATRIZES CONCEITO: Um conjunto de elementos algébricos dispostos em uma tabela retangular com linhas e colunas é uma Matriz. A seguir, vemos um exemplo de Matriz de 3 linhas e 4 colunas, e que representaremos
MATRIZES CONCEITO: Um conjunto de elementos algébricos dispostos em uma tabela retangular com linhas e colunas é uma Matriz. A seguir, vemos um exemplo de Matriz de 3 linhas e 4 colunas, e que representaremos
Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones)
 Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones) A geometria é um ramo da matemática que se dedica ao estudo do espaço e das figuras que podem
Volumes (prismas e cilindros) Áreas (prismas e cilindros) Volumes (pirâmides e cones) Áreas (pirâmides e cones) A geometria é um ramo da matemática que se dedica ao estudo do espaço e das figuras que podem
Quantos números pares, formados por algarismos distintos, existem entre 500 e 2000?
 PROVA DE MATEMÁTICA - TURMAS DO 3 O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - AGOSTO DE 011. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 01 Quantos
PROVA DE MATEMÁTICA - TURMAS DO 3 O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - AGOSTO DE 011. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 01 Quantos
MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: Observe os dados do quadro a seguir.
 MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x cos x : cosseno de x x : módulo de x log x : logaritmo de x na base 10 6. Um
MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x cos x : cosseno de x x : módulo de x log x : logaritmo de x na base 10 6. Um
MATEMÁTICA MÓDULO 13 FUNDAMENTOS 1. INTRODUÇÃO 1.1. POSTULADOS PRINCIPAIS 1.2. DETERMINAÇÃO DO PLANO. Conceitos primitivos: ponto, reta e plano.
 FUNDAMENTOS 1. INTRODUÇÃO Conceitos primitivos: ponto, reta e plano. 1.1. POSTULADOS PRINCIPAIS Dois pontos distintos determinam uma única reta que passa por eles. Três pontos não colineares determinam
FUNDAMENTOS 1. INTRODUÇÃO Conceitos primitivos: ponto, reta e plano. 1.1. POSTULADOS PRINCIPAIS Dois pontos distintos determinam uma única reta que passa por eles. Três pontos não colineares determinam
2 CILINDRO E ESFERA 1 CUBO E ESFERA. 2.1 Cilindro inscrito. 1.1 Cubo inscrito. 2.2 Cilindro circunscrito. 1.2 Cubo circunscrito
 Matemática Pedro Paulo GEOMETRIA ESPACIAL XI A seguir, nós vamos analisar a relação entre alguns sólidos e as esferas. Os sólidos podem estar inscritos ou circunscritos a uma esfera. Lembrando: A figura
Matemática Pedro Paulo GEOMETRIA ESPACIAL XI A seguir, nós vamos analisar a relação entre alguns sólidos e as esferas. Os sólidos podem estar inscritos ou circunscritos a uma esfera. Lembrando: A figura
Matemática. Questão 1. 7 o ano do Ensino Fundamental Turma. 2 o Bimestre de 2016 Data / / Escola Aluno RESOLUÇÃO:
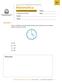 EF AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 7 o ano do Ensino Fundamental Turma GOVERNO DO ESTADO DE SÃO PAULO SECRETARIA DA EDUCAÇÃO 2 o Bimestre de 2016 Data / / Escola Aluno Questão 1 Qual é
EF AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 7 o ano do Ensino Fundamental Turma GOVERNO DO ESTADO DE SÃO PAULO SECRETARIA DA EDUCAÇÃO 2 o Bimestre de 2016 Data / / Escola Aluno Questão 1 Qual é
Segunda Etapa 2ª ETAPA 2º DIA 11/12/2006
 Segunda Etapa ª ETP º DI 11/1/006 CDERNO DE PROVS FÍSIC MTEMÁTIC GEOMETRI GRÁFIC IOLOGI GEOGRFI PORTUGUÊS LITERTUR INGLÊS ESPNHOL FRNCÊS TEORI MUSICL COMISSÃO DE PROCESSOS SELETIVOS E TREINMENTOS Geometria
Segunda Etapa ª ETP º DI 11/1/006 CDERNO DE PROVS FÍSIC MTEMÁTIC GEOMETRI GRÁFIC IOLOGI GEOGRFI PORTUGUÊS LITERTUR INGLÊS ESPNHOL FRNCÊS TEORI MUSICL COMISSÃO DE PROCESSOS SELETIVOS E TREINMENTOS Geometria
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2017.1 Gabarito Questão 01 [ 1,25 ] Determine as equações das duas retas tangentes à parábola de equação y = x 2 2x + 4 que passam pelo ponto (2,
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2017.1 Gabarito Questão 01 [ 1,25 ] Determine as equações das duas retas tangentes à parábola de equação y = x 2 2x + 4 que passam pelo ponto (2,
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
MATEMÁTICA SARGENTO DA FAB
 MATEMÁTICA BRUNA PAULA 1 COLETÂNEA DE QUESTÕES DE MATEMÁTICA DA EEAr (QUESTÕES RESOLVIDAS) QUESTÃO 1 (EEAr 2013) Se x é um arco do 1º quadrante, com sen x a e cosx b, então é RESPOSTA: d QUESTÃO 2 (EEAr
MATEMÁTICA BRUNA PAULA 1 COLETÂNEA DE QUESTÕES DE MATEMÁTICA DA EEAr (QUESTÕES RESOLVIDAS) QUESTÃO 1 (EEAr 2013) Se x é um arco do 1º quadrante, com sen x a e cosx b, então é RESPOSTA: d QUESTÃO 2 (EEAr
Geometria Espacial: Sólidos Geométricos
 Aluno(a): POLIEDROS E PRISMA (1º BIM) Noções Sobre Poliedros Denominam-se sólidos geométricos as figuras geométricas do espaço. Entre os sólidos geométricos, destacamos os poliedros e os corpos redondos.
Aluno(a): POLIEDROS E PRISMA (1º BIM) Noções Sobre Poliedros Denominam-se sólidos geométricos as figuras geométricas do espaço. Entre os sólidos geométricos, destacamos os poliedros e os corpos redondos.
- Plano Anual 4º Ano de Escolaridade -
 Números e Operações TEM A - Plano Anual 4º Ano de Escolaridade - Matemática Domínios de Referência Contar 1.Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de construção
Números e Operações TEM A - Plano Anual 4º Ano de Escolaridade - Matemática Domínios de Referência Contar 1.Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de construção
4. Superfícies e sólidos geométricos
 4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
4. Superfícies e sólidos geométricos Geometria Descritiva 2006/2007 4.1 Classificação das superfícies e sólidos geométricos Geometria Descritiva 2006/2007 1 Classificação das superfícies Linha Lugar das
Geometria Descritiva 28/08/2012. Elementos Primitivos da Geometria
 Geometria Descritiva Prof. Luiz Antonio do Nascimento ladnascimento@gmail.com www.lnascimento.com.br A Geometria, como qualquer outra ciência, fundamenta-se em observações e experiências para estabelecer
Geometria Descritiva Prof. Luiz Antonio do Nascimento ladnascimento@gmail.com www.lnascimento.com.br A Geometria, como qualquer outra ciência, fundamenta-se em observações e experiências para estabelecer
DEPARTAMENTO DE MATEMÁTICA Matemática 7 MA07A TURMA T51 Prof. Luiz Antonio Kretzschmar
 DEPARTAMENTO DE MATEMÁTICA Matemática 7 MA07A TURMA T51 Prof. Luiz Antonio Kretzschmar PARTE 2 PONTO, RETA, PLANO Def. : Uma reta é paralela a um plano se, e somente se, eles não têm ponto comum Uma reta
DEPARTAMENTO DE MATEMÁTICA Matemática 7 MA07A TURMA T51 Prof. Luiz Antonio Kretzschmar PARTE 2 PONTO, RETA, PLANO Def. : Uma reta é paralela a um plano se, e somente se, eles não têm ponto comum Uma reta
ATIVIDADES COM GEOPLANO ISOMÉTRICO
 ATIVIDADES COM GEOPLANO ISOMÉTRICO Observações. Os pinos ou pregos do geoplano isométrico são chamados de pontos. A menor distância entre dois pontos consecutivos é estabelecida como a unidade de comprimento
ATIVIDADES COM GEOPLANO ISOMÉTRICO Observações. Os pinos ou pregos do geoplano isométrico são chamados de pontos. A menor distância entre dois pontos consecutivos é estabelecida como a unidade de comprimento
Se os tubos opostos forem de mesmo comprimento, teremos as várias possibilidades de paralelogramos, incluindo o retângulo.
 Ernesto Rosa Poliedros de canudinhos rígidos possuem muitas vantagens: são fáceis de se fazer com sucata como tubinhos de canetas, bambus etc. (mas no mercado há tubos plásticos à venda), são ótimos nas
Ernesto Rosa Poliedros de canudinhos rígidos possuem muitas vantagens: são fáceis de se fazer com sucata como tubinhos de canetas, bambus etc. (mas no mercado há tubos plásticos à venda), são ótimos nas
ESTUDANDO MATEMÁTICA COM O AUXÍLIO DO GEOGEBRA UTILIZANDO AS JANELAS CAS E 3D
 ESTUDANDO MATEMÁTICA COM O AUXÍLIO DO GEOGEBRA UTILIZANDO AS JANELAS CAS E 3D Ministrantes: Bruno Santos Pereira, Ellen Cristina Barbosa dos Santos, Marrythiely Rodrigues Oliveira, Lucas Diêgo de Lima,
ESTUDANDO MATEMÁTICA COM O AUXÍLIO DO GEOGEBRA UTILIZANDO AS JANELAS CAS E 3D Ministrantes: Bruno Santos Pereira, Ellen Cristina Barbosa dos Santos, Marrythiely Rodrigues Oliveira, Lucas Diêgo de Lima,
Poliedros AULA Introdução Denições
 AULA 13 13.1 Introdução Nesta aula estudaremos os sólidos formados por regiões do espaço (faces), chamados poliedros. O conceito de poliedro está para o espaço assim como o conceito de polígono está para
AULA 13 13.1 Introdução Nesta aula estudaremos os sólidos formados por regiões do espaço (faces), chamados poliedros. O conceito de poliedro está para o espaço assim como o conceito de polígono está para
POLIEDROS REGULARES. São os poliedros cujas faces são polígonos regulares iguais entre si, e cujos ângulos poliédricos são todos iguais.
 1 POLIEDROS REGULARES DEFINIÇÃO E CLASSIFICAÇÃO DE POLIEDROS Do grego - poly (muitas) + edro (face). Os poliedros fazem parte do pensamento grego, foram estudados pelos grandes filósofos da antiguidade
1 POLIEDROS REGULARES DEFINIÇÃO E CLASSIFICAÇÃO DE POLIEDROS Do grego - poly (muitas) + edro (face). Os poliedros fazem parte do pensamento grego, foram estudados pelos grandes filósofos da antiguidade
Apostila de Matemática II 3º bimestre/2016. Professora : Cristiane Fernandes
 Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
MATEMÁTICA 6.º ANO SEGUNDO CICLO ANTÓNIO SOUSA MARIA JOÃO MATOS SÓNIA MONTEIRO TERESA PINTO
 MATEMÁTICA 6.º ANO SEGUNDO CICLO ANTÓNIO SOUSA MARIA JOÃO MATOS SÓNIA MONTEIRO TERESA PINTO ÍNDICE Figuras geométricas planas Sólidos geométricos Relacionar circunferências com ângulos, retas e polígonos
MATEMÁTICA 6.º ANO SEGUNDO CICLO ANTÓNIO SOUSA MARIA JOÃO MATOS SÓNIA MONTEIRO TERESA PINTO ÍNDICE Figuras geométricas planas Sólidos geométricos Relacionar circunferências com ângulos, retas e polígonos
Aula 10 Produto interno, vetorial e misto -
 MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
MÓDULO 2 - AULA 10 Aula 10 Produto interno, vetorial e misto - Aplicações II Objetivos Estudar as posições relativas entre retas no espaço. Obter as expressões para calcular distância entre retas. Continuando
PROPOSTA DIDÁTICA. 3. Desenvolvimento da proposta didática (10 min) - Acomodação dos alunos, apresentação dos bolsistas e realização da chamada.
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: André da Silva Alves 1.2 Série/Ano/Turma: 6º e 7º ano 1.3 Turno: manhã 1.4 Data: 10/07 Lauro Dornelles e 15/07 Oswaldo Aranha 1.5 Tempo
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: André da Silva Alves 1.2 Série/Ano/Turma: 6º e 7º ano 1.3 Turno: manhã 1.4 Data: 10/07 Lauro Dornelles e 15/07 Oswaldo Aranha 1.5 Tempo
