Ressonância Magnética Nuclear: Ecos, Imagens e Computação Quântica
|
|
|
- Glória Prada Regueira
- 9 Há anos
- Visualizações:
Transcrição
1 Ressonância Magnética Nuclear: Ecos, Imagens e Computação Quântica Jair C. C. Freitas Departamento de Física - UFES
2 Fundamentos de RMN Sumário Pulsos Ecos Espectroscopia Imagens por RMN (MRI) Princípios Métodos de contraste Computação Quântica via RMN Fundamentos de computação quântica. Implementações simples Problemas e perspectivas
3 RMN Ecos, Imagens e Computação Quântica
4 Alguns marcos históricos da RMN Rabi (1937): ressonância em feixes de moléculas de H 2. Prêmio Nobel de Física F Bloch (1946): absorção de RF em água. Prêmio Nobel de Física F Purcell (1946): absorção de RF em parafina. Prêmio Nobel de Física F Hahn (1949): ecos de spin. Packard (1951): deslocamento químico em etanol. Andrew, Lowe (1959): RMN no estado sólido. s Ernst (1964): RMN com transformada de Fourier. Prêmio Nobel de Química Wüthrich (1968): RMN aplicada ao estudo de macromoléculas culas biológicas. Prêmio Nobel de Química Lauterbur, Mansfeld (1973): imagem por RMN (MRI). Prêmio Nobel de Medicina
5 Spin nuclear e momento de dipolo magnético nuclear Ι = l s A k = 1 ( k + k ) O spin nuclear: Número quântico I. Inteiro ou semi-inteiro. Z Z A µ = ( µ N / ħ) lk + gspsk + gsns k = 1 k = 1 k = Z+ 1 k µ I µ I µ = I = γi I ( I + 1) ħ µ // efetivo 2 Fator giromagnético
6 Nuclídeo Alguns núcleos de interesse para RMN Abundância Natural (%) I µ (múltiplos de µ N ) Q (barns) 1 H 99,99 1/2 2, C 1,11 1/2 0, N 99,63 1 0,4036 0,01 15 N 0,37 1/2 0, F 100 1/2 2, Al 100 5/2 3,6414 0, Si 4,70 1/2 0, P 100 1/2 1, Mn 100 5/2 3,4680 0, Co 100 7/2 4,6490 0, Gd 14,73 3/2 0,2700 1, Gd 15,68 3/2 0,3600 1,500
7 Fundamentos de RMN Núcleo atômico na presença de um campo magnético estático: τ = r mg ω = mgr L µ = γi = µ B 0 τ ωl = γb0
8 Paramagnetismo nuclear 2 Nµ B 3kT 0 M0 = E n n = + = µ B = γmħb = mħω ( e 0 ħω L / kt ) 0 L
9 Transições de spin nuclear ħω Absorção ħω L Relaxação Equilíbrio Saturação Equilíbrio Probabilidade de transição: P m n = Pn m γ 2 B 2 1 m I x n 2 δ( ω ω L )
10 Excitação do sistema de spins B 0 ~ 1T f L ~ 43 MHz ( 1 H) f L ~ 28 GHz (elétron) Campo de RF: B 1 ~ 10G = 10-3 T Campo da Terra: B T ~ 10-5 T B 0 = B 0 zˆ B ( 2B cos t) xˆ 1 = 1 ω
11 B ( 2B cos t) xˆ 1 = 1 ω ω ω L Condição de ressonância B B [(cosω t) xˆ + (sen t) yˆ ] + 1 = B1 ω [(cosωt ) xˆ (sen t) yˆ ] 1 = B1 ω
12 Efeitos do campo de RF sobre a magnetização Z M 0 z υ 1 M 0 υ 0 FIG.3 B 1 FIG.4 B ef Sistema girante de coordenadas: ω = ω ẑ ω) zˆ B xˆ 1 = γ ( ωl + 1 FIG.5 x B 1 B 0 M 0 z Direction of rotation of M 0 about B 1 y
13 Pulsos de RF a) z b) c) z z M 0 90 o M o M 0 θ = γ Β 1 t y y y B 1 M xy B 1 B 1 M xy x x x FIG.6 M xy = M 0 M xy = 0 M xy < M 0 Pulso π/2 Pulso π Pulso θ Controle Duração ( ~ µs) Amplitude ( ~ 10 2 khz) Fase
14 Spin ½ em um campo magnético I z α = + 1 α I 2 z β = 1 2 β
15 Alguns vetores de estado
16 Pulsos de RF: matrizes de rotação Solução da equação de Shrödinger no sistema girante de coordenadas: θ = γ B t ω 1 P (ângulo de nutação) = γ B nut 1 (freqüência de nutação) ψ = R φp ( θ ) ψ 2 1 R φ P ( θ ) 1 1 iφ P cos 2θ isen 2θe = 1 iφ P 1 isen 2θe cos 2θ
17 Pulsos de RF: matrizes de rotação R x ( θ ) 1 1 cos 2θ isen 2θ = 1 1 isen 2θ cos 2θ θ = γ B t 1 P (ângulo de nutação) Exemplo 1: R x 1 1 i ( π / 2) α = = = e 2 i i iπ / 4 y Pulso π/2 na direção x atuando sobre estado inicial com spin na direção z:
18 Pulsos de RF: matrizes de rotação R x ( θ ) 1 1 cos 2θ isen 2θ = 1 1 isen 2θ cos 2θ θ = γ B t 1 P (ângulo de nutação) Exemplo 2: 0 i 1 0 Rx ( π ) α = = i = i i β Pulso π na direção x atuando sobre estado inicial com spin na direção z:
19 Outros exemplos
20 Ensemble de spins ½ Estado de um spin: ψ cα = c β Matriz densidade para um spin: ψ ψ * * cαcα cαc β = * * cβcα cβc β
21 Ensemble de spins ½ Matriz densidade para o ensemble: * * ραα ραβ cαcα cαc β ρ= = ρ ρ c c c c * * βα ββ β α β β Cálculos de valores médios para o ensemble: A =Tr{ ρa}
22 Populações e coerências ραα ρ ρ ρ αβ α + ρ= = ρ ρ ρ ρ βα ββ β Populações: ρ α ρ β ρ +ρ = 1 α β Coerências: ρ + ρ ρ =ρ + *
23 Interpretação física das populações α α 1 0 = 0 0 β β 0 0 = 0 1
24 Interpretação física das coerências x x = y y 1 1 i = 2 i 1
25 Equilíbrio térmico ρ eq e H / kt = ρeq Z 1 1 H Z Z kt UρeqU UHU Z Z kt Desvio ε ρ eq = 1 1 = I 0 2 4ε z ħγ B kt 0 4 ε = 10 Magnetização: ρ α = + ε M z ρ = β 2 4 ε M z 1 1 ρ = 4ε( M x im y ) ρ = 4ε( M + x im y )
26 Atuação de pulsos de RF ρ = + ε 0 0 ε π i ρ 2 = 1 1 4iε 2 ( / 2) x ε
27 Atuação de pulsos de RF ρ = + ε 0 0 ε π ρ 2= ( ) x ε 0 0 ε
28 Detecção do sinal de RMN FID = decaimeno livre de indução ω L f L Transformada de Fourier (FT) f L FID Espectro
29 Um experimento simples de RMN (1D) Experimento de pulso simples ou decaimento de Bloch: Sinal detectado com frequência: f = f L f RF (áudio) Sinal em ressonância: f = 0 f L FID Espectro
30 Método da transformada de Fourier
31 Espectros de RMN de 1 H - etanol Packard et al. (1951) CH 3 CH 2 OH Deslocamento químico: ( 1 ~ = σ ) B f B loc γbloc = = f (1 σ ) 2π obs L iso 0 δ = f obs f ref f ref Valores típicos ( 1 H): f ref 400MHz (TMS) f obs ν ref Hz δ 10-6 : partes por milhão (ppm)
32 Interações de spin nuclear f L fl = γb / 2 0 π Núcleo atômico isolado: medida de f L fornece B 0 ou γ. Núcleo atômico na matéria: espectros de RMN (contendo vários valores ou distribuições de f L ) fornecem informações sobre a estrutura da matéria.
33 Interações de spin nuclear Materiais isolantes e diamagnéticos: Deslocamento químico: Termo isotrópico + parte anisotrópica Interação dipolar direta: Homonuclear ou heteronuclear. Acoplamento escalar (J): Termo isotrópico. Interação quadrupolar: I > 1/2.
34 Deslocamento químico ( chemical shift ) Em líquidos: ω = γb = γ(1 σ ) B loc iso δ = ( f f ) / f obs ref ref 0 ppm TMS
35 Interação dipolar internuclear B ( loc) z = µ r 3 ij 2 (3cos θ 1) Interação através do espaço
36 Acoplamento escalar ou indireto (J ) Interação através de ligações químicas
37 Acoplamento escalar ou indireto (J ) H ω I + ω I + 2π JI I 1 1z 2 2z 1z 2z Termo isotrópico. Importante principalmente em líquidos.
38 Interação quadrupolar elétrica Núcleos quadrupolares (I > ½): 2 H, 23 Na, 25 Mg, 27 Al, 35 Cl, 55 Mn,... +q (0,0,d) z θ z -q -q -q y x -q (d,0,0) +q (0,d,0) EQ 3 2 ( eqq / d )(3cos θ 1) =
39 Interações de spin nuclear: resumo
40 Espectrômetro de RMN
41 Espectrômetro de RMN
42 RMN no estado sólido: probes e rotores Rotores menores: Frequências de MAS maiores. 7mm: f MAS < 8 khz. 2,5mm: f MAS < 35 khz. Menor sensibilidade.
43 Relaxação do sistema de spins M z = M 0 M z = 0 x ω L y x y x y M z < M 0 M z = M 0 x M x, M y = 0 y x y
44 Relaxação do sistema de spins Relaxação longitudinal (T 1 ): Trocas de energia entre spins e rede. Existência de campos flutuantes com freqüências ~ ω L. Restauração do equilíbrio térmico. Relaxação transversal (T 2 ): Perda de coerência entre os spins no plano transversal. Distribuições de freqüências de precessão. Interações entre os spins. Magnetization FIG.24 M 0 Longitudinal relaxation M z = M 0 ( 1 - e - t / T 1 ) Líquidos: T 1 T 2 Sólidos: T 1 >> T 2 T 1 T M M 0 Transverse relaxation M y = M 0 e - t / T 2 90 o pulse T 1 = T 2 t
45 Técnica dos ecos de spin ( spin-echoes ) Hahn (1950)
46 Formação dos ecos de spin
47 Formação de imagens por RMN (MRI) Utilização de gradientes de campo magnético: Discriminação espacial de freqüências. Distribuição de densidade de prótons.
48 Excitação seletiva
49 Seleção de planos - tomografia (a) seleção de um plano G z
50 Seqüência de pulsos TF 2D
51 Técnicas de contraste Contraste pela densidade de prótons. Contraste por T 1 (relaxação longitudinal). Contraste por T 2 (relaxação transversal). Tórax Pele Fígado Pulmão Próstata Ossos T 1 (s) Tumoral 1,08 1,05 0,83 1,11 1,11 1,03 T 1 (s) Normal 0,37 0,62 0,57 0,79 0,80 0,55
52 Contraste por T 1 Métodos: saturação/recuperação; inversão/recuperação; spin-eco
53 Exemplo de contraste por T 1
54 Exemplo de contraste por T 1
55 Exemplo de contraste por T 2 AVC (corte transversal)
56 Princípios de Informação Quântica Feynman (1980): Dificuldade de simular sistemas quânticos em computadores clássicos. Grupo com N spins 1/2 O(2 N ). Sistemas quânticos controlados podem ser usados nas simulações de outros sistemas quânticos. Computadores quânticos analógicos.
57 Lei de Moore: limites da computação clássica
58 Algoritmos quânticos Algoritmo de Deutsch (1986): Avaliação de funções binárias em apenas uma iteração. Algoritmo de Shor (1994): Fatoração de números grandes (milhares de dígitos) em tempo polinomial. N dígitos O(N 2 ) quântico O(10 N/2 ) clássico. Implicação em criptografia de sistemas de segurança. Algoritmo de Grover (1997): Busca de itens em uma lista desordenada. N itens O(N 1/2 ) quântico O(N/2) clássico.
59 Base computacional Bits clássicos 0 1 Bits quânticos (q-bits) 0 1 Estados da base ψ = α 0 + β 1 Superposição coerente Informação oculta. Evolução de estados coerentes. Paralelismo quântico. Possibilidade de emaranhamento ( entanglement ). Colapso do estado ao se efetuar uma medida.
60 Algumas portas lógicasl
61 Estados emaranhados (estados de Bell)
62 O emaranhamento e seus mistérios
63 Sistema de dois níveis: Implementações de q-bitsq Spin nuclear em um campo magnético. Spin eletrônico em um campo magnético. Polarizações de um fóton. Estados eletrônicos em um átomo. B 0 S = 1 / 2 0 1
64 Características de um computador quântico Superposição de estados. Operações reversíveis. Conservação do número de q-bits. Portas lógicas operadores unitários. Requisitos de um candidato a computador quântico Sistema de dois níveis (no mínimo) para cada q-bit. Atuação sobre os q-bits individualmente. Criação de estados puros e de superposições. Operações lógicas condicionais. Isolamento de interações com o ambiente.
65 Comparação entre candidatos à implementação de q-bitsq Sistema Tempo de Tempo de Número máximo descoerência (s) operação (s) de operações Spin nuclear Spin eletrônico Armadilha iônica (In + ) Elétron Au Elétron GaAs Ponto quântico Cavidade ótica Cavidade de microondas
66 Implementação experimental: armadilha iônica
67 Computação quântica via RMN Gershenfeld & Chuang (1997): RMN em amostras líquidas macroscópicas. Moléculas contendo N núcleos (I = 1/2) acoplados. O(10 20 ) computadores em paralelo com N q-bits. Operações unitárias sobre o ensemble. Preparação de estados pseudo-puros. Resultado das operações: espectro com amplitudes e fases relacionadas aos estados de saída.
68 Descrição com matriz densidade ρ eq e H / kt = ρeq Z 1 1 H Z Z kt UρeqU UHU Z Z kt Desvio Exemplo para N = 2: Equilíbrio térmico ρ eq , , , , 75 Estado pseudo-puro ρeq 0,
69 Implementação de algoritmos via RMN Preparação do estado inicial. Realização de operações unitárias (portas lógicas). Leitura do resultado final (espectro de RMN). Operadores unitários Operadores de rotação (campos de RF seletivos ou não): R( θ) = e iθi ± x, ± y Operadores de evolução temporal: T ( t, H int ) = e ih int t
70 Implementação com 2 núcleos (I = 1/2) acoplados H ω I + ω I + 2π JI I int 1 1z 2 2z 1z 2z
71 Exemplo de criação de estados pseudo-puros Estados pseudo-puros
72 Exemplo de sistema com 2 núcleos (I = 1/2) acoplados Molécula de clorofórmio: Cl 13 C 1 H 1 2 ω C ω C 13 C 1 H Cl 13 C 1 H Cl H ω I + ω I + 2π J I I C Cz H Hz CH Cz Hz π 1 ω C = ωc + JCH π J 2 ω C = ωc CH B0 = 11,8 T 2π ω 500 MHz H 2πω 125 MHz J CH C 215 Hz T T 25 s T 18 s 1C 1H 300 ms T 7 s 2C 2H 1/ 2J 2,3 ms CH
73 Implementação com 2 núcleos (I = 1/2) acoplados Porta Não-controlado (CNOT) ou Ou-Exclusivo (XOR): = +π J 1 ω C 1 ω C ωc CH 2 ω C ωc CH CH = + π J = π J Sistema girante: = π J 2 ω C 13 C 1 H 13 C 1 H CH ω C (1/ 2 ) T J CH R ( / 2) x π R ( π / 2) y
74 Implementação com 2 núcleos (I = 1/2) acoplados = +π J 1 ω C 13 C 1 H CH = π J 2 ω C 13 C 1 H CH R ( / 2) x π (1/ 2 ) T J CH R ( π / 2) y Inversão condicional do spin do núcleo 13 C
75 Exemplo de implementação da porta CNOT Porta CNOT (ou XOR):
76 Uso de núcleos quadrupolares (I > 1/2)
77 RMN de 23 Na (I = 3/2) em cristal líquido Sistema com 2 q-bits por núcleo
78 Experimentos em computação quântica via RMN Algoritmo de Grover: Chuang et al., Phys. Rev. Lett. (1998). 2 q-bits (molécula de clorofórmio, 1 H e 13 C). Algoritmo de Shor: 15 = 3 5 Vandersypen et al., Nature (2001). 7 q-bits ( 1 H e 13 C). Teleporte quântico: Nielsen et al., Nature (1998). 3 q-bits ( 1 H e 13 C).
79 Implementação experimental com 12 q-bits
80 Proposta experimental: dispositivos microeletrônicos
81 Proposta experimental: dispositivos microeletrônicos
82 Proposta experimental: dispositivos microeletrônicos
83 Proposta experimental: detecção por MRFM
84 Proposta experimental: detecção por MRFM
85 Limitações Computação quântica via RMN Vantagens e Perspectivas Manipulação de q-bits com técnicas bem estabelecidas. Implementação com sucesso de algoritmos em sistemas simples (única!!). Simulação bem sucedida de sistemas quânticos. É possível aumentar o número de q-bits......número máximo de q-bits limitado. Tempos de coerência curtos (relaxação). É possível criar emaranhamento ( entanglement ) em estados pseudo-puros??
86 Computadores do futuro = Espectrômetros de RMN? Sci. Amer., Junho 1998
87 Bibliografia recomendada Fundamentos de RMN: Spin Dynamics, M. H. Levitt, John Wiley & Sons, (Excelentes figuras!!!) Principles of Magnetic Resonance, C. P. Slichter, Springer, Imagens por RMN: Novas Imagens do Corpo, H. Panepucci et al. Ciência Hoje, 4, 46-56, Computação Quântica: Computação Quântica e Informação Quântica, M. A. Nielsen, I. L. Chuang Bookman NMR Quantum Information Processing", I. S. Oliveira, T. J. Bonagamba, R. S. Sarthour, J. C. C. Freitas, E. R. de Azevedo. Elsevier, Contato: [email protected]
Ressonância Magnética Nuclear: fundamentos e aplicações
 Ressonância Magnética Nuclear: fundamentos e aplicações Departamento de Física - UFES Sumário Fundamentos de RMN: Princípios físicos. Pulsos, ecos, espectros. Técnicas experimentais. Interações de spin
Ressonância Magnética Nuclear: fundamentos e aplicações Departamento de Física - UFES Sumário Fundamentos de RMN: Princípios físicos. Pulsos, ecos, espectros. Técnicas experimentais. Interações de spin
RMN: Fundamentos e Aplicações - Biotecnologia e áreas afins
 Ressonância Magnética Nuclear: fundamentos e aplicações em Biotecnologia e áreas afins Departamento de Física - UFES Sumário Fundamentos e aplicações de RMN: Princípios físicos. Detalhes experimentais.
Ressonância Magnética Nuclear: fundamentos e aplicações em Biotecnologia e áreas afins Departamento de Física - UFES Sumário Fundamentos e aplicações de RMN: Princípios físicos. Detalhes experimentais.
Métodos de RMN no estado sólido
 Métodos de RMN no estado sólido Jair C. C. Freitas Programa de Pós-graduação em Física UFES Programa de Pós-graduação em Química - UFES Sumário Interações de spin nuclear: Hamiltoniano de spin nuclear.
Métodos de RMN no estado sólido Jair C. C. Freitas Programa de Pós-graduação em Física UFES Programa de Pós-graduação em Química - UFES Sumário Interações de spin nuclear: Hamiltoniano de spin nuclear.
no âmbito da história da Física Moderna e suas atuais aplicaçõ
 A Ressonância ncia Magnética Nuclear no âmbito da história da Física Moderna e suas atuais aplicaçõ ções Tito J. Bonagamba LEAR / IFSC / USP Ressonância Magnética Nuclear (RMN) História Ressonância Magnética
A Ressonância ncia Magnética Nuclear no âmbito da história da Física Moderna e suas atuais aplicaçõ ções Tito J. Bonagamba LEAR / IFSC / USP Ressonância Magnética Nuclear (RMN) História Ressonância Magnética
Resumo dos pontos importantes
 Resumo dos pontos importantes Equação básica da espectroscopia de RMN. γ X o ν X = B (1 σ X ) π Espectros de RMN e deslocamentos químicos. v X ν ref 6 δ ( ppm) = 10 ν ref 2 δ ( Hz) = δ ( ppm) ν 10 = 6
Resumo dos pontos importantes Equação básica da espectroscopia de RMN. γ X o ν X = B (1 σ X ) π Espectros de RMN e deslocamentos químicos. v X ν ref 6 δ ( ppm) = 10 ν ref 2 δ ( Hz) = δ ( ppm) ν 10 = 6
Resumo sobre magnetização nuclear [ ] o = !!!! Frequência de Larmor = frequencia do movimento de precessão = frequencia de ressonancia RMN!!!
![Resumo sobre magnetização nuclear [ ] o = !!!! Frequência de Larmor = frequencia do movimento de precessão = frequencia de ressonancia RMN!!! Resumo sobre magnetização nuclear [ ] o = !!!! Frequência de Larmor = frequencia do movimento de precessão = frequencia de ressonancia RMN!!!](/thumbs/83/87093138.jpg) Resumo sobre magnetização nuclear M = µ N ( ) N ( ) [ ] 0 mag ω o = γ B o ν o = o γ B 2π!!!! Frequência de Larmor = frequencia do movimento de precessão = frequencia de ressonancia RMN!!! Magnetização
Resumo sobre magnetização nuclear M = µ N ( ) N ( ) [ ] 0 mag ω o = γ B o ν o = o γ B 2π!!!! Frequência de Larmor = frequencia do movimento de precessão = frequencia de ressonancia RMN!!! Magnetização
ν L : frequência de Larmor.
 Ressonância Magnética Nuclear β (+) N β = N α e - E/KT Núcleo de spin I= ½ ( 1 H, 13 C, 15 N, 19 F, 31 P) α β E = hν rf = γhb 0 α (-) N α sem campo com campo B 0 Campo estático externo B 0 desdobramento
Ressonância Magnética Nuclear β (+) N β = N α e - E/KT Núcleo de spin I= ½ ( 1 H, 13 C, 15 N, 19 F, 31 P) α β E = hν rf = γhb 0 α (-) N α sem campo com campo B 0 Campo estático externo B 0 desdobramento
Imagens por Ressonância Magnética: Princípios e Aplicações
 UNIVERSIDADE DE SÃO PAULO Instituto de Física de São Carlos Centro de Imagens e Espectroscopia In Vivo por Ressonância Magnética Imagens por Ressonância Magnética: Princípios e Aplicações Fernando F Paiva
UNIVERSIDADE DE SÃO PAULO Instituto de Física de São Carlos Centro de Imagens e Espectroscopia In Vivo por Ressonância Magnética Imagens por Ressonância Magnética: Princípios e Aplicações Fernando F Paiva
Métodos de RMN no estado sólido
 Métodos de RMN no estado sólido Jair C. C. Freitas Programa de Pós-graduação em Física UFES Programa de Pós-graduação em Química - UFES Sumário Interações de spin nuclear: Interação quadrupolar elétrica.
Métodos de RMN no estado sólido Jair C. C. Freitas Programa de Pós-graduação em Física UFES Programa de Pós-graduação em Química - UFES Sumário Interações de spin nuclear: Interação quadrupolar elétrica.
Métodos de RMN no estado sólido
 Métodos de RMN no estado sólido Jair C. C. Freitas Programa de Pós-graduação em Física UFES Programa de Pós-graduação em Química - UFES Sumário Técnicas de alta resolução em RMN de sólidos: Ressonância
Métodos de RMN no estado sólido Jair C. C. Freitas Programa de Pós-graduação em Física UFES Programa de Pós-graduação em Química - UFES Sumário Técnicas de alta resolução em RMN de sólidos: Ressonância
RMN de sólidos Aplicações ao estudo de meios porosos Jair C. C. Freitas
 RMN de sólidos Aplicações ao estudo de meios porosos Jair C. C. Freitas Departamento de Física - UFES Sumário Fundamentos sobre RMN de sólidos: Introdução geral. Interações anisotrópicas. Alargamento homogêneo
RMN de sólidos Aplicações ao estudo de meios porosos Jair C. C. Freitas Departamento de Física - UFES Sumário Fundamentos sobre RMN de sólidos: Introdução geral. Interações anisotrópicas. Alargamento homogêneo
ESPECTROSCOPIA DE RESSONANCIA MAGNÉTICA NUCLEAR
 ESPECTROSCOPIA DE RESSONANCIA MAGNÉTICA NUCLEAR Histórico 1924: W. Pauli descreveu a base teórica da RMN; 1946: Bloch (Stanford) e Purcell (Harvard) demonstraram a teoria de absorção de radiação eletromagnética
ESPECTROSCOPIA DE RESSONANCIA MAGNÉTICA NUCLEAR Histórico 1924: W. Pauli descreveu a base teórica da RMN; 1946: Bloch (Stanford) e Purcell (Harvard) demonstraram a teoria de absorção de radiação eletromagnética
Bioinformática RESSONÂNCIA MAGNÉTICA NUCLEAR - RMN. Disciplina de Bioinformática Alunas: Rayssa H Arruda Pereira Taciane Barbosa Henriques
 Bioinformática RESSONÂNCIA MAGNÉTICA NUCLEAR - RMN Disciplina de Bioinformática Alunas: Rayssa H Arruda Pereira Taciane Barbosa Henriques Introdução A espectroscopia por Ressonância Magnética Nuclear (RMN)
Bioinformática RESSONÂNCIA MAGNÉTICA NUCLEAR - RMN Disciplina de Bioinformática Alunas: Rayssa H Arruda Pereira Taciane Barbosa Henriques Introdução A espectroscopia por Ressonância Magnética Nuclear (RMN)
Introdução à Computação Quântica
 Introdução à Computação Quântica Aula 3 Computação quântica: portas lógicas e circuitos Renato de Oliveira Violin José Hiroki Saito Departamento de Computação - UFSCar Conteúdo Portas lógicas e circuitos.
Introdução à Computação Quântica Aula 3 Computação quântica: portas lógicas e circuitos Renato de Oliveira Violin José Hiroki Saito Departamento de Computação - UFSCar Conteúdo Portas lógicas e circuitos.
Computação quântica com íons aprisionados
 Computação quântica com íons aprisionados Alessandro S. Villar Instituto de Física Universidade de São Paulo Departamento de Física Centro de Ciências Exatas e da Natureza Universidade Federal de Pernambuco
Computação quântica com íons aprisionados Alessandro S. Villar Instituto de Física Universidade de São Paulo Departamento de Física Centro de Ciências Exatas e da Natureza Universidade Federal de Pernambuco
Fundamentos da Ressonância Magnética Nuclear
 Fundamentos da Ressonância Magnética Nuclear José Daniel Figueroa-Villar Grupo de Química Medicinal Departamento de Química Instituto Militar de Engenharia Rio de Janeiro, Brasil [email protected] Por
Fundamentos da Ressonância Magnética Nuclear José Daniel Figueroa-Villar Grupo de Química Medicinal Departamento de Química Instituto Militar de Engenharia Rio de Janeiro, Brasil [email protected] Por
NOME: QFL ª Prova (15 pontos) Tabela de deslocamentos químicos de 13 C em sistemas orgânicos
 NOME: QFL 2144 2008 3ª Prova (15 pontos) Tabela de deslocamentos químicos de 13 C em sistemas orgânicos Fragmentações e fragmentos comuns em espectrometria de massa Íon fragmento Neutro Perdido Massa do
NOME: QFL 2144 2008 3ª Prova (15 pontos) Tabela de deslocamentos químicos de 13 C em sistemas orgânicos Fragmentações e fragmentos comuns em espectrometria de massa Íon fragmento Neutro Perdido Massa do
Análise de Compostos Orgânicos RESSONÂNCIA MAGNÉTICA NUCLEAR
 Análise de Compostos Orgânicos Capítulo III O Retorno de Jedi RESSONÂNCIA MAGNÉTICA NUCLEAR Prof. Dr. Roberto Berlinck História: Kekulé, 854: Chemistry will never reveal the structure of the molecules,
Análise de Compostos Orgânicos Capítulo III O Retorno de Jedi RESSONÂNCIA MAGNÉTICA NUCLEAR Prof. Dr. Roberto Berlinck História: Kekulé, 854: Chemistry will never reveal the structure of the molecules,
Seminarios de Ressonância Magnetica Nuclear
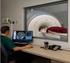 Universidade de São Paulo Instituto de Física de São Carlos - IFSC Seminarios de Ressonância Magnetica Nuclear Introdução Prof. Dr. José Pedro Donoso Ressonância Magnética Nuclear Nos núcleos onde o número
Universidade de São Paulo Instituto de Física de São Carlos - IFSC Seminarios de Ressonância Magnetica Nuclear Introdução Prof. Dr. José Pedro Donoso Ressonância Magnética Nuclear Nos núcleos onde o número
Mini-curso de Spintrônica
 Mini-curso de Spintrônica V Escola de Matogrossense de Física Tatiana G. Rappoport UFRJ http://www.if.ufrj.br/~tgrappoport I. Introdução II. Background III. Spintrônica em metais IV. Spintrônica em semicondutores
Mini-curso de Spintrônica V Escola de Matogrossense de Física Tatiana G. Rappoport UFRJ http://www.if.ufrj.br/~tgrappoport I. Introdução II. Background III. Spintrônica em metais IV. Spintrônica em semicondutores
SPI5814 Física atômica e molecular - Equações de Bloch ópticas
 SPI5814 Física atômica e molecular - Equações de Bloch ópticas Rafael Bruno Barbosa Lima Instituto de Física de São Carlos, Universidade de São Paulo, São Carlos, Brasil (Dated: Novembro de 2015) 1 I.
SPI5814 Física atômica e molecular - Equações de Bloch ópticas Rafael Bruno Barbosa Lima Instituto de Física de São Carlos, Universidade de São Paulo, São Carlos, Brasil (Dated: Novembro de 2015) 1 I.
SFI 5800 Espectroscopia Física. Ressonância Magnética Nuclear
 Universidade de São Paulo Instituto de Física de São Carlos - IFSC SFI 5800 Espectroscopia Física Ressonância Magnética Nuclear Prof. Dr. José Pedro Donoso Ressonância Magnética Nuclear Nos núcleos onde
Universidade de São Paulo Instituto de Física de São Carlos - IFSC SFI 5800 Espectroscopia Física Ressonância Magnética Nuclear Prof. Dr. José Pedro Donoso Ressonância Magnética Nuclear Nos núcleos onde
RM: PRINCÍPIOS FÍSICOS QUAL É A MÁGICA? PTC2892 Princípios da Formação e Processamento de Imagens Médicas. Ressonância Magnética
 Plano da aula de hoje PTC2892 Princípios da Formação e Processamento de Imagens Médicas Ressonância Magnética Prof. S Furuie Princípios físicos de Ressonância Magnética Formação de imagens em Ressonância
Plano da aula de hoje PTC2892 Princípios da Formação e Processamento de Imagens Médicas Ressonância Magnética Prof. S Furuie Princípios físicos de Ressonância Magnética Formação de imagens em Ressonância
Simulação numérica de experimentos de ressonância magnética de núcleos quadrupolares com aplicações em Computação Quântica.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS PROGRAMA DE PÓS-GRADUÇÃO EM FÍSICA Denimar Possa Simulação numérica de experimentos de ressonância magnética de núcleos quadrupolares com
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS PROGRAMA DE PÓS-GRADUÇÃO EM FÍSICA Denimar Possa Simulação numérica de experimentos de ressonância magnética de núcleos quadrupolares com
IMAGEM POR RESSONÂNCIA MAGNÉTICA (MRI) Prof. Sérgio Francisco Pichorim
 IMAGEM POR RESSONÂNCIA MAGNÉTICA (MRI) Prof. Sérgio Francisco Pichorim Imagem por Ressonância Magnética Não usa radiação ionizante Efeito biológico não mensurável Aparentemente seguro Imagens em cortes
IMAGEM POR RESSONÂNCIA MAGNÉTICA (MRI) Prof. Sérgio Francisco Pichorim Imagem por Ressonância Magnética Não usa radiação ionizante Efeito biológico não mensurável Aparentemente seguro Imagens em cortes
Momento Magnético Momento de Dipolo
 Propriedades Magnéticas I Magnetismo Fenômeno pelo qual certos materiais exercem uma força ou influência atrativa e repulsiva sobre outros materiais Aplicações mais importantes Geradores de potência elétrica
Propriedades Magnéticas I Magnetismo Fenômeno pelo qual certos materiais exercem uma força ou influência atrativa e repulsiva sobre outros materiais Aplicações mais importantes Geradores de potência elétrica
Imagem de Ressonância Magnética
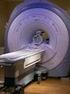 Universidade Técnica de Lisboa Instituto Superior Técnico Mestrado Integrado em Engenharia Biomédica Imagem de Ressonância Magnética Técnicas de Imagiologia Nuno Santos n.º 55746, [email protected] Rúben
Universidade Técnica de Lisboa Instituto Superior Técnico Mestrado Integrado em Engenharia Biomédica Imagem de Ressonância Magnética Técnicas de Imagiologia Nuno Santos n.º 55746, [email protected] Rúben
Cap. 5 Espectroscopia Molecular ESPECTROSCOPIA DE RESSONÂNCIA MAGNÉTICA NUCLEAR
 Cap. 5 Espectroscopia Molecular ESPECTROSCOPIA DE RESSONÂNCIA MAGNÉTICA NUCLEAR Espectro RMN de baixa resolução O-C 2 -C 3 5.1ppm 3.7 ppm 1.2 ppm Campo alto, Campo baixo O espectro explica-se pelo efeito
Cap. 5 Espectroscopia Molecular ESPECTROSCOPIA DE RESSONÂNCIA MAGNÉTICA NUCLEAR Espectro RMN de baixa resolução O-C 2 -C 3 5.1ppm 3.7 ppm 1.2 ppm Campo alto, Campo baixo O espectro explica-se pelo efeito
TOMOGRAFIA POR RESSONÂNCIA MAGNÉTICA NUCLEAR. Prof. Dr. Paulo Mazzoncini de Azevedo Marques Centro de Ciências das Imagens e Física Médica FMRP/USP
 TOMOGRAFIA POR RESSONÂNCIA MAGNÉTICA NUCLEAR Prof. Dr. Paulo Mazzoncini de Azevedo Marques Centro de Ciências das Imagens e Física Médica FMRP/USP Ressonância Magnética nuclear (RMN) permite obter estudos
TOMOGRAFIA POR RESSONÂNCIA MAGNÉTICA NUCLEAR Prof. Dr. Paulo Mazzoncini de Azevedo Marques Centro de Ciências das Imagens e Física Médica FMRP/USP Ressonância Magnética nuclear (RMN) permite obter estudos
Aula 1. Organic Chemistry 4 th Edition Paula Yurkanis Bruice. Espectroscopia de RMN
 Aula 1 Espectroscopia de RMN Organic Chemistry 4 th Edition Paula Yurkanis Bruice Irene Lee Case Western Reserve University Cleveland, OH 2004, Prentice Hall Ressonância Magnética Nuclear (RMN) Identifica
Aula 1 Espectroscopia de RMN Organic Chemistry 4 th Edition Paula Yurkanis Bruice Irene Lee Case Western Reserve University Cleveland, OH 2004, Prentice Hall Ressonância Magnética Nuclear (RMN) Identifica
Informa. Quântica. com. Quebrando Códigos com Computadores Quânticos
 Informa formação Quântica com Átomos e FótonsF Quebrando Códigos com Computadores Quânticos Prof. Marcelo Martinelli Laboratório de Manipulação Coerente de Átomos e Luz A página: http://axpfep1.if.usp.br/~mmartine
Informa formação Quântica com Átomos e FótonsF Quebrando Códigos com Computadores Quânticos Prof. Marcelo Martinelli Laboratório de Manipulação Coerente de Átomos e Luz A página: http://axpfep1.if.usp.br/~mmartine
UMA INTRODUÇÃO AO ESTUDO DA RESSONÂNCIA MAGNÉTICA NUCLEAR. Por Renata Bressane Sob orientação das profas. Dras. Marcia Rizzutto e Elisabeth Yoshimura
 UMA INTRODUÇÃO AO ESTUDO DA RESSONÂNCIA MAGNÉTICA NUCLEAR Por Renata Bressane Sob orientação das profas. Dras. Marcia Rizzutto e Elisabeth Yoshimura OBJETIVOS Conhecer o equipamento de RMN Utilidades didáticas
UMA INTRODUÇÃO AO ESTUDO DA RESSONÂNCIA MAGNÉTICA NUCLEAR Por Renata Bressane Sob orientação das profas. Dras. Marcia Rizzutto e Elisabeth Yoshimura OBJETIVOS Conhecer o equipamento de RMN Utilidades didáticas
Universidade de São Paulo Instituto de Física de São Carlos
 Universidade de São Paulo Instituto de Física de São Carlos Márcio Fernando Cobo Exploração de técnicas de RMN dipolar e aproximações analíticas no estudo de reorientações de segmentos moleculares São
Universidade de São Paulo Instituto de Física de São Carlos Márcio Fernando Cobo Exploração de técnicas de RMN dipolar e aproximações analíticas no estudo de reorientações de segmentos moleculares São
QFL (a) Aqui se trata de mero uso de fórmula e uso da constante magnetogírica do próton. 2πν
 QFL-2144-2013 Roteiro da 1 a Lista de exercícios de RMN 1.) A maioria dos espectrômetros de RMN utilizados para estudos em Química utiliza campos magnéticos fixos tais que a freqüência de ressonância de
QFL-2144-2013 Roteiro da 1 a Lista de exercícios de RMN 1.) A maioria dos espectrômetros de RMN utilizados para estudos em Química utiliza campos magnéticos fixos tais que a freqüência de ressonância de
Ressonância Magnética. Prof. Luciano Santa Rita
 Ressonância Magnética Prof. Luciano Santa Rita [email protected] www.lucianosantarita.pro.br Sumário Introdução e Histórico Princípio de funcionamento de ressonância magnética - RM (abordagem
Ressonância Magnética Prof. Luciano Santa Rita [email protected] www.lucianosantarita.pro.br Sumário Introdução e Histórico Princípio de funcionamento de ressonância magnética - RM (abordagem
Experimentos com Estados Emaranhados de Fótons
 Experimentos com Estados Emaranhados de Fótons Paulo Henrique Souto Ribeiro Instituto de Física - UFRJ Universidade Federal de Sergipe Aracaju Julho, 2009 Grupo de Óptica Quântica do IF - UFRJ Grupo de
Experimentos com Estados Emaranhados de Fótons Paulo Henrique Souto Ribeiro Instituto de Física - UFRJ Universidade Federal de Sergipe Aracaju Julho, 2009 Grupo de Óptica Quântica do IF - UFRJ Grupo de
A Experiência de Stern-Gerlach e o Spin do Elétron
 UFPR 28 de Abril de 2014 Figura: Placa Comemorativa. ela foi realizada em 1922; ela investiga os possíveis valores do momento de dipolo magnético, µ, de um átomo de prata; ela explora a dinâmica do dipolo
UFPR 28 de Abril de 2014 Figura: Placa Comemorativa. ela foi realizada em 1922; ela investiga os possíveis valores do momento de dipolo magnético, µ, de um átomo de prata; ela explora a dinâmica do dipolo
Exame não invasivo I: Imagem por. Ressonância. Magnética. Nuclear
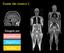 Exame não invasivo I: Imagem por Ressonância Magnética Nuclear Histórico da IRMN 1873 Maxwell - Equações para campos elétricos e magnéticos 1887 Hertz - Radiofreqüência 1924 Pauli - Magnetismo Nuclear
Exame não invasivo I: Imagem por Ressonância Magnética Nuclear Histórico da IRMN 1873 Maxwell - Equações para campos elétricos e magnéticos 1887 Hertz - Radiofreqüência 1924 Pauli - Magnetismo Nuclear
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/2 e de Dois Níveis
 Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
Aplicações dos Postulados da Mecânica Quântica Para Simples Casos: Sistema de Spin 1/ e de Dois Níveis Bruno Felipe Venancio 8 de abril de 014 1 Partícula de Spin 1/: Quantização do Momento Angular 1.1
OBI Uso de imagens no planejamento radioterápico
 OBI Uso de imagens no planejamento radioterápico CBCT Kv / Kv Ressonância Magnética Flávia Aparecida Franck Dosimetrista Téc. Fernando Assi Introdução Núcleos ativos em RM Escolha do hidrogênio Aspectos
OBI Uso de imagens no planejamento radioterápico CBCT Kv / Kv Ressonância Magnética Flávia Aparecida Franck Dosimetrista Téc. Fernando Assi Introdução Núcleos ativos em RM Escolha do hidrogênio Aspectos
Aula-11. (quase) Tudo sobre os átomos
 Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
Aula-11 (quase) Tudo sobre os átomos Algumas propriedades: Átomos são estáveis (quase sempre) Os átomos se combinam (como o fazem é descrito pela mecânica quântica) Os átomos podem ser agrupados em famílias
 ν ν α α π θ θ δ α α α + + α + α α + α + φ Γ φ θ θ θφ Γ δ = α ν α α ν + ν ν + ν + ν + δ + ν ν + δ + + + + + δ + + ν ν + + ν + + + ν ν ν + + ν + ν + = θ β β + Γ δ Γ δ β µ µ µµ µ µ µ µ α ν α µ
ν ν α α π θ θ δ α α α + + α + α α + α + φ Γ φ θ θ θφ Γ δ = α ν α α ν + ν ν + ν + ν + δ + ν ν + δ + + + + + δ + + ν ν + + ν + + + ν ν ν + + ν + ν + = θ β β + Γ δ Γ δ β µ µ µµ µ µ µ µ α ν α µ
Ressonância Magnética Nuclear
 Ressonância Magnética Nuclear Bibliografia: Pavia, D.L. et al., Introdução à Espectroscopia, Ed. Cengage Learning, 2010. Bruice, P.Y. et al., Química Orgânica, Ed. Prendice Hall, 2004. Raios-X são as radiações
Ressonância Magnética Nuclear Bibliografia: Pavia, D.L. et al., Introdução à Espectroscopia, Ed. Cengage Learning, 2010. Bruice, P.Y. et al., Química Orgânica, Ed. Prendice Hall, 2004. Raios-X são as radiações
Introdução à Computação Quântica
 Introdução à Computação Quântica Aula 2 Computação quântica: princípios matemáticos e físicos Renato de Oliveira Violin José Hiroki Saito Departamento de Computação - UFSCar Conteúdo Bits quânticos (qubits).
Introdução à Computação Quântica Aula 2 Computação quântica: princípios matemáticos e físicos Renato de Oliveira Violin José Hiroki Saito Departamento de Computação - UFSCar Conteúdo Bits quânticos (qubits).
Métodos Físicos de Análise - RESSONÂNCIA MAGNÉTICA NUCLEAR. Métodos Físicos de Análise. Métodos Físicos de Análise
 - RESSONÂNCIA MAGNÉTICA NUCLEAR Prof. Dr. Leonardo Lucchetti Mestre e Doutor em Ciências Química de Produtos Naturais NPPN/UFRJ Depto. de Química de Produtos Naturais Farmanguinhos Fiocruz Docente do Programa
- RESSONÂNCIA MAGNÉTICA NUCLEAR Prof. Dr. Leonardo Lucchetti Mestre e Doutor em Ciências Química de Produtos Naturais NPPN/UFRJ Depto. de Química de Produtos Naturais Farmanguinhos Fiocruz Docente do Programa
Princípios Básicos de Ressonância Magnética Nuclear do Estado Sólido André Luis Bonfim Bathista e Silva São Carlos, 2005 (Edição do Autor)
 do Estado Sólido André Luis Bonfim Bathista e Silva São Carlos, 2005 (Edição do Autor) Licença:
do Estado Sólido André Luis Bonfim Bathista e Silva São Carlos, 2005 (Edição do Autor) Licença:
Quantização. Quantização da energia (Planck, 1900) hc h. Efeito fotoelétrico (Einstein, 1905) Espectros atômicos (linhas discretas) v 2
 Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
Introdução à Computação Quântica
 Introdução à Computação Quântica Aula 1 Revisão da computação clássica Renato de Oliveira Violin José Hiroki Saito Departamento de Computação - UFSCar Conteúdo Dígitos binários. Portas lógicas e circuitos.
Introdução à Computação Quântica Aula 1 Revisão da computação clássica Renato de Oliveira Violin José Hiroki Saito Departamento de Computação - UFSCar Conteúdo Dígitos binários. Portas lógicas e circuitos.
Aula 12. (quase) Tudo sobre os átomos. Física Geral F-428
 Aula 1 (quase) Tudo sobre os átomos Física Geral F-48 1 Algumas propriedades atômicas: Átomos são estáveis (quase sempre); Os átomos podem ser agrupados em famílias (propriedades periódicas, com o número
Aula 1 (quase) Tudo sobre os átomos Física Geral F-48 1 Algumas propriedades atômicas: Átomos são estáveis (quase sempre); Os átomos podem ser agrupados em famílias (propriedades periódicas, com o número
Revisão do conceito de acoplamento indireto spin-spin
 Revisão do conceito de acoplamento indireto spin-spin 1) Espectros de RMN (substancias em solução) podem apresentar desdobramento de sinais ( estrutura fina ). 2) O desdobramento dos sinais se deve a interação
Revisão do conceito de acoplamento indireto spin-spin 1) Espectros de RMN (substancias em solução) podem apresentar desdobramento de sinais ( estrutura fina ). 2) O desdobramento dos sinais se deve a interação
UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA DE SÃO CARLOS ÉVERTON LUCAS DE OLIVEIRA
 UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA DE SÃO CARLOS ÉVERTON LUCAS DE OLIVEIRA Difusão de spins nucleares em meios porosos - uma abordagem computacional da RMN São Carlos 2015 ÉVERTON LUCAS DE
UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA DE SÃO CARLOS ÉVERTON LUCAS DE OLIVEIRA Difusão de spins nucleares em meios porosos - uma abordagem computacional da RMN São Carlos 2015 ÉVERTON LUCAS DE
Modelagem de Sistemas com. Histerese. Curso de Pós-Graduação TE 747. Universidade Federal do Paraná Jean Vianei Leite
 Modelagem de Sistemas com Histerese TE 747 Curso de Pós-Graduação Universidade Federal do Paraná Jean Vianei Leite Dados da Disciplina TE 747 Métodos Avançados em Sistemas Eletrônicos : Modelagem de Sistemas
Modelagem de Sistemas com Histerese TE 747 Curso de Pós-Graduação Universidade Federal do Paraná Jean Vianei Leite Dados da Disciplina TE 747 Métodos Avançados em Sistemas Eletrônicos : Modelagem de Sistemas
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 2016 14 de outubro de 2015 Parte 1 Instruções ˆ Não escreva seu nome na prova. Ela deverá ser identificada apenas através do
EUF Exame Unificado das Pós-graduações em Física Para o primeiro semestre de 2016 14 de outubro de 2015 Parte 1 Instruções ˆ Não escreva seu nome na prova. Ela deverá ser identificada apenas através do
