Daniel de Matos Alves Métodos Computacionais Aplicados no Estudo de Fármacos
|
|
|
- Dalila Castel-Branco
- 5 Há anos
- Visualizações:
Transcrição
1 Daniel de Matos Alves Métodos Computacionais Aplicados no Estudo de Fármacos Fortaleza 16/09/2011
2 Daniel de Matos Alves Métodos Computacionais Aplicados no Estudo de Fármacos Tese submetida à Coordenação do Curso de Pós-Graduação em Física, da Universidade Federal do Ceará, como requisito parcial para a obtenção do grau de Doutor em Física Orientador: Alejandro Pedro Ayala UNIVERSIDADE FEDERAL DO CEARÁ - DEPARTAMENTO DE FÍSICA Fortaleza 16/09/2011
3 Daniel de Matos Alves Métodos Computacionais Aplicados no Estudo de Fármacos Tese submetida à Coordenação do Curso de Pós-Graduação em Física, da Universidade Federal do Ceará, como requisito parcial para a obtenção do grau de Doutor em Física Aprovada em 16/09/2011 BANCA EXAMINADORA Profa. Dra. Silvete Coradi Guerini Departamento de Física, Universidade Federal do Maranhão Prof. Dr. Waldeci Paraguassu Feio Departamento de Física, Universidade Federal do Pará Prof. Dr. Paulo de Tarso Cavalcante Freire Departamento de Física, Universidade Federal do Ceará Prof. Dr. José Alves de Lima Júnior Departamento de Física, Universidade Federal do Ceará
4 Ao meu filho, Daniel, e à minha esposa, Elizabeth.
5 Agradecimentos A formação de um profissional da área de física demanda muito esforço. Não somente do estudante, mas também de todas as pessoas envolvidas, órgãos financiadores e universidade. Tendo em vista as condições sócio-econômicas da maior parte da população de nosso país, acredito que a formação de nível superior e principalmente de nível de pós-graduação é um privilégio de poucos. Classifico o ato de agradecer todos que de alguma forma contribuíram para minha formação profissional como extremamente prazeroso, já que ao longo dos anos, muito do que sou e tenho é devido em grande parte ao esforço de outros. Agradeço à CAPES pela provisão da bolsa de doutorado. Também agradeço ao Grupo de Espalhamento de Luz da UFC pelo suporte, pela disposição dos laboratórios, equipamentos e pessoal, que foram essenciais durante a realização desse trabalho. Também agradeço ao professor Josué Mendes Filho, por ser um grande incentivador, por compartilhar a sua vasta experiência científica e por seu esforço incessante de proporcionar o ambiente adequado para a proliferação do conhecimento científico no Departamento de Física da Universidade Federal do Ceará. Não me permito esquecer de agradecer queridos professores que tanto contribuíram durante esses mais de 10 anos que me dedico à Física: Francisco Erivan de Abreu Melo, Paulo de Tarso Cavalcante Freire, Maria Marlúcia Freitas Santiago, Gil de Aquino Farias, Eloneid Felipe Nobre e Antônio Gomes Souza Filho. Agradeço em especial ao professor Alejandro Pedro Ayala por acreditar no meu potencial, pela orientação acadêmica, pela dedicação constante e concelhos valiosos. Obrigado aos amigos e à minha família pelo apoio incondicional.
6 Resumo Nesse trabalho realizamos cálculos ab initio em dois fármacos, benzonidazol e mebendazol, usados no combate de infecções por parasitas. Os cálculos foram divididos em obtenção dos espectros vibracionais Raman e infravermelho, dinâmica molécular e cálculo da distribuição da energia potencial. Desenvolvemos o software PEDCALC para calcular a distribuição da energia potencial e classificar os modos de vibração. A classificação dos modos de vibração é realizada pela comparação dos espectros calculados com espectros experimentais e a distribuição da energia potencial. Mostramos que o software PEDCALC pode produzir resultados exatos da distribuição da energia potencial, e, é ferramenta essencial na classificação dos modos de vibração de qualquer molécula. Realizamos cálculo de dinâmica molecular no dímero de mebendazol para mostrar a troca de átomos de hidrogênio entre seus monômeros, observamos assim a dinâmica do tautomerismo dessa molécula.
7 Abstract In this work we performed ab initio calculations on two drugs, benzonidazole and mebendazole, used on the treatment of parasitic infections. The calculations were divided into obtaining the vibrational modes Raman and infrared spectra, molecular dynamics and calculation of the potential energy distribution. We developed the software PEDCALC to calculate the potential energy distribution and classify the vibrational modes. The classification of the vibrational modes is done by comparing the calculated spectra with experimental spectra and the potential energy distribution. We showed that software PEDCALC can produce accurate results of the potential energy distribution, and it is essential tool in the classification of vibrational modes of any molecule. We performed molecular dynamics calculations in the dimer of mebendazole to show the exchange of hydrogen atoms between its monomers, so we observed the dynamics of the tautomerism of this molecule.
8 Sumário Lista de Abreviaturas Lista de Figuras Lista de Tabelas 1 INTRODUÇÃO p CÁLCULOS DE PRIMEIROS PRINCÍPIOS p DFT p Aproximação de Born-Oppenheimer p Equação de Schrödinger p Teorema de Kohn e Hohenberg p Funcional de Correlação e Troca p Cálculo de Frequências p Intensidade dos Espectros Raman e Infravermelho p Dinâmica Molecular p Teoria de Car-Parrinello p MODOS NORMAIS DE VIBRAÇÃO p Introdução p. 34
9 3.2 Equação Secular p Coordenadas Internas p Estiramento p Deformação no Plano p Torção p Deformação Fora do Plano p Equação Secular em Coordenadas Internas p Aplicação da Matriz L para Obter a Distribuição da Energia Potencial.... p Mudança de Sistema de Coordenadas p PEDCALC p Coordenadas Naturais p Identificação de Coordenadas Redundantes p Constantes de Força p Esquema de Cores para o PED p Esquema do cálculo do PED p BENZONIDAZOL p Introdução p Estrutura Cristalina p Conformação Geométrica p Espectroscopia Vibracional p Procedimento de Classificação dos Modos Normais de Vibração... p Distribuição da Energia Potencial p Classificação das Bandas Vibracionais p. 82
10 4.7 Conclusões p MEBENDAZOL p Introdução p Otimização da Geometria p Introdução p Investigações Sobre a Geometria do Mebendazol-C p Varreduras p Nova Geometria p Espectro Vibracional do Mebendazol p PED do Mebendazol p Dinâmica Molecular p Dinâmica Molecular - Dímero Livre p Dinâmica Molecular - Novas Condições de Contorno p Conclusão p CONCLUSÕES E PERSPECTIVAS p. 134 Apêndice A -- Unidades Atômicas p. 136 Apêndice B -- Notação das coordenadas naturais p. 137 Referências Bibliográficas p. 139
11 Lista de Abreviaturas CPMD Dinâmica molecular de Car-Parrinello MBZ Fármaco mebendazol MBZ-C Polimorfo C do fármaco mebendazol LDA Aproximação de densidade local GGA Aproximação generalizada do gradiente DFT Teoria da funcional da densidade KH Kohn e Hohenberg KS Kohn e Sham PED Distribuição da energia potencial
12 Lista de Figuras 3.1 Representação da coordenada interna estiramento p Representação da coordenada interna deformação no plano p Representação da coordenada interna de torção p Representação da coordenada de deformação fora do plano p Tabela das coordenadas naturais como apresentada na interface gráfica do software PEDCALC p Tabela com a contribuição das coordenadas internas para um modo de vibração p Vibração em 606 cm 1 da molécula de benzonidazol p Esquema do PEDCALC p Fórmula estrutural da molécula de benzonidazol p Conformação molecular do benzonidazol com cada átomo identificado... p Cela unitária do benzonidazol p Ligações intermoleculares entre moléculas do BZN p Superposição das conformações moleculares teórica (laranja) e experimental (colorida) p Funções de ajuste dos espectros Raman calculados. Os gráficos são mostrados para diferentes intervalos de número de onda p Funções de ajuste dos espectros infravermelho calculados. Os gráficos são mostrados para diferentes intervalos de número de onda p. 70
13 4.8 Espectros Raman calculado (C) e experimental (E) do BZN na região entre 2500 e 3500cm p Espectros Raman calculado (C) e experimental (E) do BZN na região entre 1000 e 2000cm p Espectros Raman calculado (C) e experimental (E) do BZN na região entre 500 e 1000cm p Espectros Raman calculado (C) e experimental (E) do BZN na região entre 0 e 500cm p Espectros infravermelho calculado (C) e experimental (E) do BZN na região entre 2500 e 3600cm p Espectros infravermelho calculado (C) e experimental (E) do BZN na região entre 1000 e 2000cm p Espectros infravermelho calculado (C) e experimental (E) do BZN na região entre 500 e 1000cm p Modo vibracional de 3272 cm 1 do BZN - G2(ν[N H 100]) p Modo vibracional de 1661 cm 1 do BZN - G2(ν[CN 11]+ν[CO72])..... p Modo vibracional de 946 cm 1 (R) do BZN - G4(ν[CN 12]+δ[ONO45]).. p Modo vibracional de 960 cm 1 (R) do BZN - G1 oop[ch 99] p Modo vibracional de 38 cm 1 (R) do BZN - G2(τ[CC 36]+τ[CN 39]).... p Modo vibracional de 49 cm 1 (R) do BZN - G2(τ[CC 59]) p Molécula de mebendazol-c p Geometria inicial da molécula de mebendazol-c p Variação da energia relativa durante o varredura da torção C(5)-N(26)- C(1)-O(30) p Variação da energia relativa durante o varredura da torção N(28)-C(5)- N(26)-C(1) p. 98
14 5.5 Nova configuração da molécula de Mebendazol-C p Tautômeros da molécula de MBZ-C p Dímeros tautômeros de MBZ-C p Funções de ajuste do dímero D A para o espectro Raman p Funções de ajuste do dímero D B para o espectro Raman p Espectros Raman calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 2000 e 3500cm p Espectros Raman calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 1000 e 1800cm p Espectros Raman calculado dos dímeros D A e D B, e experimental (E) do MBZ na região entre 500 e 1000cm p Espectros Raman calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 0 e 500cm p Espectros infravermelho calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 2000 e 4000cm p Espectros infravermelho calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 1000 e 1800cm p Espectros infravermelho calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 500 e 1000cm p Modo vibracional de 3404 cm 1 do MBZ - G13(ν[N H 31]), G3(ν[N H 68]).. p Modo vibracional de 2956 cm 1 do MBZ - G1-11 ν metil sym. [97] p Modo vibracional de 1596 cm 1 do MBZ - G2-12(ν[CO18]), G5-15(ν[CO30]).p Modo vibracional de 608 cm 1 do MBZ - G4 δ 6-ring* asym. [37] p Modo vibracional de 934 cm 1 do MBZ - G4-14 τ[cc 11]+oop[CH 70]... p Dímero D B do MBZ usado como configuração inicial da dinâmica molecular p. 128
15 5.23 Dinâmica Molecular com dímero D B de MBZ a temperatura 600k p Distância dos átomos N63-H48...N p Distâncias dos átomos N60-H35...N p. 131
16 Lista de Tabelas 3.1 Principais tipos de coordenadas internas p Coordenadas Naturais propostas por Baker p Parâmetros geométricos das ligações de hidrogênio p Funções de ajuste e regiões do espectro Raman calculado da molécula isolada de BZN p Classificação dos modos vibracionais do BZN de acordo com as coordenadas de simetria p Varredura da torção C(5)-N(26)-C(1)-O(30) p Varredura N(28)-C(5)-N(26)-C(1) p Ângulos de interesse da primeira otimização de geometria p Funções de ajuste e regiões do espectro calculado Raman do dímero D A do MBZ-C p Funções de ajuste e regiões do espectro calculado Raman do dímero D B do MBZ-C p Coordenadas Intermoleculares - Dímero D B p Classificação dos modos vibracionais do dímero D B do MBZ de acordo com as coordenadas de simetria p. 117 A.1 Unidades atômicas e fatores de conversão p. 136 B.1 Representação das contribuições das coordenadas naturais para o PED mostrado nas tabelas 4.3 e p. 137
17 16 1 INTRODUÇÃO A aplicação da Teoria do Funcional da Densidade[1] (DFT) e da dinâmica molecular na física, química[2] e ciência dos materiais é cada vez mais presente. DFT é considerada uma teoria fundamental no cálculo de propriedades de sistemas quânticos de muitos corpos. Enquanto a dinâmica molecular pode nos dar informações valiosas a respeito da dinâmica desses sistemas. Existem muitas áreas da física e da engenharia onde o progresso científico e tecnológico é limitado somente pelo entendimento das propriedades da matéria a nível atômico. DFT é ferramenta fundamental para obtenção de soluções da equação de Schrödinger, e assim entender o comportamento quântico de átomos e moléculas. DFT é uma teoria de aplicação geral podendo ser aplicado na maioria dos sistemas. Como todos os métodos computacionais, DFT é melhor aplicado a um conjunto limitado de problemas: cálculos de reações (termodinâmica, caminho de reações), cálculos envolvendo metais, catálise, etc. A teoria DFT também pode ser utilizado para prever geometria e espectros vibracionais de moléculas. Cálculos de otimização de geometria juntamente com cálculos para obtenção de espectros vibracionais são ferramentas padrão na classificação de modos de vibração de moléculas de fármacos. A dinâmica molecular por sua vez pode ser aplicada em diversos campos da física, química e biologia. Dentre as aplicações da dinâmica molecular destacamos: fenômenos de transporte e viscosidade em fluídos, defeitos em cristais, fraturas, biomoléculas e propriedades eletrônicas. Dinâmica de fluídos e gases foram as aplicações iniciais da dinâmica molecular. Defeitos em cristais e fraturas em sólidos podem ser estudados com o auxílio da dinâmica molecular, e têm importante papel no avanço tecnológico. A criação de novos componentes eletrônicos de estado sólido e novos materiais mais resistentes ou flexíveis,
18 17 também são aplicações da dinâmica molecular. A dinâmica molecular aplicada no estudo de biomoléculas investiga propriedades dinâmicas de proteínas, ácidos nucleicos e membranas celulares. Com o auxílio da dinâmica molecular, podemos estudar as propriedades dinâmicas desses sistemas biológicos sem sintetizar essas estruturas, reduzindo custo e tempo. A dinâmica molecular é dividida em duas áreas de cálculo: dinâmica molecular usando mecânica clássica e aproximações, e dinâmica molecular usando métodos da mecânica quântica. Dentre os métodos quânticos da dinâmica molecular, destacamos o método Car-Parrinello[3]. A dinâmica molecular de Car-Parrinello é um método eficiente de dinâmica molecular onde o potencial de interação é definido pelo princípio variacional. Ao contrário da dinâmica molecular de Born-Oppenheimer[4] onde os graus de liberdade dos núcleos atômicos são calculados usando forças iônicas que são calculadas a cada iteração com a solução aproximada do problema eletrônico, o método de Car-Parrinello introduz graus de liberdade do problema eletrônico como um conjunto de variáveis dinâmicas e fictícias. Na teoria de Car- Parrinello um sistema de muitos corpos é descrito por um conjunto de equações acopladas, tanto para núcleos atômicos quanto para elétrons. Na dinâmica molecular de Born-Oppenheimer a minimização do problema eletrônico ao estado fundamental é realizada a cada incremento temporal 1. Já na dinâmica molecular de Car-Parrinello a minimização ao estado fundamental é feita uma única vez. A dinâmica fictícia dos elétrons mantem o estado eletrônico fundamental correspondente durante a dinâmica dos núcleos atômicos. Para que os graus de liberdade dos elétrons não interfiram com os graus de liberdade dos núcleos atômicos, a massa fictícia dos elétrons deve ser suficientemente pequena, e como consequência a integração das equações de movimento é feita em incrementos temporais muito pequenos 2. Na prática, a dinâmica molecular de Car-Parrinello é mais eficiente que outros métodos baseados na aproximação adiabática. Porém, métodos baseados na mecânica clássica ainda são mais eficientes computacionalmente para uma série de problemas que envolvem macro-moléculas, como proteínas. Isso se deve ao fato de que métodos baseados na mecânica clássica somente calculam a dinâmica dos núcleos atômicos. Ao classificar modos de vibração de uma molécula, calculamos os espectros vibracionais, geralmente usando DFT. Os espectros calculados são comparados com espectros obtidos ex- 1 Um incremento temporal corresponde a um passo na dinâmica molecular. 2 Os incrementos temporais são da ordem de s.
19 18 perimentalmente para que possamos classificar os espectros experimentais em função dos calculados. Geralmente, o processo de classificação dos modos normais consiste em comparar os espectros calculados e experimentais usando funções de ajuste, e a partir da visualização dos modos de vibração, determinar quais coordenadas internas contribuem mais para a energia potencial. Esse modelo de classificação dos modos de vibração pode levar a erros difíceis de detectar. Ao visualizar um modo de vibração com o auxílio de um software, observamos o movimento dos átomos sem quantizar a contribuição de cada coordenada interna à energia potencial. Com esse método de associação, a tendência é que façamos associação da energia potencial com os átomos que mais se movimentam na molécula. Mas em alguns casos os átomos que mais se vibram não são os que mais contribuem para a energia potencial. Para quantizar a contribuição de cada coordenada interna à energia potencial de um modo de vibração usamos o método da Distribuição da Energia Potencial[5] (Potential Energy Distribution, PED). Esse método calcula a distribuição de probabilidade de cada coordenada interna para cada modo de vibração de uma molécula. Sendo assim, podemos associar com segurança quais as coordenadas internas contribuem mais para cada modo de vibração e classificar propriamente os modos de vibração. Nesse Trabalho desenvolvemos um software de cálculo do PED chamado PEDCALC. Desenvolvemos o software PEDCALC usando as linguagem TCL[6, 7] (Tool Command Language) e C[8 11]. PEDCALC utiliza as constantes de força e coordenadas atômicas como parâmetros de entrada, que podem ser obtidos através de cálculo de otimização de geometria (usamos para isso o software Gaussian), além da descrição das coordenadas internas fornecidas pelo usuário. Dados os parâmetros de entrada, PEDCALC calcula a distribuição da energia potencial, além de exibir os modos de vibração em uma interface 3D. As coordenadas internas fornecidas pelo usuário são verificadas pelo software para que não haja redundância no sistema de coordenadas. Com o auxílio do software PEDCALC podemos classificar modos de vibração de moléculas com segurança, já que obtemos a contribuição exata de cada coordenada interna. Antes de desenvolvermos o software PEDCALC, o único software disponível para cálculo da distribuição da energia potencial era o GAR2PED[12]. Como GAR2PED não apresenta interface gráfica, não verifica a redundância de coordenadas e se apresenta como um software de difícil utilização, decidimos desenvolver PEDCALC para
20 19 superar as dificuldades encontradas com o uso de GAR2PED e também propor um novo modelo de visualização da distribuição da energia potencial baseado em um gradiente de cores no modelo tridimensional da molécula em estudo. Os métodos de cálculo DFT, Car-Parrinello e PED foram aplicados à classificação dos modos de vibração e dinâmica molecular de dois fármacos: benzonidazol e mebendazol. A geometria otimizada da molécula de benzonidazol e os espectros calculados Raman e infravermelho foram obtidos pelo método DFT usando o software Gaussian, enquanto a classificação dos modos de vibração foi realizada com o auxílio do software PEDCALC. Ao estudar as característica físicas do fármaco mebendazol também utilizamos os softwares Gaussian e PEDCALC para os mesmos propósitos, porém não calculamos otimizações de geometria somente para a molécula de mebenzadol, mas também para o dímero de mebenzadol formado a partir de ligações de hidrogênio do tipo N-H...N entre grupos carbamato e benzimidazol de monômeros opostos dos dímeros de mebendazol. Também calculamos dinâmica molecular do dímero de mebendazol a fim de mostrar a transferência de prótons nas pontes de hidrogênio N-H...N. A trajetória da dinâmica molecular foi obtida usando o software CPMD (Car-Parrinello Molecular Dynamics) que é uma implementação do método Car-Parrinello. Os fármacos mebenzadol e benzonidazol são, geralmente, utilizados em regiões onde há precárias condições sanitárias, e existe maior proliferação de doenças parasitárias tropicais. Esses fármacos combatem doenças que podem ser classificadas como doenças negligenciadas. Não existem incentivos para o desenvolvimento de pesquisa que levem ao aprimoramento dos fármacos utilizados no tratamento dessas doenças. Os medicamentos utilizados hoje no controle dessas doenças foram, em geral, desenvolvidos há muitos anos. Benzonidazol e mebendazol são usados para o tratamento de infecções causadas pelos parasitas, Trypanosoma cruzi[13] e nematódeos gastrointestinais, respectivamente. Trypanosoma cruzi é o parasita que causa à Doença de Chagas[14]. Essa doença foi inicialmente descoberta pelo infectologista Carlos Chagas, em O principal vetor da Doença de Chagas é o inseto Triatoma Infestans, popularmente conhecido no Brasil como barbeiro. A proliferação do vetor dessa doença se dá em áreas rurais e de florestas. Como a população atingida está afastada dos grandes centros urbanos, as autoridades sanitárias tendem a negligenciar o diagnóstico e o tratamento dessa doença.
21 20 A proliferação da infecção por nematódeos gastrointestinais ocorre em locais onde as condições sanitárias são precárias, incluindo áreas rurais e urbanas. Geralmente, o vetor desses parasitas é o próprio homem. As áreas endêmicas são, em geral, associadas a pobreza e a ausência de políticas governamentais para a saúde pública. Os capítulos desse trabalho são divididos da seguinte forma: no Capítulo 2 discutiremos os métodos de cálculo usados nesse trabalho, incluindo método DFT e dinâmica molecular de Car-Parrinello. Mostraremos os princípios físicos que nos levaram a usar o método DFT para calcular otimização de geometria e espectros vibracionais dos fármacos mebendazol e benzonidazol. Também mostraremos as vantagens do método de dinâmica molecular de Car- Parrinello frente os métodos de dinâmica molecular de Born-Oppenheimer. No Capítulo 3 discutiremos a importância da classificação dos espectros vibracionais em termos dos modos normais de vibração. Para isso introduziremos a notação das coordenadas internas, a relação da equação secular com as vibrações moleculares e um método para obter a distribuição da energia potencial em função das coordenadas internas. Também no capítulo 3 mostraremos o software PEDCALC, o método de cálculo usado para detectar redundância no sistema de coordenadas internas, além de um novo método de visualização da distribuição da energia potencial através de uma interface em três dimensões. No capítulo 4 mostraremos resultados da aplicação do método da análise dos modos normais sobre a molécula do fármaco benzonidazol. Calculamos os espectros vibracionais Raman e infravermelho da molécula de benzonidazol usando a teoria DFT. Os espectros calculados foram ajustados aos espectros experimentais, e a classificação dos modos de vibração foi obtida com o software PEDCALC. No capítulo 5 realizamos um estudo sobre a geometria da molécula do fármaco mebendazol. Calculamos os espectros Raman e infravermelho de dímeros de mebendazol que foram comparados com os espectros experimentais. A classificação dos modos de vibração foi realizada com o auxílio do software PEDCALC. Também realizamos dinâmica molecular sobre dímero do mebendazol, com o objetivo de demonstrar a transferência de hidrogênio entre seus monômeros.
22 21 2 CÁLCULOS DE PRIMEIROS PRINCÍPIOS 2.1 DFT A teoria do funcional da densidade[15 17] (Density Funtional Theory, DFT) é uma teoria do estado fundamental da estrutura eletrônica em termos da distribuição da densidade de elétrons. Métodos alternativos ao DFT, como Hartree-Fock[18], são baseados na função de onda de muitos elétrons. A maior vantagem da teoria DFT frente a teoria Hartree-Fock é o aumento da precisão nos cálculos computacionais, que depende da escolha do funcional de troca e correlação[19], sem um grande aumento no tempo computacional. Isso se deve ao fato das teorias baseadas na função de onda necessitarem de uma base muito grande para representar as funções de onda, enquanto DFT usa a densidade da nuvem eletrônica para derivar outras grandezas físicas Aproximação de Born-Oppenheimer Dado um sistema de M átomos, uma molécula por exemplo, a propriedade física mais interessante desse sistema é como a energia muda em função da posição dos átomos. Ao definir a posição de um átomo devemos saber a posição do núcleo atômico e dos elétrons associados. Um núcleo atômico é aproximadamente 1800 vezes mais pesado que um elétron. Logo, os elétrons têm uma inércia muito menor, e podem reagir à mudanças de sua vizinhança muito mais rápido que os núcleos atômicos. Dessa forma, podemos separar o problema de determinar as mudanças de energia do sistema em duas partes: o movimento dos núcleos atômicos e o movimento dos elétrons. Fixando os núcleos atômicos, podemos
23 22 resolver as equações de movimento dos elétrons usando a Mecânica Quântica. Dada uma configuração dos núcleos atômicos, a solução das equações de movimento dos elétrons nos dá a configuração de menor energia, que chamamos de estado fundamental. A separação dos núcleos atômicos e dos elétrons em dois problemas distintos é chamada de aproximação de Born-Oppenheimer[20] (aproximação BO). Se nosso sistema tem M núcleos atômicos nas posições R 1,..., R M, então a energia do estado fundamental dos elétrons como função da configuração dos núcleos atômicos é E R 1,..., R M. Essa função é conhecida como superfície adiabática. A superfície adiabática nos diz quanto a energia do estado fundamental dos elétrons muda de acordo com a configuração dos núcleos atômicos. Para entender como obter a energia do estado fundamental devemos resolver a equação de Schrödinger Equação de Schrödinger A equação de Schrödinger, independente do tempo e não relativística para um sistema de N elétrons é dada por Hψ= Eψ (2.1) onde H é o operador Hamiltoniano,ψéum conjunto de soluções, ou auto-estados do sistema, e E é um conjunto de números reais que representam a energia do sistema para cada auto-estado, ou autovalores do sistema. A equação de Schrödinger com o Hamiltoniano expandido, para um sistema de N elétrons interagindo com núcleos atômicos é dada por h2 N N 2 i 2m + V N r i + U r i,r j ψ= Eψ. (2.2) i=1 i=1 i=1 j<i O Hamiltoniano é dividido em três termos, em ordem: a energia cinética de cada elétron (m na equação acima é a massa do elétron), a energia potencial (potencial externo), e interação elétron-elétron. Na equação 2.2 a função de onda é função das coordenadas dos N elétrons, ψ=ψ r 1,..., r N, e E é a energia do estado fundamental. A função de onda é função das coordenadas dos N elétrons do sistema, mas é possível fazer uma aproximação dessa função de onda usando o produto de funções de onda de único elétron,ψ=ψ r 1 ψ r2,...,ψ rn. Essa aproximação é conhecida como aproximação de Hartree. Geralmente o número de elé-
24 23 trons em uma molécula é muito maior que o número de núcleos atômicos, N M. Dessa forma, o problema quântico demanda maior capacidade de cálculo dos sistemas computacionais. Devido à interação elétron-elétron presente no Hamiltoniano da equação 2.2, os orbitais de único elétron,ψ r i, não podem ser determinados isoladamente sem considerarmos as interações associadas aos outros elétrons. Com isso, podemos definir a equação de Schrödinger para N elétrons como um problema de muitos corpos. Na equação de Schrödinger ψ i as funções de onda não determinam a posição exata dos elétrons, mas sim a probabilidade, r1,..., r N ψi r1,..., r N, que os elétrons estejam em um determinado conjunto de coordenadas, r 1,..., r N. Não podemos determinar a posição exata dos elétrons e muito menos distinguir um elétron do outro. De forma que não é possível mapear a trajetória de elétrons individuais. Então,ψ i r1,..., r N ψi r1,..., r N nos dá a probabilidade de encontrarmos N elétrons (independente da ordem) nas coordenadas r 1,..., r N. As funções de ondaψ r i não são a única maneira de descrevermos um sistema de N elétrons. Mostraremos que a densidade de carga pode ser usada para determinar unicamente o potencial V r i e assim simplificar a descrição do sistema de N elétrons Teorema de Kohn e Hohenberg A densidade de elétrons em uma posição r é relacionada com a função de onda da seguinte forma n(r)=2 ψ i (r)ψ i(r), (2.3) i ondeψ i (r)ψ i(r) é definido como a probabilidade de que um elétron esteja na posição r. A somatória é multiplicada por um fator 2 devido ao princípio de exclusão de Pauli, onde cada função de onda de único elétron pode ser ocupada por dois elétrons de spins diferentes. A densidade de elétrons é uma função de três coordenadas, enquanto a função de onda é uma função de 3N coordenadas. Porém, segundo os dois teoremas desenvolvidos por Kohn e Hohenberg (KH) a densidade de elétrons tem informação suficiente para resolver a equação de Schrödinger. Os teoremas de Kohn e Hohenberg foram desenvolvidos na década de 1960, sendo o
25 24 primeiro teorema: O estado fundamental de energia da equação de Schrödinger é um funcional única da densidade de elétrons. Dessa forma o primeiro teorema de KH implica que a densidade de elétrons do estado fundamental determina todas as propriedades físicas do estado fundamental: energia, função de onda, etc. Como a densidade de elétrons é uma função de três variáveis, o problema de resolver a equação de Schrödinger passa de um problema de 3N variáveis (no formalismo da função de onda) para um problema de somente três variáveis. Embora o primeiro teorema de KH prove que o funcional da densidade de elétrons existe, não diz como podemos obter esse funcional. O segundo teorema de Kohn e Hohenberg define uma importante propriedade do funcional da densidade de elétrons: o funcional da energia nos dá o estado fundamental de energia do sistema, se e somente se, a densidade de elétrons for a densidade de elétrons do estado fundamental. Ou seja, a energia passa a ser a energia do estado fundamental somente se a densidade de elétrons for a densidade de elétrons do estado fundamental. Se o verdadeiro funcional da energia fosse conhecido, bastaria variar a densidade de elétrons até que a energia do sistema fosse mínima. Não existe ainda uma forma analítica do funcional da energia, mas existem aproximações que podem ser usadas para calcular soluções para a equação de Schrödinger. O funcional da energia pode ser escrito separando os termos conhecidos analiticamente dos termos de troca e correlação: E[n(r)]= E C [n(r)]+ E XC [n(r)] (2.4) onde E C [n(r)] são os termos cuja forma analítica é conhecida e E XC [n(r)] são todos os outros tipos de interação que não podem ser descritos analiticamente. Os termos de energia conhecidos analiticamente são: E C [n(r)]= h2 ψ i m 2 ψ i d 3 r+ V(r)n(r)d 3 r+ e2 n(r)n r 2 r r d 3 r d 3 r + E íons, i (2.5) onde os termos a direita da igualdade são, em ordem: a energia cinética dos elétrons, a interação Coulombiana entre elétrons e os núcleos atômicos, a interação Coulombiana entre pares de elétrons, e a interação entre pares de núcleos. O termo de troca e correlação do funcional da energia na equação 2.4 pode ser calculado usando um conjunto de equações de
26 25 Kohn e Sham (equações KS). As equações KS têm a forma: h 2 2m 2 +V(r)+V H (r)+v XC (r) ψ i (r)=ǫ i ψ i (r) (2.6) onde V(r) é o potencial de correlação entre elétrons e núcleos atômicos, V H (r) é o potencial de Hartree e V XC (r) é o potencial de troca e correlação. A solução da equação 2.6 é a função de onda de um único elétron que depende somente de três coordenadas espaciais. n r V H (r)= e 2 r r d 3 r. (2.7) O potencial de Hartree da equação 2.7 descreve a repulsão elétrica entre um elétron (o elétron de índice i considerado na equação 2.6) e todos os elétrons do problema. O potencial de Hartree inclui termo de auto-repulsão, ou seja, termo em que o elétron aplica uma força de repulsão em si mesmo. O termo de auto-repulsão do potencial de Hartree é um efeito não físico desse modelo de cálculo, que é corrigido no termo de troca e correlação. O potencial de troca e correlação pode ser visto como a derivada da energia de troca e correlação: V XC (r)= δe XC[r] δn(r) (2.8) onde a derivada em questão não é exata, já que não é derivada de uma função simples, mas de um funcional. A solução das equações KS ocorre da seguinte forma: inicialmente um potencial de Hartree deve ser definido, e para definir um potencial de Hartree é necessário conhecer a densidade de elétrons. Para calcular a densidade de elétrons é necessário conhecer as funções de onda de único elétron e para calcular essas funções de onda devemos resolver as equações KS. Sendo assim, a solução das equações KS deve ser obtida de forma iterativa: inicialmente é definida uma densidade de elétrons (não necessariamente a densidade de elétrons do estado fundamental), depois as equações KS são resolvidas tendo como solução as funções de onda de único elétron (ψ(r)), seguido do cálculo da nova densidade de elétrons (n(r)=2 ψ i (r)ψ i(r)). O processo iterativo termina quando a mudança na i densidade de elétrons entre iterações consecutivas é insignificante.
27 Funcional de Correlação e Troca Para resolver as equações KS devemos ter um funcional de troca e correlação, E XC [n(r)]. A teoria de Hohenberg e Kohn garante a existência de um funcional de troca e correlação, mas não diz como obter uma. Existe um caso onde o funcional de troca e correlação é conhecida: o gás de elétrons uniforme. Em um gás de elétrons uniforme a distribuição da densidade de elétrons é uma constante, n(r) = constante. Então, podemos definir o potencial de troca e correlação como: V XC (r)=v gás XC [n(r)] (2.9) onde V gás XC [n(r)] é o potencial do gás de elétrons para uma determinada densidade de elétrons. Essa aproximação usa a densidade local de elétrons para definir o potencial de troca e correlação, e é conhecida como aproximação de densidade local (local density approximation, LDA). A aproximação LDA nos dá uma solução aproximada da equação de Schrödinger. Para obter a solução exata da equação de Schrödinger seria necessário conhecer o termo de troca e correlação exato. Existem outros esquemas de aproximação do termo de troca e correlação mais complexos. A pesquisa para o desenvolvimento de novas funcionais, que se aproximem mais do verdadeiro funcional de troca e correlação, é um campo de pesquisa de grande interesse na física e na química. O conjunto mais conhecido de funcionais é aproximação generalizada do gradiente (generalized gradient approximation, GGA). GGA inclui mais informação do que LDA, já que inclui o gradiente local da densidade de elétrons Cálculo de Frequências Como as vibrações de uma molécula podem ser medidas experimentalmente, é de grande interesse o cálculo das frequências de vibração usando DFT. O espectro vibracional é uma ferramenta importante na classificação e identificação de sólidos e outras substâncias. Consideremos uma molécula diatômica com átomos fictícios A 1 e A 2, e a ligação química que mantem esses átomos ligados. A ligação química está sobre o eixo x, logo o estiramento associado a vibração dessa molécula diatômica é s= x 2 x 1. A expansão de Taylor da energia
28 27 em função do estiramento s na posição de equilíbrio s 0 é dada por: E=E 0 + de s s d 2 E s s0 ds s s 0 2 ds (2.10) s s 0 A derivada primeira na equação 2.10 é zero já que a expansão de Taylor é em torno de um ponto de mínima energia. Para pequenos deslocamentos, negligenciamos termos de ordem maior que dois. Essa aproximação é chamada de aproximação harmônica. A expressão reduzida da energia em função do comprimento do estiramento da ligação química entre os átomos A 1 e A 2 é: ondeα= d 2 E ds 2 s s 0. A equação de movimento do estiramento é: E=E 0 + α 2 s s0 2, (2.11) d 2 s(t) m2 +m 1 s s0 dt 2 =α m 2 m 1 (2.12) onde m 1 e m 2 são as massas dos átomos A 1 e A 2, respectivamente. A solução da equação m2 +m é conhecida s= s 0 +acosωt, onde a é uma constante arbitrária eω= α. m 2 m 1 A frequência de vibração é dada por ν= ω 2π = 1 m2 +m 1 α. (2.13) 2π m 2 m 1 Para calcular a frequência de vibração da molécula diatômica usando DFT duas informações são necessárias: o comprimento da ligação química que minimiza a energia da molécula e a segunda derivada da energia. Em cálculos DFT não dispomos de uma expressão analítica para a segunda derivada da energia, mas podemos aproximar a derivada segunda usando a seguinte expressão: d 2 E E s0 +δs 2E s 0 + E s0 δs = ds 2 2 (2.14) s δs0 0 que é válida para pequenos estiramentosδs.
29 28 Além da aproximação dada ao cálculo da frequência na teoria DFT, a equação de Schrödinger não tem solução exata nesse método. Dessa forma, os valores das frequências observados não são iguais aos valores calculados usando o método DFT, mas suficientemente próximos para uma boa descrição dos modos de vibração. Uma solução mais geral para o cálculo das frequências de uma molécula pode ser obtido se considerarmos uma molécula com N átomos, com 3N coordenadas cartesianas associadas aos N átomos escritas em um vetor, q= q 1,...,q 3N. Se o vetor de coordenadas cartesianas no qual a molécula se encontra em um mínimo local de energia é q 0, podemos definir uma nova coordenada como sendo x=q q 0. A expansão da série de Taylor em torno da posição de mínimo de energia para uma molécula de N átomos é E=E N 3N i=1 j=1 2 E x i x j x=0 x j x j. (2.15) As derivadas parciais da equação 2.15 podem ser substituídas por uma matriz com 3N linhas e 3N colunas conhecida como matriz Hessiana, cujos elementos são 2 E H i j =. (2.16) x i x j Se considerarmos as forças agindo sobre o sistema de N átomos, temos: x=0 d 2 x dt2= Ax, (2.17) onde A é uma matriz de 3N linhas e 3N colunas cujos elementos são A i j = H i j m i. A solução da equação 2.17 é dada como uma combinação dos modos normais de vibração x(t)= 3N i=0 ai cos(ωt)+ b i sen(ωt) e i, (2.18) onde a i e b i são constantes. Os modos normais de vibração podem ser vistos como uma descrição completa dos átomos de uma molécula. Para calcular os modos normais de vibração usando o método DFT, a matriz Hessiana
30 29 deve ser calculada usando a seguinte aproximação: H i j = 2 E x i x j x=0 = E δx i,δx j 2E0 + E δx i, δx j, (2.19) δx i δx j onde E δx i,δx j é a energia quando somente as coordenadas xi e x j não são nulas. A partir dos elementos da matriz Hessiano, a matriz A pode ser calculada e por consequência os λi autovalores,ν i =, e os autovetores que por sua vez definem o movimento da molécula 2π para as 3N 6 frequências Intensidade dos Espectros Raman e Infravermelho Além das frequências dos modos de vibração, para obter o espectro completo pela teoria DFT, geralmente são calculadas as intensidades de espectros Raman e infravermelho. A espectroscopia Raman é uma técnica baseada no espalhamento inelástico da luz. Como o espalhamento é feito de forma inelástica, a luz monocromática incidente (geralmente laser monocromático) muda após interação com a amostra. Fótons da luz incidente são absorvidos pela amostra e depois emitidos com uma frequência diferente da luz absorvida. A mudança da frequência de luz emitida em relação a frequência da luz absorvida é chamado de efeito Raman. O efeito Raman é baseado na deformação da distribuição eletrônica determinada pela polarizabilidade α. A luz incidente pode ser considerada como uma onda eletromagnética com vetor campo elétrico E oscilante, que após interagir com a amostra induz uma polarização P=αE que é capaz de deformar a distruibuição eletrônica. A luz monocromática, de um laser por exemplo, transforma as moléculas da amostra em dipolos oscilantes. As moléculas excitadas pela luz monocromática podem emitir luz com três frequências diferentes: Espalhamento Rayleigh: onde a luz incidente de frequênciaν 0 não é absorvida e é emitida sem deslocamento de frequência. Espalhamento Stokes: esse tipo de espalhamento é um espalhamento do tipo Raman, onde um fóton de frequênciaν 0 é absorvido pelo modo Raman ativo, e a luz emitida tem frequênciaν 0 ν m, ondeν m é a frequência de vibração da molécula.
31 30 Espalhamento Anti-Stokes: esse tipo de espalhamento também é um espalhamento Raman, onde um fóton de frequênciaν 0 é absorvido por uma molécula Raman ativa que já se encontra em um estado excitado de energia. Nesse caso, a molécula emite a energia em excesso em forma de luz com frequênciaν 0 +ν m. A maior parte do espalhamento de luz, mais de 99,9%, é do tipo espalhamento Rayleigh, enquanto menos de 1% é espalhamento inelástico (Raman ativo). A intensidade do espalhamento[21 23] é dada por I= N l 64π 2 3c 2 ν0 ± ν 4 Plm 2, (2.20) onde N l é o número de moléculas no estado inicial l,ν 0 é a frequência de radiação incidente, ν é o deslocamento da frequência, e P lm é a probabilidade de transição de um estado quântico. Quando l= m não temos o espalhamento elástico de Rayleigh. Nos cálculos do espectro vibracional usando DFT a intensidade de espalhamento Raman pode ser estimada com a derivada da polarizabilidade em relação a uma coordenada normal. A intensidade Raman calculada usando a aproximação harmônica é dada por 4 I Raman = (2π)4 45 h ω0 ω i 8π 2 cω i 1 e T) S i, (2.21) ( hcω i/k B onde S i é o fator de espalhamento Raman calculado em função das derivadas da polarizabilidade. Moléculas absorvem a radiação infravermelha em frequências características de sua estrutura. As absorções ocorrem em frequências ressonantes onde a frequência de vibração da molécula é a mesma da radiação incidente, sendo que sua intensidade é calculada como a derivada do momento de dipolo em relação a uma coordenada normal. 2.2 Dinâmica Molecular O objetivo da Dinâmica Molecular é modelar, com rigor de detalhes, propriedades física e químicas de sistemas de muitos corpos. A Dinâmica Molecular é uma técnica usada para investigar o equilíbrio e transporte de partículas em sistemas de muitos corpos. O movi-
32 31 mento dos núcleos atômicos é geralmente modelado usando-se as leis da Mecânica Clássica. Existem aplicações da Mecânica Quântica na Dinâmica Molecular, mas muitos problemas podem ser resolvidos com boa aproximação aos resultados experimentais usando-se somente a Mecânica Clássica. O método da Dinâmica Molecular foi primeiro introduzido por Alder e Wainwright[24], no final da década de 50, ao estudar a interação de esferas rígidas. Muitos estudos importantes surgiram a partir da contribuição de Alder e Wainwright, principalmente no estudo de líquidos simples. Outra grande contribuição para a Dinâmica Molecular ocorreu em 1964 quando Rahman[25] conduziu a primeira simulação usando um potencial não fictício para argônio líquido. A primeira simulação de uma molécula foi realizada por Rahman e Stillinger[26] para água em estado líquido. A primeira simulação de proteína ocorreu em 1977 com a simulação de um inibidor da tripsina pancreática bovina[27]. Hoje, encontramos na literatura uma grande variedade de métodos e aplicações em Dinâmica Molecular Teoria de Car-Parrinello A teoria de Car-Parrinello combina a descrição quântica da dinâmica dos elétrons com a descrição clássica da dinâmica dos núcleos atômicos em uma única estrutura. Devido a grande diferença nas massas e escalas de tempo entre elétrons e núcleos atômicos, podemos separar a dinâmica dos núcleos atômicos e a dinâmica dos elétrons por meio da aproximação adiabática. O movimento dos núcleos atômicos pode ser considerado clássico. Então a dinâmica dessas partículas é regida pelas equações de Newton, enquanto a dinâmica dos elétrons recebe um tratamento quântico. A ideia principal por traz da teoria de Car-Parrinello é tratar a evolução dos graus de liberdade eletrônicos usando um sistema fictício para os graus de liberdade eletrônicos, sendo a dinâmica dos elétrons e dos núcleos atômicos descrita por equações acopladas de Lagrange extendidas. A aproximação adiabática é mantida com a escolha correta da massa fictícia dos elétrons, onde as equações de movimento dos estados eletrônicos não interferem diretamente na dinâmica dos núcleos atômicos. Ao contrário da dinâmica molecular de Born-Oppenheimer (BO), a minimização eletrônica ocorre somente no início da dinâmica molecular. A dinâmica fictícia dos elétrons os mantêm próximos ao estado fundamental a
33 32 cada nova configuração dos núcleos atômicos. Para que a condição adiabática se mantenha durante a dinâmica molecular é necessário que a massa fictícia dos elétrons seja pequena o suficiente para que não haja grande transferência de energia entre os graus de liberdade eletrônico e iônico. Além disso, as equações de movimento devem ser integradas em pequenos tempos discretos da ordem de fs (10 15 segundos). Car e Parrinello[3] postularam o Lagrangiano dado pela equação abaixo 1 = 2 µ d 3 r ψi MIṘ2 I µ v α 2 v E {ψ i },{R I },{α v }, (2.22) i Ω I onde os orbitaisψ i devem obedecer à condição de ortonormalidade v d 3 rψ i (r, t)ψ j(r, t)=δ i j. (2.23) Ω Os termos a direita da equação 2.22 são, em ordem: a energia cinética dos orbitais (parte eletrônica do problema), a energia cinética dos núcleos atômicos, energia cinética das restrições ao sistema (volume, por exemplo) e energia potencial. Onde M I é a massa de cada núcleo atômico,µeµ v são parâmetros arbitrários. O Lagrangiano da equação 2.22 gera as seguintes equações de movimento: µ ψ i (r, t)= δe δψ i (r, t)+ Λ ik ψ k (r, t), (2.24) k M I R i (t)= Ri E, (2.25) µ v α v = E α v. (2.26) ondeλ ik são os multiplicadores de Lagrange que são introduzidos para satisfazer a condição de ortonormalidade da equação A dinâmica dos núcleos atômicos da equação 2.25 tem significado físico, enquanto as dinâmicas dos orbitais, ψ i, e das restrições ao sistema (como o volume, por exemplo), α v, são fictícias. Dadas as seguintes condições: (i) se a massa fictícia µ for suficientemente pequena, e (ii) se as equações de movimento forem integradas em intervalos de tempo discretos da ordem de f s, na condição de mínimo de energia a Lagrangiana da equação 2.22 descreve um sistema físico sobre a superfície adiabática.
34 33 Em termos gerais, uma dinâmica molecular de Car-Parrinello evolui seguindo os seguintes passos: (i) a solução das equações KS garante que o sistema esteja no estado fundamental (os orbitais são minimizados), (ii) forças são aplicadas sobre os núcleos atômicos, atualizando o tempo, t, para os núcleos, ao mesmo tempo, as forças fictícias são aplicadas sobre os orbitais, atualizando o tempo para os orbitais. O sistema é levado a uma nova configuração sobre a superfície adiabática. (iii) repete o processo a partir do passo (ii). Cada passo na dinâmica nuclear é acompanhado de um passo na dinâmica eletrônica. A completa minimização dos orbitais ocorre somente no início da simulação. Se µ for pequeno o suficiente, a nova configuração eletrônica permanece próxima do estado fundamental durante a evolução da dinâmica dos núcleos atômicos. Por outro lado, µ deve ser grande o suficiente para que os incrementos de tempo, t, não sejam muito pequenos, resultando em um menor custo computacional da integração das equações de movimento. Então Car-Parrinello se resume a uma técnica de simulação que faz o sistema evoluir sempre próximo ao seu estado fundamental, mas que o real estado fundamental nunca é alcançado. A distância do estado eletrônico comparado com o estado fundamental é controlado pela massa fictíciaµ.
35 34 3 MODOS NORMAIS DE VIBRAÇÃO 3.1 Introdução Os espectros Raman e infravermelho são ferramentas importantes no estudo da matéria sólida. Os espectros obtidos de um material são função de características estruturais e geométricas das moléculas constituintes da matéria. Sendo assim, entender a estrutura e a geometria das moléculas constituintes da matéria sólida é de grande importância na classificação dos espectros Raman e infravermelho. Podemos, sem exageros, nos referir ao espectro vibracional como impressão digital da estrutura molecular da matéria. Apesar dos avanços tecnológicos da espectroscopia Raman e infravermelho, somente algumas moléculas de poucos átomos podem ter seus espectros vibracionais classificados de forma analítica. Existem dificuldades experimentais na classificação dos espectros vibracionais, como a sobreposição de linhas espectrais ou a pouca simetria de moléculas. Como consequência das dificuldades experimentais, existe um grande interesse no desenvolvimento de técnicas de cálculo que possam determinar as frequências e intensidades de vibração. A análise das coordenadas normais é uma ferramenta de cálculo das frequências de vibração que são relacionadas com a geometria e constantes de força da molécula. A análise das coordenadas normais é feita usado a distribuição de energia potencial[5, 28] (Potential Energy Distribution, PED) que é a distribuição da energia em cada modo de vibração de uma molécula. PED é usada na análise do espectro vibracional, com o objetivo de classificar os modos vibracionais, relacionando o espectro observado com o espectro obtido através de cálculos de primeiros princípios e um conjunto de coordenadas internas. Dessa forma, a análise das coordenadas normais depende do conjunto de constantes de força e da geometria da molécula em estudo. Geralmente obtemos as constantes de força e a geometria da molécula
36 35 através de cálculos de primeiros princípios como cálculos ab initio usando a técnica DFT. No cálculo do PED usamos o método da mecânica clássica onde as vibrações são calculadas usando a aproximação harmônica e as frequências são determinadas pela solução da equação secular que relaciona energia cinética e potencial. Na nossa análise, usamos coordenadas internas que representam os graus de liberdade de uma molécula, menos as translações e rotações da molécula como um todo, ou seja, as coordenadas internas representam unicamente as vibrações de uma molécula. PED quantifica a contribuição de cada coordenada interna[29] aos modos vibracionais. Dessa forma, o problema de classificação dos modos vibracionais passa a ser um procedimento simples, principalmente se o cálculo é conduzido com o auxílio do software PEDCALC que desenvolvemos durante esse trabalho. 3.2 Equação Secular Uma molécula não linear tem 3N 6 modos normais de vibração, onde N é o número de átomos, enquanto uma molécula linear tem 3N 5 modos normais de vibração. Não incluímos nesses números os movimentos de translação e rotação da molécula como um todo. Cada modo normal de vibração pode ser descrito por uma série de coordenadas, podendo ser uma combinação de comprimentos das ligações químicas e ângulos entre essas ligações. Nesse caso, os 3N 6 graus de liberdade do sistema podem ser representados por coordenadas internas ou combinação dessas. Dentre as vantagens do uso das coordenadas internas destacamos: (i) capacidade de representar com maior clareza os movimentos internos de uma molécula, (ii) facilidade de tranferência, já que não necessitam de um referencial específico. Os deslocamentos dos átomos em uma molécula a partir da posição de equilíbrio podem ser representados pelo conjunto de coordenadas cartesianas X 1, Y 1, Z 1 para o átomo 1, X 2, Y 2, Z 2 para o átomo 2, X N, Y N, Z N para o átomo N, ou de maneira mais geral, q 1, q 2, q 3,..., q 3N. Usamos 3N coordenadas porque essas representam os graus de liberdade do sistema. Os átomos podem se movimentar nos três eixos cartesianos. Por conveniência 1, ex- 1 Assim não precisamos escrever as massas na equação secular, o que simplifica a equação matricial 3.10.
37 36 pressamos as coordenadas q i na forma q 1 = m 1 X 1, q 2 = m 1 Y 1, q 3 = m 1 Z 1, q 4 = m 2 X 2, etc. (3.1) onde m 1, m 2,..., m N são as massas dos átomos. As 3N coordenadas q i, onde i= 1, 2, 3,... 3N, são usadas para expressar a energia cinética T em termos da derivada temporal 2T= 3N i=1 q 2 i onde q i = dq i dt. (3.2) A energia potencial é uma função do deslocamento. Se os deslocamentos forem pequenos, podemos expandir a energia potencial V em função das coordenadas q em uma série de potências em torno da configuração de equilíbrio: 2V = 2V 0 +2 = 2V N i=1 3N i=1 V q i + q i f i q i + 0 3N i, j=1 3N i, j=1 2 V q i q j 0 q i q i +... f i j q i q i (3.3) Como temos liberdade para escolher o referencial de energia, para simplificar a expressão da energia potencial fazemos V= 0 na origem. Aplicando a derivada na origem, onde temos um mínimo de energia, teremos: V = 0 f i = 0 i= 1, 2, 3,... 3N. q i Para amplitudes de vibração suficientemente pequenas podemos negligenciar os termos maiores que o quadrado de q i, então 2V= 3N i, j=1 f i j q i q j, (3.4) onde as constantes de força são dadas por 2 V f i j = f ji =. (3.5) q i q j 0
38 37 As equações de Euler-Lagrange podem ser escritas como: d dt T q i + V q i = 0 i= 1, 2, 3,... 3N. (3.6) Podemos simplificar a equação 3.6 com uma substituição simples da energia cinética e energia potencial q j + 3N i=1 f i j q i = 0 j= 1, 2, 3,... 3N. (3.7) Essa é a equação de um oscilador harmônico de ordem 3N, cuja solução é conhecida q i = A i cos λ 1 2 t+ε, (3.8) ondeλ, A i eεsão constantes. Substituindo o valor de q i da equação 3.8 na equação 3.7 obtemos 3N i=1 fi j δ i j λ A i = 0 j= 1, 2, 3,... 3N, (3.9) ondeδ i j = 0 quando i j, eδ i j = 1 quando i= j. A equação 3.9 pode ser vista na forma matricial como f 11 λ f f 1,3N f 21 f 22 λ... f 2,3N = 0. (3.10) f 3N,1 f 3N,2... f 3N,3N λ Na equação 3.10 temos a equação secular na forma matricial em coordenadas cartesianas. Com isso podemos aplicar propriedades de determinantes para obter soluções. Devemos observar que devido à maneira que escolhemos as coordenadas f i j = F i j mi m j, (3.11) onde F i j é uma constante de força conhecida. Os F i j são constantes de força geralmente obtidas através de cálculos ab initio, já os f i j são constantes de força ajustadas para o conjunto de coordenadas q i de forma que a equação secular não apresente termos explicitos das massas dos átomos envolvidos. A equação secular tem 3N soluções, sendo que para molécu-
39 38 las não lineares seis 2 soluções não representam vibrações. Essas soluções em queλ=0 são translações e rotações da molécula como um todo. 3.3 Coordenadas Internas Os tipos de coordenadas internas mais comuns são mudanças nos comprimentos das ligações químicas e os ângulos entre essas ligações a partir de uma posição de equilíbrio. O uso dessas coordenadas é apropriado, pois a ideia de forças químicas mostra que essas forças produzem uma resistência às mudanças dos comprimentos das ligações químicas e aos ângulos entre essas ligações de suas posições de equilíbrio. Os principais tipos de coordenadas internas são apresentadas na tabela 3.1. Tabela 3.1: Principais tipos de coordenadas internas. Coordenada estiramento deformação no plano torção deformação fora do plano Descrição mudança no comprimento de uma ligação química mudança no ângulo entre ligações químicas mudança em um ângulo diedral formado pelas ligações químicas mudança no ângulo entre ligação química e o plano da molécula A relação entre coordenadas internas e coordenadas cartesianas é dada pela seguinte transformação de coordenadas S t = 3N i=1 B ti q i t= 1, 2, 3,..., 3N 6, (3.12) e de forma simplificada S=BX, (3.13) 2 Para moléculas lineares são cinco soluções comλ=0.
40 39 que podemos expandir como S 1 B 11 B q 1 S 2 = B 21 B q 2. (3.14) Como mostra a equação 3.12, as coordenadas internas são uma combinação das coordenadas cartesianas, onde B ti são constantes que dependem da geometria da molécula. A matriz B é a matriz de transformação do sistema de coordenadas cartesiano para o sistema de coordenadas internas. A matriz B tem 3N 6 linhas e 3N colunas para moléculas não lineares, ou 3N 5 linhas e 3N colunas para moléculas lineares. Cada linha da matriz B representa a mudança nas coordenadas cartesianas para uma coordenada interna, sendo as coordenadas cartesianas de cada átomo indexadas de três em três em cada linha. Ou seja, em uma linha as três primeiras colunas são coordenadas cartesianas do primeiro átomo, e as três colunas seguintes são coordenadas cartesianas do segundo átomo e assim por diante. Para tornar a notação mais compacta, usamos um vetor α que representa o deslocamento em coordenadas cartesianas do átomoα, substituindo as coordenadas cartesianas q i, q i+1 e q i+2. Assim obtemos uma notação mais simples para a definição das coordenadas internas: N S t = s tα α, (3.15) α=1 onde s tα e α são vetores. O significado físico de s tα é a direção em que o átomoαdeve ser deslocado para produzir a maior mudança na coordenada interna S t. Abaixo listamos as quatro principais coordenadas internas e os respectivos vetores s tα que compõem a matriz B Estiramento O estiramento é uma coordenada interna muito simples, mostrada na figura 3.1, que representa a mudança na distância entre os átomos. Os vetores s t1 e s t2 representam a mudança na distância interatômica. É evidente que a direção mais favorável é dada pelos vetores unitários e 12 e e 21, que têm a mesma direção dos vetores s t1 e s t2, respectivamente.
41 40 s t1 r s t2 Figura 3.1: Representação da coordenada interna estiramento. Nessa coordenada, os átomos 1 e 2 se deslocam de acordo com os vetores s t1 e s t2, respectivamente. s t1 = e 21 = e 12 s t2 = e 12. (3.16) A notação de vetores unitários foi escolhida de tal forma que e x y aponta do átomo x para o átomo y Deformação no Plano A coordenada de deformação no plano, ou simplesmente deformação, é dada pelo ângulo formado pela interseção de duas ligações químicas que têm um átomo em comum. Essas ligações químicas são representadas pelos segmentos de reta r 31 e r 32, como mostrado na figura 3.2. Três átomos estão envolvidos nesse tipo de coordenada, um átomo central, aqui representado pelo átomo 3, e outros dois átomos, 1 e 2, sendo os três átomos não colineares. Os vetores s t1, s t2 e s t3 mostram a direção do movimento desses átomos que induz a maior variação da coordenada S t = φ 3 s t1 r 31 s t3 r 32 s t2 1 φ 2 Figura 3.2: Representação da coordenada interna deformação no plano. Nessa coordenada, os átomos 1, 2 e 3 vibram de acordo com os vetores s t1, s t2 e s t3,
42 41 respectivamente. Como a deformação no plano é uma coordenada interna, o centro de massa da molécula não deve ser afetado, logo a soma de todos os vetores s ti deve ser nula 3. s t3 = s t1 s t2, (3.17) Os vetores s t1 e s t2 são perpendiculares a r 31 e r 32, respectivamente. O comprimento do vetor s t1 é de 1, já que um deslocamento de uma unidade na direção de s t1 aumenta o r 31 ânguloφ de 1. De maneira análoga, s t2 tem comprimento 1, e de acordo com a equação r 31 r s t3 tem comprimento s t1 +s t2. Os vetores unitários e 31 e e 32 têm a mesma direção que os vetores s t1 e s t2, respectivamente. Podemos definir os deslocamentos dos átomos na coordenada deformação em função desses vetores unitários. s t1 = e 31 e 31 e 32 r 31 sinφ = e 31 e31 e 32 e32 e31 e 31 r 31 sinφ = e 31cosφ e 32 r 31 sinφ. (3.18) Realizando um cálculo similar para o caso do vetor s t2 e com o auxílio da equação 3.17 para o vetor s t3, podemos obter as seguintes relações: s t1 = cosφe 31 e 32 r 31 sinφ, (3.19) s t2 = cosφe 32 e 31 r 32 sinφ, (3.20) r31 r 32 cosφ e 31 + r 32 r 31 cosφ e 32 s t3 = r 31 r 32 sinφ 3 Aqui estamos considerando o caso simples e uma molécula de três átomos.. (3.21)
43 Torção A coordenada interna de torção é dada pela mudança do ângulo diedral, τ, formado pelos planosπ 1,2,3 eπ 2,3,4, respectivamente, onde 1, 2, 3 e 4 são átomos representados na figura φ 2 r r 23 r 34 φ 3 4 Figura 3.3: Representação da coordenada interna de torção. A definição da coordenada interna torção,τ, é dada pela seguinte relação: e12 e 12 e23 e 34 cosτ=, (3.22) sinφ 2 sinφ 3 onde o ânguloτestá compreendido no intervalo π<τ π, de forma queτépositivo quando o átomo 2 estiver mais perto do observador do que o átomo 3, quando visto ao longo da ligação química 2, 3. O ângulo τ é visto como a projeção de 2, 1 e 3, 4 na direção horária. s t1 = e 12 e 23 r 12 sin 2 φ 2, (3.23) s t2 = r 23 r 12 cosφ 2 r 23 r 12 sinφ 2 e 12 e 23 sinφ 2 + cosφ 3 r 23 sinφ 3 e 43 e 32 sinφ 3, (3.24) s t3 = r 32 r 43 cosφ 3 r 32 r 43 sinφ 3 e 43 e 32 sinφ 3 + cosφ 2 r 32 sinφ 2 e 12 e 23 sinφ 2, (3.25) s t4 = e 43 e 32 r 43 sin 2 φ 3. (3.26)
44 Deformação Fora do Plano É a coordenada formada pelo ângulo entre uma ligação química e o plano de três átomos. A figura 3.4 mostra que o átomo 1 está fora do planoπformado pelos átomos 2, 3 e 4. A ligação química, representada por r 41, forma um ânguloθ com o planoπ. O ânguloθ é a coordenada de interesse, sendo s t1, s t2, s t3 e s t4 os vetores que mostram a direção preferencial de deslocamento dos átomos 1, 2, 3 e 4, respectivamente. Como definimos anteriormente, as vibrações em estudo são muito pequenas. No caso da coordenada deformação fora do plano, a vibração é tão pequena que podemos definir o comprimento do vetor s t1 como sendo o mesmo que o comprimento do arco formado quando o átomo 1 deixa o planoπ, s t1 = 1 r 41. s t1 = 1 r 41, (3.27) s t2 = sinφ 2 r 42 sinφ 1, (3.28) s t3 = sinφ 3 r 43 sinφ 1, (3.29) s t3 = 1 r 41 sinφ 2 r 42 sinφ 1 sinφ 3 r 43 sinφ 1. (3.30) 3.4 Equação Secular em Coordenadas Internas A energia cinética e a energia potencial em coordenadas internas são dadas pelas duas equações abaixo 2T= Ṡ G 1 Ṡ, (3.31) 2V= S FS (3.32) onde S e Ṡ são as coordenadas internas e derivada temporal das coordenadas internas, respectivamente. A matriz G 1 depende da geometria e massas atômicas. A matriz G é definida
45 44 3 r 43 φ 2 φ 1 1 r 41 4 φ 3 r 42 2 Figura 3.4: Representação da coordenada de deformação fora do plano. como ou na forma matricial G t t = 3N i=1 1 m i B ti B t i t, t = 1, 2,..., 3N 6, (3.33) G=BM 1 B, (3.34) onde M é um vetor coluna de 3N elementos representado a massa dos átomos da molécula, sendo os elementos da forma m i = m i+1 = m i+2 para o átomo de índice i de um total de N átomos. As coordenadas internas são definidas em função das coordenadas normais através da transformação de coordenadas S=LQ, (3.35) onde S são as coordenadas internas, Q são coordenadas normais e L é a matriz de transformação das coordenadas normais em coordenadas internas. Para cada coordenada normal Q j todos os átomos de uma molécula vibram com mesma frequência e passam simultaneamente pela posição de equilíbrio. Cada modo normal de vibração é caracterizado por uma única coordenada normal e autovetor L j que determina a direção de vibração de cada átomo para o dado modo normal. A principal vantagem do uso das coordenadas normais é que a
46 45 equação secular na forma matricial é diagonalizada e cada linha representa uma vibração independente. Assim como as coordenadas internas, as coordenadas normais são linearmente independentes e formam uma base completa. Logo, a energia cinética e a energia potencial podem ser escritas no sistema de coordenadas normais: 2T= Q E Q, (3.36) 2V= Q ΛQ, (3.37) onde E é a matriz identidade,λéuma matriz cujos elementos diagonais são soluçõesλ j da equação secular, e Q é a derivada temporal das coordenadas normais Q. Substituindo a equação 3.35 nas equações 3.31 e 3.32 obtemos 2T= Q L G 1 L Q, (3.38) 2V= Q L FL Q, (3.39) que ao comparar com as equações 3.36 e 3.37 obtemos L G 1 L=E, (3.40) L FL=Λ. (3.41) As equações 3.40 e 3.41 combinadas dão origem à equação secular GFL = LΛ (3.42) onde o Hamiltoniano do sistema é dado por H=GF. Os parâmetrosλ j são autovalores da equação secular cuja relação com as frequências de vibração é dada por λ j = 4π2 c 2 ν j, (3.43) N onde N é o número de Avogadro, ν é o número de onda em cm 1 e c é a velocidade da luz. Soluções triviais para a equação secular não representam vibrações, já que nesse caso o parâmetroλ j é nulo. GF Eλ =0. (3.44)
47 46 As soluções da equação 3.9 são autovaloresλ j que são relacionados diretamente com as frequências de vibração e os autovetores L que representam a direção dos deslocamentos dos átomos para os 3N 6 modos normais de vibração. Podemos reescrever a equação 3.35 na forma matricial para especificar a relação entre autovetores e autovalores da equação secular S 1 l 11 l l 1N S 2 l = 21 l l 2N.... l i1 l i2... l in S N Q 1 Q 2. Q N. (3.45) Para cada autovalorλ N existe um autovetor dado por uma coluna da matriz L cujos elementos são l 1N,l 2N,...,l in. Cada coordenada normal Q N oscila com frequência relacionada com o parâmetroλ N, e as coordenadas internas oscilam com a mesma frequência cujas amplitudes relativas de oscilação são dadas pela razão dos componentes do autovetor daquela vibração. Sendo assim, se algum componente l ik do autovetor for muito maior que as outras componentes, o modo normal de vibração é atribuído à coordenada interna associada com essa componente do autovetor. Ou, no caso de duas (ou mais) componentes do autovetor terem valores muito maiores que as outras componentes, o modo normal é dito acoplado de duas (ou mais) vibrações de coordenadas internas S i e S j. 3.5 Aplicação da Matriz L para Obter a Distribuição da Energia Potencial A matriz L determina a direção de vibração dos átomos para cada modo normal de vibração. Sendo assim, podemos relacionar a energia potencial de cada modo vibracional com os elementos da matriz L. A distribuição da energia potencial determina a contribuição de cada coordenada interna à energia potencial. Logo, podemos relacionar os elementos da matriz L com a distribuição da energia potencial. Então, dadas as constantes de força e a solução da equação secular, podemos calcular o PED. Para desenvolver a relação dos elementos da matriz L com o PED, inicialmente escreve-
48 47 mos a energia potencial no sistema de coordenadas internas como 2V= S FS, (3.46) onde F é a matriz das constantes de força no sistema de coordenadas internas. Se substituirmos na equação 3.46, S=LQ e S = Q L, obtemos 2V= Q L FLQ. (3.47) A equação 3.47 pode ser reescrita como 2V k = Q 2 k F i j l ik l jk (3.48) i j para um dado modo normal de vibração. A energia potencial também pode ser escrita como 2V= λ i Q 2 i. (3.49) Comparando as equações 3.48 e 3.49 obtemos a seguinte relação i λ k = n F i j l ik l jk (3.50) i,j onde F i j l ik l jk é a energia potencial devido a uma coordenada interna, então, proporcionalmente a contribuição para o PED de uma coordenada interna é F i j l ik l jk PED= F i j l ik l jk. (3.51) i,j Como os termos diagonais das constantes de força contribuem muito mais que os outros termos, definimos a distribuição de energia potencial aproximada como F ii l 2 ik PED diagonal = F ii l 2. (3.52) ik i
49 48 A equação 3.52 é a fração de contribuição para a energia potencial de uma única coordenada interna. Esse fato é consequência da relação de uma linha da matriz L (autovetor) e o vetor de coordenadas normais, Q, da equação Mudança de Sistema de Coordenadas As constantes de força obtidas em cálculos de primeiros princípios estão geralmente no sistema de coordenadas cartesiano. Como o cálculo da distribuição da energia potencial é realizado sobre o sistema de coordenadas internas, devemos mudar o conjunto de constantes de força de forma que o cálculo da equação secular seja realizado no sistema de coordenadas internas. A mudança de sistema de coordenadas é realizado com uma transformação de similaridade[30]. As transformações de similaridade ocorrem de acordo com a equação abaixo F = AFA (3.53) onde A=mB BmB 1, e m é uma matriz 3N 3N das massas, diagonal, em que cada 3 elementos diagonais sequenciais representam as contribuições em termos de massa nas coordenadas x, y e z de um dado átomo. Na equação 3.53, F é uma matriz das constantes de força em coordenadas cartesianas, enquanto F é a matriz das constantes de força em coordenadas internas. 3.6 PEDCALC PEDCALC é um software desenvolvido durante esse trabalho com o objetivo de calcular a distribuição da energia potencial (PED) e assim facilitar a classificação dos modos de vibração de uma molécula. PEDCALC é um ferramente importante na classificação dos modos normais de vibração, já que obtemos um resultado numérico, exato, da contribuição de cada coordenada natural nos modos normais de vibração. PEDCALC dispõe de uma interface gráfica amigável. As vibrações moleculares podem ser observadas em tempo real, ou as imagens estáticas referentes às vibrações podem ser processadas por um software traçador de raios, usando setas para destacar o movimento dos átomos e um gradiente de cores para destacar a distribuição da energia potencial.
50 49 Como veremos a seguir, alguns cuidados devem ser tomados no procedimento de cálculo da distribuição da energia potencial. Mostraremos a estratégia que adotamos no software PEDCALC para evitar resultados falsos devido a possíveis coordenadas redundantes Coordenadas Naturais Os deslocamentos dos átomos em uma molécula podem ser representados por um conjunto de coordenadas internas, completo, e não redundante S i [5]. Sendo S i um sistema de coordenadas completo e não redundante, garantimos que a função potencial na equação 3.3 é única. Além disso, a transformação de coordenadas S=BX (3.54) não deve ser singular, ou aproximadamente singular[31], ou seja, a matriz simétrica BB não deve apresentar uma singularidade. Como mostraremos mais adiante, usaremos possíveis singularidades na matriz BB para detectar e remover coordenadas redundantes do nosso sistema. Como apontado por Baker[32] as coordenadas que satisfazem essas condições são coordenadas de valência, internas e locais, isto é, formadas por deformações, estiramentos, e suas combinações. Dizer que um sistema de coordenadas é local, significa que cada coordenada somente envolve um pequeno conjunto de átomos. Por outro lado, o sistema de coordenadas mais usual, o sistema de coordenadas cartesiano, não suporta facilmente transferência de coordenadas, já que na maior parte dos casos a origem dos sistema de coordenadas não coincide com o centro geométrico da molécula. Em termos gerais, damos preferência às coordenadas local-simétricas, ou seja, coordenadas naturais. Muitas das coordenadas naturais utilizadas nesse trabalho estão definidas na tabela 3.2. Devemos observar que: estiramentos devem ser incluídos nesse sistema de coordenadas como coordenadas individuais, combinações de estiramentos C H são permitidas no metil e metileno devido a simetria, e coordenadas em anéis (simetria D nh ) devem ser combinadas com o objetivo de manter a unidade e a alta simetria. No software PEDCALC as coordenadas internas quando adicionadas são listadas em uma
51 50 tabela na interface gráfica como mostrado na figura 3.5. Nessa tabela a primeira coluna é referente ao número da coordenada, a segunda coluna é uma etiqueta ou grupo associado a coordenada, a terceira coluna é o nome da coordenada. A quarta coluna é referente ao tipo de coordenada e a última coluna lista os átomos participantes de cada coordenada. A etiqueta ou grupo da coordenada pode ser usada para separar coordenadas semelhantes em diferentes regiões da molécula. Por exemplo, na figura 3.5 muitas coordenadas podem ser identificadas como sendo as listadas na tabela 3.2. Figura 3.5: Tabela das coordenadas naturais como apresentada na interface gráfica do software PEDCALC.
52 51 Tabela 3.2: Coordenadas Naturais propostas por Baker. Coordenadas Naturais torção torções devem somar todos os ângulos X i A BY j sym def=α 1 +α 2 +α 3 β 1 β 2 β 3 asym def=2α 1 α 2 α 3 metil asym def =α 2 α 3 rocking=2β 1 β 2 β 3 rocking =β 2 β 3 CH 2 scissoring=5α+γ CX Y scissoring=α 1 +5γ metileno(sp 3 ) CH 2 rocking=β 1 β 2 +β 3 β 4 CH 2 wagging=β 1 +β 2 β 3 β 4 CH 2 twisting=β 1 β 2 β 3 +β 4 sym def=2α β 1 β 2 metileno(sp 2 ) rocking=β 1 β 2 wagging=x fora do plano CH 2 CH rocking=β 1 β 2 metina(sp 2 ) XCY def=2α β 1 β 2 CH wagging=h fora do plano XCY CH rocking=2β 1 β 2 β 3 metina(sp 3 CH rocking =β ) 2 β 3 XCY def=4α X CY +α X C Z +α Y C Z deformações X C Z e Y Z C são definidas analogamente scissoring=2α β 1 β 2 amina rocking=β 1 β 2 wagging=x fora do plano NH 2 NH rocking=β 1 β 2 imina(sp 3 ) X NY def=2α β 1 β 2 wagging=h fora do plano X NY ring def=α anel - 4 átomos 1 α 2 +α 3 α 4 puckering=τ 1 τ 2 +τ 3 τ 4 ring def=α 1 +a α2 +α 5 + b α3 +α 4 anel - 5 átomos a ring def =(a b) α 2 α 5 +(1 a) α3 α 4 torsion= b τ 1 +τ 5 +a τ2 +τ 4 +τ3 torsion =(a b) τ 4 τ 2 +(1 a) τ5 τ 1 trigonal def=α 1 α 2 +α 3 α 4 +α 5 α 6 asym def=2α 1 α 2 α 3 +α 4 α 5 α 6 asym def =α anel - 6 átomos 2 α 3 +α 4 α 5 puckering=τ 1 τ 2 +τ 3 τ 4 +τ 5 τ 6 asym torsion=τ 1 τ 3 +τ 4 τ 6 asym torsion = τ 1 +2τ 2 τ 3 τ 4 +2τ 5 τ 6 a a= cos(144 ) b= cos(72 )
53 Identificação de Coordenadas Redundantes PEDCALC utiliza as coordenadas naturais introduzidas inicialmente por Baker et al[32] no cálculo do PED. Usamos essas coordenadas porque são intuitivas e transferíveis. O sistema de coordenadas naturais deve ser de tal forma que BB seja invertível para que não haja redundância no sistema de coordenadas. Dada uma matriz quadrada e simétrica K, podemos construir sua inversa usando os autovaloresλeautovetores R de forma que: K 1 = RΛ 1 R onde Λ 1 i j =λ 1 i δ i j. (3.55) BB também é uma matriz quadrada e simétrica, de forma que a inversa pode ser calculada usando a equação BB R=RΛ onde(λ) i j =λ i δ i j. (3.56) Com a solução da equação 3.56, obtemos autovalores de forma que a matriz BB possa ser invertida. Os autovetores R devem ser ortonormais: RR = R R=1. (3.57) Cada autovalor nulo obtido na equação 3.56 corresponde a uma coordenada redundante que deve ser removida pelo software PEDCALC. O auto-sistema pode ser rescrito colocando Λ em evidência usando a equação 3.57: R BB R =Λ. (3.58)
54 53 Se o autovalor de índice n 0 é zero: R i n0 BB i j R =Λ j n n0 = 0 0 i j = R i n0 B il R jl X j n 0 i j = X j n0 B jl l = R j n0 B jl = 0. j j l 2 Na última equação as coordenadas são linearmente dependentes. Para obter a coordenada redundante de índice j 0, para o autovalor nulo de índice n 0, PEDCALC obtém j 0 usando a condição R j0 n 0 =max R j n0 (3.59) onde max R j n0 significa o maior valor em uma linha da matriz de autovetores. PEDCALC força com que o usuário use somente coordenadas não-redundantes. A cada coordenada inserida, uma verificação da redundância da nova coordenada em relação as anteriores é realizada Constantes de Força PEDCALC importa dados do software Gaussian necessários para o cálculo da equação secular. Geralmente em um cálculo de otimização de geometria usando a teoria DFT no software Gaussian, obtemos as posições dos átomos na molécula em estudo, além do conjunto de constantes de força. Com o cálculo da equação secular obtemos autovetores usados no cálculo de PED. Os seguintes itens são importados do software Gaussian : coordenadas cartesianas de todos os átomos e contantes de força no sistema de coordenadas cartesiano. PEDCALC importa outros dados do software Gaussian, mas que não são utilizados diretamente na solução da equação secular. Usando os nomes dos átomos, PEDCALC importa os valores das massas de todos os átomos usando a tabela periódica interna ao software. Ao
55 Figura 3.6: Tabela com a contribuição das coordenadas internas para um modo de vibração. 54
56 55 montar a equação secular 3.10, ajustamos as constantes de força da seguinte forma: F i j f i j = mi m j onde F i j são elementos da matriz de constantes de força importadas do software Gaussian e m i, m j são massas dos átomos i e j. Com a solução da equação secular obtemos os autovetores e autovalores do sistema Esquema de Cores para o PED Na figura 3.7 temos um modo de vibração da molécula de benzonidazol 4 com número de onda calculado de 606 cm 1. Essa figura é obtida pela técnica de traçamento de raios. A cor vermelha representa a distribuição da energia potencial, enquanto as setas representam os autovetores calculados na equação secular. Quanto maior a seta, maior o autovetor, e portanto maior a amplitude da vibração do átomo tomado como origem da seta. E quanto mais próximo da cor vermelha for a cor de um determinado átomo, maior será a contribuição daquele átomo na distribuição da energia potencial. Cada átomo pode participar de uma ou mais coordenadas internas. Se um átomo participa de mais de uma coordenada, a contribuição de cada coordenada para o PED é adicionada em forma de cor do átomo. Assim, formamos um gradiente de cores do verde ao vermelho, onde a cor verde representa pouca ou nenhuma contribuição para o PED e a cor vermelha representa grande contribuição de um átomo para o PED. No cálculo do esquema de cores do PED cada átomo contribui com a porcentagem das coordenadas as quais pertence. De forma que um único átomo não pode contribuir mais do que 100%. Porém, uma coordenada interna é composta pela participação de pelo menos dois átomos. Sendo assim, se somarmos a contribuição de todos os átomos, certamente obteremos uma soma maior do que 100%. Por exemplo, para uma molécula diatômica, temos somente um modo de vibração caracterizado pela coordenada de estiramento. A coordenada de estiramento em questão contribui com 100% já que é a única coordenada interna. Se atribuirmos uma contribuição de 100% para o primeiro átomo e uma contribuição de 100% para o segundo átomo, os átomos juntos contribuem com 200%. Estamos interessados em uma 4 Os cálculos sobre a molécula de benzonidazol serão discutidos no próximo capítulo.
57 56 comparação das contribuições relativas de cada átomo em um modo de vibração. Para isso normalizamos a contribuição de cada átomo, e os valores normalizados dessas contribuições são atribuídos as intensidades de cor de cada átomo. Sendo assim, para uma molécula diatômica, cada átomo tem a mesma intensidade de cor. Já para moléculas maiores, as intensidades de cores dos átomos podem ser distribuídas em forma de um gradiente. Um exemplo de aplicação do cálculo da intensidade de cores é mostrado na figura 3.7, onde o grupo benzil da molécula de BZN contribui mais para a energia potencial que os demais grupos funcionais da molécula. Na figura 3.6 temos o resultado do cálculo do PED em 606 cm 1 mostrado em uma tela do software PEDCALC. A etiqueta G01 na tabela mostrada na figura 3.6 é referente ao grupo benzil. As cores dos átomos em modos de vibração diferentes não podem ser comparados, já que a normalização é feita para cada modo de vibração individualmente. Então, o esquema de cores para o PED resulta em uma ferramente de visualização das regiões de uma molécula que mais contribuem para a distribuição da energia potencial. Figura 3.7: Vibração em 606 cm 1 da molécula de benzonidazol.
58 Esquema do cálculo do PED A metodologia do cálculo empregado pelo software PEDCALC é esquematizada na figura 3.8. Inicialmente PEDCALC importa a conformação molecular e as constantes de força. Numa primeira etapa foram utilizados resultados do software Gaussian, mas essa metodologia pode ser estendida para outros software de cálculo ab initio ou semi-empírico. Depois o software PEDCALC calcula as coordenadas naturais fornecidas pelo usuário. O usuário deve entrar com um conjunto de 3N 6 coordenadas internas de acordo com a lista de coordenadas suportadas pelo software PEDCALC. Antes de calcular o PED, verifica-se redundâncias nas coordenadas fornecidas pelo usuário. Se as coordenadas satisfizerem as condições necessárias para o cálculo da distribuição potencial, a equação secular é resolvida e as matrizes de força e autovetores são transformadas para coordenadas internas, de forma que o PED é calculado sobre os autovetores das coordenadas internas. No software PEDCALC as coordenadas naturais não redundantes são adicionadas a uma tabela como a mostrada na figura 3.5.
59 58 início Gaussian e coordenadas internas entrada de dados processamento gera coord. internas redundância? sim não sistema em coord. internas S=BX organiza saída/tabelas PED fim Figura 3.8: Esquema do PEDCALC
60 59 4 BENZONIDAZOL 4.1 Introdução No Brasil e outros países da América Latina, doenças parasitárias afetam milhões de pessoas, sendo um sério problema de saúde pública que muitas vezes é negligenciado por autoridades sanitárias ou mesmo instituições privadas ligadas à saúde. Dentre as doenças parasitárias mais prevalentes da América Latina[33], podemos citar a Doença de Chagas, que está presente principalmente em áreas rurais ou de florestas, onde as populações locais são expostas com maior facilidade ao inseto vetor. Decorrido um século da sua descoberta, em 1909, pelo pesquisador brasileiro Carlos Chagas[34], a Doença de Chagas ainda constitui um dos maiores problemas de saúde pública da América Latina[35]. A Doença de Chagas, também conhecida como Tripanossomíase Americana ou esquizotripanose, é causada pela infecção por um protozoário, Trypanosoma cruzi. Esse parasita é geralmente encontrado em insetos hematófagos, e pequenos mamíferos em grandes porções da América Latina. O principal vetor da Doença de Chagas para humanos é o inseto hematófago Triatoma infestans, conhecido no Brasil como barbeiro. Outras formas menos comuns de transmissão da doença são a transfusão de sangue e o transplante de órgãos de pessoas infectadas com o Trypanosoma cruzi[36]. Novos casos de infecção pelo Trypanosoma cruzi geralmente ocorrem devido à exposição às fezes do Triatoma infestans. Ao chupar o sangue de humanos ou animais domésticos, os insetos depositam suas fezes[37] (contaminadas com o parasita) sobre a pele. Nesse processo, a infecção por Trypanosoma cruzi ocorre quando as fezes do inseto entram em contato com feridas na pele e superfícies mucosas (como a boca e os olhos). A infecção por Trypano-
61 60 soma cruzi é duradoura, permanecendo no indivíduo infectado por toda a vida. Sendo que na fase crônica da doença, as pessoas infectadas desenvolvem problemas cardíacos[38, 39] e gastrointestinais[40] graves. Estudos epidemiológicos da Doença de Chagas foram realizados em áreas endêmicas e não endêmicas. Mas devido à constante migração[41] das populações rurais para os grandes centros urbanos, foram observadas áreas heterogêneas quanto à proliferação da doença. O controle sobre a proliferação da Doença de Chagas[42, 43] é feito através do combate ao inseto vetor Triatoma infestans e a aplicação de testes em doadores de sangue. Devido aos esforços internacionais realizados nos últimos 25 anos para controlar a proliferação da Doença de Chagas, a incidência da doença caiu de casos por ano para casos por ano, e a mortalidade anual caiu de para em todo o mundo[44]. Contudo, a epidemiologia da doença tem se tornado mais complexa devido aos múltiplos vetores e ainda devido as condições geopolíticas, econômicas e ecológicas das áreas endêmicas. A Doença de Chagas é caracterizada por duas fases[45]: fase aguda e fase crônica. Na fase aguda, que dura entre 6 e 8 semanas[46], a presença do parasita pode ser detectada por alguns sintomas[33]. No curto período de tempo da fase aguda da doença, o indivíduo infectado pode apresentar inchaço no local da infecção (geralmente próximo a picada do mosquito transmissor), febre, linfadenopatia, anorexia, hepatoesplenomegalia e miocardite brandas. Alguns desses sintomas podem ser confundidos com sintomas de outras doenças típicas das regiões endêmicas, tornando o diagnóstico[47] nessa fase da doença menos eficiente. A fase crônica da doença é desenvolvida ao longo dos anos, podendo ficar o parasita encubado, sem que o indivíduo infectado apresente sintomas específicos por um período de 10 à 30 anos[48]. Entretanto, durante o tempo de incubação, o parasita se reproduz de forma lenta e gradual causando danos irreversíveis ao sistema nervoso e ao coração[48] do indivíduo infectado. A infecção pode ser verificada por métodos de diagnóstico clínicos, incluindo testes sorológicos e parasitológicos[49]. Um dos fármacos usados no tratamento da Doença de Chagas é o benzonidazol[50 53], N-benzil-2-(2-nitroimidazol-1-il) acetamida (BZN), C 12 H 12 N 4 O 3, sendo mais efetivo sua aplicação no início da infecção (fase aguda)[54]. Já na fase crônica da doença, BZN não
62 61 apresenta a mesma eficácia no tratamento[46]. Além disso, efeitos colaterais se apresentam como um forte obstáculo ao tratamento contínuo da doença na fase crônica, levando à interrupção do tratamento em muitos casos[54]. Dentre os efeitos colaterais podemos citar: anorexia, dermatite alérgica e vômitos. A fórmula estrutural da molécula de BZN é mostrada na figura 4.1. Embora os mecanismos bioquímicos que expliquem a atividade do benzonidazol ainda não sejam completamente entendidos, estudos experimentais sugerem que BZN poderia interferir diretamente na síntese de macromoléculas através de ligações covalentes ou outros tipos de interação entre a nitro redução de intermediários e várias componentes celulares como DNA, lipídios e proteínas do Trypanosoma cruzi[55]. O H 2 C C NH CH 2 N N NO 2 Figura 4.1: Fórmula estrutural da molécula de benzonidazol. Na figura 4.2 temos a conformação molecular do benzonidazol com cada átomo unicamente identificado. Usaremos essa numeração dos átomos para nos referirmos a ligações químicas, ângulos e outras características físicas e geométricas dessa molécula. A molécula é dividida em três fragmentos planares: o grupo imidazol (fragmento A: N 5, C10, C9, N 4, C8, N 7, O1, O2), o grupo benzil (fragmento B: C14, C15, C16, C17, C18, C19), e o fragmento de acetamida (fragmento C: N6, C11, C12,C13, O3).
63 62 C19 O1 C18 O2 C17 C14 C15 C13 N6 C11 N5 N7 C8 N4 C9 C16 C12 C10 Figura 4.2: Conformação molecular do benzonidazol com cada átomo identificado. O3 Nesse capítulo, serão aplicadas as metodologias previamente descritas para o estudo do espectro vibracional do benzonidazol. Deste modo, cálculos de primeiros princípios serão empregados para obter a conformação molecular mais estável[30, 56, 57] e o espectro vibracional. Estes resultados serão comparados com aqueles obtidos experimentalmente. 4.2 Estrutura Cristalina As amostras de benzonidazol usadas nesse trabalho foram fornecidas pelo Instituto de Tecnologia em Fármacos-Farmanguinhos/Fiocruz. As amostras de BZN foram submetidas a um processo de recristalização por Sara B. Honorato[58]. No processo de recristalização, foi usado como solvente etanol em baixa temperatura. Foram obtidos pequenos cristais de BZN. A técnica de difração de raios X foi aplicada nos monocristais de BZN obtidos na recristalização. A técnica de difração de raios X em monocristais foi usada na determinação da estrutura cristalina.
64 63 Figura 4.3: Cela unitária do benzonidazol. A determinação da estrutura cristalina foi realizada no grupo de pesquisa do Professor Javier Ellena do Instituto de Física de São Carlos. O BZN cristaliza em um sistema monoclínico não-centrossimétrico com grupo espacial P2 1 e Z= 2, sendo os parâmetros de cela cristalina a=4.68å, b=10.98å, c= 11.9Å,β= A célula unitária do benzimidazol obtida à temperatura de 150K é mostrada na figura 4.3. De acordo com a estrutura cristalina pode ser observado que o radical nitro ligado ao imidazol é praticamente coplanar ao anel apresentando uma pequena torção de A ressonância no grupo acetamida é caracterizada pelas distâncias O-C= 1.23Å, C-N= 1.336Åe O-N= 2.273Å. Os ângulos observados em torno do nitrogênio ( ) são maiores que os esperados para uma hibridização sp 3 (109.5 ). Isso sugere que a estrutura apresenta um caráter sp 2 devido a um deslocamento de elétrons livres do nitrogênio presente no grupo acetamida. As cadeias formadas no cristal de BZN são de dois tipos: intermoleculares do tipo N6 H22...O3,C11 H23...O3 e C18 H28...O2, que possibilita a formação de cadeias infinitas no eixo a, e intramolecular do tipo C11 H23...O2.
65 64 Figura 4.4: Ligações intermoleculares entre moléculas do BZN. Tabela 4.1: Parâmetros geométricos das ligações de hidrogênio. D-H...A D-H (Å) (medido) H..A (Å) D..A (Å) D-H..A ( ) Interações Intermoleculares N6 H22...O3 0,873 2,012 2, C11 H23...O3 1,0 2,371 3, C18 H28...O2 0, , Interações Intramoleculares C11 H23...O2 1,0 2,413 2, Conformação Geométrica A partir da conformação molecular do BZN determinada pela difração de raios-x, realizamos uma otimização de geometria da molécula isolada. Essa otimização de geometria foi feita usando a técnica DFT e o software gaussian 03[59], com a combinação de funcional e base B3LYP/6-31G++(d,p).
66 65 Figura 4.5: Superposição das conformações moleculares teórica (laranja) e experimental (colorida). A conformação observada experimentalmente está determinada pela formação das ligações de hidrogênio intermoleculares que dão origem as cadeias ao longo do eixo a. Na figura 4.5 temos uma comparação das geometrias da molécula de BZN na célula cristalina (multicolorida) e da otimização de geometria (cor laranja). As diferenças entre as conformações da molécula na figura 4.5 ocorrem no centro da molécula. 4.4 Espectroscopia Vibracional A partir dos resultados da otimização de geometria foram realizados cálculos dos espectros Raman e infravermelho da molécula isolada de BZN. Para isso, usamos o software Gaussian e a combinação funcional/base B3LYP/6-31G++(d,p). A comparação entre espectros vibracionais calculados e experimentais deve ser realizada após um ajuste dos espectros calculados, de forma que reproduzam melhor os espectros experimentais.
67 Procedimento de Classificação dos Modos Normais de Vibração Ajuste de Frequências Nos cálculos de otimização de geometria que realizamos usando a teoria DFT, os modos normais de vibração têm valores em torno de 10% maiores que os valores correspondentes experimentais. Isso se deve a deficiência da Teoria da Funcional da Densidade de calcular com exatidão os termos anarmônicos[60] dos modos normais de vibração. Frequências fundamentais são relacionadas com as frequências harmônicas pela equação 4.1 ν=ω e 2ω e x e + (4.1) ondeν é a frequência fundamental,ω e é a frequência vibracional harmônica, e 2ω e x e é o termo anarmônico. Na teoria DFT, o termo anarmônico difere do valor esperado por um valor relativamente pequeno. Com isso, o espectro calculado deve sofrer um pequeno ajuste para melhor comparação com valores experimentais. O ajuste das frequências[61] é feito usando a relação ν obs ν calc = b av calc (4.2) ondeν obs é o número de onda observado,ν calc é o número de onda calculado, e a e b são constantes que devem ser determinadas durante o ajuste da curva f ν calc =νcalc b aνcalc, onde o valor da função f ν calc é a frequência observada (na verdade número de onda), v obs ; os números de onda estão em cm 1. Os valores de a e b dependem da base usada no cálculo ab initio. Sendo assim, deve ser usada a mesma função de ajuste para todos os cálculos que usem a mesma base. Os ajustes são feitos usando o método dos mínimos quadrados. Para os espectros calculados da molécula isolada de BZN, dividimos os espectros em regiões de intervalo de número de onda. Para cada região temos uma função de ajuste diferente que fornece resultados satisfatórios. A tabela 4.2 lista as diferentes regiões do espectro e as correspondentes funções de ajuste. Como pode ser visto na tabela 4.2, algumas regiões se sobrepõem devido as diferentes funções de ajuste usadas. Na região de baixa frequência (0 cm cm 1 ) foi medido somente o espectro Raman, já que a região de baixa frequência não é facilmente acessível à
68 67 espectroscopia infravermelho. Tabela 4.2: Funções de ajuste e regiões do espectro Raman calculado da molécula isolada de BZN. Região do Espectro cm 1 Função de Ajuste f(x)= x(ax+ b), a= e b= f(x)= x(ax+ b), a= e b= f(x)= x(ax+ b), a= e b= 1.2 A associação dos modos normais de vibração com o espectro vibracional pode ser feita através da comparação dos espectros calculado e observado. Quando associamos um pico do espectro calculado com o observado, podemos usar as animações referentes aos modos normais de vibração calculados para determinar o tipo de vibração envolvida. Mas podem existir modos normais calculados muito complexos, o que torna a tarefa de determinar o tipo de vibração muito complicada. A ferramenta adequada para a determinação das características das vibrações de uma molécula é a distribuição da energia potencial (PED, Potential Energy Distribuction). Com o auxílio de um cálculo de distribuição da energia potencial, podemos determinar quais coordenadas internas contribuem para um modo de vibração da molécula, e então classificamos a vibração em função dessas coordenadas. A tabela 4.3 mostra os resultados obtidos do cálculo da distribuição da energia potencial da molécula de BZN. Essa tabela mostra os valores do número de onda calculados sem a aplicação de ajuste (S.A., sem ajuste), os valores de número de onda calculados com a aplicação de ajuste (C.A., com ajuste), os valores associados dos observáveis, Raman e infravermelho, e a descrição da vibração associada (PED). Alguns números de onda não puderam ser associados ao espectro calculado. Isso porque nem sempre há similaridade entre os espectros calculados e experimentais, mesmo depois dos ajustes. Devemos lembrar que o espectro calculado é referente a uma molécula isolada de BZN, enquanto o espectro experimental é referente a BZN na forma cristalina.
69 68 Ajuste de Intensidades Raman As intensidades relativas Raman e infravermelho também devem ser levadas em consideração ao se comparar os modos normais de vibração calculados com os espectros experimentais. Nos espectros vibracionais teóricos, as intensidades Raman não são calculadas diretamente pelo software Gaussian, mas sim a atividade de espalhamento Raman. A intensidade Raman depende no entanto, de fatores experimentais que não são previstos por cálculos ab initio. A seção de choque de espalhamento, σ j [62], que é proporcional à intensidade, pode ser calculada com o auxílio da atividade de espalhamento das Ω frequências previstas pelo cálculo ab initio através da seguinte relação σ j Ω = 2 4 π 4 4 ν0 ν j h 45 hcνj 8π 2 S j (4.3) cν j 1 exp kt ondeν 0 é o número de onda do laser,ν j é número de onda do j-ésimo modo normal de vibração (calculado), h, c, k são constantes universais, e S j é a atividade de espalhamento Raman (obtida no cálculo ab initio). Após o ajuste dos números de onda e das intensidades do espectro vibracional calculado, aplicamos uma função de convolução Lorentziana para obter o espectro Raman. O mesmo procedimento é aplicado no caso do espectro calculado infravermelho, com a exceção de que não é necessário ajuste das intensidades infravermelho. Esse último ajuste foi realizado com o auxílio do software Gausssum[63] que foi modificado para fornecer os fatores de espalhamento Raman, σ j, além de convolucionar os espectros vibracionais Raman e Ω infravermelho usando a função Lorentziana. A identificação dos modos normais de vibração de uma molécula é grandemente simplificada com o auxílio de softwares adequados. Nesse contexto, nosso software (PEDCALC) se apresenta como uma alternativa viável. Como esse software podemos identificar modos normais de vibração muito complexos e visualizar esses modos normais em uma interface gráfica amigável.
70 Número de Onda Experimental (cm -1 ) Número de Onda Experimental (cm -1 ) Número de Onda Experimental (cm -1 ) Número de Onda Calculado (cm -1 ) Número de Onda Calculado (cm -1 ) (a) (b) Número de Onda Calculado (cm -1 ) (c) 69 Figura 4.6: Funções de ajuste dos espectros Raman calculados. Os gráficos são mostrados para diferentes intervalos de número de onda.
71 Número de Onda Experimental (cm -1 ) Número de Onda Experimental (cm -1 ) Número de Onda Calculado (cm -1 ) Número de Onda Experimental (cm -1 ) (a) (b) Figura 4.7: Funções de ajuste dos espectros infravermelho calculados. Os gráficos são mostrados para diferentes intervalos de número de onda. 70
72 C E Número de Onda (cm -1 ) 71 Figura 4.8: Espectros Raman calculado (C) e experimental (E) do BZN na região entre 2500 e 3500cm 1.
73 C E Número de Onda (cm -1 ) 72 Figura 4.9: Espectros Raman calculado (C) e experimental (E) do BZN na região entre 1000 e 2000cm 1.
74 C E Número de Onda (cm -1 ) 73 Figura 4.10: Espectros Raman calculado (C) e experimental (E) do BZN na região entre 500 e 1000cm 1.
75 C E Número de Onda (cm -1 ) 74 Figura 4.11: Espectros Raman calculado (C) e experimental (E) do BZN na região entre 0 e 500cm 1.
76 C E Número de Onda (cm -1 ) 75 Figura 4.12: Espectros infravermelho calculado (C) e experimental (E) do BZN na região entre 2500 e 3600cm 1.
77 C E Número de Onda (cm -1 ) 76 Figura 4.13: Espectros infravermelho calculado (C) e experimental (E) do BZN na região entre 1000 e 2000cm 1.
78 C E Número de Onda (cm -1 ) 77 Figura 4.14: Espectros infravermelho calculado (C) e experimental (E) do BZN na região entre 500 e 1000cm 1.
79 Distribuição da Energia Potencial Na tabela 4.3 são apresentadas as contribuições das coordenadas internas do BZN para cada modo vibracional. Muitas coordenadas podem contribuir com pequenas frações à energia potencial, o que tornaria a tabela demasiadamente longa. Sendo assim, levamos em consideração somente coordenadas que contribuíssem com pelo menos um décimo de toda a energia potencial de cada modo de vibração. Na tabela 4.3 podemos observar coordenadas simples como: estiramentos, dobramentos e torções. Mas também temos coordenadas mais complexas, que na verdade são combinações lineares das coordenadas internas mais simples. Ainda na tabela 4.3 relacionamos modos vibracionais calculados durante a otimização de geometria da molécula isolada de BZN com aqueles observados. A molécula de BZN foi dividida em quatro regiões: G1, G2, G3 e G4. A região G1 é referente ao grupo funcional benzil, a região G2 é referente ao grupo acetamida, a região G3 é referente ao grupo imidazol, e G4 é referente ao grupo NO 2 ligado ao imidazol. Dividimos a molécula em regiões para identificar diferentes vibrações em diferentes regiões da molécula. Por exemplo: a contribuição para o PED de um estiramento CC do grupo benzil não seria diretamente somada a contribuição de uma vibração CC do grupo acetamida. Tabela 4.3: Classificação dos modos vibracionais do BZN de acordo com as coordenadas de simetria Experimental cm 1 DFT cm 1 PED a Raman Infravermelho C.A. b S.A. c G2(τ[CC 36]+τ[CN 39]) G2(τ[C C 59]) G2(τ[CN 27]+τ[CC 32]), G4(τ[CN 24]) G2(ω[N H 25]+τ[CN 52]) continua na próxima página a Distribuição da energia potencial como uma soma da contribuição de cada coordenada cuja notação é apresentada no apêndice B. b C.A. significa número de onda calculado com ajuste. c S.A. significa número de onda calculado sem ajuste.
80 79 continuação da página anterior Experimental cm 1 DFT cm 1 Raman Infravermelho C.A. S.A. PED G2(τ[CN 26]+τ[CC 19]+ω[N H 23]), G4(τ[CN 22]) G2 scissor cxy [CCN 18]+τ[CN 45], G3 oop[n C 16] G2(ω[N H 13]), G4(τ[CN 53]) G2(ω[N H 12]+τ[CN 18]), G3 oop[cn 30], G4(τ[CN 10]) G1 τ 6-ring asym, [11] G2(ω[N H 10]+τ[CN 23]), G3 oop[cn 21] G2 τ[cn 10]+δ xny [CCN 17]+δ xny [CN C 10], G3 ρ[cn 12]+oop[CN 25] G1 ρ[cc 16], G2 τ[cn 19]+δ xny [CN C 24] G2(τ[CN 10]), G3 ρ[cn 11]+oop[N C 15]+oop[CN 32] G3 ρ[cn 16]+ρ[N C 34], G4(23) G1 τ 6-ring asym [18]+ρ[CC 25] G1 τ 6-ring asym, [14]+ρ[CC 12] G2(τ[CN 12]), G3 ρ[n C 15] G1 τ[ch 16]+τ 6-ring asym* [84] G1 τ 6-ring asym, [10] G2 δ xny [CCN 12], G3 ρ[n C 11], G4(ν[CN 13]) G1 τ 6-ring asym, [20] G2 δ xny [CCN 12], G4(ν[CN 20]) G1 oop[cc 14]+δ 6-ring asym [21]+τ6-ring asym, [21] G2 ρ[co11] G2(ω[N C 13]+ω[CC 15]), G3 ρ[n C 11]+ρ[CN 11], G4 ρ[n C 17] continua na próxima página
81 80 continuação da página anterior Experimental cm 1 DFT cm 1 PED Raman Infravermelho C.A. S.A G2(ω[N C 10]+ω[CN 29]), G3 ρ[cn 12], G4 ρ[n C 15] G1 pk 6-ring [13]+δ 6-ring asym, [24] G2 scissor cxy [CCN 10], G3 τ 5-ring* [17] G2(ω[N H 17]), G3 τ 5-ring* [39] G1 δ 6-ring* asym [83] G2(ω[N H 27]), G3 oop[n C 10]+τ 5-ring* [28] G3 oop[cn 21]+τ 5-ring [62] G1 pk 6-ring [10], G2 ρ[co15]+ν[cn 22], G3 δ 5-ring [13] G1 oop[ch 34]+pk 6-ring [55] G3 oop[cn 32], G4(ω[N C 51]) G1 oop[ch 39]+pk 6-ring [28] G3 oop[ch 82] G2 scissor cxy [CN C 11]+ω[CO29], G4(δ[ONO12]) G1(ν[CC 35]), G2 scissor cxy [CN C 10] G4(ν[CN 12]+δ[ONO45]) G1 oop[ch 99] G2 ν[cn 20]+ν[CC 14]+scissor CH2 [23] G3 oop[ch 83] G3 ν[cn 20]+δ 5-ring* [59] G1 oop[ch 77] G2 scissor CH2 [42] G1 oop[ch 91] G1 oop[ch 84]+pk 6-ring [14] G1 ν[cc 31]+trig[62] G1(ν[CC 16]), continua na próxima página
82 81 continuação da página anterior Experimental cm 1 DFT cm 1 PED Raman Infravermelho C.A. S.A. G2 δ xny [CN C 10]+ν[CC 10]+ρ CH2 [30] G1 ν[cc 63]+ρ[CH 19]+trig[12] G2(ν[C N 51]) G2(ν[C N 11]), G3 δ 5-ring [14]+ν[CC 16]+ρ[CH 48] G1 ν[cc 44]+ρ[CH 41] G2 ν[cn 12]+tw CH2 [19], G3 ν[cn 23]+ρ[CH 14] G1 ν[cc 18]+ρ[CH 82] G3 ν[cn 39]+ρ[CH 13]+δ 5-ring [12] G1 ν[cc 21]+ρ[CH 78] G2(ν[CC 16]), G3 ρ[ch 11]+ν[CN 13] G1(ν[CC 14]), G2(ν[CC 28]) G2 tw CH2 [51] G2 ν[cn 26]+ρ[CO10]+ρ[N H 16] G2(ν[C N 17]), G3 ν[cn 26]+ρ[CH 19], G4(ν[NO12]) G1(ν[C C 75]) G1 ν[cc 11]+ρ[CH 70] G2 ω CH2 [35], G3(ν[CN 12]) G2 ω CH2 [27], G3(ν[CN 26]) G2 ω CH2 [17], G3(ν[CN 10]+δ[OCO10]), G4(ν[CN 17]+ν[NO26]) G2 ω CH2 [66] G3(ν[C N 65]) G2 scissor CH2 [73] G2 scissor CH2 [92] G1 ν[cc 34]+ρ[CH 53] continua na próxima página
83 82 continuação da página anterior Experimental cm 1 DFT cm 1 PED Raman Infravermelho C.A. S.A G2 ω CH2 [10], G3(ν[CN 51]) G3 ν[cn 19]+ρ[CH 24]+ν[CC 42] G1 ν[cc 34]+ρ[CH 60] G2 ν[cn 28]+ρ[N H 50] G4(ν[N O 74]) G1 ρ[ch 18]+ν[CC 69] G1 ρ[ch 22]+ν[CC 68]+δ 6-ring asym [10] G2(ν[CN 11]+ν[CO72]) G2(ν[C H 100]) G2(ν[C H 100]) G2(ν[C H 99]) G1(ν[C H 99]) G1(ν[C H 99]) G1(ν[C H 66]), G2(ν[C H 33]) G1(ν[C H 32]), G2(ν[C H 67]) G1(ν[C H 99]) G1(ν[C H 99]) G3(ν[C H 99]) G3(ν[C H 99]) G2(ν[N H 100]) 4.6 Classificação das Bandas Vibracionais Com o auxílio do PED mostrado na tabela 4.3, temos uma classificação mais detalhada das bandas vibracionais de BZN em função dos modos normais de vibração. Os modos normais de vibração e as respectivas distribuições de energia potencial estão listados nessa tabela. As figuras 4.15, 4.16, 4.17, 4.18, 4.19, 4.20 obtidas com o software PEDCALC repre-
84 83 sentam alguns modos de vibração: suas respectivas distribuições da energia potencial e autovetores da molécula BZN. Os autovetores são representados pelas setas verdes, enquanto a distribuição da energia potencial é exibida como um gradiente de cores, da cor verde até a cor vermelha, onde a cor vermelha representa maior energia potencial. Os autovetores estão associados ao movimento dos átomos da molécula de BZN, mas em muitos casos o módulo elevado de um autovetor não representa necessariamente elevada contribuição à distribuição de energia potencial no mesmo átomo ou região da molécula. A distribuição da energia potencial depende diretamente dos autovetores, mas também depende das constantes de força das ligações químicas da molécula. Sendo assim, para um determinado modo de vibração uma região da molécula contribuirá significativamente para a distribuição da energia potencial, somente se os produtos das constantes de força pelos respectivos autovetores for maior do que os produtos de outras regiões da molécula. Região de alto número de onda (2500 cm 1 até 3500 cm 1 ): nos gráficos 4.8 e 4.12 temos a comparação dos espectros calculado e experimental Raman e infravermelho do benzonidazol, respectivamente. Esses gráficos mostram que existem muitos picos similares entre espectros calculados e observados, principalmente no espectro Raman. Nessa região do espectro temos uma série de estiramentos CH de diferentes regiões da molécula de BZN e um estiramento NH. Os modos vibracionais relacionados às ligações do tipo NH têm suas frequências calculadas sobrestimadas em relação às frequências experimentais devido ao fato que este grupo molecular participa das ligações de hidrogênio que estabilizam a estrutura cristalina. Deste modo o estiramento NH exibe o efeito típico deste tipo de interação, isto é, o deslocamento para baixas energias. Em 3272 cm 1 (R) e 3273 cm 1 (IR), temos estiramento NH correspondente ao grupo G2, como mostrado na figura Os estiramentos CH do grupo imidazol são observados a 3132 cm 1 (R) e 3130 cm 1 (IR), e 3115 cm 1 (R) e 3113 cm 1 (IR). Estiramento CH do grupo benzil aparece nos números de onda 3035 cm 1 e 3013 cm 1 (R). Em 2952 cm 1 e 2890 cm 1 observamos estiramentos CH do grupo G2. Em 3059 cm 1 temos dois modos de estiramento CH do grupo benzil e do hidrocarboneto CH 2 do grupo G2. Em um desses modos a contribuição sobre a energia potencial pelo grupo benzil é o dobro da contribuição do estiramento do grupo CH 2, enquanto no outro modo a contribuição do grupo benzil é metade da contribuição do grupo CH 2, como mostrado na tabela 4.3.
85 84 Figura 4.15: Modo vibracional de 3272 cm 1 do BZN - G2(ν[N H 100]). Região de médio número de onda (500 cm 1 até 2000 cm 1 ): esta região do espectro é apresentada nos gráficos 4.9, 4.10, 4.13 e 4.14 que relacionam espectros calculados e experimentais Raman e infravermelho do benzonidazol. Observamos nessa região do espectro uma série de vibrações relacionadas com o grupo metileno que se encontra na região G2 da molécula e dos grupos benzil e imidazol. Em 1556 cm 1 (IR) observamos os estiramentos NO do grupo NO 2. Em 1537 cm 1 (IR) observamos deformação rocking NH (G2) enquanto em 1541 cm 1 (R) observamos rocking CH do grupo benzil. Em 1485 cm 1 (IR) são observados estiramentos CN do grupo imidazol. A vibração 1358 cm 1 (R e IR) corresponde a um modo normal complexo que divide a energia potencial entre as regiões G2 e G3 da molécula: apresentando estiramento CN no grupos imidazol, dobramento OCO no grupo imidazol, e wagging no grupo metileno (G2). Em 1216 cm 1 Raman temos o modo twisting do grupo metileno (G2). Em 960 cm 1 observamos a deformação fora do plano dos átomos CH do grupo benzil, como mostrado na figura Em 958 cm 1 (IR) observamos dobramento (bending) ONO do grupo NO 2 como mostrado na figura O modo de 918 cm 1 (IR) corresponde às deformações CNC, CO e NO 2 da região G2. A vibração Raman de 871 cm 1 é devido à deformação fora do plano CH do grupo imidazol.
86 85 Figura 4.16: Modo vibracional de 1661 cm 1 do BZN - G2(ν[CN 11]+ν[CO72]). O modo de vibração 841 cm 1 (R) corresponde às deformações CH fora do plano e puckering do grupo benzil. O mesmo ocorre em 781 cm 1 (IR). Outra vibração complexa é a de 743 cm 1 (R) e 746 cm 1 (IR) correspondente à deformação punckering do grupo benzil, deformação CO e estiramento CN do grupo G2, e deformação do grupo imidazol. Em 698 cm 1 infravermelho temos wagging NH na região G2 e torção do grupo imidazol. Região de baixo número de onda (0 cm 1 até 500 cm 1 ): na região de baixa energia do espectro medimos somente espectro Raman como mostrado no gráfico As vibrações Raman mais intensas nessa região do espectro são: 73 cm 1 correspondente à torções CN e CC do grupo G2, deformação fora do plano do grupo G2 e torção CN do grupo NO 2, 49 cm 1 corresponde à torções CC (G2), 38 cm 1 corresponde à torções CN e CC (G2), como mostrado na figura A vibração em 38 cm 1 mostrada na figura 4.19 é complexa. A região da molécula de BZN com maiores vetores de deslocamento (representada pelas setas verdes) não é a que tem maior contribuição à energia potencial (representada por átomos de cor avermelhada). A diferenciação entre movimento e distribuição da energia potencial fica evidente com a utilização do software PEDCALC. A energia potencial depende tanto dos autovetores quanto
87 86 Figura 4.17: Modo vibracional de 946 cm 1 (R) do BZN - G4(ν[CN 12]+δ[ONO45]). Figura 4.18: Modo vibracional de 960 cm 1 (R) do BZN - G1 oop[ch 99].
88 87 Figura 4.19: Modo vibracional de 38 cm 1 (R) do BZN - G2(τ[CC 36]+τ[CN 39]). das constantes de força envolvidas. Se as constantes de força forem muito fracas, mesmo que os autovetores sejam relativamente grandes, a energia potencial associada deve ser pequena. Já na vibração Raman de 49 cm 1 um dos átomos que mais contribui para a vibração, também contribui significativamente para a energia potencial. Figura 4.20: Modo vibracional de 49 cm 1 (R) do BZN - G2(τ[CC 59]). Devido as diferenças conformacionais experimental e teórica da molécula de BZN são esperadas diferenças nas distribuição de energia potencial em relação as torções e deformações da região marcada na figura 4.5, correspondente ao grupo G2 na tabela 4.3. As principais diferenças na distribuição da energia potencial são esperadas nas torções CN e CC do grupro G2, deformação fora do plano CO do grupo G2 e deformação CCN e CNC do grupo G2. Nesse contexto, dentre as vibrações mais afetadas, podemos citar: 38 cm 1, 49 cm 1 e
89 cm Conclusões Nesse capítulo realizamos uma análise físico-computacional detalhada com cálculos de primeiros princípios baseada na teoria DFT da estrutura do BZN. Conseguimos obter os espectros Raman e infravermelho e compará-los com os obtidos experimentalmente. Apesar dos cálculos ab initio serem realizados na molécula isolada, os espectros calculados são uma boa aproximação dos espectros experimentais. Para melhor entender as bandas dos espectros experimentais, calculamos as diversas vibrações Raman e infravermelho e a distribuição da energia potencial em termos das coordenadas de simetria. Levamos em consideração as diferenças conformacionais entre experimental e calculado apresentadas no início do capítulo, e apontamos as principais diferenças esperadas na tabela 4.3.
90 89 5 MEBENDAZOL 5.1 Introdução Mebendazol, C 6 H 13 N 3 O 3,[(5-benzoyl-1H-benzimidazole-2-yl)-carbamic acid methyl ester, MBZ], é um fármaco derivado dos benzimidazóis. O fármaco é praticamente insolúvel em água e um estudo sobre seu polimorfismo levou a caracterização e identificação de três formas polimórficas (A, B, C) que apresentam diferenças significativas em relação à solubilidade e uso terapêutico[43, 64]. Muitos fármacos apresentam polimorfismo[65, 66], que é definido como a habilidade de uma substância existir em uma ou mais fases cristalinas[67] que têm diferentes conformações das moléculas dentro de sua estrutura. Então, podemos dizer que polimorfos são formas cristalinas da mesma substância pura nas quais se evidencia diferentes arranjos e/ou conformações das moléculas. O resultado das diferenças estruturais entre os polimorfos[68], são as diferentes propriedades físicas, incluindo propriedades termodinâmicas, espectroscópicas, etc. Na industria farmacêutica[69], o polimorfismo[66] de uma fármaco é muito relevante porque afeta a solubilidade[70] e em alguns casos a biodisponibilidade[71]. Há um grande esforço por parte das autoridades reguladoras para determinar a existência de novos polimorfos e caracterizar polimorfos conhecidos. Técnicas de espectroscopia, difração de raios-x e análise térmica foram empregadas no estudo do polimorfismo do mebendazol[72]. O efeito do polimorfismo[73] na solubilidade é de tal forma que a razão da dissolução do composto é ditada pelo balanço das forças atrativas e repulsivas existentes na interface cristal-solvente. Se o sólido tiver uma alta energia livre de rede, ou seja, um polimorfo menos estável, tenderá a dissolver mais rápido, porque ao liberar grandes quantidades de
91 90 energia que estava acumulada como energia livre da rede, aumentará a solubilidade e por consequência a taxa de dissolução. A variação nas taxas de dissolução dos polimorfos de uma mesma droga produz diferentes graus de biodisponibilidade. A biodisponibilidade de drogas injetáveis é de 100%, enquanto que para drogas administradas por via oral 1, a biodisponibilidade depende do processo de absorção no organismo do paciente. Muitos autores apontam diferenças na biodisponibilidade dos polimorfos do MBZ (polimorfos A, B e C)[70, 74]. Existem discrepâncias quanto a solubilidade relativa dos polimorfos B e C, reportadas por alguns autores, mas todos os autores concordam que a menos solúvel é a forma A[72, 75, 76]. A forma C é a preferida, já que apresenta uma solubilidade suficiente para uma boa biodisponibilidade, sem exibir a toxidade da forma B[72, 75, 77]. Em um estudo, 958 crianças tailandesas foram expostas a um tratamento com um placebo e MBZ das formas A e C, ficou evidente que a forma A tem a mesma eficácia que o placebo[75]. Outros autores propõem que 30% da forma A em uma formulação junto com a forma C é suficiente para suprimir a atividade farmacológica desejada[78]. A caracterização dos polimorfos do MBZ é feita através da difração de raios-x[79] em amostras na forma de pó. Monocristais de MBZ são difíceis de se obter, e com isso determinar a forma cristalina dos polimorfos do MBZ é um problema complexo. Estudo recente[79] mostrou que a recristalização da forma C, obtida de uma amostra disponível comercialmente, resultou na obtenção de monocristais e na determinação da estrutura do mebendazol-c (MBZ-C). Dentre as formas polimórficas do mebendazol[80], MBZ-C é o polimorfo que tem aplicação na industria farmacêutica sendo usado como medicamento anti-helmíntico, potente no tratamento de nematódeos gastrointestinais[81] 2. Os nematódeos são o grupo de metazoários mais abundantes na biosfera. O mebendazol é usado para combater diversas infecções, únicas ou mistas, dos seguintes agentes parasitas: ascaridíase, teníase, oxiurose, triquinose, e capilaríase intestinal. O combate a essas infecções é extremamente importante, dado que recentes estimativas indicam que um quarto da população mundial está contaminada com um ou mais desses 1 Mebendazol-C é administrado por via oral. 2 Também chamados de vermes cilíndricos.
92 91 parasitas, superando o número de ocorrências de malária ou tuberculose[82]. MBZ-C age sobre os agentes parasitas inibindo o ciclo de glicose e de outros nutrientes, resultando na imobilização e morte do parasita. Infecções intestinais por parasitas como os ancilostomídeos são difíceis de serem erradicadas em áreas onde é presente a pobreza e condições sanitárias precárias. Estudos mostram que existe uma relação do surgimento dessas infecções com as precárias condições socioeconômicas de uma região[81]. Sendo assim, o combate a infecções por vermes é tido como um problema mundial. Indivíduos infectados com vermes tendem a apresentar diversos problemas[83] de saúde. Dentre eles, deficiência de ferro, hemorragia, desnutrição, etc. Em crianças, a infecção pode levar a um retardamento no crescimento e uma baixa capacidade intelectual. Em mulheres grávidas, podem ocorrer problemas no desenvolvimento do feto. Devido a eficácia, largo espectro de aplicação, fácil administração e baixo custo, MBZ-C é utilizado em larga escala por programas de saúde pública com o objetivo de combater as infecções por agentes helmínticos, focados principalmente em pacientes na idade escolar de países em desenvolvimento. O O CH3 N O NH Figura 5.1: Molécula de mebendazol-c. N Sendo derivado dos benzimidazóis[84, 85], o mebendazol é um composto orgânico heterociclo aromático. Fazem parte dos benzimidazóis: albendazol, mebendazol, triclabendazol, etc. A molécula de mebendazol é composta pelos grupos benzil, benzimidazol e metil. Sendo que o plano do grupo benzil não corresponde ao mesmo plano que o grupo benzimidazol como mostrado na figura 5.2. Nesse estudo focamos nossa atenção no espectro vibracional, na classificação dos modos normais de vibração e propriedades dinâmicas do MBZ-C. Nosso estudo da molécula de MBZ-C se divide nas seguintes etapas: obtenção dos espectros vibracionais Raman e infravermelho experimentalmente, otimização de geometria da molécula isolada e do dímero de
93 92 MBZ-C, cálculo dos espectros vibracionais usando DFT, cálculo da distribuição da energia potencial (PED), classificação dos modos normais de vibração e dinâmica molecular. 5.2 Otimização da Geometria Introdução Aplicamos a teoria DFT na otimização de geometria da molécula mebendazol, usando o software gaussian 03[59]. Gaussian minimiza os parâmetros de geometria da molécula em estudo, de forma que podemos obter uma superfície potencial com pontos de mínimo local ou mínimo global que representam possíveis configurações meta-estáveis ou estáveis da molécula, respectivamente. Otimizações de geometria devem partir de uma geometria inicial, seja uma geometria obtida experimentalmente, geralmente por difração de raios X, ou de cálculos anteriores. Muitos fatores podem afetar a geometria final da molécula, e o quanto essa geometria condiz com resultados experimentais. Dentre os diversos fatores, os mais importantes são: base e funcionais usadas no cálculo DFT, forças intermoleculares. As bases e funcionais usadas em um cálculo de otimização de geometria governam como as ligações químicas são estabelecidas, e muitas vezes superestimam ou subestimam os comprimentos dessas ligações químicas. A escolha das bases e funcionais corretas é necessária para obtermos melhores resultados. Na maioria dos cálculos envolvendo moléculas orgânicas onde se fazem presentes ligações químicas C C ou ligações químicas C N, a funcional de Becke[15] de troca e correlação (não local, hibrida, de três parâmetros) é usada juntamente com a formula de correlação de Lee-Yang-Parr[86]. Essa funcional é conhecida como B3LYP (Becke, três parâmetros, Lee-Yang-Parr). A base 6-31G é geralmente usada nesses casos[87]. Forças intermoleculares são de grande importância para a exata determinação da geometria de uma molécula. Muitas vezes pontes de hidrogênio, responsáveis pelo empacotamento da molécula em uma rede cristalina, influenciam na conformação da molécula. Cálculos onde moléculas estão isoladas excluem as forças de interação entre as moléculas
94 93 da rede cristalina. Dessa forma, cálculos de otimização de geometria de moléculas isoladas, seguidos de cálculo do espectro vibracional, não podem ser vistos como a exata descrição dos modos normais de vibração da rede cristalina, mas sim uma aproximação suficiente para a maioria dos casos 3. Um cálculo de otimização de geometria é geralmente seguido de cálculo dos espectros vibracionais Raman e infravermelho. O software Gaussian é capaz de calcular os espectros vibracionais Raman e infravermelho. Mas temos que levar em consideração que devido as limitações da Teoria da Densidade Funcional, os modos normais de vibração são, geralmente, superestimados. Ajustes dos modos normais calculados aos modos normais experimentais podem ser feitos usando uma função de ajuste Investigações Sobre a Geometria do Mebendazol-C O cálculo de otimização de geometria tomou como partida as conformações moleculares observadas no hidroclorato de mebendazol (MBZ-HCl)[88, 89] e no polimorfo C (MBZ-C) [79], cujas estruturas cristalinas foram determinadas através de medidas de raios X em monocristais. A partir da estrutura experimental proposta do MBZ-C, calculamos usando a funcional/base B3LYP/6-31++g(d,p), uma geometria para a molécula isolada de mebendazol-c. A primeira otimização da geometria resultou na estrutura molecular mostrada na figura 5.2. A estrutura mostrada na figura 5.2 serviu como ponto de partida para o estudo das possíveis conformações estáveis e metaestáveis da molécula de mebendazol-c. A figura 5.2 representa a conformação da molécula MBZ-C obtida a partir do cálculo de primeiros princípios sem restrições. Ou seja, nenhuma restrição existe nas coordenadas absolutas que definem as posições dos átomos, nem mesmo restrições sobre coordenadas relativas dos átomos. Durante o cálculo a molécula MBZ-C é mantida isolada. Durante uma otimização de geometria[90, 91], geralmente, existem uma ou mais configurações moleculares que apresentam mínimos de energia potencial. Esses mínimos de energia potencial podem significar novas configurações metaestáveis ou estáveis da molé- 3 Devemos levar em consideração que parte dos cálculos realizados com a molécula de MBZ-C foram realizados com moléculas isoladas devido ao alto custo computacional de agregar mais moléculas ao cálculo.
95 94 C 2 C 3 C 4 C 32 C 15 C 6 O 30 H 18 H 17 C 9 H 21 N 27 C 14 C13 C 1 C 7 N 26 C 10 O 29 C 5 O 31 H 16 N 28 C 8 C 11 C 12 Figura 5.2: Geometria inicial da molécula de mebendazol-c. cula. Algumas dessas configurações podem não representar a forma na estrutura cristalina da molécula, já que durante o cálculo negligenciamos as forças de interação da rede cristalina, uma vez que os cálculos de otimização de geometria não incluem a vizinhança da molécula em estudo. Muitas vezes, no final da otimização de geometria, a configuração molecular resultante não representa o mínimo absoluto de energia potencial, que é, em geral, o alvo do procedimento de otimização de energia. Contudo, podemos investigar, usando restrições nas coordenadas relativas da molécula, outros possíveis mínimos de energia potencial. A investigação de outras possíveis configurações da estrutura molecular se dá pelo procedimento de varredura (scan), em que variamos gradativamente alguma coordenada interna/relativa dos átomos e observamos mudança na energia. Geralmente, as coordenadas escolhidas são ângulos e torções, enquanto distâncias são deixadas livres para serem otimizadas pelo software Varreduras A partir da primeira estrutura da molécula MBZ-C mostrada na figura 5.2, realizamos algumas varreduras (scans) em ângulos diedrais (torções) da molécula de Mebendazol com o objetivo de encontrar outras possíveis conformações. Para melhor descrever as varreduras e os átomos envolvidos, usaremos uma simples
96 95 notação. Nessa notação usaremos a figura 5.2 como referência. Como descreveremos torções, nomeamos quatro átomos na ordem que esses produzem os dois planos envolvidos no ângulo de torção. Teremos torções definidas por exemplo como: C(5)-N(26)-C(1)-O(30). Significando que os átomos C(5)-N(26)-C(1) formam o primeiro plano e os átomos N(26)- C(1)-O(30) formam o segundo plano que juntos definem um ângulo de torção. Varredura C(5)-N(26)-C(1)-O(30) A primeira varredura foi realizada sobre a torção C(5)-N(26)-C(1)-O(30). O ângulo de torção foi variado de 360 no total, usando um passo de 10, ou seja, a torção aumenta de 10 em 10, até que tenhamos uma volta completa. O software Gaussian calculou a energia total a cada passo da torção C(5)-N(26)-C(1)-O(30) após a otimização de geometria. Aqui comparamos as mudanças na energia em função do ângulo de torção C(5)-N(26)-C(1)- O(30). O gráfico 5.3 mostra os pontos de maior interesse, ou seja, mínimos e máximos de energia que também são listados na tabela SCAN 36 passos 16 M1 M energia (u.a.) P1 P2 P ângulo (10 ) Figura 5.3: Variação da energia relativa durante o varredura da torção C(5)-N(26)-C(1)- O(30). É fácil destacar do gráfico da figura 5.3 quais os pontos de máximo e mínimo. Os pontos
97 96 P 1, P 2 e P 3 são pontos de mínimo, enquanto os pontos M 1 e M 2 são pontos de máximo. Lembramos que, os pontos de mínimo representam pontos de maior estabilidade da molécula, enquanto pontos de máximo representam pontos improváveis para a configuração da estrutura molecular do Mebendazol. Esses pontos de mínimo e máximo podem ser interpretados por formação de ligações químicas ou repulsão entre os átomos, como mostraremos a seguir. O ponto P 1 na figura 5.3 é um mínimo local, referente a aproximação de O(30) e H(17). Esse mínimo local é o ponto de partida da varredura. Como o ponto de partida é uma otimização de geometria, é esperado o aparecimento de um mínimo local logo no início da varredura. É fácil ver que esse mínimo local é devido a formação da ligação de hidrogênio intramolecular entre O(30) e H(17) (1.963Å). Ligações de hidrogênio tendem a deixar a estrutura molecular mais estável. Tabela 5.1: Varredura da torção C(5)-N(26)-C(1)-O(30). P1 P2 P3 M1 M2 energia (u.a.) ângulo passo Os pontos P 1 e P 3 são equivalentes quando comparamos os valores da torção C(5)-N(26)- C(1)-O(30), mas esses têm uma diferença quanto a torção C(1)-O(30)-C(32)-H(35) (eixo do metil), em que para P 1 e P 3 têm valores, e , respectivamente. Essa última torção gira de 60 o grupo metil em seu eixo de simetria, entre os pontos P 1 e P 3. Devemos lembrar que uma varredura impõe restrições somente a um grupo pequeno de átomos, os outros átomos estão livres. Dessa forma, o software Gaussian posiciona os átomos livres de forma a obter a menor energia. Por isso, apesar dos pontos P 1 e P 3 serem equivalentes em relação a torção C(5)-N(26)-C(1)-O(30), as outras partes da molécula são ajustadas de forma a obter a menor energia possível. Sendo assim, o grupo metil gira de 60 em torno de seu eixo de simetria quando a torção C(5)-N(26)-C(1)-O(30) passar do ponto P 1 para P 3. O ponto P 2 é um mínimo global, referente a proximidade dos átomos O(29) e H(17). P 2 é o ponto em que a energia da molécula é mais favorável a estabilidade. Isso é devido a formação da forte ligação de hidrogênio entre os átomos O(29) e H(17). Os pontos M 1 e M 2 correspondem ao afastamento dos átomos O(29) e O(30) do átomo
98 97 H(17), fazendo com que seja impossível a formação das ligações de hidrogênio. Por isso, são máximos de energia, já que as ligações de hidrogênio não se formam em M 1 e M 2. A tabela 5.1 mostra os valores de intensidades relativas da energia da molécula de Mebendazol quando variamos o ângulo de torção C(5)-N(26)-C(1)-O(30). Além disso, essa tabela mostra em que passo da varredura cada ângulo de torção C(5)-N(26)-C(1)-O(30) ocorre. Varredura N(28)-C(5)-N(26)-C(1) A periferia de moléculas orgânicas consiste basicamente de átomos de hidrogênios. As interações de repulsão H-H dominam a energia de repulsão intermolecular e até mesmo na energia de interação de partes distantes de uma molécula orgânica. Dessa forma, repulsão do tipo H-H têm papel importante no dobramento de uma molécula orgânica[92]. A segunda varredura é associada à torção N(28)-C(5)-N(26)-C(1). A varredura dessa torção nos mostra a forte repulsão da estereoquímica intramolecular responsável por parte do dobramento da molécula de mebendazol-c. A relação entre energia e passos da varredura é mostrada no gráfico da figura 5.4 e na tabela 5.2. Tabela 5.2: Varredura N(28)-C(5)-N(26)-C(1). P1 P2 M1 energia (u.a.) ângulo passo Os pontos P 1 e P 2 têm o mesmo ângulo de torção, claramente são o ponto inicial e final da varredura, respectivamente. O ponto M 1 é devido a forte repulsão entre H 16 e H 17 numa distância de Å. Ou seja, M 1 representa a repulsão do tipo H-H que causa o dobramento visto no grupo cetona. Tabela 5.3: Ângulos de interesse da primeira otimização de geometria. torção valor C(5)-N(26)-C(1)-O(30) 0.15 N(28)-C(5)-N(26)-C(1)
99 98 11 SCAN 36 passos M energia (u.a.) P1 P ângulo (10 ) Figura 5.4: Variação da energia relativa durante o varredura da torção N(28)-C(5)-N(26)- C(1). As torções mais interessantes, da molécula de Mebendazol-C são mostradas na tabela 5.3. Dados esses valores das torções C(5)-N(26)-C(1)-O(30) e N(28)-C(5)-N(26)-C(1), calculamos uma nova otimização de geometria que garante uma maior estabilidade frente a primeira otimização de geometria, como mostraremos a seguir Nova Geometria As varreduras das torções C(5)-N(26)-C(1)-O(30) e N(28)-C(5)-N(26)-C(1) nos levaram a entender que a estrutura do mebendazol-c obtida na primeira otimização de geometria não era a estrutura mais estável. É evidente, que estamos levando em conta somente interações intramoleculares, já que a primeira otimização de geometria foi realizada sobre uma molécula de MBZ-C isolada. No entanto, as forças intramoleculares são, em geral, responsáveis pelos dobramentos da molécula, principalmente devido a ligações de hidrogênio e repulsões do tipo H-H. Fortes ligações de hidrogênio significam maior estabilidade à molécula. Dessa forma, a ligação de hidrogênio formada pelos átomos O29 e H17 é mais favorável que a ligação de hidrogênio entre os átomos O30 e H17. Durante a varredura da torção C(5)-
100 99 N(26)-C(1)-O(30) podemos observar mínimos de energia devido a formação dessas ligações de hidrogênio, sendo o mínimo global devido a formação da ligação de hidrogênio O29 e H17. Outro fator responsável pelo dobramento da molécula de mebendazol-c é a repulsão H-H entre os átomos H16 e H17, sendo a torção N(28)-C(5)-N(26)-C(1) mais estável em um ângulo 4 aproximadamente igual a 180. Isso sugere que os átomos H16 e H17 devem estar afastados o máximo possível um do outro para garantir maior estabilidade à molécula. Os ângulos de torção mais interessantes da primeira otimização de geometria são mostrados na tabela 5.3. Esses ângulos são referentes as varreduras de torções da molécula de mebendazol-c, cujos valores são mais favoráveis energeticamente. Usando os valores de torções da tabela 5.3 obtemos uma nova configuração para a molécula de mebendazol-c, mostrada na figura 5.5. Essa nova configuração também foi submetida a uma otimização de geometria, de forma a verificar se um mínimo de energia ocorre quando as torções da tabela 5.3 são aplicadas juntas. Figura 5.5: Nova configuração da molécula de Mebendazol-C. Na nova configuração da molécula de mebendazol mostrada na figura 5.5 o átomo H17 foi removido e relocado para formar ligação química junto ao átomo N28. Nessa nova configuração a molécula está mais estável devido a forte ligação de hidrogênio entre O29 e o átomo H17. A figura 5.6 mostra duas estruturas derivadas da estrutura inicial da figura 5.2. A diferença básica entre essas estruturas é o posicionamento de um átomo de hidrogênio, devido ao tautomerismo sugerido em outro estudo[79]. O tautomerismo no mebendazol-c se dá em torno de ligações N-H, onde o átomo de hidrogênio pode assumir diferentes posições 4 Ângulo de torção em relação ao inicio da varredura N(28)-C(5)-N(26)-C(1).
101 100 na molécula em torno do grupo benzimidazol. As moléculas de mebenzadol mostradas na figura 5.6 também passaram pelo procedimento de otimização de geometria seguido de cálculo dos espectros vibracionais Raman e infravermelho. Os dois cálculos de geometria e respectivos espectros vibracionais foram calculados usando a teoria DFT, com funcional e base, B3LYP[93] e g. (a) Molécula A (b) Molécula B Figura 5.6: Tautômeros da molécula de MBZ-C. Usamos as moléculas de MBZ-C mostradas na figura 5.6 para formar dímeros, tautômeros, como observado na estrutura cristalina deste polimorfo[79]. Os dímeros de mebendazol são mostrados na figura 5.7. Veja que esses dímeros diferem somente pelo posicionamento de dois átomos de hidrogênio que formam pontes de hidrogênio do tipo N-H...H entre os grupos benzimidazol de cada monômero. Os dímeros de MBZ-C (D A e D B ) mostrados na figura 5.7 foram obtidos após otimização de geometria. As otimizações de geometria foram seguidas de cálculos dos espectros vibracionais Raman e infravermelho. Usamos uma base diferente para o cálculo da geometria e espectros vibracionais dos dímeros de MBZ-C em comparação com a base usada para os cálculos de geometria das moléculas A e B. Usamos o par funcional/base B3LYP/6-31g, além de incluir o termo de correção do erro na superposição de bases[94] (Basis Set Superposition Error, BSSE). Houve tentativa de cálculo da geometria dos dímeros de MBZ-C usando a base g, mas o software gaussian apontou falha nos critérios de convergência dos orbitais moleculares. BSSE é consequência da truncagem da base usada em um cálculo DFT. Ou seja, o erro na superposição de bases é uma consequência do fato de que as bases em um cálculo DFT são finitas. BSSE é um efeito não físico devido a melhor descrição dos fragmentos (moléculas em um dímero, por exemplo) de um sistema quântico quando colocado na composição de um sistema maior. Com o método de correção chamado counterpoise (CP) os fragmentos de um
102 101 sistema quântico são descritos em função de orbitais estendidos, incluindo orbitais vazios e orbitais ocupados por elétrons de outros fragmentos. Então, a energia, por exemplo, de um dímero AB é dada por V CC AB (G)= E AB(G,AB) E A (G,AB) E B (G,AB) (5.1) onde E A (G,AB) e E B (G,AB) são a energia total de cada monômero na base AB (base do dímero) e geometria G (geometria do dímero). A dinâmica das ligações de hidrogênio entre os monômeros dos dímeros D A e D B da figura 5.7 serão estudadas mais adiante nesse capítulo com o auxílio da técnica de dinâmica molecular de Car-Parrinello. (a) Dímero D A (b) Dímero D B Figura 5.7: Dímeros tautômeros de MBZ-C Espectro Vibracional do Mebendazol Após obtermos a geometria dos dímeros do MBZ-C, D A e D B, seguimos com cálculos dos espectros vibracionais dos mesmos. Os espectros vibracionais são uma importante ferramenta para comparação dos dímeros de MBZ-C com espectro vibracional obtido experimentalmente. Nesse contexto, o espectro vibracional experimental é usado para validar os cálculos DFT. Comparamos os espectros vibracionais Raman e infravermelho dos cálculos de primeiros princípios dos dímeros D A e D B da figura 5.7 com os espectros obtidos experimentalmente. Os cálculos desses espectros sofreram ajustes de intensidade (no caso dos espectros Raman) e ajuste nos valores dos números de onda, como mostrado na seção
103 102 Ajustes dos Espectros Calculados Os espectros Raman e infravermelho calculados sofreram ajustes quanto aos valores dos números de onda[61]. Isso porque a teoria DFT tende a superestimar os valores de número de onda, como discutido anteriormente. O ajuste é feito por um fator de escala da forma v obs v calc = a bv calc (5.2) onde a e b são constantes que devem ser determinadas, e v obs e v calc são os números de onda observado e calculado, respectivamente. Obtemos os valores de a e b usando os modos normais de vibração de diferentes regiões do espectro vibracional, comparados com o espectro calculado mais próximo do espectro experimental e depois ajustamos esses valores a curva dada pela equação 5.2. Outro ajuste nos espectros calculados foi quanto à intensidade da atividade Raman. Mas, como mencionado anteriormente na seção 4.4.1, esse ajuste só se faz necessário nos espectros Raman calculados. Tabela 5.4: Funções de ajuste e regiões do espectro calculado Raman do dímero D A do MBZ-C. Região do Espectro (cm 1 ) Função de Ajuste f(x)= x(ax+ b), a= e b= f(x)= x(ax+ b), a= e b= f(x)= x(ax+ b), a= e b= Nos gráficos das figuras 5.10, 5.11, 5.12, 5.14, 5.15 e 5.16 temos espectros Raman e infravermelho dos dímeros D A e D B de MBZ-C comparados com os respectivos espectros experimentais. Podemos identificar diversos picos correspondentes entre o dímero D B e o espectro experimental. Não identificamos tantas semelhanças entre os espectros do dímero D A e os respectivos espectros experimentais. Dessa forma, calculamos a distribuição da energia potencial (PED) para o dímero D B. Com o auxílio do PED comparamos espectros
104 103 calculados e experimentais para identificar e classificar as vibrações correspondentes. Tabela 5.5: Funções de ajuste e regiões do espectro calculado Raman do dímero D B do MBZ-C. Região do Espectro (cm 1 ) Função de Ajuste f(x)= x(ax+ b), a= e b= f(x)= x(ax+ b), a= e b= f(x)= x(ax+ b), a= e b= Os gráficos das figuras 5.10, 5.11, 5.12, 5.14, 5.15 e 5.16 foram divididos em regiões. Para cada região do espectro temos uma função de ajuste diferente do espectro calculado. As funções de ajuste por região do espectro estão listadas nas tabelas 5.4 e 5.5. As funções de ajuste são quadráticas e diferem somente por valores das constantes a e b referentes à equação 4.2.
105 Número de Onda Experimental (cm -1 ) Número de Onda Experimental (cm -1 ) Número de Onda Experimental (cm -1 ) Número de Onda Calculado (cm -1 ) Número de Onda Calculado (cm -1 ) (a) (b) Número de Onda Calculado (cm -1 ) (c) 104 Figura 5.8: Funções de ajuste do dímero D A para o espectro Raman.
106 Número de Onda Experimental (cm -1 ) Número de Onda Experimental (cm -1 ) Número de Onda Experimental (cm -1 ) Número de Onda Calculado (cm -1 ) Número de Onda Calculado (cm -1 ) (a) (b) Número de Onda Calculado (cm -1 ) (c) 105 Figura 5.9: Funções de ajuste do dímero D B para o espectro Raman.
107 D A D B E Número de Onda (cm -1 ) Figura 5.10: Espectros Raman calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 2000 e 3500cm
108 D A D B E Número de Onda (cm -1 ) Figura 5.11: Espectros Raman calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 1000 e 1800cm
109 D A D B E Número de Onda (cm -1 ) Figura 5.12: Espectros Raman calculado dos dímeros D A e D B, e experimental (E) do MBZ na região entre 500 e 1000cm
110 D A D B E Número de Onda (cm -1 ) Figura 5.13: Espectros Raman calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 0 e 500cm
111 D A D B E Número de Onda (cm -1 ) Figura 5.14: Espectros infravermelho calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 2000 e 4000cm
112 D A D B E Número de Onda (cm -1 ) Figura 5.15: Espectros infravermelho calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 1000 e 1800cm
113 D A D B E Número de Onda (cm -1 ) Figura 5.16: Espectros infravermelho calculados dos dímeros D A e D B, e experimental (E) do MBZ na região entre 500 e 1000cm
114 PED do Mebendazol A distribuição da energia potencial mostrada na tabela 5.7 é referente ao dímero D B do MBZ-C. Calculamos o PED usando o software PEDCALC. O cálculo do PED resultou em 3N 6 modos de vibração, onde N é o número de átomos do dímero D B. A molécula isolada de MBZ-C tem 35 átomos e por consequência o seu dímero tem 70 átomos. Logo, existem 204 modos normais de vibração. No cálculo do PED usamos um total de 204 coordenadas naturais, listadas na tabela 3.2. Cada molécula do dímero D B tem 35 átomos, sendo necessário 99 coordenadas simétricas para descrever as vibrações de um monômero do dímero D B. Duas moléculas de Mebendazol isoladas precisam de 198 coordenadas, sendo as 6 coordenadas restantes intermoleculares, completando o total de 204 coordenadas. As seis coordenadas intermoleculares usadas aqui são listadas na tabela 5.6. Tabela 5.6: Coordenadas Intermoleculares - Dímero D B. Tipo de coordenada Bending Stretching Torção Átomos CNN NN (duas coordenadas) CNNC (duas coordenadas) e NNCN Região de Alta Energia (2000 cm 1 até 4000 cm 1 ): os gráficos 5.10 e 5.14 representam os espectros calculados Raman e infravermelho dos dímeros D A e D B em comparação com os respectivos espectros experimentais. Essa região do espectro é marcada por vibrações de estiramentos CH e NH, principalmente dos grupos benzil e benzimidazol. Identificamos nos espectros experimentais estiramentos CH dos grupos benzimidazol e benzil em 3084 cm 1 (R). Foi observado estiramento CH do grupo benzil em 3067 cm 1 (R). Estiramentos simétricos do grupo metil ocorrem em 2957(6) cm 1 (R/IR), enquanto estiramentos assimétricos ocorrem em 3024 cm 1 (IR) e 3026 cm 1 (R). Também identificamos estiramentos NH no espectro em 3404 cm 1 (IR) do grupo benzimidazol. Região de Média Energia (1000 cm 1 até 1800 cm 1 ): os gráficos 5.11 e 5.15 repre-
115 114 Figura 5.17: Modo vibracional de 3404 cm 1 do MBZ - G13(ν[N H 31]), G3(ν[N H 68]). sentam os espectros calculados Raman e infravermelho de média energia dos dímeros D A e D B em comparação com os respectivos espectros experimentais. Em 1597 cm 1 (R) foram observados estiramentos CO dos grupos carbamato e cetona. Em 1371 cm 1 (IR) observamos estiramento CN e deformação CN do grupo benzimidazol. Em 1319 cm 1 (IR) temos estiramentos CN e CC do grupo benzimidazol. Em 1300 cm 1 (R/IR) são observados estiramento CC e deformação CH. Já em 1279 cm 1 (IR) o grupo carbamato apresenta estiramento CO. Em 1255 cm 1 (IR) o grupo carbamato apresenta estiramentos CO e CN, e deformação CO, enquanto o grupo benzimidazol apresenta estiramentos CN e CC. Em 1242 cm 1 (IR) são observados estiramentos CC e CN, e deformação CH do grupo benzimidazol. No número de onda 1223 cm 1 (R/IR) temos estiramento CN dos grupos cetona e benzimidazol, estiramento CC do grupo benzimidazol e deformações NH e CH do grupo benzimidazol. Em 1088 cm 1 (R) são observados estiramentos CN e CC, e deformação CH do grupo benzimidazol, e estiramento CC do grupo benzil. Em 1001 cm 1 (R) são observados deformação trigonal (Trigonal Deformation) do grupo benzil combinada com fortes estiramentos CC e CH. Região de Média Energia (500 cm 1 até 1000 cm 1 ): em 536 cm 1 (R/IR) o grupo carbamato apresenta deformações CO e CN, enquanto o grupo benzimidazol apresenta deformação CC. Em 608 cm 1 (R) é observada a deformação assimétrica do anel de benzeno do grupo
116 115 benzimidazol. Em 619 cm 1 (R) observamos torções CC dos grupos benzimidazol e benzil, além de deformações fora do plano CC do grupo benzimidazol. Em 695 cm 1 (R) e 696 cm 1 (IR) o menor anel do grupo benzimidazol é deformado, enquanto o grupo cetona apresenta deformação CO e observamos deformação assimétrica do grupo benzil. Em 720 cm 1 (R) o grupo benzil apresenta modo normal que é a combinação de puckering e deformação CH fora do plano. Em 934 cm 1 (R) observamos torções CC e deformação CH fora do plano do grupo benzimidazol. Região de Baixa Energia (0 cm 1 até 500 cm 1 ): no gráfico 5.13 observamos estiramento NN de 190 cm 1 (R). Em 203 cm 1 (R) é observado torção CO. Em 405 cm 1 (R) o grupo benzimidazol também apresenta deformações CC. Figura 5.18: Modo vibracional de 2956 cm 1 do MBZ - G1-11 ν metil sym [97].
117 116 Figura 5.19: Modo vibracional de 1596 cm 1 do MBZ - G2-12(ν[CO18]), G5-15(ν[CO30]). Figura 5.20: Modo vibracional de 608 cm 1 do MBZ - G4 δ 6-ring* asym [37].
118 117 Figura 5.21: Modo vibracional de 934 cm 1 do MBZ - G4-14 τ[cc 11]+oop[CH 70]. Tabela 5.7: Classificação dos modos vibracionais do dímero D B do MBZ de acordo com as coordenadas de simetria. Experimental cm 1 DFT cm 1 PED a Raman Infravermelho C.A. b S.A. c G99(τ[N N 79]+τ[CN 16]) G5-15(τ[CC 36]), G99(τ[N N 17]+τ[CN 31]) G5-15(τ[CC 56]) G5-15(τ[CC 28]), G99(ν[N N 19]) G5-15(τ[C C 57]), G99(δ[C N N 15]) G3-13 oop[n H 15], G5-15(τ[CC 21]) continua na próxima página a Distribuição da energia potencial como uma soma da contribuição de cada coordenada cuja notação é apresentada no apêndice B. b C.A. significa número de onda calculado com ajuste. c S.A. significa número de onda calculado sem ajuste.
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Livro texto: Modern Quantum Chemistry Introduction to Advanced Elecronic Structure Theory
Geralmente, fazemos simplificações e desenvolvemos modelos. A matéria é composta por átomos e moléculas
 Disciplina: SiComLíMol 1 A matéria é composta por átomos e moléculas Geralmente, fazemos simplificações e desenvolvemos modelos O estudo teórico não permite tratar quantidades macroscópicas da matéria.
Disciplina: SiComLíMol 1 A matéria é composta por átomos e moléculas Geralmente, fazemos simplificações e desenvolvemos modelos O estudo teórico não permite tratar quantidades macroscópicas da matéria.
O Método de Hartree-Fock
 O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
O Método de Hartree-Fock CF740 Tópicos Especiais de Física Atômica e Molecular Cálculos de Estrutura Eletrônica Utilizando Funcionais de Densidade Departamento de Física Universidade Federal do Paraná
Introdução à Modelagem Molecular
 Introdução à Modelagem Molecular Prof. Alex Fabiano C. Campos, Dr Introdução Métodos teóricos e técnicas computacionais para modelar ou imitar o comportamento de moléculas e sistemas atômicos. Empregados
Introdução à Modelagem Molecular Prof. Alex Fabiano C. Campos, Dr Introdução Métodos teóricos e técnicas computacionais para modelar ou imitar o comportamento de moléculas e sistemas atômicos. Empregados
Fundamentos da modelagem Molecular - 1
 Fundamentos da modelagem Molecular - 1 Departamento de Física UFPel ufpellogo Introdução Rotas para a pesquisa Conexão entre experimento, simulação e teoria Sistema real Fazer modelos do sistema Fazer
Fundamentos da modelagem Molecular - 1 Departamento de Física UFPel ufpellogo Introdução Rotas para a pesquisa Conexão entre experimento, simulação e teoria Sistema real Fazer modelos do sistema Fazer
Introdução ao Método de Hartree-Fock
 Introdução ao Método de Hartree-Fock CF352 - Fundamentos de Física Atômica e Molecular Departamento de Física Universidade Federal do Paraná M. H. F. Bettega (UFPR) CF352 1 / 24 Preliminares Aproximação
Introdução ao Método de Hartree-Fock CF352 - Fundamentos de Física Atômica e Molecular Departamento de Física Universidade Federal do Paraná M. H. F. Bettega (UFPR) CF352 1 / 24 Preliminares Aproximação
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto 1o. Semestre de 2008 1 MQ átomos > < Moléculas moléculas e sólidos núcleos e partículas Moléculas
Disciplina: FGE5748 Simulação Computacional de Líquidos Moleculares 1
 Disciplina: FGE5748 Simulação Computacional de Líquidos Moleculares 1 A matéria é composta por átomos e moléculas Geralmente, fazemos simplificações e desenvolvemos modelos O estudo teórico não permite
Disciplina: FGE5748 Simulação Computacional de Líquidos Moleculares 1 A matéria é composta por átomos e moléculas Geralmente, fazemos simplificações e desenvolvemos modelos O estudo teórico não permite
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Teorema de Hohenberg-Kohn
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Teorema de Hohenberg-Kohn
Operadores e Função de Onda para Muitos Elétrons. Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros
 Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Aproximação de Hartree-Fock A maior preocupação da química quântica é encontrar e descrever
Operadores e Função de Onda para Muitos Elétrons Introdução à Física Atômica e Molecular UEG Prof. Renato Medeiros Aproximação de Hartree-Fock A maior preocupação da química quântica é encontrar e descrever
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos HF Dois elétrons N elétrons Thomas Fermi Átomo de Hélio 1D Energia exata: 3,154 H Vamos resolver este problema usando o método
2 Teoria do Funcional da Densidade
 2 Teoria do Funcional da Densidade A Mecânica Quântica teve seu início com a equação de Schrödinger (1926). Esta equação determina a função de onda quântica de um sistema, seja ele um átomo, uma molécula
2 Teoria do Funcional da Densidade A Mecânica Quântica teve seu início com a equação de Schrödinger (1926). Esta equação determina a função de onda quântica de um sistema, seja ele um átomo, uma molécula
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos Teorema de Hohenberg-Kohn Equações de Kohn-Sham Problema de N elétrons Aproximação de Born-Oppenheimer: os núcleos estão totalmente
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos Teorema de Hohenberg-Kohn Equações de Kohn-Sham Problema de N elétrons Aproximação de Born-Oppenheimer: os núcleos estão totalmente
Disciplina: SiComLíMol 1
 Disciplina: SiComLíMol 1 A matéria é composta por átomos e moléculas Geralmente, fazemos simplificações e desenvolvemos modelos O estudo teórico não permite tratar quantidades macroscópicas da matéria.
Disciplina: SiComLíMol 1 A matéria é composta por átomos e moléculas Geralmente, fazemos simplificações e desenvolvemos modelos O estudo teórico não permite tratar quantidades macroscópicas da matéria.
AULA 01 TEORIA ATÔMICA COMPLETA
 AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. QUÍMICA estudo
AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. QUÍMICA estudo
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Hartree-Fock Caso de N
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tema de hoje: Hartree-Fock e Thomas-Fermi Hartree-Fock Caso de N
CÁLCULO DA ESTRUTURA ELETRÔNICA DO ÓXIDO DE GRAFENO
 CÁLCULO DA ESTRUTURA ELETRÔNICA DO ÓXIDO DE GRAFENO Nome do Aluno 1 ; Nome do Orientador 2 ; Nome do Co-orientador 3 (apenas quando estiver oficialmente cadastrado como co-orientador junto ao PIBIC/PIVIC)
CÁLCULO DA ESTRUTURA ELETRÔNICA DO ÓXIDO DE GRAFENO Nome do Aluno 1 ; Nome do Orientador 2 ; Nome do Co-orientador 3 (apenas quando estiver oficialmente cadastrado como co-orientador junto ao PIBIC/PIVIC)
Maxwell Severo da COSTA; Freddy Fernandes GUIMARÃES
 Comparação entre a aproximação Z+1 e o cálculo de buraco de camada real no estudo da dinâmica nuclear dos isômeros do dicloroetileno induzida pela foto-ionização dos elétrons da camada K do cloro (ClK)
Comparação entre a aproximação Z+1 e o cálculo de buraco de camada real no estudo da dinâmica nuclear dos isômeros do dicloroetileno induzida pela foto-ionização dos elétrons da camada K do cloro (ClK)
Análise de alimentos II Introdução aos Métodos Espectrométricos
 Análise de alimentos II Introdução aos Métodos Espectrométricos Profª Drª Rosemary Aparecida de Carvalho Pirassununga/SP 2018 Introdução Métodos espectrométricos Abrangem um grupo de métodos analíticos
Análise de alimentos II Introdução aos Métodos Espectrométricos Profª Drª Rosemary Aparecida de Carvalho Pirassununga/SP 2018 Introdução Métodos espectrométricos Abrangem um grupo de métodos analíticos
Fundamentos de Química Quântica
 Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Aula 3 Professora: Melissa Soares Caetano Átomo de Hidrogênio Um núcleo
Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Fundamentos de Química Quântica Aula 3 Professora: Melissa Soares Caetano Átomo de Hidrogênio Um núcleo
Fundamentos da modelagem Molecular - 1
 Fundamentos da modelagem Molecular - 1 Departamento de Física UFPel Introdução Rotas para a pesquisa Conexão entre experimento, simulação e teoria Sistema real Fazer modelos do sistema Fazer experimentos
Fundamentos da modelagem Molecular - 1 Departamento de Física UFPel Introdução Rotas para a pesquisa Conexão entre experimento, simulação e teoria Sistema real Fazer modelos do sistema Fazer experimentos
Física para Ciências Biológicas Lista de Exercícios 5 - CASA Data: 22/05/2014
 Física para Ciências Biológicas - 2014 Lista de Exercícios 5 - CASA Data: 22/05/2014 1. Abaixo representamos a energia de interação dos átomos de K e Cl em função da distância interatômica. A energia de
Física para Ciências Biológicas - 2014 Lista de Exercícios 5 - CASA Data: 22/05/2014 1. Abaixo representamos a energia de interação dos átomos de K e Cl em função da distância interatômica. A energia de
ASPECTOS GERAIS. Prof. Harley P. Martins filho
 /6/08 ASPECTOS GERAIS Prof. Harley P. Martins filho Aspectos Gerais Espectroscopia por emissão: Abaixamento de energia de um sistema de um nível permitido para outro, com emissão da energia perdida na
/6/08 ASPECTOS GERAIS Prof. Harley P. Martins filho Aspectos Gerais Espectroscopia por emissão: Abaixamento de energia de um sistema de um nível permitido para outro, com emissão da energia perdida na
FF-296: Teoria do Funcional da Densidade I. Ronaldo Rodrigues Pela
 FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
FF-296: Teoria do Funcional da Densidade I Ronaldo Rodrigues Pela Tópicos O problema de 1 elétron O princípio variacional Função de onda tentativa Átomo de H unidimensional Íon H2 + unidimensional Equação
Moléculas. Usamos a aproximação de Born- Oppenheimer, que considera os núcleos fixos, apenas o e - se movimenta.
 Moléculas Moléculas é uma coleção de 2 ou mais núcleos e seus elétrons associados, com todas as ligações complexas unidas pelas forças Os tipos mais importantes de ligação molecular são: covalente, iônica
Moléculas Moléculas é uma coleção de 2 ou mais núcleos e seus elétrons associados, com todas as ligações complexas unidas pelas forças Os tipos mais importantes de ligação molecular são: covalente, iônica
4 e 6/Maio/2016 Aulas 17 e 18
 9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
9/Abril/016 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA
 NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 11 MOLÉCULAS Primeira Edição junho de 2005 CAPÍTULO 11 MOLÉCULAS ÍNDICE 11-1- Introdução 11.2- Ligação por Tunelamento e a Molécula
NOTAS DE AULAS DE ESTRUTURA DA MATÉRIA Prof. Carlos R. A. Lima CAPÍTULO 11 MOLÉCULAS Primeira Edição junho de 2005 CAPÍTULO 11 MOLÉCULAS ÍNDICE 11-1- Introdução 11.2- Ligação por Tunelamento e a Molécula
Quantização. Quantização da energia (Planck, 1900) hc h. Efeito fotoelétrico (Einstein, 1905) Espectros atômicos (linhas discretas) v 2
 Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
Mecânica Quântica Quantização e o modelo de Bohr (revisão) Dualidade Onda-Partícula Princípio da Incerteza Equação de Schrödinger Partícula na Caixa Átomo de Hidrogênio Orbitais Atômicos Números Quânticos
Métodos de Química Computacional
 Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Métodos de Química Computacional Professora: Melissa Soares Caetano Dinâmica molecular Conhecendo posições
Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Métodos de Química Computacional Professora: Melissa Soares Caetano Dinâmica molecular Conhecendo posições
QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White
 QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White Natureza ondulatória da luz Todas as ondas têm um comprimento de onda característico, λ, e uma amplitude, A.
QUÍMICA A Ciência Central 9ª Edição Capítulo 6 Estrutura eletrônica dos átomos David P. White Natureza ondulatória da luz Todas as ondas têm um comprimento de onda característico, λ, e uma amplitude, A.
Átomos e Moléculas. Ligações moleculares. Energia do ion. A molécula de hidrogênio H 2
 Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Ligações moleculares Átomos e Moléculas Energia do ion H 2 + A molécula de hidrogênio Ligações moleculares Uma molécula é formada por um conjunto de átomos que interagem formando um sistema com energia
Energia certa significa: quando a energia do fóton corresponde à diferença nos níveis de energia entre as duas órbitas permitidas do átomo de H.
 ESPECTROSCOPIA II A relação da luz com as linhas espectrais O que acontece se átomos de H forem bombardeados por fótons? R. Existem três possibilidades: 1) a maioria dos fótons passa sem nenhuma interação
ESPECTROSCOPIA II A relação da luz com as linhas espectrais O que acontece se átomos de H forem bombardeados por fótons? R. Existem três possibilidades: 1) a maioria dos fótons passa sem nenhuma interação
UMA SIMPLIFICAÇÃO DO MÉTODO HARTREE-FOCK
 UMA SIMPLIFICAÇÃO DO MÉTODO HARTREE-FOCK Lucas Modesto da Costa Instituto de Física - DFGE - USP 8 de outubro de 2008 1 / 39 Slater, J. C. Época Aproximação de Thomas-Fermi 2 / 39 Slater, J. C. Slater,
UMA SIMPLIFICAÇÃO DO MÉTODO HARTREE-FOCK Lucas Modesto da Costa Instituto de Física - DFGE - USP 8 de outubro de 2008 1 / 39 Slater, J. C. Época Aproximação de Thomas-Fermi 2 / 39 Slater, J. C. Slater,
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 4 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA Edição de junho de 2014 CAPÍTULO 4 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA ÍNDICE 4.1- Postulados de
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 4 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA Edição de junho de 2014 CAPÍTULO 4 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA ÍNDICE 4.1- Postulados de
Técnicas de Caracterização de Materiais
 Técnicas de Caracterização de Materiais 4302504 2º Semestre de 2016 Instituto de Física Universidade de São Paulo Professores: Antonio Domingues dos Santos Manfredo H. Tabacniks 20 de setembro Caracterização
Técnicas de Caracterização de Materiais 4302504 2º Semestre de 2016 Instituto de Física Universidade de São Paulo Professores: Antonio Domingues dos Santos Manfredo H. Tabacniks 20 de setembro Caracterização
AULA 01 TEORIA ATÔMICA COMPLETA
 AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. Estrutura Eletrônica
AULA 01 TEORIA ATÔMICA COMPLETA - ESTRUTURA ATÔMICA; - MODELOS ATÔMICOS; - ESPECTROSCOPIA ATÔMICA; - PROPRIEDADES ONDULATÓRIAS DOS ELÉTRONS; - NÚMEROS QUÂNTICOS E DISTRIBUIÇÃO ELETRÔNICA. Estrutura Eletrônica
Seminário. Teoria de Ligação de Valência - TLV UMA ABORDAGEM MECÂNICO QUÂNTICA DAS LIGAÇÕES COVALENTES
 Seminário Teoria de Ligação de Valência - TLV UMA ABORDAGEM MECÂNICO QUÂNTICA DAS LIGAÇÕES COVALENTES Autor: Marcelo Alves de Souza Mestrando UFABC 2015 Disciplina Química Integrada 1 O modelo de repulsão
Seminário Teoria de Ligação de Valência - TLV UMA ABORDAGEM MECÂNICO QUÂNTICA DAS LIGAÇÕES COVALENTES Autor: Marcelo Alves de Souza Mestrando UFABC 2015 Disciplina Química Integrada 1 O modelo de repulsão
Equações autoconsistentes incluindo efeitos de troca e correlação.
 Equações autoconsistentes incluindo efeitos de troca e correlação. W. Kohn e L. J. Sham, Phys. Rev. 137, A1697 (1965) Elton Carvalho Departamento de Física de materiais e Mecânica Instituto de Física Universidade
Equações autoconsistentes incluindo efeitos de troca e correlação. W. Kohn e L. J. Sham, Phys. Rev. 137, A1697 (1965) Elton Carvalho Departamento de Física de materiais e Mecânica Instituto de Física Universidade
A Estrutura Eletrônica dos Átomos. Prof. Fernando R. Xavier
 A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
A Estrutura Eletrônica dos Átomos Prof. Fernando R. Xavier UDESC 2015 Estrutura Atômica, Antencedentes... Modelos de Demócrito, Dalton, Thomson, etc 400 a.c. até 1897 d.c. Nascimento da Mecânica Quântica
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Física Quântica. Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli. Pieter Westera
 Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Física Quântica Aula 11: Spin do Elétron, Princípio de Exclusão de Pauli Pieter Westera pieter.westera@ufabc.edu.br http://professor.ufabc.edu.br/~pieter.westera/quantica.html Quantização do Momento Angular
Apresentações com base no material disponível no livro: Atkins, P.; de Paula, J.; Friedman, R. Physical Chemistry Quanta, Matter, and Change
 Físico-Química 01 Apresentações com base no material disponível no livro: Atkins, P.; de Paula, J.; Friedman, R. Physical Chemistry Quanta, Matter, and Change, 2nd Ed., Oxford, 2014 Prof. Dr. Anselmo E
Físico-Química 01 Apresentações com base no material disponível no livro: Atkins, P.; de Paula, J.; Friedman, R. Physical Chemistry Quanta, Matter, and Change, 2nd Ed., Oxford, 2014 Prof. Dr. Anselmo E
Espectroscopia no infravermelho e Raman
 Espectroscopia no infravermelho e Raman Tópicos Especiais em Química XII Métodos Físicos em Química Inorgânica Prof. Edson Nossol Uberlândia, 21/03/2017 Espectroscopia no infravermelho ACIK, M., LEE, G.,
Espectroscopia no infravermelho e Raman Tópicos Especiais em Química XII Métodos Físicos em Química Inorgânica Prof. Edson Nossol Uberlândia, 21/03/2017 Espectroscopia no infravermelho ACIK, M., LEE, G.,
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA Edição de janeiro de 2009 CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA ÍNDICE 5.1- Postulados
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA Edição de janeiro de 2009 CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA ÍNDICE 5.1- Postulados
Data de entrega dos resumos
 Data de entrega dos resumos Primeiro resumo Até 25 de abril de 2018 quarta-feira Segundo resumo Até 20 de junho de 2018 quarta-feira Cap. 3 Terceira parte Teorema de Koopmans Teorema de Brillouin Hamiltoniano
Data de entrega dos resumos Primeiro resumo Até 25 de abril de 2018 quarta-feira Segundo resumo Até 20 de junho de 2018 quarta-feira Cap. 3 Terceira parte Teorema de Koopmans Teorema de Brillouin Hamiltoniano
1.1 Interações de van der Waals. Quem inclue eficientemente?
 Interações de van der Waals: Quem inclue eficientemente? Amaury Melo, Evanildo Gomes Lacerda Júnior, José Maximiano F. Pinheiro Júnior Física At^omica e Molecular, IFUSP, 2009/1 Docente: Prof. Sylvio Canuto.
Interações de van der Waals: Quem inclue eficientemente? Amaury Melo, Evanildo Gomes Lacerda Júnior, José Maximiano F. Pinheiro Júnior Física At^omica e Molecular, IFUSP, 2009/1 Docente: Prof. Sylvio Canuto.
Átomos multi-eletrônicos. Indistinguibilidade
 Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli 1. Em um átomo multi-eletrônico nunca pode haver mais de 1 e- ocupando o mesmo estado quântico.. Um sistema constituído de vários
Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli 1. Em um átomo multi-eletrônico nunca pode haver mais de 1 e- ocupando o mesmo estado quântico.. Um sistema constituído de vários
Princípios Gerais da Mecânica Quântica
 Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Princípios Gerais da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ)
Aplicação do Método Variacional na Mecânica Quântica:
 Aplicação do Método Variacional na Mecânica Quântica: Átomo de Hélio Milena Menezes Carvalho 1 1 Instituto de Física de São Carlos, Universidade de São Paulo E-mail: glowingsea@gmail.com 1. Introdução
Aplicação do Método Variacional na Mecânica Quântica: Átomo de Hélio Milena Menezes Carvalho 1 1 Instituto de Física de São Carlos, Universidade de São Paulo E-mail: glowingsea@gmail.com 1. Introdução
Física Moderna II - FNC376
 Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Universidade de São Paulo Instituto de Física Física Moderna II - FNC376 Profa. Márcia de Almeida Rizzutto o. Semestre de 008 Conteúdo (P) Cap. 7, 8 e 9 Eisberg (/ do 9.7), Cap. 7 do Tipler, Cap. 7 e parte
Raios atômicos Física Moderna 2 Aula 6
 Raios atômicos 1 2 8 8 18 18 32 2 Energias de ionização 3 Espectros de R-X A organização da tabela periódica reflete a distribuição dos e - nas camadas mais externas dos átomos. No entanto, é importante
Raios atômicos 1 2 8 8 18 18 32 2 Energias de ionização 3 Espectros de R-X A organização da tabela periódica reflete a distribuição dos e - nas camadas mais externas dos átomos. No entanto, é importante
Problemas de Duas Partículas
 Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
Problemas de Duas Partículas Química Quântica Prof a. Dr a. Carla Dalmolin Massa reduzida Rotor Rígido Problemas de Duas Partículas Partícula 1: coordenadas x 1, y 1, z 1 Partícula 2: coordenadas x 2,
QUÍMICA I. Teoria atômica Capítulo 6. Aula 2
 QUÍMICA I Teoria atômica Capítulo 6 Aula 2 Natureza ondulatória da luz A teoria atômica moderna surgiu a partir de estudos sobre a interação da radiação com a matéria. A radiação eletromagnética se movimenta
QUÍMICA I Teoria atômica Capítulo 6 Aula 2 Natureza ondulatória da luz A teoria atômica moderna surgiu a partir de estudos sobre a interação da radiação com a matéria. A radiação eletromagnética se movimenta
1.1. Motivação Objetivos
 1 Introdução As Unidades de Processamento Gráfico (GPUs), ou Placas Gráficas, foram originalmente desenvolvidas com o propósito de renderização gráfica. Contudo, nos últimos anos, o desempenho na realização
1 Introdução As Unidades de Processamento Gráfico (GPUs), ou Placas Gráficas, foram originalmente desenvolvidas com o propósito de renderização gráfica. Contudo, nos últimos anos, o desempenho na realização
Teoria do Funcional de Densidade
 Teoria do Funcional de Densidade Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br M. H. F. Bettega (UFPR) PG Física 1 / 23 Kohn recebendo seu Prêmio Nobel
Teoria do Funcional de Densidade Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br M. H. F. Bettega (UFPR) PG Física 1 / 23 Kohn recebendo seu Prêmio Nobel
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 2017 04 de abril de 2017 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código.
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 2017 04 de abril de 2017 Parte 1 Instruções Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código.
h mc 2 =hν mc 2 =hc/ λ
 Louis de Broglie investigou as propriedades ondulatórias da matéria na década de 30. Ele supôs que o e-, em seu movimento ao redor do núcleo, tinha associado a ele um λ. Ele igualou as duas expressões
Louis de Broglie investigou as propriedades ondulatórias da matéria na década de 30. Ele supôs que o e-, em seu movimento ao redor do núcleo, tinha associado a ele um λ. Ele igualou as duas expressões
Estudo Teórico das Propriedades Cinéticas da Reação NF+F = N+F 2
 SIMPOETS, CEFET-GO, 121-130, 2008 Estudo Teórico das Propriedades Cinéticas da Reação NF+F = N+F 2 Danielle Maria Fernandes Do Prado 1 Graduanda de Licenciatura em Química daniellemarfe@hotmail.com Simone
SIMPOETS, CEFET-GO, 121-130, 2008 Estudo Teórico das Propriedades Cinéticas da Reação NF+F = N+F 2 Danielle Maria Fernandes Do Prado 1 Graduanda de Licenciatura em Química daniellemarfe@hotmail.com Simone
3 N(4) metil tiossemicarbazonas derivadas de 4- nitrobenzaldeído e 4-nitroacetofenona: estudos estruturais
 45 3 N(4) metil tiossemicarbazonas derivadas de 4- nitrobenzaldeído e 4-nitroacetofenona: estudos estruturais Nesse capítulo relatamos o estudo estrutural de N(4)-metil tiossemicarbazonas derivadas de
45 3 N(4) metil tiossemicarbazonas derivadas de 4- nitrobenzaldeído e 4-nitroacetofenona: estudos estruturais Nesse capítulo relatamos o estudo estrutural de N(4)-metil tiossemicarbazonas derivadas de
Aspectos Quânticos da Óptica Não Linear
 Curso: Introdução à Física Atômica Molecular Professor: Phillipe Wilhelm Courteille Autor: Tiago Gualberto Bezerra de Souza Aspectos Quânticos da Óptica Não Linear Introdução Óptica não linear é o ramo
Curso: Introdução à Física Atômica Molecular Professor: Phillipe Wilhelm Courteille Autor: Tiago Gualberto Bezerra de Souza Aspectos Quânticos da Óptica Não Linear Introdução Óptica não linear é o ramo
CF373-Mecânica Quântica II (Uma Abordagem Elementar à Teoria Quântica do Espalhamento)
 CF373-Mecânica Quântica II (Uma Abordagem Elementar à Teoria Quântica do Espalhamento) Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Espalhamento por
CF373-Mecânica Quântica II (Uma Abordagem Elementar à Teoria Quântica do Espalhamento) Márcio H. F. Bettega Departamento de Física Universidade Federal do Paraná bettega@fisica.ufpr.br Espalhamento por
2. No instante t = 0, o estado físico de uma partícula livre em uma dimensão é descrito pela seguinte função de onda:
 Universidade Federal do Pará Instituto de Ciências Exatas e Naturais Programa de Pós-Graduação em Física Exame de Seleção - Data: 03/08/2011 Nome do Candidato: Nível: Mestrado Doutorado 1. No cálculo da
Universidade Federal do Pará Instituto de Ciências Exatas e Naturais Programa de Pós-Graduação em Física Exame de Seleção - Data: 03/08/2011 Nome do Candidato: Nível: Mestrado Doutorado 1. No cálculo da
Universidade Estadual de Santa Cruz (UESC) Segunda prova de seleção para ingresso em 2012/2. Nome: Data: 13/08/2012
 Universidade Estadual de Santa Cruz (UESC) Programa de Pós-Graduação em Física Segunda prova de seleção para ingresso em 2012/2 Nome: Data: 13/08/2012 1 Seção A: Mecânica Clássica Uma nave espacial cilíndrica,
Universidade Estadual de Santa Cruz (UESC) Programa de Pós-Graduação em Física Segunda prova de seleção para ingresso em 2012/2 Nome: Data: 13/08/2012 1 Seção A: Mecânica Clássica Uma nave espacial cilíndrica,
Laboratório de Física Moderna Espectroscopia do H. Marcelo Gameiro Munhoz
 Laboratório de Física Moderna Espectroscopia do H Marcelo Gameiro Munhoz munhoz@if.usp.br 1 Contextualização Para iniciar nosso experimento, vamos compreender o contexto que o cerca Qual o tipo de fenômeno
Laboratório de Física Moderna Espectroscopia do H Marcelo Gameiro Munhoz munhoz@if.usp.br 1 Contextualização Para iniciar nosso experimento, vamos compreender o contexto que o cerca Qual o tipo de fenômeno
Fundamentos da Mecânica Quântica
 Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
Fundamentos da Mecânica Quântica Vitor Oguri Departamento de Física Nuclear e Altas Energias (DFNAE) Instituto de Física Armando Dias Tavares (IFADT) Universidade do Estado do Rio de Janeiro (UERJ) Rio
O espectro eletromagnético
 Difração de Raios X O espectro eletromagnético luz visível raios-x microondas raios gama UV infravermelho ondas de rádio Comprimento de onda (nm) Raios Absorção, um fóton de energia é absorvido promovendo
Difração de Raios X O espectro eletromagnético luz visível raios-x microondas raios gama UV infravermelho ondas de rádio Comprimento de onda (nm) Raios Absorção, um fóton de energia é absorvido promovendo
Estrutura Atômica. Química Quântica Prof a. Dr a. Carla Dalmolin. Átomos Polieletrônicos
 Estrutura Atômica Química Quântica Prof a. Dr a. Carla Dalmolin Átomos Polieletrônicos Átomos Polieletrônicos Átomos que possuem mais de 1 elétron A Eq. de Schrödinger pode ser resolvida exatamente apenas
Estrutura Atômica Química Quântica Prof a. Dr a. Carla Dalmolin Átomos Polieletrônicos Átomos Polieletrônicos Átomos que possuem mais de 1 elétron A Eq. de Schrödinger pode ser resolvida exatamente apenas
Mecânica Quântica. Química Quântica Prof a. Dr a. Carla Dalmolin. A Equação de Schrödinger Postulados da Mecânica Quântica
 Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin A Equação de Schrödinger Postulados da Mecânica Quântica Mecânica Clássica O movimento de uma partícula é governado pela Segunda Lei de Newton:
Mecânica Quântica Química Quântica Prof a. Dr a. Carla Dalmolin A Equação de Schrödinger Postulados da Mecânica Quântica Mecânica Clássica O movimento de uma partícula é governado pela Segunda Lei de Newton:
2.2.1 Efeito Hall e Magnetoresistência Condutividade Elétrica AC Corrente Elétrica em um Campo Magnético
 Conteúdo 1 Revisão de Física Moderna 1 1.1 Equação de Schrödinger; Autoestados e Valores Esperados.. 1 1.2 O Poço de Potencial Innito:Quantização da Energia.............................. 7 1.3 O Oscilador
Conteúdo 1 Revisão de Física Moderna 1 1.1 Equação de Schrödinger; Autoestados e Valores Esperados.. 1 1.2 O Poço de Potencial Innito:Quantização da Energia.............................. 7 1.3 O Oscilador
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de junho de 2014 CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 5.1- Introdução 5.2- Equação
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER Edição de junho de 2014 CAPÍTULO 5 MECÂNICA QUÂNTICA DE SCHRÖDINGER ÍNDICE 5.1- Introdução 5.2- Equação
QUI346 QUÍMICA ANALÍTICA INSTRUMENTAL
 QUI346 QUÍMICA ANALÍTICA INSTRUMENTAL Prof. Mauricio Xavier Coutrim DEQUI RADIAÇÃO ELETROMAGNÉTICA Onda eletromagnética (vácuo: v = 2,99792.10 8 m.s -1 ) l = comprimento de onda A = amplitude da onda v
QUI346 QUÍMICA ANALÍTICA INSTRUMENTAL Prof. Mauricio Xavier Coutrim DEQUI RADIAÇÃO ELETROMAGNÉTICA Onda eletromagnética (vácuo: v = 2,99792.10 8 m.s -1 ) l = comprimento de onda A = amplitude da onda v
Tabela Periódica dos elementos
 Tabela Periódica dos elementos 8 8 Alcalinos, um elétron livre na camada (pode ser facilmente removido), bons condutores Todos possuem subcamada fechada 18 18 3 1 ATENÇÃO 0 Ca (Z=0 A=40) tem camadas completas,
Tabela Periódica dos elementos 8 8 Alcalinos, um elétron livre na camada (pode ser facilmente removido), bons condutores Todos possuem subcamada fechada 18 18 3 1 ATENÇÃO 0 Ca (Z=0 A=40) tem camadas completas,
Átomo de Hidrogênio 1
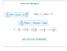 Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
Átomo de Hidrogênio 1 Potencial central Solução: separação de variáveis satisfaz a equação para qualquer valor de m l. g() deve satisfazer a condição m l deve ser inteiro. 3 Solução: separação de variáveis
INTRODUÇÃO DOS MÉTODOS COMPUTACIONAIS DE PRIMEIROS PRINCÍPIOS PARA O ESTUDO TEÓRICO DE MATERIAIS
 1 INTRODUÇÃO DOS MÉTODOS COMPUTACIONAIS DE PRIMEIROS PRINCÍPIOS PARA O ESTUDO TEÓRICO DE MATERIAIS Fábio Rogério S. Nascimento 1 - Unifesspa Jeânderson de Melo Dantas 2 Unifesspa Agência Financiadora:
1 INTRODUÇÃO DOS MÉTODOS COMPUTACIONAIS DE PRIMEIROS PRINCÍPIOS PARA O ESTUDO TEÓRICO DE MATERIAIS Fábio Rogério S. Nascimento 1 - Unifesspa Jeânderson de Melo Dantas 2 Unifesspa Agência Financiadora:
Aplicações de Semicondutores em Medicina
 Aplicações de Semicondutores em Medicina A estrutura dos cristais semicondutores Luiz Antonio Pereira dos Santos CNEN-CRCN PRÓ-ENGENHARIAS UFS-IPEN-CRCN Aracaju Março - 010 Como é a estrutura da matéria?
Aplicações de Semicondutores em Medicina A estrutura dos cristais semicondutores Luiz Antonio Pereira dos Santos CNEN-CRCN PRÓ-ENGENHARIAS UFS-IPEN-CRCN Aracaju Março - 010 Como é a estrutura da matéria?
Física Moderna 2. Aula 9. Moléculas. Tipos de ligações. Íon H2 + Iônica Covalente Outras: ponte de hidrogênio van der Waals
 Física Moderna 2 Aula 9 Moléculas Tipos de ligações Iônica Covalente Outras: Íon H2 + ponte de hidrogênio van der Waals 1 Moléculas Uma molécula é um arranjo estável de dois ou mais átomos. Por estável
Física Moderna 2 Aula 9 Moléculas Tipos de ligações Iônica Covalente Outras: Íon H2 + ponte de hidrogênio van der Waals 1 Moléculas Uma molécula é um arranjo estável de dois ou mais átomos. Por estável
Minicurso: Dinâmica Quântica. Aula 01
 Curso de Verão 2015 Minicurso: Dinâmica Quântica Aula 01 Prof. Márcio Varella Departamento de Física geral mvarella@if.usp.br Grupo de Física Molecular e Modelagem Interações com Fótons, Elétrons e Prótons
Curso de Verão 2015 Minicurso: Dinâmica Quântica Aula 01 Prof. Márcio Varella Departamento de Física geral mvarella@if.usp.br Grupo de Física Molecular e Modelagem Interações com Fótons, Elétrons e Prótons
Sabrina Silva Carara
 Estudo de Defeitos em Camadas de Grafeno usando Dinâmica Molecular por Primeiros Princípios Sabrina Silva Carara Sabrina Silva Carara Estudo de Defeitos em Camadas de Grafeno usando Dinâmica Molecular
Estudo de Defeitos em Camadas de Grafeno usando Dinâmica Molecular por Primeiros Princípios Sabrina Silva Carara Sabrina Silva Carara Estudo de Defeitos em Camadas de Grafeno usando Dinâmica Molecular
A Radiação do Corpo Negro e sua Influência sobre os Estados dos Átomos
 Universidade de São Paulo Instituto de Física de São Carlos A Radiação do Corpo Negro e sua Influência sobre os Estados dos Átomos Nome: Mirian Denise Stringasci Disciplina: Mecânica Quântica Aplicada
Universidade de São Paulo Instituto de Física de São Carlos A Radiação do Corpo Negro e sua Influência sobre os Estados dos Átomos Nome: Mirian Denise Stringasci Disciplina: Mecânica Quântica Aplicada
Física IV - FAP2204 Escola Politécnica GABARITO DA P3 8 de dezembro de 2009
 P3 Física IV - FAP2204 Escola Politécnica - 2009 GABARITO DA P3 8 de dezembro de 2009 Questão 1 Numaexperiência deespalhamentocompton, umelétrondemassam 0 emrepousoespalha um fóton de comprimento de onda
P3 Física IV - FAP2204 Escola Politécnica - 2009 GABARITO DA P3 8 de dezembro de 2009 Questão 1 Numaexperiência deespalhamentocompton, umelétrondemassam 0 emrepousoespalha um fóton de comprimento de onda
Métodos de Química Computacional
 Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Métodos de Química Computacional Professora: Melissa Soares Caetano Métodos Semi-empíricos Expressão
Universidade Federal de Ouro Preto Instituto de Ciências Exatas e Biológicas Departamento de Química Métodos de Química Computacional Professora: Melissa Soares Caetano Métodos Semi-empíricos Expressão
3 Espectroscopia Molecular
 3 Espectroscopia Molecular 3.1. Aspectos gerais Todos os espectros se devem às transições entre estados de energia. A espectroscopia molecular fornece o valor da variação da energia interna quando uma
3 Espectroscopia Molecular 3.1. Aspectos gerais Todos os espectros se devem às transições entre estados de energia. A espectroscopia molecular fornece o valor da variação da energia interna quando uma
EUF. Exame Unificado
 EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 2015 14 de abril 2015 Parte 1 Instruções ˆ Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código
EUF Exame Unificado das Pós-graduações em Física Para o segundo semestre de 2015 14 de abril 2015 Parte 1 Instruções ˆ Não escreva seu nome na prova. Ela deverá ser identificada apenas através do código
Equação de Schrödinger em 3D
 Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Equação de Schrödinger em 3D Conteúdo básico: extensão do que foi feito em 1D: p 2 /2m + V(x,y,z) = E; Equação independente do tempo: 2m 2 ψ +V(x, y, z)ψ = Eψ A interpretação probabilística envolve a integração
Átomo de Hélio. Tiago Santiago. 2 de novembro de Resumo
 Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
Átomo de Hélio Tiago Santiago de novembro d015 Resumo Nesse trabalho o átomo de Hélio é abordado definindo-se o hamiltoniano e utilizando métodos de aproximação para estimar a energia do ground state.
POSTULADOS DA MECÂNICA QUÂNTICA
 UNIVERSIDADE FEDERAL DO ABC POSTULADOS DA MECÂNICA QUÂNTICA FERNANDA MARIA RODRIGUEZ ABRIL/2015 Resumo da Apresentação O que é Mecânica Quântica? Cenário no fim do século XIX; Radiação do corpo negro;
UNIVERSIDADE FEDERAL DO ABC POSTULADOS DA MECÂNICA QUÂNTICA FERNANDA MARIA RODRIGUEZ ABRIL/2015 Resumo da Apresentação O que é Mecânica Quântica? Cenário no fim do século XIX; Radiação do corpo negro;
Capítulo 1. Introdução
 Capítulo 1 Introdução O desenvolvimento e a construção de lasers marcaram um período importante no desenvolvimento da Física em meados do século passado. A geração de um gás quase totalmente ionizado (plasma)
Capítulo 1 Introdução O desenvolvimento e a construção de lasers marcaram um período importante no desenvolvimento da Física em meados do século passado. A geração de um gás quase totalmente ionizado (plasma)
Oswaldo Sala Departamento de Química Fundamental, Universidade de São Paulo, CP 26077, São Paulo - SP
 Quim. Nova, Vol. 31, No. 4, 914-920, 2008 - UMA MOLÉCULA DIDÁTICA Educação Oswaldo Sala Departamento de Química Fundamental, Universidade de São Paulo, CP 26077, 05513-970 São Paulo - SP Recebido em 14/6/07;
Quim. Nova, Vol. 31, No. 4, 914-920, 2008 - UMA MOLÉCULA DIDÁTICA Educação Oswaldo Sala Departamento de Química Fundamental, Universidade de São Paulo, CP 26077, 05513-970 São Paulo - SP Recebido em 14/6/07;
(Versão 2014/2) (b) (d)
 MOVIMENTO HARMÔNICO SIMPLES (Versão 2014/2) 1. INTRODUÇÃO Um dos movimentos mais importantes que observamos na natureza é o movimento oscilatório. Chamado também movimento periódico ou vibracional. Em
MOVIMENTO HARMÔNICO SIMPLES (Versão 2014/2) 1. INTRODUÇÃO Um dos movimentos mais importantes que observamos na natureza é o movimento oscilatório. Chamado também movimento periódico ou vibracional. Em
Química Orgânica Ambiental
 Química Orgânica Ambiental Aula 1 Estrutura Eletrônica e ligação química Prof. Dr. Leandro Vinícius Alves Gurgel 1. Introdução: O átomo Os átomos são formados por nêutrons, prótons e elétrons: Prótons
Química Orgânica Ambiental Aula 1 Estrutura Eletrônica e ligação química Prof. Dr. Leandro Vinícius Alves Gurgel 1. Introdução: O átomo Os átomos são formados por nêutrons, prótons e elétrons: Prótons
Universidade de São Paulo Instituto de Física. Física Moderna II. Profa. Márcia de Almeida Rizzutto 2 o Semestre de Física Moderna 2 Aula 8
 Universidade de São Paulo Instituto de Física Física Moderna II Profa. Márcia de Almeida Rizzutto o Semestre de 04 Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli. Em um átomo
Universidade de São Paulo Instituto de Física Física Moderna II Profa. Márcia de Almeida Rizzutto o Semestre de 04 Átomos multi-eletrônicos Indistinguibilidade Princípio de exclusão, de Pauli. Em um átomo
FF-296: Teoria do Funcional da Densidade I. Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785
 FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tópicos Escala Funções de onda Funcionais da densidade Termo de
FF-296: Teoria do Funcional da Densidade I Prof. Dr. Ronaldo Rodrigues Pelá Sala 2602A-1 Ramal 5785 rrpela@ita.br www.ief.ita.br/~rrpela Tópicos Escala Funções de onda Funcionais da densidade Termo de
Tópicos em Métodos Espectroquímicos. Aula 2 Revisão Conceitos Fundamentais
 Universidade Federal de Juiz de Fora (UFJF) Instituto de Ciências Exatas Depto. de Química Tópicos em Métodos Espectroquímicos Aula 2 Revisão Conceitos Fundamentais Julio C. J. Silva Juiz de For a, 2013
Universidade Federal de Juiz de Fora (UFJF) Instituto de Ciências Exatas Depto. de Química Tópicos em Métodos Espectroquímicos Aula 2 Revisão Conceitos Fundamentais Julio C. J. Silva Juiz de For a, 2013
Instituto de Física USP. Física V - Aula 24. Professora: Mazé Bechara
 Instituto de Física USP Física V - Aula 24 Professora: Mazé Bechara Aula 24 Princípio de correspondênciam Experimento de Franck e Hertz, e regra de quantização de Wilson-Sommerfeld 1. O princípio de correspondência
Instituto de Física USP Física V - Aula 24 Professora: Mazé Bechara Aula 24 Princípio de correspondênciam Experimento de Franck e Hertz, e regra de quantização de Wilson-Sommerfeld 1. O princípio de correspondência
Tópicos em Métodos Espectroquímicos. Aula 2 Revisão Conceitos Fundamentais
 Universidade Federal de Juiz de Fora (UFJF) Instituto de Ciências Exatas Depto. de Química Tópicos em Métodos Espectroquímicos Aula 2 Revisão Conceitos Fundamentais Julio C. J. Silva Juiz de For a, 2015
Universidade Federal de Juiz de Fora (UFJF) Instituto de Ciências Exatas Depto. de Química Tópicos em Métodos Espectroquímicos Aula 2 Revisão Conceitos Fundamentais Julio C. J. Silva Juiz de For a, 2015
Mecânica Quântica. Veremos hoje: Dualidade onda partícula Princípio da Incerteza Formulações da MQ Equação de Schrodinger Partícula numa caixa
 Mecânica Quântica Veremos hoje: Dualidade onda partícula Princípio da Incerteza Formulações da MQ Equação de Schrodinger Partícula numa caixa Limitações do modelo de Bohr A teoria de Bohr não era capaz
Mecânica Quântica Veremos hoje: Dualidade onda partícula Princípio da Incerteza Formulações da MQ Equação de Schrodinger Partícula numa caixa Limitações do modelo de Bohr A teoria de Bohr não era capaz
Uma breve história do mundo dos quanta. Érica Polycarpo Equipe de Física Coordenação: Prof. Marta Barroso
 Uma breve história do mundo dos Érica Polycarpo Equipe de Física Coordenação: Prof. Marta Barroso Tópicos da Terceira Aula Espectros atômicos Evolução dos modelos atômicos Thomson Rutherford Bohr Princípio
Uma breve história do mundo dos Érica Polycarpo Equipe de Física Coordenação: Prof. Marta Barroso Tópicos da Terceira Aula Espectros atômicos Evolução dos modelos atômicos Thomson Rutherford Bohr Princípio
Física Moderna II Aula 07
 Universidade de São Paulo Instituto de Física 1 º Semestre de 015 Profa. Márcia de Almeida Rizzutto Oscar Sala sala 0 rizzutto@if.usp.br Física Moderna II Aula 07 Monitor: Gabriel M. de Souza Santos Sala
Universidade de São Paulo Instituto de Física 1 º Semestre de 015 Profa. Márcia de Almeida Rizzutto Oscar Sala sala 0 rizzutto@if.usp.br Física Moderna II Aula 07 Monitor: Gabriel M. de Souza Santos Sala
SUGESTÕES DE EXERCÍCIOS PARA A SEGUNDA AVALIAÇÃO
 FÍSICA IV PROF. DR. DURVAL RODRIGUES JUNIOR SUGESTÕES DE EXERCÍCIOS PARA A SEGUNDA AVALIAÇÃO Como na Biblioteca do Campus I e do Campus II temos bom número de cópias do Halliday e poucas do Serway, os
FÍSICA IV PROF. DR. DURVAL RODRIGUES JUNIOR SUGESTÕES DE EXERCÍCIOS PARA A SEGUNDA AVALIAÇÃO Como na Biblioteca do Campus I e do Campus II temos bom número de cópias do Halliday e poucas do Serway, os
