Curso Básico HEC-RAS
|
|
|
- Talita Camilo Sintra
- 8 Há anos
- Visualizações:
Transcrição
1 Curso Básico HEC-RAS Elaborado por: Rubens Gomes Dias Campos Engenheiro Civil UFMG Msc. Recursos Hídricos UFMG Apoio Logístico: Eng Marcos Jabor DER MG Versão 1.1 Belo Horizonte, 7 e 8 de Maio de
2 SUMÁRIO SUMÁRIO... 2 OBJETIVO... 4 INTRODUÇÃO... 4 INSTALANDO OS SOFTWARES... 4 HEC-RAS... 4 SOBRE O HEC-RAS... 5 BASE TEÓRICA... 5 FORMULAÇÃO MATEMÁTICA ESCOAMENTO PERMANENTE... 5 MÉTODOS NUMÉRICOS PARA CÁLCULO DO ESCOAMENTO PERMANENTE... 7 FORMULAÇÃO MATEMÁTICA ESCOAMENTO TRANSITÓRIO... 8 MÉTODOS NUMÉRICOS PARA CÁLCULO DO ESCOAMENTO TRANSITÓRIO... 9 INTERFACES INTERFACE PRIMÁRIA PARTE I INTERFACE PRIMÁRIA PARTE II GEOMETRIA INTERFACE GEOMETRIA - INTRODUÇÃO SEÇÃO GEOMÉTRICA JUNÇÕES O SISTEMA SIG E O HEC-RAS FERRAMENTA INTERPOLAÇÃO POR TRECHO POR SEÇÃO ENTRADA DE DADOS POR TABELAS DADOS DE VAZÃO E CONDIÇÕES DE CONTORNO REGIME PERMANENTE ANÁLISE PERMANENTE DADOS DE VAZÃO E CONDIÇÕES DE CONTORNO REGIME TRANSITÓRIO ANÁLISE TRANSITÓRIO ERROS, ADVERTÊNCIAS E NOTAS GEOMETRIA - FERRAMENTA PONTES E BUEIROS LEVEES RESULTADOS GRÁFICOS PERFIS DOS TRECHOS DOS MODELOS GRÁFICOS DE DADOS HIDRÁULICOS
3 TABELA DE PROPRIEDADES HIDRÁULICAS CURVA CHAVE TABELA DE DADOS DE SAÍDA VISUALIZAÇÃO 3D FIGURAS DE FUNDO PLANOS REGIME PERMANENTE REGIME TRANSITÓRIO APLICAÇÕES ENTRADA DE DADOS SUPERFÍCIE LÍQUIDA BUEIROS PONTES ÁREAS BLOQUEADAS E ÁREAS INEFETIVAS LIMITAÇÕES DO SOFTWARE BIBLIOGRAFIA
4 OBJETIVO O Objetivo do curso é que, após este, cada engenheiro participante tenha domínio suficiente para desenvolver de forma plena o uso deste recurso computacional, de forma a ser capaz de entrar com dados proceder a análises e interpretar resultados. Para tanto são abordados não somente feições sobre o software, mas também teoria sobre o funcionamento teórico dos mesmos. INTRODUÇÃO Esta apostila foi desenvolvida para ser utilizada durante o curso, com exposição simultânea, do software HEC-RAS e as instruções seguem anotadas em figuras que representam a interface do programa. Procurou-se adotar a sequência de exposições destas figuras a serem seguidas no curso. O objetivo do curso é fornecer aos alunos noções básicas do HEC-RAS para que, com os conhecimentos de engenharia, possam desenvolver de forma independente projetos e estudos com a utilização do mesmo. Serão desenvolvidos, durante o curso, passo a passo com as interfaces expostas nesta apostila, exemplos. A apostila visa a descrever as principais interfaces que serão utilizadas. INSTALANDO OS SOFTWARES HEC-RAS Executar o aplicativo e definir prioridades para instalação dos exemplos fornecidos e Sistema Internacional de Unidades. 4
5 Figura 01 Exemplos a serem instalados. Figura 02 Definição do sistema de unidades adotado. SOBRE O HEC-RAS Basicamente, possui uma interface primária por onde pode-se acessar várias outras interfaces para entrada, consulta e verificação de dados. Este software armazena os dados em vários arquivos de forma independente. Assim, criam-se arquivos somente de geometria, vazões, sedimentos, etc. Estes arquivos de dados podem ser analisados por diferentes combinações de forma a se criar vários planos de análise. BASE TEÓRICA FORMULAÇÃO MATEMÁTICA ESCOAMENTO PERMANENTE A equação de energia sentencia que: Uma partícula de água em escoamento com peso específico γ, massa específica ρ, massa m e situada a uma cota z em relação a um Datum, e considerando esta partícula submetida a um campo gravitacional, levando-se em conta as energias cinéticas e potenciais de posição e de pressão. Para a determinação do escoamento permanente a solução da equação de energia, creditada à Bernoulli, é dada pela seguinte formulação: 5
6 2 2 α 2V2 α1v1 Y 2 + Z 2 + = Y1 + Z g 2g h e (1) Onde os termos são os seguintes, respectivamente; Y 1,Y 2 Profundidade líquida na seção; Z 1,Z 2 Cota do fundo do canal em relação a um Datum; V 1,V 2 Velocidade média na seção; α1,α 2 Coeficientes de Coriolis; g Aceleração da gravidade; he Perda de carga no trecho. A Figura a seguir demonstra os termos da equação de energia. Figura 03 Perfis das linhas de água e energia e termos da equação de energia. 6
7 MÉTODOS NUMÉRICOS PARA CÁLCULO DO ESCOAMENTO PERMANENTE Os perfis da superfície líquida são calculados de uma seção para a próxima pela resolução da equação de energia por um processo iterativo conhecido como Método Passo Padrão, introduzido por CHOW (1959). Para escoamentos na grande maioria dos canais naturais em condições normais, o perfil em trechos de canais curtos é muito semelhante ao perfil para o escoamento uniforme, A determinação da superfície líquida é feita pelo uso das equações 1 e 2, em um processo iterativo, sendo este processo computacional o seguinte; Calcula-se uma determinada elevação da superfície de água, WS1, na seção à montante (ou na seção à jusante se um perfil supercrítico está sendo calculado); Baseado na elevação de superfície de água calculada determina-se a condutância e velocidade correspondente; h 2 para e ; Com os valores do passo 2, podem se calcular S f e resolver a equação Com valores dos passos 2 e 3 é possível calcular a equação 1 para WS2; Comparam-se os valores assumidos, WS1, e calculado, WS2, até o momento no qual a diferença convirja para 0,003 m, ou outro valor definido. A perda de carga entre duas seções é devida às perdas por atrito e por perdas por contração e expansão. A equação de perda de carga proposta é a seguinte; h e = LS f 2 α V V C 2 2 α g 2g 2 (2) Onde; L Comprimento do trecho; S f Coeficiente de perda de carga representativo do trecho; expansão; C Coeficientes representativo de perda de carga por contração e 7
8 O comprimento do trecho, L, é calculado como segue: L = L lob. Q lob Q + L lob ch + Q. Q ch ch + L + Q rob rob. Q rob (3) Onde; L lob, Lch, Lrob Comprimentos dos trechos para as seções especificadas em suas margem esquerda, canal principal e margem direita. Q lob, Q ch, Q rob Média aritmética das vazões entre as seções especificadas em sua margem esquerda, canal principal e margem direita. Em geral, quando não se consegue balancear a equação de energia em uma seção, as causas comuns disto são normalmente um número inadequado de seções (seções muito espaçadas) ou dados inconsistentes, presentes nas seções. FORMULAÇÃO MATEMÁTICA ESCOAMENTO TRANSITÓRIO As premissas adotadas para a formulação das equações de Saint- Venant são as seguintes, de acordo com CHAUDHRY (1993): A distribuição de pressões no escoamento é tratada como hidrostática. Esta premissa é válida se superfície líquida não tem curvatura acentuada. A declividade do leito é pequena, o canal é de leito fixo e, portanto, a profundidade medida normalmente ao canal e verticalmente são praticamente a mesma. O escoamento é unidimensional, ou seja, a velocidade (u) do escoamento é uniforme na seção. O canal é prismático. A seção transversal do canal pode variar ao longo do escoamento, porém variações desse tipo são tratadas pela restrição de vários pequenos segmentos prismáticos. Os coeficientes de rugosidade utilizados em equações de escoamento turbulento e uniforme são aplicáveis ao escoamento não permanente para cálculo da perda de carga. As equações de Manning ou Chézy podem ser utilizadas para descrever efeitos de rugosidade e perdas de carga; O fluido é incompressível e de densidade constante. Três leis da conservação Massa, momento e energia são usadas para descrever o escoamento em canais abertos, CHAUDHRY (1993). Duas variáveis do escoamento, como a profundidade e velocidade ou a profundidade e a vazão, são suficientes para descrever as condições do escoamento em uma 8
9 seção do canal. Entretanto, duas equações devem ser usadas para analisar uma situação típica de escoamento. Para a forma reduzida temos a equação de conservação da quantidade de momento (TUCCI, 1998): v v y + v + g t x x ( ) = g S o S f (4) Para a conservação de massa a equação é escrita como (TUCCI, 1998): y y y b + A + vb t x x = 0 (5) Entre as simplificações das equações do escoamento as que possuem maior relevância quanto as suas influências sobre esta pesquisa é sobre o escoamento ser admitido como unidimensional e sobre a continuidade da função. Segundo TUCCI (1998) nas deduções das equações foram desprezadas as variações de velocidade nas direções transversal e vertical, sendo assim, a velocidade média é representativa da variabilidade de velocidades na seção e o processo é considerado, preponderantemente, longitudinal, na direção do rio ou de uma declividade principal. Tratando-se de uma região onde a planície de inundação tem uma seção larga, que foi ocupada por equipamentos urbanos e existem várias ilhas devido ao processo de assoreamento, pode-se observar a formação de vários trechos preferenciais de escoamento, bem como de áreas de armazenamento, caracterizadas aqui pelos equipamentos urbanos (quarteirões). MÉTODOS NUMÉRICOS PARA CÁLCULO DO ESCOAMENTO TRANSITÓRIO Segundo CHOW et al. (1988) as equações de Saint-Venant para escoamentos distribuídos não são facilmente resolvidas por soluções analíticas, exceto em poucos casos especiais muito simples. Existem equações diferenciais parciais que, em geral, devem ser resolvidas utilizando-se métodos numéricos. Tais métodos são classificados como Métodos Numéricos Diretos ou Métodos Característicos. Para os Métodos Diretos as equações das diferenças finitas são formuladas a partir das equações diferenciais parciais originadas da continuidade e momento. A 9
10 solução para a taxa de escoamento e elevação da superfície líquida são então obtidas para tempos e distâncias incrementais ao longo do rio. Em métodos numéricos para resolução das equações parciais os cálculos são executados em um malha localizada sobre o plano x-t. O plano x- t é uma rede de pontos definidos por incrementos de distância de comprimento x e incrementos de tempo de duração t. A partir da Figura 4.2, os pontos de distância são denotados pelo índice i e os pontos de tempo pelo índice j. A linha do tempo seria uma linha paralela ao eixo x por todas as distâncias e para um valor de tempo concedido. Esquemas numéricos transformam as equações diferenciais governantes em um esquema de equações de diferenças finitas algébricas, que pode ser linear ou não linear. As equações de diferenças finitas representam as derivadas espaciais e temporais em termos de variáveis desconhecidas em ambas as linhas do tempo, j + 1, e sua linha precedente, j, onde todos os valores são conhecidos de um cálculo anterior (ver Figura 4.2). A solução das equações de Saint-Venant avançam de uma linha do tempo para a próxima. Figura 04 - Malha de plano x-t usada para solução numérica das equações de Saint-Venant por diferenças finitas - Adaptado de CHOW et al. (1988). A aproximação para o esquema de diferenças finitas pode ser aproximado pela função u(x) como mostrado na Figura 4.3. Por um processo de expansão da série de Taylor de u(x) em um ponto x + x produz: 10
11 Figura 05 - Aproximações por diferenças finitas para a função u(x)- Adaptado de CHOW et al. (1988) u( x + x) = u( x) + xu'( x) + x u''( x) + x u'''( x) (6) Onde u (x) = u/ x, u (x) = 2u/ x2, e daí em diante. A expansão da série de Taylor em x - x produz: u( x x) = u( x) xu'( x) x 2 1 u''( x) x 6 u'''( x) (7) Uma aproximação pela Diferença Central utiliza a diferença subtraindo 4.7 de 4.6: u( x + x) u( x x) = 2. x. u' ( x) + 0.( x 3 ) (8) 3 Onde 0.( x ) representa um residual contendo os temos de terceira e maiores ordens. Resolvendo para u (x) e assumindo 0.( x 3 ) 0 resulta em: u( x + x) u( x x) u'( x) 2. x (9) Que possui um erro de aproximação de ordem de x2. Este erro de aproximação, devido à eliminação dos termos de ordem maior, é também referido como erro truncado. 11
12 A aproximação para a Diferença Progressiva é definida pela subtração da equação 4.6 de u(x): u( x + x) u( x) = x. u'( x) + 0.( x 2 ) (10) Assumindo que termos de segunda e ordens maiores são negligenciáveis, solucionando para u (x) resulta: u( x + x) u( x) u'( x) x (11) Que apresenta um erro de aproximação da ordem de x. A aproximação para a Diferença Regressiva é definida pela subtração de u(x) da equação 4.7: u( x) u( x x) = x. u'( x) + 0.( x 2 ) (12) Assumindo que termos de segunda e ordens maiores são negligenciáveis, solucionando para u (x) resulta: u( x) u( x x) u'( x) x (13) O método das diferenças finitas pode utilizar o esquema implícito ou o esquema explícito. A principal diferença entre os dois é que para o método na forma explícita os valores desconhecidos são obtidos de forma sequencial ao longo do eixo do tempo de um ponto de distância para outro, enquanto que o método na forma implícita os valores desconhecidos em uma linha do tempo são todos obtidos simultaneamente. A forma explícita é mais simples, mas pode ser instável, o que significa que valores de x e t pequenos são necessários para a convergência numérica do procedimento. A forma explícita é mais conveniente por que os resultados são fornecidos em pontos de uma malha, e assim pode-se tratar variações sutis do canal de uma seção para outra, mas, é menos eficiente que a forma implícita, e assim não adequado para simulação de vazões por longos períodos. A forma implícita é matematicamente mais complicada, mas com o uso de computadores isto não é um problema sério quando se pode programar o método. Este método é estável para longos intervalos com baixa perda de precisão e assim trabalha mais rápido que o método explícito. Este método também pode suportar variações significativas entre as seções que descrevem o canal. 12
13 O software utilizado no trabalho proposto, HEC-RAS 4.1, possui em seus algoritmos, a forma implícita de quatro pontos para resolução do método das diferenças finitas, conhecido como esquema caixa (USACE a, 2008). Os esquemas implícitos usam as aproximações por diferenças finitas para ambas derivações temporal e espacial em termos da variável dependente em uma linha do tempo desconhecida. Com um exemplo simples as derivadas de tempo e espaço podem ser escritas para um ponto desconhecido (i + 1, j + 1) como: j ui+ x u = j+ 1 i+ 1 u x j+ 1 i (14) j ui t u = u t + 1 j+ 1 j + 1 i+ 1 i + 1 (15) 13
14 INTERFACES INTERFACE PRIMÁRIA PARTE I Interface por meio da qual pode se acessar as demais interfaces. Dados Escoamento Permanente Dados Quasi-Transitórios Dados escoamento Transitórios Simulação de transporte de sedimentos Simular Simulação Transitória Simulação Permanente Dados de temperatura Dados de sedimentos Simulação de qualidade de água Dados de geometria Salvar arquivos Abrir arquivos Figura 06 Interface do HEC-RAS. 14
15 INTERFACE PRIMÁRIA PARTE II Visualização da Visualização do Plotagem de dados Curvas chave Visualização 3d Hidrogramas Tabela de propriedades Dados de saída de Sumário Erros, notas e Visualização DSS Figura 07 Interface do HEC-RAS. 15
16 GEOMETRIA INTERFACE GEOMETRIA - INTRODUÇÃO Junção Imagens Seção Pontes e bueiros Estruturas alinhadas Estruturas laterais Ferramenta trechos - Áreas de armazenamento - Conexões de áreas de armazenamento- Bombas- desenho Adicionar nós em trechos e Áreas de armazenamento Conexões de áreas de Bombas Tabela de parâmetros Figuras Figura 08 Interface da geometria HEC-RAS. 16
17 SEÇÃO GEOMÉTRICA Os coeficientes de Manning podem ser definidos por faixas ou pelas margens. Coeficiente de Manning por faixas Áreas inefetivas. Figura 09 Visualização das seções no HEC-RAS. 17
18 Com estas opções podem se definir quais variações dos coeficientes de rugosidade. Variação Horizontal de n e K, ou vertical de n. Figura 10 Opções de variação coeficientes de rugosidade. Rio e trecho a ser Seçã Distância até a próxima seção Coeficiente de Manning para as Margens Coeficientes de Variação horizontal de n. Estação / Figura 11 Entrada de dados para as seções. 18
19 Ferramentas Figura 12 Interface ferramentas. 19
20 JUNÇÕES Devem ser delimitadas pára afluências e defluências. Figura 13 Modelo com junção. Figura 14 Entrada de dados para as junções. 20
21 As seções de montante têm as distâncias para a próxima seção igual a zero. A distância deve ser inserida na junção, bem como o ângulo, se este for significativo e de acordo com o método. O SISTEMA SIG E O HEC-RAS O HEC-RAS utiliza as projeções UTM sem definir a zona de projeção, mas com definição das coordenadas dos pontos das seções. Somente dados com definições SIG podem ser exportados, para uma posterior análise, em softwares SIG. A Figura ilustra a idéia do sistema de projeções de Mercator (UTM). Figura 15 Idealização da Projeção de Mercator. A Figura ilustra as zonas que interceptam o Brasil, e em Minas Gerias. Porém, para o HEC-RAS somente são consideradas as coordenadas. O HEC-RAS avisa sobre as condições de georreferenciamento das seções, Figura 16. Assim, podem haver seções georreferenciadas ou não, subtipos que podem ser originais ou interpoladas. Figura 16 Alerta sobre dados não georreferenciados. 21
22 O HEC-RAS 4.1 possui a ferramenta RAS-Mapper que necessita de arquivo.prj (com definições de projeção). No material fornecido segue o arquivo SAD_1969_UTM_Zone_23S.prj para ser utilizado com o RAS-Mapper. Obviamente outras projeções podem ser necessárias de acordo com a área de estudo. Figura 17 Zonas de projeção UTM sobre Brasil e Minas Gerais. 22
23 Figura 18 Entrada da interface de coordenadas dos pontos das seções. Entrar com as coordenadas das seções, ponto a ponto, para georreferenciamento das seções. Figura 19 Interface para inserir as coordenadas dos pontos das seções. OBSERVAÇÃO: Se as seções não forem georreferenciadas os resultados não podem ser exportados para outras bases SIG, apesar de apresentarem resultados corretos hidraulicamente. Dados que são importados de softwares de SIG, como o ArcGIS, pelo HEC-GeoRAS, já possuem dados de 23
24 coordenadas,e podem ser exportados diretamente para geração de mapas ou figuras. FERRAMENTA INTERPOLAÇÃO POR TRECHO São dois tipos de interpolação; entre duas seções ou em um trecho completo e a escolha depende da qualidade dos dados, da geometria a ser interpolada e do objetivo em estudo. Na interpolação por trecho o controle é menor. Basicamente escolhe-se a distância entre as seções, tipo de coordenadas SIG que serão adotadas, e as casas decimais. Permite-se que sejam apagadas a qualquer momento se não forem convertidas em definitivas. Ferramenta Em um trecho Entre duas seções Figura 20 Interface da ferramenta de interpolação. 24
25 Figura 21 Interpolação por trecho. POR SEÇÃO Na interpolação por seção o controle é muito mais definido. Podem-se definir os pontos que serão ligados para direcionar a interpolação. As condições de controle são as mesmas: Basicamente escolhe-se a distância entre as seções, tipo de coordenadas SIG que serão adotadas, e as casas decimais. 25
26 Figura 22 Interpolação por seção. ENTRADA DE DADOS POR TABELAS Uma opção muito interessante para trabalhar com um grande número de seções é o trabalho com tabelas, que permite a entrada de dados de forma massiva. 26
27 Figura 23 Entrada de dados por tabelas. 27
28 Figura 24 Entrada de dados por tabelas Coeficientes de Manning. 28
29 Figura 25 Entrada de dados por tabelas distância para seção de jusante. 29
30 Figura 26 Entrada de dados por tabelas coeficientes de expansão e contração. DADOS DE VAZÃO E CONDIÇÕES DE CONTORNO REGIME PERMANENTE Condições de contorno Número de perfis de Vazão Figura 27 Definição do número de dados e vazões e valores. 30
31 Entrada da Condição de contorno. Declividade da Figura 28 Condições de contorno para os dados de vazões definidos. Entrada da Condição de contorno. Declividade para a profundidade normal. Figura 29 Condições de contorno para os dados de vazões definidos. Entrada da Condição de contorno. Profundidade Figura 30 Condições de contorno para os dados de vazões definidos. 31
32 ANÁLISE PERMANENTE Nome e abreviação do plano Arquivo de geometria. Arquivo de vazões e condições de Regime de análise que deve ser selecionado pelo usuário de acordo com critérios hidráulicos. Figura 31 Interface para análise permanente. 32
33 DADOS DE VAZÃO E CONDIÇÕES DE CONTORNO REGIME TRANSITÓRIO Condição Seções com as respectivas condições de Condição de contorno: Curva chave de hidrograma, Hidrograma, Profundidade Figura 32 Condições de contorno para análise transitória. Condição de contorno inicial para cada trecho. Figura 33 Condições iniciais para análise transitória. 33
34 Dados dos hidrogramas. Figura 34 Definição do hidrograma para análise transitória. 34
35 ANÁLISE TRANSITÓRIO Figura 35 Interface para análise transitória. 35
36 ERROS, ADVERTÊNCIAS E NOTAS Ao final de uma simulação em regimes permanentes ou transitório deve-se procurar avaliar possíveis erros, advertências ou notas que o HEC-RAS verifica durante os cálculos, como por exemplo, a distância entre as seções. Figura 36 Interface de erros, advertências e notas. 36
37 GEOMETRIA - FERRAMENTA PONTES E BUEIROS Interface para entrada de dados de bueiros e pontes. Tabuleiro da ponte Pilares Taludes de pontes Modelo de cálculo da ponte Bueiros Figura 37 Interface de pontes e bueiros. Utilize os campos Station, low chord e high chord para definir os tabuleiros das pontes e bueiros. 37
38 Largura da ponte Distância até a seção de montante. Figura 38 Interface para entrada de dados das pontes. Figura 39 - Interface para entrada de dados dos pilares das pontes. 38
39 Figura 40 Interface para tipo de modelagem das pontes. 39
40 Figura 41 Interface para entrada de dados de Bueiros. 40
41 LEVEES Levees não são os diques, como sugere a tradução literal, mas sim um recurso para que não ocorra o extravasamento para regiões da geometria que esteja fora de análise. NÃO CONFUNDIR COM DIQUES (TRADUÇÃO). Figura 42 Resultado sem o uso da ferramenta Levee. Figura 43 Resultado com o uso da ferramenta Levee. 41
42 RESULTADOS GRÁFICOS Existem várias formas gráficas de visualização dos resultados. A seguir segue como operar para esta visualização. PERFIS DOS TRECHOS DOS MODELOS Figura 44 Visualização dos perfis de superfície líquida e dados correlatos. 42
43 Botão options ou clique com botão direito do mouse sobre a interface. GRÁFICOS DE DADOS HIDRÁULICOS Figura 45 Opções de interface. Avalia os dados, como por exemplo; velocidade, profundidade, em forma gráfica, ao longo de um trecho. Figura 46 Variação dos dados em forma gráfica. 43
44 Os controles são; opções, gráficos padrões, e gráficos definidos pelo usuário. Botão options ou clique com botão direito do mouse sobre a interface. Figura 47 Opções de interface. TABELA DE PROPRIEDADES HIDRÁULICAS Figura 48 Variação das propriedades por seção. 44
45 CURVA CHAVE Figura 49 Curvas chaves. 45
46 TABELA DE DADOS DE SAÍDA Figura 50 Saída de dados em forma de Tabela. 46
47 VISUALIZAÇÃO 3D Esta interface permite a exposição em perspectiva do modelo UNIDIMENSIONAL. Não confundir com modelos bi e tridimensionais. Figura 51 Visualização em 3D. Existem vários recursos que para este aplicativo que serão abordados na aula, incluindo a criação de FILMES de inundação. 47
48 FIGURAS DE FUNDO Uma ferramenta muito útil para trabalhar com informações georreferenciadas é a locação de figuras de fundo. Estas podem auxiliar para as seguintes definições: Distância entre seções topobatimétricas; Valores de coeficientes de Manning; A Figura 52 ilustra a colocação de figuras de fundo. Botão para figuras de Seleção de Figuras de Figura 52 Figuras de fundo. 48
49 PLANOS O HEC-RAS possui em sua interface os botões de planos permanente e transitório, que permitem que possam avaliados diferentes arquivos de geometria por diferentes arquivos de dados de vazão ou de hidrogramas, como apresentado na Figura 6. REGIME PERMANENTE Figura 53 Plano para escoamento permanente. REGIME TRANSITÓRIO Para a propagação de hidrogramas o ajuste da data e horas deve ser procedido após entrada de dados. 49
50 Figura 54 Plano para escoamento transitório. A utilização da propagação em regime transitório deve ser mais cautelosa. Em uma primeira rodada processa a geometria, para em uma segunda propagar o hidrograma e pós-processar. Este método pode apresentar INSTABILIDADE devido aos recursos do método numérico adotado pelo software. APLICAÇÕES Após a introdução sobre a interface básica será dirigida à aplicação de exemplos práticos para utilizando os recursos aprendidos. 50
51 Curso Básico HEC-RAS ENTRADA DE DADOS As seções devem ser entradas em ordem decrescente. As distâncias entre as seções devem ser tomadas em três pontos característicos: Margens esquerda, direita e canal principal, como demonstrado na Figura 53. Figura 55 Figuras de fundo. Principais informações que devem ser levantadas: Distância entre as seções; Coeficientes de Manning; Limite das margens; Estações e cotas (forma do canal); Outras informações pertinentes serão abordadas dependendo da característica geométrica que está se estudando. 51
52 SUPERFÍCIE LÍQUIDA Exemplo prático desenvolvido no curso. Utiliza um arquivo de geometria, um de vazão e um arquivo de Plano Permanente. BUEIROS A representação dos bueiros é bem similar a da ponte. Porém para pontes para qualquer característica geométrica pode ser aceita, porém para bueiros existem tipos pré-definidos que devem ser selecionados. Figura 56 Condições de funcionamento dos bueiros. 52
53 Figura 57 - Interface de entrada de dados dos bueiros. PONTES Para a representação de pontes deve-se entrar com os seguintes dados, de acordo com as Figuras 37 e 58. São as principais características geométricas das pontes para entrada no HEC- RAS: Distância de montante (upstream distance); Largura da ponte (Width); Pilares; Tipo de cálculo. 53
54 Figura 58 Interface de entrada de dados das pontes. Nota-se, pela figura 59 que algumas aproximações sobre o funcionamento das pontes devem ser abordadas. Assim, exige-se o uso de áreas inefetivas. Figura 59 Áreas inefetivas próximas às pontes. 54
55 Figura 60 Definições da geometria da ponte. Coeficientes de contração e expansão para pontes e bueiros são valores mais altos devido ao direcionamento do fluxo, Figura 61. Figura 61 Definições da geometria da ponte. 55
56 ÁREAS BLOQUEADAS E ÁREAS INEFETIVAS O uso das áreas inefetivas permite definir locais onde a água não está sendo efetivamente conduzida. São áreas onde ocorrerá o armazenamento, mas a velocidade da água, na direção de jusante, será próxima de zero. Esta porção líquida está incluída nos cálculos de armazenamento e outros parâmetros da área molhada da seção, mas, não está incluída como parte da área de escoamento efetivo. A área bloqueada considera regiões funcionando como uma área que não tem condutância, e não armazena água. Figura 62 - Áreas bloqueadas. 56
57 Figura 63 - Áreas inefetivas. LIMITAÇÕES DO SOFTWARE A principal limitação do software, a respeito de recursos gráficos, é o número de pontos que podem ser inseridos por seção, com um máximo de 500 pontos, inclusive pontos de recursos gráficos adicionais, como áreas bloqueadas e inefetivas. O software é unidimensional, ou seja, é considerada a velocidade de fluxo somente em uma direção e sentido. Assim, a representação da velocidade é definida em somente uma direção, e, consequentemente, o cálculo das propriedades hidráulicas. Na prática vários tipos de estruturas hidráulicas apresentam, preponderantemente, o escoamento em uma direção. Contudo, algumas estruturas hidráulicas apresentam escoamento caracterizado por escoamento em mais de uma direção. 57
58 BIBLIOGRAFIA USACE a - U.S. Army Corps of Engineers. HEC-RAS River Analysis System User s Manual. Version p USACE a - U.S. Army Corps of Engineers. HEC-RAS River Analysis System Hydraulic Reference Manual. Version p USACE b - U.S. Army Corps of Engineers. HEC-RAS River Analysis System Application Guide. Version p CAMPOS, R.G.D. Análise da Representatividade de Diferentes Hipóteses de Modelagem Matemática para Definição de Manchas de Inundações em Áreas Urbanas - Estudo de Caso da Cidade de Governador Valadares MG. UFMG No prelo. 58
Mecânica dos Fluidos Ambiental II
 Estágio docência Mecânica dos Fluidos Ambiental II Aluna: Lediane Marcon Prof.: Dr.-Ing Tobias Bleninger Medições - elevação http://defesacivil.itajai.sc.gov.br/telemetria/tele metria.php#chuva_modal_4
Estágio docência Mecânica dos Fluidos Ambiental II Aluna: Lediane Marcon Prof.: Dr.-Ing Tobias Bleninger Medições - elevação http://defesacivil.itajai.sc.gov.br/telemetria/tele metria.php#chuva_modal_4
ESCOAMENTOS UNIFORMES EM CANAIS
 ESCOAMENTOS UNIFORMES EM CANAIS Nome: nº turma INTRODUÇÃO Um escoamento em canal aberto é caracterizado pela existência de uma superfície livre. Esta superfície é na realidade uma interface entre dois
ESCOAMENTOS UNIFORMES EM CANAIS Nome: nº turma INTRODUÇÃO Um escoamento em canal aberto é caracterizado pela existência de uma superfície livre. Esta superfície é na realidade uma interface entre dois
HIDROLOGIA E HIDRÁULICA APLICADAS (LOB1216) G Aula 6 Escoamento em condutos livres
 HIDROLOGIA E HIDRÁULICA APLICADAS (LOB1216) G Aula 6 Escoamento em condutos livres 1 Canais Condutos livres Canais 2 Canais Condutos livres Canais Cursos de água naturais; Canais artificiais de irrigação
HIDROLOGIA E HIDRÁULICA APLICADAS (LOB1216) G Aula 6 Escoamento em condutos livres 1 Canais Condutos livres Canais 2 Canais Condutos livres Canais Cursos de água naturais; Canais artificiais de irrigação
Capítulo 6 Fluxo de água em canais abertos
 Capítulo 6 Fluxo de água em canais abertos slide 1 Fluxo de água em canais abertos O fluxo em canais abertos possui uma superfície livre que se ajusta dependendo das condições de fluxo. Essa superfície
Capítulo 6 Fluxo de água em canais abertos slide 1 Fluxo de água em canais abertos O fluxo em canais abertos possui uma superfície livre que se ajusta dependendo das condições de fluxo. Essa superfície
4 Modelagem Numérica. 4.1 Método das Diferenças Finitas
 4 Modelagem Numérica Para se obter a solução numérica das equações diferenciais que regem o processo de absorção de CO 2,desenvolvido no capitulo anterior, estas precisam ser transformadas em sistemas
4 Modelagem Numérica Para se obter a solução numérica das equações diferenciais que regem o processo de absorção de CO 2,desenvolvido no capitulo anterior, estas precisam ser transformadas em sistemas
Hidráulica Geral (ESA024A)
 Departamento de Engenharia Sanitária e Ambiental Hidráulica Geral (ESA04A) 1º semestre 013 Terças: 10 às 1 h Sextas: 13às 15h 14/08/013 1 Escoamentos Livres - Canais Objetivos -Estudar as características
Departamento de Engenharia Sanitária e Ambiental Hidráulica Geral (ESA04A) 1º semestre 013 Terças: 10 às 1 h Sextas: 13às 15h 14/08/013 1 Escoamentos Livres - Canais Objetivos -Estudar as características
Aula prática 09 a 12: CONDUTOS LIVRES
 Aula prática 09 a 1: CONDUTOS LIVRES INTRODUÇÃO O escoamento em condutos livres é caracterizado por apresentar uma superfície livre na qual reina a pressão atmosférica. Estes escoamentos têm um grande
Aula prática 09 a 1: CONDUTOS LIVRES INTRODUÇÃO O escoamento em condutos livres é caracterizado por apresentar uma superfície livre na qual reina a pressão atmosférica. Estes escoamentos têm um grande
Comentários sobre a densidade de operação
 Comentários sobre a densidade de operação A densidade de operação, ou densidade de referência, no software ANSYS CFD, tem grande importância na robustez e convergência de uma simulação de fluidodinâmica
Comentários sobre a densidade de operação A densidade de operação, ou densidade de referência, no software ANSYS CFD, tem grande importância na robustez e convergência de uma simulação de fluidodinâmica
RESUMO MECFLU P3. REVER A MATÉRIA DA P2!!!!! Equação da continuidade Equação da energia 1. TEOREMA DO TRANSPORTE DE REYNOLDS
 RESUMO MECFLU P3 REVER A MATÉRIA DA P2!!!!! Equação da continuidade Equação da energia 1. TEOREMA DO TRANSPORTE DE REYNOLDS Equação do Teorema do Transporte de Reynolds: : variação temporal da propriedade
RESUMO MECFLU P3 REVER A MATÉRIA DA P2!!!!! Equação da continuidade Equação da energia 1. TEOREMA DO TRANSPORTE DE REYNOLDS Equação do Teorema do Transporte de Reynolds: : variação temporal da propriedade
Condutos livres ou canais Movimento uniforme
 Condutos livres ou canais Movimento uniforme São considerados Canais todos os condutos que conduzem àguas com uma superficie livre, com secção aberta ou fechada. Os cursos de aguas naturais constituem
Condutos livres ou canais Movimento uniforme São considerados Canais todos os condutos que conduzem àguas com uma superficie livre, com secção aberta ou fechada. Os cursos de aguas naturais constituem
MODELAGEM DE ÁREAS SUSCETÍVEIS À INUNDAÇÃO NA BACIA HIDROGRÁFICA DO RIO CUBATÃO SUL
 MODELAGEM DE ÁREAS SUSCETÍVEIS À INUNDAÇÃO NA BACIA HIDROGRÁFICA DO RIO CUBATÃO SUL Acadêmico: Lucas Mauro Rosa da Luz Orientador: Pedro Luiz Borges Chaffe Coorientador: Gustavo Andrei Speckhann Trabalho
MODELAGEM DE ÁREAS SUSCETÍVEIS À INUNDAÇÃO NA BACIA HIDROGRÁFICA DO RIO CUBATÃO SUL Acadêmico: Lucas Mauro Rosa da Luz Orientador: Pedro Luiz Borges Chaffe Coorientador: Gustavo Andrei Speckhann Trabalho
Introdução aos Métodos Numéricos
 Métodos Numéricos para Mecânica dos Fluidos Introdução aos Métodos Numéricos Introdução aos Métodos Numéricos Bibliografia: J. H. Ferziger and M. Peric, 'Computational Methods for Fluid Dynamics', Springer
Métodos Numéricos para Mecânica dos Fluidos Introdução aos Métodos Numéricos Introdução aos Métodos Numéricos Bibliografia: J. H. Ferziger and M. Peric, 'Computational Methods for Fluid Dynamics', Springer
Hidrodinâmica. A hidrodinâmica objetiva o estudo do movimento dos fluidos
 Hidrodinâmica A hidrodinâmica objetiva o estudo do movimento dos fluidos 1. Vazão ou Descarga. Vazão ou descarga numa determinada seção é o volume do líquido que atravessa essa seção, na unidade de tempo.
Hidrodinâmica A hidrodinâmica objetiva o estudo do movimento dos fluidos 1. Vazão ou Descarga. Vazão ou descarga numa determinada seção é o volume do líquido que atravessa essa seção, na unidade de tempo.
3.1 CRIAR A GEOMETRIA/MALHA;
 72 3 METODOLOGIA A metodologia adotada no presente trabalho foi a de utilizar a ferramenta de dinâmica dos fluidos computacional (CFD) para simular dispositivos microfluídicos de diferentes geometrias
72 3 METODOLOGIA A metodologia adotada no presente trabalho foi a de utilizar a ferramenta de dinâmica dos fluidos computacional (CFD) para simular dispositivos microfluídicos de diferentes geometrias
DETERMINAÇÃO DO COEFICIENTE DE MANNING EM CANAL EXPERIMENTAL
 DETERMINAÇÃO DO COEFICIENTE DE MANNING EM CANAL EXPERIMENTAL Úrsula Raianny Lacerda da Silva 1 Joseilson Oliveira Rodrigues 2 Paulo Roberto Lacerda Tavares 3 RESUMO: Este trabalho refere-se ao estudo sobre
DETERMINAÇÃO DO COEFICIENTE DE MANNING EM CANAL EXPERIMENTAL Úrsula Raianny Lacerda da Silva 1 Joseilson Oliveira Rodrigues 2 Paulo Roberto Lacerda Tavares 3 RESUMO: Este trabalho refere-se ao estudo sobre
Definição. Escoamento permanente gradualmente variado. Aplicações 14/06/2012
 14/6/1 Escoamento permanente gradualmente variado Definição Um escoamento é definido como gradualmente variado quando os seus parâmetros hidráulicos variam progressivamente ao longo da corrente. Quando
14/6/1 Escoamento permanente gradualmente variado Definição Um escoamento é definido como gradualmente variado quando os seus parâmetros hidráulicos variam progressivamente ao longo da corrente. Quando
HIDROLOGIA AULA semestre - Engenharia Civil. MEDIÇÃO DE VAZÃO Profª. Priscila Pini
 HIDROLOGIA AULA 13 5 semestre - Engenharia Civil MEDIÇÃO DE VAZÃO Profª. Priscila Pini [email protected] INTRODUÇÃO Vazão: volume de água que passa por uma determinada seção de um rio ao longo
HIDROLOGIA AULA 13 5 semestre - Engenharia Civil MEDIÇÃO DE VAZÃO Profª. Priscila Pini [email protected] INTRODUÇÃO Vazão: volume de água que passa por uma determinada seção de um rio ao longo
Capítulo 1. INTRODUÇÃO
 Capítulo 1. INTRODUÇÃO A simulação numérica de problemas de engenharia ocupa atualmente uma posição de destaque no cenário mundial de pesquisa e desenvolvimento de novas tecnologias. O crescente interesse,
Capítulo 1. INTRODUÇÃO A simulação numérica de problemas de engenharia ocupa atualmente uma posição de destaque no cenário mundial de pesquisa e desenvolvimento de novas tecnologias. O crescente interesse,
Saneamento Ambiental I
 Universidade Federal do Paraná Engenharia Ambiental Saneamento Ambiental I Aula 23 O Sistema de Esgoto Sanitário: dimensionamento Profª Heloise G. Knapik 1 EXERCÍCIO ESTIMATIVA DE VAZÕES E CARGA DE ESGOTO
Universidade Federal do Paraná Engenharia Ambiental Saneamento Ambiental I Aula 23 O Sistema de Esgoto Sanitário: dimensionamento Profª Heloise G. Knapik 1 EXERCÍCIO ESTIMATIVA DE VAZÕES E CARGA DE ESGOTO
VIII Simpósio Brasileiro sobre Pequenas e Médias Centrais Hidrelétricas 01 a 04/05/2012
 PCH Paracambi Modelagem Hidrodinâmica VIII Simpósio Brasileiro sobre Pequenas e Médias Centrais Hidrelétricas 1 a 4/5/212 PCH Paracambi Modelagem Hidrodinâmica Antecedentes e Objetivos Atividades de desvio
PCH Paracambi Modelagem Hidrodinâmica VIII Simpósio Brasileiro sobre Pequenas e Médias Centrais Hidrelétricas 1 a 4/5/212 PCH Paracambi Modelagem Hidrodinâmica Antecedentes e Objetivos Atividades de desvio
UNIVERSIDADE DE SÃO PAULO ENGENHARIA QUÍMICA LOQ4085 OPERAÇÕES UNITÁRIAS I
 UNIVERSIDADE DE SÃO PAULO ENGENHARIA QUÍMICA LOQ4085 OPERAÇÕES UNITÁRIAS I Profa. Lívia Chaguri E-mail: [email protected] Conteúdo Bombas Parte 1 - Introdução - Classificação - Bombas sanitárias - Condições
UNIVERSIDADE DE SÃO PAULO ENGENHARIA QUÍMICA LOQ4085 OPERAÇÕES UNITÁRIAS I Profa. Lívia Chaguri E-mail: [email protected] Conteúdo Bombas Parte 1 - Introdução - Classificação - Bombas sanitárias - Condições
3 Fluxo Permanente Não Confinado 3.1. Introdução
 51 3 Fluxo Permanente Não Confinado 3.1. Introdução O fenômeno da percolação de fluidos em meios porosos é estudado em várias áreas da engenharia. Na engenharia geotécnica, em particular, o conhecimento
51 3 Fluxo Permanente Não Confinado 3.1. Introdução O fenômeno da percolação de fluidos em meios porosos é estudado em várias áreas da engenharia. Na engenharia geotécnica, em particular, o conhecimento
Mecânica dos Fluidos. Perda de Carga
 Mecânica dos Fluidos Perda de Carga Introdução Na engenharia trabalhamos com energia dos fluidos por unidade de peso, a qual denominamos carga (H); No escoamento de fluidos reais, parte de sua energia
Mecânica dos Fluidos Perda de Carga Introdução Na engenharia trabalhamos com energia dos fluidos por unidade de peso, a qual denominamos carga (H); No escoamento de fluidos reais, parte de sua energia
As forças que atuam em um meio contínuo: Forças de massa ou de corpo: todo o corpo peso e centrífuga Forças de superfície: sobre certas superfícies
 Hidráulica Revisão de alguns conceitos Propriedades Físicas dos Fluidos Forças, esforços e pressão (tensão) As forças que atuam em um meio contínuo: Forças de massa ou de corpo: distribuídas de maneira
Hidráulica Revisão de alguns conceitos Propriedades Físicas dos Fluidos Forças, esforços e pressão (tensão) As forças que atuam em um meio contínuo: Forças de massa ou de corpo: distribuídas de maneira
FENÔMENOS DE TRANSPORTES AULA 7 E 8 EQUAÇÕES DA ENERGIA PARA REGIME PERMANENTE
 FENÔMENOS DE TRANSPORTES AULA 7 E 8 EQUAÇÕES DA ENERGIA PARA REGIME PERMANENTE PROF.: KAIO DUTRA Equação de Euler Uma simplificação das equações de Navier-Stokes, considerando-se escoamento sem atrito
FENÔMENOS DE TRANSPORTES AULA 7 E 8 EQUAÇÕES DA ENERGIA PARA REGIME PERMANENTE PROF.: KAIO DUTRA Equação de Euler Uma simplificação das equações de Navier-Stokes, considerando-se escoamento sem atrito
Hidráulica para Engenharia Civil e Ambiental
 Hidráulica para Engenharia Civil e Ambiental Sumário Agradecimentos v Prefácio vii Uma Breve História da Hidráulica ix Notas Introdutórias xi Principais Símbolos xv Parte I Princípios e Aplicações Básicas
Hidráulica para Engenharia Civil e Ambiental Sumário Agradecimentos v Prefácio vii Uma Breve História da Hidráulica ix Notas Introdutórias xi Principais Símbolos xv Parte I Princípios e Aplicações Básicas
Fluidodinâmica. Carlos Marlon Santos
 Fluidodinâmica Carlos Marlon Santos Fluidodinâmica Os fluidos podem ser analisados utilizando-se o conceito de sistema ou de volume de controle O sistema é definido quando uma certa quantidade de matéria
Fluidodinâmica Carlos Marlon Santos Fluidodinâmica Os fluidos podem ser analisados utilizando-se o conceito de sistema ou de volume de controle O sistema é definido quando uma certa quantidade de matéria
Escoamento em uma curva:
 Escoamento em uma curva: A vazão de ar nas condições padrões, num duto plano, deve ser determinada pela instalação de tomadas de pressão numa curva. O duto tem 0,3 m de profundidade por 0,1 m de largura.
Escoamento em uma curva: A vazão de ar nas condições padrões, num duto plano, deve ser determinada pela instalação de tomadas de pressão numa curva. O duto tem 0,3 m de profundidade por 0,1 m de largura.
Fundamentos da Mecânica dos Fluidos
 Fundamentos da Mecânica dos Fluidos 1 - Introdução 1.1. Algumas Características dos Fluidos 1.2. Dimensões, Homogeneidade Dimensional e Unidades 1.2.1. Sistemas de Unidades 1.3. Análise do Comportamentos
Fundamentos da Mecânica dos Fluidos 1 - Introdução 1.1. Algumas Características dos Fluidos 1.2. Dimensões, Homogeneidade Dimensional e Unidades 1.2.1. Sistemas de Unidades 1.3. Análise do Comportamentos
HIDRÁULICA Condutos Livres ou canais
 HIDRÁULICA Condutos Livres ou canais -Aqueles em que o escoamento ocorre à pressão atmosférica local. - Seção transversal é aberta ou fechada. - Denominados condutos livres (Canais) - O que são condutos
HIDRÁULICA Condutos Livres ou canais -Aqueles em que o escoamento ocorre à pressão atmosférica local. - Seção transversal é aberta ou fechada. - Denominados condutos livres (Canais) - O que são condutos
RECURSOS HÍDRICOS AVALIAÇÃO DA EXTENSÃO DE ZONAS DE MISTURA DE EFLUENTES PARA A PORÇÃO SUPERIOR DA BACIA HIDROGRÁFICA DO RIO SANTA MARIA DA VITÓRIA
 RECURSOS HÍDRICOS AVALIAÇÃO DA EXTENSÃO DE ZONAS DE MISTURA DE EFLUENTES PARA A PORÇÃO SUPERIOR DA BACIA HIDROGRÁFICA DO RIO SANTA MARIA DA VITÓRIA Bárbara Moreto Fim [email protected] Universidade
RECURSOS HÍDRICOS AVALIAÇÃO DA EXTENSÃO DE ZONAS DE MISTURA DE EFLUENTES PARA A PORÇÃO SUPERIOR DA BACIA HIDROGRÁFICA DO RIO SANTA MARIA DA VITÓRIA Bárbara Moreto Fim [email protected] Universidade
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL GEOTECNIA III
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL GEOTECNIA III Aula 01 Fluxo no Solo Introdução Eng. Civil Augusto Romanini (FACET
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL GEOTECNIA III Aula 01 Fluxo no Solo Introdução Eng. Civil Augusto Romanini (FACET
UNIVERSIDADE DE SÃO PAULO ESCOLA SUPERIOR DE AGRICULTURA LUIZ DE QUEIROZ DEPARTAMENTO DE ENGENHARIA DE BIOSSISTEMAS AULA 3 ROTEIRO
 1 UNIVERSIDADE DE SÃO PAULO ESCOLA SUPERIOR DE AGRICULTURA LUIZ DE QUEIROZ DEPARTAMENTO DE ENGENHARIA DE BIOSSISTEMAS LEB 047 HIDRÁULICA Prof. Fernando Campos Mendonça AULA 3 ROTEIRO Tópicos da aula 3:
1 UNIVERSIDADE DE SÃO PAULO ESCOLA SUPERIOR DE AGRICULTURA LUIZ DE QUEIROZ DEPARTAMENTO DE ENGENHARIA DE BIOSSISTEMAS LEB 047 HIDRÁULICA Prof. Fernando Campos Mendonça AULA 3 ROTEIRO Tópicos da aula 3:
Experiência 6 - Perda de Carga Distribuída ao Longo de
 Experiência 6 - Perda de Carga Distribuída ao Longo de Tubulações Prof. Vicente Luiz Scalon 1181 - Lab. Mecânica dos Fluidos Objetivo: Medida de perdas de carga linear ao longo de tubos lisos e rugosos.
Experiência 6 - Perda de Carga Distribuída ao Longo de Tubulações Prof. Vicente Luiz Scalon 1181 - Lab. Mecânica dos Fluidos Objetivo: Medida de perdas de carga linear ao longo de tubos lisos e rugosos.
4 Deslocamentos gerados pela escavação
 4 Deslocamentos gerados pela escavação 4.1. Introdução Neste capítulo são analisados os campos de deslocamentos gerados no maciço rochoso devido à escavação da mineração Pampa de Pongo, Peru, que atualmente
4 Deslocamentos gerados pela escavação 4.1. Introdução Neste capítulo são analisados os campos de deslocamentos gerados no maciço rochoso devido à escavação da mineração Pampa de Pongo, Peru, que atualmente
4 Metodologia Método de elementos distintos/discretos
 4 Metodologia Para a análise numérica foi utilizado o software comercial 3DEC (Itasca, 2007), versão 4.10. O método numérico que o programa utiliza é o método de elemento distinto, este também apresenta
4 Metodologia Para a análise numérica foi utilizado o software comercial 3DEC (Itasca, 2007), versão 4.10. O método numérico que o programa utiliza é o método de elemento distinto, este também apresenta
VENHA PARA ESSE MUNDO.
 VENHA PARA ESSE MUNDO. https://www.tratamentodeagua.com.br/ar-agua-potavel/?utm_source=newsletter&utm_medium=rd_abril1&utm_campaign=rd_abril&utm_term=%c%a1gua%0pot%c%a1vel&utm_content=%c%a1gua%0pot%c%a1vel
VENHA PARA ESSE MUNDO. https://www.tratamentodeagua.com.br/ar-agua-potavel/?utm_source=newsletter&utm_medium=rd_abril1&utm_campaign=rd_abril&utm_term=%c%a1gua%0pot%c%a1vel&utm_content=%c%a1gua%0pot%c%a1vel
Universidade Tecnológica Federal do Paraná. CC54Z - Hidrologia. Medição de vazão e curva-chave. Prof. Fernando Andrade Curitiba, 2014
 Universidade Tecnológica Federal do Paraná CC54Z - Hidrologia Medição de vazão e curva-chave Prof. Fernando Andrade Curitiba, 2014 Objetivos da aula Conhecer um método analítico de estimar vazão em escoamento
Universidade Tecnológica Federal do Paraná CC54Z - Hidrologia Medição de vazão e curva-chave Prof. Fernando Andrade Curitiba, 2014 Objetivos da aula Conhecer um método analítico de estimar vazão em escoamento
4º Laboratório de EME 502 MEDIDAS DE VAZÃO
 Universidade Federal de Uberlândia Instituto de Engenharia Mecânica 4º Laboratório de EME 502 MEDIDAS DE VAZÃO Profa. Ana Lúcia Fernandes de Lima e Silva http://www.iem.unifei.edu.br/labtc/ana.html Objetivos
Universidade Federal de Uberlândia Instituto de Engenharia Mecânica 4º Laboratório de EME 502 MEDIDAS DE VAZÃO Profa. Ana Lúcia Fernandes de Lima e Silva http://www.iem.unifei.edu.br/labtc/ana.html Objetivos
DESENVOLVIMENTO DE UM SISTEMA DE PREDIÇÃO DE INUNDAÇÕES PARA AS BACIAS PILOTO DOS RIOS PIABANHA E PAQUEQUER, RJ (Código 11126)
 DESENVOLVIMENTO DE UM SISTEMA DE PREDIÇÃO DE INUNDAÇÕES PARA AS BACIAS PILOTO DOS RIOS PIABANHA E PAQUEQUER, RJ (Código 11126) Daniele Pereira Batista Amaral; José Edson Falcão de Farias Júnior; Leonardo
DESENVOLVIMENTO DE UM SISTEMA DE PREDIÇÃO DE INUNDAÇÕES PARA AS BACIAS PILOTO DOS RIOS PIABANHA E PAQUEQUER, RJ (Código 11126) Daniele Pereira Batista Amaral; José Edson Falcão de Farias Júnior; Leonardo
5 Formulação Dinâmica Não Linear no Domínio da Frequência
 129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
Perda de Carga. Representa a Energia Mecânica convertida em Energia Térmica; Expressa como a perda de pressão
 Perda de Carga Representa a Energia Mecânica convertida em Energia Térmica; Expressa como a perda de pressão h lt h ld h lm Perdas Distribuídas devido ao efeito de atrito (parede do tubo) Perdas Localizadas
Perda de Carga Representa a Energia Mecânica convertida em Energia Térmica; Expressa como a perda de pressão h lt h ld h lm Perdas Distribuídas devido ao efeito de atrito (parede do tubo) Perdas Localizadas
Capítulo 5 Validação Numérica. 5 Validação Numérica
 Capítulo 5 Validação Numérica 5 Validação Numérica Neste capítulo são mostradas as comparações das respostas numéricas e analíticas para várias condições de contorno, com o objetivo de validar numericamente
Capítulo 5 Validação Numérica 5 Validação Numérica Neste capítulo são mostradas as comparações das respostas numéricas e analíticas para várias condições de contorno, com o objetivo de validar numericamente
Dimensionamento de Bueiros
 Universidade Regional do Cariri URCA Pró Reitoriade Ensino de Graduação Coordenação da Construção Civil Drenagem de Rodovias Dimensionamento de Bueiros Prof. MSc. Renato de Oliveira Fernandes Professor
Universidade Regional do Cariri URCA Pró Reitoriade Ensino de Graduação Coordenação da Construção Civil Drenagem de Rodovias Dimensionamento de Bueiros Prof. MSc. Renato de Oliveira Fernandes Professor
4 Fluxo na barragem de terra de Macusani - Peru
 78 4 Fluxo na barragem de terra de Macusani - Peru 4.1. Introdução Neste capítulo são feitas previsões de fluxo permanente e transiente na barragem de terra Macusani (Peru) utilizando como ferramentas
78 4 Fluxo na barragem de terra de Macusani - Peru 4.1. Introdução Neste capítulo são feitas previsões de fluxo permanente e transiente na barragem de terra Macusani (Peru) utilizando como ferramentas
Estruturas hidráulicas
 Universidade Regional do Cariri URCA Pró Reitoria de Ensino de Graduação Coordenação da Construção Civil Disciplina: Estradas II Estruturas hidráulicas Dimensionamento Hidráulico de Bueiros Renato de Oliveira
Universidade Regional do Cariri URCA Pró Reitoria de Ensino de Graduação Coordenação da Construção Civil Disciplina: Estradas II Estruturas hidráulicas Dimensionamento Hidráulico de Bueiros Renato de Oliveira
ASPECTOS DO DIMENSIONAMENTO HIDRÁULICO DO CANAL DE DERIVAÇÃO DA UHE BELO MONTE
 ASPECTOS DO DIMENSIONAMENTO HIDRÁULICO DO CANAL DE DERIVAÇÃO DA UHE BELO MONTE AMAZONAS PARÁ VOLTA GRANDE DO XINGÚ MATOGROSSO ALTAMIRA UHE BELO MONTE - LOCALIZAÇÃO UHE BELO MONTE - ARRANJO GERAL CANAL
ASPECTOS DO DIMENSIONAMENTO HIDRÁULICO DO CANAL DE DERIVAÇÃO DA UHE BELO MONTE AMAZONAS PARÁ VOLTA GRANDE DO XINGÚ MATOGROSSO ALTAMIRA UHE BELO MONTE - LOCALIZAÇÃO UHE BELO MONTE - ARRANJO GERAL CANAL
ENGENHARIA FÍSICA. Fenômenos de Transporte A (Mecânica dos Fluidos)
 ENGENHARIA FÍSICA Fenômenos de Transporte A (Mecânica dos Fluidos) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] MECÂNICA DOS FLUIDOS ENGENHARIA FÍSICA AULA 7 ESCOAMENTO
ENGENHARIA FÍSICA Fenômenos de Transporte A (Mecânica dos Fluidos) Prof. Dr. Sérgio R. Montoro [email protected] [email protected] MECÂNICA DOS FLUIDOS ENGENHARIA FÍSICA AULA 7 ESCOAMENTO
Escoamentos em Superfícies Livres
 Escoamentos em Superfícies Livres Prof. Alexandre Silveira Universidade Federal de Alfenas Instituto de Ciência e Tecnologia Campus Avançado de Poços de Caldas-MG Curso Engenharia Ambiental e Urbana ICT
Escoamentos em Superfícies Livres Prof. Alexandre Silveira Universidade Federal de Alfenas Instituto de Ciência e Tecnologia Campus Avançado de Poços de Caldas-MG Curso Engenharia Ambiental e Urbana ICT
3. Metodologia utilizada na modelagem numérica dos conglomerados
 52 3. Metodologia utilizada na modelagem numérica dos conglomerados Neste capítulo apresenta-se a metodologia utilizada para a determinação das propriedades mecânicas dos conglomerados, utilizando a interpretação
52 3. Metodologia utilizada na modelagem numérica dos conglomerados Neste capítulo apresenta-se a metodologia utilizada para a determinação das propriedades mecânicas dos conglomerados, utilizando a interpretação
3 Modelos matemáticos e formulação numérica
 3 Modelos matemáticos e formulação numérica Os modelos matemáticos para fluxos em meios porosos fraturados que transformam os modelos conceituais em equações seguem basicamente a equação de Richards que
3 Modelos matemáticos e formulação numérica Os modelos matemáticos para fluxos em meios porosos fraturados que transformam os modelos conceituais em equações seguem basicamente a equação de Richards que
Departamento de Engenharia Mecânica. ENG 1011: Fenômenos de Transporte I
 Departamento de Engenharia Mecânica ENG 1011: Fenômenos de Transporte I Aula 9: Formulação diferencial Exercícios 3 sobre instalações hidráulicas; Classificação dos escoamentos (Formulação integral e diferencial,
Departamento de Engenharia Mecânica ENG 1011: Fenômenos de Transporte I Aula 9: Formulação diferencial Exercícios 3 sobre instalações hidráulicas; Classificação dos escoamentos (Formulação integral e diferencial,
Sumári"o. Capitulo 1 INTRODUÇÃO AOS MÉTODOS NUMÉRICOS Luis Carlos Wrobel Introdução Método das Diferenças Finitas...
 Sumári"o Capitulo 1 INTRODUÇÃO AOS MÉTODOS NUMÉRICOS Luis Carlos Wrobel 1 1.1 Introdução... 2 1.2 Método das Diferenças Finitas... 4 1.2.1 Derivadas de Ordem Superior.. 7 1.2.2 Problemas Bidimensionais....
Sumári"o Capitulo 1 INTRODUÇÃO AOS MÉTODOS NUMÉRICOS Luis Carlos Wrobel 1 1.1 Introdução... 2 1.2 Método das Diferenças Finitas... 4 1.2.1 Derivadas de Ordem Superior.. 7 1.2.2 Problemas Bidimensionais....
Hidráulica II (HID2001) 2 Escoamentos em Superfície Livre. Prof. Dr. Doalcey Antunes Ramos
 Hidráulica II (HID2001) 2 Escoamentos em Superfície Livre Prof. Dr. Doalcey Antunes Ramos SUMÁRIO 2.1 Introdução 2.2 Características geométricas e hidráulicas dos canais 2.3 Distribuição de pressões 2.4
Hidráulica II (HID2001) 2 Escoamentos em Superfície Livre Prof. Dr. Doalcey Antunes Ramos SUMÁRIO 2.1 Introdução 2.2 Características geométricas e hidráulicas dos canais 2.3 Distribuição de pressões 2.4
ANÁLISE DE PERDAS EM ESCOAMENTOS DENTRO DE
 Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade [email protected] ANÁLISE DE PERDAS EM ESCOAMENTOS DENTRO DE TUBULAÇÕES
Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade [email protected] ANÁLISE DE PERDAS EM ESCOAMENTOS DENTRO DE TUBULAÇÕES
https://www.youtube.com/watch?v=aiymdywghfm
 Exercício 106: Um medidor de vazão tipo venturi é ensaiado num laboratório, obtendose a curva característica abaixo. O diâmetro de aproximação e o da garganta são 60 mm e 0 mm respectivamente. O fluido
Exercício 106: Um medidor de vazão tipo venturi é ensaiado num laboratório, obtendose a curva característica abaixo. O diâmetro de aproximação e o da garganta são 60 mm e 0 mm respectivamente. O fluido
Ottobacias 2012_v.1.1. Programa para delimitação e subdivisão de bacias hidrográficas segundo o método de Otto Pfafsteter MANUAL DO USUÁRIO
 Ottobacias 2012_v.1.1 Programa para delimitação e subdivisão de bacias hidrográficas segundo o método de Otto Pfafsteter MANUAL DO USUÁRIO Eng. Dante Gama Larentis Porto Alegre, junho de 2013. 1 ÍNDICE
Ottobacias 2012_v.1.1 Programa para delimitação e subdivisão de bacias hidrográficas segundo o método de Otto Pfafsteter MANUAL DO USUÁRIO Eng. Dante Gama Larentis Porto Alegre, junho de 2013. 1 ÍNDICE
RESUMO MECFLU P2. 1. EQUAÇÃO DE BERNOULLI Estudo das propriedades de um escoamento ao longo de uma linha de corrente.
 RESUMO MECFLU P2 1. EQUAÇÃO DE BERNOULLI Estudo das propriedades de um escoamento ao longo de uma linha de corrente. Hipóteses Fluido invíscido (viscosidade nula) não ocorre perda de energia. Fluido incompressível
RESUMO MECFLU P2 1. EQUAÇÃO DE BERNOULLI Estudo das propriedades de um escoamento ao longo de uma linha de corrente. Hipóteses Fluido invíscido (viscosidade nula) não ocorre perda de energia. Fluido incompressível
Décima quinta aula de hidráulica
 CONDUTO FORÇADO Décima quinta aula de hidráulica Primeiro semestre de 2016 CONDUTO LIVRE OU CANAL Introdução aos estudos relacionados aos canais (ou condutos livres) 1. Conceito de canal ou conduto livre
CONDUTO FORÇADO Décima quinta aula de hidráulica Primeiro semestre de 2016 CONDUTO LIVRE OU CANAL Introdução aos estudos relacionados aos canais (ou condutos livres) 1. Conceito de canal ou conduto livre
MEC UFRGS IPH LISTA DE EXERCÍCIOS DHH IPH CANAIS A SUPERFÍCIE LIVRE 26/11/2007
 1) MOVIMENTO UNIFORME 1.1) Um canal tem taludes com m=1,5, declividade de fundo de 1/1600 e largura de fundo igual a 4m. Se a profundidade é igual a 1,20 m calcule a vazão, a largura superficial e a profundidade
1) MOVIMENTO UNIFORME 1.1) Um canal tem taludes com m=1,5, declividade de fundo de 1/1600 e largura de fundo igual a 4m. Se a profundidade é igual a 1,20 m calcule a vazão, a largura superficial e a profundidade
Mecânica dos Fluidos I
 Mecânica dos Fluidos I Aula prática 11 (Semana de 2 a 5 de Dezembro de 2008) EXERCÍCIO 1 A figura 1 representa esquematicamente uma pequena central mini-hídrica com uma conduta de descarga para a atmosfera.
Mecânica dos Fluidos I Aula prática 11 (Semana de 2 a 5 de Dezembro de 2008) EXERCÍCIO 1 A figura 1 representa esquematicamente uma pequena central mini-hídrica com uma conduta de descarga para a atmosfera.
ESTUDO DA ENERGIA ESPECÍFICA EM CANAL EXPERIMENTAL
 ESTUDO DA ENERGIA ESPECÍFICA EM CANAL EXPERIMENTAL Michelly Matos Pereira 1 Antonio Italcy de Oliveira Júnior 2 Paulo Fernando Matos de Santana 3 Rodrigo Alencar Ferreira 4 Paulo Roberto Lacerda Tavares
ESTUDO DA ENERGIA ESPECÍFICA EM CANAL EXPERIMENTAL Michelly Matos Pereira 1 Antonio Italcy de Oliveira Júnior 2 Paulo Fernando Matos de Santana 3 Rodrigo Alencar Ferreira 4 Paulo Roberto Lacerda Tavares
IV ANÁLISE DO ROMPIMENTO HIPOTÉTICO DE UMA BARRAGEM DE REGULARIZAÇÃO DE VAZÃO NO MUNICÍPIO DE RIO PARANAÍBA MG
 IV-088 - ANÁLISE DO ROMPIMENTO HIPOTÉTICO DE UMA BARRAGEM DE REGULARIZAÇÃO DE VAZÃO NO MUNICÍPIO DE RIO PARANAÍBA MG Marco Antônio de Andrade Júnior (1) Engenheiro Civil pela Universidade Federal de Viçosa
IV-088 - ANÁLISE DO ROMPIMENTO HIPOTÉTICO DE UMA BARRAGEM DE REGULARIZAÇÃO DE VAZÃO NO MUNICÍPIO DE RIO PARANAÍBA MG Marco Antônio de Andrade Júnior (1) Engenheiro Civil pela Universidade Federal de Viçosa
DIRETRIZES PARA PROJETO
 ELABORAÇÃO EQUIPE TÉCNICA USHI: Ely Carlos de Alvarenga Josete de Fátima de Sá Nicolás Lopardo 1 INTRODUÇÃO Esta Diretriz tem como função principal indicar critérios técnicos necessários para permitir
ELABORAÇÃO EQUIPE TÉCNICA USHI: Ely Carlos de Alvarenga Josete de Fátima de Sá Nicolás Lopardo 1 INTRODUÇÃO Esta Diretriz tem como função principal indicar critérios técnicos necessários para permitir
SOLUÇÃO DE UM PROBLEMA UNIDIMENSIONAL DE CONDUÇÃO DE CALOR
 SOLUÇÃO DE UM ROBLEMA UNIDIMENSIONAL DE CONDUÇÃO DE CALOR Marcelo M. Galarça ós Graduação em Engenharia Mecânica Universidade Federal do Rio Grande do Sul ransferência de Calor e Mecânica dos Fluidos Computacional
SOLUÇÃO DE UM ROBLEMA UNIDIMENSIONAL DE CONDUÇÃO DE CALOR Marcelo M. Galarça ós Graduação em Engenharia Mecânica Universidade Federal do Rio Grande do Sul ransferência de Calor e Mecânica dos Fluidos Computacional
HIDRÁULICA. REVISÃO 1º Bimestre
 REVISÃO 1º Bimestre ROTEIRO Condutos Livres Tipos de Movimentos Carga Específica Elementos geométricos e dimensionamento Vazão Velocidade Perda de Carga Adutora Aspectos construtivos ROTEIRO Condutos Livres
REVISÃO 1º Bimestre ROTEIRO Condutos Livres Tipos de Movimentos Carga Específica Elementos geométricos e dimensionamento Vazão Velocidade Perda de Carga Adutora Aspectos construtivos ROTEIRO Condutos Livres
AULA 6 ESCOAMENTO PERMANENTE DE FLUIDO INCOMPRESSÍVEL EM CONDUTOS FORÇADOS. Prof. Geronimo Virginio Tagliaferro
 AULA 6 ESCOAMENTO PERMANENTE DE FLUIDO INCOMPRESSÍVEL EM CONDUTOS FORÇADOS Prof. Geronimo Virginio Tagliaferro DEFINIÇÕES DEFINIÇÕES A seguir, serão introduzidas definições e conceitos utilizados ao longo
AULA 6 ESCOAMENTO PERMANENTE DE FLUIDO INCOMPRESSÍVEL EM CONDUTOS FORÇADOS Prof. Geronimo Virginio Tagliaferro DEFINIÇÕES DEFINIÇÕES A seguir, serão introduzidas definições e conceitos utilizados ao longo
Resumo de exercícios de bombas. Exercício 1
 Resumo de exercícios de bombas Exercício 1 Considere uma bomba centrífuga cuja geometria e condições de escoamento são : Raio de entrada do rotor = 37,5 mm, raio de saída = 150 mm, largura do rotor = 12,7
Resumo de exercícios de bombas Exercício 1 Considere uma bomba centrífuga cuja geometria e condições de escoamento são : Raio de entrada do rotor = 37,5 mm, raio de saída = 150 mm, largura do rotor = 12,7
ESTUDO DE CHEIAS RIO VELHO. Loteamento José Alencar Joinville / Santa Catarina. Responsável Técnico CURITIBA MARÇO / 2014
 ESTUDO DE CHEIAS RIO VELHO Loteamento José Alencar Joinville / Santa Catarina Responsável Técnico Engª Candice Schauffert Garcia, M.Sc. CREA-PR 67059/D CURITIBA MARÇO / 2014 SUMÁRIO 1. OBJETIVO... 3 2.
ESTUDO DE CHEIAS RIO VELHO Loteamento José Alencar Joinville / Santa Catarina Responsável Técnico Engª Candice Schauffert Garcia, M.Sc. CREA-PR 67059/D CURITIBA MARÇO / 2014 SUMÁRIO 1. OBJETIVO... 3 2.
4 Os Experimentos de Túnel de Vento e o Método Numérico
 4 Os Experimentos de Túnel de Vento e o Método Numérico 4.1 Descrição dos Experimentos de Túnel de Vento Para realizar a modelagem numérica do campo de escoamento médio e turbulento sobre superfícies vegetadas,
4 Os Experimentos de Túnel de Vento e o Método Numérico 4.1 Descrição dos Experimentos de Túnel de Vento Para realizar a modelagem numérica do campo de escoamento médio e turbulento sobre superfícies vegetadas,
USANDO O MODELLUS. Aula 3
 USANDO O MODELLUS Aula 3 A evolução temporal é dada pela solução numérica de equações diferenciais. Exemplo: Movimento Retilíneo Uniforme Exemplo: Movimento Retilíneo Uniformemente variado As derivadas
USANDO O MODELLUS Aula 3 A evolução temporal é dada pela solução numérica de equações diferenciais. Exemplo: Movimento Retilíneo Uniforme Exemplo: Movimento Retilíneo Uniformemente variado As derivadas
MÉTODOS NUMÉRICOS APLICADOS À ENGENHARIA
 UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MECÂNICA CURSO DE ENGENHARIA MECÂNICA MÉTODOS NUMÉRICOS APLICADOS À ENGENHARIA INTRODUÇÃO AOS MÉTODOS DE DIFERENÇAS FINITAS E DE VOLUMES
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MECÂNICA CURSO DE ENGENHARIA MECÂNICA MÉTODOS NUMÉRICOS APLICADOS À ENGENHARIA INTRODUÇÃO AOS MÉTODOS DE DIFERENÇAS FINITAS E DE VOLUMES
SUMÁRIO PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3. PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação...
 PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3 PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação... 7 CAPÍTULO 1 Modelagem matemática e resolução de problemas de engenharia...10
PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3 PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação... 7 CAPÍTULO 1 Modelagem matemática e resolução de problemas de engenharia...10
PROPAGAÇÃO DE ONDAS DE CHEIA À JUSANTE DA BARRAGEM DE XINGÓ LOCALIZADA NO RIO SÃO FRANCISCO
 PROPAGAÇÃO DE ONDAS DE CHEIA À JUSANTE DA BARRAGEM DE XINGÓ LOCALIZADA NO RIO SÃO FRANCISCO Ingridy Souza dos Santos (1) Graduada em Ciências Exatas e Tecnológicas, graduanda de Engenharia Civil. e-mail:
PROPAGAÇÃO DE ONDAS DE CHEIA À JUSANTE DA BARRAGEM DE XINGÓ LOCALIZADA NO RIO SÃO FRANCISCO Ingridy Souza dos Santos (1) Graduada em Ciências Exatas e Tecnológicas, graduanda de Engenharia Civil. e-mail:
Escoamento Superficial Curva-Chave
 Universidade de São Paulo PHA 3307 Hidrologia Aplicada Escola Politécnica da Departamento de Engenharia Hidráulica e Ambiental Escoamento Superficial Curva-Chave Aula 9 Prof. Dr. Arisvaldo Méllo Prof.
Universidade de São Paulo PHA 3307 Hidrologia Aplicada Escola Politécnica da Departamento de Engenharia Hidráulica e Ambiental Escoamento Superficial Curva-Chave Aula 9 Prof. Dr. Arisvaldo Méllo Prof.
Computação Gráfica - 10
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 10 Prof. Jorge Cavalcanti [email protected] www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 10 Prof. Jorge Cavalcanti [email protected] www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
ESTE Aula 2- Introdução à convecção. As equações de camada limite
 Universidade Federal do ABC ESTE013-13 Aula - Introdução à convecção. As equações de camada limite EN 41: Aula As equações de camada limite Análise das equações que descrevem o escoamento em camada limite:
Universidade Federal do ABC ESTE013-13 Aula - Introdução à convecção. As equações de camada limite EN 41: Aula As equações de camada limite Análise das equações que descrevem o escoamento em camada limite:
UFC6 Manual de Utilização
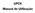 UFC6 Manual de Utilização C.1 INTRODUÇÃO O programa UFC6 Versão 1.0 é parte integrante da Dissertação de Mestrado intitulada Modelagem Computacional de Dispositivos de Atenuação do Golpe de Aríete em Adutoras.
UFC6 Manual de Utilização C.1 INTRODUÇÃO O programa UFC6 Versão 1.0 é parte integrante da Dissertação de Mestrado intitulada Modelagem Computacional de Dispositivos de Atenuação do Golpe de Aríete em Adutoras.
Modelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff
 Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /[email protected] A teoria clássica ou teoria de Kirchhoff
Resumo odelagem Numérica de Flexão de Placas Segundo a Teoria de Kirchhoff aniel ias onnerat 1 1 Hiperestática Engenharia e Projetos Ltda. /[email protected] A teoria clássica ou teoria de Kirchhoff
a) [10] Determine a vazão que escoa na meia pista caso a profundidade do escoamento seja y = 15 cm.
![a) [10] Determine a vazão que escoa na meia pista caso a profundidade do escoamento seja y = 15 cm. a) [10] Determine a vazão que escoa na meia pista caso a profundidade do escoamento seja y = 15 cm.](/thumbs/97/132109521.jpg) TEA14 - Mecânica dos Fluidos Ambiental II Curso de Graduação em Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P4, Novembro 1 Prof. Michael Mannich NOME: GABARITO Assinatura: P4 1 [4]
TEA14 - Mecânica dos Fluidos Ambiental II Curso de Graduação em Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P4, Novembro 1 Prof. Michael Mannich NOME: GABARITO Assinatura: P4 1 [4]
Mecânica dos Fluidos I
 Mecânica dos Fluidos I Aula prática 6 (Semana de 26 a 30 de Outubro de 2009) EXERCÍCIO 1 Um jacto de ar, escoando-se na atmosfera, incide perpendicularmente a uma placa e é deflectido na direcção tangencial
Mecânica dos Fluidos I Aula prática 6 (Semana de 26 a 30 de Outubro de 2009) EXERCÍCIO 1 Um jacto de ar, escoando-se na atmosfera, incide perpendicularmente a uma placa e é deflectido na direcção tangencial
4 Estabilidade estática do aterro reforçado
 4 Estabilidade estática do aterro reforçado 4.1. Introdução Neste capítulo apresenta-se a avaliação da estabilidade estática de um aterro de rejeitos de mineração reforçado com geossintéticos. A obra está
4 Estabilidade estática do aterro reforçado 4.1. Introdução Neste capítulo apresenta-se a avaliação da estabilidade estática de um aterro de rejeitos de mineração reforçado com geossintéticos. A obra está
Determinação da Curva-Chave da Vazão do Rio Manoel Alves Grande, Goiatins-To.
 Determinação da Curva-Chave da Vazão do Rio Manoel Alves Grande, Goiatins-To. BARBOSA 1, Guilherme Silva; IOST 2, Caroline; SCHIESSL 3, Maikon Adão; FEITOSA 4, Thaiana Brunes. RESUMO No planejamento e
Determinação da Curva-Chave da Vazão do Rio Manoel Alves Grande, Goiatins-To. BARBOSA 1, Guilherme Silva; IOST 2, Caroline; SCHIESSL 3, Maikon Adão; FEITOSA 4, Thaiana Brunes. RESUMO No planejamento e
Hidráulica Geral (ESA024A)
 Departamento de Engenharia Sanitária e Ambiental Hidráulica Geral (ESA04A) Aula 04 Escoamento Uniforme Escoamento Uniforme Condições de ocorrência do regime uniforme ) São constantes ao longo do conduto:
Departamento de Engenharia Sanitária e Ambiental Hidráulica Geral (ESA04A) Aula 04 Escoamento Uniforme Escoamento Uniforme Condições de ocorrência do regime uniforme ) São constantes ao longo do conduto:
