A) 4 B) 14 C) 60 D) 120 E) 24
|
|
|
- Alice Ribas Lagos
- 6 Há anos
- Visualizações:
Transcrição
1 XXIII OLIMPÍD RSILEIR DE MTEMÁTI Primeira Fase Nível - Prova de 0 questões. - Duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas a notas ou livros. - Você pode solicitar papel para rascunho. - Entregue apenas a folha de respostas. a. Fase Olimpíada Regional M GO P RJ RS S 09 de junho de 00. onsidere dois números naturais, cada um deles com três algarismos diferentes. O maior deles só tem algarismos pares e o menor só tem algarismos ímpares. O menor valor possível para a diferença entre eles é: ) ) 49 ) 9 D) 69 E) 5. Na figura abaixo, temos 4 circunferências e alguns pontos destacados no interior dessas circunferências. Escolhendo exatamente um desses pontos dentro de cada uma das circunferências, e unindo-os por segmentos de reta que não se cruzam, formamos um quadrilátero. Quantos quadriláteros diferentes seremos capazes de desenhar nessas condições? ) 4 ) 4 ) 60 D) 0 E) 4 3. Joana escreve a seqüência de números naturais, 6,,..., onde cada número, com exceção do primeiro, é igual ao anterior mais cinco. Joana pára quando encontra o primeiro número de três algarismos. Esse número é: ) 00 ) 04 ) 0 D) 03 E) 0 4. Quantos números de dois algarismos não são primos nem múltiplos de, 3 ou 5? ) ) 3 ) D) 4 E) mais de 4 5. No conjunto {0, 00, 0 00,..., } cada elemento é um número formado pelo algarismo nas extremidades e por algarismos 0 entre eles. lguns desses elementos são números primos e outros são compostos. Sobre a quantidade de números compostos podemos afirmar que: ) é igual ) é igual a 4 ) é menor do que 3 D) é maior do que 4 e menor do que E) é 3 6. Uma pera tem cerca de 90% de água e 0% de matéria sólida. Um produtor coloca 00 quilogramas de pera para desidratar até o ponto em que a água represente 60% da massa total. Quantos litros de água serão evaporados? (lembre-se: litro de água tem massa de quilograma). ) 5 litros ) 45 litros ) 75 litros D) 80 litros E) 30 litros
2 7. O triângulo equilátero T à direita tem lado. Juntando triângulos congruentes a esse, podemos formar outros triângulos equiláteros maiores, conforme indicado no desenho abaixo. Qual é o lado do triângulo equilátero formado por 49 dos triângulos T? ) 7 ) 49 ) 3 D) E) é impossível formar um triângulo equilátero com esse número de triângulos T 8. Os números inteiros positivos de a 000 são escritos lado a lado, em ordem crescente, formando a seqüência Nesta seqüência, quantas vezes aparece o grupo 89? ) 98 ) 3 ) D) 89 E) 9. Um serralheiro tem 0 pedaços de 3 elos de ferro cada um, mostrados abaixo. Ele quer fazer uma única corrente de 30 elos. Para abrir e depois soldar um elo o serralheiro leva 5 minutos. Quantos minutos no mínimo ele levará para fazer a corrente? ) 30 ) 35 ) 40 D) 45 E) Escrevem-se os números naturais numa faixa decorativa, da seguinte maneira: ssinale a figura correta: a) ) ) b) ) c) d) 00 e) D) E) melancias custam o mesmo que 9 laranjas mais 6 bananas; além disso, meia dúzia de bananas custa a metade de uma melancia. Portanto, o preço pago por uma dúzia de laranjas e uma dúzia de bananas é igual ao preço de: ) 3 melancias ) 4 melancias ) 6 melancias D) 5 melancias E) melancias. Qual é o último algarismo da soma de 70 números inteiros positivos consecutivos? ) 4 ) 0 ) 7 D) 5 E) Faltam dados
3 3. Em Tumbólia, um quilograma de moedas de 50 centavos equivale em dinheiro a dois quilogramas de moedas de 0 centavos. Sendo 8 gramas o peso de uma moeda de 0 centavos, uma moeda de 50 centavos pesará: ) 5 gramas ) 0 gramas ) gramas D) 0 gramas E) gramas 4. s medidas dos lados de um retângulo são números inteiros distintos. O perímetro e a área do retângulo se exprimem pelo mesmo número. Determine esse número. ) 8 ) ) 4 D) 9 E) O número N de três algarismos multiplicado por 7 deu como resultado um número que termina em 7. soma dos algarismos de N é: ) 0 ) ) D) 3 E) 4 6. Em um tabuleiro retangular com 6 linhas e 9 colunas, 3 casas estão ocupadas. Podemos afirmar que: ) Todas as colunas têm pelo menos 3 casas ocupadas. ) Nenhuma coluna tem mais de 3 casas ocupadas. ) lguma coluna não tem casas ocupadas. D) lguma linha tem pelo menos 6 casas ocupadas. E) Todas as linhas têm pelo menos 4 casas ocupadas. 7. ontando-se os alunos de uma classe de 4 em 4 sobram, e contando-se de 5 em 5 sobra. Sabendo-se que 5 alunos são meninas e que nesta classe o número de meninas é maior que o número de meninos, o número de meninos nesta classe é: ) 7 ) 8 ) 9 D) 0 E) 8. São escritos todos os números de a 999 nos quais o algarismo aparece exatamente vezes (tais como,,, 4, etc). soma de todos estes números é: ) 688 ) 5994 ) 4668 D) 74 E) inco animais,,, D, e E, são cães ou são lobos. ães sempre contam a verdade e lobos sempre mentem. diz que é um cão. diz que é um lobo. diz que D é um lobo. D diz que e E são animais de espécies diferentes. E diz que é um cão. Quantos lobos há entre os cinco animais? ) ) ) 3 D) 4 E) 5 0. om azulejos quadrados brancos e pretos todos do mesmo tamanho, construímos os seguintes mosaicos. regra para se construir estes mosaicos é a seguinte: inicialmente formamos um quadrado com azulejo branco cercado por azulejos pretos; e em seguida, outro quadrado, este com 4 azulejos brancos, também cercado por azulejos pretos; e assim sucessivamente. om 80 azulejos pretos, quantos azulejos brancos serão necessários para se fazer uma seqüência de mosaicos como esta? ) 55 ) 65 ) 75 D) 85 E) 00
4 GRITO Este é o gabarito para os três níveis. Observe que algumas questões são utilizadas em mais de um nível e a solução é dada apenas uma vez. onsideramos o uso de uma mesma questão em mais de um nível como um fator interessante e que reflete o caráter da Olimpíada de Matemática como uma prova de raciocínio e não de verificação do aprendizado de material ao qual o aluno tenha sido exposto recentemente. NÍVEL (5 a. e 6 a. séries) ) E 6) ) 6) D ) D 7) ) D 7) E 3) 8) 3) 8) 4) 9) 4) 9) D 5) D 0) D 5) 0) RESUMO DS SOLUÇÕES. (E) Para que a diferença seja a menor possível, os algarismos das centenas desses números devem diferir em uma unidade. lém disso, o número formado apenas por algarismos pares deve ter a menor dezena possível, ou seja, 0; o número formado apenas por algarismos ímpares deve ter a maior dezena possível, ou seja 97. ssim o menor valor possível para a diferença ocorre quando os números são 40 e 397 ou 60 e 597, e, portanto, é 5.. (D) asta escolher um ponto de cada circunferência. Isso pode ser feito de 435=0 maneiras diferentes (no enunciado subentende-se que dos quatro pontos escolhidos de cada vez, não haja três alinhados). 3. () Os números da seqüência, quando divididos por 5, deixam resto igual a. O menor número de três algarismos nessas condições é o () omo os números devem ser compostos e ter dois algarismos, eles devem ser múltiplos de 7, mas não múltiplos de, de 3 nem de 5. Só podem ser 77 = 49, 7 = 77 e 73 = (D) O conjunto dado tem números. Os números com quantidade par de zeros são divisíveis por. Por exemplo, 00 é igual a 9 (na verdade, basta aplicar o critério de divisibilidade por ). Há 5 números nessas condições; além disso, o número 0 é primo, logo a quantidade de números compostos é maior do que 4 e menor do que. (na verdade, 0 é primo e os dez outros números são compostos). 6. () Inicialmente, há 90 kg de água e 0 kg de matéria sólida. s peras devem ser desidratadas até o ponto em que esses 0 kg representem 00% 60% = 40% da massa total, ou seja, até que a massa total seja igual a % 0,4 kg. Logo 90 (5 0) = 75 litros de água serão evaporados. 7. () Para formar um triângulo de lado, são necessários 4 T, para formar um triângulo de lado 3 são necessários 9 T, etc. Pode-se provar que para formar um triângulo de lado n, são necessários n triângulos T. Logo o triângulo formado por 49 triângulos T tem lado () Na seqüência aparecem os números de um algarismo 8,9; com números de dois algarismos aparece uma vez o 89 e o agrupamento 98,99; com números de três algarismos que terminam com 89 temos 89, 89,..., 989 num total de 9 números; com números que começam com 89, temos 890, 89,..., 899 num total de 0 números; os agrupamentos 908, 909; 98, 99;...; 998,999 também aparecem, num total de 0 números. Portanto, 89 aparece = 3 vezes. 9. () brindo uma cadeia de três elos, o serralheiro emenda 4 cadeias de 3 elos, formando um pedaço de 5 elos. Por isso, com 6 elos, ele forma dois pedaços de 5 elos; abrindo mais um elo de um desses pedaços, ele emenda 5 com 4, formando a corrente de 30 elos. Levará portanto 75= 35 minutos. Para verificar que não é possível em menos tempo, basta observar que, abrindo 6 elos, restam pelo menos 8 pedaços formados por, ou 3 elos fechados e que necessitam de pelos menos 7 elos abertos para serem ligados.
5 0. (D) Observando como os números aparecem nos cantos, percebemos que aparecem omo 000 é, a resposta correta é: mais mais 3 mais mais. () Se 6 bananas = melancia então 4 bananas = melancias = 9 laranjas + 6 bananas. Portanto, 8 bananas = 9 laranjas, ou seja, bananas = laranja. ssim, laranjas + bananas = 4 bananas + bananas = 36 bananas = 3 melancias.. (D) cada 0 inteiros consecutivos aparecem todos os algarismos 0,,,, 9 como último algarismo. omo sua soma é 45, que termina em 5, e 7 5 = 35, que também termina em 5, a soma de 70 números inteiros positivos consecutivos sempre termina em () quilogramas de moedas de 0 centavos correspondem a moedas de 0 8 centavos, que valem o mesmo que 00 moedas de 50 centavos. ssim, 00 moedas de 50 centavos pesam quilograma, logo cada moeda pesa 0 gramas. 4. () b a a Trace retas paralelas aos lados a uma distância. O perímetro é igual em valor numérico à soma das áreas dos quatro retângulos finos junto aos lados. omo esta soma é igual à área total do retângulo vemos que a área do pequeno retângulo central é igual à soma das áreas dos quatro quadrados nos cantos. ssim ( a )( b ) 4. omo a b temos a = 4, b = ou a =, b = () = (D) Se cada linha tiver 5 casas ocupadas teremos 30 casas ocupadas, apenas. Logo, alguma linha tem 6 ou mais casas ocupadas. 7. (E) O número total de alunos da turma é menor que 30, é par, é maior que 5 e deixa resto quando dividido por 5. Logo, é 6. Temos meninos. 8. () Os números formados são da forma a, a ou a, onde a é um dos nove algarismos restantes. Para um dado a, a soma dos três números acima é aaa + = (a+). Logo, a sua soma para todos os nove valores possíveis de a é: S = [( ) + (9 )] = (44 + 8) = (D) Se é cão, é cão, é lobo, D é cão, E é lobo, o que é absurdo, pois E diria que é um lobo. ssim, é lobo, é lobo, é cão, D é lobo e E é lobo, e portanto há quatro lobos no grupo de animais. 0. () No primeiro mosaico, temos = 8 azulejos pretos; no segundo, temos = ; no terceiro, temos = 6; não é difícil perceber ( e verificar) que os próximos mosaicos têm 0 e 4 azulejos pretos. omo = 80, é possível construir exatamente 5 mosaicos. ssim serão necessários = = 55 azulejos brancos.
6 NÍVEL (7 a. e 8 a. séries) ) 6) ) 6) ) ) E 7) ) D 7) E ) D 3) D 8) D 3) 8) 3) 4) 9) nulada 4) E 9) D 4) D 5) 0) 5) D 0) 5) RESUMO DS SOLUÇÕES. () Veja a solução do problema 4 do nível.. (E), logo D. omo m( ˆ D) 90 o, temos m( D ˆ ) m( Dˆ ) 45 o. Mas m( ˆ ) m( Dˆ E) 80 o. Portanto, = 80 o (45 o + 80 o ) = 55 o. 3. Veja a solução do problema 5 do nível. 4. Veja a solução do problema 6 do nível. 5. Veja a solução do problema 8 do nível. 6. Veja a solução do problema 9 do nível. 7. Veja a solução do problema do nível. 8. Veja a solução do problema do nível. 9. nulada 0. Veja a solução do problema 5 do nível.. () Seja x o número de arcos percorridos e y o número de voltas dadas. P P r 35x 360 y 7x 7y x 7. Logo, n = 73.. Veja a solução do problema 6 do nível. 3. () ˆ ˆ 80(5 ) D ˆ ˆ ˆ F 60, F 48, F 66. FD ˆ Logo 4. Veja a solução do problema 7 do nível. 5. (D) Uma reta determina o número máximo de regiões no círculo quando corta o número máximo de setores (ou seja, o maior número possível de raios). figura mostra uma reta que corta n+ raios, ou seja, n+ setores, determinando assim n+ novas regiões, para um total de 3n+3 regiões. Este número é máximo, já que as extremidades dos raios extremos cortados por uma reta estão sempre em um mesmo semiplano determinado pela paralela à reta passando pelo centro do círculo. 3 n n+
7 6. () Paulo tem x reais e ezar tem y reais x 5 ( y 5) 8, ( y 5) Logo, x = 4 e y =. y x = (E) Tomemos como unidade a quantidade de ração que vaca come em dia n n Veja a solução do problema 8 do nível. 9. (D) mesa pode ser empurrada pelo corredor de dois modos: utilizando apenas movimentos de translação ou girando-a em torno do ponto de encontro dos dois corredores. No primeiro caso, é preciso um corredor de largura igual à maior dimensão da mesa (ou seja b). No segundo caso, a posição crítica ocorre quando a mesa está igualmente inclinada em relação aos dois corredores (isto é, faz um ângulo de 45 com a horizontal). Neste caso, a largura mínima deve ser igual a b a (a b). omo a < b, este valor é menor que b 4 menor que b. Logo, a largura mínima do corredor deve ser igual a ( a b). 4 a a e, portanto, b b () O plano que secciona o cubo no item é aquele que contém os segmentos que ligam os pontos médios de arestas paralelas não coincidentes de duas faces adjacentes. Pode-se verificar que as demais planificações não contém representações de interseções de planos com o cubo.. () Seja n o quadrado perfeito. omo ele termina com 00, temos n = 0000m + 00 n = 000(5m + ) (n )(n + ) = (5m + ). omo mdc(n ; n + ) = mdc(n + ; n + (n )) = mdc(n +, ) = (pois n é ímpar), n ou n + é divisível por 5 3 = 5, assim n = 5t + ou n = 5t, onde t é inteiro positivo. omo n é ímpar, t é par, logo o menor valor possível para t é. Para n = 5 = 49, temos n = 600, que termina em 00. Logo o menor quadrado perfeito cujos últimos quatro dígitos são 00 é 49 = 600 que tem 5 dígitos.. (D) Seja S a extensão do circuito, t 0 o tempo gasto pelo Papa-Léguas para dar a primeira volta e s t' 0 o tempo gasto para dar as outras 99 voltas. Temos 00 e a velocodade média do Papat 00S 0000t Léguas na corrida é Por outro lado, como nada sabemos sobre o t t' t t' 00s valor de t, se t' 9t teremos 000. ssim a opção correta é D. t t' 3. Veja a solução do problema 0 do nível. 4. Veja a solução do problema 9 do nível. 5. () Sejam M, N, O, P, Q e R os pontos de tangência dos lados,, D, DE, EF e F na circunferência inscrita, respectivamente, e seja x = M. Temos R = M = x, M = x, N = M = x, N = ( x) = + x, O = N = + x, OD = 3 ( + x) = x, DP = OD = x, PE = 4 ( x) = + x, EQ = PE = + x, QF = 5 ( + x) = 3 x e FR = QF = 3 x. Logo F = FR + R = 3 x + x = 3.
8 NÍVEL 3 (Ensino médio) ) 6) ) D 6) D ) ) E 7) ) D 7) ) 3) D 8) 3) 8) 3) 4) 9) 4) D 9) 4) 5) 0) D 5) 0) 5) E RESUMO DS SOLUÇÕES. Veja a solução do problema 4 do nível.. Veja a solução do problema do nível. 3. Veja a solução do problema 3 do nível. 4. Veja a solução do problema 4 do nível. 5. Veja a solução do problema 5 do nível. 6. Veja a solução do problema 9 do nível. 7. Veja a solução do problema 5 do nível. 8. Veja a solução do problema do nível. 9. Veja a solução do problema 3 do nível. 0. Veja a solução do problema 5 do nível.. Veja a solução do problema do nível.. (D) Observemos que a base da potência no lado esquerdo da igualdade é par. omo o expoente da potência é inteiro e positivo (é igual a (x ) + ), temos que a base, em módulo, é menor ou igual a 4, sendo então igual a, ou 4. ssim, a equação dada é equivalente a ( 6x + x = e x x + = ) ou ( 6x + x = e x x + = ) ou ( 6x + x = 4 e x x + = ). Na primeira possibilidade, temos x = 0 ou x = ; a segunda possibilidade não apresenta solução; a terceira possibilidade nos fornece x =. ssim, a equação admite três soluções inteiras distintas. 3. () O fato de que todos os alunos têm a mesma probabilidade de serem sorteados não é alterado pela perda da primeira bola sorteada. ssim, Pedro continua com uma probabilidade igual a /30 de ser sorteado. 4. Veja a solução do problema 9 do nível. 5. Veja a solução do problema 8 do nível. 6. Veja a solução do problema 9 do nível. 7. Veja a solução do problema 0 do nível. 8. () onsidere a equação f(g(x)) =. Temos (g(x)) 3g (x) + 4 = g(x) = ou g(x) =. o resolvermos f(h(x)) =, temos (h(x)) 3h(x) + 4 =, que não tem solução. ssim, sendo g(x) = f(f...(x)) (com f aplicada 999 vezes), temos que resolver f(f(g(x))) = f(g(x)) = ou f(g(x)) =. omo f(g(x)) = não tem solução, temos g(x) = ou g(x) =. Repetindo esta idéia sucessivamente, obtemos f(x) = ou f(x) = x 3x + 4 = ou x 3x + 4 = x = ou x =. ssim a equação tem soluções, a saber, e. 9. Veja a solução do problema do nível. 0. onsidere a figura a seguir (na qual assumimos, sem perda de generalidade, que < D). E M N F D Seja EF a paralela a por N. Temos que m(emf) =. lém disso, m ( ME ˆ ) = ( MF ˆ ) onsidere P sobre MF tal que PF = ME. omo PF = ME, m ( DF ˆ P) = m ( MF ˆ ) = m( ME ˆ ) e ( FP ˆ D m( Mˆ E) m ( MP ˆ ) > m ( PM ˆ D) (observe o triângulo MPD) m ( M ˆ E) > m ( FM ˆ D). P m < 90 o. FD = E, pelo caso LL temos que os triângulos ME e PFD são congruentes. Logo m ) = e PD = M. omo MD = D + M > + M = M, temos MD > M MD > PD
9 ˆ ˆ Logo = m ( EMF) m ( FMD) + m ( ME) = + m ( ME) m ( FMD) >. Outra solução: Pela lei dos senos aplicada ao triângulo ME, temos E M (I) sen ( Mˆ E ) sen ( M Eˆ ) plicando a lei dos senos agora ao triângulo MFD, temos FD MD MD sen ( F Mˆ D ) sen ( M Fˆ D ) sen ( M Fˆ ) De (I) e (II), temos sen ( FMD ˆ ) M sen ( ME ˆ ) MD omo M < MD, temos ( FMD) ˆ sen ˆ < sen ( M ˆ E). omo estes ângulos são agudos, ( FM ˆ D) m ( Mˆ E). Logo = m ( EM ˆ F) m ( FM ˆ D) + m ( M ˆ E) = + m ( M ˆ E) m ( FM ˆ D) >. ˆ (II) ˆ m <. () Seja y = x + x. Temos x + x + = 56/(x + x) y + = 56/y y + y 56 = 0 y = ou y = 3 x + x = ou x + x = 3 x + x = 0 ou x + x + 3 = 0. segunda equação não tem solução, assim a soma das soluções reais da equação original é / =.. () Seja um triângulo acutângulo, no qual supomos que a seja o menor lado. soma das S S S distâncias de um ponto P aos lados é d d d, onde S, S e S são a b c as áreas dos triângulos P, P e P, respectivamente. omo S S S é constante, d d d é máxima quando a única parcela não nula é relativa ao maior coeficiente 0, que é. a Logo, o máximo da soma ocorre quando P é o vértice oposto ao menor lado e é, portanto, igual à maior altura do triângulo. d dc P b d a 3. () Temos a = 00, a = 003,, a 9 = 00, a 0 = 0, a = 0,, a 9 = 0, a 0 =, a =,, a 9 = 30, a 30 = 3, a 3 = 4,, a 37 = 0 e finalmente a 38 =. 4. Veja a solução do problema 5 do nível. 5. (E) onsidere que os pontos e estão fixos e que gira em torno de. ssim, está na circunferência com centro e raio 5. Temos que o ângulo Ĉ é máximo quando tangencia a circunferência. Neste caso, temos que o ângulo  é reto. Logo, pelo teorema de Pitágoras, = = 6 5 = =. ssim, a área do triângulo é / = 5 /.
1. Quantos números de dois algarismos não são primos nem múltiplos de 2, 3 ou 5? A) 1 B) 3 C) 2 D) 4 E) mais de 4
 XXIII OLIMPÍD RSILEIR DE MTEMÁTI Primeira Fase Nível - Prova de 5 questões. - duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas a notas ou livros. - Você pode solicitar
XXIII OLIMPÍD RSILEIR DE MTEMÁTI Primeira Fase Nível - Prova de 5 questões. - duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas a notas ou livros. - Você pode solicitar
1. Quantos números de dois algarismos não são primos nem múltiplos de 2, 3 ou 5? A) 1 B) 3 C) 2 D) 4 E) mais de 4
 XXIII OLIMPÍD RSILEIR DE MTEMÁTI Primeira Fase Nível 3 - Prova de 5 questões. - duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas a notas ou livros. - Você pode solicitar
XXIII OLIMPÍD RSILEIR DE MTEMÁTI Primeira Fase Nível 3 - Prova de 5 questões. - duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas a notas ou livros. - Você pode solicitar
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 36ª Olimpíada rasileira de Matemática GRITO Segunda Fase Soluções Nível 3 Segunda Fase Parte RITÉRIO E ORREÇÃO: PRTE Na parte serão atribuídos pontos para cada resposta correta e a pontuação máxima para
36ª Olimpíada rasileira de Matemática GRITO Segunda Fase Soluções Nível 3 Segunda Fase Parte RITÉRIO E ORREÇÃO: PRTE Na parte serão atribuídos pontos para cada resposta correta e a pontuação máxima para
36ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 3 (Ensino Médio) GABARITO
 6ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (Ensino Médio) GABARITO GABARITO NÍVEL ) C 6) A ) D 6) A ) D ) A 7) A ) E 7) B ) E ) A 8) E ) B 8) E ) A ) C 9) C ) D 9) E ) B ) A 0) B ) A 0)
6ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (Ensino Médio) GABARITO GABARITO NÍVEL ) C 6) A ) D 6) A ) D ) A 7) A ) E 7) B ) E ) A 8) E ) B 8) E ) A ) C 9) C ) D 9) E ) B ) A 0) B ) A 0)
MATEMÁTICA SARGENTO DA FAB
 MATEMÁTICA BRUNA PAULA 1 COLETÂNEA DE QUESTÕES DE MATEMÁTICA DA EEAr (QUESTÕES RESOLVIDAS) QUESTÃO 1 (EEAr 2013) Se x é um arco do 1º quadrante, com sen x a e cosx b, então é RESPOSTA: d QUESTÃO 2 (EEAr
MATEMÁTICA BRUNA PAULA 1 COLETÂNEA DE QUESTÕES DE MATEMÁTICA DA EEAr (QUESTÕES RESOLVIDAS) QUESTÃO 1 (EEAr 2013) Se x é um arco do 1º quadrante, com sen x a e cosx b, então é RESPOSTA: d QUESTÃO 2 (EEAr
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MTEMÁTI - 3o ciclo 01 - a hamada Proposta de resolução 1. 1.1. omo a soma das frequências relativas é sempre 1, temos que Resposta: Opção 0, 3 0, 3 + a + 0, 4 = 1 a = 1 0, 3 0, 4 a = 1 0,
Prova final de MTEMÁTI - 3o ciclo 01 - a hamada Proposta de resolução 1. 1.1. omo a soma das frequências relativas é sempre 1, temos que Resposta: Opção 0, 3 0, 3 + a + 0, 4 = 1 a = 1 0, 3 0, 4 a = 1 0,
XXIX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 2 (7ª. e 8ª. séries) GABARITO
 XXIX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (ª e ª séries) GABARITO GABARITO NÍVEL ) E ) E ) B ) D ) E ) E ) C ) D ) B ) D ) E ) C ) C ) A ) B ) D ) A ) C ) B ) Anulada ) B 0) E ) A 0)
XXIX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (ª e ª séries) GABARITO GABARITO NÍVEL ) E ) E ) B ) D ) E ) E ) C ) D ) B ) D ) E ) C ) C ) A ) B ) D ) A ) C ) B ) Anulada ) B 0) E ) A 0)
Prova da segunda fase - Nível 3
 Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
XXXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 2 (8º e 9º. anos) GABARITO
 XXXIII OLIMPÍD RSILEIR DE MTEMÁTI PRIMEIR FSE NÍVEL (8º e 9º. anos) GRITO GRITO NÍVEL ) ) D ) E ) D ) D ) 7) ) 7) ) ) D 8) D ) 8) ) 4) 9) D 4) 9) D 4) 5) 0) 5) E 0) 5) ada questão da Primeira Fase vale
XXXIII OLIMPÍD RSILEIR DE MTEMÁTI PRIMEIR FSE NÍVEL (8º e 9º. anos) GRITO GRITO NÍVEL ) ) D ) E ) D ) D ) 7) ) 7) ) ) D 8) D ) 8) ) 4) 9) D 4) 9) D 4) 5) 0) 5) E 0) 5) ada questão da Primeira Fase vale
INSTRUÇÕES. Esta prova é individual e sem consulta à qualquer material.
 OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
Lugares geométricos básicos I
 Lugares geométricos básicos I M13 - Unidade 5 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Definição Lugar Geométrico da propriedade P é o conjunto
Lugares geométricos básicos I M13 - Unidade 5 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Definição Lugar Geométrico da propriedade P é o conjunto
RESPOSTAS ESPERADAS MATEMÁTICA
 RESPOSTS ESPERDS MTEMÁTI Questão 1 a) omo o ângulo de giro do ponteiro é diretamente proporcional à velocidade, podemos escrever 10 40km x 104 km Desse modo, x 104 10 / 40 91 Resposta: O ângulo mede 91º
RESPOSTS ESPERDS MTEMÁTI Questão 1 a) omo o ângulo de giro do ponteiro é diretamente proporcional à velocidade, podemos escrever 10 40km x 104 km Desse modo, x 104 10 / 40 91 Resposta: O ângulo mede 91º
Questão 2. Questão 1. Questão 3. Resposta. Resposta. Resposta
 ATENÇÃO: Escreva a resolução COMPLETA de cada questão no espaço a ela reservado. Não basta escrever apenas o resultado final: é necessário mostrar os cálculos ou o raciocínio utilizado. Questão Emumasalaháumalâmpada,umatelevisão
ATENÇÃO: Escreva a resolução COMPLETA de cada questão no espaço a ela reservado. Não basta escrever apenas o resultado final: é necessário mostrar os cálculos ou o raciocínio utilizado. Questão Emumasalaháumalâmpada,umatelevisão
Prova da UFRGS
 01. expressão (0,15) 15 é equivalente a a) 5 5. b) 5-5. c) 5. d) -5. e) (-) 5. 0. O algarismo das unidades de 9 99 é a) 1. b). c). d). e) 5. Prova da UFRGS - 015 0. Por qual potência de deve ser multiplicado
01. expressão (0,15) 15 é equivalente a a) 5 5. b) 5-5. c) 5. d) -5. e) (-) 5. 0. O algarismo das unidades de 9 99 é a) 1. b). c). d). e) 5. Prova da UFRGS - 015 0. Por qual potência de deve ser multiplicado
XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 2. 1 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP
 XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 2 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP - A duração da prova é de horas. - Não é permitido o uso de calculadoras nem
XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 2 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP - A duração da prova é de horas. - Não é permitido o uso de calculadoras nem
Matemática B Extensivo V. 7
 GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
GRITO Matemática Etensivo V. 7 Eercícios ) D ) D ) I. Falso. O diâmetro é dado por. r. cm. II. Verdadeiro. o volume é dado por π. r² π. ² π cm² III. Verdadeiro. (, ) (, ) e assim, ( )² + ( )² r² fica ²
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MTMÁTI - o ciclo 014-1 a hamada Proposta de resolução aderno 1 1. omo as grandezas x e y são inversamente proporcionais, sabemos que x y é um valor constante. ntão temos que 15 0 = 1 a 00
Prova final de MTMÁTI - o ciclo 014-1 a hamada Proposta de resolução aderno 1 1. omo as grandezas x e y são inversamente proporcionais, sabemos que x y é um valor constante. ntão temos que 15 0 = 1 a 00
MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: Observe os dados do quadro a seguir.
 MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x cos x : cosseno de x x : módulo de x log x : logaritmo de x na base 10 6. Um
MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x cos x : cosseno de x x : módulo de x log x : logaritmo de x na base 10 6. Um
UNICAMP Você na elite das universidades! MATEMÁTICA ELITE SEGUNDA FASE
 www.elitecampinas.com.br Fone: (19) -71 O ELITE RESOLVE IME 004 PORTUGUÊS/INGLÊS Você na elite das universidades! UNICAMP 004 SEGUNDA FASE MATEMÁTICA www.elitecampinas.com.br Fone: (19) 51-101 O ELITE
www.elitecampinas.com.br Fone: (19) -71 O ELITE RESOLVE IME 004 PORTUGUÊS/INGLÊS Você na elite das universidades! UNICAMP 004 SEGUNDA FASE MATEMÁTICA www.elitecampinas.com.br Fone: (19) 51-101 O ELITE
38ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 2 (8º e 9º anos do Ensino Fundamental) GABARITO
 38ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 2 (8º e 9º anos do Ensino Fundamental) GABARITO GABARITO NÍVEL 2 1) C 6) B 11) B 16) D 21) A 2) C 7) C 12) C 17) D 22) A 3) D 8) E 13) D 18) C
38ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 2 (8º e 9º anos do Ensino Fundamental) GABARITO GABARITO NÍVEL 2 1) C 6) B 11) B 16) D 21) A 2) C 7) C 12) C 17) D 22) A 3) D 8) E 13) D 18) C
XXXVII OLIMPÍADA PAULISTA DE MATEMÁTICA Prova da Primeira Fase 9 de agosto de 2014 Nível (6º e 7º anos do Ensino Fundamental)
 XXXVII OLIMPÍADA PAULISTA DE MATEMÁTICA Prova da Primeira Fase 9 de agosto de 2014 Nível (6º e 7º anos do Ensino Fundamental) Resoluções www.opm.mat.br PROBLEMA 1 a) O total de segundos destinados à visualização
XXXVII OLIMPÍADA PAULISTA DE MATEMÁTICA Prova da Primeira Fase 9 de agosto de 2014 Nível (6º e 7º anos do Ensino Fundamental) Resoluções www.opm.mat.br PROBLEMA 1 a) O total de segundos destinados à visualização
14 a ORMUB/2006 OLIMPÍADA REGIONAL DE MATEMÁTICA PROVA PARA OS ALUNOS DO 2º ANO DO ENSINO MÉDIO NOME: ESCOLA: CIDADE:
 14 a ORMUB/2006 OLIMPÍADA REGIONAL DE MATEMÁTICA PROVA PARA OS ALUNOS DO 2º ANO DO ENSINO MÉDIO NOME: ESCOLA: CIDADE: INSTRUÇÕES AVALIAÇÃO Este caderno contém 5 (cinco) questões). A solução de cada questão,
14 a ORMUB/2006 OLIMPÍADA REGIONAL DE MATEMÁTICA PROVA PARA OS ALUNOS DO 2º ANO DO ENSINO MÉDIO NOME: ESCOLA: CIDADE: INSTRUÇÕES AVALIAÇÃO Este caderno contém 5 (cinco) questões). A solução de cada questão,
Agrupamento de Escolas de Diogo Cão, Vila Real
 Agrupamento de Escolas de Diogo Cão, Vila Real MATEMÁTICA - 9º ANO JUNHO 016 PROVA FINAL DA ª CHAMADA DE 01 PROPOSTA DE RESOLUÇÃO EM MUITAS DAS RESPOSTAS HÁ EXPLICAÇÕES ADICIONAIS E NÃO APENAS A SOLUÇÃO
Agrupamento de Escolas de Diogo Cão, Vila Real MATEMÁTICA - 9º ANO JUNHO 016 PROVA FINAL DA ª CHAMADA DE 01 PROPOSTA DE RESOLUÇÃO EM MUITAS DAS RESPOSTAS HÁ EXPLICAÇÕES ADICIONAIS E NÃO APENAS A SOLUÇÃO
RESOLUÇÃO DA PROVA DE MATEMÁTICA - UFRGS 2019
 RESOLUÇÃO DA PROVA DE MATEMÁTICA - UFRGS 2019 26. Resposta (D) I. Falsa II. Correta O número 2 é o único primo par. Se a é um número múltiplo de 3, e 2a sendo um número par, logo múltiplo de 2. Então 2a
RESOLUÇÃO DA PROVA DE MATEMÁTICA - UFRGS 2019 26. Resposta (D) I. Falsa II. Correta O número 2 é o único primo par. Se a é um número múltiplo de 3, e 2a sendo um número par, logo múltiplo de 2. Então 2a
Teste Intermédio 2012
 Teste Intermédio 01 1. Uma escola básica tem duas turmas de 9. ano: a turma e a turma. Os alunos da turma distribuem-se, por idades, de acordo com o seguinte diagrama circular. Idades dos alunos da turma
Teste Intermédio 01 1. Uma escola básica tem duas turmas de 9. ano: a turma e a turma. Os alunos da turma distribuem-se, por idades, de acordo com o seguinte diagrama circular. Idades dos alunos da turma
VESTIBULAR UFPE UFRPE / ª ETAPA NOME DO ALUNO: ESCOLA: SÉRIE: TURMA: MATEMÁTICA 2
 VESTIULR UFPE UFRPE / 1998 2ª ETP NOME DO LUNO: ESOL: SÉRIE: TURM: MTEMÁTI 2 01. nalise as afirmações: 0-0) 4 + 2 + 4 2 = 12 (as raízes quadradas são as positivas) 4 1-1) = 0,666... 11 log 2-2) 2 = 2 2
VESTIULR UFPE UFRPE / 1998 2ª ETP NOME DO LUNO: ESOL: SÉRIE: TURM: MTEMÁTI 2 01. nalise as afirmações: 0-0) 4 + 2 + 4 2 = 12 (as raízes quadradas são as positivas) 4 1-1) = 0,666... 11 log 2-2) 2 = 2 2
Exercícios de Revisão
 Professor: Cassio Kiechaloski Mello Disciplina: Matemática Exercícios de Revisão Geometria Analítica Geometria Plana Geometria Espacial Números Complexos Polinômios Na prova de recuperação final, não será
Professor: Cassio Kiechaloski Mello Disciplina: Matemática Exercícios de Revisão Geometria Analítica Geometria Plana Geometria Espacial Números Complexos Polinômios Na prova de recuperação final, não será
a. 0 b. 1 c. 2 d. 3 e. 5
 X OM NÍVEL ª OPM. Maria foi à feira e comprou duas dúzias de laranjas, duas dúzias de bananas e uma dúzia de maçãs, gastando R$ 5,80. Na outra semana, quando voltou à feira, comprou três dúzias de laranjas,
X OM NÍVEL ª OPM. Maria foi à feira e comprou duas dúzias de laranjas, duas dúzias de bananas e uma dúzia de maçãs, gastando R$ 5,80. Na outra semana, quando voltou à feira, comprou três dúzias de laranjas,
05. Um retângulo ABCD está dividido em quatro retângulos menores. As áreas de três deles estão na figura abaixo. Qual é a área do retângulo ABCD?
 XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 3 1 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras
XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 3 1 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras
,12 2, = , ,12 = = (2012) 2.
 1 QUESTÃO 1 Usando a comutatividade da multiplicação, podemos escrever 1000 0,1,01 100 = 1000,01 00 0,1 = 01 01 = (01). QUESTÃO Observe que para obter o primeiro retângulo foi necessário escrever quatro
1 QUESTÃO 1 Usando a comutatividade da multiplicação, podemos escrever 1000 0,1,01 100 = 1000,01 00 0,1 = 01 01 = (01). QUESTÃO Observe que para obter o primeiro retângulo foi necessário escrever quatro
Prova da UFRGS
 Prova da UFRGS - 01 01. O algarismo das unidades de 9 10 é a) 0. b) 1.. d). e) 9. 0. A atmosfera terrestre contém 1.900 quilômetros cúbicos de água. Esse valor corresponde, em litros, a a) 1,9.10 9. b)
Prova da UFRGS - 01 01. O algarismo das unidades de 9 10 é a) 0. b) 1.. d). e) 9. 0. A atmosfera terrestre contém 1.900 quilômetros cúbicos de água. Esse valor corresponde, em litros, a a) 1,9.10 9. b)
Soluções Simulado OBMEP 2017 Nível 1 6º e 7º anos do Ensino Fundamental. = 7 cm. Logo, ela parou na marca de = 13 cm.
 Soluções Simulado OBMEP 2017 Nível 1 6º e 7º anos do Ensino Fundamental 1. ALTERNATIVA C Alvimar recebeu de troco 5,00 3,50 = 1,50 reais. Dividindo 1,50 por 0,25, obtemos o número de moedas de 25 centavos
Soluções Simulado OBMEP 2017 Nível 1 6º e 7º anos do Ensino Fundamental 1. ALTERNATIVA C Alvimar recebeu de troco 5,00 3,50 = 1,50 reais. Dividindo 1,50 por 0,25, obtemos o número de moedas de 25 centavos
XXI Olimpíada de Matemática do Estado do Rio Grande do Norte. Prova do Nível I Em 25/09/2010
 XXI Olimpíada de Matemática do Estado do Rio Grande do Norte Prova do Nível I Em 25/09/2010 Problema 1 Um professor de Matemática definiu a seguinte operação entre dois números naturais: Ele exemplificou
XXI Olimpíada de Matemática do Estado do Rio Grande do Norte Prova do Nível I Em 25/09/2010 Problema 1 Um professor de Matemática definiu a seguinte operação entre dois números naturais: Ele exemplificou
VESTIBULAR UFPE UFRPE / ª ETAPA
 VSTIULR UFP UFRP / 1999 2ª TP NOM O LUNO: SOL: SÉRI: TURM: MTMÁTI 2 01. O triângulo da ilustração abaixo é isósceles ( = ) e = = (isto é,, trissectam ): nalise as afirmações: 0-0) Os ângulos, e são congruentes.
VSTIULR UFP UFRP / 1999 2ª TP NOM O LUNO: SOL: SÉRI: TURM: MTMÁTI 2 01. O triângulo da ilustração abaixo é isósceles ( = ) e = = (isto é,, trissectam ): nalise as afirmações: 0-0) Os ângulos, e são congruentes.
2ª. Lista de Revisão Geometria Plana Prof. Kátia Curso SER - Poliedro
 ª. Lista de Revisão Geometria Plana Prof. Kátia Curso SER - Poliedro 1. (G1 - cps 016) A erosão é o processo de desgaste, transporte e sedimentação das rochas e, principalmente, dos solos. Ela pode ocorrer
ª. Lista de Revisão Geometria Plana Prof. Kátia Curso SER - Poliedro 1. (G1 - cps 016) A erosão é o processo de desgaste, transporte e sedimentação das rochas e, principalmente, dos solos. Ela pode ocorrer
2ª. Lista de Revisão Geometria Plana Prof. Kátia Curso SER - Poliedro
 ª. Lista de Revisão Geometria Plana Prof. Kátia Curso SER - Poliedro 1. (G1 - cps 016) A erosão é o processo de desgaste, transporte e sedimentação das rochas e, principalmente, dos solos. Ela pode ocorrer
ª. Lista de Revisão Geometria Plana Prof. Kátia Curso SER - Poliedro 1. (G1 - cps 016) A erosão é o processo de desgaste, transporte e sedimentação das rochas e, principalmente, dos solos. Ela pode ocorrer
Prova final de MATEMÁTICA - 3o ciclo Época especial
 Prova final de MTEMÁTI - 3o ciclo 015 - Época especial Proposta de resolução aderno 1 1. omo foi escolhido um dos convidados que gostam de gelatina, existem escolhas possíveis (a na, o Paulo, o Rui, a
Prova final de MTEMÁTI - 3o ciclo 015 - Época especial Proposta de resolução aderno 1 1. omo foi escolhido um dos convidados que gostam de gelatina, existem escolhas possíveis (a na, o Paulo, o Rui, a
Canguru Matemático sem Fronteiras 2012
 http://wwwmatucpt/canguru/ Destinatários: alunos dos 10 o e 11 o anos de escolaridade Nome: Turma: Duração: 1h 0min Não podes usar calculadora Em cada questão deves assinalar a resposta correta As questões
http://wwwmatucpt/canguru/ Destinatários: alunos dos 10 o e 11 o anos de escolaridade Nome: Turma: Duração: 1h 0min Não podes usar calculadora Em cada questão deves assinalar a resposta correta As questões
Polos Olímpicos de Treinamento. Aula 13. Curso de Geometria - Nível 3. Prof. Cícero Thiago
 Polos Olímpicos de Treinamento urso de Geometria - Nível 3 Prof. ícero Thiago ula 13 Revisão I Problema 1. Em um triângulo, = 100 e =. Seja D a bissetriz de, com D sobre o lado. Prove que D +D =. É fácil
Polos Olímpicos de Treinamento urso de Geometria - Nível 3 Prof. ícero Thiago ula 13 Revisão I Problema 1. Em um triângulo, = 100 e =. Seja D a bissetriz de, com D sobre o lado. Prove que D +D =. É fácil
35ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 2 (8º e 9º anos do Ensino Fundamental) GABARITO
 5ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (8º e 9º anos do Ensino Fundamental) GABARITO GABARITO NÍVEL 1) D) 6) D) 11) E) 16) B) 1) Anulada ) A) 7) D) 1) C) 17) C) ) B) ) D) 8) E) 1) D)
5ª OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (8º e 9º anos do Ensino Fundamental) GABARITO GABARITO NÍVEL 1) D) 6) D) 11) E) 16) B) 1) Anulada ) A) 7) D) 1) C) 17) C) ) B) ) D) 8) E) 1) D)
Projeto Jovem Nota 10 Áreas de Figuras Planas Lista 4 Professor Marco Costa
 1 Projeto Jovem Nota 10 1. (Ufscar 2001) Considere o triângulo de vértices A, B, C, representado a seguir. a) Dê a expressão da altura h em função de c (comprimento do lado AB) e do ângulo A (formado pelos
1 Projeto Jovem Nota 10 1. (Ufscar 2001) Considere o triângulo de vértices A, B, C, representado a seguir. a) Dê a expressão da altura h em função de c (comprimento do lado AB) e do ângulo A (formado pelos
A) são da mesma cor. B) são vermelhas. C) uma é vermelha e duas são brancas. D) uma é branca e duas são vermelhas. E) pelo menos uma é vermelha.
 XXII OLIMPÍADA BRASILEIRA DE MATEMÁTIA Primeira Fase Nível 1 - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas a notas ou livros. - Você pode solicitar papel para
XXII OLIMPÍADA BRASILEIRA DE MATEMÁTIA Primeira Fase Nível 1 - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas a notas ou livros. - Você pode solicitar papel para
Universidade do Algarve
 Universidade do Algarve Olimpíadas oncelhias da Matemática Ensino da Matemática na óptica da resolução de problemas: Uma parceria entre a Universidade e as Escolas 1. Na figura, [ABD] é um quadrado e [DP]
Universidade do Algarve Olimpíadas oncelhias da Matemática Ensino da Matemática na óptica da resolução de problemas: Uma parceria entre a Universidade e as Escolas 1. Na figura, [ABD] é um quadrado e [DP]
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MATEMÁTA - 3o ciclo 005-1 a hamada Proposta de resolução 1. Fazendo a contagem dos alunos que se enquadram em cada uma das opções apresentadas, temos: Ter lido menos do que um livro, ou
Prova final de MATEMÁTA - 3o ciclo 005-1 a hamada Proposta de resolução 1. Fazendo a contagem dos alunos que se enquadram em cada uma das opções apresentadas, temos: Ter lido menos do que um livro, ou
Colégio Nossa Senhora de Lourdes. Matemática - Professor: Leonardo Maciel
 Colégio Nossa Senhora de Lourdes Matemática - Professor: Leonardo Maciel 1. (Pucrj 015) Uma pesquisa realizada com 45 atletas, sobre as atividades praticadas nos seus treinamentos, constatou que 15 desses
Colégio Nossa Senhora de Lourdes Matemática - Professor: Leonardo Maciel 1. (Pucrj 015) Uma pesquisa realizada com 45 atletas, sobre as atividades praticadas nos seus treinamentos, constatou que 15 desses
1. Se x e y são números reais positivos, qual dos números a seguir é o maior?
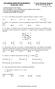 XXII OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 3 - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consulta a notas ou livros. - Você pode solicitar papel para
XXII OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 3 - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consulta a notas ou livros. - Você pode solicitar papel para
Teorema de Pitágoras
 Teorema de Pitágoras Luan Arjuna 1 Introdução Uma das maiores preocupações dos matemáticos da antiguidade era a determinação de comprimentos: desde a altura de um edifício até a distância entre duas cidades,
Teorema de Pitágoras Luan Arjuna 1 Introdução Uma das maiores preocupações dos matemáticos da antiguidade era a determinação de comprimentos: desde a altura de um edifício até a distância entre duas cidades,
QUESTÃO 1 ALTERNATIVA B
 1 QUESTÃO 1 O tabuleiro 7 7 pode ser facilmente preenchido e constata-se que na casa central deve aparecer o número 25, mas existe uma maneira melhor de fazer isto: no tabuleiro quadrado de casas, a quantidade
1 QUESTÃO 1 O tabuleiro 7 7 pode ser facilmente preenchido e constata-se que na casa central deve aparecer o número 25, mas existe uma maneira melhor de fazer isto: no tabuleiro quadrado de casas, a quantidade
Assinale as proposições verdadeiras some os resultados e marque na Folha de Respostas.
 PROVA DE MATEMÁTICA a AVALIAÇÃO UNIDADE 8 a SÉRIE E M _ COLÉGIO ANCHIETA-A ELAORAÇÃO DA PROVA: PROF OCTAMAR MARQUES PROFA MARIA ANTÔNIA CONCEIÇÃO GOUVEIA QUESTÕES DE A 8 Assinale as proposições verdadeiras
PROVA DE MATEMÁTICA a AVALIAÇÃO UNIDADE 8 a SÉRIE E M _ COLÉGIO ANCHIETA-A ELAORAÇÃO DA PROVA: PROF OCTAMAR MARQUES PROFA MARIA ANTÔNIA CONCEIÇÃO GOUVEIA QUESTÕES DE A 8 Assinale as proposições verdadeiras
Simulado 1 Matemática IME Soluções Propostas
 Simulado 1 Matemática IME 2012 Soluções Propostas 1 Para 0, temos: para cada um dos elementos de, valores possíveis em (não precisam ser distintos entre si, apenas precisam ser pertencentes a, pois não
Simulado 1 Matemática IME 2012 Soluções Propostas 1 Para 0, temos: para cada um dos elementos de, valores possíveis em (não precisam ser distintos entre si, apenas precisam ser pertencentes a, pois não
QUESTÃO 16 Sabendo que o volume do paralelepípedo abaixo é 12x 5 y 4, qual é o monômio que representa sua altura?
 Colégio Nome: N.º: Endereço: Data: Telefone: E-mail: Disciplina: MATEMÁTICA Prova: DESAFIO PARA QUEM CURSA A 1 ạ SÉRIE DO ENSINO MÉDIO EM 2019 QUESTÃO 16 Sabendo que o volume do paralelepípedo abaixo é
Colégio Nome: N.º: Endereço: Data: Telefone: E-mail: Disciplina: MATEMÁTICA Prova: DESAFIO PARA QUEM CURSA A 1 ạ SÉRIE DO ENSINO MÉDIO EM 2019 QUESTÃO 16 Sabendo que o volume do paralelepípedo abaixo é
MA13 Geometria I Avaliação
 13 eometria I valiação 011 abarito Questão 1 (,0) figura abaixo mostra um triângulo equilátero e suas circunferências inscrita e circunscrita. circunferência menor tem raio 1. alcule a área da região sombreada.
13 eometria I valiação 011 abarito Questão 1 (,0) figura abaixo mostra um triângulo equilátero e suas circunferências inscrita e circunscrita. circunferência menor tem raio 1. alcule a área da região sombreada.
XXV OLIMPÍADA BRASILEIRA DE MATEMÁTICA Segunda Fase Nível 2 (7 a. ou 8 a. séries)
 PROBLEMA No desenho ao lado, o quadrado ABCD tem área de 30 cm e o quadrado FHIJ tem área de 0 cm. Os vértices A, D, E, H e I dos três quadrados pertencem a uma mesma reta. Calcule a área do quadrado BEFG.
PROBLEMA No desenho ao lado, o quadrado ABCD tem área de 30 cm e o quadrado FHIJ tem área de 0 cm. Os vértices A, D, E, H e I dos três quadrados pertencem a uma mesma reta. Calcule a área do quadrado BEFG.
MATEMÁTICA - 3o ciclo Posição relativa de retas e planos (9 o ano) Propostas de resolução
 MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) Propostas de resolução xercícios de provas nacionais e testes intermédios 1. nalisando as quatro retas indicadas podemos ver que a reta é paralela
MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) Propostas de resolução xercícios de provas nacionais e testes intermédios 1. nalisando as quatro retas indicadas podemos ver que a reta é paralela
XXXVII OLIMPÍADA PAULISTA DE MATEMÁTICA Prova da Primeira Fase 10 de agosto de 2013 Nível (6º e 7º anos do Ensino Fundamental)
 nstruções: XXXV OLMPÍ PULST MTMÁT Prova da Primeira ase 0 de agosto de 203 Nível (6º e º anos do nsino undamental) olha de Perguntas duração da prova é de 3h30min. O tempo mínimo de permanência é de h30min.
nstruções: XXXV OLMPÍ PULST MTMÁT Prova da Primeira ase 0 de agosto de 203 Nível (6º e º anos do nsino undamental) olha de Perguntas duração da prova é de 3h30min. O tempo mínimo de permanência é de h30min.
Matemática. 3-3) As diagonais do cubo medem x / ) As diagonais da face do cubo medem 2 y 1/3. Resposta: VFFVV.
 Matemática 01. Seja x a área total da superfície de um cubo, e y, o volume do mesmo cubo. Analise as afirmações a seguir, considerando essas informações. 0-0) Se x = 54 então y = 27. 1-1) 6y = x 3 2-2)
Matemática 01. Seja x a área total da superfície de um cubo, e y, o volume do mesmo cubo. Analise as afirmações a seguir, considerando essas informações. 0-0) Se x = 54 então y = 27. 1-1) 6y = x 3 2-2)
Soluções das Questões de Matemática do Processo Seletivo de Admissão à Escola de Aprendizes- Marinheiros PSAEAM
 Soluções das Questões de Matemática do Processo Seletivo de Admissão à Escola de Aprendizes- Marinheiros PSAEAM Questão 1 Concurso 010 Sabendo que 1 grosa é equivalente a 1 dúzias, é correto afirmar que
Soluções das Questões de Matemática do Processo Seletivo de Admissão à Escola de Aprendizes- Marinheiros PSAEAM Questão 1 Concurso 010 Sabendo que 1 grosa é equivalente a 1 dúzias, é correto afirmar que
Prova final de MATEMÁTICA - 3o ciclo Época especial
 Prova final de MTEMÁTI - o ciclo 018 - Época especial Proposta de resolução aderno 1 1. omo os dados da tabela já estão ordenados podemos verificar que os valores centrais, são 61,6 e 6,4. Logo a mediana,
Prova final de MTEMÁTI - o ciclo 018 - Época especial Proposta de resolução aderno 1 1. omo os dados da tabela já estão ordenados podemos verificar que os valores centrais, são 61,6 e 6,4. Logo a mediana,
NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.
![NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo. NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.](/thumbs/74/70891793.jpg) R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
Prova da segunda fase - Nível 2
 Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
XXX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 3 (Ensino Médio) GABARITO
 XXX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (Ensino Médio) GABARITO GABARITO NÍVEL ) D 6) C ) D 6) C ) B ) A 7) B ) B 7) B ) C ) D 8) C ) E 8) B ) B 4) D 9) E 4) D 9) C 4) D ) D 0) A ou
XXX OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (Ensino Médio) GABARITO GABARITO NÍVEL ) D 6) C ) D 6) C ) B ) A 7) B ) B 7) B ) C ) D 8) C ) E 8) B ) B 4) D 9) E 4) D 9) C 4) D ) D 0) A ou
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MATEMÁTICA - 3o ciclo 013 - a Chamada Proposta de resolução 1. 1.1. Como se escolhe um aluno do primeiro turno, ou seja, um aluno com um número ímpar, existem 1 escolhas possíveis (1, 3,
Prova final de MATEMÁTICA - 3o ciclo 013 - a Chamada Proposta de resolução 1. 1.1. Como se escolhe um aluno do primeiro turno, ou seja, um aluno com um número ímpar, existem 1 escolhas possíveis (1, 3,
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MTEMÁTI - 3o ciclo 01 - a hamada Proposta de resolução aderno 1 1. 1.1. omo o ponto de coordenadas (,) pertence ao gráfico de f, então f() = 1.. omo a função f é uma função de proporcionalidade
Prova final de MTEMÁTI - 3o ciclo 01 - a hamada Proposta de resolução aderno 1 1. 1.1. omo o ponto de coordenadas (,) pertence ao gráfico de f, então f() = 1.. omo a função f é uma função de proporcionalidade
INSTRUÇÕES. Esta prova é individual e sem consulta à qualquer material.
 OPRM 09 Nível Primeira Fase 4 ou 5 de Junho de 09 uração: horas e 30 minutos Nome: scola: Fiscal: INSTRUÇÕS screva seu nome, o nome da sua escola e nome do FISL (pessoa que está aplicando a prova) nos
OPRM 09 Nível Primeira Fase 4 ou 5 de Junho de 09 uração: horas e 30 minutos Nome: scola: Fiscal: INSTRUÇÕS screva seu nome, o nome da sua escola e nome do FISL (pessoa que está aplicando a prova) nos
Portanto, o percentual de meninas na turma deste ano será:
 PROFMAT EXAME NACIONAL DE ACESSO 2018 (21/10/2017) [01] No ano passado uma turma tinha 31 estudantes. Neste ano o número de meninas aumentou em 20% e o de meninos diminuiu em 25%. Como resultado, a turma
PROFMAT EXAME NACIONAL DE ACESSO 2018 (21/10/2017) [01] No ano passado uma turma tinha 31 estudantes. Neste ano o número de meninas aumentou em 20% e o de meninos diminuiu em 25%. Como resultado, a turma
GEOMETRIA PLANA. 1) (UFRGS) Na figura abaixo, o vértice A do retângulo OABC está a 6 cm do vértice C. O raio do círculo mede
 GEOMETRI PLN 1) (UFRGS) Na figura abaixo, o vértice do retângulo O está a 6 cm do vértice. O raio do círculo mede O (a) 5 cm (b) 6 cm (c) 8 cm (d) 9 cm (e) 10 cm ) (UFRGS) Na figura abaixo, é o centro
GEOMETRI PLN 1) (UFRGS) Na figura abaixo, o vértice do retângulo O está a 6 cm do vértice. O raio do círculo mede O (a) 5 cm (b) 6 cm (c) 8 cm (d) 9 cm (e) 10 cm ) (UFRGS) Na figura abaixo, é o centro
XXVI OLIMPÍADA BRASILEIRA DE MATEMÁTICA TERCEIRA FASE NÍVEL 1 (5ª e 6ª séries - Ensino Fundamental)
 TERCEIRA FASE NÍVEL 1 (5ª e 6ª séries - Ensino Fundamental) PROBLEMA 1 Encontre todos os números naturais n de três algarismos que possuem todas as propriedades abaixo: n é ímpar; n é um quadrado perfeito;
TERCEIRA FASE NÍVEL 1 (5ª e 6ª séries - Ensino Fundamental) PROBLEMA 1 Encontre todos os números naturais n de três algarismos que possuem todas as propriedades abaixo: n é ímpar; n é um quadrado perfeito;
Aula 11 Conseqüências da semelhança de
 onseqüências da semelhança de triângulos MÓULO 1 - UL 11 ula 11 onseqüências da semelhança de triângulos Objetivos presentar o Teorema de Pitágoras presentar o teorema da bissetriz interna. O Teorema de
onseqüências da semelhança de triângulos MÓULO 1 - UL 11 ula 11 onseqüências da semelhança de triângulos Objetivos presentar o Teorema de Pitágoras presentar o teorema da bissetriz interna. O Teorema de
XX OLIMPÍADA DE MATEMÁTICA DO ESTADO DO RIO GRANDE DO NORTE - Em 19/09/2009
 XX OLIMPÍADA DE MATEMÁTICA DO ESTADO DO RIO GRANDE DO NORTE - Em 19/09/2009 PROVA DA SEGUNDA ETAPA NÍVEL I (Estudantes da 6 a e 7 a Séries) Problema 1 A expressão E, a seguir, é o produto de 20 números:
XX OLIMPÍADA DE MATEMÁTICA DO ESTADO DO RIO GRANDE DO NORTE - Em 19/09/2009 PROVA DA SEGUNDA ETAPA NÍVEL I (Estudantes da 6 a e 7 a Séries) Problema 1 A expressão E, a seguir, é o produto de 20 números:
1. A imagem da função real f definida por f(x) = é a) R {1} b) R {2} c) R {-1} d) R {-2}
 1. A imagem da função real f definida por f(x) = é R {1} R {2} R {-1} R {-2} 2. Dadas f e g, duas funções reais definidas por f(x) = x 3 x e g(x) = sen x, pode-se afirmar que a expressão de (f o g)(x)
1. A imagem da função real f definida por f(x) = é R {1} R {2} R {-1} R {-2} 2. Dadas f e g, duas funções reais definidas por f(x) = x 3 x e g(x) = sen x, pode-se afirmar que a expressão de (f o g)(x)
DATA DA APLICAÇÃO: 23/06/2017. Boa Prova!
 ª OLIMPÍADA D MATMÁTIA DO DISTRITO FDRAL Primeira Fase - Nível (8º e 9º Anos) DATA DA APLIAÇÃO: /06/07 aro(a) aluno(a): a) A duração da prova é de horas. ) Você poderá, se necessário, solicitar papel para
ª OLIMPÍADA D MATMÁTIA DO DISTRITO FDRAL Primeira Fase - Nível (8º e 9º Anos) DATA DA APLIAÇÃO: /06/07 aro(a) aluno(a): a) A duração da prova é de horas. ) Você poderá, se necessário, solicitar papel para
XXXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL 1 (6º. e 7º. anos) GABARITO
 XXXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (6º. e 7º. anos) GABARITO GABARITO NÍVEL ) A 6) A ) D 6) E ) B 7) E ) D 7) C ) E 8) C ) D 8) D 4) B 9) E 4) A 9) B 5) B 0) D 5) A 0) C Cada
XXXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (6º. e 7º. anos) GABARITO GABARITO NÍVEL ) A 6) A ) D 6) E ) B 7) E ) D 7) C ) E 8) C ) D 8) D 4) B 9) E 4) A 9) B 5) B 0) D 5) A 0) C Cada
AUTOR: SÍLVIO CARLOS PEREIRA TODO O CONTEÚDO DESTE MATERIAL DIDÁTICO ENCONTRA-SE REGISTRADO. PROTEÇÃO AUTORAL VIDE LEI 9.610/98.
 AUTOR: SÍLVIO CARLOS PEREIRA TODO O CONTEÚDO DESTE MATERIAL DIDÁTICO ENCONTRA-SE REGISTRADO. PROTEÇÃO AUTORAL VIDE LEI 9.610/98. ÍNDICE: Estatística e conteúdos abordados na prova de 2018 1... 5 Prova
AUTOR: SÍLVIO CARLOS PEREIRA TODO O CONTEÚDO DESTE MATERIAL DIDÁTICO ENCONTRA-SE REGISTRADO. PROTEÇÃO AUTORAL VIDE LEI 9.610/98. ÍNDICE: Estatística e conteúdos abordados na prova de 2018 1... 5 Prova
RESPOSTAS ESPERADAS MATEMÁTICA
 Questão 1 O trapézio em questão tem,8 m de base maior e m de base menor A diferença entre as bases é de 0,8 m, o que, dada a simetria do trapézio, implica uma diferença de 0,4 m de cada lado, como mostrado
Questão 1 O trapézio em questão tem,8 m de base maior e m de base menor A diferença entre as bases é de 0,8 m, o que, dada a simetria do trapézio, implica uma diferença de 0,4 m de cada lado, como mostrado
Prova da UFRGS
 Prova da UFRGS - 2013 01. Um adulto humano saudável abriga cerca de 100 bilhões de bactérias, somente em seu trato digestivo. Esse número de bactérias pode ser escrito como a) 10 9. b) 10 10. c) 10 11.
Prova da UFRGS - 2013 01. Um adulto humano saudável abriga cerca de 100 bilhões de bactérias, somente em seu trato digestivo. Esse número de bactérias pode ser escrito como a) 10 9. b) 10 10. c) 10 11.
CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES
 CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES CÍRCULO E CIRCUNFERÊNCIA Circunferência: é uma linha. Exemplos: argola, roda de bicicleta... Círculo: é uma superfície. Exemplos: moeda, mesa redonda... CIRCUNFERÊNCIA
CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES CÍRCULO E CIRCUNFERÊNCIA Circunferência: é uma linha. Exemplos: argola, roda de bicicleta... Círculo: é uma superfície. Exemplos: moeda, mesa redonda... CIRCUNFERÊNCIA
MATEMÁTICA - 3o ciclo Teorema de Pitágoras (8 o ano) Propostas de resolução
 MTEMÁTI - 3o ciclo Teorema de Pitágoras (8 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. omo a reta T P é tangente à circunferência no ponto T é perpendicular ao
MTEMÁTI - 3o ciclo Teorema de Pitágoras (8 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. omo a reta T P é tangente à circunferência no ponto T é perpendicular ao
FICHA de AVALIAÇÃO de MATEMÁTICA A 11.º Ano Versão 4
 FICHA de AVALIAÇÃO de MATEMÁTICA A º Ano Versão Nome: Nº Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias Quando,
FICHA de AVALIAÇÃO de MATEMÁTICA A º Ano Versão Nome: Nº Turma: Apresente o seu raciocínio de forma clara, indicando todos os cálculos que tiver de efetuar e todas as justificações necessárias Quando,
CONSTRUÇÕES GEOMÉTRICAS E DEMONSTRAÇÕES nível 2
 Prof. Élio Mega ONSTRUÇÕES GEOMÉTRIS E DEMONSTRÇÕES nível 2 partir do século V a, os matemáticos gregos desenvolveram uma parte da Matemática, intimamente ligada à Geometria, conhecida como onstruções
Prof. Élio Mega ONSTRUÇÕES GEOMÉTRIS E DEMONSTRÇÕES nível 2 partir do século V a, os matemáticos gregos desenvolveram uma parte da Matemática, intimamente ligada à Geometria, conhecida como onstruções
UFBA / UFRB a Fase Matemática RESOLUÇÃO: Professora Maria Antônia Gouveia. QUESTÕES de 01 a 08
 UFBA / UFRB 008 1a Fase Matemática Professora Maria Antônia Gouveia QUESTÕES de 01 a 08 INSTRUÇÃO: Assinale as proposições verdadeiras, some os números a elas associados e marque o resultado na Folha de
UFBA / UFRB 008 1a Fase Matemática Professora Maria Antônia Gouveia QUESTÕES de 01 a 08 INSTRUÇÃO: Assinale as proposições verdadeiras, some os números a elas associados e marque o resultado na Folha de
C A r. GABARITO MA13 Geometria I - Avaliação /2. A área de um triângulo ABC será denotada por (ABC).
 GRITO 13 Geometria I - valiação 3-01/ área de um triângulo será denotada por (). Questão 1. (pontuação: ) figura abaio mostra as semirretas perpendiculares r e s, três circunferências pequenas cada uma
GRITO 13 Geometria I - valiação 3-01/ área de um triângulo será denotada por (). Questão 1. (pontuação: ) figura abaio mostra as semirretas perpendiculares r e s, três circunferências pequenas cada uma
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
RESOLUÇÃO DA PROVA DO COLÉGIO NAVAL DE 2006 (PROVA VERDE):
 RESOLUÇÃO DA PROVA DO COLÉGIO NAVAL DE 006 (PROVA VERDE): 1) Observe o sistema de equações lineares abaixo. x y 3 1 S 1: x 7y Sendo (x 1,y 1 ) solução de S 1, o resultado de (6 )x1 (1 3)y1 é igual a a)
RESOLUÇÃO DA PROVA DO COLÉGIO NAVAL DE 006 (PROVA VERDE): 1) Observe o sistema de equações lineares abaixo. x y 3 1 S 1: x 7y Sendo (x 1,y 1 ) solução de S 1, o resultado de (6 )x1 (1 3)y1 é igual a a)
Matemática Cada quadrado pequeno ilustrado na figura tem lado 2. Qual é a área do polígono ABCDE?
 Matemática 01. ada quadrado pequeno ilustrado na figura tem lado. Qual é a área do polígono E? E Resposta: 64 O polígono pode ser decomposto no triângulo E e no quadrado E que tem lado 4 + 6. Logo, a área
Matemática 01. ada quadrado pequeno ilustrado na figura tem lado. Qual é a área do polígono E? E Resposta: 64 O polígono pode ser decomposto no triângulo E e no quadrado E que tem lado 4 + 6. Logo, a área
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MATEMÁTICA - o ciclo 006-1 a Chamada Proposta de resolução 1. 1.1. Como a Marta pesa 45 kg, e para evitar lesões na coluna vertebral, o peso de uma mochila e o do material que se transporta
Prova final de MATEMÁTICA - o ciclo 006-1 a Chamada Proposta de resolução 1. 1.1. Como a Marta pesa 45 kg, e para evitar lesões na coluna vertebral, o peso de uma mochila e o do material que se transporta
Exemplos e Contra-Exemplos
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 1 Prof. Bruno Holanda Aula 7 Exemplos e Contra-Exemplos Você que já tentou resolver alguns problemas de provas anteriores de Olimpíada de Matemática
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 1 Prof. Bruno Holanda Aula 7 Exemplos e Contra-Exemplos Você que já tentou resolver alguns problemas de provas anteriores de Olimpíada de Matemática
Colégio Santa Dorotéia
 Colégio Santa Dorotéia Área de Disciplina: Série: ª - Ensino Médio Professor: Elias Atividades para Estudos Autônomos Data: 8 / 3 / 016 QUESTÃO 1 (UEMG) O desenho ao lado representa uma caixa de madeira
Colégio Santa Dorotéia Área de Disciplina: Série: ª - Ensino Médio Professor: Elias Atividades para Estudos Autônomos Data: 8 / 3 / 016 QUESTÃO 1 (UEMG) O desenho ao lado representa uma caixa de madeira
MATEMÁTICA - 3o ciclo Teorema de Pitágoras (8 o ano) Propostas de resolução
 MTEMÁTI - 3o ciclo Teorema de Pitágoras (8 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. omo a base do prisma é um quadrado, os lados adjacentes são perpendiculares,
MTEMÁTI - 3o ciclo Teorema de Pitágoras (8 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. omo a base do prisma é um quadrado, os lados adjacentes são perpendiculares,
Número de ocorrências. a O 2. Determina a ordenada do ponto do gráfico que tem abcissa 6.
 _Prova PROV FINL MODELO É permitido o uso da calculadora Um dos trabalhos realizados pelo João para a disciplina de Matemática consistiu no registo das pontuações obtidas em dezoito lançamentos de um dado
_Prova PROV FINL MODELO É permitido o uso da calculadora Um dos trabalhos realizados pelo João para a disciplina de Matemática consistiu no registo das pontuações obtidas em dezoito lançamentos de um dado
1. Onze cubinhos, todos de mesma aresta, foram colados conforme a figura a seguir.
 XXV OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível a. Fase Olimpíada Regional AL BA GO PA PB PI RS RN SC - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas
XXV OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível a. Fase Olimpíada Regional AL BA GO PA PB PI RS RN SC - A duração da prova é de 3 horas. - Não é permitido o uso de calculadoras nem consultas
Prova final de MATEMÁTICA - 3o ciclo a Chamada
 Prova final de MATEMÁTICA - o ciclo 011 - a Chamada Proposta de resolução 1. 1.1. A função de proporcionalidade direta é a representada por parte de uma reta que contém a origem. Como a reta que contém
Prova final de MATEMÁTICA - o ciclo 011 - a Chamada Proposta de resolução 1. 1.1. A função de proporcionalidade direta é a representada por parte de uma reta que contém a origem. Como a reta que contém
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 06 - a Fase Proposta de resolução GRUPO I. Como P A B ) P A B ) P A B), temos que: P A B ) 0,6 P A B) 0,6 P A B) 0,6 P A B) 0,4 Como P A B) P A) + P B) P A B) P A
Prova Escrita de MATEMÁTICA A - o Ano 06 - a Fase Proposta de resolução GRUPO I. Como P A B ) P A B ) P A B), temos que: P A B ) 0,6 P A B) 0,6 P A B) 0,6 P A B) 0,4 Como P A B) P A) + P B) P A B) P A
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 99 / 00 PROVA DE CIÊNCIAS EXATAS DA. 1 a é equivalente a a
 13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
Paralelismo. MA13 - Unidade 3. Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria.
 Paralelismo M13 - Unidade 3 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Nomes tradicionais reta t corta as retas r e s. Dizemos que a reta t é uma
Paralelismo M13 - Unidade 3 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Nomes tradicionais reta t corta as retas r e s. Dizemos que a reta t é uma
Treino Matemático. 1. Em qual das figuras podes observar um polígono inscrito numa circunferência? (A) (B) (C) (D)
 Treino Matemático ssunto: ircunferência e círculo. 6º ano Ficha de trabalho 1. Em qual das figuras podes observar um polígono inscrito numa circunferência? () () () (). Na figura sabe-se a reta é tangente
Treino Matemático ssunto: ircunferência e círculo. 6º ano Ficha de trabalho 1. Em qual das figuras podes observar um polígono inscrito numa circunferência? () () () (). Na figura sabe-se a reta é tangente
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2017.1 Gabarito Questão 01 [ 1,25 ] Determine as equações das duas retas tangentes à parábola de equação y = x 2 2x + 4 que passam pelo ponto (2,
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2017.1 Gabarito Questão 01 [ 1,25 ] Determine as equações das duas retas tangentes à parábola de equação y = x 2 2x + 4 que passam pelo ponto (2,
Colégio MATEMÁTICA DESAFIO. QUESTÃO 16 No quadro abaixo, as estrelinhas substituem números reais.
 Nome: N.º: Endereço: Data: Telefone: E-mail: Colégio PARA QUEM CURSA O 6 Ọ ANO DO ENSINO FUNDAMENTAL EM 017 Disciplina: MATEMÁTICA Prova: DESAFIO NOTA: QUESTÃO 16 No quadro abaixo, as estrelinhas substituem
Nome: N.º: Endereço: Data: Telefone: E-mail: Colégio PARA QUEM CURSA O 6 Ọ ANO DO ENSINO FUNDAMENTAL EM 017 Disciplina: MATEMÁTICA Prova: DESAFIO NOTA: QUESTÃO 16 No quadro abaixo, as estrelinhas substituem
