SOBRE EQUAÇÕES DIFERENCIAIS
|
|
|
- Evelyn Nobre Neiva
- 8 Há anos
- Visualizações:
Transcrição
1 SOBRE EQUAÇÕES DIFERENCIAIS
2 PROBLEMA: É um fato da física que os elementos radioativos se desintegram espontaneamente em um processo chamado decaimento radioativo. Os experimentos têm mostrado que a taxa de desintegração é proporcional à quantidade de elemento presente. Sabe-se que a meia-vida específica do carbono-14 radioativo está em torno de 5730 anos. Em 1988, o Vaticano autorizou o Museu Britânico a datar a relíquia de pano conhecida como o Sudário de Turim, possivelmente o sudário de Jesus de Nazaré. Este pano, que apareceu em 1356, contém o negativo da imagem de um corpo humano que se acreditava no mundo inteiro ser o de Jesus. O relatório do Museu mostrou que as fibras no pano continham entre 92 e 93% do carbono- 14 original. Use esta informação para estimar a idade do sudário.
3 PROBLEMA: Um indivíduo é encontrado morto em seu escritório pela secretária que liga imediatamente para a polícia. Quando a polícia chega, 2 horas depois da chamada, examina o cadáver e o ambiente tirando os seguintes dados: A temperatura do escritório era de 20 o C, o cadáver inicialmente tinha uma temperatura de 35 o C. Uma hora depois medindo novamente a temperatura do corpo obteve 34.2 o C. O investigador, supondo que a temperatura de uma pessoa viva é de 36.5 o C, prende a secretária. Por quê? No dia seguinte, o advogado da secretária a liberta, alegando o quê?
4 EQUAÇÃO DIFERENCIAL Equação que envolve as derivadas (diferenciais) de uma função
5
6 EQUAÇÃO DIFERENCIAL Equação que envolve as derivadas (diferenciais) de uma função
7 Classificação: Se uma equação contiver apenas derivadas ordinárias de uma função (função de uma variável), ela será chamada de equação diferencial ordinária (EDO).
8 Classificação: Uma equação que envolve derivadas parciais (derivadas de funções de várias variáveis) será chamada de equação diferencial parcial (EDP).
9 Ordem
10 Grau
11 Solução de uma equação diferencial Resolver uma equação diferencial significa encontrar todas as funções que introduzidas juntamente com suas derivadas na equação dada, a verificam identicamente para todo valor da variável independente x, pelo menos num certo intervalo aberto I. Tais funções são chamadas soluções primitivas da equação diferencial dada. Exemplo: Verifique se a função indicada é uma solução da equação diferencial dada:
12 EQUAÇÕES DIFERENCIAIS COMO MODELOS MATEMÁTICOS É comum desejarmos descrever o comportamento de algum sistema ou fenômeno da vida real em termos matemáticos, quer sejam eles físicos, sociológicos ou mesmo econômicos. A descrição matemática de um sistema ou fenômeno é chamado modelagem matemática. A construção de um modelo matemático de um sistema começa com a identificação das variáveis responsáveis pela variação do sistema. A seguir, elaboramos um conjunto de hipóteses ou pressuposições sobre o sistema. Essas hipóteses deverão incluir também leis empíricas que podem ser obtidas experimentalmente. Como as hipóteses sobre um sistema envolvem, na maioria das vezes, taxa de variação de uma ou mais variáveis, a descrição matemática de todas essas hipóteses pode ser uma ou mais equações envolvendo derivadas. Assim, o modelo matemático pode ser uma equação diferencial ou um sistema formado por equações diferenciais. As etapas de um processo de modelagem podem ser dispostas conforme o diagrama a seguir:
13 Um modelo matemático de um sistema físico, na maioria das vezes, envolve a variável tempo. Uma solução do modelo oferece então o estado do sistema, ou seja, o sistema pode ser descrito no passado, presente e futuro.
14 Referências: Notas de aula - Professor: Altemir José Borges, UTFPR, departamento de Matemática, agosto de Equações Diferenciais com Aplicações em Modelagem Dennis G. Zill Ed. Thomson
SOBRE A DATAÇÃO POR DECAIMENTO RADIOATIVO
 33 SOBRE A DATAÇÃO POR DECAIMENTO RADIOATIVO Resumo Wendel Botelho Alves Este artigo apresenta a aplicabilidade das Equações Diferenciais no processo de datação por Decaimento Radioativo. Tomaremos como
33 SOBRE A DATAÇÃO POR DECAIMENTO RADIOATIVO Resumo Wendel Botelho Alves Este artigo apresenta a aplicabilidade das Equações Diferenciais no processo de datação por Decaimento Radioativo. Tomaremos como
Cálculo Diferencial e Integral C. Me. Aline Brum Seibel
 Cálculo Diferencial e Integral C Me. Aline Brum Seibel Em ciências, engenharia, economia e até mesmo em psicologia, frequentemente desejamos descrever ou modelar o comportamento de algum sistema ou fenômeno
Cálculo Diferencial e Integral C Me. Aline Brum Seibel Em ciências, engenharia, economia e até mesmo em psicologia, frequentemente desejamos descrever ou modelar o comportamento de algum sistema ou fenômeno
Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais)
 Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais) Vejamos o seguinte exemplo retirado do livro de Kaplan e Glass (veja a bibliografia
Exemplos de Aplicações das Funções Exponencial e Logarítmica em Biologia (com uma introdução às equações diferenciais) Vejamos o seguinte exemplo retirado do livro de Kaplan e Glass (veja a bibliografia
APLICAÇÃO DA LEI DO RESRIAMENTO DE NEWTON EM BLOCOS CERÂMICOS: MODELAGEM, RESOLUÇÃO ANALÍTICA E COMPARAÇÃO PRÁTICA DOS RESULTADOS RESUMO
 APLICAÇÃO DA LEI DO RESRIAMENTO DE NEWTON EM BLOCOS CERÂMICOS: MODELAGEM, RESOLUÇÃO ANALÍTICA E COMPARAÇÃO PRÁTICA DOS RESULTADOS Pedro Bonfim Segobia Universidade Tecnológica Federal do Paraná - UTFPR
APLICAÇÃO DA LEI DO RESRIAMENTO DE NEWTON EM BLOCOS CERÂMICOS: MODELAGEM, RESOLUÇÃO ANALÍTICA E COMPARAÇÃO PRÁTICA DOS RESULTADOS Pedro Bonfim Segobia Universidade Tecnológica Federal do Paraná - UTFPR
Aula: Equações diferenciais lineares de ordem superior
 Aula: Equações diferenciais lineares de ordem superior Profa. Ariane Piovezan Entringer DMA - UFV Problema de Valor Inicial - EDO de ordem n Problema de Valor Inicial - EDO de ordem n a n (x) d n y dx
Aula: Equações diferenciais lineares de ordem superior Profa. Ariane Piovezan Entringer DMA - UFV Problema de Valor Inicial - EDO de ordem n Problema de Valor Inicial - EDO de ordem n a n (x) d n y dx
Na Física (em módulo) é uma Lei
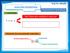 1 a interpretação Interpretações matemáticas Na Física (em módulo) é uma Lei Elementos de uma expressão matemática Variável dependente Coeficiente Variável independente 2 a interpretação Interpretações
1 a interpretação Interpretações matemáticas Na Física (em módulo) é uma Lei Elementos de uma expressão matemática Variável dependente Coeficiente Variável independente 2 a interpretação Interpretações
Equações Diferenciais
 IFBA Equações Diferenciais Versão 1 Allan de Sousa Soares Graduação: Licenciatura em Matemática - UESB Especilização: Matemática Pura - UESB Mestrado: Matemática Pura - UFMG Vitória da Conquista - BA 2013
IFBA Equações Diferenciais Versão 1 Allan de Sousa Soares Graduação: Licenciatura em Matemática - UESB Especilização: Matemática Pura - UESB Mestrado: Matemática Pura - UFMG Vitória da Conquista - BA 2013
O CRESCIMENTO POPULACIONAL DO MUNICÍPIO DE ERECHIM REPRESENTADO ATRAVÉS DE MODELAGEM MATEMÁTICA
 O CRESCIMENTO POPULACIONAL DO MUNICÍPIO DE ERECHIM REPRESENTADO ATRAVÉS DE MODELAGEM MATEMÁTICA Nelize Fracaro 1, Dionatan Breskovit de Matos 2, Eduardo Post 3, Manuel Martín Pérez Reimbold 4 1 UNIJUÍ/DECEEng/Mestrado
O CRESCIMENTO POPULACIONAL DO MUNICÍPIO DE ERECHIM REPRESENTADO ATRAVÉS DE MODELAGEM MATEMÁTICA Nelize Fracaro 1, Dionatan Breskovit de Matos 2, Eduardo Post 3, Manuel Martín Pérez Reimbold 4 1 UNIJUÍ/DECEEng/Mestrado
Resoluções de Equações Diferenciais Ordinárias (EDOs) por Séries de Potências
 Resoluções de Equações Diferenciais Ordinárias (EDOs) por Séries de Potências Hudson Umbelino dos Anjos 1, Julia de Paula Borges 2 1 Mestre em Matemática IFTO. e-mail: [email protected] 2 Graduanda
Resoluções de Equações Diferenciais Ordinárias (EDOs) por Séries de Potências Hudson Umbelino dos Anjos 1, Julia de Paula Borges 2 1 Mestre em Matemática IFTO. e-mail: [email protected] 2 Graduanda
Equações Diferenciais: Modelagem de problemas. Palavras chave: aplicações, equações diferenciais de primeira ordem, variáveis separáveis.
 Equações Diferenciais: Modelagem de problemas Cleber de Oliveira dos Santos 1 Faculdade capivari - FUCAP, Capivari de Baixo, SC [email protected] Resumo: Este artigo apresenta algumas modelagens matemática
Equações Diferenciais: Modelagem de problemas Cleber de Oliveira dos Santos 1 Faculdade capivari - FUCAP, Capivari de Baixo, SC [email protected] Resumo: Este artigo apresenta algumas modelagens matemática
UNIVERSIDADE CATÓLICA DE GOIÀS Pro- Reitoria de Graduação PLANO DE ENSINO
 UNIVERSIDADE CATÓLICA DE GOIÀS Pro- Reitoria de Graduação PLANO DE ENSINO DISCIPLINA Equações Diferenciais CÓDIGO MAF-2010-C01 PROFESSOR CRISTIAN PATRICIO NOVOA BUSTOS CURSO Engenharia PERÍODO CRÉDITO
UNIVERSIDADE CATÓLICA DE GOIÀS Pro- Reitoria de Graduação PLANO DE ENSINO DISCIPLINA Equações Diferenciais CÓDIGO MAF-2010-C01 PROFESSOR CRISTIAN PATRICIO NOVOA BUSTOS CURSO Engenharia PERÍODO CRÉDITO
CÁLCULO I. 1 Crescimento e Decaimento Exponencial
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 27: Aplicações da Derivada: Decaimento Radioativo, Crescimento Populacional e Lei de Resfriamento de Newton Objetivos da Aula Aplicar derivada
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 27: Aplicações da Derivada: Decaimento Radioativo, Crescimento Populacional e Lei de Resfriamento de Newton Objetivos da Aula Aplicar derivada
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
Guia de Atividades para Introduzir Equações Diferenciais Ordinárias usando o Software Powersim
 Guia de Atividades para Introduzir Equações Diferenciais Ordinárias usando o Software Powersim Nestas atividades temos como objetivo abordar a definição, solução e notação de uma equação diferencial e,
Guia de Atividades para Introduzir Equações Diferenciais Ordinárias usando o Software Powersim Nestas atividades temos como objetivo abordar a definição, solução e notação de uma equação diferencial e,
Química Geral e Experimental II: Cinética Química. Prof. Fabrício Ronil Sensato
 Química Geral e Experimental II: Cinética Química Prof. Fabrício Ronil Sensato Resolução comentada de exercícios selecionados. Versão v2_2005 2 1) Para a reação em fase gasosa N 2 + 3H 2 2NH 3, 2) A decomposição,
Química Geral e Experimental II: Cinética Química Prof. Fabrício Ronil Sensato Resolução comentada de exercícios selecionados. Versão v2_2005 2 1) Para a reação em fase gasosa N 2 + 3H 2 2NH 3, 2) A decomposição,
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
FÍSICA MÉDICA. Aula 04 Desintegração Nuclear. Prof. Me. Wangner Barbosa da Costa
 FÍSICA MÉDICA Aula 04 Desintegração Nuclear Prof. Me. Wangner Barbosa da Costa Desintegração Nuclear Núcleos prótons e nêutrons. Elemento com diferentes nº de nêutrons são chamados de isótopos. Núcleos
FÍSICA MÉDICA Aula 04 Desintegração Nuclear Prof. Me. Wangner Barbosa da Costa Desintegração Nuclear Núcleos prótons e nêutrons. Elemento com diferentes nº de nêutrons são chamados de isótopos. Núcleos
MAT Aula 14/ 30/04/2014. Sylvain Bonnot (IME-USP)
 MAT 0143 Aula 14/ 30/04/2014 Sylvain Bonnot (IME-USP) 2014 1 Resumo: 1 Site: http://www.ime.usp.br/~sylvain/courses.html 2 Derivada de sen, cos 3 Regra da cadeia 4 Funções inversas 5 Derivada da função
MAT 0143 Aula 14/ 30/04/2014 Sylvain Bonnot (IME-USP) 2014 1 Resumo: 1 Site: http://www.ime.usp.br/~sylvain/courses.html 2 Derivada de sen, cos 3 Regra da cadeia 4 Funções inversas 5 Derivada da função
EQUAÇÕES DIFERENCIAIS: UMA ABORDAGEM PARA GRADUAÇÃO
 EQUAÇÕES DIFERENCIAIS: UMA ABORDAGEM PARA GRADUAÇÃO Marcelo F. de Oliveira 1 ; Licéia A. Pires 1 Universidade Federal do Paraná Faculdade Educacional Araucária RESUMO A análise do comportamento de um fenômeno
EQUAÇÕES DIFERENCIAIS: UMA ABORDAGEM PARA GRADUAÇÃO Marcelo F. de Oliveira 1 ; Licéia A. Pires 1 Universidade Federal do Paraná Faculdade Educacional Araucária RESUMO A análise do comportamento de um fenômeno
Equações Lineares de 1 a Ordem - Aplicações
 Equações Lineares de 1 a Ordem - Aplicações Maria João Resende www.professores.uff.br/mjoao 2016-2 M. J. Resende (UFF) www.professores.uff.br/mjoao 2016-2 1 / 14 Modelos Matemáticos Chamamos de modelo
Equações Lineares de 1 a Ordem - Aplicações Maria João Resende www.professores.uff.br/mjoao 2016-2 M. J. Resende (UFF) www.professores.uff.br/mjoao 2016-2 1 / 14 Modelos Matemáticos Chamamos de modelo
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano [email protected] Aula 22 07/2014 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano [email protected] Aula 22 07/2014 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando
4 UNIJUÍ/DECEEng/Mestrado em Modelagem Matemática Campus Ijuí,
 MODELAGEM MATEMÁTICA DA CONSERVAÇÃO DE TEMPERATURAS DE LÍQUIDOS EM UMA GARRAFA TÉRMICA COM AMPOLA DE VIDRO: UMA APLICAÇÃO DA LEI DE RESFRIAMENTO DE NEWTON Dionatan Breskovit de Matos 1, Eduardo Post 2,
MODELAGEM MATEMÁTICA DA CONSERVAÇÃO DE TEMPERATURAS DE LÍQUIDOS EM UMA GARRAFA TÉRMICA COM AMPOLA DE VIDRO: UMA APLICAÇÃO DA LEI DE RESFRIAMENTO DE NEWTON Dionatan Breskovit de Matos 1, Eduardo Post 2,
Guia de Atividades usando o método de Euler para encontrar a solução de uma Equação Diferencial Ordinária
 Guia de Atividades usando o método de Euler para encontrar a solução de uma Equação Diferencial Ordinária Para algumas situações-problema, cuja formulação matemática envolve equações diferenciais, é possível
Guia de Atividades usando o método de Euler para encontrar a solução de uma Equação Diferencial Ordinária Para algumas situações-problema, cuja formulação matemática envolve equações diferenciais, é possível
Matemática Aplicada à Economia II Lista 1 Equações Diferenciais Ordinárias
 Matemática Aplicada à Economia II Lista 1 Equações Diferenciais Ordinárias 1) Encontre: g) h) 2) Calcule as seguintes integrais definidas: 3) Diz-se que a integral definida representa uma área sob uma
Matemática Aplicada à Economia II Lista 1 Equações Diferenciais Ordinárias 1) Encontre: g) h) 2) Calcule as seguintes integrais definidas: 3) Diz-se que a integral definida representa uma área sob uma
Aplicação dos Métodos de Runge-Kutta de primeira, segunda, terceira e quarta ordem na Resolução de uma Equação Diferencial Ordinária.
 1 Aplicação dos Métodos de Runge-Kutta de primeira, segunda, terceira e quarta ordem na Resolução de uma Equação Diferencial Ordinária. Rodrigo Romais (FCSGN) 1 [email protected] Resumo: Métodos numéricos
1 Aplicação dos Métodos de Runge-Kutta de primeira, segunda, terceira e quarta ordem na Resolução de uma Equação Diferencial Ordinária. Rodrigo Romais (FCSGN) 1 [email protected] Resumo: Métodos numéricos
AULA 7- FUNÇÕES EXPONENCIAIS E LOGARÍTMICAS VERSÃO 1 - MAIO DE 2018
 CURSO DE BIOMEDICINA CENTRO DE CIÊNCIAS DA SAÚDE UNIVERSIDADE CATÓLICA DE PETRÓPOLIS MATEMÁTICA AULA 7- FUNÇÕES EXPONENCIAIS E LOGARÍTMICAS VERSÃO 1 - MAIO DE 2018 Professor: Luís Rodrigo E-mail: [email protected]
CURSO DE BIOMEDICINA CENTRO DE CIÊNCIAS DA SAÚDE UNIVERSIDADE CATÓLICA DE PETRÓPOLIS MATEMÁTICA AULA 7- FUNÇÕES EXPONENCIAIS E LOGARÍTMICAS VERSÃO 1 - MAIO DE 2018 Professor: Luís Rodrigo E-mail: [email protected]
MAT Cálculo Diferencial e Integral I Bacharelado em Matemática
 MAT- - Cálculo Diferencial e Integral I Bacharelado em Matemática - 200 a Lista de eercícios I. Limite de funções. Calcule os seguintes ites, caso eistam: 2 3 + 9 2 + 2 + 4 2 + 6 5 ) 2 3 2 2 2) + 4 + 8
MAT- - Cálculo Diferencial e Integral I Bacharelado em Matemática - 200 a Lista de eercícios I. Limite de funções. Calcule os seguintes ites, caso eistam: 2 3 + 9 2 + 2 + 4 2 + 6 5 ) 2 3 2 2 2) + 4 + 8
Equações Ordinarias 1ªOrdem - Lineares
 Nome: Nº Curso: Licenciatura em Matemática Disciplina: Equações Diferenciais Ordinárias 7ºPeríodo Prof. Leonardo Data: / /2018 Equações Ordinarias 1ªOrdem - Lineares 1. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
Nome: Nº Curso: Licenciatura em Matemática Disciplina: Equações Diferenciais Ordinárias 7ºPeríodo Prof. Leonardo Data: / /2018 Equações Ordinarias 1ªOrdem - Lineares 1. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
Aços Alta Liga Resistentes a Corrosão IV
 Aços Alta Liga Resistentes a Corrosão IV Muitos casos são importantes para estimar ou mesmo para calcular a composição química do metal de solda antecipadamente. Se o metal de base e o metal de enchimento
Aços Alta Liga Resistentes a Corrosão IV Muitos casos são importantes para estimar ou mesmo para calcular a composição química do metal de solda antecipadamente. Se o metal de base e o metal de enchimento
Exercícios Complementares 5.2
 Exercícios Complementares 5.2 5.2A Veri que se a função dada é ou não solução da EDO indicada: (a) y = 2e x + xe x ; y 00 + 2y 0 + y = 0: (b) x = C 1 e 2t + C 2 e 3t ; :: x 10 : x + 6x = 0: (c) y = ln
Exercícios Complementares 5.2 5.2A Veri que se a função dada é ou não solução da EDO indicada: (a) y = 2e x + xe x ; y 00 + 2y 0 + y = 0: (b) x = C 1 e 2t + C 2 e 3t ; :: x 10 : x + 6x = 0: (c) y = ln
Introdução aos Métodos Numéricos
 Introdução aos Métodos Numéricos Instituto de Computação UFF Departamento de Ciência da Computação Otton Teixeira da Silveira Filho Conteúdo específico Introdução à Resolução de Equações Diferenciais Ordinárias
Introdução aos Métodos Numéricos Instituto de Computação UFF Departamento de Ciência da Computação Otton Teixeira da Silveira Filho Conteúdo específico Introdução à Resolução de Equações Diferenciais Ordinárias
Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas. Cálculo Combinatório: Introdução ao cálculo combinatório
 DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (12º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (13 de setembro a 15 de dezembro) Cálculo Combinatório: Introdução ao cálculo combinatório
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (12º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (13 de setembro a 15 de dezembro) Cálculo Combinatório: Introdução ao cálculo combinatório
MODELAGEM MATEMÁTICA COMO ESTRATÉGIA PARA O ENSINO DE EDO: UM EXPERIMENTO COM AMPULHETA
 1 MODELAGEM MATEMÁTICA COMO ESTRATÉGIA PARA O ENSINO DE EDO: UM EXPERIMENTO COM AMPULHETA Ives Lima Pereira 1 ; José Arteiro Claudino Chaves 2 ; Neurivan Humberto Cardoso de Castro 3 ; Roberto Arruda Lima
1 MODELAGEM MATEMÁTICA COMO ESTRATÉGIA PARA O ENSINO DE EDO: UM EXPERIMENTO COM AMPULHETA Ives Lima Pereira 1 ; José Arteiro Claudino Chaves 2 ; Neurivan Humberto Cardoso de Castro 3 ; Roberto Arruda Lima
O termo modelo é utilizado freqüentemente como sinônimo de edo quando referida a aplicações. A seguir, apresentaremos alguns modelos:
 Capítulo 2 Modelos O termo modelo é utilizado freqüentemente como sinônimo de edo quando referida a aplicações. A seguir, apresentaremos alguns modelos: 2.1 Molas Considere uma mola, de massa desprezível,
Capítulo 2 Modelos O termo modelo é utilizado freqüentemente como sinônimo de edo quando referida a aplicações. A seguir, apresentaremos alguns modelos: 2.1 Molas Considere uma mola, de massa desprezível,
Aplicação dos Métodos de Euler e de Euler Melhorado na Resolução de uma Equação Diferencial Ordinária.
 Aplicação dos Métodos de Euler e de Euler Melhorado na Resolução de uma Equação Diferencial Ordinária. Rodrigo Romais (FCSGN) * [email protected] Resumo: Métodos numéricos são extremamente úteis na resolução
Aplicação dos Métodos de Euler e de Euler Melhorado na Resolução de uma Equação Diferencial Ordinária. Rodrigo Romais (FCSGN) * [email protected] Resumo: Métodos numéricos são extremamente úteis na resolução
Lista 2 Funções: Definição e exemplos
 Lista Funções: Definição e exemplos. Seja f : R R definida por f(x) = x 3. Qual é o elemento do dominio que 5 tem 3 como imagem? 4. É dada uma função real tal que: (a) f(x) f(y) = f(x + y) (b) f() = (c)
Lista Funções: Definição e exemplos. Seja f : R R definida por f(x) = x 3. Qual é o elemento do dominio que 5 tem 3 como imagem? 4. É dada uma função real tal que: (a) f(x) f(y) = f(x + y) (b) f() = (c)
Exercícios Matemática I (M193)
 Exercícios Matemática I (M93) Funções. Associe a cada uma das seguintes funções o gráfico que a representa. a) f(x) = 2x + 4. b) f(x) = 3x +. c) f(x) = x 2. d) f(x) = 2x 3. e) f(x) = 0 x. f) f(x) = (0,
Exercícios Matemática I (M93) Funções. Associe a cada uma das seguintes funções o gráfico que a representa. a) f(x) = 2x + 4. b) f(x) = 3x +. c) f(x) = x 2. d) f(x) = 2x 3. e) f(x) = 0 x. f) f(x) = (0,
ELEMENTOS DE EQUAÇÕES DIFERENCIAIS
 ELEMENTOS DE EQUAÇÕES DIFERENCIAIS AULA 05: MODELAGEM E PROBLEMAS DIVERSOS TÓPICO 01: MODELAGEM No tópico 03 da aula 01 vimos alguns exemplos de equações diferenciais que serviam de modelo matemático para
ELEMENTOS DE EQUAÇÕES DIFERENCIAIS AULA 05: MODELAGEM E PROBLEMAS DIVERSOS TÓPICO 01: MODELAGEM No tópico 03 da aula 01 vimos alguns exemplos de equações diferenciais que serviam de modelo matemático para
Experiência VI (aula 10) Resfriamento de um líquido
 Experiência VI (aula 10) Resfriamento de um líquido 1. Objetivos 2. Introdução 3. Arranjo e procedimento experimental 4. Análise de dados 5. Referências 1. Objetivos A partir de um arranjo experimental
Experiência VI (aula 10) Resfriamento de um líquido 1. Objetivos 2. Introdução 3. Arranjo e procedimento experimental 4. Análise de dados 5. Referências 1. Objetivos A partir de um arranjo experimental
MAT EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17
 MAT 340 - EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17 Bulmer Mejía García 2010-II Universidade Federal de Viçosa EDO de Cauchy-Euler É uma EDO da seguinte forma a n (ax+b) n y (n) (x)+a n 1 (ax+b) n
MAT 340 - EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Aulas 14-17 Bulmer Mejía García 2010-II Universidade Federal de Viçosa EDO de Cauchy-Euler É uma EDO da seguinte forma a n (ax+b) n y (n) (x)+a n 1 (ax+b) n
Potenciação Equação Exponencial Função Exponencial. Prof.: Joni Fusinato 1
 Potenciação Equação Exponencial Função Exponencial Prof.: Joni Fusinato [email protected] [email protected] 1 Potenciação ou Exponenciação Operação usada para simplificar a multiplicação de números
Potenciação Equação Exponencial Função Exponencial Prof.: Joni Fusinato [email protected] [email protected] 1 Potenciação ou Exponenciação Operação usada para simplificar a multiplicação de números
étodos uméricos AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA
étodos uméricos AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA
Introdução à Matemática Discreta
 Introdução à Matemática Discreta Matemática Discreta Prof. Vilson Heck Junior [email protected] Condução da disciplina Aulas: Quartas: 10:10 12:00 Sextas: 08:00 09:50 Haverá troca de professores:
Introdução à Matemática Discreta Matemática Discreta Prof. Vilson Heck Junior [email protected] Condução da disciplina Aulas: Quartas: 10:10 12:00 Sextas: 08:00 09:50 Haverá troca de professores:
LISTA dy dx y x + y3 cos x = y = ky ay 3. dizemos que F (x, y) é homogênea de grau 0. Neste caso a equação diferencial y =
 MAT 01167 LISTA Equações Diferenciais Resolva: 1. y = y x + x y, y ( ) 1 8 =. (1 x ) dy dx (1 + x) y = y. dy dx y x + y cos x = 0 4. y = ky ay. Se uma função F (x, y) satisfaz a condição F (t x, t y) =
MAT 01167 LISTA Equações Diferenciais Resolva: 1. y = y x + x y, y ( ) 1 8 =. (1 x ) dy dx (1 + x) y = y. dy dx y x + y cos x = 0 4. y = ky ay. Se uma função F (x, y) satisfaz a condição F (t x, t y) =
Disciplina: Sistemas Térmicos
 Disciplina: Sistemas Térmicos Definição de Substância Pura Equilíbrio de Fases Líquido-Vapor de uma Substância Pura Diagrama de Temperatura versus Volume Específico Título de uma Substância com Fases Líquida
Disciplina: Sistemas Térmicos Definição de Substância Pura Equilíbrio de Fases Líquido-Vapor de uma Substância Pura Diagrama de Temperatura versus Volume Específico Título de uma Substância com Fases Líquida
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 16 PROCESSOS E REAÇÕES NUCLEARES Edição Agosto de 2007 CAPÍTULO 08 PROCESSOS E REAÇÕES NUCLEARES ÍNDICE 16.1- Introdução 16.2- Radioatividade
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 16 PROCESSOS E REAÇÕES NUCLEARES Edição Agosto de 2007 CAPÍTULO 08 PROCESSOS E REAÇÕES NUCLEARES ÍNDICE 16.1- Introdução 16.2- Radioatividade
1 A Equação Fundamental Áreas Primeiras definições Uma questão importante... 7
 Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
O USO DE EQUAÇÕES DIFERENCIAIS NO CRESCIMENTO DE BACTÉRIAS
 O USO DE EQUAÇÕES DIFERENCIAIS NO CRESCIMENTO DE BACTÉRIAS E. CIMADON 1 ;L. TRES ;M. P. PERGHER ;P. P. RUSEZYT 4 ; S. D. STROSCHEIN 5 Resumo: Este artigo tem por objetivo apresentar um problema com o intuito
O USO DE EQUAÇÕES DIFERENCIAIS NO CRESCIMENTO DE BACTÉRIAS E. CIMADON 1 ;L. TRES ;M. P. PERGHER ;P. P. RUSEZYT 4 ; S. D. STROSCHEIN 5 Resumo: Este artigo tem por objetivo apresentar um problema com o intuito
Lista de Exercícios 2 Cálculo Numérico - Professor Daniel
 Lista de Exercícios 2 Cálculo Numérico - Professor Daniel Observação: Esta lista abrange integração numérica e resolução numérica de EDO s. Em outras palavras, ela abrange toda a matéria da terceira prova.
Lista de Exercícios 2 Cálculo Numérico - Professor Daniel Observação: Esta lista abrange integração numérica e resolução numérica de EDO s. Em outras palavras, ela abrange toda a matéria da terceira prova.
Sessão 1: Generalidades
 Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
CURSO DE CIÊNCIAS CONTÁBEIS Autorizado pela Portaria no de 04/07/01 DOU de 09/07/01 Componente Curricular: MATEMÁTICA PLANO DE CURSO
 CURSO DE CIÊNCIAS CONTÁBEIS Autorizado pela Portaria no 1.393 de 04/07/01 DOU de 09/07/01 Componente Curricular: MATEMÁTICA Código: CTB - 120 Pré-requisito: ---------- Período Letivo: 2016.1 Professor:
CURSO DE CIÊNCIAS CONTÁBEIS Autorizado pela Portaria no 1.393 de 04/07/01 DOU de 09/07/01 Componente Curricular: MATEMÁTICA Código: CTB - 120 Pré-requisito: ---------- Período Letivo: 2016.1 Professor:
7- Equações Diferenciais Ordinárias de 1 a Ordem Redutíveis
 7- Equações Diferenciais Ordinárias de 1 a Ordem Redutíveis 7.1-Equação de Bernoulli A equação de Bernoulli é uma equação diferencial de primeira ordem do tipo: onde é uma constante sendo e e e quaisquer
7- Equações Diferenciais Ordinárias de 1 a Ordem Redutíveis 7.1-Equação de Bernoulli A equação de Bernoulli é uma equação diferencial de primeira ordem do tipo: onde é uma constante sendo e e e quaisquer
MÉTODOS MATEMÁTICOS. Prof. Dr. Paulo H. D. Santos.
 MÉTODOS MATEMÁTICOS Prof. Dr. Paulo H. D. Santos [email protected] AULA 1 10/03/2015 Apresentação do Plano de Ensino; EDOs de 1ª Ordem Parte 1. Sumário Conteúdo Programático Metodologia Avaliação Critério
MÉTODOS MATEMÁTICOS Prof. Dr. Paulo H. D. Santos [email protected] AULA 1 10/03/2015 Apresentação do Plano de Ensino; EDOs de 1ª Ordem Parte 1. Sumário Conteúdo Programático Metodologia Avaliação Critério
Séries e Equações Diferenciais Lista 04 EDO s de Primeira Ordem e Aplicações
 Séries e Equações Diferenciais Lista 04 EDO s de Primeira Ordem e Aplicações Professor: Daniel Henrique Silva Introdução às Equações Diferenciais 1) Defina equação diferencial. 2) Seja f(x; y) uma função
Séries e Equações Diferenciais Lista 04 EDO s de Primeira Ordem e Aplicações Professor: Daniel Henrique Silva Introdução às Equações Diferenciais 1) Defina equação diferencial. 2) Seja f(x; y) uma função
Cinética Química. c) A opção (C) está correta. B 3+ e B 4+ não aparecem na reação global, portanto, são intermediários da reação.
 Capítulo 6 Cinética Química 1. (ITA) Considere o seguinte mecanismo de reação genérica: A 4+ + B 2+ A 3+ + B 3+ (etapa lenta) A 4+ + B 3+ A 3+ + B 4+ (etapa rápida) C + + B 4+ C 3+ + B 2+ (etapa rápida)
Capítulo 6 Cinética Química 1. (ITA) Considere o seguinte mecanismo de reação genérica: A 4+ + B 2+ A 3+ + B 3+ (etapa lenta) A 4+ + B 3+ A 3+ + B 4+ (etapa rápida) C + + B 4+ C 3+ + B 2+ (etapa rápida)
MAT 1351 : Cálculo para Funções de Uma Variável Real I. Sylvain Bonnot (IME-USP)
 MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Aplicação das derivadas: Equações diferenciais Teorema As soluções da equação y = 0 num intervalo (a, b) são exatamente
MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Aplicação das derivadas: Equações diferenciais Teorema As soluções da equação y = 0 num intervalo (a, b) são exatamente
c c podem ser eliminados e os dois calores específicos
 ENERGIA INTERNA, ENTALPIA E CALORES ESPECÍFICOS DE SÓLIDOS E LÍQUIDOS Uma substância cujo volume específico (ou densidade) é constante é chamada de substância incompressível. Os volumes específicos de
ENERGIA INTERNA, ENTALPIA E CALORES ESPECÍFICOS DE SÓLIDOS E LÍQUIDOS Uma substância cujo volume específico (ou densidade) é constante é chamada de substância incompressível. Os volumes específicos de
Uma Equação Diferencial Ordinária (abrevia-se EDO) de primeira ordem se apresenta sob duas formas equivalentes: (i) FORMA NORMAL:
 5. EDO DE PRIMEIRA ORDEM SÉRIES & EDO - 2017.2 5.1. :::: :::::::::::::::::::::::::::: FUNDAMENTOS GERAIS Uma Equação Diferencial Ordinária (abrevia-se EDO) de primeira ordem se apresenta sob duas formas
5. EDO DE PRIMEIRA ORDEM SÉRIES & EDO - 2017.2 5.1. :::: :::::::::::::::::::::::::::: FUNDAMENTOS GERAIS Uma Equação Diferencial Ordinária (abrevia-se EDO) de primeira ordem se apresenta sob duas formas
FUNÇÕES EXPONENCIAIS Leia e descubra que eu não vim do além
 FUNÇÕES EXPONENCIAIS Leia e descubra que eu não vim do além Coordenação da Matemática 1 De potência em potência Os primeiros registros de cálculos utilizando potências são encontrados em tabelas babilônicas,
FUNÇÕES EXPONENCIAIS Leia e descubra que eu não vim do além Coordenação da Matemática 1 De potência em potência Os primeiros registros de cálculos utilizando potências são encontrados em tabelas babilônicas,
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano [email protected] Aula 6 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando métodos
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano [email protected] Aula 6 Resolução Numérica de Equações Diferenciais Ordinárias Objetivo: Resolver Equações Diferenciais Ordinárias utilizando métodos
Sistemas de Controle 1
 Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap3 Modelagem no Domínio do Tempo Prof. Dr. Marcos Lajovic Carneiro Sistemas de Controle 1 Prof. Dr. Marcos Lajovic
Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap3 Modelagem no Domínio do Tempo Prof. Dr. Marcos Lajovic Carneiro Sistemas de Controle 1 Prof. Dr. Marcos Lajovic
Equações Diferenciais Ordinárias
 Equações Diferenciais Ordinárias Prof. Guilherme Jahnecke Wemar AULA 03 Equações diferenciais de primeira ordem Equações separáveis Fonte: Material Daniela Buske, Boce, Bronson, Zill, diversos internet
Equações Diferenciais Ordinárias Prof. Guilherme Jahnecke Wemar AULA 03 Equações diferenciais de primeira ordem Equações separáveis Fonte: Material Daniela Buske, Boce, Bronson, Zill, diversos internet
MODELAGEM DE PROCESSOS INDUSTRIAIS II. Prof. Pierre Vilar Dantas Turma: 0072-A Horário: 3N ENCONTRO DE 29/05/2018
 MODELAGEM DE PROCESSOS INDUSTRIAIS II Prof. Pierre Vilar Dantas Turma: 0072-A Horário: 3N ENCONTRO DE 29/05/2018 1 Objetivos Considerar o artigo em anexo; Analisar os experimentos; Reproduzir os experimentos
MODELAGEM DE PROCESSOS INDUSTRIAIS II Prof. Pierre Vilar Dantas Turma: 0072-A Horário: 3N ENCONTRO DE 29/05/2018 1 Objetivos Considerar o artigo em anexo; Analisar os experimentos; Reproduzir os experimentos
Conceitos matemáticos:
 Conceitos matemáticos: Para entender as possíveis mudanças quantitativas que ocorrem, ao nível de uma amostra de sementes, é preciso compreender alguns princípios básicos de cálculo. Tendo sido desenvolvido
Conceitos matemáticos: Para entender as possíveis mudanças quantitativas que ocorrem, ao nível de uma amostra de sementes, é preciso compreender alguns princípios básicos de cálculo. Tendo sido desenvolvido
Soluções dos Problemas do Capítulo 3
 48 Temas e Problemas Soluções dos Problemas do Capítulo 3. A cada período de 5 anos, a população da cidade é multiplicada por,0. Logo, em 0 anos, ela é multiplicada por,0 4 =,084. Assim, o crescimento
48 Temas e Problemas Soluções dos Problemas do Capítulo 3. A cada período de 5 anos, a população da cidade é multiplicada por,0. Logo, em 0 anos, ela é multiplicada por,0 4 =,084. Assim, o crescimento
Notas de Aula de Cálculo Numérico
 IM-Universidade Federal do Rio de Janeiro Departamento de Ciência da Computação Notas de Aula de Cálculo Numérico Lista de Exercícios Prof. a Angela Gonçalves 3 1. Erros 1) Converta os seguintes números
IM-Universidade Federal do Rio de Janeiro Departamento de Ciência da Computação Notas de Aula de Cálculo Numérico Lista de Exercícios Prof. a Angela Gonçalves 3 1. Erros 1) Converta os seguintes números
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Prof. Lino Marcos da Silva Atividade 1 - Números Reais Objetivos De um modo geral, o objetivo dessa atividade é fomentar o estudo de conceitos relacionados aos números
Cálculo Diferencial e Integral I Prof. Lino Marcos da Silva Atividade 1 - Números Reais Objetivos De um modo geral, o objetivo dessa atividade é fomentar o estudo de conceitos relacionados aos números
Introdução às Equações Diferenciais Ordinárias e Suas Aplicações.
 Universidade Federal de Campina Grande UFCG Centro de Ciências e Tecnologia CCT Unidade Acadêmica de Matemática UAMat Programa de Educação Tutorial PET Introdução às Equações Diferenciais Ordinárias e
Universidade Federal de Campina Grande UFCG Centro de Ciências e Tecnologia CCT Unidade Acadêmica de Matemática UAMat Programa de Educação Tutorial PET Introdução às Equações Diferenciais Ordinárias e
Álgumas palavras sobre as Equações de Navier-Stokes
 Álgumas palavras sobre as Equações de Navier-Stokes As equações de Navier-Stokes foram derivadas inicialmente por M. Navier em 1827 e por S.D. Poisson em 1831, baseando-se num argumento envolvendo considerações
Álgumas palavras sobre as Equações de Navier-Stokes As equações de Navier-Stokes foram derivadas inicialmente por M. Navier em 1827 e por S.D. Poisson em 1831, baseando-se num argumento envolvendo considerações
FCM Física I. Prof. Rodrigo Gonçalves Pereira. Tuesday, 6 March, 12
 FCM0101 - Física I Prof. Rodrigo Gonçalves Pereira www.ifsc.usp.br/~rpereira/fcm0101 Método científico A Física é uma ciência experimental. teoria experimento Modelos Um modelo é uma versão simplificada
FCM0101 - Física I Prof. Rodrigo Gonçalves Pereira www.ifsc.usp.br/~rpereira/fcm0101 Método científico A Física é uma ciência experimental. teoria experimento Modelos Um modelo é uma versão simplificada
Figura 4.1: Circuito elétrico tipo RL com o indutor inicialmente carregado.
 Guia de Atividades para abordar Equações Diferenciais Ordinárias através da exploração de situações-problema que envolvem queda de corpos e circuitos elétricos. Nestas atividades temos como objetivo abordar
Guia de Atividades para abordar Equações Diferenciais Ordinárias através da exploração de situações-problema que envolvem queda de corpos e circuitos elétricos. Nestas atividades temos como objetivo abordar
Lista 1 - Conceitos Iniciais e EDO s de Primeira Ordem
 Lista - Conceitos Iniciais e EDO s de Primeira Ordem. Classi que as EDO s como lineares ou não-lineares. E ainda, determine a ordem e o grau de cada equação diferencial. (a) x 2 00 + x + 2 = sen(x) ; (b)
Lista - Conceitos Iniciais e EDO s de Primeira Ordem. Classi que as EDO s como lineares ou não-lineares. E ainda, determine a ordem e o grau de cada equação diferencial. (a) x 2 00 + x + 2 = sen(x) ; (b)
Manual de Experimentos de Sistemas de Controle
 Manual de Experimentos de Sistemas de Controle Laboratório de Automação Industrial e Robótica 29 de setembro de 2017 Universidade Federal do Amazonas Sumário 1 Representação e Simulação de Sistemas em
Manual de Experimentos de Sistemas de Controle Laboratório de Automação Industrial e Robótica 29 de setembro de 2017 Universidade Federal do Amazonas Sumário 1 Representação e Simulação de Sistemas em
Equações Diferenciais Ordinárias
 Universidade Estadual Paulista Instituto de Química de Araraquara Equações Diferenciais Ordinárias Jorge Manuel Vieira Capela Marisa Veiga Capela Material de apoio à disciplina Equações Diferenciais Ordinárias
Universidade Estadual Paulista Instituto de Química de Araraquara Equações Diferenciais Ordinárias Jorge Manuel Vieira Capela Marisa Veiga Capela Material de apoio à disciplina Equações Diferenciais Ordinárias
LEI DO RESFRIAMENTO DE NEWTON: APLICAÇÃO EM BLOCOS CERÂMICOS
 LEI DO RESFRIAMENTO DE NEWTON: APLICAÇÃO EM BLOCOS CERÂMICOS Daniele Lima Santos 1 Regivaldo Vieira Lima 2 Renisson Andrade Ramos 3 Tassia MillenaCarvalho Barros 4 Aislan Primo 5 Maria Anita S. S. de mendonça
LEI DO RESFRIAMENTO DE NEWTON: APLICAÇÃO EM BLOCOS CERÂMICOS Daniele Lima Santos 1 Regivaldo Vieira Lima 2 Renisson Andrade Ramos 3 Tassia MillenaCarvalho Barros 4 Aislan Primo 5 Maria Anita S. S. de mendonça
Funções de várias variáveis
 GOVERNO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO CÂMPUS JUAZEIRO/BA COLEG. DE ENG. ELÉTRICA PROF. PEDRO MACÁRIO DE MOURA CÁLCULO II 2015.2 Funções de várias variáveis
GOVERNO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO CÂMPUS JUAZEIRO/BA COLEG. DE ENG. ELÉTRICA PROF. PEDRO MACÁRIO DE MOURA CÁLCULO II 2015.2 Funções de várias variáveis
Controlo Em Espaço de Estados. Trabalho de Laboratório nº 3
 Mestrado em Engenharia Electrotécnica e de Computadores Controlo Em Espaço de Estados 2008/09 Trabalho de Laboratório nº 3 Controlo Adaptativo do Nível de um Tanque J. Miranda Lemos e Alexandre Bernardino
Mestrado em Engenharia Electrotécnica e de Computadores Controlo Em Espaço de Estados 2008/09 Trabalho de Laboratório nº 3 Controlo Adaptativo do Nível de um Tanque J. Miranda Lemos e Alexandre Bernardino
