10 Relatividade de Galileu a Einstein
|
|
|
- Madalena Desconhecida das Neves
- 9 Há anos
- Visualizações:
Transcrição
1 10 Relatividade de Galileu a Einstein 1. Uma massa m está suspensa do teto de uma arruagem de omboio por um fio. Um passageiro na mesma arruagem regista que, quando o omboio arrana da estação, o fio que suspende a massa faz um ângulo α om a vertial (i.e, om a normal ao teto da arruagem). (a) Determine as forças que atuam na massa m do ponto de vista de um observador que está a analisar as imagens da massa m a partir de uma âmara video loalizada no interior da arruagem. O observador está fora do omboio. Relaione a resposta om o ângulo α. Do ponto de vista desse observador, qual o estado de repouso ou movimento de m? (b) Determine as forças que atuam na massa m do ponto de vista de uma pessoa que permanee na plataforma da estação e vê o omboio arranar. O que poderá dizer relativamente à aeleração do omboio? 2. Um passageiro num elevador deixa air uma moeda. Nesse instante o elevador enontrava-se em movimento desendente om veloidade v elevador = 0,5 m /s. (a) Se no instante em que a moeda adquire uma veloidade de 1 m /s em relação ao passageiro, se partirem os abos do elevador, qual o movimento posterior da moeda em relação ao passageiro. Resolução: A aeleração da moeda no referenial do passageiro, a relaiona-se om a aeleração no referenial laboratório, a por a = a a R onde a R é a aeleração relativa do elevador em relação ao referenial laboratório. Como a = a R = g, a aeleração da moeda vista pelo passageiro do elevador é a = 0 e o passageiro verá a moeda a desloar-se om veloidade uniforme v = 1 m /s. (b) No instante em que se partiram os abos a moeda estava a 20 m do hão do elevador. A moeda atingirá o hão do elevador? Resolução: Uma vez que a moeda se desloa om veloidade uniforme, aabará por atingir o hão, ao fim de t = x/v = 0,2 s. () Qual o movimento da moeda antes de se partirem os abos e após se terem partido os abos do elevador, do ponto de vista do funionário da empresa que tinha preisamente aabado de arranjar o elevador e estava no patamar do último piso? 1
2 Resolução: Do ponto de vista do funionário a moeda terá sempre um movimento uniformemente aelerado om aeleração de módulo g. 3. Num simulador de vôo de um Boeing 737 pretende-se simular uma travagem do avião após uma aterragem. O omandante tem 1000 m de pista para parar e toou a pista a 180 km /h. A sensação de travagem é onseguida inlinando o módulo do simulador. Qual o ângulo a que se deve inlinar o módulo do simulador para simular esta travagem e para que o piloto sinta a mesma desaeleração? Resolução: 180km/h = 50m/s. A aeleração relativa à travagem do avião na pista de 1000m é dada por: x = v2 f v2 i 2a a = = 1.25m/s2. A força resultante de inlinar o simulador por um dado ângulo θ é dada por mg sin θ = ma sin θ = a/g θ = arsin(a/g) 7.3 o Quais as forças qua atuam no piloto durante a travagem real e no simulador? Para pensar: quais as onlusões desta experiênia no que diz respeito à omparação entre a massa gravitaional e a massa inerial? 4. (*) Uma pessoa (A) enontra-se no entro de um simulador (arroel om a parte lateral e superior ompletamente fehada) e pretende atirar uma bola para uma outra pessoa (B) loalizada a uma distânia d = 6 m do entro. O arroel é posto a girar om uma veloidade angular onstante ω = 2 rad /s. No hão do arroel enontam-se desenhadas linhas radiais. As paredes do arroel têm um vidro que permite ver de fora para dentro mas não permitem ver de dentro para fora. (a) Suponha que A atira a bola para B de modo que esta desliza pelo hão pratiamente sem atrito. A veloidade da bola do ponto de vista de A é v. A veloidade iniial da bola tem a mesma direção de uma linha radial representada no hão do arroel. Qual a trajetoria da bola do ponto de vista de A? Indique que forças atuam na bola. (b) Na situação da alínea anterior, qual a trajetória da bola do ponto de vista de um observador C, situado fora do arroel? Qual a veloidade da bola? () Suponha que agora é B que atira uma bola para A. A veloidade iniial da bola, do ponto de vista de B ( v ) é radial e na direção de A. Qual a trajetória da bola do ponto de vists de A? Indique que forças atuam na bola. (d) E do ponto de vista de C? 2
3 5. Os abos de elevador suportam, sem partir, uma força máxima de 1000 Kgf. Qual o maior peso de passageiros que o elevador pode suportar se arranar e travar om uma aeleração 10 vezes inferior à da gravidade (9,8 m /s 2 ). Resolução: Como 1 Kgf = gn, T max = 1000 Kgf = 1000 g N, onde g = 9.8 é o valor da aeleração da gravidade à superfíie da Terra. Consideremos agora o movimento de subida do elevador num referenial orientado de baixo para ima. As equações de Newton são dadas por: T max mg = ma 1000g mg = m0.1g m = 909.1kg. 6. (*) Um/a futuro/a engenheiro/a de testes oloa uma roda inerial num suporte dentro de uma box (aixa) que por sua vez será oloada no interior de um satélite. Numa abordagem simplifiada onsidere que a roda inerial é um diso om momento de inéria I = 5 kg /m 2 relativamente ao eixo de rotação que passa pelo seu entro e é perpendiular ao plano do diso. Quando o sistema é fixo na estrutura verifia-se que gira a 5000 rpm. O satélite é ilíndrio, tem massa M = 20 kg, densidade uniforme (inluindo já a roda inerial), altura h = 2 m e raio r = 1 m. A roda inerial é oloada no entro do satélite, fiando om o momento angular paralelo ao maior eixo do ilindro. A/O Engenheira/o está preoupada/o porque não sabe se há algum atrito, assoiado ao peso da roda inerial, no ontato entre o suporte e a roda inerial que possa estar a diminuir a veloidade de rotação da roda. Temese que, em situação de imponderabilidade no espaço, esse atrito desapareça dando origem a que a roda passe a girar até 5050 rpm. O que aonteerá ao satélite se, de fato, a roda inerial no espaço passar a girar a 5050 rpm? Se fosse responsável pelos testes à roda inerial, sugeriria testá-la em vôo parabólio? Porquê? O Engenheiro, que está oloado em ima de uma plataforma rotativa deide inverter o aparelho. Considere que o aparelho e o engenheiro têm um momento de inéria em relação ao eixo de rotação de 1 kg /m 2 e 35 kg /m 2, respetivamente. O que aontee ao engenheiro? 7. Um avião, que se desloa om uma veloidade v = 900 km /h a uma altitude h = m, tem que fazer uma urva de raio R = 5000 m. A massa do avião om o piloto é kg. (a) Represente esquematiamente quais as forças que atuam no avião, do ponto de vista do piloto (referenial não inerial S ) e do ponto de vista de um ontrolador aéreo situado numa torre de ontrolo de um aeroporto (referenial inerial S). Qual a expressão para a aeleração do avião relativamente a ada um dos refereniais? 3
4 Solução: No referenial fixo S (o do ontrolador aéreo) identifiamos omo forças o peso ( P ) e a força de sutentação ( F s ), tal omo sugerido na figura. Como o avião faz uma urva, movimento possível devido à inlinação α que o mesmo realiza om a horizontal, temos: F s os α = P F s sin α = F = ma. Do ponto de vista do piloto, no referenial S, o somatório das forças é zero, a aeleração é também zero. De fato no piloto, para além das forças P e F s atuam ainda uma força entrífuga. Esta força é uma força fitíia que aponta para fora e é sentida pelo piloto. O valor é dado por F I = ma R onde a R tem o signifiado da aeleração do avião, ou seja do referenial S em relação a S, e que neste aso é a aeleração do avião em relaão ao ontrolador aéreo, ou seja a R = a. Assim, no referenial S o somatório das forças é zero. (b) Seja α o ângulo que as asas do avião fazem om o horizonte durante a manobra. Qual o valor de α para que durante a manobra o módulo da veloidade do avião se mantenha igual á veloidade em ruzeiro v = 900 km /h? Solução: Da alínea anterior, temos tan α = F P = mv2 RP, onde R é o raio da trajetória. O módulo do peso para uma altitude de h = 12000m é dado por P = GM T m r 2 = N = mg, onde r = R Terra + h. Assim, ( ) mv α = tan , 2 o P R () Qual a relação entre a força de sustentação do avião durante a manobra e anteriormente à manobra indiada? 4
5 Solução: A força de sustentação é superior durante a manobra uma vez que F s os α = P e omo P é onstante, F s é mínima para α = 0 a aumenta om α. (d) Qual seria o raio de urvatura da trajétoria se a veloidade do avião fosse 1480 km /h e o piloto sentisse uma aeleração entrífuga a = 6 g durante uma urva? Solução: 1480km/h = 411m/s. No referenial do avião (S ) a aeleração é nula sendo dada pela expressão: a = a a R = 0, onde a é a aeleração medida no referenial fixo e a R é a aeleração do referenial S em relação ao referenial fixo S. Assim, a = a R v2 R = a I r = v2 a I = g = 2874m. 8. (a) Compare o valor da força gravítia que atua num astronauta à superfíie da Terra om o valor da força gravítia que atua nesse astronauta quando se enontra numa nave numa órbita irular om 6900 km de raio em torno da Terra. Considere que o astronauta tem massa M = 75 kg. Solução: e F g.superfiie = mg = 75 9, 8 = 735N F g,r=6900km = G M T m r 2 = 627, 5N. (b) Represente esquematiamente (e alule) as forças que atuam num astronauta numa estação orbital a 500 km de altitude (órbita irular om R=6900 km de raio) do ponto de vista de: um astronauta na estação orbital, se o astronauta estiver sentado aos omandos da nave; Solução: Atua a força gravítia e a orça entrifuga, a soma das duas é zero. de um Engenheiro na sala de ontrolo de vôo. Solução: Atua a força gravítia, que é a força entrípeta, responsável pela trajetória da estação espaial e da sua órbita em torno da Terra. 5
6 () Calule as forças que atuam nesse mesmo astronauta durante um vôo parabólio do ponto de vista de um passageiro no interior do avião e para o ontrolador aéreo. Considere que o avião sobe até m. (d) Qual a diferença fundamental entre as duas situações, i.e, omo explia a imponderabilidade nestes dois asos: estação orbital e vôo parabólio? Solução: Na estação orbital a força gravítia e a força entrífuga anulam-se. No vôo parabólio, referenial ligado ao avião, soma da força da gravidade e a força de inéria (que é igual a F I = ma R, sendo a R = g) é zero. (e) Por que motivo não sentimos semelhante gravidade zero num avião em vôo ruzeiro a 900 km /h e a uma altitude onstante? Solução: A força de inéria num avião em vôo ruzeiro à volta da Terra a uma altitude onstante é F I = ma R, e a R = v 2 /R, onde R a distânia ao entro da Terra. Esta força teria que anular F = mg. Porém a veloidade v = 900 km/ não é sufiiente para anular a força gravítia. 9. Um feixe de muões, µ, em raios ósmios, move-se à veloidade v = 0,992. Qual a fração que sobrevive após um perurso de 1920 metros? (T 1/2 = 1, s, no referenial próprio S, isto é no referenial em que o muão está parado). Solução: Comeemos por determinar o tempo de vida do muão no ref. do laboratório, isto é no referenial S em relação ao qual o muão se desloa: T 1/2lab = T 1/2 r.proprio = 12, s. Da Lei do deaimento radioativo sabemos que, N(t) = N 0 e λt, λ = ln 2 ln 2 = T 1/2 12, = 57190, 5 s 1. Resta determinar qual o tempo (t) que os muões demoram a perorrer o perurso de 1920m om a veloidade onstante v = 0,992, o que pode ser feito do seguinte modo: t = = 6, s. Assim, a fração de núleos que sobrevive no instante t = 6, s é dada por: N(t) N 0 = e λt = exp ( 57190, 5 6, ) 60%. 6
7 10. Um motoilista desloa-se om veloidade v = 0,8 em relação à Terra e dispara uma bola om veloidade vbola = 0,7 relativamente a ele e no sentido de v. Qual a veloidade da bola em relação à Terra? Solução: v bola = v bola + v 1 + v v 2 bola (0, 7 + 0, 8) = 1 + 0,8 0, 7 = 0, Três lâmpadas A 1 vermelha, A 2 amarela e A 3 verde aendem simultaneamente no referenial de uma nave S que se desloa em relação a outra nave S om uma veloidade v na direção X. As lâmpadas aendem no instante t = 0 s, nos pontos om oordenadas x 1 = 0, x 2 = l e x 3 = 2l, respetivamente. Determine as oordenadas das lâmpadas relativamente a S e indique qual a ordem pela qual o astronauta da nave S vê as lâmpadas a aeder. Resolução: O astronauta em S não verá o aendimento das três lâmpadas nem na mesma posição nem no mesmo instante e tempo que no referenial próprio S. A transformação de Lorentz para o espaço é x = x + vt 1 ( v Assim ele verá as lâmpadas nas posições ) 2 x 1 = 0 x 2 = l 1 ( v x 3 = 2l 1 ( v Por sua vez a transformação de Lorentz para o tempo é t = t + v x 2 1 ( v Logo ele verá ada um dos aonteimentos nos instantes ) 2 ) 2 ) 2 t 1 = 0 t 2 = v/ 2 1 ( ) l v 2 t 3 = v/ 2 1 ( ) 2l v 2 7
8 Ele verá as lâmpadas a aender na sequênia vermelho, amarelo e verde. 12. Numa base espaial enontra-se estaionada a nave Pegaso om 20 m de omprimento. A nave parte para uma viagem e quando atinge a veloidade de ruzeiro o seu omprimento, medido a partir da base, é de l = 10 m. (a) Qual a veloidade da nave Pegaso em relação à base? Solução: l = l 1 (v/) 2 v = 1 ( ) 2 l l = (b) Qual o omprimento da nave para os seus tripulantes? Solução: O omprimento da nave para os seus tripulantes é l = 20m. () As partíulas de alta energia são detetadas no laboratório pela impressão que deixam nas hapas fotográfias dos detetores. Uma partíula movendo-se à veloidade de 0,995 produz um rasto de 1,25 mm. Qual o tempo de vida da partíula no referenial próprio? Resolução: Podemos alular o tempo de vida no referenial laboratório a partir do omprimento do rasto, x, e da veloidade, v: t = x v = 1, , = 4, s Por sua vez, no referenial próprio da partíula o seu tempo é ( v ) 2 t t = 1 = 0, 0999 t = 0, s 13. Duas lâmpadas (1 e 2) são aesas simultaneamente para um observador que se enontra em repouso em relação a estas; o mesmo observador mede a distânia entre as lâmpadas e obtém 10 m. (a) As duas lâmpadas aendem simultaneamente para um observador que se desloque num avião a 600 m /s? Qual o intervalo de tempo deorrido entre o aender das lâmpadas? 8
9 Resolução: Seja x 1 = 0 e x 2 = 10, tal que x 2 x 1 = l = 10m, a posição da lâmpada 1 e 2, respetivamente. Se o observador no avião se desloar no sentido positivo do eixo dos xx irá ver a lâmpada 2 a aender primeiro. Para determinar o tempo até a lâmpada 1 aender para este observador, omeemos por determinar a lei da ontração do espaço no referenial do observador no avião (ref. S ): x = γ(x + vt ) x = x γ vt, já o tempo, é dado de aordo om ) t = γ (t + vx 2 = γ (t + v ( )) xγ 2 vt Assim, Então, t 1 = γ ( t = γ t vx ) 2. ( t 1 vx ) ( 1 2 = 0; t 2 = γ t 2 vx ) 2 2 = γ vl 2 t = t 1 t 2 = 0 + γ vl 2 6, s. (b) Qual a distânia espaial entre os dois aonteimentos (aender das lâmpadas) para o observador no avião da alínea a)? Resolução: x = x 2 x 1 = x 2 γ vt 2 x 1 γ + vt 1 = l γ + γ v2 l = 10, 012m Um eletrão e um positrão animados om veloidades 0,99 e 0,99, respetivamente, olidem frontalmente. (a) Pode obter-se omo produto desta reação um par protão antiprotão? Resolução: Para poder obter um par protão anti-protão é neessário que a energia libertada pela aniquilação do par eletrão positrão seja maior ou igual à energia equivalente à massa do par protão antiprotão. Consultamos a tabela de onstantes para obter os valores das massas das partíulas e podemos alular a energia libertada na aniquilação através de: m e E = 2 1 ( ) 2 14, 18 m e 2 2 m p 2 v 2 Logo, verifiamos que a energia libertada é insufiiente para a produção de um par protão anti-protão. 9
10 (b) O eletrão e o positrão podem hoar dando origem a dois fotões (aniquilação). Qual a energia de ada um dos fotões, supondo que o par eletrão-positrão tem a energia da alínea a)? Resolução: Cada fotão terá uma energia de E/2. Isto é E γ = 7, 09 9, ( ) 2 = 5, J = 3, 6 MeV, onde 1 MeV = 10 9 ev ; 1 ev = 1, J. () Qual é a massa iniial e final dos intervenientes no hoque da alínea b)? (Note que o fotão é uma partíula sem massa). Há onservação da massa em Relatividade? Resolução: A massa em repouso iniial é de 2 m e. Após o hoque essa massa foi onvertida na energia transportada pelos fotões; isto é a massa final é zero. Obviamente a massa não se onserva mas onserva-se a energia total, tendo havido onversão de massa em energia. 15. A energia emitida pelo Sol resulta, numa abordagem simplifiada, da fusão de quatro núleos de Hidrogénio num núleo de Hélio. (a) Qual a energia libertada para a estrela na sequênia da produção de ada núleo de Hélio? Solução: A reação que dá origem ao Hélio é: 4 1 H 4 He + 2e + + 2ν e + Energia Assim, a diferença de massa entre 4 átomos de hidrogénio e a massa de 1 átomo de hélio é (reorrendo à tabela das onstantes) 4m H m He = = = = kg. Usando a fórmula de Einstein E = m 2, vem E = ( ) 2 = J. (b) Conheida a luminosidade solar (ver tabela), determine o número de reações nuleares que devem oorrer no Sol por segundo para expliar essa luminosidade. 10
11 Solução: O número de núleos de He produzidos por segundo orresponde ao número de reações de fusão que oorrem no Sol. Assim, W (J/rea.) = rea.s 1. Relembre que W = J/s. () A Terra demora em média 365 dias a umprir uma órbita em torno do Sol. Calule a massa solar e faça uma estimativa sobre a taxa a que o Sol perde massa (dm /dt) assoiada apenas à luminosidade. Compare o valor obtido om o valor da massa solar. Solução: Podemos estimar a massa solar a partir 3 a Lei de Kepler (nota: pode ir ver à tabela): T 2 = 4π 2 G(M + m T erra ) r3 M = T 2 onde T india o período da Terra em torno do Sol. 4π 2 Gr 3 m T erra kg, Por ada reação de fusão, a diferença de massa omo vimos na alínea (a) é de kg = kg, para uma massa original de Assim, a taxa de perda de massa por reação nulear é de = 0.7% Como oorrem rea.s 1, isto orresponde a uma perda de massa por segundo de: dm dt = = kgs 1. Assim, = (d) Para ser mais exato, onvém referir que no proesso de formação de um núleo de Hélio é neessário que dois dos protões se transformem em dois neutrões de que resulta a libertação dos dois positrões (antipartíulas do eletrão) e dois neutrinos. Faça uma estimativa do fluxo de neutrinos (o número de neutrinos por segundo e por unidade de área) que se pode esperar detetar na Terra vindos diretamente interior do Sol, e que são um teste ruial aos modelos solares, inluindo à taxa de reações nuleares. 11
12 Solução: Se por ada núleo de Hélio são libertados 2 neutrinos ν e, então usando o resultado da alínea (b), sabemos que são produzidos Φ T otal,νe = ν e.s 1. Para saber o número de neutrinos que hega à Terra por unidade de área, temos de dividir o fluxo obtido pela área total da superfíie esféria ujo raio orresponde à distânia da Terra ao Sol: Φ νe = π ( ) 2 = ν e.s 1 m 2. Constantes: Constante de Gravitação Universal, G: Veloidade da luz no váuo, : m H : m Hélio : m protão = m anti protão : m eletrão = m positrão : Distânia da Terra ao Sol, D: Luminosidade solar, L = de/dt: 6, Nm 2 Kg m/s 1,0081 u.m.a. 4,0039 u.m.a. 1, kg 9, kg 1, m 3, W 1 u.m.a = 1, kg 12
10 Relatividade de Galileu a Einstein
 10.1. Uma massa m está suspensa do tecto de uma carruagem de comboio por um fio. Um passageiro na mesma carruagem regista que, quando o comboio arranca da estação, o fio que suspende a massa faz um ângulo
10.1. Uma massa m está suspensa do tecto de uma carruagem de comboio por um fio. Um passageiro na mesma carruagem regista que, quando o comboio arranca da estação, o fio que suspende a massa faz um ângulo
MAS AFINAL O QUE É A FORÇA CENTRÍFUGA?
 5º DESAIO MAS AINAL O QUE É A ORÇA CENTRÍUGA? Aabámos de ver o filme relativo ao tereiro desafio proposto e, antes sequer de pensar no problema em ausa, demos por nós (e passando a expressão) a ROERMO-NOS
5º DESAIO MAS AINAL O QUE É A ORÇA CENTRÍUGA? Aabámos de ver o filme relativo ao tereiro desafio proposto e, antes sequer de pensar no problema em ausa, demos por nós (e passando a expressão) a ROERMO-NOS
COEFICIENTES DE ATRITO
 Físia Geral I MIEET Protoolos das Aulas Prátias Departamento de Físia Universidade do Algarve COEFICIENTES DE ATRITO 1. Resumo Corpos de diferentes materiais são deixados, sem veloidade iniial, sobre um
Físia Geral I MIEET Protoolos das Aulas Prátias Departamento de Físia Universidade do Algarve COEFICIENTES DE ATRITO 1. Resumo Corpos de diferentes materiais são deixados, sem veloidade iniial, sobre um
Física I Lista 2: resolver até
 Universidade de São Paulo Instituto de Físia de São Carlos Físia I Lista : resolver até 18.3.013 Nome: Matriula: Questão 16: Tensor de Levi-Civita Sejam dados os vetores a, b,, d R 3. A definição do símbolo
Universidade de São Paulo Instituto de Físia de São Carlos Físia I Lista : resolver até 18.3.013 Nome: Matriula: Questão 16: Tensor de Levi-Civita Sejam dados os vetores a, b,, d R 3. A definição do símbolo
Séries de Problemas. Mecânica e Ondas LEIC-TP. Pedro Abreu, adaptado de original de Ana Maria Mourão (Coordenadora) e Nuno Pinhão
 Mecânica e Ondas LEIC-TP Séries de Problemas Enunciados Pedro Abreu, adaptado de original de Ana Maria Mourão (Coordenadora) e Nuno Pinhão Ano Lectivo: 2016/2017, 1 o semestre Alguns exercícios são seleccionados
Mecânica e Ondas LEIC-TP Séries de Problemas Enunciados Pedro Abreu, adaptado de original de Ana Maria Mourão (Coordenadora) e Nuno Pinhão Ano Lectivo: 2016/2017, 1 o semestre Alguns exercícios são seleccionados
Problemas de Mecânica e Ondas 10
 Problemas de Mecânica e Ondas 10 P. 10.1. Um comboio rápido de passageiros, viajando inicialmente a uma velocidade de 240 km/h é forçado a realizar uma travagem até uma velocidade de 60 km/h para evitar
Problemas de Mecânica e Ondas 10 P. 10.1. Um comboio rápido de passageiros, viajando inicialmente a uma velocidade de 240 km/h é forçado a realizar uma travagem até uma velocidade de 60 km/h para evitar
3.Um feixe de luz laser, de comprimento de onda 400nm m, tem intensidade
 1.Em um laboratório de físia, estudantes fazem um experimento em que radiação eletromagnétia de omprimento de onda λ 300 nm inide em uma plaa de sódio, provoando a emissão de elétrons. Os elétrons esapam
1.Em um laboratório de físia, estudantes fazem um experimento em que radiação eletromagnétia de omprimento de onda λ 300 nm inide em uma plaa de sódio, provoando a emissão de elétrons. Os elétrons esapam
Torção Deformação por torção de um eixo circular
 Torção Deformação por torção de um eixo irular Torque é um momento que tende a torer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o omprimento e o raio do eixo permaneerão
Torção Deformação por torção de um eixo irular Torque é um momento que tende a torer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o omprimento e o raio do eixo permaneerão
Electromagnetismo e Óptica 1º Semestre 2º Exame 29/01/ :00h
 Lieniatura em Engenharia e Arquitetura Naval Mestrado Integrado em Engenharia Aeroespaial Eletromagnetismo e Óptia º Semestre º Exame 9//3 5:h Duração do exame: :3h Leia o enuniado om atenção. Justifique
Lieniatura em Engenharia e Arquitetura Naval Mestrado Integrado em Engenharia Aeroespaial Eletromagnetismo e Óptia º Semestre º Exame 9//3 5:h Duração do exame: :3h Leia o enuniado om atenção. Justifique
Gabarito (Exame )
 Gabarito (Exame 010.1) 1 A) Alternativa (d) O fluxo do ampo elétrio através de uma superfíie Gaussiana qualquer é = E nda A interseção da superfíie Gaussiana om o plano arregado é uma irunferênia de raio
Gabarito (Exame 010.1) 1 A) Alternativa (d) O fluxo do ampo elétrio através de uma superfíie Gaussiana qualquer é = E nda A interseção da superfíie Gaussiana om o plano arregado é uma irunferênia de raio
10ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT, LEGM, LMAC
 10ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT, LEGM, LMAC 1. A vida média de uma partícula é 100 ns no seu referencial próprio. 1.a) Qual a duração da partícula no laboratório, sabendo
10ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT, LEGM, LMAC 1. A vida média de uma partícula é 100 ns no seu referencial próprio. 1.a) Qual a duração da partícula no laboratório, sabendo
8ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT e LMAC
 8ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT e LMAC 1. A vida média de uma partícula é 100 ns no seu referencial próprio. 1.a) Qual a duração da partícula no laboratório, sabendo que
8ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT e LMAC 1. A vida média de uma partícula é 100 ns no seu referencial próprio. 1.a) Qual a duração da partícula no laboratório, sabendo que
3. Considere as duas diferentes situações em que uma mala está suspensa por dois dinamómetros como representado na Fig.1.
 1 II. 2. Mecânica de Newton 1. Um partícula carregada com carga q quando colocada num campo eléctrico E fica sujeita a uma força F = q E. Considere o movimento de um electrão e um protão colocados num
1 II. 2. Mecânica de Newton 1. Um partícula carregada com carga q quando colocada num campo eléctrico E fica sujeita a uma força F = q E. Considere o movimento de um electrão e um protão colocados num
3. Mecânica de Newton
 3. Mecânica de Newton 3.1. Uma partícula carregada com carga q, quando colocada num campo eléctrico E, fica sujeita a uma força F = q E. Considere o movimento de um electrão e um protão colocados num campo
3. Mecânica de Newton 3.1. Uma partícula carregada com carga q, quando colocada num campo eléctrico E, fica sujeita a uma força F = q E. Considere o movimento de um electrão e um protão colocados num campo
11ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT, LEGM, LMAC
 11ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT, LEGM, LMAC 1. A vida média de uma partícula é 100 ns no seu referencial próprio. 1.a) Qual a duração da partícula no laboratório, sabendo
11ª Série de Problemas Mecânica e Ondas (Relatividade) MEBM, MEFT, LEGM, LMAC 1. A vida média de uma partícula é 100 ns no seu referencial próprio. 1.a) Qual a duração da partícula no laboratório, sabendo
MATEMÁTICA 1ª QUESTÃO. O domínio da função real = 2ª QUESTÃO. O valor de lim +3 1 é C) 2/3 D) 1 E) 4/3 3ª QUESTÃO B) 3 4ª QUESTÃO
 MATEMÁTICA 1ª QUESTÃO O domínio da função real = 9 é A) R B) R 3
MATEMÁTICA 1ª QUESTÃO O domínio da função real = 9 é A) R B) R 3
ESPAÇO PARA RESPOSTA COM DESENVOLVIMENTO
 Parte 2 - P3 de Física I - 2018-1 NOME: DRE Teste 0 Assinatura: Questão 1 - [2,5 pontos] Um bloco de massamestá pendurado por um fio ideal que está enrolado em uma polia fixa, mas que pode girar em torno
Parte 2 - P3 de Física I - 2018-1 NOME: DRE Teste 0 Assinatura: Questão 1 - [2,5 pontos] Um bloco de massamestá pendurado por um fio ideal que está enrolado em uma polia fixa, mas que pode girar em torno
MATEMÁTICA 1ª QUESTÃO. O valor do número real que satisfaz a equação =5 é. A) ln5. B) 3 ln5. C) 3+ln5. D) ln5 3. E) ln5 2ª QUESTÃO
 MATEMÁTICA 1ª QUESTÃO O valor do número real que satisfaz a equação =5 é A) ln5 B) 3 ln5 C) 3+ln5 D) ln5 3 E) ln5 ª QUESTÃO O domínio da função real = 64 é o intervalo A) [,] B) [, C), D), E), 3ª QUESTÃO
MATEMÁTICA 1ª QUESTÃO O valor do número real que satisfaz a equação =5 é A) ln5 B) 3 ln5 C) 3+ln5 D) ln5 3 E) ln5 ª QUESTÃO O domínio da função real = 64 é o intervalo A) [,] B) [, C), D), E), 3ª QUESTÃO
PSVS/UFES 2014 MATEMÁTICA 1ª QUESTÃO. O valor do limite 2ª QUESTÃO. O domínio da função real definida por 3ª QUESTÃO
 MATEMÁTICA 1ª QUESTÃO O valor do limite 3 x 8 lim é x 2 x 2 2ª QUESTÃO O domínio da função real definida por é 3ª QUESTÃO A imagem da função real definida por, para todo, é GRUPO 1 PROVA DE MATEMÁTICA
MATEMÁTICA 1ª QUESTÃO O valor do limite 3 x 8 lim é x 2 x 2 2ª QUESTÃO O domínio da função real definida por é 3ª QUESTÃO A imagem da função real definida por, para todo, é GRUPO 1 PROVA DE MATEMÁTICA
Fundamentos de Mecânica 15ª Lista de Exercícios Junho de 2019
 Sumário Aplicações das leis de Newton ao Movimento Circular... 2 Um corpo em movimento circular uniforme... 2 1) RHK E4.21 Lançamento de funda... 2 2) Velocidade e aceleração dos ponteiros do relógio...
Sumário Aplicações das leis de Newton ao Movimento Circular... 2 Um corpo em movimento circular uniforme... 2 1) RHK E4.21 Lançamento de funda... 2 2) Velocidade e aceleração dos ponteiros do relógio...
Série IV - Momento Angular (Resoluções Sucintas)
 Mecânica e Ondas, 0 Semestre 006-007, LEIC Série IV - Momento Angular (Resoluções Sucintas) 1. O momento angular duma partícula em relação à origem é dado por: L = r p a) Uma vez que no movimento uniforme
Mecânica e Ondas, 0 Semestre 006-007, LEIC Série IV - Momento Angular (Resoluções Sucintas) 1. O momento angular duma partícula em relação à origem é dado por: L = r p a) Uma vez que no movimento uniforme
Energia potencial (para um campo de forças conservativo).
 UNIVERSIDDE DO PORTO Faculdade de Engenharia Departamento de Engenharia Civil Mecânica II Ficha 5 (V3.99) Dinâmica da Partícula Conceitos F = m a p = m v Princípio fundamental. Quantidade de movimento.
UNIVERSIDDE DO PORTO Faculdade de Engenharia Departamento de Engenharia Civil Mecânica II Ficha 5 (V3.99) Dinâmica da Partícula Conceitos F = m a p = m v Princípio fundamental. Quantidade de movimento.
Física 1. Resumo e Exercícios P1
 Física 1 Resumo e Exercícios P1 Fórmulas e Resumo Teórico Parte 1 Derivada de polinômios - Considerando um polinômio P x = ax %, temos: d P x = anx%() dx Integral de polinômios - Considerando um polinômio
Física 1 Resumo e Exercícios P1 Fórmulas e Resumo Teórico Parte 1 Derivada de polinômios - Considerando um polinômio P x = ax %, temos: d P x = anx%() dx Integral de polinômios - Considerando um polinômio
FAP151 Fundamentos de Mecânica. 8ª Lista de Exercícios. Maio de 2008 Movimento Circular Uniforme e Movimento relativo
 FAP151 Fundamentos de Mecânica. 8ª Lista de Exercícios. Maio de 008 Movimento Circular Uniforme e Movimento relativo Entregue as soluções dos exercícios 5 e 5. Note que não é suficiente fornecer apenas
FAP151 Fundamentos de Mecânica. 8ª Lista de Exercícios. Maio de 008 Movimento Circular Uniforme e Movimento relativo Entregue as soluções dos exercícios 5 e 5. Note que não é suficiente fornecer apenas
Mecânica e Ondas. Docentes da disciplina: João Seixas e Mario J. Pinheiro MeMEC Departmento de Física e Instituto de Plasma e Fusão Nuclear,
 Mecânica e Ondas Série 5 Docentes da disciplina: João Seixas e Mario J. Pinheiro MeMEC Departmento de Física e Instituto de Plasma e Fusão Nuclear, Instituto Superior Técnico, Av. & 1049-001 Lisboa, Portugal
Mecânica e Ondas Série 5 Docentes da disciplina: João Seixas e Mario J. Pinheiro MeMEC Departmento de Física e Instituto de Plasma e Fusão Nuclear, Instituto Superior Técnico, Av. & 1049-001 Lisboa, Portugal
TA Teste de Avaliação 1
 TA Escola Data Nome N.º Turma Professor Classificação Utilize apenas caneta ou esferográfica de tinta indelével azul ou preta. Pode utilizar régua, esquadro, transferidor e máquina de calcular gráfica.
TA Escola Data Nome N.º Turma Professor Classificação Utilize apenas caneta ou esferográfica de tinta indelével azul ou preta. Pode utilizar régua, esquadro, transferidor e máquina de calcular gráfica.
1) O vetor posição de uma partícula que se move no plano XZ e dado por: r = (2t 3 + t 2 )i + 3t 2 k
 1) O vetor posição de uma partícula que se move no plano XZ e dado por: r = (2t + t 2 )i + t 2 k onde r é dado em metros e t em segundos. Determine: (a) (1,0) o vetor velocidade instantânea da partícula,
1) O vetor posição de uma partícula que se move no plano XZ e dado por: r = (2t + t 2 )i + t 2 k onde r é dado em metros e t em segundos. Determine: (a) (1,0) o vetor velocidade instantânea da partícula,
FÍSICA PROFº JAISON MATTEI
 FÍSICA PROFº JAISON MATTEI QUEDA LIVRE Fórmulas: V h V. g. h Aceleração constante e igual g = 1 m/s Velocidade inicial sempre igual a zero. Despreza a resistência do ar. Objetos com formatos e massas diferentes,
FÍSICA PROFº JAISON MATTEI QUEDA LIVRE Fórmulas: V h V. g. h Aceleração constante e igual g = 1 m/s Velocidade inicial sempre igual a zero. Despreza a resistência do ar. Objetos com formatos e massas diferentes,
PROVA G2 FIS /05/2008 FLUIDOS E TERMODINÂMICA
 PROV G FIS 04 /05/008 FLUIDOS E TERMODINÂMIC NOME N O TURM QUESTÃO VLOR GRU REVISÃO,5,0,5 TOTL 0,0 O tempo de proa é de h 50 min. Mantenha o elular desligado e seu doumento de identidade sobre a arteira:
PROV G FIS 04 /05/008 FLUIDOS E TERMODINÂMIC NOME N O TURM QUESTÃO VLOR GRU REVISÃO,5,0,5 TOTL 0,0 O tempo de proa é de h 50 min. Mantenha o elular desligado e seu doumento de identidade sobre a arteira:
Avaliação individual. Questões: 1) Apresente a leitura completa correspondente a cada uma das medidas abaixo ilustradas:
 Engenharia de Controle e Automação Físia Experimental para Engenharia 1 (N1FE1) Professor Osvaldo Canato Júnior e Wilson Elmer Avaliação individual Formulário: s v 1 1 1 vm ; am ; s s0 vt; s s0 v0t at
Engenharia de Controle e Automação Físia Experimental para Engenharia 1 (N1FE1) Professor Osvaldo Canato Júnior e Wilson Elmer Avaliação individual Formulário: s v 1 1 1 vm ; am ; s s0 vt; s s0 v0t at
Universidade Federal do Rio de Janeiro Instituto de Física Lista de Revisão Física 1. prof. Daniel Kroff e Daniela Szilard 17 de abril de 2015
 Universidade Federal do Rio de Janeiro Instituto de Física Lista de Revisão Física 1 prof. Daniel Kroff e Daniela Szilard 17 de abril de 2015 1. Uma partícula move-se em linha reta, partindo do repouso
Universidade Federal do Rio de Janeiro Instituto de Física Lista de Revisão Física 1 prof. Daniel Kroff e Daniela Szilard 17 de abril de 2015 1. Uma partícula move-se em linha reta, partindo do repouso
DISCURSIVAS. Solução: (a) Com os eixos escolhidos conforme a figura, a altura instantânea da caixa a partir do instante t=0 em que começa a cair é
 DISCURSIVAS 1. Um pequeno avião monomotor, à altitude de 500m, deixa cair uma caixa. No instante em que a caixa é largada, o avião voava a 60,0m/s inclinado de 30,0 0 acima da horizontal. (a) A caixa atinge
DISCURSIVAS 1. Um pequeno avião monomotor, à altitude de 500m, deixa cair uma caixa. No instante em que a caixa é largada, o avião voava a 60,0m/s inclinado de 30,0 0 acima da horizontal. (a) A caixa atinge
Física I. Lista de Exercícios LIVE: Exercícios P3
 Física I Lista de Exercícios LIVE: Exercícios P3 Lista de Exercícios 1. Centro de Massa P2 2016.1 Diurno Exercício 9 Uma chapa metálica de densidade superficial uniforme (I) pode ser cortada das formas
Física I Lista de Exercícios LIVE: Exercícios P3 Lista de Exercícios 1. Centro de Massa P2 2016.1 Diurno Exercício 9 Uma chapa metálica de densidade superficial uniforme (I) pode ser cortada das formas
1ª Prova de Física I - FCM0101
 1ª Prova de Física I - FCM11 #USP: Nome: Instruções: 1. Escreva seu nome e número USP no espaço acima.. A duração da prova é de horas. A prova tem 4 questões. 3. Não é permitido consultar livros, anotações
1ª Prova de Física I - FCM11 #USP: Nome: Instruções: 1. Escreva seu nome e número USP no espaço acima.. A duração da prova é de horas. A prova tem 4 questões. 3. Não é permitido consultar livros, anotações
Capítulo 5 DINÂMICA θ α
 Capítulo 5 DINÂMICA θ α DISCIPLINA DE FÍSICA CAPÍTULO 5 - DINÂMICA 5.1 Considere um pêndulo cónico com uma massa m 1 suspensa por um cabo de comprimento igual a 2,5 metros. 5.1.1 Determine a velocidade
Capítulo 5 DINÂMICA θ α DISCIPLINA DE FÍSICA CAPÍTULO 5 - DINÂMICA 5.1 Considere um pêndulo cónico com uma massa m 1 suspensa por um cabo de comprimento igual a 2,5 metros. 5.1.1 Determine a velocidade
REA DILATAÇÃO DO TEMPO
 Bloo III - Postulados e suas Consequênias REA.3.3.. ILATAÇÃO O TEPO Para a relatividade, o tempo é uma grandeza que depende do referenial. Isso signifia que o funionamento dos relógios (nossos instrumentos
Bloo III - Postulados e suas Consequênias REA.3.3.. ILATAÇÃO O TEPO Para a relatividade, o tempo é uma grandeza que depende do referenial. Isso signifia que o funionamento dos relógios (nossos instrumentos
EXERCÍCIOS DE INTRODUÇÃO À DINÂMICA
 ESCOLA DE ENSINO FUND. E MÉDIO TEN. RÊGO BARROS. DIRETOR: CESAR ALVES DE ALMEIDA COSTA - CEL. INT. R1 PROFESSORES: CÁSSIO - POMPEU ALUNO (A): N º SÉRIE: 9 a TURMA: 9A EXERCÍCIOS DE INTRODUÇÃO À DINÂMICA
ESCOLA DE ENSINO FUND. E MÉDIO TEN. RÊGO BARROS. DIRETOR: CESAR ALVES DE ALMEIDA COSTA - CEL. INT. R1 PROFESSORES: CÁSSIO - POMPEU ALUNO (A): N º SÉRIE: 9 a TURMA: 9A EXERCÍCIOS DE INTRODUÇÃO À DINÂMICA
Exame Mecânica e Ondas Curso: MIEET data: 02/05/12. Nome:... Número:... Grupo I (10 valores)
 Exame Mecânica e Ondas Curso: MIEET data: 02/05/12 Nome:... Número:... Pode utilizar uma calculadora e uma folha A4 (duas páginas) com fórmulas. Utilize g = 9,80 m/s 2. Grupo I (10 valores) Assinalar a
Exame Mecânica e Ondas Curso: MIEET data: 02/05/12 Nome:... Número:... Pode utilizar uma calculadora e uma folha A4 (duas páginas) com fórmulas. Utilize g = 9,80 m/s 2. Grupo I (10 valores) Assinalar a
LISTA 05 FUNDAMENTOS DE MECÂNICA
 LISTA 05 FUNDAMENTOS DE MECÂNICA 01) Em 72s um móvel cuja velocidade escalar é 20km/h descreve uma trajetória circular de raio 0,10km. Determine o ângulo descrito pelo móvel nesse intervalo. R: Δ φ= 4,0rad
LISTA 05 FUNDAMENTOS DE MECÂNICA 01) Em 72s um móvel cuja velocidade escalar é 20km/h descreve uma trajetória circular de raio 0,10km. Determine o ângulo descrito pelo móvel nesse intervalo. R: Δ φ= 4,0rad
m 1 m 2 FIG. 1: Máquina de Atwood m 1 m 2 g (d) Qual a relação entre as massas para que o sistema esteja em equilíbrio?
 1 II.5. Corpo rígido (versão: 20 de Maio, com respostas) 1. Determine o momento de inércia de uma régua de comprimento L e densidade uniforme nas seguintes situações : (a) em relação ao eixo que passa
1 II.5. Corpo rígido (versão: 20 de Maio, com respostas) 1. Determine o momento de inércia de uma régua de comprimento L e densidade uniforme nas seguintes situações : (a) em relação ao eixo que passa
Tipos de forças fundamentais na Natureza
 Tipos de Forças Tipos de forças fundamentais na Natureza Existem quatro tipos de interações/forças fundamentais na Natureza que atuam entre partículas a uma certa distância umas das outras: Gravitacional
Tipos de Forças Tipos de forças fundamentais na Natureza Existem quatro tipos de interações/forças fundamentais na Natureza que atuam entre partículas a uma certa distância umas das outras: Gravitacional
Grupo I. 4. Determine a distância percorrida pela bola desde o instante em que foi lançada até chegar ao solo. Apresente todas as etapas de resolução.
 Ficha 3 Forças e movimentos Considere g = 10 m s -2 Grupo I De uma janela a 6,0 m de altura do solo, uma bola, de massa 100 g, é lançada verticalmente para cima, com velocidade de módulo A força de resistência
Ficha 3 Forças e movimentos Considere g = 10 m s -2 Grupo I De uma janela a 6,0 m de altura do solo, uma bola, de massa 100 g, é lançada verticalmente para cima, com velocidade de módulo A força de resistência
FEP Física Geral e Experimental para Engenharia I
 FEP2195 - Física Geral e Experimental para Engenharia I Prova P1-10/04/2008 - Gabarito 1. A luz amarela de um sinal de transito em um cruzamento fica ligada durante 3 segundos. A largura do cruzamento
FEP2195 - Física Geral e Experimental para Engenharia I Prova P1-10/04/2008 - Gabarito 1. A luz amarela de um sinal de transito em um cruzamento fica ligada durante 3 segundos. A largura do cruzamento
Gravitação IME. Lista de Exercícios 3
 Gravitação 4300156 IME Lista de Exercícios 3 Q1 Considere as afimações abaixo e considere se são corretas ou incorretas, justificando. a) A segunda Lei de Kepler implica que velocidade dos planetas ao
Gravitação 4300156 IME Lista de Exercícios 3 Q1 Considere as afimações abaixo e considere se são corretas ou incorretas, justificando. a) A segunda Lei de Kepler implica que velocidade dos planetas ao
Distâncias inacessíveis
 U UL L esse: http://fuvestibular.om.br/ Distânias inaessíveis Introdução Na ula 20 aprendemos a alular distânias que não podiam ser medidas diretamente. Nessa aula, os oneitos utilizados foram a semelhança
U UL L esse: http://fuvestibular.om.br/ Distânias inaessíveis Introdução Na ula 20 aprendemos a alular distânias que não podiam ser medidas diretamente. Nessa aula, os oneitos utilizados foram a semelhança
Mecânica 2007/ ª Série
 Mecânica 007/008 ª Série Questões: 1. Se a velocidade média é nula durante um intervalo de tempo t e se v(t) é uma função contínua, mostre que a velocidade instantânea se deve anular em algum instante
Mecânica 007/008 ª Série Questões: 1. Se a velocidade média é nula durante um intervalo de tempo t e se v(t) é uma função contínua, mostre que a velocidade instantânea se deve anular em algum instante
Lista de exercícios e Mais Vetores
 Lista de exercícios 11... e Mais Vetores Fís1 04/1 G.4 Ex. 11 p. 4 tons IF UFRJ 2004/1 Física 1 IFA (prof. Marta) 1. O produto vetorial de dois vetores é uma operação que associa a dois vetores ~a e ~
Lista de exercícios 11... e Mais Vetores Fís1 04/1 G.4 Ex. 11 p. 4 tons IF UFRJ 2004/1 Física 1 IFA (prof. Marta) 1. O produto vetorial de dois vetores é uma operação que associa a dois vetores ~a e ~
Física I Prova 3 29/11/2014
 Nota Física I Prova 3 9/11/014 NOME MATRÍCULA TURMA PROF. Lembrete: A prova consta de 6 questões discursivas (que deverão ter respostas justificadas, desenvolvidas e demonstradas matematicamente) e 8 questões
Nota Física I Prova 3 9/11/014 NOME MATRÍCULA TURMA PROF. Lembrete: A prova consta de 6 questões discursivas (que deverão ter respostas justificadas, desenvolvidas e demonstradas matematicamente) e 8 questões
FEP2195-Física Geral e Exp. para a Engenharia I - 1 a Prova - Gabarito 11/04/2013
 FEP2195-Física Geral e Exp. para a Engenharia I - 1 a Prova - Gabarito 11/04/2013 1) Sabendo-se que a posição de uma partícula, em relação à origem O do plano xy, é determinada pelo vetor: ( ) 1 m r (t)
FEP2195-Física Geral e Exp. para a Engenharia I - 1 a Prova - Gabarito 11/04/2013 1) Sabendo-se que a posição de uma partícula, em relação à origem O do plano xy, é determinada pelo vetor: ( ) 1 m r (t)
Lista 12: Rotação de corpos rígidos
 Lista 12: Rotação de Corpos Rígidos Importante: i. Ler os enunciados com atenção. ii. Responder a questão de forma organizada, mostrando o seu raciocínio de forma coerente. iii. iv. Siga a estratégia para
Lista 12: Rotação de Corpos Rígidos Importante: i. Ler os enunciados com atenção. ii. Responder a questão de forma organizada, mostrando o seu raciocínio de forma coerente. iii. iv. Siga a estratégia para
Parte 2 - P1 de Física I NOME: ABID LOHAN DA SILVA FERREIRA DOS SANTOS. DRE Teste 1
 Assinatura: Nota Q1 Questão 1 - [1,5 ponto] Num laboratório, são lançados simultaneamente dois projéteis de dimensões desprezíveis. No instante t = 0 de lançamento, os projéteis ocupam as posições r 1
Assinatura: Nota Q1 Questão 1 - [1,5 ponto] Num laboratório, são lançados simultaneamente dois projéteis de dimensões desprezíveis. No instante t = 0 de lançamento, os projéteis ocupam as posições r 1
Cada questão objetiva vale 0,7 ponto
 Instituto de Física Segunda Prova de Física I 2017/1 Nas questões em que for necessário, considere que: todos os fios e molas são ideais; os fios permanecem esticados durante todo o tempo; a resistência
Instituto de Física Segunda Prova de Física I 2017/1 Nas questões em que for necessário, considere que: todos os fios e molas são ideais; os fios permanecem esticados durante todo o tempo; a resistência
Lista 12: Rotação de corpos rígidos
 Lista 12: Rotação de Corpos Rígidos Importante: i. Ler os enunciados com atenção. ii. Responder a questão de forma organizada, mostrando o seu raciocínio de forma coerente. iii. Siga a estratégia para
Lista 12: Rotação de Corpos Rígidos Importante: i. Ler os enunciados com atenção. ii. Responder a questão de forma organizada, mostrando o seu raciocínio de forma coerente. iii. Siga a estratégia para
1ª. Prova de Física 1 FCM Gabarito Valor das Questões 1ª. a) 1,0 b) 1,0 c) 0,5 2ª. 2,5...3,0 3ª. a) 0,75 b) 0,75 c) 1,00 4ª.
 1ª. Prova de Física 1 FCM 0501- Gabarito 2013 Nome do Aluno Número USP Valor das Questões 1ª. a) 1,0 b) 1,0 c) 0,5 2ª. 2,5...3,0 3ª. a) 0,75 b) 0,75 c) 1,00 4ª. 2,5 Nota Nota Final Boa Prova! A prova é
1ª. Prova de Física 1 FCM 0501- Gabarito 2013 Nome do Aluno Número USP Valor das Questões 1ª. a) 1,0 b) 1,0 c) 0,5 2ª. 2,5...3,0 3ª. a) 0,75 b) 0,75 c) 1,00 4ª. 2,5 Nota Nota Final Boa Prova! A prova é
Instituto Montessori - Ponte Nova
 Instituto Montessori - Ponte Nova Estudos Orientados para a Avaliação II 1) Na figura, cada quadrado tem lado de 1 unidade. Sobre os vetores mostrados ali, determine: a) Quais têm a mesma direção? b) Quais
Instituto Montessori - Ponte Nova Estudos Orientados para a Avaliação II 1) Na figura, cada quadrado tem lado de 1 unidade. Sobre os vetores mostrados ali, determine: a) Quais têm a mesma direção? b) Quais
Física I Prova 1 09/01/2016
 Nota Física I Prova 1 09/01/2016 NOME MATRÍCULA TURMA PROF. Lembrete: A prova consta de 3 questões discursivas (que deverão ter respostas justificadas, desenvolvidas e demonstradas matematicamente) e 10
Nota Física I Prova 1 09/01/2016 NOME MATRÍCULA TURMA PROF. Lembrete: A prova consta de 3 questões discursivas (que deverão ter respostas justificadas, desenvolvidas e demonstradas matematicamente) e 10
INSTITUTO GEREMÁRIO DANTAS COMPONENTE CURRICULAR: FÍSICA CIOS DE RECUPERAÇÃO FINAL
 INSTITUTO GEREMÁRIO DANTAS Educação Infantil, Ensino Fundamental e Médio Fone: (21) 21087900 Rio de Janeiro RJ www.igd.com.br Aluno(a): 1º Ano: C11 Nº Professora: Saionara Chagas Data: / /2016 COMPONENTE
INSTITUTO GEREMÁRIO DANTAS Educação Infantil, Ensino Fundamental e Médio Fone: (21) 21087900 Rio de Janeiro RJ www.igd.com.br Aluno(a): 1º Ano: C11 Nº Professora: Saionara Chagas Data: / /2016 COMPONENTE
3 a prova de F 128 Diurno 30/06/2014
 30/06/2014 Nome: RA: Turma: Esta prova contém 14 questões de múltipla escolha e 1 questão discursiva. Não esqueça de passar as respostas das questões de múltipla escolha para o cartão de respostas. Obs:
30/06/2014 Nome: RA: Turma: Esta prova contém 14 questões de múltipla escolha e 1 questão discursiva. Não esqueça de passar as respostas das questões de múltipla escolha para o cartão de respostas. Obs:
1.(UFB - adaptado) Determine a intensidade da Força Resultante necessária para manter um trem de 5 toneladas com velocidade constante de 5 m/s.
 1.(UFB - adaptado) Determine a intensidade da Força Resultante necessária para manter um trem de 5 toneladas com velocidade constante de 5 m/s. 2. -(PUC-RJ - adaptado) Considere as seguintes afirmações
1.(UFB - adaptado) Determine a intensidade da Força Resultante necessária para manter um trem de 5 toneladas com velocidade constante de 5 m/s. 2. -(PUC-RJ - adaptado) Considere as seguintes afirmações
~é a força normal do bloco de cima sobre o bloco de baixo É o peso do bloco de cima (baixo)
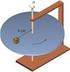 Q1. (2,0 pontos) O coeficiente de atrito estático entre os blocos da figura vale 0,60. O coeficiente de atrito cinético entre o bloco inferior e o piso é de 0,20. A força F, aplicada ao bloco superior,
Q1. (2,0 pontos) O coeficiente de atrito estático entre os blocos da figura vale 0,60. O coeficiente de atrito cinético entre o bloco inferior e o piso é de 0,20. A força F, aplicada ao bloco superior,
Lista de exercícios Mecânica Geral III
 Lista de exercícios Mecânica Geral III 12.5 Uma partícula está se movendo ao longo de uma linha reta com uma aceleração de a = (12t 3t 1/2 ) m/s 2, onde t é dado em segundos. Determine a velocidade e a
Lista de exercícios Mecânica Geral III 12.5 Uma partícula está se movendo ao longo de uma linha reta com uma aceleração de a = (12t 3t 1/2 ) m/s 2, onde t é dado em segundos. Determine a velocidade e a
FÍSICA LISTA 4 QUANTIDADE DE MOVIMENTO, GRAVITAÇÃO UNIVERSAL E EQUILÍBRIO
 FÍSICA Prof. Bruno Roberto LISTA 4 QUANTIDADE DE MOVIMENTO, GRAVITAÇÃO UNIVERSAL E EQUILÍBRIO QUANTIDADE DE MOVIMENTO 1. (Pucrj 2013) Uma massinha de 0,3 kg é lançada horizontalmente com velocidade de
FÍSICA Prof. Bruno Roberto LISTA 4 QUANTIDADE DE MOVIMENTO, GRAVITAÇÃO UNIVERSAL E EQUILÍBRIO QUANTIDADE DE MOVIMENTO 1. (Pucrj 2013) Uma massinha de 0,3 kg é lançada horizontalmente com velocidade de
ESPAÇO PARA RESPOSTA COM DESENVOLVIMENTO
 Parte 2 - P2 de Física I - 2016-2 NOME: DRE Teste 1 Nota Q1 Assinatura: Questão 1 - [2,4 ponto] Dois pequenos discos (que podem ser considerados como partículas), de massas m e 2m, se deslocam sobre uma
Parte 2 - P2 de Física I - 2016-2 NOME: DRE Teste 1 Nota Q1 Assinatura: Questão 1 - [2,4 ponto] Dois pequenos discos (que podem ser considerados como partículas), de massas m e 2m, se deslocam sobre uma
Problemas propostos. Questões Demonstrativas
 Problemas propostos Módulo 01 Nota: (i)ler atentamente o enunciado três ou mais vezes. (ii)traduzir o enunciado em um diagrama. (iii) Nomear as grandezas citadas e colocar seus valores, quando houver.
Problemas propostos Módulo 01 Nota: (i)ler atentamente o enunciado três ou mais vezes. (ii)traduzir o enunciado em um diagrama. (iii) Nomear as grandezas citadas e colocar seus valores, quando houver.
Lista de exercícios 1 Mecânica Geral III
 UNIVERSIDADE FEDERAL DO PARANÁ Setor de Tecnologia Departamento de Construção Civil TC027 Mecânica Geral III 1 0 Semestre de 2018 Ressalta-se que os testes serão baseados nas listas de exercícios. Portanto,
UNIVERSIDADE FEDERAL DO PARANÁ Setor de Tecnologia Departamento de Construção Civil TC027 Mecânica Geral III 1 0 Semestre de 2018 Ressalta-se que os testes serão baseados nas listas de exercícios. Portanto,
Universidade Federal do Rio de Janeiro Instituto de Física Física 1 - Turmas de 6 horas 2015/2 Oficinas de Física 1 Exercícios E3
 Universidade Federal do Rio de Janeiro Instituto de Física Física 1 - Turmas de 6 horas 2015/2 Oficinas de Física 1 Exercícios E3 1) Uma pessoa puxa horizontalmente o bloco B da figura 1, fazendo com que
Universidade Federal do Rio de Janeiro Instituto de Física Física 1 - Turmas de 6 horas 2015/2 Oficinas de Física 1 Exercícios E3 1) Uma pessoa puxa horizontalmente o bloco B da figura 1, fazendo com que
Física I Prova 1 04/06/2016a
 Física I Prova 1 04/06/016a NOME MATRÍCULA TURMA PROF. Lembrete: A prova consta de 0 questões de múltipla escolha valendo 0,5 ponto cada. Utilize: g = 9,80 m/s, exceto se houver alguma indicação em contrário.
Física I Prova 1 04/06/016a NOME MATRÍCULA TURMA PROF. Lembrete: A prova consta de 0 questões de múltipla escolha valendo 0,5 ponto cada. Utilize: g = 9,80 m/s, exceto se houver alguma indicação em contrário.
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 1 TEORIA DA RELATIVIDADE ESPECIAL Primeira Edição junho de 2005 CAPÍTULO 1 TEORIA DA RELATIVIDADE ESPECIAL ÍNDICE 1.1- Introdução 1.2-
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 1 TEORIA DA RELATIVIDADE ESPECIAL Primeira Edição junho de 2005 CAPÍTULO 1 TEORIA DA RELATIVIDADE ESPECIAL ÍNDICE 1.1- Introdução 1.2-
Lista4: Trabalho e Energia
 Lista 4: Trabalho e Energia NOME: Matrícula: Turma: Prof. : Importante: i. Nas cinco páginas seguintes contém problemas para se resolver e entregar. ii. Ler os enunciados com atenção. iii.responder a questão
Lista 4: Trabalho e Energia NOME: Matrícula: Turma: Prof. : Importante: i. Nas cinco páginas seguintes contém problemas para se resolver e entregar. ii. Ler os enunciados com atenção. iii.responder a questão
Halliday Fundamentos de Física Volume 2
 Halliday Fundamentos de Física Volume 2 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica, LTC, Forense,
Halliday Fundamentos de Física Volume 2 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica, LTC, Forense,
ESCOLA SECUNDÁRIA DE CASQUILHOS 2.º Teste sumativo de FQA 24. nov Versão 1
 ESCOLA SECUNDÁRIA DE CASQUILHOS 2.º Teste sumativo de FQA 24. nov. 2015 Versão 1 11.º Ano Turma A e B Duração da prova: 90 minutos. Este teste é constituído por 8 páginas e termina na palavra FIM Nome:
ESCOLA SECUNDÁRIA DE CASQUILHOS 2.º Teste sumativo de FQA 24. nov. 2015 Versão 1 11.º Ano Turma A e B Duração da prova: 90 minutos. Este teste é constituído por 8 páginas e termina na palavra FIM Nome:
Movimento Circular Uniforme
 Movimento Circular Uniforme Objeto em trajetória circular (raio R) a uma velocidade constante v. Período do movimento T: tempo de uma volta na circunferência comprimento da circunferência: Velocidade instantânea:
Movimento Circular Uniforme Objeto em trajetória circular (raio R) a uma velocidade constante v. Período do movimento T: tempo de uma volta na circunferência comprimento da circunferência: Velocidade instantânea:
Física. Física Módulo 1 Velocidade Relativa, Movimento de Projéteis, Movimento Circular
 Física Módulo 1 Velocidade Relativa, Movimento de Projéteis, Movimento Circular Velocidade Relativa Um Gedankenexperiment Imagine-se agora em um avião, a 350 km/h. O destino (a direção) é por conta de
Física Módulo 1 Velocidade Relativa, Movimento de Projéteis, Movimento Circular Velocidade Relativa Um Gedankenexperiment Imagine-se agora em um avião, a 350 km/h. O destino (a direção) é por conta de
