Fenómenos Transitórios
|
|
|
- Renato Vilanova Lisboa
- 9 Há anos
- Visualizações:
Transcrição
1 Fnónos Transóros Dfnção fnónos ransóros São fnónos q ocorr crcos lécrcos nr os saos rg rann. Noraln, os fnónos ransóros ocorr crcos lécrcos ran as anobras abrra fcho nrrors. Po abé aconcr vo a oras casas, as coo lgaçõs fosas. Noraln ss fnónos ra algns écos, cnésos o lésos sgno. Fnónos Transóros Os fnónos ransoros ra saln algns écos, cnésos o lésos sgno, cono o s so é oran, os osra co ancênca qal o ano rgoso nsão o nnsa a corrn q o ocorrr váras scçõs crco lécrco. análs os fnónos ransóros r abé rvr as sorçõs nas as ona o al os snas qano assa aravés alfcaors, flros o oros lnos. Fg. Fcho abrra nrror NS D TOS_24 NS D TOS_24 2 s a coação Fnónos Transóros Sob qasqr conçõs ransóras o saconáras há os ascos báscos a consrar: a corrn aravés a nânca a nsão aravés a caaca não o varas brscan. ª a coação corrn aravés a nânca aan ans a coação é gal à corrn aravés a sa nânca aan os a coação. 2ª a coação Fnónos Transóros nsão aravés a caaca aan ans a coação é gal à nsão aravés a sa caaca aan os a coação. onçõs ncas c c c s conçõs ncas são lzaas ara a rnação as consans nas solçõs as qaçõs frncas. Para a rnação as consans são alcaas as ls a coação. NS D TOS_24 3 NS D TOS_24 4
2 Méoos cálclo rocssos ransóros Para o cálclo crcos rg ransóros v sr rsolvas qaçõs frncas lnars. rsolção as qaçõs o sr fa or rês éoos:. lássco 2. Oraconal 3. ngral Dhal No nosso so alcaros o éoo clássco, q conss :. onsr as qaçõs frncas ara o crco lécrco os a coação 2. Drnar a solção gral coo a soa as coonns: a. oonn saconára o çaa q corrson à solção arclar a qação frncal não hoogéna, qano. NS D TOS_24 5 Méoos cálclo rocssos ransóros b. oonn lvr q corrson à solção gral a qação frncal hoogéna. Solção cola é consa or as coonns: s 3. Drnar as razs as qaçõs caracríscas. 4. Drnar as consans ngração sano as conçõs ncas. Ns caso o crco é analsao ans a coação. lv NS D TOS_24 6 Fnónos Transóros Procssos ransóros no crco co fon conína scrvaos a qação a 2ª l Krchoff ara o crco a fgra aa, co o nrror fchao: Traa-s a qação frncal lnar co cofcns consans, os são consans. NS D TOS_24 7 Fnónos Transóros sosa çaa naral Da aáca sab-s q a solção gral a qação frncal lnar é a soa a solção arclar a qação não hoogéna co a solção gral a qação hoogéna. solção arclar çaa é: çaa qação hoogéna obé-s galano o sgno bro a zro é: NS D TOS_24 8 2
3 Fnónos Transóros sosa çaa naral solção a qação hoogéna é a fnção xonncal a a: Fazno: lvr rsolvno a qação hogna or a, obos: onsraos q ara oos os fnónos ransóros o o = corrson ao nsan q o nrror é lvao a osção a ora. são consans nnns o o. NS D TOS_24 9 Fnónos Transóros sosa çaa naral ss a solção cola a qação frncal srá: lv onsan o: [s] Drnação a consan ngração: NS D TOS_24 Fnónos Transóros Procssos ransóros no crco co fon alrnaa snsoal scrvaos a qação a 2ª l Krchoff ara o crco a fgra aa, co o nrror fchao: sn Traa-s a qação frncal lnar co cofcns consans, os são consans. NS D TOS_24 Fnónos Transóros sosa çaa naral Ns caso a rsosa çaa ara a obnção sa solção, vos analsar crco corrn alrnaa snsoal onofásca: çaa Z j X 2 2 sn Z X Z qação hoogéna obé-s galano o sgno bro a zro é: NS D TOS_24 2 3
4 Fnónos Transóros sosa çaa naral Fnónos Transóros Drnação a consan ngração: solção a qação hoogéna é a fnção xonncal a a: lvr sn sn solção cola, srá: sn sn sn lv onsan o: [s] NS D TOS_24 3 NS D TOS_24 4 Fnónos Transóros Dslgação crco a fon conína scrvaos a qação a 2ª l Krchoff ara o crco a fgra aa, co o nrror fchao: on: Fnónos Transóros Drnação a consan ngração: solção sa qação hoogéna é a fnção xonncal a a: NS D TOS_24 5 NS D TOS_24 6 4
5 Fnónos Transóros NS D TOS_24 7 on: Drnação a consan ngração: Procssos ransóros nos crcos - NS D TOS_24 8 c lv s lv s Drnação a consan ngração: Procssos ransóros nos crcos - NS D TOS_24 9 Drnação a raíz a qação caracrísca: s, rans 5 3 rans Procssos ransóros nos crcos - NS D TOS_24 2 Dscarga consnsaor aravés a rssênca: c lv lv lv s
6 Procssos ransóros nos crcos - NS D TOS_24 2 s,
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1/3
 FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsn o s raciocínio d orma clara, indicando odos os cálclos q ivr d ar odas as jsiicaçõs ncssárias. Qando, para m rslado, não é pdida ma aproimação,
FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsn o s raciocínio d orma clara, indicando odos os cálclos q ivr d ar odas as jsiicaçõs ncssárias. Qando, para m rslado, não é pdida ma aproimação,
2 Modelagem de uma Colisão
 Moag a osão Moag a osão Ns aaho opo-s po oa son o íco a ão. Tano a psa qano o an q cca a ão não foa aaos. ncsão ss faos naa afaá o agoo ozação q coo sco no póo capío é oso spoa anças no pogaa sação s q
Moag a osão Moag a osão Ns aaho opo-s po oa son o íco a ão. Tano a psa qano o an q cca a ão não foa aaos. ncsão ss faos naa afaá o agoo ozação q coo sco no póo capío é oso spoa anças no pogaa sação s q
Aula 6. Sistemas mecânicos discretos e contínuos. Oscilador linear de um grau de liberdade (OL1GL) Princípio de D Alembert. Equação de equilíbrio.
 Ala 6 Ssmas mcâcos scros coíos. Osclaor lar m ra lbra OLGL rcípo Almbr. Eqação qlíbro. m lvr amorco. NL FCT EC Ehara Sísmca / sposávl: João. Blé Srra Acao 3 r r r r f m ; rcípo Almbr Força aca f f f f
Ala 6 Ssmas mcâcos scros coíos. Osclaor lar m ra lbra OLGL rcípo Almbr. Eqação qlíbro. m lvr amorco. NL FCT EC Ehara Sísmca / sposávl: João. Blé Srra Acao 3 r r r r f m ; rcípo Almbr Força aca f f f f
r R a) Aplicando a lei das malhas ao circuito, temos: ( 1 ) b) A tensão útil na bateria é: = 5. ( 2 ) c) A potência fornecida pela fonte é: .
 Aula xploraóra 07. Qusão 0: Um rssor d Ω é lgado aos rmnas d uma bara com fm d 6V rssênca nrna d Ω. Drmn: (a) a corrn; (b) a nsão úl da bara (so é, V V ); a b (c) a poênca forncda pla fon da fm ; (d) a
Aula xploraóra 07. Qusão 0: Um rssor d Ω é lgado aos rmnas d uma bara com fm d 6V rssênca nrna d Ω. Drmn: (a) a corrn; (b) a nsão úl da bara (so é, V V ); a b (c) a poênca forncda pla fon da fm ; (d) a
EXPERIÊNCIA 7 MEDIDA DE INDUTÂNCIA POR ONDA RETANGULAR
 UMCCE Eng. Elérca m - ab. Crco Elérco Prof. Wlon Yamag EXPEÊNC 7 MEDD DE NDUÂNC PO OND ENGU NODUÇÃO O objvo báco da xprênca é mdr a ndânca a rênca d ma bobna zando ma onda ranglar. O prncípo da mdção é
UMCCE Eng. Elérca m - ab. Crco Elérco Prof. Wlon Yamag EXPEÊNC 7 MEDD DE NDUÂNC PO OND ENGU NODUÇÃO O objvo báco da xprênca é mdr a ndânca a rênca d ma bobna zando ma onda ranglar. O prncípo da mdção é
Novo Espaço Matemática A, 12.º ano Proposta de teste de avaliação [março 2019]
![Novo Espaço Matemática A, 12.º ano Proposta de teste de avaliação [março 2019] Novo Espaço Matemática A, 12.º ano Proposta de teste de avaliação [março 2019]](/thumbs/98/137257708.jpg) Nom: Ao / Trma: Nº: Data: - - Não é prmitido o so d corrtor Dvs riscar aqilo q prtds q ão sja classificado A prova icli m formlário As cotaçõs dos its cotram-s o fial do ciado da prova CADERNO (É prmitido
Nom: Ao / Trma: Nº: Data: - - Não é prmitido o so d corrtor Dvs riscar aqilo q prtds q ão sja classificado A prova icli m formlário As cotaçõs dos its cotram-s o fial do ciado da prova CADERNO (É prmitido
y z CC2: na saída do reator: z = 1: 0. Pe dz Os valores característicos do problema são as raízes de: Da Pe 0 Pe Pe
 COQ-86 Méodos Nuércos para Ssas Dsrbuídos Explos Ilusravos d EDO co Problas d Valors o Cooro -) Modlo sacoáro do raor co dsprsão soérco Coo o obvo ds sudo d caso é lusrar o ovo procdo avalar o su dspo
COQ-86 Méodos Nuércos para Ssas Dsrbuídos Explos Ilusravos d EDO co Problas d Valors o Cooro -) Modlo sacoáro do raor co dsprsão soérco Coo o obvo ds sudo d caso é lusrar o ovo procdo avalar o su dspo
( ) π π. Corolário (derivada da função inversa): Seja f uma função diferenciável e injectiva definida num intervalo I IR.
 Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
MODELAGEM DE FENÔMENOS ACOPLADOS EM MEIOS POROSOS
 MOLAGM FNÔMNOS ACOLAOS M MOS OROSOS Morno, Rosângla Zanon rvsan, Osvar Val Unvrsa saal Camnas, Fala ngnhara Mâna C.. 605 308-970 Camnas, S, Brasl Rsmo. s rabalho arsna ma srra onssn ara o so nômnos ros
MOLAGM FNÔMNOS ACOLAOS M MOS OROSOS Morno, Rosângla Zanon rvsan, Osvar Val Unvrsa saal Camnas, Fala ngnhara Mâna C.. 605 308-970 Camnas, S, Brasl Rsmo. s rabalho arsna ma srra onssn ara o so nômnos ros
EEN300-MÉTODOS MATEMÁTICOS EM ENGENHARIA NAVAL. Série No. 2
 N3-MÉODOS MAMÁICOS M NGNHARIA NAVAL Sér No.. Faça ma aáls d sabldad lar d vo Nma o sqma crado plíco mosrado abao lzado para rsolvr a qação da oda m ma dmsão drm o rvalo do úmro d CFL para a sabldad ds
N3-MÉODOS MAMÁICOS M NGNHARIA NAVAL Sér No.. Faça ma aáls d sabldad lar d vo Nma o sqma crado plíco mosrado abao lzado para rsolvr a qação da oda m ma dmsão drm o rvalo do úmro d CFL para a sabldad ds
Dinâmica das Estruturas
 Dnâca das Esrras Dnâca das Esrras Redção a Ssea co Gra de Lberdade Dnâca das Esrras Dnâca das Esrras Vbrações e Sseas co Gra de Lberdade lvres não - aorecdas aorecdas c forçadas não - aorecdas aorecdas
Dnâca das Esrras Dnâca das Esrras Redção a Ssea co Gra de Lberdade Dnâca das Esrras Dnâca das Esrras Vbrações e Sseas co Gra de Lberdade lvres não - aorecdas aorecdas c forçadas não - aorecdas aorecdas
EEL-001 CIRCUITOS ELÉTRICOS ENGENHARIA DA COMPUTAÇÃO
 L IRUITOS LÉTRIOS 8 UNIFI,VFS, Re. BDB PRT L IRUITOS LÉTRIOS NGNHRI D OMPUTÇÃO PÍTULO 5 PITORS INDUTORS: omporameno com Snas onínuos e com Snas lernaos 5. INTRODUÇÃO Ressor elemeno que sspa poênca. 5.
L IRUITOS LÉTRIOS 8 UNIFI,VFS, Re. BDB PRT L IRUITOS LÉTRIOS NGNHRI D OMPUTÇÃO PÍTULO 5 PITORS INDUTORS: omporameno com Snas onínuos e com Snas lernaos 5. INTRODUÇÃO Ressor elemeno que sspa poênca. 5.
( ) Novo Espaço Matemática A 11.º ano Proposta de Teste [abril 2018] V x =, 3. CADERNO 1 (É permitido o uso de calculadora gráfica) π x 0, 2 0, 2
![( ) Novo Espaço Matemática A 11.º ano Proposta de Teste [abril 2018] V x =, 3. CADERNO 1 (É permitido o uso de calculadora gráfica) π x 0, 2 0, 2 ( ) Novo Espaço Matemática A 11.º ano Proposta de Teste [abril 2018] V x =, 3. CADERNO 1 (É permitido o uso de calculadora gráfica) π x 0, 2 0, 2](/thumbs/84/89051569.jpg) Novo Espaço Matmática A 11.º ao Proposta d Tst [abril 018] Nom: Ao / Trma: N.º: Data: - - Não é prmitido o so d corrtor. Dvs riscar aqilo q prtds q ão sja classificado. A prova icli m formlário. As cotaçõs
Novo Espaço Matmática A 11.º ao Proposta d Tst [abril 018] Nom: Ao / Trma: N.º: Data: - - Não é prmitido o so d corrtor. Dvs riscar aqilo q prtds q ão sja classificado. A prova icli m formlário. As cotaçõs
Novo Espaço Matemática A 11.º ano Proposta de teste de avaliação [novembro 2018]
![Novo Espaço Matemática A 11.º ano Proposta de teste de avaliação [novembro 2018] Novo Espaço Matemática A 11.º ano Proposta de teste de avaliação [novembro 2018]](/thumbs/93/114280552.jpg) Novo Espaço Matmática A.º ao Proposta d tst d avaliação [ovmbro 08] Nom: Ao / Trma: N.º: Data: - - Não é prmitido o so d corrtor. Dvs riscar aqilo q prtds q ão sja classificado. A prova icli m formlário.
Novo Espaço Matmática A.º ao Proposta d tst d avaliação [ovmbro 08] Nom: Ao / Trma: N.º: Data: - - Não é prmitido o so d corrtor. Dvs riscar aqilo q prtds q ão sja classificado. A prova icli m formlário.
A formulação representada pelas equações (4.1)-(4.3) no método de elementos finitos é denominada de formulação forte (strong formulation).
 4. Fomlção Mcl o Méoo Elmos Fos s cpílo sá ps fomlção mcl o méoo lmos fos pos plcção o méoo lv ssms lgécos q pom s ogzos fom mcl p poso solção po éccs mécs pops p c po qção fcl: lípc pólc o hpólc. O poo
4. Fomlção Mcl o Méoo Elmos Fos s cpílo sá ps fomlção mcl o méoo lmos fos pos plcção o méoo lv ssms lgécos q pom s ogzos fom mcl p poso solção po éccs mécs pops p c po qção fcl: lípc pólc o hpólc. O poo
ESZO Fenômenos de Transporte
 Univridad Fdral do ABC ESZO 001-15 Fnôno d Tranpor Profa. Dra. Ana Maria Prira No [email protected] Bloco A, orr 1, ala 637 1ª Li da Trodinâica para olu d Conrol ESZO 001-15_Ana Maria Prira No 1ª Li da
Univridad Fdral do ABC ESZO 001-15 Fnôno d Tranpor Profa. Dra. Ana Maria Prira No [email protected] Bloco A, orr 1, ala 637 1ª Li da Trodinâica para olu d Conrol ESZO 001-15_Ana Maria Prira No 1ª Li da
Escola Básica e Secundária Dr. Ângelo Augusto da Silva
 Escola Básica Scdária Dr. Âglo Agsto da Silva Tst d MATEMÁTICA A 1º Ao Dração: 9 mitos Março/ 9 Nom Nº T: Classificação O Prof. (Lís Abr) 1ª PARTE Para cada ma das sgits qstõs d scolha múltipla, slccio
Escola Básica Scdária Dr. Âglo Agsto da Silva Tst d MATEMÁTICA A 1º Ao Dração: 9 mitos Março/ 9 Nom Nº T: Classificação O Prof. (Lís Abr) 1ª PARTE Para cada ma das sgits qstõs d scolha múltipla, slccio
Equações de Conservação
 Eqaçõs d Consação Toma d Tanspo d Rnolds Eqação d Consação d Massa (conndad) Eqação d Consação d Qandad d Momno Lna ( a L d Non) Eqação d Na-Soks Eqação d Enga Mcânca Eqação d Consação d Qandad d Momno
Eqaçõs d Consação Toma d Tanspo d Rnolds Eqação d Consação d Massa (conndad) Eqação d Consação d Qandad d Momno Lna ( a L d Non) Eqação d Na-Soks Eqação d Enga Mcânca Eqação d Consação d Qandad d Momno
PMR Mecânica Computacional para Mecatrônica. Elemento Isoparamétrico de 4 nós
 PMR3 - Mcâca opacoal para Mcarôca Elo Isoparaérco d ós osdros cal a fção rpoladora para lo raglar osrado a fgra: 3 sdo a arál d sado os cofcs as arás dpds. osdrado os alors dssa fção os ós do râglo os:
PMR3 - Mcâca opacoal para Mcarôca Elo Isoparaérco d ós osdros cal a fção rpoladora para lo raglar osrado a fgra: 3 sdo a arál d sado os cofcs as arás dpds. osdrado os alors dssa fção os ós do râglo os:
Vieiras com palmito pupunha ao molho de limão
 Vs o to nh o oho d ão Oá, ss ntd fo ns dos tos fz s gost. Aé d nd dd, obnção d sbos sson té os s xgnts. A t s dfí v s onsg vs fss. Ingdnts: 1 to nh; 3 dúzs d vs; s nt t; d do. Modo d fz: t s tbhos é bs
Vs o to nh o oho d ão Oá, ss ntd fo ns dos tos fz s gost. Aé d nd dd, obnção d sbos sson té os s xgnts. A t s dfí v s onsg vs fss. Ingdnts: 1 to nh; 3 dúzs d vs; s nt t; d do. Modo d fz: t s tbhos é bs
CARGA E DESCARGA DE CAPACITORES
 ARGA E DESARGA DE APAITORES O assuno dscudo ns argo, a carga a dscarga d capacors, aparcu dos anos conscuvos m vsbulars do Insuo Mlar d Engnhara ( 3). Ns sudo, srão mosradas as dduçõs das uaçõs d carga
ARGA E DESARGA DE APAITORES O assuno dscudo ns argo, a carga a dscarga d capacors, aparcu dos anos conscuvos m vsbulars do Insuo Mlar d Engnhara ( 3). Ns sudo, srão mosradas as dduçõs das uaçõs d carga
A DERIVADA DE UM INTEGRAL
 A DERIVADA DE UM INTEGRAL HÉLIO BERNARDO LOPES Rsumo. O cálculo o valor a rivaa um ingral ocorr com cra frquência na via profissional físicos, químicos, ngnhiros, conomisas ou biólogos. É frqun, conuo,
A DERIVADA DE UM INTEGRAL HÉLIO BERNARDO LOPES Rsumo. O cálculo o valor a rivaa um ingral ocorr com cra frquência na via profissional físicos, químicos, ngnhiros, conomisas ou biólogos. É frqun, conuo,
# D - D - D - - -
 1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
Integrais de Funções Trigonométricas. Integrais de Funções Trigonométricas
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. As seis integrais
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. As seis integrais
Novo Espaço Matemática A 11.º ano Proposta de teste de avaliação [maio 2019]
![Novo Espaço Matemática A 11.º ano Proposta de teste de avaliação [maio 2019] Novo Espaço Matemática A 11.º ano Proposta de teste de avaliação [maio 2019]](/thumbs/99/142100261.jpg) Novo Espaço Matmática A º ao Nom: Ao / Trma: Nº: Data: - - Não é prmitido o so d corrtor Dvs riscar aqilo q prtds q ão sja classificado A prova icli m formlário As cotaçõs dos its cotram-s o fial do ciado
Novo Espaço Matmática A º ao Nom: Ao / Trma: Nº: Data: - - Não é prmitido o so d corrtor Dvs riscar aqilo q prtds q ão sja classificado A prova icli m formlário As cotaçõs dos its cotram-s o fial do ciado
Capítulo 6 Decaimento Radioativo
 Física das Radiaçõs Dosimria Capíulo 6 Dcaimno Radioaivo Dra. Luciana Tourinho Campos Programa acional d Formação m Radiorapia Inrodução Inrodução Consan d dcaimno Vida-média mia-vida Rlaçõs nr núclo pai
Física das Radiaçõs Dosimria Capíulo 6 Dcaimno Radioaivo Dra. Luciana Tourinho Campos Programa acional d Formação m Radiorapia Inrodução Inrodução Consan d dcaimno Vida-média mia-vida Rlaçõs nr núclo pai
3º) Equação do tipo = f ( y) dx Solução: 2. dy dx. 2 =. Integrando ambos os membros, dx. dx dx dy dx dy. vem: Ex: Resolva a equação 6x + 7 = 0.
 0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
E S T A T U T O D O C L U B E D E R E G A T A S B R A S I L
 E S T A T U T O D O C L U B E D E R E G A T A S B R A S I L H I N O O F I C I A L J a y m e d e A l t a v i l a I A o r e m o! Po i s n o s s o n o r t e D e g l ó r i a s t r a ç a d o e s t á. F a ç
E S T A T U T O D O C L U B E D E R E G A T A S B R A S I L H I N O O F I C I A L J a y m e d e A l t a v i l a I A o r e m o! Po i s n o s s o n o r t e D e g l ó r i a s t r a ç a d o e s t á. F a ç
Escola Básica e Secundária Dr. Ângelo Augusto da Silva Teste de MATEMÁTICA A 12º Ano
 Escola Básica Scdária Dr. Âglo Agsto da Silva Tst d MATEMÁTICA A º Ao Dração: 9 mitos Maio/ Nom Nº T: ª PARTE Para cada ma das sgits qstõs d scolha múltipla, slccio a rsposta corrcta d tr as altrativas
Escola Básica Scdária Dr. Âglo Agsto da Silva Tst d MATEMÁTICA A º Ao Dração: 9 mitos Maio/ Nom Nº T: ª PARTE Para cada ma das sgits qstõs d scolha múltipla, slccio a rsposta corrcta d tr as altrativas
Capítulo 6. Misturas de Gases
 Caítlo 6 stras de Gases Objetvos Desenvolver regras ara se estdar as roredades de stras de gases não-reatvos co base no conhecento da coosção da stra e das roredades dos coonentes ndvdas Defnr grandezas
Caítlo 6 stras de Gases Objetvos Desenvolver regras ara se estdar as roredades de stras de gases não-reatvos co base no conhecento da coosção da stra e das roredades dos coonentes ndvdas Defnr grandezas
UNIVERSIDADE CATÓLICA DE BRASÍLIA
 UNIVERSIDADE CATÓLICA DE BRASÍLIA PRÓ-REITORIA DE GRADUAÇÃO TRABALHO DE CONCLUSÃO DE CURSO Crso d Físa OSCILADORES ACOPLADOS: SISTEMA COM DOIS GRAUS DE LIBERDADE Aor: Danl d Carvalho Olvra Ornador: Prof.
UNIVERSIDADE CATÓLICA DE BRASÍLIA PRÓ-REITORIA DE GRADUAÇÃO TRABALHO DE CONCLUSÃO DE CURSO Crso d Físa OSCILADORES ACOPLADOS: SISTEMA COM DOIS GRAUS DE LIBERDADE Aor: Danl d Carvalho Olvra Ornador: Prof.
Ainda há Tempo, Volta
 Ainda há empo, Volta Letra e Música: Diogo Marques oprano ontralto Intro Envolvente (q = 60) enor aixo Piano Ó Œ. R.. F m7 2 A b 2 E b.. 2 Ó Œ É 2 Ó Œ F m7 2.. 2 2 A b 2 2 Ainda há empo, Volta Estrofe
Ainda há empo, Volta Letra e Música: Diogo Marques oprano ontralto Intro Envolvente (q = 60) enor aixo Piano Ó Œ. R.. F m7 2 A b 2 E b.. 2 Ó Œ É 2 Ó Œ F m7 2.. 2 2 A b 2 2 Ainda há empo, Volta Estrofe
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas Licenciatura em Engenharia Física
 Análise e Processameno e Bio-Sinais Mesrao Inegrao em Engenaria Bioméica Sinais e Sisemas Licenciara em Engenaria Física Deparameno e Engenaria Elecroécnica e Compaores Faclae e Ciências e Tecnologia Universiae
Análise e Processameno e Bio-Sinais Mesrao Inegrao em Engenaria Bioméica Sinais e Sisemas Licenciara em Engenaria Física Deparameno e Engenaria Elecroécnica e Compaores Faclae e Ciências e Tecnologia Universiae
Técnicas de Linearização de Sistemas
 EA66 Pro. Vo Ze DCA/FEEC/Uc éccs e Lerzção e Sses Iroção ese óco vos recorrer reqüeeee éccs e lerzção e sse ão-ler e oro e oo e oerção. Iso ere qe o sse ler resle se lso co se s oeross erres e álse váls
EA66 Pro. Vo Ze DCA/FEEC/Uc éccs e Lerzção e Sses Iroção ese óco vos recorrer reqüeeee éccs e lerzção e sse ão-ler e oro e oo e oerção. Iso ere qe o sse ler resle se lso co se s oeross erres e álse váls
(Às Co missões de Re la ções Exteriores e Defesa Na ci o nal e Comissão Diretora.)
 32988 Quarta-feira 22 DIÁRIO DO SENADO FEDERAL Ou tu bro de 2003 Art. 3º O Gru po Parlamentar reger-se-á pelo seu regulamento in ter no ou, na falta deste, pela decisão da ma i o ria absoluta de seus mem
32988 Quarta-feira 22 DIÁRIO DO SENADO FEDERAL Ou tu bro de 2003 Art. 3º O Gru po Parlamentar reger-se-á pelo seu regulamento in ter no ou, na falta deste, pela decisão da ma i o ria absoluta de seus mem
Análise de Sensibilidade. Fernando Nogueira Análise de Sensibilidade 1
 Análise de Sensibilidade Fernando Nogeira Análise de Sensibilidade Consiste em esqisar a estabilidade da solção em vista de ossíveis variações dos arâmetros a ij, b i e c j tilizados na Programação Linear,
Análise de Sensibilidade Fernando Nogeira Análise de Sensibilidade Consiste em esqisar a estabilidade da solção em vista de ossíveis variações dos arâmetros a ij, b i e c j tilizados na Programação Linear,
A solução mais geral da equação anterior tem a forma: α 2 2. Aplicando estes resultados na equação do MHS, temos que:
 . qação para o MHS Qano o oino corpo cr a rajória, a parir cro inan coça a rpir a rajória, izo q oino é prióico. O po q o corpo gaa para olar a prcorrr o o pono a rajória é chaao príoo. No noo coiiano
. qação para o MHS Qano o oino corpo cr a rajória, a parir cro inan coça a rpir a rajória, izo q oino é prióico. O po q o corpo gaa para olar a prcorrr o o pono a rajória é chaao príoo. No noo coiiano
Equações de Conservação
 Eqaçõs d Consação Toma d Tanspo d Rnolds Eqação d Consação d Massa (conndad) Eqação d Consação d Qandad d Momno Lna ( a L d Non) Eqação d Na-Soks Eqação d Enga Mcânca Eqação d Consação d Qandad d Momno
Eqaçõs d Consação Toma d Tanspo d Rnolds Eqação d Consação d Massa (conndad) Eqação d Consação d Qandad d Momno Lna ( a L d Non) Eqação d Na-Soks Eqação d Enga Mcânca Eqação d Consação d Qandad d Momno
Lista de exercícios Micro III 03/09/2008. Externalidades e Bens Públicos
 Lsta de exercícos Mcro III 03/09/008 Prof. Afonso A. de Mello Franco Neto Externaldades e Bens Públcos Exercícos Mas-Colell:.B a.b.5,.c.,.c.,.d. a.d.5,.d.7. QUESTÃO Nma economa exstem ma frma e dos consmdores.
Lsta de exercícos Mcro III 03/09/008 Prof. Afonso A. de Mello Franco Neto Externaldades e Bens Públcos Exercícos Mas-Colell:.B a.b.5,.c.,.c.,.d. a.d.5,.d.7. QUESTÃO Nma economa exstem ma frma e dos consmdores.
P R O J E T O P E R S E U
 P R O J E T O P E R S E U U M A F E R R A M E N T A C O M P U T A C I O N A L P A R A A U X Í L I O N A R E D U Ç Ã O D E D O R T D E V I D O A O U S O D O C O M P U T A D O R A n a E s t h e r V i c t
P R O J E T O P E R S E U U M A F E R R A M E N T A C O M P U T A C I O N A L P A R A A U X Í L I O N A R E D U Ç Ã O D E D O R T D E V I D O A O U S O D O C O M P U T A D O R A n a E s t h e r V i c t
(rad/s), onde f é frequência cíclica em Hz=1/s, período: Vibrações livres não-amortecidas Equação do movimento (equilíbrio dinâmico): m & u
 SISEMAS DE GRA DE IBERDADE êc ccl: π (/s, oe é êc cíclc e Hz/s, peíoo: Vções lves ão-oecs Eqção o oveo (lío âco: + k Solção: As( + Bcos(, A e B s coções cs: esloceo cl, v veloce cl v s( + cos( o ecee:
SISEMAS DE GRA DE IBERDADE êc ccl: π (/s, oe é êc cíclc e Hz/s, peíoo: Vções lves ão-oecs Eqção o oveo (lío âco: + k Solção: As( + Bcos(, A e B s coções cs: esloceo cl, v veloce cl v s( + cos( o ecee:
MECÂNICA APLICADA - Pilotagem Texto de apoio UNIDADES pag. 1 de 5
 MECÂNICA APICADA - Piloage Texo de apoio UNIDADES pag. de 5 BREVE REFERÊNCIA AOS SISTEMAS DE UNIDADES 0 Generalidades U sisea de unidades copora: unidades undaenais unidades derivadas. A ixação das unidades
MECÂNICA APICADA - Piloage Texo de apoio UNIDADES pag. de 5 BREVE REFERÊNCIA AOS SISTEMAS DE UNIDADES 0 Generalidades U sisea de unidades copora: unidades undaenais unidades derivadas. A ixação das unidades
Novo Espaço Matemática A 11.º ano Proposta de Teste [março ]
![Novo Espaço Matemática A 11.º ano Proposta de Teste [março ] Novo Espaço Matemática A 11.º ano Proposta de Teste [março ]](/thumbs/77/76110011.jpg) Novo Espaço Matmática A.º ao Proposta d Tst [março - 08] Nom: Ao / Trma: N.º: Data: / / Não é prmitido o so d corrtor. Dvs riscar aqilo q prtds q ão sja classificado. A prova icli m formlário. As cotaçõs
Novo Espaço Matmática A.º ao Proposta d Tst [março - 08] Nom: Ao / Trma: N.º: Data: / / Não é prmitido o so d corrtor. Dvs riscar aqilo q prtds q ão sja classificado. A prova icli m formlário. As cotaçõs
CÁLCULO I. 1 Teorema do Confronto. Objetivos da Aula
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Ala n o 07: Teorema do Confronto. Limite Fndamental Trigonométrico. Teorema do Valor Intermediário.
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Ala n o 07: Teorema do Confronto. Limite Fndamental Trigonométrico. Teorema do Valor Intermediário.
 !" # " $% $ : %. ( "- # 6 (( '.. '.. ( #5 (, (' 2!' 3 4 5 2 "! =!. # ( +!'! "!. # ( #! "!. # (9, 1( 9 1 9 + -. ' 6 "-! = 1( 9 1 9 % "(- ( E= + 2 F M. (( 6 (( 1 1 7 8 9 2; 22 # (' ' ". = 2 + 9 6 ( +
!" # " $% $ : %. ( "- # 6 (( '.. '.. ( #5 (, (' 2!' 3 4 5 2 "! =!. # ( +!'! "!. # ( #! "!. # (9, 1( 9 1 9 + -. ' 6 "-! = 1( 9 1 9 % "(- ( E= + 2 F M. (( 6 (( 1 1 7 8 9 2; 22 # (' ' ". = 2 + 9 6 ( +
Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e :
 INSCRIÇÕES ABERTAS ATÉ 13 DE JULH DE 2015! Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e : Caso vo cê nunca t e nh a pa
INSCRIÇÕES ABERTAS ATÉ 13 DE JULH DE 2015! Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e : Caso vo cê nunca t e nh a pa
MATEMÁTICA ATUARIAL DE VIDA Modelos de Sobrevivência
 EAC 44 Maáica Auaria II Ciêcia Auariai Nouro FEA USP Prof. Dr. Ricaro Pachco MAEMÁICA AUARIAL DE VIDA Moo Sobrvivêcia Uivria São Pauo º Sr 5 A ábua oraia u oo icro obrvivêcia. Daa a ábua Moraia hipoéica:
EAC 44 Maáica Auaria II Ciêcia Auariai Nouro FEA USP Prof. Dr. Ricaro Pachco MAEMÁICA AUARIAL DE VIDA Moo Sobrvivêcia Uivria São Pauo º Sr 5 A ábua oraia u oo icro obrvivêcia. Daa a ábua Moraia hipoéica:
f (x) Antiderivadas de f (x) ; 3 8x ; 8
 INTEGRAIS Definição: Uma fnção F é ma antierivaa e f em m intervalo I se F' ) f ) para too em I Chamaremos tamém F ) ma antierivaa e f ) eterminação e F, o F ), é chamao ANTIDIFERENCIAÇÃO O processo e
INTEGRAIS Definição: Uma fnção F é ma antierivaa e f em m intervalo I se F' ) f ) para too em I Chamaremos tamém F ) ma antierivaa e f ) eterminação e F, o F ), é chamao ANTIDIFERENCIAÇÃO O processo e
Medley Forró 4 Tenho Sede Dominguinhos e Anastácia
 TENOR Medley Forró 4 Tenho Sede Dominguinhos e Anastácia q # = 0 # # 4 # c. # n 8. iá. Lá lá lá iá lá iá lá lá iá lá iá lá iá lá iá... A iá Tra -ga me'um co - po dá - gua gan ta pe de'um pou te - nho -
TENOR Medley Forró 4 Tenho Sede Dominguinhos e Anastácia q # = 0 # # 4 # c. # n 8. iá. Lá lá lá iá lá iá lá lá iá lá iá lá iá lá iá... A iá Tra -ga me'um co - po dá - gua gan ta pe de'um pou te - nho -
Montagem de Redes de Distribuição Compacta Protegida ESTRUTURA DE TRANSIÇÃO N3 C3 NS PR
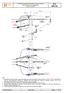 N C NS PR 855 10 OBS.: 1. Na tensão de 4,5 kv utilizar alça pré-formada para cabos de alumínio coberto 4,5 kv, 812155/59. Na tensão de 1,8 kv, alternativamente poderá ser utilizada alça pré-formada para
N C NS PR 855 10 OBS.: 1. Na tensão de 4,5 kv utilizar alça pré-formada para cabos de alumínio coberto 4,5 kv, 812155/59. Na tensão de 1,8 kv, alternativamente poderá ser utilizada alça pré-formada para
Actividade Laboratorial TL 01. Assunto: Força de atrito estático e cinético
 Dparano d Maáia Ciênias Exprinais Curso d Eduação oração Tipo 6 Nívl Aividad Laboraorial TL 0 Assuno: orça d ario sáio inéio Objivo: Esudar as forças d ario sáio inéio drinando os faors d qu dpnd. Inrodução
Dparano d Maáia Ciênias Exprinais Curso d Eduação oração Tipo 6 Nívl Aividad Laboraorial TL 0 Assuno: orça d ario sáio inéio Objivo: Esudar as forças d ario sáio inéio drinando os faors d qu dpnd. Inrodução
Aerodinâmica. Aproximações de Camada Limite (Boundary-Layer) Equação Integral de von Kármán
 Arodinâmica Aproimaçõs d Camada Limit (Bondar-Lar) Eqação Intgral d von Kármán Intgrar qaçõs d camada limit na dircção normal à pard > Eqação da continidad v + d v d ( ) Mstrado Intgrado m Engnaria Mcânica
Arodinâmica Aproimaçõs d Camada Limit (Bondar-Lar) Eqação Intgral d von Kármán Intgrar qaçõs d camada limit na dircção normal à pard > Eqação da continidad v + d v d ( ) Mstrado Intgrado m Engnaria Mcânica
Representação de Curvas
 CI8 Ssemas Gráfcos para Engenhara 5. Represenação e Crvas Lz Fernano Marha Anré Perera Baseao em maeral preparao por Marcelo Gaass Depo. e Informáca PUC-Ro aapao para a scplna CI8 Represenações e Crvas
CI8 Ssemas Gráfcos para Engenhara 5. Represenação e Crvas Lz Fernano Marha Anré Perera Baseao em maeral preparao por Marcelo Gaass Depo. e Informáca PUC-Ro aapao para a scplna CI8 Represenações e Crvas
Escola Básica e Secundária Dr. Ângelo Augusto da Silva
 Escla Básica Scdária Dr. Âgl Agst da Silva Tst d MATEMÁTICA A º A Draçã: 9 mits Març/ Nm Nº T: Classificaçã O Prf. (Lís Abr) ª PARTE Para cada ma das sgits qstõs d sclha múltipla, slcci a rspsta crrcta
Escla Básica Scdária Dr. Âgl Agst da Silva Tst d MATEMÁTICA A º A Draçã: 9 mits Març/ Nm Nº T: Classificaçã O Prf. (Lís Abr) ª PARTE Para cada ma das sgits qstõs d sclha múltipla, slcci a rspsta crrcta
Universidade Federal de Santa Catarina UFSC. Centro de Ciências Físicas e Matemáticas CFM. Departamento de Matemática.
 Univrsidad Fdral d Sana Caarina UFSC. Cnro d Ciências Físicas Mamáicas CFM. Dparamno d Mamáica. Trabalo d Conclsão II TCC II. Problmas d ransmissão ópica gomérica Florianópolis, jlo d 9. Problmas d ransmissão
Univrsidad Fdral d Sana Caarina UFSC. Cnro d Ciências Físicas Mamáicas CFM. Dparamno d Mamáica. Trabalo d Conclsão II TCC II. Problmas d ransmissão ópica gomérica Florianópolis, jlo d 9. Problmas d ransmissão
